Reteaching , or 37.5% 360. Geometric Probability. Name Date Class
|
|
|
- Tracy Berry
- 6 years ago
- Views:
Transcription
1 Name ate lass Reteaching Geometric Probability INV 6 You have calculated probabilities of events that occur when coins are tossed and number cubes are rolled. Now you will learn about geometric probability. Geometric Probability You can find the probability of an event occurring by dividing the number of ways the event can occur by the total number of outcomes. To know the probability of something falling into a part of a whole area or region, you can use geometric probability, which is the ratio of the size of the partial region to that of the whole region. epending on the situation, size can be measured in degrees, length, area, or volume. size of partial region P(partial region) size of whole region small meteor lands in the field to the right. What is the probability that it has landed in the flower garden? 0 IEL 50 m LOWER GREN 100 m area of the flower garden (0 m)(50 m) 1000 m area of the field (100 m)(100 m) 10,000 m P(meteor lands in flower garden) 1000 m % 10,000 m 100 m ompete the steps to find the probability. 1. ind the probability that a dart thrown at the dartboard lands in region 3. The degree measure of region 3 is 135. The dartboard is in the shape of a circle. The number of degrees in a circle is 360. region 3 The probability of a dart hitting region 3 is total degrees ind the probabilities. Region Region º 135º Region , or 37.5% 360. t the local pizza shop, if you drop a coin in the little bowl in the fish tank, you get a free slice of pizza. What is the probability of getting the coin in the fish tank if you have to drop it in while blindfolded? approximately 17.4% 1.5 ft 8 ft 3 ft 0.5 ft 3. ind the probability that a soccer ball kicked on goal goes over the goalie s head % 4 ft 4.5 ft Saxon. ll rights reserved. 131 Saxon Geometry
2 Reteaching continued INV 6 Experimental Probability When you say that the probability of flipping a coin and getting heads is 1, you are talking about the theoretical probability of flipping heads. If we flipped a coin 50 times, the experimental probability of heads would be the actual percentage of flips that resulted in heads. If a coin is tossed 50 times and heads occurs 6 times, what is the experimental probability of heads? P(heads) number of heads 6 heads 0.5 5% number of tosses 50 tosses In general, the experimental probability of an event is the number of times it occurs divided by the total number of trials: experimental probability # of times the event occurred # of trials s the number of trials goes up, an event s experimental probability will get closer and closer to its theoretical probability. ind the experimental probabilities. 4. Kyle rolled a number cube 50 times and got a one 9 times. ind the experimental probability of a one. experimental probability of a one number of ones number of trials % 50 What fraction will the experimental probability get closer to if the cube is tossed more? The experimental probability will get closer to the theoretical probability of 1 because experimental probability approaches theoretical probability 6 as the number of trials increases. 5. Make a spinner like the one to the right. Spin it 50 times and record the number of times it lands on three. ind the experimental probability of landing on three after 10, 5, and 50 spins. What number does it look like the experimental probability is getting closer to? Would it get closer to it if you performed more trials? Why? nswers will vary for the probabilities. The experimental probabilities should be getting closer to 1 8, or 0.15 and will get closer if more trials are performed because the experimental probability should approach the theoretical probability, 0.15, as the number of trials increases Saxon. ll rights reserved. 13 Saxon Geometry
3 Name ate lass Reteaching Quadrilateral Is a Parallelogram 61 You have worked with quadrilaterals. Now you will determine whether a quadrilateral is a parallelogram. Identifying Parallelograms parallelogram is a quadrilateral with two pairs of parallel sides. ll parallelograms have the following properties: Opposite sides are congruent. _ G _ HJ _ GH _ G J J H Opposite angles are congruent. H G J G H J Example: In quadrilateral JKLM, _ JK _ ML. Is JKLM a parallelogram? Step 1: Solve for x. _ JK _ J ML Given 3x 1 x 4 Substitute. x 3 Solve. Step : Substitute x 3 to find JM and KL. JM 4(3) 5 7 KL Since _ JK _ ML and JM _ KL _ M, JKLM is a parallelogram. x + 4 3x + 1 4x 5 x + 5 L K omplete the statements. 1. _ _ ; _ _ ; 63 The figure is a parallelogram since opposite angles and sides are congruent. 63 Use the given information to determine whether the figures are parallelograms. State the reason.. Given: _ _ 3. Given: _ PR _ QS x 18 P (4x + 6) (5x 4) x + 15 Q 6x x (3x + 6) (6x 4) x + 6 yes; x 4; Opposite angles are congruent R 7x 0 no; x 5; Opposite sides are not congruent. S Saxon. ll rights reserved. 133 Saxon Geometry
4 Reteaching continued 61 More on Identifying Parallelograms One pair of opposite sides of a quadrilateral are both parallel and congruent to each other. _ _ The diagonals bisect each other. P PH G P GP PJ J H Example: Use the given information to decide whether JLKM is a parallelogram. Given: _ JK _ LM and _ JK _ J LM Step 1: Is there a relationship between the sides? Opposite sides are both parallel and congruent to each other. M Step : If one pair of corresponding sides of a quadrilateral are both parallel and congruent to each other, the figure is a parallelogram. L K omplete the statements. 4. _ TZ _ ZV ; WZ _ ZU The diagonals of the quadrilateral bisect each other. The figure is a parallelogram. Use the given information to determine whether the figure is a parallelogram. State the reason. 5. _ VZ _ ZX and _ YZ _ ZW 6. _ _ and _ _ V W W T Z 8 V U Z E Y yes; iagonals bisect each other. 7. _ PT _ QT and _ ST _ RT 8. _ _ and _ _ P X Q yes; Opposite sides are both parallel and congruent. T E S R no no Saxon. ll rights reserved. 134 Saxon Geometry
5 Name ate lass Reteaching inding Surface rea and Volume of ylinders 6 You have learned how to find the surface area and the volume of prisms. Now you will find the surface area and the volume of cylinders. To find the surface area of a cylinder, use the formula S r rh to combine the lateral area and the area of the two bases. 9 in ind the area of the cylinder in terms of. S r rh S (9) (9)() S S 558 in in omplete the steps to find the surface area of the cylinder in terms of. 1. S (7 ) (7 )(1 ) S S 66 cm ind the surface area of each cylinder in terms of. 14 cm 1 cm. 5 yd 3. ft 14 yd 18 ft 190 yd 638 ft 4. 8 m 5. 6 mm 1 m 3 mm 00 m 456 mm Saxon. ll rights reserved. 135 Saxon Geometry
6 Reteaching continued 6 oth right cylinders and oblique cylinders each use the same formula, V r h, for volume. ind the volume of the right cylinder in terms of. V r h V (15) (10) 10 mm 15 mm V 50 mm 3 ind the volume of the oblique cylinder in terms of. V r h 8 ft V (8) (5) V 30 ft 3 5 ft omplete the steps to find the volume of each cylinder in terms of. 6. V (5 ) (7 ) 7. V (18 ) (5 ) V 175 in 3 V 8100 yd 3 10 in 18 yd 7 in 5 yd ind the volume of each cylinder in terms of mm 9. 4 cm 9 mm 1 cm mm cm ft cm 0 ft 7 cm ft cm Saxon. ll rights reserved. 136 Saxon Geometry
7 Name ate lass Reteaching Introduction to Vectors 63 You have learned how to find points on a coordinate plane. Now you will determine vectors and their magnitudes. ind r. Step 1: Place M on the origin. y Step : N will be 4 units to the right and 5 units up, so the coordinates of the terminal point N are (4, 5). Step 3: Use the distance formula to find the distance between M(0, 0) and N(4, 5). d ( x x 1 ) ( y y 1 ) M ř N d (4 0) (5 0) d Therefore, r is 41. omplete the steps to find the magnitude of the vector. y N 1. ind p. M ρˇ Place M on the origin. N is now at (3, 4). d (3 0) (4 0) d (3) (4) 5 So, p 5. ind the magnitude of each vector in simplified radical form.. m y 3. d y m d e 5. g y y e g 8 85 Saxon. ll rights reserved. 137 Saxon Geometry
8 Reteaching continued 63 dd vectors v and w. Step 1: Write v in component form. The horizontal change is 7. The vertical change is 1. y The component form of v is 7, 1. Step : Write w in component form. The component form of w is 4, 3. v w Step 3: dd the components: 7 4, , 4. The resultant vector from adding v and w is 11, 4. dd vectors s and t. The component form of s is, 1. The component form of t is, 1. The components of s and t sum of 0 because they are opposite vectors. The resultant vector is 0, 0. t y s omplete the steps to find the sum of the vectors. y 6. dd vectors h and k. The component form of h is 5, 4. The component form of k is 3, 6. dd the components: 5 3, 4 6. The resultant vector is 8, dd vectors a and b. The component form of a is 3, 8. The component form of b is 3, 8. h b y k dd the components: 3 3, 8 8. a The resultant vector is 0, 0. Saxon. ll rights reserved. 138 Saxon Geometry
9 Name ate lass Reteaching ngles Interior to ircles 64 You have learned how to construct a tangent line on a circle. Now you will determine the measure of an angle formed by a chord and a line tangent to a circle. The measure of an angle formed by a chord and a tangent is equal to half the measure of the arc that subtends it. m 1 m E Given: _ YZ and _ HI are tangent lines. E ind the indicated measure. a. m XYZ m XYZ 1 m XY m XYZ 1 (170 ) m XYZ 85 x Y 170 Z b. m GH m GHI 1 m GH 75 1 m GH 150 m GH I G 75 H omplete the steps to find each measure. 1. m 40 m 1 m 1 (40 ) I m 10. m PQR Q P m PRT 1 m PQR m PQR T 135 R 70 m PQR ind the value of x in each figure. 3. x x 66 x 18 x p 133 q Saxon. ll rights reserved. 139 Saxon Geometry
10 Reteaching continued 64 The measure of an angle formed by two chords intersecting in a circle is equal to half the sum of the intersected arcs. m 1 1 (m m ) ind the measure of angle x. x 1 (m m E ) x 1 (60 56) x 58 1 x E omplete the steps to find the measure of angle x. 5. x 1 ( m HJ m Lk ) x 1 ( ) x 146 H L 110 x J K x 1 ( m PS m QR ) x 1 ( 45 73) x 59 ind the measure of angle x for each circle. 7. x x 49.5 W 5 T U x 81 V 9. x x L P S P x x M Q 73 R 6 N Z x 153 x E Y Y G 33 Saxon. ll rights reserved. 140 Saxon Geometry
11 Name ate lass Reteaching istinguishing Types of Parallelograms 65 parallelogram is a rectangle if it has one 90 angle. Example: Is this parallelogram a rectangle? Since the consecutive angles of a parallelogram are supplementary, we know that the measure of the two given expressions must add up to 180. Solve for x. (7x+6) (8x 6) (7x 6) x 180 x 1 Substitute the value of x into one of the expressions to find the measure of the angle. 8(1) 6 90 One of the angle measures of the parallelogram is 90, so the parallelogram is a rectangle. omplete the statements to distinguish the parallelogram. (8x-6) 1. Is parallelogram MNOP a rectangle? or a parallelogram to be a rectangle, it must have one 90 angle. 6x x 60 4x 60 x 15 M 6x P (6x + 60) N O If x 15, M 6x , and MNOP is a rectangle.. Is this parallelogram a rectangle? no 3. Is this parallelogram a rectangle? yes (5x + 5) (8x + 18) (6x + 4) (11x - 9) 4. If y 10, is this parallelogram a rectangle? 5. If y 3, is this parallelogram a rectangle? W X (5x - y) (3x + y) (4x + 10) (4x - 37) Z yes Y no Saxon. ll rights reserved. 141 Saxon Geometry
12 Reteaching continued 65 parallelogram is a rhombus if it has two consecutive sides that are congruent. Example: E If x 14, is parallelogram EGH a rhombus? Since we know x 14, we can find the length of side G: G 4x 16 H G 4(16) 16 G 40 Since E and G have the same length, they are congruent. G Since E and G are consecutive sides of equal length, parallelogram EGH is a rhombus. 40 4x If x, is the parallelogram a rhombus? or a parallelogram to be a rhombus, consecutive sides must have equal length. 4x 1 9 4() 1 9 X U 4x + 1 W V 9 Since UV and VW are consecutive sides that have equal lengths, the parallelogram is a rhombus. 7. If x 19, is this parallelogram 8. If a 3, b 5, c 4, and d 4, a rhombus? is this parallelogram a rhombus? J K Q R 3x + 18 a + b I 75 ft L yes P yes c + d S 9. If x y, is this parallelogram a rhombus? no 10. Is this parallelogram a rhombus? yes W X n 50 x n Y y + 5 Saxon. ll rights reserved. 14 Saxon Geometry
13 Name ate lass Reteaching inding Perimeters and reas of Regular Polygons 66 You have learned how to find perimeter and area of many types of figures. Now you will use formulas to find perimeters and areas of regular polygons. The perimeter of a regular polygon can be found by multiplying the length of one of its sides by the number of sides it has. ind the perimeter of the regular octagon. ecause this is a regular octagon, the length of each side is the same as that of the labeled side, 7 centimeters. n octagon has 8 sides, so we can find the area by multiplying 8 by 7. P ns P (8)(7 cm) P 56 cm The perimeter of the regular octagon is 56 centimeters. 7 cm omplete the steps to find the perimeter of the regular polygon. 1. P (5)(9). P (6)(4.) 9 cm 4. ft P 45 cm P 5. ft ind the perimeter of each regular polygon m mm 1 m 11.5 mm yd in. 5.7 yd 1 in. Saxon. ll rights reserved. 143 Saxon Geometry
14 Reteaching continued 66 The area of a regular polygon is equal to its perimeter times the length of the apothem, divided by ( 1 ap ). Here we are not given the length of the apothem, so we have to find it. When the figure is a regular hexagon, we can form an equilateral triangle with the center of the hexagon as the top vertex. The apothem forms a with the side and hypotenuse. Use the Pythagorean Theorem to find that the length of the apothem is 7 3 millimeters. ind the perimeter: P ns P (6)(14) 84 ind the area: 1 ap 1 (7 3 )(84) 94 3 The area of this regular hexagon is 94 3 mm mm 7 mm a 14 mm omplete the steps to find the area of the regular polygon. 7. apothem 4 3 ft P (6)(8) 1 (4 3 )(48) 19 3 ft 8. apothem 11.5 cm P (7)(11) 1 (11.5 cm)(77 cm) cm a 8 ft 11 cm ind the area of each regular polygon in 1 m 10 in m 6.9 in m yd 4 yd ft 7 ft 9.6 ft Saxon. ll rights reserved. 144 Saxon Geometry
15 Name ate lass Reteaching Introduction to Transformations You have worked with different figures in the coordinate plane. Now you will work with moving those figures around. 67 Transformations n isometry is a transformation that does not change the size or the shape of a figure. There are different types of isometries. translation or a slide is a transformation in which all the points of a figure are moved the same distance in the same direction. ' ' ' ' reflection or a flip is a transformation that flips a figure across a line. E' ' ' E rotation is a transformation that turns a figure around a fixed point, which is called the center of rotation. center of rotation ' Rotation ' Example: Identify the type of transformation. E ' ' E' ' ' ' The figure is rotated about a point. ' omplete the statement to determine the type of transformation. 1. ll the points of the figure are moved the same distance in the L' M' same direction. L N' The transformation is a translation or a slide. M etermine the type of transformation.. reflection 3. rotation N E ' ' E' G G' ' ' Saxon. ll rights reserved. 145 Saxon Geometry '
16 Reteaching continued 67 Performing Transformations or a translation or a slide, move each point of the preimage the indicated distance and direction. ' ' or a reflection or a flip, move each point across the line of reflection so that the point and its image are the same distance from the line. ' ' ' ' ' To rotate a figure about a point, keep point fixed and turn each point on a circular path around, as shown. ' ' Example: Reflect the figure across the line. ' ' E E' ' ' omplete each translation. 4. raw the translation of the figure along the given path. 5. raw the rotation of the figure about point P. R' Q' ' P' P R ' ' Q 6. raw the translation of the figure along the given path. 7. raw the rotation of the figure across the line. ' G' ' I' G H' ' I H ' Saxon. ll rights reserved. 146 Saxon Geometry
17 Name ate lass Reteaching Introduction to Trigonometric unctions 68 You have worked with right triangles. Now you will work with special relationships between the angles and sides in a right triangle. Trigonometric Ratios leg opposite sin leg cos adjacent to hypotenuse hypotenuse Example: Write each trigonometric ratio as a fraction. leg opposite sin 4 hypotenuse 5 cos tan leg adjacent to hypotenuse 3 5 leg opposite 4 leg adjacent to 3 tan hypotenuse 5 leg opposite leg adjacent to 3 4 leg adjacent to leg opposite omplete the statement to determine the given trigonometric ratio. 1. sin K leg opposite K hypotenuse cos K leg adjacent to K hypotenuse 8 17 K 8 J H tan K leg opposite K leg adjacent to K 15 8 Use the diagram from Exercise 1 to write each trigonometric ratio as a fraction.. sin H cos H tan H 8 15 Write each trigonometric ratio as a fraction. 5. sin cos tan sin tan cos Saxon. ll rights reserved. 147 Saxon Geometry
18 Reteaching continued 68 Trigonometric Ratios (continued) You can use a calculator to find the value of trigonometric ratios: cos , or about Example: ind WY. adjacent leg cos W Write a trigonometric ratio that involves WY. hypotenuse cos cm x Substitute the given values. x cos Multiply both sides by x. x 7.5 ivide both sides by os 39 cos 39 x 9.65 cm Simplify. The length of WY is approximately 9.65 centimeters. W 7.5 cm 39 Y X omplete the steps to find E. 11. E sine opposite leg hypotenuse sin 7 18 x x sin m 7 E x 18 sin 7 x m Use your calculator to find each trigonometric ratio. Round to the nearest hundredth. 1. sin cos tan ind each length. Round to the nearest hundredth. 15. H 6.01 in. 16. JK 3.91 mm 17. US 55.3 cm 10 in. 31 G K 34.6 mm 18 L J S 66 T.5 cm U H Saxon. ll rights reserved. 148 Saxon Geometry
19 Name ate lass Reteaching Properties of Trapezoids and Kites 69 You have worked with triangles. Now you will find the lengths of sides of trapezoids and kites. Trapezoid Midsegment Theorem trapezoid is a quadrilateral with one pair of parallel sides. The midsegment of a trapezoid is the segment whose endpoints are the midpoints of the legs. The midsegment of a trapezoid is parallel to each base. M N _ _ MN and _ _ LP The length of the midsegment is one-half of the sum of L the length of the bases. 1 (MN LP ) Use the formula to find the length of the midsegment _ KL. G KL 1 (GH J ) K KL 1 (18 6) Substitute. KL 1 (44) Simplify. KL Simplify. P is the midsegment of LMNP H L J omplete the steps to find each length. 1. MN. J MN 1 ( ) M MN 1 3 ( 3 17) N XY 1 (J GH ) G X (J 48) MN 1 ( 40) 80 J 48 MN 0 J 3 ind each length. 3. KL 4. TV J Y H K N J M P L 14 S P V T Q 5.6 R Saxon. ll rights reserved. 149 Saxon Geometry
20 Reteaching continued 69 iagonals of Kites kite is a quadrilateral with two pairs of congruent adjacent sides. The diagonals of a kite are perpendicular to each other. _ _ ecause the diagonals of a kite are perpendicular to each other, you can use the Pythagorean theorem to find the length of each side. ind the length of _. Use the Pythagorean theorem to find the length of the side. E E 1 5 Substitute Simplify. 1 E Simplify Solve. So, the Length of _ is 13. omplete the steps to find the lengths of _ JK and _ JM. Round each length to the nearest tenth. K 5. Use the Pythagorean theorem to find the length of each side. JK JN NK JM JN NM JK 6 15 JM 6 8 JK 36 5 JM JK 61 JM 100 J 15 6 N 6 8 L JK 61 JM 100 M JK 16. JM 10 ind each length. Round to the nearest tenth. 6. ind the length of _. 7. ind the length of _ E. 7.4 E E Saxon. ll rights reserved. 150 Saxon Geometry
21 Name ate lass Reteaching inding Surface reas and Volumes of Pyramids 70 You have worked with surface area and volume of prisms. Now you will find the lateral area, the surface area, and the volume of pyramids. Lateral and Surface rea of a Regular Pyramid The lateral area of a regular pyramid with base perimeter P and slant height is L 1 P. The surface area of a regular pyramid with lateral area L and base area is S L or S 1 P. ind the lateral area and the surface area of the regular pyramid. L 1 P Lateral area formula L 1 (3)(1) Substitute. 1 m L 19 m Simplify. S L Surface area formula S 19 6 Substitute. S 56 m Simplify. The lateral area is 19 square meters. The surface area is 56 square meters. l 8 m base height 8 m base omplete the steps to find the lateral area and the surface area of the regular pyramid. Round your answer to the nearest tenth. 1. L 1 P 1 (48)(1) 88 ft 1 s 3 P ft S L ft 1 ft 8 ft 3 ft ind the lateral area and the surface area of the regular pyramid. Round to the nearest tenth.. L 98.0 in 3. L cm S 4.1 in S cm 1.9 in. 13 cm 8.5 in in. 1 cm 1 cm Saxon. ll rights reserved. 151 Saxon Geometry
22 Reteaching continued 70 Volume of a Pyramid The altitude, or height, of a pyramid is the perpendicular segment that measures from the vertex of the pyramid to the base of the pyramid. The volume of a pyramid with base area and h height h is V 1 3 h. ind the volume of the pyramid. Round to the nearest tenth if necessary. V 1 3 h 8 in. V 1 (5)(8) Substitute. 3 V 1 (00) Simplify. 3 V 66.7 in 3 Solve. The volume of the pyramid is 66.7 cubic inches. 5 in. 5 in. omplete the steps to find the volume of the pyramid. Round to the nearest tenth. 4. V 1 3 h 11 cm V cm 6 cm 5. V 1 3 h V 1 (84) (11) 3 V 1 (54.) (16.6) 3 (94) V 1 3 (899.7) V 308 cm 3 V 99.9 in 3 ind the volume of the pyramid. Round to the nearest tenth ft m in. 1.9 in. 8.4 in. 10 ft.6 m 7 ft 7 ft 18.1 m 33.8 m Saxon. ll rights reserved. 15 Saxon Geometry
Name Score Period Date. m = 2. Find the geometric mean of the two numbers. Copy and complete the statement.
 Chapter 6 Review Geometry Name Score Period Date Solve the proportion. 3 5 1. = m 1 3m 4 m = 2. 12 n = n 3 n = Find the geometric mean of the two numbers. Copy and complete the statement. 7 x 7? 3. 12
Chapter 6 Review Geometry Name Score Period Date Solve the proportion. 3 5 1. = m 1 3m 4 m = 2. 12 n = n 3 n = Find the geometric mean of the two numbers. Copy and complete the statement. 7 x 7? 3. 12
Geometry Honors Final Exam Review June 2018
 Geometry Honors Final Exam Review June 2018 1. Determine whether 128 feet, 136 feet, and 245 feet can be the lengths of the sides of a triangle. 2. Casey has a 13-inch television and a 52-inch television
Geometry Honors Final Exam Review June 2018 1. Determine whether 128 feet, 136 feet, and 245 feet can be the lengths of the sides of a triangle. 2. Casey has a 13-inch television and a 52-inch television
Section 5.1. Perimeter and Area
 Section 5.1 Perimeter and Area Perimeter and Area The perimeter of a closed plane figure is the distance around the figure. The area of a closed plane figure is the number of non-overlapping squares of
Section 5.1 Perimeter and Area Perimeter and Area The perimeter of a closed plane figure is the distance around the figure. The area of a closed plane figure is the number of non-overlapping squares of
Geometry Final Review. Chapter 1. Name: Per: Vocab. Example Problems
 Geometry Final Review Name: Per: Vocab Word Acute angle Adjacent angles Angle bisector Collinear Line Linear pair Midpoint Obtuse angle Plane Pythagorean theorem Ray Right angle Supplementary angles Complementary
Geometry Final Review Name: Per: Vocab Word Acute angle Adjacent angles Angle bisector Collinear Line Linear pair Midpoint Obtuse angle Plane Pythagorean theorem Ray Right angle Supplementary angles Complementary
Geometry Final Exam REVIEW
 Name: Class: _ Date: _ Geometry Final Exam 09-10 - REVIEW Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the perimeter and area of the parallelogram.
Name: Class: _ Date: _ Geometry Final Exam 09-10 - REVIEW Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the perimeter and area of the parallelogram.
Name: GEOMETRY: EXAM (A) A B C D E F G H D E. 1. How many non collinear points determine a plane?
 GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
Geometry Cumulative Review
 Geometry Cumulative Review Name 1. Find a pattern for the sequence. Use the pattern to show the next term. 1, 3, 9, 27,... A. 81 B. 45 C. 41 D. 36 2. If EG = 42, find the value of y. A. 5 B. C. 6 D. 7
Geometry Cumulative Review Name 1. Find a pattern for the sequence. Use the pattern to show the next term. 1, 3, 9, 27,... A. 81 B. 45 C. 41 D. 36 2. If EG = 42, find the value of y. A. 5 B. C. 6 D. 7
A. 180 B. 108 C. 360 D. 540
 Part I - Multiple Choice - Circle your answer: 1. Find the area of the shaded sector. Q O 8 P A. 2 π B. 4 π C. 8 π D. 16 π 2. An octagon has sides. A. five B. six C. eight D. ten 3. The sum of the interior
Part I - Multiple Choice - Circle your answer: 1. Find the area of the shaded sector. Q O 8 P A. 2 π B. 4 π C. 8 π D. 16 π 2. An octagon has sides. A. five B. six C. eight D. ten 3. The sum of the interior
Name: Class: Date: c. WZ XY and XW YZ. b. WZ ZY and XW YZ. d. WN NZ and YN NX
 Class: Date: 2nd Semester Exam Review - Geometry CP 1. Complete this statement: A polygon with all sides the same length is said to be. a. regular b. equilateral c. equiangular d. convex 3. Which statement
Class: Date: 2nd Semester Exam Review - Geometry CP 1. Complete this statement: A polygon with all sides the same length is said to be. a. regular b. equilateral c. equiangular d. convex 3. Which statement
Chapter 6. Worked-Out Solutions. Chapter 6 Maintaining Mathematical Proficiency (p. 299)
 hapter 6 hapter 6 Maintaining Mathematical Proficiency (p. 99) 1. Slope perpendicular to y = 1 x 5 is. y = x + b 1 = + b 1 = 9 + b 10 = b n equation of the line is y = x + 10.. Slope perpendicular to y
hapter 6 hapter 6 Maintaining Mathematical Proficiency (p. 99) 1. Slope perpendicular to y = 1 x 5 is. y = x + b 1 = + b 1 = 9 + b 10 = b n equation of the line is y = x + 10.. Slope perpendicular to y
Indicate whether the statement is true or false.
 PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
1 st Preparatory. Part (1)
 Part (1) (1) omplete: 1) The square is a rectangle in which. 2) in a parallelogram in which m ( ) = 60, then m ( ) =. 3) The sum of measures of the angles of the quadrilateral equals. 4) The ray drawn
Part (1) (1) omplete: 1) The square is a rectangle in which. 2) in a parallelogram in which m ( ) = 60, then m ( ) =. 3) The sum of measures of the angles of the quadrilateral equals. 4) The ray drawn
Chapter 7 Sect. 2. A pythagorean triple is a set of three nonzero whole numbers a, b, and c, that satisfy the equation a 2 + b 2 = c 2.
 Chapter 7 Sect. 2 The well-known right triangle relationship called the Pythagorean Theorem is named for Pythagoras, a Greek mathematician who lived in the sixth century b.c. We now know that the Babylonians,
Chapter 7 Sect. 2 The well-known right triangle relationship called the Pythagorean Theorem is named for Pythagoras, a Greek mathematician who lived in the sixth century b.c. We now know that the Babylonians,
0110ge. Geometry Regents Exam Which expression best describes the transformation shown in the diagram below?
 0110ge 1 In the diagram below of trapezoid RSUT, RS TU, X is the midpoint of RT, and V is the midpoint of SU. 3 Which expression best describes the transformation shown in the diagram below? If RS = 30
0110ge 1 In the diagram below of trapezoid RSUT, RS TU, X is the midpoint of RT, and V is the midpoint of SU. 3 Which expression best describes the transformation shown in the diagram below? If RS = 30
Replacement for a Carpenter s Square
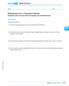 Lesson.1 Skills Practice Name Date Replacement for a arpenter s Square Inscribed and ircumscribed Triangles and Quadrilaterals Vocabulary nswer each question. 1. How are inscribed polygons and circumscribed
Lesson.1 Skills Practice Name Date Replacement for a arpenter s Square Inscribed and ircumscribed Triangles and Quadrilaterals Vocabulary nswer each question. 1. How are inscribed polygons and circumscribed
0112ge. Geometry Regents Exam Line n intersects lines l and m, forming the angles shown in the diagram below.
 Geometry Regents Exam 011 011ge 1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT. Which value of x would
Geometry Regents Exam 011 011ge 1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT. Which value of x would
Practice Test Student Answer Document
 Practice Test Student Answer Document Record your answers by coloring in the appropriate bubble for the best answer to each question. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Practice Test Student Answer Document Record your answers by coloring in the appropriate bubble for the best answer to each question. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
b) Parallelogram Opposite Sides Converse c) Parallelogram Diagonals Converse d) Opposite sides Parallel and Congruent Theorem
 Chapter 7 1. State which theorem you can use to show that the quadrilateral is a parallelogram. a) Parallelogram Opposite Angles Converse b) Parallelogram Opposite Sides Converse c) Parallelogram Diagonals
Chapter 7 1. State which theorem you can use to show that the quadrilateral is a parallelogram. a) Parallelogram Opposite Angles Converse b) Parallelogram Opposite Sides Converse c) Parallelogram Diagonals
Geometry: Hutschenreuter Semester II. Select the best answer for each question. Show expected work. MAKE A SUPPORTING SKETCH!
 Geometry: Hutschenreuter Semester II Review B Name Period Date Select the best answer for each question. Show expected work. MAKE A SUPPORTING SKETCH! 1. A parallelogram has a diagonal of 41 cm and side
Geometry: Hutschenreuter Semester II Review B Name Period Date Select the best answer for each question. Show expected work. MAKE A SUPPORTING SKETCH! 1. A parallelogram has a diagonal of 41 cm and side
Geometry. A. Right Triangle. Legs of a right triangle : a, b. Hypotenuse : c. Altitude : h. Medians : m a, m b, m c. Angles :,
 Geometry A. Right Triangle Legs of a right triangle : a, b Hypotenuse : c Altitude : h Medians : m a, m b, m c Angles :, Radius of circumscribed circle : R Radius of inscribed circle : r Area : S 1. +
Geometry A. Right Triangle Legs of a right triangle : a, b Hypotenuse : c Altitude : h Medians : m a, m b, m c Angles :, Radius of circumscribed circle : R Radius of inscribed circle : r Area : S 1. +
Which statement is true about parallelogram FGHJ and parallelogram F ''G''H''J ''?
 Unit 2 Review 1. Parallelogram FGHJ was translated 3 units down to form parallelogram F 'G'H'J '. Parallelogram F 'G'H'J ' was then rotated 90 counterclockwise about point G' to obtain parallelogram F
Unit 2 Review 1. Parallelogram FGHJ was translated 3 units down to form parallelogram F 'G'H'J '. Parallelogram F 'G'H'J ' was then rotated 90 counterclockwise about point G' to obtain parallelogram F
Introduction - Geometry
 L I F O R N I S T N R S T E S T Introduction - The following released test questions are taken from the Standards Test. This test is one of the alifornia Standards Tests administered as part of the Standardized
L I F O R N I S T N R S T E S T Introduction - The following released test questions are taken from the Standards Test. This test is one of the alifornia Standards Tests administered as part of the Standardized
Practice Test Geometry 1. Which of the following points is the greatest distance from the y-axis? A. (1,10) B. (2,7) C. (3,5) D. (4,3) E.
 April 9, 01 Standards: MM1Ga, MM1G1b Practice Test Geometry 1. Which of the following points is the greatest distance from the y-axis? (1,10) B. (,7) C. (,) (,) (,1). Points P, Q, R, and S lie on a line
April 9, 01 Standards: MM1Ga, MM1G1b Practice Test Geometry 1. Which of the following points is the greatest distance from the y-axis? (1,10) B. (,7) C. (,) (,) (,1). Points P, Q, R, and S lie on a line
Geometry Pre-Unit 1 Intro: Area, Perimeter, Pythagorean Theorem, Square Roots, & Quadratics. P-1 Square Roots and SRF
 Geometry Pre-Unit 1 Intro: Area, Perimeter, Pythagorean Theorem, Square Roots, & Quadratics P-1 Square Roots and SRF Square number the product of a number multiplied by itself. 1 * 1 = 1 1 is a square
Geometry Pre-Unit 1 Intro: Area, Perimeter, Pythagorean Theorem, Square Roots, & Quadratics P-1 Square Roots and SRF Square number the product of a number multiplied by itself. 1 * 1 = 1 1 is a square
Chapter 3 Cumulative Review Answers
 Chapter 3 Cumulative Review Answers 1a. The triangle inequality is violated. 1b. The sum of the angles is not 180º. 1c. Two angles are equal, but the sides opposite those angles are not equal. 1d. The
Chapter 3 Cumulative Review Answers 1a. The triangle inequality is violated. 1b. The sum of the angles is not 180º. 1c. Two angles are equal, but the sides opposite those angles are not equal. 1d. The
Skills Practice Skills Practice for Lesson 11.1
 Skills Practice Skills Practice for Lesson.1 Name ate Riding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. circle X T 2. center of the circle H I
Skills Practice Skills Practice for Lesson.1 Name ate Riding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. circle X T 2. center of the circle H I
Find the area of the triangle. You try: D C. Determine whether each of the following statements is true or false. Solve for the variables.
 lameda USD Geometr enchmark Stud Guide ind the area of the triangle. 9 4 5 D or all right triangles, a + b c where c is the length of the hpotenuse. 5 4 a + b c 9 + b 5 + b 5 b 5 b 44 b 9 he area of a
lameda USD Geometr enchmark Stud Guide ind the area of the triangle. 9 4 5 D or all right triangles, a + b c where c is the length of the hpotenuse. 5 4 a + b c 9 + b 5 + b 5 b 5 b 44 b 9 he area of a
0809ge. Geometry Regents Exam Based on the diagram below, which statement is true?
 0809ge 1 Based on the diagram below, which statement is true? 3 In the diagram of ABC below, AB AC. The measure of B is 40. 1) a b ) a c 3) b c 4) d e What is the measure of A? 1) 40 ) 50 3) 70 4) 100
0809ge 1 Based on the diagram below, which statement is true? 3 In the diagram of ABC below, AB AC. The measure of B is 40. 1) a b ) a c 3) b c 4) d e What is the measure of A? 1) 40 ) 50 3) 70 4) 100
New Jersey Center for Teaching and Learning. Progressive Mathematics Initiative
 Slide 1 / 150 New Jersey Center for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
Slide 1 / 150 New Jersey Center for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
0114ge. Geometry Regents Exam 0114
 0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
NORTH THURSTON PUBLIC SCHOOLS END OF COURSE GEOMETRY PRACTICE TEST. Name: Date:
 NORTH THURSTON PUBLIC SCHOOLS END OF COURSE GEOMETRY PRACTICE TEST Name: Date: Day 1 1. Determine the value of x if ΔABC is equilateral. B 7.5x 6x + 3 A Write your answer on the line. 10x 5 C What is the
NORTH THURSTON PUBLIC SCHOOLS END OF COURSE GEOMETRY PRACTICE TEST Name: Date: Day 1 1. Determine the value of x if ΔABC is equilateral. B 7.5x 6x + 3 A Write your answer on the line. 10x 5 C What is the
Ready To Go On? Skills Intervention 11-1 Lines That Intersect Circles
 Name ate lass STION 11 Ready To Go On? Skills Intervention 11-1 Lines That Intersect ircles ind these vocabulary words in Lesson 11-1 and the Multilingual Glossary. Vocabulary interior of a circle exterior
Name ate lass STION 11 Ready To Go On? Skills Intervention 11-1 Lines That Intersect ircles ind these vocabulary words in Lesson 11-1 and the Multilingual Glossary. Vocabulary interior of a circle exterior
Final Exam Review Packet
 Final Exam Review Packet Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the length of the missing side. The triangle is not drawn to scale. 6 8 a.
Final Exam Review Packet Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the length of the missing side. The triangle is not drawn to scale. 6 8 a.
0610ge. Geometry Regents Exam The diagram below shows a right pentagonal prism.
 0610ge 1 In the diagram below of circle O, chord AB chord CD, and chord CD chord EF. 3 The diagram below shows a right pentagonal prism. Which statement must be true? 1) CE DF 2) AC DF 3) AC CE 4) EF CD
0610ge 1 In the diagram below of circle O, chord AB chord CD, and chord CD chord EF. 3 The diagram below shows a right pentagonal prism. Which statement must be true? 1) CE DF 2) AC DF 3) AC CE 4) EF CD
Use this space for computations. 1 In trapezoid RSTV below with bases RS and VT, diagonals RT and SV intersect at Q.
 Part I Answer all 28 questions in this part. Each correct answer will receive 2 credits. For each statement or question, choose the word or expression that, of those given, best completes the statement
Part I Answer all 28 questions in this part. Each correct answer will receive 2 credits. For each statement or question, choose the word or expression that, of those given, best completes the statement
1 = 1, b d and c d. Chapter 7. Worked-Out Solutions Chapter 7 Maintaining Mathematical Proficiency (p. 357) Slope of line b:
 hapter 7 aintaining athematical Proficienc (p. 357) 1. (7 x) = 16 (7 x) = 16 7 x = 7 = 7 x = 3 x 1 = 3 1 x = 3. 7(1 x) + = 19 = 7(1 x) = 1 7(1 x) 7 = 1 7 1 x = 3 1 = 1 x = x 1 = 1 x = 3. 3(x 5) + 8(x 5)
hapter 7 aintaining athematical Proficienc (p. 357) 1. (7 x) = 16 (7 x) = 16 7 x = 7 = 7 x = 3 x 1 = 3 1 x = 3. 7(1 x) + = 19 = 7(1 x) = 1 7(1 x) 7 = 1 7 1 x = 3 1 = 1 x = x 1 = 1 x = 3. 3(x 5) + 8(x 5)
CP Geometry Final Exam Review Packet
 CP Geometry Final Exam Review Packet 016-017 This packet reviews the basic concepts that you learned in each of the units taught this semester that will be assessed on the final exam. You should complete
CP Geometry Final Exam Review Packet 016-017 This packet reviews the basic concepts that you learned in each of the units taught this semester that will be assessed on the final exam. You should complete
Grade 11 Mathematics Practice Test
 Grade Mathematics Practice Test Nebraska Department of Education 204 Directions: On the following pages are multiple-choice questions for the Grade Practice Test, a practice opportunity for the Nebraska
Grade Mathematics Practice Test Nebraska Department of Education 204 Directions: On the following pages are multiple-choice questions for the Grade Practice Test, a practice opportunity for the Nebraska
4.! ABC ~ DEF,! AC = 6 ft, CB = 3 ft, AB = 7 ft, DF = 9 ft.! What is the measure of EF?
 Name:!!!!!!!!!!!!! Geo(2) GEOMETRY (2) REVIEW FOR FINAL EXAM #2 1. If ABC is similar to ADE, then AB AD =? AE. Which replaces the? to make the statement true? A. AC!! B. AE!! C. DE!! D. BC 2. In ABC,
Name:!!!!!!!!!!!!! Geo(2) GEOMETRY (2) REVIEW FOR FINAL EXAM #2 1. If ABC is similar to ADE, then AB AD =? AE. Which replaces the? to make the statement true? A. AC!! B. AE!! C. DE!! D. BC 2. In ABC,
Geometry Final Exam Review
 Name: Date: Period: Geometry Final Exam Review 1. Fill in the flow chart below with the properties that belong to each polygon. 2. Find the measure of each numbered angle: 3. Find the value of x 4. Calculate
Name: Date: Period: Geometry Final Exam Review 1. Fill in the flow chart below with the properties that belong to each polygon. 2. Find the measure of each numbered angle: 3. Find the value of x 4. Calculate
Geometry Simulation Test 2014 Region 1
 Geometry Simulation Test 2014 Region 1 1 etermine the inverse of Mark Twain s quote If you tell the truth, you don t have to remember anything. You don t have to remember anything if you tell the truth.
Geometry Simulation Test 2014 Region 1 1 etermine the inverse of Mark Twain s quote If you tell the truth, you don t have to remember anything. You don t have to remember anything if you tell the truth.
9.3. Practice C For use with pages Tell whether the triangle is a right triangle.
 LESSON 9.3 NAME DATE For use with pages 543 549 Tell whether the triangle is a right triangle. 1. 21 2. 3. 75 6 2 2 17 72 63 66 16 2 4. 110 5. 4.3 6. 96 2 4.4 10 3 3 4.5 Decide whether the numbers can
LESSON 9.3 NAME DATE For use with pages 543 549 Tell whether the triangle is a right triangle. 1. 21 2. 3. 75 6 2 2 17 72 63 66 16 2 4. 110 5. 4.3 6. 96 2 4.4 10 3 3 4.5 Decide whether the numbers can
~ 1 ~ Geometry 2 nd Semester Review Find the value for the variable for each of the following situations
 Geometry nd Semester Review 018 Find the value for the variable for each of the following situations. 7. 400 m 1. 7 8. y. 8.9 cm 0 0 9.. 19 6 60 1 11 10. 45 4. 58 5 11. 5. 11 6. 18 1 slide 4.1 meters long
Geometry nd Semester Review 018 Find the value for the variable for each of the following situations. 7. 400 m 1. 7 8. y. 8.9 cm 0 0 9.. 19 6 60 1 11 10. 45 4. 58 5 11. 5. 11 6. 18 1 slide 4.1 meters long
Geometry Honors: Midterm Exam Review January 2018
 Name: Period: The midterm will cover Chapters 1-6. Geometry Honors: Midterm Exam Review January 2018 You WILL NOT receive a formula sheet, but you need to know the following formulas Make sure you memorize
Name: Period: The midterm will cover Chapters 1-6. Geometry Honors: Midterm Exam Review January 2018 You WILL NOT receive a formula sheet, but you need to know the following formulas Make sure you memorize
H. Math 2 Benchmark 1 Review
 H. Math 2 enchmark 1 Review Name: ate: 1. Parallelogram C was translated to parallelogram C. 2. Which of the following is a model of a scalene triangle?.. How many units and in which direction were the
H. Math 2 enchmark 1 Review Name: ate: 1. Parallelogram C was translated to parallelogram C. 2. Which of the following is a model of a scalene triangle?.. How many units and in which direction were the
Integrated Mathematics II
 Integrated Mathematics II This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet
Integrated Mathematics II This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet
0811ge. Geometry Regents Exam BC, AT = 5, TB = 7, and AV = 10.
 0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 2) 8 3) 3 4) 6 2 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 2) 8 3) 3 4) 6 2 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
Correlation of 2012 Texas Essential Knowledge and Skills (TEKS) for Algebra I and Geometry to Moving with Math SUMS Moving with Math SUMS Algebra 1
 Correlation of 2012 Texas Essential Knowledge and Skills (TEKS) for Algebra I and Geometry to Moving with Math SUMS Moving with Math SUMS Algebra 1 ALGEBRA I A.1 Mathematical process standards. The student
Correlation of 2012 Texas Essential Knowledge and Skills (TEKS) for Algebra I and Geometry to Moving with Math SUMS Moving with Math SUMS Algebra 1 ALGEBRA I A.1 Mathematical process standards. The student
Geometry. Midterm Review
 Geometry Midterm Review Class: Date: Geometry Midterm Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1 A plumber knows that if you shut off the water
Geometry Midterm Review Class: Date: Geometry Midterm Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1 A plumber knows that if you shut off the water
Kansas City Area Teachers of Mathematics 2013 KCATM Math Competition GEOMETRY GRADES 7-8
 Kansas City Area Teachers of Mathematics 2013 KCATM Math Competition GEOMETRY GRADES 7-8 INSTRUCTIONS Do not open this booklet until instructed to do so. Time limit: 20 minutes You may use calculators.
Kansas City Area Teachers of Mathematics 2013 KCATM Math Competition GEOMETRY GRADES 7-8 INSTRUCTIONS Do not open this booklet until instructed to do so. Time limit: 20 minutes You may use calculators.
1 What is the solution of the system of equations graphed below? y = 2x + 1
 1 What is the solution of the system of equations graphed below? y = 2x + 1 3 As shown in the diagram below, when hexagon ABCDEF is reflected over line m, the image is hexagon A'B'C'D'E'F'. y = x 2 + 2x
1 What is the solution of the system of equations graphed below? y = 2x + 1 3 As shown in the diagram below, when hexagon ABCDEF is reflected over line m, the image is hexagon A'B'C'D'E'F'. y = x 2 + 2x
Answers. Chapter 9 A92. Angles Theorem (Thm. 5.6) then XZY. Base Angles Theorem (Thm. 5.6) 5, 2. then WV WZ;
 9 9. M, 0. M ( 9, 4) 7. If WZ XZ, then ZWX ZXW ; Base Angles Theorem (Thm..6). M 9,. M ( 4, ) 74. If XZ XY, then XZY Y; Base Angles Theorem (Thm..6). M, 4. M ( 9, ) 7. If V WZV, then WV WZ; Converse of
9 9. M, 0. M ( 9, 4) 7. If WZ XZ, then ZWX ZXW ; Base Angles Theorem (Thm..6). M 9,. M ( 4, ) 74. If XZ XY, then XZY Y; Base Angles Theorem (Thm..6). M, 4. M ( 9, ) 7. If V WZV, then WV WZ; Converse of
Geometry Note Cards EXAMPLE:
 Geometry Note Cards EXAMPLE: Lined Side Word and Explanation Blank Side Picture with Statements Sections 12-4 through 12-5 1) Theorem 12-3 (p. 790) 2) Theorem 12-14 (p. 790) 3) Theorem 12-15 (p. 793) 4)
Geometry Note Cards EXAMPLE: Lined Side Word and Explanation Blank Side Picture with Statements Sections 12-4 through 12-5 1) Theorem 12-3 (p. 790) 2) Theorem 12-14 (p. 790) 3) Theorem 12-15 (p. 793) 4)
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Student Name:
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, August 17, 2011 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, August 17, 2011 8:30 to 11:30 a.m., only Student Name: School Name: Print your name and the name of
0116ge. Geometry Regents Exam RT and SU intersect at O.
 Geometry Regents Exam 06 06ge What is the equation of a circle with its center at (5, ) and a radius of 3? ) (x 5) + (y + ) = 3 ) (x 5) + (y + ) = 9 3) (x + 5) + (y ) = 3 4) (x + 5) + (y ) = 9 In the diagram
Geometry Regents Exam 06 06ge What is the equation of a circle with its center at (5, ) and a radius of 3? ) (x 5) + (y + ) = 3 ) (x 5) + (y + ) = 9 3) (x + 5) + (y ) = 3 4) (x + 5) + (y ) = 9 In the diagram
0811ge. Geometry Regents Exam
 0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 ) 8 3) 3 4) 6 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 ) 8 3) 3 4) 6 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
ACTM Regional Geometry Exam 2009
 TM Regional Geometry xam 009 In each of the following questions choose the best answer and bubble the corresponding letter on the answer sheet. Note: The geometric figures on this exam are not necessarily
TM Regional Geometry xam 009 In each of the following questions choose the best answer and bubble the corresponding letter on the answer sheet. Note: The geometric figures on this exam are not necessarily
Ohio s State Tests ITEM RELEASE SPRING 2018 GEOMETRY
 Ohio s State Tests ITEM RELEASE SPRING 2018 GEOMETRY Table of Contents Content Summary and Answer Key... iii Question 4: Question and Scoring Guidelines... 1 Question 4: Sample Response... 4 Question 8:
Ohio s State Tests ITEM RELEASE SPRING 2018 GEOMETRY Table of Contents Content Summary and Answer Key... iii Question 4: Question and Scoring Guidelines... 1 Question 4: Sample Response... 4 Question 8:
9. AD = 7; By the Parallelogram Opposite Sides Theorem (Thm. 7.3), AD = BC. 10. AE = 7; By the Parallelogram Diagonals Theorem (Thm. 7.6), AE = EC.
 3. Sample answer: Solve 5x = 3x + 1; opposite sides of a parallelogram are congruent; es; You could start b setting the two parts of either diagonal equal to each other b the Parallelogram Diagonals Theorem
3. Sample answer: Solve 5x = 3x + 1; opposite sides of a parallelogram are congruent; es; You could start b setting the two parts of either diagonal equal to each other b the Parallelogram Diagonals Theorem
JEFFERSON MATH PROJECT REGENTS AT RANDOM
 JEFFERSON MATH PROJECT REGENTS AT RANDOM The NY Geometry Regents Exams Fall 2008-August 2009 Dear Sir I have to acknolege the reciept of your favor of May 14. in which you mention that you have finished
JEFFERSON MATH PROJECT REGENTS AT RANDOM The NY Geometry Regents Exams Fall 2008-August 2009 Dear Sir I have to acknolege the reciept of your favor of May 14. in which you mention that you have finished
126 Holt McDougal Geometry
 test prep 51. m Q = m S 3x + 5 = 5x - 5 30 = x x = 15 5. J 53. 6.4 P = + + + = + + + = (5 + 8.) = 6.4 challenge and extend 54. Let given pts. be (0, 5), (4, 0), (8, 5), and possible 4th pts. be X, Y, Z.
test prep 51. m Q = m S 3x + 5 = 5x - 5 30 = x x = 15 5. J 53. 6.4 P = + + + = + + + = (5 + 8.) = 6.4 challenge and extend 54. Let given pts. be (0, 5), (4, 0), (8, 5), and possible 4th pts. be X, Y, Z.
resources Symbols < is less than > is greater than is less than or equal to is greater than or equal to = is equal to is not equal to
 Symbols < is less than > is greater than is less than or equal to is greater than or equal to resources = is equal to is not equal to is approximately equal to similar a absolute value: = ; - = (x, y)
Symbols < is less than > is greater than is less than or equal to is greater than or equal to resources = is equal to is not equal to is approximately equal to similar a absolute value: = ; - = (x, y)
Los Angeles Unified School District Periodic Assessments. Geometry. Assessment 2 ASSESSMENT CODE LA08_G_T2_TST_31241
 Los Angeles Unified School District Periodic Assessments Assessment 2 2008 2009 Los Angeles Unified School District Periodic Assessments LA08_G_T2_TST_31241 ASSESSMENT ODE 1100209 The test items contained
Los Angeles Unified School District Periodic Assessments Assessment 2 2008 2009 Los Angeles Unified School District Periodic Assessments LA08_G_T2_TST_31241 ASSESSMENT ODE 1100209 The test items contained
Name Geometry Common Core Regents Review Packet - 3. Topic 1 : Equation of a circle
 Name Geometry Common Core Regents Review Packet - 3 Topic 1 : Equation of a circle Equation with center (0,0) and radius r Equation with center (h,k) and radius r ( ) ( ) 1. The endpoints of a diameter
Name Geometry Common Core Regents Review Packet - 3 Topic 1 : Equation of a circle Equation with center (0,0) and radius r Equation with center (h,k) and radius r ( ) ( ) 1. The endpoints of a diameter
Objectives To find the measure of an inscribed angle To find the measure of an angle formed by a tangent and a chord
 1-3 Inscribed ngles ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. lso G-..3, G-..4 M 1, M 3, M 4, M 6 bjectives To find the measure of an
1-3 Inscribed ngles ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. lso G-..3, G-..4 M 1, M 3, M 4, M 6 bjectives To find the measure of an
Skills Practice Skills Practice for Lesson 9.1
 Skills Practice Skills Practice for Lesson.1 Name Date Meeting Friends The Distance Formula Vocabular Define the term in our own words. 1. Distance Formula Problem Set Archaeologists map the location of
Skills Practice Skills Practice for Lesson.1 Name Date Meeting Friends The Distance Formula Vocabular Define the term in our own words. 1. Distance Formula Problem Set Archaeologists map the location of
MT - MATHEMATICS (71) GEOMETRY - PRELIM II - PAPER - 6 (E)
 04 00 Seat No. MT - MTHEMTIS (7) GEOMETRY - PRELIM II - (E) Time : Hours (Pages 3) Max. Marks : 40 Note : ll questions are compulsory. Use of calculator is not allowed. Q.. Solve NY FIVE of the following
04 00 Seat No. MT - MTHEMTIS (7) GEOMETRY - PRELIM II - (E) Time : Hours (Pages 3) Max. Marks : 40 Note : ll questions are compulsory. Use of calculator is not allowed. Q.. Solve NY FIVE of the following
Unit 2 Review. Determine the scale factor of the dilation below.
 Unit 2 Review 1. oes the graph below represent a dilation? Why or why not? y 10 9 8 7 (0, 7) 6 5 4 3 (0, 3.5) 2 1 (5, 7) (5, 3.5) -10-9 -8-7 -6-5 -4-3 -2-1 0 1 2 3 4 5 6 7 8 9 10-1 F -2 (5, 0) -3-4 -5-6
Unit 2 Review 1. oes the graph below represent a dilation? Why or why not? y 10 9 8 7 (0, 7) 6 5 4 3 (0, 3.5) 2 1 (5, 7) (5, 3.5) -10-9 -8-7 -6-5 -4-3 -2-1 0 1 2 3 4 5 6 7 8 9 10-1 F -2 (5, 0) -3-4 -5-6
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXMINTION GEOMETRY Thursday, January 26, 2012 9:15 a.m. to 12:15 p.m., only Student Name: Notice School Name: Print your name and the
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXMINTION GEOMETRY Thursday, January 26, 2012 9:15 a.m. to 12:15 p.m., only Student Name: Notice School Name: Print your name and the
Incoming Magnet Precalculus / Functions Summer Review Assignment
 Incoming Magnet recalculus / Functions Summer Review ssignment Students, This assignment should serve as a review of the lgebra and Geometry skills necessary for success in recalculus. These skills were
Incoming Magnet recalculus / Functions Summer Review ssignment Students, This assignment should serve as a review of the lgebra and Geometry skills necessary for success in recalculus. These skills were
1. Use. What are the vertices of A.,, B.,, C.,, D.,,
 1. Use. What are the vertices of A.,, B.,, C.,, D.,, 2. Given, how are the distances to the origin from each image point related to the distance to the origin from each corresponding preimage point? A.
1. Use. What are the vertices of A.,, B.,, C.,, D.,, 2. Given, how are the distances to the origin from each image point related to the distance to the origin from each corresponding preimage point? A.
Final Exam Review. Multiple Choice Identify the choice that best completes the statement or answers the question.
 ( Final Exam Review Multiple hoice Identify the choice that best completes the statement or answers the question. 1. is an isosceles triangle. is the longest side with length. = and =. Find. 4 x + 4 7
( Final Exam Review Multiple hoice Identify the choice that best completes the statement or answers the question. 1. is an isosceles triangle. is the longest side with length. = and =. Find. 4 x + 4 7
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Student Name:
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, January 27, 2011 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, January 27, 2011 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
Name: Class: Date: 5. If the diagonals of a rhombus have lengths 6 and 8, then the perimeter of the rhombus is 28. a. True b.
 Indicate whether the statement is true or false. 1. If the diagonals of a quadrilateral are perpendicular, the quadrilateral must be a square. 2. If M and N are midpoints of sides and of, then. 3. The
Indicate whether the statement is true or false. 1. If the diagonals of a quadrilateral are perpendicular, the quadrilateral must be a square. 2. If M and N are midpoints of sides and of, then. 3. The
+2 u, 2s ) [D] ( r+ t + u, 2s )
![+2 u, 2s ) [D] ( r+ t + u, 2s ) +2 u, 2s ) [D] ( r+ t + u, 2s )](/thumbs/74/70220114.jpg) 1. Isosceles trapezoid JKLM has legs JK and LM, and base KL. If JK = 3x + 6, KL = 9x 3, and LM = 7x 9. Find the value of x. [A] 15 4 [] 3 4 [] 3 [] 3 4. Which best describes the relationship between the
1. Isosceles trapezoid JKLM has legs JK and LM, and base KL. If JK = 3x + 6, KL = 9x 3, and LM = 7x 9. Find the value of x. [A] 15 4 [] 3 4 [] 3 [] 3 4. Which best describes the relationship between the
Name Date Period Notes Formal Geometry Chapter 8 Right Triangles and Trigonometry 8.1 Geometric Mean. A. Definitions: 1.
 Name Date Period Notes Formal Geometry Chapter 8 Right Triangles and Trigonometry 8.1 Geometric Mean A. Definitions: 1. Geometric Mean: 2. Right Triangle Altitude Similarity Theorem: If the altitude is
Name Date Period Notes Formal Geometry Chapter 8 Right Triangles and Trigonometry 8.1 Geometric Mean A. Definitions: 1. Geometric Mean: 2. Right Triangle Altitude Similarity Theorem: If the altitude is
Geometry Honors Final Exam REVIEW
 Class: Date: Geometry Honors Final Exam 2010-11 REVIEW Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Determine whether the quadrilateral is a parallelogram.
Class: Date: Geometry Honors Final Exam 2010-11 REVIEW Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Determine whether the quadrilateral is a parallelogram.
Geometry Final Exam Review
 Name: Period: Geometry Final Eam Review 1. Find the volume and surface area of the following figures. a) 5' b) c) Square base, all edges of the pyramid have length of ", h = 5.66". 1' 5 9 16. Find the
Name: Period: Geometry Final Eam Review 1. Find the volume and surface area of the following figures. a) 5' b) c) Square base, all edges of the pyramid have length of ", h = 5.66". 1' 5 9 16. Find the
123 Holt McDougal Geometry
 44. - 0 - -4 y x heck students estimates; possible answer: pentagon is not equiangular; m = 100 ; m = 113 ; m = 113 ; m = 101 ; m = 113 ; yes, pentagon is not equiangular. 45a. heptagon b. (7 - )180 =
44. - 0 - -4 y x heck students estimates; possible answer: pentagon is not equiangular; m = 100 ; m = 113 ; m = 113 ; m = 101 ; m = 113 ; yes, pentagon is not equiangular. 45a. heptagon b. (7 - )180 =
GM1.1 Answers. Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
 Cambridge Essentials Mathematics Extension 8 GM1.1 Answers GM1.1 Answers Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
Cambridge Essentials Mathematics Extension 8 GM1.1 Answers GM1.1 Answers Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
Skills Practice Skills Practice for Lesson 3.1
 Skills Practice Skills Practice for Lesson.1 Name Date Get Radical or (Be)! Radicals and the Pythagorean Theorem Vocabulary Write the term that best completes each statement. 1. An expression that includes
Skills Practice Skills Practice for Lesson.1 Name Date Get Radical or (Be)! Radicals and the Pythagorean Theorem Vocabulary Write the term that best completes each statement. 1. An expression that includes
To construct the roof of a house, an architect must determine the measures of the support beams of the roof.
 Metric Relations Practice Name : 1 To construct the roof of a house, an architect must determine the measures of the support beams of the roof. m = 6 m m = 8 m m = 10 m What is the length of segment F?
Metric Relations Practice Name : 1 To construct the roof of a house, an architect must determine the measures of the support beams of the roof. m = 6 m m = 8 m m = 10 m What is the length of segment F?
ACT MATH MUST-KNOWS Pre-Algebra and Elementary Algebra: 24 questions
 Pre-Algebra and Elementary Algebra: 24 questions Basic operations using whole numbers, integers, fractions, decimals and percents Natural (Counting) Numbers: 1, 2, 3 Whole Numbers: 0, 1, 2, 3 Integers:
Pre-Algebra and Elementary Algebra: 24 questions Basic operations using whole numbers, integers, fractions, decimals and percents Natural (Counting) Numbers: 1, 2, 3 Whole Numbers: 0, 1, 2, 3 Integers:
MCA/GRAD Formula Review Packet
 MCA/GRAD Formula Review Packet 1 2 3 4 5 6 The MCA-II / BHS 2 Math Plan GRAD Page 1 of 16 Portions Copyright 2005 by Claude Paradis 8 9 10 12 11 13 14 15 16 1 18 19 20 21 The MCA-II / BHS 2 Math Plan GRAD
MCA/GRAD Formula Review Packet 1 2 3 4 5 6 The MCA-II / BHS 2 Math Plan GRAD Page 1 of 16 Portions Copyright 2005 by Claude Paradis 8 9 10 12 11 13 14 15 16 1 18 19 20 21 The MCA-II / BHS 2 Math Plan GRAD
Name: Date: Period: 1. In the diagram below,. [G.CO.6] 2. The diagram below shows a pair of congruent triangles, with and. [G.CO.
![Name: Date: Period: 1. In the diagram below,. [G.CO.6] 2. The diagram below shows a pair of congruent triangles, with and. [G.CO. Name: Date: Period: 1. In the diagram below,. [G.CO.6] 2. The diagram below shows a pair of congruent triangles, with and. [G.CO.](/thumbs/78/77420594.jpg) Name: Date: Period: Directions: Read each question carefully and choose the best answer for each question. You must show LL of your work to receive credit. 1. In the diagram below,. [G.CO.6] Which statement
Name: Date: Period: Directions: Read each question carefully and choose the best answer for each question. You must show LL of your work to receive credit. 1. In the diagram below,. [G.CO.6] Which statement
UNIT 5 SIMILARITY, RIGHT TRIANGLE TRIGONOMETRY, AND PROOF Unit Assessment
 Unit 5 ircle the letter of the best answer. 1. line segment has endpoints at (, 5) and (, 11). point on the segment has a distance that is 1 of the length of the segment from endpoint (, 5). What are the
Unit 5 ircle the letter of the best answer. 1. line segment has endpoints at (, 5) and (, 11). point on the segment has a distance that is 1 of the length of the segment from endpoint (, 5). What are the
1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT.
 1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT. Which value of x would prove l m? 1) 2.5 2) 4.5 3)
1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT. Which value of x would prove l m? 1) 2.5 2) 4.5 3)
Warm-Up Exercises. Use the figure to answer the questions. 1. What are the values of x and y? ANSWER 125, 125
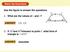 Warm-Up Exercises Use the figure to answer the questions. 1. What are the values of x and y? 125, 125 2. If AX and BY intersect at point P, what kind of triangle is XPY? isosceles EXAMPLE Warm-Up 1Exercises
Warm-Up Exercises Use the figure to answer the questions. 1. What are the values of x and y? 125, 125 2. If AX and BY intersect at point P, what kind of triangle is XPY? isosceles EXAMPLE Warm-Up 1Exercises
MCAS Review - Measurement Session 4A
 lass: ate: I: MS Review - Measurement Session 4 Multiple hoice Identify the choice that best completes the statement or answers the question. 1 circle has an area of 16π square centimeters. What is the
lass: ate: I: MS Review - Measurement Session 4 Multiple hoice Identify the choice that best completes the statement or answers the question. 1 circle has an area of 16π square centimeters. What is the
Chapter 18 Exercise 18.1
 hapter 18 Eercise 18.1 Q. 1. (i) 180 37 = 143 ( = 143 ) (ii) 180 117 = 63 ( = 63 ) 180 90 = 90 (y = 90 ) (iii) + + 3 + 45 = 180 4.5 = 135 (iv) 180 90 = y 90 = y = 30 45 = y 66 + ( + y) + 47 = 180 + y =
hapter 18 Eercise 18.1 Q. 1. (i) 180 37 = 143 ( = 143 ) (ii) 180 117 = 63 ( = 63 ) 180 90 = 90 (y = 90 ) (iii) + + 3 + 45 = 180 4.5 = 135 (iv) 180 90 = y 90 = y = 30 45 = y 66 + ( + y) + 47 = 180 + y =
Chapter 9. b: 196:1 c: 9:1
 9.1.1: Chapter 9 9-7. a: Solutions vary. Here is a possibility: b: Answers vary. Assuming there are no hidden cubes, V = 11!un 3 9-8. a: 4 25 b: 196:1 c: 9:1 9-9. Since the perimeter is 100, each side
9.1.1: Chapter 9 9-7. a: Solutions vary. Here is a possibility: b: Answers vary. Assuming there are no hidden cubes, V = 11!un 3 9-8. a: 4 25 b: 196:1 c: 9:1 9-9. Since the perimeter is 100, each side
Park Forest Math Team. Meet #4. Geometry. Self-study Packet
 Park Forest Math Team Meet #4 Self-study Packet Problem Categories for this Meet: 1. Mystery: Problem solving 2. : ngle measures in plane figures including supplements and complements 3. Number Theory:
Park Forest Math Team Meet #4 Self-study Packet Problem Categories for this Meet: 1. Mystery: Problem solving 2. : ngle measures in plane figures including supplements and complements 3. Number Theory:
Trigonometric ratios:
 0 Trigonometric ratios: The six trigonometric ratios of A are: Sine Cosine Tangent sin A = opposite leg hypotenuse adjacent leg cos A = hypotenuse tan A = opposite adjacent leg leg and their inverses:
0 Trigonometric ratios: The six trigonometric ratios of A are: Sine Cosine Tangent sin A = opposite leg hypotenuse adjacent leg cos A = hypotenuse tan A = opposite adjacent leg leg and their inverses:
2. A diagonal of a parallelogram divides it into two congruent triangles. 5. Diagonals of a rectangle bisect each other and are equal and vice-versa.
 QURILTERLS 1. Sum of the angles of a quadrilateral is 360. 2. diagonal of a parallelogram divides it into two congruent triangles. 3. In a parallelogram, (i) opposite sides are equal (ii) opposite angles
QURILTERLS 1. Sum of the angles of a quadrilateral is 360. 2. diagonal of a parallelogram divides it into two congruent triangles. 3. In a parallelogram, (i) opposite sides are equal (ii) opposite angles
GEOMETRY & MEASUREMENT
 GEOMETRY & MESUREMENT 1 1. The measure for a stud for a wall must be 72. Which of the following studs is allowed? 4 a. 72.7 in b. 72.31 in c. 71.81 in d. 71.2 in 2. t a bolt manufacturing company, 6 bolts
GEOMETRY & MESUREMENT 1 1. The measure for a stud for a wall must be 72. Which of the following studs is allowed? 4 a. 72.7 in b. 72.31 in c. 71.81 in d. 71.2 in 2. t a bolt manufacturing company, 6 bolts
2015 Arkansas Council of Teachers of Mathematics State Mathematics Contest Geometry Test
 2015 rkansas ouncil of Teachers of Mathematics State Mathematics ontest Geometry Test In each of the following choose the EST answer and record your choice on the answer sheet provided. To insure correct
2015 rkansas ouncil of Teachers of Mathematics State Mathematics ontest Geometry Test In each of the following choose the EST answer and record your choice on the answer sheet provided. To insure correct
02)
 GRE / GMATmath,! abscissa, scalene, intercept, markup, such that, break even. abscissa. (4, 2) 4abscissa, 2ordinate absolute value acre add adjacent angles altitude ; angle () acute angle (90 ) right angle
GRE / GMATmath,! abscissa, scalene, intercept, markup, such that, break even. abscissa. (4, 2) 4abscissa, 2ordinate absolute value acre add adjacent angles altitude ; angle () acute angle (90 ) right angle
Pre-Test. Use the following figure to answer Questions 1 through 6. B C. 1. What is the center of the circle? The center of the circle is point G.
 Pre-Test Name Date Use the following figure to answer Questions 1 through 6. A B C F G E D 1. What is the center of the circle? The center of the circle is point G. 2. Name a radius of the circle. A radius
Pre-Test Name Date Use the following figure to answer Questions 1 through 6. A B C F G E D 1. What is the center of the circle? The center of the circle is point G. 2. Name a radius of the circle. A radius
2013 ACTM Regional Geometry Exam
 2013 TM Regional Geometry Exam In each of the following choose the EST answer and record your choice on the answer sheet provided. To insure correct scoring, be sure to make all erasures completely. The
2013 TM Regional Geometry Exam In each of the following choose the EST answer and record your choice on the answer sheet provided. To insure correct scoring, be sure to make all erasures completely. The
#2216 Formal Geometry S2
 Instructional Materials for WCSD Math Common Finals The Instructional Materials are for student and teacher use and are aligned to the 2017-2018 Course Guides for the following course: High School #2216
Instructional Materials for WCSD Math Common Finals The Instructional Materials are for student and teacher use and are aligned to the 2017-2018 Course Guides for the following course: High School #2216
