1 st Preparatory. Part (1)
|
|
|
- Griffin Washington
- 5 years ago
- Views:
Transcription
1 Part (1) (1) omplete: 1) The square is a rectangle in which. 2) in a parallelogram in which m ( ) = 60, then m ( ) =. 3) The sum of measures of the angles of the quadrilateral equals. 4) The ray drawn parallel to one side of a triangle and passing through the mid-point of another side. 5) The rhombus is a parallelogram in which. 6) ach two opposite angles in a parallelogram are. 7) The line segment joining the midpoint of two sides of a triangle is. 8) The quadrilateral is a parallelogram if. 9) The parallelogram whose diagonals are perpendicular in. 10) If the measure of an interior angle of a triangle is equals to the sum of the measures of the other two interior angles, then the triangle is. 11) ny triangle has at least two. interior angles. 12) The measure of the exterior angle of a triangle is. 13) The parallelogram whose diagonals are perpendicular and equal in length is. 14) The sum of measures of the interior angles of a hexagon equals. 1
2 15) The rectangle is a parallelogram in which one of its angles is. 16) The parallelogram whose perimeter 24 cm and the length of its sides is 7 cm. Then the length of the adjacent side equal. 17) If is a rhombus, then 18) In the parallelogram XYZL, if m (x) = m ( Y) then m ( Y) = 19) ach of the two diagonals of the. makes an angle of measure 45 with the adjacent side. 20) The side length of a rhombus whose perimeter 42 cm equals. cm. 21) The sum of measure of interior angles of pentagon =. 22) The measure of one interior angle of regular pentagon =. 23) The number of sides of regular polygon if the measure of one interior angle 144 =. 24) The number of the diagonals of a pentagon is. 25) The measure of each angle of regular hexagon equals. 26) If the measure of an angle of a triangle is greater than the sum of the other two angles then the triangle is. 27) The sum of measure of the exterior angles of a triangle equals. 28) The measure of any of the exterior angle of an equilateral triangle equals. 2
3 (2) In the opposite figure: //, bisect 50, m ( ) = 50, m ( ) = 65 Prove that is a parallelogram 65 (3) In the opposite figure: is a triangle in which, and F are midpoints of, and respectively = 12 cm, = 10 cm Find the perimeter of the quadrilateral F 10 cm F \\ / // // 12 cm \\ / (4) In the opposite figure: is a triangle, m ( ) = m ( ) and is the bisector of prove that: = (5) In the opposite figure:, are perpendicular to, = { } 30 m ( ) = 30, m ( O) = 120 Find m ( ) 120 O 3
4 (6) In the opposite figure: is a triangle in which m ( ) = 75 m ( ) = 60, X and Y such that: // Y 75 X Find: m ( YX) 60 (7) In the opposite figure: is a square. raw // to intersect at H 1- Prove that: H = 2- Find: m ( H) 4
5 Part (2) (1) omplete: 1) The sum of measures of the interior angles of a polygon is then the number of its sides is. 2) The ray drawn from a midpoint of a side of a triangle parallel to another side then. 3), if m ( ) + m ( ) = m ( ) then m ( ) =. 4) The line segment joining the midpoints of two sides of a triangle is. and its length is equal to. 5) The regular polygon is. 6) The regular polygon is. 7) The image of (-3, 7) by rotation about the origin with an angle of measure 180 is 8) The point (4, 2) is the image of by reflection on y-axis. 9) The image of (-2, 2) by translation (x, y) (x + 4, y 2) is 10) The sum of the measures of the exterior angles of a convex polygon the number of its sides n is 11) Measure of the interior angle of the regular hexagon is 12) The image of point (2, 1) by reflection in x-axis is 13) The image of point (2, -1) by rotation about the origin 180 is 14) (-3, 2) is the image of point (3, 2) by reflection in axis. 15) The image of point (4, 6) by transformation (x, y) (-x, y - 7) is 5
6 16) The image of point (5, -3) by translation 3 units in negative direction of x-axis is 17) The image of the point (2, 3) by translation MN in direction MN where M (2, -1), N (5, 1) is (2) hoose the correct answer from the given ones: 1) The two diagonals of a rectangle a) are perpendicular b) are equal in length. c) are perpendicular and equal in length. d) bisect its interior angles 2) The two diagonals of a rhombus are a) perpendicular and are not equal. b) equal in length and are not perpendicular. c) perpendicular and equal in length. d) not equal in length and are not perpendicular. 3) The two diagonals of the square, are a) just perpendicular. b) just equal in length c) perpendicular and equal in length d) not equal in length and are not perpendicular 4) If two adjacent sides are equal in length in a parallelogram, then the figure is a a) square b) rhombus c) rectangle d) trapezium 6
7 5) If: is a rectangle in which = 5 cm, then: = cm. a) 2.5 b) 5 c) 10 d) 20 6) If: is a square, then: m ( ) = a) 90 b) 45 c) 60 d) 30 7) If: is a parallelogram in which m ( ) = m ( ), then: is a a) rectangle b) rhombus c) square d) trapezium 8) If: is a rhombus in which m ( ) = 32, then: m ( ) = a) 32 b) 64 c) 116 d) 26 9) The image of point (-1, 3) by translation (4, -2) is a) (3, 1) b) (3, -1) c) (5, 1) d) (5, -5) 10) The number of the diagonals of a pentagon is a) 3 b) 5 c) 7 d) 9 11) The image of point (2, -5) by reflection in x-axis is a) b) c) d) 12) The area of shaded part from the area of all shape is a) b) c) d) 13) The number of diagonals of a quadrilateral is a) 2 b) 3 c) 4 d) 5 14) The image of point (3, -5) by reflection in y-axis is a) (3, 5) b) (-3, -5) c) (-3, 5) d) (-5, 3) 7
8 (3) a) In the opposite figure: In, m ( ) = m ( ) such that: bisects ( ) Prove that: = b) In the opposite figure: //, m ( ) = 40 H 70 m ( H) = 70, Find: m ( ) 40 c) In the opposite figure: and,, F are midpoints of,, respectively F = 3 cm, = 4 cm, F = 5 cm Find the perimeter of F // // d) In the opposite figure: is a midpoint of, O is a midpoint of // F Prove that: // H G 8
9 // \ // \ e) In the opposite figure:, X, Y are the midpoint of, respectively, H where H = Prove that: XHY is a parallelogram. F f) In the opposite figure: Find with proof: m ( M) M 80 g) is a quadrilateral where: = {M}, 30 //, m ( M) = 70, m ( M) = 40 and m ( M) = 30 Prove that: is a parallelogram M (4) In the opposite figure: 9 cm is a trapezium, where //, m ( ) = 90, = = 17 cm, = 9 cm Find the length of, the area of trapezium 9
10 (5) In the opposite figure:, m ( ) = 90, // If = 12 cm, = 20 cm, = 9 cm, = 2 9 cm Find the length of, 12 cm (6) In the opposite figure: is a triangle m ( ) = 90,, = 11 cm if = 12 cm, = 13 cm Find the length of, 12 cm (7) Find: a) The image of OL by translation 3 cm in direction b) Find the image of OL by reflection in M O L c) Find the image of OL by rotation about O with angle (-90 ) N (8) raw the right angled triangle at, where = 3 cm, = 4 cm find the image by translation of magnitude 4 cm in direction (9) Find the image of O where (4, 1), (1, 5), (0, 0) by rotation about the origin with an angle 90 10
11 Model nswers Part (1) (1) omplete: 1) iagonals are perpendicular 2) 120 3) 360 4) bisect the third side 5) diagonals are perpendicular 6) equal in measure 7) parallel to the third side 8) each two opposite sides are equal and parallel 9) rhombus 10) right-angled triangle 11) acute 12) equal to the sum of the measure of the other two interior opposite angles. 13) square 14) ) 5 cm 17) 18) ) rectangle 20) 10.5 cm 21) ) ) 10 sides 24) 2 diagonals 25) ) obtuse angled 27) )
12 (2) Proof: // m ( ) = m ( ) = 50 (alternate angles) ( ) is a straight angle m ( ) = = 130 bisect m ( ) = = 65 m ( ) = = 115 m ( ) + m ( ) = = 180, and they are interior angles // // & // is a parallelogram (3) Proof: is the midpoint of, F is the midpoint of //, F = = 6 cm is the midpoint of, is the midpoint of //, = = 5 cm F =, c = The perimeter of the quadrilateral F = = 22 cm 12
13 (4) Proof: In the and is the bisector of m ( ) = m ( ) and m ( ) = m ( ) m ( ) = m ( ) (1) 1- m ( ) = m ( ) 2- is a common side 3- m ( ) = m ( ) = (5) Proof: The sum of measures of interior angle of = 180 m ( ) = ( ) = 60 and are vertically opposite angles. m ( ) = m ( ) = 60 The sum of measures the interior angles of the quadrilateral = (4-2) 180 = = 360 m ( ) = ( ) = 90 (6) Proof: m ( ) = 75 and m ( ) = 60 (given), the sum of measures of the interior angle of = 180 m ( ) = ( ) = = 45 // and is a transversal m ( YX) = m ( ) = 45 (corresponding angles) 13
14 (7) Proof: // (two opposite sides in the square) and H // // (given) H is a parallelogram H = ut = (two opposite side in the square) H = is a diagonal in the square bisects m ( ) = 90 2 = 45 // & is their transversal m ( H) = m ( ) = 45 (Two alternate angles), ( ) = 90 m ( H) = m ( ) + m ( H) = =
15 Part (2) 1) omplete : 1) 20 2) its length = half of the third side 3) 90 4) Parallel - half 5) has sides equals in length 6) has sides equals in length 7) ( 3, -7 ) 8) ( - 4, 2 ) 9) ( 2, 0 ) 10) ) ) (2, -1) 13) (-2, 1) 14) y 15) (-4, -1) 16) (2, -3) 17) (5, 5) 2) hoose : 1) equal in length 2) Perpendicular and not equal 3) Perpendicular and equal in length 4) Rhombus 5) 5 6) 45 7) rectangle 8) 116 9) (3, 1) 10) 5 11) (2, 5) 12) 13) 2 14) 2 15) (-3, -5) 15
16 (3) ) Proof by yourself ) m (< ) = 70 ) Perimeter of = 24 cm ) Try by yourself F) m (< M) = 120 G) Proof by your self (4) is right () 2 = () 2 - () 2 = () 2 = = 225 = = 15 cm rea of = 17 8 = 68 cm 2 rea of rectangle = 9 15 = 135 cm 2 rea of trapezium = = 203 cm 2 m = m = 90 // is a rectangle = = 15 cm 16
17 (5) In right () 2 = () 2 - () 2 = = 256 = = 16 cm = 16-9 = 7 cm = 2 = 12 2 = 24 cm In right () 2 = () 2 + () 2 = = = 625 = = 25 cm (6) In right () 2 = () 2 - () 2 = = = 25 = = 5 cm = = 16 cm In right () 2 = () 2 + () 2 = = = 400 = = 20 cm (7) a) LO b) OM c) ON 17
GEOMETRY. Similar Triangles
 GOMTRY Similar Triangles SIMILR TRINGLS N THIR PROPRTIS efinition Two triangles are said to be similar if: (i) Their corresponding angles are equal, and (ii) Their corresponding sides are proportional.
GOMTRY Similar Triangles SIMILR TRINGLS N THIR PROPRTIS efinition Two triangles are said to be similar if: (i) Their corresponding angles are equal, and (ii) Their corresponding sides are proportional.
2. A diagonal of a parallelogram divides it into two congruent triangles. 5. Diagonals of a rectangle bisect each other and are equal and vice-versa.
 QURILTERLS 1. Sum of the angles of a quadrilateral is 360. 2. diagonal of a parallelogram divides it into two congruent triangles. 3. In a parallelogram, (i) opposite sides are equal (ii) opposite angles
QURILTERLS 1. Sum of the angles of a quadrilateral is 360. 2. diagonal of a parallelogram divides it into two congruent triangles. 3. In a parallelogram, (i) opposite sides are equal (ii) opposite angles
CLASS IX GEOMETRY MOCK TEST PAPER
 Total time:3hrs darsha vidyalay hunashyal P. M.M=80 STION- 10 1=10 1) Name the point in a triangle that touches all sides of given triangle. Write its symbol of representation. 2) Where is thocenter of
Total time:3hrs darsha vidyalay hunashyal P. M.M=80 STION- 10 1=10 1) Name the point in a triangle that touches all sides of given triangle. Write its symbol of representation. 2) Where is thocenter of
Alg. Exercise (1) Department : Math Form : 1 st prep. Sheet. [1] Complete : 1) Rational number is 2) The set of integer is.. 3) If. is rational if x.
![Alg. Exercise (1) Department : Math Form : 1 st prep. Sheet. [1] Complete : 1) Rational number is 2) The set of integer is.. 3) If. is rational if x. Alg. Exercise (1) Department : Math Form : 1 st prep. Sheet. [1] Complete : 1) Rational number is 2) The set of integer is.. 3) If. is rational if x.](/thumbs/88/117810047.jpg) airo Governorate Nozha irectorate of Education Nozha Language Schools Ismailia Road epartment : Math Form : 1 st prep. Sheet [1] omplete : lg. Exercise (1) 1) Rational number is ) The set of integer is..
airo Governorate Nozha irectorate of Education Nozha Language Schools Ismailia Road epartment : Math Form : 1 st prep. Sheet [1] omplete : lg. Exercise (1) 1) Rational number is ) The set of integer is..
Exercise. and 13x. We know that, sum of angles of a quadrilateral = x = 360 x = (Common in both triangles) and AC = BD
 9 Exercise 9.1 Question 1. The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral. Solution Given, the ratio of the angles of quadrilateral are 3 : 5 : 9
9 Exercise 9.1 Question 1. The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral. Solution Given, the ratio of the angles of quadrilateral are 3 : 5 : 9
Pythagoras Theorem and Its Applications
 Lecture 10 Pythagoras Theorem and Its pplications Theorem I (Pythagoras Theorem) or a right-angled triangle with two legs a, b and hypotenuse c, the sum of squares of legs is equal to the square of its
Lecture 10 Pythagoras Theorem and Its pplications Theorem I (Pythagoras Theorem) or a right-angled triangle with two legs a, b and hypotenuse c, the sum of squares of legs is equal to the square of its
Downloaded from
 Triangles 1.In ABC right angled at C, AD is median. Then AB 2 = AC 2 - AD 2 AD 2 - AC 2 3AC 2-4AD 2 (D) 4AD 2-3AC 2 2.Which of the following statement is true? Any two right triangles are similar
Triangles 1.In ABC right angled at C, AD is median. Then AB 2 = AC 2 - AD 2 AD 2 - AC 2 3AC 2-4AD 2 (D) 4AD 2-3AC 2 2.Which of the following statement is true? Any two right triangles are similar
Theorems on Area. Introduction Axioms of Area. Congruence area axiom. Addition area axiom
 3 Theorems on rea Introduction We know that Geometry originated from the need of measuring land or recasting/refixing its boundaries in the process of distribution of certain land or field among different
3 Theorems on rea Introduction We know that Geometry originated from the need of measuring land or recasting/refixing its boundaries in the process of distribution of certain land or field among different
Triangles. Exercise 4.1
 4 Question. xercise 4. Fill in the blanks using the correct word given in brackets. (i) ll circles are....(congruent, similar) (ii) ll squares are....(similar, congruent) (iii) ll... triangles are similar.
4 Question. xercise 4. Fill in the blanks using the correct word given in brackets. (i) ll circles are....(congruent, similar) (ii) ll squares are....(similar, congruent) (iii) ll... triangles are similar.
Circles. Exercise 9.1
 9 uestion. Exercise 9. How many tangents can a circle have? Solution For every point of a circle, we can draw a tangent. Therefore, infinite tangents can be drawn. uestion. Fill in the blanks. (i) tangent
9 uestion. Exercise 9. How many tangents can a circle have? Solution For every point of a circle, we can draw a tangent. Therefore, infinite tangents can be drawn. uestion. Fill in the blanks. (i) tangent
Part (1) Second : Trigonometry. Tan
 Part (1) Second : Trigonometry (1) Complete the following table : The angle Ratio 42 12 \ Sin 0.3214 Cas 0.5321 Tan 2.0625 (2) Complete the following : 1) 46 36 \ 24 \\ =. In degrees. 2) 44.125 = in degrees,
Part (1) Second : Trigonometry (1) Complete the following table : The angle Ratio 42 12 \ Sin 0.3214 Cas 0.5321 Tan 2.0625 (2) Complete the following : 1) 46 36 \ 24 \\ =. In degrees. 2) 44.125 = in degrees,
Name: GEOMETRY: EXAM (A) A B C D E F G H D E. 1. How many non collinear points determine a plane?
 GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
Questions. Exercise (1)
 Questions Exercise (1) (1) hoose the correct answer: 1) The acute angle supplements. angle. a) acute b) obtuse c) right d) reflex 2) The right angle complements angle whose measure is. a) 0 b) 45 c) 90
Questions Exercise (1) (1) hoose the correct answer: 1) The acute angle supplements. angle. a) acute b) obtuse c) right d) reflex 2) The right angle complements angle whose measure is. a) 0 b) 45 c) 90
Geometry Honors Review for Midterm Exam
 Geometry Honors Review for Midterm Exam Format of Midterm Exam: Scantron Sheet: Always/Sometimes/Never and Multiple Choice 40 Questions @ 1 point each = 40 pts. Free Response: Show all work and write answers
Geometry Honors Review for Midterm Exam Format of Midterm Exam: Scantron Sheet: Always/Sometimes/Never and Multiple Choice 40 Questions @ 1 point each = 40 pts. Free Response: Show all work and write answers
8. Quadrilaterals. If AC = 21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
 8. Quadrilaterals Q 1 Name a quadrilateral whose each pair of opposite sides is equal. Mark (1) Q 2 What is the sum of two consecutive angles in a parallelogram? Mark (1) Q 3 The angles of quadrilateral
8. Quadrilaterals Q 1 Name a quadrilateral whose each pair of opposite sides is equal. Mark (1) Q 2 What is the sum of two consecutive angles in a parallelogram? Mark (1) Q 3 The angles of quadrilateral
Name: Class: Date: 5. If the diagonals of a rhombus have lengths 6 and 8, then the perimeter of the rhombus is 28. a. True b.
 Indicate whether the statement is true or false. 1. If the diagonals of a quadrilateral are perpendicular, the quadrilateral must be a square. 2. If M and N are midpoints of sides and of, then. 3. The
Indicate whether the statement is true or false. 1. If the diagonals of a quadrilateral are perpendicular, the quadrilateral must be a square. 2. If M and N are midpoints of sides and of, then. 3. The
GEO REVIEW TEST #1. 1. In which quadrilateral are the diagonals always congruent?
 GEO REVIEW TEST #1 Name: Date: 1. In which quadrilateral are the diagonals always congruent? (1) rectangle (3) rhombus 4. In the accompanying diagram, lines AB and CD intersect at point E. If m AED = (x+10)
GEO REVIEW TEST #1 Name: Date: 1. In which quadrilateral are the diagonals always congruent? (1) rectangle (3) rhombus 4. In the accompanying diagram, lines AB and CD intersect at point E. If m AED = (x+10)
GM1.1 Answers. Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
 Cambridge Essentials Mathematics Extension 8 GM1.1 Answers GM1.1 Answers Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
Cambridge Essentials Mathematics Extension 8 GM1.1 Answers GM1.1 Answers Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
Geometry First Semester Exam Review
 Geometry First Semester Exam Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Name three points that are collinear. a. points T, Q, and R c. points
Geometry First Semester Exam Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Name three points that are collinear. a. points T, Q, and R c. points
Prove that a + b = x + y. Join BD. In ABD, we have AOB = 180º AOB = 180º ( 1 + 2) AOB = 180º A
 bhilasha lasses lass- IX ate: 03- -7 SLUTIN (hap 8,9,0) 50 ob no.-947967444. The sides and of a quadrilateral are produced as shown in fig. rove that a + b = x + y. Join. In, we have y a + + = 80º = 80º
bhilasha lasses lass- IX ate: 03- -7 SLUTIN (hap 8,9,0) 50 ob no.-947967444. The sides and of a quadrilateral are produced as shown in fig. rove that a + b = x + y. Join. In, we have y a + + = 80º = 80º
2. In ABC, the measure of angle B is twice the measure of angle A. Angle C measures three times the measure of angle A. If AC = 26, find AB.
 2009 FGCU Mathematics Competition. Geometry Individual Test 1. You want to prove that the perpendicular bisector of the base of an isosceles triangle is also the angle bisector of the vertex. Which postulate/theorem
2009 FGCU Mathematics Competition. Geometry Individual Test 1. You want to prove that the perpendicular bisector of the base of an isosceles triangle is also the angle bisector of the vertex. Which postulate/theorem
Name: Date: Period: 1. In the diagram below,. [G.CO.6] 2. The diagram below shows a pair of congruent triangles, with and. [G.CO.
![Name: Date: Period: 1. In the diagram below,. [G.CO.6] 2. The diagram below shows a pair of congruent triangles, with and. [G.CO. Name: Date: Period: 1. In the diagram below,. [G.CO.6] 2. The diagram below shows a pair of congruent triangles, with and. [G.CO.](/thumbs/78/77420594.jpg) Name: Date: Period: Directions: Read each question carefully and choose the best answer for each question. You must show LL of your work to receive credit. 1. In the diagram below,. [G.CO.6] Which statement
Name: Date: Period: Directions: Read each question carefully and choose the best answer for each question. You must show LL of your work to receive credit. 1. In the diagram below,. [G.CO.6] Which statement
Honors Geometry Mid-Term Exam Review
 Class: Date: Honors Geometry Mid-Term Exam Review Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Classify the triangle by its sides. The
Class: Date: Honors Geometry Mid-Term Exam Review Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Classify the triangle by its sides. The
B C. You try: What is the definition of an angle bisector?
 US Geometry 1 What is the definition of a midpoint? The midpoint of a line segment is the point that divides the segment into two congruent segments. That is, M is the midpoint of if M is on and M M. 1
US Geometry 1 What is the definition of a midpoint? The midpoint of a line segment is the point that divides the segment into two congruent segments. That is, M is the midpoint of if M is on and M M. 1
Midterm Review Packet. Geometry: Midterm Multiple Choice Practice
 : Midterm Multiple Choice Practice 1. In the diagram below, a square is graphed in the coordinate plane. A reflection over which line does not carry the square onto itself? (1) (2) (3) (4) 2. A sequence
: Midterm Multiple Choice Practice 1. In the diagram below, a square is graphed in the coordinate plane. A reflection over which line does not carry the square onto itself? (1) (2) (3) (4) 2. A sequence
1. How many planes can be drawn through any three noncollinear points? a. 0 b. 1 c. 2 d. 3. a cm b cm c cm d. 21.
 FALL SEMESTER EXAM REVIEW (Chapters 1-6) CHAPTER 1 1. How many planes can be drawn through any three noncollinear points? a. 0 b. 1 c. 2 d. 3 2. Find the length of PQ. a. 50.9 cm b. 46.3 cm c. 25.7 cm
FALL SEMESTER EXAM REVIEW (Chapters 1-6) CHAPTER 1 1. How many planes can be drawn through any three noncollinear points? a. 0 b. 1 c. 2 d. 3 2. Find the length of PQ. a. 50.9 cm b. 46.3 cm c. 25.7 cm
Mathematics. Sample Question Paper. Class 9th. (Detailed Solutions) 2. From the figure, ADB ACB We have [( 16) ] [( 2 ) ] 3.
![Mathematics. Sample Question Paper. Class 9th. (Detailed Solutions) 2. From the figure, ADB ACB We have [( 16) ] [( 2 ) ] 3. Mathematics. Sample Question Paper. Class 9th. (Detailed Solutions) 2. From the figure, ADB ACB We have [( 16) ] [( 2 ) ] 3.](/thumbs/85/92233599.jpg) 6 Sample Question Paper (etailed Solutions) Mathematics lass 9th. Given equation is ( k ) ( k ) y 0. t and y, ( k ) ( k ) 0 k 6k 9 0 4k 8 0 4k 8 k. From the figure, 40 [ angles in the same segment are
6 Sample Question Paper (etailed Solutions) Mathematics lass 9th. Given equation is ( k ) ( k ) y 0. t and y, ( k ) ( k ) 0 k 6k 9 0 4k 8 0 4k 8 k. From the figure, 40 [ angles in the same segment are
8-6. a: 110 b: 70 c: 48 d: a: no b: yes c: no d: yes e: no f: yes g: yes h: no
 Lesson 8.1.1 8-6. a: 110 b: 70 c: 48 d: 108 8-7. a: no b: yes c: no d: yes e: no f: yes g: yes h: no 8-8. b: The measure of an exterior angle of a triangle equals the sum of the measures of its remote
Lesson 8.1.1 8-6. a: 110 b: 70 c: 48 d: 108 8-7. a: no b: yes c: no d: yes e: no f: yes g: yes h: no 8-8. b: The measure of an exterior angle of a triangle equals the sum of the measures of its remote
Geometry GENERAL GEOMETRY
 Geometry GENERAL GEOMETRY Essential Vocabulary: point, line, plane, segment, segment bisector, midpoint, congruence I can use the distance formula to determine the area and perimeters of triangles and
Geometry GENERAL GEOMETRY Essential Vocabulary: point, line, plane, segment, segment bisector, midpoint, congruence I can use the distance formula to determine the area and perimeters of triangles and
8-6. a: 110 b: 70 c: 48 d: a: no b: yes c: no d: yes e: no f: yes g: yes h: no
 Lesson 8.1.1 8-6. a: 110 b: 70 c: 48 d: 108 8-7. a: no b: yes c: no d: yes e: no f: yes g: yes h: no 8-8. b: The measure of an exterior angle of a triangle equals the sum of the measures of its remote
Lesson 8.1.1 8-6. a: 110 b: 70 c: 48 d: 108 8-7. a: no b: yes c: no d: yes e: no f: yes g: yes h: no 8-8. b: The measure of an exterior angle of a triangle equals the sum of the measures of its remote
COURSE STRUCTURE CLASS -IX
 environment, observance of small family norms, removal of social barriers, elimination of gender biases; mathematical softwares. its beautiful structures and patterns, etc. COURSE STRUCTURE CLASS -IX Units
environment, observance of small family norms, removal of social barriers, elimination of gender biases; mathematical softwares. its beautiful structures and patterns, etc. COURSE STRUCTURE CLASS -IX Units
0811ge. Geometry Regents Exam BC, AT = 5, TB = 7, and AV = 10.
 0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 2) 8 3) 3 4) 6 2 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 2) 8 3) 3 4) 6 2 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
Class 9 Quadrilaterals
 ID : in-9-quadrilaterals [1] Class 9 Quadrilaterals For more such worksheets visit www.edugain.com Answer t he quest ions (1) The diameter of circumcircle of a rectangle is 13 cm and rectangle's width
ID : in-9-quadrilaterals [1] Class 9 Quadrilaterals For more such worksheets visit www.edugain.com Answer t he quest ions (1) The diameter of circumcircle of a rectangle is 13 cm and rectangle's width
Chapter 19 Exercise 19.1
 hapter 9 xercise 9... (i) n axiom is a statement that is accepted but cannot be proven, e.g. x + 0 = x. (ii) statement that can be proven logically: for example, ythagoras Theorem. (iii) The logical steps
hapter 9 xercise 9... (i) n axiom is a statement that is accepted but cannot be proven, e.g. x + 0 = x. (ii) statement that can be proven logically: for example, ythagoras Theorem. (iii) The logical steps
0811ge. Geometry Regents Exam
 0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 ) 8 3) 3 4) 6 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 ) 8 3) 3 4) 6 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
Plane geometry Circles: Problems with some Solutions
 The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
CBSE Class IX Syllabus. Mathematics Class 9 Syllabus
 Mathematics Class 9 Syllabus Course Structure First Term Units Unit Marks I Number System 17 II Algebra 25 III Geometry 37 IV Co-ordinate Geometry 6 V Mensuration 5 Total 90 Second Term Units Unit Marks
Mathematics Class 9 Syllabus Course Structure First Term Units Unit Marks I Number System 17 II Algebra 25 III Geometry 37 IV Co-ordinate Geometry 6 V Mensuration 5 Total 90 Second Term Units Unit Marks
Los Angeles Unified School District Periodic Assessments. Geometry. Assessment 2 ASSESSMENT CODE LA08_G_T2_TST_31241
 Los Angeles Unified School District Periodic Assessments Assessment 2 2008 2009 Los Angeles Unified School District Periodic Assessments LA08_G_T2_TST_31241 ASSESSMENT ODE 1100209 The test items contained
Los Angeles Unified School District Periodic Assessments Assessment 2 2008 2009 Los Angeles Unified School District Periodic Assessments LA08_G_T2_TST_31241 ASSESSMENT ODE 1100209 The test items contained
Test Corrections for Unit 1 Test
 MUST READ DIRECTIONS: Read the directions located on www.koltymath.weebly.com to understand how to properly do test corrections. Ask for clarification from your teacher if there are parts that you are
MUST READ DIRECTIONS: Read the directions located on www.koltymath.weebly.com to understand how to properly do test corrections. Ask for clarification from your teacher if there are parts that you are
Geometry Note Cards EXAMPLE:
 Geometry Note Cards EXAMPLE: Lined Side Word and Explanation Blank Side Picture with Statements Sections 12-4 through 12-5 1) Theorem 12-3 (p. 790) 2) Theorem 12-14 (p. 790) 3) Theorem 12-15 (p. 793) 4)
Geometry Note Cards EXAMPLE: Lined Side Word and Explanation Blank Side Picture with Statements Sections 12-4 through 12-5 1) Theorem 12-3 (p. 790) 2) Theorem 12-14 (p. 790) 3) Theorem 12-15 (p. 793) 4)
GEOMETRY. Part I. _,_ c. August 2010
 GEOMETRY Part I nswer all 28 questions in this part. Each correct answer will receive,',"eliits. No partial credit will be allowed. For each question, write on the "pnce provided the numeral preceding
GEOMETRY Part I nswer all 28 questions in this part. Each correct answer will receive,',"eliits. No partial credit will be allowed. For each question, write on the "pnce provided the numeral preceding
MT - GEOMETRY - SEMI PRELIM - II : PAPER - 4
 017 1100 MT.1. ttempt NY FIVE of the following : (i) In STR, line l side TR S SQ T = RQ x 4.5 = 1.3 3.9 x = MT - GEOMETRY - SEMI RELIM - II : ER - 4 Time : Hours Model nswer aper Max. Marks : 40 4.5 1.3
017 1100 MT.1. ttempt NY FIVE of the following : (i) In STR, line l side TR S SQ T = RQ x 4.5 = 1.3 3.9 x = MT - GEOMETRY - SEMI RELIM - II : ER - 4 Time : Hours Model nswer aper Max. Marks : 40 4.5 1.3
0610ge. Geometry Regents Exam The diagram below shows a right pentagonal prism.
 0610ge 1 In the diagram below of circle O, chord AB chord CD, and chord CD chord EF. 3 The diagram below shows a right pentagonal prism. Which statement must be true? 1) CE DF 2) AC DF 3) AC CE 4) EF CD
0610ge 1 In the diagram below of circle O, chord AB chord CD, and chord CD chord EF. 3 The diagram below shows a right pentagonal prism. Which statement must be true? 1) CE DF 2) AC DF 3) AC CE 4) EF CD
Introduction - Geometry
 L I F O R N I S T N R S T E S T Introduction - The following released test questions are taken from the Standards Test. This test is one of the alifornia Standards Tests administered as part of the Standardized
L I F O R N I S T N R S T E S T Introduction - The following released test questions are taken from the Standards Test. This test is one of the alifornia Standards Tests administered as part of the Standardized
PRACTICE QUESTIONS CLASS IX: CHAPTER 4 LINEAR EQUATION IN TWO VARIABLES
 PRACTICE QUESTIONS CLASS IX: CHAPTER 4 LINEAR EQUATION IN TWO VARIABLES 1. Find the value of k, if x =, y = 1 is a solution of the equation x + 3y = k.. Find the points where the graph of the equation
PRACTICE QUESTIONS CLASS IX: CHAPTER 4 LINEAR EQUATION IN TWO VARIABLES 1. Find the value of k, if x =, y = 1 is a solution of the equation x + 3y = k.. Find the points where the graph of the equation
Nozha Directorate of Education Form : 2 nd Prep. Nozha Language Schools Ismailia Road Branch
 Cairo Governorate Department : Maths Nozha Directorate of Education Form : 2 nd Prep. Nozha Language Schools Sheet Ismailia Road Branch Sheet ( 1) 1-Complete 1. in the parallelogram, each two opposite
Cairo Governorate Department : Maths Nozha Directorate of Education Form : 2 nd Prep. Nozha Language Schools Sheet Ismailia Road Branch Sheet ( 1) 1-Complete 1. in the parallelogram, each two opposite
+2 u, 2s ) [D] ( r+ t + u, 2s )
![+2 u, 2s ) [D] ( r+ t + u, 2s ) +2 u, 2s ) [D] ( r+ t + u, 2s )](/thumbs/74/70220114.jpg) 1. Isosceles trapezoid JKLM has legs JK and LM, and base KL. If JK = 3x + 6, KL = 9x 3, and LM = 7x 9. Find the value of x. [A] 15 4 [] 3 4 [] 3 [] 3 4. Which best describes the relationship between the
1. Isosceles trapezoid JKLM has legs JK and LM, and base KL. If JK = 3x + 6, KL = 9x 3, and LM = 7x 9. Find the value of x. [A] 15 4 [] 3 4 [] 3 [] 3 4. Which best describes the relationship between the
1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle?
 1 For all problems, NOTA stands for None of the Above. 1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle? (A) 40 (B) 60 (C) 80 (D) Cannot be determined
1 For all problems, NOTA stands for None of the Above. 1. If two angles of a triangle measure 40 and 80, what is the measure of the other angle of the triangle? (A) 40 (B) 60 (C) 80 (D) Cannot be determined
QUESTION BANK ON STRAIGHT LINE AND CIRCLE
 QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
QUESTION BANK ON STRAIGHT LINE AND CIRCLE Select the correct alternative : (Only one is correct) Q. If the lines x + y + = 0 ; 4x + y + 4 = 0 and x + αy + β = 0, where α + β =, are concurrent then α =,
Integer (positive or negative whole numbers or zero) arithmetic
 Integer (positive or negative whole numbers or zero) arithmetic The number line helps to visualize the process. The exercises below include the answers but see if you agree with them and if not try to
Integer (positive or negative whole numbers or zero) arithmetic The number line helps to visualize the process. The exercises below include the answers but see if you agree with them and if not try to
Chapter 1. Some Basic Theorems. 1.1 The Pythagorean Theorem
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
Unit 8. ANALYTIC GEOMETRY.
 Unit 8. ANALYTIC GEOMETRY. 1. VECTORS IN THE PLANE A vector is a line segment running from point A (tail) to point B (head). 1.1 DIRECTION OF A VECTOR The direction of a vector is the direction of the
Unit 8. ANALYTIC GEOMETRY. 1. VECTORS IN THE PLANE A vector is a line segment running from point A (tail) to point B (head). 1.1 DIRECTION OF A VECTOR The direction of a vector is the direction of the
0116ge. Geometry Regents Exam RT and SU intersect at O.
 Geometry Regents Exam 06 06ge What is the equation of a circle with its center at (5, ) and a radius of 3? ) (x 5) + (y + ) = 3 ) (x 5) + (y + ) = 9 3) (x + 5) + (y ) = 3 4) (x + 5) + (y ) = 9 In the diagram
Geometry Regents Exam 06 06ge What is the equation of a circle with its center at (5, ) and a radius of 3? ) (x 5) + (y + ) = 3 ) (x 5) + (y + ) = 9 3) (x + 5) + (y ) = 3 4) (x + 5) + (y ) = 9 In the diagram
7. m JHI = ( ) and m GHI = ( ) and m JHG = 65. Find m JHI and m GHI.
 1. Name three points in the diagram that are not collinear. 2. If RS = 44 and QS = 68, find QR. 3. R, S, and T are collinear. S is between R and T. RS = 2w + 1, ST = w 1, and RT = 18. Use the Segment Addition
1. Name three points in the diagram that are not collinear. 2. If RS = 44 and QS = 68, find QR. 3. R, S, and T are collinear. S is between R and T. RS = 2w + 1, ST = w 1, and RT = 18. Use the Segment Addition
Chapter (Circle) * Circle - circle is locus of such points which are at equidistant from a fixed point in
 Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Chapter - 10 (Circle) Key Concept * Circle - circle is locus of such points which are at equidistant from a fixed point in a plane. * Concentric circle - Circle having same centre called concentric circle.
Reteaching , or 37.5% 360. Geometric Probability. Name Date Class
 Name ate lass Reteaching Geometric Probability INV 6 You have calculated probabilities of events that occur when coins are tossed and number cubes are rolled. Now you will learn about geometric probability.
Name ate lass Reteaching Geometric Probability INV 6 You have calculated probabilities of events that occur when coins are tossed and number cubes are rolled. Now you will learn about geometric probability.
iii (a, c), (a, e), (c, e), (b, d), (b, f), (d, f), (l, h), (l, j), (h, j), (g, i), (g, k), (i, k)
 Cambridge Essentials Mathematics Core 8 GM1.1 Answers GM1.1 Answers 1 a There is more than one valid reason for each statement; those given are the simplest. i Corresponding angles ii Vertically opposite
Cambridge Essentials Mathematics Core 8 GM1.1 Answers GM1.1 Answers 1 a There is more than one valid reason for each statement; those given are the simplest. i Corresponding angles ii Vertically opposite
Start at the compass direction North and draw the rotations asked for. Write down the angle formed by the arms of the clock in right angles.
 ee Lesson Plans for Year at MP Primary Practice ook b WR Imagine that this shape continues in any direction without ending, so it represents a plane. The rays a and b are drawn from the same starting point,
ee Lesson Plans for Year at MP Primary Practice ook b WR Imagine that this shape continues in any direction without ending, so it represents a plane. The rays a and b are drawn from the same starting point,
Chapter 3 Cumulative Review Answers
 Chapter 3 Cumulative Review Answers 1a. The triangle inequality is violated. 1b. The sum of the angles is not 180º. 1c. Two angles are equal, but the sides opposite those angles are not equal. 1d. The
Chapter 3 Cumulative Review Answers 1a. The triangle inequality is violated. 1b. The sum of the angles is not 180º. 1c. Two angles are equal, but the sides opposite those angles are not equal. 1d. The
Name Geometry Common Core Regents Review Packet - 3. Topic 1 : Equation of a circle
 Name Geometry Common Core Regents Review Packet - 3 Topic 1 : Equation of a circle Equation with center (0,0) and radius r Equation with center (h,k) and radius r ( ) ( ) 1. The endpoints of a diameter
Name Geometry Common Core Regents Review Packet - 3 Topic 1 : Equation of a circle Equation with center (0,0) and radius r Equation with center (h,k) and radius r ( ) ( ) 1. The endpoints of a diameter
Year 9 Term 3 Homework
 Yimin Math Centre Year 9 Term 3 Homework Student Name: Grade: Date: Score: Table of contents 5 Year 9 Term 3 Week 5 Homework 1 5.1 Geometry (Review)................................... 1 5.1.1 Angle sum
Yimin Math Centre Year 9 Term 3 Homework Student Name: Grade: Date: Score: Table of contents 5 Year 9 Term 3 Week 5 Homework 1 5.1 Geometry (Review)................................... 1 5.1.1 Angle sum
9. Areas of Parallelograms and Triangles
 9. Areas of Parallelograms and Triangles Q 1 State true or false : A diagonal of a parallelogram divides it into two parts of equal areas. Mark (1) Q 2 State true or false: Parallelograms on the same base
9. Areas of Parallelograms and Triangles Q 1 State true or false : A diagonal of a parallelogram divides it into two parts of equal areas. Mark (1) Q 2 State true or false: Parallelograms on the same base
For Primary Six. Name:.. Class:... Cairo governorate Nasr city educational zone Alsun modern school. Alsun Modern School
 airo governorate Nasr city educational zone lsun modern school For Primary Six Name:.. lass:... 1 Q1: hoose the correct answer from those given: 1) If the sum of the edge lengths of a cube = 144 cm, then
airo governorate Nasr city educational zone lsun modern school For Primary Six Name:.. lass:... 1 Q1: hoose the correct answer from those given: 1) If the sum of the edge lengths of a cube = 144 cm, then
Common Core Readiness Assessment 4
 ommon ore Readiness ssessment 4 1. Use the diagram and the information given to complete the missing element of the two-column proof. 2. Use the diagram and the information given to complete the missing
ommon ore Readiness ssessment 4 1. Use the diagram and the information given to complete the missing element of the two-column proof. 2. Use the diagram and the information given to complete the missing
Mathematics Class 9 Syllabus. Course Structure. I Number System 17 II Algebra 25 III Geometry 37 IV Co-ordinate Geometry 6 V Mensuration 5 Total 90
 Mathematics Class 9 Syllabus Course Structure First Term Units Unit Marks I Number System 17 II Algebra 25 III Geometry 37 IV Co-ordinate Geometry 6 V Mensuration 5 Total 90 Second Term Units Unit Marks
Mathematics Class 9 Syllabus Course Structure First Term Units Unit Marks I Number System 17 II Algebra 25 III Geometry 37 IV Co-ordinate Geometry 6 V Mensuration 5 Total 90 Second Term Units Unit Marks
Angles and Transformations - Ms Buerckner
 Angles and Transformations - Ms Buerckner Question 1 The marked angle is: a revolution a reflex angle Question 2 This rectangle has: four right angles four obtuse angles four acute angles Question 3 Each
Angles and Transformations - Ms Buerckner Question 1 The marked angle is: a revolution a reflex angle Question 2 This rectangle has: four right angles four obtuse angles four acute angles Question 3 Each
Homework Answers. b = 58 (alternate angles are equal or vertically opposite angles are equal)
 Cambridge Essentials Mathematics Extension 8 GM1.1 Homework Answers GM1.1 Homework Answers 1 a a = 58 (corresponding angles are equal) b = 58 (alternate angles are equal or vertically opposite angles are
Cambridge Essentials Mathematics Extension 8 GM1.1 Homework Answers GM1.1 Homework Answers 1 a a = 58 (corresponding angles are equal) b = 58 (alternate angles are equal or vertically opposite angles are
Theorem 1.2 (Converse of Pythagoras theorem). If the lengths of the sides of ABC satisfy a 2 + b 2 = c 2, then the triangle has a right angle at C.
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
Geometry Cumulative Review
 Geometry Cumulative Review Name 1. Find a pattern for the sequence. Use the pattern to show the next term. 1, 3, 9, 27,... A. 81 B. 45 C. 41 D. 36 2. If EG = 42, find the value of y. A. 5 B. C. 6 D. 7
Geometry Cumulative Review Name 1. Find a pattern for the sequence. Use the pattern to show the next term. 1, 3, 9, 27,... A. 81 B. 45 C. 41 D. 36 2. If EG = 42, find the value of y. A. 5 B. C. 6 D. 7
Arkansas Council of Teachers of Mathematics 2012 State Competition Geometry Exam. B. 28 (5x-41) 3 m (2x+25)
 rkansas ouncil of Teachers of Mathematics 2012 State ompetition Geometry Exam For questions 1 through 25, mark your answer choice on the answer sheet provided. (Figures may not be drawn to scale.) fter
rkansas ouncil of Teachers of Mathematics 2012 State ompetition Geometry Exam For questions 1 through 25, mark your answer choice on the answer sheet provided. (Figures may not be drawn to scale.) fter
Section 8.1 Objective: Students will be able to solve equations to find angle measures (supplementary and complementary).
 Lincoln Public Schools Math 8 McDougall Littell Middle School Math Course 3 Chapter 8 Items marked A, B, C are increasing in difficulty. Group A questions are the most basic while Group C are the most
Lincoln Public Schools Math 8 McDougall Littell Middle School Math Course 3 Chapter 8 Items marked A, B, C are increasing in difficulty. Group A questions are the most basic while Group C are the most
TENTH YEAR MATHEMATICS
 The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION TENTH YEAR MATHEMATICS Thursday, January 26, 1989-1:1.5 to 4:1.5 p.m., only The last page of the booklet is the answer sheet. Fold
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION TENTH YEAR MATHEMATICS Thursday, January 26, 1989-1:1.5 to 4:1.5 p.m., only The last page of the booklet is the answer sheet. Fold
Nozha Directorate of Education Form : 2 nd Prep
 Cairo Governorate Department : Maths Nozha Directorate of Education Form : 2 nd Prep Nozha Language Schools Geometry Revision Sheet Ismailia Road Branch Sheet ( 1) 1-Complete 1. In the parallelogram, each
Cairo Governorate Department : Maths Nozha Directorate of Education Form : 2 nd Prep Nozha Language Schools Geometry Revision Sheet Ismailia Road Branch Sheet ( 1) 1-Complete 1. In the parallelogram, each
Euclidian Geometry Grade 10 to 12 (CAPS)
 Euclidian Geometry Grade 10 to 12 (CAPS) Compiled by Marlene Malan marlene.mcubed@gmail.com Prepared by Marlene Malan CAPS DOCUMENT (Paper 2) Grade 10 Grade 11 Grade 12 (a) Revise basic results established
Euclidian Geometry Grade 10 to 12 (CAPS) Compiled by Marlene Malan marlene.mcubed@gmail.com Prepared by Marlene Malan CAPS DOCUMENT (Paper 2) Grade 10 Grade 11 Grade 12 (a) Revise basic results established
SEMESTER REVIEW 1: Chapters 1 and 2
 Geometry Fall emester Review (13-14) EEER REVIEW 1: hapters 1 and 2 1. What is Geometry? 2. What are the three undefined terms of geometry? 3. Find the definition of each of the following. a. Postulate
Geometry Fall emester Review (13-14) EEER REVIEW 1: hapters 1 and 2 1. What is Geometry? 2. What are the three undefined terms of geometry? 3. Find the definition of each of the following. a. Postulate
MATH 243 Winter 2008 Geometry II: Transformation Geometry Solutions to Problem Set 1 Completion Date: Monday January 21, 2008
 MTH 4 Winter 008 Geometry II: Transformation Geometry Solutions to Problem Set 1 ompletion Date: Monday January 1, 008 Department of Mathematical Statistical Sciences University of lberta Question 1. Let
MTH 4 Winter 008 Geometry II: Transformation Geometry Solutions to Problem Set 1 ompletion Date: Monday January 1, 008 Department of Mathematical Statistical Sciences University of lberta Question 1. Let
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Student Name:
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, January 27, 2011 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, January 27, 2011 9:15 a.m. to 12:15 p.m., only Student Name: School Name: Print your name and the name
+ 10 then give the value
 1. Match each vocabulary word to the picture. A. Linear Pair B. Vertical Angles P1 C. Angle Bisector D. Parallel Lines E. Orthocenter F. Centroid For questions 3 4 use the diagram below. Y Z X U W V A
1. Match each vocabulary word to the picture. A. Linear Pair B. Vertical Angles P1 C. Angle Bisector D. Parallel Lines E. Orthocenter F. Centroid For questions 3 4 use the diagram below. Y Z X U W V A
TENTH YEAR MATHEMATICS
 The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION TENTH YEAR MATHEMATICS Tuesday, June 16,1987-1:15 to 4:15 p.m., only The last page of the booklet is the answer sheet. Fold the last
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION TENTH YEAR MATHEMATICS Tuesday, June 16,1987-1:15 to 4:15 p.m., only The last page of the booklet is the answer sheet. Fold the last
NCERT Solutions for Class 7 Maths Chapter 14
 NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Class 7 Chapter 14 Symmetry Exercise 14.1, 14.2, 14.3 Solutions Exercise 14.1 : Solutions of Questions on Page Number : 268 Q1 : Copy the figures with
NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Class 7 Chapter 14 Symmetry Exercise 14.1, 14.2, 14.3 Solutions Exercise 14.1 : Solutions of Questions on Page Number : 268 Q1 : Copy the figures with
TOPIC 4 Line and Angle Relationships. Good Luck To. DIRECTIONS: Answer each question and show all work in the space provided.
 Good Luck To Period Date DIRECTIONS: Answer each question and show all work in the space provided. 1. Name a pair of corresponding angles. 1 3 2 4 5 6 7 8 A. 1 and 4 C. 2 and 7 B. 1 and 5 D. 2 and 4 2.
Good Luck To Period Date DIRECTIONS: Answer each question and show all work in the space provided. 1. Name a pair of corresponding angles. 1 3 2 4 5 6 7 8 A. 1 and 4 C. 2 and 7 B. 1 and 5 D. 2 and 4 2.
CHAPTER 11 AREAS OF PLANE FIGURES
 CHAPTER 11 AREAS OF PLANE FIGURES EXERCISE 45, Page 106 1. Find the angles p and q in diagram (a) below. p = 180-75 = 105 (interior opposite angles of a parallelogram are equal) q = 180-105 - 40 = 35.
CHAPTER 11 AREAS OF PLANE FIGURES EXERCISE 45, Page 106 1. Find the angles p and q in diagram (a) below. p = 180-75 = 105 (interior opposite angles of a parallelogram are equal) q = 180-105 - 40 = 35.
Geometry: A Complete Course
 eometry: omplete ourse with rigonometry) odule - tudent Worket Written by: homas. lark Larry. ollins 4/2010 or ercises 20 22, use the diagram below. 20. ssume is a rectangle. a) f is 6, find. b) f is,
eometry: omplete ourse with rigonometry) odule - tudent Worket Written by: homas. lark Larry. ollins 4/2010 or ercises 20 22, use the diagram below. 20. ssume is a rectangle. a) f is 6, find. b) f is,
Pre-Algebra Chapter 9 Spatial Thinking
 Pre-Algebra Chapter 9 Spatial Thinking SOME NUMBERED QUESTIONS HAVE BEEN DELETED OR REMOVED. YOU WILL NOT BE USING A CALCULATOR FOR PART I MULTIPLE-CHOICE QUESTIONS, AND THEREFORE YOU SHOULD NOT USE ONE
Pre-Algebra Chapter 9 Spatial Thinking SOME NUMBERED QUESTIONS HAVE BEEN DELETED OR REMOVED. YOU WILL NOT BE USING A CALCULATOR FOR PART I MULTIPLE-CHOICE QUESTIONS, AND THEREFORE YOU SHOULD NOT USE ONE
Geometry Honors: Midterm Exam Review January 2018
 Name: Period: The midterm will cover Chapters 1-6. Geometry Honors: Midterm Exam Review January 2018 You WILL NOT receive a formula sheet, but you need to know the following formulas Make sure you memorize
Name: Period: The midterm will cover Chapters 1-6. Geometry Honors: Midterm Exam Review January 2018 You WILL NOT receive a formula sheet, but you need to know the following formulas Make sure you memorize
A. 180 B. 108 C. 360 D. 540
 Part I - Multiple Choice - Circle your answer: 1. Find the area of the shaded sector. Q O 8 P A. 2 π B. 4 π C. 8 π D. 16 π 2. An octagon has sides. A. five B. six C. eight D. ten 3. The sum of the interior
Part I - Multiple Choice - Circle your answer: 1. Find the area of the shaded sector. Q O 8 P A. 2 π B. 4 π C. 8 π D. 16 π 2. An octagon has sides. A. five B. six C. eight D. ten 3. The sum of the interior
2013 ACTM Regional Geometry Exam
 2013 TM Regional Geometry Exam In each of the following choose the EST answer and record your choice on the answer sheet provided. To insure correct scoring, be sure to make all erasures completely. The
2013 TM Regional Geometry Exam In each of the following choose the EST answer and record your choice on the answer sheet provided. To insure correct scoring, be sure to make all erasures completely. The
0114ge. Geometry Regents Exam 0114
 0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
0114ge 1 The midpoint of AB is M(4, 2). If the coordinates of A are (6, 4), what are the coordinates of B? 1) (1, 3) 2) (2, 8) 3) (5, 1) 4) (14, 0) 2 Which diagram shows the construction of a 45 angle?
Circles. II. Radius - a segment with one endpoint the center of a circle and the other endpoint on the circle.
 Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
1 What is the solution of the system of equations graphed below? y = 2x + 1
 1 What is the solution of the system of equations graphed below? y = 2x + 1 3 As shown in the diagram below, when hexagon ABCDEF is reflected over line m, the image is hexagon A'B'C'D'E'F'. y = x 2 + 2x
1 What is the solution of the system of equations graphed below? y = 2x + 1 3 As shown in the diagram below, when hexagon ABCDEF is reflected over line m, the image is hexagon A'B'C'D'E'F'. y = x 2 + 2x
Q.2 A, B and C are points in the xy plane such that A(1, 2) ; B (5, 6) and AC = 3BC. Then. (C) 1 1 or
 STRAIGHT LINE [STRAIGHT OBJECTIVE TYPE] Q. A variable rectangle PQRS has its sides parallel to fied directions. Q and S lie respectivel on the lines = a, = a and P lies on the ais. Then the locus of R
STRAIGHT LINE [STRAIGHT OBJECTIVE TYPE] Q. A variable rectangle PQRS has its sides parallel to fied directions. Q and S lie respectivel on the lines = a, = a and P lies on the ais. Then the locus of R
NCERT SOLUTIONS OF Mensuration Exercise 2
 NCERT SOLUTIONS OF Mensuration Exercise 2 1 Question 1 The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them
NCERT SOLUTIONS OF Mensuration Exercise 2 1 Question 1 The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them
(b) the equation of the perpendicular bisector of AB. [3]
![(b) the equation of the perpendicular bisector of AB. [3] (b) the equation of the perpendicular bisector of AB. [3]](/thumbs/95/126119012.jpg) HORIZON EDUCATION SINGAPORE Additional Mathematics Practice Questions: Coordinate Geometr 1 Set 1 1 In the figure, ABCD is a rhombus with coordinates A(2, 9) and C(8, 1). The diagonals AC and BD cut at
HORIZON EDUCATION SINGAPORE Additional Mathematics Practice Questions: Coordinate Geometr 1 Set 1 1 In the figure, ABCD is a rhombus with coordinates A(2, 9) and C(8, 1). The diagonals AC and BD cut at
TERMWISE SYLLABUS SESSION CLASS-IX SUBJECT : MATHEMATICS. Course Structure. Schedule for Periodic Assessments and CASExam. of Session
 TERMWISE SYLLABUS SESSION-2018-19 CLASS-IX SUBJECT : MATHEMATICS Course Structure Units Unit Name Marks I NUMBER SYSTEMS 08 II ALGEBRA 17 III COORDINATE GEOMETRY 04 IV GEOMETRY 28 V MENSURATION 13 VI STATISTICS
TERMWISE SYLLABUS SESSION-2018-19 CLASS-IX SUBJECT : MATHEMATICS Course Structure Units Unit Name Marks I NUMBER SYSTEMS 08 II ALGEBRA 17 III COORDINATE GEOMETRY 04 IV GEOMETRY 28 V MENSURATION 13 VI STATISTICS
21. Prove that If one side of the cyclic quadrilateral is produced then the exterior angle is equal to the interior opposite angle.
 21. Prove that If one side of the cyclic quadrilateral is produced then the exterior angle is equal to the interior opposite angle. 22. Prove that If two sides of a cyclic quadrilateral are parallel, then
21. Prove that If one side of the cyclic quadrilateral is produced then the exterior angle is equal to the interior opposite angle. 22. Prove that If two sides of a cyclic quadrilateral are parallel, then
MT - GEOMETRY - SEMI PRELIM - II : PAPER - 5
 017 1100 MT MT - GEOMETRY - SEMI PRELIM - II : PPER - 5 Time : Hours Model nswer Paper Max. Marks : 40.1. ttempt NY FIVE of the following : (i) X In XYZ, ray YM bisects XYZ XY YZ XM MZ Y Z [Property of
017 1100 MT MT - GEOMETRY - SEMI PRELIM - II : PPER - 5 Time : Hours Model nswer Paper Max. Marks : 40.1. ttempt NY FIVE of the following : (i) X In XYZ, ray YM bisects XYZ XY YZ XM MZ Y Z [Property of
Circle Theorems. Angles at the circumference are equal. The angle in a semi-circle is x The angle at the centre. Cyclic Quadrilateral
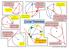 The angle in a semi-circle is 90 0 Angles at the circumference are equal. A B They must come from the same arc. Look out for a diameter. 2x Cyclic Quadrilateral Opposite angles add up to 180 0 A They must
The angle in a semi-circle is 90 0 Angles at the circumference are equal. A B They must come from the same arc. Look out for a diameter. 2x Cyclic Quadrilateral Opposite angles add up to 180 0 A They must
1. Sample answer: A, B, D. 3. D, E, F 4. plane C 6. C, E 7. E. 8. Sample answer: C ray infinite; zero. 4. no; yes 5.
 nswers hapter 1 1.1 Start Thinking When the vertex of the triangle is moved in an direction, its angle measure also changes. ecause all three sides of the triangle are connected, this also affects the
nswers hapter 1 1.1 Start Thinking When the vertex of the triangle is moved in an direction, its angle measure also changes. ecause all three sides of the triangle are connected, this also affects the
REVISED vide circular No.63 on
 Circular no. 63 COURSE STRUCTURE (FIRST TERM) CLASS -IX First Term Marks: 90 REVISED vide circular No.63 on 22.09.2015 UNIT I: NUMBER SYSTEMS 1. REAL NUMBERS (18 Periods) 1. Review of representation of
Circular no. 63 COURSE STRUCTURE (FIRST TERM) CLASS -IX First Term Marks: 90 REVISED vide circular No.63 on 22.09.2015 UNIT I: NUMBER SYSTEMS 1. REAL NUMBERS (18 Periods) 1. Review of representation of
10. Circles. Q 5 O is the centre of a circle of radius 5 cm. OP AB and OQ CD, AB CD, AB = 6 cm and CD = 8 cm. Determine PQ. Marks (2) Marks (2)
 10. Circles Q 1 True or False: It is possible to draw two circles passing through three given non-collinear points. Mark (1) Q 2 State the following statement as true or false. Give reasons also.the perpendicular
10. Circles Q 1 True or False: It is possible to draw two circles passing through three given non-collinear points. Mark (1) Q 2 State the following statement as true or false. Give reasons also.the perpendicular
