Objectives To find the measure of an inscribed angle To find the measure of an angle formed by a tangent and a chord
|
|
|
- Willa Hart
- 6 years ago
- Views:
Transcription
1 1-3 Inscribed ngles ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. lso G-..3, G-..4 M 1, M 3, M 4, M 6 bjectives To find the measure of an inscribed angle To find the measure of an angle formed by a tangent and a chord raw a large diagram and draw the angle each point makes with the goal posts. Three high-school soccer players practice kicking goals from the points shown in the diagram. ll three points are along an arc of a circle. layer says she is in the best position because the angle of her kicks toward the goal is wider than the angle of the other players kicks. o you agree? Explain. layer MTHEMTIL RTIES layer layer Lesson Vocabulary inscribed angle intercepted arc n angle whose vertex is on the circle and whose sides are chords of the circle is an inscribed angle. n arc with endpoints on the sides of an inscribed angle, and its other points in the interior of the angle is an intercepted arc. In the diagram, inscribed intercepts. Intercepted arc Inscribed angle Essential Understanding ngles formed by intersecting lines have a special relationship to the arcs the intersecting lines intercept. In this lesson, you will study arcs formed by inscribed angles. Theorem 1-11 Inscribed ngle Theorem The measure of an inscribed angle is half the measure of its intercepted arc. m = 1 m 780 hapter 1 ircles
2 To prove Theorem 1-11, there are three cases to consider. I: The center is on a side of the angle. II: The center is inside the angle. III: The center is outside the angle. elow is a proof of ase I. You will prove ase II and ase III in Exercises 6 and 7. of Theorem 1-11, ase I Given: } with inscribed and diameter rove: m = 1 m raw radius to form isosceles with = and, hence, m = m (Isosceles Triangle Theorem). m = m + m Triangle Exterior ngle Theorem m = m efinition of measure of an arc m = m + m Substitute. m = m Substitute and simplify. 1 m = m ivide each side by. Which variable should you solve for first? You know the inscribed angle that intercepts T, which has the measure a. You need a to find b. So find a first. roblem 1 What are the values of a and b? m QT = 1 m T Using the Inscribed ngle Theorem 60 = 1 a Substitute. Inscribed ngle Theorem 10 = a Multiply each side by. m RS = 1 m S Inscribed ngle Theorem m RS = 1 (m T + m TS ) rc ddition ostulate Q 60 R T 30 S b = 1 ( ) Substitute. b = 75 Simplify. Got It? 1. a. In }, what is m? b. What are m, m, m, and m? c. What do you notice about the sums of the measures of the opposite angles in the quadrilateral in part (b)? Lesson 1-3 Inscribed ngles 781
3 You will use three corollaries to the Inscribed ngle Theorem to find measures of angles in circles. The first corollary may confirm an observation you made in the Solve It. orollaries to Theorem 1-11: The Inscribed ngle Theorem orollary 1 Two inscribed angles that intercept the same arc are congruent. orollary n angle inscribed in a semicircle is a right angle. orollary 3 The opposite angles of a quadrilateral inscribed in a circle are supplementary. You will prove these corollaries in Exercises Is there too much information? Each diagram has more information than you need. Focus on what you need to find. roblem Using orollaries to Find ngle Measures What is the measure of each numbered angle? is inscribed in a semicircle. and the 38 angle intercept the y orollary, 1 is a right angle, so same arc. y orollary 1, the angles m 1 = 90. are congruent, so m = 38. Got It?. In the diagram at the right, what is the measure of each numbered angle? The following diagram shows point moving along the circle until a tangent is formed. From the Inscribed ngle Theorem, you know that in the first three diagrams m is 1 m. s the last diagram suggests, this is also true when and coincide. 78 hapter 1 ircles
4 Theorem 1-1 The measure of an angle formed by a tangent and a chord is half the measure of the intercepted arc. m = 1 m You will prove Theorem 1-1 in Exercise 34. roblem 3 Using rc Measure In the diagram, < SR > is a tangent to the circle at Q. If mmq = 1, what is mjqr? S Q < SR > is tangent to the circle at Q m MQ = 1 M R m QR m QS + m QR = 180. So first find m QS using MQ. How can you check the answer? ne way is to use m QR to find m Q. onfirm that m Q + m MQ = mmq = m QS 1 (1) = m QS Substitute. 106 = m QS Simplify. m QS + m QR = 180 Linear air ostulate m QR = 180 Substitute. m QR = 74 Simplify. The measure of an formed by a tangent and a chord is 1 the measure of the intercepted arc. Got It? 3. a. In the diagram at the right, KJ is tangent to }. What are the values of x and y? b. Reasoning In part (a), an inscribed angle ( Q) and an angle formed by a tangent and chord ( KJL) intercept the same arc. What is always true of these angles? Explain. Q 35 y L J x K Lesson 1-3 Inscribed ngles 783
5 Lesson heck o you know HW? Use the diagram for Exercises Which arc does intercept?. Which angle intercepts? 3. Which angles of quadrilateral are supplementary? MTHEMTIL RTIES o you UNERSTN? 4. Vocabulary What is the relationship between an inscribed angle and its intercepted arc? 5. Error nalysis classmate says that m = 90. What is your classmate s error? ractice and roblem-solving Exercises MTHEMTIL RTIES ractice Find the value of each variable. For each circle, the dot represents the center. See roblems 1 and d x 7 y p 58 q Find the value of each variable. Lines that appear to be tangent are tangent. See roblem y x w e f pply 19. Writing parallelogram inscribed in a circle must be what kind of parallelogram? Explain. 784 hapter 1 ircles
6 Find each indicated measure for. 0. a. m a. m b. m b. m E 48 c. m c. m d. m d. m e. m E E. Think bout a lan What kind of trapezoid can be inscribed in a circle? Justify your response. raw several diagrams to make a conjecture. How can parallel lines help? Find the value of each variable. For each circle, the dot represents the center e d 56 Write a proof for Exercises 6 and Inscribed ngle Theorem, ase II Given: } with inscribed rove: m = 1 m (Hint: Use the Inscribed ngle Theorem, ase I.) 7. Inscribed ngle Theorem, ase III Given: }S with inscribed QR rove: m QR = 1 m R R S T (Hint: Use the Inscribed ngle Theorem, ase I.) 8. Television The director of a telecast wants the option of showing the same scene from three different views. a. Explain why cameras in the positions shown in the diagram will transmit the same scene. b. Reasoning Will the scenes look the same when the director views them on the control room monitors? Explain. Q Scene amera 1 amera 3 amera Lesson 1-3 Inscribed ngles 785
7 9. Reasoning an a rhombus that is not a square be inscribed in a circle? Justify your answer. 30. onstructions The diagrams below show the construction of a tangent to a circle from a point outside the circle. Explain why < > must be tangent to }. (Hint: opy the third diagram and draw.) Given: and point onstruct the midpoint of. Label the point. onstruct a semicircle with radius and center. Label its intersection with as. raw. Write a proof for Exercises Inscribed ngle Theorem, orollary 1 Given: }, intercepts, intercepts. rove: 33. Inscribed ngle Theorem, orollary 3 Given: Quadrilateral inscribed in } rove: and are supplementary. and are supplementary. 3. Inscribed ngle Theorem, orollary Given: } with inscribed in a semicircle rove: is a right angle. 34. Theorem 1-1 Given: GH and tangent / intersecting }E at H rove: m GHI = 1 m GFH G E F H I hallenge Reasoning Is the statement true or false? If it is true, give a convincing argument. If it is false, give a counterexample. 35. If two angles inscribed in a circle are congruent, then they intercept the same arc. 36. If an inscribed angle is a right angle, then it is inscribed in a semicircle. 37. circle can always be circumscribed about a quadrilateral whose opposite angles are supplementary. 786 hapter 1 ircles
8 38. rove that if two arcs of a circle are included between parallel chords, then the arcs are congruent. 39. onstructions raw two segments. Label their lengths x and y. onstruct the geometric mean of x and y. (Hint: Recall a theorem about a geometric mean.) ERFRMNE TSK pply What You ve Learned Look back at the information given on page 761 about the logo for the showroom display. The diagram of the logo is shown again below. onsider relationships of angles and arcs in the diagram. Select all of the following that are true. Explain your reasoning. MTHEMTIL RTIES M 1 9 ft E G 7. ft 15 ft 7 ft. is an inscribed angle in }.. G is an inscribed angle in }.. G intercepts G.. G intercepts E. E. The measure of G is half the measure of G. F. G is a right triangle. G. G G Lesson 1-3 Inscribed ngles 787
Chords and Arcs. Objectives To use congruent chords, arcs, and central angles To use perpendicular bisectors to chords
 - hords and rcs ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. M, M bjectives To use congruent chords, arcs, and central angles To use perpendicular
- hords and rcs ommon ore State Standards G-.. Identify and describe relationships among inscribed angles, radii, and chords. M, M bjectives To use congruent chords, arcs, and central angles To use perpendicular
Circles and Arcs. Objectives To find the measures of central angles and arcs To find the circumference and arc length
 10-6 ircles and rcs ommon ore tate tandards G-..1 Know precise definitions of... circle... G-..1 rove that all circles are similar. lso G-..2, G-..5 M 1, M 3, M 4, M 6, M 8 bjectives o find the measures
10-6 ircles and rcs ommon ore tate tandards G-..1 Know precise definitions of... circle... G-..1 rove that all circles are similar. lso G-..2, G-..5 M 1, M 3, M 4, M 6, M 8 bjectives o find the measures
Geometry: A Complete Course
 eometry: omplete ourse with rigonometry) odule - tudent Worket Written by: homas. lark Larry. ollins 4/2010 or ercises 20 22, use the diagram below. 20. ssume is a rectangle. a) f is 6, find. b) f is,
eometry: omplete ourse with rigonometry) odule - tudent Worket Written by: homas. lark Larry. ollins 4/2010 or ercises 20 22, use the diagram below. 20. ssume is a rectangle. a) f is 6, find. b) f is,
Proportions in Triangles
 - roportions in Triangles ontent tandard G.RT. rove theorems about triangles...a line parallel to one side of a triangle divides the other two proportionally... Objective To use the ide-plitter Theorem
- roportions in Triangles ontent tandard G.RT. rove theorems about triangles...a line parallel to one side of a triangle divides the other two proportionally... Objective To use the ide-plitter Theorem
Arcs and Inscribed Angles of Circles
 Arcs and Inscribed Angles of Circles Inscribed angles have: Vertex on the circle Sides are chords (Chords AB and BC) Angle ABC is inscribed in the circle AC is the intercepted arc because it is created
Arcs and Inscribed Angles of Circles Inscribed angles have: Vertex on the circle Sides are chords (Chords AB and BC) Angle ABC is inscribed in the circle AC is the intercepted arc because it is created
Solve problems involving tangents to a circle. Solve problems involving chords of a circle
 8UNIT ircle Geometry What You ll Learn How to Solve problems involving tangents to a circle Solve problems involving chords of a circle Solve problems involving the measures of angles in a circle Why Is
8UNIT ircle Geometry What You ll Learn How to Solve problems involving tangents to a circle Solve problems involving chords of a circle Solve problems involving the measures of angles in a circle Why Is
Circles-Tangent Properties
 15 ircles-tangent roperties onstruction of tangent at a point on the circle. onstruction of tangents when the angle between radii is given. Tangents from an external point - construction and proof Touching
15 ircles-tangent roperties onstruction of tangent at a point on the circle. onstruction of tangents when the angle between radii is given. Tangents from an external point - construction and proof Touching
14.3 Tangents and Circumscribed Angles
 Name lass Date 14.3 Tangents and ircumscribed ngles Essential uestion: What are the key theorems about tangents to a circle? Explore G.5. Investigate patterns to make conjectures about geometric relationships,
Name lass Date 14.3 Tangents and ircumscribed ngles Essential uestion: What are the key theorems about tangents to a circle? Explore G.5. Investigate patterns to make conjectures about geometric relationships,
radii: AP, PR, PB diameter: AB chords: AB, CD, AF secant: AG or AG tangent: semicircles: ACB, ARB minor arcs: AC, AR, RD, BC,
 h 6 Note Sheets L Shortened Key Note Sheets hapter 6: iscovering and roving ircle roperties eview: ircles Vocabulary If you are having problems recalling the vocabulary, look back at your notes for Lesson
h 6 Note Sheets L Shortened Key Note Sheets hapter 6: iscovering and roving ircle roperties eview: ircles Vocabulary If you are having problems recalling the vocabulary, look back at your notes for Lesson
Lesson 1.7 circles.notebook. September 19, Geometry Agenda:
 Geometry genda: Warm-up 1.6(need to print of and make a word document) ircle Notes 1.7 Take Quiz if you were not in class on Friday Remember we are on 1.7 p.72 not lesson 1.8 1 Warm up 1.6 For Exercises
Geometry genda: Warm-up 1.6(need to print of and make a word document) ircle Notes 1.7 Take Quiz if you were not in class on Friday Remember we are on 1.7 p.72 not lesson 1.8 1 Warm up 1.6 For Exercises
Circles. Exercise 9.1
 9 uestion. Exercise 9. How many tangents can a circle have? Solution For every point of a circle, we can draw a tangent. Therefore, infinite tangents can be drawn. uestion. Fill in the blanks. (i) tangent
9 uestion. Exercise 9. How many tangents can a circle have? Solution For every point of a circle, we can draw a tangent. Therefore, infinite tangents can be drawn. uestion. Fill in the blanks. (i) tangent
Using Properties of Segments that Intersect Circles
 ig Idea 1 H UY I I Using roperties of egments that Intersect ircles or Your otebook You learned several relationships between tangents, secants, and chords. ome of these relationships can help you determine
ig Idea 1 H UY I I Using roperties of egments that Intersect ircles or Your otebook You learned several relationships between tangents, secants, and chords. ome of these relationships can help you determine
Introduction Circle Some terms related with a circle
 141 ircle Introduction In our day-to-day life, we come across many objects which are round in shape, such as dials of many clocks, wheels of a vehicle, bangles, key rings, coins of denomination ` 1, `
141 ircle Introduction In our day-to-day life, we come across many objects which are round in shape, such as dials of many clocks, wheels of a vehicle, bangles, key rings, coins of denomination ` 1, `
( ) Chapter 10 Review Question Answers. Find the value of x mhg. m B = 1 2 ( 80 - x) H x G. E 30 = 80 - x. x = 50. Find m AXB and m Y A D X 56
 hapter 10 Review Question nswers 1. ( ) Find the value of mhg 30 m = 1 2 ( 30) = 15 F 80 m = 1 2 ( 80 - ) H G E 30 = 80 - = 50 2. Find m X and m Y m X = 1 120 + 56 2 ( ) = 88 120 X 56 Y m Y = 1 120-56
hapter 10 Review Question nswers 1. ( ) Find the value of mhg 30 m = 1 2 ( 30) = 15 F 80 m = 1 2 ( 80 - ) H G E 30 = 80 - = 50 2. Find m X and m Y m X = 1 120 + 56 2 ( ) = 88 120 X 56 Y m Y = 1 120-56
10.4 Explore Inscribed Angles
 Investigating g eometry IIY se before esson 0.4 0.4 Eplore Inscribed ngles E I compass straightedge protractor Q E I O N How are inscribed angles related to central angles? he verte of a central angle
Investigating g eometry IIY se before esson 0.4 0.4 Eplore Inscribed ngles E I compass straightedge protractor Q E I O N How are inscribed angles related to central angles? he verte of a central angle
To find and compare lengths of segments
 1-3 Measuring Segments ommon ore State Standards G-O..1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment... lso G-GPE..6 MP 2, MP 3, MP 4, MP 6 Objective To
1-3 Measuring Segments ommon ore State Standards G-O..1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment... lso G-GPE..6 MP 2, MP 3, MP 4, MP 6 Objective To
Chapter 1. Some Basic Theorems. 1.1 The Pythagorean Theorem
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a 2 + b 2 = c 2. roof. b a a 3 2 b 2 b 4 b a b
15.3 Tangents and Circumscribed Angles
 Name lass ate 15.3 Tangents and ircumscribed ngles Essential uestion: What are the key theorems about tangents to a circle? esource Locker Explore Investigating the Tangent-adius Theorem tangent is a line
Name lass ate 15.3 Tangents and ircumscribed ngles Essential uestion: What are the key theorems about tangents to a circle? esource Locker Explore Investigating the Tangent-adius Theorem tangent is a line
Theorem 1.2 (Converse of Pythagoras theorem). If the lengths of the sides of ABC satisfy a 2 + b 2 = c 2, then the triangle has a right angle at C.
 hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
hapter 1 Some asic Theorems 1.1 The ythagorean Theorem Theorem 1.1 (ythagoras). The lengths a b < c of the sides of a right triangle satisfy the relation a + b = c. roof. b a a 3 b b 4 b a b 4 1 a a 3
Common Core Readiness Assessment 4
 ommon ore Readiness ssessment 4 1. Use the diagram and the information given to complete the missing element of the two-column proof. 2. Use the diagram and the information given to complete the missing
ommon ore Readiness ssessment 4 1. Use the diagram and the information given to complete the missing element of the two-column proof. 2. Use the diagram and the information given to complete the missing
Indicate whether the statement is true or false.
 PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
PRACTICE EXAM IV Sections 6.1, 6.2, 8.1 8.4 Indicate whether the statement is true or false. 1. For a circle, the constant ratio of the circumference C to length of diameter d is represented by the number.
Geometry Honors Homework
 Geometry Honors Homework pg. 1 12-1 Practice Form G Tangent Lines Algebra Assume that lines that appear to be tangent are tangent. O is the center of each circle. What is the value of x? 1. 2. 3. The circle
Geometry Honors Homework pg. 1 12-1 Practice Form G Tangent Lines Algebra Assume that lines that appear to be tangent are tangent. O is the center of each circle. What is the value of x? 1. 2. 3. The circle
Chapter-wise questions
 hapter-wise questions ircles 1. In the given figure, is circumscribing a circle. ind the length of. 3 15cm 5 2. In the given figure, is the center and. ind the radius of the circle if = 18 cm and = 3cm
hapter-wise questions ircles 1. In the given figure, is circumscribing a circle. ind the length of. 3 15cm 5 2. In the given figure, is the center and. ind the radius of the circle if = 18 cm and = 3cm
Geometry: A Complete Course
 Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas E. lark Larry E. ollins Geometry: omplete ourse (with Trigonometry) Module Student Worktext opyright 2014 by VideotextInteractive
Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas E. lark Larry E. ollins Geometry: omplete ourse (with Trigonometry) Module Student Worktext opyright 2014 by VideotextInteractive
Name Date Period. Notes - Tangents. 1. If a line is a tangent to a circle, then it is to the
 Name ate Period Notes - Tangents efinition: tangent is a line in the plane of a circle that intersects the circle in eactly one point. There are 3 Theorems for Tangents. 1. If a line is a tangent to a
Name ate Period Notes - Tangents efinition: tangent is a line in the plane of a circle that intersects the circle in eactly one point. There are 3 Theorems for Tangents. 1. If a line is a tangent to a
Circles. II. Radius - a segment with one endpoint the center of a circle and the other endpoint on the circle.
 Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
Answers. Chapter10 A Start Thinking. and 4 2. Sample answer: no; It does not pass through the center.
 hapter10 10.1 Start Thinking 6. no; is not a right triangle because the side lengths do not satisf the Pthagorean Theorem (Thm. 9.1). 1. (3, ) 7. es; is a right triangle because the side lengths satisf
hapter10 10.1 Start Thinking 6. no; is not a right triangle because the side lengths do not satisf the Pthagorean Theorem (Thm. 9.1). 1. (3, ) 7. es; is a right triangle because the side lengths satisf
Ready To Go On? Skills Intervention 11-1 Lines That Intersect Circles
 Name ate lass STION 11 Ready To Go On? Skills Intervention 11-1 Lines That Intersect ircles ind these vocabulary words in Lesson 11-1 and the Multilingual Glossary. Vocabulary interior of a circle exterior
Name ate lass STION 11 Ready To Go On? Skills Intervention 11-1 Lines That Intersect ircles ind these vocabulary words in Lesson 11-1 and the Multilingual Glossary. Vocabulary interior of a circle exterior
Replacement for a Carpenter s Square
 Lesson.1 Skills Practice Name Date Replacement for a arpenter s Square Inscribed and ircumscribed Triangles and Quadrilaterals Vocabulary nswer each question. 1. How are inscribed polygons and circumscribed
Lesson.1 Skills Practice Name Date Replacement for a arpenter s Square Inscribed and ircumscribed Triangles and Quadrilaterals Vocabulary nswer each question. 1. How are inscribed polygons and circumscribed
What You ll Learn. Why It s Important. We see circles in nature and in design. What do you already know about circles?
 We see circles in nature and in design. What do you already know about circles? What You ll Learn ircle properties that relate: a tangent to a circle and the radius of the circle a chord in a circle, its
We see circles in nature and in design. What do you already know about circles? What You ll Learn ircle properties that relate: a tangent to a circle and the radius of the circle a chord in a circle, its
Chapter 3. The angle bisectors. 3.1 The angle bisector theorem
 hapter 3 The angle bisectors 3.1 The angle bisector theorem Theorem 3.1 (ngle bisector theorem). The bisectors of an angle of a triangle divide its opposite side in the ratio of the remaining sides. If
hapter 3 The angle bisectors 3.1 The angle bisector theorem Theorem 3.1 (ngle bisector theorem). The bisectors of an angle of a triangle divide its opposite side in the ratio of the remaining sides. If
Plane geometry Circles: Problems with some Solutions
 The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
The University of Western ustralia SHL F MTHMTIS & STTISTIS UW MY FR YUNG MTHMTIINS Plane geometry ircles: Problems with some Solutions 1. Prove that for any triangle, the perpendicular bisectors of the
What is the longest chord?.
 Section: 7-6 Topic: ircles and rcs Standard: 7 & 21 ircle Naming a ircle Name: lass: Geometry 1 Period: Date: In a plane, a circle is equidistant from a given point called the. circle is named by its.
Section: 7-6 Topic: ircles and rcs Standard: 7 & 21 ircle Naming a ircle Name: lass: Geometry 1 Period: Date: In a plane, a circle is equidistant from a given point called the. circle is named by its.
1.2 Perpendicular Lines
 Name lass ate 1.2 erpendicular Lines Essential Question: What are the key ideas about perpendicular bisectors of a segment? 1 Explore onstructing erpendicular isectors and erpendicular Lines You can construct
Name lass ate 1.2 erpendicular Lines Essential Question: What are the key ideas about perpendicular bisectors of a segment? 1 Explore onstructing erpendicular isectors and erpendicular Lines You can construct
Honors Geometry Circle Investigation - Instructions
 Honors Geometry ircle Investigation - Instructions 1. On the first circle a. onnect points and O with a line segment. b. onnect points O and also. c. Measure O. d. Estimate the degree measure of by using
Honors Geometry ircle Investigation - Instructions 1. On the first circle a. onnect points and O with a line segment. b. onnect points O and also. c. Measure O. d. Estimate the degree measure of by using
C=2πr C=πd. Chapter 10 Circles Circles and Circumference. Circumference: the distance around the circle
 10.1 Circles and Circumference Chapter 10 Circles Circle the locus or set of all points in a plane that are A equidistant from a given point, called the center When naming a circle you always name it by
10.1 Circles and Circumference Chapter 10 Circles Circle the locus or set of all points in a plane that are A equidistant from a given point, called the center When naming a circle you always name it by
10-1 Study Guide and Intervention
 opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10-1 tudy Guide and Intervention ircles and ircumference arts of ircles circle consists of all points in a plane that are
opyright Glencoe/McGraw-Hill, a division of he McGraw-Hill ompanies, Inc. NM I 10-1 tudy Guide and Intervention ircles and ircumference arts of ircles circle consists of all points in a plane that are
Example 1: Finding angle measures: I ll do one: We ll do one together: You try one: ML and MN are tangent to circle O. Find the value of x
 Ch 1: Circles 1 1 Tangent Lines 1 Chords and Arcs 1 3 Inscribed Angles 1 4 Angle Measures and Segment Lengths 1 5 Circles in the coordinate plane 1 1 Tangent Lines Focused Learning Target: I will be able
Ch 1: Circles 1 1 Tangent Lines 1 Chords and Arcs 1 3 Inscribed Angles 1 4 Angle Measures and Segment Lengths 1 5 Circles in the coordinate plane 1 1 Tangent Lines Focused Learning Target: I will be able
Chapter 6. Worked-Out Solutions. Chapter 6 Maintaining Mathematical Proficiency (p. 299)
 hapter 6 hapter 6 Maintaining Mathematical Proficiency (p. 99) 1. Slope perpendicular to y = 1 x 5 is. y = x + b 1 = + b 1 = 9 + b 10 = b n equation of the line is y = x + 10.. Slope perpendicular to y
hapter 6 hapter 6 Maintaining Mathematical Proficiency (p. 99) 1. Slope perpendicular to y = 1 x 5 is. y = x + b 1 = + b 1 = 9 + b 10 = b n equation of the line is y = x + 10.. Slope perpendicular to y
Reteaching , or 37.5% 360. Geometric Probability. Name Date Class
 Name ate lass Reteaching Geometric Probability INV 6 You have calculated probabilities of events that occur when coins are tossed and number cubes are rolled. Now you will learn about geometric probability.
Name ate lass Reteaching Geometric Probability INV 6 You have calculated probabilities of events that occur when coins are tossed and number cubes are rolled. Now you will learn about geometric probability.
Riding a Ferris Wheel
 Lesson.1 Skills Practice Name ate iding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. center of the circle 6. central angle T H I 2. chord 7. inscribed
Lesson.1 Skills Practice Name ate iding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. center of the circle 6. central angle T H I 2. chord 7. inscribed
Skills Practice Skills Practice for Lesson 11.1
 Skills Practice Skills Practice for Lesson.1 Name ate Riding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. circle X T 2. center of the circle H I
Skills Practice Skills Practice for Lesson.1 Name ate Riding a Ferris Wheel Introduction to ircles Vocabulary Identify an instance of each term in the diagram. 1. circle X T 2. center of the circle H I
New Jersey Center for Teaching and Learning. Progressive Mathematics Initiative
 Slide 1 / 150 New Jersey Center for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
Slide 1 / 150 New Jersey Center for Teaching and Learning Progressive Mathematics Initiative This material is made freely available at www.njctl.org and is intended for the non-commercial use of students
Chapter 19 Exercise 19.1
 hapter 9 xercise 9... (i) n axiom is a statement that is accepted but cannot be proven, e.g. x + 0 = x. (ii) statement that can be proven logically: for example, ythagoras Theorem. (iii) The logical steps
hapter 9 xercise 9... (i) n axiom is a statement that is accepted but cannot be proven, e.g. x + 0 = x. (ii) statement that can be proven logically: for example, ythagoras Theorem. (iii) The logical steps
Chapter 10. Properties of Circles
 Chapter 10 Properties of Circles 10.1 Use Properties of Tangents Objective: Use properties of a tangent to a circle. Essential Question: how can you verify that a segment is tangent to a circle? Terminology:
Chapter 10 Properties of Circles 10.1 Use Properties of Tangents Objective: Use properties of a tangent to a circle. Essential Question: how can you verify that a segment is tangent to a circle? Terminology:
Triangles. Exercise 4.1
 4 Question. xercise 4. Fill in the blanks using the correct word given in brackets. (i) ll circles are....(congruent, similar) (ii) ll squares are....(similar, congruent) (iii) ll... triangles are similar.
4 Question. xercise 4. Fill in the blanks using the correct word given in brackets. (i) ll circles are....(congruent, similar) (ii) ll squares are....(similar, congruent) (iii) ll... triangles are similar.
DO NOW #1. Please: Get a circle packet
 irclengles.gsp pril 26, 2013 Please: Get a circle packet Reminders: R #10 due Friday Quiz Monday 4/29 Quiz Friday 5/3 Quiz Wednesday 5/8 Quiz Friday 5/10 Initial Test Monday 5/13 ctual Test Wednesday 5/15
irclengles.gsp pril 26, 2013 Please: Get a circle packet Reminders: R #10 due Friday Quiz Monday 4/29 Quiz Friday 5/3 Quiz Wednesday 5/8 Quiz Friday 5/10 Initial Test Monday 5/13 ctual Test Wednesday 5/15
Lesson 2B: Thales Theorem
 Lesson 2B: Thales Theorem Learning Targets o I can identify radius, diameter, chords, central circles, inscribed circles and semicircles o I can explain that an ABC is a right triangle, then A, B, and
Lesson 2B: Thales Theorem Learning Targets o I can identify radius, diameter, chords, central circles, inscribed circles and semicircles o I can explain that an ABC is a right triangle, then A, B, and
Geometry Unit 1 Practice
 Lesson 1-1 1. Persevere in solving problems. Identify each figure. hen give all possible names for the figure. a. S Geometry Unit 1 Practice e. P S G Q. What is a correct name for this plane? W R Z X b..
Lesson 1-1 1. Persevere in solving problems. Identify each figure. hen give all possible names for the figure. a. S Geometry Unit 1 Practice e. P S G Q. What is a correct name for this plane? W R Z X b..
Page 1 Central Angles & Arc Measures
 Geometry/Trig Unit 8 ll bout ircles! Name: ate: Page 1 entral ngles & rc Measures Example 1: JK is a diameter of ircle. Name two examples for each: K Minor rc:, Major rc:, M Semicircle:, Name Pair of djacent
Geometry/Trig Unit 8 ll bout ircles! Name: ate: Page 1 entral ngles & rc Measures Example 1: JK is a diameter of ircle. Name two examples for each: K Minor rc:, Major rc:, M Semicircle:, Name Pair of djacent
Geometry Note Cards EXAMPLE:
 Geometry Note Cards EXAMPLE: Lined Side Word and Explanation Blank Side Picture with Statements Sections 12-4 through 12-5 1) Theorem 12-3 (p. 790) 2) Theorem 12-14 (p. 790) 3) Theorem 12-15 (p. 793) 4)
Geometry Note Cards EXAMPLE: Lined Side Word and Explanation Blank Side Picture with Statements Sections 12-4 through 12-5 1) Theorem 12-3 (p. 790) 2) Theorem 12-14 (p. 790) 3) Theorem 12-15 (p. 793) 4)
1 = 1, b d and c d. Chapter 7. Worked-Out Solutions Chapter 7 Maintaining Mathematical Proficiency (p. 357) Slope of line b:
 hapter 7 aintaining athematical Proficienc (p. 357) 1. (7 x) = 16 (7 x) = 16 7 x = 7 = 7 x = 3 x 1 = 3 1 x = 3. 7(1 x) + = 19 = 7(1 x) = 1 7(1 x) 7 = 1 7 1 x = 3 1 = 1 x = x 1 = 1 x = 3. 3(x 5) + 8(x 5)
hapter 7 aintaining athematical Proficienc (p. 357) 1. (7 x) = 16 (7 x) = 16 7 x = 7 = 7 x = 3 x 1 = 3 1 x = 3. 7(1 x) + = 19 = 7(1 x) = 1 7(1 x) 7 = 1 7 1 x = 3 1 = 1 x = x 1 = 1 x = 3. 3(x 5) + 8(x 5)
MT EDUCARE LTD. MATHEMATICS SUBJECT : Q L M ICSE X. Geometry STEP UP ANSWERSHEET
 IS X MT UR LT. SUJT : MTHMTIS Geometry ST U NSWRSHT 003 1. In QL and RM, LQ MR [Given] LQ RM [Given] QL ~ RM [y axiom of similarity] (i) Since, QL ~ RM QL M L RM QL RM L M (ii) In QL and RQ, we have Q
IS X MT UR LT. SUJT : MTHMTIS Geometry ST U NSWRSHT 003 1. In QL and RM, LQ MR [Given] LQ RM [Given] QL ~ RM [y axiom of similarity] (i) Since, QL ~ RM QL M L RM QL RM L M (ii) In QL and RQ, we have Q
Essential Question How can you use a flowchart to prove a mathematical statement?
 .6 Proving Geometric Relationships OMMON OR Learning Standard HSG-O..9 MOLING WITH MTHMTIS To be proficient in math, you need to map relationships using such tools as diagrams, two-way tables, graphs,
.6 Proving Geometric Relationships OMMON OR Learning Standard HSG-O..9 MOLING WITH MTHMTIS To be proficient in math, you need to map relationships using such tools as diagrams, two-way tables, graphs,
SM2H Unit 6 Circle Notes
 Name: Period: SM2H Unit 6 Circle Notes 6.1 Circle Vocabulary, Arc and Angle Measures Circle: All points in a plane that are the same distance from a given point, called the center of the circle. Chord:
Name: Period: SM2H Unit 6 Circle Notes 6.1 Circle Vocabulary, Arc and Angle Measures Circle: All points in a plane that are the same distance from a given point, called the center of the circle. Chord:
12.1 Triangle Proportionality Theorem
 ame lass Date 12.1 Triangle roportionality Theorem ssential Question: When a line parallel to one side of a triangle intersects the other two sides, how does it divide those sides? Resource ocker xplore
ame lass Date 12.1 Triangle roportionality Theorem ssential Question: When a line parallel to one side of a triangle intersects the other two sides, how does it divide those sides? Resource ocker xplore
Unit 10 Geometry Circles. NAME Period
 Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
Unit 10 Geometry Circles NAME Period 1 Geometry Chapter 10 Circles ***In order to get full credit for your assignments they must me done on time and you must SHOW ALL WORK. *** 1. (10-1) Circles and Circumference
Review for Grade 9 Math Exam - Unit 8 - Circle Geometry
 Name: Review for Grade 9 Math Exam - Unit 8 - ircle Geometry Date: Multiple hoice Identify the choice that best completes the statement or answers the question. 1. is the centre of this circle and point
Name: Review for Grade 9 Math Exam - Unit 8 - ircle Geometry Date: Multiple hoice Identify the choice that best completes the statement or answers the question. 1. is the centre of this circle and point
Affine Transformations
 Solutions to hapter Problems 435 Then, using α + β + γ = 360, we obtain: ( ) x a = (/2) bc sin α a + ac sin β b + ab sin γ c a ( ) = (/2) bc sin α a 2 + (ac sin β)(ab cos γ ) + (ab sin γ )(ac cos β) =
Solutions to hapter Problems 435 Then, using α + β + γ = 360, we obtain: ( ) x a = (/2) bc sin α a + ac sin β b + ab sin γ c a ( ) = (/2) bc sin α a 2 + (ac sin β)(ab cos γ ) + (ab sin γ )(ac cos β) =
Name Geometry Common Core Regents Review Packet - 3. Topic 1 : Equation of a circle
 Name Geometry Common Core Regents Review Packet - 3 Topic 1 : Equation of a circle Equation with center (0,0) and radius r Equation with center (h,k) and radius r ( ) ( ) 1. The endpoints of a diameter
Name Geometry Common Core Regents Review Packet - 3 Topic 1 : Equation of a circle Equation with center (0,0) and radius r Equation with center (h,k) and radius r ( ) ( ) 1. The endpoints of a diameter
Geometry: A Complete Course
 Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas. lark Larry. ollins RRT 4/2010 6. In the figure below, and share the common segment. Prove the following conditional
Geometry: omplete ourse (with Trigonometry) Module - Student WorkText Written by: Thomas. lark Larry. ollins RRT 4/2010 6. In the figure below, and share the common segment. Prove the following conditional
Chapter 10 Worksheet 1 Name: Honors Accelerated Geometry Hour:
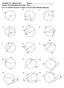 hapter 10 Worksheet 1 Name: Honors ccelerated Geometry Hour: For 1-15, find the measure of angle in each of the following diagrams. 1. 2.. 258 84 140 40 4. 5. 6. 2 y 80 y 72 7. 8. 9. 50 X 40 140 4 y 10.
hapter 10 Worksheet 1 Name: Honors ccelerated Geometry Hour: For 1-15, find the measure of angle in each of the following diagrams. 1. 2.. 258 84 140 40 4. 5. 6. 2 y 80 y 72 7. 8. 9. 50 X 40 140 4 y 10.
Tangent Lines Unit 10 Lesson 1 Example 1: Tell how many common tangents the circles have and draw them.
 Tangent Lines Unit 10 Lesson 1 EQ: How can you verify that a segment is tangent to a circle? Circle: Center: Radius: Chord: Diameter: Secant: Tangent: Tangent Lines Unit 10 Lesson 1 Example 1: Tell how
Tangent Lines Unit 10 Lesson 1 EQ: How can you verify that a segment is tangent to a circle? Circle: Center: Radius: Chord: Diameter: Secant: Tangent: Tangent Lines Unit 10 Lesson 1 Example 1: Tell how
So, PQ is about 3.32 units long Arcs and Chords. ALGEBRA Find the value of x.
 ALGEBRA Find the value of x. 1. Arc ST is a minor arc, so m(arc ST) is equal to the measure of its related central angle or 93. and are congruent chords, so the corresponding arcs RS and ST are congruent.
ALGEBRA Find the value of x. 1. Arc ST is a minor arc, so m(arc ST) is equal to the measure of its related central angle or 93. and are congruent chords, so the corresponding arcs RS and ST are congruent.
Geometry Final Review. Chapter 1. Name: Per: Vocab. Example Problems
 Geometry Final Review Name: Per: Vocab Word Acute angle Adjacent angles Angle bisector Collinear Line Linear pair Midpoint Obtuse angle Plane Pythagorean theorem Ray Right angle Supplementary angles Complementary
Geometry Final Review Name: Per: Vocab Word Acute angle Adjacent angles Angle bisector Collinear Line Linear pair Midpoint Obtuse angle Plane Pythagorean theorem Ray Right angle Supplementary angles Complementary
Mth 076: Applied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE
 Mth 076: pplied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE INTRODUTION TO GEOMETRY Pick up Geometric Formula Sheet (This sheet may be used while testing) ssignment Eleven: Problems Involving
Mth 076: pplied Geometry (Individualized Sections) MODULE FOUR STUDY GUIDE INTRODUTION TO GEOMETRY Pick up Geometric Formula Sheet (This sheet may be used while testing) ssignment Eleven: Problems Involving
2 Explain 1 Proving the Intersecting Chords Angle Measure Theorem
 xplain 1 Proving the Intersecting hords ngle easure Theorem In the xplore section, you discovered the effects that line segments, such as chords and secants, have on angle measures and their intercepted
xplain 1 Proving the Intersecting hords ngle easure Theorem In the xplore section, you discovered the effects that line segments, such as chords and secants, have on angle measures and their intercepted
Integrated Math II. IM2.1.2 Interpret given situations as functions in graphs, formulas, and words.
 Standard 1: Algebra and Functions Students graph linear inequalities in two variables and quadratics. They model data with linear equations. IM2.1.1 Graph a linear inequality in two variables. IM2.1.2
Standard 1: Algebra and Functions Students graph linear inequalities in two variables and quadratics. They model data with linear equations. IM2.1.1 Graph a linear inequality in two variables. IM2.1.2
MODULE. (40 + 8x) + (5x -16) = 180. STUDY GUIDE REVIEW Angles and Segments in Circles. Key Vocabulary
 STUDY GUIDE REVIEW Angles and Segments in ircles ODULE 15 Essential Question: How can you use angles and segments in circles to solve real-world problems? EY EXALE (Lesson 15.1) Determine m DE, m BD, m
STUDY GUIDE REVIEW Angles and Segments in ircles ODULE 15 Essential Question: How can you use angles and segments in circles to solve real-world problems? EY EXALE (Lesson 15.1) Determine m DE, m BD, m
Essential Question How can you prove a mathematical statement?
 .5 TEXS ESSENTIL KNOWLEDGE ND SKILLS Preparing for G.6. G.6. G.6.D G.6.E RESONING To be proficient in math, you need to know and be able to use algebraic properties. Proving Statements about Segments and
.5 TEXS ESSENTIL KNOWLEDGE ND SKILLS Preparing for G.6. G.6. G.6.D G.6.E RESONING To be proficient in math, you need to know and be able to use algebraic properties. Proving Statements about Segments and
Integrated Math 3 Math 3 Course Description:
 Course Description: Integrated Math 3 Math 3 Course Description: Integrated strands include algebra, functions, geometry, trigonometry, statistics, probability and discrete math. Scope and sequence includes
Course Description: Integrated Math 3 Math 3 Course Description: Integrated strands include algebra, functions, geometry, trigonometry, statistics, probability and discrete math. Scope and sequence includes
Name: Class: Date: 5. If the diagonals of a rhombus have lengths 6 and 8, then the perimeter of the rhombus is 28. a. True b.
 Indicate whether the statement is true or false. 1. If the diagonals of a quadrilateral are perpendicular, the quadrilateral must be a square. 2. If M and N are midpoints of sides and of, then. 3. The
Indicate whether the statement is true or false. 1. If the diagonals of a quadrilateral are perpendicular, the quadrilateral must be a square. 2. If M and N are midpoints of sides and of, then. 3. The
( ) Find the value of x mhg. H x G. Find m AXB and m Y A D X 56. Baroody Page 1 of 18
 1. ( ) Find the value of x mhg 30 F 80 H x G E 2. Find m X and m Y 120 X 56 Y aroody age 1 of 18 3. Find mq X 70 30 Y Q 4. Find the radius of a circle in which a 48 cm. chord is 8 cm closer to the center
1. ( ) Find the value of x mhg 30 F 80 H x G E 2. Find m X and m Y 120 X 56 Y aroody age 1 of 18 3. Find mq X 70 30 Y Q 4. Find the radius of a circle in which a 48 cm. chord is 8 cm closer to the center
The circumcircle and the incircle
 hapter 4 The circumcircle and the incircle 4.1 The Euler line 4.1.1 nferior and superior triangles G F E G D The inferior triangle of is the triangle DEF whose vertices are the midpoints of the sides,,.
hapter 4 The circumcircle and the incircle 4.1 The Euler line 4.1.1 nferior and superior triangles G F E G D The inferior triangle of is the triangle DEF whose vertices are the midpoints of the sides,,.
b. Find the measures of the two angles formed by the chord and the tangent line.
 0.5 NI NOW N I.5... ngle Relationships in ircles ssential Question When a chord intersects a tangent line or another chord, what relationships exist aong the angles and arcs fored? ngles ored by a hord
0.5 NI NOW N I.5... ngle Relationships in ircles ssential Question When a chord intersects a tangent line or another chord, what relationships exist aong the angles and arcs fored? ngles ored by a hord
Geo - CH11 Practice Test
 Geo - H11 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. 1. Identify the secant that intersects ñ. a. c. b. l d. 2. satellite rotates 50 miles
Geo - H11 Practice Test Multiple hoice Identify the choice that best completes the statement or answers the question. 1. Identify the secant that intersects ñ. a. c. b. l d. 2. satellite rotates 50 miles
8.2 Investigate Parallelograms
 Investigating g Geometry TIVITY 8.2 Investigate arallelograms T E I graphing calculator or computer Use before esson 8.2 classzone.com Keystrokes Q U E T I O N What are some of the properties of a parallelogram?
Investigating g Geometry TIVITY 8.2 Investigate arallelograms T E I graphing calculator or computer Use before esson 8.2 classzone.com Keystrokes Q U E T I O N What are some of the properties of a parallelogram?
TOPICS IN GEOMETRY: THE GEOMETRY OF THE EUCLIDEAN PLANE. 1. Introduction
 TOPIS IN GEOMETRY: THE GEOMETRY OF THE EULIEN PLNE TUGHT Y PIOTR PRZYTYKI. NOTES Y YLN NT. Note. These course notes are based on a course taught by Piotr Przytycki at McGill University in the fall of 2016.
TOPIS IN GEOMETRY: THE GEOMETRY OF THE EULIEN PLNE TUGHT Y PIOTR PRZYTYKI. NOTES Y YLN NT. Note. These course notes are based on a course taught by Piotr Przytycki at McGill University in the fall of 2016.
Assignment. Riding a Ferris Wheel Introduction to Circles. 1. For each term, name all of the components of circle Y that are examples of the term.
 ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to ircles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. hord GM, R,
ssignment ssignment for Lesson.1 Name Date Riding a Ferris Wheel Introduction to ircles 1. For each term, name all of the components of circle Y that are examples of the term. G R Y O T M a. hord GM, R,
KEY STANDARDS ADDRESSED: MM2G3. Students will understand the properties of circles.
 KEY STANDARDS ADDRESSED:. Students will understand the properties of circles. a. Understand and use properties of chords, tangents, and secants an application of triangle similarity. b. Understand and
KEY STANDARDS ADDRESSED:. Students will understand the properties of circles. a. Understand and use properties of chords, tangents, and secants an application of triangle similarity. b. Understand and
Using Chords. Essential Question What are two ways to determine when a chord is a diameter of a circle?
 10.3 Using hords ssential uestion What are two ways to determine when a chord is a diameter of a circle? rawing iameters OOKI O UU o be proficient in math, you need to look closely to discern a pattern
10.3 Using hords ssential uestion What are two ways to determine when a chord is a diameter of a circle? rawing iameters OOKI O UU o be proficient in math, you need to look closely to discern a pattern
C Given that angle BDC = 78 0 and DCA = Find angles BAC and DBA.
 UNERSTNING IRLE THEREMS-PRT NE. ommon terms: (a) R- ny portion of a circumference of a circle. (b) HR- line that crosses a circle from one point to another. If this chord passes through the centre then
UNERSTNING IRLE THEREMS-PRT NE. ommon terms: (a) R- ny portion of a circumference of a circle. (b) HR- line that crosses a circle from one point to another. If this chord passes through the centre then
Inequalities for Triangles and Pointwise Characterizations
 Inequalities for Triangles and Pointwise haracterizations Theorem (The Scalene Inequality): If one side of a triangle has greater length than another side, then the angle opposite the longer side has the
Inequalities for Triangles and Pointwise haracterizations Theorem (The Scalene Inequality): If one side of a triangle has greater length than another side, then the angle opposite the longer side has the
10.1 Tangents to Circles. Geometry Mrs. Spitz Spring 2005
 10.1 Tangents to Circles Geometry Mrs. Spitz Spring 2005 Objectives/Assignment Identify segments and lines related to circles. Use properties of a tangent to a circle. Assignment: Chapter 10 Definitions
10.1 Tangents to Circles Geometry Mrs. Spitz Spring 2005 Objectives/Assignment Identify segments and lines related to circles. Use properties of a tangent to a circle. Assignment: Chapter 10 Definitions
15.5 Angle Relationships in Circles
 ame lass ate 15.5 ngle Relationships in ircles ssential uestion: What are the relationships between angles formed by lines that intersect a circle? xplore xploring ngle Measures in ircles The sundial is
ame lass ate 15.5 ngle Relationships in ircles ssential uestion: What are the relationships between angles formed by lines that intersect a circle? xplore xploring ngle Measures in ircles The sundial is
Study Guide. Exploring Circles. Example: Refer to S for Exercises 1 6.
 9 1 Eploring ircles A circle is the set of all points in a plane that are a given distance from a given point in the plane called the center. Various parts of a circle are labeled in the figure at the
9 1 Eploring ircles A circle is the set of all points in a plane that are a given distance from a given point in the plane called the center. Various parts of a circle are labeled in the figure at the
Circles in Neutral Geometry
 Everything we do in this set of notes is Neutral. Definitions: 10.1 - Circles in Neutral Geometry circle is the set of points in a plane which lie at a positive, fixed distance r from some fixed point.
Everything we do in this set of notes is Neutral. Definitions: 10.1 - Circles in Neutral Geometry circle is the set of points in a plane which lie at a positive, fixed distance r from some fixed point.
Correlation of 2012 Texas Essential Knowledge and Skills (TEKS) for Algebra I and Geometry to Moving with Math SUMS Moving with Math SUMS Algebra 1
 Correlation of 2012 Texas Essential Knowledge and Skills (TEKS) for Algebra I and Geometry to Moving with Math SUMS Moving with Math SUMS Algebra 1 ALGEBRA I A.1 Mathematical process standards. The student
Correlation of 2012 Texas Essential Knowledge and Skills (TEKS) for Algebra I and Geometry to Moving with Math SUMS Moving with Math SUMS Algebra 1 ALGEBRA I A.1 Mathematical process standards. The student
( ) ( ) Geometry Team Solutions FAMAT Regional February = 5. = 24p.
 . A 6 6 The semi perimeter is so the perimeter is 6. The third side of the triangle is 7. Using Heron s formula to find the area ( )( )( ) 4 6 = 6 6. 5. B Draw the altitude from Q to RP. This forms a 454590
. A 6 6 The semi perimeter is so the perimeter is 6. The third side of the triangle is 7. Using Heron s formula to find the area ( )( )( ) 4 6 = 6 6. 5. B Draw the altitude from Q to RP. This forms a 454590
Key Concept Trigonometric Ratios. length of leg opposite A length of hypotenuse. = a c. length of leg adjacent to A length of hypotenuse
 8-3 Trigonometry ommon ore State Standards G-SRT..8 Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems. lso, G-SRT..7, G-MG..1 MP 1, MP 3, MP 4, MP Objective
8-3 Trigonometry ommon ore State Standards G-SRT..8 Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems. lso, G-SRT..7, G-MG..1 MP 1, MP 3, MP 4, MP Objective
Name: GEOMETRY: EXAM (A) A B C D E F G H D E. 1. How many non collinear points determine a plane?
 GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
GMTRY: XM () Name: 1. How many non collinear points determine a plane? ) none ) one ) two ) three 2. How many edges does a heagonal prism have? ) 6 ) 12 ) 18 ) 2. Name the intersection of planes Q and
0112ge. Geometry Regents Exam Line n intersects lines l and m, forming the angles shown in the diagram below.
 Geometry Regents Exam 011 011ge 1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT. Which value of x would
Geometry Regents Exam 011 011ge 1 Line n intersects lines l and m, forming the angles shown in the diagram below. 4 In the diagram below, MATH is a rhombus with diagonals AH and MT. Which value of x would
0811ge. Geometry Regents Exam BC, AT = 5, TB = 7, and AV = 10.
 0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 2) 8 3) 3 4) 6 2 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
0811ge 1 The statement "x is a multiple of 3, and x is an even integer" is true when x is equal to 1) 9 2) 8 3) 3 4) 6 2 In the diagram below, ABC XYZ. 4 Pentagon PQRST has PQ parallel to TS. After a translation
Intermediate Math Circles Wednesday October Problem Set 3
 The CETRE for EDUCTI in MTHEMTICS and CMPUTIG Intermediate Math Circles Wednesday ctober 24 2012 Problem Set 3.. Unless otherwise stated, any point labelled is assumed to represent the centre of the circle.
The CETRE for EDUCTI in MTHEMTICS and CMPUTIG Intermediate Math Circles Wednesday ctober 24 2012 Problem Set 3.. Unless otherwise stated, any point labelled is assumed to represent the centre of the circle.
UNIT OBJECTIVES. unit 9 CIRCLES 259
 UNIT 9 ircles Look around whatever room you are in and notice all the circular shapes. Perhaps you see a clock with a circular face, the rim of a cup or glass, or the top of a fishbowl. ircles have perfect
UNIT 9 ircles Look around whatever room you are in and notice all the circular shapes. Perhaps you see a clock with a circular face, the rim of a cup or glass, or the top of a fishbowl. ircles have perfect
Theorems on Area. Introduction Axioms of Area. Congruence area axiom. Addition area axiom
 3 Theorems on rea Introduction We know that Geometry originated from the need of measuring land or recasting/refixing its boundaries in the process of distribution of certain land or field among different
3 Theorems on rea Introduction We know that Geometry originated from the need of measuring land or recasting/refixing its boundaries in the process of distribution of certain land or field among different
Circles and Volume. Circle Theorems. Essential Questions. Module Minute. Key Words. What To Expect. Analytical Geometry Circles and Volume
 Analytical Geometry Circles and Volume Circles and Volume There is something so special about a circle. It is a very efficient shape. There is no beginning, no end. Every point on the edge is the same
Analytical Geometry Circles and Volume Circles and Volume There is something so special about a circle. It is a very efficient shape. There is no beginning, no end. Every point on the edge is the same
Evaluate: Homework and Practice
 valuate: Homework and Practice Identify the chord (s), inscribed angle (s), and central angle (s) in the figure. The center of the circles in xercises 1, 2, and 4 is. Online Homework Hints and Help xtra
valuate: Homework and Practice Identify the chord (s), inscribed angle (s), and central angle (s) in the figure. The center of the circles in xercises 1, 2, and 4 is. Online Homework Hints and Help xtra
8.5 Use Properties of Trapezoids
 8.5 Use Properties of Trapezoids and Kites Goal p Use properties of trapezoids and kites. Your otes VOULY Trapezoid ases of a trapezoid ase angles of a trapezoid Legs of a trapezoid Isosceles trapezoid
8.5 Use Properties of Trapezoids and Kites Goal p Use properties of trapezoids and kites. Your otes VOULY Trapezoid ases of a trapezoid ase angles of a trapezoid Legs of a trapezoid Isosceles trapezoid
Geometry First Semester Exam Review
 Geometry First Semester Exam Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Name three points that are collinear. a. points T, Q, and R c. points
Geometry First Semester Exam Review Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Name three points that are collinear. a. points T, Q, and R c. points
