Sudden death testing versus traditional censored life testing. A Monte-Carlo study

Transcription

1 Control nd Cyernetics vol. 6 (7) No. Sudden deth testing versus trditionl censored life testing. A Monte-Crlo study y Ryszrd Motyk Pomernin Pedgogicl Acdemy, Chir of Computer Science nd Sttistics Arciszewskiego, 76- Słupsk, Polnd Astrct: This pper considers two competing methods intended to shorten lifetime tests. The first method, due to L.G. Johnson, is known in reliility engineering s sudden deth testing. Its competitor is widely known time-terminted, right-censored test. Times of tests crried out ccording to these methods re set equl. Then, methods re compred in terms of vrinces nd ises of lifetime prmeter estimtors. In ddition, medin, mode, skewness nd kurtosis of estimtor distriutions re lso clculted nd compred. All dt needed cme from lrge-scle Monte-Crlo numericl experiment. Keywords: sudden deth testing, time terminted life test, Weiull distriution, Monte Crlo method.. Introduction Since yers one of the most wnted solutions tht reliility engineers wit for is ny method of shortening reliility tests. Accelerted testing through overstressing ws drem tht hightiled since VLSI components hve een commonly pplied. One hs two wys to shorten life tests without overstressing. The first wy is to pply sudden deth testing method () originlly proposed y L.G. Johnson (964) descried in O Connor () nd pplied in Chi-Hyuck, Blmuurli, Sng-Ho (6), Pscul, Meeker (996), Vlecek, Hendricks (4), Suzuki et l. (99). According to Johnson smple of n items is divided into k su-smples of m items ech. Ech su-smple is tested until the first filure occurs. The second wy is trditionl time-terminted life test () crried-out on the whole smple of n items. The is especilly pplicle when lifetimes follow the Weiull distriution. Rememer tht the Weiull distriution hs the reliility function of the form [ ( ) ] t R (t) = exp, ()

2 4 R. MOTYKA where, re the scle nd shpe prmeters, respectively. Time to the first filure in the su-smple is the rndom vrile tht lso follows the Weiull distriution. In fct it is the leftmost order sttistics in the smple of m. { [ ( ) ]} m [ ( ) t m / ] t F (t) = exp = exp = [ ( ) ] t = exp ; =. () m/ An interprettion tht ppels to imgintion is tht mkes test run m / times fster. Lifetimes of most ctive nd pssive electronic components stisfctorily fit the Weiull distriution with.5. Even smll su-smple of m = gives n exciting figure of /.5 = times! Time of testing T is equl to the rightmost order sttistics t (k) in the smple of k. An pproprite cumultive distriution function hs the form { [ ( ) ]} k T F (T ) = exp. () Time of testing T is equl to the rightmost order sttistics t (n) in the smple of n. An pproprite cumultive distriution functions hs the form { [ ( ) ]} n T F (T ) = exp. () Both times re rndom vriles. The following quntile-sed shortening coefficient ptterned fter definition of the confidence intervl. SC = q,.95 /q,.95 (4) ws proposed in Motyk (6). In the cse of the Weiull distriution SC = m /. It is noteworthy tht SC does not depend on the numer of su-smples k.. Comprison rules This pper ims t compring to ojectively with respect to properties of prmeter estimtes tht nd produce. For the comprison to e ojective two min properties of the methods in question, nmely time of testing nd smple size were intentionlly set the sme. This mde estimtors properties comprle. Figurtively speking, two nchors were dropped nd the methods cn differ in smple rrngement only. The produces non-censored dt. In contrst, produces right-censored dt. Presumly, this differentites estimtors properties. Tle lists min properties of nd.

3 Sudden deth vs. censored life testing 4 Tle. Property Numer of smples k Smple size m n = m k Numer of filures m Rndom Time of testing Numer of items tested The sme for oth methods nd equl to t (m) The sme for oth methods nd equl to n Producing non-censored dt ws gret dvntge of in the precomputer er, when the method ws put forwrd. Both goodness-of-fit test nd prmeter estimtion could e performed with the proility pper nd hnd-held clcultor. An old-fshioned estimtion method y fitting stright line to points of empiricl cumultive filure function plotted on the Weiull proility pper is still commonly used. The method ws on purpose uilt into numericl experiment s the third nchor.. An outline of numericl results The entire numericl experiment ws composed of seven component experiments tht differ in smple rrngement, s it is shown in Tle. The component experiments re ordered ccording to tendency of mking test shorter nd shorter. This cn e chieved y splitting the smple into smll numer of lrge susmples s it is shown in Tle where moderte nd extreme rrngements were distinguished. Tle. Arrgement Numer of Smple Arrngement type smples size code Moderte Extreme 5 4 5X4 5 X X7 X 7 4 7X4 5 5X Ech component experiment ws performed in three phses. Prticulr phses consisted of one or more steps s it is shown in Tle.

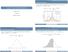
4 44 R. MOTYKA Tle. Phse Numer Description Consists of Steps Generting dt Modelling,, 4 Modelling 5, 6 4 Prmeter estimtion 7,8 The experiments were performed ssuming the scle nd shpe prmeters equl to. Ech component experiment repets the following sequence, times! Step : Crete two sets of n= pseudo-rndom numers coming from the Weiull generl popultion. These numers denoted t (i) will then e treted s oserved lifetimes of items tested in this virtul reliility test. Denote the sets WRN nd WRN. Step : Split WRN into k su-smples of m items ech. Denote corresponding lifetimes s t SD i,j, i =,,..., m,, j =,,..., k. Step : Find the shortest lifetime in ech su-smple. Denote it t SD (),j, j =,,..., k. Step 4: Determine how long it took to find t SD mx = mx Step 5: Set time of s t TT = t SD mx. j {t SD (),j }. Step 6: Determine the numer of filures NoF y counting ll TTD (time terminted dt) t (i) ttt, i =,,..., n. Step 7: Tret t SD (),j s the non-censored smple. Determine the empiricl reliility function. Plce the points on the Weiull proility pper. Fit the stright line to the points with the lest squre method. Clculte estimtes SD, SD of unknown vlues of the scle prmeter nd shpe prmeter. Step 8: Tret memers of WRN s memers of right-censored smple. Select these t (i) ttt. Determine the left-hnd segment of the empiricl reliility function. From this point repet Step 7. The results re estimtes denoted TT nd TT. 4. The results otined Figs. nd show how test rrngements influence medins nd extreme order sttistics. It is redily seen in terms of order sttistics how estimte distriutions

5 Sudden deth vs. censored life testing 45 spred-out drmticlly when one strives to increse the shortening coefficient. Figs. nd 4 complement previous figures in terms of sic smple moments. In turn, Figs. 5 nd 6 show estimte distriutions otined with computer implementtion of Przen s ide of kernel density estimtion, Drpell (). Leftmost Medin Rightmost Vlues of odred sttistics 5X4 X5 4X7 X 7X4 5X 5X4 X5 4X7 X 7X4 5X, Test rrgement Figure. Order sttistics of the shpe prmeter estimtes. Leftmost Medin Rightmost Vlues of odred sttistics, 5X4 X5 4X7 X 7X4 5X 5X4 X5 4X7 X 7X4 5X,, Test rrgement Figure. Order sttistics of the scle prmeter estimtes.

6 46 R. MOTYKA Men vlue,6,4,,,8,6,4, Men vlue,, 5X4 X5 4X7 X 7X4 5X, 5X4 X5 4X7 X 7X4 5X Test rrgement Test rrgement Stndrd devition Stndrd devition, 5X4 X5 4X7 X 7X4 5X, 5X4 X5 4X7 X 7X4 5X Test rrgement Test rrgement Skewness Skewness, 5X4 X5 4X7 X 7X4 5X 5X4 X5 4X7 X 7X4 5X Test rrgement Test rrgement Kurtosis Kurtosis, 5X4 X5 4X7 X 7X4 5X 5X4 X5 4X7 X 7X4 5X Test rrgement Test rrgement Figure. Moments of shpe estimtes. Figure 4. Moments of scle estimtes

7 Sudden deth vs. censored life testing 47 5X4 X X5 7X4 4X7 5X Figure 5. Densities of shpe estimtes.

8 48 R. MOTYKA 5X4 X f() f() X5 7X4 f() f() X7 5X f() f() Figure 6. Densities of scle estimtes.

9 Sudden deth vs. censored life testing Conclusions Let us consider ll the test rrngements nd compre SDMT nd in different terms. Conclusions we come to fll into two ctegories: conclusions of generl nture (I) nd conclusions strictly relted to nd (II): Ctegory I: A concept of estimtion is ws intended to mesure deprture of point, round witch distriution of prmeter estimtor is concentrted, from ctul prmeter vlue. A clssic definition of is involves the men vlue. Figs. - nd -4 emrrss us, ecuse the men vlue is not point of concentrtion. These evidently re the medin nd the mode. For moderte rrngements medin nd mode fit the ctul prmeter vlues. Stepping from moderte to extreme rerrngements cuse mode move to the left, the men vlue move to the right nd leve the medin unmoved. Regrdless of whether compred in terms of moments or order sttistics the shpe prmeter estimtor hs etter properties thn the scle prmeter estimtor. Moreover the scle prmeter estimtor is much sensitive to rerrngement thn tht of shpe. Ctegory II: Two seprte comprisons cn e mde, nmely in terms of moments nd in terms of order sttistics. If test methods re compred in terms of order sttistics, is to e recommended for ll rrngements. If test methods re compred in terms of moments, only extreme rrngements re to e recommended. Tests rrnged in n extreme mnner hve short durtion. However, extreme rrngements my put producer in dnger of offering product with specified MTTF even severl times greter thn the ctul. It mens tht the rrngements re only for risk-tkers, when time fctor is of importnce rther thn the estimtion precision fctor. References Chi-Hyuck, J., Blmuurli, S. nd Sng-Ho, L. (6) Vriles smpling plns for Weiull distriuted lifetimes under sudden deth testing. IEEE Trnsction on Reliility 55 (). Drpell, A. () Lifetime Models nd Renewl Processes. Numericl tretment with Mthcd. Pomernin Pedgogicl Acdemy, Słupsk. Motyk, R. (6) Extending sudden deth testing on non-weiull popultions. Conference: Metod reprezentcyjn w dnich ekonomicznospołecznych. Ktowice - Septemer 6. Nelson, L.G. (964) Theory nd Technique of Vrition Reserch. Elsevier.

10 5 R. MOTYKA O Connor, P.D.T. () Prcticl Reliility Engineering. Wiley. Pscul, F. nd Meeker, W.Q. (996) The modified sudden deth test. Journl of Testing nd Evlution 6 (6). Suzuki, K. et l. (99) On comprison etween sudden deth testing nd type II numer fixed life testing. Journl of Jpnese Society for Qulity Control, 5-. Vlecek, B.L. nd Hendricks, R.C. (4) Monte Crlo simultion of sudden deth ering testing. Triology Trnsctions 47,