The steps of the hypothesis test
|
|
|
- Camron Hutchinson
- 5 years ago
- Views:
Transcription
1 ttisticl Methods I (EXT 7005) Pge 78 Mosquito species Time of dy A B C Mid morning Mid Afternoon Dusk The Chi squre test sttistic is the sum of the chi squre vlues in ech cell. Observed Expected with d. f. = (rows )*(col ) =* = 4 The steps of the hypothesis test Expected ) Mosquito species occurrence is independent of time of dy ) Mosquito occurrence is NOT independent 3) Assume IID r.v. 4) 0.05, the criticl vlue with (r )(c ) = 4 d.f. for 0.05 is ) From the smple we get clculted = ) The clculted test sttistic exceeds the tbulr vlue with (r )(c ) = 4 d.f.. The criticl tbulr vlues re; 0.05, = sttisticlly significnt 0.0, = highly significnt 0.00, = Wow! Using this terminology we see we hve highly significnt deprture in this cse. o wht is the P vlue, the chnce of finding vlue of or greter by rndom chnce? This is P(> )= , bout in million. 7) o we conclude tht the occurrence of mosquito species is not independent of the time of dy. It ppers to be very dependent. A exmple 3 of the Chi squre Test of Independence in A Two vrieties of prticulr moth species occur in two colors (brown nd white). A biologist in North Crolin wnts to know if the distribution of the two vrieties vries with the re of the stte. He collects individuls from ech region of the stte nd note the number of ech vriety. ee computer output Jmes P. Geghn Copyright 0
2 ttisticl Methods I (EXT 7005) Pge 79 Chi qure Goodness of Fit This test is similr to the Chi qure test of independence, but insted of deriving the expected vlues from the row nd column sums, the expected vlues re derived from some theoreticl distribution. In flowering plnt with incomplete dominnce cross between red flowered prent (RR) nd white flowered prent (rr) is expected to yield offspring with pink flowers (Rr). If the offspring re then crossed with ech other, rtio of 9:6: or red to pink to white flowered offspring should result. In one prticulr experiment the offspring produced the observed results of 53 red, 7 pink nd 7 white plnts. Does this result conform to the expected results? ) H 0 : Results follow the expected proportions ) H : Results do not follow the expected proportions 3) Assume IID r.v. 4) et (t sy 0.05 or 0.0 s before). Clculte the criticl vlue where the chi squre results for this test hve c = degrees of freedom (where c is the number of column or the number of ctegories, 3 in this cse). The criticl vlue for = 0.05 is 5.99 nd for = 0.0 it is ) Conduct n experiment to obtin results. We got 4 flowers from our experiment. Red Pink White Totl Expected rtio Expected proportions Observed numbers Expected numbers Chi squre ) Compre the clculted chi squre vlue to the test sttistic. The clculted vlue (6.) does exceeds the test sttistic vlue of = 0.05, but not for = 0.0. Tbulr Chi squre vlues lph Chi squre vlue n = d.f. = Actul P(> ) ) In this cse we reject the null hypothesis nd might term our result s sttisticlly significnt deprture from the expected result under the null hypothesis. As published result we my wish to stte tht the P vlue ws 0.045, clerly indicting tht our result ws significnt t the 0.05 level of, but not t higher level. A exmple 3b of the Chi squre Goodness of Fit test in A ee computer output A exmple 3c testing simple rtio with Chi squre ee computer output Jmes P. Geghn Copyright 0
3 ttisticl Methods I (EXT 7005) Pge 80 A finl note on the Chi squre tests of hypothesis. Although tests of hypothesis bout vrinces my be either directionl or non-directionl, the chi squre tests of independence re directionl. mll vlues of the chi squre sttistics for these tests indicte tht the null hypothesis is met very well since the observed vlues re very close to the expected vlues. It is only with lrger deprtures of the expected vlues from the observed vlues tht the chi squre sttistic should be rejected. Therefore, it is only excessively lrge chi squre vlues tht cuse the null hypothesis to be rejected nd this would be one tiled test. ummry The Chi squre distribution The Chi squre distribution cn be derived s the squre of the Z distribution. mple vrinces re Chi squre distributed The Chi squre distribution cn be used to test hypotheses bout vrinces. The distribution hs only one prmeter,, (nd is different for every ) the distribution is non negtive nd symmetricl. The vrince of the distribution is. Hypothesis testing employs the form of the distribution For testing vrince we ssume the vrible i is Normlly nd Independently distributed rndom vrible (NID r.v.) In the Chi squre tbles Degrees of freedom re on the left nd different distribution is given in ech row. elected probbilities in the upper TAIL of the distribution is given in the row t the top of the tble. The distribution is NOT symmetric, so the probbilities t the top must be used for both upper nd lower limits. In ddition to tests of vrinces, the Chi squre cn be used to do Test of Independence Test of Goodness of Fit For these tests we ssume i is n Identiclly nd Independently distributed rndom vrible (IID r.v.) In A the Chi squre test of independence cn be done with PROC FREQ. 0 Jmes P. Geghn Copyright 0
4 ttisticl Methods I (EXT 7005) Pge 8 The F test This test cn be used to either, test the equlity of popultion vrinces our present topic test the equlity of popultion mens (this will be discussed lter under ANOVA) The F test is the rtio of two vrinces (the rtio of two chi squre distributions) Given two popultions Men Vrince Popultion Popultion Drw smple from ech popultion Popultion Popultion mple size n n d.f. mple men mple vrince To test the Hypothesis H: 0 H: (directionl, or one sided, hypotheses re lso possible) The test sttistic is F which hs n expected vlue of under the null hypothesis. In prctice there will be some vribility, so we need to define some resonble limits nd this will require nother sttisticl distribution. The F distribution ) The F distribution is nother fmily of distributions, ech specified by PAIR of degrees of freedom, nd. is the d. f. for the numertor is the d. f. for the denomintor Note: the two smples do not hve to be of the sme size nd usully re not of the sme size. ) The F distribution is n symmetricl distribution with vlues rnging from 0 to, so [0 F ]. 3) There is different F distribution for every possible pir of degrees of freedom. 4) In generl, n F vlue with nd d.f. is not the sme s n F vlue with nd d.f., so order is importnt. i.e. F, F, usully Jmes P. Geghn Copyright 0
5 ttisticl Methods I (EXT 7005) Pge 8 5) The expected vlue of ny F distribution is if the null hypothesis is true. The F distribution F distribution with, 5 d.f. F distribution with 00, 00 d.f. F distribution with 5, 0 d.f. The F tbles The numertor d.f. ( ) re given long the top of the pge, nd the denomintor d.f. ( ) re given long the left side of the pge. ome tbles give only one F vlue t ech intersection of nd. The whole pge would be for single vlue nd usully severl pges would be given. Our tbles will give four vlues t the intersection of ech nd, ech for different vlue. These vlues re given in the second column from the left. Our tbles will hve two pges. Only very few probbilities will be vilble, usully 0.05, 0.05, 0.0 nd 0.005, nd sometimes Only the upper til of the distribution is given. Prtil F tble d.f. P>F Jmes P. Geghn Copyright 0
6 ttisticl Methods I (EXT 7005) Pge 83 Working with F tbles The F tbles re used in fshion similr to other sttisticl tbles. elect probbility vlue t the intersection of the two degrees of freedom. Be sure to keep trck of which one is the numertor degrees of freedom (top of tble) nd which is the denomintor degrees of freedom (left side of tble). At the intersection of the degrees of freedom there re four F vlues corresponding to vlues of 0.05, 0.5, 0.0 nd Find the corresponding F vlue for the desired. Exmple of F tble use, one tiled exmple: Find F with (5,0) d.f. for 0.05 find F 0.05 such tht P[F F 0.05, 5, 0 d.f. ] = where = 5 nd = 0 For F 5, 0 d.f. The tbulr vlues re listed s 3.33, 4.4, 5.64, 6.87 These represent P[F 5, 0 d.f..5] = 0.00 (Not in your tble) P[F 5, 0 d.f. 3.33] = P[F 5, 0 d.f. 4.4] = 0.05 P[F 5, 0 d.f. 5.64] = 0.00 P[F 5, 0 d.f. 6.87] = so the vlue we re looking for is For this vlue P[F 5, 0 d.f. 3.33] = Note tht since this is tiled vlue, then P[F 5, 0 d.f. 3.33] = 0.950, so the two sides sum to Also note tht if we reverse the d.f., the tble shows tht P[F 0, 5 d.f. 4.74] = 0.050, so the F vlues generlly differ when d.f. re reversed More working with F tbles Only the upper til of the distribution is given. There re three resons for this. Most F tests, including those for Anlysis of Vrince (ANOVA), re one tiled tests, where the lower til is not needed. The need to clculte the lower til cn be eliminted in some two-tiled cses. The vlue of F for the lower til cn be found by trnsformtion of vlues from the upper til. Clculting lower til vlues for the F distribution To obtin the lower til for vlue F, for prticulr vlue of First obtin the vlue in the upper til for F, for the sme vlue of (note the chnge in order of the d.f.) Then clculte /F, to get the lower til. Jmes P. Geghn Copyright 0
7 ttisticl Methods I (EXT 7005) Pge 84 F tble : two-tiled exmple Find both upper nd lower limits for F with (8, 0) d.f. for 0.05 Find F, 8, 0 lower nd F, 8, 0 such tht P[F 0.975, 8, 0 F F 0.05, 8, 0 ]=0.950 where = 8 nd = 0 For the upper til, the vlue we re looking for cn be red directly from the tble. It is P[F 8, ] = 0.05 note tht we use only s the probbility for one of the two tils To find the lower til, we reverse the d.f., we find tht P[F 0, ] = 0.05 nd then clculte F 8, 0 d.f. lower limit = /F 0,8 = /4.30 = 0.36 Note the reversl of the order of the degrees of freedom Numericl exmple of n F-test of hypothesis The concentrtion of blue green lge ws obtined for 7 phytoplnkton-density smples tken from ech of two lke hbitts. Determine if there is difference in the vribility of phytoplnkton density between the two hbitts. ) ) H: 0 H: 3) Assume: Independence (rndomly selected smples) nd tht BOTH popultions re normlly distributed. 4) 0.05 nd the criticl limit is Clculte P[F lower F F upper ] = P[F lower F] P[F F upper ] = = 0.95 P[F F upper ] = 0.05 we cn get directly from the tble, F =0.05, 6, 6 = 5.8 P[F lower F] = 0.05 we clculte s /P[F F upper ] = /5.8 = 0.78 P[0.78 F 5.8] = 0.95 This cse is uncommon becuse d.f. upper = d.f. lower, so the F vlues re the sme. 5) Drw smple of 7 from ech hbitt; clculte the vrinces nd the F rtio. Jmes P. Geghn Copyright 0
8 ttisticl Methods I (EXT 7005) Pge 85 mple dt ummry sttistics Hbitt Hbitt Observtion Observtion Observtion Observtion Observtion Observtion Observtion ttistic Hbitt Hbitt i i Men ( ) Then clculte the F vlue s F = = 6.95 = ) Compre the clculted vlue (0.73) to the criticl region. Given = 0.05 nd TWO TAILED lterntive, nd knowing tht the degrees of freedom re =6 nd =6, (note tht both re equl), the criticl limits re P[0.78 F 5.8] = ince our clculted F vlue is between these limit vlues we would fil to reject the null hypothesis, concluding tht the dt is consistent with the null hypothesis. But it ws close. Mybe there is difference nd we did not hve enough power. ome notes on F tests NOTE tht in this exmple the smller vlue fell in the numertor. As result, we were compring the F vlue to the lower limit. However, for two tiled tests, it mkes no difference which flls in the numertor, nd which in the denomintor. As result, we cn ARBITRARIL decide to plce the lrger vlue in the numertor, nd compre the F vlue to the upper limit. lrger The need to clculte the lower limit cn be eliminted if we clculte F. smller However, don't forget tht this rbitrry plcing of the lrger vrince estimte in the numertor is done for TWO TAILED TET ONL, nd therefore we wnt to test ginst F. There re three common cses in F testing (ctully two common nd one not so common). ) Frequently, prticulrly in ANOVA (to be covered lter), we will test H: 0 ginst the lterntive, H:. In this cse we ALWA form the F vlue s F =. Jmes P. Geghn Copyright 0
9 ttisticl Methods I (EXT 7005) Pge 86 We put the vrince tht is expected to be lrger in the numertor for one tiled test! Don t forget tht this is one tiled nd ll of is plced in the upper til. In the event tht F < we don't even need to look up vlue in the tble, it cnnot be significnt. ) Norml tiled tests (used in smple t-tests to be covered lter) will test the lterntive, H:. Here we cn form the F vlue s F H: ginst 0 lrger. Don t forget tht this is -tiled test nd it is tested ginst the upper til with only hlf of (i.e. ) in the upper til. When the lrger vlue is plced in the numertor there is no wy tht we cn get clculted F <. 3) If both the upper nd lower bounds re required (not common, found mostly on EXAM in bsic sttistics) then we will be testing H: 0 ginst the lterntive H:. We cn form the F vlue ny wy we wnt, with either the lrger or smller vrince in the numertor. This is tiled test with in ech til, nd F cn ssume ny positive vlue (0 to ) ummry smller The F distribution is rtio of two vrinces (i.e. two Chi squre distributions) nd is used test used to test two vrinces for equlity. The null hypothesis is H:. 0 The distribution is n symmetricl distribution with vlues rnging from 0 to, nd n expected vlue of under the null hypothesis. The F tbles require two d.f. (numertor nd denomintor) nd give only very few criticl vlues. Mny, perhps most, F tests will be directionl. For the tests the vrince tht is expected to be lrger nd hypothesized to be lrger goes in the numertor whether it is ctully lrger or not. This vlue is tested ginst the upper til with probbility equl to. For the non-directionl lterntive we my rbitrrily plce the lrger vrince in the numertor nd test ginst the upper til, but don't forget to test ginst. Probbility Distribution interreltionships The probbility tbles tht we hve been exmining re interrelted. One of these interreltionships is ctully pretty importnt! If you exmine the F tble it turns out tht in ddition to F vlues the first column is equl to vlues of t, the lst vlue in the first column corresponds to Z nd the lst row is Chi squre vlue divided by degrees of freedom. Jmes P. Geghn Copyright 0
10 ttisticl Methods I (EXT 7005) Pge 87 d.f t (two tiled) (4.96) Z (3.84) F vlues =0.83 more F vlues The distributions nd reltionships we hve discussed re: i 0 ) Zi for observtions nd Z for testing hypothesis bout mens. n ) = Z with d.f. = Z with n d.f. = / with n d.f. 3) t with n d.f. n 4) F = Interreltionships with n, n d.f. ) / with d.f. = F with, d.f. which follows n F distribution with, d.f. ) F with, d.f. if H 0 is true given from prt bove Jmes P. Geghn Copyright 0
11 ttisticl Methods I (EXT 7005) Pge 88 then nd therefore, nd with d.f. F with n, n =, d.f. if H 0 is true, then, then F with, or n, n d.f. 3) t with = follows Z distribution, since s increses the smple vrince ( ) pproches the popultion vrince ( ). Tht is, s the smple size pproches infinity the t distribution, i t pproches the Z distribution i Z. 4) Z = F with, d.f. we sw tht Z = with d.f. we sw tht / = F with, d.f. then F = / = Z / = Z / = Z. 5) t with d.f. = F with, d.f. This cn be shown in severl wys. First, we just sw tht Z = F with, d.f. This suggests tht t = F with, d.f. Another type of proof is given below. F with, d.f. i with n d.f., nd where ˆi is the men of subgroup of the dt prtitioned into two (or more) groups (the bsis of Anlysis of Vrince). recll, n n ˆ ˆ ˆ ˆ i i i i i i i d.f re n = (n ) + Let n i i with d.f. n i Let i with n d.f. n both of which re unbised estimtes, n then F with, n d.f. nd n F t n n with n d.f. Jmes P. Geghn Copyright 0
12 ttisticl Methods I (EXT 7005) Pge 89 ummry ) / with d.f. = F with, d.f. ) F with, d.f. if Ho is true 3) t with = follows Z distribution 4) Z = F with, d.f. 5) t with d.f. = F with, d.f. ome Exmples in the F tbles (ll 0.05, two tils for Z nd t vlues since sign is lost in squring) F with, 0 d.f. = 4.96 = t with 0 d.f. = (.8) = 4.96 F with, d.f. = 3.84 = Z = (.96) = 3.84 F with 0, d.f. =.83 = / = 8.3 / 0 =.83 with 0 d.f. Confidence intervls nd mrgin of error The confidence intervl is n expression of wht we believe to be rnge of vlues tht is likely to contin the true vlue of some prmeter is clled confidence intervl. The width of this intervl bove nd below the prmeter estimte is clled the mrgin of error. We cn clculte confidence intervls for mens () nd vrinces ( ). Confidence intervls for t nd Z distributions t nd Z distribution confidence intervls strt with t or Z probbility sttement. P( t t t ) cn lso be written P( t t ) which is modified to express n intervl bout insted of t (or Z). P( t t ) P( t t ) The finl form is given below. P ( t t ) The expression for Z hs n identicl derivtion. P ( Z Z ) Jmes P. Geghn Copyright 0
13 ttisticl Methods I (EXT 7005) Pge 90 A common short nottion for the intervl in the probbility sttement is given s t the probbility sttement is preferble s finl result. The vlue t mens nd t for intervls on for intervls on individul observtions is hlf of the intervl width from the lower limit to the upper limit nd is clled the mrgin of error. Confidence intervls for vrince Vrinces follow Chi squre distribution. The confidence intervl for vrince is bsed on the Chi qure distribution. P or ( lower upper ) P( lower ) upper which is solved to isolte. P( ) P lower upper ( ) upper lower giving the expression, ( ) P upper lower Notice tht the upper tbulr Chi squre vlue comes out in the lower bound nd the lower Chi squre in the upper bound. ( ) P upper lower Notes on confidence intervls One sided intervls re possible, but uncommon. Confidence intervls re one of the most common expressions in sttistics, frequently occurring in publictions. Mrgins of error nd confidence intervls re not lwys clculted in sttisticl softwre progrms, but they cn esily be done by hnd. From the previous A Exmple c We receive shipment of pples tht re supposed to be premium pples, with dimeter of t lest.5 inches. We will tke smple of pples, nd plce confidence intervl on the men. The smple vlues for the pples re;.9,.,.4,.8, 3.,.8,.7, 3.0,.4, 3.,.3, 3.4, but Jmes P. Geghn Copyright 0
For the percentage of full time students at RCC the symbols would be:
 Mth 17/171 Chpter 7- ypothesis Testing with One Smple This chpter is s simple s the previous one, except it is more interesting In this chpter we will test clims concerning the sme prmeters tht we worked
Mth 17/171 Chpter 7- ypothesis Testing with One Smple This chpter is s simple s the previous one, except it is more interesting In this chpter we will test clims concerning the sme prmeters tht we worked
Section 11.5 Estimation of difference of two proportions
 ection.5 Estimtion of difference of two proportions As seen in estimtion of difference of two mens for nonnorml popultion bsed on lrge smple sizes, one cn use CLT in the pproximtion of the distribution
ection.5 Estimtion of difference of two proportions As seen in estimtion of difference of two mens for nonnorml popultion bsed on lrge smple sizes, one cn use CLT in the pproximtion of the distribution
Student Activity 3: Single Factor ANOVA
 MATH 40 Student Activity 3: Single Fctor ANOVA Some Bsic Concepts In designed experiment, two or more tretments, or combintions of tretments, is pplied to experimentl units The number of tretments, whether
MATH 40 Student Activity 3: Single Fctor ANOVA Some Bsic Concepts In designed experiment, two or more tretments, or combintions of tretments, is pplied to experimentl units The number of tretments, whether
Tests for the Ratio of Two Poisson Rates
 Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
Chapter 9: Inferences based on Two samples: Confidence intervals and tests of hypotheses
 Chpter 9: Inferences bsed on Two smples: Confidence intervls nd tests of hypotheses 9.1 The trget prmeter : difference between two popultion mens : difference between two popultion proportions : rtio of
Chpter 9: Inferences bsed on Two smples: Confidence intervls nd tests of hypotheses 9.1 The trget prmeter : difference between two popultion mens : difference between two popultion proportions : rtio of
Non-Linear & Logistic Regression
 Non-Liner & Logistic Regression If the sttistics re boring, then you've got the wrong numbers. Edwrd R. Tufte (Sttistics Professor, Yle University) Regression Anlyses When do we use these? PART 1: find
Non-Liner & Logistic Regression If the sttistics re boring, then you've got the wrong numbers. Edwrd R. Tufte (Sttistics Professor, Yle University) Regression Anlyses When do we use these? PART 1: find
MIXED MODELS (Sections ) I) In the unrestricted model, interactions are treated as in the random effects model:
 1 2 MIXED MODELS (Sections 17.7 17.8) Exmple: Suppose tht in the fiber breking strength exmple, the four mchines used were the only ones of interest, but the interest ws over wide rnge of opertors, nd
1 2 MIXED MODELS (Sections 17.7 17.8) Exmple: Suppose tht in the fiber breking strength exmple, the four mchines used were the only ones of interest, but the interest ws over wide rnge of opertors, nd
Goals: Determine how to calculate the area described by a function. Define the definite integral. Explore the relationship between the definite
 Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
Chapter 5 : Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
Lecture 3 Gaussian Probability Distribution
 Introduction Lecture 3 Gussin Probbility Distribution Gussin probbility distribution is perhps the most used distribution in ll of science. lso clled bell shped curve or norml distribution Unlike the binomil
Introduction Lecture 3 Gussin Probbility Distribution Gussin probbility distribution is perhps the most used distribution in ll of science. lso clled bell shped curve or norml distribution Unlike the binomil
Acceptance Sampling by Attributes
 Introduction Acceptnce Smpling by Attributes Acceptnce smpling is concerned with inspection nd decision mking regrding products. Three spects of smpling re importnt: o Involves rndom smpling of n entire
Introduction Acceptnce Smpling by Attributes Acceptnce smpling is concerned with inspection nd decision mking regrding products. Three spects of smpling re importnt: o Involves rndom smpling of n entire
Design and Analysis of Single-Factor Experiments: The Analysis of Variance
 13 CHAPTER OUTLINE Design nd Anlysis of Single-Fctor Experiments: The Anlysis of Vrince 13-1 DESIGNING ENGINEERING EXPERIMENTS 13-2 THE COMPLETELY RANDOMIZED SINGLE-FACTOR EXPERIMENT 13-2.1 An Exmple 13-2.2
13 CHAPTER OUTLINE Design nd Anlysis of Single-Fctor Experiments: The Anlysis of Vrince 13-1 DESIGNING ENGINEERING EXPERIMENTS 13-2 THE COMPLETELY RANDOMIZED SINGLE-FACTOR EXPERIMENT 13-2.1 An Exmple 13-2.2
approaches as n becomes larger and larger. Since e > 1, the graph of the natural exponential function is as below
 . Eponentil nd rithmic functions.1 Eponentil Functions A function of the form f() =, > 0, 1 is clled n eponentil function. Its domin is the set of ll rel f ( 1) numbers. For n eponentil function f we hve.
. Eponentil nd rithmic functions.1 Eponentil Functions A function of the form f() =, > 0, 1 is clled n eponentil function. Its domin is the set of ll rel f ( 1) numbers. For n eponentil function f we hve.
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
4.4 Areas, Integrals and Antiderivatives
 . res, integrls nd ntiderivtives 333. Ares, Integrls nd Antiderivtives This section explores properties of functions defined s res nd exmines some connections mong res, integrls nd ntiderivtives. In order
. res, integrls nd ntiderivtives 333. Ares, Integrls nd Antiderivtives This section explores properties of functions defined s res nd exmines some connections mong res, integrls nd ntiderivtives. In order
How can we approximate the area of a region in the plane? What is an interpretation of the area under the graph of a velocity function?
 Mth 125 Summry Here re some thoughts I ws hving while considering wht to put on the first midterm. The core of your studying should be the ssigned homework problems: mke sure you relly understnd those
Mth 125 Summry Here re some thoughts I ws hving while considering wht to put on the first midterm. The core of your studying should be the ssigned homework problems: mke sure you relly understnd those
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
 Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Comparison Procedures
 Comprison Procedures Single Fctor, Between-Subects Cse /8/ Comprison Procedures, One-Fctor ANOVA, Between Subects Two Comprison Strtegies post hoc (fter-the-fct) pproch You re interested in discovering
Comprison Procedures Single Fctor, Between-Subects Cse /8/ Comprison Procedures, One-Fctor ANOVA, Between Subects Two Comprison Strtegies post hoc (fter-the-fct) pproch You re interested in discovering
Before we can begin Ch. 3 on Radicals, we need to be familiar with perfect squares, cubes, etc. Try and do as many as you can without a calculator!!!
 Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
CS667 Lecture 6: Monte Carlo Integration 02/10/05
 CS667 Lecture 6: Monte Crlo Integrtion 02/10/05 Venkt Krishnrj Lecturer: Steve Mrschner 1 Ide The min ide of Monte Crlo Integrtion is tht we cn estimte the vlue of n integrl by looking t lrge number of
CS667 Lecture 6: Monte Crlo Integrtion 02/10/05 Venkt Krishnrj Lecturer: Steve Mrschner 1 Ide The min ide of Monte Crlo Integrtion is tht we cn estimte the vlue of n integrl by looking t lrge number of
CS 188 Introduction to Artificial Intelligence Fall 2018 Note 7
 CS 188 Introduction to Artificil Intelligence Fll 2018 Note 7 These lecture notes re hevily bsed on notes originlly written by Nikhil Shrm. Decision Networks In the third note, we lerned bout gme trees
CS 188 Introduction to Artificil Intelligence Fll 2018 Note 7 These lecture notes re hevily bsed on notes originlly written by Nikhil Shrm. Decision Networks In the third note, we lerned bout gme trees
SUMMER KNOWHOW STUDY AND LEARNING CENTRE
 SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
SUMMER KNOWHOW STUDY AND LEARNING CENTRE Indices & Logrithms 2 Contents Indices.2 Frctionl Indices.4 Logrithms 6 Exponentil equtions. Simplifying Surds 13 Opertions on Surds..16 Scientific Nottion..18
The graphs of Rational Functions
 Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
Lecture 4 5A: The its of Rtionl Functions s x nd s x + The grphs of Rtionl Functions The grphs of rtionl functions hve severl differences compred to power functions. One of the differences is the behvior
Improper Integrals. Type I Improper Integrals How do we evaluate an integral such as
 Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Discrete Mathematics and Probability Theory Summer 2014 James Cook Note 17
 CS 70 Discrete Mthemtics nd Proility Theory Summer 2014 Jmes Cook Note 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion, y tking
CS 70 Discrete Mthemtics nd Proility Theory Summer 2014 Jmes Cook Note 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion, y tking
The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).
![The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a). The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).](/thumbs/78/77467690.jpg) The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
MATH 144: Business Calculus Final Review
 MATH 144: Business Clculus Finl Review 1 Skills 1. Clculte severl limits. 2. Find verticl nd horizontl symptotes for given rtionl function. 3. Clculte derivtive by definition. 4. Clculte severl derivtives
MATH 144: Business Clculus Finl Review 1 Skills 1. Clculte severl limits. 2. Find verticl nd horizontl symptotes for given rtionl function. 3. Clculte derivtive by definition. 4. Clculte severl derivtives
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Recitation 3: More Applications of the Derivative
 Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
Discrete Mathematics and Probability Theory Spring 2013 Anant Sahai Lecture 17
 EECS 70 Discrete Mthemtics nd Proility Theory Spring 2013 Annt Shi Lecture 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion,
EECS 70 Discrete Mthemtics nd Proility Theory Spring 2013 Annt Shi Lecture 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion,
Math 8 Winter 2015 Applications of Integration
 Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Mth 8 Winter 205 Applictions of Integrtion Here re few importnt pplictions of integrtion. The pplictions you my see on n exm in this course include only the Net Chnge Theorem (which is relly just the Fundmentl
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Preparation for A Level Wadebridge School
 Preprtion for A Level Mths @ Wdebridge School Bridging the gp between GCSE nd A Level Nme: CONTENTS Chpter Removing brckets pge Chpter Liner equtions Chpter Simultneous equtions 6 Chpter Fctorising 7 Chpter
Preprtion for A Level Mths @ Wdebridge School Bridging the gp between GCSE nd A Level Nme: CONTENTS Chpter Removing brckets pge Chpter Liner equtions Chpter Simultneous equtions 6 Chpter Fctorising 7 Chpter
Is there an easy way to find examples of such triples? Why yes! Just look at an ordinary multiplication table to find them!
 PUSHING PYTHAGORAS 009 Jmes Tnton A triple of integers ( bc,, ) is clled Pythgoren triple if exmple, some clssic triples re ( 3,4,5 ), ( 5,1,13 ), ( ) fond of ( 0,1,9 ) nd ( 119,10,169 ). + b = c. For
PUSHING PYTHAGORAS 009 Jmes Tnton A triple of integers ( bc,, ) is clled Pythgoren triple if exmple, some clssic triples re ( 3,4,5 ), ( 5,1,13 ), ( ) fond of ( 0,1,9 ) nd ( 119,10,169 ). + b = c. For
Duality # Second iteration for HW problem. Recall our LP example problem we have been working on, in equality form, is given below.
 Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
Dulity #. Second itertion for HW problem Recll our LP emple problem we hve been working on, in equlity form, is given below.,,,, 8 m F which, when written in slightly different form, is 8 F Recll tht we
Solution for Assignment 1 : Intro to Probability and Statistics, PAC learning
 Solution for Assignment 1 : Intro to Probbility nd Sttistics, PAC lerning 10-701/15-781: Mchine Lerning (Fll 004) Due: Sept. 30th 004, Thursdy, Strt of clss Question 1. Bsic Probbility ( 18 pts) 1.1 (
Solution for Assignment 1 : Intro to Probbility nd Sttistics, PAC lerning 10-701/15-781: Mchine Lerning (Fll 004) Due: Sept. 30th 004, Thursdy, Strt of clss Question 1. Bsic Probbility ( 18 pts) 1.1 (
Normal Distribution. Lecture 6: More Binomial Distribution. Properties of the Unit Normal Distribution. Unit Normal Distribution
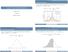 Norml Distribution Lecture 6: More Binomil Distribution If X is rndom vrible with norml distribution with men µ nd vrince σ 2, X N (µ, σ 2, then P(X = x = f (x = 1 e 1 (x µ 2 2 σ 2 σ Sttistics 104 Colin
Norml Distribution Lecture 6: More Binomil Distribution If X is rndom vrible with norml distribution with men µ nd vrince σ 2, X N (µ, σ 2, then P(X = x = f (x = 1 e 1 (x µ 2 2 σ 2 σ Sttistics 104 Colin
Best Approximation. Chapter The General Case
 Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Name Solutions to Test 3 November 8, 2017
 Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
Nme Solutions to Test 3 November 8, 07 This test consists of three prts. Plese note tht in prts II nd III, you cn skip one question of those offered. Some possibly useful formuls cn be found below. Brrier
Jim Lambers MAT 169 Fall Semester Lecture 4 Notes
 Jim Lmbers MAT 169 Fll Semester 2009-10 Lecture 4 Notes These notes correspond to Section 8.2 in the text. Series Wht is Series? An infinte series, usully referred to simply s series, is n sum of ll of
Jim Lmbers MAT 169 Fll Semester 2009-10 Lecture 4 Notes These notes correspond to Section 8.2 in the text. Series Wht is Series? An infinte series, usully referred to simply s series, is n sum of ll of
Math 360: A primitive integral and elementary functions
 Mth 360: A primitive integrl nd elementry functions D. DeTurck University of Pennsylvni October 16, 2017 D. DeTurck Mth 360 001 2017C: Integrl/functions 1 / 32 Setup for the integrl prtitions Definition:
Mth 360: A primitive integrl nd elementry functions D. DeTurck University of Pennsylvni October 16, 2017 D. DeTurck Mth 360 001 2017C: Integrl/functions 1 / 32 Setup for the integrl prtitions Definition:
Numerical integration
 2 Numericl integrtion This is pge i Printer: Opque this 2. Introduction Numericl integrtion is problem tht is prt of mny problems in the economics nd econometrics literture. The orgniztion of this chpter
2 Numericl integrtion This is pge i Printer: Opque this 2. Introduction Numericl integrtion is problem tht is prt of mny problems in the economics nd econometrics literture. The orgniztion of this chpter
1 The Riemann Integral
 The Riemnn Integrl. An exmple leding to the notion of integrl (res) We know how to find (i.e. define) the re of rectngle (bse height), tringle ( (sum of res of tringles). But how do we find/define n re
The Riemnn Integrl. An exmple leding to the notion of integrl (res) We know how to find (i.e. define) the re of rectngle (bse height), tringle ( (sum of res of tringles). But how do we find/define n re
Math 113 Fall Final Exam Review. 2. Applications of Integration Chapter 6 including sections and section 6.8
 Mth 3 Fll 0 The scope of the finl exm will include: Finl Exm Review. Integrls Chpter 5 including sections 5. 5.7, 5.0. Applictions of Integrtion Chpter 6 including sections 6. 6.5 nd section 6.8 3. Infinite
Mth 3 Fll 0 The scope of the finl exm will include: Finl Exm Review. Integrls Chpter 5 including sections 5. 5.7, 5.0. Applictions of Integrtion Chpter 6 including sections 6. 6.5 nd section 6.8 3. Infinite
Riemann is the Mann! (But Lebesgue may besgue to differ.)
 Riemnn is the Mnn! (But Lebesgue my besgue to differ.) Leo Livshits My 2, 2008 1 For finite intervls in R We hve seen in clss tht every continuous function f : [, b] R hs the property tht for every ɛ >
Riemnn is the Mnn! (But Lebesgue my besgue to differ.) Leo Livshits My 2, 2008 1 For finite intervls in R We hve seen in clss tht every continuous function f : [, b] R hs the property tht for every ɛ >
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
1 Probability Density Functions
 Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
W. We shall do so one by one, starting with I 1, and we shall do it greedily, trying
 Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Vitli covers 1 Definition. A Vitli cover of set E R is set V of closed intervls with positive length so tht, for every δ > 0 nd every x E, there is some I V with λ(i ) < δ nd x I. 2 Lemm (Vitli covering)
Problem. Statement. variable Y. Method: Step 1: Step 2: y d dy. Find F ( Step 3: Find f = Y. Solution: Assume
 Functions of Rndom Vrible Problem Sttement We know the pdf ( or cdf ) of rndom r vrible. Define new rndom vrible Y = g. Find the pdf of Y. Method: Step : Step : Step 3: Plot Y = g( ). Find F ( y) by mpping
Functions of Rndom Vrible Problem Sttement We know the pdf ( or cdf ) of rndom r vrible. Define new rndom vrible Y = g. Find the pdf of Y. Method: Step : Step : Step 3: Plot Y = g( ). Find F ( y) by mpping
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
NUMERICAL INTEGRATION. The inverse process to differentiation in calculus is integration. Mathematically, integration is represented by.
 NUMERICAL INTEGRATION 1 Introduction The inverse process to differentition in clculus is integrtion. Mthemticlly, integrtion is represented by f(x) dx which stnds for the integrl of the function f(x) with
NUMERICAL INTEGRATION 1 Introduction The inverse process to differentition in clculus is integrtion. Mthemticlly, integrtion is represented by f(x) dx which stnds for the integrl of the function f(x) with
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
Equations and Inequalities
 Equtions nd Inequlities Equtions nd Inequlities Curriculum Redy ACMNA: 4, 5, 6, 7, 40 www.mthletics.com Equtions EQUATIONS & Inequlities & INEQUALITIES Sometimes just writing vribles or pronumerls in
Equtions nd Inequlities Equtions nd Inequlities Curriculum Redy ACMNA: 4, 5, 6, 7, 40 www.mthletics.com Equtions EQUATIONS & Inequlities & INEQUALITIES Sometimes just writing vribles or pronumerls in
UNIFORM CONVERGENCE. Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3
 UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
List all of the possible rational roots of each equation. Then find all solutions (both real and imaginary) of the equation. 1.
 Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
Scientific notation is a way of expressing really big numbers or really small numbers.
 Scientific Nottion (Stndrd form) Scientific nottion is wy of expressing relly big numbers or relly smll numbers. It is most often used in scientific clcultions where the nlysis must be very precise. Scientific
Scientific Nottion (Stndrd form) Scientific nottion is wy of expressing relly big numbers or relly smll numbers. It is most often used in scientific clcultions where the nlysis must be very precise. Scientific
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
Chapter 0. What is the Lebesgue integral about?
 Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Chpter 0. Wht is the Lebesgue integrl bout? The pln is to hve tutoril sheet ech week, most often on Fridy, (to be done during the clss) where you will try to get used to the ides introduced in the previous
Consolidation Worksheet
 Cmbridge Essentils Mthemtics Core 8 NConsolidtion Worksheet N Consolidtion Worksheet Work these out. 8 b 7 + 0 c 6 + 7 5 Use the number line to help. 2 Remember + 2 2 +2 2 2 + 2 Adding negtive number is
Cmbridge Essentils Mthemtics Core 8 NConsolidtion Worksheet N Consolidtion Worksheet Work these out. 8 b 7 + 0 c 6 + 7 5 Use the number line to help. 2 Remember + 2 2 +2 2 2 + 2 Adding negtive number is
Week 10: Line Integrals
 Week 10: Line Integrls Introduction In this finl week we return to prmetrised curves nd consider integrtion long such curves. We lredy sw this in Week 2 when we integrted long curve to find its length.
Week 10: Line Integrls Introduction In this finl week we return to prmetrised curves nd consider integrtion long such curves. We lredy sw this in Week 2 when we integrted long curve to find its length.
Predict Global Earth Temperature using Linier Regression
 Predict Globl Erth Temperture using Linier Regression Edwin Swndi Sijbt (23516012) Progrm Studi Mgister Informtik Sekolh Teknik Elektro dn Informtik ITB Jl. Gnesh 10 Bndung 40132, Indonesi 23516012@std.stei.itb.c.id
Predict Globl Erth Temperture using Linier Regression Edwin Swndi Sijbt (23516012) Progrm Studi Mgister Informtik Sekolh Teknik Elektro dn Informtik ITB Jl. Gnesh 10 Bndung 40132, Indonesi 23516012@std.stei.itb.c.id
ARITHMETIC OPERATIONS. The real numbers have the following properties: a b c ab ac
 REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
Lesson 1: Quadratic Equations
 Lesson 1: Qudrtic Equtions Qudrtic Eqution: The qudrtic eqution in form is. In this section, we will review 4 methods of qudrtic equtions, nd when it is most to use ech method. 1. 3.. 4. Method 1: Fctoring
Lesson 1: Qudrtic Equtions Qudrtic Eqution: The qudrtic eqution in form is. In this section, we will review 4 methods of qudrtic equtions, nd when it is most to use ech method. 1. 3.. 4. Method 1: Fctoring
Main topics for the First Midterm
 Min topics for the First Midterm The Midterm will cover Section 1.8, Chpters 2-3, Sections 4.1-4.8, nd Sections 5.1-5.3 (essentilly ll of the mteril covered in clss). Be sure to know the results of the
Min topics for the First Midterm The Midterm will cover Section 1.8, Chpters 2-3, Sections 4.1-4.8, nd Sections 5.1-5.3 (essentilly ll of the mteril covered in clss). Be sure to know the results of the
Vyacheslav Telnin. Search for New Numbers.
 Vycheslv Telnin Serch for New Numbers. 1 CHAPTER I 2 I.1 Introduction. In 1984, in the first issue for tht yer of the Science nd Life mgzine, I red the rticle "Non-Stndrd Anlysis" by V. Uspensky, in which
Vycheslv Telnin Serch for New Numbers. 1 CHAPTER I 2 I.1 Introduction. In 1984, in the first issue for tht yer of the Science nd Life mgzine, I red the rticle "Non-Stndrd Anlysis" by V. Uspensky, in which
ECO 317 Economics of Uncertainty Fall Term 2007 Notes for lectures 4. Stochastic Dominance
 Generl structure ECO 37 Economics of Uncertinty Fll Term 007 Notes for lectures 4. Stochstic Dominnce Here we suppose tht the consequences re welth mounts denoted by W, which cn tke on ny vlue between
Generl structure ECO 37 Economics of Uncertinty Fll Term 007 Notes for lectures 4. Stochstic Dominnce Here we suppose tht the consequences re welth mounts denoted by W, which cn tke on ny vlue between
Indefinite Integral. Chapter Integration - reverse of differentiation
 Chpter Indefinite Integrl Most of the mthemticl opertions hve inverse opertions. The inverse opertion of differentition is clled integrtion. For exmple, describing process t the given moment knowing the
Chpter Indefinite Integrl Most of the mthemticl opertions hve inverse opertions. The inverse opertion of differentition is clled integrtion. For exmple, describing process t the given moment knowing the
5.7 Improper Integrals
 458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
P 3 (x) = f(0) + f (0)x + f (0) 2. x 2 + f (0) . In the problem set, you are asked to show, in general, the n th order term is a n = f (n) (0)
 1 Tylor polynomils In Section 3.5, we discussed how to pproximte function f(x) round point in terms of its first derivtive f (x) evluted t, tht is using the liner pproximtion f() + f ()(x ). We clled this
1 Tylor polynomils In Section 3.5, we discussed how to pproximte function f(x) round point in terms of its first derivtive f (x) evluted t, tht is using the liner pproximtion f() + f ()(x ). We clled this
14.3 comparing two populations: based on independent samples
 Chpter4 Nonprmetric Sttistics Introduction: : methods for mking inferences bout popultion prmeters (confidence intervl nd hypothesis testing) rely on the ssumptions bout probbility distribution of smpled
Chpter4 Nonprmetric Sttistics Introduction: : methods for mking inferences bout popultion prmeters (confidence intervl nd hypothesis testing) rely on the ssumptions bout probbility distribution of smpled
Bridging the gap: GCSE AS Level
 Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Bridging the gp: GCSE AS Level CONTENTS Chpter Removing rckets pge Chpter Liner equtions Chpter Simultneous equtions 8 Chpter Fctors 0 Chpter Chnge the suject of the formul Chpter 6 Solving qudrtic equtions
Chapter 4 Contravariance, Covariance, and Spacetime Diagrams
 Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Chpter 4 Contrvrince, Covrince, nd Spcetime Digrms 4. The Components of Vector in Skewed Coordintes We hve seen in Chpter 3; figure 3.9, tht in order to show inertil motion tht is consistent with the Lorentz
Line Integrals. Partitioning the Curve. Estimating the Mass
 Line Integrls Suppose we hve curve in the xy plne nd ssocite density δ(p ) = δ(x, y) t ech point on the curve. urves, of course, do not hve density or mss, but it my sometimes be convenient or useful to
Line Integrls Suppose we hve curve in the xy plne nd ssocite density δ(p ) = δ(x, y) t ech point on the curve. urves, of course, do not hve density or mss, but it my sometimes be convenient or useful to
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER /2019
 ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS MATH00030 SEMESTER 208/209 DR. ANTHONY BROWN 7.. Introduction to Integrtion. 7. Integrl Clculus As ws the cse with the chpter on differentil
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS MATH00030 SEMESTER 208/209 DR. ANTHONY BROWN 7.. Introduction to Integrtion. 7. Integrl Clculus As ws the cse with the chpter on differentil
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
Review of basic calculus
 Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
APPROXIMATE INTEGRATION
 APPROXIMATE INTEGRATION. Introduction We hve seen tht there re functions whose nti-derivtives cnnot be expressed in closed form. For these resons ny definite integrl involving these integrnds cnnot be
APPROXIMATE INTEGRATION. Introduction We hve seen tht there re functions whose nti-derivtives cnnot be expressed in closed form. For these resons ny definite integrl involving these integrnds cnnot be
Infinite Geometric Series
 Infinite Geometric Series Finite Geometric Series ( finite SUM) Let 0 < r < 1, nd let n be positive integer. Consider the finite sum It turns out there is simple lgebric expression tht is equivlent to
Infinite Geometric Series Finite Geometric Series ( finite SUM) Let 0 < r < 1, nd let n be positive integer. Consider the finite sum It turns out there is simple lgebric expression tht is equivlent to
Lecture 3. Limits of Functions and Continuity
 Lecture 3 Limits of Functions nd Continuity Audrey Terrs April 26, 21 1 Limits of Functions Notes I m skipping the lst section of Chpter 6 of Lng; the section bout open nd closed sets We cn probbly live
Lecture 3 Limits of Functions nd Continuity Audrey Terrs April 26, 21 1 Limits of Functions Notes I m skipping the lst section of Chpter 6 of Lng; the section bout open nd closed sets We cn probbly live
Chapter 6 Notes, Larson/Hostetler 3e
 Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
8 Laplace s Method and Local Limit Theorems
 8 Lplce s Method nd Locl Limit Theorems 8. Fourier Anlysis in Higher DImensions Most of the theorems of Fourier nlysis tht we hve proved hve nturl generliztions to higher dimensions, nd these cn be proved
8 Lplce s Method nd Locl Limit Theorems 8. Fourier Anlysis in Higher DImensions Most of the theorems of Fourier nlysis tht we hve proved hve nturl generliztions to higher dimensions, nd these cn be proved
State space systems analysis (continued) Stability. A. Definitions A system is said to be Asymptotically Stable (AS) when it satisfies
 Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
Stte spce systems nlysis (continued) Stbility A. Definitions A system is sid to be Asymptoticlly Stble (AS) when it stisfies ut () = 0, t > 0 lim xt () 0. t A system is AS if nd only if the impulse response
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
Interpreting Integrals and the Fundamental Theorem
 Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
The Fundamental Theorem of Calculus. The Total Change Theorem and the Area Under a Curve.
 Clculus Li Vs The Fundmentl Theorem of Clculus. The Totl Chnge Theorem nd the Are Under Curve. Recll the following fct from Clculus course. If continuous function f(x) represents the rte of chnge of F
Clculus Li Vs The Fundmentl Theorem of Clculus. The Totl Chnge Theorem nd the Are Under Curve. Recll the following fct from Clculus course. If continuous function f(x) represents the rte of chnge of F
MORE FUNCTION GRAPHING; OPTIMIZATION. (Last edited October 28, 2013 at 11:09pm.)
 MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
Unit #9 : Definite Integral Properties; Fundamental Theorem of Calculus
 Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Reversals of Signal-Posterior Monotonicity for Any Bounded Prior
 Reversls of Signl-Posterior Monotonicity for Any Bounded Prior Christopher P. Chmbers Pul J. Hely Abstrct Pul Milgrom (The Bell Journl of Economics, 12(2): 380 391) showed tht if the strict monotone likelihood
Reversls of Signl-Posterior Monotonicity for Any Bounded Prior Christopher P. Chmbers Pul J. Hely Abstrct Pul Milgrom (The Bell Journl of Economics, 12(2): 380 391) showed tht if the strict monotone likelihood
Lecture 21: Order statistics
 Lecture : Order sttistics Suppose we hve N mesurements of sclr, x i =, N Tke ll mesurements nd sort them into scending order x x x 3 x N Define the mesured running integrl S N (x) = 0 for x < x = i/n for
Lecture : Order sttistics Suppose we hve N mesurements of sclr, x i =, N Tke ll mesurements nd sort them into scending order x x x 3 x N Define the mesured running integrl S N (x) = 0 for x < x = i/n for
Lecture Note 9: Orthogonal Reduction
 MATH : Computtionl Methods of Liner Algebr 1 The Row Echelon Form Lecture Note 9: Orthogonl Reduction Our trget is to solve the norml eution: Xinyi Zeng Deprtment of Mthemticl Sciences, UTEP A t Ax = A
MATH : Computtionl Methods of Liner Algebr 1 The Row Echelon Form Lecture Note 9: Orthogonl Reduction Our trget is to solve the norml eution: Xinyi Zeng Deprtment of Mthemticl Sciences, UTEP A t Ax = A
Math 135, Spring 2012: HW 7
 Mth 3, Spring : HW 7 Problem (p. 34 #). SOLUTION. Let N the number of risins per cookie. If N is Poisson rndom vrible with prmeter λ, then nd for this to be t lest.99, we need P (N ) P (N ) ep( λ) λ ln(.)
Mth 3, Spring : HW 7 Problem (p. 34 #). SOLUTION. Let N the number of risins per cookie. If N is Poisson rndom vrible with prmeter λ, then nd for this to be t lest.99, we need P (N ) P (N ) ep( λ) λ ln(.)
A-Level Mathematics Transition Task (compulsory for all maths students and all further maths student)
 A-Level Mthemtics Trnsition Tsk (compulsory for ll mths students nd ll further mths student) Due: st Lesson of the yer. Length: - hours work (depending on prior knowledge) This trnsition tsk provides revision
A-Level Mthemtics Trnsition Tsk (compulsory for ll mths students nd ll further mths student) Due: st Lesson of the yer. Length: - hours work (depending on prior knowledge) This trnsition tsk provides revision
INTRODUCTION TO INTEGRATION
 INTRODUCTION TO INTEGRATION 5.1 Ares nd Distnces Assume f(x) 0 on the intervl [, b]. Let A be the re under the grph of f(x). b We will obtin n pproximtion of A in the following three steps. STEP 1: Divide
INTRODUCTION TO INTEGRATION 5.1 Ares nd Distnces Assume f(x) 0 on the intervl [, b]. Let A be the re under the grph of f(x). b We will obtin n pproximtion of A in the following three steps. STEP 1: Divide
AQA Further Pure 1. Complex Numbers. Section 1: Introduction to Complex Numbers. The number system
 Complex Numbers Section 1: Introduction to Complex Numbers Notes nd Exmples These notes contin subsections on The number system Adding nd subtrcting complex numbers Multiplying complex numbers Complex
Complex Numbers Section 1: Introduction to Complex Numbers Notes nd Exmples These notes contin subsections on The number system Adding nd subtrcting complex numbers Multiplying complex numbers Complex
Riemann Integrals and the Fundamental Theorem of Calculus
 Riemnn Integrls nd the Fundmentl Theorem of Clculus Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University September 16, 2013 Outline Grphing Riemnn Sums
Riemnn Integrls nd the Fundmentl Theorem of Clculus Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University September 16, 2013 Outline Grphing Riemnn Sums
