Hyperbolic Functions 6D
|
|
|
- Rosa McKinney
- 5 years ago
- Views:
Transcription
1 Hyperbolic Functions 6D a (sinh cosh b (cosh 5 5sinh 5 c (tanh sech (sinh cosh e f (coth cosech (sech sinh (cosh sinh cosh cosh tanh sech g (e sinh e sinh e + cosh e (cosh sinh h ( cosh cosh + sinh sinh cosh sinh cosh sinh i ( cosh cosh + sinh (cosh + sinh j k l (sinh cosh cosh cosh + sinh sinh cosh cosh + sinh sinh (ln cosh sinh cosh tanh Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free.
2 m (sinh cosh (cosh cosh sinh cosh sinh n ( ( o p (e cosh sinh e cosh cosh (cosech sinh sinh coth cosech y a coshn+ b sinhn Differentiate with respect to ansinhn+ nbcoshn an coshn+ bn sinhn n ( a coshn+ bsinh n n y To fin the stationary point of the curve y cosh sinh, we ifferentiate an set equal to. sinh cosh tanh artanh. + Using the formula artanh ln, we fin that + ln ln Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free.
3 Substituting this value for back into the given equation for y, we obtain y cosh ln sinh ln + +. So the coorinates of the stationary point are ln,. y cosh sinh sinh sinh+ cosh cosh 9 cosh sinh+ sinh cosh+ sinh cosh+ cosh sinh cosh sinh+ 6 sinh cosh (5cosh sinh+ sinh cosh 5 a Let y arcosh then coshy Differentiate with respect to sinh y y sinhy but coshy cosh y so b Let y arsinh( + then sinhy + coshy coshy but sinhy + sinh y+ so ( + + Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free.
4 5 c Let y artanh tanhy y sech y sech tanh 9 Let y arsech sechy cosh y coshy Differentiate with respect to coshy+ sinhy sinhy coshy coshy sinhy tanhy y ( sech y ( e Let y arcosh Let t y arcosht t t t ( Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free.
5 5 f y arcosh Let t y arcosht t t t 9 ( g y arcosh arcosh+ h y arsinh Lett y arsinht t t t + t t t i y e arsinh e e arsinh+ + j y arsinharcosh arcosh+ arsinh + k y arcoshsech sech arcosh tanhsech sech arcosh tanh l y arcosh arcosh+ 9 arcosh+ 9 Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free. 5
6 6 a y arcosh coshy sinhy y y sinh cosh but coshy so b y artanh tanhy y sech tanh sech y y but tanh y so 7 e y artanh e Lett y artanht t e t t t e t t Then e e e e ( e e ( e e Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free. 6
7 8 y arsinh ( + + ( + 5 ( + ( ( ( ( + ( + ( + ( + + ( + ( + ( + ( + ( y (arcosh arcosh ( arcosh ( arcosh+ ( arcosh + ( + y artanh y ln ln 5 ln Tangent is 69 ( y ln 5 5 5y 5 ln ( Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free. 7
8 In orer to fin the normal to the curve y arcosh at the point, we first must fin the value of at that point., so at,. 5 The graient of the normal at this point is therefore is arcosh ( + 5 The y value at ln. So now we substitute our values for, y, m into y m+ c in orer to fin c. y m+ c ( 5 ( 5 ln + + c c ln So we have y + 5+ ln( a We ifferentiate an evaluate at until we have non-zero terms. f ( cosh f ( f '( sinh f '( f ''( cosh f ''( f '''( sinh f '''( ( ( f ( cosh f (. Now we use the stanar Maclaurin series epansion an obtain cosh + +!! b Using the approimation, cosh (6.p..!! cosh. error cosh %. Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free. 8
9 a We ifferentiate an evaluate at until we have non-zero terms. f ( sinh f ( f '( cosh f '( f ''( sinh f ''( f '''( cosh f '''( ( ( f ( sinh f ( (5 (5 f ( cosh f (. Now we use the stanar Maclaurin series epansion an obtain 5 sinh + +! 5! b Since for all integers n, ( n (n f ( sinh f (, ( n (n f ( cosh f (. We can conclue that only the o erivatives will contribute to the Maclaurin series epansion, each with a enominator of (n!. The first non-zero term occurs when n with this choice of superscript an so we can conclue n that the nth non-zero term is. (n! a We ifferentiate an evaluate at until we have non-zero terms. f ( tanh f ( f '( sech f '( f ''( tanh sech f ''( f '''( tanh sech sech f '''(. Now we use the stanar Maclaurin series epansion an obtain tanh!. b Using the approimation,.8 tanh (6.p..69 tanh.8 error tanh.8 5.%( s.f. Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free. 9
10 5 a We ifferentiate an evaluate at until we have three non-zero terms. f ( ar tanh f ( f '( f '( f ''( f ''( f '''( ( ( ( ( ( f ( + ( (5 (5 5 ( f '''( ( + f ( (5 + + f ( f (. Now we use the stanar Maclaurin series epansion an obtain 5 artanh + +! 5! b By observation, the n th non-zero term in the series epansion appears to be n. n Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free.
11 5 c We ifferentiate an evaluate at until we have two non-zero terms. f( cosh artanh f( cosh f '( + sinh artanh f '( sinh cosh f ''( + + cosh artanh f ''( ( f '''( + 6sinh+ cosh 8 cosh ( ( cosh + + sinh artanh f '''( 5. Now we use the stanar Maclaurin series epansion an obtain 5 cosh artanh +! A less teious way of oing this woul be to take the epansions of cosh an artanh then multiply together, omitting higher orer terms. cosh artanh cosh artanh We ifferentiate an evaluate at until we have three non-zero terms. f( sinh cosh f( f '( cosh cosh+ sinh sinh f '( f ''( 5sinh cosh+ cosh sinh f ''( f '''( cosh cosh+ sinh sinh f '''( ( ( f ( sinh cosh+ cosh sinh f ( (5 (5 f ( cosh cosh+ sinh sinh f (. Now we use the stanar Maclaurin series epansion an obtain 5 sinh cosh + +! 5! Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free.
12 7 a We ifferentiate y cos cosh with respect to four times. y cos cosh cos sinh sin cosh sin sinh cos si h + sin cosh cos cosh y. ( n b We evaluate the ifferentials at until we have three non-zero terms. f ( cos cosh f ( f '( cos sinh sin cosh f '( f ''( sin sinh f ''( ( f '''( cos sinh + sin cosh f '''( ( ( f ( cos cosh f ( f (. Since we have the relation y, we can conclue that all ifferentials that are not of the n form, (where n is an integer is when evaluate at. So our thir non-zero term is n 8 8 6y ( y (8 6cos cosh f ( 6. Now we use the stanar Maclaurin series epansion an obtain 8 6 cos cosh +! 8! Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free.
13 n 7 c From the previous question, we know that the n terms are the only non-zero contributions. ( k f ( Recalling that the Maclaurin series epansion is f ( k an consiering k! n n ( n n n n ( y n 8 n 8 n 8 n 8 n y, ( y along with all ifferentials that are not of the form evaluate at, we can write an epression. ( k f ( k f ( k! cos cosh k r r r r ( r! ( r r ( ( ( r! ( ( r r r! r y + r Challenge We ifferentiate an evaluate at until we have three non-zero terms. f ( sech f ( f '( tanh sech f '( f ''( tanh sech sech f '''( tanh sech tanh sech tanh sech 5 tanh sech f '''( tanh sech f ( 5sech 5 tanh sech ( 5 f ''( ( tanh sech + tan h sech f ( 5. Now we use the stanar Maclaurin series epansion an obtain 5 sinh cosh +!! 5 + k n n (where n is an integer is when Pearson Eucation Lt 8. Copying permitte for purchasing institution only. This material is not copyright free.
( 2) ( ) Hyperbolic Functions 6E. cosh d (cosh sech ) d sinh tanh. cosh. x x x x x x C. x 1 x. 2 a. x x x = + = + cosh dx sinh C 3sinh C.
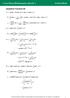Hyperolic Functions 6E a (sinh+ cosh ) cosh+ sinh+ + cosh cosh (cosh sech ) sinh tanh sinh sinh sechtanh sech+ cosh cosh cosh c a a sinh cosh+ cosh sinh sinh + + ( ) + + ( ) ( ) ( ) ( ) arcosh + ( ) +
cosh x sinh x So writing t = tan(x/2) we have 6.4 Integration using tan(x/2) 2t 1 + t 2 cos x = 1 t2 sin x =
6.4 Integration using tan/ We will revisit the ouble angle ientities: sin = sin/ cos/ = tan/ sec / = tan/ + tan / cos = cos / sin / tan = = tan / sec / tan/ tan /. = tan / + tan / So writing t = tan/ we
cosh x sinh x So writing t = tan(x/2) we have 6.4 Integration using tan(x/2) = 2 2t 1 + t 2 cos x = 1 t2 We will revisit the double angle identities:
6.4 Integration using tanx/) We will revisit the ouble angle ientities: sin x = sinx/) cosx/) = tanx/) sec x/) = tanx/) + tan x/) cos x = cos x/) sin x/) tan x = = tan x/) sec x/) tanx/) tan x/). = tan
2 4 Substituting 2 into gives 2(2) 4. + x + x +...= + + x ! 4! Substituting x= 0 and =1 into (1 + x ) + x = 0, gives 0
Talor Series 6C 1 Differentiating = +, with respect to, gives = 1+ (1) Differentiating (1) gives = () =, = 1 into = +, gives = + (1), so = 1 1 = into (1) gives =1+ = into gives () = () = = Sousing the
Integration Exercises - Part 3 (Sol'ns) (Hyperbolic Functions) (12 pages; 6/2/18) (The constant of integration has been omitted throughout.
Integration Eercises - Part (Sol'ns) (Hyperbolic Functions) ( pages; 6//8) (The constant of integration has been omitted throughout.) () cosech Given that d tanh = sech, we could investigate d coth = d
Taylor Series 6B. lim s x. 1 a We can evaluate the limit directly since there are no singularities: b Again, there are no singularities, so:
Taylor Series 6B a We can evaluate the it directly since there are no singularities: 7+ 7+ 7 5 5 5 b Again, there are no singularities, so: + + c Here we should divide through by in the numerator and denominator
Hyperbolic Functions. Notice: this material must not be used as a substitute for attending. the lectures
Hyperbolic Functions Notice: this material must not be use as a substitute for attening the lectures 0. Hyperbolic functions sinh an cosh The hyperbolic functions sinh (pronounce shine ) an cosh are efine
Differentiation 9I. 1 a. sin x 0 for 0 x π. So f ( x ) is convex on the interval. [0, π]. f ( x) 6x 6 0 for x 1. So f ( x ) is concave for all x
![Differentiation 9I. 1 a. sin x 0 for 0 x π. So f ( x ) is convex on the interval. [0, π]. f ( x) 6x 6 0 for x 1. So f ( x ) is concave for all x](/thumbs/87/95085126.jpg "Differentiation 9I. 1 a. sin x 0 for 0 x π. So f ( x ) is convex on the interval. [0, π]. f ( x) 6x 6 0 for x 1. So f ( x ) is concave for all x")
Differentiation 9I a f ( ) f ( ) 6 6 f ( ) 6 ii f ( ) is concave when f ( ) sin for π So f ( ) is concave on the interval [, π]. i f ( ) is conve when f ( ) 6 6 for So f ( ) is conve for all or on the
Today: 5.6 Hyperbolic functions
Toay: 5.6 Hyerbolic functions Warm u: Let f() = (e ) an g() = (e + ) Verify the following ientities: () f 0 () =g() () g 0 () =f() (3) f() is an o function (i.e. f(-) = -f()) (4) g() is an even function
Hyperbolic Functions: Exercises - Sol'ns (9 pages; 13/5/17)
Hyperbolic Functions: Exercises - Sol'ns (9 pages; 3/5/7) () (i) Prove, using exponential functions, that (a) cosh x sinh x = (b) sinhx = sinhxcoshx (ii) By differentiating the result from (i)(b), obtain
10.7. DIFFERENTIATION 7 (Inverse hyperbolic functions) A.J.Hobson
JUST THE MATHS SLIDES NUMBER 0.7 DIFFERENTIATION 7 (Inverse hyperbolic functions) by A.J.Hobson 0.7. Summary of results 0.7.2 The erivative of an inverse hyperbolic sine 0.7.3 The erivative of an inverse
Summary: Differentiation
Techniques of Differentiation. Inverse Trigonometric functions The basic formulas (available in MF5 are: Summary: Differentiation ( sin ( cos The basic formula can be generalize as follows: Note: ( sin
We define hyperbolic functions cosech, sech and coth in a similar way to the definitions of trigonometric functions cosec, sec and cot respectively:
3 Chapter 5 SECTION F Hyperbolic properties By the end of this section you will be able to: evaluate other hyperbolic functions show hyperbolic identities understand inverse hyperbolic functions F Other
Some functions and their derivatives
Chapter Some functions an their erivatives. Derivative of x n for integer n Recall, from eqn (.6), for y = f (x), Also recall that, for integer n, Hence, if y = x n then y x = lim δx 0 (a + b) n = a n
Chapter 2 Derivatives
Chapter Derivatives Section. An Intuitive Introuction to Derivatives Consier a function: Slope function: Derivative, f ' For each, the slope of f is the height of f ' Where f has a horizontal tangent line,
6675/01 Edexcel GCE Pure Mathematics P5 Further Mathematics FP2 Advanced/Advanced Subsidiary
6675/1 Edecel GCE Pure Mathematics P5 Further Mathematics FP Advanced/Advanced Subsidiary Monday June 5 Morning Time: 1 hour 3 minutes 1 1. (a) Find d. (1 4 ) (b) Find, to 3 decimal places, the value of.3
Hyperbolics. Scott Morgan. Further Mathematics Support Programme - WJEC A-Level Further Mathematics 31st March scott3142.
Hyperbolics Scott Morgan Further Mathematics Support Programme - WJEC A-Level Further Mathematics 3st March 208 scott342.com @Scott342 Topics Hyperbolic Identities Calculus with Hyperbolics - Differentiation
UNIT NUMBER DIFFERENTIATION 7 (Inverse hyperbolic functions) A.J.Hobson
JUST THE MATHS UNIT NUMBER 0.7 DIFFERENTIATION 7 (Inverse hyperbolic functions) by A.J.Hobson 0.7. Summary of results 0.7.2 The erivative of an inverse hyperbolic sine 0.7.3 The erivative of an inverse
FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS
Page of 6 FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS 6. HYPERBOLIC FUNCTIONS These functions which are defined in terms of e will be seen later to be related to the trigonometic functions via comple
Differentiation ( , 9.5)
Chapter 2 Differentiation (8.1 8.3, 9.5) 2.1 Rate of Change (8.2.1 5) Recall that the equation of a straight line can be written as y = mx + c, where m is the slope or graient of the line, an c is the
CHAPTER 1. DIFFERENTIATION 18. As x 1, f(x). At last! We are now in a position to sketch the curve; see Figure 1.4.
CHAPTER. DIFFERENTIATION 8 and similarly for x, As x +, fx), As x, fx). At last! We are now in a position to sketch the curve; see Figure.4. Figure.4: A sketch of the function y = fx) =/x ). Observe the
23 Implicit differentiation
23 Implicit ifferentiation 23.1 Statement The equation y = x 2 + 3x + 1 expresses a relationship between the quantities x an y. If a value of x is given, then a corresponing value of y is etermine. For
( ) = 1 t + t. ( ) = 1 cos x + x ( sin x). Evaluate y. MTH 111 Test 1 Spring Name Calculus I
MTH Test Spring 209 Name Calculus I Justify all answers by showing your work or by proviing a coherent eplanation. Please circle your answers.. 4 z z + 6 z 3 ez 2 = 4 z + 2 2 z2 2ez Rewrite as 4 z + 6
Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions
Chapter 5 Logarithmic, Exponential, an Other Transcenental Functions 5.1 The Natural Logarithmic Function: Differentiation 5.2 The Natural Logarithmic Function: Integration 5.3 Inverse Functions 5.4 Exponential
Mark Scheme (Results) Summer 2008
(Results) Summer 8 GCE GCE Mathematics (75/) Edecel Limited. Registered in England and Wales No. 975 Registered Office: One9 High Holborn, London WCV 7BH Further Pure Mathematics FP d. ( ln( tanh ) ) sech
Chapter 3 Differentiation Rules (continued)
Chapter 3 Differentiation Rules (continued) Sec 3.5: Implicit Differentiation (continued) Implicit Differentiation What if you want to find the slope of the tangent line to a curve that is not the graph
Additional Exercises for Chapter 10
Aitional Eercises for Chapter 0 About the Eponential an Logarithm Functions 6. Compute the area uner the graphs of i. f() =e over the interval [ 3, ]. ii. f() =e over the interval [, 4]. iii. f() = over
Section The Chain Rule and Implicit Differentiation with Application on Derivative of Logarithm Functions
Section 3.4-3.6 The Chain Rule an Implicit Differentiation with Application on Derivative of Logarithm Functions Ruipeng Shen September 3r, 5th Ruipeng Shen MATH 1ZA3 September 3r, 5th 1 / 3 The Chain
Strauss PDEs 2e: Section Exercise 6 Page 1 of 5
Strauss PDEs 2e: Section 4.3 - Exercise 6 Page 1 of 5 Exercise 6 If a 0 = a l = a in the Robin problem, show that: (a) There are no negative eigenvalues if a 0, there is one if 2/l < a < 0, an there are
Methods in differential equations mixed exercise 7
Methos in ifferential equations mie eercise 7 tan lnsec The integrating factor is e = e = sec Multiplying the equation by this factor gives: sec + ysectan= sec ( sec sec y = y sec= sec = tan+ c y= sin+
MTH 133 Solutions to Exam 1 February 21, Without fully opening the exam, check that you have pages 1 through 11.
MTH Solutions to Eam February, 8 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the eam, check that you have pages through. Show all
Hyperbolic Functions Mixed Exercise 6
Hyprbolic Functions Mid Ercis 6 a b c ln ln sinh(ln ) ln ln + cosh(ln ) + ln tanh ln ln + ( 6 ) ( + ) 6 7 ln ln ln,and ln ln ln,and ln ln 6 artanh artanhy + + y ln ln y + y ln + y + y y ln + y y + y y
Differential Equations DIRECT INTEGRATION. Graham S McDonald
Differential Equations DIRECT INTEGRATION Graham S McDonald A Tutorial Module introducing ordinary differential equations and the method of direct integration Table of contents Begin Tutorial c 2004 g.s.mcdonald@salford.ac.uk
Derivatives and Its Application
Chapter 4 Derivatives an Its Application Contents 4.1 Definition an Properties of erivatives; basic rules; chain rules 3 4. Derivatives of Inverse Functions; Inverse Trigonometric Functions; Hyperbolic
Math 180, Exam 2, Fall 2012 Problem 1 Solution. (a) The derivative is computed using the Chain Rule twice. 1 2 x x
. Fin erivatives of the following functions: (a) f() = tan ( 2 + ) ( ) 2 (b) f() = ln 2 + (c) f() = sin() Solution: Math 80, Eam 2, Fall 202 Problem Solution (a) The erivative is compute using the Chain
Revision Checklist. Unit FP3: Further Pure Mathematics 3. Assessment information
Revision Checklist Unit FP3: Further Pure Mathematics 3 Unit description Further matrix algebra; vectors, hyperbolic functions; differentiation; integration, further coordinate systems Assessment information
Further Pure Mathematics 3 GCE Further Mathematics GCE Pure Mathematics and Further Mathematics (Additional) A2 optional unit
Unit FP3 Further Pure Mathematics 3 GCE Further Mathematics GCE Pure Mathematics and Further Mathematics (Additional) A optional unit FP3.1 Unit description Further matrix algebra; vectors, hyperbolic
Hyperbolic functions
Roberto s Notes on Differential Calculus Chapter 5: Derivatives of transcendental functions Section Derivatives of Hyperbolic functions What you need to know already: Basic rules of differentiation, including
Math 115 (W1) Solutions to Assignment #4
Math 5 (W Solutions to Assignment #. ( marks Fin the erivative of the following. Provie reasonable simplification. a f( 3 + e sec ( ; ( ( b f( log + tan ; ( c f( tanh ; + f( ln(sinh. a f( ( 3 + 3 ln( 3
ENGI 3425 Review of Calculus Page then
ENGI 345 Review of Calculus Page 1.01 1. Review of Calculus We begin this course with a refresher on ifferentiation an integration from MATH 1000 an MATH 1001. 1.1 Reminer of some Derivatives (review from
WJEC Core 2 Integration. Section 1: Introduction to integration
WJEC Core Integration Section : Introuction to integration Notes an Eamples These notes contain subsections on: Reversing ifferentiation The rule for integrating n Fining the arbitrary constant Reversing
We want to look at some special functions that can arise, especially in trying to solve certain types of rather simple equations.
Chapter 9 Special Functions We want to look at some special functions that can arise, especially in trying to solve certain types of rather simple equations. 9.1 Hyperbolic Trigonometric Functions The
Differential and Integral Calculus
School of science an engineering El Akhawayn University Monay, March 31 st, 2008 Outline 1 Definition of hyperbolic functions: The hyperbolic cosine an the hyperbolic sine of the real number x are enote
FP3 mark schemes from old P4, P5, P6 and FP1, FP2, FP3 papers (back to June 2002)
FP mark schemes from old P, P5, P6 and FP, FP, FP papers (back to June ) Please note that the following pages contain mark schemes for questions from past papers. Where a question reference is marked with
L Hôpital s Rule was discovered by Bernoulli but written for the first time in a text by L Hôpital.
7.5. Ineterminate Forms an L Hôpital s Rule L Hôpital s Rule was iscovere by Bernoulli but written for the first time in a text by L Hôpital. Ineterminate Forms 0/0 an / f(x) If f(x 0 ) = g(x 0 ) = 0,
CHAPTER 23 MACLAURIN S SERIES
EXERCISE 97 Page 9 CHAPTER MACLAURIN S SERIES. Determine the irst our terms o the power series or sin using Maclaurin s series. Let () sin () sin () cos () cos () sin () sin () 8 cos () 8 cos 8 i( ) 6
Extra FP3 past paper - A
Mark schemes for these "Extra FP3" papers at https://mathsmartinthomas.files.wordpress.com/04//extra_fp3_markscheme.pdf Extra FP3 past paper - A More FP3 practice papers, with mark schemes, compiled from
1. Find the equation of a line passing through point (5, -2) with slope ¾. (State your answer in slope-int. form)
INTRO TO CALCULUS REVIEW FINAL EXAM NAME: DATE: A. Equations of Lines (Review Chapter) y = m + b (Slope-Intercept Form) A + By = C (Stanar Form) y y = m( ) (Point-Slope Form). Fin the equation of a line
4. Functions of one variable
4. Functions of one variable These lecture notes present my interpretation of Ruth Lawrence s lecture notes (in Hebrew) 1 In this chapter we are going to meet one of the most important concepts in mathematics:
THEOREM: THE CONSTANT RULE
MATH /MYERS/ALL FORMULAS ON THIS REVIEW MUST BE MEMORIZED! DERIVATIVE REVIEW THEOREM: THE CONSTANT RULE The erivative of a constant function is zero. That is, if c is a real number, then c 0 Eample 1:
90 Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions. Name Class. (a) (b) ln x (c) (a) (b) (c) 1 x. y e (a) 0 (b) y.
90 Chapter 5 Logarithmic, Eponential, and Other Transcendental Functions Test Form A Chapter 5 Name Class Date Section. Find the derivative: f ln. 6. Differentiate: y. ln y y y y. Find dy d if ey y. y
Unit #6 - Families of Functions, Taylor Polynomials, l Hopital s Rule
Unit # - Families of Functions, Taylor Polynomials, l Hopital s Rule Some problems an solutions selecte or aapte from Hughes-Hallett Calculus. Critical Points. Consier the function f) = 54 +. b) a) Fin
MATHEMATICS C1-C4 and FP1-FP3
MS WELSH JOINT EDUCATION COMMITTEE. CYD-BWYLLGOR ADDYSG CYMRU General Certificate of Eucation Avance Subsiiary/Avance Tystysgrif Aysg Gyffreinol Uwch Gyfrannol/Uwch MARKING SCHEMES SUMMER 6 MATHEMATICS
Chapter 9: Complex Numbers
Chapter 9: Comple Numbers 9.1 Imaginary Number 9. Comple Number - definition - argand diagram - equality of comple number 9.3 Algebraic operations on comple number - addition and subtraction - multiplication
6.2. The Hyperbolic Functions. Introduction. Prerequisites. Learning Outcomes
The Hyperbolic Functions 6. Introduction The hyperbolic functions cosh x, sinh x, tanh x etc are certain combinations of the exponential functions e x and e x. The notation implies a close relationship
(a) 82 (b) 164 (c) 81 (d) 162 (e) 624 (f) 625 None of these. (c) 12 (d) 15 (e)
Math 2 (Calculus I) Final Eam Form A KEY Multiple Choice. Fill in the answer to each problem on your computer-score answer sheet. Make sure your name, section an instructor are on that sheet.. Approimate
1 Lecture 20: Implicit differentiation
Lecture 20: Implicit ifferentiation. Outline The technique of implicit ifferentiation Tangent lines to a circle Derivatives of inverse functions by implicit ifferentiation Examples.2 Implicit ifferentiation
Breakout Session 13 Solutions
Problem True or False: If f = 2, then f = 2 False Any time that you have a function of raise to a function of, in orer to compute the erivative you nee to use logarithmic ifferentiation or something equivalent
4.1 Exponential and Logarithmic Functions
. Exponential and Logarithmic Functions Joseph Heavner Honors Complex Analysis Continued) Chapter July, 05 3.) Find the derivative of f ) e i e i. d d e i e i) d d ei ) d d e i ) e i d d i) e i d d i)
REVISION SHEET FP2 (MEI) CALCULUS. x x 0.5. x x 1.5. π π. Standard Calculus of Inverse Trig and Hyperbolic Trig Functions = + = + arcsin x = +
the Further Mathematics network www.fmnetwork.org.uk V 07 REVISION SHEET FP (MEI) CALCULUS The main ideas are: Calculus using inverse trig functions & hperbolic trig functions and their inverses. Maclaurin
Using the definition of the derivative of a function is quite tedious. f (x + h) f (x)
Derivative Rules Using te efinition of te erivative of a function is quite teious. Let s prove some sortcuts tat we can use. Recall tat te efinition of erivative is: Given any number x for wic te limit
d dx But have you ever seen a derivation of these results? We ll prove the first result below. cos h 1
Lecture 5 Some ifferentiation rules Trigonometric functions (Relevant section from Stewart, Seventh Eition: Section 3.3) You all know that sin = cos cos = sin. () But have you ever seen a erivation of
LINEAR DIFFERENTIAL EQUATIONS OF ORDER 1. where a(x) and b(x) are functions. Observe that this class of equations includes equations of the form
LINEAR DIFFERENTIAL EQUATIONS OF ORDER 1 We consier ifferential equations of the form y + a()y = b(), (1) y( 0 ) = y 0, where a() an b() are functions. Observe that this class of equations inclues equations
The Explicit Form of a Function
Section 3 5 Implicit Differentiation The Eplicit Form of a Function The normal way we see function notation has f () on one sie of an equation an an epression in terms of on the other sie. We know the
Math 1720 Final Exam Review 1
Math 70 Final Eam Review Remember that you are require to evaluate this class by going to evaluate.unt.eu an filling out the survey before minight May 8. It will only take between 5 an 0 minutes, epening
MTH 133 Exam 1 February 21, Without fully opening the exam, check that you have pages 1 through 11.
Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the eam, check that you have pages through. Show all your work on the stanar response
Math 1A Midterm 2 Fall 2015 Riverside City College (Use this as a Review)
Name Date Miterm Score Overall Grae Math A Miterm 2 Fall 205 Riversie City College (Use this as a Review) Instructions: All work is to be shown, legible, simplifie an answers are to be boxe in the space
x = c of N if the limit of f (x) = L and the right-handed limit lim f ( x)
Limit We say the limit of f () as approaches c equals L an write, lim L. One-Sie Limits (Left an Right-Hane Limits) Suppose a function f is efine near but not necessarily at We say that f has a left-hane
Pure Further Mathematics 1. Revision Notes
Pure Further Mathematics Revision Notes June 20 2 FP JUNE 20 SDB Further Pure Complex Numbers... 3 Definitions an arithmetical operations... 3 Complex conjugate... 3 Properties... 3 Complex number plane,
7. Differentiation of Trigonometric Function
7. Differentiation of Trigonoetric Fnction RADIAN MEASURE. Let s enote the length of arc AB intercepte y the central angle AOB on a circle of rais r an let S enote the area of the sector AOB. (If s is
MTH 133 Solutions to Exam 1 October 10, Without fully opening the exam, check that you have pages 1 through 11.
MTH 33 Solutions to Eam October 0, 08 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the eam, check that you have pages through. Show
Math 1271 Solutions for Fall 2005 Final Exam
Math 7 Solutions for Fall 5 Final Eam ) Since the equation + y = e y cannot be rearrange algebraically in orer to write y as an eplicit function of, we must instea ifferentiate this relation implicitly
Higher. Further Calculus 149
hsn.uk.net Higher Mathematics UNIT 3 OUTCOME 2 Further Calculus Contents Further Calculus 49 Differentiating sinx an cosx 49 2 Integrating sinx an cosx 50 3 The Chain Rule 5 4 Special Cases of the Chain
1 Functions and Inverses
October, 08 MAT86 Week Justin Ko Functions and Inverses Definition. A function f : D R is a rule that assigns each element in a set D to eactly one element f() in R. The set D is called the domain of f.
MAS153/MAS159. MAS153/MAS159 1 Turn Over SCHOOL OF MATHEMATICS AND STATISTICS hours. Mathematics (Materials) Mathematics For Chemists
Data provided: Formula sheet MAS53/MAS59 SCHOOL OF MATHEMATICS AND STATISTICS Mathematics (Materials Mathematics For Chemists Spring Semester 203 204 3 hours All questions are compulsory. The marks awarded
CONTINUITY AND DIFFERENTIABILITY
CONTINUITY AND DIFFERENTIABILITY Revision Assignment Class 1 Chapter 5 QUESTION1: Check the continuity of the function f given by f () = 7 + 5at = 1. The function is efine at the given point = 1 an its
Monday 20 June 2005 Morning Time: 1 hour 30 minutes
Paper Reference(s) 6675/01 Edecel GCE Pure Mathematics P5 Further Mathematics FP Advanced/Advanced Subsidiary Monday 0 June 005 Morning Time: 1 hour 30 minutes Materials required for eamination Mathematical
The Explicit Form of a Function
Section 3 5 Implicit Differentiation The Eplicit Form of a Function Function Notation requires that we state a function with f () on one sie of an equation an an epression in terms of on the other sie
QF101: Quantitative Finance September 5, Week 3: Derivatives. Facilitator: Christopher Ting AY 2017/2018. f ( x + ) f(x) f(x) = lim
QF101: Quantitative Finance September 5, 2017 Week 3: Derivatives Facilitator: Christopher Ting AY 2017/2018 I recoil with ismay an horror at this lamentable plague of functions which o not have erivatives.
Completion Date: Monday February 11, 2008
MATH 4 (R) Winter 8 Intermediate Calculus I Solutions to Problem Set #4 Completion Date: Monday February, 8 Department of Mathematical and Statistical Sciences University of Alberta Question. [Sec..9,
STEP Support Programme. STEP III Hyperbolic Functions: Solutions
STEP Spport Programme STEP III Hyperbolic Fnctions: Soltions Start by sing the sbstittion t cosh x. This gives: sinh x cosh a cosh x cosh a sinh x t sinh x dt t dt t + ln t ln t + ln cosh a ln ln cosh
Linear and quadratic approximation
Linear an quaratic approximation November 11, 2013 Definition: Suppose f is a function that is ifferentiable on an interval I containing the point a. The linear approximation to f at a is the linear function
ARAB ACADEMY FOR SCIENCE TECHNOLOGY AND MARITIME TRANSPORT
ARAB ACADEMY FOR SCIENCE TECHNOLOGY AND MARITIME TRANSPORT Course: Math For Engineering Winter 8 Lecture Notes By Dr. Mostafa Elogail Page Lecture [ Functions / Graphs of Rational Functions] Functions
UNDERSTANDING INTEGRATION
UNDERSTANDING INTEGRATION Dear Reaer The concept of Integration, mathematically speaking, is the "Inverse" of the concept of result, the integration of, woul give us back the function f(). This, in a way,
10 Non-routine Problems To Sharpen Your Mathematical Thinking
Have you thought about it differently? 0 Non-routine Problems To Sharpen Your Mathematical Thinking Wee Wen Shih PGDE (Credit), MSc (Research) Page Introduction This electronic book presents the second
School of Distance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION. B Sc Mathematics. (2011 Admission Onwards) IV Semester.
School of Dtance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION B Sc Mathematics 0 Admsion Onwards IV Semester Core Course CALCULUS AND ANALYTIC GEOMETRY QUESTION BANK The natural logarithm
Math Implicit Differentiation. We have discovered (and proved) formulas for finding derivatives of functions like
Math 400 3.5 Implicit Differentiation Name We have iscovere (an prove) formulas for fining erivatives of functions like f x x 3x 4x. 3 This amounts to fining y for 3 y x 3x 4x. Notice that in this case,
JUST THE MATHS UNIT NUMBER DIFFERENTIATION 2 (Rates of change) A.J.Hobson
JUST THE MATHS UNIT NUMBER 10.2 DIFFERENTIATION 2 (Rates of change) by A.J.Hobson 10.2.1 Introuction 10.2.2 Average rates of change 10.2.3 Instantaneous rates of change 10.2.4 Derivatives 10.2.5 Exercises
DIFFERENTIATION TECHNIQUES CHAIN, PRODUCT & QUOTIENT RULES
Mathematics Revision Guies Differentiation: Chain, Proct an Quotient Rules Page of 0 MK HOME TUITION Mathematics Revision Guies Level: A-Level Year DIFFERENTIATION TECHNIQUES CHAIN, PRODUCT & QUOTIENT
Transcendental Functions
78 Chapter 9 Transcenental Functions º½ 9 Transcenental Functions ÁÒÚ Ö ÙÒØ ÓÒ Informally, two functions f an g are inverses if each reverses, or unoes, the other More precisely: DEFINITION 9 Two functions
TOTAL NAME DATE PERIOD AP CALCULUS AB UNIT 4 ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT /6 10/8 10/9 10/10 X X X X 10/11 10/12
NAME DATE PERIOD AP CALCULUS AB UNIT ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT 0 0 0/6 0/8 0/9 0/0 X X X X 0/ 0/ 0/5 0/6 QUIZ X X X 0/7 0/8 0/9 0/ 0/ 0/ 0/5 UNIT EXAM X X X TOTAL AP Calculus
11.7. Implicit Differentiation. Introduction. Prerequisites. Learning Outcomes
Implicit Differentiation 11.7 Introuction This Section introuces implicit ifferentiation which is use to ifferentiate functions expresse in implicit form (where the variables are foun together). Examples
Integration by Parts
Integration by Parts 6-3-207 If u an v are functions of, the Prouct Rule says that (uv) = uv +vu Integrate both sies: (uv) = uv = uv + u v + uv = uv vu, vu v u, I ve written u an v as shorthan for u an
Pure Further Mathematics 3. Revision Notes
Pure Further Mathematics Revision Notes June 6 FP JUNE 6 SDB Hyperbolic functions... Definitions and graphs... Addition formulae, double angle formulae etc.... Osborne s rule... Inverse hyperbolic functions...
Mathematics Notes for Class 12 chapter 7. Integrals
1 P a g e Mathematics Notes for Class 12 chapter 7. Integrals Let f(x) be a function. Then, the collection of all its primitives is called the indefinite integral of f(x) and is denoted by f(x)dx. Integration
Hyperbolic functions
Hyperbolic functions Attila Máté Brooklyn College of the City University of New York January 5, 206 Contents Hyperbolic functions 2 Connection with the unit hyperbola 2 2. Geometric meaning of the parameter...........................
JUST THE MATHS UNIT NUMBER DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) A.J.Hobson
JUST THE MATHS UNIT NUMBER 104 DIFFERENTIATION 4 (Products and quotients) & (Logarithmic differentiation) by AJHobson 1041 Products 1042 Quotients 1043 Logarithmic differentiation 1044 Exercises 1045 Answers
Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE Mathematics and Further Mathematics
Pearson Edecel Level 3 Advanced Subsidiary and Advanced GCE Mathematics and Further Mathematics Mathematical formulae and statistical tables First certification from 08 Advanced Subsidiary GCE in Mathematics
Math 20B. Lecture Examples.
Math 20B. Lecture Eamples. (7/8/08) Comple eponential functions A comple number is an epression of the form z = a + ib, where a an b are real numbers an i is the smbol that is introuce to serve as a square
A. Incorrect! The letter t does not appear in the expression of the given integral
AP Physics C - Problem Drill 1: The Funamental Theorem of Calculus Question No. 1 of 1 Instruction: (1) Rea the problem statement an answer choices carefully () Work the problems on paper as neee (3) Question