Methods in differential equations mixed exercise 7

Section The Chain Rule and Implicit Differentiation with Application on Derivative of Logarithm Functions

Section 3.4-3.6 The Chain Rule an Implicit Differentiation with Application on Derivative of Logarithm Functions Ruipeng Shen September 3r, 5th Ruipeng Shen MATH 1ZA3 September 3r, 5th 1 / 3 The Chain

Math 180, Exam 2, Fall 2012 Problem 1 Solution. (a) The derivative is computed using the Chain Rule twice. 1 2 x x

. Fin erivatives of the following functions: (a) f() = tan ( 2 + ) ( ) 2 (b) f() = ln 2 + (c) f() = sin() Solution: Math 80, Eam 2, Fall 202 Problem Solution (a) The erivative is compute using the Chain

2 4 Substituting 2 into gives 2(2) 4. + x + x +...= + + x ! 4! Substituting x= 0 and =1 into (1 + x ) + x = 0, gives 0

Talor Series 6C 1 Differentiating = +, with respect to, gives = 1+ (1) Differentiating (1) gives = () =, = 1 into = +, gives = + (1), so = 1 1 = into (1) gives =1+ = into gives () = () = = Sousing the

cosh x sinh x So writing t = tan(x/2) we have 6.4 Integration using tan(x/2) 2t 1 + t 2 cos x = 1 t2 sin x =

6.4 Integration using tan/ We will revisit the ouble angle ientities: sin = sin/ cos/ = tan/ sec / = tan/ + tan / cos = cos / sin / tan = = tan / sec / tan/ tan /. = tan / + tan / So writing t = tan/ we

Differentiation 9I. 1 a. sin x 0 for 0 x π. So f ( x ) is convex on the interval. [0, π]. f ( x) 6x 6 0 for x 1. So f ( x ) is concave for all x

Differentiation 9I a f ( ) f ( ) 6 6 f ( ) 6 ii f ( ) is concave when f ( ) sin for π So f ( ) is concave on the interval [, π]. i f ( ) is conve when f ( ) 6 6 for So f ( ) is conve for all or on the

Hyperbolic Functions 6D

Hyperbolic Functions 6D a (sinh cosh b (cosh 5 5sinh 5 c (tanh sech (sinh cosh e f (coth cosech (sech sinh (cosh sinh cosh cosh tanh sech g (e sinh e sinh e + cosh e (cosh sinh h ( cosh cosh + sinh sinh

Chapter 2 Derivatives

Chapter Derivatives Section. An Intuitive Introuction to Derivatives Consier a function: Slope function: Derivative, f ' For each, the slope of f is the height of f ' Where f has a horizontal tangent line,

L Hôpital s Rule was discovered by Bernoulli but written for the first time in a text by L Hôpital.

7.5. Ineterminate Forms an L Hôpital s Rule L Hôpital s Rule was iscovere by Bernoulli but written for the first time in a text by L Hôpital. Ineterminate Forms 0/0 an / f(x) If f(x 0 ) = g(x 0 ) = 0,

Unit #6 - Families of Functions, Taylor Polynomials, l Hopital s Rule

Unit # - Families of Functions, Taylor Polynomials, l Hopital s Rule Some problems an solutions selecte or aapte from Hughes-Hallett Calculus. Critical Points. Consier the function f) = 54 +. b) a) Fin

Edexcel Further Pure 2

Edecel Further Pure Second order differential equations Section : Non-homogeneous second order differential equations Notes and Eamples These notes contain subsections on Finding particular integrals Finding

cosh x sinh x So writing t = tan(x/2) we have 6.4 Integration using tan(x/2) = 2 2t 1 + t 2 cos x = 1 t2 We will revisit the double angle identities:

6.4 Integration using tanx/) We will revisit the ouble angle ientities: sin x = sinx/) cosx/) = tanx/) sec x/) = tanx/) + tan x/) cos x = cos x/) sin x/) tan x = = tan x/) sec x/) tanx/) tan x/). = tan

1 Applications of the Chain Rule

November 7, 08 MAT86 Week 6 Justin Ko Applications of the Chain Rule We go over several eamples of applications of the chain rule to compute erivatives of more complicate functions. Chain Rule: If z =

Inverse Functions. Review from Last Time: The Derivative of y = ln x. [ln. Last time we saw that

Inverse Functions Review from Last Time: The Derivative of y = ln Last time we saw that THEOREM 22.0.. The natural log function is ifferentiable an More generally, the chain rule version is ln ) =. ln

2 nd ORDER O.D.E.s SUBSTITUTIONS

nd ORDER O.D.E.s SUBSTITUTIONS Question 1 (***+) d y y 8y + 16y = d d d, y 0, Find the general solution of the above differential equation by using the transformation equation t = y. Give the answer in

Chapter 5 Logarithmic, Exponential, and Other Transcendental Functions

Chapter 5 Logarithmic, Exponential, an Other Transcenental Functions 5.1 The Natural Logarithmic Function: Differentiation 5.2 The Natural Logarithmic Function: Integration 5.3 Inverse Functions 5.4 Exponential

18 EVEN MORE CALCULUS

8 EVEN MORE CALCULUS Chapter 8 Even More Calculus Objectives After stuing this chapter you shoul be able to ifferentiate an integrate basic trigonometric functions; unerstan how to calculate rates of change;

Hyperbolic Functions. Notice: this material must not be used as a substitute for attending. the lectures

Hyperbolic Functions Notice: this material must not be use as a substitute for attening the lectures 0. Hyperbolic functions sinh an cosh The hyperbolic functions sinh (pronounce shine ) an cosh are efine

y. ( sincos ) (sin ) (cos ) + (cos ) (sin ) sin + cos cos. 5. 6.. y + ( )( ) ( + )( ) ( ) ( ) s [( t )( t + )] t t [ t ] t t s t + t t t ( t )( t) ( t + )( t) ( t ) t ( t ) y + + / / ( + + ) / / /....

LINEAR DIFFERENTIAL EQUATIONS OF ORDER 1. where a(x) and b(x) are functions. Observe that this class of equations includes equations of the form

LINEAR DIFFERENTIAL EQUATIONS OF ORDER 1 We consier ifferential equations of the form y + a()y = b(), (1) y( 0 ) = y 0, where a() an b() are functions. Observe that this class of equations inclues equations

Math Implicit Differentiation. We have discovered (and proved) formulas for finding derivatives of functions like

Math 400 3.5 Implicit Differentiation Name We have iscovere (an prove) formulas for fining erivatives of functions like f x x 3x 4x. 3 This amounts to fining y for 3 y x 3x 4x. Notice that in this case,

THEOREM: THE CONSTANT RULE

MATH /MYERS/ALL FORMULAS ON THIS REVIEW MUST BE MEMORIZED! DERIVATIVE REVIEW THEOREM: THE CONSTANT RULE The erivative of a constant function is zero. That is, if c is a real number, then c 0 Eample 1:

Trigonometric Functions Mixed Exercise

Trigonometric Functions Mied Eercise tan = cot, -80 90 Þ tan = tan Þ tan = Þ tan = ± Calculator value for tan = + is 54.7 ( d.p.) 4 a i cosecq = cotq, 0

Module FP2. Further Pure 2. Cambridge University Press Further Pure 2 and 3 Hugh Neill and Douglas Quadling Excerpt More information

5548993 - Further Pure an 3 Moule FP Further Pure 5548993 - Further Pure an 3 Differentiating inverse trigonometric functions Throughout the course you have graually been increasing the number of functions

µ Differential Equations MAΘ National Convention 2017 For all questions, answer choice E) NOTA means that none of the above answers is correct.

µ Differential Equations MAΘ National Convention 07 For all questions, answer choice E) NOTA means that none of the above answers is correct.. C) Since f (, ) = +, (0) = and h =. Use Euler s method, we

Section 7.2 Addition and Subtraction Identities. In this section, we begin expanding our repertoire of trigonometric identities.

Section 7. Addition and Subtraction Identities 47 Section 7. Addition and Subtraction Identities In this section, we begin expanding our repertoire of trigonometric identities. Identities The sum and difference

(a) 82 (b) 164 (c) 81 (d) 162 (e) 624 (f) 625 None of these. (c) 12 (d) 15 (e)

Math 2 (Calculus I) Final Eam Form A KEY Multiple Choice. Fill in the answer to each problem on your computer-score answer sheet. Make sure your name, section an instructor are on that sheet.. Approimate

CONTINUITY AND DIFFERENTIABILITY

CONTINUITY AND DIFFERENTIABILITY Revision Assignment Class 1 Chapter 5 QUESTION1: Check the continuity of the function f given by f () = 7 + 5at = 1. The function is efine at the given point = 1 an its

Candidates sitting FP2 may also require those formulae listed under Further Pure Mathematics FP1 and Core Mathematics C1 C4. e π.

F Further IAL Pure PAPERS: Mathematics FP 04-6 AND SPECIMEN Candidates sitting FP may also require those formulae listed under Further Pure Mathematics FP and Core Mathematics C C4. Area of a sector A

MA 242 Review Exponential and Log Functions Notes for today s class can be found at

MA 242 Review Exponential and Log Functions Notes for today s class can be found at www.xecu.net/jacobs/index242.htm Example: If y = x n If y = x 2 then then dy dx = nxn 1 dy dx = 2x1 = 2x Power Function

x f(x) x f(x) approaching 1 approaching 0.5 approaching 1 approaching 0.

Engineering Mathematics 2 26 February 2014 Limits of functions Consier the function 1 f() = 1. The omain of this function is R + \ {1}. The function is not efine at 1. What happens when is close to 1?

Computing Derivatives Solutions

Stuent Stuy Session Solutions We have intentionally inclue more material than can be covere in most Stuent Stuy Sessions to account for groups that are able to answer the questions at a faster rate. Use

d dx But have you ever seen a derivation of these results? We ll prove the first result below. cos h 1

Lecture 5 Some ifferentiation rules Trigonometric functions (Relevant section from Stewart, Seventh Eition: Section 3.3) You all know that sin = cos cos = sin. () But have you ever seen a erivation of

Outline. MS121: IT Mathematics. Differentiation Rules for Differentiation: Part 1. Outline. Dublin City University 4 The Quotient Rule

MS2: IT Mathematics Differentiation Rules for Differentiation: Part John Carroll School of Mathematical Sciences Dublin City University Pattern Observe You may have notice the following pattern when we

x f(x) x f(x) approaching 1 approaching 0.5 approaching 1 approaching 0.

Engineering Mathematics 2 26 February 2014 Limits of functions Consier the function 1 f() = 1. The omain of this function is R + \ {1}. The function is not efine at 1. What happens when is close to 1?

( ) = 1 t + t. ( ) = 1 cos x + x ( sin x). Evaluate y. MTH 111 Test 1 Spring Name Calculus I

MTH Test Spring 209 Name Calculus I Justify all answers by showing your work or by proviing a coherent eplanation. Please circle your answers.. 4 z z + 6 z 3 ez 2 = 4 z + 2 2 z2 2ez Rewrite as 4 z + 6

Introduction to Differential Equations Math 286 X1 Fall 2009 Homework 2 Solutions

Introuction to Differential Equations Math 286 X1 Fall 2009 Homewk 2 Solutions 1. Solve each of the following ifferential equations: (a) y + 3xy = 0 (b) y + 3y = 3x (c) y t = cos(t)y () x 2 y x y = 3 Solution:

Math 1271 Solutions for Fall 2005 Final Exam

Math 7 Solutions for Fall 5 Final Eam ) Since the equation + y = e y cannot be rearrange algebraically in orer to write y as an eplicit function of, we must instea ifferentiate this relation implicitly

MATH 1010E University Mathematics Lecture Notes (week 8) Martin Li

MATH 1010E University Mathematics Lecture Notes (week 8) Martin Li 1 L Hospital s Rule Another useful application of mean value theorems is L Hospital s Rule. It helps us to evaluate its of indeterminate

MA Midterm Exam 1 Spring 2012

MA Miterm Eam Spring Hoffman. (7 points) Differentiate g() = sin( ) ln(). Solution: We use the quotient rule: g () = ln() (sin( )) sin( ) (ln()) (ln()) = ln()(cos( ) ( )) sin( )( ()) (ln()) = ln() cos(

The Explicit Form of a Function

Section 3 5 Implicit Differentiation The Eplicit Form of a Function Function Notation requires that we state a function with f () on one sie of an equation an an epression in terms of on the other sie

Additional Exercises for Chapter 10

Aitional Eercises for Chapter 0 About the Eponential an Logarithm Functions 6. Compute the area uner the graphs of i. f() =e over the interval [ 3, ]. ii. f() =e over the interval [, 4]. iii. f() = over

Taylor Series 6B. lim s x. 1 a We can evaluate the limit directly since there are no singularities: b Again, there are no singularities, so:

Taylor Series 6B a We can evaluate the it directly since there are no singularities: 7+ 7+ 7 5 5 5 b Again, there are no singularities, so: + + c Here we should divide through by in the numerator and denominator

MATH Non-Euclidean Geometry Exercise Set #9 Solutions

MATH 6118-090 Non-Euclidean Geometry Exercise Set #9 Solutions 1. Consider the doubly asymptotic triangle AMN in H where What is the image of AMN under the isometry γ 1? Use this to find the hyperbolic

SECTION 3.2 THE PRODUCT AND QUOTIENT RULES 1 8 3

SECTION 3.2 THE PRODUCT AND QUOTIENT RULES 8 3 L P f Q L segments L an L 2 to be tangent to the parabola at the transition points P an Q. (See the figure.) To simplify the equations you ecie to place the

PhysicsAndMathsTutor.com PMT

PhysicsAnMathsTutor.com Version.0: 006 General Certificate of Eucation abc Mathematics 660 MFP Further Pure Mark Scheme 006 eamination - January series Mark schemes are prepare by the Principal Eaminer

Some functions and their derivatives

Chapter Some functions an their erivatives. Derivative of x n for integer n Recall, from eqn (.6), for y = f (x), Also recall that, for integer n, Hence, if y = x n then y x = lim δx 0 (a + b) n = a n

2 a Substituting (1,4,7) and the coefficients. c The normal vector of the plane

Exam-style practice: Paper 1 1 a First we find y and d x. y t t ( = + y = t t + 1 1 y t t t t = + + 1. x= t+ t = 1+ t. We now find the limits in terms of t. x= t = x=.75= t+ t t t +.75= 1± 1+ 15 t = We

Basics Concepts and Ideas First Order Differential Equations. Dr. Omar R. Daoud

Basics Concepts and Ideas First Order Differential Equations Dr. Omar R. Daoud Differential Equations Man Phsical laws and relations appear mathematicall in the form of Differentia Equations The are one

Differentiation ( , 9.5)

Chapter 2 Differentiation (8.1 8.3, 9.5) 2.1 Rate of Change (8.2.1 5) Recall that the equation of a straight line can be written as y = mx + c, where m is the slope or graient of the line, an c is the

( 2) ( ) Hyperbolic Functions 6E. cosh d (cosh sech ) d sinh tanh. cosh. x x x x x x C. x 1 x. 2 a. x x x = + = + cosh dx sinh C 3sinh C.

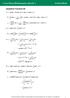Hyperolic Functions 6E a (sinh+ cosh ) cosh+ sinh+ + cosh cosh (cosh sech ) sinh tanh sinh sinh sechtanh sech+ cosh cosh cosh c a a sinh cosh+ cosh sinh sinh + + ( ) + + ( ) ( ) ( ) ( ) arcosh + ( ) +

Chapter 3 Elementary Functions

Chapter 3 Elementary Functions In this chapter, we will consier elementary functions of a complex variable. We will introuce complex exponential, trigonometric, hyperbolic, an logarithmic functions. 23.

Integration: Using the chain rule in reverse

Mathematics Learning Centre Integration: Using the chain rule in reverse Mary Barnes c 999 University of Syney Mathematics Learning Centre, University of Syney Using the Chain Rule in Reverse Recall that

11.4. Differentiating ProductsandQuotients. Introduction. Prerequisites. Learning Outcomes

Differentiating ProductsandQuotients 11.4 Introduction We have seen, in the first three Sections, how standard functions like n, e a, sin a, cos a, ln a may be differentiated. In this Section we see how

INSTRUCTOR S SOLUTIONS MANUAL SECTION 17.1 (PAGE 902)

INSTRUCTOR S SOLUTIONS MANUAL SECTION 7 PAGE 90 CHAPTER 7 ORDINARY DIFFEREN- TIAL EQUATIONS Section 7 Classifing Differential Equations page 90 = 5: st order, linear, homogeneous d d + = : nd order, linear,

6.1: Reciprocal, Quotient & Pythagorean Identities

Math Pre-Calculus 6.: Reciprocal, Quotient & Pythagorean Identities A trigonometric identity is an equation that is valid for all values of the variable(s) for which the equation is defined. In this chapter

FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS

Page of 6 FUNCTIONS OF ONE VARIABLE FUNCTION DEFINITIONS 6. HYPERBOLIC FUNCTIONS These functions which are defined in terms of e will be seen later to be related to the trigonometic functions via comple

Tutorial 1 Differentiation

Tutorial 1 Differentiation What is Calculus? Calculus 微積分 Differential calculus Differentiation 微分 y lim 0 f f The relation of very small changes of ifferent quantities f f y y Integral calculus Integration

A. Incorrect! The letter t does not appear in the expression of the given integral

AP Physics C - Problem Drill 1: The Funamental Theorem of Calculus Question No. 1 of 1 Instruction: (1) Rea the problem statement an answer choices carefully () Work the problems on paper as neee (3) Question

Lectures - Week 10 Introduction to Ordinary Differential Equations (ODES) First Order Linear ODEs

Lectures - Week 10 Introuction to Orinary Differential Equations (ODES) First Orer Linear ODEs When stuying ODEs we are consiering functions of one inepenent variable, e.g., f(x), where x is the inepenent

x = c of N if the limit of f (x) = L and the right-handed limit lim f ( x)

Limit We say the limit of f () as approaches c equals L an write, lim L. One-Sie Limits (Left an Right-Hane Limits) Suppose a function f is efine near but not necessarily at We say that f has a left-hane

Differentiation Rules Derivatives of Polynomials and Exponential Functions

Derivatives of Polynomials an Exponential Functions Differentiation Rules Derivatives of Polynomials an Exponential Functions Let s start with the simplest of all functions, the constant function f(x)

Solutions to Math 41 Second Exam November 4, 2010

Solutions to Math 41 Secon Exam November 4, 2010 1. (13 points) Differentiate, using the metho of your choice. (a) p(t) = ln(sec t + tan t) + log 2 (2 + t) (4 points) Using the rule for the erivative of

Breakout Session 13 Solutions

Problem True or False: If f = 2, then f = 2 False Any time that you have a function of raise to a function of, in orer to compute the erivative you nee to use logarithmic ifferentiation or something equivalent

2 ODEs Integrating Factors and Homogeneous Equations

2 ODEs Integrating Factors an Homogeneous Equations We begin with a slightly ifferent type of equation: 2.1 Exact Equations These are ODEs whose general solution can be obtaine by simply integrating both

February 21 Math 1190 sec. 63 Spring 2017

February 21 Math 1190 sec. 63 Spring 2017 Chapter 2: Derivatives Let s recall the efinitions an erivative rules we have so far: Let s assume that y = f (x) is a function with c in it s omain. The erivative

IMPLICIT DIFFERENTIATION

Mathematics Revision Guies Implicit Differentiation Page 1 of Author: Mark Kulowski MK HOME TUITION Mathematics Revision Guies Level: AS / A Level AQA : C4 Eecel: C4 OCR: C4 OCR MEI: C3 IMPLICIT DIFFERENTIATION

The derivative of a constant function is 0. That is,

NOTES 3: DIFFERENTIATION RULES Name: Date: Perio: LESSON 3. DERIVATIVE OF POLYNOMIALS AND EXPONENTIAL FUNCTIONS Eample : Prove f ( ) 6 is not ifferentiable at 4. Practice Problems: Fin f '( ) using the

TOTAL NAME DATE PERIOD AP CALCULUS AB UNIT 4 ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT /6 10/8 10/9 10/10 X X X X 10/11 10/12

NAME DATE PERIOD AP CALCULUS AB UNIT ADVANCED DIFFERENTIATION TECHNIQUES DATE TOPIC ASSIGNMENT 0 0 0/6 0/8 0/9 0/0 X X X X 0/ 0/ 0/5 0/6 QUIZ X X X 0/7 0/8 0/9 0/ 0/ 0/ 0/5 UNIT EXAM X X X TOTAL AP Calculus

The Explicit Form of a Function

Section 3 5 Implicit Differentiation The Eplicit Form of a Function The normal way we see function notation has f () on one sie of an equation an an epression in terms of on the other sie. We know the

Summary: Differentiation

Techniques of Differentiation. Inverse Trigonometric functions The basic formulas (available in MF5 are: Summary: Differentiation ( sin ( cos The basic formula can be generalize as follows: Note: ( sin

Inverse Circular Functions and Trigonometric Equations. Copyright 2017, 2013, 2009 Pearson Education, Inc.

6 Inverse Circular Functions and Trigonometric Equations Copyright 2017, 2013, 2009 Pearson Education, Inc. 1 6.2 Trigonometric Equations Linear Methods Zero-Factor Property Quadratic Methods Trigonometric

Using the definition of the derivative of a function is quite tedious. f (x + h) f (x)

Derivative Rules Using te efinition of te erivative of a function is quite teious. Let s prove some sortcuts tat we can use. Recall tat te efinition of erivative is: Given any number x for wic te limit

The derivative of a constant function is 0. That is,

NOTES : DIFFERENTIATION RULES Name: LESSON. DERIVATIVE OF POLYNOMIALS AND EXPONENTIAL FUNCTIONS Date: Perio: Mrs. Nguyen s Initial: Eample : Prove f ( ) 4 is not ifferentiable at. Practice Problems: Fin

6.003 Homework #7 Solutions

6.003 Homework #7 Solutions Problems. Secon-orer systems The impulse response of a secon-orer CT system has the form h(t) = e σt cos(ω t + φ)u(t) where the parameters σ, ω, an φ are relate to the parameters

1. Find the equation of a line passing through point (5, -2) with slope ¾. (State your answer in slope-int. form)

INTRO TO CALCULUS REVIEW FINAL EXAM NAME: DATE: A. Equations of Lines (Review Chapter) y = m + b (Slope-Intercept Form) A + By = C (Stanar Form) y y = m( ) (Point-Slope Form). Fin the equation of a line

Section 7.1: Integration by Parts

Section 7.1: Integration by Parts 1. Introuction to Integration Techniques Unlike ifferentiation where there are a large number of rules which allow you (in principle) to ifferentiate any function, the

Math 1A Midterm 2 Fall 2015 Riverside City College (Use this as a Review)

Name Date Miterm Score Overall Grae Math A Miterm 2 Fall 205 Riversie City College (Use this as a Review) Instructions: All work is to be shown, legible, simplifie an answers are to be boxe in the space

Mathematics 116 HWK 14 Solutions Section 4.5 p305. Note: This set of solutions also includes 3 problems from HWK 12 (5,7,11 from 4.5).

Mathematics 6 HWK 4 Solutions Section 4.5 p305 Note: This set of solutions also includes 3 problems from HWK 2 (5,7, from 4.5). Find the indicated it. Use l Hospital s Rule where appropriate. Consider

Math 115 Section 018 Course Note

Course Note 1 General Functions Definition 1.1. A function is a rule that takes certain numbers as inputs an assigns to each a efinite output number. The set of all input numbers is calle the omain of

3) sin 265 cos 25 - cos 265 sin 25 C) Find the exact value by using a sum or difference identity. 4) sin 165 C) - 627

Bonus Assignment Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Use the given information to find the exact value of the expression. 1) sin

Solutions to Problem Sheet for Week 6

THE UNIVERSITY OF SYDNEY SCHOOL OF MATHEMATICS AND STATISTICS Solutions to Problem Sheet for Week 6 MATH90: Differential Calculus (Advanced) Semester, 07 Web Page: sydney.edu.au/science/maths/u/ug/jm/math90/

Chapter 1 Overview: Review of Derivatives

Chapter Overview: Review of Derivatives The purpose of this chapter is to review the how of ifferentiation. We will review all the erivative rules learne last year in PreCalculus. In the net several chapters,

Linear First-Order Equations

5 Linear First-Orer Equations Linear first-orer ifferential equations make up another important class of ifferential equations that commonly arise in applications an are relatively easy to solve (in theory)

23 Implicit differentiation

23 Implicit ifferentiation 23.1 Statement The equation y = x 2 + 3x + 1 expresses a relationship between the quantities x an y. If a value of x is given, then a corresponing value of y is etermine. For

Section 2.1 The Derivative and the Tangent Line Problem

Chapter 2 Differentiation Course Number Section 2.1 The Derivative an the Tangent Line Problem Objective: In this lesson you learne how to fin the erivative of a function using the limit efinition an unerstan

Brief Notes on Differential Equations

Brief Notes on Differential Equations (A) Searable First-Order Differential Equations Solve the following differential equations b searation of variables: (a) (b) Solution ( 1 ) (a) The ODE becomes d and

Implicit Differentiation and Inverse Trigonometric Functions

Implicit Differentiation an Inverse Trigonometric Functions MATH 161 Calculus I J. Robert Buchanan Department of Mathematics Summer 2018 Explicit vs. Implicit Functions 0.5 1 y 0.0 y 2 0.5 3 4 1.0 0.5

HIGHER-ORDER LINEAR DIFFERENTIAL EQUATIONS

CHAPTER 5 HIGHER-ORDER LINEAR DIFFERENTIAL EQUATIONS SECTION 5. INTRODUCTION: SECOND-ORDER LINEAR EQUATIONS In this section the central ideas of the theory of linear differential equations are introduced

1 Functions and Inverses

October, 08 MAT86 Week Justin Ko Functions and Inverses Definition. A function f : D R is a rule that assigns each element in a set D to eactly one element f() in R. The set D is called the domain of f.

Table of Common Derivatives By David Abraham

Prouct an Quotient Rules: Table of Common Derivatives By Davi Abraham [ f ( g( ] = [ f ( ] g( + f ( [ g( ] f ( = g( [ f ( ] g( g( f ( [ g( ] Trigonometric Functions: sin( = cos( cos( = sin( tan( = sec

Math 190 Chapter 3 Lecture Notes. Professor Miguel Ornelas

Math 190 Chapter 3 Lecture Notes Professor Miguel Ornelas 1 M. Ornelas Math 190 Lecture Notes Section 3.1 Section 3.1 Derivatives of Polynomials an Exponential Functions Derivative of a Constant Function

Integration Techniques for the AB exam

For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior

Chapter 9: Complex Numbers

Chapter 9: Comple Numbers 9.1 Imaginary Number 9. Comple Number - definition - argand diagram - equality of comple number 9.3 Algebraic operations on comple number - addition and subtraction - multiplication

3.2 Differentiability

Section 3 Differentiability 09 3 Differentiability What you will learn about How f (a) Might Fail to Eist Differentiability Implies Local Linearity Numerical Derivatives on a Calculator Differentiability

TOPIC 4 CONTINUITY AND DIFFRENTIABILITY SCHEMATIC DIAGRAM

TOPIC 4 CONTINUITY AND DIFFRENTIABILITY SCHEMATIC DIAGRAM Topic Concepts Degree of importance Refrences NCERT Tet Book XII E 007 Continuity& Differentiability Limit of a function Continuity *** E 5 QNo-,

Exercise Set 4.3: Unit Circle Trigonometry

Eercise Set.: Unit Circle Trigonometr Sketch each of the following angles in standard position. (Do not use a protractor; just draw a quick sketch of each angle. Sketch each of the following angles in

Ordinary Differential Equations

Orinary Differential Equations Example: Harmonic Oscillator For a perfect Hooke s-law spring,force as a function of isplacement is F = kx Combine with Newton s Secon Law: F = ma with v = a = v = 2 x 2

1 Lecture 20: Implicit differentiation

Lecture 20: Implicit ifferentiation. Outline The technique of implicit ifferentiation Tangent lines to a circle Derivatives of inverse functions by implicit ifferentiation Examples.2 Implicit ifferentiation

First Order Linear Differential Equations

LECTURE 8 First Orer Linear Differential Equations We now turn our attention to the problem of constructing analytic solutions of ifferential equations; that is to say,solutions that can be epresse in

The derivative of a function f(x) is another function, defined in terms of a limiting expression: f(x + δx) f(x)

Y. D. Chong (2016) MH2801: Complex Methos for the Sciences 1. Derivatives The erivative of a function f(x) is another function, efine in terms of a limiting expression: f (x) f (x) lim x δx 0 f(x + δx)