INSTRUCTOR S SOLUTIONS MANUAL SECTION 17.1 (PAGE 902)
|
|
|
- Sharlene Barber
- 5 years ago
- Views:
Transcription
1 INSTRUCTOR S SOLUTIONS MANUAL SECTION 7 PAGE 90 CHAPTER 7 ORDINARY DIFFEREN- TIAL EQUATIONS Section 7 Classifing Differential Equations page 90 = 5: st order, linear, homogeneous d d + = : nd order, linear, nonhomogeneous d 3 = : st order, nonlinear d 4 + = sin : 3rd order, linear, nonhomogeneous 5 + sin = : nd order, linear, homogeneous = : nd order, nonlinear 7 d 3 dt 3 + t dt + t = t 3 : 3rd order, linear, nonhomogeneous 8 cos d + sin t = 0: st order, nonlinear, homogeneous dt e = 3 : 4th order, linear, homogeneous 0 + e = : nd order, nonlinear If = cos, then + = cos + cos = 0 If = sin, then + = sin + sin = 0 Thus = cos and = sin are both solutions of + = 0 This DE is linear and homogeneous, so an function of the form = A cos + B sin, where A and B are constants, is a solution also Therefore sin cos is a solution A =, B =, and sin + 3 = sin 3 cos + cos 3 sin is a solution, but sin is not since it cannot be represented in the form A cos + B sin If = e, then = e e = 0; if = e, then = e e = 0 Thus e and e are both solutions of = 0 Since = 0 is linear and homogeneous, an function of the form = Ae + Be is also a solution Thus cosh = e + e is a solution, but neither cos nor e is a solution 3 Given that = cosk is a solution of + k = 0, we suspect that = sink is also a solution This is easil verified since Since the DE is linear and homogeneous, = A + B = A cosk + B sink is a solution for an constants A and B It will satisf 3 = π/k = A cosπ + B sinπ = A 3 = π/k = Ak sinπ + Bk cosπ = Bk, provided A = 3 and B = 3/k The required solution is = 3cosk 3 k sink 4 Given that = e k is a solution of k = 0, we suspect that = e k is also a solution This is easil verified since k = k e k k e k = 0 Since the DE is linear and homogeneous, = A + B = Ae k + Be k is a solution for an constants A and B It will satisf 0 = = Ae k + Be k = = Ake k Bke k, provided A = e k /k and B = e k /k The required solution is = k ek k e k 5 B Eercise, = A cos + B sin is a solution of + = 0 for an choice of the constants A and B This solution will satisf 0 = π/ 0 = B A, 3 = π/4 = A + B, provided A = and B = The required solution is = cos + sin + k = k sink + k sink = 0 67
2 SECTION 7 PAGE 90 R A ADAMS: CALCULUS 6 = e r is a solution of the equation = 0if r e r re r e r = 0, that is, if r r = 0 This quadratic has two roots, r =, and r = Since the DE is linear and homogeneous, the function = Ae + Be is a solution for an constants A and B This solution satisfies = 0 = A + B, = 0 = A B, provided A = and B = 0 Thus, the required solution is = e 7 If = =, then = and = 0 Thus + = 0 + = B Eercise we know that = A cos + B sin satisfies the homogeneous DE + = 0 Therefore, b Theorem, = + = + A cos + B sin is a solution of + = This solution satisfies = π = π A, 0 = π = B, provided A = π and B = Thus the required solution is = + π cos + sin 8 If = = e, then = 0 and = 0 Thus = 0 + e = e B Eercise we know that = Ae + Be satisfies the homogeneous DE = 0 Therefore, b Theorem, = + = e + Ae + Be is a solution of = e This solution satisfies 3 d = + Let = v v + dv d = v + v dv d = v v3 v = + v + v + v v 3 dv = d v + ln v = ln +C + ln =C 4 ln =C d = + + v + dv d = + v + v dv d + v = tan v = ln +C = tan ln +C = tan ln +C Let = v 0 = = Ae + B e e, = = Ae B e, provided A = e + /e and B = ee / Thus the required solution is = e+ e+e + e e Section 7 page 907 d = + Solving First-Order Equations Let = v v + dv + v = d v dv d = + v v v = + v v v + v dv = d tan v ln + v = ln +C tan / ln + = ln +C tan / ln + = C 4 d = Let = v v + dv d = 3 + 3v 3 3v + v 3 dv d = + 3v 3v + v 3 v = v4 v3 + v 3 + v v dv d v 4 = Let u = v du = v dv 3 + u u du = ln +C 3 4 ln u + u 4 ln u =ln +C 3ln + ln = 4ln +C + 3 ln 4 4 = C ln + 4 = C + = C 68
3 INSTRUCTOR S SOLUTIONS MANUAL SECTION 7 PAGE d = + cos let = v v + dv d = v + cos v dv d = cos v sec v dv = d tan v = ln +ln C tan = ln C 6 = tan ln C d = e / v + dv d = v e v e v dv = d e v = ln +ln C e / = ln C = ln ln C let =v 7 We require d = + Thus 8 + = d = + C Since, 3 lies on the curve, = 4 + C Thus C = 8 and = 8, or = 4 d = + v + dv d = + v dv d = + v dv d + v = ln + v =ln +C Let = v + = C + = C Since, 3 lies on the curve, 4 = C Thus the curve has equation + = 4 9 If ξ = 0, η = 0, and d = a + b + c e + f+ g, then dη dξ = d = aξ bη c eξ f η g = aξ + bη + a 0 + b 0 + c eξ + f η + e 0 + f 0 + g aξ + bη = eξ + f η provided 0 and 0 are chosen such that a 0 + b 0 + c = 0, and e 0 + f 0 + g = 0 0 The sstem = 0, = 0 has solution 0 =, 0 = Thus, if ξ = and η =, where then dη dξ = ξ + η ξ η d = + 4 3, Let η = vξ v + ξ dv dξ = + v v ξ dv dξ = + v v v = + v v v dξ + v dv = ξ tan v ln + v = ln ξ +C 4 tan η ξ lnξ + η = C Hence the solution of the original equation is 4 tan ln + = C + d + + = 0 d + = 0 + = C e sin + d + e cos + = 0 de sin + + = 0 e sin + + = C 3 e + d + e = 0 d e = 0 e = C 4 + d + = 0 d + + = = C 69
4 SECTION 7 PAGE 907 R A ADAMS: CALCULUS 5 + d = 0 M = +, N = M N N = 3 indep of dµ µ = 3 d µ = d = 0 d ln = 0 ln = C = ln +C 6 e + ln + d + + ln + sin = 0 M = e + ln +, N = + ln + sin M = +, N = + ln + + sin M N N = N ln sin = dµ µ = d µ = d + e + ln + + ln + sin d e + ln + ln cos = 0 e + ln + ln cos = C 7 If µm, d + µn, is eact, then µm, = µn, µ M + µ M = µ N µ µ = M N M Thus M and N must be such that depends onl on N M M 8 + d = µ d µ = 0 M = µ µ N = + 63 µ For eactness we require + 4 µ = [ ]µ + 3 µ = + 3 µ µ = µ µ = + 3 d = 0 d + 3 = = C 9 Consider d + 3 e = 0 Here M =, N = 3 e, M Thus µ =, and N = µ = 3 µ = 3 d 3 + e = 0 d e = 0 e = C, or e = C 0 If µ is an integrating factor for Md+ N = 0, then µm = µn, µ M + µ M = µ N + µ N Thus M and N will have to be such that the right-hand side of the equation µ µ = N M N M depends onl on the product For cos + sin d or + we have M = cos +, sin N = M =, N = sin cos N M sin = + cos + M N = cos + + sin + M N N M = 630
5 INSTRUCTOR S SOLUTIONS MANUAL SECTION 73 PAGE 95 Thus, an integrating factor is given b µ t µt = t µt = t We multipl the original equation b / to make it eact: cos + sin d + = 0 sin d = 0 sin = C The solution is sin = C Section 73 Eistence, Uniqueness, and Numerical Methods page 95 A computer spreadsheet was used in Eercises The intermediate results appearing in the spreadsheet are not shown in these solutions We start with 0 =, 0 = 0, and calculate n+ = n + h, n+ = n + h n + n a For h = 0 we get 5 =, 5 = b For h = 0 we get 0 =, 0 = c For h = 005 we get 0 =, 0 = We start with 0 =, 0 = 0, and calculate n+ = n + h, u n+ = n + h n + n n+ = n + h n + n + n+ + u n+ a For h = 0 we get 5 =, 5 = b For h = 0 we get 0 =, 0 = 486 c For h = 005 we get 0 =, 0 = We start with 0 =, 0 = 0, and calculate n+ = n + h p n = n + n q n = n + h + n + h p n r n = n + h + n + h q n q n = n + h + n + hr n n+ = n + h 6 p n + q n + r n + s n a For h = 0 we get 5 =, 5 = b For h = 0 we get 0 =, 0 = c For h = 005 we get 0 =, 0 = We start with 0 = 0, 0 = 0, and calculate n+ = n + h, n+ = h n e n a For h = 0 we get 0 =, 0 = b For h = 0 we get 0 =, 0 = We start with 0 = 0, 0 = 0, and calculate n+ = n + h, u n+ = n + h n e n n+ = n + h ne n + n+ e u n+ a For h = 0 we get 0 =, 0 = b For h = 0 we get 0 =, 0 = We start with 0 = 0, 0 = 0, and calculate n+ = n + h p n = n e n q n = n + h e n+h/ p n r n = n + h e n+h/q n s n = n + he n+hr n n+ = n + h 6 p n + q n + r n + s n a For h = 0 we get 0 =, 0 = b For h = 0 we get 0 =, 0 = We start with 0 = 0, 0 = 0, and calculate n+ = n + h, n+ = n + h cos n a For h = 0 we get 5 =, 5 = b For h = 0 we get 0 =, 0 = c For h = 005 we get 0 =, 0 = We start with 0 = 0, 0 = 0, and calculate n+ = n + h, u n+ = n + h cos n n+ = n + h cos n + cos u n+ a For h = 0 we get 5 =, 5 = 0868 b For h = 0 we get 0 =, 0 = c For h = 005 we get 0 =, 0 =
6 SECTION 73 PAGE 95 R A ADAMS: CALCULUS 9 We start with 0 = 0, 0 = 0, and calculate n+ = n + h p n = cos n q n = cos n + h/p n r n = cos n + h/q n q n = cos n + hr n n+ = n + h 6 p n + q n + r n + s n a For h = 0 we get 5 =, 5 = b For h = 0 we get 0 =, 0 = c For h = 005 we get 0 =, 0 = We start with 0 = 0, 0 = 0, and calculate n+ = n + h, n+ = n + h cos n a For h = 0 we get 5 =, 5 = b For h = 0 we get 0 =, 0 = c For h = 005 we get 0 =, 0 = We start with 0 = 0, 0 = 0, and calculate n+ = n + h, u n+ = n + h cos n n+ = n + h cos n + cos n+ a For h = 0 we get 5 =, 5 = b For h = 0 we get 0 =, 0 = 0903 c For h = 005 we get 0 =, 0 = We start with 0 = 0, 0 = 0, and calculate n+ = n + h p n = cos n q n = cos n + h/ r n = cos n + h/ q n = cos n + h n+ = n + h 6 p n + q n + r n + s n a For h = 0 we get 5 =, 5 = b For h = 0 we get 0 =, 0 = c For h = 005 we get 0 =, 0 = = + t dt, d = = + 0 = = d = + C = + C C = 3 = 3/ = 3 4 u = + 3 t ut dt du d = 3 u, u = + 0 = du u = 3 d ln u = 3 + C 0 = ln = ln u = 3 + C C = 8 u = e For the problem = f, a = 0, the -step Runge- Kutta method with h = b a gives: 0 = a, 0 = 0, = 0 + h = b p 0 = f a, q 0 = f a + h a + b = f = r 0 s 0 = f a + h = f b = 0 + h 6 p 0 + q 0 + r 0 + s 0 = b a a + b f a + 4 f + f b, 6 which is the Simpson s Rule approimation to b a f d based on subintervals of length h/ 6 If φ0 = A 0 and φ kφ on an interval [0, X], where k > 0 and X > 0, then d d φ e k = ek φ ke k φ e k 0 Thus φ/e k is increasing on [0, X] Since its value at = 0isφ0 = A 0, therefore φ/e k A on [0, X], and φ Ae k there 7 a Suppose u = u, = +, and v = + v on [0, X], where u0 = 0 = v0 =, and X > 0 is such that v is defined on [0, X] In part b below, we will show that X <, and we assume this fact now Since all three functions are increasing on [0, X], we have u,, and v on [0, X] 63
7 INSTRUCTOR S SOLUTIONS MANUAL SECTION 74 PAGE 99 If φ = u, then φ0 = 0 and φ = + u u + u u φ on [0, X] B Eercise 6, φ 0on[0, X], and so u there Similarl, since X <, if φ = v, then φ0 = 0 and φ = + v v v + v φ on [0, X], so v there b The IVP u = u, u0 = has solution u =, obtained b separation of variables This solution is valid for < The IVP v = + v, v0 = has solution v = tan + π 4, also obtained b separation of variables It is valid onl for 3π/4 < <π/4 Observe that π/4 <, proving the assertion made about v in part a B the result of part a, the solution of the IVP = +, 0 =, increases on an interval [0, X] and as X from the left, where X is some number in the interval [π/4, ] c Here are some approimations to for values of near 09 obtained b the Runge-Kutta method with 0 = 0 and 0 = : For h = 005 n = 7 n = 085 n = 3739 n = 8 n = 090 n = n = 9 n = 095 n = For h = 00 n = 43 n = 086 n = n = 44 n = 088 n = n = 45 n = 090 n = n = 46 n = 09 n = n = 47 n = 094 n = For h = 00 n = 86 n = 086 n = n = 87 n = 087 n = n = 88 n = 088 n = n = 89 n = 089 n = n = 90 n = 090 n = n = 9 n = 09 n = n = 9 n = 09 n = n = 93 n = 093 n = n = 94 n = 094 n = The values are still in reasonable agreement at = 09, but the start to diverge quickl thereafter This suggests that X is slightl greater than 09 Section 74 Differential Equations of Second Order page 99 If = e, then 3 + = e 3 + = 0, so is a solution of the DE 3 + = 0 Let = e v Then = e v + v, = e v + v + v 3 + = e v + v + v 3v 3v + v = e v v satisfies 3 + = 0 provided w = v satisfies w w = 0 This equation has solution v = w = C e, so v = C e + C Thus the given DE has solution = e v = C e + C e If = e, then 6 = e = 0, so is a solution of the DE 6 = 0 Let = e v Then = e v v, = e v 4v + 4v 6 = e v 4v + 4v v + v 6v = e v 5v satisfies 6 = 0 provided w = v satisfies w 5w = 0 This equation has solution v = w = C /5e 5,sov = C e 5 + C Thus the given DE has solution = e v = C e 3 + C e 3 If = on 0,, then + = 0 + = 0, so is a solution of the DE + = 0 Let = v Then = v + v, = v + v + = 3 v + v + v + v v = v + 4v satisfies + = 0 provided w = v satisfies w + 4w = 0 This equation has solution v = w = 3C 4 obtained b separation of variables, so v = C 3 + C Thus the given DE has solution = v = C + C 633
8 SECTION 74 PAGE 99 R A ADAMS: CALCULUS 4 If = on 0,, then = = 0, so is a solution of the DE = 0 Let = v Then Therefore = / cos is a solution of the Bessel equation + + = 0 4 Now let = / cos v Then = v + v, = v + 4v + v = 4 v v + v 3 3 v 6 v + 4 v = 3 v + v satisfies = 0 provided w = v satisfies w + w = 0 This equation has solution v = w = C / obtained b separation of variables, so v = C ln + C Thus the given DE has solution = v = C ln + C 5 If =, then = and = 0 Thus = 0 Now let = v Then = v + v, = v + v Substituting these epressions into the differential equation we get v + 3 v v v 3 v v + v + v = 0 3 v 3 v = 0, or v v = 0, which has solution v = C + C e Hence the general solution of the given differential equation is 6 If = / cos, then Thus = C + C e = 3/ cos / sin = 3 4 5/ cos + 3/ sin / cos = 3 4 / cos + / sin 3/ cos = 0 / cos / sin + 3/ cos 4 / cos = 3/ cos v / sin v + / cos v = 3 4 5/ cos v + 3/ sin v 3/ cos v / cos v / sin v + / cos v If we substitute these epressions into the equation, man terms cancel out and we are left with the equation cos v sin v = 0 Substituting u = v, we rewrite this equation in the form cos du = sin u d du u = tan d ln u =ln sec +C 0 Thus v = u = C sec, from which we obtain v = C tan + C Thus the general solution of the Bessel equation is = / cos v = C / sin + C / cos 7 If = and = where satisfies + a + a 0 = f, then = and = a 0 a + f Thus d 0 0 = + d a 0 a f 8 If satisfies n + a n n + +a + a 0 = f, then let =, =, 3 =, n = n Therefore =, = 3, n = n, and n = a 0 a a 3 a n n + f, 634
9 INSTRUCTOR S SOLUTIONS MANUAL SECTION 75 PAGE 93 and we have d d n + = f 9 If = C e λ v, then a 0 a a a n n Section 75 Linear Differential Equations with Constant Coefficients page = 0 Auiliar: r 3 4r + 3r = 0 rr r 3 = 0 r = 0,, 3 General solution: = C + C e t + C 3 e 3t 4 + = 0 Auiliar: r 4 r + = 0 r = 0 r =,,, General solution: = C e t + C te t + C 3 e t + C 4 te t 0 = C λe λ v = C e λ Av = A provided λ and v satisf Av = λv λ 3 λ = 6 5λ + λ = λ 5λ + 4 = λ λ 4 = 0 if λ = orλ = 4 Let A = 3 If λ = and Av = v, then v A = = 3 v v v v + v = 0 Thus we ma take v = v = If λ = 4 and Av = 4v, then v v A = = 4 v 3 v = 0 v Thus we ma take v = v = v B the result of Eercise 9, = e v and = e 4 v are solutions of the homogeneous linear sstem = A Therefore the general solution of the sstem is that is = C e v + C e 4 v, = C e = C e + C e 4 = C e + C e 4 + C e 4, or = 0 Auiliar: r 4 + r + = 0 r + = 0 r = i, i, i, i General solution: = C cos t + C sin t + C 3 t cos t + C 4 t sin t = 0 Auiliar: r 4 + 4r 3 + 6r + 4r + = 0 r + 4 = 0 r =,,, General solution: = e t C + C t + C 3 t + C 4 t 3 5 If = e t, then 4 = e t = 0 The auiliar equation for the DE is r 3 r 4 = 0, for which we alrea know that r = is a root Dividing the left side b r, we obtain the quotient r + r + Hence the other two auiliar roots are ± i General solution: = C e t + C e t cos t + C 3 e t sin t 6 Au eqn: r r r 4 = 0 r + r r r + = 0 r =,,,,,,, The general solution is = e t C + C t + C 3 t + C 4 t 3 + e t C 5 + C 6 t + e t C 7 + C 8 t 7 + = 0 au: rr r + = 0 r r + = 0 r = 0, r =, Thus = A + B ln 8 3 = 0 rr r 3 = 0 r r 3 = 0 r 3r + = 0 r = and r = 3 Thus, = A + B 3 635
10 SECTION 75 PAGE 93 R A ADAMS: CALCULUS 9 + = 0 au: rr + r = 0 r =± = A + B 0 Consider + 5 = 0 Since a =, b =, and c = 5, therefore b a < 4ac Then k = a b/a = and ω = 4 Thus, the general solution is = A cosln + B sinln + = 0 au: rr + r = 0 r = 0, 0 Thus = A + B ln Given that + + = 0 Since a =, b =, c = therefore b a < 4ac Then k = a b/a = 0 and ω = Thus, the general solution is = A cosln + B sinln = 0 Tring = r leads to the auiliar equation rr r + r = 0 r 3 3r + 3r = 0 r 3 = 0 r =,, Thus = is a solution To find the general solution, tr = v Then = v + v, = v + v, = v + 3v Now 3 + = 4 v v + v + v v = v + 3v + v, and is a solution of the given equation if v = w is a solution of w + 3w + w = 0 This equation has auiliar equation rr + 3r + = 0, that is r + = 0, so its solutions are v = w = C + C 3 ln v = C + C ln + C 3 ln The general solution of the given equation is, therefore, = C + C ln + C 3 ln For a particular solution p of the given equation tr = A This satisfies the given equation if A = / Thus the general solution of the given equation is = + C e + C e + = The complementar function is h = C e + C e,as shown in Eercise For a particular solution tr = A + B Then = A and = 0, so satisfies the given equation if = A A + B = A B A We require A B = 0 and A =, so A = / and B = /4 The general solution of the given equation is = C e + C e 3 + = e The complementar function is h = C e + C e,as shown in Eercise For a particular solution tr = Ae Then = Ae and = Ae,so satisfies the given equation if e = e A A A = Ae We require A = / The general solution of the given equation is = e + C e + C e 4 + = e The complementar function is h = C e + C e,as shown in Eercise For a particular solution tr = Ae Then = Ae +, = Ae +, Section 76 Nonhomogeneous Linear Equations page 99 + = The auiliar equation for + = 0is r + r = 0, which has roots r = and r = Thus the complementar function is h = C e + C e so satisfies the given equation if e = Ae = 3Ae We require A = /3 The general solution of the given equation is = 3 e + C e + C 3 e 636
11 INSTRUCTOR S SOLUTIONS MANUAL SECTION 76 PAGE = The homogeneous equation has auiliar equation r + r + 5 = 0 with roots r = ± i Thus the complementar function is h = C e cos + C e sin For a particular solution, tr = A + B + C Then = A + B and = A We have = = A + 4A + B + 5A + 5B + 5C Thus we require 5A =, 4A + 5B = 0, and A + B + 5C = 0 This gives A = /5, B = 4/5, and C = /5 The given equation has general solution = e C cos + C sin = e The homogeneous equation has auiliar equation r + 4r + 4 = 0 with roots r =, Thus the complementar function is h = C e + C e For a particular solution, tr = A e Then = e A A and = e A 8A+4A We have e = = e A 8A + 4A + 8A 8A + 4A = Ae Thus we require A = / The given equation has general solution = e + C + C = The complementar function is = C cos + C sin For the given equation, tr = A + B + C Then = + 4 = A + 4A + 4B + 4C Thus A + 4C = 0, 4A =, 4B = 0, and we have A = 4, B = 0, and C = The given equation has 8 general solution = C cos + C sin 7 6 = e The homogeneous equation has auiliar equation r r 6 = 0 with roots r = and r = 3 Thus the complementar function is h = C e + C e 3 For a particular solution, tr = Ae Then = e A A and = e 4A + 4A We have e = 6 = e 4A + 4A A + A 6A = 5Ae Thus we require A = /5 The given equation has general solution = 5 e + C e + C e = e sin The homogeneous equation has auiliar equation r + r + = 0 with roots r = ± i Thus the complementar function is h = C e cos + C e sin For a particular solution, tr = Ae cos + Be sin Then = A + Be cos + B Ae sin = Be cos Ae sin This satisfies the nonhomogeneous DE if e sin = + + = e cos B + A + B + A + e sin A + B A + B = e cos 4A + 4B + e sin 4B 4A Thus we require A + B = 0 and 4B A =, that is, B = A = /8 The given equation has general solution = e 8 sin cos + e C cos + C sin = e sin The complementar function is the same as in Eercise 9, but for a particular solution we tr = Ae cos + Be sin = e cos A A + B + e sin B B A = e cos B B A + e sin A A B 637
12 SECTION 76 PAGE 99 R A ADAMS: CALCULUS This satisfies the nonhomogeneous DE if e sin = + + = Be cos Ae sin Thus we require B = 0 and A = / The given equation has general solution = e cos + e C cos + C sin + = e The homogeneous equation has auiliar equation r + r = 0 with roots r = 0 and r = Thus the complementar function is h = C + C e For a particular solution, tr = A + B + Ce Then = A + B + e C C = B + e C + C This satisfies the nonhomogeneous DE if e = + = A + B + B Ce Thus we require A + B = 4, B =, and C =, that is, A =, B =, C = The given equation has general solution = + e + C + C e + + = e The homogeneous equation has auiliar equation r + r + = 0 with roots r = and r = Thus the complementar function is h = C e + C e For a particular solution, tr = e A + B 3 Then = e A + 3B A B 3 = e A + 6B 4A 6B A + B 3 This satisfies the nonhomogeneous DE if e = + + = e A + 6B Thus we require A = 0 and B = /6 The given equation has general solution = 6 3 e + C e + C e 3 + = e The complementar function is h = C e + C e For a particular solution use p = e u + e u, where the coefficients u and u satisf Thus e u + e u = e u = 3 e u = 3 e Thus p = 3 e 6 e e u + e u = 0 solution of the given equation is u = 3 e u = 6 e = e The general = e + C e + C e 4 + = e The complementar function is h = C e + C e For a particular solution use p = e u + e u, where the coefficients u and u satisf Thus e u + e u = e e u + e u = 0 u = 3 e3 u = 9 e3 u = 3 u = 3 Thus p = 9 e + 3 e The general solution of the given equation is = 9 e + 3 e + C e + C e = 3 e + C e + C 3 e 5 + = If = A, then = A and = A Thus = + = A + A A = 3A, 638
13 INSTRUCTOR S SOLUTIONS MANUAL SECTION 76 PAGE 99 so A = /3 A particular solution of the given equation is = /3 The auiliar equation for the homogeneous equation + = 0is4rr + r = 0, or r = 0, which has solutions r =± Thus the general solution of the given equation is = 3 + C + C 6 + = r has a solution of the form = A r provided r = ± If this is the case, then r = A r rr + r = A r r Thus A = /r and a particular solution of the DE is = r r 7 + = Tr = A ln Then = Aln + and = A/ We have = A + Aln + A ln = A Thus A = / The complementar function was obtained in Eercise 5 The given equation has general solution = ln + C + C 8 + = Tr = u + u, where u and u satisf u + u = 0, u u = Solving these equations for u and u, we get u =, u = Thus u = ln and u = A particular solution is 4 = ln 4 The term /4 can be absorbed into the term C in the complementar function, so the general solution is = ln + C + C = 3 Since and e are independent solutions of the corresponding homogeneous equation, we can write a solution of the given equation in the form = u + e u, where u and u are chosen to satisf u + e u = 0, u + + e u = Solving these equations for u and u, we get u = and u = e Thus u = and u = e The particular solution is = Since is a solution of the homogeneous equation, we can absorb that term into the complementar function and write the general solution of the given DE as = + C + C e = 3/ 4 A particular solution can be obtained in the form = / cos u + / sin u, where u and u satisf / cos u + / sin u = 0 3/ cos / sin u 3/ sin / cos u = / We can simplif these equations b dividing the first b /, and adding the first to times the second, then dividing the result b / The resulting equations are cos u + sin u = 0 sin u + cos u =, which have solutions u = sin, u = cos, so that u = cos and u = sin Thus a particular solution of the given equation is = / cos + / sin = / The general solution is = / + C cos + C sin 639
14 SECTION 76 PAGE 99 R A ADAMS: CALCULUS Section 77 Series Solutions of Differential Equations page 933 = Tr = = = a n n nn a n n n= n + n + a n+ n 0 = = n + n + a n+ n a n n+ = n + n + a n+ n a n n n= = a + 6a 3 ] + [n + n + a n+ a n n n= a n Thus a = a 3 = 0, and a n+ = for n n + n + Given a 0 and a we have a 4 = a a 8 = a 4 a 4n = = 7 8 = a a n 4n a 0 4 n n! 3 7 4n a 5 = a 4 5 a 9 = a 5 a 4n+ = 8 9 = a n4n + a = 4 n n! 5 9 4n + a 4n+3 = a 4n+ = =a 3 = a = 0 The solution is = a a + a 4n 4 n n! 3 7 4n 4n+ 4 n n! 5 9 4n + = Tr a n n Then = na n n = na n n n= = nn a n n = n + n + a n+ n Thus we have 0 = = n + n + a n+ n a n n+ = n + n + a n+ n a n n = a + ] [n + n + a n+ a n n a n Thus a = 0 and a n+ = for n n + n + Given a 0 and a,wehave a 3 = a 0 3 a 6 = a = a = 4 a 0 6! a 9 = a = 4 7 a 0 9! a 3n = 4 3n a 0 3n! a 4 = a 3 4 = a 4! a 7 = a = 5 a 7! a 3n+ = 5 3n a 3n +! 0 = a = a 5 = a 8 = =a 3n+ Thus the general solution of the given equation is = a a 4 3n 3n 3n! 5 3n 3n+ 3n +! 640
15 INSTRUCTOR S SOLUTIONS MANUAL SECTION 77 PAGE Let + + = 0 0 = 0 = = a n n = na n n n= = nn a n n = n + n + a n+ n Substituting these epressions into the differential equation, we get n + n + a n+ n + na n n + a n n = 0, a + + so [n + n + a n+ + n + a n ] n = 0 It follows that a =, a n+ = a n, n =,, 3, n + Since a 0 = 0 =, and a = 0 =, we have Thus, 0 = + + = n + n + a n+ n + na n n + a n n = a + a 0 + ] [n + n + a n+ + n + a n n Since coefficients of all powers of must vanish, therefore a + a 0 = 0 and, for n, that is, n + n + a n+ + n + a n = 0, a n+ = a n n + If 0 =, then a 0 =, a =, a 4 =!, a 6 = 3 3!, a 8 = 4 4!, If 0 = 0, then a = a 3 = a 5 = = 0 Hence, = = 5 + sin = 0, 0 =, 0 = 0 Tr n n n! n = a 0 + a + a + a a a a 0 = a = a 4 = 3 a 6 = 3 5 a 8 = The patterns here are obvious: a = n a n = 3 5 n = n n n! n! Thus = n [ n n! n 4 If = a 3 = a 5 = 4 a 7 = 4 6 a 9 = n! a n+ = n n n! ] + n+ n n! a n n, then = na n n and = nn a n n = n + n + a n+ n n= Then a 0 = and a = 0 We have = a + 6a 3 + a 4 + 0a sin = a + a a a = + a 3 + a a 4 6 a Hence we must have a = 0, 6a 3 + = 0, a 4 = 0, 0a 5 + a 6 = 0, That is, a = 0, a 4 = 0, a 3 = 6, a 5 = The solution is 0 = = 0, 0 = 0, 0 = Tr = a n n 64
16 SECTION 77 PAGE 933 R A ADAMS: CALCULUS Then a 0 = 0 and a = We have = = na n n nn a n n n= 0 = + 9 = n + n + a n+ n nn a n n na n n + 9 a n n n= = a + 9a 0 + 6a 3 + 8a ] + [n + n + a n+ n 9a n n n= Thus a + 9a 0 = 0, 6a 3 + 8a = 0, and Therefore we have a n+ = n 9a n n + n + a = a 4 = a 6 = =0 a 3 = 4 3, a 5 = 0 = a 7 = a 9 = The initial-value problem has solution = = 0 Since = 0 is a regular singular point of this equation, tr = a n n+µ a 0 = = = Then we have n + µa n n+µ n + µn + µ a n n+µ 0 = [ ] = 3n + µ n + µ a n n+µ + a n n+µ = 3µ µ µ [ ] + 3n + µ n + µ a n + a n n+µ a n Thus 3µ µ = 0 and a n = 3n + µ n + µ for n There are two cases: µ = 0 and µ = /3 a n CASE I µ = 0 Then a n = n3n Since a 0 = we have a =, a = 5 a 3 = a n = One series solution is = n n! 5 3n CASE II µ = 3 Then n n n! 5 3n a n a n = 3 n + = a n 3 n + n3n + 3 Since a 0 = wehave a = 4, a = 4 7 a 3 = a n = n n! 4 7 3n + A second series solution is = /3 n n + n! 4 7 3n = 0 Since = 0 is a regular singular point of this equation, tr = a n n+µ a 0 = = = n + µa n n+µ n + µn + µ a n n+µ 64
17 INSTRUCTOR S SOLUTIONS MANUAL REVIEW EXERCISES 7 PAGE Then we have 0 = + + [ ] = n + µn + µ + n + µ a n n+µ + a n n+µ+ = n + µ a n n+µ + a n n+µ n= = µ µ + + µ a µ ] + [n + µ a n + a n n+µ n= Thus µ = 0, a = 0, and a n = a n n for n It follows that 0 = a = a 3 = a 5 =, and, since a 0 =, One series solution is a =, a 4 = 4, n a n = 4 n = n n n! = + n n n n! Review Eercises 7 page 934 d = = d ln = + C = Ce d = e sin e = sin d e = cos + C = lnc cos d = + d = d d e = e d = e e = e d = e 4 e + C = 4 + Ce d = + v + dv d = + v v dv d = + v v v dv v = d let = v v = v v lnv = ln + ln C = ln C = C = C d = + + d + = 0 eact d + = 0 + = C + e = d + e + e d + + e = 0 eact d + e + e = 0 + e + e = C d dt = dp dt let p = /dt dt = p dp p = dt p = C t dt = p = C t = dt C t = ln t C +C 8 d dt + 5 dt + = 0 Au: r + 5r + = 0 r = /, = C e t/ + C e t = 0 Au: 4r 4r + 5 = 0 r + 4 = 0 r = ± i = C e / cos + C e / sin 0 + = 0 Au: rr + = 0 r r + = 0 r = ± i = C / cos ln + C / sin ln 643
18 REVIEW EXERCISES 7 PAGE 934 R A ADAMS: CALCULUS t d dt t dt + 5 = 0 Au: rr r + 5 = 0 3 r + 4 = 0 r = ± i = C t cosln t + C t sinln t d 3 dt d + 6 = 0 dt dt Au: r 3 + 8r + 6r = 0 rr + 4 = 0 r = 0, 4, 4 = C + C e 4t + C 3 te 4t d d 5 d + 6 = e + e 3 Au: r 5r + 6 = 0 r =, 3 Complementar function: = C e + C e 3 Particular solution: = Ae + Be 3 = Ae + B + 3e 3 = Ae + B6 + 9e 3 Thus A =, B = 4, C = 6 The general solution is = C e + C e 6 d d = 3 The corresponding homogeneous equation has auiliar equation rr = 0, with roots r = and r =, so the complementar function is = C + C / A particular solution of the nonhomogeneous equation can have the form = A 3 Substituting this into the DE gives 6A 3 A 3 = 3, so that A = /4 The general solution is = C + C 4 e + e 3 = Ae Be = Ae + Be 3 Thus A = / and B = The general solution is = e + e 3 + C e + C e 3 d d = e d Same complementar function as in Eercise 3: C e + C e 3 For a particular solution we tr = A + Be Substituting this into the given DE leads to e = A Be Ae, d =, = = d 3 = 3 + C = 8 + C C = 7 3 = 3 7 = 3 7 /3 d =, = = d = C = + C C = = + = + d =, 0 = Let = v Then + 5 so that we need A = / and B = A = The general solution is = + e + C e + C e 3 d d + d + = Au: r + r + = 0 has solutions r =, Complementar function: = C e + C e Particular solution: tr = A + B + C Then v + dv d = v + v dv d = v v3 v = + v + v + v v 3 dv = d ln v =ln +ln C v = v = lncv = lnc C = e /, 0 = C = = A + A + B + A + B + C = e /, or = e / 644
19 INSTRUCTOR S SOLUTIONS MANUAL REVIEW EXERCISES 7 PAGE cos = cos, π = d d e sin = e sin + cos = cos e sin d d e sin = e sin + C = + Ce sin = + Ce 0 C = = e sin = 0, 0 =, 0 = Au: r + 3r + = 0 r =, = Ae + Be = A + B = Ae Be = A B Thus B = 3, A = 4 The solution is = 4e 3e π = 0, = 0, = π Au: r + r + + π = 0 r = ± πi = Ae cosπ + Be sinπ = e cosπ A + Bπ+ e sinπ B Aπ Thus Ae = 0 and A Bπe = π, so that A = 0 and B = e The solution is = e sinπ = 0, = e 5, = 0 Au: r + 0r + 5 = 0 r = 5, 5 = Ae 5 + Be 5 = 5Ae 5 + B 5e 5 We require e 5 = A + Be 5 and 0 = e 5 5A 4B Thus A + B = and 5A = 4B, so that B = 5 and A = 4 The solution is = 4e 5 + 5e = 0, e = e, e = 0 Au: rr 3r + 4 = 0, or r = 0, so that r =, 5 = A + B ln = A + B ln + B We require e = Ae + Be and 0 = Ae + 3Be Thus A + B = and A = 3B, so that A = 3 and B = The solution is = 3 ln, valid for > 0 d dt + 4 = 8et, 0 =, 0 = Complementar function: = C cost + C sint Particular solution: = Ae t, provided 4A + 4A = 8, that is, A = Thus = e t + C cost + C sint = e t C sint + C cost We require = 0 = + C and = 0 = + C Thus C = 0 and C = The solution is = e t sint 6 d d + 5 d 3 = 6 + 7e/, 0 = 0, 0 = Au: r + 5r 3 = 0 r = /, 3 Complementar function: = C e / + C e 3 Particular solution: = A + Be / = Be / + = Be / + 4 We need Be / A = 6 + 7e / This is satisfied if A = and B = The general solution of the DE is = + e / + C e / + C e 3 Now the initial conditions impl that 0 = 0 = + C + C = 0 = + C 3C, which give C = /7, C = /7 Thus the IVP has solution = + e / + 7 e/ + e 3 7 [ + Ae sin + cos ] d + [e cos + B sin ] = 0 is Md+ N We have M = + Ae cos sin N = e cos + B sin + e cos These epressions are equal and the DE is eact if A = and B = If so, the left side of the DE is dφ,, where φ, = e sin + cos The general solution is e sin + cos = C d + = 0 Multipl b n : n + 3 d + n+ = 0 is eact provided 6 n = n + n, that is, provided n = 5 In this case the left side is dφ, where φ, =
20 REVIEW EXERCISES 7 PAGE 934 R A ADAMS: CALCULUS The general solution of the given DE is = C 9 + cot + + cot = 0 If =, then = and = 0, so the DE is clearl satisfied b To find a second, independent solution, tr = v Then = v + v, and = v + v Substituting these epressions into the given DE, we obtain v + 3 v v + v + cot + v + cot = 0 3 v 3 v cot = 0, or, putting w = v, w = cot w, that is, dw cos d = w sin ln w = ln sin + ln C v = w = C sin v = C C cos A second solution of the DE is cos, and the general solution is = C + C cos 30 + cot + + cot = 3 sin Look for a particular solution of the form = u + cos u, where u + cos u = 0 u + cos sin u = sin Divide the first equation b and subtract from the second equation to get sin u = sin Thus u = and u = The first equation now gives u = cos, so that u = sin The general solution of the DE is = sin cos + C + C cos 3 Suppose = f, and 0 = 0, where f, is continuous on the whole -plane and satisfies f, K there B the Fundamental Theorem of Calculus, we have Therefore, 0 = 0 = 0 t dt = 0 0 K 0 f t, t dt Thus is bounded above and below b the lines = 0 ± K 0, and cannot have a vertical asmptote anwhere Remark: we don t seem to have needed the continuit of f/, onl the continuit of f to enable the use of the Fundamental Theorem 646
4.317 d 4 y. 4 dx d 2 y dy. 20. dt d 2 x. 21. y 3y 3y y y 6y 12y 8y y (4) y y y (4) 2y y 0. d 4 y 26.
 38 CHAPTER 4 HIGHER-ORDER DIFFERENTIAL EQUATIONS sstems are also able, b means of their dsolve commands, to provide eplicit solutions of homogeneous linear constant-coefficient differential equations.
38 CHAPTER 4 HIGHER-ORDER DIFFERENTIAL EQUATIONS sstems are also able, b means of their dsolve commands, to provide eplicit solutions of homogeneous linear constant-coefficient differential equations.
Practice Midterm Solutions
 Practice Midterm Solutions Math 4B: Ordinary Differential Equations Winter 20 University of California, Santa Barbara TA: Victoria Kala DO NOT LOOK AT THESE SOLUTIONS UNTIL YOU HAVE ATTEMPTED EVERY PROBLEM
Practice Midterm Solutions Math 4B: Ordinary Differential Equations Winter 20 University of California, Santa Barbara TA: Victoria Kala DO NOT LOOK AT THESE SOLUTIONS UNTIL YOU HAVE ATTEMPTED EVERY PROBLEM
Math3B Exam #02 Solution Fall 2017
 . Integrate. a) 8 MathB Eam # Solution Fall 7 e d b) ln e e d . Integrate. 6 d . Integrate. sin cos d 4. Use Simpsons Rule with n 6 to approimate sin d. Then use integration to get the eact value. 6 6
. Integrate. a) 8 MathB Eam # Solution Fall 7 e d b) ln e e d . Integrate. 6 d . Integrate. sin cos d 4. Use Simpsons Rule with n 6 to approimate sin d. Then use integration to get the eact value. 6 6
67. (a) Use a computer algebra system to find the partial fraction CAS. 68. (a) Find the partial fraction decomposition of the function CAS
 SECTION 7.5 STRATEGY FOR INTEGRATION 483 6. 2 sin 2 2 cos CAS 67. (a) Use a computer algebra sstem to find the partial fraction decomposition of the function 62 63 Find the area of the region under the
SECTION 7.5 STRATEGY FOR INTEGRATION 483 6. 2 sin 2 2 cos CAS 67. (a) Use a computer algebra sstem to find the partial fraction decomposition of the function 62 63 Find the area of the region under the
Higher Order Linear Equations
 C H A P T E R 4 Higher Order Linear Equations 4.1 1. The differential equation is in standard form. Its coefficients, as well as the function g(t) = t, are continuous everywhere. Hence solutions are valid
C H A P T E R 4 Higher Order Linear Equations 4.1 1. The differential equation is in standard form. Its coefficients, as well as the function g(t) = t, are continuous everywhere. Hence solutions are valid
Additional Topics in Differential Equations
 0537_cop6.qd 0/8/08 :6 PM Page 3 6 Additional Topics in Differential Equations In Chapter 6, ou studied differential equations. In this chapter, ou will learn additional techniques for solving differential
0537_cop6.qd 0/8/08 :6 PM Page 3 6 Additional Topics in Differential Equations In Chapter 6, ou studied differential equations. In this chapter, ou will learn additional techniques for solving differential
SEPARABLE EQUATIONS 2.2
 46 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 4. Chemical Reactions When certain kinds of chemicals are combined, the rate at which the new compound is formed is modeled b the autonomous differential equation
46 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 4. Chemical Reactions When certain kinds of chemicals are combined, the rate at which the new compound is formed is modeled b the autonomous differential equation
Basics Concepts and Ideas First Order Differential Equations. Dr. Omar R. Daoud
 Basics Concepts and Ideas First Order Differential Equations Dr. Omar R. Daoud Differential Equations Man Phsical laws and relations appear mathematicall in the form of Differentia Equations The are one
Basics Concepts and Ideas First Order Differential Equations Dr. Omar R. Daoud Differential Equations Man Phsical laws and relations appear mathematicall in the form of Differentia Equations The are one
2.2 SEPARABLE VARIABLES
 44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
9 11 Solve the initial-value problem Evaluate the integral. 1. y sin 3 x cos 2 x dx. calculation. 1 + i i23
 Mock Exam 1 5 8 Solve the differential equation. 7. d dt te t s1 Mock Exam 9 11 Solve the initial-value problem. 9. x ln x, 1 3 6 Match the differential equation with its direction field (labeled I IV).
Mock Exam 1 5 8 Solve the differential equation. 7. d dt te t s1 Mock Exam 9 11 Solve the initial-value problem. 9. x ln x, 1 3 6 Match the differential equation with its direction field (labeled I IV).
Math 181, Exam 2, Fall 2014 Problem 1 Solution. sin 3 (x) cos(x) dx.
 Math 8, Eam 2, Fall 24 Problem Solution. Integrals, Part I (Trigonometric integrals: 6 points). Evaluate the integral: sin 3 () cos() d. Solution: We begin by rewriting sin 3 () as Then, after using the
Math 8, Eam 2, Fall 24 Problem Solution. Integrals, Part I (Trigonometric integrals: 6 points). Evaluate the integral: sin 3 () cos() d. Solution: We begin by rewriting sin 3 () as Then, after using the
µ Differential Equations MAΘ National Convention 2017 For all questions, answer choice E) NOTA means that none of the above answers is correct.
 µ Differential Equations MAΘ National Convention 07 For all questions, answer choice E) NOTA means that none of the above answers is correct.. C) Since f (, ) = +, (0) = and h =. Use Euler s method, we
µ Differential Equations MAΘ National Convention 07 For all questions, answer choice E) NOTA means that none of the above answers is correct.. C) Since f (, ) = +, (0) = and h =. Use Euler s method, we
First Order Equations
 10 1 Linear and Semilinear Equations Chapter First Order Equations Contents 1 Linear and Semilinear Equations 9 Quasilinear Equations 19 3 Wave Equation 6 4 Sstems of Equations 31 1 Linear and Semilinear
10 1 Linear and Semilinear Equations Chapter First Order Equations Contents 1 Linear and Semilinear Equations 9 Quasilinear Equations 19 3 Wave Equation 6 4 Sstems of Equations 31 1 Linear and Semilinear
2016 FAMAT Convention Mu Integration 1 = 80 0 = 80. dx 1 + x 2 = arctan x] k2
![2016 FAMAT Convention Mu Integration 1 = 80 0 = 80. dx 1 + x 2 = arctan x] k2 2016 FAMAT Convention Mu Integration 1 = 80 0 = 80. dx 1 + x 2 = arctan x] k2](/thumbs/96/127235785.jpg) 6 FAMAT Convention Mu Integration. A. 3 3 7 6 6 3 ] 3 6 6 3. B. For quadratic functions, Simpson s Rule is eact. Thus, 3. D.. B. lim 5 3 + ) 3 + ] 5 8 8 cot θ) dθ csc θ ) dθ cot θ θ + C n k n + k n lim
6 FAMAT Convention Mu Integration. A. 3 3 7 6 6 3 ] 3 6 6 3. B. For quadratic functions, Simpson s Rule is eact. Thus, 3. D.. B. lim 5 3 + ) 3 + ] 5 8 8 cot θ) dθ csc θ ) dθ cot θ θ + C n k n + k n lim
Engineering Mathematics I
 Engineering Mathematics I_ 017 Engineering Mathematics I 1. Introduction to Differential Equations Dr. Rami Zakaria Terminolog Differential Equation Ordinar Differential Equations Partial Differential
Engineering Mathematics I_ 017 Engineering Mathematics I 1. Introduction to Differential Equations Dr. Rami Zakaria Terminolog Differential Equation Ordinar Differential Equations Partial Differential
SPS Mathematical Methods
 SPS 2281 - Mathematical Methods Assignment No. 2 Deadline: 11th March 2015, before 4:45 p.m. INSTRUCTIONS: Answer the following questions. Check our answer for odd number questions at the back of the tetbook.
SPS 2281 - Mathematical Methods Assignment No. 2 Deadline: 11th March 2015, before 4:45 p.m. INSTRUCTIONS: Answer the following questions. Check our answer for odd number questions at the back of the tetbook.
Lecture 2: Separable Ordinary Differential Equations
 Lecture : Separable Ordinar Differential Equations Dr. Michael Doughert Januar 8, 00 Some Terminolog: ODE s, PDE s, IVP s The differential equations we have looked at so far are called ordinar differential
Lecture : Separable Ordinar Differential Equations Dr. Michael Doughert Januar 8, 00 Some Terminolog: ODE s, PDE s, IVP s The differential equations we have looked at so far are called ordinar differential
Regent College Maths Department. Core Mathematics 4 Trapezium Rule. C4 Integration Page 1
 Regent College Maths Department Core Mathematics Trapezium Rule C Integration Page Integration It might appear to be a bit obvious but you must remember all of your C work on differentiation if you are
Regent College Maths Department Core Mathematics Trapezium Rule C Integration Page Integration It might appear to be a bit obvious but you must remember all of your C work on differentiation if you are
Solutions to Homework Assignment #2
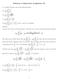 Solutions to Homework Assignment #. [4 marks] Evaluate each of the following limits. n i a lim n. b lim c lim d lim n i. sin πi n. a i n + b, where a and b are constants. n a There are ways to do this
Solutions to Homework Assignment #. [4 marks] Evaluate each of the following limits. n i a lim n. b lim c lim d lim n i. sin πi n. a i n + b, where a and b are constants. n a There are ways to do this
MATH MIDTERM 4 - SOME REVIEW PROBLEMS WITH SOLUTIONS Calculus, Fall 2017 Professor: Jared Speck. Problem 1. Approximate the integral
 MATH 8. - MIDTERM 4 - SOME REVIEW PROBLEMS WITH SOLUTIONS 8. Calculus, Fall 7 Professor: Jared Speck Problem. Approimate the integral 4 d using first Simpson s rule with two equal intervals and then the
MATH 8. - MIDTERM 4 - SOME REVIEW PROBLEMS WITH SOLUTIONS 8. Calculus, Fall 7 Professor: Jared Speck Problem. Approimate the integral 4 d using first Simpson s rule with two equal intervals and then the
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
Fitting Integrands to Basic Rules. x x 2 9 dx. Solution a. Use the Arctangent Rule and let u x and a dx arctan x 3 C. 2 du u.
 58 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8 Basic Integration Rules Review proceres for fitting an integrand to one of the basic integration rules Fitting Integrands
58 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8 Basic Integration Rules Review proceres for fitting an integrand to one of the basic integration rules Fitting Integrands
Particular Solutions
 Particular Solutions Our eamples so far in this section have involved some constant of integration, K. We now move on to see particular solutions, where we know some boundar conditions and we substitute
Particular Solutions Our eamples so far in this section have involved some constant of integration, K. We now move on to see particular solutions, where we know some boundar conditions and we substitute
z = 1 2 x 3 4 y + 3 y dt
 Exact First Order Differential Equations This Lecture covers material in Section 2.6. A first order differential equations is exact if it can be written in the form M(x, ) + N(x, ) d dx = 0, where M =
Exact First Order Differential Equations This Lecture covers material in Section 2.6. A first order differential equations is exact if it can be written in the form M(x, ) + N(x, ) d dx = 0, where M =
2326 Problem Sheet 1. Solutions 1. First Order Differential Equations. Question 1: Solve the following, given an explicit solution if possible:
 2326 Problem Sheet. Solutions First Order Differential Equations Question : Solve the following, given an explicit solution if possible:. 2 x = 4x3, () = 3, ( ) The given equation is a first order linear
2326 Problem Sheet. Solutions First Order Differential Equations Question : Solve the following, given an explicit solution if possible:. 2 x = 4x3, () = 3, ( ) The given equation is a first order linear
Section B. Ordinary Differential Equations & its Applications Maths II
 Section B Ordinar Differential Equations & its Applications Maths II Basic Concepts and Ideas: A differential equation (D.E.) is an equation involving an unknown function (or dependent variable) of one
Section B Ordinar Differential Equations & its Applications Maths II Basic Concepts and Ideas: A differential equation (D.E.) is an equation involving an unknown function (or dependent variable) of one
Exercise 3.3. MA 111: Prepared by Dr. Archara Pacheenburawana 26
 MA : Prepared b Dr. Archara Pacheenburawana 6 Eercise.. For each of the numbers a, b, c, d, e, r, s, and t, state whether the function whose graphisshown hasanabsolutemaimum orminimum, a localmaimum orminimum,
MA : Prepared b Dr. Archara Pacheenburawana 6 Eercise.. For each of the numbers a, b, c, d, e, r, s, and t, state whether the function whose graphisshown hasanabsolutemaimum orminimum, a localmaimum orminimum,
y sin n x dx cos x sin n 1 x n 1 y sin n 2 x cos 2 x dx y sin n xdx cos x sin n 1 x n 1 y sin n 2 x dx n 1 y sin n x dx
 SECTION 7. INTEGRATION BY PARTS 57 EXAPLE 6 Prove the reduction formula N Equation 7 is called a reduction formula because the eponent n has been reduced to n and n. 7 sin n n cos sinn n n sin n where
SECTION 7. INTEGRATION BY PARTS 57 EXAPLE 6 Prove the reduction formula N Equation 7 is called a reduction formula because the eponent n has been reduced to n and n. 7 sin n n cos sinn n n sin n where
Core Mathematics C3 Advanced Level
 Paper Reference(s) 666/0 Edecel GCE Core Mathematics C Advanced Level Wednesda 0 Januar 00 Afternoon Time: hour 0 minutes Materials required for eamination Mathematical Formulae (Pink or Green) Items included
Paper Reference(s) 666/0 Edecel GCE Core Mathematics C Advanced Level Wednesda 0 Januar 00 Afternoon Time: hour 0 minutes Materials required for eamination Mathematical Formulae (Pink or Green) Items included
11.4. Differentiating ProductsandQuotients. Introduction. Prerequisites. Learning Outcomes
 Differentiating ProductsandQuotients 11.4 Introduction We have seen, in the first three Sections, how standard functions like n, e a, sin a, cos a, ln a may be differentiated. In this Section we see how
Differentiating ProductsandQuotients 11.4 Introduction We have seen, in the first three Sections, how standard functions like n, e a, sin a, cos a, ln a may be differentiated. In this Section we see how
CHAPTER 5 Logarithmic, Exponential, and Other Transcendental Functions
 CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Differentiation.... 9 Section 5. The Natural Logarithmic Function: Integration...... 98
CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Differentiation.... 9 Section 5. The Natural Logarithmic Function: Integration...... 98
2 nd ORDER O.D.E.s SUBSTITUTIONS
 nd ORDER O.D.E.s SUBSTITUTIONS Question 1 (***+) d y y 8y + 16y = d d d, y 0, Find the general solution of the above differential equation by using the transformation equation t = y. Give the answer in
nd ORDER O.D.E.s SUBSTITUTIONS Question 1 (***+) d y y 8y + 16y = d d d, y 0, Find the general solution of the above differential equation by using the transformation equation t = y. Give the answer in
Fitting Integrands to Basic Rules
 6_8.qd // : PM Page 8 8 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Basic Integration Rules Review proceres for fitting an integrand to one of the basic integration
6_8.qd // : PM Page 8 8 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Basic Integration Rules Review proceres for fitting an integrand to one of the basic integration
Ex. 1. Find the general solution for each of the following differential equations:
 MATH 261.007 Instr. K. Ciesielski Spring 2010 NAME (print): SAMPLE TEST # 2 Solve the following exercises. Show your work. (No credit will be given for an answer with no supporting work shown.) Ex. 1.
MATH 261.007 Instr. K. Ciesielski Spring 2010 NAME (print): SAMPLE TEST # 2 Solve the following exercises. Show your work. (No credit will be given for an answer with no supporting work shown.) Ex. 1.
39. (a) Use trigonometric substitution to verify that. 40. The parabola y 2x divides the disk into two
 35. Prove the formula A r for the area of a sector of a circle with radius r and central angle. [Hint: Assume 0 and place the center of the circle at the origin so it has the equation. Then is the sum
35. Prove the formula A r for the area of a sector of a circle with radius r and central angle. [Hint: Assume 0 and place the center of the circle at the origin so it has the equation. Then is the sum
Additional Topics in Differential Equations
 6 Additional Topics in Differential Equations 6. Eact First-Order Equations 6. Second-Order Homogeneous Linear Equations 6.3 Second-Order Nonhomogeneous Linear Equations 6.4 Series Solutions of Differential
6 Additional Topics in Differential Equations 6. Eact First-Order Equations 6. Second-Order Homogeneous Linear Equations 6.3 Second-Order Nonhomogeneous Linear Equations 6.4 Series Solutions of Differential
Math 4381 / 6378 Symmetry Analysis
 Math 438 / 6378 Smmetr Analsis Elementar ODE Review First Order Equations Ordinar differential equations of the form = F(x, ( are called first order ordinar differential equations. There are a variet of
Math 438 / 6378 Smmetr Analsis Elementar ODE Review First Order Equations Ordinar differential equations of the form = F(x, ( are called first order ordinar differential equations. There are a variet of
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
Introduction to Differential Equations
 Math0 Lecture # Introduction to Differential Equations Basic definitions Definition : (What is a DE?) A differential equation (DE) is an equation that involves some of the derivatives (or differentials)
Math0 Lecture # Introduction to Differential Equations Basic definitions Definition : (What is a DE?) A differential equation (DE) is an equation that involves some of the derivatives (or differentials)
Unit 3. Integration. 3A. Differentials, indefinite integration. y x. c) Method 1 (slow way) Substitute: u = 8 + 9x, du = 9dx.
 Unit 3. Integration 3A. Differentials, indefinite integration 3A- a) 7 6 d. (d(sin ) = because sin is a constant.) b) (/) / d c) ( 9 8)d d) (3e 3 sin + e 3 cos)d e) (/ )d + (/ y)dy = implies dy = / d /
Unit 3. Integration 3A. Differentials, indefinite integration 3A- a) 7 6 d. (d(sin ) = because sin is a constant.) b) (/) / d c) ( 9 8)d d) (3e 3 sin + e 3 cos)d e) (/ )d + (/ y)dy = implies dy = / d /
Methods in differential equations mixed exercise 7
 Methos in ifferential equations mie eercise 7 tan lnsec The integrating factor is e = e = sec Multiplying the equation by this factor gives: sec + ysectan= sec ( sec sec y = y sec= sec = tan+ c y= sin+
Methos in ifferential equations mie eercise 7 tan lnsec The integrating factor is e = e = sec Multiplying the equation by this factor gives: sec + ysectan= sec ( sec sec y = y sec= sec = tan+ c y= sin+
Answer Key 1973 BC 1969 BC 24. A 14. A 24. C 25. A 26. C 27. C 28. D 29. C 30. D 31. C 13. C 12. D 12. E 3. A 32. B 27. E 34. C 14. D 25. B 26.
 Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
1 Exponential Functions Limit Derivative Integral... 5
 Contents Eponential Functions 3. Limit................................................. 3. Derivative.............................................. 4.3 Integral................................................
Contents Eponential Functions 3. Limit................................................. 3. Derivative.............................................. 4.3 Integral................................................
Coordinate geometry. + bx + c. Vertical asymptote. Sketch graphs of hyperbolas (including asymptotic behaviour) from the general
 A Sketch graphs of = a m b n c where m = or and n = or B Reciprocal graphs C Graphs of circles and ellipses D Graphs of hperbolas E Partial fractions F Sketch graphs using partial fractions Coordinate
A Sketch graphs of = a m b n c where m = or and n = or B Reciprocal graphs C Graphs of circles and ellipses D Graphs of hperbolas E Partial fractions F Sketch graphs using partial fractions Coordinate
1.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS
 .6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
.6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
Exact Differential Equations. The general solution of the equation is f x, y C. If f has continuous second partials, then M y 2 f
 APPENDIX C Additional Topics in Differential Equations APPENDIX C. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Chapter 6, ou studied applications
APPENDIX C Additional Topics in Differential Equations APPENDIX C. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Chapter 6, ou studied applications
9Logarithmic. functions using calculus UNCORRECTED PAGE PROOFS
 9Logarithmic functions using calculus 9. Kick off with CAS 9. The derivative of f () = log e () 9. The antiderivative of f () = 9.4 Applications 9.5 Review 9. Kick off with CAS To come Please refer to
9Logarithmic functions using calculus 9. Kick off with CAS 9. The derivative of f () = log e () 9. The antiderivative of f () = 9.4 Applications 9.5 Review 9. Kick off with CAS To come Please refer to
Math 1B Final Exam, Solution. Prof. Mina Aganagic Lecture 2, Spring (6 points) Use substitution and integration by parts to find:
 Math B Final Eam, Solution Prof. Mina Aganagic Lecture 2, Spring 20 The eam is closed book, apart from a sheet of notes 8. Calculators are not allowed. It is your responsibility to write your answers clearly..
Math B Final Eam, Solution Prof. Mina Aganagic Lecture 2, Spring 20 The eam is closed book, apart from a sheet of notes 8. Calculators are not allowed. It is your responsibility to write your answers clearly..
Mathematics 104 Fall Term 2006 Solutions to Final Exam. sin(ln t) dt = e x sin(x) dx.
 Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
f ax ; a 0 is a periodic function b is a periodic function of x of p b. f which is assumed to have the period 2 π, where
 (a) (b) If () Year - Tutorial: Toic: Fourier series Time: Two hours π π n Find the fundamental eriod of (i) cos (ii) cos k k f a ; a is a eriodic function b is a eriodic function of of b. f is a eriodic
(a) (b) If () Year - Tutorial: Toic: Fourier series Time: Two hours π π n Find the fundamental eriod of (i) cos (ii) cos k k f a ; a is a eriodic function b is a eriodic function of of b. f is a eriodic
Einstein Classes, Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road New Delhi , Ph. : ,
 C1 Order and Degree of a Differential Equation : Order : Order is the highest differential appearing in a differential equation. MDE 1 DIFFERENTIAL EQUATION Degree : It is determined b the degree of the
C1 Order and Degree of a Differential Equation : Order : Order is the highest differential appearing in a differential equation. MDE 1 DIFFERENTIAL EQUATION Degree : It is determined b the degree of the
University of Bergen. Solutions to Exam in MAT111 - Calculus 1
 Universit of Bergen The Facult of Mathematics and Natural Sciences English Solutions to Eam in MAT - Calculus Wednesda Ma 0, 07, 09.00-4.00 Eercise. a) Find the real numbers and such that the comple variable
Universit of Bergen The Facult of Mathematics and Natural Sciences English Solutions to Eam in MAT - Calculus Wednesda Ma 0, 07, 09.00-4.00 Eercise. a) Find the real numbers and such that the comple variable
Review of Essential Skills and Knowledge
 Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
DIFFERENTIAL EQUATION. Contents. Theory Exercise Exercise Exercise Exercise
 DIFFERENTIAL EQUATION Contents Topic Page No. Theor 0-0 Eercise - 04-0 Eercise - - Eercise - - 7 Eercise - 4 8-9 Answer Ke 0 - Sllabus Formation of ordinar differential equations, solution of homogeneous
DIFFERENTIAL EQUATION Contents Topic Page No. Theor 0-0 Eercise - 04-0 Eercise - - Eercise - - 7 Eercise - 4 8-9 Answer Ke 0 - Sllabus Formation of ordinar differential equations, solution of homogeneous
11.4 Polar Coordinates
 11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
DIFFERENTIAL EQUATIONS First Order Differential Equations. Paul Dawkins
 DIFFERENTIAL EQUATIONS First Order Paul Dawkins Table of Contents Preface... First Order... 3 Introduction... 3 Linear... 4 Separable... 7 Eact... 8 Bernoulli... 39 Substitutions... 46 Intervals of Validit...
DIFFERENTIAL EQUATIONS First Order Paul Dawkins Table of Contents Preface... First Order... 3 Introduction... 3 Linear... 4 Separable... 7 Eact... 8 Bernoulli... 39 Substitutions... 46 Intervals of Validit...
Introduction to Differential Equations. National Chiao Tung University Chun-Jen Tsai 9/14/2011
 Introduction to Differential Equations National Chiao Tung Universit Chun-Jen Tsai 9/14/011 Differential Equations Definition: An equation containing the derivatives of one or more dependent variables,
Introduction to Differential Equations National Chiao Tung Universit Chun-Jen Tsai 9/14/011 Differential Equations Definition: An equation containing the derivatives of one or more dependent variables,
ENGI 3424 First Order ODEs Page 1-01
 ENGI 344 First Order ODEs Page 1-01 1. Ordinary Differential Equations Equations involving only one independent variable and one or more dependent variables, together with their derivatives with respect
ENGI 344 First Order ODEs Page 1-01 1. Ordinary Differential Equations Equations involving only one independent variable and one or more dependent variables, together with their derivatives with respect
MATH 250 TOPIC 13 INTEGRATION. 13B. Constant, Sum, and Difference Rules
 Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
EXACT EQUATIONS AND INTEGRATING FACTORS
 MAP- EXACT EQUATIONS AND INTEGRATING FACTORS First-order Differential Equations for Which We Can Find Eact Solutions Stu the patterns carefully. The first step of any solution is correct identification
MAP- EXACT EQUATIONS AND INTEGRATING FACTORS First-order Differential Equations for Which We Can Find Eact Solutions Stu the patterns carefully. The first step of any solution is correct identification
Name Please print your name as it appears on the class roster.
 Berkele Cit College Practice Problems Math 1 Precalculus - Final Eam Preparation Name Please print our name as it appears on the class roster. SHORT ANSWER. Write the word or phrase that best completes
Berkele Cit College Practice Problems Math 1 Precalculus - Final Eam Preparation Name Please print our name as it appears on the class roster. SHORT ANSWER. Write the word or phrase that best completes
MB4018 Differential equations
 MB4018 Differential equations Part II http://www.staff.ul.ie/natalia/mb4018.html Prof. Natalia Kopteva Spring 2015 MB4018 (Spring 2015) Differential equations Part II 0 / 69 Section 1 Second-Order Linear
MB4018 Differential equations Part II http://www.staff.ul.ie/natalia/mb4018.html Prof. Natalia Kopteva Spring 2015 MB4018 (Spring 2015) Differential equations Part II 0 / 69 Section 1 Second-Order Linear
First Order Linear Ordinary Differential Equations
 First Order Linear Ordinary Differential Equations The most general first order linear ODE is an equation of the form p t dy dt q t y t f t. 1 Herepqarecalledcoefficients f is referred to as the forcing
First Order Linear Ordinary Differential Equations The most general first order linear ODE is an equation of the form p t dy dt q t y t f t. 1 Herepqarecalledcoefficients f is referred to as the forcing
Math 201 Solutions to Assignment 1. 2ydy = x 2 dx. y = C 1 3 x3
 Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
Math 201 Solutions to Assignment 1 1. Solve the initial value problem: x 2 dx + 2y = 0, y(0) = 2. x 2 dx + 2y = 0, y(0) = 2 2y = x 2 dx y 2 = 1 3 x3 + C y = C 1 3 x3 Notice that y is not defined for some
McKinney High School AP Calculus Summer Packet
 McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
Mathematics. Mathematics 2. hsn.uk.net. Higher HSN22000
 hsn.uk.net Higher Mathematics UNIT Mathematics HSN000 This document was produced speciall for the HSN.uk.net website, and we require that an copies or derivative works attribute the work to Higher Still
hsn.uk.net Higher Mathematics UNIT Mathematics HSN000 This document was produced speciall for the HSN.uk.net website, and we require that an copies or derivative works attribute the work to Higher Still
SOLUTIONS BY SUBSTITUTIONS
 25 SOLUTIONS BY SUBSTITUTIONS 71 25 SOLUTIONS BY SUBSTITUTIONS REVIEW MATERIAL Techniques of integration Separation of variables Solution of linear DEs INTRODUCTION We usually solve a differential equation
25 SOLUTIONS BY SUBSTITUTIONS 71 25 SOLUTIONS BY SUBSTITUTIONS REVIEW MATERIAL Techniques of integration Separation of variables Solution of linear DEs INTRODUCTION We usually solve a differential equation
Math K (24564) - Homework Solutions 02
 Math 39100 K (24564) - Homework Solutions 02 Ethan Akin Office: NAC 6/287 Phone: 650-5136 Email: ethanakin@earthlink.net Spring, 2018 Contents Reduction of Order, B & D Chapter 3, p. 174 Constant Coefficient
Math 39100 K (24564) - Homework Solutions 02 Ethan Akin Office: NAC 6/287 Phone: 650-5136 Email: ethanakin@earthlink.net Spring, 2018 Contents Reduction of Order, B & D Chapter 3, p. 174 Constant Coefficient
1.3 LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION
 . Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
. Limits at Infinit; End Behavior of a Function 89. LIMITS AT INFINITY; END BEHAVIOR OF A FUNCTION Up to now we have been concerned with its that describe the behavior of a function f) as approaches some
كلية العلوم قسم الرياضيات المعادالت التفاضلية العادية
 الجامعة اإلسالمية كلية العلوم غزة قسم الرياضيات المعادالت التفاضلية العادية Elementary differential equations and boundary value problems المحاضرون أ.د. رائد صالحة د. فاتن أبو شوقة 1 3 4 5 6 بسم هللا
الجامعة اإلسالمية كلية العلوم غزة قسم الرياضيات المعادالت التفاضلية العادية Elementary differential equations and boundary value problems المحاضرون أ.د. رائد صالحة د. فاتن أبو شوقة 1 3 4 5 6 بسم هللا
MA304 Differential Geometry
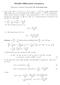 MA34 Differential Geometr Homework solutions, Spring 8, 3% of the final mark Let I R, where I = (a, b) or I = [a, b] Let α : I R 3 be a regular parameterised differentiable curve (not necessaril b arc
MA34 Differential Geometr Homework solutions, Spring 8, 3% of the final mark Let I R, where I = (a, b) or I = [a, b] Let α : I R 3 be a regular parameterised differentiable curve (not necessaril b arc
20D - Homework Assignment 4
 Brian Bowers (TA for Hui Sun) MATH 0D Homework Assignment November, 03 0D - Homework Assignment First, I will give a brief overview of how to use variation of parameters. () Ensure that the differential
Brian Bowers (TA for Hui Sun) MATH 0D Homework Assignment November, 03 0D - Homework Assignment First, I will give a brief overview of how to use variation of parameters. () Ensure that the differential
Brief Notes on Differential Equations
 Brief Notes on Differential Equations (A) Searable First-Order Differential Equations Solve the following differential equations b searation of variables: (a) (b) Solution ( 1 ) (a) The ODE becomes d and
Brief Notes on Differential Equations (A) Searable First-Order Differential Equations Solve the following differential equations b searation of variables: (a) (b) Solution ( 1 ) (a) The ODE becomes d and
Integral Calculus, dealing with areas and volumes, and approximate areas under and between curves.
 Calculus can be divided into two ke areas: Differential Calculus dealing wit its, rates of cange, tangents and normals to curves, curve sketcing, and applications to maima and minima problems Integral
Calculus can be divided into two ke areas: Differential Calculus dealing wit its, rates of cange, tangents and normals to curves, curve sketcing, and applications to maima and minima problems Integral
CHAPTER 5 Logarithmic, Exponential, and Other Transcendental Functions
 CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Dierentiation.... Section 5. The Natural Logarithmic Function: Integration...... Section
CHAPTER 5 Logarithmic, Eponential, and Other Transcendental Functions Section 5. The Natural Logarithmic Function: Dierentiation.... Section 5. The Natural Logarithmic Function: Integration...... Section
Section 1.2: A Catalog of Functions
 Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
VANDERBILT UNIVERSITY MAT 155B, FALL 12 SOLUTIONS TO THE PRACTICE FINAL.
 VANDERBILT UNIVERSITY MAT 55B, FALL SOLUTIONS TO THE PRACTICE FINAL. Important: These solutions should be used as a guide on how to solve the problems and they do not represent the format in which answers
VANDERBILT UNIVERSITY MAT 55B, FALL SOLUTIONS TO THE PRACTICE FINAL. Important: These solutions should be used as a guide on how to solve the problems and they do not represent the format in which answers
Preface. Computing Definite Integrals. 3 cos( x) dx. x 3
 Preface Here are the solutions to the practice problems for my Calculus I notes. Some solutions will have more or less detail than other solutions. The level of detail in each solution will depend up on
Preface Here are the solutions to the practice problems for my Calculus I notes. Some solutions will have more or less detail than other solutions. The level of detail in each solution will depend up on
A MATH 1225 Practice Test 4 NAME: SOLUTIONS CRN:
 A MATH 5 Practice Test 4 NAME: SOLUTIONS CRN: Multiple Choice No partial credit will be given. Clearly circle one answer. No calculator!. Which of the following must be true (you may select more than one
A MATH 5 Practice Test 4 NAME: SOLUTIONS CRN: Multiple Choice No partial credit will be given. Clearly circle one answer. No calculator!. Which of the following must be true (you may select more than one
INTRODUCTION TO DIFFERENTIAL EQUATIONS
 INTRODUCTION TO DIFFERENTIAL EQUATIONS. Definitions and Terminolog. Initial-Value Problems.3 Differential Equations as Mathematical Models CHAPTER IN REVIEW The words differential and equations certainl
INTRODUCTION TO DIFFERENTIAL EQUATIONS. Definitions and Terminolog. Initial-Value Problems.3 Differential Equations as Mathematical Models CHAPTER IN REVIEW The words differential and equations certainl
Mark Scheme (Results) Summer 2009
 Mark (Results) Summer 009 GCE GCE Mathematics (6668/0) June 009 6668 Further Pure Mathematics FP (new) Mark Q (a) = rr ( + ) r ( r+ ) r ( r+ ) B aef () (b) n n r = r = = rr ( + ) r r+ = + +...... + + n
Mark (Results) Summer 009 GCE GCE Mathematics (6668/0) June 009 6668 Further Pure Mathematics FP (new) Mark Q (a) = rr ( + ) r ( r+ ) r ( r+ ) B aef () (b) n n r = r = = rr ( + ) r r+ = + +...... + + n
Name Class. 5. Find the particular solution to given the general solution y C cos x and the. x 2 y
 10 Differential Equations Test Form A 1. Find the general solution to the first order differential equation: y 1 yy 0. 1 (a) (b) ln y 1 y ln y 1 C y y C y 1 C y 1 y C. Find the general solution to the
10 Differential Equations Test Form A 1. Find the general solution to the first order differential equation: y 1 yy 0. 1 (a) (b) ln y 1 y ln y 1 C y y C y 1 C y 1 y C. Find the general solution to the
First Order Differential Equations f ( x,
 Chapter d dx First Order Differential Equations f ( x, ).1 Linear Equations; Method of Integrating Factors Usuall the general first order linear equations has the form p( t ) g ( t ) (1) where pt () and
Chapter d dx First Order Differential Equations f ( x, ).1 Linear Equations; Method of Integrating Factors Usuall the general first order linear equations has the form p( t ) g ( t ) (1) where pt () and
Lecture 4. Properties of Logarithmic Function (Contd ) y Log z tan constant x. It follows that
 Lecture 4 Properties of Logarithmic Function (Contd ) Since, Logln iarg u Re Log ln( ) v Im Log tan constant It follows that u v, u v This shows that Re Logand Im Log are (i) continuous in C { :Re 0,Im
Lecture 4 Properties of Logarithmic Function (Contd ) Since, Logln iarg u Re Log ln( ) v Im Log tan constant It follows that u v, u v This shows that Re Logand Im Log are (i) continuous in C { :Re 0,Im
8 Differential Calculus 1 Introduction
 8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
Math 2300 Calculus II University of Colorado
 Math 3 Calculus II University of Colorado Spring Final eam review problems: ANSWER KEY. Find f (, ) for f(, y) = esin( y) ( + y ) 3/.. Consider the solid region W situated above the region apple apple,
Math 3 Calculus II University of Colorado Spring Final eam review problems: ANSWER KEY. Find f (, ) for f(, y) = esin( y) ( + y ) 3/.. Consider the solid region W situated above the region apple apple,
Questions. x 2 e x dx. Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the functions g(x) = x cost2 dt.
 Questions. Evaluate the Riemann sum for f() =,, with four subintervals, taking the sample points to be right endpoints. Eplain, with the aid of a diagram, what the Riemann sum represents.. If f() = ln,
Questions. Evaluate the Riemann sum for f() =,, with four subintervals, taking the sample points to be right endpoints. Eplain, with the aid of a diagram, what the Riemann sum represents.. If f() = ln,
Exam. Name. Domain: (0, ) Range: (-, ) Domain: (0, ) Range: (-, ) Domain: (-, ) Range: (0, ) Domain: (-, ) Range: (0, ) y
 Eam Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Graph the function and write the domain and range in interval notation. ) f () = 5 B) 0 0
Eam Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Graph the function and write the domain and range in interval notation. ) f () = 5 B) 0 0
MA 113 Calculus I Fall 2009 Exam 4 December 15, 2009
 MA 3 Calculus I Fall 009 Eam December 5, 009 Answer all of the questions - 7 and two of the questions 8-0. Please indicate which problem is not to be graded b crossing through its number in the table below.
MA 3 Calculus I Fall 009 Eam December 5, 009 Answer all of the questions - 7 and two of the questions 8-0. Please indicate which problem is not to be graded b crossing through its number in the table below.
6 = 1 2. The right endpoints of the subintervals are then 2 5, 3, 7 2, 4, 2 9, 5, while the left endpoints are 2, 5 2, 3, 7 2, 4, 9 2.
 5 THE ITEGRAL 5. Approimating and Computing Area Preliminar Questions. What are the right and left endpoints if [, 5] is divided into si subintervals? If the interval [, 5] is divided into si subintervals,
5 THE ITEGRAL 5. Approimating and Computing Area Preliminar Questions. What are the right and left endpoints if [, 5] is divided into si subintervals? If the interval [, 5] is divided into si subintervals,
Unit #3 Rules of Differentiation Homework Packet
 Unit #3 Rules of Differentiation Homework Packet In the table below, a function is given. Show the algebraic analysis that leads to the derivative of the function. Find the derivative by the specified
Unit #3 Rules of Differentiation Homework Packet In the table below, a function is given. Show the algebraic analysis that leads to the derivative of the function. Find the derivative by the specified
Polytechnic Institute of NYU MA 2132 Final Practice Answers Fall 2012
 Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
Polytechnic Institute of NYU MA Final Practice Answers Fall Studying from past or sample exams is NOT recommended. If you do, it should be only AFTER you know how to do all of the homework and worksheet
AP Calculus AB Summer Assignment Mrs. Berkson
 AP Calculus AB Summer Assignment Mrs. Berkson The purpose of the summer assignment is to prepare ou with the necessar Pre- Calculus skills required for AP Calculus AB. Net ear we will be starting off the
AP Calculus AB Summer Assignment Mrs. Berkson The purpose of the summer assignment is to prepare ou with the necessar Pre- Calculus skills required for AP Calculus AB. Net ear we will be starting off the
STEP Support Programme. Pure STEP 3 Solutions
 STEP Support Programme Pure STEP 3 Solutions S3 Q6 Preparation Completing the square on gives + + y, so the centre is at, and the radius is. First draw a sketch of y 4 3. This has roots at and, and you
STEP Support Programme Pure STEP 3 Solutions S3 Q6 Preparation Completing the square on gives + + y, so the centre is at, and the radius is. First draw a sketch of y 4 3. This has roots at and, and you
Solutions to Problem Sheet for Week 6
 THE UNIVERSITY OF SYDNEY SCHOOL OF MATHEMATICS AND STATISTICS Solutions to Problem Sheet for Week 6 MATH90: Differential Calculus (Advanced) Semester, 07 Web Page: sydney.edu.au/science/maths/u/ug/jm/math90/
THE UNIVERSITY OF SYDNEY SCHOOL OF MATHEMATICS AND STATISTICS Solutions to Problem Sheet for Week 6 MATH90: Differential Calculus (Advanced) Semester, 07 Web Page: sydney.edu.au/science/maths/u/ug/jm/math90/
Andrew s handout. 1 Trig identities. 1.1 Fundamental identities. 1.2 Other identities coming from the Pythagorean identity
 Andrew s handout Trig identities. Fundamental identities These are the most fundamental identities, in the sense that ou should probabl memorize these and use them to derive the rest (or, if ou prefer,
Andrew s handout Trig identities. Fundamental identities These are the most fundamental identities, in the sense that ou should probabl memorize these and use them to derive the rest (or, if ou prefer,
Chapter 5: Integrals
 Chapter 5: Integrals Section 5.3 The Fundamental Theorem of Calculus Sec. 5.3: The Fundamental Theorem of Calculus Fundamental Theorem of Calculus: Sec. 5.3: The Fundamental Theorem of Calculus Fundamental
Chapter 5: Integrals Section 5.3 The Fundamental Theorem of Calculus Sec. 5.3: The Fundamental Theorem of Calculus Fundamental Theorem of Calculus: Sec. 5.3: The Fundamental Theorem of Calculus Fundamental
Math 170 Calculus I Final Exam Review Solutions
 Math 70 Calculus I Final Eam Review Solutions. Find the following its: (a (b (c (d 3 = + = 6 + 5 = 3 + 0 3 4 = sin( (e 0 cos( = (f 0 ln(sin( ln(tan( = ln( (g (h 0 + cot( ln( = sin(π/ = π. Find any values
Math 70 Calculus I Final Eam Review Solutions. Find the following its: (a (b (c (d 3 = + = 6 + 5 = 3 + 0 3 4 = sin( (e 0 cos( = (f 0 ln(sin( ln(tan( = ln( (g (h 0 + cot( ln( = sin(π/ = π. Find any values
2.5. Infinite Limits and Vertical Asymptotes. Infinite Limits
 . Infinite Limits and Vertical Asmptotes. Infinite Limits and Vertical Asmptotes In this section we etend the concept of it to infinite its, which are not its as before, but rather an entirel new use of
. Infinite Limits and Vertical Asmptotes. Infinite Limits and Vertical Asmptotes In this section we etend the concept of it to infinite its, which are not its as before, but rather an entirel new use of
