1 Exponential Functions Limit Derivative Integral... 5
|
|
|
- Toby Wood
- 5 years ago
- Views:
Transcription
1 Contents Eponential Functions 3. Limit Derivative Integral Logarithmic Functions 6. Limit Derivative Integral Inverse Trigonometric Functions 9 3. Integral l Hospital s Rule 4. Indeterminate Limit Techniques of Integration 5. Integration by Parts Trigonometric Integrals Trigonometric Substitution Partial Fractions Integral U-Substitution Improper Integrals 6 6. Infinite Bounds Discontinuous Integrands Comparison Test Parametric Curves 9 7. Derivatives Areas Polar Coordinates Areas in Polar Coordinates Applications of Integration 3 8. Arc Length Parametric Arc Length Polar Coordinates Arc Length Surface Area of Revolutions Surface Area of Revolution Revisited Infinite Sequences and Series 8 9. Sequences Series Integral Test Limit Comparison Test Alternating Series Root Test
2 9.7 Ratio Test Power Series More Power Series Maclaurin Series
3 66 Eam Jam Eponential Functions. Limit Evaluate the following limit: e e lim e + e To evaluate the limit, we first multiply the top and bottom by e to reduce the problem. (same as dividing the top and bottom by e ) As, e, so we can conclude that e e e lim e + e = lim e lim e + e e e e e = lim + e + e = = 3
4 66 Eam Jam. Derivative Differentiate the function: y = e e e + e Here, we simply use the quotient rule to compute the derivative: y = (e + e )(e + e ) (e e )(e e ) (e + e ) At this point, students should be advised to stop, unless the problem eplicitly calls for simplification. y = (e + e ) (e e ) (e + e ) Note: You could also epand the terms in the numerators and achieve the same result. y = (e + e + (e e ))(e + e (e e )) (e + e ) y = (e )(e ) (e + e ) y 4 = (e + e ) 4
5 66 Eam Jam.3 Integral Evaluate: + e d e Rewriting the integral in a more convenient fashion makes a u-substitution more evident: e + e d Note: Remember to change the limits of integration u = + e du = e d +e = u du = u du +e = 3 u 3 +e and thus, the result is: + e e d = 3 ( ( + e ) + e ) 5
6 66 Eam Jam Logarithmic Functions. Limit Evaluate the following limit: lim [ln( + ) ln( + )] Here, we will rely on one of the properties of the logarithmic functions, namely: ( ) + lim [ln( + ) ln( + )] = lim ln + Now, rewriting the argument of the natural logarithm (this trick only works when since ): ( ) = lim ln ( + ) ( + ) ( = lim + ) Therefore: = ln ln ( + + ) + = ln() = lim [ln( + ) ln( + )] = 6
7 66 Eam Jam. Derivative Find y if: y = y,, y > Since there is no algebraic way of isolating y, we will resort to logarithmic differentiation by first applying the natural (or any) logarithm to both sides and using some of the logarithm s common properties: Now, using implicit differentiation and product rule: ln( y ) = ln(y ) y ln() = ln(y) y ln() + y = ln(y) + y y Finally, what is left is manipulating the equation above to isolate y : y ln() y y = ln(y) y y (ln() y ) = ln(y) y y = ln(y) y ln() y y = y ln(y) y y ln() Note: since there is no algebraic way of eplicitly solving for y, we cannot epress the final solution in terms of the independent variable only, and thus, we have to leave our solution in the form shown above. 7
8 66 Eam Jam.3 Integral Evaluate: + d + Notice that the degree of the polynomial in the numerator is higher than that of the polynomial in the denominator. Thus, we can use long division to simplify our integrand. + ) + We rewrite our integral as follows: ( = + ) d + = d + d Here, we see that the first integral is easy to compute, while the second integral requires a simple u- substitution (namely, u = + du = d): + + d = ln + + C 8
9 66 Eam Jam 3 Inverse Trigonometric Functions 3. Integral Evaluate: d This really looks like a trigonometric substitution, but we can manipulate this integral thanks to the term in the numerator. To simplify the integral stated above, first notice that we can rewrite the integral and make the following substitution: d = ( ) + 9 d u = du = d du = d = du u + 9 Hopefully, by now you recognize this integral: = du 8 ( u 3 ) + w = u 3 dw = du 3 = 3 dw 8 w + = 6 arctan w + C d = 6 arctan 3 dw = du ( ) + C 3 9
10 66 Eam Jam 4 l Hospital s Rule 4. Indeterminate Limit Find the limit: ( lim + a b, a, b ) It is easy to see that if we attempt to evaluate the limit, we end up with an indeterminate value (namely, ), and thus, we define the following function: ( Let y = + a ) b ( ln(y) = ln + a ) b ( ln(y) = b ln + a ) Now we see that the limit as approaches results in ln(y) approaching which is an indeterminate form that is not desirable. Thus, we decide to rearrange the equation in the following manner: ) ln(y) = ln ( + a b lim ln(y) = Now we see that we can apply l Hospital s Rule: Thus: lim ln(y) = lim + a b a = lim ab + a = ab lim y = lim eln(y) = e ab ( lim + a ) b = e ab
11 66 Eam Jam 5 Techniques of Integration 5. Integration by Parts Evaluate: sin(ln()) d At this point,we have no obvious options for any sort of substitution, leaving integration by parts as the only feasible option: Let I = sin(ln()) d Set u = sin(ln()) dv = d du = cos(ln()) d v = I = uv v du = sin(ln()) cos(ln()) d To evaluate the integral on the left hand side of the equation, we must now apply the integration by parts technique once more (do you see the pattern?): Set u = cos(ln()) dv = d du = sin(ln()) d v = [ I = sin(ln()) cos(ln()) + ] sin(ln()) d I = sin(ln()) cos(ln()) I I = [sin(ln() cos(ln())] sin(ln()) d = [sin(ln() cos(ln())] + C
12 66 Eam Jam 5. Trigonometric Integrals Evaluate: dφ cos φ + To evaluate this integral, we will use an old trick, that is multiplying by the conjugate in the numerator and denominator and using the difference of squares identity (do you remember the identity?): dφ cos φ cos φ + = cos φ dφ Now, we apply the Pythagorean Identity, namely: cos φ = sin φ dφ cos φ = sin φ dφ csc φ dφ Let u = sin φ du = cos φdφ du = u cot φ + C = u du cot φ + C = u cot φ + C dφ = csc φ cot φ + C cos φ +
13 66 Eam Jam 5.3 Trigonometric Substitution Evaluate: π cos t + sin t dt At first, it is not obvious what the best approach is, however, a simplifying u-substitution helps: Let = u = sin t du = cos t dt du + u It is now evident that a trigonometric substitution will help us evaluate the integral: Let = = π 4 π 4 u = tan θ du = sec θ dθ sec θ + tan θ dθ sec θ dθ = ln sec θ + tan θ π 4 = ln + ln π cos t + sin t dt = ln + Note: Here we assume that the student has the anti-derivative of the secant function committed to memory (how do you arrive to that formula?). 3
14 66 Eam Jam 5.4 Partial Fractions Integral Evaluate: d + e Here, we will attempt a u-substitution since no other routes seem reasonable. Let u = + e du = e d = (u )d du u = d d + e = du u(u ) Now, to compute the right hand side, we use the partial fractions epansion: u(u ) = A u + B u = A(u ) + Bu F or u =, F or u =, B = = A A = Thus, our integral simplifies to: du du u(u ) = u + du u = ln(u) + ln(u ) + C d + e = ln + e + ln e + C 4
15 66 Eam Jam 5.5 U-Substitution Evaluate: I = d + 3 Once again, we will use a u-substitution to simplify the problem: Let du = u = + 3 d 3( 3 ) Note here that we can use our u-substitution to back substitute for the cubic root term: 3(u ) du = d 3(u ) I = du u As you can see, the integral becomes a simple one from here on: 3u 6u + 3 = du u = (3u u ) du = 3u 6u + 3 ln u + C I = 3( + 3 ) 6( + 3 ) + 3 ln C 5
16 66 Eam Jam 6 Improper Integrals 6. Infinite Bounds Determine whether the integral converges or diverges. If it converges, evaluate the integral: 3 e 4 d To evaluate this integral, we must first introduce an auiliary variable and take the bounds as limits. This is done as follows; t lim t 3 e 4 d Now, we will introduce a u-substitution to make the integral a bit more friendly: Let u = 4 du = 4 3 d du 4 = 3 d Now, we must study what happens to the limits under this substitution: and therefore, As t, t 4 lim t t 3 e 4 d = 4 lim t = 4 lim t [ e t4 + ] = 4 [ + ] = 4 3 e 4 d = 4 t 4 e u du 6
17 66 Eam Jam 6. Discontinuous Integrands Determine whether the integral converges or diverges. If it converges, evaluate the integral: 3 ( 8) 3 d Note that the integrand is discontinuous at =. epression at hand: First, let us make a u-substitution to simplify the Let u = 8 du = 4 d du 4 = d 3 ( 8) 3 d = 4 du 6 u 3 = 4 6 u 3 du Notice that now, we must deal with the discontinuity at u = (which comes from the original discontinuity): 4 6 = 4 lim t u 3 du = 4 [ t = [ 4 lim t 6 u 3 du + u 3 du 4 [ ] u 3 du ] u 3 du lim s + ] 3u 3 t lim ] = [ 4 lim 3( 3 t 3 6) t [ 3u 3 s + s s ] + [ 4 lim 3( 3 3 s) s + Now, we can plug in values for both t and s, and the integral converges to: ] 3 ( 8) 3 d = 3 4 [ ] 7
18 66 Eam Jam 6.3 Comparison Test Determine whether this integral converges or diverges: 3 + d Evaluating this integral is quite difficult. However, a simple comparison will give us the answer we need since we are NOT looking to evaluate the integral: 3 + d 3 d = d As is (hopefully) evident, this is a convergent p-integral since p = >. Thus, by comparison: 3 + d converges 8
19 66 Eam Jam 7 Parametric Curves 7. Derivatives Find the equation of the tangent to the curve at the given point by two methods: (a) without eliminating the parameter and (b) by first eliminating the parameter. = + t, y = e t ; (, e) a) First, we must find the derivative of and y with respect to t and take the ratio of those to arrive at the needed derivative as follows: d dt = t, dy dt = tet dy d = dy/dt d/dt = tet t = 4t 3 e t Now, we must determine the value of the parameter t when = : Equation of the tangent line becomes: = = + t t = t = dy d = 4e slope = 4e t= y e = 4e( ) y = e(4 7) b) We will now attempt the same problem by eliminating the parameter. Thus, we begin by solving for t in the first parametric equation and then plugging the result into the second equation: = + t t = ( ) y = e ( )4 dy d = 4( )3 e ( ) 4 dy d = 4e = Now we see that we achieve the same equation for the tangent line to the curve (which is good!): y e = 4e( ) y = e(4 7) 9
20 66 Eam Jam 7. Areas Find the area enclosed by an ellipse using the following parametric equations: = a cos θ, y = b sin θ, θ π To be able to calculate the area at hand, we must compute the following integral: Area = Where y is the part of the ellipse in the first quadrant ( a) and then multiply the result by 4 to arrive at the total area. However, note that we can use the equations we have to rewrite the integral: y d = a cos θ d = a sin θ dθ When =, θ = π When = a, θ = y d = π b sin θ( a sin θ) dθ Now, we can get rid of the negative sign by flipping the bounds of integration, which will make the integral look a bit more friendly: = π π ab sin θ dθ = ab sin θ dθ Finally, we will use the following trigonometric identity to evaluate the integral: π = ab = ab ( cos(θ)) dθ [ θ 4 sin(θ) Area = 4 πab 4 = πab ] π = πab 4
21 66 Eam Jam 7.3 Polar Coordinates Find the points (in polar coordinates) on the given curve where the tangent line is horizontal or vertical r = e θ To be able to do so, we will first need to compute the derivative ( dy d ) using the same method we used a few problems back as well as the following equations: = r cos θ, y = r sin θ; dy d = dy/dθ (dr/dθ) sin θ + r cos θ = d/dθ (dr/dθ) cos θ r sin θ dr dθ = eθ dy d = eθ (sin θ + cos θ) e θ (cos θ sin θ) Since e θ is never equal to zero, we can simply cancel it out. From here, to find the points at which the curve has a horizontal tangent, we set the derivative equal to zero. To find vertical tangents, we will look for discontinuities in the derivative (i.e. set the denominator equal to zero): dy sin θ + cos θ = d cos θ sin θ Horizontal tangents : dy = sin θ + cos θ = d sin θ = cos θ θ = 3π 4 + nπ or θ = 7π 4 + nπ Vertical tangents : cos θ sin θ = cos θ = sin θ θ = π 4 + nπ or θ = 5π 4 + nπ Thus, the points of interest (in the interval θ π) are: ( ) Horizontal tangents : e 3π 3π 4, and 4 ( ) Vertical tangents : e π π 4, and 4 ( e 5π 4, ( e 7π 7π 4, 4 ) 5π 4 )
22 66 Eam Jam 7.4 Areas in Polar Coordinates Find the area one loop of the curve: r = sin(θ) To do so, we must first find the values at which r goes to zero (i.e. determine the limits of integration for our problem). However, note that: r = sin(θ) = θ = and θ = π Thus, we can now compute the area using the following formula: Area = π b a π r dθ = = ( cos(4θ)) dθ 4 = 4 θ π 6 sin(4θ) Area in one loop = π 8 sin (θ) dθ
23 66 Eam Jam 8 Applications of Integration 8. Arc Length Find the arc length of the curve on the given interval: y = 3 ( + ) 3/, To find the arc length, we must evaluate the following integral: ( ) dy L = + d d We compute the derivative to be dy d = + Plugging this into our formula, we get ( L = + ) + d = d = = ( + ) d = + d = = = 4 3 3
24 66 Eam Jam 8. Parametric Arc Length Find the total length of the astroid with the following parametric equations: = a cos 3 θ, y = a sin 3 θ To do so, we will use the following form of the arc length integral: L = b a ds = b d dθ = 3a cos θ sin θ, a (d ) + dθ ( ) dy dθ dθ dy dθ = 3a sin θ cos θ Because of the symmetry of the problem (and one more reason, to be seen after some simplification), we will only compute the length in the first quadrant and then multiply the result by 4: π L 4 = = 3a = 3a = 3a π π π ( 3a cos θ sin θ) + (3a sin θ cos θ) dθ cos 4 θ sin θ + sin 4 θ cos θ dθ (cos θ sin θ)(cos θ + sin θ) dθ π cos θ sin θ dθ = 3a cos θ sin θ dθ We pause here for a second to understand the situation. The fact that we applied the square root operation to a square quantity resulted in the appearance of the absolute value. However, since we are in the first quadrant (this is the second reason referred to earlier), the sine and cosine values are both positive, which allows us to drop the absolute values and move on by using the double angle identity from trigonometry to further simplify the integrand: π L 4 = 3a cos θ sin θ dθ = 3a = 3a π 4 cos θ = 3a L = 4 3a = 6a π sin θ dθ 4
25 66 Eam Jam 8.3 Polar Coordinates Arc Length Find the arc length of the following polar curve: r = ( + cos θ) To compute the arc length, we will use the following form of the arc length integral: b ( ) dr L = r + dθ dθ a dr = sin θ dθ To find the arc length, we will use the symmetry of the problem (and one more reason to be seen after some work) and integrate for θ π : L = = = π π π 4( + cos θ) + 4 sin θ dθ cos θ + 4 cos θ + 4 sin θ dθ = π π cos θ dθ = + cos θ dθ cos θ + 4(cos θ + sin θ) dθ Here, we will use the half-angle identity to simplify the integrand: L π ( ) θ π ( ) = cos θ dθ = 4 cos dθ We pause here to understand how to deal with this absolute value that appeared. Taking the square root of a square quantity ( resulted ) in the appearance of the absolute value sign. However, notice that for θ π cos. Since the cosine is always positive on this interval (which the reason we θ chose to use symmetry) we can simply drop the absolute value. L = 4 π cos L = 8 = 6 ( ) ( ) θ θ π dθ = 4 sin = 8( ) 5
26 66 Eam Jam 8.4 Surface Area of Revolutions Find the epression for the surface area of a sphere with radius r. to be able to compute this epression, we will find the surface area of half a sphere by viewing it as the surface area of a quarter of a circle with radius r revolved about the y-ais. The equation of the circle is: + y = r Now, we will use the following epression to compute the surface area: b b ( ) dy SA = π y ds = π y + d d a y = r dy d = r Note that we only considered the positive square root when solving for y since we are restricting our circle to the first quadrant. Now that we have the epressions we need, we will evaluate the integral for r (do you see why that is?). SA = π r r a + ( r ) d Now, to simplify the integrand, we will combine the terms inside the larger square root by finding a common denominator. The results is as follows: = π r SA r = πr r r r d = π r d = πr = πr r r d SA = πr = 4πr 6
27 66 Eam Jam 8.5 Surface Area of Revolution Revisited Find the epression for the surface area of a sphere with radius r. This time, we will attempt to compute the formula for the surface area of the sphere by rotating one quarter of the circle ( θ π ) about the -ais and multiplying the result by two. Also, we will do so by using the following parametric equations of the circle. = r cos θ, y = r sin θ, θ π This time around, the integral that will help us arrive at the surface area is of the following form: b b (d ) ( ) dy SA = π ds = π + dθ dθ dθ a d dy = r sin θ, dθ dθ = r cos θ π SA = π r cos θ ( r sin θ) + (r cos θ) dθ π = π r cos θ r (sin θ + cos θ) dθ = πr π cos θ dθ = πr sinθ SA = πr = 4πr a π = πr ( ) 7
28 66 Eam Jam 9 Infinite Sequences and Series 9. Sequences Determine whether the following sequences converge or diverge.. a n = ln(n) ln(n) When considering any infinite sequence, we want to see the behavior as n tends towards infinity. lim a ln(n) n = lim n n ln(n) = Given the indeterminant form, we can see that this would be a good time to employ L Hospital s Rule. lim n ln(n) ln(n) = lim n ( ln(n) ) ( ln(n) ) = lim n /n /n = lim n n n = This tells us that our sequence is convergent.. b n = sin(n) + n By imagining what happens to sin(n) as n grows, we can see that sin(n) oscillates between and. Knowing this, let us consider the following. + n sin(n) + n + n Again, we are concerned with the behavior of our sequences as n approaches infinity. lim n + n lim sin(n) n + n lim n + n sin(n) lim n + n Thus, our sequence converges to zero by squeeze theorem. 8
29 66 Eam Jam 9. Series Determine whether the following series is convergent or divergent. If it is convergent, find its sum. n= 3 n(n + 3) When testing to see if series are divergent, one of the easiest tests to use is the Test for Divergence. We can clearly see that the argument of the sum approaches as n approaches infinity. What does this mean? Inconclusive. Do not make the mistake of trying to use the converse of the Test for Divergence. The Harmonic Series is a perfect eample of this not working. What we can see is the following: 3 n(n + 3) = 3 n + 3n 3 n Now the right hand side is convergent by p-test. Since each of these terms and our original terms are all positive, our series is then convergent by comparison test. To find the sum of this series we ll have to work a bit harder. The series is not a geometric series so we don t have a convenient formula for the sum. Instead, we will eamine the partial sums. We can find its partial fraction composition to see if that helps before we tackle the partial sums. 3 n(n + 3) = A n + B n = A(n + 3) + B(n) We can see by two easy substitutions that A = and B =. So s n = ( 4) + n= ( 5) + 3 n(n + 3) = n n + 3 ( 3 6) + n= ( 4 7) + ( 5 ( ) n ) n + 3 Note that terms begin to cancel. And, in fact, our partial sum collapses. ( s n = ) ( + 4 ) ( ) ( ) ( ) ( n ) n + 3 s n = n + 3 Finally, we know that if the limit of the partial sum eists, then it is the sum of our series. 3 n(n + 3) = lim s n = lim n n n + 3 = = 6 n= 9
30 66 Eam Jam 9.3 Integral Test Determine whether the series is convergent or divergent. n= n ln n The first detail we can notice is that the argument goes to as n approaches infinity. Net, we consider what tests to use. This appears to be a reasonable Integral Test application. It is important to note that the argument is positive and decreasing for all n. So we now take the integral. d ln = lim t t d ln t lim t d ln(t) ln = lim du t ln() u = lim t Let u = ln(). So du = d ln(t) ln() Now, by the Integral Test, = lim t ln(t) + ln() = + ln() < n= n ln n converges d ln converges. Therefore, our summation converges. 3
31 66 Eam Jam 9.4 Limit Comparison Test Determine whether the following series converges or diverges. n (+/n) n= When we see summation that incorporate strange terms such as this, we drastically limit which tests we can employ. In this case, we will attempt to solve this with the Limit Comparison Test. n= n = (+/n) n n n We have two pieces to work with here. If we were to choose b n = n n then the resulting quotient will be the harmonic sequence which goes to. Knowing that a limit of is inconclusive, we ll try the other piece. Let b n = n. a n lim = lim n b n n n n n n n= = lim n n n Let y = n n so lim n y = lim n n n = lim n n /n lim ln(y) = lim ln(n) = lim n n n ln(n) n n [ ] = L H lim n n = So lim ln(y) = then lim y = lim a n = e = > n n n b n By Limit Comparison Test, both series diverge or both series converge. b n was the harmonic sequence and therefore, its series would diverge. Thus, our original series diverges. 3
32 66 Eam Jam 9.5 Alternating Series Determine whether the following series converges or diverges. ( ) n ( n + n) n= This alternating series poses a few problems that prevent us from trying most of our tests, but fortunately, we simply use the Alternating Series Test. First, we must see if the sequence without the alternator, b n = ( n + n) is decreasing. Since this is not trivial, let us use some calculus for f() = ( + ). f () = + + = + f() then has critical values at = and =. Since = is outside our domain, we can ignore it. Similarly, we are only concerned with n > so can consider our function monotone for all n >. By plugging in any positive value, it is easy to see that the denominator is always positive while the numerator is negative. Thus f() is decreasing and our sequence will decrease for all n. Now we must eamine the limit. lim b n = lim ( n + n) = n n This is an indeterminate form but we ve got plenty of practice with these limits. Let us use the conjugate method. lim ( n + ( n + n) n + + n n) = lim n n n + + n = lim n n + n n + + n = lim n Then, by the Alternating Series Test, our series is convergent. n + + n = 3
33 66 Eam Jam 9.6 Root Test Determine whether the following series converges or diverges. n= ( n ) 5n n + The eponent is a red flag that we should use the Root Test. ( n n lim n n + = lim n ) 5n ( = lim n n n n + ( n n + ) 5 = lim n 5n ) = lim n ( n n n + 5 n 5 (n + ) 5 = 5 = 3 > Then, by the Root Test, the summation is divergent. ) 5n 33
34 66 Eam Jam 9.7 Ratio Test Determine whether the following series converges or diverges. n= ( ) n 4 n+ (n + ) With several components to juggle, Ratio Test is always a strong option. lim a n+ = lim n a n = lim n n ( ) n+ 4 (n+)+ (n++) ( ) n 4 n+ (n+) () n+ 4 n+3 (n + ) 4n+ (n + ) () n = lim n ( ) n+ = lim n 4 n+3 (n + ) 4n+ (n + ) = ( ) n (n + ) = lim n 4 (n + ) = 6 = 5 8 < n 4 n+ 4 (n + ) 4n+ (n + ) n Then, by Ratio Test, our series is absolutely convergent and therefore, convergent. 34
35 66 Eam Jam 9.8 Power Series Find the radius of convergence and the interval of convergence of the series: n= n (n ) To determine the radius of convergence, we simply use the ratio test to arrive at an inequality involving : lim a n+ n a n = lim n (n ) n ((n + ) ) n We now see that many terms cancel out for the quotient to now become: = lim n+ n (n ) ((n + ) ) (n ) n = lim n (n + ) Now, since we know that n [, ), we can drop the absolute values from that term. Also, since the limit is independent of, we can pull the outside the limit = lim n (n + ) = lim = = for all values. n n + Thus, since the series converges no matter what the value is: R =, Interval of convergence : (, ) 35
36 66 Eam Jam 9.9 More Power Series Find the radius of convergence and the interval of convergence of the series: n= n b n ( a)n, b > As is always the case, we will use the ratio test to determine the radius of convergence as well as the interval of convergence: lim a n+ n a n = lim (n + )( a) n+ b n n b n+ n( a) n = lim (n + )( a) n+ b n n b n+ n ( a) n = lim n + n ( a) bn Now, since the limit does not affect nor a, we can pul the ( a) term outside the limit (do not forget about the absolute value!) and the limit becomes: = a lim n + n bn = a b Since b >, we can simply remove the absolute value signs from around b. Also, since the convergence of the series at hand requires the ratio test to result in a value less than, we will impose that restriction and see what happens: a < a < b Radius of convergence = b b From the radius of convergence, we see that the series will converge for all values of in the interval a b < < a + b. However, we need to check whether or not the series converges at the boundaries of the interval shown. Thus, we plug in the corresponding values and test for convergence/divergence: For = a b : n= For = a + b : n b n ((a b) a)n = n= n= n b n ((a + b) a)n = n b n ( b)n = n= Thus Interval of Convergence = (a b, a + b) n b n (b)n = ( ) n n Diverges by the Test for Divergence n= n Diverges by the Test for Divergence n= 36
37 66 Eam Jam 9. Maclaurin Series Find the Maclaurin series for the following function: f() = sin To complete this problem, one is tempted to use the Maclaurin series for the sine function and then squaring it. However, epanding an infinite series after having squared it is very difficult. However, we can utilize the following identity for another approach: sin = ( cos()) Knowing that the Maclaurin epansion of the cosine function is the following will also be important: cos = n= ( ) n n (n)! cos = ( ) n ()n = ( ) n n n (n)! (n)! n= cos = ( ) n+ n n (n)! = ( ) n+ n n (n)! n= n= n= Note that when n =, the values of the last summation above is. Thus, is added, the inde will simply start from rather than. sin = ( cos ) = ( ) n+ n n (n)! n= 37
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals 8. Basic Integration Rules In this section we will review various integration strategies. Strategies: I. Separate
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals 8. Basic Integration Rules In this section we will review various integration strategies. Strategies: I. Separate
3 Applications of Derivatives Instantaneous Rates of Change Optimization Related Rates... 13
 Contents Limits Derivatives 3. Difference Quotients......................................... 3. Average Rate of Change...................................... 4.3 Derivative Rules...........................................
Contents Limits Derivatives 3. Difference Quotients......................................... 3. Average Rate of Change...................................... 4.3 Derivative Rules...........................................
APPM 1360 Final Exam Spring 2016
 APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
VII. Techniques of Integration
 VII. Techniques of Integration Integration, unlike differentiation, is more of an art-form than a collection of algorithms. Many problems in applied mathematics involve the integration of functions given
VII. Techniques of Integration Integration, unlike differentiation, is more of an art-form than a collection of algorithms. Many problems in applied mathematics involve the integration of functions given
Summer Review Packet for Students Entering AP Calculus BC. Complex Fractions
 Summer Review Packet for Students Entering AP Calculus BC Comple Fractions When simplifying comple fractions, multiply by a fraction equal to 1 which has a numerator and denominator composed of the common
Summer Review Packet for Students Entering AP Calculus BC Comple Fractions When simplifying comple fractions, multiply by a fraction equal to 1 which has a numerator and denominator composed of the common
Calculus 2 - Examination
 Calculus - Eamination Concepts that you need to know: Two methods for showing that a function is : a) Showing the function is monotonic. b) Assuming that f( ) = f( ) and showing =. Horizontal Line Test:
Calculus - Eamination Concepts that you need to know: Two methods for showing that a function is : a) Showing the function is monotonic. b) Assuming that f( ) = f( ) and showing =. Horizontal Line Test:
The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. sin
 Math : Practice Final Answer Key Name: The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. Problem : Consider the definite integral I = 5 sin ( ) d.
Math : Practice Final Answer Key Name: The answers below are not comprehensive and are meant to indicate the correct way to solve the problem. Problem : Consider the definite integral I = 5 sin ( ) d.
Math 1B Final Exam, Solution. Prof. Mina Aganagic Lecture 2, Spring (6 points) Use substitution and integration by parts to find:
 Math B Final Eam, Solution Prof. Mina Aganagic Lecture 2, Spring 20 The eam is closed book, apart from a sheet of notes 8. Calculators are not allowed. It is your responsibility to write your answers clearly..
Math B Final Eam, Solution Prof. Mina Aganagic Lecture 2, Spring 20 The eam is closed book, apart from a sheet of notes 8. Calculators are not allowed. It is your responsibility to write your answers clearly..
Feedback D. Incorrect! Exponential functions are continuous everywhere. Look for features like square roots or denominators that could be made 0.
 Calculus Problem Solving Drill 07: Trigonometric Limits and Continuity No. of 0 Instruction: () Read the problem statement and answer choices carefully. () Do your work on a separate sheet of paper. (3)
Calculus Problem Solving Drill 07: Trigonometric Limits and Continuity No. of 0 Instruction: () Read the problem statement and answer choices carefully. () Do your work on a separate sheet of paper. (3)
Chapter 5: Limits, Continuity, and Differentiability
 Chapter 5: Limits, Continuity, and Differentiability 63 Chapter 5 Overview: Limits, Continuity and Differentiability Derivatives and Integrals are the core practical aspects of Calculus. They were the
Chapter 5: Limits, Continuity, and Differentiability 63 Chapter 5 Overview: Limits, Continuity and Differentiability Derivatives and Integrals are the core practical aspects of Calculus. They were the
Learning Objectives for Math 166
 Learning Objectives for Math 166 Chapter 6 Applications of Definite Integrals Section 6.1: Volumes Using Cross-Sections Draw and label both 2-dimensional perspectives and 3-dimensional sketches of the
Learning Objectives for Math 166 Chapter 6 Applications of Definite Integrals Section 6.1: Volumes Using Cross-Sections Draw and label both 2-dimensional perspectives and 3-dimensional sketches of the
6.5 Trigonometric Equations
 6. Trigonometric Equations In this section, we discuss conditional trigonometric equations, that is, equations involving trigonometric functions that are satisfied only by some values of the variable (or
6. Trigonometric Equations In this section, we discuss conditional trigonometric equations, that is, equations involving trigonometric functions that are satisfied only by some values of the variable (or
West Essex Regional School District. AP Calculus AB. Summer Packet
 West Esse Regional School District AP Calculus AB Summer Packet 05-06 Calculus AB Calculus AB covers the equivalent of a one semester college calculus course. Our focus will be on differential and integral
West Esse Regional School District AP Calculus AB Summer Packet 05-06 Calculus AB Calculus AB covers the equivalent of a one semester college calculus course. Our focus will be on differential and integral
Troy High School AP Calculus Summer Packet
 Troy High School AP Calculus Summer Packet As instructors of AP Calculus, we have etremely high epectations of students taking our courses. We epect a certain level of independence to be demonstrated by
Troy High School AP Calculus Summer Packet As instructors of AP Calculus, we have etremely high epectations of students taking our courses. We epect a certain level of independence to be demonstrated by
GEORGE ANDROULAKIS THE 7 INDETERMINATE FORMS OF LIMITS : usually we use L Hospital s rule. Two important such limits are lim
 MATH 4 (CALCULUS II) IN ORDER TO OBTAIN A PERFECT SCORE IN ANDROULAKIS MATH 4 CLASS YOU NEED TO MEMORIZE THIS HANDOUT AND SOLVE THE ASSIGNED HOMEWORK ON YOUR OWN GEORGE ANDROULAKIS TRIGONOMETRY θ sin(θ)
MATH 4 (CALCULUS II) IN ORDER TO OBTAIN A PERFECT SCORE IN ANDROULAKIS MATH 4 CLASS YOU NEED TO MEMORIZE THIS HANDOUT AND SOLVE THE ASSIGNED HOMEWORK ON YOUR OWN GEORGE ANDROULAKIS TRIGONOMETRY θ sin(θ)
Inverse Relations. 5 are inverses because their input and output are switched. For instance: f x x. x 5. f 4
 Inverse Functions Inverse Relations The inverse of a relation is the set of ordered pairs obtained by switching the input with the output of each ordered pair in the original relation. (The domain of the
Inverse Functions Inverse Relations The inverse of a relation is the set of ordered pairs obtained by switching the input with the output of each ordered pair in the original relation. (The domain of the
AP Calculus AB Summer Assignment
 AP Calculus AB Summer Assignment Name: When you come back to school, it is my epectation that you will have this packet completed. You will be way behind at the beginning of the year if you haven t attempted
AP Calculus AB Summer Assignment Name: When you come back to school, it is my epectation that you will have this packet completed. You will be way behind at the beginning of the year if you haven t attempted
1993 AP Calculus AB: Section I
 99 AP Calculus AB: Section I 90 Minutes Scientific Calculator Notes: () The eact numerical value of the correct answer does not always appear among the choices given. When this happens, select from among
99 AP Calculus AB: Section I 90 Minutes Scientific Calculator Notes: () The eact numerical value of the correct answer does not always appear among the choices given. When this happens, select from among
Part I: Multiple Choice Mark the correct answer on the bubble sheet provided. n=1. a) None b) 1 c) 2 d) 3 e) 1, 2 f) 1, 3 g) 2, 3 h) 1, 2, 3
 Math (Calculus II) Final Eam Form A Fall 22 RED KEY Part I: Multiple Choice Mark the correct answer on the bubble sheet provided.. Which of the following series converge absolutely? ) ( ) n 2) n 2 n (
Math (Calculus II) Final Eam Form A Fall 22 RED KEY Part I: Multiple Choice Mark the correct answer on the bubble sheet provided.. Which of the following series converge absolutely? ) ( ) n 2) n 2 n (
MATH 101 Midterm Examination Spring 2009
 MATH Midterm Eamination Spring 9 Date: May 5, 9 Time: 7 minutes Surname: (Please, print!) Given name(s): Signature: Instructions. This is a closed book eam: No books, no notes, no calculators are allowed!.
MATH Midterm Eamination Spring 9 Date: May 5, 9 Time: 7 minutes Surname: (Please, print!) Given name(s): Signature: Instructions. This is a closed book eam: No books, no notes, no calculators are allowed!.
sin cos 1 1 tan sec 1 cot csc Pre-Calculus Mathematics Trigonometric Identities and Equations
 Pre-Calculus Mathematics 12 6.1 Trigonometric Identities and Equations Goal: 1. Identify the Fundamental Trigonometric Identities 2. Simplify a Trigonometric Expression 3. Determine the restrictions on
Pre-Calculus Mathematics 12 6.1 Trigonometric Identities and Equations Goal: 1. Identify the Fundamental Trigonometric Identities 2. Simplify a Trigonometric Expression 3. Determine the restrictions on
Review (2) Calculus II (201-nyb-05/05,06) Winter 2019
 Review () Calculus II (-nyb-5/5,6) Winter 9 Note. You should also review the integrals eercises on the first review sheet. Eercise. Evaluate each of the following integrals. a. sin 3 ( )cos ( csc 3 (log)cot
Review () Calculus II (-nyb-5/5,6) Winter 9 Note. You should also review the integrals eercises on the first review sheet. Eercise. Evaluate each of the following integrals. a. sin 3 ( )cos ( csc 3 (log)cot
Part Two. Diagnostic Test
 Part Two Diagnostic Test AP Calculus AB and BC Diagnostic Tests Take a moment to gauge your readiness for the AP Calculus eam by taking either the AB diagnostic test or the BC diagnostic test, depending
Part Two Diagnostic Test AP Calculus AB and BC Diagnostic Tests Take a moment to gauge your readiness for the AP Calculus eam by taking either the AB diagnostic test or the BC diagnostic test, depending
171, Calculus 1. Summer 1, CRN 50248, Section 001. Time: MTWR, 6:30 p.m. 8:30 p.m. Room: BR-43. CRN 50248, Section 002
 171, Calculus 1 Summer 1, 018 CRN 5048, Section 001 Time: MTWR, 6:0 p.m. 8:0 p.m. Room: BR-4 CRN 5048, Section 00 Time: MTWR, 11:0 a.m. 1:0 p.m. Room: BR-4 CONTENTS Syllabus Reviews for tests 1 Review
171, Calculus 1 Summer 1, 018 CRN 5048, Section 001 Time: MTWR, 6:0 p.m. 8:0 p.m. Room: BR-4 CRN 5048, Section 00 Time: MTWR, 11:0 a.m. 1:0 p.m. Room: BR-4 CONTENTS Syllabus Reviews for tests 1 Review
Answer Key 1973 BC 1969 BC 24. A 14. A 24. C 25. A 26. C 27. C 28. D 29. C 30. D 31. C 13. C 12. D 12. E 3. A 32. B 27. E 34. C 14. D 25. B 26.
 Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
DuVal High School Summer Review Packet AP Calculus
 DuVal High School Summer Review Packet AP Calculus Welcome to AP Calculus AB. This packet contains background skills you need to know for your AP Calculus. My suggestion is, you read the information and
DuVal High School Summer Review Packet AP Calculus Welcome to AP Calculus AB. This packet contains background skills you need to know for your AP Calculus. My suggestion is, you read the information and
Integration Techniques for the AB exam
 For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
For the AB eam, students need to: determine antiderivatives of the basic functions calculate antiderivatives of functions using u-substitution use algebraic manipulation to rewrite the integrand prior
AP Calculus AB Summer Assignment
 AP Calculus AB Summer Assignment Name: When you come back to school, you will be epected to have attempted every problem. These skills are all different tools that you will pull out of your toolbo this
AP Calculus AB Summer Assignment Name: When you come back to school, you will be epected to have attempted every problem. These skills are all different tools that you will pull out of your toolbo this
Section 8.2: Integration by Parts When you finish your homework, you should be able to
 Section 8.2: Integration by Parts When you finish your homework, you should be able to π Use the integration by parts technique to find indefinite integral and evaluate definite integrals π Use the tabular
Section 8.2: Integration by Parts When you finish your homework, you should be able to π Use the integration by parts technique to find indefinite integral and evaluate definite integrals π Use the tabular
Harbor Creek School District
 Unit 1 Days 1-9 Evaluate one-sided two-sided limits, given the graph of a function. Limits, Evaluate limits using tables calculators. Continuity Evaluate limits using direct substitution. Differentiability
Unit 1 Days 1-9 Evaluate one-sided two-sided limits, given the graph of a function. Limits, Evaluate limits using tables calculators. Continuity Evaluate limits using direct substitution. Differentiability
Spring 2011 solutions. We solve this via integration by parts with u = x 2 du = 2xdx. This is another integration by parts with u = x du = dx and
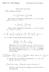 Math - 8 Rahman Final Eam Practice Problems () We use disks to solve this, Spring solutions V π (e ) d π e d. We solve this via integration by parts with u du d and dv e d v e /, V π e π e d. This is another
Math - 8 Rahman Final Eam Practice Problems () We use disks to solve this, Spring solutions V π (e ) d π e d. We solve this via integration by parts with u du d and dv e d v e /, V π e π e d. This is another
Mathematics 116 HWK 14 Solutions Section 4.5 p305. Note: This set of solutions also includes 3 problems from HWK 12 (5,7,11 from 4.5).
 Mathematics 6 HWK 4 Solutions Section 4.5 p305 Note: This set of solutions also includes 3 problems from HWK 2 (5,7, from 4.5). Find the indicated it. Use l Hospital s Rule where appropriate. Consider
Mathematics 6 HWK 4 Solutions Section 4.5 p305 Note: This set of solutions also includes 3 problems from HWK 2 (5,7, from 4.5). Find the indicated it. Use l Hospital s Rule where appropriate. Consider
AP Calculus BC Summer Assignment 2018
 AP Calculus BC Summer Assignment 018 Name: When you come back to school, I will epect you to have attempted every problem. These skills are all different tools that we will pull out of our toolbo at different
AP Calculus BC Summer Assignment 018 Name: When you come back to school, I will epect you to have attempted every problem. These skills are all different tools that we will pull out of our toolbo at different
Core Mathematics 2 Unit C2 AS
 Core Mathematics 2 Unit C2 AS compulsory unit for GCE AS and GCE Mathematics, GCE AS and GCE Pure Mathematics C2.1 Unit description Algebra and functions; coordinate geometry in the (, y) plane; sequences
Core Mathematics 2 Unit C2 AS compulsory unit for GCE AS and GCE Mathematics, GCE AS and GCE Pure Mathematics C2.1 Unit description Algebra and functions; coordinate geometry in the (, y) plane; sequences
1985 AP Calculus AB: Section I
 985 AP Calculus AB: Section I 9 Minutes No Calculator Notes: () In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e). () Unless otherwise specified, the domain of
985 AP Calculus AB: Section I 9 Minutes No Calculator Notes: () In this eamination, ln denotes the natural logarithm of (that is, logarithm to the base e). () Unless otherwise specified, the domain of
dx dx x sec tan d 1 4 tan 2 2 csc d 2 ln 2 x 2 5x 6 C 2 ln 2 ln x ln x 3 x 2 C Now, suppose you had observed that x 3
 CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial fraction decomposition with
CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial fraction decomposition with
(ii) y = ln 1 ] t 3 t x x2 9
![(ii) y = ln 1 ] t 3 t x x2 9 (ii) y = ln 1 ] t 3 t x x2 9](/thumbs/89/100579300.jpg) Study Guide for Eam 1 1. You are supposed to be able to determine the domain of a function, looking at the conditions for its epression to be well-defined. Some eamples of the conditions are: What is inside
Study Guide for Eam 1 1. You are supposed to be able to determine the domain of a function, looking at the conditions for its epression to be well-defined. Some eamples of the conditions are: What is inside
Review of elements of Calculus (functions in one variable)
 Review of elements of Calculus (functions in one variable) Mainly adapted from the lectures of prof Greg Kelly Hanford High School, Richland Washington http://online.math.uh.edu/houstonact/ https://sites.google.com/site/gkellymath/home/calculuspowerpoints
Review of elements of Calculus (functions in one variable) Mainly adapted from the lectures of prof Greg Kelly Hanford High School, Richland Washington http://online.math.uh.edu/houstonact/ https://sites.google.com/site/gkellymath/home/calculuspowerpoints
Methods of Integration
 Methods of Integration Essential Formulas k d = k +C sind = cos +C n d = n+ n + +C cosd = sin +C e d = e +C tand = ln sec +C d = ln +C cotd = ln sin +C + d = tan +C lnd = ln +C secd = ln sec + tan +C cscd
Methods of Integration Essential Formulas k d = k +C sind = cos +C n d = n+ n + +C cosd = sin +C e d = e +C tand = ln sec +C d = ln +C cotd = ln sin +C + d = tan +C lnd = ln +C secd = ln sec + tan +C cscd
Math156 Review for Exam 4
 Math56 Review for Eam 4. What will be covered in this eam: Representing functions as power series, Taylor and Maclaurin series, calculus with parametric curves, calculus with polar coordinates.. Eam Rules:
Math56 Review for Eam 4. What will be covered in this eam: Representing functions as power series, Taylor and Maclaurin series, calculus with parametric curves, calculus with polar coordinates.. Eam Rules:
Amherst College, DEPARTMENT OF MATHEMATICS Math 11, Final Examination, May 14, Answer Key. x 1 x 1 = 8. x 7 = lim. 5(x + 4) x x(x + 4) = lim
 Amherst College, DEPARTMENT OF MATHEMATICS Math, Final Eamination, May 4, Answer Key. [ Points] Evaluate each of the following limits. Please justify your answers. Be clear if the limit equals a value,
Amherst College, DEPARTMENT OF MATHEMATICS Math, Final Eamination, May 4, Answer Key. [ Points] Evaluate each of the following limits. Please justify your answers. Be clear if the limit equals a value,
Algebra/Trigonometry Review Notes
 Algebra/Trigonometry Review Notes MAC 41 Calculus for Life Sciences Instructor: Brooke Quinlan Hillsborough Community College ALGEBRA REVIEW FOR CALCULUS 1 TOPIC 1: POLYNOMIAL BASICS, POLYNOMIAL END BEHAVIOR,
Algebra/Trigonometry Review Notes MAC 41 Calculus for Life Sciences Instructor: Brooke Quinlan Hillsborough Community College ALGEBRA REVIEW FOR CALCULUS 1 TOPIC 1: POLYNOMIAL BASICS, POLYNOMIAL END BEHAVIOR,
APPLICATIONS OF DIFFERENTIATION
 4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION 4.4 Indeterminate Forms and L Hospital s Rule In this section, we will learn: How to evaluate functions whose values cannot be found at
4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION 4.4 Indeterminate Forms and L Hospital s Rule In this section, we will learn: How to evaluate functions whose values cannot be found at
MATH141: Calculus II Exam #4 review solutions 7/20/2017 Page 1
 MATH4: Calculus II Exam #4 review solutions 7/0/07 Page. The limaçon r = + sin θ came up on Quiz. Find the area inside the loop of it. Solution. The loop is the section of the graph in between its two
MATH4: Calculus II Exam #4 review solutions 7/0/07 Page. The limaçon r = + sin θ came up on Quiz. Find the area inside the loop of it. Solution. The loop is the section of the graph in between its two
Friday 09/15/2017 Midterm I 50 minutes
 Fa 17: MATH 2924 040 Differential and Integral Calculus II Noel Brady Friday 09/15/2017 Midterm I 50 minutes Name: Student ID: Instructions. 1. Attempt all questions. 2. Do not write on back of exam sheets.
Fa 17: MATH 2924 040 Differential and Integral Calculus II Noel Brady Friday 09/15/2017 Midterm I 50 minutes Name: Student ID: Instructions. 1. Attempt all questions. 2. Do not write on back of exam sheets.
Math 230 Mock Final Exam Detailed Solution
 Name: Math 30 Mock Final Exam Detailed Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and
Name: Math 30 Mock Final Exam Detailed Solution Disclaimer: This mock exam is for practice purposes only. No graphing calulators TI-89 is allowed on this test. Be sure that all of your work is shown and
(x 3)(x + 5) = (x 3)(x 1) = x + 5
 RMT 3 Calculus Test olutions February, 3. Answer: olution: Note that + 5 + 3. Answer: 3 3) + 5) = 3) ) = + 5. + 5 3 = 3 + 5 3 =. olution: We have that f) = b and f ) = ) + b = b + 8. etting these equal
RMT 3 Calculus Test olutions February, 3. Answer: olution: Note that + 5 + 3. Answer: 3 3) + 5) = 3) ) = + 5. + 5 3 = 3 + 5 3 =. olution: We have that f) = b and f ) = ) + b = b + 8. etting these equal
Some commonly encountered sets and their notations
 NATIONAL UNIVERSITY OF SINGAPORE DEPARTMENT OF MATHEMATICS (This notes are based on the book Introductory Mathematics by Ng Wee Seng ) LECTURE SETS & FUNCTIONS Some commonly encountered sets and their
NATIONAL UNIVERSITY OF SINGAPORE DEPARTMENT OF MATHEMATICS (This notes are based on the book Introductory Mathematics by Ng Wee Seng ) LECTURE SETS & FUNCTIONS Some commonly encountered sets and their
INTEGRATING RADICALS
 INTEGRATING RADICALS MATH 53, SECTION 55 (VIPUL NAIK) Corresponding material in the book: Section 8.4. What students should already know: The definitions of inverse trigonometric functions. The differentiation
INTEGRATING RADICALS MATH 53, SECTION 55 (VIPUL NAIK) Corresponding material in the book: Section 8.4. What students should already know: The definitions of inverse trigonometric functions. The differentiation
Math 102 Spring 2008: Solutions: HW #3 Instructor: Fei Xu
 Math Spring 8: Solutions: HW #3 Instructor: Fei Xu. section 7., #8 Evaluate + 3 d. + We ll solve using partial fractions. If we assume 3 A + B + C, clearing denominators gives us A A + B B + C +. Then
Math Spring 8: Solutions: HW #3 Instructor: Fei Xu. section 7., #8 Evaluate + 3 d. + We ll solve using partial fractions. If we assume 3 A + B + C, clearing denominators gives us A A + B B + C +. Then
Chapter 06: Analytic Trigonometry
 Chapter 06: Analytic Trigonometry 6.1: Inverse Trigonometric Functions The Problem As you recall from our earlier work, a function can only have an inverse function if it is oneto-one. Are any of our trigonometric
Chapter 06: Analytic Trigonometry 6.1: Inverse Trigonometric Functions The Problem As you recall from our earlier work, a function can only have an inverse function if it is oneto-one. Are any of our trigonometric
Solution. Using the point-slope form of the equation we have the answer immediately: y = 4 5 (x ( 2)) + 9 = 4 (x +2)+9
 Chapter Review. Lines Eample. Find the equation of the line that goes through the point ( 2, 9) and has slope 4/5. Using the point-slope form of the equation we have the answer immediately: y = 4 5 ( (
Chapter Review. Lines Eample. Find the equation of the line that goes through the point ( 2, 9) and has slope 4/5. Using the point-slope form of the equation we have the answer immediately: y = 4 5 ( (
Solutions to Math 41 Exam 2 November 10, 2011
 Solutions to Math 41 Eam November 10, 011 1. (1 points) Find each of the following its, with justification. If the it does not eist, eplain why. If there is an infinite it, then eplain whether it is or.
Solutions to Math 41 Eam November 10, 011 1. (1 points) Find each of the following its, with justification. If the it does not eist, eplain why. If there is an infinite it, then eplain whether it is or.
Solutions to Problem Sheet for Week 6
 THE UNIVERSITY OF SYDNEY SCHOOL OF MATHEMATICS AND STATISTICS Solutions to Problem Sheet for Week 6 MATH90: Differential Calculus (Advanced) Semester, 07 Web Page: sydney.edu.au/science/maths/u/ug/jm/math90/
THE UNIVERSITY OF SYDNEY SCHOOL OF MATHEMATICS AND STATISTICS Solutions to Problem Sheet for Week 6 MATH90: Differential Calculus (Advanced) Semester, 07 Web Page: sydney.edu.au/science/maths/u/ug/jm/math90/
First Midterm Examination
 Çankaya University Department of Mathematics 016-017 Fall Semester MATH 155 - Calculus for Engineering I First Midterm Eamination 1) Find the domain and range of the following functions. Eplain your solution.
Çankaya University Department of Mathematics 016-017 Fall Semester MATH 155 - Calculus for Engineering I First Midterm Eamination 1) Find the domain and range of the following functions. Eplain your solution.
Solutions to Math 41 Final Exam December 9, 2013
 Solutions to Math 4 Final Eam December 9,. points In each part below, use the method of your choice, but show the steps in your computations. a Find f if: f = arctane csc 5 + log 5 points Using the Chain
Solutions to Math 4 Final Eam December 9,. points In each part below, use the method of your choice, but show the steps in your computations. a Find f if: f = arctane csc 5 + log 5 points Using the Chain
Math 181, Exam 2, Fall 2014 Problem 1 Solution. sin 3 (x) cos(x) dx.
 Math 8, Eam 2, Fall 24 Problem Solution. Integrals, Part I (Trigonometric integrals: 6 points). Evaluate the integral: sin 3 () cos() d. Solution: We begin by rewriting sin 3 () as Then, after using the
Math 8, Eam 2, Fall 24 Problem Solution. Integrals, Part I (Trigonometric integrals: 6 points). Evaluate the integral: sin 3 () cos() d. Solution: We begin by rewriting sin 3 () as Then, after using the
Essex County College Division of Mathematics MTH-122 Assessments. Honor Code
 Essex County College Division of Mathematics MTH-22 Assessments Last Name: First Name: Phone or email: Honor Code The Honor Code is a statement on academic integrity, it articulates reasonable expectations
Essex County College Division of Mathematics MTH-22 Assessments Last Name: First Name: Phone or email: Honor Code The Honor Code is a statement on academic integrity, it articulates reasonable expectations
Calculus 1: Sample Questions, Final Exam
 Calculus : Sample Questions, Final Eam. Evaluate the following integrals. Show your work and simplify your answers if asked. (a) Evaluate integer. Solution: e 3 e (b) Evaluate integer. Solution: π π (c)
Calculus : Sample Questions, Final Eam. Evaluate the following integrals. Show your work and simplify your answers if asked. (a) Evaluate integer. Solution: e 3 e (b) Evaluate integer. Solution: π π (c)
Precalculus Review. Functions to KNOW! 1. Polynomial Functions. Types: General form Generic Graph and unique properties. Constants. Linear.
 Precalculus Review Functions to KNOW! 1. Polynomial Functions Types: General form Generic Graph and unique properties Constants Linear Quadratic Cubic Generalizations for Polynomial Functions - The domain
Precalculus Review Functions to KNOW! 1. Polynomial Functions Types: General form Generic Graph and unique properties Constants Linear Quadratic Cubic Generalizations for Polynomial Functions - The domain
TRIG REVIEW NOTES. Co-terminal Angles: Angles that end at the same spot. (sines, cosines, and tangents will equal)
 TRIG REVIEW NOTES Convert from radians to degrees: multiply by 0 180 Convert from degrees to radians: multiply by 0. 180 Co-terminal Angles: Angles that end at the same spot. (sines, cosines, and tangents
TRIG REVIEW NOTES Convert from radians to degrees: multiply by 0 180 Convert from degrees to radians: multiply by 0. 180 Co-terminal Angles: Angles that end at the same spot. (sines, cosines, and tangents
Partial Fractions. dx dx x sec tan d 1 4 tan 2. 2 csc d. csc cot C. 2x 5. 2 ln. 2 x 2 5x 6 C. 2 ln. 2 ln x
 460_080.qd //04 :08 PM Page CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial
460_080.qd //04 :08 PM Page CHAPTER 8 Integration Techniques, L Hôpital s Rule, and Improper Integrals Section 8. Partial Fractions Understand the concept of a partial fraction decomposition. Use partial
Fall 2016, MA 252, Calculus II, Final Exam Preview Solutions
 Fall 6, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card, and
Fall 6, MA 5, Calculus II, Final Exam Preview Solutions I will put the following formulas on the front of the final exam, to speed up certain problems. You do not need to put them on your index card, and
APPLICATIONS OF DIFFERENTIATION
 4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION 4.4 Indeterminate Forms and L Hospital s Rule In this section, we will learn: How to evaluate functions whose values cannot be found at
4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION 4.4 Indeterminate Forms and L Hospital s Rule In this section, we will learn: How to evaluate functions whose values cannot be found at
Department of Mathematical x 1 x 2 1
 Contents Limits. Basic Factoring Eample....................................... One-Sided Limit........................................... 3.3 Squeeze Theorem.......................................... 4.4
Contents Limits. Basic Factoring Eample....................................... One-Sided Limit........................................... 3.3 Squeeze Theorem.......................................... 4.4
Preface. Computing Definite Integrals. 3 cos( x) dx. x 3
 Preface Here are the solutions to the practice problems for my Calculus I notes. Some solutions will have more or less detail than other solutions. The level of detail in each solution will depend up on
Preface Here are the solutions to the practice problems for my Calculus I notes. Some solutions will have more or less detail than other solutions. The level of detail in each solution will depend up on
C. Finding roots of trinomials: 1st Example: x 2 5x = 14 x 2 5x 14 = 0 (x 7)(x + 2) = 0 Answer: x = 7 or x = -2
 AP Calculus Students: Welcome to AP Calculus. Class begins in approimately - months. In this packet, you will find numerous topics that were covered in your Algebra and Pre-Calculus courses. These are
AP Calculus Students: Welcome to AP Calculus. Class begins in approimately - months. In this packet, you will find numerous topics that were covered in your Algebra and Pre-Calculus courses. These are
Analytic Trigonometry. Copyright Cengage Learning. All rights reserved.
 Analytic Trigonometry Copyright Cengage Learning. All rights reserved. 7.1 Trigonometric Identities Copyright Cengage Learning. All rights reserved. Objectives Simplifying Trigonometric Expressions Proving
Analytic Trigonometry Copyright Cengage Learning. All rights reserved. 7.1 Trigonometric Identities Copyright Cengage Learning. All rights reserved. Objectives Simplifying Trigonometric Expressions Proving
CONTINUITY AND DIFFERENTIABILITY
 5. Introduction The whole of science is nothing more than a refinement of everyday thinking. ALBERT EINSTEIN This chapter is essentially a continuation of our stu of differentiation of functions in Class
5. Introduction The whole of science is nothing more than a refinement of everyday thinking. ALBERT EINSTEIN This chapter is essentially a continuation of our stu of differentiation of functions in Class
The definite integral gives the area under the curve. Simplest use of FTC1: derivative of integral is original function.
 5.3: The Fundamental Theorem of Calculus EX. Given the graph of f, sketch the graph of x 0 f(t) dt. The definite integral gives the area under the curve. EX 2. Find the derivative of g(x) = x 0 + t 2 dt.
5.3: The Fundamental Theorem of Calculus EX. Given the graph of f, sketch the graph of x 0 f(t) dt. The definite integral gives the area under the curve. EX 2. Find the derivative of g(x) = x 0 + t 2 dt.
Chapter 7: Techniques of Integration
 Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
Chapter 7: Techniques of Integration MATH 206-01: Calculus II Department of Mathematics University of Louisville last corrected September 14, 2013 1 / 43 Chapter 7: Techniques of Integration 7.1. Integration
Mathematics 104 Fall Term 2006 Solutions to Final Exam. sin(ln t) dt = e x sin(x) dx.
 Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
Mathematics 14 Fall Term 26 Solutions to Final Exam 1. Evaluate sin(ln t) dt. Solution. We first make the substitution t = e x, for which dt = e x. This gives sin(ln t) dt = e x sin(x). To evaluate the
Mat104 Fall 2002, Improper Integrals From Old Exams
 Mat4 Fall 22, Improper Integrals From Old Eams For the following integrals, state whether they are convergent or divergent, and give your reasons. () (2) (3) (4) (5) converges. Break it up as 3 + 2 3 +
Mat4 Fall 22, Improper Integrals From Old Eams For the following integrals, state whether they are convergent or divergent, and give your reasons. () (2) (3) (4) (5) converges. Break it up as 3 + 2 3 +
Integrals. D. DeTurck. January 1, University of Pennsylvania. D. DeTurck Math A: Integrals 1 / 61
 Integrals D. DeTurck University of Pennsylvania January 1, 2018 D. DeTurck Math 104 002 2018A: Integrals 1 / 61 Integrals Start with dx this means a little bit of x or a little change in x If we add up
Integrals D. DeTurck University of Pennsylvania January 1, 2018 D. DeTurck Math 104 002 2018A: Integrals 1 / 61 Integrals Start with dx this means a little bit of x or a little change in x If we add up
Math 1272 Solutions for Fall 2005 Final Exam
 Math 7 Solutions for Fall 5 Final Exam ) This fraction appears in Problem 5 of the undated-? exam; a solution can be found in that solution set. (E) ) This integral appears in Problem 6 of the Fall 4 exam;
Math 7 Solutions for Fall 5 Final Exam ) This fraction appears in Problem 5 of the undated-? exam; a solution can be found in that solution set. (E) ) This integral appears in Problem 6 of the Fall 4 exam;
EXAM. Practice for Second Exam. Math , Fall Nov 4, 2003 ANSWERS
 EXAM Practice for Second Eam Math 135-006, Fall 003 Nov 4, 003 ANSWERS i Problem 1. In each part, find the integral. A. d (4 ) 3/ Make the substitution sin(θ). d cos(θ) dθ. We also have Then, we have d/dθ
EXAM Practice for Second Eam Math 135-006, Fall 003 Nov 4, 003 ANSWERS i Problem 1. In each part, find the integral. A. d (4 ) 3/ Make the substitution sin(θ). d cos(θ) dθ. We also have Then, we have d/dθ
Notes 3.2: Properties of Limits
 Calculus Maimus Notes 3.: Properties of Limits 3. Properties of Limits When working with its, you should become adroit and adept at using its of generic functions to find new its of new functions created
Calculus Maimus Notes 3.: Properties of Limits 3. Properties of Limits When working with its, you should become adroit and adept at using its of generic functions to find new its of new functions created
Math 181, Exam 2, Study Guide 2 Problem 1 Solution. 1 + dx. 1 + (cos x)2 dx. 1 + cos2 xdx. = π ( 1 + cos π 2
 Math 8, Exam, Study Guide Problem Solution. Use the trapezoid rule with n to estimate the arc-length of the curve y sin x between x and x π. Solution: The arclength is: L b a π π + ( ) dy + (cos x) + cos
Math 8, Exam, Study Guide Problem Solution. Use the trapezoid rule with n to estimate the arc-length of the curve y sin x between x and x π. Solution: The arclength is: L b a π π + ( ) dy + (cos x) + cos
Chapter 2 Overview: Anti-Derivatives. As noted in the introduction, Calculus is essentially comprised of four operations.
 Chapter Overview: Anti-Derivatives As noted in the introduction, Calculus is essentially comprised of four operations. Limits Derivatives Indefinite Integrals (or Anti-Derivatives) Definite Integrals There
Chapter Overview: Anti-Derivatives As noted in the introduction, Calculus is essentially comprised of four operations. Limits Derivatives Indefinite Integrals (or Anti-Derivatives) Definite Integrals There
Math 2250 Final Exam Practice Problem Solutions. f(x) = ln x x. 1 x. lim. lim. x x = lim. = lim 2
 Math 5 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
Math 5 Final Eam Practice Problem Solutions. What are the domain and range of the function f() = ln? Answer: is only defined for, and ln is only defined for >. Hence, the domain of the function is >. Notice
McKinney High School AP Calculus Summer Packet
 McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
McKinne High School AP Calculus Summer Packet (for students entering AP Calculus AB or AP Calculus BC) Name:. This packet is to be handed in to our Calculus teacher the first week of school.. ALL work
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
a x a y = a x+y a x a = y ax y (a x ) r = a rx and log a (xy) = log a (x) + log a (y) log a ( x y ) = log a(x) log a (y) log a (x r ) = r log a (x).
 You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
You should prepare the following topics for our final exam. () Pre-calculus. (2) Inverses. (3) Algebra of Limits. (4) Derivative Formulas and Rules. (5) Graphing Techniques. (6) Optimization (Maxima and
Math 2300 Calculus II University of Colorado
 Math 3 Calculus II University of Colorado Spring Final eam review problems: ANSWER KEY. Find f (, ) for f(, y) = esin( y) ( + y ) 3/.. Consider the solid region W situated above the region apple apple,
Math 3 Calculus II University of Colorado Spring Final eam review problems: ANSWER KEY. Find f (, ) for f(, y) = esin( y) ( + y ) 3/.. Consider the solid region W situated above the region apple apple,
Math Test #3 Info and Review Exercises
 Math 181 - Test #3 Info and Review Exercises Fall 2018, Prof. Beydler Test Info Date: Wednesday, November 28, 2018 Will cover sections 10.1-10.4, 11.1-11.7. You ll have the entire class to finish the test.
Math 181 - Test #3 Info and Review Exercises Fall 2018, Prof. Beydler Test Info Date: Wednesday, November 28, 2018 Will cover sections 10.1-10.4, 11.1-11.7. You ll have the entire class to finish the test.
MATH 250 TOPIC 13 INTEGRATION. 13B. Constant, Sum, and Difference Rules
 Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
Math 5 Integration Topic 3 Page MATH 5 TOPIC 3 INTEGRATION 3A. Integration of Common Functions Practice Problems 3B. Constant, Sum, and Difference Rules Practice Problems 3C. Substitution Practice Problems
Algebra/Pre-calc Review
 Algebra/Pre-calc Review The following pages contain various algebra and pre-calculus topics that are used in the stud of calculus. These pages were designed so that students can refresh their knowledge
Algebra/Pre-calc Review The following pages contain various algebra and pre-calculus topics that are used in the stud of calculus. These pages were designed so that students can refresh their knowledge
Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document
 Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document Background knowledge: (a) The arithmetic of integers (including HCFs and LCMs), of fractions, and of real numbers.
Core A-level mathematics reproduced from the QCA s Subject criteria for Mathematics document Background knowledge: (a) The arithmetic of integers (including HCFs and LCMs), of fractions, and of real numbers.
Midterm Exam #1. (y 2, y) (y + 2, y) (1, 1)
 Math 5B Integral Calculus March 7, 7 Midterm Eam # Name: Answer Key David Arnold Instructions. points) This eam is open notes, open book. This includes any supplementary tets or online documents. You are
Math 5B Integral Calculus March 7, 7 Midterm Eam # Name: Answer Key David Arnold Instructions. points) This eam is open notes, open book. This includes any supplementary tets or online documents. You are
Pure Core 2. Revision Notes
 Pure Core Revision Notes June 06 Pure Core Algebra... Polynomials... Factorising... Standard results... Long division... Remainder theorem... 4 Factor theorem... 5 Choosing a suitable factor... 6 Cubic
Pure Core Revision Notes June 06 Pure Core Algebra... Polynomials... Factorising... Standard results... Long division... Remainder theorem... 4 Factor theorem... 5 Choosing a suitable factor... 6 Cubic
3.3 Limits and Infinity
 Calculus Maimus. Limits Infinity Infinity is not a concrete number, but an abstract idea. It s not a destination, but a really long, never-ending journey. It s one of those mind-warping ideas that is difficult
Calculus Maimus. Limits Infinity Infinity is not a concrete number, but an abstract idea. It s not a destination, but a really long, never-ending journey. It s one of those mind-warping ideas that is difficult
October 27, 2018 MAT186 Week 3 Justin Ko. We use the following notation to describe the limiting behavior of functions.
 October 27, 208 MAT86 Week 3 Justin Ko Limits. Intuitive Definitions of Limits We use the following notation to describe the iting behavior of functions.. (Limit of a Function A it is written as f( = L
October 27, 208 MAT86 Week 3 Justin Ko Limits. Intuitive Definitions of Limits We use the following notation to describe the iting behavior of functions.. (Limit of a Function A it is written as f( = L
MATH141: Calculus II Exam #1 review 6/8/2017 Page 1
 MATH: Calculus II Eam # review /8/7 Page No review sheet can cover everything that is potentially fair game for an eam, but I tried to hit on all of the topics with these questions, as well as show you
MATH: Calculus II Eam # review /8/7 Page No review sheet can cover everything that is potentially fair game for an eam, but I tried to hit on all of the topics with these questions, as well as show you
Review Problems for the Final
 Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
Review Problems for the Final Math -3 5 7 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the
MATH 31B: BONUS PROBLEMS
 MATH 31B: BONUS PROBLEMS IAN COLEY LAST UPDATED: JUNE 8, 2017 7.1: 28, 38, 45. 1. Homework 1 7.2: 31, 33, 40. 7.3: 44, 52, 61, 71. Also, compute the derivative of x xx. 2. Homework 2 First, let me say
MATH 31B: BONUS PROBLEMS IAN COLEY LAST UPDATED: JUNE 8, 2017 7.1: 28, 38, 45. 1. Homework 1 7.2: 31, 33, 40. 7.3: 44, 52, 61, 71. Also, compute the derivative of x xx. 2. Homework 2 First, let me say
Core Mathematics 3 A2 compulsory unit for GCE Mathematics and GCE Pure Mathematics Mathematics. Unit C3. C3.1 Unit description
 Unit C3 Core Mathematics 3 A2 compulsory unit for GCE Mathematics and GCE Pure Mathematics Mathematics C3. Unit description Algebra and functions; trigonometry; eponentials and logarithms; differentiation;
Unit C3 Core Mathematics 3 A2 compulsory unit for GCE Mathematics and GCE Pure Mathematics Mathematics C3. Unit description Algebra and functions; trigonometry; eponentials and logarithms; differentiation;
A BRIEF REVIEW OF ALGEBRA AND TRIGONOMETRY
 A BRIEF REVIEW OF ALGEBRA AND TRIGONOMETR Some Key Concepts:. The slope and the equation of a straight line. Functions and functional notation. The average rate of change of a function and the DIFFERENCE-
A BRIEF REVIEW OF ALGEBRA AND TRIGONOMETR Some Key Concepts:. The slope and the equation of a straight line. Functions and functional notation. The average rate of change of a function and the DIFFERENCE-
Coach Stones Expanded Standard Pre-Calculus Algorithm Packet Page 1 Section: P.1 Algebraic Expressions, Mathematical Models and Real Numbers
 Coach Stones Expanded Standard Pre-Calculus Algorithm Packet Page 1 Section: P.1 Algebraic Expressions, Mathematical Models and Real Numbers CLASSIFICATIONS OF NUMBERS NATURAL NUMBERS = N = {1,2,3,4,...}
Coach Stones Expanded Standard Pre-Calculus Algorithm Packet Page 1 Section: P.1 Algebraic Expressions, Mathematical Models and Real Numbers CLASSIFICATIONS OF NUMBERS NATURAL NUMBERS = N = {1,2,3,4,...}
Name: Date: Period: Calculus Honors: 4-2 The Product Rule
 Name: Date: Period: Calculus Honors: 4- The Product Rule Warm Up: 1. Factor and simplify. 9 10 0 5 5 10 5 5. Find ' f if f How did you go about finding the derivative? Let s Eplore how to differentiate
Name: Date: Period: Calculus Honors: 4- The Product Rule Warm Up: 1. Factor and simplify. 9 10 0 5 5 10 5 5. Find ' f if f How did you go about finding the derivative? Let s Eplore how to differentiate
