Hyperbolic Functions Mixed Exercise 6

Size: px

Start display at page:

Download "Hyperbolic Functions Mixed Exercise 6"

Ronald Bryant
5 years ago
Views:

1 Hyprbolic Functions Mid Ercis 6 a b c ln ln sinh(ln ) ln ln + cosh(ln ) + ln tanh ln ln + ( 6 ) ( + ) 6 7 ln ln ln,and ln ln ln,and ln ln 6 artanh artanhy + + y ln ln y + y ln + y + y y ln + y y + y y ln + y y + y y So + y y + y y + y y + y y + y y y 6y 6 y( ) y Us lna lnb ln a b Us ln a ln a Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr.

2 HS sinhacoshb coshasinhb A A B B A A B B A B A+ B ( ) A B ( A B) sinh( A B) LHS A+ B A+ B A B A B A+ B A+ B A B A B tanh HS tanh tanh ( ) tanh + + ( + ) ( ) ( + ) ( + ) ( ) ( + ) SoHS + ( )( + ) sinh LHS Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr.

3 9cosh sinh ( + ) ( ) ( )( 7) 0, 7 ln, ln 7 Multiply throughout by. Solv as a quadratic in. 6 sinh 7cosh ( ) ( + ) ( )( + ) 0 ln Multiply throughout by. is not possibl for ral. 7 cosh + sinh 7 Using cosh sinh ( + sinh ) + sinh 7 sinh + sinh 0 (sinh + )(sinh ) 0 sinh,sinh arsinh, arsinh 96 ln ln ln( + + ) Us arsinh ln( + + ). ln( + ) Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr.

4 8 a b At th intraction, 6+ sinh sinh 6+ sinh sinh + sinh sinh + sinh 6 0 sinh + sinh 0 (sinh )(sinh + sinh + ) 0 You can s, by inspction that sinh satisfis this quation. Th quation b ac < 0. sinh sinh 0 Th only intrsction is whr sinh For sinh, arsinh + + ln( ) ln( + ) Using y 6+ sinh y has no ral roots, bcaus Coordinats of th point of intrsction ar (ln(+ ), 7) Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr.

5 9 a cosh + sinh coshcoshα + sinhsinhα Socoshα sinhα cosh α sinh α α α (cosh sinh ) sinhα coshα tanhα α 0.0 Us th idntity cosh A sinh A. Dirct from calculator. b cosh + sinh cosh( + 0.0) For any valu A,coshA. 0 a Th minimum valu of cosh + sinh is. cosh+ sinh sinhcoshα+ coshsinhα Socoshα sinhα cosh α sinh α α α (cosh sinh ) 6 6 sinhα coshα tanhα α 0.69 cosh + sinh sinh( ) Us th idntity cosh A sinh A. Dirct from calculator. b sinh( ) 8 sinh( ) arsinh. (s.f.) 0.7 ( d.p.) Dirct from calculator. Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr.

6 0 c cosh + sinh 8 ( + ) ( ) ± ± ± 8 + ln ( d.p.) Multiply throughout by. Solv as a quadratic in. is ngativ, so not possibl for ral. y cosh sinh a y arsinh Ltt y arsinht dt dt t + t b y arsinh Lt t y arsinht dt t t dt t + + d + Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr. 6

7 c y arcosh Ltt y arcosht dt dt t t d y arcosh arcosh + arcosh + y (arsinh ) (arsinh ) ( + ) arsinh ( + ) + 0 ( + ) ( + ) ( + ) arsinh d y d a Diffrntiating with rspct to givs us f'( ) sinh cosh. b y f( ) has a turning point whn f'( ) 0. f'( ) sinh cosh 0 sinh cosh tanh tanh artanh ln Thus, ln, an cosh(ln ) sinh(ln ) Thrfor (ln,) ar th coordinats of th turning point. Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr. 7

8 y arcosh(sinh ) Ltt sinh y arcosht dt cosh t t cosh t cosh sinh d 6 a Diffrntiatingywith rspct tofour tims and applying th product rul whr ncssary givs coscosh+ sinsinh, cossi nh, sinsinh + coscosh, sincosh. So, y b Evaluating th prssions w found in part a at 0givs y(0) 0, (0), (0) 0, (0), (0) 0. Sinc w know that y, w conclud. This givs us th first thr trms in th Maclaurin pansion as 0 0 y !!!! y + 0 Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr. 8

9 7 Diffrntiating y with rspct to fiv tims and applying th product rul whr ncssary giv coshcosh + sinhsinh, sinhcosh + coshsinh, coshcosh + sinhsinh, sinhcosh + 0coshsinh, coshcosh + sinhsinh. Evaluating ths prssions at0givs y( 0) 0 (0) (0) 0 (0) (0) 0 (0) 7 6 So y ( a+ b) + c, a > 0 a ( + b) + c a b b c Comparing cofficint of : b Comparing constant trm: 7 + c c 6 Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr. 9

10 8 b Using a, ( + ) + 6 Lt + tan,thnd sc d θ θ θ sc θ and dθ ( + ) + 6 6tanθ + 6 sc θ d θ 6sc θ θ 8 + arctan ( + C) 8. So [ arctan arctan 0] π 9 Using th dfinitions of sinh and cosh sinhcosh6 0 0 ( ) d C C 0 0 cosh0 cosh + C 0 You could us hyprbolic idntitis to split up into a diffrnc of two sinh s. a + as cosha a b You cannot us by parts for sinh Using th dfinition of sinh sinh ( ) d + C + C Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr. 0

11 0 0 Ara undr curv y arsinh 0 arsinh 0 al ara arsinh m. 0 Using + a arsinh a + 0 ( ) + 9 So + 0 ( ) + 9 Lt sinh u,thn coshudu coshu so d u + 0 coshu u + C arsinh + C a Using th ponntial forms sinh + cosh + + ( ) ( ) + + du Using th substitution u,thn u u du So d d u + u + u u + du u + ( ) arctan( ) u + C arctan ( ) + C Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr.

12 b + 0 ( ) + 9 So lt sinh u,thn coshudu 9sinhu + and cosh d u u + 0 9sinh u + 9 9sinhu + cosh u d u coshu 9coshu + u + C arsinh + C So 9 + arsinh [9] + 0 ( ) 9 + arsinh a An infinitsimal rgion clos to th point of intrsction can b sn in this diagram. d So tan θ. W diffrntiat with rspct to and obtain sinh That is, d. sinh So at, θ arctan 9. (s.f.) sinh b cosh d sinh 8.8 m. Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr.

13 a b cosh ( + ), ( 8+ sinh 8 + ), w find th intrsction points by stting ths prssions qual to ach othr and solving for. ( ) 8 ( + + ) Multiplying through by and using th substitutionz, w obtain th quadratic quation z 8z + 0, with solutionsz, z +. Thrfor, th solutions ar ln( ) and ln( + ). ln ( + ) (8+ sinh cosh ) ln ( ) 8+ cosh sinh 6. ( s.f.) ( + ) ln ( ) ln First w find th cross-sctional ara of th loaf. Not that sinc a unit is cm, w will hav a numbr which w will multiply by( cm) cm as opposd to th usualcm. LtAdnot cross-sctional ara. A + ( ) + Lt sinh u, so that th intgral bcoms arsinh() A cosh d u u (sinh u) + arsinh( ) arsinh() du arsinh( ) [ u] arsinh() arsinh( ) 0arsinh() units 0arsinh() (cm) 0arsinh() cm. Thn th volum, V, is calculatd by multiplying th cross-sctional ara in cntimtrs by th lngth in cntimtrs. V 0arsinh() 0 700arsinh() 660cm Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr.

14 6 a y sinh crosss th ais whn arsinh() ln ( + + ) ln( + 0). So th coordinats ar ( + ) ( ) ln 0,0. b Th volum of rvolution, V, is found by ln( + 0) V π( sinh ) 0 ln( + 0) π ( V ) d 0 ln( + 0) π 9 ( ) + ( + ) 0 ln( + 0) π 9 ( + ) (s.f.) Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr.

15 Challng First w find th ara btwn two arbitrarily larg valus quidistant from th origin; w will call ths valus and. So ara sch du W convrt to ponntial form and us th substitution u, noting that u. schd + + u u + du u du u + ( u) arctan ( ) arctan Now that w hav this prssion for arbitrarily larg, w tak th limit as. A lim arctan ( ) ( ( ) ( )) lim arctan arctan π 0 π Parson Education Ltd 08. Copying prmittd for purchasing institution only. This matrial is not copyright fr.

( 2) ( ) Hyperbolic Functions 6E. cosh d (cosh sech ) d sinh tanh. cosh. x x x x x x C. x 1 x. 2 a. x x x = + = + cosh dx sinh C 3sinh C.

( 2) ( ) Hyperbolic Functions 6E. cosh d (cosh sech ) d sinh tanh. cosh. x x x x x x C. x 1 x. 2 a. x x x = + = + cosh dx sinh C 3sinh C. 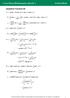Hyperolic Functions 6E a (sinh+ cosh ) cosh+ sinh+ + cosh cosh (cosh sech ) sinh tanh sinh sinh sechtanh sech+ cosh cosh cosh c a a sinh cosh+ cosh sinh sinh + + ( ) + + ( ) ( ) ( ) ( ) arcosh + ( ) +