Fractional Topological Insulators A Bosonization Approach
|
|
|
- Helen Wilson
- 5 years ago
- Views:
Transcription
1 Journl of Modrn Physis Publishd Onlin Jnury 06 in Sis. rtionl Topoloil Insultors A Boniztion Approh D. Shmltzr Physis Dprtmnt City Coll of th City Univrsity of w Yor w Yor Y USA ivd Otobr 05; ptd 8 Jnury 06; publishd Jnury 06 Copyriht 06 by uthor nd Sintifi srh Publishin In. This wor is linsd undr th Crtiv Commons Attribution Intrntionl ins (CC BY). Abstrt A mtlli dis with stron spin orbit intrtion is invstitd. Th finit dis omtry introdus onfinin potntil. Du to th stron spin-orbit intrtion nd onfinin potntil th mtl dis is dsribd by n fftiv on-dimnsionl modl with hrmoni potntil. Th hrmoni potntil ivs ris to lssil turnin points. As rsult opn boundry onditions must b usd. W boniz th modl nd obtin hirl Bons for h spin on th d of th dis. Whn th fillin frtion is rdud to ν th ltron-ltron intrtions r studid by usin th Jordn Winr phs for omposit frmions whih iv ris to uttinr liquid. Whn th mtlli dis is in th proimity with suprondutor rtionl Topoloil Insultor is obtind. An primntl rliztion is proposd. W show tht by tunnin th hmil potntil w ontrol th lssil turnin points for whih rtionl Topoloil Insultor is rlizd. Kywords Spin-Orbit Chirl Bons Chins Mtlli Dis Topoloil Insultors. Introdution Th prsn of th spin-orbit intrtion in onfind omtris ivs ris to Topoloil Insultor (T.I.). ollowin rf. [] on mps th spin-orbit intrtion to spin dpndnt mnti fild B z. As rsult th non intrtin ltrons r mppd to two fftiv Quntum Hll problms for h spis of spin. Whn th ltron dnsity is tund to n intr ndu fillin ν (for h spin) th round stt is md up of two doupld spin spis whih form n intr Quntum Hll stt with opposit hirlitis. Whn is odd th systm is TI nd whn is vn w hv trivil insultor. Whn ν th prsn of ltron-ltron How to it this ppr: Shmltzr D. (06) rtionl Topoloil Insultors A Boniztion Approh. Journl of Modrn Physis
2 D. Shmltzr intrtion for h spis of spin ivs ris to rtionl Topoloil Insultor (.T.I.). Usin th proposl for th rtionl Quntum Hll whih is built on n rry of quntum wirs [] th uthors [] [4] hv shown tht by fin tunin th spin orbit intrtion for onfiurtion of oupld hins Topoloil Insultor (T.I.) mrs. Whn th fillin ftor is suh tht it orrsponds to omposit rmions rtionl Topoloil Insultor (.T.I.) hs bn introdud in rf. []. It hs bn shown tht for modl of oupld hins in th y dirtion th spin orbit intrtion n b ud wy rsultin in twistd boundry onditions for whih.t.i. ws obtind. Th purpos of this ppr is to dmonstt tht two-dimnsionl mtlli dis with spin-orbit intrtion nd ltron ltron intrtion ivs ris ithr to Topoloil Insultor or rtionl Topoloil whn th dis is in th proimity to suprondutor. W boniz [5] [6] th modl in th limit of stron spin orbit intrtions nd omtril onfinmnt. W find tht th d of th dis is quivlnt to on-dimnsionl modl with hrmoni potntil. W obtin hirl Boni modl [7] nd show tht T.I. mrs for th fillin ftor ν. or th fillin ftor ν w us th omposit ltrons mthod [8] [9] nd show tht th omposit Jordn Winr phs [0] ivs ris to n intrtin on-dimnsionl modl in th Boni form. W obtin uttinr liquid with th uttinr prmtr κ ν whih is th proimity to supr ondutor thn w obtin.t.i. An primntl vrifition is proposd. W show tht th.t.i. is obtind by tunnin th hmil potntil th intrtions nd th rdius of th dis. Th pln of th ppr is s follows. In Stion w prsnt th spin-orbit intrtions in mtls. In Stion. nd. w rviw th modl introdud in rf. []. W find it dvntous to us opn boundry onditions nd study th modl in th frmwor of Boniztion. In Stion. w introdu our nw modl. W onsidr mtlli dis with sron spin orbit intrtion nd onfinmnt. In Stion. w study th mtlli dis with stron spin orbit intrtions nd onfinmnt for th fillin ftor ν. Usin th omposit rmion mthod w obtin uttinr liquid whih in th proimity with suprondutor rprsnts.t.i. At th nd of this stion w onsidr th primntl rliztion of th modl. Stion 4 is dvotd to onlusions.. Th Spin Orbit in Two Dimnsions in th Prsn of Confinin Potntil Th Hmiltonin for two dimnsionl mtl in th prsn of prboli onfinin potntil is ivn by: ˆ µ H µ V ( ) m p E + y () γ Usin th onfinin potntil V ( y ) ( + y ) w obtin th ltri fild: E γ Ey γ y nd E z 0. W introdu fititious mnti fild µ B. As rsult th Hmiltonin in Eqution () is funtion of th spin orbit momntum nd ts th form: y H i z + i y + z m µ + V ( y) () is th ltti onstnt nd A y Ay r th u filds. 9
3 D. Shmltzr.. Th Emrin Topoloil Insultor for Two-Dimnsionl Modl Priodi in th y Dirtion with th illin tor ν for Systm of Coupld Chins In this stion w will rviw th modl introdud in rf. []. W find ssntil to modify th modl nd us opn boundry onditions. This modifition is importnt for voidin omplitions usd by th twist introdud by th spin-orbit intrtion. Th opn boundry onditions impos onstrint on th Boni filds (th riht nd lft Boni fild r not indpndnt). or th rminin prt w will boniz [7] th modl ivn in rf. [] usin th opn boundry onditions. W will us opn boundry onditions l for th mtli dis (s Stions.-.) Th mthodoloy for both modl will b sm thrfor w find it nssry to prsnt th dtils of th Boniztion mthod (for opn boundry onditions). Th modl onsidrd in rf. [] is s follows: In th y dirtion w hv hins with th tunnlin mtri lmnt t. Th onfinin potntil V( y ) obys for 0 < < V( y ) 0 nd for > V( y ). W will ssum opn boundry onditions in th dirtion. In th y dirtion th onfind potntil is fftivly zro for 0 < y < nd V( y ) for y > ( r th numbr of hins). W will us th onditions A y nd A y 0. H H + H 0 t γ y 0 d z µ n m γ H Ψ i + V Ψ t n+ n H t d Ψ Ψ + h.. H 0 is th on dimnsionl modl for h hin nd H t dsribs th tunnlin btwn th hins. Th V y nfors th opn boundry onditions. Ψ 0 Ψ 0 n (4) onfinin potntil Th opn boundry onditions void th twist. y y i i z z ; ( 0) ( ) 0 n Ψ Ψ Ψ Ψ Ψ Ψ As rsult th Hmiltonin is trnsformd H H0 + Ht γ y H0 dψ i z Ψ n γ dψ ( i ) µ Ψ n µ t d Ψ Ψ n+ +.. n ( yn yn ) z i + n n+ n H t h t dψ Ψ + h.. y n t w us th mppin n for n introdud by [] []. This prmtriztion rmovs th osilltin phs for rtin hnnls nn+ nd thrfor ps r opnd. () (5) 0
4 D. Shmltzr In th nt stp w boniz th modl for th fillin ftor nd th Boni phs is th spin orbit strnth). ν usin th ltroni dnsity n ϕ for h hin ( µ is th hmil potntil is th rmi momntum nd i dn i ± ϕ Ψ n n n + θ ( ) ( ) n θ p θ p iδ δ δ i ( θ ) n ϕn i 4 θ n nn i( θ + ϕ ( )) i 4θn n Ψ i i + r nti ommutin Klin ftors [0] [] []. Du to th boundry onditions th lft nd riht movrs r not indpndnt. Th Boni rprsnttion of. Th lft movrs r ivn by th rmion fild Ψ is ivn in trms of th riht movrs ( ). i i Ψ (7) W dfin nw hirl (riht movin) rmi fild Ω for > 0 nd Ω ( ) <. This implis tht th hirl rmioni fild Ω obys Ω ( ) Ω ( ). Ω is for 0 priodi in th domin < < (th domin 0 < < hs b nlrd to < < ). Usin th stp Ω. funtion θ [ ] w writ th rprsnttion of th hirl fild θ[ ] + ( ) θ[ ] W find: Ω (8) H H + H H H + H 0 t t t t 0 Ω n t 0 n+ n n t 0 n+ n n Ω H d i ; H t d + h.. ; H t d + h.. ; Th bul is pd nd only four hirl mods rmin plss ( ) ( ) Ω Ω Ω Ω (0) n n n n Th hirl d Hmiltonin is ivn by H hirl n H lft-d Hhirl n Hriht-d : H H + H ; hirl lft-d riht-d lft-d d Ω Ω + Ω n Ω H i i riht-d d Ω Ω + Ω Ω H i i Usin th proimity to suprondutor with th pirin fild stts r pd) without brin tim rvrsl symmtry. (6) (9) () w n p out th ds (th bul
5 D. Shmltzr H ˆ ˆ ˆ ˆ d i i Ω Ω + Ω Ω iδ ( ) ˆ ˆ iδ ˆ ˆ Ω Ω Ω Ω HC In th prsn of mnt whih brs rvrsl-symmtry th sptrum will l b pd out []... Th rtionl Topoloil Insultor for th illin tor ν t w will onsidr th modl t th fillin ftor ν. W us omposit rmions in on dimnsions nd Boniz th modl round (w mntion tht in on dimnsions w n Boniz round ny odd numbr of rmi momntum ). In this stion w will show how th mthod of omposit rmions wors in on dimnsions. Aordin to Eqution (6) omposit rmions is obtind whnvr n vn numbr of Jordn Winr d phss is tthd to rmion. If ± i nn i ϕn dsribs n ltrons omposit frmions ( ) d is obtind by modifyin th Jordn Winr phs to ± i n + nn i ϕn. As rsult on n + is obtind for obsrvs tht th Boni rprsnttion for th omposit frmions with ( ) ν. As rsult th Boniztion is invrint undr th frmi momntum nd fillin ftor mppin: nd ν ν. ollowin th stps ivn in Eqution (6) for th fillin ftor i dn i ; ± ϕ Ψ n n n + θ n θ p p ( ) i ( ) θn n δ δnn δ i ( θ ) i 4( ( n n ) ( ϕ θ + θ )) ; i ( θ ) i 4 ( n + ϕn θ + θ ) ; n i i Ψ + ; ; ; ptin th formultion ivn in Equtions (7)-(8) w hv i i Ψ Ω θ[ ] + ( ) θ[ ] ; ; ; ; ; ; () ν w find: In th nt stp w us th rltion nd obtin similr prssions to Equtions (8)-(). Th bul is pd nd only four hirl mods rmin plss ( ) ( ) n ; n ; n ; n ; () (4) Ω Ω Ω Ω (5) Th hirl d Hmiltonin is ivn by Hhirl n ; Hlft-d; Hhirl n ; Hriht-d; : H H + H ; hirl; lft-d; riht-d; lft-d; d Ω ; Ω + Ω ; ; Ω n ; riht-d d Ω Ω + Ω ; ; Ω ; H i i H ( i ) ( i ) (6)
6 D. Shmltzr Usin th rltion imposd by th opn boundry onditions with only on indpndnt Boni fild θ w hv: θ η θ η (7) W build from η nd η ( ) non-hirl Boni filds Θ Φ : η η η η Θ + Φ (8) v Hlft-d; d κ Φ n + Θ n κ ( ) v Hriht-d d κ ( n ) ( n ) Φ + Θ κ (9) v v0 κ ν This shows tht modl is uttinr liquid with th prmtr κ ν. Whn th hins r in th proimity with suprondutor w dd to th uttinr liquid Hmiltonin in Eqution (9) th pirin prt ivn in Eqution () (sond lin in Eqution ()). As rsult th modl of th oupld hins in proimity to suprondutor ivs ris to.t.i.. ollowin rf. [] th.t.i. is idntifid with th hlp of th Josphn priodiity whih msur th dnry of th round stt.. Th Mtlli Dis in th Prsn of th Spin Orbit Intrtion A liztion of Topoloil Insultor In this stion w prsnt our modl. it ws shown tht in stron mnti w n us th limit of lr mnti fild study th physis of ltrons in stron mnti filds [4]. w Usin th nloy with th stron mnti fild w propos to study th spin -orbit intrtion in th limit. As rsult on m dimnsionl modl in onfinin potntil mrs. or prboli potntil V( y ) with th ondition m w find onstrind Hmiltoni y h i + ( i ) µ + V ( y) m z y In th limit m w obtin V y z µ is rpld by on dimnsionl modl with prboli potntil... A liztion of Topoloil Insultor for th Mtlli Dis t illin tor ν In th sond quntizd formultion w find: H Ψ V y Ψ Du to th onstrind m modl. Th oordint y ts s th momntum. Th two dimnsionl prboli potntil V( y ) d z µ (0) + is rpld by on dimnsionl nd only rmins th oordint. W find: th potntil V( y ) ( y)
7 D. Shmltzr i H Ψ V y Ψ Ψ i + Ψ d z d µ µ () In th sond lin of Eqution () w hv usd th onstrint rltion whih mrs from th stron spin-orbit intrtion y This rsult is intrprtd s sond lss onstrind [5] [6] Th on dimnsionl fftiv modl ivn in Eqution () with th potntil llows to introdu sp µ µ dpndnt rmi momntum ˆ whr ˆ ± r th lssilly turnin points. W n mp this problm to th d of th dis. W introdu th nulr vribls for th d ( is th nulr vribl for th d whih is funtion of th oriinl oordint ). Th mppin btwn th sp dpndnt rmi momntum nd th nulr vribl is ivn by th funtion sin : Th turnin point ˆ µ sin for 0 ˆ sin for. ˆ ± uss th vnishin of th fild Ψ boundry onditions. As rsult w Boniz Ψ in trms of sinl movr. ± i dn ( ) i ϕ Ψ n n n + θ i ˆ d ( ) i ˆ d ( ). or this rn w must us opn Ψ Th rmi momntum is funtion of th hmil potntil µ instd of two rmi points ± th rmi momntum ( ) is dpndnt. Th vnishin points ( ) 0 iv ris to th fftiv d for th dis. is ivn by µ Du to th ft tht th rmi momntum is dpndnt w tht rmi vloity is l sp dpndnt ˆ () µ v ˆ In th nt stp w obtin th Boni rprsnttion for th mtlli dis. ( y> 0) ( y< 0) H H + H ( y> 0 ) ˆ ˆ H d y ; > 0 v i y ; > 0 y ; > 0 v i y ; > 0 ( y< 0 ) ˆ ˆ H d y ; < 0 v i y ; < 0 y ; < 0 v i y ; < 0 () ( y 0) H > rprsnts th Hmiltonin for th uppr hlf dis nd ( y 0) H < is th Hmiltonin for th lowr hlf. 4
8 D. Shmltzr Du to th turnin points w hv th rltions: ( ; 0 ) ( ; 0 ) ( ; 0 ) ( ; 0) y> y> y< y< (4) Usin th boundry onditions ivn in Eqution (4) w obtin for Eqution () th rprsnttion: ( y> 0 ) ˆ ˆ H d y ; > 0 v i y ; > 0 y ; > 0 v i y ; > 0 ˆ d ; 0 ; 0 ˆ y v i y > > ( y< 0 ) ˆ ˆ H d y ; < 0 v i y ; < 0 y ; < 0 v i y ; < 0 ˆ d ( y ; 0) v ( i ) ( y ; < 0) < ˆ t w mp th problm to th d of th dis. W find from th mppin th rltion d. Th trm v is rpld by th drivtiv on th boundry of th dis. d sin ˆ d v v d d ˆ df f ( ) ˆ dsin f ( ) ˆ d f ( ) ˆ 0 d 0 0 d W prss th Hmiltonin in Eqution (5) in trms of th hirl rmions on th boundry of th dis. W hv th mppin T ( ) ( ) T nd find: µ d ( )( ) ( ) + ( )( ) ( ) (7) H i i st w onsidr th proimity fft of suprondutor with th pirin fild ( ) iδ. As rsult of th pirin fild suprondutin p is opn on th ds. As rsults th Hmiltonin with th pirin fild ( ) iδ ivs ris to th Bonizd form of th T.I. Hmiltonin: (5) (6) µ H d i + i 8µ iδ + d ( ) ( ( ) ( ) + ( ) ( ) ) + HC.. (8).. Th Mtlli Dis in th Prsn of th Spin Orbit Intrtion A Composit rmion ormultion for.t.i. or prtiulr dnsitis th omposit frmions onstrution introdud by [8] n b usd. In on dimnsions th Jordn Winr onstrution llows to obtin omposit rmions. ptin th produr of sp dpndnt rmi momntum introdud in Stion. w find tht th turnin points dpnds on th hmil µ µ potntil. By hnin th hmil potntil to s > w obtin s µ ˆ µ. Th turnin points drss to. s s s Th onstrution of th omposit frmions lvs th position of th turnin point invrint. Th Jordn 5
9 D. Shmltzr Winr onstrution is bsd on th ft tht both Jordn Winr rprsnttions ± i dn ( ) ± i dn ( ) dsrib rmion. Th first rprsnttion rprsnts n intrtin rmion modl with th fillin ftor. Th sond on rprsnts non intrtin rmion modl with th fillin ftor. or th hmil potntil µ s ˆ µ. µ th omposit rmion with th momntum s. or s w obtin µ nd will oby th rltion ivin th sm turnin point or this s w rpt th formultion ivn in Eqution (). W rpl θ nd hirl bons θ θ. Du to th boundry onditions t th points ( ). W introdu θ ( ) η ( ) nd θ η ( ) ; ; i dn i ; ± ϕ Ψ n n n + θ + i ( θ ) i 4( ϕ θ + θ ) i 4 η + η( ) θ θ θ ϕ θ θ ; ; Ψ ϕ with th ˆ ± w us th rltions i ( θ + ϕ ) i 4 θ + θ i 4( η + η ) ˆ d ˆ d ; i ; i ; µ W mploy th mppin to th d of th dis. Whn w suprondutor is in th proimity of th dis th prin fild ( ) iδ will nrt p W introdu th filds: µ d H i + i 8µ iδ + d ( ) ( ( ) ( ) + ( ) ( ) ) + HC.. 9 η η η η Θ +Θ ( ) Θ + Φ Θ Φ +Φ Φ (9) (0) () 6
10 D. Shmltzr Θ msurs th hr dnsity whih is onjutd to Φ. W mp th Boni filds Θ nd Φ to th d of th dis: Θ Θ ( ) Φ Φ ( ). Th Boni form of th Hmiltonin in Eqution (9) rvls th uttinr liquid struturs with th intrtin prmtr κ ν. As rsult th hr stor rprsnts n.t.i.. v H µ d κ Φ + Θ κ ( ) ( ) 8µ + d ( ) os Θ( ) os Φ ( ) + δ 9 () v µ κ ν Comprin th rsults in Eqution () with th on ivn in Eqution (7) w noti tht κ nd th pirin oprtor is rpld by th symmtri form os Θ( ) os Φ ( ) + δ. As rsult th Josphn urrnt will b diffrnt for th two ss. Th us of th zro mod oprtors ivn in rf. [0] [7] n rvl th Josphn priodiity of th dnrt round stt. Whn th suprondutor is rpld by mnti systm p on th d of th dis vi spin-flippin bsttrin will ppr. In this s th Josphn hr urrnt will b rpld by Josphn spin urrnt []. Th primntl vrifition is don by msurin th Josphn urrnt btwn th mtlli dis nd th suprondutor whih will show diffrnt rsults for th T.I. nd th.t.i. Th primntl qustion is how to driv th dis to b ithr T.I. or.t.i. Our rsults show tht for th two ss w hv diffrnt turnin points µ for T.I. nd µ for.t.i. Th physil rdius of th 9 µ dis dtrmins wht stt n b obtind. Whn th rdius obys > th T.I. nd th.t.i. r possibl. W will hv ohrnt or mitur of th two phss. In ordr obsrv sinl phs w hv to µ µ hos th rdius to stisfy. or this s th phs with ν is not possibl ( th rin 9 rdius is shortr thn th turnin point ) from th othr-hnd th.t.i. with ν is possibl to obsrv. 4. Conlusions In th first prt of this ppr w hv prsntd th Boniztion for th modl introdud in rf. []. W hv found tht it is ssntil to us opn boundry onditions. This rsults r obtind by usin hirl Boniztion. Th rtionl s hs bn obtind with th hlp of th Jordn Winr trnsformtion for omposit rmions. In th sond prt w propos nw modl for rtionl Topoloil Insultor. W onsidr mtlli dis nd t dvnt of th stron spin orbit intrtion in th prsn of prboli potntil. W mp th problm to n on-dimnsionl modl with hrmoni potntil. On th d of th dis w find hirl frmion modl whih in th proimity to suprondutor ivs ris to rtionl Topoloil Insultor whn th rdius of th dis is tund to b lrr thn th frtionl turnin point. Th mppin to th on dimnsion llows showin tht th rtionl Topoloil Insultor mrs s n fftiv uttinr liquid modl for th fillin ftor ν. A possibl primntl rliztion of th modl is sustd bsd on tunnin of th hmil potntil nd th rdius of th dis. 7
11 D. Shmltzr frns [] vi M. nd Str A. (009) Physil viw ttrs [] Kn C.. Muhopdhyy. nd ubnsy T.C. (00) Physil viw ttrs [] Si E. Or Y. Str A. nd Hlpri B.I. (05) [4] Klinovj J. nd Tsrovny Y. (04) Physil viw B [5] Hldn.D.M. (98) Physil viw ttrs [6] uthr A. nd Emry V.J. (974) Physil viw ttrs 589. [7] lorni. nd Jiw. (887) Physil viw ttrs [8] Ji J.K. (007) Composit rmions. Cmbrid Univrsity Prss Cmbrid. [9] Bsu B. nd Bndyophdhyy P. [0] Shmltzr D. Kulov A. nd Mlrd M. (00) Journl of Physis: Condnsd Mttr [] Si E. nd Or Y. (04) Physil viw B [] uprt T. Sntos. yu S. Chmo C. nd Mudry C. (0) Physil viw B [] Ston M. (994) Boniztion. World Sintifi Publishin Co. Pt. td. Sinpor w Jrsy ondon nd Hon Kon. [4] I S. Krbli D. nd Sit B. (99) Physis ttrs B [5] Shmltzr D. (0) Journl of Physis: Condnsd Mttr [6] Winbr S. (0) turs on Quntum Mhnis. Cmbrid Univrsity Prss Cmbrid. [7] Boynovsy D. (989) Physil viw B
, each of which is a tree, and whose roots r 1. , respectively, are children of r. Data Structures & File Management
 nrl tr T is init st o on or mor nos suh tht thr is on sint no r, ll th root o T, n th rminin nos r prtition into n isjoint susts T, T,, T n, h o whih is tr, n whos roots r, r,, r n, rsptivly, r hilrn o
nrl tr T is init st o on or mor nos suh tht thr is on sint no r, ll th root o T, n th rminin nos r prtition into n isjoint susts T, T,, T n, h o whih is tr, n whos roots r, r,, r n, rsptivly, r hilrn o
Lecture 11 Waves in Periodic Potentials Today: Questions you should be able to address after today s lecture:
 Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
HIGHER ORDER DIFFERENTIAL EQUATIONS
 Prof Enriqu Mtus Nivs PhD in Mthmtis Edution IGER ORDER DIFFERENTIAL EQUATIONS omognous linr qutions with onstnt offiints of ordr two highr Appl rdution mthod to dtrmin solution of th nonhomognous qution
Prof Enriqu Mtus Nivs PhD in Mthmtis Edution IGER ORDER DIFFERENTIAL EQUATIONS omognous linr qutions with onstnt offiints of ordr two highr Appl rdution mthod to dtrmin solution of th nonhomognous qution
QUESTIONS BEGIN HERE!
 Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt o Computr n Inormtion Sins CSCI 2710 (Trno) Disrt Struturs TEST or Sprin Smstr, 2005 R this or strtin! This tst is los ook
Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt o Computr n Inormtion Sins CSCI 2710 (Trno) Disrt Struturs TEST or Sprin Smstr, 2005 R this or strtin! This tst is los ook
Outline. Binary Tree
 Outlin Similrity Srh Th Binry Brnh Distn Nikolus Austn nikolus.ustn@s..t Dpt. o Computr Sins Univrsity o Slzur http://rsrh.uni-slzur.t 1 Binry Brnh Distn Binry Rprsnttion o Tr Binry Brnhs Lowr Boun or
Outlin Similrity Srh Th Binry Brnh Distn Nikolus Austn nikolus.ustn@s..t Dpt. o Computr Sins Univrsity o Slzur http://rsrh.uni-slzur.t 1 Binry Brnh Distn Binry Rprsnttion o Tr Binry Brnhs Lowr Boun or
The Angular Momenta Dipole Moments and Gyromagnetic Ratios of the Electron and the Proton
 Journl of Modrn hysics, 014, 5, 154-157 ublishd Onlin August 014 in SciRs. htt://www.scir.org/journl/jm htt://dx.doi.org/.436/jm.014.51415 Th Angulr Momnt Diol Momnts nd Gyromgntic Rtios of th Elctron
Journl of Modrn hysics, 014, 5, 154-157 ublishd Onlin August 014 in SciRs. htt://www.scir.org/journl/jm htt://dx.doi.org/.436/jm.014.51415 Th Angulr Momnt Diol Momnts nd Gyromgntic Rtios of th Elctron
Lecture 14 (Oct. 30, 2017)
 Ltur 14 8.31 Quantum Thory I, Fall 017 69 Ltur 14 (Ot. 30, 017) 14.1 Magnti Monopols Last tim, w onsidrd a magnti fild with a magnti monopol onfiguration, and bgan to approah dsribing th quantum mhanis
Ltur 14 8.31 Quantum Thory I, Fall 017 69 Ltur 14 (Ot. 30, 017) 14.1 Magnti Monopols Last tim, w onsidrd a magnti fild with a magnti monopol onfiguration, and bgan to approah dsribing th quantum mhanis
QUESTIONS BEGIN HERE!
 Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt of Computr n Informtion Sins CSCI 710 (Trnoff) Disrt Struturs TEST for Fll Smstr, 00 R this for strtin! This tst is los ook
Points miss: Stunt's Nm: Totl sor: /100 points Est Tnnss Stt Univrsity Dprtmnt of Computr n Informtion Sins CSCI 710 (Trnoff) Disrt Struturs TEST for Fll Smstr, 00 R this for strtin! This tst is los ook
Similarity Search. The Binary Branch Distance. Nikolaus Augsten.
 Similrity Srh Th Binry Brnh Distn Nikolus Augstn nikolus.ugstn@sg..t Dpt. of Computr Sins Univrsity of Slzurg http://rsrh.uni-slzurg.t Vrsion Jnury 11, 2017 Wintrsmstr 2016/2017 Augstn (Univ. Slzurg) Similrity
Similrity Srh Th Binry Brnh Distn Nikolus Augstn nikolus.ugstn@sg..t Dpt. of Computr Sins Univrsity of Slzurg http://rsrh.uni-slzurg.t Vrsion Jnury 11, 2017 Wintrsmstr 2016/2017 Augstn (Univ. Slzurg) Similrity
Layer construction of threedimensional. String-String braiding statistics. Xiao-Liang Qi Stanford University Vienna, Aug 29 th, 2014
 Layr onstrution of thrdimnsional topologial stats and String-String braiding statistis Xiao-Liang Qi Stanford Univrsity Vinna, Aug 29 th, 2014 Outlin Part I 2D topologial stats and layr onstrution Gnralization
Layr onstrution of thrdimnsional topologial stats and String-String braiding statistis Xiao-Liang Qi Stanford Univrsity Vinna, Aug 29 th, 2014 Outlin Part I 2D topologial stats and layr onstrution Gnralization
ECE COMBINATIONAL BUILDING BLOCKS - INVEST 13 DECODERS AND ENCODERS
 C 24 - COMBINATIONAL BUILDING BLOCKS - INVST 3 DCODS AND NCODS FALL 23 AP FLZ To o "wll" on this invstition you must not only t th riht nswrs ut must lso o nt, omplt n onis writups tht mk ovious wht h
C 24 - COMBINATIONAL BUILDING BLOCKS - INVST 3 DCODS AND NCODS FALL 23 AP FLZ To o "wll" on this invstition you must not only t th riht nswrs ut must lso o nt, omplt n onis writups tht mk ovious wht h
CSE 373: AVL trees. Warmup: Warmup. Interlude: Exploring the balance invariant. AVL Trees: Invariants. AVL tree invariants review
 rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
Outline. 1 Introduction. 2 Min-Cost Spanning Trees. 4 Example
 Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim's Alorithm Introution Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #33 3 Alorithm Gnrl Constrution Mik Joson (Univrsity o Clry)
Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim's Alorithm Introution Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #33 3 Alorithm Gnrl Constrution Mik Joson (Univrsity o Clry)
APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS
 Intrntionl Journl o Sintii nd Rrh Publition Volum, Iu 5, M ISSN 5-353 APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS S.M.Khirnr, R.M.Pi*, J.N.Slun** Dprtmnt o Mthmti Mhrhtr
Intrntionl Journl o Sintii nd Rrh Publition Volum, Iu 5, M ISSN 5-353 APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS S.M.Khirnr, R.M.Pi*, J.N.Slun** Dprtmnt o Mthmti Mhrhtr
CIVL 8/ D Boundary Value Problems - Rectangular Elements 1/7
 CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
Lecture contents. Bloch theorem k-vector Brillouin zone Almost free-electron model Bands Effective mass Holes. NNSE 508 EM Lecture #9
 Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
TOPIC 5: INTEGRATION
 TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
1 Introduction to Modulo 7 Arithmetic
 1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
Theoretical study of quantization of magnetic flux in a superconducting ring
 Thortial study of quantization of magnti flux in a supronduting ring DaHyon Kang Bagunmyon offi, Jinan 567-880, Kora -mail : samplmoon@hanmail.nt W rfind th onpts of ltri urrnt and fluxoid, and London
Thortial study of quantization of magnti flux in a supronduting ring DaHyon Kang Bagunmyon offi, Jinan 567-880, Kora -mail : samplmoon@hanmail.nt W rfind th onpts of ltri urrnt and fluxoid, and London
Page 1. Question 19.1b Electric Charge II Question 19.2a Conductors I. ConcepTest Clicker Questions Chapter 19. Physics, 4 th Edition James S.
 ConTst Clikr ustions Chtr 19 Physis, 4 th Eition Jms S. Wlkr ustion 19.1 Two hrg blls r rlling h othr s thy hng from th iling. Wht n you sy bout thir hrgs? Eltri Chrg I on is ositiv, th othr is ngtiv both
ConTst Clikr ustions Chtr 19 Physis, 4 th Eition Jms S. Wlkr ustion 19.1 Two hrg blls r rlling h othr s thy hng from th iling. Wht n you sy bout thir hrgs? Eltri Chrg I on is ositiv, th othr is ngtiv both
Chapter 16. 1) is a particular point on the graph of the function. 1. y, where x y 1
 Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Math 61 : Discrete Structures Final Exam Instructor: Ciprian Manolescu. You have 180 minutes.
 Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Walk Like a Mathematician Learning Task:
 Gori Dprtmnt of Euction Wlk Lik Mthmticin Lrnin Tsk: Mtrics llow us to prform mny usful mthmticl tsks which orinrily rquir lr numbr of computtions. Som typs of problms which cn b on fficintly with mtrics
Gori Dprtmnt of Euction Wlk Lik Mthmticin Lrnin Tsk: Mtrics llow us to prform mny usful mthmticl tsks which orinrily rquir lr numbr of computtions. Som typs of problms which cn b on fficintly with mtrics
Designing A Concrete Arch Bridge
 This is th mous Shwnh ri in Switzrln, sin y Rort Millrt in 1933. It spns 37.4 mtrs (122 t) n ws sin usin th sm rphil mths tht will monstrt in this lsson. To pro with this lsson, lik on th Nxt utton hr
This is th mous Shwnh ri in Switzrln, sin y Rort Millrt in 1933. It spns 37.4 mtrs (122 t) n ws sin usin th sm rphil mths tht will monstrt in this lsson. To pro with this lsson, lik on th Nxt utton hr
Present state Next state Q + M N
 Qustion 1. An M-N lip-lop works s ollows: I MN=00, th nxt stt o th lip lop is 0. I MN=01, th nxt stt o th lip-lop is th sm s th prsnt stt I MN=10, th nxt stt o th lip-lop is th omplmnt o th prsnt stt I
Qustion 1. An M-N lip-lop works s ollows: I MN=00, th nxt stt o th lip lop is 0. I MN=01, th nxt stt o th lip-lop is th sm s th prsnt stt I MN=10, th nxt stt o th lip-lop is th omplmnt o th prsnt stt I
Lecture 12 Quantum chromodynamics (QCD) WS2010/11: Introduction to Nuclear and Particle Physics
 Lctur Quntum chromodynmics (QCD) WS/: Introduction to Nuclr nd Prticl Physics QCD Quntum chromodynmics (QCD) is thory of th strong intrction - bsd on color forc, fundmntl forc dscribing th intrctions of
Lctur Quntum chromodynmics (QCD) WS/: Introduction to Nuclr nd Prticl Physics QCD Quntum chromodynmics (QCD) is thory of th strong intrction - bsd on color forc, fundmntl forc dscribing th intrctions of
I. The Connection between Spectroscopy and Quantum Mechanics
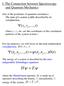 I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
Hardy Spaces, Hyperfunctions, Pseudo-Differential Operators and Wavelets
 Hrdy Sps, Hyprfuntions, Psudo-Diffrntil Oprtors nd Wvlts Colltions from lrtur Th Hrdy Sp nd Hilbrt Sls Lt : s /, t thn th Rimnn Hypothsis is th sttmnt tht / ( s is nlyti on th hlf-pln Th ppropr Hilbrt
Hrdy Sps, Hyprfuntions, Psudo-Diffrntil Oprtors nd Wvlts Colltions from lrtur Th Hrdy Sp nd Hilbrt Sls Lt : s /, t thn th Rimnn Hypothsis is th sttmnt tht / ( s is nlyti on th hlf-pln Th ppropr Hilbrt
Seven-Segment Display Driver
 7-Smnt Disply Drivr, Ron s in 7-Smnt Disply Drivr, Ron s in Prolm 62. 00 0 0 00 0000 000 00 000 0 000 00 0 00 00 0 0 0 000 00 0 00 BCD Diits in inry Dsin Drivr Loi 4 inputs, 7 outputs 7 mps, h with 6 on
7-Smnt Disply Drivr, Ron s in 7-Smnt Disply Drivr, Ron s in Prolm 62. 00 0 0 00 0000 000 00 000 0 000 00 0 00 00 0 0 0 000 00 0 00 BCD Diits in inry Dsin Drivr Loi 4 inputs, 7 outputs 7 mps, h with 6 on
Constructive Geometric Constraint Solving
 Construtiv Gomtri Constrint Solving Antoni Soto i Rir Dprtmnt Llngutgs i Sistms Inormàtis Univrsitt Politèni Ctluny Brlon, Sptmr 2002 CGCS p.1/37 Prliminris CGCS p.2/37 Gomtri onstrint prolm C 2 D L BC
Construtiv Gomtri Constrint Solving Antoni Soto i Rir Dprtmnt Llngutgs i Sistms Inormàtis Univrsitt Politèni Ctluny Brlon, Sptmr 2002 CGCS p.1/37 Prliminris CGCS p.2/37 Gomtri onstrint prolm C 2 D L BC
Lecture 6 Thermionic Engines
 Ltur 6 hrmioni ngins Rviw Rihrdson formul hrmioni ngins Shotty brrir nd diod pn juntion nd diod disussion.997 Copyright Gng Chn, MI For.997 Dirt Solr/hrml to ltril nrgy Convrsion WARR M. ROHSOW HA AD MASS
Ltur 6 hrmioni ngins Rviw Rihrdson formul hrmioni ngins Shotty brrir nd diod pn juntion nd diod disussion.997 Copyright Gng Chn, MI For.997 Dirt Solr/hrml to ltril nrgy Convrsion WARR M. ROHSOW HA AD MASS
ME 321 Kinematics and Dynamics of Machines S. Lambert Winter 2002
 3.4 Forc Analysis of Linkas An undrstandin of forc analysis of linkas is rquird to: Dtrmin th raction forcs on pins, tc. as a consqunc of a spcifid motion (don t undrstimat th sinificanc of dynamic or
3.4 Forc Analysis of Linkas An undrstandin of forc analysis of linkas is rquird to: Dtrmin th raction forcs on pins, tc. as a consqunc of a spcifid motion (don t undrstimat th sinificanc of dynamic or
Instructions for Section 1
 Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
(2) If we multiplied a row of B by λ, then the value is also multiplied by λ(here lambda could be 0). namely
 . DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
. DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
Research Scholar, Vinoba Bhave University, Hazaribag, Jharkhand
 Volum Issu July 0 ISSN: X Intrntionl Journl of Advnd Rsrh in Computr Sin nd Softwr Enginring Rsrh Ppr Avill onlin t: www.ijrss.om Dominting Funtion Thory from Nwton to Linitz s Approh of Indfinit Intgrtion
Volum Issu July 0 ISSN: X Intrntionl Journl of Advnd Rsrh in Computr Sin nd Softwr Enginring Rsrh Ppr Avill onlin t: www.ijrss.om Dominting Funtion Thory from Nwton to Linitz s Approh of Indfinit Intgrtion
EE1000 Project 4 Digital Volt Meter
 Ovrviw EE1000 Projt 4 Diitl Volt Mtr In this projt, w mk vi tht n msur volts in th rn o 0 to 4 Volts with on iit o ury. Th input is n nlo volt n th output is sinl 7-smnt iit tht tlls us wht tht input s
Ovrviw EE1000 Projt 4 Diitl Volt Mtr In this projt, w mk vi tht n msur volts in th rn o 0 to 4 Volts with on iit o ury. Th input is n nlo volt n th output is sinl 7-smnt iit tht tlls us wht tht input s
Problem 22: Journey to the Center of the Earth
 Problm : Journy to th Cntr of th Earth Imagin that on drilld a hol with smooth sids straight through th ntr of th arth If th air is rmod from this tub (and it dosn t fill up with watr, liquid rok, or iron
Problm : Journy to th Cntr of th Earth Imagin that on drilld a hol with smooth sids straight through th ntr of th arth If th air is rmod from this tub (and it dosn t fill up with watr, liquid rok, or iron
Sensors and Actuators Sensor Physics
 Snsors and Atuators Snsor Physis Sandr Stuijk (s.stuijk@tu.nl) Dpartmnt of ltrial ninrin ltroni Systms PN-JUNCON SNSOS (Chaptr 6.5) 3 mpratur snsors plamnt xitation physial fft matrial thrmal snsor ontat
Snsors and Atuators Snsor Physis Sandr Stuijk (s.stuijk@tu.nl) Dpartmnt of ltrial ninrin ltroni Systms PN-JUNCON SNSOS (Chaptr 6.5) 3 mpratur snsors plamnt xitation physial fft matrial thrmal snsor ontat
, between the vertical lines x a and x b. Given a demand curve, having price as a function of quantity, p f (x) at height k is the curve f ( x,
 Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
Practice Final Exam. 3.) What is the 61st term of the sequence 7, 11, 15, 19,...?
 Discrt mth Prctic Fl Em.) Fd 4 (i ) i=.) Fd i= 6 i.) Wht is th 6st trm th squnc 7,, 5, 9,...? 4.) Wht s th 57th trm, 6,, 4,...? 5.) Wht s th sum th first 60 trms th squnc, 5, 7, 9,...? 6.) Suppos st A
Discrt mth Prctic Fl Em.) Fd 4 (i ) i=.) Fd i= 6 i.) Wht is th 6st trm th squnc 7,, 5, 9,...? 4.) Wht s th 57th trm, 6,, 4,...? 5.) Wht s th sum th first 60 trms th squnc, 5, 7, 9,...? 6.) Suppos st A
INTEGRALS. Chapter 7. d dx. 7.1 Overview Let d dx F (x) = f (x). Then, we write f ( x)
 Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Theoretical Study on the While Drilling Electromagnetic Signal Transmission of Horizontal Well
 7 nd ntrntionl Confrnc on Softwr, Multimdi nd Communiction Enginring (SMCE 7) SBN: 978--6595-458-5 Thorticl Study on th Whil Drilling Elctromgntic Signl Trnsmission of Horizontl Wll Y-huo FAN,,*, Zi-ping
7 nd ntrntionl Confrnc on Softwr, Multimdi nd Communiction Enginring (SMCE 7) SBN: 978--6595-458-5 Thorticl Study on th Whil Drilling Elctromgntic Signl Trnsmission of Horizontl Wll Y-huo FAN,,*, Zi-ping
ENGR 323 BHW 15 Van Bonn 1/7
 ENGR 33 BHW 5 Van Bonn /7 4.4 In Eriss and 3 as wll as man othr situations on has th PDF o X and wishs th PDF o Yh. Assum that h is an invrtibl untion so that h an b solvd or to ild. Thn it an b shown
ENGR 33 BHW 5 Van Bonn /7 4.4 In Eriss and 3 as wll as man othr situations on has th PDF o X and wishs th PDF o Yh. Assum that h is an invrtibl untion so that h an b solvd or to ild. Thn it an b shown
Utilizing exact and Monte Carlo methods to investigate properties of the Blume Capel Model applied to a nine site lattice.
 Utilizing xat and Mont Carlo mthods to invstigat proprtis of th Blum Capl Modl applid to a nin sit latti Nik Franios Writing various xat and Mont Carlo omputr algorithms in C languag, I usd th Blum Capl
Utilizing xat and Mont Carlo mthods to invstigat proprtis of th Blum Capl Modl applid to a nin sit latti Nik Franios Writing various xat and Mont Carlo omputr algorithms in C languag, I usd th Blum Capl
2. Laser physics - basics
 . Lasr physics - basics Spontanous and stimulatd procsss Einstin A and B cofficints Rat quation analysis Gain saturation What is a lasr? LASER: Light Amplification by Stimulatd Emission of Radiation "light"
. Lasr physics - basics Spontanous and stimulatd procsss Einstin A and B cofficints Rat quation analysis Gain saturation What is a lasr? LASER: Light Amplification by Stimulatd Emission of Radiation "light"
b. How many ternary words of length 23 with eight 0 s, nine 1 s and six 2 s?
 MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
Numbering Boundary Nodes
 Numring Bounry Nos Lh MBri Empori Stt Univrsity August 10, 2001 1 Introution Th purpos of this ppr is to xplor how numring ltril rsistor ntworks ffts thir rspons mtrix, Λ. Morovr, wht n lrn from Λ out
Numring Bounry Nos Lh MBri Empori Stt Univrsity August 10, 2001 1 Introution Th purpos of this ppr is to xplor how numring ltril rsistor ntworks ffts thir rspons mtrix, Λ. Morovr, wht n lrn from Λ out
ME 522 PRINCIPLES OF ROBOTICS. FIRST MIDTERM EXAMINATION April 19, M. Kemal Özgören
 ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
Why the Junction Tree Algorithm? The Junction Tree Algorithm. Clique Potential Representation. Overview. Chris Williams 1.
 Why th Juntion Tr lgorithm? Th Juntion Tr lgorithm hris Willims 1 Shool of Informtis, Univrsity of Einurgh Otor 2009 Th JT is gnrl-purpos lgorithm for omputing (onitionl) mrginls on grphs. It os this y
Why th Juntion Tr lgorithm? Th Juntion Tr lgorithm hris Willims 1 Shool of Informtis, Univrsity of Einurgh Otor 2009 Th JT is gnrl-purpos lgorithm for omputing (onitionl) mrginls on grphs. It os this y
CSE 373: More on graphs; DFS and BFS. Michael Lee Wednesday, Feb 14, 2018
 CSE 373: Mor on grphs; DFS n BFS Mihl L Wnsy, F 14, 2018 1 Wrmup Wrmup: Disuss with your nighor: Rmin your nighor: wht is simpl grph? Suppos w hv simpl, irt grph with x nos. Wht is th mximum numr of gs
CSE 373: Mor on grphs; DFS n BFS Mihl L Wnsy, F 14, 2018 1 Wrmup Wrmup: Disuss with your nighor: Rmin your nighor: wht is simpl grph? Suppos w hv simpl, irt grph with x nos. Wht is th mximum numr of gs
THE SPINOR FIELD THEORY OF THE PHOTON
 Romnin Rports in Physics, Vol. 66, No., P. 9 5, 4 THE SPINOR FIELD THEORY OF THE PHOTON RUO PENG WANG Pking Univrsity, Physics Dprtmnt, Bijing 87, P.R. Chin E-mil: rpwng@pku.du.cn Rcivd Octobr 8, Abstrct.
Romnin Rports in Physics, Vol. 66, No., P. 9 5, 4 THE SPINOR FIELD THEORY OF THE PHOTON RUO PENG WANG Pking Univrsity, Physics Dprtmnt, Bijing 87, P.R. Chin E-mil: rpwng@pku.du.cn Rcivd Octobr 8, Abstrct.
Binomials and Pascal s Triangle
 Binomils n Psl s Tringl Binomils n Psl s Tringl Curriulum R AC: 0, 0, 08 ACS: 00 www.mthltis.om Binomils n Psl s Tringl Bsis 0. Intif th prts of th polnomil: 8. (i) Th gr. Th gr is. (Sin is th highst
Binomils n Psl s Tringl Binomils n Psl s Tringl Curriulum R AC: 0, 0, 08 ACS: 00 www.mthltis.om Binomils n Psl s Tringl Bsis 0. Intif th prts of th polnomil: 8. (i) Th gr. Th gr is. (Sin is th highst
Engineering 323 Beautiful HW #13 Page 1 of 6 Brown Problem 5-12
 Enginring Bautiful HW #1 Pag 1 of 6 5.1 Two componnts of a minicomputr hav th following joint pdf for thir usful liftims X and Y: = x(1+ x and y othrwis a. What is th probability that th liftim X of th
Enginring Bautiful HW #1 Pag 1 of 6 5.1 Two componnts of a minicomputr hav th following joint pdf for thir usful liftims X and Y: = x(1+ x and y othrwis a. What is th probability that th liftim X of th
Fr Carrir : Carrir onntrations as a funtion of tmpratur in intrinsi S/C s. o n = f(t) o p = f(t) W will find that: n = NN i v g W want to dtrmin how m
 MS 0-C 40 Intrinsi Smiondutors Bill Knowlton Fr Carrir find n and p for intrinsi (undopd) S/Cs Plots: o g() o f() o n( g ) & p() Arrhnius Bhavior Fr Carrir : Carrir onntrations as a funtion of tmpratur
MS 0-C 40 Intrinsi Smiondutors Bill Knowlton Fr Carrir find n and p for intrinsi (undopd) S/Cs Plots: o g() o f() o n( g ) & p() Arrhnius Bhavior Fr Carrir : Carrir onntrations as a funtion of tmpratur
Errata for Second Edition, First Printing
 Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 71: Eqution (.3) should rd B( R) = θ R 1 x= [1 G( x)] pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1
Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 71: Eqution (.3) should rd B( R) = θ R 1 x= [1 G( x)] pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1
( ) Geometric Operations and Morphing. Geometric Transformation. Forward v.s. Inverse Mapping. I (x,y ) Image Processing - Lesson 4 IDC-CG 1
 Img Procssing - Lsson 4 Gomtric Oprtions nd Morphing Gomtric Trnsformtion Oprtions dpnd on Pil s Coordints. Contt fr. Indpndnt of pil vlus. f f (, ) (, ) ( f (, ), f ( ) ) I(, ) I', (,) (, ) I(,) I (,
Img Procssing - Lsson 4 Gomtric Oprtions nd Morphing Gomtric Trnsformtion Oprtions dpnd on Pil s Coordints. Contt fr. Indpndnt of pil vlus. f f (, ) (, ) ( f (, ), f ( ) ) I(, ) I', (,) (, ) I(,) I (,
Algorithmic and NP-Completeness Aspects of a Total Lict Domination Number of a Graph
 Intrntionl J.Mth. Comin. Vol.1(2014), 80-86 Algorithmi n NP-Compltnss Aspts of Totl Lit Domintion Numr of Grph Girish.V.R. (PES Institut of Thnology(South Cmpus), Bnglor, Krntk Stt, Ini) P.Ush (Dprtmnt
Intrntionl J.Mth. Comin. Vol.1(2014), 80-86 Algorithmi n NP-Compltnss Aspts of Totl Lit Domintion Numr of Grph Girish.V.R. (PES Institut of Thnology(South Cmpus), Bnglor, Krntk Stt, Ini) P.Ush (Dprtmnt
AP Calculus BC Problem Drill 16: Indeterminate Forms, L Hopital s Rule, & Improper Intergals
 AP Calulus BC Problm Drill 6: Indtrminat Forms, L Hopital s Rul, & Impropr Intrgals Qustion No. of Instrutions: () Rad th problm and answr hois arfully () Work th problms on papr as ndd () Pik th answr
AP Calulus BC Problm Drill 6: Indtrminat Forms, L Hopital s Rul, & Impropr Intrgals Qustion No. of Instrutions: () Rad th problm and answr hois arfully () Work th problms on papr as ndd () Pik th answr
Lecture 1 - Introduction and Basic Facts about PDEs
 * 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
* 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
Limits Indeterminate Forms and L Hospital s Rule
 Limits Indtrmint Forms nd L Hospitl s Rul I Indtrmint Form o th Tp W hv prviousl studid its with th indtrmint orm s shown in th ollowin mpls: Empl : Empl : tn [Not: W us th ivn it ] Empl : 8 h 8 [Not:
Limits Indtrmint Forms nd L Hospitl s Rul I Indtrmint Form o th Tp W hv prviousl studid its with th indtrmint orm s shown in th ollowin mpls: Empl : Empl : tn [Not: W us th ivn it ] Empl : 8 h 8 [Not:
COMP108 Algorithmic Foundations
 Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
Errata for Second Edition, First Printing
 Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1 G( x)] = θp( R) + ( θ R)[1 G( R)] pg 15, problm 6: dmnd of
Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1 G( x)] = θp( R) + ( θ R)[1 G( R)] pg 15, problm 6: dmnd of
Module graph.py. 1 Introduction. 2 Graph basics. 3 Module graph.py. 3.1 Objects. CS 231 Naomi Nishimura
 Moul grph.py CS 231 Nomi Nishimur 1 Introution Just lik th Python list n th Python itionry provi wys of storing, ssing, n moifying t, grph n viw s wy of storing, ssing, n moifying t. Bus Python os not
Moul grph.py CS 231 Nomi Nishimur 1 Introution Just lik th Python list n th Python itionry provi wys of storing, ssing, n moifying t, grph n viw s wy of storing, ssing, n moifying t. Bus Python os not
Module 2 Motion Instructions
 Moul 2 Motion Instrutions CAUTION: Bor you strt this xprimnt, unrstn tht you r xpt to ollow irtions EXPLICITLY! Tk your tim n r th irtions or h stp n or h prt o th xprimnt. You will rquir to ntr t in prtiulr
Moul 2 Motion Instrutions CAUTION: Bor you strt this xprimnt, unrstn tht you r xpt to ollow irtions EXPLICITLY! Tk your tim n r th irtions or h stp n or h prt o th xprimnt. You will rquir to ntr t in prtiulr
Hermite-Hadamard Inequality for Geometrically Quasiconvex Functions on a Rectangular Box
 Mth. Si. Ltt. 5, No., 59-69 (26 59 Mthmtil Sins Lttrs An Intrntionl Journl http://d.doi.or/.8576/msl/58 Hrmit-Hdmrd Inulit for Gomtrill Qusionv Funtions on Rtnulr Bo Ali Brni nd Ftmh Mlmir Dprtmnt of Mthmtis,
Mth. Si. Ltt. 5, No., 59-69 (26 59 Mthmtil Sins Lttrs An Intrntionl Journl http://d.doi.or/.8576/msl/58 Hrmit-Hdmrd Inulit for Gomtrill Qusionv Funtions on Rtnulr Bo Ali Brni nd Ftmh Mlmir Dprtmnt of Mthmtis,
Outline. Computer Science 331. Computation of Min-Cost Spanning Trees. Costs of Spanning Trees in Weighted Graphs
 Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim s Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #34 Introution Min-Cost Spnnin Trs 3 Gnrl Constrution 4 5 Trmintion n Eiiny 6 Aitionl
Outlin Computr Sin 33 Computtion o Minimum-Cost Spnnin Trs Prim s Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #34 Introution Min-Cost Spnnin Trs 3 Gnrl Constrution 4 5 Trmintion n Eiiny 6 Aitionl
Ch 1.2: Solutions of Some Differential Equations
 Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
Assignment 4 Biophys 4322/5322
 Assignmnt 4 Biophys 4322/5322 Tylr Shndruk Fbruary 28, 202 Problm Phillips 7.3. Part a R-onsidr dimoglobin utilizing th anonial nsmbl maning rdriv Eq. 3 from Phillips Chaptr 7. For a anonial nsmbl p E
Assignmnt 4 Biophys 4322/5322 Tylr Shndruk Fbruary 28, 202 Problm Phillips 7.3. Part a R-onsidr dimoglobin utilizing th anonial nsmbl maning rdriv Eq. 3 from Phillips Chaptr 7. For a anonial nsmbl p E
Formal Concept Analysis
 Forml Conpt Anlysis Conpt intnts s losd sts Closur Systms nd Implitions 4 Closur Systms 0.06.005 Nxt-Closur ws dvlopd y B. Gntr (984). Lt M = {,..., n}. A M is ltilly smllr thn B M, if B A if th smllst
Forml Conpt Anlysis Conpt intnts s losd sts Closur Systms nd Implitions 4 Closur Systms 0.06.005 Nxt-Closur ws dvlopd y B. Gntr (984). Lt M = {,..., n}. A M is ltilly smllr thn B M, if B A if th smllst
Some Results on Interval Valued Fuzzy Neutrosophic Soft Sets ISSN
 Som Rsults on ntrval Valud uzzy Nutrosophi Soft Sts SSN 239-9725. rokiarani Dpartmnt of Mathmatis Nirmala ollg for Womn oimbator amilnadu ndia. R. Sumathi Dpartmnt of Mathmatis Nirmala ollg for Womn oimbator
Som Rsults on ntrval Valud uzzy Nutrosophi Soft Sts SSN 239-9725. rokiarani Dpartmnt of Mathmatis Nirmala ollg for Womn oimbator amilnadu ndia. R. Sumathi Dpartmnt of Mathmatis Nirmala ollg for Womn oimbator
HUGO ROSMAN * Gheorghe Asachi Technical University of Iaşi, Faculty of Electrical Engineering, Energetics and Applied Informatics
 BULETNUL NSTTUTULU POLTEHNC DN Ş Pulit d Univrsitt Thniă Ghorgh shi din şi Toul LV L Fs. 0 SŃi ELECTOTEHNCĂ. ENEGETCĂ. ELECTONCĂ THE CTVE ENEGY TNSMSSON EFFCENCY THOUGH LNE NON-UTONOMOUS ND PSSVE TWO-POTS
BULETNUL NSTTUTULU POLTEHNC DN Ş Pulit d Univrsitt Thniă Ghorgh shi din şi Toul LV L Fs. 0 SŃi ELECTOTEHNCĂ. ENEGETCĂ. ELECTONCĂ THE CTVE ENEGY TNSMSSON EFFCENCY THOUGH LNE NON-UTONOMOUS ND PSSVE TWO-POTS
Background: We have discussed the PIB, HO, and the energy of the RR model. In this chapter, the H-atom, and atomic orbitals.
 Chaptr 7 Th Hydrogn Atom Background: W hav discussd th PIB HO and th nrgy of th RR modl. In this chaptr th H-atom and atomic orbitals. * A singl particl moving undr a cntral forc adoptd from Scott Kirby
Chaptr 7 Th Hydrogn Atom Background: W hav discussd th PIB HO and th nrgy of th RR modl. In this chaptr th H-atom and atomic orbitals. * A singl particl moving undr a cntral forc adoptd from Scott Kirby
Junction Tree Algorithm 1. David Barber
 Juntion Tr Algorithm 1 David Barbr Univrsity Collg London 1 Ths slids aompany th book Baysian Rasoning and Mahin Larning. Th book and dmos an b downloadd from www.s.ul.a.uk/staff/d.barbr/brml. Fdbak and
Juntion Tr Algorithm 1 David Barbr Univrsity Collg London 1 Ths slids aompany th book Baysian Rasoning and Mahin Larning. Th book and dmos an b downloadd from www.s.ul.a.uk/staff/d.barbr/brml. Fdbak and
VECTOR ANALYSIS APPLICATION IN ROTATING MAGNETIC FIELDS
 22-578 VECTOR ANALYSIS APPLICATION IN ROTATING MAGNETIC FIELDS runo Osorno Dprtnt of Eltril And Coputr Enginring Cliforni Stt Univrsity Northridg 18111 Nordhoff St Northridg CA 9133-8436 Eil:runo@s.sun.du
22-578 VECTOR ANALYSIS APPLICATION IN ROTATING MAGNETIC FIELDS runo Osorno Dprtnt of Eltril And Coputr Enginring Cliforni Stt Univrsity Northridg 18111 Nordhoff St Northridg CA 9133-8436 Eil:runo@s.sun.du
V Envelope wave functions
 V Envlop wav funtions 5. atoriation of Bloh stat W onsidr htrountion of two matrials A and B. Th disussion applis as suh also for quantum wll strutur in whih A is th arrir and B th wll matrial. To mak
V Envlop wav funtions 5. atoriation of Bloh stat W onsidr htrountion of two matrials A and B. Th disussion applis as suh also for quantum wll strutur in whih A is th arrir and B th wll matrial. To mak
CS September 2018
 Loil los Distriut Systms 06. Loil los Assin squn numrs to msss All ooprtin prosss n r on orr o vnts vs. physil los: rport tim o y Assum no ntrl tim sour Eh systm mintins its own lol lo No totl orrin o
Loil los Distriut Systms 06. Loil los Assin squn numrs to msss All ooprtin prosss n r on orr o vnts vs. physil los: rport tim o y Assum no ntrl tim sour Eh systm mintins its own lol lo No totl orrin o
Aquauno Video 6 Plus Page 1
 Connt th timr to th tp. Aquuno Vio 6 Plus Pg 1 Usr mnul 3 lik! For Aquuno Vio 6 (p/n): 8456 For Aquuno Vio 6 Plus (p/n): 8413 Opn th timr unit y prssing th two uttons on th sis, n fit 9V lklin ttry. Whn
Connt th timr to th tp. Aquuno Vio 6 Plus Pg 1 Usr mnul 3 lik! For Aquuno Vio 6 (p/n): 8456 For Aquuno Vio 6 Plus (p/n): 8413 Opn th timr unit y prssing th two uttons on th sis, n fit 9V lklin ttry. Whn
( ) Differential Equations. Unit-7. Exact Differential Equations: M d x + N d y = 0. Verify the condition
 Diffrntial Equations Unit-7 Eat Diffrntial Equations: M d N d 0 Vrif th ondition M N Thn intgrat M d with rspt to as if wr onstants, thn intgrat th trms in N d whih do not ontain trms in and quat sum of
Diffrntial Equations Unit-7 Eat Diffrntial Equations: M d N d 0 Vrif th ondition M N Thn intgrat M d with rspt to as if wr onstants, thn intgrat th trms in N d whih do not ontain trms in and quat sum of
# 1 ' 10 ' 100. Decimal point = 4 hundred. = 6 tens (or sixty) = 5 ones (or five) = 2 tenths. = 7 hundredths.
 How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
VTU NOTES QUESTION PAPERS NEWS RESULTS FORUMS
 Diffrntial Equations Unit-7 Eat Diffrntial Equations: M d N d 0 Vrif th ondition M N Thn intgrat M d with rspt to as if wr onstants, thn intgrat th trms in N d whih do not ontain trms in and quat sum of
Diffrntial Equations Unit-7 Eat Diffrntial Equations: M d N d 0 Vrif th ondition M N Thn intgrat M d with rspt to as if wr onstants, thn intgrat th trms in N d whih do not ontain trms in and quat sum of
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,
![MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx, MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1. 1 [(y ) 2 + yy + y 2 ] dx,](/thumbs/89/98261542.jpg) MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
MATH3403: Green s Funtions, Integrl Equtions nd the Clulus of Vritions 1 Exmples 5 Qu.1 Show tht the extreml funtion of the funtionl I[y] = 1 0 [(y ) + yy + y ] dx, where y(0) = 0 nd y(1) = 1, is y(x)
Introduction to Condensed Matter Physics
 Introduction to Condnsd Mattr Physics pcific hat M.P. Vaughan Ovrviw Ovrviw of spcific hat Hat capacity Dulong-Ptit Law Einstin modl Dby modl h Hat Capacity Hat capacity h hat capacity of a systm hld at
Introduction to Condnsd Mattr Physics pcific hat M.P. Vaughan Ovrviw Ovrviw of spcific hat Hat capacity Dulong-Ptit Law Einstin modl Dby modl h Hat Capacity Hat capacity h hat capacity of a systm hld at
u x v x dx u x v x v x u x dx d u x v x u x v x dx u x v x dx Integration by Parts Formula
 7. Intgration by Parts Each drivativ formula givs ris to a corrsponding intgral formula, as w v sn many tims. Th drivativ product rul yilds a vry usful intgration tchniqu calld intgration by parts. Starting
7. Intgration by Parts Each drivativ formula givs ris to a corrsponding intgral formula, as w v sn many tims. Th drivativ product rul yilds a vry usful intgration tchniqu calld intgration by parts. Starting
Problem solving by search
 Prolm solving y srh Tomáš voo Dprtmnt o Cyrntis, Vision or Roots n Autonomous ystms Mrh 5, 208 / 3 Outlin rh prolm. tt sp grphs. rh trs. trtgis, whih tr rnhs to hoos? trtgy/algorithm proprtis? Progrmming
Prolm solving y srh Tomáš voo Dprtmnt o Cyrntis, Vision or Roots n Autonomous ystms Mrh 5, 208 / 3 Outlin rh prolm. tt sp grphs. rh trs. trtgis, whih tr rnhs to hoos? trtgy/algorithm proprtis? Progrmming
Lecture 37 (Schrödinger Equation) Physics Spring 2018 Douglas Fields
 Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Lctur 37 (Schrödingr Equation) Physics 6-01 Spring 018 Douglas Filds Rducd Mass OK, so th Bohr modl of th atom givs nrgy lvls: E n 1 k m n 4 But, this has on problm it was dvlopd assuming th acclration
Formulation of Seismic Active Earth Pressure of Inclined Retaining Wall Supporting c-ф Backfill
 01 IACSIT Coimbtor Confrns IPCSIT ol. 8 (01 (01 IACSIT Prss, Singpor Formultion of Sismi Ati Erth Prssur of Inlind Rtining Wll Supporting -Ф Bkfill Sim Ghosh 1 nd Strup Sngupt + 1 Assistnt Profssor, Ciil
01 IACSIT Coimbtor Confrns IPCSIT ol. 8 (01 (01 IACSIT Prss, Singpor Formultion of Sismi Ati Erth Prssur of Inlind Rtining Wll Supporting -Ф Bkfill Sim Ghosh 1 nd Strup Sngupt + 1 Assistnt Profssor, Ciil
Search sequence databases 3 10/25/2016
 Sarch squnc databass 3 10/25/2016 Etrm valu distribution Ø Suppos X is a random variabl with probability dnsity function p(, w sampl a larg numbr S of indpndnt valus of X from this distribution for an
Sarch squnc databass 3 10/25/2016 Etrm valu distribution Ø Suppos X is a random variabl with probability dnsity function p(, w sampl a larg numbr S of indpndnt valus of X from this distribution for an
Hydrogen Atom and One Electron Ions
 Hydrogn Atom and On Elctron Ions Th Schrödingr quation for this two-body problm starts out th sam as th gnral two-body Schrödingr quation. First w sparat out th motion of th cntr of mass. Th intrnal potntial
Hydrogn Atom and On Elctron Ions Th Schrödingr quation for this two-body problm starts out th sam as th gnral two-body Schrödingr quation. First w sparat out th motion of th cntr of mass. Th intrnal potntial
Electromagnetism Notes, NYU Spring 2018
 Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
Eletromgnetism Notes, NYU Spring 208 April 2, 208 Ation formultion of EM. Free field desription Let us first onsider the free EM field, i.e. in the bsene of ny hrges or urrents. To tret this s mehnil system
Majorana Neutrino Oscillations in Vacuum
 Journl of odrn Pysis 0 80-84 tt://dx.doi.org/0.46/jm.0.805 Publisd Onlin August 0 (tt://www.sip.org/journl/jm) jorn Nutrino Osilltions in Vuum Yubr Frny Prz Crlos Jos Quimby Esul d Físi Univrsidd Pdgógi
Journl of odrn Pysis 0 80-84 tt://dx.doi.org/0.46/jm.0.805 Publisd Onlin August 0 (tt://www.sip.org/journl/jm) jorn Nutrino Osilltions in Vuum Yubr Frny Prz Crlos Jos Quimby Esul d Físi Univrsidd Pdgógi
5/9/13. Part 10. Graphs. Outline. Circuits. Introduction Terminology Implementing Graphs
 Prt 10. Grphs CS 200 Algorithms n Dt Struturs 1 Introution Trminology Implmnting Grphs Outlin Grph Trvrsls Topologil Sorting Shortst Pths Spnning Trs Minimum Spnning Trs Ciruits 2 Ciruits Cyl A spil yl
Prt 10. Grphs CS 200 Algorithms n Dt Struturs 1 Introution Trminology Implmnting Grphs Outlin Grph Trvrsls Topologil Sorting Shortst Pths Spnning Trs Minimum Spnning Trs Ciruits 2 Ciruits Cyl A spil yl
12/3/12. Outline. Part 10. Graphs. Circuits. Euler paths/circuits. Euler s bridge problem (Bridges of Konigsberg Problem)
 12/3/12 Outlin Prt 10. Grphs CS 200 Algorithms n Dt Struturs Introution Trminology Implmnting Grphs Grph Trvrsls Topologil Sorting Shortst Pths Spnning Trs Minimum Spnning Trs Ciruits 1 Ciruits Cyl 2 Eulr
12/3/12 Outlin Prt 10. Grphs CS 200 Algorithms n Dt Struturs Introution Trminology Implmnting Grphs Grph Trvrsls Topologil Sorting Shortst Pths Spnning Trs Minimum Spnning Trs Ciruits 1 Ciruits Cyl 2 Eulr
Decimals DECIMALS.
 Dimls DECIMALS www.mthltis.o.uk ow os it work? Solutions Dimls P qustions Pl vlu o imls 0 000 00 000 0 000 00 0 000 00 0 000 00 0 000 tnths or 0 thousnths or 000 hunrths or 00 hunrths or 00 0 tn thousnths
Dimls DECIMALS www.mthltis.o.uk ow os it work? Solutions Dimls P qustions Pl vlu o imls 0 000 00 000 0 000 00 0 000 00 0 000 00 0 000 tnths or 0 thousnths or 000 hunrths or 00 hunrths or 00 0 tn thousnths
Multi-Section Coupled Line Couplers
 /0/009 MultiSction Coupld Lin Couplrs /8 Multi-Sction Coupld Lin Couplrs W cn dd multipl coupld lins in sris to incrs couplr ndwidth. Figur 7.5 (p. 6) An N-sction coupld lin l W typiclly dsign th couplr
/0/009 MultiSction Coupld Lin Couplrs /8 Multi-Sction Coupld Lin Couplrs W cn dd multipl coupld lins in sris to incrs couplr ndwidth. Figur 7.5 (p. 6) An N-sction coupld lin l W typiclly dsign th couplr
Cycles and Simple Cycles. Paths and Simple Paths. Trees. Problem: There is No Completely Standard Terminology!
 Outlin Computr Sin 331, Spnnin, n Surphs Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #30 1 Introution 2 3 Dinition 4 Spnnin 5 6 Mik Joson (Univrsity o Clry) Computr Sin 331 Ltur #30 1 / 20 Mik
Outlin Computr Sin 331, Spnnin, n Surphs Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #30 1 Introution 2 3 Dinition 4 Spnnin 5 6 Mik Joson (Univrsity o Clry) Computr Sin 331 Ltur #30 1 / 20 Mik
5/7/13. Part 10. Graphs. Theorem Theorem Graphs Describing Precedence. Outline. Theorem 10-1: The Handshaking Theorem
 Thorm 10-1: Th Hnshkin Thorm Lt G=(V,E) n unirt rph. Thn Prt 10. Grphs CS 200 Alorithms n Dt Struturs v V (v) = 2 E How mny s r thr in rph with 10 vrtis h of r six? 10 * 6 /2= 30 1 Thorm 10-2 An unirt
Thorm 10-1: Th Hnshkin Thorm Lt G=(V,E) n unirt rph. Thn Prt 10. Grphs CS 200 Alorithms n Dt Struturs v V (v) = 2 E How mny s r thr in rph with 10 vrtis h of r six? 10 * 6 /2= 30 1 Thorm 10-2 An unirt
Integration Continued. Integration by Parts Solving Definite Integrals: Area Under a Curve Improper Integrals
 Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
fiziks Forum for CSIR-UGC JRF/NET, GATE, IIT-JAM, GRE in PHYSICAL SCIENCES
 fizis /o Annd Institut of mthmtis, 8-B/6 Ji Sri Nr IIT, Huz Khs, Nw Dlhi, PIN- 6 (INDIA) Phon: -78565, +9-98745498 Wbsit: http://www.physisbyfizis.om GATE-8 (PHYSICS).. rry on mr h.. For rbitrry mtris
fizis /o Annd Institut of mthmtis, 8-B/6 Ji Sri Nr IIT, Huz Khs, Nw Dlhi, PIN- 6 (INDIA) Phon: -78565, +9-98745498 Wbsit: http://www.physisbyfizis.om GATE-8 (PHYSICS).. rry on mr h.. For rbitrry mtris
MA1506 Tutorial 2 Solutions. Question 1. (1a) 1 ) y x. e x. 1 exp (in general, Integrating factor is. ye dx. So ) (1b) e e. e c.
 MA56 utorial Solutions Qustion a Intgrating fator is ln p p in gnral, multipl b p So b ln p p sin his kin is all a Brnoulli quation -- st Sin w fin Y, Y Y, Y Y p Qustion Dfin v / hn our quation is v μ
MA56 utorial Solutions Qustion a Intgrating fator is ln p p in gnral, multipl b p So b ln p p sin his kin is all a Brnoulli quation -- st Sin w fin Y, Y Y, Y Y p Qustion Dfin v / hn our quation is v μ
Garnir Polynomial and their Properties
 Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
