Mathacle. PSet Stats, Concepts In Statistics Level Number Name: Date: , the DeMoivre-Laplace Theorem states: ( ) n x.
|
|
|
- Coleen Greer
- 5 years ago
- Views:
Transcription
1 6.4. Approimtion of Binomil Distriution y the Norml Distriution n n [MATH] When np ( p) >>, y using the Stirling s formul n! n e πn, the DeMoivre-Lplce Theorem sttes: ( ) ( n, p, ) = C p p n n e π np( p) ( np) np( p) = e np( p) π np np( p) = e σ π µ σ z where σ = Vr( ) = np( p), µ = np. Let φ( z) = e, the stndrd norml π distriution function or the Z-distriution function: µ ( n, p, ) φ σ σ 84
2 µ If z =, which is known s the z-scores, the inomil distriution cn e σ pproimted y the Z-distriution ( n, p, ) φ ( z) = φ ( z) z σ Where z = cn e viewed s the increments. σ In prctice, the conditions np > 0 nd n ( p) > 0 re good pproimtion for the conditions np ( p) >>. Let q = p, nd rememer tht 0 q, p. The 99% of re of the distriution is symmetriclly spnned within 6 stndrd devitions, so µ > 3σ is good pproimtion. Tht is, np > 3 npq or n p > npq np > 9q So, select np > 0 should e sufficient to stisfy the ove inequlity. Similrly, So nq > 0 is the other condition. nq > npq > 0q 85
3 Pr when the conditions re µ stisfied, where nd re different non-negtive integers, let z = nd σ µ z = : σ [MATH] To pproimte the inomil proility ( X ) z ( X ) = ( n p ) Pr,, = µ φ d σ σ µ z= σ z z ( z ) φ( z) dz = Φ Φ( z ) = Pr( z < z < z ) Where Φ ( z) = φ( z) dz, the CDF of the Z-distriution. The pproimtion of the integrl cn e viewed s to find the re under the curve with increments µ =, z = =. Since nd re integers, ± or ± my e used σ σ for etter pproimtion of the ounds when it comes to different cses:.) = =, use, +.), use s the lower ound. 86
4 c.), use + s the upper ound. d.), use, + s the ounds. Emple For the following given inomil distriutions, use the inomil formul nd norml formul to clculte the proilities when.) n = 0, p = 0. 5, X = 3, np =, nq = Binomil: Norml:.) n = 0, p = 0. 5, 4 X 7, np =, nq = Binomil: Norml: c.) n = 00, p = 0. 5, X = 30, np =, nq = Binomil: 87
5 Norml: d.) n = 00, p = 0. 5, 40 X 70, np =, nq = Binomil: Norml: Emple Estimte the proility of ectly 55 heds in 00 tosses of coin. Given: n = 00, = 55, p = 0. 5, q = 0. 5 The conditions for using norml pproimtion: np = 50 >> 0, nd n ( p) = 50 >> 0 The men nd stndrd devition: µ = np = = 50, σ = np( p) = ( 0.5) = (00, 0.5,55) φ( ) = φ() = e π 88
6 Emple You re plnning smple survey of smll usinesses in your re. You will choose n SRS of usinesses listed in the telephone ook s Yellow Pges. Eperience shows tht only out hlf the usinesses you contct will respond. Suppose tht you contct 50 usinesses..) Is it resonle to use the inomil distriutions or norml distriutions to study the numer rndom vrile X s the numer of responses?.) Wht is the proility tht 70 or fewer will respond? (Use oth inomil nd norml distriutions, if they re pplicle).) It is resonle to ssume s inomil ecuse B: Respond or not respond I: Assume the clls re independent N: n = 50 S: p = 0.5, q = 0.5 It is resonle to use norml distriution ecuse np = 50(0.5) = 75 0, n( p) = 50( 0.5) = 75 0 The men is µ = np = 50(0.5) = 75, nd stndrd devition is σ npq = 50(0.5)(0.5) = 6.4 = = 0.5, = = 70.5.) ( ) P 0 X 70 inomcdf (75, 0.5, 70) P ( 0 X 70) Φ Φ
7 Emple Are ttitudes towrd shopping chnging? Smple surveys show tht fewer people enjoy shopping thn in the pst. A recent survey sked ntionwide rndom smple of 500 dults if they greed or disgreed tht I like uying new cloths, ut shopping is often frustrting nd time-consuming. The popultion tht the poll wnts to drw conclusions out is ll U.S. residents ged 8 or over. Suppose tht in fct 60% of ll dults U.S. residents would sy Agree if sked the sme question..) Wht is the proility tht 50 or more of the smple gree?.) Wht is the proility tht t most 468 people in the smple would gree? n = 500, = 50, = 468, p = 0.6, np > 0, n( p) > 0, n < 0% N, µ = np = 500(0.6) = 500, σ = npq = 500(0.6)(0.4) = = = 59.5, = = ) z µ = = = 0.796, Φ( Z z ) = σ Direct inomil clcultion is P( X 50) = P( X 59) = inomcdf (500, 0.6,59) = = 0.3 µ ) z = = =.859, Φ( Z z ) = Direct inomil σ clcultion is P( X 468) = inomcdf (500,0.6,468) =
8 Modeling Discrete Distriution with Norml Distriution Binomil distriution cn e pproimted y the norml distriution when np > 0 nd n ( p) > 0. Another cse is when the smple size is lrge enough (>30), the smple mens re pproimted y the norml distriution y the Centrl Limit Theorem, which will e discussed lter. The emple elow illustrtes how distriution cn e curvefitted in norml distriution. The following histogrm grph displys 0,000 rndom digits of,, 3,, 9 generted from specific rndom digit genertor. Assume tht smple with size of 0000 ws lrge enough, so the histogrm reflects the true distriution of this rndom digit genertor. Curve-fit the distriution into the norml distriution model is sed on the fcts tht 99% of the dt should e covered within the rnge of 6σ nd the men is locted t the center. Since the mode is t 4 nd 99% of digits lie within to 7 inclusive, then the men nd 7 stndrd devition cn e pproimted y µ = 4, 6σ = 7 σ =, p( ) = e. Some of dt otined from oth distriution nd the model. 7 π distriution model Think pro p( ) = p( ) under the norml distriution, where =. The model seems resonle. The model is more ccurte towrd the men thn towrd the tils. More dvnced techniques eyond this notes cn e used to verify the ccurcy of the modeling. Norml distriution is widely used, or used, in mny pplictions. A good prctice is to t lest understnd why nd how norml distriution is implemented. 9
9 Quick-Check Approimtion of Binomil Distriution By Norml Distriution QC Suppose smple of 600 tires of the sme type is otined t rndom from n ongoing production process in which 8% of ll such tires produced re defective. Wht is the proility tht in such smple50 or fewer tires will e defective? QC Premture ies re those orn efore 37 weeks, nd those orn efore 34 weeks re most t risk. It ws reported tht % of irths in US occur efore 34 weeks. If,000 irths re selected rndomly, wht is the proility there re 0 to 5 ies, inclusive, re t risk? 9
10 Answers QC Given: n = 600, = 50, p = 0. 08, 0 X 50, = = 0. 5, = = The conditions for using norml pproimtion: np = = 8 >> 0, nd n ( p) = = 47 >> 0 The men nd stndrd devition: QC µ = np = = 8, σ = np( p) = ( 0.08) = P ( 0 X 50) = Φ Φ n = 000, = 0, = 5, p = 0.0, = = 9.5, = = 5.5 np = 000(0.0) > 0, nq = 000(0.98) > 0, µ = np = 000(0.0) = 0, µ σ = npq = 000(0.0)(0.98) = 4.47, z = = =.37, σ 4.47 µ z = = =.4, P( z Z z ) = σ
11 6.5. The Norml Distriution nd Its Z-Scores The norml distriutions, commonly known ell curve, re derived from the inomil distriutions under certin conditions. The curve is only chrcterized y the men nd stndrd devition. A specil cse is when the men is zero nd stndrd devition is one. This distriution is clled the Stndrd Norml Distriution, or Z-Distriution. Other norml distriutions cn e trnsformed into the stndrd norml distriution y using Z- scores trnsformtion. Stndrd Norml Distriution or Z Distriution N (0,) The stndrd norml proility density function (pdf) of rndom vrile Z is given y (z) φ : z φ(z) = e π The distriution hs men of zero nd stndrd devition of one. It is denoted s Z ~ N(0,). 94
12 [MATH] Proility for the Z-distriution is the re under the φ(z) curve: z z z Pr( z Z z ) = φ(z) dz = e dz z z π In terms of CDF function Φ ( z) : z Where ( z) φ( z) dz Φ =. Pr( z Z z ) = Φ( z ) Φ ( z ) [Ti-84] The re under the curve φ (z) for given intervl z, z ) ( Pr( z < z < z ) = normlcdf ( z, z,0,) cn e clculted y The vrile z vlue for given re A = Pr( < z < z ) cn e clculted y z = invnorm(a, 0,) Note tht Pr( < z < + ) =, Tht is, the entire re under the curve φ (z) is one. For the clcultion purposes, when z or z re infinity, lrge numer such s 000 cn e used in the plce of infinity. Emple Given the Z-distriution N (0,), solve ech of the prolems elow. Lel the domin (intervl) nd shde the proility re..) Pr( < z < ).) Pr( z < ) 95
13 3.) Pr( z < ) 4.) Pr( < z < ) 5.) Find z, where Pr( < z < z ) = 0.05, or the proility tht is elow 5 th percentile, 6.) Find z, where Pr( z < z < + ) = 0., or the proility tht is ove 80 th percentile. 96
14 7.) Find z *, where Pr( z < z*) = ) Find z *, where Pr( z > z*) = ) Find the integer n such tht.96 0 Pr z < = n 0.) Find σ such tht.64σ Pr( z < ) = ) Pr( < z < ) = normlcdf (,, 0, ) = ) Pr( z < ) = AREA( < z < )
15 3.) Pr( z < ) = AREA(0 < z < ) ) The cn e pproimted y reltive lrge numer such s 00. Therefore, Pr( < z < ) Pr( 00 < z < ) = normlcdf ( 00,, 0, ) = ) z = Since Pr( < z < z ) = 0.05, z = invnorm( 0.05, 0, ) = ) z = The proility on the left side is 0. = 0. 8, z = invnorm( 0.8,0,) = ) z * =. 96. Since z * < z < z *, z = z * nd z = z *. The proility on the left 0.05 side is = , z* = z = invnorm(0.975,0,) = ) z * =. 64. Since z * > z or z > z *. The proility on the left side for clculting 0. the z * is = 0. 95, z * = invnorm(0.95,0,) =
16 ) n = 400. Since =.96 n = 400 n.64σ 0.) σ =0 0. Since =.64 σ = Norml Distriution (, ) N µ σ nd Z-Scores A continuous rndom vrile X hs norml distriution with prmeter µ nd σ, denoted y N ( µ, σ ), if the proility density function is given y µ σ p( ) = e, for R σ π Where µ = E[X ] nd σ = Vr[X ]. Tht is, the men, vrince nd stndrd devition of the norml distriutions re µ, σ ndσ, respectively. The norml density function p( ) stisfies the following properties: p( ) is symmetric to = µ ; p( ) increses, nd then decreses with mode = µ ; p( ) chnges concvity t = µ ± σ. Pr( X ) = p() d = F( ) F( ), where F( ) = p() d is the CDF. 99
17 The function φ (z) is ssocited with function p () through the liner trnsformtion: µ z = σ [MATH] The functions nd p nd φ re connected in following formul: µ p( ) = φ = φ ( z) σ σ σ The z-scores re the normlized rndom vrile with zero s the men. The proility µ µ Pr( X ) = F( ) F( ) = Φ Φ = Φ z Φ z σ σ Or simply, Pr( X ) = Pr( z Z z ) ( ) ( ) [Ti-84] Clculte the proility of rndom vrile with norml-distriution N ( µ, σ ) for given intervl (, ) : ( ) Pr( X ) = p() d = normlcdf,, µ, σ When F( ) = p( ) d is given, the upper ound cn e found y ( ( ),, ) = invnorm F µ σ 00
18 The proility under φ (z) in the intervl I z is the sme s the proility under p() in I, where I [ z, z ] = nd I [, ] [ µ z σ, µ z σ ] z = = + +. Emple Given the proility under the φ (z) is Pr( < z < z ) = 0.95, µ = 0 nd σ =, find, nd Pr( < < ) for the proility under p( )? From the given, z =, = invnorm( 0.95, 0, ) = Becuse z z = µ, σ 3. = µ + z σ = 0 + ( )() =, nd = µ + z * σ = () = 9. Since z =, choose lrge numer such s 000 s pproimtion for z. Then, Pr( < < 3.9) = normlcdf ( 000, 3.9, 0, ) Emple Given Pr( z < z*) = 0.95, µ = 0 nd σ =, find nd. Since z * < z < z *, this implies z = z *, z = z *, nd Pr( < z < z*) = The z * = invnorm(0.975, 0, ) =.96, = µ + ( z*) σ = 0.96() = 6.08, = µ + z * σ = () = 3.9, nd I z = [.96,.96], I = [6.08, 3.93]. The proility Pr(6.08 < < 3.93) = normlcdf (6.08, 3.95, 0, ) Emple The verge nnul rinfll t El Yunque Rinforest on the islnd of Puerto Rico is 00 inches. Assume the vrince to e 5 inches nd the distriution is pproimtely norml. Wht is the proility tht the rinfll there net yer will e etween 85 nd 30 inches? 0
19 Pr(85 X 30) = F(30) F(85) = normlcdf (85, 30, 00, 5) Or, use the z-scores, z85 =.34, z30 =.68, nd the proility is 5 5 Pr(85 30) = Pr(.34 < z <.68) = normlcdf (.34,.68, 0.) Emple The verge Mth SAT score for grduting seniors t THS is 640 with stndrd devition of 30. In terms of SAT mth score, wht Mth SAT score would e needed to e in the top 0% of grduting senior students? Assume the scores re pproimte normlly distriuted. µ = 640 nd σ = 30. The z-score for 90 th percentile is z = invnnorm(0.9,0,).8. So, the scores tht re greter thn 90 th percentile is > µ + zσ = (.8) = 678. Emple At THS the men numer of colleges tht seniors pply to is 5.6 with stndrd devition of.3. Assuming the distriution is pproimtely norml, wht percent of seniors t THS pply to more thn 8 schools? µ = 5.6 nd σ =.3. The z-score for equls to 8 is z =.0434 nd.3 proility Pr( > 8) = Pr( z >.0434) = normlcdf (.0434,000, 0,0) 4.8%. Emple The verge time it tkes for men to run mrthon is 4 hours nd 4 minutes with stndrd devition of hour nd minutes. The verge time it tkes for women to run mrthon is 4 hours nd 5 minutes with stndrd devition of hour nd 7 minutes. Ptrick Mku of Keny holds the world record for men with hours nd 3 minutes nd Pul Rdcliffe of UK holds the world record for women with hours nd 0
20 5 minutes. Reltive to other mrthoners of like gender, who hs etter world record time? Justify your nswer sttisticlly. For Ptrick, For Pul, z ptrick z pul Pul hs etter time. 3/ / 60 =.7, or.7σ elow the men. 6 / / 60 9 / 60 =.34, or.34σ elow the men. 67 / 60 Emple Hens usully egin lying eggs when they re out 6 months old. Young hens tend to ly smller eggs, often weighing less thn the desired minimum weight of 54 grms..) The verge weight of the eggs produced y the young hens is 50.9 grms, nd only 8% of their eggs eceed the desired minimum weight. If norml model is pproprite, wht would the stndrd devition of the eggs weights e?.) By the time these hens hve reched the ge of yer, the eggs tht they produce verge 67. grms, nd 98% of them re ove the minimum weight. Wht is the stndrd devition for the pproprite norml model for these older hens? c.) A certin poultry frmer finds tht 8% of his eggs re underweight nd tht % weigh over 70 grms. Estimte the men nd stndrd devition of his eggs. 03
21 µ ). µ = 50.9, = 54, only 8% ove 54, so z = 0.588, σ = = = 5.38 z µ ). µ = 54, = 67, only 98% ove 54, so z =.05, σ = = = 6.39 z.05 c.). = 54, the underweight, = 70, z =.405, z =.749, µ 54 µ µ 70 µ = =.405, = =.749 σ σ σ σ µ = 6.7, σ = 6. Emple [CB] Some descriptive sttistics for set of test scores re shown elow. For this test, certin student hs stndrdized score of z =.. Wht score did this student receive on the test? =.9 = Emple [MC4] A distriution of scores is pproimtely norml with men of 78 nd stndrd devition of 8.6. Which of the following equtions cn e used to find the score ove which 33 percent of the scores fll? 04
22 The nswer is D. The criticl z vlue for 33% of the re is ( z * = invnorm( 33%) = ) Emple [FRQ0M] A chrity fundriser hs Spin the Pointer gme tht uses fund rising. Bsed on lst yer s event, the chrity nticiptes tht the Spin the Pointer gme will e plyed 000 times. The chrity would like to know the proility of otining net contriution of t lest $500 in 000 plys of the gme. The men nd stndrd devition of the net contriution to the chrity in 000 plys of the gme re $700 nd $9.79, respectively. Use the norml distriution to pproimte the proility tht the chrity would otin net contriution of t lest $500 in 000 plys of the gme. µ = 700, σ = 9.79, = z = = P( Z >.55) = 98.44% 05
23 Quick-Check The Norml Distriution nd Z Scores QC Given the Z-distriution N (0,), solve ech of the prolems elow. Lel the domin (intervl) nd shde the proility re. Round your nswers to three digits..) Proility: Pr( Z 3) =.) Proility: 97.5 th percentile or Pr( Z z*) = 0.05, z* = c.) Proility: the middle 95% or Pr( Z z*) = 0.95, z* = QC The heights of mle students t THS re pproimtely norml with men of 68 inches nd stndrd devition of.5 inches. Aout 0% of these mle students re tller thn wht height? 06
24 QC Jenn tkes three SAT suject tests. She scores 600 on ll three. Using stndrd scores, or z-scores, rnk her performnce on the three tests from the est to worst if mens nd stndrd devitions for the tests re s follows: Men Stndrd Devition Test I Test II Test III QC A student in Science Reserch clss interested in the ge t which women re hving their first child surveyed simple rndom smple (SRS) of 50 women hving t lest one child nd found n pproimtely norml distriution with men ge of 7.3 nd stndrd devition of 5.4. Approimtely the middle of 95% of women hd their first child etween wht ges? QC Luren scored n 8 on Wissler s geometry test for which the clss men ws 74 with the stndrd devition of 3.. She scored n 86 on Nelson s iology test for which the clss men ws 77 with stndrd devition of.9. In comprison to other memers of ech of these clsses, in which clss did Luren perform etter? QC To get into Science Reserch clss, freshmen t THS require to score in the upper 0% on mth plcement test. If the men score on the test is 50 nd the stndrd devition of the scores is 80, wht is the minimum score tht student cn ern on the test to meet the dmission requirement? Scores on the test re normlly distriuted nd re reported in the intervls of 0. 07
25 QC The GPAs re normlly distriuted with stndrd devition of 0.7. Wht is the men GPA if 5% of the students hve GPA ove 4.75? QC A survey ws tken to determine the numer of hours per week students studied mth nd sciences. The distriution ws pproimtely norml with men of 0 hours nd stndrd devition of 4 hours. Approimtely wht percent of the students studied etween 7 nd 30 hours? QC Grdes on sttistics test re normlly distriuted with men of 76 nd stndrd devition of 8. The top 0% students will receive n A, the net 0% B, the net 40% C, the net 0% D, nd the ottom 0 n F. The students who received F s in course hd no higher thn wht score? QC The men score on Trig & Stts test ws 75 with stndrd devition of four. Wht would e the z-score for Alejndro who scored n 8? QC John needs to hve tree cut down in his ckyrd. A tree service gives him n estimte of $6500. John feels this is too high nd clls the Better Business Bureu which reports the verge cost for tht service in his re is $400 with stndrd devition of $750. Assuming tht the costs re normlly distriuted, John concludes tht pproimtely 95% of the time, the cost should roughly fll etween which two vlues? 08
26 Answers QC ) 0.997,.).96, c.) z*=.96 QC in. µ = 68, σ = 8.5, z* = invnorm(0.8, 0.) = 0.34, 68 > 0.84 = in Pr > 0.84 = 0., 8.5 QC III>I>II. The higher the z-scores, the etter she did in the test. z I = =.5, 80 z II = =.08, 0 z I = = QC (6.7, 37.88) QC She did etter in Biology clss. QC QC QC QC QC QC (730, 5670) 09
Continuous Random Variable X:
 Continuous Rndom Vrile : The continuous rndom vrile hs its vlues in n intervl, nd it hs proility distriution unction or proility density unction p.d. stisies:, 0 & d Which does men tht the totl re under
Continuous Rndom Vrile : The continuous rndom vrile hs its vlues in n intervl, nd it hs proility distriution unction or proility density unction p.d. stisies:, 0 & d Which does men tht the totl re under
Discrete Mathematics and Probability Theory Spring 2013 Anant Sahai Lecture 17
 EECS 70 Discrete Mthemtics nd Proility Theory Spring 2013 Annt Shi Lecture 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion,
EECS 70 Discrete Mthemtics nd Proility Theory Spring 2013 Annt Shi Lecture 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion,
4.1. Probability Density Functions
 STT 1 4.1-4. 4.1. Proility Density Functions Ojectives. Continuous rndom vrile - vers - discrete rndom vrile. Proility density function. Uniform distriution nd its properties. Expected vlue nd vrince of
STT 1 4.1-4. 4.1. Proility Density Functions Ojectives. Continuous rndom vrile - vers - discrete rndom vrile. Proility density function. Uniform distriution nd its properties. Expected vlue nd vrince of
Continuous Random Variables Class 5, Jeremy Orloff and Jonathan Bloom
 Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Lerning Gols Continuous Rndom Vriles Clss 5, 8.05 Jeremy Orloff nd Jonthn Bloom. Know the definition of continuous rndom vrile. 2. Know the definition of the proility density function (pdf) nd cumultive
Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 217 Néhémy Lim Continuous Rndom Vribles Nottion. The indictor function of set S is rel-vlued function defined by : { 1 if x S 1 S (x) if x S Suppose tht
Discrete Mathematics and Probability Theory Summer 2014 James Cook Note 17
 CS 70 Discrete Mthemtics nd Proility Theory Summer 2014 Jmes Cook Note 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion, y tking
CS 70 Discrete Mthemtics nd Proility Theory Summer 2014 Jmes Cook Note 17 I.I.D. Rndom Vriles Estimting the is of coin Question: We wnt to estimte the proportion p of Democrts in the US popultion, y tking
Normal Distribution. Lecture 6: More Binomial Distribution. Properties of the Unit Normal Distribution. Unit Normal Distribution
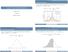 Norml Distribution Lecture 6: More Binomil Distribution If X is rndom vrible with norml distribution with men µ nd vrince σ 2, X N (µ, σ 2, then P(X = x = f (x = 1 e 1 (x µ 2 2 σ 2 σ Sttistics 104 Colin
Norml Distribution Lecture 6: More Binomil Distribution If X is rndom vrible with norml distribution with men µ nd vrince σ 2, X N (µ, σ 2, then P(X = x = f (x = 1 e 1 (x µ 2 2 σ 2 σ Sttistics 104 Colin
Continuous Random Variables
 CPSC 53 Systems Modeling nd Simultion Continuous Rndom Vriles Dr. Anirn Mhnti Deprtment of Computer Science University of Clgry mhnti@cpsc.uclgry.c Definitions A rndom vrile is sid to e continuous if there
CPSC 53 Systems Modeling nd Simultion Continuous Rndom Vriles Dr. Anirn Mhnti Deprtment of Computer Science University of Clgry mhnti@cpsc.uclgry.c Definitions A rndom vrile is sid to e continuous if there
Lecture 3 Gaussian Probability Distribution
 Introduction Lecture 3 Gussin Probbility Distribution Gussin probbility distribution is perhps the most used distribution in ll of science. lso clled bell shped curve or norml distribution Unlike the binomil
Introduction Lecture 3 Gussin Probbility Distribution Gussin probbility distribution is perhps the most used distribution in ll of science. lso clled bell shped curve or norml distribution Unlike the binomil
Chapter 6 Continuous Random Variables and Distributions
 Chpter 6 Continuous Rndom Vriles nd Distriutions Mny economic nd usiness mesures such s sles investment consumption nd cost cn hve the continuous numericl vlues so tht they cn not e represented y discrete
Chpter 6 Continuous Rndom Vriles nd Distriutions Mny economic nd usiness mesures such s sles investment consumption nd cost cn hve the continuous numericl vlues so tht they cn not e represented y discrete
Chapter 9 Definite Integrals
 Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Chpter 9 Definite Integrls In the previous chpter we found how to tke n ntiderivtive nd investigted the indefinite integrl. In this chpter the connection etween ntiderivtives nd definite integrls is estlished
Chapter 5 : Continuous Random Variables
 STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
STAT/MATH 395 A - PROBABILITY II UW Winter Qurter 216 Néhémy Lim Chpter 5 : Continuous Rndom Vribles Nottions. N {, 1, 2,...}, set of nturl numbers (i.e. ll nonnegtive integers); N {1, 2,...}, set of ll
2.4 Linear Inequalities and Interval Notation
 .4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
.4 Liner Inequlities nd Intervl Nottion We wnt to solve equtions tht hve n inequlity symol insted of n equl sign. There re four inequlity symols tht we will look t: Less thn , Less thn or
Interpreting Integrals and the Fundamental Theorem
 Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
Interpreting Integrls nd the Fundmentl Theorem Tody, we go further in interpreting the mening of the definite integrl. Using Units to Aid Interprettion We lredy know tht if f(t) is the rte of chnge of
y = f(x) This means that there must be a point, c, where the Figure 1
 Clculus Investigtion A Men Slope TEACHER S Prt 1: Understnding the Men Vlue Theorem The Men Vlue Theorem for differentition sttes tht if f() is defined nd continuous over the intervl [, ], nd differentile
Clculus Investigtion A Men Slope TEACHER S Prt 1: Understnding the Men Vlue Theorem The Men Vlue Theorem for differentition sttes tht if f() is defined nd continuous over the intervl [, ], nd differentile
M344 - ADVANCED ENGINEERING MATHEMATICS
 M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
FORM FIVE ADDITIONAL MATHEMATIC NOTE. ar 3 = (1) ar 5 = = (2) (2) (1) a = T 8 = 81
 FORM FIVE ADDITIONAL MATHEMATIC NOTE CHAPTER : PROGRESSION Arithmetic Progression T n = + (n ) d S n = n [ + (n )d] = n [ + Tn ] S = T = T = S S Emple : The th term of n A.P. is 86 nd the sum of the first
FORM FIVE ADDITIONAL MATHEMATIC NOTE CHAPTER : PROGRESSION Arithmetic Progression T n = + (n ) d S n = n [ + (n )d] = n [ + Tn ] S = T = T = S S Emple : The th term of n A.P. is 86 nd the sum of the first
0.1 THE REAL NUMBER LINE AND ORDER
 6000_000.qd //0 :6 AM Pge 0-0- CHAPTER 0 A Preclculus Review 0. THE REAL NUMBER LINE AND ORDER Represent, clssify, nd order rel numers. Use inequlities to represent sets of rel numers. Solve inequlities.
6000_000.qd //0 :6 AM Pge 0-0- CHAPTER 0 A Preclculus Review 0. THE REAL NUMBER LINE AND ORDER Represent, clssify, nd order rel numers. Use inequlities to represent sets of rel numers. Solve inequlities.
Goals: Determine how to calculate the area described by a function. Define the definite integral. Explore the relationship between the definite
 Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Unit #8 : The Integrl Gols: Determine how to clculte the re described by function. Define the definite integrl. Eplore the reltionship between the definite integrl nd re. Eplore wys to estimte the definite
Section 4: Integration ECO4112F 2011
 Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Reding: Ching Chpter Section : Integrtion ECOF Note: These notes do not fully cover the mteril in Ching, ut re ment to supplement your reding in Ching. Thus fr the optimistion you hve covered hs een sttic
Linear Inequalities. Work Sheet 1
 Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
1B40 Practical Skills
 B40 Prcticl Skills Comining uncertinties from severl quntities error propgtion We usully encounter situtions where the result of n experiment is given in terms of two (or more) quntities. We then need
B40 Prcticl Skills Comining uncertinties from severl quntities error propgtion We usully encounter situtions where the result of n experiment is given in terms of two (or more) quntities. We then need
APPENDIX. Precalculus Review D.1. Real Numbers and the Real Number Line
 APPENDIX D Preclculus Review APPENDIX D.1 Rel Numers n the Rel Numer Line Rel Numers n the Rel Numer Line Orer n Inequlities Asolute Vlue n Distnce Rel Numers n the Rel Numer Line Rel numers cn e represente
APPENDIX D Preclculus Review APPENDIX D.1 Rel Numers n the Rel Numer Line Rel Numers n the Rel Numer Line Orer n Inequlities Asolute Vlue n Distnce Rel Numers n the Rel Numer Line Rel numers cn e represente
Chapter 9: Inferences based on Two samples: Confidence intervals and tests of hypotheses
 Chpter 9: Inferences bsed on Two smples: Confidence intervls nd tests of hypotheses 9.1 The trget prmeter : difference between two popultion mens : difference between two popultion proportions : rtio of
Chpter 9: Inferences bsed on Two smples: Confidence intervls nd tests of hypotheses 9.1 The trget prmeter : difference between two popultion mens : difference between two popultion proportions : rtio of
10. AREAS BETWEEN CURVES
 . AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
. AREAS BETWEEN CURVES.. Ares etween curves So res ove the x-xis re positive nd res elow re negtive, right? Wrong! We lied! Well, when you first lern out integrtion it s convenient fiction tht s true in
Polynomial Approximations for the Natural Logarithm and Arctangent Functions. Math 230
 Polynomil Approimtions for the Nturl Logrithm nd Arctngent Functions Mth 23 You recll from first semester clculus how one cn use the derivtive to find n eqution for the tngent line to function t given
Polynomil Approimtions for the Nturl Logrithm nd Arctngent Functions Mth 23 You recll from first semester clculus how one cn use the derivtive to find n eqution for the tngent line to function t given
1 Probability Density Functions
 Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
MA 15910, Lessons 2a and 2b Introduction to Functions Algebra: Sections 3.5 and 7.4 Calculus: Sections 1.2 and 2.1
 MA 15910, Lessons nd Introduction to Functions Alger: Sections 3.5 nd 7.4 Clculus: Sections 1. nd.1 Representing n Intervl Set of Numers Inequlity Symol Numer Line Grph Intervl Nottion ) (, ) ( (, ) ]
MA 15910, Lessons nd Introduction to Functions Alger: Sections 3.5 nd 7.4 Clculus: Sections 1. nd.1 Representing n Intervl Set of Numers Inequlity Symol Numer Line Grph Intervl Nottion ) (, ) ( (, ) ]
LINEAR ALGEBRA APPLIED
 5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
Chapter 1: Logarithmic functions and indices
 Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
Chpter : Logrithmic functions nd indices. You cn simplify epressions y using rules of indices m n m n m n m n ( m ) n mn m m m m n m m n Emple Simplify these epressions: 5 r r c 4 4 d 6 5 e ( ) f ( ) 4
For the percentage of full time students at RCC the symbols would be:
 Mth 17/171 Chpter 7- ypothesis Testing with One Smple This chpter is s simple s the previous one, except it is more interesting In this chpter we will test clims concerning the sme prmeters tht we worked
Mth 17/171 Chpter 7- ypothesis Testing with One Smple This chpter is s simple s the previous one, except it is more interesting In this chpter we will test clims concerning the sme prmeters tht we worked
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Solution for Assignment 1 : Intro to Probability and Statistics, PAC learning
 Solution for Assignment 1 : Intro to Probbility nd Sttistics, PAC lerning 10-701/15-781: Mchine Lerning (Fll 004) Due: Sept. 30th 004, Thursdy, Strt of clss Question 1. Bsic Probbility ( 18 pts) 1.1 (
Solution for Assignment 1 : Intro to Probbility nd Sttistics, PAC lerning 10-701/15-781: Mchine Lerning (Fll 004) Due: Sept. 30th 004, Thursdy, Strt of clss Question 1. Bsic Probbility ( 18 pts) 1.1 (
Chapter 3 Single Random Variables and Probability Distributions (Part 2)
 Chpter 3 Single Rndom Vriles nd Proilit Distriutions (Prt ) Contents Wht is Rndom Vrile? Proilit Distriution Functions Cumultive Distriution Function Proilit Densit Function Common Rndom Vriles nd their
Chpter 3 Single Rndom Vriles nd Proilit Distriutions (Prt ) Contents Wht is Rndom Vrile? Proilit Distriution Functions Cumultive Distriution Function Proilit Densit Function Common Rndom Vriles nd their
5.1 How do we Measure Distance Traveled given Velocity? Student Notes
 . How do we Mesure Distnce Trveled given Velocity? Student Notes EX ) The tle contins velocities of moving cr in ft/sec for time t in seconds: time (sec) 3 velocity (ft/sec) 3 A) Lel the x-xis & y-xis
. How do we Mesure Distnce Trveled given Velocity? Student Notes EX ) The tle contins velocities of moving cr in ft/sec for time t in seconds: time (sec) 3 velocity (ft/sec) 3 A) Lel the x-xis & y-xis
2 b. , a. area is S= 2π xds. Again, understand where these formulas came from (pages ).
 AP Clculus BC Review Chpter 8 Prt nd Chpter 9 Things to Know nd Be Ale to Do Know everything from the first prt of Chpter 8 Given n integrnd figure out how to ntidifferentite it using ny of the following
AP Clculus BC Review Chpter 8 Prt nd Chpter 9 Things to Know nd Be Ale to Do Know everything from the first prt of Chpter 8 Given n integrnd figure out how to ntidifferentite it using ny of the following
7.1 Integral as Net Change and 7.2 Areas in the Plane Calculus
 7.1 Integrl s Net Chnge nd 7. Ares in the Plne Clculus 7.1 INTEGRAL AS NET CHANGE Notecrds from 7.1: Displcement vs Totl Distnce, Integrl s Net Chnge We hve lredy seen how the position of n oject cn e
7.1 Integrl s Net Chnge nd 7. Ares in the Plne Clculus 7.1 INTEGRAL AS NET CHANGE Notecrds from 7.1: Displcement vs Totl Distnce, Integrl s Net Chnge We hve lredy seen how the position of n oject cn e
Coimisiún na Scrúduithe Stáit State Examinations Commission
 M 30 Coimisiún n Scrúduithe Stáit Stte Exmintions Commission LEAVING CERTIFICATE EXAMINATION, 005 MATHEMATICS HIGHER LEVEL PAPER ( 300 mrks ) MONDAY, 3 JUNE MORNING, 9:30 to :00 Attempt FIVE questions
M 30 Coimisiún n Scrúduithe Stáit Stte Exmintions Commission LEAVING CERTIFICATE EXAMINATION, 005 MATHEMATICS HIGHER LEVEL PAPER ( 300 mrks ) MONDAY, 3 JUNE MORNING, 9:30 to :00 Attempt FIVE questions
7.1 Integral as Net Change Calculus. What is the total distance traveled? What is the total displacement?
 7.1 Integrl s Net Chnge Clculus 7.1 INTEGRAL AS NET CHANGE Distnce versus Displcement We hve lredy seen how the position of n oject cn e found y finding the integrl of the velocity function. The chnge
7.1 Integrl s Net Chnge Clculus 7.1 INTEGRAL AS NET CHANGE Distnce versus Displcement We hve lredy seen how the position of n oject cn e found y finding the integrl of the velocity function. The chnge
Advanced Algebra & Trigonometry Midterm Review Packet
 Nme Dte Advnced Alger & Trigonometry Midterm Review Pcket The Advnced Alger & Trigonometry midterm em will test your generl knowledge of the mteril we hve covered since the eginning of the school yer.
Nme Dte Advnced Alger & Trigonometry Midterm Review Pcket The Advnced Alger & Trigonometry midterm em will test your generl knowledge of the mteril we hve covered since the eginning of the school yer.
Math 259 Winter Solutions to Homework #9
 Mth 59 Winter 9 Solutions to Homework #9 Prolems from Pges 658-659 (Section.8). Given f(, y, z) = + y + z nd the constrint g(, y, z) = + y + z =, the three equtions tht we get y setting up the Lgrnge multiplier
Mth 59 Winter 9 Solutions to Homework #9 Prolems from Pges 658-659 (Section.8). Given f(, y, z) = + y + z nd the constrint g(, y, z) = + y + z =, the three equtions tht we get y setting up the Lgrnge multiplier
Tests for the Ratio of Two Poisson Rates
 Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
Chpter 437 Tests for the Rtio of Two Poisson Rtes Introduction The Poisson probbility lw gives the probbility distribution of the number of events occurring in specified intervl of time or spce. The Poisson
Chapter 6 Notes, Larson/Hostetler 3e
 Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
5.7 Improper Integrals
 458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
458 pplictions of definite integrls 5.7 Improper Integrls In Section 5.4, we computed the work required to lift pylod of mss m from the surfce of moon of mss nd rdius R to height H bove the surfce of the
Improper Integrals. Introduction. Type 1: Improper Integrals on Infinite Intervals. When we defined the definite integral.
 Improper Integrls Introduction When we defined the definite integrl f d we ssumed tht f ws continuous on [, ] where [, ] ws finite, closed intervl There re t lest two wys this definition cn fil to e stisfied:
Improper Integrls Introduction When we defined the definite integrl f d we ssumed tht f ws continuous on [, ] where [, ] ws finite, closed intervl There re t lest two wys this definition cn fil to e stisfied:
Review of Probability Distributions. CS1538: Introduction to Simulations
 Review of Proility Distriutions CS1538: Introduction to Simultions Some Well-Known Proility Distriutions Bernoulli Binomil Geometric Negtive Binomil Poisson Uniform Exponentil Gmm Erlng Gussin/Norml Relevnce
Review of Proility Distriutions CS1538: Introduction to Simultions Some Well-Known Proility Distriutions Bernoulli Binomil Geometric Negtive Binomil Poisson Uniform Exponentil Gmm Erlng Gussin/Norml Relevnce
Math 1431 Section 6.1. f x dx, find f. Question 22: If. a. 5 b. π c. π-5 d. 0 e. -5. Question 33: Choose the correct statement given that
 Mth 43 Section 6 Question : If f d nd f d, find f 4 d π c π- d e - Question 33: Choose the correct sttement given tht 7 f d 8 nd 7 f d3 7 c d f d3 f d f d f d e None of these Mth 43 Section 6 Are Under
Mth 43 Section 6 Question : If f d nd f d, find f 4 d π c π- d e - Question 33: Choose the correct sttement given tht 7 f d 8 nd 7 f d3 7 c d f d3 f d f d f d e None of these Mth 43 Section 6 Are Under
Section 6.1 INTRO to LAPLACE TRANSFORMS
 Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Math 135, Spring 2012: HW 7
 Mth 3, Spring : HW 7 Problem (p. 34 #). SOLUTION. Let N the number of risins per cookie. If N is Poisson rndom vrible with prmeter λ, then nd for this to be t lest.99, we need P (N ) P (N ) ep( λ) λ ln(.)
Mth 3, Spring : HW 7 Problem (p. 34 #). SOLUTION. Let N the number of risins per cookie. If N is Poisson rndom vrible with prmeter λ, then nd for this to be t lest.99, we need P (N ) P (N ) ep( λ) λ ln(.)
Improper Integrals. The First Fundamental Theorem of Calculus, as we ve discussed in class, goes as follows:
 Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Topics Covered AP Calculus AB
 Topics Covered AP Clculus AB ) Elementry Functions ) Properties of Functions i) A function f is defined s set of ll ordered pirs (, y), such tht for ech element, there corresponds ectly one element y.
Topics Covered AP Clculus AB ) Elementry Functions ) Properties of Functions i) A function f is defined s set of ll ordered pirs (, y), such tht for ech element, there corresponds ectly one element y.
Operations with Polynomials
 38 Chpter P Prerequisites P.4 Opertions with Polynomils Wht you should lern: How to identify the leding coefficients nd degrees of polynomils How to dd nd subtrct polynomils How to multiply polynomils
38 Chpter P Prerequisites P.4 Opertions with Polynomils Wht you should lern: How to identify the leding coefficients nd degrees of polynomils How to dd nd subtrct polynomils How to multiply polynomils
Section 6: Area, Volume, and Average Value
 Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Review of Gaussian Quadrature method
 Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Calculus AB. For a function f(x), the derivative would be f '(
 lculus AB Derivtive Formuls Derivtive Nottion: For function f(), the derivtive would e f '( ) Leiniz's Nottion: For the derivtive of y in terms of, we write d For the second derivtive using Leiniz's Nottion:
lculus AB Derivtive Formuls Derivtive Nottion: For function f(), the derivtive would e f '( ) Leiniz's Nottion: For the derivtive of y in terms of, we write d For the second derivtive using Leiniz's Nottion:
Definite Integrals. The area under a curve can be approximated by adding up the areas of rectangles = 1 1 +
 Definite Integrls --5 The re under curve cn e pproximted y dding up the res of rectngles. Exmple. Approximte the re under y = from x = to x = using equl suintervls nd + x evluting the function t the left-hnd
Definite Integrls --5 The re under curve cn e pproximted y dding up the res of rectngles. Exmple. Approximte the re under y = from x = to x = using equl suintervls nd + x evluting the function t the left-hnd
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
Math 131. Numerical Integration Larson Section 4.6
 Mth. Numericl Integrtion Lrson Section. This section looks t couple of methods for pproimting definite integrls numericlly. The gol is to get good pproimtion of the definite integrl in problems where n
Mth. Numericl Integrtion Lrson Section. This section looks t couple of methods for pproimting definite integrls numericlly. The gol is to get good pproimtion of the definite integrl in problems where n
1 ELEMENTARY ALGEBRA and GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE
 ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
ELEMENTARY ALGEBRA nd GEOMETRY READINESS DIAGNOSTIC TEST PRACTICE Directions: Study the exmples, work the prolems, then check your nswers t the end of ech topic. If you don t get the nswer given, check
Bob Brown Math 251 Calculus 1 Chapter 5, Section 4 1 CCBC Dundalk
 Bo Brown Mth Clculus Chpter, Section CCBC Dundlk The Fundmentl Theorem of Clculus Informlly, the Fundmentl Theorem of Clculus (FTC) sttes tht differentition nd definite integrtion re inverse opertions
Bo Brown Mth Clculus Chpter, Section CCBC Dundlk The Fundmentl Theorem of Clculus Informlly, the Fundmentl Theorem of Clculus (FTC) sttes tht differentition nd definite integrtion re inverse opertions
METHODS OF APPROXIMATING THE RIEMANN INTEGRALS AND APPLICATIONS
 Journl of Young Scientist Volume III 5 ISSN 44-8; ISSN CD-ROM 44-9; ISSN Online 44-5; ISSN-L 44 8 METHODS OF APPROXIMATING THE RIEMANN INTEGRALS AND APPLICATIONS An ALEXANDRU Scientific Coordintor: Assist
Journl of Young Scientist Volume III 5 ISSN 44-8; ISSN CD-ROM 44-9; ISSN Online 44-5; ISSN-L 44 8 METHODS OF APPROXIMATING THE RIEMANN INTEGRALS AND APPLICATIONS An ALEXANDRU Scientific Coordintor: Assist
Suppose we want to find the area under the parabola and above the x axis, between the lines x = 2 and x = -2.
 Mth 43 Section 6. Section 6.: Definite Integrl Suppose we wnt to find the re of region tht is not so nicely shped. For exmple, consider the function shown elow. The re elow the curve nd ove the x xis cnnot
Mth 43 Section 6. Section 6.: Definite Integrl Suppose we wnt to find the re of region tht is not so nicely shped. For exmple, consider the function shown elow. The re elow the curve nd ove the x xis cnnot
Genetic Programming. Outline. Evolutionary Strategies. Evolutionary strategies Genetic programming Summary
 Outline Genetic Progrmming Evolutionry strtegies Genetic progrmming Summry Bsed on the mteril provided y Professor Michel Negnevitsky Evolutionry Strtegies An pproch simulting nturl evolution ws proposed
Outline Genetic Progrmming Evolutionry strtegies Genetic progrmming Summry Bsed on the mteril provided y Professor Michel Negnevitsky Evolutionry Strtegies An pproch simulting nturl evolution ws proposed
Section 5.1 #7, 10, 16, 21, 25; Section 5.2 #8, 9, 15, 20, 27, 30; Section 5.3 #4, 6, 9, 13, 16, 28, 31; Section 5.4 #7, 18, 21, 23, 25, 29, 40
 Mth B Prof. Audrey Terrs HW # Solutions by Alex Eustis Due Tuesdy, Oct. 9 Section 5. #7,, 6,, 5; Section 5. #8, 9, 5,, 7, 3; Section 5.3 #4, 6, 9, 3, 6, 8, 3; Section 5.4 #7, 8,, 3, 5, 9, 4 5..7 Since
Mth B Prof. Audrey Terrs HW # Solutions by Alex Eustis Due Tuesdy, Oct. 9 Section 5. #7,, 6,, 5; Section 5. #8, 9, 5,, 7, 3; Section 5.3 #4, 6, 9, 3, 6, 8, 3; Section 5.4 #7, 8,, 3, 5, 9, 4 5..7 Since
Calculus Module C21. Areas by Integration. Copyright This publication The Northern Alberta Institute of Technology All Rights Reserved.
 Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Clculus Module C Ares Integrtion Copright This puliction The Northern Alert Institute of Technolog 7. All Rights Reserved. LAST REVISED Mrch, 9 Introduction to Ares Integrtion Sttement of Prerequisite
Math 1431 Section M TH 4:00 PM 6:00 PM Susan Wheeler Office Hours: Wed 6:00 7:00 PM Online ***NOTE LABS ARE MON AND WED
 Mth 43 Section 4839 M TH 4: PM 6: PM Susn Wheeler swheeler@mth.uh.edu Office Hours: Wed 6: 7: PM Online ***NOTE LABS ARE MON AND WED t :3 PM to 3: pm ONLINE Approimting the re under curve given the type
Mth 43 Section 4839 M TH 4: PM 6: PM Susn Wheeler swheeler@mth.uh.edu Office Hours: Wed 6: 7: PM Online ***NOTE LABS ARE MON AND WED t :3 PM to 3: pm ONLINE Approimting the re under curve given the type
Experiments, Outcomes, Events and Random Variables: A Revisit
 Eperiments, Outcomes, Events nd Rndom Vriles: A Revisit Berlin Chen Deprtment o Computer Science & Inormtion Engineering Ntionl Tiwn Norml University Reerence: - D. P. Bertseks, J. N. Tsitsiklis, Introduction
Eperiments, Outcomes, Events nd Rndom Vriles: A Revisit Berlin Chen Deprtment o Computer Science & Inormtion Engineering Ntionl Tiwn Norml University Reerence: - D. P. Bertseks, J. N. Tsitsiklis, Introduction
( ) as a fraction. Determine location of the highest
 AB Clculus Exm Review Sheet - Solutions A. Preclculus Type prolems A1 A2 A3 A4 A5 A6 A7 This is wht you think of doing Find the zeros of f ( x). Set function equl to 0. Fctor or use qudrtic eqution if
AB Clculus Exm Review Sheet - Solutions A. Preclculus Type prolems A1 A2 A3 A4 A5 A6 A7 This is wht you think of doing Find the zeros of f ( x). Set function equl to 0. Fctor or use qudrtic eqution if
Comparison Procedures
 Comprison Procedures Single Fctor, Between-Subects Cse /8/ Comprison Procedures, One-Fctor ANOVA, Between Subects Two Comprison Strtegies post hoc (fter-the-fct) pproch You re interested in discovering
Comprison Procedures Single Fctor, Between-Subects Cse /8/ Comprison Procedures, One-Fctor ANOVA, Between Subects Two Comprison Strtegies post hoc (fter-the-fct) pproch You re interested in discovering
The Fundamental Theorem of Calculus. The Total Change Theorem and the Area Under a Curve.
 Clculus Li Vs The Fundmentl Theorem of Clculus. The Totl Chnge Theorem nd the Are Under Curve. Recll the following fct from Clculus course. If continuous function f(x) represents the rte of chnge of F
Clculus Li Vs The Fundmentl Theorem of Clculus. The Totl Chnge Theorem nd the Are Under Curve. Recll the following fct from Clculus course. If continuous function f(x) represents the rte of chnge of F
Mathematics. Area under Curve.
 Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
Mthemtics Are under Curve www.testprepkrt.com Tle of Content 1. Introduction.. Procedure of Curve Sketching. 3. Sketching of Some common Curves. 4. Are of Bounded Regions. 5. Sign convention for finding
( ) where f ( x ) is a. AB Calculus Exam Review Sheet. A. Precalculus Type problems. Find the zeros of f ( x).
 AB Clculus Exm Review Sheet A. Preclculus Type prolems A1 Find the zeros of f ( x). This is wht you think of doing A2 A3 Find the intersection of f ( x) nd g( x). Show tht f ( x) is even. A4 Show tht f
AB Clculus Exm Review Sheet A. Preclculus Type prolems A1 Find the zeros of f ( x). This is wht you think of doing A2 A3 Find the intersection of f ( x) nd g( x). Show tht f ( x) is even. A4 Show tht f
Farey Fractions. Rickard Fernström. U.U.D.M. Project Report 2017:24. Department of Mathematics Uppsala University
 U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
U.U.D.M. Project Report 07:4 Frey Frctions Rickrd Fernström Exmensrete i mtemtik, 5 hp Hledre: Andres Strömergsson Exmintor: Jörgen Östensson Juni 07 Deprtment of Mthemtics Uppsl University Frey Frctions
Before we can begin Ch. 3 on Radicals, we need to be familiar with perfect squares, cubes, etc. Try and do as many as you can without a calculator!!!
 Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
Nme: Algebr II Honors Pre-Chpter Homework Before we cn begin Ch on Rdicls, we need to be fmilir with perfect squres, cubes, etc Try nd do s mny s you cn without clcultor!!! n The nth root of n n Be ble
Chapter 2. Random Variables and Probability Distributions
 Rndom Vriles nd Proilit Distriutions- 6 Chpter. Rndom Vriles nd Proilit Distriutions.. Introduction In the previous chpter, we introduced common topics of proilit. In this chpter, we trnslte those concepts
Rndom Vriles nd Proilit Distriutions- 6 Chpter. Rndom Vriles nd Proilit Distriutions.. Introduction In the previous chpter, we introduced common topics of proilit. In this chpter, we trnslte those concepts
The Trapezoidal Rule
 _.qd // : PM Pge 9 SECTION. Numericl Integrtion 9 f Section. The re of the region cn e pproimted using four trpezoids. Figure. = f( ) f( ) n The re of the first trpezoid is f f n. Figure. = Numericl Integrtion
_.qd // : PM Pge 9 SECTION. Numericl Integrtion 9 f Section. The re of the region cn e pproimted using four trpezoids. Figure. = f( ) f( ) n The re of the first trpezoid is f f n. Figure. = Numericl Integrtion
12Continuous ONLINE PAGE PROOFS. probability distributions Kick off with CAS
 Continuous proility distriutions. Kick off with CAS. Continuous rndom vriles nd proility functions. The continuous proility density function.4 Mesures of centre nd spred.5 Liner trnsformtions.6 Review
Continuous proility distriutions. Kick off with CAS. Continuous rndom vriles nd proility functions. The continuous proility density function.4 Mesures of centre nd spred.5 Liner trnsformtions.6 Review
Section 6.1 Definite Integral
 Section 6.1 Definite Integrl Suppose we wnt to find the re of region tht is not so nicely shped. For exmple, consider the function shown elow. The re elow the curve nd ove the x xis cnnot e determined
Section 6.1 Definite Integrl Suppose we wnt to find the re of region tht is not so nicely shped. For exmple, consider the function shown elow. The re elow the curve nd ove the x xis cnnot e determined
Chapter 7: Applications of Integrals
 Chpter 7: Applictions of Integrls 78 Chpter 7 Overview: Applictions of Integrls Clculus, like most mthemticl fields, egn with tring to solve everd prolems. The theor nd opertions were formlized lter. As
Chpter 7: Applictions of Integrls 78 Chpter 7 Overview: Applictions of Integrls Clculus, like most mthemticl fields, egn with tring to solve everd prolems. The theor nd opertions were formlized lter. As
QUADRATIC EQUATIONS OBJECTIVE PROBLEMS
 QUADRATIC EQUATIONS OBJECTIVE PROBLEMS +. The solution of the eqution will e (), () 0,, 5, 5. The roots of the given eqution ( p q) ( q r) ( r p) 0 + + re p q r p (), r p p q, q r p q (), (d), q r p q.
QUADRATIC EQUATIONS OBJECTIVE PROBLEMS +. The solution of the eqution will e (), () 0,, 5, 5. The roots of the given eqution ( p q) ( q r) ( r p) 0 + + re p q r p (), r p p q, q r p q (), (d), q r p q.
Unit #9 : Definite Integral Properties; Fundamental Theorem of Calculus
 Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
An Overview of Integration
 An Overview of Integrtion S. F. Ellermeyer July 26, 2 The Definite Integrl of Function f Over n Intervl, Suppose tht f is continuous function defined on n intervl,. The definite integrl of f from to is
An Overview of Integrtion S. F. Ellermeyer July 26, 2 The Definite Integrl of Function f Over n Intervl, Suppose tht f is continuous function defined on n intervl,. The definite integrl of f from to is
1 Part II: Numerical Integration
 Mth 4 Lb 1 Prt II: Numericl Integrtion This section includes severl techniques for getting pproimte numericl vlues for definite integrls without using ntiderivtives. Mthemticll, ect nswers re preferble
Mth 4 Lb 1 Prt II: Numericl Integrtion This section includes severl techniques for getting pproimte numericl vlues for definite integrls without using ntiderivtives. Mthemticll, ect nswers re preferble
2015 SRJC H2 Mathematics Prelim Paper 2
 05 SRJC H Mthemtics Prelim Pper Section A: Pure Mthemtics [40 mrks] Functions f nd g re defined s elow. f :, g : ln( ), (i) Sketch the grph of g() nd stte its ect rnge. [] (ii) Determine whether the composite
05 SRJC H Mthemtics Prelim Pper Section A: Pure Mthemtics [40 mrks] Functions f nd g re defined s elow. f :, g : ln( ), (i) Sketch the grph of g() nd stte its ect rnge. [] (ii) Determine whether the composite
Things to Memorize: A Partial List. January 27, 2017
 Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
AB Calculus Review Sheet
 AB Clculus Review Sheet Legend: A Preclculus, B Limits, C Differentil Clculus, D Applictions of Differentil Clculus, E Integrl Clculus, F Applictions of Integrl Clculus, G Prticle Motion nd Rtes This is
AB Clculus Review Sheet Legend: A Preclculus, B Limits, C Differentil Clculus, D Applictions of Differentil Clculus, E Integrl Clculus, F Applictions of Integrl Clculus, G Prticle Motion nd Rtes This is
The steps of the hypothesis test
 ttisticl Methods I (EXT 7005) Pge 78 Mosquito species Time of dy A B C Mid morning 0.0088 5.4900 5.5000 Mid Afternoon.3400 0.0300 0.8700 Dusk 0.600 5.400 3.000 The Chi squre test sttistic is the sum of
ttisticl Methods I (EXT 7005) Pge 78 Mosquito species Time of dy A B C Mid morning 0.0088 5.4900 5.5000 Mid Afternoon.3400 0.0300 0.8700 Dusk 0.600 5.400 3.000 The Chi squre test sttistic is the sum of
Unit 1 Exponentials and Logarithms
 HARTFIELD PRECALCULUS UNIT 1 NOTES PAGE 1 Unit 1 Eponentils nd Logrithms (2) Eponentil Functions (3) The number e (4) Logrithms (5) Specil Logrithms (7) Chnge of Bse Formul (8) Logrithmic Functions (10)
HARTFIELD PRECALCULUS UNIT 1 NOTES PAGE 1 Unit 1 Eponentils nd Logrithms (2) Eponentil Functions (3) The number e (4) Logrithms (5) Specil Logrithms (7) Chnge of Bse Formul (8) Logrithmic Functions (10)
p-adic Egyptian Fractions
 p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
p-adic Egyptin Frctions Contents 1 Introduction 1 2 Trditionl Egyptin Frctions nd Greedy Algorithm 2 3 Set-up 3 4 p-greedy Algorithm 5 5 p-egyptin Trditionl 10 6 Conclusion 1 Introduction An Egyptin frction
The area under the graph of f and above the x-axis between a and b is denoted by. f(x) dx. π O
 1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
1 Section 5. The Definite Integrl Suppose tht function f is continuous nd positive over n intervl [, ]. y = f(x) x The re under the grph of f nd ove the x-xis etween nd is denoted y f(x) dx nd clled the
Equations and Inequalities
 Equtions nd Inequlities Equtions nd Inequlities Curriculum Redy ACMNA: 4, 5, 6, 7, 40 www.mthletics.com Equtions EQUATIONS & Inequlities & INEQUALITIES Sometimes just writing vribles or pronumerls in
Equtions nd Inequlities Equtions nd Inequlities Curriculum Redy ACMNA: 4, 5, 6, 7, 40 www.mthletics.com Equtions EQUATIONS & Inequlities & INEQUALITIES Sometimes just writing vribles or pronumerls in
I1 = I2 I1 = I2 + I3 I1 + I2 = I3 + I4 I 3
 2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
2 The Prllel Circuit Electric Circuits: Figure 2- elow show ttery nd multiple resistors rrnged in prllel. Ech resistor receives portion of the current from the ttery sed on its resistnce. The split is
CS667 Lecture 6: Monte Carlo Integration 02/10/05
 CS667 Lecture 6: Monte Crlo Integrtion 02/10/05 Venkt Krishnrj Lecturer: Steve Mrschner 1 Ide The min ide of Monte Crlo Integrtion is tht we cn estimte the vlue of n integrl by looking t lrge number of
CS667 Lecture 6: Monte Crlo Integrtion 02/10/05 Venkt Krishnrj Lecturer: Steve Mrschner 1 Ide The min ide of Monte Crlo Integrtion is tht we cn estimte the vlue of n integrl by looking t lrge number of
APPLICATIONS OF DEFINITE INTEGRALS
 Chpter 6 APPICATIONS OF DEFINITE INTEGRAS OVERVIEW In Chpter 5 we discovered the connection etween Riemnn sums ssocited with prtition P of the finite closed intervl [, ] nd the process of integrtion. We
Chpter 6 APPICATIONS OF DEFINITE INTEGRAS OVERVIEW In Chpter 5 we discovered the connection etween Riemnn sums ssocited with prtition P of the finite closed intervl [, ] nd the process of integrtion. We
The Shortest Confidence Interval for the Mean of a Normal Distribution
 Interntionl Journl of Sttistics nd Proility; Vol. 7, No. 2; Mrch 208 ISSN 927-7032 E-ISSN 927-7040 Pulished y Cndin Center of Science nd Eduction The Shortest Confidence Intervl for the Men of Norml Distriution
Interntionl Journl of Sttistics nd Proility; Vol. 7, No. 2; Mrch 208 ISSN 927-7032 E-ISSN 927-7040 Pulished y Cndin Center of Science nd Eduction The Shortest Confidence Intervl for the Men of Norml Distriution
AT100 - Introductory Algebra. Section 2.7: Inequalities. x a. x a. x < a
 Section 2.7: Inequlities In this section, we will Determine if given vlue is solution to n inequlity Solve given inequlity or compound inequlity; give the solution in intervl nottion nd the solution 2.7
Section 2.7: Inequlities In this section, we will Determine if given vlue is solution to n inequlity Solve given inequlity or compound inequlity; give the solution in intervl nottion nd the solution 2.7
u( t) + K 2 ( ) = 1 t > 0 Analyzing Damped Oscillations Problem (Meador, example 2-18, pp 44-48): Determine the equation of the following graph.
 nlyzing Dmped Oscilltions Prolem (Medor, exmple 2-18, pp 44-48): Determine the eqution of the following grph. The eqution is ssumed to e of the following form f ( t) = K 1 u( t) + K 2 e!"t sin (#t + $
nlyzing Dmped Oscilltions Prolem (Medor, exmple 2-18, pp 44-48): Determine the eqution of the following grph. The eqution is ssumed to e of the following form f ( t) = K 1 u( t) + K 2 e!"t sin (#t + $
Chapter 8.2: The Integral
 Chpter 8.: The Integrl You cn think of Clculus s doule-wide triler. In one width of it lives differentil clculus. In the other hlf lives wht is clled integrl clculus. We hve lredy eplored few rooms in
Chpter 8.: The Integrl You cn think of Clculus s doule-wide triler. In one width of it lives differentil clculus. In the other hlf lives wht is clled integrl clculus. We hve lredy eplored few rooms in
List all of the possible rational roots of each equation. Then find all solutions (both real and imaginary) of the equation. 1.
 Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
Mth Anlysis CP WS 4.X- Section 4.-4.4 Review Complete ech question without the use of grphing clcultor.. Compre the mening of the words: roots, zeros nd fctors.. Determine whether - is root of 0. Show
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
