Differential Geometry of Surfaces
|
|
|
- Giles Wheeler
- 5 years ago
- Views:
Transcription
1 Differential Geometry of urfaces Jordan mith and Carlo équin C Diision, UC Berkeley Introduction These are notes on differential geometry of surfaces ased on reading Greiner et al. n. d.. Differential Geometry of urfaces Differential geometry of a D manifold or surface emedded in 3D is the study of the intrinsic properties of the surface as well as the effects of a gien parameterization on the surface. For the discussion elow, we will consider the local ehaior of a surface at a single point p with a gien local parameterization (u, ), see Figure. We would like to calculate the principle curature alues (κ, κ ), the maximum and minimum curature alues at p, as well as the local orthogonal arc length parameterization (s, t) which is aligned with the directions of maximum and minimum curature. N T fundamental form I. This measures the length of a tangent ector on a gien parametric asis y examining the quantity T T. T T ( ) + ( ) + ( ) () E + F + G (3) (4) (5) E F (6) F G U t I U (7) Equation 7 defines I. u I g ij u u E F F G (8) (9) (0) Figure : Tangent plane of 3 The First Fundamental Form With the gien parameterization, we can compute a pair of tangent ectors assuming the u and directions are distinct. These two ectors locally parameterize the tangent plane to at p. general tangent ector T can e constructed as a linear comination of scaled y infinitesimal coefficients U t. T + Consider rotating the direction of the tangent T around p y setting cos θ sin θ. In general, the magnitude and direction of T will ary ased on the skew and scale of the asis ectors, see Figure 3(a). The distortion of the local parameterization is descried y the metric tensor or the first (jordans sequin)@cs.erkeley.edu () If an orthonormal arc length parameterization (s, t) is chosen then there will e no local metric distortion and I will reduce to the identity matrix. 4 The econd Fundamental Form The unit normal N of a surface at p is the ector perpendicular to, i.e. the tangent plane of, at p. N can e calculated gien a general nondegenerate parametrization (u, ). N u () The curature of a surface at a point p is defined y the rate that N rotates in response to a unit tangential displacement as in Figure. normal section cure at p is constructed y intersecting with a plane normal to it, i.e a plane that contains N and a tangent direction T. The curature of this cure is the curature of in the direction T. The curature κ of a cure is the reciprocal of the radius ρ of the est fitting osculating circle, i.e. κ. The directional deriatie N T of N in the direction T is a linear comination ρ of the partial deriatie ectors N u N N N and is parallel to the tangent plane.
2 (uu ) + (u u) u N u + ( ) () N (u ) + (u ) N T N u + N N u N N u + ( ) (3) (4) N T Figure : Normal section of s with the tangent ector T, N T is suject to scaling y the metric of the parameter space. In an arc length parameter direction s, s N s is the curature of the normal section. Gien a general parameterization (u, ), we can compute T N T. This quantity defines the second fundamental form II which descries curature information distorted y the local metric. T N T ( N u) ( N + N u) ( N ) (5) N N (6) N u N N u N (7) U t II U (8) Equation 8 defines II. II can e simplified to a set of quanties which are easier to compute y sustituting the expressions in Equations,3 for N u and N respectiely. Two of the terms of in of the entries of the matrix in Equation anish due to the dot product of orthogonal ectors. Further simplification using properties of the ox product of ectors yields Equation. Equation 3 is deried y susituting N from Equation and shows that II can e computed simply y the dot product of the second partial deriaties of with N. Equation 3 also demonstrates that II is a symmetric matrix. T u II h ij N N u N u N N u N (u ) u u (u ) (u u) (u ) uu ( u ) ( ) u ( ) ( ) uu N u N N N L M M N (9) (0) () () (3) (4) Equations 3,4 can e sustituted for II to yield alternate formulas for T N T. T N T (u N) + ( N) + ( N) (5) L + M + N (6) u N N u N N L M M N (7) (8) II contains information aout the curature of, ut it will e distorted y the metric if the gien parameterization is not an arc length parameterization. It is still necessary to counter act this distortion in order to compute the curature of the. 5 Coordinate Transformations Our purpose in studying differential geometry and the fundamental forms has een to compute the principle curature alues (κ, κ ) and directions ( k, k ) of a parametric surface at a point p. Thus far we hae deried II which contains curature information ut can e distorted y the metric of the parameterization. I descries this metric information. We must comine II and I to find the arc length curature alues. The gien parameterization (u, ) defines a set of asis tangent ectors. We can construct an orthonormal asis s t due to an arc length parameterization (s, t) where s and are aligned, see Figure 3(a). point T can e expressed in either coordinate system, see Figure 3(). T s s t (9) The coordinates s measure the length of T as opposed to the coordinates. T T s + + (30) We would like to work in the s t, so we must find the transformations to and from. The quantities a,, and θ in Figure 3(a) are defined y.
3 t θ a (a) Constructing an orthonormal asis on top of the gien parametric asis s t θ a Figure 3: Effects of the metric s s u T () point T in (u, ) and (s, t) coordinates t T T I s ( I ) t s s ( t) ( ) t s s s (4) (43) (44) (45) (46) s + (47) It is now possile to transform our gien parameters to coordinates on an orthonormal asis where we can measure lengths. We can also transform coordinates on the orthonormal asis ack to coordinates on our gien parameterization. 6 Curature a 0 s cos θ sin θ t s t sin θ 0 u t a sin θ cos θ a u u s (3) (3) (33) (34) The first fundamental form I can e represented y these coordinate transformations. I u s t s t t 0 0 (35) (36) t (37) t (38) a a cos θ a cos θ (39) The curature at a point p on the surface in any tangential direction T is T N T. T N T N N (48) II (49) This function is parameterized y the gien parameterization. We would like to study the function that sweeps a unit length tangent around p, so it is more conenient to use arc length coordinates. We must transform coordinates so that setting the arc length coordinates s cos φ sin φ sweeps out the curature alues. T N T s ( II ) t s s s IIŜ E t E (50) (5) We can also derie transformations etween coordinates of the different sets of asis ectors y sustituting Equations 3,34 respectiely into Equation 9. a θ φ s s (40) s (4) To erify that this makes sense, consider T T again and transform the coordinates using Equations 40,4. Figure 4: The relationship etween the principle parameter directions (E, E ), the gien general parameter directions (, ), and the constructed orthonormal asis ( s, t)in the tangent plane to at p The curature function will hae maximum and minimum alues that occur at directions that are orthogonal to each other. The eigenalues of IIŜ are the principle curature alues (κ, κ ). The
4 eigenectors of IIŜ are the coordinates of the principle curature directions in the arc length coordinates. These coordinates will not e directly useful ecause we only know the ectors, so we would actually prefer the eigenectors in coordinates on this asis. IIŜ II ( ) t a sin θ sin θ 0 cos θ a L M M N a sin θ sin θ sin θ ( cos θl + am) sin θ cos θ 0 a (5) (53) sin θ ( cos θl + am) cos θl a cos θm + a N (54) oling for the eigenalues, we find the characteristic equation. The principle curature alues are the eigenalues. 0 ( a (a cos θ) ) λ ( L a cos θm + a N ) λ + ( LN M ) (55) 0 ( EG F ) λ (GL F M + EN) λ + ( LN M ) 7 The Weingarten Operator (56) n alternate way of computing the principle curature alues and directions is y using the Weingarten Operator W, also known as the shape operator. W is the inerse of the first fundamental form multiplied y the second fundamental form. I W I II (57) is the inerse of the first fundamental form. I ( t) ( ) t G F EG F F E (58) (59) We will proe that W has the same eigenalues as IIŜ, i.e. the same principle curature alues. We will also proe that the eigenectors of W are transformed ersions of the eigenectors of IIŜ to coordinates on the gien asis. eigenalue matrix as for IIŜ, so the eigenalues of W are the principle curature alues. ( )t V ( V t), so the columns of ( )t V are the eigenectors of W. This is a transformed ersion of V, the eigenectors of IIŜ oer the arc length asis. The transformation transforms the arc length coordinates to coordinates oer the gien asis, see Equation 4. s s V t t ( ) t ( V ) t s s t t u u (67) (68) (69) To sole for the principle curature alues and directions using the gien parameterization, we sustitute Equations 4,59 into Equation 57 and simplify to derie W written as the coefficients of the first and second fundamental forms. W I II (70) G F L M (7) EG F F E M N GL F M GM F N (7) EG F EM F L EN F M Then we use the representation of W in Equation 7 and compute the eigendecomposition. The eigenalues are the principle curatures, and the eigenectors are the coordinate coefficients oer the gien parametric asis ectors. GL F M + EN κ, λ, (EG F ) (GL F M + EN) 4 (EG F ) (LN M ) (EG F ) (73) κ M κ + κ GL F M + EN (EG F ) T race (W ) (74) κ G κ κ LN M Det (W ) (75) EG F References GREINER, G., LOO, J., ND WEELINK, W. Data Dependent Thin Plate Energy and its use in Interactie urface Modeling. IIŜ V ΛV (60) II IIŜ t (6) W I II (6) ( ) t II (63) ( ) t IIŜ t (64) ( ) t IIŜ t (65) W ( ) t V ΛV t (66) Equation 66 is the eigendecomposition of W. The diagonal matrix Λ has the eigenalues of W on its diagonal. It is the same
5 quare Matrices: Quick Reference. General Matrices We will e manipulating the matrices I and II, so it is important to reiew some fundamental properties. Matrix B in Equation - is a general matrix. The inerse, B, can e computed in closed form as shown in Equation -, if the determinant of B, Det (B) (ad c), does not equal to zero. α. Eigenalues B a α c d B α d ad c c a (-) (-) For a general n n square matrix, the eigenalues of are n special scalar alues λ i (i :, n) such that for special corresponding eigenectors i (i :, n), multiplication of with i is the same as scaling i y λ i, Equation -3. By sustituting i with itself multiplied y the identity matrix I in Equation -4, we can then comine terms in Equation -5. λ i i i λ i (I i) i (-3) (-4) λ ii i i 0 ( λ ii) i (-5) i is in the nullspace of the matrix ( λ ii), ut the ector i 0 always satisfies Equation -5. We are interested in nonzero eigenectors i only, so ( λ ii) must e singular so that its nullspace will e nonempty. ( λ ii) is singular if its determinant is zero. Equation -6 is the characteristic equation of, and the n roots of this equation define the eigenalues λ i (i :, n). 0 Det ( λ ii) (-6) For the case of the general matrix B, the characteristic equation, Equation -7 can e expanded analytically to yield an equation that is quadratic in λ i, Equation -. 0 Det (B λ ii) (-7) ( ) a λi 0 0 Det (-8) α c d 0 λ i 0 ( ) a α Det αλi 0 (-9) c d 0 αλ i 0 α a αλi (-0) c d αλ i 0 ( α λ i α (a + d) λ i (ad c) ) (-) α Equation - can e soled analytically using the quadratic equation to yield the eigenalues λ and λ in Equation -. λ, a + d ± (a d) + 4c α (-).3 Eigenectors For a general n n square matrix, once the eigenalues λ i (i :, n) hae een computed, the corresponding eigenectors i (i :, n) are computed y finding the nullspace of the matrix ( λ ii). The null space is computed for each λ i y sustituting its alue into the matrix ( λ ii) and then performing Gaussian elimination. The matrix will e singular, so at least one row will ecome all zeroes. It is then possile to sole for the components of i as parametric equations of a suset of free components. The parametric nature of the i s show that the eigenectors are not unique. In Equation -3, i can e replaced with itself multiplied y an aitrary scalar. This aritrary scaling of the eigenectors is the only degree of freedom if the eigenalues are unique, i.e. their algeraic multiplicities are all one. In this case, the nullspaces are all -dimensional suspaces, lines through the origin. If there are multiple roots to the characteristic equation, then the algeraic multiplicity m of some of the eigenalues will e greater than one. The m eigenectors corresponding to such an eigenalue will e a set of linearly independent ectors that span the m-dimensional suspace. The choice of these ectors has more degrees of freedom than the scaling in the -dimension case. If m, then the suspace is a plane through the origin, and there is a rotational degree of freedom for choosing the eigenectors as well as the scaling degree of freedom. In general, there are some matrices with eigenalues of algeraic multiplicity m > that do not hae a complete set of m associated eigenectors, i.e. the geometric multiplicity is less than the algeraic multiplicity. These matrices are defectie. For our purposes for the case of matrices, we will assume that the matrices are non-defectie. For the case of a non-defectie matrix B, we will try to sole for the eigenectors analytically y sustituting the eigenalues from Equation - into the matrix in Equation -0 and then performing Gaussian elimination. 0 a αλi α c d αλ i i a αλi i,x 0 c d αλ i i,y 0 a a+d± c d a+d± 0 (a d) c (a d) (a d) c i,x i,y (-3) (-4) i,x i,y (-5) i,x i,y (-6) (-7) Equation -7 shows that the matrix ( λ ii) is singular. We will let i,y then we can sole for i,y, Equation -8., (a d)± c (-8) In Equation -8, if c 0, then the eigenector is not well defined. We must handle the case where c 0 or 0 separately. In this case the eigenalues simplify to λ a α and λ d α, and gaussian elimination will produce a matrix with a single nonzero element. Hence, 0 t and 0 t, respectiely.
6 .4 Eigen Decomposition For a non-defectie n n square matrix, the geometric multiplicity equals the algeraic multiplicity for all of the eigenalues λ i (i :, n), so there is a corresponding set of n linearly independent eigenectors i (i :, n). It is then possile to diagonalize y transforming y the eigenectors and their inerse. Rememering Equation -9 that defines each eigenector, we can write all n equations as columns next to each other in Equation -0. i iλ i (-9)... n λ λ... nλ n (-0) We will define V as the matrix of column eigenectors. We can rewrite the right side of Equation -0 as the eigenector matrix V multiplied y a diagonal matrix Λ that has the n eigenalues along its diagonal, Equation -. fter right multiplying V, we derie the eigen decomposition of, Equation -4. V V V Λ V V V ΛV... n V ΛV λ λ λ n (-) (-) (-3) (-4) The eigen decomposition of, Equation -4, makes it ery efficient to raise to an integer exponent e. Consider first squaring, Equation -5. λ + λ λ λ a + d α ad c α T race () (-3) Det () (-3) We rememer that the determinant of the multiplication of two matrices is the product of their determinants. Det (B) Det () Det (B) (-33) We can then proe that the determinant of a matrix is equal to the product of its eigenalues. V ΛV Det () Det ( V ΛV ) (-34) (-35) Det (V ) Det (Λ) Det ( V ) (-36) Det ( V V Λ ) (-37) Det (Λ) (-38) λ i (-39) V ΛV V ΛV V ΛΛV V Λ V (-5) Equation -6 for to an integer exponent e is then deried y induction. This is ery efficient to compute ecause raising Λ to the exponent e can e computed y simply raising the n diagonal elements to e. e V Λ e V (-6) For the matrix B, the eigen decomposition is the following: B V Λ V (-7) a d c a d+ c V Λ a+d 0 α a+d+ 0 V c a d+ (a d) a d + 4c α c c (-8) (-9) (-30)
1.3.3 Basis sets and Gram-Schmidt Orthogonalization
 .. Basis sets and Gram-Schmidt Orthogonalization Before we address the question of existence and uniqueness, we must estalish one more tool for working with ectors asis sets. Let R, with (..-) : We can
.. Basis sets and Gram-Schmidt Orthogonalization Before we address the question of existence and uniqueness, we must estalish one more tool for working with ectors asis sets. Let R, with (..-) : We can
EIGENVALUES AND EIGENVECTORS
 CHAPTER 6 EIGENVALUES AND EIGENVECTORS SECTION 6. INTRODUCTION TO EIGENVALUES In each of Problems we first list the characteristic polynomial p( λ) A λi of the gien matrix A and then the roots of p( λ
CHAPTER 6 EIGENVALUES AND EIGENVECTORS SECTION 6. INTRODUCTION TO EIGENVALUES In each of Problems we first list the characteristic polynomial p( λ) A λi of the gien matrix A and then the roots of p( λ
Sample Solutions from the Student Solution Manual
 1 Sample Solutions from the Student Solution Manual 1213 If all the entries are, then the matrix is certainly not invertile; if you multiply the matrix y anything, you get the matrix, not the identity
1 Sample Solutions from the Student Solution Manual 1213 If all the entries are, then the matrix is certainly not invertile; if you multiply the matrix y anything, you get the matrix, not the identity
Expansion formula using properties of dot product (analogous to FOIL in algebra): u v 2 u v u v u u 2u v v v u 2 2u v v 2
 Least squares: Mathematical theory Below we provide the "vector space" formulation, and solution, of the least squares prolem. While not strictly necessary until we ring in the machinery of matrix algera,
Least squares: Mathematical theory Below we provide the "vector space" formulation, and solution, of the least squares prolem. While not strictly necessary until we ring in the machinery of matrix algera,
A Geometric Review of Linear Algebra
 A Geometric Reiew of Linear Algebra The following is a compact reiew of the primary concepts of linear algebra. The order of presentation is unconentional, with emphasis on geometric intuition rather than
A Geometric Reiew of Linear Algebra The following is a compact reiew of the primary concepts of linear algebra. The order of presentation is unconentional, with emphasis on geometric intuition rather than
1 :: Mathematical notation
 1 :: Mathematical notation x A means x is a member of the set A. A B means the set A is contained in the set B. {a 1,..., a n } means the set hose elements are a 1,..., a n. {x A : P } means the set of
1 :: Mathematical notation x A means x is a member of the set A. A B means the set A is contained in the set B. {a 1,..., a n } means the set hose elements are a 1,..., a n. {x A : P } means the set of
A Geometric Review of Linear Algebra
 A Geometric Reiew of Linear Algebra The following is a compact reiew of the primary concepts of linear algebra. I assume the reader is familiar with basic (i.e., high school) algebra and trigonometry.
A Geometric Reiew of Linear Algebra The following is a compact reiew of the primary concepts of linear algebra. I assume the reader is familiar with basic (i.e., high school) algebra and trigonometry.
10 Lorentz Group and Special Relativity
 Physics 129 Lecture 16 Caltech, 02/27/18 Reference: Jones, Groups, Representations, and Physics, Chapter 10. 10 Lorentz Group and Special Relativity Special relativity says, physics laws should look the
Physics 129 Lecture 16 Caltech, 02/27/18 Reference: Jones, Groups, Representations, and Physics, Chapter 10. 10 Lorentz Group and Special Relativity Special relativity says, physics laws should look the
6.1.1 Angle between Two Lines Intersection of Two lines Shortest Distance from a Point to a Line
 CHAPTER 6 : VECTORS 6. Lines in Space 6.. Angle between Two Lines 6.. Intersection of Two lines 6..3 Shortest Distance from a Point to a Line 6. Planes in Space 6.. Intersection of Two Planes 6.. Angle
CHAPTER 6 : VECTORS 6. Lines in Space 6.. Angle between Two Lines 6.. Intersection of Two lines 6..3 Shortest Distance from a Point to a Line 6. Planes in Space 6.. Intersection of Two Planes 6.. Angle
Review of Matrices and Vectors 1/45
 Reiew of Matrices and Vectors /45 /45 Definition of Vector: A collection of comple or real numbers, generally put in a column [ ] T "! Transpose + + + b a b a b b a a " " " b a b a Definition of Vector
Reiew of Matrices and Vectors /45 /45 Definition of Vector: A collection of comple or real numbers, generally put in a column [ ] T "! Transpose + + + b a b a b b a a " " " b a b a Definition of Vector
ES.1803 Topic 16 Notes Jeremy Orloff
 ES803 Topic 6 Notes Jerem Orloff 6 Eigenalues, diagonalization, decoupling This note coers topics that will take us seeral classes to get through We will look almost eclusiel at 2 2 matrices These hae
ES803 Topic 6 Notes Jerem Orloff 6 Eigenalues, diagonalization, decoupling This note coers topics that will take us seeral classes to get through We will look almost eclusiel at 2 2 matrices These hae
Unit 11: Vectors in the Plane
 135 Unit 11: Vectors in the Plane Vectors in the Plane The term ector is used to indicate a quantity (such as force or elocity) that has both length and direction. For instance, suppose a particle moes
135 Unit 11: Vectors in the Plane Vectors in the Plane The term ector is used to indicate a quantity (such as force or elocity) that has both length and direction. For instance, suppose a particle moes
CHAPTER 3 : VECTORS. Definition 3.1 A vector is a quantity that has both magnitude and direction.
 EQT 101-Engineering Mathematics I Teaching Module CHAPTER 3 : VECTORS 3.1 Introduction Definition 3.1 A ector is a quantity that has both magnitude and direction. A ector is often represented by an arrow
EQT 101-Engineering Mathematics I Teaching Module CHAPTER 3 : VECTORS 3.1 Introduction Definition 3.1 A ector is a quantity that has both magnitude and direction. A ector is often represented by an arrow
Conceptual Questions for Review
 Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
Conceptual Questions for Review Chapter 1 1.1 Which vectors are linear combinations of v = (3, 1) and w = (4, 3)? 1.2 Compare the dot product of v = (3, 1) and w = (4, 3) to the product of their lengths.
1 2 2 Circulant Matrices
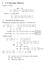 Circulant Matrices General matrix a c d Ax x ax + cx x x + dx General circulant matrix a x ax + x a x x + ax. Evaluating the Eigenvalues Find eigenvalues and eigenvectors of general circulant matrix: a
Circulant Matrices General matrix a c d Ax x ax + cx x x + dx General circulant matrix a x ax + x a x x + ax. Evaluating the Eigenvalues Find eigenvalues and eigenvectors of general circulant matrix: a
UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS
 SUBAREA I. COMPETENCY 1.0 UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS MECHANICS Skill 1.1 Calculating displacement, aerage elocity, instantaneous elocity, and acceleration in a gien frame of reference
SUBAREA I. COMPETENCY 1.0 UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS MECHANICS Skill 1.1 Calculating displacement, aerage elocity, instantaneous elocity, and acceleration in a gien frame of reference
Worksheet 9. Math 1B, GSI: Andrew Hanlon. 1 Ce 3t 1/3 1 = Ce 3t. 4 Ce 3t 1/ =
 Worksheet 9 Math B, GSI: Andrew Hanlon. Show that for each of the following pairs of differential equations and functions that the function is a solution of a differential equation. (a) y 2 y + y 2 ; Ce
Worksheet 9 Math B, GSI: Andrew Hanlon. Show that for each of the following pairs of differential equations and functions that the function is a solution of a differential equation. (a) y 2 y + y 2 ; Ce
Solutions to Final Practice Problems Written by Victoria Kala Last updated 12/5/2015
 Solutions to Final Practice Problems Written by Victoria Kala vtkala@math.ucsb.edu Last updated /5/05 Answers This page contains answers only. See the following pages for detailed solutions. (. (a x. See
Solutions to Final Practice Problems Written by Victoria Kala vtkala@math.ucsb.edu Last updated /5/05 Answers This page contains answers only. See the following pages for detailed solutions. (. (a x. See
Matrices and Matrix Algebra.
 Matrices and Matrix Algebra 3.1. Operations on Matrices Matrix Notation and Terminology Matrix: a rectangular array of numbers, called entries. A matrix with m rows and n columns m n A n n matrix : a square
Matrices and Matrix Algebra 3.1. Operations on Matrices Matrix Notation and Terminology Matrix: a rectangular array of numbers, called entries. A matrix with m rows and n columns m n A n n matrix : a square
Math 215 HW #9 Solutions
 Math 5 HW #9 Solutions. Problem 4.4.. If A is a 5 by 5 matrix with all a ij, then det A. Volumes or the big formula or pivots should give some upper bound on the determinant. Answer: Let v i be the ith
Math 5 HW #9 Solutions. Problem 4.4.. If A is a 5 by 5 matrix with all a ij, then det A. Volumes or the big formula or pivots should give some upper bound on the determinant. Answer: Let v i be the ith
Review of Linear Algebra
 Review of Linear Algebra Definitions An m n (read "m by n") matrix, is a rectangular array of entries, where m is the number of rows and n the number of columns. 2 Definitions (Con t) A is square if m=
Review of Linear Algebra Definitions An m n (read "m by n") matrix, is a rectangular array of entries, where m is the number of rows and n the number of columns. 2 Definitions (Con t) A is square if m=
CHAPTER 5. Linear Operators, Span, Linear Independence, Basis Sets, and Dimension
 A SERIES OF CLASS NOTES TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS LINEAR CLASS NOTES: A COLLECTION OF HANDOUTS FOR REVIEW AND PREVIEW OF LINEAR THEORY
A SERIES OF CLASS NOTES TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS LINEAR CLASS NOTES: A COLLECTION OF HANDOUTS FOR REVIEW AND PREVIEW OF LINEAR THEORY
Ideal Classes and Matrix Conjugation over F q [X]
![Ideal Classes and Matrix Conjugation over F q [X] Ideal Classes and Matrix Conjugation over F q [X]](/thumbs/85/92274574.jpg) Ideal lasses and Matrix onjugation oer F q [X] hristian Berghoff, Georg-August-Uniersität Göttingen Trais Morrison, Penn State Uniersity Yujia Qiu, Ruprecht-Karls-Uniersität Heidelerg Thomas Sicking, Georg-August-Uniersität
Ideal lasses and Matrix onjugation oer F q [X] hristian Berghoff, Georg-August-Uniersität Göttingen Trais Morrison, Penn State Uniersity Yujia Qiu, Ruprecht-Karls-Uniersität Heidelerg Thomas Sicking, Georg-August-Uniersität
CS 246 Review of Linear Algebra 01/17/19
 1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Notes on Linear Minimum Mean Square Error Estimators
 Notes on Linear Minimum Mean Square Error Estimators Ça gatay Candan January, 0 Abstract Some connections between linear minimum mean square error estimators, maximum output SNR filters and the least square
Notes on Linear Minimum Mean Square Error Estimators Ça gatay Candan January, 0 Abstract Some connections between linear minimum mean square error estimators, maximum output SNR filters and the least square
Math 425 Lecture 1: Vectors in R 3, R n
 Math 425 Lecture 1: Vectors in R 3, R n Motiating Questions, Problems 1. Find the coordinates of a regular tetrahedron with center at the origin and sides of length 1. 2. What is the angle between the
Math 425 Lecture 1: Vectors in R 3, R n Motiating Questions, Problems 1. Find the coordinates of a regular tetrahedron with center at the origin and sides of length 1. 2. What is the angle between the
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
The value of a problem is not so much coming up with the answer as in the ideas and attempted ideas it forces on the would be solver I.N.
 Math 410 Homework Problems In the following pages you will find all of the homework problems for the semester. Homework should be written out neatly and stapled and turned in at the beginning of class
Math 410 Homework Problems In the following pages you will find all of the homework problems for the semester. Homework should be written out neatly and stapled and turned in at the beginning of class
Elementary maths for GMT
 Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that
![58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that 58. The Triangle Inequality for vectors is. dot product.] 59. The Parallelogram Law states that](/thumbs/86/94310732.jpg) 786 CAPTER 12 VECTORS AND TE GEOETRY OF SPACE 0, 0, 1, and 1, 1, 1 as shown in the figure. Then the centroid is. ( 1 2, 1 2, 1 2 ) ] x z C 54. If c a a, where a,, and c are all nonzero vectors, show that
786 CAPTER 12 VECTORS AND TE GEOETRY OF SPACE 0, 0, 1, and 1, 1, 1 as shown in the figure. Then the centroid is. ( 1 2, 1 2, 1 2 ) ] x z C 54. If c a a, where a,, and c are all nonzero vectors, show that
MIT Final Exam Solutions, Spring 2017
 MIT 8.6 Final Exam Solutions, Spring 7 Problem : For some real matrix A, the following vectors form a basis for its column space and null space: C(A) = span,, N(A) = span,,. (a) What is the size m n of
MIT 8.6 Final Exam Solutions, Spring 7 Problem : For some real matrix A, the following vectors form a basis for its column space and null space: C(A) = span,, N(A) = span,,. (a) What is the size m n of
45. The Parallelogram Law states that. product of a and b is the vector a b a 2 b 3 a 3 b 2, a 3 b 1 a 1 b 3, a 1 b 2 a 2 b 1. a c. a 1. b 1.
 SECTION 10.4 THE CROSS PRODUCT 537 42. Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular. 43.
SECTION 10.4 THE CROSS PRODUCT 537 42. Suppose that all sides of a quadrilateral are equal in length and opposite sides are parallel. Use vector methods to show that the diagonals are perpendicular. 43.
MA 266 Review Topics - Exam # 2 (updated)
 MA 66 Reiew Topics - Exam # updated Spring First Order Differential Equations Separable, st Order Linear, Homogeneous, Exact Second Order Linear Homogeneous with Equations Constant Coefficients The differential
MA 66 Reiew Topics - Exam # updated Spring First Order Differential Equations Separable, st Order Linear, Homogeneous, Exact Second Order Linear Homogeneous with Equations Constant Coefficients The differential
Linear Algebra Primer
 Linear Algebra Primer David Doria daviddoria@gmail.com Wednesday 3 rd December, 2008 Contents Why is it called Linear Algebra? 4 2 What is a Matrix? 4 2. Input and Output.....................................
Linear Algebra Primer David Doria daviddoria@gmail.com Wednesday 3 rd December, 2008 Contents Why is it called Linear Algebra? 4 2 What is a Matrix? 4 2. Input and Output.....................................
Outline. Linear Algebra for Computer Vision
 Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
Glossary of Linear Algebra Terms. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB
 Glossary of Linear Algebra Terms Basis (for a subspace) A linearly independent set of vectors that spans the space Basic Variable A variable in a linear system that corresponds to a pivot column in the
Glossary of Linear Algebra Terms Basis (for a subspace) A linearly independent set of vectors that spans the space Basic Variable A variable in a linear system that corresponds to a pivot column in the
Vectors and Matrices
 Chapter Vectors and Matrices. Introduction Vectors and matrices are used extensively throughout this text. Both are essential as one cannot derive and analyze laws of physics and physical measurements
Chapter Vectors and Matrices. Introduction Vectors and matrices are used extensively throughout this text. Both are essential as one cannot derive and analyze laws of physics and physical measurements
Linear Algebra (Review) Volker Tresp 2017
 Linear Algebra (Review) Volker Tresp 2017 1 Vectors k is a scalar (a number) c is a column vector. Thus in two dimensions, c = ( c1 c 2 ) (Advanced: More precisely, a vector is defined in a vector space.
Linear Algebra (Review) Volker Tresp 2017 1 Vectors k is a scalar (a number) c is a column vector. Thus in two dimensions, c = ( c1 c 2 ) (Advanced: More precisely, a vector is defined in a vector space.
Linear Algebra: Matrix Eigenvalue Problems
 CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
CHAPTER8 Linear Algebra: Matrix Eigenvalue Problems Chapter 8 p1 A matrix eigenvalue problem considers the vector equation (1) Ax = λx. 8.0 Linear Algebra: Matrix Eigenvalue Problems Here A is a given
Chapter 5 Eigenvalues and Eigenvectors
 Chapter 5 Eigenvalues and Eigenvectors Outline 5.1 Eigenvalues and Eigenvectors 5.2 Diagonalization 5.3 Complex Vector Spaces 2 5.1 Eigenvalues and Eigenvectors Eigenvalue and Eigenvector If A is a n n
Chapter 5 Eigenvalues and Eigenvectors Outline 5.1 Eigenvalues and Eigenvectors 5.2 Diagonalization 5.3 Complex Vector Spaces 2 5.1 Eigenvalues and Eigenvectors Eigenvalue and Eigenvector If A is a n n
Chapter 1: Kinematics of Particles
 Chapter 1: Kinematics of Particles 1.1 INTRODUCTION Mechanics the state of rest of motion of bodies subjected to the action of forces Static equilibrium of a body that is either at rest or moes with constant
Chapter 1: Kinematics of Particles 1.1 INTRODUCTION Mechanics the state of rest of motion of bodies subjected to the action of forces Static equilibrium of a body that is either at rest or moes with constant
1 Systems of Differential Equations
 March, 20 7- Systems of Differential Equations Let U e an open suset of R n, I e an open interval in R and : I R n R n e a function from I R n to R n The equation ẋ = ft, x is called a first order ordinary
March, 20 7- Systems of Differential Equations Let U e an open suset of R n, I e an open interval in R and : I R n R n e a function from I R n to R n The equation ẋ = ft, x is called a first order ordinary
Chap 3. Linear Algebra
 Chap 3. Linear Algebra Outlines 1. Introduction 2. Basis, Representation, and Orthonormalization 3. Linear Algebraic Equations 4. Similarity Transformation 5. Diagonal Form and Jordan Form 6. Functions
Chap 3. Linear Algebra Outlines 1. Introduction 2. Basis, Representation, and Orthonormalization 3. Linear Algebraic Equations 4. Similarity Transformation 5. Diagonal Form and Jordan Form 6. Functions
Algebra I Notes Unit Nine: Exponential Expressions
 Algera I Notes Unit Nine: Eponential Epressions Syllaus Ojectives: 7. The student will determine the value of eponential epressions using a variety of methods. 7. The student will simplify algeraic epressions
Algera I Notes Unit Nine: Eponential Epressions Syllaus Ojectives: 7. The student will determine the value of eponential epressions using a variety of methods. 7. The student will simplify algeraic epressions
Algebra I Notes Concept 00b: Review Properties of Integer Exponents
 Algera I Notes Concept 00: Review Properties of Integer Eponents In Algera I, a review of properties of integer eponents may e required. Students egin their eploration of power under the Common Core in
Algera I Notes Concept 00: Review Properties of Integer Eponents In Algera I, a review of properties of integer eponents may e required. Students egin their eploration of power under the Common Core in
Mathematics 2203, Test 1 - Solutions
 Mathematics 220, Test 1 - Solutions F, 2010 Philippe B. Laval Name 1. Determine if each statement below is True or False. If it is true, explain why (cite theorem, rule, property). If it is false, explain
Mathematics 220, Test 1 - Solutions F, 2010 Philippe B. Laval Name 1. Determine if each statement below is True or False. If it is true, explain why (cite theorem, rule, property). If it is false, explain
Linear Algebra - Part II
 Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
Linear Algebra (Review) Volker Tresp 2018
 Linear Algebra (Review) Volker Tresp 2018 1 Vectors k, M, N are scalars A one-dimensional array c is a column vector. Thus in two dimensions, ( ) c1 c = c 2 c i is the i-th component of c c T = (c 1, c
Linear Algebra (Review) Volker Tresp 2018 1 Vectors k, M, N are scalars A one-dimensional array c is a column vector. Thus in two dimensions, ( ) c1 c = c 2 c i is the i-th component of c c T = (c 1, c
MTH 2032 SemesterII
 MTH 202 SemesterII 2010-11 Linear Algebra Worked Examples Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education December 28, 2011 ii Contents Table of Contents
MTH 202 SemesterII 2010-11 Linear Algebra Worked Examples Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education December 28, 2011 ii Contents Table of Contents
BASIC ALGORITHMS IN LINEAR ALGEBRA. Matrices and Applications of Gaussian Elimination. A 2 x. A T m x. A 1 x A T 1. A m x
 BASIC ALGORITHMS IN LINEAR ALGEBRA STEVEN DALE CUTKOSKY Matrices and Applications of Gaussian Elimination Systems of Equations Suppose that A is an n n matrix with coefficents in a field F, and x = (x,,
BASIC ALGORITHMS IN LINEAR ALGEBRA STEVEN DALE CUTKOSKY Matrices and Applications of Gaussian Elimination Systems of Equations Suppose that A is an n n matrix with coefficents in a field F, and x = (x,,
Eigenvalues and Eigenvectors
 Sec. 6.1 Eigenvalues and Eigenvectors Linear transformations L : V V that go from a vector space to itself are often called linear operators. Many linear operators can be understood geometrically by identifying
Sec. 6.1 Eigenvalues and Eigenvectors Linear transformations L : V V that go from a vector space to itself are often called linear operators. Many linear operators can be understood geometrically by identifying
Matrices and Vectors. Definition of Matrix. An MxN matrix A is a two-dimensional array of numbers A =
 30 MATHEMATICS REVIEW G A.1.1 Matrices and Vectors Definition of Matrix. An MxN matrix A is a two-dimensional array of numbers A = a 11 a 12... a 1N a 21 a 22... a 2N...... a M1 a M2... a MN A matrix can
30 MATHEMATICS REVIEW G A.1.1 Matrices and Vectors Definition of Matrix. An MxN matrix A is a two-dimensional array of numbers A = a 11 a 12... a 1N a 21 a 22... a 2N...... a M1 a M2... a MN A matrix can
0 a 3 a 2 a 3 0 a 1 a 2 a 1 0
 Chapter Flow kinematics Vector and tensor formulae This introductory section presents a brief account of different definitions of ector and tensor analysis that will be used in the following chapters.
Chapter Flow kinematics Vector and tensor formulae This introductory section presents a brief account of different definitions of ector and tensor analysis that will be used in the following chapters.
SOLUTIONS: ASSIGNMENT Use Gaussian elimination to find the determinant of the matrix. = det. = det = 1 ( 2) 3 6 = 36. v 4.
 SOLUTIONS: ASSIGNMENT 9 66 Use Gaussian elimination to find the determinant of the matrix det 1 1 4 4 1 1 1 1 8 8 = det = det 0 7 9 0 0 0 6 = 1 ( ) 3 6 = 36 = det = det 0 0 6 1 0 0 0 6 61 Consider a 4
SOLUTIONS: ASSIGNMENT 9 66 Use Gaussian elimination to find the determinant of the matrix det 1 1 4 4 1 1 1 1 8 8 = det = det 0 7 9 0 0 0 6 = 1 ( ) 3 6 = 36 = det = det 0 0 6 1 0 0 0 6 61 Consider a 4
1Number ONLINE PAGE PROOFS. systems: real and complex. 1.1 Kick off with CAS
 1Numer systems: real and complex 1.1 Kick off with CAS 1. Review of set notation 1.3 Properties of surds 1. The set of complex numers 1.5 Multiplication and division of complex numers 1.6 Representing
1Numer systems: real and complex 1.1 Kick off with CAS 1. Review of set notation 1.3 Properties of surds 1. The set of complex numers 1.5 Multiplication and division of complex numers 1.6 Representing
On some properties of the Lyapunov equation for damped systems
 On some properties of the Lyapuno equation for damped systems Ninosla Truhar, Uniersity of Osijek, Department of Mathematics, 31 Osijek, Croatia 1 ntruhar@mathos.hr Krešimir Veselić Lehrgebiet Mathematische
On some properties of the Lyapuno equation for damped systems Ninosla Truhar, Uniersity of Osijek, Department of Mathematics, 31 Osijek, Croatia 1 ntruhar@mathos.hr Krešimir Veselić Lehrgebiet Mathematische
Math 102, Winter Final Exam Review. Chapter 1. Matrices and Gaussian Elimination
 Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
Math 0, Winter 07 Final Exam Review Chapter. Matrices and Gaussian Elimination { x + x =,. Different forms of a system of linear equations. Example: The x + 4x = 4. [ ] [ ] [ ] vector form (or the column
Linear Algebra for Machine Learning. Sargur N. Srihari
 Linear Algebra for Machine Learning Sargur N. srihari@cedar.buffalo.edu 1 Overview Linear Algebra is based on continuous math rather than discrete math Computer scientists have little experience with it
Linear Algebra for Machine Learning Sargur N. srihari@cedar.buffalo.edu 1 Overview Linear Algebra is based on continuous math rather than discrete math Computer scientists have little experience with it
Vector Spaces. EXAMPLE: Let R n be the set of all n 1 matrices. x 1 x 2. x n
 Vector Spaces DEFINITION: A vector space is a nonempty set V of ojects, called vectors, on which are defined two operations, called addition and multiplication y scalars (real numers), suject to the following
Vector Spaces DEFINITION: A vector space is a nonempty set V of ojects, called vectors, on which are defined two operations, called addition and multiplication y scalars (real numers), suject to the following
Math 302 Outcome Statements Winter 2013
 Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Math 302 Outcome Statements Winter 2013 1 Rectangular Space Coordinates; Vectors in the Three-Dimensional Space (a) Cartesian coordinates of a point (b) sphere (c) symmetry about a point, a line, and a
Then x 1,..., x n is a basis as desired. Indeed, it suffices to verify that it spans V, since n = dim(v ). We may write any v V as r
 Practice final solutions. I did not include definitions which you can find in Axler or in the course notes. These solutions are on the terse side, but would be acceptable in the final. However, if you
Practice final solutions. I did not include definitions which you can find in Axler or in the course notes. These solutions are on the terse side, but would be acceptable in the final. However, if you
Representation theory of SU(2), density operators, purification Michael Walter, University of Amsterdam
 Symmetry and Quantum Information Feruary 6, 018 Representation theory of S(), density operators, purification Lecture 7 Michael Walter, niversity of Amsterdam Last week, we learned the asic concepts of
Symmetry and Quantum Information Feruary 6, 018 Representation theory of S(), density operators, purification Lecture 7 Michael Walter, niversity of Amsterdam Last week, we learned the asic concepts of
2. Every linear system with the same number of equations as unknowns has a unique solution.
 1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
1. For matrices A, B, C, A + B = A + C if and only if A = B. 2. Every linear system with the same number of equations as unknowns has a unique solution. 3. Every linear system with the same number of equations
MIDTERM 1 - SOLUTIONS
 MIDTERM - SOLUTIONS MATH 254 - SUMMER 2002 - KUNIYUKI CHAPTERS, 2, GRADED OUT OF 75 POINTS 2 50 POINTS TOTAL ) Use either Gaussian elimination with back-substitution or Gauss-Jordan elimination to solve
MIDTERM - SOLUTIONS MATH 254 - SUMMER 2002 - KUNIYUKI CHAPTERS, 2, GRADED OUT OF 75 POINTS 2 50 POINTS TOTAL ) Use either Gaussian elimination with back-substitution or Gauss-Jordan elimination to solve
33AH, WINTER 2018: STUDY GUIDE FOR FINAL EXAM
 33AH, WINTER 2018: STUDY GUIDE FOR FINAL EXAM (UPDATED MARCH 17, 2018) The final exam will be cumulative, with a bit more weight on more recent material. This outline covers the what we ve done since the
33AH, WINTER 2018: STUDY GUIDE FOR FINAL EXAM (UPDATED MARCH 17, 2018) The final exam will be cumulative, with a bit more weight on more recent material. This outline covers the what we ve done since the
235 Final exam review questions
 5 Final exam review questions Paul Hacking December 4, 0 () Let A be an n n matrix and T : R n R n, T (x) = Ax the linear transformation with matrix A. What does it mean to say that a vector v R n is an
5 Final exam review questions Paul Hacking December 4, 0 () Let A be an n n matrix and T : R n R n, T (x) = Ax the linear transformation with matrix A. What does it mean to say that a vector v R n is an
Elementary maths for GMT
 Elementary maths for GMT Linear Algebra Part 1: Vectors, Representations Algebra and Linear Algebra Algebra: numbers and operations on numbers 2 + 3 = 5 3 7 = 21 Linear Algebra: tuples, triples... of numbers
Elementary maths for GMT Linear Algebra Part 1: Vectors, Representations Algebra and Linear Algebra Algebra: numbers and operations on numbers 2 + 3 = 5 3 7 = 21 Linear Algebra: tuples, triples... of numbers
Geometry review, part I
 Geometr reie, part I Geometr reie I Vectors and points points and ectors Geometric s. coordinate-based (algebraic) approach operations on ectors and points Lines implicit and parametric equations intersections,
Geometr reie, part I Geometr reie I Vectors and points points and ectors Geometric s. coordinate-based (algebraic) approach operations on ectors and points Lines implicit and parametric equations intersections,
1. What is the determinant of the following matrix? a 1 a 2 4a 3 2a 2 b 1 b 2 4b 3 2b c 1. = 4, then det
 What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
What is the determinant of the following matrix? 3 4 3 4 3 4 4 3 A 0 B 8 C 55 D 0 E 60 If det a a a 3 b b b 3 c c c 3 = 4, then det a a 4a 3 a b b 4b 3 b c c c 3 c = A 8 B 6 C 4 D E 3 Let A be an n n matrix
Chapter 3 Transformations
 Chapter 3 Transformations An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Linear Transformations A function is called a linear transformation if 1. for every and 2. for every If we fix the bases
Chapter 3 Transformations An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Linear Transformations A function is called a linear transformation if 1. for every and 2. for every If we fix the bases
Information About Ellipses
 Information About Ellipses David Eberly, Geometric Tools, Redmond WA 9805 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License. To view
Information About Ellipses David Eberly, Geometric Tools, Redmond WA 9805 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License. To view
Linear Algebra V = T = ( 4 3 ).
 Linear Algebra Vectors A column vector is a list of numbers stored vertically The dimension of a column vector is the number of values in the vector W is a -dimensional column vector and V is a 5-dimensional
Linear Algebra Vectors A column vector is a list of numbers stored vertically The dimension of a column vector is the number of values in the vector W is a -dimensional column vector and V is a 5-dimensional
MATH 221, Spring Homework 10 Solutions
 MATH 22, Spring 28 - Homework Solutions Due Tuesday, May Section 52 Page 279, Problem 2: 4 λ A λi = and the characteristic polynomial is det(a λi) = ( 4 λ)( λ) ( )(6) = λ 6 λ 2 +λ+2 The solutions to the
MATH 22, Spring 28 - Homework Solutions Due Tuesday, May Section 52 Page 279, Problem 2: 4 λ A λi = and the characteristic polynomial is det(a λi) = ( 4 λ)( λ) ( )(6) = λ 6 λ 2 +λ+2 The solutions to the
Vectors in R n. P. Danziger
 1 Vectors in R n P. Danziger 1 Vectors The standard geometric definition of ector is as something which has direction and magnitude but not position. Since ectors hae no position we may place them whereer
1 Vectors in R n P. Danziger 1 Vectors The standard geometric definition of ector is as something which has direction and magnitude but not position. Since ectors hae no position we may place them whereer
Problem 3 Solution Page 1. 1A. Assuming as outlined in the text that the orbit is circular, and relating the radial acceleration
 Prolem 3 Solution Page Solution A. Assug as outlined in the text that the orit is circular, and relating the radial acceleration V GM S to the graitational field (where MS is the solar mass we otain Jupiter's
Prolem 3 Solution Page Solution A. Assug as outlined in the text that the orit is circular, and relating the radial acceleration V GM S to the graitational field (where MS is the solar mass we otain Jupiter's
On computing Gaussian curvature of some well known distribution
 Theoretical Mathematics & Applications, ol.3, no.4, 03, 85-04 ISSN: 79-9687 (print), 79-9709 (online) Scienpress Ltd, 03 On computing Gaussian curature of some well known distribution William W.S. Chen
Theoretical Mathematics & Applications, ol.3, no.4, 03, 85-04 ISSN: 79-9687 (print), 79-9709 (online) Scienpress Ltd, 03 On computing Gaussian curature of some well known distribution William W.S. Chen
Duke University, Department of Electrical and Computer Engineering Optimization for Scientists and Engineers c Alex Bronstein, 2014
 Duke University, Department of Electrical and Computer Engineering Optimization for Scientists and Engineers c Alex Bronstein, 2014 Linear Algebra A Brief Reminder Purpose. The purpose of this document
Duke University, Department of Electrical and Computer Engineering Optimization for Scientists and Engineers c Alex Bronstein, 2014 Linear Algebra A Brief Reminder Purpose. The purpose of this document
Section 6: PRISMATIC BEAMS. Beam Theory
 Beam Theory There are two types of beam theory aailable to craft beam element formulations from. They are Bernoulli-Euler beam theory Timoshenko beam theory One learns the details of Bernoulli-Euler beam
Beam Theory There are two types of beam theory aailable to craft beam element formulations from. They are Bernoulli-Euler beam theory Timoshenko beam theory One learns the details of Bernoulli-Euler beam
Econ Slides from Lecture 7
 Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
Econ 205 Sobel Econ 205 - Slides from Lecture 7 Joel Sobel August 31, 2010 Linear Algebra: Main Theory A linear combination of a collection of vectors {x 1,..., x k } is a vector of the form k λ ix i for
Matrices. A matrix is a method of writing a set of numbers using rows and columns. Cells in a matrix can be referenced in the form.
 Matrices A matrix is a method of writing a set of numbers using rows and columns. 1 2 3 4 3 2 1 5 7 2 5 4 2 0 5 10 12 8 4 9 25 30 1 1 Reading Information from a Matrix Cells in a matrix can be referenced
Matrices A matrix is a method of writing a set of numbers using rows and columns. 1 2 3 4 3 2 1 5 7 2 5 4 2 0 5 10 12 8 4 9 25 30 1 1 Reading Information from a Matrix Cells in a matrix can be referenced
Linear Algebra & Geometry why is linear algebra useful in computer vision?
 Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
MATH Spring 2011 Sample problems for Test 2: Solutions
 MATH 304 505 Spring 011 Sample problems for Test : Solutions Any problem may be altered or replaced by a different one! Problem 1 (15 pts) Let M, (R) denote the vector space of matrices with real entries
MATH 304 505 Spring 011 Sample problems for Test : Solutions Any problem may be altered or replaced by a different one! Problem 1 (15 pts) Let M, (R) denote the vector space of matrices with real entries
1 - Systems of Linear Equations
 1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
1 - Systems of Linear Equations 1.1 Introduction to Systems of Linear Equations Almost every problem in linear algebra will involve solving a system of equations. ü LINEAR EQUATIONS IN n VARIABLES We are
When two letters name a vector, the first indicates the and the second indicates the of the vector.
 8-8 Chapter 8 Applications of Trigonometry 8.3 Vectors, Operations, and the Dot Product Basic Terminology Algeraic Interpretation of Vectors Operations with Vectors Dot Product and the Angle etween Vectors
8-8 Chapter 8 Applications of Trigonometry 8.3 Vectors, Operations, and the Dot Product Basic Terminology Algeraic Interpretation of Vectors Operations with Vectors Dot Product and the Angle etween Vectors
Definitions for Quizzes
 Definitions for Quizzes Italicized text (or something close to it) will be given to you. Plain text is (an example of) what you should write as a definition. [Bracketed text will not be given, nor does
Definitions for Quizzes Italicized text (or something close to it) will be given to you. Plain text is (an example of) what you should write as a definition. [Bracketed text will not be given, nor does
Symmetric and anti symmetric matrices
 Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
Symmetric and anti symmetric matrices In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, matrix A is symmetric if. A = A Because equal matrices have equal
KIST DP Course Descriptions
 Grade: 11 Unit Number: 1 Unit Title: Algebra Sequence and Series; Exponents and Logarithms; The Binomial Theorem Deductive vs. Inductive reasoning Mathematics begins with axioms and uses deductive reasoning
Grade: 11 Unit Number: 1 Unit Title: Algebra Sequence and Series; Exponents and Logarithms; The Binomial Theorem Deductive vs. Inductive reasoning Mathematics begins with axioms and uses deductive reasoning
Classical differential geometry of two-dimensional surfaces
 Classical differential geometry of two-dimensional surfaces 1 Basic definitions This section gives an overview of the basic notions of differential geometry for twodimensional surfaces. It follows mainly
Classical differential geometry of two-dimensional surfaces 1 Basic definitions This section gives an overview of the basic notions of differential geometry for twodimensional surfaces. It follows mainly
Linear Algebra Highlights
 Linear Algebra Highlights Chapter 1 A linear equation in n variables is of the form a 1 x 1 + a 2 x 2 + + a n x n. We can have m equations in n variables, a system of linear equations, which we want to
Linear Algebra Highlights Chapter 1 A linear equation in n variables is of the form a 1 x 1 + a 2 x 2 + + a n x n. We can have m equations in n variables, a system of linear equations, which we want to
Chapter 2 Canonical Correlation Analysis
 Chapter 2 Canonical Correlation Analysis Canonical correlation analysis CCA, which is a multivariate analysis method, tries to quantify the amount of linear relationships etween two sets of random variales,
Chapter 2 Canonical Correlation Analysis Canonical correlation analysis CCA, which is a multivariate analysis method, tries to quantify the amount of linear relationships etween two sets of random variales,
Lec 2: Mathematical Economics
 Lec 2: Mathematical Economics to Spectral Theory Sugata Bag Delhi School of Economics 24th August 2012 [SB] (Delhi School of Economics) Introductory Math Econ 24th August 2012 1 / 17 Definition: Eigen
Lec 2: Mathematical Economics to Spectral Theory Sugata Bag Delhi School of Economics 24th August 2012 [SB] (Delhi School of Economics) Introductory Math Econ 24th August 2012 1 / 17 Definition: Eigen
Solution. The relationship between cartesian coordinates (x, y) and polar coordinates (r, θ) is given by. (x, y) = (r cos θ, r sin θ).
 Problem 1. Let p 1 be the point having polar coordinates r = 1 and θ = π. Let p 2 be the point having polar coordinates r = 1 and θ = π/2. Find the Euclidean distance between p 1 and p 2. The relationship
Problem 1. Let p 1 be the point having polar coordinates r = 1 and θ = π. Let p 2 be the point having polar coordinates r = 1 and θ = π/2. Find the Euclidean distance between p 1 and p 2. The relationship
Math 4A Notes. Written by Victoria Kala Last updated June 11, 2017
 Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
Math 4A Notes Written by Victoria Kala vtkala@math.ucsb.edu Last updated June 11, 2017 Systems of Linear Equations A linear equation is an equation that can be written in the form a 1 x 1 + a 2 x 2 +...
Ph12b Solution Set 4
 Ph Solution Set 4 Feruary 5, 00 The state ψ S un E is transforme to p ψ S un E + p a 0 S γ E + S η E Since γ E an η E aren t mutually orthogonal, we can t use this equation irectly to compute the new ensity
Ph Solution Set 4 Feruary 5, 00 The state ψ S un E is transforme to p ψ S un E + p a 0 S γ E + S η E Since γ E an η E aren t mutually orthogonal, we can t use this equation irectly to compute the new ensity
Section 2.1: Reduce Rational Expressions
 CHAPTER Section.: Reduce Rational Expressions Section.: Reduce Rational Expressions Ojective: Reduce rational expressions y dividing out common factors. A rational expression is a quotient of polynomials.
CHAPTER Section.: Reduce Rational Expressions Section.: Reduce Rational Expressions Ojective: Reduce rational expressions y dividing out common factors. A rational expression is a quotient of polynomials.
Eigenvalues and Eigenvectors
 /88 Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-sen University Linear Algebra Eigenvalue Problem /88 Eigenvalue Equation By definition, the eigenvalue equation for matrix
/88 Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-sen University Linear Algebra Eigenvalue Problem /88 Eigenvalue Equation By definition, the eigenvalue equation for matrix
Math Computation Test 1 September 26 th, 2016 Debate: Computation vs. Theory Whatever wins, it ll be Huuuge!
 Math 5- Computation Test September 6 th, 6 Debate: Computation vs. Theory Whatever wins, it ll be Huuuge! Name: Answer Key: Making Math Great Again Be sure to show your work!. (8 points) Consider the following
Math 5- Computation Test September 6 th, 6 Debate: Computation vs. Theory Whatever wins, it ll be Huuuge! Name: Answer Key: Making Math Great Again Be sure to show your work!. (8 points) Consider the following
6 EIGENVALUES AND EIGENVECTORS
 6 EIGENVALUES AND EIGENVECTORS INTRODUCTION TO EIGENVALUES 61 Linear equations Ax = b come from steady state problems Eigenvalues have their greatest importance in dynamic problems The solution of du/dt
6 EIGENVALUES AND EIGENVECTORS INTRODUCTION TO EIGENVALUES 61 Linear equations Ax = b come from steady state problems Eigenvalues have their greatest importance in dynamic problems The solution of du/dt
MATH 369 Linear Algebra
 Assignment # Problem # A father and his two sons are together 00 years old. The father is twice as old as his older son and 30 years older than his younger son. How old is each person? Problem # 2 Determine
Assignment # Problem # A father and his two sons are together 00 years old. The father is twice as old as his older son and 30 years older than his younger son. How old is each person? Problem # 2 Determine
