Ideal Classes and Matrix Conjugation over F q [X]
|
|
|
- Kerrie Garrison
- 5 years ago
- Views:
Transcription
1 Ideal lasses and Matrix onjugation oer F q [X] hristian Berghoff, Georg-August-Uniersität Göttingen Trais Morrison, Penn State Uniersity Yujia Qiu, Ruprecht-Karls-Uniersität Heidelerg Thomas Sicking, Georg-August-Uniersität Göttingen Decemer 10, Introduction In a commutatie ring R two matrices M, N M n (R) are called conjugate, when there is a matrix S GL n (R), such that M = S 1 NS. Howeer, gien two matrices M and N as aoe, it is not always easy to see whether they are conjugate or not. onjugate matrices will hae the same characteristic polynomial, ut if two matrices hae the same characteristic polynomial, they are not necessarily conjugate. So the question is: Gien a polynomial f(x) R[X], how many conjugacy classes of matrices with that characteristic polynomial do we hae and how can we find them? In the case when R = Z it is known from a paper y. Latimer and.. MacDuffee (see [2]) that the conjugacy classes of matrices in M n (Z) with a characteristic polynomial f(x) Z[X] of degree n are in one-to-one correspondence with the Z[α]-ideal classes in Q(α) with α a root of f. In the following paper we will deal with that prolem when the ring R is F q [X] =: A, the polynomial ring oer a finite field with q elements. F will denote the quotient field of A, so F = F q (X), and it will turn out that the theorem of Latimer and MacDuffee also holds if we exchange Z y A and Q y F. This is asically due to the fact that A, like Z, is a unique factorization domain. In the proof of the theorem the map giing the one-to-one correspondence will e explicitly gien, so gien a polynomial we will e ale to compute the conjugacy classes of matrices with that polynomial as their characteristic polynomial, and the other way round, gien a matrix we will find the class of fractional ideals corresponding to its conjugacy class (see section 3). The proof of the main theorem is asically adapted from Keith onrad s paper [1], which can e found on his home page. 2 Main section Theorem 1. Let K e a field and f(t ) K[T ] e monic and irreducile of degree n. Then (a) For a matrix M in M n (K), the characteristic polynomial of M is f(t ) if and only if f(m) = 0. 1
2 () All matrices in M n (K) with characteristic polynomial f(t ) are conjugate in M n (K). We can make K n into a K[T ]-module y defining g(t ) 0 = g(m) 0. Denote such a module y V M. To proe the aoe theorem, we will make use of the following lemma: Lemma 2. For M, N M n (K), V M = VN if and only if M and N are conjugate oer M n (K). Proof (of the lemma). Let M, N M n (K) e conjugate with N = S 1 MS. S induces a linear isomorphism of K n as a ector space oer K; we use this to define a map φ : V N V M y φ() = S. We check that this is indeed an isomorphism of modules. We need only show that for g(t ) K[T ], φ(g(t ) VN ) = g(t ) VM φ(). Using the fact that N = S 1 MS, we hae SN k = M k S for k N, so Sg(N) = g(m)s. Thus φ(g(t ) VN ) = φ(g(n)) = Sg(N) = g(m)s = g(m)φ() = g(t ) VM φ() and we conclude that V M = VN as modules oer K[T ]. Now, let V M and V N e two K[T ]-modules, with φ : V M V N a module isomorphism. Fix a asis B = (x 1,..., x n ) for V M oer K as a ector space, then φ(b) is a asis of V N as a ector space. Let S = [φ] e the matrix representatie of φ as a linear transformation. We claim that S 1 NS = M. Let K n. Then we hae S 1 NS() = S 1 N(φ()) = S 1 (T VN φ()) = φ 1 φ(t VM ) = T VM = M and since was aritrary, we conclude S 1 NS = M and the matrices M and N are conjugate. Proof of Theorem 1. (a) Suppose M has characteristic polynomial f(t ); then y the ayley-hamilton theorem, f(m) = 0. onersely, if f(m) = 0, then f(t ) diides χ M (T ) (the characteristic polynomial of M) since f(t ) must e the minimal polynomial of M in F [T ] as it is monic and irreducile. Because oth polynomials are monic and of the same degree, they must e equal. () The idea to proe this is to show that V M and K[T ]/f(t ) are isomorphic as K[T ]-modules, and therefore y our lemma any other matrix N M n (K) with characteristic polynomial f(t ) is conjugate to M, since we would hae V M = VN. Let M M n (K) hae f(t ) as its characteristic polynomial and let V M e the K[T ]-module defined aoe. Since we hae f(t ) = 0 for any K n, we can instead consider this as a module oer K[T ]/(f(t )), where g(t ) = g(m) for g(t ) K[T ]/(f(t )). This in fact makes K n a K[T ]/(f(t ))-ector space, since K[T ]/(f(t )) is a field ecause f(t ) is irreducile. For an aritrary nonzero 0 K n, the multiples K[T ] 0 = (K[T ]/(f(t )) 0 are suspaces of K n ; the K-dimension is dim K (K[T ]/(f(t ))) = n and therefore (K[T ]/(f(t )) 0 = K n. Since 0 is nonzero and K[T ]/(f(t )) is a field, we also hae K[T ]/(f(t )) = K[T ]/(f(t )) 0 as K[T ]-modules. Thus K n = K[T ]/(f(t )) as K[T ]-modules, as desired. 2
3 From Theorem 1 we can conclude that all matrices in M n (F ) (recall F = F q (X)) sharing the same characteristic polynomial are conjugate oer F, ut unfortunately it is not true for general surings of F, in particular, the ring we want to work on, A = F q [X]. So the following theorem is on our inestigation into the additional criteria when two matrices in M n (A) which hae the same characteristic polynomial, say f(t ) A[T ], are conjugate oer A. And it turns out to e strongly related to the A[α]-ideal classes in F (α) with α a root of the characteristic polynomial f in a certain extension of F. This theorem is an analogon for A and F of what Latimer and MacDuffee proed for Z and Q. Theorem 3. Let f(t ) A[T ] e monic irreducile of degree n. (a) A matrix M M n (A) has characteristic polynomial f(t ) if and only if f(m) = 0. () onjugacy classes of matrices in M n (A) with characteristic polynomial f(t ) are in ijection with the A[α]-ideal classes in F (α), where α denotes a root of f(t ). Proof. To proe theorem 3a, we need the following fact: Let R e an integrally closed domain, K its field of fractions, and f(t ) R[T ] e monic. Then if f is reducile in K[T ], it is reducile in R[T ]. This gies us that if f R[T ] is monic and irreducile oer R[T ], it is irreducile in K[T ]. Once we hae this, the proof of Theorem 1a follows through word for word, since the ayley-hamilton theorem holds in any commutatie ring. To proe this, we need the following: Suppose f(t ) R[T ] is monic and irreducile, L e a field extension oer K such that f has a root α L. Then the minimal polynomial g(t ) oer K for α in fact has coefficients from R. Indeed, if α L is a zero of the monic polynomial f(t ) R[T ], then its minimal polynomial g(t ) diides f(t ) in K[T ] (write f(t ) = g(t )q(t ) + r(t ), with deg(r) < deg(g) or r = 0, then we see r(α) = 0 and thus r(t ) = 0 since g is minimal and monic). Thus the zeroes of g(t ) are integral oer R, since they are also zeroes of f R[T ]. Then we hae g(t ) = (T β 1 )... (T β k ) with β i R. The coefficients of g(t ) are sums and products of the β i and are therefore in R as well, thus g(t ) (R K)[T ] = R[T ], since R is integrally closed. Suppose now that f(t ) R[T ] and f(t ) = k i=1 pei i (T ) with p i(t ) irreducile oer K[T ]. Then we know there is a field extension L such that each p i has a root α i in L. Then α i is also a root of f, and since f R[T ], α i is integral oer R. By our lemma, we know that this implies that in fact, p i (T ) R[T ]. Thus f(t ) is reducile oer R[T ]. () For any A[α]-fractional ideal F (α) multiplication y α gies an A- linear map m α :. hoosing an A-asis of (which is an A-module of rank n), we can represent m α y a matrix [m α ] M n (A). A different A-asis gies a conjugate matrix, so independent of the choice of a asis we can associate to a fractional ideal a conjugacy class in M n (A), namely the conjugacy class of a matrix representation of m α. For any M in this conjugacy class we hae f(m) = f([m α ]) = [m f(α) ] = [m 0 ] = 0. For an equialent fractional ideal c = x with x F the conjugacy class is the same as the one for, ecause the matrix for m α with respect to the A-asis {e 1,..., e n } of is the same as the matrix for m α with respect to the A-asis 3
4 {xe 1,..., xe n } of c, so the map A[α]-ideal classes in F (α) conjugacy classes of M M n (A) such that f(m) = 0 (1) gien y the rule: pick a fractional ideal of an ideal class and write a matrix representation for m α with respect to a asis and map the ideal class of the ideal to the conjugacy class of the matrix is well defined. We will show that this map is a ijection. We show surjectiity first. Let B M n (A) with characteristic polynomial f(t ) and let K = F (α) = F [α]. Make F n into a K-ector space in the following way: For c K write c = g(α) for a g(t ) F [T ]. For F n set c = g(α) := g(b) (2) This is well defined, as for a different polynomial h(t ) F [T ] satisfying c = h(α), we hae g(α) = h(α), so g(t ) h(t ) is diisile y the minimal polynomial of α, namely f(t ). But f(b) = 0, so g(b) = h(b) and g(b) = h(b). If A n then α = B A n, so A n is a finitely generated A[α]-sumodule of F n. The equation α = B and the way F n is defined as a K-ector space tells us that the matrix representation of m α with respect to the standard asis of A n is B. We then hae n = dim F (F n ) = [K : F ] dim K (F n ) = n dim K (F n ) (3) so F n is a 1-dimensional K-ector space. Thus for any 0 F n that is nonzero the K-linear map ϕ 0 : K F n gien y ϕ 0 (c) = c 0 is an isomorphism of 1-dimensional ector spaces. The inerse image := ϕ 1 0 (A n ) = {c K : c 0 A n } is a finitely generated A[α]-sumodule of K, i.e. a fractional ideal, since A n has these properties inside F n. Since B is the matrix representation of m α on A n with respect to the standard asis {e 1,..., e n }, B is also the matrix representation of m α on with respect to the A-asis {ϕ 1 0 (e 1 ),..., ϕ 1 0 (e n )} of. So the matrix B is indeed a representation for m α on a fractional A[α]-ideal, so the map (1) is onto. Now we intend to show that (1) is injectie. To do so, suppose and c are two fractional A[α]-ideals in K, for which the matrices B and representing m α with respect to A-ases of and c are conjugate in M n (A). Injectiity of (1) is equialent to and c eing in the same ideal class, i. e. z K : = zc. Since we know B represents the map m α : with respect to a certain A-asis B of we otain the following commutatie diagram m α [ ] B [ ] B B where the map [ ] B is the coordinate isomorphism identifying B with the standard asis A n. onsidering the asis of c with respect to which m α : c c is represented y the matrix, we derie the commutatie diagram 4
5 m α c c [ ] [ ] in an analog way. Furthermore, the conjugacy of B and in M n (A) implies = UBU 1, U GL n (A), i. e. the diagram A n U B A n U commutes. Juxtaposing these diagrams yields: [ ] B U [ ] 1 c m α B [ ] B U [ ] 1 The whole diagramm commutes ecause each of its squares is commutatie. The top and ottom maps are A-linear isomorphisms. Hence, the composite map c on the top and ottom is an A-linear isomorphism which also commutes with m α y commutatiity of the diagram. This property implies the composite map c is not only A-linear, ut een A[α]-linear which means and c are isomorphic as A[α]-modules. Isomorphic fractional A[α]-ideals are scalar multiples of each other, i. e. z K : = zc. So we hae proed that map (1) is injectie. c m α 3 Examples In this section, we are going to present four examples with different class numers and different structures of the class groups. To simplify the computation, we only choose examples in which the characteristic polynomial has degree 2. The examples 2-4 were detected y making extensie calculations with the computer algera system Magma. Example 4. As the first example, we take A to e the polynomial ring oer F 2 and we look at the following polynomial oer A: f(y) = y 2 + y + x 5 + x 3 + 1, and we denote y α a zero of f. As one of the examples gien in [3], Hayes showed that the class numer of A[α] is 1. Thus, all matrices in M 2 (A) haing f as their characteristic polynomial are conjugate. The same situation applies to the other three cures with class numer 1 gien in [3]. 5
6 Example 5. Let us denote y A the polynomial ring oer F 3 and we look at the following polynomial oer A: f(y) = y 2 x 3 + x 2 + 1, which has α as a zero. We are looking for the conjugacy classes of matrices M M 2 (A) satisfying M 2 + ( x 3 + x 2 + 1)I 2 = 0. The class numer of A[α] is 2 and the representaties of classes of fractional ideals are (1), (x + 1, α), for which we can compute the corresponding representing matrices associated to the map m α. We hae an A-asis of the ideal (1) as {1, α}, and multiplying y α yields: 1 α = α; α α = (x 3 x 2 1) α. So the multiplication y α is represented y the matrix M 1 := ( ) 0 x 3 x The matrix corresponding to the ideal class (x+1, α) has A-asis {x+1, α}, thus we can compute the representing matrix as follows: (x + 1) α = 0 (x + 1) + (x + 1) α; α α = (x 2 + x 1) (x + 1) + 0 α. So the multiplication y α is represented y the matrix M 2 := ( ) 0 x 2 +x 1 x+1 0. Thus, y theorem 3, any M in M 2 (A) haing f as its characteristic polynomial is conjugate to exactly one of those two matrices. Example 6. Now we want to erify the calculations we just made y going the other way round, i. e. conerting our matrices into fractional ideals y using the proof of the surjectiity of map (1). In example 5 we hae computed that the matrices M 1 := ( ) 0 x 3 x and M2 := ( ) 0 x 2 +x 1 x+1 0 satisfy the polynomial M 2 + ( x 3 + x 2 + 1)I 2 = 0. Let s start with M 1. First make F 2 into a F (α)-ector space, where α denotes a root of the polynomial f(y) = y 2 x 3 + x 2 + 1, y defining ( ) ( ) ( ( )) ( ) u u 0 x (a + α) := (a + M 1 ) = a + 3 x 2 1 u 1 0 ( ) ( ) a (x = 3 x 2 1) u a Set 0 = ( 1 0 ), so there is an isomorphism F (α) F 2 as F (α)-ector spaces y c c 0. The fractional ideal we are interested in is the inerse image of A 2 under this isomorphism F (α) F 2. This is {c F (α) : c 0 A 2 }. Writing c = a + α we otain ( 1 c 0 = (a + M 1 ) 0 ) ( a = Therefore, haing c 0 A 2 is equialent to c = a + α for some a, A, so the A(α)-fractional ideal in F (α) corresponding to M 1 is A + αa = (1, α) ). 6
7 and this is exactly the ideal that gae rise to M 1 in example 5. Turning to M 2 we proceed as follows. F 2 is made into a F (α)-ector space y defining ( ) ( ) ( ) ( ) u u a (x (a + α) := (a + M 2 ) = 2 + x 1) u. (x + 1) a As efore, we set 0 = ( 1 0 ) and compute {c F (α) : c 0 A 2 }. Writing c = a + α we otain ( ) ( ) ( ) ( ) 1 a 1 0 a c 0 = (a + M 2 ) = =, 0 (x + 1) 0 x + 1 so c 0 A 2 ( a ) ( x + 1 ) 1 A 2 = ( x+1 ) A 2. This means c 0 A 2 is equialent to c = u+ x+1α, u, A. Thus, the fractional ideal we get is {u + α : u, A} = A + α x + 1 x + 1 A. Another ideal from the same class is (x + 1)A + αa = (x + 1, α), which is the ideal used in example 5 to derie M 2. Example 7. Take A to e F 5 [x] and we look at the following polynomial oer A: f(y) = y 2 x 3 + x + 2, which has α as a zero. We are looking for the conjugacy classes of matrices M M 2 (A) satisfying M 2 + ( x 3 + x + 2)I 2 = 0. The class numer of A[α] is 3 and the representaties of classes of fractional ideals are (1), ((x + 3) 2, x α), ((x 2 + x 1) 2, x 3 x 2 + 3x α), to which we can compute the corresponding representing matrices associated to the map m α. We hae an A-asis of the ideal (1) as {1, α}, and multiplying y α yields: 1 α = α; α α = (x 3 x 2) α. So the multiplication y α is represented y the matrix M 1 := ( ) 0 x 3 x The matrix corresponding to the ideal class ((x + 3) 2, x α) has A-asis {(x + 3) 2, x α}, thus we can compute the representing matrix as follows: (x + 3) 2 α = ( (x + 1)) (x + 3) 2 + (x + 3) 2 (x α); (x α) α = (x + 3) (x + 3) 2 + (x + 1) (x α). 7
8 So the multiplication y α is represented y the matrix M 2 := ( (x+1) x+3 ) (x+3) 2 x+1. In a similar manner, we can also compute the matrices corresponding to the third ideal class, namely M 3 := ( (x 3 x 2 +3x+3) x 4 +2x 3 +x 2 1 ) (x 2 +x 1) 2 x 3 x 2 +3x+3. Thus, y theorem 3, any M in M 2 (A) haing f as its characteristic polynomial is conjugate to exactly one of M 1, M 2 and M 3. Example 8. Take q to e 7 and we look at the following polynomial in A[y]: f(y) = y 2 + y x 4 x + 2, which has α as a zero. We are looking for the conjugacy classes of matrices M M 2 (A) satisfying M 2 + M + ( x 4 x + 2)I 2 = 0. The class numer of A[α] is 4 and the class group is isomorphic to Z/2Z Z/2Z. The representaties of classes of fractional ideals are (1), (x(x + 5), x α), (x(x + 1), 4 + α), (x 2 + 6x + 5, 3x + α), to which we can compute the corresponding representing matrices associated to the map m α. We hae an A-asis of the ideal (1) as (1, α), and multiplying y α yields: 1 α = α; α α = (x 4 + x 2) 1 1 α. So the multiplication y α is represented y the matrix M 1 := ( ) 0 x 4 +x The matrix corresponding to the ideal class (x(x + 5), x α) can e computed as follows: x(x + 5) α = ( (x + 4)) x(x + 5) + x(x + 5) (x α); (x α) α = (x 2 + 2x + 3) x(x + 5) + (x + 3) (x α). So the multiplication y α is represented y the matrix M 2 := ( ) (x+4) x 2 +2x+3 x(x+5) x+3. In a similar manner, we can also compute the matrices corresponding to the other two ideal classes, namely M 3 := ( ) 4 x 2 x+1 x(x+1) 3 and M4 := ( ) 3x (x 2 +x+1) x 2 +6x+5 3x 1. Thus, y theorem 3, any M in M 2 (A) haing f as its characteristic polynomial is conjugate to exactly one of the four aoe matrices. References [1] K. onrad: Ideal classes and matrix conjugation oer Z [2]. Latimer,.. MacDuffee: A correspondence etween classes of ideals and classes of matrices, Ann. of Math. 34 pp , 1933 [3] D. Hayes: Explicit class field theory in gloal function fields, Rota, G.., Studies in Algera and Numer theory, pp , New York London: Academic Press
Math 581 Problem Set 9
 Math 581 Prolem Set 9 1. Let m and n e relatively prime positive integers. (a) Prove that Z/mnZ = Z/mZ Z/nZ as RINGS. (Hint: First Isomorphism Theorem) Proof: Define ϕz Z/mZ Z/nZ y ϕ(x) = ([x] m, [x] n
Math 581 Prolem Set 9 1. Let m and n e relatively prime positive integers. (a) Prove that Z/mnZ = Z/mZ Z/nZ as RINGS. (Hint: First Isomorphism Theorem) Proof: Define ϕz Z/mZ Z/nZ y ϕ(x) = ([x] m, [x] n
Differential Geometry of Surfaces
 Differential Geometry of urfaces Jordan mith and Carlo équin C Diision, UC Berkeley Introduction These are notes on differential geometry of surfaces ased on reading Greiner et al. n. d.. Differential
Differential Geometry of urfaces Jordan mith and Carlo équin C Diision, UC Berkeley Introduction These are notes on differential geometry of surfaces ased on reading Greiner et al. n. d.. Differential
TOTALLY RAMIFIED PRIMES AND EISENSTEIN POLYNOMIALS. 1. Introduction
 TOTALLY RAMIFIED PRIMES AND EISENSTEIN POLYNOMIALS KEITH CONRAD A (monic) polynomial in Z[T ], 1. Introduction f(t ) = T n + c n 1 T n 1 + + c 1 T + c 0, is Eisenstein at a prime p when each coefficient
TOTALLY RAMIFIED PRIMES AND EISENSTEIN POLYNOMIALS KEITH CONRAD A (monic) polynomial in Z[T ], 1. Introduction f(t ) = T n + c n 1 T n 1 + + c 1 T + c 0, is Eisenstein at a prime p when each coefficient
TOTALLY RAMIFIED PRIMES AND EISENSTEIN POLYNOMIALS. 1. Introduction
 TOTALLY RAMIFIED PRIMES AND EISENSTEIN POLYNOMIALS KEITH CONRAD A (monic) polynomial in Z[T ], 1. Introduction f(t ) = T n + c n 1 T n 1 + + c 1 T + c 0, is Eisenstein at a prime p when each coefficient
TOTALLY RAMIFIED PRIMES AND EISENSTEIN POLYNOMIALS KEITH CONRAD A (monic) polynomial in Z[T ], 1. Introduction f(t ) = T n + c n 1 T n 1 + + c 1 T + c 0, is Eisenstein at a prime p when each coefficient
Mon Apr dot product, length, orthogonality, projection onto the span of a single vector. Announcements: Warm-up Exercise:
 Math 2270-004 Week 2 notes We will not necessarily finish the material from a gien day's notes on that day. We may also add or subtract some material as the week progresses, but these notes represent an
Math 2270-004 Week 2 notes We will not necessarily finish the material from a gien day's notes on that day. We may also add or subtract some material as the week progresses, but these notes represent an
Review for Exam 2/Solutions
 MTH 310-3 Astract Algera I and Numer Theory S18 Review for Eam 2/Solutions 1. Let n e an integer. (a) For 0 n 10, verify that n 2 n + 11 is a prime. () If n 0, 1 and n 0, 1 (mod 11), show that n 2 n +
MTH 310-3 Astract Algera I and Numer Theory S18 Review for Eam 2/Solutions 1. Let n e an integer. (a) For 0 n 10, verify that n 2 n + 11 is a prime. () If n 0, 1 and n 0, 1 (mod 11), show that n 2 n +
Theorem 5.3. Let E/F, E = F (u), be a simple field extension. Then u is algebraic if and only if E/F is finite. In this case, [E : F ] = deg f u.
![Theorem 5.3. Let E/F, E = F (u), be a simple field extension. Then u is algebraic if and only if E/F is finite. In this case, [E : F ] = deg f u. Theorem 5.3. Let E/F, E = F (u), be a simple field extension. Then u is algebraic if and only if E/F is finite. In this case, [E : F ] = deg f u.](/thumbs/81/83685479.jpg) 5. Fields 5.1. Field extensions. Let F E be a subfield of the field E. We also describe this situation by saying that E is an extension field of F, and we write E/F to express this fact. If E/F is a field
5. Fields 5.1. Field extensions. Let F E be a subfield of the field E. We also describe this situation by saying that E is an extension field of F, and we write E/F to express this fact. If E/F is a field
Quivers. Virginia, Lonardo, Tiago and Eloy UNICAMP. 28 July 2006
 Quivers Virginia, Lonardo, Tiago and Eloy UNICAMP 28 July 2006 1 Introduction This is our project Throughout this paper, k will indicate an algeraically closed field of characteristic 0 2 Quivers 21 asic
Quivers Virginia, Lonardo, Tiago and Eloy UNICAMP 28 July 2006 1 Introduction This is our project Throughout this paper, k will indicate an algeraically closed field of characteristic 0 2 Quivers 21 asic
MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION
 MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION 1. Polynomial rings (review) Definition 1. A polynomial f(x) with coefficients in a ring R is n f(x) = a i x i = a 0 + a 1 x + a 2 x 2 + + a n x n i=0
MATH 431 PART 2: POLYNOMIAL RINGS AND FACTORIZATION 1. Polynomial rings (review) Definition 1. A polynomial f(x) with coefficients in a ring R is n f(x) = a i x i = a 0 + a 1 x + a 2 x 2 + + a n x n i=0
The Riemann-Roch Theorem: a Proof, an Extension, and an Application MATH 780, Spring 2019
 The Riemann-Roch Theorem: a Proof, an Extension, and an Application MATH 780, Spring 2019 This handout continues the notational conentions of the preious one on the Riemann-Roch Theorem, with one slight
The Riemann-Roch Theorem: a Proof, an Extension, and an Application MATH 780, Spring 2019 This handout continues the notational conentions of the preious one on the Riemann-Roch Theorem, with one slight
Topics in linear algebra
 Chapter 6 Topics in linear algebra 6.1 Change of basis I want to remind you of one of the basic ideas in linear algebra: change of basis. Let F be a field, V and W be finite dimensional vector spaces over
Chapter 6 Topics in linear algebra 6.1 Change of basis I want to remind you of one of the basic ideas in linear algebra: change of basis. Let F be a field, V and W be finite dimensional vector spaces over
Representations and Linear Actions
 Representations and Linear Actions Definition 0.1. Let G be an S-group. A representation of G is a morphism of S-groups φ G GL(n, S) for some n. We say φ is faithful if it is a monomorphism (in the category
Representations and Linear Actions Definition 0.1. Let G be an S-group. A representation of G is a morphism of S-groups φ G GL(n, S) for some n. We say φ is faithful if it is a monomorphism (in the category
QUALIFYING EXAM IN ALGEBRA August 2011
 QUALIFYING EXAM IN ALGEBRA August 2011 1. There are 18 problems on the exam. Work and turn in 10 problems, in the following categories. I. Linear Algebra 1 problem II. Group Theory 3 problems III. Ring
QUALIFYING EXAM IN ALGEBRA August 2011 1. There are 18 problems on the exam. Work and turn in 10 problems, in the following categories. I. Linear Algebra 1 problem II. Group Theory 3 problems III. Ring
Parvati Shastri. 2. Kummer Theory
 Reciprocity Laws: Artin-Hilert Parvati Shastri 1. Introduction In this volume, the early reciprocity laws including the quadratic, the cuic have een presented in Adhikari s article [1]. Also, in that article
Reciprocity Laws: Artin-Hilert Parvati Shastri 1. Introduction In this volume, the early reciprocity laws including the quadratic, the cuic have een presented in Adhikari s article [1]. Also, in that article
THE MINIMAL POLYNOMIAL AND SOME APPLICATIONS
 THE MINIMAL POLYNOMIAL AND SOME APPLICATIONS KEITH CONRAD. Introduction The easiest matrices to compute with are the diagonal ones. The sum and product of diagonal matrices can be computed componentwise
THE MINIMAL POLYNOMIAL AND SOME APPLICATIONS KEITH CONRAD. Introduction The easiest matrices to compute with are the diagonal ones. The sum and product of diagonal matrices can be computed componentwise
 Algebra Qualifying Exam August 2001 Do all 5 problems. 1. Let G be afinite group of order 504 = 23 32 7. a. Show that G cannot be isomorphic to a subgroup of the alternating group Alt 7. (5 points) b.
Algebra Qualifying Exam August 2001 Do all 5 problems. 1. Let G be afinite group of order 504 = 23 32 7. a. Show that G cannot be isomorphic to a subgroup of the alternating group Alt 7. (5 points) b.
1 :: Mathematical notation
 1 :: Mathematical notation x A means x is a member of the set A. A B means the set A is contained in the set B. {a 1,..., a n } means the set hose elements are a 1,..., a n. {x A : P } means the set of
1 :: Mathematical notation x A means x is a member of the set A. A B means the set A is contained in the set B. {a 1,..., a n } means the set hose elements are a 1,..., a n. {x A : P } means the set of
Factorization in Polynomial Rings
 Factorization in Polynomial Rings These notes are a summary of some of the important points on divisibility in polynomial rings from 17 and 18. PIDs Definition 1 A principal ideal domain (PID) is an integral
Factorization in Polynomial Rings These notes are a summary of some of the important points on divisibility in polynomial rings from 17 and 18. PIDs Definition 1 A principal ideal domain (PID) is an integral
SPRING 2006 PRELIMINARY EXAMINATION SOLUTIONS
 SPRING 006 PRELIMINARY EXAMINATION SOLUTIONS 1A. Let G be the subgroup of the free abelian group Z 4 consisting of all integer vectors (x, y, z, w) such that x + 3y + 5z + 7w = 0. (a) Determine a linearly
SPRING 006 PRELIMINARY EXAMINATION SOLUTIONS 1A. Let G be the subgroup of the free abelian group Z 4 consisting of all integer vectors (x, y, z, w) such that x + 3y + 5z + 7w = 0. (a) Determine a linearly
Math 120 HW 9 Solutions
 Math 120 HW 9 Solutions June 8, 2018 Question 1 Write down a ring homomorphism (no proof required) f from R = Z[ 11] = {a + b 11 a, b Z} to S = Z/35Z. The main difficulty is to find an element x Z/35Z
Math 120 HW 9 Solutions June 8, 2018 Question 1 Write down a ring homomorphism (no proof required) f from R = Z[ 11] = {a + b 11 a, b Z} to S = Z/35Z. The main difficulty is to find an element x Z/35Z
Vector Spaces. EXAMPLE: Let R n be the set of all n 1 matrices. x 1 x 2. x n
 Vector Spaces DEFINITION: A vector space is a nonempty set V of ojects, called vectors, on which are defined two operations, called addition and multiplication y scalars (real numers), suject to the following
Vector Spaces DEFINITION: A vector space is a nonempty set V of ojects, called vectors, on which are defined two operations, called addition and multiplication y scalars (real numers), suject to the following
FACTORING AFTER DEDEKIND
 FACTORING AFTER DEDEKIND KEITH CONRAD Let K be a number field and p be a prime number. When we factor (p) = po K into prime ideals, say (p) = p e 1 1 peg g, we refer to the data of the e i s, the exponents
FACTORING AFTER DEDEKIND KEITH CONRAD Let K be a number field and p be a prime number. When we factor (p) = po K into prime ideals, say (p) = p e 1 1 peg g, we refer to the data of the e i s, the exponents
D-MATH Algebra I HS 2013 Prof. Brent Doran. Exercise 11. Rings: definitions, units, zero divisors, polynomial rings
 D-MATH Algebra I HS 2013 Prof. Brent Doran Exercise 11 Rings: definitions, units, zero divisors, polynomial rings 1. Show that the matrices M(n n, C) form a noncommutative ring. What are the units of M(n
D-MATH Algebra I HS 2013 Prof. Brent Doran Exercise 11 Rings: definitions, units, zero divisors, polynomial rings 1. Show that the matrices M(n n, C) form a noncommutative ring. What are the units of M(n
Representation theory of SU(2), density operators, purification Michael Walter, University of Amsterdam
 Symmetry and Quantum Information Feruary 6, 018 Representation theory of S(), density operators, purification Lecture 7 Michael Walter, niversity of Amsterdam Last week, we learned the asic concepts of
Symmetry and Quantum Information Feruary 6, 018 Representation theory of S(), density operators, purification Lecture 7 Michael Walter, niversity of Amsterdam Last week, we learned the asic concepts of
Generalized Reed-Solomon Codes
 Chapter 5 Generalized Reed-Solomon Codes In 1960, I.S. Reed and G. Solomon introduced a family of error-correcting codes that are douly lessed. The codes and their generalizations are useful in practice,
Chapter 5 Generalized Reed-Solomon Codes In 1960, I.S. Reed and G. Solomon introduced a family of error-correcting codes that are douly lessed. The codes and their generalizations are useful in practice,
IUPUI Qualifying Exam Abstract Algebra
 IUPUI Qualifying Exam Abstract Algebra January 2017 Daniel Ramras (1) a) Prove that if G is a group of order 2 2 5 2 11, then G contains either a normal subgroup of order 11, or a normal subgroup of order
IUPUI Qualifying Exam Abstract Algebra January 2017 Daniel Ramras (1) a) Prove that if G is a group of order 2 2 5 2 11, then G contains either a normal subgroup of order 11, or a normal subgroup of order
RINGS: SUMMARY OF MATERIAL
 RINGS: SUMMARY OF MATERIAL BRIAN OSSERMAN This is a summary of terms used and main results proved in the subject of rings, from Chapters 11-13 of Artin. Definitions not included here may be considered
RINGS: SUMMARY OF MATERIAL BRIAN OSSERMAN This is a summary of terms used and main results proved in the subject of rings, from Chapters 11-13 of Artin. Definitions not included here may be considered
Solutions of exercise sheet 8
 D-MATH Algebra I HS 14 Prof. Emmanuel Kowalski Solutions of exercise sheet 8 1. In this exercise, we will give a characterization for solvable groups using commutator subgroups. See last semester s (Algebra
D-MATH Algebra I HS 14 Prof. Emmanuel Kowalski Solutions of exercise sheet 8 1. In this exercise, we will give a characterization for solvable groups using commutator subgroups. See last semester s (Algebra
Total 100
 Math 542 Midterm Exam, Spring 2016 Prof: Paul Terwilliger Your Name (please print) SOLUTIONS NO CALCULATORS/ELECTRONIC DEVICES ALLOWED. MAKE SURE YOUR CELL PHONE IS OFF. Problem Value 1 10 2 10 3 10 4
Math 542 Midterm Exam, Spring 2016 Prof: Paul Terwilliger Your Name (please print) SOLUTIONS NO CALCULATORS/ELECTRONIC DEVICES ALLOWED. MAKE SURE YOUR CELL PHONE IS OFF. Problem Value 1 10 2 10 3 10 4
ALGEBRAIC TOPOLOGY IV. Definition 1.1. Let A, B be abelian groups. The set of homomorphisms ϕ: A B is denoted by
 ALGEBRAIC TOPOLOGY IV DIRK SCHÜTZ 1. Cochain complexes and singular cohomology Definition 1.1. Let A, B be abelian groups. The set of homomorphisms ϕ: A B is denoted by Hom(A, B) = {ϕ: A B ϕ homomorphism}
ALGEBRAIC TOPOLOGY IV DIRK SCHÜTZ 1. Cochain complexes and singular cohomology Definition 1.1. Let A, B be abelian groups. The set of homomorphisms ϕ: A B is denoted by Hom(A, B) = {ϕ: A B ϕ homomorphism}
A Geometric Review of Linear Algebra
 A Geometric Reiew of Linear Algebra The following is a compact reiew of the primary concepts of linear algebra. The order of presentation is unconentional, with emphasis on geometric intuition rather than
A Geometric Reiew of Linear Algebra The following is a compact reiew of the primary concepts of linear algebra. The order of presentation is unconentional, with emphasis on geometric intuition rather than
GALOIS GROUPS AS PERMUTATION GROUPS
 GALOIS GROUPS AS PERMUTATION GROUPS KEITH CONRAD 1. Introduction A Galois group is a group of field automorphisms under composition. By looking at the effect of a Galois group on field generators we can
GALOIS GROUPS AS PERMUTATION GROUPS KEITH CONRAD 1. Introduction A Galois group is a group of field automorphisms under composition. By looking at the effect of a Galois group on field generators we can
1. Group Theory Permutations.
 1.1. Permutations. 1. Group Theory Problem 1.1. Let G be a subgroup of S n of index 2. Show that G = A n. Problem 1.2. Find two elements of S 7 that have the same order but are not conjugate. Let π S 7
1.1. Permutations. 1. Group Theory Problem 1.1. Let G be a subgroup of S n of index 2. Show that G = A n. Problem 1.2. Find two elements of S 7 that have the same order but are not conjugate. Let π S 7
Homework 7 Solutions to Selected Problems
 Homework 7 Solutions to Selected Prolems May 9, 01 1 Chapter 16, Prolem 17 Let D e an integral domain and f(x) = a n x n +... + a 0 and g(x) = m x m +... + 0 e polynomials with coecients in D, where a
Homework 7 Solutions to Selected Prolems May 9, 01 1 Chapter 16, Prolem 17 Let D e an integral domain and f(x) = a n x n +... + a 0 and g(x) = m x m +... + 0 e polynomials with coecients in D, where a
Solutions for Math 225 Assignment #5 1
 Solutions for Math 225 Assignment #5 1 (1) Find a polynomial f(x) of degree at most 3 satisfying that f(0) = 2, f( 1) = 1, f(1) = 3 and f(3) = 1. Solution. By Lagrange Interpolation, ( ) (x + 1)(x 1)(x
Solutions for Math 225 Assignment #5 1 (1) Find a polynomial f(x) of degree at most 3 satisfying that f(0) = 2, f( 1) = 1, f(1) = 3 and f(3) = 1. Solution. By Lagrange Interpolation, ( ) (x + 1)(x 1)(x
φ(xy) = (xy) n = x n y n = φ(x)φ(y)
 Groups 1. (Algebra Comp S03) Let A, B and C be normal subgroups of a group G with A B. If A C = B C and AC = BC then prove that A = B. Let b B. Since b = b1 BC = AC, there are a A and c C such that b =
Groups 1. (Algebra Comp S03) Let A, B and C be normal subgroups of a group G with A B. If A C = B C and AC = BC then prove that A = B. Let b B. Since b = b1 BC = AC, there are a A and c C such that b =
Honors Algebra 4, MATH 371 Winter 2010 Assignment 4 Due Wednesday, February 17 at 08:35
 Honors Algebra 4, MATH 371 Winter 2010 Assignment 4 Due Wednesday, February 17 at 08:35 1. Let R be a commutative ring with 1 0. (a) Prove that the nilradical of R is equal to the intersection of the prime
Honors Algebra 4, MATH 371 Winter 2010 Assignment 4 Due Wednesday, February 17 at 08:35 1. Let R be a commutative ring with 1 0. (a) Prove that the nilradical of R is equal to the intersection of the prime
Longitudinal Dispersion Coefficient in Estuaries
 Journal of Coastal Research SI 9 57-5 ICS (Proceedings) Brazil ISSN 79-8 Longitudinal ispersion Coefficient in Estuaries E. Jaari ; R. Bozorgi anda. Etemad-Shahidi College of Ciil Engineering Iran Uniersity
Journal of Coastal Research SI 9 57-5 ICS (Proceedings) Brazil ISSN 79-8 Longitudinal ispersion Coefficient in Estuaries E. Jaari ; R. Bozorgi anda. Etemad-Shahidi College of Ciil Engineering Iran Uniersity
GEOMETRIC CONSTRUCTIONS AND ALGEBRAIC FIELD EXTENSIONS
 GEOMETRIC CONSTRUCTIONS AND ALGEBRAIC FIELD EXTENSIONS JENNY WANG Abstract. In this paper, we study field extensions obtained by polynomial rings and maximal ideals in order to determine whether solutions
GEOMETRIC CONSTRUCTIONS AND ALGEBRAIC FIELD EXTENSIONS JENNY WANG Abstract. In this paper, we study field extensions obtained by polynomial rings and maximal ideals in order to determine whether solutions
Resultants. Chapter Elimination Theory. Resultants
 Chapter 9 Resultants 9.1 Elimination Theory We know that a line and a curve of degree n intersect in exactly n points if we work in the projective plane over some algebraically closed field K. Using the
Chapter 9 Resultants 9.1 Elimination Theory We know that a line and a curve of degree n intersect in exactly n points if we work in the projective plane over some algebraically closed field K. Using the
A PROOF OF BURNSIDE S p a q b THEOREM
 A PROOF OF BURNSIDE S p a q b THEOREM OBOB Abstract. We prove that if p and q are prime, then any group of order p a q b is solvable. Throughout this note, denote by A the set of algebraic numbers. We
A PROOF OF BURNSIDE S p a q b THEOREM OBOB Abstract. We prove that if p and q are prime, then any group of order p a q b is solvable. Throughout this note, denote by A the set of algebraic numbers. We
Review of Matrices and Vectors 1/45
 Reiew of Matrices and Vectors /45 /45 Definition of Vector: A collection of comple or real numbers, generally put in a column [ ] T "! Transpose + + + b a b a b b a a " " " b a b a Definition of Vector
Reiew of Matrices and Vectors /45 /45 Definition of Vector: A collection of comple or real numbers, generally put in a column [ ] T "! Transpose + + + b a b a b b a a " " " b a b a Definition of Vector
IRREDUCIBILITY TESTS IN Q[T ]
![IRREDUCIBILITY TESTS IN Q[T ] IRREDUCIBILITY TESTS IN Q[T ]](/thumbs/77/74724906.jpg) IRREDUCIBILITY TESTS IN Q[T ] KEITH CONRAD 1. Introduction For a general field F there is no simple way to determine if an arbitrary polynomial in F [T ] is irreducible. Here we will focus on the case
IRREDUCIBILITY TESTS IN Q[T ] KEITH CONRAD 1. Introduction For a general field F there is no simple way to determine if an arbitrary polynomial in F [T ] is irreducible. Here we will focus on the case
ALGEBRA QUALIFYING EXAM SPRING 2012
 ALGEBRA QUALIFYING EXAM SPRING 2012 Work all of the problems. Justify the statements in your solutions by reference to specific results, as appropriate. Partial credit is awarded for partial solutions.
ALGEBRA QUALIFYING EXAM SPRING 2012 Work all of the problems. Justify the statements in your solutions by reference to specific results, as appropriate. Partial credit is awarded for partial solutions.
UNIVERSAL IDENTITIES. b = det
 UNIVERSAL IDENTITIES KEITH CONRAD 1 Introduction We want to describe an idea which reduces the verification of algebraic identities valid over all commutative rings to the verification over the complex
UNIVERSAL IDENTITIES KEITH CONRAD 1 Introduction We want to describe an idea which reduces the verification of algebraic identities valid over all commutative rings to the verification over the complex
MATH 8253 ALGEBRAIC GEOMETRY WEEK 12
 MATH 8253 ALGEBRAIC GEOMETRY WEEK 2 CİHAN BAHRAN 3.2.. Let Y be a Noetherian scheme. Show that any Y -scheme X of finite type is Noetherian. Moreover, if Y is of finite dimension, then so is X. Write f
MATH 8253 ALGEBRAIC GEOMETRY WEEK 2 CİHAN BAHRAN 3.2.. Let Y be a Noetherian scheme. Show that any Y -scheme X of finite type is Noetherian. Moreover, if Y is of finite dimension, then so is X. Write f
MA 266 Review Topics - Exam # 2 (updated)
 MA 66 Reiew Topics - Exam # updated Spring First Order Differential Equations Separable, st Order Linear, Homogeneous, Exact Second Order Linear Homogeneous with Equations Constant Coefficients The differential
MA 66 Reiew Topics - Exam # updated Spring First Order Differential Equations Separable, st Order Linear, Homogeneous, Exact Second Order Linear Homogeneous with Equations Constant Coefficients The differential
1 Systems of Differential Equations
 March, 20 7- Systems of Differential Equations Let U e an open suset of R n, I e an open interval in R and : I R n R n e a function from I R n to R n The equation ẋ = ft, x is called a first order ordinary
March, 20 7- Systems of Differential Equations Let U e an open suset of R n, I e an open interval in R and : I R n R n e a function from I R n to R n The equation ẋ = ft, x is called a first order ordinary
1 2 2 Circulant Matrices
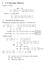 Circulant Matrices General matrix a c d Ax x ax + cx x x + dx General circulant matrix a x ax + x a x x + ax. Evaluating the Eigenvalues Find eigenvalues and eigenvectors of general circulant matrix: a
Circulant Matrices General matrix a c d Ax x ax + cx x x + dx General circulant matrix a x ax + x a x x + ax. Evaluating the Eigenvalues Find eigenvalues and eigenvectors of general circulant matrix: a
ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA
 ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA Kent State University Department of Mathematical Sciences Compiled and Maintained by Donald L. White Version: August 29, 2017 CONTENTS LINEAR ALGEBRA AND
ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA Kent State University Department of Mathematical Sciences Compiled and Maintained by Donald L. White Version: August 29, 2017 CONTENTS LINEAR ALGEBRA AND
g(x) = 1 1 x = 1 + x + x2 + x 3 + is not a polynomial, since it doesn t have finite degree. g(x) is an example of a power series.
 6 Polynomial Rings We introduce a class of rings called the polynomial rings, describing computation, factorization and divisibility in such rings For the case where the coefficients come from an integral
6 Polynomial Rings We introduce a class of rings called the polynomial rings, describing computation, factorization and divisibility in such rings For the case where the coefficients come from an integral
3.2 Modules of Fractions
 3.2 Modules of Fractions Let A be a ring, S a multiplicatively closed subset of A, and M an A-module. Define a relation on M S = { (m, s) m M, s S } by, for m,m M, s,s S, 556 (m,s) (m,s ) iff ( t S) t(sm
3.2 Modules of Fractions Let A be a ring, S a multiplicatively closed subset of A, and M an A-module. Define a relation on M S = { (m, s) m M, s S } by, for m,m M, s,s S, 556 (m,s) (m,s ) iff ( t S) t(sm
Chapter 3. Rings. The basic commutative rings in mathematics are the integers Z, the. Examples
 Chapter 3 Rings Rings are additive abelian groups with a second operation called multiplication. The connection between the two operations is provided by the distributive law. Assuming the results of Chapter
Chapter 3 Rings Rings are additive abelian groups with a second operation called multiplication. The connection between the two operations is provided by the distributive law. Assuming the results of Chapter
Math 121 Homework 4: Notes on Selected Problems
 Math 121 Homework 4: Notes on Selected Problems 11.2.9. If W is a subspace of the vector space V stable under the linear transformation (i.e., (W ) W ), show that induces linear transformations W on W
Math 121 Homework 4: Notes on Selected Problems 11.2.9. If W is a subspace of the vector space V stable under the linear transformation (i.e., (W ) W ), show that induces linear transformations W on W
MATH 361: NUMBER THEORY TENTH LECTURE
 MATH 361: NUMBER THEORY TENTH LECTURE The subject of this lecture is finite fields. 1. Root Fields Let k be any field, and let f(x) k[x] be irreducible and have positive degree. We want to construct a
MATH 361: NUMBER THEORY TENTH LECTURE The subject of this lecture is finite fields. 1. Root Fields Let k be any field, and let f(x) k[x] be irreducible and have positive degree. We want to construct a
Group Theory. 1. Show that Φ maps a conjugacy class of G into a conjugacy class of G.
 Group Theory Jan 2012 #6 Prove that if G is a nonabelian group, then G/Z(G) is not cyclic. Aug 2011 #9 (Jan 2010 #5) Prove that any group of order p 2 is an abelian group. Jan 2012 #7 G is nonabelian nite
Group Theory Jan 2012 #6 Prove that if G is a nonabelian group, then G/Z(G) is not cyclic. Aug 2011 #9 (Jan 2010 #5) Prove that any group of order p 2 is an abelian group. Jan 2012 #7 G is nonabelian nite
THE DIVISION THEOREM IN Z AND F [T ]
![THE DIVISION THEOREM IN Z AND F [T ] THE DIVISION THEOREM IN Z AND F [T ]](/thumbs/87/95592691.jpg) THE DIVISION THEOREM IN Z AND F [T ] KEITH CONRAD 1. Introduction In the integers we can carry out a process of division with remainder, as follows. Theorem 1.1. For any integers a and b, with b 0 there
THE DIVISION THEOREM IN Z AND F [T ] KEITH CONRAD 1. Introduction In the integers we can carry out a process of division with remainder, as follows. Theorem 1.1. For any integers a and b, with b 0 there
Math Midterm Solutions
 Math 145 - Midterm Solutions Problem 1. (10 points.) Let n 2, and let S = {a 1,..., a n } be a finite set with n elements in A 1. (i) Show that the quasi-affine set A 1 \ S is isomorphic to an affine set.
Math 145 - Midterm Solutions Problem 1. (10 points.) Let n 2, and let S = {a 1,..., a n } be a finite set with n elements in A 1. (i) Show that the quasi-affine set A 1 \ S is isomorphic to an affine set.
(Rgs) Rings Math 683L (Summer 2003)
 (Rgs) Rings Math 683L (Summer 2003) We will first summarise the general results that we will need from the theory of rings. A unital ring, R, is a set equipped with two binary operations + and such that
(Rgs) Rings Math 683L (Summer 2003) We will first summarise the general results that we will need from the theory of rings. A unital ring, R, is a set equipped with two binary operations + and such that
1.3.3 Basis sets and Gram-Schmidt Orthogonalization
 .. Basis sets and Gram-Schmidt Orthogonalization Before we address the question of existence and uniqueness, we must estalish one more tool for working with ectors asis sets. Let R, with (..-) : We can
.. Basis sets and Gram-Schmidt Orthogonalization Before we address the question of existence and uniqueness, we must estalish one more tool for working with ectors asis sets. Let R, with (..-) : We can
MATH 205 HOMEWORK #3 OFFICIAL SOLUTION. Problem 1: Find all eigenvalues and eigenvectors of the following linear transformations. (a) F = R, V = R 3,
 MATH 205 HOMEWORK #3 OFFICIAL SOLUTION Problem 1: Find all eigenvalues and eigenvectors of the following linear transformations. a F = R, V = R 3, b F = R or C, V = F 2, T = T = 9 4 4 8 3 4 16 8 7 0 1
MATH 205 HOMEWORK #3 OFFICIAL SOLUTION Problem 1: Find all eigenvalues and eigenvectors of the following linear transformations. a F = R, V = R 3, b F = R or C, V = F 2, T = T = 9 4 4 8 3 4 16 8 7 0 1
Math 3450 Homework Solutions
 Math 3450 Homework Solutions I have decided to write up all the solutions to prolems NOT assigned from the textook first. There are three more sets to write up and I am doing those now. Once I get the
Math 3450 Homework Solutions I have decided to write up all the solutions to prolems NOT assigned from the textook first. There are three more sets to write up and I am doing those now. Once I get the
MATH 326: RINGS AND MODULES STEFAN GILLE
 MATH 326: RINGS AND MODULES STEFAN GILLE 1 2 STEFAN GILLE 1. Rings We recall first the definition of a group. 1.1. Definition. Let G be a non empty set. The set G is called a group if there is a map called
MATH 326: RINGS AND MODULES STEFAN GILLE 1 2 STEFAN GILLE 1. Rings We recall first the definition of a group. 1.1. Definition. Let G be a non empty set. The set G is called a group if there is a map called
Graduate Preliminary Examination
 Graduate Preliminary Examination Algebra II 18.2.2005: 3 hours Problem 1. Prove or give a counter-example to the following statement: If M/L and L/K are algebraic extensions of fields, then M/K is algebraic.
Graduate Preliminary Examination Algebra II 18.2.2005: 3 hours Problem 1. Prove or give a counter-example to the following statement: If M/L and L/K are algebraic extensions of fields, then M/K is algebraic.
Bc. Dominik Lachman. Bruhat-Tits buildings
 MASTER THESIS Bc. Dominik Lachman Bruhat-Tits buildings Department of Algebra Superisor of the master thesis: Study programme: Study branch: Mgr. Vítězsla Kala, Ph.D. Mathematics Mathematical structure
MASTER THESIS Bc. Dominik Lachman Bruhat-Tits buildings Department of Algebra Superisor of the master thesis: Study programme: Study branch: Mgr. Vítězsla Kala, Ph.D. Mathematics Mathematical structure
Polynomial Rings : Linear Algebra Notes
 Polynomial Rings : Linear Algebra Notes Satya Mandal September 27, 2005 1 Section 1: Basics Definition 1.1 A nonempty set R is said to be a ring if the following are satisfied: 1. R has two binary operations,
Polynomial Rings : Linear Algebra Notes Satya Mandal September 27, 2005 1 Section 1: Basics Definition 1.1 A nonempty set R is said to be a ring if the following are satisfied: 1. R has two binary operations,
EXERCISES AND SOLUTIONS IN LINEAR ALGEBRA
 EXERCISES AND SOLUTIONS IN LINEAR ALGEBRA Mahmut Kuzucuoğlu Middle East Technical University matmah@metu.edu.tr Ankara, TURKEY March 14, 015 ii TABLE OF CONTENTS CHAPTERS 0. PREFACE..................................................
EXERCISES AND SOLUTIONS IN LINEAR ALGEBRA Mahmut Kuzucuoğlu Middle East Technical University matmah@metu.edu.tr Ankara, TURKEY March 14, 015 ii TABLE OF CONTENTS CHAPTERS 0. PREFACE..................................................
8 Appendix: Polynomial Rings
 8 Appendix: Polynomial Rings Throughout we suppose, unless otherwise specified, that R is a commutative ring. 8.1 (Largely) a reminder about polynomials A polynomial in the indeterminate X with coefficients
8 Appendix: Polynomial Rings Throughout we suppose, unless otherwise specified, that R is a commutative ring. 8.1 (Largely) a reminder about polynomials A polynomial in the indeterminate X with coefficients
Math 121 Homework 2 Solutions
 Math 121 Homework 2 Solutions Problem 13.2 #16. Let K/F be an algebraic extension and let R be a ring contained in K that contains F. Prove that R is a subfield of K containing F. We will give two proofs.
Math 121 Homework 2 Solutions Problem 13.2 #16. Let K/F be an algebraic extension and let R be a ring contained in K that contains F. Prove that R is a subfield of K containing F. We will give two proofs.
Math 203A - Solution Set 3
 Math 03A - Solution Set 3 Problem 1 Which of the following algebraic sets are isomorphic: (i) A 1 (ii) Z(xy) A (iii) Z(x + y ) A (iv) Z(x y 5 ) A (v) Z(y x, z x 3 ) A Answer: We claim that (i) and (v)
Math 03A - Solution Set 3 Problem 1 Which of the following algebraic sets are isomorphic: (i) A 1 (ii) Z(xy) A (iii) Z(x + y ) A (iv) Z(x y 5 ) A (v) Z(y x, z x 3 ) A Answer: We claim that (i) and (v)
MATH 196, SECTION 57 (VIPUL NAIK)
 TAKE-HOME CLASS QUIZ: DUE MONDAY NOVEMBER 25: SUBSPACE, BASIS, DIMENSION, AND ABSTRACT SPACES: APPLICATIONS TO CALCULUS MATH 196, SECTION 57 (VIPUL NAIK) Your name (print clearly in capital letters): PLEASE
TAKE-HOME CLASS QUIZ: DUE MONDAY NOVEMBER 25: SUBSPACE, BASIS, DIMENSION, AND ABSTRACT SPACES: APPLICATIONS TO CALCULUS MATH 196, SECTION 57 (VIPUL NAIK) Your name (print clearly in capital letters): PLEASE
M.6. Rational canonical form
 book 2005/3/26 16:06 page 383 #397 M.6. RATIONAL CANONICAL FORM 383 M.6. Rational canonical form In this section we apply the theory of finitely generated modules of a principal ideal domain to study the
book 2005/3/26 16:06 page 383 #397 M.6. RATIONAL CANONICAL FORM 383 M.6. Rational canonical form In this section we apply the theory of finitely generated modules of a principal ideal domain to study the
Notes on Linear Minimum Mean Square Error Estimators
 Notes on Linear Minimum Mean Square Error Estimators Ça gatay Candan January, 0 Abstract Some connections between linear minimum mean square error estimators, maximum output SNR filters and the least square
Notes on Linear Minimum Mean Square Error Estimators Ça gatay Candan January, 0 Abstract Some connections between linear minimum mean square error estimators, maximum output SNR filters and the least square
School of Mathematics and Statistics. MT5836 Galois Theory. Handout 0: Course Information
 MRQ 2017 School of Mathematics and Statistics MT5836 Galois Theory Handout 0: Course Information Lecturer: Martyn Quick, Room 326. Prerequisite: MT3505 (or MT4517) Rings & Fields Lectures: Tutorials: Mon
MRQ 2017 School of Mathematics and Statistics MT5836 Galois Theory Handout 0: Course Information Lecturer: Martyn Quick, Room 326. Prerequisite: MT3505 (or MT4517) Rings & Fields Lectures: Tutorials: Mon
Extension theorems for homomorphisms
 Algebraic Geometry Fall 2009 Extension theorems for homomorphisms In this note, we prove some extension theorems for homomorphisms from rings to algebraically closed fields. The prototype is the following
Algebraic Geometry Fall 2009 Extension theorems for homomorphisms In this note, we prove some extension theorems for homomorphisms from rings to algebraically closed fields. The prototype is the following
Math 611 Homework 6. Paul Hacking. November 19, All rings are assumed to be commutative with 1.
 Math 611 Homework 6 Paul Hacking November 19, 2015 All rings are assumed to be commutative with 1. (1) Let R be a integral domain. We say an element 0 a R is irreducible if a is not a unit and there does
Math 611 Homework 6 Paul Hacking November 19, 2015 All rings are assumed to be commutative with 1. (1) Let R be a integral domain. We say an element 0 a R is irreducible if a is not a unit and there does
Algebra Exam, Spring 2017
 Algebra Exam, Spring 2017 There are 5 problems, some with several parts. Easier parts count for less than harder ones, but each part counts. Each part may be assumed in later parts and problems. Unjustified
Algebra Exam, Spring 2017 There are 5 problems, some with several parts. Easier parts count for less than harder ones, but each part counts. Each part may be assumed in later parts and problems. Unjustified
Ph.D. Qualifying Examination in Algebra Department of Mathematics University of Louisville January 2018
 Ph.D. Qualifying Examination in Algebra Department of Mathematics University of Louisville January 2018 Do 6 problems with at least 2 in each section. Group theory problems: (1) Suppose G is a group. The
Ph.D. Qualifying Examination in Algebra Department of Mathematics University of Louisville January 2018 Do 6 problems with at least 2 in each section. Group theory problems: (1) Suppose G is a group. The
MULTILINEAR ALGEBRA: THE TENSOR PRODUCT
 MULTILINEAR ALGEBRA: THE TENSOR PRODUCT This writeup is drawn closely from chapter 27 of Paul Garrett s text Abstract Algebra, available from Chapman and Hall/CRC publishers and also available online at
MULTILINEAR ALGEBRA: THE TENSOR PRODUCT This writeup is drawn closely from chapter 27 of Paul Garrett s text Abstract Algebra, available from Chapman and Hall/CRC publishers and also available online at
LINEAR ALGEBRA BOOT CAMP WEEK 2: LINEAR OPERATORS
 LINEAR ALGEBRA BOOT CAMP WEEK 2: LINEAR OPERATORS Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F has characteristic zero. The following are facts
LINEAR ALGEBRA BOOT CAMP WEEK 2: LINEAR OPERATORS Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F has characteristic zero. The following are facts
Homework problems from Chapters IV-VI: answers and solutions
 Homework problems from Chapters IV-VI: answers and solutions IV.21.1. In this problem we have to describe the field F of quotients of the domain D. Note that by definition, F is the set of equivalence
Homework problems from Chapters IV-VI: answers and solutions IV.21.1. In this problem we have to describe the field F of quotients of the domain D. Note that by definition, F is the set of equivalence
A Geometric Review of Linear Algebra
 A Geometric Reiew of Linear Algebra The following is a compact reiew of the primary concepts of linear algebra. I assume the reader is familiar with basic (i.e., high school) algebra and trigonometry.
A Geometric Reiew of Linear Algebra The following is a compact reiew of the primary concepts of linear algebra. I assume the reader is familiar with basic (i.e., high school) algebra and trigonometry.
LECTURE 2: CROSS PRODUCTS, MULTILINEARITY, AND AREAS OF PARALLELOGRAMS
 LECTURE : CROSS PRODUCTS, MULTILINEARITY, AND AREAS OF PARALLELOGRAMS MA1111: LINEAR ALGEBRA I, MICHAELMAS 016 1. Finishing up dot products Last time we stated the following theorem, for which I owe you
LECTURE : CROSS PRODUCTS, MULTILINEARITY, AND AREAS OF PARALLELOGRAMS MA1111: LINEAR ALGEBRA I, MICHAELMAS 016 1. Finishing up dot products Last time we stated the following theorem, for which I owe you
CHAPTER 10: POLYNOMIALS (DRAFT)
 CHAPTER 10: POLYNOMIALS (DRAFT) LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN The material in this chapter is fairly informal. Unlike earlier chapters, no attempt is made to rigorously
CHAPTER 10: POLYNOMIALS (DRAFT) LECTURE NOTES FOR MATH 378 (CSUSM, SPRING 2009). WAYNE AITKEN The material in this chapter is fairly informal. Unlike earlier chapters, no attempt is made to rigorously
OVERVIEW OF TATE S THESIS
 OVERVIEW O TATE S THESIS ALEX MINE Abstract. This paper gies an oeriew of the main idea of John Tate s 1950 PhD thesis. I will explain the methods he used without going into too much technical detail.
OVERVIEW O TATE S THESIS ALEX MINE Abstract. This paper gies an oeriew of the main idea of John Tate s 1950 PhD thesis. I will explain the methods he used without going into too much technical detail.
SU(N) representations
 Appendix C SU(N) representations The group SU(N) has N 2 1 generators t a which form the asis of a Lie algera defined y the commutator relations in (A.2). The group has rank N 1 so there are N 1 Casimir
Appendix C SU(N) representations The group SU(N) has N 2 1 generators t a which form the asis of a Lie algera defined y the commutator relations in (A.2). The group has rank N 1 so there are N 1 Casimir
IDENTIFYING THE MATRIX RING: ALGORITHMS FOR QUATERNION ALGEBRAS AND QUADRATIC FORMS
 IDENTIYING THE MATRIX RING: ALGORITHMS OR QUATERNION ALGEBRAS AND QUADRATIC ORMS JOHN VOIGHT Abstract. We discuss the relationship between quaternion algebras and quadratic forms with a focus on computational
IDENTIYING THE MATRIX RING: ALGORITHMS OR QUATERNION ALGEBRAS AND QUADRATIC ORMS JOHN VOIGHT Abstract. We discuss the relationship between quaternion algebras and quadratic forms with a focus on computational
Math 429/581 (Advanced) Group Theory. Summary of Definitions, Examples, and Theorems by Stefan Gille
 Math 429/581 (Advanced) Group Theory Summary of Definitions, Examples, and Theorems by Stefan Gille 1 2 0. Group Operations 0.1. Definition. Let G be a group and X a set. A (left) operation of G on X is
Math 429/581 (Advanced) Group Theory Summary of Definitions, Examples, and Theorems by Stefan Gille 1 2 0. Group Operations 0.1. Definition. Let G be a group and X a set. A (left) operation of G on X is
Math 4320, Spring 2011
 Math 4320, Spring 2011 Prelim 2 with solutions 1. For n =16, 17, 18, 19 or 20, express Z n (A product can have one or more factors.) as a product of cyclic groups. Solution. For n = 16, G = Z n = {[1],
Math 4320, Spring 2011 Prelim 2 with solutions 1. For n =16, 17, 18, 19 or 20, express Z n (A product can have one or more factors.) as a product of cyclic groups. Solution. For n = 16, G = Z n = {[1],
REPRESENTATION THEORY OF S n
 REPRESENTATION THEORY OF S n EVAN JENKINS Abstract. These are notes from three lectures given in MATH 26700, Introduction to Representation Theory of Finite Groups, at the University of Chicago in November
REPRESENTATION THEORY OF S n EVAN JENKINS Abstract. These are notes from three lectures given in MATH 26700, Introduction to Representation Theory of Finite Groups, at the University of Chicago in November
Exam 2 Solutions. (a) Is W closed under addition? Why or why not? W is not closed under addition. For example,
 Exam 2 Solutions. Let V be the set of pairs of real numbers (x, y). Define the following operations on V : (x, y) (x, y ) = (x + x, xx + yy ) r (x, y) = (rx, y) Check if V together with and satisfy properties
Exam 2 Solutions. Let V be the set of pairs of real numbers (x, y). Define the following operations on V : (x, y) (x, y ) = (x + x, xx + yy ) r (x, y) = (rx, y) Check if V together with and satisfy properties
33 Idempotents and Characters
 33 Idempotents and Characters On this day I was supposed to talk about characters but I spent most of the hour talking about idempotents so I changed the title. An idempotent is defined to be an element
33 Idempotents and Characters On this day I was supposed to talk about characters but I spent most of the hour talking about idempotents so I changed the title. An idempotent is defined to be an element
THROUGH THE FIELDS AND FAR AWAY
 THROUGH THE FIELDS AND FAR AWAY JONATHAN TAYLOR I d like to thank Prof. Stephen Donkin for helping me come up with the topic of my project and also guiding me through its various complications. Contents
THROUGH THE FIELDS AND FAR AWAY JONATHAN TAYLOR I d like to thank Prof. Stephen Donkin for helping me come up with the topic of my project and also guiding me through its various complications. Contents
1. Introduction to commutative rings and fields
 1. Introduction to commutative rings and fields Very informally speaking, a commutative ring is a set in which we can add, subtract and multiply elements so that the usual laws hold. A field is a commutative
1. Introduction to commutative rings and fields Very informally speaking, a commutative ring is a set in which we can add, subtract and multiply elements so that the usual laws hold. A field is a commutative
Johns Hopkins University, Department of Mathematics Abstract Algebra - Spring 2009 Midterm
 Johns Hopkins University, Department of Mathematics 110.401 Abstract Algebra - Spring 2009 Midterm Instructions: This exam has 8 pages. No calculators, books or notes allowed. You must answer the first
Johns Hopkins University, Department of Mathematics 110.401 Abstract Algebra - Spring 2009 Midterm Instructions: This exam has 8 pages. No calculators, books or notes allowed. You must answer the first
3.5 Solving Quadratic Equations by the
 www.ck1.org Chapter 3. Quadratic Equations and Quadratic Functions 3.5 Solving Quadratic Equations y the Quadratic Formula Learning ojectives Solve quadratic equations using the quadratic formula. Identify
www.ck1.org Chapter 3. Quadratic Equations and Quadratic Functions 3.5 Solving Quadratic Equations y the Quadratic Formula Learning ojectives Solve quadratic equations using the quadratic formula. Identify
January 2016 Qualifying Examination
 January 2016 Qualifying Examination If you have any difficulty with the wording of the following problems please contact the supervisor immediately. All persons responsible for these problems, in principle,
January 2016 Qualifying Examination If you have any difficulty with the wording of the following problems please contact the supervisor immediately. All persons responsible for these problems, in principle,
Lecture 6 January 15, 2014
 Advanced Graph Algorithms Jan-Apr 2014 Lecture 6 January 15, 2014 Lecturer: Saket Sourah Scrie: Prafullkumar P Tale 1 Overview In the last lecture we defined simple tree decomposition and stated that for
Advanced Graph Algorithms Jan-Apr 2014 Lecture 6 January 15, 2014 Lecturer: Saket Sourah Scrie: Prafullkumar P Tale 1 Overview In the last lecture we defined simple tree decomposition and stated that for
ADVANCED COMMUTATIVE ALGEBRA: PROBLEM SETS
 ADVANCED COMMUTATIVE ALGEBRA: PROBLEM SETS UZI VISHNE The 11 problem sets below were composed by Michael Schein, according to his course. Take into account that we are covering slightly different material.
ADVANCED COMMUTATIVE ALGEBRA: PROBLEM SETS UZI VISHNE The 11 problem sets below were composed by Michael Schein, according to his course. Take into account that we are covering slightly different material.
A connection between number theory and linear algebra
 A connection between number theory and linear algebra Mark Steinberger Contents 1. Some basics 1 2. Rational canonical form 2 3. Prime factorization in F[x] 4 4. Units and order 5 5. Finite fields 7 6.
A connection between number theory and linear algebra Mark Steinberger Contents 1. Some basics 1 2. Rational canonical form 2 3. Prime factorization in F[x] 4 4. Units and order 5 5. Finite fields 7 6.
