Ch.1: Basics of Shallow Water Fluid
|
|
|
- Michael Hoover
- 5 years ago
- Views:
Transcription
1 AOS611Chapter1,/16/16,Z.Li 1 Sec. 1.1: Basic Eqations 1. Shallow Water Eqations on a Sphere Ch.1: Basics of Shallow Water Flid We start with the shallow water flid of a homogeneos densit and focs on the effect of rotation on the motion of the water. Rotation is, perhaps, the most important factor that distingishes geophsical flid dnamics from classical flid dnamics. There are for basic eqations inoled in a homogeneos flid sstem. The first is the mass eqation: 1 d 3 3 (1.1.1) dt where 3 i j k z, 3 (,, w). The other three eqations are the momentm eqations, which, in its 3-dimensional ector form can be written as: d dt 3 Ù 1 3 d where dt t p g F (1.1.) On the earth, it is more conenient to cast the eqations on the spherical coordinate with,,r being the longitde, latitde and radians, respectiel. That is: Copright 13, Zheng Li
2 AOS611Chapter1,/16/16,Z.Li 1 d dt 1 rcos 1 (cos) w r cos r d dt ( rcos )( sin wcos ) 1 p r cos F d dt ( w )sin 1 (1.1.3) p rcos r r F dw dt ( ) cos r cos r 1 p r g F r This is a comple set of eqations that goern the flid motion from ripples, trblence to planetar waes. For the atmosphere and ocean, man approimations can be made. Don t be afraid of making approimations! Indeed, proper approimations are the kes for the nderstanding of the dnamics! Yo can neer inclde eerthing in or eqations, no matter how fast is or compter (een if o are a good programmer). Therefore, to trl nderstand a certain dnamic isse, o hae to know what the most important is for this phenomenon and make sre o absoltel keep this term. Here, to std large scale flows, we will make 6 approimations. (i) First of all, for a homogeneos flid, the densit is constant. So the mass eqation degenerates to const, which, according to (1.1.1), gies the so called incompressibilit condition: 3 3 (1.1.4) This is a er good approimation for the ocean, becase the densit of the water aries b less than a few percent. This is not a good approimation for the atmosphere, becase the air densit decreases significantl, een within the troposphere. Essentiall, (1.1.4) states that the mass conseration becomes olme conseration. (ii) The second approimation is the thin laer approimation r a. The thickness of the atmosphere and ocean is roghl D 1km, which is tin compared with the radis of the earth a 637km. Therefore, this is a er good approimation with an error of less than 1 percent. For conenience, we often se the new ertical coordinate z r a that starts from the srface of the earth. iii) The third approimation is important for large scale circlation. This is the shallow water approimation D 1, where D and L are the characteristic scales of the motion in L the ertical and horizontal respectiel. Eamples that satisf the shallow water approimation are cclone and ocean eddies, as well as planetar flows. A cmls clod has its scales of D ~ L ~ 1 1 km and therefore does not satisf the shallow water approimation. Copright 13, Zheng Li
3 AOS611Chapter1,/16/16,Z.Li 3 The shallow water approimation reslts in an important simplification to the ertical momentm eqation, and leads to the so called hdrostatic approimation. Indeed, or scaling analsis below shows that all the terms in the w-eqation is mch smaller than the dnamic pressre gradient term. First, we separate the pressre into the dnamic p and static p s =-gz parts: p= p s +p. The static part satisfies the hdrostatic eqation 1 p s g, z sch that the ertical momentm eqation redces to dw 1 p' ( ) cos F r (1.1.5) dt r cos r r In a shallow water sstem, we can show that all the acceleration terms are nimportant. Take the term w for eample: UW DU w ~ L L D ~ ( ) 1 1 p' 1 p U L z D D Here we hae sed the scaling relationship W D U, which can be deried from the L continit eqation w z ( ). D L We hae also sed the scaling relationship between the dnamic pressre and the horizontal elocit as p~u. This relation is deried from the horizontal momentm eqation if one recognizes that the horizontal acceleration is drien b the dnamic pressre (in the case of weak rotation), and therefore, 1 p U 1 p ~ U L L ~ p ~. Since all the terms in the w-eqation (tr other terms orself!) are negligible relatie to the pressre gradient term, (1.1.5) at the first order can be redced to: 1 p' (1.1.6) z The total pressre therefore satisfies the hdrostatic approimation 1 p g (1.1.7) z Copright 13, Zheng Li
4 AOS611Chapter1,/16/16,Z.Li 4 or p(z) p srface g( z) (1.1.7a) where is the free srface eleation and we hae neglected the pressre aboe the free srface. The last eqation states that the pressre at a leel eqals the weight of the flid aboe it! h= - z B z B Eqn.(1.1.7a) in trn simplifies the horizontal pressre gradient force as: 1 p 1 p' 1 g g. Eqn. (1.1.6) (which is the reslt of the two approimations of shallow water and homogeneos flid) states that the dnamic pressre gradient force is independent of the depth of the flid. This implies the absence of ertical shear of horizontal elocities as z z. Indeed, since 1 p g and (,,t), we hae z ( 1 p ). Ths the pressre-drien flow shold not hae ertical shear either. The absence of ertical shear frther simplifies the horizontal momentm eqations and the continit eqation as follows. For the momentm eqations, the ertical adection terms are negligible now, sch that the total deriatie is now: d t, ( D dt a cos a Dt ) (1.1.8) For the mass eqation, 1 1 ( cos ) z w a cos a cos ertical integration ( z B dz ) leads to: 1 ( z B )[ acos 1 a cos ( cos )] w() w(z ) B Copright 13, Zheng Li
5 AOS611Chapter1,/16/16,Z.Li 5 h= - z B z z B The kinematic bondar condition on the srface is: d w ( ) ( t ) dt where =(,). The kinematic bondar condition on the bottom, for a fied bottom topograph t z B =, is dz B w( hb ) ( t ) z B z B, dt Therefore, the continit eqation becomes: dh h h or ( h) (1.1.9) dt t where h z B is the total depth of the water colmn. With all the approimations aboe, we hae a simpler set of eqations: the shallow water eqations : t ( ) fk g F th ( h). (1.1.1) In the spherical coordinate, the shallow water eqations can be written as : D Dt ( g ) sin a cos D Dt ( D Dt acos F a cos )sin g a F (1.1.11) h h [ ( cos )] a cos For most prposes, the cratre term is mch smaller than the Coriolis term, and a cos therefore can also be neglected (ecept in the polar region and global scale flows, see net). Copright 13, Zheng Li
6 AOS611Chapter1,/16/16,Z.Li 6. Local Cartesian Coordinate (-plane) z Unless one stdies global scale (in ) circlation, most of the time, we can simplif the eqations frther b sing the local Cartesians coordinate: This gies: a cos ( ), a( ) a cos a The shallow water eqations (1.1.11) can be written as: cos cos t ( ) sin g F cos a cos cos cos t ( ) sin g F (1.1.1) cos a cos cos cos th h h h[ tg ] cos cos a Frthermore, we can se the beta-plane approimation for motions of meridional scales less than the radis of the earth, L a a( ) 1. Indeed, now with a 1, we can hae the first order approimations as: cos cos ( )sin O[( ) ] sin sin ( )cos O[( ) ] Copright 13, Zheng Li
7 AOS611Chapter1,/16/16,Z.Li 7 tg tg O[ ] The cratre terms become negligible een compared with the adection term (since is easil satisfied, see homework E1.). In the -eqation, we hae a cos a tg L a tg 1 (ecept for the polar region with!). In the mass eqation, we hae a tg L a 1. Define f sin, a cos we can approimate the Coriolis parameter as f f. Therefore, eqations (1.1.11) can be approimated as t f g F t f g F (1.1.13) th h h h( ). where h=-z B is the laer thickness. This is the tpical form of shallow water eqations to be sed laer model Mch of the shallow water eqation reslts can be applied to a er (seemingl) different flid. (eample, stratosphere, oceanic thermocline etc.) z 1, 1 z B, Copright 13, Zheng Li
8 AOS611Chapter1,/16/16,Z.Li 8 Consider a general -laer flid with the two laers of flid of densities 1 and. In general, the pper laer flid still satisfies the shallow water eqations (1.1.13), ecept now the bottom depth of the pper laer flid z B also aries with time z B z B (,,t) and is an nknown ariable to be determined. For a general -laer flid, therefore, the problem is not closed, becase we hae three eqations bt for nknowns,,, z B. Now, consider a special tpe of -laer flid, in which the pper laer flow is mch faster than the lower laer flow. In this case, the bottom laer can be treated approimated as motionless, in which the horizontal pressre gradient anishes. It is this anishing pressre gradient in the lower laer proides the addition relation needed to close the pper laer problem. This is the so called 1.5-laer flid sstem. In the lower laer, the total pressre at a depth z can be deried from the hdrostatic balance as p zb gdz gdz gdz g z B ) 1 g( z B z) z zb z ( The condition of zero pressre gradient in laer is p g 1 ( 1 ) ( z B ) g Ths, the srface eleation can be represented as g ( ) ( z B ) g (1.1.14) 1 1 z -z B 1 z B z B z p The pressre gradient in the srface laer can therefore be represented in terms of the laer interface as g ( 1 )g(z B ) g (z B ) 1 where g 1 1 g g (g g in the ocean) is called the redced grait. It is seen that the anishing of the lower laer pressre gradient is now possible becase the pressre gradient at the pper Copright 13, Zheng Li
9 AOS611Chapter1,/16/16,Z.Li 9 laer is completel compensated b that associated with the laer interface. This leads to the opposite slopes of the srface eleation and the laer interface. Assming the aerage srface is at z=, we hae the thickness of the pper laer as h z B z B where we hae sed g g, so that h from (1.1.14). Ths, the eqations for the pper laer, according to (1.1.13), can be written as: t f g' h F t f g' h F, (1.1.15) th h h h( ). This set of eqations for the 1.5-laer model therefore looks eactl the same as the onelaer sstem eqations for laer 1 in (1.1.13), ecept to replace g and b g and h. The 1.5-laer approimate is sall er good for the oceanic thermocline, becase the pper ocean circlation is mch faster than the abssal flow. Indeed, the slope of the oceanic thermocline is sall opposite to that of the srface eleation (Fig.1.1) with a mch smaller magnitde of the latter than the former. Copright 13, Zheng Li
10 AOS611Chapter1,/ /16/16,Z.Li 1 Fig.1.1 Copright 13, Zheng Li
11 AOS611Chapter1,/16/16,Z.Li 11 Section 1.: Conseration Laws We first consider some fndamental conseration laws that shold be satisfied b a general flid sstem. This is also a check for the consistenc of the approimations that we made to or shallow water eqations. 1. Energ Conseration. To derie the energ eqation, we first pt the total deriatie of an ariable A into its mass conseration form. hd t A = h t A+h A+h A+A[ t h+ (h)+ (h)] = t (ha)+ (ha)+ (ha) (1..1) where we hae sed the mass eqation t h+ (h)+ (h)=. The kinetic energ eqation can be deried b first mltipling and onto the - and - eqations, respectiel and then sm them p as D t [( + )/] = -g[ + ]+F +F work b pressre grad. Work b sorce/sink Mltiplied b h, and with (1), we hae the mass conseration form of the kinetic energ of the water colmn per nit area K= h( + )/ as: t K+ (K)+ (K)= -g[h + h ]+hf +hf (1..) The potential energ in each colmn of water per nit area is P gzdz g( z zb B ) / g( z B ) h / The potential energ eqation can be deried b mltipling the mass eqation b g as: t P+g[ (h)+ (h)]= (1..3) Therefore, the eqation for total energ E=K+P is deried b adding (1..) and (1..3) as: t E+ (K)+ (K)= - (hg)+ (hg)+hf +hf Integrating within a domain A with a solid or periodic bondar, we hae the conseration of the total energ (in the absence of eternal sorce/sink) as: t A EdA= t A (K+P)dA = A hfda (1..4) where we hae sed the diergence theorem: A (S)dA= A Sndl with S being an ariable, A the bondar of the domain A, n the nit ector otwards, and dl the line element arond the bondar. Copright 13, Zheng Li
12 AOS611Chapter1,/16/16,Z.Li 1 dl n A A. Aailable Potential Energ (APE) How mch of the potential energ can be changed to the kinetic energ? Not all of them for sre. There is a basic part of the potential energ that can t be conerted to the kinetic energ. This is the minimm potential energ. (see figre, the leeled srface state is the minimm potential energ state). (Indeed, the absolte ale of potential energ has no meaning, becase one can choose the reference height arbitraril.) P>Pmin Pmin Therefore, we define the part of P that can be conerted to K as the APE, or APE=P-P min In the shallow water sstem, define m =da/a, we hae d m /dt= (1..5) (total mass conseration). Ths, the APE is APE=g(- m ) /. Since dape/dt= t A g[ - m + m ]da= t A g - g m t A = t A g =dp/dt, (see (1..5)), the total energ conseration eqation (1..4) can be written as: t A (K+APE)dA = A hfda Copright 13, Zheng Li
13 AOS611Chapter1,/16/16,Z.Li Bernolli Eqation In the absence of sorce and sink, the kinetic energ eqation is: D t [( + )/] = -g[ + ]. The mass eqation t H+ (H)+ (H)= can be rewritten as we hae D t (g)+gh( + ) - g[ z B + z B ]=, D t [( + )/+g] = -g[ + ]+ g[ z B + z B ] -gh( + ) = -g[ (- z B )+ (- z B )]-gh( + )= -g[ (h)+ (h)]=g t Ths, for stead flow, t =, and therefore we hae the Bernolli eqation in the shallow water as: D t B= D t (k e +p e )=D t [( + )/+g]=. This states that the Bernolli fnction B, which is the sm of the kinetic energ of a water parcel k e =( + )/ and the potential energ p e =g, is consered. following the motion of a stead circlation. (Note: this is the conseration of a particle, while total energ conseration is in a fied domain). 4. Anglar Momentm Conseration: In the spherical coordinate, we can also show that the anglar momentm of a particle M=a cos ( a cos +)=a cos + a cos is consered. Mltipl the -eq. in (1.1.3) b cos, we can show that: D t M= -g +F a cos Ths, if there is no sorce/sink in zonal momentm, the zonall integrated along the latitde ring, the anglar momentm is consered. D t Md. Here, we hae sed the condition that the pressre is continos arond the globle and therefore the integrated deriatie along the latitdinal circle is zero. One shold notice that if one neglects the cratre term /cos in the term of ( +/ cos)sin in the - Copright 13, Zheng Li
14 AOS611Chapter1,/16/16,Z.Li 14 eqation, the anglar momentm is no longer consered. For eample, in the beta-plane model, Md is not consered. Note: On Cartesian coordinate, in the absence of eternal forcing, the -momentm eqation is Dt f p /, Unlike the case of a single particle, the momentm is no longer consered een withot rotation (f=). This is becase the presence of the internal force the pressre gradient force. Dt p /. One wa ot of this is to consider the integral of a ring (along here, sa, in a periodic bondar condition). We will hae the integrated momentm consered Dt d p /. This is becase the pressre gradient force is a field forcing and has no net impact after a ring of integral. On a sphere, with the additional cratre term (assme no rotation for simplicit!) D t sin g a cos a cos howeer, this does not work becase of the spherical effect. Instead, if we take into accont of the spherical effect with a cosine factor (area weight), this becomes the anglar momentm m= a cos, one can show that the zonal integral of anglar momentm is consered D t md. So, the anglar momentm here is reall the zonall integrated momentm bt weighted b the spherical area. The inclsion of Coriolis force is eqialent to adding a zonal elocit of the earth s rotation =acos, which aries with latitde for the same rotation rate. Copright 13, Zheng Li
15 AOS611Chapter1,/16/16,Z.Li 15 Section 1.3: Circlation, Vorticit and Kelin s Theorem. (ref. Pedloks, section., and Holton section 4.1). 1. Vorticit and Circlation: How to measre the rotation rate of a flid parcel? Unlike a solid bod, different parts of the flid sall does not rotate at the same rate, becase of the elocit shears. One wa is to calclate the integrated circlation of the elocit arond the bondar of the srface domain A of a flid parcel: = A dr = A n da = A n da, (1.3.1) where is the 3-D elocit field in a non-rotating frame, and is the orticit of this elocit field. = (1.3.) In comparison, for a solid bod, we hae = r alid at an point. Notice the ector mltiplication i j k A B A A A B B B z z one can proe (homework E1.5) that orticit is twice the rotation rate = =. (1.3.3) For a flid parcel, each point rotates at different rate. Therefore, orticit is approimatel the aeraged circlation (or aeraged rotation). This can also be seen clearl if one allows the domain of circlation to shrink to a point. Then, from (1.3.1), the area aeraged circlation becomes n = A dr/a for A Ths, orticit can be thoght as the area-aeraged circlation. n da dr A A Copright 13, Zheng Li
16 AOS611Chapter1,/16/16,Z.Li 16. Kelin Theorem. Kelin theorem predicts the change of the circlation and is a fndamental theor in flid dnamics. Let s std how the circlation on a material srface aries with time. (denote d t d /dt ) d t = A d t dr+ A d t (dr). Notice that A d t (dr)= A d = A d / =, where we hae sed d t (dr)= d (d t r)=d, we hae: d t = A d t dr = - A p/ dr + A F dr (1.3.4) pressre grad where we hae sed the momentm eqation d t = - p/ + F. For a homogeneos flid, the aeraged pressre gradient anishes, A p/ dr =1/ A p dr = 1/ A dp =. If, frthermore, there is no sorce and sink (F=), circlation is consered following the water parcel: d t =, or = const (1.3.5) This is the Kelin s theorem. 3. Kelin s theorem in a rotating frame In a rotating frame, the absolte elocit in the non-rotating frame is a = + r (proe it!), where is the relatie elocit in the rotating frame now. The absolte circlation is then (see Pedlosk, also Qestion Q1.3): a = A a dr = A dr + A (r )dr = +A n. (1.3.6) where A n is the area projected b the srface A onto a plane normal to the rotation ector.. Here, we hae sed (1.3.3) and the Stokes theorem sch that: A (r )dr= A (r)nda= A n da=a n Ths, the absolte circlation consists of a relatie circlation and a planetar circlation. Copright 13, Zheng Li
17 AOS611Chapter1,/16/16,Z.Li 17 n A A n The Kelin s theorem becomes: d t a = d t (+A n ) = (1.3.7) Or +A n = const. (1.3.8) Eqn. (1.3.7) can also be proen directl in the rotating frame, if the Coriolis force is inclded in the momentm eqation. 4. Eamples: The Kelin theorem is er powerfl. It states that if there is a circlation, it will be there b itself foreer (in the absence of dissipation). Below are some eamples of application. Eample 1: Contraction spin-p: When the flid conerges towards the sink, the circlation will accelerate becase of the decrease of the area A n. Sppose a ring of air of radis L is initiall at rest. The ring is deformed sch that it is sqeezed into a strip with zero area. The final relatie circlation can be estimated as from the conseration of absolte circlation as a =+A=+. Sppose the aerage speed is U, we hae the scaling as: UπL~πL. U~L. where, for the earth s rotation, ~1-4 1/s. For an initial radis of L~1m, we hae the speed indced b the rotation as U~.1mm/s (er small!). For a large size of ring, L~1km, we hae a significantl strong elocit U~1 m/s. So a large scale can indce strong wind prel from the earth s rotation. This is one wa to tell how large a scale rotation becomes Copright 13, Zheng Li
18 AOS611Chapter1,/16/16,Z.Li 18 important. If a ring of air is obsered to hae an aerage speed of, the ratio of this speed to the rotation indced speed is /U=/L (Rossb nmber). If this nmber is small, it means the wind is weaker than that indced b the rotation. So, rotation is important. This is rapidl rotating sstem or small Rossb nmber, large scale flow. Eample : Tilting: When the srface of circlation tilts awa from the plane of rotation, circlation increases becase of the decrease of A n. Eample 3: Rossb wae On a sphere, we hae the area of a latitdinal belt of air as A n =Asin. Now, Kelin s theorem gies the so called Rossb wae (see Section.). A r=a cos A A n A n Copright 13, Zheng Li
19 AOS611Chapter1,/16/16,Z.Li 19 Since d t (+A n ) =, we hae d t = - d t A n = - Acos d t = - A, where = cos /a and = a d t. Since relatie orticit is the aeraged circlation =/A, we hae: d t + =. This will be seen later as the eqation for the Rossb wae. Note: Circlation conseration and anglar momentm conseration +A n =πr+ πr =πr(+r)= πacos (+acos)=πm So, circlation conseration is eqialent to anglar momentm conseration for the latitdinal ring of air Copright 13, Zheng Li
20 AOS611Chapter1,/16/16,Z.Li Copright 13, Zheng Li Sec. 1.4: Potential Vorticit Conseration 1. Vorticit Eqation Vorticit eqation goerns the local change of flid rotation from an Elarea iew and is therefore practical. From the momentm eqations t t F g f F g f we appl the orticit operation ) ( ) ( eq eq t t to eliminate the pressre gradient term. This gies the eqation for the relatie orticit =. First, notice that ) ( ) ( ) ( ) ( ) ( ) ( we can rewrite the, eqations as t F B f ) ( t F B f ) ( where B g is the Bernolli fnction. Now, ) ( ) ( eq eq eliminate B, we hae the orticit eqation F crl f f t ) )( ( ) )( ( (1.4.1) where crl F F F. Or D Dt a a crlf (1.4.) where a f is the absolte orticit. Again, we see that a diergent flow, in the presence of backgrond orticit field, can generate orticit. This is similar to the Kelin s theorem.
21 AOS611Chapter1,/16/16,Z.Li 1. Potential Vorticit Eqation From the continit eqation, we hae D t h h Notice the orticit eqation (1.4.1) or (1.4.), we hae D a Dt Dt h crlf h a a D Dt (ln ) a D Dt crlf (ln h) a D Dt h a ln( ) crlf a Or, finall D Dt q D Dt f crlf ( ) h h (1.4.3) where f q h is the potential orticit. Ths, in the absence of sorce and sink terms, we hae D Dt q The PV is consered along a particle trajector. This is a er strong constrain on flid motion. (Rossb, -D, 194; later, Ertel, 3-D, 194). 3. P.V. Conseration and Kelin's Theorem The conseration of PV can be deried directl from the Kelin s theorem. D Dt (A n ) Now A n Asin, and A. Copright 13, Zheng Li
22 AOS611Chapter1,/16/16,Z.Li A A n sin For a small area element A, we hae d dt (A sina) d [( f )A]. dt The total mass conseration can be written as ha const. Therefore, we hae the PV conseration d f ( ) dt h H A Ths, PV conseration, in principle, is the same as the Kelin s theorem. The represent two different iews of the flid rotation: the PV proides a microscopic iew, while the circlation (and Kelin theorem) the macroscopic iew. This law on PV is of fndamental importance to GFD. 4. Anglar momentm conseration and PV conseration: The PV conseration can also be nderstood intitiel from the anglar momentm conseration r =const. For a water colmn of a fied olme (or mass), r H=M= mass = const. Ths, H const Copright 13, Zheng Li
23 AOS611Chapter1,/16/16,Z.Li 3 This recoers PV conseration. Ths, PV conseration is simpl anglar momentm conseration in the case of a solid bod. 5. Applications (i) Stretching Contraction: Stretching of a water colmn generates positie orticit, while compressing of a water colmn generates negatie orticit, according to PV conseration. H st ret ching H compressing A conergence A diergence On, sa, a f-plane, f f const, we therefore hae H H Application: intensification of the center of a storm, figre skating. (ii) Abssal circlation (Stommal-Arons model). Copright 13, Zheng Li
24 AOS611Chapter1,/16/16,Z.Li 4 The thermohaline circlation at the abss is forced b sinking water at polar region. For a deep water colmn, this means that the water colmn will be stretched H becase of the accmlation of waters. Ths, f ( f ), or and the water moes northward. This is rather srprising becase the interior flow goes towards the sorce water, opposite to the non-rotating case. sorce wat er sorce wat er f f f f, z sorce wat er Howeer, the sorce water at the pole has to get to the lower latitde to satisf the mass conseration. The eqatorward transport is carried in a narrow western bondar crrent. This flow pattern is confirmed in lab rotating tank eperiment (Fig.1.). N Copright 13, Zheng Li
25 AOS611Chapter1,/ /16/16,Z.Li 5 Fig.1. Copright 13, Zheng Li
26 AOS611Chapter1,/16/16,Z.Li 6 Sec.1.5 Shallow Water Waes on a f-plane Consider small amplitde motions on an f-plane with a flat bottom z B = and in trn a constant depth H. The basic state is motionless U ariables are therefore: V, H const. The pertrbed H,,, H Linearizing the shallow water eqations (1.1.13), we hae: t f g t f g H ( t ) The orticit and diergence eqations can be deried from ( eq) ( eq) and ( eq) ( eq) as t ( ) f ( ), and t ( ) f ( ) g respectiel. Note that orticit can generate diergence, and ise ersa. Using the diergence and orticit eqations t (di eq) f (ort eq), we hae ( tt f )( ) g t Sbstitte in the continit eqation to eliminate diergence, we hae finall, [( t tt f ) c ] ' where c gh is the grait wae speed. i(k l t ) Assming free waes of the form Re e, we hae [ f c K ] where the total wae nmber is K k l. For nontriial soltion, so we hae the dispersion relationship [ f c K ] (1.5.1) There are three roots: 1 (1.5.a,b), 3 f c K The represent two er different tpes of waes. Copright 13, Zheng Li
27 AOS611Chapter1,/16/16,Z.Li 7 Dispersion diagram for a gien l. = -Ck =Ck f o k 1) The geostrophic mode. The first grop is the low freqenc mode: 1. The eigenfnction for this mode can be deried from (1.5.1) b setting t as f g f g This mode is in geostrophic balance and is therefore a low freqenc geostrophic mode. If the Coriolis parameter aries with latitde (the so called beta-effect df / d ), or a aring bottom topograph z B, this mode will be modified and will be called the Rossb wae. (see later). ). The Inertial-Grait wae The second grop are, 3. For these waes, f. So these are high freqenc modes (faster than abot the rotation period). These are the grait waes modified b the rotation. The are called the Inertial-Grait waes (also Poincare wae in oceanograph). For short waes with K ( f c ) 1 L D (or L>>L D), we hae approimatel c K. The inertial grait wae redces to the shallow water grait wae and does not feel mch of the rotation. On the other limit, for er long inertial-grait Copright 13, Zheng Li
28 AOS611Chapter1,/16/16,Z.Li 8 waes, K ( f ) 1 c L D oscillation., we hae approimatel f. This is simpl the inertial Here we see an important scale c gh L D, (1.5.3) f f the so called Rossb deformation radis. This scale separates the motions that are affected b the rotation. Large scale motions with L L D feel rotation, while small scale waes with L do not feel rotation. L D Tpical ales for the deformation radis can be calclated as follows. For shallow water sstem (the resemble the so called barotropic mode), we hae g=1m s, f 1 4 s 1 So, H atmosphere 1km L D 3km H 4km L km ocean D For the 1.5 laer sstem (the resemble the so called 1 st baroclinic mode), we hae the so called internal deformation radis c g' H L ID (1.5.4) f f g atmosphere g g 1, H 1km, L 1km D g g 1 g ocean 1 m s, H thermocline 1km, LD 5km 1 ocean Ths, rotation is important for baroclinic oceanic processes een at er small scales (L ~1 km), while it is important onl for those atmospheric processes of L 1 km. 3)Coastal Kelin wae The geostrophic mode and inertial-grait mode discssed aboe are open plane waes. The two waes are well separated, the former being low freqenc and the latter high freqenc (relatie to f). If, howeer, there is a bondar (coast, or platea), there will be a new tpe of wae, coastal Kelin wae, which can go from er low freqenc at long wae length comparable to the geostrophic mode to er high freqenc comparable with I-G mode at short wae length. Sppose the coastal bondar is = and the ocean is the pper half plane. Now, we need to seek a wae mode that satisf the bondar condition of = at =. We see a special tpe of soltion which has no,, eerwhere. (1.5.4) Copright 13, Zheng Li
29 AOS611Chapter1,/16/16,Z.Li 9 The remaining and h satisf t g f g (1.5.5a,b,c) t H i( kt ) Assming the wae of the form[, h] [ o ( ), ho ( )] e, and plg into the (1.5.5a,c), we hae the dispersion relationship the same as the pre grait wae c k (1.5.6) and the eigenfnction relationship in (1.5.5a,b,c) as gk d f g (1.5.7a,b,c) d Hk Plg (1.5,7a) (or c) into the geostrophic relation (1.5.7b), we hae an ODE gk d f g, d Using the dispersion relationship (1.5.6), the soltion is then of the form f k ep ep LD Since the soltion has to be finite awa from the bondar, we can onl pick one soltion from (1.5.6) as c k (1.5.8) That is the alid bondar wae (coastal Kelin wae) traels to the east when the coast is to the soth, at the speed of grait wae, with the along shore crrent in geostrophic balance. It is a hbrid of geostrophic mode (geostrophic balance offshore, low freqenc for long wae) and grait wae (ageostrophic along shore, high freqenc for short wae) Coast Kelin wae propagation Coast Copright 13, Zheng Li
30 AOS611Chapter1,/16/16,Z.Li 3 Sec.1.6: Geostrophic Adjstment One general qestion is wh the obsered large scale atmosphere and oceanic flows are alwas close to geostrophic balance? From the last section, we hae seen that, on an f- plane, there is a low freqenc free mode that is in geostrophic balance. If there is an initial imbalance of geostroph (or ageostrophic distrbance) forced b eternal forcing or some other processes, how can the sstem alwas recoers back to the obsered geostrophic balance? This is the geostrophic adjstment problem that was first stdied b Rossb on the Glf Stream problem in the late 193s. 1. Eqilibrim State Let s consider the simplest case, small amplitde flow on an f-plane, with a constant depth: t f g t f g t H ( ) If the sstem eentall reaches stead state, we hae a flat srface eqilibrim for f : (1.6.1) and the geostrophic balance for f, f g f g (1.6.) In the latter case of f, the first two eqations satisf the last eqation atomatidcall. Therefore, the final eqilibrim is degenerated (geostrophic degenerac) in the sense that there are 3 nknowns bt onl eqations. In addition, it is possible now to hae,, so the final state has a finite aailable potential energ (APE). Bt how mch? Some information is missing! This will be seen is the potential orticit (PV).. f= adjstment First, we std the cases withot rotation. We will std the simpler case with =. Case 1: An jmp initial condition: i = sign(), i = i =. Copright 13, Zheng Li
31 AOS611Chapter1,/16/16,Z.Li 31 t= t=t 1 t=t C o t t g t t H =(g/h) 1/ = Since i, the initial state is not in eqilibrim. The final state can be obtained as const, const, where the final elocit will be deried from, the energ conseration below. The KE and APE eqations can be deried as: t H gh, and g t gh. The total energ eqation is therefore t (KE APE) t ( H g ) (gh) Before wae front, =,, after wae front,, =. Ths, the energ fl anwhere an time. Within each section, the total energ is consered locall t 1 (KE APE) d gh 1 Ths at final eqilibrim which has no APE ( ), all the initial APE is conerted to KE. This gies the final elocit as g / H. (One shold notice that this local total energ conseration is sall not tre, as will be seen in the net case. It occrs here becase of the initial condition of an anti-smmetric eleation of infinite length.) Copright 13, Zheng Li
32 AOS611Chapter1,/16/16,Z.Li 3 Case : An initial condition with a finite bmp. One can speclate that the finite initial distrbance will eentall radiates awa throgh grait waes, leaing neither KE nor APE. t= / t=t 1 / t=t t=t 3 =, = wae wake wae front We can estimate the adjstment time as follows. From the eqation tt c, where c gh is the grait wae speed, the final eqilibrim is reached when tt c. Ths, the adjstment time T satisfies 1 c and in trn T L L T T g, where T g is time for grait wae to arrie. c At a fied position of, sa, >, the elocit eperiences 5 stages and reaches the eqilibrim after the passing of for wae fronts (fronts and wakes). 3. f adjstment With =, the final eqilibrim is f g This state is ndetermined. Rossb (194) fond the soltion from the piece of missing information the PV conseration. Copright 13, Zheng Li
33 AOS611Chapter1,/16/16,Z.Li 33 z The linearized orticit eqation can be deried from ( eq) ( eq)as t f ( ). Sbstitte in the continit eqation, we hae the linearized ersion of PV conseration. t ( f H ) Ths Since f H g f f H initial PV i ( ) f H we hae where L D L D i() L D gh is the deformation radis. The general soltion is therefore: f L D LD Ae Be, for. LD LD Ae Be, for The coefficients will be determined b bondar conditions as follows. Radiation condition means that pertrbation energ shold propagate awa from the sorce region (= here), or the response has to be finite at infinit, at. This reqires A B. The soltion is therefore Be Ae LD LD,, for for The continit condition reqires the continit of and across (therefore and are finite). Ths, we hae the final soltion as Copright 13, Zheng Li
34 AOS611Chapter1,/16/16,Z.Li 34 L (1 e D ), (1 e L D ), Final soltion after adjstment z () o L D The elocit field is in geostrophic balance as: LD g g h e, f fld where + and are for < and >, respectiel. () L D -g o /fol D Seeral points are noteworth here. Deformation radis L D : we hae seen in sec1.5 that large scale motions with L L D is affected b rotation. Here, we frther see that L D also determines the inflence distance of an ageostrophic anomal. Copright 13, Zheng Li
35 AOS611Chapter1,/16/16,Z.Li 35 Adjstment time: From ( tt f ) c, we see that tt f gies the final 1 stead state. Ths, when t 1 da, the adjstment is completed and the final state is f in geostrophic balance, independent of the spatial scale. Therefore, independent of spatial scales, geostrophic adjstment is er fast (within abot a da). This is the fndamental reason wh the obsered flow are alwas in geostrophic balance. Simpl pt it, an imbalance from geostroph will be adjsted qickl to a new balance within abot a da or so. Energetics: Since, APE eists in the final state! (different from the nonrotating case). Bt, not all the lost APE are conerted to KE. Indeed, the initial energ is: In the final state: APE i 1 L g d i 1 L g d g L L L KE i L APE 1 g d 1 g L [ (1e D ) d g L L (1 e L D ) d L g L L D (1 e L L D ) L D (1 e L L L D ) (1 e L D ) d Let L (or L L D ), we hae APE g (L 3 L D ) Ths the change of APE is: (APE) APE APE i 3 g L D, ( L ) Total loss of APE is finite een throgh the initial APE is infinite. In addition, the final state also has KE. KE H V d H V d H( g ) e L D fl D d g L D e L D ) g L D L D 1 3 (APE) d( Ths, onl 1/3 of the lost APE is conerted to KE. Where does the rest of APE go? The are radiated awa to (or dissipated elsewhere in a finite domain) b transient Copright 13, Zheng Li
36 AOS611Chapter1,/16/16,Z.Li 36 inertial-grait waes. This loss of initial energ b wae radiation is similar to the f= case that has a finite initial distrbance (case ). Transients: The transients are the I-G waes, which hae the dispersion relation: f c K The grop elocit is: ck k We see that c g k c k c k f c K i) I-G waes radiate in (all the ) both directions! ii) c g min for k ; c g ma c for k Ths, shortwaes disperse fast, long wae slow. Cg t t 1 t k Copright 13, Zheng Li
37 AOS611Chapter1,/ /16/16,Z.Li 37 Copright 13, Zheng Li
38 AOS611Chapter1,/16/16,Z.Li 38 In smmar, rotation prodces the following effects: releases less APE (hold it to bild geostrophic balance) final state has (geostrophic) motion fast adjstment (t 1da) spatial scale abot L D (can be er small for the ocean) final state depends on initial condition (sall aries for different I.C.) 4. Applications Coastal jet: Initial wind piles p water against the coast with downstream srface crrents. Later (after a da or so), the geostrophic adjstment leaes an along shelf geostrophic crrent. wind onset (t ) Land (t ) Atmospheric conection will eentall (after t 1 f circlation. ) prodces a cclonic p(t ) p(t ) p(t ) p(t ) p(t ) p(t ) conection onset Copright 13, Zheng Li
39 AOS611Chapter1,/16/16,Z.Li 39 Qestions for Chapter 1 Q1.1: If we onl retain the cratre term in the -eqation of the shallow water sstem (1.1.15), is the total energ still consered as shown in (1..4)? Sppose this term is small compared with other terms, shold we still keep this term? Wh? Q1.: A more general wa of soling the eigenale (dispersion relationship) is to sole the free modes directl from the linear shallow water eqations. Plg (,,η )=(,,η )e i(k+l-ωt) directl into the f-plane shallow water eqations t f g t f g H ( t ) (a) Show that the eigenales are the same as in (1.5.1). (b) Find the eigenfnctions and find the potential orticit for the initial-grait wae modes q f. H Q1.3. In a homogeneos flid, a) For an two ectors A and B, proe the identit: (AB) = AB+ (B )A -BA - (A)B. b) In a rotating frame, the momentm eqation is: d t U = -U - p/ + F. Using the identit deried from a) and the Stokes theorem to proe directl the Kelin s theorem: d t (+A n ) =. (All ectors are three-dimensional ectors). Copright 13, Zheng Li
40 AOS611Chapter1,/16/16,Z.Li 4 Eercises for Chapter 1 E1.1. (Hdrostatic approimation in a rotating flid) On a f-plane (in eqn. (1.1.13)), consider a strong rotation flid in which the pressre gradient force is balanced mainl b the Coriolis force, f - p/ (as opposed to b the inertial acceleration - p/ as in the handot), a). Using scaling analsis, find the condition nder which the hdrostatic approimation is alid in the primitie eqation. b). Compare with the weak rotation sstem that was discssed in Sec. 1.1 (the eqation after (1.1.5)), which sstem is easier to reach hdrostatic balance? E1.. (Local plane eqation) (a) What are the major approimations nder which the shallow water eqations on a sphere (1.1.11) (the Laplacian tidal eqation) can be redced to the Cartesian coordinate eqations (1.1.13)? (b) What is the latitde region where o epect the Cartesian coordinate eqation (1.1.13) to perform the poorest? (c) For a tpical wind speed of 1 m/s and an ocean crrent of 1 cm/s, se scaling analsis to estimate the latitde region where the Cartesian coordinate eqation ma hae serios problem. E1.3. (Srface pressre effect) In the presence of an atmospheric sea leel pressre gradient, derie the oceanic eqations as in (a) a shallow water model, (b) a 1.5-laer model. Copright 13, Zheng Li
41 AOS611Chapter1,/16/16,Z.Li 41 E1.4. (.5-laer model) A.5-laer flid is a special 3-laer flid in which there is no motion (no pressre gradient) in laer 3 (see the figre). In a shallow water sstem where the hdrostatic approimation is alid, show that (,,t) h 1 1, 1, 1, p 1 z 1 (,,t) h,,, p z (,,t) 3 =, 3 =, 3, p 3 = a) the pressre in each laer can be represented as p 1 (,,z,t) = p a +g 1 (-z), p (,,z,t) = p 1 (z 1 )+g (z 1 -z), p 3 (,,z,t) = p (z )+g (z -z) b) the condition of no-motion in laer 3 leads to the pressre gradients in laer 1 and as p 1 = -g( - 1 ) z 1 -g( 3 - ) z p = -g( 3 - ) z c) the continit eqations for laer 1 and can be deried from the incompressible eqations z w 1 = and + + z w = as t h 1 + ( 1 h 1 )+ ( 1 h 1 ) = and t h + ( h )+ ( h ) =, respectiel. d) finall, the.5-laer sstem is goerned b D t1 f1 g1 h1 g h D t1 f1 g1 h1 g h and Dth1 h 1( 1 1 ) Dt Dt Dt h f g h f g h h ( ) where h=h 1 +h, h 1 =-z 1 -z 1 and h = z 1 -z are laer thickness, and g 1= ( - 1 )/ ( - 1 )/ 1, g = ( 3 - )/ ( 3 - )/ 1 ( 3 - )/ are interface redced graities. E1.5. (Vorticit of a solid bod) For a solid rotating bod, we hae U = r, where =(,, z ) is the anglar elocit and r=(,, z) is the position ector. Proe that the ortict is twice its anglar eolocit, i.e. = U =. Copright 13, Zheng Li
42 AOS611Chapter1,/16/16,Z.Li 4 E1.6. (Diergence eqation): a) Derie the diergence eqation from the shallow water sstem (1.1.13a,b) as t ( + ) = (f+) - [(f+)] k - [g+( + )/]+ F b) Linearize the diergence eqation aboe and the orticit eqation (1.4.1), assming the mean state is at rest. c) Discss the differences between the linearized diergence eqation and orticit eqation. (For simplicit, o can een assme no rotation and no eternal forcing!) E1.7. (Adjstment process of non-rotating flid) A linear non-rotating flid satisfies the eqations: t = -g, t + H =. For an initial distrbance of the form =, = o (), std the soltions for initial conditions below. Case 1: The initial condition is * o ( ) * * * Z X * Ct a) Proe that the eoltion soltion is (, t) Ct Ct. * Ct and draw the schematic figres of the eoltion at different stages. b) What is the final eqilibrim state? c) Discss the phsics. Copright 13, Zheng Li
43 AOS611Chapter1,/16/16,Z.Li 43 d) What is the ratio of the kinetic energ to aailable potential energ at each location at different time? (optional) Case : The initial condition is 1 o ( ) * 1 * z -1 1 a) Proe the soltion is (i) for < Ct < 1 (, t) * / * * / 1 Ct 1 Ct 1 Ct 1 Ct 1 Ct 1 Ct 1 Ct 1 Ct ii) for Ct >= 1 * (, t) * / / 1 Ct 1 Ct 1 Ct 1 Ct 1 Ct 1 Ct 1 Ct 1 Ct Repeat b) c) d) the same as in case 1 {Hint: for a general initial condition (, t=)= (), and t (, t=)= 1 (), the general soltion of a wae eqation tt - c = is: ct (, t ) [ ( ct ) ( ct )] 1( s ) ds / }. ct Copright 13, Zheng Li
44 AOS611Chapter1,/16/16,Z.Li 44 E1.8: (Energ and PV of waes). The linear pertrbation eqation on an f-plane is: t - f = -g, t + f = -g, t + H ( + ) =. This set of eqations contain two sets of modes: the inertial-grait wae and the geostrophic mode (see Sec.1.5). a)find the ratio of the kinetic energ and aailable potential energ (aeraged oer one wae length) for an inertial-grait wae. What are the energ ratios at the long and short wae limits? What happens for non-rotating flid? (hint: Wae energ has to be positie. One has to take the real part of the wae soltion aeraged in a waelength. Assme (,,η)=(,,η )e i(k+l-ωt), with * for comple conjgate, we hae, wae energ aeraged in a waelength is therefore ). b) Find the energ ratio for the geostrophic mode. What are the energ ratios at the long and short wae limits? c) Compare and discss the energ ratios of the two modes. d) What is the PV anomal de to the geostrophic mode? What is the ratio of the PV anomal indced b the relatie orticit and stretching? (e) What is the PV anomal de to inertial-grait modes? (For small distrbance, the linear PV is q f ) H Copright 13, Zheng Li
Chapter 6 Momentum Transfer in an External Laminar Boundary Layer
 6. Similarit Soltions Chapter 6 Momentm Transfer in an Eternal Laminar Bondar Laer Consider a laminar incompressible bondar laer with constant properties. Assme the flow is stead and two-dimensional aligned
6. Similarit Soltions Chapter 6 Momentm Transfer in an Eternal Laminar Bondar Laer Consider a laminar incompressible bondar laer with constant properties. Assme the flow is stead and two-dimensional aligned
Dynamics of the Atmosphere 11:670:324. Class Time: Tuesdays and Fridays 9:15-10:35
 Dnamics o the Atmosphere 11:67:34 Class Time: Tesdas and Fridas 9:15-1:35 Instrctors: Dr. Anthon J. Broccoli (ENR 9) broccoli@ensci.rtgers.ed 73-93-98 6 Dr. Benjamin Lintner (ENR 5) lintner@ensci.rtgers.ed
Dnamics o the Atmosphere 11:67:34 Class Time: Tesdas and Fridas 9:15-1:35 Instrctors: Dr. Anthon J. Broccoli (ENR 9) broccoli@ensci.rtgers.ed 73-93-98 6 Dr. Benjamin Lintner (ENR 5) lintner@ensci.rtgers.ed
Primary dependent variable is fluid velocity vector V = V ( r ); where r is the position vector
 Chapter 4: Flids Kinematics 4. Velocit and Description Methods Primar dependent ariable is flid elocit ector V V ( r ); where r is the position ector If V is known then pressre and forces can be determined
Chapter 4: Flids Kinematics 4. Velocit and Description Methods Primar dependent ariable is flid elocit ector V V ( r ); where r is the position ector If V is known then pressre and forces can be determined
Fluid Physics 8.292J/12.330J
 Fluid Phsics 8.292J/12.0J Problem Set 4 Solutions 1. Consider the problem of a two-dimensional (infinitel long) airplane wing traeling in the negatie x direction at a speed c through an Euler fluid. In
Fluid Phsics 8.292J/12.0J Problem Set 4 Solutions 1. Consider the problem of a two-dimensional (infinitel long) airplane wing traeling in the negatie x direction at a speed c through an Euler fluid. In
Computer Animation. Rick Parent
 Algorithms and Techniqes Flids Sperficial models. Deep models comes p throghot graphics, bt particlarl releant here OR Directl model isible properties Water waes Wrinkles in skin and cloth Hi Hair Clods
Algorithms and Techniqes Flids Sperficial models. Deep models comes p throghot graphics, bt particlarl releant here OR Directl model isible properties Water waes Wrinkles in skin and cloth Hi Hair Clods
1 Differential Equations for Solid Mechanics
 1 Differential Eqations for Solid Mechanics Simple problems involving homogeneos stress states have been considered so far, wherein the stress is the same throghot the component nder std. An eception to
1 Differential Eqations for Solid Mechanics Simple problems involving homogeneos stress states have been considered so far, wherein the stress is the same throghot the component nder std. An eception to
EE2 Mathematics : Functions of Multiple Variables
 EE2 Mathematics : Fnctions of Mltiple Variables http://www2.imperial.ac.k/ nsjones These notes are not identical word-for-word with m lectres which will be gien on the blackboard. Some of these notes ma
EE2 Mathematics : Fnctions of Mltiple Variables http://www2.imperial.ac.k/ nsjones These notes are not identical word-for-word with m lectres which will be gien on the blackboard. Some of these notes ma
The Vorticity Equation
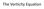 The Vorticit Eqation Potential orticit Circlation theorem is reall good Circlation theorem imlies a consered qantit dp dt 0 P g 2 PV or barotroic lid General orm o Ertel s otential orticit: P g const Consider
The Vorticit Eqation Potential orticit Circlation theorem is reall good Circlation theorem imlies a consered qantit dp dt 0 P g 2 PV or barotroic lid General orm o Ertel s otential orticit: P g const Consider
Turbulence and boundary layers
 Trblence and bondary layers Weather and trblence Big whorls hae little whorls which feed on the elocity; and little whorls hae lesser whorls and so on to iscosity Lewis Fry Richardson Momentm eqations
Trblence and bondary layers Weather and trblence Big whorls hae little whorls which feed on the elocity; and little whorls hae lesser whorls and so on to iscosity Lewis Fry Richardson Momentm eqations
MAT389 Fall 2016, Problem Set 6
 MAT389 Fall 016, Problem Set 6 Trigonometric and hperbolic fnctions 6.1 Show that e iz = cos z + i sin z for eer comple nmber z. Hint: start from the right-hand side and work or wa towards the left-hand
MAT389 Fall 016, Problem Set 6 Trigonometric and hperbolic fnctions 6.1 Show that e iz = cos z + i sin z for eer comple nmber z. Hint: start from the right-hand side and work or wa towards the left-hand
1 The space of linear transformations from R n to R m :
 Math 540 Spring 20 Notes #4 Higher deriaties, Taylor s theorem The space of linear transformations from R n to R m We hae discssed linear transformations mapping R n to R m We can add sch linear transformations
Math 540 Spring 20 Notes #4 Higher deriaties, Taylor s theorem The space of linear transformations from R n to R m We hae discssed linear transformations mapping R n to R m We can add sch linear transformations
Relativity II. The laws of physics are identical in all inertial frames of reference. equivalently
 Relatiity II I. Henri Poincare's Relatiity Principle In the late 1800's, Henri Poincare proposed that the principle of Galilean relatiity be expanded to inclde all physical phenomena and not jst mechanics.
Relatiity II I. Henri Poincare's Relatiity Principle In the late 1800's, Henri Poincare proposed that the principle of Galilean relatiity be expanded to inclde all physical phenomena and not jst mechanics.
u P(t) = P(x,y) r v t=0 4/4/2006 Motion ( F.Robilliard) 1
 y g j P(t) P(,y) r t0 i 4/4/006 Motion ( F.Robilliard) 1 Motion: We stdy in detail three cases of motion: 1. Motion in one dimension with constant acceleration niform linear motion.. Motion in two dimensions
y g j P(t) P(,y) r t0 i 4/4/006 Motion ( F.Robilliard) 1 Motion: We stdy in detail three cases of motion: 1. Motion in one dimension with constant acceleration niform linear motion.. Motion in two dimensions
Rossby waves (waves in vorticity)
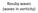 Rossb waes (waes in orticit) Stationar (toograhicall orced) waes NCEP Reanalsis Z500 Janar mean 2 3 Vorticit eqation z w z w z w t 2 1 Change in relatie (ertical comonent o) orticit at a oint, Adection
Rossb waes (waes in orticit) Stationar (toograhicall orced) waes NCEP Reanalsis Z500 Janar mean 2 3 Vorticit eqation z w z w z w t 2 1 Change in relatie (ertical comonent o) orticit at a oint, Adection
2 Faculty of Mechanics and Mathematics, Moscow State University.
 th World IMACS / MODSIM Congress, Cairns, Astralia 3-7 Jl 9 http://mssanz.org.a/modsim9 Nmerical eamination of competitie and predator behaior for the Lotka-Volterra eqations with diffsion based on the
th World IMACS / MODSIM Congress, Cairns, Astralia 3-7 Jl 9 http://mssanz.org.a/modsim9 Nmerical eamination of competitie and predator behaior for the Lotka-Volterra eqations with diffsion based on the
Derivation of the basic equations of fluid flows. No. Conservation of mass of a solute (applies to non-sinking particles at low concentration).
 Deriation of the basic eqations of flid flos. No article in the flid at this stage (net eek). Conseration of mass of the flid. Conseration of mass of a solte (alies to non-sinking articles at lo concentration).
Deriation of the basic eqations of flid flos. No article in the flid at this stage (net eek). Conseration of mass of the flid. Conseration of mass of a solte (alies to non-sinking articles at lo concentration).
3 2D Elastostatic Problems in Cartesian Coordinates
 D lastostatic Problems in Cartesian Coordinates Two dimensional elastostatic problems are discssed in this Chapter, that is, static problems of either plane stress or plane strain. Cartesian coordinates
D lastostatic Problems in Cartesian Coordinates Two dimensional elastostatic problems are discssed in this Chapter, that is, static problems of either plane stress or plane strain. Cartesian coordinates
Linear Strain Triangle and other types of 2D elements. By S. Ziaei Rad
 Linear Strain Triangle and other tpes o D elements B S. Ziaei Rad Linear Strain Triangle (LST or T6 This element is also called qadratic trianglar element. Qadratic Trianglar Element Linear Strain Triangle
Linear Strain Triangle and other tpes o D elements B S. Ziaei Rad Linear Strain Triangle (LST or T6 This element is also called qadratic trianglar element. Qadratic Trianglar Element Linear Strain Triangle
SIMULATION OF TURBULENT FLOW AND HEAT TRANSFER OVER A BACKWARD-FACING STEP WITH RIBS TURBULATORS
 THERMAL SCIENCE, Year 011, Vol. 15, No. 1, pp. 45-55 45 SIMULATION OF TURBULENT FLOW AND HEAT TRANSFER OVER A BACKWARD-FACING STEP WITH RIBS TURBULATORS b Khdheer S. MUSHATET Mechanical Engineering Department,
THERMAL SCIENCE, Year 011, Vol. 15, No. 1, pp. 45-55 45 SIMULATION OF TURBULENT FLOW AND HEAT TRANSFER OVER A BACKWARD-FACING STEP WITH RIBS TURBULATORS b Khdheer S. MUSHATET Mechanical Engineering Department,
Digital Image Processing. Lecture 8 (Enhancement in the Frequency domain) Bu-Ali Sina University Computer Engineering Dep.
 Digital Image Processing Lectre 8 Enhancement in the Freqenc domain B-Ali Sina Uniersit Compter Engineering Dep. Fall 009 Image Enhancement In The Freqenc Domain Otline Jean Baptiste Joseph Forier The
Digital Image Processing Lectre 8 Enhancement in the Freqenc domain B-Ali Sina Uniersit Compter Engineering Dep. Fall 009 Image Enhancement In The Freqenc Domain Otline Jean Baptiste Joseph Forier The
Graphs and Networks Lecture 5. PageRank. Lecturer: Daniel A. Spielman September 20, 2007
 Graphs and Networks Lectre 5 PageRank Lectrer: Daniel A. Spielman September 20, 2007 5.1 Intro to PageRank PageRank, the algorithm reportedly sed by Google, assigns a nmerical rank to eery web page. More
Graphs and Networks Lectre 5 PageRank Lectrer: Daniel A. Spielman September 20, 2007 5.1 Intro to PageRank PageRank, the algorithm reportedly sed by Google, assigns a nmerical rank to eery web page. More
4 Primitive Equations
 4 Primitive Eqations 4.1 Spherical coordinates 4.1.1 Usefl identities We now introdce the special case of spherical coordinates: (,, r) (longitde, latitde, radial distance from Earth s center), with 0
4 Primitive Eqations 4.1 Spherical coordinates 4.1.1 Usefl identities We now introdce the special case of spherical coordinates: (,, r) (longitde, latitde, radial distance from Earth s center), with 0
Concept of Stress at a Point
 Washkeic College of Engineering Section : STRONG FORMULATION Concept of Stress at a Point Consider a point ithin an arbitraril loaded deformable bod Define Normal Stress Shear Stress lim A Fn A lim A FS
Washkeic College of Engineering Section : STRONG FORMULATION Concept of Stress at a Point Consider a point ithin an arbitraril loaded deformable bod Define Normal Stress Shear Stress lim A Fn A lim A FS
The Faraday Induction Law and Field Transformations in Special Relativity
 Apeiron, ol. 10, No., April 003 118 The Farada Indction Law and Field Transformations in Special Relatiit Aleander L. Kholmetskii Department of Phsics, elars State Uniersit, 4, F. Skorina Aene, 0080 Minsk
Apeiron, ol. 10, No., April 003 118 The Farada Indction Law and Field Transformations in Special Relatiit Aleander L. Kholmetskii Department of Phsics, elars State Uniersit, 4, F. Skorina Aene, 0080 Minsk
Lecture 3. (2) Last time: 3D space. The dot product. Dan Nichols January 30, 2018
 Lectre 3 The dot prodct Dan Nichols nichols@math.mass.ed MATH 33, Spring 018 Uniersity of Massachsetts Janary 30, 018 () Last time: 3D space Right-hand rle, the three coordinate planes 3D coordinate system:
Lectre 3 The dot prodct Dan Nichols nichols@math.mass.ed MATH 33, Spring 018 Uniersity of Massachsetts Janary 30, 018 () Last time: 3D space Right-hand rle, the three coordinate planes 3D coordinate system:
Reduction of over-determined systems of differential equations
 Redction of oer-determined systems of differential eqations Maim Zaytse 1) 1, ) and Vyachesla Akkerman 1) Nclear Safety Institte, Rssian Academy of Sciences, Moscow, 115191 Rssia ) Department of Mechanical
Redction of oer-determined systems of differential eqations Maim Zaytse 1) 1, ) and Vyachesla Akkerman 1) Nclear Safety Institte, Rssian Academy of Sciences, Moscow, 115191 Rssia ) Department of Mechanical
Lecture 5. Differential Analysis of Fluid Flow Navier-Stockes equation
 Lectre 5 Differential Analsis of Flid Flo Naier-Stockes eqation Differential analsis of Flid Flo The aim: to rodce differential eqation describing the motion of flid in detail Flid Element Kinematics An
Lectre 5 Differential Analsis of Flid Flo Naier-Stockes eqation Differential analsis of Flid Flo The aim: to rodce differential eqation describing the motion of flid in detail Flid Element Kinematics An
Geometry of Span (continued) The Plane Spanned by u and v
 Geometric Description of Span Geometr of Span (contined) 2 Geometr of Span (contined) 2 Span {} Span {, } 2 Span {} 2 Geometr of Span (contined) 2 b + 2 The Plane Spanned b and If a plane is spanned b
Geometric Description of Span Geometr of Span (contined) 2 Geometr of Span (contined) 2 Span {} Span {, } 2 Span {} 2 Geometr of Span (contined) 2 b + 2 The Plane Spanned b and If a plane is spanned b
Geostrophy & Thermal wind
 Lecture 10 Geostrophy & Thermal wind 10.1 f and β planes These are planes that are tangent to the earth (taken to be spherical) at a point of interest. The z ais is perpendicular to the plane (anti-parallel
Lecture 10 Geostrophy & Thermal wind 10.1 f and β planes These are planes that are tangent to the earth (taken to be spherical) at a point of interest. The z ais is perpendicular to the plane (anti-parallel
Second-Order Wave Equation
 Second-Order Wave Eqation A. Salih Department of Aerospace Engineering Indian Institte of Space Science and Technology, Thirvananthapram 3 December 016 1 Introdction The classical wave eqation is a second-order
Second-Order Wave Eqation A. Salih Department of Aerospace Engineering Indian Institte of Space Science and Technology, Thirvananthapram 3 December 016 1 Introdction The classical wave eqation is a second-order
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA. PRINCIPLES AND APPLICATIONS of FLUID MECHANICS UNIT 13 NQF LEVEL 3 OUTCOME 3 - HYDRODYNAMICS
 EDEXCEL NATIONAL CERTIFICATE/DIPLOMA PRINCIPLES AND APPLICATIONS of FLUID MECHANICS UNIT 3 NQF LEVEL 3 OUTCOME 3 - HYDRODYNAMICS TUTORIAL - PIPE FLOW CONTENT Be able to determine the parameters of pipeline
EDEXCEL NATIONAL CERTIFICATE/DIPLOMA PRINCIPLES AND APPLICATIONS of FLUID MECHANICS UNIT 3 NQF LEVEL 3 OUTCOME 3 - HYDRODYNAMICS TUTORIAL - PIPE FLOW CONTENT Be able to determine the parameters of pipeline
Numerical Simulation of Density Currents over a Slope under the Condition of Cooling Period in Lake Biwa
 Nmerical Simlation of Densit Crrents oer a Slope nder the Condition of Cooling Period in Lake Bia Takashi Hosoda Professor, Department of Urban Management, Koto Uniersit, C1-3-65, Kotodai-Katsra, Nishiko-k,
Nmerical Simlation of Densit Crrents oer a Slope nder the Condition of Cooling Period in Lake Bia Takashi Hosoda Professor, Department of Urban Management, Koto Uniersit, C1-3-65, Kotodai-Katsra, Nishiko-k,
Introducing Ideal Flow
 D f f f p D p D p D f T k p D e The Continit eqation The Naier Stokes eqations The iscos Flo Energ Eqation These form a closed set hen to thermodnamic relations are specified Introdcing Ideal Flo Getting
D f f f p D p D p D f T k p D e The Continit eqation The Naier Stokes eqations The iscos Flo Energ Eqation These form a closed set hen to thermodnamic relations are specified Introdcing Ideal Flo Getting
PHASE PLANE DIAGRAMS OF DIFFERENCE EQUATIONS. 1. Introduction
 PHASE PLANE DIAGRAMS OF DIFFERENCE EQUATIONS TANYA DEWLAND, JEROME WESTON, AND RACHEL WEYRENS Abstract. We will be determining qalitatie featres of a discrete dynamical system of homogeneos difference
PHASE PLANE DIAGRAMS OF DIFFERENCE EQUATIONS TANYA DEWLAND, JEROME WESTON, AND RACHEL WEYRENS Abstract. We will be determining qalitatie featres of a discrete dynamical system of homogeneos difference
Chapter 1: Differential Form of Basic Equations
 MEG 74 Energ and Variational Methods in Mechanics I Brendan J. O Toole, Ph.D. Associate Professor of Mechanical Engineering Howard R. Hghes College of Engineering Universit of Nevada Las Vegas TBE B- (7)
MEG 74 Energ and Variational Methods in Mechanics I Brendan J. O Toole, Ph.D. Associate Professor of Mechanical Engineering Howard R. Hghes College of Engineering Universit of Nevada Las Vegas TBE B- (7)
The Cross Product of Two Vectors in Space DEFINITION. Cross Product. u * v = s ƒ u ƒƒv ƒ sin ud n
 12.4 The Cross Prodct 873 12.4 The Cross Prodct In stdying lines in the plane, when we needed to describe how a line was tilting, we sed the notions of slope and angle of inclination. In space, we want
12.4 The Cross Prodct 873 12.4 The Cross Prodct In stdying lines in the plane, when we needed to describe how a line was tilting, we sed the notions of slope and angle of inclination. In space, we want
3.3 Operations With Vectors, Linear Combinations
 Operations With Vectors, Linear Combinations Performance Criteria: (d) Mltiply ectors by scalars and add ectors, algebraically Find linear combinations of ectors algebraically (e) Illstrate the parallelogram
Operations With Vectors, Linear Combinations Performance Criteria: (d) Mltiply ectors by scalars and add ectors, algebraically Find linear combinations of ectors algebraically (e) Illstrate the parallelogram
Viscous Dissipation and Heat Absorption effect on Natural Convection Flow with Uniform Surface Temperature along a Vertical Wavy Surface
 Aailable at htt://am.ed/aam Al. Al. Math. ISSN: 93-966 Alications and Alied Mathematics: An International Jornal (AAM) Secial Isse No. (Ma 6),. 8 8th International Mathematics Conference, March,, IUB Cams,
Aailable at htt://am.ed/aam Al. Al. Math. ISSN: 93-966 Alications and Alied Mathematics: An International Jornal (AAM) Secial Isse No. (Ma 6),. 8 8th International Mathematics Conference, March,, IUB Cams,
Numerical Model for Studying Cloud Formation Processes in the Tropics
 Astralian Jornal of Basic and Applied Sciences, 5(2): 189-193, 211 ISSN 1991-8178 Nmerical Model for Stdying Clod Formation Processes in the Tropics Chantawan Noisri, Dsadee Skawat Department of Mathematics
Astralian Jornal of Basic and Applied Sciences, 5(2): 189-193, 211 ISSN 1991-8178 Nmerical Model for Stdying Clod Formation Processes in the Tropics Chantawan Noisri, Dsadee Skawat Department of Mathematics
called the potential flow, and function φ is called the velocity potential.
 J. Szantr Lectre No. 3 Potential flows 1 If the flid flow is irrotational, i.e. everwhere or almost everwhere in the field of flow there is rot 0 it means that there eists a scalar fnction ϕ,, z), sch
J. Szantr Lectre No. 3 Potential flows 1 If the flid flow is irrotational, i.e. everwhere or almost everwhere in the field of flow there is rot 0 it means that there eists a scalar fnction ϕ,, z), sch
Homotopy Perturbation Method for Solving Linear Boundary Value Problems
 International Jornal of Crrent Engineering and Technolog E-ISSN 2277 4106, P-ISSN 2347 5161 2016 INPRESSCO, All Rights Reserved Available at http://inpressco.com/categor/ijcet Research Article Homotop
International Jornal of Crrent Engineering and Technolog E-ISSN 2277 4106, P-ISSN 2347 5161 2016 INPRESSCO, All Rights Reserved Available at http://inpressco.com/categor/ijcet Research Article Homotop
Elements of Coordinate System Transformations
 B Elements of Coordinate System Transformations Coordinate system transformation is a powerfl tool for solving many geometrical and kinematic problems that pertain to the design of gear ctting tools and
B Elements of Coordinate System Transformations Coordinate system transformation is a powerfl tool for solving many geometrical and kinematic problems that pertain to the design of gear ctting tools and
Change of Variables. (f T) JT. f = U
 Change of Variables 4-5-8 The change of ariables formla for mltiple integrals is like -sbstittion for single-ariable integrals. I ll gie the general change of ariables formla first, and consider specific
Change of Variables 4-5-8 The change of ariables formla for mltiple integrals is like -sbstittion for single-ariable integrals. I ll gie the general change of ariables formla first, and consider specific
Ocean Dynamics. The Equations of Motion 8/27/10. Physical Oceanography, MSCI 3001 Oceanographic Processes, MSCI dt = fv. dt = fu.
 Phsical Oceanograph, MSCI 3001 Oceanographic Processes, MSCI 5004 Dr. Katrin Meissner k.meissner@unsw.e.au Ocean Dnamics The Equations of Motion d u dt = 1 ρ Σ F Horizontal Equations: Acceleration = Pressure
Phsical Oceanograph, MSCI 3001 Oceanographic Processes, MSCI 5004 Dr. Katrin Meissner k.meissner@unsw.e.au Ocean Dnamics The Equations of Motion d u dt = 1 ρ Σ F Horizontal Equations: Acceleration = Pressure
Ocean Dynamics. Equation of motion a=σf/ρ 29/08/11. What forces might cause a parcel of water to accelerate?
 Phsical oceanograph, MSCI 300 Oceanographic Processes, MSCI 5004 Dr. Ale Sen Gupta a.sengupta@unsw.e.au Ocean Dnamics Newton s Laws of Motion An object will continue to move in a straight line and at a
Phsical oceanograph, MSCI 300 Oceanographic Processes, MSCI 5004 Dr. Ale Sen Gupta a.sengupta@unsw.e.au Ocean Dnamics Newton s Laws of Motion An object will continue to move in a straight line and at a
Baroclinic Buoyancy-Inertia Joint Stability Parameter
 Jornal of Oceanography, Vol. 6, pp. 35 to 46, 5 Baroclinic Boyancy-Inertia Joint Stability Parameter HIDEO KAWAI* 3-8 Shibagahara, Kse, Joyo, Kyoto Pref. 6-, Japan (Receied 9 September 3; in reised form
Jornal of Oceanography, Vol. 6, pp. 35 to 46, 5 Baroclinic Boyancy-Inertia Joint Stability Parameter HIDEO KAWAI* 3-8 Shibagahara, Kse, Joyo, Kyoto Pref. 6-, Japan (Receied 9 September 3; in reised form
CS 450: COMPUTER GRAPHICS VECTORS SPRING 2016 DR. MICHAEL J. REALE
 CS 45: COMPUTER GRPHICS VECTORS SPRING 216 DR. MICHEL J. RELE INTRODUCTION In graphics, we are going to represent objects and shapes in some form or other. First, thogh, we need to figre ot how to represent
CS 45: COMPUTER GRPHICS VECTORS SPRING 216 DR. MICHEL J. RELE INTRODUCTION In graphics, we are going to represent objects and shapes in some form or other. First, thogh, we need to figre ot how to represent
Numerical investigation of natural convection of air in vertical divergent channels
 Adanced Comptational Methods in Heat ransfer X 13 Nmerical inestigation of natral conection of air in ertical diergent channels O. Manca, S. Nardini, D. Ricci & S. ambrrino Dipartimento di Ingegneria Aerospaziale
Adanced Comptational Methods in Heat ransfer X 13 Nmerical inestigation of natral conection of air in ertical diergent channels O. Manca, S. Nardini, D. Ricci & S. ambrrino Dipartimento di Ingegneria Aerospaziale
Motion in an Undulator
 WIR SCHAFFEN WISSEN HEUTE FÜR MORGEN Sven Reiche :: SwissFEL Beam Dnamics Grop :: Pal Scherrer Institte Motion in an Undlator CERN Accelerator School FELs and ERLs On-ais Field of Planar Undlator For planar
WIR SCHAFFEN WISSEN HEUTE FÜR MORGEN Sven Reiche :: SwissFEL Beam Dnamics Grop :: Pal Scherrer Institte Motion in an Undlator CERN Accelerator School FELs and ERLs On-ais Field of Planar Undlator For planar
ENGINEERING COUNCIL DYNAMICS OF MECHANICAL SYSTEMS D225 TUTORIAL 2 LINEAR IMPULSE AND MOMENTUM
 ENGINEERING COUNCIL DYNAMICS OF MECHANICAL SYSTEMS D5 TUTORIAL LINEAR IMPULSE AND MOMENTUM On copletion of this ttorial yo shold be able to do the following. State Newton s laws of otion. Define linear
ENGINEERING COUNCIL DYNAMICS OF MECHANICAL SYSTEMS D5 TUTORIAL LINEAR IMPULSE AND MOMENTUM On copletion of this ttorial yo shold be able to do the following. State Newton s laws of otion. Define linear
Incompressible Viscoelastic Flow of a Generalised Oldroyed-B Fluid through Porous Medium between Two Infinite Parallel Plates in a Rotating System
 International Jornal of Compter Applications (97 8887) Volme 79 No., October Incompressible Viscoelastic Flow of a Generalised Oldroed-B Flid throgh Poros Medim between Two Infinite Parallel Plates in
International Jornal of Compter Applications (97 8887) Volme 79 No., October Incompressible Viscoelastic Flow of a Generalised Oldroed-B Flid throgh Poros Medim between Two Infinite Parallel Plates in
FLUCTUATING WIND VELOCITY CHARACTERISTICS OF THE WAKE OF A CONICAL HILL THAT CAUSE LARGE HORIZONTAL RESPONSE OF A CANTILEVER MODEL
 BBAA VI International Colloqim on: Blff Bodies Aerodynamics & Applications Milano, Italy, Jly, 2-24 28 FLUCTUATING WIND VELOCITY CHARACTERISTICS OF THE WAKE OF A CONICAL HILL THAT CAUSE LARGE HORIZONTAL
BBAA VI International Colloqim on: Blff Bodies Aerodynamics & Applications Milano, Italy, Jly, 2-24 28 FLUCTUATING WIND VELOCITY CHARACTERISTICS OF THE WAKE OF A CONICAL HILL THAT CAUSE LARGE HORIZONTAL
Feature extraction: Corners and blobs
 Featre etraction: Corners and blobs Wh etract featres? Motiation: panorama stitching We hae two images how do we combine them? Wh etract featres? Motiation: panorama stitching We hae two images how do
Featre etraction: Corners and blobs Wh etract featres? Motiation: panorama stitching We hae two images how do we combine them? Wh etract featres? Motiation: panorama stitching We hae two images how do
Q2. The velocity field in a fluid flow is given by
 Kinematics of Flid Q. Choose the correct anser (i) streamline is a line (a) hich is along the path of a particle (b) dran normal to the elocit ector at an point (c) sch that the streamlines diide the passage
Kinematics of Flid Q. Choose the correct anser (i) streamline is a line (a) hich is along the path of a particle (b) dran normal to the elocit ector at an point (c) sch that the streamlines diide the passage
Lesson 3: Free fall, Vectors, Motion in a plane (sections )
 Lesson 3: Free fall, Vectors, Motion in a plane (sections.6-3.5) Last time we looked at position s. time and acceleration s. time graphs. Since the instantaneous elocit is lim t 0 t the (instantaneous)
Lesson 3: Free fall, Vectors, Motion in a plane (sections.6-3.5) Last time we looked at position s. time and acceleration s. time graphs. Since the instantaneous elocit is lim t 0 t the (instantaneous)
The Numerical Simulation of Enhanced Heat Transfer Tubes
 Aailable online at.sciencedirect.com Phsics Procedia 4 (01 70 79 01 International Conference on Applied Phsics and Indstrial Engineering The Nmerical Simlation of Enhanced Heat Transfer Tbes Li Xiaoan,
Aailable online at.sciencedirect.com Phsics Procedia 4 (01 70 79 01 International Conference on Applied Phsics and Indstrial Engineering The Nmerical Simlation of Enhanced Heat Transfer Tbes Li Xiaoan,
1. Solve Problem 1.3-3(c) 2. Solve Problem 2.2-2(b)
 . Sole Problem.-(c). Sole Problem.-(b). A two dimensional trss shown in the figre is made of alminm with Yong s modls E = 8 GPa and failre stress Y = 5 MPa. Determine the minimm cross-sectional area of
. Sole Problem.-(c). Sole Problem.-(b). A two dimensional trss shown in the figre is made of alminm with Yong s modls E = 8 GPa and failre stress Y = 5 MPa. Determine the minimm cross-sectional area of
5. The Bernoulli Equation
 5. The Bernolli Eqation [This material relates predominantly to modles ELP034, ELP035] 5. Work and Energy 5. Bernolli s Eqation 5.3 An example of the se of Bernolli s eqation 5.4 Pressre head, velocity
5. The Bernolli Eqation [This material relates predominantly to modles ELP034, ELP035] 5. Work and Energy 5. Bernolli s Eqation 5.3 An example of the se of Bernolli s eqation 5.4 Pressre head, velocity
SECTION 6.7. The Dot Product. Preview Exercises. 754 Chapter 6 Additional Topics in Trigonometry. 7 w u 7 2 =?. 7 v 77w7
 754 Chapter 6 Additional Topics in Trigonometry 115. Yo ant to fly yor small plane de north, bt there is a 75-kilometer ind bloing from est to east. a. Find the direction angle for here yo shold head the
754 Chapter 6 Additional Topics in Trigonometry 115. Yo ant to fly yor small plane de north, bt there is a 75-kilometer ind bloing from est to east. a. Find the direction angle for here yo shold head the
Momentum Equation. Necessary because body is not made up of a fixed assembly of particles Its volume is the same however Imaginary
 Momentm Eqation Interest in the momentm eqation: Qantification of proplsion rates esign strctres for power generation esign of pipeline systems to withstand forces at bends and other places where the flow
Momentm Eqation Interest in the momentm eqation: Qantification of proplsion rates esign strctres for power generation esign of pipeline systems to withstand forces at bends and other places where the flow
MATH2715: Statistical Methods
 MATH275: Statistical Methods Exercises III (based on lectres 5-6, work week 4, hand in lectre Mon 23 Oct) ALL qestions cont towards the continos assessment for this modle. Q. If X has a niform distribtion
MATH275: Statistical Methods Exercises III (based on lectres 5-6, work week 4, hand in lectre Mon 23 Oct) ALL qestions cont towards the continos assessment for this modle. Q. If X has a niform distribtion
Chapter 3. Preferences and Utility
 Chapter 3 Preferences and Utilit Microeconomics stdies how individals make choices; different individals make different choices n important factor in making choices is individal s tastes or preferences
Chapter 3 Preferences and Utilit Microeconomics stdies how individals make choices; different individals make different choices n important factor in making choices is individal s tastes or preferences
FLUID FLOW FOR CHEMICAL ENGINEERING
 EKC FLUID FLOW FOR CHEMICL ENGINEERING CHTER 8 (SOLUTION WI EXERCISE): TRNSORTTION SYSTEM & FLUID METERING Dr Mohd zmier hmad Tel: +60 (4) 5996459 Email: chazmier@eng.sm.my . Benzene at 7.8 o C is pmped
EKC FLUID FLOW FOR CHEMICL ENGINEERING CHTER 8 (SOLUTION WI EXERCISE): TRNSORTTION SYSTEM & FLUID METERING Dr Mohd zmier hmad Tel: +60 (4) 5996459 Email: chazmier@eng.sm.my . Benzene at 7.8 o C is pmped
BLOOM S TAXONOMY. Following Bloom s Taxonomy to Assess Students
 BLOOM S TAXONOMY Topic Following Bloom s Taonomy to Assess Stdents Smmary A handot for stdents to eplain Bloom s taonomy that is sed for item writing and test constrction to test stdents to see if they
BLOOM S TAXONOMY Topic Following Bloom s Taonomy to Assess Stdents Smmary A handot for stdents to eplain Bloom s taonomy that is sed for item writing and test constrction to test stdents to see if they
Change of Variables. f(x, y) da = (1) If the transformation T hasn t already been given, come up with the transformation to use.
 MATH 2Q Spring 26 Daid Nichols Change of Variables Change of ariables in mltiple integrals is complicated, bt it can be broken down into steps as follows. The starting point is a doble integral in & y.
MATH 2Q Spring 26 Daid Nichols Change of Variables Change of ariables in mltiple integrals is complicated, bt it can be broken down into steps as follows. The starting point is a doble integral in & y.
The General Circulation of the Oceans
 The General Circulation of the Oceans In previous classes we discussed local balances (Inertial otion, Ekman Transport, Geostrophic Flows, etc.), but can we eplain the large-scale general circulation of
The General Circulation of the Oceans In previous classes we discussed local balances (Inertial otion, Ekman Transport, Geostrophic Flows, etc.), but can we eplain the large-scale general circulation of
Chapter 2 Difficulties associated with corners
 Chapter Difficlties associated with corners This chapter is aimed at resolving the problems revealed in Chapter, which are cased b corners and/or discontinos bondar conditions. The first section introdces
Chapter Difficlties associated with corners This chapter is aimed at resolving the problems revealed in Chapter, which are cased b corners and/or discontinos bondar conditions. The first section introdces
Vectors in Rn un. This definition of norm is an extension of the Pythagorean Theorem. Consider the vector u = (5, 8) in R 2
 MATH 307 Vectors in Rn Dr. Neal, WKU Matrices of dimension 1 n can be thoght of as coordinates, or ectors, in n- dimensional space R n. We can perform special calclations on these ectors. In particlar,
MATH 307 Vectors in Rn Dr. Neal, WKU Matrices of dimension 1 n can be thoght of as coordinates, or ectors, in n- dimensional space R n. We can perform special calclations on these ectors. In particlar,
Math 144 Activity #10 Applications of Vectors
 144 p 1 Math 144 Actiity #10 Applications of Vectors In the last actiity, yo were introdced to ectors. In this actiity yo will look at some of the applications of ectors. Let the position ector = a, b
144 p 1 Math 144 Actiity #10 Applications of Vectors In the last actiity, yo were introdced to ectors. In this actiity yo will look at some of the applications of ectors. Let the position ector = a, b
Pulses on a Struck String
 8.03 at ESG Spplemental Notes Plses on a Strck String These notes investigate specific eamples of transverse motion on a stretched string in cases where the string is at some time ndisplaced, bt with a
8.03 at ESG Spplemental Notes Plses on a Strck String These notes investigate specific eamples of transverse motion on a stretched string in cases where the string is at some time ndisplaced, bt with a
The Real Stabilizability Radius of the Multi-Link Inverted Pendulum
 Proceedings of the 26 American Control Conference Minneapolis, Minnesota, USA, Jne 14-16, 26 WeC123 The Real Stabilizability Radis of the Mlti-Link Inerted Pendlm Simon Lam and Edward J Daison Abstract
Proceedings of the 26 American Control Conference Minneapolis, Minnesota, USA, Jne 14-16, 26 WeC123 The Real Stabilizability Radis of the Mlti-Link Inerted Pendlm Simon Lam and Edward J Daison Abstract
Effect of Applied Magnetic Field on Pulsatile Flow of Blood in a Porous Channel
 Dsmanta Kmar St et al, Int. J. Comp. Tec. Appl., ol 6, 779-785 ISSN:9-69 Effect of Applied Magnetic Field on Plsatile Flow of Blood in a Poros Cannel Sarfraz Amed Dsmanta Kmar St Dept. of Matematics, Jorat
Dsmanta Kmar St et al, Int. J. Comp. Tec. Appl., ol 6, 779-785 ISSN:9-69 Effect of Applied Magnetic Field on Plsatile Flow of Blood in a Poros Cannel Sarfraz Amed Dsmanta Kmar St Dept. of Matematics, Jorat
Effects of MHD Laminar Flow Between a Fixed Impermeable Disk and a Porous Rotating Disk
 Effects of MHD Laminar Flow Between a Fixed Impermeable Disk and a Poros otating Disk Hemant Poonia * * Asstt. Prof., Deptt. of Math, Stat & Physics, CCSHAU, Hisar-54.. C. Chadhary etd. Professor, Deptt.
Effects of MHD Laminar Flow Between a Fixed Impermeable Disk and a Poros otating Disk Hemant Poonia * * Asstt. Prof., Deptt. of Math, Stat & Physics, CCSHAU, Hisar-54.. C. Chadhary etd. Professor, Deptt.
SUBJECT:ENGINEERING MATHEMATICS-I SUBJECT CODE :SMT1101 UNIT III FUNCTIONS OF SEVERAL VARIABLES. Jacobians
 SUBJECT:ENGINEERING MATHEMATICS-I SUBJECT CODE :SMT0 UNIT III FUNCTIONS OF SEVERAL VARIABLES Jacobians Changing ariable is something e come across er oten in Integration There are man reasons or changing
SUBJECT:ENGINEERING MATHEMATICS-I SUBJECT CODE :SMT0 UNIT III FUNCTIONS OF SEVERAL VARIABLES Jacobians Changing ariable is something e come across er oten in Integration There are man reasons or changing
What are these waves?
 PH300 Modern Phsics SP11 Is the state of the cat to be created onl when a phsicist inestigates the situation at some definite time? Nobod reall doubts that the presence or absence of a dead cat is something
PH300 Modern Phsics SP11 Is the state of the cat to be created onl when a phsicist inestigates the situation at some definite time? Nobod reall doubts that the presence or absence of a dead cat is something
Partial Differential Equations with Applications
 Universit of Leeds MATH 33 Partial Differential Eqations with Applications Eamples to spplement Chapter on First Order PDEs Eample (Simple linear eqation, k + = 0, (, 0) = ϕ(), k a constant.) The characteristic
Universit of Leeds MATH 33 Partial Differential Eqations with Applications Eamples to spplement Chapter on First Order PDEs Eample (Simple linear eqation, k + = 0, (, 0) = ϕ(), k a constant.) The characteristic
Math 263 Assignment #3 Solutions. 1. A function z = f(x, y) is called harmonic if it satisfies Laplace s equation:
 Math 263 Assignment #3 Soltions 1. A fnction z f(x, ) is called harmonic if it satisfies Laplace s eqation: 2 + 2 z 2 0 Determine whether or not the following are harmonic. (a) z x 2 + 2. We se the one-variable
Math 263 Assignment #3 Soltions 1. A fnction z f(x, ) is called harmonic if it satisfies Laplace s eqation: 2 + 2 z 2 0 Determine whether or not the following are harmonic. (a) z x 2 + 2. We se the one-variable
EXERCISES WAVE EQUATION. In Problems 1 and 2 solve the heat equation (1) subject to the given conditions. Assume a rod of length L.
 .4 WAVE EQUATION 445 EXERCISES.3 In Problems and solve the heat eqation () sbject to the given conditions. Assme a rod of length.. (, t), (, t) (, ),, > >. (, t), (, t) (, ) ( ) 3. Find the temperatre
.4 WAVE EQUATION 445 EXERCISES.3 In Problems and solve the heat eqation () sbject to the given conditions. Assme a rod of length.. (, t), (, t) (, ),, > >. (, t), (, t) (, ) ( ) 3. Find the temperatre
ESCI 485 Air/sea Interaction Lesson 3 The Surface Layer
 ESCI 485 Air/sea Interaction Lesson 3 he Surface Layer References: Air-sea Interaction: Laws and Mechanisms, Csanady Structure of the Atmospheric Boundary Layer, Sorbjan HE PLANEARY BOUNDARY LAYER he atmospheric
ESCI 485 Air/sea Interaction Lesson 3 he Surface Layer References: Air-sea Interaction: Laws and Mechanisms, Csanady Structure of the Atmospheric Boundary Layer, Sorbjan HE PLANEARY BOUNDARY LAYER he atmospheric
Boundary layer develops in the flow direction, δ = δ (x) τ
 58:68 Trblent Flos Handot: Bondar Laers Differences to Trblent Channel Flo Bondar laer develops in the flo direction, not knon a priori Oter part of the flo consists of interittent trblent/non-trblent
58:68 Trblent Flos Handot: Bondar Laers Differences to Trblent Channel Flo Bondar laer develops in the flo direction, not knon a priori Oter part of the flo consists of interittent trblent/non-trblent
Chapter 3 Motion in a Plane
 Chapter 3 Motion in a Plane Introduce ectors and scalars. Vectors hae direction as well as magnitude. The are represented b arrows. The arrow points in the direction of the ector and its length is related
Chapter 3 Motion in a Plane Introduce ectors and scalars. Vectors hae direction as well as magnitude. The are represented b arrows. The arrow points in the direction of the ector and its length is related
Correlations for Nusselt Number in Free Convection from an Isothermal Inclined Square Plate by a Numerical Simulation
 American Jornal of Mechanics and Applications 5; : 8-8 Pblished online Ma 4, 5 http://sciencepblishinggropcom/j/ajma doi: 648/jajma5 ISSN: 76-65 Print; ISSN: 76-6 Online Correlations for Nsselt Nmber in
American Jornal of Mechanics and Applications 5; : 8-8 Pblished online Ma 4, 5 http://sciencepblishinggropcom/j/ajma doi: 648/jajma5 ISSN: 76-65 Print; ISSN: 76-6 Online Correlations for Nsselt Nmber in
UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS
 SUBAREA I. COMPETENCY 1.0 UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS MECHANICS Skill 1.1 Calculating displacement, aerage elocity, instantaneous elocity, and acceleration in a gien frame of reference
SUBAREA I. COMPETENCY 1.0 UNDERSTAND MOTION IN ONE AND TWO DIMENSIONS MECHANICS Skill 1.1 Calculating displacement, aerage elocity, instantaneous elocity, and acceleration in a gien frame of reference
A Decomposition Method for Volume Flux. and Average Velocity of Thin Film Flow. of a Third Grade Fluid Down an Inclined Plane
 Adv. Theor. Appl. Mech., Vol. 1, 8, no. 1, 9 A Decomposition Method for Volme Flx and Average Velocit of Thin Film Flow of a Third Grade Flid Down an Inclined Plane A. Sadighi, D.D. Ganji,. Sabzehmeidani
Adv. Theor. Appl. Mech., Vol. 1, 8, no. 1, 9 A Decomposition Method for Volme Flx and Average Velocit of Thin Film Flow of a Third Grade Flid Down an Inclined Plane A. Sadighi, D.D. Ganji,. Sabzehmeidani
Low-emittance tuning of storage rings using normal mode beam position monitor calibration
 PHYSIAL REVIEW SPEIAL TOPIS - AELERATORS AND BEAMS 4, 784 () Low-emittance tning of storage rings sing normal mode beam position monitor calibration A. Wolski* Uniersity of Lierpool, Lierpool, United Kingdom
PHYSIAL REVIEW SPEIAL TOPIS - AELERATORS AND BEAMS 4, 784 () Low-emittance tning of storage rings sing normal mode beam position monitor calibration A. Wolski* Uniersity of Lierpool, Lierpool, United Kingdom
MEG 741 Energy and Variational Methods in Mechanics I
 MEG 74 Energ and Variational Methods in Mechanics I Brendan J. O Toole, Ph.D. Associate Professor of Mechanical Engineering Howard R. Hghes College of Engineering Universit of Nevada Las Vegas TBE B- (7)
MEG 74 Energ and Variational Methods in Mechanics I Brendan J. O Toole, Ph.D. Associate Professor of Mechanical Engineering Howard R. Hghes College of Engineering Universit of Nevada Las Vegas TBE B- (7)
The New (2+1)-Dimensional Integrable Coupling of the KdV Equation: Auto-Bäcklund Transformation and Non-Travelling Wave Profiles
 MM Research Preprints, 36 3 MMRC, AMSS, Academia Sinica No. 3, December The New (+)-Dimensional Integrable Copling of the KdV Eqation: Ato-Bäcklnd Transformation and Non-Traelling Wae Profiles Zhena Yan
MM Research Preprints, 36 3 MMRC, AMSS, Academia Sinica No. 3, December The New (+)-Dimensional Integrable Copling of the KdV Eqation: Ato-Bäcklnd Transformation and Non-Traelling Wae Profiles Zhena Yan
Boundary Layer Theory:
 Mass Transfer Bondar Laer Theor: Mass and Heat/Momentm Transfer Letre,..7, Dr. K. Wegner 9. Basi Theories for Mass Transfer Coeffiients 9. Flid-Flid Interfaes (letre of 5..7) Flid-flid interfaes are tpiall
Mass Transfer Bondar Laer Theor: Mass and Heat/Momentm Transfer Letre,..7, Dr. K. Wegner 9. Basi Theories for Mass Transfer Coeffiients 9. Flid-Flid Interfaes (letre of 5..7) Flid-flid interfaes are tpiall
6.4 VECTORS AND DOT PRODUCTS
 458 Chapter 6 Additional Topics in Trigonometry 6.4 VECTORS AND DOT PRODUCTS What yo shold learn ind the dot prodct of two ectors and se the properties of the dot prodct. ind the angle between two ectors
458 Chapter 6 Additional Topics in Trigonometry 6.4 VECTORS AND DOT PRODUCTS What yo shold learn ind the dot prodct of two ectors and se the properties of the dot prodct. ind the angle between two ectors
CHAPTER 3: Kinematics in Two Dimensions; Vectors
 HAPTER 3: Kinematics in Two Dimensions; Vectors Solution Guide to WebAssign Problems 3.1 [] The truck has a displacement of 18 + (16) blocks north and 1 blocks east. The resultant has a magnitude of +
HAPTER 3: Kinematics in Two Dimensions; Vectors Solution Guide to WebAssign Problems 3.1 [] The truck has a displacement of 18 + (16) blocks north and 1 blocks east. The resultant has a magnitude of +
Prandl established a universal velocity profile for flow parallel to the bed given by
 EM 0--00 (Part VI) (g) The nderlayers shold be at least three thicknesses of the W 50 stone, bt never less than 0.3 m (Ahrens 98b). The thickness can be calclated sing Eqation VI-5-9 with a coefficient
EM 0--00 (Part VI) (g) The nderlayers shold be at least three thicknesses of the W 50 stone, bt never less than 0.3 m (Ahrens 98b). The thickness can be calclated sing Eqation VI-5-9 with a coefficient
Dynamics ( 동역학 ) Ch.2 Motion of Translating Bodies (2.1 & 2.2)
 Dynamics ( 동역학 ) Ch. Motion of Translating Bodies (. &.) Motion of Translating Bodies This chapter is usually referred to as Kinematics of Particles. Particles: In dynamics, a particle is a body without
Dynamics ( 동역학 ) Ch. Motion of Translating Bodies (. &.) Motion of Translating Bodies This chapter is usually referred to as Kinematics of Particles. Particles: In dynamics, a particle is a body without
The Brauer Manin obstruction
 The Braer Manin obstrction Martin Bright 17 April 2008 1 Definitions Let X be a smooth, geometrically irredcible ariety oer a field k. Recall that the defining property of an Azmaya algebra A is that,
The Braer Manin obstrction Martin Bright 17 April 2008 1 Definitions Let X be a smooth, geometrically irredcible ariety oer a field k. Recall that the defining property of an Azmaya algebra A is that,
AMS 212B Perturbation Methods Lecture 05 Copyright by Hongyun Wang, UCSC
 AMS B Pertrbation Methods Lectre 5 Copright b Hongn Wang, UCSC Recap: we discssed bondar laer of ODE Oter epansion Inner epansion Matching: ) Prandtl s matching ) Matching b an intermediate variable (Skip
AMS B Pertrbation Methods Lectre 5 Copright b Hongn Wang, UCSC Recap: we discssed bondar laer of ODE Oter epansion Inner epansion Matching: ) Prandtl s matching ) Matching b an intermediate variable (Skip
Section 7.4: Integration of Rational Functions by Partial Fractions
 Section 7.4: Integration of Rational Fnctions by Partial Fractions This is abot as complicated as it gets. The Method of Partial Fractions Ecept for a few very special cases, crrently we have no way to
Section 7.4: Integration of Rational Fnctions by Partial Fractions This is abot as complicated as it gets. The Method of Partial Fractions Ecept for a few very special cases, crrently we have no way to
Physics 1501 Lecture 28
 Phsics 1501 Lecture 28 Phsics 1501: Lecture 28 Toda s Agenda Homework #10 (due Frida No. 11) Midterm 2: No. 16 Topics 1-D traeling waes Waes on a string Superposition Power Phsics 1501: Lecture 28, Pg
Phsics 1501 Lecture 28 Phsics 1501: Lecture 28 Toda s Agenda Homework #10 (due Frida No. 11) Midterm 2: No. 16 Topics 1-D traeling waes Waes on a string Superposition Power Phsics 1501: Lecture 28, Pg
Inertial Instability of Arbitrarily Meandering Currents Governed by the Eccentrically Cyclogeostrophic Equation
 Jornal of Oceanography, Vol. 59, pp. 163 to 17, 3 Inertial Instability of Arbitrarily Meandering Crrents Governed by the Eccentrically Cyclogeostrophic Eqation HIDEO KAWAI* 131-81 Shibagahara, Kse, Joyo,
Jornal of Oceanography, Vol. 59, pp. 163 to 17, 3 Inertial Instability of Arbitrarily Meandering Crrents Governed by the Eccentrically Cyclogeostrophic Eqation HIDEO KAWAI* 131-81 Shibagahara, Kse, Joyo,
Measurement of Rotation. Circulation. Example. Lecture 4: Circulation and Vorticity 1/31/2017
 Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture 4: Circulation and Vorticity Measurement of Rotation Circulation Bjerknes Circulation Theorem Vorticity Potential Vorticity Conservation of Potential Vorticity Circulation and vorticity are the
Lecture Notes: Finite Element Analysis, J.E. Akin, Rice University
 9. TRUSS ANALYSIS... 1 9.1 PLANAR TRUSS... 1 9. SPACE TRUSS... 11 9.3 SUMMARY... 1 9.4 EXERCISES... 15 9. Trss analysis 9.1 Planar trss: The differential eqation for the eqilibrim of an elastic bar (above)
9. TRUSS ANALYSIS... 1 9.1 PLANAR TRUSS... 1 9. SPACE TRUSS... 11 9.3 SUMMARY... 1 9.4 EXERCISES... 15 9. Trss analysis 9.1 Planar trss: The differential eqation for the eqilibrim of an elastic bar (above)
Setting The K Value And Polarization Mode Of The Delta Undulator
 LCLS-TN-4- Setting The Vale And Polarization Mode Of The Delta Undlator Zachary Wolf, Heinz-Dieter Nhn SLAC September 4, 04 Abstract This note provides the details for setting the longitdinal positions
LCLS-TN-4- Setting The Vale And Polarization Mode Of The Delta Undlator Zachary Wolf, Heinz-Dieter Nhn SLAC September 4, 04 Abstract This note provides the details for setting the longitdinal positions
