Archimedes and Continued Fractions* John G. Thompson University of Cambridge
|
|
|
- Brenda Gregory
- 5 years ago
- Views:
Transcription
1 Archimedes and Continued Fractions* John G. Thompson University of Cambridge It is to Archimedes that we owe the inequalities The letter r is the first letter of the Greek word for perimeter, and is understood to mean the circumference of the circle of diameter. Continued fractions were invented, perhaps one should say discovered, as the most efficient way to find rational numbers close to a given number x. The most important ingredient in defining continued fractions is the "bracket function" : [x] is the largest integer < x. It might be helpful to consider a picture X 5 For the x in the picture, [x] = 4. From the definition of [x], we see that 0 ~ x- [x] <, and it is convenient to set so that {x} = x- [x], x = [x] + {x}, and we have decomposed x into the sum of two numbers, [x], the integral part of x, and { x}, the fractional part of x. * Lecture given on 3 August 987 at the prize-giving ceremony for the Interschool Mathematical Competition
2 Suppose { x} =I= 0, so that O<{x}<l. Then {!} >, and we can thus form the integral part [{!}] of {!},and we see that x = [x] + [- ] {- } {.z} + {.z} If { {!} } =/= 0, we can repeat the preceding construction. Perhaps it is worthwhile to take an example. Suppose x = ~:. We have 5 x=+- 3 ' [x] =, 5 {x}= 3 Then so 3 3 {x}=s= 2 +5, ' 3= +3' -=+- 2=2+0, 5 x=+-=+- 3 g 5 =+--3 = = ~ 3 2 =
3 This suggests the following definition: If n is an integer 2:, set [n] = n; if n, n 2,, nr are integers 2:, and [n,..., nr] has been defined, set Example. n With this definition, we get that 8 3 = [, 2,,, 2] ' and we say that [,2,,,2] is the continued fraction for ~:. It is an important property of numbers that if xis any number;::::, then x has a representation as a continued fraction, provided we allow continued fractions to continue indefinitely. If x is a rational number ;::::, then there are integers n,, nr 2: such that 69
4 and these integers n,, nr are uniquely determined by x (as we saw in examining ~= ). If x is not a rational number (i.e., if x is not a ratio of two integers), then there are integers n, n 2,, nr,... (continuing forever) such that for each r =, 2,..., [n,, nr] is the rational number represented by taking only the first r terms of the continued fraction expansion for x. Thus, n = [x], etc. Let's play this game with a famous irrational number: yl3. We have < J3 < 2, and so [ J3] =, { V3} = J3-. v'3+ V3+ V3-=(V3+).(v'3-)= v'3 +V3 ( + J3) 70 2 (v'3-) =+v'3.
5 So J3=+(J3-) =+--- V3- =+-----= -+V = V3 J ' = =--- 2+(V3-) and we see that The numbers J3 = [,,2,,2,,2,,2,... ] (forever). J [], [, ], [,, 2], [,, 2, ], are called the convergents to y'3, and the rth number in the sequence is 7
6 called the rth convergent. We have [] = = [,,2] = 5/3 = [,,2,,2] = 9/ = [,,2,,2,,2] = 7/4 = [,,2,,2,,2,,2] = 265/53 = [,,2,,2,,2,,2,,2] = 989/57 = v'3 = [,,2,,2,,2,,2,,2,] = 35/780 = [,,2,,2,,2,,2,] = 362/209 = [,,2,,2,,2,] = 97/56 = [,,2,,2,] = 26/5 = [,,2,] = 7/4 = [,] =2 = Let's now consider Archimedes' paper "The Measurement of a Circle". The idea, which did not originate with Archimedes, is to approximate the circumference of a circle by inscribed polygons and by circumscribed polygons, and to obtain estimates for the perimeter of a polygon. Archimedes uses regular polygons of 96 sides in his final construction, but he starts with hexagons. The inscribed hexagon has a perimeter of 6 x t = 3, so 3 < r. 72
7 / / 2o/ / a 2 3a =-, 4 J3 a=- -=-. J3 2 6 The perimeter of the circumscribed hexagon is 2 X v; = 2VJ so 7r < 2v'3. Out of the blue, apparently, Archimedes states that 265 v' < 3 <
8 Of course, it is easy to check that these inequalities are true. Simply square the terms and check that ( 265)2 <3 (35)2. 53 < 780 But one may ask where these particular rational numbers come from. Note that ~:~ is the 9th convergent to J3 and \ 3 5 is the 2th convergent. I 8 0 think it is safe to infer that Archimedes knew about continued fractions in some form, probably not in the same way we understand them now. For example, it would be better to take the th convergent rather than the 9th convergent, but even so, the fact remains that Archimedes chose convergents, not arbitrary rational numbers. Given the initial approximation to J3, the remaining problem, which is an exercise in plane geometry; is to determine a when we know b. We have the equations a=~, 74
9 and so Archimedes' treatment of the problem is beautiful, and is worth reading over two thousand years later. Biographical Note. Professor J. G. Thompson obtained his PhD from the University of Chicago, and was Professor of Mathematics there before assuming his current appointment as Rouse Ball Professor of Mathematics at the University of Cambridge. He is a member of the US National Academy of Sciences and a Fellow of the Royal Society. In 970, he was awarded a Fields Medal (the highest honour that can be bestowed on a mathematician) by the International Mathematical Union for fundamental work in group theory that recently led to the complete classification of finite simple groups. He was conferred an honorary doctorate by the University of Oxford in June 987. Professor Thompson was a Visiting Professor at the Mathematics Department, National University of Singapore, from June to August
Explain any relationship you see between the length of the diameter and the circumference.
 Level A π Problem of the Month Circular Reasoning π Janet and Lydia want to learn more about circles. They decide to measure different size circles that they can find. They measure the circles in two ways.
Level A π Problem of the Month Circular Reasoning π Janet and Lydia want to learn more about circles. They decide to measure different size circles that they can find. They measure the circles in two ways.
r=1 Our discussion will not apply to negative values of r, since we make frequent use of the fact that for all non-negative numbers x and t
 Chapter 2 Some Area Calculations 2.1 The Area Under a Power Function Let a be a positive number, let r be a positive number, and let S r a be the set of points (x, y) in R 2 such that 0 x a and 0 y x r.
Chapter 2 Some Area Calculations 2.1 The Area Under a Power Function Let a be a positive number, let r be a positive number, and let S r a be the set of points (x, y) in R 2 such that 0 x a and 0 y x r.
π is a mathematical constant that symbolizes the ratio of a circle s circumference to its
 Ziya Chen Math 4388 Shanyu Ji Origin of π π is a mathematical constant that symbolizes the ratio of a circle s circumference to its diameter, which is approximately 3.14159265 We have been using this symbol
Ziya Chen Math 4388 Shanyu Ji Origin of π π is a mathematical constant that symbolizes the ratio of a circle s circumference to its diameter, which is approximately 3.14159265 We have been using this symbol
Exact Value of pi π (17-8 3)
 IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 2319-765X. Volume 12, Issue 6 Ver. I (Nov. - Dec.2016), PP 04-08 www.iosrjournals.org Exact Value of pi π (17-8 3) Mr. Laxman S. Gogawale
IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 2319-765X. Volume 12, Issue 6 Ver. I (Nov. - Dec.2016), PP 04-08 www.iosrjournals.org Exact Value of pi π (17-8 3) Mr. Laxman S. Gogawale
A π day celebration! Everyone s favorite geometric constant!
 A π day celebration! Everyone s favorite geometric constant! Math Circle March 10, 2019 The circumference of a circle is another word for its perimeter. A circle s circumference is proportional to its
A π day celebration! Everyone s favorite geometric constant! Math Circle March 10, 2019 The circumference of a circle is another word for its perimeter. A circle s circumference is proportional to its
Calculus: Area. Mathematics 15: Lecture 22. Dan Sloughter. Furman University. November 12, 2006
 Calculus: Area Mathematics 15: Lecture 22 Dan Sloughter Furman University November 12, 2006 Dan Sloughter (Furman University) Calculus: Area November 12, 2006 1 / 7 Area Note: formulas for the areas of
Calculus: Area Mathematics 15: Lecture 22 Dan Sloughter Furman University November 12, 2006 Dan Sloughter (Furman University) Calculus: Area November 12, 2006 1 / 7 Area Note: formulas for the areas of
Integer (positive or negative whole numbers or zero) arithmetic
 Integer (positive or negative whole numbers or zero) arithmetic The number line helps to visualize the process. The exercises below include the answers but see if you agree with them and if not try to
Integer (positive or negative whole numbers or zero) arithmetic The number line helps to visualize the process. The exercises below include the answers but see if you agree with them and if not try to
Exact Value of Pi Π (17 8 3)
 International OPEN ACCESS Journal Of Modern Engineering Research (IJMER) Exact Value of Pi Π (17 8 3) Mr. Laxman S. Gogawale Fulora co-operative society, Dhankawadi, Pune-43 (India) Corresponding Author:
International OPEN ACCESS Journal Of Modern Engineering Research (IJMER) Exact Value of Pi Π (17 8 3) Mr. Laxman S. Gogawale Fulora co-operative society, Dhankawadi, Pune-43 (India) Corresponding Author:
Prepared by Sa diyya Hendrickson. Package Summary
 Introduction Prepared by Sa diyya Hendrickson Name: Date: Package Summary Defining Decimal Numbers Things to Remember Adding and Subtracting Decimals Multiplying Decimals Expressing Fractions as Decimals
Introduction Prepared by Sa diyya Hendrickson Name: Date: Package Summary Defining Decimal Numbers Things to Remember Adding and Subtracting Decimals Multiplying Decimals Expressing Fractions as Decimals
WEEK 7 NOTES AND EXERCISES
 WEEK 7 NOTES AND EXERCISES RATES OF CHANGE (STRAIGHT LINES) Rates of change are very important in mathematics. Take for example the speed of a car. It is a measure of how far the car travels over a certain
WEEK 7 NOTES AND EXERCISES RATES OF CHANGE (STRAIGHT LINES) Rates of change are very important in mathematics. Take for example the speed of a car. It is a measure of how far the car travels over a certain
Section 1: Sets and Interval Notation
 PART 1 From Sets to Functions Section 1: Sets and Interval Notation Introduction Set concepts offer the means for understanding many different aspects of mathematics and its applications to other branches
PART 1 From Sets to Functions Section 1: Sets and Interval Notation Introduction Set concepts offer the means for understanding many different aspects of mathematics and its applications to other branches
At first numbers were used only for counting, and 1, 2, 3,... were all that was needed. These are called positive integers.
 1 Numers One thread in the history of mathematics has een the extension of what is meant y a numer. This has led to the invention of new symols and techniques of calculation. When you have completed this
1 Numers One thread in the history of mathematics has een the extension of what is meant y a numer. This has led to the invention of new symols and techniques of calculation. When you have completed this
Circles & Interval & Set Notation.notebook. November 16, 2009 CIRCLES. OBJECTIVE Graph a Circle given the equation in standard form.
 OBJECTIVE Graph a Circle given the equation in standard form. Write the equation of a circle in standard form given a graph or two points (one being the center). Students will be able to write the domain
OBJECTIVE Graph a Circle given the equation in standard form. Write the equation of a circle in standard form given a graph or two points (one being the center). Students will be able to write the domain
Math Number 842 Professor R. Roybal MATH History of Mathematics 24th October, Project 1 - Proofs
 Math Number 842 Professor R. Roybal MATH 331 - History of Mathematics 24th October, 2017 Project 1 - Proofs Mathematical proofs are an important concept that was integral to the development of modern mathematics.
Math Number 842 Professor R. Roybal MATH 331 - History of Mathematics 24th October, 2017 Project 1 - Proofs Mathematical proofs are an important concept that was integral to the development of modern mathematics.
Why does pi keep popping up? Undergraduate Colloquium, October 2007 I. Definitions and Archimedes. II. Digits and some silliness (and Ramanujan)
 Why does pi keep popping up? Undergraduate Colloquium, October 7 I. Definitions and Archimedes II. Digits and some silliness (and Ramanujan III. Antidote: pi is irrational. IV. Pi popping up in factorials.
Why does pi keep popping up? Undergraduate Colloquium, October 7 I. Definitions and Archimedes II. Digits and some silliness (and Ramanujan III. Antidote: pi is irrational. IV. Pi popping up in factorials.
What is proof? Lesson 1
 What is proof? Lesson The topic for this Math Explorer Club is mathematical proof. In this post we will go over what was covered in the first session. The word proof is a normal English word that you might
What is proof? Lesson The topic for this Math Explorer Club is mathematical proof. In this post we will go over what was covered in the first session. The word proof is a normal English word that you might
Grade 8 Chapter 7: Rational and Irrational Numbers
 Grade 8 Chapter 7: Rational and Irrational Numbers In this chapter we first review the real line model for numbers, as discussed in Chapter 2 of seventh grade, by recalling how the integers and then the
Grade 8 Chapter 7: Rational and Irrational Numbers In this chapter we first review the real line model for numbers, as discussed in Chapter 2 of seventh grade, by recalling how the integers and then the
Another Algorithm for Computing π Attributable to Archimedes: Avoiding Cancellation Errors
 POLYTECHNIC UNIVERSITY Department of Computer and Information Science Another Algorithm for Computing π Attributable to Archimedes: Avoiding Cancellation Errors K. Ming Leung Abstract: We illustrate how
POLYTECHNIC UNIVERSITY Department of Computer and Information Science Another Algorithm for Computing π Attributable to Archimedes: Avoiding Cancellation Errors K. Ming Leung Abstract: We illustrate how
Lecture 8. Eudoxus and the Avoidance of a Fundamental Conflict
 Lecture 8. Eudoxus and the Avoidance of a Fundamental Conflict Eudoxus of Cnidus Eudoxus, 480 BC - 355 BC, was a Greek philosopher, mathematician and astronomer who contributed to Euclid s Elements. His
Lecture 8. Eudoxus and the Avoidance of a Fundamental Conflict Eudoxus of Cnidus Eudoxus, 480 BC - 355 BC, was a Greek philosopher, mathematician and astronomer who contributed to Euclid s Elements. His
Chapter 1. Areas, volumes and simple sums Summation notation. Answer the following questions:
 Chapter 1 Areas, volumes and simple sums 1.1 Answer the following questions: (a) What is the value of the fifth term of the sum S = 0 (5 + 3k)/k? (b) How many terms are there in total in the sum S = 17
Chapter 1 Areas, volumes and simple sums 1.1 Answer the following questions: (a) What is the value of the fifth term of the sum S = 0 (5 + 3k)/k? (b) How many terms are there in total in the sum S = 17
Homework 2 from lecture 11 to lecture 20
 Homework 2 from lecture 11 to lecture 20 June 14, 2016 Lecture 11 1. Take a look at Apollonius Conics in the appendices. 2. UseCalculus toproveapropertyinapollonius book: LetC beapointonahyperbola. Let
Homework 2 from lecture 11 to lecture 20 June 14, 2016 Lecture 11 1. Take a look at Apollonius Conics in the appendices. 2. UseCalculus toproveapropertyinapollonius book: LetC beapointonahyperbola. Let
The Computation of π by Archimedes. Bill McKeeman Dartmouth College
 The Computation of π by Archimedes Bill McKeeman Dartmouth College 2012.02.15 Abstract It is famously known that Archimedes approximated π by computing the perimeters of manysided regular polygons, one
The Computation of π by Archimedes Bill McKeeman Dartmouth College 2012.02.15 Abstract It is famously known that Archimedes approximated π by computing the perimeters of manysided regular polygons, one
Connections between Geometry and Number Theory
 techspace Connections between Geometry and Number Theory Some oddities of the number 7 A well-known fact is that a week has 7 days. In six days God made the heaven and the earth, the sea, and all that
techspace Connections between Geometry and Number Theory Some oddities of the number 7 A well-known fact is that a week has 7 days. In six days God made the heaven and the earth, the sea, and all that
Indian Mathematicians and Their Contributions
 Indian Mathematicians and Their Contributions By: G. Nagamani M.sc,M.Ed Teacher, Nalgonda-Telangana State ABSTRACT Indian mathematics has its roots in Vedic literature. Between 1000 B.C. and 1800 A.D.
Indian Mathematicians and Their Contributions By: G. Nagamani M.sc,M.Ed Teacher, Nalgonda-Telangana State ABSTRACT Indian mathematics has its roots in Vedic literature. Between 1000 B.C. and 1800 A.D.
In today s world, people with basic calculus knowledge take the subject for granted. As
 Ziya Chen Math 4388 Shanyu Ji Calculus In today s world, people with basic calculus knowledge take the subject for granted. As long as they plug in numbers into the right formula and do the calculation
Ziya Chen Math 4388 Shanyu Ji Calculus In today s world, people with basic calculus knowledge take the subject for granted. As long as they plug in numbers into the right formula and do the calculation
Phasor mathematics. Resources and methods for learning about these subjects (list a few here, in preparation for your research):
 Phasor mathematics This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Phasor mathematics This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Basic Ideas in Greek Mathematics
 previous index next Basic Ideas in Greek Mathematics Michael Fowler UVa Physics Department Closing in on the Square Root of 2 In our earlier discussion of the irrationality of the square root of 2, we
previous index next Basic Ideas in Greek Mathematics Michael Fowler UVa Physics Department Closing in on the Square Root of 2 In our earlier discussion of the irrationality of the square root of 2, we
On Various Ways of Approximating the Quadrature of a Circle by Numbers. 1 Author Leonh. Euler
 On Various Ways of Approximating the Quadrature of a Circle by Numbers. Author Leonh. Euler Translated and Annotated by Thomas W. Polaski. Archimedes and those who followed him investigated the approximate
On Various Ways of Approximating the Quadrature of a Circle by Numbers. Author Leonh. Euler Translated and Annotated by Thomas W. Polaski. Archimedes and those who followed him investigated the approximate
SYMMETRIES AND COUNTING
 SYMMETRIES AND COUNTING I. COUNTING BRACELETS Problem 1. (a) How many different ways can you color the circles in this figure black and white? (There are pages with copies of this figure attached at the
SYMMETRIES AND COUNTING I. COUNTING BRACELETS Problem 1. (a) How many different ways can you color the circles in this figure black and white? (There are pages with copies of this figure attached at the
Chapter 1. Introduction
 Chapter 1 Introduction 1.1 Areas Modern integration theory is the culmination of centuries of refinements and extensions of ideas dating back to the Greeks. It evolved from the ancient problem of calculating
Chapter 1 Introduction 1.1 Areas Modern integration theory is the culmination of centuries of refinements and extensions of ideas dating back to the Greeks. It evolved from the ancient problem of calculating
Let π and e be trancendental numbers and consider the case:
 Jonathan Henderson Abstract: The proposed question, Is π + e an irrational number is a pressing point in modern mathematics. With the first definition of transcendental numbers coming in the 1700 s there
Jonathan Henderson Abstract: The proposed question, Is π + e an irrational number is a pressing point in modern mathematics. With the first definition of transcendental numbers coming in the 1700 s there
Take It To The Limit. Calculus H Mr. Russo Reaction to Take It To The Limit
 Calculus H Mr. Russo Reaction to Take It To The Limit For Tuesday, I am asking you to read the article below, Take It To The Limit by Steven Strogatz, and to write a brief reaction paper to this reading.
Calculus H Mr. Russo Reaction to Take It To The Limit For Tuesday, I am asking you to read the article below, Take It To The Limit by Steven Strogatz, and to write a brief reaction paper to this reading.
We saw in Section 5.1 that a limit of the form. arises when we compute an area.
 INTEGRALS 5 INTEGRALS Equation 1 We saw in Section 5.1 that a limit of the form n lim f ( x *) x n i 1 i lim[ f ( x *) x f ( x *) x... f ( x *) x] n 1 2 arises when we compute an area. n We also saw that
INTEGRALS 5 INTEGRALS Equation 1 We saw in Section 5.1 that a limit of the form n lim f ( x *) x n i 1 i lim[ f ( x *) x f ( x *) x... f ( x *) x] n 1 2 arises when we compute an area. n We also saw that
CHAPTER 1 NUMBER SYSTEMS. 1.1 Introduction
 N UMBER S YSTEMS NUMBER SYSTEMS CHAPTER. Introduction In your earlier classes, you have learnt about the number line and how to represent various types of numbers on it (see Fig..). Fig.. : The number
N UMBER S YSTEMS NUMBER SYSTEMS CHAPTER. Introduction In your earlier classes, you have learnt about the number line and how to represent various types of numbers on it (see Fig..). Fig.. : The number
Infinity and Infinite Series
 Infinity and Infinite Series Numbers rule the Universe Pythagoras (-580-500 BC) God is a geometer Plato (-427-347 BC) God created everything by numbers Isaac Newton (1642-1727) The Great Architect of
Infinity and Infinite Series Numbers rule the Universe Pythagoras (-580-500 BC) God is a geometer Plato (-427-347 BC) God created everything by numbers Isaac Newton (1642-1727) The Great Architect of
The Dynamics of Continued Fractions
 The Dynamics of Continued Fractions Evan O Dorney May 3, 20 The Story I was first introduced to the Intel Science Talent Search in ninth grade. I knew I would have no trouble entering this contest, as
The Dynamics of Continued Fractions Evan O Dorney May 3, 20 The Story I was first introduced to the Intel Science Talent Search in ninth grade. I knew I would have no trouble entering this contest, as
Mathematical Induction. Part Two
 Mathematical Induction Part Two Announcements Problem Set due Friday, January 8 at the start of class. Problem Set checkpoints graded, will be returned at end of lecture. Afterwards, will be available
Mathematical Induction Part Two Announcements Problem Set due Friday, January 8 at the start of class. Problem Set checkpoints graded, will be returned at end of lecture. Afterwards, will be available
UNM - PNM STATEWIDE MATHEMATICS CONTEST. February 2, 2019 Second Round Three Hours
 UNM - PNM STTEWIDE MTHEMTICS CONTEST February, 09 Second Round Three Hours. certain bacterium splits into two identical bacteria every second. flask containing one such bacterium gets filled with the bacteria
UNM - PNM STTEWIDE MTHEMTICS CONTEST February, 09 Second Round Three Hours. certain bacterium splits into two identical bacteria every second. flask containing one such bacterium gets filled with the bacteria
How can you find decimal approximations of square roots that are not rational? ACTIVITY: Approximating Square Roots
 . Approximating Square Roots How can you find decimal approximations of square roots that are not rational? ACTIVITY: Approximating Square Roots Work with a partner. Archimedes was a Greek mathematician,
. Approximating Square Roots How can you find decimal approximations of square roots that are not rational? ACTIVITY: Approximating Square Roots Work with a partner. Archimedes was a Greek mathematician,
10.1 Radical Expressions and Functions Math 51 Professor Busken
 0. Radical Expressions and Functions Math 5 Professor Busken Objectives Find square roots without a calculator Simplify expressions of the form n a n Evaluate radical functions and find the domain of radical
0. Radical Expressions and Functions Math 5 Professor Busken Objectives Find square roots without a calculator Simplify expressions of the form n a n Evaluate radical functions and find the domain of radical
1.1.1 Algebraic Operations
 1.1.1 Algebraic Operations We need to learn how our basic algebraic operations interact. When confronted with many operations, we follow the order of operations: Parentheses Exponentials Multiplication
1.1.1 Algebraic Operations We need to learn how our basic algebraic operations interact. When confronted with many operations, we follow the order of operations: Parentheses Exponentials Multiplication
CHAPTER 1 NUMBER SYSTEMS. 1.1 Introduction
 N UMBER S YSTEMS NUMBER SYSTEMS CHAPTER. Introduction In your earlier classes, you have learnt about the number line and how to represent various types of numbers on it (see Fig..). Fig.. : The number
N UMBER S YSTEMS NUMBER SYSTEMS CHAPTER. Introduction In your earlier classes, you have learnt about the number line and how to represent various types of numbers on it (see Fig..). Fig.. : The number
Calculus (Math 1A) Lecture 4
 Calculus (Math 1A) Lecture 4 Vivek Shende August 30, 2017 Hello and welcome to class! Hello and welcome to class! Last time Hello and welcome to class! Last time We discussed shifting, stretching, and
Calculus (Math 1A) Lecture 4 Vivek Shende August 30, 2017 Hello and welcome to class! Hello and welcome to class! Last time Hello and welcome to class! Last time We discussed shifting, stretching, and
Pell s Equation Claire Larkin
 Pell s Equation is a Diophantine equation in the form: Pell s Equation Claire Larkin The Equation x 2 dy 2 = where x and y are both integer solutions and n is a positive nonsquare integer. A diophantine
Pell s Equation is a Diophantine equation in the form: Pell s Equation Claire Larkin The Equation x 2 dy 2 = where x and y are both integer solutions and n is a positive nonsquare integer. A diophantine
Calculus (Math 1A) Lecture 4
 Calculus (Math 1A) Lecture 4 Vivek Shende August 31, 2017 Hello and welcome to class! Last time We discussed shifting, stretching, and composition. Today We finish discussing composition, then discuss
Calculus (Math 1A) Lecture 4 Vivek Shende August 31, 2017 Hello and welcome to class! Last time We discussed shifting, stretching, and composition. Today We finish discussing composition, then discuss
Key competencies (student abilities)
 Year 9 Mathematics Cambridge IGCSE Mathematics is accepted by universities and employers as proof of mathematical knowledge and understanding. Successful Cambridge IGCSE Mathematics candidates gain lifelong
Year 9 Mathematics Cambridge IGCSE Mathematics is accepted by universities and employers as proof of mathematical knowledge and understanding. Successful Cambridge IGCSE Mathematics candidates gain lifelong
Sets. 1.1 What is a set?
 Section 1 Sets 1 Sets After working through this section, you should be able to: (a) use set notation; (b) determine whether two given sets are equal and whether one given set is a subset of another; (c)
Section 1 Sets 1 Sets After working through this section, you should be able to: (a) use set notation; (b) determine whether two given sets are equal and whether one given set is a subset of another; (c)
Natural Numbers: Also called the counting numbers The set of natural numbers is represented by the symbol,.
 Name Period Date: Topic: Real Numbers and Their Graphs Standard: 9-12.A.1.3 Objective: Essential Question: What is the significance of a point on a number line? Determine the relative position on the number
Name Period Date: Topic: Real Numbers and Their Graphs Standard: 9-12.A.1.3 Objective: Essential Question: What is the significance of a point on a number line? Determine the relative position on the number
Algebra 2 Semester Test Review
 Algebra 2 Semester Test Review Name This semester review covers everything from Semester 1. It is due. You will have a semester test that covers everything from the semester on. This packet is meant as
Algebra 2 Semester Test Review Name This semester review covers everything from Semester 1. It is due. You will have a semester test that covers everything from the semester on. This packet is meant as
The number π. Rajendra Bhatia. December 20, Indian Statistical Institute, Delhi India 1 / 78
 1 / 78 The number π Rajendra Bhatia Indian Statistical Institute, Delhi India December 20, 2012 2 / 78 CORE MATHEMATICS Nature of Mathematics Reasoning and Proofs in Mathematics History of Mathematics
1 / 78 The number π Rajendra Bhatia Indian Statistical Institute, Delhi India December 20, 2012 2 / 78 CORE MATHEMATICS Nature of Mathematics Reasoning and Proofs in Mathematics History of Mathematics
Math Practice Exam 2 - solutions
 C Roettger, Fall 205 Math 66 - Practice Exam 2 - solutions State clearly what your result is. Show your work (in particular, integrand and limits of integrals, all substitutions, names of tests used, with
C Roettger, Fall 205 Math 66 - Practice Exam 2 - solutions State clearly what your result is. Show your work (in particular, integrand and limits of integrals, all substitutions, names of tests used, with
1 Continued Fractions
 Continued Fractions To start off the course, we consider a generalization of the Euclidean Algorithm which has ancient historical roots and yet still has relevance and applications today.. Continued Fraction
Continued Fractions To start off the course, we consider a generalization of the Euclidean Algorithm which has ancient historical roots and yet still has relevance and applications today.. Continued Fraction
MA 180 Lecture. Chapter 0. College Algebra and Calculus by Larson/Hodgkins. Fundamental Concepts of Algebra
 0.) Real Numbers: Order and Absolute Value Definitions: Set: is a collection of objections in mathematics Real Numbers: set of numbers used in arithmetic MA 80 Lecture Chapter 0 College Algebra and Calculus
0.) Real Numbers: Order and Absolute Value Definitions: Set: is a collection of objections in mathematics Real Numbers: set of numbers used in arithmetic MA 80 Lecture Chapter 0 College Algebra and Calculus
GAUSS CIRCLE PROBLEM
 GAUSS CIRCLE PROBLEM 1. Gauss circle problem We begin with a very classical problem: how many lattice points lie on or inside the circle centered at the origin and with radius r? (In keeping with the classical
GAUSS CIRCLE PROBLEM 1. Gauss circle problem We begin with a very classical problem: how many lattice points lie on or inside the circle centered at the origin and with radius r? (In keeping with the classical
Mu Alpha Theta State 2007 Euclidean Circles
 Mu Alpha Theta State 2007 Euclidean Circles 1. Joe had a bet with Mr. Federer saying that if Federer can solve the following problem in one minute, Joe would be his slave for a whole month. The problem
Mu Alpha Theta State 2007 Euclidean Circles 1. Joe had a bet with Mr. Federer saying that if Federer can solve the following problem in one minute, Joe would be his slave for a whole month. The problem
4 Pictorial proofs. 1. I convert 40 C to Fahrenheit: = I react: Wow, 104 F. That s dangerous! Get thee to a doctor!
 4 Pictorial proofs 4. Adding odd numbers 58 4. Arithmetic and geometric means 60 4. Approximating the logarithm 66 4.4 Bisecting a triangle 70 4.5 Summing series 7 4.6 Summary and further problems 75 Have
4 Pictorial proofs 4. Adding odd numbers 58 4. Arithmetic and geometric means 60 4. Approximating the logarithm 66 4.4 Bisecting a triangle 70 4.5 Summing series 7 4.6 Summary and further problems 75 Have
( ) = 28. 2r = d 2 = = r d = r. 2 = r or 1. Free Pre-Algebra Lesson 33! page 1. Lesson 33 Formulas for Circles
 Free Pre-Algebra Lesson 33! page 1 Lesson 33 Formulas for Circles What is a Circle? Everyone knows what a circle looks like. A sprinkler line rotates around a center pivot, forming circles of irrigated
Free Pre-Algebra Lesson 33! page 1 Lesson 33 Formulas for Circles What is a Circle? Everyone knows what a circle looks like. A sprinkler line rotates around a center pivot, forming circles of irrigated
Discrete Mathematics. (c) Marcin Sydow. Sets. Set operations. Sets. Set identities Number sets. Pair. Power Set. Venn diagrams
 Contents : basic definitions and notation A set is an unordered collection of its elements (or members). The set is fully specified by its elements. Usually capital letters are used to name sets and lowercase
Contents : basic definitions and notation A set is an unordered collection of its elements (or members). The set is fully specified by its elements. Usually capital letters are used to name sets and lowercase
A Presentation By: Charlotte Lenz
 A Presentation By: Charlotte Lenz http://www.math.nyu.edu/~crorres/archimedes/pictures/ ArchimedesPictures.html Born: 287 BC to an Astronomer named Phidias Grew up in Syracuse, Sicily Only left Sicily
A Presentation By: Charlotte Lenz http://www.math.nyu.edu/~crorres/archimedes/pictures/ ArchimedesPictures.html Born: 287 BC to an Astronomer named Phidias Grew up in Syracuse, Sicily Only left Sicily
PHASE 9 Ali PERFECT ALI-PI.
 PHASE 9 PERFECT ALI-PI Pi as a Fraction pi is written and expressed as definite fraction and ratio of two numbers: pi = 19 /6 = 3.16666666. pi = 3 + 1/6 Any rational number which cannot be expressed as
PHASE 9 PERFECT ALI-PI Pi as a Fraction pi is written and expressed as definite fraction and ratio of two numbers: pi = 19 /6 = 3.16666666. pi = 3 + 1/6 Any rational number which cannot be expressed as
Some Elementary Problems (Solved and Unsolved) in Number Theory and Geometry
 Some Elementary Problems (Solved and Unsolved) in Number Theory and Geometry Paul Erdös The Hungarian Academy of Science and Technion, Haifa Dedicated to the memory of Prof. J. Gillis Mathematics is full
Some Elementary Problems (Solved and Unsolved) in Number Theory and Geometry Paul Erdös The Hungarian Academy of Science and Technion, Haifa Dedicated to the memory of Prof. J. Gillis Mathematics is full
Robert McGee, Professor Emeritus, Cabrini College Carol Serotta, Cabrini College Kathleen Acker, Ph.D.
 Robert McGee, Professor Emeritus, Cabrini College Carol Serotta, Cabrini College Kathleen Acker, Ph.D. 1 2 At the end of about 18 pages of discussion of the history of Chinese mathematics, Victor Katz
Robert McGee, Professor Emeritus, Cabrini College Carol Serotta, Cabrini College Kathleen Acker, Ph.D. 1 2 At the end of about 18 pages of discussion of the history of Chinese mathematics, Victor Katz
Math 137 Calculus 1 for Honours Mathematics. Course Notes
 Math 37 Calculus for Honours Mathematics Course Notes Barbara A. Forrest and Brian E. Forrest Fall 07 / Version. Copyright c Barbara A. Forrest and Brian E. Forrest. All rights reserved. August, 07 All
Math 37 Calculus for Honours Mathematics Course Notes Barbara A. Forrest and Brian E. Forrest Fall 07 / Version. Copyright c Barbara A. Forrest and Brian E. Forrest. All rights reserved. August, 07 All
For math conventions used on the GRE, refer to this link:
 GRE Review ISU Student Success Center Quantitative Workshop One Quantitative Section: Overview Your test will include either two or three 35-minute quantitative sections. There will be 20 questions in
GRE Review ISU Student Success Center Quantitative Workshop One Quantitative Section: Overview Your test will include either two or three 35-minute quantitative sections. There will be 20 questions in
SAT & ACT Foundations
 E SAT & ACT Foundations SA M PL MATHEMATICS (800) MY TUTOR Focusing on the Individual Student MYTUTOR.COM Copyright Statement The ACT & SAT Skills Book, along with all Summit Educational Group Course Materials,
E SAT & ACT Foundations SA M PL MATHEMATICS (800) MY TUTOR Focusing on the Individual Student MYTUTOR.COM Copyright Statement The ACT & SAT Skills Book, along with all Summit Educational Group Course Materials,
Counting Methods. CSE 191, Class Note 05: Counting Methods Computer Sci & Eng Dept SUNY Buffalo
 Counting Methods CSE 191, Class Note 05: Counting Methods Computer Sci & Eng Dept SUNY Buffalo c Xin He (University at Buffalo) CSE 191 Discrete Structures 1 / 48 Need for Counting The problem of counting
Counting Methods CSE 191, Class Note 05: Counting Methods Computer Sci & Eng Dept SUNY Buffalo c Xin He (University at Buffalo) CSE 191 Discrete Structures 1 / 48 Need for Counting The problem of counting
GEOMETRICAL DEFINITION OF π AND ITS APPROXIMATIONS BY NESTED RADICALS. Milan Janjić. 1. Introduction
 THE TECHING OF THETICS 008, Vol. XI,, pp. 5 34 GEOETRICL DEFINITION OF π ND ITS PPROXITIONS Y NESTED RDICLS ilan Janjić bstract. In this paper the length of the arc of a circle and the area of a circular
THE TECHING OF THETICS 008, Vol. XI,, pp. 5 34 GEOETRICL DEFINITION OF π ND ITS PPROXITIONS Y NESTED RDICLS ilan Janjić bstract. In this paper the length of the arc of a circle and the area of a circular
Understanding and Using Variables
 Algebra is a powerful tool for understanding the world. You can represent ideas and relationships using symbols, tables and graphs. In this section you will learn about Understanding and Using Variables
Algebra is a powerful tool for understanding the world. You can represent ideas and relationships using symbols, tables and graphs. In this section you will learn about Understanding and Using Variables
Chapter 1 Test Review
 Name Per ID: A Chapter 1 Test Review Short Answer Insert , or = to make the sentence true. 1. 7 12 2. 5 9 1 8 3. 16 + 6 8 + 7 Name the property of real numbers illustrated by the equation. 4. 2(x +
Name Per ID: A Chapter 1 Test Review Short Answer Insert , or = to make the sentence true. 1. 7 12 2. 5 9 1 8 3. 16 + 6 8 + 7 Name the property of real numbers illustrated by the equation. 4. 2(x +
A History of Modern Mathematical Symbols (In Twenty Slides)
 A History of Modern Mathematical Symbols (In Twenty Slides) Jeremiah A. Gilbert, Ph.D. Associate Professor, Mathematics San Bernardino Valley College + These symbols first appeared in print in a text by
A History of Modern Mathematical Symbols (In Twenty Slides) Jeremiah A. Gilbert, Ph.D. Associate Professor, Mathematics San Bernardino Valley College + These symbols first appeared in print in a text by
Methods in Mathematics
 Write your name here Surname Other names Edexcel GCSE Centre Number Candidate Number Methods in Mathematics Unit 2: Methods 2 For Approved Pilot Centres ONLY Foundation Tier Tuesday 21 June 2011 Morning
Write your name here Surname Other names Edexcel GCSE Centre Number Candidate Number Methods in Mathematics Unit 2: Methods 2 For Approved Pilot Centres ONLY Foundation Tier Tuesday 21 June 2011 Morning
Chapter 1/3 Rational Inequalities and Rates of Change
 Chapter 1/3 Rational Inequalities and Rates of Change Lesson Package MHF4U Chapter 1/3 Outline Unit Goal: By the end of this unit, you will be able to solve rational equations and inequalities algebraically.
Chapter 1/3 Rational Inequalities and Rates of Change Lesson Package MHF4U Chapter 1/3 Outline Unit Goal: By the end of this unit, you will be able to solve rational equations and inequalities algebraically.
Math Requirements for applicants by Innopolis University
 Math Requirements for applicants by Innopolis University Contents 1: Algebra... 2 1.1 Numbers, roots and exponents... 2 1.2 Basics of trigonometry... 2 1.3 Logarithms... 2 1.4 Transformations of expressions...
Math Requirements for applicants by Innopolis University Contents 1: Algebra... 2 1.1 Numbers, roots and exponents... 2 1.2 Basics of trigonometry... 2 1.3 Logarithms... 2 1.4 Transformations of expressions...
Circles. II. Radius - a segment with one endpoint the center of a circle and the other endpoint on the circle.
 Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
Circles Circles and Basic Terminology I. Circle - the set of all points in a plane that are a given distance from a given point (called the center) in the plane. Circles are named by their center. II.
Euler s Identity: why and how does e πi = 1?
 Euler s Identity: why and how does e πi = 1? Abstract In this dissertation, I want to show how e " = 1, reviewing every element that makes this possible and explore various examples of explaining this
Euler s Identity: why and how does e πi = 1? Abstract In this dissertation, I want to show how e " = 1, reviewing every element that makes this possible and explore various examples of explaining this
Problem 1. Solve the equation 3 x + 9 x = 27 x. Solution: 3 x + 3 2x = 3 3x. Denote: y = 3 x, then. y + y 2 = y 3. y 3 y 2 y = 0. y(y 2 y 1) = 0.
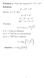 Problem 1. Solve the equation 3 x + 9 x = 7 x. Solution: 3 x + 3 x = 3 3x. Denote: y = 3 x, then Therefore, y + y = y 3. y 3 y y = 0. y(y y 1) = 0. y = 0 or y = 1 ± 5. i) 3 x = 0 has no solutions, ii)
Problem 1. Solve the equation 3 x + 9 x = 7 x. Solution: 3 x + 3 x = 3 3x. Denote: y = 3 x, then Therefore, y + y = y 3. y 3 y y = 0. y(y y 1) = 0. y = 0 or y = 1 ± 5. i) 3 x = 0 has no solutions, ii)
Math 3 Quarter 4 Overview
 Math 3 Quarter 4 Overview EO5 Rational Functions 13% EO6 Circles & Circular Functions 25% EO7 Inverse Functions 25% EO8 Normal Distribution 12% Q4 Final 10% EO5 Opp #1 Fri, Mar 24th Thu, Mar 23rd ML EO5
Math 3 Quarter 4 Overview EO5 Rational Functions 13% EO6 Circles & Circular Functions 25% EO7 Inverse Functions 25% EO8 Normal Distribution 12% Q4 Final 10% EO5 Opp #1 Fri, Mar 24th Thu, Mar 23rd ML EO5
2.2 Some Consequences of the Completeness Axiom
 60 CHAPTER 2. IMPORTANT PROPERTIES OF R 2.2 Some Consequences of the Completeness Axiom In this section, we use the fact that R is complete to establish some important results. First, we will prove that
60 CHAPTER 2. IMPORTANT PROPERTIES OF R 2.2 Some Consequences of the Completeness Axiom In this section, we use the fact that R is complete to establish some important results. First, we will prove that
Chapter 1. Areas, volumes and simple sums Summation notation. Answer the following questions:
 Chapter 1 Areas, volumes and simple sums 1.1 Answer the following questions: (a) What is the value of the fifth term of the sum S = 20 (5 + 3k)/k? (b) How many terms are there in total in the sum S = 17
Chapter 1 Areas, volumes and simple sums 1.1 Answer the following questions: (a) What is the value of the fifth term of the sum S = 20 (5 + 3k)/k? (b) How many terms are there in total in the sum S = 17
Integrated Mathematics I, II, III 2016 Scope and Sequence
 Mathematics I, II, III 2016 Scope and Sequence I Big Ideas Math 2016 Mathematics I, II, and III Scope and Sequence Number and Quantity The Real Number System (N-RN) Properties of exponents to rational
Mathematics I, II, III 2016 Scope and Sequence I Big Ideas Math 2016 Mathematics I, II, and III Scope and Sequence Number and Quantity The Real Number System (N-RN) Properties of exponents to rational
Constructions with ruler and compass.
 Constructions with ruler and compass. Semyon Alesker. 1 Introduction. Let us assume that we have a ruler and a compass. Let us also assume that we have a segment of length one. Using these tools we can
Constructions with ruler and compass. Semyon Alesker. 1 Introduction. Let us assume that we have a ruler and a compass. Let us also assume that we have a segment of length one. Using these tools we can
5.3 Multiplying Decimals
 370 CHAPTER 5. DECIMALS 5.3 Multiplying Decimals Multiplying decimal numbers involves two steps: (1) multiplying the numbers as whole numbers, ignoring the decimal point, and (2) placing the decimal point
370 CHAPTER 5. DECIMALS 5.3 Multiplying Decimals Multiplying decimal numbers involves two steps: (1) multiplying the numbers as whole numbers, ignoring the decimal point, and (2) placing the decimal point
MSM 707 Number Systems for Middle School Teachers Semester Project
 MSM 707 Number Systems for Middle School Teachers Semester Project During the course of the semester, we will discuss some important concepts of Number Theory. The following projects are designed to give
MSM 707 Number Systems for Middle School Teachers Semester Project During the course of the semester, we will discuss some important concepts of Number Theory. The following projects are designed to give
LECTURE 22: COUNTABLE AND UNCOUNTABLE SETS
 LECTURE 22: COUNTABLE AND UNCOUNTABLE SETS 1. Introduction To end the course we will investigate various notions of size associated to subsets of R. The simplest example is that of cardinality - a very
LECTURE 22: COUNTABLE AND UNCOUNTABLE SETS 1. Introduction To end the course we will investigate various notions of size associated to subsets of R. The simplest example is that of cardinality - a very
1 5 π 2. 5 π 3. 5 π π x. 5 π 4. Figure 1: We need calculus to find the area of the shaded region.
 . Area In order to quantify the size of a 2-dimensional object, we use area. Since we measure area in square units, we can think of the area of an object as the number of such squares it fills up. Using
. Area In order to quantify the size of a 2-dimensional object, we use area. Since we measure area in square units, we can think of the area of an object as the number of such squares it fills up. Using
Chapter 0. Introduction. An Overview of the Course
 Chapter 0 Introduction An Overview of the Course In the first part of these notes we consider the problem of calculating the areas of various plane figures. The technique we use for finding the area of
Chapter 0 Introduction An Overview of the Course In the first part of these notes we consider the problem of calculating the areas of various plane figures. The technique we use for finding the area of
Class 8: Numbers Exercise 3B
 Class : Numbers Exercise B 1. Compare the following pairs of rational numbers: 1 1 i First take the LCM of. LCM = 96 Therefore: 1 = 96 Hence we see that < 6 96 96 1 1 1 1 = 6 96 1 or we can say that
Class : Numbers Exercise B 1. Compare the following pairs of rational numbers: 1 1 i First take the LCM of. LCM = 96 Therefore: 1 = 96 Hence we see that < 6 96 96 1 1 1 1 = 6 96 1 or we can say that
Secondary 1 - Secondary 3 CCSS Vocabulary Word List Revised Vocabulary Word Sec 1 Sec 2 Sec 3 absolute value equation
 Vocabulary Word Sec 1 Sec 2 Sec 3 absolute value equation (optional) absolute value function absolute value inequality (optional) acute angle addition rule algebraic representation alternate exterior angles
Vocabulary Word Sec 1 Sec 2 Sec 3 absolute value equation (optional) absolute value function absolute value inequality (optional) acute angle addition rule algebraic representation alternate exterior angles
College Algebra. Basics to Theory of Equations. Chapter Goals and Assessment. John J. Schiller and Marie A. Wurster. Slide 1
 College Algebra Basics to Theory of Equations Chapter Goals and Assessment John J. Schiller and Marie A. Wurster Slide 1 Chapter R Review of Basic Algebra The goal of this chapter is to make the transition
College Algebra Basics to Theory of Equations Chapter Goals and Assessment John J. Schiller and Marie A. Wurster Slide 1 Chapter R Review of Basic Algebra The goal of this chapter is to make the transition
FLORIDA STANDARDS TO BOOK CORRELATION FOR GRADE 7 ADVANCED
 FLORIDA STANDARDS TO BOOK CORRELATION FOR GRADE 7 ADVANCED After a standard is introduced, it is revisited many times in subsequent activities, lessons, and exercises. Domain: The Number System 8.NS.1.1
FLORIDA STANDARDS TO BOOK CORRELATION FOR GRADE 7 ADVANCED After a standard is introduced, it is revisited many times in subsequent activities, lessons, and exercises. Domain: The Number System 8.NS.1.1
184/09 MATHEMATICS HIGHER TIER PAPER 1. P.M. MONDAY, 4 June (2 Hours) CALCULATORS ARE NOT TO BE USED FOR THIS PAPER
 Candidate Name Centre Number Candidate Number WELSH JOINT EDUCATION COMMITTEE General Certificate of Secondary Education CYD-BWYLLGOR ADDYSG CYMRU Tystysgrif Gyffredinol Addysg Uwchradd 184/09 MATHEMATICS
Candidate Name Centre Number Candidate Number WELSH JOINT EDUCATION COMMITTEE General Certificate of Secondary Education CYD-BWYLLGOR ADDYSG CYMRU Tystysgrif Gyffredinol Addysg Uwchradd 184/09 MATHEMATICS
MATH Spring 2010 Topics per Section
 MATH 101 - Spring 2010 Topics per Section Chapter 1 : These are the topics in ALEKS covered by each Section of the book. Section 1.1 : Section 1.2 : Ordering integers Plotting integers on a number line
MATH 101 - Spring 2010 Topics per Section Chapter 1 : These are the topics in ALEKS covered by each Section of the book. Section 1.1 : Section 1.2 : Ordering integers Plotting integers on a number line
Introduction to Trigonometry: Grade 9
 Introduction to Trigonometry: Grade 9 Andy Soper October 6, 2013 This document was constructed and type-set using P C T E X (a dielect of L A T E X) 1 1 Before you start 1.1 About these notes. These notes
Introduction to Trigonometry: Grade 9 Andy Soper October 6, 2013 This document was constructed and type-set using P C T E X (a dielect of L A T E X) 1 1 Before you start 1.1 About these notes. These notes
Atomic Theories Chapter 4.1. How do we know about atoms when no one has ever seen inside an atom?
 Atomic Theories Chapter 4.1 How do we know about atoms when no one has ever seen inside an atom? Greek Philosopher Democritus Lived 460 370 BCE Believed it is IMPOSSIBLE to divide matter ad infinitum.
Atomic Theories Chapter 4.1 How do we know about atoms when no one has ever seen inside an atom? Greek Philosopher Democritus Lived 460 370 BCE Believed it is IMPOSSIBLE to divide matter ad infinitum.
CONTENTS NUMBER SYSTEMS. Number Systems
 NUMBER SYSTEMS CONTENTS Introduction Classification of Numbers Natural Numbers Whole Numbers Integers Rational Numbers Decimal expansion of rational numbers Terminating decimal Terminating and recurring
NUMBER SYSTEMS CONTENTS Introduction Classification of Numbers Natural Numbers Whole Numbers Integers Rational Numbers Decimal expansion of rational numbers Terminating decimal Terminating and recurring
Chapter 9: Roots and Irrational Numbers
 Chapter 9: Roots and Irrational Numbers Index: A: Square Roots B: Irrational Numbers C: Square Root Functions & Shifting D: Finding Zeros by Completing the Square E: The Quadratic Formula F: Quadratic
Chapter 9: Roots and Irrational Numbers Index: A: Square Roots B: Irrational Numbers C: Square Root Functions & Shifting D: Finding Zeros by Completing the Square E: The Quadratic Formula F: Quadratic
2. Two binary operations (addition, denoted + and multiplication, denoted
 Chapter 2 The Structure of R The purpose of this chapter is to explain to the reader why the set of real numbers is so special. By the end of this chapter, the reader should understand the difference between
Chapter 2 The Structure of R The purpose of this chapter is to explain to the reader why the set of real numbers is so special. By the end of this chapter, the reader should understand the difference between
Metric spaces and metrizability
 1 Motivation Metric spaces and metrizability By this point in the course, this section should not need much in the way of motivation. From the very beginning, we have talked about R n usual and how relatively
1 Motivation Metric spaces and metrizability By this point in the course, this section should not need much in the way of motivation. From the very beginning, we have talked about R n usual and how relatively
Years, Calendars and Continued Fractions
 Years, Calendars and Continued Fractions Chris Sawer Liverpool University Maths Club, 6th January 00 Everybody is familiar with π, the ratio of a circle s diameter to its circumference; a little larger
Years, Calendars and Continued Fractions Chris Sawer Liverpool University Maths Club, 6th January 00 Everybody is familiar with π, the ratio of a circle s diameter to its circumference; a little larger
LECTURE 10: REVIEW OF POWER SERIES. 1. Motivation
 LECTURE 10: REVIEW OF POWER SERIES By definition, a power series centered at x 0 is a series of the form where a 0, a 1,... and x 0 are constants. For convenience, we shall mostly be concerned with the
LECTURE 10: REVIEW OF POWER SERIES By definition, a power series centered at x 0 is a series of the form where a 0, a 1,... and x 0 are constants. For convenience, we shall mostly be concerned with the
