Solutions Manual for Introductory Linear Algebra
|
|
|
- Ethel Holland
- 5 years ago
- Views:
Transcription
1 جايعت انقذس ان فتىحت QUDS OPEN UNIVESITY Solutions Mnul for Introdutor iner lger uthordrmhmoud l-bei
2 l-quds Open Universit SolutionsMnul forintrodutor iner lger uthordrmhmoud l-bei Evlutor DrMuhtr l-shellh
3
4 Introdution The SolutionsMnul for Introdutor iner lger hs een prepredto e omplementr to the tetoo to help students to understnd the sientifi mteril In this Mnul there re mn eerises nd solutions on eh setion of eh units well s the glossr hs een prepred in oth ri nd English lnguges in ddition to the tle of ontents whih lso shows therequired mteril from the tetoo In ddition to this mnul nd the tetoo there is prtil Mnulfor Mthd nd QSBprogrms DrMhmoud l-bei pril
5
6 Tetoo Introdutor iner lger with pplitions Contents equired Mteril from The Tetoo Chpteriner Equtions nd Mtries Eerises 9 Eerises Eerises Eerises Eerises 6nswers to Eerises8 7Glossr 9 ChpterDeterminnts Eerises Eerises nswers to Eerises8 Glossr ChpterVetors nd Vetor Spes Eerises 9 Eerises Eerises Eerises
7 6Eerises 7Eerises 8nswers to Eerises 9 Glossr69 Chpteriner Trnsformtions nd Mtries Eerises 7 Eerises 7 Eerises 7 nswers to Eerises77 Glossr89 ChpterEigenvlues nd Eigenvetors Eerises 9 Eerises 9 nswers to Eerises96 Glossr 6 Chpter6iner Progrmming 6Eerises 6nswers to Eerises7 6 Glossr 6
8 7
9 8
10 Eerises Solve the given liner sstems the method of elimintion -=8 += ++= ++ =8 -+ = += - = + =7 n oil refiner proesses low-sulfur nd high-sulfur fueleh ton of low-sulfur fuel requires minutes in the lending plnt nd minutes in the refining plnteh ton of high sulfer fuel requires minutes in the plending plnt nd minutes in the refining plnt If the plending plnt is ville for houresnd the refining plnt is ville for houres how mn tons of eh tp of fuel should e mnuftured? dietiin is prepring mel onsisting of foods B nd CEh oune of food ontins units of protien units offt nd units of rohdrteeh unit of food B ontins units of protein units of ft nd unit of rohdrte Eh unit of food C ontins units of protein units of ft nd unit of rohdrteif the mel must provide etl units of protein units of ft nd units of rohdrtehow mn ounes of eh tpe of food should e used? 9
11 Eerises et C nd B If possile ompute B T C+ If d nd find d d Consider the following liner sstem 7 w Find the oeffiient mtri Write the liner sstem in mtri form Find the ugmented mtri Write the liner sstem with ugmented mtri? mnufturer mes two inds of produtsp nd Qt eh of two plnts nd YIn ming these produts the pollutnts sulfurdioidenitri oidend prtiulte mtter re produedthe mounts of pollutnts produed re given in ilogrms the mtri
12 SulfurNitriPrtiulte Dioideoidemtter ProdutP ProdutQ Sttend federl ordinnes require tht these pollutntse removedthe dil ost of removing eh ilogrm of pollutnt is given in dollrs the mtri Plnt Plnt Y 8 B 7 Sulfur 9 Nitri Prtiulte dioide Oide mtter Wht do the entries in the mtri ProdutB tell the mnufturer? 6 photogrph usiness hs store in eh of the following ities New YorDenvernd os ngelespriulr me of mer is ville in utomtisemiutomindnonutomtimodelsmoreovereh mer hs mthed flsh unit nd mer is usull sold together with the orresponding flsh unitthe selling pries of the mers nd flsh units re given in dollrs the mtri utomtisemiutomtinonutomti Cmer Flsh unit The numer of sets mer nd flshunit ville t eh store is given the mtri
13 New Yor Denver os ngeles B 8 utomti Semiutomti Noutomti Wht is the totl vlue of the Cmer in New Yor? Wht is the totl vlue of the flsh units in os ngeles? Eerises If nd B show tht B= 6 If nd B nd C show tht B = C Consider two qui food ompniesm nd NEh er ompnm eeps of its ustomerswhile swith to NEh er N eeps of its ustomerswhile swith to MSuppose tht the initil distriution of the mret is given Find the distriution of the mret fter er Find the stle distriution of the mret
14 et nd B e smmetri mtries Show tht +B is smmetri Show tht B is smmetri if nd onl ifb=b If is nnn mtri prove tht T nd T re smmetri + T is smmetri - T is sew smmetri Eerises Whih of the following mtries re in redued row ehelon form? B C D E F
15 G H et Find the mtries otined performing the followingelements row opertions on Interhnging the seond nd fourth rows Multipling the third row dding - times the first row to the fourth row If Find mtri Cin redued row ehelon form tht is row equivlent to Find ll solutions to the given liner sstem Find ll vlues of for whih the resulting of the following liner sstemhs
16 No solution unique solution Infinit mn solutions 6 Solve the liner sstem with thefollowing given ugmented mtri 7 furniture mnufturer mes hirs offee tles nd diningroom tles Eh hir requires minutes of snding 6 minutes of stining nd minutes of vrnishing Eh offee tle requires minutes of snding 8 minutesof stiningnd minutes of vrnishingeh dining room tle requires minutes of snding minutesof stiningnd 8 minutes of vrnishing The snding enh is ville 6 hours per wee the stining enh hours per wee nd the vrnishing enh 8 hours per wee How mn per wee of eh tpe of furniture should e mde? Eerises Show tht is non-singulr Show tht
17 6 is singulr Find the inverse of the following mtri if possile Whih of the following liner sstems hve nontrivil solution? Consider n industril proess whose mtri is Find the input mtri for the following output mtri C B
18 6For wht vlues of does the homogeneous sstem hve nontrivil solution? 7 Suppose tht nd B re squre mtries nd B=If B is nonsingulr find 8 et e nnmtriprove tht if is non-singulr then the homogeneous sstem =O hs trivil solution 7
19 8 8 8 se / 8 is solution The eqution ond the to dd Then eqution the Multipl Mens 6 8 / / 6 nswers to Eerises Eerises
20 / 6 + = / Suppose tht low- sulfur high- sulfurnd note tht hours = 6= minutes nd hours = 6=8 minutes 8
21 ton 6 / 8 ton Suppose tht food food B food C 9 / 7 7 / 9 Eerises 8 7 C B B T T 6 8 C B T
22 / / d d d d The oeffiient mtri is Theliner sstem in mtri form w = 7 C The ugmented mtri 7
23 7 6 8 For eh produt P or Q the dil ost of pollution ontrol t plnt or t Plnt Y 6 $ $6 Eerises 6 B
24 C B C B The informtion n edispled in mtri form s The distriution of the mret fter er is 9 9 o The stle distriution of the mret is += 7 7 +B is smmetri mtri if +B=+B T
25 +B T = T + B T But = T nd B = B T euse nd B re smmetri mtries so +B T = T + B T =+B - Suppose tht B=B B is smmetri mtri if B=B T B T =B T T =B=B B is smmetri mtri - Suppose thtb is smmetri mtri Te B=B T =B T T =B s oth nd B re smmetri mtries B B T issmmetri if T = T T T T = T T T = T Similrl for T + T is smmetri if + T =+ T T + T T = T T + T = + T - T is sew smmetri if - T = - - T T - - T T = - T - T T =- T +=- T Eerises EG
26 6 6 7 = =667 =-667
27 6 No solution unique solution Infinit mn solutions 6 =- = = - 7 et =numer of hirs =numer of offee tles = numer of dining room tles /
28 7 = = = Eerises is non-singulr mtri euse there eist mtri B suh tht B=B=I Suppose tht Is n inverse of Then Equting orresponding elements of these two mtries we otined the liner sstem d B I d d d B /
29 8 So this liner sstem hs no solution Hene there is no suh mtri B nd is singulr mtri = - B 6 C 6 B solution nontrivil hs sstem The Mtri Singulr solution nontrivil hs sstem The Mtri Singulr 7 7 7
30 7 B O B B O B O O 8 O O O 7Glossr يصفىفت Mtri يصفىفت صفريت mtri Zero يصفىفت يربعت Mtri Squre انشكم انصفي ان يز form edued ow Ehelon ان صفىفت انقطريت Mtri Digonl يصفىفت انىحذة Mtri Identit يصفىفت يثهثيت Mtri Tringulr يصفىفت ان عايالث Mtri Coeffiient ان صفىفت ان تذة Mtri ugmented ان ظاو انخطي Sstem iner ان ظير انضربي نه صفىفت يعكىس ان صفىفت Mtri Inverse of ي قىل ان صفىفت Mtri Trnspose of رتبت ان صفىفت Mtri n of ع هياث انصف انبسيظ Opertions Elementr ow 9
31
32
33
34 Eerises Find the numer of inversions in eh of following permuttions of s Determinte whether eh of the following permuttions of s Is even or odd Compute thefollowing determinnts If
35 Find the determinnts of the following mtries nd Evlute the following determinnts using the properties of this Setion B C D 6 8 B C
36 6 If nd B re mtries with Clulte nd B d B B T B e 7 Show tht if = - then 8Show tht if T = then 9 Show tht This determinnt is lled Vndermonde determinnt Eerises et Compute ll the oftors Compute the determinnts of the following mtries
37 6 et Find dj Compute Compute dj Compute the inverse of the following mtri Use theorem to determine whih of the following mtries re non-singulr B B 7 C
38 d D 6 Use Corollr to find out whether the following homogeneous sstems hve nontrivil solutions +-= ++= -+= +++w= -+-w= +++w= --+w= 7 Solve the following liner sstem Crmer's rule ++-w=- ++w= +-+w= -+w= 8 Prove tht dj n 7
39 nswers to Eerises Eerises five inversions Seven inversions Fourinversions evenn= Odd n= Even n= --=7 -=- B C 8 D
40 9 6 7 B B B B B B C
41 7 Eerises 7 7 B B B B B d T T e 9 8 T T 9 7
42 7 B
43 9 6 C 9 T C dj I dj 8 6 6
44 C T C dj dj Mtri Singulr Mtri Singulr B Mtri Singulr C Mtri gulr Non D d sin Solution Nontrivil Hs
45 7 8 Solution Trivil Hs B 6 w n n n n dj I dj I dj I dj
46 Glossr ان حذد ان ت ى نهع صر The Minor of ij ij ان تعايم Coftor ان حذد Determinnt قري ان صفىفت Mtri djoint of قاعذة كراي ر Crmer's ule
47 6
48 7
49 8
50 Eerises Determine the hed of the vetor whose til is t Determine the til of the vetor whose hed is t et = Y=-Z=nd U=-Find nd so tht Z= U Y Z U Find the length of the following vetors -- Find the distne etween pirs of points -- 6 Find unit vetor in the diretion of = 9
51 =- 7 Find Y =-Y= = Y = - 8 Write eh of the following vetors in terms of i nd j -- 9 ship is eing pushed tugot with fore of pounds long the negtive -is while nother tugot is pushing long the negtive -is with fore of ponds Find the mgnitude nd seth the diretion of the resultnt fore Eerises Find +Y-Y nd -Y if =-Y=- et =-Y=--Z=-nd U=uFind nd u so tht Z+Y= Z+U=Y Find the length of the following vetors - Find the distne etween the following pirs of points - -6 Find Y =Y=-
52 =-Y=-- 6Whih of the following vetors =6-8 =--- =--- = =- 6 =-re Orthogonl? Prllel? In the sme diretion? 7 Find unit vetor in the diretion of = - = 8Write eh of the following vetorsin in terms of ijnd - - 9Write eh of the following vetorsin s mtri i+j- i+j lrge steel mnufturer who hs emploees lists eh emploee's slr s omponent of vetor S in If n 8 perent ross-the-ord slr inrese hs een pproved find n epression involving S giving ll the new slries Eerises Determine whether thegiven set together with the given opertions is vetor spe If it is not vetor spe list the properties of Definition tht fil to hold The set of ll ordered triples of rel numers with the opertions nd
53 The set of ll ordered triples of rel numers of the form with the opertions nd The set of ll positive rel numers with the opertions nd Whih of the following susets of re suspes of? The set of ll vetors of the form dwhere -= dwhere =+ nd d=- dwhere = nd = -d Whih of the following susets of the vetor spe of ll mtries under the usul opertions of mtri ddition nd slr multiplition re suspes? d where d e where nd f e d f Eerises Whih of the following vetors re liner omintions of =- =-nd =--? Whih of the following vetors re liner omintions of P t=t +t+ p t=t + p t=t-? t +t+
54 -t +t- Whih of the following sets of vetors spn? d- Do the polnomils t +t+t -t+t +-t +t -t+ spn P? Whih of the following sets of vetors in re linerl dependent? For those tht re epress one vetor s liner omintion of the rest = =6- =- =- = = = = =66 d = = = 6Eerises Whih of the following vetors re ses for? Whih of the following vetors re ses for P? t +t +t t + 6t +8t +6t+ t +t +t+ t +t +t+ t +t +t+ t +t +t+ t +t +t+ et W e the suspe of P spnned t t t t t tt t t
55 Find sis for Wht is the dimension of W? Find sis for tht inludes the vetors nd - Find the dimension of the solution spe of 7Eerises Find sis for the suspe V of spnned the vetors Find the row nd olumn rns of Is linerl independent set of vetors in? Determine whih of the liner sstems hve solution ompring the rns of the oeffiient nd ugmented mtries nd 8 7 S
56 8nswers to Eerises Eerises = +m=+-= = +n=+=7 The hed of the vetor is 7 = -m=-=- = -n=-=- The til of the vetor is -- == = 8 6
57 6 6 ˆ ˆ 7 Y = +-= Y= +-= 8 iˆ ˆj iˆ ˆj 9 Eerises +Y=-+-=- -Y=---=- 6
58 =-6 -Y=---= = - --+=- -= = + = = -+u= -- +u-+= -- +=- =-6 u-=- u= +== = = --- = = - 6 nd nd 6 nd nd 6 nd 6 = 6 = = 6 = 6 = nd euse C None ˆ 6 euse ˆ ˆ ˆ ˆ 7 i j i j
59 S Eerises et = Y = Z nd d in Not vetor Spe d nd f do not hold Vetor Spe Vetor Spe et = - = Y = - = ˆ j i ˆ ˆ ˆ j i ˆ ˆ ˆ Y Y Z Y Z Y d d d d d d d d
60 9 +Y= = = - = So W is not suspe of is Suspe of issuspe of et W is suspe Suspe Eerises = =-- W Y W d d Y d d Y W Y d W /
61 6 To show tht spns we let =d e n vetor in We now see onstnts nd suh tht K =d K =d-+ K =- K =- K =- So spns To show tht-spns we let =d e n vetor in We now see onstnts nd suh tht K + -+ =d t t t P t P t P t t t P t P t P d d
62 6 To show tht spns we let =d e n vetor in We now see onstnts nd suh tht K =d So the vetor is not spnned the vetors not do vetors these - ; ; spns vetors the spnned not is vetor the so d d d 6 6 d d 6 6
63 6 These vetors do not spns dto show tht - spns we let =d e n vetor in We now see onstnts nd nd suh tht K =d K + + = K + + = = K + + =d So the vetors - spns To show tht t +t+t -t+t +-t +t -t+ spns Pwe let =t +t +t+d e n vetor in P We now see onstnts nd suh tht K t +t++ t -t+t ++ t ++ -t +t -t+=t +t +t+d K =d d d d d d d d d d d d d d d
64 6 So vetor lie t +t +t+ is not spnned the vetorst +t+t - t+t +-t +t -t+ The vetors t +t+t -t+t +-t +t -t+ do not spns P To show tht = =6- =- re linerl depenent we see onstnts nd suh tht K = + + = +6 - = K - + = Te To show tht =- = re linerl independent we see onstnts nd suh tht K -+ = The vetors =- = re linerl independent t t t t 6 dependent linerl re vetors given The
65 6 To show tht = = = =66 re linerl dependent we see onstnts nd suh tht K = K + + = K = + +6 = et = K = =- = - The vetors = = = =66 re linerl dependent d To show tht = = = re linerl independent we see onstnts nd suh tht K + + = K + + = + = + + = 6 6
66 6 K = = = The vetors = = = re linerl independent 6Eerises To show tht - is linerl independent we form the Eqution + =O + - =O + - = So - is linerl independent To show tht - spns we let = e n vetor in We now see onstnts nd suh tht K + -== + - =
67 66 So spns nd is sis for To show tht - is linerl independent weform the eqution + + = O = = + + = - + This sstem hs infinit mn solutions s Showing tht is linerl dependent Hene S does not spn nd is not sis for is sis for Possile nswer dimw= Possile nswer S S t t t t
68 67 The solution set is The dimension is ero 7Eerises Possile nswer The row nd olumn rn re inerl dependent S S
69 68 The rn of the oeffiient nd ugmented mtries re So the liner sstem hs solution The rn of the oeffiient mtri is The rn of the ugmented mtri oeffiient mtri is So the liner sstem hs no solution
70 9Glossr يتجه Vetor رو بعذ N-dimensionln فضاء خطي Spe iner فضاء جزئي Suspe يج ىعت يىنذة Set Spnning يستقهت خطيا Independent inerl يرتبطت خطيا dependent inerl كثير حذود Polnomil تركيبت خطيت Comintion iner أساس Bsis بعذ Dimension 69
71 7
72 7
73 7 Eerises Whih of the following re liner trnsformtion? Whih of the following re liner trnsformtion? et e liner trnsformtion for whih we now tht Wht is Wht is nd??
74 7 et p p e liner trnsformtion for whih we now tht = t =t nd t =t +t Find t -t+ Find t +t+ Eerises et e defined? Find er Is one to one? Is onto? et e defined? Find sis for er Find sis for rnge Verif Theorem 7 et 6 e iner trnsformtion? If dim er = wht is dim rnge? If dim rnge = wht is dim er? Determine the dimension of the solution spe to the homogeneous sstem = for the given mtri
75 7 = Eerises et S = e sis for Find the oordinte vetors of the following vetors with respet to S et e sis for P Find the oordinte vetors of the following vetors with respet to S t + t et e defined et S nd T e the nturl ses for nd respetivel lso et 7 7 t t t S T nd S
76 7 e ses for nd respetivel Find the mtri of with respet to S nd T Compute et e defined et S nd T e the nturl ses for nd respetivel lso let e ses for nd respetivel Find the representtion of with respet to S nd T Compute using oth representtions ete liner trnsformtion Suppose tht themtri of with respet to the sis is sin nd in otined mtries the g u T nd S T nd S T nd S S
77 76 where Compute Compute Compute 6 et e defined Find the mtri of with respet to the nturl sis S for Using the definition of nd lso using the mtri otined in \ Find nd S S nd nd
78 77 nswers to Eerises Eerises et Then lso if is rel numer then Hene is liner trnsformtion et Y Y Y Y Y Y Y Y
79 78 Hene is not liner trnsformtion et lso if is rel numer then Hene is liner trnsformtion Hene is not liner trnsformtion Y Y Y Y Y Y 9
80 79 We n solve this question using 9
81 8 t -t+=t -t+ t -t+= t +t-t + = t -t +t+ t +t+=t +t+ t +t+= t +t+t + = t +t +t+ Eerises = + = = == is one - to one euse Given n re n rel numers n we find in so tht we re seeing solution to the liner sstem er er nd where in Y? Y Y
82 8 We re seeing solution to the liner sstem The redued row ehelon form of the ugmented mtri is Thus solution eists onl for nd so is not onto
83 8 dimer +dimrnge =dim V t t t t t t s s s t s t t t t t s t er for sis posssile rnge for sis posssile
84 8 + = dimrnge =-= dimer =-= The solution spe The dimension of the solution spe to the homogeneous sstem = for the given mtri is Eerises The oordinte vetor of the vetor with respet to S 7 s s s s s s 7 7 s s s s
85 8 The oordinte vetor of the vetor with respet to S t + = t ++ t-+ t= t + + t+ - = - = = - + = = - = The oordinte vetor of the vetor t + with respet To S The mtri of with respet to S nd T 7 7
86 8 The mtri of with respet to S` nd T ` - For - For The representtion of with respet to S nd T 7 8 7
87 86 S T T T T
88 87 The representtion of with respet to - For - For S T s s T nd S 7
89 88 6 -Using the definition of - Using the mtri otined in * * * * * * 8 * *
90 Glossr تحىيم خطي Trnsformtion iner ان ىاة Kernel ان ذي nge واحذ نىاحذ One One to شايم Onto ا عكاس efletion دورا ottion تركيب انتحىيالث انخطيت Trnsformtion Composition of iner ان صفىفت ان اقهت Mtri Trnsition ت ثيم انتحىيم انخطي ب صفىفت Trnsformtion Mtri epresenttion of iner 89
91 9
92 9
93 9
94 9 Eerises Find the hrteristi polnomil of eh mtri Find the hrteristi polnomileigenvlues nd eigenvetors of eh mtri Find whih of the mtries re digonlile
95 9 Find for eh mtri if possile non-singulr mtri Psuh tht P - P is digonl Prove tht if nd B re similr mtries the hve the sme hrteristi polnomils nd hene the sme eigenvlues Eerises Verif tht P = Is n orthogonl mtri Digonlile eh given mtri nd find n orthogonl mtri P suh tht P - P is digonl Digonlile eh given mtri
96 9 Show tht if is n orthogonl mtri then Show tht if is n orthogonl mtri then is orthogonl
97 96 nswers to Eerises Eerises 7 I 6 9 I f I s et s s s s I s s s I
98 97 s et s s I 6 f I s et s s I s et s s I digonlile not is mtri the theorem g u B Eigenves Eigenvls sin
99 98 So nd B hve the sme hrteristi polnomils nd hene the sme eigenvlues Eerises Digonlile is mtri the theorem g u Eigenves Eigenvls sin digonlile not is mtri the theorem g u Eigenves Eigenvls sin sin P or P theorem g U Digonlile Eigenves Eigenvls I B I I P I P P I P P I P P P IP P P P I B I P P B P P T
100 99 P Is orthogonlmtri eigenves eigenvls P D eigenves eigenvls P D sin D theorem g U eigenvls I
101 sin D theorem g U eigenvls I * * * I
102 sin D theorem g U eigenvls if is n orthogonl mtri then - = t Need to show tht - - = - T Suppose tht is n orthogonl mtri B ting the trnspose oth sides of equtionwe get - T = T T == = - T So T T mtri orthogonl n is
103 Glossr قي ت ي يزة Vlue Eigen يتجه ي يز Vetor Eigen كثير انحذود ان يز Polnomil Chrteristi ان عادنت ان يزة Eqution Chrteristi انفضاء ان يز Spe Eigen انتشابه Similrit يصفىفاث يتشابهت mtries Similr ان صفىفت انقابهت نهتحىيم ان يصفىفت قطريت Mtri Digonlile
104
105
106 6Eerises Steel produer mes two tpes of steel regulr nd speil ton of regulr steel requires hours in the open herth furne nd hours in the soing pit ; ton of speil steel requires hours in the openherth furne nd hours in the soing pit The open- herth furne is ville 8 hours per d nd the soing pit is ville hours per d The profit on tonof regulr steel is$ nd it is $ on ton of speil steeldetermine how mn tons of eh tpe of steel should e mde to mimie the profit television produer designs progrm sed on omedin nd time for ommerils The dvertiser insists on t lest minutes of dvertising time the sttion insists on no more thn minutes of dvertising time nd the omedin insists on t lest minutes of the omed progrm lso the totl time llotted for the dvertising nd omed portions of the progrm nnot eeed minutes If it hs een determined tht eh minute of dvertisingver retive ttrts viewers nd eh minute of the omed progrm ttrts viewers how should the time e divided etween dvertising nd progrmming to mimie the numer of viewerminutes? The protein Diet Clu serves lunheon onsisting of two dishes nd B Suppose tht eh unit of hs grm of ft grm of rohdrte nd grms of protein wheres eh unit of B hs grms of ft grm of rohdrte nd 6 grms of protein If the dietiin plnning the lunheon wnts to provide no more thn
107 6 grms of ft or more thn 7 grms of rohdrte how mn units of nd how mn units of B should e served to mimie the mount of protein onsumed? Seth the set of points stisfing the given sstem of inequlities Minimie = - Sujet to 6 Formulte the following liner progrmming prolem s new prolem with sl vriles Mimie = sujet to
108 6 nswers to Eerises 6 Eerises Supposetht is the mount of regulr steel nd is the mount of speil steel Mimie Z= + Sujet to Suppose tht is dvertising time nd is the time of the omed progrm Mimie Z= + Sujet to 8 7
109 Suppose tht is the mount units of tpe nd is the the mount units of tpe B Mimie Z = +6 Sujet to 7 8
110 The point 8 9 Z
111 min Mimie = + +7 Sujet to
112 6 Glossr ان تباي ت انخطيت Inequlit iner اقترا انهذف Funtion Ojetive قيىد شروط Constrints
113 The End
114
Reference : Croft & Davison, Chapter 12, Blocks 1,2. A matrix ti is a rectangular array or block of numbers usually enclosed in brackets.
 I MATRIX ALGEBRA INTRODUCTION TO MATRICES Referene : Croft & Dvison, Chpter, Blos, A mtri ti is retngulr rr or lo of numers usull enlosed in rets. A m n mtri hs m rows nd n olumns. Mtri Alger Pge If the
I MATRIX ALGEBRA INTRODUCTION TO MATRICES Referene : Croft & Dvison, Chpter, Blos, A mtri ti is retngulr rr or lo of numers usull enlosed in rets. A m n mtri hs m rows nd n olumns. Mtri Alger Pge If the
Worksheet #2 Math 285 Name: 1. Solve the following systems of linear equations. The prove that the solutions forms a subspace of
 Worsheet # th Nme:. Sole the folloing sstems of liner equtions. he proe tht the solutions forms suspe of ) ). Find the neessr nd suffiient onditions of ll onstnts for the eistene of solution to the sstem:.
Worsheet # th Nme:. Sole the folloing sstems of liner equtions. he proe tht the solutions forms suspe of ) ). Find the neessr nd suffiient onditions of ll onstnts for the eistene of solution to the sstem:.
Linear Algebra Introduction
 Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Introdution Wht is Liner Alger out? Liner Alger is rnh of mthemtis whih emerged yers k nd ws one of the pioneer rnhes of mthemtis Though, initilly it strted with solving of the simple liner eqution x +
Unit-VII: Linear Algebra-I. To show what are the matrices, why they are useful, how they are classified as various types and how they are solved.
 Unit-VII: Liner lger-i Purpose of lession : To show wht re the mtries, wh the re useful, how the re lssified s vrious tpes nd how the re solved. Introdution: Mtries is powerful tool of modern Mthemtis
Unit-VII: Liner lger-i Purpose of lession : To show wht re the mtries, wh the re useful, how the re lssified s vrious tpes nd how the re solved. Introdution: Mtries is powerful tool of modern Mthemtis
HOMEWORK FOR CLASS XII ( )
 HOMEWORK FOR CLASS XII 8-9 Show tht the reltion R on the set Z of ll integers defined R,, Z,, is, divisile,, is n equivlene reltion on Z Let f: R R e defined if f if Is f one-one nd onto if If f, g : R
HOMEWORK FOR CLASS XII 8-9 Show tht the reltion R on the set Z of ll integers defined R,, Z,, is, divisile,, is n equivlene reltion on Z Let f: R R e defined if f if Is f one-one nd onto if If f, g : R
Matrices SCHOOL OF ENGINEERING & BUILT ENVIRONMENT. Mathematics (c) 1. Definition of a Matrix
 tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
tries Definition of tri mtri is regulr rry of numers enlosed inside rkets SCHOOL OF ENGINEERING & UIL ENVIRONEN Emple he following re ll mtries: ), ) 9, themtis ), d) tries Definition of tri Size of tri
Section 2.3. Matrix Inverses
 Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
Mtri lger Mtri nverses Setion.. Mtri nverses hree si opertions on mtries, ition, multiplition, n sutrtion, re nlogues for mtries of the sme opertions for numers. n this setion we introue the mtri nlogue
are coplanar. ˆ ˆ ˆ and iˆ
 SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
SML QUSTION Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor ii The question pper onsists of 6 questions divided into three Setions, B nd C iii Question No
CHAPTER 4: DETERMINANTS
 CHAPTER 4: DETERMINANTS MARKS WEIGHTAGE 0 mrks NCERT Importnt Questions & Answers 6. If, then find the vlue of. 8 8 6 6 Given tht 8 8 6 On epnding both determinnts, we get 8 = 6 6 8 36 = 36 36 36 = 0 =
CHAPTER 4: DETERMINANTS MARKS WEIGHTAGE 0 mrks NCERT Importnt Questions & Answers 6. If, then find the vlue of. 8 8 6 6 Given tht 8 8 6 On epnding both determinnts, we get 8 = 6 6 8 36 = 36 36 36 = 0 =
Worksheet : Class XII Matrices & Determinants
 Worksheet : Clss XII Mtries & Determinnts Prepred B:Mr. durhimn K Mth Teher l-hej Interntionl Shool, Jeddh (IGCSE). rhmnrk@gmil.om #00966007900# MTHEMTICS WKSHEET I Nme: Mrh 0. If 8 LGEBR (Mtries nd Determinnts)
Worksheet : Clss XII Mtries & Determinnts Prepred B:Mr. durhimn K Mth Teher l-hej Interntionl Shool, Jeddh (IGCSE). rhmnrk@gmil.om #00966007900# MTHEMTICS WKSHEET I Nme: Mrh 0. If 8 LGEBR (Mtries nd Determinnts)
SECTION A STUDENT MATERIAL. Part 1. What and Why.?
 SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
SECTION A STUDENT MATERIAL Prt Wht nd Wh.? Student Mteril Prt Prolem n > 0 n > 0 Is the onverse true? Prolem If n is even then n is even. If n is even then n is even. Wht nd Wh? Eploring Pure Mths Are
Matrix- System of rows and columns each position in a matrix has a purpose. 5 Ex: 5. Ex:
 Mtries Prelulus Mtri- Sstem of rows n olumns eh position in mtri hs purpose. Element- Eh vlue in the mtri mens the element in the n row, r olumn Dimensions- How mn rows b number of olumns Ientif the element:
Mtries Prelulus Mtri- Sstem of rows n olumns eh position in mtri hs purpose. Element- Eh vlue in the mtri mens the element in the n row, r olumn Dimensions- How mn rows b number of olumns Ientif the element:
LINEAR ALGEBRA APPLIED
 5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
5.5 Applictions of Inner Product Spces 5.5 Applictions of Inner Product Spces 7 Find the cross product of two vectors in R. Find the liner or qudrtic lest squres pproimtion of function. Find the nth-order
Tutorial Worksheet. 1. Find all solutions to the linear system by following the given steps. x + 2y + 3z = 2 2x + 3y + z = 4.
 Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
Mth 5 Tutoril Week 1 - Jnury 1 1 Nme Setion Tutoril Worksheet 1. Find ll solutions to the liner system by following the given steps x + y + z = x + y + z = 4. y + z = Step 1. Write down the rgumented mtrix
April 8, 2017 Math 9. Geometry. Solving vector problems. Problem. Prove that if vectors and satisfy, then.
 pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
pril 8, 2017 Mth 9 Geometry Solving vetor prolems Prolem Prove tht if vetors nd stisfy, then Solution 1 onsider the vetor ddition prllelogrm shown in the Figure Sine its digonls hve equl length,, the prllelogrm
Things to Memorize: A Partial List. January 27, 2017
 Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
Things to Memorize: A Prtil List Jnury 27, 2017 Chpter 2 Vectors - Bsic Fcts A vector hs mgnitude (lso clled size/length/norm) nd direction. It does not hve fixed position, so the sme vector cn e moved
m A 1 1 A ! and AC 6
 REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
REVIEW SET A Using sle of m represents units, sketh vetor to represent: NON-CALCULATOR n eroplne tking off t n ngle of 8 ± to runw with speed of 6 ms displement of m in north-esterl diretion. Simplif:
TOPIC: LINEAR ALGEBRA MATRICES
 Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
Interntionl Blurete LECTUE NOTES for FUTHE MATHEMATICS Dr TOPIC: LINEA ALGEBA MATICES. DEFINITION OF A MATIX MATIX OPEATIONS.. THE DETEMINANT deta THE INVESE A -... SYSTEMS OF LINEA EQUATIONS. 8. THE AUGMENTED
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk out solving systems of liner equtions. These re prolems tht give couple of equtions with couple of unknowns, like: 6= x + x 7=
H (2a, a) (u 2a) 2 (E) Show that u v 4a. Explain why this implies that u v 4a, with equality if and only u a if u v 2a.
 Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
Chpter Review 89 IGURE ol hord GH of the prol 4. G u v H (, ) (A) Use the distne formul to show tht u. (B) Show tht G nd H lie on the line m, where m ( )/( ). (C) Solve m for nd sustitute in 4, otining
GRAND PLAN. Visualizing Quaternions. I: Fundamentals of Quaternions. Andrew J. Hanson. II: Visualizing Quaternion Geometry. III: Quaternion Frames
 Visuliing Quternions Andrew J. Hnson Computer Siene Deprtment Indin Universit Siggrph Tutoril GRAND PLAN I: Fundmentls of Quternions II: Visuliing Quternion Geometr III: Quternion Frmes IV: Clifford Algers
Visuliing Quternions Andrew J. Hnson Computer Siene Deprtment Indin Universit Siggrph Tutoril GRAND PLAN I: Fundmentls of Quternions II: Visuliing Quternion Geometr III: Quternion Frmes IV: Clifford Algers
THREE DIMENSIONAL GEOMETRY
 MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
MD THREE DIMENSIONAL GEOMETRY CA CB C Coordintes of point in spe There re infinite numer of points in spe We wnt to identif eh nd ever point of spe with the help of three mutull perpendiulr oordintes es
+ = () i =, find the values of x & y. 4. Write the function in the simplifies from. ()tan i. x x. 5. Find the derivative of. 6.
 Summer vtions Holid Home Work 7-8 Clss-XII Mths. Give the emple of reltion, whih is trnsitive ut neither refleive nor smmetri.. Find the vlues of unknown quntities if. + + () i =, find the vlues of & 7
Summer vtions Holid Home Work 7-8 Clss-XII Mths. Give the emple of reltion, whih is trnsitive ut neither refleive nor smmetri.. Find the vlues of unknown quntities if. + + () i =, find the vlues of & 7
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
 PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES. Two liner equtions in the sme two vriles re lled pir of liner equtions in two vriles. The most generl form of pir of liner equtions is x + y + 0 x + y + 0 where,,,,,,
A Primer on Continuous-time Economic Dynamics
 Eonomis 205A Fll 2008 K Kletzer A Primer on Continuous-time Eonomi Dnmis A Liner Differentil Eqution Sstems (i) Simplest se We egin with the simple liner first-orer ifferentil eqution The generl solution
Eonomis 205A Fll 2008 K Kletzer A Primer on Continuous-time Eonomi Dnmis A Liner Differentil Eqution Sstems (i) Simplest se We egin with the simple liner first-orer ifferentil eqution The generl solution
MATRICES AND VECTORS SPACE
 MATRICES AND VECTORS SPACE MATRICES AND MATRIX OPERATIONS SYSTEM OF LINEAR EQUATIONS DETERMINANTS VECTORS IN -SPACE AND -SPACE GENERAL VECTOR SPACES INNER PRODUCT SPACES EIGENVALUES, EIGENVECTORS LINEAR
MATRICES AND VECTORS SPACE MATRICES AND MATRIX OPERATIONS SYSTEM OF LINEAR EQUATIONS DETERMINANTS VECTORS IN -SPACE AND -SPACE GENERAL VECTOR SPACES INNER PRODUCT SPACES EIGENVALUES, EIGENVECTORS LINEAR
Core 2 Logarithms and exponentials. Section 1: Introduction to logarithms
 Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
Core Logrithms nd eponentils Setion : Introdution to logrithms Notes nd Emples These notes ontin subsetions on Indies nd logrithms The lws of logrithms Eponentil funtions This is n emple resoure from MEI
VECTOR ALGEBRA. Syllabus :
 MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
MV VECTOR ALGEBRA Syllus : Vetors nd Slrs, ddition of vetors, omponent of vetor, omponents of vetor in two dimensions nd three dimensionl spe, slr nd vetor produts, slr nd vetor triple produt. Einstein
University of Sioux Falls. MAT204/205 Calculus I/II
 University of Sioux Flls MAT204/205 Clulus I/II Conepts ddressed: Clulus Textook: Thoms Clulus, 11 th ed., Weir, Hss, Giordno 1. Use stndrd differentition nd integrtion tehniques. Differentition tehniques
University of Sioux Flls MAT204/205 Clulus I/II Conepts ddressed: Clulus Textook: Thoms Clulus, 11 th ed., Weir, Hss, Giordno 1. Use stndrd differentition nd integrtion tehniques. Differentition tehniques
AP Calculus BC Chapter 8: Integration Techniques, L Hopital s Rule and Improper Integrals
 AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
AP Clulus BC Chpter 8: Integrtion Tehniques, L Hopitl s Rule nd Improper Integrls 8. Bsi Integrtion Rules In this setion we will review vrious integrtion strtegies. Strtegies: I. Seprte the integrnd into
Learning Objectives of Module 2 (Algebra and Calculus) Notes:
 67 Lerning Ojetives of Module (Alger nd Clulus) Notes:. Lerning units re grouped under three res ( Foundtion Knowledge, Alger nd Clulus ) nd Further Lerning Unit.. Relted lerning ojetives re grouped under
67 Lerning Ojetives of Module (Alger nd Clulus) Notes:. Lerning units re grouped under three res ( Foundtion Knowledge, Alger nd Clulus ) nd Further Lerning Unit.. Relted lerning ojetives re grouped under
NON-DETERMINISTIC FSA
 Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
MATHEMATICS FOR MANAGEMENT BBMP1103
 T o p i c M T R I X MTHEMTICS FOR MNGEMENT BBMP Ojectives: TOPIC : MTRIX. Define mtri. ssess the clssifictions of mtrices s well s know how to perform its opertions. Clculte the determinnt for squre mtri
T o p i c M T R I X MTHEMTICS FOR MNGEMENT BBMP Ojectives: TOPIC : MTRIX. Define mtri. ssess the clssifictions of mtrices s well s know how to perform its opertions. Clculte the determinnt for squre mtri
Lecture Solution of a System of Linear Equation
 ChE Lecture Notes, Dept. of Chemicl Engineering, Univ. of TN, Knoville - D. Keffer, 5/9/98 (updted /) Lecture 8- - Solution of System of Liner Eqution 8. Why is it importnt to e le to solve system of liner
ChE Lecture Notes, Dept. of Chemicl Engineering, Univ. of TN, Knoville - D. Keffer, 5/9/98 (updted /) Lecture 8- - Solution of System of Liner Eqution 8. Why is it importnt to e le to solve system of liner
( ) { } [ ] { } [ ) { } ( ] { }
![( ) { } [ ] { } [ ) { } ( ] { } ( ) { } [ ] { } [ ) { } ( ] { }](/thumbs/96/129291861.jpg) Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Mth 65 Prelulus Review Properties of Inequlities 1. > nd > >. > + > +. > nd > 0 > 4. > nd < 0 < Asolute Vlue, if 0, if < 0 Properties of Asolute Vlue > 0 1. < < > or
Probability. b a b. a b 32.
 Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
Proility If n event n hppen in '' wys nd fil in '' wys, nd eh of these wys is eqully likely, then proility or the hne, or its hppening is, nd tht of its filing is eg, If in lottery there re prizes nd lnks,
y z A left-handed system can be rotated to look like the following. z
 Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
Chpter 2 Crtesin Coördintes The djetive Crtesin bove refers to René Desrtes (1596 1650), who ws the first to oördintise the plne s ordered pirs of rel numbers, whih provided the first sstemti link between
1.3 SCALARS AND VECTORS
 Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
Bridge Course Phy I PUC 24 1.3 SCLRS ND VECTORS Introdution: Physis is the study of nturl phenomen. The study of ny nturl phenomenon involves mesurements. For exmple, the distne etween the plnet erth nd
are coplanar. ˆ ˆ ˆ and iˆ
 SMLE QUESTION ER Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor. ii The question pper onsists of 6 questions divided into three Setions, B nd C. iii Question
SMLE QUESTION ER Clss XII Mthemtis Time llowed: hrs Mimum Mrks: Generl Instrutions: i ll questions re ompulsor. ii The question pper onsists of 6 questions divided into three Setions, B nd C. iii Question
September 13 Homework Solutions
 College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
College of Engineering nd Computer Science Mechnicl Engineering Deprtment Mechnicl Engineering 5A Seminr in Engineering Anlysis Fll Ticket: 5966 Instructor: Lrry Cretto Septemer Homework Solutions. Are
Vibration with more (than one) degrees of freedom (DOF) a) longitudinal vibration with 3 DOF. b) rotational (torsional) vibration with 3 DOF
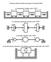 irtion with ore (thn one) degrees of freedo (DOF) ) longitudinl irtion with DOF ) rottionl (torsionl) irtion with DOF ) ending irtion with DOF d) the D (plnr) irtion of the fleil supported rigid od with
irtion with ore (thn one) degrees of freedo (DOF) ) longitudinl irtion with DOF ) rottionl (torsionl) irtion with DOF ) ending irtion with DOF d) the D (plnr) irtion of the fleil supported rigid od with
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
Lecture Notes No. 10
 2.6 System Identifition, Estimtion, nd Lerning Leture otes o. Mrh 3, 26 6 Model Struture of Liner ime Invrint Systems 6. Model Struture In representing dynmil system, the first step is to find n pproprite
2.6 System Identifition, Estimtion, nd Lerning Leture otes o. Mrh 3, 26 6 Model Struture of Liner ime Invrint Systems 6. Model Struture In representing dynmil system, the first step is to find n pproprite
MATRIX INVERSE ON CONNEX PARALLEL ARCHITECTURE
 U.P.B. Si. Bull., Series C, Vol. 75, Iss. 2, ISSN 86 354 MATRIX INVERSE ON CONNEX PARALLEL ARCHITECTURE An-Mri CALFA, Gheorghe ŞTEFAN 2 Designed for emedded omputtion in system on hip design, the Connex
U.P.B. Si. Bull., Series C, Vol. 75, Iss. 2, ISSN 86 354 MATRIX INVERSE ON CONNEX PARALLEL ARCHITECTURE An-Mri CALFA, Gheorghe ŞTEFAN 2 Designed for emedded omputtion in system on hip design, the Connex
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
CLASS XII. AdjA A. x X. a etc. B d
 CLASS XII The syllus is divided into three setions A B nd C Setion A is ompulsory for ll ndidtes Cndidtes will hve hoie of ttempting questions from either Setion B or Setion C There will e one pper of
CLASS XII The syllus is divided into three setions A B nd C Setion A is ompulsory for ll ndidtes Cndidtes will hve hoie of ttempting questions from either Setion B or Setion C There will e one pper of
Einstein Classes, Unit No. 102, 103, Vardhman Ring Road Plaza, Vikas Puri Extn., Outer Ring Road New Delhi , Ph. : ,
 Dte :... IIT/AIEEE APPEARING 0 MATRICES AND DETERMINANTS PART & PART Red the following Instrutions very refully efore you proeed for PART Time : hrs. M.M. : 40 There re 0 questions in totl. Questions to
Dte :... IIT/AIEEE APPEARING 0 MATRICES AND DETERMINANTS PART & PART Red the following Instrutions very refully efore you proeed for PART Time : hrs. M.M. : 40 There re 0 questions in totl. Questions to
50 AMC Lectures Problem Book 2 (36) Substitution Method
 0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
0 AMC Letures Prolem Book Sustitution Metho PROBLEMS Prolem : Solve for rel : 9 + 99 + 9 = Prolem : Solve for rel : 0 9 8 8 Prolem : Show tht if 8 Prolem : Show tht + + if rel numers,, n stisf + + = Prolem
QUADRATIC EQUATION. Contents
 QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
QUADRATIC EQUATION Contents Topi Pge No. Theory 0-04 Exerise - 05-09 Exerise - 09-3 Exerise - 3 4-5 Exerise - 4 6 Answer Key 7-8 Syllus Qudrti equtions with rel oeffiients, reltions etween roots nd oeffiients,
Chapter 2. Determinants
 Chpter Determinnts The Determinnt Function Recll tht the X mtrix A c b d is invertible if d-bc0. The expression d-bc occurs so frequently tht it hs nme; it is clled the determinnt of the mtrix A nd is
Chpter Determinnts The Determinnt Function Recll tht the X mtrix A c b d is invertible if d-bc0. The expression d-bc occurs so frequently tht it hs nme; it is clled the determinnt of the mtrix A nd is
Algebra 2 Semester 1 Practice Final
 Alger 2 Semester Prtie Finl Multiple Choie Ientify the hoie tht est ompletes the sttement or nswers the question. To whih set of numers oes the numer elong?. 2 5 integers rtionl numers irrtionl numers
Alger 2 Semester Prtie Finl Multiple Choie Ientify the hoie tht est ompletes the sttement or nswers the question. To whih set of numers oes the numer elong?. 2 5 integers rtionl numers irrtionl numers
2. There are an infinite number of possible triangles, all similar, with three given angles whose sum is 180.
 SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
SECTION 8-1 11 CHAPTER 8 Setion 8 1. There re n infinite numer of possile tringles, ll similr, with three given ngles whose sum is 180. 4. If two ngles α nd β of tringle re known, the third ngle n e found
16z z q. q( B) Max{2 z z z z B} r z r z r z r z B. John Riley 19 October Econ 401A: Microeconomic Theory. Homework 2 Answers
 John Riley 9 Otober 6 Eon 4A: Miroeonomi Theory Homework Answers Constnt returns to sle prodution funtion () If (,, q) S then 6 q () 4 We need to show tht (,, q) S 6( ) ( ) ( q) q [ q ] 4 4 4 4 4 4 Appeling
John Riley 9 Otober 6 Eon 4A: Miroeonomi Theory Homework Answers Constnt returns to sle prodution funtion () If (,, q) S then 6 q () 4 We need to show tht (,, q) S 6( ) ( ) ( q) q [ q ] 4 4 4 4 4 4 Appeling
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Operations with Matrices
 Section. Equlit of Mtrices Opertions with Mtrices There re three ws to represent mtri.. A mtri cn be denoted b n uppercse letter, such s A, B, or C.. A mtri cn be denoted b representtive element enclosed
Section. Equlit of Mtrices Opertions with Mtrices There re three ws to represent mtri.. A mtri cn be denoted b n uppercse letter, such s A, B, or C.. A mtri cn be denoted b representtive element enclosed
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
1. Twelve less than five times a number is thirty three. What is the number
 Alger 00 Midterm Review Nme: Dte: Directions: For the following prolems, on SEPARATE PIECE OF PAPER; Define the unknown vrile Set up n eqution (Include sketch/chrt if necessr) Solve nd show work Answer
Alger 00 Midterm Review Nme: Dte: Directions: For the following prolems, on SEPARATE PIECE OF PAPER; Define the unknown vrile Set up n eqution (Include sketch/chrt if necessr) Solve nd show work Answer
m m m m m m m m P m P m ( ) m m P( ) ( ). The o-ordinte of the point P( ) dividing the line segment joining the two points ( ) nd ( ) eternll in the r
 CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
CO-ORDINTE GEOMETR II I Qudrnt Qudrnt (-.+) (++) X X - - - 0 - III IV Qudrnt - Qudrnt (--) - (+-) Region CRTESIN CO-ORDINTE SSTEM : Retngulr Co-ordinte Sstem : Let X' OX nd 'O e two mutull perpendiulr
SCHOOL OF ENGINEERING & BUILT ENVIRONMENT
 SCHOOL OF ENGINEERING & BUIL ENVIRONMEN MARICES FOR ENGINEERING Dr Clum Mcdonld Contents Introduction Definitions Wht is mtri? Rows nd columns of mtri Order of mtri Element of mtri Equlity of mtrices Opertions
SCHOOL OF ENGINEERING & BUIL ENVIRONMEN MARICES FOR ENGINEERING Dr Clum Mcdonld Contents Introduction Definitions Wht is mtri? Rows nd columns of mtri Order of mtri Element of mtri Equlity of mtrices Opertions
8 THREE PHASE A.C. CIRCUITS
 8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
8 THREE PHSE.. IRUITS The signls in hpter 7 were sinusoidl lternting voltges nd urrents of the so-lled single se type. n emf of suh type n e esily generted y rotting single loop of ondutor (or single winding),
Discrete Structures Lecture 11
 Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Introdution Good morning. In this setion we study funtions. A funtion is mpping from one set to nother set or, perhps, from one set to itself. We study the properties of funtions. A mpping my not e funtion.
Lecture 2e Orthogonal Complement (pages )
 Lecture 2e Orthogonl Complement (pges -) We hve now seen tht n orthonorml sis is nice wy to descrie suspce, ut knowing tht we wnt n orthonorml sis doesn t mke one fll into our lp. In theory, the process
Lecture 2e Orthogonl Complement (pges -) We hve now seen tht n orthonorml sis is nice wy to descrie suspce, ut knowing tht we wnt n orthonorml sis doesn t mke one fll into our lp. In theory, the process
Chapter 3. Vector Spaces. 3.1 Images and Image Arithmetic
 Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
Chpter 3 Vetor Spes In Chpter 2, we sw tht the set of imges possessed numer of onvenient properties. It turns out tht ny set tht possesses similr onvenient properties n e nlyzed in similr wy. In liner
ENERGY AND PACKING. Outline: MATERIALS AND PACKING. Crystal Structure
 EERGY AD PACKIG Outline: Crstlline versus morphous strutures Crstl struture - Unit ell - Coordintion numer - Atomi pking ftor Crstl sstems on dense, rndom pking Dense, regulr pking tpil neighor ond energ
EERGY AD PACKIG Outline: Crstlline versus morphous strutures Crstl struture - Unit ell - Coordintion numer - Atomi pking ftor Crstl sstems on dense, rndom pking Dense, regulr pking tpil neighor ond energ
Mathematics SKE: STRAND F. F1.1 Using Formulae. F1.2 Construct and Use Simple Formulae. F1.3 Revision of Negative Numbers
 Mthemtis SKE: STRAND F UNIT F1 Formule: Tet STRAND F: Alger F1 Formule Tet Contents Setion F1.1 Using Formule F1. Construt nd Use Simple Formule F1.3 Revision of Negtive Numers F1.4 Sustitution into Formule
Mthemtis SKE: STRAND F UNIT F1 Formule: Tet STRAND F: Alger F1 Formule Tet Contents Setion F1.1 Using Formule F1. Construt nd Use Simple Formule F1.3 Revision of Negtive Numers F1.4 Sustitution into Formule
21.1 Using Formulae Construct and Use Simple Formulae Revision of Negative Numbers Substitution into Formulae
 MEP Jmi: STRAND G UNIT 1 Formule: Student Tet Contents STRAND G: Alger Unit 1 Formule Student Tet Contents Setion 1.1 Using Formule 1. Construt nd Use Simple Formule 1.3 Revision of Negtive Numers 1.4
MEP Jmi: STRAND G UNIT 1 Formule: Student Tet Contents STRAND G: Alger Unit 1 Formule Student Tet Contents Setion 1.1 Using Formule 1. Construt nd Use Simple Formule 1.3 Revision of Negtive Numers 1.4
( ) 1. 1) Let f( x ) = 10 5x. Find and simplify f( 2) and then state the domain of f(x).
 Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Mth 15 Fettermn/DeSmet Gustfson/Finl Em Review 1) Let f( ) = 10 5. Find nd simplif f( ) nd then stte the domin of f(). ) Let f( ) = +. Find nd simplif f(1) nd then stte the domin of f(). ) Let f( ) = 8.
Matrix Algebra. Matrix Addition, Scalar Multiplication and Transposition. Linear Algebra I 24
 Mtrix lger Mtrix ddition, Sclr Multipliction nd rnsposition Mtrix lger Section.. Mtrix ddition, Sclr Multipliction nd rnsposition rectngulr rry of numers is clled mtrix ( the plurl is mtrices ) nd the
Mtrix lger Mtrix ddition, Sclr Multipliction nd rnsposition Mtrix lger Section.. Mtrix ddition, Sclr Multipliction nd rnsposition rectngulr rry of numers is clled mtrix ( the plurl is mtrices ) nd the
Technische Universität München Winter term 2009/10 I7 Prof. J. Esparza / J. Křetínský / M. Luttenberger 11. Februar Solution
 Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
12.4 Similarity in Right Triangles
 Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
Nme lss Dte 12.4 Similrit in Right Tringles Essentil Question: How does the ltitude to the hpotenuse of right tringle help ou use similr right tringles to solve prolems? Eplore Identifing Similrit in Right
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
18.06 Problem Set 4 Due Wednesday, Oct. 11, 2006 at 4:00 p.m. in 2-106
 8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
Introduction to Olympiad Inequalities
 Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
Introdution to Olympid Inequlities Edutionl Studies Progrm HSSP Msshusetts Institute of Tehnology Snj Simonovikj Spring 207 Contents Wrm up nd Am-Gm inequlity 2. Elementry inequlities......................
M344 - ADVANCED ENGINEERING MATHEMATICS
 M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
M3 - ADVANCED ENGINEERING MATHEMATICS Lecture 18: Lplce s Eqution, Anltic nd Numericl Solution Our emple of n elliptic prtil differentil eqution is Lplce s eqution, lso clled the Diffusion Eqution. If
Exercise 3 Logic Control
 Exerise 3 Logi Control OBJECTIVE The ojetive of this exerise is giving n introdution to pplition of Logi Control System (LCS). Tody, LCS is implemented through Progrmmle Logi Controller (PLC) whih is lled
Exerise 3 Logi Control OBJECTIVE The ojetive of this exerise is giving n introdution to pplition of Logi Control System (LCS). Tody, LCS is implemented through Progrmmle Logi Controller (PLC) whih is lled
CS311 Computational Structures Regular Languages and Regular Grammars. Lecture 6
 CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
Green s Theorem. (2x e y ) da. (2x e y ) dx dy. x 2 xe y. (1 e y ) dy. y=1. = y e y. y=0. = 2 e
 Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Green s Theorem. Let be the boundry of the unit squre, y, oriented ounterlokwise, nd let F be the vetor field F, y e y +, 2 y. Find F d r. Solution. Let s write P, y e y + nd Q, y 2 y, so tht F P, Q. Let
Ch. 2.3 Counting Sample Points. Cardinality of a Set
 Ch..3 Counting Smple Points CH 8 Crdinlity of Set Let S e set. If there re extly n distint elements in S, where n is nonnegtive integer, we sy S is finite set nd n is the rdinlity of S. The rdinlity of
Ch..3 Counting Smple Points CH 8 Crdinlity of Set Let S e set. If there re extly n distint elements in S, where n is nonnegtive integer, we sy S is finite set nd n is the rdinlity of S. The rdinlity of
Review Topic 14: Relationships between two numerical variables
 Review Topi 14: Reltionships etween two numeril vriles Multiple hoie 1. Whih of the following stterplots est demonstrtes line of est fit? A B C D E 2. The regression line eqution for the following grph
Review Topi 14: Reltionships etween two numeril vriles Multiple hoie 1. Whih of the following stterplots est demonstrtes line of est fit? A B C D E 2. The regression line eqution for the following grph
Forces on curved surfaces Buoyant force Stability of floating and submerged bodies
 Stti Surfe ores Stti Surfe ores 8m wter hinge? 4 m ores on plne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tpes of problems Horizontl surfes (pressure
Stti Surfe ores Stti Surfe ores 8m wter hinge? 4 m ores on plne res ores on urved surfes Buont fore Stbilit of floting nd submerged bodies ores on Plne res Two tpes of problems Horizontl surfes (pressure
EXPECTED ANSWERS/VALUE POINTS SECTION - A
 6 QUESTION PPE ODE 65// EXPETED NSWES/VLUE POINTS SETION - -.... 6. / 5. 5 6. 5 7. 5. ( ) { } ( ) kˆ ĵ î kˆ ĵ î r 9. or ( ) kˆ ĵ î r. kˆ ĵ î m SETION - B.,, m,,, m O Mrks m 9 5 os θ 9, θ eing ngle etween
6 QUESTION PPE ODE 65// EXPETED NSWES/VLUE POINTS SETION - -.... 6. / 5. 5 6. 5 7. 5. ( ) { } ( ) kˆ ĵ î kˆ ĵ î r 9. or ( ) kˆ ĵ î r. kˆ ĵ î m SETION - B.,, m,,, m O Mrks m 9 5 os θ 9, θ eing ngle etween
The Ellipse. is larger than the other.
 The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
The Ellipse Appolonius of Perg (5 B.C.) disovered tht interseting right irulr one ll the w through with plne slnted ut is not perpendiulr to the is, the intersetion provides resulting urve (oni setion)
Chapter 8 Roots and Radicals
 Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Chpter 8 Roots nd Rdils 7 ROOTS AND RADICALS 8 Figure 8. Grphene is n inredily strong nd flexile mteril mde from ron. It n lso ondut eletriity. Notie the hexgonl grid pttern. (redit: AlexnderAIUS / Wikimedi
Appendix C Partial discharges. 1. Relationship Between Measured and Actual Discharge Quantities
 Appendi Prtil dishrges. Reltionship Between Mesured nd Atul Dishrge Quntities A dishrging smple my e simply represented y the euilent iruit in Figure. The pplied lternting oltge V is inresed until the
Appendi Prtil dishrges. Reltionship Between Mesured nd Atul Dishrge Quntities A dishrging smple my e simply represented y the euilent iruit in Figure. The pplied lternting oltge V is inresed until the
Unit 4. Combinational Circuits
 Unit 4. Comintionl Ciruits Digitl Eletroni Ciruits (Ciruitos Eletrónios Digitles) E.T.S.I. Informáti Universidd de Sevill 5/10/2012 Jorge Jun 2010, 2011, 2012 You re free to opy, distriute
Unit 4. Comintionl Ciruits Digitl Eletroni Ciruits (Ciruitos Eletrónios Digitles) E.T.S.I. Informáti Universidd de Sevill 5/10/2012 Jorge Jun 2010, 2011, 2012 You re free to opy, distriute
Figure XX.1.1 Plane truss structure
 Truss Eements Formution. TRUSS ELEMENT.1 INTRODUTION ne truss struture is ste struture on the sis of tringe, s shown in Fig..1.1. The end of memer is pin juntion whih does not trnsmit moment. As for the
Truss Eements Formution. TRUSS ELEMENT.1 INTRODUTION ne truss struture is ste struture on the sis of tringe, s shown in Fig..1.1. The end of memer is pin juntion whih does not trnsmit moment. As for the
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
Logic Synthesis and Verification
 Logi Synthesis nd Verifition SOPs nd Inompletely Speified Funtions Jie-Hong Rolnd Jing 江介宏 Deprtment of Eletril Engineering Ntionl Tiwn University Fll 2010 Reding: Logi Synthesis in Nutshell Setion 2 most
Logi Synthesis nd Verifition SOPs nd Inompletely Speified Funtions Jie-Hong Rolnd Jing 江介宏 Deprtment of Eletril Engineering Ntionl Tiwn University Fll 2010 Reding: Logi Synthesis in Nutshell Setion 2 most
Applications of Definite Integral
 Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Chpter 5 Applitions of Definite Integrl 5.1 Are Between Two Curves In this setion we use integrls to find res of regions tht lie between the grphs of two funtions. Consider the region tht lies between
Lecture 1 - Introduction and Basic Facts about PDEs
 * 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
* 18.15 - Introdution to PDEs, Fll 004 Prof. Gigliol Stffilni Leture 1 - Introdution nd Bsi Fts bout PDEs The Content of the Course Definition of Prtil Differentil Eqution (PDE) Liner PDEs VVVVVVVVVVVVVVVVVVVV
System Validation (IN4387) November 2, 2012, 14:00-17:00
 System Vlidtion (IN4387) Novemer 2, 2012, 14:00-17:00 Importnt Notes. The exmintion omprises 5 question in 4 pges. Give omplete explntion nd do not onfine yourself to giving the finl nswer. Good luk! Exerise
System Vlidtion (IN4387) Novemer 2, 2012, 14:00-17:00 Importnt Notes. The exmintion omprises 5 question in 4 pges. Give omplete explntion nd do not onfine yourself to giving the finl nswer. Good luk! Exerise
CS434a/541a: Pattern Recognition Prof. Olga Veksler. Lecture 2
 CS434/54: Pttern Recognition Prof. Olg Veksler Lecture Outline Review of Liner Algebr vectors nd mtrices products nd norms vector spces nd liner trnsformtions eigenvlues nd eigenvectors Introduction to
CS434/54: Pttern Recognition Prof. Olg Veksler Lecture Outline Review of Liner Algebr vectors nd mtrices products nd norms vector spces nd liner trnsformtions eigenvlues nd eigenvectors Introduction to
Something found at a salad bar
 Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Nme PP Something found t sld r 4.7 Notes RIGHT TRINGLE hs extly one right ngle. To solve right tringle, you n use things like SOH-H-TO nd the Pythgoren Theorem. n OLIQUE TRINGLE hs no right ngles. To solve
Calculus Cheat Sheet. Integrals Definitions. where F( x ) is an anti-derivative of f ( x ). Fundamental Theorem of Calculus. dx = f x dx g x dx
 Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Hybrid Systems Modeling, Analysis and Control
 Hyrid Systems Modeling, Anlysis nd Control Rdu Grosu Vienn University of Tehnology Leture 5 Finite Automt s Liner Systems Oservility, Rehility nd More Miniml DFA re Not Miniml NFA (Arnold, Diky nd Nivt
Hyrid Systems Modeling, Anlysis nd Control Rdu Grosu Vienn University of Tehnology Leture 5 Finite Automt s Liner Systems Oservility, Rehility nd More Miniml DFA re Not Miniml NFA (Arnold, Diky nd Nivt
Bases for Vector Spaces
 Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
Activities. 4.1 Pythagoras' Theorem 4.2 Spirals 4.3 Clinometers 4.4 Radar 4.5 Posting Parcels 4.6 Interlocking Pipes 4.7 Sine Rule Notes and Solutions
 MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
MEP: Demonstrtion Projet UNIT 4: Trigonometry UNIT 4 Trigonometry tivities tivities 4. Pythgors' Theorem 4.2 Spirls 4.3 linometers 4.4 Rdr 4.5 Posting Prels 4.6 Interloking Pipes 4.7 Sine Rule Notes nd
Counting intersections of spirals on a torus
 Counting intersections of spirls on torus 1 The problem Consider unit squre with opposite sides identified. For emple, if we leve the centre of the squre trveling long line of slope 2 (s shown in the first
Counting intersections of spirls on torus 1 The problem Consider unit squre with opposite sides identified. For emple, if we leve the centre of the squre trveling long line of slope 2 (s shown in the first
A Lower Bound for the Length of a Partial Transversal in a Latin Square, Revised Version
 A Lower Bound for the Length of Prtil Trnsversl in Ltin Squre, Revised Version Pooy Htmi nd Peter W. Shor Deprtment of Mthemtil Sienes, Shrif University of Tehnology, P.O.Bo 11365-9415, Tehrn, Irn Deprtment
A Lower Bound for the Length of Prtil Trnsversl in Ltin Squre, Revised Version Pooy Htmi nd Peter W. Shor Deprtment of Mthemtil Sienes, Shrif University of Tehnology, P.O.Bo 11365-9415, Tehrn, Irn Deprtment
