EPIPOLAR GEOMETRY WITH MANY DETAILS
|
|
|
- Sybil Nelson
- 6 years ago
- Views:
Transcription
1 EPIPOLAR GEOMERY WIH MANY DEAILS
2 hank ou for the slides. he come mostl from the following source. Marc Pollefes U. of North Carolina
3 hree questions: (i) Correspondence geometr: Given an image point in the first view, how does this constrain the position of the corresponding point in the second image? (ii) Camera geometr (motion): Given a set of corresponding image points { i i }, i,,n, what are the cameras P and P for the two views? (iii) Scene geometr (structure): Given corresponding image points i i and cameras P, P, what is the position of (their pre-image) X in space?
4 he epipolar geometr C,C,, and X are coplanar
5 he epipolar geometr What if onl C,C, are known?
6 he epipolar geometr All points on π project on l and l
7 he epipolar geometr Famil of planes π and lines l and l Intersection in e and e
8 he epipolar geometr epipoles e,e intersection of baseline with image plane projection of projection center in other image vanishing point of camera motion direction an epipolar plane plane containing baseline (-D famil) an epipolar line intersection of epipolar plane with image (alwas come in corresponding pairs)
9 Eample: converging cameras
10 Eample: motion parallel with image plane
11 Eample: forward motion e e
12 he fundamental matri F algebraic representation of epipolar geometr a l' we will see that mapping is (singular) correlation (i.e. projective mapping from points to lines) represented b the fundamental matri F
13 he fundamental matri F geometric derivation ' H π [ e' ] Hπ F l' e' ' mapping from -D to -D famil (rank )
14 he fundamental matri F algebraic derivation ( λ) P λc X + + ( + P P I) l P'C P' P + P + X( λ) F [ ] + e' P' P (note: doesn t work for CC F0)
15 he fundamental matri F correspondence condition he fundamental matri satisfies the condition that for an pair of corresponding points in the two images ' F 0 ( ' l' 0)
16 he fundamental matri F F is the unique 33 rank matri that satisfies F0 for all (i) ranspose: if F is fundamental matri for (P,P ), then F is fundamental matri for (P,P) (ii) Epipolar lines: l F & lf (iii) Epipoles: on all epipolar lines, thus e F0, e F0, similarl Fe0 (iv) F has 7 d.o.f., i.e. 33-(homogeneous)-(rank) (v) F is a correlation, projective mapping from a point to a line l F (not a proper correlation, i.e. not invertible)
17 Epipolar line homograph for e, for e, 3 for homograph of a line from e to e
18 he epipolar line geometr l,l epipolar lines, k line not through e l F[k] l and smmetricall lf [k ] l l l k k e e' l Fk (pick ke, since e e 0) F[ e] l l F [ e' ] l' l'
19 Fundamental matri for pure translation
20 Fundamental matri for pure translation
21 Fundamental matri for pure translation [ e' ] H [ ] F e' ( H K RK) eample: e' (,0,0) F ' F 0 ' PX ' P' X K[I 0]X K - K[I t] Z ( X,Y,Z) - K /Z ' + Kt/Z motion starts at and moves towards e, faster depending on Z pure translation: F onl d.o.f., [e] 0 auto-epipolar
22 General motion [ e' ] H 0 [ e' ] ˆ 0 ' ' ' K'RK - + K' t/z
23 Projective transformation and invariance Derivation based purel on projective concepts ˆ H, ˆ' H' ' Fˆ PX ( )( - PH H X) Pˆ Xˆ ( )( - P' H H X) Pˆ' Xˆ H' - FH - F invariant to transformations of projective 3-space ' P' X ( P, P' ) a F F a ( P,P' ) canonical form P [I 0] P' [M m] unique not unique [ m] M F
24 Projective ambiguit of cameras given F previous slide: at least projective ambiguit this slide: not more! ~ ~ Show that if F is same for (P,P ) and (P,P ), there eists a projective transformation H so that ~ ~ PHP and P HP lemma: H P' H ~ P [I 0] P' [A a] P [I 0] P ~ ' F [ a] A [ ~ a] A ~ ~ A ~ a ka k A + av ( ) rank [A ~ ~ a] af a[] a A 0 ~ af ~ a ka a A ~ a A ~ a ka ~ - A 0 ka ~ - A av [ ] [ ] [ ] ( ) ( ) k I 0 k v k [A a] k I k v 0 k [ k ( A - av ) ka] P ~ ' (-57, ok)
25 Canonical cameras given F F matri corresponds to P,P iff P FP is skew-smmetric ( X P' FPX 0, X) F matri, S skew-smmetric matri P [I 0] P' [SF e'] [SF e'] (fund.matrif) F[I 0] F S F e' F 0 0 F S 0 F 0 0 Possible choice: P [I 0] P' [[e'] F e'] Canonical representation: P [I 0] P' [[e'] F + e' v λe']
26 he essential matri ~fundamental matri for calibrated cameras (remove K) E ˆ ' [ t] R R[R t] Eˆ ( ˆ K ; ˆ' K ' ) E K' FK 5 d.o.f. (3 for R; for t up to scale) E is essential matri if and onl if two singularvalues are equal (and third0) E Udiag(,,0)V
27 Four possible reconstructions from E (onl one solution where points is in front of both cameras)
28 Epipolar geometr: basic equation ' F 0 ' f + ' f + ' f3 + ' f + ' f + ' f3 + f3 + f3 + f33 0 separate known from unknown [ ', ', ', ', ', ',,,][ f, f, f, f, f, f, f, f, f ] 0 (data) (unknowns) (linear) ' ' ' ' ' ' M M M M M M M M ' n n ' n n ' n ' n n ' n n ' n n n M f 0 Af 0
29 f f f f f f f f f n n n n n n n n n n n n M M M M M M M M M ~0000 ~0000 ~0000 ~0000 ~00 ~00 ~00 ~00! Orders of magnitude difference Between column of data matri least-squares ields poor results the NO normalized 8-point algorithm
30 the normalized 8-point algorithm ransform image to ~[-,][-,] (0,500) (700,500) (-,) (0,0) (,) (0,0) (700,0) (-,-) (,-) Least squares ields good results (Hartle, PAMI 97)
31 the singularit constraint 0 F e' 0 Fe 0 detf F rank V U σ V U σ U σ V V σ σ σ U F + + SVD from linearl computed F matri (rank 3) V U σ U σ V V 0 σ σ U F' + F min F- F' Compute closest rank- approimation
32
33 the minimum case 7 point correspondences 0 f ' ' ' ' ' ' ' ' ' ' ' ' M M M M M M M M M ( ) V,0,0,...,σ diag σ A U V ] A[V ( ) 8 [ ] V e.g.v...7 0, λf ) (F + i i i one parameter famil of solutions but F +λf not automaticall rank
34 the minimum case impose rank σ 3 (obtain or 3 solutions) F 7pts F F F 3 det( F + λf ) a 3λ + aλ + aλ + a0 0 (cubic equation) - det( F + λf ) det F det(f F + λi) 0 - F F Compute possible λ as eigenvalues of (onl real solutions are potential solutions)
35 Gold standard Maimum Likelihood Estimation (, ˆ ) d( ', ˆ' ) d i i + i i i ( least-squares for Gaussian noise) subject to ˆ' Fˆ 0 Initialize: normalized 8-point, (P,P ) from F, reconstruct X i Parameterize: P [I 0],P' [M t],x i ˆ PX, ˆ i i i P' X Minimize cost using Levenberg-Marquardt (preferabl sparse LM, see book) i (overparametrized)
36 Gold standard Alternative, minimal parametrization (with a) (note (,,) and (,,) are epipoles) problems: a0 pick largest of a,b,c,d to fi epipole at infinit pick largest of,,w and of,,w parametrizations! reparametrize at ever iteration, to be sure
37 First-order geometric error (Sampson error) ( ) e JJ e e e JJ (one eq./point JJ scalar) e ' F 0 e i ' F0 0 ( ' F) + ( ' F) + ( F) ( ) F JJ + e e JJ ( ' F) + ( ' F) + ( F) + ( F) ' F (problem if some is located at epipole) advantage: no subsidiar variables required
38 Smmetric epipolar error ( F ) d( ',, F ' ) d i i + i i ' F + ( ' F) + ( ) ( F) + ( F) ' F i
39 Some eperiments:
40 Some eperiments:
41 Some eperiments:
42 Some eperiments: Residual error: ( F ) d( ',, F ' ) d i i + i (for all points!) i i
43 Recommendations:. Do not use unnormalized algorithms. Quick and eas to implement: 8-point normalized 3. Better: enforce rank- constraint during minimization 4. Best: Maimum Likelihood Estimation (minimal parameterization, sparse implementation)
44 Feature points Etract feature points to relate images Required properties: Well-defined (i.e. neigboring points should all be different) Stable across views (i.e. same 3D point should be etracted as feature for neighboring viewpoints)
45 Degenerate cases: Degenerate cases Planar scene Pure rotation No unique solution Remaining DOF filled b noise Use simpler model (e.g. homograph) Model selection (orr et al., ICCV 98, Kanatani, Akaike) Compare H and F according to epected residual error (compensate for model compleit)
46 More problems: Absence of sufficient features (no teture) Repeated structure ambiguit Robust matcher also finds support for wrong hpothesis solution: detect repetition (Schaffalitzk and Zisserman, BMVC 98)
47 two-view geometr geometric relations between two views is full described b recovered 33 matri F
48 Image pair rectification simplif stereo matching b warping the images Appl projective transformation so that epipolar lines correspond to horizontal scanlines e e map epipole e to (,0,0) tr to minimize image distortion problem when epipole in (or close to) the image
49 Planar rectification (standard approach) ~ image size (calibrated) Bring two views to standard stereo setup (moves epipole to ) (not possible when in/close to image) Distortion minimization (uncalibrated)
50
51
Vision par ordinateur
 Vision par ordinateur Géométrie épipolaire Frédéric Devernay Avec des transparents de Marc Pollefeys Epipolar geometry π Underlying structure in set of matches for rigid scenes C1 m1 l1 M L2 L1 l T 1 l
Vision par ordinateur Géométrie épipolaire Frédéric Devernay Avec des transparents de Marc Pollefeys Epipolar geometry π Underlying structure in set of matches for rigid scenes C1 m1 l1 M L2 L1 l T 1 l
Camera: optical system
 Camera: optical system Y dαα α ρ ρ curvature radius Z thin lens small angles: α Y ρ α Y ρ lens refraction inde: n Y incident light beam deviated beam θ '' α θ ' α sin( θ '' α ) sin( θ ' α ) n θ α θ α deviation
Camera: optical system Y dαα α ρ ρ curvature radius Z thin lens small angles: α Y ρ α Y ρ lens refraction inde: n Y incident light beam deviated beam θ '' α θ ' α sin( θ '' α ) sin( θ ' α ) n θ α θ α deviation
Multiple View Geometry in Computer Vision
 Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Scene Planes & Homographies Lecture 19 March 24, 2005 2 In our last lecture, we examined various
Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Scene Planes & Homographies Lecture 19 March 24, 2005 2 In our last lecture, we examined various
Lecture 5. Epipolar Geometry. Professor Silvio Savarese Computational Vision and Geometry Lab. 21-Jan-15. Lecture 5 - Silvio Savarese
 Lecture 5 Epipolar Geometry Professor Silvio Savarese Computational Vision and Geometry Lab Silvio Savarese Lecture 5-21-Jan-15 Lecture 5 Epipolar Geometry Why is stereo useful? Epipolar constraints Essential
Lecture 5 Epipolar Geometry Professor Silvio Savarese Computational Vision and Geometry Lab Silvio Savarese Lecture 5-21-Jan-15 Lecture 5 Epipolar Geometry Why is stereo useful? Epipolar constraints Essential
CSE 252B: Computer Vision II
 CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Hamed Masnadi Shirazi, Solmaz Alipour LECTURE 5 Relationships between the Homography and the Essential Matrix 5.1. Introduction In practice,
CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Hamed Masnadi Shirazi, Solmaz Alipour LECTURE 5 Relationships between the Homography and the Essential Matrix 5.1. Introduction In practice,
Camera calibration. Outline. Pinhole camera. Camera projection models. Nonlinear least square methods A camera calibration tool
 Outline Camera calibration Camera projection models Camera calibration i Nonlinear least square methods A camera calibration tool Applications Digital Visual Effects Yung-Yu Chuang with slides b Richard
Outline Camera calibration Camera projection models Camera calibration i Nonlinear least square methods A camera calibration tool Applications Digital Visual Effects Yung-Yu Chuang with slides b Richard
CS4495/6495 Introduction to Computer Vision. 3D-L3 Fundamental matrix
 CS4495/6495 Introduction to Computer Vision 3D-L3 Fundamental matrix Weak calibration Main idea: Estimate epipolar geometry from a (redundant) set of point correspondences between two uncalibrated cameras
CS4495/6495 Introduction to Computer Vision 3D-L3 Fundamental matrix Weak calibration Main idea: Estimate epipolar geometry from a (redundant) set of point correspondences between two uncalibrated cameras
CSE 252B: Computer Vision II
 CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Tasha Vanesian LECTURE 3 Calibrated 3D Reconstruction 3.1. Geometric View of Epipolar Constraint We are trying to solve the following problem:
CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Tasha Vanesian LECTURE 3 Calibrated 3D Reconstruction 3.1. Geometric View of Epipolar Constraint We are trying to solve the following problem:
Parameterizing the Trifocal Tensor
 Parameterizing the Trifocal Tensor May 11, 2017 Based on: Klas Nordberg. A Minimal Parameterization of the Trifocal Tensor. In Computer society conference on computer vision and pattern recognition (CVPR).
Parameterizing the Trifocal Tensor May 11, 2017 Based on: Klas Nordberg. A Minimal Parameterization of the Trifocal Tensor. In Computer society conference on computer vision and pattern recognition (CVPR).
Vision 3D articielle Session 2: Essential and fundamental matrices, their computation, RANSAC algorithm
 Vision 3D articielle Session 2: Essential and fundamental matrices, their computation, RANSAC algorithm Pascal Monasse monasse@imagine.enpc.fr IMAGINE, École des Ponts ParisTech Contents Some useful rules
Vision 3D articielle Session 2: Essential and fundamental matrices, their computation, RANSAC algorithm Pascal Monasse monasse@imagine.enpc.fr IMAGINE, École des Ponts ParisTech Contents Some useful rules
LESSON 35: EIGENVALUES AND EIGENVECTORS APRIL 21, (1) We might also write v as v. Both notations refer to a vector.
 LESSON 5: EIGENVALUES AND EIGENVECTORS APRIL 2, 27 In this contet, a vector is a column matri E Note 2 v 2, v 4 5 6 () We might also write v as v Both notations refer to a vector (2) A vector can be man
LESSON 5: EIGENVALUES AND EIGENVECTORS APRIL 2, 27 In this contet, a vector is a column matri E Note 2 v 2, v 4 5 6 () We might also write v as v Both notations refer to a vector (2) A vector can be man
Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s =
 Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s = cotα), and the lens distortion (radial distortion coefficient
Camera Calibration The purpose of camera calibration is to determine the intrinsic camera parameters (c 0,r 0 ), f, s x, s y, skew parameter (s = cotα), and the lens distortion (radial distortion coefficient
Identifying second degree equations
 Chapter 7 Identifing second degree equations 71 The eigenvalue method In this section we appl eigenvalue methods to determine the geometrical nature of the second degree equation a 2 + 2h + b 2 + 2g +
Chapter 7 Identifing second degree equations 71 The eigenvalue method In this section we appl eigenvalue methods to determine the geometrical nature of the second degree equation a 2 + 2h + b 2 + 2g +
Two-View Multibody Structure from Motion
 International Journal of Computer Vision 68(), 7 5, 006 c 006 Springer Science + Business Media, LLC Manufactured in he Netherlands DOI: 0007/s63-005-4839-7 wo-view Multibody Structure from Motion RENÉ
International Journal of Computer Vision 68(), 7 5, 006 c 006 Springer Science + Business Media, LLC Manufactured in he Netherlands DOI: 0007/s63-005-4839-7 wo-view Multibody Structure from Motion RENÉ
Algorithms for Computing a Planar Homography from Conics in Correspondence
 Algorithms for Computing a Planar Homography from Conics in Correspondence Juho Kannala, Mikko Salo and Janne Heikkilä Machine Vision Group University of Oulu, Finland {jkannala, msa, jth@ee.oulu.fi} Abstract
Algorithms for Computing a Planar Homography from Conics in Correspondence Juho Kannala, Mikko Salo and Janne Heikkilä Machine Vision Group University of Oulu, Finland {jkannala, msa, jth@ee.oulu.fi} Abstract
Method 1: Geometric Error Optimization
 Method 1: Geometric Error Optimization we need to encode the constraints ŷ i F ˆx i = 0, rank F = 2 idea: reconstruct 3D point via equivalent projection matrices and use reprojection error equivalent projection
Method 1: Geometric Error Optimization we need to encode the constraints ŷ i F ˆx i = 0, rank F = 2 idea: reconstruct 3D point via equivalent projection matrices and use reprojection error equivalent projection
A Study of Kruppa s Equation for Camera Self-calibration
 Proceedings of the International Conference of Machine Vision and Machine Learning Prague, Czech Republic, August 14-15, 2014 Paper No. 57 A Study of Kruppa s Equation for Camera Self-calibration Luh Prapitasari,
Proceedings of the International Conference of Machine Vision and Machine Learning Prague, Czech Republic, August 14-15, 2014 Paper No. 57 A Study of Kruppa s Equation for Camera Self-calibration Luh Prapitasari,
Statistical Geometry Processing Winter Semester 2011/2012
 Statistical Geometry Processing Winter Semester 2011/2012 Linear Algebra, Function Spaces & Inverse Problems Vector and Function Spaces 3 Vectors vectors are arrows in space classically: 2 or 3 dim. Euclidian
Statistical Geometry Processing Winter Semester 2011/2012 Linear Algebra, Function Spaces & Inverse Problems Vector and Function Spaces 3 Vectors vectors are arrows in space classically: 2 or 3 dim. Euclidian
Trinocular Geometry Revisited
 Trinocular Geometry Revisited Jean Pounce and Martin Hebert 报告人 : 王浩人 2014-06-24 Contents 1. Introduction 2. Converging Triplets of Lines 3. Converging Triplets of Visual Rays 4. Discussion 1. Introduction
Trinocular Geometry Revisited Jean Pounce and Martin Hebert 报告人 : 王浩人 2014-06-24 Contents 1. Introduction 2. Converging Triplets of Lines 3. Converging Triplets of Visual Rays 4. Discussion 1. Introduction
The Multibody Trifocal Tensor: Motion Segmentation from 3 Perspective Views
 The Multibody Trifocal Tensor: Motion Segmentation from 3 Perspective Views Richard Hartley 1,2 and RenéVidal 2,3 1 Dept. of Systems Engineering 3 Center for Imaging Science Australian National University
The Multibody Trifocal Tensor: Motion Segmentation from 3 Perspective Views Richard Hartley 1,2 and RenéVidal 2,3 1 Dept. of Systems Engineering 3 Center for Imaging Science Australian National University
Lines and points. Lines and points
 omogeneous coordinates in the plane Homogeneous coordinates in the plane A line in the plane a + by + c is represented as (a, b, c). A line is a subset of points in the plane. All vectors (ka, kb, kc)
omogeneous coordinates in the plane Homogeneous coordinates in the plane A line in the plane a + by + c is represented as (a, b, c). A line is a subset of points in the plane. All vectors (ka, kb, kc)
Linear Algebra & Geometry why is linear algebra useful in computer vision?
 Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Eigenvectors and Eigenvalues 1
 Ma 2015 page 1 Eigenvectors and Eigenvalues 1 In this handout, we will eplore eigenvectors and eigenvalues. We will begin with an eploration, then provide some direct eplanation and worked eamples, and
Ma 2015 page 1 Eigenvectors and Eigenvalues 1 In this handout, we will eplore eigenvectors and eigenvalues. We will begin with an eploration, then provide some direct eplanation and worked eamples, and
Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix
 ECCV Workshop on Vision and Modeling of Dynamic Scenes, Copenhagen, Denmark, May 2002 Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix René Vidal Dept of EECS, UC Berkeley Berkeley,
ECCV Workshop on Vision and Modeling of Dynamic Scenes, Copenhagen, Denmark, May 2002 Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix René Vidal Dept of EECS, UC Berkeley Berkeley,
Two-View Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix
 Two-View Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix René Vidal Stefano Soatto Shankar Sastry Department of EECS, UC Berkeley Department of Computer Sciences, UCLA 30 Cory Hall,
Two-View Segmentation of Dynamic Scenes from the Multibody Fundamental Matrix René Vidal Stefano Soatto Shankar Sastry Department of EECS, UC Berkeley Department of Computer Sciences, UCLA 30 Cory Hall,
6.869 Advances in Computer Vision. Prof. Bill Freeman March 1, 2005
 6.869 Advances in Computer Vision Prof. Bill Freeman March 1 2005 1 2 Local Features Matching points across images important for: object identification instance recognition object class recognition pose
6.869 Advances in Computer Vision Prof. Bill Freeman March 1 2005 1 2 Local Features Matching points across images important for: object identification instance recognition object class recognition pose
Mathematics 309 Conic sections and their applicationsn. Chapter 2. Quadric figures. ai,j x i x j + b i x i + c =0. 1. Coordinate changes
 Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
Mathematics 309 Conic sections and their applicationsn Chapter 2. Quadric figures In this chapter want to outline quickl how to decide what figure associated in 2D and 3D to quadratic equations look like.
Geometric Modeling Summer Semester 2010 Mathematical Tools (1)
 Geometric Modeling Summer Semester 2010 Mathematical Tools (1) Recap: Linear Algebra Today... Topics: Mathematical Background Linear algebra Analysis & differential geometry Numerical techniques Geometric
Geometric Modeling Summer Semester 2010 Mathematical Tools (1) Recap: Linear Algebra Today... Topics: Mathematical Background Linear algebra Analysis & differential geometry Numerical techniques Geometric
Camera Projection Model
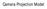 amera Projection Model 3D Point Projection (Pixel Space) O ( u, v ) ccd ccd f Projection plane (, Y, Z ) ( u, v ) img Z img (0,0) w img ( u, v ) img img uimg f Z p Y v img f Z p x y Zu f p Z img img x
amera Projection Model 3D Point Projection (Pixel Space) O ( u, v ) ccd ccd f Projection plane (, Y, Z ) ( u, v ) img Z img (0,0) w img ( u, v ) img img uimg f Z p Y v img f Z p x y Zu f p Z img img x
PAijpam.eu EPIPOLAR GEOMETRY WITH A FUNDAMENTAL MATRIX IN CANONICAL FORM Georgi Hristov Georgiev 1, Vencislav Dakov Radulov 2
 International Journal of Pure and Applied Mathematics Volume 105 No. 4 2015, 669-683 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: http://dx.doi.org/10.12732/ijpam.v105i4.8
International Journal of Pure and Applied Mathematics Volume 105 No. 4 2015, 669-683 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: http://dx.doi.org/10.12732/ijpam.v105i4.8
Computation of the Quadrifocal Tensor
 Computation of the Quadrifocal Tensor Richard I. Hartley G.E. Corporate Research and Development Research Circle, Niskayuna, NY 2309, USA Abstract. This paper gives a practical and accurate algorithm for
Computation of the Quadrifocal Tensor Richard I. Hartley G.E. Corporate Research and Development Research Circle, Niskayuna, NY 2309, USA Abstract. This paper gives a practical and accurate algorithm for
A Practical Method for Decomposition of the Essential Matrix
 Applied Mathematical Sciences, Vol. 8, 2014, no. 176, 8755-8770 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.410877 A Practical Method for Decomposition of the Essential Matrix Georgi
Applied Mathematical Sciences, Vol. 8, 2014, no. 176, 8755-8770 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.410877 A Practical Method for Decomposition of the Essential Matrix Georgi
Camera Models and Affine Multiple Views Geometry
 Camera Models and Affine Multiple Views Geometry Subhashis Banerjee Dept. Computer Science and Engineering IIT Delhi email: suban@cse.iitd.ac.in May 29, 2001 1 1 Camera Models A Camera transforms a 3D
Camera Models and Affine Multiple Views Geometry Subhashis Banerjee Dept. Computer Science and Engineering IIT Delhi email: suban@cse.iitd.ac.in May 29, 2001 1 1 Camera Models A Camera transforms a 3D
MMJ1153 COMPUTATIONAL METHOD IN SOLID MECHANICS PRELIMINARIES TO FEM
 B Course Content: A INTRODUCTION AND OVERVIEW Numerical method and Computer-Aided Engineering; Phsical problems; Mathematical models; Finite element method;. B Elements and nodes, natural coordinates,
B Course Content: A INTRODUCTION AND OVERVIEW Numerical method and Computer-Aided Engineering; Phsical problems; Mathematical models; Finite element method;. B Elements and nodes, natural coordinates,
Linear Algebra & Geometry why is linear algebra useful in computer vision?
 Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Linear Algebra & Geometry why is linear algebra useful in computer vision? References: -Any book on linear algebra! -[HZ] chapters 2, 4 Some of the slides in this lecture are courtesy to Prof. Octavia
Pose estimation from point and line correspondences
 Pose estimation from point and line correspondences Giorgio Panin October 17, 008 1 Problem formulation Estimate (in a LSE sense) the pose of an object from N correspondences between known object points
Pose estimation from point and line correspondences Giorgio Panin October 17, 008 1 Problem formulation Estimate (in a LSE sense) the pose of an object from N correspondences between known object points
Robert Collins CSE486, Penn State. Lecture 25: Structure from Motion
 Lecture 25: Structure from Motion Structure from Motion Given a set of flow fields or displacement vectors from a moving camera over time, determine: the sequence of camera poses the 3D structure of the
Lecture 25: Structure from Motion Structure from Motion Given a set of flow fields or displacement vectors from a moving camera over time, determine: the sequence of camera poses the 3D structure of the
Camera calibration by Zhang
 Camera calibration by Zhang Siniša Kolarić September 2006 Abstract In this presentation, I present a way to calibrate a camera using the method by Zhang. NOTE. This
Camera calibration by Zhang Siniša Kolarić September 2006 Abstract In this presentation, I present a way to calibrate a camera using the method by Zhang. NOTE. This
Single view metrology
 EECS 44 Computer vision Single view metrology Review calibration Lines and planes at infinity Absolute conic Estimating geometry from a single image Etensions Reading: [HZ] Chapters,3,8 Calibration Problem
EECS 44 Computer vision Single view metrology Review calibration Lines and planes at infinity Absolute conic Estimating geometry from a single image Etensions Reading: [HZ] Chapters,3,8 Calibration Problem
15. Eigenvalues, Eigenvectors
 5 Eigenvalues, Eigenvectors Matri of a Linear Transformation Consider a linear ( transformation ) L : a b R 2 R 2 Suppose we know that L and L Then c d because of linearit, we can determine what L does
5 Eigenvalues, Eigenvectors Matri of a Linear Transformation Consider a linear ( transformation ) L : a b R 2 R 2 Suppose we know that L and L Then c d because of linearit, we can determine what L does
Motion estimation. Digital Visual Effects Yung-Yu Chuang. with slides by Michael Black and P. Anandan
 Motion estimation Digital Visual Effects Yung-Yu Chuang with slides b Michael Black and P. Anandan Motion estimation Parametric motion image alignment Tracking Optical flow Parametric motion direct method
Motion estimation Digital Visual Effects Yung-Yu Chuang with slides b Michael Black and P. Anandan Motion estimation Parametric motion image alignment Tracking Optical flow Parametric motion direct method
Instance-level l recognition. Cordelia Schmid INRIA
 nstance-level l recognition Cordelia Schmid NRA nstance-level recognition Particular objects and scenes large databases Application Search photos on the web for particular places Find these landmars...in
nstance-level l recognition Cordelia Schmid NRA nstance-level recognition Particular objects and scenes large databases Application Search photos on the web for particular places Find these landmars...in
Vector and Affine Math
 Vector and Affine Math Computer Science Department The Universit of Teas at Austin Vectors A vector is a direction and a magnitude Does NOT include a point of reference Usuall thought of as an arrow in
Vector and Affine Math Computer Science Department The Universit of Teas at Austin Vectors A vector is a direction and a magnitude Does NOT include a point of reference Usuall thought of as an arrow in
Final Exam Due on Sunday 05/06
 Final Exam Due on Sunday 05/06 The exam should be completed individually without collaboration. However, you are permitted to consult with the textbooks, notes, slides and even internet resources. If you
Final Exam Due on Sunday 05/06 The exam should be completed individually without collaboration. However, you are permitted to consult with the textbooks, notes, slides and even internet resources. If you
Demonstrate solution methods for systems of linear equations. Show that a system of equations can be represented in matrix-vector form.
 Chapter Linear lgebra Objective Demonstrate solution methods for sstems of linear equations. Show that a sstem of equations can be represented in matri-vector form. 4 Flowrates in kmol/hr Figure.: Two
Chapter Linear lgebra Objective Demonstrate solution methods for sstems of linear equations. Show that a sstem of equations can be represented in matri-vector form. 4 Flowrates in kmol/hr Figure.: Two
Multiple View Geometry in Computer Vision
 Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Trifocal Tensor Lecture 21 March 31, 2005 2 Lord Shiva is depicted as having three eyes. The
Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Trifocal Tensor Lecture 21 March 31, 2005 2 Lord Shiva is depicted as having three eyes. The
Interest Operators. All lectures are from posted research papers. Harris Corner Detector: the first and most basic interest operator
 Interest Operators All lectures are from posted research papers. Harris Corner Detector: the first and most basic interest operator SIFT interest point detector and region descriptor Kadir Entrop Detector
Interest Operators All lectures are from posted research papers. Harris Corner Detector: the first and most basic interest operator SIFT interest point detector and region descriptor Kadir Entrop Detector
Instance-level l recognition. Cordelia Schmid & Josef Sivic INRIA
 nstance-level l recognition Cordelia Schmid & Josef Sivic NRA nstance-level recognition Particular objects and scenes large databases Application Search photos on the web for particular places Find these
nstance-level l recognition Cordelia Schmid & Josef Sivic NRA nstance-level recognition Particular objects and scenes large databases Application Search photos on the web for particular places Find these
Background Mathematics (2/2) 1. David Barber
 Background Mathematics (2/2) 1 David Barber University College London Modified by Samson Cheung (sccheung@ieee.org) 1 These slides accompany the book Bayesian Reasoning and Machine Learning. The book and
Background Mathematics (2/2) 1 David Barber University College London Modified by Samson Cheung (sccheung@ieee.org) 1 These slides accompany the book Bayesian Reasoning and Machine Learning. The book and
6.801/866. Affine Structure from Motion. T. Darrell
 6.801/866 Affine Structure from Motion T. Darrell [Read F&P Ch. 12.0, 12.2, 12.3, 12.4] Affine geometry is, roughly speaking, what is left after all ability to measure lengths, areas, angles, etc. has
6.801/866 Affine Structure from Motion T. Darrell [Read F&P Ch. 12.0, 12.2, 12.3, 12.4] Affine geometry is, roughly speaking, what is left after all ability to measure lengths, areas, angles, etc. has
Augmented Reality VU Camera Registration. Prof. Vincent Lepetit
 Augmented Reality VU Camera Registration Prof. Vincent Lepetit Different Approaches to Vision-based 3D Tracking [From D. Wagner] [From Drummond PAMI02] [From Davison ICCV01] Consider natural features Consider
Augmented Reality VU Camera Registration Prof. Vincent Lepetit Different Approaches to Vision-based 3D Tracking [From D. Wagner] [From Drummond PAMI02] [From Davison ICCV01] Consider natural features Consider
Some linear transformations on R 2 Math 130 Linear Algebra D Joyce, Fall 2013
 Some linear transformations on R 2 Math 3 Linear Algebra D Joce, Fall 23 Let s look at some some linear transformations on the plane R 2. We ll look at several kinds of operators on R 2 including reflections,
Some linear transformations on R 2 Math 3 Linear Algebra D Joce, Fall 23 Let s look at some some linear transformations on the plane R 2. We ll look at several kinds of operators on R 2 including reflections,
Optimisation on Manifolds
 Optimisation on Manifolds K. Hüper MPI Tübingen & Univ. Würzburg K. Hüper (MPI Tübingen & Univ. Würzburg) Applications in Computer Vision Grenoble 18/9/08 1 / 29 Contents 2 Examples Essential matrix estimation
Optimisation on Manifolds K. Hüper MPI Tübingen & Univ. Würzburg K. Hüper (MPI Tübingen & Univ. Würzburg) Applications in Computer Vision Grenoble 18/9/08 1 / 29 Contents 2 Examples Essential matrix estimation
Visual Object Recognition
 Visual Object Recognition Lecture 2: Image Formation Per-Erik Forssén, docent Computer Vision Laboratory Department of Electrical Engineering Linköping University Lecture 2: Image Formation Pin-hole, and
Visual Object Recognition Lecture 2: Image Formation Per-Erik Forssén, docent Computer Vision Laboratory Department of Electrical Engineering Linköping University Lecture 2: Image Formation Pin-hole, and
M3: Multiple View Geometry
 M3: Multiple View Geometry L18: Projective Structure from Motion: Iterative Algorithm based on Factorization Based on Sections 13.4 C. V. Jawahar jawahar-at-iiit.net Mar 2005: 1 Review: Reconstruction
M3: Multiple View Geometry L18: Projective Structure from Motion: Iterative Algorithm based on Factorization Based on Sections 13.4 C. V. Jawahar jawahar-at-iiit.net Mar 2005: 1 Review: Reconstruction
arxiv: v1 [hep-ph] 8 May 2013
![arxiv: v1 [hep-ph] 8 May 2013 arxiv: v1 [hep-ph] 8 May 2013](/thumbs/85/91742837.jpg) Analtic solutions for neutrino momenta in deca of top quarks at hadron colliders Burton A. Betchart, Regina Demina, Amnon Harel Universit of Rochester arxiv:1305.1878v1 [hep-ph] 8 Ma 013 Ma 9, 013 Abstract
Analtic solutions for neutrino momenta in deca of top quarks at hadron colliders Burton A. Betchart, Regina Demina, Amnon Harel Universit of Rochester arxiv:1305.1878v1 [hep-ph] 8 Ma 013 Ma 9, 013 Abstract
Affine transformations. Brian Curless CSE 557 Fall 2014
 Affine transformations Brian Curless CSE 557 Fall 2014 1 Reading Required: Shirle, Sec. 2.4, 2.7 Shirle, Ch. 5.1-5.3 Shirle, Ch. 6 Further reading: Fole, et al, Chapter 5.1-5.5. David F. Rogers and J.
Affine transformations Brian Curless CSE 557 Fall 2014 1 Reading Required: Shirle, Sec. 2.4, 2.7 Shirle, Ch. 5.1-5.3 Shirle, Ch. 6 Further reading: Fole, et al, Chapter 5.1-5.5. David F. Rogers and J.
First Order Equations
 10 1 Linear and Semilinear Equations Chapter First Order Equations Contents 1 Linear and Semilinear Equations 9 Quasilinear Equations 19 3 Wave Equation 6 4 Sstems of Equations 31 1 Linear and Semilinear
10 1 Linear and Semilinear Equations Chapter First Order Equations Contents 1 Linear and Semilinear Equations 9 Quasilinear Equations 19 3 Wave Equation 6 4 Sstems of Equations 31 1 Linear and Semilinear
4.7. Newton s Method. Procedure for Newton s Method HISTORICAL BIOGRAPHY
 4. Newton s Method 99 4. Newton s Method HISTORICAL BIOGRAPHY Niels Henrik Abel (18 189) One of the basic problems of mathematics is solving equations. Using the quadratic root formula, we know how to
4. Newton s Method 99 4. Newton s Method HISTORICAL BIOGRAPHY Niels Henrik Abel (18 189) One of the basic problems of mathematics is solving equations. Using the quadratic root formula, we know how to
Linear Algebra 2 More on determinants and Evalues Exercises and Thanksgiving Activities
 Linear Algebra 2 More on determinants and Evalues Exercises and Thanksgiving Activities 2. Determinant of a linear transformation, change of basis. In the solution set of Homework 1, New Series, I included
Linear Algebra 2 More on determinants and Evalues Exercises and Thanksgiving Activities 2. Determinant of a linear transformation, change of basis. In the solution set of Homework 1, New Series, I included
COMPLEX ALGEBRAIC SURFACES CLASS 15
 COMPLEX ALGEBRAIC SURFACES CLASS 15 RAVI VAKIL CONTENTS 1. Every smooth cubic has 27 lines, and is the blow-up of P 2 at 6 points 1 1.1. An alternate approach 4 2. Castelnuovo s Theorem 5 We now know that
COMPLEX ALGEBRAIC SURFACES CLASS 15 RAVI VAKIL CONTENTS 1. Every smooth cubic has 27 lines, and is the blow-up of P 2 at 6 points 1 1.1. An alternate approach 4 2. Castelnuovo s Theorem 5 We now know that
Instance-level recognition: Local invariant features. Cordelia Schmid INRIA, Grenoble
 nstance-level recognition: ocal invariant features Cordelia Schmid NRA Grenoble Overview ntroduction to local features Harris interest points + SSD ZNCC SFT Scale & affine invariant interest point detectors
nstance-level recognition: ocal invariant features Cordelia Schmid NRA Grenoble Overview ntroduction to local features Harris interest points + SSD ZNCC SFT Scale & affine invariant interest point detectors
Corners, Blobs & Descriptors. With slides from S. Lazebnik & S. Seitz, D. Lowe, A. Efros
 Corners, Blobs & Descriptors With slides from S. Lazebnik & S. Seitz, D. Lowe, A. Efros Motivation: Build a Panorama M. Brown and D. G. Lowe. Recognising Panoramas. ICCV 2003 How do we build panorama?
Corners, Blobs & Descriptors With slides from S. Lazebnik & S. Seitz, D. Lowe, A. Efros Motivation: Build a Panorama M. Brown and D. G. Lowe. Recognising Panoramas. ICCV 2003 How do we build panorama?
Uncertainty Models in Quasiconvex Optimization for Geometric Reconstruction
 Uncertainty Models in Quasiconvex Optimization for Geometric Reconstruction Qifa Ke and Takeo Kanade Department of Computer Science, Carnegie Mellon University Email: ke@cmu.edu, tk@cs.cmu.edu Abstract
Uncertainty Models in Quasiconvex Optimization for Geometric Reconstruction Qifa Ke and Takeo Kanade Department of Computer Science, Carnegie Mellon University Email: ke@cmu.edu, tk@cs.cmu.edu Abstract
Homework Notes Week 6
 Homework Notes Week 6 Math 24 Spring 24 34#4b The sstem + 2 3 3 + 4 = 2 + 2 + 3 4 = 2 + 2 3 = is consistent To see this we put the matri 3 2 A b = 2 into reduced row echelon form Adding times the first
Homework Notes Week 6 Math 24 Spring 24 34#4b The sstem + 2 3 3 + 4 = 2 + 2 + 3 4 = 2 + 2 3 = is consistent To see this we put the matri 3 2 A b = 2 into reduced row echelon form Adding times the first
Lecture 20: Quantization and Rate-Distortion
 Lecture 20: Quantization and Rate-Distortion Quantization Introduction to rate-distortion theorem Dr. Yao Xie, ECE587, Information Theory, Duke University Approimating continuous signals... Dr. Yao Xie,
Lecture 20: Quantization and Rate-Distortion Quantization Introduction to rate-distortion theorem Dr. Yao Xie, ECE587, Information Theory, Duke University Approimating continuous signals... Dr. Yao Xie,
INF Introduction to classifiction Anne Solberg Based on Chapter 2 ( ) in Duda and Hart: Pattern Classification
 INF 4300 151014 Introduction to classifiction Anne Solberg anne@ifiuiono Based on Chapter 1-6 in Duda and Hart: Pattern Classification 151014 INF 4300 1 Introduction to classification One of the most challenging
INF 4300 151014 Introduction to classifiction Anne Solberg anne@ifiuiono Based on Chapter 1-6 in Duda and Hart: Pattern Classification 151014 INF 4300 1 Introduction to classification One of the most challenging
Singular Value Decomposition
 Singular Value Decomposition Motivatation The diagonalization theorem play a part in many interesting applications. Unfortunately not all matrices can be factored as A = PDP However a factorization A =
Singular Value Decomposition Motivatation The diagonalization theorem play a part in many interesting applications. Unfortunately not all matrices can be factored as A = PDP However a factorization A =
Sparse Levenberg-Marquardt algorithm.
 Sparse Levenberg-Marquardt algorithm. R. I. Hartley and A. Zisserman: Multiple View Geometry in Computer Vision. Cambridge University Press, second edition, 2004. Appendix 6 was used in part. The Levenberg-Marquardt
Sparse Levenberg-Marquardt algorithm. R. I. Hartley and A. Zisserman: Multiple View Geometry in Computer Vision. Cambridge University Press, second edition, 2004. Appendix 6 was used in part. The Levenberg-Marquardt
Reading. 4. Affine transformations. Required: Watt, Section 1.1. Further reading:
 Reading Required: Watt, Section.. Further reading: 4. Affine transformations Fole, et al, Chapter 5.-5.5. David F. Rogers and J. Alan Adams, Mathematical Elements for Computer Graphics, 2 nd Ed., McGraw-Hill,
Reading Required: Watt, Section.. Further reading: 4. Affine transformations Fole, et al, Chapter 5.-5.5. David F. Rogers and J. Alan Adams, Mathematical Elements for Computer Graphics, 2 nd Ed., McGraw-Hill,
VECTORS IN THREE DIMENSIONS
 1 CHAPTER 2. BASIC TRIGONOMETRY 1 INSTITIÚID TEICNEOLAÍOCHTA CHEATHARLACH INSTITUTE OF TECHNOLOGY CARLOW VECTORS IN THREE DIMENSIONS 1 Vectors in Two Dimensions A vector is an object which has magnitude
1 CHAPTER 2. BASIC TRIGONOMETRY 1 INSTITIÚID TEICNEOLAÍOCHTA CHEATHARLACH INSTITUTE OF TECHNOLOGY CARLOW VECTORS IN THREE DIMENSIONS 1 Vectors in Two Dimensions A vector is an object which has magnitude
6. Vector Random Variables
 6. Vector Random Variables In the previous chapter we presented methods for dealing with two random variables. In this chapter we etend these methods to the case of n random variables in the following
6. Vector Random Variables In the previous chapter we presented methods for dealing with two random variables. In this chapter we etend these methods to the case of n random variables in the following
LU Factorization. A m x n matrix A admits an LU factorization if it can be written in the form of A = LU
 LU Factorization A m n matri A admits an LU factorization if it can be written in the form of Where, A = LU L : is a m m lower triangular matri with s on the diagonal. The matri L is invertible and is
LU Factorization A m n matri A admits an LU factorization if it can be written in the form of Where, A = LU L : is a m m lower triangular matri with s on the diagonal. The matri L is invertible and is
Induced Planar Homologies in Epipolar Geometry
 Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 12, Number 4 (2016), pp. 3759 3773 Research India Publications http://www.ripublication.com/gjpam.htm Induced Planar Homologies in
Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 12, Number 4 (2016), pp. 3759 3773 Research India Publications http://www.ripublication.com/gjpam.htm Induced Planar Homologies in
Mathematics. Mathematics 2. hsn.uk.net. Higher HSN22000
 hsn.uk.net Higher Mathematics UNIT Mathematics HSN000 This document was produced speciall for the HSN.uk.net website, and we require that an copies or derivative works attribute the work to Higher Still
hsn.uk.net Higher Mathematics UNIT Mathematics HSN000 This document was produced speciall for the HSN.uk.net website, and we require that an copies or derivative works attribute the work to Higher Still
Outline. Linear Algebra for Computer Vision
 Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
Outline Linear Algebra for Computer Vision Introduction CMSC 88 D Notation and Basics Motivation Linear systems of equations Gauss Elimination, LU decomposition Linear Spaces and Operators Addition, scalar
Basic Math for
 Basic Math for 16-720 August 23, 2002 1 Linear Algebra 1.1 Vectors and Matrices First, a reminder of a few basic notations, definitions, and terminology: Unless indicated otherwise, vectors are always
Basic Math for 16-720 August 23, 2002 1 Linear Algebra 1.1 Vectors and Matrices First, a reminder of a few basic notations, definitions, and terminology: Unless indicated otherwise, vectors are always
6.4 graphs OF logarithmic FUnCTIOnS
 SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
Cubic and quartic functions
 3 Cubic and quartic functions 3A Epanding 3B Long division of polnomials 3C Polnomial values 3D The remainder and factor theorems 3E Factorising polnomials 3F Sum and difference of two cubes 3G Solving
3 Cubic and quartic functions 3A Epanding 3B Long division of polnomials 3C Polnomial values 3D The remainder and factor theorems 3E Factorising polnomials 3F Sum and difference of two cubes 3G Solving
Eigenvalues and Eigenvectors
 5 Eigenvalues and Eigenvectors 5.2 THE CHARACTERISTIC EQUATION DETERMINANATS nn Let A be an matrix, let U be any echelon form obtained from A by row replacements and row interchanges (without scaling),
5 Eigenvalues and Eigenvectors 5.2 THE CHARACTERISTIC EQUATION DETERMINANATS nn Let A be an matrix, let U be any echelon form obtained from A by row replacements and row interchanges (without scaling),
Chapter 1. Perspective Geometry. 1.1 Shifting Perspective The Geometric Perspective
 Chapter Perspective Geometry When we move our bodies, heads, and eyes in space (often referred to as R 3 ), the appearance of our environment changes in predictable ways. When one moves closer to an object
Chapter Perspective Geometry When we move our bodies, heads, and eyes in space (often referred to as R 3 ), the appearance of our environment changes in predictable ways. When one moves closer to an object
Visual SLAM Tutorial: Bundle Adjustment
 Visual SLAM Tutorial: Bundle Adjustment Frank Dellaert June 27, 2014 1 Minimizing Re-projection Error in Two Views In a two-view setting, we are interested in finding the most likely camera poses T1 w
Visual SLAM Tutorial: Bundle Adjustment Frank Dellaert June 27, 2014 1 Minimizing Re-projection Error in Two Views In a two-view setting, we are interested in finding the most likely camera poses T1 w
Affine transformations
 Reading Optional reading: Affine transformations Brian Curless CSE 557 Autumn 207 Angel and Shreiner: 3., 3.7-3. Marschner and Shirle: 2.3, 2.4.-2.4.4, 6..-6..4, 6.2., 6.3 Further reading: Angel, the rest
Reading Optional reading: Affine transformations Brian Curless CSE 557 Autumn 207 Angel and Shreiner: 3., 3.7-3. Marschner and Shirle: 2.3, 2.4.-2.4.4, 6..-6..4, 6.2., 6.3 Further reading: Angel, the rest
Instance-level recognition: Local invariant features. Cordelia Schmid INRIA, Grenoble
 nstance-level recognition: ocal invariant features Cordelia Schmid NRA Grenoble Overview ntroduction to local features Harris interest points + SSD ZNCC SFT Scale & affine invariant interest point detectors
nstance-level recognition: ocal invariant features Cordelia Schmid NRA Grenoble Overview ntroduction to local features Harris interest points + SSD ZNCC SFT Scale & affine invariant interest point detectors
Math Computation Test 1 September 26 th, 2016 Debate: Computation vs. Theory Whatever wins, it ll be Huuuge!
 Math 5- Computation Test September 6 th, 6 Debate: Computation vs. Theory Whatever wins, it ll be Huuuge! Name: Answer Key: Making Math Great Again Be sure to show your work!. (8 points) Consider the following
Math 5- Computation Test September 6 th, 6 Debate: Computation vs. Theory Whatever wins, it ll be Huuuge! Name: Answer Key: Making Math Great Again Be sure to show your work!. (8 points) Consider the following
LECTURE 7. Least Squares and Variants. Optimization Models EE 127 / EE 227AT. Outline. Least Squares. Notes. Notes. Notes. Notes.
 Optimization Models EE 127 / EE 227AT Laurent El Ghaoui EECS department UC Berkeley Spring 2015 Sp 15 1 / 23 LECTURE 7 Least Squares and Variants If others would but reflect on mathematical truths as deeply
Optimization Models EE 127 / EE 227AT Laurent El Ghaoui EECS department UC Berkeley Spring 2015 Sp 15 1 / 23 LECTURE 7 Least Squares and Variants If others would but reflect on mathematical truths as deeply
3D from Photographs: Camera Calibration. Dr Francesco Banterle
 3D from Photographs: Camera Calibration Dr Francesco Banterle francesco.banterle@isti.cnr.it 3D from Photographs Automatic Matching of Images Camera Calibration Photographs Surface Reconstruction Dense
3D from Photographs: Camera Calibration Dr Francesco Banterle francesco.banterle@isti.cnr.it 3D from Photographs Automatic Matching of Images Camera Calibration Photographs Surface Reconstruction Dense
D u f f x h f y k. Applying this theorem a second time, we have. f xx h f yx k h f xy h f yy k k. f xx h 2 2 f xy hk f yy k 2
 93 CHAPTER 4 PARTIAL DERIVATIVES We close this section b giving a proof of the first part of the Second Derivatives Test. Part (b) has a similar proof. PROOF OF THEOREM 3, PART (A) We compute the second-order
93 CHAPTER 4 PARTIAL DERIVATIVES We close this section b giving a proof of the first part of the Second Derivatives Test. Part (b) has a similar proof. PROOF OF THEOREM 3, PART (A) We compute the second-order
Linear Algebra Review. Fei-Fei Li
 Linear Algebra Review Fei-Fei Li 1 / 51 Vectors Vectors and matrices are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightnesses, etc. A vector
Linear Algebra Review Fei-Fei Li 1 / 51 Vectors Vectors and matrices are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightnesses, etc. A vector
Factor Analysis. Qian-Li Xue
 Factor Analysis Qian-Li Xue Biostatistics Program Harvard Catalyst The Harvard Clinical & Translational Science Center Short course, October 7, 06 Well-used latent variable models Latent variable scale
Factor Analysis Qian-Li Xue Biostatistics Program Harvard Catalyst The Harvard Clinical & Translational Science Center Short course, October 7, 06 Well-used latent variable models Latent variable scale
Handout for Adequacy of Solutions Chapter SET ONE The solution to Make a small change in the right hand side vector of the equations
 Handout for dequac of Solutions Chapter 04.07 SET ONE The solution to 7.999 4 3.999 Make a small change in the right hand side vector of the equations 7.998 4.00 3.999 4.000 3.999 Make a small change in
Handout for dequac of Solutions Chapter 04.07 SET ONE The solution to 7.999 4 3.999 Make a small change in the right hand side vector of the equations 7.998 4.00 3.999 4.000 3.999 Make a small change in
Review: critical point or equivalently f a,
 Review: a b f f a b f a b critical point or equivalentl f a, b A point, is called a of if,, 0 A local ma or local min must be a critical point (but not conversel) 0 D iscriminant (or Hessian) f f D f f
Review: a b f f a b f a b critical point or equivalentl f a, b A point, is called a of if,, 0 A local ma or local min must be a critical point (but not conversel) 0 D iscriminant (or Hessian) f f D f f
CEE598 - Visual Sensing for Civil Infrastructure Eng. & Mgmt.
 CEE598 - Visual Sensing for Civil nfrastructure Eng. & Mgmt. Session 9- mage Detectors, Part Mani Golparvar-Fard Department of Civil and Environmental Engineering 3129D, Newmark Civil Engineering Lab e-mail:
CEE598 - Visual Sensing for Civil nfrastructure Eng. & Mgmt. Session 9- mage Detectors, Part Mani Golparvar-Fard Department of Civil and Environmental Engineering 3129D, Newmark Civil Engineering Lab e-mail:
6. Linear transformations. Consider the function. f : R 2 R 2 which sends (x, y) (x, y)
 Consider the function 6 Linear transformations f : R 2 R 2 which sends (x, ) (, x) This is an example of a linear transformation Before we get into the definition of a linear transformation, let s investigate
Consider the function 6 Linear transformations f : R 2 R 2 which sends (x, ) (, x) This is an example of a linear transformation Before we get into the definition of a linear transformation, let s investigate
A new constrained parameter estimator: experiments in fundamental matrix computation
 A ne constrained parameter estimator: experiments in fundamental matrix computation Anton van den Hengel, Wojciech Chojnacki, Michael J. Brooks, Darren Galey School of Computer Science, University of Adelaide
A ne constrained parameter estimator: experiments in fundamental matrix computation Anton van den Hengel, Wojciech Chojnacki, Michael J. Brooks, Darren Galey School of Computer Science, University of Adelaide
Least Squares with Examples in Signal Processing 1. 2 Overdetermined equations. 1 Notation. The sum of squares of x is denoted by x 2 2, i.e.
 Least Squares with Eamples in Signal Processing Ivan Selesnick March 7, 3 NYU-Poly These notes address (approimate) solutions to linear equations by least squares We deal with the easy case wherein the
Least Squares with Eamples in Signal Processing Ivan Selesnick March 7, 3 NYU-Poly These notes address (approimate) solutions to linear equations by least squares We deal with the easy case wherein the
Scalar functions of several variables (Sect. 14.1)
 Scalar functions of several variables (Sect. 14.1) Functions of several variables. On open, closed sets. Functions of two variables: Graph of the function. Level curves, contour curves. Functions of three
Scalar functions of several variables (Sect. 14.1) Functions of several variables. On open, closed sets. Functions of two variables: Graph of the function. Level curves, contour curves. Functions of three
Chapter 3 Numerical Methods
 Chapter 3 Numerical Methods Part 2 3.2 Systems of Equations 3.3 Nonlinear and Constrained Optimization 1 Outline 3.2 Systems of Equations 3.3 Nonlinear and Constrained Optimization Summary 2 Outline 3.2
Chapter 3 Numerical Methods Part 2 3.2 Systems of Equations 3.3 Nonlinear and Constrained Optimization 1 Outline 3.2 Systems of Equations 3.3 Nonlinear and Constrained Optimization Summary 2 Outline 3.2
1 HOMOGENEOUS TRANSFORMATIONS
 HOMOGENEOUS TRANSFORMATIONS Purpose: The purpose of this chapter is to introduce ou to the Homogeneous Transformation. This simple 4 4 transformation is used in the geometr engines of CAD sstems and in
HOMOGENEOUS TRANSFORMATIONS Purpose: The purpose of this chapter is to introduce ou to the Homogeneous Transformation. This simple 4 4 transformation is used in the geometr engines of CAD sstems and in
Name: Student ID: Math 314 (Calculus of Several Variables) Exam 3 May 24 28, Instructions:
 Name: Student ID: Section: Instructor: _00 Scott Glasgow Math 314 (Calculus of Several Variables) RED Eam 3 Ma 4 8, 013 Instructions: For questions which require a written answer, show all our work. Full
Name: Student ID: Section: Instructor: _00 Scott Glasgow Math 314 (Calculus of Several Variables) RED Eam 3 Ma 4 8, 013 Instructions: For questions which require a written answer, show all our work. Full
