Electric circuit analysis by means of optimization criteria Part I the simple circuits
|
|
|
- Roberta Adams
- 6 years ago
- Views:
Transcription
1 BULLETIN OF THE OLISH ACADEMY OF SCIENCES TECHNICAL SCIENCES Vol. 5, No. 4, 004 Electric circuit analysis by means of optimization criteria art I the simple circuits M. SIWCZYŃSKI* and M. JARACZEWSKI** Institute of Circuits and Control They, Cracow University of Technology, 4 Warszawska St., 3 55 Kraków, oland Abstract. One of the main problems of electrical power quality is to ensure a constant power flux from the supply system to the receiver, keeping in the same time the undisturbed wave fm of the current and voltage signals. Disttion of signals are caused by nonlinear time varying receivers, voltage changes power losses in a supply system. The wave-fm of the voltage of the source may also be defmed. This study seeks the optimal current and voltage wave-fm by means of an optimization criteria. The optimization problem is defined in Hilbert space and the special functionals are minimized. The source inner impedance operat is linear and time-varying. Some examples of calculations are presented. Keywds: electrical circuits, power they, optimization in Hilbert spaces.. Introduction The transmission of electric power from the source to the load is perfmed in one loop circuit, and despite its simplicity there are many unsolved problems related to it. They result from the fact that in the energy transpting process there are two signals involved the voltage and current, and they can produce the same power with various, sometimes unpredictable, wave fms. Applying some quality criteria we can find the optimal wave shape of the voltage and current signals. The power quality discipline usually deals with this crucial problem. Let us consider a simple one loop circuit depicted in Fig.. Fig.. The power transfer circuit Such a circuit serves to transpt power from the source e to the receiver. The problem, which seems to be easy, is to find such a signal i to assure a given prescribed power and it can be solved only by means of optimization technique. Thesourcepowerequation =(e, i ( obviously leads to an abundance of solutions since there is an infinite amount of such signals e and i which lead to the same dot product, equal to active power.inder to choose the unique solution from their infinite set, we * e-3@pk.edu.pl ** jaracz@usk.pk.edu.pl must put one me optimum condition: i =(i, i min ( The task ( ( has only one solution which we get by minimizing the Lagrange functional f(i, λ =(i, i+λ (e, i] min (3 where λ is real. Indeed, calculating the variation of the functional (3 caused by the variation of current δi weget: f(i + δi, λ f(i, λ =(i, δi (λe, δi+(λri, δi+(δi, δi =(i λe, δi+(δi, δi. (4 From the previous equation it follows that the sufficient and necessary condition f the minimum (3 exists i λe =0 i λ =0.5λe. (5 Nowit is necessary to choose one i λ from the abundance of solutions accding to the assumption ( i.e. =(e, 0.5λe =0.5λ(e, e =0.5λ e thus λ = e. So the optimal current signal meeting condition ( ( is i =: i opt = e. (6 e. One loop circuit power distribution In me complex problems the source has a passive linear inner impedance determined by the Z operat. In such a circuit the relation between u and i is determined by U = e Zi 359
2 M. Siwczyński, M. Jaraczewski which we can use to calculate the balance of the circuit power =(u, i =(e, i (Zi,i. If we notice that (Zi,i=(i, iz, where * stands f conjugating operation, we get =(u, i =(e, i (Ri, i (7 where R =0.5(Z + Z (8 is a positively defined linear operat. The power balance consists of three power flux: (e, i the power of the source, Z =(Ri, i thepower losses in the source, the developed absbed power. The (Ri, i is positive f any current signal (is positively defined whereas the two others can be both positive negative it is depicted in Fig.. Fig.. ower distribution The Eq. (7 with the unknown current vect also has infinitely many solutions. But the optimization task (i, i min (9 (e, i (Ri, i = as it is easy to prove, will have the unique solution i. We can find it by minimizing the functional f(i, λ =(i, i+λ(ri, i (e, i+ ] min (0 which difference δf(i,λ=f(i + δi,λ f(i,λ =(i,δi +(λri,δi (λe,δi +(δi,δi +(λrδi,δi =((i + λri λe,δi+(δi + λrδi,δi ( is positive f all δi. It will be true when the current signal i meets (i + λri λe =0 ( + λri =0.5λe ( where: denotes an identity operat, 0 zero signal. The Eq. ( includes ( + λr operat w ith a λ parameter. The same operat appears in a quadratic fm fming the second part of the increment (. F λ that ( + λr operat is positively defined, there exists a solution of ( and simultaneously it is the minimum point of (0. The λ f which the solution of ( i λ exists also determines the function F (λ =(e, i λ (Ri λ, i λ (3 But there are also such values of λ f which F (λ is undefined. To find them we must use the operat spectrum of R. The operat spectrum of R is the set of λ such that the ( + λr operat is non-reversible. It means that the equation (λ Rx =0 has a non-zero solution. Hence multiplying this equation by the scalar x weget: λ x =(Rx, x (4 then the operat R spectrum consists uniquely of the positive real numbers, because the R is a self-adjoint, positively defined operat. It results from (4 that the spectrum is a non-empty closed and bounded set because the R is bounded. In der to study F (λ function we must calculate the derivative of i λ signal (the i λ exists in the determinate set of F (λ, by differentiate equation ( in the λ direction ( + λri λ =0.5(e Ri λ (5 From (3 follows the derivative fmula f F (λ: F (λ =(e, i λ (Ri λ, i λ=(e Ri λ, i λ =(( + λri λ, i λ the resulting quadratic fm is positively negatively definite, only when ( + λr is positively negatively definite i.e. when the functional (0 has maximum minimum value. It follows that the F (λ function has two branches: ascending and decreasing. F the prescribed power < max drawn from the source the equation F (λ = (6 has two solutions of λ multipliers f which the functional (0 has respectively: a minimum f λ from the ascending branch of F (λ and maximum from decreasing one. The function F (λ with the power fluxes f appropriate λ ranges is depicted in Fig. 3. It entails the existence of two extreme source currents: i min and i max, which minimize maximize respectively the functional (. From the practical point of viewme imptant is the i min current. The F (λ function shows the relation between the delivered power of the source and the λ coefficient and it can be called a power characteristics of the source. 360 Bull. ol. Ac.: Tech. 5(4 004
3 Electric circuit analysis by means of optimization criteria art I Fig. 3. The power characteristics of the source Monotonic branch a ascending, b decreasing, c singular The me detailed examination of the F (λ function shows that f λ =0 (i λ =0,F (0 = 0, az (i λ = 0.5e, F (0 = 0.5 e the function is zero and has a positive derivation. Whereas f λ ± (i λ =0.5R e, F (λ =0.5(R e, e = max which also results from the limits of the functional (0 f(i,λ (Ri, i (e, i+ ] min f(i,λ (Ri, i (e, i+ ] max and using the variation method we get Ri =0.5e. It is equivalent to the solution of the so called receiver matching problem accding to the maximum power given and it is discussed in the literature f various particular current spaces and impedance operats of the source. F the lossless source with the zero loss operat R : R =0, Eq. ( gives i λ =0.5λe and F (λ =0.5 e λ which means that the power characteristics of the source is linear and unlimited. The lossy source has always the power characteristics limited by the maximum power max. Example. Let us find the power characteristic of the source with the time varying inner impedance (Fig. 4. Fig. 4. Theequivalent circuit diagram of thesourcewith thetime varying resist-inductance inner impedance In this case Z = r(t+l(t d ] and it affects a current signal accding to the fmula Zi(t = r(ti(t+l(t di ]. In der to define the conjugated operat Z wecalculate the quadratic fm (Zi, i = r(ti(t] + l(t di i(t. After applying the Liouville s transfmation in integration by parts of the second component we get (Zi, i = r(ti(t] dl(ti(t] i(t =(Z i, i of which results the conjugated operat of the fm Z = r(t l(t d dl(t ]. Therefe the loss operat has the fm R =0.5(Z + Z = r(t 0.5 dl(t ]. (7 The operat equation to calculate the optimal current signal ( has nowthe algebraic fm ( +λ r(t 0.5 dl(t ] i(t =0.5λe(t. Thus the power characteristics of the source F (λ is F (λ = λ +0.5ρ(t + λρ(t] e(t] where ρ(t =r(t 0.5 dl(t. Analyzing the fegoing denominat of the integral we find the singularities f λ<0 when f the positively defined two terminal netwks is r(t 0.5 dl(t > 0 f any t. Example. In the case of a stationary circuit the operat (8 is defined with the single variable function of s R(s =0.5(Z(s+Z( s where Z(s is an dinary operat function of the source inner impedance, and Z( s is its conjugated operat. It follows from the Liouville s transfmation of a single difference operat (sx(ty(t = x(t( sy]. Thus f the conjugated operat the following fmula is in fce s = s. The operat Eq. ( has then the following fm + λr(s]i(s = 0.5λE(s (8 Bull. ol. Ac.: Tech. 5(
4 where I(s, E(s stand f the two-sided Laplace transfmation of the source current and voltage. Equation (8 instantly gives the solution I λ (s = 0.5λE(s +λr(s. M. Siwczyński, M. Jaraczewski The power characteristics of the source (3 is defined by the arsevall s fmula: F (λ =(e, i λ (Ri λ, i λ = πj j j πj = πj πj = πj = 8πj E(jωI λ ( jωd(jω j j Re(s=0 Re(s=0 Re(s=0 Re(s=0 R(jωI λ (jωi λ ( jωd(jω E(sI λ ( sds R(sI λ (si λ ( sds ( +λr(s λr(s + λr(s] E(sE( sds ( +λr(s + λr(s] E(sE( sds. From the Jdan lemma the integrals along the imaginary axis are substituted by the integrals along the contour including the right left half plain i.e. the contour consists of an imaginary axis and an appropriate semi circle with the (0,0 center point and a radius approaching to infinity. These contours are marked as and. Thus F (λ = 8πj ( +λr(s + λr(s] E(sE( sds. (9 The fmula (9 is suitable f a rational function in integral, when we can use the Cauchy integral fmula. The derivative of F (λ has the fm F (λ = 4πj ( E(sE( s + λr(s] 3 ds. The root λ of the Eq. (6 f the prescribed power (, max is on the ascending branch of F (λ and determines a particular case of the current signal i.e. the optimal current. The root can be found both graphically analytically using the Newton s method. λ k+ = λ k + F (λ k F (λ k This procedure is always convergent f λ>0 = Γ (λ k. (0 Fig. 5. Γ (λ function subsequent and consecutive iteration points It results from the shape of the Γ (λ function its graph and consecutive iteration points are shown in Fig. 5, ]. 3. ower analysis of the circuit by means of other evaluation functionals In der to calculate the optimal source current other practical functionals, besides (9, can be used. Introducing the prescribed reference signal i 0 we minimize the functional of the current deviation i = i i 0. We can create optimization task in the fm ( i, i min (e, i (Ri, i = ( The task ( has a similar solution to the task (9 considered in the preceding chapter. By analogy we can prove that the minimum condition of ( result from equation ( + λri =0.5λe + i 0. ( The power characteristics of the source (3 is similar to the previous one from the Section. From the practical point of viewit is imptant to minimize the voltage deviation on the source terminals referred to the prescribed signal u 0 : u = u 0 u. It leads to the following minimizing problem: ( u, u min (e, i (Ri, i =. (3 If we note that u = Zi e where: e = e u 0, Z the inner source impedance operat, we can fm the Lagrange functional depended on the current f λ (i =( u, u+λ(ri, i (e, i+ ] min (4 and its deviation (noting that δ( u = Zδi gives δf λ (i =f λ (i + δi f λ (i =(Z u +λri λe,δi +((Z Z + λrδi,δi... (5 36 Bull. ol. Ac.: Tech. 5(4 004
5 Electric circuit analysis by means of optimization criteria art I From (5 results the sufficient and necessary condition f the minimum (4 to exist. Z u + λri =0.5λe (Z Z + λri =0.5λe + Z e. (6 The operat Eq. (6 gives the optimal current f the (4 criterion i λ =(Z Z + λr (0.5λe + Z e. (7 The characteristics F (λ is defined in λ points f which the solution of (6 exists i.e. when the invert operat (Z Z + λr exists. The function F (λ has a derivative F (λ =(e Ri λ, i λ where i λ is the current derivative in λ and is calculated by differencing the Eq. (6 (Z Z + λri λ =0.5(e Ri λ. (8 From (7, (8 it results that F (λ is a quadratic fm F (λ =((Z Z + λri λ, i λ (9 with (Z Z + λr operat, which also appear in (5. The positive definition of this operat means the monotonically ascending branch of F (λ and the existence of the minimum of the functional (4 there. Whereas the negative definition of this operat means the monotonically decreasing branch of F (λ and the existence of the minimum of the functional (4 there. The F (λ function has the following quality f λ =0 (Z Z Z e = Z e = Ye F (0 = (e, Y e (Y RY e, e λ F (λ 0.5(R e, e = max The graph 6 shows F (λ function Fig. 6. The power characteristic of a source The calculated optimal current signal (7 f (3 condition can be written in a fm i opt = G opt e + j 0 (30 where: G opt =0.5λe(Z Z + λr, j 0 =(Z Z + λr Z e. G opt self-adjoint, positively defined linear operat, j 0 additional current signal. This result is depicted in Fig. 7. Fig. 7. The equivalent circuit diagram of the optimal current It is wth considering the particular optimal solutions when the source is lossless i.e. when R is the zero operat. In that case the Eq. (6 is reduced to Z Zi =0.5λe + Z e (3 and can be solved directly i λ =0.5λYY e + Y e (3 where Y = Z is the inner admittance of the source. The power characteristics F (λ =0.5λ(Y Y e, e+(y e, e (33 is then an affine function. The solution of (6 is a point λ = (YY (34 e, e where =(Y e, e. So the optimal current of a lossless but flexible source, giving the closest voltage to u 0, is given by the fmula: i opt = (YY e, e YY e + Y e. (35 These results even get reduced f u 0 = e, when e =0 and the fmulas (9 (34 take the fm i λ =0.5λY Y e The F (λ function is linear F (λ =0.5λ(Y Y e, e. (36 Thus the optimal source current giving the minimal voltage drop on terminals is i opt = (YY e, e YY e. (37 It is wth comparing the fegoing current fm to the result (6, f the current nm criterion i min : i opt = (e, e e which exists in the literature as a Fryze current,, 3 8, 9] and it is a particular case of the current (37, which is easy to see after substituting YY e = e. Therefe the optimal current assuring the minimal inner RMS voltage drop(( u, u min is given by i opt = (e,e e. (38 Bull. ol. Ac.: Tech. 5(
6 M. Siwczyński, M. Jaraczewski Example 3. It is easy to showa definite example of the result (37. Let s take the two terminal netwk with a time invariant and reactive elements. Its impedance function is then an odd function Z(s :=sx(s (39 where X(s even rational function. Thus the loss function is R(s =0.5(Z(s+Z( s =0.5sX(s +( sx((s ] = 0. The (39 operat has the inversion (admittance then Y (s = sx(s Y (sy (s =Y (sy ( s = (Y Y e, e = πj = π j j s X(s ] E(sE( s s X(s ] ds E(jω ω X( ω dω. (40 ] Applying (39 and (40 in (37 we get the two sided Laplace transfmation of the optimal current I opt (s = π E(jω ω X( ω ] dω E(s s X(s ]. (4 Given result (4 can be reduced e.g. f the almost periodic signals. In that case the function F (s hasthe values Z(jω=jωX( ω where ω {ω n : n =0,,,...} is a countable set of harmonic components making signal e(t: ] e(t =real En e jωnt = n=0 n= E n e jωnt (4 where: E n = En, ω n = ω n. (43 Defining the inner product of the almost periodic signals (u, i = lim T T T 0 u(ti(t (44 and using (4 in (44 we get a particular fm of the arsevall fmula: (u, i = = n,m= n= U ni m lim T T n=0 T 0 e j(ωn+ωmt U n In = real U n In = real UnI n n=0 where I n = I n because lim T T T 0 e j(ωn+ωmt = { dla n + m =0 0 dla n + m 0. In such a case the quadratic fm (40 gives (YY E n e, e = ωnx n n=0 where: X n = X( ωn whereas the spectrum of the almost periodic current signal a counterpart of the current (4 isgivenby I opt n = m=0 E m ω m X m E n ω n X n. (46 Note that the fms (45 and (46 remain valid f periodic signals. 4. ower analysis of the circuit by means of multi criterion optimization tasks In the previous chapter we have fmulated some practical quality criterions concerning power transmission in a one loop circuit. In der to satisfy many individual receivers at the same time, we need to fm some mixed optimization criterions to give reasonable compromises. They can be e.g. the two criterion optimization tasks like: (i, i min (e, i (Ri, i = (47 ( i, i =Q (i, i min (e, i (Ri, i = (48 ( u, u =Q where: i = i i 0, u = u u 0 current and voltage deviations, i 0, u 0 prescribed signals of the current and voltage. In the condition (47 Q is the acceptable disttion measure of i regarding i 0 acceptable disttion measure of u regarding u 0 (48. It is obvious that these are not the unique practical optimization conditions of the source signals. As further examples we can fmulate ( i, i min (e, i (Ri, i = (49 ( i, i =Q ( i, i min (e, i (Ri, i = (50 ( u, u =Q These tasks are fmulated crectly and all of theme have a unique solution 60]. The task (47 is equivalent to 364 Bull. ol. Ac.: Tech. 5(4 004
7 Electric circuit analysis by means of optimization criteria art I minimize the Lagrange s functional f λ,µ (i =(i, i+λ(ri, i (e, i] + µ( i, i min (5 which difference in the minimum point is f λ,µ (i =f λ,µ (i + δi f λ,µ (i =(i + λri +µ i λe,δi + (( + µ+λrδi,δi > 0 (5 f any variation of the current signal δi. Thuswegetthe necessary minimum condition ( + µ+λri =0.5λe + µi 0. (53 F the positively defined operat A λ,µ =: + µ+λr (54 the equation has the solution i λ,µ. Then the vect function is defined ] Fλ (λ,µ F (λ, µ = F µ (λ, µ ] (e, iλ,µ (Ri = λ,µ,i λ,µ. (55 (i λ,µ i 0,i λ,µ i 0 The first component of the fegoing function is the source active power and the second is the deviation nm of the current. This function can be called a power-disttion characteristics. The search of λ and µ which determine the optimal current i opt := i λ,µ is perfmed using the following set of equations F (λ, µ = Q = A λ,µ (0.5λ e + µ i 0 (56 ]. (57 It is the counterpart of the power Eq. (6, which appear in the one criterion optimization task. It is proved ] that there exist such and Q that above equation has the unique solution. Example 4. The optimization equation which solves the problem (47 has fm (53 but f lossless source it get reduced to ( + µi =0.5λe + µi 0 (58 and it can be solved directly i =0.5 λ +µ e +µ i 0 + i 0 (59 therefe i = 0.5λ +µ e +µ i 0. (60 The component functions in (55 gives the fm F λ (λ, µ =0.5 e +µ λ +µ (e, i 0+(e, i 0 F µ (λ, µ =0.5 e λ 4λ(e, i 0 +4 i 0 ( + µ. (6 It turns out that f the lossless source the set of Eq. (57 can be unequivocally solved to λ and µ. Ittakes the following fm 0.5 e λ (e, i 0 =(+µ(e, i e λ 4(e, i 0 λ +4 i 0 =4 i ( + µ. (6 The solution of Eq. (6 is ] λ = e (e, i 0 ± (e, i K 0 K µ = ± K 0 K (63 where K 0 and K meet the Schwarz inequality K = e i (e, i > 0 (64 K0 = e i 0 (e, i 0 > 0. (65 These coefficients have a characteristic fm. They stand f the residual nonnative powers in the geometric differences between the active and apparent powers. They can be associated with the reactive powers of the source signals i and i 0 respectively. The minimum point demands that ( + µ > 0 and it assures a positive definition of the operat (54. Then the solution (63 of (6 is unequivocal λ = e (e, i 0 +(e, i K ] 0 K µ =+ K 0 K (66 The optimal current is given by i opt = (0.5λ e i 0 +i 0 +µ = K 0.5λ e + ( KK0 K 0 = ( K K 0 i 0 ] e (e, i 0 + e + ] ( KK0 i 0. Finally it will be convenient to rearrange it to the fm ] i opt = ( KK0 e 0 ( e + KK0 i 0 (67 where: 0 =(e, i 0 power of the ideal source giving the reference signal i 0 ; K 0 = e i 0 0 remaining (reactive power of the ideal source; K = β e i 0 ( 0 (68 β = Q i 0 = i i0 i 0 relative coefficient of the distted current. (69 From the (68 results a certain existence condition of the minimization solution β e i 0 ( 0 0 Bull. ol. Ac.: Tech. 5(
8 M. Siwczyński, M. Jaraczewski β 0 (70 e i 0 From (69 and (70 results one me fm of the condition Q ( 0 e. (7 Inequality (7 can be treated as an existence condition of the solution f the lossless source with the arbitrary assumed signals e, i and scalars, Q. The assumed relative disttion value cannot be too small. The signal (67 is then the minimal RMS current with a prescribed disttion level, giving the prescribed source power. This result can be treated as one me generalization of the so called Fryze current (6 with an additional condition defining the signal disttion level. Example 5. We will consider the minimal RMS current problem of the source with the prescribed voltage disttion (48. The appropriate solution of the optimization equation has the fm ( + µz Z + λri λ =0.5λe + µz e (7 where e = e u 0, u 0 prescribed voltage signals. In a particular case of the lossless source and f u 0 = e (the prescribed voltage equals to the open state voltage we get the problem of finding the minimal RMS current having the prescribed RMS voltage drop in the source. Thus the Eq. (7 reduces to ( + µz Zi =0.5λe. (73 This problem is a little me complex then in the Example 4. In the fegoing equation there is µz Z operat instead of the µ scalar. The Eq. (73 has the solution i λµ =0.5λ( + µz Z e =0.5λK(µe where K(µ =(+µz Z (74 is a linear self-adjoint operat, positively defined f µ>0. F µ =0is K(0 = (identityoperat thus: F λ (λ, µ =0.5λ(K(µe, e F µ (λ, µ =(0.5λ (Z ZK(µe, K(µe (75 From the equation F λ (λ, µ = (76 weget λ (µ = (K(µe, e, from this results the function µ F µ λ (µ,µ]= (K(µZ ZK(µe, e (K(µe, e. (78 A me detailed examination of the function (78 shows that F µ λ (0, 0] = (Z Ze,e e 4 (79 f µ : K(µ µ YY λ (µ (YY e, e µ F µ λ (µ,µ] (YY e, e. (80 Thus we get the function increase F µ λ (0, 0] F µ λ (µ,µ] µ = (Z Ze,e(YY e, e (e, e (YY e, e ( e > 0. (8 The proof of the inequality (8 will be carried out f the convolution operat. In a general situation the use of the spectral they is needed. If the sequence {E n } n=0,±,±,... stands f the appropriate voltage harmonics of the source and {b n } n=0,±,±,... the module components of the Z spectrum then (Z Ze,e(YY e, e (e, e ( ( = b n E n b E m n m m ( ( E n E m n m = a nm E n E m n>m where: ( a nm = b n b + b m b m b = n b m > 0. n b n b m This completes the proof. Then f Q between (YY e, e <Q< (Z Ze,e e 4 (8 there exist a unique root µ which is calculated from (K(µZ ZK(µe, e = Q. (83 (K(µe, e Fig. 8. The root determining process f the equation set ( Bull. ol. Ac.: Tech. 5(4 004
9 Electric circuit analysis by means of optimization criteria art I Therefe the second codinate of the optimum point (λ,µ the root of the power-disttion equations (56 is λ = (K(µ e, e. (84 To complete the F µ λ (µ,µ] investigation it should be proved that it is monotonic and unequivocal, what is carried out in ]. In a periodic steady state µ is the root of the convolution case of Eq. (83 ( Xn En n n,m +µx n = Q (85 E n E m (+µxn (+µx m Then the second codinate of the optimum point (λ,µ is: λ =. (86 n E n +µ X n Where X n stands f the spectrum of the inner source reactance (see ex. 3. The frequency distribution of the optimal current is given by 5. Conclusion In opt = 0.5λ +µ Xn E n. (87 The afe presented results are connected with the problem of matching the load to the source. This issue is presented in many disciplines connected not only with electrical energy transptation. It consists in the appropriate choice of the load to obtain the maximum power from the source. In the electrical domain this problem is reduced to the choice of an appropriate current signal which maximize source power functional i.e. (e, i (Ri, i max. Its solution is well known and leads to the operat equation,, 7 0]: Ri =0.5e. This is used to determine the power balance equation max =(e, i dop 0.5(e, i dop where i dop =0.5R e is the matching current signal. From the fegoing power balance it results that exactly one half of source power is lost. This fact makes such matching method extremely impractical. Nevertheless, the knowledge of possible maximum source power is useful. It is possible to fmulate a lot of me useful matching problems. In the case of e.g. stiff sources keeping invariable voltage signal regardless of the current, there exists the unique current signal giving prescribed source power. This result is of a great practical imptance and is known as the Fryze current. In the present article this signal is defined in the (6. However the problem becomes me sophisticated when we take in consideration the inner impedance Z operat of the source. It causes the source becomes lossy and flexible. Nevertheless we can still get a great variety of appropriate optimal currents using the minimum criteria, concerning the power balance of the circuit shape restriction of signals. These results can be applied to improve power quality when transmitting it to many individual receivers. Obviously, to get the optimal currents, some modification of the load is needed. It is carried out by compensat circuits but this is the problem which is not under the consideration in this article. References ] M. Siwczyński, Optimal methods in the they of electric circuits, Electrical Engineering, ublishing Houseof Cracow University of Technology, Kraków, 995 (in olish. ] M. Siwczyński, ower Engineering Circuit They, Kraków, 003 (in olish. 3] L. S. Czarnecki, Interpretation, identification and modification of power properties of one-phase circuits with deflection course, Scientific Exercises of Silesian University of Technology, Electrotechnics 9, Gliwice, 984 (in olish. 4] L. S. Czarnecki, ower and compensation in circuits with periodic current and voltage courses part 3, ower roperties of Linear One-phase Circuits, 9 40 (998, (in olish. 5] L. S. Czarnecki, ower and compensation in circuits with periodic current and voltage courses part 6, owers in Uncompensated Three-phase Circuits with eriodic Sinusoidal Current and Voltage Courses, 7 0 (000, (in olish. 6] L. S. Czarnecki, ower and compensation in circuits with periodic current and voltage courses part 7, ower roperties of Linear Three-wire, Three-phase Circuits, 8 (000, (in olish. 7] M. asko, Selection of compensats optimizing wk conditions of one-phase and multi-phase voltage sources with periodic deflection courses, Scientific Exercises of Silesian University of Technology, Electrotechnics 35, Gliwice, 994 (in olish. 8] M. asko and J. Walczak, Optimization of power-quality properties of electrical circuits with periodic non-sinusoidal courses, Scientific Exercises of Silesian University of Technology, Electrotechnics 50, Gliwice, 996 (in olish. 9] J. Walczak, Optimization of power-quality properties of electrical circuits in Hilbert spaces, Scientific Exercises of Silesian University of Technology, Electrotechnics 5, Gliwice, 99 (in olish. 0] C. A. Desoer, The maximum power transfer theem f n-pts, IEEE Trans. CT-0, 8 30 (979. Bull. ol. Ac.: Tech. 5(
Scattering Parameters
 Berkeley Scattering Parameters Prof. Ali M. Niknejad U.C. Berkeley Copyright c 2016 by Ali M. Niknejad September 7, 2017 1 / 57 Scattering Parameters 2 / 57 Scattering Matrix Voltages and currents are
Berkeley Scattering Parameters Prof. Ali M. Niknejad U.C. Berkeley Copyright c 2016 by Ali M. Niknejad September 7, 2017 1 / 57 Scattering Parameters 2 / 57 Scattering Matrix Voltages and currents are
CHAPTER 6 STEADY-STATE ANALYSIS OF SINGLE-PHASE SELF-EXCITED INDUCTION GENERATORS
 79 CHAPTER 6 STEADY-STATE ANALYSIS OF SINGLE-PHASE SELF-EXCITED INDUCTION GENERATORS 6.. INTRODUCTION The steady-state analysis of six-phase and three-phase self-excited induction generators has been presented
79 CHAPTER 6 STEADY-STATE ANALYSIS OF SINGLE-PHASE SELF-EXCITED INDUCTION GENERATORS 6.. INTRODUCTION The steady-state analysis of six-phase and three-phase self-excited induction generators has been presented
No. 5 Discrete variational principle the first integrals of the In view of the face that only the momentum integrals can be obtained by the abo
 Vol 14 No 5, May 005 cfl 005 Chin. Phys. Soc. 1009-1963/005/14(05)/888-05 Chinese Physics IOP Publishing Ltd Discrete variational principle the first integrals of the conservative holonomic systems in
Vol 14 No 5, May 005 cfl 005 Chin. Phys. Soc. 1009-1963/005/14(05)/888-05 Chinese Physics IOP Publishing Ltd Discrete variational principle the first integrals of the conservative holonomic systems in
Resonant Matching Networks
 Chapter 1 Resonant Matching Networks 1.1 Introduction Frequently power from a linear source has to be transferred into a load. If the load impedance may be adjusted, the maximum power theorem states that
Chapter 1 Resonant Matching Networks 1.1 Introduction Frequently power from a linear source has to be transferred into a load. If the load impedance may be adjusted, the maximum power theorem states that
Module 4. Single-phase AC Circuits
 Module 4 Single-phase AC Circuits Lesson 14 Solution of Current in R-L-C Series Circuits In the last lesson, two points were described: 1. How to represent a sinusoidal (ac) quantity, i.e. voltage/current
Module 4 Single-phase AC Circuits Lesson 14 Solution of Current in R-L-C Series Circuits In the last lesson, two points were described: 1. How to represent a sinusoidal (ac) quantity, i.e. voltage/current
Transmission Lines. Plane wave propagating in air Y unguided wave propagation. Transmission lines / waveguides Y. guided wave propagation
 Transmission Lines Transmission lines and waveguides may be defined as devices used to guide energy from one point to another (from a source to a load). Transmission lines can consist of a set of conductors,
Transmission Lines Transmission lines and waveguides may be defined as devices used to guide energy from one point to another (from a source to a load). Transmission lines can consist of a set of conductors,
Some of the different forms of a signal, obtained by transformations, are shown in the figure. jwt e z. jwt z e
 Transform methods Some of the different forms of a signal, obtained by transformations, are shown in the figure. X(s) X(t) L - L F - F jw s s jw X(jw) X*(t) F - F X*(jw) jwt e z jwt z e X(nT) Z - Z X(z)
Transform methods Some of the different forms of a signal, obtained by transformations, are shown in the figure. X(s) X(t) L - L F - F jw s s jw X(jw) X*(t) F - F X*(jw) jwt e z jwt z e X(nT) Z - Z X(z)
Chapter 2 Voltage-, Current-, and Z-source Converters
 Chapter 2 Voltage-, Current-, and Z-source Converters Some fundamental concepts are to be introduced in this chapter, such as voltage sources, current sources, impedance networks, Z-source, two-port network,
Chapter 2 Voltage-, Current-, and Z-source Converters Some fundamental concepts are to be introduced in this chapter, such as voltage sources, current sources, impedance networks, Z-source, two-port network,
Two Dimensional Linear Systems of ODEs
 34 CHAPTER 3 Two Dimensional Linear Sstems of ODEs A first-der, autonomous, homogeneous linear sstem of two ODEs has the fm x t ax + b, t cx + d where a, b, c, d are real constants The matrix fm is 31
34 CHAPTER 3 Two Dimensional Linear Sstems of ODEs A first-der, autonomous, homogeneous linear sstem of two ODEs has the fm x t ax + b, t cx + d where a, b, c, d are real constants The matrix fm is 31
Imaginary Impedance Axis. Real Impedance Axis. Smith Chart. The circles, tangent to the right side of the chart, are constant resistance circles
 The Smith Chart The Smith Chart is simply a graphical calculator for computing impedance as a function of reflection coefficient. Many problems can be easily visualized with the Smith Chart The Smith chart
The Smith Chart The Smith Chart is simply a graphical calculator for computing impedance as a function of reflection coefficient. Many problems can be easily visualized with the Smith Chart The Smith chart
ADAPTIVE NEAR-OPTIMAL COMPENSATION IN LOSSY POLYPHASE POWER SYSTEMS. Ronald Didier Hernández G.
 ADAPTIVE NEAR-OPTIMAL COMPENSATION IN LOSSY POLYPHASE POWER SYSTEMS A thesis presented by Ronald Didier Hernández G. to The Department of Electrical and Computer Engineering in partial fulfillment of the
ADAPTIVE NEAR-OPTIMAL COMPENSATION IN LOSSY POLYPHASE POWER SYSTEMS A thesis presented by Ronald Didier Hernández G. to The Department of Electrical and Computer Engineering in partial fulfillment of the
Subject: Optimal Control Assignment-1 (Related to Lecture notes 1-10)
 Subject: Optimal Control Assignment- (Related to Lecture notes -). Design a oil mug, shown in fig., to hold as much oil possible. The height and radius of the mug should not be more than 6cm. The mug must
Subject: Optimal Control Assignment- (Related to Lecture notes -). Design a oil mug, shown in fig., to hold as much oil possible. The height and radius of the mug should not be more than 6cm. The mug must
1 Unified Power Flow Controller (UPFC)
 Power flow control with UPFC Rusejla Sadikovic Internal report 1 Unified Power Flow Controller (UPFC) The UPFC can provide simultaneous control of all basic power system parameters ( transmission voltage,
Power flow control with UPFC Rusejla Sadikovic Internal report 1 Unified Power Flow Controller (UPFC) The UPFC can provide simultaneous control of all basic power system parameters ( transmission voltage,
MODULE-4 RESONANCE CIRCUITS
 Introduction: MODULE-4 RESONANCE CIRCUITS Resonance is a condition in an RLC circuit in which the capacitive and inductive Reactance s are equal in magnitude, there by resulting in purely resistive impedance.
Introduction: MODULE-4 RESONANCE CIRCUITS Resonance is a condition in an RLC circuit in which the capacitive and inductive Reactance s are equal in magnitude, there by resulting in purely resistive impedance.
Linear Systems Theory
 ME 3253 Linear Systems Theory Review Class Overview and Introduction 1. How to build dynamic system model for physical system? 2. How to analyze the dynamic system? -- Time domain -- Frequency domain (Laplace
ME 3253 Linear Systems Theory Review Class Overview and Introduction 1. How to build dynamic system model for physical system? 2. How to analyze the dynamic system? -- Time domain -- Frequency domain (Laplace
Optimizing Power Flows in Lossy Polyphase Systems: Effects of Source Impedance
 Optimizing Power Flows in Lossy Polyphase Systems: Effects of Source Impedance HANOCH LEVARI, ALEKSANDAR M. STANKOVIĆ Department of Electrical and Computer Engineering, Northeastern University, Boston,
Optimizing Power Flows in Lossy Polyphase Systems: Effects of Source Impedance HANOCH LEVARI, ALEKSANDAR M. STANKOVIĆ Department of Electrical and Computer Engineering, Northeastern University, Boston,
International Journal of Scientific & Engineering Research, Volume 7, Issue 7, July-2016 ISSN
 36 Solution of Coupled Electromagnetic and Thermal roblems in Gas Insulated Bus Bar Suad Ibrahim Shahl, Anwer Fouad mohammed Ali 2 University of Technology, Department of Electrical Engineering, Baghdad
36 Solution of Coupled Electromagnetic and Thermal roblems in Gas Insulated Bus Bar Suad Ibrahim Shahl, Anwer Fouad mohammed Ali 2 University of Technology, Department of Electrical Engineering, Baghdad
Microwave Phase Shift Using Ferrite Filled Waveguide Below Cutoff
 Microwave Phase Shift Using Ferrite Filled Waveguide Below Cutoff CHARLES R. BOYD, JR. Microwave Applications Group, Santa Maria, California, U. S. A. ABSTRACT Unlike conventional waveguides, lossless
Microwave Phase Shift Using Ferrite Filled Waveguide Below Cutoff CHARLES R. BOYD, JR. Microwave Applications Group, Santa Maria, California, U. S. A. ABSTRACT Unlike conventional waveguides, lossless
Name. Section. Short Answer Questions. 1. (20 Pts) 2. (10 Pts) 3. (5 Pts) 4. (10 Pts) 5. (10 Pts) Regular Questions. 6. (25 Pts) 7.
 Name Section Short Answer Questions 1. (20 Pts) 2. (10 Pts) 3. (5 Pts). (10 Pts) 5. (10 Pts) Regular Questions 6. (25 Pts) 7. (20 Pts) Notes: 1. Please read over all questions before you begin your work.
Name Section Short Answer Questions 1. (20 Pts) 2. (10 Pts) 3. (5 Pts). (10 Pts) 5. (10 Pts) Regular Questions 6. (25 Pts) 7. (20 Pts) Notes: 1. Please read over all questions before you begin your work.
1.5. Inequalities. Equations and Inequalities. Box (cont.) Sections
 1 Equations and Inequalities Sections 1.5 1.8 2008 Pearson Addison-Wesley. All rights reserved 1 Equations and Inequalities 1.5 Applications and Modeling with Quadratic Equations 1.6 Other Types of Equations
1 Equations and Inequalities Sections 1.5 1.8 2008 Pearson Addison-Wesley. All rights reserved 1 Equations and Inequalities 1.5 Applications and Modeling with Quadratic Equations 1.6 Other Types of Equations
Module 4. Single-phase AC Circuits. Version 2 EE IIT, Kharagpur 1
 Module 4 Single-phase A ircuits ersion EE IIT, Kharagpur esson 4 Solution of urrent in -- Series ircuits ersion EE IIT, Kharagpur In the last lesson, two points were described:. How to represent a sinusoidal
Module 4 Single-phase A ircuits ersion EE IIT, Kharagpur esson 4 Solution of urrent in -- Series ircuits ersion EE IIT, Kharagpur In the last lesson, two points were described:. How to represent a sinusoidal
EE 742 Chapter 3: Power System in the Steady State. Y. Baghzouz
 EE 742 Chapter 3: Power System in the Steady State Y. Baghzouz Transmission Line Model Distributed Parameter Model: Terminal Voltage/Current Relations: Characteristic impedance: Propagation constant: π
EE 742 Chapter 3: Power System in the Steady State Y. Baghzouz Transmission Line Model Distributed Parameter Model: Terminal Voltage/Current Relations: Characteristic impedance: Propagation constant: π
SPECTRAL THEOREM FOR SYMMETRIC OPERATORS WITH COMPACT RESOLVENT
 SPECTRAL THEOREM FOR SYMMETRIC OPERATORS WITH COMPACT RESOLVENT Abstract. These are the letcure notes prepared for the workshop on Functional Analysis and Operator Algebras to be held at NIT-Karnataka,
SPECTRAL THEOREM FOR SYMMETRIC OPERATORS WITH COMPACT RESOLVENT Abstract. These are the letcure notes prepared for the workshop on Functional Analysis and Operator Algebras to be held at NIT-Karnataka,
INTEGRATION WORKSHOP 2003 COMPLEX ANALYSIS EXERCISES
 INTEGRATION WORKSHOP 23 COMPLEX ANALYSIS EXERCISES DOUGLAS ULMER 1. Meromorphic functions on the Riemann sphere It s often useful to allow functions to take the value. This exercise outlines one way to
INTEGRATION WORKSHOP 23 COMPLEX ANALYSIS EXERCISES DOUGLAS ULMER 1. Meromorphic functions on the Riemann sphere It s often useful to allow functions to take the value. This exercise outlines one way to
12. Introduction and Chapter Objectives
 Real Analog - Circuits 1 Chapter 1: Steady-State Sinusoidal Power 1. Introduction and Chapter Objectives In this chapter we will address the issue of power transmission via sinusoidal or AC) signals. This
Real Analog - Circuits 1 Chapter 1: Steady-State Sinusoidal Power 1. Introduction and Chapter Objectives In this chapter we will address the issue of power transmission via sinusoidal or AC) signals. This
) Rotate L by 120 clockwise to obtain in!! anywhere between load and generator: rotation by 2d in clockwise direction. d=distance from the load to the
 3.1 Smith Chart Construction: Start with polar representation of. L ; in on lossless lines related by simple phase change ) Idea: polar plot going from L to in involves simple rotation. in jj 1 ) circle
3.1 Smith Chart Construction: Start with polar representation of. L ; in on lossless lines related by simple phase change ) Idea: polar plot going from L to in involves simple rotation. in jj 1 ) circle
Chapter 7: The z-transform
 Chapter 7: The -Transform ECE352 1 The -Transform - definition Continuous-time systems: e st H(s) y(t) = e st H(s) e st is an eigenfunction of the LTI system h(t), and H(s) is the corresponding eigenvalue.
Chapter 7: The -Transform ECE352 1 The -Transform - definition Continuous-time systems: e st H(s) y(t) = e st H(s) e st is an eigenfunction of the LTI system h(t), and H(s) is the corresponding eigenvalue.
Compensator Design to Improve Transient Performance Using Root Locus
 1 Compensator Design to Improve Transient Performance Using Root Locus Prof. Guy Beale Electrical and Computer Engineering Department George Mason University Fairfax, Virginia Correspondence concerning
1 Compensator Design to Improve Transient Performance Using Root Locus Prof. Guy Beale Electrical and Computer Engineering Department George Mason University Fairfax, Virginia Correspondence concerning
CHAPTER 5 STEADY-STATE ANALYSIS OF THREE-PHASE SELF-EXCITED INDUCTION GENERATORS
 6 CHAPTER 5 STEADY-STATE ANALYSIS OF THREE-PHASE SELF-EXCITED INDUCTION GENERATORS 5.. INTRODUCTION The steady-state analysis of six-phase SEIG has been discussed in the previous chapters. In this chapter,
6 CHAPTER 5 STEADY-STATE ANALYSIS OF THREE-PHASE SELF-EXCITED INDUCTION GENERATORS 5.. INTRODUCTION The steady-state analysis of six-phase SEIG has been discussed in the previous chapters. In this chapter,
Finite. U-46 Curriculum Scope and Sequence. Reporting Strand Instructional Focus Standards Semester. Represent linear equations in matrices.
 Finite U-46 Curriculum Scope and Sequence Repting Strand Instructional Focus Standards Semester Represent linear equations in matrices. A.REI.8, A.REI.9 Matrices Perfm operations on matrices and use matrices
Finite U-46 Curriculum Scope and Sequence Repting Strand Instructional Focus Standards Semester Represent linear equations in matrices. A.REI.8, A.REI.9 Matrices Perfm operations on matrices and use matrices
Chapter 3. Loop and Cut-set Analysis
 Chapter 3. Loop and Cut-set Analysis By: FARHAD FARADJI, Ph.D. Assistant Professor, Electrical Engineering, K.N. Toosi University of Technology http://wp.kntu.ac.ir/faradji/electriccircuits2.htm References:
Chapter 3. Loop and Cut-set Analysis By: FARHAD FARADJI, Ph.D. Assistant Professor, Electrical Engineering, K.N. Toosi University of Technology http://wp.kntu.ac.ir/faradji/electriccircuits2.htm References:
Chapter 2 Direct Current Circuits
 Chapter 2 Direct Current Circuits 2.1 Introduction Nowadays, our lives are increasingly dependent upon the availability of devices that make extensive use of electric circuits. The knowledge of the electrical
Chapter 2 Direct Current Circuits 2.1 Introduction Nowadays, our lives are increasingly dependent upon the availability of devices that make extensive use of electric circuits. The knowledge of the electrical
Sinusoidal Steady State Analysis (AC Analysis) Part II
 Sinusoidal Steady State Analysis (AC Analysis) Part II Amin Electronics and Electrical Communications Engineering Department (EECE) Cairo University elc.n102.eng@gmail.com http://scholar.cu.edu.eg/refky/
Sinusoidal Steady State Analysis (AC Analysis) Part II Amin Electronics and Electrical Communications Engineering Department (EECE) Cairo University elc.n102.eng@gmail.com http://scholar.cu.edu.eg/refky/
We consider systems of differential equations of the form. x 1 = ax 1 + bx 2,
 Chapter 5 Systems We consider systems of differential equations of the fm (5) a + b, c + d, where a, b, c, and d are real numbers At first glance the system may seem to be first-der; however, it is coupled,
Chapter 5 Systems We consider systems of differential equations of the fm (5) a + b, c + d, where a, b, c, and d are real numbers At first glance the system may seem to be first-der; however, it is coupled,
Laplace Transform Analysis of Signals and Systems
 Laplace Transform Analysis of Signals and Systems Transfer Functions Transfer functions of CT systems can be found from analysis of Differential Equations Block Diagrams Circuit Diagrams 5/10/04 M. J.
Laplace Transform Analysis of Signals and Systems Transfer Functions Transfer functions of CT systems can be found from analysis of Differential Equations Block Diagrams Circuit Diagrams 5/10/04 M. J.
Two-Layer Network Equivalent for Electromagnetic Transients
 1328 IEEE TRANSACTIONS ON POWER DELIVERY, VOL. 18, NO. 4, OCTOBER 2003 Two-Layer Network Equivalent for Electromagnetic Transients Mohamed Abdel-Rahman, Member, IEEE, Adam Semlyen, Life Fellow, IEEE, and
1328 IEEE TRANSACTIONS ON POWER DELIVERY, VOL. 18, NO. 4, OCTOBER 2003 Two-Layer Network Equivalent for Electromagnetic Transients Mohamed Abdel-Rahman, Member, IEEE, Adam Semlyen, Life Fellow, IEEE, and
GATE EE Topic wise Questions SIGNALS & SYSTEMS
 www.gatehelp.com GATE EE Topic wise Questions YEAR 010 ONE MARK Question. 1 For the system /( s + 1), the approximate time taken for a step response to reach 98% of the final value is (A) 1 s (B) s (C)
www.gatehelp.com GATE EE Topic wise Questions YEAR 010 ONE MARK Question. 1 For the system /( s + 1), the approximate time taken for a step response to reach 98% of the final value is (A) 1 s (B) s (C)
Chapter 6: The Laplace Transform. Chih-Wei Liu
 Chapter 6: The Laplace Transform Chih-Wei Liu Outline Introduction The Laplace Transform The Unilateral Laplace Transform Properties of the Unilateral Laplace Transform Inversion of the Unilateral Laplace
Chapter 6: The Laplace Transform Chih-Wei Liu Outline Introduction The Laplace Transform The Unilateral Laplace Transform Properties of the Unilateral Laplace Transform Inversion of the Unilateral Laplace
A system that is both linear and time-invariant is called linear time-invariant (LTI).
 The Cooper Union Department of Electrical Engineering ECE111 Signal Processing & Systems Analysis Lecture Notes: Time, Frequency & Transform Domains February 28, 2012 Signals & Systems Signals are mapped
The Cooper Union Department of Electrical Engineering ECE111 Signal Processing & Systems Analysis Lecture Notes: Time, Frequency & Transform Domains February 28, 2012 Signals & Systems Signals are mapped
Basic. Theory. ircuit. Charles A. Desoer. Ernest S. Kuh. and. McGraw-Hill Book Company
 Basic C m ш ircuit Theory Charles A. Desoer and Ernest S. Kuh Department of Electrical Engineering and Computer Sciences University of California, Berkeley McGraw-Hill Book Company New York St. Louis San
Basic C m ш ircuit Theory Charles A. Desoer and Ernest S. Kuh Department of Electrical Engineering and Computer Sciences University of California, Berkeley McGraw-Hill Book Company New York St. Louis San
EECS 117 Lecture 3: Transmission Line Junctions / Time Harmonic Excitation
 EECS 117 Lecture 3: Transmission Line Junctions / Time Harmonic Excitation Prof. Niknejad University of California, Berkeley University of California, Berkeley EECS 117 Lecture 3 p. 1/23 Transmission Line
EECS 117 Lecture 3: Transmission Line Junctions / Time Harmonic Excitation Prof. Niknejad University of California, Berkeley University of California, Berkeley EECS 117 Lecture 3 p. 1/23 Transmission Line
1.2 LECTURE 2. Scalar Product
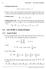 6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
6 CHAPTER 1. VECTOR ALGEBRA Pythagean theem. cos 2 α 1 + cos 2 α 2 + cos 2 α 3 = 1 There is a one-to-one crespondence between the components of the vect on the one side and its magnitude and the direction
CHAPTER VIII HILBERT SPACES
 CHAPTER VIII HILBERT SPACES DEFINITION Let X and Y be two complex vector spaces. A map T : X Y is called a conjugate-linear transformation if it is a reallinear transformation from X into Y, and if T (λx)
CHAPTER VIII HILBERT SPACES DEFINITION Let X and Y be two complex vector spaces. A map T : X Y is called a conjugate-linear transformation if it is a reallinear transformation from X into Y, and if T (λx)
Transmission lines. Shouri Chatterjee. October 22, 2014
 Transmission lines Shouri Chatterjee October 22, 2014 The transmission line is a very commonly used distributed circuit: a pair of wires. Unfortunately, a pair of wires used to apply a time-varying voltage,
Transmission lines Shouri Chatterjee October 22, 2014 The transmission line is a very commonly used distributed circuit: a pair of wires. Unfortunately, a pair of wires used to apply a time-varying voltage,
y(d) = j
 Problem 2.66 A 0-Ω transmission line is to be matched to a computer terminal with Z L = ( j25) Ω by inserting an appropriate reactance in parallel with the line. If f = 800 MHz and ε r = 4, determine the
Problem 2.66 A 0-Ω transmission line is to be matched to a computer terminal with Z L = ( j25) Ω by inserting an appropriate reactance in parallel with the line. If f = 800 MHz and ε r = 4, determine the
Microwave Oscillators Design
 Microwave Oscillators Design Oscillators Classification Feedback Oscillators β Α Oscillation Condition: Gloop = A β(jω 0 ) = 1 Gloop(jω 0 ) = 1, Gloop(jω 0 )=2nπ Negative resistance oscillators Most used
Microwave Oscillators Design Oscillators Classification Feedback Oscillators β Α Oscillation Condition: Gloop = A β(jω 0 ) = 1 Gloop(jω 0 ) = 1, Gloop(jω 0 )=2nπ Negative resistance oscillators Most used
Sinusoidal Steady State Analysis (AC Analysis) Part I
 Sinusoidal Steady State Analysis (AC Analysis) Part I Amin Electronics and Electrical Communications Engineering Department (EECE) Cairo University elc.n102.eng@gmail.com http://scholar.cu.edu.eg/refky/
Sinusoidal Steady State Analysis (AC Analysis) Part I Amin Electronics and Electrical Communications Engineering Department (EECE) Cairo University elc.n102.eng@gmail.com http://scholar.cu.edu.eg/refky/
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra
 Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
TRANSMISSION LINES AND MATCHING
 TRANSMISSION LINES AND MATCHING for High-Frequency Circuit Design Elective by Michael Tse September 2003 Contents Basic models The Telegrapher s equations and solutions Transmission line equations The
TRANSMISSION LINES AND MATCHING for High-Frequency Circuit Design Elective by Michael Tse September 2003 Contents Basic models The Telegrapher s equations and solutions Transmission line equations The
RLC Circuit (3) We can then write the differential equation for charge on the capacitor. The solution of this differential equation is
 RLC Circuit (3) We can then write the differential equation for charge on the capacitor The solution of this differential equation is (damped harmonic oscillation!), where 25 RLC Circuit (4) If we charge
RLC Circuit (3) We can then write the differential equation for charge on the capacitor The solution of this differential equation is (damped harmonic oscillation!), where 25 RLC Circuit (4) If we charge
6.1 Moment Generating and Characteristic Functions
 Chapter 6 Limit Theorems The power statistics can mostly be seen when there is a large collection of data points and we are interested in understanding the macro state of the system, e.g., the average,
Chapter 6 Limit Theorems The power statistics can mostly be seen when there is a large collection of data points and we are interested in understanding the macro state of the system, e.g., the average,
Algebraic Varieties. Chapter Algebraic Varieties
 Chapter 12 Algebraic Varieties 12.1 Algebraic Varieties Let K be a field, n 1 a natural number, and let f 1,..., f m K[X 1,..., X n ] be polynomials with coefficients in K. Then V = {(a 1,..., a n ) :
Chapter 12 Algebraic Varieties 12.1 Algebraic Varieties Let K be a field, n 1 a natural number, and let f 1,..., f m K[X 1,..., X n ] be polynomials with coefficients in K. Then V = {(a 1,..., a n ) :
Mathematical foundations - linear algebra
 Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
EE 205 Dr. A. Zidouri. Electric Circuits II. Two-Port Circuits Two-Port Parameters. Lecture #42
 EE 05 Dr. A. Zidouri Electric Circuits Two-Port Circuits Two-Port Parameters Lecture #4-1 - EE 05 Dr. A. Zidouri The material to be covered in this lecture is as follows: o ntroduction to two-port circuits
EE 05 Dr. A. Zidouri Electric Circuits Two-Port Circuits Two-Port Parameters Lecture #4-1 - EE 05 Dr. A. Zidouri The material to be covered in this lecture is as follows: o ntroduction to two-port circuits
Electromagnetic Waves
 Electromagnetic Waves Maxwell s equations predict the propagation of electromagnetic energy away from time-varying sources (current and charge) in the form of waves. Consider a linear, homogeneous, isotropic
Electromagnetic Waves Maxwell s equations predict the propagation of electromagnetic energy away from time-varying sources (current and charge) in the form of waves. Consider a linear, homogeneous, isotropic
Control Systems. Frequency Method Nyquist Analysis.
 Frequency Method Nyquist Analysis chibum@seoultech.ac.kr Outline Polar plots Nyquist plots Factors of polar plots PolarNyquist Plots Polar plot: he locus of the magnitude of ω vs. the phase of ω on polar
Frequency Method Nyquist Analysis chibum@seoultech.ac.kr Outline Polar plots Nyquist plots Factors of polar plots PolarNyquist Plots Polar plot: he locus of the magnitude of ω vs. the phase of ω on polar
Return Difference Function and Closed-Loop Roots Single-Input/Single-Output Control Systems
 Spectral Properties of Linear- Quadratic Regulators Robert Stengel Optimal Control and Estimation MAE 546 Princeton University, 2018! Stability margins of single-input/singleoutput (SISO) systems! Characterizations
Spectral Properties of Linear- Quadratic Regulators Robert Stengel Optimal Control and Estimation MAE 546 Princeton University, 2018! Stability margins of single-input/singleoutput (SISO) systems! Characterizations
An improved convergence theorem for the Newton method under relaxed continuity assumptions
 An improved convergence theorem for the Newton method under relaxed continuity assumptions Andrei Dubin ITEP, 117218, BCheremushinsaya 25, Moscow, Russia Abstract In the framewor of the majorization technique,
An improved convergence theorem for the Newton method under relaxed continuity assumptions Andrei Dubin ITEP, 117218, BCheremushinsaya 25, Moscow, Russia Abstract In the framewor of the majorization technique,
GCSE Mathematics. Paper 2 Higher Tier. Mark scheme November Version: 1.0 Final
 GCSE Mathematics Paper Higher Tier Mark scheme 8300 November 017 Version: 1.0 Final MARK SCHEME GCSE MATHEMATICS 8300/H NOVEMBER 017 Mark schemes are prepared by the Lead Assessment Writer and considered,
GCSE Mathematics Paper Higher Tier Mark scheme 8300 November 017 Version: 1.0 Final MARK SCHEME GCSE MATHEMATICS 8300/H NOVEMBER 017 Mark schemes are prepared by the Lead Assessment Writer and considered,
The Impedance Matrix
 0/0/09 The mpedance Matrix.doc /7 The mpedance Matrix Consider the -port microwave device shown below: z ( z ) z z port z z port 0 -port 0 microwave 0 device P z z P z port z P z ( z ) z port 0 ( z ) z
0/0/09 The mpedance Matrix.doc /7 The mpedance Matrix Consider the -port microwave device shown below: z ( z ) z z port z z port 0 -port 0 microwave 0 device P z z P z port z P z ( z ) z port 0 ( z ) z
EE 581 Power Systems. Admittance Matrix: Development, Direct and Iterative solutions
 EE 581 Power Systems Admittance Matrix: Development, Direct and Iterative solutions Overview and HW # 8 Chapter 2.4 Chapter 6.4 Chapter 6.1-6.3 Homework: Special Problem 1 and 2 (see handout) Overview
EE 581 Power Systems Admittance Matrix: Development, Direct and Iterative solutions Overview and HW # 8 Chapter 2.4 Chapter 6.4 Chapter 6.1-6.3 Homework: Special Problem 1 and 2 (see handout) Overview
Introduction to Network Analysis of Microwave Circuits
 1 Introduction to Network Analysis of Microwave Circuits ABSTRACT Network presentation has been used as a technique in the analysis of lowfrequency electrical electronic circuits. The same technique is
1 Introduction to Network Analysis of Microwave Circuits ABSTRACT Network presentation has been used as a technique in the analysis of lowfrequency electrical electronic circuits. The same technique is
. -2 (ZL+jZotanf3l) Zo + jzl J31 _ (60+j20)+j50tan(21trad/mx2.5m))
 CHAPTER 8 277 Section 8-6: Input Impedance Problem 8.17 At an operating frequency of 300 MHz, a loss less 50-0. air-spaced transmission line 2.501 in length is terminated with an impedance 4'. = (60+ j20)
CHAPTER 8 277 Section 8-6: Input Impedance Problem 8.17 At an operating frequency of 300 MHz, a loss less 50-0. air-spaced transmission line 2.501 in length is terminated with an impedance 4'. = (60+ j20)
Module 3F2: Systems and Control EXAMPLES PAPER 2 ROOT-LOCUS. Solutions
 Cambridge University Engineering Dept. Third Year Module 3F: Systems and Control EXAMPLES PAPER ROOT-LOCUS Solutions. (a) For the system L(s) = (s + a)(s + b) (a, b both real) show that the root-locus
Cambridge University Engineering Dept. Third Year Module 3F: Systems and Control EXAMPLES PAPER ROOT-LOCUS Solutions. (a) For the system L(s) = (s + a)(s + b) (a, b both real) show that the root-locus
A new passivity property of linear RLC circuits with application to Power Shaping Stabilization
 A new passivity property of linear RLC circuits with application to Power Shaping Stabilization Eloísa García Canseco and Romeo Ortega Abstract In this paper we characterize the linear RLC networks for
A new passivity property of linear RLC circuits with application to Power Shaping Stabilization Eloísa García Canseco and Romeo Ortega Abstract In this paper we characterize the linear RLC networks for
Math 2233 Homework Set 8
 Math 2233 Homewk Set 8. Determine the lower bound f the radius of convergence of series solutions about each given point xo. (a) y +4y +6xy =,x = Since the coefficient functions 4 6x are perfectly analytic
Math 2233 Homewk Set 8. Determine the lower bound f the radius of convergence of series solutions about each given point xo. (a) y +4y +6xy =,x = Since the coefficient functions 4 6x are perfectly analytic
ECE145A/218A Course Notes
 ECE145A/218A Course Notes Last note set: Introduction to transmission lines 1. Transmission lines are a linear system - superposition can be used 2. Wave equation permits forward and reverse wave propagation
ECE145A/218A Course Notes Last note set: Introduction to transmission lines 1. Transmission lines are a linear system - superposition can be used 2. Wave equation permits forward and reverse wave propagation
The Tuning of Robust Controllers for Stable Systems in the CD-Algebra: The Case of Sinusoidal and Polynomial Signals
 The Tuning of Robust Controllers for Stable Systems in the CD-Algebra: The Case of Sinusoidal and Polynomial Signals Timo Hämäläinen Seppo Pohjolainen Tampere University of Technology Department of Mathematics
The Tuning of Robust Controllers for Stable Systems in the CD-Algebra: The Case of Sinusoidal and Polynomial Signals Timo Hämäläinen Seppo Pohjolainen Tampere University of Technology Department of Mathematics
Linear Fractionally Damped Oscillator. Mark Naber a) Department of Mathematics. Monroe County Community College. Monroe, Michigan,
 Linear Fractionally Damped Oscillator Mark Naber a) Department of Mathematics Monroe County Community College Monroe, Michigan, 48161-9746 In this paper the linearly damped oscillator equation is considered
Linear Fractionally Damped Oscillator Mark Naber a) Department of Mathematics Monroe County Community College Monroe, Michigan, 48161-9746 In this paper the linearly damped oscillator equation is considered
ECE Branch GATE Paper The order of the differential equation + + = is (A) 1 (B) 2
 Question 1 Question 20 carry one mark each. 1. The order of the differential equation + + = is (A) 1 (B) 2 (C) 3 (D) 4 2. The Fourier series of a real periodic function has only P. Cosine terms if it is
Question 1 Question 20 carry one mark each. 1. The order of the differential equation + + = is (A) 1 (B) 2 (C) 3 (D) 4 2. The Fourier series of a real periodic function has only P. Cosine terms if it is
3.1 Energy minimum principle
 Ashley Robison My Preferences Site Tools FAQ Sign Out If you like us, please share us on social media. The latest UCD Hyperlibrary newsletter is now complete, check it out. ChemWiki BioWiki GeoWiki StatWiki
Ashley Robison My Preferences Site Tools FAQ Sign Out If you like us, please share us on social media. The latest UCD Hyperlibrary newsletter is now complete, check it out. ChemWiki BioWiki GeoWiki StatWiki
Projection Theorem 1
 Projection Theorem 1 Cauchy-Schwarz Inequality Lemma. (Cauchy-Schwarz Inequality) For all x, y in an inner product space, [ xy, ] x y. Equality holds if and only if x y or y θ. Proof. If y θ, the inequality
Projection Theorem 1 Cauchy-Schwarz Inequality Lemma. (Cauchy-Schwarz Inequality) For all x, y in an inner product space, [ xy, ] x y. Equality holds if and only if x y or y θ. Proof. If y θ, the inequality
Numerical Methods for Differential Equations Mathematical and Computational Tools
 Numerical Methods for Differential Equations Mathematical and Computational Tools Gustaf Söderlind Numerical Analysis, Lund University Contents V4.16 Part 1. Vector norms, matrix norms and logarithmic
Numerical Methods for Differential Equations Mathematical and Computational Tools Gustaf Söderlind Numerical Analysis, Lund University Contents V4.16 Part 1. Vector norms, matrix norms and logarithmic
Notes on Equidistribution
 otes on Equidistribution Jacques Verstraëte Department of Mathematics University of California, San Diego La Jolla, CA, 92093. E-mail: jacques@ucsd.edu. Introduction For a real number a we write {a} for
otes on Equidistribution Jacques Verstraëte Department of Mathematics University of California, San Diego La Jolla, CA, 92093. E-mail: jacques@ucsd.edu. Introduction For a real number a we write {a} for
Module 2 : Transmission Lines. Lecture 10 : Transmisssion Line Calculations Using Smith Chart. Objectives. In this course you will learn the following
 Objectives In this course you will learn the following What is a constant VSWR circle on the - plane? Properties of constant VSWR circles. Calculations of load reflection coefficient. Calculation of reflection
Objectives In this course you will learn the following What is a constant VSWR circle on the - plane? Properties of constant VSWR circles. Calculations of load reflection coefficient. Calculation of reflection
A Note on Inverse Iteration
 A Note on Inverse Iteration Klaus Neymeyr Universität Rostock, Fachbereich Mathematik, Universitätsplatz 1, 18051 Rostock, Germany; SUMMARY Inverse iteration, if applied to a symmetric positive definite
A Note on Inverse Iteration Klaus Neymeyr Universität Rostock, Fachbereich Mathematik, Universitätsplatz 1, 18051 Rostock, Germany; SUMMARY Inverse iteration, if applied to a symmetric positive definite
A new approach to uniqueness for linear problems of wave body interaction
 A new approach to uniqueness for linear problems of wave body interaction Oleg Motygin Laboratory for Mathematical Modelling of Wave Phenomena, Institute of Problems in Mechanical Engineering, Russian
A new approach to uniqueness for linear problems of wave body interaction Oleg Motygin Laboratory for Mathematical Modelling of Wave Phenomena, Institute of Problems in Mechanical Engineering, Russian
Lecture 9. The Smith Chart and Basic Impedance-Matching Concepts
 ecture 9 The Smith Chart and Basic Impedance-Matching Concepts The Smith Chart: Γ plot in the Complex Plane Smith s chart is a graphical representation in the complex Γ plane of the input impedance, the
ecture 9 The Smith Chart and Basic Impedance-Matching Concepts The Smith Chart: Γ plot in the Complex Plane Smith s chart is a graphical representation in the complex Γ plane of the input impedance, the
Annexure-I. network acts as a buffer in matching the impedance of the plasma reactor to that of the RF
 Annexure-I Impedance matching and Smith chart The output impedance of the RF generator is 50 ohms. The impedance matching network acts as a buffer in matching the impedance of the plasma reactor to that
Annexure-I Impedance matching and Smith chart The output impedance of the RF generator is 50 ohms. The impedance matching network acts as a buffer in matching the impedance of the plasma reactor to that
POWER SYSTEM STABILITY
 LESSON SUMMARY-1:- POWER SYSTEM STABILITY 1. Introduction 2. Classification of Power System Stability 3. Dynamic Equation of Synchronous Machine Power system stability involves the study of the dynamics
LESSON SUMMARY-1:- POWER SYSTEM STABILITY 1. Introduction 2. Classification of Power System Stability 3. Dynamic Equation of Synchronous Machine Power system stability involves the study of the dynamics
Fault Locating PRESENTED BY ERIK SCHELLENBERG IDAHO POWER
 Fault Locating PRESENTED BY ERIK SCHELLENBERG IDAHO POWER Topics Impedance Based Reactance Method Takagi Method Modifications to Takagi Method TWS & Double Ended Negative Sequence One Line Equivalent Thevenin
Fault Locating PRESENTED BY ERIK SCHELLENBERG IDAHO POWER Topics Impedance Based Reactance Method Takagi Method Modifications to Takagi Method TWS & Double Ended Negative Sequence One Line Equivalent Thevenin
Berkeley. The Smith Chart. Prof. Ali M. Niknejad. U.C. Berkeley Copyright c 2017 by Ali M. Niknejad. September 14, 2017
 Berkeley The Smith Chart Prof. Ali M. Niknejad U.C. Berkeley Copyright c 17 by Ali M. Niknejad September 14, 17 1 / 29 The Smith Chart The Smith Chart is simply a graphical calculator for computing impedance
Berkeley The Smith Chart Prof. Ali M. Niknejad U.C. Berkeley Copyright c 17 by Ali M. Niknejad September 14, 17 1 / 29 The Smith Chart The Smith Chart is simply a graphical calculator for computing impedance
Enhanced Newton Method Based Radial Distribution System Load Flow Analysis with Extrapolation Techniques
 Enhanced Newton Method Based Radial Distribution System Load Flow Analysis with Extrapolation Techniques Asst. Prof. Dr. Hassan Kuhba Electrical Engineering Department, Engineering College/Baghdad University,
Enhanced Newton Method Based Radial Distribution System Load Flow Analysis with Extrapolation Techniques Asst. Prof. Dr. Hassan Kuhba Electrical Engineering Department, Engineering College/Baghdad University,
Transient stability analysis and control of power systems with considering flux decay by energy function approach
 BULLETIN OF THE POLISH ACADEMY OF SCIENCES TECHNICAL SCIENCES, Vol. 60, No. 1, 2012 DOI: 10.2478/v10175-012-0001-1 Transient stability analysis and control of power systems with considering flux decay
BULLETIN OF THE POLISH ACADEMY OF SCIENCES TECHNICAL SCIENCES, Vol. 60, No. 1, 2012 DOI: 10.2478/v10175-012-0001-1 Transient stability analysis and control of power systems with considering flux decay
Lecture Notes 6: Dynamic Equations Part C: Linear Difference Equation Systems
 University of Warwick, EC9A0 Maths for Economists Peter J. Hammond 1 of 45 Lecture Notes 6: Dynamic Equations Part C: Linear Difference Equation Systems Peter J. Hammond latest revision 2017 September
University of Warwick, EC9A0 Maths for Economists Peter J. Hammond 1 of 45 Lecture Notes 6: Dynamic Equations Part C: Linear Difference Equation Systems Peter J. Hammond latest revision 2017 September
Review of Linear Time-Invariant Network Analysis
 D1 APPENDIX D Review of Linear Time-Invariant Network Analysis Consider a network with input x(t) and output y(t) as shown in Figure D-1. If an input x 1 (t) produces an output y 1 (t), and an input x
D1 APPENDIX D Review of Linear Time-Invariant Network Analysis Consider a network with input x(t) and output y(t) as shown in Figure D-1. If an input x 1 (t) produces an output y 1 (t), and an input x
Smith Chart Figure 1 Figure 1.
 Smith Chart The Smith chart appeared in 1939 as a graph-based method of simplifying the complex math (that is, calculations involving variables of the form x + jy) needed to describe the characteristics
Smith Chart The Smith chart appeared in 1939 as a graph-based method of simplifying the complex math (that is, calculations involving variables of the form x + jy) needed to describe the characteristics
(amperes) = (coulombs) (3.1) (seconds) Time varying current. (volts) =
 3 Electrical Circuits 3. Basic Concepts Electric charge coulomb of negative change contains 624 0 8 electrons. Current ampere is a steady flow of coulomb of change pass a given point in a conductor in
3 Electrical Circuits 3. Basic Concepts Electric charge coulomb of negative change contains 624 0 8 electrons. Current ampere is a steady flow of coulomb of change pass a given point in a conductor in
ELEC4612 Power System Analysis Power Flow Analysis
 ELEC462 Power Sstem Analsis Power Flow Analsis Dr Jaashri Ravishankar jaashri.ravishankar@unsw.edu.au Busbars The meeting point of various components of a PS is called bus. The bus or busbar is a conductor
ELEC462 Power Sstem Analsis Power Flow Analsis Dr Jaashri Ravishankar jaashri.ravishankar@unsw.edu.au Busbars The meeting point of various components of a PS is called bus. The bus or busbar is a conductor
POWER flow studies are the cornerstone of power system
 University of Wisconsin-Madison Department of Electrical and Computer Engineering. Technical Report ECE-2-. A Sufficient Condition for Power Flow Insolvability with Applications to Voltage Stability Margins
University of Wisconsin-Madison Department of Electrical and Computer Engineering. Technical Report ECE-2-. A Sufficient Condition for Power Flow Insolvability with Applications to Voltage Stability Margins
EDEXCEL NATIONAL CERTIFICATE UNIT 28 FURTHER MATHEMATICS FOR TECHNICIANS OUTCOME 2- ALGEBRAIC TECHNIQUES TUTORIAL 2 - COMPLEX NUMBERS
 EDEXCEL NATIONAL CERTIFICATE UNIT 8 FURTHER MATHEMATICS FOR TECHNICIANS OUTCOME - ALGEBRAIC TECHNIQUES TUTORIAL - COMPLEX NUMBERS CONTENTS Be able to apply algebraic techniques Arithmetic progression (AP):
EDEXCEL NATIONAL CERTIFICATE UNIT 8 FURTHER MATHEMATICS FOR TECHNICIANS OUTCOME - ALGEBRAIC TECHNIQUES TUTORIAL - COMPLEX NUMBERS CONTENTS Be able to apply algebraic techniques Arithmetic progression (AP):
KINGS COLLEGE OF ENGINEERING Punalkulam
 KINGS COLLEGE OF ENGINEERING Punalkulam 613 303 DEPARTMENT OF ELECTRICAL AND ELECTRONICS ENGINEERING POWER SYSTEM ANALYSIS QUESTION BANK UNIT I THE POWER SYSTEM AN OVERVIEW AND MODELLING PART A (TWO MARK
KINGS COLLEGE OF ENGINEERING Punalkulam 613 303 DEPARTMENT OF ELECTRICAL AND ELECTRONICS ENGINEERING POWER SYSTEM ANALYSIS QUESTION BANK UNIT I THE POWER SYSTEM AN OVERVIEW AND MODELLING PART A (TWO MARK
7.4 STEP BY STEP PROCEDURE TO DRAW THE ROOT LOCUS DIAGRAM
 ROOT LOCUS TECHNIQUE. Values of on the root loci The value of at any point s on the root loci is determined from the following equation G( s) H( s) Product of lengths of vectors from poles of G( s)h( s)
ROOT LOCUS TECHNIQUE. Values of on the root loci The value of at any point s on the root loci is determined from the following equation G( s) H( s) Product of lengths of vectors from poles of G( s)h( s)
Nonlinear Circuit Analysis in Time and Frequency-domain Example: A Pure LC Resonator
 Nonlinear Circuit Analysis in Time and Frequency-domain Example: A Pure LC Resonator AWR Microwave Office Application Note INTRODUCTION Nonlinear circuits are known to have multiple mathematical solutions
Nonlinear Circuit Analysis in Time and Frequency-domain Example: A Pure LC Resonator AWR Microwave Office Application Note INTRODUCTION Nonlinear circuits are known to have multiple mathematical solutions
ELECTRICAL ENGINEERING
 ELECTRICAL ENGINEERING Subject Code: EE Course Structure Sections/Units Section A Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Section B Section C Section D Section E Section F Section G Section H
ELECTRICAL ENGINEERING Subject Code: EE Course Structure Sections/Units Section A Unit 1 Unit 2 Unit 3 Unit 4 Unit 5 Unit 6 Unit 7 Section B Section C Section D Section E Section F Section G Section H
Transmission Lines in the Frequency Domain
 Berkeley Transmission Lines in the Frequency Domain Prof. Ali M. Niknejad U.C. Berkeley Copyright c 2016 by Ali M. Niknejad August 30, 2017 1 / 38 Why Sinusoidal Steady-State? 2 / 38 Time Harmonic Steady-State
Berkeley Transmission Lines in the Frequency Domain Prof. Ali M. Niknejad U.C. Berkeley Copyright c 2016 by Ali M. Niknejad August 30, 2017 1 / 38 Why Sinusoidal Steady-State? 2 / 38 Time Harmonic Steady-State
MAS107 Control Theory Exam Solutions 2008
 MAS07 CONTROL THEORY. HOVLAND: EXAM SOLUTION 2008 MAS07 Control Theory Exam Solutions 2008 Geir Hovland, Mechatronics Group, Grimstad, Norway June 30, 2008 C. Repeat question B, but plot the phase curve
MAS07 CONTROL THEORY. HOVLAND: EXAM SOLUTION 2008 MAS07 Control Theory Exam Solutions 2008 Geir Hovland, Mechatronics Group, Grimstad, Norway June 30, 2008 C. Repeat question B, but plot the phase curve
PID control of FOPDT plants with dominant dead time based on the modulus optimum criterion
 Archives of Control Sciences Volume 6LXII, 016 No. 1, pages 5 17 PID control of FOPDT plants with dominant dead time based on the modulus optimum criterion JAN CVEJN The modulus optimum MO criterion can
Archives of Control Sciences Volume 6LXII, 016 No. 1, pages 5 17 PID control of FOPDT plants with dominant dead time based on the modulus optimum criterion JAN CVEJN The modulus optimum MO criterion can
A Concise Course on Stochastic Partial Differential Equations
 A Concise Course on Stochastic Partial Differential Equations Michael Röckner Reference: C. Prevot, M. Röckner: Springer LN in Math. 1905, Berlin (2007) And see the references therein for the original
A Concise Course on Stochastic Partial Differential Equations Michael Röckner Reference: C. Prevot, M. Röckner: Springer LN in Math. 1905, Berlin (2007) And see the references therein for the original
Lecture 13 Date:
 ecture 3 Date: 6.09.204 The Signal Flow Graph (Contd.) Impedance Matching and Tuning Tpe Matching Network Example Signal Flow Graph (contd.) Splitting Rule Now consider the three equations SFG a a b 2
ecture 3 Date: 6.09.204 The Signal Flow Graph (Contd.) Impedance Matching and Tuning Tpe Matching Network Example Signal Flow Graph (contd.) Splitting Rule Now consider the three equations SFG a a b 2
