n n! In general: Geometric series: n n n n Harmonic series: n kn n n n k k k m
|
|
|
- Lisa Norman
- 6 years ago
- Views:
Transcription
1 f() O(g()) f() (g()) Detos 9 ostve 0 suh tht 0 f() g() ostve 0 suh tht f() g() f() (g()) f() O(g()) d f() (g()) f() o(g()) l! f()g() 0 l! 8 R, 9 0 suh tht j ; j <, 8 0 su S lest b R suh tht b s, 8s S Theoretl Couter See Chet Sheet I geerl ; ( +) + + Geoetr seres ( +) + ; ; ; 6 ; Seres ( +)( +) 6 3 ( +) 4 ; ( +) + ; + ; ( +) B +; ; ; < + ; ( +) f S gretest b R suh tht b ( ; ) ( ; ) < s, 8s S Hro seres l f! l! ff j Ng H ( +) ( ; ) H H ; l su l 4!! suf j Ng ; + Cobtos Sze subsets of sze set + + H ( +)H ; H H + ; Strlg ubers (st d)! Arrgeets of eleet setto yles ( ; )!! 3 ; 0 4 ; ; ; 5 + Strlg ubers (d d) ; ; rttos of eleet ; r + r + + set to o-ety sets 6 7 ; st order Euler ubers + r s r + s eruttos o 8 9 f g wth sets + ; (;) ; ; d order Euler ubers C Ctl Nubers Bry ; ; trees wth + vertes ; ; 3 + ; 4 ( ; )! 5 ( ; )!H ; 6 7 ; ; 8 ( ; ) + 9 0! C ; ; ; + 0 ; ; 3 4 ( +) +( ; ) 0 ; ; ; ; 0 5 f 0, 6 ; ; 7 3 ; ( +) otherwse ( +; ) (;) 30! ; ; 3 (;) ;;! for ; ; 34 ( +) +( ; ; ) 35 () ; 0 + ; ; ( +) ; ; + 0 0
2 Theoretl Couter See Chet Sheet Idettes Cot + ; +! 39 +! ; (;) ; + 4 (;) ; ( + ) (;) ; + 45 ( ; )! (;) ; for, + + ; + + ; ; + + ; + + ` + ; ` + ; 49 ` + ` ` ` + ` ` Trees Every tree wth vertes hs ; edges Krft equlty If the deths of the leves of bry tree re d d ;d d equlty holds oly f every terl ode hs sos Mster ethod T () T (b)+f() b> If 9 >0 suh tht f() O( log b ; ) the T () ( log b ) If f() ( log b )the T () ( log b log ) If 9 >0 suh tht f() ( log b + ), d 9 < suh tht f(b) f() for lrge, the T () (f()) Substtuto (ele) Cosder the followg reurree T + T T Note tht T s lwys ower of two Let t log T The we hve t + +t t Let u t Dvdg both sdes of the revous equto by + weget t t + Substtutg we d u + + u u whh s sly u So we d tht T hs the losed for T ; Sug ftors (ele) Cosder the followg reurree T 3T + T Rewrte so tht ll ters volvg T re o the left sde T ; 3T Now ed the reurree, d hoose ftor whh es the left sde \telesoe" Reurrees ; T () ; 3T () 3 ; T () ; 3T (4) 3 log ; ; T () ; 3T () 3 log ; T () ; 0 Sug the left sde we get T () Sug the rght sde we get log 3 Let 3 d log Thewehve + ; ; ( log ; ) ( log ; ) + ; ; 3 where (log ); Full hstory reurrees ofte be hged to lted hstory oes (ele) Cosder the followg reurree Note tht T + ; j0 T + + Subtrtg we d T + ; T + T T j T 0 j0 j0 Ad so T + T + T j T j ; ; ; j0 T j Geertg futos Multly both sdes of the equto by Su both sdes over ll for whh the equto s vld 3 Choose geertg futo G() Usully G() 3 Rewrte the equto ters of the geertg futo G() 4 Solve for G() 5 The oeet of G() sg Ele g + g + g 0 0 Multly d su 0 g + 0 g + 0 We hoose G() 0 Rewrte ters of G() G() ; g 0 G()+ 0 Slfy G() G()+ ; Solve forg() G() ( ; )( ; ) Ed ths usg rtl frtos G() ; ; ; So g ; 0 ; 0 0( + ; ) + A
3 Theoretl Couter See Chet Sheet 3459, e 788, 0577, , ^ ; 5 ;6803 Geerl robblty Beroull Nubers (B 0,odd 6 ) ,04 9, , , , , , , , , ,048,576 7,097,5 73 4,94, ,388, ,777, ,554, ,08, ,7,78 03 B 0,B ;, B, B 6 4 ;, 30 B 6, 4 B 8 ;, 30 B Chge of bse, qudrt forul log b log log b ;b b ; 4 Euler's uber e ; + e l ; +! + e ; <e< ; O 3 e ; e + e Hro ubers, 3,, 5, 37, 49, 363, 76, l <H < l + H l + + O Ftorl, Strlg's roto,, 6, 4, 0, 70, 5040, 4030, 36880,! + e Aer's 8 futo d verse < j ( j) ( ; ) j ( ; ( j ; )) j () fj j (j j) g 8 68,435, Bol dstrbuto 9 536,870,9 09 r[ ] q ; q ; 30,073,74,84 3 3,47,483,648 7 E[] q ; 3 4,94,967,96 3 osso dstrbuto sl's Trgle r[ ] e; E[]! Norl (Guss) dstrbuto () e ;(;) E[] The \ouo olletor" We re gve rdo ouo eh dy, d there re deret tyes of ouos The dstrbuto of ouos s ufor The eeted uberofdys to ss before we toollet ll tyes s H Cotuous dstrbutos If b r[ <<b] () the s the robblty desty futo of If r[ <] () the s the dstrbuto futo of If d both est the () () ; Eetto If s dsrete E[g()] g()r[ ] If otuous the E[g()] ; g()() Vre, stdrd devto VAR[] E[ ] ; E[] g() d () ; VAR[] Bss r[ _ Y ] r[] + r[y ] ; r[ ^ Y ] r[ ^ Y ] r[] r[y ] d Y re deedet r[jy ] r[ ^ Y ] r[b] E[ Y ]E[] E[Y ] d Y re deedet E[ + Y ]E[]+E[Y ] E[] E[] Byes' theore r[bja ] r[a ] r[a jb] j r[a j]r[bja j ] Iluso-eluso r h _ Moet equltes r r[ ]+ (;) + << r r jj E[] h ; E[] Geoetr dstrbuto r[ ] ; q E[] q ; h ^ j q ; j
4 A b C B ythgore theore C A + B Theoretl Couter See Chet Sheet Trgooetry Mtres More Trg Detos s AC s CA (0,) (-,0) (,0) (0,-) os BC se CB t s os A B os ot s B A Are, rdus of srbed rle AB AB A + B + C Idettes s s os se t ot s +os + t se +ot s s os ; ; s s( ; ) os ; os( ; ) ot ; ot( ; ) s( y) s os y os s y os( y) os os y s s y t ot ; ; s ot ; ot t t y t( y) t t y ot ot y ot( y) ot ot y s s os s t +t os os ; s os os ; os ; s os ; t +t t t ; t ot ot ; ot s( + y) s( ; y) s ; s y os( + y) os( ; y) os ; s y Euler's equto e os + s e ; 994 by Steve Sede ssede@suedu htt//wwwsuedu/~ssede Multlto C A B j b j (os s ) Deterts det A 0A s o-sgulr det A B detadet B Y det A sg() () d33 detert b d e f g h erets g b e Detos sh e ; e ; b d f d ; b ; h d f + e + bfg + dh ; eg ; fh ; bd Y er A () Hyerbol Futos osh e + e ; th e ; e ; e sh + e ; sh seh osh oth th Idettes osh ; sh th + seh oth ; sh osh(;) osh d b e sh(;) ; sh th(;) ; th sh( + y) sh osh y + osh sh y osh( + y) osh osh y + sh sh y sh sh osh osh osh + sh osh + sh e osh ; sh e ; (osh +sh) osh +sh sh osh ; osh osh + s os t thets you do't uderstd thgs, you just get used to the {Jvo Neu A b C h Lw of oses B +b ;b os C Are A h b s C s A s B sc Hero's forul A s s s b s s ( + b + ) s s ; s b s ; b s s ; More dettes r ; os s r + os os t r ; os + os ; os s s +os ot r + os ; os +os s s ; os s e ; e ; os e + e ; t ; e ; e ; e + e ; ; e ; e + sh s os osh th t
5 Nuber Theory The Chese reder theore There ests uber C suh tht C r od C r od f d j re reltvely re for 6 j Euler's futo () s the uber of ostve tegers Q less th reltvely re to If e s the re ftorzto of the () Y e; ( ; ) Euler's theore If d b re reltvely re the (b) od b Fert's theore ; od The Eulde lgorth f >bre tegers the gd( b) gd( od b b) Q If e the s the re ftorzto of S() dj d Y e+ ; ; erfet Nubers s eve erfet uber ; ( ;) d ;sre Wlso's theore s re ( ; )! ;od 8 Mobus verso f >< 0 f s ot squre-free () > (;) r f s the rodut of r dstt res If the G() F (d) dj F () (d)g d dj re ubers l l l + l l ; + l + O l () l + (l ) +! (l ) 3 + O (l ) 4 Theoretl Couter See Chet Sheet Grh Theory Detos Loo A edge oetg verte to tself Dreted Eh edge hs dreto Sle Grh wth o loos or ult-edges Wl A sequee v 0 e v e`v` Trl Awl wth dstt edges th A trl wth dstt vertes Coeted A grh where there ests th betwee y two vertes Cooet A l oeted subgrh Tree A oeted yl grh Free tree A tree wth o root DAG Dreted yl grh Euler Grh wth trl vstg eh edge etly oe Hlto Grh wth th vstg eh verte etly oe Cut A set of edges whose reovl reses the uber of ooets Cut-set A l ut Cut edge A sze ut -Coeted A grh oeted wth the reovl of y ; vertes -Tough 8S V S 6 we hve (G ; S) jsj -Regulr A grh where ll vertes hve degree -Ftor A -regulr sg subgrh Mthg A set of edges, o two of whh re djet Clque A set of vertes, ll of whh re djet Id set A set of vertes, oe of whh re djet Verte over A set of vertes whh over ll edges lr grh A grh whh be ebeded the le le grh A ebeddg of lr grh vv deg(v) If G s lr the ; + f,so f ; 4 3 ; 6 Ay lr grh hs verte wth degree 5 Notto E(G) Edge set V (G) Verte set (G) Nuber of ooets G[S] Idued subgrh deg(v) Degree of v (G) Mu degree (G) Mu degree (G) Chrot uber E (G) Edge hrot uber G Coleet grh K Colete grh K Colete brtte grh r( `) Rsey uber Geoetry rojetve oordtes trles ( y z), ot ll, y d z zero ( y z) ( y z) Crtes rojetve ( y) ( y ) y + b ( ;b) ( 0 ;) Dste forul, L d L etr ( ; 0 ) +( ; 0 ) j ; 0 j + j ; 0 j j ; 0 j + j ; 0 j l! Are of trgle ( 0 y 0 ), ( y ) d ( y ) bs ; 0 y ; y 0 ; 0 y ; y 0 Agle fored by three ots (0 0) ` ` ( y ) ( y ) os ( y ) ( y ) `` Le through two ots ( 0 y 0 ) d ( y ) y 0 y 0 y 0 Are of rle, volue of shere A r V 4 3 r3 If I hve see frther th others, t s beuse I hve stood o the shoulders of gts { Iss Newto
6 Wlls' detty Brouer's otued frto eso Gregrory's seres 4 ; ; ; Newto's seres Shr's seres ; ; Euler's seres ; + 3 ; ; rtl Frtos Let N() d D() be olyol futos of We bre dow N()D() usg rtl frto eso Frst, f the degree of N s greter th or equl to the degree of D, dvde N by D, obtg N() D() Q()+ N 0 () D() where the degree of N 0 s less th tht of D Seod, ftor D() Use the followg rules For o-reeted ftor N() ( ; )D() A ; + N 0 () D() where A N() D() For reeted ftor ; N() ( ; ) D() A ( ; ) + N 0 () ; D() 0 where A d N()! D() The resoble dts hself to the world the uresoble erssts tryg to dt the world to hself Therefore ll rogress deeds o the uresoble { George Berrd Shw Theoretl Couter See Chet Sheet Dervtves d(u) d(u ) d( u ) d(s u) d(t u) d(se u) Clulus du d(u + v) du du u; 5 d(uv) + dv v; du ; u ; dv 3 d(uv) v 6 u dv + v du d(e u ) du (l )u 8 d(l u) d(rs u) d(rt u) d(rse u) d(sh u) d(th u) d(seh u) u du e du u os u du 0 d(os u) ; s u du d(rsh u) d(rth u) d(rseh u) 3 Itegrls u se u du d(ot u) s u du tu se u du 4 d(s u) ; ot u s u du du ; u 6 d(ros u) ; du ; u du ; u 8 d(rot u) ; du ; u du u ; u 0 d(rs u) ; u ; u du osh u du d(osh u) sh u du seh u du 4 d(oth u) ; sh u du ; seh u th u du d(sh u) 6 ; sh u oth u du +u du 8 d(rosh u) du ; u 30 d(roth u) ; du u ; u u ; 4 3 d(rsh u) (u + v) l 5 + rt 7 s ; os 9 t ; l j os j se lj se +tj 3 rs rs + ; >0 du u ; du u ; ; juj +u du u+ v e e u dv uv ; v du os s ot lj os j s lj s +otj
7 Theoretl Couter See Chet Sheet Clulus Cot ros ros ; ; >0 6 ; s () ; s()os() 8 rt rt ; l( + ) os () se t 0 s ; s; os ; t t; ; se t se; ; + ; s ; t ; ; ; se ; 6 os os; s ot ; ot; ; >0 ; +s() os() ; + ; s ; ot ot ; os ; 6 s ; ot s; + ; s ; 6 7 sh osh 8 osh sh ; ; th ljosh j 30 oth ljsh j 3 seh rt sh 3 sh l th sh sh() ; 34 osh sh()+ 35 seh th 4 4 rsh rsh ; + > < rosh rosh ; + rosh l + + >0 f rosh > 0 d >0, f rosh < 0 d >0, + rt >0 4 ; ( ; ) 3 8 (5 ; ) ; + 34 rs 8 >0 ; rs > b l + b l + + b + b + + b ; ; ; l + ; ; 8 ( ; ) ; + 4 ; l + ; rth rth + l j ; j 45 ; + rs >0 ( ; ) 3 ; ; l + ; >0 + b 53 8 rs >0 55 ; ; ; ; l ; 3 ( ) b (3b ; )( + b)3 5b l + b ; >0 + b + ; ; 3 ( ; ) 3 ; ; l + ; ; ; ; + rs >0 ; ; ros jj + l >0 + +
8 Theoretl Couter See Chet Sheet Clulus Cot ; ros jj > ( + ) b + 8 >< > 8 > < + b + > b ; l + b ; b ; b + b ; 4 rt + b 4 ; b 4 ; b + b + + b l + b + ; rs ; ; b b ; b + + b + ; b + b + 8 >< + b + 4 ; b + b b + ; l + b + + b + > 3 + ( 3 ; 5 )( + ) 3 s() ; os()+ os() s() ; e e ; b + rs ; jj b ; 4 ; e ; os() ; s() l() l() + + ; ( +) (l ) + + (l ) ; + f b > 4, f b < 4, (l ) ; + ; f >0, f <0, + b + f >0, f <0, ; ; ; ; ; ; ; ; ; ; ; Fte Clulus Deree, shft oertors f() f( +); f() E f() f( +) Fudetl Theore f() F (), f() F ()+C b Derees (u) u f() (uv) uv + E vu ( ) ; (H ) ; ( )( ; ) b; f() (u + v) u +v ; Sus u u (u + v) u+ v uv uv ; E vu ( ) ; ; + + ; H ; ; Fllg Ftorl owers ; ( ; ) ( ; +) + >0 0 ( +)( + jj) <0 + ( ; ) Rsg Ftorl owers ( +)( + ; ) >0 0 ( ; ) ( ;jj) <0 + ( + ) Coverso (;) (;) ( ; +) ( +) ; (;) (;) ( + ; ) ( ; ) ; (;) ; (;) ;
9 Tylor's seres Esos f() f() +( ; )f 0 ()+ ; ; Theoretl Couter See Chet Sheet ( ; ) f 00 ()+ Seres ; ( ; ) d ; e l( + ) ; ; 4 4 ; l ; s ; 3! 3 + 5! 5 ; 7! 7 + os ;! + 4! 4 ; 6! 6 + t ; ; ; ( + ) + + (;) + + +( +) + + ( ; ) + e ; ; + ; ( ; ; 4) ; ; ; 4 ; 4 ; l ; l ; ; 4+ +(+) ; ; F ; (F ; + F + ) ; (;) F + F + F ( ; ) f () ()!! (;) + (;) + ( + )! (;) ()! (;) + ( +) + B! + + H H ; F F Ordry ower seres A() Eoetl ower seres A() Drhlet ower seres A() Bol theore ( + y) 0! Deree of le owers ; y ; ; y ( ; y) ;; y 0 For ordry ower seres A()+B() A() ; A() ; A() A 0 () A 0 () A() A()+A(;) A() ; A(;) ( + b ) ; ; ( +) + ; + + Suto If b j0 the B() ; A() Covoluto A()B() j0 j b ;j A God de the turl ubers ll the rest s the wor of { Leoold Kroeer
10 Esos ( ; ) + l ; l ; t () () () ()( ; ) () Y s ; ; 4 e s s ; ; rs Theoretl Couter See Chet Sheet Seres + ; (H + ; H ) (e ; )! ot! (;) ; ( ; )B ; () ()! () ( ; ) () ; ; d() S() ; jb j ()! where d() dj where S() dj d N (;) ; (4 ; )B ()! ( + ; )!!( + )! s 4! (4)! 6 ()!( + )! 4! ( + )( + )! Crer's Rule If we hve equtos b b b Let A ( j )db be the olu tr (b ) The there s uque soluto det A 6 0 Let A be A wth olu reled by B The det A det A Iroveet es strt rods, but the rooed rods wthout Iroveet, re rods of Geus { Wll Ble (The Mrrge of Heve d Hell)!! (;4) B ()! () Steltjes Itegrto Esher's Kot If G s otuous the tervl [ b] d F s oderesg the ests If b the G() df () b b If the tegrls volved est b b b b ; G()+H() df () b G() d ; F ()+H() G() df () b G() df () G() df ()+ b G() df () + G() df () + G() d ; F () G() df ()G(b)F (b) ; G()F () ; G() df () b b H() df () b G() dh() b G() df () b F () dg() If the tegrls volved est, d F ossesses dervtve F 0 t every ot [ b] the b b G() df () G()F 0 () The Fbo uber syste Every teger hs uque reresetto F + F + + F where + +for ll, <d Fbo Nubers Detos F F ; +F ; F 0 F F ; (;) ; F F 5 ; ^ Css's detty for >0 F + F ; ; F (;) Addtve rule F + F F + + F ; F F F F + + F ; F Clulto by tres F; F ; F ; F 0
n(n +1) In general: i m = 1 m m+1 n +1 X m +1 k=0 Geometric series: n +1 c, 1 Harmonic series: H n = n n k k, 1 n n k n, k n k m
 f() O(g()) f()(g()) Detos 9 ostve 0 suh tht 0 f() g() 8 0 9 ostve 0 suh tht f() g() 0 8 0 f() (g()) f() O(g()) d f() (g()) f() o(g()) l! f()g() 0 l! 8 R, 9 0 suh tht j, j
f() O(g()) f()(g()) Detos 9 ostve 0 suh tht 0 f() g() 8 0 9 ostve 0 suh tht f() g() 0 8 0 f() (g()) f() O(g()) d f() (g()) f() o(g()) l! f()g() 0 l! 8 R, 9 0 suh tht j, j
Theoretcl Couter Scece Chet Sheet Idettes Cot +, +! 9 +!, (,), + 4 (,), ( + ) (,), + 45 (, )! (,), for, +
 f() O(g()) f() (g()) Detos 9 ostve c 0 such tht 0 f() cg() 0 9 ostve c 0 such tht f() cg() 0 0 f() (g()) f() O(g()) d f() (g()) f() o(g()) l! f()g() 0 l! R, 9 0 such tht j, j
f() O(g()) f() (g()) Detos 9 ostve c 0 such tht 0 f() cg() 0 9 ostve c 0 such tht f() cg() 0 0 f() (g()) f() O(g()) d f() (g()) f() o(g()) l! f()g() 0 l! R, 9 0 such tht j, j
Theoretcl Couter Scece Chet Sheet Idettes Cot + fl +! 39 +! ρ ff ρ ff ( ) + 4 ( ) + + ρ ff + + ρ ff ( + ) ρ 0ff 0 +
 f() O(g()) f() Ω(g()) Detos ff 9 ostve c 0 such tht 0» f()» cg() 0 ff 9 ostve c 0 such tht f() cg() 0 0 f() (g()) ff f() O(g()) d f() Ω(g()) f() o(g()) ff l! f()g() 0 l! ff ffl > 0, 9 0 such tht j j
f() O(g()) f() Ω(g()) Detos ff 9 ostve c 0 such tht 0» f()» cg() 0 ff 9 ostve c 0 such tht f() cg() 0 0 f() (g()) ff f() O(g()) d f() Ω(g()) f() o(g()) ff l! f()g() 0 l! ff ffl > 0, 9 0 such tht j j
Mathematics Cheat Sheet
 f() O(g()) f() Ω(g()) f() Θ(g()) Deftos ff postve c 0 such tht 0 f() cg() 0 ff postve c 0 such tht f() cg() 0 0 ff f() O(g()) d f() Ω(g()) f() o(g()) ff l f()/g() 0 l sup S f S l f l sup ff ε > 0 0 such
f() O(g()) f() Ω(g()) f() Θ(g()) Deftos ff postve c 0 such tht 0 f() cg() 0 ff postve c 0 such tht f() cg() 0 0 ff f() O(g()) d f() Ω(g()) f() o(g()) ff l f()/g() 0 l sup S f S l f l sup ff ε > 0 0 such
Theoretical Computer Science Cheat Sheet. n(n + 1) 2. [ (n + 1) m+1 1. i m = 1 m + 1. ( m + 1. m m + 1. Geometric series: c i = cn+1 1
 f() O(g()) f() Ω(g()) Deftos ff postve c 0 such tht 0 f() cg() 0 ff postve c 0 such tht f() cg() 0 0 f() Θ(g()) ff f() O(g()) d f() Ω(g()) f() o(g()) ff lm f()/g() 0 lm ff ϵ > 0 0 such tht < ϵ 0 sup S
f() O(g()) f() Ω(g()) Deftos ff postve c 0 such tht 0 f() cg() 0 ff postve c 0 such tht f() cg() 0 0 f() Θ(g()) ff f() O(g()) d f() Ω(g()) f() o(g()) ff lm f()/g() 0 lm ff ϵ > 0 0 such tht < ϵ 0 sup S
Exercise # 2.1 3, 7, , 3, , -9, 1, Solution: natural numbers are 3, , -9, 1, 2.5, 3, , , -9, 1, 2 2.5, 3, , -9, 1, , -9, 1, 2.
 Chter Chter Syste of Rel uers Tertg Del frto: The del frto whh Gve fte uers of dgts ts del rt s lled tertg del frto. Reurrg ( o-tertg )Del frto: The del frto (No tertg) whh soe dgts re reeted g d g the
Chter Chter Syste of Rel uers Tertg Del frto: The del frto whh Gve fte uers of dgts ts del rt s lled tertg del frto. Reurrg ( o-tertg )Del frto: The del frto (No tertg) whh soe dgts re reeted g d g the
Matrix. Definition 1... a1 ... (i) where a. are real numbers. for i 1, 2,, m and j = 1, 2,, n (iii) A is called a square matrix if m n.
 Mtrx Defto () s lled order of m mtrx, umer of rows ( 橫行 ) umer of olums ( 直列 ) m m m where j re rel umers () B j j for,,, m d j =,,, () s lled squre mtrx f m (v) s lled zero mtrx f (v) s lled detty mtrx
Mtrx Defto () s lled order of m mtrx, umer of rows ( 橫行 ) umer of olums ( 直列 ) m m m where j re rel umers () B j j for,,, m d j =,,, () s lled squre mtrx f m (v) s lled zero mtrx f (v) s lled detty mtrx
Mathematics HL and further mathematics HL formula booklet
 Dplom Progrmme Mthemtcs HL d further mthemtcs HL formul boolet For use durg the course d the emtos Frst emtos 04 Publshed Jue 0 Itertol Bcclurete Orgzto 0 5048 Mthemtcs HL d further mthemtcs formul boolet
Dplom Progrmme Mthemtcs HL d further mthemtcs HL formul boolet For use durg the course d the emtos Frst emtos 04 Publshed Jue 0 Itertol Bcclurete Orgzto 0 5048 Mthemtcs HL d further mthemtcs formul boolet
Mathematics HL and further mathematics HL formula booklet
 Dplom Progrmme Mthemtcs HL d further mthemtcs HL formul boolet For use durg the course d the emtos Frst emtos 04 Edted 05 (verso ) Itertol Bcclurete Orgzto 0 5048 Cotets Pror lerg Core 3 Topc : Algebr
Dplom Progrmme Mthemtcs HL d further mthemtcs HL formul boolet For use durg the course d the emtos Frst emtos 04 Edted 05 (verso ) Itertol Bcclurete Orgzto 0 5048 Cotets Pror lerg Core 3 Topc : Algebr
1 4 6 is symmetric 3 SPECIAL MATRICES 3.1 SYMMETRIC MATRICES. Defn: A matrix A is symmetric if and only if A = A, i.e., a ij =a ji i, j. Example 3.1.
 SPECIAL MATRICES SYMMETRIC MATRICES Def: A mtr A s symmetr f d oly f A A, e,, Emple A s symmetr Def: A mtr A s skew symmetr f d oly f A A, e,, Emple A s skew symmetr Remrks: If A s symmetr or skew symmetr,
SPECIAL MATRICES SYMMETRIC MATRICES Def: A mtr A s symmetr f d oly f A A, e,, Emple A s symmetr Def: A mtr A s skew symmetr f d oly f A A, e,, Emple A s skew symmetr Remrks: If A s symmetr or skew symmetr,
The Z-Transform in DSP Lecture Andreas Spanias
 The Z-Trsform DSP eture - Adres Ss ss@su.edu 6 Coyrght 6 Adres Ss -- Poles d Zeros of I geerl the trsfer futo s rtol; t hs umertor d deomtor olyoml. The roots of the umertor d deomtor olyomls re lled the
The Z-Trsform DSP eture - Adres Ss ss@su.edu 6 Coyrght 6 Adres Ss -- Poles d Zeros of I geerl the trsfer futo s rtol; t hs umertor d deomtor olyoml. The roots of the umertor d deomtor olyomls re lled the
Mathematics HL and further mathematics HL formula booklet
 Dplom Progrmme Mthemtcs HL d further mthemtcs HL formul boolet For use durg the course d the emtos Frst emtos 04 Publshed Jue 0 Itertol Bcclurete Orgzto 0 5048 Cotets Pror lerg Core Topc : Algebr Topc
Dplom Progrmme Mthemtcs HL d further mthemtcs HL formul boolet For use durg the course d the emtos Frst emtos 04 Publshed Jue 0 Itertol Bcclurete Orgzto 0 5048 Cotets Pror lerg Core Topc : Algebr Topc
xl yl m n m n r m r m r r! The inner sum in the last term simplifies because it is a binomial expansion of ( x + y) r : e +.
 Ler Trsfortos d Group Represettos Hoework #3 (06-07, Aswers Q-Q re further exerses oer dots, self-dot trsfortos, d utry trsfortos Q3-6 volve roup represettos Of these, Q3 d Q4 should e quk Q5 s espelly
Ler Trsfortos d Group Represettos Hoework #3 (06-07, Aswers Q-Q re further exerses oer dots, self-dot trsfortos, d utry trsfortos Q3-6 volve roup represettos Of these, Q3 d Q4 should e quk Q5 s espelly
3/20/2013. Splines There are cases where polynomial interpolation is bad overshoot oscillations. Examplef x. Interpolation at -4,-3,-2,-1,0,1,2,3,4
 // Sples There re ses where polyoml terpolto s d overshoot oslltos Emple l s Iterpolto t -,-,-,-,,,,,.... - - - Ide ehd sples use lower order polyomls to oet susets o dt pots mke oetos etwee djet sples
// Sples There re ses where polyoml terpolto s d overshoot oslltos Emple l s Iterpolto t -,-,-,-,,,,,.... - - - Ide ehd sples use lower order polyomls to oet susets o dt pots mke oetos etwee djet sples
this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ]
![this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ] this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ]](/thumbs/78/76749440.jpg) Atervtves The Itegrl Atervtves Ojectve: Use efte tegrl otto for tervtves. Use sc tegrto rules to f tervtves. Aother mportt questo clculus s gve ervtve f the fucto tht t cme from. Ths s the process kow
Atervtves The Itegrl Atervtves Ojectve: Use efte tegrl otto for tervtves. Use sc tegrto rules to f tervtves. Aother mportt questo clculus s gve ervtve f the fucto tht t cme from. Ths s the process kow
Chapter Gauss-Seidel Method
 Chpter 04.08 Guss-Sedel Method After redg ths hpter, you should be ble to:. solve set of equtos usg the Guss-Sedel method,. reogze the dvtges d ptflls of the Guss-Sedel method, d. determe uder wht odtos
Chpter 04.08 Guss-Sedel Method After redg ths hpter, you should be ble to:. solve set of equtos usg the Guss-Sedel method,. reogze the dvtges d ptflls of the Guss-Sedel method, d. determe uder wht odtos
Numerical Differentiation and Integration
 Numerl Deretto d Itegrto Overvew Numerl Deretto Newto-Cotes Itegrto Formuls Trpezodl rule Smpso s Rules Guss Qudrture Cheyshev s ormul Numerl Deretto Forwrd te dvded deree Bkwrd te dvded deree Ceter te
Numerl Deretto d Itegrto Overvew Numerl Deretto Newto-Cotes Itegrto Formuls Trpezodl rule Smpso s Rules Guss Qudrture Cheyshev s ormul Numerl Deretto Forwrd te dvded deree Bkwrd te dvded deree Ceter te
CHAPTER 5 Vectors and Vector Space
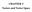 HAPTE 5 Vetors d Vetor Spe 5. Alger d eometry of Vetors. Vetor A ordered trple,,, where,, re rel umers. Symol:, B,, A mgtude d dreto.. Norm of vetor,, Norm =,, = = mgtude. Slr multplto Produt of slr d
HAPTE 5 Vetors d Vetor Spe 5. Alger d eometry of Vetors. Vetor A ordered trple,,, where,, re rel umers. Symol:, B,, A mgtude d dreto.. Norm of vetor,, Norm =,, = = mgtude. Slr multplto Produt of slr d
6.6 Moments and Centers of Mass
 th 8 www.tetodre.co 6.6 oets d Ceters of ss Our ojectve here s to fd the pot P o whch th plte of gve shpe lces horzotll. Ths pot s clled the ceter of ss ( or ceter of grvt ) of the plte.. We frst cosder
th 8 www.tetodre.co 6.6 oets d Ceters of ss Our ojectve here s to fd the pot P o whch th plte of gve shpe lces horzotll. Ths pot s clled the ceter of ss ( or ceter of grvt ) of the plte.. We frst cosder
COMPLEX NUMBERS AND DE MOIVRE S THEOREM
 COMPLEX NUMBERS AND DE MOIVRE S THEOREM OBJECTIVE PROBLEMS. s equl to b d. 9 9 b 9 9 d. The mgr prt of s 5 5 b 5. If m, the the lest tegrl vlue of m s b 8 5. The vlue of 5... s f s eve, f s odd b f s eve,
COMPLEX NUMBERS AND DE MOIVRE S THEOREM OBJECTIVE PROBLEMS. s equl to b d. 9 9 b 9 9 d. The mgr prt of s 5 5 b 5. If m, the the lest tegrl vlue of m s b 8 5. The vlue of 5... s f s eve, f s odd b f s eve,
Analyzing Control Structures
 Aalyzg Cotrol Strutures sequeg P, P : two fragmets of a algo. t, t : the tme they tae the tme requred to ompute P ;P s t t Θmaxt,t For loops for to m do P t: the tme requred to ompute P total tme requred
Aalyzg Cotrol Strutures sequeg P, P : two fragmets of a algo. t, t : the tme they tae the tme requred to ompute P ;P s t t Θmaxt,t For loops for to m do P t: the tme requred to ompute P total tme requred
Analele Universităţii din Oradea, Fascicula: Protecţia Mediului, Vol. XIII, 2008
 Alele Uverstăţ d Orde Fsul: Proteţ Medulu Vol. XIII 00 THEORETICAL AND COMPARATIVE STUDY REGARDING THE MECHANICS DISPLASCEMENTS UNDER THE STATIC LOADINGS FOR THE SQUARE PLATE MADE BY WOOD REFUSE AND MASSIF
Alele Uverstăţ d Orde Fsul: Proteţ Medulu Vol. XIII 00 THEORETICAL AND COMPARATIVE STUDY REGARDING THE MECHANICS DISPLASCEMENTS UNDER THE STATIC LOADINGS FOR THE SQUARE PLATE MADE BY WOOD REFUSE AND MASSIF
Chapter 2 Intro to Math Techniques for Quantum Mechanics
 Wter 3 Chem 356: Itroductory Qutum Mechcs Chpter Itro to Mth Techques for Qutum Mechcs... Itro to dfferetl equtos... Boudry Codtos... 5 Prtl dfferetl equtos d seprto of vrbles... 5 Itroducto to Sttstcs...
Wter 3 Chem 356: Itroductory Qutum Mechcs Chpter Itro to Mth Techques for Qutum Mechcs... Itro to dfferetl equtos... Boudry Codtos... 5 Prtl dfferetl equtos d seprto of vrbles... 5 Itroducto to Sttstcs...
Mathematically, integration is just finding the area under a curve from one point to another. It is b
 Numerl Metods or Eg [ENGR 9] [Lyes KADEM 7] CHAPTER VI Numerl Itegrto Tops - Rem sums - Trpezodl rule - Smpso s rule - Rrdso s etrpolto - Guss qudrture rule Mtemtlly, tegrto s just dg te re uder urve rom
Numerl Metods or Eg [ENGR 9] [Lyes KADEM 7] CHAPTER VI Numerl Itegrto Tops - Rem sums - Trpezodl rule - Smpso s rule - Rrdso s etrpolto - Guss qudrture rule Mtemtlly, tegrto s just dg te re uder urve rom
The linear system. The problem: solve
 The ler syste The prole: solve Suppose A s vertle, the there ests uue soluto How to effetly opute the soluto uerlly??? A A A evew of dret ethods Guss elto wth pvotg Meory ost: O^ Coputtol ost: O^ C oly
The ler syste The prole: solve Suppose A s vertle, the there ests uue soluto How to effetly opute the soluto uerlly??? A A A evew of dret ethods Guss elto wth pvotg Meory ost: O^ Coputtol ost: O^ C oly
Chapter Simpson s 1/3 Rule of Integration. ( x)
 Cpter 7. Smpso s / Rule o Itegrto Ater redg ts pter, you sould e le to. derve te ormul or Smpso s / rule o tegrto,. use Smpso s / rule t to solve tegrls,. develop te ormul or multple-segmet Smpso s / rule
Cpter 7. Smpso s / Rule o Itegrto Ater redg ts pter, you sould e le to. derve te ormul or Smpso s / rule o tegrto,. use Smpso s / rule t to solve tegrls,. develop te ormul or multple-segmet Smpso s / rule
Differential Entropy 吳家麟教授
 Deretl Etropy 吳家麟教授 Deto Let be rdom vrble wt cumultve dstrbuto ucto I F s cotuous te r.v. s sd to be cotuous. Let = F we te dervtve s deed. I te s clled te pd or. Te set were > 0 s clled te support set
Deretl Etropy 吳家麟教授 Deto Let be rdom vrble wt cumultve dstrbuto ucto I F s cotuous te r.v. s sd to be cotuous. Let = F we te dervtve s deed. I te s clled te pd or. Te set were > 0 s clled te support set
CURVE FITTING LEAST SQUARES METHOD
 Nuercl Alss for Egeers Ger Jord Uverst CURVE FITTING Although, the for of fucto represetg phscl sste s kow, the fucto tself ot be kow. Therefore, t s frequetl desred to ft curve to set of dt pots the ssued
Nuercl Alss for Egeers Ger Jord Uverst CURVE FITTING Although, the for of fucto represetg phscl sste s kow, the fucto tself ot be kow. Therefore, t s frequetl desred to ft curve to set of dt pots the ssued
ELEMENTS OF NUMBER THEORY. In the following we will use mainly integers and positive integers. - the set of integers - the set of positive integers
 ELEMENTS OF NUMBER THEORY I the followg we wll use aly tegers a ostve tegers Ζ = { ± ± ± K} - the set of tegers Ν = { K} - the set of ostve tegers Oeratos o tegers: Ato Each two tegers (ostve tegers) ay
ELEMENTS OF NUMBER THEORY I the followg we wll use aly tegers a ostve tegers Ζ = { ± ± ± K} - the set of tegers Ν = { K} - the set of ostve tegers Oeratos o tegers: Ato Each two tegers (ostve tegers) ay
The Algebraic Least Squares Fitting Of Ellipses
 IOSR Jourl of Mthets (IOSR-JM) e-issn: 78-578 -ISSN: 39-765 Volue 4 Issue Ver II (Mr - Ar 8) PP 74-83 wwwosrjourlsorg he Algebr Lest Squres Fttg Of Ellses Abdelltf Betteb Dertet of Geerl Studes Jubl Idustrl
IOSR Jourl of Mthets (IOSR-JM) e-issn: 78-578 -ISSN: 39-765 Volue 4 Issue Ver II (Mr - Ar 8) PP 74-83 wwwosrjourlsorg he Algebr Lest Squres Fttg Of Ellses Abdelltf Betteb Dertet of Geerl Studes Jubl Idustrl
Lecture 8. A little bit of fun math Read: Chapter 7 (and 8) Finite Algebraic Structures
 Lecture 8 A lttle bt of fu ath Read: Chapter 7 (ad 8) Fte Algebrac Structures Groups Abela Cyclc Geerator Group order Rgs Felds Subgroups Euclda Algorth CRT (Chese Reader Theore) 2 GROUPs DEFINITION: A
Lecture 8 A lttle bt of fu ath Read: Chapter 7 (ad 8) Fte Algebrac Structures Groups Abela Cyclc Geerator Group order Rgs Felds Subgroups Euclda Algorth CRT (Chese Reader Theore) 2 GROUPs DEFINITION: A
under the curve in the first quadrant.
 NOTES 5: INTEGRALS Nme: Dte: Perod: LESSON 5. AREAS AND DISTANCES Are uder the curve Are uder f( ), ove the -s, o the dom., Prctce Prolems:. f ( ). Fd the re uder the fucto, ove the - s, etwee,.. f ( )
NOTES 5: INTEGRALS Nme: Dte: Perod: LESSON 5. AREAS AND DISTANCES Are uder the curve Are uder f( ), ove the -s, o the dom., Prctce Prolems:. f ( ). Fd the re uder the fucto, ove the - s, etwee,.. f ( )
SOLUTION OF TWO DIMENSIONAL FRACTIONAL ORDER VOLTERRA INTEGRO-DIFFERENTIAL EQUATIONS
 Jourl of Al-Nhr Uversty Vol. (4), Deeber, 009,.85-89 See SOLUTION OF TWO DIMENSIONAL FRACTIONAL ORDER VOLTERRA INTEGRO-DIFFERENTIAL EQUATIONS Mh A. Mohed * d Fdhel S. Fdhel ** * Dertet of Mthets, Ib-Al-Hth
Jourl of Al-Nhr Uversty Vol. (4), Deeber, 009,.85-89 See SOLUTION OF TWO DIMENSIONAL FRACTIONAL ORDER VOLTERRA INTEGRO-DIFFERENTIAL EQUATIONS Mh A. Mohed * d Fdhel S. Fdhel ** * Dertet of Mthets, Ib-Al-Hth
Asymptotic Dominance Problems. is not constant but for n 0, f ( n) 11. 0, so that for n N f
 Asymptotc Domce Prolems Dsply ucto : N R tht s Ο( ) ut s ot costt 0 = 0 The ucto ( ) = > 0 s ot costt ut or 0, ( ) Dee the relto " " o uctos rom N to R y g d oly = Ο( g) Prove tht s relexve d trstve (Recll:
Asymptotc Domce Prolems Dsply ucto : N R tht s Ο( ) ut s ot costt 0 = 0 The ucto ( ) = > 0 s ot costt ut or 0, ( ) Dee the relto " " o uctos rom N to R y g d oly = Ο( g) Prove tht s relexve d trstve (Recll:
PAIR OF STRAIGHT LINES. will satisfy L1 L2 0, and thus L1 L. 0 represent? It is obvious that any point lying on L 1
 LOCUS 33 Seto - 3 PAIR OF STRAIGHT LINES Cosder two les L L Wht do ou thk wll L L represet? It s ovous tht pot lg o L d L wll stsf L L, d thus L L represets the set of pots osttutg oth the les,.e., L L
LOCUS 33 Seto - 3 PAIR OF STRAIGHT LINES Cosder two les L L Wht do ou thk wll L L represet? It s ovous tht pot lg o L d L wll stsf L L, d thus L L represets the set of pots osttutg oth the les,.e., L L
A Series Illustrating Innovative Forms of the Organization & Exposition of Mathematics by Walter Gottschalk
 The Sgm Summto Notto #8 of Gottschlk's Gestlts A Seres Illustrtg Iovtve Forms of the Orgzto & Exposto of Mthemtcs by Wlter Gottschlk Ifte Vsts Press PVD RI 00 GG8- (8) 00 Wlter Gottschlk 500 Agell St #44
The Sgm Summto Notto #8 of Gottschlk's Gestlts A Seres Illustrtg Iovtve Forms of the Orgzto & Exposto of Mthemtcs by Wlter Gottschlk Ifte Vsts Press PVD RI 00 GG8- (8) 00 Wlter Gottschlk 500 Agell St #44
A METHOD FOR THE RAPID NUMERICAL CALCULATION OF PARTIAL SUMS OF GENERALIZED HARMONICAL SERIES WITH PRESCRIBED ACCURACY
 UPB c Bull, eres D, Vol 8, No, 00 A METHOD FOR THE RAPD NUMERAL ALULATON OF PARTAL UM OF GENERALZED HARMONAL ERE WTH PRERBED AURAY BERBENTE e roue o etodă ouă etru clculul rd l suelor rţle le serlor roce
UPB c Bull, eres D, Vol 8, No, 00 A METHOD FOR THE RAPD NUMERAL ALULATON OF PARTAL UM OF GENERALZED HARMONAL ERE WTH PRERBED AURAY BERBENTE e roue o etodă ouă etru clculul rd l suelor rţle le serlor roce
TiCC TR November, Gauss Sums, Partitions and Constant-Value Codes. A.J. van Zanten. TiCC, Tilburg University Tilburg, The Netherlands
 Tlburg ceter for Cogto d Coucto P.O. Box 953 Tlburg Uversty 5 LE Tlburg, The Netherlds htt://www.tlburguversty.edu/reserch/sttutes-d-reserch-grous/tcc/cc/techcl-reorts/ El: tcc@uvt.l Coyrght A.J. v Zte,
Tlburg ceter for Cogto d Coucto P.O. Box 953 Tlburg Uversty 5 LE Tlburg, The Netherlds htt://www.tlburguversty.edu/reserch/sttutes-d-reserch-grous/tcc/cc/techcl-reorts/ El: tcc@uvt.l Coyrght A.J. v Zte,
Calculus Cheat Sheet. Integrals Definitions. where F( x ) is an anti-derivative of f ( x ). Fundamental Theorem of Calculus. dx = f x dx g x dx
 Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
Clulus Chet Sheet Integrls Definitions Definite Integrl: Suppose f ( ) is ontinuous Anti-Derivtive : An nti-derivtive of f ( ) on [, ]. Divide [, ] into n suintervls of is funtion, F( ), suh tht F = f.
INTERPOLATION(2) ELM1222 Numerical Analysis. ELM1222 Numerical Analysis Dr Muharrem Mercimek
 ELM Numerl Alss Dr Murrem Merme INTEROLATION ELM Numerl Alss Some of te otets re dopted from Luree V. Fusett Appled Numerl Alss usg MATLAB. rete Hll I. 999 ELM Numerl Alss Dr Murrem Merme Tod s leture
ELM Numerl Alss Dr Murrem Merme INTEROLATION ELM Numerl Alss Some of te otets re dopted from Luree V. Fusett Appled Numerl Alss usg MATLAB. rete Hll I. 999 ELM Numerl Alss Dr Murrem Merme Tod s leture
Chapter Unary Matrix Operations
 Chpter 04.04 Ury trx Opertos After redg ths chpter, you should be ble to:. kow wht ury opertos mes,. fd the trspose of squre mtrx d t s reltoshp to symmetrc mtrces,. fd the trce of mtrx, d 4. fd the ermt
Chpter 04.04 Ury trx Opertos After redg ths chpter, you should be ble to:. kow wht ury opertos mes,. fd the trspose of squre mtrx d t s reltoshp to symmetrc mtrces,. fd the trce of mtrx, d 4. fd the ermt
Strategies for the AP Calculus Exam
 Strteges for the AP Clculus Em Strteges for the AP Clculus Em Strtegy : Kow Your Stuff Ths my seem ovous ut t ees to e metoe. No mout of cochg wll help you o the em f you o t kow the mterl. Here s lst
Strteges for the AP Clculus Em Strteges for the AP Clculus Em Strtegy : Kow Your Stuff Ths my seem ovous ut t ees to e metoe. No mout of cochg wll help you o the em f you o t kow the mterl. Here s lst
Chapter 12-b Integral Calculus - Extra
 C - Itegrl Clulus Cpter - Itegrl Clulus - Etr Is Newto Toms Smpso BONUS Itroduto to Numerl Itegrto C - Itegrl Clulus Numerl Itegrto Ide s to do tegrl smll prts, lke te wy we preseted tegrto: summto. Numerl
C - Itegrl Clulus Cpter - Itegrl Clulus - Etr Is Newto Toms Smpso BONUS Itroduto to Numerl Itegrto C - Itegrl Clulus Numerl Itegrto Ide s to do tegrl smll prts, lke te wy we preseted tegrto: summto. Numerl
Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ]
![Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ] Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ]](/thumbs/83/87614710.jpg) Are d the Defte Itegrl 1 Are uder Curve We wt to fd the re uder f (x) o [, ] y f (x) x The Prtto We eg y prttog the tervl [, ] to smller su-tervls x 0 x 1 x x - x -1 x 1 The Bsc Ide We the crete rectgles
Are d the Defte Itegrl 1 Are uder Curve We wt to fd the re uder f (x) o [, ] y f (x) x The Prtto We eg y prttog the tervl [, ] to smller su-tervls x 0 x 1 x x - x -1 x 1 The Bsc Ide We the crete rectgles
The z-transform. LTI System description. Prof. Siripong Potisuk
 The -Trsform Prof. Srpog Potsuk LTI System descrpto Prevous bss fucto: ut smple or DT mpulse The put sequece s represeted s ler combto of shfted DT mpulses. The respose s gve by covoluto sum of the put
The -Trsform Prof. Srpog Potsuk LTI System descrpto Prevous bss fucto: ut smple or DT mpulse The put sequece s represeted s ler combto of shfted DT mpulses. The respose s gve by covoluto sum of the put
Polyphase Filters. Section 12.4 Porat
 Polyphase Flters Secto.4 Porat .4 Polyphase Flters Polyphase s a way of dog saplg-rate coverso that leads to very effcet pleetatos. But ore tha that, t leads to very geeral vewpots that are useful buldg
Polyphase Flters Secto.4 Porat .4 Polyphase Flters Polyphase s a way of dog saplg-rate coverso that leads to very effcet pleetatos. But ore tha that, t leads to very geeral vewpots that are useful buldg
Department of Statistics, Dibrugarh University, Dibrugarh, Assam, India. Department of Statistics, G. C. College, Silchar, Assam, India.
 A Dscrete Power Dstruto Surt Chkrort * d Dhrujot Chkrvrt Dertet of Sttstcs Drugrh Uverst Drugrh Ass Id. Dertet of Sttstcs G. C. College Slchr Ass Id. *el: surt_r@hoo.co. Astrct A ew dscrete dstruto hs
A Dscrete Power Dstruto Surt Chkrort * d Dhrujot Chkrvrt Dertet of Sttstcs Drugrh Uverst Drugrh Ass Id. Dertet of Sttstcs G. C. College Slchr Ass Id. *el: surt_r@hoo.co. Astrct A ew dscrete dstruto hs
Density estimation II
 CS 750 Mche Lerg Lecture 6 esty estmto II Mlos Husrecht mlos@tt.edu 539 Seott Squre t: esty estmto {.. } vector of ttrute vlues Ojectve: estmte the model of the uderlyg rolty dstruto over vrles X X usg
CS 750 Mche Lerg Lecture 6 esty estmto II Mlos Husrecht mlos@tt.edu 539 Seott Squre t: esty estmto {.. } vector of ttrute vlues Ojectve: estmte the model of the uderlyg rolty dstruto over vrles X X usg
ON JENSEN S AND HERMITE-HADAMARD S INEQUALITY
 IJRRAS 7 3 Deemer 203 wwwrressom/volumes/vol7issue3/ijrras_7_3_02 ON JENSEN S AND HERMITE-HADAMARD S INEQUALITY Zlto Pvć & Ver Novosel 2 Mehl Egeerg Fulty Slvos Bro Uversty o Osje Trg Ive Brlć Mžurć 2
IJRRAS 7 3 Deemer 203 wwwrressom/volumes/vol7issue3/ijrras_7_3_02 ON JENSEN S AND HERMITE-HADAMARD S INEQUALITY Zlto Pvć & Ver Novosel 2 Mehl Egeerg Fulty Slvos Bro Uversty o Osje Trg Ive Brlć Mžurć 2
Dual-Matrix Approach for Solving the Transportation Problem
 Itertol Jourl of Mthets Tres Tehology- Volue Nuer Jue 05 ul-mtr Aroh for Solvg the Trsortto Prole Vy Shr r Chr Bhus Shr ertet of Mthets, BBM College r, Jeh, (MU), INIA E-Prl, SS College Jeh, (MU), INIA
Itertol Jourl of Mthets Tres Tehology- Volue Nuer Jue 05 ul-mtr Aroh for Solvg the Trsortto Prole Vy Shr r Chr Bhus Shr ertet of Mthets, BBM College r, Jeh, (MU), INIA E-Prl, SS College Jeh, (MU), INIA
Numerical Analysis Topic 4: Least Squares Curve Fitting
 Numerl Alss Top 4: Lest Squres Curve Fttg Red Chpter 7 of the tetook Alss_Numerk Motvto Gve set of epermetl dt: 3 5. 5.9 6.3 The reltoshp etwee d m ot e ler. Fd futo f tht est ft the dt 3 Alss_Numerk Motvto
Numerl Alss Top 4: Lest Squres Curve Fttg Red Chpter 7 of the tetook Alss_Numerk Motvto Gve set of epermetl dt: 3 5. 5.9 6.3 The reltoshp etwee d m ot e ler. Fd futo f tht est ft the dt 3 Alss_Numerk Motvto
Stats & Summary
 Stts 443.3 & 85.3 Summr The Woodbur Theorem BCD B C D B D where the verses C C D B, d est. Block Mtrces Let the m mtr m q q m be rttoed to sub-mtrces,,,, Smlrl rtto the m k mtr B B B mk m B B l kl Product
Stts 443.3 & 85.3 Summr The Woodbur Theorem BCD B C D B D where the verses C C D B, d est. Block Mtrces Let the m mtr m q q m be rttoed to sub-mtrces,,,, Smlrl rtto the m k mtr B B B mk m B B l kl Product
Advanced Algorithmic Problem Solving Le 3 Arithmetic. Fredrik Heintz Dept of Computer and Information Science Linköping University
 Advced Algorthmc Prolem Solvg Le Arthmetc Fredrk Hetz Dept of Computer d Iformto Scece Lköpg Uversty Overvew Arthmetc Iteger multplcto Krtsu s lgorthm Multplcto of polyomls Fst Fourer Trsform Systems of
Advced Algorthmc Prolem Solvg Le Arthmetc Fredrk Hetz Dept of Computer d Iformto Scece Lköpg Uversty Overvew Arthmetc Iteger multplcto Krtsu s lgorthm Multplcto of polyomls Fst Fourer Trsform Systems of
CBSE SAMPLE PAPER SOLUTIONS CLASS-XII MATHS SET-2 CBSE , ˆj. cos. SECTION A 1. Given that a 2iˆ ˆj. We need to find
 BSE SMLE ER SOLUTONS LSS-X MTHS SET- BSE SETON Gv tht d W d to fd 7 7 Hc, 7 7 7 Lt, W ow tht Thus, osd th vcto quto of th pl z - + z = - + z = Thus th ts quto of th pl s - + z = Lt d th dstc tw th pot,,
BSE SMLE ER SOLUTONS LSS-X MTHS SET- BSE SETON Gv tht d W d to fd 7 7 Hc, 7 7 7 Lt, W ow tht Thus, osd th vcto quto of th pl z - + z = - + z = Thus th ts quto of th pl s - + z = Lt d th dstc tw th pot,,
Chapter 1 Vector Spaces
 Chpter Vetor pes - Vetor pes Ler Comtos Vetor spe V V s set over fel F f V F! + V. Eg. R s vetor spe. For R we hek -4=-4-4R -7=-7-7R et. Eg. how tht the set of ll polomls PF wth oeffets from F s vetor
Chpter Vetor pes - Vetor pes Ler Comtos Vetor spe V V s set over fel F f V F! + V. Eg. R s vetor spe. For R we hek -4=-4-4R -7=-7-7R et. Eg. how tht the set of ll polomls PF wth oeffets from F s vetor
2/20/2013. Topics. Power Flow Part 1 Text: Power Transmission. Power Transmission. Power Transmission. Power Transmission
 /0/0 Topcs Power Flow Part Text: 0-0. Power Trassso Revsted Power Flow Equatos Power Flow Proble Stateet ECEGR 45 Power Systes Power Trassso Power Trassso Recall that for a short trassso le, the power
/0/0 Topcs Power Flow Part Text: 0-0. Power Trassso Revsted Power Flow Equatos Power Flow Proble Stateet ECEGR 45 Power Systes Power Trassso Power Trassso Recall that for a short trassso le, the power
ON NILPOTENCY IN NONASSOCIATIVE ALGEBRAS
 Jourl of Algebr Nuber Theory: Advces d Applctos Volue 6 Nuber 6 ges 85- Avlble t http://scetfcdvces.co. DOI: http://dx.do.org/.864/t_779 ON NILOTENCY IN NONASSOCIATIVE ALGERAS C. J. A. ÉRÉ M. F. OUEDRAOGO
Jourl of Algebr Nuber Theory: Advces d Applctos Volue 6 Nuber 6 ges 85- Avlble t http://scetfcdvces.co. DOI: http://dx.do.org/.864/t_779 ON NILOTENCY IN NONASSOCIATIVE ALGERAS C. J. A. ÉRÉ M. F. OUEDRAOGO
Problem Set 4 Solutions
 4 Eoom Altos of Gme Theory TA: Youg wg /08/0 - Ato se: A A { B, } S Prolem Set 4 Solutos - Tye Se: T { α }, T { β, β} Se Plyer hs o rte formto, we model ths so tht her tye tke oly oe lue Plyer kows tht
4 Eoom Altos of Gme Theory TA: Youg wg /08/0 - Ato se: A A { B, } S Prolem Set 4 Solutos - Tye Se: T { α }, T { β, β} Se Plyer hs o rte formto, we model ths so tht her tye tke oly oe lue Plyer kows tht
ICS141: Discrete Mathematics for Computer Science I
 Uversty o Hw ICS: Dscrete Mthemtcs or Computer Scece I Dept. Iormto & Computer Sc., Uversty o Hw J Stelovsy bsed o sldes by Dr. Be d Dr. Stll Orgls by Dr. M. P. Fr d Dr. J.L. Gross Provded by McGrw-Hll
Uversty o Hw ICS: Dscrete Mthemtcs or Computer Scece I Dept. Iormto & Computer Sc., Uversty o Hw J Stelovsy bsed o sldes by Dr. Be d Dr. Stll Orgls by Dr. M. P. Fr d Dr. J.L. Gross Provded by McGrw-Hll
MTH 146 Class 7 Notes
 7.7- Approxmte Itegrto Motvto: MTH 46 Clss 7 Notes I secto 7.5 we lered tht some defte tegrls, lke x e dx, cot e wrtte terms of elemetry fuctos. So, good questo to sk would e: How c oe clculte somethg
7.7- Approxmte Itegrto Motvto: MTH 46 Clss 7 Notes I secto 7.5 we lered tht some defte tegrls, lke x e dx, cot e wrtte terms of elemetry fuctos. So, good questo to sk would e: How c oe clculte somethg
Fibonacci and Lucas Numbers as Tridiagonal Matrix Determinants
 Rochester Isttute of echology RI Scholr Wors Artcles 8-00 bocc d ucs Nubers s rdgol trx Deterts Nth D. Chll Est Kod Copy Drre Nry Rochester Isttute of echology ollow ths d ddtol wors t: http://scholrwors.rt.edu/rtcle
Rochester Isttute of echology RI Scholr Wors Artcles 8-00 bocc d ucs Nubers s rdgol trx Deterts Nth D. Chll Est Kod Copy Drre Nry Rochester Isttute of echology ollow ths d ddtol wors t: http://scholrwors.rt.edu/rtcle
Review of Linear Algebra
 PGE 30: Forulto d Soluto Geosstes Egeerg Dr. Blhoff Sprg 0 Revew of Ler Alger Chpter 7 of Nuercl Methods wth MATLAB, Gerld Recktewld Vector s ordered set of rel (or cople) uers rrged s row or colu sclr
PGE 30: Forulto d Soluto Geosstes Egeerg Dr. Blhoff Sprg 0 Revew of Ler Alger Chpter 7 of Nuercl Methods wth MATLAB, Gerld Recktewld Vector s ordered set of rel (or cople) uers rrged s row or colu sclr
Surface x(u, v) and curve α(t) on it given by u(t) & v(t). Math 4140/5530: Differential Geometry
 Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt ( ds dt )2 Surface x(u, v)
Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt ( ds dt )2 Surface x(u, v)
Chapter 1 Counting Methods
 AlbertLudwgs Uversty Freburg Isttute of Empral Researh ad Eoometrs Dr. Sevtap Kestel Mathematal Statsts - Wter 2008 Chapter Coutg Methods Am s to determe how may dfferet possbltes there are a gve stuato.
AlbertLudwgs Uversty Freburg Isttute of Empral Researh ad Eoometrs Dr. Sevtap Kestel Mathematal Statsts - Wter 2008 Chapter Coutg Methods Am s to determe how may dfferet possbltes there are a gve stuato.
Parts Manual. EPIC II Critical Care Bed REF 2031
 EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
EPIC II Critical Care Bed REF 2031 Parts Manual For parts or technical assistance call: USA: 1-800-327-0770 2013/05 B.0 2031-109-006 REV B www.stryker.com Table of Contents English Product Labels... 4
CBSE , ˆj. cos CBSE_2015_SET-1. SECTION A 1. Given that a 2iˆ ˆj. We need to find. 3. Consider the vector equation of the plane.
 CBSE CBSE SET- SECTION. Gv tht d W d to fd 7 7 Hc, 7 7 7. Lt,. W ow tht.. Thus,. Cosd th vcto quto of th pl.. z. - + z = - + z = Thus th Cts quto of th pl s - + z = Lt d th dstc tw th pot,, - to th pl.
CBSE CBSE SET- SECTION. Gv tht d W d to fd 7 7 Hc, 7 7 7. Lt,. W ow tht.. Thus,. Cosd th vcto quto of th pl.. z. - + z = - + z = Thus th Cts quto of th pl s - + z = Lt d th dstc tw th pot,, - to th pl.
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
 A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
Ruin Probability-Based Initial Capital of the Discrete-Time Surplus Process
 Ru Probablty-Based Ital Captal of the Dsrete-Tme Surplus Proess by Parote Sattayatham, Kat Sagaroo, ad Wathar Klogdee AbSTRACT Ths paper studes a surae model uder the regulato that the surae ompay has
Ru Probablty-Based Ital Captal of the Dsrete-Tme Surplus Proess by Parote Sattayatham, Kat Sagaroo, ad Wathar Klogdee AbSTRACT Ths paper studes a surae model uder the regulato that the surae ompay has
( ) ( ) ( ( )) ( ) ( ) ( ) ( ) ( ) = ( ) ( ) + ( ) ( ) = ( ( )) ( ) + ( ( )) ( ) Review. Second Derivatives for f : y R. Let A be an m n matrix.
 Revew + v, + y = v, + v, + y, + y, Cato! v, + y, + v, + y geeral Let A be a atr Let f,g : Ω R ( ) ( ) R y R Ω R h( ) f ( ) g ( ) ( ) ( ) ( ( )) ( ) dh = f dg + g df A, y y A Ay = = r= c= =, : Ω R he Proof
Revew + v, + y = v, + v, + y, + y, Cato! v, + y, + v, + y geeral Let A be a atr Let f,g : Ω R ( ) ( ) R y R Ω R h( ) f ( ) g ( ) ( ) ( ) ( ( )) ( ) dh = f dg + g df A, y y A Ay = = r= c= =, : Ω R he Proof
2. Elementary Linear Algebra Problems
 . Eleety e lge Pole. BS: B e lge Suoute (Pog pge wth PCK) Su of veto opoet:. Coputto y f- poe: () () () (3) N 3 4 5 3 6 4 7 8 Full y tee Depth te tep log()n Veto updte the f- poe wth N : ) ( ) ( ) ( )
. Eleety e lge Pole. BS: B e lge Suoute (Pog pge wth PCK) Su of veto opoet:. Coputto y f- poe: () () () (3) N 3 4 5 3 6 4 7 8 Full y tee Depth te tep log()n Veto updte the f- poe wth N : ) ( ) ( ) ( )
14.2 Line Integrals. determines a partition P of the curve by points Pi ( xi, y
 4. Le Itegrls I ths secto we defe tegrl tht s smlr to sgle tegrl except tht sted of tegrtg over tervl [ ] we tegrte over curve. Such tegrls re clled le tegrls lthough curve tegrls would e etter termology.
4. Le Itegrls I ths secto we defe tegrl tht s smlr to sgle tegrl except tht sted of tegrtg over tervl [ ] we tegrte over curve. Such tegrls re clled le tegrls lthough curve tegrls would e etter termology.
Journal Of Inequalities And Applications, 2008, v. 2008, p
 Ttle O verse Hlbert-tye equaltes Authors Chagja, Z; Cheug, WS Ctato Joural Of Iequaltes Ad Alcatos, 2008, v. 2008,. 693248 Issued Date 2008 URL htt://hdl.hadle.et/0722/56208 Rghts Ths work s lcesed uder
Ttle O verse Hlbert-tye equaltes Authors Chagja, Z; Cheug, WS Ctato Joural Of Iequaltes Ad Alcatos, 2008, v. 2008,. 693248 Issued Date 2008 URL htt://hdl.hadle.et/0722/56208 Rghts Ths work s lcesed uder
MULTIOBJECTIVE NONLINEAR FRACTIONAL PROGRAMMING PROBLEMS INVOLVING GENERALIZED d - TYPE-I n -SET FUNCTIONS
 THE PUBLIHING HOUE PROCEEDING OF THE ROMANIAN ACADEMY, eres A OF THE ROMANIAN ACADEMY Volue 8, Nuber /27,.- MULTIOBJECTIVE NONLINEAR FRACTIONAL PROGRAMMING PROBLEM INVOLVING GENERALIZED d - TYPE-I -ET
THE PUBLIHING HOUE PROCEEDING OF THE ROMANIAN ACADEMY, eres A OF THE ROMANIAN ACADEMY Volue 8, Nuber /27,.- MULTIOBJECTIVE NONLINEAR FRACTIONAL PROGRAMMING PROBLEM INVOLVING GENERALIZED d - TYPE-I -ET
DATA FITTING. Intensive Computation 2013/2014. Annalisa Massini
 DATA FITTING Itesve Computto 3/4 Als Mss Dt fttg Dt fttg cocers the problem of fttg dscrete dt to obt termedte estmtes. There re two geerl pproches two curve fttg: Iterpolto Dt s ver precse. The strteg
DATA FITTING Itesve Computto 3/4 Als Mss Dt fttg Dt fttg cocers the problem of fttg dscrete dt to obt termedte estmtes. There re two geerl pproches two curve fttg: Iterpolto Dt s ver precse. The strteg
Chapter 2: Probability and Statistics
 Wter 4 Che 35: Sttstcl Mechcs Checl Ketcs Itroucto to sttstcs... 7 Cotuous Dstrbutos... 9 Guss Dstrbuto (D)... Coutg evets to etere probbltes... Bol Coeffcets (Dstrbuto)... 3 Strlg s Appoto... 4 Guss Approto
Wter 4 Che 35: Sttstcl Mechcs Checl Ketcs Itroucto to sttstcs... 7 Cotuous Dstrbutos... 9 Guss Dstrbuto (D)... Coutg evets to etere probbltes... Bol Coeffcets (Dstrbuto)... 3 Strlg s Appoto... 4 Guss Approto
Chapter 2 Intro to Math Techniques for Quantum Mechanics
 Fll 4 Chem 356: Itroductory Qutum Mechcs Chpter Itro to Mth Techques for Qutum Mechcs... Itro to dfferetl equtos... Boudry Codtos... 5 Prtl dfferetl equtos d seprto of vrbles... 5 Itroducto to Sttstcs...
Fll 4 Chem 356: Itroductory Qutum Mechcs Chpter Itro to Mth Techques for Qutum Mechcs... Itro to dfferetl equtos... Boudry Codtos... 5 Prtl dfferetl equtos d seprto of vrbles... 5 Itroducto to Sttstcs...
A New Method for Solving Fuzzy Linear. Programming by Solving Linear Programming
 ppled Matheatcal Sceces Vol 008 o 50 7-80 New Method for Solvg Fuzzy Lear Prograg by Solvg Lear Prograg S H Nasser a Departet of Matheatcs Faculty of Basc Sceces Mazadara Uversty Babolsar Ira b The Research
ppled Matheatcal Sceces Vol 008 o 50 7-80 New Method for Solvg Fuzzy Lear Prograg by Solvg Lear Prograg S H Nasser a Departet of Matheatcs Faculty of Basc Sceces Mazadara Uversty Babolsar Ira b The Research
Chapter 5 Properties of a Random Sample
 Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Non-degenerate Perturbation Theory
 No-degeerate Perturbato Theory Proble : H E ca't solve exactly. But wth H H H' H" L H E Uperturbed egevalue proble. Ca solve exactly. E Therefore, kow ad. H ' H" called perturbatos Copyrght Mchael D. Fayer,
No-degeerate Perturbato Theory Proble : H E ca't solve exactly. But wth H H H' H" L H E Uperturbed egevalue proble. Ca solve exactly. E Therefore, kow ad. H ' H" called perturbatos Copyrght Mchael D. Fayer,
Modeling uncertainty using probabilities
 S 1571 Itroduto to I Leture 23 Modelg uertty usg probbltes Mlos Huskreht mlos@s.ptt.edu 5329 Seott Squre dmstrto Fl exm: Deember 11 2006 12:00-1:50pm 5129 Seott Squre Uertty To mke dgost feree possble
S 1571 Itroduto to I Leture 23 Modelg uertty usg probbltes Mlos Huskreht mlos@s.ptt.edu 5329 Seott Squre dmstrto Fl exm: Deember 11 2006 12:00-1:50pm 5129 Seott Squre Uertty To mke dgost feree possble
An Extended Mixture Inverse Gaussian Distribution
 Avlble ole t htt://wwwssstjscssructh Su Sudh Scece d Techology Jourl 016 Fculty o Scece d Techology, Su Sudh Rjbht Uversty A Eteded Mture Iverse Guss Dstrbuto Chookt Pudrommrt * Fculty o Scece d Techology,
Avlble ole t htt://wwwssstjscssructh Su Sudh Scece d Techology Jourl 016 Fculty o Scece d Techology, Su Sudh Rjbht Uversty A Eteded Mture Iverse Guss Dstrbuto Chookt Pudrommrt * Fculty o Scece d Techology,
Sebastián Martín Ruiz. Applications of Smarandache Function, and Prime and Coprime Functions
 Sebastá Martí Ruz Alcatos of Saradache Fucto ad Pre ad Core Fuctos 0 C L f L otherwse are core ubers Aerca Research Press Rehoboth 00 Sebastá Martí Ruz Avda. De Regla 43 Choa 550 Cadz Sa Sarada@telele.es
Sebastá Martí Ruz Alcatos of Saradache Fucto ad Pre ad Core Fuctos 0 C L f L otherwse are core ubers Aerca Research Press Rehoboth 00 Sebastá Martí Ruz Avda. De Regla 43 Choa 550 Cadz Sa Sarada@telele.es
MATRIX AND VECTOR NORMS
 Numercl lyss for Egeers Germ Jord Uversty MTRIX ND VECTOR NORMS vector orm s mesure of the mgtude of vector. Smlrly, mtr orm s mesure of the mgtude of mtr. For sgle comoet etty such s ordry umers, the
Numercl lyss for Egeers Germ Jord Uversty MTRIX ND VECTOR NORMS vector orm s mesure of the mgtude of vector. Smlrly, mtr orm s mesure of the mgtude of mtr. For sgle comoet etty such s ordry umers, the
Sequences and summations
 Lecture 0 Sequeces d summtos Istructor: Kgl Km CSE) E-ml: kkm0@kokuk.c.kr Tel. : 0-0-9 Room : New Mleum Bldg. 0 Lb : New Egeerg Bldg. 0 All sldes re bsed o CS Dscrete Mthemtcs for Computer Scece course
Lecture 0 Sequeces d summtos Istructor: Kgl Km CSE) E-ml: kkm0@kokuk.c.kr Tel. : 0-0-9 Room : New Mleum Bldg. 0 Lb : New Egeerg Bldg. 0 All sldes re bsed o CS Dscrete Mthemtcs for Computer Scece course
VECTORS VECTORS VECTORS VECTORS. 2. Vector Representation. 1. Definition. 3. Types of Vectors. 5. Vector Operations I. 4. Equal and Opposite Vectors
 1. Defnton A vetor s n entt tht m represent phsl quntt tht hs mgntude nd dreton s opposed to slr tht ls dreton.. Vetor Representton A vetor n e represented grphll n rrow. The length of the rrow s the mgntude
1. Defnton A vetor s n entt tht m represent phsl quntt tht hs mgntude nd dreton s opposed to slr tht ls dreton.. Vetor Representton A vetor n e represented grphll n rrow. The length of the rrow s the mgntude
ES240 Solid Mechanics Z. Suo. Principal stress. . Write in the matrix notion, and we have
 ES4 Sold Mehs Z Suo Prpl stress Prpl Stress Imge mterl prtle stte o stress The stte o stress s xed, but we represet the mterl prtle my wys by uttg ubes deret orettos For y gve stte o stress, t s lwys possble
ES4 Sold Mehs Z Suo Prpl stress Prpl Stress Imge mterl prtle stte o stress The stte o stress s xed, but we represet the mterl prtle my wys by uttg ubes deret orettos For y gve stte o stress, t s lwys possble
18.413: Error Correcting Codes Lab March 2, Lecture 8
 18.413: Error Correctg Codes Lab March 2, 2004 Lecturer: Dael A. Spelma Lecture 8 8.1 Vector Spaces A set C {0, 1} s a vector space f for x all C ad y C, x + y C, where we take addto to be compoet wse
18.413: Error Correctg Codes Lab March 2, 2004 Lecturer: Dael A. Spelma Lecture 8 8.1 Vector Spaces A set C {0, 1} s a vector space f for x all C ad y C, x + y C, where we take addto to be compoet wse
Math 2414 Activity 16 (Due by end of class August 13) 1. Let f be a positive, continuous, decreasing function for x 1, and suppose that
 Mth Actvty 6 (Due y ed of clss August ). Let f e ostve, cotuous, decresg fucto for x, d suose tht f. If the seres coverges to s, d we cll the th rtl sum of the seres the the remder doule equlty r 0 s,
Mth Actvty 6 (Due y ed of clss August ). Let f e ostve, cotuous, decresg fucto for x, d suose tht f. If the seres coverges to s, d we cll the th rtl sum of the seres the the remder doule equlty r 0 s,
CS321. Introduction to Numerical Methods
 CS Itroducto to Numercl Metods Lecture Revew Proessor Ju Zg Deprtmet o Computer Scece Uversty o Ketucky Legto, KY 6 6 Mrc 7, Number Coverso A geerl umber sould be coverted teger prt d rctol prt seprtely
CS Itroducto to Numercl Metods Lecture Revew Proessor Ju Zg Deprtmet o Computer Scece Uversty o Ketucky Legto, KY 6 6 Mrc 7, Number Coverso A geerl umber sould be coverted teger prt d rctol prt seprtely
MATH 371 Homework assignment 1 August 29, 2013
 MATH 371 Homework assgmet 1 August 29, 2013 1. Prove that f a subset S Z has a smallest elemet the t s uque ( other words, f x s a smallest elemet of S ad y s also a smallest elemet of S the x y). We kow
MATH 371 Homework assgmet 1 August 29, 2013 1. Prove that f a subset S Z has a smallest elemet the t s uque ( other words, f x s a smallest elemet of S ad y s also a smallest elemet of S the x y). We kow
SUMMARY OF THE ZETA REGULARIZATION METHOD APPLIED TO THE CALCULATION OF DIVERGENT SERIES
 SUMMARY OF THE ZETA REGULARIZATION METHOD APPLIED TO THE CALCULATION OF DIVERGENT SERIES AND DIVERGENT INTEGRALS s d s Jose Jver Grc Moret Grdute studet of Physcs t the UPV/EHU (Uversty of Bsque coutry
SUMMARY OF THE ZETA REGULARIZATION METHOD APPLIED TO THE CALCULATION OF DIVERGENT SERIES AND DIVERGENT INTEGRALS s d s Jose Jver Grc Moret Grdute studet of Physcs t the UPV/EHU (Uversty of Bsque coutry
More Regression Lecture Notes CE 311K - McKinney Introduction to Computer Methods Department of Civil Engineering The University of Texas at Austin
 More Regresso Lecture Notes CE K - McKe Itroducto to Coputer Methods Deprtet of Cvl Egeerg The Uverst of Tes t Aust Polol Regresso Prevousl, we ft strght le to os dt (, ), (, ), (, ) usg the lest-squres
More Regresso Lecture Notes CE K - McKe Itroducto to Coputer Methods Deprtet of Cvl Egeerg The Uverst of Tes t Aust Polol Regresso Prevousl, we ft strght le to os dt (, ), (, ), (, ) usg the lest-squres
Discrete random walk with barriers on a locally infinite graph
 Drete rdo wl wth rrer o loll fte grh Theo Ue Aterd Shool of Teholog Weeerde 9 97 DZ Aterd The etherld El: te@hl Atrt We ot eeted er of rrl orto rolte d eeted te efore orto for etr drete rdo wl o loll fte
Drete rdo wl wth rrer o loll fte grh Theo Ue Aterd Shool of Teholog Weeerde 9 97 DZ Aterd The etherld El: te@hl Atrt We ot eeted er of rrl orto rolte d eeted te efore orto for etr drete rdo wl o loll fte
å 1 13 Practice Final Examination Solutions - = CS109 Dec 5, 2018
 Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Section 2:00 ~ 2:50 pm Thursday in Maryland 202 Sep. 29, 2005
 Seto 2:00 ~ 2:50 pm Thursday Marylad 202 Sep. 29, 2005. Homework assgmets set ad 2 revews: Set : P. A box otas 3 marbles, red, gree, ad blue. Cosder a expermet that ossts of takg marble from the box, the
Seto 2:00 ~ 2:50 pm Thursday Marylad 202 Sep. 29, 2005. Homework assgmets set ad 2 revews: Set : P. A box otas 3 marbles, red, gree, ad blue. Cosder a expermet that ossts of takg marble from the box, the
ROOT-LOCUS ANALYSIS. Lecture 11: Root Locus Plot. Consider a general feedback control system with a variable gain K. Y ( s ) ( ) K
 ROOT-LOCUS ANALYSIS Coder a geeral feedback cotrol yte wth a varable ga. R( Y( G( + H( Root-Locu a plot of the loc of the pole of the cloed-loop trafer fucto whe oe of the yte paraeter ( vared. Root locu
ROOT-LOCUS ANALYSIS Coder a geeral feedback cotrol yte wth a varable ga. R( Y( G( + H( Root-Locu a plot of the loc of the pole of the cloed-loop trafer fucto whe oe of the yte paraeter ( vared. Root locu
Mu Sequences/Series Solutions National Convention 2014
 Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
= lim. (x 1 x 2... x n ) 1 n. = log. x i. = M, n
 .. Soluto of Problem. M s obvously cotuous o ], [ ad ], [. Observe that M x,..., x ) M x,..., x ) )..) We ext show that M s odecreasg o ], [. Of course.) mles that M s odecreasg o ], [ as well. To show
.. Soluto of Problem. M s obvously cotuous o ], [ ad ], [. Observe that M x,..., x ) M x,..., x ) )..) We ext show that M s odecreasg o ], [. Of course.) mles that M s odecreasg o ], [ as well. To show
Math 153: Lecture Notes For Chapter 1
 Mth : Lecture Notes For Chpter Sectio.: Rel Nubers Additio d subtrctios : Se Sigs: Add Eples: = - - = - Diff. Sigs: Subtrct d put the sig of the uber with lrger bsolute vlue Eples: - = - = - Multiplictio
Mth : Lecture Notes For Chpter Sectio.: Rel Nubers Additio d subtrctios : Se Sigs: Add Eples: = - - = - Diff. Sigs: Subtrct d put the sig of the uber with lrger bsolute vlue Eples: - = - = - Multiplictio
Handout 11. Energy Bands in Graphene: Tight Binding and the Nearly Free Electron Approach
 Hdout rg ds Grh: Tght dg d th Nrl Fr ltro roh I ths ltur ou wll lr: rg Th tght bdg thod (otd ) Th -bds grh FZ C 407 Srg 009 Frh R Corll Uvrst Grh d Crbo Notubs: ss Grh s two dsol sgl to lr o rbo tos rrgd
Hdout rg ds Grh: Tght dg d th Nrl Fr ltro roh I ths ltur ou wll lr: rg Th tght bdg thod (otd ) Th -bds grh FZ C 407 Srg 009 Frh R Corll Uvrst Grh d Crbo Notubs: ss Grh s two dsol sgl to lr o rbo tos rrgd
