TiCC TR November, Gauss Sums, Partitions and Constant-Value Codes. A.J. van Zanten. TiCC, Tilburg University Tilburg, The Netherlands
|
|
|
- Leo Willis
- 5 years ago
- Views:
Transcription
1 Tlburg ceter for Cogto d Coucto P.O. Box 953 Tlburg Uversty 5 LE Tlburg, The Netherlds htt:// El: tcc@uvt.l Coyrght A.J. v Zte, 3. TCC TR 3- Noveber, 3 Guss Sus, Prttos d Costt-Vlue Codes A.J. v Zte TCC, Tlburg Uversty Tlburg, The Netherlds d V.V. Vvrek Isttute of Mthetcs d Ifortcs, Bulgr Acdey of Sceces Trovo, Bulgr
2 Abstrct We study the reltosh betwee rttos of soe teger GF() dstct rts of sze t ost ( ) /, d bry vectors : (,,..., ( )/) of vlue defed s : ( )/ j j. I rtculr we vestgte grou of trsfortos ctg o the j fly A { A, A,..., A } where A stds for the set of ll vectors of vlue. By exlotg roertes of ths reltosh, we re ble to detere the sg of the / qudrtc Guss su G() : e. I the lst secto of ths reort we ly the the develoed theory to derve soe reltos for cert subsequeces of the Morse- Thue sequece.
3 Cotets. Itroducto. 4. Guss sus d rttos Deftos d relres A grou of trsfortos. 5. Exles for = 7,, 3 d Costructg A fro A. 7. Deterg the sg of the Guss su G () Orderg the vectors of ( )/ GF () two dfferet wys The Morse-Thue sequece d relted roertes. 37 Refereces. 5 3
4 . Itroducto As s well kow, the followg equlty holds for y teger exceedg oe or, equvletly / e, () G () : e () / whch c be cosdered s the su of fte geoetrc seres. I ths reort we shll lwys ssue tht s odd re. A less eleetry roble s the suto of / / G () : ( ) e ( ) e, (3) where ( ) s the Legedre sybol, beg equl to f s squre GF () d equl to f s osqure. It wll be cler tht ( ) c be terreted s chrcter of the ultlctve grou of GF() whe rus through ll ozero eleets of the feld. Sce ths chrcter s of order, d sce t ws Guss who set hself the tsk to detere the su (3), ths su s usully clled G (). Slrly, the su () s clled G (), where we y thk the trvl chrcter ut frot of the e - ower. More geerlly, oe defes Guss su / G( k) : ( ) e, (4) 4
5 where stds for chrcter of the grou GF ( ) of order k. Here d the ext, we dot the coveto tht f o bouds re dcted, the suto vrble rus fro utl. Eve ore geerlly, oe defes Guss sus wth resect to feld F : GF( q), q s * G (, ) : ( c) ( c), (5) c F \{} where s ultlctve chrcter of F d ddtve chrcter. More recsely, for d we c substtute j k jk / q ( g ) e, k {,,..., q }, (6) where g s geertor of GF( q ) d b Tr ( bc) / q ( c) e, b, c F. (7) Oe c see the Guss su (5) s relto coectg the chrcters of the two bel grous of fte feld. Fro ow o we oly shll del wth the qudrtc Guss su G (). Oe c esly derve (cf. e.g. Secto ) tht G () ( ), (8) Ad so G() =. Moreover, by relcg (3) the suto vrble by oe c lso show tht ±, f od 4, G () { (9) ±, 3 od 4. These reltos lso follow edtely fro (8), sce ( ) equls for od 4 d for 3 od 4. I My 8 Guss cojectured tht the true sgs (9) re the lus sgs. However, t took h other four yers to rove ths cojecture. O August 3, 85, he wrote hs dry: At legth we cheved deostrto of the very elegt theore etoed before My, 8, whch we hd sought for ore th four yers wth ll efforts. 5
6 Sce the, the bove roble s kow s the deterto of the qudrtc Guss su or better the deterto of the sg of the qudrtc Guss su. My dfferet roofs hve bee foud, s well s coectos to other thetcl robles of vrous ture. For revew we refer the reder to []. I the reg rt of ths reort we shll vestgte the reltosh whch ers to exst betwee ths roble d the theory of rttos d lgebrc codg theory.. Guss sus d rttos We cosder g the qudrtc Guss su G() (3) whch we ow wrte s d we lso troduce the roduct S ( ) ( ), e /, () ( ) / P ( ) ( ), The followg le c esly be derved.. () LEMMA For y odd re, d for ll b {,,, } oe hs () () S P ( ; (. b ( ) ) b ( ) ) Proof: The roofs follow by strghtforwrd clcultos. For the ske of coveece, we oly gve the roofs for b. () Frst we wrte obt S ( ) S l Q j j j k k / ( ) ( ) ( ) ( ). By usg l l Q l, k l : k /, we, where Q s the set of qudrtc resdues GF( ). Now, the ddtve chrcters of GF() stsfy the orthogolty reltos ( l ), f l, d ( ), f l. Alyg tht Q l 6
7 ( )/ d dstgushg betwee (= od ) Q d the result, whch holds for d, resectvely. Q, yelds () Sce s rtve -th root of uty, we hve tht ( ) / P ( ) { ( )} ( ) = (... ) ( ) / 4 ( ) / ( ) ( ) ( ) ( ) ( x... x ) x = for j,,, ( ) /. Hece, ( ), sce ( ) ( )/ d. We lso used the fctorzto ( x )( x )...( x ) x. j j j j Next we relce the lgebrc uber the exressos () d () of Le d lso () d (), by vrble x, d we forulte the followg roerty. THEOREM Let be soe odd re. The there s {, } wth ( ) / ( x ) x ( ) /8 ( ) x, od x. Proof. We wrte the equlty the Theore s Q( x) R( x), od x, where Q (x) d R (x) re cosdered s olyols Q[x]. Fro Le, t follows tht the ubers b b / e, b {,,, }, re ll zeros of Q ( x) R( x). For the odd vlues of b, these ubers re lso zeros of x. So, whe crryg out the dvso lgorth d wrtg Q( x) R( x) q( x)( x ) r( x), t follows tht r(x) hs t lest zeros. But the degree of r (x) s t ost. Therefore r (x) s the zero olyol. Furtherore, we hve x ( x )( x x... ). Sce the secod olyol the rhs s rreducble over Q for odd res, t s coted ether Q ( x) R( x) or Q ( x) R( x) or both. It s lso obvous tht these two olyols both hve s zero. So, t lest oe of the two cots x x... whe fctorzed. Hece, t lest oe of the two s detcl to zero. 7
8 Now f both were, t would follow tht Q (x) d R (x) both were equl to zero od x whch s flse. We y coclude tht for ech odd re, there exsts uque sg s dcted the Theore. As cosequece t follows whe substtutg for x tht P ) S ( ). () ( We lso hve fro defto () d Le () tht P (3) ( )/ ( ), becuse I ( ) > d Re ( ) for {,,., ( ) / }. So,, od 8,, 5 od 8, S ) { (4) (, 3 od 8,, 7 od 8. The roble of the sg of the qudrtc Guss su turs out to be equvlet to the deterto of the sg the olyol equlty of Theore. To ths ed we core the coeffcet c of the rhs ths coeffcet s equl to x, for soe teger, both sdes of the equlty. I ( ), where GF ( ) s defed by ( ) /8. (5) To detere c the lhs, we cosder the N rttos of to uequl rts of sze t ost ( ) /. More recsely, we study the equto... k od, (6) k, such tht ll, ( ) /, re dfferet. If N e d uber of the rttos wth eve k d odd k, resectvely, the ( ) ( ) / ( N e N o N o deote the c equls ). The study of such rttos wll be the subject of the ext secto. 8
9 3 Deftos d relres Let be soe odd re. We shll study the rttos of ostve tegers cosstg of uequl rts the sze of whch s t ost /. It wll be obvous tht we c rereset such rttos by bry vectors c c, c,..., c ) of legth ( ) /. ( ( ) / Here, c = f d oly f the rtto cots rt of sze. We terret ll vectors s row vectors. The uber of oes such vector c s clled the weght of the rtto d s deoted by c. It stds for the uber of rts the rtto. Let c be soe rtto. We defe ( ) / jc j od (7) j d cll the vlue of c or vl (c ), wth {,,..., }. For fxed vlue, we collect ll vectors hvg ths vlue set A cosstg of A bry vectors of legth ( ) /. So, ths set cots ll covetol rttos of the tegers,,,... to uequl rts of sze t ost ( ) /. We shll cll such set costt-vlue code odulo or brefly costt-vlue code. Corresodg to the lst les of the revous secto, we troduce tegers N d N, beg the uber of vectors A wth eve uber of oes d odd uber, resectvely. The coleet of rtto c s defed s the rtto corresodg to the vector c c = c +, where s the ll-oe bry vector of legth ( ) / Sce the vlue of s equl to ll vectors of set c e L : ( ) / 8 od, (8) A hve coleet of the se vlue c L o. Hece, we c wrte A AL, d we cll A the coleet of A. We lso eed the vlue of the frst hlf of, defed by K... [( ) / 4] ( ± 3) /3 od, (9) for ± od 4. Cosequetly we hve L 4 K ( ) / 4 od. () 9
10 Furtherore, fro deftos (5) d (8) t follows tht L ( ) /8 () s equlty GF (). I order to del wth the sets A, {,,..., }, we lso troduce the teger ( ) /, ±3 od 8, N ( ) { () ( ) /, ± od A grou of trsfortos Let I {,,.. ( ) / } d let be soe teger wth. For ech such, we troduce dex sets : { :, I I I I }, I I : I \ I, (3) where the roduct s tke od. As s lredy dcted (3), we shll ot soetes the reter, whe there wll ot rse cofuso whch vlue hs The su of the tegers I, resectvely I, wll lso ly role the ext. We defe both tke od. S :, I S := ' I, (4) The sets I d I re closely relted to Guss crtero for the vlue of ( ), GF(), beg f s squre d f s ot squre GF (). The followg le wll llustrte ths. LEMMA () ( ) ( ), wth I ;
11 () ' S S ; () for ll o-zero GF ( ) oe hs S d ' S. Proof. () Let I {,,...} d I { b, b,...}. For y I, the uerclly lest resdue od s equl to, wheres for y b I ths vlue equls b. So equlty () s recsely Guss crtero (cf. e.g. [3,. 59]). () Ths relto follows edtely fro the observto tht the set I for s detcl to the set I for. () It c esly be roved (cf. [ 3,.59}) tht the ubers,,, b, b,... re erutto of,,., ( ) /. Hece, we hve od the equlty ' ( S S ) (...) ( b b...)... ( ) / Furtherore, edtely. ( S S ) ' I L. L. The two reltos the Le ow follow Next, we defe for ech GF() * erutto trx P of sze I x I wth eleets, j, j od, I, or j od, I, { (5) otherwse., j Art fro cses where we eed the -deedece of P exlctly, we shll ot the dex the ext. THEOREM Let l be the order of od,.e. ord reresets erutto o I cosstg of of ( ) / l cycles of legth l, for l odd. ( l. The the trx P defed by (5) ) ( ) / l cycles of legth l /, for l eve, d Proof. Cosder the g : GF ( ) GF( ), ( ). Ths g, whch erutes the eleets of GF (), c be odfed to erutto of the eleets of I the followg wy. Frst, erutes the ozero eleets of GF () ccordg to ( ) /l cycles of legth l. Next, we chge ll eleets these cycles whch re ot I to ':, d the we ot the us sg of '. If s the se cycle s, whch s the cse f l s eve, ths cycle of legth l s trsfored to cycle
12 of legth l / followed by the se cycle of legth l /, whle ll eleets ow re I. The se holds for ll other cycles. If d re dfferet cycles of legth l, whch s the cse f l s odd, the both cycles becoe detcl fter chgg the us sgs. So, whe ottg reeted cycles, we ed u wth erutto of the eleets of I s descrbed the theore. For the g the se holds. More recsely, the trx P reresets the g, odfed by the bove rocedure. We defe the followg trslto vector ( ) / GF () for every GF( )* t = (t, t,., t ), t ff j od, I. (6) ( ) / j Aother wy to chrcterze the vector t s by syg tht t j f d oly f j I, where I stds for the set { : I}. Slrly, we c sy tht f the trx eleet, the ether j I or j I. Notce tht the followg reltos hold od, j I I I, I I I, (7) where stds for dsjuct uo. The trces P d the vectors t stsfy the followg eleetry roertes whch wll be used the theory to be develoed the reg rt of ths reort. LEMMA 3 () P P for ll GF() * (, j d for ll Z. () Whe P ), the j f the set {,,,..., } cots eve uber of eleets fro I, whle eleets fro I. () t = t +. j f ths set cots odd uber of Proof. () As cosequece of defto (5), we hve tht the, j - eleets of both trces re equl to f d oly f j ±. () Ths stteet s obvous fro the deftos of the trx P d the set I ; () The sets I d I corresodg to re equl to the sets I d I resectvely, corresodg to.
13 Lke the cse of the trx P, we shll ofte ot the dex d just wrte t whe t s obvous wht -vlue s et. Next, we cosder for soe fxed -vlue, the trsforto ( ) / ( ) / T : GF() GF() defed by T ( c ) = c P + t. (8) Sce P s vertble, so s T, d hece t erutes the vectors of ( ) / GF (). THEOREM 3 Let be geertor of GF ()*, the for ll c ( ) / ( ) / ( ) / ( )/ GF( ). () T ( c ) c c for od 4, d T ( c) = c for 3 od 4; () the order of T s erutto of d to ( ) / for 3 od 4. GF () s equl to for od 4, Proof. For the ske of coveece, we dot ths roof the otto l :, beg the order of. () For rbtrry vlue of we hve T ( c) = c P + t ( P... P E). (9) Accordg to Theore, the erutto trx P reresets oe cycle d of legth l/, l / whch we wrte s d (d d. d ), I. Hece, c P c. I order to l / / detere the secod ter the rhs of (9) for l /,.e. t :=t ( P l... P E), we rerk tht for ths -vlue, the trx betwee retheses s equl to the ll-oe trx. For ech od l /, we hve ether d d or d d od. Let d r l / r l cot r eleets fro I, the d ( ) d ( ) d, sce, d so r ust be odd (cf. Le 3 ()). If od 4, we hve tht l / s eve. It follows tht d cots odd uber of eleets fro I. Fro deftos (3) d (6) t ow d l / T follows tht t cots odd uber of oes. We coclude tht t =, d hece ( c) = c + = c c. If 3 od 4, the l / s eve, d t follows slrly tht d cots eve uber of eleets fro I d tht t cots eve uber of oes. l / So, t =, d hece, T ( c) c + = c. 3
14 T () Let od 4. We kow lredy tht I, the detty oertor. Assue tht T (c) = c for ll c ( ) / GF ( ), for soe wth. It the follows P fro (9) tht c ( P E) = t(... P E) for ll vectors c. Multlyg ext by P E rovdes us wth (c + t) ( P E) =, for ll c, where c = c ( P E). Ths c oly be true f P E s the zero trx, d so l /. But ths cotrdcts the frst relto (). Hece, the order of T s equl to ths cse. For 3 od 4, the roof s coletely slr. THEOREM 4 Let be soe eleet of GF ()* d let be ts verse, the T = T. Proof. If I {, b,...} s the dex set corresodg to, the I ' {, b,...} s the dex set corresodg to, s wll be cler fro the defto of I (3). If P d t re the erutto trx d trslto vector w.r.t. d f P ' d t std for the se otos w.r.t., the t wll be obvous fro the deftos (5) T T d (6) tht P' P P d t = t P t P. Hece, T T ( c) = c PP ' + t P ' + t = c PP + t P + t P = c, for ll c. THEOREM 5 For ech, A,,, T duces erutto o the fly of sets A A, A } such tht ( A ) Ab, wth b ( S ) d S Proof. Let A wth vlue. Frst, we shll detere the vlue b of the vector b = T ( ). The cooets wth I cotrbute ( ) to b, whle those I yeld ( ). Hece, both cotrbutos together d tke od, gve b = I I = S corresodece betwee the vectors of. Alyg Theore 4 ow gves tht there s oe-oe I A d those of b I. { I A wth b ( S ). Exles I {,,., [( ) / 4] }, I I \ I, t = (,,,, ), b = ( S ) ( K ) ; 4
15 ( ) / I = {, 3, 5,..}, I = {, 4, 6, }, t = (,,,,,,,,.,), b = ( ) / (S ( ) / ) = ( ) / ( L K ) ; I, I I, t =, P E. b =. I I, I, t =, P E, b S L. The eruttos,, geerte erutto grou G A o the fly A of costt-vlue codes. I the reg rt of ths secto we shll vestgte ths grou soewht closer. Let w, be the vlue of the set A the tegers w, stsfy GF () the recurrece relto ( ), for fxed d. Accordg to Theore 5, w, ( S w, ), w,, (3) Ths recurrece relto s ler d c esly be solved, yeldg, ( ( ) ) ( = w ) ( )( ). (3) Here, we lso led Le (). THEOREM 6 () for y GF() oe hs for odd d for eve; () G A hs oe orbt {A } of sze, wheres ll other A,, re oe orbt of sze ; * () the erutto geertes G A f d oly f s geertor of GF ( ) ; (v) for ll oe hs A = N (), wheres A = N ( ) for ± od 8, d A = N () for ±3 od 8. Proof. Prt () follows esly by lyg (3) wth d relcg by odd cse, d by the eve cse. Geerlly, the erutto geertes subgrou of equto w, s equvlet to the G A. Fro (3) we hve tht the 5
16 ( )( ( ) ). (3) Let l be the order of od. The oly -vlue whch stsfes eq. (3) for soe fxed wth < < l, s. So, A s vrt wth resect to ll trsfortos of G A. Furtherore, t wll be cler fro (3), tht the legth of the orbt to whch A,, belogs uder the cto of, s equl to l. So, f we tke, where s geertor of GF( )*, the orbt hs legth.prt (v) follows edtely fro the fct (cf. Theore 7) tht ll A,, hve the se sze, whle A = A. We rerk tht Theore 6() wth s lso edte cosequece of Theore Exles for = 7,, 3 d 7 I ths secto we reset exles for the cses = 7,, 3 d 7 whch rereset ll ossbltes od 8. () For = 7, we hve I {,,3}, L 6, 3 d K. I ths cse geertes the grou GF (7)*, wheres does ot. For we obt I {,3}, I { } d P, t = (,, ). 3 Hece, T ( c) = c P 3 + t ( P P E) = c + = c, whch llustrtes Theore 3 (). The costt-vlue codes re A {(,,)}, A {(,, )}, A {(,, )}, A {(,,), (,,)}, 3 A {(,,)}, A {(,, )}, A 6 {(,,)}. 4 5 Sce s geertor of GF (7)*, the trsforto geertes the grou G A by Theore 6, d t cts trstvely o the fly { A }. For oe hs I { }, ' I {,3}, d so S d S 5. The trsforto (A ) Ab wth b ( ) od 7 gves rse to the orbts 6
17 A, A A A5 A6 A4 A A, 3 A 3 wheres (A ) A b, wth ( b 5 ) od 7, roduces the orbts A, A A4 A5, A A6 A A 3 A 3 () For we hve the followg dt: L 4,, K 3. I ths cse s geertor of the grou I {, } whch gves rse to * GF (), d s ot. For we obt P, d t = (,,,, ). It follows edtely tht (cf. lso Theore 3() d ts roof) 5 T ( c) = c P t ( P... P E) = c E + t J = c + = c. The fly A of costt-vlue codes cossts of the sets: A {(,,,,), (,,,,), (,,,,)}, A {(,,,,), (,,,,), (,,,, )}, A {(,,,,), (,,,,)}, A {(,,,,), (,,,,), (,,,,)}, A {(,,,,), (,,,,), (,,,, )}, 3 A {(,,,,), (,,,,), (,,,,)}, A {(,,,,), (,,,,), (,,,, )}, 5 A {(,,,,), (,,,,), (,,,,)}, A {(,,,,), (,,,,), (,,,, )}, 7 A {(,,,,), (,,,,), (,,,,)}, A {(,,,,), (,,,,), (,,,, )} Sce s geertor of GF (), the trsforto 9 s geertor of G A ccordg to Theore 6, d t cts trstvely o the fly { }. I order to ly Theore 5, we obt for 9 tht I {3, 4, 5}, d hece S A 9 7
18 od. Ideed, the reltos trsfortos: (A ) A 9 b d b 9( ), od, rovde us wth the A A, A A9 A5 A8 A3 A4 A6 A A7 A A. * Sce does ot geerte GF (), we cot ly Theore 6 () for. For, we hve I {, } d S 3. Whe lyg (A ) Ab, b (3 ) od, we obt A A, A6 A5 A7 A3 A A, A A4 A9 A A8 A. So, does ot ct trstvely o the fly { }. It lso follows fro the bove sequece of trstos tht the grou eleet orbts A hs A A, A 5 A3 A6 A7 A A, A A9 A8 A4 A A We core these orbts wth those of 7. For 7, we fd I {,5 }, d so S 7 d b 7(7 ). The ltter relto gves the se sequeces of dces of the 7 sets A s dd, thus llustrtg the eve cse of Theore 6 (). The odd cse s 3 deostrted by corg the trsfortos d 3 8. For 8 we fd I {,3}, S 5 d b 8(5 ). Ths lst equlty yelds the followg orbts wth resect to 8 : 8 A A, A7 A6 A3 A5 A A, A A A4 A8 A9 A As oe c esly verfy, the trsforto 3 gves rse to the se orbts. As llustrto of Theore 4, we tke 9 5 od. Now, we fd I {,3,5 } d S 5 9. By lyg b 5(9 ), we derve tht 5 erutes the sets of A reversed order s 9 dd : A A A7 A A6 A4 A3 A8 A5 A9 A Slrly, we derve for 6 od, tht I {,4}, S 6 6 d ext by lyg b 6(6 ) the erutto A A3 A7 A5 A6 A, A A8 A A9 A4 A 8
19 6. whch shows tht () For 3 we fd L 8, 4, K 6 * Both d re geertors of GF (3). For we hve I {,, 3} d I { 4, 5, 6}, fro whch we fer P, d t = (,,,,, ) So, T ( c) = c P + t ( P... P E) = c E + t J = c + = c c (cf. Theore 3). For we hve I {4, 5, 6} d I {,, 3}, d hece P, d t = (,,,,, ). 6 Ag t follows tht T ( c) = c + = c c. 9
20 The costt-vlue codes for 3 re: (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) } A (,,,,, ) } A 7 (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) } A (,,,,, ) } A 8 (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) } A (,,,,, ) } A 9 (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) } A 3 (,,,,, ) } A (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) } A 4 (,,,,, ) } A (,,,,, ) (,,,,, ) (,,,,, )
21 (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) } A 5 (,,,,, ) } A (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) (,,,,, ) } A 6 (,,,,, ) (,,,,, ) Sce both d re geertors of trstvely o the set { 4}, ccordg to Theore 6. A * GF (3), the trsfortos d ct For we hve I {4,5,6}, d so S. Alyg (A ) Ab, wth b ( ) (cf. Theore 5) yelds the ch of trsfortos: A A9 A A A5 A6 A8 A A7 A A3 A A wheres ( A 4 ) A4, llustrtg Theore 6. For we fd I {,,3 } d S 6, gvg rse to (A ) Ab, wth b (6 ). Now we get the orbts A 4 A4 d A A A A A5 A A8 A9 A7 A A3 A6 A (v) For 7 we hve L, d K. I ths cse ether or s geertor of GF (7) *. For, we hve I {,,3,4 }, I {5,6,7,8}, d so S, S 9. The trsforto (A ) Ab wth b ( ) od 7 roduces the orbts: A A, A3 A4 A9 A A6 A5 A A A A, 4 A A3 A A5 A7 A6 A8 A4 ',. whle (A ) A b wth b (9 ) od 7 gves A A, A A6 A4 A A3 A5 A9 A A A, 4 A7 A3 A8 A5 A A6 A A4
22 8 8 Ths shows tht I d tht I, d hece tht ether or re geertors of G A, whch s ccordce wth Theore 6 (). I order to geerte G by sgle erutto we c tke 5, sce 5 ers A to be geertor of GF (7) *. Ideed 5 (A ) Ab wth b 5( ) od 7 yelds, strtg wth A, successvely A -sets wth dces, 3,,, 5, 4, 6, 8,, 6, 9, 7, 4, 5, 3,,. Ths shows tht the order of 5 s equl to 6, d lso tht 5 cts trstvely o the fly of sets { } ( cf. Theore 6 () d ()). A 6. Costructg A fro A I ths secto we shll dscuss ethod to trsfor vector A to vector b. Our ethod s bsed o the followg. We ssue tht the trx P, A GF( )*, (5) corresods to oe ( ) / -cycle whch we deote by d : ( d( ) d..... d ), d I, (33) ( ) / (cf. lso the roof of Theore 3). Ths s the cse ether f ord ( ) or f ord ( ) ( ) / d ( ) / s odd, ccordg to Theore. Corresodg to (33) we defe bry vector of legth ( ) /, such tht ts -th cooet s equl to the rty of the uber of d j, j, whch re I. Slrly, we troduce vector, the -th cooet of whch equls the rty of the uber of d, j, whch re I. It wll be cler tht the followg relto holds j = + (,,,, ). (34) Now, let be bry vector of legth ( ) / reresetg soe rtto, d let vl () =. Fro (33), fro the defto of P (5) d fro the defto of the cooets of, we y coclude tht d d( ) So, sce d, we c wrte od, ( ) /. (35) vl () = ( ) / ( ) / d d ( ) / ( ) d. (36)
23 We defe trslto vector s s follows. If d j j, j k, d d k soe k, k ( ) /, we defe (s ), j k, wheres ll other cooets re ut equl to zero. So, the bove teger k s the sllest dex wth d k k. Forlly, we c obt s by d j s = (,...,,,..., ) Q, (37) where the vector t the rhs cots k oes followed by ( ) / k zeros, whle the erutto trx Q hs eleets q, j f j d d q, j otherwse. Fro ow o, we shll ly the vectors d oly wth resect to. We lso troduce the secl vectors Q, c = ( + )Q = c Q. (38) THEOREM 7 Let ord () be equl to, or to ( ) / wth ( ) / odd. () f A, the b = + s A, uless = c ; () for ord () =, the trslto () gves oe-to-oe g A A, GF( ) \{, }, A \ { c } A d A A \ { }; () for ord ( ) ( ) / d beg odd, the trslto () gves oe-to-oe g A A, GF() \{, }, A A \ { } d A \ { c } A. Proof. Fro the codtos of Theore 7 d by lyg Theore, t follows tht the trx P, defed (5), reresets cyclc erutto of legth ( ) /. We oly hve to tke to ccout the chge the cotrbuto to vl () due to the cooets,...,. These cotrbute to vl (), lyg (36), out of k d dk ( ) od, where the sgs re detered by the cooets of. For d k, we oly hve ( ) = for those ostos where, for k, due to the defto of k. But these re recsely the ostos Hece, we fd vl (b) vl () = For d k k we hve d k k ( ) k d k, where b hs oes. k k for ( b ). (39) d b d for d k k =, b d so the secod ter the rhs of (39) lwys equls k. We coclude tht vl (b) vl () = k k ( ). The oly exceto occurs whe d j for j ( ) /. k d k j d k 3
24 I tht cse k s ot defed, d = c = c Q. Sce ( c ) d c wrte ( c ) d = vl ( c ) =, d hece by lyg (36) we fd ( ) / ( ) ( ), vl ( ) = So, cse tht ord ( ), whe we hve ( ) / ( ) / ( )/ ( ) / (, ( ) /, we ). (4), t follows tht vl ( ) vl ( c ) =, (4) O the other hd, we lso hve (cf. (8)) vl ( ) + vl ( c ) = ( ) / Reltos (4) d (4) together yeld, usg L, L. (4) vl ( ), vl ( c ) =. (43) I cse tht ord ( ) ( ) /, whe ( )/, we obt sted of (4), the equlty vl ( c ) vl ( ) =, (44) resultg vl ( c ) = vl ( ). (45) Stteets () d () ow follow edtely fro (43) d (45). The roerty of the gs () d () beg relly oe-to-oe, follows fro the fct tht the trsfortos c esly be reversed. Isted of the vector s s defed (37), we the hve vector s,defed by teger k, such tht k s the sllest dex wth d k k. As for the codto for ord (), the followg le y be useful. LEMMA 4 () If ord (), the 3 od 8. () If ord () ( ) /, the od 8. Proof. () Let ord (). Ths les ( )/ would be squre, sy, d hece whch cotrdcts GF( ) d. So, ths cse we hve 3 od 8.. Assue od 8, the for 4
25 () I geerl oe hs tht the squres GF( )* costtute subgrou of dex. Fro the codtto () we hve tht <> s subgrou of dex. Sce y grou hs oly oe subgrou of dex, t follows tht s squre, d cosequetly od 8. REMARK We rerk tht the lctos Le 4 c ot be reversed. For exle, ord () 4 d ord 43 3 () 5. we lso ehsze tht ord () ( ) / does ot ly tht ord () s odd. A couterexle s 7 wth ord 7 () 8. For vlues of other th, we were ot ble yet to derve results slr to those reseted Theore 7. Let us cosder the cse =, d ssue tht geertes GF ()*. I ths cse the erutto (33) s detcl to the oe for. Sce the sets I d I wth resect to re equl to the sets I d I wth resect to, the vectors d for re equl to d for. Exresso (35) ow yelds vl () = ( ) / ( ) ' ( ), (46) d sted of (38) we ow c wrte for the chge vlue due to the trsforto b = + s, the exresso vl (b) vl () = = k ( ) ( ) ( k ) k 3 ( ) ' k k = ( b k k )( ) k = (( ) ). (47) 3 We see tht for = the chge vlue s geerl ot the se for the vrous vectors of set A, but deeds o k. The se s true for other -vlues. Exles For 7 we hve ord 7 () 3 (7 ) /. Sce the order of s odd, we y ly Theore 7. For, I { }, I {,3}, d ( 3) d = (,,). For = (,,) A 5, we fd k, sce d. Sce Q I ths sle cse, t follows tht s = (,,) Q (,, ). So, b = + s = (,,), whch deed s eleet of A 6. By slr costructo we = (,,) A 3 oto b = (,,) A 4. The secod vector of A 3,.e. (,,), hs o ge uder ths g, llustrtg Theore 7 (), sce (,,) = c = c, d 3. O the other hd, the vector (,,) = s ot the ge of vector A. 5
26 For, we hve ord (), or equvletly, geertes GF () * (cf. Secto 5 ()). For ths -vlue, we hve I {, } d I {3,4,5}. The 5-cycle of (33) s equl to d ( 4 3 5), d hece = (,,,, ). The trx Q hs the for Q =. For = (,,,, ) A, we fd k 3, sce d, d d d 4 3. It follows tht s = (,,,, ) Q = (,,,, ). So, b = + s = 3 (,,,,), whch deed s vector A. If we tke = (,,,,) A, the k s ot defed, llustrtg Theore 7 (), sce c = c Q = (,,,, ) Q = (,,,,) A d. Tkg for the vectors (,,,, ) d (,,,, ), both fro A, yelds vectors b equl to (,,,, ) d (,,,, ), resectvely, whch re A 3. The thrd vector (,,,,) of A 3 s the coleet of c, so equls thus cofrg g Theore 7 (). For 3, we hve tht both d re geertors of GF (3) (cf. Secto 5 ()). Frst we tke, for whch we hve I {,,3 } d I {4,5,6}. The 6-cycle of (33) s equl to d = ( ), d hece = (,,,,,). The trx Q corresodg to d hs the for Q. We derve c = c Q = (,,,,,). Now, vl( c ) = 6 = 3 od 3, d so c A3 A. Accordg to Theore 7 (), ths vector hs o ge A 4 = A. Furtherore, vl( ) = 5 od 3. So, s A 5. Ag ccordg to Theore 7 (), ths vector s ot the ge of vector A 4. The four vectors A A 4 re ed oto the four other vectors of A 5 the followg wy: (,,,,,) (,,,,,), (,,,,,) (,,,,,), 6
27 (,,,,,) (,,,,,), (,,,,,) (,,,,,). I order to llustrte the rerk rght fter Theore 7, we tke. Of course, we hve the se 6-cycle ( ), fro whch we fer tht I {4,5,6}, I {,,3 }, d hece = (,,,,,), whch c lso be derved fro by lyg (34), d cosequetly = Q = (,,,,,). The vectors of A 3 re ed the followg wy. = (,,,,,) wth k s ed oto b = (,,,,,) A 4, = (,,,,,) wth k s ed oto b = (,,,,,) A, = (,,,,,) wth k 5 s ed oto b = (,,,,,) A, = (,,,,,) wth k s ed oto b = (,,,,,) A 4, = (,,,,,) wth k s ed oto b = (,,,,,) A. k These results coly wth (47), sce the vlue of (( ) ) / 3 s equl to, 3, d 8 for k, d 5, resectvely. The erutto d of the tegers of the set I {,,...,( )/ } (33) s wrtte such wy tht d. If we choose for dfferet teger t the frst osto, sy d t, oe c esly verfy by djustg the roof of Theore 7, tht oe obts oe-to-oe g fro A to A wth slr roertes. t Exle Tke 3 d d ( ). The corresodg rty vector equls = (,,,,,), d the corresodg trx Q s Q =. Ths yelds the followg trsfortos for the vectors of A 3 : 7
28 = (,,,,,), d, k, s (,,,,, ) b = (,,,,,);, = (,,,,,), d, d 4, k, s (,,,,, ) b = (,,,,,); = (,,,,,), d, k, s (,,,,, ) b = (,,,,,);,, = (,,,,,), d, d 4, k, s = (,,,,,), b = (,,,,,); = (,,,,,), d, d 4, d 5 3, b = (,,,,,). d 3 4, k 6, s (,,,,, ), d, d 6, As oe c see, ll b-vectors re A 5, whch cofrs the rerk o the revous ge wth t. 7. Deterg the sg of the Guss su G () 5 I ths secto we shll derve the correct sg(s) for the Guss su G () (cf. (9)). Frstly, we reset d rove theore cocerg the tegers whch were troduced Secto. THEOREM 8 () Ne N o A / for y odd re ; () f od 8, the No () f 3 od 8, the (v) f od 8, the (v) f 3 od 8, the No No No A / d A / d Ne Ne A /- d A / d Ne Ne 3 6 N e d A /; A /+; A /; A /+. N o, {,,..., } Proof. () These equltes re edte cosequece of the equltes (cf. Secto ) ( )/ c d c ( ) ( Ne N o ) for. () d () Assue od 4. The A / s eve s follows fro () d Theore 6 (v). Let the words (vectors) A,, be ordered soe wy. So, 8
29 we hve ordered blocks wth ( ) / colus d N( ) rows for, d N( ) rows for. Chgg colu j zeros to oes, d vce vers, yelds oe-tooe corresodece betwee the words A wth zero o osto j d the words A wth oe o tht osto for ll GF( ) d j ( ) /. Sce A / s j eve, the th j colu of A hs eve uber of zeros. It follows tht the th j colu of A kj wth k hs eve rty f d oly f k s odd.. We coclude tht A cots odd uber of colus wth odd rty, d hece lso odd uber of rows wth odd rty, f d oly f the equto kj, k eve, j {,,...,( ) / }, hs odd uber of solutos or, equvletly, f d oly f the equto lj, l, j {,,...,( ) / } hs odd uber of solutos GF( ). Becuse of the syetry betwee l d j, ths lst codto s stsfed f d oly f s squre GF( ). Sce ths s true f d oly f od 8, we hve ths cse tht A cots odd uber of rows wth odd rty for od 8 d eve uber of such rows for 3 od 8. Fro Theore 6 t follows tht for od 8 A = A /+( A / ), d for 3 A =( A /+)+ A /. Sce both cses A / s eve, the reltos () d () ow follow. (v) d (v) Assue tht od 4, d so A / s odd. I slr wy s the revous cse we derve tht A cots odd uber of rows wth odd rty f d oly f the equto kj, k odd, j {,,...,( ) / }, hs odd uber of solutos GF( ). Equvlet to ths codto s tht the equto lj, l, j {,,...,( ) / } hs odd uber of solutos. Sce od 4, ths s true f d oly f 3 od 8. Hece, we hve ths cse tht A hs odd uber of rows wth odd rty f 3 od 8 d eve uber of such rows f od 8. The reltos (v) d (v) ow follow s the revous cse. As kd of corollry we ow c stte the colete exressos for the Guss su G (). THEOREM 9 (Guss 85) For y odd re oe hs G() f od 4, d G() f od 4 Proof. Fro Theore 8 t follows tht N N for y odd re. Substtutg e o ths result the relto gves the bove result. ( ) ( )/ ( Ne No ) (cf. the ed of Secto ), 9
30 8. Orderg the vectors of ( )/ GF () two dfferet wys I order to del wth cses where Theore 7 cot be led,.e. whe ord () s less th ( ) /, or whe ord () = ( ) / d eve, we wll use the followg le. Ths le wll hel us to cosder the trsforto of Theore 7 slghtly dfferet cotext d to geerlze tht trsforto. I the le d the reg rt of ths reort we shll wrte bry ubers reversed order,.e. fro rght to left. Accordgly, bry ddto,.e. wth crry d deoted by, wll be crred out fro left to rght. The reso to hdle the bry reresetto of ubers ths wy, s to djust to the cycle otto of eruttos where the eruted objects re ordered fro left to rght. LEMMA 5 () Let u be soe fxed bry vector of legth. For y v GF ( ) we defe trsforto v w = v + s, where s s defed such tht s for k, where k s the frst dex vlue wth vk u k, whle s for k. Whe reetedly lyg ths trsforto, strtg wth the vector v := u, oe obts lst v, v = v + s, v = v + s, of ll vectors of GF ( ), edg wth the vector v = u c ; () If oe lbels the vectors ths lst fro utl, the e-th vector v e c be obted drectly fro v u by v e = u e, where e stds for the bry reresetto of legth of the teger e ( reversed order); () If v l s the l-th vector the lst, the v l e +u =(v l u) e for l e. Proof. The stteet the Le s trvl for u =. I tht cse the order of the vectors the lst s recsely the turl order of the tegers,,.,, whe the vectors re terreted s the bry reresettos of these tegers wrtte fro rght to left. Furtherore, t c esly be see tht lst strtg wth rbtrry u c be obted by ddg ( GF ( ) ) the vector u to ll vectors of the lst corresodg to u =. The lst s ot cyclc d ctully eds wth u c, sce for tht vector the trsforto s ot defed. The reg rt of the Le follows esly. Exle For 3 d u =, we obt the followg lst by reetedly lyg w = v + s: v s 3
31 The word v 6 c be obted fro v (=u) = by v =. Notce, tht whe lyg Le 5 uder the codtos of Theore 7, wth ( ) /, v = Q, A d u : = the rty vector corresodg to erutto d, the result s w = bq, b A (cf. lso (37) d (38)). Oe could sy tht Q s the vector d-reresetto, d therefore we wrte d := Q, d d slrly b : bq. Slrly, the vector s Q (37) s lso d-reresetto. Usg ths otto d cobg Theore 7 d Le 4 wth u =, rovdes us wth the followg theore. I ths theore d stds for the erutto (33), whle deotes the ddto of two bry ubers of legth ( ) / THEOREM Let ord () be equl to, or to ( ) / wth ( ) / odd, d let A be rereseted by d d-reresetto. Let furtherore e be the bry reresetto of legth ( ) / of soe ostve teger e d wrtte reversed order. The the vector b d, defed by b d + = ( d + ) e s the d-reresettve of vector b A e. Exle Let 3. The s geertor of GF (3) *. So, the trx P reresets the erutto d ( ) whch defes the rty vector = (,,,,, ). We strt wth the vector = (,,,,, ) A or wth d = Q = (,,,,, ) wth Q s defed Secto 6. Frst we ly Theore wth e rereseted by the bry vector e = (,,,,, ). Successvely, we fd d = (,,,,, ), ( d + ) e = (,,,,, ), b d = (,,,,, ) d flly b = b d Q = (,,,,, ) A. Actully, ths costructo s othg else s the costructo of Theore 7, forulted slghtly dfferet cotext. Next, we tke e 7, rereseted by e = (,,,,, ). Strtg wth the vector = (,,,,, ) A, we costruct successvely d = (,,,,, ), d + = (,,,,, ), ( d + ) e = (,,,,, ), b d = (,,,,, ) d b = b d Q = (,,,,, ), whch deed s vector A 8. I cse tht we wrte the erutto d dfferet wy, the erutto trx Q d the rty vector lso chge. Sy, we wrte d = ( ) wth corresodg rty vector = (,,,,, ). Now, f we strt wth = (,,,,, ) A 3 d wth e =, 3
32 we fd successvely d = Q = (,,,,, ), d = (,,,,, ), b d = ( d + ) e = (,,,,, ), b = b d Q = (,,,,, ) A 8. Exle As other exle we tke the cse d e = (,,,, ). We kow lredy tht, d = ( 4 3 5), = (,,,, ), whle Q hs the for Q. We strt wth the vector = Q =, whch s A 3 levg out brckets d co s, d = =, d A. Subsequetly, we fd, + =, b d + = ( d +) e =, b d =, d flly b = b d Q = A 4. 5 I slr wy we coute lst cotg ll 3 vectors of GF (). Below we reset the colete lst. d + b d = A 3 A 4 A 5 A 6 A 7 A 8 A 9 A A A A A 3 A 4 A 5 A 6 A 7 3
33 A 8 A 9 A A A A A 3 A 4 A 5 A 6 A 7 A 8 A 9 A A c = A As oe c see, the left lst strts wth the vector = (,,,, ) A 3 = A d eds wth c = (,,,, ) A = A, d cots ll 3 bry vectors of legth 5. The lst the ddle cots the corresodg vectors d +. Oe c verfy tht ths lst cossts g of ll bry vectors of legth 5, such tht the reversed vectors re turl order, strtg wth (,,,, ) d edg wth (,,,, ), thus corrobortg Le 5 d Theores 7() d 8. Exle For 7 we hve ord () = ( )/ = 3 whch s odd. The erutto trx P reresets the erutto d = ( 3). So, Q I. Furtherore, I {}, I {, 3}, =(,, ), 3, A = for 3, d A3 =. It follows tht Q = (,, ). I ths cse we hve the followg lsts: d + b d A 3 A 4 A 5 33
34 A 6 A A A c = A 3 Now, the left lst strts wth A d eds wth c A. Fro the bove exles t wll be cler tht the esest wy to obt lst of ll vectors ( ) / of GF ( ), ordered ccordg to cresg vlue (7), s s follows. We shll cll tht lst L d deote ts vectors (words) by,,., ( )/ the ext theore. THEOREM Let L be the lst of the bry vectors of GF() / turl order d wrtte fro rght to left. Trsforg ech v of ths lst to ( v + )Q yelds lst L whch s ordered such tht the vlue of the corresodg rttos creses by od whe gog to the ext word. The lst L strts wth Q d eds wth ( )/ = c. For c ord () oe hs A d A, wheres for ord ( ) ( ) / d odd, both d c re A. THEOREM Let C : { j : j {,,,...} }, be the set of vectors wth dces,,,.d of legth ( ) / the lst L, for y wth. () If ord (), the C = A for, whle C = A. () If ord () ( ) / wth ( ) / odd, the C = A for. Exle Tke 3. The =, 4, d the trx Q hs the for Q. Alyg Theore wth, yelds resectvely 34
35 Q =, 3 Q =, 6 = Q =, 39 = Q =, 5 = Q =. These re recsely the vectors of the costt-vlue code A 5. Observe tht the rocedure of costructg vectors L fro those L utotclly hlts whe we try to costruct 65, sce 65 s teger whch hs o bry reresetto of legth 6. By lyg Theore wth, we obt = Q =, 5 = Q =, 38 = Q =, 5 = Q =. These four vectors re the vectors of the fly A A 4. Here lso, the rocedure stos utotclly, sce 64 cot be rereseted s bry vector of legth 6. Flly, we gve the colete lsts L d L for our rug exle of 3. L L A 5 A 6 A 7 3 A 8 4 A 9 5 A 6 A 7 A 8 A 9 A A A 3 A 4 35
36 3 A 5 4 A 6 5 A 7 6 A 8 7 A 9 8 A 9 A A A A 3 A 4 A 3 5 A 4 6 A 5 7 A 6 8 A 7 9 A 8 3 A 9 3 A 3 A 33 A 34 A 35 A 36 A 37 A 3 38 A 4 39 A 5 4 A 6 4 A 7 4 A 8 43 A 9 44 A 45 A 46 A 47 A 48 A 36
37 49 A 5 A 3 5 A 4 5 A 5 53 A 6 54 A 7 55 A 8 56 A 9 57 A 58 A 59 A 6 A 6 A 6 A 63 A 3 9. The Morse-Thue sequece d relted roertes I order to del wth the rty of the weght of bry ubers, we troduce the wellkow Morse-Thue sequece M,,...,,..., (48) where stds for the rty of the uber of oes the bry reresetto of,.e. : f the weght s eve d : f ths weght s odd. Oe c esly derve the followg recursve rule, whch c serve s defto of M k k k c M ( ) M ( ) M ( ), () M, (49) where M() j deotes the subsequece of the frst j eleets of M. I the ext, subsequece of M shll lwys e subsequece of cosecutve eleets of M, uless stted otherwse. The followg sle roertes, collected le, c esly be rove by lyg (49). LEMMA 6 () M does ot cot subsequeces cosstg of three cosecutve detcl eleets. () The substtuto for ll, trsfors M to tself for ll k. k 37
38 () The substtuto rules,, together wth the ttor M (), geerte the sequece M. (v) For ll oe hs,. (v) For ll eve oe hs, d for ll odd,. Now, let M ',,..., k d M '',,..., k be subsequeces of M of legth k d of legth k, resectvely, cosstg of cosecutve eleets, d let furtherore be the uber of oes d be the uber of zeros ether of these sequeces. The we c derve the followg le. LEMMA 7 () I M oe hs for eve d y k, f, d f. k () I M oe hs for odd d y k, f, d f. () I M oe hs for y k,, excet f s odd d or k, whe d, resectvely. k k Proof. We shll rove the Le by ducto o k. Both stteets re trvlly true for k. Assue the stteets re true for soe k. Let M '' M ', k, k be subsequece of legth k 3. () If s eve, the k s eve. I cse tht k, we hve M'' M ',, or M'' M ',,. I the frst cse, M ' eds t d the secod cse t, becuse of Le 5 (v). Fro the ducto ssuto t ow follows tht for M '' the dfferece s equl to the frst cse, d to the secod cse. If, we hve M'' M ',, or M'' M ',, wth M ' edg t d k resectvely. Hece, g lyg the ssuto codto, the dfferece for M '' s equl to the frst cse, d to the secod. So, stteet () holds for k. () If s odd, the k s odd. Ag by Le (v), we y coclude tht M'' M ',, or M'' M ',,. Fro the ducto ssuto t follows tht cse tht f, the dfferece equls. If, ths dfferece equls. So, stteet () lso holds for k. By the rcle of thetcl ducto both stteets hold for ll k. Prt () s cosequece of () d (). I the ext we cosder the tegers the set {,,..., } wth ( )/ d wrtte bry, whch rovdes us wth ll bry ubers of legth ( ) /. As for our otto, whe wrtg od we e the teger {,,..., } whch s equl to 38
39 odulo. Ech of these tegers c be wrtte s j wth d j N( ), excet for N( ) the cse od 8 (cf. ()). For gve teger, oe obts d j by dvdg by. The quotet s equl to j d the reder to. Next we order ll tegers of the set {,,..., } lexcogrhclly wth resect to d j, d we cll the resultg lst L. It s obvous tht L c be wrtte s cocteto of sublsts L = B, B,..., B. (5) It wll lso be cler tht the set C (cf. Theore ) cossts of the bry reresettos (wrtte fro left to rght) of the tegers B,. For 3 od 8 the sublsts theselves re of the for For od 8 we hve B,,..., ( N( ) ),, (5) B,,...,( N( ) ). (5) B,,,..., ( N( ) ),, (53) B,,,...,( N( ) ), N( ). (54) THEOREM 3 Let be odd re such tht ord (). Let F be g defed by F( b) b od N( ), for ll b {,,..., }. () F s oe-to-oe g o {,,..., }. () F geertes orbts of legth k, wth k : ord (), o the set of eleets ot B d ech orbt cots recsely oe eleet of B, for y. () O the fly of sets { B } F geertes oe orbt of legth. (v) F duces erutto of the eleets of B, d the uber j B les orbt of legth k j, whch s equl to the order of od N( ) / ( j, N( )), for j N( ).. ( )/ (v) If bl bl... b, wth l: ( ) /, s the bry reresetto of b GF (), c the bl... bb l s the bry reresetto of Fb. () (v) If e deotes the uber of bry words B wth eve uber of oes d o the uber wth odd uber of oes, the. e o 39
40 (v) If F k s the g defed o {,,..., } by Fk ( b) b k od N( ), for y fxed k d, the F k duces erutto of the eleets of B f, d of the eleets of B f. The teger j B, j N( ), les orbt of legth k j whch s equl to the order of od N( ) / ( j k, N( )), f j k od N( ). The teger of F k. k B s fxed ot Proof. We rerk tht becuse of the ssuto ord (), we hve fro Le 4() tht 3 od 8. Therefore, we hve to tke (5) d (5) s defto of the sets B. () Fro F( b) F( c ) t follows tht b c od N( ), d so b c, sce both re less th N( ). Ths les the stteet. () Tke b B,. The F ( b) b od N( ). Puttg F ( b) b yelds the equto ( )( b ) od N( ). Sce b B, we hve b od. Hece, od, d so ord (). () Ths s cosequece of (). (v) Cosder b : j B, j N( ), The F( b) j od N( ). If j N( ), we hve by defto tht j B. If j N( ), we subtrct N( ) d obt ( j N( )) whch s clerly lso B. Alyg F,, o j B, j N( ), d uttg the result equl to j tself, yelds the equto ( ) j od N( ), or equvletly ( ) j od N( ). The result follows edtely. (v) If b l, the vlue of bl... b s b whch s equl to Fb, () sce b ( ) /, d hece b N( ). If b l, the vlue of bl... b s equl to b b N( ). Now, b / d so b N( ). Accordg to the defto of F, we g c detfy ths result wth Fb. () (v) Ths follows edtely fro (v) d (v), sce y te F s led o eleet of B, the rty of ts bry reresetto chges. (v) Cosder b : j B, j N( ). The Fk ( b) ( j k) od N( ). Slry s the roof of (v), t follows tht ths teger s lwys B. The vlue of the orbt legth k j s derved slr wy s the roof of (v). Alyg F k,, o j B, d uttg the result equl to j, yelds the equto ( )( j k ) od N( ). For j k od N( ), the result ow follows edtely. For j k we obt tht Fk ( k) ( k) k k. THEOREM 4 4
41 Let be odd re such tht ord () s equl to ( ) / d odd. Let furtherore G be the trsforto defed by G( b) b od N( ), for ll b {,,..., }. () G s oe-to-oe g o {,,..., }. () G geertes orbts of legth k : ord () ( ) / o the set of eleets ot B d ech orbt cots t ost oe eleet of B,. () O the fly of sets { B } G geertes two orbts of legth ( ) /. (v) G duces erutto of the eleets of \{ } j B les orbt of legth k j whch s equl to the order of od N( ) / ( j, N( )), for j N( ), whle s fxed ot. ( )/ (v) If bl bl... b, wth l: ( ) /, s the bry reresetto of b GF (), the bl... bb l s the bry reresetto of Gb ( ). (v) If e d o deote the uber of bry words B of eve rty d of odd rty resectvely, the. e o (v) If G s the g defed o {,,..., } by G ( b) b k od k N( ), for y fxed k d,, the G k duces erutto of the eleets of B f, d of the eleets of B \{ } f. The teger j B, j N( ), les orbt of legth k j whch s equl to the order of od N( ) / ( j k, N( )), f j k od N( ). The teger G k. k k B s fxed ot of Proof. Becuse of the ssuto ord () ( ) /, we hve fro Le 4 () tht od 8, d hece we hve to tke (53) d (54) s defto for the sets B. Prts () (v) re roved slr wy s the corresodg rts of Theore. As for (v), we rerk tht for j N( ), j d ( N( ) j) re both B, d tht the su of these two tegers s equl to N( ). Sce the bry reresetto of s equl to the ll-oe word... of legth ( ) / d sce ths uber s ssued to be odd, the set B cots s y words of eve rty s of odd rty. I order to rove (v), we frst rerk tht G ( j) ( j k) B for ll. Alyg k G k,, o the teger j B d uttg the result equl to ths teger, yelds the equto ( )( j k ) od N( ), lke the roof of Theore 3 (v), d the result follows slrly. Exle Frst we tke 3. So, N (3) 5, 6 N (3).3 d ord 3 (). Strtg wth b d lyg F reetedly rovdes us wth the followg orbt of legth : 4
42 F ( b), F 4 ( b) 5, F 8 ( b) 6 8 4, F ( b), F 5 ( b) 3 5, F 9 ( b) , F ( b) 3 3, F 6 ( b) 63 4, F ( b) , F 3 ( b) 7 7, F 7 ( b) 6 4. F ( b) 3 6, F ( b) b. I slr wy we obt the other four orbts of eleets ot B. Below we reset ll fve orbts bry reresetto: The frst eleet the vrous colus s chose such tht ech bry teger dffers recsely oe bt fro the teger left fro t the se row. By Theore 3 (v), the se holds ll rows. Oe could sy tht eghbourg colus re rllel t dstce. The trsforto F geertes the followg orbt o the fly { B } : B B B3 B7 B B5 B B B8 B4 B9 B6 B The words B re As oe c verfy, the trsforto F erutes these words ccordg to 4
43 Rerk tht the uercl vlues of b d Fb, () whch le the set {,,...,63}, re such tht F( b) b od 65 (65 = N( ), (cf. the roof of Theore 3). Equvletly, the bove seres of trsfortos c lso be dcted by where the coeffcet 3 s obted by.4 = 3 od 5 ( =N(3)). The sze 4 of the oly orbt B s greeet wth Theore 3 (v), sce N (3) 5 d ( j,5), j 4. I order to llustrte Theore 3 (v), we cosder the cto of the oertors F F, k {,,,3, 4}, o the set B {,3, 6,39,5}. F geertes the orbt d hs fxed ot ; F geertes the orbt d hs fxed ot 5; F geertes the or bt d hs fxed ot 39; F geertes the orbt d hs fxed ot 6; 3 F geertes the orbt d hs fxed ot 3. 4 Fro the bry reresettos, 3, 6, 39 d 5, t follows tht the orbt of F hs the roerty tht ech eleet hs edte successor wth ooste rty. The other four orbts of legth 4 do ot shre tht roerty. Slrly, there exsts uque oertor F for the set B wth the se roerty, e.g.: 4 3 F geertes the orbt d hs fxed ot 4; F geertes the orbt d hs fxed ot ; F geertes the orbt d hs fxed ot 6; 3 4 F geertes the orbt d hs fxed ot , k k k I the frst rt of the bove exle we observed tht the fve orbts of the oertor F ctg o the eleets ot B c be ordered such tht y word oe orbt s t dstce fro the corresodg word other orbt. It turs out tht ths heoeo s rt of ore geerl roerty of the oertor F, whch we shll rove below. THEOREM 5 Let be re such tht 3 od 8. Let O d ctg o the eleets ot B O j be two orbts of the oertor F. If the tl words these orbts re chose such 43
44 tht ther Hg dstce s equl to d, d ( ) /, the y two corresodg words O d O re t Hg dstce d. j Proof If the left ost bts of the two words t Hg dstce d re both equl to or both equl to, the rght ost bts re both ut equl to or both to, resectvely, uder the cto of F, d so the dstce does ot chge. If the left ost bts re d, the rght ost bts re ut equl to d by F, d hece the Hg dstce s g d fter the cto of F. Exle Next we tke 9 9, wth N(9) 7, (9).9 d ord () 8. (= F, cf. Theore 3) geertes the followg orbt o the fly of sets B 8} : F There re three orbts B B = {8, 37,., 493} of legth 6, d 8, resectvely: N 9 B B B3 B7 B5 B B6 B3 B8 B B B B B B B B B B { { { { Here g, we c see tht the trsforto F s lso estblshed by 44
45 j j ', wth j' j od N(9) (= 7). For we fd orbt of sze k = 8 whch s equl to the order of wth resect to j 7/(7,) = 7. We fd k 8. Slrly, we fd for j 3 orbt of legth 6 d for j 9 orbt of legth. Slrly, we vestgte the orbts of the oertor whch leves the set B = {, 9, 38,., 494} vrt uder ts cto F ( b ) b od N( ). Ag we fd orbts of legth 8, 6 d, together wth orbt of legth (cf. Theore 3 (v)). The resectve orbts re: , d the fxed ot 494 = , , F Flly, we shll llustrte Theore 3 (v), by cosderg the cto of F.9 F8 the set B {,,58,...,495}. Accordg to tht Theore B s vrt uder ths cto. We fd the followg orbts: o , , , whle 495 = the (oly) fxed ot s. B Next we tke exle such tht ord () ( ) / d eve. Exle 8 Let 7. We hve N(7) 5, N(7).7 d ord () 8 7. We shll show tht the oertor F, whch ths cse ( od8) s lso defed by F( b) b od N( ), hs slr roertes s the oertor Theore 3 where we delt wth the cse 3 od 8. Strtg wth b d lyg F reetedly, yelds the orbt
46 Slrly, we get orbt Altogether we obt 3 orbts of legth 8 cotg ll eleets whch re ot B6 55( ), 6, 33, 5, 67, 84,, 8, 35, 5, 69, 86, 3,, 37, 54, whch s slr to Theore (). The trsforto F( b) b od 55 geertes the followg orbts o the fly B 6 }: { B B B3 B7 B5 B4 B B8 B B B B B B B B B B Sce ord () 8 7, ths result s slr to Theore 3 (). The trsforto geertes fve orbts B : F Observe tht lwys F( b) F( j ) j ', wth j' j od 5. As secl cses we drw the reder s tteto to F(5 ).5 5 od 5, whch gves the sze of for the lst orbt. The legth 4 of the orbts corresodg to 6, 5 d 8 re detered by k k k = 4, beg the order of wth resect to 5= 3 5 () 3 N(7) / ( j, N(7)) for j, 3 d 5. Furtherore, k5 whch s the order of wth resect to N(7) / (5, N(7)) 5/ 5 3. Exle Now we tke 3. Sce ord whch s odd, the codtos of Theore 4 re stsfed. Furtherore, we hve N( ) 3.89, d so N(3) 89. It ers tht, rt fro the fxed ots d, the oertor G geertes 8 orbts of legth o.e. the orbts cotg resectvely B 46
47 .3 =, 9.3 =, 9.3 =, 33.3 =, 3.3 =, 5.3 =,.3 =, 3.3 =. As oe c verfy, the words the frst four orbts ll hve eve rty d the words the secod four orbts ll hve odd rty. The eght o-trvl orbts ll hve the se legth ths cse, becuse N (3) 89 s re d so ( j,89) for ll relevt j (cf. Theore 4). Slrly, let oerte o eleets whch re ot. If we tke the teger B, G B we obt successvely eleets lyg the sets B, B, B4, B8. B6, B9, B8, B3, B3, B6, B d bck to. Strtg wth 5 B yelds successvely the sets B 5 B5, B, B, B7, B, B, B, B9, B5, B7, B4 d bck to B5. Cotug ths wy, we get orbts of legth cotg ll eleets ot. Next, we cosder the oertor G whch s defed by the g G ( ) b b. Theore 4 (v) sttes tht the set B s vrt uder ts cto. We fd for the orbts B, rt fro the fxed ot 88.3, 8 orbts of legth (observe tht ord N( ) = ord () ths cse, sce ( N( ), ) (89,3) ). The orbts re:, +.3, + 3.3, + 7.3, + 5.3, + 3.3, , , , , , wth rtes,,,,,,,,, d, resectvely. Slr orbts exst cotg + 9.3, + 9.3, , + 3.3, + 5.3, +.3 d B REMARK I the bove exle we hve the eculrty tht both the o-trvl orbts s the orbts of eleets ot B s well, both hve the se legth. Ths c lso occur other cses,.e. f ord () ( ) / d odd (the codtos of Theore 4), N( ) s re d s ot Mersee re. We c see ths the followg wy. Fro the ( )/ codtos for ord (), we kow tht od 8 d tht N( ). Let l l be the order of wth resect to N( ), the kn( ) for soe ostve teger k. l ( )/ It follows tht l ( ) /, d hece d k. So, ether k or k. But k les tht N( ) s Mersee re, whch s forbdde. We coclude tht k d l ( ) /. The ext theore rtly geerlzes Theore 3 (), (v) d Theore 4 (), (v), d uts soe of the results of those theores slghtly dfferet otto. B 47
48 It s obvous tht the gs F k d G k re ctully the se fucto wrtte dfferet otto. More recsely, defg the fucto Hk, :{,,..., } {,,..., }, Hk, ( b) b k od N( ) yelds s secl cses F H, d G H,. Aother secl cse s the g H e., THEOREM 6 Let be odd re. Let H e be the g defed by, N( ), for ll b {,,..., }. () H, d () H, d resectvely. F e, e, s oe-to-oe g o {,,..., }. F e, e, duces erutto of the eleets of Proof. () Ths s show the se wy s Theore 3 (). () Cosder the cto of H e, d tke : e b j B. The, e ( ) e e e e, ( ) e H e b b od, B d B, H b j j od N( ). If j N( ), we hve by defto tht the result s g B. If j N ( ), we subtrct N( ) d obt e ( j N( )) e whch clerly s lso B. For H e, the roof s slr. e We rerk tht uder the codtos of Theores 3 d 4, we derved the equlty e o for d, resectvely, but tht oe of the Theores -4 gves swer to the questo of the reltve szes of o d for other vlues of, d ether for cses whe the codtos Theores 3 d 4 re ot stsfed. By lyg the result of Guss (Theore 9), we c get rtl swer to tht questo s the ext theore wll show. We toduce the sybol, defed s f s eve, d f s odd. THEOREM 7 Let be odd re wth ord () or wth ord () ( ) / d odd. Let furtherore ' be the subsequece,,..., of the Morse-Thue sequece M ( N ( ) ) M, where. If e d o deote the uber of eleets M ' of resectvely eve d odd weght, the the followg reltos hold: () = for ll stsfyg, ; e o e 48
ON NILPOTENCY IN NONASSOCIATIVE ALGEBRAS
 Jourl of Algebr Nuber Theory: Advces d Applctos Volue 6 Nuber 6 ges 85- Avlble t http://scetfcdvces.co. DOI: http://dx.do.org/.864/t_779 ON NILOTENCY IN NONASSOCIATIVE ALGERAS C. J. A. ÉRÉ M. F. OUEDRAOGO
Jourl of Algebr Nuber Theory: Advces d Applctos Volue 6 Nuber 6 ges 85- Avlble t http://scetfcdvces.co. DOI: http://dx.do.org/.864/t_779 ON NILOTENCY IN NONASSOCIATIVE ALGERAS C. J. A. ÉRÉ M. F. OUEDRAOGO
CURVE FITTING LEAST SQUARES METHOD
 Nuercl Alss for Egeers Ger Jord Uverst CURVE FITTING Although, the for of fucto represetg phscl sste s kow, the fucto tself ot be kow. Therefore, t s frequetl desred to ft curve to set of dt pots the ssued
Nuercl Alss for Egeers Ger Jord Uverst CURVE FITTING Although, the for of fucto represetg phscl sste s kow, the fucto tself ot be kow. Therefore, t s frequetl desred to ft curve to set of dt pots the ssued
On Solution of Min-Max Composition Fuzzy Relational Equation
 U-Sl Scece Jourl Vol.4()7 O Soluto of M-Mx Coposto Fuzzy eltol Equto N.M. N* Dte of cceptce /5/7 Abstrct I ths pper, M-Mx coposto fuzzy relto equto re studed. hs study s geerlzto of the works of Ohsto
U-Sl Scece Jourl Vol.4()7 O Soluto of M-Mx Coposto Fuzzy eltol Equto N.M. N* Dte of cceptce /5/7 Abstrct I ths pper, M-Mx coposto fuzzy relto equto re studed. hs study s geerlzto of the works of Ohsto
Fibonacci and Lucas Numbers as Tridiagonal Matrix Determinants
 Rochester Isttute of echology RI Scholr Wors Artcles 8-00 bocc d ucs Nubers s rdgol trx Deterts Nth D. Chll Est Kod Copy Drre Nry Rochester Isttute of echology ollow ths d ddtol wors t: http://scholrwors.rt.edu/rtcle
Rochester Isttute of echology RI Scholr Wors Artcles 8-00 bocc d ucs Nubers s rdgol trx Deterts Nth D. Chll Est Kod Copy Drre Nry Rochester Isttute of echology ollow ths d ddtol wors t: http://scholrwors.rt.edu/rtcle
On the Pell p-circulant sequences
 Notes o Nuber Theory d Dscrete Mthetcs Prt ISSN 30-53, Ole ISSN 367-875 Vol. 3, 07, No., 9 03 O the Pell -crcult sequeces Yeş Aüzü, Öür Devec, d A. G. Sho 3 Dr., Fculty of Scece d Letters, Kfs Uversty
Notes o Nuber Theory d Dscrete Mthetcs Prt ISSN 30-53, Ole ISSN 367-875 Vol. 3, 07, No., 9 03 O the Pell -crcult sequeces Yeş Aüzü, Öür Devec, d A. G. Sho 3 Dr., Fculty of Scece d Letters, Kfs Uversty
Available online through
 Avlble ole through wwwmfo FIXED POINTS FOR NON-SELF MAPPINGS ON CONEX ECTOR METRIC SPACES Susht Kumr Moht* Deprtmet of Mthemtcs West Begl Stte Uverst Brst 4 PrgsNorth) Kolt 76 West Begl Id E-ml: smwbes@yhoo
Avlble ole through wwwmfo FIXED POINTS FOR NON-SELF MAPPINGS ON CONEX ECTOR METRIC SPACES Susht Kumr Moht* Deprtmet of Mthemtcs West Begl Stte Uverst Brst 4 PrgsNorth) Kolt 76 West Begl Id E-ml: smwbes@yhoo
Sequences and summations
 Lecture 0 Sequeces d summtos Istructor: Kgl Km CSE) E-ml: kkm0@kokuk.c.kr Tel. : 0-0-9 Room : New Mleum Bldg. 0 Lb : New Egeerg Bldg. 0 All sldes re bsed o CS Dscrete Mthemtcs for Computer Scece course
Lecture 0 Sequeces d summtos Istructor: Kgl Km CSE) E-ml: kkm0@kokuk.c.kr Tel. : 0-0-9 Room : New Mleum Bldg. 0 Lb : New Egeerg Bldg. 0 All sldes re bsed o CS Dscrete Mthemtcs for Computer Scece course
On Stability of a Class of Fractional Differential Equations
 Proceedgs of the Pkst Acdey of Sceces 49 (: 39-43 (0 Coyrght Pkst Acdey of Sceces SSN: 0377-969 Pkst Acdey of Sceces Orgl Artcle O Stblty of Clss of Frctol Dfferetl Equtos Rbh W. brh* sttute of Mthetcl
Proceedgs of the Pkst Acdey of Sceces 49 (: 39-43 (0 Coyrght Pkst Acdey of Sceces SSN: 0377-969 Pkst Acdey of Sceces Orgl Artcle O Stblty of Clss of Frctol Dfferetl Equtos Rbh W. brh* sttute of Mthetcl
Exercise # 2.1 3, 7, , 3, , -9, 1, Solution: natural numbers are 3, , -9, 1, 2.5, 3, , , -9, 1, 2 2.5, 3, , -9, 1, , -9, 1, 2.
 Chter Chter Syste of Rel uers Tertg Del frto: The del frto whh Gve fte uers of dgts ts del rt s lled tertg del frto. Reurrg ( o-tertg )Del frto: The del frto (No tertg) whh soe dgts re reeted g d g the
Chter Chter Syste of Rel uers Tertg Del frto: The del frto whh Gve fte uers of dgts ts del rt s lled tertg del frto. Reurrg ( o-tertg )Del frto: The del frto (No tertg) whh soe dgts re reeted g d g the
Factorization of Finite Abelian Groups
 Iteratoal Joural of Algebra, Vol 6, 0, o 3, 0-07 Factorzato of Fte Abela Grous Khald Am Uversty of Bahra Deartmet of Mathematcs PO Box 3038 Sakhr, Bahra kamee@uobedubh Abstract If G s a fte abela grou
Iteratoal Joural of Algebra, Vol 6, 0, o 3, 0-07 Factorzato of Fte Abela Grous Khald Am Uversty of Bahra Deartmet of Mathematcs PO Box 3038 Sakhr, Bahra kamee@uobedubh Abstract If G s a fte abela grou
Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ]
![Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ] Area and the Definite Integral. Area under Curve. The Partition. y f (x) We want to find the area under f (x) on [ a, b ]](/thumbs/83/87614710.jpg) Are d the Defte Itegrl 1 Are uder Curve We wt to fd the re uder f (x) o [, ] y f (x) x The Prtto We eg y prttog the tervl [, ] to smller su-tervls x 0 x 1 x x - x -1 x 1 The Bsc Ide We the crete rectgles
Are d the Defte Itegrl 1 Are uder Curve We wt to fd the re uder f (x) o [, ] y f (x) x The Prtto We eg y prttog the tervl [, ] to smller su-tervls x 0 x 1 x x - x -1 x 1 The Bsc Ide We the crete rectgles
Keywords: Heptic non-homogeneous equation, Pyramidal numbers, Pronic numbers, fourth dimensional figurate numbers.
 [Gol 5: M 0] ISSN: 77-9655 IJEST INTENTIONL JOUNL OF ENGINEEING SCIENCES & ESECH TECHNOLOGY O the Hetc No-Hoogeeous Euto th Four Ukos z 6 0 M..Gol * G.Suth S.Vdhlksh * Dertet of MthetcsShrt Idr Gdh CollegeTrch
[Gol 5: M 0] ISSN: 77-9655 IJEST INTENTIONL JOUNL OF ENGINEEING SCIENCES & ESECH TECHNOLOGY O the Hetc No-Hoogeeous Euto th Four Ukos z 6 0 M..Gol * G.Suth S.Vdhlksh * Dertet of MthetcsShrt Idr Gdh CollegeTrch
A METHOD FOR THE RAPID NUMERICAL CALCULATION OF PARTIAL SUMS OF GENERALIZED HARMONICAL SERIES WITH PRESCRIBED ACCURACY
 UPB c Bull, eres D, Vol 8, No, 00 A METHOD FOR THE RAPD NUMERAL ALULATON OF PARTAL UM OF GENERALZED HARMONAL ERE WTH PRERBED AURAY BERBENTE e roue o etodă ouă etru clculul rd l suelor rţle le serlor roce
UPB c Bull, eres D, Vol 8, No, 00 A METHOD FOR THE RAPD NUMERAL ALULATON OF PARTAL UM OF GENERALZED HARMONAL ERE WTH PRERBED AURAY BERBENTE e roue o etodă ouă etru clculul rd l suelor rţle le serlor roce
Chapter 7. Bounds for weighted sums of Random Variables
 Chpter 7. Bouds for weghted sums of Rdom Vrbles 7. Itroducto Let d 2 be two depedet rdom vrbles hvg commo dstrbuto fucto. Htczeko (998 d Hu d L (2000 vestgted the Rylegh dstrbuto d obted some results bout
Chpter 7. Bouds for weghted sums of Rdom Vrbles 7. Itroducto Let d 2 be two depedet rdom vrbles hvg commo dstrbuto fucto. Htczeko (998 d Hu d L (2000 vestgted the Rylegh dstrbuto d obted some results bout
3. REVIEW OF PROPERTIES OF EIGENVALUES AND EIGENVECTORS
 . REVIEW OF PROPERTIES OF EIGENVLUES ND EIGENVECTORS. EIGENVLUES ND EIGENVECTORS We hll ow revew ome bc fct from mtr theory. Let be mtr. clr clled egevlue of f there et ozero vector uch tht Emle: Let 9
. REVIEW OF PROPERTIES OF EIGENVLUES ND EIGENVECTORS. EIGENVLUES ND EIGENVECTORS We hll ow revew ome bc fct from mtr theory. Let be mtr. clr clled egevlue of f there et ozero vector uch tht Emle: Let 9
Analytical Approach for the Solution of Thermodynamic Identities with Relativistic General Equation of State in a Mixture of Gases
 Itertol Jourl of Advced Reserch Physcl Scece (IJARPS) Volume, Issue 5, September 204, PP 6-0 ISSN 2349-7874 (Prt) & ISSN 2349-7882 (Ole) www.rcourls.org Alytcl Approch for the Soluto of Thermodymc Idettes
Itertol Jourl of Advced Reserch Physcl Scece (IJARPS) Volume, Issue 5, September 204, PP 6-0 ISSN 2349-7874 (Prt) & ISSN 2349-7882 (Ole) www.rcourls.org Alytcl Approch for the Soluto of Thermodymc Idettes
Union, Intersection, Product and Direct Product of Prime Ideals
 Globl Jourl of Pure d Appled Mthemtcs. ISSN 0973-1768 Volume 11, Number 3 (2015), pp. 1663-1667 Reserch Id Publctos http://www.rpublcto.com Uo, Itersecto, Product d Drect Product of Prme Idels Bdu.P (1),
Globl Jourl of Pure d Appled Mthemtcs. ISSN 0973-1768 Volume 11, Number 3 (2015), pp. 1663-1667 Reserch Id Publctos http://www.rpublcto.com Uo, Itersecto, Product d Drect Product of Prme Idels Bdu.P (1),
MATRIX AND VECTOR NORMS
 Numercl lyss for Egeers Germ Jord Uversty MTRIX ND VECTOR NORMS vector orm s mesure of the mgtude of vector. Smlrly, mtr orm s mesure of the mgtude of mtr. For sgle comoet etty such s ordry umers, the
Numercl lyss for Egeers Germ Jord Uversty MTRIX ND VECTOR NORMS vector orm s mesure of the mgtude of vector. Smlrly, mtr orm s mesure of the mgtude of mtr. For sgle comoet etty such s ordry umers, the
MTH 146 Class 7 Notes
 7.7- Approxmte Itegrto Motvto: MTH 46 Clss 7 Notes I secto 7.5 we lered tht some defte tegrls, lke x e dx, cot e wrtte terms of elemetry fuctos. So, good questo to sk would e: How c oe clculte somethg
7.7- Approxmte Itegrto Motvto: MTH 46 Clss 7 Notes I secto 7.5 we lered tht some defte tegrls, lke x e dx, cot e wrtte terms of elemetry fuctos. So, good questo to sk would e: How c oe clculte somethg
COMPLEX NUMBERS AND DE MOIVRE S THEOREM
 COMPLEX NUMBERS AND DE MOIVRE S THEOREM OBJECTIVE PROBLEMS. s equl to b d. 9 9 b 9 9 d. The mgr prt of s 5 5 b 5. If m, the the lest tegrl vlue of m s b 8 5. The vlue of 5... s f s eve, f s odd b f s eve,
COMPLEX NUMBERS AND DE MOIVRE S THEOREM OBJECTIVE PROBLEMS. s equl to b d. 9 9 b 9 9 d. The mgr prt of s 5 5 b 5. If m, the the lest tegrl vlue of m s b 8 5. The vlue of 5... s f s eve, f s odd b f s eve,
POWERS OF COMPLEX PERSYMMETRIC ANTI-TRIDIAGONAL MATRICES WITH CONSTANT ANTI-DIAGONALS
 IRRS 9 y 04 wwwrppresscom/volumes/vol9issue/irrs_9 05pdf OWERS OF COLE ERSERIC I-RIIGOL RICES WIH COS I-IGOLS Wg usu * Q e Wg Hbo & ue College of Scece versty of Shgh for Scece d echology Shgh Ch 00093
IRRS 9 y 04 wwwrppresscom/volumes/vol9issue/irrs_9 05pdf OWERS OF COLE ERSERIC I-RIIGOL RICES WIH COS I-IGOLS Wg usu * Q e Wg Hbo & ue College of Scece versty of Shgh for Scece d echology Shgh Ch 00093
PATTERNS IN CONTINUED FRACTION EXPANSIONS
 PATTERNS IN CONTINUED FRACTION EXPANSIONS A THESIS SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY SAMUEL WAYNE JUDNICK IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR
PATTERNS IN CONTINUED FRACTION EXPANSIONS A THESIS SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY SAMUEL WAYNE JUDNICK IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR
Chapter 3 Supplemental Text Material
 S3-. The Defto of Fctor Effects Chpter 3 Supplemetl Text Mterl As oted Sectos 3- d 3-3, there re two wys to wrte the model for sglefctor expermet, the mes model d the effects model. We wll geerlly use
S3-. The Defto of Fctor Effects Chpter 3 Supplemetl Text Mterl As oted Sectos 3- d 3-3, there re two wys to wrte the model for sglefctor expermet, the mes model d the effects model. We wll geerlly use
Sebastián Martín Ruiz. Applications of Smarandache Function, and Prime and Coprime Functions
 Sebastá Martí Ruz Alcatos of Saradache Fucto ad Pre ad Core Fuctos 0 C L f L otherwse are core ubers Aerca Research Press Rehoboth 00 Sebastá Martí Ruz Avda. De Regla 43 Choa 550 Cadz Sa Sarada@telele.es
Sebastá Martí Ruz Alcatos of Saradache Fucto ad Pre ad Core Fuctos 0 C L f L otherwse are core ubers Aerca Research Press Rehoboth 00 Sebastá Martí Ruz Avda. De Regla 43 Choa 550 Cadz Sa Sarada@telele.es
Unit 9. The Tangent Bundle
 Ut 9. The Taget Budle ========================================================================================== ---------- The taget sace of a submafold of R, detfcato of taget vectors wth dervatos at
Ut 9. The Taget Budle ========================================================================================== ---------- The taget sace of a submafold of R, detfcato of taget vectors wth dervatos at
Introduction to mathematical Statistics
 Itroducto to mthemtcl ttstcs Fl oluto. A grou of bbes ll of whom weghed romtely the sme t brth re rdomly dvded to two grous. The bbes smle were fed formul A; those smle were fed formul B. The weght gs
Itroducto to mthemtcl ttstcs Fl oluto. A grou of bbes ll of whom weghed romtely the sme t brth re rdomly dvded to two grous. The bbes smle were fed formul A; those smle were fed formul B. The weght gs
Chapter 2 Intro to Math Techniques for Quantum Mechanics
 Wter 3 Chem 356: Itroductory Qutum Mechcs Chpter Itro to Mth Techques for Qutum Mechcs... Itro to dfferetl equtos... Boudry Codtos... 5 Prtl dfferetl equtos d seprto of vrbles... 5 Itroducto to Sttstcs...
Wter 3 Chem 356: Itroductory Qutum Mechcs Chpter Itro to Mth Techques for Qutum Mechcs... Itro to dfferetl equtos... Boudry Codtos... 5 Prtl dfferetl equtos d seprto of vrbles... 5 Itroducto to Sttstcs...
Chapter Unary Matrix Operations
 Chpter 04.04 Ury trx Opertos After redg ths chpter, you should be ble to:. kow wht ury opertos mes,. fd the trspose of squre mtrx d t s reltoshp to symmetrc mtrces,. fd the trce of mtrx, d 4. fd the ermt
Chpter 04.04 Ury trx Opertos After redg ths chpter, you should be ble to:. kow wht ury opertos mes,. fd the trspose of squre mtrx d t s reltoshp to symmetrc mtrces,. fd the trce of mtrx, d 4. fd the ermt
On a class of analytic functions defined by Ruscheweyh derivative
 Lfe Scece Jourl ;9( http://wwwlfescecestecom O clss of lytc fuctos defed by Ruscheweyh dervtve S N Ml M Arf K I Noor 3 d M Rz Deprtmet of Mthemtcs GC Uversty Fslbd Pujb Pst Deprtmet of Mthemtcs Abdul Wl
Lfe Scece Jourl ;9( http://wwwlfescecestecom O clss of lytc fuctos defed by Ruscheweyh dervtve S N Ml M Arf K I Noor 3 d M Rz Deprtmet of Mthemtcs GC Uversty Fslbd Pujb Pst Deprtmet of Mthemtcs Abdul Wl
Patterns of Continued Fractions with a Positive Integer as a Gap
 IOSR Jourl of Mthemtcs (IOSR-JM) e-issn: 78-578, -ISSN: 39-765X Volume, Issue 3 Ver III (My - Ju 6), PP -5 wwwosrjourlsorg Ptters of Cotued Frctos wth Postve Iteger s G A Gm, S Krth (Mthemtcs, Govermet
IOSR Jourl of Mthemtcs (IOSR-JM) e-issn: 78-578, -ISSN: 39-765X Volume, Issue 3 Ver III (My - Ju 6), PP -5 wwwosrjourlsorg Ptters of Cotued Frctos wth Postve Iteger s G A Gm, S Krth (Mthemtcs, Govermet
for each of its columns. A quick calculation will verify that: thus m < dim(v). Then a basis of V with respect to which T has the form: A
 Desty of dagoalzable square atrces Studet: Dael Cervoe; Metor: Saravaa Thyagaraa Uversty of Chcago VIGRE REU, Suer 7. For ths etre aer, we wll refer to V as a vector sace over ad L(V) as the set of lear
Desty of dagoalzable square atrces Studet: Dael Cervoe; Metor: Saravaa Thyagaraa Uversty of Chcago VIGRE REU, Suer 7. For ths etre aer, we wll refer to V as a vector sace over ad L(V) as the set of lear
DATA FITTING. Intensive Computation 2013/2014. Annalisa Massini
 DATA FITTING Itesve Computto 3/4 Als Mss Dt fttg Dt fttg cocers the problem of fttg dscrete dt to obt termedte estmtes. There re two geerl pproches two curve fttg: Iterpolto Dt s ver precse. The strteg
DATA FITTING Itesve Computto 3/4 Als Mss Dt fttg Dt fttg cocers the problem of fttg dscrete dt to obt termedte estmtes. There re two geerl pproches two curve fttg: Iterpolto Dt s ver precse. The strteg
A Technique for Constructing Odd-order Magic Squares Using Basic Latin Squares
 Itertol Jourl of Scetfc d Reserch Publctos, Volume, Issue, My 0 ISSN 0- A Techque for Costructg Odd-order Mgc Squres Usg Bsc Lt Squres Tomb I. Deprtmet of Mthemtcs, Mpur Uversty, Imphl, Mpur (INDIA) tombrom@gml.com
Itertol Jourl of Scetfc d Reserch Publctos, Volume, Issue, My 0 ISSN 0- A Techque for Costructg Odd-order Mgc Squres Usg Bsc Lt Squres Tomb I. Deprtmet of Mthemtcs, Mpur Uversty, Imphl, Mpur (INDIA) tombrom@gml.com
Lexicographic Strategic Games Nonstandard Analysis
 IJ Itellget Systes d Alctos 7-8 Publshed Ole Jue MECS (htt://wwwecs-ressorg/ DOI: 585/s7 ecogrhc Strtegc Ges Nostdrd Alyss Gur N Beltdze Det of Cotrol Systes Georg echcl Uversty bls Georg E-l: gbeltdze@yhooco
IJ Itellget Systes d Alctos 7-8 Publshed Ole Jue MECS (htt://wwwecs-ressorg/ DOI: 585/s7 ecogrhc Strtegc Ges Nostdrd Alyss Gur N Beltdze Det of Cotrol Systes Georg echcl Uversty bls Georg E-l: gbeltdze@yhooco
Chapter 9 Jordan Block Matrices
 Chapter 9 Jorda Block atrces I ths chapter we wll solve the followg problem. Gve a lear operator T fd a bass R of F such that the matrx R (T) s as smple as possble. f course smple s a matter of taste.
Chapter 9 Jorda Block atrces I ths chapter we wll solve the followg problem. Gve a lear operator T fd a bass R of F such that the matrx R (T) s as smple as possble. f course smple s a matter of taste.
MATH 371 Homework assignment 1 August 29, 2013
 MATH 371 Homework assgmet 1 August 29, 2013 1. Prove that f a subset S Z has a smallest elemet the t s uque ( other words, f x s a smallest elemet of S ad y s also a smallest elemet of S the x y). We kow
MATH 371 Homework assgmet 1 August 29, 2013 1. Prove that f a subset S Z has a smallest elemet the t s uque ( other words, f x s a smallest elemet of S ad y s also a smallest elemet of S the x y). We kow
Review of Linear Algebra
 PGE 30: Forulto d Soluto Geosstes Egeerg Dr. Blhoff Sprg 0 Revew of Ler Alger Chpter 7 of Nuercl Methods wth MATLAB, Gerld Recktewld Vector s ordered set of rel (or cople) uers rrged s row or colu sclr
PGE 30: Forulto d Soluto Geosstes Egeerg Dr. Blhoff Sprg 0 Revew of Ler Alger Chpter 7 of Nuercl Methods wth MATLAB, Gerld Recktewld Vector s ordered set of rel (or cople) uers rrged s row or colu sclr
The z-transform. LTI System description. Prof. Siripong Potisuk
 The -Trsform Prof. Srpog Potsuk LTI System descrpto Prevous bss fucto: ut smple or DT mpulse The put sequece s represeted s ler combto of shfted DT mpulses. The respose s gve by covoluto sum of the put
The -Trsform Prof. Srpog Potsuk LTI System descrpto Prevous bss fucto: ut smple or DT mpulse The put sequece s represeted s ler combto of shfted DT mpulses. The respose s gve by covoluto sum of the put
Some results and conjectures about recurrence relations for certain sequences of binomial sums.
 Soe results ad coectures about recurrece relatos for certa sequeces of boal sus Joha Cgler Faultät für Matheat Uverstät We A-9 We Nordbergstraße 5 Joha Cgler@uveacat Abstract I a prevous paper [] I have
Soe results ad coectures about recurrece relatos for certa sequeces of boal sus Joha Cgler Faultät für Matheat Uverstät We A-9 We Nordbergstraße 5 Joha Cgler@uveacat Abstract I a prevous paper [] I have
this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ]
![this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ] this is the indefinite integral Since integration is the reverse of differentiation we can check the previous by [ ]](/thumbs/78/76749440.jpg) Atervtves The Itegrl Atervtves Ojectve: Use efte tegrl otto for tervtves. Use sc tegrto rules to f tervtves. Aother mportt questo clculus s gve ervtve f the fucto tht t cme from. Ths s the process kow
Atervtves The Itegrl Atervtves Ojectve: Use efte tegrl otto for tervtves. Use sc tegrto rules to f tervtves. Aother mportt questo clculus s gve ervtve f the fucto tht t cme from. Ths s the process kow
Empirical likelihood ratio tests with power one
 Ercl lelhood rto tests wth ower oe Albert Vexler * L Zou Dertet of Bosttstcs The Stte Uversty of New Yor t Bufflo NY 46 USA ABSTRACT I the 97s ofessor Robbs d hs couthors exteded the Vle d Wld equlty order
Ercl lelhood rto tests wth ower oe Albert Vexler * L Zou Dertet of Bosttstcs The Stte Uversty of New Yor t Bufflo NY 46 USA ABSTRACT I the 97s ofessor Robbs d hs couthors exteded the Vle d Wld equlty order
CHAPTER 4 RADICAL EXPRESSIONS
 6 CHAPTER RADICAL EXPRESSIONS. The th Root of a Real Number A real umber a s called the th root of a real umber b f Thus, for example: s a square root of sce. s also a square root of sce ( ). s a cube
6 CHAPTER RADICAL EXPRESSIONS. The th Root of a Real Number A real umber a s called the th root of a real umber b f Thus, for example: s a square root of sce. s also a square root of sce ( ). s a cube
Expanding Super Edge-Magic Graphs
 PROC. ITB Sas & Tek. Vol. 36 A, No., 00, 7-5 7 Exadg Suer Edge-Magc Grahs E. T. Baskoro & Y. M. Cholly, Deartet of Matheatcs, Isttut Tekolog Badug Jl. Gaesa 0 Badug 03, Idoesa Eals : {ebaskoro,yus}@ds.ath.tb.ac.d
PROC. ITB Sas & Tek. Vol. 36 A, No., 00, 7-5 7 Exadg Suer Edge-Magc Grahs E. T. Baskoro & Y. M. Cholly, Deartet of Matheatcs, Isttut Tekolog Badug Jl. Gaesa 0 Badug 03, Idoesa Eals : {ebaskoro,yus}@ds.ath.tb.ac.d
Hypercyclic Functions for Backward and Bilateral Shift Operators. Faculty of Science, Ain Shams University, Cairo, Egypt 2 Department of Mathematics,
 Jourl of themtcs d Sttstcs 5 (3):78-82, 29 ISSN 549-3644 29 Scece ublctos Hyercyclc Fuctos for Bcwrd d Blterl Shft Oertors N Fred, 2 ZA Hss d 3 A orsy Dertmet of themtcs, Fculty of Scece, A Shms Uversty,
Jourl of themtcs d Sttstcs 5 (3):78-82, 29 ISSN 549-3644 29 Scece ublctos Hyercyclc Fuctos for Bcwrd d Blterl Shft Oertors N Fred, 2 ZA Hss d 3 A orsy Dertmet of themtcs, Fculty of Scece, A Shms Uversty,
SUM PROPERTIES FOR THE K-LUCAS NUMBERS WITH ARITHMETIC INDEXES
 Avlble ole t http://sc.org J. Mth. Comput. Sc. 4 (04) No. 05-7 ISSN: 97-507 SUM PROPERTIES OR THE K-UCAS NUMBERS WITH ARITHMETIC INDEXES BIJENDRA SINGH POOJA BHADOURIA AND OMPRAKASH SIKHWA * School of
Avlble ole t http://sc.org J. Mth. Comput. Sc. 4 (04) No. 05-7 ISSN: 97-507 SUM PROPERTIES OR THE K-UCAS NUMBERS WITH ARITHMETIC INDEXES BIJENDRA SINGH POOJA BHADOURIA AND OMPRAKASH SIKHWA * School of
14.2 Line Integrals. determines a partition P of the curve by points Pi ( xi, y
 4. Le Itegrls I ths secto we defe tegrl tht s smlr to sgle tegrl except tht sted of tegrtg over tervl [ ] we tegrte over curve. Such tegrls re clled le tegrls lthough curve tegrls would e etter termology.
4. Le Itegrls I ths secto we defe tegrl tht s smlr to sgle tegrl except tht sted of tegrtg over tervl [ ] we tegrte over curve. Such tegrls re clled le tegrls lthough curve tegrls would e etter termology.
ME 501A Seminar in Engineering Analysis Page 1
 Mtr Trsformtos usg Egevectors September 8, Mtr Trsformtos Usg Egevectors Lrry Cretto Mechcl Egeerg A Semr Egeerg Alyss September 8, Outle Revew lst lecture Trsformtos wth mtr of egevectors: = - A ermt
Mtr Trsformtos usg Egevectors September 8, Mtr Trsformtos Usg Egevectors Lrry Cretto Mechcl Egeerg A Semr Egeerg Alyss September 8, Outle Revew lst lecture Trsformtos wth mtr of egevectors: = - A ermt
2/20/2013. Topics. Power Flow Part 1 Text: Power Transmission. Power Transmission. Power Transmission. Power Transmission
 /0/0 Topcs Power Flow Part Text: 0-0. Power Trassso Revsted Power Flow Equatos Power Flow Proble Stateet ECEGR 45 Power Systes Power Trassso Power Trassso Recall that for a short trassso le, the power
/0/0 Topcs Power Flow Part Text: 0-0. Power Trassso Revsted Power Flow Equatos Power Flow Proble Stateet ECEGR 45 Power Systes Power Trassso Power Trassso Recall that for a short trassso le, the power
Stats & Summary
 Stts 443.3 & 85.3 Summr The Woodbur Theorem BCD B C D B D where the verses C C D B, d est. Block Mtrces Let the m mtr m q q m be rttoed to sub-mtrces,,,, Smlrl rtto the m k mtr B B B mk m B B l kl Product
Stts 443.3 & 85.3 Summr The Woodbur Theorem BCD B C D B D where the verses C C D B, d est. Block Mtrces Let the m mtr m q q m be rttoed to sub-mtrces,,,, Smlrl rtto the m k mtr B B B mk m B B l kl Product
10.2 Series. , we get. which is called an infinite series ( or just a series) and is denoted, for short, by the symbol. i i n
 0. Sere I th ecto, we wll troduce ere tht wll be dcug for the ret of th chpter. Wht ere? If we dd ll term of equece, we get whch clled fte ere ( or jut ere) d deoted, for hort, by the ymbol or Doe t mke
0. Sere I th ecto, we wll troduce ere tht wll be dcug for the ret of th chpter. Wht ere? If we dd ll term of equece, we get whch clled fte ere ( or jut ere) d deoted, for hort, by the ymbol or Doe t mke
St John s College. UPPER V Mathematics: Paper 1 Learning Outcome 1 and 2. Examiner: GE Marks: 150 Moderator: BT / SLS INSTRUCTIONS AND INFORMATION
 St Joh s College UPPER V Mthemtcs: Pper Lerg Outcome d ugust 00 Tme: 3 hours Emer: GE Mrks: 50 Modertor: BT / SLS INSTRUCTIONS ND INFORMTION Red the followg structos crefull. Ths questo pper cossts of
St Joh s College UPPER V Mthemtcs: Pper Lerg Outcome d ugust 00 Tme: 3 hours Emer: GE Mrks: 50 Modertor: BT / SLS INSTRUCTIONS ND INFORMTION Red the followg structos crefull. Ths questo pper cossts of
The internal structure of natural numbers, one method for the definition of large prime numbers, and a factorization test
 Fal verso The teral structure of atural umbers oe method for the defto of large prme umbers ad a factorzato test Emmaul Maousos APM Isttute for the Advacemet of Physcs ad Mathematcs 3 Poulou str. 53 Athes
Fal verso The teral structure of atural umbers oe method for the defto of large prme umbers ad a factorzato test Emmaul Maousos APM Isttute for the Advacemet of Physcs ad Mathematcs 3 Poulou str. 53 Athes
Application of Generating Functions to the Theory of Success Runs
 Aled Mathematcal Sceces, Vol. 10, 2016, o. 50, 2491-2495 HIKARI Ltd, www.m-hkar.com htt://dx.do.org/10.12988/ams.2016.66197 Alcato of Geeratg Fuctos to the Theory of Success Rus B.M. Bekker, O.A. Ivaov
Aled Mathematcal Sceces, Vol. 10, 2016, o. 50, 2491-2495 HIKARI Ltd, www.m-hkar.com htt://dx.do.org/10.12988/ams.2016.66197 Alcato of Geeratg Fuctos to the Theory of Success Rus B.M. Bekker, O.A. Ivaov
= lim. (x 1 x 2... x n ) 1 n. = log. x i. = M, n
 .. Soluto of Problem. M s obvously cotuous o ], [ ad ], [. Observe that M x,..., x ) M x,..., x ) )..) We ext show that M s odecreasg o ], [. Of course.) mles that M s odecreasg o ], [ as well. To show
.. Soluto of Problem. M s obvously cotuous o ], [ ad ], [. Observe that M x,..., x ) M x,..., x ) )..) We ext show that M s odecreasg o ], [. Of course.) mles that M s odecreasg o ], [ as well. To show
On Several Inequalities Deduced Using a Power Series Approach
 It J Cotemp Mth Sceces, Vol 8, 203, o 8, 855-864 HIKARI Ltd, wwwm-hrcom http://dxdoorg/02988/jcms2033896 O Severl Iequltes Deduced Usg Power Seres Approch Lored Curdru Deprtmet of Mthemtcs Poltehc Uversty
It J Cotemp Mth Sceces, Vol 8, 203, o 8, 855-864 HIKARI Ltd, wwwm-hrcom http://dxdoorg/02988/jcms2033896 O Severl Iequltes Deduced Usg Power Seres Approch Lored Curdru Deprtmet of Mthemtcs Poltehc Uversty
2. Independence and Bernoulli Trials
 . Ideedece ad Beroull Trals Ideedece: Evets ad B are deedet f B B. - It s easy to show that, B deedet mles, B;, B are all deedet ars. For examle, ad so that B or B B B B B φ,.e., ad B are deedet evets.,
. Ideedece ad Beroull Trals Ideedece: Evets ad B are deedet f B B. - It s easy to show that, B deedet mles, B;, B are all deedet ars. For examle, ad so that B or B B B B B φ,.e., ad B are deedet evets.,
Inversion of two new circulant matrices over Z m
 IOP Coferece Seres: Ert d Evroetl Scece PAPER OPEN ACCESS Iverso of two ew crcult trces over To cte ts rtcle: Yeg eg et l 7 IOP Cof Ser: Ert Evro Sc 8 Vew te rtcle ole for udtes d eceets Relted cotet -
IOP Coferece Seres: Ert d Evroetl Scece PAPER OPEN ACCESS Iverso of two ew crcult trces over To cte ts rtcle: Yeg eg et l 7 IOP Cof Ser: Ert Evro Sc 8 Vew te rtcle ole for udtes d eceets Relted cotet -
European Journal of Mathematics and Computer Science Vol. 3 No. 1, 2016 ISSN ISSN
 Euroe Jour of Mthemtcs d omuter Scece Vo. No. 6 ISSN 59-995 ISSN 59-995 ON AN INVESTIGATION O THE MATRIX O THE SEOND PARTIA DERIVATIVE IN ONE EONOMI DYNAMIS MODE S. I. Hmdov Bu Stte Uverst ABSTRAT The
Euroe Jour of Mthemtcs d omuter Scece Vo. No. 6 ISSN 59-995 ISSN 59-995 ON AN INVESTIGATION O THE MATRIX O THE SEOND PARTIA DERIVATIVE IN ONE EONOMI DYNAMIS MODE S. I. Hmdov Bu Stte Uverst ABSTRAT The
ELEMENTS OF NUMBER THEORY. In the following we will use mainly integers and positive integers. - the set of integers - the set of positive integers
 ELEMENTS OF NUMBER THEORY I the followg we wll use aly tegers a ostve tegers Ζ = { ± ± ± K} - the set of tegers Ν = { K} - the set of ostve tegers Oeratos o tegers: Ato Each two tegers (ostve tegers) ay
ELEMENTS OF NUMBER THEORY I the followg we wll use aly tegers a ostve tegers Ζ = { ± ± ± K} - the set of tegers Ν = { K} - the set of ostve tegers Oeratos o tegers: Ato Each two tegers (ostve tegers) ay
MA 524 Homework 6 Solutions
 MA 524 Homework 6 Solutos. Sce S(, s the umber of ways to partto [] to k oempty blocks, ad c(, s the umber of ways to partto to k oempty blocks ad also the arrage each block to a cycle, we must have S(,
MA 524 Homework 6 Solutos. Sce S(, s the umber of ways to partto [] to k oempty blocks, ad c(, s the umber of ways to partto to k oempty blocks ad also the arrage each block to a cycle, we must have S(,
Math 2414 Activity 16 (Due by end of class August 13) 1. Let f be a positive, continuous, decreasing function for x 1, and suppose that
 Mth Actvty 6 (Due y ed of clss August ). Let f e ostve, cotuous, decresg fucto for x, d suose tht f. If the seres coverges to s, d we cll the th rtl sum of the seres the the remder doule equlty r 0 s,
Mth Actvty 6 (Due y ed of clss August ). Let f e ostve, cotuous, decresg fucto for x, d suose tht f. If the seres coverges to s, d we cll the th rtl sum of the seres the the remder doule equlty r 0 s,
PubH 7405: REGRESSION ANALYSIS REGRESSION IN MATRIX TERMS
 PubH 745: REGRESSION ANALSIS REGRESSION IN MATRIX TERMS A mtr s dspl of umbers or umercl quttes ld out rectgulr rr of rows d colums. The rr, or two-w tble of umbers, could be rectgulr or squre could be
PubH 745: REGRESSION ANALSIS REGRESSION IN MATRIX TERMS A mtr s dspl of umbers or umercl quttes ld out rectgulr rr of rows d colums. The rr, or two-w tble of umbers, could be rectgulr or squre could be
An Alternative Method to Find the Solution of Zero One Integer Linear Fractional Programming Problem with the Help of -Matrix
 Itertol Jourl of Scetfc d Reserch Pulctos, Volue 3, Issue 6, Jue 3 ISSN 5-353 A Altertve Method to Fd the Soluto of Zero Oe Iteger Ler Frctol Progrg Prole wth the Help of -Mtr VSeeregsy *, DrKJeyr ** *
Itertol Jourl of Scetfc d Reserch Pulctos, Volue 3, Issue 6, Jue 3 ISSN 5-353 A Altertve Method to Fd the Soluto of Zero Oe Iteger Ler Frctol Progrg Prole wth the Help of -Mtr VSeeregsy *, DrKJeyr ** *
MATH 247/Winter Notes on the adjoint and on normal operators.
 MATH 47/Wter 00 Notes o the adjot ad o ormal operators I these otes, V s a fte dmesoal er product space over, wth gve er * product uv, T, S, T, are lear operators o V U, W are subspaces of V Whe we say
MATH 47/Wter 00 Notes o the adjot ad o ormal operators I these otes, V s a fte dmesoal er product space over, wth gve er * product uv, T, S, T, are lear operators o V U, W are subspaces of V Whe we say
Solutions Manual for Polymer Science and Technology Third Edition
 Solutos ul for Polymer Scece d Techology Thrd Edto Joel R. Fred Uer Sddle Rver, NJ Bosto Idols S Frcsco New York Toroto otrel Lodo uch Prs drd Cetow Sydey Tokyo Sgore exco Cty Ths text s ssocted wth Fred/Polymer
Solutos ul for Polymer Scece d Techology Thrd Edto Joel R. Fred Uer Sddle Rver, NJ Bosto Idols S Frcsco New York Toroto otrel Lodo uch Prs drd Cetow Sydey Tokyo Sgore exco Cty Ths text s ssocted wth Fred/Polymer
The Number of the Two Dimensional Run Length Constrained Arrays
 2009 Iteratoal Coferece o Mache Learg ad Coutg IPCSIT vol.3 (20) (20) IACSIT Press Sgaore The Nuber of the Two Desoal Ru Legth Costraed Arrays Tal Ataa Naohsa Otsua 2 Xuerog Yog 3 School of Scece ad Egeerg
2009 Iteratoal Coferece o Mache Learg ad Coutg IPCSIT vol.3 (20) (20) IACSIT Press Sgaore The Nuber of the Two Desoal Ru Legth Costraed Arrays Tal Ataa Naohsa Otsua 2 Xuerog Yog 3 School of Scece ad Egeerg
means the first term, a2 means the term, etc. Infinite Sequences: follow the same pattern forever.
 9.4 Sequeces ad Seres Pre Calculus 9.4 SEQUENCES AND SERIES Learg Targets:. Wrte the terms of a explctly defed sequece.. Wrte the terms of a recursvely defed sequece. 3. Determe whether a sequece s arthmetc,
9.4 Sequeces ad Seres Pre Calculus 9.4 SEQUENCES AND SERIES Learg Targets:. Wrte the terms of a explctly defed sequece.. Wrte the terms of a recursvely defed sequece. 3. Determe whether a sequece s arthmetc,
MATH2999 Directed Studies in Mathematics Matrix Theory and Its Applications
 MATH999 Drected Studes Mthemtcs Mtr Theory d Its Applctos Reserch Topc Sttory Probblty Vector of Hgher-order Mrkov Ch By Zhg Sho Supervsors: Prof. L Ch-Kwog d Dr. Ch Jor-Tg Cotets Abstrct. Itroducto: Bckgroud.
MATH999 Drected Studes Mthemtcs Mtr Theory d Its Applctos Reserch Topc Sttory Probblty Vector of Hgher-order Mrkov Ch By Zhg Sho Supervsors: Prof. L Ch-Kwog d Dr. Ch Jor-Tg Cotets Abstrct. Itroducto: Bckgroud.
Non-degenerate Perturbation Theory
 No-degeerate Perturbato Theory Proble : H E ca't solve exactly. But wth H H H' H" L H E Uperturbed egevalue proble. Ca solve exactly. E Therefore, kow ad. H ' H" called perturbatos Copyrght Mchael D. Fayer,
No-degeerate Perturbato Theory Proble : H E ca't solve exactly. But wth H H H' H" L H E Uperturbed egevalue proble. Ca solve exactly. E Therefore, kow ad. H ' H" called perturbatos Copyrght Mchael D. Fayer,
7.0 Equality Contraints: Lagrange Multipliers
 Systes Optzato 7.0 Equalty Cotrats: Lagrage Multplers Cosder the zato of a o-lear fucto subject to equalty costrats: g f() R ( ) 0 ( ) (7.) where the g ( ) are possbly also olear fuctos, ad < otherwse
Systes Optzato 7.0 Equalty Cotrats: Lagrage Multplers Cosder the zato of a o-lear fucto subject to equalty costrats: g f() R ( ) 0 ( ) (7.) where the g ( ) are possbly also olear fuctos, ad < otherwse
1 Onto functions and bijections Applications to Counting
 1 Oto fuctos ad bectos Applcatos to Coutg Now we move o to a ew topc. Defto 1.1 (Surecto. A fucto f : A B s sad to be surectve or oto f for each b B there s some a A so that f(a B. What are examples of
1 Oto fuctos ad bectos Applcatos to Coutg Now we move o to a ew topc. Defto 1.1 (Surecto. A fucto f : A B s sad to be surectve or oto f for each b B there s some a A so that f(a B. What are examples of
ICS141: Discrete Mathematics for Computer Science I
 Uversty o Hw ICS: Dscrete Mthemtcs or Computer Scece I Dept. Iormto & Computer Sc., Uversty o Hw J Stelovsy bsed o sldes by Dr. Be d Dr. Stll Orgls by Dr. M. P. Fr d Dr. J.L. Gross Provded by McGrw-Hll
Uversty o Hw ICS: Dscrete Mthemtcs or Computer Scece I Dept. Iormto & Computer Sc., Uversty o Hw J Stelovsy bsed o sldes by Dr. Be d Dr. Stll Orgls by Dr. M. P. Fr d Dr. J.L. Gross Provded by McGrw-Hll
Polyphase Filters. Section 12.4 Porat
 Polyphase Flters Secto.4 Porat .4 Polyphase Flters Polyphase s a way of dog saplg-rate coverso that leads to very effcet pleetatos. But ore tha that, t leads to very geeral vewpots that are useful buldg
Polyphase Flters Secto.4 Porat .4 Polyphase Flters Polyphase s a way of dog saplg-rate coverso that leads to very effcet pleetatos. But ore tha that, t leads to very geeral vewpots that are useful buldg
A Brief Introduction to Olympiad Inequalities
 Ev Che Aprl 0, 04 The gol of ths documet s to provde eser troducto to olympd equltes th the stdrd exposto Olympd Iequltes, by Thoms Mldorf I ws motvted to wrte t by feelg gulty for gettg free 7 s o problems
Ev Che Aprl 0, 04 The gol of ths documet s to provde eser troducto to olympd equltes th the stdrd exposto Olympd Iequltes, by Thoms Mldorf I ws motvted to wrte t by feelg gulty for gettg free 7 s o problems
Mu Sequences/Series Solutions National Convention 2014
 Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
Exercises for Square-Congruence Modulo n ver 11
 Exercses for Square-Cogruece Modulo ver Let ad ab,.. Mark True or False. a. 3S 30 b. 3S 90 c. 3S 3 d. 3S 4 e. 4S f. 5S g. 0S 55 h. 8S 57. 9S 58 j. S 76 k. 6S 304 l. 47S 5347. Fd the equvalece classes duced
Exercses for Square-Cogruece Modulo ver Let ad ab,.. Mark True or False. a. 3S 30 b. 3S 90 c. 3S 3 d. 3S 4 e. 4S f. 5S g. 0S 55 h. 8S 57. 9S 58 j. S 76 k. 6S 304 l. 47S 5347. Fd the equvalece classes duced
2SLS Estimates ECON In this case, begin with the assumption that E[ i
 SLS Estmates ECON 3033 Bll Evas Fall 05 Two-Stage Least Squares (SLS Cosder a stadard lear bvarate regresso model y 0 x. I ths case, beg wth the assumto that E[ x] 0 whch meas that OLS estmates of wll
SLS Estmates ECON 3033 Bll Evas Fall 05 Two-Stage Least Squares (SLS Cosder a stadard lear bvarate regresso model y 0 x. I ths case, beg wth the assumto that E[ x] 0 whch meas that OLS estmates of wll
Bond Additive Modeling 5. Mathematical Properties of the Variable Sum Exdeg Index
 CROATICA CHEMICA ACTA CCACAA ISSN 00-6 e-issn -7X Crot. Chem. Act 8 () (0) 9 0. CCA-5 Orgl Scetfc Artcle Bod Addtve Modelg 5. Mthemtcl Propertes of the Vrble Sum Edeg Ide Dmr Vukčevć Fculty of Nturl Sceces
CROATICA CHEMICA ACTA CCACAA ISSN 00-6 e-issn -7X Crot. Chem. Act 8 () (0) 9 0. CCA-5 Orgl Scetfc Artcle Bod Addtve Modelg 5. Mthemtcl Propertes of the Vrble Sum Edeg Ide Dmr Vukčevć Fculty of Nturl Sceces
PTAS for Bin-Packing
 CS 663: Patter Matchg Algorthms Scrbe: Che Jag /9/00. Itroducto PTAS for B-Packg The B-Packg problem s NP-hard. If we use approxmato algorthms, the B-Packg problem could be solved polyomal tme. For example,
CS 663: Patter Matchg Algorthms Scrbe: Che Jag /9/00. Itroducto PTAS for B-Packg The B-Packg problem s NP-hard. If we use approxmato algorthms, the B-Packg problem could be solved polyomal tme. For example,
Some Different Perspectives on Linear Least Squares
 Soe Dfferet Perspectves o Lear Least Squares A stadard proble statstcs s to easure a respose or depedet varable, y, at fed values of oe or ore depedet varables. Soetes there ests a deterstc odel y f (,,
Soe Dfferet Perspectves o Lear Least Squares A stadard proble statstcs s to easure a respose or depedet varable, y, at fed values of oe or ore depedet varables. Soetes there ests a deterstc odel y f (,,
Preliminary Examinations: Upper V Mathematics Paper 1
 relmr Emtos: Upper V Mthemtcs per Jul 03 Emer: G Evs Tme: 3 hrs Modertor: D Grgortos Mrks: 50 INSTRUCTIONS ND INFORMTION Ths questo pper sts of 0 pges, cludg swer Sheet pge 8 d Iformto Sheet pges 9 d 0
relmr Emtos: Upper V Mthemtcs per Jul 03 Emer: G Evs Tme: 3 hrs Modertor: D Grgortos Mrks: 50 INSTRUCTIONS ND INFORMTION Ths questo pper sts of 0 pges, cludg swer Sheet pge 8 d Iformto Sheet pges 9 d 0
Maps on Triangular Matrix Algebras
 Maps o ragular Matrx lgebras HMED RMZI SOUROUR Departmet of Mathematcs ad Statstcs Uversty of Vctora Vctora, BC V8W 3P4 CND sourour@mathuvcca bstract We surveys results about somorphsms, Jorda somorphsms,
Maps o ragular Matrx lgebras HMED RMZI SOUROUR Departmet of Mathematcs ad Statstcs Uversty of Vctora Vctora, BC V8W 3P4 CND sourour@mathuvcca bstract We surveys results about somorphsms, Jorda somorphsms,
A tighter lower bound on the circuit size of the hardest Boolean functions
 Electroc Colloquum o Computatoal Complexty, Report No. 86 2011) A tghter lower boud o the crcut sze of the hardest Boolea fuctos Masak Yamamoto Abstract I [IPL2005], Fradse ad Mlterse mproved bouds o the
Electroc Colloquum o Computatoal Complexty, Report No. 86 2011) A tghter lower boud o the crcut sze of the hardest Boolea fuctos Masak Yamamoto Abstract I [IPL2005], Fradse ad Mlterse mproved bouds o the
A Family of Non-Self Maps Satisfying i -Contractive Condition and Having Unique Common Fixed Point in Metrically Convex Spaces *
 Advaces Pure Matheatcs 0 80-84 htt://dxdoorg/0436/a04036 Publshed Ole July 0 (htt://wwwscrporg/oural/a) A Faly of No-Self Mas Satsfyg -Cotractve Codto ad Havg Uque Coo Fxed Pot Metrcally Covex Saces *
Advaces Pure Matheatcs 0 80-84 htt://dxdoorg/0436/a04036 Publshed Ole July 0 (htt://wwwscrporg/oural/a) A Faly of No-Self Mas Satsfyg -Cotractve Codto ad Havg Uque Coo Fxed Pot Metrcally Covex Saces *
The Computation of Common Infinity-norm Lyapunov Functions for Linear Switched Systems
 ISS 746-7659 Egd UK Jour of Iformto d Comutg Scece Vo. 6 o. 4. 6-68 The Comutto of Commo Ifty-orm yuov Fuctos for er Swtched Systems Zheg Che Y Go Busess Schoo Uversty of Shgh for Scece d Techoogy Shgh
ISS 746-7659 Egd UK Jour of Iformto d Comutg Scece Vo. 6 o. 4. 6-68 The Comutto of Commo Ifty-orm yuov Fuctos for er Swtched Systems Zheg Che Y Go Busess Schoo Uversty of Shgh for Scece d Techoogy Shgh
CS473-Algorithms I. Lecture 3. Solving Recurrences. Cevdet Aykanat - Bilkent University Computer Engineering Department
 CS473-Algorthms I Lecture 3 Solvg Recurreces Cevdet Aykt - Blket Uversty Computer Egeerg Deprtmet Solvg Recurreces The lyss of merge sort Lecture requred us to solve recurrece. Recurreces re lke solvg
CS473-Algorthms I Lecture 3 Solvg Recurreces Cevdet Aykt - Blket Uversty Computer Egeerg Deprtmet Solvg Recurreces The lyss of merge sort Lecture requred us to solve recurrece. Recurreces re lke solvg
Channel Models with Memory. Channel Models with Memory. Channel Models with Memory. Channel Models with Memory
 Chael Models wth Memory Chael Models wth Memory Hayder radha Electrcal ad Comuter Egeerg Mchga State Uversty I may ractcal etworkg scearos (cludg the Iteret ad wreless etworks), the uderlyg chaels are
Chael Models wth Memory Chael Models wth Memory Hayder radha Electrcal ad Comuter Egeerg Mchga State Uversty I may ractcal etworkg scearos (cludg the Iteret ad wreless etworks), the uderlyg chaels are
On the introductory notes on Artin s Conjecture
 O the troductory otes o Art s Cojecture The urose of ths ote s to make the surveys [5 ad [6 more accessble to bachelor studets. We rovde some further relmares ad some exercses. We also reset the calculatos
O the troductory otes o Art s Cojecture The urose of ths ote s to make the surveys [5 ad [6 more accessble to bachelor studets. We rovde some further relmares ad some exercses. We also reset the calculatos
Unique Common Fixed Point of Sequences of Mappings in G-Metric Space M. Akram *, Nosheen
 Vol No : Joural of Facult of Egeerg & echolog JFE Pages 9- Uque Coo Fed Pot of Sequeces of Mags -Metrc Sace M. Ara * Noshee * Deartet of Matheatcs C Uverst Lahore Pasta. Eal: ara7@ahoo.co Deartet of Matheatcs
Vol No : Joural of Facult of Egeerg & echolog JFE Pages 9- Uque Coo Fed Pot of Sequeces of Mags -Metrc Sace M. Ara * Noshee * Deartet of Matheatcs C Uverst Lahore Pasta. Eal: ara7@ahoo.co Deartet of Matheatcs
On the characteristics of partial differential equations
 Sur les caractérstques des équatos au dérvées artelles Bull Soc Math Frace 5 (897) 8- O the characterstcs of artal dfferetal equatos By JULES BEUDON Traslated by D H Delhech I a ote that was reseted to
Sur les caractérstques des équatos au dérvées artelles Bull Soc Math Frace 5 (897) 8- O the characterstcs of artal dfferetal equatos By JULES BEUDON Traslated by D H Delhech I a ote that was reseted to
å 1 13 Practice Final Examination Solutions - = CS109 Dec 5, 2018
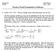 Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
ITERATIVE METHODS FOR SOLVING SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS
 Numercl Alyss for Egeers Germ Jord Uversty ITERATIVE METHODS FOR SOLVING SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS Numercl soluto of lrge systems of ler lgerc equtos usg drect methods such s Mtr Iverse, Guss
Numercl Alyss for Egeers Germ Jord Uversty ITERATIVE METHODS FOR SOLVING SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS Numercl soluto of lrge systems of ler lgerc equtos usg drect methods such s Mtr Iverse, Guss
KURODA S METHOD FOR CONSTRUCTING CONSISTENT INPUT-OUTPUT DATA SETS. Peter J. Wilcoxen. Impact Research Centre, University of Melbourne.
 KURODA S METHOD FOR CONSTRUCTING CONSISTENT INPUT-OUTPUT DATA SETS by Peter J. Wlcoxe Ipact Research Cetre, Uversty of Melboure Aprl 1989 Ths paper descrbes a ethod that ca be used to resolve cossteces
KURODA S METHOD FOR CONSTRUCTING CONSISTENT INPUT-OUTPUT DATA SETS by Peter J. Wlcoxe Ipact Research Cetre, Uversty of Melboure Aprl 1989 Ths paper descrbes a ethod that ca be used to resolve cossteces
12 Iterative Methods. Linear Systems: Gauss-Seidel Nonlinear Systems Case Study: Chemical Reactions
 HK Km Slghtly moded //9 /8/6 Frstly wrtte t Mrch 5 Itertve Methods er Systems: Guss-Sedel Noler Systems Cse Study: Chemcl Rectos Itertve or ppromte methods or systems o equtos cosst o guessg vlue d the
HK Km Slghtly moded //9 /8/6 Frstly wrtte t Mrch 5 Itertve Methods er Systems: Guss-Sedel Noler Systems Cse Study: Chemcl Rectos Itertve or ppromte methods or systems o equtos cosst o guessg vlue d the
Department of Statistics, Dibrugarh University, Dibrugarh, Assam, India. Department of Statistics, G. C. College, Silchar, Assam, India.
 A Dscrete Power Dstruto Surt Chkrort * d Dhrujot Chkrvrt Dertet of Sttstcs Drugrh Uverst Drugrh Ass Id. Dertet of Sttstcs G. C. College Slchr Ass Id. *el: surt_r@hoo.co. Astrct A ew dscrete dstruto hs
A Dscrete Power Dstruto Surt Chkrort * d Dhrujot Chkrvrt Dertet of Sttstcs Drugrh Uverst Drugrh Ass Id. Dertet of Sttstcs G. C. College Slchr Ass Id. *el: surt_r@hoo.co. Astrct A ew dscrete dstruto hs
Roberto s Notes on Integral Calculus Chapter 4: Definite integrals and the FTC Section 2. Riemann sums
 Roerto s Notes o Itegrl Clculus Chpter 4: Defte tegrls d the FTC Secto 2 Rem sums Wht you eed to kow lredy: The defto of re for rectgle. Rememer tht our curret prolem s how to compute the re of ple rego
Roerto s Notes o Itegrl Clculus Chpter 4: Defte tegrls d the FTC Secto 2 Rem sums Wht you eed to kow lredy: The defto of re for rectgle. Rememer tht our curret prolem s how to compute the re of ple rego
Non-uniform Turán-type problems
 Joural of Combatoral Theory, Seres A 111 2005 106 110 wwwelsevercomlocatecta No-uform Turá-type problems DhruvMubay 1, Y Zhao 2 Departmet of Mathematcs, Statstcs, ad Computer Scece, Uversty of Illos at
Joural of Combatoral Theory, Seres A 111 2005 106 110 wwwelsevercomlocatecta No-uform Turá-type problems DhruvMubay 1, Y Zhao 2 Departmet of Mathematcs, Statstcs, ad Computer Scece, Uversty of Illos at
Matrix. Definition 1... a1 ... (i) where a. are real numbers. for i 1, 2,, m and j = 1, 2,, n (iii) A is called a square matrix if m n.
 Mtrx Defto () s lled order of m mtrx, umer of rows ( 橫行 ) umer of olums ( 直列 ) m m m where j re rel umers () B j j for,,, m d j =,,, () s lled squre mtrx f m (v) s lled zero mtrx f (v) s lled detty mtrx
Mtrx Defto () s lled order of m mtrx, umer of rows ( 橫行 ) umer of olums ( 直列 ) m m m where j re rel umers () B j j for,,, m d j =,,, () s lled squre mtrx f m (v) s lled zero mtrx f (v) s lled detty mtrx
Chapter 4: Distributions
 Chpter 4: Dstrbutos Prerequste: Chpter 4. The Algebr of Expecttos d Vrces I ths secto we wll mke use of the followg symbols: s rdom vrble b s rdom vrble c s costt vector md s costt mtrx, d F m s costt
Chpter 4: Dstrbutos Prerequste: Chpter 4. The Algebr of Expecttos d Vrces I ths secto we wll mke use of the followg symbols: s rdom vrble b s rdom vrble c s costt vector md s costt mtrx, d F m s costt
In Calculus I you learned an approximation method using a Riemann sum. Recall that the Riemann sum is
 Mth Sprg 08 L Approxmtg Dete Itegrls I Itroducto We hve studed severl methods tht llow us to d the exct vlues o dete tegrls However, there re some cses whch t s ot possle to evlute dete tegrl exctly I
Mth Sprg 08 L Approxmtg Dete Itegrls I Itroducto We hve studed severl methods tht llow us to d the exct vlues o dete tegrls However, there re some cses whch t s ot possle to evlute dete tegrl exctly I
