Encoding of Pointers for Hardware Synthesis
|
|
|
- Alyson Cannon
- 5 years ago
- Views:
Transcription
1 Enong of Ponters for Hrwre Synthess Lu Sémér Govnn De Mhel Computer System Lortory, Stnfor Unversty Stnfor, CA 9405 ABSTRACT In the reent pst, susets of C n C++ hve een efne to moel n synthesze eletron systems s well s reusle IP loks. In orer to synthesze s muh s possle of the C syntx, we hve een reserhng the prolem of syntheszng n optmzng oe wth ponters. In ths pper, we fous on enong the ponters vlues to mnmze the sze of the ruts mplementng the ress trnsltons. After efnng the enong prolem, we present soluton se on heursts n grph-emeng tehnques. The lgorthm hs een ntegrte n our SpC flow whh syntheszes C oe wth ponters. 1. INTRODUCTION 1.1 Synthess from C For yers, esgners hve een wrtng system-level moels usng progrmmng lnguges, suh s C n C++, to estmte the system performne n verfy the funtonl orretness of the esgn. However, to mplement prts of ther esgn n hrwre usng synthess tools, they must mnully trnslte ther oe nto syntheszle suset of hrwre esrpton lnguge (HDL). Ths proess s oth tme onsumng n errorprone. The use of C or suset of C to esre oth hrwre n softwre woul elerte the esgn proess n fltte the softwre/hrwre mgrton. Desgners oul esre ther system n IP omponents usng C. C-se omponent moelng woul mprove esgn reuse n retrgetng to hrwre n softwre mplementtons. However, the tsks of syntheszng hrwre from C turns out to e prtulrly omplte euse of ynm memory lloton, funton ll, reurson, type stng n ponters. In our reserh, we hve een fousng on the prolem of syntheszng oe wth ponters. 1.2 Synthess of Ponters The prolem of syntheszng ponters hs een lrey ntroue n [1] n [6]. The e n [1] s to use ponter nlyss to efne the pont-to set (sets of vrles the ponter my pont to) of eh ponter n the progrm. Then the los (...=*p) n stores (*p=...) n e reple y se sttements n whh the vrles of the pont-to set re expltly referene. Furthermore, to reue the sze of the eoer ssote wth these se sttements n to mnmze the numer of regster use, the vlues of the ponters re enoe. For ponter p, we ll ts enoe vlue ts tg, note p_tg. Exmple 1. Let us onser ponter p tht my pont to the vrles or (result of the ponter nlyss). Conser the followng lne of oe whh mplements lo: out=*p; Ths lo nstruton n e reple y se sttement: swth(p_tg) { se 0: out=; rek; se 1: out=; rek; However, fter enong the ponters vlues n the fnl hrwre mplementton, some omntonl rut my e neee to trnslte the vlues of the ponters nvolve n ssgnments or omprsons. Exmple 2. Conser the ssgnment p=q, where the ponters p n q my pont to or. For p, (resp. ) s ssote wth the vlue 0 (resp. 1), wheres for q, (resp. ) s ssote wth 1 (resp. 0). After enong, the ssgnment p=q s reple y the followng oe segment: swth(q_tg) { se 0: p_tg = 1; rek; se 1: p_tg = 0; rek; In ths se, etter enong n e foun y hvng the sme enong for oth p n q. Then p=q woul retly e reple y p_tg=q_tg. To mnmze the orresponng omntonl rut, the oes hve to e equl or sufel of one nother. Ths pper presents soluton for the enong of ponters vlues. In Seton 2, we re gong to formulte the prolem. In orer to reue the omplexty, we show n Seton how the enong prolem n e smplfe n solve usng grph-emeng tehnques. In Setons 4 n 5, we present two optmzton tehnques lle folng n splttng. The lgorthm s then esre n Seton 6. Fnlly, n Seton 7, we show how the enong of ponters hs een ntegrte n our tool for the synthess of ponters n C (SpC) n present some results. 2. ENCODING OF POINTER 2.1 Defnton of the Prolem Defnton 1. We efne ponter-epenene grph s grph n whh the noes re the ponters n the eges re the reltons etween the ponters. An ege etween two noes s efne when the two orresponng ponters re ssgne or ompre.
2 Exmple. Conser the followng oe segment: nt *, *, *, *q1, *q2;... f(==0) { =&; =&; =&; else { =&; =&; =&; f(j==0) { q1=; q2=; else { q1=; q2=;... In ths exmple, we onser the ponters {,,, q1, q2 n the vrles {,,,. The ponters re efne s follows: my pont to the vrles or, my pont to the or n my pont to or. Then, q1 my tke the vlue of or n q2 my tke the vlue of or. Consequently, q1 ponts to, or, n q2 ponts to, or. Ths les to the ponter-epenene grph on Fgure 1. {, {, {, q1 {,, q1 q2 q2 {,, Fgure 1: exmple of ponter-epenene grph Our gol s to enoe eh ponter wth the mnmum numer of ts. An, when ponter s ssgne or ompre to nother ponter, we wnt the orresponng tgs to e equl (e.g. p_tg=q_tg) or s lose s possle to eh other. If two tgs hve fferent numer of ts, one tg n e equl to sufel of the other. Assgnments woul then e performe y ontentng or removng ts, wheres omprsons woul only e exeute on the ts ommon to the two oes. Ths reues the sze of the rut tht trnsltes or ompres the tgs whle keepng the numer of ts to mnmum. The enong prolem n e formulte s follows. For eh ponter we efne set of symols orresponng to the vrles the ponter my pont to. As result we hve n ensemle of sets of symols n the epenenes mong the sets. The prolem onssts of enong the symols n the sets. The onstrnts on the enong re two: 1) the superue 1 of the symols n eh set must hve mnmum sze; 2) the symols tht orrespon to the sme vrle n two epenent sets must e enoe s lose s possle. The reson for the frst onstrnt s to mnmze the numer of ts to store, whle the reson for the seon one s to reue the sze of the omntonl rut mplementng the ponter ssgnment n omprson. Exmple 4. In Exmple, the ponters, n my pont to two fferent vrles n q1, q2 my pont to three fferent vrles. We wnt to oe, n on 1 t n q1, q2 on 2 ts. Then we wnt the oe of n to e sufels of the oe of q1 n the oe of n to e sufels of the oe of q2. An enong verfyng these propertes s shown on Fgure Fgure 2: exmple of enong 1. The superue of set of ues s the smllest ue ontnng ll the ues n the set [8]. q1,q2 For, vlue 0 s ssgne to n vlue 1 to. For, 1 wll e ssgne to n 0 to. As result, q1= wll e reple y q1_tg={_tg,0 n q1= wll e reple y q1_tg={0,_tg (where {, s the ontenton opertor). 2.2 Prolem Formulton Let s efne P ponters { p 1, p 2,, p P. We efne the ponter epenene relton s follows. For two ponters, p n p j, r( p, p j ) = 1 f n only f the two ponters re ssgne or ompre, r( p, p j ) = 0 otherwse. For eh ponter p we efne ts pont-to set Π to e the set of vrles the ponter my pont to. The pont-to set Π s set of N symols { s 1, s 2,, s N, where eh symol s ssote wth vrle. After enong, we efne E, the set of the enoe symols of the pont-to set Π. The enoe vlues of the symols n eh set re note { e 1, e 2,, e N. Defnton 2. Two sets Π n Π j re s to e epenent f ther ssote ponters re ssgne or ompre (.e. r( p, p j ) = 1 ). Our frst gol s to mnmze the numer of regsters s well s the sze of the eoers requre to store n eoe the ponters vlues. We wnt the mnmze the menson of the superue of the enoe symols n eh set. Ths mnmum s heve when the sum of the mensons of the superues s lso mnmze: P mn m( superue( E )) (1) = 1 When two ponters re ssgne or ompre, we lso wnt to mnmze the sze of the rut mplementng the trnslton of the oes. For ths purpose, the stne etween enoe symols n two epenent sets hs to e mnmum: P P mn r( p, p j )st( E, E j ) (2) = 1 j = 1 where st( ) s the stne etween the two enoe sets. When the ponters hve the sme pont-to set, st( ) s efne s: N j st( E, E j ) = H( e k, e k ) () k = 1 where N s the numer of symols n the pont-to set n j H( e k, e k ) s the Hmmng stne etween the oes of the j symols s k = s k. In generl, the szes of the oes n the pont-to sets my ffer. The omputton of the stne s then more omplex: we hve to onser the fferent sufels n the symols ssote wth the sme vrles n the two sets. Our gol s to mnmze Eq. 1 n Eq. 2. There s tre-off etween the storge re (numer of regsters) n the mount of log use to trnslte the oes. For exmple, one my optmze the sze of the ponters keepng the mount of log mnmum y mnmzng frst Eq. 2 n then Eq. 1. In generl, we n st the prolem s follows: P P P mn β m( sup. ( E )) + γ r( p, p j )st( E, E j ) (4) = 1 = 1 j = 1 where β n γ re two oeffents.
3 Sne ths prolem s omputtonlly hr to solve usng ext methos, we hve een lookng t heursts for solvng the enong of ponters.. SIMPLIFIED PROBLEM.1 Formlsm for Glol Soluton In the generl formulton of the prolem presente n Seton 2, fferent oes my e ssote wth the symols n eh set. Therefore the enong hs to e foun lolly, n eh set. The prolem n e smplfe y onstrnng ll symols ssote wth the sme vrle to shre the sme oe. Eq. 2 s then rrelevnt euse the stne etween the oes of the symols tht orrespon to the sme vrle n the fferent pont-to sets s null (.e. st( E, E j ) = 0 (, j) { 1, 2,..., P 2 ). Our gol eomes to mnmze Eq. 1 only. The enong s then foun glolly for ll the symols whh orrespon to the sme vrle n the sets. We re now onserng the symols (.e. vrles) n the unon Π of the pont-to sets. These symols wll e enote: Π = { s 1, s 2,, s N. The omplexty s reue: nste of elng wth O(P*N) symols { s j suh tht { 1, 2,..., P n j { 1, 2,..., N we only el wth N symols { s 1, s 2,, s N, where N s the numer of vrles. We ntroue now formlsm whh hs een use to solve other enong prolems [8], [7], [14]. Defnton. The relton mtrx A s efne s the mtrx n whh the rows represent the pont-to sets n the olumns the symols. The entry, j of A s 1 f n only f the symol s j s n the set Π. Exmple 5. Let s tke the se of Exmple. We n onstrut the followng relton mtrx: q1 q2 For exmple, the frst row of the mtrx shows tht my pont to or. We re lookng for n enong mtrx E, tht stsfes the enong onstrnts represente y A. The onstrnts expresse y the relton mtrx A s the followng. Eh row n A orrespons to pont-to set. For eh row α of A, we wnt the superues of the rows of E orresponng to the 1s n α to hve mnmum sze. Ths orrespons to the onstrnt expresse n Eq. 1. Ths prolem ffers from the nput enong prolem [8]. The relton mtrx s not nry onstrnt mtrx, s efne for the generl enong prolem [8], n the sense tht we on t hve the tonl onstrnt tht, for eh row α of the onstrnt mtrx, the superue of the rows of E orresponng to the 1s n α oes not nterset ny of the rows of E orresponng to the 0s n α. The 0s n the relton mtrx n then e onsere s on t re n the onstrnt mtrx..2 Generl Enong Algorthm The prolem of nput enong hs een extensvely stue ([1] [4] [7] [9] [10] [11] [12] [14]). We use n pproh remnsent of MUSTANG [9] n POW [1]. Defnton 4. An ffnty grph s n unrete weghte grph n whh the noes re the symols Π = { s 1, s 2,, s N n the eges re the reltons etween the symols n Π. The weght w, j on the ege { s, s j s efne s: P w, j = k, ( 1 + k, j Log 2 N Log 2 N k ) (5) k = 1 where P s the numer of ponters, N s the totl numer of symols, N k the numer of symols n the set Π k, n, j s n element of the relton mtrx. The weght w, j n the ffnty grph nreses wth the numer of sets tht ontn oth s n s j : when two vrles re n mny pont-to sets, we wnt ther oe to e lose. Ths s even more mportnt for smll pont-to sets. For exmple, f we hve N k = 2 symols n the pont-to set Π k, ther oe must e next to eh other to mnmze the menson of the superue of the enoe set E k, wheres f we hve N k = 10 symols n the pont-to set Π k, the Hmmng stne etween the enong of the symols n the pont-to set n e s muh s Log 2 ( N k ) = 4. Therefore, the weght w, j s the sum of the ontrutons of the pont-to sets tht ontn oth s n s j, where the ontruton of eh pont-to set Π k s ( 1 + Log 2 N Log 2 N k ). The ponter enong prolem n e solve s n emeng of the ffnty grph n the Boolen hyperspe s one n [10],[9],[1]. Exmple 6. The relton mtrx presente n Exmple 5 n e use to generte the ffnty grph on Fgure Fgure : Exmple of Affnty Grph Let s look t w, the weght on the ege {,. The vrles n re oth n the pont-to sets of n q1. The weght w, s, sum of 2, ontruton from, n 1, ontruton from q1. After grph-emeng, the enong presente n Fgure 2 n e foun. These lgorthms however o not onser the ft tht two symols n shre the sme oe. We re gong to use ths property n Seton 4 for tehnque lle folng. One symol n lso hve multple oes. The noton of splttng presente n Seton 5 wll e se on ths property. 4. ENCODING WITH FOLDING Defnton 5. We efne s folng the ton of ssgnng the sme oe to two symols. Proposton 1. Two symols n e fole f n only f they re not oth n the sme pont-to set n not n two epenent pontto sets. The rtonle for ths proposton s tht we wnt to stngush eh symol nse pont-to set n, n the se of omprson, we wnt to stngush the symols n the two epenent pont-to sets. In the relton mtrx A, folng the symols s n s j s equvlent to replng the olumns n j y one olumn k suh tht: k, l =, l jl, for l n {1, 2,..., N. (6)
4 In the ffnty grph, folng s one y mergng (or fusng 1 ) the noes orresponng to the symols s, s j nto one new noe orresponng to s k. The weghts on the eges nent to ths new noe orresponng to s k re then efne s: w k, l = w, l + w jl, for l n {1, 2,..., N. (7) Grph-emeng tehnques n e mofe to norporte folng. In Seton 6, we present olumn-se metho wth folng. Exmple 7. Let s onser the ponter-epenene grph on Fgure 4 where,, n pont respetvely to {,,, {,, n {,,e. The relton mtrx n the ssote ffnty grph re represente n Fgure 5. {,, {,, {,,e q1 {,,, q1 q2 q2 {,,,e Fgure 4: Ponter-epenene grph e q q2 Fgure 5: Enong prolem efore folng The numer of vrles n eh pont-to set s ether (for,, n ) or 4 (for q1 n q2). Therefore, we wnt to oe the symols ssote wth the vrles on 2 ts. However, sne we hve 5 symols, n enong wth less thn ts nnot e foun wthout folng. The symol s n the pont-to set of n q1, wheres the symol e s the pont-to set of n q2. Aorng to the ponter-epenene grph, these pont-to sets re not epenent. The symols ssote wth n e n e fole. After folng we en up wth the grph on Fgure 6. e q1 q2,e Fgure 6: Enong prolem fter folng n e Ths les to n enong tht requres only two ts: 00,, 01 q1,q e 00,e Fgure 7: Result of the enong fter folng n e 1. A pr of vertes, n grph re s to e fuse (merge or entfe) f the two vertes re reple y sngle vertex suh tht every ege tht ws nent on ether or or on oth s nent on the new vertex [2] e 5. SPLITTING TECHNIQUE Defnton 6. We efne s splttng the ton of ssgnng two or more oes to one vrle (or symol). In Seton n 4, eh vrle ws ssote wth unque symol tht ws enoe. After splttng, one vrle my e ssote wth more thn one symol: splttng symol s s equvlent to retng new symol s ' whh orrespons to the sme vrle. The orgnl symol s n the newly rete s ' re then enoe nto e n e ' respetvely. Proposton 2. A pont-to set Π k tht ontns symol s my, fter splttng s, ontn the newly rete symol s ' f n only f there s no oe equl to e ' n the enoe set E k or n ny enoe set epene of Π k. As esre n Seton 2.2 the symols n eh set n hve fferent oes. Therefore, to mnmze the menson of the superue of the enoe symols n set (.e. Eq. 1), we n rete new symols ssote wth the sme vrles, for ths set. Note tht, f we splt the symols for eh pont-to set, we en up wth lol enong sheme s presente n Seton 2.2. However, to lmt the nrese n omplexty, we re tryng to splt s few symols s possle. In the relton mtrx A, splttng s one y ng olumn ' reltve to s '. For eh row α reltve to the pont-to set ' k Π k, the entry k n e set to 1 f Proposton 2 s verfe. The pont-to set Π k my then ontn s, s ' or oth s n s '. In orer to mnmze Eq. 1, for set tht my ontn s or s ', the followng expresson my e onsere: mn( m( superue( ( E k { e ) E' ))) (8) E' where E' s ether { e, { e ' or { e, e '. For exmple, f Eq. 8 s mnmum for E' = { e ', the menson of the superue of the enoe symols n the pontto set Π k s mnmum when k s set to 0 n k s set to 1. ' The new ffnty grph n then e reompute from the relton mtrx. Splttng s well s folng n e norporte n our grph-emeng lgorthm s presente n Seton 6. Exmple 8. Let s onser the ponter-epenene grph on Fgure 8 where, n my respetvely pont to {,, {, n {,. {, {, q {, q {,, A = q Fgure 8: enong prolem efore splttng We woul lke to enoe, n wth 1 t n q wth 2 ts. We lso wnt the oes of, n to e sufels of the oe of q. Usng the enong tehnque wthout splttng symols, we n fn the enong on Fgure 9. In ths se n re enoe on 1 t ut the enong of requres 2 ts.
5 00 q, Fgure 9: enong wthout splttng After splttng the symol, we en up wth the two symols n. We n fn the enong on Fgure 10 where the symol s n the pont-to set of, n q n n the pont-to set of n q. A = ' The enong n Fgure 10 s optml:, n re enoe on 1 t n the ssgnments to q (q=, q=, q=) on t requre ny tonl log. 6. ALGORITHM q q 11 Fgure 10: result fter splttng symol We propose olumn-se pproh (whh mens tht the enong mtrx n e foun olumn y olumn []). Our lgorthm wthout folng n splttng s smlr to the one use n [1]. A pseuo oe of the lgorthm wth folng n splttng s presente on Fgure 11. We onser one t of the oe t the tme. For symol s k ssote wth the oe e, we onser the ts e for k={1, 2,..., n where n s typlly n = log. At eh terton k, we onstrut the k th 2 ( N ) olumn of the enong mtrx E: the vlue k of e (0 or 1) s ssgne n wy tht mnmzes the stne etween the enoe symol e n ts neghors n the ffnty grph. The ssgnment s one for the symols on every ege strtng wth the eges wth hghest weghts. For the symols nent to the eges { s, s, we re tryng to ssgn the sme vlue j to oth e n e j. However, f the symols s n s jw re lso nent to other eges whose weghts re hgher thn, the, j vlues of e n e j my lrey e ssgne to fferent vlues. Moreover, t eh terton of k, the numer of symols hvng the sme oe s lso lmte. Defnton 7. An ege { s, s s s to e volte t terton k j f the vlues e n e j ssote wth the two symols nent to the ege, hve fferent vlues. Defnton 8. A lss volton s efne t terton k, when more thn 2 n k symols hve the sme oe so fr. (At terton k, we re only onserng the k frst ts of the oes, sne the other ones hven t een ssgne yet). The rtonle for efnng lss volton s tht we ultmtely wnt to stngush ll the symols. Therefore, n our greey lgorthm, we hve to mke sure tht, t eh terton of k, we hve less thn 2 n k symols ssote wth the sme oe. For exmple for k=(n-1), we nnot hve more thn 2 symols wth the sme oe. Proposton. An ege { s, s j s volte t terton k f ether one of the followng ontons pples: there s lss volton (n therefore, e n e j nee to hve fferent vlues), the vlues e n e j ssote wth the two symols nent to the ege hve lrey een ssgne to fferent vlues (y Defnton 7). In the se of lss volton, we try to fol one of the symols on the ege { s, s j wth ny of the prevously ssgne symols. At ths stge, two symols re fole f Proposton 1 s verfe n f they hve the sme prtl oe so fr. In the se when fferent vlues hve een ssgne to the two symols s, s j (.e. e e j ), we try to splt the symols on the ege. One symol n e splt f the newly rete symol oes use ny lss volton or n e fole wth nother symol. In our lgorthm, for symol s, we rete new symol l l s ' ssote wth oe e ' suh tht e' = e for l>k n e' = e j. In se of lss volton, we try to fol ths new symol s one prevously. If folng nnot e one, the symol s not splt. enoe ponter() { /* onstrut mtrx E one olumn t tme */ for k=1 to n ssgn_oe(k); ssgn_oe(k) { sort eges y weght n eresng orer; foreh ege { s, s j { f( e n e j not ssgne) { e = e j = selet_t( s, s j ); f(lss volton) { try_fol( s ); try_fol( s j ); f( s or s j not ssgne) { s h =unssgne( s, s j ); s l =ssgne( s, s j ); e h = e l ; f(no lss volton) { try_fol( s ); try_fol( s j ); else /* s n s ssgne */ j f( e h!= e l ) volte_eges->({ s, s j ) sort volte eges y weght n eresng orer; foreh volte ege { s, s j { try_splt( s ); try_splt( s j ); try_splt( s ) { rete s ' e ' = e xor(1<<k); f(lss volton) try_fol( s ' ); try_fol( s ) { f( s j s.t. Proposton 1 verfe n e == e j ){ fol( s, s j ); remove s ; Fgure 11: lgorthm wth splttng n folng
6 Exmple 9. Conser the prolem presente on Fgure 12. The ssote relton mtrx n ffnty grph re presente on Fgure 1. r4 r5 {, {, q1 q2 {, r4 {, r5 {, Fgure 12: enong prolem r4 r5 q1 q2 Fgure 1: relton mtrx n ffnty grph Sne we hve 4 symols, we wnt to enoe them on n=2 ts. At terton k=1, we ssgn the vlue 0 to, n 1 to,. The volte eges re {,, {,, {, n {, ut folng n splttng nnot e one. For exmple, for the ege {,, nnot e fole wth (resp. ) euse oth symols re n the pont-to set of n q1(resp. n q1). At terton k=2, we ssgn 00 to, 01 to, 10 to n 11 to. All the eges re volte n some symols n e splt. The vrle n e splt n the new symol n e fole wth. The vrle n lso e splt n the new symol n e fole wth. Fnlly, we en up wth the enong on Fgure 14 n whh ll the onstrnts re verfe. q1,q2 7. IMPLEMENTATION IN SPC In [1], we presente SpC soluton for the synthess of ponters n C. The toolflow s presente on Fgure 15. Our mplementton tkes funton wth ponters n C n genertes moule n Verlog. Ths moule n then e synthesze usng the Behvorl Compler TM of Synopsys. The trnslton from C to Verlog onssts of fferent psses. After the front-en, we nlne the funtons n perform the ponter nlyss. Then the lsng nformton s use to remove n optmze ponters n the followng orer: - efne the pont-to-set of eh ponter; - reple the los n stores; - optmze los n stores; - enoe ponters; - e-oe elmnton. The ntermete oe wthout ponters s then trnslte nto Verlog ,, 01,r4,r5 1- Fgure 14: enong fter splttng n folng C funton Verlog Moule Netlst Toy, SpC supports only ponters to vrles n rry elements. Nevertheless, our lgorthm for ponter enong oul e use for ponters to ponters, ponters to funtons, n reursve t strutures s well. The heurst lgorthm esre n Seton 6 hs een mplemente n pple to some test ses. The results re llustrte n Tle 1 n hve een otne s follows. The regster fle s well s the log neessry to trnslte the vlues of the ponters hs een synthesze usng Synopsys Desgn Compler TM n the tsm.5 lrry. We present the results for three fferent shemes. Frst we present the results for strghtforwr mnmumlength enong of the symols. In ths suoptml enong, eh vrle n eh pont-to set s smply ssote wth numer (0 for the frst vrle, 1 for the seon vrle, et...). The numer of ts use to enoe eh tg s then mnmum ut the sze of the rut whh trnsltes the vlues of the ponters s not. The seon sheme s the mplementton of the lgorthm wthout splttng n folng. The sze of the rut trnsltng the vlues of the ponters s then reue. However, the numer of ts use for the enong s not lwys mnml, whh les to lrger eong ruts (omntonl re) n more regsters (non-omntonl re). Fnlly, the lst olumn shows the results for the lgorthm wth folng n splttng. The length of the oes s then lose from the mnmum n the sze of the omntonl rut s reue, whh gves etter results. exmple P N. front-en ponter nlyss remove ponters eoe Csuf2Verlog.v Behvorl Compler. set pont-to-set reple * opt lo/store enoe ponters remove & Fgure 15: Toolflow for the Synthess of Ponters n C mn. length smple lgorthm spt n fol omn. non-. omn. non-. omn. non-. test test test Tle 1: results fter synthess n optmzton usng tsm.5 lrry: omntonl re n non-omntonl re n lrry unts.
7 8. CONCLUSION We hve presente the prolem of enong ponters for the synthess of hrwre. After smplfton, the prolem n e solve usng grph-emeng tehnques. These tehnques n e further optmze: two symols n shre the sme oe (folng) n one symol n hve multple oes (splttng). The lgorthm presente hs een suessfully mplemente for the synthess of C oe wth ponters. Our tehnque oul lso e pple to other lnguges n ojet-orente progrms. 9. ACKNOWLEDGMENTS Ths reserh s supporte y DARPA uner grnt DATB6-95-C0049 n y Synopsys In. We woul lso lke to thnk Murzo Dmn for ts preous omments n suggestons. 10.REFERENCES [1] L.Benn n G.De Mhel, Stte ssgnment for low power sspton Custom Integrte Cruts Conferene, 1994, pp [2] Nrsngh Deo Grph Theory wth ppltons to Engneerng n Computer Sene, Prente-Hll, Englewoo Clffs, NJ, [] T.A Dolott n E.J. MCluskey. The Enong of Internl Sttes of Sequentl Mhnes. n IEEE Trnstons on Eletron Computers, volume EC-1, pp , Otoer [4] C. Duff, Coge utomtes et théore es ues ntersetnts, These, Insttut Ntonl Polytehnque e Grenole, Frne, Mrh [5] Evgue Golerg, Tzno Vll, Roert Bryton, Alerto Sngovnn-Vnentell, Theory n Algorthms for Fe Hyperue Emeng Trnston on CAD, volume 17(6), June [6] Hwyong Km, Kyoung Cho, Trnsformton from C to Syntheszle VHDL n Proeengs of As Pf Conf. on HDL APCHDL 98, July [7] Govnn De Mhel. Symol Desgn of Comntonl n Sequentl Log Cruts Implemente y Two-Level Log Mros. IEEE Trnston on CAD, volume 5(4), pp , [8] Govnn De Mhel Synthess n Optmzton of Dgtl Cruts, M Grw Hll, Hghtstown, NJ, [9] A. R. Newton, S. Devrs, H-keung M n A. Sngovnn- Vnentell. MUSTANG: Stte Assgnment of Fnte Stte Mhnes Trgetng Multlevel Log Implementtons. IEEE Trnston on CAD, volume 7(12), pp , [10] G. Suer, Stte Assgnment of Asynhronous Sequentl Mhnes usng Grph Tehnques, IEEE Trnston on Computer, Mrh [11] G. Suer, C. Duff, F. Porot, Stte ssgnment usng new emeng metho se on ntersetng ue theory, n Proeeng of Desgn Automton Conf., pp , June [12] G. Suer, M.C. Depulet n P. Sr, ASYL: A rulese system for ontroller synthess, IEEE Trnstons on CAD, volume CAD-6, pp , Novemer [1] Lu Sémér, Govnn De Mhel, SpC: Synthess of Ponters n C. Applton of Ponter Anlyss to the Behvorl Synthess from C, proeeng of the 1998 ICCAD, pp , Novemer [14] Tzno Vll, Alerto Sngovnn-Vnentelly, NOVA: Stte Assgnment of Fnte Stte Mhnes for Optml Two- Level Log Implementton, IEEE Trnstons on Computer-Ae Desgn, Vol. 9, pp , Septemer 1990.
MCA-205: Mathematics II (Discrete Mathematical Structures)
 MCA-05: Mthemts II (Dsrete Mthemtl Strutures) Lesson No: I Wrtten y Pnkj Kumr Lesson: Group theory - I Vette y Prof. Kulp Sngh STRUCTURE.0 OBJECTIVE. INTRODUCTION. SOME DEFINITIONS. GROUP.4 PERMUTATION
MCA-05: Mthemts II (Dsrete Mthemtl Strutures) Lesson No: I Wrtten y Pnkj Kumr Lesson: Group theory - I Vette y Prof. Kulp Sngh STRUCTURE.0 OBJECTIVE. INTRODUCTION. SOME DEFINITIONS. GROUP.4 PERMUTATION
Abhilasha Classes Class- XII Date: SOLUTION (Chap - 9,10,12) MM 50 Mob no
 hlsh Clsses Clss- XII Dte: 0- - SOLUTION Chp - 9,0, MM 50 Mo no-996 If nd re poston vets of nd B respetvel, fnd the poston vet of pont C n B produed suh tht C B vet r C B = where = hs length nd dreton
hlsh Clsses Clss- XII Dte: 0- - SOLUTION Chp - 9,0, MM 50 Mo no-996 If nd re poston vets of nd B respetvel, fnd the poston vet of pont C n B produed suh tht C B vet r C B = where = hs length nd dreton
Lecture 6: Coding theory
 Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Leture 6: Coing theory Biology 429 Crl Bergstrom Ferury 4, 2008 Soures: This leture loosely follows Cover n Thoms Chpter 5 n Yeung Chpter 3. As usul, some of the text n equtions re tken iretly from those
Greedy Algorithms. Greedy Algorithms. Piyush Kumar
 Gree s goo. Gree s rght. Gree works. Gree lrfes, uts through, n ptures the essene of the evolutonry sprt. - Goron Geko (Mhel Dougls) Anlyss of Algorthms Pyush Kumr (Leture 4: Greey Algorthms) Welome to
Gree s goo. Gree s rght. Gree works. Gree lrfes, uts through, n ptures the essene of the evolutonry sprt. - Goron Geko (Mhel Dougls) Anlyss of Algorthms Pyush Kumr (Leture 4: Greey Algorthms) Welome to
Factorising FACTORISING.
 Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
Ftorising FACTORISING www.mthletis.om.u Ftorising FACTORISING Ftorising is the opposite of expning. It is the proess of putting expressions into rkets rther thn expning them out. In this setion you will
CS 491G Combinatorial Optimization Lecture Notes
 CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
CS 491G Comintoril Optimiztion Leture Notes Dvi Owen July 30, August 1 1 Mthings Figure 1: two possile mthings in simple grph. Definition 1 Given grph G = V, E, mthing is olletion of eges M suh tht e i,
Rank One Update And the Google Matrix by Al Bernstein Signal Science, LLC
 Introducton Rnk One Updte And the Google Mtrx y Al Bernsten Sgnl Scence, LLC www.sgnlscence.net here re two dfferent wys to perform mtrx multplctons. he frst uses dot product formulton nd the second uses
Introducton Rnk One Updte And the Google Mtrx y Al Bernsten Sgnl Scence, LLC www.sgnlscence.net here re two dfferent wys to perform mtrx multplctons. he frst uses dot product formulton nd the second uses
Trigonometry. Trigonometry. Curriculum Ready ACMMG: 223, 224, 245.
 Trgonometry Trgonometry Currulum Rey ACMMG: 223, 22, 2 www.mthlets.om Trgonometry TRIGONOMETRY Bslly, mny stutons n the rel worl n e relte to rght ngle trngle. Trgonometry souns ffult, ut t s relly just
Trgonometry Trgonometry Currulum Rey ACMMG: 223, 22, 2 www.mthlets.om Trgonometry TRIGONOMETRY Bslly, mny stutons n the rel worl n e relte to rght ngle trngle. Trgonometry souns ffult, ut t s relly just
Partially Observable Systems. 1 Partially Observable Markov Decision Process (POMDP) Formalism
 CS294-40 Lernng for Rootcs nd Control Lecture 10-9/30/2008 Lecturer: Peter Aeel Prtlly Oservle Systems Scre: Dvd Nchum Lecture outlne POMDP formlsm Pont-sed vlue terton Glol methods: polytree, enumerton,
CS294-40 Lernng for Rootcs nd Control Lecture 10-9/30/2008 Lecturer: Peter Aeel Prtlly Oservle Systems Scre: Dvd Nchum Lecture outlne POMDP formlsm Pont-sed vlue terton Glol methods: polytree, enumerton,
The DOACROSS statement
 The DOACROSS sttement Is prllel loop similr to DOALL, ut it llows prouer-onsumer type of synhroniztion. Synhroniztion is llowe from lower to higher itertions sine it is ssume tht lower itertions re selete
The DOACROSS sttement Is prllel loop similr to DOALL, ut it llows prouer-onsumer type of synhroniztion. Synhroniztion is llowe from lower to higher itertions sine it is ssume tht lower itertions re selete
An Efficient Implementation of LZW Decompression in the FPGA
 An Effent Implementton of LZW Deompresson n the FPGA Xn Zhou, Ysuk Ito, n Koj Nkno Deprtment of Informton Engneerng, Hroshm Unversty Kgmym --, Hgsh-Hroshm, Hroshm, 739-857 Jpn Astrt LZW lgorthm s one of
An Effent Implementton of LZW Deompresson n the FPGA Xn Zhou, Ysuk Ito, n Koj Nkno Deprtment of Informton Engneerng, Hroshm Unversty Kgmym --, Hgsh-Hroshm, Hroshm, 739-857 Jpn Astrt LZW lgorthm s one of
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
Representing Curves. Representing Curves. 3D Objects Representation. Objects Representation. General Techniques. Curves Representation
 Reresentng Crves Fole & n Dm, Chter Reresentng Crves otvtons ehnqes for Ojet Reresentton Crves Reresentton Free Form Reresentton Aromton n Interolton Prmetr Polnomls Prmetr n eometr Contnt Polnoml Slnes
Reresentng Crves Fole & n Dm, Chter Reresentng Crves otvtons ehnqes for Ojet Reresentton Crves Reresentton Free Form Reresentton Aromton n Interolton Prmetr Polnomls Prmetr n eometr Contnt Polnoml Slnes
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
CS311 Computational Structures Regular Languages and Regular Grammars. Lecture 6
 CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
Now we must transform the original model so we can use the new parameters. = S max. Recruits
 MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
MODEL FOR VARIABLE RECRUITMENT (ontinue) Alterntive Prmeteriztions of the pwner-reruit Moels We n write ny moel in numerous ifferent ut equivlent forms. Uner ertin irumstnes it is onvenient to work with
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
22: Union Find. CS 473u - Algorithms - Spring April 14, We want to maintain a collection of sets, under the operations of:
 22: Union Fin CS 473u - Algorithms - Spring 2005 April 14, 2005 1 Union-Fin We wnt to mintin olletion of sets, uner the opertions of: 1. MkeSet(x) - rete set tht ontins the single element x. 2. Fin(x)
22: Union Fin CS 473u - Algorithms - Spring 2005 April 14, 2005 1 Union-Fin We wnt to mintin olletion of sets, uner the opertions of: 1. MkeSet(x) - rete set tht ontins the single element x. 2. Fin(x)
New Algorithms: Linear, Nonlinear, and Integer Programming
 New Algorthms: ner, Nonlner, nd Integer Progrmmng Dhnnjy P. ehendle Sr Prshurmhu College, Tl Rod, Pune-400, Ind dhnnjy.p.mehendle@gml.om Astrt In ths pper we propose new lgorthm for lner progrmmng. Ths
New Algorthms: ner, Nonlner, nd Integer Progrmmng Dhnnjy P. ehendle Sr Prshurmhu College, Tl Rod, Pune-400, Ind dhnnjy.p.mehendle@gml.om Astrt In ths pper we propose new lgorthm for lner progrmmng. Ths
Chapter Newton-Raphson Method of Solving a Nonlinear Equation
 Chpter.4 Newton-Rphson Method of Solvng Nonlner Equton After redng ths chpter, you should be ble to:. derve the Newton-Rphson method formul,. develop the lgorthm of the Newton-Rphson method,. use the Newton-Rphson
Chpter.4 Newton-Rphson Method of Solvng Nonlner Equton After redng ths chpter, you should be ble to:. derve the Newton-Rphson method formul,. develop the lgorthm of the Newton-Rphson method,. use the Newton-Rphson
Numbers and indices. 1.1 Fractions. GCSE C Example 1. Handy hint. Key point
 GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
GCSE C Emple 7 Work out 9 Give your nswer in its simplest form Numers n inies Reiprote mens invert or turn upsie own The reiprol of is 9 9 Mke sure you only invert the frtion you re iviing y 7 You multiply
Trigonometry. Trigonometry. Solutions. Curriculum Ready ACMMG: 223, 224, 245.
 Trgonometry Trgonometry Solutons Currulum Redy CMMG:, 4, 4 www.mthlets.om Trgonometry Solutons Bss Pge questons. Identfy f the followng trngles re rght ngled or not. Trngles,, d, e re rght ngled ndted
Trgonometry Trgonometry Solutons Currulum Redy CMMG:, 4, 4 www.mthlets.om Trgonometry Solutons Bss Pge questons. Identfy f the followng trngles re rght ngled or not. Trngles,, d, e re rght ngled ndted
Counting Paths Between Vertices. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs. Isomorphism of Graphs
 Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Isomorphism of Grphs Definition The simple grphs G 1 = (V 1, E 1 ) n G = (V, E ) re isomorphi if there is ijetion (n oneto-one n onto funtion) f from V 1 to V with the property tht n re jent in G 1 if
Intermediate Math Circles Wednesday, November 14, 2018 Finite Automata II. Nickolas Rollick a b b. a b 4
 Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Surds and Indices. Surds and Indices. Curriculum Ready ACMNA: 233,
 Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
Surs n Inies Surs n Inies Curriulum Rey ACMNA:, 6 www.mthletis.om Surs SURDS & & Inies INDICES Inies n surs re very losely relte. A numer uner (squre root sign) is lle sur if the squre root n t e simplifie.
CARLETON UNIVERSITY. 1.0 Problems and Most Solutions, Sect B, 2005
 RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
RLETON UNIVERSIT eprtment of Eletronis ELE 2607 Swithing iruits erury 28, 05; 0 pm.0 Prolems n Most Solutions, Set, 2005 Jn. 2, #8 n #0; Simplify, Prove Prolem. #8 Simplify + + + Reue to four letters (literls).
Equivalent fractions have the same value but they have different denominators. This means they have been divided into a different number of parts.
 Frtions equivlent frtions Equivlent frtions hve the sme vlue ut they hve ifferent enomintors. This mens they hve een ivie into ifferent numer of prts. Use the wll to fin the equivlent frtions: Wht frtions
Frtions equivlent frtions Equivlent frtions hve the sme vlue ut they hve ifferent enomintors. This mens they hve een ivie into ifferent numer of prts. Use the wll to fin the equivlent frtions: Wht frtions
Dennis Bricker, 2001 Dept of Industrial Engineering The University of Iowa. MDP: Taxi page 1
 Denns Brcker, 2001 Dept of Industrl Engneerng The Unversty of Iow MDP: Tx pge 1 A tx serves three djcent towns: A, B, nd C. Ech tme the tx dschrges pssenger, the drver must choose from three possble ctons:
Denns Brcker, 2001 Dept of Industrl Engneerng The Unversty of Iow MDP: Tx pge 1 A tx serves three djcent towns: A, B, nd C. Ech tme the tx dschrges pssenger, the drver must choose from three possble ctons:
INTRODUCTION TO COMPLEX NUMBERS
 INTRODUCTION TO COMPLEX NUMBERS The numers -4, -3, -, -1, 0, 1,, 3, 4 represent the negtve nd postve rel numers termed ntegers. As one frst lerns n mddle school they cn e thought of s unt dstnce spced
INTRODUCTION TO COMPLEX NUMBERS The numers -4, -3, -, -1, 0, 1,, 3, 4 represent the negtve nd postve rel numers termed ntegers. As one frst lerns n mddle school they cn e thought of s unt dstnce spced
Data Structures LECTURE 10. Huffman coding. Example. Coding: problem definition
 Dt Strutures, Spring 24 L. Joskowiz Dt Strutures LEURE Humn oing Motivtion Uniquel eipherle oes Prei oes Humn oe onstrution Etensions n pplitions hpter 6.3 pp 385 392 in tetook Motivtion Suppose we wnt
Dt Strutures, Spring 24 L. Joskowiz Dt Strutures LEURE Humn oing Motivtion Uniquel eipherle oes Prei oes Humn oe onstrution Etensions n pplitions hpter 6.3 pp 385 392 in tetook Motivtion Suppose we wnt
for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx
![for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx for all x in [a,b], then the area of the region bounded by the graphs of f and g and the vertical lines x = a and x = b is b [ ( ) ( )] A= f x g x dx](/thumbs/74/70408252.jpg) Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Applitions of Integrtion Are of Region Between Two Curves Ojetive: Fin the re of region etween two urves using integrtion. Fin the re of region etween interseting urves using integrtion. Desrie integrtion
Welcome. Balanced search trees. Balanced Search Trees. Inge Li Gørtz
 Welome nge Li Gørt. everse tehing n isussion of exerises: 02110 nge Li Gørt 3 tehing ssistnts 8.00-9.15 Group work 9.15-9.45 isussions of your solutions in lss 10.00-11.15 Leture 11.15-11.45 Work on exerises
Welome nge Li Gørt. everse tehing n isussion of exerises: 02110 nge Li Gørt 3 tehing ssistnts 8.00-9.15 Group work 9.15-9.45 isussions of your solutions in lss 10.00-11.15 Leture 11.15-11.45 Work on exerises
NON-DETERMINISTIC FSA
 Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Solutions for HW9. Bipartite: put the red vertices in V 1 and the black in V 2. Not bipartite!
 Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Solutions for HW9 Exerise 28. () Drw C 6, W 6 K 6, n K 5,3. C 6 : W 6 : K 6 : K 5,3 : () Whih of the following re iprtite? Justify your nswer. Biprtite: put the re verties in V 1 n the lk in V 2. Biprtite:
Lecture 11 Binary Decision Diagrams (BDDs)
 C 474A/57A Computer-Aie Logi Design Leture Binry Deision Digrms (BDDs) C 474/575 Susn Lyseky o 3 Boolen Logi untions Representtions untion n e represente in ierent wys ruth tle, eqution, K-mp, iruit, et
C 474A/57A Computer-Aie Logi Design Leture Binry Deision Digrms (BDDs) C 474/575 Susn Lyseky o 3 Boolen Logi untions Representtions untion n e represente in ierent wys ruth tle, eqution, K-mp, iruit, et
The Schur-Cohn Algorithm
 Modelng, Estmton nd Otml Flterng n Sgnl Processng Mohmed Njm Coyrght 8, ISTE Ltd. Aendx F The Schur-Cohn Algorthm In ths endx, our m s to resent the Schur-Cohn lgorthm [] whch s often used s crteron for
Modelng, Estmton nd Otml Flterng n Sgnl Processng Mohmed Njm Coyrght 8, ISTE Ltd. Aendx F The Schur-Cohn Algorthm In ths endx, our m s to resent the Schur-Cohn lgorthm [] whch s often used s crteron for
Section 1.3 Triangles
 Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
Se 1.3 Tringles 21 Setion 1.3 Tringles LELING TRINGLE The line segments tht form tringle re lled the sides of the tringle. Eh pir of sides forms n ngle, lled n interior ngle, nd eh tringle hs three interior
CSE 332. Sorting. Data Abstractions. CSE 332: Data Abstractions. QuickSort Cutoff 1. Where We Are 2. Bounding The MAXIMUM Problem 4
 Am Blnk Leture 13 Winter 2016 CSE 332 CSE 332: Dt Astrtions Sorting Dt Astrtions QuikSort Cutoff 1 Where We Are 2 For smll n, the reursion is wste. The onstnts on quik/merge sort re higher thn the ones
Am Blnk Leture 13 Winter 2016 CSE 332 CSE 332: Dt Astrtions Sorting Dt Astrtions QuikSort Cutoff 1 Where We Are 2 For smll n, the reursion is wste. The onstnts on quik/merge sort re higher thn the ones
Convert the NFA into DFA
 Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Necessary and sucient conditions for some two. Abstract. Further we show that the necessary conditions for the existence of an OD(44 s 1 s 2 )
 Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
Neessry n suient onitions for some two vrile orthogonl esigns in orer 44 C. Koukouvinos, M. Mitrouli y, n Jennifer Seerry z Deite to Professor Anne Penfol Street Astrt We give new lgorithm whih llows us
LASER: A Hardware/Software Approach to Accelerate Complicated Loops on CGRAs
 Appers n the Proeengs of the Desgn Automton n Test n Europe (DATE), 208 LASER: A Hrwre/Softwre Approh to Aelerte Complte Loops on CGRAs Mhesh Blsurmnn, Shl Dve, Avrl Shrvstv, Reley Jeypul Compler Mrorhteture
Appers n the Proeengs of the Desgn Automton n Test n Europe (DATE), 208 LASER: A Hrwre/Softwre Approh to Aelerte Complte Loops on CGRAs Mhesh Blsurmnn, Shl Dve, Avrl Shrvstv, Reley Jeypul Compler Mrorhteture
ORTHOGONAL APPROXIMATELY HARMONIC PROJECTION FOR FACE RECOGNITION
 Journl of heoretl n Apple Informton ehnology 5 th Novemer 202. Vol. 45 No. 2005-202 JAI & LLS. All rghts reserve. ISSN: 992-8645 www.tt.org E-ISSN: 87-395 ORHOGONAL APPROXIMAELY HARMONIC PROJECION FOR
Journl of heoretl n Apple Informton ehnology 5 th Novemer 202. Vol. 45 No. 2005-202 JAI & LLS. All rghts reserve. ISSN: 992-8645 www.tt.org E-ISSN: 87-395 ORHOGONAL APPROXIMAELY HARMONIC PROJECION FOR
Regular Language. Nonregular Languages The Pumping Lemma. The pumping lemma. Regular Language. The pumping lemma. Infinitely long words 3/17/15
 Regulr Lnguge Nonregulr Lnguges The Pumping Lemm Models of Comput=on Chpter 10 Recll, tht ny lnguge tht cn e descried y regulr expression is clled regulr lnguge In this lecture we will prove tht not ll
Regulr Lnguge Nonregulr Lnguges The Pumping Lemm Models of Comput=on Chpter 10 Recll, tht ny lnguge tht cn e descried y regulr expression is clled regulr lnguge In this lecture we will prove tht not ll
Lecture 7 Circuits Ch. 27
 Leture 7 Cruts Ch. 7 Crtoon -Krhhoff's Lws Tops Dret Current Cruts Krhhoff's Two ules Anlyss of Cruts Exmples Ammeter nd voltmeter C ruts Demos Three uls n rut Power loss n trnsmsson lnes esstvty of penl
Leture 7 Cruts Ch. 7 Crtoon -Krhhoff's Lws Tops Dret Current Cruts Krhhoff's Two ules Anlyss of Cruts Exmples Ammeter nd voltmeter C ruts Demos Three uls n rut Power loss n trnsmsson lnes esstvty of penl
18.06 Problem Set 4 Due Wednesday, Oct. 11, 2006 at 4:00 p.m. in 2-106
 8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
8. Problem Set Due Wenesy, Ot., t : p.m. in - Problem Mony / Consier the eight vetors 5, 5, 5,..., () List ll of the one-element, linerly epenent sets forme from these. (b) Wht re the two-element, linerly
Chapter Newton-Raphson Method of Solving a Nonlinear Equation
 Chpter 0.04 Newton-Rphson Method o Solvng Nonlner Equton Ater redng ths chpter, you should be ble to:. derve the Newton-Rphson method ormul,. develop the lgorthm o the Newton-Rphson method,. use the Newton-Rphson
Chpter 0.04 Newton-Rphson Method o Solvng Nonlner Equton Ater redng ths chpter, you should be ble to:. derve the Newton-Rphson method ormul,. develop the lgorthm o the Newton-Rphson method,. use the Newton-Rphson
BINARY LAMBDA-SET FUNCTION AND RELIABILITY OF AIRLINE
 BINARY LAMBDA-SET FUNTION AND RELIABILITY OF AIRLINE Y. Paramonov, S. Tretyakov, M. Hauka Ra Tehnal Unversty, Aeronautal Insttute, Ra, Latva e-mal: yur.paramonov@mal.om serejs.tretjakovs@mal.om mars.hauka@mal.om
BINARY LAMBDA-SET FUNTION AND RELIABILITY OF AIRLINE Y. Paramonov, S. Tretyakov, M. Hauka Ra Tehnal Unversty, Aeronautal Insttute, Ra, Latva e-mal: yur.paramonov@mal.om serejs.tretjakovs@mal.om mars.hauka@mal.om
REGULAR CUBIC LANGUAGE AND REGULAR CUBIC EXPRESSION
 Advnes n Fuzzy ets nd ystems 05 Pushp Pulshng House Allhd nd Pulshed Onlne: Novemer 05 http://dx.do.org/0.7654/afde05_097_3 Volume 0 Numer 05 Pges 97-3 N: 0973-4X REGUAR CUBC ANGUAGE AND REGUAR CUBC EXPREON
Advnes n Fuzzy ets nd ystems 05 Pushp Pulshng House Allhd nd Pulshed Onlne: Novemer 05 http://dx.do.org/0.7654/afde05_097_3 Volume 0 Numer 05 Pges 97-3 N: 0973-4X REGUAR CUBC ANGUAGE AND REGUAR CUBC EXPREON
Implication Graphs and Logic Testing
 Implition Grphs n Logi Testing Vishwni D. Agrwl Jmes J. Dnher Professor Dept. of ECE, Auurn University Auurn, AL 36849 vgrwl@eng.uurn.eu www.eng.uurn.eu/~vgrwl Joint reserh with: K. K. Dve, ATI Reserh,
Implition Grphs n Logi Testing Vishwni D. Agrwl Jmes J. Dnher Professor Dept. of ECE, Auurn University Auurn, AL 36849 vgrwl@eng.uurn.eu www.eng.uurn.eu/~vgrwl Joint reserh with: K. K. Dve, ATI Reserh,
ECE 522 Power Systems Analysis II 2 Power System Modeling
 ECE 522 Power Systems Analyss II 2 Power System Moelng Sprng 218 Instrutor: Ka Sun 1 Outlne 2.1 Moelng of synhronous generators for Stablty Stues Synhronous Mahne Moelng Smplfe Moels for Stablty Stues
ECE 522 Power Systems Analyss II 2 Power System Moelng Sprng 218 Instrutor: Ka Sun 1 Outlne 2.1 Moelng of synhronous generators for Stablty Stues Synhronous Mahne Moelng Smplfe Moels for Stablty Stues
Variable time amplitude amplification and quantum algorithms for linear algebra. Andris Ambainis University of Latvia
 Vrble tme mpltude mplfcton nd quntum lgorthms for lner lgebr Andrs Ambns Unversty of Ltv Tlk outlne. ew verson of mpltude mplfcton;. Quntum lgorthm for testng f A s sngulr; 3. Quntum lgorthm for solvng
Vrble tme mpltude mplfcton nd quntum lgorthms for lner lgebr Andrs Ambns Unversty of Ltv Tlk outlne. ew verson of mpltude mplfcton;. Quntum lgorthm for testng f A s sngulr; 3. Quntum lgorthm for solvng
Digital Electronics Part I Combinational and Sequential Logic
 9//24 Dgtl Eletrons Prt I Comntonl nd Sequentl Log Dr I J Wssell Introduton 9//24 Ams To fmlrse students wth Comntonl log ruts Sequentl log ruts How dgtl log gtes re ult usng trnsstors Desgn nd uld of
9//24 Dgtl Eletrons Prt I Comntonl nd Sequentl Log Dr I J Wssell Introduton 9//24 Ams To fmlrse students wth Comntonl log ruts Sequentl log ruts How dgtl log gtes re ult usng trnsstors Desgn nd uld of
9.1 Day 1 Warm Up. Solve the equation = x x 2 = March 1, 2017 Geometry 9.1 The Pythagorean Theorem 1
 9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
9.1 Dy 1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 1, 2017 Geometry 9.1 The Pythgoren Theorem 1 9.1 Dy 2 Wrm Up Use the Pythgoren
Minimal DFA. minimal DFA for L starting from any other
 Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
= x x 2 = 25 2
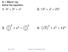 9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
9.1 Wrm Up Solve the eqution. 1. 4 2 + 3 2 = x 2 2. 13 2 + x 2 = 25 2 3. 3 2 2 + x 2 = 5 2 2 4. 5 2 + x 2 = 12 2 Mrh 7, 2016 Geometry 9.1 The Pythgoren Theorem 1 Geometry 9.1 The Pythgoren Theorem 9.1
CS 310 (sec 20) - Winter Final Exam (solutions) SOLUTIONS
 CS 310 (sec 20) - Winter 2003 - Finl Exm (solutions) SOLUTIONS 1. (Logic) Use truth tles to prove the following logicl equivlences: () p q (p p) (q q) () p q (p q) (p q) () p q p q p p q q (q q) (p p)
CS 310 (sec 20) - Winter 2003 - Finl Exm (solutions) SOLUTIONS 1. (Logic) Use truth tles to prove the following logicl equivlences: () p q (p p) (q q) () p q (p q) (p q) () p q p q p p q q (q q) (p p)
ECE 422 Power System Operations & Planning 2 Synchronous Machine Modeling
 ECE 422 Power System Operatons & Plannng 2 Synhronous Mahne Moelng Sprng 219 Instrutor: Ka Sun 1 Outlne 2.1 Moelng of synhronous generators for Stablty Stues Synhronous Mahne Moelng Smplfe Moels for Stablty
ECE 422 Power System Operatons & Plannng 2 Synhronous Mahne Moelng Sprng 219 Instrutor: Ka Sun 1 Outlne 2.1 Moelng of synhronous generators for Stablty Stues Synhronous Mahne Moelng Smplfe Moels for Stablty
Section 6: Area, Volume, and Average Value
 Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
Chpter The Integrl Applied Clculus Section 6: Are, Volume, nd Averge Vlue Are We hve lredy used integrls to find the re etween the grph of function nd the horizontl xis. Integrls cn lso e used to find
A Developed Method of Tuning PID Controllers with Fuzzy Rules for Integrating Processes
 A Develope Metho of Tunng PID Controllers wth Fuzzy Rules for Integratng Proesses Janmng Zhang, Nng Wang an Shuqng Wang Abstrat The proportonal ntegral ervatve (PID) ontrollers are wely apple n nustral
A Develope Metho of Tunng PID Controllers wth Fuzzy Rules for Integratng Proesses Janmng Zhang, Nng Wang an Shuqng Wang Abstrat The proportonal ntegral ervatve (PID) ontrollers are wely apple n nustral
First Midterm Examination
 24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
A Efficiently Estimating Motif Statistics of Large Networks
 A Effently Estmtng Motf Sttsts of Lrge Networks Pnghu Wng, Huwe Noh s Ark L John C.S. Lu, The Chnese Unversty of Hong Kong Bruno Rero, Crnege Mellon Unversty Don Towsley, Unversty of Msshusetts Amherst
A Effently Estmtng Motf Sttsts of Lrge Networks Pnghu Wng, Huwe Noh s Ark L John C.S. Lu, The Chnese Unversty of Hong Kong Bruno Rero, Crnege Mellon Unversty Don Towsley, Unversty of Msshusetts Amherst
Data Compression Techniques (Spring 2012) Model Solutions for Exercise 4
 58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
58487 Dt Compressio Tehiques (Sprig 0) Moel Solutios for Exerise 4 If you hve y fee or orretios, plese ott jro.lo t s.helsii.fi.. Prolem: Let T = Σ = {,,, }. Eoe T usig ptive Huffm oig. Solutio: R 4 U
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Exam Review. John Knight Electronics Department, Carleton University March 2, 2009 ELEC 2607 A MIDTERM
 riting Exms: Exm Review riting Exms += riting Exms synhronous iruits Res, yles n Stte ssignment Synhronous iruits Stte-Grph onstrution n Smll Prolems lso Multiple Outputs, n Hrer omintionl Prolem riting
riting Exms: Exm Review riting Exms += riting Exms synhronous iruits Res, yles n Stte ssignment Synhronous iruits Stte-Grph onstrution n Smll Prolems lso Multiple Outputs, n Hrer omintionl Prolem riting
set is not closed under matrix [ multiplication, ] and does not form a group.
![set is not closed under matrix [ multiplication, ] and does not form a group. set is not closed under matrix [ multiplication, ] and does not form a group.](/thumbs/78/78412113.jpg) Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
Prolem 2.3: Which of the following collections of 2 2 mtrices with rel entries form groups under [ mtrix ] multipliction? i) Those of the form for which c d 2 Answer: The set of such mtrices is not closed
REGULARIZATION IN QUANTUM GAUGE THEORY OF GRAVITATION WITH DE SITTER INNER SYMMETRY
 THEORETICAL PHYSICS REGULARIZATION IN QUANTUM GAUGE THEORY OF GRAVITATION WITH DE SITTER INNER SYMMETRY V. CHIRIÞOIU 1, G. ZET 1 Poltehn Unversty Tmºor, Tehnl Physs Deprtment, Romn E-ml: vorel.hrtou@et.upt.ro
THEORETICAL PHYSICS REGULARIZATION IN QUANTUM GAUGE THEORY OF GRAVITATION WITH DE SITTER INNER SYMMETRY V. CHIRIÞOIU 1, G. ZET 1 Poltehn Unversty Tmºor, Tehnl Physs Deprtment, Romn E-ml: vorel.hrtou@et.upt.ro
Bases for Vector Spaces
 Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
Bses for Vector Spces 2-26-25 A set is independent if, roughly speking, there is no redundncy in the set: You cn t uild ny vector in the set s liner comintion of the others A set spns if you cn uild everything
7.2 Volume. A cross section is the shape we get when cutting straight through an object.
 7. Volume Let s revew the volume of smple sold, cylnder frst. Cylnder s volume=se re heght. As llustrted n Fgure (). Fgure ( nd (c) re specl cylnders. Fgure () s rght crculr cylnder. Fgure (c) s ox. A
7. Volume Let s revew the volume of smple sold, cylnder frst. Cylnder s volume=se re heght. As llustrted n Fgure (). Fgure ( nd (c) re specl cylnders. Fgure () s rght crculr cylnder. Fgure (c) s ox. A
6.5 Improper integrals
 Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Eerpt from "Clulus" 3 AoPS In. www.rtofprolemsolving.om 6.5. IMPROPER INTEGRALS 6.5 Improper integrls As we ve seen, we use the definite integrl R f to ompute the re of the region under the grph of y =
Spacetime and the Quantum World Questions Fall 2010
 Spetime nd the Quntum World Questions Fll 2010 1. Cliker Questions from Clss: (1) In toss of two die, wht is the proility tht the sum of the outomes is 6? () P (x 1 + x 2 = 6) = 1 36 - out 3% () P (x 1
Spetime nd the Quntum World Questions Fll 2010 1. Cliker Questions from Clss: (1) In toss of two die, wht is the proility tht the sum of the outomes is 6? () P (x 1 + x 2 = 6) = 1 36 - out 3% () P (x 1
Controller Design for Networked Control Systems in Multiple-packet Transmission with Random Delays
 Appled Mehans and Materals Onlne: 03-0- ISSN: 66-748, Vols. 78-80, pp 60-604 do:0.408/www.sentf.net/amm.78-80.60 03 rans eh Publatons, Swtzerland H Controller Desgn for Networed Control Systems n Multple-paet
Appled Mehans and Materals Onlne: 03-0- ISSN: 66-748, Vols. 78-80, pp 60-604 do:0.408/www.sentf.net/amm.78-80.60 03 rans eh Publatons, Swtzerland H Controller Desgn for Networed Control Systems n Multple-paet
CS103B Handout 18 Winter 2007 February 28, 2007 Finite Automata
 CS103B ndout 18 Winter 2007 Ferury 28, 2007 Finite Automt Initil text y Mggie Johnson. Introduction Severl childrens gmes fit the following description: Pieces re set up on plying ord; dice re thrown or
CS103B ndout 18 Winter 2007 Ferury 28, 2007 Finite Automt Initil text y Mggie Johnson. Introduction Severl childrens gmes fit the following description: Pieces re set up on plying ord; dice re thrown or
Optimality of Strategies for Collapsing Expanded Random Variables In a Simple Random Sample Ed Stanek
 Optmlt of Strteges for Collpsg Expe Rom Vrles Smple Rom Smple E Stek troucto We revew the propertes of prectors of ler comtos of rom vrles se o rom vrles su-spce of the orgl rom vrles prtculr, we ttempt
Optmlt of Strteges for Collpsg Expe Rom Vrles Smple Rom Smple E Stek troucto We revew the propertes of prectors of ler comtos of rom vrles se o rom vrles su-spce of the orgl rom vrles prtculr, we ttempt
Name Ima Sample ASU ID
 Nme Im Smple ASU ID 2468024680 CSE 355 Test 1, Fll 2016 30 Septemer 2016, 8:35-9:25.m., LSA 191 Regrding of Midterms If you elieve tht your grde hs not een dded up correctly, return the entire pper to
Nme Im Smple ASU ID 2468024680 CSE 355 Test 1, Fll 2016 30 Septemer 2016, 8:35-9:25.m., LSA 191 Regrding of Midterms If you elieve tht your grde hs not een dded up correctly, return the entire pper to
Introduction to Numerical Integration Part II
 Introducton to umercl Integrton Prt II CS 75/Mth 75 Brn T. Smth, UM, CS Dept. Sprng, 998 4/9/998 qud_ Intro to Gussn Qudrture s eore, the generl tretment chnges the ntegrton prolem to ndng the ntegrl w
Introducton to umercl Integrton Prt II CS 75/Mth 75 Brn T. Smth, UM, CS Dept. Sprng, 998 4/9/998 qud_ Intro to Gussn Qudrture s eore, the generl tretment chnges the ntegrton prolem to ndng the ntegrl w
ME 501A Seminar in Engineering Analysis Page 1
 More oundr-vlue Prolems nd genvlue Prolems n Os ovemer 9, 7 More oundr-vlue Prolems nd genvlue Prolems n Os Lrr retto Menl ngneerng 5 Semnr n ngneerng nlss ovemer 9, 7 Outlne Revew oundr-vlue prolems Soot
More oundr-vlue Prolems nd genvlue Prolems n Os ovemer 9, 7 More oundr-vlue Prolems nd genvlue Prolems n Os Lrr retto Menl ngneerng 5 Semnr n ngneerng nlss ovemer 9, 7 Outlne Revew oundr-vlue prolems Soot
The University of Nottingham SCHOOL OF COMPUTER SCIENCE A LEVEL 2 MODULE, SPRING SEMESTER MACHINES AND THEIR LANGUAGES ANSWERS
 The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
TELCOM 2130 Time Varying Queues. David Tipper Associate Professor Graduate Telecommunications and Networking Program University of Pittsburgh Slides 7
 TELOM 3 Tme Vryng Queues Dvd Tpper Assote Professor Grdute Teleommuntons nd Networkng Progrm Unversty of Pttsburgh ldes 7 Tme Vryng Behvor Teletrff typlly hs lrge tme of dy vrtons Men number of lls per
TELOM 3 Tme Vryng Queues Dvd Tpper Assote Professor Grdute Teleommuntons nd Networkng Progrm Unversty of Pttsburgh ldes 7 Tme Vryng Behvor Teletrff typlly hs lrge tme of dy vrtons Men number of lls per
Rewiring World Trade. Part I: A Binary Network Analysis
 Rewrng Worl Tre. Prt I: A Bnry Networ Anlyss Tzno Squrtn CSC n Deprtment of Physs, Unversty of Sen, V Rom 56, 53 Sen (Itly) Gorgo Fgolo LEM, Snt Ann Shool of Avne Stues, 56127 Ps (Itly) Dego Grlshell LEM,
Rewrng Worl Tre. Prt I: A Bnry Networ Anlyss Tzno Squrtn CSC n Deprtment of Physs, Unversty of Sen, V Rom 56, 53 Sen (Itly) Gorgo Fgolo LEM, Snt Ann Shool of Avne Stues, 56127 Ps (Itly) Dego Grlshell LEM,
Principle Component Analysis
 Prncple Component Anlyss Jng Go SUNY Bufflo Why Dmensonlty Reducton? We hve too mny dmensons o reson bout or obtn nsghts from o vsulze oo much nose n the dt Need to reduce them to smller set of fctors
Prncple Component Anlyss Jng Go SUNY Bufflo Why Dmensonlty Reducton? We hve too mny dmensons o reson bout or obtn nsghts from o vsulze oo much nose n the dt Need to reduce them to smller set of fctors
Previously on GLT. Basic technologies. Lexical analysis. Basic technologies ASF+SDF. Concepts of programming languages
 Prevously on GLT Generc Lnguge Technology: Bsc technologes Pro.dr. Mrk vn den Brnd ASF+SDF syntx descrptons semntc descrptons: type checkng nlyss trnsormtons t so to s Concepts o progrmmng lnguges syntctc
Prevously on GLT Generc Lnguge Technology: Bsc technologes Pro.dr. Mrk vn den Brnd ASF+SDF syntx descrptons semntc descrptons: type checkng nlyss trnsormtons t so to s Concepts o progrmmng lnguges syntctc
Censored Models. Li Gan. April, Examples of censored regression: (1) stadium attendance= min(attendance *, capacity)
 Censore Moels L Gn Aprl 8 mples o ensore regresson: stm ttenne mn(ttenne pt) Here gropng (those oservtons wth ttenne rtes less thn one vs those oservtons wth ttenne rtes t one) re lerl se on oserve tors.
Censore Moels L Gn Aprl 8 mples o ensore regresson: stm ttenne mn(ttenne pt) Here gropng (those oservtons wth ttenne rtes less thn one vs those oservtons wth ttenne rtes t one) re lerl se on oserve tors.
PHYSICS 212 MIDTERM II 19 February 2003
 PHYSICS 1 MIDERM II 19 Feruary 003 Exam s losed ook, losed notes. Use only your formula sheet. Wrte all work and answers n exam ooklets. he aks of pages wll not e graded unless you so request on the front
PHYSICS 1 MIDERM II 19 Feruary 003 Exam s losed ook, losed notes. Use only your formula sheet. Wrte all work and answers n exam ooklets. he aks of pages wll not e graded unless you so request on the front
CS 2204 DIGITAL LOGIC & STATE MACHINE DESIGN SPRING 2014
 S 224 DIGITAL LOGI & STATE MAHINE DESIGN SPRING 214 DUE : Mrh 27, 214 HOMEWORK III READ : Relte portions of hpters VII n VIII ASSIGNMENT : There re three questions. Solve ll homework n exm prolems s shown
S 224 DIGITAL LOGI & STATE MAHINE DESIGN SPRING 214 DUE : Mrh 27, 214 HOMEWORK III READ : Relte portions of hpters VII n VIII ASSIGNMENT : There re three questions. Solve ll homework n exm prolems s shown
Lecture 2: Cayley Graphs
 Mth 137B Professor: Pri Brtlett Leture 2: Cyley Grphs Week 3 UCSB 2014 (Relevnt soure mteril: Setion VIII.1 of Bollos s Moern Grph Theory; 3.7 of Gosil n Royle s Algeri Grph Theory; vrious ppers I ve re
Mth 137B Professor: Pri Brtlett Leture 2: Cyley Grphs Week 3 UCSB 2014 (Relevnt soure mteril: Setion VIII.1 of Bollos s Moern Grph Theory; 3.7 of Gosil n Royle s Algeri Grph Theory; vrious ppers I ve re
Nondeterministic Finite Automata
 Nondeterministi Finite utomt The Power of Guessing Tuesdy, Otoer 4, 2 Reding: Sipser.2 (first prt); Stoughton 3.3 3.5 S235 Lnguges nd utomt eprtment of omputer Siene Wellesley ollege Finite utomton (F)
Nondeterministi Finite utomt The Power of Guessing Tuesdy, Otoer 4, 2 Reding: Sipser.2 (first prt); Stoughton 3.3 3.5 S235 Lnguges nd utomt eprtment of omputer Siene Wellesley ollege Finite utomton (F)
Definite Integrals. The area under a curve can be approximated by adding up the areas of rectangles = 1 1 +
 Definite Integrls --5 The re under curve cn e pproximted y dding up the res of rectngles. Exmple. Approximte the re under y = from x = to x = using equl suintervls nd + x evluting the function t the left-hnd
Definite Integrls --5 The re under curve cn e pproximted y dding up the res of rectngles. Exmple. Approximte the re under y = from x = to x = using equl suintervls nd + x evluting the function t the left-hnd
3/6/00. Reading Assignments. Outline. Hidden Markov Models: Explanation and Model Learning
 3/6/ Hdden Mrkov Models: Explnton nd Model Lernng Brn C. Wllms 6.4/6.43 Sesson 2 9/3/ courtesy of JPL copyrght Brn Wllms, 2 Brn C. Wllms, copyrght 2 Redng Assgnments AIMA (Russell nd Norvg) Ch 5.-.3, 2.3
3/6/ Hdden Mrkov Models: Explnton nd Model Lernng Brn C. Wllms 6.4/6.43 Sesson 2 9/3/ courtesy of JPL copyrght Brn Wllms, 2 Brn C. Wllms, copyrght 2 Redng Assgnments AIMA (Russell nd Norvg) Ch 5.-.3, 2.3
2.4 Theoretical Foundations
 2 Progrmming Lnguge Syntx 2.4 Theoretil Fountions As note in the min text, snners n prsers re se on the finite utomt n pushown utomt tht form the ottom two levels of the Chomsky lnguge hierrhy. At eh level
2 Progrmming Lnguge Syntx 2.4 Theoretil Fountions As note in the min text, snners n prsers re se on the finite utomt n pushown utomt tht form the ottom two levels of the Chomsky lnguge hierrhy. At eh level
Intermediate Math Circles Wednesday 17 October 2012 Geometry II: Side Lengths
 Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Intermedite Mth Cirles Wednesdy 17 Otoer 01 Geometry II: Side Lengths Lst week we disussed vrious ngle properties. As we progressed through the evening, we proved mny results. This week, we will look t
Situation Calculus. Situation Calculus Building Blocks. Sheila McIlraith, CSC384, University of Toronto, Winter Situations Fluents Actions
 Plnning gent: single gent or multi-gent Stte: complete or Incomplete (logicl/probbilistic) stte of the worl n/or gent s stte of knowlege ctions: worl-ltering n/or knowlege-ltering (e.g. sensing) eterministic
Plnning gent: single gent or multi-gent Stte: complete or Incomplete (logicl/probbilistic) stte of the worl n/or gent s stte of knowlege ctions: worl-ltering n/or knowlege-ltering (e.g. sensing) eterministic
Chapter 4 State-Space Planning
 Leture slides for Automted Plnning: Theory nd Prtie Chpter 4 Stte-Spe Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Motivtion Nerly ll plnning proedures re serh proedures Different
Leture slides for Automted Plnning: Theory nd Prtie Chpter 4 Stte-Spe Plnning Dn S. Nu CMSC 722, AI Plnning University of Mrylnd, Spring 2008 1 Motivtion Nerly ll plnning proedures re serh proedures Different
I 3 2 = I I 4 = 2A
 ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
ECE 210 Eletril Ciruit Anlysis University of llinois t Chigo 2.13 We re ske to use KCL to fin urrents 1 4. The key point in pplying KCL in this prolem is to strt with noe where only one of the urrents
GM1 Consolidation Worksheet
 Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
Cmridge Essentils Mthemtis Core 8 GM1 Consolidtion Worksheet GM1 Consolidtion Worksheet 1 Clulte the size of eh ngle mrked y letter. Give resons for your nswers. or exmple, ngles on stright line dd up
VECTORS VECTORS VECTORS VECTORS. 2. Vector Representation. 1. Definition. 3. Types of Vectors. 5. Vector Operations I. 4. Equal and Opposite Vectors
 1. Defnton A vetor s n entt tht m represent phsl quntt tht hs mgntude nd dreton s opposed to slr tht ls dreton.. Vetor Representton A vetor n e represented grphll n rrow. The length of the rrow s the mgntude
1. Defnton A vetor s n entt tht m represent phsl quntt tht hs mgntude nd dreton s opposed to slr tht ls dreton.. Vetor Representton A vetor n e represented grphll n rrow. The length of the rrow s the mgntude
GAUSS ELIMINATION. Consider the following system of algebraic linear equations
 Numercl Anlyss for Engneers Germn Jordnn Unversty GAUSS ELIMINATION Consder the followng system of lgebrc lner equtons To solve the bove system usng clsscl methods, equton () s subtrcted from equton ()
Numercl Anlyss for Engneers Germn Jordnn Unversty GAUSS ELIMINATION Consder the followng system of lgebrc lner equtons To solve the bove system usng clsscl methods, equton () s subtrcted from equton ()
CIS587 - Artificial Intelligence. Uncertainty CIS587 - AI. KB for medical diagnosis. Example.
 CIS587 - rtfcl Intellgence Uncertnty K for medcl dgnoss. Exmple. We wnt to uld K system for the dgnoss of pneumon. rolem descrpton: Dsese: pneumon tent symptoms fndngs, l tests: Fever, Cough, leness, WC
CIS587 - rtfcl Intellgence Uncertnty K for medcl dgnoss. Exmple. We wnt to uld K system for the dgnoss of pneumon. rolem descrpton: Dsese: pneumon tent symptoms fndngs, l tests: Fever, Cough, leness, WC
Finite State Automata and Determinisation
 Finite Stte Automt nd Deterministion Tim Dworn Jnury, 2016 Lnguges fs nf re df Deterministion 2 Outline 1 Lnguges 2 Finite Stte Automt (fs) 3 Non-deterministi Finite Stte Automt (nf) 4 Regulr Expressions
Finite Stte Automt nd Deterministion Tim Dworn Jnury, 2016 Lnguges fs nf re df Deterministion 2 Outline 1 Lnguges 2 Finite Stte Automt (fs) 3 Non-deterministi Finite Stte Automt (nf) 4 Regulr Expressions
Linear Inequalities. Work Sheet 1
 Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
Work Sheet 1 Liner Inequlities Rent--Hep, cr rentl compny,chrges $ 15 per week plus $ 0.0 per mile to rent one of their crs. Suppose you re limited y how much money you cn spend for the week : You cn spend
6. Suppose lim = constant> 0. Which of the following does not hold?
 CSE 0-00 Nme Test 00 points UTA Stuent ID # Multiple Choie Write your nswer to the LEFT of eh prolem 5 points eh The k lrgest numers in file of n numers n e foun using Θ(k) memory in Θ(n lg k) time using
CSE 0-00 Nme Test 00 points UTA Stuent ID # Multiple Choie Write your nswer to the LEFT of eh prolem 5 points eh The k lrgest numers in file of n numers n e foun using Θ(k) memory in Θ(n lg k) time using
