REGULAR CUBIC LANGUAGE AND REGULAR CUBIC EXPRESSION
|
|
|
- Richard Skinner
- 6 years ago
- Views:
Transcription
1 Advnes n Fuzzy ets nd ystems 05 Pushp Pulshng House Allhd nd Pulshed Onlne: Novemer 05 Volume 0 Numer 05 Pges 97-3 N: X REGUAR CUBC ANGUAGE AND REGUAR CUBC EXPREON Thr Mhmood leem Adullh nd Qsr Khn Deprtment of Mthemts nterntonl slm Unversty slmd Pkstn e-ml: thrkht@yhoo.om qsrkhn4@gml.om Deprtment of Mthemts Qud--Azm Unversty slmd Pkstn e-ml: sleemdullh8@yhoo.om Astrt n ths pper usng u set we ntrodue u lnguge regulr u grmmr regulr u lnguge fnte stte utomt wth u trnstons fnte stte utomt wth u fnl sttes Myhll- Nerode theorem for u lnguges nd defne n lgorthm for mnmzton of fnte stte utomt wth u fnl stte nd progrmme n Mtl.. ntroduton n 965 Zdeh ntrodued the onept of fuzzy set [7] whh s the generlzton of mthemtl log. Fuzzy set s new mthemtl tool to Reeved: Jnury 3 05; Revsed: Mrh 0 05; Aepted: Aprl Mthemts ujet Clssfton: 68Q70 68Q45 03D05 65Y04 08A70. Keywords nd phrses: u lnguge regulr u grmmr fnte stte utomt regulr u expresson Myhll-Nerode theorem for u lnguge.
2 98 Thr Mhmood leem Adullh nd Qsr Khn desre the unertnty. n [5 6] Zdeh mde n extenson of the onept of fuzzy sets y n ntervl-vlued fuzzy set.e. fuzzy set wth n ntervlvlued memershp funton. n trdtonl fuzzy log to represent e.g. the expert s degree of ertnty n dfferent sttements numers from the ntervl [ 0 ] re used. After ths Atnssov ntrodued the ntutonst fuzzy set n 986 [ ] n whh he gve the onept of memershp funton nd nonmemershp funton to represent the unertnty. And then Gu nd Buehrer ntrodued the onept of vgue set n 993 nd Bustne nd Burllo proved tht vgue set s n ntutonst fuzzy set [9 3]. t s often dffult for n expert to extly quntfy hs or her ertnty; therefore nsted of rel numer t s more dequte to represent ths degree of ertnty y n ntervl or even y fuzzy set. n the frst se we get n ntervl-vlued fuzzy set. n the seond se we get seond order fuzzy set. ntervl-vlued fuzzy sets hve een tvely used n rel-lfe pplton. n 0 Jun et l. [0] ntrodued the onept of u set. Cu set s n ordered pr of ntervl-vlued fuzzy set nd fuzzy set. These ll re mthemtl modelng to solve the prolems n our dly lfe. These tools hve ts own nherent prolems to solve these types of unertnty whle the u set s more nformtve tool to solve ths unertnty. Fuzzy grmmr nd fuzzy lnguges were ntrodued y ee nd Zdeh n 969 []. ne Wee [4] n 967 ntrodued the onept of fuzzy utomt followng ee nd Zdeh [] fuzzy utomt theory hs een developed y mny reserhers. After the ntroduton of fuzzy lnguge nd fuzzy utomt there re mny generlztons of fuzzy lnguge nd fuzzy utomt. ntervl-vlued fuzzy vgue nd ntutonst fuzzy regulr lnguges were ntrodued y Chouey nd Rv [4 6 7]. Mteesu et l. ntrodued fnte fuzzy utomt wth fuzzy trnston nd fnte fuzzy utomt wth fuzzy fnl stte nd fuzzy regulr expresson n 995 [3]. n 009 Chouey nd Rv ntrodued ntutonst fuzzy utomt nd ntutonst fuzzy regulr expressons [5]. n 03 Chouey nd Rv ntrodued the onept of mnmzng fnte stte utomt wth vgue fnl stte nd ntutonst fuzzy fnl sttes [8].
3 Regulr Cu nguge nd Regulr Cu Expresson 99 The rest of the pper s dvded n the followng setons. Prelmnres re dsussed n eton. n eton 3 u regulr lnguge u grmmr some lger operton on u regulr lnguge nd relted results re dsussed. n eton 4 we dsussed fnte utomt wth u trnston fnte utomt wth u fnl stte u regulr expresson nd relted results. n eton 5 we gve Myhll-Nerode theorem for u lnguges nd defned n lgorthm for mnmzton of fnte stte utomt wth u fnl stte nd progrmme n Mtl. Also the lst seton onssts of onluson nd referenes.. Prelmnres Defnton. [3]. et U e n lphet set nd ω ( ) : U [ 0 ] s funton. Then the set of the form = { ω ( ) U } s lled fuzzy lnguge over U nd ω ( ) the memershp funton of. Defnton. [3]. et e fuzzy lnguge over U the fnte lphet set wth ω ( ) : U [ 0 ] s ts memershp funton. Then s lled fuzzy regulr lnguge f; () the set { [ 0 ] M ( ) } s fnte nd () for eh [ 0 ] the strng M ( ) s regulr. Defnton.3 [0]. et X e non-empty set. Then the set of the form A = { x A( x) λ( x) } s u set n whh A ( x) s ntervl-vlued fuzzy set nd λ ( x) s fuzzy set n X. For smplty we wrte A = A λ nsted of A = { x A( x) λ( x) x X}. Defnton.4 [0]. For ny A = { A ( x) λ ( x) x X} we defne P-unon P-nterseton R-unon nd R-nterseton s follows:
4 00 Thr Mhmood leem Adullh nd Qsr Khn A B { x ( A )( x) ( λ ) ( x) x X} (P-unon) p = Λ Λ A B { x ( A )( x) ( λ ) ( x) x X} (p-nterseton) p = Λ Λ A B { x ( A )( x) ( λ ) ( x) x X} (R-unon) R = Λ Λ A B { x ( A )( x) ( λ ) ( x) x X} (R-nterseton). R = Λ Λ 3. Cu Regulr nguge Defnton 3.. et U e non-empty set of lphets. A u lnguge over U s n ojet of the form n whh A ( x) : U [] = {( x A ( x) λ ( x) x U )} nd λ ( x) : U represent respetvely ntervl-vlued fuzzy nd fuzzy memershp funtons of for ll x U. Here [] represents the set of ll losed su-ntervl n [ 0 ] nd represents the losed ntervl [ 0 ]. A ( x) ssgns ntervl-vlue nd λ ( x) ssgns rel numers n the losed ntervl [ 0 ] to eh strng of the lnguge. et e u lnguge over the lphet U nd A ( x) : U [] nd λ ( x) : U re respetvely ntervl-vlued fuzzy nd fuzzy memershp funtons of. Then for eh [ ] [ ] denoted y ([ ] ) the set ([ ] ) = { x x U nd A ( x) = [ ]} nd for eh the set { x x U nd λ ( x) = } s denoted y ( ). Note tht s n nverse funton of memershp funtons. Exmple 3.. et U = { x y} nd A ( x) : U []. Then nd λ ( x ): U
5 Regulr Cu nguge nd Regulr Cu Expresson 0 = {( x [ ] 0.4)( x y [ ] 0.5) x x y U } represent u lnguge. Cu lnguge s generted y u grmmr. The defnton of u grmmr s gven elow. Defnton 3.3. A four-tuple G = ( UT U N P ) s lled u grmmr where () The elements of U T represent termnl symols. U N () The elements of =. U N represent non-termnl symols nd U T () The elements of P re lled produtons. s the strtng symol nd U N. The elements of P re expressons of the form α ( β γ) = ([ ϑ ρ] δ) for [ ϑ ρ] [ ] nd δ where β nd γ re strngs n ( U ) nd T U N [ ϑ ρ] δ represents the grde of memershps of γ for gven β. For smplty the ove expresson n lso e wrtten s α ( β γ) = ([ ϑ ρ] δ) to [ ϑ ρ] \ δ β γ or β γ. The produtons of P re of the form C [ ϑ ρ] \ δ D or C [ ϑ ρ] \ δ C D U N U T s llowed n u regulr grmmr nd lso the produton Λ s llowed wth memershp vlues nd 0 respetvely. Cu grmmr s generlzton of fuzzy grmmr. For termnl strng x s sd to e n ( G) f nd only f x s dervle from strtng symol.
6 0 Thr Mhmood leem Adullh nd Qsr Khn Defnton 3.4. Two u lnguges nd re sd to e equl nd wrtten s A ( x) = A ( x) f nd only f λ ( x) = λ( x) for ll x U. Defnton 3.5. A u lnguge s suset of u lnguge denoted y f nd only f A ( x) A ( x) nd λ ( x) λ( x) for ll x U. n the ove defnton A ( x) A ( x) nd λ ( x) λ ( x) represent respetvely the ntervl-vlued fuzzy nd fuzzy memershp funtons of nd. These lnguges re onstruted over n lphet U ome lger opertons over u lnguges et nd e two u lnguges over n lphet U. et A A nd λ λ e the memershps funtons of nd respetvely. Then the followng s opertons suh s unon omplement nterseton ontenton str on the lnguges nd wll hold. () Unon. The unon of the lnguges nd s denoted nd defned s = = {( x { A ( x) A ( x) } { λ ( x) λ ( x) } x U )}. () nterseton. The nterseton of the lnguges nd s denoted nd defned s = = {( x { A ( x) A ( x) } { λ ( x) λ ( x) } x U )}. () Complement. The omplement of the lnguges s denoted nd defned s = {( A ( x) λ ( x)) x U } x U = {( x [ A ( x) A ( x)] λ ( x)) x U }.
7 Regulr Cu nguge nd Regulr Cu Expresson 03 (d) Contenton. The ontenton of the lnguges nd s denoted nd defned s = = {( x { ( A ( ) A ( ) )} { ( λ ( ) λ ( ) )} x = U nd x U )}. s (e) tr. The str operton of the lnguges s denoted nd defned = ( x { ( A ( ) A ( )... A ( ))} { ( λ ( ) λ ( )... λ ( ))}) x = (f)... n... n U n n 0} x U. + denotes the lnguge for the operton + on nd defned s = ( x { ( A ( ) A ( )... A ( n ))} { ( λ( ) λ( )... λ( n ))}) x =... n... n U n } x U. Defnton 3.7. et e u lnguge over the lphet U nd A ( x) : U [] nd λ ( x) : U re respetvely ntervl-vlued fuzzy nd fuzzy memershp funtons of. Then we ll u regulr lnguge f () the sets {[ ] [ ] [ ] nd ([ ] ) φ} nd { nd ( ) φ} re fnte nd () for eh [ ] [ ] ([ ] ) nd ( ) s regulr. Exmple 3.8. et e u lnguge over the lphet U = { x y} nd the memershp funtons A nd λ re gven elow: n
8 04 Thr Mhmood leem Adullh nd Qsr Khn f x 0 f x A ( x) = [ ] f x yx nd λ ( x) = 0.5 f x yx 0 otherwse otherwse. Then = {( x 0) ( x yx [ ] 0.5) x x yx U } s u regulr lnguge s ts strngs re regulr wth memershp funtons re fnte vlues. Theorem 3.9. Cu regulr lnguges re losed under nterseton unon omplement ontenton nd str opertons. Proof. et nd e two u lnguges over n lphet U. et A : U [] A : U [] nd λ : U λ : U e the ntervl-vlued fuzzy nd fuzzy memershp funtons of nd respetvely. et e the resultng u lnguge fter the opertons (unon nterseton str) wth A U : [] nd λ : U s ts ntervlvlued fuzzy nd fuzzy memershp funtons respetvely. Then lerly [] [] [] nd (n the se of unon nterseton ontenton nd str opertons) or [ ] = {[ ] [ ] [ ] } nd = { } (n se of omplement) re fnte for whh the orrespondng strngs re regulr. et [ ] nd e fnte vlues n [ ] nd respetvely. Then ([ ] ) nd ( ) re defned s follows: Unon [ ] [ ] [ ] [ ] [ ] [ ] f > [ ] [ ] [ ] [ ] [ ] [ ] [ ] f > [ ] ([ ] ) = ( [ ] [ ]) [ ] [ ] > [ ] [ ] [ ] [ ] [ ] [ ] f > [ ]
9 Regulr Cu nguge nd Regulr Cu Expresson 05 ( ) ( ) ( ) ( ) ( ) (( ( ) ( )) ( ) ( ) ( ) = < < < <. f f f nterseton [ ] ( ) [ ] [ ] [ ] [ ] [ ] [] [] [ ] [ ] [ ] [ ] [ ] [] [] (( [ ] [ ]) [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] = < < < < f f f nd ( ) ( ) ( ) ( ) ( ) (( ( ) ( )) ( ) ( ) ( ) = > > > >. f f f Complementton [] [ ][ ] [ ] { } = nd { } = [ ] ( ) [ ] ( ) = nd ( ) ( ). = Contenton [ ] ( ) [ ] [ ] ( ) [ ] [ ] [ ] [ ] [ ] [ ] ( ) [ ] ( ) = = [ ] [ ] ( ) [ ] [ ] [ ] [ ] [ ] [ ] ( ) [ ] ( ) >
10 06 Thr Mhmood leem Adullh nd Qsr Khn nd ([ ] ) = ( ) ( ) ( ) ( ) tr Assumng tht 3 4. ( ) = ( ) < [] = {[ ][ ]... [ k ]} k [ ] [ ] > [ ] > > [ k ] [ 0 0] k {... } 0 < < < = k k ([ ] ) = ( ([ ] ) f [ ] = [ ] ([ ] ) = { Λ} + ([ ]) = ( ([ ]) { Λ} f [ ] [ ] ([ m m ]) = ([ ]) ([ ] ) { Λ} n m n n l< m l + f m k nd ( ) = ( ( ) f = 0 ( 0) = { Λ} nd + ( ) = ( ) { Λ} f 0 + ( m ) = ( ) ( ) { Λ} n m n l > m l f m k. Therefore Kleene losure s stsfed.
11 4.. Defnton Regulr Cu nguge nd Regulr Cu Expresson Fnte Automt wth Cu Trnstons A nondetermnst fnte utomt wth u trnstons s 5-tuple M = ( M U A s F ) where the elements of M re fnte set of sttes. The elements of U re fnte set of nput symols A = A λ s u set n M U M A : M U M nd λ : M U M re ntervl-vlued fuzzy nd fuzzy memershp funtons of M respetvely s denotes the ntl stte nd F M s the set of fnl stte. tht s [ ] For U nd r s M defne the exted memershp funtons of stte trnstons s 0 f = Λ nd r s f = Λ nd r = s A ( r s) = u M { A ( r u) A( u s)} = for ll U U otherwse nd 0 λ ( r s) = u M { λ ( r u) λ( u r)} = for ll U U f = Λ nd f = Λ nd otherwse. r r = s s Then we sy tht d[ ] M ( ) nd d M ( ) where d U s reognzed y M wth degrees of memershp [ ] M ( ) = { A ( s u) u F} nd d M ( ) = { λ ( s u) u F}. We denote the lnguge epted y M s ( M) nd s gven to e the set ( M) = {( d[ ] ( ) d ( )) X }. M M
12 08 Thr Mhmood leem Adullh nd Qsr Khn 4.. Exmple et M = ( M U A s F ) e nondetermnst fnte utomt wth u trnston s shown n the fgure elow where M = { s r u} U = { x y} ntl stte = s fnl stte = {u}. Also u trnstons re defned s follows: A ( s x r) = [ ] λ( s x r) = 0.3 A( s x u) = [ ] λ( s x u) = 0.4 A ( r y r) = [ ] λ( r y r) = 0.5 A( r x u) = [ ] λ( r x u) = 0.6 A ( u y u) = [ ] λ( u y u) = 0.7. The u regulr lnguge epted y the non-determnst fnte utomt wth u trnstons s ( M) = {( [ ] 0.7) xy xy } {( [ ] 0.7) xy }. The trnston dgrm of the ove non-determnst fnte utomt wth u trnston s gven y Defnton 4.3. A determnst fnte utomt wth u trnstons s non-determnst fnte utomt wth u trnston wth the ondton tht for eh r u M nd for eh x U f A( r x u) > 0 λ( r x u) < nd A( r x v) > 0 λ( r x v) < then u = v. Theorem 4.4. e u regulr lnguge f nd only f t s reognzed y non-determnst fnte utomton wth u trnston wth the reognton of Λ the empty word.
13 Regulr Cu nguge nd Regulr Cu Expresson 09 Proof. et e u regulr lnguge over n lphet U. et A : U [] nd λ : U e ntervl-vlued fuzzy nd fuzzy memershp funtons of respetvely. et [] = {... k } nd = {... k } e the fnte sets of ntervl-vlued fuzzy nd fuzzy memershp funtons of respetvely. As s u regulr lnguge so for eh [ ] we hve ( ) nd ( ) re regulr where k. ( ) ( ) = nd ( ) ( ) = for j sne re funtons. nd Also note tht A nd et M = ( M U A s F ) e determnst fnte utomton wth u trnston (or non-determnst fnte utomton wth u trnston) suh tht ( ) = ( M ) nd ( ) = ( M ) where k. Now we onstrut M ι = ( M U A s F ) where λ A ( r x u) = 0 f ( r x u) A otherwse nd ( ) λ λ f r x u ( r x u) = otherwse represent the ntervl-vlued fuzzy nd fuzzy memershp funtons of respetvely. We suppose tht ( M U A s F ) suh tht M M j = for j. et us defne M =
14 0 Thr Mhmood leem Adullh nd Qsr Khn M = { s} s M M M M M M n n F = F F Fn A( r x u) Aι ( r x u) A ( s x u) 0 = ι f r u M k f r = s u M k otherwse λι( r x u) f r u M k λ( r x u) = λι( s x u) f r = s u M k otherwse. Hene M reognzes wth the exepton of Λ the empty strng. Conversely let M = ( M U A s F ) e non-determnst fnte utomt wth u trnston. et us defne u lnguge wth A ( x) = d[ ] ( x) nd λ ( x) = d M ( x) s ts ntervl-vlued fuzzy nd fuzzy memershp funtons respetvely ( A ( Λ) = 0 nd λ ( Λ) = ). M Now we hve to prove tht s u regulr lnguge. et [ ]= {[ ] A( r x u) = [ ] r u M x U } nd = { λ( r x u) = r u M x U }. Then [] nd re fnte. Now suppose tht [ ] = {... k } wth > > > k k nd = {... k } wth < < < k k. et us defne M = ( M U A s F ) e non-determnst fnte utomton where A = {( r x u) A( r x u) } nd λ = {( r x u) λ( r x u) }. Now defne the lnguges of s for k for the nresng sequene
15 Regulr Cu nguge nd Regulr Cu Expresson = ( M ) = ( M ) ( ) M = ( M ) ( ( M ) ( )) 3 3 M ( ) = M ( M ). j= j Therefore ( ) = nd s u regulr lnguge for every k. Theorem 4.5. et e u regulr lnguge. Then s reognzed y determnst fnte utomton wth u trnston f nd only f t + + stsfes the followng xoms for eh U U = nd A ( ) > 0 λ( ) < mply tht A( ) A( ) nd λ ( ) λ( ). Proof. et M = ( M U A s F ) e determnst fnte utomton wth u trnstons whh reognzed the u regulr lnguge. We prove tht stsfes the ove ondton. + et U + U suh tht =. f d[ ] ( ) = 0 M nd ( ) = then A( ) A( ) nd λ ( ) λ( ) re true otherwse lso A( ) = d ( ) = { A ( r) A( r u) r u F} M A ( r) = d[ ] ( ) = A( ) M λ( ) = d ( ) = { λ ( r) λ( r u) r u F} M λ ( r) = d ( ) = λ( ). M d M
16 Thr Mhmood leem Adullh nd Qsr Khn λ Conversely let e u regulr lnguge nd A : U [] nd : U e ntervl-vlued fuzzy nd fuzzy memershp funtons of respetvely stsfyng the gven ondton. uppose tht [ ] = {... k } nd = {... k }. Construt determnst fnte utomton M = ( M U A s F ) suh tht ( ) = ( M ) nd ( ) = ( M ) where k. ( M ) ( M ) = ( ) ( ) = nd ( M ) ( M ) ( ) ( ) = for every j. j j = j Now we defne determnst fnte utomton M = ( M U A s F ) where M = M M M s = { s s... s } A : M U M s defned y k k A( ( p p... p ) x) ( A ( p x) A ( p x)... A ( p x)) k = k k j nd λ : M U M s defned y λ (( p p... p ) x) = ( λ ( p x) λ ( p x)... ( p )) k λ k k x nd F = F F F where k Fk = {( p p... p ) ( p p... p ) k k M p F nd p j Fj for j} j = n. Note tht F F = for j nd j ( ) = { x x U nd A ( s x) F } nd ( ) = { x x U nd λ ( s x) F }.
17 Regulr Cu nguge nd Regulr Cu Expresson 3 Bsed on the ove determnst fnte utomton M we n defne determnst fnte utomt wth u trnston M s M = ( M U A s F ) suh tht A ( r x u) = 0 f A( r x) = u F f A ( r x) = u F otherwse nd λ( r x u) = 0 f λ( r x) = u F f λ ( r x) = u F otherwse. We re now only to prove tht [ ] ( x) = A ( x) nd ( x) = λ ( x) + for ll x U. d M et us show tht M hs the followng property. d M For ll + x U wth x = for eh U U d [ ] ( x) = > 0 ff A ( s r) nd A( r u) = M for some u F k nd d ( x) = < ff λ ( s r) nd λ( r u) = M for some u F k. (E) Then f prt n e proved esly. For the only f prt t holds trvlly when = Λ. For Λ we re ssumng the ontrry tht s A ( s r) = nd A ( r u) = j > for k j. Also λ ( s r) = nd λ ( r u) = j < for k j. Then there exsts deomposton of = def for ll suh tht d f U nd e U
18 4 Thr Mhmood leem Adullh nd Qsr Khn A ( d v) A( v e z) = nd A( z f r) lso λ ( d v) λ( v e z) = nd λ ( z f r). By the defnton of M we know tht z nd u. F F j Thus we hve A ( de) = nd A ( x) = j lso λ ( de ) = nd λ ( x ) = j. ne we ssume tht gven ondton. Hene (E) holds. > nd < ths ontrdton to the j j Agn (E) mples ( ) tht s A ( x) = nd ( ) tht s λ ( x ) =. Hene the theorem s proved. Fnte utomt wth u (fnl) sttes Defnton 4.6. A 7-tuple M = ( M U A λ q F [ ] F ) s lled fnte utomt wth u fnl sttes where the elements of U re fnte set of sttes the elements of re fnte set of nput letters nd M A λ : M U re the trnston funtons q s the u ntl stte nd F [ ] : M [] M M M F M : M re the ntervl-vlued fuzzy nd fuzzy memershp funtons of the u (fnl) sttes set respetvely. Defne d [ ] ( ) = { F [ ] ( q r) A } M M nd d ( ) = { F ( q r) λ } M M M where A λ : M U respetvely denotes the reflexve nd trnstve losure A of λ. The strng s epted y M wth the ntervlvlued fuzzy nd fuzzy degrees of memershp d [ ] M ( ) nd d M ( ).
19 Regulr Cu nguge nd Regulr Cu Expresson 5 The u regulr lnguge epted y M s denoted y ( M ) defned s ( ) {( [ ] ( ) M = d d ( )) U }. M M nd Defnton 4.7. A determnst fnte utomton wth u fnl sttes s 7-tuple M = ( M U A λ q F [ ] F ) M M s non-determnst utomton wth u fnl stte wth A λ : M U M s funtons. For eh U d [ ] ( ) = F [ ] ( r ) where r = A ( q ) M M nd ( ) = F ( ) where r = λ ( q 0 ). d r M M Defne d [ ] M ( ) = 0 nd d M ( ) = f A ( q0 ) not defned. nd λ ( q ) re 0 Theorem 4.8. et e u lnguge. Then s u regulr lnguge f nd only f t s reognzed y determnst fnte utomton wth u fnl stte. A Proof. et e u regulr lnguge over n lphet U wth : U [] nd λ : U s ts ntervl-vlued fuzzy nd fuzzy memershp funtons where [ ] represents the set of ll losed su-ntervls n the losed ntervl [ 0 ] nd represents the losed ntervl [ 0 ]. ne s u regulr lnguge so for every [ ] nd the sets ( ) nd ( ) re regulr. uppose tht = {... k } nd = {... k } where k. Now we defne determnst fnte utomton wth u fnl stte M = ( M U A λ s F [ ] M F ) ι M suh ι tht ( M ) = ( ) nd ( M ) ( ). =
20 6 Thr Mhmood leem Adullh nd Qsr Khn Now we onstrut determnst fnte utomton wth u fnl sttes M = ( M U A λ s F [ ] F ) M M to e the ross produt of M k wth F [ ] ( p ( ) p ( )... p ( ) ) M k () ( ) j p F [ ] for some k nd p F = M M 0 j j otherwse nd F ( p () p ( )... p ( ) ) M k () ( ) j p F for some k nd p F j = M M j otherwse. k Now f ( p () p ( )... p ( ) ) s rehle from ( s s... s k ) for every k n M then t s not possle to get ( p ) ( F [ ] F ) nd M M ( j p ) ( F [ ] F ) for j euse ( M ) ( ) = for j k. Mj M j M j Hene M reognzes. Conversely let M = ( M U A λ s F [ ] F ) e determnst fnte utomt wth u fnl stte. Defne nd M M [] = { F [ ] ( p) = for some p M} M = { F ( p) = for some p M}. M Thus [ ] nd re fnte sets. For eh [ ] nd defne M = ( M U A λ s F F )
21 Regulr Cu nguge nd Regulr Cu Expresson 7 where F = { p F [ ] ( p) } M nd F = { p F ( p ) = }. = M et = ( M) tht s A = d [ nd λ = d. ]M M Hene for eh [] the set ( ) nd the set ( ) re regulr. Therefore s u regulr lnguge. Theorem 4.9. A u regulr lnguge s reognzed y nondetermnst fnte utomton wth u fnl stte f nd only f t s reognzed y determnst fnte utomton wth u fnl stte. Proof. et M e u lnguge. Here we hve to prove f M s non-determnst fnte utomt wth u fnl stte nd = ( M) then = ( M ) where M s determnst fnte utomt wth u fnl stte. et M = ( M U A λ s F [ ] F ) represent non-determnst M M fnte utomt wth u fnl stte. We defne determnst fnte utomton wth u fnl stte M = ( M U A λ s F [ ] M F M ) usng the method of stndrd suset onstruton nd for eh Q M ( Q M ) defne nd F [ ] ( Q) = { F [ ] ( p) = p Q} mx M M ( Q) = mn { F ( p) = p } F Q M M where nd represent respetvely the ntervl-vlued fuzzy nd fuzzy memershp vlues of the strng n the lnguge. Therefore = ( M ).
22 8 Thr Mhmood leem Adullh nd Qsr Khn Cu regulr expresson Eh strng n u regulr lnguge hs fnte ntervl-vlued fuzzy nd fuzzy memershp vlues. The set of fnte words ssoted wth these vlues forms regulr lnguge. Therefore u regulr lnguge my e represented y modfed u regulr expresson. et U = { x y} e n lphet. f { Λ x xx xxx...} [ ] 0.5 { y xy yx xyx...} [ ] 0. 4 represents u regulr lnguge then we n represent t y u regulr expresson s x [ ] x yx [ ] 0.4. The forml defnton of u regulr expresson s defned elow s. Defnton 4.0. et U e n lphet nd [ ] e fnte sets of ntervlvlued fuzzy nd fuzzy vlues n [ 0 ]. et e regulr expresson over U nd [ d] [ ] nd. Then we ll = [ d] n u regulr expresson where [ d] nd respetvely represent ntervl-vlued fuzzy nd fuzzy vlues of. et nd e two u regulr expressons over n lphet U. Then the followng hold: () elongs to u regulr expresson wth memershp vlues nd 0 () Λ elongs to u regulr expresson wth memershp vlues nd 0 (3) elongs to u regulr expresson wth ntervl-vlued fuzzy nd fuzzy memershp vlues n [ 0 ] for ll X (4) for ll nd elong to u regulr expressons ( + ) elongs to u regulr expressons ( ) elongs to u regulr expressons ( ) elongs to u regulr expressons.
23 Regulr Cu nguge nd Regulr Cu Expresson 9 By pplyng the ove mentoned steps (() nd ()) fnte numer of tmes we otned u regulr expresson. Defnton 4.. et e u regulr expresson over n lphet U. Then the orrespondng lnguge tht s u regulr lnguge ( ) s defned y ( ) = {( [ d e] h) ( )}. Here ( ) represents the lnguge for regulr expresson. f ( ) ( ) ( ) ( = + = = ) then ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ( = = = )) respetvely. Defnton 4.. A u regulr expresson over n lphet U s sd to e normlzed u regulr expresson f t s of the form... k k k where... k re regulr expressons over U nd... k nd... k re ntervl-vlued fuzzy nd fuzzy memershp vlues n [ 0 ]. Note tht f = nd = 0 then n smply e wrtten s. We ssumed nd hs hgher prortes thn /. o ertn prs of prenthess n e omtted. Exmple 4.3. The followng re ll vld u regulr expressons: () x y [ ] x yx [ ] () xy [ ] x [ ] (3) ( x + y) xx( x + y) [ ] 0. 6 (4) ( y + Λ)( x + xy) [ ] 0. 47
24 0 Thr Mhmood leem Adullh nd Qsr Khn (5) ( x + xy) [ ] (6) ( y xy [ ] 0.6) ( x yx [ ] 0.59) + x + y. The ove from () to (5) re normlzed nd (6) s not normlzed. The followng re not vld u regulr expressons: () x y [ ] 0.49 [ ] zy [ ] 0. 3 () ( x [ ] 0.46) [ ] x yx [ ] 0. Defnton 4.4. A u regulr expresson over n lphet s strtly normlzed u regulr expresson f t s normlzed: =... k k k nd for ny j nd j ( ) ( ) =. j Exmple 4.5. () xy [ ] xz [ ] yz [ ] 0.59 () (( yy + yyx) [ ] ({ x y} { yx}} [ ] 0.6 () x y [ ] ( x + y) x( x + y) y [ ] 0.7 (v) x x [ ] ( x + y) y( x + ) x [ ] Myhll-Nerode Theorem For Cu Regulr nguge Theorem 5.. The followng three sttements re equvlent to one nother: () A u regulr lnguge over n lphet U s epted y some determnst fnte utomton wth u (fnl) sttes. () s the unon of some of the equvlene lsses of rght nvrnt equvlene relton of fnte ndex.
25 A Regulr Cu nguge nd Regulr Cu Expresson (3) The relton U U E s defned y E ff for ll U ( ) = A ( ) nd λ ( ) = λ ( ) then of fnte ndex. E s n equvlene relton Proof. () () et e u regulr lnguge over n lphet U. uppose tht s reognzed y some determnst fnte utomton wth u fnl stte M = ( M U A λ s F [ ] M F M ). et E M e the equvlene relton E M f nd only f A ( ) = A( ) nd λ ( ) = λ( ). ne E M s rght nvrnt so for ny A ( ) = A( ) f A ( ) = A( ) nd λ ( ) = λ( ) f λ ( ) = λ( ). Then the ndex of E M s fnte sne the ndex s t most the numer of sttes n M. Furthermore s the unon of those equvlene lsses hvng strng suh tht A ( ) nd λ ( ) re respetvely n F [ ]M nd F M. Tht s the equvlene lsses orrespondng to the fnl sttes. () () We prove tht ny equvlene relton R stsfyng () s refnement of E ; tht s some equvlene lsses of E wll e superset of every equvlene lss R. Thus the ndex of E nnot e greter thn the ndex of R nd so s fnte. Assume tht R for eh X R nd thus ( ) = ( ) sne R s rght nvrnt. Hene E. We onlude tht eh equvlene lss of R s the suset of some equvlene lsses of E. () () To prove tht E s rght nvrnt ssume E nd let U we must show tht E ; tht s for ny d ( d ) = ( d ). ne E for ny e ( e) = ( e) (y the defnton of E ). uppose e = d to show E s rght nvrnt.
26 Thr Mhmood leem Adullh nd Qsr Khn Now we present the mnmzed determnst fnte utomt wth u fnl stte y defnng equvlene lsses of E. et M e fnte set of equvlene lsses of ontnng. E nd M Defne A ( h) = h nd λ ( h) = h. Ths defnton s onsstent s E s rght nvrnt. f we hoose nsted of from then we wll hve A ( h) = h nd λ ( ) = h. But E so ( ) = ( d ). n prtulr f d = hd ( h d ) = ( hd ) so he h nd h = h. et s = Λ F [ ] = { } nd F = { }. M M The fnte utomton M = ( M U A λ s F [ ] F ) epts therefore A ( s ) = A ( Λ ) = nd λ ( s ) = λ ( Λ ) =. Hene ( M ) = ( M). 5.. Algorthm for mnmzng determnst fnte stte utomton wth u fnl stte et M = ( M U A λ s F [ ] F ) e determnst fnte utomton M M wt u fnl sttes. uppose tht M = { s m m... mk } k 0 nd let P = {( m m j ) m m j M nd 0 < j k}. egn tep : for eh pr ( m m j ) P nd F [ ] M( m ) F[ ] M( m j ) or ( m ) F ( m ) FM M j M M
27 Regulr Cu nguge nd Regulr Cu Expresson 3 do mrk ( m m j ); tep : for eh unmrked pr ( m m ) P do j f for some U ( A( m ) A( m j )) nd ( λ ( m ) λ ( m j )) s mrked then tep.: mrk ( m m j ); tep.. reursvely mrked ll unmrked prs on the lst of ( m m j ) nd the lst of other prs tht re mrked on ths step. else tep.3: for ll nput symols do put ( m m j ) on the lst for ( A( m ) A( m j )) nd ( λ ( m ) λ( m )) unless ( A( m ) A( m )) nd j ( λ ( m ) λ( m )) j j tep 3: Equvlene lsses of M re onstruted s follows; For = 0 to k do For j = + to k do tep 4: Defne mnmum determnst fnte stte utomton wth u fnl stte M = ( M U A λ s F F ) s follows;. M M M = { m m M} A ( m x) = A( m x) nd λ ( m x) = λ( m x) nd F ( m ) = F ( m ). A A s F [ ] A( m ) = F [ ] A( m ) s =
28 4 Thr Mhmood leem Adullh nd Qsr Khn Exmple 5.3. et M = ( M U A λ s F[ ] F ) e determnst M M fnte utomton wth u fnl sttes. M = { s u v w y z} U = { } u ntl stte s s wth ntervl-vlued fuzzy memershp vlue F[ ] M ( s) = [ ] nd fuzzy memershp vlue F M ( s) = 0.3 A λ : M U M re the trnston funtons gven elow: A ( s ) = v A( s ) = u A( u ) = w A( u ) = s A( v ) = z A( v ) = y A ( w ) = z A( w ) = y A( y ) = z A( y ) = y A( z ) = z A( z ) = z λ ( s ) = v λ( s ) = u λ( u ) = w λ( u ) = s λ( v ) = z λ( v ) = y λ ( w ) = z λ( w ) = y λ( y ) = z λ( y ) = y λ( z ) = z λ( z ) = z nd FM ( u) = [ ] FM ( u) = 0.4 F[ ] M( v) = [ ] FM ( v) = 0.5 F[ ] M ( w) = [ ] FM ( w) = 0.5 F[ ] M( y) = [ ] FM ( v) = 0.6 F[ ] M ( z) = [ ] FM ( z) = 0. 7 show the ntervl-vlued fuzzy nd fuzzy memershp funtons of { u } { v } { w } { y} { z} respetvely. The trnston dgrm of determnst fnte stte utomton s gven elow:
29 Regulr Cu nguge nd Regulr Cu Expresson 5 The trnston dgrm of the mnmzed determnst fnte stte utomton wth u fnl stte: The lnguge reognzed y the ove determnst fnte utomton wth u fnl stte nd mnmzed fnte utomton wth u fnl stte s gven elow: ( M) = {( ) \[ ] 0.3 ( ) \[ ] 0.4 [ ] \[ ] 0.6 ( + ) [ ] 0.7 ( + ) \[ ] 0.7} Progrmme n Mtl for mnmzng determnst fnte utomton wth u fnl stte noofsttes=nput( Enter the numer of sttes of DFA-CF... ); sttes=[noofsttes]; lower=[noofsttes]; upper=[noofsttes]; fuzzy=[noofsttes]; sttes()=nput('enter the ntl stte nme...''s'); lower()=nput('enter lower ound of ntervl for ntl stte...');
30 6 Thr Mhmood leem Adullh nd Qsr Khn upper()=nput('enter upper ound of ntervl for ntl stte...'); fuzzy()=nput('enter fuzzy vlue for ntl stte...'); for k=:noofsttes sttes(k)=nput(strt('enter the stte nme...'strt(numstr(k)'...'))'s'); lower(k)=nput(strt('enter lower ound of ntervl for stte...'strt(numstr(k)'...'))); upper(k)=nput(strt('enter upper ound of ntervl for stte...'strt(numstr(k)'...'))); fuzzy(k)=nput(strt('enter fuzzy vlue for stte...'strt(numstr(k)'...'))); noofnputs=nput('enter the numer of nput symols of DFA-CF...'); nputsymols=[noofnputs]; for k=:noofnputs nputsymols(k)=nput(strt('enter the nme of nput symol...' strt (numstr(k)'...'))'s'); trnstons=[noofsttesnoofnputs]; for k=:noofsttes for p=:noofnputs trnstons(kp)=nput(strt(strt(strt('enter trget stte for stte...' sttes(k))'... nd for nput symol...')strt(nputsymols(p)'...'))'s'); for =:noofsttes f (sttes()==trnstons(kp)) trnstons(kp)=;
31 Regulr Cu nguge nd Regulr Cu Expresson 7 ps=[noofsttesnoofsttes]; lst=[noofsttesnoofsttesnoofsttesnoofsttes]; for k=:noofsttes for j=:noofsttes for l=:noofsttes for m=:noofsttes lst(kjlm)=0; for k=:noofsttes for j=:noofsttes ps(kj)=3; f (k<j) ps(kj)=0; f(lower(k)=lower(j)&&upper(k)=upper(j)&&fuzzy(k)=fuzzy(j)) ps(kj)=;
32 8 Thr Mhmood leem Adullh nd Qsr Khn for k=:noofsttes for j=:noofsttes f (ps(kj)==0) temp=0; for =:noofnputs f (ps(trnstons(k)trnstons(j))==) ps(kj)=; lstout=[noofsttes]; [lstout ur]=lstmrk(kjlstnoofstteslstout); for m=:ur- ps(lstout(m)lstout(m))=; temp=; f temp==0 for =:noofnputs f trnstons(k)=trnstons(j)&&k<j lst(kjtrnstons(k)trnstons(j))=;
33 Regulr Cu nguge nd Regulr Cu Expresson 9 eqlsses=[noofsttes*noofsttes]; urr=; for k=:noofsttes- for j=k+:noofsttes f(ps(kj)==0) eqlsses(urr)=k; eqlsses(urr)=j; urr=urr+; fprntf('the nput symols re...\n') for k=:noofnputs fprntf('%...'nputsymols(k)); fprntf('\nthe output sttes re...\n') for k=:noofsttes for l=:urr- f k=eqlsses(l) fprntf('%...%f...%f...%f...'sttes(k)lower(k)upper(k)fuzzy(k)); fprntf('\nthe trget sttes re...\n') for k=:noofsttes
34 30 Thr Mhmood leem Adullh nd Qsr Khn for l=:urr- f k=eqlsses(l) for j=:noofnputs f trnstons(kj)==eqlsses(l) fprntf('for the stte...%...nd nput...%...trget stte s...%...'sttes(k) nputsymols(j)eqlsses(l)); else fprntf('for the stte...%...nd nput...%...trget stte s...%...' sttes(k) nputsymols(j)trnstons(kj)); eond progrm funton [lstouturrent ] = lstmrk(kjlststteslstouturrent) for =:sttes for l=:sttes f(lst(kjl)==) lstout(urrent)=; lstout(urrent)=l; urrent=urrent+; lstmrk(llststteslstouturrent);
35 Regulr Cu nguge nd Regulr Cu Expresson 3 6. Conluson We ntrodued u lnguge whh s the generlzton of fuzzy lnguge. We lso ntrodue u grmmr nd u regulr lnguge nd show tht u regulr lnguge s losed under unon nterseton ontenton nd str opertons. We ntrodue fnte stte utomton wth u trnstons nd fnte stte utomton wth u fnl sttes. We lso gve Myhll-Nerode theorem for u regulr lnguge. We lso ntrodue lgorthm for mnmzton of fnte stte utomton wth u fnl sttes nd onstrut progrmme n Mtl. Referenes [] K. T. Atnssov ntutonst fuzzy sets Fuzzy ets nd ystems 0() (986) [] K. T. Atnssov More on ntutonst fuzzy sets Fuzzy ets nd ystems 33() (989) [3] H. Bustne nd P. Burllo Vgue sets re ntutonst fuzzy sets Fuzzy ets nd ystems 79(3) (996) [4] A. Chouey nd K. M. Rv ntutonst fuzzy regulr lnguge Proeedngs of nterntonl Conferene on Modellng nd multon CTCOM pp [5] A. Chouey nd K. M. Rv ntutonst fuzzy utomt nd ntutonst fuzzy regulr expressons J. Appl. Mth. nformts 7(-) (009) [6] A. Chouey nd K. M. Rv Vgue regulr lnguge Advnes n Fuzzy Mthemts 4() (009) [7] A. Chouey ntervl-vlued fuzzy regulr lnguge J. Appl. Mth. nformts 8(3-4) (00) [8] A. Chouey nd K. M. Rv Mnmzton of determnst fnte utomt wth vgue fnl stte nd ntutonst fuzzy fnl stte rnn Journl of Fuzzy ystems 0() (03) [9] W.. Gu nd D. J. Buehrer Vgue sets EEE Trnstons on ystems Mn nd Cyernets 3() (993) [0] Y. B. Jun C.. Km nd K. O. Yng Cu sets Ann. Fuzzy Mth. nform. 4 (0)
36 3 Thr Mhmood leem Adullh nd Qsr Khn [] Edwrd T. ee nd otf A. Zdeh Note on fuzzy lnguges nform.. 4 (969) [] Y. nd W. Pedryz Fuzzy fnte utomt nd fuzzy regulr expressons wth memershp vlues n ltte-ordered monods Fuzzy ets nd ystems 56() (005) [3] A. Mteesu A. lom K. lom nd. Yu exl nlyss wth smple fnte-fuzzy-utomton model The Journl of Unversl Computer ene (995) 9-3. [4] Wllm Go Wee On Generlztons of Adptve Algorthms nd Applton of the Fuzzy ets Conept to Pttern Clssfton Pulsher Purdue Unversty West fyette UA pp. [5] otf A. Zdeh Fuzzy sets nformton nd Control 8(3) (965) [6] otf A. Zdeh The onept of lngust vrle nd ts pplton to pproxmte resonng- nform.. 8(3) (975) [7] otf A. Zdeh The onept of lngust vrle nd ts pplton to pproxmte resonng- nform.. 8(4) (975)
CS311 Computational Structures Regular Languages and Regular Grammars. Lecture 6
 CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
Prefix-Free Regular-Expression Matching
 Prefix-Free Regulr-Expression Mthing Yo-Su Hn, Yjun Wng nd Derik Wood Deprtment of Computer Siene HKUST Prefix-Free Regulr-Expression Mthing p.1/15 Pttern Mthing Given pttern P nd text T, find ll sustrings
Prefix-Free Regulr-Expression Mthing Yo-Su Hn, Yjun Wng nd Derik Wood Deprtment of Computer Siene HKUST Prefix-Free Regulr-Expression Mthing p.1/15 Pttern Mthing Given pttern P nd text T, find ll sustrings
The University of Nottingham SCHOOL OF COMPUTER SCIENCE A LEVEL 2 MODULE, SPRING SEMESTER MACHINES AND THEIR LANGUAGES ANSWERS
 The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
The University of ottinghm SCHOOL OF COMPUTR SCIC A LVL 2 MODUL, SPRIG SMSTR 2015 2016 MACHIS AD THIR LAGUAGS ASWRS Time llowed TWO hours Cndidtes my omplete the front over of their nswer ook nd sign their
Regular languages refresher
 Regulr lnguges refresher 1 Regulr lnguges refresher Forml lnguges Alphet = finite set of letters Word = sequene of letter Lnguge = set of words Regulr lnguges defined equivlently y Regulr expressions Finite-stte
Regulr lnguges refresher 1 Regulr lnguges refresher Forml lnguges Alphet = finite set of letters Word = sequene of letter Lnguge = set of words Regulr lnguges defined equivlently y Regulr expressions Finite-stte
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Technische Universität München Winter term 2009/10 I7 Prof. J. Esparza / J. Křetínský / M. Luttenberger 11. Februar Solution
 Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
Tehnishe Universität Münhen Winter term 29/ I7 Prof. J. Esprz / J. Křetínský / M. Luttenerger. Ferur 2 Solution Automt nd Forml Lnguges Homework 2 Due 5..29. Exerise 2. Let A e the following finite utomton:
Chapter 4 Regular Grammar and Regular Sets. (Solutions / Hints)
 C K Ngpl Forml Lnguges nd utomt Theory Chpter 4 Regulr Grmmr nd Regulr ets (olutions / Hints) ol. (),,,,,,,,,,,,,,,,,,,,,,,,,, (),, (c) c c, c c, c, c, c c, c, c, c, c, c, c, c c,c, c, c, c, c, c, c, c,
C K Ngpl Forml Lnguges nd utomt Theory Chpter 4 Regulr Grmmr nd Regulr ets (olutions / Hints) ol. (),,,,,,,,,,,,,,,,,,,,,,,,,, (),, (c) c c, c c, c, c, c c, c, c, c, c, c, c, c c,c, c, c, c, c, c, c, c,
Previously on GLT. Basic technologies. Lexical analysis. Basic technologies ASF+SDF. Concepts of programming languages
 Prevously on GLT Generc Lnguge Technology: Bsc technologes Pro.dr. Mrk vn den Brnd ASF+SDF syntx descrptons semntc descrptons: type checkng nlyss trnsormtons t so to s Concepts o progrmmng lnguges syntctc
Prevously on GLT Generc Lnguge Technology: Bsc technologes Pro.dr. Mrk vn den Brnd ASF+SDF syntx descrptons semntc descrptons: type checkng nlyss trnsormtons t so to s Concepts o progrmmng lnguges syntctc
First Midterm Examination
 24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
Regular expressions, Finite Automata, transition graphs are all the same!!
 CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
MCA-205: Mathematics II (Discrete Mathematical Structures)
 MCA-05: Mthemts II (Dsrete Mthemtl Strutures) Lesson No: I Wrtten y Pnkj Kumr Lesson: Group theory - I Vette y Prof. Kulp Sngh STRUCTURE.0 OBJECTIVE. INTRODUCTION. SOME DEFINITIONS. GROUP.4 PERMUTATION
MCA-05: Mthemts II (Dsrete Mthemtl Strutures) Lesson No: I Wrtten y Pnkj Kumr Lesson: Group theory - I Vette y Prof. Kulp Sngh STRUCTURE.0 OBJECTIVE. INTRODUCTION. SOME DEFINITIONS. GROUP.4 PERMUTATION
Nondeterministic Automata vs Deterministic Automata
 Nondeterministi Automt vs Deterministi Automt We lerned tht NFA is onvenient model for showing the reltionships mong regulr grmmrs, FA, nd regulr expressions, nd designing them. However, we know tht n
Nondeterministi Automt vs Deterministi Automt We lerned tht NFA is onvenient model for showing the reltionships mong regulr grmmrs, FA, nd regulr expressions, nd designing them. However, we know tht n
The Schur-Cohn Algorithm
 Modelng, Estmton nd Otml Flterng n Sgnl Processng Mohmed Njm Coyrght 8, ISTE Ltd. Aendx F The Schur-Cohn Algorthm In ths endx, our m s to resent the Schur-Cohn lgorthm [] whch s often used s crteron for
Modelng, Estmton nd Otml Flterng n Sgnl Processng Mohmed Njm Coyrght 8, ISTE Ltd. Aendx F The Schur-Cohn Algorthm In ths endx, our m s to resent the Schur-Cohn lgorthm [] whch s often used s crteron for
Interval Valued Neutrosophic Soft Topological Spaces
 8 Interval Valued Neutrosoph Soft Topologal njan Mukherjee Mthun Datta Florentn Smarandah Department of Mathemats Trpura Unversty Suryamannagar gartala-7990 Trpura Indamal: anjan00_m@yahooon Department
8 Interval Valued Neutrosoph Soft Topologal njan Mukherjee Mthun Datta Florentn Smarandah Department of Mathemats Trpura Unversty Suryamannagar gartala-7990 Trpura Indamal: anjan00_m@yahooon Department
NON-DETERMINISTIC FSA
 Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Tw o types of non-determinism: NON-DETERMINISTIC FS () Multiple strt-sttes; strt-sttes S Q. The lnguge L(M) ={x:x tkes M from some strt-stte to some finl-stte nd ll of x is proessed}. The string x = is
Formal Languages and Automata
 Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
Moile Computing nd Softwre Engineering p. 1/5 Forml Lnguges nd Automt Chpter 2 Finite Automt Chun-Ming Liu cmliu@csie.ntut.edu.tw Deprtment of Computer Science nd Informtion Engineering Ntionl Tipei University
Chapter Five: Nondeterministic Finite Automata. Formal Language, chapter 5, slide 1
 Chpter Five: Nondeterministic Finite Automt Forml Lnguge, chpter 5, slide 1 1 A DFA hs exctly one trnsition from every stte on every symol in the lphet. By relxing this requirement we get relted ut more
Chpter Five: Nondeterministic Finite Automt Forml Lnguge, chpter 5, slide 1 1 A DFA hs exctly one trnsition from every stte on every symol in the lphet. By relxing this requirement we get relted ut more
Finite State Automata and Determinisation
 Finite Stte Automt nd Deterministion Tim Dworn Jnury, 2016 Lnguges fs nf re df Deterministion 2 Outline 1 Lnguges 2 Finite Stte Automt (fs) 3 Non-deterministi Finite Stte Automt (nf) 4 Regulr Expressions
Finite Stte Automt nd Deterministion Tim Dworn Jnury, 2016 Lnguges fs nf re df Deterministion 2 Outline 1 Lnguges 2 Finite Stte Automt (fs) 3 Non-deterministi Finite Stte Automt (nf) 4 Regulr Expressions
Rank One Update And the Google Matrix by Al Bernstein Signal Science, LLC
 Introducton Rnk One Updte And the Google Mtrx y Al Bernsten Sgnl Scence, LLC www.sgnlscence.net here re two dfferent wys to perform mtrx multplctons. he frst uses dot product formulton nd the second uses
Introducton Rnk One Updte And the Google Mtrx y Al Bernsten Sgnl Scence, LLC www.sgnlscence.net here re two dfferent wys to perform mtrx multplctons. he frst uses dot product formulton nd the second uses
= state, a = reading and q j
 4 Finite Automt CHAPTER 2 Finite Automt (FA) (i) Derterministi Finite Automt (DFA) A DFA, M Q, q,, F, Where, Q = set of sttes (finite) q Q = the strt/initil stte = input lphet (finite) (use only those
4 Finite Automt CHAPTER 2 Finite Automt (FA) (i) Derterministi Finite Automt (DFA) A DFA, M Q, q,, F, Where, Q = set of sttes (finite) q Q = the strt/initil stte = input lphet (finite) (use only those
Let's start with an example:
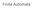 Finite Automt Let's strt with n exmple: Here you see leled circles tht re sttes, nd leled rrows tht re trnsitions. One of the sttes is mrked "strt". One of the sttes hs doule circle; this is terminl stte
Finite Automt Let's strt with n exmple: Here you see leled circles tht re sttes, nd leled rrows tht re trnsitions. One of the sttes is mrked "strt". One of the sttes hs doule circle; this is terminl stte
Fuzzy Rings and Anti Fuzzy Rings With Operators
 OSR Journal of Mathemats (OSR-JM) e-ssn: 2278-5728, p-ssn: 2319-765X. Volume 11, ssue 4 Ver. V (Jul - ug. 2015), PP 48-54 www.osrjournals.org Fuzzy Rngs and nt Fuzzy Rngs Wth Operators M.Z.lam Department
OSR Journal of Mathemats (OSR-JM) e-ssn: 2278-5728, p-ssn: 2319-765X. Volume 11, ssue 4 Ver. V (Jul - ug. 2015), PP 48-54 www.osrjournals.org Fuzzy Rngs and nt Fuzzy Rngs Wth Operators M.Z.lam Department
5. (±±) Λ = fw j w is string of even lengthg [ 00 = f11,00g 7. (11 [ 00)± Λ = fw j w egins with either 11 or 00g 8. (0 [ ffl)1 Λ = 01 Λ [ 1 Λ 9.
 Regulr Expressions, Pumping Lemm, Right Liner Grmmrs Ling 106 Mrch 25, 2002 1 Regulr Expressions A regulr expression descries or genertes lnguge: it is kind of shorthnd for listing the memers of lnguge.
Regulr Expressions, Pumping Lemm, Right Liner Grmmrs Ling 106 Mrch 25, 2002 1 Regulr Expressions A regulr expression descries or genertes lnguge: it is kind of shorthnd for listing the memers of lnguge.
Myhill-Nerode Theorem
 Overview Myhill-Nerode Theorem Correspondence etween DA s nd MN reltions Cnonicl DA for L Computing cnonicl DFA Myhill-Nerode Theorem Deepk D Souz Deprtment of Computer Science nd Automtion Indin Institute
Overview Myhill-Nerode Theorem Correspondence etween DA s nd MN reltions Cnonicl DA for L Computing cnonicl DFA Myhill-Nerode Theorem Deepk D Souz Deprtment of Computer Science nd Automtion Indin Institute
Harvard University Computer Science 121 Midterm October 23, 2012
 Hrvrd University Computer Science 121 Midterm Octoer 23, 2012 This is closed-ook exmintion. You my use ny result from lecture, Sipser, prolem sets, or section, s long s you quote it clerly. The lphet is
Hrvrd University Computer Science 121 Midterm Octoer 23, 2012 This is closed-ook exmintion. You my use ny result from lecture, Sipser, prolem sets, or section, s long s you quote it clerly. The lphet is
Nondeterministic Finite Automata
 Nondeterministi Finite utomt The Power of Guessing Tuesdy, Otoer 4, 2 Reding: Sipser.2 (first prt); Stoughton 3.3 3.5 S235 Lnguges nd utomt eprtment of omputer Siene Wellesley ollege Finite utomton (F)
Nondeterministi Finite utomt The Power of Guessing Tuesdy, Otoer 4, 2 Reding: Sipser.2 (first prt); Stoughton 3.3 3.5 S235 Lnguges nd utomt eprtment of omputer Siene Wellesley ollege Finite utomton (F)
First Midterm Examination
 Çnky University Deprtment of Computer Engineering 203-204 Fll Semester First Midterm Exmintion ) Design DFA for ll strings over the lphet Σ = {,, c} in which there is no, no nd no cc. 2) Wht lnguge does
Çnky University Deprtment of Computer Engineering 203-204 Fll Semester First Midterm Exmintion ) Design DFA for ll strings over the lphet Σ = {,, c} in which there is no, no nd no cc. 2) Wht lnguge does
The Number of Rows which Equal Certain Row
 Interntonl Journl of Algebr, Vol 5, 011, no 30, 1481-1488 he Number of Rows whch Equl Certn Row Ahmd Hbl Deprtment of mthemtcs Fcult of Scences Dmscus unverst Dmscus, Sr hblhmd1@gmlcom Abstrct Let be X
Interntonl Journl of Algebr, Vol 5, 011, no 30, 1481-1488 he Number of Rows whch Equl Certn Row Ahmd Hbl Deprtment of mthemtcs Fcult of Scences Dmscus unverst Dmscus, Sr hblhmd1@gmlcom Abstrct Let be X
Theory of Computation Regular Languages. (NTU EE) Regular Languages Fall / 38
 Theory of Computtion Regulr Lnguges (NTU EE) Regulr Lnguges Fll 2017 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of Finite Automt A finite utomton hs finite set of control
Theory of Computtion Regulr Lnguges (NTU EE) Regulr Lnguges Fll 2017 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of Finite Automt A finite utomton hs finite set of control
On Implicative and Strong Implicative Filters of Lattice Wajsberg Algebras
 Glol Journl of Mthemtil Sienes: Theory nd Prtil. ISSN 974-32 Volume 9, Numer 3 (27), pp. 387-397 Interntionl Reserh Pulition House http://www.irphouse.om On Implitive nd Strong Implitive Filters of Lttie
Glol Journl of Mthemtil Sienes: Theory nd Prtil. ISSN 974-32 Volume 9, Numer 3 (27), pp. 387-397 Interntionl Reserh Pulition House http://www.irphouse.om On Implitive nd Strong Implitive Filters of Lttie
Abhilasha Classes Class- XII Date: SOLUTION (Chap - 9,10,12) MM 50 Mob no
 hlsh Clsses Clss- XII Dte: 0- - SOLUTION Chp - 9,0, MM 50 Mo no-996 If nd re poston vets of nd B respetvel, fnd the poston vet of pont C n B produed suh tht C B vet r C B = where = hs length nd dreton
hlsh Clsses Clss- XII Dte: 0- - SOLUTION Chp - 9,0, MM 50 Mo no-996 If nd re poston vets of nd B respetvel, fnd the poston vet of pont C n B produed suh tht C B vet r C B = where = hs length nd dreton
AUTOMATA AND LANGUAGES. Definition 1.5: Finite Automaton
 25. Finite Automt AUTOMATA AND LANGUAGES A system of computtion tht only hs finite numer of possile sttes cn e modeled using finite utomton A finite utomton is often illustrted s stte digrm d d d. d q
25. Finite Automt AUTOMATA AND LANGUAGES A system of computtion tht only hs finite numer of possile sttes cn e modeled using finite utomton A finite utomton is often illustrted s stte digrm d d d. d q
Finite-State Automata: Recap
 Finite-Stte Automt: Recp Deepk D Souz Deprtment of Computer Science nd Automtion Indin Institute of Science, Bnglore. 09 August 2016 Outline 1 Introduction 2 Forml Definitions nd Nottion 3 Closure under
Finite-Stte Automt: Recp Deepk D Souz Deprtment of Computer Science nd Automtion Indin Institute of Science, Bnglore. 09 August 2016 Outline 1 Introduction 2 Forml Definitions nd Nottion 3 Closure under
Formal languages, automata, and theory of computation
 Mälrdlen University TEN1 DVA337 2015 School of Innovtion, Design nd Engineering Forml lnguges, utomt, nd theory of computtion Thursdy, Novemer 5, 14:10-18:30 Techer: Dniel Hedin, phone 021-107052 The exm
Mälrdlen University TEN1 DVA337 2015 School of Innovtion, Design nd Engineering Forml lnguges, utomt, nd theory of computtion Thursdy, Novemer 5, 14:10-18:30 Techer: Dniel Hedin, phone 021-107052 The exm
Nondeterminism and Nodeterministic Automata
 Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
Closure Properties of Regular Languages
 Closure Properties of Regulr Lnguges Regulr lnguges re closed under mny set opertions. Let L 1 nd L 2 e regulr lnguges. (1) L 1 L 2 (the union) is regulr. (2) L 1 L 2 (the conctention) is regulr. (3) L
Closure Properties of Regulr Lnguges Regulr lnguges re closed under mny set opertions. Let L 1 nd L 2 e regulr lnguges. (1) L 1 L 2 (the union) is regulr. (2) L 1 L 2 (the conctention) is regulr. (3) L
Homework 3 Solutions
 CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
Minimal DFA. minimal DFA for L starting from any other
 Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Complement of an Extended Fuzzy Set
 Internatonal Journal of Computer pplatons (0975 8887) Complement of an Extended Fuzzy Set Trdv Jyot Neog Researh Sholar epartment of Mathemats CMJ Unversty, Shllong, Meghalaya usmanta Kumar Sut ssstant
Internatonal Journal of Computer pplatons (0975 8887) Complement of an Extended Fuzzy Set Trdv Jyot Neog Researh Sholar epartment of Mathemats CMJ Unversty, Shllong, Meghalaya usmanta Kumar Sut ssstant
CSCI 340: Computational Models. Kleene s Theorem. Department of Computer Science
 CSCI 340: Computtionl Models Kleene s Theorem Chpter 7 Deprtment of Computer Science Unifiction In 1954, Kleene presented (nd proved) theorem which (in our version) sttes tht if lnguge cn e defined y ny
CSCI 340: Computtionl Models Kleene s Theorem Chpter 7 Deprtment of Computer Science Unifiction In 1954, Kleene presented (nd proved) theorem which (in our version) sttes tht if lnguge cn e defined y ny
Assignment 1 Automata, Languages, and Computability. 1 Finite State Automata and Regular Languages
 Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
CHAPTER 1 Regular Languages. Contents
 Finite Automt (FA or DFA) CHAPTE 1 egulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, euivlence of NFAs nd DFAs, closure under regulr
Finite Automt (FA or DFA) CHAPTE 1 egulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, euivlence of NFAs nd DFAs, closure under regulr
Chapter 2 Finite Automata
 Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
Compression of Palindromes and Regularity.
 Compression of Plinromes n Regulrity. Kyoko Shikishim-Tsuji Center for Lierl Arts Eution n Reserh Tenri University 1 Introution In [1], property of likstrem t t view of tse is isusse n it is shown tht
Compression of Plinromes n Regulrity. Kyoko Shikishim-Tsuji Center for Lierl Arts Eution n Reserh Tenri University 1 Introution In [1], property of likstrem t t view of tse is isusse n it is shown tht
Theory of Computation Regular Languages
 Theory of Computtion Regulr Lnguges Bow-Yw Wng Acdemi Sinic Spring 2012 Bow-Yw Wng (Acdemi Sinic) Regulr Lnguges Spring 2012 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of
Theory of Computtion Regulr Lnguges Bow-Yw Wng Acdemi Sinic Spring 2012 Bow-Yw Wng (Acdemi Sinic) Regulr Lnguges Spring 2012 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of
Grammar. Languages. Content 5/10/16. Automata and Languages. Regular Languages. Regular Languages
 5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
Intermediate Math Circles Wednesday, November 14, 2018 Finite Automata II. Nickolas Rollick a b b. a b 4
 Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
Intermedite Mth Circles Wednesdy, Novemer 14, 2018 Finite Automt II Nickols Rollick nrollick@uwterloo.c Regulr Lnguges Lst time, we were introduced to the ide of DFA (deterministic finite utomton), one
CS241 Week 6 Tutorial Solutions
 241 Week 6 Tutoril olutions Lnguges: nning & ontext-free Grmmrs Winter 2018 1 nning Exerises 1. 0x0x0xd HEXINT 0x0 I x0xd 2. 0xend--- HEXINT 0xe I nd ER -- MINU - 3. 1234-120x INT 1234 INT -120 I x 4.
241 Week 6 Tutoril olutions Lnguges: nning & ontext-free Grmmrs Winter 2018 1 nning Exerises 1. 0x0x0xd HEXINT 0x0 I x0xd 2. 0xend--- HEXINT 0xe I nd ER -- MINU - 3. 1234-120x INT 1234 INT -120 I x 4.
Module 3: Element Properties Lecture 5: Solid Elements
 Modue : Eement Propertes eture 5: Sod Eements There re two s fmes of three-dmenson eements smr to two-dmenson se. Etenson of trngur eements w produe tetrhedrons n three dmensons. Smr retngur preeppeds
Modue : Eement Propertes eture 5: Sod Eements There re two s fmes of three-dmenson eements smr to two-dmenson se. Etenson of trngur eements w produe tetrhedrons n three dmensons. Smr retngur preeppeds
Fundamentals of Computer Science
 Fundmentls of Computer Science Chpter 3: NFA nd DFA equivlence Regulr expressions Henrik Björklund Umeå University Jnury 23, 2014 NFA nd DFA equivlence As we shll see, it turns out tht NFA nd DFA re equivlent,
Fundmentls of Computer Science Chpter 3: NFA nd DFA equivlence Regulr expressions Henrik Björklund Umeå University Jnury 23, 2014 NFA nd DFA equivlence As we shll see, it turns out tht NFA nd DFA re equivlent,
CS 373, Spring Solutions to Mock midterm 1 (Based on first midterm in CS 273, Fall 2008.)
 CS 373, Spring 29. Solutions to Mock midterm (sed on first midterm in CS 273, Fll 28.) Prolem : Short nswer (8 points) The nswers to these prolems should e short nd not complicted. () If n NF M ccepts
CS 373, Spring 29. Solutions to Mock midterm (sed on first midterm in CS 273, Fll 28.) Prolem : Short nswer (8 points) The nswers to these prolems should e short nd not complicted. () If n NF M ccepts
1 PYTHAGORAS THEOREM 1. Given a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
 1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
1 PYTHAGORAS THEOREM 1 1 Pythgors Theorem In this setion we will present geometri proof of the fmous theorem of Pythgors. Given right ngled tringle, the squre of the hypotenuse is equl to the sum of the
VECTORS VECTORS VECTORS VECTORS. 2. Vector Representation. 1. Definition. 3. Types of Vectors. 5. Vector Operations I. 4. Equal and Opposite Vectors
 1. Defnton A vetor s n entt tht m represent phsl quntt tht hs mgntude nd dreton s opposed to slr tht ls dreton.. Vetor Representton A vetor n e represented grphll n rrow. The length of the rrow s the mgntude
1. Defnton A vetor s n entt tht m represent phsl quntt tht hs mgntude nd dreton s opposed to slr tht ls dreton.. Vetor Representton A vetor n e represented grphll n rrow. The length of the rrow s the mgntude
Partially Observable Systems. 1 Partially Observable Markov Decision Process (POMDP) Formalism
 CS294-40 Lernng for Rootcs nd Control Lecture 10-9/30/2008 Lecturer: Peter Aeel Prtlly Oservle Systems Scre: Dvd Nchum Lecture outlne POMDP formlsm Pont-sed vlue terton Glol methods: polytree, enumerton,
CS294-40 Lernng for Rootcs nd Control Lecture 10-9/30/2008 Lecturer: Peter Aeel Prtlly Oservle Systems Scre: Dvd Nchum Lecture outlne POMDP formlsm Pont-sed vlue terton Glol methods: polytree, enumerton,
CMPSCI 250: Introduction to Computation. Lecture #31: What DFA s Can and Can t Do David Mix Barrington 9 April 2014
 CMPSCI 250: Introduction to Computtion Lecture #31: Wht DFA s Cn nd Cn t Do Dvid Mix Brrington 9 April 2014 Wht DFA s Cn nd Cn t Do Deterministic Finite Automt Forml Definition of DFA s Exmples of DFA
CMPSCI 250: Introduction to Computtion Lecture #31: Wht DFA s Cn nd Cn t Do Dvid Mix Brrington 9 April 2014 Wht DFA s Cn nd Cn t Do Deterministic Finite Automt Forml Definition of DFA s Exmples of DFA
CS 330 Formal Methods and Models
 CS 330 Forml Methods nd Models Dn Richrds, section 003, George Mson University, Fll 2017 Quiz Solutions Quiz 1, Propositionl Logic Dte: Septemer 7 1. Prove (p q) (p q), () (5pts) using truth tles. p q
CS 330 Forml Methods nd Models Dn Richrds, section 003, George Mson University, Fll 2017 Quiz Solutions Quiz 1, Propositionl Logic Dte: Septemer 7 1. Prove (p q) (p q), () (5pts) using truth tles. p q
NFAs continued, Closure Properties of Regular Languages
 lgorithms & Models of omputtion S/EE 374, Spring 209 NFs continued, losure Properties of Regulr Lnguges Lecture 5 Tuesdy, Jnury 29, 209 Regulr Lnguges, DFs, NFs Lnguges ccepted y DFs, NFs, nd regulr expressions
lgorithms & Models of omputtion S/EE 374, Spring 209 NFs continued, losure Properties of Regulr Lnguges Lecture 5 Tuesdy, Jnury 29, 209 Regulr Lnguges, DFs, NFs Lnguges ccepted y DFs, NFs, nd regulr expressions
Homework 4. 0 ε 0. (00) ε 0 ε 0 (00) (11) CS 341: Foundations of Computer Science II Prof. Marvin Nakayama
 CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 4 1. UsetheproceduredescriedinLemm1.55toconverttheregulrexpression(((00) (11)) 01) into n NFA. Answer: 0 0 1 1 00 0 0 11 1 1 01 0 1 (00)
CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 4 1. UsetheproceduredescriedinLemm1.55toconverttheregulrexpression(((00) (11)) 01) into n NFA. Answer: 0 0 1 1 00 0 0 11 1 1 01 0 1 (00)
1. For each of the following theorems, give a two or three sentence sketch of how the proof goes or why it is not true.
 York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
Talen en Automaten Test 1, Mon 7 th Dec, h45 17h30
 Tlen en Automten Test 1, Mon 7 th Dec, 2015 15h45 17h30 This test consists of four exercises over 5 pges. Explin your pproch, nd write your nswer to ech exercise on seprte pge. You cn score mximum of 100
Tlen en Automten Test 1, Mon 7 th Dec, 2015 15h45 17h30 This test consists of four exercises over 5 pges. Explin your pproch, nd write your nswer to ech exercise on seprte pge. You cn score mximum of 100
Instructions. An 8.5 x 11 Cheat Sheet may also be used as an aid for this test. MUST be original handwriting.
 ID: B CSE 2021 Computer Orgniztion Midterm Test (Fll 2009) Instrutions This is losed ook, 80 minutes exm. The MIPS referene sheet my e used s n id for this test. An 8.5 x 11 Chet Sheet my lso e used s
ID: B CSE 2021 Computer Orgniztion Midterm Test (Fll 2009) Instrutions This is losed ook, 80 minutes exm. The MIPS referene sheet my e used s n id for this test. An 8.5 x 11 Chet Sheet my lso e used s
Lecture 08: Feb. 08, 2019
 4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
New Algorithms: Linear, Nonlinear, and Integer Programming
 New Algorthms: ner, Nonlner, nd Integer Progrmmng Dhnnjy P. ehendle Sr Prshurmhu College, Tl Rod, Pune-400, Ind dhnnjy.p.mehendle@gml.om Astrt In ths pper we propose new lgorthm for lner progrmmng. Ths
New Algorthms: ner, Nonlner, nd Integer Progrmmng Dhnnjy P. ehendle Sr Prshurmhu College, Tl Rod, Pune-400, Ind dhnnjy.p.mehendle@gml.om Astrt In ths pper we propose new lgorthm for lner progrmmng. Ths
In-depth introduction to main models, concepts of theory of computation:
 CMPSCI601: Introduction Lecture 1 In-depth introduction to min models, concepts of theory of computtion: Computility: wht cn e computed in principle Logic: how cn we express our requirements Complexity:
CMPSCI601: Introduction Lecture 1 In-depth introduction to min models, concepts of theory of computtion: Computility: wht cn e computed in principle Logic: how cn we express our requirements Complexity:
CMSC 330: Organization of Programming Languages
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 CMSC 330 1 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All exmples so fr Nondeterministic
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 CMSC 330 1 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All exmples so fr Nondeterministic
The University of Nottingham SCHOOL OF COMPUTER SCIENCE A LEVEL 2 MODULE, SPRING SEMESTER LANGUAGES AND COMPUTATION ANSWERS
 The University of Nottinghm SCHOOL OF COMPUTER SCIENCE LEVEL 2 MODULE, SPRING SEMESTER 2016 2017 LNGUGES ND COMPUTTION NSWERS Time llowed TWO hours Cndidtes my complete the front cover of their nswer ook
The University of Nottinghm SCHOOL OF COMPUTER SCIENCE LEVEL 2 MODULE, SPRING SEMESTER 2016 2017 LNGUGES ND COMPUTTION NSWERS Time llowed TWO hours Cndidtes my complete the front cover of their nswer ook
Converting Regular Expressions to Discrete Finite Automata: A Tutorial
 Converting Regulr Expressions to Discrete Finite Automt: A Tutoril Dvid Christinsen 2013-01-03 This is tutoril on how to convert regulr expressions to nondeterministic finite utomt (NFA) nd how to convert
Converting Regulr Expressions to Discrete Finite Automt: A Tutoril Dvid Christinsen 2013-01-03 This is tutoril on how to convert regulr expressions to nondeterministic finite utomt (NFA) nd how to convert
CS 310 (sec 20) - Winter Final Exam (solutions) SOLUTIONS
 CS 310 (sec 20) - Winter 2003 - Finl Exm (solutions) SOLUTIONS 1. (Logic) Use truth tles to prove the following logicl equivlences: () p q (p p) (q q) () p q (p q) (p q) () p q p q p p q q (q q) (p p)
CS 310 (sec 20) - Winter 2003 - Finl Exm (solutions) SOLUTIONS 1. (Logic) Use truth tles to prove the following logicl equivlences: () p q (p p) (q q) () p q (p q) (p q) () p q p q p p q q (q q) (p p)
NFAs continued, Closure Properties of Regular Languages
 Algorithms & Models of Computtion CS/ECE 374, Fll 2017 NFAs continued, Closure Properties of Regulr Lnguges Lecture 5 Tuesdy, Septemer 12, 2017 Sriel Hr-Peled (UIUC) CS374 1 Fll 2017 1 / 31 Regulr Lnguges,
Algorithms & Models of Computtion CS/ECE 374, Fll 2017 NFAs continued, Closure Properties of Regulr Lnguges Lecture 5 Tuesdy, Septemer 12, 2017 Sriel Hr-Peled (UIUC) CS374 1 Fll 2017 1 / 31 Regulr Lnguges,
A Study on the Properties of Rational Triangles
 Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Interntionl Journl of Mthemtis Reserh. ISSN 0976-5840 Volume 6, Numer (04), pp. 8-9 Interntionl Reserh Pulition House http://www.irphouse.om Study on the Properties of Rtionl Tringles M. Q. lm, M.R. Hssn
Convert the NFA into DFA
 Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Controller Design for Networked Control Systems in Multiple-packet Transmission with Random Delays
 Appled Mehans and Materals Onlne: 03-0- ISSN: 66-748, Vols. 78-80, pp 60-604 do:0.408/www.sentf.net/amm.78-80.60 03 rans eh Publatons, Swtzerland H Controller Desgn for Networed Control Systems n Multple-paet
Appled Mehans and Materals Onlne: 03-0- ISSN: 66-748, Vols. 78-80, pp 60-604 do:0.408/www.sentf.net/amm.78-80.60 03 rans eh Publatons, Swtzerland H Controller Desgn for Networed Control Systems n Multple-paet
CS 275 Automata and Formal Language Theory
 CS 275 utomt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Prolem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) nton Setzer (Bsed on ook drft y J. V. Tucker nd K. Stephenson)
CS 275 utomt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Prolem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) nton Setzer (Bsed on ook drft y J. V. Tucker nd K. Stephenson)
1.4 Nonregular Languages
 74 1.4 Nonregulr Lnguges The number of forml lnguges over ny lphbet (= decision/recognition problems) is uncountble On the other hnd, the number of regulr expressions (= strings) is countble Hence, ll
74 1.4 Nonregulr Lnguges The number of forml lnguges over ny lphbet (= decision/recognition problems) is uncountble On the other hnd, the number of regulr expressions (= strings) is countble Hence, ll
Matrix. Definition 1... a1 ... (i) where a. are real numbers. for i 1, 2,, m and j = 1, 2,, n (iii) A is called a square matrix if m n.
 Mtrx Defto () s lled order of m mtrx, umer of rows ( 橫行 ) umer of olums ( 直列 ) m m m where j re rel umers () B j j for,,, m d j =,,, () s lled squre mtrx f m (v) s lled zero mtrx f (v) s lled detty mtrx
Mtrx Defto () s lled order of m mtrx, umer of rows ( 橫行 ) umer of olums ( 直列 ) m m m where j re rel umers () B j j for,,, m d j =,,, () s lled squre mtrx f m (v) s lled zero mtrx f (v) s lled detty mtrx
NFA DFA Example 3 CMSC 330: Organization of Programming Languages. Equivalence of DFAs and NFAs. Equivalence of DFAs and NFAs (cont.
 NFA DFA Exmple 3 CMSC 330: Orgniztion of Progrmming Lnguges NFA {B,D,E {A,E {C,D {E Finite Automt, con't. R = { {A,E, {B,D,E, {C,D, {E 2 Equivlence of DFAs nd NFAs Any string from {A to either {D or {CD
NFA DFA Exmple 3 CMSC 330: Orgniztion of Progrmming Lnguges NFA {B,D,E {A,E {C,D {E Finite Automt, con't. R = { {A,E, {B,D,E, {C,D, {E 2 Equivlence of DFAs nd NFAs Any string from {A to either {D or {CD
Table of contents: Lecture N Summary... 3 What does automata mean?... 3 Introduction to languages... 3 Alphabets... 3 Strings...
 Tle of contents: Lecture N0.... 3 ummry... 3 Wht does utomt men?... 3 Introduction to lnguges... 3 Alphets... 3 trings... 3 Defining Lnguges... 4 Lecture N0. 2... 7 ummry... 7 Kleene tr Closure... 7 Recursive
Tle of contents: Lecture N0.... 3 ummry... 3 Wht does utomt men?... 3 Introduction to lnguges... 3 Alphets... 3 trings... 3 Defining Lnguges... 4 Lecture N0. 2... 7 ummry... 7 Kleene tr Closure... 7 Recursive
Name Ima Sample ASU ID
 Nme Im Smple ASU ID 2468024680 CSE 355 Test 1, Fll 2016 30 Septemer 2016, 8:35-9:25.m., LSA 191 Regrding of Midterms If you elieve tht your grde hs not een dded up correctly, return the entire pper to
Nme Im Smple ASU ID 2468024680 CSE 355 Test 1, Fll 2016 30 Septemer 2016, 8:35-9:25.m., LSA 191 Regrding of Midterms If you elieve tht your grde hs not een dded up correctly, return the entire pper to
11.1 Finite Automata. CS125 Lecture 11 Fall Motivation: TMs without a tape: maybe we can at least fully understand such a simple model?
 CS125 Lecture 11 Fll 2016 11.1 Finite Automt Motivtion: TMs without tpe: mybe we cn t lest fully understnd such simple model? Algorithms (e.g. string mtching) Computing with very limited memory Forml verifiction
CS125 Lecture 11 Fll 2016 11.1 Finite Automt Motivtion: TMs without tpe: mybe we cn t lest fully understnd such simple model? Algorithms (e.g. string mtching) Computing with very limited memory Forml verifiction
PYTHAGORAS THEOREM WHAT S IN CHAPTER 1? IN THIS CHAPTER YOU WILL:
 PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
PYTHAGORAS THEOREM 1 WHAT S IN CHAPTER 1? 1 01 Squres, squre roots nd surds 1 02 Pythgors theorem 1 03 Finding the hypotenuse 1 04 Finding shorter side 1 05 Mixed prolems 1 06 Testing for right-ngled tringles
State Complexity of Union and Intersection of Binary Suffix-Free Languages
 Stte Complexity of Union nd Intersetion of Binry Suffix-Free Lnguges Glin Jirásková nd Pvol Olejár Slovk Ademy of Sienes nd Šfárik University, Košie 0000 1111 0000 1111 Glin Jirásková nd Pvol Olejár Binry
Stte Complexity of Union nd Intersetion of Binry Suffix-Free Lnguges Glin Jirásková nd Pvol Olejár Slovk Ademy of Sienes nd Šfárik University, Košie 0000 1111 0000 1111 Glin Jirásková nd Pvol Olejár Binry
Designing finite automata II
 Designing finite utomt II Prolem: Design DFA A such tht L(A) consists of ll strings of nd which re of length 3n, for n = 0, 1, 2, (1) Determine wht to rememer out the input string Assign stte to ech of
Designing finite utomt II Prolem: Design DFA A such tht L(A) consists of ll strings of nd which re of length 3n, for n = 0, 1, 2, (1) Determine wht to rememer out the input string Assign stte to ech of
Non Deterministic Automata. Linz: Nondeterministic Finite Accepters, page 51
 Non Deterministic Automt Linz: Nondeterministic Finite Accepters, pge 51 1 Nondeterministic Finite Accepter (NFA) Alphbet ={} q 1 q2 q 0 q 3 2 Nondeterministic Finite Accepter (NFA) Alphbet ={} Two choices
Non Deterministic Automt Linz: Nondeterministic Finite Accepters, pge 51 1 Nondeterministic Finite Accepter (NFA) Alphbet ={} q 1 q2 q 0 q 3 2 Nondeterministic Finite Accepter (NFA) Alphbet ={} Two choices
CSE 401 Compilers. Today s Agenda
 CSE 401 Compilers Leture 3: Regulr Expressions & Snning, on?nued Mihel Ringenurg Tody s Agend Lst?me we reviewed lnguges nd grmmrs, nd riefly strted disussing regulr expressions. Tody I ll restrt the regulr
CSE 401 Compilers Leture 3: Regulr Expressions & Snning, on?nued Mihel Ringenurg Tody s Agend Lst?me we reviewed lnguges nd grmmrs, nd riefly strted disussing regulr expressions. Tody I ll restrt the regulr
Non-deterministic Finite Automata
 Non-deterministic Finite Automt Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd T. vn Lrhoven Institute for Computing nd Informtion Sciences Intelligent
Non-deterministic Finite Automt Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd T. vn Lrhoven Institute for Computing nd Informtion Sciences Intelligent
Types of Finite Automata. CMSC 330: Organization of Programming Languages. Comparing DFAs and NFAs. NFA for (a b)*abb.
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
Types of Finite Automata. CMSC 330: Organization of Programming Languages. Comparing DFAs and NFAs. Comparing DFAs and NFAs (cont.) Finite Automata 2
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
CS 330 Formal Methods and Models
 CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2017 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 2 1. Prove ((( p q) q) p) is tutology () (3pts) y truth tle. p q p q
CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2017 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 2 1. Prove ((( p q) q) p) is tutology () (3pts) y truth tle. p q p q
Running an NFA & the subset algorithm (NFA->DFA) CS 350 Fall 2018 gilray.org/classes/fall2018/cs350/
 Running n NFA & the suset lgorithm (NFA->DFA) CS 350 Fll 2018 gilry.org/lsses/fll2018/s350/ 1 NFAs operte y simultneously exploring ll pths nd epting if ny pth termintes t n ept stte.!2 Try n exmple: L
Running n NFA & the suset lgorithm (NFA->DFA) CS 350 Fll 2018 gilry.org/lsses/fll2018/s350/ 1 NFAs operte y simultneously exploring ll pths nd epting if ny pth termintes t n ept stte.!2 Try n exmple: L
Scanner. Specifying patterns. Specifying patterns. Operations on languages. A scanner must recognize the units of syntax Some parts are easy:
 Scnner Specifying ptterns source code tokens scnner prser IR A scnner must recognize the units of syntx Some prts re esy: errors mps chrcters into tokens the sic unit of syntx x = x + y; ecomes
Scnner Specifying ptterns source code tokens scnner prser IR A scnner must recognize the units of syntx Some prts re esy: errors mps chrcters into tokens the sic unit of syntx x = x + y; ecomes
Al-Zangana Iraqi Journal of Science, 2016, Vol. 57, No.2A, pp:
 Results n Projetve Geometry PG( r,), r, Emd Bkr Al-Zngn* Deprtment of Mthemts, College of Sene, Al-Mustnsryh Unversty, Bghdd, Ir Abstrt In projetve plne over fnte feld F, on s the unue omplete ( ) r nd
Results n Projetve Geometry PG( r,), r, Emd Bkr Al-Zngn* Deprtment of Mthemts, College of Sene, Al-Mustnsryh Unversty, Bghdd, Ir Abstrt In projetve plne over fnte feld F, on s the unue omplete ( ) r nd
CS103B Handout 18 Winter 2007 February 28, 2007 Finite Automata
 CS103B ndout 18 Winter 2007 Ferury 28, 2007 Finite Automt Initil text y Mggie Johnson. Introduction Severl childrens gmes fit the following description: Pieces re set up on plying ord; dice re thrown or
CS103B ndout 18 Winter 2007 Ferury 28, 2007 Finite Automt Initil text y Mggie Johnson. Introduction Severl childrens gmes fit the following description: Pieces re set up on plying ord; dice re thrown or
Project 6: Minigoals Towards Simplifying and Rewriting Expressions
 MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
MAT 51 Wldis Projet 6: Minigols Towrds Simplifying nd Rewriting Expressions The distriutive property nd like terms You hve proly lerned in previous lsses out dding like terms ut one prolem with the wy
CSE : Exam 3-ANSWERS, Spring 2011 Time: 50 minutes
 CSE 260-002: Exm 3-ANSWERS, Spring 20 ime: 50 minutes Nme: his exm hs 4 pges nd 0 prolems totling 00 points. his exm is closed ook nd closed notes.. Wrshll s lgorithm for trnsitive closure computtion is
CSE 260-002: Exm 3-ANSWERS, Spring 20 ime: 50 minutes Nme: his exm hs 4 pges nd 0 prolems totling 00 points. his exm is closed ook nd closed notes.. Wrshll s lgorithm for trnsitive closure computtion is
CS 330 Formal Methods and Models Dana Richards, George Mason University, Spring 2016 Quiz Solutions
 CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2016 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 9 1. (4pts) ((p q) (q r)) (p r), prove tutology using truth tles. p
CS 330 Forml Methods nd Models Dn Richrds, George Mson University, Spring 2016 Quiz Solutions Quiz 1, Propositionl Logic Dte: Ferury 9 1. (4pts) ((p q) (q r)) (p r), prove tutology using truth tles. p
Data Structures and Algorithm. Xiaoqing Zheng
 Dt Strutures nd Algorithm Xioqing Zheng zhengxq@fudn.edu.n String mthing prolem Pttern P ours with shift s in text T (or, equivlently, tht pttern P ours eginning t position s + in text T) if T[s +... s
Dt Strutures nd Algorithm Xioqing Zheng zhengxq@fudn.edu.n String mthing prolem Pttern P ours with shift s in text T (or, equivlently, tht pttern P ours eginning t position s + in text T) if T[s +... s
KULLBACK-LEIBLER DISTANCE BETWEEN COMPLEX GENERALIZED GAUSSIAN DISTRIBUTIONS
 0th Europen Sgnl Proessng Conferene (EUSIPCO 0) uhrest, Romn, August 7-3, 0 KULLACK-LEILER DISTANCE ETWEEN COMPLEX GENERALIZED GAUSSIAN DISTRIUTIONS Corn Nfornt, Ynnk erthoumeu, Ion Nfornt, Alexndru Isr
0th Europen Sgnl Proessng Conferene (EUSIPCO 0) uhrest, Romn, August 7-3, 0 KULLACK-LEILER DISTANCE ETWEEN COMPLEX GENERALIZED GAUSSIAN DISTRIUTIONS Corn Nfornt, Ynnk erthoumeu, Ion Nfornt, Alexndru Isr
Thoery of Automata CS402
 Thoery of Automt C402 Theory of Automt Tle of contents: Lecture N0. 1... 4 ummry... 4 Wht does utomt men?... 4 Introduction to lnguges... 4 Alphets... 4 trings... 4 Defining Lnguges... 5 Lecture N0. 2...
Thoery of Automt C402 Theory of Automt Tle of contents: Lecture N0. 1... 4 ummry... 4 Wht does utomt men?... 4 Introduction to lnguges... 4 Alphets... 4 trings... 4 Defining Lnguges... 5 Lecture N0. 2...
CS375: Logic and Theory of Computing
 CS375: Logic nd Theory of Computing Fuhu (Frnk) Cheng Deprtment of Computer Science University of Kentucky 1 Tle of Contents: Week 1: Preliminries (set lger, reltions, functions) (red Chpters 1-4) Weeks
CS375: Logic nd Theory of Computing Fuhu (Frnk) Cheng Deprtment of Computer Science University of Kentucky 1 Tle of Contents: Week 1: Preliminries (set lger, reltions, functions) (red Chpters 1-4) Weeks
Regular Languages and Applications
 Regulr Lnguges nd Applictions Yo-Su Hn Deprtment of Computer Science Yonsei University 1-1 SNU 4/14 Regulr Lnguges An old nd well-known topic in CS Kleene Theorem in 1959 FA (finite-stte utomton) constructions:
Regulr Lnguges nd Applictions Yo-Su Hn Deprtment of Computer Science Yonsei University 1-1 SNU 4/14 Regulr Lnguges An old nd well-known topic in CS Kleene Theorem in 1959 FA (finite-stte utomton) constructions:
