Previously on GLT. Basic technologies. Lexical analysis. Basic technologies ASF+SDF. Concepts of programming languages
|
|
|
- Scot Hood
- 6 years ago
- Views:
Transcription
1 Prevously on GLT Generc Lnguge Technology: Bsc technologes Pro.dr. Mrk vn den Brnd ASF+SDF syntx descrptons semntc descrptons: type checkng nlyss trnsormtons t so to s Concepts o progrmmng lnguges syntctc ssues semntc ssues Met modelng nd model trnsormtons / Fcultet Wskunde en Inormtc PAGE 1 Bsc technologes Syntctcl nlyss Prser genertors Rewrte engnes Tsks nd orgnzton o lexcl nlyzer Speccton o lexcl tokens v regulr expressons Implementton o regulr expressons (non-)determnstc nte utomt trnslton o regulr expresson to utomton / Fcultet Wskunde en Inormtc PAGE 2 / Fcultet Wskunde en Inormtc PAGE 3
2 progrm text (chrcters) Syntctcl nlyss prse tree Tsks o the lexcl nlyzer: redng the nput nd producton o tokens elmnton o lyout nd comments keepng trck o poston normton Lexcl nlyzer get next token token Prser Symol tle / Fcultet Wskunde en Inormtc PAGE 4 / Fcultet Wskunde en Inormtc PAGE 5 A regulr expresson (r.e.) r over n lphet Σ corresponds to the lnguge L(r) 1. s r.e. nd corresponds to {} 2. Σ s r.e. nd corresponds to {} 3. Suppose r nd s re r.e. s correspondng to the lnguges L(r) nd L(s). lterntve (r) (s) s r.e. L(r) L(s). conctenton (r) (s) s r.e. L(r) L(s) c. Kleene closure (r)* s r.e. (L(r))* d. rckets (r) s r.e. L(r) Opertors re let-ssoctve nd prortes re * > conctenton > A regulr denton over lphet Σ hs the orm: re 1 -> d 1 re 2 -> d 2 re n -> d n where d re derent nmes nd ech re s r.e. over lphet Σ {d 1, d 2,, d -1 } Thus, n re occur only nmes whch re lredy dened / Fcultet Wskunde en Inormtc PAGE 6 / Fcultet Wskunde en Inormtc PAGE 7
3 A regulr expresson cn e compled nto nte utomton (FA = nte utomton) whch s recognzer or the correspondng regulr lnguge A nte utomton s non-determnstc severl derent trnstons re possle or one nput symol n stte (NFA) There re two possle wys o trnsormng r.e. nto determnstc nte utomton: 1. r.e. NFA DFA 2. re r.e. DFA The generted DFA hs to e optmzed Otherwse the nte utomton s determnstc (DFA) / Fcultet Wskunde en Inormtc PAGE 8 / Fcultet Wskunde en Inormtc PAGE 9 Non-determnstc nte utomton conssts o: 1. Set o sttes S 2. Input lphet Σ 3. Trnston uncton whch tkes stte/symol pr nd yelds set o new sttes 4. The strt stte s 0 S 5. A set F o cceptng sttes Exmple: S = {0,1,2,3} Σ = {, } S 0 = 0 F = {3} Ths utomton ccepts: ( )* Trnston uncton: Stte 0 {0,1} {0} 1 {2} 2 {3} / Fcultet Wskunde en Inormtc PAGE 10 / Fcultet Wskunde en Inormtc PAGE 11
4 Trnstons my lso e lelled wth NFA ccepts strng x There exsts pth n the trnston dgrm rom strt to nl stte such tht the conctenton o the lels on the pth equl x For exmple s ccepted y the prevous NFA Pth: Lels: = The regulr expresson s: * * / Fcultet Wskunde en Inormtc PAGE 12 / Fcultet Wskunde en Inormtc PAGE 13 Regulr expresson NFA Input: regulr expresson r over lphet Σ Output: NFA N whch ccepts L(r) 1. r = 2. r = where Σ 1. Suppose N(s) nd N(t) re NFAs or the r.e. s nd t. r = s t. r=st N(s) N(s) N(t) N(t) Ths operton s only possle the nl stte o N(s) hs no outgong trnstons nd the strt stte o N(t) hs no ncomng trnstons / Fcultet Wskunde en Inormtc PAGE 14 / Fcultet Wskunde en Inormtc PAGE 15
5 c. r = s* N(s) d. r =(s) thenn(r) =N(s) Converson NFA DFA Regulr expresson cn e trnsormed nto NFAs DFAs cn e smulted/mplemented ecently Trnsormton o NFA nto DFA: construct DFA where ech stte represents suset o the sttes o the sttes o the NFA ter redng the nput 1 2 n the NFA s n set o sttes T, whch corresponds to one stte o the DFA / Fcultet Wskunde en Inormtc PAGE 16 / Fcultet Wskunde en Inormtc PAGE 17 Auxlry unctons: -closure(s) yelds set o NFA sttes rechle rom stte s n NFA v -trnstons only -closure(t) yelds set o NFA sttes rechle rom stte s n T v -trnstons only move(t, ) yelds set o NFA sttes rechle rom stte s n T v nput Intlly, -closure(s 0 ) s the only stte n Dsttes nd unmrked whle there s n unmrked stte T n Dsttes do mrk T; or ech nput symol do U := -closure(move(t, )) U s not n Dsttes then dd U s n unmrked stte to Dsttes; end Dtrns[T,] := U; end end / Fcultet Wskunde en Inormtc PAGE 18 / Fcultet Wskunde en Inormtc PAGE 19
6 Suset constructon (Rn & Scott) NFA = (Q, V, γ, q 0, F) NFA N or ( )* Equvlent DFA = (P(Q), V, δ, {q 0 }, F ) ) δ P(Q) V P(Q) δ(qq, ) ) = ( q:q qq : γ(q, ( )) F = {qq P(Q) qq F } δ({q 0 }, w) = set o ll sttes n whch the orgnl NFA cn e ter processng strng w / Fcultet Wskunde en Inormtc PAGE 20 / Fcultet Wskunde en Inormtc PAGE 21 A = {0, 1, 4, 5, 7} (= -closure(0)) B = {1, 2, 3, 4, 6, 7, 8} (= move({0, 1, 4, 5, 7}, )) C = {1, 2, 4, 5, 6, 7} (= move({0, 1, 4, 5, 7}, )) D = {1,2,4,5,6,7,9}(= move({1, 2, 3, 4, 6, 7, 8}, )) E = {1, 2, 4, 5, 6, 7, 10} (= move({1, 2, 3, 4, 6, 7, 9}, )) Resultng DFA A B D E Trnston tle stte A B C B B D C B C D B E E B C C / Fcultet Wskunde en Inormtc PAGE 22 / Fcultet Wskunde en Inormtc PAGE 23
7 LEX s scnner genertor whch trnsorms regulr expressons nto nte utomton: r.e. NFA re 0 {cton 0 } re 1 {cton 1 } 0 0 re k {cton k } strt F = { 0,, k } NFA DFA cceptng sttes hve the orm {,,,,, c, } wth correspondng cton: cton mn(,,c) k k Resoluton o mgutes Longest mtch s preerred I two lterntves recognze the sme sequence o chrcters, the lterntve occurrng rst n the speccton s chosen BEGIN [sym := egnsym] IF [sym := sym] letter.(letter dgt)* [sym := dsym] dgt.(dgt)* [sym := ntrepsym] := [sym := ecomessym] / Fcultet Wskunde en Inormtc PAGE 24 / Fcultet Wskunde en Inormtc PAGE 25 Syntctcl nlyss Syntctcl nlyss Context-ree grmmrs Dervtons Prse Trees Let-recursve grmmrs Top-down prsng non-recursve predctve prsers constructon o prse tles Bottom-up prsng sht/reduce prsers LR prsers GLR prsers SGLR prsers A context-ree grmmr s 4-tuple G = (N, Σ, P, S) 1. N s set o non termnls 2. Σ s set o termnls (dsjont rom N) 3. P s suset o (N Σ)* N An element (α, A) P s clled producton A ::= α or α A 4. S N s the strt symol The sets N, Σ, P re nte / Fcultet Wskunde en Inormtc PAGE 26 / Fcultet Wskunde en Inormtc PAGE 27
8 Syntctcl nlyss Syntctcl nlyss A context-ree grmmr cn e consder s smple rewrte system: A A P (,, (N Σ)*, A N) Exmple N = {E}, Σ = {+,*,(,),-, }, S = E, P = { E + E E E * E E ( E ) E - E E E} } Dervton: E -E -(E) -(E+E) -(+E) -(+) The lnguge L(G) generted y the context-ree grmmr G = (N, Σ, P, S) s: L(G) = {w Σ* S + w} A sentence w L(G) contns only termnls A sententl orm s strng o termnls nd nontermnls whch cn e derved rom S: S * wth (N Σ) * A sentence n L(G) s sententl orm n whch no non-termnls occur / Fcultet Wskunde en Inormtc PAGE 28 / Fcultet Wskunde en Inormtc PAGE 29 Syntctcl nlyss Syntctcl nlyss Let/rght dervtons There re choces to e mde or ech dervton step: whch non-termnl must e replced? whch lterntve o the selected non-termnl must e ppled? Alwys selectng the letmost non-termnl n the sententl orm gves letmost dervton: lm There exsts lso rghtmost dervton: rm Consder the context-ree grmmr or expressons: Letmost dervton or -(+) E -E -(E) -(E+E) -(+E) -(+) Rghtmost t dervton or -(+) E -E -(E) -(E+E) -(E+) -(+) A prse tree or context-ree grmmr s G = (N, Σ, P, S) tree: 1. The root s leled wth S (the strt non-termnl) 2. Ech le s leled wth termnl ( Σ)or 3. All other nodes re leled wth non-termnl I A s the lel o node nd X 1,,X n re the lels o the chldren (rom let to rght) then X 1,,X n A must e producton rule n G (wth X s ether termnl or non-termnl) Specl cse: A wth lel A whch hs exctly one chld wth lel / Fcultet Wskunde en Inormtc PAGE 30 / Fcultet Wskunde en Inormtc PAGE 31
9 Syntctcl nlyss Syntctcl nlyss Exmple: E -E -(E) -(E+E) -(+E) -(+) E E E E E E E - E - E - E - E - E - E ( E ) ( E ) ( E ) ( E ) ( E ) E + E E + E E + E The prse tree strcts rom the dervton order Acceptor nd prser For ech grmmr G there exsts decson procedure (cceptor) AG or L(G): AG: STRING {true, lse} such tht AG(w) =true w L(G) A prser s n cceptor whch constructs prse tree s well. A top-down prser constructs the tree strtng rom the root A ottom-up prser constructs the tree strtng rom the les / Fcultet Wskunde en Inormtc PAGE 32 / Fcultet Wskunde en Inormtc PAGE 33
Scanner. Specifying patterns. Specifying patterns. Operations on languages. A scanner must recognize the units of syntax Some parts are easy:
 Scnner Specifying ptterns source code tokens scnner prser IR A scnner must recognize the units of syntx Some prts re esy: errors mps chrcters into tokens the sic unit of syntx x = x + y; ecomes
Scnner Specifying ptterns source code tokens scnner prser IR A scnner must recognize the units of syntx Some prts re esy: errors mps chrcters into tokens the sic unit of syntx x = x + y; ecomes
Java II Finite Automata I
 Jv II Finite Automt I Bernd Kiefer Bernd.Kiefer@dfki.de Deutsches Forschungszentrum für künstliche Intelligenz Finite Automt I p.1/13 Processing Regulr Expressions We lredy lerned out Jv s regulr expression
Jv II Finite Automt I Bernd Kiefer Bernd.Kiefer@dfki.de Deutsches Forschungszentrum für künstliche Intelligenz Finite Automt I p.1/13 Processing Regulr Expressions We lredy lerned out Jv s regulr expression
Lexical Analysis Part III
 Lexicl Anlysis Prt III Chpter 3: Finite Automt Slides dpted from : Roert vn Engelen, Florid Stte University Alex Aiken, Stnford University Design of Lexicl Anlyzer Genertor Trnslte regulr expressions to
Lexicl Anlysis Prt III Chpter 3: Finite Automt Slides dpted from : Roert vn Engelen, Florid Stte University Alex Aiken, Stnford University Design of Lexicl Anlyzer Genertor Trnslte regulr expressions to
Regular Expressions (RE) Regular Expressions (RE) Regular Expressions (RE) Regular Expressions (RE) Kleene-*
 Regulr Expressions (RE) Regulr Expressions (RE) Empty set F A RE denotes the empty set Opertion Nottion Lnguge UNIX Empty string A RE denotes the set {} Alterntion R +r L(r ) L(r ) r r Symol Alterntion
Regulr Expressions (RE) Regulr Expressions (RE) Empty set F A RE denotes the empty set Opertion Nottion Lnguge UNIX Empty string A RE denotes the set {} Alterntion R +r L(r ) L(r ) r r Symol Alterntion
Lexical Analysis Finite Automate
 Lexicl Anlysis Finite Automte CMPSC 470 Lecture 04 Topics: Deterministic Finite Automt (DFA) Nondeterministic Finite Automt (NFA) Regulr Expression NFA DFA A. Finite Automt (FA) FA re grph, like trnsition
Lexicl Anlysis Finite Automte CMPSC 470 Lecture 04 Topics: Deterministic Finite Automt (DFA) Nondeterministic Finite Automt (NFA) Regulr Expression NFA DFA A. Finite Automt (FA) FA re grph, like trnsition
Non-deterministic Finite Automata
 Non-deterministic Finite Automt Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd T. vn Lrhoven Institute for Computing nd Informtion Sciences Intelligent
Non-deterministic Finite Automt Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd T. vn Lrhoven Institute for Computing nd Informtion Sciences Intelligent
AUTOMATA AND LANGUAGES. Definition 1.5: Finite Automaton
 25. Finite Automt AUTOMATA AND LANGUAGES A system of computtion tht only hs finite numer of possile sttes cn e modeled using finite utomton A finite utomton is often illustrted s stte digrm d d d. d q
25. Finite Automt AUTOMATA AND LANGUAGES A system of computtion tht only hs finite numer of possile sttes cn e modeled using finite utomton A finite utomton is often illustrted s stte digrm d d d. d q
Fundamentals of Computer Science
 Fundmentls of Computer Science Chpter 3: NFA nd DFA equivlence Regulr expressions Henrik Björklund Umeå University Jnury 23, 2014 NFA nd DFA equivlence As we shll see, it turns out tht NFA nd DFA re equivlent,
Fundmentls of Computer Science Chpter 3: NFA nd DFA equivlence Regulr expressions Henrik Björklund Umeå University Jnury 23, 2014 NFA nd DFA equivlence As we shll see, it turns out tht NFA nd DFA re equivlent,
CS415 Compilers. Lexical Analysis and. These slides are based on slides copyrighted by Keith Cooper, Ken Kennedy & Linda Torczon at Rice University
 CS415 Compilers Lexicl Anlysis nd These slides re sed on slides copyrighted y Keith Cooper, Ken Kennedy & Lind Torczon t Rice University First Progrmming Project Instruction Scheduling Project hs een posted
CS415 Compilers Lexicl Anlysis nd These slides re sed on slides copyrighted y Keith Cooper, Ken Kennedy & Lind Torczon t Rice University First Progrmming Project Instruction Scheduling Project hs een posted
CMSC 330: Organization of Programming Languages
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 CMSC 330 1 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All exmples so fr Nondeterministic
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 CMSC 330 1 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All exmples so fr Nondeterministic
CHAPTER 1 Regular Languages. Contents
 Finite Automt (FA or DFA) CHAPTE 1 egulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, euivlence of NFAs nd DFAs, closure under regulr
Finite Automt (FA or DFA) CHAPTE 1 egulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, euivlence of NFAs nd DFAs, closure under regulr
FABER Formal Languages, Automata and Models of Computation
 DVA337 FABER Forml Lnguges, Automt nd Models of Computtion Lecture 5 chool of Innovtion, Design nd Engineering Mälrdlen University 2015 1 Recp of lecture 4 y definition suset construction DFA NFA stte
DVA337 FABER Forml Lnguges, Automt nd Models of Computtion Lecture 5 chool of Innovtion, Design nd Engineering Mälrdlen University 2015 1 Recp of lecture 4 y definition suset construction DFA NFA stte
Non-deterministic Finite Automata
 Non-deterministic Finite Automt From Regulr Expressions to NFA- Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion
Non-deterministic Finite Automt From Regulr Expressions to NFA- Eliminting non-determinism Rdoud University Nijmegen Non-deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion
Harvard University Computer Science 121 Midterm October 23, 2012
 Hrvrd University Computer Science 121 Midterm Octoer 23, 2012 This is closed-ook exmintion. You my use ny result from lecture, Sipser, prolem sets, or section, s long s you quote it clerly. The lphet is
Hrvrd University Computer Science 121 Midterm Octoer 23, 2012 This is closed-ook exmintion. You my use ny result from lecture, Sipser, prolem sets, or section, s long s you quote it clerly. The lphet is
Types of Finite Automata. CMSC 330: Organization of Programming Languages. Comparing DFAs and NFAs. NFA for (a b)*abb.
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
Types of Finite Automata. CMSC 330: Organization of Programming Languages. Comparing DFAs and NFAs. Comparing DFAs and NFAs (cont.) Finite Automata 2
 CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
CMSC 330: Orgniztion of Progrmming Lnguges Finite Automt 2 Types of Finite Automt Deterministic Finite Automt () Exctly one sequence of steps for ech string All exmples so fr Nondeterministic Finite Automt
NFAs continued, Closure Properties of Regular Languages
 Algorithms & Models of Computtion CS/ECE 374, Fll 2017 NFAs continued, Closure Properties of Regulr Lnguges Lecture 5 Tuesdy, Septemer 12, 2017 Sriel Hr-Peled (UIUC) CS374 1 Fll 2017 1 / 31 Regulr Lnguges,
Algorithms & Models of Computtion CS/ECE 374, Fll 2017 NFAs continued, Closure Properties of Regulr Lnguges Lecture 5 Tuesdy, Septemer 12, 2017 Sriel Hr-Peled (UIUC) CS374 1 Fll 2017 1 / 31 Regulr Lnguges,
NFAs and Regular Expressions. NFA-ε, continued. Recall. Last class: Today: Fun:
 CMPU 240 Lnguge Theory nd Computtion Spring 2019 NFAs nd Regulr Expressions Lst clss: Introduced nondeterministic finite utomt with -trnsitions Tody: Prove n NFA- is no more powerful thn n NFA Introduce
CMPU 240 Lnguge Theory nd Computtion Spring 2019 NFAs nd Regulr Expressions Lst clss: Introduced nondeterministic finite utomt with -trnsitions Tody: Prove n NFA- is no more powerful thn n NFA Introduce
CS 301. Lecture 04 Regular Expressions. Stephen Checkoway. January 29, 2018
 CS 301 Lecture 04 Regulr Expressions Stephen Checkowy Jnury 29, 2018 1 / 35 Review from lst time NFA N = (Q, Σ, δ, q 0, F ) where δ Q Σ P (Q) mps stte nd n lphet symol (or ) to set of sttes We run n NFA
CS 301 Lecture 04 Regulr Expressions Stephen Checkowy Jnury 29, 2018 1 / 35 Review from lst time NFA N = (Q, Σ, δ, q 0, F ) where δ Q Σ P (Q) mps stte nd n lphet symol (or ) to set of sttes We run n NFA
Deterministic Finite Automata
 Finite Automt Deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion Sciences Version: fll 2016 J. Rot Version: fll 2016 Tlen en Automten 1 / 21 Outline Finite Automt Finite
Finite Automt Deterministic Finite Automt H. Geuvers nd J. Rot Institute for Computing nd Informtion Sciences Version: fll 2016 J. Rot Version: fll 2016 Tlen en Automten 1 / 21 Outline Finite Automt Finite
Converting Regular Expressions to Discrete Finite Automata: A Tutorial
 Converting Regulr Expressions to Discrete Finite Automt: A Tutoril Dvid Christinsen 2013-01-03 This is tutoril on how to convert regulr expressions to nondeterministic finite utomt (NFA) nd how to convert
Converting Regulr Expressions to Discrete Finite Automt: A Tutoril Dvid Christinsen 2013-01-03 This is tutoril on how to convert regulr expressions to nondeterministic finite utomt (NFA) nd how to convert
Minimal DFA. minimal DFA for L starting from any other
 Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
Miniml DFA Among the mny DFAs ccepting the sme regulr lnguge L, there is exctly one (up to renming of sttes) which hs the smllest possile numer of sttes. Moreover, it is possile to otin tht miniml DFA
1.3 Regular Expressions
 56 1.3 Regulr xpressions These hve n importnt role in describing ptterns in serching for strings in mny pplictions (e.g. wk, grep, Perl,...) All regulr expressions of lphbet re 1.Ønd re regulr expressions,
56 1.3 Regulr xpressions These hve n importnt role in describing ptterns in serching for strings in mny pplictions (e.g. wk, grep, Perl,...) All regulr expressions of lphbet re 1.Ønd re regulr expressions,
Assignment 1 Automata, Languages, and Computability. 1 Finite State Automata and Regular Languages
 Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
Deprtment of Computer Science, Austrlin Ntionl University COMP2600 Forml Methods for Softwre Engineering Semester 2, 206 Assignment Automt, Lnguges, nd Computility Smple Solutions Finite Stte Automt nd
Convert the NFA into DFA
 Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Convert the NF into F For ech NF we cn find F ccepting the sme lnguge. The numer of sttes of the F could e exponentil in the numer of sttes of the NF, ut in prctice this worst cse occurs rrely. lgorithm:
Theory of Computation Regular Languages. (NTU EE) Regular Languages Fall / 38
 Theory of Computtion Regulr Lnguges (NTU EE) Regulr Lnguges Fll 2017 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of Finite Automt A finite utomton hs finite set of control
Theory of Computtion Regulr Lnguges (NTU EE) Regulr Lnguges Fll 2017 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of Finite Automt A finite utomton hs finite set of control
1.4 Nonregular Languages
 74 1.4 Nonregulr Lnguges The number of forml lnguges over ny lphbet (= decision/recognition problems) is uncountble On the other hnd, the number of regulr expressions (= strings) is countble Hence, ll
74 1.4 Nonregulr Lnguges The number of forml lnguges over ny lphbet (= decision/recognition problems) is uncountble On the other hnd, the number of regulr expressions (= strings) is countble Hence, ll
Homework 3 Solutions
 CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 3 Solutions 1. Give NFAs with the specified numer of sttes recognizing ech of the following lnguges. In ll cses, the lphet is Σ = {,1}.
Lecture 6 Regular Grammars
 Lecture 6 Regulr Grmmrs COT 4420 Theory of Computtion Section 3.3 Grmmr A grmmr G is defined s qudruple G = (V, T, S, P) V is finite set of vribles T is finite set of terminl symbols S V is specil vrible
Lecture 6 Regulr Grmmrs COT 4420 Theory of Computtion Section 3.3 Grmmr A grmmr G is defined s qudruple G = (V, T, S, P) V is finite set of vribles T is finite set of terminl symbols S V is specil vrible
NFA DFA Example 3 CMSC 330: Organization of Programming Languages. Equivalence of DFAs and NFAs. Equivalence of DFAs and NFAs (cont.
 NFA DFA Exmple 3 CMSC 330: Orgniztion of Progrmming Lnguges NFA {B,D,E {A,E {C,D {E Finite Automt, con't. R = { {A,E, {B,D,E, {C,D, {E 2 Equivlence of DFAs nd NFAs Any string from {A to either {D or {CD
NFA DFA Exmple 3 CMSC 330: Orgniztion of Progrmming Lnguges NFA {B,D,E {A,E {C,D {E Finite Automt, con't. R = { {A,E, {B,D,E, {C,D, {E 2 Equivlence of DFAs nd NFAs Any string from {A to either {D or {CD
CSCI 340: Computational Models. Kleene s Theorem. Department of Computer Science
 CSCI 340: Computtionl Models Kleene s Theorem Chpter 7 Deprtment of Computer Science Unifiction In 1954, Kleene presented (nd proved) theorem which (in our version) sttes tht if lnguge cn e defined y ny
CSCI 340: Computtionl Models Kleene s Theorem Chpter 7 Deprtment of Computer Science Unifiction In 1954, Kleene presented (nd proved) theorem which (in our version) sttes tht if lnguge cn e defined y ny
Lecture 08: Feb. 08, 2019
 4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
4CS4-6:Theory of Computtion(Closure on Reg. Lngs., regex to NDFA, DFA to regex) Prof. K.R. Chowdhry Lecture 08: Fe. 08, 2019 : Professor of CS Disclimer: These notes hve not een sujected to the usul scrutiny
Overview HC9. Parsing: Top-Down & LL(1) Context-Free Grammars (1) Introduction. CFGs (3) Context-Free Grammars (2) Vertalerbouw HC 9: Ch.
 Overview H9 Vertlerouw H 9: Prsing: op-down & LL(1) do 3 mei 2001 56 heo Ruys h. 8 - Prsing 8.1 ontext-free Grmmrs 8.2 op-down Prsing 8.3 LL(1) Grmmrs See lso [ho, Sethi & Ullmn 1986] for more thorough
Overview H9 Vertlerouw H 9: Prsing: op-down & LL(1) do 3 mei 2001 56 heo Ruys h. 8 - Prsing 8.1 ontext-free Grmmrs 8.2 op-down Prsing 8.3 LL(1) Grmmrs See lso [ho, Sethi & Ullmn 1986] for more thorough
CS375: Logic and Theory of Computing
 CS375: Logic nd Theory of Computing Fuhu (Frnk) Cheng Deprtment of Computer Science University of Kentucky 1 Tle of Contents: Week 1: Preliminries (set lger, reltions, functions) (red Chpters 1-4) Weeks
CS375: Logic nd Theory of Computing Fuhu (Frnk) Cheng Deprtment of Computer Science University of Kentucky 1 Tle of Contents: Week 1: Preliminries (set lger, reltions, functions) (red Chpters 1-4) Weeks
First Midterm Examination
 24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
24-25 Fll Semester First Midterm Exmintion ) Give the stte digrm of DFA tht recognizes the lnguge A over lphet Σ = {, } where A = {w w contins or } 2) The following DFA recognizes the lnguge B over lphet
Formal Language and Automata Theory (CS21004)
 Forml Lnguge nd Automt Forml Lnguge nd Automt Theory (CS21004) Khrgpur Khrgpur Khrgpur Forml Lnguge nd Automt Tle of Contents Forml Lnguge nd Automt Khrgpur 1 2 3 Khrgpur Forml Lnguge nd Automt Forml Lnguge
Forml Lnguge nd Automt Forml Lnguge nd Automt Theory (CS21004) Khrgpur Khrgpur Khrgpur Forml Lnguge nd Automt Tle of Contents Forml Lnguge nd Automt Khrgpur 1 2 3 Khrgpur Forml Lnguge nd Automt Forml Lnguge
ɛ-closure, Kleene s Theorem,
 DEGefW5wiGH2XgYMEzUKjEmtCDUsRQ4d 1 A nice pper relevnt to this course is titled The Glory of the Pst 2 NICTA Resercher, Adjunct t the Austrlin Ntionl University nd Griffith University ɛ-closure, Kleene
DEGefW5wiGH2XgYMEzUKjEmtCDUsRQ4d 1 A nice pper relevnt to this course is titled The Glory of the Pst 2 NICTA Resercher, Adjunct t the Austrlin Ntionl University nd Griffith University ɛ-closure, Kleene
First Midterm Examination
 Çnky University Deprtment of Computer Engineering 203-204 Fll Semester First Midterm Exmintion ) Design DFA for ll strings over the lphet Σ = {,, c} in which there is no, no nd no cc. 2) Wht lnguge does
Çnky University Deprtment of Computer Engineering 203-204 Fll Semester First Midterm Exmintion ) Design DFA for ll strings over the lphet Σ = {,, c} in which there is no, no nd no cc. 2) Wht lnguge does
Worked out examples Finite Automata
 Worked out exmples Finite Automt Exmple Design Finite Stte Automton which reds inry string nd ccepts only those tht end with. Since we re in the topic of Non Deterministic Finite Automt (NFA), we will
Worked out exmples Finite Automt Exmple Design Finite Stte Automton which reds inry string nd ccepts only those tht end with. Since we re in the topic of Non Deterministic Finite Automt (NFA), we will
Theory of Computation Regular Languages
 Theory of Computtion Regulr Lnguges Bow-Yw Wng Acdemi Sinic Spring 2012 Bow-Yw Wng (Acdemi Sinic) Regulr Lnguges Spring 2012 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of
Theory of Computtion Regulr Lnguges Bow-Yw Wng Acdemi Sinic Spring 2012 Bow-Yw Wng (Acdemi Sinic) Regulr Lnguges Spring 2012 1 / 38 Schemtic of Finite Automt control 0 0 1 0 1 1 1 0 Figure: Schemtic of
Grammar. Languages. Content 5/10/16. Automata and Languages. Regular Languages. Regular Languages
 5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
5//6 Grmmr Automt nd Lnguges Regulr Grmmr Context-free Grmmr Context-sensitive Grmmr Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Regulr Lnguges Context Free Lnguges Context Sensitive
CSC 311 Theory of Computation
 CSC 11 Theory of Computtion Tutoril on DFAs, NFAs, regulr expressions, regulr grmmr, closure of regulr lnguges, context-free grmmrs, non-deterministic push-down utomt, Turing mchines,etc. Tutoril 2 Second
CSC 11 Theory of Computtion Tutoril on DFAs, NFAs, regulr expressions, regulr grmmr, closure of regulr lnguges, context-free grmmrs, non-deterministic push-down utomt, Turing mchines,etc. Tutoril 2 Second
Finite Automata-cont d
 Automt Theory nd Forml Lnguges Professor Leslie Lnder Lecture # 6 Finite Automt-cont d The Pumping Lemm WEB SITE: http://ingwe.inghmton.edu/ ~lnder/cs573.html Septemer 18, 2000 Exmple 1 Consider L = {ww
Automt Theory nd Forml Lnguges Professor Leslie Lnder Lecture # 6 Finite Automt-cont d The Pumping Lemm WEB SITE: http://ingwe.inghmton.edu/ ~lnder/cs573.html Septemer 18, 2000 Exmple 1 Consider L = {ww
2. Lexical Analysis. Oscar Nierstrasz
 2. Lexicl Anlysis Oscr Nierstrsz Thnks to Jens Plserg nd Tony Hosking for their kind permission to reuse nd dpt the CS132 nd CS502 lecture notes. http://www.cs.ucl.edu/~plserg/ http://www.cs.purdue.edu/homes/hosking/
2. Lexicl Anlysis Oscr Nierstrsz Thnks to Jens Plserg nd Tony Hosking for their kind permission to reuse nd dpt the CS132 nd CS502 lecture notes. http://www.cs.ucl.edu/~plserg/ http://www.cs.purdue.edu/homes/hosking/
Finite-State Automata: Recap
 Finite-Stte Automt: Recp Deepk D Souz Deprtment of Computer Science nd Automtion Indin Institute of Science, Bnglore. 09 August 2016 Outline 1 Introduction 2 Forml Definitions nd Nottion 3 Closure under
Finite-Stte Automt: Recp Deepk D Souz Deprtment of Computer Science nd Automtion Indin Institute of Science, Bnglore. 09 August 2016 Outline 1 Introduction 2 Forml Definitions nd Nottion 3 Closure under
a,b a 1 a 2 a 3 a,b 1 a,b a,b 2 3 a,b a,b a 2 a,b CS Determinisitic Finite Automata 1
 CS4 45- Determinisitic Finite Automt -: Genertors vs. Checkers Regulr expressions re one wy to specify forml lnguge String Genertor Genertes strings in the lnguge Deterministic Finite Automt (DFA) re nother
CS4 45- Determinisitic Finite Automt -: Genertors vs. Checkers Regulr expressions re one wy to specify forml lnguge String Genertor Genertes strings in the lnguge Deterministic Finite Automt (DFA) re nother
1. For each of the following theorems, give a two or three sentence sketch of how the proof goes or why it is not true.
 York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
York University CSE 2 Unit 3. DFA Clsses Converting etween DFA, NFA, Regulr Expressions, nd Extended Regulr Expressions Instructor: Jeff Edmonds Don t chet y looking t these nswers premturely.. For ech
NFAs continued, Closure Properties of Regular Languages
 lgorithms & Models of omputtion S/EE 374, Spring 209 NFs continued, losure Properties of Regulr Lnguges Lecture 5 Tuesdy, Jnury 29, 209 Regulr Lnguges, DFs, NFs Lnguges ccepted y DFs, NFs, nd regulr expressions
lgorithms & Models of omputtion S/EE 374, Spring 209 NFs continued, losure Properties of Regulr Lnguges Lecture 5 Tuesdy, Jnury 29, 209 Regulr Lnguges, DFs, NFs Lnguges ccepted y DFs, NFs, nd regulr expressions
Automata Theory 101. Introduction. Outline. Introduction Finite Automata Regular Expressions ω-automata. Ralf Huuck.
 Outline Automt Theory 101 Rlf Huuck Introduction Finite Automt Regulr Expressions ω-automt Session 1 2006 Rlf Huuck 1 Session 1 2006 Rlf Huuck 2 Acknowledgement Some slides re sed on Wolfgng Thoms excellent
Outline Automt Theory 101 Rlf Huuck Introduction Finite Automt Regulr Expressions ω-automt Session 1 2006 Rlf Huuck 1 Session 1 2006 Rlf Huuck 2 Acknowledgement Some slides re sed on Wolfgng Thoms excellent
Chapter Five: Nondeterministic Finite Automata. Formal Language, chapter 5, slide 1
 Chpter Five: Nondeterministic Finite Automt Forml Lnguge, chpter 5, slide 1 1 A DFA hs exctly one trnsition from every stte on every symol in the lphet. By relxing this requirement we get relted ut more
Chpter Five: Nondeterministic Finite Automt Forml Lnguge, chpter 5, slide 1 1 A DFA hs exctly one trnsition from every stte on every symol in the lphet. By relxing this requirement we get relted ut more
Exercises Chapter 1. Exercise 1.1. Let Σ be an alphabet. Prove wv = w + v for all strings w and v.
 1 Exercises Chpter 1 Exercise 1.1. Let Σ e n lphet. Prove wv = w + v for ll strings w nd v. Prove # (wv) = # (w)+# (v) for every symol Σ nd every string w,v Σ. Exercise 1.2. Let w 1,w 2,...,w k e k strings,
1 Exercises Chpter 1 Exercise 1.1. Let Σ e n lphet. Prove wv = w + v for ll strings w nd v. Prove # (wv) = # (w)+# (v) for every symol Σ nd every string w,v Σ. Exercise 1.2. Let w 1,w 2,...,w k e k strings,
Talen en Automaten Test 1, Mon 7 th Dec, h45 17h30
 Tlen en Automten Test 1, Mon 7 th Dec, 2015 15h45 17h30 This test consists of four exercises over 5 pges. Explin your pproch, nd write your nswer to ech exercise on seprte pge. You cn score mximum of 100
Tlen en Automten Test 1, Mon 7 th Dec, 2015 15h45 17h30 This test consists of four exercises over 5 pges. Explin your pproch, nd write your nswer to ech exercise on seprte pge. You cn score mximum of 100
Let's start with an example:
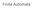 Finite Automt Let's strt with n exmple: Here you see leled circles tht re sttes, nd leled rrows tht re trnsitions. One of the sttes is mrked "strt". One of the sttes hs doule circle; this is terminl stte
Finite Automt Let's strt with n exmple: Here you see leled circles tht re sttes, nd leled rrows tht re trnsitions. One of the sttes is mrked "strt". One of the sttes hs doule circle; this is terminl stte
CS 314 Principles of Programming Languages
 C 314 Principles of Progrmming Lnguges Lecture 6: LL(1) Prsing Zheng (Eddy) Zhng Rutgers University Ferury 5, 2018 Clss Informtion Homework 2 due tomorrow. Homework 3 will e posted erly next week. 2 Top
C 314 Principles of Progrmming Lnguges Lecture 6: LL(1) Prsing Zheng (Eddy) Zhng Rutgers University Ferury 5, 2018 Clss Informtion Homework 2 due tomorrow. Homework 3 will e posted erly next week. 2 Top
12.1 Nondeterminism Nondeterministic Finite Automata. a a b ε. CS125 Lecture 12 Fall 2016
 CS125 Lecture 12 Fll 2016 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
CS125 Lecture 12 Fll 2016 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
Regular expressions, Finite Automata, transition graphs are all the same!!
 CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
CSI 3104 /Winter 2011: Introduction to Forml Lnguges Chpter 7: Kleene s Theorem Chpter 7: Kleene s Theorem Regulr expressions, Finite Automt, trnsition grphs re ll the sme!! Dr. Neji Zgui CSI3104-W11 1
CS 275 Automata and Formal Language Theory
 CS 275 utomt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Prolem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) nton Setzer (Bsed on ook drft y J. V. Tucker nd K. Stephenson)
CS 275 utomt nd Forml Lnguge Theory Course Notes Prt II: The Recognition Prolem (II) Chpter II.5.: Properties of Context Free Grmmrs (14) nton Setzer (Bsed on ook drft y J. V. Tucker nd K. Stephenson)
Context-Free Grammars and Languages
 Context-Free Grmmrs nd Lnguges (Bsed on Hopcroft, Motwni nd Ullmn (2007) & Cohen (1997)) Introduction Consider n exmple sentence: A smll ct ets the fish English grmmr hs rules for constructing sentences;
Context-Free Grmmrs nd Lnguges (Bsed on Hopcroft, Motwni nd Ullmn (2007) & Cohen (1997)) Introduction Consider n exmple sentence: A smll ct ets the fish English grmmr hs rules for constructing sentences;
CISC 4090 Theory of Computation
 9/6/28 Stereotypicl computer CISC 49 Theory of Computtion Finite stte mchines & Regulr lnguges Professor Dniel Leeds dleeds@fordhm.edu JMH 332 Centrl processing unit (CPU) performs ll the instructions
9/6/28 Stereotypicl computer CISC 49 Theory of Computtion Finite stte mchines & Regulr lnguges Professor Dniel Leeds dleeds@fordhm.edu JMH 332 Centrl processing unit (CPU) performs ll the instructions
Speech Recognition Lecture 2: Finite Automata and Finite-State Transducers. Mehryar Mohri Courant Institute and Google Research
 Speech Recognition Lecture 2: Finite Automt nd Finite-Stte Trnsducers Mehryr Mohri Cournt Institute nd Google Reserch mohri@cims.nyu.com Preliminries Finite lphet Σ, empty string. Set of ll strings over
Speech Recognition Lecture 2: Finite Automt nd Finite-Stte Trnsducers Mehryr Mohri Cournt Institute nd Google Reserch mohri@cims.nyu.com Preliminries Finite lphet Σ, empty string. Set of ll strings over
CHAPTER 1 Regular Languages. Contents. definitions, examples, designing, regular operations. Non-deterministic Finite Automata (NFA)
 Finite Automt (FA or DFA) CHAPTER Regulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, equivlence of NFAs DFAs, closure under regulr
Finite Automt (FA or DFA) CHAPTER Regulr Lnguges Contents definitions, exmples, designing, regulr opertions Non-deterministic Finite Automt (NFA) definitions, equivlence of NFAs DFAs, closure under regulr
Anatomy of a Deterministic Finite Automaton. Deterministic Finite Automata. A machine so simple that you can understand it in less than one minute
 Victor Admchik Dnny Sletor Gret Theoreticl Ides In Computer Science CS 5-25 Spring 2 Lecture 2 Mr 3, 2 Crnegie Mellon University Deterministic Finite Automt Finite Automt A mchine so simple tht you cn
Victor Admchik Dnny Sletor Gret Theoreticl Ides In Computer Science CS 5-25 Spring 2 Lecture 2 Mr 3, 2 Crnegie Mellon University Deterministic Finite Automt Finite Automt A mchine so simple tht you cn
3 Regular expressions
 3 Regulr expressions Given n lphet Σ lnguge is set of words L Σ. So fr we were le to descrie lnguges either y using set theory (i.e. enumertion or comprehension) or y n utomton. In this section we shll
3 Regulr expressions Given n lphet Σ lnguge is set of words L Σ. So fr we were le to descrie lnguges either y using set theory (i.e. enumertion or comprehension) or y n utomton. In this section we shll
CSE : Exam 3-ANSWERS, Spring 2011 Time: 50 minutes
 CSE 260-002: Exm 3-ANSWERS, Spring 20 ime: 50 minutes Nme: his exm hs 4 pges nd 0 prolems totling 00 points. his exm is closed ook nd closed notes.. Wrshll s lgorithm for trnsitive closure computtion is
CSE 260-002: Exm 3-ANSWERS, Spring 20 ime: 50 minutes Nme: his exm hs 4 pges nd 0 prolems totling 00 points. his exm is closed ook nd closed notes.. Wrshll s lgorithm for trnsitive closure computtion is
Nondeterminism and Nodeterministic Automata
 Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
Nondeterminism nd Nodeterministic Automt 61 Nondeterminism nd Nondeterministic Automt The computtionl mchine models tht we lerned in the clss re deterministic in the sense tht the next move is uniquely
Designing finite automata II
 Designing finite utomt II Prolem: Design DFA A such tht L(A) consists of ll strings of nd which re of length 3n, for n = 0, 1, 2, (1) Determine wht to rememer out the input string Assign stte to ech of
Designing finite utomt II Prolem: Design DFA A such tht L(A) consists of ll strings of nd which re of length 3n, for n = 0, 1, 2, (1) Determine wht to rememer out the input string Assign stte to ech of
Finite Automata. Informatics 2A: Lecture 3. John Longley. 22 September School of Informatics University of Edinburgh
 Lnguges nd Automt Finite Automt Informtics 2A: Lecture 3 John Longley School of Informtics University of Edinburgh jrl@inf.ed.c.uk 22 September 2017 1 / 30 Lnguges nd Automt 1 Lnguges nd Automt Wht is
Lnguges nd Automt Finite Automt Informtics 2A: Lecture 3 John Longley School of Informtics University of Edinburgh jrl@inf.ed.c.uk 22 September 2017 1 / 30 Lnguges nd Automt 1 Lnguges nd Automt Wht is
CS375: Logic and Theory of Computing
 CS375: Logic nd Theory of Computing Fuhu (Frnk) Cheng Deprtment of Computer Science University of Kentucky 1 Tble of Contents: Week 1: Preliminries (set lgebr, reltions, functions) (red Chpters 1-4) Weeks
CS375: Logic nd Theory of Computing Fuhu (Frnk) Cheng Deprtment of Computer Science University of Kentucky 1 Tble of Contents: Week 1: Preliminries (set lgebr, reltions, functions) (red Chpters 1-4) Weeks
CMSC 330: Organization of Programming Languages. DFAs, and NFAs, and Regexps (Oh my!)
 CMSC 330: Orgniztion of Progrmming Lnguges DFAs, nd NFAs, nd Regexps (Oh my!) CMSC330 Spring 2018 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All
CMSC 330: Orgniztion of Progrmming Lnguges DFAs, nd NFAs, nd Regexps (Oh my!) CMSC330 Spring 2018 Types of Finite Automt Deterministic Finite Automt (DFA) Exctly one sequence of steps for ech string All
Nondeterminism. Nondeterministic Finite Automata. Example: Moves on a Chessboard. Nondeterminism (2) Example: Chessboard (2) Formal NFA
 Nondeterminism Nondeterministic Finite Automt Nondeterminism Subset Construction A nondeterministic finite utomton hs the bility to be in severl sttes t once. Trnsitions from stte on n input symbol cn
Nondeterminism Nondeterministic Finite Automt Nondeterminism Subset Construction A nondeterministic finite utomton hs the bility to be in severl sttes t once. Trnsitions from stte on n input symbol cn
Some Theory of Computation Exercises Week 1
 Some Theory of Computtion Exercises Week 1 Section 1 Deterministic Finite Automt Question 1.3 d d d d u q 1 q 2 q 3 q 4 q 5 d u u u u Question 1.4 Prt c - {w w hs even s nd one or two s} First we sk whether
Some Theory of Computtion Exercises Week 1 Section 1 Deterministic Finite Automt Question 1.3 d d d d u q 1 q 2 q 3 q 4 q 5 d u u u u Question 1.4 Prt c - {w w hs even s nd one or two s} First we sk whether
12.1 Nondeterminism Nondeterministic Finite Automata. a a b ε. CS125 Lecture 12 Fall 2014
 CS125 Lecture 12 Fll 2014 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
CS125 Lecture 12 Fll 2014 12.1 Nondeterminism The ide of nondeterministic computtions is to llow our lgorithms to mke guesses, nd only require tht they ccept when the guesses re correct. For exmple, simple
Review for the Midterm
 Review for the Midterm Stephen A. Edwrds Columi University Fll 2018 The Midterm Structure of Compiler Scnning Lnguges nd Regulr Expressions NFAs Trnslting REs into NFAs: Thompson s Construction Building
Review for the Midterm Stephen A. Edwrds Columi University Fll 2018 The Midterm Structure of Compiler Scnning Lnguges nd Regulr Expressions NFAs Trnslting REs into NFAs: Thompson s Construction Building
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automt Theory nd Forml Lnguges TMV027/DIT321 LP4 2018 Lecture 10 An Bove April 23rd 2018 Recp: Regulr Lnguges We cn convert between FA nd RE; Hence both FA nd RE ccept/generte regulr lnguges; More
Finite Automt Theory nd Forml Lnguges TMV027/DIT321 LP4 2018 Lecture 10 An Bove April 23rd 2018 Recp: Regulr Lnguges We cn convert between FA nd RE; Hence both FA nd RE ccept/generte regulr lnguges; More
Chapter 2 Finite Automata
 Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
Chpter 2 Finite Automt 28 2.1 Introduction Finite utomt: first model of the notion of effective procedure. (They lso hve mny other pplictions). The concept of finite utomton cn e derived y exmining wht
Speech Recognition Lecture 2: Finite Automata and Finite-State Transducers
 Speech Recognition Lecture 2: Finite Automt nd Finite-Stte Trnsducers Eugene Weinstein Google, NYU Cournt Institute eugenew@cs.nyu.edu Slide Credit: Mehryr Mohri Preliminries Finite lphet, empty string.
Speech Recognition Lecture 2: Finite Automt nd Finite-Stte Trnsducers Eugene Weinstein Google, NYU Cournt Institute eugenew@cs.nyu.edu Slide Credit: Mehryr Mohri Preliminries Finite lphet, empty string.
Finite Automata. Informatics 2A: Lecture 3. Mary Cryan. 21 September School of Informatics University of Edinburgh
 Finite Automt Informtics 2A: Lecture 3 Mry Cryn School of Informtics University of Edinburgh mcryn@inf.ed.c.uk 21 September 2018 1 / 30 Lnguges nd Automt Wht is lnguge? Finite utomt: recp Some forml definitions
Finite Automt Informtics 2A: Lecture 3 Mry Cryn School of Informtics University of Edinburgh mcryn@inf.ed.c.uk 21 September 2018 1 / 30 Lnguges nd Automt Wht is lnguge? Finite utomt: recp Some forml definitions
CS 373, Spring Solutions to Mock midterm 1 (Based on first midterm in CS 273, Fall 2008.)
 CS 373, Spring 29. Solutions to Mock midterm (sed on first midterm in CS 273, Fll 28.) Prolem : Short nswer (8 points) The nswers to these prolems should e short nd not complicted. () If n NF M ccepts
CS 373, Spring 29. Solutions to Mock midterm (sed on first midterm in CS 273, Fll 28.) Prolem : Short nswer (8 points) The nswers to these prolems should e short nd not complicted. () If n NF M ccepts
Compiler Design. Fall Lexical Analysis. Sample Exercises and Solutions. Prof. Pedro C. Diniz
 University of Southern Cliforni Computer Science Deprtment Compiler Design Fll Lexicl Anlysis Smple Exercises nd Solutions Prof. Pedro C. Diniz USC / Informtion Sciences Institute 4676 Admirlty Wy, Suite
University of Southern Cliforni Computer Science Deprtment Compiler Design Fll Lexicl Anlysis Smple Exercises nd Solutions Prof. Pedro C. Diniz USC / Informtion Sciences Institute 4676 Admirlty Wy, Suite
1 From NFA to regular expression
 Note 1: How to convert DFA/NFA to regulr expression Version: 1.0 S/EE 374, Fll 2017 Septemer 11, 2017 In this note, we show tht ny DFA cn e converted into regulr expression. Our construction would work
Note 1: How to convert DFA/NFA to regulr expression Version: 1.0 S/EE 374, Fll 2017 Septemer 11, 2017 In this note, we show tht ny DFA cn e converted into regulr expression. Our construction would work
Overview. Regular Languages. Finite Automata. A finite automaton. Startstate : q Acceptstate : q. Transitions
 Overvew Regulr Lnguges Andres Krwth & Mlte Helmert Determnstc fnte utomt Regulr lnguges Nondetermnstc fnte utomt Closure oertons Regulr exressons Nonregulr lnguges The umng lemm 2 Fnte Automt A fnte utomton
Overvew Regulr Lnguges Andres Krwth & Mlte Helmert Determnstc fnte utomt Regulr lnguges Nondetermnstc fnte utomt Closure oertons Regulr exressons Nonregulr lnguges The umng lemm 2 Fnte Automt A fnte utomton
Homework 4. 0 ε 0. (00) ε 0 ε 0 (00) (11) CS 341: Foundations of Computer Science II Prof. Marvin Nakayama
 CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 4 1. UsetheproceduredescriedinLemm1.55toconverttheregulrexpression(((00) (11)) 01) into n NFA. Answer: 0 0 1 1 00 0 0 11 1 1 01 0 1 (00)
CS 341: Foundtions of Computer Science II Prof. Mrvin Nkym Homework 4 1. UsetheproceduredescriedinLemm1.55toconverttheregulrexpression(((00) (11)) 01) into n NFA. Answer: 0 0 1 1 00 0 0 11 1 1 01 0 1 (00)
1 Nondeterministic Finite Automata
 1 Nondeterministic Finite Automt Suppose in life, whenever you hd choice, you could try oth possiilities nd live your life. At the end, you would go ck nd choose the one tht worked out the est. Then you
1 Nondeterministic Finite Automt Suppose in life, whenever you hd choice, you could try oth possiilities nd live your life. At the end, you would go ck nd choose the one tht worked out the est. Then you
CMPSCI 250: Introduction to Computation. Lecture #31: What DFA s Can and Can t Do David Mix Barrington 9 April 2014
 CMPSCI 250: Introduction to Computtion Lecture #31: Wht DFA s Cn nd Cn t Do Dvid Mix Brrington 9 April 2014 Wht DFA s Cn nd Cn t Do Deterministic Finite Automt Forml Definition of DFA s Exmples of DFA
CMPSCI 250: Introduction to Computtion Lecture #31: Wht DFA s Cn nd Cn t Do Dvid Mix Brrington 9 April 2014 Wht DFA s Cn nd Cn t Do Deterministic Finite Automt Forml Definition of DFA s Exmples of DFA
Today s Topics Automata and Languages
 Tody s Topics Automt nd Lnguges Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn DFA to Regulr Expression GFNA DFAèGNFA GNFA è RE DFA è RE Exmples 2 DFA è RE NFA DFA -NFA REX GNFA 3 Definition
Tody s Topics Automt nd Lnguges Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn DFA to Regulr Expression GFNA DFAèGNFA GNFA è RE DFA è RE Exmples 2 DFA è RE NFA DFA -NFA REX GNFA 3 Definition
Automata and Languages
 Automt nd Lnguges Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Tody s Topics DFA to Regulr Expression GFNA DFAèGNFA GNFA è RE DFA è RE Exmples 2 DFA è RE NFA DFA -NFA REX GNFA 3 Definition
Automt nd Lnguges Prof. Mohmed Hmd Softwre Engineering L. The University of Aizu Jpn Tody s Topics DFA to Regulr Expression GFNA DFAèGNFA GNFA è RE DFA è RE Exmples 2 DFA è RE NFA DFA -NFA REX GNFA 3 Definition
Chapter 4 Regular Grammar and Regular Sets. (Solutions / Hints)
 C K Ngpl Forml Lnguges nd utomt Theory Chpter 4 Regulr Grmmr nd Regulr ets (olutions / Hints) ol. (),,,,,,,,,,,,,,,,,,,,,,,,,, (),, (c) c c, c c, c, c, c c, c, c, c, c, c, c, c c,c, c, c, c, c, c, c, c,
C K Ngpl Forml Lnguges nd utomt Theory Chpter 4 Regulr Grmmr nd Regulr ets (olutions / Hints) ol. (),,,,,,,,,,,,,,,,,,,,,,,,,, (),, (c) c c, c c, c, c, c c, c, c, c, c, c, c, c c,c, c, c, c, c, c, c, c,
CS311 Computational Structures Regular Languages and Regular Grammars. Lecture 6
 CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
CS311 Computtionl Strutures Regulr Lnguges nd Regulr Grmmrs Leture 6 1 Wht we know so fr: RLs re losed under produt, union nd * Every RL n e written s RE, nd every RE represents RL Every RL n e reognized
GNFA GNFA GNFA GNFA GNFA
 DFA RE NFA DFA -NFA REX GNFA Definition GNFA A generlize noneterministic finite utomton (GNFA) is grph whose eges re lele y regulr expressions, with unique strt stte with in-egree, n unique finl stte with
DFA RE NFA DFA -NFA REX GNFA Definition GNFA A generlize noneterministic finite utomton (GNFA) is grph whose eges re lele y regulr expressions, with unique strt stte with in-egree, n unique finl stte with
Formal languages, automata, and theory of computation
 Mälrdlen University TEN1 DVA337 2015 School of Innovtion, Design nd Engineering Forml lnguges, utomt, nd theory of computtion Thursdy, Novemer 5, 14:10-18:30 Techer: Dniel Hedin, phone 021-107052 The exm
Mälrdlen University TEN1 DVA337 2015 School of Innovtion, Design nd Engineering Forml lnguges, utomt, nd theory of computtion Thursdy, Novemer 5, 14:10-18:30 Techer: Dniel Hedin, phone 021-107052 The exm
Non-Deterministic Finite Automata. Fall 2018 Costas Busch - RPI 1
 Non-Deterministic Finite Automt Fll 2018 Costs Busch - RPI 1 Nondeterministic Finite Automton (NFA) Alphbet ={} q q2 1 q 0 q 3 Fll 2018 Costs Busch - RPI 2 Nondeterministic Finite Automton (NFA) Alphbet
Non-Deterministic Finite Automt Fll 2018 Costs Busch - RPI 1 Nondeterministic Finite Automton (NFA) Alphbet ={} q q2 1 q 0 q 3 Fll 2018 Costs Busch - RPI 2 Nondeterministic Finite Automton (NFA) Alphbet
Non Deterministic Automata. Linz: Nondeterministic Finite Accepters, page 51
 Non Deterministic Automt Linz: Nondeterministic Finite Accepters, pge 51 1 Nondeterministic Finite Accepter (NFA) Alphbet ={} q 1 q2 q 0 q 3 2 Nondeterministic Finite Accepter (NFA) Alphbet ={} Two choices
Non Deterministic Automt Linz: Nondeterministic Finite Accepters, pge 51 1 Nondeterministic Finite Accepter (NFA) Alphbet ={} q 1 q2 q 0 q 3 2 Nondeterministic Finite Accepter (NFA) Alphbet ={} Two choices
Lecture 09: Myhill-Nerode Theorem
 CS 373: Theory of Computtion Mdhusudn Prthsrthy Lecture 09: Myhill-Nerode Theorem 16 Ferury 2010 In this lecture, we will see tht every lnguge hs unique miniml DFA We will see this fct from two perspectives
CS 373: Theory of Computtion Mdhusudn Prthsrthy Lecture 09: Myhill-Nerode Theorem 16 Ferury 2010 In this lecture, we will see tht every lnguge hs unique miniml DFA We will see this fct from two perspectives
Closure Properties of Regular Languages
 Closure Properties of Regulr Lnguges Regulr lnguges re closed under mny set opertions. Let L 1 nd L 2 e regulr lnguges. (1) L 1 L 2 (the union) is regulr. (2) L 1 L 2 (the conctention) is regulr. (3) L
Closure Properties of Regulr Lnguges Regulr lnguges re closed under mny set opertions. Let L 1 nd L 2 e regulr lnguges. (1) L 1 L 2 (the union) is regulr. (2) L 1 L 2 (the conctention) is regulr. (3) L
CS:4330 Theory of Computation Spring Regular Languages. Equivalences between Finite automata and REs. Haniel Barbosa
 CS:4330 Theory of Computtion Spring 208 Regulr Lnguges Equivlences between Finite utomt nd REs Hniel Brbos Redings for this lecture Chpter of [Sipser 996], 3rd edition. Section.3. Finite utomt nd regulr
CS:4330 Theory of Computtion Spring 208 Regulr Lnguges Equivlences between Finite utomt nd REs Hniel Brbos Redings for this lecture Chpter of [Sipser 996], 3rd edition. Section.3. Finite utomt nd regulr
Closure Properties of Regular Languages
 of Regulr Lnguges Dr. Neil T. Dntm CSCI-561, Colordo School of Mines Fll 2018 Dntm (Mines CSCI-561) Closure Properties of Regulr Lnguges Fll 2018 1 / 50 Outline Introduction Closure Properties Stte Minimiztion
of Regulr Lnguges Dr. Neil T. Dntm CSCI-561, Colordo School of Mines Fll 2018 Dntm (Mines CSCI-561) Closure Properties of Regulr Lnguges Fll 2018 1 / 50 Outline Introduction Closure Properties Stte Minimiztion
SWEN 224 Formal Foundations of Programming WITH ANSWERS
 T E W H A R E W Ā N A N G A O T E Ū P O K O O T E I K A A M Ā U I VUW V I C T O R I A UNIVERSITY OF WELLINGTON Time Allowed: 3 Hours EXAMINATIONS 2011 END-OF-YEAR SWEN 224 Forml Foundtions of Progrmming
T E W H A R E W Ā N A N G A O T E Ū P O K O O T E I K A A M Ā U I VUW V I C T O R I A UNIVERSITY OF WELLINGTON Time Allowed: 3 Hours EXAMINATIONS 2011 END-OF-YEAR SWEN 224 Forml Foundtions of Progrmming
Introduction to ω-autamata
 Fridy 25 th Jnury, 2013 Outline From finite word utomt ω-regulr lnguge ω-utomt Nondeterministic Models Deterministic Models Two Lower Bounds Conclusion Discussion Synthesis Preliminry From finite word
Fridy 25 th Jnury, 2013 Outline From finite word utomt ω-regulr lnguge ω-utomt Nondeterministic Models Deterministic Models Two Lower Bounds Conclusion Discussion Synthesis Preliminry From finite word
Chapter 1, Part 1. Regular Languages. CSC527, Chapter 1, Part 1 c 2012 Mitsunori Ogihara 1
 Chpter 1, Prt 1 Regulr Lnguges CSC527, Chpter 1, Prt 1 c 2012 Mitsunori Ogihr 1 Finite Automt A finite utomton is system for processing ny finite sequence of symols, where the symols re chosen from finite
Chpter 1, Prt 1 Regulr Lnguges CSC527, Chpter 1, Prt 1 c 2012 Mitsunori Ogihr 1 Finite Automt A finite utomton is system for processing ny finite sequence of symols, where the symols re chosen from finite
CS 573 Automata Theory and Formal Languages
 Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
Non-determinism Automt Theory nd Forml Lnguges Professor Leslie Lnder Leture # 3 Septemer 6, 2 To hieve our gol, we need the onept of Non-deterministi Finite Automton with -moves (NFA) An NFA is tuple
