Near-Optimal Solutions and Large Integrality Gaps for Almost All Instances of Single-Machine Precedence-Constrained Scheduling

Transcription

1 Near-Optimal Solutio ad Large Itegrality Gap for Almot All Itace of Sigle-Machie Precedece-Cotraied Schedulig Adrea S. Schulz a Nelo A. Uha b Jue 200 Abtract We coider the problem of miimizig the weighted um of completio time o a igle machie ubject to bipartite precedece cotrait where all miimal job have uit proceig time ad zero weight, ad all maximal job have zero proceig time ad uit weight. For variou probability ditributio over thee itace icludig the uiform ditributio we how everal almot all -type reult. Firt, we how that almot all itace are prime with repect to a well-tudied decompoitio for thi chedulig problem. Secod, we how that for almot all itace, every feaible chedule i arbitrarily cloe to optimal. Fially, for almot all itace, we give a lower boud o the itegrality gap of variou liear programmig relaxatio of thi problem. a Sloa School of Maagemet ad Operatio Reearch Ceter, Maachuett Ititute of Techology, Cambridge, MA. e- mail: chulz@mit.edu b School of Idutrial Egieerig, Purdue Uiverity, Wet Lafayette, IN. uha@purdue.edu

2 Itroductio We coider the followig claic chedulig problem. We have a et of job N D f; : : : ; g that eed to be cheduled opreemptively o a igle machie, which ca proce at mot oe job at a time. Each job i 2 N ha a proceig time p i 2 R 0 ad weight w i 2 R 0. Precedece cotrait are repreeted by a acyclic, traitively cloed directed graph G D.N; A/: if.i; j / 2 A, the job i mut be proceed before job j. The objective i to chedule thee job i a way that repect the precedece cotrait ad miimize the um of weighted completio time. I the otatio of Graham et al. [0], thi problem i deoted a j prec j P w j C j. The chedulig problem j prec j P w j C j i trogly NP-hard [4, 5]. Curretly, the bet ow approximatio algorithm all have a performace guaratee of 2 [, 4, 3, 9, 6]. O the iapproximability frot, Ambühl et al. [] howed that a PTAS i ot poible, aumig NP-complete problem caot be olved i radomized ub-expoetial time. Baal ad Khot [2] howed that it i NP-hard to compute a.2 "/-approximate chedule for ay " > 0, aumig a troger verio of the Uique Game Cojecture [3] hold. I thi wor, we focu o 0- bipartite itace. I a 0- bipartite itace.n ; N 2 ; A/, the et of job i partitioed ito N D N P[N 2, ad precedece cotrait tae the form of a directed bipartite graph.n P[N 2 ; A/ where.i; j / 2 A implie i 2 N ad j 2 N 2. The job i N have uit proceig time ad zero weight, ad the job i N 2 have zero proceig time ad uit weight. Thi chedulig problem o 0- bipartite itace ca equivaletly be viewed a a liear orderig problem o a mixed bipartite graph, i which there i a udirected edge betwee every pair of ode i 2 N, j 2 N 2, for which.i; j / 62 A. The goal i to fid a orietatio B of the udirected edge, uch that the reultig directed graph.n [ N 2 ; A [ B/ i acyclic ad ha a few arc that are directed from N to N 2 a poible. Thee 0- bipartite itace have further appeal tha their imple combiatorial tructure: it tur out that thee imple itace effectively capture the iheret difficulty of j prec j P w j C j. Cheuri ad Motwai [3] ued a cla of 0- bipartite itace to how that the liear programmig relaxatio i liear orderig variable due to Pott [9] ha a itegrality gap of 2. Moreover, Woegiger [23] howed that a -approximatio algorithm for 0- bipartite itace of j prec j P w j C j implie a. C "/-approximatio algorithm for arbitrary itace of j prec j P w j C j ; that i, the approximability behavior of 0- bipartite itace ad arbitrary itace are virtually idetical. I fact, the previouly metioed iapproximability reult due to Baal ad Khot [2] wa proved uig 0- bipartite itace. We tudy 0- bipartite itace of j prec j P w j C j with a probabilitic le. Oe appealig feature of 0- bipartite itace i that they are completely defied by their precedece cotrait. Sice precedece relatio i bipartite partial order are idepedet, we ca apply the model of Erdö ad Réyi [7] ofte ued i radom graph theory to defie clae of radom 0- bipartite itace. Our aalyi of thee radom 0- bipartite itace yield everal almot all -type reult. We how that almot all 0- bipartite itace are o-sidey-decompoable. Sidey [2] decompoitio techique plit a itace of j prec j P w j C j ito maller itace o that the cocateatio of optimal chedule for the maller part yield a optimal chedule for the etire itace. Together with the wor of Cheuri ad Motwai [3], Margot et al. [6], ad Goema ad Williamo [9], our reult alo implie that for almot all 0- bipartite itace, ay feaible chedule i a 2-approximatio. Uig two-dimeioal Gatt chart, we how that for almot all 0- bipartite itace, all feaible chedule are actually arbitrarily cloe to optimal. I particular, we how that for ay give " > 0, ay feaible chedule i a. C"/-approximatio with high probability, whe the umber of job i ufficietly large. We give a lower boud o the itegrality gap of variou liear programmig relaxatio of j prec j P w j C j for almot all 0- bipartite itace. For the radom model of 0- bipartite itace

3 that we tudy, thi lower boud approache 2 a the precedece cotrait become parer i expectatio. Thi reult geeralize a reult of Cheuri ad Motwai [3]. 2 Model for radom 0- bipartite itace We form a model for radom 0- bipartite itace a follow. Let 2 Z >0 ad q 2.0; /. I additio, let 2 R C 0 be a probability vector; that i, P D0 D. We defie B.; ; q/ a the probability pace of 0- bipartite itace.n ; N 2 ; A/ with job uch that P.jN j D ; jn 2 j D / D for D 0; : : : ; ad each arc.i; j / 2 N N 2 appear i A idepedetly with probability q. I thi wor, we coider radom model of balaced 0- bipartite itace.n ; N 2 ; A/, i the ee that the ratio betwee the ize of N ad the ize of N 2 i ot too far from./ with high probability. I particular, we loo at model B.; ; q/ with probability vector 2 R C 0 that atify D0 c c 2 2 ad C c 3 c 4 2 (2.) for ome fuctio W Z >0 Z >0 uch that 2.log / for ome fixed, ad for ome cotat c ; c 2 ; c 3 ; c 4 2 R >0, whe i ufficietly large. Thee coditio o the probability vector are atified for two atural model of radom 0- bipartite itace i particular. Firt, coider B.; N; q/, where N D.=2/ for D 0; : : : ; : job are aiged to N ad N 2 with equal probability. Note that B.; N; =2/ i the uiform ditributio over all 0- bipartite itace. There exit cotat c ; c 2 ; c 3 ; c 4 2 R >0 o that the probability vector N atifie (2.) for ay 2.log / with, ice D0 C N D N D D0 2 2 ; 2 D C C 2 2 : Secod, coider B.; O; q/ where O D if D, ad O D 0 otherwie, for ome fixed 2.0; / uch that 2 Z >0 ad. / 2 Z >0. For ay itace.n ; N 2 ; A/ from B.; O; q/, the proportio betwee the umber of job i N ad the umber of job i N 2 i alway fixed. Clearly, there exit cotat c ; c 2 ; c 3 ; c 4 2 R >0 o that the probability vector O atifie (2.) for ay 2.log / with, whe i ufficietly large. 3 Sidey-decompoability ad 0- bipartite itace Sidey [2] itroduced a very ueful characterizatio of optimal chedule to j prec j P w j C j. We defie ( P j 2S w j = P j 2S p j for ay ubet of job S N uch that P j 2S p j > 0,.S/ WD C otherwie. A et of job I N i called iitial if j 2 I ad.i; j / 2 A imply i 2 I. A iitial et I i aid to be -maximal if I 2 arg maxf.i / W I i a oempty iitial etg. Sidey howed that there exit a optimal chedule i which all job i a -maximal iitial et S are cheduled before thoe i N S. By recurively applyig thi reult, we aturally obtai a partitio of job.s ; : : : ; S / with.s /.S /. Such 2

4 a partitio i called a Sidey decompoitio. Sidey decompoitio theory ca be ee a a geeralizatio of Smith [22] rule for the problem without precedece cotrait. A itace of j prec j P w j C j i o-sidey-decompoable if the oly -maximal iitial et i N ; otherwie the itace i called Sideydecompoable. A itace i called tiff if.n /.I / for all oempty iitial et I ; ote that tiffe i a eceary coditio for a itace to be o-sidey-decompoable. A Sidey decompoitio ca be computed i polyomial time [4, 8, 8, 6]. Idepedetly, Cheuri ad Motwai [3] ad Margot et al. [6] howed that for tiff itace, every feaible chedule i already a 2-approximatio. A geometric proof of thi reult wa ubequetly give by Goema ad Williamo [9]. I thi ectio, we how that almot all 0- bipartite itace are o-sidey-decompoable. We begi by givig the followig characterizatio of Sidey-decompoability for 0- bipartite itace. For ay directed graph.n; A/ ad ay ubet of vertice N, we defie./ WD fi 2 N W.i; j / 2 A or.j; i/ 2 A for ome j 2 g; i word,./ i the et of eighbor of. Lemma 3.. A 0- bipartite itace.n ; N 2 ; A/ of j prec j P w j C j with jn j D, jn 2 j D 2, ad C 2 2 i Sidey-decompoable if ad oly if oe of the followig three coditio hold: (SD) D 0; (SD2) 2 D 0; (SD3) (i) there exit a ubet Y N 2 uch that Y ;; N 2 ad 2 j.y /j jy j, (ii) or j.n 2 /j. Proof. Firt, ote that a 0- bipartite itace with C 2 2 i Sidey-decompoable whe D 0 or 2 D 0, ice ay oempty ubet of job I i iitial ad atifie.i / D.N /. Now uppoe a 0- bipartite itace with > 0 ad 2 > 0 i Sidey-decompoable. By defiitio, thi occur if ad oly if there exit a -maximal iitial et I N uch that.i / 2 =. (3.) Recall that by defiitio, a -maximal iitial et i oempty. Suppoe (3.) i atified with a iitial et I uch that I N [ N 2, but I 6 N. Sice I i -maximal, I D.Y / [ Y for ome Y N 2 uch that Y ;. We coider the followig cae. If Y N 2, the (3.) hold if ad oly if jy j=j.y /j 2 =. Otherwie, we have Y D N 2. I thi cae, (3.) hold if ad oly if j.n 2 /j. Note that (3.) caot be atified if I N, ice i thi cae,.i / D 0 < 2 = D.N /. Note that (SD3) implie that a 0- bipartite itace.n ; N 2 ; A/ with jn j D jn 2 j i o-sideydecompoable if ad oly if j.n 2 /j D jn j D jn 2 j ad j.y /j > jy j for all Y N 2 uch that Y ;; N 2. Thi i very imilar to Hall [2] marriage theorem, which ay that a udirected bipartite graph.n P[N 2 ; A/ with jn j D jn 2 j ha a perfect matchig if ad oly if j.y /j jy j for all Y N 2. We ow give a aalogou characterizatio of Sidey-decompoable 0- bipartite itace that coider ubet of N itead. Lemma 3.2. The coditio (SD3) i Lemma 3. hold if ad oly if the followig coditio hold: (SD3 0 ) (i) There exit a ubet N uch that ;; N ad j./j 2 jj, or (ii) j.n /j 2. Proof. We how that (SD3) implie (SD3 0 ). Suppoe that (SD3) hold becaue there exit a ubet Y N 2 uch that Y ;; N 2 ad 2 j.y /j jy j. Let D N.Y /. We coider the followig cae:.y / D ;. I thi cae, D N. Sice Y ;, thi implie that j.n /j D j./j 2..Y / ;; N. I thi cae, ;; N. I additio, we have that jj D j.y /j, ad j./j 2 jy j. Thee two obervatio, i additio to the aumptio that 2 j.y /j jy j, implie that j./j 2 jj. 3

5 .Y / D N. I thi cae, ice 2 j.y /j jy j, we have that jy j 2, which i a cotradictio, ice Y N 2. Now uppoe that (SD3) hold becaue j.n 2 /j. Let D N.N 2 /. Note that ice j.n 2 /j, we have that ;. I additio, ice \.N 2 / D ;, we have that j./j D ;. We coider the followig cae..n 2 / ;. The ;; N, ad j./j D 0 2 jj..n 2 / D ;. The D N, ad j.n /j D j./j D 0 2. Showig the revere directio wor i a imilar maer. Uig the characterizatio of Sidey-decompoability i Lemma 3. ad Lemma 3.2, we ca how that almot all 0- bipartite itace are o-sidey-decompoable. Theorem 3.3. Fix q 2.0; /, >, ad 2.log /. Let 2 R C 0 be a probability vector that atifie (2.) for ad ome cotat c ; c 2 ; c 3 ; c 4 2 R >0, whe i ufficietly large. The, lim P B 2 B.; ; q/ i o-sidey-decompoable D : Proof. Let B D.N ; N 2 ; A/ be a radom 0- bipartite itace from B.; ; q/ with probability vector that atifie (2.) for ad for ome cotat c ; c 2 ; c 3 ; c 4 2 R >0, whe i ufficietly large. We how that the probability that B atifie ay of the coditio (SD)-(SD3) goe to zero a approache ifiity. For the remaider of thi proof, we coider ufficietly large o that 2 ad b=2c. Firt, we coider (SD). We have that P B 2 B.; ; q/ atifie (SD) D P B 2 B.; ; q/ ha D 0 D 0 c c 2 2 ; ad o lim P.B 2 B.; ; q/ atifie (SD)/ D 0. Similarly, for (SD2), we have that P B 2 B.; ; q/ atifie (SD2) D P B 2 B.; ; q/ ha 2 D 0 D c 3 c 4 2 ; ad therefore lim P.B 2 B.; ; q/ atifie (SD2)/ D 0. Now we coider (SD3). Oberve that ay bipartite graph.n [N 2 ; A/ with jn j D ad jn 2 j D with a ubet Y of N 2 of ize uch that j.y /j ca be cotructed a follow. Chooe a ubet Y of N 2 of ize, ad a ubet of N of ize b c, ad forbid all edge betwee Y ad N. Ay bipartite graph.n [ N 2 ; A/ with jn j D ad jn 2 j D with a ubet of N of ize uch that j./j ca be cotructed imilarly. Therefore, by coditioig o the ize of N ad N 2 ad uig a uio boud, we have P B 2 B.; ; q/ atifie (SD3/ D P B 2 B.; ; q/ atifie (SD3) j jn j D ; jn 2 j D b=2c D b=2c D C B 2 B.; ; q/ P atifie (SD3) Dd=2e D D ˇ D jn j D ; jn 2 j D b c b c C Dd=2e B 2 B.; ; q/ P atifie (SD3 0 ). q/. b c/ C. q/. q/. b c/ C. /. q/ : 4 ˇ jn j D ; jn 2 j D

6 o that We defie D WD D b c. q/. b c/ for D ; : : : ; b=2c; E WD. q/ for D ; : : : ; b=2c; F WD c. q/. b c/ for D d=2e; : : : ; ; D b G WD. /. q/ for D d=2e; : : : ; ; P B 2 B.; ; q/ atifie (SD3/ b=2c D b=2c D C D E C Dd=2e F C Dd=2e For the remaider of thi proof, let r D. q/. Note that r >. Firt, we coider the expreio F i the regime D d=2e; : : : ;. By Lemma A. i Appedix A (lettig a D ), for all D d=2e; : : : ;, we have that G : F D 2. q/. b c/ D 2. q/. / : For all D d=2e; : : : ; ad D ; : : : ;, defie H ; WD 2. q/. / ; ad ote that H ; D H ;. We would lie to how that H ; H ;C for all D d=2e; : : : ; ad D ; : : : ; b=2c, or equivaletly, 2 log r C. 2 / for D ; : : : ; b=2c ad D d=2e; : : : ; : (3.2) Defie.x/ WD. 2x / 2 log r. x/ C 2 log r.x C /: Taig derivative, D 2. / C 2 log r x C ; x 2 D 2 log r. x/ 2.x C / 2 Note that for x 2 Œ0;. /=2, we have 2 =@x 2 0, o.x/ i cocave o Œ0;. /=2. We have that.0/ 0 for all D d=2e; : : : ;, ice.0/ D. / 2 log r C 2 log r D 2 log r 2 log r (ice ad ) 5 :

7 2 log r (ice ) 0 (ice 2.log / ad > ): I additio, we have that.. /=2/ D 0. Sice.x/ i cocave o Œ0;. /=2, it follow that whe D d=2e; : : : ;,.x/ 0 for all x 2 Œ0;. /=2, which etablihe (3.2). Therefore, H ; H ;C for D d=2e; : : : ; ad D ; : : : ; b=2c. Sice H ; D H ;, it follow that H ; H ; for D d=2e; : : : ; ad D ; : : : ;. So, for D d=2e; : : : ;, we have that Therefore, F D 2. q/. / 2. q/. / D 3. q/. / 3. q/ 2 (ice 2 for 2). Dd=2e F Dd=2e 3. q/ 2 Dd=2e 3. q/ 2 4. q/ =2 : Now we coider F i the regime D C ; : : : ;. Note that F D b c. q/. b c/ 2. q/ 2.2 q/ : D It follow that D C F We alo have that C 2.2 q/ C 2.2 q/ c 3.2 c 4 / q : 2 Dd=2e G D Dd=2e Dd=2e. /. q/ Dd=2e 2. q/= q/=2 : l 2 m. q/ d=2e Uig imilar techique to above, we ca alo how that D D c.2 c 2 / q ; 2 b=2c D D 4. q/ =2 ; b=2c D E 2 2. q/=2 : Therefore, P B 2 B.; ; q/ atifie (SD3/ b=2c D b=2c D C 6 D E C Dd=2e F C Dd=2e G

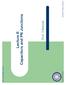
8 c.2 c 2 / q C c3.2 c 4 / 2 Sice 2.log / for ome fixed >, it follow that Fially, we put all the piece together: lim P.B 2 B.; ; q/ atifie (SD3)/ D 0: q C 2 4. q/ =2 C 2. q/ =2 : 2 lim P B 2 B.; ; q/ i Sidey decompoable D lim P B 2 B.; ; q/ atifie (SD/ C lim P B 2 B.; ; q/ atifie (SD2/ C lim P B 2 B.; ; q/ atifie (SD3/ D 0: I radom model of balaced 0- bipartite itace, the umber of job i N ad the umber of job i N 2 grow together a the total umber of job grow. Thi pheomeo i importat for the validity of Theorem 3.3. For example, coider B.; Q; q/ with Q D if D ad Q D 0 otherwie: the cla of itace i which N coit of oe job, ad N 2 coit of job. I thi cae, a itace B 2 B.; Q; q/ i o-sidey-decompoable if ad oly if the job i N mut precede all job i N 2. Thi occur with probability q, which goe to zero a the total umber of job grow. Fially, we ote that Theorem 3.3 till hold for parer precedece cotrait. It i traightforward to how that if the probability q of a precedece cotrait appearig i a fuctio of the umber of job o that q 2.= log /, the the aalyi i the proof of Theorem 3.3 hold. 4 Two-dimeioal Gatt chart ad 0- bipartite itace Two-dimeioal (2D) Gatt chart [6] provide a elegat, geometric way of udertadig igle-machie completio-time-objective chedulig problem. I a traditioal Gatt chart, the horizotal axi correpod to proceig time. I a 2D Gatt chart, the horizotal axi correpod to proceig time, ad the vertical axi correpod to weight. Suppoe we have a itace.n; A;.p i / i2n ;.w i / i2n / of j prec j P w j C j. The 2D Gatt chart i cotructed for a permutatio chedule.; : : : ; / a follow. Each job j 2 N i repreeted by a rectagle of width p j ad height w j, whoe poitio i the chart i defied by a tartpoit ad a edpoit. The tartpoit of the firt job (job ) i the chedule i.0; P j 2N w j /, ad it edpoit i.p ; P j 2N w j w /. For all ubequet job i the chedule, the tartpoit.t; w/ of job j i the edpoit of the previou job j, ad it edpoit i.t C p j ; w w j /. The completio time of a job i thi chedule i the time compoet of it edpoit. The wor curve W.t/ formed by the upper ide of each rectagle i the total weight of job that have ot bee completed by time t. The area uder the wor curve i equal to the um of weighted completio time for the chedule repreeted by the 2D Gatt chart. It tur out that the area uder the optimal wor curve for almot all 0- bipartite itace i large. We formalize thi otio ow. Coider the 2D Gatt chart for a optimal chedule of a 0- bipartite itace B D.N ; N 2 ; A/ with jn j D ad jn 2 j D 2. Note that ay 2D Gatt chart for uch a itace tart at.0; 2 / ad ed at. ; 0/. Alo oberve that all job i N are repreeted by a horizotal lie egmet of legth, ad that all job i N 2 are repreeted by a vertical lie egmet of legth. We defie R B to be the regio betwee the optimal wor curve ad the frotier formed by the lie f.t; w/ W t D g ad f.t; w/ W w D 2 g. See Figure for a example. We defie the followig parametrized coditio o a 0- bipartite itace B, for ay 2.0; /: (R- ) A rectagle of width ad height 2 caot fit i R B. 7

9 weight wor curve W.t/ 2 2 R B proceig time Figure : A example of a 2D Gatt chart for a 0- bipartite itace. We ow how that for ay fixed 2.0; /, the coditio (R- ) i atified for almot all 0- bipartite itace. Theorem 4.. Fix q 2.0; /, 2.0; /,, ad 2.log /. Let 2 R C 0 be a probability vector that atifie (2.) for ad ome cotat c ; c 2 ; c 3 ; c 4 2 R >0, whe i ufficietly large. The, lim P B 2 B.; ; q/ atifie (R- ) D : Proof. Fix a 0- bipartite itace B D.N ; N 2 ; A/ with jn j D ad jn 2 j D 2. If B doe ot atify (R- ), that i, a rectagle of width ad height 2 ca fit i R B, the there exit a et of d 2 e job from N 2 that ha at mot d e predeceor i N. I other word, if a rectagle of width ad height 2 ca fit i R B, the there exit a et of d 2 e job from N 2 ad a et of d e job from N with o precedece cotrait betwee them. Therefore, we have that P B 2 B.; ; q/ doe ot atify (R- ) j jn j D ; jn 2 j D 0 jj D d e; jy j D d. /e; 9 N ; Y N 2 W o precedece cotrait betwee ad Y ˇ jn j D ; jn 2 j D A. q/ d ed. /e. q/ 2. / : d e d. /e d e d. /e So, by coditioig o the ize of N ad N 2, P B 2 B.; ; q/ doe ot atify (R- ) B 2 B.; ; q/ D P jn j D ; doe ot atify (R- ) ˇ jn 2 j D Let o that D D D d e d. /e D. q/ 2. / d e d. for D ; : : : ; P B 2 B.; ; q/ doe ot atify (R- ) D : 8 D. q/ 2. / : /e

10 Firt, for the regime D ; : : : ;, we have that D D. q/ 2. / d e d. /e D D D Similarly, we ca how that For the regime D ; : : : ; Therefore, D D 2. q/ 2. / c c 2. q/ 2. / : D D C, we have that d e D D D c 3 c 4. q/ 2. / : d. P B 2 B.; ; q/ doe ot atify (R- ) /e. q/ 2. / 2. q/ 2. / 2. q/ 2. / : D D 2. q/ 2. / c c 2. q/ 2. / C c 3 c 4. q/ 2. / C 2. q/ 2. / : Sice 2.log / for a fixed, it follow that lim P.B 2 B.; ; q/ doe ot atify (R- )/ D 0: A with the o-sidey-decompoability reult i Sectio 3, the balacede of the radom 0- bipartite itace we coider play a ey role i the validity of the theorem above. To illutrate thi, a before, fix q 2.0; / ad coider B.; Q; q/ with Q D if D ad Q D 0 otherwie: the cla of itace i which N coit of oe job, ad N 2 coit of job. Tae to be arbitrarily mall: i particular, < q. I thi cae, a itace B 2 B.; Q; q/ doe ot atify (R- ) if ad oly if there exit at leat d. /e job i N 2 that do ot have ay predeceor i N. Let Z be a biomial radom variable with trial ad probability of ucce q. The, by the lower tail Cheroff boud i Lemma A.2(b), P.B 2 B.; Q; q/ doe ot atify (R- )/ D P.Z d. D P.Z d. /e / P.Z. // D P Z. q/. / exp q 2 /e/ 2. q/. / : q Therefore, P.B 2 B.; Q; q/ atifie (R- )/ goe to zero a the total umber of job grow. With Theorem 4. i had, we ca how that for almot all 0- bipartite itace, all feaible chedule are arbitrarily cloe to optimal. Let opt.b/ deote the optimal value of itace B, ad let val.b; S/ deote the objective value of (feaible) chedule S for itace B. 9

11 Theorem 4.2. Fix q 2.0; /, 2.0; /,, ad 2.log /. Let 2 R C 0 be a probability vector that atifie (2.) for ad ome cotat c ; c 2 ; c 3 ; c 4 2 R >0, whe i ufficietly large. The, lim P val.b; S/ B 2 B.; ; q/ atifie. / 2 for all feaible chedule S D : opt.b/ Proof. Coider ome 0- bipartite itace B with jn j D ad jn 2 j D 2. If (R- ) i atified that i, if a rectagle of width ad height 2 caot fit i the regio R B the opt.b/ > 2. / 2. Sice the objective value of ay feaible chedule of a itace B i at mot 2, thi implie that if (R- ) i atified, val.b;s/ opt.b/ 2 2. / 2 D. / 2, which implie the claim. I additio, Theorem 4. alo implie a o-trivial lower boud o the itegrality gap of variou liear programmig relaxatio of j prec j P w j C j, for almot all 0- bipartite itace. Pott [9] propoed the followig iteger programmig formulatio. Defie the deciio variable.ı ij / i;j 2N Wi j a follow: for all i; j 2 N uch that i j, ı ij i equal to if job i i proceed before job j, ad 0 otherwie. The j prec j P w j C j ca be formulated a [P] miimize p j w j C p i w j ı ij (4.a) j 2N i;j 2N Wi j ubject to ı ij C ı j i D for all i; j 2 N W i j; (4.b) ı ij C ı j C ı i 2 for all i; j; 2 N W i j i; (4.c) ı ij D for all.i; j / 2 A; (4.d) ı ij 2 f0; g for all i; j 2 N W i j: (4.e) It i traightforward to chec that [P] i a correct formulatio of j prec j P w j C j. We deote the LP relaxatio of [P] obtaied by replacig the biary cotrait (4.e) with oegativity cotrait ı ij 0 for all i; j 2 N a [P-LP]. Let lp.b/ deote the optimal value of [P-LP]. Theorem 4.3. Fix q 2.0; /, 2.0; /, ı 2.0; /,, ad 2.log /. Let 2 R C 0 be a probability vector that atifie (2.) for ad ome cotat c ; c 2 ; c 3 ; c 4 2 R >0, whe i ufficietly large. The, lim P B 2 B.; ; q/ atifie opt.b/ 2. /2 > D : lp.b/ C. C ı/q Proof. Coider a 0- bipartite itace B D.N ; N 2 ; A/ with jn j D ad jn 2 j D 2. It i traightforward to how that ettig ı ij D if.i; j / 2 A, ad ı ij D 2 otherwie, i a feaible olutio to [P-LP], ad that thi olutio ha objective value 2. 2 C jaj/. Therefore, lp.b/ 2. 2 C jaj/. I the proof of Theorem 4.2, we howed that if B atifie (R- ), the opt.b/ > 2. / 2. Therefore, if B atifie (R- ) ad jaj <. C ı/q 2, the ad o opt.b/ lp.b/ > 2. / C jaj/ > 2. / C. C ı/q 2 / P B 2 B.; ; q/ atifie opt.b/ lp.b/ 2. /2 C. C ı/q D 2. /2 C. C ı/q ; P B 2 B.; ; q/ doe ot atify (R- ) C P B 2 B.; ; q/ atifie jaj. C ı/q 2 : 0

12 By coditioig o the ize of N ad N 2, ad uig the upper tail Cheroff boud from Lemma A.2(a), we obtai P B 2 B.; ; q/ atifie jaj. C ı/q 2 B 2 B.; ; q/ atifie D P jaj. C ı/q 2 D e q. D /ı2 =3 ˇ D ; 2 D e q. /ı2 =3 e q. /ı2 =3 : D Therefore, lim P B 2 B.; ; q/ atifie jaj. C ı/q 2 D 0. By Theorem 4., we have that lim P B 2 B.; ; q/ doe ot atify (R- ) D 0. It follow that lim P B 2 B.; ; q/ atifie opt.b/ 2. /2 D 0: lp.b/ C. C ı/q We ote that the above reult alo applie to other formulatio of j prec j P w j C j, icludig the further relaxatio of [P] due to Chuda ad Hochbaum [4] ad Correa ad Schulz [5], ad the LP relaxatio of j prec j P w j C j baed o completio-time variable due to Queyrae ad Wag [20], ice all thee relaxatio are o troger tha [P-LP]. Fially, we ote that Theorem 4.2 ad Theorem 4.3 remai valid a log a the probability q of a precedece cotrait appearig i a fuctio of the umber of job o that q 2.= log /. Acowledgemet The author would lie to tha the aociate editor, three aoymou referee, a well a David Gamari, Moaldo Matrolilli, ad Maurice Queyrae for their helpful commet. A Ueful lemma Lemma A.. For ay a 2.0; uch that a 2 Z >0 ad D ; : : : ;, Proof. Note that x x for ay x D ; : : : ;. It follow that for ay x D ; : : : ;. Sice x x a bac. Cbac bac. Alo ote that C bac D C ba a. /c C ba. /c D C a. / D a; the claim follow. Lemma A.2 (Cheroff boud, ee Mitzemacher ad Upfal [7]). Let ; : : : ; m be idepedet radom variable uch that for i D ; : : : ; m, P. i D / D q ad P. i D 0/ D q with q 2.0; /. The for S D P m id i, D E.S/ D qm, ad ay ı 2.0; /, (a) P.S. C ı// e ı2 =3 ; (b) P.S. ı// e ı2 =2.

13 Referece [] C. Ambühl, M. Matrolilli, O. Sveo Iapproximability reult for paret cut, optimal liear arragemet, ad precedece cotraied chedulig. I Proceedig of the 48th Aual IEEE Sympoium o Foudatio of Computer Sciece (FOCS 2007), pp [2] N. Baal, S. Khot Optimal log code tet with oe free bit. I Proceedig of the 50th Aual IEEE Sympoium o Foudatio of Computer Sciece (FOCS 2009), pp [3] C. Cheuri, R. Motwai Precedece cotraied chedulig to miimize um of weighted completio time o a igle machie. Dicrete Applied Mathematic 98: [4] F. A. Chuda, D. S. Hochbaum A half-itegral liear programmig relaxatio for chedulig precedece-cotraied job o a igle machie. Operatio Reearch Letter 25: [5] J. R. Correa, A. S. Schulz Sigle-machie chedulig with precedece cotrait. Mathematic of Operatio Reearch 30: [6] W. L. Eatma, S. Eve, I. M. Iaac Boud for the optimal chedulig of job o m proceor. Maagemet Sciece : [7] P. Erdö, A. Réyi O radom graph. Publicatioe Mathematicae 6: [8] G. Gallo, M. D. Grigoriadi, R. E. Tarja A fat parametric maximum flow algorithm ad applicatio. SIAM Joural o Computig 8: [9] M.. Goema, D. P. Williamo Two-dimeioal Gatt chart ad a chedulig algorithm of Lawler. SIAM Joural o Dicrete Mathematic 3: [0] R. L. Graham, E. L. Lawler, J. K. Letra, A. H. G. Riooy Ka Optimizatio ad approximatio i determiitic equecig ad chedulig: a urvey. Aal of Dicrete Mathematic 5: [] L. A. Hall, A. S. Schulz, D. B. Shmoy, J. Wei Schedulig to miimize average completio time: off-lie ad o-lie approximatio algorithm. Mathematic of Operatio Reearch 22: [2] P. Hall O repreetative of ubet. Joural of the Lodo Mathematical Society 0: [3] S. Khot O the power of uique 2-prover -roud game. I Proceedig of the 34th Aual ACM Sympoium o Theory of Computig (STOC 2002), pp [4] E. L. Lawler Sequecig job to miimize total weighted completio time ubject to precedece cotrait. Aal of Dicrete Mathematic 2: [5] J. K. Letra, A. H. G. Riooy Ka Complexity of chedulig uder precedece cotrait. Operatio Reearch 26: [6] F. Margot, M. Queyrae, Y. Wag Decompoitio, etwor flow, ad a precedece cotraied igle-machie chedulig problem. Operatio Reearch 5: [7] M. Mitzemacher, E. Upfal Probability ad Computig: Radomized Algorithm ad Probabilitic Aalyi. Cambridge Uiverity Pre. 2

14 [8] J.-C. Picard, M. Queyrae O the tructure of all miimum cut i a etwor ad applicatio. Mathematical Programmig Study 3:8 6. [9] C. N. Pott A algorithm for the igle machie equecig problem with precedece cotrait. Mathematical Programmig Study 3: [20] M. Queyrae, Y. Wag. 99. Sigle-machie chedulig polyhedra with precedece cotrait. Mathematic of Operatio Reearch 6: 20. [2] J. B. Sidey Decompoitio algorithm for igle-machie equecig with precedece cotrait ad deferral cot. Operatio Reearch 23: [22] W. E. Smith Variou optimizer for igle-tage productio. Naval Reearch Logitic Quarterly 3: [23] G. J. Woegiger O the approximability of average completio time chedulig uder precedece cotrait. Dicrete Applied Mathematic 3: