ROLL CUTTING PROBLEMS UNDER STOCHASTIC DEMAND
|
|
|
- Erica Cox
- 6 years ago
- Views:
Transcription
1 Pacific-Asia Joural of Mathematics, Volume 5, No., Jauary-Jue 20 ROLL CUTTING PROBLEMS UNDER STOCHASTIC DEMAND SHAKEEL JAVAID, Z. H. BAKHSHI & M. M. KHALID ABSTRACT: I this paper, the roll cuttig problem uder ucertai demad with ow probability distributios is discussed. This stochastic problem is coverted ito a determiistic problem. The problem turs out to be that of liear programmig uder ucertai demad. A solutio procedure is preseted by exploitig the special structure of the problem i which there is o optimizatio problem i the secod stage as the first stage variables ad the values of the radom elemets uiquely determie the secod stage variables.. INTRODUCTION I this paper, we study the applicatio of stochastic programmig to the roll cuttig problem which is ecoutered quite frequetly i real life situatio. I may situatios a material is required to be cut ito pieces accordig to the demads. Some examples are the problems of cuttig the paper, glass, leather ad log etc. The obective is to miimize wastage while the requiremets are met. I this paper, the roll cuttig problem uder ucertai demad with ow probability distributios is discussed. This stochastic problem is the coverted ito a determiistic oe. The problem turs out to be that of liear programmig uder ucertai demad. A solutio procedure is preseted by exploitig the special structure of the problem i which there is o optimizatio problem i the secod stage as the first stage variables ad the values of the radom elemets uiquely determie the secod stage variables. Several authors have give liear programmig formulatios to this cuttig stoc problem, e.g., Gilmore ad Gomory (96, 963). May heuristic methods are developed to miimize the wastage i cuttig stoc problems such as, Coverdale et al., (976), Golde (976), Roberts (984). 2. STATEMENT OF THE PROBLEM UNDER UNCERTAIN DEMAND Give m rolls of legths l, l 2, l 3, l m. These rolls are to be cut ito stadard sizes of size s, s 2, s 3, s. The cost of the roll of legth s is c. Let the value of the roll of size s cut from i th roll be give by c s. The problem may be stated i the followig form: Keywords: Cuttig plae method, Determiistic equivalet, Ucertaity.
2 56 Shaeel Javaid, Z. H. Bahshi & M. M. Khalid Problem P : Fid x i, i =, 2,..., m;, 2,..., which maximizes Subect to m S = c s x () i = i s x l i =, 2,..., m (2) i i xi d, 2,..., (3) ad x i o-egative itegers (4) The d demad for the umber of pieces of size s is ot exactly ow, but there is a ow probability distributio p (d ) for each of them. The problem of cuttig the rolls ito stadard legth is formulated ad solved as the apsac problem i Gilmore ad Gomory (96, 963). Here we treat the problem where o each stadard legth there is a ucertai demad with ow discrete probability distributio. The problem turs out to be that of liear programmig uder ucertai demads. For its solutio we give it a two stage liear programmig uder ucertai demad, Madasy (962). Let us deote by x i, the umber of pieces of size s tae from the i th roll. The total supply of the pieces of size s is xi = x (say). Let a uder-supply of a pieces of size s icur a loss of f [e.g. it is purchased from the local maret ad supplied to the customer o loss]. Defie L () d x 0 for d x = f () d xfor d > x. (5) The expected pealty cost from the discrepacies i the pieces of size is the, L () x = {()} E L d {()} x = E f d x. (6) d d
3 Roll Cuttig Problems uder Stochastic Demad 57 The problem may be ow beig stated as follows: Problem P 2 : Maximize Subect to c x L () x (7) s xi li i =, 2,..., m (8) xi d, 2,..., (9) ad x i itegers 0. (0) Here x i are the first stage variables. These are to be determied before the demad d is actually ow. At the secod stage we do ot have to solve a optimizatio problem, sice the secod stage variables y = d x are uiquely determied for each x, whe x are observed. This fact is explicated i the ext sectio. 3. EQUIVALENT DETERMINISTIC PROBLEM Note that for each the oly possible values of d are itegers. Let these values be 0,,..., d. The expected pealty cost from the uder-supply is the d L ()()() x = f d x p d. () d = x Let us determie L (x ) for, 2,..., ad also the icremetal values L (x ) L (x + ) for each, where x rages from 0 to d. Observe that the sum of the icremetal values startig from x = d ad goig up to x equals L (x ). It is clear from () that L (x ) is decreasig fuctio of x. We may also prove that L (x ) is covex. Sice x are itegers, it is sufficiet to solve (Wager 977) that,
4 58 Shaeel Javaid, Z. H. Bahshi & M. M. Khalid L (( d ))()()(( x + L )) d x L d x L d x i.e. f (( d )) x + 2()(( f )) d x f d x or f 0 which is true. Thus, L () x = {()}()() E L d x = f D x p d = D (2) d D > x beig a covex liear combiatio of L (d x ) is also covex. From that fact that L (x ) is decreasig ad covex, it follows that the icremetal values L (x ) L (x + ) are decreasig. that The maximum possible demad that may occur is d s is greater tha the total availability Let d s li = a0 m i = ai. d s. We may assume. (3) For each piece tae from the slac there is a pealty associated with it. Let us choose the pieces from the slac such that the pealty is miimized. This is the same thig as to miimize. L () y (4) subect to y s = a0. Where y (o-egative iteger) is the umber of pieces of size s tae from the slac. The fact that L () y is covex ad decreasig may be exploited to apply a techique for the apsac problem (Saaty 970), for solvig the problem (4).
5 Roll Cuttig Problems uder Stochastic Demad 59 Let us put the problem i the followig form: Problem P 3 : Maximize d L d y = 0 (5) where d (6) subect to y s = a0 = 0 ad y = 0 or (7) d = 0 y = y The total umber of variables y is ( ) d + = N, say. We arrage the variables y accordig to the descedig values of s s + L d y L d y = 0 = 0. Problem P 3 may ow be solved by eumeratig the solutio vector i lexicographic orderig of the apsac problem with costraits (6) ad (7) of problem P 3 ad their liear obective fuctio i which the cost coefficiet of y s is {()(( L d ))} s L d s +. Note that i the optimal solutio, the sum of the costs associated with allocatig a 0 (ufilled demad) to the pieces of size s will equal the value of d L d y = 0. Let the optimal distributio of slac amogst various sizes be y,, 2,...,. After distributig the slac i this way we subtract y from d ad the solve the followig problem:
6 60 Shaeel Javaid, Z. H. Bahshi & M. M. Khalid Problem P 4 : Maximize Subect to m c xi (8) i = s xi = li i =, 2,..., m (9) xi = d y, 2,..., (20) ad x i itegers 0 (2) This is the determiistic problem of cuttig the rolls uder ucertai demad. 4. SOLUTION PROCEDURE FOR EQUIVALENT DETERMINISTIC PROBLEM The parameters of the Problem P 4 ca be arraged i the followig form as: Table Structure of the Problem P 4 Size (s ) s.... s Supply Slac y.... y a o c c l x : : : : : : : : : : c m.... c m l x m x Maximum c m.... c m demad x m x x We call the problem to be balaced if m l = d y ; otherwise we call it ubalaced. i i = The solutio procedure for the above problem P 4, with ow demad is give below, (Bari, 980).
7 Roll Cuttig Problems uder Stochastic Demad 6 Let us arrage the parameters of the problem P 4 as: l l... l 2 m s s2... s. (22) We fid the solutios to the equatios (9) by tur i =, 2,..., m, which also satisfy (20) ad (2). The solutio to the equatios i (9) are sought through lexicographic orderig. (a lexicographic orderig of a set of solutios is a orderig of the solutios accordig to the first compoets, ad if, there is a tie, the accordig to the secod compoets, ad so o, the solutio with the larger compoets beig larger). The first lexicographic vectors are tae to be the solutios. Note that the first lexicographic vectors may ot maximize the correspodig obective fuctios, but as stated a feasible solutio will serve our purpose ad we eed ot proceed the first lexicographic solutio. For i =, =, 2,..., m, we fid the o-egative itegers x,, 2,...,, such that s x = li (23) x () d y x,, 2,..., m (24) i i = We assume for the preset that the itegers exist which satisfy (23) ad (24). The followig procedure (Sasty 970) may be used for fidig the first lexicographic solutios x,..., x, =, 2,..., m. Step : Allocate the maximum possible to the left most cell, say, th, for which xi () d y. i = Step 2: Allocate the maximum possible of the remaider to the cell ext to the th, say *th, such that x * () * * i d y i =. This process is cotiued for the other cells i the th row util a slac less tha s is left. If the slac is zero, the the first lexicographic solutio to the th row is obtaied.
8 62 Shaeel Javaid, Z. H. Bahshi & M. M. Khalid Step 3: If the slac, say β, is ot zero, the the positive allocatio of the right most cell, say i th, is reduced by s t ad s t = β is ow distributed as i step ad step 2 i the cells other tha the i th. If a slac, say β 2, is still left the reduce the allocatio of the i th cell by 2s t ad 2s t = β 2 is ow similarly attempted to be distributed ad so o. The cotributio of the purpose i step 3 will yield a solutio, if oe exists. This is because the solutio of the i th row, which is the first lexicographic, gives more freedom for the solutio of the i + I st row as compared to the freedom give by ay other solutio. I step 3 of the above procedure oe may ot fid zero slac for some. I this case, i order to obtai a feasible solutio to the origial problem, we bac trac ad chage the solutio of the ( ) th row to the secod lexicographic solutio ad proceed with the remaiig rows as i step to 3 above. Every time we ecouter a solutio of a o zero slac i ay row we will have to bac trac ad proceed with the ext ad proceed with the remaiig rows lexicographic solutio i the previous row. Let the total umber of zero slac lexicographic solutios i the i th row be z. A exhaustive search for explorig a feasible solutio i the th row will require z z 2... z permutatios of the lexicographic solutios i the previous ( ) rows. However, the umber of zero slac lexicographic solutios is geerally ot large. Further, i the search of a feasible solutio for the + st row oe eed ot explore those permutatios of the lexicographic solutios i the rows which have already bee explored durig the search for a feasible solutio of the th row. If a feasible solutio exists the above search beig (implicitly) exhaustive, must yield it. For the maximum, oe should go through the other solutios i lexicographic orderig. However, as stated above, a feasible solutio suffices for the balaced case. Thus we may use the first lexicographic solutios. 5. NUMERICAL EXAMPLE Cosider the problem with the followig data. m = 3, = 4, s = (, 7, 4, 2) ad a = (a, a 2, a 3 ), where s ad a are vectors. The correspodig cost is give i the followig Table 2. Table 2 Costs of the Stadard Rolls
9 Roll Cuttig Problems uder Stochastic Demad 63 The demad d, d 2, d 3 ad d 4 are ucertai with their probability distributios as: We have P ( d = )( = P d2)( = = 3)( P d = 4) = P d = = 4 P ( d2 = )( = P d2)( 2 = = 3) P d2 = = 3 P ( d 3 = 4) =, P ( d3 = 5)( = P d6) 3 = = 2 4 P ( d 4 = 6) =, P ( d 4 = ) =, 2 2 m d s l = 0. i i = Let the losses from uder supply be as: f = f 2 =, = = 2. By usig equatio (3) we fid L (x ), ad the L (x + ) for all, 2,...,. We write values i the followig tabular form i Table (3): Table 3 Calculated Values of L (x ), ad L (x + ), ( ) x L (x ) L (x ) L (x + ) L 2 (x 2 ) L 2 (x 2 ) L 2 (x 2 + ) 0 5/2 f f 2 f 2 f 2 2 6/4 f 3/4 f f 2 2/3 f /4 f /2 f /3 f 2 /3 f /4 f /4 f x L 3 (x 3 ) L 3 (x 3 ) L 3 (x 3 + ) L 4 (x 4 ) L 4 (x 4 ) L 4 (x 4 + ) 0 9/4 3/2 2 5/4 /2 3 2 /4 9/ /4 7/ /4 /2 5/2 6 5 /4 /4 3/ /2 /
10 64 Shaeel Javaid, Z. H. Bahshi & M. M. Khalid Now we solve the problem Maximize d L d y = 0 subect to y s = a0 d = 0 ad y = 0 or The pealty fuctios are arraged i ascedig order of magitude from left to right. The allocatios i followig table for solvig the problem are doe by usig the rules for ordiary Kapsac problem. f f f f f f 3 4 f f f s Allocatio f s Allocatio 2 The solutio is = 3 = 4 = y y y Now the solutio to the full problem ca be obtaied as show i Table (4) Table 4 Equivalet Determiistic Problem s Supply Slac Max. demad The first lexicographic solutio with zero slac solutio i all the rows is show i the Table (5).
11 Roll Cuttig Problems uder Stochastic Demad 65 Table 5 Zero Slac Solutio i The rows The total retur for this solutio is The obective value for the zero slac solutios with the other orderig A K s of are listed below. It is observed that the obective value goes o decreasig as we move from the order A, A 2, A 3. Table 6 Optimal Solutio of the Problem S. No. Order of A K s Obective values for the zero slac A, A 2, A A, A 3, A * A 2, A 3, A A 2, A, A * A 3, A, A * A 3, A 2, A 83.2 The orders with asteris (*) sig are the discarded oes by some precedig orders. It may be oted that oly 3 of the above orders eed to be eumerated. The optimal solutio is the zero slac solutio obtaied from the order A, A 2, A 3 as preseted i Table (6). REFERENCES [] Bari A., Slicig Optimally the Rolls of Give Legths Ito the Stadard Sizes, Pure Applied Math. Scieces, 2(-2), (980), 8. [2] Gilmore P. C., ad Gomory R. E., A Liear Programmig Approach to the Cuttig Stoc Problem Part I, Operatios Research, 9, (96), [3] Gilmore P. C., ad Gomory R. E., A Liear Programmig Approach to the Cuttig Stoc Problem Part II, Operatios Research,, (963), [4] Golde B. G., Approaches to the Cuttig Stoc Problem, AIIE Trasactios, 9, (976), [5] Coverdale I., ad Wharto F., A Improved Heuristic Procedure for a No-Liear Cuttig Stoc Problem, Math. Prog., 2, (976), 8-25.
12 66 Shaeel Javaid, Z. H. Bahshi & M. M. Khalid [6] Madasy A., Methods of Solutio of Liear Programs Uder Ucertaity, Operatios Research, 0, (962), [7] Roberts S. A., Applicatio of Heuristic Techiques to the Cuttig Stoc Problem for Worshops, Joural of Operatioal Research Society, 35(5), (984), [8] Saaty T. L., Optimizatio ad Related Exteral Problems, McGraw Hill Boo Compay, New Yor, (970). [9] Wager H. M., Priciples of Operatios Research with Applicatios to Maagerial Decisios, Pricetice Hall of Idia Pvt. Ltd., New Delhi, (977). Shaeel Javaid * & M. M. Khalid ** Departmet of Statistics & Operatios Research A.M.U., Aligarh, U.P., INDIA, s: shaeel.d@operamail.com * mmhalid2007@yahoo.com ** Z. H. Bahshi Departmet of Statistics, Meelle Uiversity, Ethiopia, Africa. bahshistat@gmail.com
Optimization Methods: Linear Programming Applications Assignment Problem 1. Module 4 Lecture Notes 3. Assignment Problem
 Optimizatio Methods: Liear Programmig Applicatios Assigmet Problem Itroductio Module 4 Lecture Notes 3 Assigmet Problem I the previous lecture, we discussed about oe of the bech mark problems called trasportatio
Optimizatio Methods: Liear Programmig Applicatios Assigmet Problem Itroductio Module 4 Lecture Notes 3 Assigmet Problem I the previous lecture, we discussed about oe of the bech mark problems called trasportatio
Zeros of Polynomials
 Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
3.2 Properties of Division 3.3 Zeros of Polynomials 3.4 Complex and Rational Zeros of Polynomials
 Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Markov Decision Processes
 Markov Decisio Processes Defiitios; Statioary policies; Value improvemet algorithm, Policy improvemet algorithm, ad liear programmig for discouted cost ad average cost criteria. Markov Decisio Processes
Markov Decisio Processes Defiitios; Statioary policies; Value improvemet algorithm, Policy improvemet algorithm, ad liear programmig for discouted cost ad average cost criteria. Markov Decisio Processes
Definitions and Theorems. where x are the decision variables. c, b, and a are constant coefficients.
 Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
A NEW APPROACH TO SOLVE AN UNBALANCED ASSIGNMENT PROBLEM
 A NEW APPROACH TO SOLVE AN UNBALANCED ASSIGNMENT PROBLEM *Kore B. G. Departmet Of Statistics, Balwat College, VITA - 415 311, Dist.: Sagli (M. S.). Idia *Author for Correspodece ABSTRACT I this paper I
A NEW APPROACH TO SOLVE AN UNBALANCED ASSIGNMENT PROBLEM *Kore B. G. Departmet Of Statistics, Balwat College, VITA - 415 311, Dist.: Sagli (M. S.). Idia *Author for Correspodece ABSTRACT I this paper I
Properties and Tests of Zeros of Polynomial Functions
 Properties ad Tests of Zeros of Polyomial Fuctios The Remaider ad Factor Theorems: Sythetic divisio ca be used to fid the values of polyomials i a sometimes easier way tha substitutio. This is show by
Properties ad Tests of Zeros of Polyomial Fuctios The Remaider ad Factor Theorems: Sythetic divisio ca be used to fid the values of polyomials i a sometimes easier way tha substitutio. This is show by
A New Solution Method for the Finite-Horizon Discrete-Time EOQ Problem
 This is the Pre-Published Versio. A New Solutio Method for the Fiite-Horizo Discrete-Time EOQ Problem Chug-Lu Li Departmet of Logistics The Hog Kog Polytechic Uiversity Hug Hom, Kowloo, Hog Kog Phoe: +852-2766-7410
This is the Pre-Published Versio. A New Solutio Method for the Fiite-Horizo Discrete-Time EOQ Problem Chug-Lu Li Departmet of Logistics The Hog Kog Polytechic Uiversity Hug Hom, Kowloo, Hog Kog Phoe: +852-2766-7410
Section 5.1 The Basics of Counting
 1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
1 Sectio 5.1 The Basics of Coutig Combiatorics, the study of arragemets of objects, is a importat part of discrete mathematics. I this chapter, we will lear basic techiques of coutig which has a lot of
Randomized Algorithms I, Spring 2018, Department of Computer Science, University of Helsinki Homework 1: Solutions (Discussed January 25, 2018)
 Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
IP Reference guide for integer programming formulations.
 IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
IP Referece guide for iteger programmig formulatios. by James B. Orli for 15.053 ad 15.058 This documet is iteded as a compact (or relatively compact) guide to the formulatio of iteger programs. For more
w (1) ˆx w (1) x (1) /ρ and w (2) ˆx w (2) x (2) /ρ.
 2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
2 5. Weighted umber of late jobs 5.1. Release dates ad due dates: maximimizig the weight of o-time jobs Oce we add release dates, miimizig the umber of late jobs becomes a sigificatly harder problem. For
Optimally Sparse SVMs
 A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
Scheduling under Uncertainty using MILP Sensitivity Analysis
 Schedulig uder Ucertaity usig MILP Sesitivity Aalysis M. Ierapetritou ad Zheya Jia Departmet of Chemical & Biochemical Egieerig Rutgers, the State Uiversity of New Jersey Piscataway, NJ Abstract The aim
Schedulig uder Ucertaity usig MILP Sesitivity Aalysis M. Ierapetritou ad Zheya Jia Departmet of Chemical & Biochemical Egieerig Rutgers, the State Uiversity of New Jersey Piscataway, NJ Abstract The aim
subject to A 1 x + A 2 y b x j 0, j = 1,,n 1 y j = 0 or 1, j = 1,,n 2
 Additioal Brach ad Boud Algorithms 0-1 Mixed-Iteger Liear Programmig The brach ad boud algorithm described i the previous sectios ca be used to solve virtually all optimizatio problems cotaiig iteger variables,
Additioal Brach ad Boud Algorithms 0-1 Mixed-Iteger Liear Programmig The brach ad boud algorithm described i the previous sectios ca be used to solve virtually all optimizatio problems cotaiig iteger variables,
TEACHER CERTIFICATION STUDY GUIDE
 COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
Lecture #20. n ( x p i )1/p = max
 COMPSCI 632: Approximatio Algorithms November 8, 2017 Lecturer: Debmalya Paigrahi Lecture #20 Scribe: Yua Deg 1 Overview Today, we cotiue to discuss about metric embeddigs techique. Specifically, we apply
COMPSCI 632: Approximatio Algorithms November 8, 2017 Lecturer: Debmalya Paigrahi Lecture #20 Scribe: Yua Deg 1 Overview Today, we cotiue to discuss about metric embeddigs techique. Specifically, we apply
Linear Programming and the Simplex Method
 Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
Liear Programmig ad the Simplex ethod Abstract This article is a itroductio to Liear Programmig ad usig Simplex method for solvig LP problems i primal form. What is Liear Programmig? Liear Programmig is
1 Duality revisited. AM 221: Advanced Optimization Spring 2016
 AM 22: Advaced Optimizatio Sprig 206 Prof. Yaro Siger Sectio 7 Wedesday, Mar. 9th Duality revisited I this sectio, we will give a slightly differet perspective o duality. optimizatio program: f(x) x R
AM 22: Advaced Optimizatio Sprig 206 Prof. Yaro Siger Sectio 7 Wedesday, Mar. 9th Duality revisited I this sectio, we will give a slightly differet perspective o duality. optimizatio program: f(x) x R
Problem 4: Evaluate ( k ) by negating (actually un-negating) its upper index. Binomial coefficient
 Problem 4: Evaluate by egatig actually u-egatig its upper idex We ow that Biomial coefficiet r { where r is a real umber, is a iteger The above defiitio ca be recast i terms of factorials i the commo case
Problem 4: Evaluate by egatig actually u-egatig its upper idex We ow that Biomial coefficiet r { where r is a real umber, is a iteger The above defiitio ca be recast i terms of factorials i the commo case
The Method of Least Squares. To understand least squares fitting of data.
 The Method of Least Squares KEY WORDS Curve fittig, least square GOAL To uderstad least squares fittig of data To uderstad the least squares solutio of icosistet systems of liear equatios 1 Motivatio Curve
The Method of Least Squares KEY WORDS Curve fittig, least square GOAL To uderstad least squares fittig of data To uderstad the least squares solutio of icosistet systems of liear equatios 1 Motivatio Curve
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
SNAP Centre Workshop. Basic Algebraic Manipulation
 SNAP Cetre Workshop Basic Algebraic Maipulatio 8 Simplifyig Algebraic Expressios Whe a expressio is writte i the most compact maer possible, it is cosidered to be simplified. Not Simplified: x(x + 4x)
SNAP Cetre Workshop Basic Algebraic Maipulatio 8 Simplifyig Algebraic Expressios Whe a expressio is writte i the most compact maer possible, it is cosidered to be simplified. Not Simplified: x(x + 4x)
M.Jayalakshmi and P. Pandian Department of Mathematics, School of Advanced Sciences, VIT University, Vellore-14, India.
 M.Jayalakshmi, P. Padia / Iteratioal Joural of Egieerig Research ad Applicatios (IJERA) ISSN: 48-96 www.iera.com Vol., Issue 4, July-August 0, pp.47-54 A New Method for Fidig a Optimal Fuzzy Solutio For
M.Jayalakshmi, P. Padia / Iteratioal Joural of Egieerig Research ad Applicatios (IJERA) ISSN: 48-96 www.iera.com Vol., Issue 4, July-August 0, pp.47-54 A New Method for Fidig a Optimal Fuzzy Solutio For
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
CALCULATION OF FIBONACCI VECTORS
 CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
CALCULATION OF FIBONACCI VECTORS Stuart D. Aderso Departmet of Physics, Ithaca College 953 Daby Road, Ithaca NY 14850, USA email: saderso@ithaca.edu ad Dai Novak Departmet of Mathematics, Ithaca College
(3) If you replace row i of A by its sum with a multiple of another row, then the determinant is unchanged! Expand across the i th row:
 Math 50-004 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig
Math 50-004 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig
Math 475, Problem Set #12: Answers
 Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
Math 475, Problem Set #12: Aswers A. Chapter 8, problem 12, parts (b) ad (d). (b) S # (, 2) = 2 2, sice, from amog the 2 ways of puttig elemets ito 2 distiguishable boxes, exactly 2 of them result i oe
In algebra one spends much time finding common denominators and thus simplifying rational expressions. For example:
 74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
Let us consider the following problem to warm up towards a more general statement.
 Lecture 4: Sequeces with repetitios, distributig idetical objects amog distict parties, the biomial theorem, ad some properties of biomial coefficiets Refereces: Relevat parts of chapter 15 of the Math
Lecture 4: Sequeces with repetitios, distributig idetical objects amog distict parties, the biomial theorem, ad some properties of biomial coefficiets Refereces: Relevat parts of chapter 15 of the Math
Lecture 7: Properties of Random Samples
 Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
Lecture 7: Properties of Radom Samples 1 Cotiued From Last Class Theorem 1.1. Let X 1, X,...X be a radom sample from a populatio with mea µ ad variace σ
OPTIMIZED SOLUTION OF PRESSURE VESSEL DESIGN USING GEOMETRIC PROGRAMMING
 OPTIMIZED SOLUTION OF PRESSURE VESSEL DESIGN USING GEOMETRIC PROGRAMMING S.H. NASSERI, Z. ALIZADEH AND F. TALESHIAN ABSTRACT. Geometric programmig is a methodology for solvig algebraic oliear optimizatio
OPTIMIZED SOLUTION OF PRESSURE VESSEL DESIGN USING GEOMETRIC PROGRAMMING S.H. NASSERI, Z. ALIZADEH AND F. TALESHIAN ABSTRACT. Geometric programmig is a methodology for solvig algebraic oliear optimizatio
Sequences, Mathematical Induction, and Recursion. CSE 2353 Discrete Computational Structures Spring 2018
 CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
Product Mix Problem with Radom Return and Preference of Production Quantity. Osaka University Japan
 Product Mix Problem with Radom Retur ad Preferece of Productio Quatity Hiroaki Ishii Osaka Uiversity Japa We call such fiace or idustrial assets allocatio problems portfolio selectio problems, ad various
Product Mix Problem with Radom Retur ad Preferece of Productio Quatity Hiroaki Ishii Osaka Uiversity Japa We call such fiace or idustrial assets allocatio problems portfolio selectio problems, ad various
Solutions to Final Exam
 Solutios to Fial Exam 1. Three married couples are seated together at the couter at Moty s Blue Plate Dier, occupyig six cosecutive seats. How may arragemets are there with o wife sittig ext to her ow
Solutios to Fial Exam 1. Three married couples are seated together at the couter at Moty s Blue Plate Dier, occupyig six cosecutive seats. How may arragemets are there with o wife sittig ext to her ow
The multi capacitated clustering problem
 The multi capacitated clusterig problem Bruo de Aayde Prata 1 Federal Uiversity of Ceará, Brazil Abstract Clusterig problems are combiatorial optimizatio problems wi several idustrial applicatios. The
The multi capacitated clusterig problem Bruo de Aayde Prata 1 Federal Uiversity of Ceará, Brazil Abstract Clusterig problems are combiatorial optimizatio problems wi several idustrial applicatios. The
Machine Learning for Data Science (CS 4786)
 Machie Learig for Data Sciece CS 4786) Lecture & 3: Pricipal Compoet Aalysis The text i black outlies high level ideas. The text i blue provides simple mathematical details to derive or get to the algorithm
Machie Learig for Data Sciece CS 4786) Lecture & 3: Pricipal Compoet Aalysis The text i black outlies high level ideas. The text i blue provides simple mathematical details to derive or get to the algorithm
Integer Linear Programming
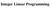 Iteger Liear Programmig Itroductio Iteger L P problem (P) Mi = s. t. a = b i =,, m = i i 0, iteger =,, c Eemple Mi z = 5 s. t. + 0 0, 0, iteger F(P) = feasible domai of P Itroductio Iteger L P problem
Iteger Liear Programmig Itroductio Iteger L P problem (P) Mi = s. t. a = b i =,, m = i i 0, iteger =,, c Eemple Mi z = 5 s. t. + 0 0, 0, iteger F(P) = feasible domai of P Itroductio Iteger L P problem
Bertrand s Postulate
 Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
(3) If you replace row i of A by its sum with a multiple of another row, then the determinant is unchanged! Expand across the i th row:
 Math 5-4 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig facts,
Math 5-4 Tue Feb 4 Cotiue with sectio 36 Determiats The effective way to compute determiats for larger-sized matrices without lots of zeroes is to ot use the defiitio, but rather to use the followig facts,
Optimization Methods MIT 2.098/6.255/ Final exam
 Optimizatio Methods MIT 2.098/6.255/15.093 Fial exam Date Give: December 19th, 2006 P1. [30 pts] Classify the followig statemets as true or false. All aswers must be well-justified, either through a short
Optimizatio Methods MIT 2.098/6.255/15.093 Fial exam Date Give: December 19th, 2006 P1. [30 pts] Classify the followig statemets as true or false. All aswers must be well-justified, either through a short
PROPERTIES OF AN EULER SQUARE
 PROPERTIES OF N EULER SQURE bout 0 the mathematicia Leoard Euler discussed the properties a x array of letters or itegers ow kow as a Euler or Graeco-Lati Square Such squares have the property that every
PROPERTIES OF N EULER SQURE bout 0 the mathematicia Leoard Euler discussed the properties a x array of letters or itegers ow kow as a Euler or Graeco-Lati Square Such squares have the property that every
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER / Statistics
 ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 018/019 DR. ANTHONY BROWN 8. Statistics 8.1. Measures of Cetre: Mea, Media ad Mode. If we have a series of umbers the
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 018/019 DR. ANTHONY BROWN 8. Statistics 8.1. Measures of Cetre: Mea, Media ad Mode. If we have a series of umbers the
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
U8L1: Sec Equations of Lines in R 2
 MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
POSSIBILISTIC OPTIMIZATION WITH APPLICATION TO PORTFOLIO SELECTION
 THE PUBLISHING HOUSE PROCEEDINGS OF THE ROMANIAN ACADEMY, Series A, OF THE ROMANIAN ACADEMY Volume, Number /, pp 88 9 POSSIBILISTIC OPTIMIZATION WITH APPLICATION TO PORTFOLIO SELECTION Costi-Cipria POPESCU,
THE PUBLISHING HOUSE PROCEEDINGS OF THE ROMANIAN ACADEMY, Series A, OF THE ROMANIAN ACADEMY Volume, Number /, pp 88 9 POSSIBILISTIC OPTIMIZATION WITH APPLICATION TO PORTFOLIO SELECTION Costi-Cipria POPESCU,
CHAPTER I: Vector Spaces
 CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
Injections, Surjections, and the Pigeonhole Principle
 Ijectios, Surjectios, ad the Pigeohole Priciple 1 (10 poits Here we will come up with a sloppy boud o the umber of parethesisestigs (a (5 poits Describe a ijectio from the set of possible ways to est pairs
Ijectios, Surjectios, ad the Pigeohole Priciple 1 (10 poits Here we will come up with a sloppy boud o the umber of parethesisestigs (a (5 poits Describe a ijectio from the set of possible ways to est pairs
Similarity Solutions to Unsteady Pseudoplastic. Flow Near a Moving Wall
 Iteratioal Mathematical Forum, Vol. 9, 04, o. 3, 465-475 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/0.988/imf.04.48 Similarity Solutios to Usteady Pseudoplastic Flow Near a Movig Wall W. Robi Egieerig
Iteratioal Mathematical Forum, Vol. 9, 04, o. 3, 465-475 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/0.988/imf.04.48 Similarity Solutios to Usteady Pseudoplastic Flow Near a Movig Wall W. Robi Egieerig
Subject: Differential Equations & Mathematical Modeling -III. Lesson: Power series solutions of Differential Equations. about ordinary points
 Power series solutio of Differetial equatios about ordiary poits Subject: Differetial Equatios & Mathematical Modelig -III Lesso: Power series solutios of Differetial Equatios about ordiary poits Lesso
Power series solutio of Differetial equatios about ordiary poits Subject: Differetial Equatios & Mathematical Modelig -III Lesso: Power series solutios of Differetial Equatios about ordiary poits Lesso
Apply change-of-basis formula to rewrite x as a linear combination of eigenvectors v j.
 Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
Polynomials with Rational Roots that Differ by a Non-zero Constant. Generalities
 Polyomials with Ratioal Roots that Differ by a No-zero Costat Philip Gibbs The problem of fidig two polyomials P(x) ad Q(x) of a give degree i a sigle variable x that have all ratioal roots ad differ by
Polyomials with Ratioal Roots that Differ by a No-zero Costat Philip Gibbs The problem of fidig two polyomials P(x) ad Q(x) of a give degree i a sigle variable x that have all ratioal roots ad differ by
arxiv: v1 [math.nt] 10 Dec 2014
![arxiv: v1 [math.nt] 10 Dec 2014 arxiv: v1 [math.nt] 10 Dec 2014](/thumbs/82/85433827.jpg) A DIGITAL BINOMIAL THEOREM HIEU D. NGUYEN arxiv:42.38v [math.nt] 0 Dec 204 Abstract. We preset a triagle of coectios betwee the Sierpisi triagle, the sum-of-digits fuctio, ad the Biomial Theorem via a
A DIGITAL BINOMIAL THEOREM HIEU D. NGUYEN arxiv:42.38v [math.nt] 0 Dec 204 Abstract. We preset a triagle of coectios betwee the Sierpisi triagle, the sum-of-digits fuctio, ad the Biomial Theorem via a
Ray-triangle intersection
 Ray-triagle itersectio ria urless October 2006 I this hadout, we explore the steps eeded to compute the itersectio of a ray with a triagle, ad the to compute the barycetric coordiates of that itersectio.
Ray-triagle itersectio ria urless October 2006 I this hadout, we explore the steps eeded to compute the itersectio of a ray with a triagle, ad the to compute the barycetric coordiates of that itersectio.
Introduction to Optimization Techniques. How to Solve Equations
 Itroductio to Optimizatio Techiques How to Solve Equatios Iterative Methods of Optimizatio Iterative methods of optimizatio Solutio of the oliear equatios resultig form a optimizatio problem is usually
Itroductio to Optimizatio Techiques How to Solve Equatios Iterative Methods of Optimizatio Iterative methods of optimizatio Solutio of the oliear equatios resultig form a optimizatio problem is usually
The picture in figure 1.1 helps us to see that the area represents the distance traveled. Figure 1: Area represents distance travelled
 1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
Topic 9: Sampling Distributions of Estimators
 Topic 9: Samplig Distributios of Estimators Course 003, 2016 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Topic 9: Samplig Distributios of Estimators Course 003, 2016 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
The Random Walk For Dummies
 The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
The Radom Walk For Dummies Richard A Mote Abstract We look at the priciples goverig the oe-dimesioal discrete radom walk First we review five basic cocepts of probability theory The we cosider the Beroulli
Homework 2. Show that if h is a bounded sesquilinear form on the Hilbert spaces X and Y, then h has the representation
 omework 2 1 Let X ad Y be ilbert spaces over C The a sesquiliear form h o X Y is a mappig h : X Y C such that for all x 1, x 2, x X, y 1, y 2, y Y ad all scalars α, β C we have (a) h(x 1 + x 2, y) h(x
omework 2 1 Let X ad Y be ilbert spaces over C The a sesquiliear form h o X Y is a mappig h : X Y C such that for all x 1, x 2, x X, y 1, y 2, y Y ad all scalars α, β C we have (a) h(x 1 + x 2, y) h(x
Theorem: Let A n n. In this case that A does reduce to I, we search for A 1 as the solution matrix X to the matrix equation A X = I i.e.
 Theorem: Let A be a square matrix The A has a iverse matrix if ad oly if its reduced row echelo form is the idetity I this case the algorithm illustrated o the previous page will always yield the iverse
Theorem: Let A be a square matrix The A has a iverse matrix if ad oly if its reduced row echelo form is the idetity I this case the algorithm illustrated o the previous page will always yield the iverse
Linear Regression Demystified
 Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
Liear Regressio Demystified Liear regressio is a importat subject i statistics. I elemetary statistics courses, formulae related to liear regressio are ofte stated without derivatio. This ote iteds to
TRANSPORTATION AND ASSIGNMENT PROBLEMS
 Trasportatio problem TRANSPORTATION AND ASSIGNMENT PROBLEMS Example P&T Compay produces caed peas. Peas are prepared at three caeries (Belligham, Eugee ad Albert Lea). Shipped by truck to four distributig
Trasportatio problem TRANSPORTATION AND ASSIGNMENT PROBLEMS Example P&T Compay produces caed peas. Peas are prepared at three caeries (Belligham, Eugee ad Albert Lea). Shipped by truck to four distributig
Research Article A New Second-Order Iteration Method for Solving Nonlinear Equations
 Abstract ad Applied Aalysis Volume 2013, Article ID 487062, 4 pages http://dx.doi.org/10.1155/2013/487062 Research Article A New Secod-Order Iteratio Method for Solvig Noliear Equatios Shi Mi Kag, 1 Arif
Abstract ad Applied Aalysis Volume 2013, Article ID 487062, 4 pages http://dx.doi.org/10.1155/2013/487062 Research Article A New Secod-Order Iteratio Method for Solvig Noliear Equatios Shi Mi Kag, 1 Arif
WORKING WITH NUMBERS
 1 WORKING WITH NUMBERS WHAT YOU NEED TO KNOW The defiitio of the differet umber sets: is the set of atural umbers {0, 1,, 3, }. is the set of itegers {, 3,, 1, 0, 1,, 3, }; + is the set of positive itegers;
1 WORKING WITH NUMBERS WHAT YOU NEED TO KNOW The defiitio of the differet umber sets: is the set of atural umbers {0, 1,, 3, }. is the set of itegers {, 3,, 1, 0, 1,, 3, }; + is the set of positive itegers;
Lecture 6 Chi Square Distribution (χ 2 ) and Least Squares Fitting
 Lecture 6 Chi Square Distributio (χ ) ad Least Squares Fittig Chi Square Distributio (χ ) Suppose: We have a set of measuremets {x 1, x, x }. We kow the true value of each x i (x t1, x t, x t ). We would
Lecture 6 Chi Square Distributio (χ ) ad Least Squares Fittig Chi Square Distributio (χ ) Suppose: We have a set of measuremets {x 1, x, x }. We kow the true value of each x i (x t1, x t, x t ). We would
You may work in pairs or purely individually for this assignment.
 CS 04 Problem Solvig i Computer Sciece OOC Assigmet 6: Recurreces You may work i pairs or purely idividually for this assigmet. Prepare your aswers to the followig questios i a plai ASCII text file or
CS 04 Problem Solvig i Computer Sciece OOC Assigmet 6: Recurreces You may work i pairs or purely idividually for this assigmet. Prepare your aswers to the followig questios i a plai ASCII text file or
( ) = p and P( i = b) = q.
 MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
x c the remainder is Pc ().
 Algebra, Polyomial ad Ratioal Fuctios Page 1 K.Paulk Notes Chapter 3, Sectio 3.1 to 3.4 Summary Sectio Theorem Notes 3.1 Zeros of a Fuctio Set the fuctio to zero ad solve for x. The fuctio is zero at these
Algebra, Polyomial ad Ratioal Fuctios Page 1 K.Paulk Notes Chapter 3, Sectio 3.1 to 3.4 Summary Sectio Theorem Notes 3.1 Zeros of a Fuctio Set the fuctio to zero ad solve for x. The fuctio is zero at these
Section 7 Fundamentals of Sequences and Series
 ectio Fudametals of equeces ad eries. Defiitio ad examples of sequeces A sequece ca be thought of as a ifiite list of umbers. 0, -, -0, -, -0...,,,,,,. (iii),,,,... Defiitio: A sequece is a fuctio which
ectio Fudametals of equeces ad eries. Defiitio ad examples of sequeces A sequece ca be thought of as a ifiite list of umbers. 0, -, -0, -, -0...,,,,,,. (iii),,,,... Defiitio: A sequece is a fuctio which
CHAPTER 5. Theory and Solution Using Matrix Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
Problem Set 4 Due Oct, 12
 EE226: Radom Processes i Systems Lecturer: Jea C. Walrad Problem Set 4 Due Oct, 12 Fall 06 GSI: Assae Gueye This problem set essetially reviews detectio theory ad hypothesis testig ad some basic otios
EE226: Radom Processes i Systems Lecturer: Jea C. Walrad Problem Set 4 Due Oct, 12 Fall 06 GSI: Assae Gueye This problem set essetially reviews detectio theory ad hypothesis testig ad some basic otios
Lecture 6 Chi Square Distribution (χ 2 ) and Least Squares Fitting
 Lecture 6 Chi Square Distributio (χ ) ad Least Squares Fittig Chi Square Distributio (χ ) Suppose: We have a set of measuremets {x 1, x, x }. We kow the true value of each x i (x t1, x t, x t ). We would
Lecture 6 Chi Square Distributio (χ ) ad Least Squares Fittig Chi Square Distributio (χ ) Suppose: We have a set of measuremets {x 1, x, x }. We kow the true value of each x i (x t1, x t, x t ). We would
14.1 Understanding Rational Exponents and Radicals
 Name Class Date 14.1 Uderstadig Ratioal Expoets ad Radicals Essetial Questio: How are radicals ad ratioal expoets related? Resource Locker Explore 1 Uderstadig Iteger Expoets Recall that powers like are
Name Class Date 14.1 Uderstadig Ratioal Expoets ad Radicals Essetial Questio: How are radicals ad ratioal expoets related? Resource Locker Explore 1 Uderstadig Iteger Expoets Recall that powers like are
Inverse Matrix. A meaning that matrix B is an inverse of matrix A.
 Iverse Matrix Two square matrices A ad B of dimesios are called iverses to oe aother if the followig holds, AB BA I (11) The otio is dual but we ofte write 1 B A meaig that matrix B is a iverse of matrix
Iverse Matrix Two square matrices A ad B of dimesios are called iverses to oe aother if the followig holds, AB BA I (11) The otio is dual but we ofte write 1 B A meaig that matrix B is a iverse of matrix
Differentiable Convex Functions
 Differetiable Covex Fuctios The followig picture motivates Theorem 11. f ( x) f ( x) f '( x)( x x) ˆx x 1 Theorem 11 : Let f : R R be differetiable. The, f is covex o the covex set C R if, ad oly if for
Differetiable Covex Fuctios The followig picture motivates Theorem 11. f ( x) f ( x) f '( x)( x x) ˆx x 1 Theorem 11 : Let f : R R be differetiable. The, f is covex o the covex set C R if, ad oly if for
Scholars Journal of Physics, Mathematics and Statistics
 Jaalakshmi M. Sch. J. Phs. Math. Stat., 015 Vol- Issue-A Mar-Ma pp-144-150 Scholars Joural of Phsics, Mathematics ad Statistics Sch. J. Phs. Math. Stat. 015 A:144-150 Scholars Academic ad Scietific Publishers
Jaalakshmi M. Sch. J. Phs. Math. Stat., 015 Vol- Issue-A Mar-Ma pp-144-150 Scholars Joural of Phsics, Mathematics ad Statistics Sch. J. Phs. Math. Stat. 015 A:144-150 Scholars Academic ad Scietific Publishers
Problem Set 2 Solutions
 CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
Lecture Overview. 2 Permutations and Combinations. n(n 1) (n (k 1)) = n(n 1) (n k + 1) =
 COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
COMPSCI 230: Discrete Mathematics for Computer Sciece April 8, 2019 Lecturer: Debmalya Paigrahi Lecture 22 Scribe: Kevi Su 1 Overview I this lecture, we begi studyig the fudametals of coutig discrete objects.
Roger Apéry's proof that zeta(3) is irrational
 Cliff Bott cliffbott@hotmail.com 11 October 2011 Roger Apéry's proof that zeta(3) is irratioal Roger Apéry developed a method for searchig for cotiued fractio represetatios of umbers that have a form such
Cliff Bott cliffbott@hotmail.com 11 October 2011 Roger Apéry's proof that zeta(3) is irratioal Roger Apéry developed a method for searchig for cotiued fractio represetatios of umbers that have a form such
Precalculus MATH Sections 3.1, 3.2, 3.3. Exponential, Logistic and Logarithmic Functions
 Precalculus MATH 2412 Sectios 3.1, 3.2, 3.3 Epoetial, Logistic ad Logarithmic Fuctios Epoetial fuctios are used i umerous applicatios coverig may fields of study. They are probably the most importat group
Precalculus MATH 2412 Sectios 3.1, 3.2, 3.3 Epoetial, Logistic ad Logarithmic Fuctios Epoetial fuctios are used i umerous applicatios coverig may fields of study. They are probably the most importat group
Quadratic Functions. Before we start looking at polynomials, we should know some common terminology.
 Quadratic Fuctios I this sectio we begi the study of fuctios defied by polyomial expressios. Polyomial ad ratioal fuctios are the most commo fuctios used to model data, ad are used extesively i mathematical
Quadratic Fuctios I this sectio we begi the study of fuctios defied by polyomial expressios. Polyomial ad ratioal fuctios are the most commo fuctios used to model data, ad are used extesively i mathematical
Rank Modulation with Multiplicity
 Rak Modulatio with Multiplicity Axiao (Adrew) Jiag Computer Sciece ad Eg. Dept. Texas A&M Uiversity College Statio, TX 778 ajiag@cse.tamu.edu Abstract Rak modulatio is a scheme that uses the relative order
Rak Modulatio with Multiplicity Axiao (Adrew) Jiag Computer Sciece ad Eg. Dept. Texas A&M Uiversity College Statio, TX 778 ajiag@cse.tamu.edu Abstract Rak modulatio is a scheme that uses the relative order
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CSE 191, Class Note 05: Counting Methods Computer Sci & Eng Dept SUNY Buffalo
 Coutig Methods CSE 191, Class Note 05: Coutig Methods Computer Sci & Eg Dept SUNY Buffalo c Xi He (Uiversity at Buffalo CSE 191 Discrete Structures 1 / 48 Need for Coutig The problem of coutig the umber
Coutig Methods CSE 191, Class Note 05: Coutig Methods Computer Sci & Eg Dept SUNY Buffalo c Xi He (Uiversity at Buffalo CSE 191 Discrete Structures 1 / 48 Need for Coutig The problem of coutig the umber
x a x a Lecture 2 Series (See Chapter 1 in Boas)
 Lecture Series (See Chapter i Boas) A basic ad very powerful (if pedestria, recall we are lazy AD smart) way to solve ay differetial (or itegral) equatio is via a series expasio of the correspodig solutio
Lecture Series (See Chapter i Boas) A basic ad very powerful (if pedestria, recall we are lazy AD smart) way to solve ay differetial (or itegral) equatio is via a series expasio of the correspodig solutio
Complex Analysis Spring 2001 Homework I Solution
 Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
a for a 1 1 matrix. a b a b 2 2 matrix: We define det ad bc 3 3 matrix: We define a a a a a a a a a a a a a a a a a a
 Math S-b Lecture # Notes This wee is all about determiats We ll discuss how to defie them, how to calculate them, lear the allimportat property ow as multiliearity, ad show that a square matrix A is ivertible
Math S-b Lecture # Notes This wee is all about determiats We ll discuss how to defie them, how to calculate them, lear the allimportat property ow as multiliearity, ad show that a square matrix A is ivertible
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
End-of-Year Contest. ERHS Math Club. May 5, 2009
 Ed-of-Year Cotest ERHS Math Club May 5, 009 Problem 1: There are 9 cois. Oe is fake ad weighs a little less tha the others. Fid the fake coi by weighigs. Solutio: Separate the 9 cois ito 3 groups (A, B,
Ed-of-Year Cotest ERHS Math Club May 5, 009 Problem 1: There are 9 cois. Oe is fake ad weighs a little less tha the others. Fid the fake coi by weighigs. Solutio: Separate the 9 cois ito 3 groups (A, B,
Axioms of Measure Theory
 MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
CSI 2101 Discrete Structures Winter Homework Assignment #4 (100 points, weight 5%) Due: Thursday, April 5, at 1:00pm (in lecture)
 CSI 101 Discrete Structures Witer 01 Prof. Lucia Moura Uiversity of Ottawa Homework Assigmet #4 (100 poits, weight %) Due: Thursday, April, at 1:00pm (i lecture) Program verificatio, Recurrece Relatios
CSI 101 Discrete Structures Witer 01 Prof. Lucia Moura Uiversity of Ottawa Homework Assigmet #4 (100 poits, weight %) Due: Thursday, April, at 1:00pm (i lecture) Program verificatio, Recurrece Relatios
Commutativity in Permutation Groups
 Commutativity i Permutatio Groups Richard Wito, PhD Abstract I the group Sym(S) of permutatios o a oempty set S, fixed poits ad trasiet poits are defied Prelimiary results o fixed ad trasiet poits are
Commutativity i Permutatio Groups Richard Wito, PhD Abstract I the group Sym(S) of permutatios o a oempty set S, fixed poits ad trasiet poits are defied Prelimiary results o fixed ad trasiet poits are
Lecture 2: April 3, 2013
 TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
A widely used display of protein shapes is based on the coordinates of the alpha carbons - - C α
 Nice plottig of proteis: I A widely used display of protei shapes is based o the coordiates of the alpha carbos - - C α -s. The coordiates of the C α -s are coected by a cotiuous curve that roughly follows
Nice plottig of proteis: I A widely used display of protei shapes is based o the coordiates of the alpha carbos - - C α -s. The coordiates of the C α -s are coected by a cotiuous curve that roughly follows
Random Matrices with Blocks of Intermediate Scale Strongly Correlated Band Matrices
 Radom Matrices with Blocks of Itermediate Scale Strogly Correlated Bad Matrices Jiayi Tog Advisor: Dr. Todd Kemp May 30, 07 Departmet of Mathematics Uiversity of Califoria, Sa Diego Cotets Itroductio Notatio
Radom Matrices with Blocks of Itermediate Scale Strogly Correlated Bad Matrices Jiayi Tog Advisor: Dr. Todd Kemp May 30, 07 Departmet of Mathematics Uiversity of Califoria, Sa Diego Cotets Itroductio Notatio
Recursive Algorithms. Recurrences. Recursive Algorithms Analysis
 Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
