Linear Convergence of Gradient and Proximal-Gradient Methods Under the Polyak- Lojasiewicz Condition
|
|
|
- Randell Wright
- 5 years ago
- Views:
Transcription
1 Linear Convergence of Gradient and Proximal-Gradient Methods Under the Polak- Lojasiewicz Condition Hamed Karimi, Julie Nutini, and Mark Schmidt Department of Computer Science, Universit of British Columbia Vancouver, British Columbia, Canada Abstract. In 963, Polak proposed a simple condition that is sufficient to show a global linear convergence rate for gradient descent. This condition is a special case of the Lojasiewicz inequalit proposed in the same ear, and it does not require strong convexit (or even convexit). In this work, we show that this much-older Polak- Lojasiewicz (PL) inequalit is actuall weaker than the main conditions that have been explored to show linear convergence rates without strong convexit over the last 5 ears. We also use the PL inequalit to give new analses of randomized and greed coordinate descent methods, sign-based gradient descent methods, and stochastic gradient methods in the classic setting (with decreasing or constant step-sizes) as well as the variancereduced setting. We further propose a generalization that applies to proximal-gradient methods for non-smooth optimization, leading to simple proofs of linear convergence of these methods. Along the wa, we give simple convergence results for a wide variet of problems in machine learning: least squares, logistic regression, boosting, resilient backpropagation, L-regularization, support vector machines, stochastic dual coordinate ascent, and stochastic variance-reduced gradient methods. Introduction Fitting most machine learning models involves solving some sort of optimization problem. Gradient descent, and variants of it like coordinate descent and stochastic gradient, are the workhorse tools used b the field to solve ver large instances of these problems. In this work we consider the basic problem of minimizing a smooth function and the convergence rate of gradient descent methods. It is wellknown that if f is strongl-convex, then gradient descent achieves a global linear convergence rate for this problem Nesterov, 4]. However, man of the fundamental models in machine learning like least squares and logistic regression ield objective functions that are convex but not strongl-convex. Further, if f is onl convex, then gradient descent onl achieves a sub-linear rate. This situation has motivated a variet of alternatives to strong convexit (SC) in the literature, in order to show that we can obtain linear convergence rates for problems like least squares and logistic regression. One of the oldest of these conditions is the error bounds (EB) of Luo and Tseng 993], but four other recentl-considered conditions are essential strong convexit (ESC) Liu et al., 4], weak strong convexit (WSC) Necoara et al., 5], the restricted secant inequalit (RSI) Zhang and Yin, 3], and the quadratic growth (QG) condition Anitescu, ]. Some of these conditions have different names in the special case of convex functions. For example, a convex function satisfing RSI is said to satisf restricted strong convexit (RSC) Zhang and Yin, 3]. Names describing convex functions satisfing QG include optimal strong convexit (OSC) Liu and Wright, 5], semi-strong convexit (SSC) Gong and Ye, 4], and (confusingl) WSC Ma et al., 5]. The proofs of linear convergence under all of these relaxations are tpicall not straightforward, and it is rarel discussed how these conditions relate to each other. In this work, we consider a much older condition that we refer to as the Polak- Lojasiewicz (PL) inequalit. This inequalit was originall introduced b Polak 963], who showed that it is a sufficient condition for gradient descent to achieve a linear convergence rate. We describe it as the PL inequalit because it is also a special case of the inequalit introduced in the same ear b Lojasiewicz 963]. We review the PL inequalit in the next section and how it leads to a trivial proof of the linear convergence rate of gradient descent. Next, in terms of showing a global linear convergence rate to the optimal solution, we show that the PL inequalit is weaker than all of the more recent conditions discussed in the previous paragraph. This suggests that we can replace the long and complicated proofs under an of the conditions above with simpler proofs based on the PL inequalit. Subsequentl, we show how
2 this result implies gradient descent achieves linear rates for standard problems in machine learning like least squares and logistic regression that are not necessaril SC, and even for some non-convex problems (Section.3). In Section 3 we use the PL inequalit to give new convergence rates for randomized and greed coordinate descent (impling a new convergence rate for certain variants of boosting), sign-based gradient descent methods, and stochastic gradient methods in either the classical or variance-reduced setting. Next we turn to the problem of minimizing the sum of a smooth function and a simple non-smooth function. We propose a generalization of the PL inequalit that allows us to show linear convergence rates for proximal-gradient methods without SC. In this setting, the new condition is equivalent to the well-known Kurdka- Lojasiewicz (KL) condition which has been used to show linear convergence of proximal-gradient methods for certain problems like support vector machines and l -regularized least squares Bolte et al., 5]. But this new alternate generalization of the PL inequalit leads to shorter and simpler proofs in these cases. Polak- Lojasiewicz Inequalit We first focus on the basic unconstrained optimization problem argmin f(x), () x R d and we assume that the first derivative of f is L-Lipschitz continuous. This means that f() f(x) + f(x), x + L x, () for all x and. For twice-differentiable objectives this assumption means that the eigenvalues of f(x) are bounded above b some L, which is tpicall a reasonable assumption. We also assume that the optimization problem has a non-empt solution set X, and we use f to denote the corresponding optimal function value. We will sa that a function satisfies the PL inequalit if the following holds for some µ >, f(x) µ(f(x) f ), x. (3) This inequalit simpl requires that the gradient grows faster than a quadratic function as we move awa from the optimal function value. Note that this inequalit implies that ever stationar point is a global minimum. But unlike SC, it does not impl that there is a unique solution. Linear convergence of gradient descent under these assumptions was first proved b Polak 963]. Below we give a simple proof of this result when using a step-size of /L. Theorem. Consider problem (), where f has an L-Lipschitz continuous gradient (), a non-empt solution set X, and satisfies the PL inequalit (3). Then the gradient method with a step-size of /L, has a global linear convergence rate, f(x k ) f x k+ = x k L f(x k), (4) ( µ L) k (f(x ) f ). Proof. B using update rule (4) in the Lipschitz inequalit condition () we have Now b using the PL inequalit (3) we get f(x k+ ) f(x k ) L f(x k). f(x k+ ) f(x k ) µ L (f(x k) f ). Re-arranging and subtracting f from both sides gives us f(x k+ ) f ( L) µ (f(xk ) f ). Appling this inequalit recursivel gives the result.
3 Note that the above result also holds if we use the optimal step-size at each iteration, because under this choice we have ( f(x k+ ) = min{f(x k α f(x k ))} f x k ) α L f(x k). A beautiful aspect of this proof is its simplicit; in fact it is simpler than the proof of the same fact under the usual SC assumption. It is certainl simpler than tpical proofs which rel on the other conditions mentioned in Section. Further, it is worth noting that the proof does not assume convexit of f. Thus, this is one of the few general results we have for global linear convergence on non-convex problems.. Relationships Between Conditions As mentioned in the Section, several other assumptions have been explored over the last 5 ears in order to show that gradient descent achieves a linear convergence rate. These tpicall assume that f is convex, and lead to more complicated proofs than the one above. However, it is rarel discussed how the conditions relate to each other. Indeed, all of the relationships that have been explored have onl been in the context of convex functions Bolte et al., 5, Liu and Wright, 5, Necoara et al., 5, Zhang, 5]. In Appendix A, we give the precise definitions of all conditions and also prove the result below giving relationships between the conditions. Theorem. For a function f with a Lipschitz-continuous gradient, the following implications hold: (SC) (ESC) (W SC) (RSI) (EB) (P L) (QG). If we further assume that f is convex then we have (RSI) (EB) (P L) (QG). Note the equivalence between EB and PL is a special case of a more general result b Bolte et al. 5, Theorem 5], while Zhang 6] independentl also recentl gave the relationships between RSI, EB, PL, and QG. This result shows that QG is the weakest assumption among those considered. However, QG allows non-global local minima so it is not enough to guarantee that gradient descent finds a global minimizer. This means that, among those considered above, PL and the equivalent EB are the most general conditions that allow linear convergence to a global minimizer. Note that in the convex case QG is called OSC or SSC, but the result above shows that in the convex case it is also equivalent to EB and PL (as well as RSI which is known as RSC in this case).. Invex and Non-Convex Functions While the PL inequalit does not impl convexit of f, it does impl the weaker condition of invexit. A function is invex if it is differentiable and there exists a vector valued function η such that for an x and in IR n, the following inequalit holds f() f(x) + f(x) T η(x, ). We obtain convex functions as the special case where η(x, ) = x. Invexit was first introduced b Hanson 98], and has been used in the context of learning output kernels Dinuzzo et al., ]. Craven and Glover 985] show that a smooth f is invex if and onl if ever stationar point of f is a global minimum. Since the PL inequalit implies that all stationar points are global minimizers, functions satisfing the PL inequalit must be invex. It is eas to see this b noting that at an stationar point x we have f( x) =, so we have = f( x) µ(f(x) f ), where the last inequalit holds because µ > and f(x) f for all x. This implies that f( x) = f and thus an stationar point must be a global minimum. Drusvatski and Lewis 6] is a recent work discussing the relationships among man of these conditions for non-smooth functions. 3
4 Theorem shows that all of the previous conditions (except QG) impl invexit. The function f(x) = x + 3 sin (x) is an example of an invex but non-convex function satisfing the PL inequalit (with µ = /3). Thus, Theorem implies gradient descent obtains a global linear convergence rate on this function. Unfortunatel, man complicated models have non-optimal stationar points. For example, tpical deep feed-forward neural networks have sub-optimal stationar points and are thus not invex. A classic wa to analze functions like this is to consider a global convergence phase and a local convergence phase. The global convergence phase is the time spent to get close to a local minimum, and then once we are close to a local minimum the local convergence phase characterizes the convergence rate of the method. Usuall, the local convergence phase starts to appl once we are locall SC around the minimizer. But this means that the local convergence phase ma be arbitraril small: for example, for f(x) = x + 3 sin (x) the local convergence rate would not even appl over the interval x, ]. If we instead defined the local convergence phase in terms of locall satisfing the PL inequalit, then we see that it can be much larger (x IR for this example)..3 Relevant Problems If f is µ-sc, then it also satisfies the PL inequalit with the same µ (see Appendix B). Further, b Theorem, f satisfies the PL inequalit if it satisfies an of ESC, WSC, RSI, or EB (while for convex f, QG is also sufficient). Although it is hard to precisel characterize the general class of functions for which the PL inequalit is satisfied, we note one important special case below. Strongl-convex composed with linear: This is the case where f has the form f(x) = g(ax) for some σ-sc function g and some matrix A. In Appendix B, we show that this class of functions satisfies the PL inequalit, and we note that this form frequentl arises in machine learning. For example, least squares problems have the form f(x) = Ax b, and b noting that g(z) z b is SC we see that least squares falls into this categor. Indeed, this class includes all convex quadratic functions. In the case of logistic regression we have f(x) = n log( + exp(b i a T i x)). i= This can be written in the form g(ax), where g is strictl convex but not SC. In cases like this where g is onl strictl convex, the PL inequalit will still be satisfied over an compact set. Thus, if the iterations of gradient descent remain bounded, the linear convergence result still applies. It is reasonable to assume that the iterates remain bounded when the set of solutions is finite, since each step must decrease the objective function. Thus, for practical purposes, we can relax the above condition to strictl-convex composed with linear and the PL inequalit implies a linear convergence rate for logistic regression. 3 Convergence of Huge-Scale Methods In this section, we use the PL inequalit to analze several variants of two of the most widel-used techniques for handling large-scale machine learning problems: coordinate descent and stochastic gradient methods. In particular, the PL inequalit ields ver simple analses of these methods that appl to more general classes of functions than previousl analzed. We also note that the PL inequalit has recentl been used b Garber and Hazan 5a] to analze the Frank-Wolfe algorithm. Further, inspired b the resilient backpropagation (RPROP) algorithm of Riedmiller and Braun 99], in Appendix C we also give a convergence rate analsis for a sign-based gradient descent method. 3. Randomized Coordinate Descent Nesterov ] shows that randomized coordinate descent achieves a faster convergence rate than gradient descent for problems where we have d variables and it is d times cheaper to update one coordinate than it is to compute the entire gradient. The expected linear convergence rates in this previous work 4
5 rel on SC, but in this section we show that randomized coordinate descent achieves an expected linear convergence rate if we onl assume that the PL inequalit holds. To analze coordinate descent methods, we assume that the gradient is coordinate-wise Lipschitz continuous, meaning that for an x and we have f(x + αe i ) f(x) + α i f(x) + L α, α R, x R d, (5) for an coordinate i, and where e i is the ith unit vector. Theorem 3. Consider problem (), where f has a coordinate-wise L-Lipschitz continuous gradient (5), a non-empt solution set X, and satisfies the PL inequalit (3). Consider the coordinate descent method with a step-size of /L, x k+ = x k L i k f(x k )e ik. (6) If we choose the variable to update i k uniforml at random, then the algorithm has an expected linear convergence rate of ( Ef(x k ) f ] µ ) k f(x ) f ]. dl Proof. B using the update rule (6) in the Lipschitz condition (5) we have f(x k+ ) f(x k ) L i k f(x k ). B taking the expectation of both sides with respect to i k we have E f(x k+ )] f(x k ) L E ik f(x k ) ] = f(x k ) L i d if(x k ) = f(x k ) dl f(x k). B using the PL inequalit (3) and subtracting f from both sides, we get ( Ef(x k+ ) f ] µ ) f(x k ) f ]. dl Appling this recursivel and using iterated expectations ields the result. As before, instead of using /L we could perform exact coordinate optimization and the result would still hold. If we have a Lipschitz constant L i for each coordinate and sample proportional to the L i as suggested b Nesterov ], then the above argument (using a step-size of /L ik ) can be used to show that we obtain a faster rate of ( Ef(x k ) f ] µ ) k f(x ) f ], d L where L = d d j= L j. 3. Greed Coordinate Descent Nutini et al. 5] have recentl analzed coordinate descent under the greed Gauss-Southwell (GS) rule, and argued that this rule ma be suitable for problems with a large degree of sparsit. The GS rule chooses i k according to the rule i k = argmax j j f(x k ). Using the fact that max i f(x k ) i d 5 d i f(x k ), i=
6 it is straightforward to show that the GS rule satisfies the rate above for the randomized method. However, Nutini et al. 5] show that a faster convergence rate can be obtained for the GS rule b measuring SC in the -norm. Since the PL inequalit is defined on the dual (gradient) space, in order to derive an analogous result we could measure the PL inequalit in the -norm, f(x) µ (f(x) f ). Because of the equivalence between norms, this is not introducing an additional assumptions beond that the PL inequalit is satisfied. Further, if f is µ -SC in the -norm, then it satisfies the PL inequalit in the -norm with the same constant µ. B using that ik f(x k ) = f(x k ) when the GS rule is used, the above argument can be used to show that coordinate descent with the GS rule achieves a convergence rate of ( f(x k ) f µ L ) k f(x ) f ], when the function satisfies the PL inequalit in the -norm with a constant of µ. B the equivalence between norms we have that µ/d µ, so this is faster than the rate with random selection. Meir and Rätsch 3] show that we can view some variants of boosting algorithms as implementations of coordinate descent with the GS rule. The use the error bound propert to argue that these methods achieve a linear convergence rate, but this propert does not lead to an explicit rate. Our simple result above thus provides the first explicit convergence rate for these variants of boosting. 3.3 Stochastic Gradient Methods Stochastic gradient (SG) methods appl to the general stochastic optimization problem argmin f(x) = Ef i (x)], (7) x IR d where the expectation is taken with respect to i. These methods are tpicall used to optimize finite sums, f(x) = n f i (x). (8) n Here, each f i tpicall represents the fit of a model on an individual training example. SG methods are suitable for cases where the number of training examples n is so large that it is infeasible to compute the gradient of all n examples more than a few times. Stochastic gradient methods use the iteration i x k+ = x k α k f ik (x k ), (9) where α k is the step size and i k is a sample from the distribution over i so that E f ik (x k )] = f(x k ). Below, we analze the convergence rate of stochastic gradient methods under standard assumptions on f, and under both a decreasing and a constant step-size scheme. Theorem 4. Consider problem (7). Assume that each f has an L-Lipschitz continuous gradient (), f has a non-empt solution set X, f satisfies the PL inequalit (3), and E f i (x k ) ] C for all x k and some C. If we use the SG algorithm (9) with α k = k+ µ(k+), then we get a convergence rate of Ef(x k ) f ] LC kµ. If instead we use a constant α k = α < µ, then we obtain a linear convergence rate up to a solution level that is proportional to α, Ef(x k ) f ] ( µα) k f(x ) f ] + LC α 4µ. 6
7 Proof. B using the update rule (9) inside the Lipschitz condition (), we have f(x k+ ) f(x k ) α k f (x k ), f ik (x k ) + Lα k f i k (x k ). Taking the expectation of both sides with respect to i k we have Ef(x k+ )] f(x k ) α k f(x k ), E f ik (x k )] + Lα k E f i(x k ) ] f(x k ) α k f (x k ) + LC α k f(x k ) µα k (f(x k ) f ) + LC αk, where the second line uses that E f ik (x k )] = f(x k ) and E f i (x k ) ] C, and the third line uses the PL inequalit. Subtracting f from both sides ields: Decreasing step size: With α k = k+ µ(k+) Ef(x k+ ) f ] ( α k µ)f(x k ) f ] + LC αk. () Ef(x k+ ) f ] in () we obtain k (k+) f(x k ) f ] + LC (k+) 8µ (k+). 4 Multipling both sides b (k + ) and letting δ f (k) k Ef(x k ) f ] we get δ f (k + ) δ f (k) + LC (k + ) 8µ (k + ) δ f (k) + LC µ, where the second line follows from k+ k+ <. Summing up this inequalit from k = to k and using the fact that δ f () = we get δ f (k + ) δ f () + LC k µ i= LC (k+) µ (k + ) Ef(x k+ ) f ] LC (k+) µ which gives the stated rate. Constant step size: Choosing α k = α for an α < /µ and appling () recursivel ields Ef(x k+ ) f ] ( αµ) k f(x ) f ] + LC α ( αµ) k f(x ) f ] + LC α = ( αµ) k f(x ) f ] + LC α 4µ, where the last line uses that α < /µ and the limit of the geometric series. k ( αµ) i i= ( αµ) i The O(/k) rate for a decreasing step size matches the convergence rate of stochastic gradient methods under SC Nemirovski et al., 9]. It was recentl shown using a non-trivial analsis that a stochastic Newton method could achieve an O(/k) rate for least squares problems Bach and Moulines, 3], but our result above shows that the basic stochastic gradient method alread achieves this propert (although the constants are worse than for this Newton-like method). Further, our result does not rel on convexit. Note that if we are happ with a solution of fixed accurac, then the result with a constant step-size is perhaps the more useful strateg in practice: it supports the often-used empirical strateg of using a constant size for a long time, then halving the step-size if the algorithm appears to have stalled (the above result indicates that halving the step-size will at least halve the sub-optimalit). i= 7
8 3.4 Finite Sum Methods In the setting of (8) where we are minimizing a finite sums, it has recentl been shown that there are methods that have the low iteration cost of stochastic gradient methods but that still have linear convergence rates for SC functions Le Roux et al., ]. While the first methods that achieved this remarkable propert required a memor of previous gradient values, the stochastic variance-reduced gradient (SVRG) method of Johnson and Zhang 3] does not have this drawback. Gong and Ye 4] show that SVRG has a linear convergence rate without SC under the weaker assumption of QG plus convexit (where QG is equivalent to PL). We review how the analsis of Johnson and Zhang 3] can be easil modified to give a similar result in Appendix D. A related result appears in Garber and Hazan 5b], who assume that f is SC but do not assume that the individual functions are convex. More recent analses b Reddi et al. 6a,b] have considered these tpes of methods under the PL inequalit without convexit assumptions. 4 Proximal-Gradient Generalization A generalization of the PL inequalit for non-smooth optimization is the KL inequalit Kurdka, 998, Bolte et al., 8]. The KL inequalit has been used to analze the convergence of the classic proximalpoint algorithm Attouch and Bolte, 9] as well as a variet of other optimization methods Attouch et al., 3]. In machine learning, a popular generalization of gradient descent is proximal-gradient methods. Bolte et al. 5] show that the proximal-gradient method has a linear convergence rate for functions satisfing the KL inequalit, while Li and Pong 6] give a related result. The set of problems satisfing the KL inequalit notabl includes problems like support vector machines and l -regularized least squares, impling that the algorithm has a linear convergence rate for these problems. In this section we propose a different generalization of the PL inequalit that leads to a simpler linear convergence rate analsis for the proximal-gradient method as well as its coordinate-wise variant. Proximal-gradient methods appl to problems of the form argmin F (x) = f(x) + g(x), () x R d where f is a differentiable function with an L-Lipschitz continuous gradient and g is a simple but potentiall non-smooth convex function. Tpical examples of simple functions g include a scaled l -norm of the parameter vectors, g(x) = λ x, and indicator functions that are zero if x lies in a simple convex set and are infinit otherwise. In order to analze proximal-gradient algorithms, a natural (though not particularl intuitive) generalization of the PL inequalit is that there exists a µ > satisfing D g(x, L) µ(f (x) F ), () where D g (x, α) α min f(x), x + α ] x + g() g(x). (3) We call this the proximal-pl inequalit, and we note that if g is constant (or linear) then it reduces to the standard PL inequalit. Below we show that this inequalit is sufficient for the proximal-gradient method to achieve a global linear convergence rate. Theorem 5. Consider problem (), where f has an L-Lipschitz continuous gradient (), F has a nonempt solution set X, g is convex, and F satisfies the proximal-pl inequalit (). Then the proximalgradient method with a step-size of /L, x k+ = argmin converges linearl to the optimal value F, f(x k ), x k + L ] x k + g() g(x k ) F (x k ) F ( µ L) k F (x ) F ]. (4) 8
9 Proof. B using Lipschitz continuit of the gradient of f we have F (x k+ ) = f(x k+ ) + g(x k ) + g(x k+ ) g(x k ) F (x k ) + f(x k ), x k+ x k + L x k+ x k + g(x k+ ) g(x k ) F (x k ) L D g(x k, L) F (x k ) µ L F (x k) F ], which uses the definition of x k+ and D g followed b the proximal-pl inequalit (). This subsequentl implies that ( F (x k+ ) F µ ) F (x k ) F ], (5) L which applied recursivel gives the result. While other conditions have been proposed to show linear convergence rates of proximal-gradient methods without SC Kadkhodaie et al., 4, Bolte et al., 5, Zhang, 5, Li and Pong, 6], their analses tend to be more complicated than the above. Further, in Appendix G we show that the proximal-pl condition is in fact equivalent to the KL condition, which itself is known to be equivalent to a proximal-gradient variant on the EB condition Bolte et al., 5]. Thus, the proximal-pl inequalit includes the standard scenarios where existing conditions appl. 4. Relevant Problems As with the PL inequalit, we now list several important function classes that satisf the proximal-pl inequalit (). We give proofs that these classes satisf the inequalit in Appendix F and G.. The inequalit is satisfied if f satisfies the PL inequalit and g is constant. Thus, the above result generalizes Theorem.. The inequalit is satisfied if f is SC. This is the usual assumption used to show a linear convergence rate for the proximal-gradient algorithm Schmidt et al., ], although we note that the above analsis is much simpler than standard arguments. 3. The inequalit is satisfied if f has the form f(x) = h(ax) for a SC function h and a matrix A, while g is an indicator function for a polhedral set. 4. The inequalit is satisfied if F is convex and satisfies the QG propert. 5. The inequalit is satisfied if F satisfies the proximal-eb condition or the KL inequalit. B the equivalence shown in Appendix G, the proximal-pl inequalit also holds for other problems where a linear convergence rate has been show like group L-regularization Tseng, ], sparse group L-regularization Zhang et al., 3], nuclear-norm regularization Hou et al., 3], and other classes of functions Zhou and So, 5, Drusvatski and Lewis, 6]. 4. Least Squares with L-Regularization Perhaps the most interesting example of problem () is the l -regularized least squares problem, argmin x IR Ax b + λ x, d where λ > is the regularization parameter. This problem has been studied extensivel in machine learning, signal processing, and statistics. This problem structure seems well-suited to using proximalgradient methods, but the first works analzing proximal-gradient methods for this problem onl showed sub-linear convergence rates Beck and Teboulle, 9]. Subsequent works show that linear convergence rates can be achieved under additional assumptions. For example, Gu et al. 3] prove that their algorithm achieves a linear convergence rate if A satisfies a restricted isometr propert (RIP) and the solution is sufficientl sparse. Xiao and Zhang 3] also assume the RIP propert and show linear convergence using a homotop method that slowl decreases the value of λ. Agarwal et al. ] give a 9
10 linear convergence rate under a modified restricted strong convexit and modified restricted smoothness assumption. But these problems have also been shown to satisf proximal variants of the KL and EB conditions Tseng,, Bolte et al., 5, Necoara and Clipici, 6], and Bolte et al. 5] in particular analzes the proximal-gradient method under KL while giving explicit bounds on the constant. This means an L-regularized least squares problem also satisfies the proximal-pl inequalit. Thus, Theorem 5 gives a simple proof of global linear convergence for these problems without making additional assumptions or making an modifications to the algorithm. 4.3 Proximal Coordinate Descent It is also possible to adapt our results on coordinate descent and proximal-gradient methods in order to give a linear convergence rate for coordinate-wise proximal-gradient methods for problem (). To do this, we require the extra assumption that g is a separable function. This means that g(x) = i g i(x i ) for a set of univariate functions g i. The update rule for the coordinate-wise proximal-gradient method is x k+ = argmin α We state the convergence rate result below. α ik f(x k ) + L ] α + g ik (x ik + α) g ik (x ik ), (6) Theorem 6. Assume the setup of Theorem 5 and that g is a separable function g(x) = i g i(x i ), where each g i is convex. Then the coordinate-wise proximal-gradient update rule (6) achieves a convergence rate ( EF (x k ) F ] µ ) k F (x ) F ], (7) dl when i k is selected uniforml at random. The proof is given in Appendix H and although it is more complicated than the proofs of Theorems 4 and 5, it is arguabl still simpler than existing proofs for proximal coordinate descent under SC Richtárik and Takáč, 4], KL Attouch et al., 3], or QG Zhang, 6]. It is also possible to analze stochastic proximal-gradient algorithms, and indeed Reddi et al. 6c] use the proximal-pl inequalit to analze finite-sum methods in the proximal stochastic case. 4.4 Support Vector Machines Another important model problem that arises in machine learning is support vector machines, argmin x IR d λ xt x + n max(, b i x T a i ). (8) i= where (a i, b i ) are the labelled training set with a i R d and b i {, }. We often solve this problem b performing coordinate optimization on its Fenchel dual, which has the form min w f( w) = wt M w w i, w i, U], (9) for a particular positive semi-definite matrix M and constant U. This convex function satisfies the QG propert and thus Theorem 6 implies that coordinate optimization achieves a linear convergence rate in terms of optimizing the dual objective. Further, note that Hush et al. 6] show that we can obtain an ɛ-accurate solution to the primal problem with an O(ɛ )-accurate solution to the dual problem. Thus this result also implies we can obtain a linear convergence rate on the primal problem b showing that stochastic dual coordinate ascent has a linear convergence rate on the dual problem. Global linear convergence rates for SVMs have also been shown b others Tseng and Yun, 9, Wang and Lin, 4, Ma et al., 5], but again we note that these works lead to more complicated analses. Although the constants in these convergence rate ma be quite bad (depending on the smallest non-zero singular value of the Gram matrix), we note that the existing sublinear rates still appl in the earl iterations while, as the algorithm begins to identif support vectors, the constants improve (depending on the smallest non-zero singular value of the block of the Gram matrix corresponding to the support vectors).
11 The result of the previous section is not onl restricted to SVMs. Indeed, the result of the previous subsection implies a linear convergence rate for man l -regularized linear prediction problems, the framework considered in the stochastic dual coordinate ascent (SDCA) work of Shalev-Shwartz and Zhang 3]. While Shalev-Shwartz and Zhang 3] show that this is true when the primal is smooth, our result gives linear rates in man cases where the primal is non-smooth. 5 Discussion We believe that this work provides a unifing and simplifing view of a variet of optimization and convergence rate issues in machine learning. Indeed, we have shown that man of the assumptions used to achieve linear convergence rates can be replaced b the PL inequalit and its proximal generalization. While we have focused on sufficient conditions for linear convergence, another recent work has turned to the question of necessar conditions for convergence Zhang, 6]. Further, while we ve focused on non-accelerated methods, Zhang 6] has recentl analzed Nesterov s accelerated gradient method without strong convexit. We also note that, while we have focused on first-order methods, Nesterov and Polak 6] have used the PL inequalit to analze a second-order Newton-stle method with cubic regularization. The also consider a generalization of the inequalit under the name gradient-dominated functions. Throughout the paper, we have pointed out how our analses impl convergence rates for a variet of machine learning models and algorithms. Some of these were previousl known, tpicall under stronger assumptions or with more complicated proofs, but man of these are novel. Note that we have not provided an experimental results in this work, since the main contributions of this work are showing that existing algorithms actuall work better on standard problems than we previousl thought. We expect that going forward efficienc will no longer be decided b the issue of whether functions are SC, but rather b whether the satisf a variant of the PL inequalit. Acknowledgments. We would like to thank Simon LaCoste-Julien, Martin Takáč, Ruou Sun, Hui Zhang, and Dmitri Drusvatski for valuable discussions. We would like to thank Ting Kei Pong and Zirui Zhou for pointing out an error in the first version of this paper, to Ting Kei Pong for discussions that lead to the addition of Appendix G, to Jérôme Bolte for an informative discussion about the KL inequalit and pointing us to related results that we had missed, and to Boris Polak for providing an English translation of his original work. This research was supported b the Natural Sciences and Engineering Research Council of Canada (NSERC RGPIN-668-5). Julie Nutini is funded b a UBC Four Year Doctoral Fellowship (4YF) and Hamed Karimi is support b a Mathematics of Information Technolog and Complex Sstems (MITACS) Elevate Fellowship. Appendix A Relationships Between Conditions We start b stating the different conditions. All of these definitions involve some constant µ > (which ma not be the same across conditions), and we ll use the convention that x p is the projection of x onto the solution set X.. Strong Convexit (SC): For all x and we have f() f(x) + f(x), x + µ x.. Essential Strong Convexit (ESC): For all x and such that x p = p we have f() f(x) + f(x), x + µ x. 3. Weak Strong Convexit (WSC): For all x we have f f(x) + f(x), x p x + µ x p x.
12 4. Restricted Secant Inequalit (RSI): For all x we have f(x), x x p µ x p x. If the function f is also convex it is called restricted strong convexit (RSC). 5. Error Bound (EB): For all x we have 6. Polak- Lojasiewicz (PL): For all x we have 7. Quadratic Growth (QG): For all x we have f(x) µ x p x. f(x) µ(f(x) f ). f(x) f µ x p x. If the function f is also convex it is called optimal strong convexit (OSC) or semi-strong convexit or sometimes WSC (but we ll reserve the expression WSC for the definition above). Below we prove a subset of the implications in Theorem. The remaining relationships in Theorem follow from these results and transitivit. SC ESC: The SC assumption implies that the ESC inequalit is satisfied for all x and, so it is also satisfied under the constraint x p = p. ESC WSC: Take = x p in the ESC inequalit (which clearl has the same projection as x) to get WSC with the same µ as a special case. WSC RSI: Re-arrange the WSC inequalit to f(x), x x p f(x) f + µ x p x. Since f(x) f, we have RSI with µ. RSI EB: Using Cauch-Schwartz on the RSI we have f(x) x x p f(x), x x p µ x p x, and dividing both sides b x x p (assuming x x p ) gives EB with the same µ (while EB clearl holds if x = x p ). EB PL: B Lipschitz continuit we have f(x) f(x p ) + f(x p ), x x p + L x p x, and using EB along with f(x p ) = f and f(x p ) = we have f(x) f L x p x L µ f(x), which is the PL inequalit with constant µ L. PL EB: Below we show that PL implies QG. Using this result, while denoting the PL constant with µ p and the QG constant with µ q, we get f(x) µ p (f(x) f ) µ pµ q x x p, which implies that EB holds with constant µ p µ q. QG + Convex RSI: B convexit we have Re-arranging and using QG we get which is RSI with constant µ. f(x p ) f(x) + f(x), x p x. f(x), x x p f(x) f µ x p x,
13 PL QG: Our argument that this implication holds is similar to the argument used in related works Bolte et al., 5, Zhang, 5] Define the function g(x) = f(x) f. If we assume that f satisfies the PL inequalit then for an x X we have or that g(x) = f(x) f(x) f µ, B the definition of g, to show QG it is sufficient to show that g(x) µ. () g(x) µ x x p. () As f is assumed to satisf the PL inequalit we have that f is an invex function and thus b definition g is a positive invex function (g(x) ) with a closed optimal solution set X such that for all X, g() =. For an point x X, consider solving the following differential equation: dx(t) = g(x(t)) dt x(t = ) = x, () for x(t) X. (This is a flow orbit starting at x and flowing along the gradient of g.) B (), g is bounded from below, and as g is a positive invex function g is also bounded from below. Thus, b moving along the path defined b () we are sufficientl reducing the function and will eventuall reach the optimal set. Thus there exists a T such that x(t ) X (and at this point the differential equation ceases to be defined). We can show this b using the steps g(x ) g(x t ) = ( ) = = = x x t g(x), dx (gradient theorem for line integrals) xt x g(x), dx (flipping integral bounds) = µt. g(x(t)), dx(t) dt (reparameterization) dt g(x(t)) dt (from ()) µdt (from ()) As g(x t ), this shows we need to have T g(x )/µ, so there must be a T with x(t ) X. The length of the orbit x(t) starting at x, which we ll denote b L(x ), is given b L(x ) = dx(t)/dt dt = g(x(t)) dt x x p, (3) where x p is the projection of x onto X and the inequalit follows because the orbit is a path from x to a point in X (and thus it must be at least as long as the projection distance). Starting from the line marked ( ) above we have g(x ) g(x T ) = µ g(x(t)) dt g(x(t)) dt (b the PL inequalit variation in ()) µ x x p. (b (3)) 3
14 As g(x T ) =, this ields our result (), or equivalentl which is QG with a different constant. f(x) f µ x x p, Appendix B Relevant Problems Strongl-convex: B minimizing both sides of the SC inequalit with respect to we get f(x ) f(x) µ f(x), which implies the PL inequalit holds with the same value µ. Thus, Theorem exactl matches the known rate for gradient descent with a step-size of /L for a µ-sc function. Strongl-convex composed with linear: To show that this class of functions satisfies the PL inequalit, we first define f(x) := g(ax) for a σ-strongl convex function g. For arbitrar x and, we define u := Ax and v := A. B the strong convexit of g, we have g(v) g(u) + g(u) T (v u) + σ v u. B our definitions of u and v, we get g(a) g(ax) + g(ax) T (A Ax) + σ A Ax, where we can write the middle term as (A T g(ax)) T ( x). B the definition of f and its gradient being f(x) = A T g(ax) b the multivariate chain rule, we obtain f() f(x) + f(x), x + σ A( x). Using x p to denote the projection of x onto the optimal solution set X, we have f(x p ) f(x) + f(x), x p x + σ A(x p x) f(x) + f(x), x p x + σθ(a) x p x f(x) + min f(x), x + σθ(a) ] x = f(x) θ(a)σ f(x). In the second line we use that X is polhedral, and use the theorem of Hoffman 95] to obtain a bound in terms of θ(a) (the smallest non-zero singular value of A). This derivation implies that the PL inequalit is satisfied with µ = σθ(a). Appendix C Sign-Based Gradient Methods The learning heuristic RPROP (Resilient backpropagation) is a classic iterative method used for supervised learning problems in feedforward neural networks Riedmiller and Braun, 99]. The general update for some vector of step sizes α k IR d is given b x k+ = x k α k sign( f(x k )), where the operator indicates coordinate-wise multiplication. Although this method has been used for man ears in the machine learning communit, we are not aware of an previous convergence rate analsis of such a method. Here we give a convergence rate when the individual step-sizes αi k are chosen 4
15 proportional to / L i, where the L i are constants such that the gradient is -Lipschitz continuous in the norm defined b z L ] z i. Li i Formall, we assume that the L i are set so that for all x and we have f() f(x) L ] x L ], and where the dual norm of the L ] norm above is given b the L ] norm, z L ] max Li z i. i We note that such L i alwas exist if the gradient is Lipschitz continuous, so this is not adding an assumptions on the function f. The particular choice of the step-sizes αi k that we will analze is α k i = f(xk ) L ] Li, which ields a linear convergence rate for problems where the PL inequalit is satisfied. The coordinate-wise iteration update under this choice of αi k is given b x k+ i = x k i f(xk ) L ] Li sign( i f(x k )). Defining a diagonal matrix Λ with / L i along the diagonal, the update can be written as x k+ = x k f(x k ) L ]Λ sign( f(x k )). Consider the function g(τ) = f(x + τ( x)) with τ IR. Then f() f(x) f(x), x = g() g() f(x), x = = = dg (τ) f(x), x dτ dτ f(x + τ( x)), x f(x), x dτ f(x + τ( x)) f(x), x dτ f(x + τ( x)) f(x) L ] x L ] dτ τ x L ] dτ = τ x L ] = x L ] = x L ]. where the second inequalit uses the Lipschitz assumption, and in the first inequalit we ve used the Cauch-Schwarz inequalit and that the dual norm of the L ] norm is the L ] norm. The above gives an upper bound on the function in terms of this L ]-norm, f() f(x) + f(x), x + x L ]. 5
16 Plugging in our iteration update we have f(x k+ ) f(x k ) + f(x k ), x k+ x k + xk+ x k L ] = f(x k ) f(x k ) L ] f(x k ), Λ sign( f(x k )) + f(xk ) L ] Λ sign( f(x k )) L ] = f(x k ) f(x k ) L ] + f(xk ) ( L ] ) max Li sign( i f(x k )) i Li = f(x k ) f(xk ) L ]. Subtracting f from both sides ields f(x k+ ) f(x ) f(x k ) f(x ) f(xk ) L ]. Appling the PL inequalit with respect to the L ]-norm (which, if the PL inequalit is satisfied, holds for some µ L ] b the equivalence between norms), we have Appendix D f(xk ) L ] µ ( L ] f(x k ) f ), f(x k+ ) f(x ) ( µ L ] ) ( f(x k ) f(x ) ). Linear Convergence Rate of SVRG Method In this section, we look at the SVRG method for the finite-sum optimization problem, f(w) = f i (w). (4) n To minimize functions of this form, the SVRG algorithm of Johnson and Zhang 3] uses iterations of the form x t = x t α f it (x t ) f it (x s ) + µ s ], (5) where i t is chosen uniforml from {,,..., n} and we assume the step-size satisfies α < /L. In this algorithm we start with some x and initiall set µ = f(x ) and x = x, but after ever m steps we set x s+ to a random x t for t {ms +,..., m(s + )}, then replace µ s with f(x s ) and x t with x s+. Analogous to Johnson and Zhang 3] for the SC case, we now show tnat SVRG has a linear convergence rate if each f i is a convex function with a Lipschitz-continuous gradient and f satisfies the PL inequalit. Following the same argument as Johnson and Zhang 3], for an solution x the assumptions on the f i mean that the outer SVRG iterations x s satisf α( Lα)mEf(x s ) f ] E x s x ] + 4Lα mef(x s ) f ]. Choosing the particular x that is the projection of x s onto the solution set and using QG (which is equivalent to PL in this convex setting) we have α( Lα)mEf(x s ) f ] µ Ef(xs ) f ] + 4Lα mef(x s ) f ]. Dividing both sides b α( Lα)m we get Ef(x s ) f ] αl i ( ) mµα + Lα Ef(x s ) f ], which is a linear convergence rate for sufficientl large m and sufficientl small α. 6
17 Appendix E Proximal-PL Lemma In this section we give a useful propert of the function D g. Lemma. For an differentiable function f and an convex function g, given µ µ > we have D g (x, µ ) D g (x, µ ). We ll prove Lemma as a corollar of a related result. We first restate the definition D g (x, λ) = λ min f(x), x + λ ] x + g() g(x), (6) and we note that we require λ >. B completing the square, we have D g (x, λ) = min f(x) + f(x) + λ f(x), x + λ x + λ(g() g(x)) ] = f(x) min λ( x) + f(x) + λ(g() g(x)) ]. Notice that if g =, then D g (x, λ) = f(x) and the proximal-pl inequalit reduces to the PL inequalit. We ll the define the proximal residual function as the second part of the above equalit, R g (λ, x, a) min λ( x) + a + λ(g() g(x) ]. (7) Lemma. If g is convex then for an x and a, and for < λ λ we have Proof. Without loss of generalit, assume x =. Then we have R g (λ, x, a) R g (λ, x, a). (8) R g (λ, a) = min λ + a + λ(g() g() ] = min ȳ + a + λ(g(ȳ/λ) g() ], (9) ȳ where in the second line we used a changed of variables ȳ = λ (note that we are minimizing over the whole space of IR n ). B the convexit of g, for an α, ] and z IR n we have B using < λ /λ and using the choices α = λ λ Adding ȳ + a to both sides, we get g(αz) αg(z) + ( α)g() g(αz) g() α(g(z) g()). (3) and z = ȳ/λ we have g(ȳ/λ ) g() λ (g(ȳ/λ ) g()) λ λ (g(ȳ/λ ) g()) λ (g(ȳ/λ ) g()), (3) ȳ + a + λ (g(ȳ/λ ) g()) ȳ + a + λ (g(ȳ/λ ) g()). (3) Taking the minimum over both sides with respect to ȳ ields Lemma due to (9). Corollar. For an differentiable function f and convex function g, given λ λ, we have D g (x, λ ) D g (x, λ ). (33) B using D g (x, λ) = f(x) R g (λ, x, f(x)), Corollar is exactl Lemma. 7
18 Appendix F Relevant Problems In this section we prove that the three classes of functions listed in Section 4. satisf the proximal-pl inequalit condition. Note that while we prove these hold for D g (x, λ) for λ L, b Lemma above the also hold for D g (x, L).. f(x), where f satisfies the PL inequalit (g is constant): As g is assumed to be constant, we have g() g(x) = and the left-hand side of the proximal-pl inequalit simplifies to D g (x, µ) = µ min f(x), x + µ x } ( = µ ) µ f(x) { = f(x), Thus, the proximal PL inequalit simplifies to f satisfing the PL inequalit, as we assumed.. F (x) = f(x) + g(x) and f is strongl convex: B the strong convexit of f we have f(x) µ (f(x) f ), f() f(x) + f(x), x + µ x, (34) which leads to F () F (x) + f(x), x + µ x + g() g(x). (35) Minimizing both sides respect to, F F (x) + min f(x), x + µ x + g() g(x) = F (x) µ D g(x, µ). (36) Rearranging, we have our result. 3. F (x) = f(ax) + g(x) and f is strongl convex, g is the indicator function for a polhedral set X, and A is a linear transformation: B defining f(x) = f(ax) and using strong convexit of f, we have f() f(x) + f(x), x + µ A( x), (37) which leads to F () F (x) + f(x), x + µ A( x) + g() g(x). (38) Since X is polhedral, it can be written as a set {x : Bx c} for a matrix B and a vector c. As before, assume that x p is the projection of x onto the optimal solution set X which in this case is 8
19 {x : Bx c, Ax = z} for some z. F = F (x p ) F (x) + f(x), x p x + µ A(x x p) + g(x p ) g(x) = F (x) + f(x), x p x + µ Ax z + g(x p ) g(x) = F (x) + f(x), x p x + µ {Ax z} + + { Ax + z} + + g(x p ) g(x) = F (x) + f(x), x p x + µ A z A x z + g(x p ) g(x) B c F (x) + f(x), µθ(a, B) x p x + x x p + g(x p ) g(x) f(x), x + F (x) + min = F (x) µθ(a, B) x + g() g(x) µ θ(a) D g(x, µθ(a, B)). (39) where we ve used the notation that { } + = max{, }, the fourth equalit follows because x was projected onto X in the previous iteration (so Bx c ), and the line after that uses Hoffman s bound Hoffman, 95]. 4. F (x) = f(x) + g(x), f is convex, and F satisfies the quadratic growth (QG) condition: A function F satisfies the QG condition if + F (x) F µ x x p. (4) ] For an λ > we have, min f(x), x + λ ] x + g() g(x) f(x), x p x + λ x p x + g(x p ) g(x) f(x p ) f(x) + λ x p x + g(x p ) g(x) = λ x p x + F F (x) ( λ ) (F F ). (4) µ The third line follows from the convexit of f, and the last inequalit uses the QG condition of F. Multipling both sides b λ, we have D g (x, λ) = λ min f(x), x + λ ] ( x + g() g(x) λ λ ) (F (x) F ). (4) µ This is true for an λ >, and b choosing λ = µ/ we have D g (x, µ/) µ (F (x) F ). (43) 5. F satisfies the KL inequalit or the proximal-eb inequalit: In the next section we show that these are equivalent to the proximal-pl inequalit. Appendix G Equivalence of Proximal-PL with KL and EB The equivalence of the KL condition and the proximal-gradient variant of the Luo-Tseng EB condition is known for convex f, see Drusvatski and Lewis, 6, Corollar 3.6] and the proof of Bolte et al., 5, Theorem 5]. Here we prove the equivalence of these conditions with the proximal-pl inequalit for non-convex f. First we review the definitions of the three conditions: 9
20 . Proximal-PL: There exists a µ > such that where D g(x, L) µ(f (x) F ) { D g (x, L) = L min f(x), x + L } x + g() g(x).. Proximal-EB: There exists c > such that we have x x p c (x x prox L g ) L f(x). (44) 3. Kurdka- Lojasiewicz: The KL condition with exponent holds if there exist µ > such that min s F (x) s µ(f (x) F ) (45) where F (x) is Frechet subdifferential. In particular, if F : H R is a real-valued function then we sa that s H is a Frechet subdifferential of F at x dom F if F () F (x) s, x lim inf x, x x. (46) Note that for differentiable f the Frechet subdifferential onl contains the gradient, f(x). In our case where F (x) = f(x) + g(x) with a differentiable f and a convex g we have F (x) = { f(x) + ξ ξ g(x)}. The KL inequalit is an intuitive generalization of the PL inequalit since, analogous to the gradient vector in the smooth case, the negation of the quantit argmin s F (x) s points in the direction of steepest descent see Bertsekas et al., 3, Section 8.4] We first derive an alternative representation of D g (x, L) in terms of the so-called forward-backward envelope F of F see Stella et al., 6, Definition.]. Indeed, L { D g (x, L) = L min f(x), x + L } x + g() g(x) { = L min f(x) + f(x), x + L } ] (47) x + g() f(x) g(x) It follows from the definition of F L = LF L (x) F (x)] = LF (x) F L (x)], F L (x) F = min (x) that we have { f(x) + f(x), x + L x + g() } f(x ) g(x ) f(x) + f(x), x x + L x x + g(x ) f(x ) g(x ) = f(x) f(x ) + f(x), x x + L x x = f(x) f(x ) + f(x), x x + L x x L x x, (48) where the second line uses that we are taking the minimizer and the last line uses the Lipschitz continuit of f as follows, f(x) f() + f(x), x f(), x + L x + f(x), x = f() f(x), x + L x (49) f() f(x) x + L x 3L x.
Linear Convergence under the Polyak-Łojasiewicz Inequality
 Linear Convergence under the Polyak-Łojasiewicz Inequality Hamed Karimi, Julie Nutini, Mark Schmidt University of British Columbia Linear of Convergence of Gradient-Based Methods Fitting most machine learning
Linear Convergence under the Polyak-Łojasiewicz Inequality Hamed Karimi, Julie Nutini, Mark Schmidt University of British Columbia Linear of Convergence of Gradient-Based Methods Fitting most machine learning
Linear Convergence under the Polyak-Łojasiewicz Inequality
 Linear Convergence under the Polyak-Łojasiewicz Inequality Hamed Karimi, Julie Nutini and Mark Schmidt The University of British Columbia LCI Forum February 28 th, 2017 1 / 17 Linear Convergence of Gradient-Based
Linear Convergence under the Polyak-Łojasiewicz Inequality Hamed Karimi, Julie Nutini and Mark Schmidt The University of British Columbia LCI Forum February 28 th, 2017 1 / 17 Linear Convergence of Gradient-Based
Coordinate Descent and Ascent Methods
 Coordinate Descent and Ascent Methods Julie Nutini Machine Learning Reading Group November 3 rd, 2015 1 / 22 Projected-Gradient Methods Motivation Rewrite non-smooth problem as smooth constrained problem:
Coordinate Descent and Ascent Methods Julie Nutini Machine Learning Reading Group November 3 rd, 2015 1 / 22 Projected-Gradient Methods Motivation Rewrite non-smooth problem as smooth constrained problem:
A. Derivation of regularized ERM duality
 A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
CPSC 540: Machine Learning
 CPSC 540: Machine Learning Proximal-Gradient Mark Schmidt University of British Columbia Winter 2018 Admin Auditting/registration forms: Pick up after class today. Assignment 1: 2 late days to hand in
CPSC 540: Machine Learning Proximal-Gradient Mark Schmidt University of British Columbia Winter 2018 Admin Auditting/registration forms: Pick up after class today. Assignment 1: 2 late days to hand in
min f(x). (2.1) Objectives consisting of a smooth convex term plus a nonconvex regularization term;
 Chapter 2 Gradient Methods The gradient method forms the foundation of all of the schemes studied in this book. We will provide several complementary perspectives on this algorithm that highlight the many
Chapter 2 Gradient Methods The gradient method forms the foundation of all of the schemes studied in this book. We will provide several complementary perspectives on this algorithm that highlight the many
Stochastic and online algorithms
 Stochastic and online algorithms stochastic gradient method online optimization and dual averaging method minimizing finite average Stochastic and online optimization 6 1 Stochastic optimization problem
Stochastic and online algorithms stochastic gradient method online optimization and dual averaging method minimizing finite average Stochastic and online optimization 6 1 Stochastic optimization problem
SVRG++ with Non-uniform Sampling
 SVRG++ with Non-uniform Sampling Tamás Kern András György Department of Electrical and Electronic Engineering Imperial College London, London, UK, SW7 2BT {tamas.kern15,a.gyorgy}@imperial.ac.uk Abstract
SVRG++ with Non-uniform Sampling Tamás Kern András György Department of Electrical and Electronic Engineering Imperial College London, London, UK, SW7 2BT {tamas.kern15,a.gyorgy}@imperial.ac.uk Abstract
Master 2 MathBigData. 3 novembre CMAP - Ecole Polytechnique
 Master 2 MathBigData S. Gaïffas 1 3 novembre 2014 1 CMAP - Ecole Polytechnique 1 Supervised learning recap Introduction Loss functions, linearity 2 Penalization Introduction Ridge Sparsity Lasso 3 Some
Master 2 MathBigData S. Gaïffas 1 3 novembre 2014 1 CMAP - Ecole Polytechnique 1 Supervised learning recap Introduction Loss functions, linearity 2 Penalization Introduction Ridge Sparsity Lasso 3 Some
Modern Stochastic Methods. Ryan Tibshirani (notes by Sashank Reddi and Ryan Tibshirani) Convex Optimization
 Modern Stochastic Methods Ryan Tibshirani (notes by Sashank Reddi and Ryan Tibshirani) Convex Optimization 10-725 Last time: conditional gradient method For the problem min x f(x) subject to x C where
Modern Stochastic Methods Ryan Tibshirani (notes by Sashank Reddi and Ryan Tibshirani) Convex Optimization 10-725 Last time: conditional gradient method For the problem min x f(x) subject to x C where
arxiv: v1 [math.oc] 1 Jul 2016
![arxiv: v1 [math.oc] 1 Jul 2016 arxiv: v1 [math.oc] 1 Jul 2016](/thumbs/78/78221552.jpg) Convergence Rate of Frank-Wolfe for Non-Convex Objectives Simon Lacoste-Julien INRIA - SIERRA team ENS, Paris June 8, 016 Abstract arxiv:1607.00345v1 [math.oc] 1 Jul 016 We give a simple proof that the
Convergence Rate of Frank-Wolfe for Non-Convex Objectives Simon Lacoste-Julien INRIA - SIERRA team ENS, Paris June 8, 016 Abstract arxiv:1607.00345v1 [math.oc] 1 Jul 016 We give a simple proof that the
Stochastic Dual Coordinate Ascent Methods for Regularized Loss Minimization
 Stochastic Dual Coordinate Ascent Methods for Regularized Loss Minimization Shai Shalev-Shwartz and Tong Zhang School of CS and Engineering, The Hebrew University of Jerusalem Optimization for Machine
Stochastic Dual Coordinate Ascent Methods for Regularized Loss Minimization Shai Shalev-Shwartz and Tong Zhang School of CS and Engineering, The Hebrew University of Jerusalem Optimization for Machine
ECS289: Scalable Machine Learning
 ECS289: Scalable Machine Learning Cho-Jui Hsieh UC Davis Sept 29, 2016 Outline Convex vs Nonconvex Functions Coordinate Descent Gradient Descent Newton s method Stochastic Gradient Descent Numerical Optimization
ECS289: Scalable Machine Learning Cho-Jui Hsieh UC Davis Sept 29, 2016 Outline Convex vs Nonconvex Functions Coordinate Descent Gradient Descent Newton s method Stochastic Gradient Descent Numerical Optimization
Randomized Coordinate Descent with Arbitrary Sampling: Algorithms and Complexity
 Randomized Coordinate Descent with Arbitrary Sampling: Algorithms and Complexity Zheng Qu University of Hong Kong CAM, 23-26 Aug 2016 Hong Kong based on joint work with Peter Richtarik and Dominique Cisba(University
Randomized Coordinate Descent with Arbitrary Sampling: Algorithms and Complexity Zheng Qu University of Hong Kong CAM, 23-26 Aug 2016 Hong Kong based on joint work with Peter Richtarik and Dominique Cisba(University
Optimizing Nonconvex Finite Sums by a Proximal Primal-Dual Method
 Optimizing Nonconvex Finite Sums by a Proximal Primal-Dual Method Davood Hajinezhad Iowa State University Davood Hajinezhad Optimizing Nonconvex Finite Sums by a Proximal Primal-Dual Method 1 / 35 Co-Authors
Optimizing Nonconvex Finite Sums by a Proximal Primal-Dual Method Davood Hajinezhad Iowa State University Davood Hajinezhad Optimizing Nonconvex Finite Sums by a Proximal Primal-Dual Method 1 / 35 Co-Authors
Finite-sum Composition Optimization via Variance Reduced Gradient Descent
 Finite-sum Composition Optimization via Variance Reduced Gradient Descent Xiangru Lian Mengdi Wang Ji Liu University of Rochester Princeton University University of Rochester xiangru@yandex.com mengdiw@princeton.edu
Finite-sum Composition Optimization via Variance Reduced Gradient Descent Xiangru Lian Mengdi Wang Ji Liu University of Rochester Princeton University University of Rochester xiangru@yandex.com mengdiw@princeton.edu
Minimizing Finite Sums with the Stochastic Average Gradient Algorithm
 Minimizing Finite Sums with the Stochastic Average Gradient Algorithm Joint work with Nicolas Le Roux and Francis Bach University of British Columbia Context: Machine Learning for Big Data Large-scale
Minimizing Finite Sums with the Stochastic Average Gradient Algorithm Joint work with Nicolas Le Roux and Francis Bach University of British Columbia Context: Machine Learning for Big Data Large-scale
Convex Optimization Lecture 16
 Convex Optimization Lecture 16 Today: Projected Gradient Descent Conditional Gradient Descent Stochastic Gradient Descent Random Coordinate Descent Recall: Gradient Descent (Steepest Descent w.r.t Euclidean
Convex Optimization Lecture 16 Today: Projected Gradient Descent Conditional Gradient Descent Stochastic Gradient Descent Random Coordinate Descent Recall: Gradient Descent (Steepest Descent w.r.t Euclidean
In applications, we encounter many constrained optimization problems. Examples Basis pursuit: exact sparse recovery problem
 1 Conve Analsis Main references: Vandenberghe UCLA): EECS236C - Optimiation methods for large scale sstems, http://www.seas.ucla.edu/ vandenbe/ee236c.html Parikh and Bod, Proimal algorithms, slides and
1 Conve Analsis Main references: Vandenberghe UCLA): EECS236C - Optimiation methods for large scale sstems, http://www.seas.ucla.edu/ vandenbe/ee236c.html Parikh and Bod, Proimal algorithms, slides and
STA141C: Big Data & High Performance Statistical Computing
 STA141C: Big Data & High Performance Statistical Computing Lecture 8: Optimization Cho-Jui Hsieh UC Davis May 9, 2017 Optimization Numerical Optimization Numerical Optimization: min X f (X ) Can be applied
STA141C: Big Data & High Performance Statistical Computing Lecture 8: Optimization Cho-Jui Hsieh UC Davis May 9, 2017 Optimization Numerical Optimization Numerical Optimization: min X f (X ) Can be applied
Conditional Gradient (Frank-Wolfe) Method
 Conditional Gradient (Frank-Wolfe) Method Lecturer: Aarti Singh Co-instructor: Pradeep Ravikumar Convex Optimization 10-725/36-725 1 Outline Today: Conditional gradient method Convergence analysis Properties
Conditional Gradient (Frank-Wolfe) Method Lecturer: Aarti Singh Co-instructor: Pradeep Ravikumar Convex Optimization 10-725/36-725 1 Outline Today: Conditional gradient method Convergence analysis Properties
Active-set complexity of proximal gradient
 Noname manuscript No. will be inserted by the editor) Active-set complexity of proximal gradient How long does it take to find the sparsity pattern? Julie Nutini Mark Schmidt Warren Hare Received: date
Noname manuscript No. will be inserted by the editor) Active-set complexity of proximal gradient How long does it take to find the sparsity pattern? Julie Nutini Mark Schmidt Warren Hare Received: date
Proximal Minimization by Incremental Surrogate Optimization (MISO)
 Proximal Minimization by Incremental Surrogate Optimization (MISO) (and a few variants) Julien Mairal Inria, Grenoble ICCOPT, Tokyo, 2016 Julien Mairal, Inria MISO 1/26 Motivation: large-scale machine
Proximal Minimization by Incremental Surrogate Optimization (MISO) (and a few variants) Julien Mairal Inria, Grenoble ICCOPT, Tokyo, 2016 Julien Mairal, Inria MISO 1/26 Motivation: large-scale machine
Frank-Wolfe Method. Ryan Tibshirani Convex Optimization
 Frank-Wolfe Method Ryan Tibshirani Convex Optimization 10-725 Last time: ADMM For the problem min x,z f(x) + g(z) subject to Ax + Bz = c we form augmented Lagrangian (scaled form): L ρ (x, z, w) = f(x)
Frank-Wolfe Method Ryan Tibshirani Convex Optimization 10-725 Last time: ADMM For the problem min x,z f(x) + g(z) subject to Ax + Bz = c we form augmented Lagrangian (scaled form): L ρ (x, z, w) = f(x)
Primal-dual coordinate descent A Coordinate Descent Primal-Dual Algorithm with Large Step Size and Possibly Non-Separable Functions
 Primal-dual coordinate descent A Coordinate Descent Primal-Dual Algorithm with Large Step Size and Possibly Non-Separable Functions Olivier Fercoq and Pascal Bianchi Problem Minimize the convex function
Primal-dual coordinate descent A Coordinate Descent Primal-Dual Algorithm with Large Step Size and Possibly Non-Separable Functions Olivier Fercoq and Pascal Bianchi Problem Minimize the convex function
Big Data Analytics: Optimization and Randomization
 Big Data Analytics: Optimization and Randomization Tianbao Yang Tutorial@ACML 2015 Hong Kong Department of Computer Science, The University of Iowa, IA, USA Nov. 20, 2015 Yang Tutorial for ACML 15 Nov.
Big Data Analytics: Optimization and Randomization Tianbao Yang Tutorial@ACML 2015 Hong Kong Department of Computer Science, The University of Iowa, IA, USA Nov. 20, 2015 Yang Tutorial for ACML 15 Nov.
Accelerating Stochastic Optimization
 Accelerating Stochastic Optimization Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem and Mobileye Master Class at Tel-Aviv, Tel-Aviv University, November 2014 Shalev-Shwartz
Accelerating Stochastic Optimization Shai Shalev-Shwartz School of CS and Engineering, The Hebrew University of Jerusalem and Mobileye Master Class at Tel-Aviv, Tel-Aviv University, November 2014 Shalev-Shwartz
Barzilai-Borwein Step Size for Stochastic Gradient Descent
 Barzilai-Borwein Step Size for Stochastic Gradient Descent Conghui Tan The Chinese University of Hong Kong chtan@se.cuhk.edu.hk Shiqian Ma The Chinese University of Hong Kong sqma@se.cuhk.edu.hk Yu-Hong
Barzilai-Borwein Step Size for Stochastic Gradient Descent Conghui Tan The Chinese University of Hong Kong chtan@se.cuhk.edu.hk Shiqian Ma The Chinese University of Hong Kong sqma@se.cuhk.edu.hk Yu-Hong
Parallel Coordinate Optimization
 1 / 38 Parallel Coordinate Optimization Julie Nutini MLRG - Spring Term March 6 th, 2018 2 / 38 Contours of a function F : IR 2 IR. Goal: Find the minimizer of F. Coordinate Descent in 2D Contours of a
1 / 38 Parallel Coordinate Optimization Julie Nutini MLRG - Spring Term March 6 th, 2018 2 / 38 Contours of a function F : IR 2 IR. Goal: Find the minimizer of F. Coordinate Descent in 2D Contours of a
Stochastic Gradient Descent. Ryan Tibshirani Convex Optimization
 Stochastic Gradient Descent Ryan Tibshirani Convex Optimization 10-725 Last time: proximal gradient descent Consider the problem min x g(x) + h(x) with g, h convex, g differentiable, and h simple in so
Stochastic Gradient Descent Ryan Tibshirani Convex Optimization 10-725 Last time: proximal gradient descent Consider the problem min x g(x) + h(x) with g, h convex, g differentiable, and h simple in so
Nesterov s Acceleration
 Nesterov s Acceleration Nesterov Accelerated Gradient min X f(x)+ (X) f -smooth. Set s 1 = 1 and = 1. Set y 0. Iterate by increasing t: g t 2 @f(y t ) s t+1 = 1+p 1+4s 2 t 2 y t = x t + s t 1 s t+1 (x
Nesterov s Acceleration Nesterov Accelerated Gradient min X f(x)+ (X) f -smooth. Set s 1 = 1 and = 1. Set y 0. Iterate by increasing t: g t 2 @f(y t ) s t+1 = 1+p 1+4s 2 t 2 y t = x t + s t 1 s t+1 (x
Optimization methods
 Lecture notes 3 February 8, 016 1 Introduction Optimization methods In these notes we provide an overview of a selection of optimization methods. We focus on methods which rely on first-order information,
Lecture notes 3 February 8, 016 1 Introduction Optimization methods In these notes we provide an overview of a selection of optimization methods. We focus on methods which rely on first-order information,
arxiv: v1 [math.oc] 10 Oct 2018
![arxiv: v1 [math.oc] 10 Oct 2018 arxiv: v1 [math.oc] 10 Oct 2018](/thumbs/89/97503904.jpg) 8 Frank-Wolfe Method is Automatically Adaptive to Error Bound ondition arxiv:80.04765v [math.o] 0 Oct 08 Yi Xu yi-xu@uiowa.edu Tianbao Yang tianbao-yang@uiowa.edu Department of omputer Science, The University
8 Frank-Wolfe Method is Automatically Adaptive to Error Bound ondition arxiv:80.04765v [math.o] 0 Oct 08 Yi Xu yi-xu@uiowa.edu Tianbao Yang tianbao-yang@uiowa.edu Department of omputer Science, The University
Accelerated Randomized Primal-Dual Coordinate Method for Empirical Risk Minimization
 Accelerated Randomized Primal-Dual Coordinate Method for Empirical Risk Minimization Lin Xiao (Microsoft Research) Joint work with Qihang Lin (CMU), Zhaosong Lu (Simon Fraser) Yuchen Zhang (UC Berkeley)
Accelerated Randomized Primal-Dual Coordinate Method for Empirical Risk Minimization Lin Xiao (Microsoft Research) Joint work with Qihang Lin (CMU), Zhaosong Lu (Simon Fraser) Yuchen Zhang (UC Berkeley)
Stochastic Optimization Algorithms Beyond SG
 Stochastic Optimization Algorithms Beyond SG Frank E. Curtis 1, Lehigh University involving joint work with Léon Bottou, Facebook AI Research Jorge Nocedal, Northwestern University Optimization Methods
Stochastic Optimization Algorithms Beyond SG Frank E. Curtis 1, Lehigh University involving joint work with Léon Bottou, Facebook AI Research Jorge Nocedal, Northwestern University Optimization Methods
Proximal Newton Method. Ryan Tibshirani Convex Optimization /36-725
 Proximal Newton Method Ryan Tibshirani Convex Optimization 10-725/36-725 1 Last time: primal-dual interior-point method Given the problem min x subject to f(x) h i (x) 0, i = 1,... m Ax = b where f, h
Proximal Newton Method Ryan Tibshirani Convex Optimization 10-725/36-725 1 Last time: primal-dual interior-point method Given the problem min x subject to f(x) h i (x) 0, i = 1,... m Ax = b where f, h
Optimization for Machine Learning
 Optimization for Machine Learning (Problems; Algorithms - A) SUVRIT SRA Massachusetts Institute of Technology PKU Summer School on Data Science (July 2017) Course materials http://suvrit.de/teaching.html
Optimization for Machine Learning (Problems; Algorithms - A) SUVRIT SRA Massachusetts Institute of Technology PKU Summer School on Data Science (July 2017) Course materials http://suvrit.de/teaching.html
6. Proximal gradient method
 L. Vandenberghe EE236C (Spring 2016) 6. Proximal gradient method motivation proximal mapping proximal gradient method with fixed step size proximal gradient method with line search 6-1 Proximal mapping
L. Vandenberghe EE236C (Spring 2016) 6. Proximal gradient method motivation proximal mapping proximal gradient method with fixed step size proximal gradient method with line search 6-1 Proximal mapping
Coordinate descent methods
 Coordinate descent methods Master Mathematics for data science and big data Olivier Fercoq November 3, 05 Contents Exact coordinate descent Coordinate gradient descent 3 3 Proximal coordinate descent 5
Coordinate descent methods Master Mathematics for data science and big data Olivier Fercoq November 3, 05 Contents Exact coordinate descent Coordinate gradient descent 3 3 Proximal coordinate descent 5
Worst-Case Complexity Guarantees and Nonconvex Smooth Optimization
 Worst-Case Complexity Guarantees and Nonconvex Smooth Optimization Frank E. Curtis, Lehigh University Beyond Convexity Workshop, Oaxaca, Mexico 26 October 2017 Worst-Case Complexity Guarantees and Nonconvex
Worst-Case Complexity Guarantees and Nonconvex Smooth Optimization Frank E. Curtis, Lehigh University Beyond Convexity Workshop, Oaxaca, Mexico 26 October 2017 Worst-Case Complexity Guarantees and Nonconvex
Fast Stochastic Optimization Algorithms for ML
 Fast Stochastic Optimization Algorithms for ML Aaditya Ramdas April 20, 205 This lecture is about efficient algorithms for minimizing finite sums min w R d n i= f i (w) or min w R d n f i (w) + λ 2 w 2
Fast Stochastic Optimization Algorithms for ML Aaditya Ramdas April 20, 205 This lecture is about efficient algorithms for minimizing finite sums min w R d n i= f i (w) or min w R d n f i (w) + λ 2 w 2
A Unified Approach to Proximal Algorithms using Bregman Distance
 A Unified Approach to Proximal Algorithms using Bregman Distance Yi Zhou a,, Yingbin Liang a, Lixin Shen b a Department of Electrical Engineering and Computer Science, Syracuse University b Department
A Unified Approach to Proximal Algorithms using Bregman Distance Yi Zhou a,, Yingbin Liang a, Lixin Shen b a Department of Electrical Engineering and Computer Science, Syracuse University b Department
Stochastic Gradient Descent with Variance Reduction
 Stochastic Gradient Descent with Variance Reduction Rie Johnson, Tong Zhang Presenter: Jiawen Yao March 17, 2015 Rie Johnson, Tong Zhang Presenter: JiawenStochastic Yao Gradient Descent with Variance Reduction
Stochastic Gradient Descent with Variance Reduction Rie Johnson, Tong Zhang Presenter: Jiawen Yao March 17, 2015 Rie Johnson, Tong Zhang Presenter: JiawenStochastic Yao Gradient Descent with Variance Reduction
Large-scale Stochastic Optimization
 Large-scale Stochastic Optimization 11-741/641/441 (Spring 2016) Hanxiao Liu hanxiaol@cs.cmu.edu March 24, 2016 1 / 22 Outline 1. Gradient Descent (GD) 2. Stochastic Gradient Descent (SGD) Formulation
Large-scale Stochastic Optimization 11-741/641/441 (Spring 2016) Hanxiao Liu hanxiaol@cs.cmu.edu March 24, 2016 1 / 22 Outline 1. Gradient Descent (GD) 2. Stochastic Gradient Descent (SGD) Formulation
Convex Optimization. Newton s method. ENSAE: Optimisation 1/44
 Convex Optimization Newton s method ENSAE: Optimisation 1/44 Unconstrained minimization minimize f(x) f convex, twice continuously differentiable (hence dom f open) we assume optimal value p = inf x f(x)
Convex Optimization Newton s method ENSAE: Optimisation 1/44 Unconstrained minimization minimize f(x) f convex, twice continuously differentiable (hence dom f open) we assume optimal value p = inf x f(x)
Proximal Newton Method. Zico Kolter (notes by Ryan Tibshirani) Convex Optimization
 Proximal Newton Method Zico Kolter (notes by Ryan Tibshirani) Convex Optimization 10-725 Consider the problem Last time: quasi-newton methods min x f(x) with f convex, twice differentiable, dom(f) = R
Proximal Newton Method Zico Kolter (notes by Ryan Tibshirani) Convex Optimization 10-725 Consider the problem Last time: quasi-newton methods min x f(x) with f convex, twice differentiable, dom(f) = R
Stochastic Optimization with Variance Reduction for Infinite Datasets with Finite Sum Structure
 Stochastic Optimization with Variance Reduction for Infinite Datasets with Finite Sum Structure Alberto Bietti Julien Mairal Inria Grenoble (Thoth) March 21, 2017 Alberto Bietti Stochastic MISO March 21,
Stochastic Optimization with Variance Reduction for Infinite Datasets with Finite Sum Structure Alberto Bietti Julien Mairal Inria Grenoble (Thoth) March 21, 2017 Alberto Bietti Stochastic MISO March 21,
NOTES ON FIRST-ORDER METHODS FOR MINIMIZING SMOOTH FUNCTIONS. 1. Introduction. We consider first-order methods for smooth, unconstrained
 NOTES ON FIRST-ORDER METHODS FOR MINIMIZING SMOOTH FUNCTIONS 1. Introduction. We consider first-order methods for smooth, unconstrained optimization: (1.1) minimize f(x), x R n where f : R n R. We assume
NOTES ON FIRST-ORDER METHODS FOR MINIMIZING SMOOTH FUNCTIONS 1. Introduction. We consider first-order methods for smooth, unconstrained optimization: (1.1) minimize f(x), x R n where f : R n R. We assume
10. Unconstrained minimization
 Convex Optimization Boyd & Vandenberghe 10. Unconstrained minimization terminology and assumptions gradient descent method steepest descent method Newton s method self-concordant functions implementation
Convex Optimization Boyd & Vandenberghe 10. Unconstrained minimization terminology and assumptions gradient descent method steepest descent method Newton s method self-concordant functions implementation
Block Coordinate Descent for Regularized Multi-convex Optimization
 Block Coordinate Descent for Regularized Multi-convex Optimization Yangyang Xu and Wotao Yin CAAM Department, Rice University February 15, 2013 Multi-convex optimization Model definition Applications Outline
Block Coordinate Descent for Regularized Multi-convex Optimization Yangyang Xu and Wotao Yin CAAM Department, Rice University February 15, 2013 Multi-convex optimization Model definition Applications Outline
Lecture 23: November 21
 10-725/36-725: Convex Optimization Fall 2016 Lecturer: Ryan Tibshirani Lecture 23: November 21 Scribes: Yifan Sun, Ananya Kumar, Xin Lu Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer:
10-725/36-725: Convex Optimization Fall 2016 Lecturer: Ryan Tibshirani Lecture 23: November 21 Scribes: Yifan Sun, Ananya Kumar, Xin Lu Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer:
Comparison of Modern Stochastic Optimization Algorithms
 Comparison of Modern Stochastic Optimization Algorithms George Papamakarios December 214 Abstract Gradient-based optimization methods are popular in machine learning applications. In large-scale problems,
Comparison of Modern Stochastic Optimization Algorithms George Papamakarios December 214 Abstract Gradient-based optimization methods are popular in machine learning applications. In large-scale problems,
SIAM Conference on Imaging Science, Bologna, Italy, Adaptive FISTA. Peter Ochs Saarland University
 SIAM Conference on Imaging Science, Bologna, Italy, 2018 Adaptive FISTA Peter Ochs Saarland University 07.06.2018 joint work with Thomas Pock, TU Graz, Austria c 2018 Peter Ochs Adaptive FISTA 1 / 16 Some
SIAM Conference on Imaging Science, Bologna, Italy, 2018 Adaptive FISTA Peter Ochs Saarland University 07.06.2018 joint work with Thomas Pock, TU Graz, Austria c 2018 Peter Ochs Adaptive FISTA 1 / 16 Some
Gradient Descent. Ryan Tibshirani Convex Optimization /36-725
 Gradient Descent Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: canonical convex programs Linear program (LP): takes the form min x subject to c T x Gx h Ax = b Quadratic program (QP): like
Gradient Descent Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: canonical convex programs Linear program (LP): takes the form min x subject to c T x Gx h Ax = b Quadratic program (QP): like
Coordinate descent. Geoff Gordon & Ryan Tibshirani Optimization /
 Coordinate descent Geoff Gordon & Ryan Tibshirani Optimization 10-725 / 36-725 1 Adding to the toolbox, with stats and ML in mind We ve seen several general and useful minimization tools First-order methods
Coordinate descent Geoff Gordon & Ryan Tibshirani Optimization 10-725 / 36-725 1 Adding to the toolbox, with stats and ML in mind We ve seen several general and useful minimization tools First-order methods
Primal-dual coordinate descent
 Primal-dual coordinate descent Olivier Fercoq Joint work with P. Bianchi & W. Hachem 15 July 2015 1/28 Minimize the convex function f, g, h convex f is differentiable Problem min f (x) + g(x) + h(mx) x
Primal-dual coordinate descent Olivier Fercoq Joint work with P. Bianchi & W. Hachem 15 July 2015 1/28 Minimize the convex function f, g, h convex f is differentiable Problem min f (x) + g(x) + h(mx) x
CPSC 540: Machine Learning
 CPSC 540: Machine Learning Gradient Descent, Newton-like Methods Mark Schmidt University of British Columbia Winter 2017 Admin Auditting/registration forms: Submit them in class/help-session/tutorial this
CPSC 540: Machine Learning Gradient Descent, Newton-like Methods Mark Schmidt University of British Columbia Winter 2017 Admin Auditting/registration forms: Submit them in class/help-session/tutorial this
Descent methods. min x. f(x)
 Gradient Descent Descent methods min x f(x) 5 / 34 Descent methods min x f(x) x k x k+1... x f(x ) = 0 5 / 34 Gradient methods Unconstrained optimization min f(x) x R n. 6 / 34 Gradient methods Unconstrained
Gradient Descent Descent methods min x f(x) 5 / 34 Descent methods min x f(x) x k x k+1... x f(x ) = 0 5 / 34 Gradient methods Unconstrained optimization min f(x) x R n. 6 / 34 Gradient methods Unconstrained
Convex Optimization. Convex Analysis - Functions
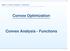 Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Convex Optimization Convex Analsis - Functions p. 1 A function f : K R n R is convex, if K is a convex set and x, K,x, λ (,1) we have f(λx+(1 λ)) λf(x)+(1 λ)f(). (x, f(x)) (,f()) x - strictl convex,
Barzilai-Borwein Step Size for Stochastic Gradient Descent
 Barzilai-Borwein Step Size for Stochastic Gradient Descent Conghui Tan Shiqian Ma Yu-Hong Dai Yuqiu Qian May 16, 2016 Abstract One of the major issues in stochastic gradient descent (SGD) methods is how
Barzilai-Borwein Step Size for Stochastic Gradient Descent Conghui Tan Shiqian Ma Yu-Hong Dai Yuqiu Qian May 16, 2016 Abstract One of the major issues in stochastic gradient descent (SGD) methods is how
Accelerated Block-Coordinate Relaxation for Regularized Optimization
 Accelerated Block-Coordinate Relaxation for Regularized Optimization Stephen J. Wright Computer Sciences University of Wisconsin, Madison October 09, 2012 Problem descriptions Consider where f is smooth
Accelerated Block-Coordinate Relaxation for Regularized Optimization Stephen J. Wright Computer Sciences University of Wisconsin, Madison October 09, 2012 Problem descriptions Consider where f is smooth
FAST DISTRIBUTED COORDINATE DESCENT FOR NON-STRONGLY CONVEX LOSSES. Olivier Fercoq Zheng Qu Peter Richtárik Martin Takáč
 FAST DISTRIBUTED COORDINATE DESCENT FOR NON-STRONGLY CONVEX LOSSES Olivier Fercoq Zheng Qu Peter Richtárik Martin Takáč School of Mathematics, University of Edinburgh, Edinburgh, EH9 3JZ, United Kingdom
FAST DISTRIBUTED COORDINATE DESCENT FOR NON-STRONGLY CONVEX LOSSES Olivier Fercoq Zheng Qu Peter Richtárik Martin Takáč School of Mathematics, University of Edinburgh, Edinburgh, EH9 3JZ, United Kingdom
Feedforward Neural Networks
 Chapter 4 Feedforward Neural Networks 4. Motivation Let s start with our logistic regression model from before: P(k d) = softma k =k ( λ(k ) + w d λ(k, w) ). (4.) Recall that this model gives us a lot
Chapter 4 Feedforward Neural Networks 4. Motivation Let s start with our logistic regression model from before: P(k d) = softma k =k ( λ(k ) + w d λ(k, w) ). (4.) Recall that this model gives us a lot
Optimization methods
 Optimization methods Optimization-Based Data Analysis http://www.cims.nyu.edu/~cfgranda/pages/obda_spring16 Carlos Fernandez-Granda /8/016 Introduction Aim: Overview of optimization methods that Tend to
Optimization methods Optimization-Based Data Analysis http://www.cims.nyu.edu/~cfgranda/pages/obda_spring16 Carlos Fernandez-Granda /8/016 Introduction Aim: Overview of optimization methods that Tend to
Fast Asynchronous Parallel Stochastic Gradient Descent: A Lock-Free Approach with Convergence Guarantee
 Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (AAAI-16) Fast Asynchronous Parallel Stochastic Gradient Descent: A Lock-Free Approach with Convergence Guarantee Shen-Yi Zhao and
Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (AAAI-16) Fast Asynchronous Parallel Stochastic Gradient Descent: A Lock-Free Approach with Convergence Guarantee Shen-Yi Zhao and
CPSC 540: Machine Learning
 CPSC 540: Machine Learning First-Order Methods, L1-Regularization, Coordinate Descent Winter 2016 Some images from this lecture are taken from Google Image Search. Admin Room: We ll count final numbers
CPSC 540: Machine Learning First-Order Methods, L1-Regularization, Coordinate Descent Winter 2016 Some images from this lecture are taken from Google Image Search. Admin Room: We ll count final numbers
ECE G: Special Topics in Signal Processing: Sparsity, Structure, and Inference
 ECE 18-898G: Special Topics in Signal Processing: Sparsity, Structure, and Inference Sparse Recovery using L1 minimization - algorithms Yuejie Chi Department of Electrical and Computer Engineering Spring
ECE 18-898G: Special Topics in Signal Processing: Sparsity, Structure, and Inference Sparse Recovery using L1 minimization - algorithms Yuejie Chi Department of Electrical and Computer Engineering Spring
Stability Analysis for Linear Systems under State Constraints
 Stabilit Analsis for Linear Sstems under State Constraints Haijun Fang Abstract This paper revisits the problem of stabilit analsis for linear sstems under state constraints New and less conservative sufficient
Stabilit Analsis for Linear Sstems under State Constraints Haijun Fang Abstract This paper revisits the problem of stabilit analsis for linear sstems under state constraints New and less conservative sufficient
Optimization. Benjamin Recht University of California, Berkeley Stephen Wright University of Wisconsin-Madison
 Optimization Benjamin Recht University of California, Berkeley Stephen Wright University of Wisconsin-Madison optimization () cost constraints might be too much to cover in 3 hours optimization (for big
Optimization Benjamin Recht University of California, Berkeley Stephen Wright University of Wisconsin-Madison optimization () cost constraints might be too much to cover in 3 hours optimization (for big
Tutorial: PART 2. Optimization for Machine Learning. Elad Hazan Princeton University. + help from Sanjeev Arora & Yoram Singer
 Tutorial: PART 2 Optimization for Machine Learning Elad Hazan Princeton University + help from Sanjeev Arora & Yoram Singer Agenda 1. Learning as mathematical optimization Stochastic optimization, ERM,
Tutorial: PART 2 Optimization for Machine Learning Elad Hazan Princeton University + help from Sanjeev Arora & Yoram Singer Agenda 1. Learning as mathematical optimization Stochastic optimization, ERM,
A Universal Catalyst for Gradient-Based Optimization
 A Universal Catalyst for Gradient-Based Optimization Julien Mairal Inria, Grenoble CIMI workshop, Toulouse, 2015 Julien Mairal, Inria Catalyst 1/58 Collaborators Hongzhou Lin Zaid Harchaoui Publication
A Universal Catalyst for Gradient-Based Optimization Julien Mairal Inria, Grenoble CIMI workshop, Toulouse, 2015 Julien Mairal, Inria Catalyst 1/58 Collaborators Hongzhou Lin Zaid Harchaoui Publication
Proximal Gradient Descent and Acceleration. Ryan Tibshirani Convex Optimization /36-725
 Proximal Gradient Descent and Acceleration Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: subgradient method Consider the problem min f(x) with f convex, and dom(f) = R n. Subgradient method:
Proximal Gradient Descent and Acceleration Ryan Tibshirani Convex Optimization 10-725/36-725 Last time: subgradient method Consider the problem min f(x) with f convex, and dom(f) = R n. Subgradient method:
Block stochastic gradient update method
 Block stochastic gradient update method Yangyang Xu and Wotao Yin IMA, University of Minnesota Department of Mathematics, UCLA November 1, 2015 This work was done while in Rice University 1 / 26 Stochastic
Block stochastic gradient update method Yangyang Xu and Wotao Yin IMA, University of Minnesota Department of Mathematics, UCLA November 1, 2015 This work was done while in Rice University 1 / 26 Stochastic
This can be 2 lectures! still need: Examples: non-convex problems applications for matrix factorization
 This can be 2 lectures! still need: Examples: non-convex problems applications for matrix factorization x = prox_f(x)+prox_{f^*}(x) use to get prox of norms! PROXIMAL METHODS WHY PROXIMAL METHODS Smooth
This can be 2 lectures! still need: Examples: non-convex problems applications for matrix factorization x = prox_f(x)+prox_{f^*}(x) use to get prox of norms! PROXIMAL METHODS WHY PROXIMAL METHODS Smooth
Learning with stochastic proximal gradient
 Learning with stochastic proximal gradient Lorenzo Rosasco DIBRIS, Università di Genova Via Dodecaneso, 35 16146 Genova, Italy lrosasco@mit.edu Silvia Villa, Băng Công Vũ Laboratory for Computational and
Learning with stochastic proximal gradient Lorenzo Rosasco DIBRIS, Università di Genova Via Dodecaneso, 35 16146 Genova, Italy lrosasco@mit.edu Silvia Villa, Băng Công Vũ Laboratory for Computational and
Relative-Continuity for Non-Lipschitz Non-Smooth Convex Optimization using Stochastic (or Deterministic) Mirror Descent
 Relative-Continuity for Non-Lipschitz Non-Smooth Convex Optimization using Stochastic (or Deterministic) Mirror Descent Haihao Lu August 3, 08 Abstract The usual approach to developing and analyzing first-order
Relative-Continuity for Non-Lipschitz Non-Smooth Convex Optimization using Stochastic (or Deterministic) Mirror Descent Haihao Lu August 3, 08 Abstract The usual approach to developing and analyzing first-order
Optimization for Machine Learning
 Optimization for Machine Learning (Lecture 3-A - Convex) SUVRIT SRA Massachusetts Institute of Technology Special thanks: Francis Bach (INRIA, ENS) (for sharing this material, and permitting its use) MPI-IS
Optimization for Machine Learning (Lecture 3-A - Convex) SUVRIT SRA Massachusetts Institute of Technology Special thanks: Francis Bach (INRIA, ENS) (for sharing this material, and permitting its use) MPI-IS
Trade-Offs in Distributed Learning and Optimization
 Trade-Offs in Distributed Learning and Optimization Ohad Shamir Weizmann Institute of Science Includes joint works with Yossi Arjevani, Nathan Srebro and Tong Zhang IHES Workshop March 2016 Distributed
Trade-Offs in Distributed Learning and Optimization Ohad Shamir Weizmann Institute of Science Includes joint works with Yossi Arjevani, Nathan Srebro and Tong Zhang IHES Workshop March 2016 Distributed
Lecture 17: October 27
 0-725/36-725: Convex Optimiation Fall 205 Lecturer: Ryan Tibshirani Lecture 7: October 27 Scribes: Brandon Amos, Gines Hidalgo Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer: These
0-725/36-725: Convex Optimiation Fall 205 Lecturer: Ryan Tibshirani Lecture 7: October 27 Scribes: Brandon Amos, Gines Hidalgo Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer: These
Robust Nash Equilibria and Second-Order Cone Complementarity Problems
 Robust Nash Equilibria and Second-Order Cone Complementarit Problems Shunsuke Haashi, Nobuo Yamashita, Masao Fukushima Department of Applied Mathematics and Phsics, Graduate School of Informatics, Koto
Robust Nash Equilibria and Second-Order Cone Complementarit Problems Shunsuke Haashi, Nobuo Yamashita, Masao Fukushima Department of Applied Mathematics and Phsics, Graduate School of Informatics, Koto
I P IANO : I NERTIAL P ROXIMAL A LGORITHM FOR N ON -C ONVEX O PTIMIZATION
 I P IANO : I NERTIAL P ROXIMAL A LGORITHM FOR N ON -C ONVEX O PTIMIZATION Peter Ochs University of Freiburg Germany 17.01.2017 joint work with: Thomas Brox and Thomas Pock c 2017 Peter Ochs ipiano c 1
I P IANO : I NERTIAL P ROXIMAL A LGORITHM FOR N ON -C ONVEX O PTIMIZATION Peter Ochs University of Freiburg Germany 17.01.2017 joint work with: Thomas Brox and Thomas Pock c 2017 Peter Ochs ipiano c 1
Greed is Good. Greedy Optimization Methods for Large-Scale Structured Problems. Julie Nutini
 Greed is Good Greedy Optimization Methods for Large-Scale Structured Problems by Julie Nutini B.Sc., The University of British Columbia (Okanagan), 2010 M.Sc., The University of British Columbia (Okanagan),
Greed is Good Greedy Optimization Methods for Large-Scale Structured Problems by Julie Nutini B.Sc., The University of British Columbia (Okanagan), 2010 M.Sc., The University of British Columbia (Okanagan),
Convergence of Fixed-Point Iterations
 Convergence of Fixed-Point Iterations Instructor: Wotao Yin (UCLA Math) July 2016 1 / 30 Why study fixed-point iterations? Abstract many existing algorithms in optimization, numerical linear algebra, and
Convergence of Fixed-Point Iterations Instructor: Wotao Yin (UCLA Math) July 2016 1 / 30 Why study fixed-point iterations? Abstract many existing algorithms in optimization, numerical linear algebra, and
Gradient descent. Barnabas Poczos & Ryan Tibshirani Convex Optimization /36-725
 Gradient descent Barnabas Poczos & Ryan Tibshirani Convex Optimization 10-725/36-725 1 Gradient descent First consider unconstrained minimization of f : R n R, convex and differentiable. We want to solve
Gradient descent Barnabas Poczos & Ryan Tibshirani Convex Optimization 10-725/36-725 1 Gradient descent First consider unconstrained minimization of f : R n R, convex and differentiable. We want to solve
Contents. 1 Introduction. 1.1 History of Optimization ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016
 ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016 LECTURERS: NAMAN AGARWAL AND BRIAN BULLINS SCRIBE: KIRAN VODRAHALLI Contents 1 Introduction 1 1.1 History of Optimization.....................................
ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016 LECTURERS: NAMAN AGARWAL AND BRIAN BULLINS SCRIBE: KIRAN VODRAHALLI Contents 1 Introduction 1 1.1 History of Optimization.....................................
Improved Optimization of Finite Sums with Minibatch Stochastic Variance Reduced Proximal Iterations
 Improved Optimization of Finite Sums with Miniatch Stochastic Variance Reduced Proximal Iterations Jialei Wang University of Chicago Tong Zhang Tencent AI La Astract jialei@uchicago.edu tongzhang@tongzhang-ml.org
Improved Optimization of Finite Sums with Miniatch Stochastic Variance Reduced Proximal Iterations Jialei Wang University of Chicago Tong Zhang Tencent AI La Astract jialei@uchicago.edu tongzhang@tongzhang-ml.org
Parallel and Distributed Stochastic Learning -Towards Scalable Learning for Big Data Intelligence
 Parallel and Distributed Stochastic Learning -Towards Scalable Learning for Big Data Intelligence oé LAMDA Group H ŒÆOŽÅ Æ EâX ^ #EâI[ : liwujun@nju.edu.cn Dec 10, 2016 Wu-Jun Li (http://cs.nju.edu.cn/lwj)
Parallel and Distributed Stochastic Learning -Towards Scalable Learning for Big Data Intelligence oé LAMDA Group H ŒÆOŽÅ Æ EâX ^ #EâI[ : liwujun@nju.edu.cn Dec 10, 2016 Wu-Jun Li (http://cs.nju.edu.cn/lwj)
Optimization and Optimal Control in Banach Spaces
 Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Optimization and Optimal Control in Banach Spaces Bernhard Schmitzer October 19, 2017 1 Convex non-smooth optimization with proximal operators Remark 1.1 (Motivation). Convex optimization: easier to solve,
Lecture: Adaptive Filtering
 ECE 830 Spring 2013 Statistical Signal Processing instructors: K. Jamieson and R. Nowak Lecture: Adaptive Filtering Adaptive filters are commonly used for online filtering of signals. The goal is to estimate
ECE 830 Spring 2013 Statistical Signal Processing instructors: K. Jamieson and R. Nowak Lecture: Adaptive Filtering Adaptive filters are commonly used for online filtering of signals. The goal is to estimate
Unconstrained minimization of smooth functions
 Unconstrained minimization of smooth functions We want to solve min x R N f(x), where f is convex. In this section, we will assume that f is differentiable (so its gradient exists at every point), and
Unconstrained minimization of smooth functions We want to solve min x R N f(x), where f is convex. In this section, we will assume that f is differentiable (so its gradient exists at every point), and
Uses of duality. Geoff Gordon & Ryan Tibshirani Optimization /
 Uses of duality Geoff Gordon & Ryan Tibshirani Optimization 10-725 / 36-725 1 Remember conjugate functions Given f : R n R, the function is called its conjugate f (y) = max x R n yt x f(x) Conjugates appear
Uses of duality Geoff Gordon & Ryan Tibshirani Optimization 10-725 / 36-725 1 Remember conjugate functions Given f : R n R, the function is called its conjugate f (y) = max x R n yt x f(x) Conjugates appear
PICONE S IDENTITY FOR A SYSTEM OF FIRST-ORDER NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS
 Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 143, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu PICONE S IDENTITY
Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 143, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu PICONE S IDENTITY
Stochastic Composition Optimization
 Stochastic Composition Optimization Algorithms and Sample Complexities Mengdi Wang Joint works with Ethan X. Fang, Han Liu, and Ji Liu ORFE@Princeton ICCOPT, Tokyo, August 8-11, 2016 1 / 24 Collaborators
Stochastic Composition Optimization Algorithms and Sample Complexities Mengdi Wang Joint works with Ethan X. Fang, Han Liu, and Ji Liu ORFE@Princeton ICCOPT, Tokyo, August 8-11, 2016 1 / 24 Collaborators
Ordinal One-Switch Utility Functions
 Ordinal One-Switch Utilit Functions Ali E. Abbas Universit of Southern California, Los Angeles, California 90089, aliabbas@usc.edu David E. Bell Harvard Business School, Boston, Massachusetts 0163, dbell@hbs.edu
Ordinal One-Switch Utilit Functions Ali E. Abbas Universit of Southern California, Los Angeles, California 90089, aliabbas@usc.edu David E. Bell Harvard Business School, Boston, Massachusetts 0163, dbell@hbs.edu
Accelerated primal-dual methods for linearly constrained convex problems
 Accelerated primal-dual methods for linearly constrained convex problems Yangyang Xu SIAM Conference on Optimization May 24, 2017 1 / 23 Accelerated proximal gradient For convex composite problem: minimize
Accelerated primal-dual methods for linearly constrained convex problems Yangyang Xu SIAM Conference on Optimization May 24, 2017 1 / 23 Accelerated proximal gradient For convex composite problem: minimize
Newton s Method. Javier Peña Convex Optimization /36-725
 Newton s Method Javier Peña Convex Optimization 10-725/36-725 1 Last time: dual correspondences Given a function f : R n R, we define its conjugate f : R n R, f ( (y) = max y T x f(x) ) x Properties and
Newton s Method Javier Peña Convex Optimization 10-725/36-725 1 Last time: dual correspondences Given a function f : R n R, we define its conjugate f : R n R, f ( (y) = max y T x f(x) ) x Properties and
A Greedy Framework for First-Order Optimization
 A Greedy Framework for First-Order Optimization Jacob Steinhardt Department of Computer Science Stanford University Stanford, CA 94305 jsteinhardt@cs.stanford.edu Jonathan Huggins Department of EECS Massachusetts
A Greedy Framework for First-Order Optimization Jacob Steinhardt Department of Computer Science Stanford University Stanford, CA 94305 jsteinhardt@cs.stanford.edu Jonathan Huggins Department of EECS Massachusetts
A Randomized Nonmonotone Block Proximal Gradient Method for a Class of Structured Nonlinear Programming
 A Randomized Nonmonotone Block Proximal Gradient Method for a Class of Structured Nonlinear Programming Zhaosong Lu Lin Xiao March 9, 2015 (Revised: May 13, 2016; December 30, 2016) Abstract We propose
A Randomized Nonmonotone Block Proximal Gradient Method for a Class of Structured Nonlinear Programming Zhaosong Lu Lin Xiao March 9, 2015 (Revised: May 13, 2016; December 30, 2016) Abstract We propose
Non-Smooth, Non-Finite, and Non-Convex Optimization
 Non-Smooth, Non-Finite, and Non-Convex Optimization Deep Learning Summer School Mark Schmidt University of British Columbia August 2015 Complex-Step Derivative Using complex number to compute directional
Non-Smooth, Non-Finite, and Non-Convex Optimization Deep Learning Summer School Mark Schmidt University of British Columbia August 2015 Complex-Step Derivative Using complex number to compute directional
Proximal and First-Order Methods for Convex Optimization
 Proximal and First-Order Methods for Convex Optimization John C Duchi Yoram Singer January, 03 Abstract We describe the proximal method for minimization of convex functions We review classical results,
Proximal and First-Order Methods for Convex Optimization John C Duchi Yoram Singer January, 03 Abstract We describe the proximal method for minimization of convex functions We review classical results,
