6-6. Fitting a Quadratic Model to Data. Vocabulary. Lesson. Mental Math
|
|
|
- Louise Miles
- 5 years ago
- Views:
Transcription
1 Chapter 6 Lesson 6-6 Fitting a Quadratic odel to Data Vocabulary quadratic regression BG DEA Quadratic regression is like linear regression in that it fi nds the model with the least sum of squares of differences from the given data points to the values predicted by the model. n Chapter 3, you learned how to find an equation for the line through two points, and how to find a linear model for data that lie approximately on a straight line. You can also fit a quadratic model to data that lie approximately on a parabola. Quadratic regression fits a model of the form y = ax 2 + bx + c to data. Activity ATERALS old CD that can get scratched up, two 8 2 inch by inch pieces of paper, quarter, CAS or graphing calculator You are going to investigate how the radius x of a circular object affects the probability y of the object landing completely in a fi xed region when dropped. ental ath Find the slope of the image of 3x + 2y = 7 under the transformation. a. T 6, b. R 9 c. R 27 d. r y = x Step A CD like the one pictured at the right has 3 circles on it. Circle represents the hole in the CD. Circle (for middle) represents the start of the silver writing surface. Circle represents the outer edge of the CD. Draw a line across the middle of your 8 2 by piece of paper, dividing it into two 5 2 by 8 2 rectangular targets. Step 2 n a separate sheet of paper, make four columns labeled Drop Number,,, and. n the Drop Number column, write the integers through 25. Place your divided sheet of 8 2 inch by inch paper on the fl oor and stand above it holding the CD waist high, parallel to the fl oor. Drop the CD. 48 Quadratic Functions
2 Lesson 6 6 f no part of the CD is touching the paper, drop it again. f any part of the CD is touching the paper, determine the score for each circle,,, and as follows: f a circle on the CD lands completely inside one of the two rectangular targets, give it point for that drop. Pictured below are the four possible situations and scores after a drop. The horizontal line represents either the edge of the paper or the line you drew on the paper. all circles and only no circles circle point Drop the CD 25 times and fi ll in your table. Step 3 Calculate the relative frequency of a circle landing completely in a target. For example, if has 6 points, then its relative frequency of points per drop is Record the frequencies in a table like the one at the right. The radii of circles on a standard CD have been fi lled in for you, but you should measure your CD to check. Step 4 Create a scatterplot with three data points (radius, frequency) for,, and on your calculator. Choose the quadratic regression option from the appropriate menu. A sample is shown at the right. n this calculator, the graph of a quadratic model for the data is added to the scatterplot. The calculator displays the equation for the quadratic model. Circle Radius Relative (in.) Frequency 5 6? 7 8? 2? Step 5 Examine the scatterplot with the graph of the regression equation on it. How well does your model fit your data? Step 6 easure the diameter of a quarter and use your regression equation to predict the relative frequency of the quarter landing inside a target rectangle. Drop the quarter 25 times and see if the relative frequency is close to your prediction. Combine your results with other classmates. Compare the combined data with the prediction. Which value is closer to the predicted value your own data or the combined data? Fitting a Quadratic odel to Data 49
3 Chapter 6 Finding the Equation of a Given Parabola You can apply the techniques of solving systems of equations you learned in Chapter 5 and the regression technique in the Activity to find an equation for any parabola on which you know three points. Example The parabola at the right contains the points (, 7), (, 3) and (5, ). Find its equation. 7 y Solution Use a system of equations. 5 Because the ordered pairs (x, y) are solutions of the equation y = ax 2 + bx + c, substitute to get 3 linear equations in a, b, and c. When x =, y = 7: When x =, y = 3: When x = 5, y = : 7 = a( ) 2 + b( ) + c 3 = a() 2 + b() + c = a(5) 2 + b(5) + c x = a - b + c So a, b, and c are solutions to the system 3 = a + b + c = 25a + 5b + c You are asked to solve this system in Question Solution 2 Use quadratic regression. Enter the x coordinates and y coordinates into lists in your calculator and apply quadratic regression. ne calculator gives the solution at the right, so the parabola has equation y = x 2-5x +. Check Substitute the points into the equation. Does ( ) 2-5( ) + = 7? Does () 2-5() + = 3? Does (5) 2-5(5) + =? Yes. Yes. Yes; it checks. Questions CVERNG THE DEAS. Refer to the Activity. a. Write an equation for the function your quadratic regression describes. b. Use the model from Part a to predict the probability of a mini CD with a radius of 4 centimeters landing completely inside one of the two rectangular targets. 4 Quadratic Functions
4 Lesson Solve the system of the Example to find an equation for the parabola that contains the given points. n 3 and 4, solve a system of equations to write an equation for the parabola that contains the given points. 3. (4, 6), ( 2, 3), (, ) 4. (, 3), (5, 8), (2, 2) n 5 and 6, use quadratic regression to find an equation for the parabola that contains the given points. 5. (3, 2), (, 5), (8, 7) 6. ( 6, 5), (, ), (3, 4) APPLYNG THE ATHEATCS 7. A quarterback threw a ball from 5 yards behind the line of scrimmage and a height of 6 feet. The ball was feet high as it crossed the line of scrimmage. t was caught 2 yards past the line of scrimmage at a height of 5 feet off the ground. a. Find an equation that gives the height y of the ball (in feet) when it was x yards beyond the line of scrimmage. b. Graph the equation. 8. n The Greedy Triangle by arilyn Burns, an equilateral triangle keeps changing shape into a regular polygon with more and more sides. As the number of sides of a polygon increase, so do the number of diagonals of the polygon. Recall the formula for the number of diagonals in a polygon. f you have forgotten, you can Peyton anning throwing for derive it using quadratic regression. the ndianapolis Colts a. Count the number of diagonals in each polygon Number Number of below and complete the table to the right. Shape of Sides Diagonals Triangle?? Quadrilateral?? b. Use quadratic regression to find a model for the number of diagonals in a polygon. c. s this model exact or approximate? d. Use the model to determine the number of diagonals in a 5-sided polygon. Pentagon?? Hexagon?? Fitting a Quadratic odel to Data 4
5 Chapter 6 9. Shown below is a table of data on the eight major planets in our solar system. For each planet, the period of the orbit is given in Earth years and the average distance from the Sun is in astronomical units (AU). ne AU is approximately the mean distance between Earth and the Sun. Each planet s distance from the Sun is not constant due to its elliptical orbit, so the average distance is given. Planet d = Avg. Distance From the Sun (AU) P = Period of rbit (in Earth years) ercury Venus Earth.. ars Jupiter Saturn Uranus Neptune a. Create a scatterplot of the data. Use average distance d as the independent variable and period P as the dependent variable. b. Fit a quadratic model to these data. Graph the model on the same axes as your scatterplot. Does the model seem like it fits the data? Why or why not? c. Pluto, a dwarf planet, is an average AU from the Sun. t takes Pluto Earth years to orbit the Sun. Does Pluto fit your model? d. Another dwarf planet, Sedna, or 23 VB2, as it was originally designated, orbits the sun at an average distance of 9 AU. Use your model from Part b to predict how long it takes Sedna to orbit the Sun. REVEW n 2, rewrite the equation in vertex form. (Lesson 6 5). y = x 2-4x y = 3x 2-9x y = x 2-4gx + 3g 2 3. Find an equation in standard form for the image of the parabola with equation y = 2x 2 under the translation T 4,.5. (Lessons 6 3, 6 ) Pluto and one of its moons, Charon, are shown above. Sunlight takes about 5 2 hours to reach Pluto. Sunlight reaches Earth in about 8 minutes. 42 Quadratic Functions
6 Lesson a. Find an equation for the line through points (a, b) and (b, a). b. Use a rotation matrix to find an equation for the image of the line from Part a under a rotation of 9 about the origin. (Lessons 4 9, 3-4) 5. The oon is much less massive than Earth, and exerts less gravity. Near the surface of the oon, the acceleration due to ft gravity is about 5.3. Suppose an astronaut drops an object sec2 on the oon from a height of 5 feet. a. How long will it take the object to fall? b. How long would it have taken the object to fall if it was dropped from the same height on Earth? (Lesson 6 4) EXPLRATN 6. Follow these steps to determine the theoretical probabilities that the circles of the CD in the Activity will be in one of the rectangular target areas. a. Find the area of the region in which the center point of the CD can land so that the CD is touching the paper. b. Find the area of the region in which the center point of the CD can land so that circle lands completely in one of the target areas. c. Let a be your answer to Part a, and b your answer to Part b. Calculate _ b a. This number is the probability that the smallest circle is in the target area. d. Repeat Parts b and c for the other two circles. e. Do the probabilities seem to agree with the relative frequencies your class found? Fitting a Quadratic odel to Data 43
NAME: PERIOD: DATE: LAB PARTNERS: LAB #39 ECCENTRICITY OF PLANETARY ORBITS
 NAME: PERIOD: DATE: LAB PARTNERS: LAB #39 ECCENTRICITY OF PLANETARY ORBITS INTRODUCTION Our sun is not exactly in the center of the orbits of the planets, and therefore the planetary orbits are not circular.
NAME: PERIOD: DATE: LAB PARTNERS: LAB #39 ECCENTRICITY OF PLANETARY ORBITS INTRODUCTION Our sun is not exactly in the center of the orbits of the planets, and therefore the planetary orbits are not circular.
Large and small planets
 Large and small planets Journey through the Solar System C 41 time 50 minutes. Preparation For the activity Planets show the planets under each other on the board, as shown in the table. learning outcomes
Large and small planets Journey through the Solar System C 41 time 50 minutes. Preparation For the activity Planets show the planets under each other on the board, as shown in the table. learning outcomes
Patterns in the Solar System (Chapter 18)
 GEOLOGY 306 Laboratory Instructor: TERRY J. BOROUGHS NAME: Patterns in the Solar System (Chapter 18) For this assignment you will require: a calculator, colored pencils, a metric ruler, and meter stick.
GEOLOGY 306 Laboratory Instructor: TERRY J. BOROUGHS NAME: Patterns in the Solar System (Chapter 18) For this assignment you will require: a calculator, colored pencils, a metric ruler, and meter stick.
Patterns in the Solar System (Chapter 18)
 GEOLOGY 306 Laboratory Instructor: TERRY J. BOROUGHS NAME: Patterns in the Solar System (Chapter 18) For this assignment you will require: a calculator, colored pencils, a metric ruler, and meter stick.
GEOLOGY 306 Laboratory Instructor: TERRY J. BOROUGHS NAME: Patterns in the Solar System (Chapter 18) For this assignment you will require: a calculator, colored pencils, a metric ruler, and meter stick.
UNIT 12 ~ More About Regression
 ***SECTION 15.1*** The Regression Model When a scatterplot shows a relationship between a variable x and a y, we can use the fitted to the data to predict y for a given value of x. Now we want to do tests
***SECTION 15.1*** The Regression Model When a scatterplot shows a relationship between a variable x and a y, we can use the fitted to the data to predict y for a given value of x. Now we want to do tests
Yes, inner planets tend to be and outer planets tend to be.
 1. Planet Density Make some general comments about inner and outer planets density Inner Planets Density Outer Planets Density Is there a pattern or a trend in planet density? Yes, inner planets tend to
1. Planet Density Make some general comments about inner and outer planets density Inner Planets Density Outer Planets Density Is there a pattern or a trend in planet density? Yes, inner planets tend to
2275 Speedway, Mail Code C9000 Austin, TX (512) Planet Fun
 Lesson Plan for Grades: Middle School Length of Lesson: 70 min Authored by: UT Environmental Science Institute Date created: 12/03/2016 Subject area/course: Mathematics, Astronomy, and Space Materials:
Lesson Plan for Grades: Middle School Length of Lesson: 70 min Authored by: UT Environmental Science Institute Date created: 12/03/2016 Subject area/course: Mathematics, Astronomy, and Space Materials:
Orbital Paths. the Solar System
 Purpose To compare the lengths of the terrestrial planets orbital paths and revolution times. Process Skills Measure, form a hypothesis, predict, observe, collect data, interpret data, communicate, draw
Purpose To compare the lengths of the terrestrial planets orbital paths and revolution times. Process Skills Measure, form a hypothesis, predict, observe, collect data, interpret data, communicate, draw
Science Skills Station
 Science Skills Station Objective 1. Describe the relationship between the distance from the sun and temperature. 2. Make inferences about how temperature impacted the solar system formation. 3. Explain
Science Skills Station Objective 1. Describe the relationship between the distance from the sun and temperature. 2. Make inferences about how temperature impacted the solar system formation. 3. Explain
3.4 Solving Quadratic Equations by Completing
 www.ck1.org Chapter 3. Quadratic Equations and Quadratic Functions 3.4 Solving Quadratic Equations by Completing the Square Learning objectives Complete the square of a quadratic expression. Solve quadratic
www.ck1.org Chapter 3. Quadratic Equations and Quadratic Functions 3.4 Solving Quadratic Equations by Completing the Square Learning objectives Complete the square of a quadratic expression. Solve quadratic
Unit: Planetary Science
 Orbital Motion Kepler s Laws GETTING AN ACCOUNT: 1) go to www.explorelearning.com 2) click on Enroll in a class (top right hand area of screen). 3) Where it says Enter class Code enter the number: MLTWD2YAZH
Orbital Motion Kepler s Laws GETTING AN ACCOUNT: 1) go to www.explorelearning.com 2) click on Enroll in a class (top right hand area of screen). 3) Where it says Enter class Code enter the number: MLTWD2YAZH
The Size of the Solar System
 The Size of the Solar System Overview Questions: My answers: Become familiar with the scale of the planets vs. their distances. Get an overview of the solar system. Introduction It is easy to flip to the
The Size of the Solar System Overview Questions: My answers: Become familiar with the scale of the planets vs. their distances. Get an overview of the solar system. Introduction It is easy to flip to the
12-1. Parabolas. Vocabulary. What Is a Parabola? Lesson. Definition of Parabola. Mental Math
 Chapter 2 Lesson 2- Parabolas BIG IDEA From the geometric defi nition of a parabola, it can be proved that the graph of the equation y = ax 2 is a parabola. Vocabulary parabola focus, directrix axis of
Chapter 2 Lesson 2- Parabolas BIG IDEA From the geometric defi nition of a parabola, it can be proved that the graph of the equation y = ax 2 is a parabola. Vocabulary parabola focus, directrix axis of
Lesson 1 The Structure of the Solar System
 Lesson 1 Student Labs and Activities Page Launch Lab 8 Content Vocabulary 9 Lesson Outline 10 MiniLab 12 Content Practice A 13 Content Practice B 14 School to Home 15 Key Concept Builders 16 Enrichment
Lesson 1 Student Labs and Activities Page Launch Lab 8 Content Vocabulary 9 Lesson Outline 10 MiniLab 12 Content Practice A 13 Content Practice B 14 School to Home 15 Key Concept Builders 16 Enrichment
Orbital Scale of the Solar System
 Unit 3: Lesson 2 Scale of the Solar System Orbital Scale of the Solar System Subject/Grade Level: Space and the Solar System / Middle School (Grades 6-8) Lesson Objective(s): To understand the scale of
Unit 3: Lesson 2 Scale of the Solar System Orbital Scale of the Solar System Subject/Grade Level: Space and the Solar System / Middle School (Grades 6-8) Lesson Objective(s): To understand the scale of
Question number Answer Notes Marks 1 correctly; (ii) Sun X should be left of the imaginary 5-7 line, reject X placed outside the orbit
 ( a) (i) omet orbit behind Sun completed Dashed or solid correctly; curved line X marked anywhere in grey area; No need to label X as Sun X should be left of the imaginary 5-7 line, reject X placed outside
( a) (i) omet orbit behind Sun completed Dashed or solid correctly; curved line X marked anywhere in grey area; No need to label X as Sun X should be left of the imaginary 5-7 line, reject X placed outside
Investigating the Solar System
 Investigating the Solar System This Workbook belongs to: Our Local Star: The Sun Location in The Solar System Interesting Facts 1. 2. 3. 4. Name of Star: THE SUN 5. Draw and Color your own Sun in the blank
Investigating the Solar System This Workbook belongs to: Our Local Star: The Sun Location in The Solar System Interesting Facts 1. 2. 3. 4. Name of Star: THE SUN 5. Draw and Color your own Sun in the blank
Quest Chapter 14. Think back to circular motion. What keeps something moving around an object instead of to it?
 1 Since the moon is gravitationally attracted to the Earth, why doesn t it simply crash into the Earth? 1.When the moon moves close to the Earth, the air on the Earth repels it. 2. The moon s tangential
1 Since the moon is gravitationally attracted to the Earth, why doesn t it simply crash into the Earth? 1.When the moon moves close to the Earth, the air on the Earth repels it. 2. The moon s tangential
Unit 9: Quadratics Intercept Form
 For Teacher Use Packet Score: Name: Period: Algebra 1 Unit 9: Quadratics Intercept Form Note & Homework Packet Date Topic/Assignment HW Page 9-A Graphing Parabolas in Intercept Form 9-B Solve Quadratic
For Teacher Use Packet Score: Name: Period: Algebra 1 Unit 9: Quadratics Intercept Form Note & Homework Packet Date Topic/Assignment HW Page 9-A Graphing Parabolas in Intercept Form 9-B Solve Quadratic
Motion and Forces Lab
 Name: Motion Newton's 1st Law 1. Define Newton s first law. Motion and Forces Lab Period: 2. What will the truck want to do at rest? Explain. 3. What will the truck want to do when moving? Explain. 4.
Name: Motion Newton's 1st Law 1. Define Newton s first law. Motion and Forces Lab Period: 2. What will the truck want to do at rest? Explain. 3. What will the truck want to do when moving? Explain. 4.
NAME: PERIOD: DATE: ECCENTRICITY OF PLANETARY ORBITS INTRODUCTION
 NAME: PERIOD: DATE: PARTNERS: Lab # ECCENTRICITY OF PLANETARY ORBITS INTRODUCTION INTRODUCTION Our sun is not exactly in the center of the orbits of the planets, and therefore the planetary orbits are
NAME: PERIOD: DATE: PARTNERS: Lab # ECCENTRICITY OF PLANETARY ORBITS INTRODUCTION INTRODUCTION Our sun is not exactly in the center of the orbits of the planets, and therefore the planetary orbits are
The Solar System LEARNING TARGETS. Scientific Language. Name Test Date Hour
 Name Test Date Hour Astronomy#3 - Notebook The Solar System LEARNING TARGETS I can describe the objects that make up our solar system. I can identify the inner and outer planets. I can explain the difference
Name Test Date Hour Astronomy#3 - Notebook The Solar System LEARNING TARGETS I can describe the objects that make up our solar system. I can identify the inner and outer planets. I can explain the difference
Key Points: Learn the relationship between gravitational attractive force, mass and distance. Understand that gravity can act as a centripetal force.
 Lesson 9: Universal Gravitation and Circular Motion Key Points: Learn the relationship between gravitational attractive force, mass and distance. Understand that gravity can act as a centripetal force.
Lesson 9: Universal Gravitation and Circular Motion Key Points: Learn the relationship between gravitational attractive force, mass and distance. Understand that gravity can act as a centripetal force.
9-4. Quadratics and Projectiles. Vocabulary. Equations for the Paths of Projectiles. Activity. Lesson
 Chapter 9 Lesson 9-4 Quadratics and Projectiles Vocabulary force of gravity initial upward velocity initial height BIG IDEA Assuming constant gravity, both the path of a projectile and the height of a
Chapter 9 Lesson 9-4 Quadratics and Projectiles Vocabulary force of gravity initial upward velocity initial height BIG IDEA Assuming constant gravity, both the path of a projectile and the height of a
Astronomy Test Review. 3 rd Grade
 Astronomy Test Review 3 rd Grade Match the vocabulary word to its definition. Outer Planets The path a planet takes around the sun. Inner Planets Orbit Sun The center of our solar system. Small, rocky
Astronomy Test Review 3 rd Grade Match the vocabulary word to its definition. Outer Planets The path a planet takes around the sun. Inner Planets Orbit Sun The center of our solar system. Small, rocky
Chapter 16 Review. 1. What is the solution set of n 2 + 5n 14 = 0? (A) n = {0, 14} (B) n = { 1, 14} (C) n = { 2, 7} (D) n = { 2, 7} (E) n = { 7, 2}
 Chapter 16 Review Directions: For each of the questions below, choose the best answer from the five choices given. 1. What is the solution set of n + 5n 14 = 0? (A) n = {0, 14} (B) n = { 1, 14} (C) n =
Chapter 16 Review Directions: For each of the questions below, choose the best answer from the five choices given. 1. What is the solution set of n + 5n 14 = 0? (A) n = {0, 14} (B) n = { 1, 14} (C) n =
Putting Earth In Its Place
 Teacher Instructions Overview: During this activity, students build a model of our Solar System to gain insight into the relative sizes and distances involved. ives: The student will: create a scale model
Teacher Instructions Overview: During this activity, students build a model of our Solar System to gain insight into the relative sizes and distances involved. ives: The student will: create a scale model
Skills Practice Skills Practice for Lesson 12.1
 Skills Practice Skills Practice for Lesson.1 Name Date Try to Stay Focused Ellipses Centered at the Origin Vocabulary Match each definition to its corresponding term. 1. an equation of the form a. ellipse
Skills Practice Skills Practice for Lesson.1 Name Date Try to Stay Focused Ellipses Centered at the Origin Vocabulary Match each definition to its corresponding term. 1. an equation of the form a. ellipse
The Solar System. Name Test Date Hour
 Name Test Date Hour Astronomy#3 - Notebook The Solar System LEARNING TARGETS I can describe the objects that make up our solar system. I can identify the inner and outer planets. I can explain the difference
Name Test Date Hour Astronomy#3 - Notebook The Solar System LEARNING TARGETS I can describe the objects that make up our solar system. I can identify the inner and outer planets. I can explain the difference
Gravitation & Kepler s Laws
 Gravitation & Kepler s Laws What causes YOU to be pulled down to the surface of the earth? THE EARTH.or more specifically the EARTH S MASS. Anything that has MASS has a gravitational pull towards it. F
Gravitation & Kepler s Laws What causes YOU to be pulled down to the surface of the earth? THE EARTH.or more specifically the EARTH S MASS. Anything that has MASS has a gravitational pull towards it. F
I. Introduction. II. An Introduction to Starry Night NAME: ORBITAL MOTION
 NAME: ORBITAL MOTION What will you learn in this Lab? You will be using some special software to simulate the motion of planets in our Solar System and across the night sky. You will be asked to try and
NAME: ORBITAL MOTION What will you learn in this Lab? You will be using some special software to simulate the motion of planets in our Solar System and across the night sky. You will be asked to try and
The Outer Planets (pages )
 The Outer Planets (pages 720 727) Gas Giants and Pluto (page 721) Key Concept: The first four outer planets Jupiter, Saturn, Uranus, and Neptune are much larger and more massive than Earth, and they do
The Outer Planets (pages 720 727) Gas Giants and Pluto (page 721) Key Concept: The first four outer planets Jupiter, Saturn, Uranus, and Neptune are much larger and more massive than Earth, and they do
Unit 2 Quadratics. Mrs. Valentine Math 3
 Unit 2 Quadratics Mrs. Valentine Math 3 2.1 Factoring and the Quadratic Formula Factoring ax 2 + bx + c when a = ±1 Reverse FOIL method Find factors of c that add up to b. Using the factors, write the
Unit 2 Quadratics Mrs. Valentine Math 3 2.1 Factoring and the Quadratic Formula Factoring ax 2 + bx + c when a = ±1 Reverse FOIL method Find factors of c that add up to b. Using the factors, write the
Developing/Secure Pathway. End of Topic Assessment. Space
 Name: Group: Year 8 Developing/Secure Pathway End of Topic Assessment Space Analysis and Targets No. Score Below/On/Above Target for next Assessment. How will you achieve it? 1 /6 2 /4 3 /6 4 /6 5 /4 6
Name: Group: Year 8 Developing/Secure Pathway End of Topic Assessment Space Analysis and Targets No. Score Below/On/Above Target for next Assessment. How will you achieve it? 1 /6 2 /4 3 /6 4 /6 5 /4 6
5. How did Copernicus s model solve the problem of some planets moving backwards?
 MODELS OF THE SOLAR SYSTEM Reading Guide: Chapter 27.2 (read text pages 691-694) 1k. Recognize the cumulative nature of scientific evidence. 1n. Know that when an observation does not agree with an accepted
MODELS OF THE SOLAR SYSTEM Reading Guide: Chapter 27.2 (read text pages 691-694) 1k. Recognize the cumulative nature of scientific evidence. 1n. Know that when an observation does not agree with an accepted
UNIT 7: Kilo Hōkū - Astronomy & Navigation Teacher s Notes for: The Ordered Solar System
 UNIT 7: Kilo Hōkū - Astronomy & Navigation Teacher s Notes for: The Ordered Solar System Before the students can begin their Tour Through the Solar System they need to have a roadmap. This exercise provides
UNIT 7: Kilo Hōkū - Astronomy & Navigation Teacher s Notes for: The Ordered Solar System Before the students can begin their Tour Through the Solar System they need to have a roadmap. This exercise provides
Unit 5 Gravitation. Newton s Law of Universal Gravitation Kepler s Laws of Planetary Motion
 Unit 5 Gravitation Newton s Law of Universal Gravitation Kepler s Laws of Planetary Motion Into to Gravity Phet Simulation Today: Make sure to collect all data. Finished lab due tomorrow!! Universal Law
Unit 5 Gravitation Newton s Law of Universal Gravitation Kepler s Laws of Planetary Motion Into to Gravity Phet Simulation Today: Make sure to collect all data. Finished lab due tomorrow!! Universal Law
GEMS Student Activity
 Girls in Engineering, Mathematics, and Science GEMS Student Activity HONEY, I SHRUNK THE SOLAR SYSTEM Solar System Predictions How big each of the planets would be if the sun was the size of the fitness
Girls in Engineering, Mathematics, and Science GEMS Student Activity HONEY, I SHRUNK THE SOLAR SYSTEM Solar System Predictions How big each of the planets would be if the sun was the size of the fitness
8 th Grade Intensive Math
 8 th Grade Intensive Math Ready Florida MAFS Student Edition August-September 2014 Lesson 1 Part 1: Introduction Properties of Integer Exponents Develop Skills and Strategies MAFS 8.EE.1.1 In the past,
8 th Grade Intensive Math Ready Florida MAFS Student Edition August-September 2014 Lesson 1 Part 1: Introduction Properties of Integer Exponents Develop Skills and Strategies MAFS 8.EE.1.1 In the past,
A2 HW Imaginary Numbers
 Name: A2 HW Imaginary Numbers Rewrite the following in terms of i and in simplest form: 1) 100 2) 289 3) 15 4) 4 81 5) 5 12 6) -8 72 Rewrite the following as a radical: 7) 12i 8) 20i Solve for x in simplest
Name: A2 HW Imaginary Numbers Rewrite the following in terms of i and in simplest form: 1) 100 2) 289 3) 15 4) 4 81 5) 5 12 6) -8 72 Rewrite the following as a radical: 7) 12i 8) 20i Solve for x in simplest
Drexel-SDP GK-12 ACTIVITY
 Drexel-SDP GK-12 ACTIVITY Subject Area(s): Astronomy, Scale Associated Unit: None Lesson Title: Putting the Solar System in Perspective Header Image 1 Description: Picture of all the planets and their
Drexel-SDP GK-12 ACTIVITY Subject Area(s): Astronomy, Scale Associated Unit: None Lesson Title: Putting the Solar System in Perspective Header Image 1 Description: Picture of all the planets and their
Chapter 2 Polynomial and Rational Functions
 SECTION.1 Linear and Quadratic Functions Chapter Polynomial and Rational Functions Section.1: Linear and Quadratic Functions Linear Functions Quadratic Functions Linear Functions Definition of a Linear
SECTION.1 Linear and Quadratic Functions Chapter Polynomial and Rational Functions Section.1: Linear and Quadratic Functions Linear Functions Quadratic Functions Linear Functions Definition of a Linear
End-of-Chapter Exercises
 End-of-Chapter Exercises Exercises 1 12 are primarily conceptual questions that are designed to see if you have understood the main concepts of the chapter. Treat all balls with mass as point masses. 1.
End-of-Chapter Exercises Exercises 1 12 are primarily conceptual questions that are designed to see if you have understood the main concepts of the chapter. Treat all balls with mass as point masses. 1.
FIFTH MIDTERM -- REVIEW PROBLEMS
 Physics 2210 Fall 2005 Paolo Gondolor FIFTH MIDTERM -- REVIEW PROBLEMS A solution set is available on the course web page in pdf format (no solutions for 27-29). 7 1. Assume that the planet Uranus has
Physics 2210 Fall 2005 Paolo Gondolor FIFTH MIDTERM -- REVIEW PROBLEMS A solution set is available on the course web page in pdf format (no solutions for 27-29). 7 1. Assume that the planet Uranus has
Math is Cool Championships
 Individual Contest Express all answers as reduced fractions unless stated otherwise. Leave answers in terms of π where applicable. Do not round any answers unless stated otherwise. Record all answers on
Individual Contest Express all answers as reduced fractions unless stated otherwise. Leave answers in terms of π where applicable. Do not round any answers unless stated otherwise. Record all answers on
PAP Algebra 2. Unit 4B. Quadratics (Part 2) Name Period
 PAP Algebra Unit 4B Quadratics (Part ) Name Period 1 After Test WS: 4.6 Solve by Factoring PAP Algebra Name Factor. 1. x + 6x + 8. 4x 8x 3 + + 3. x + 7x + 5 4. x 3x 1 + + 5. x + 7x + 6 6. 3x + 10x + 3
PAP Algebra Unit 4B Quadratics (Part ) Name Period 1 After Test WS: 4.6 Solve by Factoring PAP Algebra Name Factor. 1. x + 6x + 8. 4x 8x 3 + + 3. x + 7x + 5 4. x 3x 1 + + 5. x + 7x + 6 6. 3x + 10x + 3
Simulating the Solar System
 Simulating the Solar System Classroom Activity Simulating the Solar System Objectives The primary objective of this activity is to increase the students understanding of the appearance and movements of
Simulating the Solar System Classroom Activity Simulating the Solar System Objectives The primary objective of this activity is to increase the students understanding of the appearance and movements of
Modeling Data with Functions
 Chapter 11 Modeling Data with Functions 11.1 Data Modeling Concepts 1 11.1.1 Conceptual Explanations: Modeling Data with Functions In school, you generally start with a function and work from there to
Chapter 11 Modeling Data with Functions 11.1 Data Modeling Concepts 1 11.1.1 Conceptual Explanations: Modeling Data with Functions In school, you generally start with a function and work from there to
Graphs of Non-Linear Functions
 Classwork Exploratory Challenge 1. Plot a graphical representation of the distance of the ball down a ramp over time. https://www.youtube.com/watch?v=zinszqvhaok Discussion 2. Did everyone s graph have
Classwork Exploratory Challenge 1. Plot a graphical representation of the distance of the ball down a ramp over time. https://www.youtube.com/watch?v=zinszqvhaok Discussion 2. Did everyone s graph have
3 UCM & Gravity Student Physics Regents Date
 Student Physics Regents Date 1. Which diagram best represents the gravitational forces, Fg, between a satellite, S, and Earth? A) B) 4. Gravitational force exists between point objects and separated by
Student Physics Regents Date 1. Which diagram best represents the gravitational forces, Fg, between a satellite, S, and Earth? A) B) 4. Gravitational force exists between point objects and separated by
Learning Outcomes in Focus
 Contextual strand: E&S 3 Learning Outcomes in Focus Students should be able to interpret data to compare the Earth with other planets and moons in the solar system, with respect to properties including
Contextual strand: E&S 3 Learning Outcomes in Focus Students should be able to interpret data to compare the Earth with other planets and moons in the solar system, with respect to properties including
Algebra II Notes Quadratic Functions Unit Applying Quadratic Functions. Math Background
 Applying Quadratic Functions Math Background Previously, you Graphed and solved quadratic functions. Solved literal equations for a given variable. Found the inverse for a linear function. Verified by
Applying Quadratic Functions Math Background Previously, you Graphed and solved quadratic functions. Solved literal equations for a given variable. Found the inverse for a linear function. Verified by
October 19, NOTES Solar System Data Table.notebook. Which page in the ESRT???? million km million. average.
 Celestial Object: Naturally occurring object that exists in space. NOT spacecraft or man-made satellites Which page in the ESRT???? Mean = average Units = million km How can we find this using the Solar
Celestial Object: Naturally occurring object that exists in space. NOT spacecraft or man-made satellites Which page in the ESRT???? Mean = average Units = million km How can we find this using the Solar
KIDS HOPE AUS. THEMED MENTOR HOUR
 KIDS HOPE AUS. THEMED MENTOR HOUR OUTER SPACE SCIENCE Orbiting Planets What better way to learn about space than to make your own Orbiting Planets Solar System! Here's what you'll need... Printed Orbiting
KIDS HOPE AUS. THEMED MENTOR HOUR OUTER SPACE SCIENCE Orbiting Planets What better way to learn about space than to make your own Orbiting Planets Solar System! Here's what you'll need... Printed Orbiting
Cosmology Vocabulary
 Cosmology Vocabulary Vocabulary Words Terrestrial Planets The Sun Gravity Galaxy Lightyear Axis Comets Kuiper Belt Oort Cloud Meteors AU Nebula Solar System Cosmology Universe Coalescence Jovian Planets
Cosmology Vocabulary Vocabulary Words Terrestrial Planets The Sun Gravity Galaxy Lightyear Axis Comets Kuiper Belt Oort Cloud Meteors AU Nebula Solar System Cosmology Universe Coalescence Jovian Planets
Note: The zero function f(x) = 0 is a polynomial function. It has no degree and no leading coefficient. Sep 15 2:51 PM
 2.1 Linear and Quadratic Name: Functions and Modeling Objective: Students will be able to recognize and graph linear and quadratic functions, and use these functions to model situations and solve problems.
2.1 Linear and Quadratic Name: Functions and Modeling Objective: Students will be able to recognize and graph linear and quadratic functions, and use these functions to model situations and solve problems.
Grades K 2 Education Guide
 Written by Kim Small Illustrated by Audio Visual Imagineering Table of Contents Standards Checklist*..3 Lessons Checklist....4 Program Pre- and Post- Survey 5 Lesson 1 The Little Star That Could Vocabulary..9
Written by Kim Small Illustrated by Audio Visual Imagineering Table of Contents Standards Checklist*..3 Lessons Checklist....4 Program Pre- and Post- Survey 5 Lesson 1 The Little Star That Could Vocabulary..9
1998 Harvard/MIT Math Tournament GEOMETRY Answer Sheet
 1998 Harvard/MIT Math Tournament GEOMETRY Answer Sheet Name: School: Grade: 1 7 2 8 3 9 4 10a 5 10b 6 10c TOTAL: GEOMETRY Question One. [3 points] Quadrilateral ALEX, pictured below (but not necessarily
1998 Harvard/MIT Math Tournament GEOMETRY Answer Sheet Name: School: Grade: 1 7 2 8 3 9 4 10a 5 10b 6 10c TOTAL: GEOMETRY Question One. [3 points] Quadrilateral ALEX, pictured below (but not necessarily
ASTROMATH 101: BEGINNING MATHEMATICS IN ASTRONOMY
 Name Partner(s) Section Date ASTROMATH 101: BEGINNING MATHEMATICS IN ASTRONOMY Astronomers deal with very, very large distances, some incredible temperatures, and even really, really small wavelengths.
Name Partner(s) Section Date ASTROMATH 101: BEGINNING MATHEMATICS IN ASTRONOMY Astronomers deal with very, very large distances, some incredible temperatures, and even really, really small wavelengths.
Unit 2 Lesson 1 What Objects Are Part of the Solar System? Copyright Houghton Mifflin Harcourt Publishing Company
 Unit 2 Lesson 1 What Objects Are Part of the Solar System? Florida Benchmarks SC.5.E.5.2 Recognize the major common characteristics of all planets and compare/contrast the properties of inner and outer
Unit 2 Lesson 1 What Objects Are Part of the Solar System? Florida Benchmarks SC.5.E.5.2 Recognize the major common characteristics of all planets and compare/contrast the properties of inner and outer
A. B. C. D. Quadratics Practice Test. Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2. 3/8/2018 Print Assignment
 Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2 C. D. https://my.hrw.com/wwtb2/viewer/printall_vs23.html?umk5tfdnj31tcldd29v4nnzkclztk3w8q6wgvr262aca0a5fsymn1tfv8j1vs4qotwclvofjr8xhs0cldd29v4
Question 1. Select the graph of the quadratic function. g (x ) = 1 3 x 2 C. D. https://my.hrw.com/wwtb2/viewer/printall_vs23.html?umk5tfdnj31tcldd29v4nnzkclztk3w8q6wgvr262aca0a5fsymn1tfv8j1vs4qotwclvofjr8xhs0cldd29v4
A Walk Across the Solar System
 A Walk Across the Solar System Subject Area: Earth Science and Mathematics Grade Level: Grades 4 and 8 Lesson Objective: Duration: Students will help create a model of the solar system in which the scale
A Walk Across the Solar System Subject Area: Earth Science and Mathematics Grade Level: Grades 4 and 8 Lesson Objective: Duration: Students will help create a model of the solar system in which the scale
Radicals and Radical Functions
 0 Radicals and Radical Functions So far we have discussed polynomial and rational expressions and functions. In this chapter, we study algebraic expressions that contain radicals. For example, + 2,, or.
0 Radicals and Radical Functions So far we have discussed polynomial and rational expressions and functions. In this chapter, we study algebraic expressions that contain radicals. For example, + 2,, or.
The Solar System. Grade Level: 4 6
 The Solar System Grade Level: 4 6 Teacher Guidelines pages 1 2 Instructional Pages pages 3 5 Activity Pages pages 6 9 Crossword Puzzle page 10 Answer Key page 11 Classroom Procedure 1. Distribute the Address
The Solar System Grade Level: 4 6 Teacher Guidelines pages 1 2 Instructional Pages pages 3 5 Activity Pages pages 6 9 Crossword Puzzle page 10 Answer Key page 11 Classroom Procedure 1. Distribute the Address
AP Physics QUIZ Gravitation
 AP Physics QUIZ Gravitation Name: 1. If F1 is the magnitude of the force exerted by the Earth on a satellite in orbit about the Earth and F2 is the magnitude of the force exerted by the satellite on the
AP Physics QUIZ Gravitation Name: 1. If F1 is the magnitude of the force exerted by the Earth on a satellite in orbit about the Earth and F2 is the magnitude of the force exerted by the satellite on the
Model the Movements of the Planets
 In the Curriculum Starship Gaia Model the Movements of the Planets By Bob Albrecht and Paul Davis Subject: Science, math Audience: Teachers, teacher educators Grade Level: 5 10 (10 15) Technology: Internet/Web
In the Curriculum Starship Gaia Model the Movements of the Planets By Bob Albrecht and Paul Davis Subject: Science, math Audience: Teachers, teacher educators Grade Level: 5 10 (10 15) Technology: Internet/Web
Name Typical Applications in Algebra 1
 1. Graph the information below as a scatter plot. Turn your graph paper to landscape. Use 1960 as year 0. Let each square along the x-axis represent one year. Let each square on the y axis represent 100
1. Graph the information below as a scatter plot. Turn your graph paper to landscape. Use 1960 as year 0. Let each square along the x-axis represent one year. Let each square on the y axis represent 100
Diagnostic Test. Month Balance Change February $ March $ $13.10 April $1, $ May $ $ June $ $163.
 Diagnostic Test Select the best answer for questions 1 60. Fill in the correct bubble on your answer sheet. 1. The chart shows the balance in Neil s savings account and the change from the previous month.
Diagnostic Test Select the best answer for questions 1 60. Fill in the correct bubble on your answer sheet. 1. The chart shows the balance in Neil s savings account and the change from the previous month.
Planet Time to orbit the Sun (Earth years) Distance from the Sun (million km) Mercury Venus Earth Mars 2.
 The inner planets Burt and Duncan investigated the inner planets of our solar system. Burt compiled some information about the four inner planets. Planet Time to orbit the Sun (Earth years) Distance from
The inner planets Burt and Duncan investigated the inner planets of our solar system. Burt compiled some information about the four inner planets. Planet Time to orbit the Sun (Earth years) Distance from
11-8. Modeling Data with Polynomials. Lesson
 Chapter 11 Lesson 11-8 Modeling Data with Polynomials BIG IDEA Given n points in the plane, no two of which have the same fi rst coordinate, it is generally possible to fi nd an equation for a polynomial
Chapter 11 Lesson 11-8 Modeling Data with Polynomials BIG IDEA Given n points in the plane, no two of which have the same fi rst coordinate, it is generally possible to fi nd an equation for a polynomial
Exploring Our Solar System
 Exploring Our Solar System Our Solar System What do you think? Read the two statements below and decide whether you agree or disagree with them. Place an A in the Before column if you agree with the statement
Exploring Our Solar System Our Solar System What do you think? Read the two statements below and decide whether you agree or disagree with them. Place an A in the Before column if you agree with the statement
Physics12 Exam Review Questions
 Physics12 Exam Review Questions 1) You are making a circular turn in your car on a horizontal road when you hit a big patch of ice, causing the force of friction between the tires and the road to become
Physics12 Exam Review Questions 1) You are making a circular turn in your car on a horizontal road when you hit a big patch of ice, causing the force of friction between the tires and the road to become
Circle Theorems. Angles at the circumference are equal. The angle in a semi-circle is x The angle at the centre. Cyclic Quadrilateral
 The angle in a semi-circle is 90 0 Angles at the circumference are equal. A B They must come from the same arc. Look out for a diameter. 2x Cyclic Quadrilateral Opposite angles add up to 180 0 A They must
The angle in a semi-circle is 90 0 Angles at the circumference are equal. A B They must come from the same arc. Look out for a diameter. 2x Cyclic Quadrilateral Opposite angles add up to 180 0 A They must
Unit 6 Lesson 4 What Are the Planets in Our Solar System? Copyright Houghton Mifflin Harcourt Publishing Company
 Unit 6 Lesson 4 What Are the Planets in Our Solar System? What other objects are near Earth in this part of space? Earth and millions of other objects make up our solar system. In Our Corner of Space A
Unit 6 Lesson 4 What Are the Planets in Our Solar System? What other objects are near Earth in this part of space? Earth and millions of other objects make up our solar system. In Our Corner of Space A
VISUAL PHYSICS ONLINE
 VISUAL PHYSICS ONLINE PRACTICAL ACTIVITY HOW DO THE PANETS MOVE? One of the most important questions historically in Physics was how the planets move. Many historians consider the field of Physics to date
VISUAL PHYSICS ONLINE PRACTICAL ACTIVITY HOW DO THE PANETS MOVE? One of the most important questions historically in Physics was how the planets move. Many historians consider the field of Physics to date
TAKEN FROM HORIZONS 7TH EDITION CHAPTER 1 TUTORIAL QUIZ
 TAKEN FROM HORIZONS 7TH EDITION CHAPTER 1 TUTORIAL QUIZ 1. If the solar system is scaled down so that the Sun is represented by a basketball, a. a ping-pong ball located 500 feet away would properly represent
TAKEN FROM HORIZONS 7TH EDITION CHAPTER 1 TUTORIAL QUIZ 1. If the solar system is scaled down so that the Sun is represented by a basketball, a. a ping-pong ball located 500 feet away would properly represent
Which number listed below belongs to the interval 0,7; 0,8? c) 6 7. a) 3 5. b) 7 9. d) 8 9
 Problem 1 Which number listed below belongs to the interval 0,7; 0,8? a) 3 5 b) 7 9 c) 6 7 d) 8 9 2 Problem 2 What is the greatest common divisor of the numbers 3 2 3 5 and 2 3 3 5? a) 6 b) 15 c) 30 d)
Problem 1 Which number listed below belongs to the interval 0,7; 0,8? a) 3 5 b) 7 9 c) 6 7 d) 8 9 2 Problem 2 What is the greatest common divisor of the numbers 3 2 3 5 and 2 3 3 5? a) 6 b) 15 c) 30 d)
9J Gravity and Space ILU
 9J Gravity and Space ILU Level 3 4 5 6 7 no. of qu.s 0 1 3 5 0. Level 4 1. Lisa drew a picture of herself standing at four different positions on the Earth, A D B C not to scale (a) (i) Draw an arrow at
9J Gravity and Space ILU Level 3 4 5 6 7 no. of qu.s 0 1 3 5 0. Level 4 1. Lisa drew a picture of herself standing at four different positions on the Earth, A D B C not to scale (a) (i) Draw an arrow at
CHAPTER 11. We continue to Learn a lot about the Solar System by using Space Exploration
 CHAPTER 11 We continue to Learn a lot about the Solar System by using Space Exploration Section 11.1 The Sun page 390 -Average sized star -Millions of km away -300,000 more massive then Earth, 99% of all
CHAPTER 11 We continue to Learn a lot about the Solar System by using Space Exploration Section 11.1 The Sun page 390 -Average sized star -Millions of km away -300,000 more massive then Earth, 99% of all
AdvAlg6.4GraphingQuadratics.notebook. March 07, Newton s Formula h(t) = 1 gt 2 + v o t + h o 2. time. initial upward velocity
 Notes Lesson 6 4 Applications of Quadratic Functions Newton s Formula h(t) = 1 gt 2 + v o t + h o 2 Height of object time Constant (accel. due to gravity) *32 ft/sec 2 *9.8 m/sec 2 **MEMORIZE THESE** initial
Notes Lesson 6 4 Applications of Quadratic Functions Newton s Formula h(t) = 1 gt 2 + v o t + h o 2 Height of object time Constant (accel. due to gravity) *32 ft/sec 2 *9.8 m/sec 2 **MEMORIZE THESE** initial
Lesson 2 The Inner Planets
 Lesson 2 Student Labs and Activities Page Launch Lab 25 Content Vocabulary 26 Lesson Outline 27 MiniLab 29 Content Practice A 30 Content Practice B 31 School to Home 32 Key Concept Builders 33 Enrichment
Lesson 2 Student Labs and Activities Page Launch Lab 25 Content Vocabulary 26 Lesson Outline 27 MiniLab 29 Content Practice A 30 Content Practice B 31 School to Home 32 Key Concept Builders 33 Enrichment
1 of 5 5/2/2015 5:50 PM
 1 of 5 5/2/2015 5:50 PM 1. A comet that has a semi-major axis of 100 AU must have a period of about 10 years. 20 years. 100 years. 1000 years. 2. Astronomers believe chondrite meteorites are about 4.6
1 of 5 5/2/2015 5:50 PM 1. A comet that has a semi-major axis of 100 AU must have a period of about 10 years. 20 years. 100 years. 1000 years. 2. Astronomers believe chondrite meteorites are about 4.6
Unit 3, Lesson 1: How Well Can You Measure?
 Unit 3, Lesson 1: How Well Can You Measure? 1. Estimate the side length of a square that has a 9 cm long diagonal. 2. Select all quantities that are proportional to the diagonal length of a square. A.
Unit 3, Lesson 1: How Well Can You Measure? 1. Estimate the side length of a square that has a 9 cm long diagonal. 2. Select all quantities that are proportional to the diagonal length of a square. A.
CA Physical Science Benchmark Test 4. 1 A rocket accelerates from the launch pad. The forces on the rocket are
 Physical Science enchmark Test 4 Name: ate: 1 rocket accelerates from the launch pad. The forces on the rocket are action forces. balanced. reaction forces. unbalanced. 2 What force(s) act(s) on a rocket
Physical Science enchmark Test 4 Name: ate: 1 rocket accelerates from the launch pad. The forces on the rocket are action forces. balanced. reaction forces. unbalanced. 2 What force(s) act(s) on a rocket
Chapter 13: universal gravitation
 Chapter 13: universal gravitation Newton s Law of Gravitation Weight Gravitational Potential Energy The Motion of Satellites Kepler s Laws and the Motion of Planets Spherical Mass Distributions Apparent
Chapter 13: universal gravitation Newton s Law of Gravitation Weight Gravitational Potential Energy The Motion of Satellites Kepler s Laws and the Motion of Planets Spherical Mass Distributions Apparent
Chapter 14 Satellite Motion
 1 Academic Physics Mechanics Chapter 14 Satellite Motion The Mechanical Universe Kepler's Three Laws (Episode 21) The Kepler Problem (Episode 22) Energy and Eccentricity (Episode 23) Navigating in Space
1 Academic Physics Mechanics Chapter 14 Satellite Motion The Mechanical Universe Kepler's Three Laws (Episode 21) The Kepler Problem (Episode 22) Energy and Eccentricity (Episode 23) Navigating in Space
Name Class Date. For each pair of terms, explain how the meanings of the terms differ.
 Skills Worksheet Chapter Review USING KEY TERMS For each pair of terms, explain how the meanings of the terms differ. 1. terrestrial planet and gas giant 2. asteroid and comet 3. meteor and meteorite Complete
Skills Worksheet Chapter Review USING KEY TERMS For each pair of terms, explain how the meanings of the terms differ. 1. terrestrial planet and gas giant 2. asteroid and comet 3. meteor and meteorite Complete
The Sun s center is much hotter than the surface. The Sun looks large and bright in the sky. Other stars look much smaller.
 The Sun A star is a huge ball of hot, glowing gases. The Sun is a star. The width of the Sun is equal to the width of 100 Earths placed side by side. The Sun is extremely hot. The surface of the Sun has
The Sun A star is a huge ball of hot, glowing gases. The Sun is a star. The width of the Sun is equal to the width of 100 Earths placed side by side. The Sun is extremely hot. The surface of the Sun has
https://njctl.org/courses/science/ap-physics-c-mechanics/attachments/summerassignment-3/
 AP Physics C Summer Assignment 2017 1. Complete the problem set that is online, entitled, AP C Physics C Summer Assignment 2017. I also gave you a copy of the problem set. You may work in groups as a matter
AP Physics C Summer Assignment 2017 1. Complete the problem set that is online, entitled, AP C Physics C Summer Assignment 2017. I also gave you a copy of the problem set. You may work in groups as a matter
Completing the Square
 5-7 Completing the Square TEKS FOCUS TEKS (4)(F) Solve quadratic and square root equations. TEKS (1)(A) Apply mathematics to problems arising in everyday life, society, and the workplace. Additional TEKS
5-7 Completing the Square TEKS FOCUS TEKS (4)(F) Solve quadratic and square root equations. TEKS (1)(A) Apply mathematics to problems arising in everyday life, society, and the workplace. Additional TEKS
Learning Targets: Standard Form: Quadratic Function. Parabola. Vertex Max/Min. x-coordinate of vertex Axis of symmetry. y-intercept.
 Name: Hour: Algebra A Lesson:.1 Graphing Quadratic Functions Learning Targets: Term Picture/Formula In your own words: Quadratic Function Standard Form: Parabola Verte Ma/Min -coordinate of verte Ais of
Name: Hour: Algebra A Lesson:.1 Graphing Quadratic Functions Learning Targets: Term Picture/Formula In your own words: Quadratic Function Standard Form: Parabola Verte Ma/Min -coordinate of verte Ais of
2 P a g e. Essential Questions:
 NC Math 1 Unit 5 Quadratic Functions Main Concepts Study Guide & Vocabulary Classifying, Adding, & Subtracting Polynomials Multiplying Polynomials Factoring Polynomials Review of Multiplying and Factoring
NC Math 1 Unit 5 Quadratic Functions Main Concepts Study Guide & Vocabulary Classifying, Adding, & Subtracting Polynomials Multiplying Polynomials Factoring Polynomials Review of Multiplying and Factoring
Chapter 15 & 16 Science Review (PATTERNS IN THE SKY, OUR SOLAR SYSTEM)
 Chapter 15 & 16 Science Review (PATTERNS IN THE SKY, OUR SOLAR SYSTEM) The Milky Way the galaxy that contains our solar system Our solar system is a speck in the Milky Way galaxy Pluto is now considered
Chapter 15 & 16 Science Review (PATTERNS IN THE SKY, OUR SOLAR SYSTEM) The Milky Way the galaxy that contains our solar system Our solar system is a speck in the Milky Way galaxy Pluto is now considered
9.2 - Our Solar System
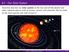 9.2 - Our Solar System Scientists describe our solar system as the Sun and all the planets and other celestial objects, such as moons, comets, and asteroids, that are held by the Sun s gravity and orbit
9.2 - Our Solar System Scientists describe our solar system as the Sun and all the planets and other celestial objects, such as moons, comets, and asteroids, that are held by the Sun s gravity and orbit
2. Very generally, describe how the Milky Way Galaxy formed. (Words or labeled picture)
 Potter Name: Date: Hour: Score: /11 Learning Check 2.1 LT 2.1 Galaxy Formation: I am able to describe the formation of the Milky Way Galaxy and our solar system and model earth s position in each. 1. Label
Potter Name: Date: Hour: Score: /11 Learning Check 2.1 LT 2.1 Galaxy Formation: I am able to describe the formation of the Milky Way Galaxy and our solar system and model earth s position in each. 1. Label
VOYAGE OF DISCOVERY TEACHER PAGE
 Background This activity has two parts. The activity has two parts. Part I looks at the sizes of the planets and takes place in the classroom. Students predict the size of Earth and Jupiter and find foods
Background This activity has two parts. The activity has two parts. Part I looks at the sizes of the planets and takes place in the classroom. Students predict the size of Earth and Jupiter and find foods
learning outcomes end product a model showing a solar eclipse
 Solar eclipse Looking at the stars * 53 time 50 minutes learning outcomes To: know that during a solar eclipse the Moon comes between the Sun and the Earth know that a solar eclipse does not take place
Solar eclipse Looking at the stars * 53 time 50 minutes learning outcomes To: know that during a solar eclipse the Moon comes between the Sun and the Earth know that a solar eclipse does not take place
NASA Explorer Schools Pre-Algebra Unit Lesson 3 Student Workbook. Solar System Math. Comparing Planetary Travel Distances
 National Aeronautics and Space Administration NASA Explorer Schools Pre-Algebra Unit Lesson 3 Student Workbook Solar System Math Comparing Planetary Travel Distances How far can humans travel in our solar
National Aeronautics and Space Administration NASA Explorer Schools Pre-Algebra Unit Lesson 3 Student Workbook Solar System Math Comparing Planetary Travel Distances How far can humans travel in our solar
5. Use the graph below to determine the displacement of the object at the end of the first seven seconds.
 Name: Hour: 1. The slope of the tangent on a position-time graph equals the: Sem 1 Exam Review Advanced Physics 2015-2016 2. The area under the curve on a velocity-time graph equals the: 3. The graph below
Name: Hour: 1. The slope of the tangent on a position-time graph equals the: Sem 1 Exam Review Advanced Physics 2015-2016 2. The area under the curve on a velocity-time graph equals the: 3. The graph below
3.2 Quadratic Equations by Graphing
 www.ck12.org Chapter 3. Quadratic Equations and Quadratic Functions 3.2 Quadratic Equations by Graphing Learning Objectives Identify the number of solutions of quadratic equations. Solve quadratic equations
www.ck12.org Chapter 3. Quadratic Equations and Quadratic Functions 3.2 Quadratic Equations by Graphing Learning Objectives Identify the number of solutions of quadratic equations. Solve quadratic equations
