UNIVERZITET U KRAGUJEVCU PRIRODNO-MATEMATIQKI FAKULTET. Marjan Mateji. Doktorska disertacija. Kragujevac, 2016.
|
|
|
- Angel McBride
- 5 years ago
- Views:
Transcription
1 UNIVERZITET U KRAGUJEVCU PRIRODNO-MATEMATIQKI FAKULTET Marjan Mateji RAZVOJ RACIONALNIH ALGORITAMA ZA KONSTRUKCIJU ORTOGONALNIH POLINOMA JEDNE PROMEN IVE Doktorska disertacija Kragujevac, 2016.
2 IDENTIFIKACIONA STRANICA DOKTORSKE DISERTACIJE I. Autor Ime i prezime: Marjan Mateji Datum i mesto roea: godine, Nix Sadaxe zaposlee: asistent na Elektronskom fakultetu u Nixu II. Doktorska disertacija Naslov: Razvoj racionalnih algoritama za konstrukciju ortogonalnih polinoma jedne promen ive Broj stranica: 92 Broj slika: 14 Broj bibliografskih podataka: 71 Ustanova i mesto gde je rad izraen: Prirodno-matematiqki fakultet, Univerzitet u Kragujevcu, Kragujevac Nauqna oblast (UDK): Matematika (Numeriqka analiza, UDK 51) Mentor: dr Gradimir V. Milovanovi, redovni qlan SANU III. Ocena i odbrana Datum prijave teme: godine Broj odluke i datum prihvataa doktorske disertacije: Komisija za ocenu podobnosti teme i kandidata: 1. dr Gradimir V. Milovanovi, redovni qlan SANU 2. dr Aleksandar S. Cvetkovi, redovni profesor Maxinskog fakulteta u Beogradu 3. dr Marija P. Stani, vanredni profesor Prirodno-matematiqkog fakulteta u Kragujevcu 4. dr Tatjana V. Tomovi, docent Prirodno-matematiqkog fakulteta u Kragujevcu Komisija za ocenu i odbranu doktorske disertacije: 1. dr Aleksandar S. Cvetkovi, redovni profesor Maxinskog fakulteta u Beogradu 2. dr Marija P. Stani, vanredni profesor Prirodno-matematiqkog fakulteta u Kragujevcu 3. dr Tatjana V. Tomovi, docent Prirodno-matematiqkog fakulteta u Kragujevcu Datum odbrane disertacije:
3 Sadraj 1 Osnovna teorija ortogonalnih polinoma na realnoj pravoj Uvod Troqlana rekurentna relacija Nule ortogonalnih polinoma Qebixev evi polinomi Ekstremalna svojstva ortogonalnih polinoma Metodi konstrukcije ortogonalnih polinoma Qebixev ev algoritam Stiltjesova procedura Modifikacioni algoritmi Transformacije teinske funkcije Racionalni algoritam za kvadratnu Kristofelovu modifikaciju mere Modifikacija kvadratnim faktorom Algoritam Primene algoritma Polinomi ortogonalni u odnosu na modifikovane Qebixev eve mere Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru prve vrste i
4 Sadraj 3.2 Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru druge vrste Linearni delioci Linearni faktori Primene u kvadraturnim procesima i L 2 -aproksimaciji Kvadraturne formule O pozitivnoj definitnosti nekih linearnih funkcionela Pomoni rezultati Dokaz glavnog rezultata Standardna L 2 -aproksimacija Polinomska L 2 -aproksimacija sa ograniqeima Literatura 87 ii
5 Lista slika 1.1 Grafici funkcija y = T n (x) za n = 0, 1, 2, 3, 4, 5 i 1 x Grafici funkcija y = U n (x) za n = 0, 1, 2, 3, 4, 5 i 1 x Grafici teinskih funkcija x ŵ(x) i x w (x) na intervalu [ 1, 1] Grafici teinskih funkcija x w(x), x w(x), x w(x) i x ŵ(x) na intervalu [ 1, 1] Grafici polinoma p n (x), n = 0, 1, 2, 3, Grafici polinoma r n (x), n = 0, 1, 2, 3, Grafici polinoma p 3,2 k (x), k = 0, 1, 2, 3, 4, Grafici polinoma p 2,4 k (x), k = 0, 1, 2, 3, 4, Grafik racionalnog dela teine u (3.6) Grafik teinske funkcije x w 3,2 (x) Grafici funkcija x w 2,4 (x), x f(x) (levo) i x f(x)w 2,4 (x) (desno) Relativna grexka pri aproksimaciji funkcije x f(x) polinomom x p(x) Grafici funkcije x f(x) i polinoma x a+(x 2 1/2)q 0 p 0 (x) i relativna grexka Relativna grexka pri aproksimaciji funkcije x f(x) polinomom x r(x) iii
6 Lista tabela 4.1 Qvorovi i teinski koeficijenti u kvadraturnoj formuli (4.5) za m = 10, n = 3 i s = Apsolutna grexka kvadraturnih formula (4.7) za n = 2, s = 4 i m = 5(5) Qvorovi i teinski koeficijenti u kvadraturnoj formuli (4.7) za n = 2, s = 4 i m = 5(5) Numeriqki rezultati u primerima i iv
7 Predgovor Predgovor Although this may seem a paradox, all exact science is dominated by the idea of approximation. "Moe se qiniti paradoksalno xto svom egzaktnom naukom dominira ideja aproksimacije." Bertrand Rasel 1 Predmet ove disertacije su ortogonalni polinomi na realnoj pravoj. Polinomi jedne promen ive u velikoj meri proimaju klasiqnu numeriqku analizu. Polinomska aproksimacija jedan je od najprirodnijih pristupa rekonstrukciji funkcija na osnovu konaqnog skupa informacija. U xirokoj paleti numeriqkih metoda polinomi imaju ulogu pomonih funkcija. Karakteristiqni polinomi uspostav aju mostove matematike sa ineerskim disciplinama. Jox neke tradicionalne oblasti intenzivne primene jesu ortogonalni razvoji (generalizovani Furijeovi redovi), numeriqka integracija (kvadraturne formule) i razliqite grane fizike i mehanike. Nexto mae poznata je veza ortogonalnih polinoma sa Padeovom aproksimacijom. Novija, savremena istraivaa iz teorije verovatnoe i stohastiqkih procesa, teorije grafova, kodiraa, itd., takoe se oslaaju na znaa iz oblasti ortogonalnih polinoma. Klasiqni ortogonalni polinomi, kao xto su Leandrovi, Lagerovi, Ermitovi i drugi, imaju xiroku primenu u svim oblastima nauke i in- eerstva. Dok je teorija klasiqnih ortogonalnih polinoma razvijena u dobroj meri, xira klasa polinoma i da e ostaje nepoznanica u vezi raqunskih aspekata kao i primene. Polinomi ortogonalni u odnosu na nestandardne teine i mere imaju mnogo mae primeenu primenu. Razlog ovome je u brojnim texkoama koje prate ihovo numeriqko generisae. 1 Bertrand Russell ( ), britanski matematiqar i filozof. v
8 Predgovor Konstrukcija ortogonalnih polinoma je priliqno jednostavna kada je eksplicitno poznata troqlana rekurentna relacija. Utvrivae nepoznatih qlanova rekurentne relacije je samo po sebi veoma teak problem. Interesantno je da je emu u literaturi pridavano malo pa- e, naroqito u razdob u pre kompjutera. Najverovatnije da je tome doprinelo postojae teorijskog rexea, datog formulom preko Henkelovih determinanata. Ovakav pristup nosi preteranu raqunsku cenu i veliku numeriqku nestabilnost prilikom konstrukcije rekurzivnih koeficijenata. Posledih qetvrt veka znaqajan napredak postignut je na ovom planu, kako u metodama vezanim za izraqunavaa neklasiqnih ortogonalnih polinoma tako i u ihovoj novoj primeni. Numeriqko izraqunavae je veoma vaan alat prilikom testiraa ideja i hipoteza u mnogim istraivaima. Primarni ci eksperimentalne matematike je unapreee teorijskog znaa. Eksperimentalni rezultati mogu dati smernice, da podstaknu ili ohrabre da e izuqavae. U oblasti istraivaa neklasiqnih ortogonalnih polinoma, eksperimentalna istraivaa su u velikoj meri olakxana postojaem specijalizovanih programskih paketa razvijanih u Matlab i Wolfram Mathematica softverima. Da i razvoj konstruktivne teorije ortogonalnih polinoma je u qvrstoj sprezi sa auriraem i unapreeem ovakvih specijalizovanih paketa. Iz svih navedenih razloga izuqavae osobina ortogonalnih polinoma qini se prikladno, u najmau ruku. Praksa pokazuje da rexavae problema konstrukcije neklasiqnih ortogonalnih polinoma dovodi vrlo brzo do ihove primene, qak i na nestandardne naqine. Da i razvoj konstruktivne teorije i istraivae raqunskih i softverskih aspekata neklasiqnih sistema ortogonalnih polinoma, nesumivo e unaprediti ihovu primenu. Takoe, nije previxe oqekivati ni zaqetke nekih potpuno novih nauqnih disciplina proizaxlih iz sliqnih istraivaa. Ova disertacija rezultat je vixegodixeg izuqavaa konstruktivne teorije neklasiqnih ortogonalnih polinoma voena mentorom akademikom Gradimirom Milovanoviem i uz blisku saradu sa profesorom Aleksandrom Cvetkoviem. Disertacija je organizovana u qetiri glave. Prva glava je preglednog karaktera i sastoji se od qetiri poglav a. U oj je razmatran opxti koncept polinoma ortogonalnih u odnosu na linearnu funkcionelu definisanu na prostoru algebarskih polinoma. Dat je kratak pregled osnovnih rezultata teorije ortogonalnih polinoma na realnoj pravoj. Kako se znaqajan deo disertacije bavi izuqavaem polinoma ortogonalnih u odnosu na modifikovane Qebixev eve mere, to je posebno poglav e prve glave posveeno Qebixev evim polinomima. vi
9 Predgovor Na kraju ove glave dati su osnovni metodi za konstrukciju ortogonalnih polinoma. Druga glava posveena je modifikacionim algoritmima. Prostor je dat rezultatima rada na problemu uticaja pojedinih modifikacija teinske funkcije na koeficijente troqlane rekurentne relacije. Razvijen je originalni racionalni algoritam za kvadratnu Kristofelovu modifikaciju teine i primeen je na generisae polinoma ortogonalnih u odnosu na neke modifikovane mere. Trea glava bavi se isk uqivo izuqavaem polinoma ortogonalnih u odnosu na modifikovane Qebixev eve mere prve i druge vrste. Za ove neklasiqne teine kao originalni rezultat dobijeni su koeficijenti troqlane rekurentne relacije u analitiqki zatvorenom obliku. U qetvrtoj glavi dat je pregled osnovnih rezultata iz kvadraturnih procesa, budui da je to oblast direktne primene teorije ortogonalnih polinoma. U drugom poglav u qetvrte glave ispitivani su potrebni i dovo ni uslovi pozitivne definitnosti nekih linearnih funkcionela definisanih na skupu algebarskih polinoma. Posmatrana je i standardna L 2 -aproksimacija. Primene modifikacionog algoritma predstav enog u drugoj glavi na polinomsku L 2 -aproksimaciju sa ograniqeima, nalaze se na kraju. Numerisae svih definicija, teorema, lema, primera, slika i tabela izvrxeno je prema rednom broju poglav a u kojem se jav aju i redosledu jav aa u okviru samog poglav a. Spisak korixene ili citirane literature, koji se sastoji od 71 reference, dat je na kraju disertacije. Ovom prilikom posebno elim da se zahvalim svom mentoru, akademiku Gradimiru Milovanoviu, na pomoi, liqnom angaovau i stalnom struqnom nadzoru. Takoe, veliku zahvalnost dugujem dr Aleksandru Cvetkoviu, jer je sarada sa im bila od presudne vanosti za nastanak ove disertacije. Na kraju zahva ujem se kolegama sa Katedre za matematiku Elektronskog fakulteta u Nixu na nesebiqnoj pomoi, razumevau i strp eu. Nix, jun Marjan Mateji vii
10 Glava 1 Osnovna teorija ortogonalnih polinoma na realnoj pravoj 1.1 Uvod Izuqavae ortogonalnih polinoma, ihova konstrukcija, analiza i primena, predstav a jednu od klasiqnih grana primeene matematike. Naznake teorije moemo pratiti sve do Leandra 1, u egovom prouqavau kretaa nebeskih tela. Formalna teorija poqie analizom Stiltjesovih 2 verinih razlomaka. Svoj doprinos oblasti dali su mnogi veliki matematiqari, od Bernulija 3 do Erdexa 4. Kao i sve specijalne funkcije, ortogonalni polinomi su i svojim poreklom i razvojem tesno vezani za praktiqnu primenu. Zbog toga ih predstav amo kao moan alat visoke tehnologije. Znaqaj istraivaa ove klasiqne teme ogleda se u impresivnom broju implikacija i primena tih istraivaa kako u primeenoj matematici tako i u mnogim drugim oblastima nauke. Spomenuemo tek neke znaqajnije: teorija operatora, numeriqka analiza, verini razlomci i teorija brojeva, kombinatorika, teorija grafova, stohastiqki procesi, statistika, teorija integralnih i diferencijalnih jednaqina, dinamiqki sistemi, teorija podataka, kompjuterska tomografija, elektrostatika, elektrotehnika, obrada digitalnih signala, teorija filtara, kvantna mehanika, nuklearna fizika, fizika qvrstog staa, teorijska hemija i dr. 1 Adrien Marie Legendre ( ), francuski matematiqar i fiziqar. 2 Thomas Joannes Stieltjes ( ), danski matematiqar. 3 Jacob Bernoulli ( ), xvajcarski matematiqar. 4 Pál Erdős ( ), matematiqar maarskog porekla. 1
11 1.1. Uvod Upravo xiroka primena ortogonalnih polinoma razlog je stalnog interesovaa istraivaqa za ovu oblast. Razvoj postojeih i novih nauqnih oblasti veoma qesto je u tesnoj sprezi sa xireem teorijskog znaa iz oblasti ortogonalnih polinoma. U novije vreme poseban podsticaj istraivaima primeene matematike, uopxte, dao je razvoj monih kompjuterskih sistema sposobnih za izvoee simboliqkih izraqunavaa (M apple, M athematica i sl.). To u izuzetnoj meri smauje neophodnost rada papir-olovka, te su moderni kompjuterski sistemi postali nezamen ivi u savremenim nauqnim istraivaima. Teorija ortogonalnih polinoma razvija se u dva pravca: algebarski i analitiqki. Svaki od dva aspekta teorije tiqe se odgovarajuih karakteristika ortogonalnih polinoma razvijanih u okviru odreene discipline, algebre ili analize. Najvei broj generalnih rezultata teorije ortogonalnih polinoma pripada dvema oblastima: ortogonalni polinomi na realnoj pravoj i na jediniqnom krugu K[0, 1] = {z z = 1}. Xiroka paleta rezultata posledica je intenzivne primene, naroqito klasiqnih ortogonalnih polinoma, kao i specijalnih pogodnih osobina samih skupova R i K[0, 1]. U disertaciji baviemo se prostorom polinoma realne promen ive x nad po em kompleksnih brojeva, u oznaci (P, C). Sa P n oznaqavamo skup svih algebarskih polinoma stepena ne veeg od n nad po em kompleksnih brojeva C, a odgovarajui linearan prostor sa (P n, C). Analogno (P, R) i (P n, R) oznaqavae odgovarajue linearne prostore algebarskih polinoma nad po em realnih brojeva R. Oznaka P n rezervisana je za skup moniqnih polinoma. Definicija Neka je m n, n N 0, niz kompleksnih brojeva i neka je L funkcija sa kompleksnim vrednostima definisana na skupu svih algebarskih polinoma sa L (x n ) = m n, n N 0, L (α 1 P 1 (x) + α 2 P 2 (x)) = α 1 L(P 1 (x)) + α 2 L(P 2 (x)) za sve kompleksne brojeve α 1, α 2 i sve polinome P 1 (x), P 2 (x). Tada se L zove moment-funkcionela definisana nizom momenata m n, n N 0. Broj m n je moment reda n. Linearna funkcionela L jedinstveno je odreena nizom momenata m k, k N 0. Za proizvo ni polinom P (x) = n k=0 a kx k imamo L(P (x)) = 2 n a k m k. k=0
12 1.1. Uvod Definicija Neka je data linearna funkcionela L : P C. Niz polinoma P k, k N 0, je niz polinoma ortogonalnih u odnosu na L ako i samo ako vai: (1) polinom P k, k N 0, je stepena k, (2) L(P k P l ) = M l δ kl, M l 0, k, l N 0, gde je δ kl Kronekerova delta. Niz polinoma P k, k N 0, je ortonormiran ako je polinom P k, k N 0, stepena k i vai L(P k P l ) = δ kl, k, l N 0. U nastavku dajemo pregled poznatih, bitnijih tvrea za karakterizaciju niza ortogonalnih polinoma (videti [11] npr.). Navedena tvrea koristiemo i u teorijskim izvoeima datim u narednim poglav ima disertacije. Teorema Neka je L moment-funkcionela i P k, k N 0, niz polinoma. Tada su sledea tvrea ekvivalentna: 1 niz P k, k N 0, je niz polinoma ortogonalnih u odnosu na L; 2 L(πP k ) = 0 za svaki polinom π stepena l < k i L(πP k ) 0 za l = k; 3 L(x l P k ) = M k δ lk, gde je M k 0, l = 0, 1,..., k. Teorema Neka je P k, k N 0, niz polinoma ortogonalnih u odnosu na funkcionelu L. Tada se svaki polinom π(x) stepena n moe predstaviti u obliku π(x) = gde su koeficijenti c k dati sa n c k P k (x), k=0 c k = L(πP k), k = 0, 1,..., n. L(Pk 2 ) Teorema Ako su P k i Q k, k N 0, dva niza polinoma ortogonalnih u odnosu na istu funkcionelu L, tada postoje brojevi c n 0 tako da je Q n (x) = c n P n (x), n N 0. Teorema Za dati niz polinoma P n, n N 0, ortogonalnih u odnosu na funkcionelu L, odgovarajui ortonormirani niz glasi p n (x) = ( L(P 2 n(x)) ) 1/2 Pn (x). 3
13 1.1. Uvod U opxtem sluqaju kvadratni koreni koji se jav aju u prethodnom izrazu ne moraju biti realni brojevi. Meutim, u najveem broju primera iz prakse ortogonalnih polinoma vai upravo L(Pn 2 (x)) > 0 i u tom sluqaju p n (x) je jedinstveno odreen uslovom da je vodei koeficijent pozitivan. Niz polinoma ortogonalnih u odnosu na datu linearnu funkcionelu u opxtem sluqaju ne mora da postoji. Linearne funkcionele L koje generixu nizove ortogonalnih polinoma se nazivaju regularne ili kvazi-definitne (videti [11, str. 11], [46, str. 96], [16]). Regularnost funkcionele L je veoma bitno pitae. Naredna tvrea daju odgovor. Teorema Neka je L : P C linearna funkcionela. Oznaqimo sa k, k N 0, sledee determinante m 0 m 1 m 2 m k m 1 m 2 m 3 m k+1 k = m 2 m 3 m 4 m k+2, k N 0, (1.1) m k m k+1 m k+2 m 2k gde su m k, k N 0, momenti funkcionele L. Niz polinoma P k ortogonalnih u odnosu na L postoji ako i samo ako je k 0, k = 0, 1, 2,.... Determinante k, k N 0, nazivamo Henkelovim 5 determinantama. Ova teorema, iako u potpunosti rexava egzistenciju niza ortogonalnih polinoma, u praksi je skoro neupotreb iva za ihovo izraqunavae. Samo u nekim specijalnim sluqajevima determinante k, k N 0, moemo odrediti analitiqki. Kao ilustraciju navedimo da u [41], koja se bavi analitiqkim izraqunavaem vrednosti determinanata, za determinante Henkelovog tipa autor savetuje da se pregleda literatura o ortogonalnim polinomima kako bi se eventualno traena determinanta prepoznala meu ve izraqunatim Henkelovim determinantama. Uglavnom, mogunost izraqunavaa determinante k u zatvorenom obliku je neophodna za postojae analitiqkih rezultata za odgovarajuu klasu ortogonalnih polinoma. Ovde pod pojmom analitiqko rexee podrazumevamo rexee koje jeste analitiqko ali takoe ima i razumnu kompleksnost. Primer Kao ilustraciju navodimo primer linearne funkcionele L(P ) = 1 1 P (x) dx, P P. π 1 x 2 5 Hermann Hankel ( ), nemaqki matematiqar. 0 4
14 1.1. Uvod Momenti date funkcionele su dati sa m k = Γ((k+1)/2)/(kΓ(k/2)), k N 0. Vrednosti prvih nekoliko Henkelovih determinanata su 0 = π 2, 1 = π2 8 8π, 2 = 9π π, 3 = π π π 2. Kako red determinante raste, izrazi postaju sve komplikovaniji. Lako se moe zak uqiti da o analitiqkom izrazu za vrednosti Henkelovih determinanata texko da i ima smisla govoriti jer bi takvi analitiqki izrazi bili previxe sloeni. Definicija Linearna funkcionela L : P C je pozitivnodefinitna ako i samo ako je L(P ) > 0 za svaki polinom P koji je nenegativan za svako realno x i nije identiqki jednak nuli. Sledea teorema daje karakterizaciju pozitivno-definitnih linearnih funkcionela. Teorema Linearna funkcionela L je pozitivno-definitna ako i samo ako su vrednosti Henkelovih determinanata k, k N 0, pozitivne i momenti funkcionele L realni. Teorema Ako je linearna funkcionela L : P C pozitivnodefinitna, onda niz ortogonalnih realnih polinoma, u smislu definicije 1.1.2, postoji. Najvaniji sluqaj linearne funkcionele L : P C je linearna funkcionela koja je definisana preko integrala. Neka je dµ mera, takva da je svaki polinom dµ-integrabilan, tada je sa L(P ) = P dµ, P P, (1.2) zadata linearna funkcionela koja slika polinome na skup kompleksnih brojeva. Vai i obrat. Teorema Neka je m k, k N 0, proizvo an niz kompleksnih brojeva. Onda postoji funkcija φ ograniqene varijacije na R, takva da vai R x n dφ = m k, k N 0. 5
15 1.1. Uvod Ako je linearna funkcionela zadata sa (1.2), onda je ona pozitivnodefinitna pod uslovom da je mera dµ pozitivna. Kod mnogih mera koje se jav aju u primenama, distribucija µ je apsolutno neprekidna funkcija. Tada se funkcija w(x) = µ (x) zove teinska funkcija. U tom sluqaju meru dµ moemo predstaviti u obliku dµ = w(x)dx, gde je w(x) nenegativna funkcija, mer iva u Lebegovom 6 smislu na R, za koju svi momenti m k, k N 0, postoje i m 0 > 0. U tom sluqaju umesto p n ( ; dµ), π n ( ; dµ), α n ( ; dµ), itd. pixemo redom p n ( ; w), π n ( ; w), α n ( ; w). Taqka x 0 je taqka rasta funkcije φ ako i samo ako je za svako ε > 0 φ(x 0 + ε) φ(x 0 ε) > 0. Inaqe, skup taqaka rasta se jox naziva i nosaqem funkcije φ (videti [11, str. 51], [12]). Nosaq funkcije φ, mere µ, oznaqavamo sa supp(φ), supp(µ), redom. Nosaq mere supp(w) je interval koji moe biti konaqan, polu-beskonaqan ili beskonaqan. Ako je supp(w) = [a, b], gde je < a < b < +, tada kaemo da je w teinska funkcija na [a, b]. Za svaku zadatu linearnu funkcionelu L moemo definisati skalarni proizvod na P. Definicija Pod L-skalarnim proizvodom, L : P 2 C podrazumevamo sledei izraz P, Q L = L(P Q), P, Q P. U sluqaju kada je L pozitivno-definitna, onda je, L pravi skalarni proizvod na (P, R) jer on verifikuje sve aksiome skalarnog proizvoda (videti [43, str. 52], [66, str. 71], [53, str. 86]). Definicijom skalarnog proizvoda na unitarnim prostorima P, Q L = L(P Q), dobijamo prirodnu ekstenziju pozitivne-definitnosti sa (P, R) na (P, C). U disertaciji koristiemo oznake p n ( ; w) i π n ( ; w) redom za ortonormirane polinome, odnosno moniqne ortogonalne polinome na (a, b) u odnosu na teinsku funkciju w. Interval (a, b) zove se interval ortogonalnosti. 6 Henri Lebesgue ( ), francuski matematiqar. 6
16 1.1. Uvod Troqlana rekurentna relacija Troqlana rekurentna relacija predstav a jednostavnu i efikasnu proceduru za rekurzivno generisae niza ortogonalnih polinoma. Ona je od suxtinske vanosti u konstruktivnoj teoriji ortogonalnih polinoma. Polazna je osnova za izvoee osobina niza ortogonalnih polinoma. Pomou koeficijenata troqlane rekurentne relacije jednostavno odreujemo ortogonalne polinome, ihove izvode, linearne kombinacije, zahtevajui poznavae samo linearnog niza parametara. Ova relacija je karakteristika polinoma na realnoj pravoj, dok se u opxtem sluqaju situacija komplikuje. Teorema Neka je L : P C regularna linearna funkcionela i neka je π k, k N 0 niz moniqnih polinoma ortogonalnih u odnosu na L. Tada postoje nizovi α k, β k 0, k N 0, takvi da vai π k+1 = (x α k )π k β k π k 1, k N 0, (1.3) i π 1 = 0. Ako je funkcionela L pozitivno-definitna, onda je α k R, k N 0, β k > 0, k N, a β 0 moe biti proizvo no. Obrnuto tvree ove teoreme je quvena Favardova 7 teorema (videti [22], [11, str. 21].) Teorema Neka su α k i β k, k N 0, dva proizvo na kompleksna niza i neka su polinomi π k, k N 0, definisani sa π k+1 = (x α k )π k β k π k 1, k N 0, gde je π 1 = 0 i π 0 = 1. Tada postoji jedinstvena linearna funkcionela L : P C takva da vai L(1) = β 0, L(π k π ν ) = 0, k ν, k, ν N 0. Funkcionela L je regularna i π k, k N 0, je odgovarajui niz moniqnih ortogonalnih polinoma ako i samo ako je β k 0, k N 0. Xtavixe, L je pozitivno-definitna i π k, k N 0, je odgovarajui niz moniqnih ortogonalnih polinoma ako i samo ako je α k R, k N 0, i β k > 0, k N 0. 7 Jean Favard ( ), francuski matematiqar. 7
17 1.1. Uvod Verzija Favardove teoreme u sluqaju kada je linearna funkcionela L zadata integralom glasi: Teorema Neka je za proizvo na dva niza kompleksnih brojeva α k i β k, k N 0, definisan niz moniqnih polinoma π k, k N 0, pomou π k+1 = (x α k )π k β k π k 1, k N 0, gde je π 0 = 1 i π 1 = 0. Tada postoji funkcija φ ograniqene varijacije na R, takva da vai n π n π k dφ = δ nk β ν, k, n N 0. R ν=1 Funkcija φ moe biti realna ako i samo ako su α k, β k R, k N 0. Funkcija φ moe biti neopadajua sa neograniqenim brojem taqaka rasta ako i samo ako je α k R i β k > 0, k N 0. Na skupu regularnih funkcionela ova tvrea su ekvivalentna. Nada e emo se u disertaciji baviti isk uqivo regularnim funkcionelama. Vezu izmeu niza momenata m k, k N 0, i koeficijenata α k i β k, k N 0 troqlane relacije (1.3), za regularnu funkcionelu L, daje sledea teorema (videti [11, str. 19]). Teorema Oznaqimo sa n, n N 0, determinante n = m 0 m 1 m n 1 m n+1 m 1 m 2 m n m n+2 m 2 m 3 m n+1 m n m n m n+1 m 2n 1 m 2n+1 Ukoliko je n 0, n N 0, onda vai α n = n n n 1 n 1,, n N 0. (1.4) β n = n n 2, n N 2 0, (1.5) n 1 gde je 1 = 0, 1 = 2 = 1, a n, n N 0, su Henkelove determinante date izrazom (1.1). Determinante n, n N 0, nazivamo modifikovanim Henkelovim determinantama. one predstav aju minor elementa na poziciji (n + 1, n) Henkelove determinante n+1. U nastavku navodimo i neke jednostavne osobine koeficijenata troqlane rekurentne relacije ([15, str. 10{11]). 8
18 1.1. Uvod Teorema Ako niz moniqnih ortogonalnih polinoma zadovo ava uslov π n (z) = ( 1) n π n ( z), n N 0, onda je Re(α k ) = Im(β k ) = 0. 2 Ako je regularna linearna funkcionela L, sa nizom moniqnih ortogonalnih polinoma π n, n N 0, zadata na sledei naqin L(P ) = a a P (x)ω(x)dx, P P, a R +, pri qemu vai ω(x) = ω( x), x R, onda je π n (z) = ( 1) n π n ( z), n N 0. 3 Ako je regularna linearna funkcionela L, sa nizom moniqnih ortogonalnih polinoma π n, n N 0, zadata na sledei naqin L(P ) = a a P (x)ω(x)dx, P P, a R +, pri qemu vai ω(x) = ω( x), x R, onda je π n (z) = ( 1) n+1 π n ( z), n N 0. Koeficijenti relacije (1.3), α k i β k, jav aju se u Jakobijevom 8 verinom razlomku povezanom sa merom dµ F (z) = R dµ(x) z x β 0 z α 0 β 1 z α 1, koji je poznat kao Stiltjesova transformacija mere dµ. Za n-ti konvergent ovog verinog razlomka vai β 0 β 1 z α 0 z α 1 β n 1 = σ n(z) z α n 1 π n (z), (1.6) gde su σ n takozvani pridrueni polinomi definisani sa σ k (z) = R π k (z) π k (x) z x dµ(x), k 0. Pridrueni polinomi zadovo avaju istu troqlanu rekurentnu relaciju kao i polinomi π k (x). Naime, vai σ k+1 (z) = (z α k )σ k (z) β k σ k 1 (z), k 0, uz poqetne vrednosti σ 0 (z) = 0, σ 1 (z) = 1. 8 Carl Gustav Jacob Jacobi ( ), nemaqki matematiqar. 9
19 Funkcija druge vrste ϱ k (z) = R 1.1. Uvod π k (x) dµ(x), k 0, z x pri qemu z ne pripada nosaqu mere dµ, takoe zadovo ava istu troqlanu rekurentnu relaciju (1.3) i predstav a eno minimalno rexee, normalizovano sa ϱ 1 (z) = 1. Racionalna funkcija (1.6) ima proste polove u nulama z = t (n) k, k = 1,..., n, polinoma π n (x). Ako sa λ n,k oznaqimo odgovarajue reziduume funkcije σ n (z)/π n (z) u ovim polovima, tj. λ n,k = lim z t (n) k (z t (n) k )σ n(z) π n (z) = 1 π n(t (n) tada za verini razlomak (1.6) vai razvoj σ n (z) π n (z) = n k=1 k ) λ n,k. z t (n) k R π n (x) x t (n) k dµ(x), (1.7) Ortonormirani polinomi p k, k N 0, zadovo avaju nexto drugaqiju rekurentnu relaciju u odnosu na (1.3) (videti [46, str. 101]), pre svega jer im je u opxtem sluqaju vodei koeficijent razliqit od 1. Za ih vai xp k (x) = β k+1 p k+1 (x) + α k p k (x) + β k p k 1 (x), k N 0, (1.8) gde je p 1 (x) = 0, p 0 (x) = 1/ β 0. Koeficijenti troqlane rekurentne relacije (1.8) osnova su teorije Jakobijevih operatora (videti ode ak 1.1.2). O ovoj formuli i enoj primeni bie vixe reqi u narednom ode ku. Jedna od vanih posledica troqlane rekurentne relacije (1.8) je Kristofel 9 -Darbuova 10 formula data u sledeem tvreu. Teorema Neka je p k, k N 0, niz ortonormiranih polinoma u odnosu na meru dµ. Tada je n k=0 p k (x)p k (t) = p n+1 (t)p n (x) p n (t)p n+1 (x) β n+1. (1.9) t x 9 Elwin Bruno Christoffel ( ), nemaqki matematiqar. 10 Jean Gaston Darboux ( ), francuski matematiqar. 10
20 1.1. Uvod Uzimajui graniqnu vrednost kada t x u (1.9) dobijamo n p k (x) 2 = ( β n+1 p n+1 (x)p n (x) p n(x)p n+1 (x) ). (1.10) k=0 Funkcija λ n (x) = λ n (x; dµ) = zove se Kristofelova funkcija. ( n 1 ) 1 p k (x) 2 k=0 (1.11) Nule ortogonalnih polinoma Ponaxae nula ortogonalnih polinoma zaokup a pau jox od godine, sa prvim radovima iz oblasti Markova 11 i Stiltjesa. Razlozi interesovaa lee u velikom znaqaju nula ortogonalnih polinoma za praktiqnu primenu. Poznata je interpretacija nula Jakobijevih, Lagerovih 12 i Ermitovih 13 polinoma u elektrostatici. Izuzetnu ulogu imaju kao qvorovi Gausovih 14 kvadraturnih formula. K uqnu ulogu igraju u dokazima nekih klasiqnih nejednakosti. Zahva ujui ima razvijene su mnoge mone analitiqke i diskretne tehnike. Spomenuemo samo Xturmovu 15 teoremu poreea za nule rexea diferencijalnih jednaqina drugog reda, Markovu teoremu o monotonosti nula ortogonalnih polinoma u zavisnosti od prirode teinske funkcije. Iz svih tih razloga bitno je poznavati geometriju nula ortogonalnih polinoma i ihove eksplicitne izraze, kada je to mogue. Nule ortogonalnih polinoma pozitivno-definitnih funkcionela pokazuju neka veoma pravilna svojstva, iskazana u narednim tvreima (videti [11], [46]). Pretpostavimo da je supp(dµ) ograniqen i obeleimo sa Co(supp(dµ)) najmai zatvoren interval koji sadri supp(dµ). Teorema Sve nule polinoma P n (x) = P n (x; dµ), n N, su realne i razliqite i lee u unutraxosti intervala Co(supp(dµ)). 11 Andre$i Andreeviq Markov (1856{1922), ruski matematiqar. 12 Edmond Nicolas Laguerre ( ), francuski matematiqar. 13 Charles Hermite ( ), francuski matematiqar. 14 Carl Friedrich Gauss ( ), nemaqki matematiqar. 15 Jacques Charles Francois Sturm ( ), xvajcarski matematiqar. 11
21 Teorema Neka su t (n) k 1.1. Uvod, k = 1,..., n, nule polinoma P n (x; dµ) u rastuem poretku, tj. t (n) 1 < t (n) 2 < < t (n) n. Nule polinoma P n i P n+1 se meusobno razdvajaju, tj. vai: t (n+1) k < t (n) k Sledea teorema moe se nai u [71]. < t (n+1) k+1, k = 1,..., n, n N. Teorema Neka je dato 2n + 1 proizvo nih realnih brojeva t (n) k i t (n+1) k tako da je a < t (n+1) k < t (n) k < t (n+1) k+1 < b, k = 1,..., n. Tada postoji niz moniqnih polinoma π k (x), st(π k ) = k, k N 0, ortogonalnih na [a, b] takvih da je π n (x) = n k=1 (x t(n) k ) i π n+1(x) = n+1 k=1 (x t(n+1) k ). Kao xto je ve napomenuto u prethodnom ode ku, ortonormirani polinomi p k, k N 0, zadovo avaju rekurentnu relaciju xp k (x) = β k+1 p k+1 (x) + α k p k (x) + β k p k 1 (x), k N 0, gde je p 1 (x) = 0, p 0 (x) = 1/ β 0. Uzimajui k = 0, 1,..., n 1, preko sledeeg sistema jednaqina uspostav a se veza spektralne teorije i nula ortogonalnih polinoma: xp n (x) = J n (dµ)p n (x) + β n p n (x)e n, (1.12) gde su J n (dµ) = α 0 β1 0 0 β1 α 1 β2 0 0 β2 α α n 1., p n (x) = p 0 (x) p 1 (x) p 2 (x). p n 1 (x), e n = Trodijagonalna matrica J n = J n (dµ) naziva se Jakobijeva matrica. Moniqni polinomi π n (x) imaju predstav ae preko Jakobijeve matrice u obliku π n (x) = det(xi n J n ), gde je I n jediniqna matrica reda n. Teorema Nule t (n) k, k = 1,..., n, polinoma p n (x; dµ) su sopstvene vrednosti trodijagonalne Jakobijeve matrice J n (dµ) reda n. Odgovarajui sopstveni vektori glase p n (t (n) k ), k = 1,..., n. 12
22 3.1. Qebixev evi polinomi Ovom teoremom je ispitivae spektralnih svojstava Jakobijevih operatora svedeno na utvrivae osobina mere dµ na osnovu troqlane rekurentne relacije. Vrednosti Kristofelove funkcije (1.11) u nulama t (n) k, k = 1,..., n, ortogonalnog polinoma P n (x; dµ), tj. brojevi λ (n) k = λ(t (n) k ; dµ), k = 1,..., n, (1.13) zovu se Kristofelovi brojevi ili Kouts 16 -Kristofelovi koeficijenti i imaju veliki znaqaj u numeriqkoj integraciji. 1.2 Qebixev evi polinomi Budui da se veliki deo ove disertacije bavi izuqavaem polinoma ortogonalnih u odnosu na modifikovane Qebixev eve 17 mere, u posebnom poglav u navodimo najvanije osobine Qebixev evih polinoma. Qebixev evi polinomi prve i druge vrste se za x 1 redom definixu na sledei naqin T n (x) = cos(n arccos x) i U n (x) = sin((n + 1) arccos x), (1.14) 1 x 2 pri qemu je T 0 (x) = 1, T 1 (x) = x i U 0 (x) = 1, U 1 (x) = 2x. Odgovarajue teine glase w(x) = 1 1 x 2 Koristei identitet i w(x) = 1 x 2, x 1. cos(n + 1)θ + cos(n 1)θ = 2 cos θ cos nθ za x = cos θ, zak uqujemo da polinomi T n i U n zadovo avaju istu troqlanu rekurentnu relaciju P n+1 (x) = 2xP n (x) P n 1 (x), n N, (1.15) 16 Roger Cotes ( ), britanski matematiqar. 17 Pafnuti$i L~voviq Qebyx ev ( ), ruski matematiqar. 13
23 3.1. Qebixev evi polinomi za razliqite poqetne uslove. Korixeem (1.15), uz poqetne uslove T 0 (x) = 1 i T 1 (x) = x ili U 0 (x) = 1 i U 1 (x) = 2x, dobijamo nizove polinoma {T n (x)} n N0 i {U n (x)} n N0. Daemo primera radi eksplicitne izraze Qebixev evih polinoma prve i druge vrste za n = 0, 1,..., 6 : T 0 (x) = 1, U 0 (x) = 1, T 1 (x) = x, U 1 (x) = 2x, T 2 (x) = 2x 2 1, U 1 (x) = 4x 2 1, T 3 (x) = 4x 3 3x, U 3 (x) = 8x 3 4x, T 4 (x) = 8x 4 8x 2 + 1, U 4 (x) = 16x 4 12x 2 + 1, T 5 (x) = 16x 5 20x 3 + 5x, U 5 (x) = 32x 5 32x 3 + 6x, T 6 (x) = 32x 6 48x x 2 1, U 6 (x) = 64x 6 80x x n 0 n 1 n 2 n n 4 n Slika 1.1: Grafici funkcija y = T n (x) za n = 0, 1, 2, 3, 4, 5 i 1 x 1 Poznati su i opxti eksplicitni izrazi Qebixev evih polinoma prve i druge vrste. Oni redom glase i T n (x) = n 2 [n/2] k=0 U n (x) = ( 1) k (n k 1)! (2x) n 2k (n 1) k!(n 2k)! [n/2] k=0 ( 1) k (n k)! (2x) n 2k. k!(n 2k)! 14
24 3.1. Qebixev evi polinomi n 0 n n 2 n 3 n 4 2 n Slika 1.2: Grafici funkcija y = U n (x) za n = 0, 1, 2, 3, 4, 5 i 1 x 1 Odgovarajui ortonormirani sistemi redom su { } 1 2 2, π π T 1, π T 2,... i { } π, π U 1, π U 2,.... Qebixev evi polinomi prve vrste T n (x) su dati na slici 1.1, dok su na slici 1.2 prikazani Qebixev evi polinomi druge vrste za n = 0, 1,..., 5. Osobine osnovnih trigonometrijskih funkcija kojima su definisani Qebixev evih polinomi (1.14) uslov avaju da e ihove osobine. Tako imamo: T n (x) 1 za svako n N 0 i 1 x 1. U n (x) n + 1 i 1 x 2 U n (x) 1 za svako 1 x 1. T 0 = π, T n = π/2, n N. U n = π/2, n N 0. Parnost funkcija T n (x) i U n (x) odgovara parnosti stepena n. Eksplicitni izraz za nule polinoma T n (x) glasi t k = t (n) (2k 1)π k = cos 2n (k = 1,..., n). 15
25 3.1. Qebixev evi polinomi Qebixev evi polinomi prve vrste T n (x) zadovo avaju diferencijalnu jednaqinu (1 x 2 )y xy + n 2 y = 0. Drugo partikularno rexee ove jednaqine S n (x) = sin(n arccos x) ( 1 x 1) moe da se izrazi preko Qebixev evih polinoma druge vrste. Naime, vai S n (x) = U n 1 (x) 1 x 2. Odgovarajua diferencijalna jednaqina za Qebixev eve polinome druge vrste U n (x) glasi (1 x 2 )y 3xy + n(n + 2)y = 0. U literaturi moe se nai mnoxtvo drugih relacija koje ovi polinomi zadovo avaju, kao na primer: U n (x) = 1 n + 1 T n+1(x) = 1 1 x (xt n+1(x) T 2 n+2 (x)), T n (x) = U n (x) xu n 1 (x) = xu n 1 (x) U n 2 (x), 1 U n (x) = 2(n + 1) (U n+1(x) U n 1(x)), U n(x) = 1 1 x 2 ((n + 1)U n 1(x) nxu n (x)). Takoe, za 2 k n vai T n (x) = T k (x)u n k (x) T k 1 (x)u n k 1 (x). Neke interesantne vrednosti su: T n (±1) = (±1) n, T 2n (0) = ( 1) n, T 2n+1 (0) = 0, T n(±1) = (±1) n n 2, n (1) = n2 (n 2 1) (n 2 (k 1) 2 ). (2k 1)!! T (k) Qebixev evi polinomi prve i druge vrste pripadaju opxtijoj klasi Gegenbauerovih 18 polinoma. Qebixev evi polinomi tree i qetvrte vrste su definisani sa V n (cos θ) = cos(n )θ cos 1 2 θ i W n (cos θ) = sin(n )θ sin 1 2 θ, a Qebixev eve mere tree i qetvrte vrste glase dµ(x) = (1 x) 1/2 (1 + x) 1/2 dx i dµ(x) = (1 x) 1/2 (1 + x) 1/2 dx 18 Karl Gegenbauer ( ), nemaqki matematiqar. 16
26 na ( 1, 1) redom Ekstremalna svojstva ortogonalnih polinoma Svi Qebixev evi kao i Gegenbauerovi polinomi jesu potklasa generalnije klase { Jakobijevih polinoma. 1.3 Ekstremalna svojstva ortogonalnih polinoma Ortogonalni polinomi se mogu definisati i preko ekstremalnih problema. Naime, moniqni ortogonalni polinom π n ( ; dµ) ima sledee ekstremalno svojstvo. Teorema Za svaki moniqni polinom p P n vai R p(x) 2 dµ(x) R π n (x; dµ) 2 dµ(x), pri qemu jednakost vai ako i samo ako je p = π n. Iz ove teoreme sledi da je polinom π n ( ; dµ) jedinstveni moniqni polinom koji minimizira L 2 (dµ) normu, tj. min p P n R p(x) 2 dµ(x) = R π n (x; dµ) 2 dµ(x). (1.16) Ekstremalno svojstvo (1.16) moe se proxiriti na L r (dµ) normu za svako r > 1. Teorema Neka je 1 < r < +. Tada postoji jedinstveni moniqni polinom πn P n tako da vai min p(x) r dµ(x) = p P n R R π n(x) r dµ(x). (1.17) Vaan specijalan sluqaj prethodne teoreme je r = 2s + 2, s N 0. Ekstremalni moniqni polinom π n(x) u (1.17) oznaqimo sa π n,s (x). Ako posmatramo integral sa leve strane jednakosti (1.17) kao funkciju koeficijenata F (a 0, a 1,..., a n 1 ) polinoma p(x) = x n + a n 1 x n a 1 x + a 0, 17
27 1.4. Metodi konstrukcije ortogonalnih polinoma tada parcijalni izvodi funkcije F po a k, k = 0, 1,..., n 1, moraju biti jednaki nuli. Odavde dobijamo R π n,s (x) 2s+1 x ν dµ(x) = 0, ν = 0, 1,..., n 1. Dakle, (2s + 1)-vi stepen polinoma π n,s (x) mora biti ortogonalan sa svim polinomima nieg stepena u odnosu na meru dµ. Polinom π n,s (x) zove se s-ortogonalan polinom u odnosu na meru dµ. Kada je s = 0, s-ortogonalni polinomi se svode na standardne ortogonalne polinome, p n,0 = p n. Za date n i s, stav ajui dµ n,s (x) = (p n,s (x)) 2s dµ(x), Milovanovi (videti [48]) je reinterpretirao ove uslove ortogonalnosti za standardne ortogonalne polinome kao R p n,s k (x)xk dµ n,s (x) = 0, k = 0, 1,..., n 1, gde je p n,s k, k N 0, niz moniqnih ortogonalnih polinoma u odnosu na novu meru dµ n,s (x) = (p n,s (x)) 2s dµ(x). Primetimo da je p n,s (x) p n,s n (x). Kao xto moemo da vidimo, polinomi p n,s k, k = 0, 1,..., su implicitno definisani, jer nova mera dµ n,s (x) zavisi od p n,s (x). Na osnovu prethodnog, da bismo naxli s-ortogonalne polinome p n,s, n = 0, 1,..., N, potrebno je konstruisati standardne polinome p n,s (x), k k n (ortogonalne u odnosu na meru dµ n,s (x) = (p n,s (x)) 2s dµ(x)) za svako n N i da uzmemo p n,s = p n,s n, n = 0, 1,..., N. Napomenimo jox i to da je Bernxtajn godine pokazao da moniqni Qebixev ev polinom T n (x) minimizira sve integrale oblika 1 1 π n (x) k+1 dx (k 0), 1 x 2 gde je π n proizvo an moniqni polinom stepena n. To znaqi da su moniqni Qebixev evi polinomi T n s-ortogonalni na [ 1, 1] za svako s Metodi konstrukcije ortogonalnih polinoma Koeficijenti troqlane rekurentne relacije poznati su eksplicitno samo za usku klasu ortogonalnih polinoma, kao xto su Jakobijevi, gene- 19 Felix Bernstein ( ), nemaqki matematiqar jevrejskog porekla. 18
28 1.4. Metodi konstrukcije ortogonalnih polinoma ralisani Lagerovi i Ermitovi polinomi. To su takozvani klasiqni ortogonalni polinomi. Ortogonalni polinomi qije koeficijente troqlane rekurentne relacije ne poznajemo zovu se strogo neklasiqni polinomi. Poznavae rekurentnih koeficijenata je neophodno za raqunsku primenu ortogonalnih polinoma. Konstruktivna teorija ortogonalnih polinoma bavi se sledeim problemom: Za datu meru dµ(x) i dati prirodan broj n odrediti prvih n koeficijenata α k (dµ(x)) i β k (dµ(x)) u troqlanoj rekurentnoj relaciji. U ovom ode ku baviemo se raqunskim metodama za generisae ortogonalnih polinoma. Fokus je pre svega na neklasiqnim teinskim funkcijama. U zavisnosti od informacija koje su dostupne o meri dµ(x) razvijeni su razliqiti algoritmi konstrukcije nepoznatih koeficijenata troqlane rekurentne relacije. Ukoliko je mera poznata jedino preko momenata, procedura izbora je Qebixev ev algoritam. U sluqaju apsolutno neprekidne mere i poznate teinske funkcije, preporuquje se Stiltjesova procedura. Vaan doprinos istraivaima iz ove oblasti dao je Gauqi 20 ([24], [25]) Qebixev ev algoritam Qebixev ev algoritam uspostav a vezu izmeu momenata m k, k N 0, i koeficijenata troqlane rekurentne relacije. Ovaj algoritam se moe iskazati na sledei naqin. Neka je data trougaona matrica qiji su elementi σ k,i = R P k (x)x i dµ(x), k, i N 0, k i, gde je P n (x) n-ti qlan niza ortogonalnih polinoma. Tada je m k = σ 0,k. Na osnovu troqlane rekurentne relacije vai σ k+1,i = σ k,i+1 α k σ k,i β k σ k 1,i, (1.18) 20 Walter Gautschi (1927 ), ameriqki matematiqar roen u Xvajcarskoj. 19
29 1.4. Metodi konstrukcije ortogonalnih polinoma pri qemu je σ 1,i = 0. Za odreivae koeficijenata troqlane rekurentne relacije koristimo jednakosti α 0 = σ 0,1 σ 0,0, β 0 = σ 0,0, α k = σ k,k+1 σ k 1,k, σ k,k σ k 1,k 1 β k = σ k,k, k N. σ k 1,k 1 (1.19) Jednaqine (1.18) i (1.19) definixu Qebixev ev algoritam. Pomou ovog algoritma mogue je jednostavno odrediti prvih n koeficijenata troqlane rekurentne relacije ako je poznato prvih 2n momenata. Jedini nedostatak Qebixev evog algoritma je egova slaba uslov enost. U ovom sluqaju dolazi do oduzimaa bliskih brojeva, pa u aritmetici konaqne mantise dolazi do gubitka znaqajnih cifara. Uvoeem pogodnih modifikovanih momenata, mogue je dobiti bo u numeriqku stabilnost. Ovaj algoritam poznat je u literaturi kao modifikovan Qebixev ev algoritam. On zahteva poznavae jox jednog niza ortogonalnih polinoma i ihove troqlane rekurentne relacije. Tada, na osnovu sledeih veliqina σ k,i = R P k (x)w i (x)x i dµ(x), gde je W i niz moniqnih ortogonalnih polinoma koji zadovo avaju troqlanu rekurentnu relaciju W k+1 (x) = (x a k )W k (x) b k W k 1 (x), k N 0, pri qemu je W 1 (x) = 0, W 0 (x) = 1, a koeficijenti a k i b k su poznati. Nepoznate koeficijente troqlane rekurente relacije odreujemo iz σ k,i = σ k 1,i+1 (α k 1 a i )σ k 1,i β k 1 σ k 2,i + b i σ k 1,i 1, α k = a k + σ k,k+1 σ k 1,k, σ k,k σ k 1,k 1 β k = σ k,k, σ k 1,k 1 gde je σ 1,i = 0 i σ 0,i = R W i(x)dµ(x). (1.20) Modifikovani Qebixev ev algoritam koristi dodatni niz ortogonalnih polinoma sa poznatim koeficijentima troqlane rekurentne relacije. U radu [25] pokazano je da se pomou modifikovanog Qebixev e- vog algoritma mogu izvrxiti konstrukcije koje imaju bo u numeriqku 20
30 1.4. Metodi konstrukcije ortogonalnih polinoma stabilnost od rezultata koji se dobijaju primenom originalnog Qebixevevog algoritma. Takoe, mogue je diskutovati za razne nizove poznatog niza ortogonalnih polinoma stabilnost algoritma. Primetimo jox da se u sluqaju W k (x) = x k, k = 0, 1,..., 2n 1, tj. a k = b k = 0, modifikovani Qebixev ev algoritam svodi na osnovni algoritam definisan pomou (1.18) i (1.19) Stiltjesova procedura Neka je P k, k N 0, moniqan niz ortogonalnih polinoma u odnosu na meru dµ. Iz troqlane rekurentne relacije koristei svojstva ortogonalnosti dobijaju se sledee formule R α k = xp k 2(x)dµ(x) R P k 2(x)dµ(x), k N 0, β 0 = dµ(x), R R β k = P k 2(x)dµ(x) R P k N. k 1 2 (x)dµ(x), (1.21) Polazei od P 0 = 1, moemo konstruisati koeficijente α 0 i β 0. Formiramo iterativni postupak kojim na osnovu dobijenih koeficijenata troqlane relacije najpre odredimo naredni qlan niza ortogonalnih polinoma P k, a zatim na osnovu relacija (1.21) odreujemo i nove koeficijente α k i β k. Proceduru nastav amo do konstrukcije prvih n koeficijenata, odnosno qlanova niza ortogonalnih polinoma. Navedeni postupak alternativne primene formula (1.21) i troqlane rekurentne relacije koju polinomi P k, k N 0, zadovo avaju naziva se Stiltjesova procedura. Odreivae vrednosti integrala koji se pojav uju u (1.21) mogue je izvrxiti numeriqki, tj. primenom neke kvadraturne formule (videti poglav e kvadraturne formule). Kako kvadraturne formule za meru dµ nisu dostupne zbog nepoznavaa koeficijenata troqlane relacije, najqexe se koristi neka druga kvadraturna formula za meru koja je sliqna meri dµ. U tom sluqaju navedeni postupak se naziva diskretizovana Stiltjesova procedura. Ovakav postupak pokazuje dobre karakteristike uslov enosti i ima prednost nad Qebixev evim algoritmom. 21
31 1.4. Metodi konstrukcije ortogonalnih polinoma Razvoj simboliqkog raquna i aritmetike promen ive preciznosti omoguili su generisae koeficijenata troqlane rekurzije Qebixev e- vom ili Stiltjesovom procedurom. U nastavku navodimo neke interesantne neklasiqne mere za koje su u literaturi dobijeni rekurzivni koeficijenti [51]. 1. Kristofelov primer w(x) = [(1 k 2 x 2 )(1 x 2 )] 1/2, 0 < k < 1, x [ 1, 1]; 2. Logaritamska teina w(x) = x α ln(1/x), α > 1, x (0, 1); 3. Generalisana logaritamska teina w(x) = x α (1 x) β ln(1/x), α, β > 1, x (0, 1); 4. Ermitova mera na polu-intervalu w(x) = e x2, x [0, ); 5. Vixe-komponentna distribucija w(x) = (1 x 2 ) 1/2 + a, a > 0, x [ 1, 1]; 6. Ejrijeva 21 teina w(x) = e x3 /3, x (0, ); 7. Reciproqna gama teina w(x) = 1/Γ(x), x (0, ); 8. Ajnxtajnova 22 teina w(x) = x, x (0, ); e x 1 9. Fermijeva teina 23 w(x) = 1, x (0, ); e x Hiperboliqke teine w(x) = 1 cosh 2 x sinh x i w(x) = cosh 2, x (0, ). x 21 George Biddell Airy ( ), britanski astronom. 22 Albert Einstein ( ), teoretski fiziqar roen u Nemaqkoj, jevrejskog porekla. 23 Enrico Fermi ( ), italijanski fiziqar. 22
32 Glava 2 Modifikacioni algoritmi Jedan od najvanijih problema konstruktivne teorije ortogonalnih polinoma jeste odreivae koeficijenata troqlane rekurentne relacije za neklasiqne teinske funkcije. U ovom poglav u baviemo se utvrivaem uticaja modifikacije teinske funkcije na koeficijente troqlane rekurentne relacije. Razmatraemo sluqaj mnoea teinske funkcije pozitivnom racionalnom funkcijom. Ispitivae ortogonalnih polinoma sa modifikovanim teinama znaqajno je prilikom konstrukcije kvadraturnih formula. Ovakav pristup u konstrukciji kvadratura xiri ihov skup taqnosti sa algebarskih na racionalne funkcije unapred definisanih polova. Neka je dµ(x) pozitivna mera sa konaqnim nosaqem supp(dµ) = [a, b] i neka su u(x) = ± l (x u k ) i v(x) = k=1 m (x v k ) dva realna uzajamno prosta polinoma koja se ne anuliraju na [a, b], pri qemu se znak + ili u izrazu za u(x) uzima tako da je u(x)/v(x) > 0 na [a, b]. Uvodimo novu meru k=1 d µ(x) = u(x) dµ(x), x [a, b]. (2.1) v(x) Potrebno je odrediti koeficijente α k = α k (d µ) i β k = β k (d µ) troqlane rekurentne relacije za meru (2.1), na osnovu poznatih koeficijenata rekurzije α k = α k (dµ) i β k = β k (dµ) vezane za poqetnu meru dµ. Metodi koji vrxe ovu transformaciju zovu se modifikacioni algoritmi. 23
33 2.1. Transformacije teinske funkcije Prvi rezultat u ovoj oblasti dolazi od Kristofela [13] koji je izrazio u(x)π n (x; d µ) (v 1 i dµ(x) = dx) u obliku determinante, kao linearnu kombinaciju polinoma π n+i (x; dµ), i = 0, 1,..., l. Sto godina kasnije Uvarov 1 [70] je rexio sluqaj kada je v(x) 1. Savremen razvoj konstruktivne teorije ortogonalnih polinoma na realnoj pravoj u mnogome dugujemo Volteru Gauqiju [51]. Razvijao je efikasne algoritme za numeriqko generisae ortogonalnih polinoma, dao ihovu deta nu analizu stabilnosti i nekoliko novih primena. Zahva ujui radu Gauqija mogua je konstrukcija mnogih novih klasa ortogonalnih polinoma i ihova primena u razliqitim oblastima primeene i numeriqke matematike kao i mnogim oblastima primeene nauke. 2.1 Transformacije teinske funkcije U ovom ode ku dajemo pregled poznatih rezultata (videti [26], [65]) modifikacionih algoritama sa dve jednostavne transformacije. Teorema Oznaqimo sa w(x) i w(x) originalnu i transformisanu teinsku funkciju, a sa π n (x), n N 0, i π n (x), n N 0, nizove moniqnih ortogonalnih polinoma u odnosu na w(x) i w(x) teinsku funkciju redom. Neka su da e α n, β n, n N 0, i α n, β n, n N 0, odgovarajui koeficijenti troqlane rekurentne relacije za originalnu i transformisanu teinsku funkciju redom. Tada vae sledee transformacione formule. 1 Ako je w(x) = Cw(x), gde je C > 0, onda vai α n = α n, n N 0 i β0 = Cβ 0, βn = β n, n N. Pri tom je π n (x) = π n (x) za svako n N 0. 2 Ako je w(x) = w(ax + b), gde je a, b R i a 0, onda vai α n = (α n b)/a, n N 0 i β0 = β 0 / a, βn = β n /a 2, n N. Osim toga je π n (x) = π n (ax + b)/a n za svako n N 0. 1 Vasili$i Borisoviq Uvarov ( ), ruski matematiqar i fiziqar. 24
34 2.1. Transformacije teinske funkcije Naredna teorema tiqe se transformacije teinske funkcije oblika gde su u(x) i v(x) realni polinomi. w(x) = u(x) v(x) w(x), Teorema Neka su π n (x) i π n (x), n N 0, moniqni ortogonalni polinomi u odnosu na teinske funkcije w(x) i w(x) = r(x)w(x) redom, gde su r(x) = u(x) v(x) i u(x) = l m (x u i ), v(x) = (x v j ). i=1 j=1 U sluqaju m n vai π n m (x) π n 1 (x) π n (x) π n+l (x) π n m (u 1 ) π n 1 (u 1 ) π n (u 1 ) π n+l (u 1 ) u(x) π n (x) = C π n m (u l ) π n 1 (u l ) π n (u l ) π n+l (u l ). (2.2) ρ n m (v 1 ) ρ n 1 (v 1 ) ρ n (v 1 ) ρ n+l (v 1 ) ρ n m (v m ) ρ n 1 (v m ) ρ n (v m ) ρ n+l (v m ) U suprotnom, ako je m > n, onda vai u(x) π n (x) = C π 0 (x) π n+l (x) π 0 (u 1 ) π n+l (u 1 ) π 0 (u l ) π n+l (u l ) 1 v 1 v1 m n 1 ρ 0 (v 1 ) ρ n+l (v 1 ) 1 v m vm m n 1 ρ 0 (v m ) ρ n+l (v m ), (2.3) gde je C normalizaciona konstanta za moniqni polinom. Sa ρ n (z) oznaqili smo Koxijeve 2 integrale polinoma π n (x) definisane sa π n (x) ρ n (z) = z x w(x)dx, n N 0. R Originalna Kristofelova teorema se dobija u sluqaju v(x) = 1, odnosno m = 0. 2 Augustin Cauchy ( ), francuski matematiqar. 25
35 2.1. Transformacije teinske funkcije Naredne transformacione formule dobijene su primenom teoreme u specijalnim sluqajevima ([26]). Teorema Neka su sve oznake kao u teoremi i neka je niz r n, n N 0, definisan sa Tada: r 0 = c α 0, r n = c α n β n r n 1, n N. (2.4) 1 Ako je w(x) = (x c)w(x), gde je c < inf supp(w), onda vai r n β 0 = w(x)dx, βn = β n, n N, r n 1 R α n = α n+1 + r n+1 r n, n N 0. 2 U sluqaju w(x) = (x c)(x c)w(x), za c C \ R vai β 0 = β 0 (β 1 + r 0 2 ), βn = β n r n+1r n 1 α n = α n+2 + r n+2 + r n+2 r n+1 gde je r n = Re r n i r n = Im r n. (r n 1) 2 r n r n 1 r n+1 (r n+1 + r 2 n+1 r r n n, n N, ), n N 0, U nekim sluqajevima je veoma texko nai rexee diferencne jednaqine (2.4) u zatvorenom obliku. U sledeem tvreu transformacione formule iz dela 1 prethodne teoreme se uproxavaju uvoeem pomonog niza. Posledica Neka su sve oznake kao u teoremi i neka je niz λ n, n N 0, definisan sa λ 1 = 0, λ 0 = 1, λ n+1 = (c α n )λ n β n λ n 1, n N, (2.5) gde je c < inf supp(w). Ako je w(x) = (x c)w(x), tada vai λ n+1 λ n 1 β 0 = w(x)dx, βn = β n, n N, R λ 2 n α n = c λ n+1 λ n β n+1 λ n λ n+1, n N 0. 26
36 2.2. Racionalni algoritam za kvadratnu Kristofelovu modifikaciju mere Teorema Neka su sve oznake kao u teoremi Neka je niz r n, n N 0, definisan sa r 1 = w(x)dx, Tada: R r n = c α n β n r n 1, n N 0. (2.6) 1 Ako je w(x) = w(x), gde je c < inf supp(w), onda vai x c α 0 = α 0 + r 0, α n = α n + r n r n 1, β 0 = r 1, βn = β n 1 r n 1 r n 2, n N. (2.7) 2 Ukoliko je w(x) = w(x), gde je c > sup supp(w), vae relacije (2.6) c x i (2.7) pri qemu je β 0 = r 1, gde je r 1 = w(x)dx. R 2.2 Racionalni algoritam za kvadratnu Kristofelovu modifikaciju mere Modifikacija kvadratnim faktorom d µ(x) := (x z) 2 dµ(x), z C, proizvodi novi niz ortogonalnih polinoma p n (x) = p n (x; d µ), n N 0, koji se moe realizovati dvostrukom uzastopnom primenom modifikacije linearnim faktorima (videti [27, str. 121{124] i [17]). Problem sa ovim pristupom nastaje kada z pripada supp(dµ). Naime, kada je z nula polinoma p n, koji je qlan niza ortogonalnih polinoma u odnosu na meru dµ, primena modifikacionog algoritma linearnim faktorom nije mogua, zbog qienice da dolazi do de ea nulom. Alternativni pristup je da se primeni jedan korak QR algoritma na Jakobijevu matricu J = J(dµ) za meru dµ. Ovaj algoritam zahteva raqunae kvadratnih korena, xto znaqi da nije racionalan. 27
37 2.2. Racionalni algoritam za kvadratnu Kristofelovu modifikaciju mere U radu [18] predstav en je algoritam koji moe da se primeni bez obzira na qienicu gde se taqka z nalazi. Takoe, taj algoritam je racionalan, kao i algoritam predstav en u [10] koji se odnosi na linearne modifikacije. Za neke druge modifikacije videti [29]. Data modifikacija kvadratnim faktorom moe biti uspexno primeena na dirigovanu polinomijalnu L 2 -aproksimaciju, za konstrukciju s- (ili σ-) ortogonalnih polinoma i odgovarajue kvadrature Turanovog 3 tipa (videti [32], [55]), itd. Tipiqna primena na L 2 -aproksimaciju sa ograniqeima zahteva polinome ortogonalne u odnosu na meru q m (x) 2 dµ(x), gde je q m moniqni polinom stepena m sa nulama τ 1,..., τ m, koje pripadaju nosaqu mere dµ(x) (videti [45, str. 388] i [52]). To se moe postii primenom datog modifikacionog algoritma m puta sa kvadratnim faktorom (x τ k ) 2, k = 1,..., m Modifikacija kvadratnim faktorom Definicija Neka je dµ pozitivna mera i p n ( ) = p n ( ; dµ) niz moniqnih ortogonalnih polinoma u odnosu na meru dµ. Neka je z C i pretpostavimo da je p n (z) 0 za n N. Tada izraz p n (x; z) = 1 x z zovemo polinomsko jezgro za meru dµ. [ p n+1 (x) p n+1(z) p n (z) p n(x) Primetimo da je p n (x; z) P n kao funkcija po x. ] (2.8) Teorema Neka je dµ pozitivna mera i z C takav da je p n (z) 0, n N. Neka je d µ(x) = (x z)dµ(x). Tada je d µ kvazi-definitna mera i polinomska jezgra p k, k N 0, su formalni moniqni ortogonalni polinomi u odnosu na meru d µ. U radu [18] dati su sledei rezultati. Lema Koeficijenti α k i β k, k N 0, koji se jav aju u troqlanoj rekurentnoj relaciji za polinome ortogonalne u odnosu na meru su neprekidne funkcije po z R. d µ(x) = (x z) 2 dµ(x), z C, 3 Pál Turán ( ), maarski matematiqar. 28
38 2.2. Racionalni algoritam za kvadratnu Kristofelovu modifikaciju mere Dokaz. Posmatrajmo niz momenata m n = x n d µ(x), n N 0. Jednostavno se pokazuje da je svaki m n polinom drugog stepena po z. Kako p n moe da se izrazi pomou p n (x) = 1 Ĥ n m 0 m 1 m n m 1 m 2 m n x x n (videti [11, str. 17]), gde je Ĥn Henkelova determinanta koja je razliqita od nule jer je mera d µ pozitivna. Dakle, koeficijenti polinoma p n su neprekidne funkcije po z R a takoe i koeficijenti u troqlanoj rekurentnoj relaciji.., Lema Ako je n n (z) = p n+1 (z)p n(z) p n (z)p n+1(z), n N 0, onda je n+1 = β n+1 n p 2 n+1(z), n N 0. (2.9) Dokaz. Prema Kristofel-Darbuovoj formuli (videti [11, str. 23{24], [27, str. 15{16]), sledi n p n 2 = n k=0 odakle, oduzimaem dobijamo Koristei identitet β n+1 = p n+1 2 p 2 k (z) i p k 2 n+1 p n+1 = n+1 p 2 k (z) 2 p k 2, p 2 n+1(z) p n+1 2 = n+1 p n+1 + n 2 p n. 2 k=0 p n 2 dobijamo tvree leme. Teorema Neka je z C takav broj da je mera d µ kvazi-definitna. Koeficijenti u troqlanoj rekurentnoj relaciji za polinome ortogonalne u odnosu na meru su dati sa α n = p2 n+1 d µ(x) = (x z) 2 dµ(x), z C, ( pn p n+1 + z n ) + βn+1 ( 2pn p n+1 n + α n+1 2 n) n n+1, (2.10) 29
39 2.2. Racionalni algoritam za kvadratnu Kristofelovu modifikaciju mere [ β 0 = β 0 β1 + (z α 0 ) 2] n 1 n+1, βn = β n, (2.11) 2 n gde smo oznaqili p n := p n (z; dµ), n N 0, i p n je niz polinoma ortogonalnih u odnosu na meru dµ. Dokaz. Primenom Kristofel-Darbuove formule dobijamo n p n 2 = p n+1p n p np n+1 p n 2 = n k=0 p 2 k p k 2 > 0, odakle sledi da je n (z) < 0 za svako n N 0 i z R. Oznaqimo sa Z n skup svih nula polinoma p n. Prema teoremi skup nula Z n, n N, sadri n realnih brojeva, pa je Z = n N Z n, skup nula svih polinoma p n, n N, prebrojiv skup. Zato je skup R \ Z neprazan i ima mo kontinuuma. Izaberimo z R \ Z. Za takvo z vai p n (z) 0, n N, i n (z) < 0, n N. Uslov p n (z) 0, n N, prema teoremi obezbeuje da je mera d µ(x) = (x z)dµ(x) kvazi-definitna i da postoji odgovarajui niz ortogonalnih polinoma dat sa (2.8). Dakle, moemo izraziti polinome p n, n N, ortogonalne u odnosu na meru d µ pomou p n (x; z) = 1 x z [ p n+1 (x) p n+1 p n (x) p n ], n N 0. Mera koju nada e ispitujemo je d µ(x) = (x z)d µ(x) = (x z) 2 dµ(x). Primenimo teoremu jox jednom i dobijamo S obzirom na p n (x; z) = 1 x z [ p n+1 (x; z) p n+1(z; z) p n (z; z) p n(x; z) ], n N 0. p n (z; z) = n(z) p n (z), uslov n (z) 0, n N 0, nam omoguuje primenu teoreme Sreivaem izraza p n (x; z) = 1 [ p n+1 (x) p ] n+1(z) x z p n (z) p n(x) = 1 { pn+2 (x) (p n+2 (z)/p n+1 (z))p n+1 (x) x z x z ( )} n+1/p n+1 (z) pn+1 (x) (p n+1 (z)/p n (z))p n (x) n /p n (z) x z 30
40 2.2. Racionalni algoritam za kvadratnu Kristofelovu modifikaciju mere dobijamo { 1 pn+1 (z)p n+2 (x) p n+2 (z)p n+1 (x) = (x z) 2 p n+1 (z) } n+1p n (z) p n+1 (x)p n (z) p n+1 (z)p n (x) n p n+1 (z) p n (z) p n+2 (x) p n+2(z) p n+1 (z) p n+1(x) ( ) n+1 pn (z) n p n+1 (z) p n+1(x) p n (x) = (x z) 2 ( ) p n+2 (z) p n+2 (x) n p n+1 (x) n p n+1 (z) + p n (z) n+1 + p n (x) n+1 p n+1 (z) =, (x z) 2 n p n (x; z) = p n+2(x) n p n+1 (x) ( ) p n+2 p n p n p n+2 + pn (x) n+1. (2.12) (x z) 2 n Zamenom (2.12) u troqlanoj rekurentnoj relaciji za polinome p n, dobijamo p n+1 (x) = (x α n ) p n (x) β n p n 1 (x), n N 0, p n+3 (x) n+1 p n+2 (x)(p n+3 p n+1 p n+1 p n+3) + p n+1 (x) n+2 (x z) 2 n+1 = (x α n ) p n+2(x) n p n+1 (x)(p n+2 p n p n p n+2) + p n (x) n+1 (x z) 2 n β n p n+1 (x) n 1 p n (x)(p n+1 (p n 1 p n 1 p n+1) + p n 1 (x) n (x z) 2 n 1. Sreivaem prethodnog izraza i zamenom u troqlanoj rekurentnoj relaciji za niz polinoma p n sledi p n+3 (x) p n+2(x) [(z α n+2 ) n+1 p n+1 p n+2 ] + p n+1 (x) n+2 n+1 ( n+1 = (x α n ) p n+2 (x) p n+1(x) [(z α n+1 ) n p n p n+1 ] + p n (x) ) n+1 n ( n β n p n+1 (x) p n(x) [(z α n ) n 1 p n 1 p n ] + p n 1 (x) ) n. n 1 n 1 Zamenom p n+3 (x) = (x α n+2 )p n+2 (x) β n+2 p n+1 (x) u prethodnoj jed- 31
41 2.2. Racionalni algoritam za kvadratnu Kristofelovu modifikaciju mere nakosti, imamo β n+2 p n+1 (x) + n+2p n+1 (x) + β n ( n+1 n p n 1 (x) p ) n(x)((z α n ) n 1 p n 1 p n ) + p n+1 (x) n 1 n 1 + (x α n+2 )p n+2 (x) (x α n ) ( n+1 p n (x) p ) n+1(x)((z α n+1 ) n p n p n+1 + p n+2 (x) n n p n+2(x)((z α n+2 ) n+1 p n+1 p n+2 ) = 0. n+1 Kako je n+2 = β n+2 n+1 p 2 n+2, p n+2 (x) = (x α n+1 )p n+1 (x) β n+1 p n (x) i p n+1 (x) = (x α n )p n (x) β n p n 1 (x), rexavaem sistema od dve jednaqine dobija se: α n = α n+1 n n+1 + n+1 p n p n+1 n p n+1 p n+2 n n+1, β n = (α n+1 z)β n n 1 n n+1 p n p n+1 + β n n 1 n+1 p 2 np 2 n+1 2 n n+1 ( n β n n 1 ) (2.13) (α n+1 z)β n n 1 2 np n+1 p n+2 + β n n 1 n p n+2 ( n p n+2 + p n p 2 n+1). 2 n n+1 ( n β n n 1 ) Sada, zamenom n+1 = β n+1 n p 2 n+1 i p n+2 (z) = (z α n+1 )p n+1 (z) β n+1 p n (z) u (2.13) dobijaju se izrazi dati sa (2.10) i (2.11). Dobijeni izrazi za koeficijente u troqlanoj relaciji α n i β n, n N 0, vae za z R \ Z. Kako je mera d µ pozitivna za z R, to polinomi ortogonalni u odnosu na d µ postoje. Sada pokazujemo da isti izrazi vae za svako z R. Prvo primetimo da smo dokazali da je n (z) < 0, z R, te su desne strane u izrazima (2.10) i (2.11) definisane za svako z R. Posmatrajmo sada niz otvorenih skupova O n = R \ Z n, n N. Svaki O n, n N, je gust u R. Kako je R kompletan metriqki prostor on je Bairov 4 prostor (videti [1, str. 31]). Na osnovu Bairove teoreme o kategorijama svaki rezidualan skup, tj. presek prebrojivo mnogo otvorenih skupova koji su gusti u R, je gust u R. Dakle, n N O n = R \ Z je gust u R. To znaqi da jednakosti (2.10) i (2.11) vae na skupu koji je gust u R. Na osnovu leme koeficijenti α n i β n, n N 0, su neprekidne funkcije po z R, i 4 René-Lous Baire ( ), francuski matematiqar. 32
42 2.2. Racionalni algoritam za kvadratnu Kristofelovu modifikaciju mere desne strane u jednakostima (2.10) i (2.11) su neprekidne po z R, jer je n (z) < 0, n N, z R. Za svako z Z, moemo konstruisati niz taqaka z n R \ Z, n N, takav da je lim z n = z, a to na osnovu qienice da je skup R \ Z gust u R. Koristei neprekidnost dobijamo da jednakosti (2.10) vae po z takoe. Kako je z Z proizvo no, sledi da jednakosti vae za svako z R. Sada, neka je z C \ R. Oznaqimo sa { } Z n = zl n C Ĥn(zl n ) = 0, l = 1,..., N(n), gde je N(n) broj nula polinoma Ĥn. Dakle, n N Zn je prebrojiv skup svih kompleksnih brojeva gde mera d µ nije kvazi-definitna. Neka je z 0 C\R takav da je mera d µ kvazi-definitna. Pretpostavimo da za neko n N vai n (z 0 ) = 0. Definiximo n 0 = min{n N n (z 0 ) = 0}. Kako je Ĥn neprekidna funkcija po z i kako je β n = Ĥn 2Ĥn/Ĥ2 n 1, sledi da je β n, n N 0, takoe neprekidna funkcija po z na C \ Z n. Zato postoji otvorena okolina taqke z 0, O 1 (z 0 ), takva da za svako z O 1 (z 0 ) vai Ĥ n 0, β n 0, za n = 0, 1,..., 4n 0. Kako je n0 (z 0 ) = 0, postoji otvorena okolina taqke z 0, O 2 (z 0 ), takva da za svako z O 2 (z 0 ) \ {z 0 } vai n0 (z) 0. Ako ne, postoji taqka z u svakoj otvorenoj okolini taqke z 0, razliqita od z 0, tako da vai n0 (z) = 0. Kako je n0 cela funkcija po z to bi znaqilo da je n0 (z) = 0, z C (videti [38, str. 168]), xto je nemogue na osnovu qienice da je n0 (z) < 0, z R. Definiximo O(z 0 ) = O 1 (z 0 ) O 2 (z 0 ). Tada je O(z 0 ) otvorena okolina taqke z 0 za koju je n0 (z) 0, z z 0, i na kojoj je β n0 neprekidna. Kako je to je {0, } lim z z0 βn0 = lim z z0 β n0 n0 1 n n 0, n0 +1(z 0 ) = 0. i S obzirom na to da je n 0 n0 (z 0 ) = p n k=0 n 0 +1 n0 +1(z 0 ) = p n k=0 p 2 k (z 0) p k 2 = 0 p 2 k (z 0) p k 2 = 0, 33
43 2.3. Algoritam dobijamo p 2 n 0 +1(z 0 ) = 0, xto je kontradikcija jer p n0 +1 ne moe imati kompleksnu nulu, kao qlan niza polinoma ortogonalnih u odnosu na pozitivnu meru dµ na realnoj pravoj. Ovim je pokazano da formule (2.10) i (2.11) vae za sve z C za koje je mera d µ kvazi-definitna. Konaqno, za neko z C za koje je mera d µ kvazi-definitna, dobijamo β 0 = (x z) 2 dµ = (x α 0 + α 0 z) 2 dµ = (x α 0 ) 2 dµ + 2 (x α 0 )(α 0 z)dµ + (α 0 z) 2 dµ = β 0 β 1 + (α 0 z) 2 β 0 = β 0 [ β1 + (z α 0 ) 2]. 2.3 Algoritam U ovom poglav u predstav amo racionalni algoritam za modifikaciju kvadratnim faktorom, d µ(x) = (x z) 2 dµ(x), pri qemu je z proizvoan kompleksan broj takav da je mera d µ kvazi-definitna. Teorema Koeficijenti α n i β n u troqlanoj rekurentnoj relaciji za niz polinoma ortogonalnih u odnosu na kvazi-definitnu meru d µ(x) = (x z) 2 dµ(x) mogu da se izraqunaju na sledei naqin: Poqetni uslovi: f 0 = 0, e 0 = 1. Izraqunavae: za i = 0, 1, 2,..., n raqunati a = α i z f i, a 2 ako je e b = i 0, e i e i 1 β i ako je e i = 0, β i = (1 e i )(b + β i+1 ), b e i+1 =, b + β i+1 f i+1 = (1 e i+1 )(a + α i+1 z), α i = a + f i+1 + z. 34
44 2.3. Algoritam Dokaz. Prvo pretpostavimo da je p i (z) 0 za sve i N 0. Dokaz se izvodi koristei matematiqku indukciju. Pokazaemo da za svako n N 0 vai: Za i = 0 imamo: e n = p2 n(z) n, f n = α n z p n(z)p n+1 (z) n. a = α 0 z f 0 = α 0 z = p 0p 1 0, b = a2 e 0 = (α 0 z) 2, β 0 = 0, e 1 = b b + β 1 = (α 0 z) 2 (α 0 z) 2 + β 1 = p2 1 1, f 1 = (1 e 1 )(a + α 1 z) = β 1(α 0 + α 1 2z) (α 0 z) 2 + β 1 = α 1 z p 1p 2 1, α 0 = a + f 1 + z = p2 1 ( p0 p 1 + z 0 ) + β1 ( 2p0 p α 1 2 0) 0 1. Neka je tvree taqno za n. Iz Algoritma za i = n + 1 sledi: a = α n+1 z f n+1 = α n+1 z ( α n a z) = α n+1 z α n + a + z = α n+1 + p np n+1 n = p n+1p n+2, n+1 b = a2 e n+1 = p2 n+2 n+1, n n+2 β n+1 = (1 e n+1 )(b + β n+2 ) = β n+1, 2 n+1 e n+2 = p 2 n+2 p 2 n+2 β n+2 n+1 = p2 n+2 n+2, f n+2 = (1 e n+2 )(a + α n+2 z) ( ) ( = 1 + p2 n+2 pn+1 p n+2 n+2 n+1 ) + α n+2 z = β n+2 (p n+1 p n+2 + α n+2 n+1 z n+1 ) n+2, α n 35
45 2.3. Primene algoritma α n+1 = a + f n+2 + z = p n+1p n+2 + β n+2 (p n+1 p n+2 + α n+2 n+1 z n+1 ) + z n+1 n+2 Iz sledi 1 ( = pn+1 p n+2 n+2 + n+1 β n+2 p n+1 p n n+1 n+1β n+2 α n+2 n+2 ) z 2 n+1β n+2 + z n+1 n+2 1 ( = pn+1 p n+2 (β n+2 n+1 p 2 n+1 n+2) + n+1 β n+2 p n+1 p n+2 n+2 ) + 2 n+1β n+2 α n+2 z n+1 p 2 n+2 ( ) ( pn p n+1 + z n + βn+1 2pn p n+1 n + α n+1 n) 2 = p2 n+1 n n+1. Ako je p i (z) = 0 za neko i, tada iz troqlane rekurentne relacije sledi Kako je to je Ovim je dokaz zavrxen. p i+1 (z) = (z α i )p i (z) β i p i 1 (z) = β i p i 1 (z). a = p ip i+1 i, e i = p2 i i a 2 e i = p2 i p 2 i+1 p 2 i i p 2 i+1 = p i+1 p i p. ip i+1 p i+1 p i p i p i+1 = β i p i 1 p i = β i (p i p i 1 p i 1 p i), a 2 = β ip 2 i 1(z) e i p i p i 1 p i 1p i = β i e i Primene algoritma U ovom delu primeujemo teoremu dva puta da bismo izraqunali koeficijente u troqlanoj rekurentnoj relaciji za niz polinoma ortogonalnih u odnosu na modifikovanu Qebixev evu meru druge vrste d µ(x) := ŵ(x)dx = ( x 2 1 2) 2 1 x2 dx, x [ 1, 1], 36
46 kao i u odnosu na meru 2.3. Primene algoritma dµ (x) := w (x)dx = x 2 ( x 2 1 2) 2 1 x2 dx, x [ 1, 1]. - - Slika 2.1: Grafici teinskih funkcija x ŵ(x) i x w (x) na intervalu [ 1, 1] - - Slika 2.2: Grafici teinskih funkcija x w(x), x w(x), x w(x) i x ŵ(x) na intervalu [ 1, 1] U prvom koraku raqunamo koeficijente α k, β k, k N 0, za niz polinoma ortogonalnih u odnosu na meru d µ(x) := w(x)dx = ( x 1 2 ) 2 1 x2 dx, x [ 1, 1]. Zatim, koristei izraqunate koeficijente α k i β k primenom 37
47 2.3. Primene algoritma teoreme dobijamo traene koeficijente α k i β k, k N 0, koristei qienicu da je d µ(x) = ( x 1 2 ) 2 d µ(x). Na slici 2.2 prikazane su teinske funkcije w(x) = 1 x 2, w(x), w(x) = (x + 1/ 2) 2 w(x) i ŵ(x). Teorema Koeficijenti u troqlanoj rekurentnoj relaciji za niz polinoma ortogonalnih u odnosu na meru ( d µ(x) = x 1 ) 2 1 x2 dx, x [ 1, 1], 2 su ) ( α k, βk = za k N 0. ( ) 2 k(k + 3),, k 0 mod 4, (k + 1)(k + 3) 4(k + 1) 2 ( 1, 2(k + 2) ) k(k + 3), k 1 mod 4, 4(k + 2) 2 ( ) k + 1 0,, k 2 mod 4, 4(k + 2) ( 1, 2(k + 2) ) k + 2, k 3 mod 4, 4(k + 1) Dokaz. Kako je ovo modifikacija Qebixev eve mere druge vrste, koeficijenti α k i β k u teoremi su α k = 0, k N 0, β 0 = π/2 i β k = 1/4, k N, a z = 1/ 2. Da bismo dokazali teoremu pokazaemo da su za svako k N 0 nizovi f k i e k u teoremi jednaki (f k, e k ) = ( k 2 2(k + 1), 1 k + 1 ( (k + 1), 2(k + 2) ), k 0 mod 4, ) 2, k 1 mod 4, k + 2 ( 1 ) 1,, k 2 mod 4, 2 k + 2 ( 1 ), 0, k 3 mod
48 2.3. Primene algoritma Dokaz sledi primenom matematiqke indukcije. Na poqetku pokazujemo taqnost tvrea za k = 0, 1, 2, 3. Direktnim izraqunavaem dobijamo: k = 0 : a = 1, b = 1 2 2, β0 = 0, e 1 = , f 1 = 3, α 0 = 3 ; k = 1 : a = 1 3 2, b = 1 12, β1 = 1 9, e 2 = 1 4, f 2 = 1 2, α 1 = ; k = 2 : a = 0, b = 0, β2 = 3 16, e 3 = 0, f 3 = 1 2, α 2 = 0; k = 3 : a = 0, b = 1 16, β3 = 5 16, e 4 = 1 5, f 4 = 2 2 5, α 3 = Neka je sada tvree taqno za k N. Na osnovu teoreme sledi: a = k 2 2(k + 1) = 1 2(k + 1), b = e k+1 = 2 k + 3, f k+1 = k + 2 2(k + 3), 1 2(k + 1), βk = 2 α k+1 = (k + 1)(k + 3), k(k + 3) 4(k + 1) 2, 1 a =, b = 2(k + 3) e k+2 = 1 k + 4, f k+2 = 1 2, (k + 1)(k + 4), 4(k + 3) 2 1 α k+2 =, 2(k + 3) 1 4(k + 3), βk+1 = a = 0, b = 0, βk+2 = k + 3 4(k + 4), e k+3 = 0, f k+3 = 1 2, α k+3 = 0, 39
49 a = 0, b = 2.3. Primene algoritma 1 4(k + 4), βk+3 = k + 5 4(k + 4), e k+4 = 1 k + 5, f k+4 = k + 4 2(k + 5), α k+4 = Ovim je dokaz zavrxen. 1 2(k + 5). Teorema Koeficijenti u troqlanoj rekurentnoj relaciji za polinome ortogonalne u odnosu na meru ( d µ(x) = x 2 2) x2 dx, x [ 1, 1], (2.14) su α k = 0, k N 0, β0 = π 16, k, k 0 mod 4, 4(k + 2) za k N 0. β k = 1 + k, k 1 mod 4, 4(k + 3) k + 4, k 2 mod 4, 4(k + 2) 5 + k, k 3 mod 4, 4(k + 3) Dokaz. Da bismo dokazali teoremu pokazaemo da su za svako k N 0 nizovi f k i e k u teoremi jednaki ( ) fk, ê k = ( k, 2(k + 1) 1 k + 2 ), k 0 mod 4, ( ) (k + 1) 2(k + 1),, k 1 mod 4, 2(k + 2) k(k + 3) ( ) 1 1 2,, k 2 mod 4, k + 1 ( ) 1 2, 0, k 3 mod 4. Ostatak dokaza je isti kao i dokaz teoreme
50 2.3. Primene algoritma Primer Prvih nekoliko polinoma p k ortogonalnih u odnosu na meru (2.14) su: p 0 (x) = 1, p 1 (x) = x, p 2 (x) = x 2 1 8, p 3 (x) = x x, p 4 (x) = x x , p 5 (x) = x 5 x x, p 6 (x) = x x x , p 7 (x) = x x x x, p 8 (x) = x x x x , p 9 (x) = x 9 2x x5 1 4 x x, p 10 (x) = x x x x x n=0 n=1 n=2 n=3 n= Slika 2.3: Grafici polinoma p n (x), n = 0, 1, 2, 3, 5 Na sliqan naqin dobijamo sledeu teoremu. 41
51 2.3. Primene algoritma Teorema Koeficijenti u troqlanoj rekurentnoj relaciji za polinome ortogonalne u odnosu na meru dµ (x) = x 2 ( x 2 1 2) 2 1 x2 dx, x [ 1, 1], (2.15) su α k = 0, k N 0, β0 = π 128, k, k 0 mod 4, 4(k + 4) za k N 0. β k = k + 7, k 1 mod 4, 4(k + 3) 1, k 2 mod 4, 4 1, k 3 mod 4, 4 Primer Prvih nekoliko polinoma r k ortogonalnih u odnosu na meru (2.15) su: r 0 (x) = 1, r 1 (x) = x, r 2 (x) = x 2 1 2, r 3 (x) = x x, r 4 (x) = x 4 x , r 5 (x) = x x x, r 6 (x) = x x x2 3 64, r 7 (x) = x x x x, r 8 (x) = x 8 2x x4 1 4 x , r 9 (x) = x x x x x, r 10 (x) = x x x x x
52 2.3. Primene algoritma - n=0 n=1 n=2 n=3 n= Slika 2.4: Grafici polinoma r n (x), n = 0, 1, 2, 3, 5 43
53 Glava 3 Polinomi ortogonalni u odnosu na modifikovane Qebixev eve mere Savremena teorija ortogonalnih polinoma bavi se konstrukcijom i analizom ihovih novih klasa. U najveem broju sluqajeva istraivaqi inspiraciju crpu upravo iz klasiqnih ortogonalnih polinoma. ihovo uopxtavae ili segregacija najqexi su pristupi u procesu konstrukcije i mogu se svesti na neki od sledeih naqina ili na ihovu kombinaciju: izmena nosaqa klasiqne mere ili modifikacija teinske funkcije. Tako su u radovima [2], [5], [33], [40], [4] razmatrane klase ortogonalnih polinoma na fragmentiranom nosaqu mere. Neki od naqina modifikacije teinske funkcije dati su u prethodnoj glavi. U ovom poglav u baviemo se parametrizacijom teinske funkcije jedne od klasiqnih mera. U [27] autori su razmatrali modifikaciju Qebixev eve mere koja je kasnije uopxtena u radu [19]. Moderna istraivaa potpomognuta su monim kompjuterskim sistemima u kojima su i specijalizovani paketi za rad sa ortogonalnim polinomima i specijalnim funkcijama, uopxte. Rezultati rada [19] u velikoj meri dobijeni su zahva ujui upotrebi programskog paketa Mathematica, a naroqito programskog paketa OrthogonalPolynomials koji je deta no opisan u [14], [17]. 44
54 3.1. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru prve vrste Neka su dati brojevi n, s N, n 2, i mera dµ n,s (x) := w n,s (x)dx = 2s T n (x) dx, (3.1) 1 x 2 gde je T n (x) = T n (x)/2 n 1 = cos(n arccos x)/2 n 1 moniqni Qebixev ev polinom prve vrste n-tog stepena. Ova mera generixe niz ortogonalnih polinoma p n,s k (x) = pn,s k (x; dµn,s ), k N 0, za koji znamo da je p n,s n = p n,s = T n. Egzistencija ovog niza polinoma je osigurana jer je dµ n,s (x) pozitivna mera. U [27] autori su razmatrali specijalan sluqaj s = 1 i dokazali sledeu teoremu, koja e biti korixena u dokazu glavnog rezultata kao baza indukcije. Teorema Za svako n 2, polinomi p n k (x) = pn k (x; dµn ), k N 0, gde je dµ n (x) = T 2 n(x)/ 1 x 2 dx, zadovo avaju rekurentnu relaciju p n k+1(x) = xp n k(x) β n k p n k 1(x), k N 0, p n 0(x) = 1, p n 1(x) = 0, pri qemu je βk n = π, 22n 1 ako je k = 0, ) 1 (1 ( 1)k/n, k/n ako je k 0 (mod n) (k 0), ) 1 (1 + ( 1)(k 1)/n, ako je k 1 (mod n), (k 1)/n 1 4, inaqe. Glavni rezultat ovog poglav a je uopxtee teoreme dato u radu [19]. 45
55 3.1. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Teorema Za svako n, s N, n 2, polinomi p n,s k N 0, zadovo avaju troqlanu rekurentnu relaciju k (x) = pn,s k (x; dµn,s ), sa i za k N (x) = xpn,s k (x) βn,s k pn,s k 1 (x), k N 0, (3.2) p n,s 0 (x) = 1, p n,s 1(x) = 0, p n,s k+1 β n,s 0 = π ( ) 2s 2 2ns s k, ako je k 0 (mod 2n), 4(k + ns) β n,s k = k + 2ns 1, ako je k 1 (mod 2n), 4(k + ns 1) k + 2ns, ako je k n (mod 2n), 4(k + ns) k 1, ako je k n + 1 (mod 2n), 4(k + ns 1) 1 4, inaqe. (3.3) Dokaz. Pretpostavimo da je za svako n, s N, n 2, niz {p n,s k } k N 0 definisan sa (3.2), pri qemu je β n,s k dato sa (3.3). Oqigledno, svaki p n,s k je moniqan polinom. Odredimo najpre koeficijent β n,s 0. Po definiciji imamo β n,s 0 = µ n,s 0 = Da e sledi (n 1)s π β n,s 0 = = 1 π 2 2(n 1)s 1 2 2(n 1)s+2s = 1 π 2 2ns 0 cos 2s nt ( sin t)dt = sin t ( ) e int + e int 2s dt 0 π 2s j=0 0 ( 2s j 2 2s j=0 ( 2s j 1 2 2(n 1)s π ) e ijnt e i(2s j)nt dt ) e 2i(s j)nt dt 0 cos 2s ntdt. 46
56 3.1. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... = 1 2 2ns = 1 2 2ns = π 2 2ns 2s j=0 2s j=0 ( 2s s ( ) 2s π e 2i(s j)nt dt j 0 ( ) 2s 1 e 2i(s j)nπ ). j 2i(s j)n U nastavku izostaviemo argument polinoma radi uproxea i preglednosti izraza. Tako emo, na primer, umesto T n (x) 2 p n,s 2nk (x) pisati T np 2 n,s 2nk. Za nastavak dokaza k uqna je taqnost tvrea iskazanih sledeim relacijama za k N 0 : T 2 np n,s 2nk = pn,s 1 2n(k+1) T 2 np n,s 2nk+j = pn,s 1 2n(k+1)+j + + (2k + 2s 2)(2k + 2s 1) + p n,s 1 2 2n 2nk, (2k + s 1)(2k + s) k + s 2 2j 1 (2k + s)(2k + s + 1) pn,s 1 2n(k+1) j (2k + 2s 1)(2k + 2s) p n,s 1 2 2n (2k + s) 2 2nk+j, j = 1,..., n 1, T np 2 n,s 2nk+n = (2k + 2s)(2k + 2s + 1) pn,s 1 2n(k+1)+n + 2 2n (2k + s)(2k + s + 1) pn,s 1 2nk+n, T np 2 n,s 2nk+n+j = pn,s 1 2n(k+1)+n+j 2k + 2s j (2k + s + 1)(2k + s + 2) pn,s 1 2n(k+1)+n j (2k + 2s)(2k + 2s + 1) + p n,s 1 2 2n (2k + s + 1) 2 2nk+n+j, j = 1,..., n 1. (3.4) Budui da niz polinoma sa leve strane jednakosti u (3.4) oqigledno zadovo ava relaciju T np 2 n,s k+1 x T np 2 n,s k + β n,s k T np 2 n,s k 1 = T n 2 ( p n,s k+1 xpn,s k + β n,s k k 1) pn,s = 0 za svako k N 0, ostaje da pokaemo da niz definisan desnom stranom jednakosti, recimo {q i } i N0, u (3.4) zadovo ava istu relaciju, kao i da vai T np 2 n,s 0 = q 0 i T np 2 n,s 1 = q 1. Da bismo pokazali jednakost q i+1 xq i + β n,s i q i 1 = 0 za svako i N, razlikovaemo osam sluqajeva. 47
57 3.1. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Sluqaj 1: i 1 (mod 2n). U ovom sluqaju treba da pokaemo da je izraz p n,s 1 2n(k+1)+2 + k + s 2 3 (2k + s)(2k + s + 1) pn,s 1 2n(k+1) 2 (2k + 2s 1)(2k + 2s) + p n,s 1 2 2n (2k + s) 2 2nk+2 ( x p n,s 1 2n(k+1)+1 + k + s 2(2k + s)(2k + s + 1) pn,s 1 2n(k+1) 1 (2k + 2s 1)(2k + 2s) ) + p n,s 1 2 2n (2k + s) 2 2nk+1 2k + 2s ( + p n,s n(k+1) (2k + s) jednak nuli. Kako ekvivalentni oblik glasi p n,s 1 2n(k+1)+2 xpn,s 1 2n(k+1)+1 + βn,s 1 2n(k+1)+1 pn,s 1 2n(k+1) + ( 2k + 2s 2 2 (2k + s) βn,s 1 2n(k+1)+1 + (2k + 2s 2)(2k + 2s 1) 2 2n (2k + s 1)(2k + s) ) p n,s 1 2nk ) ( p n,s 1 2n(k+1) + xpn,s 1 2n(k+1) 1 βn,s 1 2n(k+1) 1 pn,s 1 2n(k+1) 2 (2k + 2s 1)(2k + 2s) ( ) p n,s 1 2 2n (2k + s) 2 2nk+2 xpn,s 1 2nk+1 + βn,s 1 2nk+1 pn,s 1 2nk, tvree jednostavno zak uqujemo. Sluqaj 2: i j (mod 2n), j = 2,..., n 2. U ovom sluqaju posmatramo izraz p n,s 1 2n(k+1)+j+1 + k + s 2 2j+1 (2k + s)(2k + s + 1) pn,s 1 2n(k+1) j 1 (2k + 2s 1)(2k + 2s) + p n,s 1 2 2n (2k + s) 2 2nk+j+1 ( x p n,s 1 2n(k+1)+j + k + s 2 2j 1 (2k + s)(2k + s + 1) pn,s 1 (2k + 2s 1)(2k + 2s) ) + p n,s 1 2 2n (2k + s) 2 2nk+j + 1 ( p n,s 1 2n(k+1)+j k + s 2 2j 3 (2k + s)(2k + s + 1) pn,s 1 (2k + 2s 1)(2k + 2s) ) + p n,s 1 2 2n (2k + s) 2 2nk+j 1. 2n(k+1) j 2n(k+1) j+1 ) 48
58 3.1. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... U ekvivalentnom obliku glasi gde je u (j) k,s = p n,s 1 2n(k+1)+j+1 xpn,s 1 2n(k+1)+j + βn,s 1 2n(k+1)+1 pn,s 1 2n(k+1)+j 1 + u (j) k,s + v (n) k,s ( p n,s 1 2n(k+1) j+1 xpn,s 1 2n(k+1) j + βn,s 1 2n(k+1) j pn,s 1 2n(k+1) j 1 ( ) p n,s 1 2nk+j+1 xpn,s 1 2nk+j + βn,s 1 2nk+j pn,s 1 2nk+j 1 = 0, k + s 2 2j 1 (2k + s)(2k + s + 1) i (2k + 2s 1)(2k + 2s) v(n) k,s =. 2 2n (2k + s) 2 Jasno je da je prethodni izraz jednak nuli. Sluqaj 3: i n 1 (mod 2n). Sada dobijamo p n,s 1 (2k + 2s)(2k + 2s + 1) 2n(k+1)+n + 2 2n (2k + s)(2k + s + 1) pn,s 1 ( x p n,s 1 2n(k+1)+n 1 + (2k + 2s 1)(2k + 2s) + p n,s 1 2 2n (2k + s) 2 ( p n,s 1 2n(k+1)+n xto moemo napisati kao 2nk+n k + s 2 2n 3 (2k + s)(2k + s + 1) pn,s 1 2n(k+1) n+1 ) 2nk+n 1 (2k + 2s 1)(2k + 2s) 2 2n (2k + s) 2 p n,s 1 2nk+n 2 k + s 2 2n 5 (2k + s)(2k + s + 1) pn,s 1 2n(k+1) n+2 ) p n,s 1 2n(k+1)+n xpn,s 1 2n(k+1)+n 1 + βn,s 1 2n(k+1)+n 1 pn,s 1 2n(k+1)+n 2 + u (n) k,s + v (n) k,s pa je sve jednako nuli. Sada je u (n) k,s = ( ) p n,s 1 2n(k+1) n+2 xpn,s 1 2n(k+1) n+1 + βn,s 1 2n(k+1) n+1 pn,s 1 2n(k+1) n ( ) p n,s 1 2nk+n xpn,s 1 2nk+n 1 + βn,s 1 2nk+n 1 pn,s 1 2nk+n 2, k + s 2 2n 3 (2k + s)(2k + s + 1) i (2k + 2s 1)(2k + 2s) v(n) k,s =. 2 2n (2k + s) 2, ) 49
59 3.1. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Sluqaj 4: i n (mod 2n). Odgovarajui izrazi za ovaj sluqaj postaju p n,s 1 2n(k+1)+n+1 2k + 2s + 1 4(2k + s + 1)(2k + s + 2) pn,s 1 2n(k+1)+n 1 (2k + 2s)(2k + 2s + 1) + p n,s 1 2 2n (2k + s + 1) 2 2nk+n+1 ( x p n,s 1 (2k + 2s)(2k + 2s + 1) ) 2n(k+1)+n + 2 2n (2k + s)(2k + s + 1) pn,s 1 2nk+n 2k + 2s + 1 ( + p n,s 1 2n(k+1)+n 1 4(2k + s + 1) + + koje moemo napisati u obliku k + s 2 2n 3 (2k + s)(2k + s + 1) pn,s 1 2n(k+1) n+1 (2k + 2s 1)(2k + 2s) 2 2n (2k + s) 2 p n,s 1 2nk+n 1 p n,s 1 2n(k+1)+n+1 xpn,s 1 2n(k+1)+n + βn,s 1 2n(k+1)+n pn,s 1 2n(k+1)+n 1 + (2k + 2s)(2k + 2s + 1) ( p n,s 1 2 2n 2nk+n+1 (2k + s)(2k + s + 1) xpn,s 1 2nk+n + βn,s 1 2nk+n 2nk+n 1) pn,s 1 = 0. Jasno je da je prethodni izraz jednak nuli. Sluqaj 5: i n + 1 (mod 2n). U ovom sluqaju imamo p n,s 1 2n(k+1)+n+2 + 2k + 2s (2k + s + 1)(2k + s + 2) pn,s 1 2n(k+1)+n 2 (2k + 2s)(2k + 2s + 1) + p n,s 1 2 2n (2k + s + 1) 2 2nk+n+2 ( x p n,s 1 2n(k+1)+n+1 2k + 2s (2k + s + 1)(2k + s + 2) pn,s 1 2n(k+1)+n 1 (2k + 2s)(2k + 2s + 1) ) + p n,s 1 2 2n (2k + s + 1) 2 2nk+n+1 2k + 1 ( + p n,s 1 (2k + 2s)(2k + 2s + 1) ) 2 2 2n(k+1)+n + (2k + s + 1) 2 2n (2k + s)(2k + s + 1) pn,s 1 2nk+n ), 50
60 3.1. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... gde je u k,s = = p n,s 1 2n(k+1)+n+2 xpn,s 1 2n(k+1)+n+1 + βn,s 1 2n(k+1)+n+1 pn,s 1 2n(k+1)+n ( u k,s p n,s 1 2n(k+1)+n xpn,s 1 2n(k+1)+n 1 + βn,s 1 2n(k+1)+n 1 pn,s 1 2n(k+1)+n 2 ) ( + v (n) k,s p n,s 1 2nk+n+2 xpn,s 1 2nk+n+1 + βn,s 1 2nk+n+1 pn,s 1 2nk+n = 0, 2k + 2s + 1 (2k + s + 1)(2k + s + 2) i (2k + 2s)(2k + 2s + 1) v(n) k,s =. 2 2n (2k + s + 1) 2 ) Sluqaj 6: i n + j + 1 (mod 2n), j = 1,..., n 3. Sada imamo izraz p n,s 1 2n(k+1)+n+j+2 + 2k + 2s (j+2) (2k + s + 1)(2k + s + 2) pn,s 1 2n(k+1)+n j 2 koji se svodi na (2k + 2s)(2k + 2s + 1) + p n,s 1 2 2n (2k + s + 1) 2 2nk+n+j+2 ( x p n,s 1 2n(k+1)+n+j+1 2k + 2s (j+1) (2k + s + 1)(2k + s + 2) pn,s 1 2n(k+1)+n j 1 (2k + 2s)(2k + 2s + 1) ) + p n,s 1 2 2n (2k + s + 1) 2 2nk+n+j ( p n,s 1 2n(k+1)+n+j 4 2k + 2s j (2k + s + 1)(2k + s + 2) pn,s 1 2n(k+1)+n j (2k + 2s)(2k + 2s + 1) ) + p n,s 1 2 2n (2k + s + 1) 2 2nk+n+j, p n,s 1 2n(k+1)+n+j+2 xpn,s 1 2n(k+1)+n+j+1 + βn,s 1 2n(k+1)+n+j+1 pn,s 1 2n(k+1)+n+j u (j) k,s + v (n) k,s ( p n,s 1 2n(k+1)+n j xpn,s 1 2n(k+1)+n j 1 + βn,s 1 2n(k+1)+n j 1 pn,s 1 2n(k+1)+n j 2 ( p n,s 1 2nk+n+j+2 xpn,s 1 2nk+n+j+1 + βn,s 1 2nk+n+j+1 pn,s 1 2nk+n+j i jednak je nuli jednostavnom analizom svakog reda prethodnog izraza. U ovom sluqaju je u (j) k,s = 2k + 2s j+2 (2k + s + 1)(2k + s + 2) i (2k + 2s)(2k + 2s + 1) v(n) k,s =. 2 2n (2k + s + 1) 2 ), ) 51
61 3.1. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Sluqaj 7: i 2n 1 (mod 2n). Kako se svodi na p n,s 1 (2k + 2s)(2k + 2s + 1) 2n(k+2) + 2 2n (2k + s + 1)(2k + s + 2) pn,s 1 2n(k+1) ( x p n,s 1 2n(k+2) 1 2k + 2s n 1 (2k + s + 1)(2k + s + 2) pn,s 1 2n(k+1)+1 (2k + 2s)(2k + 2s + 1) ) + p n,s 1 2 2n (2k + s + 1) 2 2n(k+1) ( p n,s 1 2n(k+2) k + 2s n 2 (2k + s + 1)(2k + s + 2) pn,s 1 2n(k+1)+2 (2k + 2s)(2k + 2s + 1) ) + p n,s 1 2 2n (2k + s + 1) 2 2n(k+1) 2 p n,s 1 2n(k+2) xpn,s 1 2n(k+2) 1 + βn,s 1 2n(k+2) 1 pn,s 1 2n(k+2) 2 u (n) k,s + v (n) k,s ( p n,s 1 2n(k+1)+2 xpn,s 1 2n(k+1)+1 + βn,s 1 2n(k+1)+1 pn,s 1 2n(k+1) ( p n,s 1 2n(k+1) xpn,s 1 2n(k+1) 1 + βn,s 1 2n(k+1) 1 pn,s 1 2n(k+1) 2 to je poslede jednako nuli jer je svaki red jednak nuli. U ovom sluqaju je u (n) k,s = 2k + 2s n 1 (2k + s + 1)(2k + s + 2) i (2k + 2s)(2k + 2s + 1) v(n) k,s =. 2 2n (2k + s + 1) 2 Sluqaj 8: i 2n (mod 2n). Sada imamo izraz p n,s 1 2n(k+2)+1 + k + s + 1 2(2k + s + 2)(2k + s + 3) pn,s 1 2n(k+2) 1 (2k + 2s + 1)(2k + 2s + 2) + p n,s 1 2 2n (2k + s + 2) 2 2n(k+1)+1 ( x p n,s 1 (2k + 2s)(2k + 2s + 1) 2n(k+2) + 2 2n (2k + s + 1)(2k + s + 2) pn,s 1 2(k + 1) ( + p n,s 1 2n(k+2) 1 4(2k + s + 2) + 2k + 2s n 1 (2k + s + 1)(2k + s + 2) pn,s 1 2n(k+1)+1 (2k + 2s)(2k + 2s + 1) 2 2n (2k + s + 1) 2 p n,s 1 2n(k+1) 1 52 ), 2n(k+1) ) ), )
62 3.1. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... koji se svodi na p n,s 1 2n(k+2)+1 xpn,s 1 2n(k+2) + βn,s 1 2n(k+2) pn,s 1 2n(k+2) 1 + (2k + 2s)(2k + 2s + 1) 2 2n (2k + s + 1)(2k + s + 2) i jednak je nuli jer je svaki red jednak nuli. Sada emo pokazati sledeu jednakost T 2 n = p n,s 1 2n + ( p n,s 1 2n(k+1)+1 xpn,s 1 2n(k+1) + βn,s 1 2n(k+1) pn,s 1 2n(k+1) 1 (2s 2)(2s 1). (3.5) 2 2n (s 1)s Poznato je da za moniqne Qebixev eve polinome prve vrste T n vai T 2 n = 1/2 2n 1 + T 2n. Koristei rekurentnu relaciju za Qebixev eve polinome T n+1 = x T n T n 1 /4 i jednakost dobijamo p n,s n+1 = xp n,s n Ako oznaqimo sa β n,s n = 1 + 2s 4(1 + s) = s 4(1 + s), βn n,s p n,s n 1 = T s n+1 4(s + 1) T n 1, p n,s n+2 = xp n,s n+1 βn+1p n,s n,s n = T n+2 sx 4(s + 1) T n 1 + s 4(s + 1) T n. s u 0 = 4(s + 1) T n 1, u 1 = sx 4(s + 1) T s n 1 + 4(s + 1) T n, moemo da zapixemo p n,s n+k = T n+k + u k 1, gde niz polinoma u k, k = 0,..., n 1, zadovo ava relaciju u k+1 = xu k 1 4 u k 1. Primenom matematiqke indukcije lako moemo da pokaemo da vai s u k = 4(s + 1) (Ûk T n 1 Ûk 1 T n ), gde je Ûk moniqni Qebixev ev polinom druge vrste k-tog stepena. ) 53
63 3.1. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Sada imamo odakle sledi p n,s 2n = T 2n + u n 1 = T s 2n 4(s + 1) (Ûn 1 T n 1 Ûn 2 T n ) = T s 1 2n 4(s + 1) 2, 2n 3 p n,s 2n = T n s 2n 1 s + 1 xto je zapravo (3.5) za s := s + 1. Treba da pokaemo da je T 2 np n,s 1 = q 1. Imamo 1 2 = T 2 2n 1 n 1 2s n 1 s + 1, q 1 = p n,s 1 1 2n+1 + 2(s + 1) pn,s 1 2n 1 + 2s 1 2 2n 1 s pn,s 1 1 = xp n,s 1 2n = xp n,s 1 2n = β n,s 1 2n p n,s 1 1 2n 1 + 2(s + 1) pn,s 1 2n 1 + 2s 1 2 2n 1 s x 1 2(s + 1) pn,s 1 ( p n,s 1 2n + 2s 1 2 2n 1 s 2n 1 + ) x = T 2 np n,s (s + 1) pn,s 1 2n 1 + 2s 1 2 2n 1 s x Ostaje da se dokae ortogonalnost niza p n,s k, k N 0, za n, s N, n 2. Sada koristimo matematiqku indukciju po s. Sluqaj s = 1 je upravo teorema Ako pretpostavimo da je za n, s N, n 2, p n,s 1 k, k N 0, niz moniqnih polinoma koji je ortogonalan u odnosu na teinsku funkciju w n,s 1, onda ortogonalnost niza p n,s k, k N 0, jednostavno sledi iz relacije w n,s = T nw 2 n,s 1. Posle mnoea relacije (3.4) sa odgovarajuim p n,s 1 j i integra eem obe strane jednakosti dobijamo 1 1 Ovim je dokaz zavrxen. 1 p n,s m p n,s 1 j w n,s dx = T np 2 n,s m p n,s 1 j w n,s 1 dx =
64 3.1. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Slika 3.1: Grafici polinoma p 3,2 k (x), k = 0, 1, 2, 3, 4, 5 Primer Prvih nekoliko polinoma p 3,2 k (x) i p2,4 k (x) ortogonalnih u odnosu na meru (3.1) za n = 3, s = 2 i n = 2, s = 4 redom su: p 3,2 0 (x) = 1, p 3,2 1 (x) = x, p 3,2 2 (x) = x 2 1 2, p 3,2 3 (x) = x x, p 3,2 4 (x) = x x , p 3,2 5 (x) = x x x, p 3,2 6 (x) = x x x2 5 96, p 3,2 7 (x) = x x x x, p 3,2 8 (x) = x 8 2x x x , p 3,2 9 (x) = x x x x x, p 3,2 10 (x) = x x x x x
65 3.2. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Slika 3.2: Grafici polinoma p 2,4 k (x), k = 0, 1, 2, 3, 4, 5 p 2,4 0 (x) = 1, p 2,4 1 (x) = x, p 2,4 2 (x) = x 2 1 2, p 2,4 3 (x) = x x, p 2,4 4 (x) = x 4 x , p 2,4 5 (x) = x x x, p 2,4 6 (x) = x x x2 1 96, p 2,4 7 (x) = x x x x, p 2,4 8 (x) = x 8 2x x x , p 2,4 9 (x) = x x x x x, p 2,4 10 (x) = x x x x x , a ihovi grafici su prikazani na slikama 3.1 i
66 3.2. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru druge vrste Konstruixemo niz polinoma P k, k N 0, ortogonalan u odnosu na modifikovanu Qebixev evu meru druge vrste d µ(x) = x + 1c c 1 x + 1c + 1 x2 dx, x [ 1, 1], 2 2c gde je c pozitivan realan broj. Dakle, izuqavamo polinome ortogonalne u odnosu na moment-funkcionelu L(P ) = 1 1 P (x) x + 1c c 1 x + 1c + 1 x2 dx, P P, (3.6) 2 2c gde je c R\{0}. Specijalan sluqaj c = 1 razmatran je u [17]. Da bismo pojasnili sluqaj, na slici 3.3 je prikazan grafik racionalnog dela teinske funkcije za c = 2. Kada c tei ka 1 singularitet racionalnog dela tei ka 1, kada c proe 1 singularitet tei ka. Potpuno simetriqna situacija nastaje za c < 0. Naime, stav ajui c := c, i posle smene x := x, dobijamo istu linearnu funkcionelu, pa nada e razmatramo samo sluqaj c > 0. Nula racionalnog dela je uvek po modulu vea od singulariteta. y x 1 Slika 3.3: Grafik racionalnog dela teine u (3.6) 57
67 3.2. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Posmatramo modifikovanu meru d µ(x) = x γ 1 x2 dx, x [ 1, 1], x δ gde je γ = 1c 1 i δ = 1c 1. Rexavamo problem nalaea koeficijenata u rekurentnoj relaciji α k = α k (d µ), βk = β k (d µ), znajui da su 2 c 2 2c koeficijenti za Qebixev evu meru druge vrste α k = 0, β k = 1/4 za k N i α 0 = 0, β 0 = π/2. Niz ortogonalnih polinoma P k, k N 0, postoji budui da je mera d µ(x) pozitivna na [ 1, 1] i da ima konaqne sve momente L(x k ) = 1 1 x k x + 1c c 1 x + 1c + 1 x2 dx, k N c Problem rexavamo u dva koraka. Prvo, posmatramo modifikaciju Qebixev eve mere druge vrste de eem linearnim faktorom, pri qemu koristimo Algoritam 1. Na taj naqin dobijamo koeficijente α k i β k. Zatim primeujemo Algoritam 2 za odreivae koeficijenata u odnosu na modifikovanu meru koja nastaje mnoeem linearnim faktorom, d µ(x), i konaqno dobijamo α k i β k, za k N 0. Sliqne teinske funkcije, kao xto su na primer (1 x 2 )(1 k 2 x 2 ) 1/2, k 2 < 1, su izuqavane u [67]. Takoe postoji veliki broj rezultata za takozvane Sege 1 -Bernxtajn teinske funkcije date sa w 1 (x) = ρ(x), w 2(x) = ρ(x) 1 x 1 x 2, w 3 (x) = ρ(x) 1 x x, pri qemu je ρ polinom koji je pozitivan na intervalu ( 1, 1) (videti [69], [9]). Sliqna teinska funkcija w(x) = 1 x 2 1 µx 2, µ 1, takoe je izuqavana u [34]. Za Qebixev evu meru prve vrste ista modifikacija je prouqavana u [37]. Konaqno, u [5] mogu se nai sliqni rezultati qak i za sluqaj kada nosaq mere ima dve disjunktne komponente. 1 Gábor Szegő ( ), maarski matematiqar. 58
68 3.2. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru Linearni delioci Razmatramo modifikovanu meru koja se dobija de eem linearnim faktorom d µ(x) = 1 1 x2 dx, x [ 1, 1], δ R \ [ 1, 1], x δ gde je δ = 1 2 c 1 2c. Da bismo mogli da primenimo modifikacioni Algoritam 1, neophodna nam je vrednost Koxijevog integrala ρ 0 (δ) = 1 1 koji izraqunavamo u sledeoj lemi. 1 1 x2 dx, δ R \ [ 1, 1], δ x Lema Vrednost Koxijevog integrala je ρ 0 (δ) = x2 dx = ( δ δ x δ)π. Dokaz. Koristei drugu Ojlerovu 2 smenu 1 x 2 = 1 + mx, dobijamo Sada imamo x = 2m 1 + m, dx = 2(m2 1) 2 (1 + m 2 ) dm x2 dx = 2 δ x (m 2 1) 2 (δm 2 + 2m + δ)(1 + m 2 ) 2 dm. Ovaj integral moemo izraqunati kao integral racionalne funkcije. Da e imamo (m 2 1) 2 (δm 2 + 2m + δ)(1 + m 2 ) 2 = Ostatak dokaza je sada oqigledan. δ 1 + m 2m 2 (1 + m 2 ) + 1 δ 2 2 δm 2 + 2m + δ. Pre nego xto dokaemo sledeu teoremu dajemo Algoritam 1 koji emo koristiti u dokazu teoreme Oba modifikaciona algoritma mogu se nai, na primer, u [27, str. 123{129]. 2 Leonhard Euler ( ), xvajcarski matematiqar i fiziqar. 59
69 3.2. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Algoritam 1 (Modifikacija linearnim deliocem) Poqetni uslovi: α 0 = δ β 0 ρ 0 (δ), β0 = ρ 0 (δ), q 0 = β 0 ρ 0 (δ). (3.7) Izraqunavae: Za k = 1, 2,..., n 1 raqunati e k 1 = α k 1 δ q k 1, (3.8) β k = q k 1 e k 1, q k = β k /e k 1, (3.9) α k = q k + e k 1 + δ. (3.10) su i Teorema Koeficijenti u troqlanoj relaciji za meru 1 d µ(x) = 1 x + c + 1 x2 dx, 2 2c x [ 1, 1], α 0 = 1 2c, α k = 0 za k 1 β 0 = π c, βk = 1 4 za k 1. Dokaz. Koeficijenti α 0 i β 0 su izraqunati direktno pomou (3.7). Takoe, korisno je izraqunati koeficijente α 1 i β 1 kao bazu matematiqke indukcije. Primenom Algoritma 1 za k = 1 dobijamo α 1 = 0, β1 = 1 4. Ostatak dokaza sledi primenom matematiqke indukcije. Dakle, neka je tvree taqno za k i treba dokazati taqnost tvrea za k + 1. Kombinovaem (3.8) i (3.10) dobija se α k = 0 = q k + e k 1 + δ = q k δ q k 1 + δ, odakle je q k = q k 1. (3.11) Iz (3.10) sledi α k+1 = q k+1 + e k + δ = q k+1 δ q k + δ = q k+1 q k. 60
70 3.2. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Koristei (3.9) dobijamo a iz (3.11) Sada je q k+1 = 1 4e k, α k = 1 4e k 1 q k = q k q k = 0. Iz (3.11) i (3.12) sledi e k = e k 1. (3.12) β k+1 = q k e k = q k 1 e k 1 = 1 4, qime je dokaz zavrxen Linearni faktori Posmatramo modifikaciju mere linearnim faktorom gde je γ = 1 2 c 1 c. d µ(x) = (x γ)d µ(x), x [ 1, 1], γ R \ [ 1, 1], Pre nego xto predstavimo Algoritam 2, treba da naglasimo da u ovom algoritmu koristimo ve izraqunate koeficijente α k i β k da bismo izraqunali koeficijente u troqlanoj rekurentoj relaciji za meru d µ(x), α k i β k, k N 0. Algoritam 2 (Modifikacija linearnim faktorom) Poqetni uslov: e 1 = 0. Izraqunavae: Za k = 0, 1,..., n 1 raqunati q k = α k e k 1 γ, (3.13) β k = ( α 0 γ) β 0 za k = 0, β k = q k e k 1 za k > 0, (3.14) e k = β k+1 /q k, (3.15) α k = γ + q k + e k. (3.16) 61
71 3.2. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... meru su i Teorema Koeficijenti u troqlanoj rekurentnoj relaciji za gde smo oznaqili A = d µ(x) = x + c c 1 x + c + 1 x2 dx, x [ 1, 1], 2 2c Apq k α k = (1 + pq k )(1 + pq k+1 ), k N 0, (3.17) β k = (1 + pqk 1 )(1 + pq k+1 ) 4(1 + pq k ) 2, k N, (3.18) c c(2 + c 2 + c 4 + 4), p = Dokaz. Pokazaemo da je e k = 2 + c2 c c c4 + 4 c 2 c c 2, q = 2 + c2 c c 2 + c pq k 1 + pq, k N 0, (3.19) k+1 odakle ostatak dokaza ove teoreme sledi direktno. Dokaz izvodimo primenom matematiqke indukcije. Za k = 0 iz (3.19) dobijamo e 0 = c/(2+2c 2 ) xto takoe moemo dobiti iz Algoritma 2 stav ajui da je k = 0. Dakle, neka je tvree taqno za k 1. Iz (3.13) i (3.15) sledi e k = 1/4 q k Elementarnim raqunom dobijamo ( 2 + c 2 c c 1 = 4(e k 1 + γ). (3.20) 1 + pq k 1 c 1 + pq k 2 1 ) = c 4c 2 + c 2 c pq k pq k. Izraz na desnoj strani prethodne jednakosti je 1/e k, xto se upravo i tvrdilo u (3.20). Iz (3.14) i (3.15) sledi xto je zapravo (3.18). β k = q k e k 1 = β k+1 e k 1 = 1 e k 1, e k 4 e k Sada, (3.17) je direktna posledica (3.16) i (3.19). Na kraju ovog poglav a, u sledee dve teoreme dajemo eksplicitni izraz za niz polinoma P n. 62
72 3.2. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Teorema Niz polinoma ortogonalan u odnosu na meru d µ(x) moe se izraziti pomou P k (x) = U k (x) α 0 U k 1 (x), gde je α 0 = 1/(2c), a U n je Qebixev ev polinom druge vrste n-tog stepena. Dokaz. Tvree je taqno za k = 1 i k = 2. Zaista, imamo P 1 (x) = (x α 0 ) P 0 (x) = x α 0 = U 1 (x) α 0 U 0 (x) i P 2 (x) = (x α 1 ) P 1 (x) β 1 P0 (x) = x(u 1 (x) α 0 U 0 (x)) β 1 U 0 = xu 1 (x) β 1 U 0 (x) α 0 xu 0 (x) = U 2 (x) α 0 U 1 (x). Neka je tvree taqno za k 1 i k, i treba da dokaemo taqnost za k + 1. Sada je P k+1 (x) = (x α k ) P k (x) β k Pk 1 (x) = (x α k )(U k (x) α 0 U k 1 (x)) β k (U k 1 (x) α 0 U k 2 (x)) = (xu k (x) β k U k 1 (x)) α 0 (xu k 1 (x) β k U k 2 (x)) = U k+1 (x) α 0 U k (x). Konaqno, moemo da izrazimo dati niz polinoma P n direktno preko Qebixev evih polinoma druge vrste U n. Teorema Neka je d µ(x) kvazi-definitna mera i γ = 1 2 c 1 c takvo da je P k (γ) 0 za k N. Neka je d µ(x) = (x γ)d µ(x). Tada je mera d µ(x) takoe kvazi-definitna i polinomi P n su moniqni formalni ortogonalni polinomi u odnosu na d µ(x), koji se mogu izraziti pomou P n (x, γ) = = P n+1 (x) P n+1 (γ) P n (γ) x γ P n (x) U n+1 (x) α 0 U n (x) U n+1(γ) α 0 U n (γ) U n (γ) α 0 U n 1 (γ) (U n(x) α 0 U n 1 (x)). x γ Dokaz. Dokaz ove teoreme je posledica teoreme 1.55 iz [27, str. 38]. 63
73 3.2. Polinomi ortogonalni u odnosu na modifikovanu Qebixev evu meru... Primer Prvih nekoliko polinoma P k ortogonalnih u odnosu na moment-funkcionelu (3.6) za c = 2 su: P 0 (x) = 1, P 1 (x) = x , P 2 (x) = x x 11 40, P 3 (x) = x x x , P 4 (x) = x x x x , P 5 (x) = x x x x x
74 Glava 4 Primene u kvadraturnim procesima i L 2 -aproksimaciji 4.1 Kvadraturne formule Neka je dµ konaqna pozitivna Borelova 1 mera na realnoj pravoj R qiji nosaq supp(dµ) ima beskonaqno mnogo elemenata i qiji svi momenti m k = R xk dµ, k = 0, 1,..., postoje i konaqni su. Kvadraturna formula sa n taqaka oblika R f(x)dµ(x) = n A k f(τ k ) + R n (f), (4.1) k=1 koja je taqna na skupu P 2n 1 (R n (P 2n 1 ) = 0) je poznata kao Gaus-Kristofelova kvadraturna formula. To je kvadraturna formula koja ima maksimalni algebarski stepen taqnosti d max = 2n 1. Prvu formulu ovog tipa 1 0 f(x)dx = n A k f(τ k ) + R n (f) (4.2) k=1 otkrio je Karl Fridrih Gaus pre dva veka. Posle utnove 2 formule o numeriqkoj integraciji iz godine (poznato je i kao utn-koutsovo pravilo) b a f(x)dx Q n (x) = n A k f(τ k ), (4.3) k=1 1 Émile Borel ( ), francuski matematiqar. 2 Isaac Newton ( ), engleski fiziqar i matematiqar. 65
75 4.1. Kvadraturne formule koja se dobija integracijom odgovarajueg interpolacionog polinoma funkcije f(x) u n razliqitih fiksiranih taqaka (qvorova) τ 1,...,τ n (koje se najqexe biraju ekvidistantno u [a, b]), Gaus je godine razvio svoj quveni metod koji drastiqno pobo xava utnov metod. Budui da je utn-koutsova formula taqna samo za polinome stepena najvixe n 1, Gaus je postavio pitae koji maksimalan algebarski stepen taqnosti moe da se postigne u (4.3) (tj. u (4.2) stav ajui [a, b] = [0, 1]) ako su qvorovi τ 1,...,τ n slobodni. Kako kvadraturna suma Q n (f) = n A k f(τ k ) k=1 ima 2n nepoznatih parametara: τ k, A k, k = 1,..., n, Gaus je poxao od pretpostavke da kvadraturna formula (4.2) moe biti taqna za sve algebarske polinome stepena najvixe 2n 1. Oslaajui se na radove utna i Koutsa i svoj rad o hipergeometrijskim razvojima iz godine, Gaus je dokazao ovaj rezultat. Treba napomenuti da je Gaus odredio numeriqke vrednosti parametara kvadrature: qvorove τ k i teine A k, k = 1,..., n, za sve n 7 sa skoro 16 znaqajnih decimalnih cifara. Ovo otkrie je bilo jedno od najznaqajnijih u devetnaestom veku u po u numeriqke integracije, a moda i u celoj numeriqkoj analizi. Gausove rezultate je po formi pojednostavio Jakobi godine. U devetnaestom veku Gausove kvadrature su deta nije razraivali Meler 3, Radau 4, Hajne 5, Kristofel, itd. Ocenu grexke i konvergenciju su dokazali Markov i Stiltjes. Modernim jezikom reqeno, glavni rezultat ove teorije glasi: Neka je dµ(x) pozitivna mera na R sa konaqnim ili neograniqenim nosaqem qiji svi momenti m k = R xk dµ(x), k N, postoje i konaqni su i m 0 > 0. Tada, za svako n N, postoji Gaus-Kristofelova kvadraturna formula (4.1) sa n taqaka koja je taqna za sve algebarske polinome stepena 2n 1, tj. R n (f) = 0 za svako f P 2n 1. Sledeu teoremu dokazao je Jakobi godine. Teorema Za dati prirodan broj m ( n), kvadraturna formula (4.1) ima algebarski stepen taqnosti d = n 1+m ako i samo ako vai: 1 formula (4.1) je interpolaciona; 3 Gustav Ferdinand Mehler ( ), nemaqki matematiqar. 4 Jean Charles Rodolphe Radau ( ), astronom i matematiqar roen u Prusiji. 5 Heinrich Eduard Heine ( ), nemaqki matematiqar. 66
76 4.1. Kvadraturne formule 2 polinom ω n (x) = (x τ 1 ) (x τ n ) zadovo ava (p, ω n ) = p(x)ω n (x)dµ(x) = 0 za sve p P m 1. R Prema ovoj teoremi, kvadraturna formula (4.1) u odnosu na pozitivnu meru dµ(x) ima maksimalni algebarski stepen taqnosti 2n 1, tj. vrednost m = n je optimalna. Vrednosti m > n nisu mogue. Zaista, za m = n + 1 bi, zbog 2, polinom ω n morao biti ortogonalan na samom sebi, xto je nemogue. Kada je m = n 1 imamo Gaus-Radauovu formulu (jedna od krajih taqaka intervala a ili b je uk uqena u skup qvorova), dok za m = n 2 imamo Gaus-Lobatovu 6 formulu (τ 1 = a i τ n = b). U sluqaju m = n iz uslova ortogonalnosti 2 teoreme sledi da polinom ω n mora biti moniqni ortogonalni polinom π n u odnosu na meru dµ. Dakle, qvorovi Gausove kvadraturne formule su nule moniqnog ortogonalnog (ili ortonormiranog) polinoma t (n) k u odnosu na meru dµ. Teine se mogu predstaviti u sledeem obliku A k = ( n 1 ( p ν ν=1 t (n) k ) 2 ) 1, k = 1,..., n. Prema tome, sve teine A k, k = 1,..., n, su pozitivne. sledea teorema. Dakle, vai Teorema Parametri Gausove kvadraturne formule (4.1) u odnosu na pozitivnu meru dµ su τ k = t (n) k, A k = λ n,k = λ n (t (n) k ; dµ), k = 1,..., n, tj. qvorovi su nule ortogonalnog polinoma π n (x; dµ), a teine su odgovarajui Kristofelovi brojevi. Za numeriqku konstrukciju Gausovih kvadraturnih formula postoji vixe metoda, a svakako najpoznatiji je metod Goluba 7 i Velqa ([36]). i- hov metod je baziran na odreivau sopstvenih vrednosti i prvih komponenata sopstvenih vektora simetriqne trodijagonalne Jakobijeve matrice koristei QR algoritam. 6 Rehnel Lobatto ( ), danski matematiqar. 7 Gene Howard Golub ( ), ameriqki matematiqar. 67
77 4.1. Kvadraturne formule Teorema Qvorovi τ k, k = 1,..., n, u Gausovoj kvadraturnoj formuli (4.1) u odnosu na pozitivnu meru dµ su sopstvene vrednosti Jakobijeve matrice reda n α 0 β1 0 0 β1 α 1 β2 0 J n (dµ) = 0 β2 α 2 0, (4.4) α n 1 gde su α k i β k, k = 0, 1,..., n 1, koeficijenti troqlane rekurentne relacije za moniqne ortogonalne polinome π k ( ; dµ). Teine A k date su sa A k = β 0 υk,1, 2 k = 1,..., n, gde je β 0 = m 0 = dµ(x), a υ R k,1 prva komponenta normalizovanog sopstvenog vektora v k (= [υ k,1... υ k,n ] T ) koji odgovara sopstvenoj vrednosti t (n) k, tj. J n (dµ)v k = t (n) k v k, vk T v k = 1, k = 1,..., n. Pretpostavimo da je [a, b] = supp(dµ). Za ostatak R n (f) Gausove kvadraturne formule vai sledei rezultat. Teorema Ako je f C 2n [a, b], tada postoji ξ (a, b) tako da vai R n (f) = π n 2 (2n)! f (2n) (ξ), gde je π n moniqni ortogonalni polinom u odnosu na meru dµ. Primer Za izraqunavae integrala oblika 1 1 2s T n (x) f(x) dx, n, s N, n 2, 1 x 2 gde je T n (x) moniqni Qebixev ev polinom n-tog stepena prve vrste, formiramo kvadraturne formule gde su τ n,s j p n,s k 1 1 2s T n (x) f(x) dx = m A n,s 1 x 2 j f(τ n,s j ) + R m (f), (4.5) j=1, j = 1, 2,..., m, nule polinoma stepena m iz niza polinoma (x) ortogonalnih u odnosu na teinsku funkciju x w n,s (x) = T 2s n (x). (4.6) 1 x 2 68
78 4.1. Kvadraturne formule y x Slika 4.1: Grafik teinske funkcije x w 3,2 (x) Na slici 4.1 prikazan je grafik teinske funkcije (4.6) za n = 3 i s = 2. Posmatrajmo sluqaj m = 10, n = 3 i s = 2. Prema teoremi 4.1.3, qvorovi τ 3,2 j i koeficijenti A 3,2 j, j = 1, 2,..., 10, u kvadraturnoj formuli (4.5) izraqunavaju se korixeem polinoma p 3,2 10 (x), odreenog u primeru Numeriqke vrednosti qvorova i koeficijenata prikazane su u tabeli 4.1. Tabela 4.1: Qvorovi i teinski koeficijenti u kvadraturnoj formuli (4.5) za m = 10, n = 3 i s = 2 j τ 3,2 j A 3,2 j Primenom tako dobijene kvadraturne formule odreuju se, na primer, 69
79 4.1. Kvadraturne formule vrednosti integrala cos 1 1 e x2 +10x 1 ( πx ) 4 T 3 (x) dx , 2 1 x 2 ) sin 2 ( πx 2 ) 4 T 3 (x) dx , 1 x 2 ( πx cos 3 2 T 3 4 (x) dx x 2 Prema teoremi 4.1.4, procena grexke je 10 2 R 10 (f) = p3,2 20! f (20) (ξ) = f (20) (ξ), 1 < ξ < 1. U navedenim primerima, granice apsolutne grexke pri izraqunavau integrala su , i redom. Primer Za testirae kvadraturne formule (4.5) za n = 2 i s = 4 1 T 2 8 (x) f(x) dx = m 1 x 2 1 j=1 za razliqit broj qvorova m koristimo funkciju f(x) = 0.01(1 x 2 ) 1 x 2, jer se taqno moe izraqunati vrednost integrala I(f) = 1 1 T 8 2 (x) 1 f(x) dx = 1 x 2 1 A 2,4 j f(τ 2,4 j ) + R m (f), (4.7) 1 x T 8 2 (x)dx = U tabeli 4.3 prikazani su qvorovi τ 2,4 j i koeficijenti A 2,4 j, j = 1, 2,..., m, u kvadraturnoj formuli (4.5) za m = 5(5)20. Tabela 4.2: Apsolutna grexka kvadraturnih formula (4.7) za n = 2, s = 4 i m = 5(5)20 m I(f) Q 2,4 m (f) ( 8) ( 9) ( 10) ( 10) 70
80 4.1. Kvadraturne formule Apsolutne grexke pri izraqunavau integrala I(f) primenom kvadraturnih suma Q 2,4 m (f) = m j=1 A 2,4 j f(τ 2,4 j ) iz formule (4.7) za m = 5(5)20 predstav ene su u tabeli 4.2, a grafici teinske funkcije x w 2,4 (x), funkcije x f(x) i integranda x f(x)w 2,4 (x) na slici 4.2. Tabela 4.3: Qvorovi i teinski koeficijenti u kvadraturnoj formuli (4.7) za n = 2, s = 4 i m = 5(5)20 m j τ 2,4 j A 2,4 j 5 1, 5 ± , 4 ± , 10 ± , 9 ± , 8 ± ( 6) 4, 7 ± , 6 ± , 15 ± , 14 ± , 13 ± , 12 ± ( 6) 5, 11 ± , 10 ± , 9 ± , 20 ± , 19 ± , 18 ± , 17 ± , 16 ± ( 6) 6, 15 ± ( 6) 7, 14 ± , 13 ± , 12 ± , 11 ±
81 4.2. O pozitivnoj definitnosti nekih linearnih funkcionela Slika 4.2: Grafici funkcija x w 2,4 (x), x f(x) (levo) i x f(x)w 2,4 (x) (desno) 4.2 O pozitivnoj definitnosti nekih linearnih funkcionela Neka je linearna funkcionela L definisana sa L(p) = k N ω k p(z k ), p P. (4.8) Generalno govorei, ispitujemo funkcionele kod kojih je ω k, z k C \ {0}, ali sa sledeim restrikcijama. Prvo, pretpostav amo da je ω k 0, k N. Ovaj uslov je kraje prirodan, budui da ako je za neko k N, ω k = 0, onda sumirae vrximo preko skupa N \ {k}. Drugo, neemo umaiti opxtost ako pretpostavimo da je z i z j, i, j N, jer u suprotnom moemo izostaviti qlan sume sa indeksom j a uzeti ω i = ω i + ω j za taqku z i. Za skup taqaka z i, i N, uvodimo oznaku Z = {z k k N}. Pretpostaviemo da je lim z k = 0, (4.9) k + i, da bismo imali apsolutnu integrabilnost svih polinoma p P pretpostaviemo da vai ω k M < +. (4.10) k N 72
82 4.2. O pozitivnoj definitnosti nekih linearnih funkcionela Takoe, nada e emo podrazumevati da je niz z k, k N, ureen tako da je z k+1 z k, k N. Primetimo da linearna funkcionela L moe biti shvaena kao linearna funkcionela koja deluje u prostoru ograniqenih kompleksnih nizova l. Naime, prema uslovu (4.10) imamo da niz w k, k N, pripada prostoru l 1, prostoru svih apsolutno sumabilnih kompleksnih nizova (videti [66, str. 30], [43, str. 39]). Kao xto je poznato vai l 1 l, gde l oznaqava dualni prostor prostora l. Definiximo linearno preslikavae I : P l na sledei naqin I(p) = (p(z 1 ), p(z 2 ),..., p(z n ),...). Linearni prostor P moe se normirati pomou p = sup p(z k ), p P. k N Lema Linearno preslikavae I : P l je ograniqeno utapae skupa P u l. Dokaz. Za dato I svaki polinom p P dostie svoj maksimum na kompaktu Z, pa je svaki niz p(z k ), k N, p P, uniformno ograniqen po k i pripada skupu l. Osobina oquvaa norme se jednostavno pokazuje. Primetimo da ako dva polinoma zadovo avaju I(p 1 p 2 ) = 0, onda je p 1 = p 2, jer su ovo dve analitiqke funkcije jednake na skupu Z koji ima jednu taqku nagomilavaa. Dakle, I(P) l je utapae. Lako se uoqava da je I = 1. Sada definiximo linearnu funkcionelu L : l C na sledei naqin L (u) = k N ω k u k, u = (u 1, u 2,...) l. Oqigledno je funkcionela L ograniqena jer je L (u) ω k u k u ω k, u l, k N k N i L I = L na P. Zbog toga moemo identifikovati L sa L i moemo smatrati da je L ograniqena linearna ekstenzija funkcionele L na ceo skup l. 73
83 4.2. O pozitivnoj definitnosti nekih linearnih funkcionela Oznaqimo sa P + skup svih polinoma p P \ {0} koji su nenegativni na realnoj pravoj. Kao direktnu posledicu pozitivne definitnosti imamo sledeu lemu. Lema Ako je linearna funkcionela L : P C pozitivnodefinitna, onda vai L(x 2n ) > 0, L(x 2n+1 ) R, L(p) R, p P R, n N 0. (4.11) Dokaz. Kako je x 2n P +, direktno sledi da je L(x 2n ) > 0. Za neparne stepene imamo L(x 1) 2n = 2n k=0 ( ) 2n ( 1) 2n k L(x k ) > 0, k i koristei matematiqku indukciju po n 2N dobijamo L(x 2n 1 ) < 1 2n 2n k=0,k 2n 1 ( ) 2n ( 1) k L(x k ). k Konaqno, koristei linearnost funkcionele L sledi ostatak tvrea. Centralna teorema ovog poglav a glasi: Teorema Linearna funkcionela L definisana pomou (4.8) je pozitivno-definitna ako i samo ako je ω k > 0 i z k R, k N. Uvedimo jox jednu oznaku e n = (0,..., 0, 1, 0,...) l, n N, pri qemu se broj 1 nalazi na n-toj poziciji, dok su na ostalim mestima nule Pomoni rezultati U ovom delu dokazujemo nekoliko pomonih lema. Lema Izaberimo z n Z i pretpostavimo da z n / Z. Tada postoji p n C, p n = 1, takav da za svaki r n P R vai p n r n (z n )e n I(P R ). Ako je z n R \ {0}, onda je p n = 1. 74
84 4.2. O pozitivnoj definitnosti nekih linearnih funkcionela Dokaz. Konstruisaemo niz p n k P +, k, n N, takav da je lim k + I(pn k) = α n e n za neke kompleksne brojeve α n C \ {0}. Izaberimo neki z n Z i pretpostavimo da z n / Z. Da e, izaberimo neki polinom r n P R. Definiximo p n k(z) = r n (z) pri qemu smo uveli oznaku k i=1,i n Oqigledno vai p n k P +, k, n N. (z z i )(z z i ), k N, λ n i λ n i = z n z i z n z i, i n. Budui da je r n algebarski polinom, on je uniformno ograniqen na kompaktu Z. Dakle, postoji M > 0 tako da je r n (z ν ) < M, ν N. Koristei uslov (4.9), moemo izabrati neki i 01 N tako da je z n /2 < z ν z i, z n /2 < z ν z i, i > i 01, ν = 1,..., n. Fiksirajmo q (0, 1). Moemo izabrati neki i 02 N tako da vai z i < z n q/4, i > i 02. Neka je i 0 = max{i 01, i 02 }. Za k > i 0 i ν > k imamo p n k(z ν ) = r n (z ν ) M i 0 i=1,i n i 0 i=1,i n z ν z i z ν z i λ n i z ν z i z ν z i λ n i ( ) 2i0 2 2 z1 M q 2(k i0), m k i=i 0 +1 k i=i 0 +1 z ν z i z ν z i z n z i z n z i z n q/2 z n q/2 z n /2 z n /2 gde je m = min i=1,...,i0,i n{ z n z i, z n z i } > 0. Primetimo da je p n k (z ν) = 0 za ν < k, ν n. Odavde sledi da imamo uniformnu konvergenciju izraza p n k (z ν) ka nuli po ν n kada k +, tj. da za svako ε > 0 i k > k 01 = i log q log ε M vai p n k (z ν) 0 < ε, ν N \ {n}. Sada, posmatrajui p n k (z n) dobijamo p n k(z n ) = r n (z n ) 75 ( m 2 z 1 ) 2i0 2
85 4.2. O pozitivnoj definitnosti nekih linearnih funkcionela prema definiciji λ n i. Ovo znaqi da p n k (z n) ima konstantnu normu kada k +. Proizvod k i=1,i n (z n z i )(z n z i ), k N, λ n i je proizvod kompleksnih brojeva qiji je moduo 1, tj. brojeva koji se nalaze na jediniqnoj krunici u kompleksnoj ravni. Kako je jediniqna krunica kompakt u C, sledi da postoji neki podniz ovog niza koji konvergira ka nekom p n qija je norma jedan. Oznaqimo skup indeksa za taj konvergentan podniz sa N 1. Tada, za svako ε > 0 postoji k 02 N 1, tako da za svako k > k 02, k N 1, vai Sada za vektor r n (z n )p n e n imamo p n k(z n ) r n (z n )p n < ε. I(p n k) r n (z n )p n e n = sup p n k(z ν ) r n (z n )p n e n < ε ν N za k > max{k 01, k 02 }, k N 1. Dakle, ako izvrximo renumeraciju niza p n k koristei jedino indekse k N 1, dobijamo niz p n k P R takav da je lim k + I(pn k) = p n e n. Konaqno, ako je z n R \ {0} i kako je r n P R, dobijamo r n (z n ) R i p n k(z n ) = r n (z n ) k i=1,i n (z n z i )(z n z i ) λ n i R, pri qemu su izrazi u proizvodu jednaki 1, pa je p n = 1. Ovu konstrukciju moemo ponoviti za svako n N, tj. za svaku taqku z n Z za koju vai z n / Z. U sluqaju da je r n P +, jednostavno se uoqava da p n k takoe pripada prostoru P +, pa samim tim imamo sledei rezultat. Lema Pretpostavimo da vai z n / Z. Tada postoji p n C, p n = 1, takav da za svaki r n P + vai p n r n (z n )e n I(P + ). Ako je z n R \ {0}, onda je p n = 1. 76
86 4.2. O pozitivnoj definitnosti nekih linearnih funkcionela Sada emo razmotriti sluqaj kada z n Z. Bez gub ea opxtosti moemo pretpostaviti da je z n+1 = z n, xto se jednostavno postie renumeraciom niza z n, n N. Lema Neka je z n+1 = z n za neko n N. Tada postoji neki p n C, p n = 1, tako da za svaki polinom r n P + vai p n r n (z n )e n + p n r n (z n )e n+1 I(P R ). Dokaz. Posmatrajmo niz polinoma p n k(z) = r n (z) k i=1,i n,n+1 (z z i )(z z i ), λ n i pri qemu su sve oznake kao u dokazu leme Jedini problem predstav a definicija niza λ n i, ali sreom imamo z n z i z n z i = z n+1 z i z n+1 z i, jer je z n+1 = z n. Na osnovu ove qienice sledi da moemo primeniti istu definiciju. Koristei iste argumente, moemo dokazati da vai za svako p n k(z ν ) 0 < ε k > k 01 = i log q log ε ( ) 2i0 4 m. M 2 z 1 Takoe je p n k (z n) = p n k (z n+1), odakle sledi konvergencija po nekom nizu k N 1 ka meusobno konjugovanim vrednostima. Jasno je da moemo da izaberemo r n P + da bismo dobili direktnu posledicu ove leme. Lema Neka je z n+1 = z n za neko n N. Tada postoji neki p n C, p n = 1, tako da za svaki polinom r n P + vai p n r n (z n )e n + p n r n (z n )e n+1 I(P + ). 77
87 4.2. O pozitivnoj definitnosti nekih linearnih funkcionela Dokaz glavnog rezultata Sada dajemo dokaz glavne teoreme. Dokaz teoreme Jednostavno se dokazuje da ako je ω n > 0 i z n R, n N, za p P + je L(p) = k N ω k p(z k ) > 0, koristei jednostavnu qienicu da je p(z k ) 0, k N. Pretpostavimo da je L pozitivno-definitna funkcionela. Izaberimo neki n N i pretpostavimo da z n / Z. Tada, prema lemi dobijamo lim k + L(pn k) = lim k + (L I)(p n k) = L (p n r n (z n )e n ), pri qemu smo iskoristili qienicu da je L neprekidna funkcionela na l. Tada je L (p n r n (z n )e n ) = ω n r n (z n )p n. Uzimajui r n (z) = 1, r n P +, i r n (z) = z, r n P R, dobijamo L (p n e n ) = ω n p n 0 i L (p n z n e n ) = ω n z n p n R. Kako je z n 0 i prema konstrukciji p n 0, sledi da je L (p n e n ) = ω n p n > 0. Tada dobijamo z n = L (p n z n e n ) L (p n e n ) R i takoe ω n > 0, prema qienici da je p n = 1 za z n R \ {0}. Neka je sada z n = z n+1. Primetimo da u ovom sluqaju ne moe da bude z n R, jer bismo tada imali z n = z n+1, xto je nemogue prema uslovima nametnutim za skup Z. Tada, prema lemi i qienici da je L pozitivno-definitna funkcionela, za r n (z) = 1 i r n (z) = z sledi i L (p n e n + p n e n+1 ) = ω n p n + ω n+1 p n = α 0 L (p n z n e n + p n z n e n+1 ) = ω n z n p n + ω n+1 p n z n = β R. Ove dve jednakosti moemo posmatrati kao sistem linearnih jednaqina po p n i p n koji ima jedinstveno rexee dato sa p n = αz n β ω n (z n z n ), pn = 78 αz n β ω n+1 (z n z n ).
88 4.2. O pozitivnoj definitnosti nekih linearnih funkcionela Koristei ove izraze dobijamo ω n+1 = ω n a takoe sledi da ne moe da bude α 2 + β 2 = 0 jer bi to za posledicu imalo p n = 0, xto je nemogue. Stavimo sada da je r n (z) = z 2ν, ν N. Da e imamo L (p n z 2ν n e n + p n z 2ν n e n+1 ) = ω n z 2ν n p n + ω n z 2ν n p n = Re(ω n z 2ν n p n ) 0, ν N 0. Ako oznaqimo sa α n = arg(ω n ), β n = arg(p n ) i ϕ n = arg(z n ), pri qemu je ϕ n 0 i ϕ n π, sledi ω n z 2ν n p n cos(α n + β n + 2νϕ n ) 0, ν N 0. elimo da pokaemo da postoji neko ν N 0 takvo da je funkcija cos negativna, xto bi dovelo do kontradikcije. Funkcija cos x je negativna ako 2ν pripada nekom od intervala J k = ( (4k + 1)π 2(αn + β n ), (4k + 3)π 2(α ) n + β n ), k Z. 2ϕ n 2ϕ n Duina intervala J k je π/ ϕ n > 1, pa zato u svakom od ovih intervala postoji bar jedan ceo broj. Ako je π/ ϕ n > 2, onda u svakom intervalu postoje bar dva uzastopna cela broja i bar jedan od ih je paran. Uzimajui da je 2ν bax taj paran ceo broj, dobijamo kontradikciju. Zato emo pretpostaviti da je π/ ϕ n 2. Segmente oblika G k = [ (4k + 3)π 2(αn + β n ), (4k + 5)π 2(α ] n + β n ), k Z, 2ϕ n 2ϕ n zvaemo praznine. Oqigledno je R = k Z (J k G k ). sledi Ako je π/ ϕ n = 2, onda je ϕ n = ±π/2, xto znaqi da ako je cos(α n + β n ± 2 0 π/2) > 0 cos(α n + β n ± 2 1 π/2) = cos(α n + β n ) < 0, xto je kontradikcija. Ako je cos(α n + β n ± 2 0 π/2) = 0, onda dobijamo Re(ω n z 2ν n p n ) = ω n z 2ν n p n cos(α n + β n ± νπ) = 0, ν N, i, birajui r n (z) = z 2ν+1, ν N 0, sledi Re(ω n zn 2ν+1 p n ) = ω n zn 2ν+1 p n cos(α n + β n ± (2ν + 1)π/2) = ±( 1) ν ω n z 2ν+1 n p n sin(α n + β n ) 0, ν N 0. 79
89 4.3. Standardna L 2 -aproksimacija Iz uslova cos(α n + β n ) = 0 sledi sin(α n + β n ) = ±1, odakle dobijamo da prethodni izraz nije jednak nuli. Posmatrajmo sada polinome r n (z) = z 2ν (z 1) 2, ν N 0. Oqigledno je r n P +, pa mora da vai lim k + L(pn k) = lim k + (L I)(p n k) = ω n zn 2ν (z n 1) 2 p n + ω n zn 2ν (z n 1) 2 p n = Re(ω n z 2ν n (z n 1) 2 p n ) 0. Koristei linearnost dobijamo Re(ω n z 2ν n (z n 1) 2 p n ) = Re( 2ω n z 2ν+1 n p n ) Ovo je, naravno, kontradikcija. = 2( 1) ν ω n z 2ν+1 n p n sin(α n + β n ) > 0, ν N 0. Dakle, mora da vai 1 < π/ ϕ n < 2. Pretpostavimo da neki interval J k sadri ceo broj 2m + 1. Tada moemo da izaberemo ν N, tako da je π ϕ n > 2ν 2m 1 2ν 2m 2 > 1. Raqunajui od 2m + 1 do 2ν postoji taqno 2ν 2m celih brojeva koji su pokriveni sa 2ν 2m > 2ν 2m 1 π/ ϕ n intervala i praznina. Kako poqiemo i zavrxavamo sa intervalom, imamo ν m 1 praznina i ν m intervala. Prema Dirihleovom principu postoji bar jedan interval ili jedna praznina u kojem se nalaze bar dva uzastopna cela broja. Ako neki interval sadri dva uzastopna cela broja, onda je dokaz zavrxen. Zato pretpostavimo da neka praznina sadri dva cela uzastopna broja. Ako praznina sadri paran pa neparan ceo broj, onda sledei interval sadri paran ceo broj, xto je kraj dokaza. Ako praznina sadri neparan pa paran ceo broj, onda prethodni interval sadri paran ceo broj, pa je dokaz zavrxen. Zak uqujemo da ne moe da vai z n, z n Z. Ve smo dokazali da ako je z n Z, onda je z n R i ω n > 0, qime je dokaz zavrxen Standardna L 2 -aproksimacija Neka je dµ(x) data nenegativna mera na R i U n = {g 0, g 1, g 2,..., g n } dati sistem linearno nezavisnih funkcija u realnom unitarnom prostoru X 80
90 sa skalarnim proizvodom 4.3. Standardna L 2 -aproksimacija (f, g) = R f(x)g(x)dµ(x) (f, g X). (4.12) Neka je X n potprostor prostora X takav da je X n = Lin{g 0, g 1, g 2,..., g n }. Da e, pretpostavimo da momenti funkcije f u odnosu na meru dµ(x) i sistem U n m k (f, U n ) = R f(x)g k (x)dµ(x) = (f, g k ), k = 0, 1,..., n, (4.13) postoje. elimo da aproksimiramo funkciju f sa tako da vai s n = n a ν g ν X n, ν=0 m k (s n, U n ) = m k (f, U n ), k = 0, 1,..., n. (4.14) Poznato je da se standardna L 2 -aproksimacija funkcije f X sa s n X n, tj. min f s 2 = min f s X n a ν R n 2 a ν g ν = f sn 2 dostie ako i samo ako je grexka f s n ortogonalna na ceo potprostor X n, tj. ako i samo ako je ( f ν=0 n ) a ν g ν, g k = 0, k = 0, 1,..., n, (4.15) ν=0 xto je ekvivalentno sa (4.14). Dakle, standardna L 2 -aproksimacija funkcije quva momente. Napomenimo da ako je S n = {φ 0, φ 1, φ 2,..., φ n } ortonormiran (ili ortogonalan) sistem funkcija, iz uslova (4.15) direktno dobijamo Furijeove 8 koeficijente a k = (f, φ k ), k = 0, 1,..., n. U sluqaju aproksimacije algebarskim polinomima, S n je skup polinoma p k ( ; dµ) koji su ortonormirani u odnosu na meru dµ(x). Sada je L 2 -aproksimacija data sa s n (x) = n a k p k (x), a k = k=0 8 Joseph Fourier ( ), francuski matematiqar. R f(x)p k (x)dµ(x), k = 0, 1,..., n, (4.16) 81
91 4.4. Polinomska L 2 -aproksimacija sa ograniqeima a odgovarajua grexka najbo e L 2 -aproksimacije je E n (dµ, f) 2 2 = f s n 2 = f 2 n a 2 k. k=0 4.4 Polinomska L 2 -aproksimacija sa ograniqeima U nekim sluqajevima elimo da najbo a L 2 -aproksimacija s n+m oquva jox neka svojstva originalne funkcije f, na primer da ima iste vrednosti kao i funkcija f u nekim taqkama. Iako ovo moemo razmatrati u opxtem sluqaju, ovde emo se zadrati na najjednostavnijem sluqaju. Problem L 2 -aproksimacije sa ograniqeima moe se iskazati na sledei naqin. Za dati skup taqaka t 1,..., t m, m n, i funkciju f treba da vai s n+m (t i ) = f(t i ), i = 1,..., m. (4.17) Dakle, treba da minimiziramo izraz Ẽn+m(dµ, f) 2 2 = f s 2, pri qemu je s P n+m i zadovo ava uslove (4.17). Oznaqimo sa P C n+m = {p P n+m p(t i ) = f(t i ), i = 1,..., m}. Da bismo naxli najbo i L 2 -aproksimacioni polinom sa datim ograniqeima, prvo emo konstruisati interpolacioni polinom stepena najvixe m 1 koji zadovo ava uslove (4.17). To je polinom P m (x) = L m (f; x) = m q m (x) f(t i ) (x t i )q m(t i ), i=1 gde je q m (x) = m i=1 (x t i). Sada traimo najbo u kvadratnu aproksimaciju u obliku s(x) = P m (x) + q m (x)s(x), s P n, gde je s neki polinom stepena najvixe n koji emo odrediti iz sledeeg minimizacionog uslova Ẽ n+m (dµ, f) 2 2 = min f P m q m s 2 s P n = (f(x) P m (x) q m (x)s(x)) 2 dµ(x) = R R ( 2 f(x) Pm (x) s(x)) q m (x) 2 dµ(x). q m (x) 82
92 4.4. Polinomska L 2 -aproksimacija sa ograniqeima Ako su f nova funkcija i d µ nova mera date sa f(x) = f(x) P m(x) q m (x) i d µ(x) = q m (x) 2 dµ(x) redom, dobijamo sledei L 2 -aproksimacioni problem bez ograniqea Ẽ n+m (dµ, f) 2 2 = E n (d µ, f) 2 2 = min ( s P n R f(x) s(x)) 2 d µ(x). Ako je s n rexee ovog L 2 -problema, tada je s n+m (x) = P m (x) + q m (x)s n (x) rexee L 2 -aproksimacionog problema sa datim ograniqeima. Prema (4.16), rexee s n moe da se napixe u obliku s n (x) = n ã k p k (x; d µ), ã k = k=0 R f(x)p k (x; d µ)d µ(x), k = 0, 1,..., n. Zak uqujemo da je polinom s n zapravo L 2 -aproksimacija funkcije (f P m )/q m u odnosu na transformisanu meru q 2 mdµ. Da bismo ilustrovali izloenu teoriju dajemo dva primera. Primer Posmatrajmo problem dirigovane L 2 -aproksimacije u odnosu na Qebixev evu meru druge vrste sa ograniqeima datim u taqkama ±1/ 2 za funkciju f(x) = cos(πx/2). Ovde je m = 2, a polinom P 2 je interpolacioni polinom za skup taqaka ( 1/ 2, a), (1/ 2, a), pri qemu je a = cos(π/(2 2)) = , tj. P 2 (x) = a ( x + 1/ 2 2/ 2 + x 1/ 2 2/ 2 i q 2 (x) = x 2 1/2. Da bismo rexili L 2 -aproksimacioni problem sa ograniqeima treba da reximo sledei standardni L 2 -aproksimacioni problem min s P n 1 1 ) = a ( ) 2 ( f(x) a x 2 1/2 s(x) x 2 2) x2 dx Uoqavamo meru d µ iz teoreme Najbo i pristup za konstrukciju polinoma S n je da se S n dobije kao linearna kombinacija polinoma p n, 1/2. 83
93 4.4. Polinomska L 2 -aproksimacija sa ograniqeima n N 0, ortogonalnih u odnosu na meru d µ (videti primer 2.4.1). Rexee je dato u sledeem obliku S n (x) = n k=0 q k p k (x), q k = 1 p k f(x) a x 2 1/2 p k(x)d µ(x). U ovom sluqaju je q 2k+1 = 0, k 0. Koeficijenti q 2k za 0 k 8 su dati u tabeli 4.4. Sve raqunske operacije su izvoene u aritmetici dvostruke preciznosti (sa maxinskom preciznoxu m.p ). Brojevi u zagradama oznaqavaju decimalne eksponente. sa Odgovarajua apsolutna grexka dirigovane L 2 -aproksimacije p data e n+m = max 1 x 1 cos πx 2 p(x), p P C n+m, prikazana je u istoj tabeli. Na primer, apsolutna grexka odgovarajue y x Slika 4.3: Relativna grexka pri aproksimaciji funkcije x f(x) polinomom x p(x) aproksimacije za n = 6 i m = 2 p(x) = a + ( x 2 1 ) (q 0 p 0 (x) + q 2 p 2 (x) + q 4 p 4 (x) + q 6 p 6 (x)) 2 = x x x x je , a relativna grexka je predstav ena na slici 4.3. Na slici 4.4 prikazani su grafici funkcije x f(x) i polinoma x a + (x 2 1/2)q 0 p 0 (x) = x , kao i relativna grexka navedene aproksimacije. 84
94 4.4. Polinomska L 2 -aproksimacija sa ograniqeima y y x x 0.04 Slika 4.4: Grafici funkcije x f(x) i polinoma x a + (x 2 1/2)q 0 p 0 (x) i relativna grexka Tabela 4.4: Numeriqki rezultati u primerima i k q 2k e 2k+2 q 2k+1 e 2k ( 1) ( 1) 2.39( 3) ( 1) 9.74( 2) ( 2) 4.02( 5) ( 2) 1.98( 3) ( 4) 2.79( 7) ( 4) 3.68( 5) ( 5) 1.75( 9) ( 5) 2.51( 7) ( 7) 5.99( 12) ( 7) 1.64( 8) ( 9) 1.95( 14) ( 10) 5.56( 12) ( 11) m.p ( 11) 1.84( 14) ( 13) m.p ( 13) m.p ( 15) m.p. Primer Neka je opet f(x) = cos(πx/2), 1 x 1. Sliqno kao u prethodnom primeru, za skup interpolacionih ograniqea u taqkama 0, ±1/ 2 i dirigovanu L 2 -aproksimaciju u odnosu na Qebixev evu meru druge vrste, moemo da koristimo izloenu tehniku i teoremu U ovom sluqaju imamo ( ) π P 3 (x) = 1 4x 2 sin i ( q 3 (x) = x x 2 1 ). 2 Ako oznaqimo niz polinoma ortogonalnih u odnosu na meru dµ sa r k, k N 0, (videti primer 2.4.2), dobijamo R n (x) = n k=0 q kr k (x), q k = 1 1 f(x) P 3 (x) r k 2 1 x(x 2 1/2) r k(x)dµ (x). 85
95 4.4. Polinomska L 2 -aproksimacija sa ograniqeima Sada je q 2k = 0, k 0. Koeficijenti q 2k+1 za 0 k 8 i odgovarajue grexke e 2k+4 su takoe dati u tabeli 4.4. Aproksimacioni polinom je ( r(x) = P 3 (x) + x x 2 1 ) (q 2 1r 1 (x) + q 3r 3 (x) + q 5r 5 (x) + q 7r 7 (x) ) = x x x x x 2 + 1, a relativna grexka pri aproksimaciji je predstav ena na slici 4.5. y x Slika 4.5: Relativna grexka pri aproksimaciji funkcije x f(x) polinomom x r(x) 86
96 Literatura [1] R. Abraham, J.E. Marsden, T. Ratiu: Manifolds, Tensor Analysis, and Applications, Springer-Verlag, New York, [2] N.I. Akhiezer: Orthogonal polynomials on several intervals, Dokl. Akad. Nauk SSSR 134 (1960), [3] N.I. Akhiezer, I.M. Galzman: Theory of Linear Operators in Hilbert Space, vol I, Pitman, Boston, [4] W. Al-Salam, W.R. Allaway, R. Askey: Sieved ultraspherical polynomials. Trans. Amer. Math. Soc. 284 (1984), [5] G.I. Barkov: Some systems of polynomials orthogonal in two symmetric intervals, Izv. Vysš. Učebn. Zaved. Matematika 1960 no. 4 (17), 3 16 (Russian). [6] B. Beckerman: Complex Jacobi matrices, J. Comput. Appl. Math. 127 (2001), [7] B. Beckerman: On the convergence of bouded J-fractions on the resolvent set of the corresponding second order difference operator, J. Approx. Theory 99 (1999), [8] S. Bernstein: Sur les polynomes orthogonaux relatifs à un segment fini. J. Math. Pures Appl. 9(9), (1930) [9] S. Bernstein: Sur une classe de polynomes orthogonaux. Comm. de la Soc. Math. Kharkoff 4 (1930), 79 93; Complemant, Ibid. 5 (1932) [10] M.I. Bueno, F.M. Dopico: A more accurate algorithm for computing the Christoffel transformation, J. Comput. Appl. Math. 205 (2007), [11] T.S. Chihara: An Introduction to Orthogonal Polynomials, Gordon and Breach, New York,
97 Literatura [12] T.S. Chihara: The three term recurrence relation and spectral properties of orthogonal polynomials, In: P. Nevai: Orthogonal Polynomials, pp [13] E.B. Christoffel: Über die Gaußische Quadratur und eine Verallgemeinerung derselben, J. Reine Andew. Math., 55:61 82, [14] A.S. Cvetkovi: Programski paket za simboliqku i numeriqku konstrukciju ortogonalnih polinoma i kvadraturnih formula, Magistarska teza, Univerzitet u Nixu, [15] A.S. Cvetkovi: Nestandardna ortogonalnost i kvadraturne formule, Doktorska disertacija, Univerzitet u Nixu, [16] A.S. Cvetković, P. Rajković, M. Ivković: Catalan numbers, the Hankel transform, and Fibonacci numbers. Journal of Integer Sequences 5 (2002), Article [17] A.S. Cvetković, G.V. Milovanović: The Mathematica Package OrthogonalPolynomials, Facta Univ. Ser. Math. Inform. 19 (2004), [18] A.S. Cvetković, G.V. Milovanović, M.M. Matejić: Rational Algorithm for Quadratic Christoffel Modification and Applications to the Constrained L 2 -Approximation, Int. J. Comput. Math. 88 (2011), [19] A.S. Cvetković, M.M. Matejić, G.V. Milovanović: Orthogonal polynomials for modified Chebyshev measure of the first kind, Results Math. 69 (2016), [20] J. Dieudonné: Foundations of Modern Analysis. Academic Press, New York [21] J. Dombrowski: Orthogonal polynomials and functional analysis, In P. Nevai: Orthogonal Polynomials, [22] J. Favard: Sur les polynomes de Tchebycheff, C. R. Acad. Sci. Paris 200 (1935), [23] G.M. Fihtengol~c: Kurs differencial~nogo i integral~nogo isqisleni, I. Fizmatgiz, Moskva [24] W. Gautschi: On generating orthogonal polynomials, SIAM J. Sci. Statist. Comput. 3 (1982),
98 Literatura [25] W. Gautschi: Algorithm 726: ORTHPOL - A package of routines for generating orthogonal polynomials and Gauss-type quadrature rules., ACM Trans. Math. Software 20 (1994), [26] W. Gautschi: Orthogonal polynomials: applications and computations, in Acta Numerica, 1996, Cambridge University Press, 1996, pp [27] W. Gautschi: Orthogonal Polynomials: Computation and Approximation, Oxford University Press Inc., New York, [28] W. Gautschi: Orthogonal polynomials (in Matlab), J. Comput. Appl. Math. 178, (2005), [29] W. Gautschi, S. Li: A set of orthogonal polynomials induced by a given orthogonal polynomial, Aequationes Math. 46 (1993), [30] W. Gautschi, G.V. Milovanović: Gaussian quadrature involving Einstein and Fermi functions with an application to summation of series, Math. Comp. 44 (1985), [31] W. Gautschi, G.V. Milovanović: Polynomials orthogonal on the semicircle, J. Approx. Theory 46 (1986), [32] W. Gautschi, G.V. Milovanović: S orthogonality and construction of Gauss Turán type quadrature formulae, J. Comput. Appl. Math. 86 (1997), [33] J.S. Geronimo, W. Van Assche: Orthogonal polynomials on several intervals via a polynomial mapping, Trans. Amer. Math. Soc. 308 (1988) [34] J. Geronimus: On a set of orthogonal polynomials. Ann. Math. 31 (1930) [35] A. Ghizzetti, A. Ossicini: Quadrature Formulae. Akademie Verlag, Berlin (1970) [36] G.H. Golub, J.H. Welsch: Calculation of Gauss quadrature rules. Math. Comp. 23 (1969), [37] Z.S. Grinšpun: On a class of orthogonal polynomials. Vestnik Leningrad. Univ. 21 (1966), (Russian). [38] M. Heins: Complex Function Theory, Academic Press, New York- London,
99 Literatura [39] V.A. Il~in.G. Poznk: Osnovy matematiqeskogo analiza, I. Nauka, Moskva [40] M.E.H. Ismail: On sieved orthogonal polynomials, III: orthogonality on several intervals, Trans. Amer. Math. Soc. 294 (1986) [41] C. Krattenthaler: Advanced determinant calculus, The Andrews Festschhrift (Maratea, 1998), Sem. Lothar. Combin. 42 (1999), Art. B42q, 67 pp. (electronic). [42] P. Lankaster: Theory of Matrices. Academic Press, New York London [43] P.D. Lax: Functional Analysis, Wiley-Interscience, [44] A.P. Magnus: Toeplitz matrix techniques and convergence of compex weight Pade approximation, J. Comput. Appl. Math. 19 (1987), [45] G. Mastroianni, G.V. Milovanović: Interpolation Processes Basic Theory and Applications, Springer Monographs in Mathematics, Springer-Verlag, Berlin-Heidelberg, [46] G.V. Milovanovi: Numeriqka analiza, I deo, Nauqna kiga, Beograd, [47] G.V. Milovanovi: Numeriqka analiza, II deo, Nauqna kiga, Beograd, [48] G.V. Milovanović: Construction of s-orthogonal polynomials and Turan quadrature formulae, In: Numerical Methods and Approximation Theory III (Niš, 1987), Univ. Niš, Niš (1988) [49] G.V. Milovanović: Quadratures with multiple nodes, power orthogonality, and moment-preserving spline approximation, J. Comput. Appl. Math. 127, (2001) [50] G.V. Milovanović: Construction and applications of Gaussian quadratures with nonclassical and exotic weight function, Stud. Univ. Babes Bolyai Math. 60 (2015), no. 2, [51] G.V. Milovanović: Orthogonal polynomials on the real line, Walter Gautschi Volume 2, Selected works with commentaries, Editors: Claude Brezinski, Ahmed Sameh, Springer New York Heidelberg Dordrecht London, 2014, ISBN [52] G.V. Milovanović, S. Wrigge: Least squares approximation with constrains, Math. Comp. 46 (1986),
100 Literatura [53] G.V. Milovanovi, R.. orevi: Matematika za studente tehniqkih fakulteta, I deo, Elektronski fakultet, Nix, [54] G.V. Milovanović, D.S. Mitrinović, Th.M. Rassias: Topics in Polynomials: Extremal Problems, Inequalities, Zeros, World Scientific Publ. Co., Singapore - New Jersey - London - Hong Kong, [55] G.V. Milovanović, M.M. Spalević, A.S. Cvetković: Calculation of Gaussian type quadrature rules with multiple nodes, Math. Comput. Modelling 39 (2004), [56] G.V. Milovanović, A.S. Cvetković, M.M. Matejić: On positive definitness of some linear functionals, Stud. Univ. Babes Bolyai Math. 51 (2006), no. 4, [57] G.V. Milovanović, A.S. Cvetković, M.M. Matejić: Remark on orthogonal polynomials induced by the modified Chebyshev measure of the second kind, Facta Univ. Ser. Math. Inform. 21 (2006), [58] G.V. Milovanović, A.S. Cvetković: Special classes of orthogonal polynomials and corresponding quadratures of Gaussian type, Math. Balkanica 26 (2012), [59] B. Mirkovi: Teorija mera i integrala, Nauqna kiga, Beograd, [60] D.S. Mitrinovi: Predavaa o redovima, Graevinska kiga, Beograd, [61] D.S. Mitrinovi: Koxijev raqun ostataka sa primenama, Matematiqki problemi i ekspozicije, Nauqna kiga, Beograd, [62] D.S. Mitrinovi, D.D. Adamovi: Nizovi i redovi: definicije { stavovi { zadaci { problemi, Matematiqki problemi i ekspozicije, Nauqna kiga, Beograd, [63] D.S. Mitrinovi, D.. okovi: Polinomi i matrice, Graevinska kiga, Beograd, [64] J.M. Ortega, W.C. Rheinboldt: Iterative Solution of Nonlinear Equations in Several variables, Academic Press, New York, [65] M.D. Petkovi: Simboliqko izraqunavae Henkelovih determinanata i generalisanih inverza matrica, Doktorska disertacija, Univerzitet u Nixu,
101 Literatura [66] V. Rakoqevi: Funkcionalna analiza, Nauqna kiga, Beograd, [67] C.J. Rees: Eliptic orthogonal polynomials. Duke Math. J. 12 (1945), [68] H. Stahl, V. Totik: General Orthogonal Polynomials, Encyclopedia of Mathematics and its Applications, 43, Cambridge University Press, Cambridge, [69] G. Szegő: Orthogonal Polynomials, Amer. Math. Soc. Colloq. Publ., 23, 4th ed., Amer. Math. Soc., Providence, R. I., [70] V.B. Uvarov: Relation between polynomials orthogonal with different weights, Dokl. Akad. Nauk SSSR, 126(1): , [71] B. Wendroff: On Orthogonal polynomials, AMS procedings,
102 Biografija Marjan Mateji je roen u Nixu godine, gde je zavrxio osnovnu xkolu kao nosilac diplome,,vuk Karai", kao i specijalizovano matematiqko ode ee pri Gimnaziji,,Svetozar Markovi" u Nixu. Na studije na Filozofskom fakultetu u Nixu upisao se xkolske 1996/97. godine, a diplomirao na smeru za Teorijsku matematiku i primene godine, sa proseqnom ocenom u toku studija Na poslediplomske studije na Prirodno-matematiqkom fakultetu u Nixu upisao se na smeru Numeriqka matematika i optimizacija. Sve planom i programom predviene ispite poloio je sa proseqnom ocenom 10 i godine odbranio magistarsku tezu pod nazivom,,fraktalni skupovi dobijeni interpolacijom u ravni". Nakon zavrxetka osnovnih studija, godine izabran je za asistenta-pripravnika na Katedri za matematiku Elektronskog fakulteta u Nixu, gde i sada radi u zvau asistent. Kao saradnik Katedre za matematiku bio je angaovan na izvoeu raqunskih vebi iz predmeta: Linearna algebra, Matematiqka analiza, Matamatika I, Matematika II, Numeriqka analiza, Matematiqki metodi, Matematika-odabrana poglav a, Verovatnoa i statistika i laboratorijskih vebi iz predmeta Matematika III. U okviru nauqno-istraivaqkog rada na Katedri za matematiku Elektronskog fakulteta u Nixu uqestvovao je u realizaciji sledeih projekata: Primeeni ortogonalni sistemi, konstruktivne aproksimacije i numeriqki metodi (2002{2005); Ortogonalni sistemi i primene (2006{2010).
103 Summary Orthogonal polynomials, their construction, analysis and application, have an important role in the Applied mathematics. Nevertheless, the investigations in the Constructive theory of Orthogonal polynomials are still in an early development phase. The central concept is a three-term recurrence relation. Knowing its coefficients is of outmost importance. Once these are known, all other computational aspects regarding Orthogonal polynomials are easily available. Obtaining these coefficients is a fairly difficult task, thus, keeping up-to-date libraries on new developments is of high importance. The new era mighty computer packages are being built containing the readily-available results and also the tools for calculating the yet unknown parameters. Orthogonal polynomials, as all other special functions, owe their origin and development to practice in our physical and the scientific world. As Mathematics develops and awareness in its application broadens, the new horizons open in different scientific fields. Such is the case with the Constructive theory of Orthogonal polynomials. The number of its applications is augmenting on daily bases as a result of new developments in the topic. Among applications with the far most importance and longest history is the one in Numerical integration. The underlying concept is orthogonal decomposition providing the least error with a prescribed computational effort. Thus the search for the most appropriate dense subspace of approximation. This dissertation is a result of the research I was involved in under the supervision and guidance of academician Gradimir Milovanović. The research addressed the two key issues, mentioned earlier, related to the theory of Orthogonal polynomials on real line. The summary of the known and original results is given in a systematic overview through four chapters. The Bibliography contains 71 titles of scientific papers and books. The first chapter is introductory. Contains basic definitions and properties of the theory of Orthogonal polynomials. In particular, a separate Section is devoted to Chebyshev polynomials of the first and second kind. In the final section two algorithms for the construction of the three-term recurrence coefficients are enclosed. Modification algorithms are treated in the second chapter. Weight functions of the linear functional are transformed and the influence on the re-
104 currence coefficients is observed. The original algorithm for the quadratic Christoffel modification is presented along with its application. Modification of Chebyshev s measures of the first and second kind is the topic of the third chapter. Research of these non-classic weights finalized in the established recurrence coefficients for an entirely new class of orthogonal polynomials. The forth chapter is devoted to numerical integration. Necessary and sufficient conditions for the positive definiteness of certain class of linear functionals is presented. A standard L 2 -approximation is also treated. As an example, the modification algorithm from the second chapter is applied to a polynomial L 2 -approximation.
105 !\('SUits. J\.lat ll. ()!) (201()). Jtl:j 20Hi SpriH!(cr Inlornatiounl Publi l$hing H22-G3S3/ 1G/ 030,143-l3 p~~.bl:t:shed ouli'iu!.jmmary 2S, 201{) DO I / :; J (). 05 :.W-8 I Results in Mathematics Cross Mark Orth.ogonal Polynomials for Modified Chebyshev Measure of the First Kind.. lelksawlar s. Cvetkovic) rv:[arjan IvL rviatcji(:, and Gn1dhuir V. iviilcvano\ ic Abstract. Given nmnhers n >.'$ E Pi 1 n ;;;: 2, aud th ~ nth-degrhe mohk ChebysiHw polynomifl.l of the first kind 1~, (:r), the polynomial systern "ill(htc<jd" by f:, (:r;) il'> the syst:orn of or thogonal polynmnialh {p~ ' } col' respondiug to the tuodhiej mc~tl:}ul'e du 11 ' ~< (x) = T,:If (:r.:) d<1(: }, where da(. :) = 1/ J'f - :t::t &r: is the hcbysh v mea. -mre of the first kind. Here we n,re conccnwd with the problem of determining the co flicient.r iu tho thrco-term reenrroue' relation for th' polynomials ij~. ~. Tho de~ir!d co (lffidcnt t< ar... obt.uimui am.t1ytically iu a losoo fm m. Mathematics Suhjed Classification. I dmary :l:jct15. Kcywot ds. Orthogonal polyuomials, 'hebysh v tucasur ~, Cheby. hev polynomial~, n~cm..-enen relation. 1. Introduction Let dci(:r) he a positiw~ measure on R\ \Vtt.h finite or nnbohnd d support lmving fmi te Inomcnt:H of all ordcrs 1 and let { P&} I k E No, he Lh" corro~pondiug (monic) orthogonal poly ton ia.ls) JJJ,:(;t:) = J.iJ, (!t:; da)l k E No~ which satisfy the following three-f. 'rm recurrence relation (cf. [5} p.. 07]) Plt t,(:c) = (:t - a,.;)pj.:(:1;) ~ f h,.tjtr - l(:r} ~ po(:l;) = I' JL I ( : r ~) = ol k No, T he work WH!i Sll}J}lOrt.ed in part by tim Serbi<m I\' filli ~ 1, ry or [~dw.;atioh f Sden(:e r~lld Tech 110logknl DevrloptuChL. ~ Birkhiiuse:r
106 International Journal of Computer Mathematics Vol. 88, No. 14, September 2011, Q Taylor & Francis ~ Taylor&FrantisGroup Rational algorithm for quadratic Christoffel modification and applications to the constrained L 2 -approximation A.S. Cvetkovica, G.V. Milovanovicb* and M.M. Matejicc a Faculty of Sciences and Mathematics, University of Nis, P. 0. Box 224, Nis, Serbia; b Faculty of Computer Sciences, Megatrend University Belgrade, Bulevar umetnosti 29, Novi Beograd, Serbia; c Faculty of Electronic Engineering, University of Nis, P. 0. Box 73, Nis, Serbia (Received 10 May 2010; final version received 17 February 2011) In this paper, we consider a rational algorithm for modification of a positive measure by quadratic factor, da (t) = (t - z) 2 da (t), where it is allowed z to be in supp(da). Also, we present an application of modified ~is the algorithm to the measures da(t) = T}(t) da(t) and da'(t) = t 2 Tl(t) da(t), where T2(t) = t 2 - second degree monic Chebyshev polynomial of the first kind and da (f) =.JT"=t2 dt, t E [ -1, 1], is the Chebyshev measure of the second kind. Also, we present an application to the constrained L 2 -polynomial approximation. Keywords: orthogonal polynomials; Chebyshev polynomials; positive measure; Christoffel algorithm; three-term recurrence relation; constrained L 2 -approximation 20JOAMS Subject Classifications: 33C45; 33C47; 41A10; 41A29; 65F25 1. Introduction Let dcr be a positive measure on IR with an infinite support such that polynomials are integrable and let {p 11 }, n E N 0, be a sequence of the corresponding monic orthogonal polynomials, Pn(t) = Pn(dcr; t), n E No. It is known that they satisfy a three-term recurrence relation of the form Pn+I (t) = (t- an)pn(t)- f3npn-l (t), Po(t) = 1, P-1 (t) = 0, n E No, where 0'. 11 = 0'. 11 ( dcr) E IR, {3 11 = {3 11 ( dcr) > 0, and by convention, f3o = f3o ( dcr) = a (IR). *Corresponding author. gvm@megatrend.edu.rs ISSN print/issn online 2011 Taylor & Francis DOl: / http: I jwww.informaworld.com
107 STUDIA UNIV. "BABE:'j-BOLYA I", MATHEMATICA, Volume Ll, Number 4, December 2006 ON POSITIVE DEFINITENESS OF SOME LINEAR FUNCTIONALS G.V. MILOVANOVIC, A.S. CVETKOVIC AND M.M. M ATEJIC Dedicated to Prof essor Gheorghe Coman at his 70th anniversary Abstract. In this paper we investigate the positive defini teness of linear functionals.c defined on t he space of all algebraic polynomials P by.c(p) = L Wk p( zk), p E P. ken 1. Introduction Let P b e the space of all algebraic polynomials. In this paper we investigate linear functionals L defin ed by J:(p) = L wkp(zk ), p E P. (1) ken In general, we investigate functi onals for which wk, Zk E C\ {0}, but wi th the foll owing restri t:tions. First, we assume that Wk # 0, k E N. T his condition is rat her natural, since', assuming Wk = 0, for some k E N, simply produces a linear functional where summation is p erformed over N\ { k}. Additionally, we will not loose any generality if we assume that Zi # Zj, i, j E N, since, for example, we may skip summation over j and use w ~ = wi + Wj at point Zi. For the set of nodes zi, i EN, we introduce the notation Z = {zk I k EN}. Second we are going to assume that lim z ~;. = 0 k~+oo (2) Received by t he editors: Mathematics Subject Classifi cation. 5tlC50, 32A 05. KP.U wnrd.~ fnulphro.:h~.<l linear fu ncl.ionals, algebraic polynom ials. 157
108 FACT A UNIVERSITATIS (NIS) SER. MATH. INFORM. 21 (2006), REMARK ON ORTHOGONAL POLYNOMIALS INDUCED BY THE MODIFIED CHEBYSHEV MEASURE OF THE SECOND KIND* G. V. Milovanovic, A. S. Cvetkovic, M. M. Matejic Abstract. In this note we introduce a system of polynomials {Pi.:} orthogonal wit h respect to t he modified Chebyshev measure of the second kind, ~ t + l c + l t + -2 c + -2c d>. (t) = 12 ~ Jl=t2" dt, t E [-1, 1], where c is a positive real number, and determine the coefficients in the corresponding three-term recurrence relation for these polynomials in an analytical form. 1. Introduction In this note we investigate polynomials ort hogonal with respect to the moment functional (1.1) P E P, where c E IR\{0}. The special case c = 1 has been considered in [4]. To make it more clear, Figure 1 displays graph of the rational part of t he weight for c = J2. As c tends to 1, t he singularity of t he rational part tends Received J anuary 18, Mathem atics Subject Classification. 33C45, 33C47. *The authors were supported in part by the Serbian Ministry of Science and Environmental Protection (Project: Orthogonal Systems and Applications, grant number #144004) and t he Swiss National Science Foundation (SCOPES Joint Research Project No. IB "New Iviethods for Quadrature" ). 13
109 05PA3AU 1. ~3jasa 0 aytopctby nornlllcahi!i-a _M'--- -~_~f>_j_ ~_._\+-_-JM----'~..ft-~-=-==-' \A. -'--'--h_. _ 6p~yn111ca ~3jaslbyjeM pe3yntat concrsehor I!ICTpa)I(I!!BaYKor paaa, Aa npeajto)i(eha AlllcepTal..ll!lja y uemthi-1 Hlil y AellOBI!!Ma Hvtje a npea!lo)i(eha 3a A06111jat-be Koje Al!lnnoMe npema CTYAI-1jCKvtM nporpami-1ma,apyr1-1x Bl-1COKOWKOI1CKV1X yctahoba,,aa cy pe3yi1tatiii KOpeKTHO HaBeAeHlil lil Aa HV1CaM KpwV1o/na aytopc t<a npasa 1-1 KOPIIICTV10 l-1htenektyanhy csojl!ihy APYrli1X Y Kparyjesuy, 20. Ob',2CJlQ.,...,
110 06PA3AL.t 2. IJ13jaoa 0 HCTOBeTHOCTH WTaMnaHe H ejlektpohcke Bep3Hje,QOKTOpCKOr pa,qa VI Me 11 npe311me ayropa ~~~ M*-\ :1 \A-h.. 6poj yn11ca Cry,Qii1jCKII1 nporpam ~:~~~~ P-A~frJ~~tr;~~~~t flomu\qh!=;ia\jh;;: n?ontm~l{l5t li13jab!byjem.qa je WTaMnaHa Bep31i1ja MOr.QOKTOpCKOr pa,aa 11CTOBeTHa enektpohckoj sep31i1jvt Kojy cam npe,aao/na 3a o6jasfbvtbal-be Ha noprany AHrHTallHOr pen03htophjyma YHHBep3HTeTa y KparyjeB4Y Ao3BO!basaM.aa ce o6jase MOjli1 M1YHV1 no.aau11 Be3aHII1 3a,Q06111jal-be aka,qemckor 3Bal-ba,llOKTOpa Hay.Ka, KaO WTO cy 11Me VI npe31!1me, ro,qii1ha V1 MeCTO pot)el-ba li1,qatym O,ll6paHe pa,qa. Oavt J111YHVI no,qauv1 Mory ce o6jabv1tvi Ha Mpe>KHVIM crpahviu.ama.qv1rv1tanhe 6V16J1VIOTeKe, y enektpohckom Karanory 11 y ny6m1kau111jama YHV~sep31t1Tera y Kparyjesuy. Y Kparyjesu.y, 20. OG..2oA!ci Td. notnhc aytopa ~
111 06PA3Al-' 3. ~3jaaa o KOpHwliet-by OsnawnyjeM YHt-~sep3!-1TeTcKy 6t-~6nt-~oTeKy Aa y At-~rt-~TallHvt peno3vttopl-1jym YHt-~sep3t-~TeTa,. _ Kparyjesuy yhece Mojy AOKTopcKy At-~cepTaut-~jy noa HacnosoM:. t'~~"\30-:l?.a-\bud\h\f\:.j\-{x. A-/\\0"?\.IT-A-~h- "S../lr \4:?~'?"1\SU..Lci'i KOja je MOje aytopcko A!10..0,1-!CepTal(l-ljy ca CBI-IM npt-~!1031-lma TpajHO apxiiibi-!pah>e. npeaao/fla CaM y fl KTpOHCKOM cpopmaty noroahoivi 3a Mojy AOKTopcKy AvtcepTaUt-~jy noxpah>ehy y Avtn1Ta11Hvt peno3t-~topl-1jym YHvtsep31-1TeTa y Kparyjesuy Mory.Qa Kopt-~cTe cs~-1 Kojt-~ nowtyjy OAPeA6e ca.qp)f(ahe y o.qa6pahom Tl'lny nvtuehue KpeaTvtBHe 3ajeAH111Lie (Creative Commons) 3a Kojy cam ce OAJJYYIIIO/na. 1. AyTOpCTBO 2. AyTOpcTso - HeKoMepul-1janHo ffiaytopctbo - HeKOMeput-~jaflHO - 6e3 npepa.qe noa IIICTI'IM ycnos1-1ma '4:' AyTopcTBO - HeKoMepul-ljanHo -.Qent-~TI-1 5. AyTopcTBO - 6e3 npepa.qe 6. AyTopcTBO - Aemnt-~ noa t-~ctt-~m ycnost-~ma (MOflliiMO Aa 3aOKpy)!(t-~Te CaMO jeahy OA W CT nohyf)ehi-1x fli-1li HUVI, 41-ljl-1 je KpaTaK onvtc.qat je Ha o6pacuy 6poj 4.). notnhc aytopa Y Kparyjesuy, 2.0. OG, QoU~.T<t - ====---====== ==.:~ ::...:==---=======:... t==== ;;==;.;;...;;.. ;;;;,
Projektovanje paralelnih algoritama II
 Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
Projektovanje paralelnih algoritama II Primeri paralelnih algoritama, I deo Paralelni algoritmi za množenje matrica 1 Algoritmi za množenje matrica Ovde su data tri paralelna algoritma: Direktan algoritam
TEORIJA SKUPOVA Zadaci
 TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
TEORIJA SKUPOVA Zadai LOGIKA 1 I. godina 1. Zapišite simbolima: ( x nije element skupa S (b) d je član skupa S () F je podskup slupa S (d) Skup S sadrži skup R 2. Neka je S { x;2x 6} = = i neka je b =
Unutraxnjost skra enih usrednjenih gausovskih kvadratura i ocena grexke Gaus-Kronrodovih kvadratura
 UNIVERZITET U KRAGUJEVCU PRIRODNO-MATEMATIQKI FAKULTET mr Duxan uki Unutraxnjost skra enih usrednjenih gausovskih kvadratura i ocena grexke Gaus-Kronrodovih kvadratura DOKTORSKA DISERTACIJA Mentor: prof.
UNIVERZITET U KRAGUJEVCU PRIRODNO-MATEMATIQKI FAKULTET mr Duxan uki Unutraxnjost skra enih usrednjenih gausovskih kvadratura i ocena grexke Gaus-Kronrodovih kvadratura DOKTORSKA DISERTACIJA Mentor: prof.
ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA. Šefket Arslanagić, Sarajevo, BiH
 MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
MAT-KOL (Banja Luka) XXIII ()(7), -7 http://wwwimviblorg/dmbl/dmblhtm DOI: 75/МК7A ISSN 5-6969 (o) ISSN 986-588 (o) ZANIMLJIV NAČIN IZRAČUNAVANJA NEKIH GRANIČNIH VRIJEDNOSTI FUNKCIJA Šefket Arslanagić,
IZVEXTAJ. 1. Biografija kandidata. 2. Nauqni i struqni rad. Nastavno nauqnom ve u Matematiqkog fakulteta Univerziteta u Beogradu
 Nastavno nauqnom ve u Matematiqkog fakulteta Univerziteta u Beogradu Na 339. toj sednici Nastavno nauqnog ve a Matematiqkog fakulteta, odrжanoj 24. februara 2017. godine, određeni smo za qlanove komisije
Nastavno nauqnom ve u Matematiqkog fakulteta Univerziteta u Beogradu Na 339. toj sednici Nastavno nauqnog ve a Matematiqkog fakulteta, odrжanoj 24. februara 2017. godine, određeni smo za qlanove komisije
Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku
 Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Valentina Volmut Ortogonalni polinomi Diplomski rad Osijek, 2016. Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku
Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Valentina Volmut Ortogonalni polinomi Diplomski rad Osijek, 2016. Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku
Eksponencijalne i logaritamske funkcije, jednaqine i nejednaqine u sredoj xkoli sa osvrtom na problemske zadatke
 Matematiqki fakultet Univerzitet u Beogradu Eksponencijalne i logaritamske funkcije, jednaqine i nejednaqine u sredoj xkoli sa osvrtom na problemske zadatke Mentor: dr Milox Arsenovi Master rad Student:
Matematiqki fakultet Univerzitet u Beogradu Eksponencijalne i logaritamske funkcije, jednaqine i nejednaqine u sredoj xkoli sa osvrtom na problemske zadatke Mentor: dr Milox Arsenovi Master rad Student:
PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU
 MAT KOL Banja Luka) ISSN 0354 6969 p) ISSN 1986 58 o) Vol. XXI )015) 105 115 http://www.imvibl.org/dmbl/dmbl.htm PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU Bernadin Ibrahimpašić 1 Senka Ibrahimpašić
MAT KOL Banja Luka) ISSN 0354 6969 p) ISSN 1986 58 o) Vol. XXI )015) 105 115 http://www.imvibl.org/dmbl/dmbl.htm PRIPADNOST RJEŠENJA KVADRATNE JEDNAČINE DANOM INTERVALU Bernadin Ibrahimpašić 1 Senka Ibrahimpašić
KLASIFIKACIJA NAIVNI BAJES. NIKOLA MILIKIĆ URL:
 KLASIFIKACIJA NAIVNI BAJES NIKOLA MILIKIĆ EMAIL: nikola.milikic@fon.bg.ac.rs URL: http://nikola.milikic.info ŠTA JE KLASIFIKACIJA? Zadatak određivanja klase kojoj neka instanca pripada instanca je opisana
KLASIFIKACIJA NAIVNI BAJES NIKOLA MILIKIĆ EMAIL: nikola.milikic@fon.bg.ac.rs URL: http://nikola.milikic.info ŠTA JE KLASIFIKACIJA? Zadatak određivanja klase kojoj neka instanca pripada instanca je opisana
Slika 1. Slika 2. Da ne bismo stalno izbacivali elemente iz skupa, mi ćemo napraviti još jedan niz markirano, gde će
 Permutacije Zadatak. U vreći se nalazi n loptica različitih boja. Iz vreće izvlačimo redom jednu po jednu lopticu i stavljamo jednu pored druge. Koliko različitih redosleda boja možemo da dobijemo? Primer
Permutacije Zadatak. U vreći se nalazi n loptica različitih boja. Iz vreće izvlačimo redom jednu po jednu lopticu i stavljamo jednu pored druge. Koliko različitih redosleda boja možemo da dobijemo? Primer
Uvod u relacione baze podataka
 Uvod u relacione baze podataka Ana Spasić 2. čas 1 Mala studentska baza dosije (indeks, ime, prezime, datum rodjenja, mesto rodjenja, datum upisa) predmet (id predmeta, sifra, naziv, bodovi) ispitni rok
Uvod u relacione baze podataka Ana Spasić 2. čas 1 Mala studentska baza dosije (indeks, ime, prezime, datum rodjenja, mesto rodjenja, datum upisa) predmet (id predmeta, sifra, naziv, bodovi) ispitni rok
Red veze za benzen. Slika 1.
 Red veze za benzen Benzen C 6 H 6 je aromatično ciklično jedinjenje. Njegove dve rezonantne forme (ili Kekuléove structure), prema teoriji valentne veze (VB) prikazuju se uobičajeno kao na slici 1 a),
Red veze za benzen Benzen C 6 H 6 je aromatično ciklično jedinjenje. Njegove dve rezonantne forme (ili Kekuléove structure), prema teoriji valentne veze (VB) prikazuju se uobičajeno kao na slici 1 a),
ZANIMLJIVI ALGEBARSKI ZADACI SA BROJEM 2013 (Interesting algebraic problems with number 2013)
 MAT-KOL (Banja Luka) ISSN 0354-6969 (p), ISSN 1986-5228 (o) Vol. XIX (3)(2013), 35-44 ZANIMLJIVI ALGEBARSKI ZADACI SA BROJEM 2013 (Interesting algebraic problems with number 2013) Nenad O. Vesi 1 Du²an
MAT-KOL (Banja Luka) ISSN 0354-6969 (p), ISSN 1986-5228 (o) Vol. XIX (3)(2013), 35-44 ZANIMLJIVI ALGEBARSKI ZADACI SA BROJEM 2013 (Interesting algebraic problems with number 2013) Nenad O. Vesi 1 Du²an
Fajl koji je korišćen može se naći na
 Machine learning Tumačenje matrice konfuzije i podataka Fajl koji je korišćen može se naći na http://www.technologyforge.net/datasets/. Fajl se odnosi na pečurke (Edible mushrooms). Svaka instanca je definisana
Machine learning Tumačenje matrice konfuzije i podataka Fajl koji je korišćen može se naći na http://www.technologyforge.net/datasets/. Fajl se odnosi na pečurke (Edible mushrooms). Svaka instanca je definisana
UNIVERZITET U KRAGUJEVCU PRIRODNO{MATEMATIQKI FAKULTET. Numeriqka aproksimacija dvodimenzionalnih paraboliqkih problema sa delta funkcijom
 UNIVERZITET U KRAGUJEVCU PRIRODNO{MATEMATIQKI FAKULTET Bratislav Sredojevi Numeriqka aproksimacija dvodimenzionalnih paraboliqkih problema sa delta funkcijom doktorska disertacija KRAGUJEVAC, 16 ИНДЕНТИФИКАЦИОНА
UNIVERZITET U KRAGUJEVCU PRIRODNO{MATEMATIQKI FAKULTET Bratislav Sredojevi Numeriqka aproksimacija dvodimenzionalnih paraboliqkih problema sa delta funkcijom doktorska disertacija KRAGUJEVAC, 16 ИНДЕНТИФИКАЦИОНА
Mathcad sa algoritmima
 P R I M J E R I P R I M J E R I Mathcad sa algoritmima NAREDBE - elementarne obrade - sekvence Primjer 1 Napraviti algoritam za sabiranje dva broja. NAREDBE - elementarne obrade - sekvence Primjer 1 POČETAK
P R I M J E R I P R I M J E R I Mathcad sa algoritmima NAREDBE - elementarne obrade - sekvence Primjer 1 Napraviti algoritam za sabiranje dva broja. NAREDBE - elementarne obrade - sekvence Primjer 1 POČETAK
BROJEVNE KONGRUENCIJE
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Vojko Nestorović BROJEVNE KONGRUENCIJE - MASTER RAD - Mentor, dr Siniša Crvenković Novi Sad, 2011. Sadržaj Predgovor...............................
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Vojko Nestorović BROJEVNE KONGRUENCIJE - MASTER RAD - Mentor, dr Siniša Crvenković Novi Sad, 2011. Sadržaj Predgovor...............................
Metrički prostori i Riman-Stiltjesov integral
 Metrički prostori i Riman-Stiltjesov integral Sadržaj 1 Metrički prostori 3 1.1 Primeri metričkih prostora................. 3 1.2 Konvergencija nizova i osobine skupova...................... 12 1.3 Kantorov
Metrički prostori i Riman-Stiltjesov integral Sadržaj 1 Metrički prostori 3 1.1 Primeri metričkih prostora................. 3 1.2 Konvergencija nizova i osobine skupova...................... 12 1.3 Kantorov
Rešenja zadataka za vežbu na relacionoj algebri i relacionom računu
 Rešenja zadataka za vežbu na relacionoj algebri i relacionom računu 1. Izdvojiti ime i prezime studenata koji su rođeni u Beogradu. (DOSIJE WHERE MESTO_RODJENJA='Beograd')[IME, PREZIME] where mesto_rodjenja='beograd'
Rešenja zadataka za vežbu na relacionoj algebri i relacionom računu 1. Izdvojiti ime i prezime studenata koji su rođeni u Beogradu. (DOSIJE WHERE MESTO_RODJENJA='Beograd')[IME, PREZIME] where mesto_rodjenja='beograd'
Metode izračunavanja determinanti matrica n-tog reda
 Osječki matematički list 10(2010), 31 42 31 STUDENTSKA RUBRIKA Metode izračunavanja determinanti matrica n-tog reda Damira Keček Sažetak U članku su opisane metode izračunavanja determinanti matrica n-tog
Osječki matematički list 10(2010), 31 42 31 STUDENTSKA RUBRIKA Metode izračunavanja determinanti matrica n-tog reda Damira Keček Sažetak U članku su opisane metode izračunavanja determinanti matrica n-tog
Algoritmi za mnoºenje i dijeljenje velikih. brojeva. Marko Pejovi UNIVERZITET CRNE GORE. Prirodno-matemati ki fakultet Podgorica. Podgorica, 2018.
 UNIVERZITET CRNE GORE Prirodno-matemati ki fakultet Podgorica Marko Pejovi Algoritmi za mnoºenje i dijeljenje velikih brojeva SPECIJALISTIƒKI RAD Podgorica, 2018. UNIVERZITET CRNE GORE Prirodno-matemati
UNIVERZITET CRNE GORE Prirodno-matemati ki fakultet Podgorica Marko Pejovi Algoritmi za mnoºenje i dijeljenje velikih brojeva SPECIJALISTIƒKI RAD Podgorica, 2018. UNIVERZITET CRNE GORE Prirodno-matemati
IMPROVEMENT OF HIPPARCOS PROPER MOTIONS IN DECLINATION
 Serb. Astron. J. 172 (2006), 41-51 UDC 521.96 DOI: 10.2298/SAJ0672041D Preliminary report IMPROVEMENT OF HIPPARCOS PROPER MOTIONS IN DECLINATION G. Damljanović 1, N. Pejović 2 and B. Jovanović 1 1 Astronomical
Serb. Astron. J. 172 (2006), 41-51 UDC 521.96 DOI: 10.2298/SAJ0672041D Preliminary report IMPROVEMENT OF HIPPARCOS PROPER MOTIONS IN DECLINATION G. Damljanović 1, N. Pejović 2 and B. Jovanović 1 1 Astronomical
UOPŠTENI INVERZI, FAKTORI USLOVLJENOSTI I PERTURBACIJE
 UNIVERZITET U NIŠU PRIRODNO MATEMATIČKI FAKULTET ODSEK ZA MATEMATIKU I INFORMATIKU Dijana Mosić UOPŠTENI INVERZI, FAKTORI USLOVLJENOSTI I PERTURBACIJE Doktorska disertacija Mentor Prof. dr Dragan Djordjević
UNIVERZITET U NIŠU PRIRODNO MATEMATIČKI FAKULTET ODSEK ZA MATEMATIKU I INFORMATIKU Dijana Mosić UOPŠTENI INVERZI, FAKTORI USLOVLJENOSTI I PERTURBACIJE Doktorska disertacija Mentor Prof. dr Dragan Djordjević
Iskazna logika 1. Matematička logika u računarstvu. oktobar 2012
 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia oktobar 2012 Iskazi, istinitost, veznici Intuitivno, iskaz je rečenica koja je ima tačno jednu jednu
Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia oktobar 2012 Iskazi, istinitost, veznici Intuitivno, iskaz je rečenica koja je ima tačno jednu jednu
SIMBOLIČKO IZRAČUNAVANJE HANKELOVIH DETERMINANTI I GENERALISANIH INVERZA MATRICA
 Univerzitet u Nišu Prirodno-Matematički fakultet Marko D. Petković SIMBOLIČKO IZRAČUNAVANJE HANKELOVIH DETERMINANTI I GENERALISANIH INVERZA MATRICA Doktorska disertacija Niš, Jun 2008 Mogućnost simboličkog
Univerzitet u Nišu Prirodno-Matematički fakultet Marko D. Petković SIMBOLIČKO IZRAČUNAVANJE HANKELOVIH DETERMINANTI I GENERALISANIH INVERZA MATRICA Doktorska disertacija Niš, Jun 2008 Mogućnost simboličkog
Klase neograničenih operatora
 Univerzitet u Nišu Prirodno- matematički fakultet Departman za matematiku Klase neograničenih operatora Master rad Mentor: Prof. dr. Dragan Đorđević Student: Milena Nikolić Niš,. Sadržaj Predgovor...2
Univerzitet u Nišu Prirodno- matematički fakultet Departman za matematiku Klase neograničenih operatora Master rad Mentor: Prof. dr. Dragan Đorđević Student: Milena Nikolić Niš,. Sadržaj Predgovor...2
Šime Šuljić. Funkcije. Zadavanje funkcije i područje definicije. š2004š 1
 Šime Šuljić Funkcije Zadavanje funkcije i područje definicije š2004š 1 Iz povijesti Dvojica Francuza, Pierre de Fermat i Rene Descartes, posebno su zadužila matematiku unijevši ideju koordinatne metode
Šime Šuljić Funkcije Zadavanje funkcije i područje definicije š2004š 1 Iz povijesti Dvojica Francuza, Pierre de Fermat i Rene Descartes, posebno su zadužila matematiku unijevši ideju koordinatne metode
Funkcijske jednadºbe
 MEMO pripreme 2015. Marin Petkovi, 9. 6. 2015. Funkcijske jednadºbe Uvod i osnovne ideje U ovom predavanju obradit emo neke poznate funkcijske jednadºbe i osnovne ideje rje²avanja takvih jednadºbi. Uobi
MEMO pripreme 2015. Marin Petkovi, 9. 6. 2015. Funkcijske jednadºbe Uvod i osnovne ideje U ovom predavanju obradit emo neke poznate funkcijske jednadºbe i osnovne ideje rje²avanja takvih jednadºbi. Uobi
Permutacije sa ograniqeƭima
 Univerzitet u Nixu Prirodno matematiqki fakultet Departman za matematiku Vladimir M. Balti Permutacije sa ograniqeƭima Doktorska disertacija Nix, 2014. University of Niš Faculty of Science and Mathematics
Univerzitet u Nixu Prirodno matematiqki fakultet Departman za matematiku Vladimir M. Balti Permutacije sa ograniqeƭima Doktorska disertacija Nix, 2014. University of Niš Faculty of Science and Mathematics
NASTAVA MATEMATIKE U OSNOVNOJ XKOLI. Dr Vladimir Mi i PRAVILA NALAЖENjA QLANOVA NIZA
 NASTAVA MATEMATIKE U OSNOVNOJ XKOLI Dr Vladimir Mi i PRAVILA NALAЖENjA QLANOVA NIZA Nastavnim programom predmeta Matematika predviđeno je da u qetvrtom razredu osnovne xkole uqenici upoznaju skup N prirodnih
NASTAVA MATEMATIKE U OSNOVNOJ XKOLI Dr Vladimir Mi i PRAVILA NALAЖENjA QLANOVA NIZA Nastavnim programom predmeta Matematika predviđeno je da u qetvrtom razredu osnovne xkole uqenici upoznaju skup N prirodnih
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Ivan Marinković Klasifikacija H-matrica metodom skaliranja i njena primena u odred ivanju oblasti konvergencije
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Ivan Marinković Klasifikacija H-matrica metodom skaliranja i njena primena u odred ivanju oblasti konvergencije
Simplektiqki kapaciteti
 Matematiqki fakultet Univerzitet u Beogradu Master rad Simplektiqki kapaciteti Student: Filip Жivanovi Mentor: dr Darko Milinkovi U Beogradu, 2015-2016. Sadraj 1 Uvod u simplektiqku topologiju 3 1.1 Simplektiqke
Matematiqki fakultet Univerzitet u Beogradu Master rad Simplektiqki kapaciteti Student: Filip Жivanovi Mentor: dr Darko Milinkovi U Beogradu, 2015-2016. Sadraj 1 Uvod u simplektiqku topologiju 3 1.1 Simplektiqke
XTAJNEROVI SISTEMI I NOVE KONSTRUKCIJE
 UNIVERZITET U BEOGRADU MATEMATIQKI FAKULTET Nebojxa T. Nikoli XTAJNEROVI SISTEMI I NOVE KONSTRUKCIJE (v,k,t)-pokrivaNja doktorska disertacija Beograd, 2015 UNIVERSITY OF BELGRADE FACULTY OF MATHEMATICS
UNIVERZITET U BEOGRADU MATEMATIQKI FAKULTET Nebojxa T. Nikoli XTAJNEROVI SISTEMI I NOVE KONSTRUKCIJE (v,k,t)-pokrivaNja doktorska disertacija Beograd, 2015 UNIVERSITY OF BELGRADE FACULTY OF MATHEMATICS
Simetrične matrice, kvadratne forme i matrične norme
 Sveučilište JJStrossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Martina Dorić Simetrične matrice, kvadratne forme i matrične norme Završni rad Osijek, 2014 Sveučilište
Sveučilište JJStrossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Martina Dorić Simetrične matrice, kvadratne forme i matrične norme Završni rad Osijek, 2014 Sveučilište
p f(p)
 NASTAVA MATEMATIKE U SREDNjOJ XKOLI Vladimir Mixi, Veljko irovi, dr Vojislav Andri VARIJACIJE NA ZADATU TEMU Vreme koje je pred nama je prostor koji e nesumnjivo pripasti kreativnim ljudima. Zato je razvijanje
NASTAVA MATEMATIKE U SREDNjOJ XKOLI Vladimir Mixi, Veljko irovi, dr Vojislav Andri VARIJACIJE NA ZADATU TEMU Vreme koje je pred nama je prostor koji e nesumnjivo pripasti kreativnim ljudima. Zato je razvijanje
Uvod u analizu (M3-02) 05., 07. i 12. XI dr Nenad Teofanov. principle) ili Dirihleov princip (engl. Dirichlet box principle).
 Uvod u analizu (M-0) 0., 07. i. XI 0. dr Nenad Teofanov. Kardinalni broj skupa R U ovom predavanju se razmatra veličina skupa realnih brojeva. Jasno, taj skup ima beskonačno mnogo elemenata. Pokazaće se,
Uvod u analizu (M-0) 0., 07. i. XI 0. dr Nenad Teofanov. Kardinalni broj skupa R U ovom predavanju se razmatra veličina skupa realnih brojeva. Jasno, taj skup ima beskonačno mnogo elemenata. Pokazaće se,
Osobine metode rezolucije: zaustavlja se, pouzdanost i kompletnost. Iskazna logika 4
 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Rezolucija 1 Metod rezolucije je postupak za dokazivanje da li je neka iskazna (ili
Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Rezolucija 1 Metod rezolucije je postupak za dokazivanje da li je neka iskazna (ili
Virtual Library of Faculty of Mathematics - University of Belgrade
 Matematiqki fakultet Univerzitet u Beogradu Master rad Spektralne invarijante u Florovoj homologiji Student: Mentor: Vukaxin Stojisavljevi dr Darko Milinkovi U Beogradu, 2014-2015. Sadraj 1 Topoloxki uvod
Matematiqki fakultet Univerzitet u Beogradu Master rad Spektralne invarijante u Florovoj homologiji Student: Mentor: Vukaxin Stojisavljevi dr Darko Milinkovi U Beogradu, 2014-2015. Sadraj 1 Topoloxki uvod
Matrice traga nula math.e Vol. 26. math.e. Hrvatski matematički elektronički časopis. Matrice traga nula. komutator linearna algebra. Sažetak.
 1 math.e Hrvatski matematički elektronički časopis komutator linearna algebra Marijana Kožul i Rajna Rajić Matrice traga nula marijana55@gmail.com, rajna.rajic@rgn.hr Rudarsko-geološko-naftni fakultet,
1 math.e Hrvatski matematički elektronički časopis komutator linearna algebra Marijana Kožul i Rajna Rajić Matrice traga nula marijana55@gmail.com, rajna.rajic@rgn.hr Rudarsko-geološko-naftni fakultet,
On the relation between Zenkevich and Wiener indices of alkanes
 J.Serb.Chem.Soc. 69(4)265 271(2004) UDC 547.21:54 12+539.6 JSCS 3152 Original scientific paper On the relation between Zenkevich and Wiener indices of alkanes IVAN GUTMAN a*, BORIS FURTULA a, BILJANA ARSI]
J.Serb.Chem.Soc. 69(4)265 271(2004) UDC 547.21:54 12+539.6 JSCS 3152 Original scientific paper On the relation between Zenkevich and Wiener indices of alkanes IVAN GUTMAN a*, BORIS FURTULA a, BILJANA ARSI]
OSCILATORNOST NELINEARNIH DIFERENCIJALNIH JEDNAČINA DRUGOG REDA
 UNIVERZIE U BEOGRADU MAEMAIČKI FAKULE Jelena V. Manojlović OSCILAORNOS NELINEARNIH DIFERENCIJALNIH JEDNAČINA DRUGOG REDA Doktorska disertacija Beograd, 999. Predgovor Ova doktorska disertacija posvećena
UNIVERZIE U BEOGRADU MAEMAIČKI FAKULE Jelena V. Manojlović OSCILAORNOS NELINEARNIH DIFERENCIJALNIH JEDNAČINA DRUGOG REDA Doktorska disertacija Beograd, 999. Predgovor Ova doktorska disertacija posvećena
Statistiqke funkcije dubine i ihova primena u otkriva u autlajera u dvodimenzionom prostoru
 UNIVERZITET U BEOGRADU MATEMATIQKI FAKULTET Katarina Jeremi Statistiqke funkcije dubine i ihova primena u otkriva u autlajera u dvodimenzionom prostoru master rad Beograd, 2017. Sadraj 1 Statistiqke funkcije
UNIVERZITET U BEOGRADU MATEMATIQKI FAKULTET Katarina Jeremi Statistiqke funkcije dubine i ihova primena u otkriva u autlajera u dvodimenzionom prostoru master rad Beograd, 2017. Sadraj 1 Statistiqke funkcije
Jedna familija trokoračnih postupaka šestog reda za rešavanje nelinearnih jednačina
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Ester Jambor Jedna familija trokoračnih postupaka šestog reda za rešavanje nelinearnih jednačina master rad
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Ester Jambor Jedna familija trokoračnih postupaka šestog reda za rešavanje nelinearnih jednačina master rad
NIZOVI I REDOVI FUNKCIJA
 SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Danijela Piškor NIZOVI I REDOVI FUNKCIJA Diplomski rad Voditelj rada: izv. prof. dr. sc. Ljiljana Arambašić Zagreb, rujan 206.
SVEUČILIŠTE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Danijela Piškor NIZOVI I REDOVI FUNKCIJA Diplomski rad Voditelj rada: izv. prof. dr. sc. Ljiljana Arambašić Zagreb, rujan 206.
UNIVERZITET U NIŠU PRIRODNO-MATEMATIČKI FAKULTET. mr Dragan Stevanović NEKE KOMPOZICIJE GRAFOVA I GRAFOVI SA CELOBROJNIM SPEKTROM
 UNIVERZITET U NIŠU PRIRODNO-MATEMATIČKI FAKULTET mr Dragan Stevanović NEKE KOMPOZICIJE GRAFOVA I GRAFOVI SA CELOBROJNIM SPEKTROM doktorska disertacija Niš, 1999. Za Sanju Sadržaj Predgovor vii I NEPS
UNIVERZITET U NIŠU PRIRODNO-MATEMATIČKI FAKULTET mr Dragan Stevanović NEKE KOMPOZICIJE GRAFOVA I GRAFOVI SA CELOBROJNIM SPEKTROM doktorska disertacija Niš, 1999. Za Sanju Sadržaj Predgovor vii I NEPS
Algoritmi i strukture podataka
 Algoritmi i strukture podataka Materijal sa predava a Miodrag ivkovi e-mail: ezivkovm@matf.bg.ac.rs URL: www.matf.bg.ac.rs/~ezivkovm Vesna Marinkovi e-mail: vesnap@matf.bg.ac.rs URL: www.matf.bg.ac.rs/~vesnap
Algoritmi i strukture podataka Materijal sa predava a Miodrag ivkovi e-mail: ezivkovm@matf.bg.ac.rs URL: www.matf.bg.ac.rs/~ezivkovm Vesna Marinkovi e-mail: vesnap@matf.bg.ac.rs URL: www.matf.bg.ac.rs/~vesnap
ANALYSIS OF INFLUENCE OF PARAMETERS ON TRANSFER FUNCTIONS OF APERIODIC MECHANISMS UDC Života Živković, Miloš Milošević, Ivan Ivanov
 UNIVERSITY OF NIŠ The scientific journal FACTA UNIVERSITATIS Series: Mechanical Engineering Vol.1, N o 6, 1999 pp. 675-681 Editor of series: Nenad Radojković, e-mail: radojkovic@ni.ac.yu Address: Univerzitetski
UNIVERSITY OF NIŠ The scientific journal FACTA UNIVERSITATIS Series: Mechanical Engineering Vol.1, N o 6, 1999 pp. 675-681 Editor of series: Nenad Radojković, e-mail: radojkovic@ni.ac.yu Address: Univerzitetski
Neke klase maksimalnih hiperklonova
 UNIVERZITET U NOVOM SDU PRIRODNO-MTEMTIČKI FKULTET DERRTMN Z MTEMTIKU I INFORMTIKU Jelena Čolić Neke klase maksimalnih hiperklonova - završni rad - MENTOR: Prof. dr Rozalija Madaras-Siladi Novi Sad, 2012.
UNIVERZITET U NOVOM SDU PRIRODNO-MTEMTIČKI FKULTET DERRTMN Z MTEMTIKU I INFORMTIKU Jelena Čolić Neke klase maksimalnih hiperklonova - završni rad - MENTOR: Prof. dr Rozalija Madaras-Siladi Novi Sad, 2012.
Krive u prostoru Minkovskog
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Maja Jolić Krive u prostoru Minkovskog - master rad - Mentor: dr Sanja Konjik Novi Sad, 2016 Predgovor Na vratima
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Maja Jolić Krive u prostoru Minkovskog - master rad - Mentor: dr Sanja Konjik Novi Sad, 2016 Predgovor Na vratima
Nilpotentni operatori i matrice
 Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Nikolina Romić Nilpotentni operatori i matrice Završni rad Osijek, 2016. Sveučilište J. J. Strossmayera
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Nikolina Romić Nilpotentni operatori i matrice Završni rad Osijek, 2016. Sveučilište J. J. Strossmayera
Hornerov algoritam i primjene
 Osječki matematički list 7(2007), 99 106 99 STUDENTSKA RUBRIKA Hornerov algoritam i primjene Zoran Tomljanović Sažetak. U ovom članku obrad uje se Hornerov algoritam za efikasno računanje vrijednosti polinoma
Osječki matematički list 7(2007), 99 106 99 STUDENTSKA RUBRIKA Hornerov algoritam i primjene Zoran Tomljanović Sažetak. U ovom članku obrad uje se Hornerov algoritam za efikasno računanje vrijednosti polinoma
Ivan Soldo. Sažetak. U članku se analiziraju različiti načini množenja matrica. Svaki od njih ilustriran je primjerom.
 Osječki matematički list 5(005), 8 Različiti načini množenja matrica Ivan Soldo Sažetak U članku se analiziraju različiti načini množenja matrica Svaki od njih ilustriran je primjerom Ključne riječi: linearni
Osječki matematički list 5(005), 8 Različiti načini množenja matrica Ivan Soldo Sažetak U članku se analiziraju različiti načini množenja matrica Svaki od njih ilustriran je primjerom Ključne riječi: linearni
Algoritam za množenje ulančanih matrica. Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek
 Algoritam za množenje ulančanih matrica Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek O problemu (1) Neka je A 1, A 2,, A n niz ulančanih matrica duljine n N, gdje su dimenzije matrice
Algoritam za množenje ulančanih matrica Alen Kosanović Prirodoslovno-matematički fakultet Matematički odsjek O problemu (1) Neka je A 1, A 2,, A n niz ulančanih matrica duljine n N, gdje su dimenzije matrice
ANALIZA PRSTENA I MODULA
 UNIVERZITET U BEOGRADU MATEMATIQKI FAKULTET Zoran S. Pucanovi ANALIZA PRSTENA I MODULA PRIDRUЖIVANjEM GRAFOVA DOKTORSKA DISERTACIJA BEOGRAD, 2012. UNIVERSITY OF BELGRADE FACULTY OF MATHEMATICS Zoran S.
UNIVERZITET U BEOGRADU MATEMATIQKI FAKULTET Zoran S. Pucanovi ANALIZA PRSTENA I MODULA PRIDRUЖIVANjEM GRAFOVA DOKTORSKA DISERTACIJA BEOGRAD, 2012. UNIVERSITY OF BELGRADE FACULTY OF MATHEMATICS Zoran S.
Teorem o reziduumima i primjene. Završni rad
 Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Matej Petrinović Teorem o reziduumima i primjene Završni rad Osijek, 207. Sveučilište J. J. Strossmayera
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Matej Petrinović Teorem o reziduumima i primjene Završni rad Osijek, 207. Sveučilište J. J. Strossmayera
Položaj nultočaka polinoma
 Osječki matematički list 4 (204), 05-6 Položaj nultočaka polinoma Mandalena Pranjić Rajna Rajić Sažetak Prema Rolleovom teoremu, bilo koji segment čiji su krajevi međusobno različite realne nultočke polinoma
Osječki matematički list 4 (204), 05-6 Položaj nultočaka polinoma Mandalena Pranjić Rajna Rajić Sažetak Prema Rolleovom teoremu, bilo koji segment čiji su krajevi međusobno različite realne nultočke polinoma
Ariana Trstenjak Kvadratne forme
 Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Ariana Trstenjak Kvadratne forme Završni rad Osijek, 014. Sveučilište Josipa Jurja Strossmayera
Sveučilište Josipa Jurja Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Ariana Trstenjak Kvadratne forme Završni rad Osijek, 014. Sveučilište Josipa Jurja Strossmayera
MODELIRANJE TEHNOLOŠKIH PROCESA U RUDARSTVU U USLOVIMA NEDOVOLJNOSTI PODATAKA PRIMENOM TEORIJE GRUBIH SKUPOVA
 UNIVERZITET U BEOGRADU RUDARSKO GEOLOŠKI FAKULTET Zoran M. Štirbanović MODELIRANJE TEHNOLOŠKIH PROCESA U RUDARSTVU U USLOVIMA NEDOVOLJNOSTI PODATAKA PRIMENOM TEORIJE GRUBIH SKUPOVA Doktorska disertacija
UNIVERZITET U BEOGRADU RUDARSKO GEOLOŠKI FAKULTET Zoran M. Štirbanović MODELIRANJE TEHNOLOŠKIH PROCESA U RUDARSTVU U USLOVIMA NEDOVOLJNOSTI PODATAKA PRIMENOM TEORIJE GRUBIH SKUPOVA Doktorska disertacija
A SPECTRAL ATLAS OF λ BOOTIS STARS
 Serb. Astron. J. 188 (2014), 75-84 UDC 524.3 355.3 DOI: 10.2298/SAJ1488075P Professional paper A SPECTRAL ATLAS OF λ BOOTIS STARS E. Paunzen 1 and U. Heiter 2 1 Department of Theoretical Physics and Astrophysics,
Serb. Astron. J. 188 (2014), 75-84 UDC 524.3 355.3 DOI: 10.2298/SAJ1488075P Professional paper A SPECTRAL ATLAS OF λ BOOTIS STARS E. Paunzen 1 and U. Heiter 2 1 Department of Theoretical Physics and Astrophysics,
Ksenija Doroslovački KOMBINATORIKA INTERPRETIRANA FUNKCIJAMA I NJIHOVIM OSOBINAMA MASTER RAD. NOVI SAD jun 2008
 1 Ksenija Doroslovački KOMBINATORIKA INTERPRETIRANA FUNKCIJAMA I NJIHOVIM OSOBINAMA MASTER RAD NOVI SAD jun 2008 2 Sadržaj 1 UVOD 5 2 FUNKCIJE 11 3 KLASIČNI KOMBINATORNI OBJEKTI 17 4 NEKI NEKLASIČNI KOMBINATORNI
1 Ksenija Doroslovački KOMBINATORIKA INTERPRETIRANA FUNKCIJAMA I NJIHOVIM OSOBINAMA MASTER RAD NOVI SAD jun 2008 2 Sadržaj 1 UVOD 5 2 FUNKCIJE 11 3 KLASIČNI KOMBINATORNI OBJEKTI 17 4 NEKI NEKLASIČNI KOMBINATORNI
PRIMENA UOPŠTENIH INVERZA U REŠAVANJU FAZI LINEARNIH SISTEMA
 UNIVERZITET U NOVOM SADU FAKULTET TEHNIČKIH NAUKA U NOVOM SADU Vera Miler Jerković PRIMENA UOPŠTENIH INVERZA U REŠAVANJU FAZI LINEARNIH SISTEMA DOKTORSKA DISERTACIJA Novi Sad, 08. УНИВЕРЗИТЕТ У НОВОМ
UNIVERZITET U NOVOM SADU FAKULTET TEHNIČKIH NAUKA U NOVOM SADU Vera Miler Jerković PRIMENA UOPŠTENIH INVERZA U REŠAVANJU FAZI LINEARNIH SISTEMA DOKTORSKA DISERTACIJA Novi Sad, 08. УНИВЕРЗИТЕТ У НОВОМ
ON ORBITS FOR A PARTICULAR CASE OF AXIAL SYMMETRY
 Serb. Astron. J. 178 (2009), 29-37 UDC 524.62 334.2 DOI: 10.2298/SAJ0978029N Original scientific paper ON ORBITS FOR A PARTICULAR CASE OF AXIAL SYMMETRY S. Ninković and B. Jovanović Astronomical Observatory,
Serb. Astron. J. 178 (2009), 29-37 UDC 524.62 334.2 DOI: 10.2298/SAJ0978029N Original scientific paper ON ORBITS FOR A PARTICULAR CASE OF AXIAL SYMMETRY S. Ninković and B. Jovanović Astronomical Observatory,
Elastic - plastic analysis of crack on bimaterial interface
 Theoret. Appl. Mech., Vol.32, No.3, pp. 193 207, Belgrade 2005 Elastic - plastic analysis of crack on bimaterial interface Ruzica R. Nikolic Jelena M. Veljkovic Abstract In this paper are presented solutions
Theoret. Appl. Mech., Vol.32, No.3, pp. 193 207, Belgrade 2005 Elastic - plastic analysis of crack on bimaterial interface Ruzica R. Nikolic Jelena M. Veljkovic Abstract In this paper are presented solutions
Karakteri konačnih Abelovih grupa
 Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Matija Klarić Karakteri konačnih Abelovih grupa Završni rad Osijek, 2015. Sveučilište J. J. Strossmayera
Sveučilište J. J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Matija Klarić Karakteri konačnih Abelovih grupa Završni rad Osijek, 2015. Sveučilište J. J. Strossmayera
Nataxa Todorovi STRMOST U SVETLU TEOREME NEHOROXEVA I NjENI NUMERIQKI ASPEKTI NA PRIMERU QETVORODIMENZIONE SIMPLEKTIQKE MAPE
 MATEMATIQKI FAKULTET UNIVERZITETA U BEOGRADU Nataxa Todorovi STRMOST U SVETLU TEOREME NEHOROXEVA I NjENI NUMERIQKI ASPEKTI NA PRIMERU QETVORODIMENZIONE SIMPLEKTIQKE MAPE DOKTORSKA TEZA Beograd 212. 2 Sadrжaj
MATEMATIQKI FAKULTET UNIVERZITETA U BEOGRADU Nataxa Todorovi STRMOST U SVETLU TEOREME NEHOROXEVA I NjENI NUMERIQKI ASPEKTI NA PRIMERU QETVORODIMENZIONE SIMPLEKTIQKE MAPE DOKTORSKA TEZA Beograd 212. 2 Sadrжaj
Karakterizacija problema zadovoljenja uslova širine 1
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Aleksandar Prokić Karakterizacija problema zadovoljenja uslova širine 1 -master rad- Mentor: dr Petar Marković
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Aleksandar Prokić Karakterizacija problema zadovoljenja uslova širine 1 -master rad- Mentor: dr Petar Marković
Zadatci sa ciklusima. Zadatak1: Sastaviti progra koji određuje z ir prvih prirod ih rojeva.
 Zadatci sa ciklusima Zadatak1: Sastaviti progra koji određuje z ir prvih prirod ih rojeva. StrToIntDef(tekst,broj) - funkcija kojom se tekst pretvara u ceo broj s tim da je uvedena automatska kontrola
Zadatci sa ciklusima Zadatak1: Sastaviti progra koji određuje z ir prvih prirod ih rojeva. StrToIntDef(tekst,broj) - funkcija kojom se tekst pretvara u ceo broj s tim da je uvedena automatska kontrola
PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK. Marina Zrno KOMUTATIVNI PRSTENI. Diplomski rad. Voditelj rada: prof.dr.sc.
 SVEUČ ILIŠ TE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Marina Zrno KOMUTATIVNI PRSTENI Diplomski rad Voditelj rada: prof.dr.sc. Ozren Perše Zagreb, 2014 Ovaj diplomski rad obranjen
SVEUČ ILIŠ TE U ZAGREBU PRIRODOSLOVNO MATEMATIČKI FAKULTET MATEMATIČKI ODSJEK Marina Zrno KOMUTATIVNI PRSTENI Diplomski rad Voditelj rada: prof.dr.sc. Ozren Perše Zagreb, 2014 Ovaj diplomski rad obranjen
Numerical Inverse Laplace Transform
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Omalkhaer Salem Elmabruk Bleblou Numerical Inverse Laplace Transform - master thesis - Novi Sad, 2011. Ovaj
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Omalkhaer Salem Elmabruk Bleblou Numerical Inverse Laplace Transform - master thesis - Novi Sad, 2011. Ovaj
AUTOMATSKE GRUPE I STRUKTURE PREDSTAVLJIVE KONAČNIM AUTOMATIMA
 AUTOMATSKE GRUPE I STRUKTURE PREDSTAVLJIVE KONAČNIM AUTOMATIMA master teza Autor: Atila Fešiš Mentor: dr Igor Dolinka Novi Sad, 2013. Sadržaj Predgovor iii 1 Osnovni pojmovi 1 1.1 Konačni automati i regularni
AUTOMATSKE GRUPE I STRUKTURE PREDSTAVLJIVE KONAČNIM AUTOMATIMA master teza Autor: Atila Fešiš Mentor: dr Igor Dolinka Novi Sad, 2013. Sadržaj Predgovor iii 1 Osnovni pojmovi 1 1.1 Konačni automati i regularni
Konstekstno slobodne gramatike
 Konstekstno slobodne gramatike Vežbe 07 - PPJ Nemanja Mićović nemanja_micovic@matfbgacrs Matematički fakultet, Univerzitet u Beogradu 4 decembar 2017 Sadržaj Konstekstno slobodne gramatike Rečenična forma
Konstekstno slobodne gramatike Vežbe 07 - PPJ Nemanja Mićović nemanja_micovic@matfbgacrs Matematički fakultet, Univerzitet u Beogradu 4 decembar 2017 Sadržaj Konstekstno slobodne gramatike Rečenična forma
Dependence of the total -electron energy on a large number of non-bonding molecular orbitals
 J. Serb. Chem. Soc. 69 (10) 777 782 (2004) UDC 54 724+537.872:519.17:54 12 JSCS 3204 Original scientific paper Dependence of the total -electron energy on a large number of non-bonding molecular orbitals
J. Serb. Chem. Soc. 69 (10) 777 782 (2004) UDC 54 724+537.872:519.17:54 12 JSCS 3204 Original scientific paper Dependence of the total -electron energy on a large number of non-bonding molecular orbitals
Geometrijski smisao rješenja sustava od tri linearne jednadžbe s tri nepoznanice
 Osječki matematički list 6(2006), 79 84 79 Geometrijski smisao rješenja sustava od tri linearne jednadžbe s tri nepoznanice Zlatko Udovičić Sažetak. Geometrijski smisao rješenja sustava od dvije linearne
Osječki matematički list 6(2006), 79 84 79 Geometrijski smisao rješenja sustava od tri linearne jednadžbe s tri nepoznanice Zlatko Udovičić Sažetak. Geometrijski smisao rješenja sustava od dvije linearne
Mirela Nogolica Norme Završni rad
 Sveučilište J.J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Mirela Nogolica Norme Završni rad Osijek, 2014. Sveučilište J.J. Strossmayera u Osijeku Odjel za
Sveučilište J.J. Strossmayera u Osijeku Odjel za matematiku Sveučilišni preddiplomski studij matematike Mirela Nogolica Norme Završni rad Osijek, 2014. Sveučilište J.J. Strossmayera u Osijeku Odjel za
Introduction to orthogonal polynomials. Michael Anshelevich
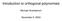 Introduction to orthogonal polynomials Michael Anshelevich November 6, 2003 µ = probability measure on R with finite moments m n (µ) = R xn dµ(x)
Introduction to orthogonal polynomials Michael Anshelevich November 6, 2003 µ = probability measure on R with finite moments m n (µ) = R xn dµ(x)
APPROPRIATENESS OF GENETIC ALGORITHM USE FOR DISASSEMBLY SEQUENCE OPTIMIZATION
 JPE (2015) Vol.18 (2) Šebo, J. Original Scientific Paper APPROPRIATENESS OF GENETIC ALGORITHM USE FOR DISASSEMBLY SEQUENCE OPTIMIZATION Received: 17 July 2015 / Accepted: 25 Septembre 2015 Abstract: One
JPE (2015) Vol.18 (2) Šebo, J. Original Scientific Paper APPROPRIATENESS OF GENETIC ALGORITHM USE FOR DISASSEMBLY SEQUENCE OPTIMIZATION Received: 17 July 2015 / Accepted: 25 Septembre 2015 Abstract: One
FIZIKALNA KOZMOLOGIJA VII. VRLO RANI SVEMIR & INFLACIJA
 FIZIKALNA KOZMOLOGIJA VII. VRLO RANI SVEMIR & INFLACIJA KOZMIČKI SAT ranog svemira Ekstra zračenje u mjerenju CMB Usporedba s rezultatima LEP-a Usporedba CMB i neutrina Vj.: Pozadinsko zračenje neutrina
FIZIKALNA KOZMOLOGIJA VII. VRLO RANI SVEMIR & INFLACIJA KOZMIČKI SAT ranog svemira Ekstra zračenje u mjerenju CMB Usporedba s rezultatima LEP-a Usporedba CMB i neutrina Vj.: Pozadinsko zračenje neutrina
Pellova jednadžba. Pell s equation
 Osječki matematički list 8(2008), 29 36 29 STUDENTSKA RUBRIKA Pellova jednadžba Ivona Mandić Ivan Soldo Sažetak. Članak sadrži riješene primjere i probleme koji se svode na analizu skupa rješenja Pellove
Osječki matematički list 8(2008), 29 36 29 STUDENTSKA RUBRIKA Pellova jednadžba Ivona Mandić Ivan Soldo Sažetak. Članak sadrži riješene primjere i probleme koji se svode na analizu skupa rješenja Pellove
Hamiltonov princip i parcijalne diferencijalne jednačine
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Nikola Dukanović Hamiltonov princip i parcijalne diferencijalne jednačine -master rad- Novi Sad, 2014. Sadržaj
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Nikola Dukanović Hamiltonov princip i parcijalne diferencijalne jednačine -master rad- Novi Sad, 2014. Sadržaj
THE BOUNDARY VALUES OF THE PUNCH DIAMETER IN THE TECHNOLOGY OF THE OPENING MANUFACTURE BY PUNCHING UDC
 FACTA UNIVERSITATIS Series: Mechanical Engineering Vol.1, N o 7, 2000, pp. 887-891 THE BOUNDARY VALUES OF THE PUNCH DIAMETER IN THE TECHNOLOGY OF THE OPENING MANUFACTURE BY PUNCHING UDC 621.962 621.744.52
FACTA UNIVERSITATIS Series: Mechanical Engineering Vol.1, N o 7, 2000, pp. 887-891 THE BOUNDARY VALUES OF THE PUNCH DIAMETER IN THE TECHNOLOGY OF THE OPENING MANUFACTURE BY PUNCHING UDC 621.962 621.744.52
Konstrukcija i analiza algoritama
 Konstrukcija i analiza algoritama 27. februar 207 Matematička indukcija Princip matematičke indukcije: Da bi za svako n N važilo tvrdjenje T (n) dovoljno je pokazati: bazu indukcije: tvrdjenje T () induktivni
Konstrukcija i analiza algoritama 27. februar 207 Matematička indukcija Princip matematičke indukcije: Da bi za svako n N važilo tvrdjenje T (n) dovoljno je pokazati: bazu indukcije: tvrdjenje T () induktivni
Kvaternioni i kvaternionsko rješenje kvadratne jednadžbe
 Kvaternioni i kvaternionsko rješenje 1 Uvod Kvaternioni i kvaternionsko rješenje kvadratne jednadžbe Željko Zrno 1 i Neven Jurić Što je matematika? Na što prvo čovjeka asocira riječ matematika? Matematika
Kvaternioni i kvaternionsko rješenje 1 Uvod Kvaternioni i kvaternionsko rješenje kvadratne jednadžbe Željko Zrno 1 i Neven Jurić Što je matematika? Na što prvo čovjeka asocira riječ matematika? Matematika
Analogne modulacije / Analog modulations
 Analogne modulacije / Analog modulations Zadatak: Na slici 1 je prikazana blok ²ema prijemnika AM-1B0 signala sa sinhronom demodulacijom. Moduli²u i signal m(t) ima spektar u opsegu ( f m f m ) i snagu
Analogne modulacije / Analog modulations Zadatak: Na slici 1 je prikazana blok ²ema prijemnika AM-1B0 signala sa sinhronom demodulacijom. Moduli²u i signal m(t) ima spektar u opsegu ( f m f m ) i snagu
Prsten cijelih brojeva
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ODJEL ZA MATEMATIKU Marijana Pravdić Prsten cijelih brojeva Diplomski rad Osijek, 2017. SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ODJEL ZA MATEMATIKU
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ODJEL ZA MATEMATIKU Marijana Pravdić Prsten cijelih brojeva Diplomski rad Osijek, 2017. SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU ODJEL ZA MATEMATIKU
Andrea Rožnjik. VaR KAO MERA RIZIKA U OPTIMIZACIJI PORTFOLIA. - magistarska teza - Novi Sad, 2008.
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Andrea Rožnjik VaR KAO MERA RIZIKA U OPTIMIZACIJI PORTFOLIA - magistarska teza - Novi Sad, 2008. Predgovor
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Andrea Rožnjik VaR KAO MERA RIZIKA U OPTIMIZACIJI PORTFOLIA - magistarska teza - Novi Sad, 2008. Predgovor
The existence theorem for the solution of a nonlinear least squares problem
 61 The existence theorem for the solution of a nonlinear least squares problem Dragan Jukić Abstract. In this paper we prove a theorem which gives necessary and sufficient conditions which guarantee the
61 The existence theorem for the solution of a nonlinear least squares problem Dragan Jukić Abstract. In this paper we prove a theorem which gives necessary and sufficient conditions which guarantee the
IV razred- matematika. U prvoj nedelji septembra planirano je obnavljanje gradiva druge godine (3 èasa), a 4-tog èasa radi se inicijalni test.
 Profesor: Ivana Obrenoviã Termini za konsultacije: IV razred- matematika U prvoj nedelji septembra planirano je obnavljanje gradiva druge godine (3 èasa), a 4-tog èasa radi se inicijalni test. TEMA 1.
Profesor: Ivana Obrenoviã Termini za konsultacije: IV razred- matematika U prvoj nedelji septembra planirano je obnavljanje gradiva druge godine (3 èasa), a 4-tog èasa radi se inicijalni test. TEMA 1.
Mehurasto sortiranje Brzo sortiranje Sortiranje učešljavanjem Sortiranje umetanjem. Overviev Problemi pretraživanja Heš tabele.
 Bubble sort Razmotrimo još jedan vrlo popularan algoritam sortiranja podataka, vrlo sličan prethodnom algoritmu. Algoritam je poznat pod nazivom Bubble sort algoritam (algoritam mehurastog sortiranja),
Bubble sort Razmotrimo još jedan vrlo popularan algoritam sortiranja podataka, vrlo sličan prethodnom algoritmu. Algoritam je poznat pod nazivom Bubble sort algoritam (algoritam mehurastog sortiranja),
Jednočlani potpuni skupovi veznika za iskaznu logiku
 Univerzitet u Beogradu Matematički fakultet Petar Maksimović Jednočlani potpuni skupovi veznika za iskaznu logiku Master teza mentor: dr Predrag Janičić Beograd 2008 2 Sadržaj 1 Uvod 7 1.1 Kratak istorijat
Univerzitet u Beogradu Matematički fakultet Petar Maksimović Jednočlani potpuni skupovi veznika za iskaznu logiku Master teza mentor: dr Predrag Janičić Beograd 2008 2 Sadržaj 1 Uvod 7 1.1 Kratak istorijat
SINTAKSNA I ALGORITAMSKA NOTACIJA
 B-1 Prilog B SINTAKSNA I ALGORITAMSKA NOTACIJA B-2 B.1 Sintaksna notacija sa zagradama U osnovi svake sintaksne notacije nalaze se slede}i elementi: sintaksni pojam: leksi~ka konstrukcija koja se defini{e;
B-1 Prilog B SINTAKSNA I ALGORITAMSKA NOTACIJA B-2 B.1 Sintaksna notacija sa zagradama U osnovi svake sintaksne notacije nalaze se slede}i elementi: sintaksni pojam: leksi~ka konstrukcija koja se defini{e;
Jacobi-Angelesco multiple orthogonal polynomials on an r-star
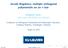 M. Leurs Jacobi-Angelesco m.o.p. 1/19 Jacobi-Angelesco multiple orthogonal polynomials on an r-star Marjolein Leurs, (joint work with Walter Van Assche) Conference on Orthogonal Polynomials and Holomorphic
M. Leurs Jacobi-Angelesco m.o.p. 1/19 Jacobi-Angelesco multiple orthogonal polynomials on an r-star Marjolein Leurs, (joint work with Walter Van Assche) Conference on Orthogonal Polynomials and Holomorphic
AN EXPERIMENTAL METHOD FOR DETERMINATION OF NATURAL CIRCULAR FREQUENCY OF HELICAL TORSIONAL SPRINGS UDC:
 UNIVERSITY OF NIŠ The scientific journal FACTA UNIVERSITATIS Series: Mechanical Engineering Vol.1, N o 5, 1998 pp. 547-554 Editor of series: Nenad Radojković, e-mail: radojkovic@ni.ac.yu Address: Univerzitetski
UNIVERSITY OF NIŠ The scientific journal FACTA UNIVERSITATIS Series: Mechanical Engineering Vol.1, N o 5, 1998 pp. 547-554 Editor of series: Nenad Radojković, e-mail: radojkovic@ni.ac.yu Address: Univerzitetski
Uvod u numericku matematiku
 Uvod u numericku matematiku M. Klaricić Bakula Oujak, 2009. Uvod u numericku matematiku 2 1 Uvod Jedan od osnovnih problema numericke matematike je rješavanje linearnih sustava jednadbi. U ovom poglavlju
Uvod u numericku matematiku M. Klaricić Bakula Oujak, 2009. Uvod u numericku matematiku 2 1 Uvod Jedan od osnovnih problema numericke matematike je rješavanje linearnih sustava jednadbi. U ovom poglavlju
5 th INTERNATIONAL CONFERENCE Contemporary achievements in civil engineering 21. April Subotica, SERBIA
 5 th INTERNATIONAL CONFERENCE Contemporary achievements in civil engineering 21. April 2017. Subotica, SERBIA COMPUTER SIMULATION OF THE ORDER FREQUENCIES AMPLITUDES EXCITATION ON RESPONSE DYNAMIC 1D MODELS
5 th INTERNATIONAL CONFERENCE Contemporary achievements in civil engineering 21. April 2017. Subotica, SERBIA COMPUTER SIMULATION OF THE ORDER FREQUENCIES AMPLITUDES EXCITATION ON RESPONSE DYNAMIC 1D MODELS
Univerzitet u Beogradu Matematiqki fakultet. Razvoj nove metode za odreiva e elemenata za kontrolu genske ekspresije kod bakterija
 Univerzitet u Beogradu Matematiqki fakultet Razvoj nove metode za odreiva e elemenata za kontrolu genske ekspresije kod bakterija - Master rad - Mentor: dr Nenad Miti Kandidat: Marko Stojievi Beograd,
Univerzitet u Beogradu Matematiqki fakultet Razvoj nove metode za odreiva e elemenata za kontrolu genske ekspresije kod bakterija - Master rad - Mentor: dr Nenad Miti Kandidat: Marko Stojievi Beograd,
4-POLITOPA. Prema Štajnicovom radu iz godine skup f vektora 3 politopa dat je sa:
 NEKE NUMERIČKE KARAKTERISTIKE 4-POLITOPA VLADIMIR TELEBAK Prirodno-matematički fakultet Univerzitet u Banjoj Luci Ul. Mladena Stojanovića 2 Banja Luka, Republika Srpska e-pošta: vladotelebak@yahoo.com
NEKE NUMERIČKE KARAKTERISTIKE 4-POLITOPA VLADIMIR TELEBAK Prirodno-matematički fakultet Univerzitet u Banjoj Luci Ul. Mladena Stojanovića 2 Banja Luka, Republika Srpska e-pošta: vladotelebak@yahoo.com
Neke primene teorije fazi skupova i fazi logike u procesiranju slika
 Univerzitet u Beogradu Matematički fakultet Neke primene teorije fazi skupova i fazi logike u procesiranju slika - Master rad - Nebojša Perić 1024/2013 Beograd, 2014. 2 Mentor: Članovi komisije: Datum
Univerzitet u Beogradu Matematički fakultet Neke primene teorije fazi skupova i fazi logike u procesiranju slika - Master rad - Nebojša Perić 1024/2013 Beograd, 2014. 2 Mentor: Članovi komisije: Datum
KVADRATNE INTERPOLACIJSKE METODE ZA JEDNODIMENZIONALNU BEZUVJETNU LOKALNU OPTIMIZACIJU 1
 MAT KOL (Banja Luka) ISSN 0354 6969 (p), ISSN 1986 5228 (o) Vol. XXII (1)(2016), 5 19 http://www.imvibl.org/dmbl/dmbl.htm KVADRATNE INTERPOLACIJSKE METODE ZA JEDNODIMENZIONALNU BEZUVJETNU LOKALNU OPTIMIZACIJU
MAT KOL (Banja Luka) ISSN 0354 6969 (p), ISSN 1986 5228 (o) Vol. XXII (1)(2016), 5 19 http://www.imvibl.org/dmbl/dmbl.htm KVADRATNE INTERPOLACIJSKE METODE ZA JEDNODIMENZIONALNU BEZUVJETNU LOKALNU OPTIMIZACIJU
Linearno uređena topologija
 Univerzitet u Novom Sadu Prirodno-matematički fakultet Departman za matematiku i informatiku Aleksandar Janjoš Linearno uređena topologija Master rad Mentor: Dr Aleksandar Pavlović 2017, Novi Sad Sadržaj
Univerzitet u Novom Sadu Prirodno-matematički fakultet Departman za matematiku i informatiku Aleksandar Janjoš Linearno uređena topologija Master rad Mentor: Dr Aleksandar Pavlović 2017, Novi Sad Sadržaj
