Nonparametric Methods for Unbalanced Multivariate Data and Many Factor Levels

Transcription

1 onprmetric Methods for Unblnced Multivrite Dt nd Mny Fctor evels Solomon W. Hrrr nd rne C. Bthke bstrct We propose different nonprmetric tests for multivrite dt nd derive their symptotic distribution for unblnced designs in which the number of fctor levels tends to infinity lrge, smll cse. Qusi grtis, some new prmetric multivrite tests suitble for the lrge symptotic cse re lso obtined. Finite smple performnces re investigted nd compred in simultion study. The nonprmetric tests re bsed on seprte rnkings for the different vribles. In the presence of outliers, the proposed nonprmetric methods hve better power thn their prmetric counterprts. ppliction of the new tests is demonstrted using dt from plnt pthology. Key words: Multivrite nlysis of Vrince, onnormlity, onprmetric Model, Ordinl Dt, Rnk sttistic, Unblnced Design. Mthemtics Subject Clssifiction 000: 6G0, 6G0, 6H0, 6H5, 6J0. ITRODUCTIO Multivrite dt occurs nturlly in severl scientific fields, s for exmple in griculture, biology, medicine, nd the socil sciences. In mny situtions, it is not resonble to ssume tht the observtions follow Gussin distribution, in prticulr when the responses re scores on n ordinl scle, nd therefore ppliction of norml theory methods is not pproprite, nd nonprmetric pproch is desirble. Recently, Munzel nd Brunner [,] see lso [3] hve proposed different tests for multivrite dt tht re completely nonprmetric nd llow for rbitrry distributions of the response vribles, including discrete distributions, nd for rbitrry dependence between the different vribles. Munzel nd Brunner s symptotic theory is imed t the sitution where the smple sizes re lrge, compred Solomon W. Hrrr is ssistnt Professor, Deprtment of Mthemticl Sciences, University of Montn, 3 Cmpus Drive, Missoul, MT 598, US; Emil: hrrr@mso.umt.edu rne C. Bthke is ssistnt Professor, Deprtment of Sttistics, University of Kentucky, 875 Ptterson Office Tower, exington, KY , US; Emil: rne@ms.uky.edu

2 to the number of smples lrge, smll. The focus of this mnuscript is the sitution which the number of smples is lrger thn the smple sizes lrge, smll. This is often the cse, for exmple, in griculturl screening trils see, e.g., [4,5], or in survey dt with lrge number of strt nd few observtions per strtum. Bthke nd Hrrr [6,7] hve proposed nd evluted different types of multivrite nonprmetric tests for blnced dt. Blnced dt fcilittes rther elegnt theory in the derivtion of tests for multivrite fctoril designs, nd for reltively simple limiting distributions of the test sttistics. However, unfortuntely, mny rel dt sets re not blnced. In the present mnuscript, we propose different nonprmetric tests for unblnced multivrite dt nd derive their symptotic distribution s, wheres is ssumed bounded. s lredy the cse in simple liner model, unblnced multivrite designs cn esily led to formidble lgebric expressions, nd to controversies bout which types of sums of squres re pproprite. Here, we investigte three different wys to define sums of squres. For ech wy, we derive the symptotic distribution of different types of sttistics, nmely Dempster-OV-Type, wley-hotelling-type, nd Brtlett-nd-Pilli-Type. In generl, none of these three types is uniformly better thn the other two. In fct, which test is preferble depends, mong other things, on the usully unknown correltion structure between the different vribles tht form the multivrite observtions. This is lso confirmed in the simultion study in the present mnuscript. In our theoreticl derivtion of the symptotic distributions, we mke use of the fct tht the three types of sttistics under considertion cn be expressed in similr wys. For ech combintion of sums of squres, we prove one generl theorem regrding the symptotic distribution of clsses of multivrite rnk sttistics, nd the results bout the individul types of tests then follow s simple corollries. Munzel nd Brunner s, s well s our pproch to define multivrite nonprmetric tests is bsed on seprte rnkings of the different vribles, s opposed to Thompson [8,9] who proposed multivrite tests bsed on overll rnkings cross the vribles. Using seprte rnkings hs some importnt dvntges. First, tests bsed on seprte rnkings re invrint under seprte monotone trnsformtions of the response vribles. Consider, for exmple, the vribles height nd weight: It should not mtter whether they re mesured in centimeters nd grms, or inches nd pounds. Seprte monotone trnsformtions of the individul vribles should not ffect the results of the tests. This cn only be chieved in seprte rnkings. Furthermore, it is commonly the cse tht the different vribles re mesured on completely different scles for which n overll rnking is not sensible. The seprte rnking pproch cn even be pplied when the different vribles re mesured on different types of scles e.g., ordinl nd quntittive. In ddition, in the cse tht mesurements of different vribles re independent, seprte rnkings preserve the independence cross the vribles, wheres n overll rnking induces dependence cross ll vribles. Erly work on multivrite nonprmetric methods includes Puri nd Sen [0,] who lso used seprte rnkings for the different vribles. They considered Wld-type sttistic, ssuming semiprmetric loction models with continuous popultion distributions. In Munzel nd Brunner [,] s well s in the present mnuscript, the model is completely nonprmetric, nd the distribution functions re llowed to be rbitrry.

3 The lrge symptotic behvior of nonprmetric multivrite tests for unblnced dt hs, to our knowledge, not been ddressed previously in the literture. In ddition, we would like to point out tht the new symptotic results in this mnuscript re pplicble not only to the rnks, but lso to the originl observtions if we ssume tht the fourth moments of the popultion distributions exist. Prmetric versions of the tests described in Sections.5 nd.6 hve not been used in the literture before. One principl dvntge of these tests is tht they could be pplied in situtions where the covrince mtrix is not constnt from group to group. Outline of the pper. In the following Section., we define the nonprmetric hypotheses under considertion this mnuscript, s well s some mtrix-vlued qudrtic forms tht we will use to test these hypotheses. Furthermore, we introduce the terms rnk trnsform nd symptotic rnk trnsform. In the subsequent sections, we derive the symptotic null distribution of severl newly proposed test sttistics tht re bsed on the mtrix-vlued qudrtic forms defined in Section.. This derivtios broken up into different prts, with some preliminry work done in Sections. nd.3. Specificlly, in Section., we prove the consistency of different covrince mtrix estimtors, wheres in Section.3, we estblish the symptotic equivlence of certin expressions defined in terms of rnk trnsforms nd the corresponding expressions in terms of symptotic rnk trnsforms. Finlly, in Sections.4-.6, we derive the symptotic s distribution of ll test sttistics under considertion, mking use of the results obtined in the previous sections. We compre the finite smple behvior of the different tests in simultion study tht is described in Section 3. Furthermore, the new results re pplied to rel dt set in Section 4. ll proofs re deferred to the ppendix. DEFIITIO D SYMPTOTIC PROPERTIES. Bsic Definitions Consider n unblnced design with independent smples of multivrite observtions. In the following, the index i =,..., denotes the group, j =,..., denotes the subjects per group, nd k =,...,p denotes the different vribles mesured on the sme subject. The observtions re modeled by independent rndom vectors X ij = X ij,...,xp ij, i =,...,, j =,...,, with possibly dependent components. The dependence structure cn be rbitrry. Denote the multivrite distributions by X ij F i, nd the mrginl distributions by X k ij mrginl distributions F k i F k i, k =,...,p. The re ssumed to be nondegenerte. Throughout the mnuscript, we use the normlized version of the cumultive distribution function, F k i x = PXk ij x + PXk ij < x [-5]. fctoril design cn be modeled within the context of this setup by imposing structure on the index i. However, this pper focuses on the one-wy lyout. The more generl symptotic results cn be trnsferred to higher-wy lyouts, but nottion nd symptotic vrince become rther involved. n exhustive tretment of higher-wy lyouts would exceed scope nd length of this mnuscript, nd it is therefore deferred to seprte tretise. 3

4 The nonprmetric hypotheses cn be stted either in terms of the multivrite distributions or in terms of the mrginl distributions. For exmple, in the nonprmetric one-wy lyout, we consider the multivrite null hypothesis H 0 : F =... = F nd the mrginl null hypothesis H 0 : F k =... = F k, k =,...,p. The multivrite hypothesis is stronger thn the mrginl hypothesis in the sense tht the first implies the ltter. Therefore, every result tht is proved under the mrginl hypothesis is lso true under the stronger multivrite hypothesis, but not vice vers, unless the mrginl distributions re independent. lso, note tht in generl the nonprmetric hypotheses formulted in terms of distribution functions imply the liner model hypotheses formulted in terms of the corresponding expected vlues. To see this, consider n rbitrry contrst defined by weights w i, i =,...,. If for the contrst in terms of distribution functions, w i F i = 0 is true, then the following holds for the sme contrst in terms of expecttions: w i µf i = w i xdf i x = xd w i F i x = 0 In the subsequent theorems, we hve strived to provide trnsprency s to which of the results re true under the weker mrginl hypothesis, nd we hve explicitly indicted when the stronger multivrite hypothesis llows for stronger results. Tht is, if result is true under the weker mrginl hypothesis H 0, then we hve stted it under H 0, in some cses followed by stronger result obtined under H 0. The test sttistics considered in this pper use seprte rnkings for the p different vribles. This is motivted by possible pplictions where ech vrible is mesured on different scle. In fct, the tests considered here cn even be used when some of the vribles re ordinl, while others re mesured on numericl scle. In such cse, it would not mke sense to rnk observtions cross ll vribles. lso, s we hve mentioned bove, only seprte rnkings llow for invrince under monotone trnsformtions of the different vribles. In ddition, in the cse where the different vribles re independent, the seprte rnking preserves this independence, while n overll rnking would introduce dependence cross the vribles. Furthermore, s n nonymous referee pointed out, both H 0 nd H 0 re invrint under the group of mrginl monotone trnsformtions G, sy. So the invrince principle suggests bsing tests on mximl invrint sttistics for G, which re the seprte componentwise rnks. Define R = R,...,R n, R,...,R n, where R ij = R ij,...,rp ij, nd R k ij mong ll = rnk of X k ij dimension p. Denote R i. = is the mid- rndom vribles X k,...,x n k. ote tht R is mtrix of R ij, R.. = R ij the weighted verge, nd R.. = R i. j= j= the unweighted verge of the rnk vectors. et I m be the m-dimensionl identity mtrix, m the m column vector consisting of ones, J m = m m the m m mtrix of ones, nd P m = I m m J m the so-clled centering mtrix. We denote by the Moore Penrose generlized inverse of. Besides its uniqueness nd existence, this inverse lso defines continuous mpping see Schott [6], Chpter 5. We hve investigted rnk-bsed versions of three different types of test sttistics tht re populr in prmetric multivrite inference, nmely wley-hotelling-type, Brtlett-nd-Pilly-Type, nd 4

5 Dempster-OV-Type. It is possible to derive coherent theory for these three types becuse they ll cn be defined similrly in terms of the following p p mtrices tht re bsed on the rnk mtrix R. H = H = G = G = = R G 3 = R i. R.. R i. R.. = R R i. R.. R i. R.. = R j= n i [ R ij R i. R ij R i. = R j= P J ni n i J R [ ] ni P n n i R i P ni R 3 R ij R i. R ij R i. ] R 4 j=r ij R i. R ij R i. = R P R 5 Ech of the different test sttistics proposed below will be bsed on one of the three pirs H, G, H, G, or H, G 3. ote tht in blnced design with n, i =,...,, the mtrices G nd G re identicl, nd furthermore, H = n H nd G 3 = n G = n G. Becuse of these reltions, in blnced design, ech of the three pirs will led to the sme test sttistic. While the first pir H, G represents strightforwrd extension of the univrite one-wy nlysis of vrince see, e.g., Scheffé [7], p.59, the multivrite test sttistics bsed on H, G hve rther complicted symptotic vrince, which led us to consider other mtrix pirs. The mtrices H, G nd G 3 cn be motivted from the MOV pproch for constructing tests. For exmple, in multivrite mixed models, it is common prctice to construct tests for fixed nd rndom effects by compring sums of squres nd cross-product mtrices under the null hypothesis. et H X, G X nd G 3 X be defined in the sme wy s H, G nd G 3, respectively, but bsed on the originl observtions mtrix X. Consider the null hypothesis H 0 : F k =... = F k, k =,...,p. et VrX ij = Ω i. Then, E H0 [H X] = E[G X] = E H0 [H X] = E[G 3 X] = Ω i. Ω i Therefore, it mkes sense to compre the mtrices in ech of the pirs H X, G X nd H X, G 3 X to construct vlid tests for H 0. For univrite designs, these sums of squres hve beenvestigted recently [8,9]. Furthermore, the OV-Type nd wley-hotelling-type test sttistics proposed in nd 5

6 [,] in the context of the lrge n symptotic setting re closely relted to those in the present mnuscript tht re bsed on the mtrix pir H, G 3. However, due to the different symptotic context, the vrince estimtors derived in [,] would not be consistent in the present mnuscript lrge symptotics. cvet in using tests bsed on ny of these pirs is tht the tests my not be invrint to ffine trnsformtions. Tht is, let RX denote the mtrix of componentwise rnks of X, nd C be p p positive definite mtrix. In generl, RCX CRX unless C is digonl mtrix. Therefore the test sttistics considered in this pper will not be ffine invrint. onprmetric ffine invrint sign nd signed rnk tests for the multi-smple loction problem hve been considered in the work of Oj nd collegues [0,,]. For comprehensive review, see lso [3]. In these mnuscripts, the popultion distributions re ssumed to belong to the clss of bsolutely continuous nd symmetric loction fmilies of distributions. For the mthemticl derivtions in the technicl proofs of this mnuscript, it is convenient to use the so-clled symptotic rnk trnsforms RT nd rnk trnsforms RT. They re formlly introduced in the following definition. The concept of RT ws proposed by krits [4]. Definition. et X ij = X ij,...,xp ij, i =,...,, j =,...,, be independent rndom vectors with possibly dependent components X k ij F k i, k =,..., p. et =. H k x = Ĥ k x = F k i x denotes the verge cdf for vrible k; 6 j= cx X k ij, where ct = 0, t < 0 /, t = 0, t > 0, denotes the verge empiricl cdf; 7 Y = Y,..., Y, where Y i = Y i,...,y ini nd Y ij = Y ij,...,y p ij, nd finlly Y k ij = H k X k ij, is the p mtrix of symptotic rnk trnsforms RT. 8 The mtrix of rnk trnsforms RT, Ŷ, is defined nlogously, with elements Ŷ k ij = Ĥk X k ij. Fur- ij is the vector of thermore, M = µ, µ,...,µ, µ i = µ i,..., µ ini where µ ij = µ ij,...,µp expecttions of the RT vector Y ij, tht is µ k ij = E Y k ij, nd Y µ = Y M, Ŷ µ = Ŷ M. The expression rnk trnsform pys tribute to the fct tht Ŷ k ij is relted to the mid-rnk R k ij of the rndom vrible X k ij mong ll observtions X k,..., X n k by Ŷ k ij = R k ij. However, the symptotic rnk trnsforms re techniclly more trctble thn the rnk trnsforms, due to the simpler covrince structure of Y s compred to Ŷ. ote tht the RT of independent rndom vribles re independent, but the RT re not. We denote the RT nlogs of the mtrices H i nd G i defined in 5 by H i nd G i, respectively. In order to prove symptotic normlity results for the rnk-bsed test sttistics considered in this pper Sections.4 to.6, we need to first estblish the symptotic equivlence of certin qudrtic forms 6

7 defined in terms of H i, G i bsed on rnk trnsforms nd the corresponding qudrtic forms defined in terms of H i, Gi bsed on symptotic rnk trnsforms. This will be done in Section.3. Before tht, we prove the consistency s tends to infinity of different vrince estimtors tht we will use lter.. Consistent Vrince Estimtion In this section, we prove tht the mtrices G i, i =,, 3, s well s liner combintion of H nd G, generte consistent estimtors of covrince mtrices of the RT. ote tht the first two theorems re proved under the stronger multivrite hypothesis, wheres for Theorem 3, the weker mrginl hypothesis is ssumed. Denote VrY i = Σ i nd ssume tht the following limits exist: lim Σ i = Σ nd lim Σ i = n Σ, i where these limits hve digonl elements σ k nd σ k, nd off-digonl elements σ kl nd σ kl, respectively. Theorem. Under the multivrite null hypothesis H 0 : F =... = F, s, bounded, p G Σ. Theorem. Under the null hypothesis nd the ssumptions of Theorem, H + G p Σ. Theorem 3. Under the mrginl null hypothesis H 0 : F k =... = F k, k =,...,p, s, bounded, where p G Σ Σ = lim p nd G 3 Σ, Σ i, Σ = lim ssuming tht the limits exist. Σ i, nd Σ i = VrY i,.3 symptotic Equivlence In the following theorems, we prepre the derivtions of symptotic distributions tht will follow in the subsequent sections by first estblishing symptotic equivlence results of certin expressions defined in terms of rnk trnsforms nd the corresponding expressions in terms of symptotic rnk trnsforms. Our finl gol is to derive symptotic results for rnk-bsed test sttistics. However, it is techniclly esier to derive those results for the symptotic rnk trnsforms tht hve much simpler covrince structure. The theorems in this section justify this pproch by providing the connection between rnk trnsforms nd symptotic rnk trnsforms. 7

8 Theorem 4. Under the multivrite null hypothesis H 0 : F =... = F, s, bounded, H G H G p 0. Theorem 5. Under the mrginl null hypothesis H 0 : F k =... = F k, k =,...,p, s, bounded, H G H G p 0. Theorem 6. Under the mrginl null hypothesis H 0 : F k =... = F k, k =,...,p, s, bounded, H G 3 H G p 3 0. In Theorems 4 6, we hve shown tht in order to obtin the symptotic distributions of H G, H G, nd H G 3, it is sufficient to derive the symptotic distribution of the corresponding expression H i G j. This is ccomplished in the following theorems. More specificlly, the next theorems provide the symptotic distribution of the trces of the rndom mtrices H G, H G, nd H G 3, where is fixed non negtive definite mtrix. Different choices of will result in the different multivrite tests under considertion wley- Hotelling, Brtlett-nd-Pilli, Dempster OV-Type..4 symptotic Distribution of Tests Bsed on H nd G In this nd the following sections, we derive concrete tests tht re bsed on the three pirs of p p- mtrices H, G, H, G, nd H, G 3. In ech cse, the symptotic distributios first derived in generl theorems covering clss of tests, nd then the results for individul multivrite tests follow in corollries. Theorem 7. et be n rbitrry fixed non negtive definite mtrix, nd ssume tht, s, bounded, lim = n nd lim = n. Then, under the multivrite null hypothesis H 0 : F =... = F, s, bounded, trh G 0, τ where τ = n n trσ n nn + µ4 trσ n trσ Σ = VrY nd µ 4 = E[Y µ Y µ ]. 8

9 In order to be ble to pply the symptotic result from Theorem 7, we need to be ble to consistently estimte the vrince τ. This is ccomplished in the following Theorem 8. Theorem 8. et the null hypothesis nd the ssumptions be s in Theorem 7, nd let τ be defined s in Theorem 7. et ˆτ = n n trg n nn + ˆµ4 trg n trg, where ˆµ 4 = j= [ Rij + Then, 4 ˆτ p τ s, bounded. R ij + ], nd G is defined in 3. The symptotic distributions of the different multivrite nonprmetric tests cn now be obtined s corollries of the previous theorems by pproprite choices of the fixed non negtive definite mtrix. In prticulr, the Dempster OV-Type sttistic corresponds to = trσ I p, while wley- Hotelling s trce nd the Brtlett-nd-Pilli criterion correspond to = Σ. Corollry. et the null hypothesis nd the ssumptions be s in Theorem 7. Denote the Dempster OV-Type sttistic by T D = tr H /tr G. Then, TD 0, τ n n nn where τ = trσ n trσ + µ4 trσ n trσ, Σ = vry, nd µ 4 = E[Y µ Y µ ]. Furthermore, the estimtor n ˆτ = trg where ˆµ 4 = n nn n trg + j= ˆµ4 trg n trg [ Rij + is consistent for τ in the sense tht ˆτ p τ s, bounded. R ij + ], nd G is defined in 3, Corollry. et the null hypothesis nd the ssumptions be s in Theorem 7. et r be the rnk of G. Denote the wley-hotelling-type sttistic by T H = tr H G. Then, T H r 0, τ, where τ = nρ n nn + n n µ 4 ρ ρ, ρ = rnkσ, Σ = vry, nd µ 4 = E[Y µ Σ Y µ ]., 9

10 Furthermore, s, bounded, the following estimtor ˆτ is consistent for τ. ˆτ = nr n nn + n n ˆµ 4 r r, where ˆµ 4 = j= [ Rij + G R ij + ], nd G is defined in 3. Corollry 3. et the null hypothesis nd the ssumptions be s in Theorem 7. et r be the rnk of H + G. Denote the Brtlett-nd-Pilli-Type sttistic by T BP = tr H H + G. Then, T BP r 0, τ, where τ = nρ n nn + n n µ 4 ρ ρ, ρ = rnkσ, Σ = vry, nd µ 4 = E[Y µ Σ Y µ ]. otice tht the expression for τ in Corollry 3 is the sme s in Corollry. Hence, the estimtor ˆτ defined in Corollry works for the Brtlett-nd-Pilli-Type sttistic, s well..5 symptotic Distribution of Tests Bsed on H nd G In this section we prove symptotic normlity results for Dempster s OV-Type nd the wley-hotelling sttistics. It is not cler how to get weighted mixture of H nd G to obtin consistent nd symptoticlly unbised estimtor of E H0 H. Therefore, there is no strightforwrd wy to define Brtlett-nd-Pilli type sttistic bsed on H nd G. Theorem 9. ssume tht the following limit exists. lim trσ i = τ. Then, under the mrginl null hypothesis H 0 : F k = F k =... = F k for ll k =,...,p, s, fixed nd ny p p 0 fixed, trh G 0, τ. Corollry 4. ssume tht the following limit exists. trσ lim trσ i = τ, 0

11 where Σ is s defined in Theorem 3. Denote the Dempster OV-Type sttistic bsed on H nd G by T D = tr H /tr G. Then, under the mrginl null hypothesis s stted in Theorem 9, T D 0, τ. Under the multivrite null hypothesis, s stted in Theorem 7, τ simplifies to τ = tr Σ tr Σ lim, which cn be consistently estimted by ˆτ = tr G tr G. Corollry 5. ssume tht the following limit exists. lim trσ i Σ = τ, where Σ is s defined in Theorem 3. et r be the rnk of G. Denote the wley-hotelling-type sttistic bsed on H nd G by T H = tr H G. Then, under the mrginl null hypothesis s stted in Theorem 9, T H r 0, τ. Under the multivrite null hypothesis, s stted in Theorem 7, τ simplifies to τ = rnkσ lim, which cn be consistently estimted by ˆτ = rnkg. It is cler from Theorem 5 tht the symptotic vrince of the test sttistics depends on the vrinces nd covrinces of the RT. Since the columns of the RT mtrix re independent, the results derived bsed on the RT mtrix cn be pplied directly to obtin the null distribution of the sme test sttistics bsed on the originl observtions, whose columns re lso independent. However, the entries of the RT mtrix re uniformly bounded, wheres it will be necessry to ssume existence of fourth moments for the prent popultions when bsing the test sttistics on the originl observtions. Unlike the tests bsed on H nd G, the symptotic null distributions presented in Corollries 4 nd 5 do not depend on the fourth order moments of the symptotic trnsforms. Hence, when the sttistics bsed on these corollries re pplied to the originl observtions, the sizes of the test will be symptoticlly invrint with regrd to the distribution of the popultions from which the smples re coming.

12 .6 symptotic Distribution of Tests Bsed on H nd G 3 Here, we clculte the symptotic distributions of Dempster s OV-Type nd the wley- Hotelling sttistics, bsed on H nd G 3. s in the previous section, there is gin no strightforwrd wy to define Brtlett-nd-Pilli type sttistic bsed on H nd G 3. Theorem 0. ssume tht the following limit exists. lim trσ i = τ 3. Then, under the mrginl null hypothesis H 0 : F k = F k =... = F k for ll k =,...,p, s, fixed nd ny p p 0 fixed, trh G 3 0, τ 3. Corollry 6. ssume tht the following limit exists. tr Σ lim trσ i = τ 3 where Σ is s defined in Theorem 3. Denote the Dempster OV-Type sttistic bsed on H nd G 3 by T 3 D = tr H /tr G 3. Then, under the mrginl null hypothesis s stted in Theorem 0, T 3 D 0, τ 3. Under the multivrite null hypothesis, s stted in Theorem 7, τ 3 simplifies to τ 3 = tr tr Σ Σ lim, which cn be consistently estimted by ˆτ 3 = tr G tr G 3. Corollry 7. ssume tht the following limit exists. lim trσ i Σ = τ 3 where Σ is s defined in Theorem 3. et r 3 be the rnk of G 3. Denote the wley-hotelling-type sttistic bsed on H nd G 3 by T 3 H = tr H G 3. Then, under the mrginl null hypothesis s stted in Theorem 0, T 3 H r3 0, τ 3.

13 Under the multivrite null hypothesis, s stted in Theorem 7, τ 3 simplifies to τ 3 = tr Σ Σ lim, which cn be consistently estimted by ˆτ 3 = tr G G 3. The symptotic distributions of tests bsed on H nd G 3 lso do not depend on the fourth order moments of the symptotic trnsforms. Therefore, s in the previous section, the corresponding procedures pplied to the originl observtions will be symptoticlly invrint with regrd to the popultion distributions. 3 SIMUTIO STUDY We investigted the finite smple performnce of the proposed nonprmetric procedures s well s its prmetric counterprts through computer simultions using SS IM SS 9.. Power functions were plotted with R [5]. For the simultions, we ssumed one-wy lyout, nd we considered the following nonprmetric rnk-bsed multivrite tests. Dempster OV type nd wley-hotelling type sttistic bsed on H, G, H, G, nd H, G 3, nd Brtlett-nd-Pilli type sttistic bsed on H, G. s prmetric competitors, we used the corresponding sttistics bsed on the originl observtions. ote tht the prmetric tests bsed on H, G nd H, G 3 re newly introduced in this mnuscript. The number of simultions ws lwys 0,000. Smple sizes per group were chosen the following wys. Hlf of the smples were of size = 4, the other hlf hd = 6. Hlf of the smples were of size = 4, the other hlf hd = 8. 3 Ten percent of the smples were of size = 4, the remining 90 percent were of size = 6 or 4 = 8. We only report the results from setting in the tbles below, becuse the other simultions hd very similr outcomes. First, we simulted the ctul α-level of ll seven test sttistics in one-wy lyout under the null hypothesis tht the multivrite distributions re the sme for ech fctor level. We set the number of fctor levels to = 0, 0, 50, 00, nd 00, while the number of replictions per fctor level followed one of the ptterns described bove, nd the number of vribles ws p = Tble nd p = 4 Tble. We hve used different underlying popultion distributions, nmely multivrite norml with positive, negtive, nd zero correltion between the vribles, s well s with nd without contmintion through 0% outliers coming from 0, distribution, nd multivrite distributions bsed on Student s t with different degrees of freedom nd different correltion. The results for some selected configurtions re summrized in Tbles nd below. 3

14 ext, we hve investigted the power of the proposed tests under loction lterntives. We re conducting the power comprison bsed on firly smll vlue of. We selected those four tests whose simulted α-levels were in generl closest to the nominl 5%. These re the Dempster OV type sttistic bsed on H, G nd H, G 3, s well s wley-hotelling nd Brtlett-nd-Pilli type sttistics bsed on H, G. However, for lrge, the other tests will rgubly hve comprble powers. For hlf of the fctor levels, the mes shifted by x where x [0, ] for ech vrible. In generl, lterntives for power simultions cn be chosen mny wys. One of the intentions of the simultion study is to compre the nonprmetric tests to ech other nd lso to their prmetric competitors. The prmetric tests re nturlly defined in the frmework of loction model. Therefore, we hve lso chosen loction model for this simultion. For the power simultions, we hve set the number of vribles to p =. The number of fctor levels is = 0, nd the number of replictions per fctor level is s described in setting bove. Plots of different simulted power functions re given Figures nd. The α-level simultions in Tbles nd suggest tht the wley-hotelling type sttistics bsed on H, G nd H, G 3 should not be recommended unless is very lrge since they re by fr exceeding the nominl α. ll tests re slightly liberl for smll to moderte. Most of the tests bsed on H, G re within two percentge points from the nominl α of 5% when the number of levels is = 0 or lrger, nd within one percentge point when = 50. The best convergence results re chieved by the Brtlett-nd-Pilli sttistic. In generl, contmintion or correltion do not seem to ffect the simulted α-levels. For p = 4, convergence to the nominl α is usully fster thn for p =. s expected, nonprmetric nd prmetric tests perform very similrly under null hypothesis. Under simulted loction lterntive, they lso perform similrly when the norml model ssumptions re met. Figure intends to demonstrte the drmtic power differences between prmetric nd nonprmetric tests when the dt contins bout 0% outliers or is from more hevy-tiled distribution such s Student s t with df = 3. From this figure, it cn lso be seen tht in generl the tests tht exceed the nominl α-level by the frthest re lso the ones tht keep the highest power in generl. Tht is, higher power is in generl chieved through higher type I error rte. Generlly, the nonprmetric tests bsed on H, G re recommended when the simulted type of lterntive is suspected. The Dempster OV type sttistic bsed on H, G 3 hs only slightly lower power thn the one bsed on H, G, but it hs the prcticl dvntge tht it cn esily be clculted using SS stndrd procedures see the dt exmple below. In cse of positive correltion between the vribles, the Dempster OV type sttistic hs higher power thn the other two types, wheres for negtively correlted vribles, the wley-hotelling nd Brtlett-nd-Pilli sttistics chieve higher simulted power. This is shown Figure. In Figure, the vribles re not correlted, nd the Dempster OV type sttistic fres best mong those tests tht lso keep the nominl level well. 4

15 umber of Vribles p = Underlying Distribution Test Sttistic = 0 = 0 = 50 = 00 = 00 OV type H,G multivrite norml OV type H,G with correltion=0 OV type H,G H type H,G H type H,G H type H,G BP type H,G OV type H,G multivrite norml OV type H,G with correltion = 0.5 OV type H,G nd 0% outliers H type H,G H type H,G H type H,G BP type H,G OV type H,G multivrite norml OV type H,G with correltion = -0.5 OV type H,G nd 0% outliers H type H,G H type H,G H type H,G BP type H,G Tble : Simulted α-levels [in percent] for the proposed nonprmetric multivrite tests in prentheses: their respective prmetric counterprts of the Dempster-OV, wley-hotelling, nd Brtlett-nd-Pilli type. ominl α is 5%. umber of simultions is 0,000 stndrd error umber of vribles is p =. Vrying numbers of fctor levels between = 0 nd = 00. In ech cse, hlf of the smples re of size = 4, the other hlf is of size = 6. 5

16 umber of Vribles p = 4 Underlying Distribution Test Sttistic = 0 = 0 = 50 = 00 = 00 OV type H,G multivrite norml OV type H,G with correltion=0 OV type H,G H type H,G H type H,G H type H,G BP type H,G OV type H,G multivrite norml OV type H,G with correltion = 0.5 OV type H,G nd 0% outliers H type H,G H type H,G H type H,G BP type H,G OV type H,G multivrite norml OV type H,G with correltion = -0.3 OV type H,G H type H,G H type H,G H type H,G BP type H,G Tble : Simulted α-levels [in percent] for the proposed nonprmetric multivrite tests in prentheses: their respective prmetric counterprts. ominl α is 5%. umber of simultions is 0,000 stndrd error umber of vribles is p = 4. Vrying numbers of fctor levels between = 0 nd = 00. In ech cse, hlf of the smples re of size = 4, the other hlf is of size = 6. 6

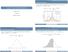
17 Underlying Multivrite orml Distribution Correltion=0 with 0% Outliers Simulted Power Functions, onprmetric versus Prmetric Multivrite Tests Simulted Power Functions, onprmetric versus Prmetric Multivrite Tests Underlying Multivrite Distribution bsed on t3 Correltion= B B nonprmetric rnk bsed bsed on originl observtions B B B B B B B B B B B B B B B B B B B nonprmetric rnk bsed bsed on originl observtions B B B B B B B B B Figure : Simulted power of proposed nonprmetric on top nd corresponding prmetric versions of four of the multivrite tests under investigtion. = 0 levels, p = vribles. Hlf of the smples re of size = 4, the other hlf is of size = 6. Underlying distributios bivrite norml with correltion=0, nd 0% outliers left or bivrite Student s t with df = 3, correltion=0, nd no outliers right. The letters,, nd B denote OV-Type, wley-hotelling, nd Brtlett-nd-Pilli, respectively, ll bsed on H,G. 7

18 Simulted Power Functions, onprmetric Multivrite Tests Underlying Multivrite orml Distribution Correltion=0.5 with 0% Outliers Simulted Power Functions, onprmetric Multivrite Tests Underlying Multivrite orml Distribution Correltion= 0.5 with 0% Outliers D H,G D H,G3 H H,G BP H,G D H,G D H,G3 H H,G BP H,G Simulted Power Functions, onprmetric Multivrite Tests Underlying Multivrite Distribution bsed on t3 positive correltion Simulted Power Functions, onprmetric Multivrite Tests Underlying Multivrite Distribution bsed on t3 negtive correltion D H,G D H,G3 H H,G BP H,G D H,G D H,G3 H H,G BP H,G Figure : Simulted power of three nonprmetric versions of the multivrite tests under investigtion. = 0 levels, p = vribles. Hlf of the smples re of size = 4, the other hlf is of size = 6. First row: Underlying distributios bivrite norml with positive correltion 0.5, left nd negtive correltion -0.5, right, nd 0% outliers. Second row: Underlying bivrite distributios bsed on Student s t with df = 3, positive left nd negtive correltion right, nd no outliers. 8

19 4 PPICTIO We pplied the methods derived in the present mnuscript to plnt pthology dt set. Chtfield et l. [4] evluted = 63 vrieties of crbpples for disese resistnce ginst pple scb t p = 4 times during the growing seson, with = 3 to 5 replictes of ech vriety. pple scb is mjor fungl disese problem tht cn severely ffect mrketbility of crbpples. The best method for control is through the use of resistnt crbpple selections [4]. One of the gols in the described tril is to find out whether the 63 vrieties differ significntly with regrd to their disese resistnce. The response vrible is ordinl, ech crbpple tree ws rted on scle from zero to five. Therefore, prmetric norml theory techniques re not pproprite for the nlysis of this type of dt, nd nonprmetric methods should be used. We tested the multivrite null hypothesis tht there is no difference in disese resistnce between the 63 vrieties. ccording to the simultion results reported in the lst section, the nonprmetric version of the Dempster OV type test is recommended for this type of dt since we would expect positive correltion between the mesurements t different time points. This ws confirmed by simultion of α-level nd power for desigmitting the crbpple experiment s closely s possible simulting high correltion of 0.9 between the vribles, nd discretizing the response to six-point ordinl scle. However, it ctully turns out tht for this dt set, ech of the prmetric nd nonprmetric versions of the multivrite tests under considertion led to the sme conclusion of high significnce p < Tht is, the different vrieties of crbpples show significntly different disese resistnce. s result, it is indeed possible to reduce the impct of pple scb through the choice of more resistnt vrieties. We hve performed the nlysis using code written SS IM tht we cn emil on request. It is possible to roughly pproximte some of the test sttistics derived in this mnuscript using SS stndrd procedures, though. For exmple, the terms T H in Corollry s well s T BP in Corollry 3 cn be obtined using the mnov option Proc Glm, fter individully rnking ech of the vribles. fter Proc Rnk outputs the rnks of the four scores into the vribles r r4, the pproprite SS code for this dt set is then: proc glm dt=; clss vriety; model r-r4=vriety; mnov h=vriety; run; The terms T H nd T BP pper in the SS output s Hotelling-wley Trce nd Pilli s Trce, respectively. s Dr. rry Mdden pointed out to us, the term T 3 D in Corollry 6 cn lso be reproduced, using Proc Mixed long with the novf option on the rnked dt. To this end, the seprte rnks of ll four vribles hve to be stcked into one new rnk vrible here clled rr, nd two more vribles representing time nd individul subject hve to be creted. Then, the effect of vriety is tested s simple fctor effect of vriety time, using the following code: proc mixed dt= novf method=mivque0; clss time vriety subject; model rr = time time*vriety / chisq noint; repeted / group=vriety sub=subject type=un; run; 9

20 However, clcultion of the stndrdized test sttistics tht cn be compred to quntiles from stndrd norml distribution still involves some progrmming. When the desigs not too fr from being blnced, rough pproximtios possible by substituting the symptotic vrince τ in Corollries nd 3 by nr / n. Some Useful Results In this section, we restte some results from Bthke nd Hrrr [6] wherein the proof cn be found. These results re used in the present mnuscript. They fcilitte determining symptotic equivlence of rnk trnsforms nd symptotic rnk trnsforms, s well s clculting the vrince of the limiting distribution.. Theorem.. et X = X,...,X be mtrix tht consists of independent rndom vectors,...,x p i with multivrite distribution X i F i, i =,...,. et Y nd Ŷ be the X i = X i corresponding mtrices of sme dimension whose components re the symptotic rnk trnsforms nd rnk trnsforms defined in Section. et C = c ik i ; k be symmetric mtrix, nd let Σ C = S C = c ik, k= k= k = c ik c ik + ii c kk + c i k c ik. Furthermore, let T = Ŷ µ CŶ µ nd V = Y µ CY µ be two p p-mtrices of qudrtic forms generted by the mtrix C. Then, T V = O P Σ C / + O P S C /. Corollry.. Suppose C is such tht ll its entries re nonnegtive. Then, Σ C = C. If in ddition ll the digonl entries of C re equl, then S C = C + trc + trc. emm.. Suppose Y = Y,...,Y n is p n rndom mtrix whose columns Y i, i =,...,n, re independently distributed with men 0 nd covrince Σ i. et = ij nd B = b ij be n n symmetric mtrices. Then, Cov vecyy, vecyby n n = ij b ij I p + K p,p Σ i Σ j + j= n ii b ii K 4 Y i 0

21 where K 4 Y i = E vecy i Y ivecy i Y i I p + K p,p Σ i Σ i vecσ i vecσ i. B Proofs Proof of Theorem ote tht under the null hypothesis, Σ i Σ, i =,...,. Define C = P ni. Then, G = ŶCŶ. Theorem. nd Corollry. in ppendix yield ŶCŶ YCY = O p Σ C / +O p S C / where Σ C = C nd S C = C + tr C +tr C. Here, C = J ni + I ni is the mtrix whose elements re the bsolute vlues of the elements of C. It immeditely follows tht Σ C = nd S C = O. Therefore, ŶCŶ YCY = O p 0 p s. ow, consider n rbitrry digonl element of YCY, σ k = Y k ij j= Ȳ k i. = n i σ k:i where E σ k:i = σ k nd Vr σ k:i < M since Yk ij is bounded rndom vrible. Thus, it follows tht σ k converges lmost surely to σ k. In the sme mnner, the off-digonl elements σ kl converge lmost surely to σ kl, which finishes the proof. Proof of Theorem otice tht under the null hypothesis µ ij = µ. Then, observe tht H + G = Ŷ ij µŷ ij µ ˆȲ.. µˆȳ.. µ j= = Ŷ µ I Ŷ µ Ŷ µ J Ŷ µ. = Ŷ µ C Ŷ µ Ŷ µ C Ŷ µ where C = I nd C = It cn be verified tht Σ C = Σ C = = O, S C = J. = O, nd S C = = O + = O s. Therefore, by Theorem., Ŷ µ C Ŷ µ Y µ C Y µ = o p nd Ŷ µ C Ŷ µ Y µ C Y µ = o p. Moreover, 9 implies tht Y µ C Y µ = o p. Thus, H + G Y µ C Y µ = o p.

22 ow, Y µ C Y µ = by the S. Y ij µy ij µ p EY µy µ = Σ j= Proof of Theorem 3 Define C = We prove the result for G. The proof for G 3 follows long the sme lines. P. Then, G = ŶCŶ. Using the techniques pplied in the p proof of Theorem, we obtin ŶCŶ YCY 0 s. Furthermore, the digonl elements of YCY re of the form σ k = σ k:i where σ k:i = Y k ij Ȳ k i., nd under the j= mrginl hypothesis, E σ k:i = σ k nd Vr σ k:i < M. Therefore, for bounded, σ k = σ k:i + o p σ p k. However, note tht for the off-digonl elements σ kl = σ kl:i, under the mrginl hypothesis, the expecttion E σ kl:i = σ kl:i still depends o, therefore σ kl = σ kl:i + o p p lim σ kl:i = σ kl. Proof of Theorem 4 H G = ˆȲ i. ˆȲ.. ˆȲ i. ˆȲ.. ˆȲ ij ˆȲ i. ˆȲ ij ˆȲ i. j= j= [ = Ŷ µ J ni ] J P Ŷ µ = ŶµC + C + C 3 Ŷ µ where C = n i C = J J ni, nd C 3 = J ni I ni, I ni. For C nd C, we cn pply Theorem. nd Corollry. stted in the ppendix to show tht Ŷµ C i Ŷ µ Y µc i Y µ 0 p s, i =,. In order to prove tht ŶµC 3 Ŷ µ Y µ C 3 Y µ p element w i j= Ŷ k ij Y k ij where w i = 0 s, consider first n rbitrry digonl. We simplify nottion by collpsing the two indices i, j into one index i =,..., nd by defining φx k i, X k j, X k l = cx k i X k j cx k i X k l H k X k i,

23 s well s ψx k i, X k j nd we obtin, X k = φx k, X k, X k E[φX k, X k, X k l w i Ŷ i Y i = i = j w i i,j,l l j= k= w i ψx k i i φx k i j, X k, X k j l l X k j, X k j, X k l + o p. ] E[φX k, X k, X k i j l X k Here, denotes the set of index triples i, j, l consisting of three distinct numbers. The summtion over the set of index triples where t lest two of the three indices re equl is term of order o p becuse w i = O/ nd the expression prentheses is bounded. lso, note tht w i = 0, so tht the sum equls zero for every v =,...,. There- of the conditionl expecttions is equl to zero, s well. The conditionl expecttion E ψx k i, X k j, X k l v fore, E w i Ŷ i Yi = 4 i,j,l i,j,l X k l ], w i w i E ψx k i, X k j, X k l ψx k i, X k j, X k l + o p = o p, becuse if the number of different indices mong i, j, l, i, j, l is either six or five, the expecttion will be equl to zero, nd thus the first term only contributes o p s. In similr wy, it cn be shown for n rbitrry off-digonl element k, k tht j= k w i Ŷ ij Ŷ l ij Y k ij Y l p ij 0. To this end, choose φx k i, X k j, X k i, X k l = cx k i X k j cx k i X k H k X k i H k X k i l, s well s ψx k i, X k j, X k i, X k = φx k i, X k j, X k i, X k E[φX k i, X k j, X k i, X k X k j ] l l E[φX k i, X k j, X k i, X k l X k l ]. l 3

24 Proof of Theorem 5 H G = = Ŷ µ [ ni ] ˆȲ i. ˆȲ.. ˆȲ i. ˆȲ.. n i ˆȲ ij ˆȲ i. ˆȲ ij ˆȲ i. n j= i j= [ J ni J n ] i P Ŷ µ = Ŷ µ C + C Ŷ µ where C = n i n i J I ni nd C = J J ni. pplying Theorem. nd Corollry., it follows tht ŶµC i Ŷ µ Y µ C i Y µ p 0 s, i =,. Proof of Theorem 6 H G 3 = Ŷ µ [ ni P n i = Ŷ µ C + C Ŷ µ where C = n i J I ni nd C = ni J I n i ] P Ŷ µ ppliction of Theorem. nd Corollry. yields tht Ŷ µ C i Ŷ µ Y µc i Y µ p 0 s, i =,.. Proof of Theorem 7 By Theorem 4, it suffices to find the symptotic distribution of H G. ow, H = Ȳ i. Ȳ.. Ȳ i. Ȳ.. Ȳ i. Ȳ.. Ȳ i. Ȳ.. = Ȳ i. µȳ i. µ Ȳ.. µȳ.. µ. 4

25 Similrly, G = Then, = Y ij Y i. Y ij Y i. j= [Y ij µ Ȳi. µ][y ij µ Ȳi. µ]. j= H G Ȳ i. µȳ i. µ Denote n [Y ij µ Ȳi. µ][y ij µ Ȳi. µ] j= Ȳ.. µȳ.. µ = Y i µ J ni Y i µ n i Q = Y µ J Y µ. n Y i µ P ni Y i µ Y µ J Y µ = Y i µ It cn esily be shown tht Y µ J Y µ J ni n P Y i µ EQ = / Σ = o. 9 Moreover, by using emm., we get vrq = I p + K p,pσ Σ + K 4 Y where K 4 Y = E[vecY Y vecy Y ] I p + K p,p Σ Σ vecσ vecσ. 0 5

26 Therefore vrq = o. This together with 9 implies Q p 0. Consequently, tr H G where Z i = tr = tr Y i µ J ni Z i Y i µ J ni n P Y i µ. It my be noted tht, EZ i = nd vrz i = where W i = Y i µ n i trσ = 0 n n P Y i µ vec vrw i vec J ni n P Y i µ. But, pplying emm., vrw i = + n i I n p + K p,p Σ Σ + n K 4 Y n where K 4 Y is s defined in 0. Substituting in nd mking some simplifictions, vrz i = + trσ + n n n µ4 trσ n n trσ 3 where n = / /. From 3 it follows tht lim / vrz i = τ. Finlly, since vrz i = nd Z i is bounded rndom vrible, the indeberg condition holds. Proof of Theorem 8 et = ij nd 0 = mx i,j ij. The consistency of G for Σ is proved in Theorem bove. Thus, we need to prove tht ˆµ 4 4 µ p 4. ote tht ˆµ 4 4 = [Ŷ ij Ŷij ]. For the corresponding expression defined in terms of the RT, we hve [Y ij µ ij Y ij µ ij ].s. E[Y µ Y µ ], j= 6 j=

27 due to the strong lw of lrge numbers. Therefore, the proof will be finished by showing tht [ Ŷ ij,µŷ ij,µ Y ij,µy ij,µ ] p 0, j= where Ŷ ij,µ = Ŷ ij nd Y ij,µ = Y ij µ ij. Indeed, ] E [Ŷ ij,µ Ŷ ij,µ Y ij,µ Y ij,µ E Ŷ ij,µ Ŷ ij,µ Y ij,µ Y ij,µ j= j= = E Ŷ ij,µ Ŷ ij,µ Y ij,µ Y ij,µ Ŷ ij,µ Ŷ ij,µ + Y ij,µ Y ij,µ = j= 4p4 0 4p4 0 = 4p p j= p E Ŷ ij,µ Ŷ ij,µ Y ij,µ Y ij,µ E Ŷ ij,µ Ŷ ij,µ Y ij,µ Y ij,µ j= p 4 0 j= p p k= j= k= l= [ p p l= k= p l= EŶ k ij,µŷ l ij,µ Y k ij,µ Y l ij,µ p k l E Ŷ ij,µ Ŷ ij,µ Y l ij,µ + Y l p j= k= l= EŶ k ij,µ Ŷ l ij,µ Y l ij,µ + k ij,µ Ŷ kl Ŷ ij,µŷ k l ij,µ + Y k ij,µ Y l ij,µ ij,µ Y k ij,µ p p j= k= l= EY l ij,µ Ŷ k ij,µ Y k ij,µ ] Proof of Corollry TD = / trh G / trg trh G. trσ Choosing = /trσ I p in Theorem 7, we get the first result. The consistency of G for Σ is proved in Theorem. The rest follows by choosing = I p in Theorem 8. Proof of Corollry T H r = trh G tr G G = tr H G G 7

28 trh G Σ The lst line follows from the fct tht / G p Σ Theorem nd the continuity of the Moore- Penrose inverse. ow, setting = Σ nd pplying Theorem 7, we get the first result. Regrding the consistency, note tht, p r = tr G G trσ Σ = ρ. Then, the result follows by choosing = Σ in Theorem 8 nd observing, [ j= Ŷ ij ] G Ŷij j= [ Y ij Σ Y ] ij = op becuse / G = Σ + o p s. Proof of Corollry 3 T BP r = tr H + G From Theorem nd continuity of the Moore-Penrose inverse we get, T BP H + G. p H + G Σ. 4 Simplifying nd using 4 yield T BP r tr H G Σ. Proof of Theorem 9 G. By Theorem 5, it suffices to derive the symptotic distribution of tr H H G = Y µ C Y µ Y µ C Y µ where C nd C re s defined in the proof of Theorem 5. Denote Q = Y µ C Y µ. 8

29 ow, EQ = k= j= l= n j c :ij:kl E Y ik µy jl µ where c :ij:kl is the k, lth entry of the i, jth block of C. otice tht c :ii:kl = 0 for i =,...,. lso tht E Y ik µy jl µ = 0 for i j. Therefore EQ = 0. pplying emm. nd noting tht c :ii:kl = 0 for i =,...,, we see tht vrq = j= k= l= c :ij:kl I p + K p,pσ i Σ j = I p + K p,p n j Σ i Σ j i j = I p + K p,p Σ i n j Σ j = O. i j The lst line follows becuse the entries of Y ij re uniformly bounded which implies tht Σ i n j Σ j = O. i j Therefore Q p 0. et us next find the distribution of try µ C Y µ = try µ C Y µ. try µ C Y µ = Z i where Z i = try i µ n i J I ni Y i µ. Since the digonl entries of J ni I ni re zeros nd Y ij s re independent, it follows tht EZ i = 0. Moreover, vrz i = vec vrw i vec where W i = Y i µ n i J I ni Y i µ. pplying emm., we get vrw i = n i n i Ip + K p,p Σ i Σ i. 9 Z i

30 Thus, lim vrz i = lim = lim = τ. n i n i vec I p + K p,p Σ i Σ i vec n i n i trσi Since the Z i re bounded rndom vribles, the theorem is proved. Proof of Corollry 4 T D = / trh G / trg trh G trσ. Choosing = /trσi p in Theorem 9, we get the desired first result. Simplifiction nd consistency under the multivrite hypothesis re strightforwrd. Proof of Corollry 5 T H r = trh G tr G G = tr H G G trh G Σ ow, setting = Σ nd pplying Theorem 9, we get the desired result. Proof of Theorem 0 Here lso it suffices to obtin the symptotic distribution of trh G 3. H G 3 = Y µ C Y µ + Y µ C Y µ where C nd C re s defined in the proof of Theorem 6. etting Q = Y µ C Y µ we cn show s in Theorems 4 nd 5 tht Q p 0. Hence, tr H G 3 Y µ C Y µ = tr Y i µ J I ni Y i µ = where Z i = tr Y i µ J I ni Y i µ. Z i Moreover, EZ i = 0 nd lim / vrz i = τ 3. 30

31 Proof of Corollry 6 3 T D = / trh G 3 / trg 3 trh G 3 tr Σ. Choosing = /tr ΣI p in Theorem 0, we get the desired result. Proof of Corollry 7 T 3 H r3 = trh G 3 tr G 3 G 3 = tr H G 3 G 3 trh G 3 Σ ow, setting = Σ nd pplying Theorem 0, we get the desired result. REFERECES [] U. Munzel, E. Brunner, onprmetric Methods in Multivrite Fctoril Designs, Journl of Sttisticl Plnning nd Inference 88, [] U. Munzel, E. Brunner, onprmetric Tests in the Unblnced Multivrite One-Wy Design, Biometricl Journl 4, [3] E. Brunner, U. Munzel, M.. Puri, Rnk-Score Tests in Fctoril Designs with Repeted Mesures, Journl of Multivrite nlysis 70, [4] J.. Chtfield, E.. Drper, K.D. Cochrn, D.. Herms, Evlution of Crbpples for pple Scb t the Secrest rboretum in Wooster, Ohio, The Ohio Stte University, Ohio griculturl Reserch nd Development Center Specil Circulr Ornmentl Plnts: nnul Reports nd Reserch Reviews. [5] M.. Omer, D.. Johnson, R.C. Rowe, Recovery of Verticillium dhlie from orth mericn Certified Seed Pottoes nd Chrcteriztion of Strins by Vegettive Comptibility nd ggressiveness, mericn Journl of Potto Reserch [6].C. Bthke, S.W. Hrrr, onprmetric Methods in Multivrite Fctoril Designs for rge umber of Fctor evels, Submitted 006. [7] S.W. Hrrr,.C. Bthke, onprmetric Version of the Brtlett-nd-Pilli Multivrite Test. symptotics, pproximtions, nd pplictions, Submitted 006. [8] G.. Thompson, symptotic Distribution of Rnk Sttistics under Dependencies with Multivrite ppliction, Journl of Multivrite nlysis [9] G.. Thompson, Unified pproch to Rnk Tests for Multivrite nd Repeted Mesures Designs, Journl of the mericn Sttisticl ssocition [0] M.. Puri, P.K. Sen, On Clss of Multivrite Multismple Rnk-Order Tests, Snkhy