Estimation of Generalized / ' / \ Negative Binomial Distribution
|
|
|
- Amelia Cook
- 5 years ago
- Views:
Transcription
1 C H A P T E R - I I I Estimation of Generalized / ' / \ Negative Binomial Distribution
2 3.1: Introduction Fish e r(l 9 2 2, ) laid the foundation o f the theory o f estimation, although m uch o f the attention w a s directed to approxim ation m easures appropriate to large sam ple. In the present age o f com puter sophistication, com putational difficulty is no lo n ger a justification for se eking alternative and inefficient estimation procedures particularly w hen there are only tw o or three parameters to be estimated. Q u ite often there are m any com peting m ethods o f estimation and specific m ethod m ay be superior to other method. The G N B D is a tri-parameter discrete distribution, w h ich have to be estimated w hen the m odel is used to describe a p h ysical situation. M u c h w o rk has been done in the direction o f estim ation o f param eters o f G N B D. V a rio u s authors have suggested v a rio u s m ethods o f estim ations o f parameters. These m ethods have been critically exam in ed in this chapter. T h e cla ssica l technique o f estim ation by the m ethod o f m axim um likelihood requires a lot o f calculation in generalized distribution, as likelihood equations do not appear to be straight forw ard to be solved. A n alternate m ethod for estim ating generalized negative binom ial distribution ( G N B D ) has been presented w here the non-zero frequency o f a
3 variable is observed o n ly upon a finite value. The m ethod is found very sim ple and q u ic k to apply. T h e m ethod, requires the estim ation o f o n ly tw o parameter 0 and P and other is obtained by linear relationship am ong the parameters by counting the non-zero frequency classes. U s in g this m ethod o f estimation, G N B D has been fitted to som e observed distribution and fit have been found quite satisfactory, [H a ssa n et al. (2004)]. In addition, w e have presented a method o f estim ation for estim ating the parameters o f size biased G N B D and zero truncated G N B D by e xplo itin g the conditions given w ith its probability m ass function. 3.2: Method Of Moments T h e generalized negative binom ial distribution contains three parameter with conditions m > 0, p = 0, or p > 1, 0 < 0 < 1, 0 P < l. F o r estim ating these parameters b y the m ethod o f m om ents, three m om ents o f G N B D are required. Su p p o se a random sam ple o f size n is taken from G N B D m odel (1.6.1), and let fj be the observed frequencies corresponding to the value o f Xj for 1 = 0, 1,2,..., k where, x k is the largest observation in sample. Let Si, s 2 and s 3 denotes the m ean, variance and third central m om ent from sample. C o n su l and F a m o ye ( ) and Fam o ye (1 997) gave fo llo w in g three different m ethods for estim ating the parameters o f G N B D u sin g moments. i) Three moments methods U s in g relation (2.3.2) (3.2.1) (3.2.2) T h is gives 82
4 p = e -i (3.2.3) Rewriting relation (2.3.7) as: ( i - e p ) 2 11 ~ e P (2 ~ 9)] Substituting the values o f (1 0p) 2 from (3.2.2) vve get ^3 = 7 M-2 Hi (1-9 ) [3(i - e) - (2-9)(i - ep)] (3.2.4) Substituting the value o f (I - ep) = [^',(1-0) a; ]'/2in (3.2.4) and replacing population m om ents b y sam ple m oments. W e get after sim plification: (2 - e ) - i - e S 1S 3-3 s : s ls 2 = k (say) (2-0 )2 = k(l - 0) (k - 4)0 - (k - 4) = 0 (3.2.5) The tw o roots o f equation (3.2.5) are - (k - 4) ± '(k - 4 ) - 4 ( k - 4 ) = , 2, V - k Since the range o f 0 is between 0 and 1, the adm issible value o f 0 is thus (3.2.6) the relation (3.2.3) w h ic h w h e n substitute w ith value o f 0 from (3.2.6) gives estimate o f p, as A A P = (0) -i 83
5 then u sin g 0 and P in (3.2.1) one get the estimate o f m, as s,[g~' - p ] ii) First two moments and proportion o f zero (MOZE) Let P 0 be the probability o f zero class in G N B D, then P = ( l - 9 ) m = = f (3.2.7) l o g f o = m l o g ( l - 0 ) (3.2.8) F ro m relation (2.3.2), w e h ave p? = ( m 0 ) 3 ( l - 0 P ) 3 (3.2.9) Substituting the value o f (I - Gp) 3 from (2.3.4) in (3.2.9) on sim plification one gets 2 ( i e )u? m =, (3.2.10) 0 2p 2 Sq u a rin g (3.2.8) and replacing population m om ents w ith their corresponding sam ple m om ents, and equating w ith (3.2.10) w e get f,(0) = s 2(log f 0) 2s (1-0)[log(l - 0)]2 = 0 (3.2.11) S o lv in g (3.2.11) iteratively to obtain estim ators 0 based on M O Z E method, the initial value o f 0 is taken as m om ent estimate. From relation (3.2.10) the estim ates o f m is obtained as m = 0 -,[ ( l - 0)s?s-,J ' 2 (3.2.12) A ls o from (2.3.2), the estimate o f p is give n as Hi, First two moments and ratio o f first two frequencies (MORA) L e t Pj be the pro b ability o f the one class in G N B D (1.6.1). T he ratio o f one class to the ze ro class is g ive n b y
6 -!- = m e ( l- e )!-, Po Let fr be the corre sponding sam ples ratio, then w hich g ive s m 0( l - 0) M = f r (3.2.14) f m = ( ) 0(1-0 ) M u sin g relation (3.2.10), replacing population m om ents w ith sam ple moments, and equating w ith (3.2.14), and after rearranging the terms, one gets s 2f r2s ' 3 = ( l - 0) 2M ( ) After a p p ly in g log, w e get f 2 (9) = (2P - 1 ) log(l - 0) - log[s2f r2s r 3 (3.2.17) A l s o fro m relation (3.2.2) p = e _ /2 (3.2.18) u sin g this relation in (3.2.17) w e get f 2(0) = 2_2 0 0 s', (1 e )s2 J /2 lllo g ( l - 9) - log(s2f r2s, 3) so lv in g f2(0 ) iteratively, the estimate o f 0 based on M O R A m ethod is obtained. M O R A estim ator for m and (3 is obtained by u sin g relation (3.2.12) and (3.2.13). 3.3: MINIMUM CHI-SQUARE ESTIMATION Suppose that sample o f size n is divided into a finite (or countably infinite) sets o f groups. Katti and Gurland (1962) suggested the use o f t statistics S = (sj, S2,.. St) for estimating r parameters (j) = (<})i, <t>r) where t > r. T h e m in im u m chi-square ( M C ) estimators for the parameters <f> can be obtained b y m in im iz in g 85
7 Qmc - ( S ~ 1(S - A) (3.3.1 ) where Q E ( S E (s))(s E (s) is the variance covariance m atrix o f S and Q is consistent estim ator o f Q. A lso, S is a consistent estimator o f X = ( X h X 2,...,^t) where V s are functions o f the V parameters in < >. (0, p, m ) are F o r the G N B D m odel, the estim ating equations for the parameters ({) r &k' n~](s-xy = o (3.3.2) and generalized variance o f the M C estim ators o f < >is given by d<\> dp (3.3.3) E x p re ss S = (k(1), k (2)>k(3),lo g P 0 ), where k (j),l,2,3 are first three factorial cum ulants and lo g P 0 is the logarithm o f the zero frequency. Q = var(c) where var (c) is the variance - convenience m atrix C. In place o f u sin g the logarithm o f the zero frequency, one m ay use the ratio o f the first tw o frequencies, but usually m ethod o f u sin g the logarithm o f the zero frequency is m ore efficient in considerably w ide range o f the parameter space. F a m o ye ( ) com pared param eters o f G N B D in case o f finite sam ple size. F o r this com parison, p seudo - random sam ples o f size n = 200, n = 1000, and n = 10,000 w ere generated from G N B D. T he M O Z E, M O R A and M C m ethods w ere used to estimate the param eters 0, p and m. In order to be able to estimate the bias and the variance o f the estimators, 1000 sam ples were generated fro m each sa m p le size. T h e b ia s w a s com puted b y subtracting the 86
8 actual parameter value from estimated value. Several parameter values were considered and results are sim ila r to those in table It w as found that param eter estimator have large biases w hen the sample size is sm all, as sam ple size increases biases goes down. The value o f parameters 0 are generally overestimated, whereas, the values o f p and m are generally underestim ated. In term s o f bias only, the M O R A estim ators are best. TABLE Bias and Variance (in parenthesis) for Parameter 6 = 0.4, p = 1.2 and m = 2.0 e P m o o<n 1 c M O Z E.2199 (0.0083) (.0077) (.1113) M O R A.2112 (0.0172) (.0488) (.5536) M C.2276 (0.0100) (.0104) (.1266) n = 1000 M O Z E.1714 (0.0080) (.0107) (.1460) M O R A.1567 (0.0161) (.0506) (.6053) M C.1756 (0.0100) (.0129) (.1683) n =10,000 M O Z E.0368 (0.0051) (.0177) (.2039) M O R A.0238 (0.0084) (.0590) (.6675) M C.0341 (0.0056) (.0200) (.2356) In com p a rin g the M O Z E, M O R A and M C m ethods. T h e M O Z E estim ators have the sm allest variance. M O R A estimator has the sm allest bias especially w hen n = 1000, or greater. W h e n both properties o f bias and variance are considered, the M O Z E m ethod seem s to be the best. 3.4: Maximum Likelihood Method of Estimation (MLE) T h e generalized negative b in o m ia l distribution is a tri-param etric m odel w ith param eters m, 0, p. L e t a random sam ple o f size n be taken from the G N B D and let the observed frequencies be fx, x 0,1,2,..., k so that k x=0 ^ 87
9 where k is the largest o f the observed value h a vin g non-zero frequencies. The likelihood function is g ive n by k L = n x=0 m m + px rm + p x x 0 x ( l - 0) m+px" x (3.4.1) v * j - n x=0 f l ( x! ) f» k {m(m + p x - l)(m + P x - 2)- m + p x - (x - 1)0X (1 - Q ) m + P x ~ x )f» k x 1 m ne n x ( i_ e ) mn+n ( M ) x n n (m + px _ j)f«x=2 j=l f l ( x!)f> x=0 The log likelih o o d function is give n by log L = n log m + nx log 0 + [mn + n(p - l)x] log(l - 0) + Z f. x=2 x 1 l o g ( m + p x - j ) - l o g ( x! ) j=i T he m a x im u m likelih o o d estim ator o f 0, p and m are obtained by partially differentiating likelih o o d function w ith respect to 0, P and m and equating to zero. T h e likelih o o d equations are d. T n[x - 0(m + px)] _ 102 J-/ 30 0(1-0) = 0 (3.4.2) k x 1 x f v A l o g L = m x log(l - 0) + X Z n ~ ap x=2 j=l P j = 0 (3.4.3) d. _ n - f, lo g L = dm m (3.4.4) 88
10 T h e eq uation s (3.4.2), (3.4.3) and (3.4.4) are so lve d sim u ltan e o u sly to A A obtain 0, p and m, the M L estim ators o f parameter 0, p and m respectively. G upta ( a ) obtained m axim um likelihood estimates for m odified pow er series distribution (1.3.1) and results were applied to obtain m axim um likelihood estim ators for G N B D. Let X j, X 2,...,X n be random sam ple o f size n from M P S D and let L be the likelihood function, then w here is m ean o f M P S D and x is sam ple mean, the solution o f likelihood equation is then give n by x = *i(0) (3.4.5) so lv in g (3.4.5) for 6 one obtains 0 = ^ ( x ) (3.4.6) provided \x is invertible. T h e in ve rsion o f p. can be justified at least w hen g(0) is increasing because in that case > 0 as variance - ^ 7 % > 0 and hence n (0 ) d0 g (0) d0 is an increasing function o f 0. T h e generalized negative binom ial distribution given by (1.6.1) being a m em ber o f M P S D w ith g (0) - 0( l - 0) M,f(0) = ( l - 0) m and ^ (0) = ^ - ^ u sin g equation (3.4.5), w e get
11 F o r b in o m ia l distribution, p 0, and hence 0 = and for negative m binom ial, p 1 and hence 0 =. T he am ount o f inform ation 1(0) contained in sam ple is 1(0) = - E ( J? L de2 lo g L = n / g (0) (3.4.7) where n 2(0) = ^ is variance o f M P S D, and in case o f G N B D it is equal to m 0( l - 0 ) ( l - e p ) g (6) V ar(0) = [l(0)]_l = %(6) (3.4.8) d0 from (3.4.8), the variance o f 0 in case o f G N B D is V a r(0) = 0(1 0)(1 0P) n In particular for b in o m ial distribution Var(0) = ^ for negative n binom ial distribution, V ar(0) = 0(1-0 ) B ( l - 0) A n d bias o f 0 is obtained as b(0) = by u sin g the relation mn n b(0) = 1 g (0) 2n i2 g '( 0), g ( e ) g '( e ) - ( g '( 0))! M " 3 ( g 'O ))2 where ja3 is third the central m om ents o f G N B D given b y (2.3.7) Amount o f bias in ML estimator using negative moments T h e M L estim ator 0 o f 0 based on the random sam ple X h X 2,...,Xn from G N B D, (1.6.1) w a s g iv e n b y G upta (1 975a) as 0 = 1 m n m + px p p J 1 Y + m n/p_ (3.4.9) 90
12 where Y denotes the su m o f sam ple values and x is the sam ple mean. The random variable Y has G N B D given by P (Y = y) = mn m n + py mn + Py {9(1-9)m }v (1-0)' y = 0, 1, 2... and zero elsewhere, m > 0, 0 < 0 < 1 and O < p < 0-1. T h e above distribution o f random variable Y is G N B D with only difference that m is replaced by mn. K u m a r and C o n su l u sin g the negative m om ents found the exact am ount o f bias in the M L estimators o f parameters in G N B D. U s in g relation (2.5.4) and (2.5.5) after changin g m by m n for the random variable Y. S in c e k = -^ ~ given = p k - m n - k is negative, thus P u sin g relation (2.5.5) replacing m by mn, w e get Y + m n mn 00 P X i=0 f V mn p \ 0 i+1o - 0) mn/p mn + i +1 p A on substituting in (3.4.9), w e get expected value o f M L estimator 0 o f 0 in G N B D, g ive n as E 0 = mn P 00 ^ m n + i l Qi+in 0 i+1 (1 _ - m 0)' mn/p X p mn t 0 + i + 1 / P (3.4.10) obtained as Subtracting 0 from both sides o f (3.4.10) the bias in M L estimator is b(0) = m n / \ m n + i v p 0 i+i( i - 0) m n/p mn T + i + l (3.4.11) H ow ever, if k = is p o sitive integer, the relation (2.5.3), reduces to 91
13 y + m n = E 1 = I - p y ( -» ' f l - 0 "l i / i\k-l 1^ / 1 a\d r i - e A + ( - 1) l o g ( l - 0)p y + k k f ^ ( k - i ) CD CD (3.4.12) F ro m (3.4.9) and (3.4.12) the expected value o f M L estim ator 9 o f 0 in mn G N B D w hen ^ = k is positive integer is give n as r ^ 1-0 ^ E (e ) = k Z ^ r ( ^ ) ' + ( - l ) k k l o g ( l - 0) N o ( k - 0 e, (3.4.13) T hus, b ias in 0 is g ive n in closed form as k-1 ( / b(0) = (l-0 ) + k]t - i\i 1) M ( k ( l) k log(l - 0) v 0 j G upta ( a ) obtained the m a xim u m likelihood estimation o f decapitated G N B D th rough M P S D as F o r decapitated G N B D give n by (1.6.4) H(0) = (1 0p)[l (1 0)m ] (3.4.14) u sing relation (3.4.5). T h e M L E o f 0 is given by mo x ~ { \ - e p ) [ \ - ( \ - d ) m ] (3.4.15) F o r p = 0,this reduces for truncated binom ial distribution, to x = m 0 (3.4.16) 1 (1 0 )m w hich agree w ith Patil (1962b), and for truncated negative binom ial distribution, m 0 x = ( l- 0 ) [ l- ( l- 0 ) m] (3.4.17) 92
14 W h eneve r the o b serve d num ber o f zero s are m ore than that given by the model, it is recom m ended that the m odel should be m odified accordingly to account for the extra zeros. Gupta, G upta and T riparthi (1 995) obtained the m axim um likelihood estimation o f param eters o f the zero inflated M P S D. The distribution o f inflated m o d ifie d pow er series is given by (1.3.13) Letting X = (1 - a ) 1 - a(0) f (0), the m odel can be written as P ( X = 0) = 1-A. x = 1, 2, 3,... (3.4.18) Let X ], X 2... X n be a random sam ple from (3.4.18) and let nj be the 00 number o f observations su ch that n = ^ n j. T hen likelihood can be written as i=0 L = n [ p ( x = o ] n i=0 00 L = o - x ) n - n i=0 1 - a(x)[g(9)]! a(0) ' f (0) f (0) lo g L = n 0 log(l - X) + ^ n j log i=l 1-00 ^ a(i)[g(9)]1 a(0) f (0) f ( 6) this gives lo g L d X 00 _ n 0 i f - 1-X X 93
15 3, _ -f'(6)(n-n0) log L h ae 5 f (9) - a(0) oo X ini. i=l 8(0) estimator o f X and 0 are g ive n by X = n - n 0 n (3.4.19) 00 Y i n i and i - a(q) n - n, f (0) (3.4.20) where n(0) = g (0) f '( 0) f ( 0) - g '( 0) is mean o f m o d ifie d p o w e r series distribution. F o r generalized negative binom ial distribution g iv e n b y (1.6.1). u sin g relation (3.4.19) and (3.4.20), the mle o f 0 and a for G N B D is w mo (i - ep){\ - (i - o))m «-«(3.4.21) a = - ( i - 0 ) m n i - (i - 0) m (3.4.22) given by F o r b in o m ia l distribution, p 0, therefore m le s 0 and a o f 0 and a are 00 m 0 Z in i i=l 1 - ( 1 0) m n - n 0 a - n, n - ( 1-0 ) m l - ( l - 0 ) m 94
16 T he results o f G upta, G upta and Tripathi (1 995) were extended by M urat and Szynal ( ) to the discrete distributions inflated at any point s. T he p robability m a ss function o f inflated m odified pow er series distribution at point s is g ive n by P(X = x) = a + (1 - a) a (x)(g(0)) f (0) a (x)(g(0))x (1 -c t ) f ( 0) X = s X * s x e N (3.4.23) where 0 < a < 1. N is set o f positive integers. Proceeding on same lines as Gupta, G upta and T rip a th i (1995), they obtained m axim u m likelihood estimator o f a and 0 as n - n, a = n (3.4.24) d Me)fi e)z,. a Le(e)i l, _! _ g in f ( 0) - a ( s ) [ g ( ) ] S n - n s i= li«(3.4.25) where m (0) = m! - f. i s m e a n o f M P S D g '( 0) - f ( 0) 0 can be obtained from (3.4.25) by iterative num erical techniques, thus using g (0 ), f{6 ) and a ( x ), w e have fo llo w in g m le o f 0 and a s!m0r(m + sp - s +1) - smp(m + ps)(l - 0p)0 (1-0) (p-l)s+m 00 1 (1-0P) s!t(m + sp - s +1) - mt(m + Ps)0s (1-0) (P-l)s+m X i n i n - n s i = li«a A a = «5 i r ( m + s/3 - s + 1 ) - nm{m + fls)6s (1-6) $5,!r(/w + sj3 - s + 1) - mt{m + fis)os (1-6) In particular w h e n p = 1, w e obtain the m le o f 0 and a for negative binom ial distribution as 95
17 m9 - (1-0) / \ 1 - m + s-1 v m+l As (1-0) 0 m + s-1 \ 0 s (1-0 ) m s 00 Z n - ru.,. s 1= 11* S i n ' a = n, ^m + s - 1^ - n "m + s-t ^ s > < s > fm + s - 0 A A n 1-0(1-0)m I s J 0 s (1-0) m 3.5: Maximum Likelihood Estimation of GNBD Using Second Order Derivatives of Likelihood Function A m o n g v a rio u s m ethods o f estimation, the m ethod o f m axim um likelihood is su p e rio r to m a n y others, but som etim es it becom es incredibly difficult to so lve M L equations on account o f intricacies involved, this is true in case o f G N B D also. H a ssa n ( ) b y m a k in g use o f second order partial derivatives o f lik e lih o o d function obtained m le o f parameters o f G N B D Let a random sam ple o f size n be taken from the G N B D and let the k observed frequencies be fx, x = 0,1,2,... k so that ] T f x = n where k is the largest o f the observe d valu e s h a v in g non-zero frequencies. T he likelihood function o f the G N B D can be written as x=0 k x i m (n-fo)0 nx (1 _ 0 ) mn+n(p-l)x (m + p x _ j) x=2 j=l i W * x=0 T h u s, the lo g lik e lih o o d function can be written as log L = (n - f 0) log m + nx log 0 + n[m + (P - l)x]log(l - 0) k x-l + E Z fx log(m + px - j) - log M x=2j=l (3.5.1) 96
18 k where M = J ^ ( x! ) f* x=0 The three likelihood equations are given as, d lo g L _ nx n[m + (p - l)x] 50 ~ 0 (1-0) (3.5.2) S L o g L _ m ^ ^ x f v,3.5.3) ,3.5.4, 5m m x=2h m + Px - J F ro m equation (3.5.2), w e get 6 = * (3.5.5) m + px S o lv in g equation (3.5.3) and (3.5.4), w e have n v k X_1 f -= IE; (3-5-6) m x = 2 j= l ( m + P x - j ) These equations do not seem to be directly solvable and hence some method o f iteration has to be applied. (3.5.4), as T h e second derivatives o f log L can be obtained from (3.5.2), (3.5.3) and d 2 lo g L nx n[m + ( P - l) x ] (3 5 7) dq2 ~ 0 2 (1 0 )2 d2u>gl _ y y ( ) ap2 5^ 2j=i (m + p x - j ) 2 d 2L o g L _ ( n - f 0 ) y y! x (3.5.9) 5m2 m 2 x=2j=i (m + p x - j) 2 97
19 d 2LogL aeap nx (1-0) (3.5.10) a 2L o g L 505m n (1-0) (3.5.11) a 2L o g L _ x f 3 P 3 m X = 2 >? ( m + p x - i ) : (3.5.12) T h e valu e s o f these second order partial derivatives can be put in the fo llo w in g equations in the m atrix form. d2 lo g L d2 lo g L d 2 lo g L dq- aeap aoam a 2 logl a2 logl a2 logl a0ap ap2 apam a2 logl a2 logl a2 logl a0am apam ^m2 0o,Po>m o 0-0 o P-Po rh - m o a lo g L a a logl a logl am 0O Po>mO (3.5.13) A A where 0, p and m are the M L estimators o f 0, P and m respectively and 0 O, po and mo are the trial values o f the parameters. For trial values, the moment estimators can be used or it can be obtained by equating the first three observed relative frequencies to the corresponding theoretical probabilities. This system o f three equations may be used repeatedly till very close estimates o f 0, p and m are obtained. 3.6: B ayesian Estim ation o f GNBD T h e B a y e s estim ators o f a num ber o f param etric functions o f 0 for G N B D w ith k n o w n m and p w a s obtained b y Isla m and C o n su l (1986). Since 0 < 0 < 1, the p rio r inform ation on 0 were sum m arized b y beta distribution B(a,b), w here the param eter a and b are know n, under the squared loss function. I f X u X 2,..., X n be a random sam ple o f size n draw n from G N B D then likelihood function o f X i, X 2,..., X n g ive n 0 is o f the form. 98
20 l(x e)= k enx (i - 9)mn+nnx-nx where K = II m m + Px =, m + (3x i V x (3.6.1) The sum m ation b e ing taken overall x = (x,...xn) such that x, = nx. t= l Sin ce prior inform ation on 0 is give n by beta distribution with probability density function X (0;a,b) = 0 a- ( l - 0) b-> B (a,b) a,b > 0, 0 < 9 < 1 (3.6.2) The posterior distribution o f 0 becom es Qnx+a-l _ 0^mn+b+(P-l)nx-l p(g x) = (3.6.3) B (nx + a, mn + b + (p - l)nx) and B a y e s estim ator o f any function <f)(0) w ith respect to squared error less function is [ 1 <f>(0)0n* + a ~ l (1-0 ) m n + b + ( P - l) n x - l ^(6) = / _ = r B (nx + a, mn + b + (P - l)nx) Bayes estimators of some parametric functions in GNBD * ( 0) m e '( i - 9 ) k B[nx + a + i, (P - l)nx + mn + b + k] I and k non-negative B [nx + a, (p - l)nx + mn + b] integers {0( l - 0)M }k B[nx + k + a, mn + b + (P - l)(nx + k)] B [nx + a, mn + b + (p - l)nx] 0' (nx + a), (pnx + m n + a + b), P(X = k) m fm + pk^ Bfk + nx + a, (p - l)(k + nx) + m (n +1) + b] m + p k ^ k J B[nx + a, ( P - l) n x + mn + b] W h e re x<n) denotes the risin g factorial x (x + l) ( x + 2)...(x + m - 1 ) 99
21 T h e y estim ated the B a y e s relative frequencies by u sin g the estimator o f P ( X - k ).A w id e range o f values from 1 to 100 were considered for a and b and values o f P ( X = k) w ere com puted for k = 0, , and for the follow ing five broad categories: i) a = 1 and b = 1, 10, 20, 30, 40, 50, 100 ii) b = 1 and a = 10, 20, 30, 40, 50, 100 iii) In cre a sin g values o f a and decreasing values o f b. iv) D e c re a sin g values o f a but increasing values o f b. v) E q u a l values o f a and b but increasing from 1 to 50. In each case the values o f estimated B a y e s frequencies were com pared with the sim ulated values. It w as discovered that the estimated B a y e s frequencies w ere quite close to the sim ulated sam ple frequencies, w hen a and b were equal and that the variation in the B a y e s frequencies w as very little as the equal values o f a and b w ere increased. It w as found that % - values between the sim ulated sam ple frequencies and the estimated B a y e s frequencies were the least w hen a = b = Bayesian Estimation in a Decapitated Generalized Negative Binomial Distribution T h e D ecapitated form o f G N B D has been extensively studied over the past 25 years. B a sa l and G an ji ( ) derived B a y e s estimate o f zero truncated G N B D. T h e p ro b ability function o f zero truncated G N B D is given by (1.6.4) as P (x ;m,0,p )= m m -f px ''m + px^ 0 X(1- O ) m + p x -x 1 (1 0) x = 1,2,... (3.7.1) o < e < i Su p p o se 0 is a random variable and m and p are fixed but u nkn ow n constants, sin ce 0 < 0 < 1, p rio r inform ation on 0 m ay be give n by a beta distribution B (a, b) w ith k n o w n hyper-param eters a > 0, and b >
22 0 a-i n g(0; a, b) = < 0 < 1, a, b > B (a,b) I f Xi, x 2,... x n be a random sam ple o f size n draw n from a decapitated G N B D. T h e lik e lih o o d function x, x 2... x n< give n 0, is o f the form L ( x i 0) = n = m + pxj v m + px j x i d - 0) m + P x.-x i i. - { 1- e r f (3.7.2) = C 0 s ( l - 0 ) mn+ps s l - j l - 0 } " ] " m + pxj and s = X x i i=l The posterior distribution o f 0 becom es 7l(0 x) = Qa+s-l (1 _ e )mn+(p-!)s+b-! 1_ }] _ 0 }m -n W (b,s,n ) (3.7.3) where W (b, s,n) = J0 a+s_1 (1-0) 0 m n+(p-l)s+b-l d0 oo ^ - / n + k - 1 k=ov n ' k - l ' = ^T B(a + s,m k + ( p - l) s + b) k=n vn - l, = r ( a + s)d (b,s,n ) where 00 D ( b, s, n ) = ^ k=nvn r(mk + (P - l)s + b) r ( m k + ps + a + b) 7t(0 X ) = 0 3+ s-l ^ _ Q-)mn+(P-l)s+b-l [l _ (j e } m " r ( a + s)d (b,s,n ) 101
23 and Bayes estimate o f 0 with respect to squared error loss function is 0(b,s, n) = Jo 7i (01 x)d0 0 1 Je a+s (i - e )mn+<p-a>s+b- ] [1 _ {! _ e jm ]~n de J _ 0 r ( a + s)d (b,s,n) J0 a+s (1-0 )mn+(p-ds+b-l k=n T(a + s)d(b,s, n) 1V _ Q^m(-n+k) de CO f i r _ i \ 1 Z k=nl n 1 L Mea*s( i - 0)mk* F (a + s)d (b,s,n ) K P -l)s + b-l de o c - i ^ E l. B(a,s + 1,m k + ( p - l ) s + b) k=n vn - l/ T(a + s)d (b,s,n ) = r (a + s + l)r(m k + (P - l)s + b) k=n r (m k + ps + a + b + 1)* T(a + s) * D(b,s, n) k=n\ (a + s)r(m k + (p - l)s + b) r (m k + ps + a + b + l)d(b, s, n) 0 = [(a + s)d (b P,s + l,n)] D (b,s,n ) 3.8 M in im u m V a r ia n c e U n b ia s e d E stim a tio n ( M V T J E ) G upta ( b ) gave the necessary and sufficient conditions for the existence o f m in im u m variance unbiased estimate ( M V U E ) o f the parameters based on sufficient statistics and obtained m in im u m variance unbiased estimates o f param eters o f a M P S D (1.3.1). Theorem : su p p o se Xi, X 2,.*->x n is a random sam ple M P S D. T hen there exists essentially a unique unbiased estim ator o f ^(0) w ith m in im u m variance if and o n ly i f ^(0)[f (0)]n is analytic at the o rig in and has an expansion o f the form 102
24 (O)[f(0)]" = C (z,n )(g (0 )); n W here z ^ X j is a com plete and sufficient for 0 and its probability i=l distribution is giv e n b y P (Z = z) = b(z,n) [g(0)p [f(0)]n T h u s m in im u m variance unbiased estimate o f ^(0) is given by C (z,n ) vj/(z,n) = b(z,n) b(z,n) * 0 (3.8.1 ) The inform ation inequality for the variance o f an unbiased estimator, (0), o f ^(0) based on random sam ple x,, x 2,...xn from M P S D is given by Var M ) > j m U (6 ) ( f ( 6 ))2 ( r ( 6 ))2 \ 2 g '( 0) dja v a r(x ) n g(0) ' d0 (3.8.2) where i(0) is m ean o f M P S D. In order to obtain the M V U E o f ^(0) = 0 r( r > l ) for G N B D Gupta (1977b) em ployed a w e ll k n o w n L a gra n g ia n form ula 00 A ( 6) = A (0 ) + - ZTt z! z=l )Z 1 -(h (e))za'(0) e=o z-1 0 h(0) (3.8.4) to expand A (0 ) = 0 r( l - 0 ) w ith h(0) = ( l - 0 ) -p+i u y er(i-e) = X 1 dz-1 Z=r ^ z! 3 0 z-1 A ( e '( i _ 0)-ra' ) 30 (g(0))! e=o r y i i! l l _ f e r- i ( i - e ) - P z+z- mn] (g (9))2 ^ z! 50 0=0 rrz!3 I 0 z-1 -pz+ z-m n-1 0 r ( i e) 0=0 (g(e))5 103
25 ^ i a z_ r 2 / I A D 7-1 Z=rz! ^ r-1 'r-f* ( - l )1(l - 0)l-Pz+z-mn (g(b))2 zt=0 0=0 ^ i az~l + m n ^ z = rz! ae z-l oo = S Cr(Z nxg(0)): Z=r t=0 w 0=0 (3.8.5) where r r_1 C r(z,n) = Y z! ^ iv (Pz + m n -t-z )! v ~ v r:» z > r (Pz + m n - t - z)! = 0, z < r Repeating the procedure em ployed to obtain C r(z, n) with r = 0, we obtain: b(z,n) = m n(pz + z n - l ) z!(pz + m n - z )! (3.8.6) and M V U E for 0 r is g ive n by b(z,n) for r = 1 _.. 1 (Pz + m n - z )! /n C,(z,n ) = - ^ ( P z + m n z - z ) o f z > l z! (pz + m n - z )! = 0 o f z < 1 T h u s M V U E o f 0 for G N B D is give n by C,(z,n ) (Pz + m n z - z ) b(z, n) m n(pz + m n - 1) (3.8.7) T h u s for P = 1, (3.8.7), g iv e s the M V U E o f parameter for negative binom ial distribution as and G uttm an (1957). z + m n - 1. T h is coincides w ith R o y and M itra (1957) 104
26 3.9: M in im u m V a r ia n c e U n b ia se d E stim a tio n fo r Left T ru n c a te d G N B D in te rm s o f M o d if ie d C - N u m b e r s Jam ( ) m ade a detailed study o f the M V U estimation in left truncated G N B D and M V U estim ators were expressed in terms o f new defined m odified C -n u m b e r. T h e p robability function o f the left truncated G N B D w ith truncation point r(r > 0) is g iv e n by P(X = x) = P ( x : r, 0) m(m + px-l)!{o(l - Q ) ^ 1 r-l x!(m + px - x)!(l- 0)~m- X(-l)k' - ( m Pk + k~'}'fefl- O)^1}X k=o (-m -p x )lk! x = r, r + 1,... (3.9.1) m (m + P x - l)! ( g ( 0 ) ) x x!(m + px -x )!H j(0,-m, r,p ) (3.9.2) where H,(0-m,r,p) = (1-0)-m - ( - l ) k-' m(-m -Pk + k - l)! ( l- 0 ) p ') (3 9 3) (-m-pk)lk! and g(0) = 0 ( l - 0 ) M. (3.9.4) Let Xi, x 2, x n be a random sam ple o f size n from (3.9.2), w hen p and r are k n o w n the distribution o f Z = is give n by 1=1 n P (Z = 2) = d (z n r P )(g (0 ))- z = m, m ( H ^ O - m ^ P ) ) " and w hen r is u n kn o w n, the joint distribution o f (Y, Z ) where Y = m in {x i,x 2...,xn} is g iv e n in Jani (1 977) as = d (Z, n y, P ) - d ( z, n, y + li P ) ( )z (3.9.6) (Hi(0,-m,r,P)) z = n y + n y + l..., y = r, r + l,
27 W here H, (0, -m, r, (5) and g(0) are as given in (3.9.3) and (3.9.4), and d(z, n, r, P) is the coefficient o f (g(0 ))' in expansion o f (H,(0,-m,r,P ))n = ]d (z,n,r,p X g (0))z ( ) z=r n C haralam b ides (1974a) obtained the probability function o f ( Y Z ) as P(y, z; r,0) = C(z>n>y) ~ C(z,n, m, y +1 )0z (1-6)Pz~z hn(0,m,r)z! for y = r, r + 1,..., z = m, m with z > ny, 0 < 0 < 1, 0 p < 1. W here C (z, n, m, r) = V f l m rcm + px,) m! r ( Xi + l)r(m + pxj - x; + 1) C haralam b ides utilized this distribution to obtain M V U estimator o f 0 s, s > 1, w here the truncation point r is assum ed to be know n, and o f rs and 0s w hen r is unknow n. In case r is k n o w n, the M V U estimator 0s is obtained as e s (y) = Zf,r ( Pk Z l )s(y ) L -. C(_z- k,n,m,r) ^ ^ m + s r((p k - k )k -s)k! C(z,n,m,r) In case r is u n k n o w n the M V U estim ators o f rs and 0 s (s > 1) are given respectively by P / =s - S _ C (z,n,m,y + 1) y C(z, n, m, y) - C(z, n, m, y +1) k= ovk, yk (3.9.8) and 0 s fv r (Pk ~ s^ y ^ C ( z - k, n, m, y ) - C ( z - k, n, m, y + l) r ( p k - k ) k - s )! k C ( z, n, m, y ) - C (z,n,m,y + 1) 3.10: Confidence Interval Estimation Fam o ye and C o n su l ( ) considered the case o f both sm all and large sam ples and obtained expression for setting 100( l - o t ) % confidence interval for parameter 0 in case o f G N B D u sin g the general case discussed for M P S D. 106
28 Let a random xj, x 2,..., xn of size n be taken from the MPSD. Its likelihood function is g ive n by (3.10.1) n T h e statistic Y ^ X j com plete and sufficient statistic for parameter and i=l its probability function is g ive n by Py(0) = b(y){g(e)}y {f(0 )}"n where b(y) = ^ a ( x, ) a ( x 2) - a ( x n) Sin ce Y is sufficient statistic for the parameter 0 in (1.3.1), one can equate the su m o f the probabilities o f the distribution o f Y on each side with a/2, thus g iv e s 00 x=y a 2 (3.10.2) Y Xb(x){g(0i)}x{f(ei)}- x=0 a 2 (3.10.3) T h e distribution o f sam ple sum in case o f G N B D is given by using (3.10.2) and (3.10.3), w e get (3.10.4) and (3.10.5) 107
29 F o r any g iv e n set o f m, n, p and Y, (3.10.4) and (3.10.5) can be solved by u sin g N e w to n -R a p h so n iteration method, w hich w ill provide 100(1 - a ) % two sided confidence interval for 0 as (0 ^,0 U). I f a/2 is replaced w ith a in (3.10.4) and (3.10.5) then their solution provide one sided low er ( l - a ) % confidence bound 0, and one sided upper 100( l - a ) % confidence bound 0 u. n F o r large sam ples the sam ple sum Y = ^Tx, is a m odified pow er series w ith m ean n\x and variance n a. T he quantity i=i W = Y -n jj. crvn (x- i)vn a has a lim itin g distribution i.e. norm al w ith mean zero and variance 1. A c c o rd in g ly tw o sided ( l - a ) % confidence interval for 0 is 1- a = P x - Z ng'(6) d 0 \ i /2 g(6) f'(6) - 7 < < x + Z g'(b) f(b) ( g(0) d \i) 1/2" V n g*(6) de J where Z a is the critical value from norm al table. T h e upper bound 0 U and the 2 low er bound 0, are the solutions o f the equation x _ j w. m ± Z a g (8) f(0) f g(0) d n ' 1'2 ng'(6) de = 0 (3.10.6) w here g '( 0) d0 is variance o f M P S D. Since sam ple variance S 2 is given by S 2 = ~ r S ( x i _ x ) 2 n - 1 : A c c o rd in g ly, the tw o sided ( l - a ) % confidence interval can also be obtained fro m 1 - a = P _ z a < ( ^ < z 0 2 J 108
30 = p x - Z f ^S -7 S < i < x + Z a (3.10.7) me O n substituting the value o f u = (i - ep) bounds for param eter 0 o f G N B D are obtained as, the two sided 100(l-a)% confidence x - Z m + p / x - Z \ x + Z (3.10.8) \ m + P v x + Z 3.11: A S im p le a n d Q u ic k E s t im a t o r T h o u g h am o n g va rio u s m ethods o f estimation, the m ethod o f m axim um likelihood is the m ost preferred one. Som etim es the likelihood equations are very com plicated and its explicit algebraic solution is not available. It is to be solved n um e rically in that, by the m ethod o f iteration. In this section w e present a sim ple m ethod for estim ating the parameters o f generalized negative binom ial distribution. T h e m ethod is found very sim ple and quick to apply. In this method, the estim ation o f o n ly tw o parameters 0 and P is needed and o f the other is obtained b y the linear relationship am ong the parameters by counting the num ber o f non-zero frequency classes. T o exam ine the unbiasedness and efficiency o f the estimates o f parameters b y u sin g this method, an intensive M o n te C a rlo technique has been applied. U s in g this m ethod o f estimation, G N B D has been fitted to som e observed distributions and the fits have been foun d quite satisfactory. 109
31 M o s t often in practice the observed distributions are obtained only up to a finite value o f a variable i.e. up to finite num ber o f classes h avin g non-zero frequencies. Let us consider that 4t is the highest observed value h avin g nonzero frequency i.e. (t+1) is the low est value h avin g zero frequency. F ro m one o f the conditions o f the p m f o f the G N B D, w e have m + pt - 1 < 0 for x > t considering the equality, w e get m + pt - 1 = 0 (3.11.1) w hich give s m = t(l - P) (3.11.2) o b viously here P < 1 as m > 0. C o n su l and G u p ta s (1980) condition that G N B D is a true probability distribution for p=0, and for all values o f p in 1< p< 6~x is o b vio u sly for the range o f x as 0(1 )oo. In case the range o f G N B D is 0(1) t, the value o f p < 1. It can be seen in Jain and C o n su l (1971) and C o n su l and Fam oye (1995) that the estimates o f p b y the m ethod o f m om ents and ML m ethod are com in g to be less than one. Substituting the value o f m from (3.11.2) in the m ean defined in (2.3.2) o f G N B D, w e get _ t(l-p)0 ^ (i-ep) to top i- e p l- e p L e t 1-0 p = a (3.11.3) w hich g ive s, t0 t( l- a ) ^ 1 = (3.11.4) 110
32 Using (2.3.2) and (2.3.4) of GNBD, we define / 2 _ 0-0 ) (1-0 ) A (1 -e/3)2 a2 Substituting the value from (3.11.4) in (3.11.5), we get (3.11.5) t o ( 1 - <? ) ( > - / /, ') 2 t2(\-e)2 - M l ) 2 t 2( \ - 0 ) 2 After a little sim plification, w e get g {t-y [)2y[ A.. (3.11.6) Substituting the value o f 6 from (3.11.6) in (3.11.4), w e get Mi R e p la c in g the population m om ents i', and ji2 by the respective sample m om ents x and s 2, w e get the estimate o f 0 as and estimate o f a as T h u s estimate o f P is obtained by u sin g relation (3.11.3) (3.11.9) Substituting the value o f p from (3.11.9) in (3.11.2), the estimate o f m is obtained as «= /( l-p) Bias and Efficiency o f suggested estimators using Monte Carlo Technique F o r evaluating the am ount o f bias and the efficiency o f the estimators o f m, 0 and p, so obtained, an intensive M o n te C a rlo T echnique has been applied as the m athem atical e xpressio ns for their m eans and variances are not know n. 111
33 Fifty random sam ples each o f size 100 have been drawn from the G N B D on com puter taking different com binations o f values o f the parameters, m, 0 and p. W h ile studying the efficiency o f the B ayesian estimators o f the G N B D, u sin g M o n te C a rlo technique, Isla m and C o n su l (1 986) selected the values o f m, 0 and p as 7, 0.3 and 2 respectively. Selecting the same com binations o f values o f m and 0 as 7 and 0.3, w e selected various different values o f p as 0.1(0.1)0.9. A fte r generating such sam ples, the estimates o f the parameters were obtained u sin g the suggested m ethod for each o f the sam ples for each com bination o f the values o f the parameters. The m ean and variance o f each o f the estimates o f each o f the parameters were computed, w hich indicates about the biased ness and efficiency o f the parameters. T he estimates o f m, 0 and p for n=7, 0 = 0.3 and p = 0.1(0.1)0.9 o f one sam ple and m ean and variance o f 50 sam ples for each com bination o f values o f parameters have been sh o w n in fo llo w in g tables. T a b le : T h e estim ates o f m, 0 a n d p fo r m =7, 0 = 0.3 a n d p = 0.1(0.1)0.9 p t E stim a te s o f m E stim a te s o f 0 E stim a te s o f P 112
34 Table: M e a n a n d v a ria n c e o f the estim ates o f m =7, 0 = 0.3 a n d p=0.1(0.1)0.9 p E stim a te s o f E stim a te s o f E stim a te s of M e a n V a r ia n c e M e a n V a ria n c e M e a n V a ria n c e The estimates w ere found alm ost unbiased and quite efficient. 3.12: G o o d n e ss o f F it A n attempt has been m ade to fit G N B D to num ber o f actual data sets, observed by other researchers, and for w h ich they had either used other m odels or the G N B D. D a ta set I is a sports data used by S in h a (1 984) for fitting the negative b in o m ia l distribution, and gives observed num ber o f w ickets taken by Sobers in 158 com plete in n in g s in test cricket. T he data set I I contains the runs scored b y V ish w a n a th in 142 com plete innings. T h e expected frequencies obtained b y the m ethod o f m om ents for G N B D have also been give n so that quick com p ariso n can be made. 113
35 Table Wickets Taken By Sobers in 158 Complete Innings in Test Cricket Data set I Wickets Observed Expected Frequency taken Frequency Methods of Moments Suggested method Total Mean j x d.f 1 2 a a p a m Table Runs Scored By Vishwanath in 142 Complete Innings Data set II Runs Observed Expected Frequency (unit of 30) Frequency Methods of Moments Suggested method J J Total 142 Mean X/V 2 d.f a 0 A s r A m \ 8.13 ~l
36 By a comparison o f two sets of expected frequencies with observed ones and a lso b y their x, va lue s, it is evident that the frequencies com puted by the suggested m ethod for G N B D are m ore or less close r to the observed ones, though the value o f % are sligh tly higher in case o f suggested method than in case o f m om ent method. H ow e ver, these differences do not seem to be m uch significant. Further, the suggested method has one definite advantage over other m ethods in certain situations. It can be applied w hen the method o f m om ents fail to g ive estim ates o f the parameter. M ore over, it is relatively very quick and so it m ay be preferred to others. 3.13: Estimation of Parameters of Size-Biased and Zero Truncated Generalized Negative Binomial Distribution T h e param eters o f size biased generalized negative binom ial distribution ( S B G N B D ) and zero truncated generalized negative binom ial distribution ( Z T G N B D ) are bit difficult to be estimated and so they are not m uch in com m on practice. In this section a sim ple and quick m ethod o f estim ating the parameters o f S B G N B D and Z T G N B D has been suggested. L e t us consid er that t* is the highest observed value h aving non-zero frequency i.e. (t+1) is the low est value h a v in g zero frequency. F ro m one o f the conditions o f the S B G N B D m odel, w e m ay have m + pt - t < 0 for x > t considering the equality, w e get this give s m + t(p - 1) = 0 (3.13.1) m = t (1 - p) (3.13.2) F ro m (2.12.4) and (2.12.6), putting 1-0 p = a, w e get (3.13.3) F ro m (3.13.2) and (3.13.3), w e have 115
37 from (3.13.4), we have (2.12.4) as x*' _ t(0--l + a) 1-6 t(q-\ + a)a + (\-Q) M, _ a ^ = ^ ~ (3-13.5) T h is g iv e s 1-0 = (M; - t)a: T ^ T (3.13.6) J D, ( M ;-t) a 2 m T (3-13-7) Substituting the value o f m and ( 1-0 ) from (3.13.2) and (3.13.6) and a = 1-0 p in ( ), w e get ( M ', - t ) M o = ( l - t a ) 2a ta -tm Ja +M; - ta - Mja + ta 2 + M',a-1 T h is g ive s M 2t2a 3 - [2tM2 - (m; - 1)2 - tm; (m; - t)ja2-2(m; - t)m;«+ (m; - 1) = o Put t - M J = R (S a y ) f(a) = M2t 2a 3 - (2tM2 - R 2 - tm',r)a2+ 2RMJa- R = 0 (3.13.8) R e p la c in g the population m om ents M', and M 2 by respective sam ple m om ents x and s 2 w e get f(a) = s2t2a 3 -(2ts2- r2- r tx ) a 2+ 2 rx a -r = 0 (3.13.9) where r = t - x Sin ce equation (3.13.9) is not directly solvable for a, som e iteration m ethod such as the N e w to n -R a p h so n m ethod can be used for estim ating a. Putting this va lu e o f a in (3.13.7) the estimate o f 0 can be obtained, substituting the estim ate o f a and 0 in (3.13.3) the estimate o f p can be obtained and fin ally from (3.13.2) an estimate o f m can be obtained.
38 Estimation o f Parameters o f Zero-truncated GNBD T he probability m ass function o f zero-truncated generalized negative binom ial distribution ( Z T G N B D ) is given by P3[X = x] = m m + px m + px v x j 0 X ( i _ 0 ) m+px-x p ^ _ e r p x = 1,2,3,... ( ) 0 < 0 < 1, 0 p < 1, m > 0 = 0, for x > t such that m + pt < t T he Z T G N B D probability m ass function as quoted in ( ) clearly assumes the value zero as m entioned in the conditions for all values o f x = t resulting into m + pt < t. T a k in g the highest observed value h aving non-zero frequency as n and c o n sid e rin g m + pn = n, w e obtain m in terms o f n and p as m = n (1 - P) ( ) Since m > 0, n > 0, the value o f p w ill alw ays lie between 0 and 1. T he first and second m om ents about origin o f Z T G N B D is given respectively b y t ; = m 0 ( i - e p ) ( i - ( i - e r ] ( ) and v 2 m9(l - 9) m?92 (i - op)3 [l - (i - e)m] (i - ep)3[i - (i - 9)3] ( ) From ( ) w e get T ' = T,' 1-0 m 0 + (1-9(3) (1 9p) J putting T I 1-9 m9 1 - e p = a, w e g e t ^ = + V ( ) w hich on sim p lific a tio n u sin g ( ) give s T' (1-0)(1 - an) - n = j t; a 2 L = (1-0)(1 - an) ( ) a 117
39 T ' where L = i - n ( ) From ( ), w e get 1-0 = 0 = 1 L a 2 (1 - a n ) L a a n ( ) A g a in from ( ) w e have, 0 + a - l = a 1 - a n 1+ (n + L )a ( ) and 0 + a - l a [ l - ( n + L )a ] a n - L a ( ) Substituting the values from ( ), ( ) and ( ) in ( ), w e get T = (1 - a n ) 1 - n [ l - ( n + L )a ] r La2 /, r 2. a n - ( n + L ) a n 1- n a / 1- a n - L a ' w hich give s on sim p lificatio n a function o f a, say f(a ) as f(a ) = L o g 1 - n[l - ( n + L )a ] (1 - na)t,' an[l-(n + L)a]Log_La 2 =0 (3, 3 2Q) 1 - a n - L a (1 - a n ) F o r estim ating the parameters, the population m om ents T,' and are replaced b y sam ple m om ents x and s'2 thus the equation becom es f (a ) = L o g 1 - n[l - (n + ^)a] (1 - n a )x a n [ l - ( n + Q a ] Lo ( a 1 - a n - t o 2 (1 - n a) = 0 w here = ^ - n ( ) x T h is is an equation in a w h ic h does not appear to be solved directly for a. It can be v e rifie d e a sily that one o f the roots o f this equation lies at a = ^ (n + K ) w h ic h im p lie s that a 1 0 and so p is alw ays unity. O b viously, 118
40 this root w ill not solve our purpose and so, we need another root o f equation. F o r this som e iteration m ethods preferably the R e gula -F a lsi method can be used. U s in g the R e g u la -F a lsi m ethod that the value o f a is obtained for w hich the value o f the function is sufficiently near to zero. Putting this value o f a in ( ) an estimate o f 9 can be obtained. U sin g the estimate o f 0 and a an estimate o f f>can be obtained and finally u sin g ( ) an estimate o f m can be obtained. 3.14: G o o d n e ss o f F it A n attempt has been m ade to study the adequacy o f the zero-truncated G N B D to describe the distribution o f the num ber o f households w hen the num ber o f h ouseholds w ith no m igrant is not available. It has also been tried to fit an alternative to zero truncated G N B D ( Z T G N B D ) and size-biased G N B D ( S B G N B D ) to the sam e data sets. O n fitting, it is found that the S B G N B D describes the distribution o f num ber o f households according to the num ber o f m igrants w hen the num ber o f households with no m igrants is not available, in a better w a y than the Z T G N B D. T h is m ay be probably because o f the general nature o f m igration, w h ich occurs in batches and it increases in proportion to its sizes. Theoretically, S B G N B D is best suited for the m igration data w hen the house h old w ith no m igrants is not know n. T he results have been show n below. 119
41 Table Observed and expected number of households of size group 10 and above having at least one migrant. Number of migrants Observed number of households Expected number of households SBGNBD ZTGNBD ^ 6.86 ^ ^ 9.95 > J 0.50 J Total M e a n x d.f 2 2 P(x2) A A P A m
42 Table Observed and expected number of households of size group 16 and above having at least one migrant. Number of Observed Expected number of households migrants number of SBGNBD ZTGNBD households ' 4.26 > 4.56 " r 6 > 7.31 > > , Total M e a n 2.56 x d.f 2 2 P (x 2) p ^ O b v io u sly, the S B G N B D provides better fits to the observed distributions than to Z T G N B D. M ore o ve r, it is relatively very quick to be obtained and so it m ay be preferred to others w here very quick results are required. 121
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
c. What is the average rate of change of f on the interval [, ]? Answer: d. What is a local minimum value of f? Answer: 5 e. On what interval(s) is f
![c. What is the average rate of change of f on the interval [, ]? Answer: d. What is a local minimum value of f? Answer: 5 e. On what interval(s) is f c. What is the average rate of change of f on the interval [, ]? Answer: d. What is a local minimum value of f? Answer: 5 e. On what interval(s) is f](/thumbs/87/95703678.jpg) Essential Skills Chapter f ( x + h) f ( x ). Simplifying the difference quotient Section. h f ( x + h) f ( x ) Example: For f ( x) = 4x 4 x, find and simplify completely. h Answer: 4 8x 4 h. Finding the
Essential Skills Chapter f ( x + h) f ( x ). Simplifying the difference quotient Section. h f ( x + h) f ( x ) Example: For f ( x) = 4x 4 x, find and simplify completely. h Answer: 4 8x 4 h. Finding the
C o r p o r a t e l i f e i n A n c i e n t I n d i a e x p r e s s e d i t s e l f
 C H A P T E R I G E N E S I S A N D GROWTH OF G U IL D S C o r p o r a t e l i f e i n A n c i e n t I n d i a e x p r e s s e d i t s e l f i n a v a r i e t y o f f o r m s - s o c i a l, r e l i g i
C H A P T E R I G E N E S I S A N D GROWTH OF G U IL D S C o r p o r a t e l i f e i n A n c i e n t I n d i a e x p r e s s e d i t s e l f i n a v a r i e t y o f f o r m s - s o c i a l, r e l i g i
The Ability C ongress held at the Shoreham Hotel Decem ber 29 to 31, was a reco rd breaker for winter C ongresses.
 The Ability C ongress held at the Shoreham Hotel Decem ber 29 to 31, was a reco rd breaker for winter C ongresses. Attended by m ore than 3 00 people, all seem ed delighted, with the lectu res and sem
The Ability C ongress held at the Shoreham Hotel Decem ber 29 to 31, was a reco rd breaker for winter C ongresses. Attended by m ore than 3 00 people, all seem ed delighted, with the lectu res and sem
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
S ca le M o d e l o f th e S o la r Sy ste m
 N a m e ' D a t e ' S ca le M o d e l o f th e S o la r Sy ste m 6.1 I n t r o d u c t i o n T h e S olar System is large, at least w hen com pared to distances we are fam iliar w ith on a day-to-day basis.
N a m e ' D a t e ' S ca le M o d e l o f th e S o la r Sy ste m 6.1 I n t r o d u c t i o n T h e S olar System is large, at least w hen com pared to distances we are fam iliar w ith on a day-to-day basis.
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
 A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
Form and content. Iowa Research Online. University of Iowa. Ann A Rahim Khan University of Iowa. Theses and Dissertations
 University of Iowa Iowa Research Online Theses and Dissertations 1979 Form and content Ann A Rahim Khan University of Iowa Posted with permission of the author. This thesis is available at Iowa Research
University of Iowa Iowa Research Online Theses and Dissertations 1979 Form and content Ann A Rahim Khan University of Iowa Posted with permission of the author. This thesis is available at Iowa Research
Procedures for Computing Classification Consistency and Accuracy Indices with Multiple Categories
 esearcli R eport Semes 2 0 0 0 Procedures for Computing Classification Consistency and Accuracy Indices with Multiple Categories Won-Chan Lee Bradley A. Hanson Robert L. Brennan ACT O c t o b e r For additional
esearcli R eport Semes 2 0 0 0 Procedures for Computing Classification Consistency and Accuracy Indices with Multiple Categories Won-Chan Lee Bradley A. Hanson Robert L. Brennan ACT O c t o b e r For additional
LSU Historical Dissertations and Theses
 Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1976 Infestation of Root Nodules of Soybean by Larvae of the Bean Leaf Beetle, Cerotoma Trifurcata
Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1976 Infestation of Root Nodules of Soybean by Larvae of the Bean Leaf Beetle, Cerotoma Trifurcata
Few thoughts on PFA, from the calorim etric point of view
 1 Few thoughts on PFA, from the calorim etric point of view discussing pad siz e, M oliere radius, distance from the interaction point. H enri Videau 2 H ave you had anytim e a close view at show ers?
1 Few thoughts on PFA, from the calorim etric point of view discussing pad siz e, M oliere radius, distance from the interaction point. H enri Videau 2 H ave you had anytim e a close view at show ers?
Grain Reserves, Volatility and the WTO
 Grain Reserves, Volatility and the WTO Sophia Murphy Institute for Agriculture and Trade Policy www.iatp.org Is v o la tility a b a d th in g? De pe n d s o n w h e re yo u s it (pro d uc e r, tra d e
Grain Reserves, Volatility and the WTO Sophia Murphy Institute for Agriculture and Trade Policy www.iatp.org Is v o la tility a b a d th in g? De pe n d s o n w h e re yo u s it (pro d uc e r, tra d e
Executive Committee and Officers ( )
 Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o
 I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
Nov Julien Michel
 Int roduct ion t o Free Ene rgy Calculat ions ov. 2005 Julien Michel Predict ing Binding Free Energies A A Recept or B B Recept or Can we predict if A or B will bind? Can we predict the stronger binder?
Int roduct ion t o Free Ene rgy Calculat ions ov. 2005 Julien Michel Predict ing Binding Free Energies A A Recept or B B Recept or Can we predict if A or B will bind? Can we predict the stronger binder?
What are S M U s? SMU = Software Maintenance Upgrade Software patch del iv ery u nit wh ich once ins tal l ed and activ ated prov ides a point-fix for
 SMU 101 2 0 0 7 C i s c o S y s t e m s, I n c. A l l r i g h t s r e s e r v e d. 1 What are S M U s? SMU = Software Maintenance Upgrade Software patch del iv ery u nit wh ich once ins tal l ed and activ
SMU 101 2 0 0 7 C i s c o S y s t e m s, I n c. A l l r i g h t s r e s e r v e d. 1 What are S M U s? SMU = Software Maintenance Upgrade Software patch del iv ery u nit wh ich once ins tal l ed and activ
LU N C H IN C LU D E D
 Week 1 M o n d a y J a n u a ry 7 - C o lo u rs o f th e R a in b o w W e w ill b e k ic k in g o ff th e h o lid a y s w ith a d a y fu ll o f c o lo u r! J o in u s fo r a ra n g e o f a rt, s p o rt
Week 1 M o n d a y J a n u a ry 7 - C o lo u rs o f th e R a in b o w W e w ill b e k ic k in g o ff th e h o lid a y s w ith a d a y fu ll o f c o lo u r! J o in u s fo r a ra n g e o f a rt, s p o rt
M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7; ;J zy U;K z< mj ]!.,,+7;
![M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7; ;J zy U;K z< mj ]!.,,+7; M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7; ;J zy U;K z< mj ]!.,,+7;](/thumbs/78/78216077.jpg) V 3U. T, SK I 1393/08/21 :,F! 1393/10/29 ::!n> 2 1 /M + - /E+4q; Z R :'!3Qi M $,7 8$ 4,!AK 4 4/ * /;K "FA ƒf\,7 /;G2 @;J\ M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7;
V 3U. T, SK I 1393/08/21 :,F! 1393/10/29 ::!n> 2 1 /M + - /E+4q; Z R :'!3Qi M $,7 8$ 4,!AK 4 4/ * /;K "FA ƒf\,7 /;G2 @;J\ M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7;
Beechwood Music Department Staff
 Beechwood Music Department Staff MRS SARAH KERSHAW - HEAD OF MUSIC S a ra h K e rs h a w t r a i n e d a t t h e R oy a l We ls h C o l le g e of M u s i c a n d D ra m a w h e re s h e ob t a i n e d
Beechwood Music Department Staff MRS SARAH KERSHAW - HEAD OF MUSIC S a ra h K e rs h a w t r a i n e d a t t h e R oy a l We ls h C o l le g e of M u s i c a n d D ra m a w h e re s h e ob t a i n e d
Last 4 Digits of USC ID:
 Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
EKOLOGIE EN SYSTEMATIEK. T h is p a p e r n o t to be c i t e d w ith o u t p r i o r r e f e r e n c e to th e a u th o r. PRIMARY PRODUCTIVITY.
 EKOLOGIE EN SYSTEMATIEK Ç.I.P.S. MATHEMATICAL MODEL OF THE POLLUTION IN NORT H SEA. TECHNICAL REPORT 1971/O : B i o l. I T h is p a p e r n o t to be c i t e d w ith o u t p r i o r r e f e r e n c e to
EKOLOGIE EN SYSTEMATIEK Ç.I.P.S. MATHEMATICAL MODEL OF THE POLLUTION IN NORT H SEA. TECHNICAL REPORT 1971/O : B i o l. I T h is p a p e r n o t to be c i t e d w ith o u t p r i o r r e f e r e n c e to
Sodium-Initiated Polymerization of Alpha- Methylstyrene in the Vicinity of Its Reported Ceiling Temperature
 Western Michigan University ScholarWorks at WMU Dissertations Graduate College 8-1976 Sodium-Initiated Polymerization of Alpha- Methylstyrene in the Vicinity of Its Reported Ceiling Temperature Shuenn-long
Western Michigan University ScholarWorks at WMU Dissertations Graduate College 8-1976 Sodium-Initiated Polymerization of Alpha- Methylstyrene in the Vicinity of Its Reported Ceiling Temperature Shuenn-long
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
S U E K E AY S S H A R O N T IM B E R W IN D M A R T Z -PA U L L IN. Carlisle Franklin Springboro. Clearcreek TWP. Middletown. Turtlecreek TWP.
 F R A N K L IN M A D IS O N S U E R O B E R T LE IC H T Y A LY C E C H A M B E R L A IN T W IN C R E E K M A R T Z -PA U L L IN C O R A O W E N M E A D O W L A R K W R E N N LA N T IS R E D R O B IN F
F R A N K L IN M A D IS O N S U E R O B E R T LE IC H T Y A LY C E C H A M B E R L A IN T W IN C R E E K M A R T Z -PA U L L IN C O R A O W E N M E A D O W L A R K W R E N N LA N T IS R E D R O B IN F
Functional pottery [slide]
![Functional pottery [slide] Functional pottery [slide]](/thumbs/89/99193754.jpg) Functional pottery [slide] by Frank Bevis Fabens A thesis submitted in partial fulfillment of the requirements for the degree of Master of Fine Arts Montana State University Copyright by Frank Bevis Fabens
Functional pottery [slide] by Frank Bevis Fabens A thesis submitted in partial fulfillment of the requirements for the degree of Master of Fine Arts Montana State University Copyright by Frank Bevis Fabens
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
 Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr
 Chemistry 05 B First Letter of PLEASE PRINT YOUR NAME IN BLOCK LETTERS Exam last Name Name: 02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr Lab TA s Name: Question Points Score Grader 2 2 9 3 9 4 2
Chemistry 05 B First Letter of PLEASE PRINT YOUR NAME IN BLOCK LETTERS Exam last Name Name: 02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr Lab TA s Name: Question Points Score Grader 2 2 9 3 9 4 2
f;g,7k ;! / C+!< 8R+^1 ;0$ Z\ \ K S;4 i!;g + 5 ;* \ C! 1+M, /A+1+> 0 /A+>! 8 J 4! 9,7 )F C!.4 ;* )F /0 u+\ 30< #4 8 J C!
 393/09/0 393//07 :,F! ::!n> b]( a.q 5 O +D5 S ١ ; ;* :'!3Qi C+0;$ < "P 4 ; M V! M V! ; a 4 / ;0$ f;g,7k ;! / C+!< 8R+^ ;0$ Z\ \ K S;4 "* < 8c0 5 *
393/09/0 393//07 :,F! ::!n> b]( a.q 5 O +D5 S ١ ; ;* :'!3Qi C+0;$ < "P 4 ; M V! M V! ; a 4 / ;0$ f;g,7k ;! / C+!< 8R+^ ;0$ Z\ \ K S;4 "* < 8c0 5 *
H STO RY OF TH E SA NT
 O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
O RY OF E N G L R R VER ritten for the entennial of th e Foundin g of t lair oun t y on ay 8 82 Y EEL N E JEN K RP O N! R ENJ F ] jun E 3 1 92! Ph in t ed b y h e t l a i r R ep u b l i c a n O 4 1922
SPU TTERIN G F R O M A LIQ U ID -PH A SE G A -IN EUTECTIC ALLOY KEVIN M A R K H U B B A R D YALE UNIVER SITY M A Y
 SPU TTERIN G F R O M A LIQ U ID -PH A SE G A -IN EUTECTIC ALLOY KEVIN M A R K H U B B A R D YALE UNIVER SITY M A Y 1 9 8 9 ABSTRACT S p u t t e r i n g f r o m a L i q u i d - P h a s e G a - I n E u t
SPU TTERIN G F R O M A LIQ U ID -PH A SE G A -IN EUTECTIC ALLOY KEVIN M A R K H U B B A R D YALE UNIVER SITY M A Y 1 9 8 9 ABSTRACT S p u t t e r i n g f r o m a L i q u i d - P h a s e G a - I n E u t
Speed of light c = m/s. x n e a x d x = 1. 2 n+1 a n π a. He Li Ne Na Ar K Ni 58.
 Physical Chemistry II Test Name: KEY CHEM 464 Spring 18 Chapters 7-11 Average = 1. / 16 6 questions worth a total of 16 points Planck's constant h = 6.63 1-34 J s Speed of light c = 3. 1 8 m/s ħ = h π
Physical Chemistry II Test Name: KEY CHEM 464 Spring 18 Chapters 7-11 Average = 1. / 16 6 questions worth a total of 16 points Planck's constant h = 6.63 1-34 J s Speed of light c = 3. 1 8 m/s ħ = h π
Class Diagrams. CSC 440/540: Software Engineering Slide #1
 Class Diagrams CSC 440/540: Software Engineering Slide # Topics. Design class diagrams (DCDs) 2. DCD development process 3. Associations and Attributes 4. Dependencies 5. Composition and Constraints 6.
Class Diagrams CSC 440/540: Software Engineering Slide # Topics. Design class diagrams (DCDs) 2. DCD development process 3. Associations and Attributes 4. Dependencies 5. Composition and Constraints 6.
REFUGEE AND FORCED MIGRATION STUDIES
 THE OXFORD HANDBOOK OF REFUGEE AND FORCED MIGRATION STUDIES Edited by ELENA FIDDIAN-QASMIYEH GIL LOESCHER KATY LONG NANDO SIGONA OXFORD UNIVERSITY PRESS C o n t e n t s List o f Abbreviations List o f
THE OXFORD HANDBOOK OF REFUGEE AND FORCED MIGRATION STUDIES Edited by ELENA FIDDIAN-QASMIYEH GIL LOESCHER KATY LONG NANDO SIGONA OXFORD UNIVERSITY PRESS C o n t e n t s List o f Abbreviations List o f
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
 Lesson seven What is a chemical reaction? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading Informational Text,
Lesson seven What is a chemical reaction? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading Informational Text,
Solutions and Ions. Pure Substances
 Class #4 Solutions and Ions CHEM 107 L.S. Brown Texas A&M University Pure Substances Pure substance: described completely by a single chemical formula Fixed composition 1 Mixtures Combination of 2 or more
Class #4 Solutions and Ions CHEM 107 L.S. Brown Texas A&M University Pure Substances Pure substance: described completely by a single chemical formula Fixed composition 1 Mixtures Combination of 2 or more
A Comparison of Two Methods of Teaching Computer Programming to Secondary Mathematics Students.
 Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1983 A Comparison of Two Methods of Teaching Computer Programming to Secondary Mathematics Students.
Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1983 A Comparison of Two Methods of Teaching Computer Programming to Secondary Mathematics Students.
STEEL PIPE NIPPLE BLACK AND GALVANIZED
 Price Sheet Effective August 09, 2018 Supersedes CWN-218 A Member of The Phoenix Forge Group CapProducts LTD. Phone: 519-482-5000 Fax: 519-482-7728 Toll Free: 800-265-5586 www.capproducts.com www.capitolcamco.com
Price Sheet Effective August 09, 2018 Supersedes CWN-218 A Member of The Phoenix Forge Group CapProducts LTD. Phone: 519-482-5000 Fax: 519-482-7728 Toll Free: 800-265-5586 www.capproducts.com www.capitolcamco.com
Ash Wednesday. First Introit thing. * Dómi- nos. di- di- nos, tú- ré- spi- Ps. ne. Dó- mi- Sál- vum. intra-vé-runt. Gló- ri-
 sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
PRISON POLICY INITIATIVE ANNUAL REPORT
 PRISON POLICY INITIATIVE 2015-2016 2016-2017 ANNUAL REPORT N 2016 2017 PO Bx 127 N MA 01061 :// (413) 527-0845 1 T Ex D 1 W 3 P k 4 C R - 7 S j 8 B j 10 P x 12 P j 14 P 16 Wk 18 C x 19 Y P Nk S R 15 B
PRISON POLICY INITIATIVE 2015-2016 2016-2017 ANNUAL REPORT N 2016 2017 PO Bx 127 N MA 01061 :// (413) 527-0845 1 T Ex D 1 W 3 P k 4 C R - 7 S j 8 B j 10 P x 12 P j 14 P 16 Wk 18 C x 19 Y P Nk S R 15 B
Rebecca G. Frederick L ouisiana State U niversity D epartm ent of E xperim ental Statistics
 USING ODS W ITH PROC UNIVARIATE Rebecca G. Frederick L ouisiana State U niversity D epartm ent of E xperim ental Statistics South CentralS A S U sers G roup 1 ABSTRACT P ro c U n iv a ria te is u se d
USING ODS W ITH PROC UNIVARIATE Rebecca G. Frederick L ouisiana State U niversity D epartm ent of E xperim ental Statistics South CentralS A S U sers G roup 1 ABSTRACT P ro c U n iv a ria te is u se d
CHEM 10113, Quiz 5 October 26, 2011
 CHEM 10113, Quiz 5 October 26, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
CHEM 10113, Quiz 5 October 26, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
Alles Taylor & Duke, LLC Bob Wright, PE RECORD DRAWINGS. CPOW Mini-Ed Conf er ence Mar ch 27, 2015
 RECORD DRAWINGS CPOW Mini-Ed Conf er ence Mar ch 27, 2015 NOMENCLATURE: Record Draw ings?????? What Hap p ened t o As- Built s?? PURPOSE: Fur n ish a Reco r d o f Co m p o n en t s Allo w Locat io n o
RECORD DRAWINGS CPOW Mini-Ed Conf er ence Mar ch 27, 2015 NOMENCLATURE: Record Draw ings?????? What Hap p ened t o As- Built s?? PURPOSE: Fur n ish a Reco r d o f Co m p o n en t s Allo w Locat io n o
(please print) (1) (18) H IIA IIIA IVA VA VIA VIIA He (2) (13) (14) (15) (16) (17)
 CHEM 10113, Quiz 3 September 28, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
CHEM 10113, Quiz 3 September 28, 2011 Name (please print) All equations must be balanced and show phases for full credit. Significant figures count, show charges as appropriate, and please box your answers!
5 questions, 3 points each, 15 points total possible. 26 Fe Cu Ni Co Pd Ag Ru 101.
 Physical Chemistry II Lab CHEM 4644 spring 2017 final exam KEY 5 questions, 3 points each, 15 points total possible h = 6.626 10-34 J s c = 3.00 10 8 m/s 1 GHz = 10 9 s -1. B= h 8π 2 I ν= 1 2 π k μ 6 P
Physical Chemistry II Lab CHEM 4644 spring 2017 final exam KEY 5 questions, 3 points each, 15 points total possible h = 6.626 10-34 J s c = 3.00 10 8 m/s 1 GHz = 10 9 s -1. B= h 8π 2 I ν= 1 2 π k μ 6 P
INSTRUCTIONS: Exam III. November 10, 1999 Lab Section
 CHEM 1215 Exam III John III. Gelder November 10, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last page includes a periodic table and
CHEM 1215 Exam III John III. Gelder November 10, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last page includes a periodic table and
Software Process Models there are many process model s in th e li t e ra t u re, s om e a r e prescriptions and some are descriptions you need to mode
 Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
What is the periodic table?
 The periodic table of the elements represents one of the greatest discoveries in the history of science that certain elements, the basic chemical substances from which all matter is made, resemble each
The periodic table of the elements represents one of the greatest discoveries in the history of science that certain elements, the basic chemical substances from which all matter is made, resemble each
Agenda Rationale for ETG S eek ing I d eas ETG fram ew ork and res u lts 2
 Internal Innovation @ C is c o 2 0 0 6 C i s c o S y s t e m s, I n c. A l l r i g h t s r e s e r v e d. C i s c o C o n f i d e n t i a l 1 Agenda Rationale for ETG S eek ing I d eas ETG fram ew ork
Internal Innovation @ C is c o 2 0 0 6 C i s c o S y s t e m s, I n c. A l l r i g h t s r e s e r v e d. C i s c o C o n f i d e n t i a l 1 Agenda Rationale for ETG S eek ing I d eas ETG fram ew ork
1K21 LED GR N +33V 604R VR? 1K0 -33V -33V 0R0 MUTE SWTH? JA? T1 T2 RL? +33V 100R A17 CB? 1N N RB? 2K0 QBI? OU T JE182 4K75 RB? 1N914 D?
 L P.O. O X 0, N L R. PROROUH, ONRIO N KJ Y PHO N (0) FX (0) 0 WWW.RYSON. ate : Size : 000 File : OVRLL SHMI.Schoc Sheet : 0 of 0 Rev : rawn : 0.0 0K K 0K K 0K0 0K0 0K0 0K0 0K0 00K R K0 R K 0R??? 00N M?
L P.O. O X 0, N L R. PROROUH, ONRIO N KJ Y PHO N (0) FX (0) 0 WWW.RYSON. ate : Size : 000 File : OVRLL SHMI.Schoc Sheet : 0 of 0 Rev : rawn : 0.0 0K K 0K K 0K0 0K0 0K0 0K0 0K0 00K R K0 R K 0R??? 00N M?
UNCLASSIFIED Reptoduced. if ike ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED
 . UNCLASSIFIED. 273207 Reptoduced if ike ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED NOTICE: When government or other drawings, specifications
. UNCLASSIFIED. 273207 Reptoduced if ike ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED NOTICE: When government or other drawings, specifications
Measure-theoretic probability
 Measure-theoretic probability Koltay L. VEGTMAM144B November 28, 2012 (VEGTMAM144B) Measure-theoretic probability November 28, 2012 1 / 27 The probability space De nition The (Ω, A, P) measure space is
Measure-theoretic probability Koltay L. VEGTMAM144B November 28, 2012 (VEGTMAM144B) Measure-theoretic probability November 28, 2012 1 / 27 The probability space De nition The (Ω, A, P) measure space is
INTERIM MANAGEMENT REPORT FIRST HALF OF 2018
 INTERIM MANAGEMENT REPORT FIRST HALF OF 2018 F r e e t r a n s l a t ion f r o m t h e o r ig ina l in S p a n is h. I n t h e e v e n t o f d i s c r e p a n c y, t h e Sp a n i s h - la n g u a g e v
INTERIM MANAGEMENT REPORT FIRST HALF OF 2018 F r e e t r a n s l a t ion f r o m t h e o r ig ina l in S p a n is h. I n t h e e v e n t o f d i s c r e p a n c y, t h e Sp a n i s h - la n g u a g e v
Circle the letters only. NO ANSWERS in the Columns!
 Chemistry 1304.001 Name (please print) Exam 5 (100 points) April 18, 2018 On my honor, I have neither given nor received unauthorized aid on this exam. Signed Date Circle the letters only. NO ANSWERS in
Chemistry 1304.001 Name (please print) Exam 5 (100 points) April 18, 2018 On my honor, I have neither given nor received unauthorized aid on this exam. Signed Date Circle the letters only. NO ANSWERS in
Lab Day and Time: Instructions. 1. Do not open the exam until you are told to start.
 Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
EC 219 SA M PLING AND INFERENCE. One and One HalfH ours (1 1 2 H ours) Answerallparts ofquestion 1,and ONE other question.
 ECONOM ICS EC 219 SA M PLING AND INFERENCE One and One HalfH ours (1 1 2 H ours) Answerallparts ofquestion 1,and ONE other question. M athem aticaland Statisticaltables are provided. An approved calculatormay
ECONOM ICS EC 219 SA M PLING AND INFERENCE One and One HalfH ours (1 1 2 H ours) Answerallparts ofquestion 1,and ONE other question. M athem aticaland Statisticaltables are provided. An approved calculatormay
The Ind ian Mynah b ird is no t fro m Vanuat u. It w as b ro ug ht here fro m overseas and is now causing lo t s o f p ro b lem s.
 The Ind ian Mynah b ird is no t fro m Vanuat u. It w as b ro ug ht here fro m overseas and is now causing lo t s o f p ro b lem s. Mynah b ird s p ush out nat ive b ird s, com p et ing for food and p laces
The Ind ian Mynah b ird is no t fro m Vanuat u. It w as b ro ug ht here fro m overseas and is now causing lo t s o f p ro b lem s. Mynah b ird s p ush out nat ive b ird s, com p et ing for food and p laces
Structural Properties of Generalized Negative Binomial
 C H A P T E R - Structural Properties of Generalized Negative Binoial \ / / Distribution 2.1. ntroduction The usefulness o f a distribution to a greater extent rests on its structural properties and the
C H A P T E R - Structural Properties of Generalized Negative Binoial \ / / Distribution 2.1. ntroduction The usefulness o f a distribution to a greater extent rests on its structural properties and the
Guide to the Extended Step-Pyramid Periodic Table
 Guide to the Extended Step-Pyramid Periodic Table William B. Jensen Department of Chemistry University of Cincinnati Cincinnati, OH 452201-0172 The extended step-pyramid table recognizes that elements
Guide to the Extended Step-Pyramid Periodic Table William B. Jensen Department of Chemistry University of Cincinnati Cincinnati, OH 452201-0172 The extended step-pyramid table recognizes that elements
THIS PAGE DECLASSIFIED IAW EO IRIS u blic Record. Key I fo mation. Ma n: AIR MATERIEL COMM ND. Adm ni trative Mar ings.
 T H S PA G E D E CLA SSFED AW E O 2958 RS u blc Recod Key fo maon Ma n AR MATEREL COMM ND D cumen Type Call N u b e 03 V 7 Rcvd Rel 98 / 0 ndexe D 38 Eneed Dae RS l umbe 0 0 4 2 3 5 6 C D QC d Dac A cesson
T H S PA G E D E CLA SSFED AW E O 2958 RS u blc Recod Key fo maon Ma n AR MATEREL COMM ND D cumen Type Call N u b e 03 V 7 Rcvd Rel 98 / 0 ndexe D 38 Eneed Dae RS l umbe 0 0 4 2 3 5 6 C D QC d Dac A cesson
Years. Marketing without a plan is like navigating a maze; the solution is unclear.
 F Q 2018 E Mk l lk z; l l Mk El M C C 1995 O Y O S P R j lk q D C Dl Off P W H S P W Sl M Y Pl Cl El M Cl FIRST QUARTER 2018 E El M & D I C/O Jff P RGD S C D M Sl 57 G S Alx ON K0C 1A0 C Tl: 6134821159
F Q 2018 E Mk l lk z; l l Mk El M C C 1995 O Y O S P R j lk q D C Dl Off P W H S P W Sl M Y Pl Cl El M Cl FIRST QUARTER 2018 E El M & D I C/O Jff P RGD S C D M Sl 57 G S Alx ON K0C 1A0 C Tl: 6134821159
CHEM 10123/10125, Exam 2
 CHEM 10123/10125, Exam 2 March 7, 2012 (50 minutes) Name (please print) Please box your answers, and remember that significant figures, phases (for chemical equations), and units do count! 1. (13 points)
CHEM 10123/10125, Exam 2 March 7, 2012 (50 minutes) Name (please print) Please box your answers, and remember that significant figures, phases (for chemical equations), and units do count! 1. (13 points)
CMSC 313 Lecture 17 Postulates & Theorems of Boolean Algebra Semiconductors CMOS Logic Gates
 CMSC 313 Lecture 17 Postulates & Theorems of Boolean Algebra Semiconductors CMOS Logic Gates UMBC, CMSC313, Richard Chang Last Time Overview of second half of this course Logic gates &
CMSC 313 Lecture 17 Postulates & Theorems of Boolean Algebra Semiconductors CMOS Logic Gates UMBC, CMSC313, Richard Chang Last Time Overview of second half of this course Logic gates &
Generating and characteristic functions. Generating and Characteristic Functions. Probability generating function. Probability generating function
 Generating and characteristic functions Generating and Characteristic Functions September 3, 03 Probability generating function Moment generating function Power series expansion Characteristic function
Generating and characteristic functions Generating and Characteristic Functions September 3, 03 Probability generating function Moment generating function Power series expansion Characteristic function
Table of C on t en t s Global Campus 21 in N umbe r s R e g ional Capac it y D e v e lopme nt in E-L e ar ning Structure a n d C o m p o n en ts R ea
 G Blended L ea r ni ng P r o g r a m R eg i o na l C a p a c i t y D ev elo p m ent i n E -L ea r ni ng H R K C r o s s o r d e r u c a t i o n a n d v e l o p m e n t C o p e r a t i o n 3 0 6 0 7 0 5
G Blended L ea r ni ng P r o g r a m R eg i o na l C a p a c i t y D ev elo p m ent i n E -L ea r ni ng H R K C r o s s o r d e r u c a t i o n a n d v e l o p m e n t C o p e r a t i o n 3 0 6 0 7 0 5
8. Relax and do well.
 CHEM 15 Exam II John II. Gelder March 4, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last two pages includes a periodic table, a solubility
CHEM 15 Exam II John II. Gelder March 4, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last two pages includes a periodic table, a solubility
(C) Pavel Sedach and Prep101 1
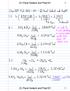 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach
(C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach
8. Relax and do well.
 CHEM 1515 Exam II John II. Gelder October 14, 1993 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 8 different pages. The last two pages include a periodic table, a
CHEM 1515 Exam II John II. Gelder October 14, 1993 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 8 different pages. The last two pages include a periodic table, a
8. Relax and do well.
 CHEM 1014 Exam I John I. Gelder September 16, 1999 Name TA's Name Lab Section Please sign your name below to give permission to post your course scores on homework, laboratories and exams. If you do not
CHEM 1014 Exam I John I. Gelder September 16, 1999 Name TA's Name Lab Section Please sign your name below to give permission to post your course scores on homework, laboratories and exams. If you do not
8. Relax and do well.
 CHEM 1225 Exam III John III. Gelder April 8, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last two pages includes a periodic table and
CHEM 1225 Exam III John III. Gelder April 8, 1999 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last two pages includes a periodic table and
HANDOUT SET GENERAL CHEMISTRY II
 HANDOUT SET GENERAL CHEMISTRY II Periodic Table of the Elements 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 IA VIIIA 1 2 H He 1.00794 IIA IIIA IVA VA VIA VIIA 4.00262 3 Li 6.941 11 Na 22.9898
HANDOUT SET GENERAL CHEMISTRY II Periodic Table of the Elements 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 IA VIIIA 1 2 H He 1.00794 IIA IIIA IVA VA VIA VIIA 4.00262 3 Li 6.941 11 Na 22.9898
30 Zn(s) 45 Rh. Pd(s) Ag(s) Cd(s) In(s) Sn(s) white. 77 Ir. Pt(s) Au. Hg(l) Tl. 109 Mt. 111 Uuu. 112 Uub. 110 Uun. 65 Tb. 62 Sm. 64 Gd. 63 Eu.
 Enthalpy changes: experimentally it is much easier to measure heat flow at const pressure - this is enthalpy q p = )H : also nearly all chemical reactions are done at constant pressure. Enthalpy (heat)
Enthalpy changes: experimentally it is much easier to measure heat flow at const pressure - this is enthalpy q p = )H : also nearly all chemical reactions are done at constant pressure. Enthalpy (heat)
8. Relax and do well.
 CHEM 1215 Exam III John III. Gelder November 11, 1998 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last page includes a periodic table and
CHEM 1215 Exam III John III. Gelder November 11, 1998 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 7 different pages. The last page includes a periodic table and
K. 27 Co. 28 Ni. 29 Cu Rb. 46 Pd. 45 Rh. 47 Ag Cs Ir. 78 Pt.
 1 IA 1 ydrogen 1.01 Atomic number Element symbol Element name Atomic mass VIIIA 1 1.01 IIA IIIA IVA VA VIA VIIA 2 e 4.00 Metalloids 3 Li 6.94 4 Be 9.01 5 B 10.81 6 C 12.01 7 N 14.01 8 O 16.00 9 F 19.00
1 IA 1 ydrogen 1.01 Atomic number Element symbol Element name Atomic mass VIIIA 1 1.01 IIA IIIA IVA VA VIA VIIA 2 e 4.00 Metalloids 3 Li 6.94 4 Be 9.01 5 B 10.81 6 C 12.01 7 N 14.01 8 O 16.00 9 F 19.00
EXPANSION OF ANALYTIC FUNCTIONS IN TERMS INVOLVING LUCAS NUMBERS OR SIMILAR NUMBER SEQUENCES
 EXPANSION OF ANALYTIC FUNCTIONS IN TERMS INVOLVING LUCAS NUMBERS OR SIMILAR NUMBER SEQUENCES PAUL F. BYRD San Jose State College, San Jose, California 1. INTRODUCTION In a previous article [_ 1J, certain
EXPANSION OF ANALYTIC FUNCTIONS IN TERMS INVOLVING LUCAS NUMBERS OR SIMILAR NUMBER SEQUENCES PAUL F. BYRD San Jose State College, San Jose, California 1. INTRODUCTION In a previous article [_ 1J, certain
CHEM 108 (Spring-2008) Exam. 3 (105 pts)
 CHEM 08 (Spring-008) Exam. (05 pts) Name: --------------------------------------------------------------------------, CLID # -------------------------------- LAST NAME, First (Circle the alphabet segment
CHEM 08 (Spring-008) Exam. (05 pts) Name: --------------------------------------------------------------------------, CLID # -------------------------------- LAST NAME, First (Circle the alphabet segment
o Alphabet Recitation
 Letter-Sound Inventory (Record Sheet #1) 5-11 o Alphabet Recitation o Alphabet Recitation a b c d e f 9 h a b c d e f 9 h j k m n 0 p q k m n 0 p q r s t u v w x y z r s t u v w x y z 0 Upper Case Letter
Letter-Sound Inventory (Record Sheet #1) 5-11 o Alphabet Recitation o Alphabet Recitation a b c d e f 9 h a b c d e f 9 h j k m n 0 p q k m n 0 p q r s t u v w x y z r s t u v w x y z 0 Upper Case Letter
Results as of 30 September 2018
 rt Results as of 30 September 2018 F r e e t r a n s l a t ion f r o m t h e o r ig ina l in S p a n is h. I n t h e e v e n t o f d i s c r e p a n c y, t h e Sp a n i s h - la n g u a g e v e r s ion
rt Results as of 30 September 2018 F r e e t r a n s l a t ion f r o m t h e o r ig ina l in S p a n is h. I n t h e e v e n t o f d i s c r e p a n c y, t h e Sp a n i s h - la n g u a g e v e r s ion
Nucleus. Electron Cloud
 Atomic Structure I. Picture of an Atom Nucleus Electron Cloud II. Subatomic particles Particle Symbol Charge Relative Mass (amu) protons p + +1 1.0073 neutrons n 0 1.0087 electrons e - -1 0.00054858 Compare
Atomic Structure I. Picture of an Atom Nucleus Electron Cloud II. Subatomic particles Particle Symbol Charge Relative Mass (amu) protons p + +1 1.0073 neutrons n 0 1.0087 electrons e - -1 0.00054858 Compare
Evolution Strategies for Optimizing Rectangular Cartograms
 Evolution Strategies for Optimizing Rectangular Cartograms Kevin Buchin 1, Bettina Speckmann 1, and Sander Verdonschot 2 1 TU Eindhoven, 2 Carleton University September 20, 2012 Sander Verdonschot (Carleton
Evolution Strategies for Optimizing Rectangular Cartograms Kevin Buchin 1, Bettina Speckmann 1, and Sander Verdonschot 2 1 TU Eindhoven, 2 Carleton University September 20, 2012 Sander Verdonschot (Carleton
CHEM Come to the PASS workshop with your mock exam complete. During the workshop you can work with other students to review your work.
 It is most beneficial to you to write this mock midterm UNDER EXAM CONDITIONS. This means: Complete the midterm in 1.5 hours. Work on your own. Keep your notes and textbook closed. Attempt every question.
It is most beneficial to you to write this mock midterm UNDER EXAM CONDITIONS. This means: Complete the midterm in 1.5 hours. Work on your own. Keep your notes and textbook closed. Attempt every question.
ORBITAL DIAGRAM - A graphical representation of the quantum number "map" of electrons around an atom.
 178 (MAGNETIC) SPIN QUANTUM NUMBER: "spin down" or "spin up" - An ORBITAL (region with fixed "n", "l" and "ml" values) can hold TWO electrons. ORBITAL DIAGRAM - A graphical representation of the quantum
178 (MAGNETIC) SPIN QUANTUM NUMBER: "spin down" or "spin up" - An ORBITAL (region with fixed "n", "l" and "ml" values) can hold TWO electrons. ORBITAL DIAGRAM - A graphical representation of the quantum
9/20/2017. Elements are Pure Substances that cannot be broken down into simpler substances by chemical change (contain Only One Type of Atom)
 CAPTER 6: TE PERIODIC TABLE Elements are Pure Substances that cannot be broken down into simpler substances by chemical change (contain Only One Type of Atom) The Periodic Table (Mendeleev) In 1872, Dmitri
CAPTER 6: TE PERIODIC TABLE Elements are Pure Substances that cannot be broken down into simpler substances by chemical change (contain Only One Type of Atom) The Periodic Table (Mendeleev) In 1872, Dmitri
INSTRUCTIONS: CHEM Exam I. September 13, 1994 Lab Section
 CHEM 1314.05 Exam I John I. Gelder September 13, 1994 Name TA's Name Lab Section Please sign your name below to give permission to post, by the last 4 digits of your student I.D. number, your course scores
CHEM 1314.05 Exam I John I. Gelder September 13, 1994 Name TA's Name Lab Section Please sign your name below to give permission to post, by the last 4 digits of your student I.D. number, your course scores
7. Relax and do well.
 CHEM 1215 Exam II John II. Gelder October 7, 1998 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 5 different pages. The last page includes a periodic table and a solubility
CHEM 1215 Exam II John II. Gelder October 7, 1998 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 5 different pages. The last page includes a periodic table and a solubility
Lab Day and Time: Instructions. 1. Do not open the exam until you are told to start.
 Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
Name: Lab Day and Time: Instructions 1. Do not open the exam until you are told to start. 2. This exam is closed note and closed book. You are not allowed to use any outside material while taking this
(308 ) EXAMPLES. 1. FIND the quotient and remainder when. II. 1. Find a root of the equation x* = +J Find a root of the equation x 6 = ^ - 1.
 (308 ) EXAMPLES. N 1. FIND the quotient and remainder when is divided by x 4. I. x 5 + 7x* + 3a; 3 + 17a 2 + 10* - 14 2. Expand (a + bx) n in powers of x, and then obtain the first derived function of
(308 ) EXAMPLES. N 1. FIND the quotient and remainder when is divided by x 4. I. x 5 + 7x* + 3a; 3 + 17a 2 + 10* - 14 2. Expand (a + bx) n in powers of x, and then obtain the first derived function of
F O R M T H R E E K enya C ertificate of Secondary E ducation
 N a m e : A d m. N o...... D a t e : C la ss:.... 565/1 FO R M 3 B U S I N E S S S T U D I E S P A P E R 1 T I M E : 2 H O U R S T R I A L 6 2 0 1 8 FO R M 3 B U S I N E S S S T U D I E S P A P E R 1 T
N a m e : A d m. N o...... D a t e : C la ss:.... 565/1 FO R M 3 B U S I N E S S S T U D I E S P A P E R 1 T I M E : 2 H O U R S T R I A L 6 2 0 1 8 FO R M 3 B U S I N E S S S T U D I E S P A P E R 1 T
 ,,,,..,,., {. (, ),, {,.,.,..,,.,.,,....... {.. : N {, Z {, Q {, Q p { p{ {. 3, R {, C {. : ord p {. 8, (k) {.42,!() { {. 24, () { {. 24, () { {. 25,., () { {. 26,. 9, () { {. 27,. 23, '() { ( ) {. 28,
,,,,..,,., {. (, ),, {,.,.,..,,.,.,,....... {.. : N {, Z {, Q {, Q p { p{ {. 3, R {, C {. : ord p {. 8, (k) {.42,!() { {. 24, () { {. 24, () { {. 25,., () { {. 26,. 9, () { {. 27,. 23, '() { ( ) {. 28,
w = X ^ = ^ ^, (i*i < ix
 A SUMMATION FORMULA FOR POWER SERIES USING EULERIAN FRACTIONS* Xinghua Wang Math. Department, Zhejiang University, Hangzhou 310028, China Leetsch C. Hsu Math. Institute, Dalian University of Technology,
A SUMMATION FORMULA FOR POWER SERIES USING EULERIAN FRACTIONS* Xinghua Wang Math. Department, Zhejiang University, Hangzhou 310028, China Leetsch C. Hsu Math. Institute, Dalian University of Technology,
600 Billy Smith Road, Athens, VT
 600 Billy Smith Road, Athens, VT Curtis Trousdale, Owner, Broker, Realtor Cell: 802-233-5589 curtis@preferredpropertiesvt.com 2004 Williston Road, South Burlington VT 05403 www.preferredpropertiesvt.com
600 Billy Smith Road, Athens, VT Curtis Trousdale, Owner, Broker, Realtor Cell: 802-233-5589 curtis@preferredpropertiesvt.com 2004 Williston Road, South Burlington VT 05403 www.preferredpropertiesvt.com
(Received March 30, 1953)
 MEMOIRS OF THE COLLEGE OF SCIENCE, UNIVERSITY OF KYOTO, SERIES, A V ol. XXVIII, Mathematics No. 1, 1953. On the Evaluation of the Derivatives of Solutions of y"=-f (x, y, y'). By Taro YOSHIZAWA (Received
MEMOIRS OF THE COLLEGE OF SCIENCE, UNIVERSITY OF KYOTO, SERIES, A V ol. XXVIII, Mathematics No. 1, 1953. On the Evaluation of the Derivatives of Solutions of y"=-f (x, y, y'). By Taro YOSHIZAWA (Received
Chemistry 2 Exam Roane State Academic Festival. Name (print neatly) School
 Name (print neatly) School There are fifteen question on this exam. Each question is weighted equally. n the answer sheet, write your name in the space provided and your answers in the blanks provided.
Name (print neatly) School There are fifteen question on this exam. Each question is weighted equally. n the answer sheet, write your name in the space provided and your answers in the blanks provided.
APPLICATION OF AUTOMATION IN THE STUDY AND PREDICTION OF TIDES AT THE FRENCH NAVAL HYDROGRAPHIC SERVICE
 APPLICATION OF AUTOMATION IN THE STUDY AND PREDICTION OF TIDES AT THE FRENCH NAVAL HYDROGRAPHIC SERVICE by L. R o u m é g o u x Ingénieur H ydrographe en Chef, C hief of the T idal Section The considerable
APPLICATION OF AUTOMATION IN THE STUDY AND PREDICTION OF TIDES AT THE FRENCH NAVAL HYDROGRAPHIC SERVICE by L. R o u m é g o u x Ingénieur H ydrographe en Chef, C hief of the T idal Section The considerable
Modified from: Larry Scheffler Lincoln High School IB Chemistry 1-2.1
 Modified from: Larry Scheffler Lincoln High School IB Chemistry 1-2.1 The development of the periodic table brought a system of order to what was otherwise an collection of thousands of pieces of information.
Modified from: Larry Scheffler Lincoln High School IB Chemistry 1-2.1 The development of the periodic table brought a system of order to what was otherwise an collection of thousands of pieces of information.
Feasibility Analysis, Dynamics, and Control of Distillation Columns With Vapor Recompression.
 Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1981 Feasibility Analysis, Dynamics, and Control of Distillation Columns With Vapor Recompression.
Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1981 Feasibility Analysis, Dynamics, and Control of Distillation Columns With Vapor Recompression.
Chemistry 126 Final Examination, Prof. Hanson, May, Section B or D (circle one) Seat Coordinate Name
 Chemistry 126 Final Examination, Prof. Hanson, May, 2004 Section B or D (circle one) Seat Coordinate Name DO NOT OPEN THIS EXAM UNTIL INSTRUCTED TO DO SO Each asterisk () is 5 points. There are 40 s, for
Chemistry 126 Final Examination, Prof. Hanson, May, 2004 Section B or D (circle one) Seat Coordinate Name DO NOT OPEN THIS EXAM UNTIL INSTRUCTED TO DO SO Each asterisk () is 5 points. There are 40 s, for
h : sh +i F J a n W i m +i F D eh, 1 ; 5 i A cl m i n i sh» si N «q a : 1? ek ser P t r \. e a & im a n alaa p ( M Scanned by CamScanner
 m m i s t r * j i ega>x I Bi 5 n ì r s w «s m I L nk r n A F o n n l 5 o 5 i n l D eh 1 ; 5 i A cl m i n i sh» si N «q a : 1? { D v i H R o s c q \ l o o m ( t 9 8 6) im a n alaa p ( M n h k Em l A ma
m m i s t r * j i ega>x I Bi 5 n ì r s w «s m I L nk r n A F o n n l 5 o 5 i n l D eh 1 ; 5 i A cl m i n i sh» si N «q a : 1? { D v i H R o s c q \ l o o m ( t 9 8 6) im a n alaa p ( M n h k Em l A ma
Dangote Flour Mills Plc
 SUMMARY OF OFFER Opening Date 6 th September 27 Closing Date 27 th September 27 Shares on Offer 1.25bn Ord. Shares of 5k each Offer Price Offer Size Market Cap (Post Offer) Minimum Offer N15. per share
SUMMARY OF OFFER Opening Date 6 th September 27 Closing Date 27 th September 27 Shares on Offer 1.25bn Ord. Shares of 5k each Offer Price Offer Size Market Cap (Post Offer) Minimum Offer N15. per share
