Beyond Chebyshev technology. Alex Townsend MIT
|
|
|
- Shawn Francis
- 6 years ago
- Views:
Transcription
1 Beyond Chebyshev technology Strthclyde, 25th June th Biennil Numericl Anlysis Conference Alex Townsend MIT Joint work with Nick Hle nd Sheehn Olver
2 Beyond Chebyshev technology Strthclyde, 25th June th Biennil Numericl Anlysis Conference Alex Townsend MIT Joint work with Nick Hle nd Sheehn Olver
3 Beyond Chebyshev technology Strthclyde, 25th June th Biennil Numericl Anlysis Conference Alex Townsend MIT Joint work with Nick Hle nd Sheehn Olver
4 Introduction Chebfun stnds for Chebyshev fun Chebfun = Chebyshev fun Chebyshev technology: A powerful pproch for numericlly computing with functions It is bsed on (piecewise) polynomil interpoltion t Chebyshev points nd Chebyshev polynomils: x j cospjπ{nq, ď j ď n, T k pxq cospk cos xq There exist fst, ccurte lgorithms for integrtion, differentition, rootfinding, minimiztion, solution of ODEs, etc Alex MIT 1/17
5 Introduction Chebyshev technology is powerful Chebyshev interpolnt of fpxq: n ÿ f px q «pn px q ck T k p x q, pn pxj q f pxj q, xj chebpts k Powerful concepts: FFT, brycentric formul, collegue mtrix, colloction SIAM digit chllenge problem v y [Trefethen, 2] Alex MIT Computing sphericl choreogrphies Inverse trnsform smpling x [Olver & T, 14] -2-2 [Montnelli & Gushterov, 15] 2/17
6 Introduction Chebyshev technology cn lso bring us together Chebyshev technology cn lso bring us together My friends: «45 peer-reviewed publictions, «5 essys, nd book clled ATAP Alex MIT 3/17
7 Introduction Chrcters: Stndrd orthogonl polynomils on r, 1s Nme Nottion wpxq Chebyshev polynomils (of 1st kind) T k pxq p1 x 2 q{2 Chebyshev polynomils (of 2nd kind) U k pxq p1 x 2 q 1{2 Legendre polynomils P k pxq 1 Ultrsphericl polynomils C pλq k pxq p1 x 2 q λ{2 Fst trnsforms now vilble for Legendre nd ultrsphericl technology [Hle & T, 214], [Hle & T, 215] Alex MIT 4/17
8 Introduction Tlk overview nd trivil exmple Fct: Chebyshev polynomils stisfy: T j pxqt k pxq 1 x 2 dx $ & π, j k, π{2, j k ą, %, j k Inconvenience: The 1st coeff of Chebyshev series is treted s specil: fpxq 1 2 T pxq ` 8ÿ k T k pxq, k 1 k 2 π Alterntive: Chebyshev polynomils of the 2nd kind: ż # 1 π{2, j k, U j pxqu k pxq 1 x 2 dx, j k Results: Sves your snity nd voids mistkes fpxqt k pxq 1 x 2 dx Alex MIT 5/17
9 Introduction Tlk overview nd trivil exmple Fct: Chebyshev polynomils stisfy: T j pxqt k pxq 1 x 2 dx $ & π, j k, π{2, j k ą, %, j k Inconvenience: The 1st coeff of Chebyshev series is treted s specil: fpxq 1 2 T pxq ` 8ÿ k T k pxq, k 1 k 2 π Alterntive: Chebyshev polynomils of the 2nd kind: ż # 1 π{2, j k, U j pxqu k pxq 1 x 2 dx, j k Results: Sves your snity nd voids mistkes fpxqt k pxq 1 x 2 dx Alex MIT 5/17
10 Introduction Tlk overview nd trivil exmple Fct: Chebyshev polynomils stisfy: T j pxqt k pxq 1 x 2 dx $ & π, j k, π{2, j k ą, %, j k Inconvenience: The 1st coeff of Chebyshev series is treted s specil: fpxq 1 2 T pxq ` 8ÿ k T k pxq, k 1 k 2 π Alterntive: Chebyshev polynomils of the 2nd kind: ż # 1 π{2, j k, U j pxqu k pxq 1 x 2 dx, j k Results: Sves your snity nd voids mistkes fpxqt k pxq 1 x 2 dx Alex MIT 5/17
11 Introduction Tlk overview nd trivil exmple Fct: Chebyshev polynomils stisfy: T j pxqt k pxq 1 x 2 dx $ & π, j k, π{2, j k ą, %, j k Inconvenience: The 1st coeff of Chebyshev series is treted s specil: fpxq 1 2 T pxq ` 8ÿ k T k pxq, k 1 k 2 π Alterntive: Chebyshev polynomils of the 2nd kind: ż # 1 π{2, j k, U j pxqu k pxq 1 x 2 dx, j k Results: Sves your snity nd voids mistkes fpxqt k pxq 1 x 2 dx Alex MIT 5/17
12 Introduction Tlk overview nd trivil exmple Fct: Chebyshev polynomils stisfy: T j pxqt k pxq 1 x 2 dx $ & π, j k, π{2, j k ą, %, j k Inconvenience: The 1st coeff of Chebyshev series is treted s specil: fpxq 1 2 T pxq ` 8ÿ k T k pxq, k 1 k 2 π Alterntive: Chebyshev polynomils of the 2nd kind: ż # 1 π{2, j k, U j pxqu k pxq 1 x 2 dx, j k Results: Sves your snity nd voids mistkes fpxqt k pxq 1 x 2 dx Alex MIT 5/17
13 Introduction Tlk overview nd trivil exmple Fct: Chebyshev polynomils stisfy: T j pxqt k pxq 1 x 2 dx $ & π, j k, π{2, j k ą, %, j k Inconvenience: The 1st coeff of Chebyshev series is treted s specil: fpxq 1 2 T pxq ` 8ÿ k T k pxq, k 1 k 2 π Alterntive: Chebyshev polynomils of the 2nd kind: ż # 1 π{2, j k, U j pxqu k pxq 1 x 2 dx, j k Results: Sves your snity nd voids mistkes fpxqt k pxq 1 x 2 dx Alex MIT 5/17
14 Introduction Tlk overview nd trivil exmple Fct: Chebyshev polynomils stisfy: T j pxqt k pxq 1 x 2 dx $ & π, j k, π{2, j k ą, %, j k Inconvenience: The 1st coeff of Chebyshev series is treted s specil: fpxq 1 2 T pxq ` 8ÿ k T k pxq, k 1 k 2 π Alterntive: Chebyshev polynomils of the 2nd kind: ż # 1 π{2, j k, U j pxqu k pxq 1 x 2 dx, j k Results: Sves your snity nd voids mistkes fpxqt k pxq 1 x 2 dx Alex MIT 5/17
15 Introduction Tlk overview nd trivil exmple Fct: Chebyshev polynomils stisfy: T j pxqt k pxq 1 x 2 dx $ & π, j k, π{2, j k ą, %, j k Inconvenience: The 1st coeff of Chebyshev series is treted s specil: fpxq 1 2 T pxq ` 8ÿ k T k pxq, k 1 k 2 π Alterntive: Chebyshev polynomils of the 2nd kind: ż # 1 π{2, j k, U j pxqu k pxq 1 x 2 dx, j k Results: Sves your snity nd voids mistkes fpxqt k pxq 1 x 2 dx Alex MIT 5/17
16 Introduction Tlk overview nd trivil exmple Fct: Chebyshev polynomils stisfy: T j pxqt k pxq 1 x 2 dx $ & π, j k, π{2, j k ą, %, j k Inconvenience: The 1st coeff of Chebyshev series is treted s specil: fpxq 1 2 T pxq ` 8ÿ k T k pxq, k 1 k 2 π Alterntive: Chebyshev polynomils of the 2nd kind: ż # 1 π{2, j k, U j pxqu k pxq 1 x 2 dx, j k Results: Sves your snity nd voids mistkes fpxqt k pxq 1 x 2 dx Alex MIT 5/17
17 Exmple 1 Convolution Fct: The Fourier trnsform of T k pxq is complicted: T k pxqe iωx dx complicted, [Foks & Smithemn, 12] Inconvenience: Convolution cnnot be bsed on the convolution theorem: hpxq pf gqpxq ż minp1,x`1q mxp,xq fptqgpx tqdt 1 t ÝÑ ÝÑ x 2 2 Qudrture is expensive Alex MIT 6/17
18 Exmple 1 Convolution Fct: The Fourier trnsform of T k pxq is complicted: T k pxqe iωx dx complicted, [Foks & Smithemn, 12] Inconvenience: Convolution cnnot be bsed on the convolution theorem: hpxq pf gqpxq ż minp1,x`1q mxp,xq fptqgpx tqdt 1 t ÝÑ ÝÑ x 2 2 Qudrture is expensive Alex MIT 6/17
19 Exmple 1 Convolution Fct: The Fourier trnsform of T k pxq is complicted: T k pxqe iωx dx complicted, [Foks & Smithemn, 12] Inconvenience: Convolution cnnot be bsed on the convolution theorem: hpxq pf gqpxq ż minp1,x`1q mxp,xq fptqgpx tqdt 1 t ÝÑ ÝÑ x 2 2 Qudrture is expensive Alex MIT 6/17
20 Exmple 1 Convolution Fct: The Fourier trnsform of T k pxq is complicted: T k pxqe iωx dx complicted, [Foks & Smithemn, 12] Inconvenience: Convolution cnnot be bsed on the convolution theorem: hpxq pf gqpxq ż minp1,x`1q mxp,xq fptqgpx tqdt 1 t ÝÑ ÝÑ x 2 2 Qudrture is expensive Alex MIT 6/17
21 Exmple 1 Convolution Fct: The Fourier trnsform of T k pxq is complicted: T k pxqe iωx dx complicted, [Foks & Smithemn, 12] Inconvenience: Convolution cnnot be bsed on the convolution theorem: hpxq pf gqpxq ż minp1,x`1q mxp,xq fptqgpx tqdt 1 t ÝÑ ÝÑ x 2 2 Qudrture is expensive Alex MIT 6/17
22 Exmple 1 Convolution (cont) Alterntive: The Fourier trnsform of P k pxq is convenient [Hle & T, 214]: P k pxqe iωx dx 2p iq k j k pωq, where j k pωq sphericl Bessel function Theorem (Convolution theorem) Let m nd n be integers Then, rdlmf, p181719qs, pp m P n qpxq 2p iqm`n π ż 8 8 f nd g in P k bsis j m pωqj n pωqe iωx, Fourier trnsform j m pωq sphericl Bessel ˆf nd ĝ in j k bsis f g in P k bsis Inverse trnsform ˆf ˆ ĝ in j k bsis Alex MIT 7/17
23 Exmple 1 Convolution (cont) Alterntive: The Fourier trnsform of P k pxq is convenient [Hle & T, 214]: P k pxqe iωx dx 2p iq k j k pωq, where j k pωq sphericl Bessel function Theorem (Convolution theorem) Let m nd n be integers Then, rdlmf, p181719qs, pp m P n qpxq 2p iqm`n π ż 8 8 f nd g in P k bsis j m pωqj n pωqe iωx, Fourier trnsform j m pωq sphericl Bessel ˆf nd ĝ in j k bsis f g in P k bsis Inverse trnsform ˆf ˆ ĝ in j k bsis Alex MIT 7/17
24 Exmple 1 Convolution (cont) Alterntive: The Fourier trnsform of P k pxq is convenient [Hle & T, 214]: P k pxqe iωx dx 2p iq k j k pωq, where j k pωq sphericl Bessel function Theorem (Convolution theorem) Let m nd n be integers Then, rdlmf, p181719qs, pp m P n qpxq 2p iqm`n π ż 8 8 f nd g in P k bsis j m pωqj n pωqe iωx, Fourier trnsform j m pωq sphericl Bessel ˆf nd ĝ in j k bsis f g in P k bsis Inverse trnsform ˆf ˆ ĝ in j k bsis Alex MIT 7/17
25 Exmple 1 Convolution (cont) Alterntive: The Fourier trnsform of P k pxq is convenient [Hle & T, 214]: P k pxqe iωx dx 2p iq k j k pωq, where j k pωq sphericl Bessel function Theorem (Convolution theorem) Let m nd n be integers Then, rdlmf, p181719qs, pp m P n qpxq 2p iqm`n π ż 8 8 f nd g in P k bsis j m pωqj n pωqe iωx, Fourier trnsform j m pωq sphericl Bessel ˆf nd ĝ in j k bsis f g in P k bsis Inverse trnsform ˆf ˆ ĝ in j k bsis Alex MIT 7/17
26 Exmple 1 Convolution (cont) Alterntive: The Fourier trnsform of P k pxq is convenient [Hle & T, 214]: P k pxqe iωx dx 2p iq k j k pωq, where j k pωq sphericl Bessel function Theorem (Convolution theorem) Let m nd n be integers Then, rdlmf, p181719qs, pp m P n qpxq 2p iqm`n π ż 8 8 f nd g in P k bsis j m pωqj n pωqe iωx, Fourier trnsform j m pωq sphericl Bessel ˆf nd ĝ in j k bsis f g in P k bsis Inverse trnsform ˆf ˆ ĝ in j k bsis Alex MIT 7/17
27 Exmple 1 Convolution (cont) Results: Computtionl timings Qudrture New Mollifiction of rough signls Computtion time OpN 3 q OpN 2 q N Now used in the conv(f, g) commnd in Chebfun Alex MIT 8/17
28 Exmple 2 Solving differentil equtions Fct: The derivtive of Chebyshev polynomil stisfies: T 1 k pxq # 2k ř k j odd T jpxq, k even, 2k ř k j even T jpxq 1, k odd Inconvenience: The Chebyshev-tu spectrl method leds to dense mtrices For exmple, du dx ` 4xu upq c, ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ u u 1 u 2 u n c Alex MIT 9/17
29 Exmple 2 Solving differentil equtions Fct: The derivtive of Chebyshev polynomil stisfies: T 1 k pxq # 2k ř k j odd T jpxq, k even, 2k ř k j even T jpxq 1, k odd Inconvenience: The Chebyshev-tu spectrl method leds to dense mtrices For exmple, du dx ` 4xu upq c, ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ u u 1 u 2 u n c Alex MIT 9/17
30 Exmple 2 Solving differentil equtions Fct: The derivtive of Chebyshev polynomil stisfies: T 1 k pxq # 2k ř k j odd T jpxq, k even, 2k ř k j even T jpxq 1, k odd Inconvenience: The Chebyshev-tu spectrl method leds to dense mtrices For exmple, du dx ` 4xu upq c, ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ u u 1 u 2 u n c Alex MIT 9/17
31 Exmple 2 Solving differentil equtions Fct: The derivtive of Chebyshev polynomil stisfies: T 1 k pxq # 2k ř k j odd T jpxq, k even, 2k ř k j even T jpxq 1, k odd Inconvenience: The Chebyshev-tu spectrl method leds to dense mtrices For exmple, du dx ` 4xu upq c, ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ u u 1 u 2 u n c Alex MIT 9/17
32 Exmple 2 Solving differentil equtions (cont) Alterntive: Let differentition convert to ultrsphericl bses [Olver & T, 213] T 1 k pxq kcp1q k pxq, T 2 k pxq 2kCp2q k 2 pxq, T 3 k pxq 8kCp3q k 3 pxq For exmple, du dx ` 4xu upq c, pq n n 3 1 n 2 1 n 1 u u 1 u 2 u n c Alex MIT 1/17
33 Exmple 2 Solving differentil equtions (cont) Alterntive: Let differentition convert to ultrsphericl bses [Olver & T, 213] T 1 k pxq kcp1q k pxq, T 2 k pxq 2kCp2q k 2 pxq, T 3 k pxq 8kCp3q k 3 pxq For exmple, du dx ` 4xu upq c, pq n n 3 1 n 2 1 n 1 u u 1 u 2 u n c Alex MIT 1/17
34 Exmple 2 Solving differentil equtions (cont) Alterntive: Let differentition convert to ultrsphericl bses [Olver & T, 213] T 1 k pxq kcp1q k pxq, T 2 k pxq 2kCp2q k 2 pxq, T 3 k pxq 8kCp3q k 3 pxq For exmple, du dx ` 4xu upq c, pq n n 3 1 n 2 1 n 1 u u 1 u 2 u n c Alex MIT 1/17
35 Exmple 2 Solving differentil equtions (cont) Results: [Olver & T, 213], [T & Olver, 215] u 1 pxq ` x 3 upxq 1 sinp2,x 2 q, upq 2 u ` 5p2 yqu, u BΩ u(x) degree(u) = 2391 time = 155s time 121s x Alex MIT 11/17
36 Exmple 2 Solving differentil equtions (future work) Results (in the pipeline, perhps?): 2 u ` 5p1 yqu, Ω penrose, u BΩ Using n extension of Hierrchicl Poincre Steklov scheme [Mrtinsson 212] Alex MIT 12/17
37 Exmple 3 Best low rnk pproximtion Fct: Chebyshev polynomils re not orthogonl in the L 2 inner-product: T j pxqt k pxqdx, j k Inconvenience: Tsks connected to L 2 -orthogonlity re wkwrd nÿ Best lest squres poly pprox: }fpxq c k T k pxq} L 2 min Best low-rnk pproximtion: }f px, yq k rÿ σ j u j pyqv j pxq} L 2 min j 1 Alex MIT 13/17
38 Exmple 3 Best low rnk pproximtion Fct: Chebyshev polynomils re not orthogonl in the L 2 inner-product: T j pxqt k pxqdx, j k Inconvenience: Tsks connected to L 2 -orthogonlity re wkwrd nÿ Best lest squres poly pprox: }fpxq c k T k pxq} L 2 min Best low-rnk pproximtion: }f px, yq k rÿ σ j u j pyqv j pxq} L 2 min j 1 Alex MIT 13/17
39 Exmple 3 Best low rnk pproximtion Fct: Chebyshev polynomils re not orthogonl in the L 2 inner-product: T j pxqt k pxqdx, j k Inconvenience: Tsks connected to L 2 -orthogonlity re wkwrd nÿ Best lest squres poly pprox: }fpxq c k T k pxq} L 2 min Best low-rnk pproximtion: }f px, yq k rÿ σ j u j pyqv j pxq} L 2 min j 1 Alex MIT 13/17
40 Exmple 3 Best low rnk pproximtion Fct: Chebyshev polynomils re not orthogonl in the L 2 inner-product: T j pxqt k pxqdx, j k Inconvenience: Tsks connected to L 2 -orthogonlity re wkwrd nÿ Best lest squres poly pprox: }fpxq c k T k pxq} L 2 min Best low-rnk pproximtion: }f px, yq k rÿ σ j u j pyqv j pxq} L 2 min j 1 Alex MIT 13/17
41 Exmple 3 Best low rnk pproximtion (cont) Alterntive: The P k pxq bsis is orthogonl wrt the L 2 inner-product: P j pxqp k pxqdx, j k For best lest squres poly pprox of degree n: fpxq 8ÿ k For best low-rnk pproximtion: fpx, yq mÿ j k leg k P k pxq ñ }f nÿ k nÿ C jk P j pyqp k pxq ñ fpx, yq leg P k k pxq} L 2 min rÿ σ j u j pyqv j pxq j 1 loooooooomoooooooon Computed vi the discrete svd of C Alex MIT 14/17
42 Exmple 3 Best low rnk pproximtion (cont) Alterntive: The P k pxq bsis is orthogonl wrt the L 2 inner-product: P j pxqp k pxqdx, j k For best lest squres poly pprox of degree n: fpxq 8ÿ k For best low-rnk pproximtion: fpx, yq mÿ j k leg k P k pxq ñ }f nÿ k nÿ C jk P j pyqp k pxq ñ fpx, yq leg P k k pxq} L 2 min rÿ σ j u j pyqv j pxq j 1 loooooooomoooooooon Computed vi the discrete svd of C Alex MIT 14/17
43 Exmple 3 Best low rnk pproximtion (cont) Alterntive: The P k pxq bsis is orthogonl wrt the L 2 inner-product: P j pxqp k pxqdx, j k For best lest squres poly pprox of degree n: fpxq 8ÿ k For best low-rnk pproximtion: fpx, yq mÿ j k leg k P k pxq ñ }f nÿ k nÿ C jk P j pyqp k pxq ñ fpx, yq leg P k k pxq} L 2 min rÿ σ j u j pyqv j pxq j 1 loooooooomoooooooon Computed vi the discrete svd of C Alex MIT 14/17
44 Exmple 3 Best low rnk function pproximtion (cont) Results: Best lest squres pprox of degree 15 Best rnk 3 pprox fpxq 1 1`1x 2 Alex MIT 15/17
![Bonus exmple Guss qudrture The rce for high order Guss Legendre qudrture, in SIAM News [T, 14] tic, [x, w] = legpts( 1 ); toc Elpsed time is 1256 seconds tic, [x, w] = legpts( 1 ); toc Elpsed time is](/docs-images/77/74932931/images/45-0.jpg "1289 seconds tic, [x, w] = legpts( 1 ); toc Elpsed time is 1418 seconds Similr dvnces in jcpts(), hermpts(), nd lgpts() [Hle & T, 14], [T, Trogdon, & Olver, 15], [Glser, Lui, & Rokhlin, 7] Ignce")
45 Bonus exmple Guss qudrture The rce for high order Guss Legendre qudrture, in SIAM News [T, 14] tic, [x, w] = legpts( 1 ); toc Elpsed time is 1256 seconds tic, [x, w] = legpts( 1 ); toc Elpsed time is 1289 seconds tic, [x, w] = legpts( 1 ); toc Elpsed time is 1418 seconds Similr dvnces in jcpts(), hermpts(), nd lgpts() [Hle & T, 14], [T, Trogdon, & Olver, 15], [Glser, Lui, & Rokhlin, 7] Ignce Bogert Alex MIT 16/17
46 Conclusion nd thnk you using Legendre technology 8% of the time use T k, otherwise use something else Alex MIT 17/17
47 Conclusion nd thnk you using Legendre technology Rnk 1 Rnk 2 Rnk 3 8% of the time use T k, otherwise use something else Rnk 4 Rnk 5 Rnk 15 Alex MIT 17/17
1 The Lagrange interpolation formula
Notes on Qudrture 1 The Lgrnge interpoltion formul We briefly recll the Lgrnge interpoltion formul. The strting point is collection of N + 1 rel points (x 0, y 0 ), (x 1, y 1 ),..., (x N, y N ), with x
Numerical Methods I Orthogonal Polynomials
Numericl Methods I Orthogonl Polynomils Aleksndr Donev Cournt Institute, NYU 1 donev@cournt.nyu.edu 1 MATH-GA 2011.003 / CSCI-GA 2945.003, Fll 2014 Nov 6th, 2014 A. Donev (Cournt Institute) Lecture IX
Chapter 3 Polynomials
Dr M DRAIEF As described in the introduction of Chpter 1, pplictions of solving liner equtions rise in number of different settings In prticulr, we will in this chpter focus on the problem of modelling
A fast Chebyshev Legendre transform using an asymptotic formula
A fast Chebyshev Legendre transform using an asymptotic formula Alex Townsend MIT (Joint work with ick Hale) SIAM OPSFA, 5th June 2015 Introduction What is the Chebyshev Legendre transform? Suppose we
Part IB Numerical Analysis
Prt IB Numericl Anlysis Theorems with proof Bsed on lectures by G. Moore Notes tken by Dexter Chu Lent 2016 These notes re not endorsed by the lecturers, nd I hve modified them (often significntly) fter
Matrices, Moments and Quadrature, cont d
Jim Lmbers MAT 285 Summer Session 2015-16 Lecture 2 Notes Mtrices, Moments nd Qudrture, cont d We hve described how Jcobi mtrices cn be used to compute nodes nd weights for Gussin qudrture rules for generl
CMDA 4604: Intermediate Topics in Mathematical Modeling Lecture 19: Interpolation and Quadrature
CMDA 4604: Intermedite Topics in Mthemticl Modeling Lecture 19: Interpoltion nd Qudrture In this lecture we mke brief diversion into the res of interpoltion nd qudrture. Given function f C[, b], we sy
Lecture 19: Continuous Least Squares Approximation
Lecture 19: Continuous Lest Squres Approximtion 33 Continuous lest squres pproximtion We begn 31 with the problem of pproximting some f C[, b] with polynomil p P n t the discrete points x, x 1,, x m for
NUMERICAL INTEGRATION. The inverse process to differentiation in calculus is integration. Mathematically, integration is represented by.
NUMERICAL INTEGRATION 1 Introduction The inverse process to differentition in clculus is integrtion. Mthemticlly, integrtion is represented by f(x) dx which stnds for the integrl of the function f(x) with
3.4 Numerical integration
3.4. Numericl integrtion 63 3.4 Numericl integrtion In mny economic pplictions it is necessry to compute the definite integrl of relvlued function f with respect to "weight" function w over n intervl [,
Lecture 14: Quadrature
Lecture 14: Qudrture This lecture is concerned with the evlution of integrls fx)dx 1) over finite intervl [, b] The integrnd fx) is ssumed to be rel-vlues nd smooth The pproximtion of n integrl by numericl
Theoretical foundations of Gaussian quadrature
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Construction of Gauss Quadrature Rules
Jim Lmbers MAT 772 Fll Semester 2010-11 Lecture 15 Notes These notes correspond to Sections 10.2 nd 10.3 in the text. Construction of Guss Qudrture Rules Previously, we lerned tht Newton-Cotes qudrture
Best Approximation in the 2-norm
Jim Lmbers MAT 77 Fll Semester 1-11 Lecture 1 Notes These notes correspond to Sections 9. nd 9.3 in the text. Best Approximtion in the -norm Suppose tht we wish to obtin function f n (x) tht is liner combintion
CAAM 453 NUMERICAL ANALYSIS I Examination There are four questions, plus a bonus. Do not look at them until you begin the exam.
Exmintion 1 Posted 23 October 2002. Due no lter thn 5pm on Mondy, 28 October 2002. Instructions: 1. Time limit: 3 uninterrupted hours. 2. There re four questions, plus bonus. Do not look t them until you
Best Approximation. Chapter The General Case
Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Orthogonal Polynomials
Mth 4401 Gussin Qudrture Pge 1 Orthogonl Polynomils Orthogonl polynomils rise from series solutions to differentil equtions, lthough they cn be rrived t in vriety of different mnners. Orthogonl polynomils
Discrete Least-squares Approximations
Discrete Lest-squres Approximtions Given set of dt points (x, y ), (x, y ),, (x m, y m ), norml nd useful prctice in mny pplictions in sttistics, engineering nd other pplied sciences is to construct curve
Advanced Computational Fluid Dynamics AA215A Lecture 3 Polynomial Interpolation: Numerical Differentiation and Integration.
Advnced Computtionl Fluid Dynmics AA215A Lecture 3 Polynomil Interpoltion: Numericl Differentition nd Integrtion Antony Jmeson Winter Qurter, 2016, Stnford, CA Lst revised on Jnury 7, 2016 Contents 3 Polynomil
Are resultant methods numerically unstable for multidimensional rootfinding? Alex Townsend MIT
Are resultant methods numerically unstable for multidimensional rootfinding? University of Oxford, 16th June 2015 NA internal seminar Alex Townsend MIT Joint work with Vanni Noferini Betteridge s law of
Fourier transforms. Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x L or L x L) as Fourier series: a n cos L
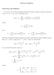ourier trnsforms Motivtion nd definition Up to now, we ve been expressing functions on finite intervls (usully the intervl 0 x or x ) s ourier series: fpxq 0 8 nπx n cos n b n sin nπx where 0» fpxq dx
Lecture 23: Interpolatory Quadrature
Lecture 3: Interpoltory Qudrture. Qudrture. The computtion of continuous lest squres pproximtions to f C[, b] required evlutions of the inner product f, φ j = fxφ jx dx, where φ j is polynomil bsis function
University of Houston, Department of Mathematics Numerical Analysis II
University of Houston, Deprtment of Mtemtics Numericl Anlysis II 6 Glerkin metod, finite differences nd colloction 6.1 Glerkin metod Consider sclr 2nd order ordinry differentil eqution in selfdjoint form
Lecture 6: Singular Integrals, Open Quadrature rules, and Gauss Quadrature
Lecture notes on Vritionl nd Approximte Methods in Applied Mthemtics - A Peirce UBC Lecture 6: Singulr Integrls, Open Qudrture rules, nd Guss Qudrture (Compiled 6 August 7) In this lecture we discuss the
ENGI 9420 Lecture Notes 7 - Fourier Series Page 7.01
ENGI 940 ecture Notes 7 - Fourier Series Pge 7.0 7. Fourier Series nd Fourier Trnsforms Fourier series hve multiple purposes, including the provision of series solutions to some liner prtil differentil
Instructor: Marios M. Fyrillas HOMEWORK ASSIGNMENT ON INTERPOLATION
AMAT 34 Numericl Methods Instructor: Mrios M. Fyrills Emil: m.fyrills@fit.c.cy Office Tel.: 34559/6 Et. 3 HOMEWORK ASSIGNMENT ON INTERPOATION QUESTION Using interpoltion by colloction-polynomil fit method
Abstract inner product spaces
WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
Numerical Analysis. Doron Levy. Department of Mathematics Stanford University
Numericl Anlysis Doron Levy Deprtment of Mthemtics Stnford University December 1, 2005 D. Levy Prefce i D. Levy CONTENTS Contents Prefce i 1 Introduction 1 2 Interpoltion 2 2.1 Wht is Interpoltion?............................
Numerical integration
2 Numericl integrtion This is pge i Printer: Opque this 2. Introduction Numericl integrtion is problem tht is prt of mny problems in the economics nd econometrics literture. The orgniztion of this chpter
1. Gauss-Jacobi quadrature and Legendre polynomials. p(t)w(t)dt, p {p(x 0 ),...p(x n )} p(t)w(t)dt = w k p(x k ),
1. Guss-Jcobi qudrture nd Legendre polynomils Simpson s rule for evluting n integrl f(t)dt gives the correct nswer with error of bout O(n 4 ) (with constnt tht depends on f, in prticulr, it depends on
A fast analysis-based discrete Hankel transform using asymptotic expansions
A fast analysis-based discrete Hankel transform using asymptotic expansions Alex Townsend MIT IMA Leslie Fox Prize Meeting, 22nd June, 2015 Based on: T., A fast analysis-based discrete Hankel transform
Interpolation. Gaussian Quadrature. September 25, 2011
Gussin Qudrture September 25, 2011 Approximtion of integrls Approximtion of integrls by qudrture Mny definite integrls cnnot be computed in closed form, nd must be pproximted numericlly. Bsic building
On the interval Legendre polynomials
Journl of Computtionl nd Applied Mthemtics 154 (003 15 7 www.elsevier.com/locte/cm On the intervl Legendre polynomils F.Ptrcio, J.A.Ferreir, F.Oliveir Deprtment of Mthemtics, University of Coimbr, Aprtdo
MAT 128A - Practice Midterm Exam
MAT 8A - Practice Midterm Exam Karry Wong October 3, 08 Problem (True or False) Given that f : r, s Ñ R is a continuous function, and that ta n u are its Chebyshev coefficients. Also, for N P N, p N pxq
Quantum Physics II (8.05) Fall 2013 Assignment 2
Quntum Physics II (8.05) Fll 2013 Assignment 2 Msschusetts Institute of Technology Physics Deprtment Due Fridy September 20, 2013 September 13, 2013 3:00 pm Suggested Reding Continued from lst week: 1.
Orthogonal Polynomials and Least-Squares Approximations to Functions
Chpter Orthogonl Polynomils nd Lest-Squres Approximtions to Functions **4/5/3 ET. Discrete Lest-Squres Approximtions Given set of dt points (x,y ), (x,y ),..., (x m,y m ), norml nd useful prctice in mny
Math 520 Final Exam Topic Outline Sections 1 3 (Xiao/Dumas/Liaw) Spring 2008
Mth 520 Finl Exm Topic Outline Sections 1 3 (Xio/Dums/Liw) Spring 2008 The finl exm will be held on Tuesdy, My 13, 2-5pm in 117 McMilln Wht will be covered The finl exm will cover the mteril from ll of
Math 270A: Numerical Linear Algebra
Mth 70A: Numericl Liner Algebr Instructor: Michel Holst Fll Qurter 014 Homework Assignment #3 Due Give to TA t lest few dys before finl if you wnt feedbck. Exercise 3.1. (The Bsic Liner Method for Liner
QUADRATURE is an old-fashioned word that refers to
World Acdemy of Science Engineering nd Technology Interntionl Journl of Mthemticl nd Computtionl Sciences Vol:5 No:7 011 A New Qudrture Rule Derived from Spline Interpoltion with Error Anlysis Hdi Tghvfrd
Chapter 3. Vector Spaces
3.4 Liner Trnsformtions 1 Chpter 3. Vector Spces 3.4 Liner Trnsformtions Note. We hve lredy studied liner trnsformtions from R n into R m. Now we look t liner trnsformtions from one generl vector spce
Review of Gaussian Quadrature method
Review of Gussin Qudrture method Nsser M. Asi Spring 006 compiled on Sundy Decemer 1, 017 t 09:1 PM 1 The prolem To find numericl vlue for the integrl of rel vlued function of rel vrile over specific rnge
Fourier transforms. Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x L or L x L) as Fourier series: a n cos L
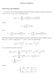ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
Numerical Integration
Numericl Integrtion Wouter J. Den Hn London School of Economics c 2011 by Wouter J. Den Hn June 3, 2011 Qudrture techniques I = f (x)dx n n w i f (x i ) = w i f i i=1 i=1 Nodes: x i Weights: w i Qudrture
CLOSED EXPRESSIONS FOR COEFFICIENTS IN WEIGHTED NEWTON-COTES QUADRATURES
Filomt 27:4 (2013) 649 658 DOI 10.2298/FIL1304649M Published by Fculty of Sciences nd Mthemtics University of Niš Serbi Avilble t: http://www.pmf.ni.c.rs/filomt CLOSED EXPRESSIONS FOR COEFFICIENTS IN WEIGHTED
NUMERICAL INTEGRATION
NUMERICAL INTEGRATION How do we evlute I = f (x) dx By the fundmentl theorem of clculus, if F (x) is n ntiderivtive of f (x), then I = f (x) dx = F (x) b = F (b) F () However, in prctice most integrls
Lecture Notes: Orthogonal Polynomials, Gaussian Quadrature, and Integral Equations
18330 Lecture Notes: Orthogonl Polynomils, Gussin Qudrture, nd Integrl Equtions Homer Reid My 1, 2014 In the previous set of notes we rrived t the definition of Chebyshev polynomils T n (x) vi the following
Math 473: Practice Problems for the Material after Test 2, Fall 2011
Mth 473: Prctice Problems for the Mteril fter Test, Fll SOLUTION. Consider the following modified het eqution u t = u xx + u x. () Use the relevnt 3 point pproximtion formuls for u xx nd u x to derive
COSC 3361 Numerical Analysis I Numerical Integration and Differentiation (III) - Gauss Quadrature and Adaptive Quadrature
COSC 336 Numericl Anlysis I Numericl Integrtion nd Dierentition III - Guss Qudrture nd Adptive Qudrture Edgr Griel Fll 5 COSC 336 Numericl Anlysis I Edgr Griel Summry o the lst lecture I For pproximting
Monte Carlo method in solving numerical integration and differential equation
Monte Crlo method in solving numericl integrtion nd differentil eqution Ye Jin Chemistry Deprtment Duke University yj66@duke.edu Abstrct: Monte Crlo method is commonly used in rel physics problem. The
Chapter 3 Solving Nonlinear Equations
Chpter 3 Solving Nonliner Equtions 3.1 Introduction The nonliner function of unknown vrible x is in the form of where n could be non-integer. Root is the numericl vlue of x tht stisfies f ( x) 0. Grphiclly,
REAL ANALYSIS II TAKE HOME EXAM. T. Tao s Lecture Notes Set 5
REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
Math& 152 Section Integration by Parts
Mth& 5 Section 7. - Integrtion by Prts Integrtion by prts is rule tht trnsforms the integrl of the product of two functions into other (idelly simpler) integrls. Recll from Clculus I tht given two differentible
Oscillatory Quadratures Based on the Tau Method
Journl of Mthemtics Reserch; Vol. 5, No. 3; 213 ISSN 1916-9795 E-ISSN 1916-989 Published by Cndin Center of Science nd Eduction Oscilltory Qudrtures Bsed on the Tu Method Mohmed K. El-Dou 1 1 Applied Sciences
Numerical Methods I. Olof Widlund Transcribed by Ian Tobasco
Numericl Methods I Olof Widlund Trnscribed by In Tobsco Abstrct. This is prt one of two semester course on numericl methods. The course ws offered in Fll 011 t the Cournt Institute for Mthemticl Sciences,
Composite Mendeleev s Quadratures for Solving a Linear Fredholm Integral Equation of The Second Kind
Globl Journl of Pure nd Applied Mthemtics. ISSN 0973-1768 Volume 12, Number (2016), pp. 393 398 Reserch Indi Publictions http://www.ripubliction.com/gjpm.htm Composite Mendeleev s Qudrtures for Solving
The Riemann Integral
Deprtment of Mthemtics King Sud University 2017-2018 Tble of contents 1 Anti-derivtive Function nd Indefinite Integrls 2 3 4 5 Indefinite Integrls & Anti-derivtive Function Definition Let f : I R be function
Review of Calculus, cont d
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Numerical Integration. 1 Introduction. 2 Midpoint Rule, Trapezoid Rule, Simpson Rule. AMSC/CMSC 460/466 T. von Petersdorff 1
AMSC/CMSC 46/466 T. von Petersdorff 1 umericl Integrtion 1 Introduction We wnt to pproximte the integrl I := f xdx where we re given, b nd the function f s subroutine. We evlute f t points x 1,...,x n
Part IB Numerical Analysis
Prt IB Numericl Anlysis Bsed on lectures by G. Moore Notes tken by Dexter Chu Lent 2016 These notes re not endorsed by the lecturers, nd I hve modified them (often significntly) fter lectures. They re
ODE: Existence and Uniqueness of a Solution
Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
63. Representation of functions as power series Consider a power series. ( 1) n x 2n for all 1 < x < 1
3 9. SEQUENCES AND SERIES 63. Representtion of functions s power series Consider power series x 2 + x 4 x 6 + x 8 + = ( ) n x 2n It is geometric series with q = x 2 nd therefore it converges for ll q =
1 Linear Least Squares
Lest Squres Pge 1 1 Liner Lest Squres I will try to be consistent in nottion, with n being the number of dt points, nd m < n being the number of prmeters in model function. We re interested in solving
DS-GA 1002: PREREQUISITES REVIEW SOLUTIONS VLADIMIR KOBZAR
DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of
Chapter 2. Numerical Integration also called quadrature. 2.2 Trapezoidal Rule. 2.1 A basic principle Extending the Trapezoidal Rule DRAWINGS
S Cpter Numericl Integrtion lso clled qudrture Te gol of numericl integrtion is to pproximte numericlly. f(x)dx Tis is useful for difficult integrls like sin(x) ; sin(x ); x + x 4 Or worse still for multiple-dimensionl
8 Laplace s Method and Local Limit Theorems
8 Lplce s Method nd Locl Limit Theorems 8. Fourier Anlysis in Higher DImensions Most of the theorems of Fourier nlysis tht we hve proved hve nturl generliztions to higher dimensions, nd these cn be proved
Key words. Numerical quadrature, piecewise polynomial, convergence rate, trapezoidal rule, midpoint rule, Simpson s rule, spectral accuracy.
O SPECTRA ACCURACY OF QUADRATURE FORMUAE BASED O PIECEWISE POYOMIA ITERPOATIO A KURGAOV AD S TSYKOV Abstrct It is well-known tt te trpezoidl rule, wile being only second-order ccurte in generl, improves
MATH 260 Final Exam April 30, 2013
MATH 60 Finl Exm April 30, 03 Let Mpn,Rq e the spce of n-y-n mtrices with rel entries () We know tht (with the opertions of mtrix ddition nd sclr multipliction), M pn, Rq is vector spce Wht is the dimension
Numerical Analysis. 10th ed. R L Burden, J D Faires, and A M Burden
Numericl Anlysis 10th ed R L Burden, J D Fires, nd A M Burden Bemer Presenttion Slides Prepred by Dr. Annette M. Burden Youngstown Stte University July 9, 2015 Chpter 4.1: Numericl Differentition 1 Three-Point
Numerical quadrature based on interpolating functions: A MATLAB implementation
SEMINAR REPORT Numericl qudrture bsed on interpolting functions: A MATLAB implementtion by Venkt Ayylsomyjul A seminr report submitted in prtil fulfillment for the degree of Mster of Science (M.Sc) in
A Nonclassical Collocation Method For Solving Two-Point Boundary Value Problems Over Infinite Intervals
Austrlin Journl of Bsic nd Applied Sciences 59: 45-5 ISS 99-878 A onclssicl Colloction Method For Solving o-oint Boundry Vlue roblems Over Infinite Intervls M Mlei nd M vssoli Kni Deprtment of Mthemtics
`an cos nπx. n 1. L `b
4 Fourier Series A periodic function on a range p,q may be decomposed into a sum of sinusoidal (sine or cosine) functions. This can be written as follows gpxq 1 2 a ` ř8 `b (4.1) The aim of this chapter
Numerical Integration
Chpter 5 Numericl Integrtion Numericl integrtion is the study of how the numericl vlue of n integrl cn be found. Methods of function pproximtion discussed in Chpter??, i.e., function pproximtion vi the
1 Ordinary Differential Equations
1 Ordinry Differentil Equtions 1. Mthemticl Bckground 1..1 Smoothness Definition 1.1 A function f defined on [, b] is continuous t x [, b] if lim x x f(x) = f(x ). Remrk Note tht this implies existence
DOING PHYSICS WITH MATLAB MATHEMATICAL ROUTINES
DOIG PHYSICS WITH MATLAB MATHEMATICAL ROUTIES COMPUTATIO OF OE-DIMESIOAL ITEGRALS In Cooper School of Physics, University of Sydney in.cooper@sydney.edu.u DOWLOAD DIRECTORY FOR MATLAB SCRIPTS mth_integrtion_1d.m
Point-based methods for estimating the length of a parametric curve
Point-bsed methods for estimting the length of prmetric curve Michel S. Floter, Atgeirr F. Rsmussen CMA, University of Oslo, P.O. Box 1053 Blindern, 0316 Oslo, Norwy Abstrct This pper studies generl method
Trapezoidal Rule, n = 1, x 0 = a, x 1 = b, h = b a. f (x)dx = h 2 (f (x 0) + f (x 1 )) h3
Trpezoidl Rule, n = 1, x 0 =, x 1 = b, h = b f (x)dx = h 2 (f (x 0) + f (x 1 )) h3 12 f (ξ). Simpson s Rule: n = 3, x 0 =, x 1 = +b 2, x 2 = b, h = b 2. Qudrture Rule, double node t x 1 P 3 (x)dx = f (x
Ordinary Differential Equations- Boundary Value Problem
Ordinry Differentil Equtions- Boundry Vlue Problem Shooting method Runge Kutt method Computer-bsed solutions o BVPFD subroutine (Fortrn IMSL subroutine tht Solves (prmeterized) system of differentil equtions
Moment-free numerical integration of highly oscillatory functions
Moment-free numericl integrtion of highly oscilltory functions Sheehn Olver September 4, 005 Abstrct The im of this pper is to derive new methods for numericlly pproximting the integrl of highly oscilltory
Improper Integrals, and Differential Equations
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
If u = g(x) is a differentiable function whose range is an interval I and f is continuous on I, then f(g(x))g (x) dx = f(u) du
Integrtion by Substitution: The Fundmentl Theorem of Clculus demonstrted the importnce of being ble to find nti-derivtives. We now introduce some methods for finding ntiderivtives: If u = g(x) is differentible
Engineering Analysis ENG 3420 Fall Dan C. Marinescu Office: HEC 439 B Office hours: Tu-Th 11:00-12:00
Engineering Anlysis ENG 3420 Fll 2009 Dn C. Mrinescu Office: HEC 439 B Office hours: Tu-Th 11:00-12:00 Lecture 13 Lst time: Problem solving in preprtion for the quiz Liner Algebr Concepts Vector Spces,
Arithmetic Mean Derivative Based Midpoint Rule
Applied Mthemticl Sciences, Vol. 1, 018, no. 13, 65-633 HIKARI Ltd www.m-hikri.com https://doi.org/10.1988/ms.018.858 Arithmetic Men Derivtive Bsed Midpoint Rule Rike Mrjulis 1, M. Imrn, Symsudhuh Numericl
The Islamic University of Gaza Faculty of Engineering Civil Engineering Department. Numerical Analysis ECIV Chapter 11
The Islmic University of Gz Fculty of Engineering Civil Engineering Deprtment Numericl Anlysis ECIV 6 Chpter Specil Mtrices nd Guss-Siedel Associte Prof Mzen Abultyef Civil Engineering Deprtment, The Islmic
A NONLINEAR OPTIMIZATION PROCEDURE FOR GENERALIZED GAUSSIAN QUADRATURES
A NONLINEAR OPTIMIZATION PROCEDURE FOR GENERALIZED GAUSSIAN QUADRATURES JAMES BREMER, ZYDRUNAS GIMBUTAS, AND VLADIMIR ROKHLIN Abstrct We present new nonliner optimiztion procedure for the computtion of
308K. 1 Section 3.2. Zelaya Eufemia. 1. Example 1: Multiplication of Matrices: X Y Z R S R S X Y Z. By associativity we have to choices:
8K Zely Eufemi Section 2 Exmple : Multipliction of Mtrices: X Y Z T c e d f 2 R S X Y Z 2 c e d f 2 R S 2 By ssocitivity we hve to choices: OR: X Y Z R S cr ds er fs X cy ez X dy fz 2 R S 2 Suggestion
Numerical Integration. Newton Cotes Formulas. Quadrature. Newton Cotes Formulas. To approximate the integral b
Numericl Integrtion Newton Cotes Formuls Given function f : R R nd two rel numbers, b R, < b, we clculte (pproximtely) the integrl I(f,, b) = f (x) dx K. Frischmuth (IfM UR) Numerics for CSE 08/09 8 /
Introduction to Numerical Analysis. Hector D. Ceniceros
Introduction to Numericl Anlysis Hector D. Ceniceros c Drft dte November 27, 2018 Contents Contents i Prefce 1 1 Introduction 3 1.1 Wht is Numericl Anlysis?.................. 3 1.2 An Illustrtive Exmple.....................
Introduction to Some Convergence theorems
Lecture Introduction to Some Convergence theorems Fridy 4, 005 Lecturer: Nti Linil Notes: Mukund Nrsimhn nd Chris Ré. Recp Recll tht for f : T C, we hd defined ˆf(r) = π T f(t)e irt dt nd we were trying
P 3 (x) = f(0) + f (0)x + f (0) 2. x 2 + f (0) . In the problem set, you are asked to show, in general, the n th order term is a n = f (n) (0)
1 Tylor polynomils In Section 3.5, we discussed how to pproximte function f(x) round point in terms of its first derivtive f (x) evluted t, tht is using the liner pproximtion f() + f ()(x ). We clled this
AMS 212A Applied Mathematical Methods I Lecture 06 Copyright by Hongyun Wang, UCSC. ( ), v (that is, 1 ( ) L i
AMS A Applied Mthemticl Methods I Lecture 6 Copyright y Hongyun Wng, UCSC Recp of Lecture 5 Clssifiction of oundry conditions Dirichlet eumnn Mixed Adjoint opertor, self-djoint opertor Sturm-Liouville
Numerical Analysis: Trapezoidal and Simpson s Rule
nd Simpson s Mthemticl question we re interested in numericlly nswering How to we evlute I = f (x) dx? Clculus tells us tht if F(x) is the ntiderivtive of function f (x) on the intervl [, b], then I =
STURM-LIOUVILLE THEORY, VARIATIONAL APPROACH
STURM-LIOUVILLE THEORY, VARIATIONAL APPROACH XIAO-BIAO LIN. Qudrtic functionl nd the Euler-Jcobi Eqution The purpose of this note is to study the Sturm-Liouville problem. We use the vritionl problem s
Harmonic Mean Derivative - Based Closed Newton Cotes Quadrature
IOSR Journl of Mthemtics (IOSR-JM) e-issn: - p-issn: 9-X. Volume Issue Ver. IV (My. - Jun. 0) PP - www.iosrjournls.org Hrmonic Men Derivtive - Bsed Closed Newton Cotes Qudrture T. Rmchndrn D.Udykumr nd
An approximation to the arithmetic-geometric mean. G.J.O. Jameson, Math. Gazette 98 (2014), 85 95
An pproximtion to the rithmetic-geometric men G.J.O. Jmeson, Mth. Gzette 98 (4), 85 95 Given positive numbers > b, consider the itertion given by =, b = b nd n+ = ( n + b n ), b n+ = ( n b n ) /. At ech
Chapter 14. Matrix Representations of Linear Transformations
Chpter 4 Mtrix Representtions of Liner Trnsformtions When considering the Het Stte Evolution, we found tht we could describe this process using multipliction by mtrix. This ws nice becuse computers cn
Fourier series. Preliminary material on inner products. Suppose V is vector space over C and (, )
Fourier series. Preliminry mteril on inner products. Suppose V is vector spce over C nd (, ) is Hermitin inner product on V. This mens, by definition, tht (, ) : V V C nd tht the following four conditions
Solving the Poisson Partial Differential Equation using Spectral Polynomial Methods
Solving the Poisson Prtil Differentil Eqution using Spectrl Polynomil Methods Seungkeol Choe April 8th, 4 Abstrct In this report, we present spectrl polynomil method for solving the Poisson eqution with
TMA 4180 Optimeringsteori Least Squares Optimization. Harald E. Krogstad, rev. 2010
TMA 48 Optimeringsteori Lest Squres Optimiztion Hrld E. Krogstd, rev. This note ws originlly prepred for erlier versions of the course. Nocedl nd Wright hs nice introduction to Lest Squre (LS) optimiztion
Elementary Linear Algebra
Elementry Liner Algebr Anton & Rorres, 1 th Edition Lecture Set 5 Chpter 4: Prt II Generl Vector Spces 163 คณ ตศาสตร ว ศวกรรม 3 สาขาว ชาว ศวกรรมคอมพ วเตอร ป การศ กษา 1/2555 163 คณตศาสตรวศวกรรม 3 สาขาวชาวศวกรรมคอมพวเตอร
Lecture 17. Integration: Gauss Quadrature. David Semeraro. University of Illinois at Urbana-Champaign. March 20, 2014
Lecture 17 Integrtion: Guss Qudrture Dvid Semerro University of Illinois t Urbn-Chmpign Mrch 0, 014 Dvid Semerro (NCSA) CS 57 Mrch 0, 014 1 / 9 Tody: Objectives identify the most widely used qudrture method