DS-GA 1002: PREREQUISITES REVIEW SOLUTIONS VLADIMIR KOBZAR
|
|
|
- Ruth McDowell
- 5 years ago
- Views:
Transcription
1 DS-GA 2: PEEQUISIES EVIEW SOLUIONS VLADIMI KOBZA he following is a selection of questions (drawn from Mr. Bernstein s notes) for reviewing the prerequisites for DS-GA 2. Questions from Ch, 8, 9 and 2 of Stewart will also be suitable for this purpose.. Sets Our model of probability will be based on set theory, and thus we will review the necessary concepts. () Let A t2, 3, 5u, B t, 3u, and suppose we are working in the universe S t, 2,..., 8u. (a) What is A Y B? What is A X B (written AB in oss)? (b) What is BzA? What is AzB? (c) What is A c (read A complement )? (d) What is A X B c? What is pa X B c q Y pa X Bq? (e) What is ta ˆ Bu? (f) Is A Ă B? Is B Ă A? Is A Ă A? (2) If A 5 and B, what can we say about A Y B? (3) If A,..., A n Ă S, for some universe S, give an expression for p Ť n A kq c in terms of an intersection. (4) What is Ť 8 np3, nq? Here p3, nq denotes the open interval tx P : 3 ă x ă nu? (5) What is Ş 8 np {n, {nq? Soln: () (a) A Y B t, 2, 3, 5u? A X B t3u. (b) BzA tu, AzB t2, 5u. (c) A c t, 4,, 7, 8u. (d) A X B c AzB t2, 5u? pa X B c q Y pa X Bq A (since B and B c partition S). (e) ta ˆ Bu tp2, q, p2, 3q, p3, q, p3, 3q, p5, q, p5, 3qu. (f) No. No. Yes. (2) ď A Y B A ` B A X B ď 5. (3) By De Morgan s laws, p Ť n A kq c Ş n Ac k. (4) Ť 8 np3, nq p3, 8q. Date: September, 2.
2 2 VLADIMI KOBZA (5) Ş 8 np {n, {nq (for every x, there is n sufficiently large s.t. x p {n, {nq, but P p {n, {nq for every n). 2. Series We will also need series/sums as they frequently occur when computing probabilities. ry proving each of the following commonly used results. () ř n k npn`q and ř n 2 k2 npn`qp2n`q. Soln: he first result follows by summing p `... ` nq ` pn `... ` q. For the second result, the base case (n=) is clear: 2 3. By the inductive hypothesis, we get n` ÿ k 2 nÿ k 2 ` pn ` q 2 npn ` qp2n ` q pn ` q2 ` pn ` qp2n2 ` 7n ` q pn ` qpn ` 2qp2pn ` q ` q as desired. (2) ř n k rk rn` for r and n ` if r. r Soln: For r, we have a telescoping series nÿ nÿ r k p rqr k r k If r, (3) For r ă, k p rq ` pr r2 q `... ` pr n r n` q r rn` r k nÿ r k k nÿ n ` k r k r, 8 ÿ k 2 r k r ` r2 p rq 3
3 DS-GA 2: PEEQUISIES EVIEW SOLUIONS 3 Soln: For the first result, lim nÿ nñ8 k r k lim nñ8 r n` r r For the second result, we use the ratio test to confirm the convergence lim a k` lim pk ` q2 r k` kñ8 kñ8 k 2 r k a k We can then expand the sum into a telescoping series though that requires slightly more algebra that the previous result. Alternatively, we can obtain the result by term-by-term differentiation. For a given r ă, let a ă be s.t. r P r a, as. Starting wth fptq t ` t ` t2 `... he term-by-term differentiated series is ř 8 krk converges uniformly on r a, as. herefore, the derivative of f is given by term-by-term differentiation, f ptq d dt p t q p tq 2 8 ÿ Multiplying by t, we get tf ptq kt k t p tq 2 kt k epeat the term-by-term differentiation to get f 2 ptq 2 pt q 3 8 ÿ kpk qt k 2 and set t 2 f 2 ptq kpk qt k
4 4 VLADIMI KOBZA Finally, set t r and observe that k 2 r k r 2 f 2 prq ` rf prq r 2 p 2 pr q q ` r 3 p rq 2 r ` r2 p rq 3 lim a k` lim kñ8 a k kñ8 x k` k! pk ` q! x k (4) e x ř 8 x k k for all x P. We define the function e x by the k! foregoing series and use the ratio test again to confirm the convergence. Since this limit is less than, the series converges (in fact, it converges absolutely). (5) he harmonic series ř 8 n diverges. he p-series ř 8 n n converges for p ą and diverges for p ď (can prove using integral n p test or Cauchy condensation test). Soln: By the integral test, if fpxq ě and f decreases monotonically on r, 8q then fpnq n converges if and only if 8 fpxqdx converges. hen, by explicit computation, ş 8 dx converges for x p p ą and diverges for p ď. Alternatively, by the Cauchy condensation test, the convergence of a monotonically decreasing sequence is determined by a condensed subsequence. Specifically, suppose a ě a 2 ě... ě. hen the series ř 8 n converges if and only if the series 2 n a 2 n a ` 2a 2 ` 4a 4 ` 8a 8 `... n converges. (For a proof, see e.g., udin, heorem 3.27.) If p ď, then lim 8 nñ8 Ñ 8. herefore the series diverges. n p If p ą, then the series is monotonically decreasing. By the condensation test, we consider
5 DS-GA 2: PEEQUISIES EVIEW SOLUIONS 5 2 n a 2 n n n 2 n 2 np 8 ÿ n 2 p n his geometric series converges if and only if 2 p ă, which is equivalent to p ă. Most of the series manipulations we have to make will involve modifying or matching the pattern with well-known series. () Give a series equal to the expression. Where does it converge? 4x 2 (2) Give a (non-series) expression for ř 8 (3) Give a (non-series) expression for ř 8 k n p qn x 3n where x ă. e tke λ λ k where λ ą and k! t P. (4) Compute a non-series expression for ř 8 k kxk when x ă. Soln: () ř 8 4x 2 k p4x2 q k converges for x ă {2. (2) ř 8 n p qn x 3n (3) ř 8 k p x 3 q. e tk e λ λ k k! e λ exppe t λq e λpet q. (4) (same as part of 2.(3) above) For a given x ă, let a ă be s.t. x P r a, as. Starting wth fptq t ` t ` t2 `... the term-by-term differentiated series is ř 8 krk. It converges uniformly on r a, as. herefore, the derivative of f is given by term-by-term differentiation, f ptq d dt p t q p tq 2 8 ÿ Multiplying by t, we get tf ptq kt k t p tq 2 kt k Letting t x kx k x p xq 2
6 VLADIMI KOBZA 3. Functions We will study random quantities (like the number of heads in a sequence of coin flips) using so-called random variables, which are realvalued functions. Here we will review basic facts about functions. ecall that a function f : X Ñ Y assigns to each element of X (the domain) exactly one element of Y (the codomain). he image (or range) of a function is the set fpxq defined by fpxq tfpxq : x P Xu Given any function (even non-invertible functions) we can form something called the preimage. More precisely, if A Ă Y, then f paq tx P X : fpxq P Au, called the preimage of A under f. We can perform algebra on real-valued functions in a natural way. For instance, if f, g : X Ñ, then pf ` gqpxq fpxq ` gpxq and pf 2 qpxq fpxq 2 () Let X 5 and Y 7. (a) How many functions f : X Ñ Y are there? (b) How many of them are injective? (ecall that a function is injective or one-to-one if fpx q fpx 2 q implies x x 2 for all x, x 2 P X. In the language of calculus/precalculus, injective functions pass the horizontal line test, and thus can be inverted, i.e., we get a function f : fpxq Ñ X.) (c) How many of them are surjective (we say that a function is surjective or onto if fpxq Y )? (d) How many have images of size 3? (2) Let f : Ñ be defined by fpxq x 2. What is f pr, 2sq? In other words, what is tx : fpxq P r, 2su? (3) Let X tpd, d 2 q : ď d i ď u and Y. If f, g : X Ñ Y with fpx, x 2 q x and fpx, x 2 q x 2, then what is pf `gq pt7uq tx P X : pf ` gqpxq 7u? Soln: () (a) Every domain element ican be mapped to any one of the 7 range elements. hus, there are 7 5 functions f : X Ñ Y. (b) Every domain element can be mapped to any one of the 7 range elements, provided that no other domain element is also mapped to that range element. hus, there are injective functions f : X Ñ Y. (c) None (since an domain element can t be mapped to more than one range element).
7 DS-GA 2: PEEQUISIES EVIEW SOLUIONS 7 (d) here are `7 3 different images, and the function needs to be surjective on each such image. here are 3 5 total functions with an image of size 3, of which, by inclusion-exclusion principle, `3 25 `3 2 5 are non-surjective on such image. hus, ˆ7 ˆ3 ˆ3 p ` 5 q 3 2 functions have images of size 3. (2) he preimage f pr, 2sq is given by r?2, s Y r,? 2s. (3) pf ` gq pt7uq tpd, d 2 q : d ` d 2 7; ď d i ď u. If the domain is a square in, then the preimage is the line interval from (,) to (,). If the domain is Z 2, then the preimage is tp, q, p2, 5q, p3, 4q, p4, 3q, p5, 2q, p, qu. 4. Single-variable calculus ecall a few results from single-variable calculus. Let f : ra, bs Ñ be integrable. If f ě then ş b f represents the area of the region a beneath f. For g : Ñ we define b gpxqdx lim añ if the limit exists. Note that if g ě then Gpbq b b a gpxqdx gpxqdx is an increasing function. he FC connects the definite integral, which computes the area, to the anti-derivative. heorem. (Version of FC) () Assume f : Ñ is integrable, and define F by F pxq x fptqdt hen F pxq fpxq where f is continuous. (2) Suppose f : pa, bq Ñ is continuous, and there is a function F : ra, bs Ñ that is continuous with F pxq fpxq for all x P pa, bq. hen b Here are a few exercises. a fpxqdx F pbq F paq
8 8 VLADIMI KOBZA () Which is bigger, or are they equal: e u du or e x2 dx (2) Let F pxq ş x fptqdt sinpex2 q for all x P. What is ş 47 fptqdt? 5 (3) Let fpxq e x. (a) What is F pxq ş x fptqdt? (b) What is F pxq? (4) If F pxq ş 3x 2 2x e t2 dt then what is F pxq? (5) Define fpxq by if x ă, $ & if ď x ă, 2 ` x if ď x ă 2, % if x ě 2. (a) What is F pxq ş x fptqdt? (b) What is F pxq? Soln: () By substitution, u x 2, du 2xdx, (2) since 2x ą e u du e x2 2xdx ą e x2 dx. fptqdt F p47q F p 5q sinpe 452 q sinpe p 5q2 q. (3) Let fpxq e x. (a) If x ď, (b) If x ą, F pxq F pxq x e t dt ` x e t dt e x e t dt 2 e x # F e x if x ď pxq e x if x ą e x
9 DS-GA 2: PEEQUISIES EVIEW SOLUIONS 9 (4) Let Gpyq ş y et2 dt. By the chain rule, F pxq G p3x 2 2xqpx 2q e p3x2 2xq 2 px 2q (5) (a) $ if x ă, & x if ď x ă, F pxq ` 2x ` % x2 if x ě if ď x ă 2, (b) By the FC F pxq fpxq except for x, and 3 where f is discontinuous. 5. Multivariate Calculus: Integrating over egions We will use multivariate calculus to study joint distributions, which show not only how random variables behave but also how they are related. () Let f : 2 Ñ be defined as follows: fpx, yq # if ď x ď y ď, otherwise. What is ş 8 ş 8 fpx, yqdxdy? (2) Consider the function fpx, yq : 4 px 2 ` y 2 q. he graph is a surface of revolution of a parabola. (a) Let tpx, yq : ď x, y ď u. What is ť fpx, yqdxdy? (b) Let S tpx, yq : ď x 2 ` y 2 ď 4u. What is ť fpx, yqdxdy? S (c) Let be the triangular region in the xy plane enclosed by the lines y x, x and y. What is ť fpx, yqdxdy? (3) Let fpx, yq e px`yq. (a) Let g be defined by # if ď x, y ď 2, gpx, yq otherwise. What is ş 8 ş 8 fpx, yqgpx, yqdxdy?
10 VLADIMI KOBZA (b) Let tpx, yq : ď x, y ď u and let 2 tpx, yq : ď x, y ď 2u. Which of the following two integrals is bigger: fpx, yqdxdy or f px{2, y{2qdxdy? (4) Let tpx, yq : ď x, y ď 4u and let tpx, yq : ď x, y ď 2u. Which of the following two integrals is bigger: f px{, y{qdxdy or fpx 2 {, y 2 {qdxdy? (5) Let gpx, yq x 2 ` 2xy ` y 3 and let f be defined by Soln: () (a) What are Bg Bx (b) What are Bf Bx fpx, yq (c) What is B2 f BxBy 8 8 x y e p2t2`u 2q dtdu Bg px, yq and px, yq? By Bf px, yq and px, yq? By px, yq? fpx, yqdxdy y dxdy x y xdy y2 2 y 2 (2) (a) 4 px 2 ` y 2 qdxdy r4x x3 3 xy2 s xdy r4 3 y2 s xdy r 3 y y3 {3 3 s ydy
11 DS-GA 2: PEEQUISIES EVIEW SOLUIONS (b) By changing to polar coordinates, we have ij 2π 2 fpx, yqdxdy p4 r 2 qrdrdθ (c) ij t (3) (a) 8 fpx, yqdxdy 8 x 2π 8π r2r 2 r4 4 s2 xdθ 4 px 2 ` y 2 qdydx r4y x 2 y y3 fpx, yqgpx, yqdxdy dx 3 s x 4p xq x 2 p xq p xqp 4x 2 ` 2x ` q dx 3 x 2 9x ` ` 4x 3 dx e px`yq dxdy 2 e x dx e y dy p xq3 dx 3 p e x 2 q 2 p e 2 q 2 (b) Let pu, vq Gpx, yq px{2, y{2q. hen, the Jacobian dpu,vq {4 dpx,yq fpu, vqdudv fpx{2, y{2q 4 dxdy herefore, since fpx, yq ą fpx, yqdxdy ă f px{2, y{2qdxdy
12 2 VLADIMI KOBZA (4) Let define the change of variables by pu, vq Gpx, yq px 2, y 2 q. hen, the Jacobian is given by dpu,vq 4xy, and we have dpx,yq f pu{, v{qdudv fpx 2 {, y 2 {q4xydxdy herefore, since fpx, yq ą ; x, y ą, (5) (a) Bg Bx f px{, y{qdxdy ą fpx 2 {, y 2 {qdxdy Bg px, yq 2x ` 2y; px, yq 2x ` 3y2 By (b) Bf Bx px, yq ş y e p2t2`x 2q dt; Bf By px, yq ş x e p2y2`u 2q du (c) B2 f BxBy px, yq e p2y2`x 2 q eferences [] Bernstein, heory of Probability lecture notes, brettb/probsum25/index.html [2] oss, A First Course in Probability (9th ed., 24) [3] Stewart, Essential Calculus: Early ranscendentals (2nd ed., 23)
ADVANCE TOPICS IN ANALYSIS - REAL. 8 September September 2011
 ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
ADVANCE TOPICS IN ANALYSIS - REAL NOTES COMPILED BY KATO LA Introductions 8 September 011 15 September 011 Nested Interval Theorem: If A 1 ra 1, b 1 s, A ra, b s,, A n ra n, b n s, and A 1 Ě A Ě Ě A n
REAL ANALYSIS II TAKE HOME EXAM. T. Tao s Lecture Notes Set 5
 REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
REAL ANALYSIS II TAKE HOME EXAM CİHAN BAHRAN T. Tao s Lecture Notes Set 5 1. Suppose that te 1, e 2, e 3,... u is a countable orthonormal system in a complex Hilbert space H, and c 1, c 2,... is a sequence
Singular integral operators and the Riesz transform
 Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
Singular integral operators and the Riesz transform Jordan Bell jordan.bell@gmail.com Department of Mathematics, University of Toronto November 17, 017 1 Calderón-Zygmund kernels Let ω n 1 be the measure
DS-GA 3001: PROBLEM SESSION 2 SOLUTIONS VLADIMIR KOBZAR
 DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
DS-GA 3: PROBLEM SESSION SOLUTIONS VLADIMIR KOBZAR Note: In this discussion we allude to the fact the dimension of a vector space is given by the number of basis vectors. We will shortly establish this
a P (A) f k(x) = A k g k " g k (x) = ( 1) k x ą k. $ & g k (x) = x k (0, 1) f k, f, g : [0, 8) Ñ R f k (x) ď g(x) k P N x P [0, 8) g(x)dx g(x)dx ă 8
 M M, d A Ď M f k : A Ñ R A a P A f kx = A k xña k P N ta k u 8 k=1 f kx = f k x. xña kñ8 kñ8 xña M, d N, ρ A Ď M f k : A Ñ N tf k u 8 k=1 f : A Ñ N A f A 8ř " x ď k, g k x = 1 k x ą k. & g k x = % g k
M M, d A Ď M f k : A Ñ R A a P A f kx = A k xña k P N ta k u 8 k=1 f kx = f k x. xña kñ8 kñ8 xña M, d N, ρ A Ď M f k : A Ñ N tf k u 8 k=1 f : A Ñ N A f A 8ř " x ď k, g k x = 1 k x ą k. & g k x = % g k
Random Variables. Andreas Klappenecker. Texas A&M University
 Random Variables Andreas Klappenecker Texas A&M University 1 / 29 What is a Random Variable? Random variables are functions that associate a numerical value to each outcome of an experiment. For instance,
Random Variables Andreas Klappenecker Texas A&M University 1 / 29 What is a Random Variable? Random variables are functions that associate a numerical value to each outcome of an experiment. For instance,
Lecture 19 - Covariance, Conditioning
 THEORY OF PROBABILITY VLADIMIR KOBZAR Review. Lecture 9 - Covariance, Conditioning Proposition. (Ross, 6.3.2) If X,..., X n are independent normal RVs with respective parameters µ i, σi 2 for i,..., n,
THEORY OF PROBABILITY VLADIMIR KOBZAR Review. Lecture 9 - Covariance, Conditioning Proposition. (Ross, 6.3.2) If X,..., X n are independent normal RVs with respective parameters µ i, σi 2 for i,..., n,
Homework for MATH 4604 (Advanced Calculus II) Spring 2017
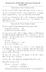 Homework for MATH 4604 (Advanced Calculus II) Spring 2017 Homework 14: Due on Tuesday 2 May 55. Let m, n P N, A P R mˆn and v P R n. Show: L A pvq 2 ď A 2 v 2. 56. Let n P N and let A P R nˆn. Let I n
Homework for MATH 4604 (Advanced Calculus II) Spring 2017 Homework 14: Due on Tuesday 2 May 55. Let m, n P N, A P R mˆn and v P R n. Show: L A pvq 2 ď A 2 v 2. 56. Let n P N and let A P R nˆn. Let I n
MATH 360 Final Exam Thursday, December 14, a n 2. a n 1 1
 MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
MATH 36 Final Exam Thursday, December 4, 27 Name. The sequence ta n u is defined by a and a n (a) Prove that lim a n exists by showing that ta n u is bounded and monotonic and invoking an appropriate result.
MAT 128A - Practice Midterm Exam
 MAT 8A - Practice Midterm Exam Karry Wong October 3, 08 Problem (True or False) Given that f : r, s Ñ R is a continuous function, and that ta n u are its Chebyshev coefficients. Also, for N P N, p N pxq
MAT 8A - Practice Midterm Exam Karry Wong October 3, 08 Problem (True or False) Given that f : r, s Ñ R is a continuous function, and that ta n u are its Chebyshev coefficients. Also, for N P N, p N pxq
arxiv: v1 [math.ca] 4 Apr 2017
![arxiv: v1 [math.ca] 4 Apr 2017 arxiv: v1 [math.ca] 4 Apr 2017](/thumbs/88/115044967.jpg) ON LOCALIZATION OF SCHRÖDINGER MEANS PER SJÖLIN Abstract. Localization properties for Schrödinger means are studied in dimension higher than one. arxiv:704.00927v [math.ca] 4 Apr 207. Introduction Let
ON LOCALIZATION OF SCHRÖDINGER MEANS PER SJÖLIN Abstract. Localization properties for Schrödinger means are studied in dimension higher than one. arxiv:704.00927v [math.ca] 4 Apr 207. Introduction Let
THEORY OF PROBABILITY VLADIMIR KOBZAR
 THEORY OF PROBABILITY VLADIMIR KOBZAR Lecture 3 - Axioms of Probability I Sample Space and Events. In probability theory, an experiment is any situation which has several possible outcomes, exactly one
THEORY OF PROBABILITY VLADIMIR KOBZAR Lecture 3 - Axioms of Probability I Sample Space and Events. In probability theory, an experiment is any situation which has several possible outcomes, exactly one
Functions. Ex. f : R 0 Ñ R 0 defined by x fiñ x 2.
 Functions Let f : X Ñ Y be a function. Recall, the image of f is fpxq ty P Y fpxq y for some x P Xu. Further, f is... injective if at most one x P X maps to each y P Y,i.e. if fpx q fpx q then x x. Ex.
Functions Let f : X Ñ Y be a function. Recall, the image of f is fpxq ty P Y fpxq y for some x P Xu. Further, f is... injective if at most one x P X maps to each y P Y,i.e. if fpx q fpx q then x x. Ex.
APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER
 APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER TOM SANDERS The purpose of this note is to highlight a question raised by Shachar Lovett [Lov], and to offer some motivation
APPROXIMATE HOMOMORPHISMS BETWEEN THE BOOLEAN CUBE AND GROUPS OF PRIME ORDER TOM SANDERS The purpose of this note is to highlight a question raised by Shachar Lovett [Lov], and to offer some motivation
Integration and Fourier Theory. Lecture 14
 Integration and Fourier Theory Lecture 4 Morten Grud Rasmussen March 5, 03 Trigonometric Series Denote the unit circle in the complex plane by T tx P C x u ( T for torus ). Note that R Q t ÞÑ e it P T
Integration and Fourier Theory Lecture 4 Morten Grud Rasmussen March 5, 03 Trigonometric Series Denote the unit circle in the complex plane by T tx P C x u ( T for torus ). Note that R Q t ÞÑ e it P T
NOTES WEEK 02 DAY 1. THEOREM 0.3. Let A, B and C be sets. Then
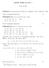 NOTES WEEK 02 DAY 1 SCOT ADAMS LEMMA 0.1. @propositions P, Q, R, rp or pq&rqs rp p or Qq&pP or Rqs. THEOREM 0.2. Let A and B be sets. Then (i) A X B B X A, and (ii) A Y B B Y A THEOREM 0.3. Let A, B and
NOTES WEEK 02 DAY 1 SCOT ADAMS LEMMA 0.1. @propositions P, Q, R, rp or pq&rqs rp p or Qq&pP or Rqs. THEOREM 0.2. Let A and B be sets. Then (i) A X B B X A, and (ii) A Y B B Y A THEOREM 0.3. Let A, B and
Introduction to computability Tutorial 7
 Introduction to computability Tutorial 7 Context free languages and Turing machines November 6 th 2014 Context-free languages 1. Show that the following languages are not context-free: a) L ta i b j a
Introduction to computability Tutorial 7 Context free languages and Turing machines November 6 th 2014 Context-free languages 1. Show that the following languages are not context-free: a) L ta i b j a
Markov Chains. Andreas Klappenecker by Andreas Klappenecker. All rights reserved. Texas A&M University
 Markov Chains Andreas Klappenecker Texas A&M University 208 by Andreas Klappenecker. All rights reserved. / 58 Stochastic Processes A stochastic process X tx ptq: t P T u is a collection of random variables.
Markov Chains Andreas Klappenecker Texas A&M University 208 by Andreas Klappenecker. All rights reserved. / 58 Stochastic Processes A stochastic process X tx ptq: t P T u is a collection of random variables.
MATH 2413 TEST ON CHAPTER 4 ANSWER ALL QUESTIONS. TIME 1.5 HRS.
 MATH 1 TEST ON CHAPTER ANSWER ALL QUESTIONS. TIME 1. HRS. M1c Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Use the summation formulas to rewrite the
MATH 1 TEST ON CHAPTER ANSWER ALL QUESTIONS. TIME 1. HRS. M1c Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Use the summation formulas to rewrite the
Approximation in the Zygmund Class
 Approximation in the Zygmund Class Odí Soler i Gibert Joint work with Artur Nicolau Universitat Autònoma de Barcelona New Developments in Complex Analysis and Function Theory, 02 July 2018 Approximation
Approximation in the Zygmund Class Odí Soler i Gibert Joint work with Artur Nicolau Universitat Autònoma de Barcelona New Developments in Complex Analysis and Function Theory, 02 July 2018 Approximation
Short Notes in Mathematics Fundamental concepts every student of Mathematics should know
 Short Notes in Mathematics Fundamental concepts every student of Mathematics should know Markus J. Pflaum October 9, 2018 Contents Titlepage 1 1 Foundations 2 Set theory........................................
Short Notes in Mathematics Fundamental concepts every student of Mathematics should know Markus J. Pflaum October 9, 2018 Contents Titlepage 1 1 Foundations 2 Set theory........................................
NOTES WEEK 11 DAY 2 SCOT ADAMS
 NOTES WEEK 11 DAY 2 SCOT ADAMS In Proposition 0.1 below, Bp0, δq is just the open interval p δ, δq and Bp0, x q is just the closed interval r x, x s. PROPOSITION 0.1. Let g : R R and let δ ą 0. Assume
NOTES WEEK 11 DAY 2 SCOT ADAMS In Proposition 0.1 below, Bp0, δq is just the open interval p δ, δq and Bp0, x q is just the closed interval r x, x s. PROPOSITION 0.1. Let g : R R and let δ ą 0. Assume
arxiv: v2 [math.ca] 13 May 2015
![arxiv: v2 [math.ca] 13 May 2015 arxiv: v2 [math.ca] 13 May 2015](/thumbs/88/114667751.jpg) ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
ON THE CLOSURE OF TRANSLATION-DILATION INVARIANT LINEAR SPACES OF POLYNOMIALS arxiv:1505.02370v2 [math.ca] 13 May 2015 J. M. ALMIRA AND L. SZÉKELYHIDI Abstract. Assume that a linear space of real polynomials
Tempered Distributions
 Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
Tempered Distributions Lionel Fiske and Cairn Overturf May 9, 26 In the classical study of partial differential equations one requires a solution to be differentiable. While intuitively this requirement
Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system
 Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system 1 Joinings and channels 1.1 Joinings Definition 1. If px, µ, T q and py, ν, Sq are MPSs, then a joining
Entropy and Ergodic Theory Notes 22: The Kolmogorov Sinai entropy of a measure-preserving system 1 Joinings and channels 1.1 Joinings Definition 1. If px, µ, T q and py, ν, Sq are MPSs, then a joining
MATH 260 Homework assignment 8 March 21, px 2yq dy. (c) Where C is the part of the line y x, parametrized any way you like.
 MATH 26 Homework assignment 8 March 2, 23. Evaluate the line integral x 2 y dx px 2yq dy (a) Where is the part of the parabola y x 2 from p, q to p, q, parametrized as x t, y t 2 for t. (b) Where is the
MATH 26 Homework assignment 8 March 2, 23. Evaluate the line integral x 2 y dx px 2yq dy (a) Where is the part of the parabola y x 2 from p, q to p, q, parametrized as x t, y t 2 for t. (b) Where is the
Introduction to Differential Equations
 Introduction to Differential Equations J. M. Veal, Ph. D. version 13.08.30 Contents 1 Introduction to Differential Equations 2 1.1 Definitions and Terminology.................... 2 1.2 Initial-Value Problems.......................
Introduction to Differential Equations J. M. Veal, Ph. D. version 13.08.30 Contents 1 Introduction to Differential Equations 2 1.1 Definitions and Terminology.................... 2 1.2 Initial-Value Problems.......................
For example, p12q p2x 1 x 2 ` 5x 2 x 2 3 q 2x 2 x 1 ` 5x 1 x 2 3. (a) Let p 12x 5 1x 7 2x 4 18x 6 2x 3 ` 11x 1 x 2 x 3 x 4,
 SOLUTIONS Math A4900 Homework 5 10/4/2017 1. (DF 2.2.12(a)-(d)+) Symmetric polynomials. The group S n acts on the set tx 1, x 2,..., x n u by σ x i x σpiq. That action extends to a function S n ˆ A Ñ A,
SOLUTIONS Math A4900 Homework 5 10/4/2017 1. (DF 2.2.12(a)-(d)+) Symmetric polynomials. The group S n acts on the set tx 1, x 2,..., x n u by σ x i x σpiq. That action extends to a function S n ˆ A Ñ A,
Basics of Probability Theory
 Basics of Probability Theory Andreas Klappenecker Texas A&M University 2018 by Andreas Klappenecker. All rights reserved. 1 / 39 Terminology The probability space or sample space Ω is the set of all possible
Basics of Probability Theory Andreas Klappenecker Texas A&M University 2018 by Andreas Klappenecker. All rights reserved. 1 / 39 Terminology The probability space or sample space Ω is the set of all possible
NOTES WEEK 15 DAY 1 SCOT ADAMS
 NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
NOTES WEEK 15 DAY 1 SCOT ADAMS We fix some notation for the entire class today: Let n P N, W : R n, : 2 P N pw q, W : LpW, W q, I : id W P W, z : 0 W 0 n. Note that W LpR n, R n q. Recall, for all T P
Probability Generating Functions
 Probability Generating Functions Andreas Klappenecker Texas A&M University 2018 by Andreas Klappenecker. All rights reserved. 1 / 27 Probability Generating Functions Definition Let X be a discrete random
Probability Generating Functions Andreas Klappenecker Texas A&M University 2018 by Andreas Klappenecker. All rights reserved. 1 / 27 Probability Generating Functions Definition Let X be a discrete random
Entropy and Ergodic Theory Notes 21: The entropy rate of a stationary process
 Entropy and Ergodic Theory Notes 21: The entropy rate of a stationary process 1 Sources with memory In information theory, a stationary stochastic processes pξ n q npz taking values in some finite alphabet
Entropy and Ergodic Theory Notes 21: The entropy rate of a stationary process 1 Sources with memory In information theory, a stationary stochastic processes pξ n q npz taking values in some finite alphabet
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES
 FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
FURSTENBERG S THEOREM ON PRODUCTS OF I.I.D. 2 ˆ 2 MATRICES JAIRO BOCHI Abstract. This is a revised version of some notes written ą 0 years ago. I thank Anthony Quas for pointing to a gap in the previous
Solutions of exercise sheet 3
 Topology D-MATH, FS 2013 Damen Calaque Solutons o exercse sheet 3 1. (a) Let U Ă Y be open. Snce s contnuous, 1 puq s open n X. Then p A q 1 puq 1 puq X A s open n the subspace topology on A. (b) I s contnuous,
Topology D-MATH, FS 2013 Damen Calaque Solutons o exercse sheet 3 1. (a) Let U Ă Y be open. Snce s contnuous, 1 puq s open n X. Then p A q 1 puq 1 puq X A s open n the subspace topology on A. (b) I s contnuous,
Variational inequality formulation of chance-constrained games
 Variational inequality formulation of chance-constrained games Joint work with Vikas Singh from IIT Delhi Université Paris Sud XI Computational Management Science Conference Bergamo, Italy May, 2017 Outline
Variational inequality formulation of chance-constrained games Joint work with Vikas Singh from IIT Delhi Université Paris Sud XI Computational Management Science Conference Bergamo, Italy May, 2017 Outline
Introduction to Numerical Analysis
 Introduction to Numerical Analysis Lecture Notes for SI 507 Authors: S. Baskar and S. Sivaji Ganesh Department of Mathematics Indian Institute of Technology Bombay Powai, Mumbai 400 076. Contents 1 Mathematical
Introduction to Numerical Analysis Lecture Notes for SI 507 Authors: S. Baskar and S. Sivaji Ganesh Department of Mathematics Indian Institute of Technology Bombay Powai, Mumbai 400 076. Contents 1 Mathematical
Asymptotic Analysis 1: Limits and Asymptotic Equality
 Asymptotic Analysis 1: Limits and Asymptotic Equality Andreas Klappenecker and Hyunyoung Lee Texas A&M University 1 / 15 Motivation In asymptotic analysis, our goal is to compare a function f pnq with
Asymptotic Analysis 1: Limits and Asymptotic Equality Andreas Klappenecker and Hyunyoung Lee Texas A&M University 1 / 15 Motivation In asymptotic analysis, our goal is to compare a function f pnq with
Introduction to Applied Algebraic Topology
 Introduction to Applied Algebraic Topology Tom Needham Last Updated: December 10, 2017 These are lecture notes for the course MATH 4570 at the Ohio State University. They are a work in progress and certainly
Introduction to Applied Algebraic Topology Tom Needham Last Updated: December 10, 2017 These are lecture notes for the course MATH 4570 at the Ohio State University. They are a work in progress and certainly
NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2
 NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2 MARCO VITTURI Contents 1. Solution to exercise 5-2 1 2. Solution to exercise 5-3 2 3. Solution to exercise 5-7 4 4. Solution to exercise 5-8 6 5. Solution
NOTES ON SOME EXERCISES OF LECTURE 5, MODULE 2 MARCO VITTURI Contents 1. Solution to exercise 5-2 1 2. Solution to exercise 5-3 2 3. Solution to exercise 5-7 4 4. Solution to exercise 5-8 6 5. Solution
1. Examples. We did most of the following in class in passing. Now compile all that data.
 SOLUTIONS Math A4900 Homework 12 11/22/2017 1. Examples. We did most of the following in class in passing. Now compile all that data. (a) Favorite examples: Let R tr, Z, Z{3Z, Z{6Z, M 2 prq, Rrxs, Zrxs,
SOLUTIONS Math A4900 Homework 12 11/22/2017 1. Examples. We did most of the following in class in passing. Now compile all that data. (a) Favorite examples: Let R tr, Z, Z{3Z, Z{6Z, M 2 prq, Rrxs, Zrxs,
`an cos nπx. n 1. L `b
 4 Fourier Series A periodic function on a range p,q may be decomposed into a sum of sinusoidal (sine or cosine) functions. This can be written as follows gpxq 1 2 a ` ř8 `b (4.1) The aim of this chapter
4 Fourier Series A periodic function on a range p,q may be decomposed into a sum of sinusoidal (sine or cosine) functions. This can be written as follows gpxq 1 2 a ` ř8 `b (4.1) The aim of this chapter
Lecture Notes 1 Basic Concepts of Mathematics MATH 352
 Lecture Notes 1 Basic Concepts of Mathematics MATH 352 Ivan Avramidi New Mexico Institute of Mining and Technology Socorro, NM 87801 June 3, 2004 Author: Ivan Avramidi; File: absmath.tex; Date: June 11,
Lecture Notes 1 Basic Concepts of Mathematics MATH 352 Ivan Avramidi New Mexico Institute of Mining and Technology Socorro, NM 87801 June 3, 2004 Author: Ivan Avramidi; File: absmath.tex; Date: June 11,
NOTES WEEK 14 DAY 2 SCOT ADAMS
 NOTES WEEK 14 DAY 2 SCOT ADAMS For this lecture, we fix the following: Let n P N, let W : R n, let : 2 P N pr n q and let I : id R n : R n Ñ R n be the identity map, defined by Ipxq x. For any h : W W,
NOTES WEEK 14 DAY 2 SCOT ADAMS For this lecture, we fix the following: Let n P N, let W : R n, let : 2 P N pr n q and let I : id R n : R n Ñ R n be the identity map, defined by Ipxq x. For any h : W W,
Singular Value Decomposition and its. SVD and its Applications in Computer Vision
 Singular Value Decomposition and its Applications in Computer Vision Subhashis Banerjee Department of Computer Science and Engineering IIT Delhi October 24, 2013 Overview Linear algebra basics Singular
Singular Value Decomposition and its Applications in Computer Vision Subhashis Banerjee Department of Computer Science and Engineering IIT Delhi October 24, 2013 Overview Linear algebra basics Singular
MATH 260 Class notes/questions January 10, 2013
 MATH 26 Class notes/questions January, 2 Linear transformations Last semester, you studied vector spaces (linear spaces) their bases, dimension, the ideas of linear dependence and linear independence Now
MATH 26 Class notes/questions January, 2 Linear transformations Last semester, you studied vector spaces (linear spaces) their bases, dimension, the ideas of linear dependence and linear independence Now
Mathematische Methoden der Unsicherheitsquantifizierung
 Mathematische Methoden der Unsicherheitsquantifizierung Oliver Ernst Professur Numerische Mathematik Sommersemester 2014 Contents 1 Introduction 1.1 What is Uncertainty Quantification? 1.2 A Case Study:
Mathematische Methoden der Unsicherheitsquantifizierung Oliver Ernst Professur Numerische Mathematik Sommersemester 2014 Contents 1 Introduction 1.1 What is Uncertainty Quantification? 1.2 A Case Study:
THEORY OF PROBABILITY VLADIMIR KOBZAR
 THEORY OF PROBABILITY VLADIMIR KOBZAR Lecture 20 - Conditional Expectation, Inequalities, Laws of Large Numbers, Central Limit Theorem This lecture is based on the materials from the Courant Institute
THEORY OF PROBABILITY VLADIMIR KOBZAR Lecture 20 - Conditional Expectation, Inequalities, Laws of Large Numbers, Central Limit Theorem This lecture is based on the materials from the Courant Institute
Eco 610 Mathematical Economics I Notes M. Jerison 8/24/14
 Eco 610 Mathematical Economics I Notes M. Jerison 8/24/14 1. Introduction Economists analyze qualitative relations (e.g., who is whose boss, or which ownership pattern is more efficient) and quantitative
Eco 610 Mathematical Economics I Notes M. Jerison 8/24/14 1. Introduction Economists analyze qualitative relations (e.g., who is whose boss, or which ownership pattern is more efficient) and quantitative
RAMSEY PARTIAL ORDERS FROM ACYCLIC GRAPHS
 RAMSEY PARTIAL ORDERS FROM ACYCLIC GRAPHS JAROSLAV NEŠETŘIL AND VOJTĚCH RÖDL Abstract. We prove that finite partial orders with a linear extension form a Ramsey class. Our proof is based on the fact that
RAMSEY PARTIAL ORDERS FROM ACYCLIC GRAPHS JAROSLAV NEŠETŘIL AND VOJTĚCH RÖDL Abstract. We prove that finite partial orders with a linear extension form a Ramsey class. Our proof is based on the fact that
q-de Rham cohomology via Λ-rings
 q-de Rham cohomology via Λ-rings J.P.Pridham arxiv:1608.07142 1 / 21 q-analogues (Gauss) rns q : qn 1 q 1 1 q... qn 1 rns q! : rns q... r2s q r1s q, ¹ n 1 i 0 n 1 ¹ i 0 p1 p1 n k q : rns q! rn ksq!rksq!
q-de Rham cohomology via Λ-rings J.P.Pridham arxiv:1608.07142 1 / 21 q-analogues (Gauss) rns q : qn 1 q 1 1 q... qn 1 rns q! : rns q... r2s q r1s q, ¹ n 1 i 0 n 1 ¹ i 0 p1 p1 n k q : rns q! rn ksq!rksq!
Draft. Chapter 2 Approximation and Interpolation. MATH 561 Numerical Analysis. Songting Luo. Department of Mathematics Iowa State University
 Chapter 2 Approximation and Interpolation Songting Luo Department of Mathematics Iowa State University MATH 561 Numerical Analysis Songting Luo ( Department of Mathematics Iowa State University[0.5in]
Chapter 2 Approximation and Interpolation Songting Luo Department of Mathematics Iowa State University MATH 561 Numerical Analysis Songting Luo ( Department of Mathematics Iowa State University[0.5in]
PRODUCT MEASURES AND FUBINI S THEOREM
 CHAPTER 6 PRODUCT MEASURES AND FUBINI S THEOREM All students learn in elementary calculus to evaluate a double integral by iteration. The theorem justifying this process is called Fubini s theorem. However,
CHAPTER 6 PRODUCT MEASURES AND FUBINI S THEOREM All students learn in elementary calculus to evaluate a double integral by iteration. The theorem justifying this process is called Fubini s theorem. However,
Approximation of Weighted Local Mean Operators
 Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
Approximation of Weighted Local ean Operators Jianzhong Wang Department of athematics and Statistics Sam Houston State University Huntsville, TX 7734 Abstract Recently, weighted local mean operators are
NONLINEAR EVOLUTION EQUATIONS SHORT NOTES WEEK #1
 NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
NONLNEA EVOLUTON EQUATONS SHOT NOTES WEEK #. Free Schrödinger Equation Let Bx 2 `...`Bx 2 n denote the Laplacian on d with d ě. The initial-value problem for the free Schrödinger equation (in d space dimensions)
NOTES WEEK 04 DAY 1 SCOT ADAMS
 NOTES WEEK 0 DAY 1 SCOT ADAMS DEFINITION 01 Let m, n P N, B P BpR m, R n q Let e 1,, e m be the standard basis of R m Let f 1,, f n be the standard basis of R n Then we define rbs P R nˆm by rbs ji Bpe
NOTES WEEK 0 DAY 1 SCOT ADAMS DEFINITION 01 Let m, n P N, B P BpR m, R n q Let e 1,, e m be the standard basis of R m Let f 1,, f n be the standard basis of R n Then we define rbs P R nˆm by rbs ji Bpe
TOPOLOGY NOTES KLINT QINAMI
 TOPOLOGY NOTES KLINT QINAMI Preamble. The following is a collection of exercises relating to point-set topology and preliminary algebraic topology, together with my proofs of those exercises. Use at your
TOPOLOGY NOTES KLINT QINAMI Preamble. The following is a collection of exercises relating to point-set topology and preliminary algebraic topology, together with my proofs of those exercises. Use at your
Fourier transforms. Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x L or L x L) as Fourier series: a n cos L
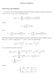 ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative
 Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative notation: H tx l l P Zu xxy, Additive notation: H tlx
Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative notation: H tx l l P Zu xxy, Additive notation: H tlx
L E C T U R E 2 1 : P R O P E RT I E S O F M AT R I X T R A N S F O R M AT I O N S I I. Wednesday, November 30
 L E C T U R E 2 1 : P R O P E RT I E S O F M AT R I X T R A N S F O R M AT I O N S I I Wednesday, November 30 1 the range of a linear transformation Let s begin by defining the range of a linear transformation.
L E C T U R E 2 1 : P R O P E RT I E S O F M AT R I X T R A N S F O R M AT I O N S I I Wednesday, November 30 1 the range of a linear transformation Let s begin by defining the range of a linear transformation.
NOTES WEEK 01 DAY 1 SCOT ADAMS
 NOTES WEEK 01 DAY 1 SCOT ADAMS Question: What is Mathematics? Answer: The study of absolute truth. Question: Why is it so hard to teach and to learn? Answer: One must learn to play a variety of games called
NOTES WEEK 01 DAY 1 SCOT ADAMS Question: What is Mathematics? Answer: The study of absolute truth. Question: Why is it so hard to teach and to learn? Answer: One must learn to play a variety of games called
Real Analysis Math 131AH Rudin, Chapter #1. Dominique Abdi
 Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Real Analysis Math 3AH Rudin, Chapter # Dominique Abdi.. If r is rational (r 0) and x is irrational, prove that r + x and rx are irrational. Solution. Assume the contrary, that r+x and rx are rational.
Ewa Marciniak, Jakub Trybuła OPTIMAL DIVIDEND POLICY IN DISCRETE TIME
 DEMONSTRATIO MATHEMATICA Vol XLVII No 1 2014 Ewa Marciniak, Jakub Trybuła OPTIMAL DIVIDEND POLICY IN DISCRETE TIME Abstract A problem of optimal dividend policy for a firm with a bank loan is considered
DEMONSTRATIO MATHEMATICA Vol XLVII No 1 2014 Ewa Marciniak, Jakub Trybuła OPTIMAL DIVIDEND POLICY IN DISCRETE TIME Abstract A problem of optimal dividend policy for a firm with a bank loan is considered
Mathematics 206 Solutions for HWK 23 Section 6.3 p358
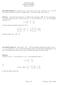 Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
Mathematics 6 Solutions for HWK Section Problem 9. Given T(x, y, z) = (x 9y + z,6x + 5y z) and v = (,,), use the standard matrix for the linear transformation T to find the image of the vector v. Note
Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY
 DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 215 Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY Communicated by E. Zadrzyńska Abstract.
DEMONSTRATIO MATHEMATICA Vol. XLVIII No 1 215 Mariusz Jurkiewicz, Bogdan Przeradzki EXISTENCE OF SOLUTIONS FOR HIGHER ORDER BVP WITH PARAMETERS VIA CRITICAL POINT THEORY Communicated by E. Zadrzyńska Abstract.
NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION. Contents 1. Overview Steenrod s construction
 NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION GUS LONERGAN Abstract. We use Steenrod s construction to prove that the quantum Coulomb branch is a Frobenius-constant quantization. Contents
NOTES FOR BEILINSON-DRINFELD SEMINAR - EVEN SHORTER VERSION GUS LONERGAN Abstract. We use Steenrod s construction to prove that the quantum Coulomb branch is a Frobenius-constant quantization. Contents
Ground States are generically a periodic orbit
 Gonzalo Contreras CIMAT Guanajuato, Mexico Ergodic Optimization and related topics USP, Sao Paulo December 11, 2013 Expanding map X compact metric space. T : X Ñ X an expanding map i.e. T P C 0, Dd P Z`,
Gonzalo Contreras CIMAT Guanajuato, Mexico Ergodic Optimization and related topics USP, Sao Paulo December 11, 2013 Expanding map X compact metric space. T : X Ñ X an expanding map i.e. T P C 0, Dd P Z`,
Numerically solving the wave equation using the finite element method
 Faculty of Science Numerically solving the wave equation using the finite element method Bachelor s Thesis Jasper Everink Mathematics Supervisor: Dr. Tristan van Leeuwen Mathematical Institute 7th June
Faculty of Science Numerically solving the wave equation using the finite element method Bachelor s Thesis Jasper Everink Mathematics Supervisor: Dr. Tristan van Leeuwen Mathematical Institute 7th June
9 < Ways to place n distinguishable objects= S(n, k) = into k indistinguishable boxes so that no box is left empty We stated in section 6.
 Math 365 Monday 4/1/19 8.5 (inclusion/exclusion) and 9.1 & 9.5 (equivalence relations) Exercise 41. Use inclusion/exclusion to answer the following questions. (a) How many elements are in A 1 [ A 2 if
Math 365 Monday 4/1/19 8.5 (inclusion/exclusion) and 9.1 & 9.5 (equivalence relations) Exercise 41. Use inclusion/exclusion to answer the following questions. (a) How many elements are in A 1 [ A 2 if
Almost Conservation Laws for KdV and Cubic NLS. UROP Final Paper, Summer 2018
 Almost Conservation Laws for KdV and Cubic NLS UROP Final Paper, Summer 2018 Zixuan Xu Mentor: Ricardo Grande Izquierdo Project suggested by: Gigliola Staffilani Abstract In this paper, we explore the
Almost Conservation Laws for KdV and Cubic NLS UROP Final Paper, Summer 2018 Zixuan Xu Mentor: Ricardo Grande Izquierdo Project suggested by: Gigliola Staffilani Abstract In this paper, we explore the
The Riemann Roch theorem for metric graphs
 The Riemann Roch theorem for metric graphs R. van Dobben de Bruyn 1 Preface These are the notes of a talk I gave at the graduate student algebraic geometry seminar at Columbia University. I present a short
The Riemann Roch theorem for metric graphs R. van Dobben de Bruyn 1 Preface These are the notes of a talk I gave at the graduate student algebraic geometry seminar at Columbia University. I present a short
PROBABILITY 2018 HANDOUT 2: GAUSSIAN DISTRIBUTION
 PROAILITY 218 HANDOUT 2: GAUSSIAN DISTRIUTION GIOVANNI PISTONE Contents 1. Standard Gaussian Distribution 1 2. Positive Definite Matrices 5 3. General Gaussian Distribution 6 4. Independence of Jointly
PROAILITY 218 HANDOUT 2: GAUSSIAN DISTRIUTION GIOVANNI PISTONE Contents 1. Standard Gaussian Distribution 1 2. Positive Definite Matrices 5 3. General Gaussian Distribution 6 4. Independence of Jointly
Crypto math II. Alin Tomescu May 27, Abstract A quick overview on group theory from Ron Rivest s course in Spring 2015.
 Crypto math II Alin Tomescu alinush@mit.edu May 7, 015 Abstract A quick overview on group theory from Ron Rivest s 6.857 course in Spring 015. 1 Overview Group theory review Diffie-Hellman (DH) key exchange
Crypto math II Alin Tomescu alinush@mit.edu May 7, 015 Abstract A quick overview on group theory from Ron Rivest s 6.857 course in Spring 015. 1 Overview Group theory review Diffie-Hellman (DH) key exchange
arxiv: v2 [cs.lg] 31 Oct 2018
![arxiv: v2 [cs.lg] 31 Oct 2018 arxiv: v2 [cs.lg] 31 Oct 2018](/thumbs/96/127998133.jpg) SOME NEGATIVE RESULTS FOR SINGLE LAYER AND MULTILAYER FEEDFORWARD NEURAL NETWORKS arxiv:1810.10032v2 [cs.lg] 31 Oct 2018 J. M. ALMIRA, P. E. LOPEZ-DE-TERUEL, D. J. ROMERO-LÓPEZ Abstract. We prove, for
SOME NEGATIVE RESULTS FOR SINGLE LAYER AND MULTILAYER FEEDFORWARD NEURAL NETWORKS arxiv:1810.10032v2 [cs.lg] 31 Oct 2018 J. M. ALMIRA, P. E. LOPEZ-DE-TERUEL, D. J. ROMERO-LÓPEZ Abstract. We prove, for
L E C T U R E 2 1 : M AT R I X T R A N S F O R M AT I O N S. Monday, November 14
 L E C T U R E 2 1 : M AT R I X T R A N S F O R M AT I O N S Monday, November 14 In this lecture we want to consider functions between vector spaces. Recall that a function is simply a rule that takes an
L E C T U R E 2 1 : M AT R I X T R A N S F O R M AT I O N S Monday, November 14 In this lecture we want to consider functions between vector spaces. Recall that a function is simply a rule that takes an
MATH 551 HOMEWORK II SOLUTIONS. Graded problems: 1,3,4,6,7. Solutions to ungraded problems abridged. Let D d
 MATH 551 HOMEWORK II SOLUTIONS Graded problems: 1,3,4,6,7. Solutions to ungraded problems abridged. Let D d dx and xf, gy ş b fpxqgpxqdx. Integration by parts is then expressed as a xdf, gy fg b a xf,
MATH 551 HOMEWORK II SOLUTIONS Graded problems: 1,3,4,6,7. Solutions to ungraded problems abridged. Let D d dx and xf, gy ş b fpxqgpxqdx. Integration by parts is then expressed as a xdf, gy fg b a xf,
TOPOLOGY OF LINE ARRANGEMENTS. Alex Suciu. Northeastern University. Workshop on Configuration Spaces Il Palazzone di Cortona September 1, 2014
 TOPOLOGY OF LINE ARRANGEMENTS Alex Suciu Northeastern University Workshop on Configuration Spaces Il Palazzone di Cortona September 1, 2014 ALEX SUCIU (NORTHEASTERN) TOPOLOGY OF LINE ARRANGEMENTS CORTONA,
TOPOLOGY OF LINE ARRANGEMENTS Alex Suciu Northeastern University Workshop on Configuration Spaces Il Palazzone di Cortona September 1, 2014 ALEX SUCIU (NORTHEASTERN) TOPOLOGY OF LINE ARRANGEMENTS CORTONA,
we can assume without loss of generality that x and y are of the form x pabcq and y pbcdq,
 1. Symmetric and alternating groups. SOLUTIONS Math A4900 Homework 9 11/1/2017 (a) In class we showed that S n is generated by T tpi jq 1 ď i ă j ď nu, the set of transpositions in S n. Show by induction
1. Symmetric and alternating groups. SOLUTIONS Math A4900 Homework 9 11/1/2017 (a) In class we showed that S n is generated by T tpi jq 1 ď i ă j ď nu, the set of transpositions in S n. Show by induction
1 (1 x) 4 by taking derivatives and rescaling appropriately. Conjecture what the general formula for the series for 1/(1 x) n.
 Math 365 Wednesday 3/20/9 8.2 and 8.4 Exercise 35. Consider the recurrence relation a n =8a n 2 6a n 4 + F (n). (a) Write the associated homogeneous recursion relation and solve for its general solution
Math 365 Wednesday 3/20/9 8.2 and 8.4 Exercise 35. Consider the recurrence relation a n =8a n 2 6a n 4 + F (n). (a) Write the associated homogeneous recursion relation and solve for its general solution
PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS
 PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS T. R. RILEY AND A. W. SALE Abstract. A group has finite palindromic width if there exists n such that every element can
PALINDROMIC WIDTH OF WREATH PRODUCTS, METABELIAN GROUPS, AND MAX-N SOLVABLE GROUPS T. R. RILEY AND A. W. SALE Abstract. A group has finite palindromic width if there exists n such that every element can
A Bowl of Kernels. By Nuriye Atasever, Cesar Alvarado, and Patrick Doherty. December 03, 2013
 December 03, 203 Introduction When we studied Fourier series we improved convergence by convolving with the Fejer and Poisson kernels on T. The analogous Fejer and Poisson kernels on the real line help
December 03, 203 Introduction When we studied Fourier series we improved convergence by convolving with the Fejer and Poisson kernels on T. The analogous Fejer and Poisson kernels on the real line help
arxiv: v1 [math.fa] 17 Feb 2014
![arxiv: v1 [math.fa] 17 Feb 2014 arxiv: v1 [math.fa] 17 Feb 2014](/thumbs/88/115476446.jpg) COORBIT SPACES WITH VOICE IN A FRÉCHET SPACE S. DAHLKE, F. DE MARI, E. DE VITO, D. LABATE,. STEIDL,. TESCHKE, AND S. VIONA arxiv:1402.3917v1 [math.fa] 17 Feb 2014 Abstract. We set up a new general coorbit
COORBIT SPACES WITH VOICE IN A FRÉCHET SPACE S. DAHLKE, F. DE MARI, E. DE VITO, D. LABATE,. STEIDL,. TESCHKE, AND S. VIONA arxiv:1402.3917v1 [math.fa] 17 Feb 2014 Abstract. We set up a new general coorbit
Dr. Marques Sophie Algebra 1 Spring Semester 2017 Problem Set 9
 Dr. Marques Sophie Algebra Spring Semester 207 Office 59 marques@cims.nyu.edu Problem Set 9 Exercise 0 : Prove that every group of order G 28 must contain a normal subgroup of order 7. (Why should it contain
Dr. Marques Sophie Algebra Spring Semester 207 Office 59 marques@cims.nyu.edu Problem Set 9 Exercise 0 : Prove that every group of order G 28 must contain a normal subgroup of order 7. (Why should it contain
LECTURE NOTES DISCRETE MATHEMATICS. Eusebius Doedel
 LECTURE NOTES on DISCRETE MATHEMATICS Eusebius Doedel 1 LOGIC Introduction. First we introduce some basic concepts needed in our discussion of logic. These will be covered in more detail later. A set is
LECTURE NOTES on DISCRETE MATHEMATICS Eusebius Doedel 1 LOGIC Introduction. First we introduce some basic concepts needed in our discussion of logic. These will be covered in more detail later. A set is
MAT 570 REAL ANALYSIS LECTURE NOTES. Contents. 1. Sets Functions Countability Axiom of choice Equivalence relations 9
 MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
MAT 570 REAL ANALYSIS LECTURE NOTES PROFESSOR: JOHN QUIGG SEMESTER: FALL 204 Contents. Sets 2 2. Functions 5 3. Countability 7 4. Axiom of choice 8 5. Equivalence relations 9 6. Real numbers 9 7. Extended
Last time: Cyclic groups. Proposition
 Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative notation: H tx` ` P Zu xxy, Additive notation: H t`x `
Warmup Recall, a group H is cyclic if H can be generated by a single element. In other words, there is some element x P H for which Multiplicative notation: H tx` ` P Zu xxy, Additive notation: H t`x `
Electronic Companion Dynamic Pricing of Perishable Assets under Competition
 1 Electronic Companion Dynamic Pricing of Perishable Assets under Competition Guillermo Gallego IEOR Department, Columbia University, New York, NY 10027 gmg2@columbia.edu Ming Hu Rotman School of Management,
1 Electronic Companion Dynamic Pricing of Perishable Assets under Competition Guillermo Gallego IEOR Department, Columbia University, New York, NY 10027 gmg2@columbia.edu Ming Hu Rotman School of Management,
Focus rules for segments. Focus and defocus rules for concatenation. Mlength with a while loop. Mlength with a while loop.
 The function nth-cell Separation Logic Part 2 Returns the i-th cell of a list: Arthur Charguéraud February 2015 let rec nth_cell (i:int) (p: a cell) = if i = 0 then p else nth_cell (i-1) (p.tl) Why is
The function nth-cell Separation Logic Part 2 Returns the i-th cell of a list: Arthur Charguéraud February 2015 let rec nth_cell (i:int) (p: a cell) = if i = 0 then p else nth_cell (i-1) (p.tl) Why is
MTH132 Exam 2 Solutions Covers: Page Total. Max
 Name: PID: A Section #: Instructor: Page 3 4 5 6 7 8 Total Score Max 30 18 4 14 150 Instructions 1. You will be given exactly 90 minutes for this exam.. No calculators, phones, or any electronic devices.
Name: PID: A Section #: Instructor: Page 3 4 5 6 7 8 Total Score Max 30 18 4 14 150 Instructions 1. You will be given exactly 90 minutes for this exam.. No calculators, phones, or any electronic devices.
Continuous r.v practice problems
 Continuous r.v practice problems SDS 321 Intro to Probability and Statistics 1. (2+2+1+1 6 pts) The annual rainfall (in inches) in a certain region is normally distributed with mean 4 and standard deviation
Continuous r.v practice problems SDS 321 Intro to Probability and Statistics 1. (2+2+1+1 6 pts) The annual rainfall (in inches) in a certain region is normally distributed with mean 4 and standard deviation
C*-algebras - a case study
 - a case study Definition Suppose that H is a Hilbert space. A C -algebra is an operator-norm closed -subalgebra of BpHq. are closed under ultraproducts and subalgebras so they should be captured by continous
- a case study Definition Suppose that H is a Hilbert space. A C -algebra is an operator-norm closed -subalgebra of BpHq. are closed under ultraproducts and subalgebras so they should be captured by continous
Separation Logic. Part 3. Arthur Charguéraud. February / 66
 Separation Logic Part 3 Arthur Charguéraud February 2014 1 / 66 Content Reasoning about loops For loops While loops Repeat-loops Total correctness Frame in a while loop Higher-order iterators for pure
Separation Logic Part 3 Arthur Charguéraud February 2014 1 / 66 Content Reasoning about loops For loops While loops Repeat-loops Total correctness Frame in a while loop Higher-order iterators for pure
Math 212-Lecture 20. P dx + Qdy = (Q x P y )da. C
 15. Green s theorem Math 212-Lecture 2 A simple closed curve in plane is one curve, r(t) : t [a, b] such that r(a) = r(b), and there are no other intersections. The positive orientation is counterclockwise.
15. Green s theorem Math 212-Lecture 2 A simple closed curve in plane is one curve, r(t) : t [a, b] such that r(a) = r(b), and there are no other intersections. The positive orientation is counterclockwise.
Lecture two. January 17, 2019
 Lecture two January 17, 2019 We will learn how to solve rst-order linear equations in this lecture. Example 1. 1) Find all solutions satisfy the equation u x (x, y) = 0. 2) Find the solution if we know
Lecture two January 17, 2019 We will learn how to solve rst-order linear equations in this lecture. Example 1. 1) Find all solutions satisfy the equation u x (x, y) = 0. 2) Find the solution if we know
L11: Algebraic Path Problems with applications to Internet Routing Lecture 15. Path Weight with functions on arcs?
 L11: Algebraic Path Problems with applications to Internet Routing Lecture 15 Timothy G. Griffin timothy.griffin@cl.cam.ac.uk Computer Laboratory University of Cambridge, UK Michaelmas Term, 2016 tgg22
L11: Algebraic Path Problems with applications to Internet Routing Lecture 15 Timothy G. Griffin timothy.griffin@cl.cam.ac.uk Computer Laboratory University of Cambridge, UK Michaelmas Term, 2016 tgg22
LECTURE NOTES DISCRETE MATHEMATICS. Eusebius Doedel
 LECTURE NOTES on DISCRETE MATHEMATICS Eusebius Doedel 1 LOGIC Introduction. First we introduce some basic concepts needed in our discussion of logic. These will be covered in more detail later. A set is
LECTURE NOTES on DISCRETE MATHEMATICS Eusebius Doedel 1 LOGIC Introduction. First we introduce some basic concepts needed in our discussion of logic. These will be covered in more detail later. A set is
Math 365 Monday 3/25/19. 1 x n n 1. 1 x = X. a k x k (Considered formally, i.e. without consideration of convergence.)
 Recall: Also, for series we have f(x)+g(x) = Math 365 Monday 3/25/9 ( + x) n = e x = f(x) = nx X x k /k!, n x k, k and x n n x = X x k, x = X X a k x k and g(x) = X (a k + b k )x k and f(x)g(x) = x k X
Recall: Also, for series we have f(x)+g(x) = Math 365 Monday 3/25/9 ( + x) n = e x = f(x) = nx X x k /k!, n x k, k and x n n x = X x k, x = X X a k x k and g(x) = X (a k + b k )x k and f(x)g(x) = x k X
Fixed Points and Contractive Transformations. Ron Goldman Department of Computer Science Rice University
 Fixed Points and Contractive Transformations Ron Goldman Department of Computer Science Rice University Applications Computer Graphics Fractals Bezier and B-Spline Curves and Surfaces Root Finding Newton
Fixed Points and Contractive Transformations Ron Goldman Department of Computer Science Rice University Applications Computer Graphics Fractals Bezier and B-Spline Curves and Surfaces Root Finding Newton
On principal eigenpair of temporal-joined adjacency matrix for spreading phenomenon Abstract. Keywords: 1 Introduction
 1,3 1,2 1 2 3 r A ptq pxq p0q 0 pxq 1 x P N S i r A ptq r A ÝÑH ptq i i ÝÑH t ptq i N t1 ÝÑ ź H ptq θ1 t 1 0 i `t1 ri ` A r ÝÑ H p0q ra ptq t ra ptq i,j 1 i j t A r ptq i,j 0 I r ś N ˆ N mś ĂA l A Ą m...
1,3 1,2 1 2 3 r A ptq pxq p0q 0 pxq 1 x P N S i r A ptq r A ÝÑH ptq i i ÝÑH t ptq i N t1 ÝÑ ź H ptq θ1 t 1 0 i `t1 ri ` A r ÝÑ H p0q ra ptq t ra ptq i,j 1 i j t A r ptq i,j 0 I r ś N ˆ N mś ĂA l A Ą m...
ETIKA V PROFESII PSYCHOLÓGA
 P r a ž s k á v y s o k á š k o l a p s y c h o s o c i á l n í c h s t u d i í ETIKA V PROFESII PSYCHOLÓGA N a t á l i a S l o b o d n í k o v á v e d ú c i p r á c e : P h D r. M a r t i n S t r o u
P r a ž s k á v y s o k á š k o l a p s y c h o s o c i á l n í c h s t u d i í ETIKA V PROFESII PSYCHOLÓGA N a t á l i a S l o b o d n í k o v á v e d ú c i p r á c e : P h D r. M a r t i n S t r o u
PRINCIPLES OF ANALYSIS - LECTURE NOTES
 PRINCIPLES OF ANALYSIS - LECTURE NOTES PETER A. PERRY 1. Constructions of Z, Q, R Beginning with the natural numbers N t1, 2, 3,...u we can use set theory to construct, successively, Z, Q, and R. We ll
PRINCIPLES OF ANALYSIS - LECTURE NOTES PETER A. PERRY 1. Constructions of Z, Q, R Beginning with the natural numbers N t1, 2, 3,...u we can use set theory to construct, successively, Z, Q, and R. We ll
