Math 365 Monday 3/25/19. 1 x n n 1. 1 x = X. a k x k (Considered formally, i.e. without consideration of convergence.)
|
|
|
- Shannon Casey
- 5 years ago
- Views:
Transcription
1 Recall: Also, for series we have f(x)+g(x) = Math 365 Monday 3/25/9 ( + x) n = e x = f(x) = nx X x k /k!, n x k, k and x n n x = X x k, x = X X a k x k and g(x) = X (a k + b k )x k and f(x)g(x) = x k X b k x k, Exercise 37. Recall that the generating function for a sequence {a 0,a,a 2,...,} is X a k x k (Considered formally, i.e. without. consideration of convergence.) X! kx a i b k i x k. ( ) Give the generating functions, in terms of their series and in their simplified (closed) form, for each of the following sequences. In many cases, you ll use your answers from Exercise 36 (from last time). (a) a n = n + for n =0,, 2,... (b) a n =3 n, for n =0,,... ( n =3k for some k 2 Z, (c) a n = for n =0,,... 0, n 6= 3k for all k 2 Z, (i.e. a n is if n is a multiple of 3, and is 0 otherwise). (d) a n =/n for n =, 2,... i=0 Exercise 38. For each of the following recursively defined sequences, (i) solve using generating functions; (ii) solve using the methods of Section 8.2 and compare to part (i); (iii) check your answers by comparing the values you get by using your formula and by computing recursively for the first three terms of the sequence. (a) a n =2a n + 3, a 0 =. (b) a n =3a n +4 n.
2 Exercise 39. (a) Consider the integer partitions of 4. (i) Write a corresponding generating function, wherein the coe integer partitions of 4. cient of x 4 is the number of (ii) Make explicit the correspondence between the monomials in the expansion of your generating function and the integer partitions of 4 (like we did for the partitions of 5 in class). (b) Describe a combinatorial problem that is solved by calculating the coe following generating functions. (i) ( + x + x 2 + x 3 ) 4 (ii) ( + x + x 2 + +)( + x 2 + x 4 + x 6 )( + x 3 + x 6 ) (iii) (x + x 2 + x 3 ) 5 cient of x 6 for the (c) For each of the following questions, give the corresponding generating function and determine k such that the coe cient of x k is the answer the question. (i) How many di erent ways can 2 identical action figures can be given to five children so that each child receives at most three action figures? (ii) How many di erent ways 0 identical balloons can be given to four children if each child receives at least two balloons? (iii) How many di erent ways are there to choose a dozen bagels from three varieties plain, onion, and raisin if at least two bagels of each kind but no more than three plain bagels are chosen? (iv) How many ways can you make change for $00 using $ bills, $5 bills, $0 bills, and $20 bills? Exercise 40. (Generating functions for partitions) (a) Write the generating function for partitions with even-sized parts, i.e. or but not or. (b) Write the generating function for partitions with no more than two parts of each size, i.e. or but not or. (c) Write the generating function for partitions parts all of prime size, i.e. or but not or. (The prime numbers are the integers p greater than that are divisible by and p but no other positive integers.)
3 Taylor series to know and love: nÿ ˆn p ` xq n x k ` k ˆn x ` x n n x ÿ x k ` x ` x 2 ` `x n x e x x k ` x ` x 2 ` x k {k! ` x ` x2 2 ` x3 3! ˆn x 2 ` `x n 2 (finite) (finite) (infinite) ` (infinite) The lefthand side of each is called the closed form for the series. New Series from old: Let fpxq a k x k and gpxq b k x k. Then f pxq`gpxq pa k ` b k qx k and fpxqgpxq kÿ a i b k i x k. You can also di erentiate and integrate series to get new series. Section 8.4: Generating functions. A generating function for a sequence ta k u,,... is the series a k x k. ( Formal : forget about convergence!) When possible, we rewrite the generating function in terms of a simple expression of elementary functions, which we call closed solutions. For example, the generating function for the sequence,,, tu,,... is x k x. The generating function for the sequence, 2, 6, t{n!u is x n {n! e x.
4 Section 8.4: Generating functions. A generating function for a sequence ta k u,,... is the series a k x k ( Formal : forget about. convergence!) When possible, we rewrite the generating function in terms of a simple expression of elementary functions, which we call closed solutions. Not every generating function has a nice closed form, butthat shouldn t stop you from writing it down. For example, the generating function for the sequence, 0, 2, 0, 3, 0,... is ` 0 x ` 2x 2 ` 0 x 3 ` 3x 4 ` pk ` q x 2k. And the generating function for the sequence0, 0, 2 2, 3 2, 0, 5 2, 0, 7 2,..., i.e. a n n 2 if n is prime and a n 0 otherwise is 2 2 x 2 ` 3 2 x 3 ` 5 2 x 5 ` 7 2 x 2 ` ÿ p 2 x p. p prime A generating function for a sequence ta k u,,... is the series a k x k. ( Formal : forget about convergence!) When possible, we rewrite the generating function in terms of a simple expression of elementary functions, which we call closed solutions. Note that a finite sequence a 0,a,...,a n is the same as the infinite sequence a 0,a,...,a n, 0, 0,...; similarly, the generating function for a finite sequence will be a finite degree polynomial: a k x k a 0 ` a x ` a 2 x 2 ` a n x n ` 0 ` 0 ` For example, for a fixed n, the generating function for the sequence t`n k u,,...,n is nÿ a k x k. ˆn x k px`q n. You try Exercise 37 k
5 First application: solving recurrence relations Take a generating function for some sequence ta n u: Notice that Gpxq a n x n a 0 ` a x ` a 2 x 2 `. xgpxq a 0 x ` a x 2 ` a 2 x 3 ` x 2 Gpxq a 0 x 2 ` a x 3 ` a 2 x 4 `. n n 2 x d Gpxq a 0 x d ` a x d` ` a 2 x d`2 ` a n x n a n 2 x n n d a n d x n. (Rewrite sums so that the power of x matches the index, tomake it easier to collect like terms when adding series!)
6 First application: solving recurrence relations So say I have a sequence ta n u that satisfies the recurrence relation a n 3a n. (Sanity check: we already know the general solution should look like a n a 0 3 n.) Let Gpxq 8 a nx n. Then Gpxq a 0 ` a x ` a 2 x 2 ` a 3 x 3 `... a 0 ` xpa ` a 2 x ` q Set aside d terms, a 0 ` x a 0 ` x a 0 ` 3x a n` x n 3a n x n a n x n (where d degree of recurrence) and factor out x d from the rest. Plug in the recurrence relation. Simplify. a 0 ` 3xGpxq. Return to closed form. Now solve for Gpxq: Gpxq a 0 ` 3xGpxq. First application: solving recurrence relations So say I have a sequence ta n u that satisfies the recurrence relation a n 3a n. (Sanity check: we already know the general solution should look like a n a 0 3 n.) Let Gpxq 8 a nx n. Then Now solve for Gpxq: and so for x {3, Gpxq a 0 ` 3xGpxq. a 0 Gpxq 3xGpxq p 3xqGpxq; Gpxq a 0 3x a 0 ÿ 8 a 0 p3xq n ˆ y ˇˇˇˇy 3x pa 0 3 n qx n. Now compare to the original formula for Gpxq! This shows that a n a 0 3 n (as expected).
7 Ex 2: suppose I have a sequence satisfying a n 9a n 2 ` 0 n 2 with a 0 3 and a 2. Let Gpxq 8 a nx n. Then Gpxq a 0 ` a x ` a 2 x 2 ` a 3 x 3 `... a 0 ` a x ` x 2 pa 2 ` a 3 x ` q Set aside d terms, a 0 ` a x ` x 2 a n`2 x n a 0 ` a x ` x 2 p9a n ` 0 n qx n a 0 ` a x ` 9x 2 8 ÿ a n x n ` x 2 (where d degree of recurrence) 8 ÿ and factor out x d from the rest. Plug in the recurrence relation. p0xq n Expand and simplify. ˆ a 0 ` a x ` 9x 2 Gpxq`x 2. Return to closed forms. 0x Ex 2: suppose I have a sequence satisfying a n 9a n 2 ` 0 n 2 with a 0 3 and a 2. Let Gpxq 8 a nx n. Then ˆ Gpxq a 0 ` a x ` 9x 2 Gpxq`x 2 0x Now solve for Gpxq: ˆ a 0 ` a x ` x 2 Gpxq 9x 2 Gpxq p 9x 2 qgpxq; 0x So Gpxq pa 0 ` a xqp 0xq`x 2 p 0xqp 9x 2 a 0 `pa 0a 0 qx `p 0a qx 2 q p 0xqp ` 3xqp 3xq 3 28x 9x 2 p 0xqp ` 3xqp 3xq ˆ ˆ46 0x ` 39 p 3xq ` 9 0x Review partial fractions decomposition!
8 Ex 2: suppose I have a sequence satisfying a n 9a n 2 ` 0 n 2 with a 0 3 and a 2. Let Gpxq 8 a nx n.then ˆ Gpxq a 0 ` a x ` 9x 2 Gpxq`x 2 0x Now solve for Gpxq: ˆ ˆ46 Gpxq 0x ` 39 p 3xq ` 9 0x Review partial fractions decomposition! Putting back into series form, we get ˆ ˆ46 Gpxq 0 n x n ` p 3q n x n ` 3 n x n 39 9 ˆ ˆ ˆ46 n 0 n ` p 3q n ` 3 x n So a n 0 n ` ˆ ˆ46 p 3q n ` 3 n Try Ex Counting problems and Generating functions Example: What is the coe cient on x 2 in px looooooooooomooooooooooon 2 ` x 3 ` x 4 ` x 5 q px loooomoooon 4 ` x 5 q px looooooomooooooon ` x 2 ` x 3 q? e, glazed e 2, choc. e 3, jelly This is equivalent to the question How many integer solutions are there to the equation e ` e 2 ` e 3 2 with 2 e 5, 4 e 2 5, e 3 3? 2 Which is the same as How many ways can you pick 2 doughnuts to bring to the o ce if you ve had requests for at least 2 glazed, 4 chocolate, and one jelly-filled, but when you get to the store, they only have 5 glazed, 5 chocolate, and 3 jelly-filled left?
9 Example: Use a generating function to answer the question How many non-negative integer solutions are there to e ` e 2 ` e 3 0 where e 2 is a multiple of 2 and e 3 is a multiple of 3? The answer is the same as the coe cient of x 0 in p loooooooooomoooooooooon ` x ` x 2 ` qp looooooooooooooomooooooooooooooon ` x 2 ` x 4 ` x 6 ` qp looooooooooooooomooooooooooooooon ` x 3 ` x 6 ` x 9 ` q e e 2 e 3, which is the same as the coe cient of x 0 in p loooooooooooooomoooooooooooooon ` x ` x 2 ` `x 0 q p looooooooooooooomooooooooooooooon ` x 2 ` x 4 ` `x 0 q p loooooooooomoooooooooon ` x 3 ` x 6 ` x 9 q e e 2 e 3, since we would never use any terms that came from x a for a 0. This is something we can plug into a calculator like WolframAlpha. Example: Use a generating function to answer the question How many non-negative integer solutions are there to e ` e 2 ` e 3 0 where e 2 is a multiple of 2 and e 3 is a multiple of 3? The answer is the same as the coe cient of x 0 in... This is something we can plug into a calculator like WolframAlpha:
10 Integer partitions How many integer partitions are there of 5? This is the same as the coe cient of x 5 in p ` x ` x 2 ` x 3 ` x 4 ` x 5 qp ` x 2 ` x 4 qp ` x 3 qp ` x 4 qp ` x 5 q `px q 0 `px q `px q 2 `px q 3 `px q 4 `px q 5 (pts of length ) `px 2 q 0 `px 2 q `px 2 q 2 (pts of length 2) `px 3 q 0 `px 3 q (pts of length 3) `px 4 q 0 `px 4 q (pts of length 4) `px 5 q 0 `px 5 q (pts of length 5) Why? For example, consider the partition.
11 Integer partitions Counting integer partitions of 5 by looking at the coe. of x 5 in p ` x ` x 2 ` x 3 ` x 4 ` x 5 qp ` x 2 ` x 4 qp ` x 3 qp ` x 4 qp ` x 5 q... corresponds to px q 2 from first factor, since there are 2 parts of length, px 2 q 0 from second factor, since there are 0 parts of length 2, px 3 q from third factor, since there is part of length 3, px 4 q 0 from fourth factor, since there are 0 parts of length 4, and px 5 q 0 from fourth factor, since there are parts of length 5. Integer partitions Counting integer partitions of 5 by looking at the coe. of x 5 in p ` x ` x 2 ` x 3 ` x 4 ` x 5 qp ` x 2 ` x 4 qp ` x 3 qp ` x 4 qp ` x 5 q... corresponds to px q 2 px 3 q. Similarly, the correspondence between the other partitions of 5 and the monomials goes like px 5 q x px 4 q px 2 q px 3 q px q px 2 q 2 px q 3 px 2 q px q 5
12 Notice that the coe cient of x 5 in the polynomial from the previous slide is the same as the coe cient of x 5 in i 2i 3i 4i 5i x x x x x 5π k x ki 5π k Which is the same as the coe cient of x 5 in i 2i 3i x x x ˆ x k. x 4i 5i 6i 7i x x x loooomoooon loooomoooon must use the term must use the term Notice that the coe cient of x 5 in the polynomial from the previous slide is the same as the coe cient of x 5 in i 2i 3i 4i x x x x 5π ki 5π ˆ x x k. k k Which is the same as the coe cient of x 5 in i 2i 3i x x x 8π k x 5i x ki So in general, the number of integer partitions of n, denoted ppnq, is the coe cient of x n in 8π ˆ ppnqx n x k. k
Section 8.4: Generating functions.
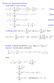 Section 8.4: Generating functions. Taylor series to know and love: nÿ ˆn ˆn p ` xq n x k ` k x ` x n n x ÿ x k ` x ` x 2 ` `x n x e x x k ` x ` x 2 ` x k {k! ` x ` x2 2 ` x3 3! Combining series: Let f
Section 8.4: Generating functions. Taylor series to know and love: nÿ ˆn ˆn p ` xq n x k ` k x ` x n n x ÿ x k ` x ` x 2 ` `x n x e x x k ` x ` x 2 ` x k {k! ` x ` x2 2 ` x3 3! Combining series: Let f
1 (1 x) 4 by taking derivatives and rescaling appropriately. Conjecture what the general formula for the series for 1/(1 x) n.
 Math 365 Wednesday 3/20/9 8.2 and 8.4 Exercise 35. Consider the recurrence relation a n =8a n 2 6a n 4 + F (n). (a) Write the associated homogeneous recursion relation and solve for its general solution
Math 365 Wednesday 3/20/9 8.2 and 8.4 Exercise 35. Consider the recurrence relation a n =8a n 2 6a n 4 + F (n). (a) Write the associated homogeneous recursion relation and solve for its general solution
Power series and Taylor series
 Power series and Taylor series D. DeTurck University of Pennsylvania March 29, 2018 D. DeTurck Math 104 002 2018A: Series 1 / 42 Series First... a review of what we have done so far: 1 We examined series
Power series and Taylor series D. DeTurck University of Pennsylvania March 29, 2018 D. DeTurck Math 104 002 2018A: Series 1 / 42 Series First... a review of what we have done so far: 1 We examined series
Elementary factoring algorithms
 Math 5330 Spring 018 Elementary factoring algorithms The RSA cryptosystem is founded on the idea that, in general, factoring is hard. Where as with Fermat s Little Theorem and some related ideas, one can
Math 5330 Spring 018 Elementary factoring algorithms The RSA cryptosystem is founded on the idea that, in general, factoring is hard. Where as with Fermat s Little Theorem and some related ideas, one can
Chapter Generating Functions
 Chapter 8.1.1-8.1.2. Generating Functions Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 8. Generating Functions Math 184A / Fall 2017 1 / 63 Ordinary Generating Functions (OGF) Let a n (n = 0, 1,...)
Chapter 8.1.1-8.1.2. Generating Functions Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 8. Generating Functions Math 184A / Fall 2017 1 / 63 Ordinary Generating Functions (OGF) Let a n (n = 0, 1,...)
Permutations and Polynomials Sarah Kitchen February 7, 2006
 Permutations and Polynomials Sarah Kitchen February 7, 2006 Suppose you are given the equations x + y + z = a and 1 x + 1 y + 1 z = 1 a, and are asked to prove that one of x,y, and z is equal to a. We
Permutations and Polynomials Sarah Kitchen February 7, 2006 Suppose you are given the equations x + y + z = a and 1 x + 1 y + 1 z = 1 a, and are asked to prove that one of x,y, and z is equal to a. We
1 What is the area model for multiplication?
 for multiplication represents a lovely way to view the distribution property the real number exhibit. This property is the link between addition and multiplication. 1 1 What is the area model for multiplication?
for multiplication represents a lovely way to view the distribution property the real number exhibit. This property is the link between addition and multiplication. 1 1 What is the area model for multiplication?
Warm up: Recall that if you require real coe cients (not complex), polynomials always factor into degree 1 or 2 parts.
 Today: 6.3 Partial fractions Warm up: Recall that if you require real coe cients (not comple), polynomials always factor into degree or parts. For eample, 3 + +3 5=( )( + i)( ++i) =( {z } )( + + 5) {z
Today: 6.3 Partial fractions Warm up: Recall that if you require real coe cients (not comple), polynomials always factor into degree or parts. For eample, 3 + +3 5=( )( + i)( ++i) =( {z } )( + + 5) {z
Chapter 2. Limits and Continuity 2.6 Limits Involving Infinity; Asymptotes of Graphs
 2.6 Limits Involving Infinity; Asymptotes of Graphs Chapter 2. Limits and Continuity 2.6 Limits Involving Infinity; Asymptotes of Graphs Definition. Formal Definition of Limits at Infinity.. We say that
2.6 Limits Involving Infinity; Asymptotes of Graphs Chapter 2. Limits and Continuity 2.6 Limits Involving Infinity; Asymptotes of Graphs Definition. Formal Definition of Limits at Infinity.. We say that
Equations with regular-singular points (Sect. 5.5).
 Equations with regular-singular points (Sect. 5.5). Equations with regular-singular points. s: Equations with regular-singular points. Method to find solutions. : Method to find solutions. Recall: The
Equations with regular-singular points (Sect. 5.5). Equations with regular-singular points. s: Equations with regular-singular points. Method to find solutions. : Method to find solutions. Recall: The
Section Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence.
 Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence. Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence. f n (0)x n Recall from
Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence. Example Determine the Maclaurin series of f (x) = e x and its the interval of convergence. f n (0)x n Recall from
Legendre s Equation. PHYS Southern Illinois University. October 18, 2016
 Legendre s Equation PHYS 500 - Southern Illinois University October 18, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 18, 2016 1 / 11 Legendre s Equation Recall We are trying
Legendre s Equation PHYS 500 - Southern Illinois University October 18, 2016 PHYS 500 - Southern Illinois University Legendre s Equation October 18, 2016 1 / 11 Legendre s Equation Recall We are trying
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS
 LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
LIMITS AT INFINITY MR. VELAZQUEZ AP CALCULUS RECALL: VERTICAL ASYMPTOTES Remember that for a rational function, vertical asymptotes occur at values of x = a which have infinite its (either positive or
n(n 1) = (n + 1)n(n 1)/ ( 1) n(n 1)(n 2) = (n + 1)n(n 1)(n 2)/4
 NOTES FROM THE FIRST TWO CLASSES MIKE ZABROCKI - SEPTEMBER 6 &, 202 main idea of this class + 2 + 3 + + n = n(n + )/2 to r + 2 r + + n r =??? Just to show what we are up against: + 2 + 3 + + n = n(n +
NOTES FROM THE FIRST TWO CLASSES MIKE ZABROCKI - SEPTEMBER 6 &, 202 main idea of this class + 2 + 3 + + n = n(n + )/2 to r + 2 r + + n r =??? Just to show what we are up against: + 2 + 3 + + n = n(n +
Finding Limits Analytically
 Finding Limits Analytically Most of this material is take from APEX Calculus under terms of a Creative Commons License In this handout, we explore analytic techniques to compute its. Suppose that f(x)
Finding Limits Analytically Most of this material is take from APEX Calculus under terms of a Creative Commons License In this handout, we explore analytic techniques to compute its. Suppose that f(x)
Notes on Paths, Trees and Lagrange Inversion
 Notes on Paths, Trees and Lagrange Inversion Today we are going to start with a problem that may seem somewhat unmotivated, and solve it in two ways. From there, we will proceed to discuss applications
Notes on Paths, Trees and Lagrange Inversion Today we are going to start with a problem that may seem somewhat unmotivated, and solve it in two ways. From there, we will proceed to discuss applications
Generating Functions
 8.30 lecture notes March, 0 Generating Functions Lecturer: Michel Goemans We are going to discuss enumeration problems, and how to solve them using a powerful tool: generating functions. What is an enumeration
8.30 lecture notes March, 0 Generating Functions Lecturer: Michel Goemans We are going to discuss enumeration problems, and how to solve them using a powerful tool: generating functions. What is an enumeration
2.5 The Fundamental Theorem of Algebra.
 2.5. THE FUNDAMENTAL THEOREM OF ALGEBRA. 79 2.5 The Fundamental Theorem of Algebra. We ve seen formulas for the (complex) roots of quadratic, cubic and quartic polynomials. It is then reasonable to ask:
2.5. THE FUNDAMENTAL THEOREM OF ALGEBRA. 79 2.5 The Fundamental Theorem of Algebra. We ve seen formulas for the (complex) roots of quadratic, cubic and quartic polynomials. It is then reasonable to ask:
Math /Foundations of Algebra/Fall 2017 Numbers at the Foundations: Real Numbers In calculus, the derivative of a function f(x) is defined
 Math 400-001/Foundations of Algebra/Fall 2017 Numbers at the Foundations: Real Numbers In calculus, the derivative of a function f(x) is defined using limits. As a particular case, the derivative of f(x)
Math 400-001/Foundations of Algebra/Fall 2017 Numbers at the Foundations: Real Numbers In calculus, the derivative of a function f(x) is defined using limits. As a particular case, the derivative of f(x)
9 < Ways to place n distinguishable objects= S(n, k) = into k indistinguishable boxes so that no box is left empty We stated in section 6.
 Math 365 Monday 4/1/19 8.5 (inclusion/exclusion) and 9.1 & 9.5 (equivalence relations) Exercise 41. Use inclusion/exclusion to answer the following questions. (a) How many elements are in A 1 [ A 2 if
Math 365 Monday 4/1/19 8.5 (inclusion/exclusion) and 9.1 & 9.5 (equivalence relations) Exercise 41. Use inclusion/exclusion to answer the following questions. (a) How many elements are in A 1 [ A 2 if
Math Lecture 18 Notes
 Math 1010 - Lecture 18 Notes Dylan Zwick Fall 2009 In our last lecture we talked about how we can add, subtract, and multiply polynomials, and we figured out that, basically, if you can add, subtract,
Math 1010 - Lecture 18 Notes Dylan Zwick Fall 2009 In our last lecture we talked about how we can add, subtract, and multiply polynomials, and we figured out that, basically, if you can add, subtract,
Course Notes for Calculus , Spring 2015
 Course Notes for Calculus 110.109, Spring 2015 Nishanth Gudapati In the previous course (Calculus 110.108) we introduced the notion of integration and a few basic techniques of integration like substitution
Course Notes for Calculus 110.109, Spring 2015 Nishanth Gudapati In the previous course (Calculus 110.108) we introduced the notion of integration and a few basic techniques of integration like substitution
Writing proofs for MATH 51H Section 2: Set theory, proofs of existential statements, proofs of uniqueness statements, proof by cases
 Writing proofs for MATH 51H Section 2: Set theory, proofs of existential statements, proofs of uniqueness statements, proof by cases September 22, 2018 Recall from last week that the purpose of a proof
Writing proofs for MATH 51H Section 2: Set theory, proofs of existential statements, proofs of uniqueness statements, proof by cases September 22, 2018 Recall from last week that the purpose of a proof
Lecture 9: Taylor Series
 Math 8 Instructor: Padraic Bartlett Lecture 9: Taylor Series Week 9 Caltech 212 1 Taylor Polynomials and Series When we first introduced the idea of the derivative, one of the motivations we offered was
Math 8 Instructor: Padraic Bartlett Lecture 9: Taylor Series Week 9 Caltech 212 1 Taylor Polynomials and Series When we first introduced the idea of the derivative, one of the motivations we offered was
Generating Function Notes , Fall 2005, Prof. Peter Shor
 Counting Change Generating Function Notes 80, Fall 00, Prof Peter Shor In this lecture, I m going to talk about generating functions We ve already seen an example of generating functions Recall when we
Counting Change Generating Function Notes 80, Fall 00, Prof Peter Shor In this lecture, I m going to talk about generating functions We ve already seen an example of generating functions Recall when we
(2) Dividing both sides of the equation in (1) by the divisor, 3, gives: =
 Dividing Polynomials Prepared by: Sa diyya Hendrickson Name: Date: Let s begin by recalling the process of long division for numbers. Consider the following fraction: Recall that fractions are just division
Dividing Polynomials Prepared by: Sa diyya Hendrickson Name: Date: Let s begin by recalling the process of long division for numbers. Consider the following fraction: Recall that fractions are just division
1 Question related to polynomials
 07-08 MATH00J Lecture 6: Taylor Series Charles Li Warning: Skip the material involving the estimation of error term Reference: APEX Calculus This lecture introduced Taylor Polynomial and Taylor Series
07-08 MATH00J Lecture 6: Taylor Series Charles Li Warning: Skip the material involving the estimation of error term Reference: APEX Calculus This lecture introduced Taylor Polynomial and Taylor Series
Math 40510, Algebraic Geometry
 Math 40510, Algebraic Geometry Problem Set 1, due February 10, 2016 1. Let k = Z p, the field with p elements, where p is a prime. Find a polynomial f k[x, y] that vanishes at every point of k 2. [Hint:
Math 40510, Algebraic Geometry Problem Set 1, due February 10, 2016 1. Let k = Z p, the field with p elements, where p is a prime. Find a polynomial f k[x, y] that vanishes at every point of k 2. [Hint:
Solving Differential Equations Using Power Series
 LECTURE 25 Solving Differential Equations Using Power Series We are now going to employ power series to find solutions to differential equations of the form (25.) y + p(x)y + q(x)y = 0 where the functions
LECTURE 25 Solving Differential Equations Using Power Series We are now going to employ power series to find solutions to differential equations of the form (25.) y + p(x)y + q(x)y = 0 where the functions
Solving Differential Equations Using Power Series
 LECTURE 8 Solving Differential Equations Using Power Series We are now going to employ power series to find solutions to differential equations of the form () y + p(x)y + q(x)y = 0 where the functions
LECTURE 8 Solving Differential Equations Using Power Series We are now going to employ power series to find solutions to differential equations of the form () y + p(x)y + q(x)y = 0 where the functions
q-series Michael Gri for the partition function, he developed the basic idea of the q-exponential. From
 q-series Michael Gri th History and q-integers The idea of q-series has existed since at least Euler. In constructing the generating function for the partition function, he developed the basic idea of
q-series Michael Gri th History and q-integers The idea of q-series has existed since at least Euler. In constructing the generating function for the partition function, he developed the basic idea of
Dr. Z s Math151 Handout #4.7 [L Hôspital s Rule]
![Dr. Z s Math151 Handout #4.7 [L Hôspital s Rule] Dr. Z s Math151 Handout #4.7 [L Hôspital s Rule]](/thumbs/89/100185618.jpg) By Doron Zeilberger Dr Z s Math151 Handout #47 [L Hôspital s Rule] Problem Type 471 : Given certain its of certain functions f(x) g(x) at a designated point x = a determine whether the its (at that very
By Doron Zeilberger Dr Z s Math151 Handout #47 [L Hôspital s Rule] Problem Type 471 : Given certain its of certain functions f(x) g(x) at a designated point x = a determine whether the its (at that very
SOLVED PROBLEMS ON TAYLOR AND MACLAURIN SERIES
 SOLVED PROBLEMS ON TAYLOR AND MACLAURIN SERIES TAYLOR AND MACLAURIN SERIES Taylor Series of a function f at x = a is ( f k )( a) ( x a) k k! It is a Power Series centered at a. Maclaurin Series of a function
SOLVED PROBLEMS ON TAYLOR AND MACLAURIN SERIES TAYLOR AND MACLAURIN SERIES Taylor Series of a function f at x = a is ( f k )( a) ( x a) k k! It is a Power Series centered at a. Maclaurin Series of a function
Notes on generating functions in automata theory
 Notes on generating functions in automata theory Benjamin Steinberg December 5, 2009 Contents Introduction: Calculus can count 2 Formal power series 5 3 Rational power series 9 3. Rational power series
Notes on generating functions in automata theory Benjamin Steinberg December 5, 2009 Contents Introduction: Calculus can count 2 Formal power series 5 3 Rational power series 9 3. Rational power series
THE DENOMINATORS OF POWER SUMS OF ARITHMETIC PROGRESSIONS. Bernd C. Kellner Göppert Weg 5, Göttingen, Germany
 #A95 INTEGERS 18 (2018) THE DENOMINATORS OF POWER SUMS OF ARITHMETIC PROGRESSIONS Bernd C. Kellner Göppert Weg 5, 37077 Göttingen, Germany b@bernoulli.org Jonathan Sondow 209 West 97th Street, New Yor,
#A95 INTEGERS 18 (2018) THE DENOMINATORS OF POWER SUMS OF ARITHMETIC PROGRESSIONS Bernd C. Kellner Göppert Weg 5, 37077 Göttingen, Germany b@bernoulli.org Jonathan Sondow 209 West 97th Street, New Yor,
LINEAR RECURSIVE SEQUENCES. The numbers in the sequence are called its terms. The general form of a sequence is
 LINEAR RECURSIVE SEQUENCES BJORN POONEN 1. Sequences A sequence is an infinite list of numbers, like 1) 1, 2, 4, 8, 16, 32,.... The numbers in the sequence are called its terms. The general form of a sequence
LINEAR RECURSIVE SEQUENCES BJORN POONEN 1. Sequences A sequence is an infinite list of numbers, like 1) 1, 2, 4, 8, 16, 32,.... The numbers in the sequence are called its terms. The general form of a sequence
Limits at Infinity. Horizontal Asymptotes. Definition (Limits at Infinity) Horizontal Asymptotes
 Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
Limits at Infinity If a function f has a domain that is unbounded, that is, one of the endpoints of its domain is ±, we can determine the long term behavior of the function using a it at infinity. Definition
CHAPTER 3 REVIEW QUESTIONS MATH 3034 Spring a 1 b 1
 . Let U = { A M (R) A = and b 6 }. CHAPTER 3 REVIEW QUESTIONS MATH 334 Spring 7 a b a and b are integers and a 6 (a) Let S = { A U det A = }. List the elements of S; that is S = {... }. (b) Let T = { A
. Let U = { A M (R) A = and b 6 }. CHAPTER 3 REVIEW QUESTIONS MATH 334 Spring 7 a b a and b are integers and a 6 (a) Let S = { A U det A = }. List the elements of S; that is S = {... }. (b) Let T = { A
CSCE 222 Discrete Structures for Computing. Dr. Hyunyoung Lee
 CSCE 222 Discrete Structures for Computing Sequences and Summations Dr. Hyunyoung Lee Based on slides by Andreas Klappenecker 1 Sequences 2 Sequences A sequence is a function from a subset of the set of
CSCE 222 Discrete Structures for Computing Sequences and Summations Dr. Hyunyoung Lee Based on slides by Andreas Klappenecker 1 Sequences 2 Sequences A sequence is a function from a subset of the set of
PUTNAM TRAINING POLYNOMIALS. Exercises 1. Find a polynomial with integral coefficients whose zeros include
 PUTNAM TRAINING POLYNOMIALS (Last updated: December 11, 2017) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
PUTNAM TRAINING POLYNOMIALS (Last updated: December 11, 2017) Remark. This is a list of exercises on polynomials. Miguel A. Lerma Exercises 1. Find a polynomial with integral coefficients whose zeros include
are the q-versions of n, n! and . The falling factorial is (x) k = x(x 1)(x 2)... (x k + 1).
 Lecture A jacques@ucsd.edu Notation: N, R, Z, F, C naturals, reals, integers, a field, complex numbers. p(n), S n,, b(n), s n, partition numbers, Stirling of the second ind, Bell numbers, Stirling of the
Lecture A jacques@ucsd.edu Notation: N, R, Z, F, C naturals, reals, integers, a field, complex numbers. p(n), S n,, b(n), s n, partition numbers, Stirling of the second ind, Bell numbers, Stirling of the
Simplifying Rational Expressions and Functions
 Department of Mathematics Grossmont College October 15, 2012 Recall: The Number Types Definition The set of whole numbers, ={0, 1, 2, 3, 4,...} is the set of natural numbers unioned with zero, written
Department of Mathematics Grossmont College October 15, 2012 Recall: The Number Types Definition The set of whole numbers, ={0, 1, 2, 3, 4,...} is the set of natural numbers unioned with zero, written
Pade Approximations and the Transcendence
 Pade Approximations and the Transcendence of π Ernie Croot March 9, 27 1 Introduction Lindemann proved the following theorem, which implies that π is transcendental: Theorem 1 Suppose that α 1,..., α k
Pade Approximations and the Transcendence of π Ernie Croot March 9, 27 1 Introduction Lindemann proved the following theorem, which implies that π is transcendental: Theorem 1 Suppose that α 1,..., α k
INFINITE SEQUENCES AND SERIES
 11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES In section 11.9, we were able to find power series representations for a certain restricted class of functions. INFINITE SEQUENCES AND SERIES
11 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES In section 11.9, we were able to find power series representations for a certain restricted class of functions. INFINITE SEQUENCES AND SERIES
Math 3 Variable Manipulation Part 3 Polynomials A
 Math 3 Variable Manipulation Part 3 Polynomials A 1 MATH 1 & 2 REVIEW: VOCABULARY Constant: A term that does not have a variable is called a constant. Example: the number 5 is a constant because it does
Math 3 Variable Manipulation Part 3 Polynomials A 1 MATH 1 & 2 REVIEW: VOCABULARY Constant: A term that does not have a variable is called a constant. Example: the number 5 is a constant because it does
Chapter REVIEW ANSWER KEY
 TEXTBOOK HELP Pg. 313 Chapter 3.2-3.4 REVIEW ANSWER KEY 1. What qualifies a function as a polynomial? Powers = non-negative integers Polynomial functions of degree 2 or higher have graphs that are smooth
TEXTBOOK HELP Pg. 313 Chapter 3.2-3.4 REVIEW ANSWER KEY 1. What qualifies a function as a polynomial? Powers = non-negative integers Polynomial functions of degree 2 or higher have graphs that are smooth
Work easier problems first. Write out your plan for harder problems before beginning them.
 Notes:??? Form R 1 of 7 Directions: For multiple choice (A, B, C, etc.), circle the letter of the best choice. For TRUE/FALSE, circle the word TRUE or the word FALSE. When a list of choices is given for
Notes:??? Form R 1 of 7 Directions: For multiple choice (A, B, C, etc.), circle the letter of the best choice. For TRUE/FALSE, circle the word TRUE or the word FALSE. When a list of choices is given for
Functions. If x 2 D, then g(x) 2 T is the object that g assigns to x. Writing the symbols. g : D! T
 Functions This is the second of three chapters that are meant primarily as a review of Math 1050. We will move quickly through this material. A function is a way of describing a relationship between two
Functions This is the second of three chapters that are meant primarily as a review of Math 1050. We will move quickly through this material. A function is a way of describing a relationship between two
Read the following definitions and match them with the appropriate example(s) using the lines provided.
 Algebraic Expressions Prepared by: Sa diyya Hendrickson Name: Date: Read the following definitions and match them with the appropriate example(s) using the lines provided. 1. Variable: A letter that is
Algebraic Expressions Prepared by: Sa diyya Hendrickson Name: Date: Read the following definitions and match them with the appropriate example(s) using the lines provided. 1. Variable: A letter that is
P-adic numbers. Rich Schwartz. October 24, 2014
 P-adic numbers Rich Schwartz October 24, 2014 1 The Arithmetic of Remainders In class we have talked a fair amount about doing arithmetic with remainders and now I m going to explain what it means in a
P-adic numbers Rich Schwartz October 24, 2014 1 The Arithmetic of Remainders In class we have talked a fair amount about doing arithmetic with remainders and now I m going to explain what it means in a
Partial Fractions. (Do you see how to work it out? Substitute u = ax + b, so du = a dx.) For example, 1 dx = ln x 7 + C, x x (x 3)(x + 1) = a
 Partial Fractions 7-9-005 Partial fractions is the opposite of adding fractions over a common denominator. It applies to integrals of the form P(x) dx, wherep(x) and Q(x) are polynomials. Q(x) The idea
Partial Fractions 7-9-005 Partial fractions is the opposite of adding fractions over a common denominator. It applies to integrals of the form P(x) dx, wherep(x) and Q(x) are polynomials. Q(x) The idea
Problem Solving in Math (Math 43900) Fall 2013
 Problem Solving in Math (Math 43900) Fall 203 Week six (October ) problems recurrences Instructor: David Galvin Definition of a recurrence relation We met recurrences in the induction hand-out. Sometimes
Problem Solving in Math (Math 43900) Fall 203 Week six (October ) problems recurrences Instructor: David Galvin Definition of a recurrence relation We met recurrences in the induction hand-out. Sometimes
Factoring Review Types of Factoring: 1. GCF: a. b.
 Factoring Review Types of Factoring: 1. GCF: a. b. Ex. A. 4 + 2 8 B. 100 + 25 2. DOS: a. b. c. Ex. A. 9 B. 2 32 3. Plain x Trinomials: Start Signs Factors 1. 2. 3. 4. Ex. A. + 7 + 12 B. 2 3 4. Non-Plain
Factoring Review Types of Factoring: 1. GCF: a. b. Ex. A. 4 + 2 8 B. 100 + 25 2. DOS: a. b. c. Ex. A. 9 B. 2 32 3. Plain x Trinomials: Start Signs Factors 1. 2. 3. 4. Ex. A. + 7 + 12 B. 2 3 4. Non-Plain
Partial Fractions. June 27, In this section, we will learn to integrate another class of functions: the rational functions.
 Partial Fractions June 7, 04 In this section, we will learn to integrate another class of functions: the rational functions. Definition. A rational function is a fraction of two polynomials. For example,
Partial Fractions June 7, 04 In this section, we will learn to integrate another class of functions: the rational functions. Definition. A rational function is a fraction of two polynomials. For example,
AP Calculus Chapter 9: Infinite Series
 AP Calculus Chapter 9: Infinite Series 9. Sequences a, a 2, a 3, a 4, a 5,... Sequence: A function whose domain is the set of positive integers n = 2 3 4 a n = a a 2 a 3 a 4 terms of the sequence Begin
AP Calculus Chapter 9: Infinite Series 9. Sequences a, a 2, a 3, a 4, a 5,... Sequence: A function whose domain is the set of positive integers n = 2 3 4 a n = a a 2 a 3 a 4 terms of the sequence Begin
Lecture 7: Sections 2.3 and 2.4 Rational and Exponential Functions. Recall that a power function has the form f(x) = x r where r is a real number.
 L7-1 Lecture 7: Sections 2.3 and 2.4 Rational and Exponential Functions Recall that a power function has the form f(x) = x r where r is a real number. f(x) = x 1/2 f(x) = x 1/3 ex. Sketch the graph of
L7-1 Lecture 7: Sections 2.3 and 2.4 Rational and Exponential Functions Recall that a power function has the form f(x) = x r where r is a real number. f(x) = x 1/2 f(x) = x 1/3 ex. Sketch the graph of
Introduction and Review of Power Series
 Introduction and Review of Power Series Definition: A power series in powers of x a is an infinite series of the form c n (x a) n = c 0 + c 1 (x a) + c 2 (x a) 2 +...+c n (x a) n +... If a = 0, this is
Introduction and Review of Power Series Definition: A power series in powers of x a is an infinite series of the form c n (x a) n = c 0 + c 1 (x a) + c 2 (x a) 2 +...+c n (x a) n +... If a = 0, this is
PRACTICE PROBLEM SET
 PRACTICE PROBLEM SET NOTE: On the exam, you will have to show all your work (unless told otherwise), so write down all your steps and justify them. Exercise. Solve the following inequalities: () x < 3
PRACTICE PROBLEM SET NOTE: On the exam, you will have to show all your work (unless told otherwise), so write down all your steps and justify them. Exercise. Solve the following inequalities: () x < 3
Lecture 19: Solving linear ODEs + separable techniques for nonlinear ODE s
 Lecture 19: Solving linear ODEs + separable techniques for nonlinear ODE s Geoffrey Cowles Department of Fisheries Oceanography School for Marine Science and Technology University of Massachusetts-Dartmouth
Lecture 19: Solving linear ODEs + separable techniques for nonlinear ODE s Geoffrey Cowles Department of Fisheries Oceanography School for Marine Science and Technology University of Massachusetts-Dartmouth
Some Review Problems for Exam 2: Solutions
 Math 5366 Fall 017 Some Review Problems for Exam : Solutions 1 Find the coefficient of x 15 in each of the following: 1 (a) (1 x) 6 Solution: 1 (1 x) = ( ) k + 5 x k 6 k ( ) ( ) 0 0 so the coefficient
Math 5366 Fall 017 Some Review Problems for Exam : Solutions 1 Find the coefficient of x 15 in each of the following: 1 (a) (1 x) 6 Solution: 1 (1 x) = ( ) k + 5 x k 6 k ( ) ( ) 0 0 so the coefficient
MATH 1231 MATHEMATICS 1B Calculus Section 4.4: Taylor & Power series.
 MATH 1231 MATHEMATICS 1B 2010. For use in Dr Chris Tisdell s lectures. Calculus Section 4.4: Taylor & Power series. 1. What is a Taylor series? 2. Convergence of Taylor series 3. Common Maclaurin series
MATH 1231 MATHEMATICS 1B 2010. For use in Dr Chris Tisdell s lectures. Calculus Section 4.4: Taylor & Power series. 1. What is a Taylor series? 2. Convergence of Taylor series 3. Common Maclaurin series
Ch. 12 Higher Degree Equations Rational Root
 Ch. 12 Higher Degree Equations Rational Root Sec 1. Synthetic Substitution ~ Division of Polynomials This first section was covered in the chapter on polynomial operations. I m reprinting it here because
Ch. 12 Higher Degree Equations Rational Root Sec 1. Synthetic Substitution ~ Division of Polynomials This first section was covered in the chapter on polynomial operations. I m reprinting it here because
Numerical Methods I: Interpolation (cont ed)
 1/20 Numerical Methods I: Interpolation (cont ed) Georg Stadler Courant Institute, NYU stadler@cims.nyu.edu November 30, 2017 Interpolation Things you should know 2/20 I Lagrange vs. Hermite interpolation
1/20 Numerical Methods I: Interpolation (cont ed) Georg Stadler Courant Institute, NYU stadler@cims.nyu.edu November 30, 2017 Interpolation Things you should know 2/20 I Lagrange vs. Hermite interpolation
+ 1 3 x2 2x x3 + 3x 2 + 0x x x2 2x + 3 4
 Math 4030-001/Foundations of Algebra/Fall 2017 Polynomials at the Foundations: Rational Coefficients The rational numbers are our first field, meaning that all the laws of arithmetic hold, every number
Math 4030-001/Foundations of Algebra/Fall 2017 Polynomials at the Foundations: Rational Coefficients The rational numbers are our first field, meaning that all the laws of arithmetic hold, every number
MTH Linear Algebra. Study Guide. Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education
 MTH 3 Linear Algebra Study Guide Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education June 3, ii Contents Table of Contents iii Matrix Algebra. Real Life
MTH 3 Linear Algebra Study Guide Dr. Tony Yee Department of Mathematics and Information Technology The Hong Kong Institute of Education June 3, ii Contents Table of Contents iii Matrix Algebra. Real Life
8. Limit Laws. lim(f g)(x) = lim f(x) lim g(x), (x) = lim x a f(x) g lim x a g(x)
 8. Limit Laws 8.1. Basic Limit Laws. If f and g are two functions and we know the it of each of them at a given point a, then we can easily compute the it at a of their sum, difference, product, constant
8. Limit Laws 8.1. Basic Limit Laws. If f and g are two functions and we know the it of each of them at a given point a, then we can easily compute the it at a of their sum, difference, product, constant
MIKE ZABROCKI - SEPTEMBER 6 & 11, 2012
 NOTES FROM THE FIRST TWO CLASSES MIKE ZABROCKI - SEPTEMBER 6 &, 202 main idea of this class +2+3+ + n = n(n + )/2 to r +2 r + + n r =??? Just to show what we are up against: +2+3+ + n = n(n + )/2 2 +2
NOTES FROM THE FIRST TWO CLASSES MIKE ZABROCKI - SEPTEMBER 6 &, 202 main idea of this class +2+3+ + n = n(n + )/2 to r +2 r + + n r =??? Just to show what we are up against: +2+3+ + n = n(n + )/2 2 +2
n=0 xn /n!. That is almost what we have here; the difference is that the denominator is (n + 1)! in stead of n!. So we have x n+1 n=0
 DISCRETE MATHEMATICS HOMEWORK 8 SOL Undergraduate Course Chukechen Honors College Zhejiang University Fall-Winter 204 HOMEWORK 8 P496 6. Find a closed form for the generating function for the sequence
DISCRETE MATHEMATICS HOMEWORK 8 SOL Undergraduate Course Chukechen Honors College Zhejiang University Fall-Winter 204 HOMEWORK 8 P496 6. Find a closed form for the generating function for the sequence
TAYLOR AND MACLAURIN SERIES
 TAYLOR AND MACLAURIN SERIES. Introduction Last time, we were able to represent a certain restricted class of functions as power series. This leads us to the question: can we represent more general functions
TAYLOR AND MACLAURIN SERIES. Introduction Last time, we were able to represent a certain restricted class of functions as power series. This leads us to the question: can we represent more general functions
CHMC: Finite Fields 9/23/17
 CHMC: Finite Fields 9/23/17 1 Introduction This worksheet is an introduction to the fascinating subject of finite fields. Finite fields have many important applications in coding theory and cryptography,
CHMC: Finite Fields 9/23/17 1 Introduction This worksheet is an introduction to the fascinating subject of finite fields. Finite fields have many important applications in coding theory and cryptography,
Math 300: Final Exam Practice Solutions
 Math 300: Final Exam Practice Solutions 1 Let A be the set of all real numbers which are zeros of polynomials with integer coefficients: A := {α R there exists p(x) = a n x n + + a 1 x + a 0 with all a
Math 300: Final Exam Practice Solutions 1 Let A be the set of all real numbers which are zeros of polynomials with integer coefficients: A := {α R there exists p(x) = a n x n + + a 1 x + a 0 with all a
Proofs. Chapter 2 P P Q Q
 Chapter Proofs In this chapter we develop three methods for proving a statement. To start let s suppose the statement is of the form P Q or if P, then Q. Direct: This method typically starts with P. Then,
Chapter Proofs In this chapter we develop three methods for proving a statement. To start let s suppose the statement is of the form P Q or if P, then Q. Direct: This method typically starts with P. Then,
Math 651 Introduction to Numerical Analysis I Fall SOLUTIONS: Homework Set 1
 ath 651 Introduction to Numerical Analysis I Fall 2010 SOLUTIONS: Homework Set 1 1. Consider the polynomial f(x) = x 2 x 2. (a) Find P 1 (x), P 2 (x) and P 3 (x) for f(x) about x 0 = 0. What is the relation
ath 651 Introduction to Numerical Analysis I Fall 2010 SOLUTIONS: Homework Set 1 1. Consider the polynomial f(x) = x 2 x 2. (a) Find P 1 (x), P 2 (x) and P 3 (x) for f(x) about x 0 = 0. What is the relation
Generating Functions
 Generating Functions Karen Ge May, 07 Abstract Generating functions gives us a global perspective when we need to study a local property. We define generating functions and present its applications in
Generating Functions Karen Ge May, 07 Abstract Generating functions gives us a global perspective when we need to study a local property. We define generating functions and present its applications in
We consider the problem of finding a polynomial that interpolates a given set of values:
 Chapter 5 Interpolation 5. Polynomial Interpolation We consider the problem of finding a polynomial that interpolates a given set of values: x x 0 x... x n y y 0 y... y n where the x i are all distinct.
Chapter 5 Interpolation 5. Polynomial Interpolation We consider the problem of finding a polynomial that interpolates a given set of values: x x 0 x... x n y y 0 y... y n where the x i are all distinct.
Exam 2 Solutions. In class questions
 Math 5330 Spring 2018 Exam 2 Solutions In class questions 1. (15 points) Solve the following congruences. Put your answer in the form of a congruence. I usually find it easier to go from largest to smallest
Math 5330 Spring 2018 Exam 2 Solutions In class questions 1. (15 points) Solve the following congruences. Put your answer in the form of a congruence. I usually find it easier to go from largest to smallest
Section 10: Counting the Elements of a Finite Group
 Section 10: Counting the Elements of a Finite Group Let G be a group and H a subgroup. Because the right cosets are the family of equivalence classes with respect to an equivalence relation on G, it follows
Section 10: Counting the Elements of a Finite Group Let G be a group and H a subgroup. Because the right cosets are the family of equivalence classes with respect to an equivalence relation on G, it follows
2a 2 4ac), provided there is an element r in our
 MTH 310002 Test II Review Spring 2012 Absractions versus examples The purpose of abstraction is to reduce ideas to their essentials, uncluttered by the details of a specific situation Our lectures built
MTH 310002 Test II Review Spring 2012 Absractions versus examples The purpose of abstraction is to reduce ideas to their essentials, uncluttered by the details of a specific situation Our lectures built
CHAPTER 2 POLYNOMIALS KEY POINTS
 CHAPTER POLYNOMIALS KEY POINTS 1. Polynomials of degrees 1, and 3 are called linear, quadratic and cubic polynomials respectively.. A quadratic polynomial in x with real coefficient is of the form a x
CHAPTER POLYNOMIALS KEY POINTS 1. Polynomials of degrees 1, and 3 are called linear, quadratic and cubic polynomials respectively.. A quadratic polynomial in x with real coefficient is of the form a x
Numerical Methods I: Polynomial Interpolation
 1/31 Numerical Methods I: Polynomial Interpolation Georg Stadler Courant Institute, NYU stadler@cims.nyu.edu November 16, 2017 lassical polynomial interpolation Given f i := f(t i ), i =0,...,n, we would
1/31 Numerical Methods I: Polynomial Interpolation Georg Stadler Courant Institute, NYU stadler@cims.nyu.edu November 16, 2017 lassical polynomial interpolation Given f i := f(t i ), i =0,...,n, we would
A SUMMARY OF RECURSION SOLVING TECHNIQUES
 A SUMMARY OF RECURSION SOLVING TECHNIQUES KIMMO ERIKSSON, KTH These notes are meant to be a complement to the material on recursion solving techniques in the textbook Discrete Mathematics by Biggs. In
A SUMMARY OF RECURSION SOLVING TECHNIQUES KIMMO ERIKSSON, KTH These notes are meant to be a complement to the material on recursion solving techniques in the textbook Discrete Mathematics by Biggs. In
10/22/16. 1 Math HL - Santowski SKILLS REVIEW. Lesson 15 Graphs of Rational Functions. Lesson Objectives. (A) Rational Functions
 Lesson 15 Graphs of Rational Functions SKILLS REVIEW! Use function composition to prove that the following two funtions are inverses of each other. 2x 3 f(x) = g(x) = 5 2 x 1 1 2 Lesson Objectives! The
Lesson 15 Graphs of Rational Functions SKILLS REVIEW! Use function composition to prove that the following two funtions are inverses of each other. 2x 3 f(x) = g(x) = 5 2 x 1 1 2 Lesson Objectives! The
ALGEBRA. 1. Some elementary number theory 1.1. Primes and divisibility. We denote the collection of integers
 ALGEBRA CHRISTIAN REMLING 1. Some elementary number theory 1.1. Primes and divisibility. We denote the collection of integers by Z = {..., 2, 1, 0, 1,...}. Given a, b Z, we write a b if b = ac for some
ALGEBRA CHRISTIAN REMLING 1. Some elementary number theory 1.1. Primes and divisibility. We denote the collection of integers by Z = {..., 2, 1, 0, 1,...}. Given a, b Z, we write a b if b = ac for some
1 The Well Ordering Principle, Induction, and Equivalence Relations
 1 The Well Ordering Principle, Induction, and Equivalence Relations The set of natural numbers is the set N = f1; 2; 3; : : :g. (Some authors also include the number 0 in the natural numbers, but number
1 The Well Ordering Principle, Induction, and Equivalence Relations The set of natural numbers is the set N = f1; 2; 3; : : :g. (Some authors also include the number 0 in the natural numbers, but number
A description of a math circle set of activities around polynomials, especially interpolation.
 A description of a math circle set of activities around polynomials, especially interpolation. Bob Sachs Department of Mathematical Sciences George Mason University Fairfax, Virginia 22030 rsachs@gmu.edu
A description of a math circle set of activities around polynomials, especially interpolation. Bob Sachs Department of Mathematical Sciences George Mason University Fairfax, Virginia 22030 rsachs@gmu.edu
Summing Series: Solutions
 Sequences and Series Misha Lavrov Summing Series: Solutions Western PA ARML Practice December, 0 Switching the order of summation Prove useful identity 9 x x x x x x Riemann s zeta function ζ is defined
Sequences and Series Misha Lavrov Summing Series: Solutions Western PA ARML Practice December, 0 Switching the order of summation Prove useful identity 9 x x x x x x Riemann s zeta function ζ is defined
Math 2233 Homework Set 7
 Math 33 Homework Set 7 1. Find the general solution to the following differential equations. If initial conditions are specified, also determine the solution satisfying those initial conditions. a y 4
Math 33 Homework Set 7 1. Find the general solution to the following differential equations. If initial conditions are specified, also determine the solution satisfying those initial conditions. a y 4
LECTURE 10: REVIEW OF POWER SERIES. 1. Motivation
 LECTURE 10: REVIEW OF POWER SERIES By definition, a power series centered at x 0 is a series of the form where a 0, a 1,... and x 0 are constants. For convenience, we shall mostly be concerned with the
LECTURE 10: REVIEW OF POWER SERIES By definition, a power series centered at x 0 is a series of the form where a 0, a 1,... and x 0 are constants. For convenience, we shall mostly be concerned with the
10.1 Sequences. Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1.
 10.1 Sequences Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1 Examples: EX1: Find a formula for the general term a n of the sequence,
10.1 Sequences Example: A sequence is a function f(n) whose domain is a subset of the integers. Notation: *Note: n = 0 vs. n = 1 Examples: EX1: Find a formula for the general term a n of the sequence,
The above statement is the false product rule! The correct product rule gives g (x) = 3x 4 cos x+ 12x 3 sin x. for all angles θ.
 Math 7A Practice Midterm III Solutions Ch. 6-8 (Ebersole,.7-.4 (Stewart DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam. You
Math 7A Practice Midterm III Solutions Ch. 6-8 (Ebersole,.7-.4 (Stewart DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam. You
We ll start today by learning how to change a repeating decimal into a fraction! Then we will do a review of Unit 1 - half of Unit 3!
 Welcome to math! We ll start today by learning how to change a repeating decimal into a fraction! Then we will do a review of Unit 1 - half of Unit 3! So grab a seat where you can focus, and get ready
Welcome to math! We ll start today by learning how to change a repeating decimal into a fraction! Then we will do a review of Unit 1 - half of Unit 3! So grab a seat where you can focus, and get ready
ZEROES OF INTEGER LINEAR RECURRENCES. 1. Introduction. 4 ( )( 2 1) n
 ZEROES OF INTEGER LINEAR RECURRENCES DANIEL LITT Consider the integer linear recurrence 1. Introduction x n = x n 1 + 2x n 2 + 3x n 3 with x 0 = x 1 = x 2 = 1. For which n is x n = 0? Answer: x n is never
ZEROES OF INTEGER LINEAR RECURRENCES DANIEL LITT Consider the integer linear recurrence 1. Introduction x n = x n 1 + 2x n 2 + 3x n 3 with x 0 = x 1 = x 2 = 1. For which n is x n = 0? Answer: x n is never
CHAPTER 7: TECHNIQUES OF INTEGRATION
 CHAPTER 7: TECHNIQUES OF INTEGRATION DAVID GLICKENSTEIN. Introduction This semester we will be looking deep into the recesses of calculus. Some of the main topics will be: Integration: we will learn how
CHAPTER 7: TECHNIQUES OF INTEGRATION DAVID GLICKENSTEIN. Introduction This semester we will be looking deep into the recesses of calculus. Some of the main topics will be: Integration: we will learn how
Partial Fraction Decomposition Honors Precalculus Mr. Velazquez Rm. 254
 Partial Fraction Decomposition Honors Precalculus Mr. Velazquez Rm. 254 Adding and Subtracting Rational Expressions Recall that we can use multiplication and common denominators to write a sum or difference
Partial Fraction Decomposition Honors Precalculus Mr. Velazquez Rm. 254 Adding and Subtracting Rational Expressions Recall that we can use multiplication and common denominators to write a sum or difference
Intermediate Math Circles February 14, 2018 Contest Prep: Number Theory
 Intermediate Math Circles February 14, 2018 Contest Prep: Number Theory Part 1: Prime Factorization A prime number is an integer greater than 1 whose only positive divisors are 1 and itself. An integer
Intermediate Math Circles February 14, 2018 Contest Prep: Number Theory Part 1: Prime Factorization A prime number is an integer greater than 1 whose only positive divisors are 1 and itself. An integer
x arctan x = x x x x2 9 +
 Math 1B Project 3 Continued Fractions. Many of the special functions that occur in the applications of mathematics are defined by infinite processes, such as series, integrals, and iterations. The continued
Math 1B Project 3 Continued Fractions. Many of the special functions that occur in the applications of mathematics are defined by infinite processes, such as series, integrals, and iterations. The continued
Homework 1 Solutions Math 587
 Homework 1 Solutions Math 587 1) Find positive functions f(x),g(x), continuous on (0, ) so that f = O(g(x)) as x 0, but lim x 0 f(x)/g(x) does not exist. One can take f(x) = sin(1/x) and g(x) = 1, for
Homework 1 Solutions Math 587 1) Find positive functions f(x),g(x), continuous on (0, ) so that f = O(g(x)) as x 0, but lim x 0 f(x)/g(x) does not exist. One can take f(x) = sin(1/x) and g(x) = 1, for
1 Review of di erential calculus
 Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
Review of di erential calculus This chapter presents the main elements of di erential calculus needed in probability theory. Often, students taking a course on probability theory have problems with concepts
1 Reductions from Maximum Matchings to Perfect Matchings
 15-451/651: Design & Analysis of Algorithms November 21, 2013 Lecture #26 last changed: December 3, 2013 When we first studied network flows, we saw how to find maximum cardinality matchings in bipartite
15-451/651: Design & Analysis of Algorithms November 21, 2013 Lecture #26 last changed: December 3, 2013 When we first studied network flows, we saw how to find maximum cardinality matchings in bipartite
Lecture 10: Powers of Matrices, Difference Equations
 Lecture 10: Powers of Matrices, Difference Equations Difference Equations A difference equation, also sometimes called a recurrence equation is an equation that defines a sequence recursively, i.e. each
Lecture 10: Powers of Matrices, Difference Equations Difference Equations A difference equation, also sometimes called a recurrence equation is an equation that defines a sequence recursively, i.e. each
