Fourier transforms. Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x L or L x L) as Fourier series: a n cos L
|
|
|
- Veronica Floyd
- 6 years ago
- Views:
Transcription
1 ourier trnsforms Motivtion nd definition Up to now, we ve been expressing functions on finite intervls (usully the intervl 0 x or x ) s ourier series: fpxq 0 8 nπx n cos n b n sin nπx where 0» fpxq dx 2 nd n» fpxq cos nπx dx, b n» fpxq sin nπx dx. We lso occsionlly thought bout the complex exponentil version of ourier series: Since e iθ cos θ i sin θ nd e iθ cos θ i sin θ, or equivlently cos θ eiθ e iθ 2 nd sin θ eiθ e iθ, 2i we cn rewrite the bove series s: fpxq 0 e 0ix 0 e 0ix 8 n 8 e nπix{ n n 8 n c n e nπix{ n ib n 2 e nπix{ 2 b n e nπix{ e nπix{ 2i e nπix{ n ib n e nπix{ 2 where $ '& c n '% 2 n ib n q for n 0 0 for n 0 2 n ib n q for n 0
2 2 fourier trnsforms Using the formuls for n nd b n given bove, we see tht, for n 0. If n 0 we hve c n 2 p n 2 2 2»»» ib n q nπx i fpxq cos dx 2 nπx fpxq cos i sin fpxqe nπix{ dx.» nπx fpxq sin dx nπx dx c n 2 p n ib n q» fpxq cos nπx dx i» 2 2» nπx nπx fpxq cos i sin 2 2» fpxqe nπix{ dx fpxq sin dx nπx dx becuse cosine is n even function nd sine is odd. So the sme formul works for ll the coefficients (even c 0 ) in this cse nd we hve 8 fpxq c n e nπix{ where c n» fpxqe nπix{ dx. 2 n Wht we wnt to do here is let tend to infinity, so we cn consider problems on the whole rel line. To see wht hppens to our ourier series formuls when we do this, we introduce two new vribles: ω nπ{ nd ω π{. Then our complex ourier series formuls become fpxq 8 n c n e iωx where c n ω» fpxqe iωx dx nd the n in the formul for c n is hiding in the vrible ω. Now, if we let c ω c n { ω, we cn rewrite these s 8 fpxq c ω e iωx ω where c ω» fpxqe iωx dx. n The vrible ω nπ{ tkes on more nd more vlues which re closer nd closer together s Ñ 8, so c ω begins to feel like function of the vrible ω defined
3 mth for ll rel ω. ikewise, the sum on the left looks n wful lot like Riemnn sum pproximting n integrl. Wht hppens in the limit s Ñ 8 is: fpxq cpωqe iωx dω where cpωq fpxqe ixω dx. The formul on the right defines the function cpωq s the ourier trnsform of fpxq, nd the formul on the left defines fpxq s the inverse ourier trnsform of cpωq. These formuls hold true (nd the inverse ourier trnsform of the ourier trnsform of f pxq is f pxq the so-clled ourier inversion formul) for resonble functions fpxq tht decy to zero s x Ñ 8 in such wy so tht fpxq nd/or fpxq 2 hs finite integrl over the whole rel line. There re mny stndrd nottions for ourier trnsforms (nd lterntive definitions with the minus sign in the ourier trnsform rther thn in the inverse, nd with the fctor in different plces, so wtch out if you re looking in books other thn our textbook!), including nd Properties nd exmples. fpωq pωq rfpxqspωq q pxq fpxq r pωqspxq fpxqe ixω dx pωqe ixω dω. The ourier trnsform is n opertion tht mps function of x, sy fpxq to function of ω, nmely rfspωq q fpωq. It is clerly liner opertor, so for functions fpxq nd gpxq nd constnts α nd β we hve rαfpxq βgpxqs α rfpxqs β rgpxqs. Some other properties of the ourier trnsform re. Trnsltion (or shifting): rfpx qs pωq e iω rfpxqs pωq. And in the other direction, re ix fpxqs pωq rfpxqs pω q. 2. Scling: f x pωq rfpxqs pωq, nd likewise rfpxqs pωq rfpxqs ω. 3. Opertionl property (derivtives): rf pxqs pωq iω rfpxqs pωq, nd rxfpxqs pωq i d p rfpxqs pωqq. dω The opertionl property is of essentil importnce for the study of differentil equtions, since it shows tht the ourier trnsform converts derivtives to multipliction
4 4 fourier trnsforms so it converts clculus to lgebr (or might reduce prtil differentil eqution to n ordinry one). Here re the proofs of the first of ech of the three pirs of formuls to give sense of how to work with ourier trnsforms, nd leve the other three s exercises. or the first shifting rule, we mke the substitution y x (so dy dx nd x y ) to clculte rfpx qs pωq fpx qe iωx dx fpyqe iωy e iω dx e iω rfpxqs pωq or the first scling rule, we mke the substitution y x{ (so dx dy) nd get x f pωq x f e iωx dx fpyqe iωy dy rfpxqs pωq or the opertionl property we first point out tht since the ourier trnsforms of both f pxq nd fpxq exist, we must hve tht fpxq Ñ 0 nd f pxq Ñ 0 s x Ñ 8. Therefore the endpoint terms will vnish when we integrte by prts (with u e iωx nd dv f pxq dx, so du iωe iωx nd v fpxq): rf pxqs pωq f pxqe iωx dx x8 eiωx fpxq 0 iω x iω rfpxqs pωq fpxqe iωx dx iωfpxqe iωx dx et s clculte few bsic exmples of ourier trnsforms: Exmple. et S pxq be the function defined by " if x S pxq 0 otherwise
5 mth Then rs pxqs pωq» e iωx dx eiω e iω iω sin ω πω. Exmple 2. et upxq e x2 {2, so the grph of upxq is Gussin or bell-shped curve. Then upxq stisfies the differentil eqution u xu 0. We cn use this fct nd the properties of the ourier trnsform to clculte û s follows: Tke the ourier trnsform of the differentil eqution nd use linerity nd both prts of property (3) bove to get 0 ru xus pωq ru s rxus d rus iω rus i dω Therefore rus stisfies the differentil eqution the solution of which is rus ω rus 0 rus Ce ω2 {p2q. The constnt C is the vlue of rus p0q, i.e., C c e x2{2 dx 2 e y2 dy?, using the substitution y x nd the fmilir (or t lest ccessible) fct tht ³ 2 8 e y2 dy? π. Therefore e x2 {2 pωq? e ω2{p2q, so the originl Gussin is trnsformed into different one. An interesting observtion is wht hppens for : Then we hve e x2 {2? e ω2{2, x2{2 so the specific Gussin e is eigenvlue {?. n eigenfunction of the ourier trnsform with Exmple 3. et fpxq e x, so fpxq " e x if x 0 e x if x 0.
6 6 fourier trnsforms Then e x pωq πp 2» 0» 0 e x e iωx dx e x e iωx dx e p iωqx dx p iωqx x0 e iω x iω ω 2 q iω 0 e ω e iωx dx e p iωqx dx 0 p iωqx x8 e iω x0 (the limiting vlues of the exponentils t 8 re zero becuse e x goes to zero s x goes to 8 nd e iωx stys bounded). An observtion. Becuse the formuls for the ourier trnsform nd the inverse ourier trnsform re so similr, we cn get inverse trnsform formuls from the direct ones nd vice vers. In prticulr, note tht if we let y x then rfpxqs pωq ikewise r pωqs pxq fpxqe iωx dx pωqe iωx dω fp yqe iωy dy rfp yqs pωq p αqe iαx dα r p αqs pxq So if we know ourier trnsform formul or n inverse ourier trnsform formul, we cn get nother one for free by reversing the inverse. or exmple, since we immeditely hve tht rs pxqs pωq sin ω πω, sin ω pxq S pxq. πω rom either of the formuls bove nd the fct tht sin x{x is n even function, we hve sin x pωq πx S pωq,
7 mth or Similrly, since we know tht sin x x e x 2 S pωq. πp 2 ω 2 q for 0, we cn immeditely write πp 2 e x. ω 2 q And since is n even function of ω, we hve πp 2 or 2 πp 2 x 2 q x 2 ω 2 q e ω, 2 e ω. Convolutions. We need one more ourier trnsform formul, nd it involves n opertion on functions tht might seem new to you. It is clled convolution nd it strts with two functions, fpxq nd gpxq nd produces new one, denoted f g or pf gqpxq (or sometimes just f gpxq), defined by pf gqpxq fpyqgpx yq dy. If you think bout it, convolution is like multipliction of polynomils or series, wherein n bn c n where c n m b n m. This motivtes the definition of convolution s n opertion tht might hve hs its ourier trnsform the product of the trnsforms of the individul functions, nd it does (up to nuisnce fctor of ), but more on tht in moment. irst some bsic properties of convolutions:
8 8 fourier trnsforms. Convolution is liner in ech of the two functions. In other words, if f, g nd h re functions nd α nd β re constnts, then pαf βgq h αf h βg h nd f pαg βhq αf g βf h. 2. Convolution is commuttive: f g g f. To prove this, we mke the substitution z x y in the integrl (so we think of x s being constnt while we re doing the integrl, nd y x z nd dy dz) nd get pf gqpxq 3. Now for the ourier trnsform:» 8 pg fqpxq fpyqgpx yq dy fpx zqgpzq dz gpzqfpx zq dz rf gs pωq rfs pωq rgs pωq or pf gqpωq fpωqĝpωq. To see this we use the substitution z x y gin, nd brek up e iωx e iωpx y yq e iωy e iωpx yq to get: pf gqpωq fpyqgpx yq dy e iωx dx fpyqgpx yqe iωx dx dy fpyqe iωy gpx yqe iωpx yq dx dy gpx yqe iωpx yq dx fpyqe iωy dy fpωqĝpωq gpzqe iωz dz gpzqe iωz dz fpyqe iωy dy fpyqe iωy dy s ikewise, the trnsform of the product of two functions is the convolution of the trnsforms, except without the fctor of, nmely r Gs pxq q pxq q Gpxq.
9 mth One lst thing: the convolution product of two functions hs n interesting property reltive to derivtives: d df pf gq dx dx g f dg dx so when you tke derivtives of convolution of two functions, you get to stick the derivtive on whichever of the two functions is more convenient (or differentible) this is n esy consequence of the commuttivity of convolution, nd it hs the powerful consequence tht the convolution of two functions hs the better of the differentibility properties of the two individul functions. So if f is discontinuous but g is smooth, then f g will be smooth. The het eqution on the whole line. Now we re redy to use ll of this for something! We seek to solve the het eqution u t ku xx for t 0 nd x 8, with initil conditions upx, 0q fpxq nd ssuming u decys to zero t x nd x 8. We ll strt by tking the ourier trnsform of both sides of the differentil eqution in the x-vrible. By this we men so û stisfies nd ûpω, tq Bû Bt kω2 û ûpω, 0q fpωq. upx, tqe ixω dx, This is n ordinry differentil eqution where the independent vrible is t nd ω should be treted s constnt. The generl solution of the differentil eqution is ûpω, tq cpωqe kω2t. Putting t 0 shows tht cpωq fqωq. Therefore ourier trnsform of the solution of our problem is ûpω, tq fpωqe kω2t. We cn now recover upx, tq by tking the inverse ourier trnsform of both sides, using the rule tht the ourier trnsform of convolution is times the product of the individul ourier trnsforms, so upx, tq fpxq e kω2 t
10 0 fourier trnsforms nd we hve to clculte the inverse ourier trnsform of e kω2t. But we hve the rule for Gussins: e x2 {2? e ω2{p2q, or e ω2 {p2q? e x2{2. Since we wnt to clculte the inverse ourier trnsform of e kω2t, we should set {p2q kt, or {p2ktq. Then we get c e kω2 t π {p4ktq kt e x2, nd so upx, tq c π fpxq {p4ktq kt e x2? 4πkt fpyqe px yq2 {p4ktq dy. The function Gpx, y, tq? 4πkt e px yq2 {p4ktq is clled the fundmentl solution of the het eqution. It is the solution to the initil vlue for the het eqution for the sitution where the initil conditions re such tht single unit of het energy is introduced t the point y t time t 0. So the bove formul for upx, tq sys tht we cn solve the het eqution for rbitrry initil conditions upx, tq by integrting together ll the contributions to the temperture t time t 0 t ll points, s described by the differentil fpyq dy. The wve eqution on the whole line. Next, let s look t the initil-vlue problem for the wve eqution on the whole line. We ll solve the wve eqution together with initil conditions u tt c 2 u xx upx, 0q fpxq nd u t px, 0q gpxq. As we did with the het eqution, we ll tke the ourier trnsform of both sides of the differentil eqution in the x-vrible. So once gin, let ûpω, tq upx, tqe iωx dx
11 so û stisfies nd mth 425 B 2 û Bt 2 c2 ω 2 û ûpω, 0q fpωq nd û t pω, 0q ĝpωq. We will gin tret this s n ordinry differentil eqution in t with ω treted s constnt. The generl solution of this eqution is nd the initil conditions imply u p ω, tq c pωq cos ωct c 2 pωq sin ωct, upω, 0q c pωq fpωq nd u t pω, 0q cωc 2 pωq ĝpωq. Therefore, c pωq fpωq nd c 2 pωq ĝpωq{pcωq nd we hve obtined the ourier trnsform of the solution: ûpω, tq fpωq ĝpωq cos ωct sin ωct. cω Therefore ĝpωq upx, tq fpωq cos ωct cω sin ωct. We ll tke the two terms one t time. or the first, we write cos ωct in complex exponentil form, so we re trying to compute fpωq eiωct e iωct fpωqre iωct e iωct se iωx dω 2 2 fpωqe iωpx ctq dx fpωqe iωpx ctq dx 2 rfpx ctq fpx ctqs 2 using the definition of the inverse ourier trnsform. or the second term, we proceed differently. Reclling tht Ŝpωq sin ω{pπωq nd tht the inverse ourier trnsform of product of two functions is their convolution (divided by q, we hve ĝpωq sin ωct cω π gpxq c S ctpxq 2c 2c 2c» ct ct» x ct x ct gpx yqs ct pyq dy gpx yq dy gpuq du
12 2 fourier trnsforms where in the lst step we mde the substitution u x y (so y x u nd dy du). We put both terms together to get the solution to our initil-vlue problem for the wve eqution: upx, tq 2 rfpx ctq fpx ctqs 2c» x ct x ct gpuq du. This is clled d Alembert s solution of the wve eqution, nd clerly shows tht signls propgte with speed c, since the vlue of the solution t point x nd time t depends only on the initil position nd velocity vlues in the intervl rx ct, x cts, nd conversely tht the initil vlues t point x influence the solution t time t only within the intervl rx ct, x cts. iner lgebric properties of the ourier trnsform: Prsevl s theorem nd Hermite functions We remrked erlier tht the ourier trnsform is liner trnsformtion from functions of x to functions of ω defined on the whole line (which cn be integrted etc.). We lso found tht the function e x2 {2 is n eigenfunction of the ourier trnsform with eigenvlue {?. We explore some further consequences of these observtions in this section. irst, we cn compre the inner product of the ourier trnsforms of two functions with the inner product of the functions themselves (remember, in the complex (or Hermitin) inner product, we hve to tke the complex conjugte of the second fctor, nd we write z for the complex conjugte of z): xf, gy fpxqpgpxqq dx fpxq ĝpωqe dω iωx dx fpxqe iωx pĝpωqq dx dω fpxqe iωx dx pĝpωqq dω fpωqpĝpωqq dω A E f, ĝ. A E In prticulr, if f g we hve tht }f} 2 xf, fy f, f } f} 2 or } f} 2 }f}2.
13 mth This is clled Prsevl s equlity or Prsevl s theorem it sys tht the ourier trnsforms shrinks the norms of ll functions by fctor of {? (so it wsn t n ccident tht we found n eigenfunction with tht eigenvlue!), nd it hs number of interesting consequences. As simple exmple. since we know tht (reclling tht S pxq is the step function for the intervl r, s, sin ω rs pxqs pωq πω we cn conclude tht 2 sin ω πω }S pxq} 2. The right side is esy to compute, it s simply» dx π. But we lern something interesting by compring this to the left side: sin 2 ω π 2 ω 2 dω π or sin 2 ω ω 2 dω π, which is certinly something we didn t know before. Now, bck to the liner lgebr. We sk curious question, relted to the observtion we mde on pge 6: Wht hppens if you tke the ourier trnsform of the ourier trnsform of function? et s see: r rfpxqss pωq fpzqe iωz dz fpzqe ip ωqz dz fp ωq, since the lst integrl is the inverse ourier trnsform evluted t ω. But this shows tht doing the ourier trnsform twice to function gives bck its reverse multiplied by {pq. So if we do the ourier trnsform four times to function we should get {p4π 2 q times the reverse of the reverse, which is the originl function. In other words, 4 rfpxqs 4π fpxq. 2 We could write this s n eqution bout the ourier trnsform opertor: 4 4π 2 I 0,
14 4 fourier trnsforms where I is the identity opertor. Knowing this, we cn see tht if f is ny eigenfunction of with eigenvlue λ, then 4 rfs 4π Irfs λ 4 f 0, 2 4π 2 which mens tht ll of the eigenvlues of the ourier trnsform must stisfy the eqution λ 4 4π 2 0, so the only possible eigenvlues of re?, i?,? nd i?. We lredy hve tht the Gussin e x2 {2 is n eigenfunction of with eigenvlue {?. Now we ll find eigenfunctions for the other eigenvlues. We hve two ourier trnsform rules tht look quite similr: df dx pωq iω fpωq nd xfpxqpωq i d f dω. So the ourier trnsforms of ech of the opertions multiply by the vrible nd tke the derivtive on the x-side is the other opertion on the ω-side (well, there re fctors of i to keep trck of, nd we will). Becuse of this, the sum nd difference of these two opertors hve specil reltionship with the ourier trnsform opertor: df d rfs d rfs xfpxq iω rfs pωq i dx dω i ω rfs pωq dω nd df dx xfpxq iω rfs pωq d rfs i dω i d rfs dω ω rfs pωq. These equtions show tht if fpxq is n eigenfunction of the ourier trnsform opertor with eigenvlue λ then f pxq xfpxq will be n eigenfunction of the ourier trnsform with eigenvlue iλ (unless f pxq xfpxq 0), nd f pxq xfpxq will be n eigenfunction of the ourier trnsform with eigenvlue iλ (unless f pxq xfpxq 0). et s try this with the eigenfunction we know, nmely fpxq e x2{2. Unfortuntely, f xf 0, but f pxq xfpxq xe x2 {2 xe x2 {2 2xe x2 {2, so 2xe x2{2 is n eigenfunction of the ourier trnsform with eigenvlue i{? : 2xe x2 {2 pωq? i p 2ωe ω2{2 q.
15 mth And we cn keep going: If we set f pxq 2xe x2 {2, then f xf 2e x2 {2 2fpxq, so we get nothing new here. But f xf p4x 2 2qe x2 {2, so we cll f 2 pxq p4x 2 2qe x2{2 nd we hve p4x 2 2qe x2 {2? p4ω 2 2qe ω2{2. We cn continue in this wy nd obtin n infinite sequence of eigenfunctions of the ourier trnsform, strting from f 0 pxq e x2 {2, where f n pxq f n pxq xf npxq, nd the eigenvlue of f n will be i n {?. There will be more to sy bout this in the homework!
Fourier transforms. Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x L or L x L) as Fourier series: a n cos L
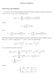 ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
ourier transforms Motivation and definition Up to now, we ve been expressing functions on finite intervals (usually the interval 0 x or x ) as ourier series: fpxq a 0 8 nπx a n cos n b n sin nπx where
Physics 116C Solution of inhomogeneous ordinary differential equations using Green s functions
 Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
Physics 6C Solution of inhomogeneous ordinry differentil equtions using Green s functions Peter Young November 5, 29 Homogeneous Equtions We hve studied, especilly in long HW problem, second order liner
The Regulated and Riemann Integrals
 Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Chpter 1 The Regulted nd Riemnn Integrls 1.1 Introduction We will consider severl different pproches to defining the definite integrl f(x) dx of function f(x). These definitions will ll ssign the sme vlue
Math 360: A primitive integral and elementary functions
 Mth 360: A primitive integrl nd elementry functions D. DeTurck University of Pennsylvni October 16, 2017 D. DeTurck Mth 360 001 2017C: Integrl/functions 1 / 32 Setup for the integrl prtitions Definition:
Mth 360: A primitive integrl nd elementry functions D. DeTurck University of Pennsylvni October 16, 2017 D. DeTurck Mth 360 001 2017C: Integrl/functions 1 / 32 Setup for the integrl prtitions Definition:
ODE: Existence and Uniqueness of a Solution
 Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Mth 22 Fll 213 Jerry Kzdn ODE: Existence nd Uniqueness of Solution The Fundmentl Theorem of Clculus tells us how to solve the ordinry differentil eqution (ODE) du = f(t) dt with initil condition u() =
Theoretical foundations of Gaussian quadrature
 Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Theoreticl foundtions of Gussin qudrture 1 Inner product vector spce Definition 1. A vector spce (or liner spce) is set V = {u, v, w,...} in which the following two opertions re defined: (A) Addition of
Improper Integrals. Type I Improper Integrals How do we evaluate an integral such as
 Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
Improper Integrls Two different types of integrls cn qulify s improper. The first type of improper integrl (which we will refer to s Type I) involves evluting n integrl over n infinite region. In the grph
7.2 The Definite Integral
 7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
7.2 The Definite Integrl the definite integrl In the previous section, it ws found tht if function f is continuous nd nonnegtive, then the re under the grph of f on [, b] is given by F (b) F (), where
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H. Thomas Shores Department of Mathematics University of Nebraska Spring 2007
 A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
A REVIEW OF CALCULUS CONCEPTS FOR JDEP 384H Thoms Shores Deprtment of Mthemtics University of Nebrsk Spring 2007 Contents Rtes of Chnge nd Derivtives 1 Dierentils 4 Are nd Integrls 5 Multivrite Clculus
1 The Riemann Integral
 The Riemnn Integrl. An exmple leding to the notion of integrl (res) We know how to find (i.e. define) the re of rectngle (bse height), tringle ( (sum of res of tringles). But how do we find/define n re
The Riemnn Integrl. An exmple leding to the notion of integrl (res) We know how to find (i.e. define) the re of rectngle (bse height), tringle ( (sum of res of tringles). But how do we find/define n re
1 1D heat and wave equations on a finite interval
 1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
1 1D het nd wve equtions on finite intervl In this section we consider generl method of seprtion of vribles nd its pplictions to solving het eqution nd wve eqution on finite intervl ( 1, 2. Since by trnsltion
f(x) dx, If one of these two conditions is not met, we call the integral improper. Our usual definition for the value for the definite integral
 Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Improper Integrls Every time tht we hve evluted definite integrl such s f(x) dx, we hve mde two implicit ssumptions bout the integrl:. The intervl [, b] is finite, nd. f(x) is continuous on [, b]. If one
Advanced Calculus: MATH 410 Notes on Integrals and Integrability Professor David Levermore 17 October 2004
 Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
Advnced Clculus: MATH 410 Notes on Integrls nd Integrbility Professor Dvid Levermore 17 October 2004 1. Definite Integrls In this section we revisit the definite integrl tht you were introduced to when
Unit #9 : Definite Integral Properties; Fundamental Theorem of Calculus
 Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Unit #9 : Definite Integrl Properties; Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Review of basic calculus
 Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
Review of bsic clculus This brief review reclls some of the most importnt concepts, definitions, nd theorems from bsic clculus. It is not intended to tech bsic clculus from scrtch. If ny of the items below
1.1. Linear Constant Coefficient Equations. Remark: A differential equation is an equation
 1 1.1. Liner Constnt Coefficient Equtions Section Objective(s): Overview of Differentil Equtions. Liner Differentil Equtions. Solving Liner Differentil Equtions. The Initil Vlue Problem. 1.1.1. Overview
1 1.1. Liner Constnt Coefficient Equtions Section Objective(s): Overview of Differentil Equtions. Liner Differentil Equtions. Solving Liner Differentil Equtions. The Initil Vlue Problem. 1.1.1. Overview
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 2013 Outline 1 Riemnn Sums 2 Riemnn Integrls 3 Properties
Bernoulli Numbers Jeff Morton
 Bernoulli Numbers Jeff Morton. We re interested in the opertor e t k d k t k, which is to sy k tk. Applying this to some function f E to get e t f d k k tk d k f f + d k k tk dk f, we note tht since f
Bernoulli Numbers Jeff Morton. We re interested in the opertor e t k d k t k, which is to sy k tk. Applying this to some function f E to get e t f d k k tk d k f f + d k k tk dk f, we note tht since f
c n φ n (x), 0 < x < L, (1) n=1
 SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
SECTION : Fourier Series. MATH4. In section 4, we will study method clled Seprtion of Vribles for finding exct solutions to certin clss of prtil differentil equtions (PDEs. To do this, it will be necessry
Main topics for the First Midterm
 Min topics for the First Midterm The Midterm will cover Section 1.8, Chpters 2-3, Sections 4.1-4.8, nd Sections 5.1-5.3 (essentilly ll of the mteril covered in clss). Be sure to know the results of the
Min topics for the First Midterm The Midterm will cover Section 1.8, Chpters 2-3, Sections 4.1-4.8, nd Sections 5.1-5.3 (essentilly ll of the mteril covered in clss). Be sure to know the results of the
Riemann Sums and Riemann Integrals
 Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Riemnn Sums nd Riemnn Integrls Jmes K. Peterson Deprtment of Biologicl Sciences nd Deprtment of Mthemticl Sciences Clemson University August 26, 203 Outline Riemnn Sums Riemnn Integrls Properties Abstrct
Abstract inner product spaces
 WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
WEEK 4 Abstrct inner product spces Definition An inner product spce is vector spce V over the rel field R equipped with rule for multiplying vectors, such tht the product of two vectors is sclr, nd the
P 3 (x) = f(0) + f (0)x + f (0) 2. x 2 + f (0) . In the problem set, you are asked to show, in general, the n th order term is a n = f (n) (0)
 1 Tylor polynomils In Section 3.5, we discussed how to pproximte function f(x) round point in terms of its first derivtive f (x) evluted t, tht is using the liner pproximtion f() + f ()(x ). We clled this
1 Tylor polynomils In Section 3.5, we discussed how to pproximte function f(x) round point in terms of its first derivtive f (x) evluted t, tht is using the liner pproximtion f() + f ()(x ). We clled this
Section 6.1 INTRO to LAPLACE TRANSFORMS
 Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Higher Checklist (Unit 3) Higher Checklist (Unit 3) Vectors
 Vectors Skill Achieved? Know tht sclr is quntity tht hs only size (no direction) Identify rel-life exmples of sclrs such s, temperture, mss, distnce, time, speed, energy nd electric chrge Know tht vector
Vectors Skill Achieved? Know tht sclr is quntity tht hs only size (no direction) Identify rel-life exmples of sclrs such s, temperture, mss, distnce, time, speed, energy nd electric chrge Know tht vector
Properties of Integrals, Indefinite Integrals. Goals: Definition of the Definite Integral Integral Calculations using Antiderivatives
 Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Block #6: Properties of Integrls, Indefinite Integrls Gols: Definition of the Definite Integrl Integrl Clcultions using Antiderivtives Properties of Integrls The Indefinite Integrl 1 Riemnn Sums - 1 Riemnn
Improper Integrals, and Differential Equations
 Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
Improper Integrls, nd Differentil Equtions October 22, 204 5.3 Improper Integrls Previously, we discussed how integrls correspond to res. More specificlly, we sid tht for function f(x), the region creted
1.2. Linear Variable Coefficient Equations. y + b "! = a y + b " Remark: The case b = 0 and a non-constant can be solved with the same idea as above.
 1 12 Liner Vrible Coefficient Equtions Section Objective(s): Review: Constnt Coefficient Equtions Solving Vrible Coefficient Equtions The Integrting Fctor Method The Bernoulli Eqution 121 Review: Constnt
1 12 Liner Vrible Coefficient Equtions Section Objective(s): Review: Constnt Coefficient Equtions Solving Vrible Coefficient Equtions The Integrting Fctor Method The Bernoulli Eqution 121 Review: Constnt
Math Lecture 23
 Mth 8 - Lecture 3 Dyln Zwick Fll 3 In our lst lecture we delt with solutions to the system: x = Ax where A is n n n mtrix with n distinct eigenvlues. As promised, tody we will del with the question of
Mth 8 - Lecture 3 Dyln Zwick Fll 3 In our lst lecture we delt with solutions to the system: x = Ax where A is n n n mtrix with n distinct eigenvlues. As promised, tody we will del with the question of
Chapter 28. Fourier Series An Eigenvalue Problem.
 Chpter 28 Fourier Series Every time I close my eyes The noise inside me mplifies I cn t escpe I relive every moment of the dy Every misstep I hve mde Finds wy it cn invde My every thought And this is why
Chpter 28 Fourier Series Every time I close my eyes The noise inside me mplifies I cn t escpe I relive every moment of the dy Every misstep I hve mde Finds wy it cn invde My every thought And this is why
The Wave Equation I. MA 436 Kurt Bryan
 1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
1 Introduction The Wve Eqution I MA 436 Kurt Bryn Consider string stretching long the x xis, of indeterminte (or even infinite!) length. We wnt to derive n eqution which models the motion of the string
MORE FUNCTION GRAPHING; OPTIMIZATION. (Last edited October 28, 2013 at 11:09pm.)
 MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
MORE FUNCTION GRAPHING; OPTIMIZATION FRI, OCT 25, 203 (Lst edited October 28, 203 t :09pm.) Exercise. Let n be n rbitrry positive integer. Give n exmple of function with exctly n verticl symptotes. Give
ARITHMETIC OPERATIONS. The real numbers have the following properties: a b c ab ac
 REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
REVIEW OF ALGEBRA Here we review the bsic rules nd procedures of lgebr tht you need to know in order to be successful in clculus. ARITHMETIC OPERATIONS The rel numbers hve the following properties: b b
Chapter 6 Notes, Larson/Hostetler 3e
 Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
Contents 6. Antiderivtives nd the Rules of Integrtion.......................... 6. Are nd the Definite Integrl.................................. 6.. Are............................................ 6. Reimnn
and that at t = 0 the object is at position 5. Find the position of the object at t = 2.
 7.2 The Fundmentl Theorem of Clculus 49 re mny, mny problems tht pper much different on the surfce but tht turn out to be the sme s these problems, in the sense tht when we try to pproimte solutions we
7.2 The Fundmentl Theorem of Clculus 49 re mny, mny problems tht pper much different on the surfce but tht turn out to be the sme s these problems, in the sense tht when we try to pproimte solutions we
Math& 152 Section Integration by Parts
 Mth& 5 Section 7. - Integrtion by Prts Integrtion by prts is rule tht trnsforms the integrl of the product of two functions into other (idelly simpler) integrls. Recll from Clculus I tht given two differentible
Mth& 5 Section 7. - Integrtion by Prts Integrtion by prts is rule tht trnsforms the integrl of the product of two functions into other (idelly simpler) integrls. Recll from Clculus I tht given two differentible
UNIFORM CONVERGENCE. Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3
 UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
UNIFORM CONVERGENCE Contents 1. Uniform Convergence 1 2. Properties of uniform convergence 3 Suppose f n : Ω R or f n : Ω C is sequence of rel or complex functions, nd f n f s n in some sense. Furthermore,
Polynomial Approximations for the Natural Logarithm and Arctangent Functions. Math 230
 Polynomil Approimtions for the Nturl Logrithm nd Arctngent Functions Mth 23 You recll from first semester clculus how one cn use the derivtive to find n eqution for the tngent line to function t given
Polynomil Approimtions for the Nturl Logrithm nd Arctngent Functions Mth 23 You recll from first semester clculus how one cn use the derivtive to find n eqution for the tngent line to function t given
approaches as n becomes larger and larger. Since e > 1, the graph of the natural exponential function is as below
 . Eponentil nd rithmic functions.1 Eponentil Functions A function of the form f() =, > 0, 1 is clled n eponentil function. Its domin is the set of ll rel f ( 1) numbers. For n eponentil function f we hve.
. Eponentil nd rithmic functions.1 Eponentil Functions A function of the form f() =, > 0, 1 is clled n eponentil function. Its domin is the set of ll rel f ( 1) numbers. For n eponentil function f we hve.
Math 1B, lecture 4: Error bounds for numerical methods
 Mth B, lecture 4: Error bounds for numericl methods Nthn Pflueger 4 September 0 Introduction The five numericl methods descried in the previous lecture ll operte by the sme principle: they pproximte the
Mth B, lecture 4: Error bounds for numericl methods Nthn Pflueger 4 September 0 Introduction The five numericl methods descried in the previous lecture ll operte by the sme principle: they pproximte the
x = b a n x 2 e x dx. cdx = c(b a), where c is any constant. a b
 CHAPTER 5. INTEGRALS 61 where nd x = b n x i = 1 (x i 1 + x i ) = midpoint of [x i 1, x i ]. Problem 168 (Exercise 1, pge 377). Use the Midpoint Rule with the n = 4 to pproximte 5 1 x e x dx. Some quick
CHAPTER 5. INTEGRALS 61 where nd x = b n x i = 1 (x i 1 + x i ) = midpoint of [x i 1, x i ]. Problem 168 (Exercise 1, pge 377). Use the Midpoint Rule with the n = 4 to pproximte 5 1 x e x dx. Some quick
n f(x i ) x. i=1 In section 4.2, we defined the definite integral of f from x = a to x = b as n f(x i ) x; f(x) dx = lim i=1
 The Fundmentl Theorem of Clculus As we continue to study the re problem, let s think bck to wht we know bout computing res of regions enclosed by curves. If we wnt to find the re of the region below the
The Fundmentl Theorem of Clculus As we continue to study the re problem, let s think bck to wht we know bout computing res of regions enclosed by curves. If we wnt to find the re of the region below the
Conservation Law. Chapter Goal. 5.2 Theory
 Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
Chpter 5 Conservtion Lw 5.1 Gol Our long term gol is to understnd how mny mthemticl models re derived. We study how certin quntity chnges with time in given region (sptil domin). We first derive the very
Infinite Geometric Series
 Infinite Geometric Series Finite Geometric Series ( finite SUM) Let 0 < r < 1, nd let n be positive integer. Consider the finite sum It turns out there is simple lgebric expression tht is equivlent to
Infinite Geometric Series Finite Geometric Series ( finite SUM) Let 0 < r < 1, nd let n be positive integer. Consider the finite sum It turns out there is simple lgebric expression tht is equivlent to
Definition of Continuity: The function f(x) is continuous at x = a if f(a) exists and lim
 Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
Mth 9 Course Summry/Study Guide Fll, 2005 [1] Limits Definition of Limit: We sy tht L is the limit of f(x) s x pproches if f(x) gets closer nd closer to L s x gets closer nd closer to. We write lim f(x)
Advanced Calculus: MATH 410 Uniform Convergence of Functions Professor David Levermore 11 December 2015
 Advnced Clculus: MATH 410 Uniform Convergence of Functions Professor Dvid Levermore 11 December 2015 12. Sequences of Functions We now explore two notions of wht it mens for sequence of functions {f n
Advnced Clculus: MATH 410 Uniform Convergence of Functions Professor Dvid Levermore 11 December 2015 12. Sequences of Functions We now explore two notions of wht it mens for sequence of functions {f n
20 MATHEMATICS POLYNOMIALS
 0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
0 MATHEMATICS POLYNOMIALS.1 Introduction In Clss IX, you hve studied polynomils in one vrible nd their degrees. Recll tht if p(x) is polynomil in x, the highest power of x in p(x) is clled the degree of
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS.
 THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
THE EXISTENCE-UNIQUENESS THEOREM FOR FIRST-ORDER DIFFERENTIAL EQUATIONS RADON ROSBOROUGH https://intuitiveexplntionscom/picrd-lindelof-theorem/ This document is proof of the existence-uniqueness theorem
MA 124 January 18, Derivatives are. Integrals are.
 MA 124 Jnury 18, 2018 Prof PB s one-minute introduction to clculus Derivtives re. Integrls re. In Clculus 1, we lern limits, derivtives, some pplictions of derivtives, indefinite integrls, definite integrls,
MA 124 Jnury 18, 2018 Prof PB s one-minute introduction to clculus Derivtives re. Integrls re. In Clculus 1, we lern limits, derivtives, some pplictions of derivtives, indefinite integrls, definite integrls,
How do we solve these things, especially when they get complicated? How do we know when a system has a solution, and when is it unique?
 XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
XII. LINEAR ALGEBRA: SOLVING SYSTEMS OF EQUATIONS Tody we re going to tlk bout solving systems of liner equtions. These re problems tht give couple of equtions with couple of unknowns, like: 6 2 3 7 4
Review of Calculus, cont d
 Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
Jim Lmbers MAT 460 Fll Semester 2009-10 Lecture 3 Notes These notes correspond to Section 1.1 in the text. Review of Clculus, cont d Riemnn Sums nd the Definite Integrl There re mny cses in which some
1 Probability Density Functions
 Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
Lis Yn CS 9 Continuous Distributions Lecture Notes #9 July 6, 28 Bsed on chpter by Chris Piech So fr, ll rndom vribles we hve seen hve been discrete. In ll the cses we hve seen in CS 9, this ment tht our
The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).
![The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a). The First Fundamental Theorem of Calculus. If f(x) is continuous on [a, b] and F (x) is any antiderivative. f(x) dx = F (b) F (a).](/thumbs/78/77467690.jpg) The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
The Fundmentl Theorems of Clculus Mth 4, Section 0, Spring 009 We now know enough bout definite integrls to give precise formultions of the Fundmentl Theorems of Clculus. We will lso look t some bsic emples
Consequently, the temperature must be the same at each point in the cross section at x. Let:
 HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
HW 2 Comments: L1-3. Derive the het eqution for n inhomogeneous rod where the therml coefficients used in the derivtion of the het eqution for homogeneous rod now become functions of position x in the
Linearity, linear operators, and self adjoint eigenvalue problems
 Linerity, liner opertors, nd self djoint eigenvlue problems 1 Elements of liner lgebr The study of liner prtil differentil equtions utilizes, unsurprisingly, mny concepts from liner lgebr nd liner ordinry
Linerity, liner opertors, nd self djoint eigenvlue problems 1 Elements of liner lgebr The study of liner prtil differentil equtions utilizes, unsurprisingly, mny concepts from liner lgebr nd liner ordinry
Recitation 3: More Applications of the Derivative
 Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
Mth 1c TA: Pdric Brtlett Recittion 3: More Applictions of the Derivtive Week 3 Cltech 2012 1 Rndom Question Question 1 A grph consists of the following: A set V of vertices. A set E of edges where ech
Anti-derivatives/Indefinite Integrals of Basic Functions
 Anti-derivtives/Indefinite Integrls of Bsic Functions Power Rule: In prticulr, this mens tht x n+ x n n + + C, dx = ln x + C, if n if n = x 0 dx = dx = dx = x + C nd x (lthough you won t use the second
Anti-derivtives/Indefinite Integrls of Bsic Functions Power Rule: In prticulr, this mens tht x n+ x n n + + C, dx = ln x + C, if n if n = x 0 dx = dx = dx = x + C nd x (lthough you won t use the second
The Riemann Integral
 Deprtment of Mthemtics King Sud University 2017-2018 Tble of contents 1 Anti-derivtive Function nd Indefinite Integrls 2 3 4 5 Indefinite Integrls & Anti-derivtive Function Definition Let f : I R be function
Deprtment of Mthemtics King Sud University 2017-2018 Tble of contents 1 Anti-derivtive Function nd Indefinite Integrls 2 3 4 5 Indefinite Integrls & Anti-derivtive Function Definition Let f : I R be function
Convergence of Fourier Series and Fejer s Theorem. Lee Ricketson
 Convergence of Fourier Series nd Fejer s Theorem Lee Ricketson My, 006 Abstrct This pper will ddress the Fourier Series of functions with rbitrry period. We will derive forms of the Dirichlet nd Fejer
Convergence of Fourier Series nd Fejer s Theorem Lee Ricketson My, 006 Abstrct This pper will ddress the Fourier Series of functions with rbitrry period. We will derive forms of the Dirichlet nd Fejer
Chapter 5. , r = r 1 r 2 (1) µ = m 1 m 2. r, r 2 = R µ m 2. R(m 1 + m 2 ) + m 2 r = r 1. m 2. r = r 1. R + µ m 1
 Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
Tor Kjellsson Stockholm University Chpter 5 5. Strting with the following informtion: R = m r + m r m + m, r = r r we wnt to derive: µ = m m m + m r = R + µ m r, r = R µ m r 3 = µ m R + r, = µ m R r. 4
MATH 174A: PROBLEM SET 5. Suggested Solution
 MATH 174A: PROBLEM SET 5 Suggested Solution Problem 1. Suppose tht I [, b] is n intervl. Let f 1 b f() d for f C(I; R) (i.e. f is continuous rel-vlued function on I), nd let L 1 (I) denote the completion
MATH 174A: PROBLEM SET 5 Suggested Solution Problem 1. Suppose tht I [, b] is n intervl. Let f 1 b f() d for f C(I; R) (i.e. f is continuous rel-vlued function on I), nd let L 1 (I) denote the completion
Best Approximation. Chapter The General Case
 Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Chpter 4 Best Approximtion 4.1 The Generl Cse In the previous chpter, we hve seen how n interpolting polynomil cn be used s n pproximtion to given function. We now wnt to find the best pproximtion to given
Review of Riemann Integral
 1 Review of Riemnn Integrl In this chpter we review the definition of Riemnn integrl of bounded function f : [, b] R, nd point out its limittions so s to be convinced of the necessity of more generl integrl.
1 Review of Riemnn Integrl In this chpter we review the definition of Riemnn integrl of bounded function f : [, b] R, nd point out its limittions so s to be convinced of the necessity of more generl integrl.
Overview of Calculus I
 Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
Overview of Clculus I Prof. Jim Swift Northern Arizon University There re three key concepts in clculus: The limit, the derivtive, nd the integrl. You need to understnd the definitions of these three things,
MATH , Calculus 2, Fall 2018
 MATH 36-2, 36-3 Clculus 2, Fll 28 The FUNdmentl Theorem of Clculus Sections 5.4 nd 5.5 This worksheet focuses on the most importnt theorem in clculus. In fct, the Fundmentl Theorem of Clculus (FTC is rgubly
MATH 36-2, 36-3 Clculus 2, Fll 28 The FUNdmentl Theorem of Clculus Sections 5.4 nd 5.5 This worksheet focuses on the most importnt theorem in clculus. In fct, the Fundmentl Theorem of Clculus (FTC is rgubly
Energy Bands Energy Bands and Band Gap. Phys463.nb Phenomenon
 Phys463.nb 49 7 Energy Bnds Ref: textbook, Chpter 7 Q: Why re there insultors nd conductors? Q: Wht will hppen when n electron moves in crystl? In the previous chpter, we discussed free electron gses,
Phys463.nb 49 7 Energy Bnds Ref: textbook, Chpter 7 Q: Why re there insultors nd conductors? Q: Wht will hppen when n electron moves in crystl? In the previous chpter, we discussed free electron gses,
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS
 STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
STURM-LIOUVILLE BOUNDARY VALUE PROBLEMS Throughout, we let [, b] be bounded intervl in R. C 2 ([, b]) denotes the spce of functions with derivtives of second order continuous up to the endpoints. Cc 2
F (x) dx = F (x)+c = u + C = du,
 35. The Substitution Rule An indefinite integrl of the derivtive F (x) is the function F (x) itself. Let u = F (x), where u is new vrible defined s differentible function of x. Consider the differentil
35. The Substitution Rule An indefinite integrl of the derivtive F (x) is the function F (x) itself. Let u = F (x), where u is new vrible defined s differentible function of x. Consider the differentil
Orthogonal Polynomials
 Mth 4401 Gussin Qudrture Pge 1 Orthogonl Polynomils Orthogonl polynomils rise from series solutions to differentil equtions, lthough they cn be rrived t in vriety of different mnners. Orthogonl polynomils
Mth 4401 Gussin Qudrture Pge 1 Orthogonl Polynomils Orthogonl polynomils rise from series solutions to differentil equtions, lthough they cn be rrived t in vriety of different mnners. Orthogonl polynomils
7. Indefinite Integrals
 7. Indefinite Integrls These lecture notes present my interprettion of Ruth Lwrence s lecture notes (in Herew) 7. Prolem sttement By the fundmentl theorem of clculus, to clculte n integrl we need to find
7. Indefinite Integrls These lecture notes present my interprettion of Ruth Lwrence s lecture notes (in Herew) 7. Prolem sttement By the fundmentl theorem of clculus, to clculte n integrl we need to find
Calculus II: Integrations and Series
 Clculus II: Integrtions nd Series August 7, 200 Integrls Suppose we hve generl function y = f(x) For simplicity, let f(x) > 0 nd f(x) continuous Denote F (x) = re under the grph of f in the intervl [,x]
Clculus II: Integrtions nd Series August 7, 200 Integrls Suppose we hve generl function y = f(x) For simplicity, let f(x) > 0 nd f(x) continuous Denote F (x) = re under the grph of f in the intervl [,x]
1 Techniques of Integration
 November 8, 8 MAT86 Week Justin Ko Techniques of Integrtion. Integrtion By Substitution (Chnge of Vribles) We cn think of integrtion by substitution s the counterprt of the chin rule for differentition.
November 8, 8 MAT86 Week Justin Ko Techniques of Integrtion. Integrtion By Substitution (Chnge of Vribles) We cn think of integrtion by substitution s the counterprt of the chin rule for differentition.
Lecture 1. Functional series. Pointwise and uniform convergence.
 1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
1 Introduction. Lecture 1. Functionl series. Pointwise nd uniform convergence. In this course we study mongst other things Fourier series. The Fourier series for periodic function f(x) with period 2π is
MATH34032: Green s Functions, Integral Equations and the Calculus of Variations 1
 MATH34032: Green s Functions, Integrl Equtions nd the Clculus of Vritions 1 Section 1 Function spces nd opertors Here we gives some brief detils nd definitions, prticulrly relting to opertors. For further
MATH34032: Green s Functions, Integrl Equtions nd the Clculus of Vritions 1 Section 1 Function spces nd opertors Here we gives some brief detils nd definitions, prticulrly relting to opertors. For further
Integrals - Motivation
 Integrls - Motivtion When we looked t function s rte of chnge If f(x) is liner, the nswer is esy slope If f(x) is non-liner, we hd to work hrd limits derivtive A relted question is the re under f(x) (but
Integrls - Motivtion When we looked t function s rte of chnge If f(x) is liner, the nswer is esy slope If f(x) is non-liner, we hd to work hrd limits derivtive A relted question is the re under f(x) (but
Math Calculus with Analytic Geometry II
 orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
orem of definite Mth 5.0 with Anlytic Geometry II Jnury 4, 0 orem of definite If < b then b f (x) dx = ( under f bove x-xis) ( bove f under x-xis) Exmple 8 0 3 9 x dx = π 3 4 = 9π 4 orem of definite Problem
Lecture 3. Limits of Functions and Continuity
 Lecture 3 Limits of Functions nd Continuity Audrey Terrs April 26, 21 1 Limits of Functions Notes I m skipping the lst section of Chpter 6 of Lng; the section bout open nd closed sets We cn probbly live
Lecture 3 Limits of Functions nd Continuity Audrey Terrs April 26, 21 1 Limits of Functions Notes I m skipping the lst section of Chpter 6 of Lng; the section bout open nd closed sets We cn probbly live
Section 6.1 INTRO to LAPLACE TRANSFORMS
 Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Section 6. INTRO to LAPLACE TRANSFORMS Key terms: Improper Integrl; diverge, converge A A f(t)dt lim f(t)dt Piecewise Continuous Function; jump discontinuity Function of Exponentil Order Lplce Trnsform
Read section 3.3, 3.4 Announcements:
 Dte: 3/1/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: 1. f x = 3x 6, find the inverse, f 1 x., Using your grphing clcultor, Grph 1. f x,f
Dte: 3/1/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: 1. f x = 3x 6, find the inverse, f 1 x., Using your grphing clcultor, Grph 1. f x,f
5.4, 6.1, 6.2 Handout. As we ve discussed, the integral is in some way the opposite of taking a derivative. The exact relationship
 5.4, 6.1, 6.2 Hnout As we ve iscusse, the integrl is in some wy the opposite of tking erivtive. The exct reltionship is given by the Funmentl Theorem of Clculus: The Funmentl Theorem of Clculus: If f is
5.4, 6.1, 6.2 Hnout As we ve iscusse, the integrl is in some wy the opposite of tking erivtive. The exct reltionship is given by the Funmentl Theorem of Clculus: The Funmentl Theorem of Clculus: If f is
Definite integral. Mathematics FRDIS MENDELU
 Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová Brno 1 Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function defined on [, b]. Wht is the re of the
Lecture 1: Introduction to integration theory and bounded variation
 Lecture 1: Introduction to integrtion theory nd bounded vrition Wht is this course bout? Integrtion theory. The first question you might hve is why there is nything you need to lern bout integrtion. You
Lecture 1: Introduction to integrtion theory nd bounded vrition Wht is this course bout? Integrtion theory. The first question you might hve is why there is nything you need to lern bout integrtion. You
Chapter 14. Matrix Representations of Linear Transformations
 Chpter 4 Mtrix Representtions of Liner Trnsformtions When considering the Het Stte Evolution, we found tht we could describe this process using multipliction by mtrix. This ws nice becuse computers cn
Chpter 4 Mtrix Representtions of Liner Trnsformtions When considering the Het Stte Evolution, we found tht we could describe this process using multipliction by mtrix. This ws nice becuse computers cn
63. Representation of functions as power series Consider a power series. ( 1) n x 2n for all 1 < x < 1
 3 9. SEQUENCES AND SERIES 63. Representtion of functions s power series Consider power series x 2 + x 4 x 6 + x 8 + = ( ) n x 2n It is geometric series with q = x 2 nd therefore it converges for ll q =
3 9. SEQUENCES AND SERIES 63. Representtion of functions s power series Consider power series x 2 + x 4 x 6 + x 8 + = ( ) n x 2n It is geometric series with q = x 2 nd therefore it converges for ll q =
Chapter 8: Methods of Integration
 Chpter 8: Methods of Integrtion Bsic Integrls 8. Note: We hve the following list of Bsic Integrls p p+ + c, for p sec tn + c p + ln + c sec tn sec + c e e + c tn ln sec + c ln + c sec ln sec + tn + c ln
Chpter 8: Methods of Integrtion Bsic Integrls 8. Note: We hve the following list of Bsic Integrls p p+ + c, for p sec tn + c p + ln + c sec tn sec + c e e + c tn ln sec + c ln + c sec ln sec + tn + c ln
4 7x =250; 5 3x =500; Read section 3.3, 3.4 Announcements: Bell Ringer: Use your calculator to solve
 Dte: 3/14/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: Use your clcultor to solve 4 7x =250; 5 3x =500; HW Requests: Properties of Log Equtions
Dte: 3/14/13 Objective: SWBAT pply properties of exponentil functions nd will pply properties of rithms. Bell Ringer: Use your clcultor to solve 4 7x =250; 5 3x =500; HW Requests: Properties of Log Equtions
We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.
![We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b. We partition C into n small arcs by forming a partition of [a, b] by picking s i as follows: a = s 0 < s 1 < < s n = b.](/thumbs/93/114277851.jpg) Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
Mth 255 - Vector lculus II Notes 4.2 Pth nd Line Integrls We begin with discussion of pth integrls (the book clls them sclr line integrls). We will do this for function of two vribles, but these ides cn
Improper Integrals. The First Fundamental Theorem of Calculus, as we ve discussed in class, goes as follows:
 Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
Improper Integrls The First Fundmentl Theorem of Clculus, s we ve discussed in clss, goes s follows: If f is continuous on the intervl [, ] nd F is function for which F t = ft, then ftdt = F F. An integrl
SYDE 112, LECTURES 3 & 4: The Fundamental Theorem of Calculus
 SYDE 112, LECTURES & 4: The Fundmentl Theorem of Clculus So fr we hve introduced two new concepts in this course: ntidifferentition nd Riemnn sums. It turns out tht these quntities re relted, but it is
SYDE 112, LECTURES & 4: The Fundmentl Theorem of Clculus So fr we hve introduced two new concepts in this course: ntidifferentition nd Riemnn sums. It turns out tht these quntities re relted, but it is
Definite integral. Mathematics FRDIS MENDELU. Simona Fišnarová (Mendel University) Definite integral MENDELU 1 / 30
 Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová (Mendel University) Definite integrl MENDELU / Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function
Definite integrl Mthemtics FRDIS MENDELU Simon Fišnrová (Mendel University) Definite integrl MENDELU / Motivtion - re under curve Suppose, for simplicity, tht y = f(x) is nonnegtive nd continuous function
Notes on length and conformal metrics
 Notes on length nd conforml metrics We recll how to mesure the Eucliden distnce of n rc in the plne. Let α : [, b] R 2 be smooth (C ) rc. Tht is α(t) (x(t), y(t)) where x(t) nd y(t) re smooth rel vlued
Notes on length nd conforml metrics We recll how to mesure the Eucliden distnce of n rc in the plne. Let α : [, b] R 2 be smooth (C ) rc. Tht is α(t) (x(t), y(t)) where x(t) nd y(t) re smooth rel vlued
df dt f () b f () a dt
 Vector lculus 16.7 tokes Theorem Nme: toke's Theorem is higher dimensionl nlogue to Green's Theorem nd the Fundmentl Theorem of clculus. Why, you sk? Well, let us revisit these theorems. Fundmentl Theorem
Vector lculus 16.7 tokes Theorem Nme: toke's Theorem is higher dimensionl nlogue to Green's Theorem nd the Fundmentl Theorem of clculus. Why, you sk? Well, let us revisit these theorems. Fundmentl Theorem
Math Fall 2006 Sample problems for the final exam: Solutions
 Mth 42-5 Fll 26 Smple problems for the finl exm: Solutions Any problem my be ltered or replced by different one! Some possibly useful informtion Prsevl s equlity for the complex form of the Fourier series
Mth 42-5 Fll 26 Smple problems for the finl exm: Solutions Any problem my be ltered or replced by different one! Some possibly useful informtion Prsevl s equlity for the complex form of the Fourier series
Calculus I-II Review Sheet
 Clculus I-II Review Sheet 1 Definitions 1.1 Functions A function is f is incresing on n intervl if x y implies f(x) f(y), nd decresing if x y implies f(x) f(y). It is clled monotonic if it is either incresing
Clculus I-II Review Sheet 1 Definitions 1.1 Functions A function is f is incresing on n intervl if x y implies f(x) f(y), nd decresing if x y implies f(x) f(y). It is clled monotonic if it is either incresing
221B Lecture Notes WKB Method
 Clssicl Limit B Lecture Notes WKB Method Hmilton Jcobi Eqution We strt from the Schrödinger eqution for single prticle in potentil i h t ψ x, t = [ ] h m + V x ψ x, t. We cn rewrite this eqution by using
Clssicl Limit B Lecture Notes WKB Method Hmilton Jcobi Eqution We strt from the Schrödinger eqution for single prticle in potentil i h t ψ x, t = [ ] h m + V x ψ x, t. We cn rewrite this eqution by using
INTRODUCTION TO INTEGRATION
 INTRODUCTION TO INTEGRATION 5.1 Ares nd Distnces Assume f(x) 0 on the intervl [, b]. Let A be the re under the grph of f(x). b We will obtin n pproximtion of A in the following three steps. STEP 1: Divide
INTRODUCTION TO INTEGRATION 5.1 Ares nd Distnces Assume f(x) 0 on the intervl [, b]. Let A be the re under the grph of f(x). b We will obtin n pproximtion of A in the following three steps. STEP 1: Divide
Math 3B Final Review
 Mth 3B Finl Review Written by Victori Kl vtkl@mth.ucsb.edu SH 6432u Office Hours: R 9:45-10:45m SH 1607 Mth Lb Hours: TR 1-2pm Lst updted: 12/06/14 This is continution of the midterm review. Prctice problems
Mth 3B Finl Review Written by Victori Kl vtkl@mth.ucsb.edu SH 6432u Office Hours: R 9:45-10:45m SH 1607 Mth Lb Hours: TR 1-2pm Lst updted: 12/06/14 This is continution of the midterm review. Prctice problems
Math Advanced Calculus II
 Mth 452 - Advnced Clculus II Line Integrls nd Green s Theorem The min gol of this chpter is to prove Stoke s theorem, which is the multivrible version of the fundmentl theorem of clculus. We will be focused
Mth 452 - Advnced Clculus II Line Integrls nd Green s Theorem The min gol of this chpter is to prove Stoke s theorem, which is the multivrible version of the fundmentl theorem of clculus. We will be focused
Section 7.1 Integration by Substitution
 Section 7. Integrtion by Substitution Evlute ech of the following integrls. Keep in mind tht using substitution my not work on some problems. For one of the definite integrls, it is not possible to find
Section 7. Integrtion by Substitution Evlute ech of the following integrls. Keep in mind tht using substitution my not work on some problems. For one of the definite integrls, it is not possible to find
f(a+h) f(a) x a h 0. This is the rate at which
 M408S Concept Inventory smple nswers These questions re open-ended, nd re intended to cover the min topics tht we lerned in M408S. These re not crnk-out-n-nswer problems! (There re plenty of those in the
M408S Concept Inventory smple nswers These questions re open-ended, nd re intended to cover the min topics tht we lerned in M408S. These re not crnk-out-n-nswer problems! (There re plenty of those in the
