Chapter 3: Kinematics and Dynamics of Multibody Systems
|
|
|
- Jeffery Bond
- 6 years ago
- Views:
Transcription
1 Chapter 3: Knematcs and Dynamcs of Multbody Systems 3. Fundamentals of Knematcs 3.2 Settng up the euatons of moton for multbody-systems II
2 3. Fundamentals of Knematcs 2 damper strut sprng chasss x z y steerng 4 rod Dsposer/te rod Wheel carrer transverse control arm
3 3. Fundamentals of Knematcs 3 opologcal basc prncples. Open knematcal chan ( tree-structure ) n B bodes (wthout reference/nertal body) n onts he route between two bodes s dstnct each body has exactly one predecessor Hence t apples: n n B Each ont has a dedcated body and connects the body wth ts predecessor n B n 7
4 3. Fundamentals of Knematcs 4 opologcal basc prncples 2. Closed knematcal chan ( loop-structure ) n B bodes (wthout reference/nertal body) n onts each loop reures one extra ont Hence : n n B +n L n B 0 n 3 n L 3
5 3. Fundamentals of Knematcs 5 Basc notaton and coherences f - degree of freedom of ont f - Sum of all degree of freedom of onts f L - degree of freedom of loop Degree of freedom (Laufgrad) durng spatal moton (rübler; Kutzbach) f n 6 nb (6 f ) n L n n B f n f f 6 n L 6 n L
6 Prncples of assemblng knematcal chans wth closed loops 3. Fundamentals of Knematcs 6. sparse method (cuttng off at all bodes) prncple: constrants: dsconnectng all onts concurrence of all ont parameters 2. vector-loop method (dsconnectng loops) prncple: constrants: dsconnectng only one ont per loop closure condtons of the loops 3. topologcal methods (loops as transference elements) prncple: constrants: knematcal loops are prepared as knematcal transfer elements ( knematcal transformators) - transfer euatons n the loop (nonlnear and local) - coupler euatons between the loops (lnear and global)
7 3. Fundamental Procedures of Knematcs II Illustraton wth the example of a double wshbone suspenson (front wheel suspenson): 7 double wshbone wheel suspenson: σ + γ γ Rgd body model P S β s R L L 2 S S solated DOF R wheel axle r s β S Mult-body system 5 bodes 7 onts 2 knematcal loops System degrees of freedom compresson (angle β) steerng ( dsplacement s) solated degree of freedom gnored
8 3. Fundamentals of Knematcs 8 System overvew n 7 n B 5 n L n -n B 2 4 f 4 7 f 7 L 2 B 5 6 f 6 3 B 4 f 6 n B n (6 f ) B 6 5 ( ) L 3 f f 5 3 R P S S f B 3 B 2 R S 2 f 2 3
9 3. Fundamentals of Knematcs 9. sparse method (cuttng of all bodes) Euaton of constrants e.g. for 5 : r 2 2 wth w + r ( w [ x y z ϕ ψ θ ] ) r r (w ) 2r B 4 4r ont 5 r 4 B 2 r 2
10 3. Fundamentals of Knematcs 0 Double wshbone wheel suspenson wth cut onts: a) sparse method (cuttng off all bodes) 5 bodes all onts dsconnected 7 onts assembly: each ont has (6 f ) constrants degrees of freedom of ont euatons of constrants are dentfed from the closure condtons for poston and orentaton: r ( r ( ) )!! r ( ( r ) )
11 2. vector-loop Methods (dsconnectng loops) he relatve moton n the onts s descrbed through 3. Fundamentals of Knematcs f n g f Jont varables β, s β 2 a 3 B β 6,, β 7, β 8 Jont 5 Closure Euatons a e.g. for 2 : a + a2( β) a3( β2 ) + a4( β6, β7, β8 ) β B 3 a 2 a 4 B 2 Jont 2
12 Double Wshbone Suspenson wth dsonted loops 3. Fundamentals of Knematcs 2 vector-loop Method (dsconnectng loops) 5 Bodes Number of ndependant loops: n 7 Jonts L n -n B Jonts 2 and 5 are dsconnected Assembly: each Jont has (6 f ) Constrants Degrees of freedom of Jont Constrant euatons from closure condtons for poston and orentaton: a! 0! Ι Identtymatrx
13 3. Fundamentals of Knematcs 3 3. topologsche Methode (Loops are consdered as tranmsson elements) Am: to calculate the moton of every body of the system usng the nput parameters (generalsed coordnates) β 2 L 2 2 s s β 2,, β 3, (β 4 ) β β (, 2 ),...4 s s ( 2 ), β 6,, β 7, β 8 β 9,, β 0, β L ββ β 3,, β 4, (β 5 )
14 3. Fundamentals of Knematcs Double Wshbone Suspenson wth transmsson elements 4 topologsche Method (loops as transmsson elements) 5 Bodes Number of ndependant loops: 7 Jonts n L n -n B Assembly: each loop s a knematc transmsson element (knematc ransformator) Constrant euatons: - local: n general 6 non-lnear contrant euatons per loop - global: lnear couplng euatons between the loops; Number depends on the order of the couplng between the loops
15 3. Fundamentals of Knematcs 5 β 2 loop f 8, n L f L f -6n L Inputs: ββ, β 6 β 6,, β 7, β 8 Outputs: β 2, β 3,, β 4, (β 5 ), β 7, β 8 L β 2 β B β 8 β B 3 β 7 β 3,, β 4, (β 5 ) redundent Degree of freedom β 3 (β 5 ) β 4 β 6 B 2
16 3. Fundamentals of Knematcs 6 β 2 Loop f g 8, n L f L f g -6n L β 6,, β 7, β 8 Inputs: ββ, β 6 Outputs: β 2, β 3,, β 4, (β 5 ), β 7, β 8 L β Knematc ransformer β β 6 L fl 2 β 3 β 4 β 7 β 8 β 2 β 3,, β 4, (β 5 ) redundant Degree of freedom
17 7 3. Fundamentals of Knematcs s β 2,, β 3, (β 4 ) Loop 2 f, n L f L2 f -6n L -6 5 β 2 L 2 Inputs: β 2, ss, β 7, β 8, (β 4 ) Outputs: β 6, β 9, β 0, β, β 2, β 3 β 9,, β 0, β β 6,, β 7, β 8 β 2 2 s B β 8 β 3 B 5 β 7 (β 4 ) β 6 β 2 B 2 B β 4 β 9 β 0
18 β 2 s L 2 β 2,, β 3, (β 4 ) 3. Fundamentals of Knematcs Loop 2 f, n l f L2 f -6n l -6 5 Inputs: β 2, ss, β 7, β 8, (β 4 ) Outputs: β 6, β 9, β 0, β, β 2, β 3 8 β 6,, β 7, β 8 β 9,, β 0, β Knematc ransformer s β 9 β β 2 0 β L β 7 2 β β 8 2 (β f L2 4(5) β 4 ) 3 β 6
19 3. Fundamentals of Knematcs opologcal descrpton of the double wshbone suspenson 9 B β 2 2 s B 5 B 2 L β 8 Β 3, (β 4 ) β 7 β B 3 β 6 β 2 (β 5 ), β 4 β B 4 β 3 β 9 β 0 L 2
20 3. Fundamentals of Knematcs 20 L + L 2 β 2 ββ β 3 L β 4 fl 2 β 3 β 4 β 9 β 0 β β 2 β 3 β 6 β 7 β 8 + s β 9 β β 2 0 β L β 7 2 β β 8 2 (β f L2 4(5) β 4 ) 3 β 6 L fl 2 ββ β 6 β 2 β 7 β 8 ss L 2 f L2 4(5) (β 4 )
21 3. Fundamentals of Knematcs 2 Knematc Net (wthout solated degree of fredom) 2 s solated DoF (gnored) β β 3 β 4 β 9 β 0 β β 2 β 3 2 knematc Loops wth (2+4) β 6 loop degrees of freedom 6 β 2 L fl 2 β 7 L 2-4 Couplng euatons between β 8 f L2 4(5) the loops -4 System degrees of freedom 2 ββ ss (β 4 )
22 Vehcle as a normal Mult-body system 3.2 Euatons of moton for Mult-Body systems 22 Is modelled as a complex mult-body system wth knematc loops, consstng of rgd bodes. o begn wth elastc characterstcs are modelled as concentrated elastctes. In the case of holonomc Constrants: Normal/Usual Mult-body systems he euatons of moton n mnmal coordnates for a system wth f degrees of freedom In the general form: M () & + b (,) & Q (,,t) & M b Q (f x ) - Vector of general coordnates (f x f) - Mass matrx (symmetrc) (f x ) - Vector of general centrfugal and gyro Forces (f x ) - Vector of general appled forces
23 3.2 Euatons of moton for Mult-Body systems Specaltes n Mult-loop Mult-body systems and Mechansms 23 Because of the knematc loops, there are comparatvely less degrees of freedom n a System wth more number of bodes and constrants. Settng up complex euatons of moton: - manually (very strenuous!) - numercally and/or usng symbols wth the help of computers
24 3.2 Euatons of moton for Mult-Body systems 24 Example: he Fve-pont Wheel Suspenson (Spatal) Euatons of moton for the sprng compresson ( f Degree of freedom multlnk rear suspenson Damler-Benz
25 Example: he Fve-pont Wheel Suspenson (Spatal) 3.2 Euatons of moton for Mult-Body systems 25 f D o F Euatons of moton n the form s Sprngr m (s)s & + b(s,s) & Q(s,s,t) & Steerng gude Usng symbols wth Programmsystem NEWEUL Steerng arm (blocked) Wheel carrer
26 3.2 Euatons of moton for Mult-Body systems 26 Fve-pont wheel suspenson: suspensonmovement f... m (s)s + b(s,s). Q (s,s,t) wheel suspenson (cont.) m(s). b(s,s). b(s,s) Q (s,s,t).
27 3.2 Euatons of moton for Mult-Body systems Methods to set up the euatons of moton for mult-body systems and mechansms Holonom Systems consdered as normal Mult-body systems 27 n Bodes r Constrants f 6 n - r Degrees of freedom Prncple of lnear momentum and Prncple of conservaton of angular momentum (Newton-Euler-Euaton) Number of euatons of moton: 6 n > f ( f) Lagrange Euatons of frst order (Method ) Number of euatons of moton : 6 n > f Lagrange Euatons of scond order (Method 2) Number of euatons of moton : f d`alembert s Prncple (Method 3) 6 n (Lagrange Multplcators) Number of euatons of moton : f (Mnmum coordnates)
28 3.2 Euatons of moton for Mult-Body systems Methods to set up the euatons of moton. Method: Based on the Fundamental euatons of dynamcs N ( F m a ) δr ( F - Appled forces) 0 Wll be then appled n the LARANE euatons frst order for pont masses: ven s a system wth 28 N Mass ponts m, r, g geometrc Constrants f α (t ; r,,r N ) 0 ; α,,g k knematc Constrants N φβ l β ( t; r,..., rn ) v + dβ (t; r,..., rn ) β,,k 0 ; Hence the System has f 3 N - g - k Degrees of freedom
29 By applyng the LARANE Multplcators λ α, µ β We get the LARANE Euatons of frst order: 3.2 Euatons of moton for Mult-Body systems 29 m f α a F + (t; r,..., rn ) 0 g f k α λα + µ β α r β l β ;,,N ; α,,g (DAE Dfferental Algebrac Euatons) N φβ l β v + dβ 0 ; β,,k (3N+g+k) Euatons for the (3N+g+k) Unknowns x,y,z, λ α, µ β 3N g k Advantages:- applcable for holonomc and non-holonomc systems - Euatons can be easly set up - Reacton forces can be calculated drectly Dsadvantages:- more euatons than degrees of freedom - euatons are numercally unstable Euatons for rgd body systems are analogous!
30 3.2 Euatons of moton for Mult-Body systems Method: By ntroducng f ndependant general coordnates (correspondng to the number of degrees of freedom), 2,, f One can obtan from the fundamental dynamc euatons he LARANE euatons of second order for holonom Systems: d dt ( ) & Q ;,..., f
31 3.2 Euatons of moton for Mult-Body systems 3. Method: Euatons of moton obtaned from the d`alembert s Prncple wth the help of knematc Dfferentals: Systematc procedure to solve the constrant euatons makng use of the solved loop knematcs. Identfyng the ndependant loops - ntroducton of natural coordnates β,s - settng up local, non-lnear constrant euatons - local solutons from the outputs Keep at hand the knematc ransformator 2. Defnng the loop network - settng up the lnear couplng euatons knematc Network 3. Choosng the structural nputs Optmsng the soluton flow 3... relatve Knematcs β. β.. β
32 Forward knematcs (recursve) 3.2 Euatons of moton for Mult-Body systems 32 Absolute coordnates, Body B w Poston: [ x, y, z, ϕ, ψ θ ], Jont Coordnate β w w ( w, w 2,, w, β, t) Velocty: B B w& w& ( w,...., w ; w&,...., w& ; β, ; t Acceleraton: β & ) It represents here translaton (s) and rotaton (β) w& w&& ( w,...., w ; w&,...., w& ; w&&,...., w& ; β, β &, β & ; t ) β β & β & absolute Knematcs w w& w& &
33 3.2 Euatons of moton for Mult-Body systems Knematcs of two bodes oned together wth a ont Parameters of Moton of B are known Parameters of moton of B J are reured Elementary standard ont 33 Rotatonal transton from B to B β ω α ω + ω α + ω ω + α v a ω r α v r a α ω r B ranslatory transton from B to B B r r r v a r + r v a + ω + α r r + v + 2ω v + ω (ω r ) + a Known Unknown Only one dmensonal onts are allowed. In the case of mult dmensonal onts, they have to be represented wth sngle dmensonal onts wth vrtual bodes nbetween them.
34 34 Used representaons r, r v, v a, a ω, ω α, α Poston vector to the reference/consdered pont, Absolute velocty of the reference/consdered pont, Absolute acceleraton of the reference/consdered pont, Absolute angular velocty of the body Absolute angular acceleraton of the body, r connectng vector between the reference/consdered ponts, v, a velocty / Acceleraton of B relatve to B, ω, α Angular velocty and angular acceleraton of B relatve B.
35 Euatons of moton for Mult-Body systems Rotatonal ont θ s β s B B B B e e s&e ranslatory ont β & e,, e e ) r ( r a r v r r r β α β ω α α ω ω ω ω + α ω + && & se a se v 0 0 a a v v r r r && & α ω +
36 3.2 Euatons of moton for Mult-Body systems 36 ranslaton v v + ω r + v v + ω (r + r ' ) + v ' v + ω (r + r ' ) + se & a a + α r + 2ω v + ω ( ω r ) + a a + α (r + r ' ) + 2ω v ' + ω ( ω (r + r ' )) + a ' a + α (r + r ' ) + 2ω se & + ω ( ω (r + r )) + && se ' Rotaton ω ω + ω ω + ω ' ω + β& e ω α + ω ω + α α + ω ω ' + α ' α + ω β& e + βe &&
37 37 Used representaton r r r ' v a ω α se & && se β& e β&& e Vektor from reference pont B to the reference pont B Vektor from reference pont B to the ont pont, Vektor vom ont pont to the reference pont B, Velocty of relatve to ( translatory Jont), Acceleraton of relatve to ( translatory ont), Angular velocty of relatve to ( rotatonal ont), Angular acceleraton of relatve to ( rotatonal ont).
38 38 x x x x x z y x z y x e e e e e e (3.23) (3.24) (3.25) ` ` (3.26) x y x z y z ` u u ) cos ( 0 u u u 0 u u u 0 sn cos ) u, ( ϕ + ϕ + ϕι ϕ (3.27) ϕ ϕ ϕ ϕ cos sn 0 sn cos ` (3.28)
39 3.2 Euatons of moton for Mult-Body systems 39 Summary of Knematcs eneralsed coordnates natural/ontcoordnates global coordnates & & & relatve Knematcs global Knematcs β β& β & absolut Knematcs w w& w& &
40 3.2 Euatons of moton for Mult-Body systems Euatons of moton derved from the d`alember Prncple 40 Reacton forces on B Reacton moments on B n B { m & F ) δs + ( θ ω& + ω θ ω ) δφ } ( s& s s 0 Vrtual work done by the Reacton forces and moments on B m, θ s : Mass und nertal tensor (relatve to the center of mass) of the body & s& ω F, ω&, δ s, δφ : acceleraton of the centre of mass of the body : angular velocty and acceleraton : resultng appled forces and moments : vrtual translaton or rotatonal orsche, bzw. rotatorsche dsplacements
41 4 3.2 Euatons of moton for Mult-Body systems Prncple of conservaton of angular momentum Prncple of lnear momentum S S R R R F m a m J F m s F F m s F F F m s + + && && && && S S S R S S R R S S a J ω + ω θ + θ θ ω θ + ω ω θ + ω θ + ω ω θ φ φ & & & & D Alembert s Prncple vrtual work of the Reacton forces vanshes ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 a J J F m a m J J J F J F s F s F s ) F (s A B B B B B B n S S S S S S n R R S n R R n R R n R R n R R ω + ω θ + θ θ + + δ + δ φ + δ δ φ + δ δφ + δ φ + δ δ φ φ φ φ && &&
42 3.2 Euatons of moton for Mult-Body systems 42 One reures the transfoematon of δ [ ] M& + b δ Q δ ndependant Euatons of moton M & & + b Q : [f x ] - Vector of generalsed coordnates (f number of degrees of freedom) M : [f x f ] - System Mass matrx (symmetrc, regular) b : [f x ] - Vector of generalsed gyro and centrfugal forces Q : [f x ] - Vector of generalsed appled forces Introducng the knematc relatons o δ δ o s φ o J o o o o s δ & s J s & ; & + bs ; J s o o o Jφδ ; o ω& Jφ & & + bφ ;.. o Jφ o s o φ Jacob- Matrces
43 Elements of the euaton of moton 3.2 Euatons of moton for Mult-Body systems 43 - Mass matrx n B o o o o o M { J s J m + θ } s J φ s J φ - eneralsed gyro forces n B o o b { s s m + [ θ + θ ] J o a } o o o o o ω ω J φ a s φ s - eneralsed appled forces n B o o o o Q { J s F + J φ }
44 3.2 Euatons of moton for Mult-Body systems Partal dfferentaton of the absolute values wth respect to the generalsed coordnates 44 Motvaton: v s s s s& ( ) & & + L+ & { { f { J s Column Column f f V s already known through the Knematcs dependant on o o s J s o ; J φ (Jacob-Matrces) o φ o a s f f k 2 o s k & & k o aφ f f k 2 o φ k & & k
45 Euatons of moton for Mult-Body systems Knematc Dfferentals φ ϕ θ ψ s z y x w w J w. Dfferentaton to determne: w w w w & & f & f. 0 0 ~ () Formal: ϕ ϕ φ f f s w x x J J J L M O M L knematc: lobal Knematc (no dfferentaton) w w&.. & & & f. 0 0 ~ ()
46 3.2 Euatons of moton for Mult-Body systems 46 knematc Dfferentals w ~ () w& ~ () & w& w& else & k 0 th Column J{ w } ~ () w& Seperated nto translaton and rotaton: s ~ () s& φ ~ () ω
47 3.2 Euatons of moton for Mult-Body systems Dfferentaton to determne: aw k 2 w k & & k Formal: ~ w w& & & & + 0 aw Knematc: & ~ & & 0 lobal Knematc (wthout dfferentaton) w w& ~ w& &
48 3.2 Euatons of moton for Mult-Body systems Knematc Dfferentals w w& ~ w & ~ w& a && 0 Seperated nto RANSLAION and ROAION a a s φ ~ && s ~ ω&
49 49 Euatons of moton wth knematc Dfferentals 3.2 Euatons of moton for Mult-Body systems Newton-Euler-euaton n B { m & F ) + ( θ ω& + θ ω ) } ( s& s δφ 0 δ s ω s! Dfferental relatonshps δs f ~ () f ~ s& δ & s& s& ().. ~ ; + & s& δφ f ~ () ω δ ; ω& f ~ ω () & ~ & + ω& M & & + b Q Dfferental euatons of moton of mnmal order
50 3.2 Euatons of moton for Mult-Body systems 50 coeffcents M,k n B { () (k) ~ () (k) + ~ ( )} m ~ s& ~ s& ω θ s ω b n B ~ ~ { m + ω [ θ ω + ω θ ω ]} s& ~ () & s& ~ () s s Q n B { s& () F + } ~ ω ()
51 3.2 Euatons of moton for Mult-Body systems Euatons of Moton of Complex Multbody System usng Knematcal Dfferentals 5 Input: Mass and Inerta m, Appled Forces and orues F, State-Varables ( t ) (t),..., θ s [ (t)] ; & ( t ) [ & (t),..., (t)] f & f k & k & && 0 0 k lobal Knematcs lobal Knematcs lobal Knematcs (Poston) (Velocty) (Acceleraton) s ~ s& ~ ω ~ ~ & s& ω& Euatons of Moton (Mnmal Order) M & & + b Q
52 3.2 Euatons of moton for Mult-Body systems 52 Double wshbone suspenson: σ + γ γ Rgd body model: P β s S R L L 2 S S r s Mult-body system: 5 bodes 7 onts 2 knematc loops R S Wheel axle 2 observable system degrees Of freedom: β - compresson (angle ) -steerng(dsplacement s) Lagrange. order Lagrange 2. order Knematc Dfferentals Dynamc und knematc Euatons are set up and worked wth n parallel. Descrpton results n Body coordnates and/or Relatve coordnates. Only dynamc euatons. Knematc euatons wll be set up Earler und ncorporated nto the Dynamc euatons. Descrpton results n Mnmal coordnates (Relatve coordnates n the most cases): Applcable only for holonomc Systems. Usng d`alembert s Prncple ranston over to dynamc Euatons n Mnmal coordnates;. e. Settng up the knematc euatons beforehand n Mnmal coordnates und ts Incorporaton nto the dynamc Euatons. & & & β Relatv- β & knematcs β & Absolute knematcs lobal Knematcs w w& w& &
53 Fundamental problems of the Dynamcs. Drect Problems gven: forces ^ generalsed forces Q [Q,, Q f ] 3.2 Euatons of moton for Mult-Body systems reured: moton ^ generalsed acceleratons & [ &&,..., & f ] and generalsed coordnates respectvely [,, f ] as a soluton of the Dfferental euaton M.... Mf && ḅ M Mf.... Mff && f bf Q f Q... reured gven Non-lnear Problem 53
54 3.2 Euatons of moton for Mult-Body systems Inverse Problem gven: moton ^ generalsed coordnates [,, f ] reured: loads ^ generalsed forces Q [Q,, Q f ] M.... M Mf M M f.... ff && && f ḅ b... Lnear Problem 3. Reactve forces (Zwangskräfte) gven: loads and moton reured: reactve forces f f gven reured Prncple of lnear momentum and prncple of conservaton of angular momentum (Newton Euler) Q Q...
Lesson 5: Kinematics and Dynamics of Particles
 Lesson 5: Knematcs and Dynamcs of Partcles hs set of notes descrbes the basc methodology for formulatng the knematc and knetc equatons for multbody dynamcs. In order to concentrate on the methodology and
Lesson 5: Knematcs and Dynamcs of Partcles hs set of notes descrbes the basc methodology for formulatng the knematc and knetc equatons for multbody dynamcs. In order to concentrate on the methodology and
coordinates. Then, the position vectors are described by
 Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Part C Dynamics and Statics of Rigid Body. Chapter 5 Rotation of a Rigid Body About a Fixed Axis
 Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Modeling of Dynamic Systems
 Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
11. Dynamics in Rotating Frames of Reference
 Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
Unversty of Rhode Island DgtalCommons@URI Classcal Dynamcs Physcs Course Materals 2015 11. Dynamcs n Rotatng Frames of Reference Gerhard Müller Unversty of Rhode Island, gmuller@ur.edu Creatve Commons
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING. Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582
 NMT EE 589 & UNM ME 48/58 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 48/58 7. Robot Dynamcs 7.5 The Equatons of Moton Gven that we wsh to fnd the path q(t (n jont space) whch mnmzes the energy
NMT EE 589 & UNM ME 48/58 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 48/58 7. Robot Dynamcs 7.5 The Equatons of Moton Gven that we wsh to fnd the path q(t (n jont space) whch mnmzes the energy
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
CHAPTER 6. LAGRANGE S EQUATIONS (Analytical Mechanics)
 CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
Chapter 11: Angular Momentum
 Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
Chapter 11: ngular Momentum Statc Equlbrum In Chap. 4 we studed the equlbrum of pontobjects (mass m) wth the applcaton of Newton s aws F 0 F x y, 0 Therefore, no lnear (translatonal) acceleraton, a0 For
MEEM 3700 Mechanical Vibrations
 MEEM 700 Mechancal Vbratons Mohan D. Rao Chuck Van Karsen Mechancal Engneerng-Engneerng Mechancs Mchgan echnologcal Unversty Copyrght 00 Lecture & MEEM 700 Multple Degree of Freedom Systems (ext: S.S.
MEEM 700 Mechancal Vbratons Mohan D. Rao Chuck Van Karsen Mechancal Engneerng-Engneerng Mechancs Mchgan echnologcal Unversty Copyrght 00 Lecture & MEEM 700 Multple Degree of Freedom Systems (ext: S.S.
Rigid body simulation
 Rgd bod smulaton Rgd bod smulaton Once we consder an object wth spacal etent, partcle sstem smulaton s no longer suffcent Problems Problems Unconstraned sstem rotatonal moton torques and angular momentum
Rgd bod smulaton Rgd bod smulaton Once we consder an object wth spacal etent, partcle sstem smulaton s no longer suffcent Problems Problems Unconstraned sstem rotatonal moton torques and angular momentum
Classical Mechanics Virtual Work & d Alembert s Principle
 Classcal Mechancs Vrtual Work & d Alembert s Prncple Dpan Kumar Ghosh UM-DAE Centre for Excellence n Basc Scences Kalna, Mumba 400098 August 15, 2016 1 Constrants Moton of a system of partcles s often
Classcal Mechancs Vrtual Work & d Alembert s Prncple Dpan Kumar Ghosh UM-DAE Centre for Excellence n Basc Scences Kalna, Mumba 400098 August 15, 2016 1 Constrants Moton of a system of partcles s often
PHYS 705: Classical Mechanics. Newtonian Mechanics
 1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
Notes on Analytical Dynamics
 Notes on Analytcal Dynamcs Jan Peters & Mchael Mstry October 7, 004 Newtonan Mechancs Basc Asssumptons and Newtons Laws Lonely pontmasses wth postve mass Newtons st: Constant velocty v n an nertal frame
Notes on Analytcal Dynamcs Jan Peters & Mchael Mstry October 7, 004 Newtonan Mechancs Basc Asssumptons and Newtons Laws Lonely pontmasses wth postve mass Newtons st: Constant velocty v n an nertal frame
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
SCHOOL OF COMPUTING, ENGINEERING AND MATHEMATICS SEMESTER 2 EXAMINATIONS 2011/2012 DYNAMICS ME247 DR. N.D.D. MICHÉ
 s SCHOOL OF COMPUTING, ENGINEERING ND MTHEMTICS SEMESTER EXMINTIONS 011/01 DYNMICS ME47 DR. N.D.D. MICHÉ Tme allowed: THREE hours nswer: ny FOUR from SIX questons Each queston carres 5 marks Ths s a CLOSED-BOOK
s SCHOOL OF COMPUTING, ENGINEERING ND MTHEMTICS SEMESTER EXMINTIONS 011/01 DYNMICS ME47 DR. N.D.D. MICHÉ Tme allowed: THREE hours nswer: ny FOUR from SIX questons Each queston carres 5 marks Ths s a CLOSED-BOOK
An Algorithm to Solve the Inverse Kinematics Problem of a Robotic Manipulator Based on Rotation Vectors
 An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
An Algorthm to Solve the Inverse Knematcs Problem of a Robotc Manpulator Based on Rotaton Vectors Mohamad Z. Al-az*, Mazn Z. Othman**, and Baker B. Al-Bahr* *AL-Nahran Unversty, Computer Eng. Dep., Baghdad,
Lecture 23: Newton-Euler Formulation. Vaibhav Srivastava
 Lecture 23: Newton-Euler Formulaton Based on Chapter 7, Spong, Hutchnson, and Vdyasagar Vabhav Srvastava Department of Electrcal & Computer Engneerng Mchgan State Unversty Aprl 10, 2017 ECE 818: Robotcs
Lecture 23: Newton-Euler Formulaton Based on Chapter 7, Spong, Hutchnson, and Vdyasagar Vabhav Srvastava Department of Electrcal & Computer Engneerng Mchgan State Unversty Aprl 10, 2017 ECE 818: Robotcs
Advanced Mechanical Elements
 May 3, 08 Advanced Mechancal Elements (Lecture 7) Knematc analyss and moton control of underactuated mechansms wth elastc elements - Moton control of underactuated mechansms constraned by elastc elements
May 3, 08 Advanced Mechancal Elements (Lecture 7) Knematc analyss and moton control of underactuated mechansms wth elastc elements - Moton control of underactuated mechansms constraned by elastc elements
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
Physics 53. Rotational Motion 3. Sir, I have found you an argument, but I am not obliged to find you an understanding.
 Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
Physcs 53 Rotatonal Moton 3 Sr, I have found you an argument, but I am not oblged to fnd you an understandng. Samuel Johnson Angular momentum Wth respect to rotatonal moton of a body, moment of nerta plays
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING. Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582
 NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582 4. Moton Knematcs 4.2 Angular Velocty Knematcs Summary From the last lecture we concluded that: If the jonts
NMT EE 589 & UNM ME 482/582 ROBOT ENGINEERING Dr. Stephen Bruder NMT EE 589 & UNM ME 482/582 4. Moton Knematcs 4.2 Angular Velocty Knematcs Summary From the last lecture we concluded that: If the jonts
Iterative General Dynamic Model for Serial-Link Manipulators
 EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
EEL6667: Knematcs, Dynamcs and Control of Robot Manpulators 1. Introducton Iteratve General Dynamc Model for Seral-Lnk Manpulators In ths set of notes, we are gong to develop a method for computng a general
BAR & TRUSS FINITE ELEMENT. Direct Stiffness Method
 BAR & TRUSS FINITE ELEMENT Drect Stness Method FINITE ELEMENT ANALYSIS AND APPLICATIONS INTRODUCTION TO FINITE ELEMENT METHOD What s the nte element method (FEM)? A technqe or obtanng approxmate soltons
BAR & TRUSS FINITE ELEMENT Drect Stness Method FINITE ELEMENT ANALYSIS AND APPLICATIONS INTRODUCTION TO FINITE ELEMENT METHOD What s the nte element method (FEM)? A technqe or obtanng approxmate soltons
In this section is given an overview of the common elasticity models.
 Secton 4.1 4.1 Elastc Solds In ths secton s gven an overvew of the common elastcty models. 4.1.1 The Lnear Elastc Sold The classcal Lnear Elastc model, or Hooean model, has the followng lnear relatonshp
Secton 4.1 4.1 Elastc Solds In ths secton s gven an overvew of the common elastcty models. 4.1.1 The Lnear Elastc Sold The classcal Lnear Elastc model, or Hooean model, has the followng lnear relatonshp
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Translational Equations of Motion for A Body Translational equations of motion (centroidal) for a body are m r = f.
 Lesson 12: Equatons o Moton Newton s Laws Frst Law: A artcle remans at rest or contnues to move n a straght lne wth constant seed there s no orce actng on t Second Law: The acceleraton o a artcle s roortonal
Lesson 12: Equatons o Moton Newton s Laws Frst Law: A artcle remans at rest or contnues to move n a straght lne wth constant seed there s no orce actng on t Second Law: The acceleraton o a artcle s roortonal
Lagrange Multipliers. A Somewhat Silly Example. Monday, 25 September 2013
 Lagrange Multplers Monday, 5 September 013 Sometmes t s convenent to use redundant coordnates, and to effect the varaton of the acton consstent wth the constrants va the method of Lagrange undetermned
Lagrange Multplers Monday, 5 September 013 Sometmes t s convenent to use redundant coordnates, and to effect the varaton of the acton consstent wth the constrants va the method of Lagrange undetermned
Indeterminate pin-jointed frames (trusses)
 Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
CHAIN DYNAMIC FORMULATIONS FOR MULTIBODY SYSTEM TRACKED VEHICLES
 2012 NDIA GROUND VEHICLE SYSEMS ENGINEERING AND ECHNOLOGY SYMOSIUM MODELING &SIMULAION, ESING AND VALIDAION (MSV) MINI-SYMOSIUM AUGUS 14-16, MICHIGAN CHAIN DYNAMIC FORMULAIONS FOR MULIBODY SYSEM RACKED
2012 NDIA GROUND VEHICLE SYSEMS ENGINEERING AND ECHNOLOGY SYMOSIUM MODELING &SIMULAION, ESING AND VALIDAION (MSV) MINI-SYMOSIUM AUGUS 14-16, MICHIGAN CHAIN DYNAMIC FORMULAIONS FOR MULIBODY SYSEM RACKED
Linear Momentum. Center of Mass.
 Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Lecture 6 Chapter 9 Physcs I 03.3.04 Lnear omentum. Center of ass. Course webste: http://faculty.uml.edu/ndry_danylov/teachng/physcsi Lecture Capture: http://echo360.uml.edu/danylov03/physcssprng.html
Mechanics Physics 151
 Mechancs Physcs 151 Lecture 3 Lagrange s Equatons (Goldsten Chapter 1) Hamlton s Prncple (Chapter 2) What We Dd Last Tme! Dscussed mult-partcle systems! Internal and external forces! Laws of acton and
Mechancs Physcs 151 Lecture 3 Lagrange s Equatons (Goldsten Chapter 1) Hamlton s Prncple (Chapter 2) What We Dd Last Tme! Dscussed mult-partcle systems! Internal and external forces! Laws of acton and
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Study Guide For Exam Two
 Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Study Gude For Exam Two Physcs 2210 Albretsen Updated: 08/02/2018 All Other Prevous Study Gudes Modules 01-06 Module 07 Work Work done by a constant force F over a dstance s : Work done by varyng force
Classical Mechanics ( Particles and Biparticles )
 Classcal Mechancs ( Partcles and Bpartcles ) Alejandro A. Torassa Creatve Commons Attrbuton 3.0 Lcense (0) Buenos Ares, Argentna atorassa@gmal.com Abstract Ths paper consders the exstence of bpartcles
Classcal Mechancs ( Partcles and Bpartcles ) Alejandro A. Torassa Creatve Commons Attrbuton 3.0 Lcense (0) Buenos Ares, Argentna atorassa@gmal.com Abstract Ths paper consders the exstence of bpartcles
Week 11: Chapter 11. The Vector Product. The Vector Product Defined. The Vector Product and Torque. More About the Vector Product
 The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
The Vector Product Week 11: Chapter 11 Angular Momentum There are nstances where the product of two vectors s another vector Earler we saw where the product of two vectors was a scalar Ths was called the
PHYS 705: Classical Mechanics. Calculus of Variations II
 1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
Physics 106a, Caltech 11 October, Lecture 4: Constraints, Virtual Work, etc. Constraints
 Physcs 106a, Caltech 11 October, 2018 Lecture 4: Constrants, Vrtual Work, etc. Many, f not all, dynamcal problems we want to solve are constraned: not all of the possble 3 coordnates for M partcles (or
Physcs 106a, Caltech 11 October, 2018 Lecture 4: Constrants, Vrtual Work, etc. Many, f not all, dynamcal problems we want to solve are constraned: not all of the possble 3 coordnates for M partcles (or
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
MEV442 Introduction to Robotics Module 2. Dr. Santhakumar Mohan Assistant Professor Mechanical Engineering National Institute of Technology Calicut
 MEV442 Introducton to Robotcs Module 2 Dr. Santhakumar Mohan Assstant Professor Mechancal Engneerng Natonal Insttute of Technology Calcut Jacobans: Veloctes and statc forces Introducton Notaton for tme-varyng
MEV442 Introducton to Robotcs Module 2 Dr. Santhakumar Mohan Assstant Professor Mechancal Engneerng Natonal Insttute of Technology Calcut Jacobans: Veloctes and statc forces Introducton Notaton for tme-varyng
Lie Group Formulation of Articulated Rigid Body Dynamics
 Le Group Formulaton of Artculated Rgd Body Dynamcs Junggon Km 11/9/2012, Ver 1.01 Abstract It has been usual n most old-style text books for dynamcs to treat the formulas descrbng lnearor translatonal
Le Group Formulaton of Artculated Rgd Body Dynamcs Junggon Km 11/9/2012, Ver 1.01 Abstract It has been usual n most old-style text books for dynamcs to treat the formulas descrbng lnearor translatonal
Chapter Eight. Review and Summary. Two methods in solid mechanics ---- vectorial methods and energy methods or variational methods
 Chapter Eght Energy Method 8. Introducton 8. Stran energy expressons 8.3 Prncpal of statonary potental energy; several degrees of freedom ------ Castglano s frst theorem ---- Examples 8.4 Prncpal of statonary
Chapter Eght Energy Method 8. Introducton 8. Stran energy expressons 8.3 Prncpal of statonary potental energy; several degrees of freedom ------ Castglano s frst theorem ---- Examples 8.4 Prncpal of statonary
Module 3 LOSSY IMAGE COMPRESSION SYSTEMS. Version 2 ECE IIT, Kharagpur
 Module 3 LOSSY IMAGE COMPRESSION SYSTEMS Verson ECE IIT, Kharagpur Lesson 6 Theory of Quantzaton Verson ECE IIT, Kharagpur Instructonal Objectves At the end of ths lesson, the students should be able to:
Module 3 LOSSY IMAGE COMPRESSION SYSTEMS Verson ECE IIT, Kharagpur Lesson 6 Theory of Quantzaton Verson ECE IIT, Kharagpur Instructonal Objectves At the end of ths lesson, the students should be able to:
LAGRANGIAN MECHANICS
 LAGRANGIAN MECHANICS Generalzed Coordnates State of system of N partcles (Newtonan vew): PE, KE, Momentum, L calculated from m, r, ṙ Subscrpt covers: 1) partcles N 2) dmensons 2, 3, etc. PE U r = U x 1,
LAGRANGIAN MECHANICS Generalzed Coordnates State of system of N partcles (Newtonan vew): PE, KE, Momentum, L calculated from m, r, ṙ Subscrpt covers: 1) partcles N 2) dmensons 2, 3, etc. PE U r = U x 1,
Modeling and Simulation of a Hexapod Machine Tool for the Dynamic Stability Analysis of Milling Processes. C. Henninger, P.
 Smpack User Meetng 27 Modelng and Smulaton of a Heapod Machne Tool for the Dynamc Stablty Analyss of Mllng Processes C. Hennnger, P. Eberhard Insttute of Engneerng project funded by the DFG wthn the framework
Smpack User Meetng 27 Modelng and Smulaton of a Heapod Machne Tool for the Dynamc Stablty Analyss of Mllng Processes C. Hennnger, P. Eberhard Insttute of Engneerng project funded by the DFG wthn the framework
CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE
 CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE Analytcal soluton s usually not possble when exctaton vares arbtrarly wth tme or f the system s nonlnear. Such problems can be solved by numercal tmesteppng
CHAPTER 5 NUMERICAL EVALUATION OF DYNAMIC RESPONSE Analytcal soluton s usually not possble when exctaton vares arbtrarly wth tme or f the system s nonlnear. Such problems can be solved by numercal tmesteppng
Conservation of Angular Momentum = "Spin"
 Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Chapter 11 Angular Momentum
 Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Our focus will be on linear systems. A system is linear if it obeys the principle of superposition and homogenity, i.e.
 SSTEM MODELLIN In order to solve a control syste proble, the descrptons of the syste and ts coponents ust be put nto a for sutable for analyss and evaluaton. The followng ethods can be used to odel physcal
SSTEM MODELLIN In order to solve a control syste proble, the descrptons of the syste and ts coponents ust be put nto a for sutable for analyss and evaluaton. The followng ethods can be used to odel physcal
Physics 106 Lecture 6 Conservation of Angular Momentum SJ 7 th Ed.: Chap 11.4
 Physcs 6 ecture 6 Conservaton o Angular Momentum SJ 7 th Ed.: Chap.4 Comparson: dentons o sngle partcle torque and angular momentum Angular momentum o a system o partcles o a rgd body rotatng about a xed
Physcs 6 ecture 6 Conservaton o Angular Momentum SJ 7 th Ed.: Chap.4 Comparson: dentons o sngle partcle torque and angular momentum Angular momentum o a system o partcles o a rgd body rotatng about a xed
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
VEHICLE DYNAMICS SIMULATION, PART 1: MATHEMATICAL MODEL
 INTERNATIONAL DESIGN CONFERENCE - DESIGN 2002 Dubrovnk, May 4-7, 2002. VEHICLE DYNAMICS SIMULATION, PART : MATHEMATICAL MODEL Iztok Cglarc and Ivan Prebl Keywords: Computatonal dynamc, multubody systems,
INTERNATIONAL DESIGN CONFERENCE - DESIGN 2002 Dubrovnk, May 4-7, 2002. VEHICLE DYNAMICS SIMULATION, PART : MATHEMATICAL MODEL Iztok Cglarc and Ivan Prebl Keywords: Computatonal dynamc, multubody systems,
Canonical transformations
 Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
November 5, 2002 SE 180: Earthquake Engineering SE 180. Final Project
 SE 8 Fnal Project Story Shear Frame u m Gven: u m L L m L L EI ω ω Solve for m Story Bendng Beam u u m L m L Gven: m L L EI ω ω Solve for m 3 3 Story Shear Frame u 3 m 3 Gven: L 3 m m L L L 3 EI ω ω ω
SE 8 Fnal Project Story Shear Frame u m Gven: u m L L m L L EI ω ω Solve for m Story Bendng Beam u u m L m L Gven: m L L EI ω ω Solve for m 3 3 Story Shear Frame u 3 m 3 Gven: L 3 m m L L L 3 EI ω ω ω
1 Derivation of Point-to-Plane Minimization
 1 Dervaton of Pont-to-Plane Mnmzaton Consder the Chen-Medon (pont-to-plane) framework for ICP. Assume we have a collecton of ponts (p, q ) wth normals n. We want to determne the optmal rotaton and translaton
1 Dervaton of Pont-to-Plane Mnmzaton Consder the Chen-Medon (pont-to-plane) framework for ICP. Assume we have a collecton of ponts (p, q ) wth normals n. We want to determne the optmal rotaton and translaton
Mathematical Preparations
 1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
Irregular vibrations in multi-mass discrete-continuous systems torsionally deformed
 (2) 4 48 Irregular vbratons n mult-mass dscrete-contnuous systems torsonally deformed Abstract In the paper rregular vbratons of dscrete-contnuous systems consstng of an arbtrary number rgd bodes connected
(2) 4 48 Irregular vbratons n mult-mass dscrete-contnuous systems torsonally deformed Abstract In the paper rregular vbratons of dscrete-contnuous systems consstng of an arbtrary number rgd bodes connected
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
UIC University of Illinois at Chicago
 DSL Dynamc Smulaton Laboratory UIC Unversty o Illnos at Chcago FINITE ELEMENT/ MULTIBODY SYSTEM ALGORITHMS FOR RAILROAD VEHICLE SYSTEM DYNAMICS Ahmed A. Shabana Department o Mechancal and Industral Engneerng
DSL Dynamc Smulaton Laboratory UIC Unversty o Illnos at Chcago FINITE ELEMENT/ MULTIBODY SYSTEM ALGORITHMS FOR RAILROAD VEHICLE SYSTEM DYNAMICS Ahmed A. Shabana Department o Mechancal and Industral Engneerng
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
9 Characteristic classes
 THEODORE VORONOV DIFFERENTIAL GEOMETRY. Sprng 2009 [under constructon] 9 Characterstc classes 9.1 The frst Chern class of a lne bundle Consder a complex vector bundle E B of rank p. We shall construct
THEODORE VORONOV DIFFERENTIAL GEOMETRY. Sprng 2009 [under constructon] 9 Characterstc classes 9.1 The frst Chern class of a lne bundle Consder a complex vector bundle E B of rank p. We shall construct
CHAPTER 10 ROTATIONAL MOTION
 CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
EN40: Dynamics and Vibrations. Homework 7: Rigid Body Kinematics
 N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
N40: ynamcs and Vbratons Homewor 7: Rgd Body Knematcs School of ngneerng Brown Unversty 1. In the fgure below, bar AB rotates counterclocwse at 4 rad/s. What are the angular veloctes of bars BC and C?.
Rotational Dynamics. Physics 1425 Lecture 19. Michael Fowler, UVa
 Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
A NUMERICAL COMPARISON OF LANGRANGE AND KANE S METHODS OF AN ARM SEGMENT
 Internatonal Conference Mathematcal and Computatonal ology 0 Internatonal Journal of Modern Physcs: Conference Seres Vol. 9 0 68 75 World Scentfc Publshng Company DOI: 0.4/S009450059 A NUMERICAL COMPARISON
Internatonal Conference Mathematcal and Computatonal ology 0 Internatonal Journal of Modern Physcs: Conference Seres Vol. 9 0 68 75 World Scentfc Publshng Company DOI: 0.4/S009450059 A NUMERICAL COMPARISON
Physics 141. Lecture 14. Frank L. H. Wolfs Department of Physics and Astronomy, University of Rochester, Lecture 14, Page 1
 Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
Physcs 141. Lecture 14. Frank L. H. Wolfs Department of Physcs and Astronomy, Unversty of Rochester, Lecture 14, Page 1 Physcs 141. Lecture 14. Course Informaton: Lab report # 3. Exam # 2. Mult-Partcle
THE EFFECT OF TORSIONAL RIGIDITY BETWEEN ELEMENTS ON FREE VIBRATIONS OF A TELESCOPIC HYDRAULIC CYLINDER SUBJECTED TO EULER S LOAD
 Journal of Appled Mathematcs and Computatonal Mechancs 7, 6(3), 7- www.amcm.pcz.pl p-issn 99-9965 DOI:.75/jamcm.7.3. e-issn 353-588 THE EFFECT OF TORSIONAL RIGIDITY BETWEEN ELEMENTS ON FREE VIBRATIONS
Journal of Appled Mathematcs and Computatonal Mechancs 7, 6(3), 7- www.amcm.pcz.pl p-issn 99-9965 DOI:.75/jamcm.7.3. e-issn 353-588 THE EFFECT OF TORSIONAL RIGIDITY BETWEEN ELEMENTS ON FREE VIBRATIONS
Study on Active Micro-vibration Isolation System with Linear Motor Actuator. Gong-yu PAN, Wen-yan GU and Dong LI
 2017 2nd Internatonal Conference on Electrcal and Electroncs: echnques and Applcatons (EEA 2017) ISBN: 978-1-60595-416-5 Study on Actve Mcro-vbraton Isolaton System wth Lnear Motor Actuator Gong-yu PAN,
2017 2nd Internatonal Conference on Electrcal and Electroncs: echnques and Applcatons (EEA 2017) ISBN: 978-1-60595-416-5 Study on Actve Mcro-vbraton Isolaton System wth Lnear Motor Actuator Gong-yu PAN,
829. An adaptive method for inertia force identification in cantilever under moving mass
 89. An adaptve method for nerta force dentfcaton n cantlever under movng mass Qang Chen 1, Mnzhuo Wang, Hao Yan 3, Haonan Ye 4, Guola Yang 5 1,, 3, 4 Department of Control and System Engneerng, Nanng Unversty,
89. An adaptve method for nerta force dentfcaton n cantlever under movng mass Qang Chen 1, Mnzhuo Wang, Hao Yan 3, Haonan Ye 4, Guola Yang 5 1,, 3, 4 Department of Control and System Engneerng, Nanng Unversty,
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
Research on the Fuzzy Control for Vehicle Semi-active Suspension. Xiaoming Hu 1, a, Wanli Li 1,b
 Advanced Materals Research Onlne: 0-0- ISSN: -9, Vol., pp -9 do:0.0/www.scentfc.net/amr.. 0 Trans Tech Publcatons, Swterland Research on the Fuy Control for Vehcle Sem-actve Suspenson Xaomng Hu, a, Wanl
Advanced Materals Research Onlne: 0-0- ISSN: -9, Vol., pp -9 do:0.0/www.scentfc.net/amr.. 0 Trans Tech Publcatons, Swterland Research on the Fuy Control for Vehcle Sem-actve Suspenson Xaomng Hu, a, Wanl
DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED.
 EE 539 Homeworks Sprng 08 Updated: Tuesday, Aprl 7, 08 DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED. For full credt, show all work. Some problems requre hand calculatons.
EE 539 Homeworks Sprng 08 Updated: Tuesday, Aprl 7, 08 DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED. For full credt, show all work. Some problems requre hand calculatons.
T f. Geometry. R f. R i. Homogeneous transformation. y x. P f. f 000. Homogeneous transformation matrix. R (A): Orientation P : Position
 Homogeneous transformaton Geometr T f R f R T f Homogeneous transformaton matr Unverst of Genova T f Phlppe Martnet = R f 000 P f 1 R (A): Orentaton P : Poston 123 Modelng and Control of Manpulator robots
Homogeneous transformaton Geometr T f R f R T f Homogeneous transformaton matr Unverst of Genova T f Phlppe Martnet = R f 000 P f 1 R (A): Orentaton P : Poston 123 Modelng and Control of Manpulator robots
Integrals and Invariants of Euler-Lagrange Equations
 Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
χ x B E (c) Figure 2.1.1: (a) a material particle in a body, (b) a place in space, (c) a configuration of the body
 Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Perfect Fluid Cosmological Model in the Frame Work Lyra s Manifold
 Prespacetme Journal December 06 Volume 7 Issue 6 pp. 095-099 Pund, A. M. & Avachar, G.., Perfect Flud Cosmologcal Model n the Frame Work Lyra s Manfold Perfect Flud Cosmologcal Model n the Frame Work Lyra
Prespacetme Journal December 06 Volume 7 Issue 6 pp. 095-099 Pund, A. M. & Avachar, G.., Perfect Flud Cosmologcal Model n the Frame Work Lyra s Manfold Perfect Flud Cosmologcal Model n the Frame Work Lyra
Lecture 6/7 (February 10/12, 2014) DIRAC EQUATION. The non-relativistic Schrödinger equation was obtained by noting that the Hamiltonian 2
 P470 Lecture 6/7 (February 10/1, 014) DIRAC EQUATION The non-relatvstc Schrödnger equaton was obtaned by notng that the Hamltonan H = P (1) m can be transformed nto an operator form wth the substtutons
P470 Lecture 6/7 (February 10/1, 014) DIRAC EQUATION The non-relatvstc Schrödnger equaton was obtaned by notng that the Hamltonan H = P (1) m can be transformed nto an operator form wth the substtutons
Salmon: Lectures on partial differential equations. Consider the general linear, second-order PDE in the form. ,x 2
 Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
ADAMS Theory in a Nutshell for Class ME543 Department of Mechanical Engineering The University of Michigan Ann Arbor March 22, 2001
 ADAMS heory n a Nutshell for Class ME543 Department of Mechancal Engneerng he Unversty of Mchgan Ann Arbor March, Dan Negrut dnegr@adams.com Brett Harrs bharrs@adams.com Defntons, Notatons, Conventons.
ADAMS heory n a Nutshell for Class ME543 Department of Mechancal Engneerng he Unversty of Mchgan Ann Arbor March, Dan Negrut dnegr@adams.com Brett Harrs bharrs@adams.com Defntons, Notatons, Conventons.
Structure and Drive Paul A. Jensen Copyright July 20, 2003
 Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
2D Motion of Rigid Bodies: Falling Stick Example, Work-Energy Principle
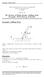 Example: Fallng Stck 1.003J/1.053J Dynamcs and Control I, Sprng 007 Professor Thomas Peacock 3/1/007 ecture 10 D Moton of Rgd Bodes: Fallng Stck Example, Work-Energy Prncple Example: Fallng Stck Fgure
Example: Fallng Stck 1.003J/1.053J Dynamcs and Control I, Sprng 007 Professor Thomas Peacock 3/1/007 ecture 10 D Moton of Rgd Bodes: Fallng Stck Example, Work-Energy Prncple Example: Fallng Stck Fgure
2010 vds-3d. Professor Kyongsu Yi. Vehicle Dynamics and Control Laboratory
 3D Dnamcs 2010 vds-3d Professor Kongsu Y 2010 VDCL Vehcle Dnamcs and Control Laborator 1 Knetcs of Rgd Bodes n Three Dmensons ma G Translatonal Dnamc Equaton of Rgd Bod (Newton Equaton F ma G Rotatonal
3D Dnamcs 2010 vds-3d Professor Kongsu Y 2010 VDCL Vehcle Dnamcs and Control Laborator 1 Knetcs of Rgd Bodes n Three Dmensons ma G Translatonal Dnamc Equaton of Rgd Bod (Newton Equaton F ma G Rotatonal
Degrees of Freedom. Spherical (ball & socket) 3 (3 rotation) Two-Angle (universal) 2 (2 rotation)
 ME 6590 Multbody Dynamcs Connectn Jonts Part I o Connectn jonts constran te relatve moton between adjonn bodes n a multbody system. Jonts rane rom allown no relatve moton (a rd jont) to allown all motons
ME 6590 Multbody Dynamcs Connectn Jonts Part I o Connectn jonts constran te relatve moton between adjonn bodes n a multbody system. Jonts rane rom allown no relatve moton (a rd jont) to allown all motons
Technical Report TR05
 Techncal Report TR05 An Introducton to the Floatng Frame of Reference Formulaton for Small Deformaton n Flexble Multbody Dynamcs Antono Recuero and Dan Negrut May 11, 2016 Abstract Ths techncal report
Techncal Report TR05 An Introducton to the Floatng Frame of Reference Formulaton for Small Deformaton n Flexble Multbody Dynamcs Antono Recuero and Dan Negrut May 11, 2016 Abstract Ths techncal report
Poisson brackets and canonical transformations
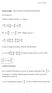 rof O B Wrght Mechancs Notes osson brackets and canoncal transformatons osson Brackets Consder an arbtrary functon f f ( qp t) df f f f q p q p t But q p p where ( qp ) pq q df f f f p q q p t In order
rof O B Wrght Mechancs Notes osson brackets and canoncal transformatons osson Brackets Consder an arbtrary functon f f ( qp t) df f f f q p q p t But q p p where ( qp ) pq q df f f f p q q p t In order
GENERALIZED LAGRANGE D ALEMBERT PRINCIPLE. Ðorđe Ðukić
 PUBLICATIONS DE L INSTITUT MATHÉMATIQUE Nouvelle sére, tome 91(105) (2012), 49 58 DOI: 10.2298/PIM1205049D GENERALIZED LAGRANGE D ALEMBERT PRINCIPLE Ðorđe Ðukć Abstract. The major ssues n the analyss of
PUBLICATIONS DE L INSTITUT MATHÉMATIQUE Nouvelle sére, tome 91(105) (2012), 49 58 DOI: 10.2298/PIM1205049D GENERALIZED LAGRANGE D ALEMBERT PRINCIPLE Ðorđe Ðukć Abstract. The major ssues n the analyss of
NON LINEAR ANALYSIS OF STRUCTURES ACCORDING TO NEW EUROPEAN DESIGN CODE
 October 1-17, 008, Bejng, Chna NON LINEAR ANALYSIS OF SRUCURES ACCORDING O NEW EUROPEAN DESIGN CODE D. Mestrovc 1, D. Czmar and M. Pende 3 1 Professor, Dept. of Structural Engneerng, Faculty of Cvl Engneerng,
October 1-17, 008, Bejng, Chna NON LINEAR ANALYSIS OF SRUCURES ACCORDING O NEW EUROPEAN DESIGN CODE D. Mestrovc 1, D. Czmar and M. Pende 3 1 Professor, Dept. of Structural Engneerng, Faculty of Cvl Engneerng,
Finite Element Modelling of truss/cable structures
 Pet Schreurs Endhoven Unversty of echnology Department of Mechancal Engneerng Materals echnology November 3, 214 Fnte Element Modellng of truss/cable structures 1 Fnte Element Analyss of prestressed structures
Pet Schreurs Endhoven Unversty of echnology Department of Mechancal Engneerng Materals echnology November 3, 214 Fnte Element Modellng of truss/cable structures 1 Fnte Element Analyss of prestressed structures
Lecture 13 APPROXIMATION OF SECOMD ORDER DERIVATIVES
 COMPUTATIONAL FLUID DYNAMICS: FDM: Appromaton of Second Order Dervatves Lecture APPROXIMATION OF SECOMD ORDER DERIVATIVES. APPROXIMATION OF SECOND ORDER DERIVATIVES Second order dervatves appear n dffusve
COMPUTATIONAL FLUID DYNAMICS: FDM: Appromaton of Second Order Dervatves Lecture APPROXIMATION OF SECOMD ORDER DERIVATIVES. APPROXIMATION OF SECOND ORDER DERIVATIVES Second order dervatves appear n dffusve
Problem Points Score Total 100
 Physcs 450 Solutons of Sample Exam I Problem Ponts Score 1 8 15 3 17 4 0 5 0 Total 100 All wor must be shown n order to receve full credt. Wor must be legble and comprehensble wth answers clearly ndcated.
Physcs 450 Solutons of Sample Exam I Problem Ponts Score 1 8 15 3 17 4 0 5 0 Total 100 All wor must be shown n order to receve full credt. Wor must be legble and comprehensble wth answers clearly ndcated.
CHEMICAL REACTIONS AND DIFFUSION
 CHEMICAL REACTIONS AND DIFFUSION A.K.A. NETWORK THERMODYNAMICS BACKGROUND Classcal thermodynamcs descrbes equlbrum states. Non-equlbrum thermodynamcs descrbes steady states. Network thermodynamcs descrbes
CHEMICAL REACTIONS AND DIFFUSION A.K.A. NETWORK THERMODYNAMICS BACKGROUND Classcal thermodynamcs descrbes equlbrum states. Non-equlbrum thermodynamcs descrbes steady states. Network thermodynamcs descrbes
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
C/CS/Phy191 Problem Set 3 Solutions Out: Oct 1, 2008., where ( 00. ), so the overall state of the system is ) ( ( ( ( 00 ± 11 ), Φ ± = 1
 C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
C/CS/Phy9 Problem Set 3 Solutons Out: Oct, 8 Suppose you have two qubts n some arbtrary entangled state ψ You apply the teleportaton protocol to each of the qubts separately What s the resultng state obtaned
Use of Non-inertial Coordinates and Implicit Integration for Efficient Solution of Multibody Systems AHMED K. ABOUBAKR
 Use of Non-nertal Coordnates and Implct Integraton for Effcent Soluton of Multbody Systems BY AHMED K. ABOUBAKR B.Sc., Caro Unversty, 2004 M.Sc., Caro Unversty, 2009 THESIS Submtted as partal fulfllment
Use of Non-nertal Coordnates and Implct Integraton for Effcent Soluton of Multbody Systems BY AHMED K. ABOUBAKR B.Sc., Caro Unversty, 2004 M.Sc., Caro Unversty, 2009 THESIS Submtted as partal fulfllment
CSci 6974 and ECSE 6966 Math. Tech. for Vision, Graphics and Robotics Lecture 21, April 17, 2006 Estimating A Plane Homography
 CSc 6974 and ECSE 6966 Math. Tech. for Vson, Graphcs and Robotcs Lecture 21, Aprl 17, 2006 Estmatng A Plane Homography Overvew We contnue wth a dscusson of the major ssues, usng estmaton of plane projectve
CSc 6974 and ECSE 6966 Math. Tech. for Vson, Graphcs and Robotcs Lecture 21, Aprl 17, 2006 Estmatng A Plane Homography Overvew We contnue wth a dscusson of the major ssues, usng estmaton of plane projectve
Homework 2: Kinematics and Dynamics of Particles Due Friday Feb 7, 2014 Max Score 45 Points + 8 Extra Credit
 EN40: Dynamcs and Vbratons School of Engneerng Brown Unversty Homework : Knematcs and Dynamcs of Partcles Due Frday Feb 7, 014 Max Score 45 Ponts + 8 Extra Credt 1. An expermental mcro-robot (see a descrpton
EN40: Dynamcs and Vbratons School of Engneerng Brown Unversty Homework : Knematcs and Dynamcs of Partcles Due Frday Feb 7, 014 Max Score 45 Ponts + 8 Extra Credt 1. An expermental mcro-robot (see a descrpton
