_ 3 jveg-f* fl2ul_-pj>" -D' Zu\ E 1 2 j / J EG F*'
|
|
|
- Cody Lewis
- 6 years ago
- Views:
Transcription
1 1901.] A CLASS OF SURFACES. 417 (1) SURFACES WHOSE FIRST AND SECOND FUN DAMENTAL FORMS ARE THE SECOND AND FIRST RESPECTIVELY OF ANOTHER SURFACE. BY DE. "L. P. EISENHABT. ( Eead bef ore the American Mathematical Society, February 23, 1901.) THE fundamental theorem in the theory of surfaces is : * Given two quadratic differential forms ƒ= Edu 2 + 2Fdudv + Gdv 2 <p = Bdu 2 + ZD'dudv + D"dv 2, of which the first is definite, in order that there exist a surface which shall have ƒ and f for its first and second fundamental forms respectively, it is necessary and sufficient that the coefficients of these forms satisfy the Codazzi equations dd d ^-{\ 2 }M{ï}-m)-+m*"= (2) and the equation of Gauss (3) i r ^IVEG-F 2 JIIU VEG l F*ldv\~ E (2j/ _ 3 jveg-f* fl2ul_-pj>" -D' Zu\ E 1 2 j / J EG F*' I rs 1 where the Christoffel symbols < > are formed with respect to the form ƒ. And, moreover, when these conditions are satisfied the corresponding surface is unique and determinate. We propose now to determine those surfaces S with fundamental forms (1) which have associated with them surfaces S v whose first and second fundamental forms are, respectively, * Bianchi, Lezioni, p. 92.
2 418 A CLASS OF SURFACES. [J u ty? Ddu 2 + 2D'dudv + D"dv\ Edu 2 + 2Fdudv + Gdv 2. Denoting by subscript x functions belonging to S v we have f x = ds 2 = E x du 2 + 2F 1 dudv + Gydv*, <P 1 = D l du 2 + 2D 1 'dudv +D^'dv 2. Comparing these with the above, we remark that for a surface S 1 satisfying the conditions of the problem, (5) E x = D, F x =- D', Q x = D"; D x = E, D/ = F, D/' = O. It is evident that the double system of lines which is conjugate for S and S ± is composed of the lines of curvature on each surface. We will refer both surfaces to these lines ; then (6) F=0, D' = 0. With this special choice of parametric lines the Codazzi equations become dd tdeid D"\_ (7) 3w and the Gauss equation 2 du\e + ~G)~ 0; (*\ DD " 9 / 1 d^g\ 9/1 *^Ë\ In order that 8 1 may be a surface the coefficients of its fundamental forms must satisfy these equations. Hence in order that S may be the kind of surface sought, it is necessary that its fundamental coefficients satisfy the conditions BE, dd IE. G dv "dv\d^d") ' (9) 36? 3D" 2 '"(1+ \-o du du \D^ D"f~ ' and HO) _??_ 9 / 1 d^w'\, 9 / 1 d>/d\
3 1901.] A CLASS OF SURFACES. 419 BE Substituting in equations (7) the expressions for -=- and ^, as given by equations (9), we get in each case ou Denote by p x and p 2 the principal radii of curvature at the point (w, v) on S ; then 1_D 1 D" P 1 JE 9 p 2 G' When these expressions for p 1 and p 2 are replaced by the latter in the equation of condition (11), it becomes (I2) k-^h)- Hence S must be a surface for which the total curvature at a point and the Casorati * curvature are equal. Developing equation (12) we remark that it is necessary that Pi = Hence, in order that the first and second fundamental forms of a surface S may determine a surface for ivhich these forms shall he respectively the second and first forms it is necessary that 8 have its two radii equal and of the same sign. This class of surfaces has been the object of a study by Monge,f and later by Forsyth. J The former has shown that the sphere is the only real surface belonging to the class. His discussion was with reference to the differential equation of the second order, characteristic of such surfaces, viz. ia + Pr q>)r-2pqs+(l+f)ty = 4(r*~s 2 )(l+p 2 +<f), for the determination of which the surface was given by the equation * " Mésure de la courbure des surfaces suivant l'idée commune ", Acta Mathematica, 14, 2. f Application de l'analyse à la géométrie, 5th éd., pp X "Note on surfaces whose radii of curvature are equal and of same sign," Messenger of Mathematics, new series, no. 321.
4 420 A CLASS OF SURFACES. [Juty? (14) *=ƒ(*, SO, and where, as originally denoted by Monge, 3s dz d 2 z d 2 z d 2 z (15) p, q, r, «, t- Wx, g-, ^ ^-, g- 2. Forsyth integrated the same equation (13) by a process differing from that used by Monge and found that all such surfaces are given by eliminating //. between the equations 16) y + fix= <p(v)i z ix{\ + fi 2 )i = (p{fi) where <p and <p are arbitrary functions. We shall now determine the forms of the functions, which correspond to surfaces furnishing a solution to our problem. To this end we remark that the notations of Gauss and of Monge have the following relations : E=l+p\ F = pq, G~l + q 2, (17) "-7TWF+? jy= ==L===., z>"= t It is evident then that our problem reduces to the finding of <p and 4' such that (18) and =pj±== = 1 + p*, Plq v 1 + q 2 : V 1 + p 2 + q (19) \+p% pq, l + g» = r» * *i sr+pf + q* where the subscript x denotes that the functions belong to the associated surface S v Substituting for the functions in (18) their expressions as derived from equations (16) and from the similar equations y -f ^== ^OO, z ix(l 4-M 1 2 )^ = ^W, corresponding to the surface S v we find on equating to zero the coefficients of x 2, x, and 1, the following relations :
5 1901.] A CLASS OF SURFACES // (20) 2<p'n + Ati\v'4>" - <p"4>') = -?>/V + 2^y r+xvm' + ASV/ 2 ; (1+A 2 )! 1 +AH" : (21) 1 - nab Vl + ^ - Atx(<p'<j>" <?"<!>') ST+ = %>/! + tffw + ^ (22) %A (1 + M')* 1 + tf' AB= 2?/ + 2iju, ^1+V.A( f V - <»") = < + «V, where, for the sake of brevity, we have written A = * = -, (23) w' + v 1 + MV B = <P" - <p'i(l + ^2) "i + i//(l + /x 2 ) -V'. The similar relations arising from equations (19) can be gotten at once from the above by giving subscripts to the terms not having them and removing them from those
6 422 A CLASS OF SURFACES. [J^ty, which have; we shall refer to these relations as (20'), (21') and (22'), respectively. From the first relations of (20), (21), and (22) we see that i\ = ^ hence these three relations and the corresponding ones in (20'), (21') (22') may be replaced, respectively, by fl<p' i\/l + tl*<p'= 04) ^ f Combining these with the second relations of (20), (21), (22) and (20') (21'), (22'), we find that the latter may be replaced by is/1 + iffy" - i(l + M 2 )-V + ifi(l+ j". 2 )"*?"] (25) ^ * S l + / is/i + itty» - i(i + i^y^cpi + ^(i + M 2 )-*<'] = +2^~2^(l + /, 2 )-i. Differentiating the second of equations (24) and combining the result with the second of equations (25) and both of (24), we find (26)?/ =?', ^ = 0', hence <p x and <f> x can differ at most from <p and 0, respectively, by an additive constant. Hence S and 8 1 are the same surface, to a translation près. Making use of the preceding results, we find that the third equations of (20), (21), (22), (20'), (21'), and (22') are equivalent to the single one (27) is/1 + nx<p'<l>'' - <*y) = / + <p'\ Expressing this relation in terms of <p and its derivatives, we find from which we get (29) 9=y/ 1 + l t + c^+c t
7 1901.] A CLASS OF SURFACES. 423 where C x and C 2 are arbitrary constants. this expression in (24), we find On substituting (30) vp=*cyi + ti* + ti + C s, C B being a third arbitrary constant. From (29) and (30) we get (31) ^? + ^ 5 S (C 1 +1)(M+^1 + P 2 ) +C 2 +C Z, ^=^-^=(0^1)^-^ FT7? ) + c 2 - c 3. It is readily seen that equations (16) can be replaced by ( ôjj ) t where $ and W have the expressions (31). Writing in these expressions C x = a, C 2 = b, C 3 = ic, and eliminating i± from the equations (32) thus obtained we get (a;_ a y + (2/_ &)2 + (,_ c ) 2 = l ; that is, a sphere of center (a, 6, c) and radius unity. Moreover, only when the radius is unity are the conditions satisfied. We have then the following results : The ruled surfaces, defined by the equations y + fix = V/FT/? + Qfi + Ci z ix */T+ /J 2 = fi+c 1 */l + fi*+ G v are the only surfaces whosefirstand second fundamental forms can be taken for the second and first fundamental forms of a surface. Further the second surface is only the first to a translation pres. And of these surfaces the only real one is the sphere of radius unity. PRINCETON UNIVERSITY, February 14, 1901.
Lecture 13 The Fundamental Forms of a Surface
 Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
Lecture 13 The Fundamental Forms of a Surface In the following we denote by F : O R 3 a parametric surface in R 3, F(u, v) = (x(u, v), y(u, v), z(u, v)). We denote partial derivatives with respect to the
Lectures on Quantum sine-gordon Models
 Lectures on Quantum sine-gordon Models Juan Mateos Guilarte 1, 1 Departamento de Física Fundamental (Universidad de Salamanca) IUFFyM (Universidad de Salamanca) Universidade Federal de Matto Grosso Cuiabá,
Lectures on Quantum sine-gordon Models Juan Mateos Guilarte 1, 1 Departamento de Física Fundamental (Universidad de Salamanca) IUFFyM (Universidad de Salamanca) Universidade Federal de Matto Grosso Cuiabá,
CS Tutorial 5 - Differential Geometry I - Surfaces
 236861 Numerical Geometry of Images Tutorial 5 Differential Geometry II Surfaces c 2009 Parameterized surfaces A parameterized surface X : U R 2 R 3 a differentiable map 1 X from an open set U R 2 to R
236861 Numerical Geometry of Images Tutorial 5 Differential Geometry II Surfaces c 2009 Parameterized surfaces A parameterized surface X : U R 2 R 3 a differentiable map 1 X from an open set U R 2 to R
COMPLEMENTARY SURFACES FOR A VECTOR FIELD
 COMPLEMENTARY SURFACES FOR A VECTOR FIELD T. K. PAN 1. Introduction. Let d be a vector field in a surface in an ordinary space. The author defined the curve of v and the asymptotic line of v and proved
COMPLEMENTARY SURFACES FOR A VECTOR FIELD T. K. PAN 1. Introduction. Let d be a vector field in a surface in an ordinary space. The author defined the curve of v and the asymptotic line of v and proved
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algo
 Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Dierential Geometry Curves and surfaces Local properties Geometric foundations (critical for visual modeling and computing) Quantitative analysis Algorithm development Shape control and interrogation Curves
Gaussian and Mean Curvatures
 Gaussian and Mean Curvatures (Com S 477/577 Notes) Yan-Bin Jia Oct 31, 2017 We have learned that the two principal curvatures (and vectors) determine the local shape of a point on a surface. One characterizes
Gaussian and Mean Curvatures (Com S 477/577 Notes) Yan-Bin Jia Oct 31, 2017 We have learned that the two principal curvatures (and vectors) determine the local shape of a point on a surface. One characterizes
Chapter 4. The First Fundamental Form (Induced Metric)
 Chapter 4. The First Fundamental Form (Induced Metric) We begin with some definitions from linear algebra. Def. Let V be a vector space (over IR). A bilinear form on V is a map of the form B : V V IR which
Chapter 4. The First Fundamental Form (Induced Metric) We begin with some definitions from linear algebra. Def. Let V be a vector space (over IR). A bilinear form on V is a map of the form B : V V IR which
GROUPS POSSESSING A SMALL NUMBER OF SETS OF CONJUGATE OPERATORS*
 GROUPS POSSESSING A SMALL NUMBER OF SETS OF CONJUGATE OPERATORS* BY G. A. MILLER 1. Introduction Some properties of a group G can perhaps be most clearly presented by representing G as a kind of independent
GROUPS POSSESSING A SMALL NUMBER OF SETS OF CONJUGATE OPERATORS* BY G. A. MILLER 1. Introduction Some properties of a group G can perhaps be most clearly presented by representing G as a kind of independent
CANONICAL EQUATIONS. Application to the study of the equilibrium of flexible filaments and brachistochrone curves. By A.
 Équations canoniques. Application a la recherche de l équilibre des fils flexibles et des courbes brachystochrones, Mem. Acad. Sci de Toulouse (8) 7 (885), 545-570. CANONICAL EQUATIONS Application to the
Équations canoniques. Application a la recherche de l équilibre des fils flexibles et des courbes brachystochrones, Mem. Acad. Sci de Toulouse (8) 7 (885), 545-570. CANONICAL EQUATIONS Application to the
Subrings and Ideals 2.1 INTRODUCTION 2.2 SUBRING
 Subrings and Ideals Chapter 2 2.1 INTRODUCTION In this chapter, we discuss, subrings, sub fields. Ideals and quotient ring. We begin our study by defining a subring. If (R, +, ) is a ring and S is a non-empty
Subrings and Ideals Chapter 2 2.1 INTRODUCTION In this chapter, we discuss, subrings, sub fields. Ideals and quotient ring. We begin our study by defining a subring. If (R, +, ) is a ring and S is a non-empty
Vectors and Fields. Vectors versus scalars
 C H A P T E R 1 Vectors and Fields Electromagnetics deals with the study of electric and magnetic fields. It is at once apparent that we need to familiarize ourselves with the concept of a field, and in
C H A P T E R 1 Vectors and Fields Electromagnetics deals with the study of electric and magnetic fields. It is at once apparent that we need to familiarize ourselves with the concept of a field, and in
(1.1) Mi= f (Z -1-)dP, i = 0, 1,,* - 1,
 ON PARALLEL HYPERSURFACES IN THE ELLIPTIC AND HYPERBOLIC w-dimensional SPACE L. A. SANTALÖ 1. Introduction. Let S"-1 be a hypersurface of class C3 in the elliptic or hyperbolic w-dimensional space, which
ON PARALLEL HYPERSURFACES IN THE ELLIPTIC AND HYPERBOLIC w-dimensional SPACE L. A. SANTALÖ 1. Introduction. Let S"-1 be a hypersurface of class C3 in the elliptic or hyperbolic w-dimensional space, which
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
Z(J5L_ + J«L+...+_«_
 ON THE LOCATION OF THE ROOTS OF THE JACOBIAN OF TWO BINARY FORMS, AND OF THE DERIVATIVE OF A RATIONAL FUNCTION* By J. L. WALSH Introduction Professor Bôcher has shown how the roots of certain algebraic
ON THE LOCATION OF THE ROOTS OF THE JACOBIAN OF TWO BINARY FORMS, AND OF THE DERIVATIVE OF A RATIONAL FUNCTION* By J. L. WALSH Introduction Professor Bôcher has shown how the roots of certain algebraic
NOTE ON A THEOREM OF JACOB. 231
 NOTE ON A THEOREM OF JACOB. 231 the limiting value of the integral of g( rj) N[( ) approaches zero. Hence Theorem II 1 is a simple special case of Theorem III. References. Bochner and Hardy, 1, " Notes
NOTE ON A THEOREM OF JACOB. 231 the limiting value of the integral of g( rj) N[( ) approaches zero. Hence Theorem II 1 is a simple special case of Theorem III. References. Bochner and Hardy, 1, " Notes
Visualisations of Gussian and Mean Curvatures by Using Mathematica and webmathematica
 6 th International Conference on Applied Informatics Eger, Hungary, January 27 31, 2004. Visualisations of Gussian and Mean Curvatures by Using Mathematica and webmathematica Vladimir Benič, Sonja Gorjanc
6 th International Conference on Applied Informatics Eger, Hungary, January 27 31, 2004. Visualisations of Gussian and Mean Curvatures by Using Mathematica and webmathematica Vladimir Benič, Sonja Gorjanc
ON THE DENSITY OF SOME SEQUENCES OF INTEGERS P. ERDOS
 ON THE DENSITY OF SOME SEQUENCES OF INTEGERS P. ERDOS Let ai
ON THE DENSITY OF SOME SEQUENCES OF INTEGERS P. ERDOS Let ai
Mechanical Theorem Proving of the Local Theory of Surfaces
 Mechanical Theorem Proving of the Local Theory of Surfaces ZIMING LI Research Institute for Symbolic Computation Johannes Kepler University, A-4040 Linz, Austria e-mail: zmli@risc.uni-linz.ac.at August
Mechanical Theorem Proving of the Local Theory of Surfaces ZIMING LI Research Institute for Symbolic Computation Johannes Kepler University, A-4040 Linz, Austria e-mail: zmli@risc.uni-linz.ac.at August
d F = (df E 3 ) E 3. (4.1)
 4. The Second Fundamental Form In the last section we developed the theory of intrinsic geometry of surfaces by considering the covariant differential d F, that is, the tangential component of df for a
4. The Second Fundamental Form In the last section we developed the theory of intrinsic geometry of surfaces by considering the covariant differential d F, that is, the tangential component of df for a
StokesI Theorem. Definition. Let F = PT + QT + $ be a continuously differentiable,
 StokesI Theorem Our text states and proves Stokes' Theorem in 12.11, but ituses the scalar form for writing both the line integral and the surface integral involved. In the applications, it is the vector
StokesI Theorem Our text states and proves Stokes' Theorem in 12.11, but ituses the scalar form for writing both the line integral and the surface integral involved. In the applications, it is the vector
Hyperbolic Geometry on Geometric Surfaces
 Mathematics Seminar, 15 September 2010 Outline Introduction Hyperbolic geometry Abstract surfaces The hemisphere model as a geometric surface The Poincaré disk model as a geometric surface Conclusion Introduction
Mathematics Seminar, 15 September 2010 Outline Introduction Hyperbolic geometry Abstract surfaces The hemisphere model as a geometric surface The Poincaré disk model as a geometric surface Conclusion Introduction
ON RESTRICTED SYSTEMS OF HIGHER INDETERMINATE EQUATIONS * E. T. BELL
 ON RESTRICTED SYSTEMS OF HIGHER INDETERMINATE EQUATIONS * BY E. T. BELL By two examples we shall illustrate a means for deriving arithmetical properties of certain restricted forms. So little being known
ON RESTRICTED SYSTEMS OF HIGHER INDETERMINATE EQUATIONS * BY E. T. BELL By two examples we shall illustrate a means for deriving arithmetical properties of certain restricted forms. So little being known
S. Lie has thrown much new light on this operation. The assumption
 600 MATHEMATICS: A. E. ROSS PRoc. N. A. S. The operation of finding the limit of an infinite series has been one of the most fruitful operations of all mathematics. While this is not a group operation
600 MATHEMATICS: A. E. ROSS PRoc. N. A. S. The operation of finding the limit of an infinite series has been one of the most fruitful operations of all mathematics. While this is not a group operation
Chapter 14. Basics of The Differential Geometry of Surfaces. Introduction. Parameterized Surfaces. The First... Home Page. Title Page.
 Chapter 14 Basics of The Differential Geometry of Surfaces Page 649 of 681 14.1. Almost all of the material presented in this chapter is based on lectures given by Eugenio Calabi in an upper undergraduate
Chapter 14 Basics of The Differential Geometry of Surfaces Page 649 of 681 14.1. Almost all of the material presented in this chapter is based on lectures given by Eugenio Calabi in an upper undergraduate
176 5 t h Fl oo r. 337 P o ly me r Ma te ri al s
 A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
A g la di ou s F. L. 462 E l ec tr on ic D ev el op me nt A i ng er A.W.S. 371 C. A. M. A l ex an de r 236 A d mi ni st ra ti on R. H. (M rs ) A n dr ew s P. V. 326 O p ti ca l Tr an sm is si on A p ps
Lectures 18: Gauss's Remarkable Theorem II. Table of contents
 Math 348 Fall 27 Lectures 8: Gauss's Remarkable Theorem II Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams.
Math 348 Fall 27 Lectures 8: Gauss's Remarkable Theorem II Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams.
COMPOSITIO MATHEMATICA
 COMPOSITIO MATHEMATICA F. LOONSTRA The classes of partially ordered groups Compositio Mathematica, tome 9 (1951), p. 130-140 Foundation Compositio Mathematica,
COMPOSITIO MATHEMATICA F. LOONSTRA The classes of partially ordered groups Compositio Mathematica, tome 9 (1951), p. 130-140 Foundation Compositio Mathematica,
Toroidal Surfaces. XVII th International Conference Geometry, Integrability and Quantization Varna, Bulgaria. Metin Gürses
 Toroidal Surfaces XVII th International Conference Geometry, Integrability and Quantization Varna, Bulgaria Metin Gürses Matematik Bölümü Bilkent Üniversitesi, Ankara Metin Gürses Toroidal Surfaces June
Toroidal Surfaces XVII th International Conference Geometry, Integrability and Quantization Varna, Bulgaria Metin Gürses Matematik Bölümü Bilkent Üniversitesi, Ankara Metin Gürses Toroidal Surfaces June
APSIDAL ANGLES FOR SYMMETRICAL DYNAMICAL SYSTEMS WITH TWO DEGREES OF FREEDOM
 APSIDAL ANGLES FOR SYMMETRICAL DYNAMICAL SYSTEMS WITH TWO DEGREES OF FREEDOM J. L. SYNGE The bob of a spherical pendulum (or particle on a smooth sphere under gravity) oscillates between two levels, and
APSIDAL ANGLES FOR SYMMETRICAL DYNAMICAL SYSTEMS WITH TWO DEGREES OF FREEDOM J. L. SYNGE The bob of a spherical pendulum (or particle on a smooth sphere under gravity) oscillates between two levels, and
Regularity for the optimal transportation problem with Euclidean distance squared cost on the embedded sphere
 Regularity for the optimal transportation problem with Euclidean distance squared cost on the embedded sphere Jun Kitagawa and Micah Warren January 6, 011 Abstract We give a sufficient condition on initial
Regularity for the optimal transportation problem with Euclidean distance squared cost on the embedded sphere Jun Kitagawa and Micah Warren January 6, 011 Abstract We give a sufficient condition on initial
Math 115 ( ) Yum-Tong Siu 1. Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives
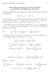 Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
Math 115 006-007 Yum-Tong Siu 1 Euler-Lagrange Equations for Many Functions and Variables and High-Order Derivatives The Case of High-Order Derivatives. The context is to find the extremal for the functional
16.5 Surface Integrals of Vector Fields
 16.5 Surface Integrals of Vector Fields Lukas Geyer Montana State University M73, Fall 011 Lukas Geyer (MSU) 16.5 Surface Integrals of Vector Fields M73, Fall 011 1 / 19 Parametrized Surfaces Definition
16.5 Surface Integrals of Vector Fields Lukas Geyer Montana State University M73, Fall 011 Lukas Geyer (MSU) 16.5 Surface Integrals of Vector Fields M73, Fall 011 1 / 19 Parametrized Surfaces Definition
ON THE NUMBER OF POSITIVE INTEGERS LESS THAN x AND FREE OF PRIME DIVISORS GREATER THAN x e
 ON THE NUMBER OF POSITIVE INTEGERS LESS THAN x AND FREE OF PRIME DIVISORS GREATER THAN x e V. RAMASWAMI Dr. Chowla recently raised the following question regarding the number of positive integers less
ON THE NUMBER OF POSITIVE INTEGERS LESS THAN x AND FREE OF PRIME DIVISORS GREATER THAN x e V. RAMASWAMI Dr. Chowla recently raised the following question regarding the number of positive integers less
A LIMITED ARITHMETIC ON SIMPLE CONTINUED FRACTIONS
 A LIMITED ARITHMETIC ON SIMPLE CONTINUED FRACTIONS C. T. L O N G and J. H. JORDAN Washington State University, Pullman, Washington -*-* Introduction,, As Is well known., a number of remarkable and interesting
A LIMITED ARITHMETIC ON SIMPLE CONTINUED FRACTIONS C. T. L O N G and J. H. JORDAN Washington State University, Pullman, Washington -*-* Introduction,, As Is well known., a number of remarkable and interesting
Introduction to Algebraic and Geometric Topology Week 14
 Introduction to Algebraic and Geometric Topology Week 14 Domingo Toledo University of Utah Fall 2016 Computations in coordinates I Recall smooth surface S = {f (x, y, z) =0} R 3, I rf 6= 0 on S, I Chart
Introduction to Algebraic and Geometric Topology Week 14 Domingo Toledo University of Utah Fall 2016 Computations in coordinates I Recall smooth surface S = {f (x, y, z) =0} R 3, I rf 6= 0 on S, I Chart
exceptional value turns out to be, "RAC" CURVATURE calling attention especially to the fundamental Theorem III, and to emphasize
 VOL. 18, 1932 V,MA THEMA TICS: E. KASNER 267 COMPLEX GEOMETRY AND RELATIVITY: "RAC" CURVATURE BY EDWARD KASNER DEPARTMENT OF MATHEMATICS, COLUMBIA UNIVERSITY Communicated February 3, 1932 THEORY OF THE
VOL. 18, 1932 V,MA THEMA TICS: E. KASNER 267 COMPLEX GEOMETRY AND RELATIVITY: "RAC" CURVATURE BY EDWARD KASNER DEPARTMENT OF MATHEMATICS, COLUMBIA UNIVERSITY Communicated February 3, 1932 THEORY OF THE
Part IB GEOMETRY (Lent 2016): Example Sheet 1
 Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
Surface x(u, v) and curve α(t) on it given by u(t) & v(t). Math 4140/5530: Differential Geometry
 Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt ( ds dt )2 Surface x(u, v)
Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt Surface x(u, v) and curve α(t) on it given by u(t) & v(t). α du dv (t) x u dt + x v dt ( ds dt )2 Surface x(u, v)
ON THE AVERAGE NUMBER OF REAL ROOTS OF A RANDOM ALGEBRAIC EQUATION
 ON THE AVERAGE NUMBER OF REAL ROOTS OF A RANDOM ALGEBRAIC EQUATION M. KAC 1. Introduction. Consider the algebraic equation (1) Xo + X x x + X 2 x 2 + + In-i^" 1 = 0, where the X's are independent random
ON THE AVERAGE NUMBER OF REAL ROOTS OF A RANDOM ALGEBRAIC EQUATION M. KAC 1. Introduction. Consider the algebraic equation (1) Xo + X x x + X 2 x 2 + + In-i^" 1 = 0, where the X's are independent random
GENERALIZED LIMITS IN GENERAL ANALYSIS* SECOND PAPER
 GENERALIZED LIMITS IN GENERAL ANALYSIS* SECOND PAPER BY CHARLES N. MOORE In a previous paper of the same titlet I have developed the fundamental principles of a general theory which includes as particular
GENERALIZED LIMITS IN GENERAL ANALYSIS* SECOND PAPER BY CHARLES N. MOORE In a previous paper of the same titlet I have developed the fundamental principles of a general theory which includes as particular
CALCULUS ON MANIFOLDS. 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M =
 CALCULUS ON MANIFOLDS 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M = a M T am, called the tangent bundle, is itself a smooth manifold, dim T M = 2n. Example 1.
CALCULUS ON MANIFOLDS 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M = a M T am, called the tangent bundle, is itself a smooth manifold, dim T M = 2n. Example 1.
Total No. of Questions : 58 ] [ Total No. of Printed Pages : 40. ê ÂŒÈ : πâä  FOR OFFICE USE ONLY
![Total No. of Questions : 58 ] [ Total No. of Printed Pages : 40. ê ÂŒÈ : πâä  FOR OFFICE USE ONLY Total No. of Questions : 58 ] [ Total No. of Printed Pages : 40. ê ÂŒÈ : πâä  FOR OFFICE USE ONLY](/thumbs/94/120871203.jpg) Roll No. Serial No. of Q. C. A. B. ÈJ ÂX applerπâ   zapplew : 58 ] [ ÈJ ÆÂÈÈåX  ÂÏ πâ   zapplew : 40 Total No. of Questions : 58 ] [ Total No. of Printed Pages : 40 ê ÂŒÈ : πâä   xë   zapplew
Roll No. Serial No. of Q. C. A. B. ÈJ ÂX applerπâ   zapplew : 58 ] [ ÈJ ÆÂÈÈåX  ÂÏ πâ   zapplew : 40 Total No. of Questions : 58 ] [ Total No. of Printed Pages : 40 ê ÂŒÈ : πâä   xë   zapplew
+ 2gx + 2fy + c = 0 if S
 CIRCLE DEFINITIONS A circle is the locus of a point which moves in such a way that its distance from a fixed point, called the centre, is always a constant. The distance r from the centre is called the
CIRCLE DEFINITIONS A circle is the locus of a point which moves in such a way that its distance from a fixed point, called the centre, is always a constant. The distance r from the centre is called the
Classical differential geometry of two-dimensional surfaces
 Classical differential geometry of two-dimensional surfaces 1 Basic definitions This section gives an overview of the basic notions of differential geometry for twodimensional surfaces. It follows mainly
Classical differential geometry of two-dimensional surfaces 1 Basic definitions This section gives an overview of the basic notions of differential geometry for twodimensional surfaces. It follows mainly
DIVISORS OF ZERO IN MATRIC RINGS
 DIVISORS OF ZERO IN MATRIC RINGS NEAL H. MCCOY 1. Introduction. An element a of a ring 6* is a divisor of zero in 5 if there exists a nonzero element x of S such that ax 0, or a nonzero element y of S
DIVISORS OF ZERO IN MATRIC RINGS NEAL H. MCCOY 1. Introduction. An element a of a ring 6* is a divisor of zero in 5 if there exists a nonzero element x of S such that ax 0, or a nonzero element y of S
A/P Warrants. June 15, To Approve. To Ratify. Authorize the City Manager to approve such expenditures as are legally due and
 T. 7 TY LS ALATS A/P rrnts June 5, 5 Pges: To Approve - 5 89, 54.3 A/P rrnts 6/ 5/ 5 Subtotl $ 89, 54. 3 To Rtify Pges: 6-, 34. 98 Advnce rrnts 5/ 6/ 5-4 3, 659. 94 Advnce rrnts 6/ / 5 4, 7. 69 June Retirees
T. 7 TY LS ALATS A/P rrnts June 5, 5 Pges: To Approve - 5 89, 54.3 A/P rrnts 6/ 5/ 5 Subtotl $ 89, 54. 3 To Rtify Pges: 6-, 34. 98 Advnce rrnts 5/ 6/ 5-4 3, 659. 94 Advnce rrnts 6/ / 5 4, 7. 69 June Retirees
ALGEBRAIC PROPERTIES OF THE LATTICE R nx
 CHAPTER 6 ALGEBRAIC PROPERTIES OF THE LATTICE R nx 6.0 Introduction This chapter continues to explore further algebraic and topological properties of the complete lattice Rnx described in Chapter 5. We
CHAPTER 6 ALGEBRAIC PROPERTIES OF THE LATTICE R nx 6.0 Introduction This chapter continues to explore further algebraic and topological properties of the complete lattice Rnx described in Chapter 5. We
On loc \ Perta\mnq To The Osculating
 C ollom On loc \ Perta\mnq To The Osculating C\rc\?5 And Spheres Of Certam ^pae
C ollom On loc \ Perta\mnq To The Osculating C\rc\?5 And Spheres Of Certam ^pae
Math 5378, Differential Geometry Solutions to practice questions for Test 2
 Math 5378, Differential Geometry Solutions to practice questions for Test 2. Find all possible trajectories of the vector field w(x, y) = ( y, x) on 2. Solution: A trajectory would be a curve (x(t), y(t))
Math 5378, Differential Geometry Solutions to practice questions for Test 2. Find all possible trajectories of the vector field w(x, y) = ( y, x) on 2. Solution: A trajectory would be a curve (x(t), y(t))
Oct : Lecture 15: Surface Integrals and Some Related Theorems
 90 MIT 3.016 Fall 2005 c W.C Carter Lecture 15 Oct. 21 2005: Lecture 15: Surface Integrals and Some Related Theorems Reading: Kreyszig Sections: 9.4 pp:485 90), 9.5 pp:491 495) 9.6 pp:496 505) 9.7 pp:505
90 MIT 3.016 Fall 2005 c W.C Carter Lecture 15 Oct. 21 2005: Lecture 15: Surface Integrals and Some Related Theorems Reading: Kreyszig Sections: 9.4 pp:485 90), 9.5 pp:491 495) 9.6 pp:496 505) 9.7 pp:505
Map Projections. Jim Emery. Revision 7/21/ The Earth Ellipsoid 2. 2 The Fundamental Quadratic Forms of a Surface 6
 Map Projections Jim Emery Revision 7/21/2004 Contents 1 The Earth Ellipsoid 2 2 The Fundamental Quadratic Forms of a Surface 6 3 Principal Directions On A Surface 9 4 Principal Normal Curvatures on the
Map Projections Jim Emery Revision 7/21/2004 Contents 1 The Earth Ellipsoid 2 2 The Fundamental Quadratic Forms of a Surface 6 3 Principal Directions On A Surface 9 4 Principal Normal Curvatures on the
Gradient Estimate of Mean Curvature Equations and Hessian Equations with Neumann Boundary Condition
 of Mean Curvature Equations and Hessian Equations with Neumann Boundary Condition Xinan Ma NUS, Dec. 11, 2014 Four Kinds of Equations Laplace s equation: u = f(x); mean curvature equation: div( Du ) =
of Mean Curvature Equations and Hessian Equations with Neumann Boundary Condition Xinan Ma NUS, Dec. 11, 2014 Four Kinds of Equations Laplace s equation: u = f(x); mean curvature equation: div( Du ) =
Lecture Notes on Minimal Surfaces January 27, 2006 by Michael Dorff
 Lecture Notes on Minimal Surfaces January 7, 6 by Michael Dorff 1 Some Background in Differential Geometry Our goal is to develop the mathematics necessary to investigate minimal surfaces in R 3. Every
Lecture Notes on Minimal Surfaces January 7, 6 by Michael Dorff 1 Some Background in Differential Geometry Our goal is to develop the mathematics necessary to investigate minimal surfaces in R 3. Every
Chapter 4 Systems of Linear Equations; Matrices
 Chapter 4 Systems of Linear Equations; Matrices Section 5 Inverse of a Square Matrix Learning Objectives for Section 4.5 Inverse of a Square Matrix The student will be able to identify identity matrices
Chapter 4 Systems of Linear Equations; Matrices Section 5 Inverse of a Square Matrix Learning Objectives for Section 4.5 Inverse of a Square Matrix The student will be able to identify identity matrices
\ABC (9) \AX BI Ci\ = 0, r; vi -iv ~*i -n*yi -o
 i 9 28.] INVERSION OF TRANSFORMATIONS 565 \ABC BiCi C1A1 Ai Bi (9) \AX BI Ci\ = 0, r; vi -iv ~*i -n*yi -o ' A 2 B2 C2 = 0, B2 C2 d Ai Ai Bi represent the two éliminants of the system (8). The two necessary
i 9 28.] INVERSION OF TRANSFORMATIONS 565 \ABC BiCi C1A1 Ai Bi (9) \AX BI Ci\ = 0, r; vi -iv ~*i -n*yi -o ' A 2 B2 C2 = 0, B2 C2 d Ai Ai Bi represent the two éliminants of the system (8). The two necessary
Practice ? b a (-a) b a b (3a)
 Practice 8- Zero and Negative Exponents. 6 0 2. -2 3. 3-3. 8-5. 6. 7. 3 8. 2 2 2 25 23 6 2 2 25 9. 3? 8 0 0. 6? 2-2. 2-2. -7-2 3. 6? 0. 9 0 5. 32 2 6. 9 8 2 2 2 7. 8 22 8. 9 2 9. 5(-6) 0 20. (3.7) 0 0
Practice 8- Zero and Negative Exponents. 6 0 2. -2 3. 3-3. 8-5. 6. 7. 3 8. 2 2 2 25 23 6 2 2 25 9. 3? 8 0 0. 6? 2-2. 2-2. -7-2 3. 6? 0. 9 0 5. 32 2 6. 9 8 2 2 2 7. 8 22 8. 9 2 9. 5(-6) 0 20. (3.7) 0 0
Stereographic projection and inverse geometry
 Stereographic projection and inverse geometry The conformal property of stereographic projections can be established fairly efficiently using the concepts and methods of inverse geometry. This topic is
Stereographic projection and inverse geometry The conformal property of stereographic projections can be established fairly efficiently using the concepts and methods of inverse geometry. This topic is
Directional Derivative and the Gradient Operator
 Chapter 4 Directional Derivative and the Gradient Operator The equation z = f(x, y) defines a surface in 3 dimensions. We can write this as z f(x, y) = 0, or g(x, y, z) = 0, where g(x, y, z) = z f(x, y).
Chapter 4 Directional Derivative and the Gradient Operator The equation z = f(x, y) defines a surface in 3 dimensions. We can write this as z f(x, y) = 0, or g(x, y, z) = 0, where g(x, y, z) = z f(x, y).
ON A SIMPLE SYSTEM OF CHARGED PARTICLES IN MILNE'S KINEMATICAL THEORY
 ON A SIMPLE SYSTEM OF CHARGED PARTICLES IN MILNE'S KINEMATICAL THEORY BY D. N. MOGHE (Research Scholar, Bombay Uni,~er.dty) Received March 9, 1939 (Communicatcd by Dr. G. S. Mahajnni) 7. Introduction IN
ON A SIMPLE SYSTEM OF CHARGED PARTICLES IN MILNE'S KINEMATICAL THEORY BY D. N. MOGHE (Research Scholar, Bombay Uni,~er.dty) Received March 9, 1939 (Communicatcd by Dr. G. S. Mahajnni) 7. Introduction IN
A NEW DEFINITION OF THE GENERAL ABELIAN LINEAR GROUP*
 A NEW DEFINITION OF THE GENERAL ABELIAN LINEAR GROUP* LEONARD EUGENE DICKSON 1. We may give a striking definition of the general Abelian group, making use of the fruitful conception of the " compounds
A NEW DEFINITION OF THE GENERAL ABELIAN LINEAR GROUP* LEONARD EUGENE DICKSON 1. We may give a striking definition of the general Abelian group, making use of the fruitful conception of the " compounds
Review Sheet for the Final
 Review Sheet for the Final Math 6-4 4 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence
Review Sheet for the Final Math 6-4 4 These problems are provided to help you study. The presence of a problem on this handout does not imply that there will be a similar problem on the test. And the absence
UNCLASSIFIED Reptoduced. if ike ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED
 . UNCLASSIFIED. 273207 Reptoduced if ike ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED NOTICE: When government or other drawings, specifications
. UNCLASSIFIED. 273207 Reptoduced if ike ARMED SERVICES TECHNICAL INFORMATION AGENCY ARLINGTON HALL STATION ARLINGTON 12, VIRGINIA UNCLASSIFIED NOTICE: When government or other drawings, specifications
ANALYTIC MAPPINGS BETWEEN ARBITRARY RIEMANN SURFACES 1 BY LEO SARIO. Communicated by John W. Green, July 10, 1962
 ANALYTIC MAPPINGS BETWEEN ARBITRARY RIEMANN SURFACES 1 BY LEO SARIO Communicated by John W. Green, July 10, 1962 1. The problem. L. Ahlfors [l] established the first and second main theorems for analytic
ANALYTIC MAPPINGS BETWEEN ARBITRARY RIEMANN SURFACES 1 BY LEO SARIO Communicated by John W. Green, July 10, 1962 1. The problem. L. Ahlfors [l] established the first and second main theorems for analytic
A PROOF OF THE GAUSS-BONNET THEOREM. Contents. 1. Introduction. 2. Regular Surfaces
 A PROOF OF THE GAUSS-BONNET THEOREM AARON HALPER Abstract. In this paper I will provide a proof of the Gauss-Bonnet Theorem. I will start by briefly explaining regular surfaces and move on to the first
A PROOF OF THE GAUSS-BONNET THEOREM AARON HALPER Abstract. In this paper I will provide a proof of the Gauss-Bonnet Theorem. I will start by briefly explaining regular surfaces and move on to the first
KENNETH F. ANDERSEN1. Df(y) = m{t: \f(t)\ > y} (y ^ 0)
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 40, Number 1, September 1973 ON V NORMS AND THE EQUIMEASURABILITY OF FUNCTIONS KENNETH F. ANDERSEN1 Abstract. For measurable functions f and g, necessary
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 40, Number 1, September 1973 ON V NORMS AND THE EQUIMEASURABILITY OF FUNCTIONS KENNETH F. ANDERSEN1 Abstract. For measurable functions f and g, necessary
Lecture III. Curvature Elasticity of Fluid Lipid Membranes. Helfrich s Approach
 Lecture III. Curvature Elasticity of Fluid Lipid Membranes. Helfrich s Approach Marina Voinova Department of Applied Physics, Chalmers University of Technology and Göteborg University, SE-412 96, Göteborg,
Lecture III. Curvature Elasticity of Fluid Lipid Membranes. Helfrich s Approach Marina Voinova Department of Applied Physics, Chalmers University of Technology and Göteborg University, SE-412 96, Göteborg,
7 Curvature of a connection
 [under construction] 7 Curvature of a connection 7.1 Theorema Egregium Consider the derivation equations for a hypersurface in R n+1. We are mostly interested in the case n = 2, but shall start from the
[under construction] 7 Curvature of a connection 7.1 Theorema Egregium Consider the derivation equations for a hypersurface in R n+1. We are mostly interested in the case n = 2, but shall start from the
Econometric modelling and forecasting of intraday electricity prices
 E y y Xv:1812.09081v1 [q-.st] 21 D 2018 M Nw Uvy Duu-E F Z Uvy Duu-E D 24, 2018 A I w w y ID 3 -P G Iy Cuu Ey M u. A uv u uy qu-uy u y. W u qu u-- vy - uy. T w u. F u v w G Iy Cuu Ey M y ID 3 -P vu. T
E y y Xv:1812.09081v1 [q-.st] 21 D 2018 M Nw Uvy Duu-E F Z Uvy Duu-E D 24, 2018 A I w w y ID 3 -P G Iy Cuu Ey M u. A uv u uy qu-uy u y. W u qu u-- vy - uy. T w u. F u v w G Iy Cuu Ey M y ID 3 -P vu. T
Grilled it ems are prepared over real mesquit e wood CREATE A COMBO STEAKS. Onion Brewski Sirloin * Our signature USDA Choice 12 oz. Sirloin.
 TT & L Gl v l q T l q TK v i f i ' i i T K L G ' T G!? Ti 10 (Pik 3) -F- L P ki - ik T ffl i zzll ik Fi Pikl x i f l $3 (li 2) i f i i i - i f i jlñ i 84 6 - f ki i Fi 6 T i ffl i 10 -i i fi & i i ffl
TT & L Gl v l q T l q TK v i f i ' i i T K L G ' T G!? Ti 10 (Pik 3) -F- L P ki - ik T ffl i zzll ik Fi Pikl x i f l $3 (li 2) i f i i i - i f i jlñ i 84 6 - f ki i Fi 6 T i ffl i 10 -i i fi & i i ffl
On Moore Graphs with Diameters 2 and 3
 .., A. J. Hoffman* R. R. Singleton On Moore Graphs with Diameters 2 and 3 Abstract: This note treats the existence of connected, undirected graphs homogeneous of degree d and of diameter k, having a number
.., A. J. Hoffman* R. R. Singleton On Moore Graphs with Diameters 2 and 3 Abstract: This note treats the existence of connected, undirected graphs homogeneous of degree d and of diameter k, having a number
Ninth Meeting, July KM, On the form in Polar co-ordinates of oertain expressions occurring in Elastic Solids and in Hydrodynamics.
 109 Ninth Meeting, July KM, 1885. A. J. G. BARCLAY, Esq., M.A., President, in thr Chair. On the form in Polar co-ordinates of oertain expressions occurring in Elastic Solids and in Hydrodynamics. By CHARLES
109 Ninth Meeting, July KM, 1885. A. J. G. BARCLAY, Esq., M.A., President, in thr Chair. On the form in Polar co-ordinates of oertain expressions occurring in Elastic Solids and in Hydrodynamics. By CHARLES
Artificial Intelligence & Neuro Cognitive Systems Fakultät für Informatik. Robot Dynamics. Dr.-Ing. John Nassour J.
 Artificial Intelligence & Neuro Cognitive Systems Fakultät für Informatik Robot Dynamics Dr.-Ing. John Nassour 25.1.218 J.Nassour 1 Introduction Dynamics concerns the motion of bodies Includes Kinematics
Artificial Intelligence & Neuro Cognitive Systems Fakultät für Informatik Robot Dynamics Dr.-Ing. John Nassour 25.1.218 J.Nassour 1 Introduction Dynamics concerns the motion of bodies Includes Kinematics
NOTE ON GREEN'S THEOREM.
 1915.] NOTE ON GREEN'S THEOREM. 17 NOTE ON GREEN'S THEOREM. BY MR. C. A. EPPERSON. (Read before the American Mathematical Society April 24, 1915.) 1. Introduction, We wish in this paper to extend Green's
1915.] NOTE ON GREEN'S THEOREM. 17 NOTE ON GREEN'S THEOREM. BY MR. C. A. EPPERSON. (Read before the American Mathematical Society April 24, 1915.) 1. Introduction, We wish in this paper to extend Green's
Bäcklund transformations for fourth-order Painlevé-type equations
 Bäcklund transformations for fourth-order Painlevé-type equations A. H. Sakka 1 and S. R. Elshamy Department of Mathematics, Islamic University of Gaza P.O.Box 108, Rimae, Gaza, Palestine 1 e-mail: asakka@mail.iugaza.edu
Bäcklund transformations for fourth-order Painlevé-type equations A. H. Sakka 1 and S. R. Elshamy Department of Mathematics, Islamic University of Gaza P.O.Box 108, Rimae, Gaza, Palestine 1 e-mail: asakka@mail.iugaza.edu
THE CONTIGUOUS FUNCTION RELATIONS FOR pf q WITH APPLICATIONS TO BATEMAN'S ƒ»«and RICE'S # n (r, p, v)
 THE CONTIGUOUS FUNCTION RELATIONS FOR pf q WITH APPLICATIONS TO BATEMAN'S ƒ»«and RICE'S # n (r, p, v) EARL D. RAIN VILLE 1. Introduction. If in the generalized 1 hypergeometric function n. a a Q. A («OnWn
THE CONTIGUOUS FUNCTION RELATIONS FOR pf q WITH APPLICATIONS TO BATEMAN'S ƒ»«and RICE'S # n (r, p, v) EARL D. RAIN VILLE 1. Introduction. If in the generalized 1 hypergeometric function n. a a Q. A («OnWn
Minimal timelike surfaces in a certain homogeneous Lorentzian 3-manifold II
 Minimal timelike surfaces in a certain homogeneous Lorentzian 3-manifold II Sungwook Lee Abstract The 2-parameter family of certain homogeneous Lorentzian 3-manifolds which includes Minkowski 3-space and
Minimal timelike surfaces in a certain homogeneous Lorentzian 3-manifold II Sungwook Lee Abstract The 2-parameter family of certain homogeneous Lorentzian 3-manifolds which includes Minkowski 3-space and
ALGEBRAS AND THEIR ARITHMETICS*
 1924.] ALGEBRAS AND THEIR ARITHMETICS 247 ALGEBRAS AND THEIR ARITHMETICS* BY L. E. DICKSON 1. Introduction. Beginning with Hamilton's discovery of quaternions eighty years ago, there has been a widespread
1924.] ALGEBRAS AND THEIR ARITHMETICS 247 ALGEBRAS AND THEIR ARITHMETICS* BY L. E. DICKSON 1. Introduction. Beginning with Hamilton's discovery of quaternions eighty years ago, there has been a widespread
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
Thermodynamic Variables and Relations
 MME 231: Lecture 10 Thermodynamic Variables and Relations A. K. M. B. Rashid Professor, Department of MME BUET, Dhaka Today s Topics Thermodynamic relations derived from the Laws of Thermodynamics Definitions
MME 231: Lecture 10 Thermodynamic Variables and Relations A. K. M. B. Rashid Professor, Department of MME BUET, Dhaka Today s Topics Thermodynamic relations derived from the Laws of Thermodynamics Definitions
DEFINITION IN TERMS OF ORDER ALONE IN THE LINEAR CONTINUUM AND IN WELL-ORDERED SETS*
 DEFINITION IN TERMS OF ORDER ALONE IN THE LINEAR CONTINUUM AND IN WELL-ORDERED SETS* BY OSWALD VEBLEN First definition of the continuum. A linear continuum is a set of elements { P} which we may call points,
DEFINITION IN TERMS OF ORDER ALONE IN THE LINEAR CONTINUUM AND IN WELL-ORDERED SETS* BY OSWALD VEBLEN First definition of the continuum. A linear continuum is a set of elements { P} which we may call points,
ASYMPTOTIC DISTRIBUTION OF THE MAXIMUM CUMULATIVE SUM OF INDEPENDENT RANDOM VARIABLES
 ASYMPTOTIC DISTRIBUTION OF THE MAXIMUM CUMULATIVE SUM OF INDEPENDENT RANDOM VARIABLES KAI LAI CHUNG The limiting distribution of the maximum cumulative sum 1 of a sequence of independent random variables
ASYMPTOTIC DISTRIBUTION OF THE MAXIMUM CUMULATIVE SUM OF INDEPENDENT RANDOM VARIABLES KAI LAI CHUNG The limiting distribution of the maximum cumulative sum 1 of a sequence of independent random variables
Boundary Conditions in Fluid Mechanics
 Boundary Conditions in Fluid Mechanics R. Shankar Subramanian Department of Chemical and Biomolecular Engineering Clarkson University The governing equations for the velocity and pressure fields are partial
Boundary Conditions in Fluid Mechanics R. Shankar Subramanian Department of Chemical and Biomolecular Engineering Clarkson University The governing equations for the velocity and pressure fields are partial
TRANSFINITE RATIONALS
 TRANSFINITE RATIONALS JOHN M. H. OLMSTED The standard method of extending a system with an operation to a system with the operation and its inverse depends heavily on the law of cancellation: ab=ac implies
TRANSFINITE RATIONALS JOHN M. H. OLMSTED The standard method of extending a system with an operation to a system with the operation and its inverse depends heavily on the law of cancellation: ab=ac implies
(x 1, y 1 ) = (x 2, y 2 ) if and only if x 1 = x 2 and y 1 = y 2.
 1. Complex numbers A complex number z is defined as an ordered pair z = (x, y), where x and y are a pair of real numbers. In usual notation, we write z = x + iy, where i is a symbol. The operations of
1. Complex numbers A complex number z is defined as an ordered pair z = (x, y), where x and y are a pair of real numbers. In usual notation, we write z = x + iy, where i is a symbol. The operations of
5.3 Surface Theory with Differential Forms
 5.3 Surface Theory with Differential Forms 1 Differential forms on R n, Click here to see more details Differential forms provide an approach to multivariable calculus (Click here to see more detailes)
5.3 Surface Theory with Differential Forms 1 Differential forms on R n, Click here to see more details Differential forms provide an approach to multivariable calculus (Click here to see more detailes)
surface area per unit time is w(x, t). Derive the partial differential
 1.2 Conduction of Heat in One-Dimension 11 1.2.4. Derive the diffusion equation for a chemical pollutant. (a) Consider the total amount of the chemical in a thin region between x and x + Ax. (b) Consider
1.2 Conduction of Heat in One-Dimension 11 1.2.4. Derive the diffusion equation for a chemical pollutant. (a) Consider the total amount of the chemical in a thin region between x and x + Ax. (b) Consider
arxiv: v1 [math.dg] 1 Jul 2014
![arxiv: v1 [math.dg] 1 Jul 2014 arxiv: v1 [math.dg] 1 Jul 2014](/thumbs/92/108978689.jpg) Constrained matrix Li-Yau-Hamilton estimates on Kähler manifolds arxiv:1407.0099v1 [math.dg] 1 Jul 014 Xin-An Ren Sha Yao Li-Ju Shen Guang-Ying Zhang Department of Mathematics, China University of Mining
Constrained matrix Li-Yau-Hamilton estimates on Kähler manifolds arxiv:1407.0099v1 [math.dg] 1 Jul 014 Xin-An Ren Sha Yao Li-Ju Shen Guang-Ying Zhang Department of Mathematics, China University of Mining
Dirac Operator. Göttingen Mathematical Institute. Paul Baum Penn State 6 February, 2017
 Dirac Operator Göttingen Mathematical Institute Paul Baum Penn State 6 February, 2017 Five lectures: 1. Dirac operator 2. Atiyah-Singer revisited 3. What is K-homology? 4. The Riemann-Roch theorem 5. K-theory
Dirac Operator Göttingen Mathematical Institute Paul Baum Penn State 6 February, 2017 Five lectures: 1. Dirac operator 2. Atiyah-Singer revisited 3. What is K-homology? 4. The Riemann-Roch theorem 5. K-theory
ν(u, v) = N(u, v) G(r(u, v)) E r(u,v) 3.
 5. The Gauss Curvature Beyond doubt, the notion of Gauss curvature is of paramount importance in differential geometry. Recall two lessons we have learned so far about this notion: first, the presence
5. The Gauss Curvature Beyond doubt, the notion of Gauss curvature is of paramount importance in differential geometry. Recall two lessons we have learned so far about this notion: first, the presence
PLANAR KINETICS OF A RIGID BODY FORCE AND ACCELERATION
 PLANAR KINETICS OF A RIGID BODY FORCE AND ACCELERATION I. Moment of Inertia: Since a body has a definite size and shape, an applied nonconcurrent force system may cause the body to both translate and rotate.
PLANAR KINETICS OF A RIGID BODY FORCE AND ACCELERATION I. Moment of Inertia: Since a body has a definite size and shape, an applied nonconcurrent force system may cause the body to both translate and rotate.
A characterisation of eccentric sequences of maximal outerplanar graphs
 AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 58(3) (2014), Pages 376 391 A characterisation of eccentric sequences of maximal outerplanar graphs P. Dankelmann Department of Mathematics University of Johannesburg
AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 58(3) (2014), Pages 376 391 A characterisation of eccentric sequences of maximal outerplanar graphs P. Dankelmann Department of Mathematics University of Johannesburg
PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2)
 PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2) We will limit our study of planar kinetics to rigid bodies that are symmetric with respect to a fixed reference plane. As discussed in Chapter 16, when
PLANAR KINETIC EQUATIONS OF MOTION (Section 17.2) We will limit our study of planar kinetics to rigid bodies that are symmetric with respect to a fixed reference plane. As discussed in Chapter 16, when
SOME APPLICATIONS H. F. BLICHFELDT
 A NEW PRINCIPLE THE GEOMETRY OF NUMBERS, WITH SOME APPLICATIONS BY H. F. BLICHFELDT 1. Minkowski has discovered a geometrical principle which he applied with success to certain important problems in the
A NEW PRINCIPLE THE GEOMETRY OF NUMBERS, WITH SOME APPLICATIONS BY H. F. BLICHFELDT 1. Minkowski has discovered a geometrical principle which he applied with success to certain important problems in the
The First Fundamental Form
 The First Fundamental Form Outline 1. Bilinear Forms Let V be a vector space. A bilinear form on V is a function V V R that is linear in each variable separately. That is,, is bilinear if αu + β v, w αu,
The First Fundamental Form Outline 1. Bilinear Forms Let V be a vector space. A bilinear form on V is a function V V R that is linear in each variable separately. That is,, is bilinear if αu + β v, w αu,
Exercise 1 (Formula for connection 1-forms) Using the first structure equation, show that
 1 Stokes s Theorem Let D R 2 be a connected compact smooth domain, so that D is a smooth embedded circle. Given a smooth function f : D R, define fdx dy fdxdy, D where the left-hand side is the integral
1 Stokes s Theorem Let D R 2 be a connected compact smooth domain, so that D is a smooth embedded circle. Given a smooth function f : D R, define fdx dy fdxdy, D where the left-hand side is the integral
CHAPTER 5. Higher Order Linear ODE'S
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 2 A COLLECTION OF HANDOUTS ON SCALAR LINEAR ORDINARY
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 2 A COLLECTION OF HANDOUTS ON SCALAR LINEAR ORDINARY
Principles of Spherical Trigonometry Drawn from the Method of the Maxima and Minima
 TRANSLATOR S NOTE In preparing this translation my assumption has been that the interested audience likely consists of both mathematicians and historians of mathematics. To satisfy the latter I have attempted
TRANSLATOR S NOTE In preparing this translation my assumption has been that the interested audience likely consists of both mathematicians and historians of mathematics. To satisfy the latter I have attempted
Gradient, Divergence and Curl in Curvilinear Coordinates
 Gradient, Divergence and Curl in Curvilinear Coordinates Although cartesian orthogonal coordinates are very intuitive and easy to use, it is often found more convenient to work with other coordinate systems.
Gradient, Divergence and Curl in Curvilinear Coordinates Although cartesian orthogonal coordinates are very intuitive and easy to use, it is often found more convenient to work with other coordinate systems.
Modern Cosmology Solutions 2: Relativistic Gravity
 Modern Cosmology Solutions 2: Relativistic Gravity Max Camenzind October 0, 2010 1. Special Relativity Relativity principle Lecture Notes. Doppler shift and the stellar aberration of light given on my
Modern Cosmology Solutions 2: Relativistic Gravity Max Camenzind October 0, 2010 1. Special Relativity Relativity principle Lecture Notes. Doppler shift and the stellar aberration of light given on my
1 Differentiable manifolds and smooth maps. (Solutions)
 1 Differentiable manifolds and smooth maps Solutions Last updated: February 16 2012 Problem 1 a The projection maps a point P x y S 1 to the point P u 0 R 2 the intersection of the line NP with the x-axis
1 Differentiable manifolds and smooth maps Solutions Last updated: February 16 2012 Problem 1 a The projection maps a point P x y S 1 to the point P u 0 R 2 the intersection of the line NP with the x-axis
