GENERALIZED LIMITS IN GENERAL ANALYSIS* SECOND PAPER
|
|
|
- Millicent Scott
- 5 years ago
- Views:
Transcription
1 GENERALIZED LIMITS IN GENERAL ANALYSIS* SECOND PAPER BY CHARLES N. MOORE In a previous paper of the same titlet I have developed the fundamental principles of a general theory which includes as particular instances the theories of Cesàro and Holder summability of divergent series and divergent integrals. I further made use of these fundamental principles to prove a general theorem which includes as special cases several important theorems in the above mentioned special theories. In the present paper the general theory referred to above is extended to the case of multiple limits and the theorem mentioned is likewise generalized. The theorem thus obtained includes as special cases the extension to multiple series of the Knopp-Schnee-Ford theorem^ on the equivalence of Cesàro and Holder summability for divergent series, the extension to multiple integrals of the analogous theorem of Landauf for the case of divergent integrals, and the extension to partial derivatives of a corresponding theorem with regard to the equivalence of certain generalized derivatives. Once the principles of the theory are set forth, the proof of this general theorem is fully as simple as the proofs of any of the special theorems would be. Thus we have exhibited the greater power of the methods of General Analysis as compared with the methods of classical analysis. The basis of our general theory may be indicated as follows : («;$»;%;...; $m;@t;@,;...; ;»*.«.«-.* «; $,««,.,,..,.to«( = 1,2,...,»»); g.on@ s..., tosi (» = 1,2,...,m); Ron,,,,..., mtoä. &on@,,,,...,»to«. «,(»»). #» *»«.!<»««**. (»' = 1,2,...,m); ^ongto^onçtos) * Presented to the Society April 14,1922. t These Transactions, vol. 24 (1922), pp For references to the literature dealing with the special theorems referred to, see Paper I
2 460 C. N. MOORE [October where 2Í = [a] denotes the class of all real numbers a, 5f3 = [pi] denotes a class of elements pi (i = 1, 2,..., m), and» = [a ] denotes a class of sets a of elements^ of the range $& ( = 1, 2,..., wi); = [y], C = [^ ] (* = 1,2,..., w), &eee[op ]( = 1,2,...,m), = [?], and g = [99] are (2»w4-3) classes of functions, y, rfu,..., t im), <pm,..., op(m>, t, and op respectively on!, to 21 (we consider only single-valued functions); op<m) is a special function of the class $; «7is a functional operation turning a function of the class into a function of the class or a function of the class & into a function of the class fa, denoted by JiY or Jii respectively; and J is a functional operation turning a function of the class into a function of the class q or a function of the class into a function of the class %, denoted by Jy or Ji respectively. In order to show the relationship of our general theorem to the special cases of it to which we have referred, we will indicate here what the general basis reduces to in the particular instances in and IV. «ß1» = [all n, = 1, 2, 3,...] ( =1,2,..., = [o"n( = (1,2,..., ni)\m] ( =1,2,..., m); = & = ft = = g = [all y,,», y,,, yons,...,,.^«] (* = 1, 2,... m); <P0m) (o«., <Jn., ffnj = «i nj «m (n,-; t = 1, 2,..., wi); A<=n< (di ö)(oml,-on ) = 2»(a»,,..., afc,..., an ) k,=n, (n<; *= 1, 2,..., m; 0 *= y, f ); *««=bk (^0)(a«,,..., a»j = J 2 Vi"*,,..., OkJ; fc,=i km=i (m; i = 1, 2,..., m; 0 = y, i ). ^ = [allaf>0] (i = 1,2,...,m);. = [a = (all^suchthato^a^a^ (at.^o; =1,2,..., m)]; = [all functions that are finite in any finite region (0<a; < a ; i 1, 2,..., m) and are integrable (Lebesgue) with respect
3 1923] GENERALIZED LIMITS 461 to each of the variables xi (i = 1,., m) on every finite interval (0 < xí <j Oí; i = 1,..., m)] ; r t. =. ail»/(*' = J y(xx,xt,...,xi,...,xm)dxi (xi>0; i= 1,..., m); o I* B?< = allç>(i) = I ^fo,;*:»,...,a*,...,xm)dxi (xi>0;i~l,...,m); > = allr/ = I I y(ici,..., Xm) (xi>0; i = 1,..., m); 0 0 Ja* -?» Il l(xi, -, xm) 0 0 (xí>0; i 1,..., mi); (q>0m))(aa,,..., oaj a* a* am (aï, * 1,..., m); r' W9) (<*a>,..., oaj = \ ddxi (oí; i = 1,..., m; 6 = y, t/<»); o a, a (Jö) (oa,,..., aaj = I I 8 (at; i = 1,..., m; $== y, ç). With regard to each of the classes i,»,..., m we make definitions analogous to those made for the class in Paper I, and we further postulate analogous properties. These properties will be referred to by the same letters as in the previous paper with a subscript or index attached to indicate the particular class to which reference is made. When any two functions 9, to SI are regarded as functions of a single set a, the other sets being held fixed, we define the notation (Df 6) (a<«..., a^) = a (a(1),..., a<m>)
4 462 C. N. MOORE [October in a manner entirely analogous to that in which the notation(z>0) (a) = a (a) was defined in Paper I. When functions of the class are regarded as functions of a single set ff(i), the other sets being held fixed, we postulate for them the properties of class of Paper 1, these properties to be referred to by the same letter with suitable index or subscript. Analogous properties for the classes ö and %, designated in similar fashion, are also postulated. Furthermore for the classes j and 3, regarded as functions of the set a alone, we postulate the properties of classes > and % of Paper I and indicate them in like manner. When the functions of classes and that are involved in the operation Ji are regarded as functions of the set a alone, we require Ji to have all the properties required of J in Paper I, which properties we shall designate by the same symbols with subscript or index i. We further postulate that any of the operations Jx, J2,..., Jm is interchangeable with any other of the set, which property we designate as (Z). We also postulate as to the relationship between J and Ji, J2,..., Jm that (N) ijv) (<*», -, a«) = ijx(j2 ( JmV)...)) (aw..., o«w). With regard to the special function xpqm) (<ß-\..., < m)) we postulate that ix) xpf» (a'«,...., a<"»)) = op0 (a«) xp0 (o»). op0 (a<»'>), where xp0 (<*(i)) as function of a, for i = 1, 2,..., m, is the same function as xp0 (a) of Paper I as function of a. We also postulate for the class that (<7i op) (a(1),..., a(m)), for i = 1, 2,..., m, is of the class g, which property we designate as (K). For the sake of brevity we shall agree to represent, in all cases where no loss of clearness is involved, the set of elements p(1\..., p(m) by the single symbol p, the set of classes $(1),..., 5ß(OT) by 5ß, the set of classes é(1),..., (TO) by, and the set of sets a(1),..., a("*> by a. Analogous to the definition of the notation lim,, 6 (a) = a in Paper I, we define the corresponding notation in the case that a represents the set of sets o(1),..., a(m) to mean that corresponding to every positive e there exist sets a<,..., a<m> such that for sets 0(0 > a( ) ( = j f 2,..., m) we have 10(a) a\ <: e. We then postulate as to the class the property (75) defined by (7J) If lim,, t (a) exists and is equal to a, then \i (a) < ai (a).
5 1923] GENERALIZED LIMITS 463 If we also for the sake of brevity agree to represent a group of properties such as Rx, B2,..., Bm by the single letter B, we may indicate the foundation of our theory as follows: V _ /or Wi ffxvar. (uonstom.lp c- on S to SI. L. P, s2j / 1 \ 2^ = \^,V; ;,Vi ' (l=l,...,m); <y,ontstow.l(pfs( ) C(â, / _. N. ç-onstosi.ipsob O t \* I, m ), <y cyonstow.lpsbcák (m)%.x û ; <Po ; j<m<stof>l.on6ttofil.jií)ms>l( >I(/l (i = 1 m)- ron to$.on$ tos.j?\ We now set (1) «C>(«) - <Pon( Wï<Pon(*2))---<Pon( (m)), where q>^ (a ), as function of a, is the same function as g>0n (a), as function of a, defined by equation (3) of Paper I. We are then ready to define the two generalized limits with which we shall be concerned. Given any function i (a), we set (2) (cnv)( )=-Mr^(Jnv)(<>) (»). (3) (Mi)(o)=-J^(JV)(a), (4) (Hni)(a)=(M*i)(o) (n). If for a fixed n lima(cn^) (a) exists, we define this limit as the generalized limit of type (Cn) for r (a). If \\ma(hnn) (a) exists, we define this limit as the generalized limit of type (Hn) for i\ (a).
6 464 C. N. MOORE [October Before proceeding to the proof of the equivalence theorem we introduce the following notations: (5) (Miy)io) = [l/opo(a )](jfy)(o) (i = l,...,m), (6) (C**"--«*f)(o) = yow(^.!.)^\a(^))^---(ji+^)---)(ct) (n)' (7) y(0(a) = 9>o(o(i))9'o(a<í))---ípo(ow_2)y(o) («>2; =l,...,m), ;f (o) = 9>o(o(i)) r( ), if 00 = y(a) ( = 1,..., m), where a, a,... are defined with regard to o in the same manner as di, Ou,... with regard to a in Paper I; (8) (5 y)(o)= ({^-Mi + j -E)y]jia) (n), (9) (S«1'2" öy)(o) = (fif(sf--(sfy)" ))(«) (n; =l,...,m), (10) (Ä y)(a) = (tf(rf'--(^'''))w («), (11) (r *y)(o) = tty(a)- ^J] ijir(»)i ) in; i= 1,..., m). We are now ready for the proof of our theorem ; we begin by proving some lemmas. LEMMA 1. If we define Sn as in (10), we have the identity (12) (Sn icn n)) (a) = (M(Cn-x V)) (a) in). We have from Lemma 1 of Paper I and the interchangeability of the various operations involved
7 1923] GENERALIZED LIMITS 465 (Sn(CnV)) (a) = (Si1'2.,*-1) (<#'.m-" (ÄS* «tf0 *)))) (*) - (-i#2. W-1) (eg»«--» (Jfm (CÍA i?)))) (o) - (ä2*-- (a«-2.m-2) ( ir» (dr" (if«(cía *)))))) (a) = ( ga-.«*-» (^2'-m-2) (üfm_i (Mm (&ZÏ'm) n))))) («) = [Ux (Mt (Mn (Cnr-i n)) )) (a) = (M(C-i n)) ( ). Our lemma is therefore established. We define 9 in a manner analogous to the definition of y in (7). We also set fon-i(a) =?>on(a ). We then prove LEMMA 2. If\imaq>(a) exists and is equal to a and \<p(o)\ < ax for every a, then limelfon (a )]-1 (J( qp ) (a) will exist and be equal to aln and we shall have \[<Pon(aW)]_1 (Ji <) ( )l < < (O,», * = 1,... ( «). Given a positive e, we choose oé so that a (e/4)<?>(o)< a + (e/4) for a^oj.* We have [^( )^(Ji»i?)(9) (13) = [^ (a )]-1 («7; y ) (a»,..., a ',..., <»<*>)] + [^ (a )]"1 [(J, 9><?) (*)-(/, <») ( (1),..., of,..., a<"«)]. * It should be remembered throughout that «is an abbreviation for («r*1*, <r,..., a ), and that <r>«j is an abbreviation for the set of relationships <r(x)>a(x),...,
8 466 c- N- MOORE [October Analogous to (18) of Paper I we have the relationship (14) mpffx«)»^^^«'-.*)»])^) Making use of (14), and postulates Mf and If, on the right hand side of (13) lies between we see that the second term %\ 4/L Von( (,,)J n\ 4/[ foni W)J From (IV) of Paper I it follows that for a proper choice of q' > aj the above expression differs from a In by a quantity that is less in absolute value than \e for all a> a". The first term on the right side of (13) is seen from (14), Mi%\ and Ij to be less in absolute value than n <p0ni li>) From IV of Paper I it follows that we can choose a"' > <s'e so as to make this expression less in absolute value than e for a > o'e". If now we choose for oe the greater of ai' and a'", it follows from (13) that for a^oe, K (o )]"1(Ji V«) (o)- («/») I < *, and the first part of our conclusion is established. Making use of (14) and M, we have «i n <[<Pon( ii))]-1(ji<p( >)i )<-%-> which establishes the second part of our conclusion.
9 1923] GENERALIZED LIMITS 467 LEMMA 3. If \\ma (p(o) exists and is equal to a, and \ q> (a) <c a^ for every a, thenlim(r(8nf)(o) will exist and be equal to a and we shall have (Sn f) (i) < at for every a. By virtue of definition (10) the operation 8n is equivalent to a succession of operations Sn for i = 1, 2,..., m. It follows from Lemma 2> for the case n = 1, that if a function (p(a) remains finite for all a and approaches a limit as to a, the same is true for the function resulting from the operation Sn applied to <p (a). Hence by a succession of m applications of Lemma 2, we obtain the conclusion of the present lemma. We now set (15) (p'i(o) = (&%)(<») (»-1,2,...,«). We then prove LEMMA 4. If for any i lim^op^o) exists and is equal to a, and f'i(a)\ < Oi for every a, then \ima(p(a) will exist and be equal to a, and we shall have 19( ) I < <h for every a. By a procedure analogous to that used in the proof of Lemma 3 of Paper I we may transform equation (15) into the form (16) (p(a) = (2 >i)( ) (*>2; t = l,...,m), where T is defined by equation (11). Our lemma then follows from Lemma 2 for n > 2. For n = 1 it is an obvious consequence of (15) and (8). LEMMA 5. If lim,, (Sn f) (a) exists and is equal to a and \(Sn f) (a)\ <c ax for every a, then lim^ gp(a) will exist and be equal to a and we shall have \f(a)\ < at for every a. Making use of the definition of Sn given in equation (10), we see that this lemma may be established by successive applications of Lemma 4. Noting that Sn and M are interchangeable operations, we have from successive applications of (12), in a manner analogous to the corresponding reductions in Paper I by means of equation (14) of that paper, (17) (Hn r ) (*) - U(&. (St (Sn-! (Sn (Cn *?))) ))) (a) («).
10 468 O. N. MOORE We are now ready to prove our theorem: THEOREM. If lima icn r ) (a) exists and is equal to a, then lim,, ihn i ) (a) will exist and be equal to a, and conversely. From (17), (7J), and successive applications of Lemma 3, we obtain the result : If there exists limff (Cn i ) (a) = a, then there exists \va\ (7J i ) (a) = a (»). From (17), (7J), and successive applications of Lemma 5, we obtain the result: If there exists limff(7j»^)(a) = a, then there exists lim0.(c»^)(a) = a(n). Our theorem is therefore established. University of Cincinnati, Cincinnati, Ohio.
T i t l e o f t h e w o r k : L a M a r e a Y o k o h a m a. A r t i s t : M a r i a n o P e n s o t t i ( P l a y w r i g h t, D i r e c t o r )
 v e r. E N G O u t l i n e T i t l e o f t h e w o r k : L a M a r e a Y o k o h a m a A r t i s t : M a r i a n o P e n s o t t i ( P l a y w r i g h t, D i r e c t o r ) C o n t e n t s : T h i s w o
v e r. E N G O u t l i n e T i t l e o f t h e w o r k : L a M a r e a Y o k o h a m a A r t i s t : M a r i a n o P e n s o t t i ( P l a y w r i g h t, D i r e c t o r ) C o n t e n t s : T h i s w o
A CONVEXITY CONDITION IN BANACH SPACES AND THE STRONG LAW OF LARGE NUMBERS1
 A CONVEXITY CONDITION IN BANACH SPACES AND THE STRONG LAW OF LARGE NUMBERS1 ANATOLE BECK Introduction. The strong law of large numbers can be shown under certain hypotheses for random variables which take
A CONVEXITY CONDITION IN BANACH SPACES AND THE STRONG LAW OF LARGE NUMBERS1 ANATOLE BECK Introduction. The strong law of large numbers can be shown under certain hypotheses for random variables which take
ASYMPTOTIC DISTRIBUTION OF THE MAXIMUM CUMULATIVE SUM OF INDEPENDENT RANDOM VARIABLES
 ASYMPTOTIC DISTRIBUTION OF THE MAXIMUM CUMULATIVE SUM OF INDEPENDENT RANDOM VARIABLES KAI LAI CHUNG The limiting distribution of the maximum cumulative sum 1 of a sequence of independent random variables
ASYMPTOTIC DISTRIBUTION OF THE MAXIMUM CUMULATIVE SUM OF INDEPENDENT RANDOM VARIABLES KAI LAI CHUNG The limiting distribution of the maximum cumulative sum 1 of a sequence of independent random variables
h : sh +i F J a n W i m +i F D eh, 1 ; 5 i A cl m i n i sh» si N «q a : 1? ek ser P t r \. e a & im a n alaa p ( M Scanned by CamScanner
 m m i s t r * j i ega>x I Bi 5 n ì r s w «s m I L nk r n A F o n n l 5 o 5 i n l D eh 1 ; 5 i A cl m i n i sh» si N «q a : 1? { D v i H R o s c q \ l o o m ( t 9 8 6) im a n alaa p ( M n h k Em l A ma
m m i s t r * j i ega>x I Bi 5 n ì r s w «s m I L nk r n A F o n n l 5 o 5 i n l D eh 1 ; 5 i A cl m i n i sh» si N «q a : 1? { D v i H R o s c q \ l o o m ( t 9 8 6) im a n alaa p ( M n h k Em l A ma
(4) cn = f f(x)ux)dx (n = 0, 1, 2, ).
 ON APPROXIMATION BY WALSH FUNCTIONS SHIGEKI yano Let
ON APPROXIMATION BY WALSH FUNCTIONS SHIGEKI yano Let
An Example file... log.txt
 # ' ' Start of fie & %$ " 1 - : 5? ;., B - ( * * B - ( * * F I / 0. )- +, * ( ) 8 8 7 /. 6 )- +, 5 5 3 2( 7 7 +, 6 6 9( 3 5( ) 7-0 +, => - +< ( ) )- +, 7 / +, 5 9 (. 6 )- 0 * D>. C )- +, (A :, C 0 )- +,
# ' ' Start of fie & %$ " 1 - : 5? ;., B - ( * * B - ( * * F I / 0. )- +, * ( ) 8 8 7 /. 6 )- +, 5 5 3 2( 7 7 +, 6 6 9( 3 5( ) 7-0 +, => - +< ( ) )- +, 7 / +, 5 9 (. 6 )- 0 * D>. C )- +, (A :, C 0 )- +,
UNIQUE FJORDS AND THE ROYAL CAPITALS UNIQUE FJORDS & THE NORTH CAPE & UNIQUE NORTHERN CAPITALS
 Q J j,. Y j, q.. Q J & j,. & x x. Q x q. ø. 2019 :. q - j Q J & 11 Y j,.. j,, q j q. : 10 x. 3 x - 1..,,. 1-10 ( ). / 2-10. : 02-06.19-12.06.19 23.06.19-03.07.19 30.06.19-10.07.19 07.07.19-17.07.19 14.07.19-24.07.19
Q J j,. Y j, q.. Q J & j,. & x x. Q x q. ø. 2019 :. q - j Q J & 11 Y j,.. j,, q j q. : 10 x. 3 x - 1..,,. 1-10 ( ). / 2-10. : 02-06.19-12.06.19 23.06.19-03.07.19 30.06.19-10.07.19 07.07.19-17.07.19 14.07.19-24.07.19
$%! & (, -3 / 0 4, 5 6/ 6 +7, 6 8 9/ 5 :/ 5 A BDC EF G H I EJ KL N G H I. ] ^ _ ` _ ^ a b=c o e f p a q i h f i a j k e i l _ ^ m=c n ^
![$%! & (, -3 / 0 4, 5 6/ 6 +7, 6 8 9/ 5 :/ 5 A BDC EF G H I EJ KL N G H I. ] ^ _ ` _ ^ a b=c o e f p a q i h f i a j k e i l _ ^ m=c n ^ $%! & (, -3 / 0 4, 5 6/ 6 +7, 6 8 9/ 5 :/ 5 A BDC EF G H I EJ KL N G H I. ] ^ _ ` _ ^ a b=c o e f p a q i h f i a j k e i l _ ^ m=c n ^](/thumbs/92/108125918.jpg) ! #" $%! & ' ( ) ) (, -. / ( 0 1#2 ' ( ) ) (, -3 / 0 4, 5 6/ 6 7, 6 8 9/ 5 :/ 5 ;=? @ A BDC EF G H I EJ KL M @C N G H I OPQ ;=R F L EI E G H A S T U S V@C N G H IDW G Q G XYU Z A [ H R C \ G ] ^ _ `
! #" $%! & ' ( ) ) (, -. / ( 0 1#2 ' ( ) ) (, -3 / 0 4, 5 6/ 6 7, 6 8 9/ 5 :/ 5 ;=? @ A BDC EF G H I EJ KL M @C N G H I OPQ ;=R F L EI E G H A S T U S V@C N G H IDW G Q G XYU Z A [ H R C \ G ] ^ _ `
GENERALIZATIONS OF MIDPOINT RULES
 ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 1, Number 4, Fall 1971 GENERALIZATIONS OF MIDPOINT RULES ROBERT E. BARNHILL ABSTRACT. A midpoint rule proposed by Jagermann and improved upon by Stetter is
ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 1, Number 4, Fall 1971 GENERALIZATIONS OF MIDPOINT RULES ROBERT E. BARNHILL ABSTRACT. A midpoint rule proposed by Jagermann and improved upon by Stetter is
ON THE EQUATION Xa=7X+/3 OVER AN ALGEBRAIC DIVISION RING
 ON THE EQUATION Xa=7X+/3 OVER AN ALGEBRAIC DIVISION RING R. E. JOHNSON 1. Introduction and notation. The main purpose of this paper is to give necessary and sufficient conditions in order that the equation
ON THE EQUATION Xa=7X+/3 OVER AN ALGEBRAIC DIVISION RING R. E. JOHNSON 1. Introduction and notation. The main purpose of this paper is to give necessary and sufficient conditions in order that the equation
ON THE HARMONIC SUMMABILITY OF DOUBLE FOURIER SERIES P. L. SHARMA
 ON THE HARMONIC SUMMABILITY OF DOUBLE FOURIER SERIES P. L. SHARMA 1. Suppose that the function f(u, v) is integrable in the sense of Lebesgue, over the square ( ir, ir; it, it) and is periodic with period
ON THE HARMONIC SUMMABILITY OF DOUBLE FOURIER SERIES P. L. SHARMA 1. Suppose that the function f(u, v) is integrable in the sense of Lebesgue, over the square ( ir, ir; it, it) and is periodic with period
I ƒii - [ Jj ƒ(*) \'dzj'.
 I93 2 -] COMPACTNESS OF THE SPACE L p 79 ON THE COMPACTNESS OF THE SPACE L p BY J. D. TAMARKIN* 1. Introduction, Let R n be the ^-dimensional euclidean space and L p (p>l) the function-space consisting
I93 2 -] COMPACTNESS OF THE SPACE L p 79 ON THE COMPACTNESS OF THE SPACE L p BY J. D. TAMARKIN* 1. Introduction, Let R n be the ^-dimensional euclidean space and L p (p>l) the function-space consisting
K E L LY T H O M P S O N
 K E L LY T H O M P S O N S E A O LO G Y C R E ATO R, F O U N D E R, A N D PA R T N E R K e l l y T h o m p s o n i s t h e c r e a t o r, f o u n d e r, a n d p a r t n e r o f S e a o l o g y, a n e x
K E L LY T H O M P S O N S E A O LO G Y C R E ATO R, F O U N D E R, A N D PA R T N E R K e l l y T h o m p s o n i s t h e c r e a t o r, f o u n d e r, a n d p a r t n e r o f S e a o l o g y, a n e x
ALGEBRAIC PROPERTIES OF SELF-ADJOINT SYSTEMS*
 ALGEBRAIC PROPERTIES OF SELF-ADJOINT SYSTEMS* BY DUNHAM JACKSON The general definition of adjoint systems of boundary conditions associated with ordinary linear differential equations was given by Birkhoff.t
ALGEBRAIC PROPERTIES OF SELF-ADJOINT SYSTEMS* BY DUNHAM JACKSON The general definition of adjoint systems of boundary conditions associated with ordinary linear differential equations was given by Birkhoff.t
necessita d'interrogare il cielo
 gigi nei necessia d'inegae i cie cic pe sax span s inuie a dispiegaa fma dea uce < affeandi ves i cen dea uce isnane " sienzi dei padi sie veic dei' anima 5 J i f H 5 f AL J) i ) L '3 J J "' U J J ö'
gigi nei necessia d'inegae i cie cic pe sax span s inuie a dispiegaa fma dea uce < affeandi ves i cen dea uce isnane " sienzi dei padi sie veic dei' anima 5 J i f H 5 f AL J) i ) L '3 J J "' U J J ö'
S U E K E AY S S H A R O N T IM B E R W IN D M A R T Z -PA U L L IN. Carlisle Franklin Springboro. Clearcreek TWP. Middletown. Turtlecreek TWP.
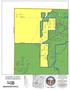 F R A N K L IN M A D IS O N S U E R O B E R T LE IC H T Y A LY C E C H A M B E R L A IN T W IN C R E E K M A R T Z -PA U L L IN C O R A O W E N M E A D O W L A R K W R E N N LA N T IS R E D R O B IN F
F R A N K L IN M A D IS O N S U E R O B E R T LE IC H T Y A LY C E C H A M B E R L A IN T W IN C R E E K M A R T Z -PA U L L IN C O R A O W E N M E A D O W L A R K W R E N N LA N T IS R E D R O B IN F
ETIKA V PROFESII PSYCHOLÓGA
 P r a ž s k á v y s o k á š k o l a p s y c h o s o c i á l n í c h s t u d i í ETIKA V PROFESII PSYCHOLÓGA N a t á l i a S l o b o d n í k o v á v e d ú c i p r á c e : P h D r. M a r t i n S t r o u
P r a ž s k á v y s o k á š k o l a p s y c h o s o c i á l n í c h s t u d i í ETIKA V PROFESII PSYCHOLÓGA N a t á l i a S l o b o d n í k o v á v e d ú c i p r á c e : P h D r. M a r t i n S t r o u
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
Lemma 8: Suppose the N by N matrix A has the following block upper triangular form:
 17 4 Determinants and the Inverse of a Square Matrix In this section, we are going to use our knowledge of determinants and their properties to derive an explicit formula for the inverse of a square matrix
17 4 Determinants and the Inverse of a Square Matrix In this section, we are going to use our knowledge of determinants and their properties to derive an explicit formula for the inverse of a square matrix
Introduction and Preliminaries
 Chapter 1 Introduction and Preliminaries This chapter serves two purposes. The first purpose is to prepare the readers for the more systematic development in later chapters of methods of real analysis
Chapter 1 Introduction and Preliminaries This chapter serves two purposes. The first purpose is to prepare the readers for the more systematic development in later chapters of methods of real analysis
ON THE SPACE OF INTEGRAL FUNCTIONS. IV
 ON THE SPACE OF INTEGRAL FUNCTIONS. IV V. GANAPATHY IYER 1. Introduction. We first recall the definitions, notations and some of the results in the previous papers [l; 2; 3].1 We denoted by V the class
ON THE SPACE OF INTEGRAL FUNCTIONS. IV V. GANAPATHY IYER 1. Introduction. We first recall the definitions, notations and some of the results in the previous papers [l; 2; 3].1 We denoted by V the class
Executive Committee and Officers ( )
 Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
Gifted and Talented International V o l u m e 2 4, N u m b e r 2, D e c e m b e r, 2 0 0 9. G i f t e d a n d T a l e n t e d I n t e r n a t i o n a2 l 4 ( 2), D e c e m b e r, 2 0 0 9. 1 T h e W o r
ON THE DENSITY OF SOME SEQUENCES OF INTEGERS P. ERDOS
 ON THE DENSITY OF SOME SEQUENCES OF INTEGERS P. ERDOS Let ai
ON THE DENSITY OF SOME SEQUENCES OF INTEGERS P. ERDOS Let ai
Chapter 3. Antimagic Gl'aphs
 Chapter 3 Antimagic Gl'aphs CHAPTER III ANTIMAGIC GRAPHS 3.1 Introduction In 1970 Kotzig and Rosa [81] defined the magic labeling of a graph G as a bijection f from VuE to {1,2,... IV u EI } such that
Chapter 3 Antimagic Gl'aphs CHAPTER III ANTIMAGIC GRAPHS 3.1 Introduction In 1970 Kotzig and Rosa [81] defined the magic labeling of a graph G as a bijection f from VuE to {1,2,... IV u EI } such that
NOTE ON GREEN'S THEOREM.
 1915.] NOTE ON GREEN'S THEOREM. 17 NOTE ON GREEN'S THEOREM. BY MR. C. A. EPPERSON. (Read before the American Mathematical Society April 24, 1915.) 1. Introduction, We wish in this paper to extend Green's
1915.] NOTE ON GREEN'S THEOREM. 17 NOTE ON GREEN'S THEOREM. BY MR. C. A. EPPERSON. (Read before the American Mathematical Society April 24, 1915.) 1. Introduction, We wish in this paper to extend Green's
ON DIVISION ALGEBRAS*
 ON DIVISION ALGEBRAS* BY J. H. M. WEDDERBURN 1. The object of this paper is to develop some of the simpler properties of division algebras, that is to say, linear associative algebras in which division
ON DIVISION ALGEBRAS* BY J. H. M. WEDDERBURN 1. The object of this paper is to develop some of the simpler properties of division algebras, that is to say, linear associative algebras in which division
ON THE GIBBS PHENOMENON FOR HARMONIC MEANS FU CHENG HSIANG. 1. Let a sequence of functions {fn(x)} converge to a function/(se)
 ON THE GIBBS PHENOMENON FOR HARMONIC MEANS FU CHENG HSIANG 1. Let a sequence of functions {fn(x)} converge to a function/(se) for x0
ON THE GIBBS PHENOMENON FOR HARMONIC MEANS FU CHENG HSIANG 1. Let a sequence of functions {fn(x)} converge to a function/(se) for x0
SOME TAÜBERIAN PROPERTIES OF HOLDER TRANSFORMATIONS AMNON JAKIMOVSKI1
 SOME TAÜBERIAN PROPERTIES OF HOLDER TRANSFORMATIONS AMNON JAKIMOVSKI1 1. Introduction. The result which follows was proved by me, recently, in [l],2 Theorem (9.2). If, for some o> 1, the sequence {sn},
SOME TAÜBERIAN PROPERTIES OF HOLDER TRANSFORMATIONS AMNON JAKIMOVSKI1 1. Introduction. The result which follows was proved by me, recently, in [l],2 Theorem (9.2). If, for some o> 1, the sequence {sn},
Lower Austria. The Big Travel Map. Big Travel Map of Lower Austria.
 v v v :,000, v v v v, v j, Z ö V v! ö +4/4/000 000 @ : / : v v V, V,,000 v v v v v v 08 V, v j?, v V v v v v v v,000, V v V, v V V vv /Z, v / v,, v v V, v x 6,000 v v 00,000 v, x v U v ( ) j v, x q J J
v v v :,000, v v v v, v j, Z ö V v! ö +4/4/000 000 @ : / : v v V, V,,000 v v v v v v 08 V, v j?, v V v v v v v v,000, V v V, v V V vv /Z, v / v,, v v V, v x 6,000 v v 00,000 v, x v U v ( ) j v, x q J J
FUNCTIONS THAT PRESERVE THE UNIFORM DISTRIBUTION OF SEQUENCES
 transactions of the american mathematical society Volume 307, Number 1, May 1988 FUNCTIONS THAT PRESERVE THE UNIFORM DISTRIBUTION OF SEQUENCES WILLIAM BOSCH ABSTRACT. In this paper, necessary and sufficient
transactions of the american mathematical society Volume 307, Number 1, May 1988 FUNCTIONS THAT PRESERVE THE UNIFORM DISTRIBUTION OF SEQUENCES WILLIAM BOSCH ABSTRACT. In this paper, necessary and sufficient
ON THE INTEGRATION OF UNBOUNDED FUNCTIONS*
 1932.] INTEGRATION OF UNBOUNDED FUNCTIONS 123 ON THE INTEGRATION OF UNBOUNDED FUNCTIONS* BY W. M. WHYBURN 1. Introduction. The author has shown f that F. Riesz' treatment of intégration} leads in every
1932.] INTEGRATION OF UNBOUNDED FUNCTIONS 123 ON THE INTEGRATION OF UNBOUNDED FUNCTIONS* BY W. M. WHYBURN 1. Introduction. The author has shown f that F. Riesz' treatment of intégration} leads in every
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
A CHARACTERIZATION OF INNER PRODUCT SPACES
 A CHARACTERIZATION OF INNER PRODUCT SPACES DAVID ALBERT SENECHALLE The well-known parallelogram law of Jordan and von Neumann [l] has been generalized in two different ways by M. M. Day [2] and E. R. Lorch
A CHARACTERIZATION OF INNER PRODUCT SPACES DAVID ALBERT SENECHALLE The well-known parallelogram law of Jordan and von Neumann [l] has been generalized in two different ways by M. M. Day [2] and E. R. Lorch
Chapter 4. Matrices and Matrix Rings
 Chapter 4 Matrices and Matrix Rings We first consider matrices in full generality, i.e., over an arbitrary ring R. However, after the first few pages, it will be assumed that R is commutative. The topics,
Chapter 4 Matrices and Matrix Rings We first consider matrices in full generality, i.e., over an arbitrary ring R. However, after the first few pages, it will be assumed that R is commutative. The topics,
A HARNACK INEQUALITY FOR NONLINEAR EQUATIONS
 A HARNACK INEQUALITY FOR NONLINEAR EQUATIONS BY JAMES SERRIN Communicated by Lawrence Markus, March 18, 1963 Recently Moser has obtained a Harnack inequality for linear divergence structure equations with
A HARNACK INEQUALITY FOR NONLINEAR EQUATIONS BY JAMES SERRIN Communicated by Lawrence Markus, March 18, 1963 Recently Moser has obtained a Harnack inequality for linear divergence structure equations with
F I N I T E T E R M I N A T I 0 N GAME S
 F I N I T E T E R M I N A T I 0 N GAME S W I T H T I E by P E T E R G. HINMAN Abstract We consider the class of finite two-person games with perfect information in which the last player who can make a
F I N I T E T E R M I N A T I 0 N GAME S W I T H T I E by P E T E R G. HINMAN Abstract We consider the class of finite two-person games with perfect information in which the last player who can make a
KAHANE'S CONSTRUCTION AND THE WEAK SEQUENTIAL COMPLETENESS OF L1 E. A. HEARD
 proceedings of the american mathematical society Volume 44, Number 1, May 1974 KAHANE'S CONSTRUCTION AND THE WEAK SEQUENTIAL COMPLETENESS OF L1 E. A. HEARD Abstract. If A is a normalized Lebesgue measure
proceedings of the american mathematical society Volume 44, Number 1, May 1974 KAHANE'S CONSTRUCTION AND THE WEAK SEQUENTIAL COMPLETENESS OF L1 E. A. HEARD Abstract. If A is a normalized Lebesgue measure
THE INVERSE OPERATION IN GROUPS
 THE INVERSE OPERATION IN GROUPS HARRY FURSTENBERG 1. Introduction. In the theory of groups, the product ab~l occurs frequently in connection with the definition of subgroups and cosets. This suggests that
THE INVERSE OPERATION IN GROUPS HARRY FURSTENBERG 1. Introduction. In the theory of groups, the product ab~l occurs frequently in connection with the definition of subgroups and cosets. This suggests that
A SYSTEM OF AXIOMATIC SET THEORY PART VI 62
 THE JOOBNAL OF SYMBOLIC LOGIC Volume 13, Number 2, June 1948 A SYSTEM OF AXIOMATIC SET THEORY PART VI 62 PAUL BEKNAYS 16. The r61e of the restrictive axiom. Comparability of classes. Till now we tried
THE JOOBNAL OF SYMBOLIC LOGIC Volume 13, Number 2, June 1948 A SYSTEM OF AXIOMATIC SET THEORY PART VI 62 PAUL BEKNAYS 16. The r61e of the restrictive axiom. Comparability of classes. Till now we tried
Optimal Starting Approximations. Newton's Method. By P. H. Sterbenz and C. T. Fike
 Optimal Starting Approximations Newton's Method for By P. H. Sterbenz and C. T. Fike Abstract. Various writers have dealt with the subject of optimal starting approximations for square-root calculation
Optimal Starting Approximations Newton's Method for By P. H. Sterbenz and C. T. Fike Abstract. Various writers have dealt with the subject of optimal starting approximations for square-root calculation
LATTICE AND BOOLEAN ALGEBRA
 2 LATTICE AND BOOLEAN ALGEBRA This chapter presents, lattice and Boolean algebra, which are basis of switching theory. Also presented are some algebraic systems such as groups, rings, and fields. 2.1 ALGEBRA
2 LATTICE AND BOOLEAN ALGEBRA This chapter presents, lattice and Boolean algebra, which are basis of switching theory. Also presented are some algebraic systems such as groups, rings, and fields. 2.1 ALGEBRA
Ç. Asma, R. Çolak ON THE KÔTHE-TOEPLITZ DUALS OF SOME GENERALIZED SETS OF DIFFERENCE SEQUENCES
 DEMONSTRATIO MATHEMATICA Vol. XXXIII No 4 2000 Ç. Asma, R. Çolak ON THE KÔTHE-TOEPLITZ DUALS OF SOME GENERALIZED SETS OF DIFFERENCE SEQUENCES Abstract. In this paper we define the sequence sets {u, A,p),
DEMONSTRATIO MATHEMATICA Vol. XXXIII No 4 2000 Ç. Asma, R. Çolak ON THE KÔTHE-TOEPLITZ DUALS OF SOME GENERALIZED SETS OF DIFFERENCE SEQUENCES Abstract. In this paper we define the sequence sets {u, A,p),
Scandinavia SUMMER / GROUPS. & Beyond 2014
 / & 2014 25 f f Fx f 211 9 Öæ Höf æ å f 807 ø 19 øø ä 2111 1 Z F ø 1328 H f fö F H å fö ö 149 H 1 ö f Hø ø Hf 1191 2089 ä ø å F ä 1907 ä 1599 H 1796 F ø ä Jä J ( ) ø F ø 19 ö ø 15 á Å f 2286 æ f ó ä H
/ & 2014 25 f f Fx f 211 9 Öæ Höf æ å f 807 ø 19 øø ä 2111 1 Z F ø 1328 H f fö F H å fö ö 149 H 1 ö f Hø ø Hf 1191 2089 ä ø å F ä 1907 ä 1599 H 1796 F ø ä Jä J ( ) ø F ø 19 ö ø 15 á Å f 2286 æ f ó ä H
GREEN'S THEOREM AND GREEN'S FUNCTIONS FOR CERTAIN SYSTEMS OF DIFFERENTIAL EQUATIONS*
 GREEN'S THEOREM AND GREEN'S FUNCTIONS FOR CERTAIN SYSTEMS OF DIFFERENTIAL EQUATIONS* BY MAX MASON The Green's function, defined originally for the potential equation, has been generalized to apply to the
GREEN'S THEOREM AND GREEN'S FUNCTIONS FOR CERTAIN SYSTEMS OF DIFFERENTIAL EQUATIONS* BY MAX MASON The Green's function, defined originally for the potential equation, has been generalized to apply to the
ON THE NUMBER OF REPRESENTATIONS OF 2n AS A SUM OF 2r SQUARES.
 1919.] REPEESENTATION AS SUM OF SQUARES. 19 ON THE NUMBER OF REPRESENTATIONS OF 2n AS A SUM OF 2r SQUARES. BY PEOFESSOR E. T. BELL. (Read before the San Francisco Section of the American Mathematical Society
1919.] REPEESENTATION AS SUM OF SQUARES. 19 ON THE NUMBER OF REPRESENTATIONS OF 2n AS A SUM OF 2r SQUARES. BY PEOFESSOR E. T. BELL. (Read before the San Francisco Section of the American Mathematical Society
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
ON THE THEORY OF ASSOCIATIVE DIVISION ALGEBRAS*
 ON THE THEORY OF ASSOCIATIVE DIVISION ALGEBRAS* BY OLIVE C. HAZLETT 1. Relation to the literature. There is a famous theorem to the effect that the only linear associative algebras over the field of all
ON THE THEORY OF ASSOCIATIVE DIVISION ALGEBRAS* BY OLIVE C. HAZLETT 1. Relation to the literature. There is a famous theorem to the effect that the only linear associative algebras over the field of all
A PROBLEM IN ADDITIVE NUMBER THEORY*
 A PROBLEM IN ADDITIVE NUMBER THEORY* BY R. D. JAMES 1. Introduction. Some time ago the author was asked by Professor D. N. Lehmer if there was anything known about the representation of an integer A in
A PROBLEM IN ADDITIVE NUMBER THEORY* BY R. D. JAMES 1. Introduction. Some time ago the author was asked by Professor D. N. Lehmer if there was anything known about the representation of an integer A in
Application: Can we tell what people are looking at from their brain activity (in real time)? Gaussian Spatial Smooth
 Application: Can we tell what people are looking at from their brain activity (in real time? Gaussian Spatial Smooth 0 The Data Block Paradigm (six runs per subject Three Categories of Objects (counterbalanced
Application: Can we tell what people are looking at from their brain activity (in real time? Gaussian Spatial Smooth 0 The Data Block Paradigm (six runs per subject Three Categories of Objects (counterbalanced
Ht) = - {/(* + t)-f(x-t)}, e(t) = - I^-á«.
 ON THE ABSOLUTE SUMMABILITY OF THE CONJUGATE SERIES OF A FOURIER SERIES T. PATI 1.1. Let/( ) be a periodic function with period 2w and integrable (L) over ( ir, it). Let 1 (1.1.1) a0 + Y (an cos nt + bn
ON THE ABSOLUTE SUMMABILITY OF THE CONJUGATE SERIES OF A FOURIER SERIES T. PATI 1.1. Let/( ) be a periodic function with period 2w and integrable (L) over ( ir, it). Let 1 (1.1.1) a0 + Y (an cos nt + bn
ON ABSOLUTE NORMAL DOUBLE MATRIX SUMMABILITY METHODS. B. E. Rhoades Indiana University, USA
 GLASNIK MATEMATIČKI Vol. 38582003, 57 73 ON ABSOLUTE NORMAL DOUBLE MATRIX SUMMABILITY METHODS B. E. Rhoades Indiana University, USA Abstract. It is shown that, if T is a row finite nonnegative double summability
GLASNIK MATEMATIČKI Vol. 38582003, 57 73 ON ABSOLUTE NORMAL DOUBLE MATRIX SUMMABILITY METHODS B. E. Rhoades Indiana University, USA Abstract. It is shown that, if T is a row finite nonnegative double summability
Error Analysis of the Algorithm for Shifting the Zeros of a Polynomial by Synthetic Division
 MATHEMATICS OF COMPUTATION, VOLUME 25, NUMBER 113, JANUARY, 1971 Error Analysis of the Algorithm for Shifting the Zeros of a Polynomial by Synthetic Division By G. W. Stewart III* Abstract. An analysis
MATHEMATICS OF COMPUTATION, VOLUME 25, NUMBER 113, JANUARY, 1971 Error Analysis of the Algorithm for Shifting the Zeros of a Polynomial by Synthetic Division By G. W. Stewart III* Abstract. An analysis
Matrix-Matrix Multiplication
 Chapter Matrix-Matrix Multiplication In this chapter, we discuss matrix-matrix multiplication We start by motivating its definition Next, we discuss why its implementation inherently allows high performance
Chapter Matrix-Matrix Multiplication In this chapter, we discuss matrix-matrix multiplication We start by motivating its definition Next, we discuss why its implementation inherently allows high performance
ON ORDER-CONVERGENCE
 ON ORDER-CONVERGENCE E. S. WÖLK1 1. Introduction. Let X be a set partially ordered by a relation ^ and possessing least and greatest elements O and I, respectively. Let {f(a), aed] be a net on the directed
ON ORDER-CONVERGENCE E. S. WÖLK1 1. Introduction. Let X be a set partially ordered by a relation ^ and possessing least and greatest elements O and I, respectively. Let {f(a), aed] be a net on the directed
PERIODIC SOLUTIONS OF SYSTEMS OF DIFFERENTIAL EQUATIONS1 IRVING J. EPSTEIN
 PERIODIC SOLUTIONS OF SYSTEMS OF DIFFERENTIAL EQUATIONS1 IRVING J. EPSTEIN Introduction and summary. Let i be an»x» matrix whose elements are continuous functions of the real variable t. Consider the system
PERIODIC SOLUTIONS OF SYSTEMS OF DIFFERENTIAL EQUATIONS1 IRVING J. EPSTEIN Introduction and summary. Let i be an»x» matrix whose elements are continuous functions of the real variable t. Consider the system
ON THE AVERAGE NUMBER OF REAL ROOTS OF A RANDOM ALGEBRAIC EQUATION
 ON THE AVERAGE NUMBER OF REAL ROOTS OF A RANDOM ALGEBRAIC EQUATION M. KAC 1. Introduction. Consider the algebraic equation (1) Xo + X x x + X 2 x 2 + + In-i^" 1 = 0, where the X's are independent random
ON THE AVERAGE NUMBER OF REAL ROOTS OF A RANDOM ALGEBRAIC EQUATION M. KAC 1. Introduction. Consider the algebraic equation (1) Xo + X x x + X 2 x 2 + + In-i^" 1 = 0, where the X's are independent random
K-0DI. flflflflflflflflflii
 flflflflflflflflflii AD-Ass7 364 TEXAS UNIV AT AUSTIN DEPT OF CHEMISTRY F/6 7/4 " POTOCATALYTIC PRODUCTION OF HYDROGEN FROM WATER AND TEXAS LIBN-ETC(U) JUM 80 S SATO, J M WHITE NOOOl,-75-C-0922 END K-0DI
flflflflflflflflflii AD-Ass7 364 TEXAS UNIV AT AUSTIN DEPT OF CHEMISTRY F/6 7/4 " POTOCATALYTIC PRODUCTION OF HYDROGEN FROM WATER AND TEXAS LIBN-ETC(U) JUM 80 S SATO, J M WHITE NOOOl,-75-C-0922 END K-0DI
Symmetry and Properties of Crystals (MSE638) Stress and Strain Tensor
 Symmetry and Properties of Crystals (MSE638) Stress and Strain Tensor Somnath Bhowmick Materials Science and Engineering, IIT Kanpur April 6, 2018 Tensile test and Hooke s Law Upto certain strain (0.75),
Symmetry and Properties of Crystals (MSE638) Stress and Strain Tensor Somnath Bhowmick Materials Science and Engineering, IIT Kanpur April 6, 2018 Tensile test and Hooke s Law Upto certain strain (0.75),
BULLETIN DE L'ACADEMIE POLONAISE DES SCIENCES Série des sci. math., astr. et phys. - Vol. VI, No. 12, 1958 On Sets Which Are Measured bar Multiples of
 BULLETIN DE L'ACADEMIE POLONAISE DES SCIENCES Série des sci. math., astr. et phys. - Vol. VI, No. 12, 1958 On Sets Which Are Measured bar Multiples of Irrational Numbers MATHEMATICS P. by ERDŐS and K.
BULLETIN DE L'ACADEMIE POLONAISE DES SCIENCES Série des sci. math., astr. et phys. - Vol. VI, No. 12, 1958 On Sets Which Are Measured bar Multiples of Irrational Numbers MATHEMATICS P. by ERDŐS and K.
Some Third Order Methods for Solving Systems of Nonlinear Equations
 Some Third Order Methods for Solving Systems of Nonlinear Equations Janak Raj Sharma Rajni Sharma International Science Index, Mathematical Computational Sciences waset.org/publication/1595 Abstract Based
Some Third Order Methods for Solving Systems of Nonlinear Equations Janak Raj Sharma Rajni Sharma International Science Index, Mathematical Computational Sciences waset.org/publication/1595 Abstract Based
AN EXTREMUM PROPERTY OF SUMS OF EIGENVALUES' HELMUT WIELANDT
 AN EXTREMUM PROPERTY OF SUMS OF EIGENVALUES' HELMUT WIELANDT We present in this note a maximum-minimum characterization of sums like at+^+aa where a^ ^a are the eigenvalues of a hermitian nxn matrix. The
AN EXTREMUM PROPERTY OF SUMS OF EIGENVALUES' HELMUT WIELANDT We present in this note a maximum-minimum characterization of sums like at+^+aa where a^ ^a are the eigenvalues of a hermitian nxn matrix. The
Chapter 2. Linear Algebra. rather simple and learning them will eventually allow us to explain the strange results of
 Chapter 2 Linear Algebra In this chapter, we study the formal structure that provides the background for quantum mechanics. The basic ideas of the mathematical machinery, linear algebra, are rather simple
Chapter 2 Linear Algebra In this chapter, we study the formal structure that provides the background for quantum mechanics. The basic ideas of the mathematical machinery, linear algebra, are rather simple
55 Separable Extensions
 55 Separable Extensions In 54, we established the foundations of Galois theory, but we have no handy criterion for determining whether a given field extension is Galois or not. Even in the quite simple
55 Separable Extensions In 54, we established the foundations of Galois theory, but we have no handy criterion for determining whether a given field extension is Galois or not. Even in the quite simple
APPH 4200 Physics of Fluids
 APPH 42 Physics of Fluids Problem Solving and Vorticity (Ch. 5) 1.!! Quick Review 2.! Vorticity 3.! Kelvin s Theorem 4.! Examples 1 How to solve fluid problems? (Like those in textbook) Ç"Tt=l I $T1P#(
APPH 42 Physics of Fluids Problem Solving and Vorticity (Ch. 5) 1.!! Quick Review 2.! Vorticity 3.! Kelvin s Theorem 4.! Examples 1 How to solve fluid problems? (Like those in textbook) Ç"Tt=l I $T1P#(
ON MIXING AND PARTIAL MIXING
 ON MIXING AND PARTIAL MIXING BY N. A. XRIEDMAN AND D. S. ORNSTEIN 1. Introduction Let (X, a, m) denote the unit interwl with Lebesgue mesure, nd let r be n invertible ergodie mesure preserving transformation
ON MIXING AND PARTIAL MIXING BY N. A. XRIEDMAN AND D. S. ORNSTEIN 1. Introduction Let (X, a, m) denote the unit interwl with Lebesgue mesure, nd let r be n invertible ergodie mesure preserving transformation
ON RESTRICTED SYSTEMS OF HIGHER INDETERMINATE EQUATIONS * E. T. BELL
 ON RESTRICTED SYSTEMS OF HIGHER INDETERMINATE EQUATIONS * BY E. T. BELL By two examples we shall illustrate a means for deriving arithmetical properties of certain restricted forms. So little being known
ON RESTRICTED SYSTEMS OF HIGHER INDETERMINATE EQUATIONS * BY E. T. BELL By two examples we shall illustrate a means for deriving arithmetical properties of certain restricted forms. So little being known
UNIFORM INTEGRABILITY AND THE POINTWTSE ERGODIC THEOREM
 UNIFORM INTEGRABILITY AND THE POINTWTSE ERGODIC THEOREM YUJI ITO Let ix, 03, m) be a finite measure space. We shall denote by L*im) (1 èp< ) the Banach space of all real-valued (B-measurable functions/
UNIFORM INTEGRABILITY AND THE POINTWTSE ERGODIC THEOREM YUJI ITO Let ix, 03, m) be a finite measure space. We shall denote by L*im) (1 èp< ) the Banach space of all real-valued (B-measurable functions/
On Weird and Pseudoperfect
 mathematics of computation, volume 28, number 126, april 1974, pages 617-623 On Weird and Pseudoperfect Numbers By S. J. Benkoski and P. Krdö.s Abstract. If n is a positive integer and
mathematics of computation, volume 28, number 126, april 1974, pages 617-623 On Weird and Pseudoperfect Numbers By S. J. Benkoski and P. Krdö.s Abstract. If n is a positive integer and
Planning for Reactive Behaviors in Hide and Seek
 University of Pennsylvania ScholarlyCommons Center for Human Modeling and Simulation Department of Computer & Information Science May 1995 Planning for Reactive Behaviors in Hide and Seek Michael B. Moore
University of Pennsylvania ScholarlyCommons Center for Human Modeling and Simulation Department of Computer & Information Science May 1995 Planning for Reactive Behaviors in Hide and Seek Michael B. Moore
\ABC (9) \AX BI Ci\ = 0, r; vi -iv ~*i -n*yi -o
 i 9 28.] INVERSION OF TRANSFORMATIONS 565 \ABC BiCi C1A1 Ai Bi (9) \AX BI Ci\ = 0, r; vi -iv ~*i -n*yi -o ' A 2 B2 C2 = 0, B2 C2 d Ai Ai Bi represent the two éliminants of the system (8). The two necessary
i 9 28.] INVERSION OF TRANSFORMATIONS 565 \ABC BiCi C1A1 Ai Bi (9) \AX BI Ci\ = 0, r; vi -iv ~*i -n*yi -o ' A 2 B2 C2 = 0, B2 C2 d Ai Ai Bi represent the two éliminants of the system (8). The two necessary
arxiv: v1 [math.at] 21 Apr 2012
![arxiv: v1 [math.at] 21 Apr 2012 arxiv: v1 [math.at] 21 Apr 2012](/thumbs/75/72822740.jpg) THE ASYMPTOTIC DENSITY OF WECKEN MAPS ON SURFACES WITH BOUNDARY arxiv:204.4808v [math.at] 2 Apr 202 SEUNG WON KIM AND P. CHRISTOPHER STAECKER Abstract. The Nielsen number N(f) is a lower bound for the
THE ASYMPTOTIC DENSITY OF WECKEN MAPS ON SURFACES WITH BOUNDARY arxiv:204.4808v [math.at] 2 Apr 202 SEUNG WON KIM AND P. CHRISTOPHER STAECKER Abstract. The Nielsen number N(f) is a lower bound for the
MODULES OVER RINGS OF WORDS
 MODULES OVER RINGS OF WORDS WILLIAM G. LEAVITT Introduction. A right module M over a ring K with unit is called a free module if it is finitely based. If the basis number of such a module is not invariant
MODULES OVER RINGS OF WORDS WILLIAM G. LEAVITT Introduction. A right module M over a ring K with unit is called a free module if it is finitely based. If the basis number of such a module is not invariant
UNDEFINABLE CLASSES AND DEFINABLE ELEMENTS IN MODELS OF SET THEORY AND ARITHMETIC
 proceedings of the american mathematical society Volume 103, Number 4, August 1988 UNDEFINABLE CLASSES AND DEFINABLE ELEMENTS IN MODELS OF SET THEORY AND ARITHMETIC ALI ENAYAT (Communicated by Thomas J.
proceedings of the american mathematical society Volume 103, Number 4, August 1988 UNDEFINABLE CLASSES AND DEFINABLE ELEMENTS IN MODELS OF SET THEORY AND ARITHMETIC ALI ENAYAT (Communicated by Thomas J.
DIFFERENTIABILITY VIA DIRECTIONAL DERIVATIVES
 PROCEEDINGS OK THE AMERICAN MATHEMATICAL SOCIETY Volume 70, Number 1, lune 1978 DIFFERENTIABILITY VIA DIRECTIONAL DERIVATIVES KA-SING LAU AND CLIFFORD E. WEIL Abstract. Let F be a continuous function from
PROCEEDINGS OK THE AMERICAN MATHEMATICAL SOCIETY Volume 70, Number 1, lune 1978 DIFFERENTIABILITY VIA DIRECTIONAL DERIVATIVES KA-SING LAU AND CLIFFORD E. WEIL Abstract. Let F be a continuous function from
AN EXTENSION OF A THEOREM OF NAGANO ON TRANSITIVE LIE ALGEBRAS
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 45, Number 3, September 197 4 AN EXTENSION OF A THEOREM OF NAGANO ON TRANSITIVE LIE ALGEBRAS HÉCTOR J. SUSSMANN ABSTRACT. Let M be a real analytic
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 45, Number 3, September 197 4 AN EXTENSION OF A THEOREM OF NAGANO ON TRANSITIVE LIE ALGEBRAS HÉCTOR J. SUSSMANN ABSTRACT. Let M be a real analytic
Fun and Fascinating Bible Reference for Kids Ages 8 to 12. starts on page 3! starts on page 163!
 F a Faa R K 8 12 a a 3! a a 163! 2013 a P, I. ISN 978-1-62416-216-9. N a a a a a, a,. C a a a a P, a 500 a a aa a. W, : F G: K Fa a Q &, a P, I. U. L aa a a a Fa a Q & a. C a 2 (M) Ta H P M (K) Wa P a
F a Faa R K 8 12 a a 3! a a 163! 2013 a P, I. ISN 978-1-62416-216-9. N a a a a a, a,. C a a a a P, a 500 a a aa a. W, : F G: K Fa a Q &, a P, I. U. L aa a a a Fa a Q & a. C a 2 (M) Ta H P M (K) Wa P a
Chapter 30 Design and Analysis of
 Chapter 30 Design and Analysis of 2 k DOEs Introduction This chapter describes design alternatives and analysis techniques for conducting a DOE. Tables M1 to M5 in Appendix E can be used to create test
Chapter 30 Design and Analysis of 2 k DOEs Introduction This chapter describes design alternatives and analysis techniques for conducting a DOE. Tables M1 to M5 in Appendix E can be used to create test
EXPANSION OF ANALYTIC FUNCTIONS IN TERMS INVOLVING LUCAS NUMBERS OR SIMILAR NUMBER SEQUENCES
 EXPANSION OF ANALYTIC FUNCTIONS IN TERMS INVOLVING LUCAS NUMBERS OR SIMILAR NUMBER SEQUENCES PAUL F. BYRD San Jose State College, San Jose, California 1. INTRODUCTION In a previous article [_ 1J, certain
EXPANSION OF ANALYTIC FUNCTIONS IN TERMS INVOLVING LUCAS NUMBERS OR SIMILAR NUMBER SEQUENCES PAUL F. BYRD San Jose State College, San Jose, California 1. INTRODUCTION In a previous article [_ 1J, certain
THE FINE SPECTRA FOR WEIGHTED MEAN OPERATORS
 PACIFIC JOURNAL OF MATHEMATICS Vol. 104, No. 1, 1983 THE FINE SPECTRA FOR WEIGHTED MEAN OPERATORS B. E. RHOADES In a recent paper [5] the fine spectra of integer powers of the Cesaro matrix were computed.
PACIFIC JOURNAL OF MATHEMATICS Vol. 104, No. 1, 1983 THE FINE SPECTRA FOR WEIGHTED MEAN OPERATORS B. E. RHOADES In a recent paper [5] the fine spectra of integer powers of the Cesaro matrix were computed.
(1) 0 á per(a) Í f[ U, <=i
 ON LOWER BOUNDS FOR PERMANENTS OF (, 1) MATRICES1 HENRYK MINC 1. Introduction. The permanent of an «-square matrix A = (a^) is defined by veria) = cesn n II «"( j. If A is a (, 1) matrix, i.e. a matrix
ON LOWER BOUNDS FOR PERMANENTS OF (, 1) MATRICES1 HENRYK MINC 1. Introduction. The permanent of an «-square matrix A = (a^) is defined by veria) = cesn n II «"( j. If A is a (, 1) matrix, i.e. a matrix
BOOLEAN MAfRICES AND GRAPH THEORY. R. S. Ledley. NBR Report No /3265. March 1968
 ?0 00 BOOLEAN MAfRICES AND GRAPH THEORY by R. S. Ledley NBR Report No. 68032/3265 March 1968 Chirac! WoAr- lzds(o0j National Biomedical Research Foundation 11200 Lockwood Drive Silver Spring, Maryland
?0 00 BOOLEAN MAfRICES AND GRAPH THEORY by R. S. Ledley NBR Report No. 68032/3265 March 1968 Chirac! WoAr- lzds(o0j National Biomedical Research Foundation 11200 Lockwood Drive Silver Spring, Maryland
4.7 The Levi-Civita connection and parallel transport
 Classnotes: Geometry & Control of Dynamical Systems, M. Kawski. April 21, 2009 138 4.7 The Levi-Civita connection and parallel transport In the earlier investigation, characterizing the shortest curves
Classnotes: Geometry & Control of Dynamical Systems, M. Kawski. April 21, 2009 138 4.7 The Levi-Civita connection and parallel transport In the earlier investigation, characterizing the shortest curves
Your Galactic Address
 How Big is the Universe? Usually you think of your address as only three or four lines long: your name, street, city, and state. But to address a letter to a friend in a distant galaxy, you have to specify
How Big is the Universe? Usually you think of your address as only three or four lines long: your name, street, city, and state. But to address a letter to a friend in a distant galaxy, you have to specify
On Regularly Generated Double Sequences
 Filomat 3:3 207, 809 822 DOI 02298/FIL703809T Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://wwwpmfniacrs/filomat On Regularly Generated Double Sequences
Filomat 3:3 207, 809 822 DOI 02298/FIL703809T Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://wwwpmfniacrs/filomat On Regularly Generated Double Sequences
ON THE NUMERICAL RANGE OF AN OPERATOR
 ON THE NUMERICAL RANGE OF AN OPERATOR CHING-HWA MENG The numerical range of an operator P in a Hubert space is defined as the set of all the complex numbers (Tx, x), where x is a unit vector in the space.
ON THE NUMERICAL RANGE OF AN OPERATOR CHING-HWA MENG The numerical range of an operator P in a Hubert space is defined as the set of all the complex numbers (Tx, x), where x is a unit vector in the space.
MOMENT SEQUENCES AND BACKWARD EXTENSIONS OF SUBNORMAL WEIGHTED SHIFTS
 J. Austral. Math. Soc. 73 (2002), 27-36 MOMENT SEQUENCES AND BACKWARD EXTENSIONS OF SUBNORMAL WEIGHTED SHIFTS THOMAS HOOVER, IL BONG JUNG and ALAN LAMBERT (Received 15 February 2000; revised 10 July 2001)
J. Austral. Math. Soc. 73 (2002), 27-36 MOMENT SEQUENCES AND BACKWARD EXTENSIONS OF SUBNORMAL WEIGHTED SHIFTS THOMAS HOOVER, IL BONG JUNG and ALAN LAMBERT (Received 15 February 2000; revised 10 July 2001)
THE LINDEBERG-LÉVY THEOREM FOR MARTINGALES1
 THE LINDEBERG-LÉVY THEOREM FOR MARTINGALES1 PATRICK BILLINGSLEY The central limit theorem of Lindeberg [7] and Levy [3] states that if {mi, m2, } is an independent, identically distributed sequence of
THE LINDEBERG-LÉVY THEOREM FOR MARTINGALES1 PATRICK BILLINGSLEY The central limit theorem of Lindeberg [7] and Levy [3] states that if {mi, m2, } is an independent, identically distributed sequence of
A PROPERTY OF CONTINUITY*
 1922.] A PEOPEETY OP CONTINUITY 245 A PROPERTY OF CONTINUITY* BY D. C. GILLESPIE If and rj are two points of the interval (a, b) in which the function f(x) is continuous, then the function takes on all
1922.] A PEOPEETY OP CONTINUITY 245 A PROPERTY OF CONTINUITY* BY D. C. GILLESPIE If and rj are two points of the interval (a, b) in which the function f(x) is continuous, then the function takes on all
Lecture 11: Introduction to Markov Chains. Copyright G. Caire (Sample Lectures) 321
 Lecture 11: Introduction to Markov Chains Copyright G. Caire (Sample Lectures) 321 Discrete-time random processes A sequence of RVs indexed by a variable n 2 {0, 1, 2,...} forms a discretetime random process
Lecture 11: Introduction to Markov Chains Copyright G. Caire (Sample Lectures) 321 Discrete-time random processes A sequence of RVs indexed by a variable n 2 {0, 1, 2,...} forms a discretetime random process
NONLOCAL PROBLEMS WITH LOCAL DIRICHLET AND NEUMANN BOUNDARY CONDITIONS BURAK AKSOYLU AND FATIH CELIKER
 NONLOCAL PROBLEMS WITH LOCAL DIRICHLET AND NEUMANN BOUNDARY CONDITIONS BURAK AKSOYLU AND FATIH CELIKER Department of Mathematics, Wayne State University, 656 W. Kirby, Detroit, MI 480, USA. Department
NONLOCAL PROBLEMS WITH LOCAL DIRICHLET AND NEUMANN BOUNDARY CONDITIONS BURAK AKSOYLU AND FATIH CELIKER Department of Mathematics, Wayne State University, 656 W. Kirby, Detroit, MI 480, USA. Department
EVENTUAL DISCONJUGACY OF A LINEAR DIFFERENTIAL EQUATION. II WILLIAM F. TRENCH
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 94. Number 4. August 1985 EVENTUAL DISCONJUGACY OF A LINEAR DIFFERENTIAL EQUATION. II WILLIAM F. TRENCH Abstract. A sufficient condition is given
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 94. Number 4. August 1985 EVENTUAL DISCONJUGACY OF A LINEAR DIFFERENTIAL EQUATION. II WILLIAM F. TRENCH Abstract. A sufficient condition is given
_ 3 jveg-f* fl2ul_-pj>" -D' Zu\ E 1 2 j / J EG F*'
 1901.] A CLASS OF SURFACES. 417 (1) SURFACES WHOSE FIRST AND SECOND FUN DAMENTAL FORMS ARE THE SECOND AND FIRST RESPECTIVELY OF ANOTHER SURFACE. BY DE. "L. P. EISENHABT. ( Eead bef ore the American Mathematical
1901.] A CLASS OF SURFACES. 417 (1) SURFACES WHOSE FIRST AND SECOND FUN DAMENTAL FORMS ARE THE SECOND AND FIRST RESPECTIVELY OF ANOTHER SURFACE. BY DE. "L. P. EISENHABT. ( Eead bef ore the American Mathematical
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A. Ήχος Πα. to os se e e na aș te e e slă ă ă vi i i i i
 CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
n = n = This is the Binomial Theorem with non-negative integer as index. Thus, a Pascal's Triangle can be written as
 Pascal's Triangle and the General Binomial Theorem by Chan Wei Min It is a well-nown fact that the coefficients of terms in the expansion of (1 + x)n for nonnegative integer n can be arranged in the following
Pascal's Triangle and the General Binomial Theorem by Chan Wei Min It is a well-nown fact that the coefficients of terms in the expansion of (1 + x)n for nonnegative integer n can be arranged in the following
Recursive Computation of the Repeated Integrals of the Error Function
 Recursive Computation of the Repeated Integrals of the Error Function By Walter Gautschi 1. This paper is concerned with a special technique, originated by J. C. P. Miller [1, p. xvii], of computing a
Recursive Computation of the Repeated Integrals of the Error Function By Walter Gautschi 1. This paper is concerned with a special technique, originated by J. C. P. Miller [1, p. xvii], of computing a
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
(308 ) EXAMPLES. 1. FIND the quotient and remainder when. II. 1. Find a root of the equation x* = +J Find a root of the equation x 6 = ^ - 1.
 (308 ) EXAMPLES. N 1. FIND the quotient and remainder when is divided by x 4. I. x 5 + 7x* + 3a; 3 + 17a 2 + 10* - 14 2. Expand (a + bx) n in powers of x, and then obtain the first derived function of
(308 ) EXAMPLES. N 1. FIND the quotient and remainder when is divided by x 4. I. x 5 + 7x* + 3a; 3 + 17a 2 + 10* - 14 2. Expand (a + bx) n in powers of x, and then obtain the first derived function of
F O R SOCI AL WORK RESE ARCH
 7 TH EUROPE AN CONFERENCE F O R SOCI AL WORK RESE ARCH C h a l l e n g e s i n s o c i a l w o r k r e s e a r c h c o n f l i c t s, b a r r i e r s a n d p o s s i b i l i t i e s i n r e l a t i o n
7 TH EUROPE AN CONFERENCE F O R SOCI AL WORK RESE ARCH C h a l l e n g e s i n s o c i a l w o r k r e s e a r c h c o n f l i c t s, b a r r i e r s a n d p o s s i b i l i t i e s i n r e l a t i o n
Sb1) = (4, Az,.-., An),
 PROBABILITY ' AND MATHEMATICAL STATISTICS VoL 20, lux. 2 (20W), pp. 359-372 DISCRETE PROBABILITY MEASURES ON 2 x 2 STOCHASTIC MATRICES AND A FUNCTIONAL EQUATION OW '[o, 11 - -. A. MUKHERJEA AND J. S. RATTI
PROBABILITY ' AND MATHEMATICAL STATISTICS VoL 20, lux. 2 (20W), pp. 359-372 DISCRETE PROBABILITY MEASURES ON 2 x 2 STOCHASTIC MATRICES AND A FUNCTIONAL EQUATION OW '[o, 11 - -. A. MUKHERJEA AND J. S. RATTI
Congruence Properties of G-Functions. By HANSRAJ GUPTA. (Received 12th February, 1934, and in revised form 22nd April, Read 3rd March, 1934.
 Congruence Properties of G-Functions By HANSRAJ GUPTA. (Received 12th February, 1934, and in revised form 22nd April, 1934. Read 3rd March, 1934.) 1. Denoting the sum of the products of the first n natural
Congruence Properties of G-Functions By HANSRAJ GUPTA. (Received 12th February, 1934, and in revised form 22nd April, 1934. Read 3rd March, 1934.) 1. Denoting the sum of the products of the first n natural
