DEPARTMENT OF MATHEMATICS BIT, MESRA, RANCHI MA2201 Advanced Engg. Mathematics Session: SP/ 2017
|
|
|
- Dana Rich
- 5 years ago
- Views:
Transcription
1 DEARMEN OF MAEMAICS BI, MESRA, RANCI MA Advad Egg. Mathatis Sssio: S/ 7 MODULE I. Cosidr th two futios f utorial Sht No. -- ad g o th itrval [,] a Show that thir Wroskia W f, g vaishs idtially. b Show that f ad g ar ot liarly idpdt.. Show that th solutios, ad of y y y ar liarly idpdt ad h or othrwis solv th quatio.. Show that is th gral solutio of y y o ay itrval ot otaiig, ad fid th partiular solutio for whih y ad y 5 4. Show that th Wroskia of th futios, log is o zro. Ca ths futios b idpdt solutios of ordiary dfrtial quatios; so dtri this quatio. Solv th followig dfrtial quatios: si 6. si 7. si 4 8. D D os 9. D 4 si. a s a. 4 si d y dy. oslog silog d d. d y dy 5 d d 4. Vry that solutio. y is o solutio of y y 4, ad fid sod solutio y ad th gral 5. Solv si, giv that ot is o solutio.
2 6. Vry that o of th solutio of th quatio is, ad fid aothr solutio valid i. Solv th followig dfrtial quatios by trasforatio or hag of idpdt variabl. 7. y ot y si os os 8. y 4 8 si os 9. si ot y si si. y ta y os MODULE II Solv th followig dfrtial quatios by rduig to Noral For:.. y. y ta y s Solv th followig dfrtial quatios by th variatio of paratrs: 4. ot ot si y y y y ' s ta, / 7. y ''' y s 8. y '''- 6 y '' y ' Fid th sigular poits of th followig dfrtial quatios ad lassy th: a b y y y y Fid th sris solutio of th followig dfrtial quatios:. 4 about =. 9 y 4 about = about =. y y y about = 4. y y y with y, y 4 about =
3 MODULE III 5. Driv th solutio of Bssl s quatio of ordr : ad prss th i trs of Bssl s futios 6. rov that a J si b J os d d 7. rov that a [ J ] J b [ J ] J d d 8. rov that a J J J b J J J 9. rov that a J J b J { J J 4. rov that J si os 5 4. rov that 48 4 J J J 4 d 4. Show that J J J J d 4. Show that J d J J 44. If α ad β ar th roots of, th show that J J J d, J, 45. rov that for itgral, J Cos Si d 46. a J b d 47. rov th followig: a b a b 48. Eprss 4 6 i a sris of Lgdr s polyoials. d 49. rov that! d
4 5. Show: 5. rov that, /! /!, for odd for v 5. rov that d,, 5. rov that d 54. rov that t d t t 55. Driv th solutio of yprgotri quatio: [ a b ] ab, a, b, ostats, i trs iit ovrgt sris about ad prss th i trs of yprgotri futios as : y F a, b, a. b ;! a a b b!....,,,... y F a, b, ;,, 4... ad th gral solutio solutios as y F a, b, ; F a, b, ;, ot a itgr. 56. rov that a F,, ; b l F /,, / ; 57. Driv th solutio of followig dfrtial quatio i trs of yprgotri futios: y 6 y rov th followig rlatios for Chbyshv polyoial os os : 58. a b 4 t rov th followig rlatios usig th gratig futio for as t, t. t t 59. b
5 6. a ' b 6. rov th orthogoality of Chbyshv polyoials as : d ; rov th followig rlatios for th rit polyoial d d, : 6. a 4 b 8 rov th followig rlatios usig th gratig futio for as t t t! 6. a b 64. rov th orthogoality of rit polyoials as! d *******************************************************************************
6 MA ADVANCED ENGINEERING MAEMAICS 4 Modul I Liar Dfrtial Equatios of ighr Ordr with ostat offiits. Dfrtial Equatios with Variabl Coffiits: Rduibl to Equatios with ostat Coffiits:- Cauhy Eulr Dfrtial Equatio. Lgdr Liar Dfrtial Equatio. Solutio of Dfrtial Equatio by trasforatio or, hag of Idpdt Variabl. Modul II Rdutio of Dfrtial Equatio to Noral For by rduig th ordr of th Dfrtial Equatio. Solutio by th thod of Variatio of aratrs. Sris Solutio of dfrtial Equatios. Modul III Bssl s dfrtial Equatio ad its Gral solutio. roprtis of Bssl s Futios. Lgdr s Dfrtial Equatio ad Lgdr olyoials. roprtis of Lgdr olyoials. Itrodutio to yprgotri Equatio. Itrodutio to rit Dfrtial Equatios. Itrodutio to Chbyshv olyoials. Modul IV Eig Valus ad Eig Futios. Stur Liouvill robls. riodi Futios. Dirihlt s Coditios o Fourir Sris. Eulr s Forula for Fourir Coffiits. alf rag Sris. Fourir Sris of Futios with Arbitrary priod. Modul V Futio of Copl Variabls. Liit, Cotiuity, Dfrtiability of a Copl Variabl. Cauhy Ria Dfrtial Equatios i Cartsia ad olar Fors. Aalyti Futio. Cauhy-Goursat tho, Cauhy s Itgral hor. Cauhy s Itgral Forula. Morra s thor. Modul VI Liouvill s thor. h fudatal thor of algbra. aylor Sris, Laurt Sris. Rsidus, ols, Rsidu hor. Rsidu at ols. Cotour Itgrals of rigootri to ad Algbrai Equatios to. Coforal Mappig ad Biliar rasforatio. Modul VII artial Dfrtial Equatio, Lagrag s Mthod, oogous ad No-hoogous ighr Ordr Equatios with Costat Coffiits. O-disioal at Equatio. O disioal Wav Equatio t Books:. Sios G. F., Dfrtial Equatios with Appliatios ad istorial Nots. M, d d.,.. R. V. Churhill ad J. W. Brow, Copl Variabls ad Appliatios, 8 th d., 9, MGraw ill.. Dis G. Zill, Warr S. Wright, Advad Egirig Mathatis,4 th d. 4. E. Kryszig, Advad Egirig Mathatis, Jho Wily ad Sos, 8 th d., 999 Rfr Books:. Edwards ad y, Dfrtial Equatios ad Boudary Valu robls, arso Edu., rd d.. Shply L. Ross, Dfrtial Equatios Wily Idia vt. Ltd., rd d.. Birkhoff ad Rota, Ordiary Dfrtial Equatios, Wily Idia vt. Ltd., 4 th d. 4. Zill, Dfrtial Equatios, hoso Larig, 5 th d., 4 5. A.D. Wush, Copl Variabls with Appliatios, arso Eduatio I., rd d. 6. M.J. Ablowitz ad A.S.Fokas, Copl Variabls Itrodutio ad Appliatios, Cabridg ts, d d.
Ordinary Differential Equations
Basi Nomlatur MAE 0 all 005 Egirig Aalsis Ltur Nots o: Ordiar Diffrtial Equatios Author: Profssor Albrt Y. Tog Tpist: Sakurako Takahashi Cosidr a gral O. D. E. with t as th idpdt variabl, ad th dpdt variabl.
PURE MATHEMATICS A-LEVEL PAPER 1
-AL P MATH PAPER HONG KONG EXAMINATIONS AUTHORITY HONG KONG ADVANCED LEVEL EXAMINATION PURE MATHEMATICS A-LEVEL PAPER 8 am am ( hours) This papr must b aswrd i Eglish This papr cosists of Sctio A ad Sctio
Australian Journal of Basic and Applied Sciences, 4(9): , 2010 ISSN
Australia Joural of Basic ad Applid Scics, 4(9): 4-43, ISSN 99-878 Th Caoical Product of th Diffrtial Equatio with O Turig Poit ad Sigular Poit A Dabbaghia, R Darzi, 3 ANaty ad 4 A Jodayr Akbarfa, Islaic
Iterative Methods of Order Four for Solving Nonlinear Equations
Itrativ Mods of Ordr Four for Solvig Noliar Equatios V.B. Kumar,Vatti, Shouri Domii ad Mouia,V Dpartmt of Egirig Mamatis, Formr Studt of Chmial Egirig Adhra Uivrsity Collg of Egirig A, Adhra Uivrsity Visakhapatam
Worksheet: Taylor Series, Lagrange Error Bound ilearnmath.net
Taylor s Thorm & Lagrag Error Bouds Actual Error This is th ral amout o rror, ot th rror boud (worst cas scario). It is th dirc btw th actual () ad th polyomial. Stps:. Plug -valu ito () to gt a valu.
Digital Signal Processing, Fall 2006
Digital Sigal Procssig, Fall 6 Lctur 9: Th Discrt Fourir Trasfor Zhg-Hua Ta Dpartt of Elctroic Systs Aalborg Uivrsity, Dar zt@o.aau.d Digital Sigal Procssig, I, Zhg-Hua Ta, 6 Cours at a glac MM Discrt-ti
After the completion of this section the student. V.4.2. Power Series Solution. V.4.3. The Method of Frobenius. V.4.4. Taylor Series Solution
Chapter V ODE V.4 Power Series Solutio Otober, 8 385 V.4 Power Series Solutio Objetives: After the ompletio of this setio the studet - should reall the power series solutio of a liear ODE with variable
Lecture contents. Density of states Distribution function Statistic of carriers. Intrinsic Extrinsic with no compensation Compensation
Ltur otts Dsity of stats Distributio futio Statisti of arrirs Itrisi trisi with o ompsatio ompsatio S 68 Ltur #7 Dsity of stats Problm: alulat umbr of stats pr uit rgy pr uit volum V() Larg 3D bo (L is
Explicit and closed formed solution of a differential equation. Closed form: since finite algebraic combination of. converges for x x0
Chapter 4 Series Solutios Epliit ad losed formed solutio of a differetial equatio y' y ; y() 3 ( ) ( 5 e ) y Closed form: sie fiite algebrai ombiatio of elemetary futios Series solutio: givig y ( ) as
NET/JRF, GATE, IIT JAM, JEST, TIFR
Istitut for NET/JRF, GATE, IIT JAM, JEST, TIFR ad GRE i PHYSICAL SCIENCES Mathmatical Physics JEST-6 Q. Giv th coditio φ, th solutio of th quatio ψ φ φ is giv by k. kφ kφ lφ kφ lφ (a) ψ (b) ψ kφ (c) ψ
1985 AP Calculus BC: Section I
985 AP Calculus BC: Sctio I 9 Miuts No Calculator Nots: () I this amiatio, l dots th atural logarithm of (that is, logarithm to th bas ). () Ulss othrwis spcifid, th domai of a fuctio f is assumd to b
SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,
![SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,](/thumbs/94/119566625.jpg "SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,")
4. Series Solutios of Differetial Equatios:Special Fuctios 4.. Illustrative examples.. 5. Obtai the geeral solutio of each of the followig differetial equatios i terms of Maclauri series: d y (a dx = xy,
15/03/1439. Lectures on Signals & systems Engineering
Lcturs o Sigals & syms Egirig Dsigd ad Prd by Dr. Ayma Elshawy Elsfy Dpt. of Syms & Computr Eg. Al-Azhar Uivrsity Email : aymalshawy@yahoo.com A sigal ca b rprd as a liar combiatio of basic sigals. Th
MONTGOMERY COLLEGE Department of Mathematics Rockville Campus. 6x dx a. b. cos 2x dx ( ) 7. arctan x dx e. cos 2x dx. 2 cos3x dx
MONTGOMERY COLLEGE Dpartmt of Mathmatics Rockvill Campus MATH 8 - REVIEW PROBLEMS. Stat whthr ach of th followig ca b itgratd by partial fractios (PF), itgratio by parts (PI), u-substitutio (U), or o of
A Review of Complex Arithmetic
/0/005 Rviw of omplx Arithmti.do /9 A Rviw of omplx Arithmti A omplx valu has both a ral ad imagiary ompot: { } ad Im{ } a R b so that w a xprss this omplx valu as: whr. a + b Just as a ral valu a b xprssd
Class #24 Monday, April 16, φ φ φ
lass #4 Moday, April 6, 08 haptr 3: Partial Diffrtial Equatios (PDE s First of all, this sctio is vry, vry difficult. But it s also supr cool. PDE s thr is mor tha o idpdt variabl. Exampl: φ φ φ φ = 0
CHAPTER:Indefinite Integrals Multiple Choice Questions with solution: 1
CHAPTER:Idfiit Itgrals Multipl Choi Qustios with solutio: 0. d = a )log( ) + b )log( ) + )log( ) + + d ) N o As : Put dt = t: d= dt d= ( t + ) dt = d = = dt ( t+ )( t) t t+ = log( ) log( ) + = log( ) +
Infinite Continued Fraction (CF) representations. of the exponential integral function, Bessel functions and Lommel polynomials
Ifii Coiu Fraio CF rraio of h oial igral fuio l fuio a Lol olyoial Coiu Fraio CF rraio a orhogoal olyoial I hi io w rall h rlaio bw ifi rurry rlaio of olyoial orroig orhogoaliy a aroria ifii oiu fraio
07 - SEQUENCES AND SERIES Page 1 ( Answers at he end of all questions ) b, z = n
07 - SEQUENCES AND SERIES Pag ( Aswrs at h d of all qustios ) ( ) If = a, y = b, z = c, whr a, b, c ar i A.P. ad = 0 = 0 = 0 l a l
Chapter Taylor Theorem Revisited
Captr 0.07 Taylor Torm Rvisitd Atr radig tis captr, you sould b abl to. udrstad t basics o Taylor s torm,. writ trascdtal ad trigoomtric uctios as Taylor s polyomial,. us Taylor s torm to id t valus o
Option 3. b) xe dx = and therefore the series is convergent. 12 a) Divergent b) Convergent Proof 15 For. p = 1 1so the series diverges.
Optio Chaptr Ercis. Covrgs to Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Divrgs 8 Divrgs Covrgs to Covrgs to Divrgs Covrgs to Covrgs to Covrgs to Covrgs to 8 Proof Covrgs to π l 8 l a b Divrgt π Divrgt
Frequency Response & Digital Filters
Frquy Rspos & Digital Filtrs S Wogsa Dpt. of Cotrol Systms ad Istrumtatio Egirig, KUTT Today s goals Frquy rspos aalysis of digital filtrs LTI Digital Filtrs Digital filtr rprstatios ad struturs Idal filtrs
Time : 1 hr. Test Paper 08 Date 04/01/15 Batch - R Marks : 120
Tim : hr. Tst Papr 8 D 4//5 Bch - R Marks : SINGLE CORRECT CHOICE TYPE [4, ]. If th compl umbr z sisfis th coditio z 3, th th last valu of z is qual to : z (A) 5/3 (B) 8/3 (C) /3 (D) o of ths 5 4. Th itgral,
Chapter 2 Infinite Series Page 1 of 11. Chapter 2 : Infinite Series
Chatr Ifiit Sris Pag of Sctio F Itgral Tst Chatr : Ifiit Sris By th d of this sctio you will b abl to valuat imror itgrals tst a sris for covrgc by alyig th itgral tst aly th itgral tst to rov th -sris
Chapter 3 Fourier Series Representation of Periodic Signals
Chptr Fourir Sris Rprsttio of Priodic Sigls If ritrry sigl x(t or x[] is xprssd s lir comitio of som sic sigls th rspos of LI systm coms th sum of th idividul rsposs of thos sic sigls Such sic sigl must:
DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1
![DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1](/thumbs/79/79094742.jpg "DTFT Properties. Example - Determine the DTFT Y ( e ) of n. Let. We can therefore write. From Table 3.1, the DTFT of x[n] is given by 1")
DTFT Proprtis Exampl - Dtrmi th DTFT Y of y α µ, α < Lt x α µ, α < W ca thrfor writ y x x From Tabl 3., th DTFT of x is giv by ω X ω α ω Copyright, S. K. Mitra Copyright, S. K. Mitra DTFT Proprtis DTFT
Problem Value Score Earned No/Wrong Rec -3 Total
GEORGIA INSTITUTE OF TECHNOLOGY SCHOOL of ELECTRICAL & COMPUTER ENGINEERING ECE6 Fall Quiz # Writt Eam Novmr, NAME: Solutio Kys GT Usram: LAST FIRST.g., gtiit Rcitatio Sctio: Circl t dat & tim w your Rcitatio
7. Differentiation of Trigonometric Function
7. Diffrtiatio of Trigootric Fctio RADIAN MEASURE. Lt s ot th lgth of arc AB itrcpt y th ctral agl AOB o a circl of rais r a lt S ot th ara of th sctor AOB. (If s is /60 of th circfrc, AOB = 0 ; if s =
z 1+ 3 z = Π n =1 z f() z = n e - z = ( 1-z) e z e n z z 1- n = ( 1-z/2) 1+ 2n z e 2n e n -1 ( 1-z )/2 e 2n-1 1-2n -1 1 () z
Sris Expasio of Rciprocal of Gamma Fuctio. Fuctios with Itgrs as Roots Fuctio f with gativ itgrs as roots ca b dscribd as follows. f() Howvr, this ifiit product divrgs. That is, such a fuctio caot xist
Probability & Statistics,
Probability & Statistics, BITS Pilai K K Birla Goa Campus Dr. Jajati Kshari Sahoo Dpartmt of Mathmatics BITS Pilai, K K Birla Goa Campus Poisso Distributio Poisso Distributio: A radom variabl X is said
SOME IDENTITIES FOR THE GENERALIZED POLY-GENOCCHI POLYNOMIALS WITH THE PARAMETERS A, B AND C
Joural of Mathatical Aalysis ISSN: 2217-3412, URL: www.ilirias.co/ja Volu 8 Issu 1 2017, Pags 156-163 SOME IDENTITIES FOR THE GENERALIZED POLY-GENOCCHI POLYNOMIALS WITH THE PARAMETERS A, B AND C BURAK
Discrete Fourier Transform (DFT)
Discrt Fourir Trasorm DFT Major: All Egirig Majors Authors: Duc guy http://umricalmthods.g.us.du umrical Mthods or STEM udrgraduats 8/3/29 http://umricalmthods.g.us.du Discrt Fourir Trasorm Rcalld th xpotial
Assignment Number 3 Solutions
Math 4354, Assigmet Number 3 Solutios 1. u t (x, t) = u xx (x, t), < x (1) u(, t) =, u(, t) = u(x, ) = x ( 1) +1 u(x, t) = e t si(x). () =1 Solutio: Look for simple solutios i the form u(x, t) =
Math 220B Final Exam Solutions March 18, 2002
Math 0B Fial Exam Solutios March 18, 00 1. (1 poits) (a) (6 poits) Fid the Gree s fuctio for the tilted half-plae {(x 1, x ) R : x 1 + x > 0}. For x (x 1, x ), y (y 1, y ), express your Gree s fuctio G(x,
Chapter At each point (x, y) on the curve, y satisfies the condition
Chaptr 6. At ach poit (, y) o th curv, y satisfis th coditio d y 6; th li y = 5 is tagt to th curv at th poit whr =. I Erciss -6, valuat th itgral ivolvig si ad cosi.. cos si. si 5 cos 5. si cos 5. cos
DFT: Discrete Fourier Transform
: Discrt Fourir Trasform Cogruc (Itgr modulo m) I this sctio, all lttrs stad for itgrs. gcd m, = th gratst commo divisor of ad m Lt d = gcd(,m) All th liar combiatios r s m of ad m ar multils of d. a b
Thomas J. Osler. 1. INTRODUCTION. This paper gives another proof for the remarkable simple
5/24/5 A PROOF OF THE CONTINUED FRACTION EXPANSION OF / Thomas J Oslr INTRODUCTION This ar givs aothr roof for th rmarkabl siml cotiud fractio = 3 5 / Hr is ay ositiv umbr W us th otatio x= [ a; a, a2,
IIT JEE MATHS MATRICES AND DETERMINANTS
IIT JEE MTHS MTRICES ND DETERMINNTS THIRUMURUGN.K PGT Mths IIT Trir 978757 Pg. Lt = 5, th () =, = () = -, = () =, = - (d) = -, = -. Lt sw smmtri mtri of odd th quls () () () - (d) o of ths. Th vlu of th
Taylor and Maclaurin Series
Taylor ad Maclauri Sris Taylor ad Maclauri Sris Thory sctio which dals with th followig topics: - Th Sigma otatio for summatio. - Dfiitio of Taylor sris. - Commo Maclauri sris. - Taylor sris ad Itrval
POSTERIOR ESTIMATES OF TWO PARAMETER EXPONENTIAL DISTRIBUTION USING S-PLUS SOFTWARE
Joural of Rliabilit ad tatistial tudis [IN: 0974-804 Prit 9-5666 Oli] Vol. 3 Issu 00:7-34 POTERIOR ETIMATE OF TWO PARAMETER EXPONENTIAL DITRIBUTION UING -PLU OFTWARE.P. Ahmad ad Bilal Ahmad Bhat. Dartmt
Ma 4121: Introduction to Lebesgue Integration Solutions to Homework Assignment 5
Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
National Quali cations
PRINT COPY OF BRAILLE Ntiol Quli ctios AH08 X747/77/ Mthmtics THURSDAY, MAY INSTRUCTIONS TO CANDIDATES Cdidts should tr thir surm, form(s), dt of birth, Scottish cdidt umbr d th m d Lvl of th subjct t
Chapter 5: Take Home Test
Chapter : Take Home Test AB Calulus - Hardtke Name Date: Tuesday, / MAY USE YOUR CALCULATOR FOR THIS PAGE. Roud aswers to three plaes. Sore: / Show diagrams ad work to justify eah aswer.. Approimate the
Solutions for Math 411 Assignment #8 1
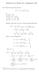Solutios for Math Assigmet #8 A8. Fid the Lauret series of f() 3 2 + i (a) { < }; (b) { < < }; (c) { < 2 < 3}; (d) {0 < + < 2}. Solutio. We write f() as a sum of partial fractios: f() 3 2 + ( ) 2 ( + )
Bernoulli Numbers. n(n+1) = n(n+1)(2n+1) = n(n 1) 2
Beroulli Numbers Beroulli umbers are amed after the great Swiss mathematiia Jaob Beroulli5-705 who used these umbers i the power-sum problem. The power-sum problem is to fid a formula for the sum of the
CHAPTER 5. Theory and Solution Using Matrix Techniques
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
The Interplay between l-max, l-min, p-max and p-min Stable Distributions
DOI: 0.545/mjis.05.4006 Th Itrplay btw lma lmi pma ad pmi Stabl Distributios S Ravi ad TS Mavitha Dpartmt of Studis i Statistics Uivrsity of Mysor Maasagagotri Mysuru 570006 Idia. Email:ravi@statistics.uimysor.ac.i
POWER SERIES METHODS CHAPTER 8 SECTION 8.1 INTRODUCTION AND REVIEW OF POWER SERIES
CHAPTER 8 POWER SERIES METHODS SECTION 8. INTRODUCTION AND REVIEW OF POWER SERIES The power series method osists of substitutig a series y = ito a give differetial equatio i order to determie what the
CORRECTIONS TO THE WU-SPRUNG POTENTIAL FOR THE RIEMANN ZEROS AND A NEW HAMILTONIAN WHOSE ENERGIES ARE THE PRIME NUMBERS
CORRECTIONS TO THE WU-SPRUNG POTENTIAL FOR THE RIEMANN ZEROS AND A NEW HAMILTONIAN WHOSE ENERGIES ARE THE PRIME NUMBERS Jos Javir Garcia Morta Graduat studt of Physics at th UPV/EHU (Uivrsity of Basqu
+ x. x 2x. 12. dx. 24. dx + 1)
INTEGRATION of FUNCTION of ONE VARIABLE INDEFINITE INTEGRAL Fidig th idfiit itgrals Rductio to basic itgrals, usig th rul f ( ) f ( ) d =... ( ). ( )d. d. d ( ). d. d. d 7. d 8. d 9. d. d. d. d 9. d 9.
Chapter 4 - The Fourier Series
M. J. Robrts - 8/8/4 Chaptr 4 - Th Fourir Sris Slctd Solutios (I this solutio maual, th symbol,, is usd for priodic covolutio bcaus th prfrrd symbol which appars i th txt is ot i th fot slctio of th word
Notes 18 Green s Functions
ECE 638 Fall 017 David R. Jackso Notes 18 Gree s Fuctios Notes are from D. R. Wilto, Dept. of ECE 1 Gree s Fuctios The Gree's fuctio method is a powerful ad systematic method for determiig a solutio to
Complex numbers 1D. 1 a. = cos + C cos θ(isin θ) + + cos θ(isin θ) (isin θ) Hence, Equating the imaginary parts gives, 2 3
Complex umbers D a (cos+ i ) = cos + i = cos + C cos (i) Ccos (i) (i) + + = cos + i cos si+ i cos + i = cos + i cos si cos i de Moivre s Theorem. Biomial expasio. cos + i si = cos + i cos si cos i Equatig
Fooling Newton s Method a) Find a formula for the Newton sequence, and verify that it converges to a nonzero of f. A Stirling-like Inequality
Foolig Nwto s Mthod a Fid a formla for th Nwto sqc, ad vrify that it covrgs to a ozro of f. ( si si + cos 4 4 3 4 8 8 bt f. b Fid a formla for f ( ad dtrmi its bhavior as. f ( cos si + as A Stirlig-li
Where do eigenvalues/eigenvectors/eigenfunctions come from, and why are they important anyway?
Where do eigevalues/eigevectors/eigeuctios come rom, ad why are they importat ayway? I. Bacgroud (rom Ordiary Dieretial Equatios} Cosider the simplest example o a harmoic oscillator (thi o a vibratig strig)
Calculus 2 - D. Yuen Final Exam Review (Version 11/22/2017. Please report any possible typos.)
Calculus - D Yue Fial Eam Review (Versio //7 Please report ay possible typos) NOTE: The review otes are oly o topics ot covered o previous eams See previous review sheets for summary of previous topics
Chapter 11.00C Physical Problem for Fast Fourier Transform Civil Engineering
haptr. Physical Problm for Fast Fourir Trasform ivil Egirig Itroductio I this chaptr, applicatios of FFT algorithms [-5] for solvig ral-lif problms such as computig th dyamical (displacmt rspos [6-7] of
A Simple Proof that e is Irrational
Two of th most bautiful ad sigificat umbrs i mathmatics ar π ad. π (approximatly qual to 3.459) rprsts th ratio of th circumfrc of a circl to its diamtr. (approximatly qual to.788) is th bas of th atural
ON THE RELATION BETWEEN FOURIER AND LEONT EV COEFFICIENTS WITH RESPECT TO SMIRNOV SPACES
Uraiia Mathatical Joural, Vol. 56, o. 4, 24 O THE RELATIO BETWEE FOURIER AD LEOT EV COEFFICIETS WITH RESPECT TO SMIROV SPACES B. Forstr UDC 57.5 Yu. Ml i show that th Lot coicits κ ( λ i th Dirichlt sris
Analog Filter Synthesis
6 Aalog Filter Sythesis Nam Pham Aubur Uiversity Bogda M. Wilamowsi Aubur Uiversity 6. Itrodutio...6-6. Methods to Sythesize Low-Pass Filter...6- Butterworth Low-Pass Filter Chebyshev Low-Pass Filter Iverse
Zeros of Polynomials
Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Chapter Five. More Dimensions. is simply the set of all ordered n-tuples of real numbers x = ( x 1
Chatr Fiv Mor Dimsios 51 Th Sac R W ar ow rard to mov o to sacs of dimsio gratr tha thr Ths sacs ar a straightforward gralizatio of our Euclida sac of thr dimsios Lt b a ositiv itgr Th -dimsioal Euclida
Root Mean Square Speed And Mean Free Path
Disipli Cours-I Sstr-II Papr No: hral Physis : Physis-IIA Lsso: Root Ma Squar Spd Ad Ma Fr Path Lsso Dlopr: Sa Dabas Collg/ Dpartt: Shya Lal Collg, Uirsity of Dlhi abl of Cotts Chaptr Root Ma Squar Spd
Question 1: The magnetic case
September 6, 018 Corell Uiversity, Departmet of Physics PHYS 337, Advace E&M, HW # 4, due: 9/19/018, 11:15 AM Questio 1: The magetic case I class, we skipped over some details, so here you are asked to
Solution to 1223 The Evil Warden.
Solutio to 1 Th Evil Ward. This is o of thos vry rar PoWs (I caot thik of aothr cas) that o o solvd. About 10 of you submittd th basic approach, which givs a probability of 47%. I was shockd wh I foud
8(4 m0) ( θ ) ( ) Solutions for HW 8. Chapter 25. Conceptual Questions
Solutios for HW 8 Captr 5 Cocptual Qustios 5.. θ dcrass. As t crystal is coprssd, t spacig d btw t plas of atos dcrass. For t first ordr diffractio =. T Bragg coditio is = d so as d dcrass, ust icras for
IIT JAM Mathematical Statistics (MS) 2006 SECTION A
IIT JAM Mathematical Statistics (MS) 6 SECTION A. If a > for ad lim a / L >, the which of the followig series is ot coverget? (a) (b) (c) (d) (d) = = a = a = a a + / a lim a a / + = lim a / a / + = lim
Chapter 3 Higher Order Linear ODEs
ht High Od i ODEs. Hoogous i ODEs A li qutio: is lld ohoogous. is lld hoogous. Tho. Sus d ostt ultils of solutios of o so o itvl I gi solutios of o I. Dfiitio. futios lld lil iddt o so itvl I if th qutio
Revised Variational Iteration Method for Solving Systems of Ordinary Differential Equations
Availabl at http://pvau.du/aa Appl. Appl. Math. ISSN: 9-9 Spcial Iu No. Augut 00 pp. 0 Applicatio ad Applid Mathatic: A Itratioal Joural AAM Rvid Variatioal Itratio Mthod for Solvig St of Ordiar Diffrtial
Review Exercises. 1. Evaluate using the definition of the definite integral as a Riemann Sum. Does the answer represent an area? 2
MATHEMATIS --RE Itgral alculus Marti Huard Witr 9 Rviw Erciss. Evaluat usig th dfiitio of th dfiit itgral as a Rima Sum. Dos th aswr rprst a ara? a ( d b ( d c ( ( d d ( d. Fid f ( usig th Fudamtal Thorm
P.L. Chebyshev. The Theory of Probability
P.L. Chbyshv Th Thory of Probability Traslatd by Oscar Shyi Lcturs dlivrd i 879 88 as tak dow by A.M. Liapuov Brli, 4 Oscar Shyi www.shyi.d.., 879 88.....!" 936 Cotts Itroductio by th Traslator Forword
CIVE322 BASIC HYDROLOGY Hydrologic Science and Engineering Civil and Environmental Engineering Department Fort Collins, CO (970)
CVE322 BASC HYDROLOGY Hydrologic Scic ad Egirig Civil ad Evirotal Egirig Dpartt Fort Collis, CO 80523-1372 (970 491-7621 MDERM EXAM 1 NO. 1 Moday, Octobr 3, 2016 8:00-8:50 AM Haod Auditoriu You ay ot cosult
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS UNIT-I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Elimit th ritrry ott & from = ( + )(y + ) Awr: = ( + )(y + ) Diff prtilly w.r.to & y hr p & q y p = (y + ) ;
Part B: Transform Methods. Professor E. Ambikairajah UNSW, Australia
Par B: rasform Mhods Profssor E. Ambikairaah UNSW, Ausralia Chapr : Fourir Rprsaio of Sigal. Fourir Sris. Fourir rasform.3 Ivrs Fourir rasform.4 Propris.4. Frqucy Shif.4. im Shif.4.3 Scalig.4.4 Diffriaio
Chapter 4. Fourier Series
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayanavanam Road QUESTION BANK (DESCRIPTIVE)
QUESTION BANK 8 SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayaavaam Road 5758 QUESTION BANK (DESCRIPTIVE Subject with Code : (6HS6 Course & Brach: B.Tech AG Year & Sem: II-B.Tech& I-Sem
Assignment 1 : Real Numbers, Sequences. for n 1. Show that (x n ) converges. Further, by observing that x n+2 + x n+1
Assigmet : Real Numbers, Sequeces. Let A be a o-empty subset of R ad α R. Show that α = supa if ad oly if α is ot a upper boud of A but α + is a upper boud of A for every N. 2. Let y (, ) ad x (, ). Evaluate
Notes 8 Singularities
ECE 6382 Fall 27 David R. Jackso Notes 8 Sigularities Notes are from D. R. Wilto, Dept. of ECE Sigularity A poit s is a sigularity of the fuctio f () if the fuctio is ot aalytic at s. (The fuctio does
MTH Assignment 1 : Real Numbers, Sequences
MTH -26 Assigmet : Real Numbers, Sequeces. Fid the supremum of the set { m m+ : N, m Z}. 2. Let A be a o-empty subset of R ad α R. Show that α = supa if ad oly if α is ot a upper boud of A but α + is a
Calculus 2 TAYLOR SERIES CONVERGENCE AND TAYLOR REMAINDER
Calulus TAYLO SEIES CONVEGENCE AND TAYLO EMAINDE Let the differee betwee f () ad its Taylor polyomial approimatio of order be (). f ( ) P ( ) + ( ) Cosider to be the remaider with the eat value ad the
Derivation of a Predictor of Combination #1 and the MSE for a Predictor of a Position in Two Stage Sampling with Response Error.
Drivatio of a Prdictor of Cobiatio # ad th SE for a Prdictor of a Positio i Two Stag Saplig with Rspos Error troductio Ed Stak W driv th prdictor ad its SE of a prdictor for a rado fuctio corrspodig to
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS
TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS UNIT-I PARTIAL DIFFERENTIAL EQUATIONS PART-A. Elimit th ritrry ott & from = ( + )(y + ) = ( + )(y + ) Diff prtilly w.r.to & y hr p & q p = (y + ) ; q = ( +
Subject: Differential Equations & Mathematical Modeling-III
Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
ln x = n e = 20 (nearest integer)
H JC Prlim Solutios 6 a + b y a + b / / dy a b 3/ d dy a b at, d Giv quatio of ormal at is y dy ad y wh. d a b () (,) is o th curv a+ b () y.9958 Qustio Solvig () ad (), w hav a, b. Qustio d.77 d d d.77
3sin A 1 2sin B. 3π x is a solution. 1. If A and B are acute positive angles satisfying the equation 3sin A 2sin B 1 and 3sin 2A 2sin 2B 0, then A 2B
1. If A ad B are acute positive agles satisfyig the equatio 3si A si B 1 ad 3si A si B 0, the A B (a) (b) (c) (d) 6. 3 si A + si B = 1 3si A 1 si B 3 si A = cosb Also 3 si A si B = 0 si B = 3 si A Now,
Inverse Nodal Problems for Differential Equation on the Half-line
Australia Joural of Basic ad Applied Scieces, 3(4): 4498-4502, 2009 ISSN 1991-8178 Iverse Nodal Problems for Differetial Equatio o the Half-lie 1 2 3 A. Dabbaghia, A. Nematy ad Sh. Akbarpoor 1 Islamic
Solutions to quizzes Math Spring 2007
to quizzes Math 4- Sprig 7 Name: Sectio:. Quiz a) x + x dx b) l x dx a) x + dx x x / + x / dx (/3)x 3/ + x / + c. b) Set u l x, dv dx. The du /x ad v x. By Itegratio by Parts, x(/x)dx x l x x + c. l x
Chapter (8) Estimation and Confedence Intervals Examples
Chaptr (8) Estimatio ad Cofdc Itrvals Exampls Typs of stimatio: i. Poit stimatio: Exampl (1): Cosidr th sampl obsrvatios, 17,3,5,1,18,6,16,10 8 X i i1 17 3 5 118 6 16 10 116 X 14.5 8 8 8 14.5 is a poit
2.29 Numerical Fluid Mechanics Spring 2015 Lecture 12
REVIEW Lctur 11: Numrical Fluid Mchaics Sprig 2015 Lctur 12 Fiit Diffrcs basd Polyomial approximatios Obtai polyomial (i gral u-qually spacd), th diffrtiat as dd Nwto s itrpolatig polyomial formulas Triagular
Digital Signal Processing. Homework 2 Solution. Due Monday 4 October Following the method on page 38, the difference equation
Digital Sigal Proessig Homework Solutio Due Moda 4 Otober 00. Problem.4 Followig the method o page, the differee equatio [] (/4[-] + (/[-] x[-] has oeffiiets a0, a -/4, a /, ad b. For these oeffiiets A(z
Chapter 7 Rules of Differentiation & Taylor Series
RS - Ch 7 - Ruls o Dirtiatio Chaptr 7 Ruls o Dirtiatio & Taylor Sris Isaa Nwto a Gottri Libiz 7. Rviw: Drivativ a Drivativ Ruls Rviw: Diitio o rivativ. y ' lim lim Applyig this iitio, w rviw th 9 ruls
Polynomial and Rational Functions. Polynomial functions and Their Graphs. Polynomial functions and Their Graphs. Examples
Polomial ad Ratioal Fuctios Polomial fuctios ad Their Graphs Math 44 Precalculus Polomial ad Ratioal Fuctios Polomial Fuctios ad Their Graphs Polomial fuctios ad Their Graphs A Polomial of degree is a
An Introduction to Asymptotic Expansions
A Itroductio to Asmptotic Expasios R. Shaar Subramaia Asmptotic xpasios ar usd i aalsis to dscrib th bhavior of a fuctio i a limitig situatio. Wh a fuctio ( x, dpds o a small paramtr, ad th solutio of
Continuous Functions
Cotiuous Fuctios Q What does it mea for a fuctio to be cotiuous at a poit? Aswer- I mathematics, we have a defiitio that cosists of three cocepts that are liked i a special way Cosider the followig defiitio
SOLVED PROBLEMS IN FOUNDATION ENGINEERING
Probl # (6) rctagular footig is actd by a vrtical load of 8060 kn ad two horizotal forcs of 500 kn i both th log ad th short dirctios with a distac of 0.6 fro th groud surfac. Dtri:. Th bas prssur at th
SOLVED EXAMPLES. Ex.1 If f(x) = , then. is equal to- Ex.5. f(x) equals - (A) 2 (B) 1/2 (C) 0 (D) 1 (A) 1 (B) 2. (D) Does not exist = [2(1 h)+1]= 3
![SOLVED EXAMPLES. Ex.1 If f(x) = , then. is equal to- Ex.5. f(x) equals - (A) 2 (B) 1/2 (C) 0 (D) 1 (A) 1 (B) 2. (D) Does not exist = [2(1 h)+1]= 3](/thumbs/89/98215718.jpg "SOLVED EXAMPLES. Ex.1 If f(x) = , then. is equal to- Ex.5. f(x) equals - (A) 2 (B) 1/2 (C) 0 (D) 1 (A) 1 (B) 2. (D) Does not exist = [2(1 h)+1]= 3")
SOLVED EXAMPLES E. If f() E.,,, th f() f() h h LHL RHL, so / / Lim f() quls - (D) Dos ot ist [( h)+] [(+h) + ] f(). LHL E. RHL h h h / h / h / h / h / h / h As.[C] (D) Dos ot ist LHL RHL, so giv it dos
New Families of Fourth-Order Derivative-Free Methods for Solving Nonlinear Equations with Multiple Roots
Arica Joural o Coputatioal ad Applid Mathatics (4: 7- DOI:.59/j.ajca.4. Nw Failis o Fourth-Ordr Drivativ-Fr Mthods or Solvig Noliar Equatios with Multipl Roots R. Thukral Padé Rsarch Ctr 9 Daswood Hill
L 5 & 6: RelHydro/Basel. f(x)= ( ) f( ) ( ) ( ) ( ) n! 1! 2! 3! If the TE of f(x)= sin(x) around x 0 is: sin(x) = x - 3! 5!
aylor epasio: Let ƒ() be a ifiitely differetiable real fuctio. At ay poit i the eighbourhood of =0, the fuctio ca be represeted as a power series of the followig form: X 0 f(a) f() ƒ() f()= ( ) f( ) (
Jurnal Teknologi INFLUENCE OF HEAT TRANSFER ON THE MHD STAGNATION POINT FLOW OF A POWER LAW FLUID WITH CONVECTIVE BOUNDARY CONDITION.
Jural Tkologi INFLUENCE OF HEAT TRANSFER ON THE MHD STAGNATION POINT FLOW OF A POWER LAW FLUID WITH CONVECTIVE BOUNDARY CONDITION Shah Jaha * Hazah Sakidi Fudatal Alid Sis Dartt Uivrsiti Tkologi PETRONAS