Analytic Solution of Nonlinear Schrödinger Equation by Means of A New Approach
|
|
|
- Lesley Lindsey
- 5 years ago
- Views:
Transcription
1 Anlytic Solution of Nonlinr Schrödingr Eqution y Mns of A Nw Approch Ali Yunus Rohdi Optoinformtics Lortory, Dprtmnt of Physics, Spuluh Nopmr Institut of Tchnology (ITS), Sukolilo, Sury, 6111 Tlp/Fx : , E-mil:rohdi@physics.its.c.id Astrct Th nonlinr Schrödingr qution (NSE) hs srvd s th govrning qution of opticl soliton in th study of its pplictions to opticl communiction nd opticl switching. Vrious schms hv n mployd for th solution of this nonlinr qution s wll s its vrints. W rport in this ppr rltivly simplr nw pproch for th nlytic solution of NSE. In this schm th qution ws first trnsformd into n rctngnt diffrntil qution, which ws thn sprtd into th linr nd nonlinr prts, with th linr prt solvd in stright forwrd mnnr. Th solution of th nonlinr qution ws writtn in th form of modultion function chrctrizd y its mplitud function A nd phs function F(A). Sustituting th linr solution for A, th rctngnt diffrntil qution ws solvd for crtin initil vlu of A. It is shown tht this mthod is pplicl to othr first-ordr nonlinr diffrntil qution such s th Kortwg d Vris qution, which cn trnsformd into n rctngnt diffrntil qution. I. Introduction Th phnomnon of th solitry wv propgtion ws osrvd for th first tim y th Scottish scintist John Scott Russll in 1844, whn on dy h ws wtching wtr wvs of crtin shp kpt on trvling without chnging thir shp for distnc s fr s his y could s. To xplin th hvior of such unsul wv, Kortwg nd d Vris govrnd modl for th wv propgtion in shllow wtr in form prtil diffrntil qution clld s KdV diffrntil qution, which its solution pproprits to th fturs of th solitry wv clld s soliton [1]. Th xistnc of solitons in opticl fir ws prdictd y Zkrov nd Zt (197) ftr thy drivd diffrntil qution for th light propgting in n opticl fir, tht dmonstrtd ltr y Hzgw in 1973 t Bll Lortory. Nxt, Mollnur nd Stoln mployd th solitons in opticl fir for gnrting supicoscond pulss. Th diffrntil qution of th soliton pulss propgtion in losslss opticl fir hs n ordinrily givn in normlizd from : U 1 U j + + N U Z T U whr U, Z, nd T r rspctivly th normlizd prmtrs of th nvlop function, th distnc nd th tim propgtion, whil N is n ordr of soliton, nd (1)
2 j 1. Th ov of th nonlinr diffrntil qution with th Z nd T xchngd is known s th nonlinr Schrödingr qution (NSE). Aftr th lightwv soliton cn gnrtd in opticl fir, th NSE hs n com th primry modling which hs lso srvd s th govrning qution of opticl soliton in th study of its pplictions to opticl communiction nd opticl switching [1],[]. Thr r vrious schm tht commonly mployd for solving th NSE, mong ths r th split Fourir trnsform [3], finit diffrnc [4], vritionl pproch [5], nd prturtion mthod [6]. Du to for N 1 th NSE rducs to n intgrl form, hnc it cn solvd xctly in nlytic solution, whr its solution corrsponds to th fundmntl soliton. Sprting oth vrils T nd Z hs n don y ssuming th NSE solution in form [1],[] : jφ( z) U( T, Z) V( T), () whr oth V nd φ nd r th rl functions. Applying th oundry conditions dv T, V nd givs φ κz whr κ is constnt, nd hnc dt th NSE rducs to th following first ordr diffrntil qution : dw dt κw w, V w (3) κ It is wll-known tht upon intgrting th oth sids of Eqs.(3) givs th solution of w in hyprolic scnt function (sch-function). But w rport in this ppr nw pproch clld Short Stl Modultion Tchniqu (S-SMT) for otining th solution of w y trnsforming Eqs.(3) into n rctngnt diffrntil qution, which ws thn sprtd into th linr nd nonlinr prts, with th linr prt solvd in stright forwrd mnnr. Th solution of th nonlinr qution ws writtn in th form of modultion function chrctrizd y its mplitud function A nd phs function F(A). Sustituting th linr solution for A, th rctngnt diffrntil qution ws solvd for crtin initil vlu of A. II. Solving n rctngnt diffrntil qution y using th common procdur In clssifying th first ordr nonlinr ordinry diffrntil qution, n rctngnt diffrntil qution is dfind s : dy y dx +, y ( x ) y (4) for oth ritrry of dn constnt cofficints nd strtd from th ordinry point (x). Th common procdur of solving Eqs.(4) ing y trnsforming into rctngnt. Rcntly, w hv rportd nothr wy for solving th rctngnt diffrntil qution using Brnoulli intgrl [7], nd y pplying th stl modultion tchniqu [8]. Solving of Eqs.(4) for oth nd r positiv constnts y trnsforming into rctngnt prformd y mking chng vril u y givs th xct solution in th form :
3 1 ( x) tn x + tn y y (5) Eqution (5) indicts tht th solution th rctngnt diffrntil qution for initil vlu y is of th form : whil th solution for ( x) tn( x) y (6) y is of th form : ( x) tn( x C) y + (7) whr C is th intgrting constnt tht must dtrmind y pplying th initil y x y. vlu ( ) II. Solving n rctngnt diffrntil qution y mns S-SMT pproch Applying th Short Stl Modultion Tchniqu (S-SMT) for solving Eqs.(4) is strtd for th cs with th initil vlu y. Th linr prt of Eqs.(4) is of form : with solution dy L dx, (8) y L x, whil th nonlinr prt is of form : dy N y N, (9) dx which its solution must writtn in th following modultion function : y y N N (1) y dx N As in th stl modultion tchniqu (SMT) sd on Brnoulli qution [8],[9], th SMT sd on rctngnt diffrntil qution is lso chrctrizd y modultion function of th nonlinr solution prt in which its initil vlu y N sids cts s mplitud A, lso modultd in th phs function F(A). Th corrsponding phs function of solving th rctngnt is of form : 1 F (A) (11) Adx Sustituting y L into y N in Eqs.(1) givs th solution of y in th form :
4 x y( x) (1) x Involving th constnt in th numrtor of Eqs.(1) is prformd y multiplying /, thn writing Eqs.(1) in form : / x y( x) (13) ( / x) Th pproch of short stl modultion is pplid to th dnomintor of Eqs.(13) y pproching th inomil into th root squr for x, thus w find : x y( x) (14) x By using n pproximtion x sin x for x, thn Eqs.(14) coms : ( ) y x tn x (15) Similr to th stps in Eqs.(6-7) for ritrry vlu of y, w tk th solution of th rctngnt diffrntil qution in th form : y (16) ( x) tn x + C whr C is dtrmind y pplying th initil vlu. Th solution of th rctngnt diffrntil qution s Rictti diffrntil of constnt cofficints [1] cn crtd sily using AF(A) digrm whn Eqs.(4) is writtn in from : Solution dy dx ( y) + (17) 1 y ( x) tn x + tn y / (18)
5 Th trm of AF(A) digrm rfrs to th xistnc of mplitud tht lso including in tngnt function of th phs function. Importnt to strssd hr tht for oth nd r positiv constnts, th trm coms, thrfor Eqs.(18) rducs to th form in Eqs.(5). Whil nlytic solution of Eqs.(18) for ritrry nd cofficints must still involving d Moivr thorm tht rltd tngnt nd rctngnt to th hyprolic of tngnt nd rctngnt [11]. III. Appliction of th S-SMT for solving th NSE of fundmntl soliton w to trnsform Eqs.(3) into nothr form of th following diffrntil qution : According to [1], w mk chng vril sin( θ) dθ dt κ sin ( θ) Th form of th rctngnt diffrntil qution is otind from Eqs.(19) ftr rprsnting th sinus function in trm of th Eulr formul, tht is of form : d dη κ ( ) 1, η T hr V to th nvlop of soliton function, th vlu of w 1 t T corrspond κ jπ / to th θ. Du to th rl of ( ), hnc th solving Eqs.() (19) () nd η r th dpndnt nd indpndnt vrils rspctivly. According π / corrsponds to th initil vlu ( ). Thrfor th procdur of solving Eqs.() is prformd schmticlly s following :
6 ( ) 1 d dη Th linr prt Th non linr prt d ( ) L d( ) N 1 ( ) dη ( ) η dη ( ) ( ) L N 1 ( ) j ( ) L ( ) N 1 ( jη) ( jη) ( jη) η θ j jtn using d Moivr thorm [11] tnh solution d j θ 1 dη tn ( ) T 1 κ κτ ( θ / ) N dη N j θ sin j sin using d Moivr rltion [11] ( jη) ( jη) Hnc, th finl solution ( ) w sinθ dw dt κw w in Eqs.(3) is of form : ( ) ( θ/) V tnθ/ k 1+ tn κτ κτ + sch ( κt) (1) Th nlytic solution of th NSE for th fundmntl soliton is in th form : U T,Z V T jφ z κsch κt () ( ) ( ) ( ) ( ) jκκ
7 III. Appliction of AF(A) digrm for solving KdV of fundmntl soliton Th KdV diffrntil qution is of form [4],[1] : y y y y + + 6y t z z t z 3 whr z nd t r rspctivly th distnc nt th tim of th soliton propgtion. Introducing th collctiv coordints [13] ξ z vt, whr v is th vlocity of soliton, nd ssuming th solution in form : y ( x,t) f ( ξ) (4) thn Eqs.(1) rducs to th form: 3 f f f ( 1 v ) + 6 f + v (5) 3 ξ ξ ξ Upon succssiv intgrtion of Eqs.(5) rspct to d ξ nd df, lso y dfining th following two prmtrs : f u 1 v 1 v 1 α w found th corrsponding of th first ordr nonlinr diffrntil qution of Eqs.(5) in th form : du αu dξ u Using u sin θ, nd rprsnting in trm of th Eulr formul to trnsform Eqs.(6) into th rctngnt diffrntil qution : d α ( ) + ( j) (7) dξ v [ ] [ ] (3) (6) Crting th solution Eqs.(7) using AF(A) digrm is otind in th form: 1 jtn jαξ+ tn ( j ) (8) or tnh 1 [ αξ + tnh ( cosθ jsin θ )] As on th NSE cs, th KdV diffrntil qution tht givs th fundmntl soliton ing corrsponding to θ π /. Hnc, ftr nglcting th imginry trm of jsin θ, w find from Eqs.(9) th rltion tnh 1 ( ) αξ, tht vntully tn θ/. This rsult llows us to writ : u sin ( θ ) sc h ξ. v Hnc, th nlytic solution of th KdV diffrntil qution for th fundmntl soliton is of form : v 1 y ( z, t ) f ( ξ ) u ( ξ ) (3) or yilding ( ) αξ 1 (9) v 1
8 v 1 1 v 1 ( z,t) sch ( z vt) y Finlly, w prsnt th visuliztion of propgtion th fundmntl soliton of solving th NSE of Eqs.() nd th KdV of Eqs.(31) in Fig.1 low. v (31) () NSE of κ 1 () KdV for v (c) KdV for v5 (d) KdV for v7.5 Fig. 1 Visuliztion of propgtion th fundmntl soliton of solving NSE nd KdV IV. Discussion W hv shown tht th solving rctngnt diffrntil dy y dx + qution for ritrry nd constnt cofficints with th initil vlu y (x ) y y mns short stl modultion tchniqu (S-SMT) givs th nlytic xct solution in AF(A) formul of modultion function, whr its mplitud in (this cs A ) modultd in tngnt function [ Ax C] tn + of th phs function, whr C is th intgrting constnt. Th AF(A) formul cn crt th nlytic xct solution of oth th NSE nd KdV for fundmntl ordr tht corrsponds to th propgtion of fundmntl soliton in losslss mdi. As ppr
9 in Eqs.() for th NSE nd Eqs.(31) for KdV, th nlyticl solution of oth intgrl nonlinr prtil diffrntil qution lso form n AF(A) formul, whr ch of mplitud trm lso modultd in hyprolic scnt nd qudrtic of scnt hyprolic of th phs function rspctivly. V. Conclusions Applying th Short Stl Modultion Tchniqu (S-SMT) sd on rctngnt diffrntil qution simplifid y AF(A) digrm pplicl to solv oth of NSE nd KdV diffrntil qution nlyticlly for fundmntl soliton. AF(A) digrm of th S-SMT cn justify th following intgrl formultion 1 dθ dθ sc h ( θ) nd ln tn( θ / ) sin θ θ θ Hnc, th AF(A) digrm is rcommndd to mployd to formult nothr intgrls tht cn trnsformd into rctngnt. Th solution of n intgrl nonlinr prtil diffrntil qution such s th NSE nd KdV diffrntil qution for soliton propgtion of fundmntl soliton in losslss mdi hv th sm fturs, tht r in modultion function of form AF(A) formul, whr its mplitud trm A lso modultd in th phs function F(A). ACKNOWLEDGMENTS : I would lik to thnk Prof. M.O. Tji (Dprtmnt of Physics, ITB, Bndung) for introducing m into th intrst lnd of solitons, nd lso for his support my suggstions in dvloping smrt mthods of solving th nonlinr diffrntil qutions. Lst, ut not lst, my grtitud gos to my prnts, my wif Sri Yulini nd my dughtrs (Astrid Dnyls nd Ndy Frmg) for thir continus support during this rsrch. REFERENCES : [1] Izuk, K, Elmnts of Photonics, Vol.II, Chptr 15, pp: , John Wily nd Sons,. [] Agrwl G.P, Fir-Optic Communiction Systm, Chptr 9, pp: , Wily Sris in Microwv nd Opticl Enginring, 199. [3] Kczmrk,T, nd Kczmrk, A Nonlinr Lightguid s A Trnsmission Mdium of Ultrshort Chirpd Hyprolic Scnt Shp nd Gussin Pulss, Scintific- Procdings of RGA Tchnicl Univrsity, Sris Computr Sicnc, 1. [4] Aguyo,L, t.l, Exploring th Bhvior of Soliton on A Dsktop Prsonl Computr, Rvist Mxin D Fisic E-5(1) [5] Rpti, Z, Kvrdikis, P.G, Smrsi, A, nd Bishop, A.R, Vritionl Approch to th Modultion Instility, rxiv:cond-mt/4461, 4. [6] Jong H.L, Anlysis nd Chrctriztion of Fir Nonlinritis with Dtrministics nd Stochstic Signl Sourcs, P.hD Dissrttion in Elctricl Enginring, Univrsity of Virgini,. [7] Rohdi,A.Y, Introducing Brnoulli Intgrl for Solving Som Prolm of Physics, Procding of Syimposium of Physics nd Its Applictions, Dprtmnt of Physics, ITS, Sury, My, 7. A6.1-5.
10 [8] Rohdi,A.Y, Applying of Modultion Schm of Solving Brnoulli Diffrntil Eqution, Journl of Physics nd Its pplictions, Vol 3, No.1, pp 1:6, Dprtmnt of Physics, ITS,Sury, 7. [9] Rohdi,A.Y, Introducing Stl Modultion Tchniqu for Solving n Inhomognous Brnoulli Diffrntil Eqution, Sumit to Symposium ICOLA 7, Univrsity of Indonsi, 7. [1] Rohdi,A.Y, Anlyticl Solution of th Rictti Diffrntil Eqution for High Frquncy using Stl Modultion Tchniqu, Prsntd on ICMNS, ITB, Bndung, Nopmr, 6. [11] Spigl,M.R,(1968)., Mthmticl Hndook of Formuls nd Tls, Schum s Outlin Sris, McGRAW-Hill Book Compny. [1] Much,S, Introduction to Mthods of Applid Mthmtics Advncd Mthmticl Mthods for Sintists nd Enginrs, Chptr 7, pp.6:63, Much Pulishing Compny, 1. [13] Louis Morls-Molin t.l, Soliton Rtchts in Homognous Nonlinr Klin Gordon Systm, rxiv:cond-mt/5174 v, Nop. 5.
INTEGRALS. Chapter 7. d dx. 7.1 Overview Let d dx F (x) = f (x). Then, we write f ( x)
 Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Ch 1.2: Solutions of Some Differential Equations
 Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
Chapter 16. 1) is a particular point on the graph of the function. 1. y, where x y 1
 Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
CIVL 8/ D Boundary Value Problems - Rectangular Elements 1/7
 CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
Integration Continued. Integration by Parts Solving Definite Integrals: Area Under a Curve Improper Integrals
 Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
TOPIC 5: INTEGRATION
 TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
Instructions for Section 1
 Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
Creating A New Planck s Formula of Spectral Density of Black-body Radiation by Means of AF(A) Diagram
 nd Jogj Interntionl Physics Conference Enhncing Network nd Collortion Developing Reserch nd Eduction in Physics nd Nucler Energy Septemer 6-9, 007, Yogykrt-Indonesi Creting A New Plnck s Formul of Spectrl
nd Jogj Interntionl Physics Conference Enhncing Network nd Collortion Developing Reserch nd Eduction in Physics nd Nucler Energy Septemer 6-9, 007, Yogykrt-Indonesi Creting A New Plnck s Formul of Spectrl
CONTINUITY AND DIFFERENTIABILITY
 MCD CONTINUITY AND DIFFERENTIABILITY NCERT Solvd mpls upto th sction 5 (Introduction) nd 5 (Continuity) : Empl : Chck th continuity of th function f givn by f() = + t = Empl : Emin whthr th function f
MCD CONTINUITY AND DIFFERENTIABILITY NCERT Solvd mpls upto th sction 5 (Introduction) nd 5 (Continuity) : Empl : Chck th continuity of th function f givn by f() = + t = Empl : Emin whthr th function f
Multi-Section Coupled Line Couplers
 /0/009 MultiSction Coupld Lin Couplrs /8 Multi-Sction Coupld Lin Couplrs W cn dd multipl coupld lins in sris to incrs couplr ndwidth. Figur 7.5 (p. 6) An N-sction coupld lin l W typiclly dsign th couplr
/0/009 MultiSction Coupld Lin Couplrs /8 Multi-Sction Coupld Lin Couplrs W cn dd multipl coupld lins in sris to incrs couplr ndwidth. Figur 7.5 (p. 6) An N-sction coupld lin l W typiclly dsign th couplr
Lecture 11 Waves in Periodic Potentials Today: Questions you should be able to address after today s lecture:
 Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 8: Effect of a Vertical Field on Tokamak Equilibrium
 .65, MHD Thory of usion Systms Prof. ridrg Lctur 8: Effct of Vrticl ild on Tokmk Equilirium Toroidl orc lnc y Mns of Vrticl ild. Lt us riw why th rticl fild is imortnt. 3. or ry short tims, th cuum chmr
.65, MHD Thory of usion Systms Prof. ridrg Lctur 8: Effct of Vrticl ild on Tokmk Equilirium Toroidl orc lnc y Mns of Vrticl ild. Lt us riw why th rticl fild is imortnt. 3. or ry short tims, th cuum chmr
Lecture contents. Bloch theorem k-vector Brillouin zone Almost free-electron model Bands Effective mass Holes. NNSE 508 EM Lecture #9
 Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
SOLVED EXAMPLES. be the foci of an ellipse with eccentricity e. For any point P on the ellipse, prove that. tan
 LOCUS 58 SOLVED EXAMPLES Empl Lt F n F th foci of n llips with ccntricit. For n point P on th llips, prov tht tn PF F tn PF F Assum th llips to, n lt P th point (, sin ). P(, sin ) F F F = (-, 0) F = (,
LOCUS 58 SOLVED EXAMPLES Empl Lt F n F th foci of n llips with ccntricit. For n point P on th llips, prov tht tn PF F tn PF F Assum th llips to, n lt P th point (, sin ). P(, sin ) F F F = (-, 0) F = (,
MASTER CLASS PROGRAM UNIT 4 SPECIALIST MATHEMATICS SEMESTER TWO 2014 WEEK 11 WRITTEN EXAMINATION 1 SOLUTIONS
 MASTER CLASS PROGRAM UNIT SPECIALIST MATHEMATICS SEMESTER TWO WEEK WRITTEN EXAMINATION SOLUTIONS FOR ERRORS AND UPDATES, PLEASE VISIT WWW.TSFX.COM.AU/MC-UPDATES QUESTION () Lt p ( z) z z z If z i z ( is
MASTER CLASS PROGRAM UNIT SPECIALIST MATHEMATICS SEMESTER TWO WEEK WRITTEN EXAMINATION SOLUTIONS FOR ERRORS AND UPDATES, PLEASE VISIT WWW.TSFX.COM.AU/MC-UPDATES QUESTION () Lt p ( z) z z z If z i z ( is
Section 3: Antiderivatives of Formulas
 Chptr Th Intgrl Appli Clculus 96 Sction : Antirivtivs of Formuls Now w cn put th is of rs n ntirivtivs togthr to gt wy of vluting finit intgrls tht is ct n oftn sy. To vlut finit intgrl f(t) t, w cn fin
Chptr Th Intgrl Appli Clculus 96 Sction : Antirivtivs of Formuls Now w cn put th is of rs n ntirivtivs togthr to gt wy of vluting finit intgrls tht is ct n oftn sy. To vlut finit intgrl f(t) t, w cn fin
, between the vertical lines x a and x b. Given a demand curve, having price as a function of quantity, p f (x) at height k is the curve f ( x,
 Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
HIGHER ORDER DIFFERENTIAL EQUATIONS
 Prof Enriqu Mtus Nivs PhD in Mthmtis Edution IGER ORDER DIFFERENTIAL EQUATIONS omognous linr qutions with onstnt offiints of ordr two highr Appl rdution mthod to dtrmin solution of th nonhomognous qution
Prof Enriqu Mtus Nivs PhD in Mthmtis Edution IGER ORDER DIFFERENTIAL EQUATIONS omognous linr qutions with onstnt offiints of ordr two highr Appl rdution mthod to dtrmin solution of th nonhomognous qution
Mathematics. Mathematics 3. hsn.uk.net. Higher HSN23000
 Highr Mthmtics UNIT Mthmtics HSN000 This documnt ws producd spcilly for th HSN.uk.nt wbsit, nd w rquir tht ny copis or drivtiv works ttribut th work to Highr Still Nots. For mor dtils bout th copyright
Highr Mthmtics UNIT Mthmtics HSN000 This documnt ws producd spcilly for th HSN.uk.nt wbsit, nd w rquir tht ny copis or drivtiv works ttribut th work to Highr Still Nots. For mor dtils bout th copyright
Elliptical motion, gravity, etc
 FW Physics 130 G:\130 lctur\ch 13 Elliticl motion.docx g 1 of 7 11/3/010; 6:40 PM; Lst rintd 11/3/010 6:40:00 PM Fig. 1 Elliticl motion, grvity, tc minor xis mjor xis F 1 =A F =B C - D, mjor nd minor xs
FW Physics 130 G:\130 lctur\ch 13 Elliticl motion.docx g 1 of 7 11/3/010; 6:40 PM; Lst rintd 11/3/010 6:40:00 PM Fig. 1 Elliticl motion, grvity, tc minor xis mjor xis F 1 =A F =B C - D, mjor nd minor xs
Lecture 4. Conic section
 Lctur 4 Conic sction Conic sctions r locus of points whr distncs from fixd point nd fixd lin r in constnt rtio. Conic sctions in D r curvs which r locus of points whor position vctor r stisfis r r. whr
Lctur 4 Conic sction Conic sctions r locus of points whr distncs from fixd point nd fixd lin r in constnt rtio. Conic sctions in D r curvs which r locus of points whor position vctor r stisfis r r. whr
PH427/PH527: Periodic systems Spring Overview of the PH427 website (syllabus, assignments etc.) 2. Coupled oscillations.
 Dy : Mondy 5 inuts. Ovrviw of th PH47 wsit (syllus, ssignnts tc.). Coupld oscilltions W gin with sss coupld y Hook's Lw springs nd find th possil longitudinl) otion of such syst. W ll xtnd this to finit
Dy : Mondy 5 inuts. Ovrviw of th PH47 wsit (syllus, ssignnts tc.). Coupld oscilltions W gin with sss coupld y Hook's Lw springs nd find th possil longitudinl) otion of such syst. W ll xtnd this to finit
1 Introduction to Modulo 7 Arithmetic
 1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
Theoretical Study on the While Drilling Electromagnetic Signal Transmission of Horizontal Well
 7 nd ntrntionl Confrnc on Softwr, Multimdi nd Communiction Enginring (SMCE 7) SBN: 978--6595-458-5 Thorticl Study on th Whil Drilling Elctromgntic Signl Trnsmission of Horizontl Wll Y-huo FAN,,*, Zi-ping
7 nd ntrntionl Confrnc on Softwr, Multimdi nd Communiction Enginring (SMCE 7) SBN: 978--6595-458-5 Thorticl Study on th Whil Drilling Elctromgntic Signl Trnsmission of Horizontl Wll Y-huo FAN,,*, Zi-ping
Garnir Polynomial and their Properties
 Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
FSA. CmSc 365 Theory of Computation. Finite State Automata and Regular Expressions (Chapter 2, Section 2.3) ALPHABET operations: U, concatenation, *
 CmSc 365 Thory of Computtion Finit Stt Automt nd Rgulr Exprssions (Chptr 2, Sction 2.3) ALPHABET oprtions: U, conctntion, * otin otin Strings Form Rgulr xprssions dscri Closd undr U, conctntion nd * (if
CmSc 365 Thory of Computtion Finit Stt Automt nd Rgulr Exprssions (Chptr 2, Sction 2.3) ALPHABET oprtions: U, conctntion, * otin otin Strings Form Rgulr xprssions dscri Closd undr U, conctntion nd * (if
Last time: introduced our first computational model the DFA.
 Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
ME 522 PRINCIPLES OF ROBOTICS. FIRST MIDTERM EXAMINATION April 19, M. Kemal Özgören
 ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
Differential Equations
 UNIT I Diffrntial Equations.0 INTRODUCTION W li in a world of intrrlatd changing ntitis. Th locit of a falling bod changs with distanc, th position of th arth changs with tim, th ara of a circl changs
UNIT I Diffrntial Equations.0 INTRODUCTION W li in a world of intrrlatd changing ntitis. Th locit of a falling bod changs with distanc, th position of th arth changs with tim, th ara of a circl changs
UNIT # 08 (PART - I)
 . r. d[h d[h.5 7.5 mol L S d[o d[so UNIT # 8 (PRT - I CHEMICL INETICS EXERCISE # 6. d[ x [ x [ x. r [X[C ' [X [[B r '[ [B [C. r [NO [Cl. d[so d[h.5 5 mol L S d[nh d[nh. 5. 6. r [ [B r [x [y r' [x [y r'
. r. d[h d[h.5 7.5 mol L S d[o d[so UNIT # 8 (PRT - I CHEMICL INETICS EXERCISE # 6. d[ x [ x [ x. r [X[C ' [X [[B r '[ [B [C. r [NO [Cl. d[so d[h.5 5 mol L S d[nh d[nh. 5. 6. r [ [B r [x [y r' [x [y r'
Continuous Random Variables: Basics
 Continuous Rndom Vrils: Bsics Brlin Chn Dprtmnt o Computr Scinc & Inormtion Enginring Ntionl Tiwn Norml Univrsit Rrnc: - D.. Brtss, J. N. Tsitsilis, Introduction to roilit, Sctions 3.-3.3 Continuous Rndom
Continuous Rndom Vrils: Bsics Brlin Chn Dprtmnt o Computr Scinc & Inormtion Enginring Ntionl Tiwn Norml Univrsit Rrnc: - D.. Brtss, J. N. Tsitsilis, Introduction to roilit, Sctions 3.-3.3 Continuous Rndom
CONIC SECTIONS. MODULE-IV Co-ordinate Geometry OBJECTIVES. Conic Sections
 Conic Sctions 16 MODULE-IV Co-ordint CONIC SECTIONS Whil cutting crrot ou might hv noticd diffrnt shps shown th dgs of th cut. Anlticll ou m cut it in thr diffrnt ws, nml (i) (ii) (iii) Cut is prlll to
Conic Sctions 16 MODULE-IV Co-ordint CONIC SECTIONS Whil cutting crrot ou might hv noticd diffrnt shps shown th dgs of th cut. Anlticll ou m cut it in thr diffrnt ws, nml (i) (ii) (iii) Cut is prlll to
10. The Discrete-Time Fourier Transform (DTFT)
 Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
However, many atoms can combine to form particular molecules, e.g. Chlorine (Cl) and Sodium (Na) atoms form NaCl molecules.
 Lctur 6 Titl: Fundmntls of th Quntum Thory of molcul formtion Pg- In th lst modul, w hv discussd out th tomic structur nd tomic physics to undrstnd th spctrum of toms. Howvr, mny toms cn comin to form
Lctur 6 Titl: Fundmntls of th Quntum Thory of molcul formtion Pg- In th lst modul, w hv discussd out th tomic structur nd tomic physics to undrstnd th spctrum of toms. Howvr, mny toms cn comin to form
NEW APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA
 NE APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA Mirca I CÎRNU Ph Dp o Mathmatics III Faculty o Applid Scincs Univrsity Polithnica o Bucharst Cirnumirca @yahoocom Abstract In a rcnt papr [] 5 th indinit intgrals
NE APPLICATIONS OF THE ABEL-LIOUVILLE FORMULA Mirca I CÎRNU Ph Dp o Mathmatics III Faculty o Applid Scincs Univrsity Polithnica o Bucharst Cirnumirca @yahoocom Abstract In a rcnt papr [] 5 th indinit intgrals
Enforcement of Opacity Security Properties Using Insertion Functions
 Enforcmnt of Opcity Scurity Proprtis Using Insrtion Functions Yi-Chin Wu nd Stéphn Lfortun EECS Dprtmnt, Univrsity of Michign CDC 12 Dc. 13 th, 2012 Motivtion Scurity nd privcy concrns in onlin srvics
Enforcmnt of Opcity Scurity Proprtis Using Insrtion Functions Yi-Chin Wu nd Stéphn Lfortun EECS Dprtmnt, Univrsity of Michign CDC 12 Dc. 13 th, 2012 Motivtion Scurity nd privcy concrns in onlin srvics
CSE303 - Introduction to the Theory of Computing Sample Solutions for Exercises on Finite Automata
 CSE303 - Introduction to th Thory of Computing Smpl Solutions for Exrciss on Finit Automt Exrcis 2.1.1 A dtrministic finit utomton M ccpts th mpty string (i.., L(M)) if nd only if its initil stt is finl
CSE303 - Introduction to th Thory of Computing Smpl Solutions for Exrciss on Finit Automt Exrcis 2.1.1 A dtrministic finit utomton M ccpts th mpty string (i.., L(M)) if nd only if its initil stt is finl
CBSE 2015 FOREIGN EXAMINATION
 CBSE 05 FOREIGN EXAMINATION (Sris SSO Cod No 65//F, 65//F, 65//F : Forign Rgion) Not tht ll th sts hv sm qustions Onl thir squnc of pprnc is diffrnt M Mrks : 00 Tim Allowd : Hours SECTION A Q0 Find th
CBSE 05 FOREIGN EXAMINATION (Sris SSO Cod No 65//F, 65//F, 65//F : Forign Rgion) Not tht ll th sts hv sm qustions Onl thir squnc of pprnc is diffrnt M Mrks : 00 Tim Allowd : Hours SECTION A Q0 Find th
Homotopy perturbation technique
 Comput. Mthods Appl. Mch. Engrg. 178 (1999) 257±262 www.lsvir.com/locat/cma Homotopy prturbation tchniqu Ji-Huan H 1 Shanghai Univrsity, Shanghai Institut of Applid Mathmatics and Mchanics, Shanghai 272,
Comput. Mthods Appl. Mch. Engrg. 178 (1999) 257±262 www.lsvir.com/locat/cma Homotopy prturbation tchniqu Ji-Huan H 1 Shanghai Univrsity, Shanghai Institut of Applid Mathmatics and Mchanics, Shanghai 272,
MERIDIAN SURFACE OF WEINGARTEN TYPE IN 4-DIMENSIONAL EUCLIDEAN SPACE E 4 arxiv: v1 [math.dg] 14 May 2013
![MERIDIAN SURFACE OF WEINGARTEN TYPE IN 4-DIMENSIONAL EUCLIDEAN SPACE E 4 arxiv: v1 [math.dg] 14 May 2013 MERIDIAN SURFACE OF WEINGARTEN TYPE IN 4-DIMENSIONAL EUCLIDEAN SPACE E 4 arxiv: v1 [math.dg] 14 May 2013](/thumbs/93/111838361.jpg) MERIDIAN SURFACE OF WEINGARTEN TYPE IN 4-DIMENSIONAL EUCLIDEAN SPACE E 4 rxiv:13053155v1 [mthdg] 14 My 2013 Astrct In this ppr, w study mridin surfcs of Wingrtn typ in Euclidn 4-spc E 4 W giv th nccssry
MERIDIAN SURFACE OF WEINGARTEN TYPE IN 4-DIMENSIONAL EUCLIDEAN SPACE E 4 rxiv:13053155v1 [mthdg] 14 My 2013 Astrct In this ppr, w study mridin surfcs of Wingrtn typ in Euclidn 4-spc E 4 W giv th nccssry
This Week. Computer Graphics. Introduction. Introduction. Graphics Maths by Example. Graphics Maths by Example
 This Wk Computr Grphics Vctors nd Oprtions Vctor Arithmtic Gomtric Concpts Points, Lins nd Plns Eploiting Dot Products CSC 470 Computr Grphics 1 CSC 470 Computr Grphics 2 Introduction Introduction Wh do
This Wk Computr Grphics Vctors nd Oprtions Vctor Arithmtic Gomtric Concpts Points, Lins nd Plns Eploiting Dot Products CSC 470 Computr Grphics 1 CSC 470 Computr Grphics 2 Introduction Introduction Wh do
MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS
 VSRT MEMO #05 MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS 01886 Fbrury 3, 009 Tlphon: 781-981-507 Fx: 781-981-0590 To: VSRT Group From: Aln E.E. Rogrs Subjct: Simplifid
VSRT MEMO #05 MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS 01886 Fbrury 3, 009 Tlphon: 781-981-507 Fx: 781-981-0590 To: VSRT Group From: Aln E.E. Rogrs Subjct: Simplifid
Engineering 323 Beautiful HW #13 Page 1 of 6 Brown Problem 5-12
 Enginring Bautiful HW #1 Pag 1 of 6 5.1 Two componnts of a minicomputr hav th following joint pdf for thir usful liftims X and Y: = x(1+ x and y othrwis a. What is th probability that th liftim X of th
Enginring Bautiful HW #1 Pag 1 of 6 5.1 Two componnts of a minicomputr hav th following joint pdf for thir usful liftims X and Y: = x(1+ x and y othrwis a. What is th probability that th liftim X of th
Math 61 : Discrete Structures Final Exam Instructor: Ciprian Manolescu. You have 180 minutes.
 Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Fourier Transforms and the Wave Equation. Key Mathematics: More Fourier transform theory, especially as applied to solving the wave equation.
 Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Linear Algebra Existence of the determinant. Expansion according to a row.
 Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
Integration by Parts
 Intgration by Parts Intgration by parts is a tchniqu primarily for valuating intgrals whos intgrand is th product of two functions whr substitution dosn t work. For ampl, sin d or d. Th rul is: u ( ) v'(
Intgration by Parts Intgration by parts is a tchniqu primarily for valuating intgrals whos intgrand is th product of two functions whr substitution dosn t work. For ampl, sin d or d. Th rul is: u ( ) v'(
temperature T speed v time t density ρ scalars may be constant or may be variable yes distributive a(b+c) = ab+ac
 Mthmtics Riw. Sclr mthmticl ntity tht hs mgnitud only.g.: tmprtur T spd tim t dnsity ρ sclrs my constnt or my ril Lws of Algr for Sclrs: ys commutti ys ssociti (c) ()c ys distriuti (c) c Fith A. Morrison,
Mthmtics Riw. Sclr mthmticl ntity tht hs mgnitud only.g.: tmprtur T spd tim t dnsity ρ sclrs my constnt or my ril Lws of Algr for Sclrs: ys commutti ys ssociti (c) ()c ys distriuti (c) c Fith A. Morrison,
cycle that does not cross any edges (including its own), then it has at least
 W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
Chapter 3 Fourier Series Representation of Periodic Signals
 Chptr Fourir Sris Rprsttio of Priodic Sigls If ritrry sigl x(t or x[] is xprssd s lir comitio of som sic sigls th rspos of LI systm coms th sum of th idividul rsposs of thos sic sigls Such sic sigl must:
Chptr Fourir Sris Rprsttio of Priodic Sigls If ritrry sigl x(t or x[] is xprssd s lir comitio of som sic sigls th rspos of LI systm coms th sum of th idividul rsposs of thos sic sigls Such sic sigl must:
Minimum Spanning Trees
 Minimum Spnning Trs Minimum Spnning Trs Problm A town hs st of houss nd st of rods A rod conncts nd only houss A rod conncting houss u nd v hs rpir cost w(u, v) Gol: Rpir nough (nd no mor) rods such tht:
Minimum Spnning Trs Minimum Spnning Trs Problm A town hs st of houss nd st of rods A rod conncts nd only houss A rod conncting houss u nd v hs rpir cost w(u, v) Gol: Rpir nough (nd no mor) rods such tht:
DIFFERENTIAL EQUATION
 MD DIFFERENTIAL EQUATION Sllabus : Ordinar diffrntial quations, thir ordr and dgr. Formation of diffrntial quations. Solution of diffrntial quations b th mthod of sparation of variabls, solution of homognous
MD DIFFERENTIAL EQUATION Sllabus : Ordinar diffrntial quations, thir ordr and dgr. Formation of diffrntial quations. Solution of diffrntial quations b th mthod of sparation of variabls, solution of homognous
The Theory of Small Reflections
 Jim Stils Th Univ. of Knss Dt. of EECS 4//9 Th Thory of Smll Rflctions /9 Th Thory of Smll Rflctions Rcll tht w nlyzd qurtr-wv trnsformr usg th multil rflction viw ot. V ( z) = + β ( z + ) V ( z) = = R
Jim Stils Th Univ. of Knss Dt. of EECS 4//9 Th Thory of Smll Rflctions /9 Th Thory of Smll Rflctions Rcll tht w nlyzd qurtr-wv trnsformr usg th multil rflction viw ot. V ( z) = + β ( z + ) V ( z) = = R
# 1 ' 10 ' 100. Decimal point = 4 hundred. = 6 tens (or sixty) = 5 ones (or five) = 2 tenths. = 7 hundredths.
 How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
INC 693, 481 Dynamics System and Modelling: Linear Graph Modeling II Dr.-Ing. Sudchai Boonto Assistant Professor
 INC 69, 48 Dynamics Systm and Modlling: Linar Graph Modling II Dr.-Ing. Sudchai Boonto Assistant Profssor Dpartmnt of Control Systm and Instrumntation Enginring King Mongkut s Unnivrsity of Tchnology Thonuri
INC 69, 48 Dynamics Systm and Modlling: Linar Graph Modling II Dr.-Ing. Sudchai Boonto Assistant Profssor Dpartmnt of Control Systm and Instrumntation Enginring King Mongkut s Unnivrsity of Tchnology Thonuri
APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS
 Intrntionl Journl o Sintii nd Rrh Publition Volum, Iu 5, M ISSN 5-353 APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS S.M.Khirnr, R.M.Pi*, J.N.Slun** Dprtmnt o Mthmti Mhrhtr
Intrntionl Journl o Sintii nd Rrh Publition Volum, Iu 5, M ISSN 5-353 APPLICATIONS OF THE LAPLACE-MELLIN INTEGRAL TRANSFORM TO DIFFERNTIAL EQUATIONS S.M.Khirnr, R.M.Pi*, J.N.Slun** Dprtmnt o Mthmti Mhrhtr
ECE COMBINATIONAL BUILDING BLOCKS - INVEST 13 DECODERS AND ENCODERS
 C 24 - COMBINATIONAL BUILDING BLOCKS - INVST 3 DCODS AND NCODS FALL 23 AP FLZ To o "wll" on this invstition you must not only t th riht nswrs ut must lso o nt, omplt n onis writups tht mk ovious wht h
C 24 - COMBINATIONAL BUILDING BLOCKS - INVST 3 DCODS AND NCODS FALL 23 AP FLZ To o "wll" on this invstition you must not only t th riht nswrs ut must lso o nt, omplt n onis writups tht mk ovious wht h
( x) On the Exponentiated Generalized Weibull Distribution: A Generalization of the Weibull Distribution. 1. Introduction.
 Indin Journl o Scinc nd Tchnology, Vol 8(35), DOI:.7485/ist/25/v8i35/676, Dcmr 25 ISSN (Print) : 974-6846 ISSN (Onlin) : 974-5645 On th Eponntitd Gnrlizd Wiull Distriution: A Gnrliztion o th Wiull Distriution
Indin Journl o Scinc nd Tchnology, Vol 8(35), DOI:.7485/ist/25/v8i35/676, Dcmr 25 ISSN (Print) : 974-6846 ISSN (Onlin) : 974-5645 On th Eponntitd Gnrlizd Wiull Distriution: A Gnrliztion o th Wiull Distriution
1 General boundary conditions in diffusion
 Gnral boundary conditions in diffusion Πρόβλημα 4.8 : Δίνεται μονοδιάτατη πλάκα πάχους, που το ένα άκρο της κρατιέται ε θερμοκραία T t και το άλλο ε θερμοκραία T 2 t. Αν η αρχική θερμοκραία της πλάκας
Gnral boundary conditions in diffusion Πρόβλημα 4.8 : Δίνεται μονοδιάτατη πλάκα πάχους, που το ένα άκρο της κρατιέται ε θερμοκραία T t και το άλλο ε θερμοκραία T 2 t. Αν η αρχική θερμοκραία της πλάκας
The Z transform techniques
 h Z trnfor tchniqu h Z trnfor h th rol in dicrt yt tht th Lplc trnfor h in nlyi of continuou yt. h Z trnfor i th principl nlyticl tool for ingl-loop dicrt-ti yt. h Z trnfor h Z trnfor i to dicrt-ti yt
h Z trnfor tchniqu h Z trnfor h th rol in dicrt yt tht th Lplc trnfor h in nlyi of continuou yt. h Z trnfor i th principl nlyticl tool for ingl-loop dicrt-ti yt. h Z trnfor h Z trnfor i to dicrt-ti yt
Math 102. Rumbos Spring Solutions to Assignment #8. Solution: The matrix, A, corresponding to the system in (1) is
 Math 12. Rumbos Spring 218 1 Solutions to Assignmnt #8 1. Construct a fundamntal matrix for th systm { ẋ 2y ẏ x + y. (1 Solution: Th matrix, A, corrsponding to th systm in (1 is 2 A. (2 1 1 Th charactristic
Math 12. Rumbos Spring 218 1 Solutions to Assignmnt #8 1. Construct a fundamntal matrix for th systm { ẋ 2y ẏ x + y. (1 Solution: Th matrix, A, corrsponding to th systm in (1 is 2 A. (2 1 1 Th charactristic
page 11 equation (1.2-10c), break the bar over the right side in the middle
 I. Corrctios Lst Updtd: Ju 00 Complx Vrils with Applictios, 3 rd ditio, A. Dvid Wusch First Pritig. A ook ought for My 007 will proly first pritig With Thks to Christi Hos of Swd pg qutio (.-0c), rk th
I. Corrctios Lst Updtd: Ju 00 Complx Vrils with Applictios, 3 rd ditio, A. Dvid Wusch First Pritig. A ook ought for My 007 will proly first pritig With Thks to Christi Hos of Swd pg qutio (.-0c), rk th
COMP108 Algorithmic Foundations
 Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
The Angular Momenta Dipole Moments and Gyromagnetic Ratios of the Electron and the Proton
 Journl of Modrn hysics, 014, 5, 154-157 ublishd Onlin August 014 in SciRs. htt://www.scir.org/journl/jm htt://dx.doi.org/.436/jm.014.51415 Th Angulr Momnt Diol Momnts nd Gyromgntic Rtios of th Elctron
Journl of Modrn hysics, 014, 5, 154-157 ublishd Onlin August 014 in SciRs. htt://www.scir.org/journl/jm htt://dx.doi.org/.436/jm.014.51415 Th Angulr Momnt Diol Momnts nd Gyromgntic Rtios of th Elctron
ELEG 413 Lecture #6. Mark Mirotznik, Ph.D. Professor The University of Delaware
 LG 43 Lctur #6 Mrk Mirtnik, Ph.D. Prfssr Th Univrsity f Dlwr mil: mirtni@c.udl.du Wv Prpgtin nd Plritin TM: Trnsvrs lctrmgntic Wvs A md is prticulr fild cnfigurtin. Fr givn lctrmgntic bundry vlu prblm,
LG 43 Lctur #6 Mrk Mirtnik, Ph.D. Prfssr Th Univrsity f Dlwr mil: mirtni@c.udl.du Wv Prpgtin nd Plritin TM: Trnsvrs lctrmgntic Wvs A md is prticulr fild cnfigurtin. Fr givn lctrmgntic bundry vlu prblm,
Quasi-Classical States of the Simple Harmonic Oscillator
 Quasi-Classical Stats of th Simpl Harmonic Oscillator (Draft Vrsion) Introduction: Why Look for Eignstats of th Annihilation Oprator? Excpt for th ground stat, th corrspondnc btwn th quantum nrgy ignstats
Quasi-Classical Stats of th Simpl Harmonic Oscillator (Draft Vrsion) Introduction: Why Look for Eignstats of th Annihilation Oprator? Excpt for th ground stat, th corrspondnc btwn th quantum nrgy ignstats
Q.28 Q.29 Q.30. Q.31 Evaluate: ( log x ) Q.32 Evaluate: ( ) Q.33. Q.34 Evaluate: Q.35 Q.36 Q.37 Q.38 Q.39 Q.40 Q.41 Q.42. Q.43 Evaluate : ( x 2) Q.
 LASS XII Q Evlut : Q sc Evlut c Q Evlut: ( ) Q Evlut: Q5 α Evlut: α Q Evlut: Q7 Evlut: { t (t sc )} / Q8 Evlut : ( )( ) Q9 Evlut: Q0 Evlut: Q Evlut : ( ) ( ) Q Evlut : / ( ) Q Evlut: / ( ) Q Evlut : )
LASS XII Q Evlut : Q sc Evlut c Q Evlut: ( ) Q Evlut: Q5 α Evlut: α Q Evlut: Q7 Evlut: { t (t sc )} / Q8 Evlut : ( )( ) Q9 Evlut: Q0 Evlut: Q Evlut : ( ) ( ) Q Evlut : / ( ) Q Evlut: / ( ) Q Evlut : )
Australian Journal of Basic and Applied Sciences. An Error Control Algorithm of Kowalsky's method for Orbit Determination of Visual Binaries
 Austrlin Journl of Bsic nd Applid Scincs, 8(7) Novmbr 04, Pgs: 640-648 AENSI Journls Austrlin Journl of Bsic nd Applid Scincs ISSN:99-878 Journl hom pg: www.bswb.com An Error Control Algorithm of Kowlsky's
Austrlin Journl of Bsic nd Applid Scincs, 8(7) Novmbr 04, Pgs: 640-648 AENSI Journls Austrlin Journl of Bsic nd Applid Scincs ISSN:99-878 Journl hom pg: www.bswb.com An Error Control Algorithm of Kowlsky's
C-Curves. An alternative to the use of hyperbolic decline curves S E R A F I M. Prepared by: Serafim Ltd. P. +44 (0)
 An ltntiv to th us of hypolic dclin cuvs Ppd y: Sfim Ltd S E R A F I M info@sfimltd.com P. +44 (02890 4206 www.sfimltd.com Contnts Contnts... i Intoduction... Initil ssumptions... Solving fo cumultiv...
An ltntiv to th us of hypolic dclin cuvs Ppd y: Sfim Ltd S E R A F I M info@sfimltd.com P. +44 (02890 4206 www.sfimltd.com Contnts Contnts... i Intoduction... Initil ssumptions... Solving fo cumultiv...
Notes on Finite Automata Department of Computer Science Professor Goldberg Textbooks: Introduction to the Theory of Computation by Michael Sipser
 Nots on Finit Automt Dprtmnt of Computr Scinc Profssor Goldrg Txtooks: Introduction to th Thory of Computtion y Michl Sipsr Elmnts of th Thory of Computtion y H. Lwis nd C. Ppdimitriou Ths nots contin
Nots on Finit Automt Dprtmnt of Computr Scinc Profssor Goldrg Txtooks: Introduction to th Thory of Computtion y Michl Sipsr Elmnts of th Thory of Computtion y H. Lwis nd C. Ppdimitriou Ths nots contin
Chapter 6 Techniques of Integration
 MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
MA Techniques of Integrtion Asst.Prof.Dr.Suprnee Liswdi Chpter 6 Techniques of Integrtion Recll: Some importnt integrls tht we hve lernt so fr. Tle of Integrls n+ n d = + C n + e d = e + C ( n ) d = ln
b. How many ternary words of length 23 with eight 0 s, nine 1 s and six 2 s?
 MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
National Quali cations
 PRINT COPY OF BRAILLE Ntiol Quli ctios AH08 X747/77/ Mthmtics THURSDAY, MAY INSTRUCTIONS TO CANDIDATES Cdidts should tr thir surm, form(s), dt of birth, Scottish cdidt umbr d th m d Lvl of th subjct t
PRINT COPY OF BRAILLE Ntiol Quli ctios AH08 X747/77/ Mthmtics THURSDAY, MAY INSTRUCTIONS TO CANDIDATES Cdidts should tr thir surm, form(s), dt of birth, Scottish cdidt umbr d th m d Lvl of th subjct t
Fundamental Algorithms for System Modeling, Analysis, and Optimization
 Fundmntl Algorithms for Sstm Modling, Anlsis, nd Optimiztion Edwrd A. L, Jijt Rohowdhur, Snjit A. Sshi UC Brkl EECS 144/244 Fll 2011 Copright 2010-11, E. A. L, J. Rohowdhur, S. A. Sshi, All rights rsrvd
Fundmntl Algorithms for Sstm Modling, Anlsis, nd Optimiztion Edwrd A. L, Jijt Rohowdhur, Snjit A. Sshi UC Brkl EECS 144/244 Fll 2011 Copright 2010-11, E. A. L, J. Rohowdhur, S. A. Sshi, All rights rsrvd
Probability and Stochastic Processes: A Friendly Introduction for Electrical and Computer Engineers Roy D. Yates and David J.
 Probability and Stochastic Procsss: A Frindly Introduction for Elctrical and Computr Enginrs Roy D. Yats and David J. Goodman Problm Solutions : Yats and Goodman,4.3. 4.3.4 4.3. 4.4. 4.4.4 4.4.6 4.. 4..7
Probability and Stochastic Procsss: A Frindly Introduction for Elctrical and Computr Enginrs Roy D. Yats and David J. Goodman Problm Solutions : Yats and Goodman,4.3. 4.3.4 4.3. 4.4. 4.4.4 4.4.6 4.. 4..7
HOMEWORK SOLUTIONS MATH 1910 Sections 7.9, 8.1 Fall 2016
 HOMEWORK SOLUTIONS MATH 9 Sections 7.9, 8. Fll 6 Problem 7.9.33 Show tht for ny constnts M,, nd, the function yt) = )) t ) M + tnh stisfies the logistic eqution: y SOLUTION. Let Then nd Finlly, y = y M
HOMEWORK SOLUTIONS MATH 9 Sections 7.9, 8. Fll 6 Problem 7.9.33 Show tht for ny constnts M,, nd, the function yt) = )) t ) M + tnh stisfies the logistic eqution: y SOLUTION. Let Then nd Finlly, y = y M
Exp-function method to solve the nonlinear dispersive K(m,n) equations
 From th SlctdWork of Ji-Hn H 8 Exp-fnction mthod to olv th nonlinr dipriv K(mn qtion Xin-Wi Zho Yi-Xin Wn Ji-Hn H Dongh Univrity Avilbl t: http://work.bpr.com/ji_hn_h/9/ Frnd Pblihing Ho Ltd. Intrntionl
From th SlctdWork of Ji-Hn H 8 Exp-fnction mthod to olv th nonlinr dipriv K(mn qtion Xin-Wi Zho Yi-Xin Wn Ji-Hn H Dongh Univrity Avilbl t: http://work.bpr.com/ji_hn_h/9/ Frnd Pblihing Ho Ltd. Intrntionl
I. The Connection between Spectroscopy and Quantum Mechanics
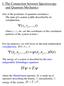 I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Limits Indeterminate Forms and L Hospital s Rule
 Limits Indtrmint Forms nd L Hospitl s Rul I Indtrmint Form o th Tp W hv prviousl studid its with th indtrmint orm s shown in th ollowin mpls: Empl : Empl : tn [Not: W us th ivn it ] Empl : 8 h 8 [Not:
Limits Indtrmint Forms nd L Hospitl s Rul I Indtrmint Form o th Tp W hv prviousl studid its with th indtrmint orm s shown in th ollowin mpls: Empl : Empl : tn [Not: W us th ivn it ] Empl : 8 h 8 [Not:
2008 AP Calculus BC Multiple Choice Exam
 008 AP Multipl Choic Eam Nam 008 AP Calculus BC Multipl Choic Eam Sction No Calculator Activ AP Calculus 008 BC Multipl Choic. At tim t 0, a particl moving in th -plan is th acclration vctor of th particl
008 AP Multipl Choic Eam Nam 008 AP Calculus BC Multipl Choic Eam Sction No Calculator Activ AP Calculus 008 BC Multipl Choic. At tim t 0, a particl moving in th -plan is th acclration vctor of th particl
Chapter 10. The singular integral Introducing S(n) and J(n)
 Chaptr Th singular intgral Our aim in this chaptr is to rplac th functions S (n) and J (n) by mor convnint xprssions; ths will b calld th singular sris S(n) and th singular intgral J(n). This will b don
Chaptr Th singular intgral Our aim in this chaptr is to rplac th functions S (n) and J (n) by mor convnint xprssions; ths will b calld th singular sris S(n) and th singular intgral J(n). This will b don
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Prelim Examination 2011 / 2012 (Assessing Units 1 & 2) MATHEMATICS. Advanced Higher Grade. Time allowed - 2 hours
 Prlim Eamination / (Assssing Units & ) MATHEMATICS Advancd Highr Grad Tim allowd - hours Rad Carfull. Calculators ma b usd in this papr.. Candidats should answr all qustions. Full crdit will onl b givn
Prlim Eamination / (Assssing Units & ) MATHEMATICS Advancd Highr Grad Tim allowd - hours Rad Carfull. Calculators ma b usd in this papr.. Candidats should answr all qustions. Full crdit will onl b givn
Einstein Equations for Tetrad Fields
 Apiron, Vol 13, No, Octobr 006 6 Einstin Equations for Ttrad Filds Ali Rıza ŞAHİN, R T L Istanbul (Turky) Evry mtric tnsor can b xprssd by th innr product of ttrad filds W prov that Einstin quations for
Apiron, Vol 13, No, Octobr 006 6 Einstin Equations for Ttrad Filds Ali Rıza ŞAHİN, R T L Istanbul (Turky) Evry mtric tnsor can b xprssd by th innr product of ttrad filds W prov that Einstin quations for
arxiv: v2 [math.ca] 24 Feb 2016
![arxiv: v2 [math.ca] 24 Feb 2016 arxiv: v2 [math.ca] 24 Feb 2016](/thumbs/74/71089459.jpg) Product of prbolic cylindr functions involving Lplc trnsforms of conflunt hyprgomtric functions Ridh Nsri rxiv:53.69v [mth.ca] 4 Fb 6 Orng Lbs, 38-4 vnu Gnrl Lclrc, 9794 Issy-ls-Moulinux, Frnc In this
Product of prbolic cylindr functions involving Lplc trnsforms of conflunt hyprgomtric functions Ridh Nsri rxiv:53.69v [mth.ca] 4 Fb 6 Orng Lbs, 38-4 vnu Gnrl Lclrc, 9794 Issy-ls-Moulinux, Frnc In this
The graph of y = x (or y = ) consists of two branches, As x 0, y + ; as x 0, y +. x = 0 is the
 Copyright itutcom 005 Fr download & print from wwwitutcom Do not rproduc by othr mans Functions and graphs Powr functions Th graph of n y, for n Q (st of rational numbrs) y is a straight lin through th
Copyright itutcom 005 Fr download & print from wwwitutcom Do not rproduc by othr mans Functions and graphs Powr functions Th graph of n y, for n Q (st of rational numbrs) y is a straight lin through th
Walk Like a Mathematician Learning Task:
 Gori Dprtmnt of Euction Wlk Lik Mthmticin Lrnin Tsk: Mtrics llow us to prform mny usful mthmticl tsks which orinrily rquir lr numbr of computtions. Som typs of problms which cn b on fficintly with mtrics
Gori Dprtmnt of Euction Wlk Lik Mthmticin Lrnin Tsk: Mtrics llow us to prform mny usful mthmticl tsks which orinrily rquir lr numbr of computtions. Som typs of problms which cn b on fficintly with mtrics
Functions and Graphs 1. (a) (b) (c) (f) (e) (d) 2. (a) (b) (c) (d)
 Functions nd Grps. () () (c) - - - O - - - O - - - O - - - - (d) () (f) - - O - 7 6 - - O - -7-6 - - - - - O. () () (c) (d) - - - O - O - O - - O - -. () G() f() + f( ), G(-) f( ) + f(), G() G( ) nd G()
Functions nd Grps. () () (c) - - - O - - - O - - - O - - - - (d) () (f) - - O - 7 6 - - O - -7-6 - - - - - O. () () (c) (d) - - - O - O - O - - O - -. () G() f() + f( ), G(-) f( ) + f(), G() G( ) nd G()
u x v x dx u x v x v x u x dx d u x v x u x v x dx u x v x dx Integration by Parts Formula
 7. Intgration by Parts Each drivativ formula givs ris to a corrsponding intgral formula, as w v sn many tims. Th drivativ product rul yilds a vry usful intgration tchniqu calld intgration by parts. Starting
7. Intgration by Parts Each drivativ formula givs ris to a corrsponding intgral formula, as w v sn many tims. Th drivativ product rul yilds a vry usful intgration tchniqu calld intgration by parts. Starting
Cycles and Simple Cycles. Paths and Simple Paths. Trees. Problem: There is No Completely Standard Terminology!
 Outlin Computr Sin 331, Spnnin, n Surphs Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #30 1 Introution 2 3 Dinition 4 Spnnin 5 6 Mik Joson (Univrsity o Clry) Computr Sin 331 Ltur #30 1 / 20 Mik
Outlin Computr Sin 331, Spnnin, n Surphs Mik Joson Dprtmnt o Computr Sin Univrsity o Clry Ltur #30 1 Introution 2 3 Dinition 4 Spnnin 5 6 Mik Joson (Univrsity o Clry) Computr Sin 331 Ltur #30 1 / 20 Mik
( ) Same as above but m = f x = f x - symmetric to y-axis. find where f ( x) Relative: Find where f ( x) x a + lim exists ( lim f exists.
 AP Clculus Finl Review Sheet solutions When you see the words This is wht you think of doing Find the zeros Set function =, fctor or use qudrtic eqution if qudrtic, grph to find zeros on clcultor Find
AP Clculus Finl Review Sheet solutions When you see the words This is wht you think of doing Find the zeros Set function =, fctor or use qudrtic eqution if qudrtic, grph to find zeros on clcultor Find
a b c cat CAT A B C Aa Bb Cc cat cat Lesson 1 (Part 1) Verbal lesson: Capital Letters Make The Same Sound Lesson 1 (Part 1) continued...
 Progrssiv Printing T.M. CPITLS g 4½+ Th sy, fun (n FR!) wy to tch cpitl lttrs. ook : C o - For Kinrgrtn or First Gr (not for pr-school). - Tchs tht cpitl lttrs mk th sm souns s th littl lttrs. - Tchs th
Progrssiv Printing T.M. CPITLS g 4½+ Th sy, fun (n FR!) wy to tch cpitl lttrs. ook : C o - For Kinrgrtn or First Gr (not for pr-school). - Tchs tht cpitl lttrs mk th sm souns s th littl lttrs. - Tchs th
Slide 1. Slide 2. Slide 3 DIGITAL SIGNAL PROCESSING CLASSIFICATION OF SIGNALS
 Slid DIGITAL SIGAL PROCESSIG UIT I DISCRETE TIME SIGALS AD SYSTEM Slid Rviw of discrt-tim signals & systms Signal:- A signal is dfind as any physical quantity that varis with tim, spac or any othr indpndnt
Slid DIGITAL SIGAL PROCESSIG UIT I DISCRETE TIME SIGALS AD SYSTEM Slid Rviw of discrt-tim signals & systms Signal:- A signal is dfind as any physical quantity that varis with tim, spac or any othr indpndnt
Derangements and Applications
 2 3 47 6 23 Journal of Intgr Squncs, Vol. 6 (2003), Articl 03..2 Drangmnts and Applications Mhdi Hassani Dpartmnt of Mathmatics Institut for Advancd Studis in Basic Scincs Zanjan, Iran mhassani@iasbs.ac.ir
2 3 47 6 23 Journal of Intgr Squncs, Vol. 6 (2003), Articl 03..2 Drangmnts and Applications Mhdi Hassani Dpartmnt of Mathmatics Institut for Advancd Studis in Basic Scincs Zanjan, Iran mhassani@iasbs.ac.ir
( ) Differential Equations. Unit-7. Exact Differential Equations: M d x + N d y = 0. Verify the condition
 Diffrntial Equations Unit-7 Eat Diffrntial Equations: M d N d 0 Vrif th ondition M N Thn intgrat M d with rspt to as if wr onstants, thn intgrat th trms in N d whih do not ontain trms in and quat sum of
Diffrntial Equations Unit-7 Eat Diffrntial Equations: M d N d 0 Vrif th ondition M N Thn intgrat M d with rspt to as if wr onstants, thn intgrat th trms in N d whih do not ontain trms in and quat sum of
5.4 The Quarter-Wave Transformer
 4//9 5_4 Th Qurtr Wv Trnsformr.doc / 5.4 Th Qurtr-Wv Trnsformr Rdg Assignmnt: pp. 73-76, 4-43 By now you v noticd tht qurtr-wv lngth of trnsmission l ( λ 4, β π ) pprs oftn microwv ngrg prolms. Anothr
4//9 5_4 Th Qurtr Wv Trnsformr.doc / 5.4 Th Qurtr-Wv Trnsformr Rdg Assignmnt: pp. 73-76, 4-43 By now you v noticd tht qurtr-wv lngth of trnsmission l ( λ 4, β π ) pprs oftn microwv ngrg prolms. Anothr
PROOF OF FIRST STANDARD FORM OF NONELEMENTARY FUNCTIONS
 Intrnational Journal Of Advanc Rsarch In Scinc And Enginring http://www.ijars.com IJARSE, Vol. No., Issu No., Fbruary, 013 ISSN-319-8354(E) PROOF OF FIRST STANDARD FORM OF NONELEMENTARY FUNCTIONS 1 Dharmndra
Intrnational Journal Of Advanc Rsarch In Scinc And Enginring http://www.ijars.com IJARSE, Vol. No., Issu No., Fbruary, 013 ISSN-319-8354(E) PROOF OF FIRST STANDARD FORM OF NONELEMENTARY FUNCTIONS 1 Dharmndra
(2) If we multiplied a row of B by λ, then the value is also multiplied by λ(here lambda could be 0). namely
 . DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
. DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
Note If the candidate believes that e x = 0 solves to x = 0 or gives an extra solution of x = 0, then withhold the final accuracy mark.
 . (a) Eithr y = or ( 0, ) (b) Whn =, y = ( 0 + ) = 0 = 0 ( + ) = 0 ( )( ) = 0 Eithr = (for possibly abov) or = A 3. Not If th candidat blivs that = 0 solvs to = 0 or givs an tra solution of = 0, thn withhold
. (a) Eithr y = or ( 0, ) (b) Whn =, y = ( 0 + ) = 0 = 0 ( + ) = 0 ( )( ) = 0 Eithr = (for possibly abov) or = A 3. Not If th candidat blivs that = 0 solvs to = 0 or givs an tra solution of = 0, thn withhold
