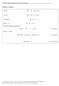
Chapter 2 Solutions. ψ 1 ψ. 16 t. ( z υt ), where υ is in the negative z direction. = 2 A. Chapter 2 Solutions = 32
|
|
|
- Roy Roland McKenzie
- 5 years ago
- Views:
Transcription
1 Chaper Soluions 1 Chaper Soluions.1 υ ( z+ υ) ψ υ( z+ υ) ψ υ I s a wice differeniable funcion of ( z υ ), where υ is in he negaive z direcion.. υ ψ ( y,) ( y 4) ( y 4 ) ψ ( y 4 ) ψ 3 Thus, υ 4, υ 16, and, 16 The velociy is ν 4 in he posiive y direcion..3 Saring wih: A ψ (, z ) ( z υ) + 1 υ ( υ ) z A z [( z υ ) + 1] ψ ( z υ) 1 A + 3 [( z υ) + 1] [( z υ) + 1] 4( z υ) ( z υ) + 1 A [( z υ) + 1] [( z υ) + 1] 3( z υ) 1 A [( z 3 υ ) + 1]
2 Chaper Soluions ( z υ) Aυ [( z υ) + 1] ψ ( z υ) Aυ [( z υ ) + 1] ν 4 ν( z υ) Aυ + ( z υ) 3 υ + υ + [( z ) 1] [( z ) 1] ν[( z υ) + 1] 4 ν( z υ) Aυ + 3 [( z υ) + 1] [( z υ) + 1] 3( z υ) 1 Aυ 3 [( z υ) + 1] Thus since υ The wave moves wih velociy υ in he posiive z direcion..4 c ν λ 3 10 m/s m Hz 474 THz.5 Saring wih: ψ ( y, ) Aexp[ a( by c) ] ψ ( y, ) Aexp[ a( by c) ] Aexp[ a( by c) ] Aa c c y exp[ a( by c) ] b b b ψ 4Aa c c y exp[ a( by c) ] 4 b b b Aa c y exp[ a( by c) ] b b ψ 4Aa c y exp[ a( by c) ] 4 b b Thus ψ ( y, ) Aexp[ a( by c ) ] is a soluion of he wave equaion wih υ cb / in he + y direcion..6 Number of waves, N d/λ ( )/( ) 1. D Nλ Nc/ν 1(3 10 )/( ) 3 m.7 c 3 10 λ v km. c 3 10 For WiFi, λ 6 cm. 9 v 5 10 c 3 10 For ligh used in he definiion of candela, λ nm. 14 v υ 343. λ 66 nm. This is comparable wih ligh waves. ν 5 10
3 Chaper Soluions s 0 waves period. Hence, τ 0.5 s and from ha ν Hz. If wo full wavelenghs fi ino 5 m, hen λ 5/.5 m. The speed is c λν 5 m/s..10 υ νλ m/s λ(94 Hz); λ» 0.4 m..11 For air: λ υ/ν 343/440; λ» 7 cm. For waer: λ υ/ν 1500/440; λ» 3.41 m..1 υ (6 m)/(1. s) 5 m/s; λ υ/ν (5 m/s)/(0 Hz) 0.5 m. Number of wavelenghs, Ν 6/0.5 4 wavelenghs..13 υ νλ (ω/π ) λ and so ω (π /λ)υ..14 q π / π /4 0 π /4 π / 3π /4 sin q 1 / 0 / 1 / cos q 0 / 1 / 0 / sin(q π /4) / 1 / 0 / 1 sin(q π /) 0 / 1 / 0 / sin(q 3π /4) / 0 / -1 / 0 sin(q + π /) 0 / 1 / 0 / q π 5π /4 3π / 7π /4 π sin q 0 / 1 / 0 cos q 1 / 0 / 1 sin(q π /4) / 0 / 1 / sin(q π /) 1 0 / 1 sin(q 3π /4) / 1 / 0 / sin(q + π /) 1 / 0 / 1 sin q leads sin(q p/) x λ/ λ/ 4 0 λ/4 λ/ 3λ/4 λ π kx x π π / 0 π / π 3π /π λ cos( kx π /4) / / / / cos( kx + 3 π /4) // / /// / τ / τ /4 0 τ /4 τ / 3 τ /4 τ ω ( πτ / ) π π / 0 π / π 3π /π sin( ω + π/4) / / / // sin( π/4 ω) /// / ///
4 4 Chaper Soluions.17 λ π /k 4 m, τ λ/ν 1.6 s, ν 1/τ 0.65 Hz and A 0.1 m..1 (a) λ ( ) m 4.0 m (b) υ νλ, so υ 0 m/s ν 5.0 Hz λ 4.0 m (c) ψ( x, ) Asin( kx ω + ε) From he figure, A 0.00 m π π 1 k 0.5π m ; ω πν π (5.0 Hz) 10π rad/ s λ 4.0 m π π π ψ( x, ) [ 0.00 m] sin x 10π 0.00 cos x 10π.19 (a) λ ( ) cm 30.0 cm. (c) υ νλ, so ν υ /λ (100 cm/s)/(30.0 cm) 3.33 Hz.0 (a) τ ( ) s 0.0 s. (b) ν 1/τ 1/(0.0 s) 5.00 Hz. (c) υ νλ, so λ υ/ν (40.0 cm/s)/(5.00 s 1 ).00 cm..1 Firs wave is of he form ψ A sin π (k x + ν). So, (a) ν, (b) λ 1/ , (c) τ 1/ 0.5, (d) A 5, (e) υ 5, and (f) negaive x. Second wave is of he form ψ A sin(kx ω). So, (a) ν 1.5/π, (b) λ π /5, (c) τ π /1.5, (d) A, (e) υ 1.5/5, and (f) posiive x.. (a) ν 0 Hz, (b) τ 1/ s, (c) A 0. m, (d) λ 1/4 0.5 m, (e) υ 5 m/s, and (f) posiive x.3 (a) λ m, (b) τ 0.05 s, (c) ν 1/ Hz, (d) A 0.5 m, (e) υ λ/τ 40 m/s, and (f) negaive y direcion..4 ψ/ x k ψ and Therefore ψ/ k υψ. ψ x υ ψ k + k ψ / (1/ ) / ( ) 0..5 ψ/ x k ψ; ψ/ ω ψ; ω / υ ( πv) / υ ( π/ λ) k ; herefore, ψ/ x (1/ υ ) ψ/ ( k + k ) ψ 0..6 From rigonomery, we know ha sin(α + π /) cosα. Therefore, he same funcion can be expressed as ψ (x, ) A sin(kx ω + π /)..7 υ y ω A cos(kx ω + ε), a y ω y. Simple harmonic moion since a y y.. τ s; herefore ν 1/τ Hz; υ νλ, λ υ /ν m and k π /λ m 1. ψ (x, ) (10 3 V/m) cos[ m 1 (x (m/s))]. I s cosine because cos y(x, ) C/[ + (x + υ ) ]..30 ψ (0, ) A cos(kυ + π) A cos(kυ ) A cos(ω), hen ψ (0, τ/) A cos(ωτ/) A cos (π) A, ψ (0, 3τ/4) A cos(3ωτ/4) A cos(3π/) None of he presened funcions can be differeniaed wice in a nonrivial way (he second derivaives are jus zero in all he cases). So, hey canno be valid wave funcions.
5 Chaper Soluions The phase is ϕ( z) π ( z ), Is parial derivaives are: ( ϕ/ ) π6 10 z 1 4 and ( ϕ/ z ) π 10 ; and as per Eq. (.3), he phase velociy is / ( ϕ/ ) ( ϕ/ z) 3 10 m/s..33 The wavelengh is λ vτ m y ψ( y, ) (0.050 m)sin π + λ τ.5 m 3.6 s ψ( y, ) (0.050 m)sin π + λ τ ψ( y, ) (0.050 m)sin π ψ( y, ) (0.050 m) sin π ( ) ( ) ψ( y, ) (0.050 m)sin π 3.09 ψ ( y, ) 0.07 m.34 dψ/ d ( / x)( dx/ d) + ( / )( dy/ d ) and le y whereupon dψ/ d / x( ± υ) +/ 0 and he desired resul follows immediaely..35 dϕ/ d ( ϕ/ x)( dx/ d) + ϕ/ k( dx/ d) k υ. This is zero when dx/d υ which is wha we mean o prove. Using i on Problem.3, we have 4 1 ( ϕ/ z)( υ) + ϕ/ 0; and hus, π 10 ( υ) π and from here υ 3 10 m/s..36 a(bx + c) ab (x + c/b) g(x + υ ) and so υ c/b and he wave ravels in he negaive x-direcion. Using Eq. (.34) ( / ) /( / x) x [ A( a)( bx + c) c exp[ a( bx + c) ]]/[ A( a)( bx + c) b exp[ a( bx + c) ]] c/ b ; he minus sign ells us ha he moion is in he negaive x-direcion..37 ψ (z, 0) A sin(kz + ε); ψ ( λ /1, 0) A sin( π /6 + ε) 0.66; ψ (λ/6, 0) A sin(π/3 + ε) 1/; ψ (λ/4, 0) A sin (π/ + ε) 0. A sin (π / + ε) A(sin π / cos ε + cos π / sin ε) A cos ε 0, ε π /. A sin(π /3 + π /) A sin(5π /6) 1/; herefore A 1, hence ψ (z, 0) sin (kz + π /)..3 Boh (a) and (b) are waves since hey are wice differeniable funcions of z υ and x + υ, respecively. Thus for (a) ψ a (z b /a) and he velociy is b/a in he posiive z-direcion. For (b) ψ a (x + b/a + c/a) and he velociy is b/a in he negaive x-direcion..39 (a) ψ (y, ) exp[ (ay b) ], a raveling wave in he +y direcion, wih speed υ ω/k b/a. (b) no a raveling wave. (c) raveling wave in he x direcion, υ a/b, (d) raveling wave in he +x direcion, υ ψ (x, ) 5.0 exp[ a( x + b/ a ) ], he propagaion direcion is negaive x; υ ba / 0.6 m/s. ψ (x, 0) 5.0 exp( 5x )..41 ω πv π(440) 763 rad/s. k π / λ πν / υ 3.14 (440/343).06 rad/m. ϕ( x, ) ( kx ω) (.06x 763 ). [ ] [ ] ϕ ϕ( x+ 0., ) ϕ( x, ).06( x+ 0.) x rad. z
6 6 Chaper Soluions x x.4 10 πrad; ϕ( x, ) ( kx ω) π v πυ v. λ c We are looking for d such ha ϕ( x+ d,) ϕ(,) x π. Afer subsiuing, we obain x d x d πυ v + πυ v π. From here, πυ v πor c c c c 3 10 d m 300 nm..43 ψ (x, ) A sin π (x/λ ± /τ), ψ 60 sin π (x/ / ), λ 400 nm, υ / m/s. ν (1/1.33) Hz, τ s..44 exp[ iα]exp[ iβ] (cosα + isin α)(cos β + i sin β) (cosαcos β sinαsin β) + i(sinαcos β + cosαsin β) cos( α + β) + isin( α + β) exp[ i ( α + β)] ψψ * A exp[iω ] A exp[ iω ] A * ; ψψ A. In erms of Euler s formula ψψ * A (cos ω + i sin ω )(cos ω i sin ω ) A (cos ω + sin ω ) A..45 If z x + iy, hen z * x iy and z z * yi..46 z 1 x1 + iy1 z x + iy z + z x + x + iy + iy Re( z + z ) x + x 1 1 Re( z ) + Re( z ) x + x.47 z 1 x1 + iy1 z x + iy 1 1 Re( z ) Re( z ) xx 1 1 Re( z z ) Re( xx + ixy + ixy yy) xx yy Thus Re( z 1) Re( z ) Re( z 1 z )..4 ψ A exp i(k xx + k yy + k zz), k x kα, k y kβ, k z kγ, 1/ 1/ k [( kα) + ( kβ) + ( kγ) ] k( α + β + γ )..49 Consider Eq. (.64), wih ψ/ x α f, ψ/ y β f, / z f, / f. ψ γ ψ υ Then (1/ ) / ( + + 1) f 0 whenever ψ υ ψ α β γ α + β + γ 1. *************************<<INSERT MATTER OF.50 IS MISSING>>***********************
7 Chaper Soluions 7.51 Consider he funcion: ψ (z, ) Aexp[ (a z + b + abz)]. Where A, a, and b are all consans. Firs facor he exponen: 1 (a z + b + abz) (az + b) b z. + a a 1 b Thus, ψ ( z, ) Aexp z + a a. This is a wice differeniable funcion of (z υ ), where υ ba /, and ravels in he z direcion..5 λ h m /( υ) ( ) 4 10 m ν υλ / 500 (4 10 ) Hz. Boh resuls are orders of magniude beyond any known wave phenomena in fac, he wavelengh is wihin an order of magniude of he so-called Planck's lengh he shores disance ha modern physics can conceive of..53 k can be consruced by forming a uni vecor in he proper direcion and muliplying i by k. The uni vecor is ˆ [(4 0) iˆ+ ( 0) ˆj+ (1 0) k]/ (4iˆ+ ˆj+ kˆ)/ 1 and ˆ ˆ ˆ k k(4i + j + k) / 1. r xiˆ+ yj ˆ+ zkˆ, hence ψ( x, y, z, ) Asin[(4 k / 1) x+ ( k/ 1) y+ ( k/ 1) z ω]..54 ˆ ˆ ˆ k (1i + 0 j + 0 k), r xˆi + yˆj + zkˆ, so, ψ Asin( k r ω+ ε) Asin( kx ω+ ε) where k π /λ (could use cos insead of sin)..55 ψ( r1,) ψ[ r ( r r1),] ψ( k r1,) ψ[ k r k ( r r1),] ψ( k r,) ψ( r,) since k ( r r1) 0.56 ψ Aexp[ ik ( r+ ω+ ε)] Aexp[ ikx ( + ky+ kz+ ω+ ε)] x y z The wave equaion is: 1 ψ ψ v where, + + x ψ ( k + k + k ) Aexp[ ikx ( + ky+ kz+ ω+ ε)] x y z x y z ψ ω Aexp ( ω + ε) i kx x ky y kz z where hen, k k + k + k x y z k k + k + k x y z ψ k Aexp[ ikx ( + ky+ kz+ ω + ε)] x y z This means ha ψ is a soluion of he wave equaion if ν ω / k ν ω/. k
8 Chaper Soluions.57 θθ ππ 3ππ/4 ππ/ ππ/4 0 ππ/4 ππ/ 3ππ/4 ππ 5ππ/4 3ππ/ 7ππ/4 ππ sin θθ sin(θθ + ππ/) sin θθ + sin(θθ + ππ/) θθ ππ 3ππ/4 ππ/ ππ/4 0 ππ/4 ππ/ 3ππ/4 ππ 5ππ/4 3ππ/ 7ππ/4 ππ sin θθ sin(θθ 3ππ/4) sin θθ + sin(θθ 3ππ/4) The new funcion will be described by ψ() ψ1() + ψ(). Using simple rigonomery, we can easily find ha ψ( ) Asin( ω + ϕ/) cos ϕ/. Wih a lile rearranging, ψ( ) (Acos ϕ/)sin( ω + ϕ/). The ampliude is A cos ϕ/ and he phase shif is ϕ /..60 x λ / λ /4 0 λ /4 λ / 3λ /4 λ kx π π / 0 π / π 3π /π cos kx cos (kx + π) cos kx + cos (kx + π)
Chapter 2 Solutions. Chapter 2 Solutions 1. 4( z t) ( z t) z t
 Chapter Solutions 1 Chapter Solutions.1. 1 z t ( z t) z z ( z t) t t It s a twice differentiable function of ( z t ), where is in the negative z direction. 1 y t ( y, t) ( y4 t) ( y 4 t) y y 8( y 4 t)
Chapter Solutions 1 Chapter Solutions.1. 1 z t ( z t) z z ( z t) t t It s a twice differentiable function of ( z t ), where is in the negative z direction. 1 y t ( y, t) ( y4 t) ( y 4 t) y y 8( y 4 t)
Maxwell s Equations and Electromagnetic Waves
 Phsics 36: Waves Lecure 3 /9/8 Maxwell s quaions and lecromagneic Waves Four Laws of lecromagneism. Gauss Law qenc all da ρdv Inegral From From he vecor ideni da dv Therefore, we ma wrie Gauss Law as ρ
Phsics 36: Waves Lecure 3 /9/8 Maxwell s quaions and lecromagneic Waves Four Laws of lecromagneism. Gauss Law qenc all da ρdv Inegral From From he vecor ideni da dv Therefore, we ma wrie Gauss Law as ρ
Traveling Waves. Chapter Introduction
 Chaper 4 Traveling Waves 4.1 Inroducion To dae, we have considered oscillaions, i.e., periodic, ofen harmonic, variaions of a physical characerisic of a sysem. The sysem a one ime is indisinguishable from
Chaper 4 Traveling Waves 4.1 Inroducion To dae, we have considered oscillaions, i.e., periodic, ofen harmonic, variaions of a physical characerisic of a sysem. The sysem a one ime is indisinguishable from
Some Basic Information about M-S-D Systems
 Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
MA 214 Calculus IV (Spring 2016) Section 2. Homework Assignment 1 Solutions
 MA 14 Calculus IV (Spring 016) Secion Homework Assignmen 1 Soluions 1 Boyce and DiPrima, p 40, Problem 10 (c) Soluion: In sandard form he given firs-order linear ODE is: An inegraing facor is given by
MA 14 Calculus IV (Spring 016) Secion Homework Assignmen 1 Soluions 1 Boyce and DiPrima, p 40, Problem 10 (c) Soluion: In sandard form he given firs-order linear ODE is: An inegraing facor is given by
Wave Motion Sections 1,2,4,5, I. Outlook II. What is wave? III.Kinematics & Examples IV. Equation of motion Wave equations V.
 Secions 1,,4,5, I. Oulook II. Wha is wave? III.Kinemaics & Eamples IV. Equaion of moion Wave equaions V. Eamples Oulook Translaional and Roaional Moions wih Several phsics quaniies Energ (E) Momenum (p)
Secions 1,,4,5, I. Oulook II. Wha is wave? III.Kinemaics & Eamples IV. Equaion of moion Wave equaions V. Eamples Oulook Translaional and Roaional Moions wih Several phsics quaniies Energ (E) Momenum (p)
WEEK-3 Recitation PHYS 131. of the projectile s velocity remains constant throughout the motion, since the acceleration a x
 WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
4.5 Constant Acceleration
 4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
Differential Equations
 Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Chapter Q1. We need to understand Classical wave first. 3/28/2004 H133 Spring
 Chaper Q1 Inroducion o Quanum Mechanics End of 19 h Cenury only a few loose ends o wrap up. Led o Relaiviy which you learned abou las quarer Led o Quanum Mechanics (1920 s-30 s and beyond) Behavior of
Chaper Q1 Inroducion o Quanum Mechanics End of 19 h Cenury only a few loose ends o wrap up. Led o Relaiviy which you learned abou las quarer Led o Quanum Mechanics (1920 s-30 s and beyond) Behavior of
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
 Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Answers to 1 Homework
 Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Section 3.5 Nonhomogeneous Equations; Method of Undetermined Coefficients
 Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
d 1 = c 1 b 2 - b 1 c 2 d 2 = c 1 b 3 - b 1 c 3
 and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
BEng (Hons) Telecommunications. Examinations for / Semester 2
 BEng (Hons) Telecommunicaions Cohor: BTEL/14/FT Examinaions for 2015-2016 / Semeser 2 MODULE: ELECTROMAGNETIC THEORY MODULE CODE: ASE2103 Duraion: 2 ½ Hours Insrucions o Candidaes: 1. Answer ALL 4 (FOUR)
BEng (Hons) Telecommunicaions Cohor: BTEL/14/FT Examinaions for 2015-2016 / Semeser 2 MODULE: ELECTROMAGNETIC THEORY MODULE CODE: ASE2103 Duraion: 2 ½ Hours Insrucions o Candidaes: 1. Answer ALL 4 (FOUR)
Problem Set #1. i z. the complex propagation constant. For the characteristic impedance:
 Problem Se # Problem : a) Using phasor noaion, calculae he volage and curren waves on a ransmission line by solving he wave equaion Assume ha R, L,, G are all non-zero and independen of frequency From
Problem Se # Problem : a) Using phasor noaion, calculae he volage and curren waves on a ransmission line by solving he wave equaion Assume ha R, L,, G are all non-zero and independen of frequency From
(1) (2) Differentiation of (1) and then substitution of (3) leads to. Therefore, we will simply consider the second-order linear system given by (4)
 Phase Plane Analysis of Linear Sysems Adaped from Applied Nonlinear Conrol by Sloine and Li The general form of a linear second-order sysem is a c b d From and b bc d a Differeniaion of and hen subsiuion
Phase Plane Analysis of Linear Sysems Adaped from Applied Nonlinear Conrol by Sloine and Li The general form of a linear second-order sysem is a c b d From and b bc d a Differeniaion of and hen subsiuion
and v y . The changes occur, respectively, because of the acceleration components a x and a y
 Week 3 Reciaion: Chaper3 : Problems: 1, 16, 9, 37, 41, 71. 1. A spacecraf is raveling wih a veloci of v0 = 5480 m/s along he + direcion. Two engines are urned on for a ime of 84 s. One engine gives he
Week 3 Reciaion: Chaper3 : Problems: 1, 16, 9, 37, 41, 71. 1. A spacecraf is raveling wih a veloci of v0 = 5480 m/s along he + direcion. Two engines are urned on for a ime of 84 s. One engine gives he
x i v x t a dx dt t x
 Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
Physics 3A: Basic Physics I Shoup - Miderm Useful Equaions A y A sin A A A y an A y A A = A i + A y j + A z k A * B = A B cos(θ) A B = A B sin(θ) A * B = A B + A y B y + A z B z A B = (A y B z A z B y
AP Calculus BC Chapter 10 Part 1 AP Exam Problems
 AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
DEPARTMENT OF ELECTRICAL AND ELECTRONIC ENGINEERING EXAMINATIONS 2008
 [E5] IMPERIAL COLLEGE LONDON DEPARTMENT OF ELECTRICAL AND ELECTRONIC ENGINEERING EXAMINATIONS 008 EEE/ISE PART II MEng BEng and ACGI SIGNALS AND LINEAR SYSTEMS Time allowed: :00 hours There are FOUR quesions
[E5] IMPERIAL COLLEGE LONDON DEPARTMENT OF ELECTRICAL AND ELECTRONIC ENGINEERING EXAMINATIONS 008 EEE/ISE PART II MEng BEng and ACGI SIGNALS AND LINEAR SYSTEMS Time allowed: :00 hours There are FOUR quesions
t + t sin t t cos t sin t. t cos t sin t dt t 2 = exp 2 log t log(t cos t sin t) = Multiplying by this factor and then integrating, we conclude that
 ODEs, Homework #4 Soluions. Check ha y ( = is a soluion of he second-order ODE ( cos sin y + y sin y sin = 0 and hen use his fac o find all soluions of he ODE. When y =, we have y = and also y = 0, so
ODEs, Homework #4 Soluions. Check ha y ( = is a soluion of he second-order ODE ( cos sin y + y sin y sin = 0 and hen use his fac o find all soluions of he ODE. When y =, we have y = and also y = 0, so
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
System of Linear Differential Equations
 Sysem of Linear Differenial Equaions In "Ordinary Differenial Equaions" we've learned how o solve a differenial equaion for a variable, such as: y'k5$e K2$x =0 solve DE yx = K 5 2 ek2 x C_C1 2$y''C7$y
Sysem of Linear Differenial Equaions In "Ordinary Differenial Equaions" we've learned how o solve a differenial equaion for a variable, such as: y'k5$e K2$x =0 solve DE yx = K 5 2 ek2 x C_C1 2$y''C7$y
Roller-Coaster Coordinate System
 Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
8. Basic RL and RC Circuits
 8. Basic L and C Circuis This chaper deals wih he soluions of he responses of L and C circuis The analysis of C and L circuis leads o a linear differenial equaion This chaper covers he following opics
8. Basic L and C Circuis This chaper deals wih he soluions of he responses of L and C circuis The analysis of C and L circuis leads o a linear differenial equaion This chaper covers he following opics
Ground Rules. PC1221 Fundamentals of Physics I. Kinematics. Position. Lectures 3 and 4 Motion in One Dimension. A/Prof Tay Seng Chuan
 Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
t is a basis for the solution space to this system, then the matrix having these solutions as columns, t x 1 t, x 2 t,... x n t x 2 t...
 Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Oscillations. Periodic Motion. Sinusoidal Motion. PHY oscillations - J. Hedberg
 Oscillaions PHY 207 - oscillaions - J. Hedberg - 2017 1. Periodic Moion 2. Sinusoidal Moion 3. How do we ge his kind of moion? 4. Posiion - Velociy - cceleraion 5. spring wih vecors 6. he reference circle
Oscillaions PHY 207 - oscillaions - J. Hedberg - 2017 1. Periodic Moion 2. Sinusoidal Moion 3. How do we ge his kind of moion? 4. Posiion - Velociy - cceleraion 5. spring wih vecors 6. he reference circle
Chapter 4 The Fourier Series and Fourier Transform
 Represenaion of Signals in Terms of Frequency Componens Chaper 4 The Fourier Series and Fourier Transform Consider he CT signal defined by x () = Acos( ω + θ ), = The frequencies `presen in he signal are
Represenaion of Signals in Terms of Frequency Componens Chaper 4 The Fourier Series and Fourier Transform Consider he CT signal defined by x () = Acos( ω + θ ), = The frequencies `presen in he signal are
Wall. x(t) f(t) x(t = 0) = x 0, t=0. which describes the motion of the mass in absence of any external forcing.
 MECHANICS APPLICATIONS OF SECOND-ORDER ODES 7 Mechanics applicaions of second-order ODEs Second-order linear ODEs wih consan coefficiens arise in many physical applicaions. One physical sysems whose behaviour
MECHANICS APPLICATIONS OF SECOND-ORDER ODES 7 Mechanics applicaions of second-order ODEs Second-order linear ODEs wih consan coefficiens arise in many physical applicaions. One physical sysems whose behaviour
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
ENGI 9420 Engineering Analysis Assignment 2 Solutions
 ENGI 940 Engineering Analysis Assignmen Soluions 0 Fall [Second order ODEs, Laplace ransforms; Secions.0-.09]. Use Laplace ransforms o solve he iniial value problem [0] dy y, y( 0) 4 d + [This was Quesion
ENGI 940 Engineering Analysis Assignmen Soluions 0 Fall [Second order ODEs, Laplace ransforms; Secions.0-.09]. Use Laplace ransforms o solve he iniial value problem [0] dy y, y( 0) 4 d + [This was Quesion
Integration Over Manifolds with Variable Coordinate Density
 Inegraion Over Manifolds wih Variable Coordinae Densiy Absrac Chrisopher A. Lafore clafore@gmail.com In his paper, he inegraion of a funcion over a curved manifold is examined in he case where he curvaure
Inegraion Over Manifolds wih Variable Coordinae Densiy Absrac Chrisopher A. Lafore clafore@gmail.com In his paper, he inegraion of a funcion over a curved manifold is examined in he case where he curvaure
Motion along a Straight Line
 chaper 2 Moion along a Sraigh Line verage speed and average velociy (Secion 2.2) 1. Velociy versus speed Cone in he ebook: fer Eample 2. Insananeous velociy and insananeous acceleraion (Secions 2.3, 2.4)
chaper 2 Moion along a Sraigh Line verage speed and average velociy (Secion 2.2) 1. Velociy versus speed Cone in he ebook: fer Eample 2. Insananeous velociy and insananeous acceleraion (Secions 2.3, 2.4)
k 1 k 2 x (1) x 2 = k 1 x 1 = k 2 k 1 +k 2 x (2) x k series x (3) k 2 x 2 = k 1 k 2 = k 1+k 2 = 1 k k 2 k series
 Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
Parametrics and Vectors (BC Only)
 Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Morning Time: 1 hour 30 minutes Additional materials (enclosed):
 ADVANCED GCE 78/0 MATHEMATICS (MEI) Differenial Equaions THURSDAY JANUARY 008 Morning Time: hour 30 minues Addiional maerials (enclosed): None Addiional maerials (required): Answer Bookle (8 pages) Graph
ADVANCED GCE 78/0 MATHEMATICS (MEI) Differenial Equaions THURSDAY JANUARY 008 Morning Time: hour 30 minues Addiional maerials (enclosed): None Addiional maerials (required): Answer Bookle (8 pages) Graph
Week 1 Lecture 2 Problems 2, 5. What if something oscillates with no obvious spring? What is ω? (problem set problem)
 Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
4.6 One Dimensional Kinematics and Integration
 4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
Physics 3A: Basic Physics I Shoup Sample Midterm. Useful Equations. x f. x i v x. a x. x i. v xi v xf. 2a x f x i. y f. a r.
 Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
MEI STRUCTURED MATHEMATICS 4758
 OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
23.2. Representing Periodic Functions by Fourier Series. Introduction. Prerequisites. Learning Outcomes
 Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
23.5. Half-Range Series. Introduction. Prerequisites. Learning Outcomes
 Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Solution: b All the terms must have the dimension of acceleration. We see that, indeed, each term has the units of acceleration
 PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
Math 333 Problem Set #2 Solution 14 February 2003
 Mah 333 Problem Se #2 Soluion 14 February 2003 A1. Solve he iniial value problem dy dx = x2 + e 3x ; 2y 4 y(0) = 1. Soluion: This is separable; we wrie 2y 4 dy = x 2 + e x dx and inegrae o ge The iniial
Mah 333 Problem Se #2 Soluion 14 February 2003 A1. Solve he iniial value problem dy dx = x2 + e 3x ; 2y 4 y(0) = 1. Soluion: This is separable; we wrie 2y 4 dy = x 2 + e x dx and inegrae o ge The iniial
THE 2-BODY PROBLEM. FIGURE 1. A pair of ellipses sharing a common focus. (c,b) c+a ROBERT J. VANDERBEI
 THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
Circuit Variables. AP 1.1 Use a product of ratios to convert two-thirds the speed of light from meters per second to miles per second: 1 ft 12 in
 Circui Variables 1 Assessmen Problems AP 1.1 Use a produc of raios o conver wo-hirds he speed of ligh from meers per second o miles per second: ( ) 2 3 1 8 m 3 1 s 1 cm 1 m 1 in 2.54 cm 1 f 12 in 1 mile
Circui Variables 1 Assessmen Problems AP 1.1 Use a produc of raios o conver wo-hirds he speed of ligh from meers per second o miles per second: ( ) 2 3 1 8 m 3 1 s 1 cm 1 m 1 in 2.54 cm 1 f 12 in 1 mile
CHAPTER 12 DIRECT CURRENT CIRCUITS
 CHAPTER 12 DIRECT CURRENT CIUITS DIRECT CURRENT CIUITS 257 12.1 RESISTORS IN SERIES AND IN PARALLEL When wo resisors are conneced ogeher as shown in Figure 12.1 we said ha hey are conneced in series. As
CHAPTER 12 DIRECT CURRENT CIUITS DIRECT CURRENT CIUITS 257 12.1 RESISTORS IN SERIES AND IN PARALLEL When wo resisors are conneced ogeher as shown in Figure 12.1 we said ha hey are conneced in series. As
1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.
![1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx. 1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.](/thumbs/71/65799522.jpg) . Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
. Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
HOMEWORK # 2: MATH 211, SPRING Note: This is the last solution set where I will describe the MATLAB I used to make my pictures.
 HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
Challenge Problems. DIS 203 and 210. March 6, (e 2) k. k(k + 2). k=1. f(x) = k(k + 2) = 1 x k
 Challenge Problems DIS 03 and 0 March 6, 05 Choose one of he following problems, and work on i in your group. Your goal is o convince me ha your answer is correc. Even if your answer isn compleely correc,
Challenge Problems DIS 03 and 0 March 6, 05 Choose one of he following problems, and work on i in your group. Your goal is o convince me ha your answer is correc. Even if your answer isn compleely correc,
In this chapter the model of free motion under gravity is extended to objects projected at an angle. When you have completed it, you should
 Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Ordinary Differential Equations
 Lecure 22 Ordinary Differenial Equaions Course Coordinaor: Dr. Suresh A. Karha, Associae Professor, Deparmen of Civil Engineering, IIT Guwahai. In naure, mos of he phenomena ha can be mahemaically described
Lecure 22 Ordinary Differenial Equaions Course Coordinaor: Dr. Suresh A. Karha, Associae Professor, Deparmen of Civil Engineering, IIT Guwahai. In naure, mos of he phenomena ha can be mahemaically described
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Physics for Scientists & Engineers 2
 Direc Curren Physics for Scieniss & Engineers 2 Spring Semeser 2005 Lecure 16 This week we will sudy charges in moion Elecric charge moving from one region o anoher is called elecric curren Curren is all
Direc Curren Physics for Scieniss & Engineers 2 Spring Semeser 2005 Lecure 16 This week we will sudy charges in moion Elecric charge moving from one region o anoher is called elecric curren Curren is all
u(x) = e x 2 y + 2 ) Integrate and solve for x (1 + x)y + y = cos x Answer: Divide both sides by 1 + x and solve for y. y = x y + cos x
 . 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
. 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
Thus the force is proportional but opposite to the displacement away from equilibrium.
 Chaper 3 : Siple Haronic Moion Hooe s law saes ha he force (F) eered by an ideal spring is proporional o is elongaion l F= l where is he spring consan. Consider a ass hanging on a he spring. In equilibriu
Chaper 3 : Siple Haronic Moion Hooe s law saes ha he force (F) eered by an ideal spring is proporional o is elongaion l F= l where is he spring consan. Consider a ass hanging on a he spring. In equilibriu
Chapter 15 Oscillatory Motion I
 Chaper 15 Oscillaory Moion I Level : AP Physics Insrucor : Kim Inroducion A very special kind of moion occurs when he force acing on a body is proporional o he displacemen of he body from some equilibrium
Chaper 15 Oscillaory Moion I Level : AP Physics Insrucor : Kim Inroducion A very special kind of moion occurs when he force acing on a body is proporional o he displacemen of he body from some equilibrium
SOLUTIONS TO ECE 3084
 SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
Chapter 7: Solving Trig Equations
 Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
( ) is the stretch factor, and x the
 (Lecures 7-8) Liddle, Chaper 5 Simple cosmological models (i) Hubble s Law revisied Self-similar srech of he universe All universe models have his characerisic v r ; v = Hr since only his conserves homogeneiy
(Lecures 7-8) Liddle, Chaper 5 Simple cosmological models (i) Hubble s Law revisied Self-similar srech of he universe All universe models have his characerisic v r ; v = Hr since only his conserves homogeneiy
Chapter 10 INDUCTANCE Recommended Problems:
 Chaper 0 NDUCTANCE Recommended Problems: 3,5,7,9,5,6,7,8,9,,,3,6,7,9,3,35,47,48,5,5,69, 7,7. Self nducance Consider he circui shown in he Figure. When he swich is closed, he curren, and so he magneic field,
Chaper 0 NDUCTANCE Recommended Problems: 3,5,7,9,5,6,7,8,9,,,3,6,7,9,3,35,47,48,5,5,69, 7,7. Self nducance Consider he circui shown in he Figure. When he swich is closed, he curren, and so he magneic field,
Lecture Outline. Introduction Transmission Line Equations Transmission Line Wave Equations 8/10/2018. EE 4347 Applied Electromagnetics.
 8/10/018 Course Insrucor Dr. Raymond C. Rumpf Office: A 337 Phone: (915) 747 6958 E Mail: rcrumpf@uep.edu EE 4347 Applied Elecromagneics Topic 4a Transmission Line Equaions Transmission These Line noes
8/10/018 Course Insrucor Dr. Raymond C. Rumpf Office: A 337 Phone: (915) 747 6958 E Mail: rcrumpf@uep.edu EE 4347 Applied Elecromagneics Topic 4a Transmission Line Equaions Transmission These Line noes
Solutions to Assignment 1
 MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
Ch.1. Group Work Units. Continuum Mechanics Course (MMC) - ETSECCPB - UPC
 Ch.. Group Work Unis Coninuum Mechanics Course (MMC) - ETSECCPB - UPC Uni 2 Jusify wheher he following saemens are rue or false: a) Two sreamlines, corresponding o a same insan of ime, can never inersec
Ch.. Group Work Unis Coninuum Mechanics Course (MMC) - ETSECCPB - UPC Uni 2 Jusify wheher he following saemens are rue or false: a) Two sreamlines, corresponding o a same insan of ime, can never inersec
From Particles to Rigid Bodies
 Rigid Body Dynamics From Paricles o Rigid Bodies Paricles No roaions Linear velociy v only Rigid bodies Body roaions Linear velociy v Angular velociy ω Rigid Bodies Rigid bodies have boh a posiion and
Rigid Body Dynamics From Paricles o Rigid Bodies Paricles No roaions Linear velociy v only Rigid bodies Body roaions Linear velociy v Angular velociy ω Rigid Bodies Rigid bodies have boh a posiion and
ln 2 1 ln y x c y C x
 Lecure 14 Appendi B: Some sample problems from Boas Here are some soluions o he sample problems assigned for Chaper 8 8: 6 Soluion: We wan o find he soluion o he following firs order equaion using separaion
Lecure 14 Appendi B: Some sample problems from Boas Here are some soluions o he sample problems assigned for Chaper 8 8: 6 Soluion: We wan o find he soluion o he following firs order equaion using separaion
Section 3.8, Mechanical and Electrical Vibrations
 Secion 3.8, Mechanical and Elecrical Vibraions Mechanical Unis in he U.S. Cusomary and Meric Sysems Disance Mass Time Force g (Earh) Uni U.S. Cusomary MKS Sysem CGS Sysem fee f slugs seconds sec pounds
Secion 3.8, Mechanical and Elecrical Vibraions Mechanical Unis in he U.S. Cusomary and Meric Sysems Disance Mass Time Force g (Earh) Uni U.S. Cusomary MKS Sysem CGS Sysem fee f slugs seconds sec pounds
Class Meeting # 10: Introduction to the Wave Equation
 MATH 8.5 COURSE NOTES - CLASS MEETING # 0 8.5 Inroducion o PDEs, Fall 0 Professor: Jared Speck Class Meeing # 0: Inroducion o he Wave Equaion. Wha is he wave equaion? The sandard wave equaion for a funcion
MATH 8.5 COURSE NOTES - CLASS MEETING # 0 8.5 Inroducion o PDEs, Fall 0 Professor: Jared Speck Class Meeing # 0: Inroducion o he Wave Equaion. Wha is he wave equaion? The sandard wave equaion for a funcion
THE WAVE EQUATION. part hand-in for week 9 b. Any dilation v(x, t) = u(λx, λt) of u(x, t) is also a solution (where λ is constant).
 THE WAVE EQUATION 43. (S) Le u(x, ) be a soluion of he wave equaion u u xx = 0. Show ha Q43(a) (c) is a. Any ranslaion v(x, ) = u(x + x 0, + 0 ) of u(x, ) is also a soluion (where x 0, 0 are consans).
THE WAVE EQUATION 43. (S) Le u(x, ) be a soluion of he wave equaion u u xx = 0. Show ha Q43(a) (c) is a. Any ranslaion v(x, ) = u(x + x 0, + 0 ) of u(x, ) is also a soluion (where x 0, 0 are consans).
9. Alternating currents
 WS 9. Alernaing currens 9.1 nroducion Besides ohmic resisors, capaciors and inducions play an imporan role in alernaing curren (AC circuis as well. n his experimen, one shall invesigae heir behaviour in
WS 9. Alernaing currens 9.1 nroducion Besides ohmic resisors, capaciors and inducions play an imporan role in alernaing curren (AC circuis as well. n his experimen, one shall invesigae heir behaviour in
Laplace transfom: t-translation rule , Haynes Miller and Jeremy Orloff
 Laplace ransfom: -ranslaion rule 8.03, Haynes Miller and Jeremy Orloff Inroducory example Consider he sysem ẋ + 3x = f(, where f is he inpu and x he response. We know is uni impulse response is 0 for
Laplace ransfom: -ranslaion rule 8.03, Haynes Miller and Jeremy Orloff Inroducory example Consider he sysem ẋ + 3x = f(, where f is he inpu and x he response. We know is uni impulse response is 0 for
556: MATHEMATICAL STATISTICS I
 556: MATHEMATICAL STATISTICS I INEQUALITIES 5.1 Concenraion and Tail Probabiliy Inequaliies Lemma (CHEBYCHEV S LEMMA) c > 0, If X is a random variable, hen for non-negaive funcion h, and P X [h(x) c] E
556: MATHEMATICAL STATISTICS I INEQUALITIES 5.1 Concenraion and Tail Probabiliy Inequaliies Lemma (CHEBYCHEV S LEMMA) c > 0, If X is a random variable, hen for non-negaive funcion h, and P X [h(x) c] E
Section 7.4 Modeling Changing Amplitude and Midline
 488 Chaper 7 Secion 7.4 Modeling Changing Ampliude and Midline While sinusoidal funcions can model a variey of behaviors, i is ofen necessary o combine sinusoidal funcions wih linear and exponenial curves
488 Chaper 7 Secion 7.4 Modeling Changing Ampliude and Midline While sinusoidal funcions can model a variey of behaviors, i is ofen necessary o combine sinusoidal funcions wih linear and exponenial curves
UCLA: Math 3B Problem set 3 (solutions) Fall, 2018
 UCLA: Mah 3B Problem se 3 (soluions) Fall, 28 This problem se concenraes on pracice wih aniderivaives. You will ge los of pracice finding simple aniderivaives as well as finding aniderivaives graphically
UCLA: Mah 3B Problem se 3 (soluions) Fall, 28 This problem se concenraes on pracice wih aniderivaives. You will ge los of pracice finding simple aniderivaives as well as finding aniderivaives graphically
72 Calculus and Structures
 72 Calculus and Srucures CHAPTER 5 DISTANCE AND ACCUMULATED CHANGE Calculus and Srucures 73 Copyrigh Chaper 5 DISTANCE AND ACCUMULATED CHANGE 5. DISTANCE a. Consan velociy Le s ake anoher look a Mary s
72 Calculus and Srucures CHAPTER 5 DISTANCE AND ACCUMULATED CHANGE Calculus and Srucures 73 Copyrigh Chaper 5 DISTANCE AND ACCUMULATED CHANGE 5. DISTANCE a. Consan velociy Le s ake anoher look a Mary s
Reading from Young & Freedman: For this topic, read sections 25.4 & 25.5, the introduction to chapter 26 and sections 26.1 to 26.2 & 26.4.
 PHY1 Elecriciy Topic 7 (Lecures 1 & 11) Elecric Circuis n his opic, we will cover: 1) Elecromoive Force (EMF) ) Series and parallel resisor combinaions 3) Kirchhoff s rules for circuis 4) Time dependence
PHY1 Elecriciy Topic 7 (Lecures 1 & 11) Elecric Circuis n his opic, we will cover: 1) Elecromoive Force (EMF) ) Series and parallel resisor combinaions 3) Kirchhoff s rules for circuis 4) Time dependence
Physics 221 Fall 2008 Homework #2 Solutions Ch. 2 Due Tues, Sept 9, 2008
 Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
Physics 221 Fall 28 Homework #2 Soluions Ch. 2 Due Tues, Sep 9, 28 2.1 A paricle moving along he x-axis moves direcly from posiion x =. m a ime =. s o posiion x = 1. m by ime = 1. s, and hen moves direcly
Introduction to Physical Oceanography Homework 5 - Solutions
 Laure Zanna //5 Inroducion o Phsical Oceanograph Homework 5 - Soluions. Inerial oscillaions wih boom fricion non-selecive scale: The governing equaions for his problem are This ssem can be wrien as where
Laure Zanna //5 Inroducion o Phsical Oceanograph Homework 5 - Soluions. Inerial oscillaions wih boom fricion non-selecive scale: The governing equaions for his problem are This ssem can be wrien as where
Harmonic oscillator in quantum mechanics
 Harmonic oscillaor in quanum mechanics PHYS400, Deparmen of Physics, Universiy of onnecicu hp://www.phys.uconn.edu/phys400/ Las modified: May, 05 Dimensionless Schrödinger s equaion in quanum mechanics
Harmonic oscillaor in quanum mechanics PHYS400, Deparmen of Physics, Universiy of onnecicu hp://www.phys.uconn.edu/phys400/ Las modified: May, 05 Dimensionless Schrödinger s equaion in quanum mechanics
Course Notes for EE227C (Spring 2018): Convex Optimization and Approximation
 Course Noes for EE7C Spring 018: Convex Opimizaion and Approximaion Insrucor: Moriz Hard Email: hard+ee7c@berkeley.edu Graduae Insrucor: Max Simchowiz Email: msimchow+ee7c@berkeley.edu Ocober 15, 018 3
Course Noes for EE7C Spring 018: Convex Opimizaion and Approximaion Insrucor: Moriz Hard Email: hard+ee7c@berkeley.edu Graduae Insrucor: Max Simchowiz Email: msimchow+ee7c@berkeley.edu Ocober 15, 018 3
The Lorentz Transformation
 The Lorenz Transformaion Relaiviy and Asrophysics Lecure 06 Terry Herer Ouline Coordinae ransformaions Lorenz Transformaion Saemen Proof Addiion of velociies Parial proof Examples of velociy addiion Proof
The Lorenz Transformaion Relaiviy and Asrophysics Lecure 06 Terry Herer Ouline Coordinae ransformaions Lorenz Transformaion Saemen Proof Addiion of velociies Parial proof Examples of velociy addiion Proof
Giambattista, Ch 3 Problems: 9, 15, 21, 27, 35, 37, 42, 43, 47, 55, 63, 76
 Giambaisa, Ch 3 Problems: 9, 15, 21, 27, 35, 37, 42, 43, 47, 55, 63, 76 9. Sraeg Le be direced along he +x-axis and le be 60.0 CCW from Find he magniude of 6.0 B 60.0 4.0 A x 15. (a) Sraeg Since he angle
Giambaisa, Ch 3 Problems: 9, 15, 21, 27, 35, 37, 42, 43, 47, 55, 63, 76 9. Sraeg Le be direced along he +x-axis and le be 60.0 CCW from Find he magniude of 6.0 B 60.0 4.0 A x 15. (a) Sraeg Since he angle
dv dt = s and t = s a = 28.7 m/s
 COSMOS: Complee Online Soluions Manual Organizaion Sysem Chaper, Soluion. Posiion: Velociy: 0 3 5 x = 0 + 0 m 3 dx v = = 0 5 0 m/s d dv Acceleraion: a = = 0 5 d When v = 0, 0 5 0 = 0 Solving he quadraic
COSMOS: Complee Online Soluions Manual Organizaion Sysem Chaper, Soluion. Posiion: Velociy: 0 3 5 x = 0 + 0 m 3 dx v = = 0 5 0 m/s d dv Acceleraion: a = = 0 5 d When v = 0, 0 5 0 = 0 Solving he quadraic
a 10.0 (m/s 2 ) 5.0 Name: Date: 1. The graph below describes the motion of a fly that starts out going right V(m/s)
 Name: Dae: Kinemaics Review (Honors. Physics) Complee he following on a separae shee of paper o be urned in on he day of he es. ALL WORK MUST BE SHOWN TO RECEIVE CREDIT. 1. The graph below describes he
Name: Dae: Kinemaics Review (Honors. Physics) Complee he following on a separae shee of paper o be urned in on he day of he es. ALL WORK MUST BE SHOWN TO RECEIVE CREDIT. 1. The graph below describes he
Book Corrections for Optimal Estimation of Dynamic Systems, 2 nd Edition
 Boo Correcions for Opimal Esimaion of Dynamic Sysems, nd Ediion John L. Crassidis and John L. Junins November 17, 017 Chaper 1 This documen provides correcions for he boo: Crassidis, J.L., and Junins,
Boo Correcions for Opimal Esimaion of Dynamic Sysems, nd Ediion John L. Crassidis and John L. Junins November 17, 017 Chaper 1 This documen provides correcions for he boo: Crassidis, J.L., and Junins,
Effects of Coordinate Curvature on Integration
 Effecs of Coordinae Curvaure on Inegraion Chrisopher A. Lafore clafore@gmail.com Absrac In his paper, he inegraion of a funcion over a curved manifold is examined in he case where he curvaure of he manifold
Effecs of Coordinae Curvaure on Inegraion Chrisopher A. Lafore clafore@gmail.com Absrac In his paper, he inegraion of a funcion over a curved manifold is examined in he case where he curvaure of he manifold
dy dx = xey (a) y(0) = 2 (b) y(1) = 2.5 SOLUTION: See next page
 Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Solutions for homework 12
 y Soluions for homework Secion Nonlinear sysems: The linearizaion of a nonlinear sysem Consider he sysem y y y y y (i) Skech he nullclines Use a disincive marking for each nullcline so hey can be disinguished
y Soluions for homework Secion Nonlinear sysems: The linearizaion of a nonlinear sysem Consider he sysem y y y y y (i) Skech he nullclines Use a disincive marking for each nullcline so hey can be disinguished
Vanishing Viscosity Method. There are another instructive and perhaps more natural discontinuous solutions of the conservation law
 Vanishing Viscosiy Mehod. There are anoher insrucive and perhaps more naural disconinuous soluions of he conservaion law (1 u +(q(u x 0, he so called vanishing viscosiy mehod. This mehod consiss in viewing
Vanishing Viscosiy Mehod. There are anoher insrucive and perhaps more naural disconinuous soluions of he conservaion law (1 u +(q(u x 0, he so called vanishing viscosiy mehod. This mehod consiss in viewing
AP Calculus BC - Parametric equations and vectors Chapter 9- AP Exam Problems solutions
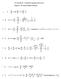 AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
EXERCISES FOR SECTION 1.5
 1.5 Exisence and Uniqueness of Soluions 43 20. 1 v c 21. 1 v c 1 2 4 6 8 10 1 2 2 4 6 8 10 Graph of approximae soluion obained using Euler s mehod wih = 0.1. Graph of approximae soluion obained using Euler
1.5 Exisence and Uniqueness of Soluions 43 20. 1 v c 21. 1 v c 1 2 4 6 8 10 1 2 2 4 6 8 10 Graph of approximae soluion obained using Euler s mehod wih = 0.1. Graph of approximae soluion obained using Euler
Robotics I. April 11, The kinematics of a 3R spatial robot is specified by the Denavit-Hartenberg parameters in Tab. 1.
 Roboics I April 11, 017 Exercise 1 he kinemaics of a 3R spaial robo is specified by he Denavi-Harenberg parameers in ab 1 i α i d i a i θ i 1 π/ L 1 0 1 0 0 L 3 0 0 L 3 3 able 1: able of DH parameers of
Roboics I April 11, 017 Exercise 1 he kinemaics of a 3R spaial robo is specified by he Denavi-Harenberg parameers in ab 1 i α i d i a i θ i 1 π/ L 1 0 1 0 0 L 3 0 0 L 3 3 able 1: able of DH parameers of
Solutions of Sample Problems for Third In-Class Exam Math 246, Spring 2011, Professor David Levermore
 Soluions of Sample Problems for Third In-Class Exam Mah 6, Spring, Professor David Levermore Compue he Laplace ransform of f e from is definiion Soluion The definiion of he Laplace ransform gives L[f]s
Soluions of Sample Problems for Third In-Class Exam Mah 6, Spring, Professor David Levermore Compue he Laplace ransform of f e from is definiion Soluion The definiion of he Laplace ransform gives L[f]s
