DCSP-3: Fourier Transform II
|
|
|
- Lynn Barker
- 5 years ago
- Views:
Transcription
1 DCSP-3: Fourier Transform II Jianfeng Feng Department of Computer Science Warwick Univ., UK
2 Fourier Theorem This representation is quite general. In fact we have the following theorem due to Fourier. Any signal x(t) of period T can be represented as the sum of a set of cosinusoidal and sinusoidal waves of different frequencies
3 This week s summary Introduce FT in layman s language (today) Applications (tomorrow)
4 This week s summary Introduce FT in layman s language (today) Applications (tomorrow) You might find the world is different!
5 100m-for-medical-imaging-tech/
6 This week s summary Introduce FT in layman s language (today) Talk about continuous FT since it is clean and simple Come back to it on how to numerically calculate it later on Intuition Fourier theorem Examples Bandwidth
7 Intuition of FT Two dimensional space (all points) (a, b) = a (1,0) + b (0,1) Signal space (all functions of t) x (t) = a sin(ω t) + b sin (2 ω t)
8 Intuition of FT Two a point in it (a, b) = a (1,0) + b (0,1)
9 Intuition of FT Two a point in it (a, b) = a (1,0) + b (0,1) Signal = coef basis coef basis
10 Intuition of FT Two a point in it (a, b) = a (1,0) + b (0,1) x(t) =? Signal = coef basis coef basis
11 Intuition of FT Two a point in it (a, b) = a (1,0) + b (0,1) x(t) = a F1(t) +b F2(t) Signal = coef basis coef basis
12 Intuition of FT It is a branch of mathematics called functional analysis: treat each function as a point in a functional space It is the starting pointe of modern mathematics It is also the actual power of mathematics Branch space, Hilbert space etc.
13 Intuition of FT How to calculate these coefficients? o (a, b) = a (1,0) + b (0,1) Functional x (t) = a cos(ω t) + b cos (2 ω t) w = 2 pi /T
14 Intuition of FT 1. Coefficient is obtained via Inner product <(x, y), (m,n)> = xm+yn 2. All bases are orthogonal <(0, 1), (1,0)> = 0, (0,1) (1, 0) (a, b) = a (1,0) + b (0,1) Therefore <(a, b), (1,0)> = a <(1,0), (1,0)> + b <(0,1), (1,0)> = a <(a, b), (0,1)> = a <(1,0), (0,1)> + b <(0,1), (0,1)> = b
15 Intuition of FT Two dimensi coefficient is obtained via Inner product (a, b) = a (1,0) + b (0,1) <(a, b), (1,0)> = a <(1,0), (1,0)> + b <(0,1), (1,0)> = a Functional coefficient is obtained via inner product x (t) = a cos(ω t) + b cos (2 ω t) <x (t), cos(ω t) > = <a cos(ω t), cos(ω t) > + <b cos (2 ω t), cos(ω t) > = a (?) If cos(ω t) and cos(2 ω t) are orthogonal
16 Intuition of FT Two dimension orthogonal basis (a, b) = a (1,0) + b (0,1) Functional space basis x (t) = a cos(ω t) + b cos (2 ω t)
17 Intuition of FT It turns out that we can define the inner product in the signal space x(t), y ( t ) 2 T T / 2 T / 2 x ( t ) y ( ) t dt 2 cos( wt ),cos(2wt ) cos( wt)cos(2wt ) dt T T T
18 Intuition of FT Cos ( 2 p t) Cos ( 2*2 p t) Cos ( 2 p t) * Cos ( 2*2 p t) 2 cos( wt ),cos(2wt ) cos( wt)cos(2wt ) dt T T T
19 they form orthogonal bases Intuition of FT Cos ( 2 p t) Cos ( 2*2 p t) Cos ( 2 p t) * Cos ( 2*2 p t) { cos (n ω t ), n=1,2 } are orthogonal
20 Intuition of FT It turns out that we can define the inner product in the signal space cos( mwt),cos( nwt) In particular, we have 2 / T, n 0, n m m x (t) = a cos(ω t) + b cos (2 ω t) a = <X(t), cos(ω t)> = b =? 2 T T /2 ò -T /2 x(t) cos( wt)dt
21 Intuition of FT X X 1 X 6 ( ) X 2 X 3 x 4 X5 ( ) ( ) ( ) ( ) ( ) In an n-dim Euclidean space, we decompose any vector X in terms of orthogonal bases Coefficient is obtained by inner product between a basis and X We sometime call x i weight X = x 1 ( ) + x 2 ( ) + + x 6 ( )
22 Intuition of FT X(t) A 1 A 6. cos (ω t ) A 2 A 3 A 4 A5 x( t) A1 cos( wt) more
23 Intuition of FT X(t) A 1 A 6. cos (ω t ) A 2 A 3 A 4 A5 cos (2 ω t ) x t) A cos( wt) A cos(2 t) more ( 1 2 w
24 Intuition of FT X(t) A 1 A 6. cos (ω t ) A 2 A 3 A 4 A5 cos (3 ω t ) cos (2 ω t ) x t) A cos( wt) A cos(2wt ) A cos(3 t) more ( w
25 Intuition of FT X(t) A 1 A 6. cos (ω t ) A 2 A 3 A 4 A5 cos (3 ω t ) cos (4 ω t ) cos (2 ω t ) x t) A cos( wt) A cos(2wt ) A cos(3wt ) A cos(4 t) more ( w
26 Intuition of FT X(t) A 1 A 6. cos (ω t ) A 2 A 3 A 4 0 cos (3 ω t ) cos (4 ω t ) cos (2 ω t ) x t) A cos( wt) A cos(2wt ) A cos(3wt ) A cos(4 t) more ( w
27 Intuition of FT X(t) A 1 A 6 cos (ω t ) A 2 A 3 A 4 0 cos (3 ω t ) cos (4 ω t ) cos (2 ω t ) x t) A cos( wt) A cos(2wt ) A cos(3wt ) A cos(4wt ) A cos(6w ) ( t
28 Intuition of FT X(t) A 1 A 6. cos (ω t ) A 2 A 3 A 4 0 cos (3 ω t ) cos (4 ω t ) cos (2 ω t ) In an n-dim Euclidean space, we decompose any vector X in terms of orthogonal bases Coefficient is obtained by inner product between a basis and X We sometime call x i weight
29 FT: Fourier Thm in terms of Sin and Cos simply a generalization of common knowledge of the Euclidean space { 1, cos (nωt), sin(nwt), n=1,2 } are orthogonal and complete they form orthogonal bases
30 FT: Fourier Thm in terms of Sin and Cos simply a generalization of common knowledge of the Euclidean space { 1, cos (nωt), sin(nwt), n=1,2 } are orthogonal and complete they form orthogonal bases
31 FT: Fourier Thm in terms of Sin and Cos simply a generalization of common knowledge of the Euclidean space { 1, cos (nωt), sin(nwt), n=1,2 } are orthogonal and complete they form orthogonal bases x(t) = A 0 + å A n cos(nwt)+ n=1 n=1 ì ï A 0 =<1, x(t) >= 1 ïï T ï í ï ïï ï ï î T /2 -T /2 B n sin(nwt) where A 0 is the d.c. term, and T is the period of the waveform. ò å x(t)dt A n =< cos(nwt), x(t) >= 2 T B n =< sin(nwt), x(t) >= 2 T w = 2p T T /2 ò -T /2 T /2 ò -T /2 x(t) cos(nwt) dt x(t)sin(nwt) dt
32 FT: Fourier Thm in terms of Sin and Cos simply a generalization of common knowledge of the Euclidean space { 1, cos (nωt), sin(nwt), n=1,2 } are orthogonal and complete they form orthogonal bases x(t) = A 0 + å A n cos(nwt)+ n=1 n=1 ì ï A 0 =<1, x(t) >= 1 ïï T ï í ï ïï ï ï î T /2 -T /2 B n sin(nwt) where A 0 is the d.c. term, and T is the period of the waveform. ò å x(t)dt A n =< cos(nwt), x(t) >= 2 T B n =< sin(nwt), x(t) >= 2 T w = 2p T T /2 ò -T /2 T /2 ò -T /2 x(t) cos(nwt) dt x(t)sin(nwt) dt
33 FT: Fourier Thm in terms of Sin and Cos simply a generalization of common knowledge of the Euclidean space { 1, cos (nωt), sin(nwt), n=1,2 } are orthogonal and complete they form orthogonal bases x(t) = A 0 + å A n cos(nwt)+ n=1 n=1 ì ï A 0 =<1, x(t) >= 1 ïï T ï í ï ïï ï ï î T /2 -T /2 B n sin(nwt) where A 0 is the d.c. term, and T is the period of the waveform. ò å x(t)dt A n =< cos(nwt), x(t) >= 2 T B n =< sin(nwt), x(t) >= 2 T w = 2p T T /2 ò -T /2 T /2 ò -T /2 x(t) cos(nwt) dt x(t)sin(nwt) dt
34 FT: Fourier Thm in terms of Sin and Cos simply a generalization of common knowledge of the Euclidean space { 1, cos (nωt), sin(nwt), n=1,2 } are orthogonal and complete they form orthogonal bases x(t) = A 0 + å A n cos(nwt)+ n=1 n=1 ì ï A 0 =<1, x(t) >= 1 ïï T ï í ï ïï ï ï î T /2 -T /2 B n sin(nwt) where A 0 is the d.c. term, and T is the period of the waveform. ò å x(t)dt A n =< cos(nwt), x(t) >= 2 T B n =< sin(nwt), x(t) >= 2 T w = 2p T T /2 ò -T /2 T /2 ò -T /2 x(t) cos(nwt) dt x(t)sin(nwt) dt
35 Example I x(t)=1, 0< t < p, 2p < t < 3p, 0 otherwise Hence x(t) is a signal with a period of 2p p 2p 3p 4p
36 Example I ì A 0 = 1 p ï ò dt = 1 ï 2p 0 2 A n = 2 p ï í ò cos(nt)dt = 1 sin(np ) = 0,n =1,2,... ï 2p 0 np ï B n = 2 p ï ò sin(nt)dt = 1 (1- cos(np )), n =1, 2,... îï 2p np 0 Finally, we have x(t) = p [sin(t)+ 1 3 sin(3t)+ 1 5 sin(5t)+...]
37 Example I X(F) 2/p Frequency domain x(t) = p [sin(t)+ 1 3 sin(3t)+ 1 5 sin(5t)+...] The description of a signal in terms of its constituent frequencies is called its frequency (power) spectrum.
38 Example I X(F) 2/p = Time domain Frequency domain
39 Example I A periodic signal is uniquely determined by its coefficients {A n, B n }. If we truncated the series into finite term, the signal can be approximated by a finite sines as shown below (compression, MP3, MP4, JPG, ) one term Two terms Three terms Five terms
40 Example II (understanding music)
41 Example II a. Pure tone: Script1_1.m This confirms our earlier believe that it is a signal with a finite bandwidth (N-S sampling Thm)
42 Example II b. Different waveforms Script1_2.m This confirms our earlier believe that it is a signal without bandlimit (N-S sampling Thm)
43 Bandwidth can be properly defined Bandwidth is the difference between the upper and lower frequencies in a set of frequencies. It is typically measured in hertz
44 Bandwidth can be properly defined Power 0 B Frequency Bandwidth is the difference between the upper and lower frequencies in a continuous set of frequencies. It is typically measured in hertz
45 Example II C. Approximation (compression) Script1_3.m Without doing much, we can compress the original data now, as in Example I.
46
47 DCSP-4: Applications Jianfeng Feng Department of Computer Science Warwick Univ., UK
48 Recap In general, a signal with T = 2p / w can be represented as follows x(t) = A 0 + å n=1 N å A n cos(wnt)+ ~ A 0 + A n cos(wnt)+ n=1 å n=1 N å n=1 B n sin(wnt) B n sin(wnt)
49 Recap In general, a signal with T=2p/w can be represented as follows T 2T X(t) ~ A 0 + A 1 cos(w t)
50 Recap In general, a signal with T=2p/w can be represented as follows T 2T X(t) ~ A 0 + A 1 cos(w t)+a 2 cos(2wt)
51 Recap In general, a signal with T=2p/w can be represented as follows T 2T X(t) ~ A 0 + A 1 cos(w t)+a 2 cos(2wt)+a 3 cos(3wt)
52 Recap In general, a signal with T=2p/w can be represented as follows T 2T X(t) ~ A 0 + A 1 cos(w t)+a 2 cos(2wt)+a 3 cos(3wt) + A 4 cos(4wt)+a 5 cos(5wt)+a 6 cos(6wt) + A 7 cos(7wt)+a 8 cos(8wt)+a 9 cos(9wt)
53 Recap In general, a signal with T=2p/w can be represented as follows T 2T X(t) = A 0 + A 1 cos(w t)+a 2 cos(2wt)+a 3 cos(3wt) + A 4 cos(4wt)+a 5 cos(5wt)+a 6 cos(6wt) + A 7 cos(7wt)+a 8 cos(8wt)+a 9 cos(9wt) +
54 Recap In general, a signal with T=2p/w can be represented as follows A 3 A 1 A 2 T 2T X(t) = A 0 + A 1 cos(w t)+a 2 cos(2wt)+a 3 cos(3wt) + A 4 cos(4wt)+a 5 cos(5wt)+a 6 cos(6wt) + A 7 cos(7wt)+a 8 cos(8wt)+a 9 cos(9wt) +
55 Recap In general, a signal with T=2p/w can be represented as follows A3 A 1 FREQUENCY TIME A 2 T 2T X(t) = A 0 + A 1 cos(w t)+a 2 cos(2wt)+a 3 cos(3wt) + A 4 cos(4wt)+a 5 cos(5wt)+a 6 cos(6wt) + A 7 cos(7wt)+a 8 cos(8wt)+a 9 cos(9wt) +
56 Recap In general, a signal with T=2p/w can be represented as follows x(t) = A 0 + å n=1 N å A n cos(wnt)+ ~ A 0 + A n cos(wnt)+ n=1 å n=1 N å n=1 B n sin(wnt) B n sin(wnt) The more terms we have, the more accurate: compression The plot of {A n, B n } against { n} is called frequency spectrum
57 Today s Summary General form of FT A few applications (6 more precisely) Noise
58 In general, a signal can be represented as follows FT: Neat Form; to remember easily ) )]exp( /(2 2 / [ ) )]exp( /(2 2 / [ ) )]/(2 exp( ) [exp( 2 )]/ exp( ) [exp( ) sin( ) cos( ) ( n n n n n n n n n n n n n n nt j j B A nt j j B A A j nt j nt j B nt j nt j A A nt B nt A A t x w w w w w w w w
59 In general, a signal can be represented as follows FT: Neat Form ) exp( ) )]exp( /(2 2 / [ ) )]exp( /(2 2 / [ ) )]/(2 exp( ) [exp( 2 )]/ exp( ) [exp( ) sin( ) cos( ) ( nt j c nt j j B A nt j j B A A j nt j nt j B nt j nt j A A nt B nt A A t x n n n n n n n n n n n n n n n n w w w w w w w w w C -n C n
60 FT : Neat Form Which is the exponential form of the Fourier series. In this expression the values C n are complex number, we have FT x(t) {C n, n=,-1,0,1,2,, } C C 2 ( A B1 )/ 4 C C 2 ( A B2 )/ 4 TIME T 2T FREQUENCY
61 FT : Neat Form Which is the exponential form of the Fourier series. In this expression the values C n are complex number, we have FT x(t) {C n, n=,-1,0,1,2,, } IFT X( nw) x( t) X( F ) F c n 1 T X( F )exp( jft) T / 2 T / 2 x( t)exp( jnwt) x( t) dt where w = (2 p) / T
62 FT in complex exponential If the periodic signal is replace with an aperiodic signal (general case) FT is given by ì ïx(f) = FT(x) = í ïx(t) = FT -1 î (X) = ò - ò - x(t)exp(-2p jft)dt X(F)exp(2p jft)df Is that deadly simple?
63 Fourier s song Integrate your function times a complex exponential It's really not so hard you can do it with your pencil yes, I agree
64 Example I Consider the case of a rectangular pulse. In particular, let us define ì ï x(t) = í îï 1, if < t < 0.5 0, otherwise Its FT is given by X(F) = 0.5 ò -0.5 x(t)exp(- j2pft)dt = sin(pf) pf Which is called the Sinc function.
65 Example I There are a number of features to note: 1. The bandwidth of the signal is only approximately finite. power Most of the energy is contained in a limited regions called the main-lobe. However, some energy is found at all frequencies. 2. The spectrum has positive and negative frequencies. These are symmetric about the origin. This may seem non-intuitive, but can be seen from equations in periodic case Frequency 3. Note that the spectrum is continuous now: X(F)= Sinc function
66 Fourier's Song Integrate your function times a complex exponential It's really not so hard you can do it with your pencil And when you're done with this calculation You've got a brand new function - the Fourier Transformation What a prism does to sunlight, what the ear does to sound Fourier does to signals, it's the coolest trick around Now filtering is easy, you don't need to convolve All you do is multiply in order to solve. From time into frequency - from frequency to time Every operation in the time domain Has a Fourier analog - that's what I claim Think of a delay, a simple shift in time It becomes a phase rotation - now that's truly sublime! And to differentiate, here's a simple trick Just multiply by J omega, ain't that slick? Integration is the inverse, what you gonna do? Divide instead of multiply - you can do it too. Or make the pulse wide, and the sinc grows dense, The uncertainty principle is just common sense. From time into frequency - from frequency to time Let's do some examples... consider a sine It's mapped to a delta, in frequency - not time Now take that same delta as a function of time Mapped into frequency - of course - it's a sine! Sine x on x is handy, let's call it a sinc. Its Fourier Transform is simpler than you think. You get a pulse that's shaped just like a top hat... Squeeze the pulse thin, and the sinc grows fat.
67 The world has changed Frequency eye This module and a few following ones will make use of the frequency information
68 This module is about practical applications Carpenter: saw, screw driver, hammer. Can you make a table for me? I doubt. How ì to use this idea? ïx(f) = FT(x) = í ï îx(t) = FT -1 (X) = ò - ò - x(t)exp(-2p jft)dt X(F)exp(2p jft)df
69 App I Time domain Frequency domain S 1 (t)= 10 cos(2pt) + cos(10*2pt) for i=1:10000 x(i)=10*cos(i*0.01)+cos(i*10*0.01); End Sound(x)
70 App I Time domain Frequency domain S 2 (t)= cos(2pt) + 10 cos(10*2pt) for i=1:10000 x(i)=1*cos(i*0.01)+10*cos(i*10*0.01); End Sound(s)
71 App I In frequency domain, the height of the spectrum indicates the energy of the corresponding signal. For example, for S 1, energy concentrating on the signal cos(2pt), a low frequency signal for S 2, energy concentrating on the signal cos(10*2pt), a high frequency signal
72 App II: Touch-tone dialing
73 App II: Touch-tone dialing Freqs 1209 Hz 1336 Hz 1477 Hz 1633 Hz 697 Hz A 770 Hz B 852 Hz C 941 Hz * 0 # D touch_tone.m (1)=A n1 cos(n1 w 0 t) +A n2 cos(n2w 0 t) 1 Hz = w 0 Your phone is a section (two terms) of a FT
74 APP III: Spread spectrum techniques In bluetooth, for example, to improve resistance to radio frequency interference by avoiding using crowded frequencies in the hopping sequence. In military use, it is a simple idea (radio guided torpedo, for example)
75 App IV: instruments We all know about pitch It is really about frequency, or cycles per seconds How about harmonics? This is what gives the timbre of an instrument!
76 App IV: instruments The played note is the frequency of the first peak: 220Hz (note A) in this case Other peaks are called harmonics: they define the typical sound of the instrument Without Fourier, we could have been lost When you play an instrument, It is a section of a FT
77 App V: MP3+MP4 How can an MP3 song sound so well, while being so compressed? Compression in a sense introduces noise. a combination of our hearing system + FT
78 App V: MP3+MP4 Original noiseless music Original musie + noise 2 SNR =13 db Same amount of noise Impressive difference of sound What is the secret? >> r = audiorecorder(22050, 16, 1); >> record(r) >> stop(r) >> myspeech = getaudiodata(r, 'int16'); % get data as int16 array >> audiowrite('compress_3.wav',myspeech,fs); load handel.mat filename = 'handel.wav'; audiowrite(filename,y,fs); clear y Fs
79 App V: MP3+MP4
80 App V: MP3+MP4 MP3: complex compression algorithm that introduces errors MP3 minimizes the perceived qaulity decay by shaping the compression errors
81 App VI: Mind Reading MRI is a medical imaging technique to visualize your internal body structure and/or activity in detail Using a physics term: it measures the oscillations of hydrogen nuclei when stimulated by different radio-frequency magnetic fields Reading you mind with FT My brain activity during one scan
82 App VI: Mind Reading MRI is a medical imaging technique to visualize your internal body structure and/or activity in detail Using a physics term: it measures the oscillations of hydrogen nuclei when stimulated by different radio-frequency magnetic fields Reading you mind with FT My brain activity during one scan It is not about sex
83 App VI: Mind Reading Using a DCSP term: it measures the FT of the internal structure and/or activity of interest How does the collected data looks like? img=(t1_image(:,:,50)); img = fftshift(img(:,:)); F = fft2(img); figure; imagesc(100*log(1+abs(fftshift(f)))); colormap(gray); title('magnitude spectrum'); figure; imagesc(angle(f)); colormap(gray); title('phase spectrum');
84 App VI: Mind Reading Little information about the subject can be gathered in the original picture An inverse Fourier transform of the data reveals the slice of a human head activity
85 App VI: Mind Reading Human Brain Project was one of the two projects with a budge of 1B Euros for ten years each (another is graphene) in 2013 The main purpose is to simulate the Brain = USA matched with a 4.5 B US Dollars in 2014 China will do as well
DCSP-2: Fourier Transform
 DCSP-2: Fourier Transform Jianfeng Feng Department of Computer Science Warwick Univ., UK Jianfeng.feng@warwick.ac.uk http://www.dcs.warwick.ac.uk/~feng/dcsp.html Data transmission Channel characteristics,
DCSP-2: Fourier Transform Jianfeng Feng Department of Computer Science Warwick Univ., UK Jianfeng.feng@warwick.ac.uk http://www.dcs.warwick.ac.uk/~feng/dcsp.html Data transmission Channel characteristics,
DCSP-5: Fourier Transform II
 DCSP-5: Fourier Transform II Jianfeng Feng Department of Computer Science Warwick Univ., UK Jianfeng.feng@warwick.ac.uk http://www.dcs.warwick.ac.uk/~feng/dcsp.html Assignment:2018 Q1: you should be able
DCSP-5: Fourier Transform II Jianfeng Feng Department of Computer Science Warwick Univ., UK Jianfeng.feng@warwick.ac.uk http://www.dcs.warwick.ac.uk/~feng/dcsp.html Assignment:2018 Q1: you should be able
ECS332: Midterm Examination (Set I) Seat
 Sirindhorn International Institute of Technology Thammasat University at Rangsit School of Information, Computer and Communication Technology ECS33: Midterm Examination (Set I) COURSE : ECS33 (Principles
Sirindhorn International Institute of Technology Thammasat University at Rangsit School of Information, Computer and Communication Technology ECS33: Midterm Examination (Set I) COURSE : ECS33 (Principles
Jianfeng Feng. DCSP-15: Wiener Filter and Kalman Filter* Department of Computer Science Warwick Univ.
 DCSP-15: Wiener Filter and Kalman Filter* Jianfeng Feng Department of Computer Science Warwick Univ., UK Jianfeng.feng@warwick.ac.uk http://www.dcs.warwick.ac.uk/~feng/dcsp.html Father of cybernetics Norbert
DCSP-15: Wiener Filter and Kalman Filter* Jianfeng Feng Department of Computer Science Warwick Univ., UK Jianfeng.feng@warwick.ac.uk http://www.dcs.warwick.ac.uk/~feng/dcsp.html Father of cybernetics Norbert
EA2.3 - Electronics 2 1
 In the previous lecture, I talked about the idea of complex frequency s, where s = σ + jω. Using such concept of complex frequency allows us to analyse signals and systems with better generality. In this
In the previous lecture, I talked about the idea of complex frequency s, where s = σ + jω. Using such concept of complex frequency allows us to analyse signals and systems with better generality. In this
ENSC327 Communications Systems 2: Fourier Representations. Jie Liang School of Engineering Science Simon Fraser University
 ENSC327 Communications Systems 2: Fourier Representations Jie Liang School of Engineering Science Simon Fraser University 1 Outline Chap 2.1 2.5: Signal Classifications Fourier Transform Dirac Delta Function
ENSC327 Communications Systems 2: Fourier Representations Jie Liang School of Engineering Science Simon Fraser University 1 Outline Chap 2.1 2.5: Signal Classifications Fourier Transform Dirac Delta Function
Notes 07 largely plagiarized by %khc
 Notes 07 largely plagiarized by %khc Warning This set of notes covers the Fourier transform. However, i probably won t talk about everything here in section; instead i will highlight important properties
Notes 07 largely plagiarized by %khc Warning This set of notes covers the Fourier transform. However, i probably won t talk about everything here in section; instead i will highlight important properties
Wave Phenomena Physics 15c
 Wave Phenomena Physics 5c Lecture Fourier Analysis (H&L Sections 3. 4) (Georgi Chapter ) What We Did Last ime Studied reflection of mechanical waves Similar to reflection of electromagnetic waves Mechanical
Wave Phenomena Physics 5c Lecture Fourier Analysis (H&L Sections 3. 4) (Georgi Chapter ) What We Did Last ime Studied reflection of mechanical waves Similar to reflection of electromagnetic waves Mechanical
Lecture 28 Continuous-Time Fourier Transform 2
 Lecture 28 Continuous-Time Fourier Transform 2 Fundamentals of Digital Signal Processing Spring, 2012 Wei-Ta Chu 2012/6/14 1 Limit of the Fourier Series Rewrite (11.9) and (11.10) as As, the fundamental
Lecture 28 Continuous-Time Fourier Transform 2 Fundamentals of Digital Signal Processing Spring, 2012 Wei-Ta Chu 2012/6/14 1 Limit of the Fourier Series Rewrite (11.9) and (11.10) as As, the fundamental
FOURIER ANALYSIS. (a) Fourier Series
 (a) Fourier Series FOURIER ANAYSIS (b) Fourier Transforms Useful books: 1. Advanced Mathematics for Engineers and Scientists, Schaum s Outline Series, M. R. Spiegel - The course text. We follow their notation
(a) Fourier Series FOURIER ANAYSIS (b) Fourier Transforms Useful books: 1. Advanced Mathematics for Engineers and Scientists, Schaum s Outline Series, M. R. Spiegel - The course text. We follow their notation
THE FOURIER TRANSFORM (Fourier series for a function whose period is very, very long) Reading: Main 11.3
 THE FOURIER TRANSFORM (Fourier series for a function whose period is very, very long) Reading: Main 11.3 Any periodic function f(t) can be written as a Fourier Series a 0 2 + a n cos( nωt) + b n sin n
THE FOURIER TRANSFORM (Fourier series for a function whose period is very, very long) Reading: Main 11.3 Any periodic function f(t) can be written as a Fourier Series a 0 2 + a n cos( nωt) + b n sin n
Fourier Transform. Find the Fourier series for a periodic waveform Determine the output of a filter when the input is a periodic function
 Objectives: Be able to Fourier Transform Find the Fourier series for a periodic waveform Determine the output of a filter when the input is a periodic function Filters with a Single Sinusoidal Input: Suppose
Objectives: Be able to Fourier Transform Find the Fourier series for a periodic waveform Determine the output of a filter when the input is a periodic function Filters with a Single Sinusoidal Input: Suppose
Physical Acoustics. Hearing is the result of a complex interaction of physics, physiology, perception and cognition.
 Physical Acoustics Hearing, auditory perception, or audition is the ability to perceive sound by detecting vibrations, changes in the pressure of the surrounding medium through time, through an organ such
Physical Acoustics Hearing, auditory perception, or audition is the ability to perceive sound by detecting vibrations, changes in the pressure of the surrounding medium through time, through an organ such
Lecture 27 Frequency Response 2
 Lecture 27 Frequency Response 2 Fundamentals of Digital Signal Processing Spring, 2012 Wei-Ta Chu 2012/6/12 1 Application of Ideal Filters Suppose we can generate a square wave with a fundamental period
Lecture 27 Frequency Response 2 Fundamentals of Digital Signal Processing Spring, 2012 Wei-Ta Chu 2012/6/12 1 Application of Ideal Filters Suppose we can generate a square wave with a fundamental period
Networks and Systems Prof V.G K. Murti Department of Electrical Engineering Indian Institute of Technology, Madras Lecture - 10 Fourier Series (10)
 Networks and Systems Prof V.G K. Murti Department of Electrical Engineering Indian Institute of Technology, Madras Lecture - 10 Fourier Series (10) What we have seen in the previous lectures, is first
Networks and Systems Prof V.G K. Murti Department of Electrical Engineering Indian Institute of Technology, Madras Lecture - 10 Fourier Series (10) What we have seen in the previous lectures, is first
MITOCW MITRES_6-007S11lec09_300k.mp4
 MITOCW MITRES_6-007S11lec09_300k.mp4 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for
MITOCW MITRES_6-007S11lec09_300k.mp4 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for
Frequency Response & Filter Analysis. Week Date Lecture Title. 4-Mar Introduction & Systems Overview 6-Mar [Linear Dynamical Systems] 2
![Frequency Response & Filter Analysis. Week Date Lecture Title. 4-Mar Introduction & Systems Overview 6-Mar [Linear Dynamical Systems] 2 Frequency Response & Filter Analysis. Week Date Lecture Title. 4-Mar Introduction & Systems Overview 6-Mar [Linear Dynamical Systems] 2](/thumbs/96/127490167.jpg) http://elec34.com Frequency Response & Filter Analysis 4 School of Information Technology and Electrical Engineering at The University of Queensland Lecture Schedule: Week Date Lecture Title 4-Mar Introduction
http://elec34.com Frequency Response & Filter Analysis 4 School of Information Technology and Electrical Engineering at The University of Queensland Lecture Schedule: Week Date Lecture Title 4-Mar Introduction
LOPE3202: Communication Systems 10/18/2017 2
 By Lecturer Ahmed Wael Academic Year 2017-2018 LOPE3202: Communication Systems 10/18/2017 We need tools to build any communication system. Mathematics is our premium tool to do work with signals and systems.
By Lecturer Ahmed Wael Academic Year 2017-2018 LOPE3202: Communication Systems 10/18/2017 We need tools to build any communication system. Mathematics is our premium tool to do work with signals and systems.
Introduction to Biomedical Engineering
 Introduction to Biomedical Engineering Biosignal processing Kung-Bin Sung 6/11/2007 1 Outline Chapter 10: Biosignal processing Characteristics of biosignals Frequency domain representation and analysis
Introduction to Biomedical Engineering Biosignal processing Kung-Bin Sung 6/11/2007 1 Outline Chapter 10: Biosignal processing Characteristics of biosignals Frequency domain representation and analysis
2.3 Oscillation. The harmonic oscillator equation is the differential equation. d 2 y dt 2 r y (r > 0). Its solutions have the form
 2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
Notes on Fourier Series and Integrals Fourier Series
 Notes on Fourier Series and Integrals Fourier Series et f(x) be a piecewise linear function on [, ] (This means that f(x) may possess a finite number of finite discontinuities on the interval). Then f(x)
Notes on Fourier Series and Integrals Fourier Series et f(x) be a piecewise linear function on [, ] (This means that f(x) may possess a finite number of finite discontinuities on the interval). Then f(x)
Review Quantitative Aspects of Networking. Decibels, Power, and Waves John Marsh
 Review Quantitative spects of Networking Decibels, ower, and Waves John Marsh Outline Review of quantitative aspects of networking Metric system Numbers with Units Math review exponents and logs Decibel
Review Quantitative spects of Networking Decibels, ower, and Waves John Marsh Outline Review of quantitative aspects of networking Metric system Numbers with Units Math review exponents and logs Decibel
Lab Fourier Analysis Do prelab before lab starts. PHSX 262 Spring 2011 Lecture 5 Page 1. Based with permission on lectures by John Getty
 Today /5/ Lecture 5 Fourier Series Time-Frequency Decomposition/Superposition Fourier Components (Ex. Square wave) Filtering Spectrum Analysis Windowing Fast Fourier Transform Sweep Frequency Analyzer
Today /5/ Lecture 5 Fourier Series Time-Frequency Decomposition/Superposition Fourier Components (Ex. Square wave) Filtering Spectrum Analysis Windowing Fast Fourier Transform Sweep Frequency Analyzer
L6: Short-time Fourier analysis and synthesis
 L6: Short-time Fourier analysis and synthesis Overview Analysis: Fourier-transform view Analysis: filtering view Synthesis: filter bank summation (FBS) method Synthesis: overlap-add (OLA) method STFT magnitude
L6: Short-time Fourier analysis and synthesis Overview Analysis: Fourier-transform view Analysis: filtering view Synthesis: filter bank summation (FBS) method Synthesis: overlap-add (OLA) method STFT magnitude
Wave Phenomena Physics 15c. Lecture 10 Fourier Transform
 Wave Phenomena Physics 15c Lecture 10 Fourier ransform What We Did Last ime Reflection of mechanical waves Similar to reflection of electromagnetic waves Mechanical impedance is defined by For transverse/longitudinal
Wave Phenomena Physics 15c Lecture 10 Fourier ransform What We Did Last ime Reflection of mechanical waves Similar to reflection of electromagnetic waves Mechanical impedance is defined by For transverse/longitudinal
Lab10: FM Spectra and VCO
 Lab10: FM Spectra and VCO Prepared by: Keyur Desai Dept. of Electrical Engineering Michigan State University ECE458 Lab 10 What is FM? A type of analog modulation Remember a common strategy in analog modulation?
Lab10: FM Spectra and VCO Prepared by: Keyur Desai Dept. of Electrical Engineering Michigan State University ECE458 Lab 10 What is FM? A type of analog modulation Remember a common strategy in analog modulation?
Direct-Sequence Spread-Spectrum
 Chapter 3 Direct-Sequence Spread-Spectrum In this chapter we consider direct-sequence spread-spectrum systems. Unlike frequency-hopping, a direct-sequence signal occupies the entire bandwidth continuously.
Chapter 3 Direct-Sequence Spread-Spectrum In this chapter we consider direct-sequence spread-spectrum systems. Unlike frequency-hopping, a direct-sequence signal occupies the entire bandwidth continuously.
SEISMIC WAVE PROPAGATION. Lecture 2: Fourier Analysis
 SEISMIC WAVE PROPAGATION Lecture 2: Fourier Analysis Fourier Series & Fourier Transforms Fourier Series Review of trigonometric identities Analysing the square wave Fourier Transform Transforms of some
SEISMIC WAVE PROPAGATION Lecture 2: Fourier Analysis Fourier Series & Fourier Transforms Fourier Series Review of trigonometric identities Analysing the square wave Fourier Transform Transforms of some
LECTURE 12 Sections Introduction to the Fourier series of periodic signals
 Signals and Systems I Wednesday, February 11, 29 LECURE 12 Sections 3.1-3.3 Introduction to the Fourier series of periodic signals Chapter 3: Fourier Series of periodic signals 3. Introduction 3.1 Historical
Signals and Systems I Wednesday, February 11, 29 LECURE 12 Sections 3.1-3.3 Introduction to the Fourier series of periodic signals Chapter 3: Fourier Series of periodic signals 3. Introduction 3.1 Historical
Communication Engineering Prof. Surendra Prasad Department of Electrical Engineering Indian Institute of Technology, Delhi
 Communication Engineering Prof. Surendra Prasad Department of Electrical Engineering Indian Institute of Technology, Delhi Lecture - 3 Brief Review of Signals and Systems My subject for today s discussion
Communication Engineering Prof. Surendra Prasad Department of Electrical Engineering Indian Institute of Technology, Delhi Lecture - 3 Brief Review of Signals and Systems My subject for today s discussion
Communication Engineering Prof. Surendra Prasad Department of Electrical Engineering Indian Institute of Technology, Delhi
 Communication Engineering Prof. Surendra Prasad Department of Electrical Engineering Indian Institute of Technology, Delhi Lecture - 41 Pulse Code Modulation (PCM) So, if you remember we have been talking
Communication Engineering Prof. Surendra Prasad Department of Electrical Engineering Indian Institute of Technology, Delhi Lecture - 41 Pulse Code Modulation (PCM) So, if you remember we have been talking
Fourier Series and Integrals
 Fourier Series and Integrals Fourier Series et f(x) beapiece-wiselinearfunctionon[, ] (Thismeansthatf(x) maypossessa finite number of finite discontinuities on the interval). Then f(x) canbeexpandedina
Fourier Series and Integrals Fourier Series et f(x) beapiece-wiselinearfunctionon[, ] (Thismeansthatf(x) maypossessa finite number of finite discontinuities on the interval). Then f(x) canbeexpandedina
MITOCW watch?v=hdyabia-dny
 MITOCW watch?v=hdyabia-dny The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To
MITOCW watch?v=hdyabia-dny The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To
ESE 250: Digital Audio Basics. Week 4 February 5, The Frequency Domain. ESE Spring'13 DeHon, Kod, Kadric, Wilson-Shah
 ESE 250: Digital Audio Basics Week 4 February 5, 2013 The Frequency Domain 1 Course Map 2 Musical Representation With this compact notation Could communicate a sound to pianist Much more compact than 44KHz
ESE 250: Digital Audio Basics Week 4 February 5, 2013 The Frequency Domain 1 Course Map 2 Musical Representation With this compact notation Could communicate a sound to pianist Much more compact than 44KHz
Chapter 2. Signals. Static and Dynamic Characteristics of Signals. Signals classified as
 Chapter 2 Static and Dynamic Characteristics of Signals Signals Signals classified as. Analog continuous in time and takes on any magnitude in range of operations 2. Discrete Time measuring a continuous
Chapter 2 Static and Dynamic Characteristics of Signals Signals Signals classified as. Analog continuous in time and takes on any magnitude in range of operations 2. Discrete Time measuring a continuous
ELEG 3124 SYSTEMS AND SIGNALS Ch. 5 Fourier Transform
 Department of Electrical Engineering University of Arkansas ELEG 3124 SYSTEMS AND SIGNALS Ch. 5 Fourier Transform Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Introduction Fourier Transform Properties of Fourier
Department of Electrical Engineering University of Arkansas ELEG 3124 SYSTEMS AND SIGNALS Ch. 5 Fourier Transform Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Introduction Fourier Transform Properties of Fourier
natural frequency of the spring/mass system is ω = k/m, and dividing the equation through by m gives
 77 6. More on Fourier series 6.. Harmonic response. One of the main uses of Fourier series is to express periodic system responses to general periodic signals. For example, if we drive an undamped spring
77 6. More on Fourier series 6.. Harmonic response. One of the main uses of Fourier series is to express periodic system responses to general periodic signals. For example, if we drive an undamped spring
Signals, Instruments, and Systems W5. Introduction to Signal Processing Sampling, Reconstruction, and Filters
 Signals, Instruments, and Systems W5 Introduction to Signal Processing Sampling, Reconstruction, and Filters Acknowledgments Recapitulation of Key Concepts from the Last Lecture Dirac delta function (
Signals, Instruments, and Systems W5 Introduction to Signal Processing Sampling, Reconstruction, and Filters Acknowledgments Recapitulation of Key Concepts from the Last Lecture Dirac delta function (
Periodogram of a sinusoid + spike Single high value is sum of cosine curves all in phase at time t 0 :
 Periodogram of a sinusoid + spike Single high value is sum of cosine curves all in phase at time t 0 : X(t) = µ + Asin(ω 0 t)+ Δ δ ( t t 0 ) ±σ N =100 Δ =100 χ ( ω ) Raises the amplitude uniformly at all
Periodogram of a sinusoid + spike Single high value is sum of cosine curves all in phase at time t 0 : X(t) = µ + Asin(ω 0 t)+ Δ δ ( t t 0 ) ±σ N =100 Δ =100 χ ( ω ) Raises the amplitude uniformly at all
Instructor (Brad Osgood)
 TheFourierTransformAndItsApplications-Lecture26 Instructor (Brad Osgood): Relax, but no, no, no, the TV is on. It's time to hit the road. Time to rock and roll. We're going to now turn to our last topic
TheFourierTransformAndItsApplications-Lecture26 Instructor (Brad Osgood): Relax, but no, no, no, the TV is on. It's time to hit the road. Time to rock and roll. We're going to now turn to our last topic
Discrete Systems & Z-Transforms. Week Date Lecture Title. 9-Mar Signals as Vectors & Systems as Maps 10-Mar [Signals] 3
![Discrete Systems & Z-Transforms. Week Date Lecture Title. 9-Mar Signals as Vectors & Systems as Maps 10-Mar [Signals] 3 Discrete Systems & Z-Transforms. Week Date Lecture Title. 9-Mar Signals as Vectors & Systems as Maps 10-Mar [Signals] 3](/thumbs/89/99446510.jpg) http:elec34.org Discrete Systems & Z-Transforms 4 School of Information Technology and Electrical Engineering at The University of Queensland Lecture Schedule: eek Date Lecture Title -Mar Introduction
http:elec34.org Discrete Systems & Z-Transforms 4 School of Information Technology and Electrical Engineering at The University of Queensland Lecture Schedule: eek Date Lecture Title -Mar Introduction
a n cos 2πnt L n=1 {1/2, cos2π/l, cos 4π/L, cos6π/l,...,sin 2π/L, sin 4π/L, sin 6π/L,...,} (2)
 Note Fourier. 30 January 2007 (as 23.II..tex) and 20 October 2009 in this form. Fourier Analysis The Fourier series First some terminology: a function f(t) is periodic if f(t + ) = f(t) for all t for some,
Note Fourier. 30 January 2007 (as 23.II..tex) and 20 October 2009 in this form. Fourier Analysis The Fourier series First some terminology: a function f(t) is periodic if f(t + ) = f(t) for all t for some,
Module 24: Outline. Expt. 8: Part 2:Undriven RLC Circuits
 Module 24: Undriven RLC Circuits 1 Module 24: Outline Undriven RLC Circuits Expt. 8: Part 2:Undriven RLC Circuits 2 Circuits that Oscillate (LRC) 3 Mass on a Spring: Simple Harmonic Motion (Demonstration)
Module 24: Undriven RLC Circuits 1 Module 24: Outline Undriven RLC Circuits Expt. 8: Part 2:Undriven RLC Circuits 2 Circuits that Oscillate (LRC) 3 Mass on a Spring: Simple Harmonic Motion (Demonstration)
Question Paper Code : AEC11T02
 Hall Ticket No Question Paper Code : AEC11T02 VARDHAMAN COLLEGE OF ENGINEERING (AUTONOMOUS) Affiliated to JNTUH, Hyderabad Four Year B. Tech III Semester Tutorial Question Bank 2013-14 (Regulations: VCE-R11)
Hall Ticket No Question Paper Code : AEC11T02 VARDHAMAN COLLEGE OF ENGINEERING (AUTONOMOUS) Affiliated to JNTUH, Hyderabad Four Year B. Tech III Semester Tutorial Question Bank 2013-14 (Regulations: VCE-R11)
Fourier Series. Spectral Analysis of Periodic Signals
 Fourier Series. Spectral Analysis of Periodic Signals he response of continuous-time linear invariant systems to the complex exponential with unitary magnitude response of a continuous-time LI system at
Fourier Series. Spectral Analysis of Periodic Signals he response of continuous-time linear invariant systems to the complex exponential with unitary magnitude response of a continuous-time LI system at
A3. Frequency Representation of Continuous Time and Discrete Time Signals
 A3. Frequency Representation of Continuous Time and Discrete Time Signals Objectives Define the magnitude and phase plots of continuous time sinusoidal signals Extend the magnitude and phase plots to discrete
A3. Frequency Representation of Continuous Time and Discrete Time Signals Objectives Define the magnitude and phase plots of continuous time sinusoidal signals Extend the magnitude and phase plots to discrete
SSSC Discovery Series NMR2 Multidimensional NMR Spectroscopy
 SSSC Discovery Series NMR2 Multidimensional NMR Spectroscopy Topics: 1. Some Common Experiments 2. Anatomy of a 2D experiment 3. 3D NMR spectroscopy no quantum mechanics! Some Common 2D Experiments Very
SSSC Discovery Series NMR2 Multidimensional NMR Spectroscopy Topics: 1. Some Common Experiments 2. Anatomy of a 2D experiment 3. 3D NMR spectroscopy no quantum mechanics! Some Common 2D Experiments Very
Summary: ISI. No ISI condition in time. II Nyquist theorem. Ideal low pass filter. Raised cosine filters. TX filters
 UORIAL ON DIGIAL MODULAIONS Part 7: Intersymbol interference [last modified: 200--23] Roberto Garello, Politecnico di orino Free download at: www.tlc.polito.it/garello (personal use only) Part 7: Intersymbol
UORIAL ON DIGIAL MODULAIONS Part 7: Intersymbol interference [last modified: 200--23] Roberto Garello, Politecnico di orino Free download at: www.tlc.polito.it/garello (personal use only) Part 7: Intersymbol
Fourier series. XE31EO2 - Pavel Máša. Electrical Circuits 2 Lecture1. XE31EO2 - Pavel Máša - Fourier Series
 Fourier series Electrical Circuits Lecture - Fourier Series Filtr RLC defibrillator MOTIVATION WHAT WE CAN'T EXPLAIN YET Source voltage rectangular waveform Resistor voltage sinusoidal waveform - Fourier
Fourier series Electrical Circuits Lecture - Fourier Series Filtr RLC defibrillator MOTIVATION WHAT WE CAN'T EXPLAIN YET Source voltage rectangular waveform Resistor voltage sinusoidal waveform - Fourier
Ch. 15 Wavelet-Based Compression
 Ch. 15 Wavelet-Based Compression 1 Origins and Applications The Wavelet Transform (WT) is a signal processing tool that is replacing the Fourier Transform (FT) in many (but not all!) applications. WT theory
Ch. 15 Wavelet-Based Compression 1 Origins and Applications The Wavelet Transform (WT) is a signal processing tool that is replacing the Fourier Transform (FT) in many (but not all!) applications. WT theory
BME 50500: Image and Signal Processing in Biomedicine. Lecture 2: Discrete Fourier Transform CCNY
 1 Lucas Parra, CCNY BME 50500: Image and Signal Processing in Biomedicine Lecture 2: Discrete Fourier Transform Lucas C. Parra Biomedical Engineering Department CCNY http://bme.ccny.cuny.edu/faculty/parra/teaching/signal-and-image/
1 Lucas Parra, CCNY BME 50500: Image and Signal Processing in Biomedicine Lecture 2: Discrete Fourier Transform Lucas C. Parra Biomedical Engineering Department CCNY http://bme.ccny.cuny.edu/faculty/parra/teaching/signal-and-image/
Tutorial Sheet #2 discrete vs. continuous functions, periodicity, sampling
 2.39 utorial Sheet #2 discrete vs. continuous functions, periodicity, sampling We will encounter two classes of signals in this class, continuous-signals and discrete-signals. he distinct mathematical
2.39 utorial Sheet #2 discrete vs. continuous functions, periodicity, sampling We will encounter two classes of signals in this class, continuous-signals and discrete-signals. he distinct mathematical
Antennas Prof. Girish Kumar Department of Electrical Engineering Indian Institute of Technology, Bombay. Module 02 Lecture 08 Dipole Antennas-I
 Antennas Prof. Girish Kumar Department of Electrical Engineering Indian Institute of Technology, Bombay Module 02 Lecture 08 Dipole Antennas-I Hello, and welcome to today s lecture. Now in the last lecture
Antennas Prof. Girish Kumar Department of Electrical Engineering Indian Institute of Technology, Bombay Module 02 Lecture 08 Dipole Antennas-I Hello, and welcome to today s lecture. Now in the last lecture
The Spectral Differences in Sounds and Harmonics. Through chemical and biological processes, we, as humans, can detect the movement and
 John Chambers Semester Project 5/2/16 The Spectral Differences in Sounds and Harmonics Through chemical and biological processes, we, as humans, can detect the movement and vibrations of molecules through
John Chambers Semester Project 5/2/16 The Spectral Differences in Sounds and Harmonics Through chemical and biological processes, we, as humans, can detect the movement and vibrations of molecules through
Reference Text: The evolution of Applied harmonics analysis by Elena Prestini
 Notes for July 14. Filtering in Frequency domain. Reference Text: The evolution of Applied harmonics analysis by Elena Prestini It all started with: Jean Baptist Joseph Fourier (1768-1830) Mathematician,
Notes for July 14. Filtering in Frequency domain. Reference Text: The evolution of Applied harmonics analysis by Elena Prestini It all started with: Jean Baptist Joseph Fourier (1768-1830) Mathematician,
19. The Fourier Transform in optics
 19. The Fourier Transform in optics What is the Fourier Transform? Anharmonic waves The spectrum of a light wave Fourier transform of an exponential The Dirac delta function The Fourier transform of e
19. The Fourier Transform in optics What is the Fourier Transform? Anharmonic waves The spectrum of a light wave Fourier transform of an exponential The Dirac delta function The Fourier transform of e
Time-Frequency Analysis
 Time-Frequency Analysis Basics of Fourier Series Philippe B. aval KSU Fall 015 Philippe B. aval (KSU) Fourier Series Fall 015 1 / 0 Introduction We first review how to derive the Fourier series of a function.
Time-Frequency Analysis Basics of Fourier Series Philippe B. aval KSU Fall 015 Philippe B. aval (KSU) Fourier Series Fall 015 1 / 0 Introduction We first review how to derive the Fourier series of a function.
Topic 3: Fourier Series (FS)
 ELEC264: Signals And Systems Topic 3: Fourier Series (FS) o o o o Introduction to frequency analysis of signals CT FS Fourier series of CT periodic signals Signal Symmetry and CT Fourier Series Properties
ELEC264: Signals And Systems Topic 3: Fourier Series (FS) o o o o Introduction to frequency analysis of signals CT FS Fourier series of CT periodic signals Signal Symmetry and CT Fourier Series Properties
Quantitative Understanding in Biology Fourier Analysis and Signal Processing
 Quantitative Understanding in Biology Fourier Analysis and Signal Processing Representing Mathematical Functions as Linear Combinations of Basis Functions Throughout this course we have seen examples of
Quantitative Understanding in Biology Fourier Analysis and Signal Processing Representing Mathematical Functions as Linear Combinations of Basis Functions Throughout this course we have seen examples of
SIGNALS AND SYSTEMS: PAPER 3C1 HANDOUT 6a. Dr David Corrigan 1. Electronic and Electrical Engineering Dept.
 SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6a. Dr David Corrigan. Electronic and Electrical Engineering Dept. corrigad@tcd.ie www.mee.tcd.ie/ corrigad FOURIER SERIES Have seen how the behaviour of systems can
SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6a. Dr David Corrigan. Electronic and Electrical Engineering Dept. corrigad@tcd.ie www.mee.tcd.ie/ corrigad FOURIER SERIES Have seen how the behaviour of systems can
Mathematics for Chemists 2 Lecture 14: Fourier analysis. Fourier series, Fourier transform, DFT/FFT
 Mathematics for Chemists 2 Lecture 14: Fourier analysis Fourier series, Fourier transform, DFT/FFT Johannes Kepler University Summer semester 2012 Lecturer: David Sevilla Fourier analysis 1/25 Remembering
Mathematics for Chemists 2 Lecture 14: Fourier analysis Fourier series, Fourier transform, DFT/FFT Johannes Kepler University Summer semester 2012 Lecturer: David Sevilla Fourier analysis 1/25 Remembering
Chapter 2: Problem Solutions
 Chapter 2: Problem Solutions Discrete Time Processing of Continuous Time Signals Sampling à Problem 2.1. Problem: Consider a sinusoidal signal and let us sample it at a frequency F s 2kHz. xt 3cos1000t
Chapter 2: Problem Solutions Discrete Time Processing of Continuous Time Signals Sampling à Problem 2.1. Problem: Consider a sinusoidal signal and let us sample it at a frequency F s 2kHz. xt 3cos1000t
Review: Continuous Fourier Transform
 Review: Continuous Fourier Transform Review: convolution x t h t = x τ h(t τ)dτ Convolution in time domain Derivation Convolution Property Interchange the order of integrals Let Convolution Property By
Review: Continuous Fourier Transform Review: convolution x t h t = x τ h(t τ)dτ Convolution in time domain Derivation Convolution Property Interchange the order of integrals Let Convolution Property By
RF Pulse Design. Multi-dimensional Excitation I. M229 Advanced Topics in MRI Kyung Sung, Ph.D Class Business
 RF Pulse Design Multi-dimensional Excitation I M229 Advanced Topics in MRI Kyung Sung, Ph.D. 2018.04.10 Class Business Office hours - Instructors: Fri 10-12pm TAs: Xinran Zhong and Zhaohuan Zhang (time:
RF Pulse Design Multi-dimensional Excitation I M229 Advanced Topics in MRI Kyung Sung, Ph.D. 2018.04.10 Class Business Office hours - Instructors: Fri 10-12pm TAs: Xinran Zhong and Zhaohuan Zhang (time:
Fourier analysis of discrete-time signals. (Lathi Chapt. 10 and these slides)
 Fourier analysis of discrete-time signals (Lathi Chapt. 10 and these slides) Towards the discrete-time Fourier transform How we will get there? Periodic discrete-time signal representation by Discrete-time
Fourier analysis of discrete-time signals (Lathi Chapt. 10 and these slides) Towards the discrete-time Fourier transform How we will get there? Periodic discrete-time signal representation by Discrete-time
Fourier Series & The Fourier Transform
 Fourier Series & The Fourier Transform What is the Fourier Transform? Anharmonic Waves Fourier Cosine Series for even functions Fourier Sine Series for odd functions The continuous limit: the Fourier transform
Fourier Series & The Fourier Transform What is the Fourier Transform? Anharmonic Waves Fourier Cosine Series for even functions Fourier Sine Series for odd functions The continuous limit: the Fourier transform
Pulse Shaping and ISI (Proakis: chapter 10.1, 10.3) EEE3012 Spring 2018
 Pulse Shaping and ISI (Proakis: chapter 10.1, 10.3) EEE3012 Spring 2018 Digital Communication System Introduction Bandlimited channels distort signals the result is smeared pulses intersymol interference
Pulse Shaping and ISI (Proakis: chapter 10.1, 10.3) EEE3012 Spring 2018 Digital Communication System Introduction Bandlimited channels distort signals the result is smeared pulses intersymol interference
ω 0 = 2π/T 0 is called the fundamental angular frequency and ω 2 = 2ω 0 is called the
 he ime-frequency Concept []. Review of Fourier Series Consider the following set of time functions {3A sin t, A sin t}. We can represent these functions in different ways by plotting the amplitude versus
he ime-frequency Concept []. Review of Fourier Series Consider the following set of time functions {3A sin t, A sin t}. We can represent these functions in different ways by plotting the amplitude versus
Unstable Oscillations!
 Unstable Oscillations X( t ) = [ A 0 + A( t ) ] sin( ω t + Φ 0 + Φ( t ) ) Amplitude modulation: A( t ) Phase modulation: Φ( t ) S(ω) S(ω) Special case: C(ω) Unstable oscillation has a broader periodogram
Unstable Oscillations X( t ) = [ A 0 + A( t ) ] sin( ω t + Φ 0 + Φ( t ) ) Amplitude modulation: A( t ) Phase modulation: Φ( t ) S(ω) S(ω) Special case: C(ω) Unstable oscillation has a broader periodogram
Chapter 4 The Fourier Series and Fourier Transform
 Chapter 4 The Fourier Series and Fourier Transform Fourier Series Representation of Periodic Signals Let x(t) be a CT periodic signal with period T, i.e., xt ( + T) = xt ( ), t R Example: the rectangular
Chapter 4 The Fourier Series and Fourier Transform Fourier Series Representation of Periodic Signals Let x(t) be a CT periodic signal with period T, i.e., xt ( + T) = xt ( ), t R Example: the rectangular
The Continuous Time Fourier Transform
 COMM 401: Signals & Systems Theory Lecture 8 The Continuous Time Fourier Transform Fourier Transform Continuous time CT signals Discrete time DT signals Aperiodic signals nonperiodic periodic signals Aperiodic
COMM 401: Signals & Systems Theory Lecture 8 The Continuous Time Fourier Transform Fourier Transform Continuous time CT signals Discrete time DT signals Aperiodic signals nonperiodic periodic signals Aperiodic
MITOCW MITRES18_005S10_DiffEqnsMotion_300k_512kb-mp4
 MITOCW MITRES18_005S10_DiffEqnsMotion_300k_512kb-mp4 PROFESSOR: OK, this lecture, this day, is differential equations day. I just feel even though these are not on the BC exams, that we've got everything
MITOCW MITRES18_005S10_DiffEqnsMotion_300k_512kb-mp4 PROFESSOR: OK, this lecture, this day, is differential equations day. I just feel even though these are not on the BC exams, that we've got everything
GATE EE Topic wise Questions SIGNALS & SYSTEMS
 www.gatehelp.com GATE EE Topic wise Questions YEAR 010 ONE MARK Question. 1 For the system /( s + 1), the approximate time taken for a step response to reach 98% of the final value is (A) 1 s (B) s (C)
www.gatehelp.com GATE EE Topic wise Questions YEAR 010 ONE MARK Question. 1 For the system /( s + 1), the approximate time taken for a step response to reach 98% of the final value is (A) 1 s (B) s (C)
ECE 3084 QUIZ 2 SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING GEORGIA INSTITUTE OF TECHNOLOGY APRIL 2, Name:
 ECE 3084 QUIZ 2 SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING GEORGIA INSTITUTE OF TECHNOLOGY APRIL 2, 205 Name:. The quiz is closed book, except for one 2-sided sheet of handwritten notes. 2. Turn off
ECE 3084 QUIZ 2 SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING GEORGIA INSTITUTE OF TECHNOLOGY APRIL 2, 205 Name:. The quiz is closed book, except for one 2-sided sheet of handwritten notes. 2. Turn off
Frequency Response and Continuous-time Fourier Series
 Frequency Response and Continuous-time Fourier Series Recall course objectives Main Course Objective: Fundamentals of systems/signals interaction (we d like to understand how systems transform or affect
Frequency Response and Continuous-time Fourier Series Recall course objectives Main Course Objective: Fundamentals of systems/signals interaction (we d like to understand how systems transform or affect
Last time: small acoustics
 Last time: small acoustics Voice, many instruments, modeled by tubes Traveling waves in both directions yield standing waves Standing waves correspond to resonances Variations from the idealization give
Last time: small acoustics Voice, many instruments, modeled by tubes Traveling waves in both directions yield standing waves Standing waves correspond to resonances Variations from the idealization give
MITOCW MITRES18_005S10_DerivOfSinXCosX_300k_512kb-mp4
 MITOCW MITRES18_005S10_DerivOfSinXCosX_300k_512kb-mp4 PROFESSOR: OK, this lecture is about the slopes, the derivatives, of two of the great functions of mathematics: sine x and cosine x. Why do I say great
MITOCW MITRES18_005S10_DerivOfSinXCosX_300k_512kb-mp4 PROFESSOR: OK, this lecture is about the slopes, the derivatives, of two of the great functions of mathematics: sine x and cosine x. Why do I say great
Assignment 3 Solutions
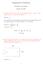 Assignment Solutions Networks and systems August 8, 7. Consider an LTI system with transfer function H(jw) = input is sin(t + π 4 ), what is the output? +jw. If the Solution : C For an LTI system with
Assignment Solutions Networks and systems August 8, 7. Consider an LTI system with transfer function H(jw) = input is sin(t + π 4 ), what is the output? +jw. If the Solution : C For an LTI system with
ENSC327 Communications Systems 2: Fourier Representations. School of Engineering Science Simon Fraser University
 ENSC37 Communications Systems : Fourier Representations School o Engineering Science Simon Fraser University Outline Chap..5: Signal Classiications Fourier Transorm Dirac Delta Function Unit Impulse Fourier
ENSC37 Communications Systems : Fourier Representations School o Engineering Science Simon Fraser University Outline Chap..5: Signal Classiications Fourier Transorm Dirac Delta Function Unit Impulse Fourier
MITOCW watch?v=pqkyqu11eta
 MITOCW watch?v=pqkyqu11eta The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To
MITOCW watch?v=pqkyqu11eta The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To
Chirp Transform for FFT
 Chirp Transform for FFT Since the FFT is an implementation of the DFT, it provides a frequency resolution of 2π/N, where N is the length of the input sequence. If this resolution is not sufficient in a
Chirp Transform for FFT Since the FFT is an implementation of the DFT, it provides a frequency resolution of 2π/N, where N is the length of the input sequence. If this resolution is not sufficient in a
Continuous Time Signal Analysis: the Fourier Transform. Lathi Chapter 4
 Continuous Time Signal Analysis: the Fourier Transform Lathi Chapter 4 Topics Aperiodic signal representation by the Fourier integral (CTFT) Continuous-time Fourier transform Transforms of some useful
Continuous Time Signal Analysis: the Fourier Transform Lathi Chapter 4 Topics Aperiodic signal representation by the Fourier integral (CTFT) Continuous-time Fourier transform Transforms of some useful
ANALOG AND DIGITAL SIGNAL PROCESSING ADSP - Chapter 8
 ANALOG AND DIGITAL SIGNAL PROCESSING ADSP - Chapter 8 Fm n N fnt ( ) e j2mn N X() X() 2 X() X() 3 W Chap. 8 Discrete Fourier Transform (DFT), FFT Prof. J.-P. Sandoz, 2-2 W W 3 W W x () x () x () 2 x ()
ANALOG AND DIGITAL SIGNAL PROCESSING ADSP - Chapter 8 Fm n N fnt ( ) e j2mn N X() X() 2 X() X() 3 W Chap. 8 Discrete Fourier Transform (DFT), FFT Prof. J.-P. Sandoz, 2-2 W W 3 W W x () x () x () 2 x ()
IB Paper 6: Signal and Data Analysis
 IB Paper 6: Signal and Data Analysis Handout 5: Sampling Theory S Godsill Signal Processing and Communications Group, Engineering Department, Cambridge, UK Lent 2015 1 / 85 Sampling and Aliasing All of
IB Paper 6: Signal and Data Analysis Handout 5: Sampling Theory S Godsill Signal Processing and Communications Group, Engineering Department, Cambridge, UK Lent 2015 1 / 85 Sampling and Aliasing All of
06EC44-Signals and System Chapter Fourier Representation for four Signal Classes
 Chapter 5.1 Fourier Representation for four Signal Classes 5.1.1Mathematical Development of Fourier Transform If the period is stretched without limit, the periodic signal no longer remains periodic but
Chapter 5.1 Fourier Representation for four Signal Classes 5.1.1Mathematical Development of Fourier Transform If the period is stretched without limit, the periodic signal no longer remains periodic but
ANALOG AND DIGITAL SIGNAL PROCESSING CHAPTER 3 : LINEAR SYSTEM RESPONSE (GENERAL CASE)
 3. Linear System Response (general case) 3. INTRODUCTION In chapter 2, we determined that : a) If the system is linear (or operate in a linear domain) b) If the input signal can be assumed as periodic
3. Linear System Response (general case) 3. INTRODUCTION In chapter 2, we determined that : a) If the system is linear (or operate in a linear domain) b) If the input signal can be assumed as periodic
Fourier Transform for Continuous Functions
 Fourier Transform for Continuous Functions Central goal: representing a signal by a set of orthogonal bases that are corresponding to frequencies or spectrum. Fourier series allows to find the spectrum
Fourier Transform for Continuous Functions Central goal: representing a signal by a set of orthogonal bases that are corresponding to frequencies or spectrum. Fourier series allows to find the spectrum
Quantitative Understanding in Biology Module IV: ODEs Lecture III: Fourier Analysis
 Quantitative Understanding in Biology Module IV: ODEs Lecture III: Fourier Analysis Introduction Throughout this course we have seen examples of complex mathematical phenomena being represented as linear
Quantitative Understanding in Biology Module IV: ODEs Lecture III: Fourier Analysis Introduction Throughout this course we have seen examples of complex mathematical phenomena being represented as linear
Randomly Modulated Periodic Signals
 Randomly Modulated Periodic Signals Melvin J. Hinich Applied Research Laboratories University of Texas at Austin hinich@mail.la.utexas.edu www.la.utexas.edu/~hinich Rotating Cylinder Data Fluid Nonlinearity
Randomly Modulated Periodic Signals Melvin J. Hinich Applied Research Laboratories University of Texas at Austin hinich@mail.la.utexas.edu www.la.utexas.edu/~hinich Rotating Cylinder Data Fluid Nonlinearity
I. Signals & Sinusoids
 I. Signals & Sinusoids [p. 3] Signal definition Sinusoidal signal Plotting a sinusoid [p. 12] Signal operations Time shifting Time scaling Time reversal Combining time shifting & scaling [p. 17] Trigonometric
I. Signals & Sinusoids [p. 3] Signal definition Sinusoidal signal Plotting a sinusoid [p. 12] Signal operations Time shifting Time scaling Time reversal Combining time shifting & scaling [p. 17] Trigonometric
Let x(t) be a finite energy signal with Fourier transform X(jω). Let E denote the energy of the signal. Thus E <. We have.
 Notes on the Uncertainty principle Let x(t) be a finite energy signal with Fourier transform X(jω). Let E denote the energy of the signal. Thus E
Notes on the Uncertainty principle Let x(t) be a finite energy signal with Fourier transform X(jω). Let E denote the energy of the signal. Thus E
A523 Signal Modeling, Statistical Inference and Data Mining in Astrophysics Spring 2011
 A523 Signal Modeling, Statistical Inference and Data Mining in Astrophysics Spring 2011 Lecture 6 PDFs for Lecture 1-5 are on the web page Problem set 2 is on the web page Article on web page A Guided
A523 Signal Modeling, Statistical Inference and Data Mining in Astrophysics Spring 2011 Lecture 6 PDFs for Lecture 1-5 are on the web page Problem set 2 is on the web page Article on web page A Guided
Homework 6 EE235, Spring 2011
 Homework 6 EE235, Spring 211 1. Fourier Series. Determine w and the non-zero Fourier series coefficients for the following functions: (a 2 cos(3πt + sin(1πt + π 3 w π e j3πt + e j3πt + 1 j2 [ej(1πt+ π
Homework 6 EE235, Spring 211 1. Fourier Series. Determine w and the non-zero Fourier series coefficients for the following functions: (a 2 cos(3πt + sin(1πt + π 3 w π e j3πt + e j3πt + 1 j2 [ej(1πt+ π
26. The Fourier Transform in optics
 26. The Fourier Transform in optics What is the Fourier Transform? Anharmonic waves The spectrum of a light wave Fourier transform of an exponential The Dirac delta function The Fourier transform of e
26. The Fourier Transform in optics What is the Fourier Transform? Anharmonic waves The spectrum of a light wave Fourier transform of an exponential The Dirac delta function The Fourier transform of e
Continuous-time Fourier Methods
 ELEC 321-001 SIGNALS and SYSTEMS Continuous-time Fourier Methods Chapter 6 1 Representing a Signal The convolution method for finding the response of a system to an excitation takes advantage of the linearity
ELEC 321-001 SIGNALS and SYSTEMS Continuous-time Fourier Methods Chapter 6 1 Representing a Signal The convolution method for finding the response of a system to an excitation takes advantage of the linearity
Basics of Radiation Fields
 Basics of Radiation Fields Initial questions: How could you estimate the distance to a radio source in our galaxy if you don t have a parallax? We are now going to shift gears a bit. In order to understand
Basics of Radiation Fields Initial questions: How could you estimate the distance to a radio source in our galaxy if you don t have a parallax? We are now going to shift gears a bit. In order to understand
MITOCW watch?v=ufu6b7ohb8m
 MITOCW watch?v=ufu6b7ohb8m The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To
MITOCW watch?v=ufu6b7ohb8m The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To
Instructor (Brad Osgood)
 TheFourierTransformAndItsApplications-Lecture05 Instructor (Brad Osgood):Okay, ready to rock and roll? All right. We ve been getting a lot of as I understand it, we ve been getting a lot of email questions
TheFourierTransformAndItsApplications-Lecture05 Instructor (Brad Osgood):Okay, ready to rock and roll? All right. We ve been getting a lot of as I understand it, we ve been getting a lot of email questions
Fun With The Fourier Series
 oo = a Σ 0 + a n cos(2nπt/t) + b n sin(2nπt/t) n=1 Presented at: Santa Clara Valley Chapter IEEE EMC Society March 10, 1998 Franz Gisin Silicon Graphics Inc 2011 North Shoreline M/S 43L 946 Phone: (415)
oo = a Σ 0 + a n cos(2nπt/t) + b n sin(2nπt/t) n=1 Presented at: Santa Clara Valley Chapter IEEE EMC Society March 10, 1998 Franz Gisin Silicon Graphics Inc 2011 North Shoreline M/S 43L 946 Phone: (415)
Differential Equations
 Differential Equations A differential equation (DE) is an equation which involves an unknown function f (x) as well as some of its derivatives. To solve a differential equation means to find the unknown
Differential Equations A differential equation (DE) is an equation which involves an unknown function f (x) as well as some of its derivatives. To solve a differential equation means to find the unknown
