Lab10: FM Spectra and VCO
|
|
|
- Moses Alexander
- 5 years ago
- Views:
Transcription
1 Lab10: FM Spectra and VCO Prepared by: Keyur Desai Dept. of Electrical Engineering Michigan State University ECE458 Lab 10
2 What is FM? A type of analog modulation Remember a common strategy in analog modulation?
3 What is FM? A type of analog modulation Remember a common strategy in analog modulation? Vary some aspect of a Carrier signal w.r.t message
4 What is FM? A type of analog modulation Remember a common strategy in analog modulation? Vary some aspect of a Carrier signal w.r.t message A simple case: When message is sinusoid (single tone) x(t) = A c cos[ω c t + φ c + A m sin(ω m t + φ m )], (1) where (A c, ω c, φ c ) describe the carrier sinusoid where (A m, ω m, φ m ) specify the modulator sinusoid
5 What is FM? x(t) = A c cos[ω c t + φ c + A m sin(ω m t + φ m )], (2) Strictly speaking, it is not the frequency of the carrier that is modulated sinusoidally, but rather the instantaneous phase of the carrier
6 What is FM? x(t) = A c cos[ω c t + φ c + A m sin(ω m t + φ m )], (2) Strictly speaking, it is not the frequency of the carrier that is modulated sinusoidally, but rather the instantaneous phase of the carrier Phase modulation is a better term
7 What is FM? Let us discuss what we understand by Phase of a sinusoid s(t) = A cos[φ(t)] (3) where, φ(t) is instantaneous phase: φ(t) = ωt + θ
8 What is FM? Let us discuss what we understand by Phase of a sinusoid s(t) = A cos[φ(t)] (3) where, φ(t) is instantaneous phase: φ(t) = ωt + θ d dt φ(t) =?
9 What is FM? Let us discuss what we understand by Phase of a sinusoid s(t) = A cos[φ(t)] (3) where, φ(t) is instantaneous phase: φ(t) = ωt + θ d dt φ(t) =? d dt φ(t) = ω
10 What is FM? Let us discuss what we understand by Phase of a sinusoid s(t) = A cos[φ(t)] (3) where, φ(t) is instantaneous phase: φ(t) = ωt + θ d dt φ(t) =? d dt φ(t) = ω In general the phase may not increase / change linearly and hence d dt φ(t) = ω(t) We call ω(t) instantaneous frequency
11 What is FM? FM signal is: ( t ) x c (t) = A cos ω c t + β m(τ) dτ 0 Instantaneous phase of this signal is:
12 What is FM? FM signal is: ( t ) x c (t) = A cos ω c t + β m(τ) dτ 0 Instantaneous phase of this signal is: ( t ) φ(t) = ω c t + β m(τ) dτ 0 Then Instantaneous frequency is:
13 What is FM? FM signal is: ( t ) x c (t) = A cos ω c t + β m(τ) dτ 0 Instantaneous phase of this signal is: ( t ) φ(t) = ω c t + β m(τ) dτ 0 Then Instantaneous frequency is: d dt φ(t) = ω c + β m(t), where β is the frequency sensitivity of the FM modulator
14 What is FM? Figure: An audio signal (top) may be carried by an AM or FM radio wave
15 What is FM? Figure: An example of frequency modulation. The top diagram shows the modulating signal superimposed on the carrier wave. The bottom diagram shows the resulting frequency-modulated signal
16 Why FM? Historical motivation was: Constant amplitude signals are easier to process
17 Why FM? Historical motivation was: Constant amplitude signals are easier to process What we mean by process?
18 Why FM? Historical motivation was: Constant amplitude signals are easier to process What we mean by process? Analog Circuit operations, such as Amplify, Multiply Amplification of AM signal is (maybe was) difficult
19 Why FM? Historical motivation was: Constant amplitude signals are easier to process What we mean by process? Analog Circuit operations, such as Amplify, Multiply Amplification of AM signal is (maybe was) difficult Bandwidth-Fidelity tradeoff: FM allows to allocate more bandwidth to improve SNR
20 Why FM? Historical motivation was: Constant amplitude signals are easier to process What we mean by process? Analog Circuit operations, such as Amplify, Multiply Amplification of AM signal is (maybe was) difficult Bandwidth-Fidelity tradeoff: FM allows to allocate more bandwidth to improve SNR How do I spend more bandwidth? Increase the frequency sensitivity β of FM modulator
21 Spectra of FM x(t) = A c cos[ω c t + φ c + A m sin(ω m t + φ m )], (4) What is the spectrum (Fourier domain representation) of the above signal?
22 Spectra of FM x(t) = A c cos[ω c t + φ c + A m sin(ω m t + φ m )], (4) What is the spectrum (Fourier domain representation) of the above signal? Answer is non-trivial and require us to go through an elegant mathematical derivation that involves Bessel functions Remember the first rule of Fourier Club: Series for periodic functions and transform for aperiodic functions
23 Bessel function We will need Bessel functions. The Bessel function is defined as (Hold your breathe):
24 Bessel function We will need Bessel functions. The Bessel function is defined as (Hold your breathe): J α (x) = 1 2π π π e i(ατ x sin τ) dτ (5)
25 Bessel function We will need Bessel functions. The Bessel function is defined as (Hold your breathe): J α (x) = 1 2π π π e i(ατ x sin τ) dτ (5) From where such a madness arises? For a while focus only on the question: Can we compute the integral
26 Bessel function We will need Bessel functions. The Bessel function is defined as (Hold your breathe): J α (x) = 1 2π π π e i(ατ x sin τ) dτ (5) From where such a madness arises? For a while focus only on the question: Can we compute the integral Remember exponential series: e x = n=0 x n n! = 1 + x + x 2 2! + x 3 3! + x 4 4! + (6)
27 Bessel function If we plug the exponential series into Bessel function definition we end up with J α (x) = m=0 ( 1) m x ) 2m+α (7) m!γ(m + α + 1)( 2
28 Bessel function If we plug the exponential series into Bessel function definition we end up with J α (x) = m=0 Where did the integral go? ( 1) m x ) 2m+α (7) m!γ(m + α + 1)( 2
29 Bessel function If we plug the exponential series into Bessel function definition we end up with J α (x) = m=0 Where did the integral go? ( 1) m x ) 2m+α (7) m!γ(m + α + 1)( 2 It is consumed by a simpler concept called Gamma function: Γ(z) = 0 t z 1 e t dt (8)
30 Spectra of FM What good is the concept of Bessel function for?
31 Spectra of FM What good is the concept of Bessel function for? e jβ sin(ωmt) = J k (β)e jkωmt. (9) What does it mean? k=
32 Spectra of FM What good is the concept of Bessel function for? e jβ sin(ωmt) = k= J k (β)e jkωmt. (9) What does it mean? J k (β) is the amplitude of the kth harmonic in the Fourier-series expansion of the periodic signal exp[jβ sin(ω m t)]
33 Bessel function Figure: Plot of Bessel function of the first kind, J α (x), for integer orders α = 0, 1, 2
34 Spectra of FM How does this signal look like in Fourier domain? x(t) = cos[ω c t + β sin(ω m t)], (10)
35 Spectra of FM How does this signal look like in Fourier domain? x(t) = cos[ω c t + β sin(ω m t)], (10) Is x(t) periodic?
36 Spectra of FM How does this signal look like in Fourier domain? x(t) = cos[ω c t + β sin(ω m t)], (10) Is x(t) periodic? Then we will have to work with Fourier series
37 Spectra of FM cos[ω c t + β sin(ω m t)] (11)
38 Spectra of FM cos[ω c t + β sin(ω m t)] (11) { = re e j[ωct+β sin(ωmt)]} (12)
39 Spectra of FM cos[ω c t + β sin(ω m t)] (11) { = re e j[ωct+β sin(ωmt)]} (12) { = re e jωct e jβ sin(ωmt)} (13)
40 Spectra of FM = re cos[ω c t + β sin(ω m t)] (11) { = re e j[ωct+β sin(ωmt)]} (12) { = re e jωct e jβ sin(ωmt)} (13) { e jωct k= J k (β)e jkωmt } (14)
41 Spectra of FM = re = re cos[ω c t + β sin(ω m t)] (11) { = re e j[ωct+β sin(ωmt)]} (12) { = re e jωct e jβ sin(ωmt)} (13) { e jωct { k= k= J k (β)e jkωmt } J k (β)e j(ωc+kωm)t } (14) (15)
42 Spectra of FM = re = re = cos[ω c t + β sin(ω m t)] (11) { = re e j[ωct+β sin(ωmt)]} (12) { = re e jωct e jβ sin(ωmt)} (13) { e jωct { k= k= k= J k (β)e jkωmt } J k (β)e j(ωc+kωm)t } (14) (15) J k (β) cos[(ω c + kω m )t] (16)
43 Fourier Series of e jβ sin(ω mt) Remember the fourier series?
44 Fourier Series of e jβ sin(ω mt) Remember the fourier series? where f (t) = + n= c ne inωot, (17)
45 Fourier Series of e jβ sin(ω mt) Remember the fourier series? f (t) = + n= c ne inωot, (17) where c n = ω π o ωo f (t)e inωot dt. (18) 2π π ωo
46 Fourier Series of e jβ sin(ω mt) Remember the fourier series? f (t) = + n= c ne inωot, (17) where c n = ω π o ωo f (t)e inωot dt. (18) 2π π ωo Let us derive fourier series of e jβ sin(ωmt).
47 Fourier Series of e jβ sin(ω mt) Remember the fourier series? f (t) = + n= c ne inωot, (17) where c n = ω π o ωo f (t)e inωot dt. (18) 2π π ωo Let us derive fourier series of e jβ sin(ωmt). c n = ω π m ωm e jβ sin(ωmt) e jn ωm t dt (19) 2π π ωm
48 Fourier Series of e jβ sin(ω mt) Remember the fourier series? f (t) = + n= c ne inωot, (17) where c n = ω π o ωo f (t)e inωot dt. (18) 2π π ωo Let us derive fourier series of e jβ sin(ωmt). c n = ω π m ωm e jβ sin(ωmt) e jn ωm t dt (19) 2π c n = ω m 2π π ωm π ωm π ωm e j(n ωm t β sin(ωmt)) dt (20)
49 Fourier Series of e jβ sin(ω mt) Remember the fourier series? f (t) = + n= c ne inωot, (17) where c n = ω π o ωo f (t)e inωot dt. (18) 2π π ωo Let us derive fourier series of e jβ sin(ωmt). c n = ω π m ωm e jβ sin(ωmt) e jn ωm t dt (19) 2π c n = ω m 2π π ωm π ωm π ωm J α (x) = 1 2π e j(n ωm t β sin(ωmt)) dt (20) π π e j(ατ x sin τ) dτ (21)
Chapter 4 The Fourier Series and Fourier Transform
 Chapter 4 The Fourier Series and Fourier Transform Fourier Series Representation of Periodic Signals Let x(t) be a CT periodic signal with period T, i.e., xt ( + T) = xt ( ), t R Example: the rectangular
Chapter 4 The Fourier Series and Fourier Transform Fourier Series Representation of Periodic Signals Let x(t) be a CT periodic signal with period T, i.e., xt ( + T) = xt ( ), t R Example: the rectangular
Chapter 4 The Fourier Series and Fourier Transform
 Chapter 4 The Fourier Series and Fourier Transform Representation of Signals in Terms of Frequency Components Consider the CT signal defined by N xt () = Acos( ω t+ θ ), t k = 1 k k k The frequencies `present
Chapter 4 The Fourier Series and Fourier Transform Representation of Signals in Terms of Frequency Components Consider the CT signal defined by N xt () = Acos( ω t+ θ ), t k = 1 k k k The frequencies `present
ELEG 3124 SYSTEMS AND SIGNALS Ch. 5 Fourier Transform
 Department of Electrical Engineering University of Arkansas ELEG 3124 SYSTEMS AND SIGNALS Ch. 5 Fourier Transform Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Introduction Fourier Transform Properties of Fourier
Department of Electrical Engineering University of Arkansas ELEG 3124 SYSTEMS AND SIGNALS Ch. 5 Fourier Transform Dr. Jingxian Wu wuj@uark.edu OUTLINE 2 Introduction Fourier Transform Properties of Fourier
Fourier transform representation of CT aperiodic signals Section 4.1
 Fourier transform representation of CT aperiodic signals Section 4. A large class of aperiodic CT signals can be represented by the CT Fourier transform (CTFT). The (CT) Fourier transform (or spectrum)
Fourier transform representation of CT aperiodic signals Section 4. A large class of aperiodic CT signals can be represented by the CT Fourier transform (CTFT). The (CT) Fourier transform (or spectrum)
Amplitude and Phase A(0) 2. We start with the Fourier series representation of X(t) in real notation: n=1
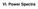 VI. Power Spectra Amplitude and Phase We start with the Fourier series representation of X(t) in real notation: A() X(t) = + [ A(n) cos(nωt) + B(n) sin(nωt)] 2 n=1 he waveform of the observed segment exactly
VI. Power Spectra Amplitude and Phase We start with the Fourier series representation of X(t) in real notation: A() X(t) = + [ A(n) cos(nωt) + B(n) sin(nωt)] 2 n=1 he waveform of the observed segment exactly
LOPE3202: Communication Systems 10/18/2017 2
 By Lecturer Ahmed Wael Academic Year 2017-2018 LOPE3202: Communication Systems 10/18/2017 We need tools to build any communication system. Mathematics is our premium tool to do work with signals and systems.
By Lecturer Ahmed Wael Academic Year 2017-2018 LOPE3202: Communication Systems 10/18/2017 We need tools to build any communication system. Mathematics is our premium tool to do work with signals and systems.
ω 0 = 2π/T 0 is called the fundamental angular frequency and ω 2 = 2ω 0 is called the
 he ime-frequency Concept []. Review of Fourier Series Consider the following set of time functions {3A sin t, A sin t}. We can represent these functions in different ways by plotting the amplitude versus
he ime-frequency Concept []. Review of Fourier Series Consider the following set of time functions {3A sin t, A sin t}. We can represent these functions in different ways by plotting the amplitude versus
Chapter 5 Frequency Domain Analysis of Systems
 Chapter 5 Frequency Domain Analysis of Systems CT, LTI Systems Consider the following CT LTI system: xt () ht () yt () Assumption: the impulse response h(t) is absolutely integrable, i.e., ht ( ) dt< (this
Chapter 5 Frequency Domain Analysis of Systems CT, LTI Systems Consider the following CT LTI system: xt () ht () yt () Assumption: the impulse response h(t) is absolutely integrable, i.e., ht ( ) dt< (this
A new class of sum rules for products of Bessel functions. G. Bevilacqua, 1, a) V. Biancalana, 1 Y. Dancheva, 1 L. Moi, 1 2, b) and T.
 A new class of sum rules for products of Bessel functions G. Bevilacqua,, a V. Biancalana, Y. Dancheva, L. Moi,, b and T. Mansour CNISM and Dipartimento di Fisica, Università di Siena, Via Roma 56, 5300
A new class of sum rules for products of Bessel functions G. Bevilacqua,, a V. Biancalana, Y. Dancheva, L. Moi,, b and T. Mansour CNISM and Dipartimento di Fisica, Università di Siena, Via Roma 56, 5300
Chapter 5 Frequency Domain Analysis of Systems
 Chapter 5 Frequency Domain Analysis of Systems CT, LTI Systems Consider the following CT LTI system: xt () ht () yt () Assumption: the impulse response h(t) is absolutely integrable, i.e., ht ( ) dt< (this
Chapter 5 Frequency Domain Analysis of Systems CT, LTI Systems Consider the following CT LTI system: xt () ht () yt () Assumption: the impulse response h(t) is absolutely integrable, i.e., ht ( ) dt< (this
EE 3054: Signals, Systems, and Transforms Summer It is observed of some continuous-time LTI system that the input signal.
 EE 34: Signals, Systems, and Transforms Summer 7 Test No notes, closed book. Show your work. Simplify your answers. 3. It is observed of some continuous-time LTI system that the input signal = 3 u(t) produces
EE 34: Signals, Systems, and Transforms Summer 7 Test No notes, closed book. Show your work. Simplify your answers. 3. It is observed of some continuous-time LTI system that the input signal = 3 u(t) produces
CMPT 318: Lecture 5 Complex Exponentials, Spectrum Representation
 CMPT 318: Lecture 5 Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University January 23, 2006 1 Exponentials The exponential is
CMPT 318: Lecture 5 Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University January 23, 2006 1 Exponentials The exponential is
Representing a Signal
 The Fourier Series Representing a Signal The convolution method for finding the response of a system to an excitation takes advantage of the linearity and timeinvariance of the system and represents the
The Fourier Series Representing a Signal The convolution method for finding the response of a system to an excitation takes advantage of the linearity and timeinvariance of the system and represents the
Continuous Time Signal Analysis: the Fourier Transform. Lathi Chapter 4
 Continuous Time Signal Analysis: the Fourier Transform Lathi Chapter 4 Topics Aperiodic signal representation by the Fourier integral (CTFT) Continuous-time Fourier transform Transforms of some useful
Continuous Time Signal Analysis: the Fourier Transform Lathi Chapter 4 Topics Aperiodic signal representation by the Fourier integral (CTFT) Continuous-time Fourier transform Transforms of some useful
THE FOURIER TRANSFORM (Fourier series for a function whose period is very, very long) Reading: Main 11.3
 THE FOURIER TRANSFORM (Fourier series for a function whose period is very, very long) Reading: Main 11.3 Any periodic function f(t) can be written as a Fourier Series a 0 2 + a n cos( nωt) + b n sin n
THE FOURIER TRANSFORM (Fourier series for a function whose period is very, very long) Reading: Main 11.3 Any periodic function f(t) can be written as a Fourier Series a 0 2 + a n cos( nωt) + b n sin n
Problem Set 8 Mar 5, 2004 Due Mar 10, 2004 ACM 95b/100b 3pm at Firestone 303 E. Sterl Phinney (2 pts) Include grading section number
 Problem Set 8 Mar 5, 24 Due Mar 1, 24 ACM 95b/1b 3pm at Firestone 33 E. Sterl Phinney (2 pts) Include grading section number Useful Readings: For Green s functions, see class notes and refs on PS7 (esp
Problem Set 8 Mar 5, 24 Due Mar 1, 24 ACM 95b/1b 3pm at Firestone 33 E. Sterl Phinney (2 pts) Include grading section number Useful Readings: For Green s functions, see class notes and refs on PS7 (esp
EECS 117 Lecture 3: Transmission Line Junctions / Time Harmonic Excitation
 EECS 117 Lecture 3: Transmission Line Junctions / Time Harmonic Excitation Prof. Niknejad University of California, Berkeley University of California, Berkeley EECS 117 Lecture 3 p. 1/23 Transmission Line
EECS 117 Lecture 3: Transmission Line Junctions / Time Harmonic Excitation Prof. Niknejad University of California, Berkeley University of California, Berkeley EECS 117 Lecture 3 p. 1/23 Transmission Line
Solutions to Problems in Chapter 4
 Solutions to Problems in Chapter 4 Problems with Solutions Problem 4. Fourier Series of the Output Voltage of an Ideal Full-Wave Diode Bridge Rectifier he nonlinear circuit in Figure 4. is a full-wave
Solutions to Problems in Chapter 4 Problems with Solutions Problem 4. Fourier Series of the Output Voltage of an Ideal Full-Wave Diode Bridge Rectifier he nonlinear circuit in Figure 4. is a full-wave
Lecture 9. PMTs and Laser Noise. Lecture 9. Photon Counting. Photomultiplier Tubes (PMTs) Laser Phase Noise. Relative Intensity
 s and Laser Phase Phase Density ECE 185 Lasers and Modulators Lab - Spring 2018 1 Detectors Continuous Output Internal Photoelectron Flux Thermal Filtered External Current w(t) Sensor i(t) External System
s and Laser Phase Phase Density ECE 185 Lasers and Modulators Lab - Spring 2018 1 Detectors Continuous Output Internal Photoelectron Flux Thermal Filtered External Current w(t) Sensor i(t) External System
06EC44-Signals and System Chapter Fourier Representation for four Signal Classes
 Chapter 5.1 Fourier Representation for four Signal Classes 5.1.1Mathematical Development of Fourier Transform If the period is stretched without limit, the periodic signal no longer remains periodic but
Chapter 5.1 Fourier Representation for four Signal Classes 5.1.1Mathematical Development of Fourier Transform If the period is stretched without limit, the periodic signal no longer remains periodic but
Fourier Series and Fourier Transforms
 Fourier Series and Fourier Transforms EECS2 (6.082), MIT Fall 2006 Lectures 2 and 3 Fourier Series From your differential equations course, 18.03, you know Fourier s expression representing a T -periodic
Fourier Series and Fourier Transforms EECS2 (6.082), MIT Fall 2006 Lectures 2 and 3 Fourier Series From your differential equations course, 18.03, you know Fourier s expression representing a T -periodic
Notes on the Periodically Forced Harmonic Oscillator
 Notes on the Periodically orced Harmonic Oscillator Warren Weckesser Math 38 - Differential Equations 1 The Periodically orced Harmonic Oscillator. By periodically forced harmonic oscillator, we mean the
Notes on the Periodically orced Harmonic Oscillator Warren Weckesser Math 38 - Differential Equations 1 The Periodically orced Harmonic Oscillator. By periodically forced harmonic oscillator, we mean the
16.362: Signals and Systems: 1.0
 16.362: Signals and Systems: 1.0 Prof. K. Chandra ECE, UMASS Lowell September 1, 2016 1 Background The pre-requisites for this course are Calculus II and Differential Equations. A basic understanding of
16.362: Signals and Systems: 1.0 Prof. K. Chandra ECE, UMASS Lowell September 1, 2016 1 Background The pre-requisites for this course are Calculus II and Differential Equations. A basic understanding of
SIGNALS AND SYSTEMS: PAPER 3C1 HANDOUT 6a. Dr David Corrigan 1. Electronic and Electrical Engineering Dept.
 SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6a. Dr David Corrigan. Electronic and Electrical Engineering Dept. corrigad@tcd.ie www.mee.tcd.ie/ corrigad FOURIER SERIES Have seen how the behaviour of systems can
SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6a. Dr David Corrigan. Electronic and Electrical Engineering Dept. corrigad@tcd.ie www.mee.tcd.ie/ corrigad FOURIER SERIES Have seen how the behaviour of systems can
ENSC327 Communications Systems 2: Fourier Representations. Jie Liang School of Engineering Science Simon Fraser University
 ENSC327 Communications Systems 2: Fourier Representations Jie Liang School of Engineering Science Simon Fraser University 1 Outline Chap 2.1 2.5: Signal Classifications Fourier Transform Dirac Delta Function
ENSC327 Communications Systems 2: Fourier Representations Jie Liang School of Engineering Science Simon Fraser University 1 Outline Chap 2.1 2.5: Signal Classifications Fourier Transform Dirac Delta Function
EE 435. Lecture 28. Data Converters Linearity INL/DNL Spectral Performance
 EE 435 Lecture 8 Data Converters Linearity INL/DNL Spectral Performance Performance Characterization of Data Converters Static characteristics Resolution Least Significant Bit (LSB) Offset and Gain Errors
EE 435 Lecture 8 Data Converters Linearity INL/DNL Spectral Performance Performance Characterization of Data Converters Static characteristics Resolution Least Significant Bit (LSB) Offset and Gain Errors
Problem 1: Lagrangians and Conserved Quantities. Consider the following action for a particle of mass m moving in one dimension
 105A Practice Final Solutions March 13, 01 William Kelly Problem 1: Lagrangians and Conserved Quantities Consider the following action for a particle of mass m moving in one dimension S = dtl = mc dt 1
105A Practice Final Solutions March 13, 01 William Kelly Problem 1: Lagrangians and Conserved Quantities Consider the following action for a particle of mass m moving in one dimension S = dtl = mc dt 1
LECTURE 12 Sections Introduction to the Fourier series of periodic signals
 Signals and Systems I Wednesday, February 11, 29 LECURE 12 Sections 3.1-3.3 Introduction to the Fourier series of periodic signals Chapter 3: Fourier Series of periodic signals 3. Introduction 3.1 Historical
Signals and Systems I Wednesday, February 11, 29 LECURE 12 Sections 3.1-3.3 Introduction to the Fourier series of periodic signals Chapter 3: Fourier Series of periodic signals 3. Introduction 3.1 Historical
CT Rectangular Function Pairs (5B)
 C Rectangular Function Pairs (5B) Continuous ime Rect Function Pairs Copyright (c) 009-013 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU
C Rectangular Function Pairs (5B) Continuous ime Rect Function Pairs Copyright (c) 009-013 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU
Introduction to Time-Frequency Distributions
 Introduction to Time-Frequency Distributions Selin Aviyente Department of Electrical and Computer Engineering Michigan State University January 19, 2010 Motivation for time-frequency analysis When you
Introduction to Time-Frequency Distributions Selin Aviyente Department of Electrical and Computer Engineering Michigan State University January 19, 2010 Motivation for time-frequency analysis When you
The Laplace Transform
 The Laplace Transform Syllabus ECE 316, Spring 2015 Final Grades Homework (6 problems per week): 25% Exams (midterm and final): 50% (25:25) Random Quiz: 25% Textbook M. Roberts, Signals and Systems, 2nd
The Laplace Transform Syllabus ECE 316, Spring 2015 Final Grades Homework (6 problems per week): 25% Exams (midterm and final): 50% (25:25) Random Quiz: 25% Textbook M. Roberts, Signals and Systems, 2nd
CHAPTER 4 FOURIER SERIES S A B A R I N A I S M A I L
 CHAPTER 4 FOURIER SERIES 1 S A B A R I N A I S M A I L Outline Introduction of the Fourier series. The properties of the Fourier series. Symmetry consideration Application of the Fourier series to circuit
CHAPTER 4 FOURIER SERIES 1 S A B A R I N A I S M A I L Outline Introduction of the Fourier series. The properties of the Fourier series. Symmetry consideration Application of the Fourier series to circuit
Lecture 8 ELE 301: Signals and Systems
 Lecture 8 ELE 30: Signals and Systems Prof. Paul Cuff Princeton University Fall 20-2 Cuff (Lecture 7) ELE 30: Signals and Systems Fall 20-2 / 37 Properties of the Fourier Transform Properties of the Fourier
Lecture 8 ELE 30: Signals and Systems Prof. Paul Cuff Princeton University Fall 20-2 Cuff (Lecture 7) ELE 30: Signals and Systems Fall 20-2 / 37 Properties of the Fourier Transform Properties of the Fourier
Review of Linear Time-Invariant Network Analysis
 D1 APPENDIX D Review of Linear Time-Invariant Network Analysis Consider a network with input x(t) and output y(t) as shown in Figure D-1. If an input x 1 (t) produces an output y 1 (t), and an input x
D1 APPENDIX D Review of Linear Time-Invariant Network Analysis Consider a network with input x(t) and output y(t) as shown in Figure D-1. If an input x 1 (t) produces an output y 1 (t), and an input x
I. Signals & Sinusoids
 I. Signals & Sinusoids [p. 3] Signal definition Sinusoidal signal Plotting a sinusoid [p. 12] Signal operations Time shifting Time scaling Time reversal Combining time shifting & scaling [p. 17] Trigonometric
I. Signals & Sinusoids [p. 3] Signal definition Sinusoidal signal Plotting a sinusoid [p. 12] Signal operations Time shifting Time scaling Time reversal Combining time shifting & scaling [p. 17] Trigonometric
Fourier Transform. Find the Fourier series for a periodic waveform Determine the output of a filter when the input is a periodic function
 Objectives: Be able to Fourier Transform Find the Fourier series for a periodic waveform Determine the output of a filter when the input is a periodic function Filters with a Single Sinusoidal Input: Suppose
Objectives: Be able to Fourier Transform Find the Fourier series for a periodic waveform Determine the output of a filter when the input is a periodic function Filters with a Single Sinusoidal Input: Suppose
E2.5 Signals & Linear Systems. Tutorial Sheet 1 Introduction to Signals & Systems (Lectures 1 & 2)
 E.5 Signals & Linear Systems Tutorial Sheet 1 Introduction to Signals & Systems (Lectures 1 & ) 1. Sketch each of the following continuous-time signals, specify if the signal is periodic/non-periodic,
E.5 Signals & Linear Systems Tutorial Sheet 1 Introduction to Signals & Systems (Lectures 1 & ) 1. Sketch each of the following continuous-time signals, specify if the signal is periodic/non-periodic,
Chapter 2: Complex numbers
 Chapter 2: Complex numbers Complex numbers are commonplace in physics and engineering. In particular, complex numbers enable us to simplify equations and/or more easily find solutions to equations. We
Chapter 2: Complex numbers Complex numbers are commonplace in physics and engineering. In particular, complex numbers enable us to simplify equations and/or more easily find solutions to equations. We
Signals and Systems Lecture Notes
 Dr. Mahmoud M. Al-Husari Signals and Systems Lecture Notes This set of lecture notes are never to be considered as a substitute to the textbook recommended by the lecturer. ii Contents Preface v 1 Introduction
Dr. Mahmoud M. Al-Husari Signals and Systems Lecture Notes This set of lecture notes are never to be considered as a substitute to the textbook recommended by the lecturer. ii Contents Preface v 1 Introduction
Signals, Instruments, and Systems W5. Introduction to Signal Processing Sampling, Reconstruction, and Filters
 Signals, Instruments, and Systems W5 Introduction to Signal Processing Sampling, Reconstruction, and Filters Acknowledgments Recapitulation of Key Concepts from the Last Lecture Dirac delta function (
Signals, Instruments, and Systems W5 Introduction to Signal Processing Sampling, Reconstruction, and Filters Acknowledgments Recapitulation of Key Concepts from the Last Lecture Dirac delta function (
ENSC327 Communications Systems 2: Fourier Representations. School of Engineering Science Simon Fraser University
 ENSC37 Communications Systems : Fourier Representations School o Engineering Science Simon Fraser University Outline Chap..5: Signal Classiications Fourier Transorm Dirac Delta Function Unit Impulse Fourier
ENSC37 Communications Systems : Fourier Representations School o Engineering Science Simon Fraser University Outline Chap..5: Signal Classiications Fourier Transorm Dirac Delta Function Unit Impulse Fourier
Fourier Series. Spectral Analysis of Periodic Signals
 Fourier Series. Spectral Analysis of Periodic Signals he response of continuous-time linear invariant systems to the complex exponential with unitary magnitude response of a continuous-time LI system at
Fourier Series. Spectral Analysis of Periodic Signals he response of continuous-time linear invariant systems to the complex exponential with unitary magnitude response of a continuous-time LI system at
Module 24: Outline. Expt. 8: Part 2:Undriven RLC Circuits
 Module 24: Undriven RLC Circuits 1 Module 24: Outline Undriven RLC Circuits Expt. 8: Part 2:Undriven RLC Circuits 2 Circuits that Oscillate (LRC) 3 Mass on a Spring: Simple Harmonic Motion (Demonstration)
Module 24: Undriven RLC Circuits 1 Module 24: Outline Undriven RLC Circuits Expt. 8: Part 2:Undriven RLC Circuits 2 Circuits that Oscillate (LRC) 3 Mass on a Spring: Simple Harmonic Motion (Demonstration)
Randomly Modulated Periodic Signals
 Randomly Modulated Periodic Signals Melvin J. Hinich Applied Research Laboratories University of Texas at Austin hinich@mail.la.utexas.edu www.la.utexas.edu/~hinich Rotating Cylinder Data Fluid Nonlinearity
Randomly Modulated Periodic Signals Melvin J. Hinich Applied Research Laboratories University of Texas at Austin hinich@mail.la.utexas.edu www.la.utexas.edu/~hinich Rotating Cylinder Data Fluid Nonlinearity
Unstable Oscillations!
 Unstable Oscillations X( t ) = [ A 0 + A( t ) ] sin( ω t + Φ 0 + Φ( t ) ) Amplitude modulation: A( t ) Phase modulation: Φ( t ) S(ω) S(ω) Special case: C(ω) Unstable oscillation has a broader periodogram
Unstable Oscillations X( t ) = [ A 0 + A( t ) ] sin( ω t + Φ 0 + Φ( t ) ) Amplitude modulation: A( t ) Phase modulation: Φ( t ) S(ω) S(ω) Special case: C(ω) Unstable oscillation has a broader periodogram
Periodic functions: simple harmonic oscillator
 Periodic functions: simple harmonic oscillator Recall the simple harmonic oscillator (e.g. mass-spring system) d 2 y dt 2 + ω2 0y = 0 Solution can be written in various ways: y(t) = Ae iω 0t y(t) = A cos
Periodic functions: simple harmonic oscillator Recall the simple harmonic oscillator (e.g. mass-spring system) d 2 y dt 2 + ω2 0y = 0 Solution can be written in various ways: y(t) = Ae iω 0t y(t) = A cos
The Harmonic Oscillator
 The Harmonic Oscillator Math 4: Ordinary Differential Equations Chris Meyer May 3, 008 Introduction The harmonic oscillator is a common model used in physics because of the wide range of problems it can
The Harmonic Oscillator Math 4: Ordinary Differential Equations Chris Meyer May 3, 008 Introduction The harmonic oscillator is a common model used in physics because of the wide range of problems it can
Physics 11b Lecture #15
 Physics 11b ecture #15 and ircuits A ircuits S&J hapter 3 & 33 Administravia Midterm # is Thursday If you can t take midterm, you MUST let us (me, arol and Shaun) know in writing before Wednesday noon
Physics 11b ecture #15 and ircuits A ircuits S&J hapter 3 & 33 Administravia Midterm # is Thursday If you can t take midterm, you MUST let us (me, arol and Shaun) know in writing before Wednesday noon
Assignment 3 Solutions
 Assignment Solutions Networks and systems August 8, 7. Consider an LTI system with transfer function H(jw) = input is sin(t + π 4 ), what is the output? +jw. If the Solution : C For an LTI system with
Assignment Solutions Networks and systems August 8, 7. Consider an LTI system with transfer function H(jw) = input is sin(t + π 4 ), what is the output? +jw. If the Solution : C For an LTI system with
SIGNALS AND SYSTEMS: PAPER 3C1 HANDOUT 6. Dr Anil Kokaram Electronic and Electrical Engineering Dept.
 SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6. Dr Anil Kokaram Electronic and Electrical Engineering Dept. anil.kokaram@tcd.ie www.mee.tcd.ie/ sigmedia FOURIER ANALYSIS Have seen how the behaviour of systems
SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6. Dr Anil Kokaram Electronic and Electrical Engineering Dept. anil.kokaram@tcd.ie www.mee.tcd.ie/ sigmedia FOURIER ANALYSIS Have seen how the behaviour of systems
Frequency Response and Continuous-time Fourier Series
 Frequency Response and Continuous-time Fourier Series Recall course objectives Main Course Objective: Fundamentals of systems/signals interaction (we d like to understand how systems transform or affect
Frequency Response and Continuous-time Fourier Series Recall course objectives Main Course Objective: Fundamentals of systems/signals interaction (we d like to understand how systems transform or affect
Discrete-time Signals and Systems in
 Discrete-time Signals and Systems in the Frequency Domain Chapter 3, Sections 3.1-39 3.9 Chapter 4, Sections 4.8-4.9 Dr. Iyad Jafar Outline Introduction The Continuous-Time FourierTransform (CTFT) The
Discrete-time Signals and Systems in the Frequency Domain Chapter 3, Sections 3.1-39 3.9 Chapter 4, Sections 4.8-4.9 Dr. Iyad Jafar Outline Introduction The Continuous-Time FourierTransform (CTFT) The
Mathematical models for class-d amplifiers
 Mathematical models for class-d amplifiers Stephen Cox School of Mathematical Sciences, University of Nottingham, UK 12 November 2012 Stephen Cox Mathematical models for class-d amplifiers 1/38 Background
Mathematical models for class-d amplifiers Stephen Cox School of Mathematical Sciences, University of Nottingham, UK 12 November 2012 Stephen Cox Mathematical models for class-d amplifiers 1/38 Background
EAS 305 Random Processes Viewgraph 1 of 10. Random Processes
 EAS 305 Random Processes Viewgraph 1 of 10 Definitions: Random Processes A random process is a family of random variables indexed by a parameter t T, where T is called the index set λ i Experiment outcome
EAS 305 Random Processes Viewgraph 1 of 10 Definitions: Random Processes A random process is a family of random variables indexed by a parameter t T, where T is called the index set λ i Experiment outcome
2.161 Signal Processing: Continuous and Discrete
 MIT OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. M MASSACHUSETTS
MIT OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. M MASSACHUSETTS
EDISP (NWL2) (English) Digital Signal Processing Transform, FT, DFT. March 11, 2015
 EDISP (NWL2) (English) Digital Signal Processing Transform, FT, DFT March 11, 2015 Transform concept We want to analyze the signal represent it as built of some building blocks (well known signals), possibly
EDISP (NWL2) (English) Digital Signal Processing Transform, FT, DFT March 11, 2015 Transform concept We want to analyze the signal represent it as built of some building blocks (well known signals), possibly
5 Analog carrier modulation with noise
 5 Analog carrier modulation with noise 5. Noisy receiver model Assume that the modulated signal x(t) is passed through an additive White Gaussian noise channel. A noisy receiver model is illustrated in
5 Analog carrier modulation with noise 5. Noisy receiver model Assume that the modulated signal x(t) is passed through an additive White Gaussian noise channel. A noisy receiver model is illustrated in
EE 435. Lecture 30. Data Converters. Spectral Performance
 EE 435 Lecture 30 Data Converters Spectral Performance . Review from last lecture. INL Often Not a Good Measure of Linearity Four identical INL with dramatically different linearity X OUT X OUT X REF X
EE 435 Lecture 30 Data Converters Spectral Performance . Review from last lecture. INL Often Not a Good Measure of Linearity Four identical INL with dramatically different linearity X OUT X OUT X REF X
Wave Phenomena Physics 15c
 Wave Phenomena Physics 5c Lecture Fourier Analysis (H&L Sections 3. 4) (Georgi Chapter ) What We Did Last ime Studied reflection of mechanical waves Similar to reflection of electromagnetic waves Mechanical
Wave Phenomena Physics 5c Lecture Fourier Analysis (H&L Sections 3. 4) (Georgi Chapter ) What We Did Last ime Studied reflection of mechanical waves Similar to reflection of electromagnetic waves Mechanical
Signals and Systems Spring 2004 Lecture #9
 Signals and Systems Spring 2004 Lecture #9 (3/4/04). The convolution Property of the CTFT 2. Frequency Response and LTI Systems Revisited 3. Multiplication Property and Parseval s Relation 4. The DT Fourier
Signals and Systems Spring 2004 Lecture #9 (3/4/04). The convolution Property of the CTFT 2. Frequency Response and LTI Systems Revisited 3. Multiplication Property and Parseval s Relation 4. The DT Fourier
5. THE CLASSES OF FOURIER TRANSFORMS
 5. THE CLASSES OF FOURIER TRANSFORMS There are four classes of Fourier transform, which are represented in the following table. So far, we have concentrated on the discrete Fourier transform. Table 1.
5. THE CLASSES OF FOURIER TRANSFORMS There are four classes of Fourier transform, which are represented in the following table. So far, we have concentrated on the discrete Fourier transform. Table 1.
Basic Electronics. Introductory Lecture Course for. Technology and Instrumentation in Particle Physics Chicago, Illinois June 9-14, 2011
 Basic Electronics Introductory Lecture Course for Technology and Instrumentation in Particle Physics 2011 Chicago, Illinois June 9-14, 2011 Presented By Gary Drake Argonne National Laboratory Session 2
Basic Electronics Introductory Lecture Course for Technology and Instrumentation in Particle Physics 2011 Chicago, Illinois June 9-14, 2011 Presented By Gary Drake Argonne National Laboratory Session 2
Review of Frequency Domain Fourier Series: Continuous periodic frequency components
 Today we will review: Review of Frequency Domain Fourier series why we use it trig form & exponential form how to get coefficients for each form Eigenfunctions what they are how they relate to LTI systems
Today we will review: Review of Frequency Domain Fourier series why we use it trig form & exponential form how to get coefficients for each form Eigenfunctions what they are how they relate to LTI systems
L = 1 2 a(q) q2 V (q).
 Physics 3550, Fall 2011 Motion near equilibrium - Small Oscillations Relevant Sections in Text: 5.1 5.6 Motion near equilibrium 1 degree of freedom One of the most important situations in physics is motion
Physics 3550, Fall 2011 Motion near equilibrium - Small Oscillations Relevant Sections in Text: 5.1 5.6 Motion near equilibrium 1 degree of freedom One of the most important situations in physics is motion
Signals & Systems. Lecture 5 Continuous-Time Fourier Transform. Alp Ertürk
 Signals & Systems Lecture 5 Continuous-Time Fourier Transform Alp Ertürk alp.erturk@kocaeli.edu.tr Fourier Series Representation of Continuous-Time Periodic Signals Synthesis equation: x t = a k e jkω
Signals & Systems Lecture 5 Continuous-Time Fourier Transform Alp Ertürk alp.erturk@kocaeli.edu.tr Fourier Series Representation of Continuous-Time Periodic Signals Synthesis equation: x t = a k e jkω
Series FOURIER SERIES. Graham S McDonald. A self-contained Tutorial Module for learning the technique of Fourier series analysis
 Series FOURIER SERIES Graham S McDonald A self-contained Tutorial Module for learning the technique of Fourier series analysis Table of contents Begin Tutorial c 24 g.s.mcdonald@salford.ac.uk 1. Theory
Series FOURIER SERIES Graham S McDonald A self-contained Tutorial Module for learning the technique of Fourier series analysis Table of contents Begin Tutorial c 24 g.s.mcdonald@salford.ac.uk 1. Theory
The Laplace Transform
 The Laplace Transform Introduction There are two common approaches to the developing and understanding the Laplace transform It can be viewed as a generalization of the CTFT to include some signals with
The Laplace Transform Introduction There are two common approaches to the developing and understanding the Laplace transform It can be viewed as a generalization of the CTFT to include some signals with
Central to this is two linear transformations: the Fourier Transform and the Laplace Transform. Both will be considered in later lectures.
 In this second lecture, I will be considering signals from the frequency perspective. This is a complementary view of signals, that in the frequency domain, and is fundamental to the subject of signal
In this second lecture, I will be considering signals from the frequency perspective. This is a complementary view of signals, that in the frequency domain, and is fundamental to the subject of signal
Sinusoidal Modeling. Yannis Stylianou SPCC University of Crete, Computer Science Dept., Greece,
 Sinusoidal Modeling Yannis Stylianou University of Crete, Computer Science Dept., Greece, yannis@csd.uoc.gr SPCC 2016 1 Speech Production 2 Modulators 3 Sinusoidal Modeling Sinusoidal Models Voiced Speech
Sinusoidal Modeling Yannis Stylianou University of Crete, Computer Science Dept., Greece, yannis@csd.uoc.gr SPCC 2016 1 Speech Production 2 Modulators 3 Sinusoidal Modeling Sinusoidal Models Voiced Speech
Damped harmonic motion
 Damped harmonic motion March 3, 016 Harmonic motion is studied in the presence of a damping force proportional to the velocity. The complex method is introduced, and the different cases of under-damping,
Damped harmonic motion March 3, 016 Harmonic motion is studied in the presence of a damping force proportional to the velocity. The complex method is introduced, and the different cases of under-damping,
SOLVING DIFFERENTIAL EQUATIONS. Amir Asif. Department of Computer Science and Engineering York University, Toronto, ON M3J1P3
 SOLVING DIFFERENTIAL EQUATIONS Amir Asif Department of Computer Science and Engineering York University, Toronto, ON M3J1P3 ABSTRACT This article reviews a direct method for solving linear, constant-coefficient
SOLVING DIFFERENTIAL EQUATIONS Amir Asif Department of Computer Science and Engineering York University, Toronto, ON M3J1P3 ABSTRACT This article reviews a direct method for solving linear, constant-coefficient
Time-Frequency Analysis
 Time-Frequency Analysis Basics of Fourier Series Philippe B. aval KSU Fall 015 Philippe B. aval (KSU) Fourier Series Fall 015 1 / 0 Introduction We first review how to derive the Fourier series of a function.
Time-Frequency Analysis Basics of Fourier Series Philippe B. aval KSU Fall 015 Philippe B. aval (KSU) Fourier Series Fall 015 1 / 0 Introduction We first review how to derive the Fourier series of a function.
Basics of Electric Circuits
 António Dente Célia de Jesus February 2014 1 Alternating Current Circuits 1.1 Using Phasors There are practical and economic reasons justifying that electrical generators produce emf with alternating and
António Dente Célia de Jesus February 2014 1 Alternating Current Circuits 1.1 Using Phasors There are practical and economic reasons justifying that electrical generators produce emf with alternating and
GUIDELINES FOR THE METHOD OF UNDETERMINED COEFFICIENTS
 GUIDELINES FOR THE METHOD OF UNDETERMINED COEFFICIENTS Given a constant coefficient linear differential equation a + by + cy = g(t), where g is an exponential, a simple sinusoidal function, a polynomial,
GUIDELINES FOR THE METHOD OF UNDETERMINED COEFFICIENTS Given a constant coefficient linear differential equation a + by + cy = g(t), where g is an exponential, a simple sinusoidal function, a polynomial,
Complex symmetry Signals and Systems Fall 2015
 18-90 Signals and Systems Fall 015 Complex symmetry 1. Complex symmetry This section deals with the complex symmetry property. As an example I will use the DTFT for a aperiodic discrete-time signal. The
18-90 Signals and Systems Fall 015 Complex symmetry 1. Complex symmetry This section deals with the complex symmetry property. As an example I will use the DTFT for a aperiodic discrete-time signal. The
The Pendulum Plain and Puzzling
 The Pendulum Plain and Puzzling Chris Sangwin School of Mathematics University of Edinburgh April 2017 Chris Sangwin (University of Edinburgh) Pendulum April 2017 1 / 38 Outline 1 Introduction and motivation
The Pendulum Plain and Puzzling Chris Sangwin School of Mathematics University of Edinburgh April 2017 Chris Sangwin (University of Edinburgh) Pendulum April 2017 1 / 38 Outline 1 Introduction and motivation
Fourier series. XE31EO2 - Pavel Máša. Electrical Circuits 2 Lecture1. XE31EO2 - Pavel Máša - Fourier Series
 Fourier series Electrical Circuits Lecture - Fourier Series Filtr RLC defibrillator MOTIVATION WHAT WE CAN'T EXPLAIN YET Source voltage rectangular waveform Resistor voltage sinusoidal waveform - Fourier
Fourier series Electrical Circuits Lecture - Fourier Series Filtr RLC defibrillator MOTIVATION WHAT WE CAN'T EXPLAIN YET Source voltage rectangular waveform Resistor voltage sinusoidal waveform - Fourier
Chapter 16 Waves. Types of waves Mechanical waves. Electromagnetic waves. Matter waves
 Chapter 16 Waves Types of waves Mechanical waves exist only within a material medium. e.g. water waves, sound waves, etc. Electromagnetic waves require no material medium to exist. e.g. light, radio, microwaves,
Chapter 16 Waves Types of waves Mechanical waves exist only within a material medium. e.g. water waves, sound waves, etc. Electromagnetic waves require no material medium to exist. e.g. light, radio, microwaves,
ECE 3084 QUIZ 2 SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING GEORGIA INSTITUTE OF TECHNOLOGY APRIL 2, Name:
 ECE 3084 QUIZ 2 SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING GEORGIA INSTITUTE OF TECHNOLOGY APRIL 2, 205 Name:. The quiz is closed book, except for one 2-sided sheet of handwritten notes. 2. Turn off
ECE 3084 QUIZ 2 SCHOOL OF ELECTRICAL AND COMPUTER ENGINEERING GEORGIA INSTITUTE OF TECHNOLOGY APRIL 2, 205 Name:. The quiz is closed book, except for one 2-sided sheet of handwritten notes. 2. Turn off
1.3 Sinusoidal Steady State
 1.3 Sinusoidal Steady State Electromagnetics applications can be divided into two broad classes: Time-domain: Excitation is not sinusoidal (pulsed, broadband, etc.) Ultrawideband communications Pulsed
1.3 Sinusoidal Steady State Electromagnetics applications can be divided into two broad classes: Time-domain: Excitation is not sinusoidal (pulsed, broadband, etc.) Ultrawideband communications Pulsed
2.3 Oscillation. The harmonic oscillator equation is the differential equation. d 2 y dt 2 r y (r > 0). Its solutions have the form
 2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
Oscillations. Simple Harmonic Motion of a Mass on a Spring The equation of motion for a mass m is attached to a spring of constant k is
 Dr. Alain Brizard College Physics I (PY 10) Oscillations Textbook Reference: Chapter 14 sections 1-8. Simple Harmonic Motion of a Mass on a Spring The equation of motion for a mass m is attached to a spring
Dr. Alain Brizard College Physics I (PY 10) Oscillations Textbook Reference: Chapter 14 sections 1-8. Simple Harmonic Motion of a Mass on a Spring The equation of motion for a mass m is attached to a spring
Frequency Response. Re ve jφ e jωt ( ) where v is the amplitude and φ is the phase of the sinusoidal signal v(t). ve jφ
 27 Frequency Response Before starting, review phasor analysis, Bode plots... Key concept: small-signal models for amplifiers are linear and therefore, cosines and sines are solutions of the linear differential
27 Frequency Response Before starting, review phasor analysis, Bode plots... Key concept: small-signal models for amplifiers are linear and therefore, cosines and sines are solutions of the linear differential
4.1 Introduction. 2πδ ω (4.2) Applications of Fourier Representations to Mixed Signal Classes = (4.1)
 4.1 Introduction Two cases of mixed signals to be studied in this chapter: 1. Periodic and nonperiodic signals 2. Continuous- and discrete-time signals Other descriptions: Refer to pp. 341-342, textbook.
4.1 Introduction Two cases of mixed signals to be studied in this chapter: 1. Periodic and nonperiodic signals 2. Continuous- and discrete-time signals Other descriptions: Refer to pp. 341-342, textbook.
Module 4. Single-phase AC Circuits
 Module 4 Single-phase AC Circuits Lesson 14 Solution of Current in R-L-C Series Circuits In the last lesson, two points were described: 1. How to represent a sinusoidal (ac) quantity, i.e. voltage/current
Module 4 Single-phase AC Circuits Lesson 14 Solution of Current in R-L-C Series Circuits In the last lesson, two points were described: 1. How to represent a sinusoidal (ac) quantity, i.e. voltage/current
A system that is both linear and time-invariant is called linear time-invariant (LTI).
 The Cooper Union Department of Electrical Engineering ECE111 Signal Processing & Systems Analysis Lecture Notes: Time, Frequency & Transform Domains February 28, 2012 Signals & Systems Signals are mapped
The Cooper Union Department of Electrical Engineering ECE111 Signal Processing & Systems Analysis Lecture Notes: Time, Frequency & Transform Domains February 28, 2012 Signals & Systems Signals are mapped
a k cos kω 0 t + b k sin kω 0 t (1) k=1
 MOAC worksheet Fourier series, Fourier transform, & Sampling Working through the following exercises you will glean a quick overview/review of a few essential ideas that you will need in the moac course.
MOAC worksheet Fourier series, Fourier transform, & Sampling Working through the following exercises you will glean a quick overview/review of a few essential ideas that you will need in the moac course.
CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation
 CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 26, 2005 1 Sinusoids Sinusoids
CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 26, 2005 1 Sinusoids Sinusoids
EE 435. Lecture 29. Data Converters. Linearity Measures Spectral Performance
 EE 435 Lecture 9 Data Converters Linearity Measures Spectral Performance Linearity Measurements (testing) Consider ADC V IN (t) DUT X IOUT V REF Linearity testing often based upon code density testing
EE 435 Lecture 9 Data Converters Linearity Measures Spectral Performance Linearity Measurements (testing) Consider ADC V IN (t) DUT X IOUT V REF Linearity testing often based upon code density testing
ECS332: Midterm Examination (Set I) Seat
 Sirindhorn International Institute of Technology Thammasat University at Rangsit School of Information, Computer and Communication Technology ECS33: Midterm Examination (Set I) COURSE : ECS33 (Principles
Sirindhorn International Institute of Technology Thammasat University at Rangsit School of Information, Computer and Communication Technology ECS33: Midterm Examination (Set I) COURSE : ECS33 (Principles
3 Chemical exchange and the McConnell Equations
 3 Chemical exchange and the McConnell Equations NMR is a technique which is well suited to study dynamic processes, such as the rates of chemical reactions. The time window which can be investigated in
3 Chemical exchange and the McConnell Equations NMR is a technique which is well suited to study dynamic processes, such as the rates of chemical reactions. The time window which can be investigated in
Laplace Transforms and use in Automatic Control
 Laplace Transforms and use in Automatic Control P.S. Gandhi Mechanical Engineering IIT Bombay Acknowledgements: P.Santosh Krishna, SYSCON Recap Fourier series Fourier transform: aperiodic Convolution integral
Laplace Transforms and use in Automatic Control P.S. Gandhi Mechanical Engineering IIT Bombay Acknowledgements: P.Santosh Krishna, SYSCON Recap Fourier series Fourier transform: aperiodic Convolution integral
First and Second Order Circuits. Claudio Talarico, Gonzaga University Spring 2015
 First and Second Order Circuits Claudio Talarico, Gonzaga University Spring 2015 Capacitors and Inductors intuition: bucket of charge q = Cv i = C dv dt Resist change of voltage DC open circuit Store voltage
First and Second Order Circuits Claudio Talarico, Gonzaga University Spring 2015 Capacitors and Inductors intuition: bucket of charge q = Cv i = C dv dt Resist change of voltage DC open circuit Store voltage
EE 505 Lecture 10. Spectral Characterization. Part 2 of 2
 EE 505 Lecture 10 Spectral Characterization Part 2 of 2 Review from last lecture Spectral Analysis If f(t) is periodic f(t) alternately f(t) = = A A ( kω t + ) 0 + Aksin θk k= 1 0 + a ksin t k= 1 k= 1
EE 505 Lecture 10 Spectral Characterization Part 2 of 2 Review from last lecture Spectral Analysis If f(t) is periodic f(t) alternately f(t) = = A A ( kω t + ) 0 + Aksin θk k= 1 0 + a ksin t k= 1 k= 1
Chapter 33. Alternating Current Circuits
 Chapter 33 Alternating Current Circuits 1 Capacitor Resistor + Q = C V = I R R I + + Inductance d I Vab = L dt AC power source The AC power source provides an alternative voltage, Notation - Lower case
Chapter 33 Alternating Current Circuits 1 Capacitor Resistor + Q = C V = I R R I + + Inductance d I Vab = L dt AC power source The AC power source provides an alternative voltage, Notation - Lower case
Answers to Problem Set Number MIT (Fall 2005).
 Answers to Problem Set Number 6. 18.305 MIT (Fall 2005). D. Margetis and R. Rosales (MIT, Math. Dept., Cambridge, MA 02139). December 12, 2005. Course TA: Nikos Savva, MIT, Dept. of Mathematics, Cambridge,
Answers to Problem Set Number 6. 18.305 MIT (Fall 2005). D. Margetis and R. Rosales (MIT, Math. Dept., Cambridge, MA 02139). December 12, 2005. Course TA: Nikos Savva, MIT, Dept. of Mathematics, Cambridge,
The Laplace Transform
 The Laplace Transform Generalizing the Fourier Transform The CTFT expresses a time-domain signal as a linear combination of complex sinusoids of the form e jωt. In the generalization of the CTFT to the
The Laplace Transform Generalizing the Fourier Transform The CTFT expresses a time-domain signal as a linear combination of complex sinusoids of the form e jωt. In the generalization of the CTFT to the
Lectures on Spectra of Continuous-Time Signals
 Lectures on Spectra of Continuous-Time Signals Principal questions to be addressed:. What, in a general sense, is the "spectrum" of a signal? 2. Why are we interested in spectra? ("spectra" = plural of
Lectures on Spectra of Continuous-Time Signals Principal questions to be addressed:. What, in a general sense, is the "spectrum" of a signal? 2. Why are we interested in spectra? ("spectra" = plural of
Dispersion (3A) 1-D Dispersion. Young W. Lim 10/15/13
 1-D Dispersion Copyright (c) 013. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1. or any later version published
1-D Dispersion Copyright (c) 013. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1. or any later version published
Problem Value
 GEORGIA INSTITUTE OF TECHNOLOGY SCHOOL of ELECTRICAL & COMPUTER ENGINEERING FINAL EXAM DATE: 30-Apr-04 COURSE: ECE-2025 NAME: GT #: LAST, FIRST Recitation Section: Circle the date & time when your Recitation
GEORGIA INSTITUTE OF TECHNOLOGY SCHOOL of ELECTRICAL & COMPUTER ENGINEERING FINAL EXAM DATE: 30-Apr-04 COURSE: ECE-2025 NAME: GT #: LAST, FIRST Recitation Section: Circle the date & time when your Recitation
