Fourier Series and Fourier Transforms
|
|
|
- Nora Francis
- 5 years ago
- Views:
Transcription
1 Fourier Series and Fourier Transforms EECS2 (6.082), MIT Fall 2006 Lectures 2 and 3
2 Fourier Series From your differential equations course, 18.03, you know Fourier s expression representing a T -periodic time function x(t) as an infinite sum of sines and cosines at the fundamental frequency and its harmonics, plus a constant term equal to the average value of the time function over a period: x(t) = a 0 + where n=1 a n cos(nω 0 t)+b n sin(nω 0 t) (1) ω 0 = 2π T a 0 = 1 T and for integer n > 0 a n = 2 T b n = 2 T T/2 x(t) dt (2) T/2 x(t) cos(nω 0t) dt (3) T/2 x(t) sin(nω 0t) dt (4) 1
3 Some comments on symmetries 1. The integrals could have been taken over any interval of length T, but the symmetric interval [ T 2, T 2 ] is most convenient for us. 2. Note from the defining expressions that if x(t) is an even function of t, i.e., if x( t) = x(t), then b n = 0 for all n > 0, so only cosine terms appear in the Fourier series. Similarly, if x(t) is an odd function of t, i.e., if x( t) = x(t), then a n = 0 for all n 0, so only sine terms appear in the Fourier series. 2
4 Recall some useful trigonometric identities cos( p) = cos p sin( p) = sin p cos(p + q) = cos p cos q sin p sin q sin(p + q) = sin p cos q + cos p sin q The latter two are most easily derived from Euler s identity: where j = 1. e jθ = cos θ + j sin θ From the cosine-sum and sine-sum identities above, various other identities can be derived, e.g., 2 cos p cos q = cos(p + q) + cos(p q) 2 sin p sin q = cos(p q) cos(p + q) 2 sin p cos q = sin(p + q) + sin(p q) 3
5 Example 1 (sanity check) Suppose x(t) = K cos ω 0 t, with ω 0 > 0. Then a 1 = 2 T T/2 K cos2 (ω 0 t) dt = K while all other a n and all b n are 0. So the Fourier series for x(t) is simply K cos ω 0 t, as it should be! Similarly, the Fourier series for x(t) = K sin(ω 0 t) is just this expression itself. 4
6 Example 2 (magnitude and phase) Suppose x(t) = a cos(ω 0 t) + b sin(ω 0 t), with ω 0 > 0. This evidently is periodic with period T = 2π/ω 0, and its Fourier series will be the same expression again. But there s an alternative representation that yields a bit more insight: Rewrite x(t) as ( x(t) = a 2 + b 2 a cos(ω 0t) + a 2 +b 2 and let so θ = arctan a = cos θ, a 2 + b 2 b a 2 +b 2 sin(ω 0t) ( ) b a ) b = sin θ a 2 + b
7 Example 2 (continued) (Construct for yourself a right-angled triangle that displays the preceding relations among a, b, and θ.) Our previous expression for x(t) then becomes ( x(t) = a 2 + b 2 cos θ cos(ω 0 t) + sin θ sin(ω 0 t) = c cos(ω 0 t θ) ) where c = a 2 + b 2 So adding a cosine and a sine of the same frequency, but possibly different amplitudes, yields (perhaps surprisingly) a pure sinusoid again, with magnitude and phase as specified above. We refer to the cosine and sine as having added in quadrature, because the two are displaced from each other by 90 degrees (π/2 radians). 6
8 Magnitude/phase form of Fourier series The transformation carried out on the x(t) in the previous example can be equally well applied to a typical term of the Fourier series in (1), to obtain = a n cos(nω 0 t) + b n sin(nω 0 t) ( a 2 n + b2 a n n b n a 2 n +b 2 n a 2 n +b 2 cos(nω 0 t) + n ) sin(nω 0 t) Letting and ( ) bn θ n = arctan a n c n = a 2 n + b2 n for n 0 (with c 0 = a 0 and θ 0 = 0), we get the following alternate form of (1) for a T -periodic function x(t): x(t) = n=0 c n cos(nω 0 t θ n ) (5) 7
9 A two-sided Fourier series It is convenient for many purposes to rewrite the Fourier series in yet another form, allowing both positive and negative multiples of the fundamental frequency. To obtain such a twosided representation, note that a n cos nω 0 t = a n 2 cos nω 0t + a n 2 cos n( ω 0)t b n sin nω 0 t = b n 2 sin nω 0t b n 2 sin n( ω 0)t Now for all integer n (negative, zero, and positive) define A n = 1 T B n = 1 T T/2 x(t) cos nω 0t dt (6) T/2 x(t) sin nω 0t dt (7) (The minus sign preceding the integral in the definition of B n serves to make our notation consistent with the notation that is widely used in engineering.)... 8
10 Two-sided Fourier series (continued) From the preceding definitions, we conclude that A 0 = a 0, and for n > 0 A n = a n 2 = A n B n = b n 2 = B n With these definitions, the Fourier series for a T -periodic function x(t) can be written in the form x(t) = n= A n cos nω 0 t B n sin nω 0 t (8) Note that the summation now runs symmetrically over all integer n (negative, zero, and positive), corresponding to terms at all integer multiples of the fundamental frequency. 9
11 Magnitude/phase form of two-sided series By defining and θ n = arctan X n = ( ) Bn A n A 2 n + B 2 n we can write A n = X n cos θ n, B n = X n sin θ n Using the now familiar procedure, we can use the preceding relations to rewrite the two-sided series in magnitude/phase form as x(t) = n= X n cos(nω 0 t + θ n ) 10
12 A step further Let s go a small step beyond where you left off in 18.03: If x(t) = a n cos(nω 0 t), then the average value of x 2 (t) over a period the mean square value of x(t) is 1 T T/2 x2 (t) dt = 1 T = a2 n 2 T/2 a2 n cos2 (nω 0 t) dt Extending this kind of calculation in a straightforward way, and invoking the standard trigonometric identities listed earlier, produces the various equivalent expressions shown on the next slide for the mean square value of a general periodic x(t)
13 Parseval s theorem The mean square value of a T -periodic signal x(t) is given in terms of its Fourier series coefficients by the following expressions: 1 T = a = c = = T/2 x2 (t) dt n= Xn 2 n= n=1 c 2 n n=1 (a 2 n + b2 n ) (A 2 n + B2 n ) 12
14 Some consequences of Parseval s 1. The mean square value of x(t) is finite (for all cases of interest to us), so the infinite sums on the previous slide are all finite, which must mean that the Fourier coefficients all decay to 0 as n in particular, X n It is often useful or necessary to approximate x(t) by a finite number of terms from its Fourier series, for instance by x N (t) = N n= N X n cos(nω 0 t + θ n ) Note that the highest frequency in this approximating signal is Nω 0. The mean square error in this case is 1 T/2 ( ) 2 x(t) x N (t) dt = Xn 2 T T/2 n >N 13
15 Complex notation for compact expressions Recall x(t) = n= A n cos nω 0 t B n sin nω 0 t where A n and B n are specified by the integrals in (6), (7). Defining so X n = A n + jb n = X n e jθ n X n = 1 T T/2 x(t)e jnω 0t dt (9) allows us to rewrite the expression for x(t) as x(t) = n= X n e jnω 0t (10) (The reason the imaginary part of the sum drops out is that A n = A n and B n = B n.) Equations (9) and (10) comprise the complex form of the Fourier series representation for a T -periodic signal. 14
16 Non-periodic signals: to Fourier transforms From Fourier series We are often interested in non-periodic signals, for instance an x(t) of finite duration, or one that decays to 0 as t. The signals of interest to us typically satisfy x(t) dt < or x(t) 2 dt < We can consider such signals to have an infinite period, and can obtain a Fourier representation by taking the limit T, ω 0 dω, nω 0 = n 2π T ω, T X n X(ω) with summations suitably replaced by integrals. The resulting X(ω) is termed the Fourier transform of x(t)
17 The Fourier transform The resulting expressions replace (10) and (9) respectively by and x(t) = 1 2π X(ω) = X(ω)e jωt dω (11) x(t)e jωt dt (12) The first of this pair of equations, (11), is the Fourier synthesis equation, showing how a general time function may be expressed as a weighted combination of exponentials of all frequencies ω; the Fourier transform X(ω) determines the weighting. The second of this pair of equations, (12), is the Fourier analysis equation, showing how to compute the Fourier transform from the signal. 16
18 Some additional observations Remember that X(ω) is in general a complex number at each ω, even though x(t) is real reflecting the earlier definition X n = A n + jb n. We shall denote the real and imaginary parts of X(ω) by A(ω) and B(ω) respectively, so X(ω) = A(ω) + jb(ω) We shall denote the magnitude and angle of X(ω) by X(ω) and θ X (ω) respectively, so X(ω) = X(ω) X(ω) = θ X (ω) Thus X(ω) = X(ω)e jθ X(ω) 17
CHAPTER 4 FOURIER SERIES S A B A R I N A I S M A I L
 CHAPTER 4 FOURIER SERIES 1 S A B A R I N A I S M A I L Outline Introduction of the Fourier series. The properties of the Fourier series. Symmetry consideration Application of the Fourier series to circuit
CHAPTER 4 FOURIER SERIES 1 S A B A R I N A I S M A I L Outline Introduction of the Fourier series. The properties of the Fourier series. Symmetry consideration Application of the Fourier series to circuit
Chapter 4 The Fourier Series and Fourier Transform
 Chapter 4 The Fourier Series and Fourier Transform Representation of Signals in Terms of Frequency Components Consider the CT signal defined by N xt () = Acos( ω t+ θ ), t k = 1 k k k The frequencies `present
Chapter 4 The Fourier Series and Fourier Transform Representation of Signals in Terms of Frequency Components Consider the CT signal defined by N xt () = Acos( ω t+ θ ), t k = 1 k k k The frequencies `present
Chapter 4 The Fourier Series and Fourier Transform
 Chapter 4 The Fourier Series and Fourier Transform Fourier Series Representation of Periodic Signals Let x(t) be a CT periodic signal with period T, i.e., xt ( + T) = xt ( ), t R Example: the rectangular
Chapter 4 The Fourier Series and Fourier Transform Fourier Series Representation of Periodic Signals Let x(t) be a CT periodic signal with period T, i.e., xt ( + T) = xt ( ), t R Example: the rectangular
CMPT 318: Lecture 5 Complex Exponentials, Spectrum Representation
 CMPT 318: Lecture 5 Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University January 23, 2006 1 Exponentials The exponential is
CMPT 318: Lecture 5 Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University January 23, 2006 1 Exponentials The exponential is
The Fourier Transform (and more )
 The Fourier Transform (and more ) imrod Peleg ov. 5 Outline Introduce Fourier series and transforms Introduce Discrete Time Fourier Transforms, (DTFT) Introduce Discrete Fourier Transforms (DFT) Consider
The Fourier Transform (and more ) imrod Peleg ov. 5 Outline Introduce Fourier series and transforms Introduce Discrete Time Fourier Transforms, (DTFT) Introduce Discrete Fourier Transforms (DFT) Consider
IB Paper 6: Signal and Data Analysis
 IB Paper 6: Signal and Data Analysis Handout 2: Fourier Series S Godsill Signal Processing and Communications Group, Engineering Department, Cambridge, UK Lent 2015 1 / 1 Fourier Series Revision of Basics
IB Paper 6: Signal and Data Analysis Handout 2: Fourier Series S Godsill Signal Processing and Communications Group, Engineering Department, Cambridge, UK Lent 2015 1 / 1 Fourier Series Revision of Basics
Amplitude and Phase A(0) 2. We start with the Fourier series representation of X(t) in real notation: n=1
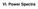 VI. Power Spectra Amplitude and Phase We start with the Fourier series representation of X(t) in real notation: A() X(t) = + [ A(n) cos(nωt) + B(n) sin(nωt)] 2 n=1 he waveform of the observed segment exactly
VI. Power Spectra Amplitude and Phase We start with the Fourier series representation of X(t) in real notation: A() X(t) = + [ A(n) cos(nωt) + B(n) sin(nωt)] 2 n=1 he waveform of the observed segment exactly
a k cos kω 0 t + b k sin kω 0 t (1) k=1
 MOAC worksheet Fourier series, Fourier transform, & Sampling Working through the following exercises you will glean a quick overview/review of a few essential ideas that you will need in the moac course.
MOAC worksheet Fourier series, Fourier transform, & Sampling Working through the following exercises you will glean a quick overview/review of a few essential ideas that you will need in the moac course.
CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation
 CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 26, 2005 1 Sinusoids Sinusoids
CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 26, 2005 1 Sinusoids Sinusoids
Lecture 27 Frequency Response 2
 Lecture 27 Frequency Response 2 Fundamentals of Digital Signal Processing Spring, 2012 Wei-Ta Chu 2012/6/12 1 Application of Ideal Filters Suppose we can generate a square wave with a fundamental period
Lecture 27 Frequency Response 2 Fundamentals of Digital Signal Processing Spring, 2012 Wei-Ta Chu 2012/6/12 1 Application of Ideal Filters Suppose we can generate a square wave with a fundamental period
Assignment 3 Solutions
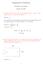 Assignment Solutions Networks and systems August 8, 7. Consider an LTI system with transfer function H(jw) = input is sin(t + π 4 ), what is the output? +jw. If the Solution : C For an LTI system with
Assignment Solutions Networks and systems August 8, 7. Consider an LTI system with transfer function H(jw) = input is sin(t + π 4 ), what is the output? +jw. If the Solution : C For an LTI system with
Review of Linear Time-Invariant Network Analysis
 D1 APPENDIX D Review of Linear Time-Invariant Network Analysis Consider a network with input x(t) and output y(t) as shown in Figure D-1. If an input x 1 (t) produces an output y 1 (t), and an input x
D1 APPENDIX D Review of Linear Time-Invariant Network Analysis Consider a network with input x(t) and output y(t) as shown in Figure D-1. If an input x 1 (t) produces an output y 1 (t), and an input x
Properties of Fourier Series - GATE Study Material in PDF
 Properties of Fourier Series - GAE Study Material in PDF In the previous article, we learnt the Basics of Fourier Series, the different types and all about the different Fourier Series spectrums. Now,
Properties of Fourier Series - GAE Study Material in PDF In the previous article, we learnt the Basics of Fourier Series, the different types and all about the different Fourier Series spectrums. Now,
Sinusoids. Amplitude and Magnitude. Phase and Period. CMPT 889: Lecture 2 Sinusoids, Complex Exponentials, Spectrum Representation
 Sinusoids CMPT 889: Lecture Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 6, 005 Sinusoids are
Sinusoids CMPT 889: Lecture Sinusoids, Complex Exponentials, Spectrum Representation Tamara Smyth, tamaras@cs.sfu.ca School of Computing Science, Simon Fraser University September 6, 005 Sinusoids are
Review of Discrete-Time System
 Review of Discrete-Time System Electrical & Computer Engineering University of Maryland, College Park Acknowledgment: ENEE630 slides were based on class notes developed by Profs. K.J. Ray Liu and Min Wu.
Review of Discrete-Time System Electrical & Computer Engineering University of Maryland, College Park Acknowledgment: ENEE630 slides were based on class notes developed by Profs. K.J. Ray Liu and Min Wu.
DSP-I DSP-I DSP-I DSP-I
 NOTES FOR 8-79 LECTURES 3 and 4 Introduction to Discrete-Time Fourier Transforms (DTFTs Distributed: September 8, 2005 Notes: This handout contains in brief outline form the lecture notes used for 8-79
NOTES FOR 8-79 LECTURES 3 and 4 Introduction to Discrete-Time Fourier Transforms (DTFTs Distributed: September 8, 2005 Notes: This handout contains in brief outline form the lecture notes used for 8-79
ω 0 = 2π/T 0 is called the fundamental angular frequency and ω 2 = 2ω 0 is called the
 he ime-frequency Concept []. Review of Fourier Series Consider the following set of time functions {3A sin t, A sin t}. We can represent these functions in different ways by plotting the amplitude versus
he ime-frequency Concept []. Review of Fourier Series Consider the following set of time functions {3A sin t, A sin t}. We can represent these functions in different ways by plotting the amplitude versus
16.362: Signals and Systems: 1.0
 16.362: Signals and Systems: 1.0 Prof. K. Chandra ECE, UMASS Lowell September 1, 2016 1 Background The pre-requisites for this course are Calculus II and Differential Equations. A basic understanding of
16.362: Signals and Systems: 1.0 Prof. K. Chandra ECE, UMASS Lowell September 1, 2016 1 Background The pre-requisites for this course are Calculus II and Differential Equations. A basic understanding of
Signals, Systems, and Society. By: Carlos E. Davila
 Signals, Systems, and Society By: Carlos E. Davila Signals, Systems, and Society By: Carlos E. Davila Online: < http://cnx.org/content/col965/.5/ > C O N N E X I O N S Rice University, Houston, Texas
Signals, Systems, and Society By: Carlos E. Davila Signals, Systems, and Society By: Carlos E. Davila Online: < http://cnx.org/content/col965/.5/ > C O N N E X I O N S Rice University, Houston, Texas
PS403 - Digital Signal processing
 PS403 - Digital Signal processing III. DSP - Digital Fourier Series and Transforms Key Text: Digital Signal Processing with Computer Applications (2 nd Ed.) Paul A Lynn and Wolfgang Fuerst, (Publisher:
PS403 - Digital Signal processing III. DSP - Digital Fourier Series and Transforms Key Text: Digital Signal Processing with Computer Applications (2 nd Ed.) Paul A Lynn and Wolfgang Fuerst, (Publisher:
EA2.3 - Electronics 2 1
 In the previous lecture, I talked about the idea of complex frequency s, where s = σ + jω. Using such concept of complex frequency allows us to analyse signals and systems with better generality. In this
In the previous lecture, I talked about the idea of complex frequency s, where s = σ + jω. Using such concept of complex frequency allows us to analyse signals and systems with better generality. In this
3 What You Should Know About Complex Numbers
 3 What You Should Know About Complex Numbers Life is complex it has a real part, and an imaginary part Andrew Koenig. Complex numbers are an extension of the more familiar world of real numbers that make
3 What You Should Know About Complex Numbers Life is complex it has a real part, and an imaginary part Andrew Koenig. Complex numbers are an extension of the more familiar world of real numbers that make
LECTURE 12 Sections Introduction to the Fourier series of periodic signals
 Signals and Systems I Wednesday, February 11, 29 LECURE 12 Sections 3.1-3.3 Introduction to the Fourier series of periodic signals Chapter 3: Fourier Series of periodic signals 3. Introduction 3.1 Historical
Signals and Systems I Wednesday, February 11, 29 LECURE 12 Sections 3.1-3.3 Introduction to the Fourier series of periodic signals Chapter 3: Fourier Series of periodic signals 3. Introduction 3.1 Historical
SIGNALS AND SYSTEMS: PAPER 3C1 HANDOUT 6. Dr Anil Kokaram Electronic and Electrical Engineering Dept.
 SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6. Dr Anil Kokaram Electronic and Electrical Engineering Dept. anil.kokaram@tcd.ie www.mee.tcd.ie/ sigmedia FOURIER ANALYSIS Have seen how the behaviour of systems
SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6. Dr Anil Kokaram Electronic and Electrical Engineering Dept. anil.kokaram@tcd.ie www.mee.tcd.ie/ sigmedia FOURIER ANALYSIS Have seen how the behaviour of systems
SIGNALS AND SYSTEMS: PAPER 3C1 HANDOUT 6a. Dr David Corrigan 1. Electronic and Electrical Engineering Dept.
 SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6a. Dr David Corrigan. Electronic and Electrical Engineering Dept. corrigad@tcd.ie www.mee.tcd.ie/ corrigad FOURIER SERIES Have seen how the behaviour of systems can
SIGNALS AND SYSTEMS: PAPER 3C HANDOUT 6a. Dr David Corrigan. Electronic and Electrical Engineering Dept. corrigad@tcd.ie www.mee.tcd.ie/ corrigad FOURIER SERIES Have seen how the behaviour of systems can
Signals and Systems Lecture (S2) Orthogonal Functions and Fourier Series March 17, 2008
 Signals and Systems Lecture (S) Orthogonal Functions and Fourier Series March 17, 008 Today s Topics 1. Analogy between functions of time and vectors. Fourier series Take Away Periodic complex exponentials
Signals and Systems Lecture (S) Orthogonal Functions and Fourier Series March 17, 008 Today s Topics 1. Analogy between functions of time and vectors. Fourier series Take Away Periodic complex exponentials
Lecture 7 ELE 301: Signals and Systems
 Lecture 7 ELE 30: Signals and Systems Prof. Paul Cuff Princeton University Fall 20-2 Cuff (Lecture 7) ELE 30: Signals and Systems Fall 20-2 / 22 Introduction to Fourier Transforms Fourier transform as
Lecture 7 ELE 30: Signals and Systems Prof. Paul Cuff Princeton University Fall 20-2 Cuff (Lecture 7) ELE 30: Signals and Systems Fall 20-2 / 22 Introduction to Fourier Transforms Fourier transform as
Music 270a: Complex Exponentials and Spectrum Representation
 Music 270a: Complex Exponentials and Spectrum Representation Tamara Smyth, trsmyth@ucsd.edu Department of Music, University of California, San Diego (UCSD) October 24, 2016 1 Exponentials The exponential
Music 270a: Complex Exponentials and Spectrum Representation Tamara Smyth, trsmyth@ucsd.edu Department of Music, University of California, San Diego (UCSD) October 24, 2016 1 Exponentials The exponential
Phasor mathematics. Resources and methods for learning about these subjects (list a few here, in preparation for your research):
 Phasor mathematics This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Phasor mathematics This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
Fourier Analysis and Spectral Representation of Signals
 MIT 6.02 DRAFT Lecture Notes Last update: April 11, 2012 Comments, questions or bug reports? Please contact verghese at mit.edu CHAPTER 13 Fourier Analysis and Spectral Representation of Signals We have
MIT 6.02 DRAFT Lecture Notes Last update: April 11, 2012 Comments, questions or bug reports? Please contact verghese at mit.edu CHAPTER 13 Fourier Analysis and Spectral Representation of Signals We have
2 Fourier Transforms and Sampling
 2 Fourier ransforms and Sampling 2.1 he Fourier ransform he Fourier ransform is an integral operator that transforms a continuous function into a continuous function H(ω) =F t ω [h(t)] := h(t)e iωt dt
2 Fourier ransforms and Sampling 2.1 he Fourier ransform he Fourier ransform is an integral operator that transforms a continuous function into a continuous function H(ω) =F t ω [h(t)] := h(t)e iωt dt
Fourier Transform. Find the Fourier series for a periodic waveform Determine the output of a filter when the input is a periodic function
 Objectives: Be able to Fourier Transform Find the Fourier series for a periodic waveform Determine the output of a filter when the input is a periodic function Filters with a Single Sinusoidal Input: Suppose
Objectives: Be able to Fourier Transform Find the Fourier series for a periodic waveform Determine the output of a filter when the input is a periodic function Filters with a Single Sinusoidal Input: Suppose
Mathematical Review for Signal and Systems
 Mathematical Review for Signal and Systems 1 Trigonometric Identities It will be useful to memorize sin θ, cos θ, tan θ values for θ = 0, π/3, π/4, π/ and π ±θ, π θ for the above values of θ. The following
Mathematical Review for Signal and Systems 1 Trigonometric Identities It will be useful to memorize sin θ, cos θ, tan θ values for θ = 0, π/3, π/4, π/ and π ±θ, π θ for the above values of θ. The following
23.6. The Complex Form. Introduction. Prerequisites. Learning Outcomes
 he Complex Form 3.6 Introduction In this Section we show how a Fourier series can be expressed more concisely if we introduce the complex number i where i =. By utilising the Euler relation: e iθ cos θ
he Complex Form 3.6 Introduction In this Section we show how a Fourier series can be expressed more concisely if we introduce the complex number i where i =. By utilising the Euler relation: e iθ cos θ
EC Signals and Systems
 UNIT I CLASSIFICATION OF SIGNALS AND SYSTEMS Continuous time signals (CT signals), discrete time signals (DT signals) Step, Ramp, Pulse, Impulse, Exponential 1. Define Unit Impulse Signal [M/J 1], [M/J
UNIT I CLASSIFICATION OF SIGNALS AND SYSTEMS Continuous time signals (CT signals), discrete time signals (DT signals) Step, Ramp, Pulse, Impulse, Exponential 1. Define Unit Impulse Signal [M/J 1], [M/J
Solutions to Problems in Chapter 4
 Solutions to Problems in Chapter 4 Problems with Solutions Problem 4. Fourier Series of the Output Voltage of an Ideal Full-Wave Diode Bridge Rectifier he nonlinear circuit in Figure 4. is a full-wave
Solutions to Problems in Chapter 4 Problems with Solutions Problem 4. Fourier Series of the Output Voltage of an Ideal Full-Wave Diode Bridge Rectifier he nonlinear circuit in Figure 4. is a full-wave
5. THE CLASSES OF FOURIER TRANSFORMS
 5. THE CLASSES OF FOURIER TRANSFORMS There are four classes of Fourier transform, which are represented in the following table. So far, we have concentrated on the discrete Fourier transform. Table 1.
5. THE CLASSES OF FOURIER TRANSFORMS There are four classes of Fourier transform, which are represented in the following table. So far, we have concentrated on the discrete Fourier transform. Table 1.
D.S.G. POLLOCK: BRIEF NOTES
 BIVARIATE SPECTRAL ANALYSIS Let x(t) and y(t) be two stationary stochastic processes with E{x(t)} = E{y(t)} =. These processes have the following spectral representations: (1) x(t) = y(t) = {cos(ωt)da
BIVARIATE SPECTRAL ANALYSIS Let x(t) and y(t) be two stationary stochastic processes with E{x(t)} = E{y(t)} =. These processes have the following spectral representations: (1) x(t) = y(t) = {cos(ωt)da
EE 3054: Signals, Systems, and Transforms Summer It is observed of some continuous-time LTI system that the input signal.
 EE 34: Signals, Systems, and Transforms Summer 7 Test No notes, closed book. Show your work. Simplify your answers. 3. It is observed of some continuous-time LTI system that the input signal = 3 u(t) produces
EE 34: Signals, Systems, and Transforms Summer 7 Test No notes, closed book. Show your work. Simplify your answers. 3. It is observed of some continuous-time LTI system that the input signal = 3 u(t) produces
Representing a Signal
 The Fourier Series Representing a Signal The convolution method for finding the response of a system to an excitation takes advantage of the linearity and timeinvariance of the system and represents the
The Fourier Series Representing a Signal The convolution method for finding the response of a system to an excitation takes advantage of the linearity and timeinvariance of the system and represents the
EE301 Signals and Systems In-Class Exam Exam 3 Thursday, Apr. 19, Cover Sheet
 EE301 Signals and Systems In-Class Exam Exam 3 Thursday, Apr. 19, 2012 Cover Sheet Test Duration: 75 minutes. Coverage: Chaps. 5,7 Open Book but Closed Notes. One 8.5 in. x 11 in. crib sheet Calculators
EE301 Signals and Systems In-Class Exam Exam 3 Thursday, Apr. 19, 2012 Cover Sheet Test Duration: 75 minutes. Coverage: Chaps. 5,7 Open Book but Closed Notes. One 8.5 in. x 11 in. crib sheet Calculators
Notes on the Periodically Forced Harmonic Oscillator
 Notes on the Periodically orced Harmonic Oscillator Warren Weckesser Math 38 - Differential Equations 1 The Periodically orced Harmonic Oscillator. By periodically forced harmonic oscillator, we mean the
Notes on the Periodically orced Harmonic Oscillator Warren Weckesser Math 38 - Differential Equations 1 The Periodically orced Harmonic Oscillator. By periodically forced harmonic oscillator, we mean the
Series FOURIER SERIES. Graham S McDonald. A self-contained Tutorial Module for learning the technique of Fourier series analysis
 Series FOURIER SERIES Graham S McDonald A self-contained Tutorial Module for learning the technique of Fourier series analysis Table of contents Begin Tutorial c 24 g.s.mcdonald@salford.ac.uk 1. Theory
Series FOURIER SERIES Graham S McDonald A self-contained Tutorial Module for learning the technique of Fourier series analysis Table of contents Begin Tutorial c 24 g.s.mcdonald@salford.ac.uk 1. Theory
Signals and Systems Spring 2004 Lecture #9
 Signals and Systems Spring 2004 Lecture #9 (3/4/04). The convolution Property of the CTFT 2. Frequency Response and LTI Systems Revisited 3. Multiplication Property and Parseval s Relation 4. The DT Fourier
Signals and Systems Spring 2004 Lecture #9 (3/4/04). The convolution Property of the CTFT 2. Frequency Response and LTI Systems Revisited 3. Multiplication Property and Parseval s Relation 4. The DT Fourier
Signals and Systems. Problem Set: The z-transform and DT Fourier Transform
 Signals and Systems Problem Set: The z-transform and DT Fourier Transform Updated: October 9, 7 Problem Set Problem - Transfer functions in MATLAB A discrete-time, causal LTI system is described by the
Signals and Systems Problem Set: The z-transform and DT Fourier Transform Updated: October 9, 7 Problem Set Problem - Transfer functions in MATLAB A discrete-time, causal LTI system is described by the
Ver 3808 E1.10 Fourier Series and Transforms (2014) E1.10 Fourier Series and Transforms. Problem Sheet 1 (Lecture 1)
 Ver 88 E. Fourier Series and Transforms 4 Key: [A] easy... [E]hard Questions from RBH textbook: 4., 4.8. E. Fourier Series and Transforms Problem Sheet Lecture. [B] Using the geometric progression formula,
Ver 88 E. Fourier Series and Transforms 4 Key: [A] easy... [E]hard Questions from RBH textbook: 4., 4.8. E. Fourier Series and Transforms Problem Sheet Lecture. [B] Using the geometric progression formula,
LOPE3202: Communication Systems 10/18/2017 2
 By Lecturer Ahmed Wael Academic Year 2017-2018 LOPE3202: Communication Systems 10/18/2017 We need tools to build any communication system. Mathematics is our premium tool to do work with signals and systems.
By Lecturer Ahmed Wael Academic Year 2017-2018 LOPE3202: Communication Systems 10/18/2017 We need tools to build any communication system. Mathematics is our premium tool to do work with signals and systems.
Discrete-time Fourier transform (DTFT) representation of DT aperiodic signals Section The (DT) Fourier transform (or spectrum) of x[n] is
![Discrete-time Fourier transform (DTFT) representation of DT aperiodic signals Section The (DT) Fourier transform (or spectrum) of x[n] is Discrete-time Fourier transform (DTFT) representation of DT aperiodic signals Section The (DT) Fourier transform (or spectrum) of x[n] is](/thumbs/89/98498368.jpg) Discrete-time Fourier transform (DTFT) representation of DT aperiodic signals Section 5. 3 The (DT) Fourier transform (or spectrum) of x[n] is X ( e jω) = n= x[n]e jωn x[n] can be reconstructed from its
Discrete-time Fourier transform (DTFT) representation of DT aperiodic signals Section 5. 3 The (DT) Fourier transform (or spectrum) of x[n] is X ( e jω) = n= x[n]e jωn x[n] can be reconstructed from its
Communication Signals (Haykin Sec. 2.4 and Ziemer Sec Sec. 2.4) KECE321 Communication Systems I
 Communication Signals (Haykin Sec..4 and iemer Sec...4-Sec..4) KECE3 Communication Systems I Lecture #3, March, 0 Prof. Young-Chai Ko 년 3 월 일일요일 Review Signal classification Phasor signal and spectra Representation
Communication Signals (Haykin Sec..4 and iemer Sec...4-Sec..4) KECE3 Communication Systems I Lecture #3, March, 0 Prof. Young-Chai Ko 년 3 월 일일요일 Review Signal classification Phasor signal and spectra Representation
The Discrete Fourier Transform
 In [ ]: cd matlab pwd The Discrete Fourier Transform Scope and Background Reading This session introduces the z-transform which is used in the analysis of discrete time systems. As for the Fourier and
In [ ]: cd matlab pwd The Discrete Fourier Transform Scope and Background Reading This session introduces the z-transform which is used in the analysis of discrete time systems. As for the Fourier and
Course Notes for Signals and Systems. Krishna R Narayanan
 Course Notes for Signals and Systems Krishna R Narayanan May 7, 018 Contents 1 Math Review 5 1.1 Trigonometric Identities............................. 5 1. Complex Numbers................................
Course Notes for Signals and Systems Krishna R Narayanan May 7, 018 Contents 1 Math Review 5 1.1 Trigonometric Identities............................. 5 1. Complex Numbers................................
2.3 Oscillation. The harmonic oscillator equation is the differential equation. d 2 y dt 2 r y (r > 0). Its solutions have the form
 2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
2. Oscillation So far, we have used differential equations to describe functions that grow or decay over time. The next most common behavior for a function is to oscillate, meaning that it increases and
Overview - Previous lecture 1/2
 Overview - Previous lecture 1/2 Derived the wave equation with solutions of the form We found that the polarization of the material affects wave propagation, and found the dispersion relation ω(k) with
Overview - Previous lecture 1/2 Derived the wave equation with solutions of the form We found that the polarization of the material affects wave propagation, and found the dispersion relation ω(k) with
The Discrete-Time Fourier
 Chapter 3 The Discrete-Time Fourier Transform 清大電機系林嘉文 cwlin@ee.nthu.edu.tw 03-5731152 Original PowerPoint slides prepared by S. K. Mitra 3-1-1 Continuous-Time Fourier Transform Definition The CTFT of
Chapter 3 The Discrete-Time Fourier Transform 清大電機系林嘉文 cwlin@ee.nthu.edu.tw 03-5731152 Original PowerPoint slides prepared by S. K. Mitra 3-1-1 Continuous-Time Fourier Transform Definition The CTFT of
Fourier Transform for Continuous Functions
 Fourier Transform for Continuous Functions Central goal: representing a signal by a set of orthogonal bases that are corresponding to frequencies or spectrum. Fourier series allows to find the spectrum
Fourier Transform for Continuous Functions Central goal: representing a signal by a set of orthogonal bases that are corresponding to frequencies or spectrum. Fourier series allows to find the spectrum
Signals & Systems. Lecture 5 Continuous-Time Fourier Transform. Alp Ertürk
 Signals & Systems Lecture 5 Continuous-Time Fourier Transform Alp Ertürk alp.erturk@kocaeli.edu.tr Fourier Series Representation of Continuous-Time Periodic Signals Synthesis equation: x t = a k e jkω
Signals & Systems Lecture 5 Continuous-Time Fourier Transform Alp Ertürk alp.erturk@kocaeli.edu.tr Fourier Series Representation of Continuous-Time Periodic Signals Synthesis equation: x t = a k e jkω
Chapter 2: Complex numbers
 Chapter 2: Complex numbers Complex numbers are commonplace in physics and engineering. In particular, complex numbers enable us to simplify equations and/or more easily find solutions to equations. We
Chapter 2: Complex numbers Complex numbers are commonplace in physics and engineering. In particular, complex numbers enable us to simplify equations and/or more easily find solutions to equations. We
ENGIN 211, Engineering Math. Fourier Series and Transform
 ENGIN 11, Engineering Math Fourier Series and ransform 1 Periodic Functions and Harmonics f(t) Period: a a+ t Frequency: f = 1 Angular velocity (or angular frequency): ω = ππ = π Such a periodic function
ENGIN 11, Engineering Math Fourier Series and ransform 1 Periodic Functions and Harmonics f(t) Period: a a+ t Frequency: f = 1 Angular velocity (or angular frequency): ω = ππ = π Such a periodic function
(Refer Slide Time: 01:28 03:51 min)
 Digital Signal Processing Prof. S. C. Dutta Roy Department of Electrical Engineering Indian Institute of Technology, Delhi Lecture 40 FIR Design by Windowing This is the 40 th lecture and our topic for
Digital Signal Processing Prof. S. C. Dutta Roy Department of Electrical Engineering Indian Institute of Technology, Delhi Lecture 40 FIR Design by Windowing This is the 40 th lecture and our topic for
Complex symmetry Signals and Systems Fall 2015
 18-90 Signals and Systems Fall 015 Complex symmetry 1. Complex symmetry This section deals with the complex symmetry property. As an example I will use the DTFT for a aperiodic discrete-time signal. The
18-90 Signals and Systems Fall 015 Complex symmetry 1. Complex symmetry This section deals with the complex symmetry property. As an example I will use the DTFT for a aperiodic discrete-time signal. The
Fourier Analysis and Spectral Representation of Signals
 MIT 6.02 DRAFT Lecture Notes Last update: November 3, 2012 CHAPTER 13 Fourier Analysis and Spectral Representation of Signals We have seen in the previous chapter that the action of an LTI system on a
MIT 6.02 DRAFT Lecture Notes Last update: November 3, 2012 CHAPTER 13 Fourier Analysis and Spectral Representation of Signals We have seen in the previous chapter that the action of an LTI system on a
MITOCW MITRES_6-007S11lec09_300k.mp4
 MITOCW MITRES_6-007S11lec09_300k.mp4 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for
MITOCW MITRES_6-007S11lec09_300k.mp4 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for
Mathematical methods and its applications Dr. S. K. Gupta Department of Mathematics Indian Institute of Technology, Roorkee
 Mathematical methods and its applications Dr. S. K. Gupta Department of Mathematics Indian Institute of Technology, Roorkee Lecture - 56 Fourier sine and cosine transforms Welcome to lecture series on
Mathematical methods and its applications Dr. S. K. Gupta Department of Mathematics Indian Institute of Technology, Roorkee Lecture - 56 Fourier sine and cosine transforms Welcome to lecture series on
Lecture 34. Fourier Transforms
 Lecture 34 Fourier Transforms In this section, we introduce the Fourier transform, a method of analyzing the frequency content of functions that are no longer τ-periodic, but which are defined over the
Lecture 34 Fourier Transforms In this section, we introduce the Fourier transform, a method of analyzing the frequency content of functions that are no longer τ-periodic, but which are defined over the
Discrete Systems & Z-Transforms. Week Date Lecture Title. 9-Mar Signals as Vectors & Systems as Maps 10-Mar [Signals] 3
![Discrete Systems & Z-Transforms. Week Date Lecture Title. 9-Mar Signals as Vectors & Systems as Maps 10-Mar [Signals] 3 Discrete Systems & Z-Transforms. Week Date Lecture Title. 9-Mar Signals as Vectors & Systems as Maps 10-Mar [Signals] 3](/thumbs/89/99446510.jpg) http:elec34.org Discrete Systems & Z-Transforms 4 School of Information Technology and Electrical Engineering at The University of Queensland Lecture Schedule: eek Date Lecture Title -Mar Introduction
http:elec34.org Discrete Systems & Z-Transforms 4 School of Information Technology and Electrical Engineering at The University of Queensland Lecture Schedule: eek Date Lecture Title -Mar Introduction
Figure 3.1 Effect on frequency spectrum of increasing period T 0. Consider the amplitude spectrum of a periodic waveform as shown in Figure 3.2.
 3. Fourier ransorm From Fourier Series to Fourier ransorm [, 2] In communication systems, we oten deal with non-periodic signals. An extension o the time-requency relationship to a non-periodic signal
3. Fourier ransorm From Fourier Series to Fourier ransorm [, 2] In communication systems, we oten deal with non-periodic signals. An extension o the time-requency relationship to a non-periodic signal
CS711008Z Algorithm Design and Analysis
 CS711008Z Algorithm Design and Analysis Lecture 5 FFT and Divide and Conquer Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / 56 Outline DFT: evaluate a polynomial
CS711008Z Algorithm Design and Analysis Lecture 5 FFT and Divide and Conquer Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / 56 Outline DFT: evaluate a polynomial
Circuits and Systems I
 Circuits and Systems I LECTURE #2 Phasor Addition lions@epfl Prof. Dr. Volkan Cevher LIONS/Laboratory for Information and Inference Systems License Info for SPFirst Slides This work released under a Creative
Circuits and Systems I LECTURE #2 Phasor Addition lions@epfl Prof. Dr. Volkan Cevher LIONS/Laboratory for Information and Inference Systems License Info for SPFirst Slides This work released under a Creative
Fourier transform representation of CT aperiodic signals Section 4.1
 Fourier transform representation of CT aperiodic signals Section 4. A large class of aperiodic CT signals can be represented by the CT Fourier transform (CTFT). The (CT) Fourier transform (or spectrum)
Fourier transform representation of CT aperiodic signals Section 4. A large class of aperiodic CT signals can be represented by the CT Fourier transform (CTFT). The (CT) Fourier transform (or spectrum)
(Refer Slide Time: 01:30)
 Networks and Systems Prof V.G K.Murti Department of Electrical Engineering Indian Institute of Technology, Madras Lecture - 11 Fourier Series (5) Continuing our discussion of Fourier series today, we will
Networks and Systems Prof V.G K.Murti Department of Electrical Engineering Indian Institute of Technology, Madras Lecture - 11 Fourier Series (5) Continuing our discussion of Fourier series today, we will
LECTURE 13 Introduction to Filtering
 MIT 6.02 DRAFT ecture Notes Fall 2010 (ast update: October 25, 2010) Comments, questions or bug reports? Please contact 6.02-staff@mit.edu ECTURE 13 Introduction to Filtering This lecture introduces the
MIT 6.02 DRAFT ecture Notes Fall 2010 (ast update: October 25, 2010) Comments, questions or bug reports? Please contact 6.02-staff@mit.edu ECTURE 13 Introduction to Filtering This lecture introduces the
2.161 Signal Processing: Continuous and Discrete
 MI OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 8 For information about citing these materials or our erms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSES INSIUE
MI OpenCourseWare http://ocw.mit.edu.6 Signal Processing: Continuous and Discrete Fall 8 For information about citing these materials or our erms of Use, visit: http://ocw.mit.edu/terms. MASSACHUSES INSIUE
Signals and Systems Lecture Notes
 Dr. Mahmoud M. Al-Husari Signals and Systems Lecture Notes This set of lecture notes are never to be considered as a substitute to the textbook recommended by the lecturer. ii Contents Preface v 1 Introduction
Dr. Mahmoud M. Al-Husari Signals and Systems Lecture Notes This set of lecture notes are never to be considered as a substitute to the textbook recommended by the lecturer. ii Contents Preface v 1 Introduction
Unstable Oscillations!
 Unstable Oscillations X( t ) = [ A 0 + A( t ) ] sin( ω t + Φ 0 + Φ( t ) ) Amplitude modulation: A( t ) Phase modulation: Φ( t ) S(ω) S(ω) Special case: C(ω) Unstable oscillation has a broader periodogram
Unstable Oscillations X( t ) = [ A 0 + A( t ) ] sin( ω t + Φ 0 + Φ( t ) ) Amplitude modulation: A( t ) Phase modulation: Φ( t ) S(ω) S(ω) Special case: C(ω) Unstable oscillation has a broader periodogram
George Mason University Signals and Systems I Spring 2016
 George Mason University Signals and Systems I Spring 206 Problem Set #6 Assigned: March, 206 Due Date: March 5, 206 Reading: This problem set is on Fourier series representations of periodic signals. The
George Mason University Signals and Systems I Spring 206 Problem Set #6 Assigned: March, 206 Due Date: March 5, 206 Reading: This problem set is on Fourier series representations of periodic signals. The
Lecture 28 Continuous-Time Fourier Transform 2
 Lecture 28 Continuous-Time Fourier Transform 2 Fundamentals of Digital Signal Processing Spring, 2012 Wei-Ta Chu 2012/6/14 1 Limit of the Fourier Series Rewrite (11.9) and (11.10) as As, the fundamental
Lecture 28 Continuous-Time Fourier Transform 2 Fundamentals of Digital Signal Processing Spring, 2012 Wei-Ta Chu 2012/6/14 1 Limit of the Fourier Series Rewrite (11.9) and (11.10) as As, the fundamental
Introduction to Fourier Transforms. Lecture 7 ELE 301: Signals and Systems. Fourier Series. Rect Example
 Introduction to Fourier ransforms Lecture 7 ELE 3: Signals and Systems Fourier transform as a limit of the Fourier series Inverse Fourier transform: he Fourier integral theorem Prof. Paul Cuff Princeton
Introduction to Fourier ransforms Lecture 7 ELE 3: Signals and Systems Fourier transform as a limit of the Fourier series Inverse Fourier transform: he Fourier integral theorem Prof. Paul Cuff Princeton
LINEAR SYSTEMS. J. Elder PSYC 6256 Principles of Neural Coding
 LINEAR SYSTEMS Linear Systems 2 Neural coding and cognitive neuroscience in general concerns input-output relationships. Inputs Light intensity Pre-synaptic action potentials Number of items in display
LINEAR SYSTEMS Linear Systems 2 Neural coding and cognitive neuroscience in general concerns input-output relationships. Inputs Light intensity Pre-synaptic action potentials Number of items in display
Today s lecture. The Fourier transform. Sampling, aliasing, interpolation The Fast Fourier Transform (FFT) algorithm
 Today s lecture The Fourier transform What is it? What is it useful for? What are its properties? Sampling, aliasing, interpolation The Fast Fourier Transform (FFT) algorithm Jean Baptiste Joseph Fourier
Today s lecture The Fourier transform What is it? What is it useful for? What are its properties? Sampling, aliasing, interpolation The Fast Fourier Transform (FFT) algorithm Jean Baptiste Joseph Fourier
Sinusoidal steady-state analysis
 Sinusoidal steady-state analysis From our previous efforts with AC circuits, some patterns in the analysis started to appear. 1. In each case, the steady-state voltages or currents created in response
Sinusoidal steady-state analysis From our previous efforts with AC circuits, some patterns in the analysis started to appear. 1. In each case, the steady-state voltages or currents created in response
Signals and Systems. Lecture 14 DR TANIA STATHAKI READER (ASSOCIATE PROFESSOR) IN SIGNAL PROCESSING IMPERIAL COLLEGE LONDON
 Signals and Systems Lecture 14 DR TAIA STATHAKI READER (ASSOCIATE PROFESSOR) I SIGAL PROCESSIG IMPERIAL COLLEGE LODO Introduction. Time sampling theorem resume. We wish to perform spectral analysis using
Signals and Systems Lecture 14 DR TAIA STATHAKI READER (ASSOCIATE PROFESSOR) I SIGAL PROCESSIG IMPERIAL COLLEGE LODO Introduction. Time sampling theorem resume. We wish to perform spectral analysis using
7. Find the Fourier transform of f (t)=2 cos(2π t)[u (t) u(t 1)]. 8. (a) Show that a periodic signal with exponential Fourier series f (t)= δ (ω nω 0
![7. Find the Fourier transform of f (t)=2 cos(2π t)[u (t) u(t 1)]. 8. (a) Show that a periodic signal with exponential Fourier series f (t)= δ (ω nω 0 7. Find the Fourier transform of f (t)=2 cos(2π t)[u (t) u(t 1)]. 8. (a) Show that a periodic signal with exponential Fourier series f (t)= δ (ω nω 0](/thumbs/96/126850209.jpg) Fourier Transform Problems 1. Find the Fourier transform of the following signals: a) f 1 (t )=e 3 t sin(10 t)u (t) b) f 1 (t )=e 4 t cos(10 t)u (t) 2. Find the Fourier transform of the following signals:
Fourier Transform Problems 1. Find the Fourier transform of the following signals: a) f 1 (t )=e 3 t sin(10 t)u (t) b) f 1 (t )=e 4 t cos(10 t)u (t) 2. Find the Fourier transform of the following signals:
Periodic functions: simple harmonic oscillator
 Periodic functions: simple harmonic oscillator Recall the simple harmonic oscillator (e.g. mass-spring system) d 2 y dt 2 + ω2 0y = 0 Solution can be written in various ways: y(t) = Ae iω 0t y(t) = A cos
Periodic functions: simple harmonic oscillator Recall the simple harmonic oscillator (e.g. mass-spring system) d 2 y dt 2 + ω2 0y = 0 Solution can be written in various ways: y(t) = Ae iω 0t y(t) = A cos
Review of Linear System Theory
 Review of Linear System Theory The following is a (very) brief review of linear system theory and Fourier analysis. I work primarily with discrete signals. I assume the reader is familiar with linear algebra
Review of Linear System Theory The following is a (very) brief review of linear system theory and Fourier analysis. I work primarily with discrete signals. I assume the reader is familiar with linear algebra
Solutions 2: Simple Harmonic Oscillator and General Oscillations
 Massachusetts Institute of Technology MITES 2017 Physics III Solutions 2: Simple Harmonic Oscillator and General Oscillations Due Wednesday June 21, at 9AM under Rene García s door Preface: This problem
Massachusetts Institute of Technology MITES 2017 Physics III Solutions 2: Simple Harmonic Oscillator and General Oscillations Due Wednesday June 21, at 9AM under Rene García s door Preface: This problem
Alternating Current (AC) Circuits
 Alternating Current (AC) Circuits We have been talking about DC circuits Constant currents and voltages Resistors Linear equations Now we introduce AC circuits Time-varying currents and voltages Resistors,
Alternating Current (AC) Circuits We have been talking about DC circuits Constant currents and voltages Resistors Linear equations Now we introduce AC circuits Time-varying currents and voltages Resistors,
Chapter 4 Discrete Fourier Transform (DFT) And Signal Spectrum
 Chapter 4 Discrete Fourier Transform (DFT) And Signal Spectrum CEN352, DR. Nassim Ammour, King Saud University 1 Fourier Transform History Born 21 March 1768 ( Auxerre ). Died 16 May 1830 ( Paris ) French
Chapter 4 Discrete Fourier Transform (DFT) And Signal Spectrum CEN352, DR. Nassim Ammour, King Saud University 1 Fourier Transform History Born 21 March 1768 ( Auxerre ). Died 16 May 1830 ( Paris ) French
SOLVING DIFFERENTIAL EQUATIONS. Amir Asif. Department of Computer Science and Engineering York University, Toronto, ON M3J1P3
 SOLVING DIFFERENTIAL EQUATIONS Amir Asif Department of Computer Science and Engineering York University, Toronto, ON M3J1P3 ABSTRACT This article reviews a direct method for solving linear, constant-coefficient
SOLVING DIFFERENTIAL EQUATIONS Amir Asif Department of Computer Science and Engineering York University, Toronto, ON M3J1P3 ABSTRACT This article reviews a direct method for solving linear, constant-coefficient
Chapter 10: Sinusoidal Steady-State Analysis
 Chapter 10: Sinusoidal Steady-State Analysis 1 Objectives : sinusoidal functions Impedance use phasors to determine the forced response of a circuit subjected to sinusoidal excitation Apply techniques
Chapter 10: Sinusoidal Steady-State Analysis 1 Objectives : sinusoidal functions Impedance use phasors to determine the forced response of a circuit subjected to sinusoidal excitation Apply techniques
Spectral Analysis. Jesús Fernández-Villaverde University of Pennsylvania
 Spectral Analysis Jesús Fernández-Villaverde University of Pennsylvania 1 Why Spectral Analysis? We want to develop a theory to obtain the business cycle properties of the data. Burns and Mitchell (1946).
Spectral Analysis Jesús Fernández-Villaverde University of Pennsylvania 1 Why Spectral Analysis? We want to develop a theory to obtain the business cycle properties of the data. Burns and Mitchell (1946).
Fourier series. Complex Fourier series. Positive and negative frequencies. Fourier series demonstration. Notes. Notes. Notes.
 Fourier series Fourier series of a periodic function f (t) with period T and corresponding angular frequency ω /T : f (t) a 0 + (a n cos(nωt) + b n sin(nωt)), n1 Fourier series is a linear sum of cosine
Fourier series Fourier series of a periodic function f (t) with period T and corresponding angular frequency ω /T : f (t) a 0 + (a n cos(nωt) + b n sin(nωt)), n1 Fourier series is a linear sum of cosine
Lecture 15: Time and Frequency Joint Perspective
 WAVELETS AND MULTIRATE DIGITAL SIGNAL PROCESSING Lecture 15: Time and Frequency Joint Perspective Prof.V.M.Gadre, EE, IIT Bombay Introduction In lecture 14, we studied steps required to design conjugate
WAVELETS AND MULTIRATE DIGITAL SIGNAL PROCESSING Lecture 15: Time and Frequency Joint Perspective Prof.V.M.Gadre, EE, IIT Bombay Introduction In lecture 14, we studied steps required to design conjugate
Signal and systems. Linear Systems. Luigi Palopoli. Signal and systems p. 1/5
 Signal and systems p. 1/5 Signal and systems Linear Systems Luigi Palopoli palopoli@dit.unitn.it Wrap-Up Signal and systems p. 2/5 Signal and systems p. 3/5 Fourier Series We have see that is a signal
Signal and systems p. 1/5 Signal and systems Linear Systems Luigi Palopoli palopoli@dit.unitn.it Wrap-Up Signal and systems p. 2/5 Signal and systems p. 3/5 Fourier Series We have see that is a signal
Lectures on Spectra of Discrete-Time Signals
 Lectures on Spectra of Discrete-Time Signals Principal questions to be addressed: What, in a general sense, is the "spectrum" of a discrete-time signal? How does one assess the spectrum of a discrete-time
Lectures on Spectra of Discrete-Time Signals Principal questions to be addressed: What, in a general sense, is the "spectrum" of a discrete-time signal? How does one assess the spectrum of a discrete-time
1 (2n)! (-1)n (θ) 2n
 Complex Numbers and Algebra The real numbers are complete for the operations addition, subtraction, multiplication, and division, or more suggestively, for the operations of addition and multiplication
Complex Numbers and Algebra The real numbers are complete for the operations addition, subtraction, multiplication, and division, or more suggestively, for the operations of addition and multiplication
Chapter 6 THE SAMPLING PROCESS 6.1 Introduction 6.2 Fourier Transform Revisited
 Chapter 6 THE SAMPLING PROCESS 6.1 Introduction 6.2 Fourier Transform Revisited Copyright c 2005 Andreas Antoniou Victoria, BC, Canada Email: aantoniou@ieee.org July 14, 2018 Frame # 1 Slide # 1 A. Antoniou
Chapter 6 THE SAMPLING PROCESS 6.1 Introduction 6.2 Fourier Transform Revisited Copyright c 2005 Andreas Antoniou Victoria, BC, Canada Email: aantoniou@ieee.org July 14, 2018 Frame # 1 Slide # 1 A. Antoniou
Lecture 04: Discrete Frequency Domain Analysis (z-transform)
 Lecture 04: Discrete Frequency Domain Analysis (z-transform) John Chiverton School of Information Technology Mae Fah Luang University 1st Semester 2009/ 2552 Outline Overview Lecture Contents Introduction
Lecture 04: Discrete Frequency Domain Analysis (z-transform) John Chiverton School of Information Technology Mae Fah Luang University 1st Semester 2009/ 2552 Outline Overview Lecture Contents Introduction
A system that is both linear and time-invariant is called linear time-invariant (LTI).
 The Cooper Union Department of Electrical Engineering ECE111 Signal Processing & Systems Analysis Lecture Notes: Time, Frequency & Transform Domains February 28, 2012 Signals & Systems Signals are mapped
The Cooper Union Department of Electrical Engineering ECE111 Signal Processing & Systems Analysis Lecture Notes: Time, Frequency & Transform Domains February 28, 2012 Signals & Systems Signals are mapped
A1 Time-Frequency Analysis
 A 20 / A Time-Frequency Analysis David Murray david.murray@eng.ox.ac.uk www.robots.ox.ac.uk/ dwm/courses/2tf Hilary 20 A 20 2 / Content 8 Lectures: 6 Topics... From Signals to Complex Fourier Series 2
A 20 / A Time-Frequency Analysis David Murray david.murray@eng.ox.ac.uk www.robots.ox.ac.uk/ dwm/courses/2tf Hilary 20 A 20 2 / Content 8 Lectures: 6 Topics... From Signals to Complex Fourier Series 2
EE3210 Lab 3: Periodic Signal Representation by Fourier Series
 City University of Hong Kong Department of Electronic Engineering EE321 Lab 3: Periodic Signal Representation by Fourier Series Prelab: Read the Background section. Complete Section 2.2(b), which asks
City University of Hong Kong Department of Electronic Engineering EE321 Lab 3: Periodic Signal Representation by Fourier Series Prelab: Read the Background section. Complete Section 2.2(b), which asks
