UNIVERSITY COLLEGE DUBLIN. An Coláiste Ollscoile, Baile Átha Cliath MOCK SEMESTER 1 EXAMINATION 2008/2009 MST30070
|
|
|
- Camron Fletcher
- 5 years ago
- Views:
Transcription
1 UNIVERSITY COLLEGE DUBLIN An Coláise Ollscoile, Baile Áha Cliah MOCK SEMESTER EXAMINATION 8/9 MST37 Inroducion o Differenial Geomery Professor P.J. Rippon Professor S. Dineen Dr. J. B. Quigley Time Allowed: hours Insrucions for Candidaes Aemp shor quesions from par one, for 4% of available marks. Aemp 4 quesions from par wo, for 6% of available marks. Noes for Invigilaors Non Programmable calculaors are permied. Mahemaical formulae are on page 4. Page of 5
2 par one: aemp of 4 quesions for 4% from par one. image, graph, conour,curves, circle, AS, cycloid Helix. Skech he conour f of fx,y x y.. Skech he conour f of fx,y x y. 3. Skech he graph of fx,y x y. 4. Compue he speed of c i /j. 5. Give a formula for he velociy vecor of c xi yj. 6. Compue he acceleraion vecor of c i /j. arc-lengh 7. For c as in 5 above wha quaniy is a ẋ τ ẏ τ dτ? 8. Wrie down he oal arc lengh L of one urn of he helix. curvaure 9. Give a formula for he curvaure c as in 5 above.. Wrie down he curvaure κ of he sraigh line y x.. Wrie down he curvaure a cos sini sin cosj of he Archimedean spiral.. Wrie down he curvaure of he circle c 3 cos7i 4 3 sin7j involue and evolue 3. Give formula for he involue of c as in Give formula for he evolue of c as in Skech he conical Helix c cosi sinj k. 6. Skech he cardioid. 7. Skech involue of he circle. 8. Skech he evolue of he cycloid. classificaion of saionary poins 9. Give he second order approximaion o fx, y expx y near i j.. Is i j a saionary poin of gx,y xy y x?. Is a local maximum poin a degenerae saionary poin?. Is a saddle poin a degenerae saionary poin? 3. Find a funcion fx,y wih a degenerae saionary poin a i j. 4. Find he Hessian of kx,y x 4xy 6y a i j. Page of 5
3 par wo: aemp 4 of 5 quesions for 6% from par wo.. Le f be he funcion fx,y xy. i Skech he conour f. ii Skech he conour f. iii Skech he conour f. iv Show, in a single skech, he 9 conours f d for d { ±, ±4, ±9, ±6}. v Draw he graph of f as a surface in R 3. Also draw he box wih 6 faces x ±,y ±,z ±. Clearly show ha he graph cus each of he four verical faces in a line. Find he equaions of all four such lines. vi [ Here f d R denoes he conour or level se on which f has value d R ]. Le Γ R be he curve paramerized by c xi yj zk i coshj, i Roughly skech Γ R he caenary. ii Compue he velociy vecor ċ. iii Compue he acceleraion vecor c. iv Compue he speed scalar ċ. v Compue he oal arc lengh L of Γ. vi Compue s he arc lengh measured along Γ from c o he general poin c. 3. Le c xi yj paramerize a curve Γ R. i Give a formula for he curvaure κ a c Γ in erms of ẋ,ẏ,ẍ and ÿ. ii Paramerize he cardioid curve. iii Roughly skech he cardioid. iv Compue, showing deails, κ for he cardioid. 4. The cardioid curve is paramerized by c?i?j, π. i Compue he velociy vecor ċ. and he acceleraion vecor c. ii Prove ha he speed ċ?. iii Compue he uni normal vecor n. iv Prove ha he curvaure κ?. Page 3 of 5
4 v Prove ha he evolue curve is paramerized by e? i? j. vi Skech he cardioid and is evolue. 5. Le f be he funcion fx,y x 3 3x 3 3xy 6y y 3 3y. i Compue he firs order parial derivaives f x and f y. ii Compue he second order parial derivaives f xx,f xy,f yx and f yy. iii Prove ha f has wo saionary poins and find boh. iv Compue boh saionary values. v Prove ha boh saionary poins are non-degenerae. vi Classify each saionary poin as local maximum, local minimum or saddle. ooo Page 4 of 5
5 MATHEMATICAL FORMULAE Noe: some formulae do no for hold for all variable values. i Trigonomeric Formulae cosx y cos xcos y sin x sin y { cos x sin x anx y an x an y/ an xan y cosx cos x sin x sinx sin x cos x anx an x/ an x an x /, an/ cos x /, an/ sin x /, an/ cos x cos x/ sin x cos x/ cos xcos y [cosx y cosx y]/ sin xcos y [sinx y sinx y]/ sin xsin y [cosx y cosx y]/ cos x cos y cos[x y/]cos[x y/] cos x cos y sin[x y/]sin[x y/] sin x sin y sin[x y/] cos[x y/] sin x sin y cos[x y/]sin[x y/] sin cos cosec co arcsec x arccos/x arccosec x arcsin/x cosh ix cos x sinh ix isin x ii Differeniaion iii Inegraion fx f x fx f x x n nx n lnx /x cos x sin x sin x cos x an x sec x sec x sec xan x cosec x cosec xco x co x cosec x e x e x a x a x log a arcsin x / x arcan x / x arcco x / x arccos x / x arcsec x /x x arccosec x /x x iv Mensuraion fx fx dx fx fx dx x n n x n /n /x log x cos x sin x sin x cos x an x logsec x sec x logsec x an x cosec x loganx/ co x log sin x e x e x a x a x /log a / x log x x / x arcsin x /x arcan x / x [log x log x]/ / x x arcsec x / x log x x Area of riangle ABC/ab sin C ss as bs c where s /a b c Cosine rule for riangle ABC: a b c bc cos A Disc, radius r: Areaπr : Circumferenceπr Cylinder, radius r,heigh h: Volumeπr h: Surface area πrh Cone, radius r, heigh h:volume/3πr h: Surface area πr r h Sphere, radius r: Volume4/3πr 3 : Surface area4πr Page 5 of 5
6 ANSWERS MOCK-EXAM ms37 Inroducion o Differenial Geomery Auumn 8 J.B.Quigley 7-3 K3 K K -8 K K Figure : iconical helix, ii cardioid par one: aemp of 4 quesions for 4% from par one. image, graph, conour,curves ec. i Skech he conour f of fx, y x y. { The conour is he se x } x y in R. This is he se { x x y } which is he uni circle cenered on he origin, skech omied. ii Skech he conour f of fx, y x y. The conour is he subse of R consising of poins which saisfy he equaion x y x y ;i.e. he single se { } conaining one poin, he origin, skech omied. iii Skech he graph of fx, y x y. Consider he graph of z x x in R which is a sraigh line hrough he origin. The graph of in R 3 consiss of he laer roaed abou he z-axis and is a cone surface, see figure3 iv Compue he speed of c i /j. ċ ẋ ẏ v Give a formula for he velociy vecor of c xi yj. Page 6 of 5
7 Figure : i cycloid and evolue, ii Archimedian spiral, involue of circle K K K5 K Figure 3: i cone surface, graph of z x y, ii conours of z xy Page 7 of 5
8 y x.5. Figure 4: i graph z xy, cus enclosing box, ii graph from Q K K K K K Figure 5: caenary cosh as average expx expx/: and sinh Page 8 of 5
9 K3 K K K3 K K K K K K Figure 6: cardioid and evolue a lile cardioid c ẋi ẏj ẋ ẏ vi Compue he acceleraion vecor of c i /j. c ẍi ÿj i j j arc-lengh vii For c as in 5 above wha quaniy is ẋ τ ẏ τdτ? a This quaniy is he arc lengh measured along he curve Γ R paramerized by c from he poin ca Γ o he poin c Γ viii Wrie down he oal arc lengh L of one urn of he helix. Wih usual paramerizaion c a cosi a sinjbk he oal arc lengh is L π a b curvaure ix Give a formula for he curvaure of c as in 5 above. κ deċ, c <ċ,ċ> 3/ ẋÿẏẍ ẋ ẏ 3/ x Wrie down he curvaure κ of he sraigh line y x. The curvaure of any line is κ /. This is because a line is a degenerae circle of radius. Alernaively use he formula of he previous wer wih c i j. xi Wrie down he curvaure a cos sini sin cosj This is he paramerizaion of he AS curve and was covered in he lecures. From memory κ /. xii Wrie down he curvaure of he circle c 3cos7i 4 3sin7j We can wrie c 3cos7i 4 3sin7j. This shows ha raversal is negaive i.e. C.W. Since he radius is 3 he curvaure is κ /3. involue and evolue xiii Give formula for he involue of c as in 5. i c s x s ẋ ẋ y ẏ ẏ where s a ẋ ẏ d. xiv Give formula for he evolue of c as in 5. e c n κ x y ẋ ẏ ẏ ẋÿ ẏÿ ẋ xv Skech he conical Helix c cosi sinj k. See figure. Page 9 of 5
10 xvi Skech he cardioid. See figure6. xvii Skech involue of he circle. See figure. xviii Skech he evolue of he cycloid. See figure. classificaion of saionary poins xix Give he second order approximaion o fx, y expx y near i j. f x f y f xx f xy f yy f expx y. A x y Thus hese are all equal o. Thus f, Df,, D f,. fx, y f, Df, x y x! x, y D f, y, x y x, y x y x y x xy y xx Is i j a saionary poin of gx,y xy y x? i j. Firs order pds are g x y a and g y x a. Thus i j is a saionary poin. xxi Is a local maximum poin a degenerae saionary poin? No. de D f >, xxii Is a saddle poin a degenerae saionary poin? No.de D f <, xxiii Find a funcion fx, y wih a degenerae saionary poin a i j. fx, y x 3 y 3, check ha Df,, and de D f,. xxiv Find he Hessian of kx, y x 4xy 6y a i j. D h hxx h xy h yx h yy 4 4 x which is so for all in paricular for y x i. y quesion Le f be he funcion fx, y xy. i Skech he conour f. ii Skech he conour f. iii Skech he conour f. iv Show, in a single skech, he 9 conours f d for d { ±, ±4, ±9, ±6}. v Draw he graph of f as a surface in R 3. Also draw he box wih 6 faces x ±, y ±, z ±. Clearly show ha he graph cus each of he four verical faces in a line. Find he equaions of all four such lines. vi [ Here f d R denoes he conour or level se on which f has value d R ]. wer The conour f R is he se {x xy } {x y } {x x } and is made up of wo sraigh lines, namely he x and y axes. See figure3.. wer The conour f R is he se {x xy } and is an hyperbola consising of wo unconeced pars, one in he second quadran and one in he fourh quadran. The lines f are asympoic o his hyperbola. See figure3.3 wer This conour is again an hyperbola bu now lying in he firs and hird quadrans. See figure3 Page of 5
11 .4 wer See figure3.5 wer See figure4. The graph is a saddle. I is he usual saddle z x y roaed by π/4. Noe ha xy X Y afer a change of variable x X Y, y X Y. This explains similariy of he graphs, boh are saddles. To see where he graph cus he verical side plane x suxsiue x ino z xy o obain x and z y. There are four verical faces x ±, y ±. Each is cu in a line x, z y x, z y y, z x y, z x Thes lines can be seen in figure4 quesion Le Γ R be he curve paramerized by c xiyjzk icoshj, i Roughly skech Γ R he caenary. ii Compue he velociy vecor ċ. iii Compue he acceleraion vecor c. iv Compue he speed scalar ċ. v Compue he oal arc lengh L of Γ. vi Compue s he arc lengh measured along Γ from c o he general poin c.. wer By definiion cosh expx expx. In figure5 we see he cosh curve as he average of growh exp x and decayexpx.. wer Firs we summarize some well known formulae. coshx expx exp x sinhx expx exp x cosh sinh We have sinh cosh cosh sinh c x y Thus he velociy is c x y cosh sinh.3 wer Also he acceleraion is c x y.4 wer Also he speed is.5 wer The oal arc-lengh is.6 wer c cosh x y sinh cosh cosh L The general arc-lengh is sinh c d cosh d sinh sinh sinh [ e ] e 3 quesion L c τ dτ coshτdτ sinhτ sinh sinh sinh [ e e ] Le c xi yj paramerize a curve Γ R. i Give a formula for he curvaure κ a c Γ in erms of ẋ,ẏ,ẍ and ÿ. ii Paramerize he cardioid curve. iii Roughly skech he cardioid. iv Compue, showing deails, κ for he cardioid. Page of 5
12 3. wer 3. wer κ deċ, c < ċ,ċ > 3/ ẋ ẏ de ẍ ÿ ẋ ẏ 3/ ẋÿ ẏẍ ẋ, ẏ 3/ The explanaion for he following parameerizaion of he cardioid will be supplied soon, when ime permis. c : [, π] Γ R x y 3.3 wer See figure6 3.4 wer cos cos sin sin The following curvaure compuaion is quie srenuous; if you can do i you will be well prepared for he much less demanding real exam. To compue κ we firs need ċ and c. x cos cos c y sin sin ẋ sin sin ċ Thus c κ ẏ ẍ ÿ cos cos cos 4cos sin 4sin sin sinsin sin 4 cos coscos cos sin sin 3/ 8 cos cos sin 3sin sin sin 4 cos 3cos cos cos sin cos 3/ 8 cos cos sin sin sin cos sin cos 3cos cos sin sin sin cos sin cos cos cos sinsin sin cos 3 cos cos 4 3 cos 8 cos 3/ 3/ 3/ ẋÿ ẏẍ ẋ, ẏ 3/ sin sinsin 4sin cos coscos 4cos sin sin 3/ cos cos sin / 84sin / 3/ 4 sin / 64 sin 3 / 3 8sin/ Page of 5
13 4 quesion This again is a srenuous quesion, he real exam quesion will be easier. The cardioid curve is paramerized by c?i?j, π. i Compue he velociy vecor ċ. and he acceleraion vecor c. ii Prove ha he speed ċ?. iii Compue he uni normal vecor n. iv Prove ha he curvaure κ?. v Prove ha he evolue curve is paramerized by e? i? j. vi Skech he cardioid and is evolue. sin cos cos cos sinsin sin cos cos cos / 4sin / / / / 4. wer c x y cos cos sin sin ẋ sin sin ċ ẏ cos cos ẍ cos 4cos c ÿ sin 4sin 4. wer The speed is ċ ẋ ẏ 4sin/ 4.3 wer The uni normal vecor is 4.4 wer n ẏ ẋ ẏ ẋ cos cos 4sin/ sin sin The curvaure was compued in wer o q3 above 3 κ 8sin/ 4.5 wer sin sin cos cos sin sin cos cos / / e c n κ See he lecure noes for his formula; for he cardioid e c n κ sin cos cos cos sin sin sin cos / c κ n cos cos sin sin Page 3 of 5
14 [ ] 3/8 sin/ cos cos sin sin [ ] 8sin/ 3 4sin/ 4sin/ cos cos sin sin 3 summary cos cos sin sin cos cos sin sin cos cos sin sin 6cos 3cos 4cos 4cos 3 6sin 3 sin 4sin 4 sin cos cos 3 sin sin cos cos c sin sin e cos cos 3 sin sin I is eviden ha he evolue is some sor of cardioid reduced in size by /3. See a maple skech, see figure6 In fac we can rearrange e e cos π cos π 3 sin π sin π This proves ha he evolue is a copy of he original cardoid bu a wih ime delay of π b scaled in size by /3 d refleced in he origin o accoun for he exra minus sign v Prove ha boh saionary poins are nondegenerae. vi Classify each saionary poin as local maximum, local minimum or saddle. 5. wer f x 3 3x 3 3xy 6y y 3 3y f x 3x 6x 3y f y 3y 6y 3x 6 5. wer 5.3 wer f xx 6x 6 f xy 3 f yx 3 Saionary ps occur when f x and f y f yy 6y 6 3x 6x 3y and 3y 6y 3x 6 x x y and y y x NOTE The soluion of hese wo equaions is very difficul, in fac more difficul han inended. The real exam will be easier The firs equaion ells us ha y x x. Subsiue his ino he second o obain x x x x x 4x 4x 3 x 4 4x x x x 4 4x 3 6x 5x x 4 4x 3 6x 5x x x 3 3x 3x x x x x The expression x x has only complex roos. Thus x or and y x x. Then x and y or x and y 5 quesion Le f be he funcion fx, y x 3 3x 3 3xy 6y y 3 3y. i Compue he firs order f x and f y. parial derivaives ii Compue he second order parial derivaives f xx, f xy, f yx and f yy. iii Prove ha f has wo saionary poins and find boh. iv Compue boh saionary values. summary There are wo saionary poins. x x and y y 5.4 wer f, Page 4 of 5
15 f, poin x 8 3 Also ded f, 93 7 ; and so y is also a nondegenerae saionary poin. summary The saionary values are f,, f, 5.5 wer ded fx, y 6x 6 3 de 3 6y 6 6x 66y 6 9 3x 3y 9 9[x y ] 9[x y ] 9[4x y ] 9[4xy 4y 4x 5] Thus ded f, ; x and so is a nondegenerae saionary y 5.6 wer Since ded f, 9 he nondegenerae saionary poin is a saddle poin. x y Since ded f, 7 > his is a loc.max. or loc.min. Bu rd f f xx f yy 6x 6y < x when. The nondegenerae saionary y x poin is a local maximum poin. y For good measure here is a maple plo of he graph of f, see figure4. Page 5 of 5
SEMESTER 1 EXAMINATION 2009/2010. MATH40060 Differential Geometry
 UNIVERSITY COLLEGE DUBLIN An Coláise Ollscoile, Baile Áha Cliah SEMESTER EXAMINATION 9/ MATH46 Differenial Geomery Professor P. J. Rippon Dr. M. Ó Searcóid Dr. J. B. Quigley Insrucions for Cidaes Time
UNIVERSITY COLLEGE DUBLIN An Coláise Ollscoile, Baile Áha Cliah SEMESTER EXAMINATION 9/ MATH46 Differenial Geomery Professor P. J. Rippon Dr. M. Ó Searcóid Dr. J. B. Quigley Insrucions for Cidaes Time
3, so θ = arccos
 Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
MEI STRUCTURED MATHEMATICS 4758
 OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
AP Calculus BC Chapter 10 Part 1 AP Exam Problems
 AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
Math 115 Final Exam December 14, 2017
 On my honor, as a suden, I have neiher given nor received unauhorized aid on his academic work. Your Iniials Only: Iniials: Do no wrie in his area Mah 5 Final Exam December, 07 Your U-M ID # (no uniqname):
On my honor, as a suden, I have neiher given nor received unauhorized aid on his academic work. Your Iniials Only: Iniials: Do no wrie in his area Mah 5 Final Exam December, 07 Your U-M ID # (no uniqname):
Math 116 Practice for Exam 2
 Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Morning Time: 1 hour 30 minutes Additional materials (enclosed):
 ADVANCED GCE 78/0 MATHEMATICS (MEI) Differenial Equaions THURSDAY JANUARY 008 Morning Time: hour 30 minues Addiional maerials (enclosed): None Addiional maerials (required): Answer Bookle (8 pages) Graph
ADVANCED GCE 78/0 MATHEMATICS (MEI) Differenial Equaions THURSDAY JANUARY 008 Morning Time: hour 30 minues Addiional maerials (enclosed): None Addiional maerials (required): Answer Bookle (8 pages) Graph
PROBLEMS FOR MATH 162 If a problem is starred, all subproblems are due. If only subproblems are starred, only those are due. SLOPES OF TANGENT LINES
 PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
Module MA1132 (Frolov), Advanced Calculus Tutorial Sheet 1. To be solved during the tutorial session Thursday/Friday, 21/22 January 2016
 Module MA113 (Frolov), Advanced Calculus Tuorial Shee 1 To be solved during he uorial session Thursday/Friday, 1/ January 16 A curve C in he xy-plane is represened by he equaion Ax + Bxy + Cy + Dx + Ey
Module MA113 (Frolov), Advanced Calculus Tuorial Shee 1 To be solved during he uorial session Thursday/Friday, 1/ January 16 A curve C in he xy-plane is represened by he equaion Ax + Bxy + Cy + Dx + Ey
Some Basic Information about M-S-D Systems
 Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
ACCUMULATION. Section 7.5 Calculus AP/Dual, Revised /26/2018 7:27 PM 7.5A: Accumulation 1
 ACCUMULATION Secion 7.5 Calculus AP/Dual, Revised 2019 vie.dang@humbleisd.ne 12/26/2018 7:27 PM 7.5A: Accumulaion 1 APPLICATION PROBLEMS A. Undersand he quesion. I is ofen no necessary o as much compuaion
ACCUMULATION Secion 7.5 Calculus AP/Dual, Revised 2019 vie.dang@humbleisd.ne 12/26/2018 7:27 PM 7.5A: Accumulaion 1 APPLICATION PROBLEMS A. Undersand he quesion. I is ofen no necessary o as much compuaion
HOMEWORK # 2: MATH 211, SPRING Note: This is the last solution set where I will describe the MATLAB I used to make my pictures.
 HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
Math 23 Spring Differential Equations. Final Exam Due Date: Tuesday, June 6, 5pm
 Mah Spring 6 Differenial Equaions Final Exam Due Dae: Tuesday, June 6, 5pm Your name (please prin): Insrucions: This is an open book, open noes exam. You are free o use a calculaor or compuer o check your
Mah Spring 6 Differenial Equaions Final Exam Due Dae: Tuesday, June 6, 5pm Your name (please prin): Insrucions: This is an open book, open noes exam. You are free o use a calculaor or compuer o check your
Homework sheet Exercises done during the lecture of March 12, 2014
 EXERCISE SESSION 2A FOR THE COURSE GÉOMÉTRIE EUCLIDIENNE, NON EUCLIDIENNE ET PROJECTIVE MATTEO TOMMASINI Homework shee 3-4 - Exercises done during he lecure of March 2, 204 Exercise 2 Is i rue ha he parameerized
EXERCISE SESSION 2A FOR THE COURSE GÉOMÉTRIE EUCLIDIENNE, NON EUCLIDIENNE ET PROJECTIVE MATTEO TOMMASINI Homework shee 3-4 - Exercises done during he lecure of March 2, 204 Exercise 2 Is i rue ha he parameerized
a. Show that these lines intersect by finding the point of intersection. b. Find an equation for the plane containing these lines.
 Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Math Final Exam Solutions
 Mah 246 - Final Exam Soluions Friday, July h, 204 () Find explici soluions and give he inerval of definiion o he following iniial value problems (a) ( + 2 )y + 2y = e, y(0) = 0 Soluion: In normal form,
Mah 246 - Final Exam Soluions Friday, July h, 204 () Find explici soluions and give he inerval of definiion o he following iniial value problems (a) ( + 2 )y + 2y = e, y(0) = 0 Soluion: In normal form,
Parametrics and Vectors (BC Only)
 Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
AP Calculus BC 2004 Free-Response Questions Form B
 AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
Applications of the Basic Equations Chapter 3. Paul A. Ullrich
 Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
Check in: 1 If m = 2(x + 1) and n = find y when. b y = 2m n 2
 7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
7 Parameric equaions This chaer will show ou how o skech curves using heir arameric equaions conver arameric equaions o Caresian equaions find oins of inersecion of curves and lines using arameric equaions
AP CALCULUS BC 2016 SCORING GUIDELINES
 6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
Solutions from Chapter 9.1 and 9.2
 Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Logistic growth rate. Fencing a pen. Notes. Notes. Notes. Optimization: finding the biggest/smallest/highest/lowest, etc.
 Opimizaion: finding he bigges/smalles/highes/lowes, ec. Los of non-sandard problems! Logisic growh rae 7.1 Simple biological opimizaion problems Small populaions AND large populaions grow slowly N: densiy
Opimizaion: finding he bigges/smalles/highes/lowes, ec. Los of non-sandard problems! Logisic growh rae 7.1 Simple biological opimizaion problems Small populaions AND large populaions grow slowly N: densiy
DE55/DC55 ENGINEERING MATHEMATICS-II DEC 2013
 DE55/DC55 ENGINEERING MATHEMATICS-II DEC Q. a. Evaluae LT sin x x sin 5x + sin 6x sin x Here we have, L x sin x + sin 6x sin 5x sin x L x L x x + 6x x 6x sin + cos 5x + x 5x x cos.sin sin 4x cos( x) cos
DE55/DC55 ENGINEERING MATHEMATICS-II DEC Q. a. Evaluae LT sin x x sin 5x + sin 6x sin x Here we have, L x sin x + sin 6x sin 5x sin x L x L x x + 6x x 6x sin + cos 5x + x 5x x cos.sin sin 4x cos( x) cos
Chapter 7: Solving Trig Equations
 Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
2.7. Some common engineering functions. Introduction. Prerequisites. Learning Outcomes
 Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Math 334 Fall 2011 Homework 11 Solutions
 Dec. 2, 2 Mah 334 Fall 2 Homework Soluions Basic Problem. Transform he following iniial value problem ino an iniial value problem for a sysem: u + p()u + q() u g(), u() u, u () v. () Soluion. Le v u. Then
Dec. 2, 2 Mah 334 Fall 2 Homework Soluions Basic Problem. Transform he following iniial value problem ino an iniial value problem for a sysem: u + p()u + q() u g(), u() u, u () v. () Soluion. Le v u. Then
Solutions of Sample Problems for Third In-Class Exam Math 246, Spring 2011, Professor David Levermore
 Soluions of Sample Problems for Third In-Class Exam Mah 6, Spring, Professor David Levermore Compue he Laplace ransform of f e from is definiion Soluion The definiion of he Laplace ransform gives L[f]s
Soluions of Sample Problems for Third In-Class Exam Mah 6, Spring, Professor David Levermore Compue he Laplace ransform of f e from is definiion Soluion The definiion of he Laplace ransform gives L[f]s
4.5 Constant Acceleration
 4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
Starting from a familiar curve
 In[]:= NoebookDirecory Ou[]= C:\Dropbox\Work\myweb\Courses\Mah_pages\Mah_5\ You can evaluae he enire noebook by using he keyboard shorcu Al+v o, or he menu iem Evaluaion Evaluae Noebook. Saring from a
In[]:= NoebookDirecory Ou[]= C:\Dropbox\Work\myweb\Courses\Mah_pages\Mah_5\ You can evaluae he enire noebook by using he keyboard shorcu Al+v o, or he menu iem Evaluaion Evaluae Noebook. Saring from a
IB Physics Kinematics Worksheet
 IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
IB Physics Kinemaics Workshee Wrie full soluions and noes for muliple choice answers. Do no use a calculaor for muliple choice answers. 1. Which of he following is a correc definiion of average acceleraion?
u(x) = e x 2 y + 2 ) Integrate and solve for x (1 + x)y + y = cos x Answer: Divide both sides by 1 + x and solve for y. y = x y + cos x
 . 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
. 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
AP Calculus BC - Parametric equations and vectors Chapter 9- AP Exam Problems solutions
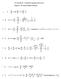 AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
10.1 EXERCISES. y 2 t 2. y 1 t y t 3. y e
 66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
23.5. Half-Range Series. Introduction. Prerequisites. Learning Outcomes
 Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Half-Range Series 2.5 Inroducion In his Secion we address he following problem: Can we find a Fourier series expansion of a funcion defined over a finie inerval? Of course we recognise ha such a funcion
Differential Geometry: Revisiting Curvatures
 Differenial Geomery: Reisiing Curaures Curaure and Graphs Recall: hus, up o a roaion in he x-y plane, we hae: f 1 ( x, y) x y he alues 1 and are he principal curaures a p and he corresponding direcions
Differenial Geomery: Reisiing Curaures Curaure and Graphs Recall: hus, up o a roaion in he x-y plane, we hae: f 1 ( x, y) x y he alues 1 and are he principal curaures a p and he corresponding direcions
Predator - Prey Model Trajectories and the nonlinear conservation law
 Predaor - Prey Model Trajecories and he nonlinear conservaion law James K. Peerson Deparmen of Biological Sciences and Deparmen of Mahemaical Sciences Clemson Universiy Ocober 28, 213 Ouline Drawing Trajecories
Predaor - Prey Model Trajecories and he nonlinear conservaion law James K. Peerson Deparmen of Biological Sciences and Deparmen of Mahemaical Sciences Clemson Universiy Ocober 28, 213 Ouline Drawing Trajecories
Math 221: Mathematical Notation
 Mah 221: Mahemaical Noaion Purpose: One goal in any course is o properly use he language o ha subjec. These noaions summarize some o he major conceps and more diicul opics o he uni. Typing hem helps you
Mah 221: Mahemaical Noaion Purpose: One goal in any course is o properly use he language o ha subjec. These noaions summarize some o he major conceps and more diicul opics o he uni. Typing hem helps you
Chapters 6 & 7: Trigonometric Functions of Angles and Real Numbers. Divide both Sides by 180
 Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
Algebra Chapers & : Trigonomeric Funcions of Angles and Real Numbers Chapers & : Trigonomeric Funcions of Angles and Real Numbers - Angle Measures Radians: - a uni (rad o measure he size of an angle. rad
AP CALCULUS AB/CALCULUS BC 2016 SCORING GUIDELINES. Question 1. 1 : estimate = = 120 liters/hr
 AP CALCULUS AB/CALCULUS BC 16 SCORING GUIDELINES Quesion 1 (hours) R ( ) (liers / hour) 1 3 6 8 134 119 95 74 7 Waer is pumped ino a ank a a rae modeled by W( ) = e liers per hour for 8, where is measured
AP CALCULUS AB/CALCULUS BC 16 SCORING GUIDELINES Quesion 1 (hours) R ( ) (liers / hour) 1 3 6 8 134 119 95 74 7 Waer is pumped ino a ank a a rae modeled by W( ) = e liers per hour for 8, where is measured
Math 333 Problem Set #2 Solution 14 February 2003
 Mah 333 Problem Se #2 Soluion 14 February 2003 A1. Solve he iniial value problem dy dx = x2 + e 3x ; 2y 4 y(0) = 1. Soluion: This is separable; we wrie 2y 4 dy = x 2 + e x dx and inegrae o ge The iniial
Mah 333 Problem Se #2 Soluion 14 February 2003 A1. Solve he iniial value problem dy dx = x2 + e 3x ; 2y 4 y(0) = 1. Soluion: This is separable; we wrie 2y 4 dy = x 2 + e x dx and inegrae o ge The iniial
Roller-Coaster Coordinate System
 Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
System of Linear Differential Equations
 Sysem of Linear Differenial Equaions In "Ordinary Differenial Equaions" we've learned how o solve a differenial equaion for a variable, such as: y'k5$e K2$x =0 solve DE yx = K 5 2 ek2 x C_C1 2$y''C7$y
Sysem of Linear Differenial Equaions In "Ordinary Differenial Equaions" we've learned how o solve a differenial equaion for a variable, such as: y'k5$e K2$x =0 solve DE yx = K 5 2 ek2 x C_C1 2$y''C7$y
Math 106: Review for Final Exam, Part II. (x x 0 ) 2 = !
 Mah 6: Review for Final Exam, Par II. Use a second-degree Taylor polynomial o esimae 8. We choose f(x) x and x 7 because 7 is he perfec cube closes o 8. f(x) x / f(7) f (x) x / f (7) x / 7 / 7 f (x) 9
Mah 6: Review for Final Exam, Par II. Use a second-degree Taylor polynomial o esimae 8. We choose f(x) x and x 7 because 7 is he perfec cube closes o 8. f(x) x / f(7) f (x) x / f (7) x / 7 / 7 f (x) 9
Applicable Mathematics 2A
 Applicable Mahemaics A Lecure Noes Revised: Augus 00 Please noe ha hese are my lecure noes: hey are no course noes. So I will be following hese noes very closely, supplemened by he homework eamples ec
Applicable Mahemaics A Lecure Noes Revised: Augus 00 Please noe ha hese are my lecure noes: hey are no course noes. So I will be following hese noes very closely, supplemened by he homework eamples ec
Solutions to Assignment 1
 MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Answers to 1 Homework
 Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
Answers o Homework. x + and y x 5 y To eliminae he parameer, solve for x. Subsiue ino y s equaion o ge y x.. x and y, x y x To eliminae he parameer, solve for. Subsiue ino y s equaion o ge x y, x. (Noe:
WEEK-3 Recitation PHYS 131. of the projectile s velocity remains constant throughout the motion, since the acceleration a x
 WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
Math 116 Second Midterm March 21, 2016
 Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
Math 334 Test 1 KEY Spring 2010 Section: 001. Instructor: Scott Glasgow Dates: May 10 and 11.
 1 Mah 334 Tes 1 KEY Spring 21 Secion: 1 Insrucor: Sco Glasgow Daes: Ma 1 and 11. Do NOT wrie on his problem saemen bookle, excep for our indicaion of following he honor code jus below. No credi will be
1 Mah 334 Tes 1 KEY Spring 21 Secion: 1 Insrucor: Sco Glasgow Daes: Ma 1 and 11. Do NOT wrie on his problem saemen bookle, excep for our indicaion of following he honor code jus below. No credi will be
10.6 Parametric Equations
 0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
0_006.qd /8/05 9:05 AM Page 77 Secion 0.6 77 Parameric Equaions 0.6 Parameric Equaions Wha ou should learn Evaluae ses of parameric equaions for given values of he parameer. Skech curves ha are represened
SOLUTIONS TO ECE 3084
 SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
Let us start with a two dimensional case. We consider a vector ( x,
 Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
AP CALCULUS AB 2003 SCORING GUIDELINES (Form B)
 SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
SCORING GUIDELINES (Form B) Quesion A blood vessel is 6 millimeers (mm) long Disance wih circular cross secions of varying diameer. x (mm) 6 8 4 6 Diameer The able above gives he measuremens of he B(x)
Matlab and Python programming: how to get started
 Malab and Pyhon programming: how o ge sared Equipping readers he skills o wrie programs o explore complex sysems and discover ineresing paerns from big daa is one of he main goals of his book. In his chaper,
Malab and Pyhon programming: how o ge sared Equipping readers he skills o wrie programs o explore complex sysems and discover ineresing paerns from big daa is one of he main goals of his book. In his chaper,
The equation to any straight line can be expressed in the form:
 Sring Graphs Par 1 Answers 1 TI-Nspire Invesigaion Suden min Aims Deermine a series of equaions of sraigh lines o form a paern similar o ha formed by he cables on he Jerusalem Chords Bridge. Deermine he
Sring Graphs Par 1 Answers 1 TI-Nspire Invesigaion Suden min Aims Deermine a series of equaions of sraigh lines o form a paern similar o ha formed by he cables on he Jerusalem Chords Bridge. Deermine he
Distance Between Two Ellipses in 3D
 Disance Beween Two Ellipses in 3D David Eberly Magic Sofware 6006 Meadow Run Cour Chapel Hill, NC 27516 eberly@magic-sofware.com 1 Inroducion An ellipse in 3D is represened by a cener C, uni lengh axes
Disance Beween Two Ellipses in 3D David Eberly Magic Sofware 6006 Meadow Run Cour Chapel Hill, NC 27516 eberly@magic-sofware.com 1 Inroducion An ellipse in 3D is represened by a cener C, uni lengh axes
Math 105 Second Midterm March 16, 2017
 Mah 105 Second Miderm March 16, 2017 UMID: Insrucor: Iniials: Secion: 1. Do no open his exam unil you are old o do so. 2. Do no wrie your name anywhere on his exam. 3. This exam has 9 pages including his
Mah 105 Second Miderm March 16, 2017 UMID: Insrucor: Iniials: Secion: 1. Do no open his exam unil you are old o do so. 2. Do no wrie your name anywhere on his exam. 3. This exam has 9 pages including his
3.6 Derivatives as Rates of Change
 3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
SMT 2014 Calculus Test Solutions February 15, 2014 = 3 5 = 15.
 SMT Calculus Tes Soluions February 5,. Le f() = and le g() =. Compue f ()g (). Answer: 5 Soluion: We noe ha f () = and g () = 6. Then f ()g () =. Plugging in = we ge f ()g () = 6 = 3 5 = 5.. There is a
SMT Calculus Tes Soluions February 5,. Le f() = and le g() =. Compue f ()g (). Answer: 5 Soluion: We noe ha f () = and g () = 6. Then f ()g () =. Plugging in = we ge f ()g () = 6 = 3 5 = 5.. There is a
Ground Rules. PC1221 Fundamentals of Physics I. Kinematics. Position. Lectures 3 and 4 Motion in One Dimension. A/Prof Tay Seng Chuan
 Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
PHYS 100: Lecture 2. Motion at Constant Acceleration. Relative Motion: Reference Frames. x x = v t + a t. x = vdt. v = adt. x Tortoise.
 a PHYS 100: Lecure 2 Moion a Consan Acceleraion a 0 0 Area a 0 a 0 v ad v v0 a0 v 0 x vd 0 A(1/2)( v) Area v 0 v v-v 0 v 0 x x v + a 1 0 0 2 0 2 Relaive Moion: Reference Frames x d Achilles Toroise x Toroise
a PHYS 100: Lecure 2 Moion a Consan Acceleraion a 0 0 Area a 0 a 0 v ad v v0 a0 v 0 x vd 0 A(1/2)( v) Area v 0 v v-v 0 v 0 x x v + a 1 0 0 2 0 2 Relaive Moion: Reference Frames x d Achilles Toroise x Toroise
( ) 2. Review Exercise 2. cos θ 2 3 = = 2 tan. cos. 2 x = = x a. Since π π, = 2. sin = = 2+ = = cotx. 2 sin θ 2+
 Review Eercise sin 5 cos sin an cos 5 5 an 5 9 co 0 a sinθ 6 + 4 6 + sin θ 4 6+ + 6 + 4 cos θ sin θ + 4 4 sin θ + an θ cos θ ( ) + + + + Since π π, < θ < anθ should be negaive. anθ ( + ) Pearson Educaion
Review Eercise sin 5 cos sin an cos 5 5 an 5 9 co 0 a sinθ 6 + 4 6 + sin θ 4 6+ + 6 + 4 cos θ sin θ + 4 4 sin θ + an θ cos θ ( ) + + + + Since π π, < θ < anθ should be negaive. anθ ( + ) Pearson Educaion
Section 3.8, Mechanical and Electrical Vibrations
 Secion 3.8, Mechanical and Elecrical Vibraions Mechanical Unis in he U.S. Cusomary and Meric Sysems Disance Mass Time Force g (Earh) Uni U.S. Cusomary MKS Sysem CGS Sysem fee f slugs seconds sec pounds
Secion 3.8, Mechanical and Elecrical Vibraions Mechanical Unis in he U.S. Cusomary and Meric Sysems Disance Mass Time Force g (Earh) Uni U.S. Cusomary MKS Sysem CGS Sysem fee f slugs seconds sec pounds
9231 FURTHER MATHEMATICS
 CAMBRIDGE INTERNATIONAL EXAMINATIONS GCE Advanced Level MARK SCHEME for he May/June series 9 FURTHER MATHEMATICS 9/ Paper, maximum raw mark This mark scheme is published as an aid o eachers and candidaes,
CAMBRIDGE INTERNATIONAL EXAMINATIONS GCE Advanced Level MARK SCHEME for he May/June series 9 FURTHER MATHEMATICS 9/ Paper, maximum raw mark This mark scheme is published as an aid o eachers and candidaes,
Section 3.5 Nonhomogeneous Equations; Method of Undetermined Coefficients
 Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
23.2. Representing Periodic Functions by Fourier Series. Introduction. Prerequisites. Learning Outcomes
 Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Solutionbank Edexcel AS and A Level Modular Mathematics
 Page of 4 Soluionbank Edexcel AS and A Level Modular Mahemaics Exercise A, Quesion Quesion: Skech he graphs of (a) y = e x + (b) y = 4e x (c) y = e x 3 (d) y = 4 e x (e) y = 6 + 0e x (f) y = 00e x + 0
Page of 4 Soluionbank Edexcel AS and A Level Modular Mahemaics Exercise A, Quesion Quesion: Skech he graphs of (a) y = e x + (b) y = 4e x (c) y = e x 3 (d) y = 4 e x (e) y = 6 + 0e x (f) y = 00e x + 0
Solutions for homework 12
 y Soluions for homework Secion Nonlinear sysems: The linearizaion of a nonlinear sysem Consider he sysem y y y y y (i) Skech he nullclines Use a disincive marking for each nullcline so hey can be disinguished
y Soluions for homework Secion Nonlinear sysems: The linearizaion of a nonlinear sysem Consider he sysem y y y y y (i) Skech he nullclines Use a disincive marking for each nullcline so hey can be disinguished
k 1 k 2 x (1) x 2 = k 1 x 1 = k 2 k 1 +k 2 x (2) x k series x (3) k 2 x 2 = k 1 k 2 = k 1+k 2 = 1 k k 2 k series
 Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
An Introduction to Malliavin calculus and its applications
 An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
SINUSOIDAL WAVEFORMS
 SINUSOIDAL WAVEFORMS The sinusoidal waveform is he only waveform whose shape is no affeced by he response characerisics of R, L, and C elemens. Enzo Paerno CIRCUIT ELEMENTS R [ Ω ] Resisance: Ω: Ohms Georg
SINUSOIDAL WAVEFORMS The sinusoidal waveform is he only waveform whose shape is no affeced by he response characerisics of R, L, and C elemens. Enzo Paerno CIRCUIT ELEMENTS R [ Ω ] Resisance: Ω: Ohms Georg
Oscillations. Periodic Motion. Sinusoidal Motion. PHY oscillations - J. Hedberg
 Oscillaions PHY 207 - oscillaions - J. Hedberg - 2017 1. Periodic Moion 2. Sinusoidal Moion 3. How do we ge his kind of moion? 4. Posiion - Velociy - cceleraion 5. spring wih vecors 6. he reference circle
Oscillaions PHY 207 - oscillaions - J. Hedberg - 2017 1. Periodic Moion 2. Sinusoidal Moion 3. How do we ge his kind of moion? 4. Posiion - Velociy - cceleraion 5. spring wih vecors 6. he reference circle
8. Basic RL and RC Circuits
 8. Basic L and C Circuis This chaper deals wih he soluions of he responses of L and C circuis The analysis of C and L circuis leads o a linear differenial equaion This chaper covers he following opics
8. Basic L and C Circuis This chaper deals wih he soluions of he responses of L and C circuis The analysis of C and L circuis leads o a linear differenial equaion This chaper covers he following opics
Math 36. Rumbos Spring Solutions to Assignment #6. 1. Suppose the growth of a population is governed by the differential equation.
 Mah 36. Rumbos Spring 1 1 Soluions o Assignmen #6 1. Suppose he growh of a populaion is governed by he differenial equaion where k is a posiive consan. d d = k (a Explain why his model predics ha he populaion
Mah 36. Rumbos Spring 1 1 Soluions o Assignmen #6 1. Suppose he growh of a populaion is governed by he differenial equaion where k is a posiive consan. d d = k (a Explain why his model predics ha he populaion
DEPARTMENT OF ELECTRICAL AND ELECTRONIC ENGINEERING EXAMINATIONS 2008
 [E5] IMPERIAL COLLEGE LONDON DEPARTMENT OF ELECTRICAL AND ELECTRONIC ENGINEERING EXAMINATIONS 008 EEE/ISE PART II MEng BEng and ACGI SIGNALS AND LINEAR SYSTEMS Time allowed: :00 hours There are FOUR quesions
[E5] IMPERIAL COLLEGE LONDON DEPARTMENT OF ELECTRICAL AND ELECTRONIC ENGINEERING EXAMINATIONS 008 EEE/ISE PART II MEng BEng and ACGI SIGNALS AND LINEAR SYSTEMS Time allowed: :00 hours There are FOUR quesions
Y 0.4Y 0.45Y Y to a proper ARMA specification.
 HG Jan 04 ECON 50 Exercises II - 0 Feb 04 (wih answers Exercise. Read secion 8 in lecure noes 3 (LN3 on he common facor problem in ARMA-processes. Consider he following process Y 0.4Y 0.45Y 0.5 ( where
HG Jan 04 ECON 50 Exercises II - 0 Feb 04 (wih answers Exercise. Read secion 8 in lecure noes 3 (LN3 on he common facor problem in ARMA-processes. Consider he following process Y 0.4Y 0.45Y 0.5 ( where
Physics 218 Exam 1. with Solutions Fall 2010, Sections Part 1 (15) Part 2 (20) Part 3 (20) Part 4 (20) Bonus (5)
 Physics 18 Exam 1 wih Soluions Fall 1, Secions 51-54 Fill ou he informaion below bu o no open he exam unil insruce o o so! Name Signaure Suen ID E-mail Secion # ules of he exam: 1. You have he full class
Physics 18 Exam 1 wih Soluions Fall 1, Secions 51-54 Fill ou he informaion below bu o no open he exam unil insruce o o so! Name Signaure Suen ID E-mail Secion # ules of he exam: 1. You have he full class
Week 1 Lecture 2 Problems 2, 5. What if something oscillates with no obvious spring? What is ω? (problem set problem)
 Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
t is a basis for the solution space to this system, then the matrix having these solutions as columns, t x 1 t, x 2 t,... x n t x 2 t...
 Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Lecture 13 RC/RL Circuits, Time Dependent Op Amp Circuits
 Lecure 13 RC/RL Circuis, Time Dependen Op Amp Circuis RL Circuis The seps involved in solving simple circuis conaining dc sources, resisances, and one energy-sorage elemen (inducance or capaciance) are:
Lecure 13 RC/RL Circuis, Time Dependen Op Amp Circuis RL Circuis The seps involved in solving simple circuis conaining dc sources, resisances, and one energy-sorage elemen (inducance or capaciance) are:
Laplace transfom: t-translation rule , Haynes Miller and Jeremy Orloff
 Laplace ransfom: -ranslaion rule 8.03, Haynes Miller and Jeremy Orloff Inroducory example Consider he sysem ẋ + 3x = f(, where f is he inpu and x he response. We know is uni impulse response is 0 for
Laplace ransfom: -ranslaion rule 8.03, Haynes Miller and Jeremy Orloff Inroducory example Consider he sysem ẋ + 3x = f(, where f is he inpu and x he response. We know is uni impulse response is 0 for
DIFFERENTIAL GEOMETRY HW 5
 DIFFERENTIAL GEOMETRY HW 5 CLAY SHONKWILER 3. Le M be a complee Riemannian manifold wih non-posiive secional curvaure. Prove ha d exp p v w w, for all p M, all v T p M and all w T v T p M. Proof. Le γ
DIFFERENTIAL GEOMETRY HW 5 CLAY SHONKWILER 3. Le M be a complee Riemannian manifold wih non-posiive secional curvaure. Prove ha d exp p v w w, for all p M, all v T p M and all w T v T p M. Proof. Le γ
dy dx = xey (a) y(0) = 2 (b) y(1) = 2.5 SOLUTION: See next page
 Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Numerical Dispersion
 eview of Linear Numerical Sabiliy Numerical Dispersion n he previous lecure, we considered he linear numerical sabiliy of boh advecion and diffusion erms when approimaed wih several spaial and emporal
eview of Linear Numerical Sabiliy Numerical Dispersion n he previous lecure, we considered he linear numerical sabiliy of boh advecion and diffusion erms when approimaed wih several spaial and emporal
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
 Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
MATH 4330/5330, Fourier Analysis Section 6, Proof of Fourier s Theorem for Pointwise Convergence
 MATH 433/533, Fourier Analysis Secion 6, Proof of Fourier s Theorem for Poinwise Convergence Firs, some commens abou inegraing periodic funcions. If g is a periodic funcion, g(x + ) g(x) for all real x,
MATH 433/533, Fourier Analysis Secion 6, Proof of Fourier s Theorem for Poinwise Convergence Firs, some commens abou inegraing periodic funcions. If g is a periodic funcion, g(x + ) g(x) for all real x,
MA 214 Calculus IV (Spring 2016) Section 2. Homework Assignment 1 Solutions
 MA 14 Calculus IV (Spring 016) Secion Homework Assignmen 1 Soluions 1 Boyce and DiPrima, p 40, Problem 10 (c) Soluion: In sandard form he given firs-order linear ODE is: An inegraing facor is given by
MA 14 Calculus IV (Spring 016) Secion Homework Assignmen 1 Soluions 1 Boyce and DiPrima, p 40, Problem 10 (c) Soluion: In sandard form he given firs-order linear ODE is: An inegraing facor is given by
Ordinary Differential Equations
 Ordinary Differenial Equaions 5. Examples of linear differenial equaions and heir applicaions We consider some examples of sysems of linear differenial equaions wih consan coefficiens y = a y +... + a
Ordinary Differenial Equaions 5. Examples of linear differenial equaions and heir applicaions We consider some examples of sysems of linear differenial equaions wih consan coefficiens y = a y +... + a
Kinematics Vocabulary. Kinematics and One Dimensional Motion. Position. Coordinate System in One Dimension. Kinema means movement 8.
 Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Finish reading Chapter 2 of Spivak, rereading earlier sections as necessary. handout and fill in some missing details!
 MAT 257, Handou 6: Ocober 7-2, 20. I. Assignmen. Finish reading Chaper 2 of Spiva, rereading earlier secions as necessary. handou and fill in some missing deails! II. Higher derivaives. Also, read his
MAT 257, Handou 6: Ocober 7-2, 20. I. Assignmen. Finish reading Chaper 2 of Spiva, rereading earlier secions as necessary. handou and fill in some missing deails! II. Higher derivaives. Also, read his
THE 2-BODY PROBLEM. FIGURE 1. A pair of ellipses sharing a common focus. (c,b) c+a ROBERT J. VANDERBEI
 THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
THE 2-BODY PROBLEM ROBERT J. VANDERBEI ABSTRACT. In his shor noe, we show ha a pair of ellipses wih a common focus is a soluion o he 2-body problem. INTRODUCTION. Solving he 2-body problem from scrach
Chapter 2 Solutions. ψ 1 ψ. 16 t. ( z υt ), where υ is in the negative z direction. = 2 A. Chapter 2 Solutions = 32
 Chaper Soluions 1 Chaper Soluions.1 υ ( z+ υ) ψ υ( z+ υ) ψ υ I s a wice differeniable funcion of ( z υ ), where υ is in he negaive z direcion.. υ ψ ( y,) ( y 4) ( y 4 ) ψ ( y 4 ) ψ 3 Thus, υ 4, υ 16, and,
Chaper Soluions 1 Chaper Soluions.1 υ ( z+ υ) ψ υ( z+ υ) ψ υ I s a wice differeniable funcion of ( z υ ), where υ is in he negaive z direcion.. υ ψ ( y,) ( y 4) ( y 4 ) ψ ( y 4 ) ψ 3 Thus, υ 4, υ 16, and,
t + t sin t t cos t sin t. t cos t sin t dt t 2 = exp 2 log t log(t cos t sin t) = Multiplying by this factor and then integrating, we conclude that
 ODEs, Homework #4 Soluions. Check ha y ( = is a soluion of he second-order ODE ( cos sin y + y sin y sin = 0 and hen use his fac o find all soluions of he ODE. When y =, we have y = and also y = 0, so
ODEs, Homework #4 Soluions. Check ha y ( = is a soluion of he second-order ODE ( cos sin y + y sin y sin = 0 and hen use his fac o find all soluions of he ODE. When y =, we have y = and also y = 0, so
