Math 221: Mathematical Notation
|
|
|
- Silvia Fox
- 5 years ago
- Views:
Transcription
1 Mah 221: Mahemaical Noaion Purpose: One goal in any course is o properly use he language o ha subjec. These noaions summarize some o he major conceps and more diicul opics o he uni. Typing hem helps you learn he maerial while eaching you o properly express mahemaics on he compuer. Par o your grade is or properly using mahemaical conen. Insrucions: Use Word or WordPerec o recreae he ollowing documens. Each aricle is worh 10 poins and should be ed o he insrucor a james@richland.edu. This is no a group assignmen, each person needs o creae and submi heir own noaion. I you urn in someone else's work as your own, you will ge a zero or he assignmen and ha person will lose poins. Do no share your work wih ohers. Type your name a he op o each documen. Include he ile as par o wha you ype. The lines around he ile aren' ha imporan, bu i you will ype a he beginning o a line and hi ener, boh Word and WordPerec will conver i o a line. For expressions or equaions, you should use he equaion edior in Word or WordPerec. The insrucor used WordPerec and a 14 p Times New oman on wih 0.75" margins, so hey may no look exacly he same as your documen. I here is an equaion, pu boh sides o he equaion ino he same equaion edior box insead o creaing wo objecs. Be sure o use he proper symbols, here are some insances where more han one symbol may look he same, bu hey have dieren meanings and don' appear he same as wha's on he assignmen. There are some useul ips on he websie a hp://people.richland.edu/james/edior/ I you ail o ype your name on he documen, you will lose 1 poin. Don' ype he hins or reminders ha appear on he pages. These noaions are due beore he beginning o class on he day o he exam or ha maerial. Lae work will be acceped bu will lose 20% o is value per class period. I I receive your ed assignmen more han one class period beore i is due and you don' receive all 10 poins, hen I will you back wih hings o correc so ha you can ge all he poins. Any correcions need o be submied by he due dae and ime or he original score will be used.
2 haper 12 - Vecors Press rl-b beore each vecor o make i bold Do Producs The do produc is a scalar and is deined as uv 1 1+ uv 2 2+ uv 3 3 u v The do produc is 0 i and only i he vecors are orhogonal. u v u v cosθ v b proj v b b W F cosθ PQ F PQ The orhogonal projecion o v ono b is b 2 Work can be ound by ross Producs i j k u v u u u v v v The cross produc is a vecor and is deined as The cross produc is orhogonal o boh vecors. u v u v sinθ The area o a parallelogram is equal o he cross produc o he adjacen side vecors. The cross produc is he zero vecor i and only i he vecors are parallel. Triple Scalar Producs The riple scalar produc is a scalar and is deined as u ( v w) u1 u2 u3 v1 v2 v3 w w w The absolue value o he riple scalar produc is he volume o a parallelpiped. The riple scalar produc is 0 i and only i he vecors are coplanar.
3 haper 13 - Vecor Valued Funcions The derivaives o do and cross producs ollow he produc rule. ( r1 r2) r 1 r2 + r1 r 2 and ( r1 r2) r 1 r2 + r1 r2 I a vecor valued uncion has consan lengh, he r and r' are orhogonal. The arc lengh o a smooh vecor valued uncion is b d L r d Hold down he shi while selecing he I symbol o ge i o grow wih he inegrand. The chain rule is d r d r d dτ d dτ The arc lengh paramerizaion is For a smooh vecor valued uncion, d s r du 0 du dr ds d d and a dr 1 ds To ind he uni angen vecor, ake he derivaive and normalize i. T() d r r To ind he uni normal vecor, ake he derivaive o he uni angen vecor and normalize i. N() T T For curves paramerized by arc lengh, T s r s and N( s) r r The binormal vecor is he cross produc o he uni angen and uni normal vecors. I is also a uni vecor and is ound by. The curvaure is deined by ( ) ( ) ( ) B T N dt κ ds ( s) r s or κ The radius o he oscillaing circle is called he radius o curvaure and is T r ( s) ( s) 1 ρ κ ( )
4 haper 14 - Parial Derivaives The irs-order parial derivaive o wih respec o x is denoed by x ( x, is ound by inding he derivaive o wih every variable oher han x reaed as a consan. The second-order parial derivaives o are, yx y x 2 2 xx, yy 2 x and and he mixed parials are. I is coninuous, he. Noice xy he ordering on he parials. The order or The order or 2 x y x y xy is righ o le, y irs and x second. is rom le o righ, x irs and y second. I z ( x, is diereniable a ( x0, y 0), hen he oal dierenial o a ( x0, y0) is dz ( x, y ) dx + ( x, y ) dy x 0 0 y 0 0 The chain rule says ha i dz dx dy + d d d z z z + u u u z ( x, and x and y are boh uncions o, hen. Furhermore, i x and y are boh uncions o u and v, hen and z z z + v v v xy yx The gradien o is a vecor deined by x, y, z xi + yj + zk x y +, xi y. is read "del ". j or The direcional derivaive o in he direcion o he uni vecor u can be wrien as (, ) (, ) D x y x y u u The applicaions o he gradien are oo numerous o i on his page. I will appear in many ormulas.
5 haper 15 - Muliple Inegrals To evaluae a deinie inegral, work rom inside o ouside. The order o he inegraion is imporan, so be sure o use proper noaion. b g2( x) d h2( 1 1 x, y da x, y dy dx x, y dx dy a g x c h y I you can spli he inegrand ino wo independen uncions o x and y and he limis are consan, hen you can spli a double (or riple) inegral up ino he produc o he b d b d inegrals. x g y dy dx x dx g y dy a c a c The area o a region is A da. The volume o a solid G is The surace area o a paramerically deined surace σ is The cener o graviy ( x, o a lamina is given by M 1 x x x y da M mass o S V G r r u v y x δ (, ), δ (, ) dv da M 1 y y x y da M mass o The Theorem o Pappus says ha he volume o a solid by revolving a region abou a line L is he area o he region imes he disance raveled by he cenroid. For polar and cylindrical coordinaes, you need o inser an exra r ino he inegrand. For spherical coordinaes, you need o inser an exra ρ 2 sinφ ino he inegrand. All o his is relaed o he Jacobian. I T is a ransormaion rom he uv-plane ino he xy-plane, hen he Jacobian o T is denoed by (, ) J u v ( xy, ) u u ( uv, ) x y v v. When applying he ransormaion, muliply he inegrand by he absolue value o he Jacobian.
6 haper 16 - Topics in Vecor alculus ( x, y, z) ( x, y, z) + g ( x, y, z) + h( x, y, z) F i j k g h F + + F z onsider he vecor uncion. The divergence o F is a scalar deined by div The curl o F is a vecor deined by curl i j k F F z g h The line inegral o wih respec o s along is he ne signed area beween he curve and he graph o and is denoed by. ( x, y ) (, ) L Arc lengh can be expressed as. ds A x y ds The value o a line inegral does no depend on is parameerizaion. However, i he orienaion is reversed, he sign o he inegral wih respec o x and y changes, bu he inegral wih respec o he arc lengh parameer s remains unchanged. The work perormed by he vecor ield is I F is a conservaive vecor ield and heorem o calculus applies o line inegrals and F ( x, d r φ( x, y ) φ( x, y ) F W F T ds F d r ( x, φ( x, hen he irs undamenal I F is a conservaive vecor ield, hen F d r 0 curve and he inegral is independen o he pah. or every piecewise smooh closed A vecor ield in 2-space is conservaive i Green's Theorem says (, ) (, ) g and in 3-space i g x y dx + g x y dy da curl F 0
Mathematical Notation Math Calculus & Analytic Geometry III
 Mathematical Notation Math 221 - alculus & Analytic Geometry III Use Word or WordPerect to recreate the ollowing documents. Each article is worth 10 points and should be emailed to the instructor at james@richland.edu.
Mathematical Notation Math 221 - alculus & Analytic Geometry III Use Word or WordPerect to recreate the ollowing documents. Each article is worth 10 points and should be emailed to the instructor at james@richland.edu.
Mathematical Notation Math Calculus & Analytic Geometry III
 Name : Mathematical Notation Math 221 - alculus & Analytic Geometry III Use Word or WordPerect to recreate the ollowing documents. Each article is worth 10 points and can e printed and given to the instructor
Name : Mathematical Notation Math 221 - alculus & Analytic Geometry III Use Word or WordPerect to recreate the ollowing documents. Each article is worth 10 points and can e printed and given to the instructor
a. Show that these lines intersect by finding the point of intersection. b. Find an equation for the plane containing these lines.
 Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
Mah A Final Eam Problems for onsideraion. Show all work for credi. Be sure o show wha you know. Given poins A(,,, B(,,, (,, 4 and (,,, find he volume of he parallelepiped wih adjacen edges AB, A, and A.
3, so θ = arccos
 Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
Mahemaics 210 Professor Alan H Sein Monday, Ocober 1, 2007 SOLUTIONS This problem se is worh 50 poins 1 Find he angle beween he vecors (2, 7, 3) and (5, 2, 4) Soluion: Le θ be he angle (2, 7, 3) (5, 2,
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
Parametrics and Vectors (BC Only)
 Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Paramerics and Vecors (BC Only) The following relaionships should be learned and memorized. The paricle s posiion vecor is r() x(), y(). The velociy vecor is v(),. The speed is he magniude of he velociy
Ground Rules. PC1221 Fundamentals of Physics I. Kinematics. Position. Lectures 3 and 4 Motion in One Dimension. A/Prof Tay Seng Chuan
 Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Ground Rules PC11 Fundamenals of Physics I Lecures 3 and 4 Moion in One Dimension A/Prof Tay Seng Chuan 1 Swich off your handphone and pager Swich off your lapop compuer and keep i No alking while lecure
Math 116 Practice for Exam 2
 Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
Mah 6 Pracice for Exam Generaed Ocober 3, 7 Name: SOLUTIONS Insrucor: Secion Number:. This exam has 5 quesions. Noe ha he problems are no of equal difficuly, so you may wan o skip over and reurn o a problem
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
AP Calculus BC - Parametric equations and vectors Chapter 9- AP Exam Problems solutions
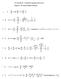 AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
AP Calculus BC - Parameric equaions and vecors Chaper 9- AP Exam Problems soluions. A 5 and 5. B A, 4 + 8. C A, 4 + 4 8 ; he poin a is (,). y + ( x ) x + 4 4. e + e D A, slope.5 6 e e e 5. A d hus d d
Challenge Problems. DIS 203 and 210. March 6, (e 2) k. k(k + 2). k=1. f(x) = k(k + 2) = 1 x k
 Challenge Problems DIS 03 and 0 March 6, 05 Choose one of he following problems, and work on i in your group. Your goal is o convince me ha your answer is correc. Even if your answer isn compleely correc,
Challenge Problems DIS 03 and 0 March 6, 05 Choose one of he following problems, and work on i in your group. Your goal is o convince me ha your answer is correc. Even if your answer isn compleely correc,
AP Calculus BC Chapter 10 Part 1 AP Exam Problems
 AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
AP Calculus BC Chaper Par AP Eam Problems All problems are NO CALCULATOR unless oherwise indicaed Parameric Curves and Derivaives In he y plane, he graph of he parameric equaions = 5 + and y= for, is a
Vector Calculus. Chapter 2
 Chaper Vecor Calculus. Elemenar. Vecor Produc. Differeniaion of Vecors 4. Inegraion of Vecors 5. Del Operaor or Nabla (Smbol 6. Polar Coordinaes Chaper Coninued 7. Line Inegral 8. Volume Inegral 9. Surface
Chaper Vecor Calculus. Elemenar. Vecor Produc. Differeniaion of Vecors 4. Inegraion of Vecors 5. Del Operaor or Nabla (Smbol 6. Polar Coordinaes Chaper Coninued 7. Line Inegral 8. Volume Inegral 9. Surface
Theory of! Partial Differential Equations-I!
 hp://users.wpi.edu/~grear/me61.hml! Ouline! Theory o! Parial Dierenial Equaions-I! Gréar Tryggvason! Spring 010! Basic Properies o PDE!! Quasi-linear Firs Order Equaions! - Characerisics! - Linear and
hp://users.wpi.edu/~grear/me61.hml! Ouline! Theory o! Parial Dierenial Equaions-I! Gréar Tryggvason! Spring 010! Basic Properies o PDE!! Quasi-linear Firs Order Equaions! - Characerisics! - Linear and
2.1: What is physics? Ch02: Motion along a straight line. 2.2: Motion. 2.3: Position, Displacement, Distance
 Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Ch: Moion along a sraigh line Moion Posiion and Displacemen Average Velociy and Average Speed Insananeous Velociy and Speed Acceleraion Consan Acceleraion: A Special Case Anoher Look a Consan Acceleraion
Theory of! Partial Differential Equations!
 hp://www.nd.edu/~gryggva/cfd-course/! Ouline! Theory o! Parial Dierenial Equaions! Gréar Tryggvason! Spring 011! Basic Properies o PDE!! Quasi-linear Firs Order Equaions! - Characerisics! - Linear and
hp://www.nd.edu/~gryggva/cfd-course/! Ouline! Theory o! Parial Dierenial Equaions! Gréar Tryggvason! Spring 011! Basic Properies o PDE!! Quasi-linear Firs Order Equaions! - Characerisics! - Linear and
THE WAVE EQUATION. part hand-in for week 9 b. Any dilation v(x, t) = u(λx, λt) of u(x, t) is also a solution (where λ is constant).
 THE WAVE EQUATION 43. (S) Le u(x, ) be a soluion of he wave equaion u u xx = 0. Show ha Q43(a) (c) is a. Any ranslaion v(x, ) = u(x + x 0, + 0 ) of u(x, ) is also a soluion (where x 0, 0 are consans).
THE WAVE EQUATION 43. (S) Le u(x, ) be a soluion of he wave equaion u u xx = 0. Show ha Q43(a) (c) is a. Any ranslaion v(x, ) = u(x + x 0, + 0 ) of u(x, ) is also a soluion (where x 0, 0 are consans).
Welcome Back to Physics 215!
 Welcome Back o Physics 215! (General Physics I) Thurs. Jan 19 h, 2017 Lecure01-2 1 Las ime: Syllabus Unis and dimensional analysis Today: Displacemen, velociy, acceleraion graphs Nex ime: More acceleraion
Welcome Back o Physics 215! (General Physics I) Thurs. Jan 19 h, 2017 Lecure01-2 1 Las ime: Syllabus Unis and dimensional analysis Today: Displacemen, velociy, acceleraion graphs Nex ime: More acceleraion
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
Lecture #6: Continuous-Time Signals
 EEL5: Discree-Time Signals and Sysems Lecure #6: Coninuous-Time Signals Lecure #6: Coninuous-Time Signals. Inroducion In his lecure, we discussed he ollowing opics:. Mahemaical represenaion and ransormaions
EEL5: Discree-Time Signals and Sysems Lecure #6: Coninuous-Time Signals Lecure #6: Coninuous-Time Signals. Inroducion In his lecure, we discussed he ollowing opics:. Mahemaical represenaion and ransormaions
2. Nonlinear Conservation Law Equations
 . Nonlinear Conservaion Law Equaions One of he clear lessons learned over recen years in sudying nonlinear parial differenial equaions is ha i is generally no wise o ry o aack a general class of nonlinear
. Nonlinear Conservaion Law Equaions One of he clear lessons learned over recen years in sudying nonlinear parial differenial equaions is ha i is generally no wise o ry o aack a general class of nonlinear
MEI STRUCTURED MATHEMATICS 4758
 OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
OXFORD CAMBRIDGE AND RSA EXAMINATIONS Advanced Subsidiary General Cerificae of Educaion Advanced General Cerificae of Educaion MEI STRUCTURED MATHEMATICS 4758 Differenial Equaions Thursday 5 JUNE 006 Afernoon
In this chapter the model of free motion under gravity is extended to objects projected at an angle. When you have completed it, you should
 Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Math 116 Second Midterm March 21, 2016
 Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
Mah 6 Second Miderm March, 06 UMID: EXAM SOLUTIONS Iniials: Insrucor: Secion:. Do no open his exam unil you are old o do so.. Do no wrie your name anywhere on his exam. 3. This exam has pages including
4.6 One Dimensional Kinematics and Integration
 4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
Operators related to the Jacobi setting, for all admissible parameter values
 Operaors relaed o he Jacobi seing, for all admissible parameer values Peer Sjögren Universiy of Gohenburg Join work wih A. Nowak and T. Szarek Alba, June 2013 () 1 / 18 Le Pn α,β be he classical Jacobi
Operaors relaed o he Jacobi seing, for all admissible parameer values Peer Sjögren Universiy of Gohenburg Join work wih A. Nowak and T. Szarek Alba, June 2013 () 1 / 18 Le Pn α,β be he classical Jacobi
1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.
![1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx. 1 1 + x 2 dx. tan 1 (2) = ] ] x 3. Solution: Recall that the given integral is improper because. x 3. 1 x 3. dx = lim dx.](/thumbs/71/65799522.jpg) . Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
. Use Simpson s rule wih n 4 o esimae an () +. Soluion: Since we are using 4 seps, 4 Thus we have [ ( ) f() + 4f + f() + 4f 3 [ + 4 4 6 5 + + 4 4 3 + ] 5 [ + 6 6 5 + + 6 3 + ]. 5. Our funcion is f() +.
I. OBJECTIVE OF THE EXPERIMENT.
 I. OBJECTIVE OF THE EXPERIMENT. Swissmero raels a high speeds hrough a unnel a low pressure. I will hereore undergo ricion ha can be due o: ) Viscosiy o gas (c. "Viscosiy o gas" eperimen) ) The air in
I. OBJECTIVE OF THE EXPERIMENT. Swissmero raels a high speeds hrough a unnel a low pressure. I will hereore undergo ricion ha can be due o: ) Viscosiy o gas (c. "Viscosiy o gas" eperimen) ) The air in
d = ½(v o + v f) t distance = ½ (initial velocity + final velocity) time
 BULLSEYE Lab Name: ANSWER KEY Dae: Pre-AP Physics Lab Projecile Moion Weigh = 1 DIRECTIONS: Follow he insrucions below, build he ramp, ake your measuremens, and use your measuremens o make he calculaions
BULLSEYE Lab Name: ANSWER KEY Dae: Pre-AP Physics Lab Projecile Moion Weigh = 1 DIRECTIONS: Follow he insrucions below, build he ramp, ake your measuremens, and use your measuremens o make he calculaions
Kinematics Vocabulary. Kinematics and One Dimensional Motion. Position. Coordinate System in One Dimension. Kinema means movement 8.
 Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Kinemaics Vocabulary Kinemaics and One Dimensional Moion 8.1 WD1 Kinema means movemen Mahemaical descripion of moion Posiion Time Inerval Displacemen Velociy; absolue value: speed Acceleraion Averages
Space-Time Electrodynamics, and Magnetic Monopoles
 Gauge Insiue Journal Space-Time lecrodnamics and Magneic Monopoles vic0@comcas.ne June 203 Absrac Mawell s lecrodnamics quaions for he 3- Space Vecor Fields disallow magneic monopoles. Those equaions could
Gauge Insiue Journal Space-Time lecrodnamics and Magneic Monopoles vic0@comcas.ne June 203 Absrac Mawell s lecrodnamics quaions for he 3- Space Vecor Fields disallow magneic monopoles. Those equaions could
Math 23 Spring Differential Equations. Final Exam Due Date: Tuesday, June 6, 5pm
 Mah Spring 6 Differenial Equaions Final Exam Due Dae: Tuesday, June 6, 5pm Your name (please prin): Insrucions: This is an open book, open noes exam. You are free o use a calculaor or compuer o check your
Mah Spring 6 Differenial Equaions Final Exam Due Dae: Tuesday, June 6, 5pm Your name (please prin): Insrucions: This is an open book, open noes exam. You are free o use a calculaor or compuer o check your
Mat 267 Engineering Calculus III Updated on 04/30/ x 4y 4z 8x 16y / 4 0. x y z x y. 4x 4y 4z 24x 16y 8z.
 Ma 67 Engineering Calcls III Updaed on 04/0/0 r. Firoz Tes solion:. a) Find he cener and radis of he sphere 4 4 4z 8 6 0 z ( ) ( ) z / 4 The cener is a (, -, 0), and radis b) Find he cener and radis of
Ma 67 Engineering Calcls III Updaed on 04/0/0 r. Firoz Tes solion:. a) Find he cener and radis of he sphere 4 4 4z 8 6 0 z ( ) ( ) z / 4 The cener is a (, -, 0), and radis b) Find he cener and radis of
10.1 EXERCISES. y 2 t 2. y 1 t y t 3. y e
 66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
66 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES SLUTIN We use a graphing device o produce he graphs for he cases a,,.5,.,,.5,, and shown in Figure 7. Noice ha all of hese curves (ecep he case a ) have
Topics covered in tutorial 01: 1. Review of definite integrals 2. Physical Application 3. Area between curves. 1. Review of definite integrals
 MATH4 Calculus II (8 Spring) MATH 4 Tuorial Noes Tuorial Noes (Phyllis LIANG) IA: Phyllis LIANG Email: masliang@us.hk Homepage: hps://masliang.people.us.hk Office: Room 3 (Lif/Lif 3) Phone number: 3587453
MATH4 Calculus II (8 Spring) MATH 4 Tuorial Noes Tuorial Noes (Phyllis LIANG) IA: Phyllis LIANG Email: masliang@us.hk Homepage: hps://masliang.people.us.hk Office: Room 3 (Lif/Lif 3) Phone number: 3587453
Finish reading Chapter 2 of Spivak, rereading earlier sections as necessary. handout and fill in some missing details!
 MAT 257, Handou 6: Ocober 7-2, 20. I. Assignmen. Finish reading Chaper 2 of Spiva, rereading earlier secions as necessary. handou and fill in some missing deails! II. Higher derivaives. Also, read his
MAT 257, Handou 6: Ocober 7-2, 20. I. Assignmen. Finish reading Chaper 2 of Spiva, rereading earlier secions as necessary. handou and fill in some missing deails! II. Higher derivaives. Also, read his
A Note on Fractional Electrodynamics. Abstract
 Commun Nonlinear Sci Numer Simula 8 (3 589 593 A Noe on Fracional lecrodynamics Hosein Nasrolahpour Absrac We invesigae he ime evoluion o he racional elecromagneic waves by using he ime racional Maxwell's
Commun Nonlinear Sci Numer Simula 8 (3 589 593 A Noe on Fracional lecrodynamics Hosein Nasrolahpour Absrac We invesigae he ime evoluion o he racional elecromagneic waves by using he ime racional Maxwell's
KEY. Math 334 Midterm I Fall 2008 sections 001 and 003 Instructor: Scott Glasgow
 1 KEY Mah 4 Miderm I Fall 8 secions 1 and Insrucor: Sco Glasgow Please do NOT wrie on his eam. No credi will be given for such work. Raher wrie in a blue book, or on our own paper, preferabl engineering
1 KEY Mah 4 Miderm I Fall 8 secions 1 and Insrucor: Sco Glasgow Please do NOT wrie on his eam. No credi will be given for such work. Raher wrie in a blue book, or on our own paper, preferabl engineering
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Physics Notes - Ch. 2 Motion in One Dimension
 Physics Noes - Ch. Moion in One Dimension I. The naure o physical quaniies: scalars and ecors A. Scalar quaniy ha describes only magniude (how much), NOT including direcion; e. mass, emperaure, ime, olume,
Physics Noes - Ch. Moion in One Dimension I. The naure o physical quaniies: scalars and ecors A. Scalar quaniy ha describes only magniude (how much), NOT including direcion; e. mass, emperaure, ime, olume,
AP Calculus BC 2004 Free-Response Questions Form B
 AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
AP Calculus BC 200 Free-Response Quesions Form B The maerials included in hese files are inended for noncommercial use by AP eachers for course and exam preparaion; permission for any oher use mus be sough
Lecture 16 (Momentum and Impulse, Collisions and Conservation of Momentum) Physics Spring 2017 Douglas Fields
 Lecure 16 (Momenum and Impulse, Collisions and Conservaion o Momenum) Physics 160-02 Spring 2017 Douglas Fields Newon s Laws & Energy The work-energy heorem is relaed o Newon s 2 nd Law W KE 1 2 1 2 F
Lecure 16 (Momenum and Impulse, Collisions and Conservaion o Momenum) Physics 160-02 Spring 2017 Douglas Fields Newon s Laws & Energy The work-energy heorem is relaed o Newon s 2 nd Law W KE 1 2 1 2 F
t 2 B F x,t n dsdt t u x,t dxdt
 Evoluion Equaions For 0, fixed, le U U0, where U denoes a bounded open se in R n.suppose ha U is filled wih a maerial in which a conaminan is being ranspored by various means including diffusion and convecion.
Evoluion Equaions For 0, fixed, le U U0, where U denoes a bounded open se in R n.suppose ha U is filled wih a maerial in which a conaminan is being ranspored by various means including diffusion and convecion.
CSE 3802 / ECE Numerical Methods in Scientific Computation. Jinbo Bi. Department of Computer Science & Engineering
 CSE 3802 / ECE 3431 Numerical Mehods in Scienific Compuaion Jinbo Bi Deparmen of Compuer Science & Engineering hp://www.engr.uconn.edu/~jinbo 1 Ph.D in Mahemaics The Insrucor Previous professional experience:
CSE 3802 / ECE 3431 Numerical Mehods in Scienific Compuaion Jinbo Bi Deparmen of Compuer Science & Engineering hp://www.engr.uconn.edu/~jinbo 1 Ph.D in Mahemaics The Insrucor Previous professional experience:
Unit Root Time Series. Univariate random walk
 Uni Roo ime Series Univariae random walk Consider he regression y y where ~ iid N 0, he leas squares esimae of is: ˆ yy y y yy Now wha if = If y y hen le y 0 =0 so ha y j j If ~ iid N 0, hen y ~ N 0, he
Uni Roo ime Series Univariae random walk Consider he regression y y where ~ iid N 0, he leas squares esimae of is: ˆ yy y y yy Now wha if = If y y hen le y 0 =0 so ha y j j If ~ iid N 0, hen y ~ N 0, he
- If one knows that a magnetic field has a symmetry, one may calculate the magnitude of B by use of Ampere s law: The integral of scalar product
 11.1 APPCATON OF AMPEE S AW N SYMMETC MAGNETC FEDS - f one knows ha a magneic field has a symmery, one may calculae he magniude of by use of Ampere s law: The inegral of scalar produc Closed _ pah * d
11.1 APPCATON OF AMPEE S AW N SYMMETC MAGNETC FEDS - f one knows ha a magneic field has a symmery, one may calculae he magniude of by use of Ampere s law: The inegral of scalar produc Closed _ pah * d
Yimin Math Centre. 4 Unit Math Homework for Year 12 (Worked Answers) 4.1 Further Geometric Properties of the Ellipse and Hyperbola...
 4 Uni Mah Homework for Year 12 (Worked Answers) Suden Name: Grade: Dae: Score: Table of conens 4 Topic 2 Conics (Par 4) 1 4.1 Furher Geomeric Properies of he Ellipse and Hyperbola............... 1 4.2
4 Uni Mah Homework for Year 12 (Worked Answers) Suden Name: Grade: Dae: Score: Table of conens 4 Topic 2 Conics (Par 4) 1 4.1 Furher Geomeric Properies of he Ellipse and Hyperbola............... 1 4.2
AP Physics 1 - Summer Assignment
 AP Physics 1 - Summer Assignmen This assignmen is due on he firs day of school. You mus show all your work in all seps. Do no wai unil he las minue o sar his assignmen. This maerial will help you wih he
AP Physics 1 - Summer Assignmen This assignmen is due on he firs day of school. You mus show all your work in all seps. Do no wai unil he las minue o sar his assignmen. This maerial will help you wih he
Solutions from Chapter 9.1 and 9.2
 Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Math 334 Test 1 KEY Spring 2010 Section: 001. Instructor: Scott Glasgow Dates: May 10 and 11.
 1 Mah 334 Tes 1 KEY Spring 21 Secion: 1 Insrucor: Sco Glasgow Daes: Ma 1 and 11. Do NOT wrie on his problem saemen bookle, excep for our indicaion of following he honor code jus below. No credi will be
1 Mah 334 Tes 1 KEY Spring 21 Secion: 1 Insrucor: Sco Glasgow Daes: Ma 1 and 11. Do NOT wrie on his problem saemen bookle, excep for our indicaion of following he honor code jus below. No credi will be
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
MA6151 MATHEMATICS I PART B UNIVERSITY QUESTIONS. (iv) ( i = 1, 2, 3,., n) are the non zero eigen values of A, then prove that (1) k i.
 UNIT MATRICES METHOD EIGEN VALUES AND EIGEN VECTORS Find he Eigen values and he Eigenvecors of he following marices (i) ** 3 6 3 (ii) 6 (iii) 3 (iv) 0 3 Prove ha he Eigen values of a real smmeric mari
UNIT MATRICES METHOD EIGEN VALUES AND EIGEN VECTORS Find he Eigen values and he Eigenvecors of he following marices (i) ** 3 6 3 (ii) 6 (iii) 3 (iv) 0 3 Prove ha he Eigen values of a real smmeric mari
Applications of the Basic Equations Chapter 3. Paul A. Ullrich
 Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
Applicaions of he Basic Equaions Chaper 3 Paul A. Ullrich paullrich@ucdavis.edu Par 1: Naural Coordinaes Naural Coordinaes Quesion: Why do we need anoher coordinae sysem? Our goal is o simplify he equaions
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Scientific Research of the Institute of Mathematics and Computer Science DIFFERENT VARIANTS OF THE BOUNDARY ELEMENT METHOD FOR PARABOLIC EQUATIONS
 Scieniic Research o he Insiue o Mahemaics and Compuer Science DIERENT VARIANTS O THE BOUNDARY ELEMENT METHOD OR PARABOLIC EQUATIONS Ewa Majchrzak,, Ewa Ładyga Jerzy Mendakiewicz, Alicja Piasecka Belkhaya
Scieniic Research o he Insiue o Mahemaics and Compuer Science DIERENT VARIANTS O THE BOUNDARY ELEMENT METHOD OR PARABOLIC EQUATIONS Ewa Majchrzak,, Ewa Ładyga Jerzy Mendakiewicz, Alicja Piasecka Belkhaya
AP CALCULUS BC 2016 SCORING GUIDELINES
 6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
6 SCORING GUIDELINES Quesion A ime, he posiion of a paricle moving in he xy-plane is given by he parameric funcions ( x ( ), y ( )), where = + sin ( ). The graph of y, consising of hree line segmens, is
dy dx = xey (a) y(0) = 2 (b) y(1) = 2.5 SOLUTION: See next page
 Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Solutions to Assignment 1
 MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
Non-uniform circular motion *
 OpenSax-CNX module: m14020 1 Non-uniform circular moion * Sunil Kumar Singh This work is produced by OpenSax-CNX and licensed under he Creaive Commons Aribuion License 2.0 Wha do we mean by non-uniform
OpenSax-CNX module: m14020 1 Non-uniform circular moion * Sunil Kumar Singh This work is produced by OpenSax-CNX and licensed under he Creaive Commons Aribuion License 2.0 Wha do we mean by non-uniform
PROBLEMS FOR MATH 162 If a problem is starred, all subproblems are due. If only subproblems are starred, only those are due. SLOPES OF TANGENT LINES
 PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
PROBLEMS FOR MATH 6 If a problem is sarred, all subproblems are due. If onl subproblems are sarred, onl hose are due. 00. Shor answer quesions. SLOPES OF TANGENT LINES (a) A ball is hrown ino he air. Is
Physics 180A Fall 2008 Test points. Provide the best answer to the following questions and problems. Watch your sig figs.
 Physics 180A Fall 2008 Tes 1-120 poins Name Provide he bes answer o he following quesions and problems. Wach your sig figs. 1) The number of meaningful digis in a number is called he number of. When numbers
Physics 180A Fall 2008 Tes 1-120 poins Name Provide he bes answer o he following quesions and problems. Wach your sig figs. 1) The number of meaningful digis in a number is called he number of. When numbers
Math Week 14 April 16-20: sections first order systems of linear differential equations; 7.4 mass-spring systems.
 Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
L p -L q -Time decay estimate for solution of the Cauchy problem for hyperbolic partial differential equations of linear thermoelasticity
 ANNALES POLONICI MATHEMATICI LIV.2 99) L p -L q -Time decay esimae for soluion of he Cauchy problem for hyperbolic parial differenial equaions of linear hermoelasiciy by Jerzy Gawinecki Warszawa) Absrac.
ANNALES POLONICI MATHEMATICI LIV.2 99) L p -L q -Time decay esimae for soluion of he Cauchy problem for hyperbolic parial differenial equaions of linear hermoelasiciy by Jerzy Gawinecki Warszawa) Absrac.
Module 2 F c i k c s la l w a s o s f dif di fusi s o i n
 Module Fick s laws of diffusion Fick s laws of diffusion and hin film soluion Adolf Fick (1855) proposed: d J α d d d J (mole/m s) flu (m /s) diffusion coefficien and (mole/m 3 ) concenraion of ions, aoms
Module Fick s laws of diffusion Fick s laws of diffusion and hin film soluion Adolf Fick (1855) proposed: d J α d d d J (mole/m s) flu (m /s) diffusion coefficien and (mole/m 3 ) concenraion of ions, aoms
Week 1 Lecture 2 Problems 2, 5. What if something oscillates with no obvious spring? What is ω? (problem set problem)
 Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
t is a basis for the solution space to this system, then the matrix having these solutions as columns, t x 1 t, x 2 t,... x n t x 2 t...
 Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Hamilton- J acobi Equation: Explicit Formulas In this lecture we try to apply the method of characteristics to the Hamilton-Jacobi equation: u t
 M ah 5 2 7 Fall 2 0 0 9 L ecure 1 0 O c. 7, 2 0 0 9 Hamilon- J acobi Equaion: Explici Formulas In his lecure we ry o apply he mehod of characerisics o he Hamilon-Jacobi equaion: u + H D u, x = 0 in R n
M ah 5 2 7 Fall 2 0 0 9 L ecure 1 0 O c. 7, 2 0 0 9 Hamilon- J acobi Equaion: Explici Formulas In his lecure we ry o apply he mehod of characerisics o he Hamilon-Jacobi equaion: u + H D u, x = 0 in R n
Constant Acceleration
 Objecive Consan Acceleraion To deermine he acceleraion of objecs moving along a sraigh line wih consan acceleraion. Inroducion The posiion y of a paricle moving along a sraigh line wih a consan acceleraion
Objecive Consan Acceleraion To deermine he acceleraion of objecs moving along a sraigh line wih consan acceleraion. Inroducion The posiion y of a paricle moving along a sraigh line wih a consan acceleraion
Suggested Practice Problems (set #2) for the Physics Placement Test
 Deparmen of Physics College of Ars and Sciences American Universiy of Sharjah (AUS) Fall 014 Suggesed Pracice Problems (se #) for he Physics Placemen Tes This documen conains 5 suggesed problems ha are
Deparmen of Physics College of Ars and Sciences American Universiy of Sharjah (AUS) Fall 014 Suggesed Pracice Problems (se #) for he Physics Placemen Tes This documen conains 5 suggesed problems ha are
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Be able to sketch a function defined parametrically. (by hand and by calculator)
 Pre Calculus Uni : Parameric and Polar Equaions (7) Te References: Pre Calculus wih Limis; Larson, Hoseler, Edwards. B he end of he uni, ou should be able o complee he problems below. The eacher ma provide
Pre Calculus Uni : Parameric and Polar Equaions (7) Te References: Pre Calculus wih Limis; Larson, Hoseler, Edwards. B he end of he uni, ou should be able o complee he problems below. The eacher ma provide
u(x) = e x 2 y + 2 ) Integrate and solve for x (1 + x)y + y = cos x Answer: Divide both sides by 1 + x and solve for y. y = x y + cos x
 . 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
. 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
Lecture 10: The Poincaré Inequality in Euclidean space
 Deparmens of Mahemaics Monana Sae Universiy Fall 215 Prof. Kevin Wildrick n inroducion o non-smooh analysis and geomery Lecure 1: The Poincaré Inequaliy in Euclidean space 1. Wha is he Poincaré inequaliy?
Deparmens of Mahemaics Monana Sae Universiy Fall 215 Prof. Kevin Wildrick n inroducion o non-smooh analysis and geomery Lecure 1: The Poincaré Inequaliy in Euclidean space 1. Wha is he Poincaré inequaliy?
Integration Over Manifolds with Variable Coordinate Density
 Inegraion Over Manifolds wih Variable Coordinae Densiy Absrac Chrisopher A. Lafore clafore@gmail.com In his paper, he inegraion of a funcion over a curved manifold is examined in he case where he curvaure
Inegraion Over Manifolds wih Variable Coordinae Densiy Absrac Chrisopher A. Lafore clafore@gmail.com In his paper, he inegraion of a funcion over a curved manifold is examined in he case where he curvaure
AP Physics 1 - Summer Assignment
 AP Physics 1 - Summer Assignmen This assignmen is due on he firs day of school. You mus show all your work in all seps. Do no wai unil he las minue o sar his assignmen. This maerial will help you wih he
AP Physics 1 - Summer Assignmen This assignmen is due on he firs day of school. You mus show all your work in all seps. Do no wai unil he las minue o sar his assignmen. This maerial will help you wih he
Instructor: Barry McQuarrie Page 1 of 5
 Procedure for Solving radical equaions 1. Algebraically isolae one radical by iself on one side of equal sign. 2. Raise each side of he equaion o an appropriae power o remove he radical. 3. Simplify. 4.
Procedure for Solving radical equaions 1. Algebraically isolae one radical by iself on one side of equal sign. 2. Raise each side of he equaion o an appropriae power o remove he radical. 3. Simplify. 4.
Physics 218 Exam 1. with Solutions Fall 2010, Sections Part 1 (15) Part 2 (20) Part 3 (20) Part 4 (20) Bonus (5)
 Physics 18 Exam 1 wih Soluions Fall 1, Secions 51-54 Fill ou he informaion below bu o no open he exam unil insruce o o so! Name Signaure Suen ID E-mail Secion # ules of he exam: 1. You have he full class
Physics 18 Exam 1 wih Soluions Fall 1, Secions 51-54 Fill ou he informaion below bu o no open he exam unil insruce o o so! Name Signaure Suen ID E-mail Secion # ules of he exam: 1. You have he full class
TEACHER NOTES MATH NSPIRED
 Naural Logarihm Mah Objecives Sudens will undersand he definiion of he naural logarihm funcion in erms of a definie inegral. Sudens will be able o use his definiion o relae he value of he naural logarihm
Naural Logarihm Mah Objecives Sudens will undersand he definiion of he naural logarihm funcion in erms of a definie inegral. Sudens will be able o use his definiion o relae he value of he naural logarihm
Traveling Waves. Chapter Introduction
 Chaper 4 Traveling Waves 4.1 Inroducion To dae, we have considered oscillaions, i.e., periodic, ofen harmonic, variaions of a physical characerisic of a sysem. The sysem a one ime is indisinguishable from
Chaper 4 Traveling Waves 4.1 Inroducion To dae, we have considered oscillaions, i.e., periodic, ofen harmonic, variaions of a physical characerisic of a sysem. The sysem a one ime is indisinguishable from
Name: Total Points: Multiple choice questions [120 points]
![Name: Total Points: Multiple choice questions [120 points] Name: Total Points: Multiple choice questions [120 points]](/thumbs/88/115221528.jpg) Name: Toal Poins: (Las) (Firs) Muliple choice quesions [1 poins] Answer all of he following quesions. Read each quesion carefully. Fill he correc bubble on your scanron shee. Each correc answer is worh
Name: Toal Poins: (Las) (Firs) Muliple choice quesions [1 poins] Answer all of he following quesions. Read each quesion carefully. Fill he correc bubble on your scanron shee. Each correc answer is worh
in Engineering Prof. Dr. Michael Havbro Faber ETH Zurich, Switzerland Swiss Federal Institute of Technology
 Risk and Saey in Engineering Pro. Dr. Michael Havbro Faber ETH Zurich, Swizerland Conens o Today's Lecure Inroducion o ime varian reliabiliy analysis The Poisson process The ormal process Assessmen o he
Risk and Saey in Engineering Pro. Dr. Michael Havbro Faber ETH Zurich, Swizerland Conens o Today's Lecure Inroducion o ime varian reliabiliy analysis The Poisson process The ormal process Assessmen o he
AP CALCULUS AB 2003 SCORING GUIDELINES (Form B)
 SCORING GUIDELINES (Form B) Quesion A ank conains 15 gallons of heaing oil a ime =. During he ime inerval 1 hours, heaing oil is pumped ino he ank a he rae 1 H ( ) = + ( 1 + ln( + 1) ) gallons per hour.
SCORING GUIDELINES (Form B) Quesion A ank conains 15 gallons of heaing oil a ime =. During he ime inerval 1 hours, heaing oil is pumped ino he ank a he rae 1 H ( ) = + ( 1 + ln( + 1) ) gallons per hour.
An Introduction to Malliavin calculus and its applications
 An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
Roller-Coaster Coordinate System
 Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
Winer 200 MECH 220: Mechanics 2 Roller-Coaser Coordinae Sysem Imagine you are riding on a roller-coaer in which he rack goes up and down, wiss and urns. Your velociy and acceleraion will change (quie abruply),
THE SINE INTEGRAL. x dt t
 THE SINE INTEGRAL As one learns in elemenary calculus, he limi of sin(/ as vanishes is uniy. Furhermore he funcion is even and has an infinie number of zeros locaed a ±n for n1,,3 Is plo looks like his-
THE SINE INTEGRAL As one learns in elemenary calculus, he limi of sin(/ as vanishes is uniy. Furhermore he funcion is even and has an infinie number of zeros locaed a ±n for n1,,3 Is plo looks like his-
Physics for Scientists and Engineers I
 Physics for Scieniss and Engineers I PHY 48, Secion 4 Dr. Beariz Roldán Cuenya Universiy of Cenral Florida, Physics Deparmen, Orlando, FL Chaper - Inroducion I. General II. Inernaional Sysem of Unis III.
Physics for Scieniss and Engineers I PHY 48, Secion 4 Dr. Beariz Roldán Cuenya Universiy of Cenral Florida, Physics Deparmen, Orlando, FL Chaper - Inroducion I. General II. Inernaional Sysem of Unis III.
Biol. 356 Lab 8. Mortality, Recruitment, and Migration Rates
 Biol. 356 Lab 8. Moraliy, Recruimen, and Migraion Raes (modified from Cox, 00, General Ecology Lab Manual, McGraw Hill) Las week we esimaed populaion size hrough several mehods. One assumpion of all hese
Biol. 356 Lab 8. Moraliy, Recruimen, and Migraion Raes (modified from Cox, 00, General Ecology Lab Manual, McGraw Hill) Las week we esimaed populaion size hrough several mehods. One assumpion of all hese
Solution: b All the terms must have the dimension of acceleration. We see that, indeed, each term has the units of acceleration
 PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
PHYS 54 Tes Pracice Soluions Spring 8 Q: [4] Knowing ha in he ne epression a is acceleraion, v is speed, is posiion and is ime, from a dimensional v poin of view, he equaion a is a) incorrec b) correc
Physics 218 Exam 1 with Solutions Spring 2011, Sections ,526,528
 Physics 18 Exam 1 wih Soluions Sprin 11, Secions 513-515,56,58 Fill ou he informaion below bu do no open he exam unil insruced o do so Name Sinaure Suden ID E- mail Secion # Rules of he exam: 1. You have
Physics 18 Exam 1 wih Soluions Sprin 11, Secions 513-515,56,58 Fill ou he informaion below bu do no open he exam unil insruced o do so Name Sinaure Suden ID E- mail Secion # Rules of he exam: 1. You have
DIFFERENTIAL GEOMETRY HW 5
 DIFFERENTIAL GEOMETRY HW 5 CLAY SHONKWILER 3. Le M be a complee Riemannian manifold wih non-posiive secional curvaure. Prove ha d exp p v w w, for all p M, all v T p M and all w T v T p M. Proof. Le γ
DIFFERENTIAL GEOMETRY HW 5 CLAY SHONKWILER 3. Le M be a complee Riemannian manifold wih non-posiive secional curvaure. Prove ha d exp p v w w, for all p M, all v T p M and all w T v T p M. Proof. Le γ
Week #13 - Integration by Parts & Numerical Integration Section 7.2
 Week #3 - Inegraion by Pars & Numerical Inegraion Secion 7. From Calculus, Single Variable by Hughes-Halle, Gleason, McCallum e. al. Copyrigh 5 by John Wiley & Sons, Inc. This maerial is used by permission
Week #3 - Inegraion by Pars & Numerical Inegraion Secion 7. From Calculus, Single Variable by Hughes-Halle, Gleason, McCallum e. al. Copyrigh 5 by John Wiley & Sons, Inc. This maerial is used by permission
Physics 3A: Basic Physics I Shoup Sample Midterm. Useful Equations. x f. x i v x. a x. x i. v xi v xf. 2a x f x i. y f. a r.
 Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
Physics 3A: Basic Physics I Shoup Sample Miderm Useful Equaions A y Asin A A x A y an A y A x A = A x i + A y j + A z k A * B = A B cos(θ) A x B = A B sin(θ) A * B = A x B x + A y B y + A z B z A x B =
Effects of Coordinate Curvature on Integration
 Effecs of Coordinae Curvaure on Inegraion Chrisopher A. Lafore clafore@gmail.com Absrac In his paper, he inegraion of a funcion over a curved manifold is examined in he case where he curvaure of he manifold
Effecs of Coordinae Curvaure on Inegraion Chrisopher A. Lafore clafore@gmail.com Absrac In his paper, he inegraion of a funcion over a curved manifold is examined in he case where he curvaure of he manifold
1 Solutions to selected problems
 1 Soluions o seleced problems 1. Le A B R n. Show ha in A in B bu in general bd A bd B. Soluion. Le x in A. Then here is ɛ > 0 such ha B ɛ (x) A B. This shows x in B. If A = [0, 1] and B = [0, 2], hen
1 Soluions o seleced problems 1. Le A B R n. Show ha in A in B bu in general bd A bd B. Soluion. Le x in A. Then here is ɛ > 0 such ha B ɛ (x) A B. This shows x in B. If A = [0, 1] and B = [0, 2], hen
HW6: MRI Imaging Pulse Sequences (7 Problems for 100 pts)
 HW6: MRI Imaging Pulse Sequences (7 Problems for 100 ps) GOAL The overall goal of HW6 is o beer undersand pulse sequences for MRI image reconsrucion. OBJECTIVES 1) Design a spin echo pulse sequence o image
HW6: MRI Imaging Pulse Sequences (7 Problems for 100 ps) GOAL The overall goal of HW6 is o beer undersand pulse sequences for MRI image reconsrucion. OBJECTIVES 1) Design a spin echo pulse sequence o image
k 1 k 2 x (1) x 2 = k 1 x 1 = k 2 k 1 +k 2 x (2) x k series x (3) k 2 x 2 = k 1 k 2 = k 1+k 2 = 1 k k 2 k series
 Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
Final Review A Puzzle... Consider wo massless springs wih spring consans k 1 and k and he same equilibrium lengh. 1. If hese springs ac on a mass m in parallel, hey would be equivalen o a single spring
4. Electric field lines with respect to equipotential surfaces are
 Pre-es Quasi-saic elecromagneism. The field produced by primary charge Q and by an uncharged conducing plane disanced from Q by disance d is equal o he field produced wihou conducing plane by wo following
Pre-es Quasi-saic elecromagneism. The field produced by primary charge Q and by an uncharged conducing plane disanced from Q by disance d is equal o he field produced wihou conducing plane by wo following
Elements of Computer Graphics
 CS580: Compuer Graphics Min H. Kim KAIST School of Compuing Elemens of Compuer Graphics Geomery Maerial model Ligh Rendering Virual phoography 2 Foundaions of Compuer Graphics A PINHOLE CAMERA IN 3D 3
CS580: Compuer Graphics Min H. Kim KAIST School of Compuing Elemens of Compuer Graphics Geomery Maerial model Ligh Rendering Virual phoography 2 Foundaions of Compuer Graphics A PINHOLE CAMERA IN 3D 3
