Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky ÚVOD DO DIFERENCIÁLNEJ GEOMETRIE
|
|
|
- Cory Pearson
- 5 years ago
- Views:
Transcription
1 Unverza Komenského v Braslave Fakula maemaky, fyzky a nformaky ÚVOD DO DIFERENCIÁLNEJ GEOMETRIE Mloš BOŽEK Braslava 015
2 Unverza Komenského v Braslave Fakula maemaky, fyzky a nformaky ÚVOD DO DIFERENCIÁLNEJ GEOMETRIE Mloš BOŽEK Braslava 015 1
3 Názov: ÚVOD DO DIFERENCIÁLNEJ GEOMETRIE Auor: doc. RNDr. Mloš Božek, CSc. Recenzen: Doc. RNDr. Vojech BÁLINT, CSc. RNDr. Ján BAKŠA, PhD.. Vydavaeľ: Knžnčné a edčné cenrum FMFI UK Braslava Vydané s fnančnou podporou granu KEGA 094UK-4/013, E-mak+, Konnuálne vzdelávane učeľov maemaky Rukops neprešel jazykovou úpravou. C Mloš BOŽEK, 015 ISBN EAN
4 M. BOŽEK: ÚVOD DO DIFERENCIÁLNEJ GEOMETRIE OBSAH Úvod... 4 Časť 1 KRIVKY Lekca 1. Kap. 1. Paramercké vyjadrene krvky 1. časť... 7 Lekca. Kap. 1. Paramercké vyjadrene krvky. časť Kap.. Doyčnca a normála krvky Lekca 3. Kap. 3. Oskulačná rovna presorovej krvky. Freneov rojhran Lekca 4. Kap. 4. Dĺžka krvky. Prrodzená paramerzáca krvky... Lekca 5. Kap. 5. Krvosť krvky Lekca 6. Kap. 6. Syk krvek Obrázky ku krvkám Úlohy k lekcám Časť PLOCHY Lekca 7 Kap. 1. Paramercké vyjadrene plochy Lekca 8 Kap.. Krvky na ploche Lekca 9 Kap. 3. Normálová krvosť plochy defníca Lekca 10 Kap. 4. Normálová krvosť plochy vlasnos Obrázky k plochám Úlohy k lekcám Prílohy Príloha 1 Vekorový súčn Príloha Knemacky zadané krvky Príloha 3 O čom je dferencálna geomera Príloha 4 Nesprávna predsava o oskulačnej kružnc rovnnej krvky
5 Úvod Celý ex, korý budeme spolu preberať, vznkol na základe sručného učebného maerálu k jednosemesrálnej voleľnej prednáške Dferencálna geomera v reťom roku šúda učeľsva maemaky na FMFI UK. Tomu odpovedá jeho rochu surová podoba. Každá lekca pozosáva z učebného exu, v korom sú voľne rozmesnené komenáre. Práve číae prvý z nch. Kvôl zreeľnému odlíšenu od vlasného exu ch píšem, ako vdíe, ným ypom písma, nou farbou a menšou veľkosťou písma. Od exu ch navyše oddeľujú vodorovné čary. Prvá lekca sa skladá z úvodu do kurzu a z prvej čas prvej kapoly. Úvod s prečíaje a prvú kapolu našuduje. V nej a aj v ďalších kapolách sa nachádzajú úlohy, e s nemusíe veľm všímať. Sú o akés pozosaky z predchádzajúcch podôb exu, bolo m ľúo ch zlkvdovať. Pre eno kurz plaa né zadana. Každý ýždeň ch nájdee v samosanom súbore. Uvedomujem s, že s písaním rešení vašch úloh v elekronckej podobe môžee mať ťažkos, ak nemáe dosaočné skúsenos so sadzbou maemackého exu. V akom prípade navrhujem jednu z dvoch náhradných možnosí: 1. Rešene napíše rukou, a ak máe možnosť, naskenuje ju a pošle ako obrázok.. Ak nemáe prísup k skeneru, rešene napíše rukou a pošle m ho klasckou pošou na fakulnú adresu. Aby sa ale dodržal formálne pravdlá evyučovana, súčasne pošle prosrednícvom Moodlu aj sručné elekroncké oznámene o odoslaní rešena v paperovej podobe. Ak o však čo len rochu pôjde, snaže sa rešena zaselať vo formáe PDF. Dferencálna geomera sa zaoberá zakrveným geomerckým objekm. Pr ch skúmaní využíva meódy a výsledky maemackej analýzy, v prvom rade ako už jej názov napovedá čerpá z dferencálneho poču. To znamená, že jej základným pracovným prosredkom sú derváce. Skúmaným objekm sú najmä krvky a plochy veľm rozmaných varov. V omo kurze sa oboznáme s ch najjednoduchším vlasnosťam. Nevyhnuným predpokladom pre použe dervácí je príomnosť funkcí, koré sa majú dervovať, preo musíme mať geomercké objeky vyjadrené prosrednícvom čísel, čže súradncam. V omo zmysle môžeme eda dferencálnu geomeru považovať za nadsavbu č pokračovane analyckej geomere. Okrem dobrého ovládana základných pravdel dferencálneho poču predpokladáme preo u účasníkov kurzu aj dôvernú znalosť analyckej geomere v jej bodovo vekorovej podobe, ako sa bežne prezenuje na vysokých školách v prvých ročníkoch šúda maemaky resp. učeľsva maemaky. Krvky a plochy sa objavujú už v učve maemackej analýzy ako grafy funkcí jednej resp. dvoch premenných, prčom mnohé výsledky analýzy sa kvôl názornos formulujú aj v geomerckej podobe. Typckou ukážkou je predsava lokálneho exrému funkce jednej premennej ako bodu, v korom je doyčnca grafu rovnobežná s osou x. Reprezenáca v podobe grafov funkcí však na vyjadrene mnohých krvek a plôch nesačí, lebo už napríklad celú! kružncu nemožno opísať ako graf funkce v akej podobe sa dajú zvládnuť ba nekoré jej čas, napríklad polkružnca. Preo ale aj z ných dôvodov budeme krvky a plochy vyjadrovať v našom kurze paramercky. Mohlo by sa zdať, že geomera čakala na vznk maemackej analýzy a poom jednoducho od nej prevzala hoové výsledky. Hsóra maemaky však ukazuje, že vec mal podsane zložejšu podobu a prebeh. Vznk a rozvoj maemackej analýzy bol z veľkej čas movovaný práve oázkam, koré kládla geomera. Veľm pekne o lusruje názov Lebnzovho článku z roku 1684, korý sa všeobecne spolu s Newonovým Maemackým základm prírodnej flozofe považuje za zrod dferencálneho a negrálneho poču: Nová meóda pre maxmá a mnmá, ako aj pre doyčnce, korá plaí aj pre raconálne a lomené 4
6 hodnoy, a pozoruhodný spôsob počíana pre eno účel. Vdíme eda, že jednou zo základných movácí vznku maemackej analýzy bola geomercká úloha o doyčnc. Dferencálna geomera v podobe, v akej ju predkladáme v omo kurze, sa usálla zhruba v polovc 19. soroča až na jej spôsob zápsu v bodovo vekorovej podobe, en je deťaťom prvej reny 0. soroča. Bežne sa jej hovorí klascká dferencálna geomera. Prblžne v rene až polovc 0. soroča vznkla moderná dferencálna geomera, korej objeky skúmana a používané meódy zasahujú veľm hlboko do vacerých oblasí súčasnej maemaky. Ako príklad objeku skúmaného v modernej dferencálnej geomer spomeňme množnu všekých zhodnosí rojrozmerného eukldovského presoru, korá okrem oho, že je grupou, má aj prrodzenú šrukúru šesťrozmerného zakrveného presoru. Obe eo šrukúry sú navzájom zosúladené, akže vznká objek, korému sa hovorí Leova grupa čía sa líova Sophus Le, nórsky maemak, 19. soroče; v dnešnej maemake sa akéo grupy nenzívne skúmajú a využívajú. Napríklad spomenuá grupa zhodnosí sa v mechanke nerpreuje ako konfguračný presor všekých polôh uhého elesa. Sručne o obsahu kurzu. Kurz pozosáva z dvoch emackých celkov. Prvý je venovaný krvkám, druhý plochám. V prvej kapole o krvkách zavedeme pojem krvky. Naprek snahe o čo najjednoduchší posup, naša defníca krvky má zložejšu podobu, ako by sa as čakalo. Nasledujú dve kapoly s opsným charakerom. Zavádzame v nch rovné objeky spojené s krvkou v každom jej bode: doyčncu, normálu, oskulačnú rovnu a Freneov rojhran. V ďalšej kapole sručne spomeneme dĺžku krvky a venujeme sa prrodzenej paramerzác krvky, korá je založená práve na dĺžke úsekov krvky. Kľúčovým pojmom pre krvky je krvosť, korej je venovaná paa kapola. Poslednú kapolu o krvkách pojednávajúcu o syku krvek sme do kurzu zaradl najmä kvôl jej veľm akuálnym aplkácám v počíačovej grafke. Temacký celok o plochách je už menej rozsahly. V prvej kapole uvádzame pojem plochy, v druhej hovoríme o doykovej rovne a o normále plochy. Ťažskové sú rea a švrá kapola o normálovej krvos plochy, prosrednícvom korej sa skúma var plochy. Kapoly sú v oboch emackých celkoch číslované samosane, eda prvá kapola o plochách má číslo 1 rovnako ako prvá kapola o krvkách. Vey, príklady, poznámky, úlohy a obrázky číslujeme samosane v podvojnej podobe eda vea 5. je druhá vea paej kapoly, v nej môže byť aj príklad č obrázok s rovnakým číslom 5.. Defníce sa neuvádzajú ako číslované exové jednoky. Poznáme ch podľa kurzívy fon alc, korou je napísaný defnovaný pojem. Najmä kvôl úspore mesa v zobrazenom exe v jeho súbore pomerne časo používame zjednodušený záps zlomkov a odmocnín v vare a/b a x. V zložejších suácách sa správne číajú a píšu pomocou závorek napr. ako: b ab ab cd a, abc ab c. cd cd Všmne s, čo by spôsobl chýbajúce závorky: b abd ab cd a d, abc a bc. c c Tex učva kurzu je poprekladaný komenárm, prezrádza ch modrá farba a menše ležaé písmo. 5
7 Z echnckých dôvodov čo je jemné vyjadrene auorovej neškovnos ne sú obrázky pramou súčasťou exu, nachádzajú sa ba v samosaných súboroch. Navyše, väčšnou sú o ba nasnímané rukou načrnué skce. V oboch emackých celkoch sa súsreďujeme ba na najzákladnejše vec a vynechávame mnohé pare, koré sú šandardnou súčasťou učva v bežných kurzoch klasckej dferencálnej geomere. Pr krvkách nenájdee najmä émy Freneove vzorce, orza, sngulárne body a obálky. Pr plochách vynechávame omnoho vac, vlasne akmer všeko rozvnueľné pramkové plochy, prvá základná forma plochy a merane na ploche, zobrazena plôch, hlavné krvos a Gaussova krvosť,... Absolven kurzu by však v prípade poreby č záujmu mal byť schopný oboznámť sa s ďalším émam klasckej dferencálnej geomere samosane. Čo sa ýka odporúčanej leraúry, korá by pokrývala a prípadne rozšrovala láku oho kurzu, pre slovenského čaeľa sú ba zlé správy. Dosupnej leraúry vlasne ne. Pre úplnosť a z dôvodu dodržana dobrých mravov predsa len uvedem nekoľko relevanných ulov: Budnský, B.: Analycká a dferencální geomere. SNTL, Praha, 1983, Pogorelov, A.V.: Geomerja. Nauka, Moskva 1983, Ruer, G.: Geomery of Curves. Chapman and Hall 000. Budnského učebnca je kurzu urče najblžša. Nelen jazykovo, ale ež z hľadska obsahu a spôsobu výkladu. Možno ju eše nájdee v nekorej knžnc. Zaujímavé nformáce o krvkách a plochách sú samozrejme aj na nernee. Najčasejše majú podobu albumov, v korých s môžeme prezerať mnoho obrázkov, časo nerakívnych č so sprevodným exom. Ak s eda chcee pozreť pekné obrázky krvek a prípadne sa o nch aj nečo zaujímavé dočíať, skúse ovorť nasledujúce sránky. Vyhľadala ch moja bývalá dplomanka Mgr. Eva Kozáková. hp://xahlee.org/pagetwo_dr/more.hml hp://www-groups.dcs.s-andrews.ac.uk/%7ehsory/curves/curves.hml hp:// Ak nájdee ďalše zaujímavé nerneové zdroje k našej éme, budem vám veľm vďačný, ak ma s nm zoznáme. Nemenej vďačný budem za všeky ohlasy a prpomenky, koré by mohl vylepšť budúce verze exu. Vo vašej prác v rámc kurzu vám prajem veľa rpezlvos, korá vám so prnese úspechy a e zasa pocy rados a uspokojena. Konaky na vyučujúceho: doc. RNDr. Mloš Božek, CSc. pracovňa: M 156 Kaedra algebry, geomere a ddakky maemaky UK FMFI : bozek@fmph.unba.sk Mlynská dolna Braslava 6
8 Lekca 1 1. Paramercké vyjadrene krvky 1. časť Ceľom prvej kapoly je oboznámť sa s pojmom krvky. Základným echnckým násrojm sú bodové a vekorové funkce jednej premennej a ch derváce. Uvedené funkce sa od bežných číselných funkcí odlšujú v podsae ba oborom hodnô je ním množna bodov resp. vekorov presoru resp. rovny. Keď body a vekory reprezenujeme súradncam, bodová č vekorová funkca jednej premennej ne je vlasne nč né ako usporadaná rojca pre rovnu dvojca obyčajných číselných funkcí so spoločným defnčným oborom je ním nerval na číselnej os. Algebracké aj analycké operáce lmy, derváce a negrály s bodovým a vekorovým funkcam, koré sú dané súradncam, vykonávame po zložkách. Prečo požívame bodové aj vekorové funkce? Bodovú funkcu porebujeme na analycké vyjadrene krvky. Keď ho zdervujeme raz, dvakrá,..., vznkajú vekorové funkce, preo je prrodzené, že sa zaoberáme aj s nm. Prečo poom krvku nevyjadrujeme vekorovou funkcou? Je pravda, že vedy by sme pracoval ba s vekorovým funkcam, eda s menším počom pomocných pojmov, a že akýo prísup nájdee v mnohých učebncach dferencálnej geomere. Neodpovedá o ale dobre reale, lebo as nko s nepredsavuje krvku zloženú z vekorov, z bodov však hádam každý. So slovom krvka sa sreávame v každodennom žvoe, v echnke, v prírodných vedách a v maemake. Kvôl ejo rôznorodos jeho výskyu nemožno očakávať unverzálnu defnícu, korá by úplne uspokojla všekých používaeľov. V dferencálnej geomer a v počíačovej grafke sa krvky v rovne resp. v presore najčasejše zadávajú paramercky prosrednícvom bodovej funkce jednej číselnej premennej, čo je funkca, korá každému reálnemu číslu z nejakého nervalu číselnej os prraďuje bod v rovne resp. v presore. Ide eda o zobrazene 1.1 P: I E, resp. P: I E 3, kde I je nerval na číselnej os R,. Klascký záps bodovej funkce jednej premennej 1.1 je 1. P = P, I. Hodnou premennej v ejo súvslos nazývame paramerom bodu P. Záps bodovej funkce 1. je analógou zápsu číselnej funkce v vare y yx, xi, korý sa používa napríklad v dferencálnych rovncach. Opro časejše sa vyskyujúcemu zápsu číselnej funkce v podobe y fx, xi má podoba y yx ú výhodu, že sa v nej ušerlo písmeno f. Rovnaký šerac efek vdíme aj v zápse bodovej funkce 1.. V súradncach vyzerá bodová funkca jednej premennej ako: 1.3a P = x, y, z, I, pre krvku v presore resp. 1.3b P = x, y, I, pre krvku v rovne, 7
9 kde x = x, y = y, z = z sú obvyklé číselné funkce so spoločným defnčným oborom I obr Ich hodnoy sú súradnce bodov krvky. Symbol rovnos vo vzorcoch 1.3a a 1.3b číame rovnako ako v analyckej geomer má súradnce. Používa sa aj akýo záps paramerckého vyjadrena krvky v presore 1.3c x = x, y = y, z = z, I Paramercky zadanú krvku v rovne môžeme považovať aj za krvku v presore, ak soožníme bod v rovne so súradncam x, y s bodom v presore so súradncam x, y, 0. Preo akmer vždy budeme spoločné vlasnos krvek v rovne a v presore formulovať ba pre presorový prípad. Bodovú funkcu jednej premennej fyzkálne nerpreujeme ako maemacké vyjadrene pohybu hmoného bodu. Premennú vedy považujeme za čas prvé písmeno lanského slova empus čas; analogcky P je prvé písmeno slova puncum bod. V súlade s ým symbol P číame bod P v momene a ne bod P v bode, ako by sa parlo podľa zvyklosí maemackej analýzy. Nasleduje séra príkladov bodových funkcí jednej premennej a odpovedajúcch krvek. Príklad 1.1 Pramka: P = A + u, R. Je o z analyckej geomere známe paramercké vyjadrene pramky určenej bodom A a vekorom u. V súradncovej podobe 1.3a má var P = a 1 + u 1, a + u, a 3 + u 3, R, kde koefcenm sú súradnce určujúceho bodu a vekora pramky: A a 1, a, a 3, u u 1, u, u 3. Symboly rovnos v zápse súradníc bodu a vekora číame má súradnce. Fyzkálne funkca P = A + u vyjadruje rovnomerný pramočary pohyb. Príklad 1. Kružnca so sredom v začaku súsavy súradníc a s polomerom r obr. 1.: P = rcos, rsn, 0,, náč zapísané: x = rcos, 0,. y = rsn, Zrejme plaí P0 = r, 0, P = r, 0, čže P = P0. Koncový bod krvky eda splýva s počaočným, čo znamená, že kružnca je uzavreá krvka. Geomercký význam paramera: je orenovaný uhol jednokového vekora e 1 os x s vekorom P O. Uvedené paramercké vyjadrene kružnce fyzkálne vyjadruje rovnomerný oáčavý pohyb bodu okolo začaku súsavy súradníc. 1. Informáca o geomerckom č fyzkálnom význame paramera v paramerckom vyjadrení krvky je dôležá nelen pre vorbu správnych nuívnych predsáv, ale aj pr aplkácách eóre krvek.. Prečo sme kružncu paramercky vyjadrl na uzavreom nervale 0, a ne na nervale 0, č 0,? Veď aj vedy by sme mal vyjadrenú celú krvku a navyše každý jej bod by odpovedal presne jednej hodnoe paramera! 8
10 Dôvody sú dva. Pr použí uzavreého nervalu, prčom obrazom jeho krajných bodov je en sý bod krvky, zdôrazňujeme, že krvka začína a končí v rovnakom bode, eda, že krvka je uzavreá. Druhý dôvod spoznáme v kapole 4, kde uvdíme, že dĺžka krvky sa defnuje pre krvky paramercky zadané na uzavreým a ohrančeným nervale. Príklad 1.3 Elpsa s osam na súradncových osach obr. 1.3, korej rovnca je x /a y /b 1 0, má paramercké vyjadrene P = acos, bsn, 0,, a b 0. Geomercký význam paramera dáva obr Príklad 1.4 Opäť elpsa: 1 P a, b,, +, a b Presvedče sa, že všeky eo body vyhovujú rovnc x /a y /b 1 0. Too paramercké vyjadrene nepokrýva celú elpsu, lebo nezachycuje ľavý vrchol so súradncam a, 0. Príklad 1.5 Dve vevy hyperboly s osam na súradncových osach obr. 1.4, korej rovnca je x /a y /b 1 0: P = acosh, bsnh,, +, a, b 0. Pre znamenko vznkne ľavá a pre pravá veva hyperboly. Prpomeňme dve menej známe funkce hyperbolcký kosínus: coshx = ½e x + e x, hyperbolcký sínus: snhx = ½e x e x a ch základné vlasnos: cosh x snh x = 1, coshx = snhx, snhx = coshx. Inverzná funkca k hyperbolckému sínusu sa nazýva aj argumen hyperbolckého sínusu a má var snh 1 x = Argsnhx = ln x x 1. Na rozdel od bežného sínusu a kosínusu, hyperbolcký kosínus, hyperbolcký sínus a k nemu nverzná funkca nepredsavujú novú redu hyperbolckých gonomerckých funkcí, lebo sú vyjadrené prosrednícvom osaných elemenárnych funkcí. Funkce snhx a coshx ne sú perodcké! Príklad 1.6 Parabola s rovncou y px = 0 obr. 1.5: P =,,, +, p 0. p Príklad 1.7 Cykloda obr. 1.6: 9
11 P = a sn, a1 cos,, +. Fyzkálne: Pohyb bodu 0, 0 kružnce x y a a 0, korá sa bez kĺzana koúľa po os x. V šarovacej polohe 0 sa kružnca zhora doýka os x v začaku súsavy súradníc. Príklad 1.8 Reťazovka obr. 1.7: P, a cosh,, +, a 0. a Fyzkálne: Krvka vyjadruje var voľne zaveseného homogénneho lana upevneného v dvoch bodoch. Možno ju pozorovať v krajne ako drôy vysokého elekrckého napäa. Pre a 1 de o graf funkce y coshx. Príklad 1.9 Trakrx obr. 1.8: Príklad 1.10 Asroda obr. 1.9: P alng cos, asn, 0,, a 0. P = acos 3, asn 3, 0,, a 0. Príklad 1.11 Skrukovca obr je v našch príkladoch jedný pramy zásupca presorových krvek: P = acos, asn, b,, +, a 0, b 0. Osou skrukovce s uvedenou paramerzácou je os z. Fyzkálne: Funkca vyjadruje pohyb bodu, korý sa rovnomerne oáča okolo os z a súčasne sa pozdĺž nej rovnomerne posúva. Príklad 1.1 Bézerova kubka: P = 1 3 A A A + 3 A 3, 0,1. Body A 0, A 1, A, A 3 sa nazývajú radace vrcholy Bézerovej kubky. Bod P je ch lneárnou kombnácou s premenným koefcenm 1 3, 31, 31, 3. Prakcky o znamená, že súradnce bodu P sú lneárnym kombnácam súradníc radacch vrcholov s uvedeným koefcenm. Táo krvka môže byť presorová aj rovnná. Rovnná je vedy, keď všeky jej radace vrcholy leža v jednej rovne, v nej poom leža všeky body krvky. Bézerove kubky hrajú obrovskú úlohu v počíačovej grafke pr vyváraní krvek a plôch ako sa rochu prehnane hovorí ľubovoľného varu. Lneárna kombnáca bodov je neúplná analóga lneárnej kombnáce vekorov. Defnovaná je ba v dvoch prípadoch: Keď je súče koefcenov 1, výsledkom je bod, keď je súče koefcenov 0, výsledkom je vekor. Súradnce lneárnej kombnáce bodov sú lneárne kombnáce súradníc kombnovaných bodov. Napríklad sred dvojce bodov A,B môžeme zapísať ako ½A ½B. Vzorec z defníce Bézerovej krvky defnuje bod, lebo na pravej srane je súče koefcenov 1: 10
12 1 [1 ] Úloha 1.1 a Napíše paramercké vyjadrene kružnce so sredom v bode S = m, n. b Napíše paramercké vyjadrene úsečky s krajným bodm A, B. Základné pojmy maemackej analýzy lmu, spojosť a dervácu preneseme na bodové funkce jednej číselnej premennej, a o prosrednícvom súradníc. Lma bodovej funkce P = x, y, z, I v momene 0 je bod lm P lm x,lm y,lm z Bodová funkca P = x, y, z, I je spojá, ak sú spojé jej súradncové zložky x, y, z. Derváca bodovej funkce P = x, y, z, I v momene 0 I je vekor P 0 = x 0, y 0, z 0. Vekorový charaker derváce P 0 sa vysveľuje v poznámke 1.1 Podobne ako bodová funkca jednej premennej sa defnuje vekorová funkca jednej premennej u: I VE 3. V programáorskom jazyku by sme mohl povedať, že návraová hodnoa bodovej funkce má yp bod a návraová hodnoa vekorovej funkce má yp vekor. Súradncové vyjadrene vekorovej funkce je rovnaké ako pre bodovú funkcu: u = x, y, z, I. Rovnako sa defnuje jej lma a derváca: lm u lm x,lm y,lm z, u 0 = x 0, y 0, z 0. Dervácou vekorovej funkce je funkca vekorová. Preože dervácou aj bodovej funkce je funkca vekorová, nelen prvá, ale aj vyšše derváce bodovej funkce sú vekorové funkce. Pr počíaní s dervácam bodových a vekorových funkcí plaa obvyklé pravdlá dferencálneho poču, napr. P + u = P + u, fu = fu + fu, u v = u v + u v, u v = u v + u v, derváca súču derváca skalárneho násobku derváca skalárneho súčnu derváca vekorového súčnu P = 0 pre všeky funkca P = P je konšanná. derváca konšany Príklad 1.13 Pre dervácu bodovej funkce P = acos 3, asn 3 ako už veme z príkladu 1.10, uvažovaná funkca vyjadruje paramercky asrodu plaí 11
13 P = 3a cos sn, 3a sn cos = 3a cos sn cos, sn. Rovnosť P = 3a cos sn cos, sn je korekná, lebo pravá srana vyjadruje v súradncach operácu násobena vekora číslom. Napro omu úprava zápsu bodovej funkce P = acos 3, asn 3 do podoby P = acos 3, sn 3 je neprípusná, lebo operáca číslo krá bod ne je defnovaná. Úloha 1. Vypočíaje prvú a druhú dervácu aspoň nekorých bodových funkcí, koré vyjadrujú krvky z príkladov Úloha 1.3 Dokáže nekoré z vyšše uvedených pravdel pre počíane s dervácam, napríklad pravdlo derváce skalárneho súčnu. [Návod: Zapíše bodové a vekorové funkce vysupujúce v pravdle prosrednícvom súradníc.] Poznámka Uvažujme bodovú funkcu P = x, y, z, I a číslo 0 I. Uvedomme s, že funkca P P P P 0, 0 je vekorová, lebo na pravej srane je súčn čísla s vekorom. Funkca má súradnce P P 0 x x 0 y y 0 z z 0,, Jej lma v momene 0 je eda vekor a jeho súradnce sú x 0, y 0, z 0. Tým sa vysveľuje, prečo je derváca bodovej funkce v každom momene vekor.. Fyzkálna nerpreáca dervácí bodovej funkce: Vekor P 0 vyjadruje okamžú rýchlosť a vekor P 0 okamžé zrýchlene pohybujúceho sa bodu P v momene 0. Vekorový charaker derváce bodovej funkce má obrovský význam, lebo pr skúmaní krvek nám umožňuje využívať bohaý apará lneárnej algebry. Ďalše úlohy na ému paramercky zadaných krvek nájdee v prloženom exe Tvorba krvek. Samozrejme, aj všeky amojše úlohy sú nepovnné. Prvú kapolu ukončíme v ďalšej lekc. 1
14 Lekca V prvej čas lekce dokončíme prvú kapolu učebného exu. Doeraz sme sa zoznáml s bodovým a vekorovým funkcam jednej premennej a s ch lmam a dervácam. Na mnohých konkrénych príkladoch sme vdel, že bodové funkce veľm úzko súvsa s krvkam. Na začaku lekce budeme posupne prpravovať defnícu krvky. Už eraz upozorňujem, že jej výsledná podoba pravdepodobne nesplní vaše očakávana. Defníca nebude mať ož var krvka je množna bodov v presore resp. v rovne, paramercky vyjadrená bodovou funkcou jednej premennej. Dôvodom je skuočnosť, že exsujú aké krvky v zmysle naznačenej defníce, koré majú pr rôznych paramerckých vyjadrenach rôzne geomercké vlasnos. Prprave sa eda na pomerne krkolomnú defnícu krvky. Od bodovej funkce P = x, y, z, I, korá paramercky určuje krvku, sa spravdla vyžaduje, že má nasledujúce dve vlasnos: 1.4a hladkosť: exsujú derváce všekých rádov.j. súradncové funkce x, y a z majú derváce všekých rádov, eda sú hladké a 1.4b regulárnosť: vekor P je nenulový pre všeky. Vekor P sa v druhej. kapole sane smerovým vekorom doyčnce krvky v bode P, preo v defníc vyžadujeme, aby bol nenulový, eda aby spolu s bodom P určoval pramku. Aby sme zachyl čo najvac krvek z rôznych oblasí aplkácí, v príkladoch na konkrénych krvkách prpúšťame výsky nekoľkých bodov, pre koré ne je podmenka regulárnos splnená. Také body, eda body P s vlasnosťou P 0, sa nazývajú sngulárne body krvky. Osané body krvky sú regulárne. Príklad 1.14 Pokračovane príkladu Bodová funkca P = acos 3, asn 3, 0,, je zrejme hladká a P = 3a cos sn cos, sn = 0 práve vedy, keď = k/, k 0, 1,, 3, 4. Asroda má eda práve šyr sngulárne body P/, P, P3/, P P0 osam bod P0 pre k 0 sme soožnl s bodom P pre k 4. Sú o presečníky krvky so súradncovým osam. Osané body asrody sú regulárne obr Úloha 1.5 Skúmaje splnene podmenky regulárnos pre cyklodu a rakrx. Príklad 1.15 obr Graf funkce y = f x, xi je krvka s paramerzácou P =, f, I. Pre hladkú funkcu f je áo paramerzáca jej grafu hladká, lebo obe funkce x a y f sú hladké. Uvedená paramerzáca je aj regulárna, lebo P = 1, f 0, 0 pre všeky kvôl prvej súradnc. 13
15 Nekedy je výhodná zmena paramerckého vyjadrena krvky: Paramerzáca krvky P, I sa zmení prosrednícvom subsúce = u, uj, kde J je nejaký nerval. Vedy nová paramerzáca krvky je Qu = P u, uj. Od subsúce sa vyžaduje, aby funkca : J R bola 1.5a hladká, čže exsujú derváce všekých rádov:,,,..., 1.5b regulárna, čže u 0 pre všeky u, 1.5c surjekívna, čže nerval J zobrazuje na nerval I,.j. J I. Vedy funkca : J R zobrazuje nerval J bjekívne na nerval I. Hovoríme ež, že v paramerzácách P, I a Qu = P u, uj s body Qu a Pu navzájom odpovedajú. Orenáca krvky je určená jej paramerzácou. Paramerzáca Qu = Pu určuje na krvke rovnakú orenácu ako pôvodná paramerzáca P práve vedy, keď u 0 pre všeky u, eda práve vedy, keď subsučná funkca u je rasúca. Orenácu krvky nuívne chápeme ako jeden z dvoch smerov pohybu po nej. Každá paramercky zadaná krvka má nekonečne veľa paramerzácí a práve dve orenáce. Príklad 1.16 obr. 1.1 Grafom funkce y b a a x paramerckým vyjadrením P, b a, xa, a je horná polelpsa s odpovedajúcm a, a, a. Subsúcou = a cos u, u0, získame paramerzácu Qu = a cos u, b sn u, u0, z príkladu 1.3. Teno komenár je dúfam zbyočný, ale predsa. V príklade 1.16 sa opro príkladu 1.3 zmenlo označene funkcí a premenných. Tam bolo P = acos, bsn a u je Qu = acosu, bsnu. To však nkomu nesme vadť.samozrejme zmenl sa aj defnčný obor paramerzáce, lebo v príklade 1.16 nepracujeme s celou elpsou. Úloha 1.6 Presvedče sa, že subsúca z predchádzajúceho príkladu je hladká, regulárna a surjekívna. Zachováva sa pr nej orenáca polelpsy? Úloha 1.7 Presvedče sa, že subsúca = gu/, u, zmení paramerzácu elpsy z príkladu 1.4 na paramerzácu z príkladu 1.3 s upraveným defnčným oborom,. 1 g x g x [Využe vzorce známe z negrovana cos x, sn x.] 1 g x 1 g x Pozorný čaeľ s mohol všmnúť, že doeraz sme nedefnoval krvku, ba jej paramerzácu. Hoc s pod krvkou nuívne predsavujeme geomercký úvar, eda množnu bodov s sým vlasnosťam, presná a prom dosaočne všeobecná defníca v akejo podobe by vyžadovala ďalšu rozsahlu prípravu. Aby sme sa jej vyhl, bude krvka defnovaná nasledovne: 14
16 1.6a Krvka je určená svojou paramerzácou, eda hladkou a akmer všade regulárnou bodovou funkcou jednej premennej. 1.6b Dve bodové funkce jednej premennej určujú rovnakú krvku, ak jedna vznkne z druhej hladkou regulárnou a surjekívnou subsúcou. Bod krvky je ľubovoľný bod z oboru hodnô jej paramerckého vyjadrena. Nameso o krvke určenej paramerzácou P, I jednoducho hovoríme krvka P, I. Je evdenné, že pr zmene paramerckého vyjadrena krvky sa množna jej bodov nezmení zaručuje o podmenka 1.5c. Tako krvka konečne súvsí s množnou bodov. Pre paramercké vyjadrene P, I je o množna {P; I}. Krvka však ne je ba množnou bodov, ale množnou bodov s paramerckým vyjadrením. Too paramercké vyjadrene môžeme mnohým spôsobm zmenť, nesmeme ho však vynechať. Sú známe príklady rôznych paramerckých vyjadrení krvek s rovnakou množnou bodov, koré majú rôzne geomercké vlasnos napr. rôznu dĺžku alebo v om som bode rôzne doyčnce. Jeden aký príklad spoznáme v kapole 4. Naším ceľom nebolo a ne je podrobne analyzovať pojem krvky, ale čím skôr začať skúmať vlasnosí krvek. Preo eše raz zdôrazňujeme: 1. Krvka ne je ba množna bodov, ale množna bodov spolu s jej paramerckým vyjadrením prosrednícvom bodovej funkce jednej premennej.. Krvka má nekonečne veľa paramerckých vyjadrení. 3. Paramercké vyjadrene krvky určuje na nej orenácu. Myslím, že na uvedené r zásady s dosť rýchlo zvyknee. Teda krvka je nečo, čo je nejako určené. Ak vám veľm chýba defníca krvky v podobe krvka je nečo, čo má nejaké vlasnos, ozve sa. Odpoveď mám prpravenú, keď vás as nepoeší. Možno ju však nájdee aj sam... Tu by mohla prvá kapola skončť. Ko chce, nemusí z nej ďalej číať an slovo a môže prejsť rovno ku kapole. Myslím s však, že nasledujúca úvaha je poučná. Poznamenajme eše, že defníca krvky má rovnakú šrukúru, ako defníca vekora v elemenárnej geomer: Vekor je určený orenovanou úsečkou. Dve orenované úsečky určujú rovnaký vekor, ak majú rovnakú dĺžku a rovnaký smer. Eše jednoduchší príklad uvedeného posupu je určovane raconálnych čísel zlomkam. Pokúse sa sformulovať defnícu raconálneho čísla, korá by začínala veou Raconálne číslo je určené zlomkom. Z prísne maemackého hľadska zlomok ne je raconálne číslo, ba ho určuje vyjadruje, reprezenuje,... Dôvod je en, že rôznym zlomkam, napr. 1/ a /4, zapsujeme rovnaké raconálne číslo. Uvedené dva zlomky sú naozaj navzájom rôzne, lebo, lebo majú rôzne čaele a rôzne menovaele. Zlomky sú vlasne usporadané dvojce celých čísel, ba ným spôsobom zapísané. Prvá zložka zlomku dvojce sa nazýva čaeľ a druhá menovaeľ. 15
17 . Doyčnca a normála krvky V druhej a v reej kapole zosrojíme v bode krvky sé pramky a rovny, koré sú s krvkou bezprosredne späé a do sej mery vyjadrujú jej var blízkos uvažovaného bodu. Najprrodzenejším akým objekom je doyčnca. Daná je krvka paramerzácou P, I a číslo 0 I. Doyčnca krvky v bode P 0 je pramka určená bodom P 0 a vekorom P 0 obr..1. Vekor P 0 sa nazýva doykový vekor krvky. Prom predpokladáme, že eno vekor je nenulový, eda, že bod P 0 je regulárny bod krvky. V sngulárnom bode doyčncu eda nedefnujeme. Ne že by sa o vôbec nedalo, ale bolo by o rochu náročné. Napríklad doyčncou asrody príklad 1.10 v sngulárnom bode P0 je os x. Príklad.1 Doyčnca elpsy P = acos, bsn, 0, v bode P/6 je určená bodom P/6 = acos/6, bsn/6 = a3/, b/ a vekorom P/6 = asn/6, bcos/6 = a/, b3/, preo má paramercké rovnce x = a3/ a/ u, y = b/ + b3/ u. Doyčnca elpsy v jej všeobecnom bode P = acos, bsn je určená bodom P a vekorom P = asn, bcos, preo jej paramercké rovnce sú x = acos ausn, y = bsn + aucos. Všmne s, že v paramerckých rovncach doyčnce krvky v jej všeobecnom bode vysupujú dva paramere. Parameer vyjadruje bod krvky, v korom určujeme doyčncu, a druhý parameer u vyjadruje polohu bodu na doyčnc. Príklad. Doyčnca grafu funkce obr... Graf funkce y = fx má paramercké vyjadrene P =, f, preo doykový vekor ejo krvky je P = 1, f. Smerncová rovnca doyčnce v bode x 0, fx 0 má eda dobre známy var y = fx 0 + f x 0 x x 0. To znamená, že defníca doyčnce paramercky zadanej krvky rozšruje pojem doyčnce grafu funkce z úvodného kurzu maemackej analýzy. Úloha.1 Napíše paramercké rovnce doyčnce reťazovky P =, acosh/a,, + v jej ľubovoľnom bode. Úloha. a Napíše paramercké rovnce doyčnce asrody v jej ľubovoľnom regulárnom bode. b Dokáže, že súradncové os vyínajú na všekých doyčncach asrody úsečky s rovnakou dĺžkou obr c Narysuje nekoľko povedzme 10, lepše vac úseček s rovnakou dĺžkou a napr. a 5 cm, korých krajné body leža na kladných polosach súradncových osí. Obálkou ýcho úseček je asroda, presnejše jeden z jej šyroch oblúkov. Skúse o naprogramovať. 16
18 d Geomercký význam paramera asrody: Dokáže, že uhol doyčnce asrody v bode P = acos 3, asn 3, 0, / s osou x je. Úloha.3 a Napíše paramercké rovnce doyčnce rakrxy P = aln g / + cos, asn, 0, v jej ľubovoľnom bode P, /. b Dokáže, že úsek na doyčnc od bodu doyku po os x má na všekých doyčncach rovnakú dĺžku obr Úloha.4 a Napíše paramercké rovnce doyčnce skrukovce v jej ľubovoľnom bode. b Presvedče sa, že všeky doyčnce skrukovce zverajú s osou skrukovce rovnaký uhol. Pr zmene paramerzáce krvky sa dĺžka a orenáca doykového vekora môže zmenť, ale jeho neorenovaný smer ne, preo je doyčnca krvky defnovaná nezávsle od akuálneho paramerckého vyjadrena krvky. Dôvodom je skuočnosť, že plaí klascký vzorec pre dervácu zloženej funkce Qu = Pu:.1 Qu = Pu u. Pravá srana má šrukúru vekor P u krá číslo u. Uvedomujeme s, že eno záps ne je z hľadska algebry úplne korekný, správne by malo byť Qu = up u. Dávame však prednosť analýze, eda šrukúre vzorca pre dervácu zloženej funkce: derváca vonkajšej zložky krá derváca vnúornej zložky. Vzorec.1 možno ľahko dokázať prosrednícvom súradníc, pre jednoduchše písane ba v rovne. Ak P x, y, ak Qu = Pu xu, yu, preo Qu xu, yu xu u, yu u = Pu u. V poslednej rovnos bolo dôležé, že obdve súradnce vekora Qu xu u, yu u obsahujú rovnaký čneľ u. Bežne sa hovorí, že doyčnca krvky je lmná poloha sečníc. Myslí sa o ako: Uvažujme pramku p, korá je určená bodm P 0 a P, 0. Keď sa číslo blíž k 0, bod P sa blíž po danej krvke k bodu P 0 a pramka p sa následne oáča okolo bodu P 0. Dá sa dokázať, že lmnou polohou pramky p je doyčnca krvky v bode P 0. Dôsledkom predošlej úvahy je vrdene: Spomedz všekých pramok, koré prechádzajú daným bodom krvky, je ku krvke najesnejše prložená doyčnca. Podrobnejše v kap. 6. Uvedená lmná vlasnosť doyčnce sa v saršej leraúre vyjadruje frázou doyčnca krvky je spojnca jej dvoch nekonečne blízkych bodov alebo ež spojnca dvoch súmedzných bodov krvky. Normála krvky v regulárnom bode krvky je každá pramka dúca bodom krvky kolmo na doyčncu v om bode. V rovne má krvka v každom bode práve jednu normálu obr..3, v presore prechádza bodom krvky nekonečne veľa normál. Teo vypĺňajú rovnu, korá prechádza bodom krvky kolmo na doyčncu. Nazývame ju normálová rovna krvky obr
19 Úloha.5 Napíše paramercké rovnce a rovncu normály v ľubovoľnom bode nekorej krvky z príkladov Úloha.6 Napíše paramercké rovnce a rovncu normálovej rovny v ľubovoľnom bode skrukovce z príkladu Treba zdôraznť, že doyčnca krvky, normála a v 3D aj normálová rovna krvky sa vždy važe na jeden bod krvky, sú o objeky v om bode krvky. 18
20 Lekca 3 Doeraz sme sa zoznáml s bodovým a vekorovým funkcam jednej premennej a s ch lmam a dervácam. Pomocou bodových funkcí určujeme paramercky krvky. Pomocou prvej derváce paramerckého vyjadrena krvky určujeme doyčncu ku krvke. V ejo lekc budeme pracovať nelen s prvou, ale aj s druhou dervácou paramerckého vyjadrena krvky. Objavuje sa v nej po prvý krá vekorový súčn. Jeho pre geomeru najdôležejše vlasnos som zhrnul do samosaného pomocného exu. 3. Oskulačná rovna presorovej krvky. Freneov rojhran Bod P rovnnej alebo presorovej krvky sa nazýva nflexný bod, k sú vekory P a P lneárne závslé. Ak sú nezávslé, P je nenflexný bod krvky. Inflexné body krvky z našch úvah spravdla vynechávame. S výrazom nflexný bod se sa urče srel v prvom ročníku vysokoškolského šúda v predmee Maemacká analýza pr skúmaní prebehu funkce jednej premennej. Tam sa nflexný bod funkce obvykle defnuje ako bod, v korom má funkca nulovú druhú dervácu. V nasledujúcom príklade sa presvedčíme, že nflexný bod krvky je prrodzeným rozšírením odpovedajúceho pojmu z maemackej analýzy. Príklad 3.1 Bod P =, f je nflexným bodom grafu funkce y = fx, xi práve vedy, keď bod je nflexným bodom funkce y = fx. Tvrdene vyplýva zo skuočnos, že vekory P = 1, f, P = 0, f sú lneárne závslé práve vedy, keď f = 0. Naozaj, vekory P, P dvojrozmerného presoru sú lneárne závslé práve vedy, keď deermnan z ch súradníc je nulový. V našom prípade ale 1 0 f f f. Preo vekory P, P dvojrozmerného presoru sú lneárne závslé práve vedy, keď f 0. Pomocou prvej derváce paramerckého vyjadrena krvky sme defnoval doyčncu krvky ako pramku, korá je v danom bode krvky ku krvke najesnejše prložená. Pomocou prvej a druhej derváce budeme defnovať ku krvke najesnejše prloženú rovnu. Aby rovna bola určená jednoznačne, musa byť určujúce vekory lneárne nezávslé, eda bod krvky musí byť nenflexný. Oskulačná rovna presorovej krvky v nenflexnom bode P je rovna určená bodom P a vekorm P a P. 19
21 Geomercký význam oskulačnej rovny: Daná je krvka P, I a jej bod P 0. Doyčncou krvky v bode P 0 označme p 0. Uvažujme rovnu prechádzajúcu pramkou p 0 a bodom krvky P, 0. Keď sa číslo blíž k 0, bod P sa po krvke blíž k bodu P 0, prčom rovna sa oáča okolo pramky p 0. Dá sa dokázať, že lmnou polohou rovny je oskulačná rovna krvky v bode P 0. Preo spomedz všekých rovín, koré prechádzajú doyčncou krvky, je ku krvke najesnejše prložená jej oskulačná rovna. Názov pochádza z lanského slova osculao = bozkávane. Názov zavedol v 18. soročí W. Lebnz. Teda an vedy nebol všec maemac suchár. Príklad 3. Oskulačná rovna skrukovce. Pre paramerzácu P = acos, asn, b máme P = asn, acos, b, P = acos, asn, 0. Za normálový vekor oskulačnej rovny môžeme eda vzať vekor P P = absn, bcos, a, eše lepše vekor s jednoduchším súradncam m bsn, bcos, a. Oskulačná rovna skrukovce v bode P má symbolckú rovncu mx P 0. Po rozpísaní je o rovnca bsnx bcosy + az ab = 0. Úloha 3.1 Dokáže, že v ľubovoľnom bode skrukovce je uhol oskulačnej rovny s osou skrukovce, eda s osou z, konšanný. Porovnaje s úlohou.4. Úloha 3. Dokáže, že pre krvku, korej všeky body leža v jednej rovne, plaí: a Vekory prvej a druhej a všekých ďalších dervácí paramerckého vyjadrena krvky sú rovnobežné s ou rovnou resp. leža v nej, resp. sú jej smerové vekory formuláca je vec vkusu. b Táo rovna je oskulačnou rovnou krvky v každom jej bode. Návod: a Dosaďe súradnce paramerckého vyjadrena krvky P = x, y, z do rovnce rovny ax by cz d 0 a dervuje. b Využe vrdene a. Prpomeňme, že normála krvky je každá pramka prechádzajúca daným bodom krvky kolmo na doyčncu v om bode krvky. Spomedz všekých nekonečne veľa normál presorovej krvky v jej nenflexnom bode sú dve významné. Prvá leží v oskulačnej rovne nazýva sa hlavná normála, druhá je na oskulačnú rovnu kolmá nazýva sa bnormála. Bnormála a doyčnca určujú rekfkačnú rovnu krvky. Tako v každom nenflexnom bode krvky vznkl r navzájom kolmé pramky doyčnca, hlavná normála a bnormála a r navzájom kolmé rovny určené ým pramkam oskulačná rovna určená doyčncou a hlavnou normálou, normálová rovna určená hlavnou normálou a bnormálou a rekfkačná rovna určená doyčncou a bnormálou obr Na doyčnc, hlavnej normále a na bnormále leža jednokové vekory, n a b, koré vznkajú oronormalzačným procesom z vekorov P, P a P P: 0
22 3.1 P, P P P P P P P n, P P P P P P P P b. P P Nazývajú sa vekor doyčnce, vekor hlavnej normály a vekor bnormály obr Podsanú časť vzorca pre vekor n sme získal rešením rovnce P up vp 0, eda rovnce P P u P P v 0. Najjednoduchším nenulovým rešením je u P P, v P P. Vzorec 3.1 pre vekor n je pomerne komplkovaný, preo sa vekory, n a b časejše počíajú v zmenenom poradí: P P P 3., b, n b P P P Porade vekorov na pravej srane posledného vzorca neslobodno zmenť, lebo b = n. Pre krvky v rovne majú zmysel ba prvé dva zo vzorcov 3.1, lebo vekorový súčn am ne je defnovaný. Podobne ako v presore aj u je k dspozíc výpočová alernaíva pre vekor n: 3.3 = P/P, n = [sgn dep, P] Prom dep, P je deermnan, korého radky sú súradnce daných vekorov, eda x y dep, P a vekor vznkne z vekora oočením o +90, eda = b, a pre x y = a, b. Konečne sgn je skraka slova sgnum, čo je znamenko. Podrobnejše, pre vekor n z 3.3 plaí: Ak dep, P 0, ak n =. Ak dep, P 0, ak n =. Prečo sme ale v 3.3 nenapísal jednoducho n =? Dôvodom je skuočnosť, že z dvoch jednokových vekorov a,koré sú kolmé na vekor, bereme za vekor n en, pre korý je báza, n orenovaná rovnako ako báza P, P. V analyckej geomer sa hovorí, že dvojce nezávslých vekorov rovny, n a P, P sú rovnako orenované práve vedy, keď deermnany de, n a dep, P majú rovnaké znamenka. Oronormálne vekory, n a b vora Freneov rojhran alebo ež Freneov repér krvky. Francúzske slovo repére znamená značka, zárez. V geomer sa slovo repér radčne používa na vyjadrene objeku, korý určuje súsavu súradníc. 1. Francúzsky maemak J. P. Frene sa okolo roku 1850 sal spoluobjaveľom dôležých vzorcov z dferencálnej geomere krvek, koré sa dnes zapsujú pomocou vekorov, n, b a ch dervácí. Preo sa eo vekory menujú po ňom.. Všmne s, že vekor bnormály b je kolmý na oskulačnú rovnu krvky v bode P, preo jej rovncu môžeme zapísať v vare bx P 0, kde X x, y, z je ľubovoľný bod presoru a jeho súradnce sú v predošlej rovnc neznámym. Vedel by se obdobným spôsobom napísať rovncu normálovej rovny? Touo lekcou sa skončla prvá časť emackého celku Krvky. Mala opsný charaker, prevládal defníce a príklady. Od budúcej lekce sa charaker kurzu začne menť, objava sa prvé vey eorémy o vlasnosach krvek. 1
23 Lekca 4 Základným ceľom ejo lekce je spoznať prrodzenú paramerzácu krvky, korá je hádam najčasejše používaným násrojom eóre krvek. Dôležý medzkrok v omo smere, korý však má aj svoj samosaný význam, je dĺžka krvky. Budeme ju defnovať analycky, čoskoro však vo vee 4.1 ukážeme, že akýo posup je v súlade s bežnou predsavou o dĺžke čary. 4. Dĺžka krvky. Prrodzená paramerzáca krvky Dĺžka krvky s paramerzácou P, a, b je negrál b l P P d. a Poznámka 4.1 Všmnme s, že dĺžka je defnovaná ba pre krvky, korých paramercké vyjadrene je defnované na uzavreom a ohrančenom nervale. Takéo krvky sa nekedy nazývajú oblúky. Hovoríme, že oblúk P, a,b spája svoje krajné body Pa, Pb. Poznámka 4. Vea o subsúc v určom negrál zabezpečuje, že dĺžka krvky nezávsí od voľby jej paramerckého vyjadrena. Presvedčme sa o om. Paramercké vyjadrene P, a,b sa po subsúc u, uc,d zmení na Qu Pu, uc,d, prčom Qu Pu u pre všeky u vzorec.1. Funkca u je monoónna, kvôl určos nech je klesajúca. Vedy c b, d a a u u pre všeky u. Preo b l P P d a 1 b 1 a c P u udu P u u du Q u du l Q. Nasledujúce r príklady ukážu, že pre jednoduché krvky dáva defníca dĺžky krvky očakávané výsledky. d d c Príklad 4.1 Dĺžka úsečky s paramerckým vyjadrením P A B A, 0,1: 1 1 l P P d B A d B A [ ] 0 B A B A
24 Príklad 4. Dĺžka kružnce s polomerom r s paramerckým vyjadrením P rcos, rsn, 0, je r, lebo l P 0 P d 0 r cos, r sn d 0 r d r [ ] 0 r Príklad 4.3 Dĺžka grafu funkce y = fx, xa,b. Krvka má paramercké vyjadrene P =, f, preo doykový vekor krvky je P = 1, f. Z defníce dĺžky krvky dosávame známy vzorec pre dĺžku grafu funkce l b a 1 f x d x. Úloha 4.1 Presvedče sa, že bodové funkce a P 1 = rcos, rsn, 0, P = rcos, rsn, 0, 4 kružnca dvakrá obehnuá kružnca neurčujú rovnakú krvku, hoc nm zadané krvky majú rovnaké množny bodov. [Návod: Vypočíaje dĺžku oboch krvek a využe vrdene z poznámky 4..] Nasledujúca vea dáva defníc dĺžky krvky geomercký zmysel. Najprv ale príde defníca. Lomená čara vpísaná do krvky P, a,b je lomená čara s vrcholm P 0, P 1,, P k 1, P k, kde a = 0 1 k 1 k = b je delene nervalu a,b obr Dĺžka lomenej čary P 0 P 1 P k 1 P k je súče dĺžok jej srán, eda číslo lp 0 P 1 P k 1 P k P 0 P 1... P k 1 P k. Prpomeňme, že suprémum množny AR je najmenše horné ohrančene množny A, eda reálne číslo c, koré vyhovuje podmenkam 1. c x pre všeky xa,. pre každé 0 exsuje xa, pre koré x c. Prvá podmenka hovorí, že číslo c je horné ohrančene množny A a druhá, že žadne číslo menše ako c už ne je horné ohrančene množny A. Suprémum množny A zapsujeme supa. Mmoradne dôležá vea z maemackej analýzy hovorí, že každá neprázdna zhora ohrančená množna reálnych čísel má práve jedno suprémum. Vea 4.1 Geomercká nerpreáca dĺžky krvky a Úsečka je najkraša krvka spájajúca dva body. b Dĺžka krvky je suprémum dĺžok do krvky vpísaných lomených čar. Dôkaz vykonáme kvôl jednoduchšemu zápsu ba pre krvky v rovne. Uvažujme eda krvku s paramerzácou P x, y, a,b. a V dôkaze oho vrdena zvoľme súsavu súradníc ak, že body Pa, Pb leža na prvej súradncovej os, eda Pa xa,0, Pb xb,0, prčom eše xa xb. Zrejme plaí 3
25 4 d d d d b P a P a x b x x x y x P P l b a b a b a b a. V nerovnosach sme využl monoónnosť určého negrálu, eda vrdene b a b a dx x g dx x f x g x f b a x, V prvej nerovnos pre premennú x a funkce y x f a x g, v druhej nerovnos pre funkce x x f a x g. b Z defníce vpísanej lomenej čary a jej dĺžky a z predchádzajúcej čas vey vyplýva, že dĺžka každej lomenej čary vpísanej do krvky je menša alebo sa rovná dĺžke krvky. Osáva dokázať, že k dĺžke krvky sa môžeme s ľubovoľnou presnosťou prblížť dĺžkou vhodne vybranej vpísanej lomenej čary. Túo časť dôkazu ba naznačíme. Zvoľme ľubovoľné delene a = 0 1 k 1 k = b nervalu a,b. Odpovedajúca lomená čara P 0 P 1 P k 1 P k má dĺžku k k y y x x P P V každom z nervalov, 1 aplkujeme na funkce x x a y y Lagrangeovu veu o srednej hodnoe. Prpomeňme Lagrangeovu veu o srednej hodnoe: Pre každú číselnú funkcu y fx, korá je spojá na nervale a, b a má dervácu na nervale a, b exsuje aké číslo ca, b, že fb fa f cb a Geomercky: V bode c, fc je doyčnca grafu funkce y fx rovnobežná s pramkou, korá spája body a, fa, b, fb, eda krajné body grafu. V ďalšom kroku dôkazu aplkujeme Lagrangeovu veu o srednej hodnoe najprv na funkcu x x na nervale, 1. Číslo c z Lagrangeovej vey označíme, aby sme zvýraznl jeho závslosť od funkce x a od -ého nervalu delena. Podobne pre funkcu y y vznkne číslo. Podľa Lagrangeovej vey exsujú v ovorenom nervale, 1 aké čísla,, že y y y x x x a, preo ] [ ] [ k k y x y y x x k y x Pre jemné delene nervalu a,b sú nervaly, 1 veľm kráke, a preože,, 1, plaí prblžná rovnosť, a eda aj y y. To nám umožňuje pokračovať: k k k P y x y x Posledná suma je negrálny súče funkce f P, a, b. Pre dosaočne jemné delene nervalu a,b sa eno súče prblžne rovná negrálu, eda dĺžke krvky. Súčasne pre všeky
26 1,..., k 1 plaí y y, eda negrálny úče sa prblžne rovná dĺžke vpísanej lomenej čary, korá vznkne na základe oho delena nervalu. Zhrnue: Pre dosaočne jemné delene nervalu a,b sa dĺžka odpovedajúcej vpísanej lomenej čary prblžne rovná dĺžke krvky P, a,b. Poznamenajme, že presný dôkaz druhej čas vey 4.1 sa dá urobť využím faku, že funkca f, x y je rovnomerne spojá na dvojrozmernom nervale a,b a,b. Paramerzáca P, I sa nazýva prrodzená paramerzáca krvky alebo paramerzáca s jednokovou rýchlosťou, ak P = 1 pre všeky. Príklad 4.4 Nájdme prrodzenú paramerzácu pramky. Začneme ľubovoľnou paramerzácou z analyckej geomere P A u. Vedy P u, preo áo paramerzáca pramky je prrodzená paramerzáca práve vedy, keď u = 1. Príklad 4.5 Nájdme prrodzenú paramerzácu kružnce P = rcos, rsn, 0,. Na základe exu za príkladom 1.15 pr zmene paramerckého vyjadrena krvky pracujeme so subsúcou = s, sj. Teraz hľadáme akú, aby Qs = Ps bola prrodzená paramerzáca, eda akú, aby vekor Qs = Ps s bol jednokový. Preože Qs = r s sns, r s coss r s sns, coss vekor Qs je jednokový práve vedy, keď r s = 1, eda práve vedy, keď s = 1/r. Vedy s = 1/rds s/r + C. Preože nehľadáme všeky prrodzené paramerzáce kružnce ale ba jednu, pre jednoduchosť zvolíme znamenko + a negračnú konšanu C = 0: Qs = rcoss/r, rsns/r, s0, r. Úloha 4.1 Nájde prrodzenú paramerzácu skrukovce P = rcos, rsn, b, 0,. [Výsledok: Qs = acos s/a b, asn s/a b, bs/a b. Návod: s = 1/a b, = s s/a b.] Kvôl nasledujúcej vee prpomeňme, že symbol Pa,b znamená zúžene funkce P, I na podmnožnu a,b defnčného oboru I. Predps funkce sa eda nemení, ba jej defnčný obor je menší. Vea 4. Geomercká nerpreáca prrodzenej paramerzáce Pre prrodzenú paramerzácu krvky P, I plaí: Pre každý podnerval a,b I sa dĺžka úseku krvky Pa,b rovná dĺžke b a odpovedajúcej čas defnčného oboru paramerzáce obr. 4.,.j. Dôkaz Pre prrodzenú paramerzácu plaí lpa,b = b a pre všeky nervaly a,b I. b b l P a, b P d 1d b a. a a 5
27 Položme vo vee 4. a 0 a b s. Vedy lp0, s s, eda s je dĺžka oblúka krvky medz bodm P0 a Ps. Iným slovam, bod pohybujúc sa po krvke z bodu P0 do bodu Ps vykoná dráhu dĺžky s, čo je v súlade s obvyklým označením v mechanke. Preo premennú v prrodzenej paramerzác krvky spravdla označujeme písmenom s a prrodzenú paramerzácu nazývame ež paramerzáca dĺžkou oblúka. Posup z príkladu 4.3 zovšeobecňuje nasledujúca vea. Kvôl jej dôkazu defnujme pre krvku P, I a pre číslo ai funkcu Pre všeky I zrejme plaí 4.1 P, s a : I R, s a P u du. s a 4. s a lpa, ak a, 4.3 s a lp,a ak a. a Rovnosť 4.1 vyplýva zo známeho vzorca pre dervácu funkce, korá je negrálom s premennou hornou hrancou: d dx x a f u du f x, ďalše dve rovnos vyplývajú z defníce dĺžky krvky a z vey o výmene hraníc určého negrálu. Vea 4.3 Nech P, I je regulárna paramerzáca krvky a nech 0 I a s 0 R sú ľubovoľné čísla. Poom exsuje aká subsúca = s, sj, že s 0 J, s 0 = 0 a Qs = Ps je prrodzená paramerzáca danej krvky, korá krvku orenuje rovnako ako pôvodná paramerzáca.j. s 0 pre všeky s. Dôkaz. Uvážme funkcu = s 0 + s a pre a = 0. Zrejme 0 = s 0 a = s a P 0 pre všeky. Preo exsuje nverzná funkca = 1 s, sj, korú označíme s. Na základe vey o dervác nverznej funkce dosávame s = 1/ s = 1/s a s = 1/Ps 0. Funkca s je eda rasúca, preo nová paramerzáca Qs = Ps orenuje krvku rovnako ako paramerzáca P. Qs je prrodzená paramerzáca, lebo pre všeky s plaí Qs = Ps s = Ps s = Ps 1/Ps = 1. Poznámka 4.3 Vea 4.3 hovorí, že každá regulárna krvka má nekonečne veľa prrodzených paramerzácí. Smunou skuočnosťou však je, že prosrednícvom elemenárnych funkcí ch možno vyjadrť len pre veľm málo krvek. Napríklad z kužeľoseček možno prrodzenú paramerzácu explcne eda vzorcom napísať ba pre kružncu príklad
28 Poznámka 4.4 Prrodzená paramerzáca krvky sa používa najmä v eoreckých úvahách, lebo pre ňu mnohé vzorce nadobúdajú jednoduchšu podobu. Vdno o napr. na nžše sa nachádzajúcom vzorc 4.6b a na dôsledku 4.1. Poznámka 4.5 Keď krvku skúmame v jednom jej bode, môžeme na základe vey 4.3 predpokladať, že krvka je vyjadrená prrodzenou paramerzácou Ps, prčom skúmaný bod je Ps 0. Kvôl jednoduchšemu zápsu časo klademe s 0 0. Úloha 4.3 Nájde prrodzenú paramerzácu a reťazovky P =, cosh. [Qs = lns s 1, s 1. Návod: = s 0 snh, = s Argsnhs lns s 1. Funkce snhx a coshx nájdee v príklade 1.5.] b krvky P = e cos, e sn, e. [Qs = s 3/3 cos lns 3/3, s 3/3 sn lns 3/3, s 3/3. Návod: = s 0 3e 1, = s lns 3/3.] Lema 4.1 Ak je dĺžka vekorovej funkce u konšanná, ak uu 0, čže u u pre všeky. Dôkaz. Ak u = c pre všeky, ak uu = c všade. Po zdervovaní oboch srán máme uu = 0 pre všeky, čže uu = 0,.j. u u pre všeky. Nasledujúce vzorce vyjadrujú základné vlasnos prrodzenej paramerzáce, budeme ch časo používať. Tu a aj neskôr skraka PP upozorňuje, že vzorec plaí ba pre prrodzenú paramerzácu krvky, pre né ypy paramerzácí už plať nemusí. 4.4 Ps = 1.j. PsPs 1 PP 4.5 Ps Ps.j. PsPs 0 PP 4.6a s = Ps PP 4.6b ns = Ps/Ps PP 4.6c bs = s ns PP Vzorce odôvodníme jednoducho: Vzorec 4.4 ba opakuje defnícu prrodzenej paramerzáce, vzorec 4.5 je vzhľadom na lemu 4.1 dôsledkom vzorca 4.4 pre funkcu u Ps. Zo vzorcov 3.1, 4.4 a 4.5 dosaneme 4.6a, 4.6b. Vzorec 4.6c plaí dokonca pre ľubovoľnú paramerzácu krvky, u ho uvádzame ba kvôl úplnos nformáce. Dôsledok 4.1 Bod Ps je nflexným bodom krvky vyjadrenej v prrodzenej paramerzác práve vedy, keď Ps = 0 PP. Dôkaz Bod Ps je nflexným bodom krvky práve vedy, keď vekory Ps a Ps sú lneárne závslé. Podľa vzorca 4.5 máme Ps Ps pre všeky s. Lenže vekor Ps je lneárne závslý s nenulovým vekorom Ps a súčasne naň kolmý práve vedy, keď je nulový. 7
29 Nasledujúca vea hovorí o rozložení bodov rovnnej krvky vzhľadom na jej doyčncu v nenflexnom bode. Pre jej dôkaz prpomíname nekoré faky o analyckom vyjadrení pramky a polrovny. V rovne môžeme rovncu pramky a, korá prechádza bodom A kolmo na vekor n, symbolcky zapísať pomocou skalárneho súčnu vekorov v vare nx A 0. Pramka a s rovncou nx A 0 je hrancou dvoch navzájom opačných polrovín. Teo sú vyjadrené nerovncam nx A 0 resp. nx A 0. Do prvej z polrovín smeruje vekor n, do druhej vekor n. Hovoríme ež, že polrovna nx A 0 je určená pramkou a vekorom n. Vea 4.4 V blízkos nenflexného bodu leží rovnná krvka v polrovne určenej doyčncou a vekorom normály. Dôkaz obr Podľa poznámky 4.5 môžeme predpokladať, že krvka je zadaná prrodzenou paramerzácou a že ju skúmame v bode P0. Doyčnca v bode P0 má rovncu n0x P0 0, polrovna určená doyčncou a vekorom normály krvky je vyjadrená nerovncou n0x P0 0. Pre funkcu hs = n0ps P0 plaí h0 n0p0 P0 0, h0 = n0p0 = n00 = 0, h0 = n0p0 = n0p0n0 = P0n0n0 = P0 0. V druhej rovnos poslednej sére sme využl obmenu vzorca 4.6b P0 P0n0. Funkca hs má eda v bode 0 osré lokálne mnmum rovné 0, preo pre s nenulové ale blízke nule je kladná. Teda pre s blízke k 0 vyhovujú body Ps nerovnc n0x P0 0, preo leža v polrovne, korá je určená doyčncou a vekorom normály krvky v bode P0. 1. Precízna podoba výroku pre s blízke k 0 vyhovujú body Ps nerovnc n0x P0 0 je: exsuje aké 0, že pre všeky s, plaí n0x P0 0. Analogcky aj nde.. Funkca hs = n0ps P0 z predchádzajúceho dôkazu vyjadruje orenovanú vzdalenosť bodu Ps od doyčnce krvky v bode P0. Ak je doyčnca vodorovná, hs je výška bodu Ps nad doyčncou. Odaľ symbol h. V súsave súradníc P0, 0, n0 je hs druhá súradnca bodu Ps. Poznámka 4.6 Pre dosaočne veľké hodnoy paramera môžu body krvky prejsť do opačnej polrovny s nerovncou n0[x P0] 0, a o aj vedy, keď všeky body krvky sú nenflexné. Typckým príkladom krvky, korá sa ak chová, je Archmedova šprála P cos, sn, 0,. Vac nformácí o nej vráane obrázka možno nájsť napríklad na sránke hps://en.wkpeda.org/wk/archmedean_spral. Poznámka 4.7 Vea 4.4 je ukážkou výsledku zv. lokálnej dferencálnej geomere, korá skúma vlasnos malých časí krvek. Pre ňu je ypcké, že z vlasnosí dervácí v jednom bode v omo prípade z vlasnos, že vekory P0 a P0 sú lneárne nezávslé sa získajú vlasnos bodov ležacch blízko skúmaného bodu u o bolo vrdene, že blízke body leža v jednej polrovne vzhľadom na doyčncu. 8
Kapitola S5. Skrutkovica na rotačnej ploche
 Kapitola S5 Skrutkovica na rotačnej ploche Nech je rotačná plocha určená osou rotácie o a meridiánom m. Skrutkový pohyb je pohyb zložený z rovnomerného rotačného pohybu okolo osi o a z rovnomerného translačného
Kapitola S5 Skrutkovica na rotačnej ploche Nech je rotačná plocha určená osou rotácie o a meridiánom m. Skrutkový pohyb je pohyb zložený z rovnomerného rotačného pohybu okolo osi o a z rovnomerného translačného
Teória grafov. RNDr. Milan Stacho, PhD.
 Teória grafov RNDr. Milan Stacho, PhD. Literatúra Plesník: Grafové algoritmy, Veda Bratislava 1983 Sedláček: Úvod do teórie grafů, Academia Praha 1981 Bosák: Grafy a ich aplikácie, Alfa Bratislava 1980
Teória grafov RNDr. Milan Stacho, PhD. Literatúra Plesník: Grafové algoritmy, Veda Bratislava 1983 Sedláček: Úvod do teórie grafů, Academia Praha 1981 Bosák: Grafy a ich aplikácie, Alfa Bratislava 1980
Kapitola P2. Rozvinuteľné priamkové plochy
 Kapitola P2 Rozvinuteľné priamkové plochy 1 Priamková plocha je rozvinuteľná, ak na nej ležia iba torzálne priamky. Rozvinuteľné priamkové plochy rozdeľujeme na: rovinu, valcové plochy, kužeľové plochy,
Kapitola P2 Rozvinuteľné priamkové plochy 1 Priamková plocha je rozvinuteľná, ak na nej ležia iba torzálne priamky. Rozvinuteľné priamkové plochy rozdeľujeme na: rovinu, valcové plochy, kužeľové plochy,
A L A BA M A L A W R E V IE W
 A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
A L A BA M A L A W R E V IE W Volume 52 Fall 2000 Number 1 B E F O R E D I S A B I L I T Y C I V I L R I G HT S : C I V I L W A R P E N S I O N S A N D TH E P O L I T I C S O F D I S A B I L I T Y I N
Matematická analýza II.
 V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prednáška 8 6. marca 2018 It has apparently not yet been observed, that...
V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prednáška 8 6. marca 2018 It has apparently not yet been observed, that...
Dokonalé a spriatelené čísla
 Dokonalé a spriatelené čísla 1. kapitola. Niektoré poznatky z teorie čísel In: Tibor Šalát (author): Dokonalé a spriatelené čísla. (Slovak). Praha: Mladá fronta, 1969. pp. 5 17. Persistent URL: http://dml.cz/dmlcz/403668
Dokonalé a spriatelené čísla 1. kapitola. Niektoré poznatky z teorie čísel In: Tibor Šalát (author): Dokonalé a spriatelené čísla. (Slovak). Praha: Mladá fronta, 1969. pp. 5 17. Persistent URL: http://dml.cz/dmlcz/403668
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
METRICKÉ ÚLOHY V PRIESTORE
 1. ÚVOD METRICKÉ ÚLOHY V PRIESTORE Monika ĎURIKOVIČOVÁ 1 Katedra Matematiky, Strojnícka fakulta STU, Abstrakt: Popisujeme možnosti použitia programového systému Mathematica pri riešení špeciálnych metrických
1. ÚVOD METRICKÉ ÚLOHY V PRIESTORE Monika ĎURIKOVIČOVÁ 1 Katedra Matematiky, Strojnícka fakulta STU, Abstrakt: Popisujeme možnosti použitia programového systému Mathematica pri riešení špeciálnych metrických
Odvodenie niektorých geometrických veličín z GPS meraní
 Acta Montanstca Slovaca Ročník 10 (2005), číslo 3, 310-316 Odvodene nektorých geometrckých velčín z GPS meraní Adel Alfrehat 1, Janka Sabová a Marcel Mozeš 2 Dervaton of some geometrc parameters from GPS
Acta Montanstca Slovaca Ročník 10 (2005), číslo 3, 310-316 Odvodene nektorých geometrckých velčín z GPS meraní Adel Alfrehat 1, Janka Sabová a Marcel Mozeš 2 Dervaton of some geometrc parameters from GPS
Metódy vol nej optimalizácie
 Matematické programovanie Metódy vol nej optimalizácie p. 1/35 Informácie o predmete Informácie o predmete p. 2/35 Informácie o predmete METÓDY VOL NEJ OPTIMALIZÁCIE Prednášajúca: M. Trnovská (M 267) Cvičiaci:
Matematické programovanie Metódy vol nej optimalizácie p. 1/35 Informácie o predmete Informácie o predmete p. 2/35 Informácie o predmete METÓDY VOL NEJ OPTIMALIZÁCIE Prednášajúca: M. Trnovská (M 267) Cvičiaci:
R a. Aeolian Church. A O g C. Air, Storm, Wind. P a h. Affinity: Clan Law. r q V a b a. R 5 Z t 6. c g M b. Atroxic Church. d / X.
 A M W A A A A R A O C A () A 6 A A G A A A A A A-C Au A A P 0 V A T < Au J Az01 Az02 A Au A A A A R 5 Z 6 M B G B B B P T Bu B B B B S B / X B A Cu A, S, W A: S Hu Ru A: C L A, S, F, S A, u F C, R C F
A M W A A A A R A O C A () A 6 A A G A A A A A A-C Au A A P 0 V A T < Au J Az01 Az02 A Au A A A A R 5 Z 6 M B G B B B P T Bu B B B B S B / X B A Cu A, S, W A: S Hu Ru A: C L A, S, F, S A, u F C, R C F
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO BRATISLAVA
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO BRATISLAVA P Í S O M N Á D I Z E R T A Č N E J Č A S Ť S K Ú Š K Y 6 Vladmír Palaj Katedra Algebry, Geometre a Ddaktky Matematky Fakulta Matematky,
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO BRATISLAVA P Í S O M N Á D I Z E R T A Č N E J Č A S Ť S K Ú Š K Y 6 Vladmír Palaj Katedra Algebry, Geometre a Ddaktky Matematky Fakulta Matematky,
P a g e 3 6 of R e p o r t P B 4 / 0 9
 P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
P a g e 3 6 of R e p o r t P B 4 / 0 9 p r o t e c t h um a n h e a l t h a n d p r o p e r t y fr om t h e d a n g e rs i n h e r e n t i n m i n i n g o p e r a t i o n s s u c h a s a q u a r r y. J
Ing. Tomasz Kanik. doc. RNDr. Štefan Peško, CSc.
 Ing. Tomasz Kanik Školiteľ: doc. RNDr. Štefan Peško, CSc. Pracovisko: Študijný program: KMMOA, FRI, ŽU 9.2.9 Aplikovaná informatika 1 identifikácia problémovej skupiny pacientov, zlepšenie kvality rozhodovacích
Ing. Tomasz Kanik Školiteľ: doc. RNDr. Štefan Peško, CSc. Pracovisko: Študijný program: KMMOA, FRI, ŽU 9.2.9 Aplikovaná informatika 1 identifikácia problémovej skupiny pacientov, zlepšenie kvality rozhodovacích
THIS PAGE DECLASSIFIED IAW E
 THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
THS PAGE DECLASSFED AW E0 2958 BL K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW E0 2958 B L K THS PAGE DECLASSFED AW E0 2958 THS PAGE DECLASSFED AW EO 2958 THS PAGE DECLASSFED AW EO 2958 THS
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
Stavba Lobačevského planimetrie
 Stavba Lobačevského planimetrie Riešenie úloh In: Ján Gatial (author); Milan Hejný (author): Stavba Lobačevského planimetrie. (Slovak). Praha: Mladá fronta, 1969. pp. 78 109. Persistent URL: http://dml.cz/dmlcz/403691
Stavba Lobačevského planimetrie Riešenie úloh In: Ján Gatial (author); Milan Hejný (author): Stavba Lobačevského planimetrie. (Slovak). Praha: Mladá fronta, 1969. pp. 78 109. Persistent URL: http://dml.cz/dmlcz/403691
«Le double : de l inquiétante étrangeté à l abjection. L Étrange Cas du docteur Jekyll et de M. Hyde de Robert Louis Stevenson»
 «u : nn n à n Én C u u J M H R u Snn» Cn Ch Pu : Ch Cn 200 «u : nn n à n Én C u u J M H R u Snn» Pu D «n ux» n En n (Cnu xx / xx / xxxx D u n : Ch Cn 200 «u : nn n à n Én C u u J M H R u
«u : nn n à n Én C u u J M H R u Snn» Cn Ch Pu : Ch Cn 200 «u : nn n à n Én C u u J M H R u Snn» Pu D «n ux» n En n (Cnu xx / xx / xxxx D u n : Ch Cn 200 «u : nn n à n Én C u u J M H R u
KATASTROFY VYBRANÉ PROBLÉMY
 16. medznárodná vedecká konferenca Rešene krízových stuácí v špecfckom prostredí, Fakulta špecálneho nžnerstva ŽU, Žlna, 1. - 2. jún 2011 KATASTROFY VYBRANÉ PROBLÉMY Klučka Jozef * ) ABSTRAKT Dôsledky
16. medznárodná vedecká konferenca Rešene krízových stuácí v špecfckom prostredí, Fakulta špecálneho nžnerstva ŽU, Žlna, 1. - 2. jún 2011 KATASTROFY VYBRANÉ PROBLÉMY Klučka Jozef * ) ABSTRAKT Dôsledky
Appendix. Title. Petr Lachout MFF UK, ÚTIA AV ČR
 Title ROBUST - Kráĺıky - únor, 2010 Definice Budeme se zabývat optimalizačními úlohami. Uvažujme metrický prostor X a funkci f : X R = [, + ]. Zajímá nás minimální hodnota funkce f na X ϕ (f ) = inf {f
Title ROBUST - Kráĺıky - únor, 2010 Definice Budeme se zabývat optimalizačními úlohami. Uvažujme metrický prostor X a funkci f : X R = [, + ]. Zajímá nás minimální hodnota funkce f na X ϕ (f ) = inf {f
PSEUDOINVERZNÁ MATICA
 PSEUDOINVERZNÁ MATICA Jozef Fecenko, Michal Páleš Abstrakt Cieľom príspevku je podať základnú informácie o pseudoinverznej matici k danej matici. Ukázať, že bázický rozklad matice na súčin matíc je skeletným
PSEUDOINVERZNÁ MATICA Jozef Fecenko, Michal Páleš Abstrakt Cieľom príspevku je podať základnú informácie o pseudoinverznej matici k danej matici. Ukázať, že bázický rozklad matice na súčin matíc je skeletným
Testy výkonnosti SKrZ
 Slovenský krasokorčuliarsky zväz Záhradnícka 95, 821 08 Bratislava 2 Testy výkonnosti SKrZ Test č. 6 a č. 5 Materiál spracovaný pre potreby SKrZ Test číslo 6 Nádeje 9 1. Oblúky vzad von (min. 6 oblúkov)
Slovenský krasokorčuliarsky zväz Záhradnícka 95, 821 08 Bratislava 2 Testy výkonnosti SKrZ Test č. 6 a č. 5 Materiál spracovaný pre potreby SKrZ Test číslo 6 Nádeje 9 1. Oblúky vzad von (min. 6 oblúkov)
1 Matice a ich vlastnosti
 Pojem sústavy a jej riešenie 1 Matice a ich vlastnosti 11 Sústavy lineárnych rovníc a matice Príklad 11 V množine reálnych čísel riešte sústavu rovníc x - 2y + 4z + t = -6 2x + 3y - z + 2t = 13 2x + 5y
Pojem sústavy a jej riešenie 1 Matice a ich vlastnosti 11 Sústavy lineárnych rovníc a matice Príklad 11 V množine reálnych čísel riešte sústavu rovníc x - 2y + 4z + t = -6 2x + 3y - z + 2t = 13 2x + 5y
Marine Harvest Herald
 Hv H T u 6-2013. u! u v v u up uu. F u - p u u u u u u pu uu x. W xu u u, u u k, O uu u u v v, u p. T, v u u u, u, k. p, u u u. v v,, G, pp u. W v p pv u x p v u v p. T v x u p u vu. u u v u u k upp, p
Hv H T u 6-2013. u! u v v u up uu. F u - p u u u u u u pu uu x. W xu u u, u u k, O uu u u v v, u p. T, v u u u, u, k. p, u u u. v v,, G, pp u. W v p pv u x p v u v p. T v x u p u vu. u u v u u k upp, p
Odhady veľkosti pokrytí náhodne indukovaných podgrafov n-rozmernej hyperkocky
 KATEDRA INFORMATIKY FAKULTA MATEMATIKY FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO Odhady veľkosti pokrytí náhodne indukovaných podgrafov nrozmernej hyperkocky Diplomová práca Bc. Ján Kliman študijný odbor:
KATEDRA INFORMATIKY FAKULTA MATEMATIKY FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO Odhady veľkosti pokrytí náhodne indukovaných podgrafov nrozmernej hyperkocky Diplomová práca Bc. Ján Kliman študijný odbor:
Univerzita Karlova v Praze Matematicko-fyzikální fakulta. Michal Kesely. Katedra matematické analýzy. Studijní program: Obecná matematika
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Michal Kesely Slavné neřešitelné problémy Katedra matematické analýzy Vedoucí bakalářské práce: RNDr. Dalibor Pražák, Ph.D. Studijní
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Michal Kesely Slavné neřešitelné problémy Katedra matematické analýzy Vedoucí bakalářské práce: RNDr. Dalibor Pražák, Ph.D. Studijní
I n t e r ku l t ú r n a ko mu n i ká c i a na hodine anglické h o jazyka. p r ostrední c tvom použitia PC
 I n t e r ku l t ú r n a ko mu n i ká c i a na hodine anglické h o jazyka p r ostrední c tvom použitia PC P e t r a J e s e n s k á A n o t á c i a V p r í s p e v k u j e r o z p r a c o v a n é š p e
I n t e r ku l t ú r n a ko mu n i ká c i a na hodine anglické h o jazyka p r ostrední c tvom použitia PC P e t r a J e s e n s k á A n o t á c i a V p r í s p e v k u j e r o z p r a c o v a n é š p e
OH BOY! Story. N a r r a t iv e a n d o bj e c t s th ea t e r Fo r a l l a g e s, fr o m th e a ge of 9
 OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
OH BOY! O h Boy!, was or igin a lly cr eat ed in F r en ch an d was a m a jor s u cc ess on t h e Fr en ch st a ge f or young au di enc es. It h a s b een s een by ap pr ox i ma t ely 175,000 sp ect at
Cataraqui Source Protection Area Stream Gauge Locations
 Cqu u P m Gu s Ts Ez K Ts u s sp E s ms P Ps s m m C Y u u I s Ts x C C u R 4 N p Ds Qu H Em us ms p G Cqu C, s Ks F I s s Gqu u Gqu s N D U ( I T Gqu C s C, 5 Rs p, Rs 15, 7 N m s m Gus - Ps P f P 1,
Cqu u P m Gu s Ts Ez K Ts u s sp E s ms P Ps s m m C Y u u I s Ts x C C u R 4 N p Ds Qu H Em us ms p G Cqu C, s Ks F I s s Gqu u Gqu s N D U ( I T Gqu C s C, 5 Rs p, Rs 15, 7 N m s m Gus - Ps P f P 1,
Matematika 17. a 18. storočia
 Matematika 17. a 18. storočia René Descartes Narodený : 31 Marec 1596 v La Haye (teraz Descartes),Touraine, France Zomrel : 11 Feb 1650 v Stockholm, Sweden Riešenie kvadratických rovníc podľa Descarta
Matematika 17. a 18. storočia René Descartes Narodený : 31 Marec 1596 v La Haye (teraz Descartes),Touraine, France Zomrel : 11 Feb 1650 v Stockholm, Sweden Riešenie kvadratických rovníc podľa Descarta
Eva Baranová, Kamil Maleček OD STREDOVÉHO PRIEMETU KRUŽNICE KU STREDOVÝM CYKLIDÁM. 1 Priemet kružnice v stredovom premietaní
 25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Eva Baranová, Kamil Maleček OD STREDOVÉHO PRIEMETU KRUŽNICE KU STREDOVÝM CYKLIDÁM Abstrakt V prvej časti príspevku odvodzujeme podmienku, kedy je v danom
25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Eva Baranová, Kamil Maleček OD STREDOVÉHO PRIEMETU KRUŽNICE KU STREDOVÝM CYKLIDÁM Abstrakt V prvej časti príspevku odvodzujeme podmienku, kedy je v danom
Ayuntamiento de Madrid
 9 v vx-xvv \ ü - v q v ó - ) q ó v Ó ü " v" > - v x -- ü ) Ü v " ñ v é - - v j? j 7 Á v ü - - v - ü
9 v vx-xvv \ ü - v q v ó - ) q ó v Ó ü " v" > - v x -- ü ) Ü v " ñ v é - - v j? j 7 Á v ü - - v - ü
Prednáška 3. Optimalizačné metódy pre funkcie n-premenných. Študujme reálnu funkciu n-premenných. f: R R
 Prednáška 3 Optimalizačné metódy pre funkcie n-premenných Študujme reálnu funkciu n-premenných n f: R R Našou úlohou bude nájsť také x opt R n, pre ktoré má funkcia f minimum x opt = arg min ( f x) Túto
Prednáška 3 Optimalizačné metódy pre funkcie n-premenných Študujme reálnu funkciu n-premenných n f: R R Našou úlohou bude nájsť také x opt R n, pre ktoré má funkcia f minimum x opt = arg min ( f x) Túto
c- : r - C ' ',. A a \ V
 HS PAGE DECLASSFED AW EO 2958 c C \ V A A a HS PAGE DECLASSFED AW EO 2958 HS PAGE DECLASSFED AW EO 2958 = N! [! D!! * J!! [ c 9 c 6 j C v C! ( «! Y y Y ^ L! J ( ) J! J ~ n + ~ L a Y C + J " J 7 = [ " S!
HS PAGE DECLASSFED AW EO 2958 c C \ V A A a HS PAGE DECLASSFED AW EO 2958 HS PAGE DECLASSFED AW EO 2958 = N! [! D!! * J!! [ c 9 c 6 j C v C! ( «! Y y Y ^ L! J ( ) J! J ~ n + ~ L a Y C + J " J 7 = [ " S!
SYSTÉMY PRE ZVÝŠENIA BEZPEČNOSTI VODIČA MOTOROVÉHO VOZIDLA - ZAZNAMENÁVANIE OKA, POHĽADU V REÁLNOM ČASE PRE MONITOROVANIE OSTRAŽITOSTI VODIČA
 Ročník 5., Číslo III., lisopad 200 SYSTÉMY PRE ZVÝŠENIA BEZPEČNOSTI VODIČA MOTOROVÉHO VOZIDLA - ZAZNAMENÁVANIE OKA, POHĽADU V REÁLNOM ČASE PRE MONITOROVANIE OSTRAŽITOSTI VODIČA SYSTEMS DRIVERS SECURITY
Ročník 5., Číslo III., lisopad 200 SYSTÉMY PRE ZVÝŠENIA BEZPEČNOSTI VODIČA MOTOROVÉHO VOZIDLA - ZAZNAMENÁVANIE OKA, POHĽADU V REÁLNOM ČASE PRE MONITOROVANIE OSTRAŽITOSTI VODIČA SYSTEMS DRIVERS SECURITY
( ) = ( ) ( ) = ( ) = + = = = ( ) Therefore: , where t. Note: If we start with the condition BM = tab, we will have BM = ( x + 2, y + 3, z 5)
 Chapter Exercise a) AB OB OA ( xb xa, yb ya, zb za),,, 0, b) AB OB OA ( xb xa, yb ya, zb za) ( ), ( ),, 0, c) AB OB OA x x, y y, z z (, ( ), ) (,, ) ( ) B A B A B A ( ) d) AB OB OA ( xb xa, yb ya, zb za)
Chapter Exercise a) AB OB OA ( xb xa, yb ya, zb za),,, 0, b) AB OB OA ( xb xa, yb ya, zb za) ( ), ( ),, 0, c) AB OB OA x x, y y, z z (, ( ), ) (,, ) ( ) B A B A B A ( ) d) AB OB OA ( xb xa, yb ya, zb za)
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
 Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
Lesson eight What are characteristics of chemical reactions? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading
ENTROPIA. Claude Elwood Shannon ( ), USA A Mathematical Theory of Communication, 1948 LOGARITMUS
 LOGARITMUS ENTROPIA Claude Elwood Shao (96-00), USA A Mathematcal Theory of Commucato, 948 7. storoče Naer, Brggs, orovae číselých ostuostí: artmetcká ostuosť 3 0 3 4 5 6 geometrcká ostuosť /8 /4 / 4 8
LOGARITMUS ENTROPIA Claude Elwood Shao (96-00), USA A Mathematcal Theory of Commucato, 948 7. storoče Naer, Brggs, orovae číselých ostuostí: artmetcká ostuosť 3 0 3 4 5 6 geometrcká ostuosť /8 /4 / 4 8
STRAIGHT LINES EXERCISE - 3
 STRAIGHT LINES EXERCISE - 3 Q. D C (3,4) E A(, ) Mid point of A, C is B 3 E, Point D rotation of point C(3, 4) by angle 90 o about E. 3 o 3 3 i4 cis90 i 5i 3 i i 5 i 5 D, point E mid point of B & D. So
STRAIGHT LINES EXERCISE - 3 Q. D C (3,4) E A(, ) Mid point of A, C is B 3 E, Point D rotation of point C(3, 4) by angle 90 o about E. 3 o 3 3 i4 cis90 i 5i 3 i i 5 i 5 D, point E mid point of B & D. So
Univerzita Karlova v Praze. Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE. Matúš Kepič
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Matúš Kepič Webová aplikace pro výuku goniometrických funkcí, rovnic a nerovnic Katedra didaktiky matematiky Vedoucí diplomové práce:
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Matúš Kepič Webová aplikace pro výuku goniometrických funkcí, rovnic a nerovnic Katedra didaktiky matematiky Vedoucí diplomové práce:
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE. Ekonomická a finančná matematika
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE Ekonomcká a fnančná maemaka EKONOMETRICKÝ MODEL AGREGÁTNEHO DOPYTU SLOVENSKEJ REPUBLIKY Dploman: Lenka Drnáková Školeľ: Doc.
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE Ekonomcká a fnančná maemaka EKONOMETRICKÝ MODEL AGREGÁTNEHO DOPYTU SLOVENSKEJ REPUBLIKY Dploman: Lenka Drnáková Školeľ: Doc.
fotón gluón WaZ A.Einstein A.Compton Richter, Ting M.Gell-Mann Ledermann Schwartz Steinberger Friedman Kendall Taylor Gross,Wilczek,Politzer
 Program pre učiteľov fyziky z členských štátov CERNu Fyzika elementárnych častíc 1. z čoho sa skladá svet Martin Mojžiš elementárne častice elementárne fermióny leptóny kvarky elementárne bozóny fotón
Program pre učiteľov fyziky z členských štátov CERNu Fyzika elementárnych častíc 1. z čoho sa skladá svet Martin Mojžiš elementárne častice elementárne fermióny leptóny kvarky elementárne bozóny fotón
ADM a logika. 4. prednáška. Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť
 ADM a logika 4. prednáška Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť 1 Odvodzovanie formúl výrokovej logiky, logický dôsledok, syntaktický prístup Logický dôsledok
ADM a logika 4. prednáška Výroková logika II, logický a sémantický dôsledok, teória a model, korektnosť a úplnosť 1 Odvodzovanie formúl výrokovej logiky, logický dôsledok, syntaktický prístup Logický dôsledok
VYHLÁSENIE O PARAMETROCH. č SK. Predpokladané použitie. stave ý h častí ako o kladov a stropov, pozri prílohu, najmä prílohy B 1 - B 3
 VYHLÁSENIE O PARAMETROCH č. 0017 SK 1. Jedi eč ý ide tifikač ý kód typu výro ku: fischer skrutka do betónu FBS, FBS A4 a FBS C 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v etó e
VYHLÁSENIE O PARAMETROCH č. 0017 SK 1. Jedi eč ý ide tifikač ý kód typu výro ku: fischer skrutka do betónu FBS, FBS A4 a FBS C 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v etó e
Časopis pro pěstování matematiky a fysiky
 Časopis pro pěstování matematiky a fysiky Norman Levinson Criteria for the limit-point case for second order linear differential operators Časopis pro pěstování matematiky a fysiky, Vol. 74 (1949), No.
Časopis pro pěstování matematiky a fysiky Norman Levinson Criteria for the limit-point case for second order linear differential operators Časopis pro pěstování matematiky a fysiky, Vol. 74 (1949), No.
Všeobecný algebraický modelovací systém - GAMS
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE Katedra aplkovane matematky a štatstky Všeobecný algebracký modelovací systém - GAMS DIPLOMOVÁ PRÁCA BRATISLAVA 2006 Jakub Drozdík
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE Katedra aplkovane matematky a štatstky Všeobecný algebracký modelovací systém - GAMS DIPLOMOVÁ PRÁCA BRATISLAVA 2006 Jakub Drozdík
Ranking accounting, banking and finance journals: A note
 MPRA Munich Personal RePEc Archive Ranking accounting, banking and finance ournals: A note George Halkos and Nickolaos Tzeremes University of Thessaly, Department of Economics January 2012 Online at https://mpra.ub.uni-muenchen.de/36166/
MPRA Munich Personal RePEc Archive Ranking accounting, banking and finance ournals: A note George Halkos and Nickolaos Tzeremes University of Thessaly, Department of Economics January 2012 Online at https://mpra.ub.uni-muenchen.de/36166/
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY HADAMARDOVE MATICE A ICH APLIKÁCIE V OPTIMÁLNOM DIZAJNE BAKALÁRSKA PRÁCA 2012 Samuel ROSA UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY HADAMARDOVE MATICE A ICH APLIKÁCIE V OPTIMÁLNOM DIZAJNE BAKALÁRSKA PRÁCA 2012 Samuel ROSA UNIVERZITA KOMENSKÉHO V BRATISLAVE
Matematická analýza II.
 V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prezentácie k prednáškam čast II 21. februára 2018 The extent of this calculus
V. Diferenciálny počet (prezentácia k prednáške MANb/10) doc. RNDr., PhD. 1 1 ondrej.hutnik@upjs.sk umv.science.upjs.sk/analyza Prezentácie k prednáškam čast II 21. februára 2018 The extent of this calculus
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A. Ήχος Πα. to os se e e na aș te e e slă ă ă vi i i i i
 CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
CATAVASII LA NAȘTEREA DOMNULUI DUMNEZEU ȘI MÂNTUITORULUI NOSTRU, IISUS HRISTOS. CÂNTAREA I-A Ήχος α H ris to os s n ș t slă ă ă vi i i i i ți'l Hris to o os di in c ru u uri, în tâm pi i n ți i'l Hris
Jádrové odhady gradientu regresní funkce
 Monika Kroupová Ivana Horová Jan Koláček Ústav matematiky a statistiky, Masarykova univerzita, Brno ROBUST 2018 Osnova Regresní model a odhad gradientu Metody pro odhad vyhlazovací matice Simulace Závěr
Monika Kroupová Ivana Horová Jan Koláček Ústav matematiky a statistiky, Masarykova univerzita, Brno ROBUST 2018 Osnova Regresní model a odhad gradientu Metody pro odhad vyhlazovací matice Simulace Závěr
1 Arithmetic calculations (calculator is not allowed)
 1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
1 ARITHMETIC CALCULATIONS (CALCULATOR IS NOT ALLOWED) 1 Arithmetic calculations (calculator is not allowed) 1.1 Check the result Problem 1.1. Problem 1.2. Problem 1.3. Problem 1.4. 78 5 6 + 24 3 4 99 1
Ash Wednesday. First Introit thing. * Dómi- nos. di- di- nos, tú- ré- spi- Ps. ne. Dó- mi- Sál- vum. intra-vé-runt. Gló- ri-
 sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
sh Wdsdy 7 gn mult- tú- st Frst Intrt thng X-áud m. ns ní- m-sr-cór- Ps. -qu Ptr - m- Sál- vum m * usqu 1 d fc á-rum sp- m-sr-t- ó- num Gló- r- Fí- l- Sp-rí- : quó-n- m ntr-vé-runt á- n-mm c * m- quó-n-
VYHLÁSENIE O PARAMETROCH. č SK. Predpokladané použitie. stave ý h častí ako o kladov a stropov, pozri prílohu, najmä prílohy B 1 - B 4
 VYHLÁSENIE O PARAMETROCH č. 0009 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: o eľová kotva fis her FAZ II 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v betóne k upev e iu ťažký
VYHLÁSENIE O PARAMETROCH č. 0009 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: o eľová kotva fis her FAZ II 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v betóne k upev e iu ťažký
TABLE OF CONTENTS 2 CHAPTER 1
 TABLE OF CONTENTS CHAPTER 1 Quadratics CHAPTER Functions 3 CHAPTER 3 Coordinate Geometry 3 CHAPTER 4 Circular Measure 4 CHAPTER 5 Trigonometry 4 CHAPTER 6 Vectors 5 CHAPTER 7 Series 6 CHAPTER 8 Differentiation
TABLE OF CONTENTS CHAPTER 1 Quadratics CHAPTER Functions 3 CHAPTER 3 Coordinate Geometry 3 CHAPTER 4 Circular Measure 4 CHAPTER 5 Trigonometry 4 CHAPTER 6 Vectors 5 CHAPTER 7 Series 6 CHAPTER 8 Differentiation
Scilab Textbook Companion for Linear Algebra and Its Applications by D. C. Lay 1
 Scilab Textbook Companion for Linear Algebra and Its Applications by D. C. Lay 1 Created by Animesh Biyani B.Tech (Pursuing) Electrical Engineering National Institute Of Technology, Karnataka College Teacher
Scilab Textbook Companion for Linear Algebra and Its Applications by D. C. Lay 1 Created by Animesh Biyani B.Tech (Pursuing) Electrical Engineering National Institute Of Technology, Karnataka College Teacher
:,,.. ;,..,.,. 90 :.. :, , «-»,, -. : -,,, -, -., ,, -, -. - «-»:,,, ,.,.
 .,.,. 2015 1 614.8 68.9 90 :,,.. ;,. 90.,.,. :.. :, 2015. 164. - - 280700, «-»,, -. : -,,, -, -.,. -. -. -,, -, -. - «-»:,,, -. 614.8 68.9.,.,., 2015, 2015 2 ... 5... 7 1.... 7 1.1.... 7 1.2.... 9 1.3....
.,.,. 2015 1 614.8 68.9 90 :,,.. ;,. 90.,.,. :.. :, 2015. 164. - - 280700, «-»,, -. : -,,, -, -.,. -. -. -,, -, -. - «-»:,,, -. 614.8 68.9.,.,., 2015, 2015 2 ... 5... 7 1.... 7 1.1.... 7 1.2.... 9 1.3....
VYHLÁSENIE O PARAMETROCH. č SK. Predpoklada é použitie. stave ý h častí ako o kladov a stropov, pozri prílohu, najmä prílohy B 1 - B 8
 VYHLÁSENIE O PARAMETROCH č. 0007 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: i jektáž y systé FIS V 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v et e k upev e iu ťažký h systé
VYHLÁSENIE O PARAMETROCH č. 0007 SK 1. Jedi eč ý ide tifikač ý k d typu výro ku: i jektáž y systé FIS V 2. )a ýšľa é použitie/použitia: Produkt O eľová kotva pre použitie v et e k upev e iu ťažký h systé
A l g o r i t m i c k y n e r i e š i t e ľ n é p r o b l é m y
 A l g o r i t m i c k y n e r i e š i t e ľ n é p r o b l é m y Lev Bukovský Ústav matematických vied, Prírodovedecká fakulta UPJŠ Košice, 20. apríla 2004 Obsah 1 Úvod 2 2 Čiastočne rekurzívne funkcie
A l g o r i t m i c k y n e r i e š i t e ľ n é p r o b l é m y Lev Bukovský Ústav matematických vied, Prírodovedecká fakulta UPJŠ Košice, 20. apríla 2004 Obsah 1 Úvod 2 2 Čiastočne rekurzívne funkcie
Company Case Study: The Market Hall. Prof.dr.ir. Mick Eekhout
 30 years of Dutch Glass Developments and Innovations Company Case Study: The Market Hall Prof.dr.ir. Po r t fo l i o : 3 0 y e a rs o f s p a c e st r u c t u re s, 25 y e a rs o f g l a s s structure
30 years of Dutch Glass Developments and Innovations Company Case Study: The Market Hall Prof.dr.ir. Po r t fo l i o : 3 0 y e a rs o f s p a c e st r u c t u re s, 25 y e a rs o f g l a s s structure
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITA KOMENSKÉHO V BRATISLAVE DIPLOMOVÁ PRÁCA Michal Polák
 FAKULA MAEMAIKY, FYZIKY A INFORMAIKY UNIVERZIA KOMENSKÉHO V BRAISLAVE DIPLOMOVÁ PRÁCA 2004 Michal Polák FAKULA MAEMAIKY, FYZIKY A INFORMAIKY UNIVERZIA KOMENSKÉHO V BRAISLAVE KAEDRA EKONOMICKÝCH A FINANČNÝCH
FAKULA MAEMAIKY, FYZIKY A INFORMAIKY UNIVERZIA KOMENSKÉHO V BRAISLAVE DIPLOMOVÁ PRÁCA 2004 Michal Polák FAKULA MAEMAIKY, FYZIKY A INFORMAIKY UNIVERZIA KOMENSKÉHO V BRAISLAVE KAEDRA EKONOMICKÝCH A FINANČNÝCH
A Probability Primer. A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes.
 A Probability Primer A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes. Are you holding all the cards?? Random Events A random event, E,
A Probability Primer A random walk down a probabilistic path leading to some stochastic thoughts on chance events and uncertain outcomes. Are you holding all the cards?? Random Events A random event, E,
N C GM L P, u u y Du J W P: u,, uy u y j S, P k v, L C k u, u GM L O v L v y, u k y v v QV v u, v- v ju, v, u v u S L v: S u E x y v O, L O C u y y, k
 Qu V vu P O B x 1361, Bu QLD 4575 C k N 96 N EWSLEE NOV/ DECE MBE 2015 E N u uu L O C 21 Nv, 2 QV v Py Cu Lv Su, 23 2 5 N v, 4 2015 u G M v y y : y quu u C, u k y Bu k v, u u vy v y y C k! u,, uu G M u
Qu V vu P O B x 1361, Bu QLD 4575 C k N 96 N EWSLEE NOV/ DECE MBE 2015 E N u uu L O C 21 Nv, 2 QV v Py Cu Lv Su, 23 2 5 N v, 4 2015 u G M v y y : y quu u C, u k y Bu k v, u u vy v y y C k! u,, uu G M u
Class IX : Math Chapter 11: Geometric Constructions Top Concepts 1. To construct an angle equal to a given angle. Given : Any POQ and a point A.
 1 Class IX : Math Chapter 11: Geometric Constructions Top Concepts 1. To construct an angle equal to a given angle. Given : Any POQ and a point A. Required : To construct an angle at A equal to POQ. 1.
1 Class IX : Math Chapter 11: Geometric Constructions Top Concepts 1. To construct an angle equal to a given angle. Given : Any POQ and a point A. Required : To construct an angle at A equal to POQ. 1.
I N A C O M P L E X W O R L D
 IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
IS L A M I C E C O N O M I C S I N A C O M P L E X W O R L D E x p l o r a t i o n s i n A g-b eanste d S i m u l a t i o n S a m i A l-s u w a i l e m 1 4 2 9 H 2 0 0 8 I s l a m i c D e v e l o p m e
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o
 I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
I M P O R T A N T S A F E T Y I N S T R U C T I O N S W h e n u s i n g t h i s e l e c t r o n i c d e v i c e, b a s i c p r e c a u t i o n s s h o u l d a l w a y s b e t a k e n, i n c l u d f o l
História nekonečne malej veličiny PROJEKTOVÁ PRÁCA. Martin Čulen. Alex Fleško. Konzultant: Vladimír Repáš
 História nekonečne malej veličiny PROJEKTOVÁ PRÁCA Martin Čulen Alex Fleško Konzultant: Vladimír Repáš Škola pre mimoriadne nadané deti a Gymnázium, Skalická 1, Bratislava BRATISLAVA 2013 1. Obsah 1. Obsah
História nekonečne malej veličiny PROJEKTOVÁ PRÁCA Martin Čulen Alex Fleško Konzultant: Vladimír Repáš Škola pre mimoriadne nadané deti a Gymnázium, Skalická 1, Bratislava BRATISLAVA 2013 1. Obsah 1. Obsah
Software Process Models there are many process model s in th e li t e ra t u re, s om e a r e prescriptions and some are descriptions you need to mode
 Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
Unit 2 : Software Process O b j ec t i ve This unit introduces software systems engineering through a discussion of software processes and their principal characteristics. In order to achieve the desireable
Exercise: concepts from chapter 3
 Reading:, Ch 3 1) The natural representation of a curve, c = c(s), satisfies the condition dc/ds = 1, where s is the natural parameter for the curve. a) Describe in words and a sketch what this condition
Reading:, Ch 3 1) The natural representation of a curve, c = c(s), satisfies the condition dc/ds = 1, where s is the natural parameter for the curve. a) Describe in words and a sketch what this condition
EXERCISE - 01 CHECK YOUR GRASP
 XRCIS - 1 CHCK YOUR GRASP SLCT TH CORRCT ALTRNATIV (ONLY ON CORRCT ANSWR) 1. If A B = 1 5 3 7 and A 3B = 5 7, then matrix B is equal to - 4 5 6 7 (B) 6 3 7 1 3 6 1. If A = cos sin sin cos, then A A is
XRCIS - 1 CHCK YOUR GRASP SLCT TH CORRCT ALTRNATIV (ONLY ON CORRCT ANSWR) 1. If A B = 1 5 3 7 and A 3B = 5 7, then matrix B is equal to - 4 5 6 7 (B) 6 3 7 1 3 6 1. If A = cos sin sin cos, then A A is
f;g,7k ;! / C+!< 8R+^1 ;0$ Z\ \ K S;4 i!;g + 5 ;* \ C! 1+M, /A+1+> 0 /A+>! 8 J 4! 9,7 )F C!.4 ;* )F /0 u+\ 30< #4 8 J C!
 393/09/0 393//07 :,F! ::!n> b]( a.q 5 O +D5 S ١ ; ;* :'!3Qi C+0;$ < "P 4 ; M V! M V! ; a 4 / ;0$ f;g,7k ;! / C+!< 8R+^ ;0$ Z\ \ K S;4 "* < 8c0 5 *
393/09/0 393//07 :,F! ::!n> b]( a.q 5 O +D5 S ١ ; ;* :'!3Qi C+0;$ < "P 4 ; M V! M V! ; a 4 / ;0$ f;g,7k ;! / C+!< 8R+^ ;0$ Z\ \ K S;4 "* < 8c0 5 *
Le classeur à tampons
 Le classeur à tampons P a s à pa s Le matériel 1 gr a n d cla s s e u r 3 pa pi e r s co o r d o n n é s. P o u r le m o d è l e pr é s e n t é P a p i e r ble u D ai s y D s, pa pi e r bor d e a u x,
Le classeur à tampons P a s à pa s Le matériel 1 gr a n d cla s s e u r 3 pa pi e r s co o r d o n n é s. P o u r le m o d è l e pr é s e n t é P a p i e r ble u D ai s y D s, pa pi e r bor d e a u x,
Contribution to Deterministic Top-Down Analysis of Context-free Languages
 KYBERNETIKA ČÍSLO 5, ROČNÍK 4/1968 Contribution to Deterministic Top-Down Analysis of Context-free Languages KAREL CULIK II In the present paper a generalization of ZX(A:)-grammars is given, the notion
KYBERNETIKA ČÍSLO 5, ROČNÍK 4/1968 Contribution to Deterministic Top-Down Analysis of Context-free Languages KAREL CULIK II In the present paper a generalization of ZX(A:)-grammars is given, the notion
2 tel
 Us. Timeless, sophisticated wall decor that is classic yet modern. Our style has no limitations; from traditional to contemporar y, with global design inspiration. The attention to detail and hand- craf
Us. Timeless, sophisticated wall decor that is classic yet modern. Our style has no limitations; from traditional to contemporar y, with global design inspiration. The attention to detail and hand- craf
1. Suppose that a, b, c and d are four different integers. Explain why. (a b)(a c)(a d)(b c)(b d)(c d) a 2 + ab b = 2018.
 New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
New Zealand Mathematical Olympiad Committee Camp Selection Problems 2018 Solutions Due: 28th September 2018 1. Suppose that a, b, c and d are four different integers. Explain why must be a multiple of
Kointegračná analýza v ekonometrii
 Koinegračná analýza v ekonomerii Marin Lukáčik Juraj Pekár Prognózovanie budúceho vývoja ekonomických ukazovaeľov, koré sú v cenre záujmu užívaeľov informácií, býva časo najdôležiejšou úlohou ekonomických
Koinegračná analýza v ekonomerii Marin Lukáčik Juraj Pekár Prognózovanie budúceho vývoja ekonomických ukazovaeľov, koré sú v cenre záujmu užívaeľov informácií, býva časo najdôležiejšou úlohou ekonomických
Hanoi Open Mathematical Olympiad
 HEXAGON inspiring minds always Let x = 6+2 + Hanoi Mathematical Olympiad 202 6 2 Senior Section 20 Find the value of + x x 7 202 2 Arrange the numbers p = 2 2, q =, t = 2 + 2 in increasing order Let ABCD
HEXAGON inspiring minds always Let x = 6+2 + Hanoi Mathematical Olympiad 202 6 2 Senior Section 20 Find the value of + x x 7 202 2 Arrange the numbers p = 2 2, q =, t = 2 + 2 in increasing order Let ABCD
CH 61 USING THE GCF IN EQUATIONS AND FORMULAS
 CH 61 USING THE GCF IN EQUATIONS AND FORMULAS Introduction A while back we studied the Quadratic Formula and used it to solve quadratic equations such as x 5x + 6 = 0; we were also able to solve rectangle
CH 61 USING THE GCF IN EQUATIONS AND FORMULAS Introduction A while back we studied the Quadratic Formula and used it to solve quadratic equations such as x 5x + 6 = 0; we were also able to solve rectangle
Dotyková rovina a normála k ploche z=f(x,y) s Matlabom
 Dotyková rovina a normála k ploche z=f(x,y) s Matlabom Jana Schusterová ABSTRACT: The aim of this article is to explain how determine a tangent plane and a normal of the surface z=f(x,y) using the programming
Dotyková rovina a normála k ploche z=f(x,y) s Matlabom Jana Schusterová ABSTRACT: The aim of this article is to explain how determine a tangent plane and a normal of the surface z=f(x,y) using the programming
On second order sufficient optimality conditions for quasilinear elliptic boundary control problems
 On second order sufficient optimality conditions for quasilinear elliptic boundary control problems Vili Dhamo Technische Universität Berlin Joint work with Eduardo Casas Workshop on PDE Constrained Optimization
On second order sufficient optimality conditions for quasilinear elliptic boundary control problems Vili Dhamo Technische Universität Berlin Joint work with Eduardo Casas Workshop on PDE Constrained Optimization
CMSC 313 Lecture 17 Postulates & Theorems of Boolean Algebra Semiconductors CMOS Logic Gates
 CMSC 313 Lecture 17 Postulates & Theorems of Boolean Algebra Semiconductors CMOS Logic Gates UMBC, CMSC313, Richard Chang Last Time Overview of second half of this course Logic gates &
CMSC 313 Lecture 17 Postulates & Theorems of Boolean Algebra Semiconductors CMOS Logic Gates UMBC, CMSC313, Richard Chang Last Time Overview of second half of this course Logic gates &
2 u Du, k Hu Dv Hu, y H. u Cu j u qu u. Nv. v uy. Cu Hu F A H. qu Cu.. Cu j 1980, u V, v Nu My O k. v u u. A G C. My u v k, 2.5 H v v u / u v u v k y
 H HE 1016 M EEING OF HE ODIE CLU 1,016 Cu 7:30.. D 11, 2007 y W L Uvy. C : Pu A y: Ov 25 x u. Hk, u k MA k D u y Hu, u G, u C C, MN C, Nk Dv Hu, MN, u K A u vu v. W y A Pku G, G u. N EW UINE: D, Cu, 22
H HE 1016 M EEING OF HE ODIE CLU 1,016 Cu 7:30.. D 11, 2007 y W L Uvy. C : Pu A y: Ov 25 x u. Hk, u k MA k D u y Hu, u G, u C C, MN C, Nk Dv Hu, MN, u K A u vu v. W y A Pku G, G u. N EW UINE: D, Cu, 22
Use precise language and domain-specific vocabulary to inform about or explain the topic. CCSS.ELA-LITERACY.WHST D
 Lesson seven What is a chemical reaction? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading Informational Text,
Lesson seven What is a chemical reaction? Science Constructing Explanations, Engaging in Argument and Obtaining, Evaluating, and Communicating Information ENGLISH LANGUAGE ARTS Reading Informational Text,
Have Metropolitan Planning Organizations improved regional policy making? The cases of Kansas City and St. Louis.
 Uv u S Lu RL @ USL D USL Gu k 5-6-00 Hv P Oz v k? K C S Lu J E C Uv u-s Lu j6@ F k : ://uu/ P P S C R C C J E "Hv P Oz v k? K C S Lu" (00) D 49 ://uu//49 D u u USL Gu k RL @ USL u D uz RL @ USL F v@uu
Uv u S Lu RL @ USL D USL Gu k 5-6-00 Hv P Oz v k? K C S Lu J E C Uv u-s Lu j6@ F k : ://uu/ P P S C R C C J E "Hv P Oz v k? K C S Lu" (00) D 49 ://uu//49 D u u USL Gu k RL @ USL u D uz RL @ USL F v@uu
0# E % D 0 D - C AB
 5-70,- 393 %& 44 03& / / %0& / / 405 4 90//7-90/8/3 ) /7 0% 0 - @AB 5? 07 5 >0< 98 % =< < ; 98 07 &? % B % - G %0A 0@ % F0 % 08 403 08 M3 @ K0 J? F0 4< - G @ I 0 QR 4 @ 8 >5 5 % 08 OF0 80P 0O 0N 0@ 80SP
5-70,- 393 %& 44 03& / / %0& / / 405 4 90//7-90/8/3 ) /7 0% 0 - @AB 5? 07 5 >0< 98 % =< < ; 98 07 &? % B % - G %0A 0@ % F0 % 08 403 08 M3 @ K0 J? F0 4< - G @ I 0 QR 4 @ 8 >5 5 % 08 OF0 80P 0O 0N 0@ 80SP
(C) Pavel Sedach and Prep101 1
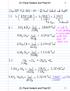 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach
(C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 1 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 2 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach and Prep101 3 (C) Pavel Sedach
Lower Austria. The Big Travel Map. Big Travel Map of Lower Austria.
 v v v :,000, v v v v, v j, Z ö V v! ö +4/4/000 000 @ : / : v v V, V,,000 v v v v v v 08 V, v j?, v V v v v v v v,000, V v V, v V V vv /Z, v / v,, v v V, v x 6,000 v v 00,000 v, x v U v ( ) j v, x q J J
v v v :,000, v v v v, v j, Z ö V v! ö +4/4/000 000 @ : / : v v V, V,,000 v v v v v v 08 V, v j?, v V v v v v v v,000, V v V, v V V vv /Z, v / v,, v v V, v x 6,000 v v 00,000 v, x v U v ( ) j v, x q J J
FICH~:s lciithyo\l~~trio~es.
 PB FCNyM UNLP T g vg wk b b y y g b y F wk v b m b v gz w my y m g E bv b g y v q y q q ó y P mv gz y b v m q m mó g FCH CTHYOTROES P W P -C b } k < HP- qe q< - - < - m T
PB FCNyM UNLP T g vg wk b b y y g b y F wk v b m b v gz w my y m g E bv b g y v q y q q ó y P mv gz y b v m q m mó g FCH CTHYOTROES P W P -C b } k < HP- qe q< - - < - m T
2-UMA-115 Teória množín. Martin Sleziak
 2-UMA-115 Teória množín Martin Sleziak 23. septembra 2010 Obsah 1 Úvod 4 1.1 Predhovor...................................... 4 1.2 Sylaby a literatúra................................. 5 1.2.1 Literatúra..................................
2-UMA-115 Teória množín Martin Sleziak 23. septembra 2010 Obsah 1 Úvod 4 1.1 Predhovor...................................... 4 1.2 Sylaby a literatúra................................. 5 1.2.1 Literatúra..................................
Last 4 Digits of USC ID:
 Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
Chemistry 05 B Practice Exam Dr. Jessica Parr First Letter of last Name PLEASE PRINT YOUR NAME IN BLOCK LETTERS Name: Last 4 Digits of USC ID: Lab TA s Name: Question Points Score Grader 8 2 4 3 9 4 0
! 94
 ! 94 4 : - : : / : : : : ( :) : : : - : / : / : : - 4 : -4 : : : : : -5 () ( ) : -6 : - - : : : () : : : :4 : -7. : : -8. (. : ( : -9 : ( ( ( (5 (4 4 : -0! : ( : ( :. : (. (. (. (4. ( ( ( : ( 4 : - : :
! 94 4 : - : : / : : : : ( :) : : : - : / : / : : - 4 : -4 : : : : : -5 () ( ) : -6 : - - : : : () : : : :4 : -7. : : -8. (. : ( : -9 : ( ( ( (5 (4 4 : -0! : ( : ( :. : (. (. (. (4. ( ( ( : ( 4 : - : :
Jádrové odhady regresní funkce pro korelovaná data
 Jádrové odhady regresní funkce pro korelovaná data Ústav matematiky a statistiky MÚ Brno Finanční matematika v praxi III., Podlesí 3.9.-4.9. 2013 Obsah Motivace Motivace Motivace Co se snažíme získat?
Jádrové odhady regresní funkce pro korelovaná data Ústav matematiky a statistiky MÚ Brno Finanční matematika v praxi III., Podlesí 3.9.-4.9. 2013 Obsah Motivace Motivace Motivace Co se snažíme získat?
8. Relax and do well.
 CHEM 1515 Exam II John II. Gelder October 14, 1993 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 8 different pages. The last two pages include a periodic table, a
CHEM 1515 Exam II John II. Gelder October 14, 1993 Name TA's Name Lab Section INSTRUCTIONS: 1. This examination consists of a total of 8 different pages. The last two pages include a periodic table, a
ADDITIONAL MATHEMATICS
 005-CE A MATH HONG KONG CERTIFICATE OF EDUCATION EXAMINATION 005 ADDITIONAL MATHEMATICS :00 pm 5:0 pm (½ hours) This paper must be answered in English 1. Answer ALL questions in Section A and any FOUR
005-CE A MATH HONG KONG CERTIFICATE OF EDUCATION EXAMINATION 005 ADDITIONAL MATHEMATICS :00 pm 5:0 pm (½ hours) This paper must be answered in English 1. Answer ALL questions in Section A and any FOUR
MEEN 618: ENERGY AND VARIATIONAL METHODS
 JN Reddy - 1 MEEN 618: ENERGY AND VARIATIONAL METHODS WORK, ENERGY, AND VARIATIONAL CALCULUS Read: Chapter 4 CONTENTS Work done External and internal work done Strain energy and strain energy density Complementary
JN Reddy - 1 MEEN 618: ENERGY AND VARIATIONAL METHODS WORK, ENERGY, AND VARIATIONAL CALCULUS Read: Chapter 4 CONTENTS Work done External and internal work done Strain energy and strain energy density Complementary
02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr
 Chemistry 05 B First Letter of PLEASE PRINT YOUR NAME IN BLOCK LETTERS Exam last Name Name: 02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr Lab TA s Name: Question Points Score Grader 2 2 9 3 9 4 2
Chemistry 05 B First Letter of PLEASE PRINT YOUR NAME IN BLOCK LETTERS Exam last Name Name: 02/05/09 Last 4 Digits of USC ID: Dr. Jessica Parr Lab TA s Name: Question Points Score Grader 2 2 9 3 9 4 2
4038/02 October/November 2009
 Additional Mathematics (408/0) version 1.1 ADDITIONAL MATHEMATIS Paper Suggested Solutions 1. Topic: Further Trigonometric Identities sin(a B) sin A cos B cos A sin B 8 5 8 cos A sin B 8 8 408/0 October/November
Additional Mathematics (408/0) version 1.1 ADDITIONAL MATHEMATIS Paper Suggested Solutions 1. Topic: Further Trigonometric Identities sin(a B) sin A cos B cos A sin B 8 5 8 cos A sin B 8 8 408/0 October/November
Advanced Placement. Chemistry. Integrated Rates
 Advanced Placement Chemistry Integrated Rates 204 47.90 9.22 78.49 (26) 50.94 92.9 80.95 (262) 52.00 93.94 83.85 (263) 54.938 (98) 86.2 (262) 55.85 0. 90.2 (265) 58.93 02.9 92.2 (266) H Li Na K Rb Cs Fr
Advanced Placement Chemistry Integrated Rates 204 47.90 9.22 78.49 (26) 50.94 92.9 80.95 (262) 52.00 93.94 83.85 (263) 54.938 (98) 86.2 (262) 55.85 0. 90.2 (265) 58.93 02.9 92.2 (266) H Li Na K Rb Cs Fr
The Golden Ratio and Signal Quantization
 The Golden Ratio and Signal Quantization Tom Hejda, tohecz@gmail.com based on the work of Ingrid Daubechies et al. Doppler Institute & Department of Mathematics, FNSPE, Czech Technical University in Prague
The Golden Ratio and Signal Quantization Tom Hejda, tohecz@gmail.com based on the work of Ingrid Daubechies et al. Doppler Institute & Department of Mathematics, FNSPE, Czech Technical University in Prague
M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7; ;J zy U;K z< mj ]!.,,+7;
![M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7; ;J zy U;K z< mj ]!.,,+7; M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7; ;J zy U;K z< mj ]!.,,+7;](/thumbs/78/78216077.jpg) V 3U. T, SK I 1393/08/21 :,F! 1393/10/29 ::!n> 2 1 /M + - /E+4q; Z R :'!3Qi M $,7 8$ 4,!AK 4 4/ * /;K "FA ƒf\,7 /;G2 @;J\ M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7;
V 3U. T, SK I 1393/08/21 :,F! 1393/10/29 ::!n> 2 1 /M + - /E+4q; Z R :'!3Qi M $,7 8$ 4,!AK 4 4/ * /;K "FA ƒf\,7 /;G2 @;J\ M $ 4 65\ K;$ 5, 65\ M $ C! 4 /2 K;$ M $ /+5\ 8$ A5 =+0,7 ;* C! 4.4/ =! K;$,7 $,+7;
