Spectral gaps for the O-U/Stochastic heat processes on path space over a Riemannian manifold with boundary
|
|
|
- Jemima Marshall
- 5 years ago
- Views:
Transcription
1 arxiv: v1 [mah.pr] 5 Dec 18 ec1 Specral gap for he O-U/Sochaic hea procee on pah pace over a Riemannian manifold wih boundary Bo Wu School of Mahemaical Science, Fudan Univeriy, Shanghai 433, China wubo@fudan.edu.cn Abrac Fang-Wu[15] preened a explici pecral gap for he O-U proce on pah pace over a Riemannian manifold wihou boundary under he bounded Ricci curvaure condiion. In hi paper, we will exend hee reul o he cae of he Riemannian manifold wih boundary. Moreover, we alo derive he imilar reul for he ochaic hea proce. Keyword: Funcional inequaliy; Ricci Curvaure; Second fundamenal form; Diffuion proce; Pah pace. 1 Inroducion Funcional inequaliy i an imporan ool o udy he pecral gap for ome diffuion operaor in he analyi/ochaic analyi field, epecially, for he cae of infinie dimenional Riemannian pah pace. For he manifold wihou boundary, Fang[1] fir eablihed he Poincaré inequaliy for he O-U operaor on Riemanian pah pace by he Clark-Ocean formula, afer ha he log-sobolev inequaliy/weakpoincaré inequaliy have alo been eablihed for he O-U Dirichle form, ee e.g. [1, 3, 9, 18, 19, 3, 4, 1, 7, 8, 5] and reference herein. Recenly Naber[1] gave ome characerizaion of he uniform bound of Ricci curvaure by he analyi of he pah pace. Moiviaed by hi work, Fang and Wu[15] gave he explici pecral gap of he O-U operaor on Suppored in par by NNSFC
2 pah pace under he Ricci curvaure condiion ha K Ric Z : Ric+ Z K 1 and K +K 1. Thi condiion K +K 1 i removed by Cheng-Thalimaier[5]. For he manifold wih boundary, Wang[6] proved he damped log-sobolev inequaliy for he O-U proce on pah pace, bu ome geomeric informaion are hidden in hi inequaliy. In hi aricle, our main aim i o preen a eimae of he pecral gap for he O-U operaor on pah pace over a manifold poible wih boundary under he curvaure and he econd fundamenal form condiion eq K Ric Z K 1, σ I σ 1 foromeconank,k 1,σ,σ 1 R. Inparicular, ourreulcover Fang-Wu reul and Cheng-Thalmaier reul. Moreover, we alo obain he eimae of he pecral gap for he ochaic hea proce. To ae our main reul, we need o inroduce ome noaion. Le M be a d- dimenional complee Riemannian manifold poibly wih a boundary M and N be he inward uni normal vecor field of M. Le L 1 +Z be he diffuion operaor for ome C 1 vecor field Z, where i he Laplace operaor on M. Denoe by he Riemannian pah pace: W T x M {γ C[,T];M : γ x}. Le ρ be he Riemannian diance on M. Then Wx T M i a Polih pace under he uniform diance ρ γ,σ : up ργ,σ, γ,σ Wx T M. [,T] Le OM be he orhonormal frame bundle over M and π : OM M be he canonical projecion. Furhermore, we chooe a canonical orhonormal bai {e i } 1 i d on R d and a andard orhonormal bai H i u : H uei 1 i d for u OM of horizonal vecor field on OM. Then he horizonal reflecing diffuion proce i he unique oluion o he SDE: eq1. 1. du x H i U x dw +H Z U x d+h NU x dlx, Ux O xm, where W i he d-dimenional Brwonian moion on a complee filraion probabiliy pace Ω,{F },P, H Z and H N are he horizonal lif of Z and N repecively, and l x i an adaped increaing proce which increae only when X x : πu x M which i called he local ime of X x on M. Then i i eay o know ha X x olve he equaion eq dx x U x dw +ZX x d+nx dl x, Xx x up o he life ime ζ he maximal ime of he oluion.
3 Le FCT be he pace of bounded Lipchiz coninuou cylinder funcion on Wx TM, i.e. for every F FC T, here exi ome N 1 and < 1 < < N T, f C Lip M N uch ha Fγ fγ 1,,γ N,γ Wx T M, where C Lip M N i he collecion of bounded Lipchiz coninuou funcion on M N. Suppoe H i he andard Cameron-Marin pace for C[,T];R d, i.e. { } H h C[,T];R d : h, h H T : h d <. In order o conruc O-U proce on pah pace by he heory of Dirichle form, we fir inroduce he damped Mallavin gradien given by Wang[5]. To do ha, we will recommend a muliplicaive funcional Q x,, which i fir inroduced by Hu [] o inveigae gradien eimae on P. For any fixed, Q x, i an adaped righ-coninuou proce on R d R d uch ha Q x, P U x if X x M and eq Q x, I Q x,r{ RicZ U x r d+iux r dlx r where P u : R d R d i he projecion along u 1 N, i.e. } I 1 {X x M}P U x, P u a,b : ua,n ub,n, a,b R d,u x M O x M. For every F FCT, by 4..1 in [5], he damped gradien i defined by eq D FX[,T] x Q x, i U 1 i i fx x 1,,X x N, [,T]. eq eq i: i > Thu, he aociaed Mallavin gradien will defined a follow: D FX[,T] x i: i > I 1 {X xi M}P U xi U 1 i i fx x 1,,X x N, [,T]. For any conan K,K 1,σ,σ 1 wih K K 1,σ σ 1 and each [,T], le µ be he random meaure on [,T] given by µ dr exp[ K r σ l x r lx ]{ K 1 K dr + σ 1 σ dl x r }} : ϕ 1,r,K 1,K,σ 1,σ dr+ϕ 1,r,K 1,K,σ 1,σ dl x r Denoe by wo meaurable funcion on W T x M A 1+µ[,T] + B 1+µ[r,T] ϕ 1 r,,k 1,K,σ 1,σ dr 1+µ[r,T] ϕ r,,k 1,K,σ 1,σ dr. 3
4 Throughou he aricle, we aume ha he reflecing if M exi L-diffuion proce i non-exploive. Le P x be he diribuion of he L-diffuion proce X x aring from a fixed poin x up o ome fixed ime T >. Then P x i a probabiliy meaure on he Riemannian pah pace Wx T M. Define he following quadraic form by eq E K 1,K σ 1,σ F,F : D F A d+b dl dp x. Wx TM The following Logarihmic Sobolev inequaliy i he main reul of hi paper. T1.1 Theorem 1.1. Aume ha K Ric Z K 1 and σ I σ 1. Then he following Logarihmic Sobolev inequaliy hold eq E F F log E K 1,K F σ 1,σ F,F, F FCT. L By he above Theorem 1.1, we obain he following Corollary for wo pecial cae. C1. Corollary 1.. a Aume ha M i a Riemannian manifold wihou a boundary and K 1 Ric Z K, hen he Logarihmic Sobolev inequaliy hold eq E F F log CT,K F 1,K D F ddp x, F FC L Wx TM b M. In paricular, when K <, we have eq Spec L eq eq When K >, we have SG L 1 1+β 1+ K 1 K [ ] 1 e K T. K β + β β +β β e K T e K T, where β K 1 K K. b Le M be Ricci fla Riemannian manifold wih boundary, and we aume ha he econd fundamenal form aifie σ I σ 1, hen When σ, we ge ha for any F FCT E F log F F L W T x M 1+σ 1 lt x D F ddp x + σ 1 1+σ 1 l x Wx TM T T 4 D F dl dp x.
5 When σ <, we ge ha for any F FCT eq E F F log 1+ σ F 1 σ exp[ σ +εl x L Wx TM T ] + σ1 σ exp[ σ +εlt] x Wx TM for ome conan ε >. D F ddp x D F dl dp x Remark Wang [5] proved ha he damped Logarihmic Sobolev inequaliy. When M i a Riemannian manifold wihou boundary, and K Ric Z K 1,K +K 1, Fang-Wu [15] fir proved 1.1, laer, hi reul had been exended o he general cae of K and K 1 by Cheng-Thalimaier[5]. The re of hi paper i organized a follow: In Secion, we will prove Theorem 1.1 and Corollary 1.. The eimae of he pecral gap for he ochaic hea proce will be preened in Secion 3. Proof of Theorem 1.1 and Corollary 1..1 Proof of Theorem 1.1 Proof of Theorem 1.1. By Theorem 4.4 in [5], we know ha he following damped logarihmic Sobolev inequaliy hold eq.1.1 E F F log D F F ddp x. L Wx TM eq.. eq.3.3 Therefore i uffice o how ha D F d D F A d+b dl. By uing he aumpion of K Ric Z K 1 and σ I σ 1, we have Combining hi wih 1.14 Q x, I Ric Z K 1 K, I σ 1 σ, Q x,r{ Ric Z U x r d+iux r dlx r and [6, Theorem 3..1], i i eay o derive ha Q x,r exp[ K r σ l x r l x ]. 5 } I 1 {X x M}P U x.
6 By he definiion of he damped gradien, we ge eq.4.4 D FX[,T] x Q x, i U 1 i i fx x 1,,X x N D FX[,T] x i: i > i i: i > Q x,r{ Ric Z U x rd+iu x rdl x r} I 1 {X x M} P U x i U 1 i i fx x 1,,X x N D FX[,T] x Q,r{ x Ric Z Ur x D rfx[,t] x dr +IUx r D rfx[,t] r} x dlx. Then we have eq.5.5 D F X[,T] x D F X[,T] x + eq.6.6 exp[ K r σ l x r lx ]{ K 1 K dr+ σ 1 σ dl x r } D rf X x [,T] } D F X[,T] x + D r F µ dr. The Hölder inequaliy implie ha Thu, we obain eq D F d D F X x [,T] 1+µ[,T] r 1+µ [,T] D F + 1+µ[,T] D F d+ D F d+ 1+µ[,T] 1+µ[,T] D r F ϕ,r,k 1,K,σ 1,σ dl r d 1+µ[,T] D F d+ r 1+µ[,T] D r F ϕ,r,k 1,K,σ 1,σ dl r d 1+µ[,T] D F d+ 1+µ[r,T] ϕ r,,k 1,K,σ 1,σ dr D F dl D F A d+b dl. D r F µ dr 1+µ[,T] D r F µ drd D r F ϕ 1,r,K 1,K,σ 1,σ drd 1+µ[,T] D r F ϕ 1,r,K 1,K,σ 1,σ drd 1+µ[r,T] ϕ 1 r,,k 1,K,σ 1,σ dr D F d 6
7 eq.8.8 Up o now, we complee he proof.. Proof of Corollary 1. To prove Corollary 1., we need ome preparaion. Le β K 1 K K and define [ ] Λ,T 1+β 1 exp[ K T ] + β +β [ ] 1 exp K and + β [exp K +T exp K T ] CT,K 1,K : up Λ,T. [,T] Similar o he proof of Propoiion 3.3 in Fang-Wu[15] for he cae of K 1 +K, in he following we will dicu monooniciy of he funcion Λ, T. p.1 Propoiion.1. 1 If K <, hen Λ,T i ricly increaing over [,T]. If K, hen he maximum i aained a a poin in,t. Proof. According o he definiion.8 of Λ,T, we ge Λ,T 1+β 1 e K T and ΛT,T 1+ β +β [ 1 exp K T ]+ β [ e K T 1 ] [ ] 1+β 1 e K T Λ,T. eq.9.9 In paricular, he econd in he above implie ha ΛT,T Λ,T. Nex, we ake he derivaive of Λ,T wih repec o, Λ,T βk e KT + β +β K e K β K [ e K +T +e ] K T. Then we have and eq.1.1 Λ,T βk e K T + β +β K β K e K T βk 1+β1 e K T ; Λ T,T βk + β +β K e KT β K [ e K T +1 ] βk 1 1+βe KT + β [ e K T +1 ] βk [1 e K T ] β K [1 e K T ]. 7
8 Noing ha eq { Λ T,T > if K <, Λ T,T < if K >. Now we look for [,T] uch ha Λ,T. We have Λ,T eq.1.1 e KT +1+βe K β [ e K +T +e ] K T e KT e K +1+β β [ e K T +e KT e ] K 1+ β e KT e K 1+β β e K T. Therefore here exi a mo one uch ha Λ,T. For he cae where K <, if here exi,t uch ha Λ,T <. Then by.9 and.11, he equaion Λ,T ha a lea wo oluion, i i impoible. Therefore for K <, Λ,T. For K >, we uppoe uch ha Λ,T, hen by.1 e K Thu he proof i compleed. 1+ β 1 e K T e KT. +β By he above Propoiion.1, i i eay o obain he following Propoiion.. p. Propoiion.. i If K >, eq up Λ,T 1+β [,T] β + β 1+ β +β β +β β e K T 1+ β +β 1 e K T T e K. 1 e K T e K T eq ii If K <, up [,T]Λ,T K 1 K [ ] 1 e K T. K 8
9 Proof of Corollary 1.. a Since M i a Riemannian manifold wihou boundary, hen he local ime l, hu we have Then µ dr : K 1 K exp[ K r ]dr. eq µ[,t] K 1 K [1 exp[ K T ]]. K Which implie ha eq ϕ 1 r,,k 1,K,σ 1,σ K 1 K exp[ K r] ϕ r,,k 1,K,σ 1,σ. Then by.15 and he fir equaliy of.16, eq µ[r,T] ϕ 1 r,,k 1,K,σ 1,σ dr K 1 K 1+ K 1 K [1 exp[ K T r]] exp[ K r]dr K K1 K + K 1 K [ 1 exp K K K ] K 1 K exp K K +TexpK 1. Thu we ge eq B A 1+µ[r,T] ϕ r,,k 1,K,σ 1,σ dr 1+µ[,T] + 1+µ[r,T] ϕ 1 r,,k 1,K,σ 1,σ dr 1+ K 1 K [1 exp[ K T ]] K K1 K + + K 1 K [ 1 exp K K K ] + K 1 K [exp K K +T exp K T ]. From which we have eq D F A d+b dl Λ,T D F d. 9
10 Then 1.9, 1.1 and 1.11 come from Theorem 1.1 and Propoiion.. b By he aumpion of M, we know ha eq.. µ dr σ 1 σ exp[ σ lr x lx ]dlx r. Thu, eq.1.1 µ[,t] σ 1 σ exp[σ l x ] exp[ σ lr x ]dlx r. In addiion,. implie ha eq.. ϕ 1 r,,k 1,K,σ 1,σ ϕ r,,k 1,K,σ 1,σ σ 1 σ exp[ σ l x lx r ]. Then, by he definiion of A and B, eq.3.3 A 1+ σ 1 σ exp[σ l x ] exp[ σ lr x ]dlx r B σ 1 σ 1+ σ 1 σ exp[σ l xr ] exp[ σ lu x ]dlx u exp[ σ l x lx r ]dr. r eq.4.4 Since l x i a increaing proce, we have A { 1+σ 1 l x T, if σ, 1+ σ 1 σ exp[ σ +εl x T ], if σ < and eq.5.5 B { σ 1 1+σ 1 l x T T, if σ, σ 1 σ exp[ σ +εl x T ], if σ < By Theorem 1.1, when σ, we ge E F F log F L eq σ 1 lt x W T x M + σ 1 1+σ 1 l x Wx TM T T D F ddp x D F dl dp x, 1
11 and when σ <, we ge E F F log F L eq σ 1 σ exp[ σ +εl x Wx TM T ] D F ddp x + σ1 σ exp[ σ +εlt] x D F dl dp x. W T x M eq.8.8 Corollary.3. Le M : { x x 1,,x d R d : a 1 x 1 + +a d x d c } for ome conan c R, hen M i a Riemannian manifold wihou boundary and Ric wih I, hu we have E F log F F L 3 Sochaic hea equaion D F ddp x. Wx TM In hi ecion, we will conider he pecral gap for he ochaic hea equaion on a Riemannian manifold wih boundary. Before moving on, le inroduce ome noaion. The ochaic hea equaion on Riemannian manifold had been udied deailed by []ee alo [17]. Here hey inroduced ome noaion. In paricular, he claical cylinder funcion depending on finie ime i no in he domain of generaor aociaed o he ochaic hea equaion. Thu, we need o inroduce a cla of new cylinder funcion FCb 1 on WT x M, i.e. for every F FC1 b, here exi ome m 1, m N, f Cb 1Rm,g i C,1 b [,1] M, i 1,...,m, uch ha 1 eq Fγ f g 1,γ d, 1 g,γ d,..., 1 g m,γ d, γ Wx T M, where C,1 b [,1] M denoe he funcion which are coninuou w.r.. he fir variable and differeniable w.r.. he econd variable wih coninuou derivaive. For any F FC 1 b wih. form and h L [,1];R d, according o Wang[5], he damped Malliavin gradien of F i given by DFγ : m j1 ˆ j fγ Q,u Uu 1 γ g j u,γ u du, γ Wx T M. 11
12 Le F be he damped L -gradien of F, and ince Then, we have Thu, DF,h F,h d d h,df H D h F h,df L F, h udu d F,h u dud Fudu,h d. F m j1 The L -gradien of F i defined by Fudu DF. u F,h u ˆ j fγq,t U 1 γ g j,γ. ddu F m j1 ˆ j fγu 1 γ g j,γ. By Lemma 4.3. in [5], we have eq3. 3. F F + F + F + DF,dB Fudu,dB Q,u Fudu,dB eq By he andard he procedure, we have E F log F F L Wx TM Q,u Fudu ddp x. 1
13 eq By.3 and Hölder inequaliy, we ge Le Q,u Fudu ϕ e Ku σlx u l x Fudu e Ku σlx u lx du e Ku σlx u lx du e Ku σlx u lx du. Then by changing he order of inegraion we obain W T x M where W T x M Q,u Fudu A F ddp x, A ddp x W T x M ϕue K u σlx lx u du. Thu, we ge he following Logarihmic Sobolev inequaliy. e Ku σlx u lx F udu e Ku σlx u lx F udu. ϕ e Ku σlx u lx F ududdp x T3.1 Theorem 3.1. Aume ha Ric Z K and I σ. Then he following Logarihmic Sobolev inequaliy hold eq E F log F F L A F ddp x, F FCb. 1 Wx T M c3. Corollary 3.. a Aume ha M i a Riemannian manifold wih a convex boundary and K Ric Z, hen he Logarihmic Sobolev inequaliy hold eq E F log F F L CT,K F ddp x, F FC Wx TM b M, where [ ] 1 e KT K CT,K e e KT e KT 1, if K, KT 1 [ 1 K 1 e KT ], if K <. 13
14 Proof. Since he boundary i convex, hu I σ. Thu and eq ϕ Then we ge e Ku σlx u lx du e Ku du 1 K [ 1 e KT ] A ϕue K u σlx l u x du 1 [ ] 1 e KT u e K u du K 1 ] [ e K +e KT+ e KT. K A, AT 1 1 e K K In he following, imilar o he argumen of Propoiion.1. Taking he derivaive of A give A 1 ] [e K e KT+ e KT. K Thu, Noing ha A 1 K [ ] 1 e K, A T 1 [ e K 1 ]. K eq { A T > if K <, A T < if K >. Now we look for [,T] uch ha A. We have c A e K e KT+ e KT e KT e KT+K e K e KT 1. Therefore here exi a mo one uch ha A. For he cae where K <, if here exi,t uch ha A <. Then by 3.7 and 3.8, he equaion A ha a lea wo oluion, i i impoible. Therefore for K <, A. For K >, we uppoe uch ha Λ,T, hen by 3.9 The proof i compleed. e K e KT 1. 14
15 Corollary 3.3. Le M be a Ricci-fla Riemannian manifold wih a convex boundary, hen we have E F F log T F ddp F x. L Reference W T x M [1] S. Aida and K. D. Elworhy, Differenial calculu on pah and loop pace. I. Logarihmic Sobolev inequaliie on pah pace, C. R. Acad. Sci. Pari Série I, , [] D. Bakry, M. Ledoux, F.-Y. Wang, Perurbaion of funcional inequaliie uing growh condiion, J. Mah. Pure Appl. 877, [3] B. Capiaine, E. P. Hu and M. Ledoux, Maringale repreenaion and a imple proof of logarihmic Sobolev inequaliie on pah pace, Elecron. Comm. Probab. 1997, [4] X. Chen, B. Wu, Funcional inequaliy on pah pace over a non-compac Riemannian manifold, J. Func. Anal. 6614, [5] L. J. Cheng, A. Thalmaier, Specral gap on Riemannian pah pace over aic and evolving manifold, J. Func. Anal V984 [6] A. B. Cruzeiro and P. Malliavin, Renormalized differenial geomery and pah pace: rucural equaion, curvaure, J. Func. Anal. 139: , [7] B. K. Driver, A Cameron-Marin ype quai-invariance heorem for Brownian moion on a compac Riemannian manifold, J. Func. Anal , [8] B. K. Driver and M. Röckner, Conrucion of diffuion on pah and loop pace of compac Riemannian manifold, C. R. Acad. Sci. Pari Série I , [9] K. D. Elworhy, X.- M. Li and Y. Lejan, On The geomery of diffuion operaor and ochaic flow, Lecure Noe in Mahemaic, , Springer-Verlag. [1] K. D. Elworhy and Z.-M. Ma, Vecor field on mapping pace and relaed Dirichle form and diffuion, Oaka. J. Mah , [11] O. Enchev and D. W. Sroock, Toward a Riemannian geomery on he pah pace over a Riemannian manifold, J. Func. Anal. 134 : 1995, [1] S.- Z. Fang, Un inéqualié du ype Poincaréur un epace de chemin, C. R. Acad. Sci. Pari Série I , [13] S.- Z. Fang and P. Malliavin, Sochaic analyi on he pah pace of a Riemannian manifold: I. Markovian ochaic calculu, J. Func. Anal. 118 : , [14] S.- Z. Fang, F.-Y. Wang and B. Wu, Tranporaion-co inequaliy on pah pace wih uniform diance, Sochaic. Proce. Appl. 118: 1 8, [15] S. Z. Fang, B. Wu, Remark on pecral gap on he Riemannian pah pace, Elecron. Commun. Probab. 17, no. 19, 1V13. 15
16 [16] M. Fukuhima, Y. Ohima and M. Takeda, Dirichle Form and Symmeric Markov Procee, Waler de Gruyer, 1. [17] M. Hairer. The moion of a random ring, arxiv:165.19, page 1-, 16. [18] E. P. Hu, Logarihmic Sobolev inequalie on pah pace over compac Riemannian manifold, Commun. Mah. Phy , [19] E. P. Hu, Analyi on pah and loop pace, in Probabiliy Theory and Applicaion E. P. Hu and S. R. S. Varadhan, Ed., LAS/PARK CITY Mahemaic Serie, 61999, , Amer. Mah. Soc. Providence. [] E. P. Hu, Muliplicaive funcional for he hea equaion on manifold wih boundary, Mich. Mah. J. 5, [1] A. Naber, Characerizaion of bounded Ricci curvaure on mooh and nonmooh pace, arxiv: v4. [] M. Röckner, B. Wu, R.C. Zhu and R.X. Zhu,Sochaic Hea Equaion wih Value in a Manifold via Dirichle Form, ubmied. [3] F.- Y. Wang, Weak poincaré Inequaliie on pah pace, In. Mah. Re. No. 44, [4] F.-Y. Wang, Second fundamenal form and gradien of Neumann emigroup, J. Func. Anal. 569, [5] F.-Y. Wang, Analyi on pah pace over Riemannian manifold wih boundary, Comm. Mah. Sci. 911, [6] F.- Y. Wang, Analyi for diffuion procee on Riemannian manifold, World Scienific, 14. [7] F.- Y. Wang and B. Wu, Poinwie Characerizaion of Curvaure and Second Fundamenal Form on Riemannian Manifold, acceped by SC. [8] B. Wu, Characerizaion of he upper bound of Bakry-Emery curvaure, arxiv: v1 16
Mathematische Annalen
 Mah. Ann. 39, 33 339 (997) Mahemaiche Annalen c Springer-Verlag 997 Inegraion by par in loop pace Elon P. Hu Deparmen of Mahemaic, Norhweern Univeriy, Evanon, IL 628, USA (e-mail: elon@@mah.nwu.edu) Received:
Mah. Ann. 39, 33 339 (997) Mahemaiche Annalen c Springer-Verlag 997 Inegraion by par in loop pace Elon P. Hu Deparmen of Mahemaic, Norhweern Univeriy, Evanon, IL 628, USA (e-mail: elon@@mah.nwu.edu) Received:
Fractional Ornstein-Uhlenbeck Bridge
 WDS'1 Proceeding of Conribued Paper, Par I, 21 26, 21. ISBN 978-8-7378-139-2 MATFYZPRESS Fracional Ornein-Uhlenbeck Bridge J. Janák Charle Univeriy, Faculy of Mahemaic and Phyic, Prague, Czech Republic.
WDS'1 Proceeding of Conribued Paper, Par I, 21 26, 21. ISBN 978-8-7378-139-2 MATFYZPRESS Fracional Ornein-Uhlenbeck Bridge J. Janák Charle Univeriy, Faculy of Mahemaic and Phyic, Prague, Czech Republic.
Fractional Brownian Bridge Measures and Their Integration by Parts Formula
 Journal of Mahemaical Reearch wih Applicaion Jul., 218, Vol. 38, No. 4, pp. 418 426 DOI:1.377/j.in:295-2651.218.4.9 Hp://jmre.lu.eu.cn Fracional Brownian Brige Meaure an Their Inegraion by Par Formula
Journal of Mahemaical Reearch wih Applicaion Jul., 218, Vol. 38, No. 4, pp. 418 426 DOI:1.377/j.in:295-2651.218.4.9 Hp://jmre.lu.eu.cn Fracional Brownian Brige Meaure an Their Inegraion by Par Formula
ESTIMATES FOR THE DERIVATIVE OF DIFFUSION SEMIGROUPS
 Elec. Comm. in Probab. 3 (998) 65 74 ELECTRONIC COMMUNICATIONS in PROBABILITY ESTIMATES FOR THE DERIVATIVE OF DIFFUSION SEMIGROUPS L.A. RINCON Deparmen of Mahemaic Univeriy of Wale Swanea Singleon Par
Elec. Comm. in Probab. 3 (998) 65 74 ELECTRONIC COMMUNICATIONS in PROBABILITY ESTIMATES FOR THE DERIVATIVE OF DIFFUSION SEMIGROUPS L.A. RINCON Deparmen of Mahemaic Univeriy of Wale Swanea Singleon Par
Ricci Curvature and Bochner Formulas for Martingales
 Ricci Curvaure and Bochner Formula for Maringale Rober Halhofer and Aaron Naber Augu 15, 16 Abrac We generalize he claical Bochner formula for he hea flow on M o maringale on he pah pace, and develop a
Ricci Curvaure and Bochner Formula for Maringale Rober Halhofer and Aaron Naber Augu 15, 16 Abrac We generalize he claical Bochner formula for he hea flow on M o maringale on he pah pace, and develop a
Introduction to SLE Lecture Notes
 Inroducion o SLE Lecure Noe May 13, 16 - The goal of hi ecion i o find a ufficien condiion of λ for he hull K o be generaed by a imple cure. I urn ou if λ 1 < 4 hen K i generaed by a imple curve. We will
Inroducion o SLE Lecure Noe May 13, 16 - The goal of hi ecion i o find a ufficien condiion of λ for he hull K o be generaed by a imple cure. I urn ou if λ 1 < 4 hen K i generaed by a imple curve. We will
An introduction to the (local) martingale problem
 An inroducion o he (local) maringale problem Chri Janjigian Ocober 14, 214 Abrac Thee are my preenaion noe for a alk in he Univeriy of Wiconin - Madion graduae probabiliy eminar. Thee noe are primarily
An inroducion o he (local) maringale problem Chri Janjigian Ocober 14, 214 Abrac Thee are my preenaion noe for a alk in he Univeriy of Wiconin - Madion graduae probabiliy eminar. Thee noe are primarily
GRADIENT ESTIMATES FOR A SIMPLE PARABOLIC LICHNEROWICZ EQUATION. Osaka Journal of Mathematics. 51(1) P.245-P.256
 Tile Auhor(s) GRADIENT ESTIMATES FOR A SIMPLE PARABOLIC LICHNEROWICZ EQUATION Zhao, Liang Ciaion Osaka Journal of Mahemaics. 51(1) P.45-P.56 Issue Dae 014-01 Tex Version publisher URL hps://doi.org/10.18910/9195
Tile Auhor(s) GRADIENT ESTIMATES FOR A SIMPLE PARABOLIC LICHNEROWICZ EQUATION Zhao, Liang Ciaion Osaka Journal of Mahemaics. 51(1) P.45-P.56 Issue Dae 014-01 Tex Version publisher URL hps://doi.org/10.18910/9195
Generalized Orlicz Spaces and Wasserstein Distances for Convex-Concave Scale Functions
 Generalized Orlicz Space and Waerein Diance for Convex-Concave Scale Funcion Karl-Theodor Surm Abrac Given a ricly increaing, coninuou funcion ϑ : R + R +, baed on he co funcional ϑ (d(x, y dq(x, y, we
Generalized Orlicz Space and Waerein Diance for Convex-Concave Scale Funcion Karl-Theodor Surm Abrac Given a ricly increaing, coninuou funcion ϑ : R + R +, baed on he co funcional ϑ (d(x, y dq(x, y, we
Explicit form of global solution to stochastic logistic differential equation and related topics
 SAISICS, OPIMIZAION AND INFOMAION COMPUING Sa., Opim. Inf. Compu., Vol. 5, March 17, pp 58 64. Publihed online in Inernaional Academic Pre (www.iapre.org) Explici form of global oluion o ochaic logiic
SAISICS, OPIMIZAION AND INFOMAION COMPUING Sa., Opim. Inf. Compu., Vol. 5, March 17, pp 58 64. Publihed online in Inernaional Academic Pre (www.iapre.org) Explici form of global oluion o ochaic logiic
Research Article Existence and Uniqueness of Solutions for a Class of Nonlinear Stochastic Differential Equations
 Hindawi Publihing Corporaion Abrac and Applied Analyi Volume 03, Aricle ID 56809, 7 page hp://dx.doi.org/0.55/03/56809 Reearch Aricle Exience and Uniquene of Soluion for a Cla of Nonlinear Sochaic Differenial
Hindawi Publihing Corporaion Abrac and Applied Analyi Volume 03, Aricle ID 56809, 7 page hp://dx.doi.org/0.55/03/56809 Reearch Aricle Exience and Uniquene of Soluion for a Cla of Nonlinear Sochaic Differenial
FIXED POINTS AND STABILITY IN NEUTRAL DIFFERENTIAL EQUATIONS WITH VARIABLE DELAYS
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 136, Number 3, March 28, Page 99 918 S 2-9939(7)989-2 Aricle elecronically publihed on November 3, 27 FIXED POINTS AND STABILITY IN NEUTRAL DIFFERENTIAL
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 136, Number 3, March 28, Page 99 918 S 2-9939(7)989-2 Aricle elecronically publihed on November 3, 27 FIXED POINTS AND STABILITY IN NEUTRAL DIFFERENTIAL
Stability in Distribution for Backward Uncertain Differential Equation
 Sabiliy in Diribuion for Backward Uncerain Differenial Equaion Yuhong Sheng 1, Dan A. Ralecu 2 1. College of Mahemaical and Syem Science, Xinjiang Univeriy, Urumqi 8346, China heng-yh12@mail.inghua.edu.cn
Sabiliy in Diribuion for Backward Uncerain Differenial Equaion Yuhong Sheng 1, Dan A. Ralecu 2 1. College of Mahemaical and Syem Science, Xinjiang Univeriy, Urumqi 8346, China heng-yh12@mail.inghua.edu.cn
, the. L and the L. x x. max. i n. It is easy to show that these two norms satisfy the following relation: x x n x = (17.3) max
 ecure 8 7. Sabiliy Analyi For an n dimenional vecor R n, he and he vecor norm are defined a: = T = i n i (7.) I i eay o how ha hee wo norm aify he following relaion: n (7.) If a vecor i ime-dependen, hen
ecure 8 7. Sabiliy Analyi For an n dimenional vecor R n, he and he vecor norm are defined a: = T = i n i (7.) I i eay o how ha hee wo norm aify he following relaion: n (7.) If a vecor i ime-dependen, hen
On the Exponential Operator Functions on Time Scales
 dvance in Dynamical Syem pplicaion ISSN 973-5321, Volume 7, Number 1, pp. 57 8 (212) hp://campu.m.edu/ada On he Exponenial Operaor Funcion on Time Scale laa E. Hamza Cairo Univeriy Deparmen of Mahemaic
dvance in Dynamical Syem pplicaion ISSN 973-5321, Volume 7, Number 1, pp. 57 8 (212) hp://campu.m.edu/ada On he Exponenial Operaor Funcion on Time Scale laa E. Hamza Cairo Univeriy Deparmen of Mahemaic
Measure-valued Diffusions and Stochastic Equations with Poisson Process 1
 Publihed in: Oaka Journal of Mahemaic 41 (24), 3: 727 744 Meaure-valued Diffuion and Sochaic quaion wih Poion Proce 1 Zongfei FU and Zenghu LI 2 Running head: Meaure-valued Diffuion and Sochaic quaion
Publihed in: Oaka Journal of Mahemaic 41 (24), 3: 727 744 Meaure-valued Diffuion and Sochaic quaion wih Poion Proce 1 Zongfei FU and Zenghu LI 2 Running head: Meaure-valued Diffuion and Sochaic quaion
Multidimensional Markovian FBSDEs with superquadratic
 Mulidimenional Markovian FBSDE wih uperquadraic growh Michael Kupper a,1, Peng Luo b,, Ludovic angpi c,3 December 14, 17 ABSRAC We give local and global exience and uniquene reul for mulidimenional coupled
Mulidimenional Markovian FBSDE wih uperquadraic growh Michael Kupper a,1, Peng Luo b,, Ludovic angpi c,3 December 14, 17 ABSRAC We give local and global exience and uniquene reul for mulidimenional coupled
Existence of Stepanov-like Square-mean Pseudo Almost Automorphic Solutions to Nonautonomous Stochastic Functional Evolution Equations
 Exience of Sepanov-like Square-mean Peudo Almo Auomorphic Soluion o Nonauonomou Sochaic Funcional Evoluion Equaion Zuomao Yan Abrac We inroduce he concep of bi-quare-mean almo auomorphic funcion and Sepanov-like
Exience of Sepanov-like Square-mean Peudo Almo Auomorphic Soluion o Nonauonomou Sochaic Funcional Evoluion Equaion Zuomao Yan Abrac We inroduce he concep of bi-quare-mean almo auomorphic funcion and Sepanov-like
Approximate Controllability of Fractional Stochastic Perturbed Control Systems Driven by Mixed Fractional Brownian Motion
 American Journal of Applied Mahemaic and Saiic, 15, Vol. 3, o. 4, 168-176 Available online a hp://pub.ciepub.com/ajam/3/4/7 Science and Educaion Publihing DOI:1.1691/ajam-3-4-7 Approximae Conrollabiliy
American Journal of Applied Mahemaic and Saiic, 15, Vol. 3, o. 4, 168-176 Available online a hp://pub.ciepub.com/ajam/3/4/7 Science and Educaion Publihing DOI:1.1691/ajam-3-4-7 Approximae Conrollabiliy
arxiv: v1 [math.pr] 2 Jan 2015
![arxiv: v1 [math.pr] 2 Jan 2015 arxiv: v1 [math.pr] 2 Jan 2015](/thumbs/95/125077488.jpg) Mean-field backward ochaic differenial equaion on Markov chain arxiv:151.955v1 [mah.pr] 2 Jan 215 Wen Lu 1 Yong Ren 2 1. School of Mahemaic and Informaional Science, Yanai Univeriy, Yanai 2645, China 2.
Mean-field backward ochaic differenial equaion on Markov chain arxiv:151.955v1 [mah.pr] 2 Jan 215 Wen Lu 1 Yong Ren 2 1. School of Mahemaic and Informaional Science, Yanai Univeriy, Yanai 2645, China 2.
First variation formula in Wasserstein spaces over compact Alexandrov spaces
 Fir variaion formula in Waerein pace over compac Alexandrov pace Nicola Gigli and Shin-ichi Oha July 29, 2010 Abrac We exend reul proven by he econd auhor Amer. J. ah., 2009 for nonnegaively curved Alexandrov
Fir variaion formula in Waerein pace over compac Alexandrov pace Nicola Gigli and Shin-ichi Oha July 29, 2010 Abrac We exend reul proven by he econd auhor Amer. J. ah., 2009 for nonnegaively curved Alexandrov
Rough Paths and its Applications in Machine Learning
 Pah ignaure Machine learning applicaion Rough Pah and i Applicaion in Machine Learning July 20, 2017 Rough Pah and i Applicaion in Machine Learning Pah ignaure Machine learning applicaion Hiory and moivaion
Pah ignaure Machine learning applicaion Rough Pah and i Applicaion in Machine Learning July 20, 2017 Rough Pah and i Applicaion in Machine Learning Pah ignaure Machine learning applicaion Hiory and moivaion
Lower and Upper Approximation of Fuzzy Ideals in a Semiring
 nernaional Journal of Scienific & Engineering eearch, Volume 3, ue, January-0 SSN 9-558 Lower and Upper Approximaion of Fuzzy deal in a Semiring G Senhil Kumar, V Selvan Abrac n hi paper, we inroduce he
nernaional Journal of Scienific & Engineering eearch, Volume 3, ue, January-0 SSN 9-558 Lower and Upper Approximaion of Fuzzy deal in a Semiring G Senhil Kumar, V Selvan Abrac n hi paper, we inroduce he
Heat kernel and Harnack inequality on Riemannian manifolds
 Hea kernel and Harnack inequaliy on Riemannian manifolds Alexander Grigor yan UHK 11/02/2014 onens 1 Laplace operaor and hea kernel 1 2 Uniform Faber-Krahn inequaliy 3 3 Gaussian upper bounds 4 4 ean-value
Hea kernel and Harnack inequaliy on Riemannian manifolds Alexander Grigor yan UHK 11/02/2014 onens 1 Laplace operaor and hea kernel 1 2 Uniform Faber-Krahn inequaliy 3 3 Gaussian upper bounds 4 4 ean-value
Coupling Homogenization and Large Deviations. Principle in a Parabolic PDE
 Applied Mahemaical Science, Vol. 9, 215, no. 41, 219-23 HIKARI Ld, www.m-hikari.com hp://dx.doi.org/1.12988/am.215.5169 Coupling Homogenizaion and Large Deviaion Principle in a Parabolic PDE Alioune Coulibaly,
Applied Mahemaical Science, Vol. 9, 215, no. 41, 219-23 HIKARI Ld, www.m-hikari.com hp://dx.doi.org/1.12988/am.215.5169 Coupling Homogenizaion and Large Deviaion Principle in a Parabolic PDE Alioune Coulibaly,
FUZZY n-inner PRODUCT SPACE
 Bull. Korean Mah. Soc. 43 (2007), No. 3, pp. 447 459 FUZZY n-inner PRODUCT SPACE Srinivaan Vijayabalaji and Naean Thillaigovindan Reprined from he Bullein of he Korean Mahemaical Sociey Vol. 43, No. 3,
Bull. Korean Mah. Soc. 43 (2007), No. 3, pp. 447 459 FUZZY n-inner PRODUCT SPACE Srinivaan Vijayabalaji and Naean Thillaigovindan Reprined from he Bullein of he Korean Mahemaical Sociey Vol. 43, No. 3,
Backward Stochastic Differential Equations and Applications in Finance
 Backward Sochaic Differenial Equaion and Applicaion in Finance Ying Hu Augu 1, 213 1 Inroducion The aim of hi hor cae i o preen he baic heory of BSDE and o give ome applicaion in 2 differen domain: mahemaical
Backward Sochaic Differenial Equaion and Applicaion in Finance Ying Hu Augu 1, 213 1 Inroducion The aim of hi hor cae i o preen he baic heory of BSDE and o give ome applicaion in 2 differen domain: mahemaical
arxiv: v1 [math.pr] 23 Apr 2018
![arxiv: v1 [math.pr] 23 Apr 2018 arxiv: v1 [math.pr] 23 Apr 2018](/thumbs/90/102208097.jpg) arxiv:184.8469v1 [mah.pr] 23 Apr 218 The Neumann Boundary Problem for Ellipic Parial ifferenial Equaion wih Nonlinear ivergence Term Xue YANG Tianjin Univeriy e-mail: xyang213@ju.edu.cn Jing ZHANG Fudan
arxiv:184.8469v1 [mah.pr] 23 Apr 218 The Neumann Boundary Problem for Ellipic Parial ifferenial Equaion wih Nonlinear ivergence Term Xue YANG Tianjin Univeriy e-mail: xyang213@ju.edu.cn Jing ZHANG Fudan
Lecture 10: The Poincaré Inequality in Euclidean space
 Deparmens of Mahemaics Monana Sae Universiy Fall 215 Prof. Kevin Wildrick n inroducion o non-smooh analysis and geomery Lecure 1: The Poincaré Inequaliy in Euclidean space 1. Wha is he Poincaré inequaliy?
Deparmens of Mahemaics Monana Sae Universiy Fall 215 Prof. Kevin Wildrick n inroducion o non-smooh analysis and geomery Lecure 1: The Poincaré Inequaliy in Euclidean space 1. Wha is he Poincaré inequaliy?
On the Benney Lin and Kawahara Equations
 JOURNAL OF MATEMATICAL ANALYSIS AND APPLICATIONS 11, 13115 1997 ARTICLE NO AY975438 On he BenneyLin and Kawahara Equaion A Biagioni* Deparmen of Mahemaic, UNICAMP, 1381-97, Campina, Brazil and F Linare
JOURNAL OF MATEMATICAL ANALYSIS AND APPLICATIONS 11, 13115 1997 ARTICLE NO AY975438 On he BenneyLin and Kawahara Equaion A Biagioni* Deparmen of Mahemaic, UNICAMP, 1381-97, Campina, Brazil and F Linare
Systems of nonlinear ODEs with a time singularity in the right-hand side
 Syem of nonlinear ODE wih a ime ingulariy in he righ-hand ide Jana Burkoová a,, Irena Rachůnková a, Svaolav Saněk a, Ewa B. Weinmüller b, Sefan Wurm b a Deparmen of Mahemaical Analyi and Applicaion of
Syem of nonlinear ODE wih a ime ingulariy in he righ-hand ide Jana Burkoová a,, Irena Rachůnková a, Svaolav Saněk a, Ewa B. Weinmüller b, Sefan Wurm b a Deparmen of Mahemaical Analyi and Applicaion of
Randomized Perfect Bipartite Matching
 Inenive Algorihm Lecure 24 Randomized Perfec Biparie Maching Lecurer: Daniel A. Spielman April 9, 208 24. Inroducion We explain a randomized algorihm by Ahih Goel, Michael Kapralov and Sanjeev Khanna for
Inenive Algorihm Lecure 24 Randomized Perfec Biparie Maching Lecurer: Daniel A. Spielman April 9, 208 24. Inroducion We explain a randomized algorihm by Ahih Goel, Michael Kapralov and Sanjeev Khanna for
FLAT CYCLOTOMIC POLYNOMIALS OF ORDER FOUR AND HIGHER
 #A30 INTEGERS 10 (010), 357-363 FLAT CYCLOTOMIC POLYNOMIALS OF ORDER FOUR AND HIGHER Nahan Kaplan Deparmen of Mahemaic, Harvard Univeriy, Cambridge, MA nkaplan@mah.harvard.edu Received: 7/15/09, Revied:
#A30 INTEGERS 10 (010), 357-363 FLAT CYCLOTOMIC POLYNOMIALS OF ORDER FOUR AND HIGHER Nahan Kaplan Deparmen of Mahemaic, Harvard Univeriy, Cambridge, MA nkaplan@mah.harvard.edu Received: 7/15/09, Revied:
Heat semigroup and singular PDEs
 Hea emigroup and ingular PDE I. BAILLEUL 1 and F. BERNICOT wih an Appendix by F. Bernico & D. Frey Abrac. We provide in hi work a emigroup approach o he udy of ingular PDE, in he line of he paraconrolled
Hea emigroup and ingular PDE I. BAILLEUL 1 and F. BERNICOT wih an Appendix by F. Bernico & D. Frey Abrac. We provide in hi work a emigroup approach o he udy of ingular PDE, in he line of he paraconrolled
Differential Harnack Estimates for Parabolic Equations
 Differenial Harnack Esimaes for Parabolic Equaions Xiaodong Cao and Zhou Zhang Absrac Le M,g be a soluion o he Ricci flow on a closed Riemannian manifold In his paper, we prove differenial Harnack inequaliies
Differenial Harnack Esimaes for Parabolic Equaions Xiaodong Cao and Zhou Zhang Absrac Le M,g be a soluion o he Ricci flow on a closed Riemannian manifold In his paper, we prove differenial Harnack inequaliies
Let. x y. denote a bivariate time series with zero mean.
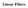 Linear Filer Le x y : T denoe a bivariae ime erie wih zero mean. Suppoe ha he ime erie {y : T} i conruced a follow: y a x The ime erie {y : T} i aid o be conruced from {x : T} by mean of a Linear Filer.
Linear Filer Le x y : T denoe a bivariae ime erie wih zero mean. Suppoe ha he ime erie {y : T} i conruced a follow: y a x The ime erie {y : T} i aid o be conruced from {x : T} by mean of a Linear Filer.
A Stochastic Representation for Fully Nonlinear PDEs and Its Application to Homogenization
 J. Mah. Sci. Univ. Tokyo 12 (2005), 467 492. A Sochaic Repreenaion for Fully Nonlinear PDE and I Applicaion o Homogenizaion By Naoyuki Ichihara Abrac. We eablih a ochaic repreenaion formula for oluion
J. Mah. Sci. Univ. Tokyo 12 (2005), 467 492. A Sochaic Repreenaion for Fully Nonlinear PDE and I Applicaion o Homogenizaion By Naoyuki Ichihara Abrac. We eablih a ochaic repreenaion formula for oluion
arxiv: v1 [math.pr] 23 Jan 2019
![arxiv: v1 [math.pr] 23 Jan 2019 arxiv: v1 [math.pr] 23 Jan 2019](/thumbs/88/115739889.jpg) Consrucion of Liouville Brownian moion via Dirichle form heory Jiyong Shin arxiv:90.07753v [mah.pr] 23 Jan 209 Absrac. The Liouville Brownian moion which was inroduced in [3] is a naural diffusion process
Consrucion of Liouville Brownian moion via Dirichle form heory Jiyong Shin arxiv:90.07753v [mah.pr] 23 Jan 209 Absrac. The Liouville Brownian moion which was inroduced in [3] is a naural diffusion process
MALLIAVIN CALCULUS FOR BACKWARD STOCHASTIC DIFFERENTIAL EQUATIONS AND APPLICATION TO NUMERICAL SOLUTIONS
 The Annal of Applied Probabiliy 211, Vol. 21, No. 6, 2379 2423 DOI: 1.1214/11-AAP762 Iniue of Mahemaical Saiic, 211 MALLIAVIN CALCULUS FOR BACKWARD STOCHASTIC DIFFERENTIAL EQUATIONS AND APPLICATION TO
The Annal of Applied Probabiliy 211, Vol. 21, No. 6, 2379 2423 DOI: 1.1214/11-AAP762 Iniue of Mahemaical Saiic, 211 MALLIAVIN CALCULUS FOR BACKWARD STOCHASTIC DIFFERENTIAL EQUATIONS AND APPLICATION TO
6.8 Laplace Transform: General Formulas
 48 HAP. 6 Laplace Tranform 6.8 Laplace Tranform: General Formula Formula Name, ommen Sec. F() l{ f ()} e f () d f () l {F()} Definiion of Tranform Invere Tranform 6. l{af () bg()} al{f ()} bl{g()} Lineariy
48 HAP. 6 Laplace Tranform 6.8 Laplace Tranform: General Formula Formula Name, ommen Sec. F() l{ f ()} e f () d f () l {F()} Definiion of Tranform Invere Tranform 6. l{af () bg()} al{f ()} bl{g()} Lineariy
Laplace Transform. Inverse Laplace Transform. e st f(t)dt. (2)
 Laplace Tranform Maoud Malek The Laplace ranform i an inegral ranform named in honor of mahemaician and aronomer Pierre-Simon Laplace, who ued he ranform in hi work on probabiliy heory. I i a powerful
Laplace Tranform Maoud Malek The Laplace ranform i an inegral ranform named in honor of mahemaician and aronomer Pierre-Simon Laplace, who ued he ranform in hi work on probabiliy heory. I i a powerful
EECE 301 Signals & Systems Prof. Mark Fowler
 EECE 31 Signal & Syem Prof. Mark Fowler Noe Se #27 C-T Syem: Laplace Tranform Power Tool for yem analyi Reading Aignmen: Secion 6.1 6.3 of Kamen and Heck 1/18 Coure Flow Diagram The arrow here how concepual
EECE 31 Signal & Syem Prof. Mark Fowler Noe Se #27 C-T Syem: Laplace Tranform Power Tool for yem analyi Reading Aignmen: Secion 6.1 6.3 of Kamen and Heck 1/18 Coure Flow Diagram The arrow here how concepual
Energy Equality and Uniqueness of Weak Solutions to MHD Equations in L (0,T; L n (Ω))
 Aca Mahemaica Sinica, Englih Serie May, 29, Vol. 25, No. 5, pp. 83 814 Publihed online: April 25, 29 DOI: 1.17/1114-9-7214-8 Hp://www.AcaMah.com Aca Mahemaica Sinica, Englih Serie The Ediorial Office of
Aca Mahemaica Sinica, Englih Serie May, 29, Vol. 25, No. 5, pp. 83 814 Publihed online: April 25, 29 DOI: 1.17/1114-9-7214-8 Hp://www.AcaMah.com Aca Mahemaica Sinica, Englih Serie The Ediorial Office of
ANSWERS TO ODD NUMBERED EXERCISES IN CHAPTER
 John Riley 6 December 200 NWER TO ODD NUMBERED EXERCIE IN CHPTER 7 ecion 7 Exercie 7-: m m uppoe ˆ, m=,, M (a For M = 2, i i eay o how ha I implie I From I, for any probabiliy vecor ( p, p 2, 2 2 ˆ ( p,
John Riley 6 December 200 NWER TO ODD NUMBERED EXERCIE IN CHPTER 7 ecion 7 Exercie 7-: m m uppoe ˆ, m=,, M (a For M = 2, i i eay o how ha I implie I From I, for any probabiliy vecor ( p, p 2, 2 2 ˆ ( p,
PATHWISE UNIQUENESS FOR STOCHASTIC DIFFERENTIAL EQUATIONS WITH SINGULAR DRIFT AND NONCONSTANT DIFFUSION. Katharina von der Lühe
 Dieraion PATHWISE UNIQUENESS FOR STOCHASTIC DIFFERENTIAL EQUATIONS WITH SINGULAR DRIFT AND NONCONSTANT DIFFUSION Kaharina on der Lühe Fakulä für Mahemaik Unieriä Bielefeld Augu 26 Conen Conen. Inroducion..
Dieraion PATHWISE UNIQUENESS FOR STOCHASTIC DIFFERENTIAL EQUATIONS WITH SINGULAR DRIFT AND NONCONSTANT DIFFUSION Kaharina on der Lühe Fakulä für Mahemaik Unieriä Bielefeld Augu 26 Conen Conen. Inroducion..
An Introduction to Backward Stochastic Differential Equations (BSDEs) PIMS Summer School 2016 in Mathematical Finance.
 1 An Inroducion o Backward Sochasic Differenial Equaions (BSDEs) PIMS Summer School 2016 in Mahemaical Finance June 25, 2016 Chrisoph Frei cfrei@ualbera.ca This inroducion is based on Touzi [14], Bouchard
1 An Inroducion o Backward Sochasic Differenial Equaions (BSDEs) PIMS Summer School 2016 in Mahemaical Finance June 25, 2016 Chrisoph Frei cfrei@ualbera.ca This inroducion is based on Touzi [14], Bouchard
LECTURE 1: GENERALIZED RAY KNIGHT THEOREM FOR FINITE MARKOV CHAINS
 LECTURE : GENERALIZED RAY KNIGHT THEOREM FOR FINITE MARKOV CHAINS We will work wih a coninuous ime reversible Markov chain X on a finie conneced sae space, wih generaor Lf(x = y q x,yf(y. (Recall ha q
LECTURE : GENERALIZED RAY KNIGHT THEOREM FOR FINITE MARKOV CHAINS We will work wih a coninuous ime reversible Markov chain X on a finie conneced sae space, wih generaor Lf(x = y q x,yf(y. (Recall ha q
Stochastic Optimal Control in Infinite Dimensions: Dynamic Programming and HJB Equations
 Sochaic Opimal Conrol in Infinie Dimenion: Dynamic Programming and HJB Equaion G. Fabbri 1 F. Gozzi 2 and A. Świe ch3 wih Chaper 6 by M. Fuhrman 4 and G. Teiore 5 1 Aix-Mareille Univeriy (Aix-Mareille
Sochaic Opimal Conrol in Infinie Dimenion: Dynamic Programming and HJB Equaion G. Fabbri 1 F. Gozzi 2 and A. Świe ch3 wih Chaper 6 by M. Fuhrman 4 and G. Teiore 5 1 Aix-Mareille Univeriy (Aix-Mareille
arxiv:math/ v2 [math.fa] 30 Jul 2006
![arxiv:math/ v2 [math.fa] 30 Jul 2006 arxiv:math/ v2 [math.fa] 30 Jul 2006](/thumbs/91/106526752.jpg) ON GÂTEAUX DIFFERENTIABILITY OF POINTWISE LIPSCHITZ MAPPINGS arxiv:mah/0511565v2 [mah.fa] 30 Jul 2006 JAKUB DUDA Abrac. We prove ha for every funcion f : X Y, where X i a eparable Banach pace and Y i a
ON GÂTEAUX DIFFERENTIABILITY OF POINTWISE LIPSCHITZ MAPPINGS arxiv:mah/0511565v2 [mah.fa] 30 Jul 2006 JAKUB DUDA Abrac. We prove ha for every funcion f : X Y, where X i a eparable Banach pace and Y i a
Reflected Solutions of BSDEs Driven by G-Brownian Motion
 Refleced Soluion of BSDE Driven by G-Brownian Moion Hanwu Li Shige Peng Abdoulaye Soumana Hima Sepember 1, 17 Abrac In hi paper, we udy he refleced oluion of one-dimenional backward ochaic differenial
Refleced Soluion of BSDE Driven by G-Brownian Moion Hanwu Li Shige Peng Abdoulaye Soumana Hima Sepember 1, 17 Abrac In hi paper, we udy he refleced oluion of one-dimenional backward ochaic differenial
FULLY COUPLED FBSDE WITH BROWNIAN MOTION AND POISSON PROCESS IN STOPPING TIME DURATION
 J. Au. Mah. Soc. 74 (23), 249 266 FULLY COUPLED FBSDE WITH BROWNIAN MOTION AND POISSON PROCESS IN STOPPING TIME DURATION HEN WU (Received 7 Ocober 2; revied 18 January 22) Communicaed by V. Sefanov Abrac
J. Au. Mah. Soc. 74 (23), 249 266 FULLY COUPLED FBSDE WITH BROWNIAN MOTION AND POISSON PROCESS IN STOPPING TIME DURATION HEN WU (Received 7 Ocober 2; revied 18 January 22) Communicaed by V. Sefanov Abrac
U T,0. t = X t t T X T. (1)
 Gauian bridge Dario Gabarra 1, ommi Soinen 2, and Eko Valkeila 3 1 Deparmen of Mahemaic and Saiic, PO Box 68, 14 Univeriy of Helinki,Finland dariogabarra@rnihelinkifi 2 Deparmen of Mahemaic and Saiic,
Gauian bridge Dario Gabarra 1, ommi Soinen 2, and Eko Valkeila 3 1 Deparmen of Mahemaic and Saiic, PO Box 68, 14 Univeriy of Helinki,Finland dariogabarra@rnihelinkifi 2 Deparmen of Mahemaic and Saiic,
NECESSARY AND SUFFICIENT CONDITIONS FOR LATENT SEPARABILITY
 NECESSARY AND SUFFICIENT CONDITIONS FOR LATENT SEPARABILITY Ian Crawford THE INSTITUTE FOR FISCAL STUDIES DEPARTMENT OF ECONOMICS, UCL cemmap working paper CWP02/04 Neceary and Sufficien Condiion for Laen
NECESSARY AND SUFFICIENT CONDITIONS FOR LATENT SEPARABILITY Ian Crawford THE INSTITUTE FOR FISCAL STUDIES DEPARTMENT OF ECONOMICS, UCL cemmap working paper CWP02/04 Neceary and Sufficien Condiion for Laen
arxiv:math/ v1 [math.nt] 3 Nov 2005
![arxiv:math/ v1 [math.nt] 3 Nov 2005 arxiv:math/ v1 [math.nt] 3 Nov 2005](/thumbs/71/66009857.jpg) arxiv:mah/0511092v1 [mah.nt] 3 Nov 2005 A NOTE ON S AND THE ZEROS OF THE RIEMANN ZETA-FUNCTION D. A. GOLDSTON AND S. M. GONEK Absrac. Le πs denoe he argumen of he Riemann zea-funcion a he poin 1 + i. Assuming
arxiv:mah/0511092v1 [mah.nt] 3 Nov 2005 A NOTE ON S AND THE ZEROS OF THE RIEMANN ZETA-FUNCTION D. A. GOLDSTON AND S. M. GONEK Absrac. Le πs denoe he argumen of he Riemann zea-funcion a he poin 1 + i. Assuming
Class Meeting # 10: Introduction to the Wave Equation
 MATH 8.5 COURSE NOTES - CLASS MEETING # 0 8.5 Inroducion o PDEs, Fall 0 Professor: Jared Speck Class Meeing # 0: Inroducion o he Wave Equaion. Wha is he wave equaion? The sandard wave equaion for a funcion
MATH 8.5 COURSE NOTES - CLASS MEETING # 0 8.5 Inroducion o PDEs, Fall 0 Professor: Jared Speck Class Meeing # 0: Inroducion o he Wave Equaion. Wha is he wave equaion? The sandard wave equaion for a funcion
arxiv: v1 [math.pr] 25 Jul 2017
![arxiv: v1 [math.pr] 25 Jul 2017 arxiv: v1 [math.pr] 25 Jul 2017](/thumbs/75/72669149.jpg) COUPLING AND A GENERALISED POLICY ITERATION ALGORITHM IN CONTINUOUS TIME SAUL D. JACKA, ALEKSANDAR MIJATOVIĆ, AND DEJAN ŠIRAJ arxiv:177.7834v1 [mah.pr] 25 Jul 217 Abrac. We analye a verion of he policy
COUPLING AND A GENERALISED POLICY ITERATION ALGORITHM IN CONTINUOUS TIME SAUL D. JACKA, ALEKSANDAR MIJATOVIĆ, AND DEJAN ŠIRAJ arxiv:177.7834v1 [mah.pr] 25 Jul 217 Abrac. We analye a verion of he policy
Network Flows: Introduction & Maximum Flow
 CSC 373 - lgorihm Deign, nalyi, and Complexiy Summer 2016 Lalla Mouaadid Nework Flow: Inroducion & Maximum Flow We now urn our aenion o anoher powerful algorihmic echnique: Local Search. In a local earch
CSC 373 - lgorihm Deign, nalyi, and Complexiy Summer 2016 Lalla Mouaadid Nework Flow: Inroducion & Maximum Flow We now urn our aenion o anoher powerful algorihmic echnique: Local Search. In a local earch
An Introduction to Malliavin calculus and its applications
 An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
An Inroducion o Malliavin calculus and is applicaions Lecure 5: Smoohness of he densiy and Hörmander s heorem David Nualar Deparmen of Mahemaics Kansas Universiy Universiy of Wyoming Summer School 214
Introduction to Congestion Games
 Algorihmic Game Theory, Summer 2017 Inroducion o Congeion Game Lecure 1 (5 page) Inrucor: Thoma Keelheim In hi lecure, we ge o know congeion game, which will be our running example for many concep in game
Algorihmic Game Theory, Summer 2017 Inroducion o Congeion Game Lecure 1 (5 page) Inrucor: Thoma Keelheim In hi lecure, we ge o know congeion game, which will be our running example for many concep in game
Parameter Estimation for Fractional Ornstein-Uhlenbeck Processes: Non-Ergodic Case
 Parameer Eimaion for Fracional Ornein-Uhlenbeck Procee: Non-Ergodic Cae R. Belfadli 1, K. E-Sebaiy and Y. Ouknine 3 1 Polydiciplinary Faculy of Taroudan, Univeriy Ibn Zohr, Taroudan, Morocco. Iniu de Mahémaique
Parameer Eimaion for Fracional Ornein-Uhlenbeck Procee: Non-Ergodic Cae R. Belfadli 1, K. E-Sebaiy and Y. Ouknine 3 1 Polydiciplinary Faculy of Taroudan, Univeriy Ibn Zohr, Taroudan, Morocco. Iniu de Mahémaique
L p -L q -Time decay estimate for solution of the Cauchy problem for hyperbolic partial differential equations of linear thermoelasticity
 ANNALES POLONICI MATHEMATICI LIV.2 99) L p -L q -Time decay esimae for soluion of he Cauchy problem for hyperbolic parial differenial equaions of linear hermoelasiciy by Jerzy Gawinecki Warszawa) Absrac.
ANNALES POLONICI MATHEMATICI LIV.2 99) L p -L q -Time decay esimae for soluion of he Cauchy problem for hyperbolic parial differenial equaions of linear hermoelasiciy by Jerzy Gawinecki Warszawa) Absrac.
CS4445/9544 Analysis of Algorithms II Solution for Assignment 1
 Conider he following flow nework CS444/944 Analyi of Algorihm II Soluion for Aignmen (0 mark) In he following nework a minimum cu ha capaciy 0 Eiher prove ha hi aemen i rue, or how ha i i fale Uing he
Conider he following flow nework CS444/944 Analyi of Algorihm II Soluion for Aignmen (0 mark) In he following nework a minimum cu ha capaciy 0 Eiher prove ha hi aemen i rue, or how ha i i fale Uing he
Heat semigroup and singular PDEs
 Hea emigroup and ingular PDE Imaël Bailleul, Frederic Bernico To cie hi verion: Imaël Bailleul, Frederic Bernico. Hea emigroup and ingular PDE: Wih an Appendix by F. Bernico and D. Frey. Journal of Funcional
Hea emigroup and ingular PDE Imaël Bailleul, Frederic Bernico To cie hi verion: Imaël Bailleul, Frederic Bernico. Hea emigroup and ingular PDE: Wih an Appendix by F. Bernico and D. Frey. Journal of Funcional
arxiv: v1 [math.ca] 15 Nov 2016
![arxiv: v1 [math.ca] 15 Nov 2016 arxiv: v1 [math.ca] 15 Nov 2016](/thumbs/90/102217337.jpg) arxiv:6.599v [mah.ca] 5 Nov 26 Counerexamples on Jumarie s hree basic fracional calculus formulae for non-differeniable coninuous funcions Cheng-shi Liu Deparmen of Mahemaics Norheas Peroleum Universiy
arxiv:6.599v [mah.ca] 5 Nov 26 Counerexamples on Jumarie s hree basic fracional calculus formulae for non-differeniable coninuous funcions Cheng-shi Liu Deparmen of Mahemaics Norheas Peroleum Universiy
Convergence of the gradient algorithm for linear regression models in the continuous and discrete time cases
 Convergence of he gradien algorihm for linear regreion model in he coninuou and dicree ime cae Lauren Praly To cie hi verion: Lauren Praly. Convergence of he gradien algorihm for linear regreion model
Convergence of he gradien algorihm for linear regreion model in he coninuou and dicree ime cae Lauren Praly To cie hi verion: Lauren Praly. Convergence of he gradien algorihm for linear regreion model
Existence of positive solution for a third-order three-point BVP with sign-changing Green s function
 Elecronic Journal of Qualiaive Theory of Differenial Equaions 13, No. 3, 1-11; hp://www.mah.u-szeged.hu/ejqde/ Exisence of posiive soluion for a hird-order hree-poin BVP wih sign-changing Green s funcion
Elecronic Journal of Qualiaive Theory of Differenial Equaions 13, No. 3, 1-11; hp://www.mah.u-szeged.hu/ejqde/ Exisence of posiive soluion for a hird-order hree-poin BVP wih sign-changing Green s funcion
CHAPTER 7: SECOND-ORDER CIRCUITS
 EEE5: CI RCUI T THEORY CHAPTER 7: SECOND-ORDER CIRCUITS 7. Inroducion Thi chaper conider circui wih wo orage elemen. Known a econd-order circui becaue heir repone are decribed by differenial equaion ha
EEE5: CI RCUI T THEORY CHAPTER 7: SECOND-ORDER CIRCUITS 7. Inroducion Thi chaper conider circui wih wo orage elemen. Known a econd-order circui becaue heir repone are decribed by differenial equaion ha
The Asymptotic Behavior of Nonoscillatory Solutions of Some Nonlinear Dynamic Equations on Time Scales
 Advances in Dynamical Sysems and Applicaions. ISSN 0973-5321 Volume 1 Number 1 (2006, pp. 103 112 c Research India Publicaions hp://www.ripublicaion.com/adsa.hm The Asympoic Behavior of Nonoscillaory Soluions
Advances in Dynamical Sysems and Applicaions. ISSN 0973-5321 Volume 1 Number 1 (2006, pp. 103 112 c Research India Publicaions hp://www.ripublicaion.com/adsa.hm The Asympoic Behavior of Nonoscillaory Soluions
BSDE's, Clark-Ocone formula, and Feynman-Kac formula for Lévy processes Nualart, D.; Schoutens, W.
 BSD', Clark-Ocone formula, and Feynman-Kac formula for Lévy procee Nualar, D.; Schouen, W. Publihed: 1/1/ Documen Verion Publiher PDF, alo known a Verion of ecord (include final page, iue and volume number)
BSD', Clark-Ocone formula, and Feynman-Kac formula for Lévy procee Nualar, D.; Schouen, W. Publihed: 1/1/ Documen Verion Publiher PDF, alo known a Verion of ecord (include final page, iue and volume number)
The Residual Graph. 11 Augmenting Path Algorithms. Augmenting Path Algorithm. Augmenting Path Algorithm
 Augmening Pah Algorihm Greedy-algorihm: ar wih f (e) = everywhere find an - pah wih f (e) < c(e) on every edge augmen flow along he pah repea a long a poible The Reidual Graph From he graph G = (V, E,
Augmening Pah Algorihm Greedy-algorihm: ar wih f (e) = everywhere find an - pah wih f (e) < c(e) on every edge augmen flow along he pah repea a long a poible The Reidual Graph From he graph G = (V, E,
ON FRACTIONAL ORNSTEIN-UHLENBECK PROCESSES
 Communicaion on Sochaic Analyi Vol. 5, No. 1 211 121-133 Serial Publicaion www.erialpublicaion.com ON FRACTIONAL ORNSTEIN-UHLENBECK PROCESSES TERHI KAARAKKA AND PAAVO SALMINEN Abrac. In hi paper we udy
Communicaion on Sochaic Analyi Vol. 5, No. 1 211 121-133 Serial Publicaion www.erialpublicaion.com ON FRACTIONAL ORNSTEIN-UHLENBECK PROCESSES TERHI KAARAKKA AND PAAVO SALMINEN Abrac. In hi paper we udy
arxiv: v5 [math.pr] 6 Oct 2015
![arxiv: v5 [math.pr] 6 Oct 2015 arxiv: v5 [math.pr] 6 Oct 2015](/thumbs/93/112727003.jpg) ON THE EXISTENCE AND UNIQUENESS OF SOLUTIONS TO STOCHASTIC DIFFERENTIAL EQUATIONS DRIVEN BY G-BROWNIAN MOTION WITH INTEGRAL-LIPSCHITZ COEFFICIENTS XUEPENG BAI AND YIQING LIN arxiv:12.146v5 mah.pr] 6 Oc
ON THE EXISTENCE AND UNIQUENESS OF SOLUTIONS TO STOCHASTIC DIFFERENTIAL EQUATIONS DRIVEN BY G-BROWNIAN MOTION WITH INTEGRAL-LIPSCHITZ COEFFICIENTS XUEPENG BAI AND YIQING LIN arxiv:12.146v5 mah.pr] 6 Oc
Backward Stochastic Partial Differential Equations with Jumps and Application to Optimal Control of Random Jump Fields
 Backward Sochaic Parial Differenial Equaion wih Jump and Applicaion o Opimal Conrol of Random Jump Field Bern Økendal 1,2, Frank Proke 1, Tuheng Zhang 1,3 June 7, 25 Abrac We prove an exience and uniquene
Backward Sochaic Parial Differenial Equaion wih Jump and Applicaion o Opimal Conrol of Random Jump Field Bern Økendal 1,2, Frank Proke 1, Tuheng Zhang 1,3 June 7, 25 Abrac We prove an exience and uniquene
Analysis of Boundedness for Unknown Functions by a Delay Integral Inequality on Time Scales
 Inernaional Conference on Image, Viion and Comuing (ICIVC ) IPCSIT vol. 5 () () IACSIT Pre, Singaore DOI:.7763/IPCSIT..V5.45 Anali of Boundedne for Unknown Funcion b a Dela Inegral Ineuali on Time Scale
Inernaional Conference on Image, Viion and Comuing (ICIVC ) IPCSIT vol. 5 () () IACSIT Pre, Singaore DOI:.7763/IPCSIT..V5.45 Anali of Boundedne for Unknown Funcion b a Dela Inegral Ineuali on Time Scale
INTEGRATION BY PARTS FORMULA AND LOGARITHMIC SOBOLEV INEQUALITY ON THE PATH SPACE OVER LOOP GROUPS. By Shizan Fang Université de Bourgogne
 The Annals of Probabiliy 1999, Vol. 27, No. 2, 664 683 INTEGRATION BY PARTS FORMULA AND LOGARITHMIC SOBOLEV INEQUALITY ON THE PATH SPACE OVER LOOP GROUPS By Shizan Fang Universié de Bourgogne The geomeric
The Annals of Probabiliy 1999, Vol. 27, No. 2, 664 683 INTEGRATION BY PARTS FORMULA AND LOGARITHMIC SOBOLEV INEQUALITY ON THE PATH SPACE OVER LOOP GROUPS By Shizan Fang Universié de Bourgogne The geomeric
The Residual Graph. 12 Augmenting Path Algorithms. Augmenting Path Algorithm. Augmenting Path Algorithm
 Augmening Pah Algorihm Greedy-algorihm: ar wih f (e) = everywhere find an - pah wih f (e) < c(e) on every edge augmen flow along he pah repea a long a poible The Reidual Graph From he graph G = (V, E,
Augmening Pah Algorihm Greedy-algorihm: ar wih f (e) = everywhere find an - pah wih f (e) < c(e) on every edge augmen flow along he pah repea a long a poible The Reidual Graph From he graph G = (V, E,
Network Flow. Data Structures and Algorithms Andrei Bulatov
 Nework Flow Daa Srucure and Algorihm Andrei Bulao Algorihm Nework Flow 24-2 Flow Nework Think of a graph a yem of pipe We ue hi yem o pump waer from he ource o ink Eery pipe/edge ha limied capaciy Flow
Nework Flow Daa Srucure and Algorihm Andrei Bulao Algorihm Nework Flow 24-2 Flow Nework Think of a graph a yem of pipe We ue hi yem o pump waer from he ource o ink Eery pipe/edge ha limied capaciy Flow
Approximation for Option Prices under Uncertain Volatility
 Approximaion for Opion Price under Uncerain Volailiy Jean-Pierre Fouque Bin Ren February, 3 Abrac In hi paper, we udy he aympoic behavior of he wor cae cenario opion price a he volailiy inerval in an uncerain
Approximaion for Opion Price under Uncerain Volailiy Jean-Pierre Fouque Bin Ren February, 3 Abrac In hi paper, we udy he aympoic behavior of he wor cae cenario opion price a he volailiy inerval in an uncerain
Research Article On Double Summability of Double Conjugate Fourier Series
 Inernaional Journal of Mahemaic and Mahemaical Science Volume 22, Aricle ID 4592, 5 page doi:.55/22/4592 Reearch Aricle On Double Summabiliy of Double Conjugae Fourier Serie H. K. Nigam and Kuum Sharma
Inernaional Journal of Mahemaic and Mahemaical Science Volume 22, Aricle ID 4592, 5 page doi:.55/22/4592 Reearch Aricle On Double Summabiliy of Double Conjugae Fourier Serie H. K. Nigam and Kuum Sharma
as representing the flow of information over time, with
 [Alraheed 4(4): April 15] ISSN: 77-9655 Scienific Journal Impac Facor: 3.449 (ISRA) Impac Facor:.114 IJSR INRNAIONAL JOURNAL OF NGINRING SCINCS & RSARCH CHNOLOGY H FINANCIAL APPLICAIONS OF RANDOM CONROL
[Alraheed 4(4): April 15] ISSN: 77-9655 Scienific Journal Impac Facor: 3.449 (ISRA) Impac Facor:.114 IJSR INRNAIONAL JOURNAL OF NGINRING SCINCS & RSARCH CHNOLOGY H FINANCIAL APPLICAIONS OF RANDOM CONROL
DIMENSIONAL REDUCTION IN NONLINEAR FILTERING: A HOMOGENIZATION APPROACH
 DIMNSIONAL RDUCION IN NONLINAR FILRING: A HOMOGNIZAION APPROACH PR IMKLLR 1, N. SRI NAMACHCHIVAYA 2, NICOLAS PRKOWSKI 1, AND HOONG C. YONG 2 Abrac. We propoe a homogenized filer for mulicale ignal, which
DIMNSIONAL RDUCION IN NONLINAR FILRING: A HOMOGNIZAION APPROACH PR IMKLLR 1, N. SRI NAMACHCHIVAYA 2, NICOLAS PRKOWSKI 1, AND HOONG C. YONG 2 Abrac. We propoe a homogenized filer for mulicale ignal, which
arxiv: v1 [math.pr] 19 Feb 2011
![arxiv: v1 [math.pr] 19 Feb 2011 arxiv: v1 [math.pr] 19 Feb 2011](/thumbs/92/110849938.jpg) A NOTE ON FELLER SEMIGROUPS AND RESOLVENTS VADIM KOSTRYKIN, JÜRGEN POTTHOFF, AND ROBERT SCHRADER ABSTRACT. Various equivalen condiions for a semigroup or a resolven generaed by a Markov process o be of
A NOTE ON FELLER SEMIGROUPS AND RESOLVENTS VADIM KOSTRYKIN, JÜRGEN POTTHOFF, AND ROBERT SCHRADER ABSTRACT. Various equivalen condiions for a semigroup or a resolven generaed by a Markov process o be of
On Delayed Logistic Equation Driven by Fractional Brownian Motion
 On Delayed Logiic Equaion Driven by Fracional Brownian Moion Nguyen Tien Dung Deparmen of Mahemaic, FPT Univeriy No 8 Ton Tha Thuye, Cau Giay, Hanoi, 84 Vienam Email: dungn@fp.edu.vn ABSTRACT In hi paper
On Delayed Logiic Equaion Driven by Fracional Brownian Moion Nguyen Tien Dung Deparmen of Mahemaic, FPT Univeriy No 8 Ton Tha Thuye, Cau Giay, Hanoi, 84 Vienam Email: dungn@fp.edu.vn ABSTRACT In hi paper
CHAPTER 7. Definition and Properties. of Laplace Transforms
 SERIES OF CLSS NOTES FOR 5-6 TO INTRODUCE LINER ND NONLINER PROBLEMS TO ENGINEERS, SCIENTISTS, ND PPLIED MTHEMTICINS DE CLSS NOTES COLLECTION OF HNDOUTS ON SCLR LINER ORDINRY DIFFERENTIL EQUTIONS (ODE")
SERIES OF CLSS NOTES FOR 5-6 TO INTRODUCE LINER ND NONLINER PROBLEMS TO ENGINEERS, SCIENTISTS, ND PPLIED MTHEMTICINS DE CLSS NOTES COLLECTION OF HNDOUTS ON SCLR LINER ORDINRY DIFFERENTIL EQUTIONS (ODE")
Semi-discrete semi-linear parabolic SPDEs
 Semi-dicree emi-linear parabolic SPDE Nico Georgiou Univeriy of Suex Davar Khohnevian Univeriy of Uah Mahew Joeph Univeriy of Sheffield Shang-Yuan Shiu Naional Cenral Univeriy La Updae: November 2, 213
Semi-dicree emi-linear parabolic SPDE Nico Georgiou Univeriy of Suex Davar Khohnevian Univeriy of Uah Mahew Joeph Univeriy of Sheffield Shang-Yuan Shiu Naional Cenral Univeriy La Updae: November 2, 213
arxiv: v1 [math.gm] 5 Jan 2019
![arxiv: v1 [math.gm] 5 Jan 2019 arxiv: v1 [math.gm] 5 Jan 2019](/thumbs/93/114385572.jpg) A FUNCTION OBSTRUCTION TO THE EXISTENCE OF COMPLEX STRUCTURES arxiv:1901.05844v1 [mah.gm] 5 Jan 2019 JUN LING Abrac. We conruc a funcion for almo-complex Riemannian manifold. Non-vanihing of he funcion
A FUNCTION OBSTRUCTION TO THE EXISTENCE OF COMPLEX STRUCTURES arxiv:1901.05844v1 [mah.gm] 5 Jan 2019 JUN LING Abrac. We conruc a funcion for almo-complex Riemannian manifold. Non-vanihing of he funcion
The multisubset sum problem for finite abelian groups
 Alo available a hp://amc-journal.eu ISSN 1855-3966 (prined edn.), ISSN 1855-3974 (elecronic edn.) ARS MATHEMATICA CONTEMPORANEA 8 (2015) 417 423 The muliube um problem for finie abelian group Amela Muraović-Ribić
Alo available a hp://amc-journal.eu ISSN 1855-3966 (prined edn.), ISSN 1855-3974 (elecronic edn.) ARS MATHEMATICA CONTEMPORANEA 8 (2015) 417 423 The muliube um problem for finie abelian group Amela Muraović-Ribić
A stability approach for solving multidimensional quadratic BSDES
 A abiliy approach for olving mulidimenional quadraic BSDES Jonahan Harer, Adrien Richou To cie hi verion: Jonahan Harer, Adrien Richou A abiliy approach for olving mulidimenional quadraic BSDES 17 HAL
A abiliy approach for olving mulidimenional quadraic BSDES Jonahan Harer, Adrien Richou To cie hi verion: Jonahan Harer, Adrien Richou A abiliy approach for olving mulidimenional quadraic BSDES 17 HAL
On certain subclasses of close-to-convex and quasi-convex functions with respect to k-symmetric points
 J. Mah. Anal. Appl. 322 26) 97 6 www.elevier.com/locae/jmaa On cerain ubclae o cloe-o-convex and quai-convex uncion wih repec o -ymmeric poin Zhi-Gang Wang, Chun-Yi Gao, Shao-Mou Yuan College o Mahemaic
J. Mah. Anal. Appl. 322 26) 97 6 www.elevier.com/locae/jmaa On cerain ubclae o cloe-o-convex and quai-convex uncion wih repec o -ymmeric poin Zhi-Gang Wang, Chun-Yi Gao, Shao-Mou Yuan College o Mahemaic
REPRESENTATION THEOREMS FOR BACKWARD STOCHASTIC DIFFERENTIAL EQUATIONS. BY JIN MA 1 AND JIANFENG ZHANG Purdue University and University of Minnesota
 The Annal of Applied Probabiliy 22, Vol. 12, No. 4, 139 1418 REPRESENTATION THEOREMS FOR BACKWARD STOCHASTIC DIFFERENTIAL EQUATIONS BY JIN MA 1 AND JIANFENG ZHANG Purdue Univeriy and Univeriy of Minneoa
The Annal of Applied Probabiliy 22, Vol. 12, No. 4, 139 1418 REPRESENTATION THEOREMS FOR BACKWARD STOCHASTIC DIFFERENTIAL EQUATIONS BY JIN MA 1 AND JIANFENG ZHANG Purdue Univeriy and Univeriy of Minneoa
Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 32 (2016), ISSN
 Aca Mahemaica Academiae Paedagogicae Nyíregyháziensis 3 6, 79 7 www.emis.de/journals ISSN 76-9 INTEGRAL INEQUALITIES OF HERMITE HADAMARD TYPE FOR FUNCTIONS WHOSE DERIVATIVES ARE STRONGLY α-preinvex YAN
Aca Mahemaica Academiae Paedagogicae Nyíregyháziensis 3 6, 79 7 www.emis.de/journals ISSN 76-9 INTEGRAL INEQUALITIES OF HERMITE HADAMARD TYPE FOR FUNCTIONS WHOSE DERIVATIVES ARE STRONGLY α-preinvex YAN
On Two Integrability Methods of Improper Integrals
 Inernaional Journal of Mahemaics and Compuer Science, 13(218), no. 1, 45 5 M CS On Two Inegrabiliy Mehods of Improper Inegrals H. N. ÖZGEN Mahemaics Deparmen Faculy of Educaion Mersin Universiy, TR-33169
Inernaional Journal of Mahemaics and Compuer Science, 13(218), no. 1, 45 5 M CS On Two Inegrabiliy Mehods of Improper Inegrals H. N. ÖZGEN Mahemaics Deparmen Faculy of Educaion Mersin Universiy, TR-33169
Fractional Method of Characteristics for Fractional Partial Differential Equations
 Fracional Mehod of Characerisics for Fracional Parial Differenial Equaions Guo-cheng Wu* Modern Teile Insiue, Donghua Universiy, 188 Yan-an ilu Road, Shanghai 51, PR China Absrac The mehod of characerisics
Fracional Mehod of Characerisics for Fracional Parial Differenial Equaions Guo-cheng Wu* Modern Teile Insiue, Donghua Universiy, 188 Yan-an ilu Road, Shanghai 51, PR China Absrac The mehod of characerisics
Existence and Global Attractivity of Positive Periodic Solutions in Shifts δ ± for a Nonlinear Dynamic Equation with Feedback Control on Time Scales
 Exience and Global Araciviy of Poiive Periodic Soluion in Shif δ ± for a Nonlinear Dynamic Equaion wih Feedback Conrol on Time Scale MENG HU Anyang Normal Univeriy School of mahemaic and aiic Xian ge Avenue
Exience and Global Araciviy of Poiive Periodic Soluion in Shif δ ± for a Nonlinear Dynamic Equaion wih Feedback Conrol on Time Scale MENG HU Anyang Normal Univeriy School of mahemaic and aiic Xian ge Avenue
On a Fractional Stochastic Landau-Ginzburg Equation
 Applied Mahemaical Sciences, Vol. 4, 1, no. 7, 317-35 On a Fracional Sochasic Landau-Ginzburg Equaion Nguyen Tien Dung Deparmen of Mahemaics, FPT Universiy 15B Pham Hung Sree, Hanoi, Vienam dungn@fp.edu.vn
Applied Mahemaical Sciences, Vol. 4, 1, no. 7, 317-35 On a Fracional Sochasic Landau-Ginzburg Equaion Nguyen Tien Dung Deparmen of Mahemaics, FPT Universiy 15B Pham Hung Sree, Hanoi, Vienam dungn@fp.edu.vn
1 Motivation and Basic Definitions
 CSCE : Deign and Analyi of Algorihm Noe on Max Flow Fall 20 (Baed on he preenaion in Chaper 26 of Inroducion o Algorihm, 3rd Ed. by Cormen, Leieron, Rive and Sein.) Moivaion and Baic Definiion Conider
CSCE : Deign and Analyi of Algorihm Noe on Max Flow Fall 20 (Baed on he preenaion in Chaper 26 of Inroducion o Algorihm, 3rd Ed. by Cormen, Leieron, Rive and Sein.) Moivaion and Baic Definiion Conider
Fréchet derivatives and Gâteaux derivatives
 Fréche derivaives and Gâeaux derivaives Jordan Bell jordan.bell@gmail.com Deparmen of Mahemaics, Universiy of Torono April 3, 2014 1 Inroducion In his noe all vecor spaces are real. If X and Y are normed
Fréche derivaives and Gâeaux derivaives Jordan Bell jordan.bell@gmail.com Deparmen of Mahemaics, Universiy of Torono April 3, 2014 1 Inroducion In his noe all vecor spaces are real. If X and Y are normed
Sobolev-type Inequality for Spaces L p(x) (R N )
 In. J. Conemp. Mah. Sciences, Vol. 2, 27, no. 9, 423-429 Sobolev-ype Inequaliy for Spaces L p(x ( R. Mashiyev and B. Çekiç Universiy of Dicle, Faculy of Sciences and Ars Deparmen of Mahemaics, 228-Diyarbakir,
In. J. Conemp. Mah. Sciences, Vol. 2, 27, no. 9, 423-429 Sobolev-ype Inequaliy for Spaces L p(x ( R. Mashiyev and B. Çekiç Universiy of Dicle, Faculy of Sciences and Ars Deparmen of Mahemaics, 228-Diyarbakir,
Existence of multiple positive periodic solutions for functional differential equations
 J. Mah. Anal. Appl. 325 (27) 1378 1389 www.elsevier.com/locae/jmaa Exisence of muliple posiive periodic soluions for funcional differenial equaions Zhijun Zeng a,b,,libi a, Meng Fan a a School of Mahemaics
J. Mah. Anal. Appl. 325 (27) 1378 1389 www.elsevier.com/locae/jmaa Exisence of muliple posiive periodic soluions for funcional differenial equaions Zhijun Zeng a,b,,libi a, Meng Fan a a School of Mahemaics
Time Varying Multiserver Queues. W. A. Massey. Murray Hill, NJ Abstract
 Waiing Time Aympoic for Time Varying Mulierver ueue wih Abonmen Rerial A. Melbaum Technion Iniue Haifa, 3 ISRAEL avim@x.echnion.ac.il M. I. Reiman Bell Lab, Lucen Technologie Murray Hill, NJ 7974 U.S.A.
Waiing Time Aympoic for Time Varying Mulierver ueue wih Abonmen Rerial A. Melbaum Technion Iniue Haifa, 3 ISRAEL avim@x.echnion.ac.il M. I. Reiman Bell Lab, Lucen Technologie Murray Hill, NJ 7974 U.S.A.
