The area-angular momentum inequality for black holes in cosmological spacetimes
|
|
|
- Victoria Margery Cooper
- 5 years ago
- Views:
Transcription
1 Hom Srch Collctions Journls Aout Contct us My IOPscinc Th r-ngulr momntum inqulity for lck hols in cosmologicl spctims This contnt hs n downlodd from IOPscinc. Pls scroll down to s th full txt. 015 Clss. Quntum Grv ( Viw th tl of contnts for this issu, or go to th journl hompg for mor Downlod dtils: IP Addrss: This contnt ws downlodd on 05/08/015 t 07:05 Pls not tht trms nd conditions pply.
2 Clssicl nd Quntum Grvity Clss. Quntum Grv. 3 (015) (3pp) doi: / /3/14/ Th r-ngulr momntum inqulity for lck hols in cosmologicl spctims Mrí Eugni Gch Clémnt 1, Mrtín Riris nd Wltr Simon 3 1 Grupo d Rltividd y Grvitción Fcultd d Mthmátic, Astronomí y Físic, FMAF Univrsidd Ncionl d Córdo, Ciudd Univrsitri, CP:X5000HUA Córdo, Argntin Mx-Plnck-Institut für Grvittionsphysik Am Mühlnrg 1, D Potsdm- Golm, Grmny 3 Grvittionsphysik Fkultät für Physik, Univrsität Win Boltzmnngss 5, A-1090 Win, Austri E-mil: wltr.simon@univi.c.t, gch@fmf.unc.du.r nd mrtin@i.mpg.d Rcivd Frury 015 Accptd for puliction 4 April 015 Pulishd 9 Jun 015 Astrct For stl, mrginlly outr trppd surfc (MOTS) in n xilly symmtric spctim with cosmologicl constnt Λ > 0 nd with mttr stisfying th dominnt nrgy condition, w prov tht th r A nd th ngulr momntum J stisfy th inqulity 8 π J A (1 ΛA 4 π)(1 ΛA 1 π), which is sturtd prcisly for th xtrm Krr d Sittr fmily of mtrics. This rsult ntils univrsl uppr ound J Jmx 0.17 Λ for such MOTS, which is sturtd for on prticulr xtrm configurtion. Our rsult shrpns th inqulity 8π J A (Din nd Riris 011 Phys. Rv. Ltt , Jrmillo, Riris nd Din 011 Phys. Rv. Ltt. D ), nd w follow th ovrll strtgy of its proof in th sns tht w first stimt th r from low in trms of th nrgy corrsponding to mss functionl, which is siclly suitly rgulrizd hrmonic mp. Howvr, in th cosmologicl cs this mss functionl cquirs n dditionl potntil trm which itslf dpnds on th r. To stimt th corrsponding nrgy in trms of th ngulr momntum nd th cosmologicl constnt w us sutl scling rgumnt, gnrlizd Crtr-idntity, nd vrious tchniqus from vritionl clculus, including th mountin pss thorm. Kywords: r inqulity, pprnt horizon, cosmologicl constnt Contnt from this work my usd undr th trms of th Crtiv Commons Attriution 3.0 licnc. Any furthr distriution of this work must mintin ttriution to th uthor(s) nd th titl of th work, journl cittion nd DOI /15/ $ IOP Pulishing Ltd Printd in th UK 1
3 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l 1. Introduction Som rmrkl r inqulitis for stl mrginlly outr trppd surfcs (MOTS) hv n provn rcntly [6 10, 14 16, 18 0]. In prticulr, for xilly symmtric configurtions with r A nd ngulr momntum J, thr is th ound [7, 14] J A 8 π, (1.1) which is sturtd for xtrm Krr lck hols. Although cosmologicl constnt Λ dos not xplicitly ntr into (1.1), this inqulity holds in th prsnc of non-ngtiv Λ. On th othr hnd, whn Λ > 0, stl MOTS oy th lowr ound 1 A 4 πλ, (1.) sturtd for th xtrm Schwrzschild d Sittr horizon [1]. This rdily implis th univrsl uppr ound J ( Λ) 1 (1.3) which, howvr, cn nvr sturtd vn in thory (lving prcticl considrtions sid 1 in viw of th fct tht Λ is of ordr Th sitution rs som nlogy to stl MOTS in (not ncssrily xilly symmtric) spctims with lctromgntic filds nd lctric nd mgntic chrgs Q E nd Q M. In this cs th inqulitis A 4πQ [9] with Q = QE + QM (sturtd for xtrm Rissnr Nordström horizons) nd 1 A 4πΛ imply th (unsturtd) ound 1 Q Λ. Thr is howvr th strongr ound [16] ΛA 4πA + 16π Q 0 (1.4) which is sturtd for xtrm Rissnr Nordström d Sittr configurtions nd, morovr, improvs th univrsl chrg ound to Q (4 Λ) 1. Rturning to th prsnt xilly symmtric cs, th min ojctiv of this rticl is to incorport xplicitly th cosmologicl constnt into inqulity (1.1) nd dtrmin how it controls th llowd vlus of th ngulr momntum. W prov th following thorm. Thorm 1.1. Lt n xilly symmtric, stl MOTS togthr with n xilly symmtric 4-nighorhood of clld (, gij). On (, gij) w rquir Einstin s qutions to hold, with Λ > 0 nd with mttr stisfying th dominnt nrgy condition (DEC). Thn th ngulr momntum J nd th r A of stisfy J J A ΛA ΛA 1 1, (1.5) 8π 4π 1π 3 J mx = 4. (1.6) Λ 13 Λ Hr (1.5) is sturtd prcisly for th 1-prmtr fmily of xtrm Krr d Sittr (KdS) horizons whil th univrsl ound (1.6) is sturtd for on prticulr such configurtion. Th proof of this thorm will sktchd in sction 4, whil dtils r postpond to sction 5. W discuss now its scop nd th min diffrncs, similritis nd difficultis comprd to th ons citd ov.
4 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l As Λ > 0, th min inqulity (1.5) is strongr thn oth (1.1) nd (1.); in prticulr it forids th lck hol to rott s fst s its non-cosmologicl countrprt. Concrning th sturtion of (1.5), w osrv th sm pttrn s in th prvious inqulitis: th xtrm solutions st ound to th mximum vlus of chrgs nd/or ngulr momntum. Th non-vnishing cosmologicl constnt dos not chng this proprty of xtrm lck hols. Inqulity (1.6) is otind in strightforwrd mnnr from (1.5) nd mks us of n intrsting ftur of th xtrm KdS fmily. Givn Λ > 0 thr xists mximum vlu for th ngulr momntum which is ttind t crtin vlu of th r A. This proprty is not shrd y xtrm Krr horizons ( Λ = 0), whr th vlu of A dtrmins th ngulr momntum s 8 π J = A. Not lso tht, s opposd to (1.3), (1.6) is shrp nd improvs th numricl fctor from 0.5 to 0.17 pproximtly. As sttd in thorm 1.1, th inqulity (1.5) holds twn th r nd ngulr momntum of stl MOTS s. Nvrthlss, du to th nlogy twn stl MOTS nd stl miniml surfcs in mximl slics, on cn prov n nlogous rsult for this typ of surfcs s wll (s [6] for discussion of th similritis of ths surfcs within th contxt of gomtric inqulitis). Not tht mttr stisfying th DEC is llowd. Th nrgy condition is rquird in ordr to dispos of th mttr trms nd to rriv t th cln inqulity (1.5) whr mttr dos not ppr xplicitly. Howvr, for lctromgntic filds w xpct to otin n inqulity twn r, ngulr momntum, lctromgntic chrgs Q E, Q M nd cosmologicl constnt which should rduc to (1.5) for Q = 0 nd to (1.4) whn J = 0. W discuss corrsponding conjctur in sction 6. W now commnt on th proof thorm 1.1 which is not strightforwrd gnrliztion of prvious rsults. To xplin this w rcll rifly th sic strtgy of [7, 14] tht lds to (1.1). Strting with th stility condition on otins lowr ound for th r of th MOTS in trms of mss functionl. This is th ky quntity in th proof, nd dpnds only on th twist potntil nd th norm of th xil Killing vctor. Th non-ngtiv cosmologicl constnt nd th mttr trms (stisfying th DEC) nithr ppr in nor ltr in th discussion in this cs. Thrfor, th prolm rducs to vcuum nd with Λ = 0. Thn, vritionl principl is usd to otin lowr ound for. Th ky point in this stp is th rltion twn nd th hrmonic nrgy of mps twn th two-sphr nd th hyprolic pln. This llows to us nd dpt powrful thorm y Hildrndt t l [13] on hrmonic mps, which givs xistnc nd uniqunss of th minimizr for. This minimizr, in turn, givs th right hnd sid of (1.1). In th prsnt work whr w strngthn (1.1) to(1.5), two importnt ostcls ppr. Firstly, th r A now pprs not only s uppr ound on th corrsponding functionl ut lso xplicitly in itslf. This mks th vritionl principl hrd to formult. W ovrcom this prolm in ssnc y frzing A s wll s J to crtin vlus corrsponding to n xtrm KdS configurtion, nd y dpting th dynmicl vrils in suitly. Scondly, th rltion of to hrmonic mps mntiond ov no longr prsists, whnc th proof of xistnc nd uniqunss of minimizr for hs to don hr from scrtch. W procd y proving first tht vry criticl point of is locl minimum. Finlly w us th mountin pss thorm in ordr to gt th corrsponding glol sttmnt. Our ppr is orgnizd s follows. In sction w rcll nd dpt som prliminry mtril, in prticulr th dfinition of ngulr momntum for gnrl -surfcs, s wll s th dfinition of stl MOTS. In sction 3 w discuss rlvnt spcts of th KdS mtric, focusing on th xtrm cs. In 3
5 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l sction 4 w sktch th proof of thorm 1.1, postponing th cor of th rgumnt to thr ky propositions which r provn in sction 5. In sction 6 w conjctur gnrliztion of our inqulity to th cs with lctromgntic fild long th lins mntiond ov lrdy, nd w lso discuss rifly th cs Λ < 0.. Prliminris.1. Th gomtric stup W considr mnifold which is topologiclly 4-nighorhood of n mddd -surfc of sphricl topology. crris mtric g ij nd Lvi-Civit connction i. (Ltin indics from i onwrds run from 0 to 3, nd th mtric hs signtur (, +, +, + )). Th fild qutions r G = Λg + 8 πt, (.1) ij ij ij whr Λ is th cosmologicl constnt, nd th nrgy momntum tnsor T ij stisfis th DEC. In sctions nd 3 w llow Λ to hv ithr sign; this nls us to compr with nd to crry ovr usful formuls from work which focuss on Krr nti-d Sittr, in prticulr [4] nd [5]. W nxt introduc null vctors l i nd k i spnning th norml pln to nd normlizd i s lki = 1. W dnot y q = g + l k th inducd mtric on, th corrsponding ij ij ( i j) Lvi-Civit connction y D i nd th Ricci sclr y R. ϵij nd ds r rspctivly th volum lmnt nd th r msur on. Th normliztion lk i i = 1 lvs (oost) rscling frdom i i l = fl, i 1 i k = f k. Whil this rscling ffcts som quntitis introducd low in n ovious wy, our ky dfinitions such s th ngulr momntum (.4) nd th dfinition of stility (.1) r invrint, nd th sm pplis to ll our rsults. Th () l xpnsion, th shr σij () l () l nd th norml fundmntl form Ω i ssocitd with th null norml l i r givn y () l ij () 1 q ilj, ij l q k l q l () l () = σ = i j k l qij, Ωi l = k j q k iklj. (.).. Twist nd ngulr momntum W now ssum tht s wll s Ωi () l r xilly symmtric, i.. thr is Killing vctor i η on such tht ij i () l q = 0 Ω = 0. (.3) η η Th fild η i is normlizd so tht its intgrl curvs hv lngth π. W dfin th ngulr momntum of s 1 J = 8π () Ωi l η i d S, (.4) which will rltd to th Komr ngulr momntum shortly. By Hodg s thorm, thr xist sclr filds ω nd λ on, dfind up to constnts, such tht Ω () hs th following dcomposition i l 4
6 Clss. Quntum Grv. 3 (015) Ω () i l From xil symmtry it follows tht = 1 Dj ij Dj. (.5) η ϵ ω + λ = 1 i 1 Dj i ij Di, (.6) η ϵη ω= η ξ ω ηiω i () l 1 whr i η = ηη i nd ξ i is unit vctor tngnt to nd orthogonl to η i. W now rcll from [7] tht on ny xilly symmtric -surfc on cn introduc coordint systm such tht i j c q dx dx = σ d + σ sin d φ (.7) ij for som function σ nd constnt c which is rltd to th r A of vi c A = 4π. In such coordint systm w cn writ J s 1 π 1 J = ω d = [ ω( π) ω(0)], (.8) whr hr nd hncforth prim dnots th drivtiv w.r.t.. From now onwrds w ssum tht th Killing vctor i η on xtnds to s Killing vctor of g ij. Of cours this implis (.3). Morovr, it follows tht i i ηl = ηk = 0. Using th first qution w otin i () η Ωi l j i i j = kl η. (.9) Insrting (.9) in(.4) w s tht it indd coincids with th Komr ngulr momntum 1 J = 8π W finlly introduc th twist vctor iη j d S. (.10) ij ω = ϵ ηj kηl. (.11) i ijkl If th nrgy momntum tnsor vnishs on, w hv [ iω j] = 0. Hnc thr xists twist potntil ω, dfind up to constnt, such tht ωi = iω. Th rstriction of this sclr fild to is sily sn to coincid with th ω introducd in (.5), which justifis th nottion. In wht follows w will rfr to th pir ( σ, ω) on s th dt..3. Stl MOTS W now tk to mrginlly trppd surfc dfind y () l = 0. W will rfr to l i s th outgoing null vctor, which lds to th nm MOTS. Morovr, following [] (sction 5) w now considr fmily of two-surfcs in nighorhood of togthr with rspctiv null normls l i nd k i nd w impos th following dditionl rquirmnts on nd its nighorhood. Dfinition.1. A mrginlly trppd surfc is stl if thr xists n outgoing ( k i - orintd) vctor X i = γl i ψk i () l, with γ 0 nd ψ > 0, such tht th vrition δ X of with rspct to X i fulfills th condition δ X () l M E Gch Clémnt t l 0. (.1) Two rmrks r in ordr hr. Firstly, it is sy to s (s sction 5 of []) tht stility of w.r.t. som dirction X i implis stility w.r.t ll dirctions tiltd wy from l i. () l () l In prticulr, sinc δ ψk δx stility w.r.t. ny X i implis stility in th 5
7 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l pst outgoing null dirction k i. rsults. This lttr condition suffics s rquirmnt for ll our Th othr rmrk concrns th rltion twn stility nd xil symmtry. W rcll tht in [7, 14], inqulity (1.1) ws provn undr th symmtry rquirmnts (.3) nd undr stility condition similr to dfinition.1 which, howvr, rquird ψ to xilly symmtric s wll. (Axil symmtry of γ ws lso ssumd ut not usd in th proof). In contrst, in th prsnt thorm (1.1) w impos th strongr symmtry rquirmnt tht s wll s its nighorhood r xilly symmtric. In this cs it suffics to impos th stility condition (.1) s ov, nmly without xplicitly rquiring xil symmtry of ψ, sinc th xistnc of n xilly symmtric function ψ thn follows utomticlly, s thorm 8.. of () l []. Morovr, for strictly stl MOTS (which stisfy δx 0 in ddition to (.1)) thr follows vn xil symmtry of th surfc itslf if its nighorhood is xilly symmtric (s thorm 8.1. of []). 3. Krr d Sittr In this sction w rviw som rlvnt proprtis of th vnt horizons of th KdS solutions, mking us of [4, 5], nd rfrncs thrin. Othr spcts of th rich nd complx structur of ths spctims cn found in [11] Th mtric, th horizon nd th ngulr momntum In Boyr Lindquist coordints, th KdS mtric is ds ζ sin ρ ρ sin r dt dϕ dr d dt d, ρ κ ζ χ χ + = ϕ ρ κ (3.1) whr ( r r Λ ζ = + ) 1 mr, ρ r cos = + (3.) 3 Λ 1 3, 1 Λ cos κ = + χ = + 3, (3.3) whr m nd stisfy crtin uppr ounds, cf. [4, 5]. As function of r, ζ hs on ngtiv root nd thr positiv roots (possily countd with multiplicitis). Th grtst root, r ch, mrks th cosmologicl horizon, whil th scond grtst, r h, mrks th vnt horizon (from now on simply clld horizon ). Th r of th horizon is 4π A = ( rh + ) κ (3.4) 6
8 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l nd th inducd mtric on it rds 4 h h ds = μ κρ d sin d, (3.5) κρh μh χ + ϕ σ q h ( h ) χ ρh h q H σ+ + c whr μ = r + nd = r + cos. Hnc r A = = = const. = κ 4π nd th mtric is in th cnonicl form (.7) of [7] q ( ϕ ) (3.6) ds = σ d + sin d (3.7) with σ + q = c = const. W now clcult th twist potntil ωη () vrywhr (not only on ), for η = d ϕ. Adpting known clcultion in th cs Λ = 0 (s.g. ppndix A of [3]) nd omitting som intrmdit stps, w find tt tϕ ( r tϕ r ϕϕ) grrgtt grrgt ζ sin ω = ω = ϵ rt rηt + ϵ ϕ ϕ ϕrt rηϕ = g g + g g κ 3 κ m sin r = g rgt gt rg r ϕϕ ϕ ϕ ϕϕ = + r + χ sin κρ ρ It follows tht ( ) ( ) m = cos3 3 cos κ m ω = cos3 3 cos κ cos sin ρ 4 cos sin ρ 4 (3.8) (3.9). (3.10). (3.11) W not tht comprd to th cs Λ = 0, ω just gts n xtr fctor 1 κ. Intgrting nd using (.8) w otin in prticulr tht J = m κ (3.1) which grs with qution (.10) of [5] nd qution (18) of [4]. 3.. Extrm horizons Whn t lst two of th thr non-ngtiv roots of ζ () r coincid, (on of which is ncssrily r h ), th horizon is clld xtrml. Whn this hppns th gomtry nr th horizon dgnrts to throt. W rfr to [5] for furthr discussion. In wht follows w will just nd th rltion twn th prmtrs m,, Λ, A nd J which w driv xplicitly. For xtrml vnt horizons th rdius of th limiting sphr r stisfis, in ddition to ζ ( r ) = 0, th qution 7
9 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l 3 1 d r ζ Λ Λ 0 = = + r 1 m. (3.13) dr 3 3 Hr nd hncforth suscript indicts xtrmlity. Eliminting m from ζ ( r ) = 0 nd (3.13) w otin Λr Λ + r 1 + = 0. (3.14) 3 4 For Λ 0 this qution hs just singl root which cn clld xtrml horizon, whil for Λ > 0 thr r two solutions r = r ± for givn J. Explicitly, for Λ > 0, ± r 1 Λ 1 Λ = 1 ± 1 4 Λ. (3.15) Λ 3 Λ 3 Whn r = r, (nd r is not tripl root), th first two positiv roots mt nd r < rch, which mns tht cosmologicl horizon prsists in spctim. On th othr hnd whn r = r +, thn th lst two positiv roots coincid nd th vnt nd th cosmologicl horizons com oth xtrml (nd mrg). Using (3.14) to limint from (3.4) wfind 8πr A = 1 + Λ r. (3.16) On th othr hnd, liminting r from (3.14) nd (3.4) givs = A 1 ΛA 4π 4π (1 ΛA 8 π)(1 ΛA 1 π). (3.17) In qution (3.1) w limint now m using (3.13), thn using (3.14) nd finlly r using (3.16). W otin th following simpl rltion twn th ngulr momntum nd th r for xtrm K()dS J A ΛA ΛA = ( A) 1 1 8π 4π 1π (3.18) which ftr trivil rformultion grs with (.3) of [5]. In th cs Λ > 0 nd J = 0 th zros of th prnthss corrspond to th lck hol horizon nd th cosmologicl horizon of Schwrzschild d Sittr, rspctivly. For Λ > 0 w r only intrstd in th domin ΛA 4π < 1 rcll tht this ound cn shown for ll stl MOTS (irrspctivly of sphricl symmtry) [1]. In this rng of A, (3.18) tks on mximl vlu J mx = 3 A π t mx 1 4 Λ 13 Λ = Λ 1 3 (3.19) which is th vlu sttd in (1.6). Morovr, for ch J with J < J mx thr r two vlus A ( J) < A+ ( J) for th r, s figur 1. W r now rdy to dscri th proof of thorm
10 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l Figur 1. Th shdd rgion rprsnts ll points stisfying J ( A). Figur. Th construction dscrid in thorm Th structur nd th proof of th min thorm Th min inqulity J ( A) (4.1) with givn in (3.18) nd Λ > 0 will not shown dirctly ut it will follow from rltd on. This is xplind in th following thorm: Thorm 4.1. For ny givn MOTS with r A, cosmologicl constnt Λ nd ngulr momntum J, thr is uniqu xtrm KdS solution with r  constnt Λ nd ngulr momntum Ĵ such tht J A Jˆ =, (4.) Aˆ nd ÂΛ 4 π. Morovr, th inqulity J ( A) is quivlnt to th inqulity Aˆ A. (4.3) 9
11 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l Proof. Th first rsult, lding to qution (4.), is intuitivly clr from figur sinc through ny point (A, J) thr is uniqu prol JA = const., nd ny such prol intrscts th xtrm curv J = ( A) prcisly onc prt from th trivil point (0, 0). To stt this rigorously, lt λ AÂ nd hnc Jˆ = λ J nd ÂΛ 4 π. Thn th httd vrsion of (3.18) givs qudrtic qution for λ ( J, A). If 3π 3 J > ΛA this qution hs uniqu solution othr thn (0, 0). Othrwis, thr r two non-trivil solutions ut only on of thm lis in th rgion of intrst ÂΛ 4 π. To prov th quivlnc twn (4.1) nd (4.3), ssum first tht Aˆ A. Thn A A A J ( A) A ˆ ˆ ˆ ( A) Aˆ λ = = =, (4.4) J J λ J whr w hv usd (4.), (3.18) nd Aˆ = λa, rspctivly. W nxt us tht th function ( λa) is monotoniclly dcrsing with λ nd thrfor, s Aˆ A w ound th lst trm s λ ( λa) ( A). Putting this togthr with (4.4) wfind λ Aˆ ( A) Aˆ J (4.5) which givs th dsird rsult, tht is, tht (4.3) implis (4.1). To prov th convrs ssum J ( A). Thn Jˆ = λ J nd (3.18) giv ( λa) = Jˆ = λ J λ ( A) (4.6) nd thrfor ( λa) λ ( A). (4.7) Agin, du to th monotonicity of th lft hnd sid with rspct to λ w otin λa A which is (4.3). Hving stlishd th quivlnc twn th min inqulity (4.1) nd (4.3), th nxt sction will dvotd to proving (4.3) for stl MOTS with r A, ngulr momntum J nd dt ( σ, ω). Th proof consists of th sm two stps s in th cs Λ = 0. Howvr, s w mntiond in th introduction nd s w will s low, whn Λ > 0 mny nw complictions ris. In gnrl trms th sic stps cn dscrid s follows. Stp I. W writ th stility inqulity (.1) in trms of th dt ( σ, ω) nd multiply it y n xilly symmtric function α whos choic is motivtd y th form of th dt ( σ, ω) of th xtrm KdS horizon. Thn w intgrt it on to otin lowr ound for A in trms of th so-clld mss functionl dpnding on th dynmic vrils ( σ, ω). Th rsult is th following proposition: Proposition 4.. Lt ( σ, ω) th dt of stl MOTS of r A nd ngulr momntum J. Thn, for ny rl numr th following inqulity holds A (,, A, ), (4.8) 4π σω β 8 κ 10
12 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l whr th functionl is givn y π (,, A, ) ω σ ω σ + + 4σ 0 η whr nd whr ( 1 + Λ cos ) A + 4 Λ σ χ sin d, 4 π χ (4.9) π χ β = 4χ + sin d (4.10) 0 χ χ ( ) hs n dfind in (3.3). At this stg th constnt is ritrry, ut it will fixd in th nxt stp. Stp II. Th difficulty now is to choos convnintly nd to show tht, with such, th rhs of (4.8) hs th lowr ound A 4 π Aˆ. This would prov (4.3), (hnc (4.1) y thorm 4.1). W choos qul to th vlu tht it would tk for th xtrm lck hol of r Â. Th xplicit form is (3.17) with A rplcd y Â. W will dnot it y â nd w dnot y κˆ, χˆ nd ˆβ, th vlus of κ, χ nd β whn is rplcd y â in (3.3),nd (4.10). Thn, for th dt ( σ, ω) of th givn MOTS dfin σˆ σ + lnλ ωˆ = λ ω, (4.11) whr (gin) λ = AÂ. With this chng of vrils w otin Thus ( ) ( ) ( ) σ, ω, A, ˆ = σˆ, ωˆ, Aˆ,ˆ 16κ ln Aˆ A. (4.1) ( σωa) A (,, A, ˆ) ˆ A 8ˆ 8ˆ (4.13) 4π σω β = β κ κ Aˆ nd w nd to prov proposition 4.3. ˆ, ˆ,ˆ, ˆ ˆ Proposition 4.3. In th stup xplind ov w hv ( σω ˆ, ˆ,ˆ, A ˆ ) β ˆ Aˆ 8ˆ κ 4 π. (4.14) W wish to mntion th following point hr. (4.14) mns tht th lowr ound is otind y minimizing th functionl ( σˆ, ωˆ, Aˆ, ˆ) mong ll pirs ( σˆ, ωˆ ) of smooth functions with 8πJˆ = ( ωˆ ( π) ωˆ (0)). A prticulr clss of such functions hs n constructd ov vi (4.11) from smooth dt ( σ, ω) on smooth MOTS of r A nd ngulr momntum J. Howvr, this dos not mn tht ( σˆ, ωˆ ) will still form smooth dt on smooth MOTS of r  nd ngulr momntum Ĵ. This cn sn s follows. In ordr for th MOTS to smooth (fr of conicl singulritis), th coordint function q must vnish t th pols, i.. q(0) = q( π) = 0 which implis tht σ A = 4π (0) = ( ) 4π σ π. But insrting th scling lw σ (4.11) in th lttr rltion contrdicts th smoothnss proprty  = 4πˆ (0) = 4π σˆ ( π) for th httd dt, (xcpt in th trivil cs λ = 1). Thrfor, ( σˆ, ωˆ, Aˆ, ˆ) should considrd s strct functionl in th sns tht its rgumnts r no longr dirctly rltd to ny 11
13 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l MOTS. Nvrthlss, xtrm KdS is not only criticl point of ( σ, ω, A, ) ut lso of ( σˆ, ω ˆ, Aˆ, ˆ), nd th proprtis of th lttr functionl nl us to prov (4.14). Nxt w prsnt th proofs of propositions 4. nd Proof of th min propositions 5.1. Proof of proposition 4. Proof. Th proof is nlogous to th cs Λ = 0 [14] to which it rducs y stting χ 1. Th strting point is th stility inqulity (.1) in which w tk ψ to xilly symmtric without loss of gnrlity (s th rmrks ftr dfinition.1). In trms of th quntitis introducd in sction w otin, intgrting (.1) ginst ny xisymmtric function α:, R ( l) D α + α α Ω Λα ds 0. (5.1) As mntiond in th prvious sction, w choos th tril function sd on th form of th xtrm KdS gomtry s α χ 1 σ =. (5.) In th coordints (3.7) th sclr curvtur tks th form σ c R = σ cos sin σ + sin ( sin σ ). (5.3) sin Using this xprssion w otin 1 R Dα + α ds = π χσ χσ cos 0 π sin 0 π χσ σ χ χ + sin d (5.4) 4 4χ χ + χ sin Intgrtion y prts nd som rrrngmnt yilds 1 R Dα + α ds = π 0 π σ 4 + σ 1 + Λ 3 ( sin σ ) d. (5.5) cos sin d (5.6) π χ + χ + π sin d χσ cos 0. (5.7) 0 4χ Using (3.6), th lst trm in lin (5.7) ov is qul to κ ln( A 4 π). Finlly, still following [14], w hv ( l) ( ) d S 1 1 π ω α Ω + Λα = χ π 4 0 σ sin 4 sin d Λ c χ σ sin d. 0 (5.8) π 1
14 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l Comining qutions (5.1), (5.6) (5.7) nd (5.9) wfind A β κ ln 4 π 4 (5.9) with β s in (4.10). This xprssion is quivlnt to (4.8) s wishd. 5.. Proof of proposition 4.3 In this sction w prov (4.14) whr th httd vrils ( σˆ, ωˆ ) rfr to th rscld quntitis introducd in (4.11). To simplify th nottion, for this sction only, w omit th hts on ths functions. With th nw nottion, inqulity (4.14) rds ( σω,, A ˆ, ˆ ) β ˆ Aˆ 8ˆ κ 4 π. (5.10) As in th proof of th inqulity in th Λ = 0 cs, this stp is don y minimizing th functionl. W find first minimum of for functions σ, ω dfind on compct intrvls [, ] (0, π) (in propositions 5.1 nd 5.), nd thn tk th limit [, ] [0, π] to find (5.10) (in proposition 5.3). Rcll tht whn Λ = 0 th xtrm Krr gomtry is th minimizr of th corrsponding functionl. In this Λ > 0 cs, w find y strightforwrd computtion tht xtrm KdS dt ( σ, ω ) is criticl point of, tht is, th xplicit functions σ ( ) 3 μˆ r r ˆ ˆ, ˆ χ ˆˆ ˆ ˆ sin = ω = + 4 κρ μρ ˆ ˆ stisfy th Eulr Lgrng qutions of : 1 sin d d ˆ χω η ( Λ ) ( ˆ χ σ sin ) = d ˆ sin χ d η ˆ cos ˆ Aˆ Λχ 4π σ (5.11) (5.1) ω = 0. (5.13) In (5.11), th quntitis ρ, ê κ ˆ, μ ê rˆ nd χˆ wr dfind in (3.), (3.3), low (3.5) nd in (3.14) ut crrying suscripts nd hts thy rfr hr to th xtrm KdS solution with prmtr â. Using (3.14) it is sy to s tht th ov ω indd coincids with (3.9) nd thrfor with (3.10). This proprty of xtrm KdS gomtry will ply fundmntl rol in th proof of (5.10), ut for going into dtils, som prliminry dfinitions r ndd. Prliminris. Lt 0 < < < π fixd. For ny function f :[, ] in H 1, dfin L f f = f d, (5.14) f 1, f H1, = ( f) + f d = f + f. (5.15) 13
15 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l Thn, for ny 1 <,( < 1 nd < ), w hv ( 1) ( ) 1 1, f f f. (5.16) This sys in prticulr tht f is uniformly continuous nd w hv {( ) [ ]} f f sup f f ( ):, π f π f, (5.17) whr f = f ( ). W will us th ffin spc Γ of H 1, pths γ:[, ], γ = ( σ, ω), such tht ( σ ω ) = ( σ ω ) ( σ ω ) = ( σ ω ) ( ), ( ) ( ), ( ) nd ( ), ( ) ( ), ( ), (5.18) whr ( σ, ω) r th dt of xtrm KdS of r Â. In lin with th nottion (5.14) w us th shorthnd γ1 γ 1, σ1 σ 1, + ω1 ω 1,. Lt = (): γ Γ th functionl givn y () γ = ( σ) + 4σ ( 1 + Λˆ cos ) ( ω) + χˆ σ sin 4 1, Aˆ + 4Λ σ χˆ sin d. 4π (5.19) Not tht this functionl is th sm s th ppring in (5.10) xcpt tht th intgrtion is ovr [, ] nd tht th rgumnts γ = ( σ, ω) vry in Γ. Th functionl. Considr th chng of vrils (, σ, ω) (, σ, ω ) givn y d sin d sin ˆ ( ), lnsin = σ = σ + χ sin, ω = ω. (5.0) Explicitly, ( ) rds, with suitl choic of th intgrtion constnt, tn 1 κˆ ˆ Λ tn xp κˆ 3 rctn ˆ Λ = 3 cos. (5.1) It follows tht th mp is diffomorphism from [0, π] into [0, π] nd tht 0 < c1 < (sin sin ) < c < for c 1 nd c dpnding only on â Λ. Th trnsformtion of th ffin spc Γ will dnotd y Γ. A strightforwrd computtion shows () γ = () γ 4cos d 4 cos ˆ Λ 4 cos sin 3 cos σ σ + 4ˆ χ cos d, (5.) sin whr th functionl = ( γ): Γ is givn y ( ) ( γ) = ( σ ) + 4σ + ω σ sin4 Aˆ 4 sin + 4Λ 4 sin ˆ ( ) sin d. π 4 χ σ (5.3) 14
16 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l Thus, th functionls : Γ nd : Γ: diffr y constnt nd oundry trms This immditly implis tht γ is criticl point of iff γ is criticl point of. In prticulr s γ is criticl point of, γ is criticl point of. As w will xplin low, th ntur of criticl points of th functionl cn sily nlysd vi crucil formul du to Crtr. A similr simpl formul to nlys th criticl points of is unknown to us. For this rson w will continu working with rthr thn with. Th rsults. Th nxt thr propositions togthr prov proposition 4.3. Propositions 5.1 nd 5. dl with th minimiztion of th rstrictd functionl. Thn, proposition 5.3 stlishs th connction twn th minimiztion of (or, quivlntly, th minimiztion of ) nd th minimiztion of th originl functionl tht ultimtly lds to (5.10) nd proposition 4.3. Th ngls, (0, π) dfining r ritrry. Proposition 5.1. For ny criticl point γc of thr r constnts ϵ > 0 nd c > 0, such tht if γ γc ϵ thn 1, In prticulr Proposition 5.. i.. Proposition 5.3. ( ) c c c 1, ( γ) γ + γ γ. (5.4) chivs strict locl minimum t ny of its criticl points. hs only on criticl point γ = γ nd ( γ ) is glol minimum, ( γ ) c ( γ). (5.5) W hv ( γ A ) ( γ A ), ˆ,ˆ,ˆ, ˆ (5.6) for functions γ = ( σ, ω) hving th oundry vlus γ, = γ., Morovr, tking th limit [, ] [0, π] w hv ( γ A ) ( γ A ), ˆ,ˆ,ˆ, ˆ. (5.7) Th xplicit form of ( γ ) givs (5.10). Not tht tking th limit (, ) (0, π) is vry dlict issu s th limit oundry vlus of σ r not ncssrily th sm s thos of σ. W will trt this prolm following th ids of [1]. Proof of proposition 5.1. For givn γ lt γ = ( σ, ω ) γ γc nd dfin th pth γτ = γc + τγ for τ in [0, 1]. Th Tylor xpnsion of ( γ τ ) t τ = 0 givs ( γ) = ( γ c) + τ( γ τ) + τ( γ τ), (5.8) 6 τ= 0 τ= τ* whr 0 τ* 1. Th proof of proposition (5.1) coms from nlysing th lst two trms on th right hnd sid of (5.8). W do tht sprtly. To simplify nottion st ( γ τ ) =. Morovr, in th prsnt proof prims on functions dnot drivtivs. Th first τ-drivtiv of s function of τ is 15
17 Clss. Quntum Grv. 3 (015) ( ) D D D ω ω σ ω Dσ D τ = σ + σ + η whr σ σ sin d, (5.9) Aˆ sin4 4Λ 4 sin ˆ π ( ) (5.30) 4 χ nd th drivtiv oprtor D nd th dot products r tkn with rspct to th stndrd mtric on. (Du to xisymmtry D = ). Evlut t τ = 0, intgrt y prts nd us th oundry conditions to otin th Eulr Lgrng qutions for, nmly ( D ω c) Δσ c + = σc, (5.31) η D D ω η c c c = 0, (5.3) whr η sin c = σ c, nd Δ is th Lplc oprtor with rspct to th stndrd mtric on. (Agin, du to xisymmtry, Δ involvs only drivtivs with rspct to ). Th scond τ-drivtiv of rds τ σ ω 4σ ω ω ω = ( D σ ) + η ( D ) D D + ( D ) Nxt, rcll Crtr s idntity in th form (s [8]) whr nd σ + σ sin d. (5.33) F + σ G + ω G + σω G η ω G = H, (5.34) G σ σ ω ω σ ( D ) ( ) () τ = Δσ + η ω, (5.35) G () τ = D η Dω, (5.36) ω ( ) G () τ = Δσ + η Dω. Dω σ D σ ω, (5.37) ( ( )) G () τ = D η Dω σ Dω, (5.38) ω 1 1 ( ) ( ) 1 ( ) ( ) F() τ = Dσ + ωη Dω + D ωη η σ Dω + η σ Dω ωη Dη, ( ) 1 1 H τ = D σdσ + ωη D( ωη ) M E Gch Clémnt t l (5.39) (). (5.40) 16
18 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l Now w cn us th xprssions for G σ nd G ω to otin, ftr simpl intgrtion y prts, 1 = G G σ sin d. (5.41) + ω σ τ σ ω σ Using (5.34), intgrting y prts onc gin nd using th oundry conditions σ ( ) = σ ( ) = 0, ω ( ) = ω ( ) = 0 to gt rid of H, yilds 1 F G G = + σω η ω + σ σ τ ω σ sin d. (5.4) Evluting t τ = 0 nd using th Eulr Lgrng qutions, w otin ( c ) 1 F 0 = c + η ω + σ σ τ τ= sin d, (5.43) which cn writtn in th form ωc ω τ τ= 0 = σ + η η c c c ω ωc + σ η ηc (5.44) σω c ωη c ω σ σc sin d. (5.45) η c η η c c W procd y tking dvntg of this formul. First w not tht cus γc is criticl point w hv ω k sin c ηc = whr k is constnt. Writ ω ω η nd disrgrd th first trm in (5.45). W gt c Lt s min { (sin ) ηc } k k c c 0 σ sin sin η ω ω η σ + + τ τ= ( σ + ω + σ ) c } sin d. (5.46) Ω nd ssum k sin d 4 σ > sin d. (5.47) s ω Ω Thn th first trm in (5.46) cn oundd s 1 k c σ + η sin d (5.48) sin ω 1 σ sin d 1 k η c sin d (5.49) sin ω 17
19 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l 1 1 k sin d σ ω sin d (5.50) s 1 1 sin d 1 σ σ sin d (5.51) 1 1 sin d min sin 1 1 = σ σ d, (5.5) whr (5.51) hs n otind using (5.47). This ound togthr with th lst trm in (5.46) givs us τ τ= 0 1 1, c σ (5.53) for som constnt c1 > 0. Now ssum tht th opposit to (5.47) holds, nmly k sin d 4 σ sin d. (5.54) s ω Ω Ω Thn from (5.46) w hv ( ) c sin d 0 ω + σ σ τ τ= (5.55) σ c { } Ω ( ) min ω + σ sin d (5.56) s min{ σ c } σ + σ sin d (5.57) 4k s min{ σ c} min 1, 4 ( ) sin d (5.58) σ + σ k which gin givs us n inqulity τ τ= 0 c σ 1, for som constnt c > 0. Thus in ithr cs w hv τ τ= 0 3 1, c σ (5.59) for som constnt c3 > 0. Now w cn intrchng th rols of σ nd ω (osrving th symmtry in (5.46)) to find gin τ τ= 0 3 1, c ω. (5.60) Using tht ω = ω ηc nd y n rgumnt similr to th prvious on w dduc from (5.60) tht τ τ= 0 4 1, c ω (5.61) for som constnt c 0. 4 > Collcting (5.59) nd (5.61) w gt for som constnt c5 > 0. τ τ= 0 5 1, c ( σ, ω ) = c γ γ (5.6) 5 18 c 1,
20 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l Hving trtd th scond trm on th right hnd sid of (5.8) w turn to th lst on. W clim tht thr is constnt c6 > 0 such tht if γ γ c 1 thn 1, 3 3 c ( σ, ω ). (5.63) τ τ= τ* 6 1, Comind with (5.8) this would show, s w wnt, tht if ( σ, ω ) 1, ϵ for ϵ sufficintly smll, thn (5.4) holds for som constnt c > 0. Th ound (5.63) is indd sily otind. A dirct computtion givs 3 τ = 6σω 1σ ω ω + 4σ ω σ 3 + σ sin d. (5.64) η 3 Bounds for ch trm in this intgrl, comptil with (5.63), r otind y using tht σ π σ 1, π ( σ, ω ) 1,, nd tht if γ γ c 1 thn σ c 1, 7 nd ω c8 for constnts c7 > 0 nd c8 > 0. For instnc th first trm is oundd s σω 1 sin d 1 1 sup c7 3 σ ω c (, ) (5.65) 3 9 σ ω 1, η sin for som constnt c 0. 9 > Th othr trms r oundd in th sm wy. Proof of proposition 5.. It will mor convnint to work with th functionl * ( γ*) of th rgumnts γ* = ( u, ω) with u = ln η, givn y whr * u u ( ) = ( u + + ) γ* ω * sin d, (5.66) * = sin. (5.67) This functionl is qul to () γ plus constnt indpndnt of th rgumnts. (Us u = ln η in (5.3)). If * is shown to stisfy th Plis Sml (PS) condition (s low), thn simpl ppliction of proposition 5.1 nd th mountin pss thorm, s xplind in th corollry on pg 187 of [15], shows tht γ* = (ln η, ω ) is th only criticl point nd tht * ( γ* ) is th strict solut minimum of *. W xplin now how to vrify th PS condition. Rcll first tht th PS condition holds iff ny squnc γ* i for which * ( γ* i ) is oundd nd for which δ * ( γi * ) 0 hs (strongly) convrgnt susqunc. Hr δ * ( γ * ) is th norm of th diffrntil of * i γ Rcll tht this norm is δ* γ { δ * X γ X 1, } ( *) = sup ( *) : = 1. Not from this dfinition tht if δ * ( γ * ) 0, thn for ny squnc X i with X K w hv t i *. Xi * i * i i 1, ( ) 0. (5.68) δ γ Now, for ny tngnt vctor X = ( u, ω ) to point γ* = ( u, ω) w comput u u u ( ) = ( uu + u + + u ) δ * γ* ω ωω sin sin d. (5.69) X This xprssion will usd low. 19
21 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l Lt γi * squnc such tht * ( γ* i ) is uniformly oundd nd such tht δ * ( γi * ) 0. From (5.66) w dduc tht u i is uniformly oundd 4 nd from this nd (5.17) tht u i is uniformly oundd nd uniformly continuous. By th thorm of Arzlà Ascoli, u i hs C 0 -convrgnt susqunc (tht w still indx y i ). As u i 1, is uniformly oundd w cn ssum tht u i convrgs wkly in H 1, too. Thn, from th C 0 -ounddnss of u i nd gin from (5.66), w dduc in similr fshion tht ωi hs susqunc convrging in C 0 1, nd wkly in H. Assum thn without loss of gnrlity tht for th ov squnc γ* i w hv ui u nd ωi ω wkly in H 1, 0 nd strongly in C. Lt c > 0 constnt such tht u c < i sin for ll i. Thn, ( i ) ( i ) c d u ω ω ω ω i sin d = ( ) ui sin d ( ) ui ω sin d i ωi ω ω ωi ω 0, (5.70) whr th first intgrl in (5.70) is sn to go to zro y tking V i = (0, ω i) with ω i = ω i ω in (5.68), whil th scond intgrl in (5.70) tnds to zro cus ωi ω wkly in H 1, nd ui u strongly in C 0 nd wkly in H 1,. From (5.17) nd (5.70) w dduc tht ωi ω 0, which togthr with (5.70) gin shows tht ωi ω in 1, H. Th convrgnc ui u in H 1, is shown in th sm fshion. Proof of proposition 5.3. Inqulity (5.6) follows from propositions 5.1 nd 5., togthr with th rltion (5.) twn th functionls nd, s thy imply tht xtrm KdS dt ( σ, ω) r th uniqu glol minimizrs of mong functions ( σ, ω) hving th sm oundry conditions s ( σ, ω) t,. Th proof of (5.7) is lin y lin idnticl to th proof whn Λ = 0 nd which ws otind in [1]. W will only sktch th rgumnt hr nd rfr th rdr to [1] for dtils. It is importnt to rmrk tht th prsnc of th cosmologicl constnt plys no importnt rol in this stp. Divid th intrvl [0, π] in thr rgions, (ln t) ΩI = {sin }, (ln t) Ω II = { sin t} nd ΩIII = { t sin }. Not tht whn t gos to zro, th rgions ΩI nd ΩII shrink towrd th pols, whil ΩIII xtnds to covr th whol intrvl [0, π]. Thn spcific prtition function f ( ) (s qutions (70)-(71) in [1]) is usd to intrpolt twn xtrm KdS horizon dt in rgion ΩI nd gnrl dt in rgion ΩIII. Dfin th uxiliry intrpolting dt γ () t = ( σ(), t ω()) t s ( ) γ( t) = f (sin ) γ + 1 f (sin ) γ, (5.71) t t thn, s mntiond for, comining propositions 5.1 nd 5. on th rgion [, ] ΩII ΩIII for functions γ (): t Γ w find ( γ( t)) ( γ ). (5.7) Morovr, s γ () t Ω = γ I Ω, w cn xtnd (5.7)to[0, π ] (rcll tht [0, π] = Ω [, ] I I ) to otin 4 Not tht thr r constnts 0 < c 1 < c < such tht c < sin < c. 1 0
22 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l ( γ( t)) ( γ ). (5.73) Th finl stp is to show tht s t gos to zro, th mss functionl for th uxiliry dt convrgs to th mss functionl for th originl gnrl dt, tht is lim ( γ( t)) = ( γ). (5.74) t 0 This is don in n idnticl mnnr s in [1] (with Λ ing irrlvnt hr), y using tht ω = ω + (sin ) nr th pols nd tht ( γ) nd ( γ ) r wll dfind. Inqulitis (5.73) nd (5.74) giv (5.7). Morovr, using th xplicit vlu w find ( σ, ω, A ˆ, ˆ ) β ˆ Aˆ 8ˆ κ = 4π ( σω,, A ˆ, ˆ ) β ˆ Aˆ 8ˆ κ which is inqulity (5.10). 4π (5.75) (5.76) 6. Possil gnrliztions W conclud discussing possil xtnsions of our min rsult to th cs with lctromgntic fild nd to th cs Λ < 0. In th formr cs w conjctur n inqulity which, in ddition to A, J nd Λ, contins lctric nd mgntic chrgs Q E nd Q M in th comintion Q = QE + Q M. Such n xtnsion is nturl from th fct tht ll spcil css r provn, in prticulr w rcll [6] th ound 4 A 16 π (4 J + Q ) in th cs Λ = 0. Morovr, xtrm Krr Nwmn d Sittr sturts (6.1) nd (6.). Conjctur 6.1. Undr th ssumptions of thorm 1.1 ut undr th prsnc of n lctromgntic fild with chrgs Q E, Q M with Q = QE + QM nd for ny Λ > 0 w hv A ΛA ΛA ΛQ Q4 J 1 1 (6.1) 64π 4π 1π 3 4 or quivlntly, ΛA A ΛA Q + 1 4J 48π 16π 6π A A A Q Λ Λ J 0. (6.) 48π 16π 6π Morovr, (6.1) nd (6.) r sturtd prcisly for xtrm Krr Nwmn d Sittr configurtions. As to th clcultions lding to (6.1) nd (6.) w md us of qution (44) of Cldrlli t l [4], whr th tmprtur T of Krr Nwmn nti-d Sittr lck hol is 1
23 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l givn in trms of l = 3 Λ, th mss M, th ntropy S = A 4, Q nd J. This clcultion is insnsitiv to th sign of Λ, nd th rquirmnt tht T 0 givs dirctly (6.1), whil (6.) is otind vi simpl lgric mnipultions. W finlly commnt on th prospcts of proving th r inqulitis (1.5), (6.1) nd (6.) for th cs Λ < 0 long th lins dscrid ov. W first rmrk tht xtrm Krr nti-d Sittr sturts (1.5) which should clr from th discussion of sction 3, nd xtrm Krr Nwmn nti-d Sittr sturts (6.1) nd (6.). Nxt, th first prt of our proof of (1.5), nmly th lowr ound for A in trms on s givn in (4.8) crris ovr to Λ < 0 strightforwrdly. Howvr, ttmpts of otining lowr ound for nlogously to (4.1) sm to in vin. Th rson is tht on cn sily construct xmpls with sufficintly smll σ (ngtiv with lrg modulus), nd suitly djustd ω for which th lst trm in (4.9), which is now ngtiv, domints th first two positiv trms. In fct ths xmpls strongly suggst tht is vn unoundd from low unlss th dt r rstrictd ppropritly. Thrfor, whil it is still possil tht (1.5), (6.1) nd (6.) hold for Λ < 0 s wll, our strtgy which ws succssful for Λ > 0 is unlikly to crry ovr. Acknowldgmnts W cknowldg hlpful discussions with Lrs Andrsson, Piotr Bizoń, Piotr Chruścil, Srgio Din, Jos Luis Jrmillo, Mrc Mrs nd Luc Nguyn. MEGC is supportd y CONICET (Argntin). WS ws fundd y th Austrin Scinc Fund (FWF): P3337-N16 nd y th Alrt Einstin Institut (Potsdm). Rfrncs [1] Acñ A, Din S nd Gch Clémnt M E 011 Horizon r-ngulr momntum inqulity for clss of xilly symmtric lck hols Clss. Quntum Grv [] Andrsson L, Mrs M nd Simon W 008 Stility of mrginlly outr trppd surfcs nd xistnc of mrginlly outr trppd tus Adv. Thor. Mth. Phys [3] Avil G A nd Din S 008 Th Ym invrint for xilly symmtric two Krr lck hols initil dt Clss. Quntum Grv [4] Cldrlli M M, Cognol G nd Klmm D 000 Thrmodynmics of Krr Nwmn AdS lck hols nd conforml fild thoris Clss. Quntum Grv [5] Cho J-H, Ko Y nd Nm S 010 Th ntropy function for th xtrml Krr-(nti-)d Sittr lck hols Ann. Phys [6] Din S nd Riris M 011 Ar-ngulr-momntum inqulity for xisymmtric lck hols Phys. Rv. Ltt [7] Din S 010 Extrm throt initil dt st nd horizon r-ngulr momntum inqulity for xisymmtric lck hols Phys. Rv. D [8] Din S, Jrmillo J L nd Riris M 01 Ar-chrg inqulity for lck hols Clss. Quntum Grv [9] Gch Clmnt M E, Jrmillo J L nd Riris M 013 Proof of th r-ngulr momntumchrg inqulity for xisymmtric lck hols Clss. Quntum Grv [10] Fjmn D nd Simon W 014 Ar inqulitis for stl mrginlly outr trppd surfcs in Einstin Mxwll-dilton thory Adv. Thor. Mth. Phys [11] Hwking S W nd Ellis G F R 1973 (Th Lrg Scl Structur of Spc-Tim (Cmridg Monogrphs on Mthmticl Physics) vol 1) (Cmridg: Cmridg Univrsity Prss) [1] Hywrd S A, Shiromizu T nd Nko K-I 1994 A cosmologicl constnt limits th siz of lck hols Phys. Rv. D [13] Hildrndt S, Kul H nd Widmn K-O 1977 An xistnc thorm for hrmonic mppings of Rimnnin mnifolds Act Mth
24 Clss. Quntum Grv. 3 (015) M E Gch Clémnt t l [14] Hollnds S 01 Horizon r-ngulr momntum inqulity in highr dimnsionl spctims Clss. Quntum Grv [15] Jrmillo J L, Riris M nd Din S 011 Blck hol r-ngulr-momntum inqulity in nonvcuum spctims Phys. Rv. Ltt. D [16] Ptz T-T nd Simon W 013 Mrginlly outr trppd surfcs in highr dimnsions Clss. Quntum Grv [17] Pucci P nd Srrin J 1984 Extnsions of th mountin pss thorm J. Funct. Anl [18] Simon W 01 Bounds on r nd chrg for mrginlly trppd surfcs with cosmologicl constnt Clss. Quntum Grv [19] Yzdjiv S 013 Ar-ngulr momntum-chrg inqulity for stl mrginlly outr trppd surfcs in 4D Einstin-Mxwll-dilton thory Phys. Rv. D [0] Yzdjiv S 013 Horizon r-ngulr momntum-chrg-mgntic fluxs inqulitis in 5D Einstin-Mxwll-dilton grvity Clss. Quntum Grv
INTEGRALS. Chapter 7. d dx. 7.1 Overview Let d dx F (x) = f (x). Then, we write f ( x)
 Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
Chptr 7 INTEGRALS 7. Ovrviw 7.. Lt d d F () f (). Thn, w writ f ( ) d F () + C. Ths intgrls r clld indfinit intgrls or gnrl intgrls, C is clld constnt of intgrtion. All ths intgrls diffr y constnt. 7..
TOPIC 5: INTEGRATION
 TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
TOPIC 5: INTEGRATION. Th indfinit intgrl In mny rspcts, th oprtion of intgrtion tht w r studying hr is th invrs oprtion of drivtion. Dfinition.. Th function F is n ntidrivtiv (or primitiv) of th function
Chapter 16. 1) is a particular point on the graph of the function. 1. y, where x y 1
 Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Prctic qustions W now tht th prmtr p is dirctl rltd to th mplitud; thrfor, w cn find tht p. cos d [ sin ] sin sin Not: Evn though ou might not now how to find th prmtr in prt, it is lws dvisl to procd
Lecture 11 Waves in Periodic Potentials Today: Questions you should be able to address after today s lecture:
 Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
Lctur 11 Wvs in Priodic Potntils Tody: 1. Invrs lttic dfinition in 1D.. rphicl rprsnttion of priodic nd -priodic functions using th -xis nd invrs lttic vctors. 3. Sris solutions to th priodic potntil Hmiltonin
Integration Continued. Integration by Parts Solving Definite Integrals: Area Under a Curve Improper Integrals
 Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
Intgrtion Continud Intgrtion y Prts Solving Dinit Intgrls: Ar Undr Curv Impropr Intgrls Intgrtion y Prts Prticulrly usul whn you r trying to tk th intgrl o som unction tht is th product o n lgric prssion
CIVL 8/ D Boundary Value Problems - Rectangular Elements 1/7
 CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
CIVL / -D Boundr Vlu Prolms - Rctngulr Elmnts / RECANGULAR ELEMENS - In som pplictions, it m mor dsirl to us n lmntl rprsnttion of th domin tht hs four sids, ithr rctngulr or qudriltrl in shp. Considr
CSE303 - Introduction to the Theory of Computing Sample Solutions for Exercises on Finite Automata
 CSE303 - Introduction to th Thory of Computing Smpl Solutions for Exrciss on Finit Automt Exrcis 2.1.1 A dtrministic finit utomton M ccpts th mpty string (i.., L(M)) if nd only if its initil stt is finl
CSE303 - Introduction to th Thory of Computing Smpl Solutions for Exrciss on Finit Automt Exrcis 2.1.1 A dtrministic finit utomton M ccpts th mpty string (i.., L(M)) if nd only if its initil stt is finl
Multi-Section Coupled Line Couplers
 /0/009 MultiSction Coupld Lin Couplrs /8 Multi-Sction Coupld Lin Couplrs W cn dd multipl coupld lins in sris to incrs couplr ndwidth. Figur 7.5 (p. 6) An N-sction coupld lin l W typiclly dsign th couplr
/0/009 MultiSction Coupld Lin Couplrs /8 Multi-Sction Coupld Lin Couplrs W cn dd multipl coupld lins in sris to incrs couplr ndwidth. Figur 7.5 (p. 6) An N-sction coupld lin l W typiclly dsign th couplr
Lecture 4. Conic section
 Lctur 4 Conic sction Conic sctions r locus of points whr distncs from fixd point nd fixd lin r in constnt rtio. Conic sctions in D r curvs which r locus of points whor position vctor r stisfis r r. whr
Lctur 4 Conic sction Conic sctions r locus of points whr distncs from fixd point nd fixd lin r in constnt rtio. Conic sctions in D r curvs which r locus of points whor position vctor r stisfis r r. whr
Instructions for Section 1
 Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
Instructions for Sction 1 Choos th rspons tht is corrct for th qustion. A corrct nswr scors 1, n incorrct nswr scors 0. Mrks will not b dductd for incorrct nswrs. You should ttmpt vry qustion. No mrks
Last time: introduced our first computational model the DFA.
 Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
Lctur 7 Homwork #7: 2.2.1, 2.2.2, 2.2.3 (hnd in c nd d), Misc: Givn: M, NFA Prov: (q,xy) * (p,y) iff (q,x) * (p,) (follow proof don in clss tody) Lst tim: introducd our first computtionl modl th DFA. Tody
Lecture contents. Bloch theorem k-vector Brillouin zone Almost free-electron model Bands Effective mass Holes. NNSE 508 EM Lecture #9
 Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
Lctur contnts Bloch thorm -vctor Brillouin zon Almost fr-lctron modl Bnds ffctiv mss Hols Trnsltionl symmtry: Bloch thorm On-lctron Schrödingr qution ch stt cn ccommo up to lctrons: If Vr is priodic function:
The Angular Momenta Dipole Moments and Gyromagnetic Ratios of the Electron and the Proton
 Journl of Modrn hysics, 014, 5, 154-157 ublishd Onlin August 014 in SciRs. htt://www.scir.org/journl/jm htt://dx.doi.org/.436/jm.014.51415 Th Angulr Momnt Diol Momnts nd Gyromgntic Rtios of th Elctron
Journl of Modrn hysics, 014, 5, 154-157 ublishd Onlin August 014 in SciRs. htt://www.scir.org/journl/jm htt://dx.doi.org/.436/jm.014.51415 Th Angulr Momnt Diol Momnts nd Gyromgntic Rtios of th Elctron
, between the vertical lines x a and x b. Given a demand curve, having price as a function of quantity, p f (x) at height k is the curve f ( x,
 Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
Clculus for Businss nd Socil Scincs - Prof D Yun Finl Em Rviw vrsion 5/9/7 Chck wbsit for ny postd typos nd updts Pls rport ny typos This rviw sht contins summris of nw topics only (This rviw sht dos hv
MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS
 VSRT MEMO #05 MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS 01886 Fbrury 3, 009 Tlphon: 781-981-507 Fx: 781-981-0590 To: VSRT Group From: Aln E.E. Rogrs Subjct: Simplifid
VSRT MEMO #05 MASSACHUSETTS INSTITUTE OF TECHNOLOGY HAYSTACK OBSERVATORY WESTFORD, MASSACHUSETTS 01886 Fbrury 3, 009 Tlphon: 781-981-507 Fx: 781-981-0590 To: VSRT Group From: Aln E.E. Rogrs Subjct: Simplifid
FSA. CmSc 365 Theory of Computation. Finite State Automata and Regular Expressions (Chapter 2, Section 2.3) ALPHABET operations: U, concatenation, *
 CmSc 365 Thory of Computtion Finit Stt Automt nd Rgulr Exprssions (Chptr 2, Sction 2.3) ALPHABET oprtions: U, conctntion, * otin otin Strings Form Rgulr xprssions dscri Closd undr U, conctntion nd * (if
CmSc 365 Thory of Computtion Finit Stt Automt nd Rgulr Exprssions (Chptr 2, Sction 2.3) ALPHABET oprtions: U, conctntion, * otin otin Strings Form Rgulr xprssions dscri Closd undr U, conctntion nd * (if
Winter 2016 COMP-250: Introduction to Computer Science. Lecture 23, April 5, 2016
 Wintr 2016 COMP-250: Introduction to Computr Scinc Lctur 23, April 5, 2016 Commnt out input siz 2) Writ ny lgorithm tht runs in tim Θ(n 2 log 2 n) in wors cs. Explin why this is its running tim. I don
Wintr 2016 COMP-250: Introduction to Computr Scinc Lctur 23, April 5, 2016 Commnt out input siz 2) Writ ny lgorithm tht runs in tim Θ(n 2 log 2 n) in wors cs. Explin why this is its running tim. I don
Section 3: Antiderivatives of Formulas
 Chptr Th Intgrl Appli Clculus 96 Sction : Antirivtivs of Formuls Now w cn put th is of rs n ntirivtivs togthr to gt wy of vluting finit intgrls tht is ct n oftn sy. To vlut finit intgrl f(t) t, w cn fin
Chptr Th Intgrl Appli Clculus 96 Sction : Antirivtivs of Formuls Now w cn put th is of rs n ntirivtivs togthr to gt wy of vluting finit intgrls tht is ct n oftn sy. To vlut finit intgrl f(t) t, w cn fin
CBSE 2015 FOREIGN EXAMINATION
 CBSE 05 FOREIGN EXAMINATION (Sris SSO Cod No 65//F, 65//F, 65//F : Forign Rgion) Not tht ll th sts hv sm qustions Onl thir squnc of pprnc is diffrnt M Mrks : 00 Tim Allowd : Hours SECTION A Q0 Find th
CBSE 05 FOREIGN EXAMINATION (Sris SSO Cod No 65//F, 65//F, 65//F : Forign Rgion) Not tht ll th sts hv sm qustions Onl thir squnc of pprnc is diffrnt M Mrks : 00 Tim Allowd : Hours SECTION A Q0 Find th
MERIDIAN SURFACE OF WEINGARTEN TYPE IN 4-DIMENSIONAL EUCLIDEAN SPACE E 4 arxiv: v1 [math.dg] 14 May 2013
![MERIDIAN SURFACE OF WEINGARTEN TYPE IN 4-DIMENSIONAL EUCLIDEAN SPACE E 4 arxiv: v1 [math.dg] 14 May 2013 MERIDIAN SURFACE OF WEINGARTEN TYPE IN 4-DIMENSIONAL EUCLIDEAN SPACE E 4 arxiv: v1 [math.dg] 14 May 2013](/thumbs/93/111838361.jpg) MERIDIAN SURFACE OF WEINGARTEN TYPE IN 4-DIMENSIONAL EUCLIDEAN SPACE E 4 rxiv:13053155v1 [mthdg] 14 My 2013 Astrct In this ppr, w study mridin surfcs of Wingrtn typ in Euclidn 4-spc E 4 W giv th nccssry
MERIDIAN SURFACE OF WEINGARTEN TYPE IN 4-DIMENSIONAL EUCLIDEAN SPACE E 4 rxiv:13053155v1 [mthdg] 14 My 2013 Astrct In this ppr, w study mridin surfcs of Wingrtn typ in Euclidn 4-spc E 4 W giv th nccssry
CONTINUITY AND DIFFERENTIABILITY
 MCD CONTINUITY AND DIFFERENTIABILITY NCERT Solvd mpls upto th sction 5 (Introduction) nd 5 (Continuity) : Empl : Chck th continuity of th function f givn by f() = + t = Empl : Emin whthr th function f
MCD CONTINUITY AND DIFFERENTIABILITY NCERT Solvd mpls upto th sction 5 (Introduction) nd 5 (Continuity) : Empl : Chck th continuity of th function f givn by f() = + t = Empl : Emin whthr th function f
Elliptical motion, gravity, etc
 FW Physics 130 G:\130 lctur\ch 13 Elliticl motion.docx g 1 of 7 11/3/010; 6:40 PM; Lst rintd 11/3/010 6:40:00 PM Fig. 1 Elliticl motion, grvity, tc minor xis mjor xis F 1 =A F =B C - D, mjor nd minor xs
FW Physics 130 G:\130 lctur\ch 13 Elliticl motion.docx g 1 of 7 11/3/010; 6:40 PM; Lst rintd 11/3/010 6:40:00 PM Fig. 1 Elliticl motion, grvity, tc minor xis mjor xis F 1 =A F =B C - D, mjor nd minor xs
cycle that does not cross any edges (including its own), then it has at least
 W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
W prov th following thorm: Thorm If a K n is drawn in th plan in such a way that it has a hamiltonian cycl that dos not cross any dgs (including its own, thn it has at last n ( 4 48 π + O(n crossings Th
Notes on Finite Automata Department of Computer Science Professor Goldberg Textbooks: Introduction to the Theory of Computation by Michael Sipser
 Nots on Finit Automt Dprtmnt of Computr Scinc Profssor Goldrg Txtooks: Introduction to th Thory of Computtion y Michl Sipsr Elmnts of th Thory of Computtion y H. Lwis nd C. Ppdimitriou Ths nots contin
Nots on Finit Automt Dprtmnt of Computr Scinc Profssor Goldrg Txtooks: Introduction to th Thory of Computtion y Michl Sipsr Elmnts of th Thory of Computtion y H. Lwis nd C. Ppdimitriou Ths nots contin
PH427/PH527: Periodic systems Spring Overview of the PH427 website (syllabus, assignments etc.) 2. Coupled oscillations.
 Dy : Mondy 5 inuts. Ovrviw of th PH47 wsit (syllus, ssignnts tc.). Coupld oscilltions W gin with sss coupld y Hook's Lw springs nd find th possil longitudinl) otion of such syst. W ll xtnd this to finit
Dy : Mondy 5 inuts. Ovrviw of th PH47 wsit (syllus, ssignnts tc.). Coupld oscilltions W gin with sss coupld y Hook's Lw springs nd find th possil longitudinl) otion of such syst. W ll xtnd this to finit
I. The Connection between Spectroscopy and Quantum Mechanics
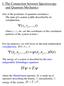 I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
I. Th Connction twn Spctroscopy nd Quntum Mchnics On of th postults of quntum mchnics: Th stt of systm is fully dscrid y its wvfunction, Ψ( r1, r,..., t) whr r 1, r, tc. r th coordints of th constitunt
Linear Algebra Existence of the determinant. Expansion according to a row.
 Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
Lir Algbr 2270 1 Existc of th dtrmit. Expsio ccordig to row. W dfi th dtrmit for 1 1 mtrics s dt([]) = (1) It is sy chck tht it stisfis D1)-D3). For y othr w dfi th dtrmit s follows. Assumig th dtrmit
Math 61 : Discrete Structures Final Exam Instructor: Ciprian Manolescu. You have 180 minutes.
 Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Nm: UCA ID Numr: Stion lttr: th 61 : Disrt Struturs Finl Exm Instrutor: Ciprin nolsu You hv 180 minuts. No ooks, nots or lultors r llow. Do not us your own srth ppr. 1. (2 points h) Tru/Fls: Cirl th right
Lecture 12 Quantum chromodynamics (QCD) WS2010/11: Introduction to Nuclear and Particle Physics
 Lctur Quntum chromodynmics (QCD) WS/: Introduction to Nuclr nd Prticl Physics QCD Quntum chromodynmics (QCD) is thory of th strong intrction - bsd on color forc, fundmntl forc dscribing th intrctions of
Lctur Quntum chromodynmics (QCD) WS/: Introduction to Nuclr nd Prticl Physics QCD Quntum chromodynmics (QCD) is thory of th strong intrction - bsd on color forc, fundmntl forc dscribing th intrctions of
SOLVED EXAMPLES. be the foci of an ellipse with eccentricity e. For any point P on the ellipse, prove that. tan
 LOCUS 58 SOLVED EXAMPLES Empl Lt F n F th foci of n llips with ccntricit. For n point P on th llips, prov tht tn PF F tn PF F Assum th llips to, n lt P th point (, sin ). P(, sin ) F F F = (-, 0) F = (,
LOCUS 58 SOLVED EXAMPLES Empl Lt F n F th foci of n llips with ccntricit. For n point P on th llips, prov tht tn PF F tn PF F Assum th llips to, n lt P th point (, sin ). P(, sin ) F F F = (-, 0) F = (,
22.615, MHD Theory of Fusion Systems Prof. Freidberg Lecture 8: Effect of a Vertical Field on Tokamak Equilibrium
 .65, MHD Thory of usion Systms Prof. ridrg Lctur 8: Effct of Vrticl ild on Tokmk Equilirium Toroidl orc lnc y Mns of Vrticl ild. Lt us riw why th rticl fild is imortnt. 3. or ry short tims, th cuum chmr
.65, MHD Thory of usion Systms Prof. ridrg Lctur 8: Effct of Vrticl ild on Tokmk Equilirium Toroidl orc lnc y Mns of Vrticl ild. Lt us riw why th rticl fild is imortnt. 3. or ry short tims, th cuum chmr
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Th Matrix Exponntial (with xrciss) by D. Klain Vrsion 207.0.05 Corrctions and commnts ar wlcom. Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix A A k I + A + k!
Construction of asymmetric orthogonal arrays of strength three via a replacement method
 isid/ms/26/2 Fbruary, 26 http://www.isid.ac.in/ statmath/indx.php?modul=prprint Construction of asymmtric orthogonal arrays of strngth thr via a rplacmnt mthod Tian-fang Zhang, Qiaoling Dng and Alok Dy
isid/ms/26/2 Fbruary, 26 http://www.isid.ac.in/ statmath/indx.php?modul=prprint Construction of asymmtric orthogonal arrays of strngth thr via a rplacmnt mthod Tian-fang Zhang, Qiaoling Dng and Alok Dy
CONIC SECTIONS. MODULE-IV Co-ordinate Geometry OBJECTIVES. Conic Sections
 Conic Sctions 16 MODULE-IV Co-ordint CONIC SECTIONS Whil cutting crrot ou might hv noticd diffrnt shps shown th dgs of th cut. Anlticll ou m cut it in thr diffrnt ws, nml (i) (ii) (iii) Cut is prlll to
Conic Sctions 16 MODULE-IV Co-ordint CONIC SECTIONS Whil cutting crrot ou might hv noticd diffrnt shps shown th dgs of th cut. Anlticll ou m cut it in thr diffrnt ws, nml (i) (ii) (iii) Cut is prlll to
( ) Geometric Operations and Morphing. Geometric Transformation. Forward v.s. Inverse Mapping. I (x,y ) Image Processing - Lesson 4 IDC-CG 1
 Img Procssing - Lsson 4 Gomtric Oprtions nd Morphing Gomtric Trnsformtion Oprtions dpnd on Pil s Coordints. Contt fr. Indpndnt of pil vlus. f f (, ) (, ) ( f (, ), f ( ) ) I(, ) I', (,) (, ) I(,) I (,
Img Procssing - Lsson 4 Gomtric Oprtions nd Morphing Gomtric Trnsformtion Oprtions dpnd on Pil s Coordints. Contt fr. Indpndnt of pil vlus. f f (, ) (, ) ( f (, ), f ( ) ) I(, ) I', (,) (, ) I(,) I (,
Mathematics. Mathematics 3. hsn.uk.net. Higher HSN23000
 Highr Mthmtics UNIT Mthmtics HSN000 This documnt ws producd spcilly for th HSN.uk.nt wbsit, nd w rquir tht ny copis or drivtiv works ttribut th work to Highr Still Nots. For mor dtils bout th copyright
Highr Mthmtics UNIT Mthmtics HSN000 This documnt ws producd spcilly for th HSN.uk.nt wbsit, nd w rquir tht ny copis or drivtiv works ttribut th work to Highr Still Nots. For mor dtils bout th copyright
The Matrix Exponential
 Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Th Matrix Exponntial (with xrciss) by Dan Klain Vrsion 28928 Corrctions and commnts ar wlcom Th Matrix Exponntial For ach n n complx matrix A, dfin th xponntial of A to b th matrix () A A k I + A + k!
Continuous Random Variables: Basics
 Continuous Rndom Vrils: Bsics Brlin Chn Dprtmnt o Computr Scinc & Inormtion Enginring Ntionl Tiwn Norml Univrsit Rrnc: - D.. Brtss, J. N. Tsitsilis, Introduction to roilit, Sctions 3.-3.3 Continuous Rndom
Continuous Rndom Vrils: Bsics Brlin Chn Dprtmnt o Computr Scinc & Inormtion Enginring Ntionl Tiwn Norml Univrsit Rrnc: - D.. Brtss, J. N. Tsitsilis, Introduction to roilit, Sctions 3.-3.3 Continuous Rndom
This Week. Computer Graphics. Introduction. Introduction. Graphics Maths by Example. Graphics Maths by Example
 This Wk Computr Grphics Vctors nd Oprtions Vctor Arithmtic Gomtric Concpts Points, Lins nd Plns Eploiting Dot Products CSC 470 Computr Grphics 1 CSC 470 Computr Grphics 2 Introduction Introduction Wh do
This Wk Computr Grphics Vctors nd Oprtions Vctor Arithmtic Gomtric Concpts Points, Lins nd Plns Eploiting Dot Products CSC 470 Computr Grphics 1 CSC 470 Computr Grphics 2 Introduction Introduction Wh do
ME 522 PRINCIPLES OF ROBOTICS. FIRST MIDTERM EXAMINATION April 19, M. Kemal Özgören
 ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
ME 522 PINCIPLES OF OBOTICS FIST MIDTEM EXAMINATION April 9, 202 Nm Lst Nm M. Kml Özgörn 2 4 60 40 40 0 80 250 USEFUL FOMULAS cos( ) cos cos sin sin sin( ) sin cos cos sin sin y/ r, cos x/ r, r 0 tn 2(
b. How many ternary words of length 23 with eight 0 s, nine 1 s and six 2 s?
 MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
MATH 3012 Finl Exm, My 4, 2006, WTT Stunt Nm n ID Numr 1. All our prts o this prolm r onrn with trnry strings o lngth n, i.., wors o lngth n with lttrs rom th lpht {0, 1, 2}.. How mny trnry wors o lngth
However, many atoms can combine to form particular molecules, e.g. Chlorine (Cl) and Sodium (Na) atoms form NaCl molecules.
 Lctur 6 Titl: Fundmntls of th Quntum Thory of molcul formtion Pg- In th lst modul, w hv discussd out th tomic structur nd tomic physics to undrstnd th spctrum of toms. Howvr, mny toms cn comin to form
Lctur 6 Titl: Fundmntls of th Quntum Thory of molcul formtion Pg- In th lst modul, w hv discussd out th tomic structur nd tomic physics to undrstnd th spctrum of toms. Howvr, mny toms cn comin to form
Einstein Equations for Tetrad Fields
 Apiron, Vol 13, No, Octobr 006 6 Einstin Equations for Ttrad Filds Ali Rıza ŞAHİN, R T L Istanbul (Turky) Evry mtric tnsor can b xprssd by th innr product of ttrad filds W prov that Einstin quations for
Apiron, Vol 13, No, Octobr 006 6 Einstin Equations for Ttrad Filds Ali Rıza ŞAHİN, R T L Istanbul (Turky) Evry mtric tnsor can b xprssd by th innr product of ttrad filds W prov that Einstin quations for
Chem 104A, Fall 2016, Midterm 1 Key
 hm 104A, ll 2016, Mitrm 1 Ky 1) onstruct microstt tl for p 4 configurtion. Pls numrt th ms n ml for ch lctron in ch microstt in th tl. (Us th formt ml m s. Tht is spin -½ lctron in n s oritl woul writtn
hm 104A, ll 2016, Mitrm 1 Ky 1) onstruct microstt tl for p 4 configurtion. Pls numrt th ms n ml for ch lctron in ch microstt in th tl. (Us th formt ml m s. Tht is spin -½ lctron in n s oritl woul writtn
temperature T speed v time t density ρ scalars may be constant or may be variable yes distributive a(b+c) = ab+ac
 Mthmtics Riw. Sclr mthmticl ntity tht hs mgnitud only.g.: tmprtur T spd tim t dnsity ρ sclrs my constnt or my ril Lws of Algr for Sclrs: ys commutti ys ssociti (c) ()c ys distriuti (c) c Fith A. Morrison,
Mthmtics Riw. Sclr mthmticl ntity tht hs mgnitud only.g.: tmprtur T spd tim t dnsity ρ sclrs my constnt or my ril Lws of Algr for Sclrs: ys commutti ys ssociti (c) ()c ys distriuti (c) c Fith A. Morrison,
Oppgavesett kap. 6 (1 av..)
 Oppgvstt kp. 6 (1 v..) hns.brnn@go.uio.no Problm 1 () Wht is homognous nucltion? Why dos Figur 6.2 in th book show tht w won't gt homognous nucltion in th tmosphr? ˆ Homognous nucltion crts cloud droplts
Oppgvstt kp. 6 (1 v..) hns.brnn@go.uio.no Problm 1 () Wht is homognous nucltion? Why dos Figur 6.2 in th book show tht w won't gt homognous nucltion in th tmosphr? ˆ Homognous nucltion crts cloud droplts
Theoretical Study on the While Drilling Electromagnetic Signal Transmission of Horizontal Well
 7 nd ntrntionl Confrnc on Softwr, Multimdi nd Communiction Enginring (SMCE 7) SBN: 978--6595-458-5 Thorticl Study on th Whil Drilling Elctromgntic Signl Trnsmission of Horizontl Wll Y-huo FAN,,*, Zi-ping
7 nd ntrntionl Confrnc on Softwr, Multimdi nd Communiction Enginring (SMCE 7) SBN: 978--6595-458-5 Thorticl Study on th Whil Drilling Elctromgntic Signl Trnsmission of Horizontl Wll Y-huo FAN,,*, Zi-ping
Minimum Spanning Trees
 Minimum Spnning Trs Minimum Spnning Trs Problm A town hs st of houss nd st of rods A rod conncts nd only houss A rod conncting houss u nd v hs rpir cost w(u, v) Gol: Rpir nough (nd no mor) rods such tht:
Minimum Spnning Trs Minimum Spnning Trs Problm A town hs st of houss nd st of rods A rod conncts nd only houss A rod conncting houss u nd v hs rpir cost w(u, v) Gol: Rpir nough (nd no mor) rods such tht:
The van der Waals interaction 1 D. E. Soper 2 University of Oregon 20 April 2012
 Th van dr Waals intraction D. E. Sopr 2 Univrsity of Orgon 20 pril 202 Th van dr Waals intraction is discussd in Chaptr 5 of J. J. Sakurai, Modrn Quantum Mchanics. Hr I tak a look at it in a littl mor
Th van dr Waals intraction D. E. Sopr 2 Univrsity of Orgon 20 pril 202 Th van dr Waals intraction is discussd in Chaptr 5 of J. J. Sakurai, Modrn Quantum Mchanics. Hr I tak a look at it in a littl mor
COMP108 Algorithmic Foundations
 Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
Grdy mthods Prudn Wong http://www.s.liv..uk/~pwong/thing/omp108/01617 Coin Chng Prolm Suppos w hv 3 typs of oins 10p 0p 50p Minimum numr of oins to mk 0.8, 1.0, 1.? Grdy mthod Lrning outoms Undrstnd wht
Why the Junction Tree Algorithm? The Junction Tree Algorithm. Clique Potential Representation. Overview. Chris Williams 1.
 Why th Juntion Tr lgorithm? Th Juntion Tr lgorithm hris Willims 1 Shool of Informtis, Univrsity of Einurgh Otor 2009 Th JT is gnrl-purpos lgorithm for omputing (onitionl) mrginls on grphs. It os this y
Why th Juntion Tr lgorithm? Th Juntion Tr lgorithm hris Willims 1 Shool of Informtis, Univrsity of Einurgh Otor 2009 Th JT is gnrl-purpos lgorithm for omputing (onitionl) mrginls on grphs. It os this y
SECTION where P (cos θ, sin θ) and Q(cos θ, sin θ) are polynomials in cos θ and sin θ, provided Q is never equal to zero.
 SETION 6. 57 6. Evaluation of Dfinit Intgrals Exampl 6.6 W hav usd dfinit intgrals to valuat contour intgrals. It may com as a surpris to larn that contour intgrals and rsidus can b usd to valuat crtain
SETION 6. 57 6. Evaluation of Dfinit Intgrals Exampl 6.6 W hav usd dfinit intgrals to valuat contour intgrals. It may com as a surpris to larn that contour intgrals and rsidus can b usd to valuat crtain
Addition of angular momentum
 Addition of angular momntum April, 0 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat th
Addition of angular momntum April, 0 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat th
Fourier Transforms and the Wave Equation. Key Mathematics: More Fourier transform theory, especially as applied to solving the wave equation.
 Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
Lur 7 Fourir Transforms and th Wav Euation Ovrviw and Motivation: W first discuss a fw faturs of th Fourir transform (FT), and thn w solv th initial-valu problm for th wav uation using th Fourir transform
(Upside-Down o Direct Rotation) β - Numbers
 Amrican Journal of Mathmatics and Statistics 014, 4(): 58-64 DOI: 10593/jajms0140400 (Upsid-Down o Dirct Rotation) β - Numbrs Ammar Sddiq Mahmood 1, Shukriyah Sabir Ali,* 1 Dpartmnt of Mathmatics, Collg
Amrican Journal of Mathmatics and Statistics 014, 4(): 58-64 DOI: 10593/jajms0140400 (Upsid-Down o Dirct Rotation) β - Numbrs Ammar Sddiq Mahmood 1, Shukriyah Sabir Ali,* 1 Dpartmnt of Mathmatics, Collg
Miscellaneous open problems in the Regular Boundary Collocation approach
 Miscllnous opn problms in th Rgulr Boundry Colloction pproch A. P. Zilińsi Crcow Univrsity of chnology Institut of Mchin Dsign pz@mch.p.du.pl rfftz / MFS Confrnc ohsiung iwn 5-8 Mrch 0 Bsic formultions
Miscllnous opn problms in th Rgulr Boundry Colloction pproch A. P. Zilińsi Crcow Univrsity of chnology Institut of Mchin Dsign pz@mch.p.du.pl rfftz / MFS Confrnc ohsiung iwn 5-8 Mrch 0 Bsic formultions
UNIT # 08 (PART - I)
 . r. d[h d[h.5 7.5 mol L S d[o d[so UNIT # 8 (PRT - I CHEMICL INETICS EXERCISE # 6. d[ x [ x [ x. r [X[C ' [X [[B r '[ [B [C. r [NO [Cl. d[so d[h.5 5 mol L S d[nh d[nh. 5. 6. r [ [B r [x [y r' [x [y r'
. r. d[h d[h.5 7.5 mol L S d[o d[so UNIT # 8 (PRT - I CHEMICL INETICS EXERCISE # 6. d[ x [ x [ x. r [X[C ' [X [[B r '[ [B [C. r [NO [Cl. d[so d[h.5 5 mol L S d[nh d[nh. 5. 6. r [ [B r [x [y r' [x [y r'
Garnir Polynomial and their Properties
 Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
Univrsity of Cliforni, Dvis Dprtmnt of Mthmtis Grnir Polynomil n thir Proprtis Author: Yu Wng Suprvisor: Prof. Gorsky Eugny My 8, 07 Grnir Polynomil n thir Proprtis Yu Wng mil: uywng@uvis.u. In this ppr,
THE SPINOR FIELD THEORY OF THE PHOTON
 Romnin Rports in Physics, Vol. 66, No., P. 9 5, 4 THE SPINOR FIELD THEORY OF THE PHOTON RUO PENG WANG Pking Univrsity, Physics Dprtmnt, Bijing 87, P.R. Chin E-mil: rpwng@pku.du.cn Rcivd Octobr 8, Abstrct.
Romnin Rports in Physics, Vol. 66, No., P. 9 5, 4 THE SPINOR FIELD THEORY OF THE PHOTON RUO PENG WANG Pking Univrsity, Physics Dprtmnt, Bijing 87, P.R. Chin E-mil: rpwng@pku.du.cn Rcivd Octobr 8, Abstrct.
Ch 1.2: Solutions of Some Differential Equations
 Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
Ch 1.2: Solutions of Som Diffrntil Equtions Rcll th fr fll nd owl/mic diffrntil qutions: v 9.8.2v, p.5 p 45 Ths qutions hv th gnrl form y' = y - b W cn us mthods of clculus to solv diffrntil qutions of
EEO 401 Digital Signal Processing Prof. Mark Fowler
 EEO 401 Digital Signal Procssing Prof. Mark Fowlr Dtails of th ot St #19 Rading Assignmnt: Sct. 7.1.2, 7.1.3, & 7.2 of Proakis & Manolakis Dfinition of th So Givn signal data points x[n] for n = 0,, -1
EEO 401 Digital Signal Procssing Prof. Mark Fowlr Dtails of th ot St #19 Rading Assignmnt: Sct. 7.1.2, 7.1.3, & 7.2 of Proakis & Manolakis Dfinition of th So Givn signal data points x[n] for n = 0,, -1
Introduction to Arithmetic Geometry Fall 2013 Lecture #20 11/14/2013
 18.782 Introduction to Arithmtic Gomtry Fall 2013 Lctur #20 11/14/2013 20.1 Dgr thorm for morphisms of curvs Lt us rstat th thorm givn at th nd of th last lctur, which w will now prov. Thorm 20.1. Lt φ:
18.782 Introduction to Arithmtic Gomtry Fall 2013 Lctur #20 11/14/2013 20.1 Dgr thorm for morphisms of curvs Lt us rstat th thorm givn at th nd of th last lctur, which w will now prov. Thorm 20.1. Lt φ:
Limiting value of higher Mahler measure
 Limiting valu of highr Mahlr masur Arunabha Biswas a, Chris Monico a, a Dpartmnt of Mathmatics & Statistics, Txas Tch Univrsity, Lubbock, TX 7949, USA Abstract W considr th k-highr Mahlr masur m k P )
Limiting valu of highr Mahlr masur Arunabha Biswas a, Chris Monico a, a Dpartmnt of Mathmatics & Statistics, Txas Tch Univrsity, Lubbock, TX 7949, USA Abstract W considr th k-highr Mahlr masur m k P )
Recall that by Theorems 10.3 and 10.4 together provide us the estimate o(n2 ), S(q) q 9, q=1
 Chaptr 11 Th singular sris Rcall that by Thorms 10 and 104 togthr provid us th stimat 9 4 n 2 111 Rn = SnΓ 2 + on2, whr th singular sris Sn was dfind in Chaptr 10 as Sn = q=1 Sq q 9, with Sq = 1 a q gcda,q=1
Chaptr 11 Th singular sris Rcall that by Thorms 10 and 104 togthr provid us th stimat 9 4 n 2 111 Rn = SnΓ 2 + on2, whr th singular sris Sn was dfind in Chaptr 10 as Sn = q=1 Sq q 9, with Sq = 1 a q gcda,q=1
u 3 = u 3 (x 1, x 2, x 3 )
 Lctur 23: Curvilinar Coordinats (RHB 8.0 It is oftn convnint to work with variabls othr than th Cartsian coordinats x i ( = x, y, z. For xampl in Lctur 5 w mt sphrical polar and cylindrical polar coordinats.
Lctur 23: Curvilinar Coordinats (RHB 8.0 It is oftn convnint to work with variabls othr than th Cartsian coordinats x i ( = x, y, z. For xampl in Lctur 5 w mt sphrical polar and cylindrical polar coordinats.
Addition of angular momentum
 Addition of angular momntum April, 07 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat
Addition of angular momntum April, 07 Oftn w nd to combin diffrnt sourcs of angular momntum to charactriz th total angular momntum of a systm, or to divid th total angular momntum into parts to valuat
# 1 ' 10 ' 100. Decimal point = 4 hundred. = 6 tens (or sixty) = 5 ones (or five) = 2 tenths. = 7 hundredths.
 How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
How os it work? Pl vlu o imls rprsnt prts o whol numr or ojt # 0 000 Tns o thousns # 000 # 00 Thousns Hunrs Tns Ons # 0 Diml point st iml pl: ' 0 # 0 on tnth n iml pl: ' 0 # 00 on hunrth r iml pl: ' 0
Derangements and Applications
 2 3 47 6 23 Journal of Intgr Squncs, Vol. 6 (2003), Articl 03..2 Drangmnts and Applications Mhdi Hassani Dpartmnt of Mathmatics Institut for Advancd Studis in Basic Scincs Zanjan, Iran mhassani@iasbs.ac.ir
2 3 47 6 23 Journal of Intgr Squncs, Vol. 6 (2003), Articl 03..2 Drangmnts and Applications Mhdi Hassani Dpartmnt of Mathmatics Institut for Advancd Studis in Basic Scincs Zanjan, Iran mhassani@iasbs.ac.ir
10. The Discrete-Time Fourier Transform (DTFT)
 Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
Th Discrt-Tim Fourir Transform (DTFT Dfinition of th discrt-tim Fourir transform Th Fourir rprsntation of signals plays an important rol in both continuous and discrt signal procssing In this sction w
(2) If we multiplied a row of B by λ, then the value is also multiplied by λ(here lambda could be 0). namely
 . DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
. DETERMINANT.. Dtrminnt. Introution:I you think row vtor o mtrix s oorint o vtors in sp, thn th gomtri mning o th rnk o th mtrix is th imnsion o th prlllppi spnn y thm. But w r not only r out th imnsion,
BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES
 BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES DONALD M. DAVIS Abstract. If p is a prim (implicit in notation and n a positiv intgr, lt ν(n dnot th xponnt of p in n, and U(n n/p ν(n, th unit
BINOMIAL COEFFICIENTS INVOLVING INFINITE POWERS OF PRIMES DONALD M. DAVIS Abstract. If p is a prim (implicit in notation and n a positiv intgr, lt ν(n dnot th xponnt of p in n, and U(n n/p ν(n, th unit
The Z transform techniques
 h Z trnfor tchniqu h Z trnfor h th rol in dicrt yt tht th Lplc trnfor h in nlyi of continuou yt. h Z trnfor i th principl nlyticl tool for ingl-loop dicrt-ti yt. h Z trnfor h Z trnfor i to dicrt-ti yt
h Z trnfor tchniqu h Z trnfor h th rol in dicrt yt tht th Lplc trnfor h in nlyi of continuou yt. h Z trnfor i th principl nlyticl tool for ingl-loop dicrt-ti yt. h Z trnfor h Z trnfor i to dicrt-ti yt
Weighted Matching and Linear Programming
 Wightd Mtching nd Linr Progrmming Jonthn Turnr Mrch 19, 01 W v sn tht mximum siz mtchings cn b found in gnrl grphs using ugmnting pths. In principl, this sm pproch cn b pplid to mximum wight mtchings.
Wightd Mtching nd Linr Progrmming Jonthn Turnr Mrch 19, 01 W v sn tht mximum siz mtchings cn b found in gnrl grphs using ugmnting pths. In principl, this sm pproch cn b pplid to mximum wight mtchings.
LINEAR DELAY DIFFERENTIAL EQUATION WITH A POSITIVE AND A NEGATIVE TERM
 Elctronic Journal of Diffrntial Equations, Vol. 2003(2003), No. 92, pp. 1 6. ISSN: 1072-6691. URL: http://jd.math.swt.du or http://jd.math.unt.du ftp jd.math.swt.du (login: ftp) LINEAR DELAY DIFFERENTIAL
Elctronic Journal of Diffrntial Equations, Vol. 2003(2003), No. 92, pp. 1 6. ISSN: 1072-6691. URL: http://jd.math.swt.du or http://jd.math.unt.du ftp jd.math.swt.du (login: ftp) LINEAR DELAY DIFFERENTIAL
CSE 373: AVL trees. Warmup: Warmup. Interlude: Exploring the balance invariant. AVL Trees: Invariants. AVL tree invariants review
 rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
rmup CSE 7: AVL trs rmup: ht is n invrint? Mihl L Friy, Jn 9, 0 ht r th AVL tr invrints, xtly? Disuss with your nighor. AVL Trs: Invrints Intrlu: Exploring th ln invrint Cor i: xtr invrint to BSTs tht
Solution: APPM 1360 Final (150 pts) Spring (60 pts total) The following parts are not related, justify your answers:
 APPM 6 Final 5 pts) Spring 4. 6 pts total) Th following parts ar not rlatd, justify your answrs: a) Considr th curv rprsntd by th paramtric quations, t and y t + for t. i) 6 pts) Writ down th corrsponding
APPM 6 Final 5 pts) Spring 4. 6 pts total) Th following parts ar not rlatd, justify your answrs: a) Considr th curv rprsntd by th paramtric quations, t and y t + for t. i) 6 pts) Writ down th corrsponding
arxiv: v2 [math.ca] 24 Feb 2016
![arxiv: v2 [math.ca] 24 Feb 2016 arxiv: v2 [math.ca] 24 Feb 2016](/thumbs/74/71089459.jpg) Product of prbolic cylindr functions involving Lplc trnsforms of conflunt hyprgomtric functions Ridh Nsri rxiv:53.69v [mth.ca] 4 Fb 6 Orng Lbs, 38-4 vnu Gnrl Lclrc, 9794 Issy-ls-Moulinux, Frnc In this
Product of prbolic cylindr functions involving Lplc trnsforms of conflunt hyprgomtric functions Ridh Nsri rxiv:53.69v [mth.ca] 4 Fb 6 Orng Lbs, 38-4 vnu Gnrl Lclrc, 9794 Issy-ls-Moulinux, Frnc In this
Finite Automata. d: Q S Q. Finite automaton is M=(Q, S, d, q 0, F) Ex: an FA that accepts all odd-length strings of zeros: q 0 q 1. q i. q k.
 Finit Automt Bsic id: FA is mchin tht chngs stts whil procssing symols, on t tim. Finit st of stts: Q = {q 0, q 1, q 3,..., q k } Trnsition function: Initil stt: Finl stts: d: Q S Q q 0 Q F Q Finit utomton
Finit Automt Bsic id: FA is mchin tht chngs stts whil procssing symols, on t tim. Finit st of stts: Q = {q 0, q 1, q 3,..., q k } Trnsition function: Initil stt: Finl stts: d: Q S Q q 0 Q F Q Finit utomton
Quasi-Classical States of the Simple Harmonic Oscillator
 Quasi-Classical Stats of th Simpl Harmonic Oscillator (Draft Vrsion) Introduction: Why Look for Eignstats of th Annihilation Oprator? Excpt for th ground stat, th corrspondnc btwn th quantum nrgy ignstats
Quasi-Classical Stats of th Simpl Harmonic Oscillator (Draft Vrsion) Introduction: Why Look for Eignstats of th Annihilation Oprator? Excpt for th ground stat, th corrspondnc btwn th quantum nrgy ignstats
page 11 equation (1.2-10c), break the bar over the right side in the middle
 I. Corrctios Lst Updtd: Ju 00 Complx Vrils with Applictios, 3 rd ditio, A. Dvid Wusch First Pritig. A ook ought for My 007 will proly first pritig With Thks to Christi Hos of Swd pg qutio (.-0c), rk th
I. Corrctios Lst Updtd: Ju 00 Complx Vrils with Applictios, 3 rd ditio, A. Dvid Wusch First Pritig. A ook ought for My 007 will proly first pritig With Thks to Christi Hos of Swd pg qutio (.-0c), rk th
ECE602 Exam 1 April 5, You must show ALL of your work for full credit.
 ECE62 Exam April 5, 27 Nam: Solution Scor: / This xam is closd-book. You must show ALL of your work for full crdit. Plas rad th qustions carfully. Plas chck your answrs carfully. Calculators may NOT b
ECE62 Exam April 5, 27 Nam: Solution Scor: / This xam is closd-book. You must show ALL of your work for full crdit. Plas rad th qustions carfully. Plas chck your answrs carfully. Calculators may NOT b
Errata for Second Edition, First Printing
 Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 71: Eqution (.3) should rd B( R) = θ R 1 x= [1 G( x)] pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1
Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 71: Eqution (.3) should rd B( R) = θ R 1 x= [1 G( x)] pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1
0.1. Exercise 1: the distances between four points in a graph
 Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 pg 1 Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 u: W, 3 My 2017, in lss or y mil (grinr@umn.u) or lss S th wsit or rlvnt mtril. Rsults provn in th nots, or in
Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 pg 1 Mth 707 Spring 2017 (Drij Grinrg): mitrm 3 u: W, 3 My 2017, in lss or y mil (grinr@umn.u) or lss S th wsit or rlvnt mtril. Rsults provn in th nots, or in
Errata for Second Edition, First Printing
 Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1 G( x)] = θp( R) + ( θ R)[1 G( R)] pg 15, problm 6: dmnd of
Errt for Scond Edition, First Printing pg 68, lin 1: z=.67 should b z=.44 pg 1: Eqution (.63) should rd B( R) = x= R = θ ( x R) p( x) R 1 x= [1 G( x)] = θp( R) + ( θ R)[1 G( R)] pg 15, problm 6: dmnd of
1 Introduction to Modulo 7 Arithmetic
 1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
1 Introution to Moulo 7 Arithmti Bor w try our hn t solvin som hr Moulr KnKns, lt s tk los look t on moulr rithmti, mo 7 rithmti. You ll s in this sminr tht rithmti moulo prim is quit irnt rom th ons w
, each of which is a tree, and whose roots r 1. , respectively, are children of r. Data Structures & File Management
 nrl tr T is init st o on or mor nos suh tht thr is on sint no r, ll th root o T, n th rminin nos r prtition into n isjoint susts T, T,, T n, h o whih is tr, n whos roots r, r,, r n, rsptivly, r hilrn o
nrl tr T is init st o on or mor nos suh tht thr is on sint no r, ll th root o T, n th rminin nos r prtition into n isjoint susts T, T,, T n, h o whih is tr, n whos roots r, r,, r n, rsptivly, r hilrn o
MASTER CLASS PROGRAM UNIT 4 SPECIALIST MATHEMATICS SEMESTER TWO 2014 WEEK 11 WRITTEN EXAMINATION 1 SOLUTIONS
 MASTER CLASS PROGRAM UNIT SPECIALIST MATHEMATICS SEMESTER TWO WEEK WRITTEN EXAMINATION SOLUTIONS FOR ERRORS AND UPDATES, PLEASE VISIT WWW.TSFX.COM.AU/MC-UPDATES QUESTION () Lt p ( z) z z z If z i z ( is
MASTER CLASS PROGRAM UNIT SPECIALIST MATHEMATICS SEMESTER TWO WEEK WRITTEN EXAMINATION SOLUTIONS FOR ERRORS AND UPDATES, PLEASE VISIT WWW.TSFX.COM.AU/MC-UPDATES QUESTION () Lt p ( z) z z z If z i z ( is
Supplementary Materials
 6 Supplmntary Matrials APPENDIX A PHYSICAL INTERPRETATION OF FUEL-RATE-SPEED FUNCTION A truck running on a road with grad/slop θ positiv if moving up and ngativ if moving down facs thr rsistancs: arodynamic
6 Supplmntary Matrials APPENDIX A PHYSICAL INTERPRETATION OF FUEL-RATE-SPEED FUNCTION A truck running on a road with grad/slop θ positiv if moving up and ngativ if moving down facs thr rsistancs: arodynamic
CSE 373: More on graphs; DFS and BFS. Michael Lee Wednesday, Feb 14, 2018
 CSE 373: Mor on grphs; DFS n BFS Mihl L Wnsy, F 14, 2018 1 Wrmup Wrmup: Disuss with your nighor: Rmin your nighor: wht is simpl grph? Suppos w hv simpl, irt grph with x nos. Wht is th mximum numr of gs
CSE 373: Mor on grphs; DFS n BFS Mihl L Wnsy, F 14, 2018 1 Wrmup Wrmup: Disuss with your nighor: Rmin your nighor: wht is simpl grph? Suppos w hv simpl, irt grph with x nos. Wht is th mximum numr of gs
ELEG 413 Lecture #6. Mark Mirotznik, Ph.D. Professor The University of Delaware
 LG 43 Lctur #6 Mrk Mirtnik, Ph.D. Prfssr Th Univrsity f Dlwr mil: mirtni@c.udl.du Wv Prpgtin nd Plritin TM: Trnsvrs lctrmgntic Wvs A md is prticulr fild cnfigurtin. Fr givn lctrmgntic bundry vlu prblm,
LG 43 Lctur #6 Mrk Mirtnik, Ph.D. Prfssr Th Univrsity f Dlwr mil: mirtni@c.udl.du Wv Prpgtin nd Plritin TM: Trnsvrs lctrmgntic Wvs A md is prticulr fild cnfigurtin. Fr givn lctrmgntic bundry vlu prblm,
Basic Polyhedral theory
 Basic Polyhdral thory Th st P = { A b} is calld a polyhdron. Lmma 1. Eithr th systm A = b, b 0, 0 has a solution or thr is a vctorπ such that π A 0, πb < 0 Thr cass, if solution in top row dos not ist
Basic Polyhdral thory Th st P = { A b} is calld a polyhdron. Lmma 1. Eithr th systm A = b, b 0, 0 has a solution or thr is a vctorπ such that π A 0, πb < 0 Thr cass, if solution in top row dos not ist
That is, we start with a general matrix: And end with a simpler matrix:
 DIAGON ALIZATION OF THE STR ESS TEN SOR INTRO DUCTIO N By th us of Cauchy s thorm w ar abl to rduc th numbr of strss componnts in th strss tnsor to only nin valus. An additional simplification of th strss
DIAGON ALIZATION OF THE STR ESS TEN SOR INTRO DUCTIO N By th us of Cauchy s thorm w ar abl to rduc th numbr of strss componnts in th strss tnsor to only nin valus. An additional simplification of th strss
Section 6.1. Question: 2. Let H be a subgroup of a group G. Then H operates on G by left multiplication. Describe the orbits for this operation.
 MAT 444 H Barclo Spring 004 Homwork 6 Solutions Sction 6 Lt H b a subgroup of a group G Thn H oprats on G by lft multiplication Dscrib th orbits for this opration Th orbits of G ar th right costs of H
MAT 444 H Barclo Spring 004 Homwork 6 Solutions Sction 6 Lt H b a subgroup of a group G Thn H oprats on G by lft multiplication Dscrib th orbits for this opration Th orbits of G ar th right costs of H
A Simple Formula for the Hilbert Metric with Respect to a Sub-Gaussian Cone
 mathmatics Articl A Simpl Formula for th Hilbrt Mtric with Rspct to a Sub-Gaussian Con Stéphan Chrétin 1, * and Juan-Pablo Ortga 2 1 National Physical Laboratory, Hampton Road, Tddinton TW11 0LW, UK 2
mathmatics Articl A Simpl Formula for th Hilbrt Mtric with Rspct to a Sub-Gaussian Con Stéphan Chrétin 1, * and Juan-Pablo Ortga 2 1 National Physical Laboratory, Hampton Road, Tddinton TW11 0LW, UK 2
a b c cat CAT A B C Aa Bb Cc cat cat Lesson 1 (Part 1) Verbal lesson: Capital Letters Make The Same Sound Lesson 1 (Part 1) continued...
 Progrssiv Printing T.M. CPITLS g 4½+ Th sy, fun (n FR!) wy to tch cpitl lttrs. ook : C o - For Kinrgrtn or First Gr (not for pr-school). - Tchs tht cpitl lttrs mk th sm souns s th littl lttrs. - Tchs th
Progrssiv Printing T.M. CPITLS g 4½+ Th sy, fun (n FR!) wy to tch cpitl lttrs. ook : C o - For Kinrgrtn or First Gr (not for pr-school). - Tchs tht cpitl lttrs mk th sm souns s th littl lttrs. - Tchs th
Problem 1. Solution: = show that for a constant number of particles: c and V. a) Using the definitions of P
 rol. Using t dfinitions of nd nd t first lw of trodynis nd t driv t gnrl rltion: wr nd r t sifi t itis t onstnt rssur nd volu rstivly nd nd r t intrnl nrgy nd volu of ol. first lw rlts d dq d t onstnt
rol. Using t dfinitions of nd nd t first lw of trodynis nd t driv t gnrl rltion: wr nd r t sifi t itis t onstnt rssur nd volu rstivly nd nd r t intrnl nrgy nd volu of ol. first lw rlts d dq d t onstnt
CS September 2018
 Loil los Distriut Systms 06. Loil los Assin squn numrs to msss All ooprtin prosss n r on orr o vnts vs. physil los: rport tim o y Assum no ntrl tim sour Eh systm mintins its own lol lo No totl orrin o
Loil los Distriut Systms 06. Loil los Assin squn numrs to msss All ooprtin prosss n r on orr o vnts vs. physil los: rport tim o y Assum no ntrl tim sour Eh systm mintins its own lol lo No totl orrin o
CS 361 Meeting 12 10/3/18
 CS 36 Mting 2 /3/8 Announcmnts. Homwork 4 is du Friday. If Friday is Mountain Day, homwork should b turnd in at my offic or th dpartmnt offic bfor 4. 2. Homwork 5 will b availabl ovr th wknd. 3. Our midtrm
CS 36 Mting 2 /3/8 Announcmnts. Homwork 4 is du Friday. If Friday is Mountain Day, homwork should b turnd in at my offic or th dpartmnt offic bfor 4. 2. Homwork 5 will b availabl ovr th wknd. 3. Our midtrm
HIGHER ORDER DIFFERENTIAL EQUATIONS
 Prof Enriqu Mtus Nivs PhD in Mthmtis Edution IGER ORDER DIFFERENTIAL EQUATIONS omognous linr qutions with onstnt offiints of ordr two highr Appl rdution mthod to dtrmin solution of th nonhomognous qution
Prof Enriqu Mtus Nivs PhD in Mthmtis Edution IGER ORDER DIFFERENTIAL EQUATIONS omognous linr qutions with onstnt offiints of ordr two highr Appl rdution mthod to dtrmin solution of th nonhomognous qution
On spanning trees and cycles of multicolored point sets with few intersections
 On spanning trs and cycls of multicolord point sts with fw intrsctions M. Kano, C. Mrino, and J. Urrutia April, 00 Abstract Lt P 1,..., P k b a collction of disjoint point sts in R in gnral position. W
On spanning trs and cycls of multicolord point sts with fw intrsctions M. Kano, C. Mrino, and J. Urrutia April, 00 Abstract Lt P 1,..., P k b a collction of disjoint point sts in R in gnral position. W
