`Anomalous dimensions for conserved currents and Noether s Second Theorem
|
|
|
- Arleen Hoover
- 5 years ago
- Views:
Transcription
1 `Anomalous dimensions for conserved currents and Noether s Second Theorem Thanks to: NSF, EFRC (DOE) Gabriele La Nave Kridsangaphong Limtragool
2 0 no order Mott insulator x
3 strange metal: experimental facts T-linear resistivity L xy = apple xy /T xy 6=#/ T (!) =C! 2 3 n e 2 m 1 1 i!
4 standard metals resistivity / T 2 Weidemann-Franz law apple xx = 2 T xx 3 optical conductivity < / 1/! 2
5 why is the problem hard?
6 single-parameter scaling / z 2 ln Z! A µ A µ 1 / T (2 d)/z (!, T) /! (d 2)/z 2/3 C v / T d/z anomalous dimension 2! 2d A
7 dimension of vector potential gauge invariance A µ!a µ µ G has no units [A µ ]= 1 L =1 vector potential cannot have an anomalous dimension conserved current
8 gauge invariance= current conservation Z S = d d x F 2 + J µ A µ + A! A Z S! S + d d xj integrate by parts Noether s Thm. µ J µ =0 current conservation
9 gauge invariance [A µ ]=1 current conservation [d d xja] =0 fixes dimension of current [J] =d 1
10 photon propagator ha i (k)a j ( k)i / ij k 2
11 strange metal explained! Hall Angle cot H xx xy T 2 T-linear resistivity Hall Lorenz ratio L xy = apple xy /T xy 6=#/ T all explained if [J µ ]=d + + z 1 Hartnoll/Karch [A µ ]=1 = 2/3
12 strange metal: strange E&M [J µ ]=d + + z 1 [A µ ]=1 = 2/3 [E] =1+z [B] =2 note r 2 B 6= flux ha i (k)a j ( k)i / ij k 2(1 ) non-local propagator
13 ha i (k)a j ( k)i / ij k 2(1 )
14 How is this possible - - if at all?
15 current algebra with an anomalous dimension? is there a direct experimental probe of this anomaly? how can A have an `anomalous dimension? what else can be explained with an anomalous dimension?
16 what is the new gauge principle? if [A µ ] 6= 1 A µ! A µ µ
17 µ J µ =0 current conservation what if [@ µ, Ŷ ]=0 new µ ŶJ µ µ J µ =0 [ J] =d 1 D Y
18 possible gauge transformations Z S = 1 d d xf 2 4 S = 1 2 Z d d k 2 d A µ(k)[k 2 µ M µ { k µ k ]A (k) k =0 zero eigenvector ik A µ! A µ µ
19 family of zero eigenvalues M µ fk =0 { generator of gauge symmetry 1.) rotational invariance 2.) A is still a 1-form 3.) [f,k µ ]=0
20 only choice f f(k 2 ) ( ) A µ! A µ +( ) ( 1) µ [A µ ]= what kind of E&M has such gauge transformations?
21 if [A µ ] 6= 1 but the current is conserved
22 extra dimensions
23 model with anomalous dimensions S = Z d d+2 x p g appler (@ µ ) 2 2 Z( ) 4 F 2 + V ( ) 8 < : Z( )!!1 Z 0 e V ( )!!1 V 0 e. e = r ±apple r F 2 Karch: Gouteraux:
24 claim [A] 6= 1 y =1 S = Z dv d dy y a F 2 + y =0 how?? F = da
25 if holography is RG then how can it lead to an anomalous dimension?
26 standard case A J Z d d xa J A(y = 0) = A bc does not satisfy A(y = 0) 6= A + d
27 alternatively (A + d = a + boundary theory has non-trivial gauge structure AdS/ Lifshitz Z dy/y = 1 large gauge transformation
28 construct boundary theory explicitly
29 S = Z dv d dy y a F 2 + eom d(y a? da) =0 y 6= 0 A! A what about the boundary?
30 Caffarelli-Silvestre extension theorem (2006) y g(x, y = 0) = f(x) xg + a y g y + g yy =0 r (y a rg(x, y)) = 0 lim y!0 y g? C d, ( ) f x g(z =0,x)=f(x) fractional Laplacian = 1 a 2
31 boundary is non-local! Z ( x) a f(x) =C d,a d (f(x) R d f( )) x d+2a Chang/Gonzalez P 2 ( ĝ) + 1 pseudo-differential operator
32 closer look r (y a ru) =0 scalar field (use CS theorem) d(y a? da) =0 holography similar equations generalize CS theorem to p-forms GL,PP: (CIMP)
33 generalize CS to p-forms y!0 ya i 1 i = C d, ( )! i1 i p fractional Maxwell equations at boundary!
34 boundary action: fractional Maxwell equations A? =0 A? = J boundary action has `anomalous dimension (non-locality)
35 if holography is RG then how can it lead to an anomalous dimension? Z S = dv d dy y a F 2 + [A] =1 a/2 dimension of A is fixed by the bulk theory: not really anomalous dimension
36 define F ij i A j A i d A = d 1 2 A, S = Z 1 4 F ijf ij integrate by parts S = Z 1 2 A i( ) 2 A i, non-local boundary action
37 fractional differential } (a 1)/2 d a = 1 2 (d(d d) (a 1)/2! +(dd ) (a 1)/2 d!) d =( 1) n(p+1)+1? d? dd : p (M)! p (M) does not change the order of the form
38 new gauge transformation A! A + d, d ( ) 1 2 d [A] = boundary does lies at infinity (large gauge transformation)
39 causality A µ =0 [, ] =0 share the same eigenfunctions e i ( ~ k ~x!t) =(k 2! 2 ) e i ( ~ k ~x!t)! = ck
40 from the bulk use CS theorem lim y!0 (x, y),y (x 0,y)] = [ (x, y, (x 0,y)] = (x x 0 )=0 no problem with causality
41 S = Z 1 2 A i( ) 2 A i, ha i (k)a j ( k)i / ij k 2
42 @ µ J µ =0 current conservation what if [@ µ, Ŷ ]=0
43 answer? µ, Ŷ ]=0 [d, ]=0 Ŷ = J! J [J] =d 1
44 current-current correlator ij k i k j C ij (k) / (k 2 ) k 2. standard Ward identity k i C ij (k) i C ij (k) =0 but k 1 k µ C µ µ ( ) 1 2 C µ =0 inherent ambiguity in E&M
45 family of zero eigenvalues M µ fk =0 most fundamental conservation µ ( r 2 ) ( 1)/2 J µ =0
46 Noether s Theorems A µ! A µ µ G +,
47 arxiv:
48 is this just a game? is there a consistent algebra for fractional currents?
49 Yes
50 Virasoro algebra L n := [L n,l m ]=(n m)l n+m + c 12 m(m2 1) m+n,0 Witt algebra central extension conformal transformations on unit disk V! W! 1
51 Fractional Virasoro algebra generators a a L a n = La n := z [L n,l m ](z ak )= (a(k + n) + 1) (a(k 1+n) + 1) (a(k + m) + 1) (a(k 1+m) + 1) L n+m (z ak ) =(A a n,m(k) L n+m )(z ak ) [L a m,l a n]=a m,n L a m+n + m,n h(n)cz a algebra for conformal nonlocal actions Z 2?(W a, H)/B 2?(W a, H)
52 experiments?
53 skin effect = r 2!µ
54 new result 1 2 r ~ B E ~ v = µ ~ J =1/k 2 = v 2! 1 2( +1) 1 sin 2( +1) + 2 n +1
55 ~B magnetic flux r 2 B should be dimensionless [B] =2 =2+2/3 6= 2 what s the resolution?
56 correct dimensionless quantity D i i e ~ a i fictitious gauge field a i [@ i,i i A i ]=@ i I i A i a µ! a µ µ A! A + d = e ~ I ~a(~r) d ~ l.
57 New Aharonov-Bohm Effect D = e p 2 ~ r2 BR (2 ) (1 2 )! ( ) ( ) sin F 1 (1, 2 ; 2; r2 R 2 )
58 is the correction large? =1+2/3 =5/3 R = eb`2 ~ L 5/3 /(0.43) 2 yes!
59 experiment Planckian dissipation = ~ k B T ybco, s
60 if in the strange metal [A µ ]=d A 6=1 1 2 r ~ B God said ~! E v 2 = µ ~ 1 2 r E ~ = 1 2 r ~ E ~ =0 1 2 r ~ B =0. Pippard Kernel Z J µ (x) = d d x 0 C µ ( x [J] 6= d 1 [A] 6= 1 x 0 )A fractional E&M in SC!! = ck
Do Cuprates Harbor Extra Dimensions?
 Do Cuprates Harbor Extra Dimensions? Thanks to: NSF, EFRC (DOE) Gabriele La Nave Kridsangaphong Limtragool How would such dimensions be detected? Do they obey the standard electricity and magnetism? standard
Do Cuprates Harbor Extra Dimensions? Thanks to: NSF, EFRC (DOE) Gabriele La Nave Kridsangaphong Limtragool How would such dimensions be detected? Do they obey the standard electricity and magnetism? standard
`Anomalous dimensions for conserved currents from holographic dilatonic models to superconductivity. Gabriele La Nave. Thanks to: NSF, EFRC (DOE)
 `Anomalous dimensions for conserved currents from holographic dilatonic models to superconductivity Thanks to: NSF, EFRC (DOE) Gabriele La Nave Kridsangaphong Limtragool Pippard s problem J s 6= c 4 2
`Anomalous dimensions for conserved currents from holographic dilatonic models to superconductivity Thanks to: NSF, EFRC (DOE) Gabriele La Nave Kridsangaphong Limtragool Pippard s problem J s 6= c 4 2
Detecting unparticles and anomalous dimensions in the Strange Metal
 Detecting unparticles and anomalous dimensions in the Strange Metal Thanks to: NSF, EFRC (DOE) Andreas Karch Brandon Langley Garrett Vanacore Kridsangaphong Limtragool Gabriele La Nave Drude metal Drude
Detecting unparticles and anomalous dimensions in the Strange Metal Thanks to: NSF, EFRC (DOE) Andreas Karch Brandon Langley Garrett Vanacore Kridsangaphong Limtragool Gabriele La Nave Drude metal Drude
Unaprticles: MEELS, ARPES and the Strange Metal
 Unaprticles: MEELS, ARPES and the Strange Metal K. Limtragool Chandan Setty Chandan Setty Zhidong Leong Zhidong Leong Bikash Padhi strange metal: experimental facts T-linear resistivity (!) =C! 2 3 L xy
Unaprticles: MEELS, ARPES and the Strange Metal K. Limtragool Chandan Setty Chandan Setty Zhidong Leong Zhidong Leong Bikash Padhi strange metal: experimental facts T-linear resistivity (!) =C! 2 3 L xy
Testing Mottness/unparticles and anomalous dimensions in the Cuprates
 Testing Mottness/unparticles and anomalous dimensions in the Cuprates Thanks to: NSF, EFRC (DOE) Brandon Langley Garrett Vanacore Kridsangaphong Limtragool / at what is strange about the strange metal?
Testing Mottness/unparticles and anomalous dimensions in the Cuprates Thanks to: NSF, EFRC (DOE) Brandon Langley Garrett Vanacore Kridsangaphong Limtragool / at what is strange about the strange metal?
Anomalous dimensions, Mottness, Bose metals, and holography. D. Dalidovich G. La Nave G. Vanacore. Wednesday, January 18, 17
 Anomalous dimensions, Mottness, Bose metals, and holography D. Dalidovich G. La Nave G. Vanacore Anomalous dimensions, Mottness, Bose metals, and holography 1 p 2 (p 2 ) d U d/2 Fermi liquids D. Dalidovich
Anomalous dimensions, Mottness, Bose metals, and holography D. Dalidovich G. La Nave G. Vanacore Anomalous dimensions, Mottness, Bose metals, and holography 1 p 2 (p 2 ) d U d/2 Fermi liquids D. Dalidovich
Optical Conductivity in the Cuprates from holography and unparticles
 Optical Conductivity in the Cuprates from holography and unparticles Thanks to: NSF, EFRC (DOE) Brandon Langley Garrett Vanacore Kridsangaphong Limtragool Properties all particles share? charge fixed mass!
Optical Conductivity in the Cuprates from holography and unparticles Thanks to: NSF, EFRC (DOE) Brandon Langley Garrett Vanacore Kridsangaphong Limtragool Properties all particles share? charge fixed mass!
Optical Conductivity in the Cuprates from Holography and Unparticles
 Optical Conductivity in the Cuprates from Holography and Unparticles Thanks to: NSF, EFRC (DOE) Brandon Langley Garrett Vanacore Kridsangaphong Limtragool Drude conductivity n e 2 1 m 1 i! (!) =C! 2 3
Optical Conductivity in the Cuprates from Holography and Unparticles Thanks to: NSF, EFRC (DOE) Brandon Langley Garrett Vanacore Kridsangaphong Limtragool Drude conductivity n e 2 1 m 1 i! (!) =C! 2 3
Optical Conductivity in the Cuprates: from Mottness to Scale Invariance
 Optical Conductivity in the Cuprates: from Mottness to Scale Invariance Thanks to: NSF, EFRC (DOE) Brandon Langley Garrett Vanacore Kridsangaphong Limtragool N e ( ) = 2mV cell e 2 Z 0 (!)d! optical
Optical Conductivity in the Cuprates: from Mottness to Scale Invariance Thanks to: NSF, EFRC (DOE) Brandon Langley Garrett Vanacore Kridsangaphong Limtragool N e ( ) = 2mV cell e 2 Z 0 (!)d! optical
Holography, Soft Theorems, and Infinite Dimensional Symmetries of Flat Space
 Holography, Soft Theorems, and Infinite Dimensional Symmetries of Flat Space Clifford Cheung w/ Anton de la Fuente & Raman Sundrum (1607.xxxxx) Asymptotic Symmetries of Yang-Mills Theory Andrew Strominger
Holography, Soft Theorems, and Infinite Dimensional Symmetries of Flat Space Clifford Cheung w/ Anton de la Fuente & Raman Sundrum (1607.xxxxx) Asymptotic Symmetries of Yang-Mills Theory Andrew Strominger
3.15. Some symmetry properties of the Berry curvature and the Chern number.
 50 Phys620.nb z M 3 at the K point z M 3 3 t ' sin 3 t ' sin (3.36) (3.362) Therefore, as long as M 3 3 t ' sin, the system is an topological insulator ( z flips sign). If M 3 3 t ' sin, z is always positive
50 Phys620.nb z M 3 at the K point z M 3 3 t ' sin 3 t ' sin (3.36) (3.362) Therefore, as long as M 3 3 t ' sin, the system is an topological insulator ( z flips sign). If M 3 3 t ' sin, z is always positive
Dimensional Reduction in the Early Universe
 Dimensional Reduction in the Early Universe Giulia Gubitosi University of Rome Sapienza References: PLB 736 (2014) 317 PRD 88 (2013) 103524 PRD 88 (2013) 041303 PRD 87 (2013) 123532 (with G. Amelino-Camelia,
Dimensional Reduction in the Early Universe Giulia Gubitosi University of Rome Sapienza References: PLB 736 (2014) 317 PRD 88 (2013) 103524 PRD 88 (2013) 041303 PRD 87 (2013) 123532 (with G. Amelino-Camelia,
Geometry and Motion Selected answers to Sections A and C Dwight Barkley 2016
 MA34 Geometry and Motion Selected answers to Sections A and C Dwight Barkley 26 Example Sheet d n+ = d n cot θ n r θ n r = Θθ n i. 2. 3. 4. Possible answers include: and with opposite orientation: 5..
MA34 Geometry and Motion Selected answers to Sections A and C Dwight Barkley 26 Example Sheet d n+ = d n cot θ n r θ n r = Θθ n i. 2. 3. 4. Possible answers include: and with opposite orientation: 5..
Field Theory Description of Topological States of Matter. Andrea Cappelli INFN, Florence (w. E. Randellini, J. Sisti)
 Field Theory Description of Topological States of Matter Andrea Cappelli INFN, Florence (w. E. Randellini, J. Sisti) Topological States of Matter System with bulk gap but non-trivial at energies below
Field Theory Description of Topological States of Matter Andrea Cappelli INFN, Florence (w. E. Randellini, J. Sisti) Topological States of Matter System with bulk gap but non-trivial at energies below
6.1 Matrices. Definition: A Matrix A is a rectangular array of the form. A 11 A 12 A 1n A 21. A 2n. A m1 A m2 A mn A 22.
 61 Matrices Definition: A Matrix A is a rectangular array of the form A 11 A 12 A 1n A 21 A 22 A 2n A m1 A m2 A mn The size of A is m n, where m is the number of rows and n is the number of columns The
61 Matrices Definition: A Matrix A is a rectangular array of the form A 11 A 12 A 1n A 21 A 22 A 2n A m1 A m2 A mn The size of A is m n, where m is the number of rows and n is the number of columns The
can be moved in energy/momentum but not individually destroyed; in general: topological Fermi surfaces
 nodes protected against gapping can be moved in energy/momentum but not individually destroyed; in general: topological Fermi surfaces physical realization: stacked 2d topological insulators C=1 3d top
nodes protected against gapping can be moved in energy/momentum but not individually destroyed; in general: topological Fermi surfaces physical realization: stacked 2d topological insulators C=1 3d top
1. (a) (5 points) Find the unit tangent and unit normal vectors T and N to the curve. r (t) = 3 cos t, 0, 3 sin t, r ( 3π
 1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P 3, 3π, r t) 3 cos t, 4t, 3 sin t 3 ). b) 5 points) Find curvature of the curve at the point P. olution:
1. a) 5 points) Find the unit tangent and unit normal vectors T and N to the curve at the point P 3, 3π, r t) 3 cos t, 4t, 3 sin t 3 ). b) 5 points) Find curvature of the curve at the point P. olution:
x + ye z2 + ze y2, y + xe z2 + ze x2, z and where T is the
 1.(8pts) Find F ds where F = x + ye z + ze y, y + xe z + ze x, z and where T is the T surface in the pictures. (The two pictures are two views of the same surface.) The boundary of T is the unit circle
1.(8pts) Find F ds where F = x + ye z + ze y, y + xe z + ze x, z and where T is the T surface in the pictures. (The two pictures are two views of the same surface.) The boundary of T is the unit circle
On higher-spin gravity in three dimensions
 On higher-spin gravity in three dimensions Jena, 6 November 2015 Stefan Fredenhagen Humboldt-Universität zu Berlin und Max-Planck-Institut für Gravitationsphysik Higher spins Gauge theories are a success
On higher-spin gravity in three dimensions Jena, 6 November 2015 Stefan Fredenhagen Humboldt-Universität zu Berlin und Max-Planck-Institut für Gravitationsphysik Higher spins Gauge theories are a success
Towards new non-geometric backgrounds
 Towards new non-geometric backgrounds Erik Plauschinn University of Padova Ringberg 30.07.204 this talk is based on... This talk is based on T-duality revisited [arxiv:30.494], and on some work in progress
Towards new non-geometric backgrounds Erik Plauschinn University of Padova Ringberg 30.07.204 this talk is based on... This talk is based on T-duality revisited [arxiv:30.494], and on some work in progress
EXAM MATHEMATICAL METHODS OF PHYSICS. TRACK ANALYSIS (Chapters I-V). Thursday, June 7th,
 EXAM MATHEMATICAL METHODS OF PHYSICS TRACK ANALYSIS (Chapters I-V) Thursday, June 7th, 1-13 Students who are entitled to a lighter version of the exam may skip problems 1, 8-11 and 16 Consider the differential
EXAM MATHEMATICAL METHODS OF PHYSICS TRACK ANALYSIS (Chapters I-V) Thursday, June 7th, 1-13 Students who are entitled to a lighter version of the exam may skip problems 1, 8-11 and 16 Consider the differential
Topological insulator part II: Berry Phase and Topological index
 Phys60.nb 11 3 Topological insulator part II: Berry Phase and Topological index 3.1. Last chapter Topological insulator: an insulator in the bulk and a metal near the boundary (surface or edge) Quantum
Phys60.nb 11 3 Topological insulator part II: Berry Phase and Topological index 3.1. Last chapter Topological insulator: an insulator in the bulk and a metal near the boundary (surface or edge) Quantum
Unparticles in High T_c Superconductors
 Unparticles in High T_c Superconductors Thanks to: NSF, EFRC (DOE) Kiaran dave Charlie Kane Brandon Langley J. A. Hutasoit Correlated Electron Matter Correlated Electron Matter What is carrying the current?
Unparticles in High T_c Superconductors Thanks to: NSF, EFRC (DOE) Kiaran dave Charlie Kane Brandon Langley J. A. Hutasoit Correlated Electron Matter Correlated Electron Matter What is carrying the current?
Holography and Unitarity in Gravitational Physics
 Holography and Unitarity in Gravitational Physics Don Marolf 01/13/09 UCSB ILQG Seminar arxiv: 0808.2842 & 0808.2845 This talk is about: Diffeomorphism Invariance and observables in quantum gravity The
Holography and Unitarity in Gravitational Physics Don Marolf 01/13/09 UCSB ILQG Seminar arxiv: 0808.2842 & 0808.2845 This talk is about: Diffeomorphism Invariance and observables in quantum gravity The
Dark energy and nonlocal gravity
 Dark energy and nonlocal gravity Michele Maggiore Vacuum 2015, Barcelona based on Jaccard, MM, Mitsou, PRD 2013, 1305.3034 MM, PRD 2014, 1307.3898 Foffa, MM, Mitsou, PLB 2014, 1311.3421 Foffa, MM, Mitsou,
Dark energy and nonlocal gravity Michele Maggiore Vacuum 2015, Barcelona based on Jaccard, MM, Mitsou, PRD 2013, 1305.3034 MM, PRD 2014, 1307.3898 Foffa, MM, Mitsou, PLB 2014, 1311.3421 Foffa, MM, Mitsou,
BMS current algebra and central extension
 Recent Developments in General Relativity The Hebrew University of Jerusalem, -3 May 07 BMS current algebra and central extension Glenn Barnich Physique théorique et mathématique Université libre de Bruxelles
Recent Developments in General Relativity The Hebrew University of Jerusalem, -3 May 07 BMS current algebra and central extension Glenn Barnich Physique théorique et mathématique Université libre de Bruxelles
Coupled differential equations
 Coupled differential equations Example: dy 1 dy 11 1 1 1 1 1 a y a y b x a y a y b x Consider the case with b1 b d y1 a11 a1 y1 y a1 ay dy y y e y 4/1/18 One way to address this sort of problem, is to
Coupled differential equations Example: dy 1 dy 11 1 1 1 1 1 a y a y b x a y a y b x Consider the case with b1 b d y1 a11 a1 y1 y a1 ay dy y y e y 4/1/18 One way to address this sort of problem, is to
Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 28, 2011
 Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 8, Solutions to Problems 5 are omitted since they involve topics no longer covered on the Comprehensive
Solutions to the Calculus and Linear Algebra problems on the Comprehensive Examination of January 8, Solutions to Problems 5 are omitted since they involve topics no longer covered on the Comprehensive
Page Problem Score Max Score a 8 12b a b 10 14c 6 6
 Fall 14 MTH 34 FINAL EXAM December 8, 14 Name: PID: Section: Instructor: DO NOT WRITE BELOW THIS LINE. Go to the next page. Page Problem Score Max Score 1 5 5 1 3 5 4 5 5 5 6 5 7 5 8 5 9 5 1 5 11 1 3 1a
Fall 14 MTH 34 FINAL EXAM December 8, 14 Name: PID: Section: Instructor: DO NOT WRITE BELOW THIS LINE. Go to the next page. Page Problem Score Max Score 1 5 5 1 3 5 4 5 5 5 6 5 7 5 8 5 9 5 1 5 11 1 3 1a
8.03 Lecture 12. Systems we have learned: Wave equation: (1) String with constant tension and mass per unit length ρ L T v p = ρ L
 8.03 Lecture 1 Systems we have learned: Wave equation: ψ = ψ v p x There are three different kinds of systems discussed in the lecture: (1) String with constant tension and mass per unit length ρ L T v
8.03 Lecture 1 Systems we have learned: Wave equation: ψ = ψ v p x There are three different kinds of systems discussed in the lecture: (1) String with constant tension and mass per unit length ρ L T v
Introduction to string theory 2 - Quantization
 Remigiusz Durka Institute of Theoretical Physics Wroclaw / 34 Table of content Introduction to Quantization Classical String Quantum String 2 / 34 Classical Theory In the classical mechanics one has dynamical
Remigiusz Durka Institute of Theoretical Physics Wroclaw / 34 Table of content Introduction to Quantization Classical String Quantum String 2 / 34 Classical Theory In the classical mechanics one has dynamical
Holographic Q-Lattices and Metal-Insulator Transitions
 Holographic Q-Lattices and Metal-Insulator Transitions Jerome Gauntlett Aristomenis Donos Holographic tools provide a powerful framework for investigating strongly coupled systems using weakly coupled
Holographic Q-Lattices and Metal-Insulator Transitions Jerome Gauntlett Aristomenis Donos Holographic tools provide a powerful framework for investigating strongly coupled systems using weakly coupled
Sturm-Liouville Theory
 More on Ryan C. Trinity University Partial Differential Equations April 19, 2012 Recall: A Sturm-Liouville (S-L) problem consists of A Sturm-Liouville equation on an interval: (p(x)y ) + (q(x) + λr(x))y
More on Ryan C. Trinity University Partial Differential Equations April 19, 2012 Recall: A Sturm-Liouville (S-L) problem consists of A Sturm-Liouville equation on an interval: (p(x)y ) + (q(x) + λr(x))y
Holographic Lattices
 Holographic Lattices Jerome Gauntlett with Aristomenis Donos Christiana Pantelidou Holographic Lattices CFT with a deformation by an operator that breaks translation invariance Why? Translation invariance
Holographic Lattices Jerome Gauntlett with Aristomenis Donos Christiana Pantelidou Holographic Lattices CFT with a deformation by an operator that breaks translation invariance Why? Translation invariance
Contents. MATH 32B-2 (18W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables. 1 Multiple Integrals 3. 2 Vector Fields 9
 MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
Local RG, Quantum RG, and Holographic RG. Yu Nakayama Special thanks to Sung-Sik Lee and Elias Kiritsis
 Local RG, Quantum RG, and Holographic RG Yu Nakayama Special thanks to Sung-Sik Lee and Elias Kiritsis Local renormalization group The main idea dates back to Osborn NPB 363 (1991) See also my recent review
Local RG, Quantum RG, and Holographic RG Yu Nakayama Special thanks to Sung-Sik Lee and Elias Kiritsis Local renormalization group The main idea dates back to Osborn NPB 363 (1991) See also my recent review
3d GR is a Chern-Simons theory
 3d GR is a Chern-Simons theory An identity in three dimensions p g R + 1`2 = abc (R ab e c + 1`2 ea e b e c )= A a da a + 13 abca a A b A Ā c a dā a + 13 abcāa Ā b Ā c + db with 1 ` ea = A a Ā a, a bc
3d GR is a Chern-Simons theory An identity in three dimensions p g R + 1`2 = abc (R ab e c + 1`2 ea e b e c )= A a da a + 13 abca a A b A Ā c a dā a + 13 abcāa Ā b Ā c + db with 1 ` ea = A a Ā a, a bc
Collective T-duality transformations and non-geometric spaces
 Collective T-duality transformations and non-geometric spaces Erik Plauschinn LMU Munich ESI Vienna 09.12.2015 based on... This talk is based on :: T-duality revisited On T-duality transformations for
Collective T-duality transformations and non-geometric spaces Erik Plauschinn LMU Munich ESI Vienna 09.12.2015 based on... This talk is based on :: T-duality revisited On T-duality transformations for
Domain Wall Brane in Eddington Inspired Born-Infeld Gravity
 2012cüWâfÔn»Æï? Domain Wall Brane in Eddington Inspired Born-Infeld Gravity µ4œ Ç =²ŒÆnØÔnïÄ Email: yangke09@lzu.edu.cn I# Ÿ 2012.05.10 Outline Introduction to Brane World Introduction to Eddington Inspired
2012cüWâfÔn»Æï? Domain Wall Brane in Eddington Inspired Born-Infeld Gravity µ4œ Ç =²ŒÆnØÔnïÄ Email: yangke09@lzu.edu.cn I# Ÿ 2012.05.10 Outline Introduction to Brane World Introduction to Eddington Inspired
AC conductivity of a holographic strange metal
 AC conductivity of a holographic strange metal F. Peña-Benítez INFN - Perugia 1507.05633 in collaboration with Elias Kiritsis Workshop on Holography and Condensed Matter 1 motivation holography is a good
AC conductivity of a holographic strange metal F. Peña-Benítez INFN - Perugia 1507.05633 in collaboration with Elias Kiritsis Workshop on Holography and Condensed Matter 1 motivation holography is a good
2.10 Saddles, Nodes, Foci and Centers
 2.10 Saddles, Nodes, Foci and Centers In Section 1.5, a linear system (1 where x R 2 was said to have a saddle, node, focus or center at the origin if its phase portrait was linearly equivalent to one
2.10 Saddles, Nodes, Foci and Centers In Section 1.5, a linear system (1 where x R 2 was said to have a saddle, node, focus or center at the origin if its phase portrait was linearly equivalent to one
Holography and Mottness: a Discrete Marriage
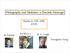 Holography and Mottness: a Discrete Marriage Thanks to: NSF, EFRC (DOE) Ka Wai Lo M. Edalati R. G. Leigh Seungmin Hong Mott Problem Mott Problem + # + Mott Problem + # + σ(ω) Ω -1 cm -1 VO 2 T=360 K T=295
Holography and Mottness: a Discrete Marriage Thanks to: NSF, EFRC (DOE) Ka Wai Lo M. Edalati R. G. Leigh Seungmin Hong Mott Problem Mott Problem + # + Mott Problem + # + σ(ω) Ω -1 cm -1 VO 2 T=360 K T=295
Proximity-induced magnetization dynamics, interaction effects, and phase transitions on a topological surface
 Proximity-induced magnetization dynamics, interaction effects, and phase transitions on a topological surface Ilya Eremin Theoretische Physik III, Ruhr-Uni Bochum Work done in collaboration with: F. Nogueira
Proximity-induced magnetization dynamics, interaction effects, and phase transitions on a topological surface Ilya Eremin Theoretische Physik III, Ruhr-Uni Bochum Work done in collaboration with: F. Nogueira
Study Guide/Practice Exam 3
 Study Guide/Practice Exam 3 This study guide/practice exam covers only the material since exam. The final exam, however, is cumulative so you should be sure to thoroughly study earlier material. The distribution
Study Guide/Practice Exam 3 This study guide/practice exam covers only the material since exam. The final exam, however, is cumulative so you should be sure to thoroughly study earlier material. The distribution
SYMMETRIES AND DISSIPATIVE MAGNETOHYDRODYNAMICS
 SAŠO GROZDANOV INSTITUUT-LORENTZ FOR THEORETICAL PHYSICS LEIDEN UNIVERSITY GENERALISED GLOBAL SYMMETRIES AND DISSIPATIVE MAGNETOHYDRODYNAMICS OXFORD, 14.7.2017 2 OUTLINE hydrodynamics generalised global
SAŠO GROZDANOV INSTITUUT-LORENTZ FOR THEORETICAL PHYSICS LEIDEN UNIVERSITY GENERALISED GLOBAL SYMMETRIES AND DISSIPATIVE MAGNETOHYDRODYNAMICS OXFORD, 14.7.2017 2 OUTLINE hydrodynamics generalised global
Analog Duality. Sabine Hossenfelder. Nordita. Sabine Hossenfelder, Nordita Analog Duality 1/29
 Analog Duality Sabine Hossenfelder Nordita Sabine Hossenfelder, Nordita Analog Duality 1/29 Dualities A duality, in the broadest sense, identifies two theories with each other. A duality is especially
Analog Duality Sabine Hossenfelder Nordita Sabine Hossenfelder, Nordita Analog Duality 1/29 Dualities A duality, in the broadest sense, identifies two theories with each other. A duality is especially
Exact Solutions of the Einstein Equations
 Notes from phz 6607, Special and General Relativity University of Florida, Fall 2004, Detweiler Exact Solutions of the Einstein Equations These notes are not a substitute in any manner for class lectures.
Notes from phz 6607, Special and General Relativity University of Florida, Fall 2004, Detweiler Exact Solutions of the Einstein Equations These notes are not a substitute in any manner for class lectures.
MAC2313 Final A. (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative.
 MAC2313 Final A (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative. ii. The vector field F = 5(x 2 + y 2 ) 3/2 x, y is radial. iii. All constant
MAC2313 Final A (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative. ii. The vector field F = 5(x 2 + y 2 ) 3/2 x, y is radial. iii. All constant
2.20 Fall 2018 Math Review
 2.20 Fall 2018 Math Review September 10, 2018 These notes are to help you through the math used in this class. This is just a refresher, so if you never learned one of these topics you should look more
2.20 Fall 2018 Math Review September 10, 2018 These notes are to help you through the math used in this class. This is just a refresher, so if you never learned one of these topics you should look more
6.0 INTRODUCTION TO DIFFERENTIAL EQUATIONS
 6.0 Introduction to Differential Equations Contemporary Calculus 1 6.0 INTRODUCTION TO DIFFERENTIAL EQUATIONS This chapter is an introduction to differential equations, a major field in applied and theoretical
6.0 Introduction to Differential Equations Contemporary Calculus 1 6.0 INTRODUCTION TO DIFFERENTIAL EQUATIONS This chapter is an introduction to differential equations, a major field in applied and theoretical
Applications of AdS/CFT correspondence to cold atom physics
 Applications of AdS/CFT correspondence to cold atom physics Sergej Moroz in collaboration with Carlos Fuertes ITP, Heidelberg Outline Basics of AdS/CFT correspondence Schrödinger group and correlation
Applications of AdS/CFT correspondence to cold atom physics Sergej Moroz in collaboration with Carlos Fuertes ITP, Heidelberg Outline Basics of AdS/CFT correspondence Schrödinger group and correlation
A Conformal Basis for Flat Space Amplitudes SABRINA GONZALEZ PASTERSKI
 A Conformal Basis for Flat Space Amplitudes SABRINA GONZALEZ PASTERSKI A scattering basis motivated by asymptotic symmetries? v Plane wave Highest weight scattering [arxiv:1701.00049, arxiv:1705.01027,
A Conformal Basis for Flat Space Amplitudes SABRINA GONZALEZ PASTERSKI A scattering basis motivated by asymptotic symmetries? v Plane wave Highest weight scattering [arxiv:1701.00049, arxiv:1705.01027,
Autocorrelators in models with Lifshitz scaling
 Autocorrelators in models with Lifshitz scaling Lárus Thorlacius based on V. Keränen & L.T.: Class. Quantum Grav. 29 (202) 94009 arxiv:50.nnnn (to appear...) International workshop on holography and condensed
Autocorrelators in models with Lifshitz scaling Lárus Thorlacius based on V. Keränen & L.T.: Class. Quantum Grav. 29 (202) 94009 arxiv:50.nnnn (to appear...) International workshop on holography and condensed
Math 350 Solutions for Final Exam Page 1. Problem 1. (10 points) (a) Compute the line integral. F ds C. z dx + y dy + x dz C
 Math 35 Solutions for Final Exam Page Problem. ( points) (a) ompute the line integral F ds for the path c(t) = (t 2, t 3, t) with t and the vector field F (x, y, z) = xi + zj + xk. (b) ompute the line
Math 35 Solutions for Final Exam Page Problem. ( points) (a) ompute the line integral F ds for the path c(t) = (t 2, t 3, t) with t and the vector field F (x, y, z) = xi + zj + xk. (b) ompute the line
3 2 6 Solve the initial value problem u ( t) 3. a- If A has eigenvalues λ =, λ = 1 and corresponding eigenvectors 1
 Math Problem a- If A has eigenvalues λ =, λ = 1 and corresponding eigenvectors 1 3 6 Solve the initial value problem u ( t) = Au( t) with u (0) =. 3 1 u 1 =, u 1 3 = b- True or false and why 1. if A is
Math Problem a- If A has eigenvalues λ =, λ = 1 and corresponding eigenvectors 1 3 6 Solve the initial value problem u ( t) = Au( t) with u (0) =. 3 1 u 1 =, u 1 3 = b- True or false and why 1. if A is
The Geometry of the Quantum Hall Effect
 The Geometry of the Quantum Hall Effect Dam Thanh Son (University of Chicago) Refs: Carlos Hoyos, DTS arxiv:1109.2651 DTS, M.Wingate cond-mat/0509786 Plan Review of quantum Hall physics Summary of results
The Geometry of the Quantum Hall Effect Dam Thanh Son (University of Chicago) Refs: Carlos Hoyos, DTS arxiv:1109.2651 DTS, M.Wingate cond-mat/0509786 Plan Review of quantum Hall physics Summary of results
Fourth Aegean Summer School: Black Holes Mytilene, Island of Lesvos September 18, 2007
 Fourth Aegean Summer School: Black Holes Mytilene, Island of Lesvos September 18, 2007 Central extensions in flat spacetimes Duality & Thermodynamics of BH dyons New classical central extension in asymptotically
Fourth Aegean Summer School: Black Holes Mytilene, Island of Lesvos September 18, 2007 Central extensions in flat spacetimes Duality & Thermodynamics of BH dyons New classical central extension in asymptotically
Complex entangled states of quantum matter, not adiabatically connected to independent particle states. Compressible quantum matter
 Complex entangled states of quantum matter, not adiabatically connected to independent particle states Gapped quantum matter Z2 Spin liquids, quantum Hall states Conformal quantum matter Graphene, ultracold
Complex entangled states of quantum matter, not adiabatically connected to independent particle states Gapped quantum matter Z2 Spin liquids, quantum Hall states Conformal quantum matter Graphene, ultracold
Phys 731: String Theory - Assignment 3
 Phys 73: String Theory - Assignment 3 Andrej Pokraka November 8, 27 Problem a) Evaluate the OPE T () :e ik (,) : using Wick s theorem. Expand the exponential, then sum over contractions between T and the
Phys 73: String Theory - Assignment 3 Andrej Pokraka November 8, 27 Problem a) Evaluate the OPE T () :e ik (,) : using Wick s theorem. Expand the exponential, then sum over contractions between T and the
Review for the First Midterm Exam
 Review for the First Midterm Exam Thomas Morrell 5 pm, Sunday, 4 April 9 B9 Van Vleck Hall For the purpose of creating questions for this review session, I did not make an effort to make any of the numbers
Review for the First Midterm Exam Thomas Morrell 5 pm, Sunday, 4 April 9 B9 Van Vleck Hall For the purpose of creating questions for this review session, I did not make an effort to make any of the numbers
Holography and Mottness: a Discrete Marriage
 Holography and Mottness: a Discrete Marriage Thanks to: NSF, EFRC (DOE) Ka Wai Lo M. Edalati R. G. Leigh Mott Problem emergent gravity Mott Problem What interacting problems can we solve in quantum mechanics?
Holography and Mottness: a Discrete Marriage Thanks to: NSF, EFRC (DOE) Ka Wai Lo M. Edalati R. G. Leigh Mott Problem emergent gravity Mott Problem What interacting problems can we solve in quantum mechanics?
Electromagnetic Waves Retarded potentials 2. Energy and the Poynting vector 3. Wave equations for E and B 4. Plane EM waves in free space
 Electromagnetic Waves 1 1. Retarded potentials 2. Energy and the Poynting vector 3. Wave equations for E and B 4. Plane EM waves in free space 1 Retarded Potentials For volume charge & current = 1 4πε
Electromagnetic Waves 1 1. Retarded potentials 2. Energy and the Poynting vector 3. Wave equations for E and B 4. Plane EM waves in free space 1 Retarded Potentials For volume charge & current = 1 4πε
Holographic Anyonic Superfluids
 Holographic Anyonic Superfluids Matt Lippert (Amsterdam) with Niko Jokela (USC) and Gilad Lifschytz (Haifa) Plan Anyons, SL(2,Z), and Quantum Hall Effect Superfluids and Anyon Superfliuds A Holographic
Holographic Anyonic Superfluids Matt Lippert (Amsterdam) with Niko Jokela (USC) and Gilad Lifschytz (Haifa) Plan Anyons, SL(2,Z), and Quantum Hall Effect Superfluids and Anyon Superfliuds A Holographic
(a p (t)e i p x +a (t)e ip x p
 5/29/3 Lecture outline Reading: Zwiebach chapters and. Last time: quantize KG field, φ(t, x) = (a (t)e i x +a (t)e ip x V ). 2Ep H = ( ȧ ȧ(t)+ 2E 2 E pa a) = p > E p a a. P = a a. [a p,a k ] = δ p,k, [a
5/29/3 Lecture outline Reading: Zwiebach chapters and. Last time: quantize KG field, φ(t, x) = (a (t)e i x +a (t)e ip x V ). 2Ep H = ( ȧ ȧ(t)+ 2E 2 E pa a) = p > E p a a. P = a a. [a p,a k ] = δ p,k, [a
21-256: Partial differentiation
 21-256: Partial differentiation Clive Newstead, Thursday 5th June 2014 This is a summary of the important results about partial derivatives and the chain rule that you should know. Partial derivatives
21-256: Partial differentiation Clive Newstead, Thursday 5th June 2014 This is a summary of the important results about partial derivatives and the chain rule that you should know. Partial derivatives
Is Strongly Correlated Electron Matter Full of Unparticles? Kiaran dave Charlie Kane Brandon Langley
 Is Strongly Correlated Electron Matter Full of Unparticles? Kiaran dave Charlie Kane Brandon Langley 2=3 goal 2 = 3 Properties all particles share? Properties all particles share? charge fixed mass! Properties
Is Strongly Correlated Electron Matter Full of Unparticles? Kiaran dave Charlie Kane Brandon Langley 2=3 goal 2 = 3 Properties all particles share? Properties all particles share? charge fixed mass! Properties
Differential equations, comprehensive exam topics and sample questions
 Differential equations, comprehensive exam topics and sample questions Topics covered ODE s: Chapters -5, 7, from Elementary Differential Equations by Edwards and Penney, 6th edition.. Exact solutions
Differential equations, comprehensive exam topics and sample questions Topics covered ODE s: Chapters -5, 7, from Elementary Differential Equations by Edwards and Penney, 6th edition.. Exact solutions
Vectors, matrices, eigenvalues and eigenvectors
 Vectors, matrices, eigenvalues and eigenvectors 1 ( ) ( ) ( ) Scaling a vector: 0.5V 2 0.5 2 1 = 0.5 = = 1 0.5 1 0.5 ( ) ( ) ( ) ( ) Adding two vectors: V + W 2 1 2 + 1 3 = + = = 1 3 1 + 3 4 ( ) ( ) a
Vectors, matrices, eigenvalues and eigenvectors 1 ( ) ( ) ( ) Scaling a vector: 0.5V 2 0.5 2 1 = 0.5 = = 1 0.5 1 0.5 ( ) ( ) ( ) ( ) Adding two vectors: V + W 2 1 2 + 1 3 = + = = 1 3 1 + 3 4 ( ) ( ) a
Black holes with AdS asymptotics and holographic RG flows
 Black holes with AdS asymptotics and holographic RG flows Anastasia Golubtsova 1 based on work with Irina Aref eva (MI RAS, Moscow) and Giuseppe Policastro (ENS, Paris) arxiv:1803.06764 (1) BLTP JINR,
Black holes with AdS asymptotics and holographic RG flows Anastasia Golubtsova 1 based on work with Irina Aref eva (MI RAS, Moscow) and Giuseppe Policastro (ENS, Paris) arxiv:1803.06764 (1) BLTP JINR,
Convergence Tests. Academic Resource Center
 Convergence Tests Academic Resource Center Series Given a sequence {a 0, a, a 2,, a n } The sum of the series, S n = A series is convergent if, as n gets larger and larger, S n goes to some finite number.
Convergence Tests Academic Resource Center Series Given a sequence {a 0, a, a 2,, a n } The sum of the series, S n = A series is convergent if, as n gets larger and larger, S n goes to some finite number.
THE MANY AVATARS OF GALILEAN CONFORMAL SYMMETRY
 THE MANY AVATARS OF GALILEAN CONFORMAL SYMMETRY Arjun Bagchi Indian Strings Meet 2014 December 18, 2014. CONFORMAL FIELD THEORY Conformal field theories are amongst the most powerful tools in modern theoretical
THE MANY AVATARS OF GALILEAN CONFORMAL SYMMETRY Arjun Bagchi Indian Strings Meet 2014 December 18, 2014. CONFORMAL FIELD THEORY Conformal field theories are amongst the most powerful tools in modern theoretical
Symmetry and Duality FACETS Nemani Suryanarayana, IMSc
 Symmetry and Duality FACETS 2018 Nemani Suryanarayana, IMSc What are symmetries and why are they important? Most useful concept in Physics. Best theoretical models of natural Standard Model & GTR are based
Symmetry and Duality FACETS 2018 Nemani Suryanarayana, IMSc What are symmetries and why are they important? Most useful concept in Physics. Best theoretical models of natural Standard Model & GTR are based
Solutions to Homework 11
 Solutions to Homework 11 Read the statement of Proposition 5.4 of Chapter 3, Section 5. Write a summary of the proof. Comment on the following details: Does the proof work if g is piecewise C 1? Or did
Solutions to Homework 11 Read the statement of Proposition 5.4 of Chapter 3, Section 5. Write a summary of the proof. Comment on the following details: Does the proof work if g is piecewise C 1? Or did
Partial differential equations (ACM30220)
 (ACM3. A pot on a stove has a handle of length that can be modelled as a rod with diffusion constant D. The equation for the temperature in the rod is u t Du xx < x
(ACM3. A pot on a stove has a handle of length that can be modelled as a rod with diffusion constant D. The equation for the temperature in the rod is u t Du xx < x
Properties of Matrices and Operations on Matrices
 Properties of Matrices and Operations on Matrices A common data structure for statistical analysis is a rectangular array or matris. Rows represent individual observational units, or just observations,
Properties of Matrices and Operations on Matrices A common data structure for statistical analysis is a rectangular array or matris. Rows represent individual observational units, or just observations,
SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2
 SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2 Here are the solutions to the additional exercises in betsepexercises.pdf. B1. Let y and z be distinct points of L; we claim that x, y and z are not
SOLUTIONS TO ADDITIONAL EXERCISES FOR II.1 AND II.2 Here are the solutions to the additional exercises in betsepexercises.pdf. B1. Let y and z be distinct points of L; we claim that x, y and z are not
Optimization Theory. Linear Operators and Adjoints
 Optimization Theory Linear Operators and Adjoints A transformation T. : X Y y Linear Operators y T( x), x X, yy is the image of x under T The domain of T on which T can be defined : D X The range of T
Optimization Theory Linear Operators and Adjoints A transformation T. : X Y y Linear Operators y T( x), x X, yy is the image of x under T The domain of T on which T can be defined : D X The range of T
Math 265H: Calculus III Practice Midterm II: Fall 2014
 Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
Name: Section #: Math 65H: alculus III Practice Midterm II: Fall 14 Instructions: This exam has 7 problems. The number of points awarded for each question is indicated in the problem. Answer each question
Groups. 3.1 Definition of a Group. Introduction. Definition 3.1 Group
 C H A P T E R t h r e E Groups Introduction Some of the standard topics in elementary group theory are treated in this chapter: subgroups, cyclic groups, isomorphisms, and homomorphisms. In the development
C H A P T E R t h r e E Groups Introduction Some of the standard topics in elementary group theory are treated in this chapter: subgroups, cyclic groups, isomorphisms, and homomorphisms. In the development
Chapter 5 Cylindrical Cavities and Waveguides
 Chapter 5 Cylindrical Cavities and Waveguides We shall consider an electromagnetic field propagating inside a hollow (in the present case cylindrical) conductor. There are no sources inside the conductor,
Chapter 5 Cylindrical Cavities and Waveguides We shall consider an electromagnetic field propagating inside a hollow (in the present case cylindrical) conductor. There are no sources inside the conductor,
MA261-A Calculus III 2006 Fall Midterm 2 Solutions 11/8/2006 8:00AM ~9:15AM
 MA6-A Calculus III 6 Fall Midterm Solutions /8/6 8:AM ~9:5AM. Find the it xy cos y (x;y)(;) 3x + y, if it exists, or show that the it does not exist. Assume that x. The it becomes (;y)(;) y cos y 3 + y
MA6-A Calculus III 6 Fall Midterm Solutions /8/6 8:AM ~9:5AM. Find the it xy cos y (x;y)(;) 3x + y, if it exists, or show that the it does not exist. Assume that x. The it becomes (;y)(;) y cos y 3 + y
Warped Penguins. Based on arxiv: In collaboration with Csaba Csáki, Yuval Grossman, Philip Tanedo. LEPP Particle Theory Seminar
 Warped Penguins Based on arxiv:1004.2037 In collaboration with Csaba Csáki, Yuval Grossman, Philip Tanedo Cornell University LEPP Particle Theory Seminar Yuhsin Tsai, Cornell University/LEPP Warped Penguins
Warped Penguins Based on arxiv:1004.2037 In collaboration with Csaba Csáki, Yuval Grossman, Philip Tanedo Cornell University LEPP Particle Theory Seminar Yuhsin Tsai, Cornell University/LEPP Warped Penguins
TC412 Microwave Communications. Lecture 8 Rectangular waveguides and cavity resonator
 TC412 Microwave Communications Lecture 8 Rectangular waveguides and cavity resonator 1 TM waves in rectangular waveguides Finding E and H components in terms of, WG geometry, and modes. From 2 2 2 xye
TC412 Microwave Communications Lecture 8 Rectangular waveguides and cavity resonator 1 TM waves in rectangular waveguides Finding E and H components in terms of, WG geometry, and modes. From 2 2 2 xye
Math 212-Lecture 8. The chain rule with one independent variable
 Math 212-Lecture 8 137: The multivariable chain rule The chain rule with one independent variable w = f(x, y) If the particle is moving along a curve x = x(t), y = y(t), then the values that the particle
Math 212-Lecture 8 137: The multivariable chain rule The chain rule with one independent variable w = f(x, y) If the particle is moving along a curve x = x(t), y = y(t), then the values that the particle
Holographic Lattices
 Holographic Lattices Jerome Gauntlett with Aristomenis Donos Christiana Pantelidou Holographic Lattices CFT with a deformation by an operator that breaks translation invariance Why? Translation invariance
Holographic Lattices Jerome Gauntlett with Aristomenis Donos Christiana Pantelidou Holographic Lattices CFT with a deformation by an operator that breaks translation invariance Why? Translation invariance
1 Linear Algebra Problems
 Linear Algebra Problems. Let A be the conjugate transpose of the complex matrix A; i.e., A = A t : A is said to be Hermitian if A = A; real symmetric if A is real and A t = A; skew-hermitian if A = A and
Linear Algebra Problems. Let A be the conjugate transpose of the complex matrix A; i.e., A = A t : A is said to be Hermitian if A = A; real symmetric if A is real and A t = A; skew-hermitian if A = A and
Partial Differential Equations for Engineering Math 312, Fall 2012
 Partial Differential Equations for Engineering Math 312, Fall 2012 Jens Lorenz July 17, 2012 Contents Department of Mathematics and Statistics, UNM, Albuquerque, NM 87131 1 Second Order ODEs with Constant
Partial Differential Equations for Engineering Math 312, Fall 2012 Jens Lorenz July 17, 2012 Contents Department of Mathematics and Statistics, UNM, Albuquerque, NM 87131 1 Second Order ODEs with Constant
Metric Spaces Math 413 Honors Project
 Metric Spaces Math 413 Honors Project 1 Metric Spaces Definition 1.1 Let X be a set. A metric on X is a function d : X X R such that for all x, y, z X: i) d(x, y) = d(y, x); ii) d(x, y) = 0 if and only
Metric Spaces Math 413 Honors Project 1 Metric Spaces Definition 1.1 Let X be a set. A metric on X is a function d : X X R such that for all x, y, z X: i) d(x, y) = d(y, x); ii) d(x, y) = 0 if and only
Linear Algebra Review (Course Notes for Math 308H - Spring 2016)
 Linear Algebra Review (Course Notes for Math 308H - Spring 2016) Dr. Michael S. Pilant February 12, 2016 1 Background: We begin with one of the most fundamental notions in R 2, distance. Letting (x 1,
Linear Algebra Review (Course Notes for Math 308H - Spring 2016) Dr. Michael S. Pilant February 12, 2016 1 Background: We begin with one of the most fundamental notions in R 2, distance. Letting (x 1,
Engg. Math. I. Unit-I. Differential Calculus
 Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
Dr. Satish Shukla 1 of 50 Engg. Math. I Unit-I Differential Calculus Syllabus: Limits of functions, continuous functions, uniform continuity, monotone and inverse functions. Differentiable functions, Rolle
Partial Derivatives Formulas. KristaKingMath.com
 Partial Derivatives Formulas KristaKingMath.com Domain and range of a multivariable function A function f of two variables is a rule that assigns to each ordered pair of real numbers (x, y) in a set D
Partial Derivatives Formulas KristaKingMath.com Domain and range of a multivariable function A function f of two variables is a rule that assigns to each ordered pair of real numbers (x, y) in a set D
Metric Spaces Math 413 Honors Project
 Metric Spaces Math 413 Honors Project 1 Metric Spaces Definition 1.1 Let X be a set. A metric on X is a function d : X X R such that for all x, y, z X: i) d(x, y) = d(y, x); ii) d(x, y) = 0 if and only
Metric Spaces Math 413 Honors Project 1 Metric Spaces Definition 1.1 Let X be a set. A metric on X is a function d : X X R such that for all x, y, z X: i) d(x, y) = d(y, x); ii) d(x, y) = 0 if and only
The Uses of Conformal Symmetry in QCD
 The Uses of Conformal Symmetry in QCD V. M. Braun University of Regensburg DESY, 23 September 2006 based on a review V.M. Braun, G.P. Korchemsky, D. Müller, Prog. Part. Nucl. Phys. 51 (2003) 311 Outline
The Uses of Conformal Symmetry in QCD V. M. Braun University of Regensburg DESY, 23 September 2006 based on a review V.M. Braun, G.P. Korchemsky, D. Müller, Prog. Part. Nucl. Phys. 51 (2003) 311 Outline
Quantum phase transitions in condensed matter
 Quantum phase transitions in condensed matter The 8th Asian Winter School on Strings, Particles, and Cosmology, Puri, India January 11-18, 2014 Subir Sachdev Talk online: sachdev.physics.harvard.edu HARVARD
Quantum phase transitions in condensed matter The 8th Asian Winter School on Strings, Particles, and Cosmology, Puri, India January 11-18, 2014 Subir Sachdev Talk online: sachdev.physics.harvard.edu HARVARD
5 Topological insulator with time-reversal symmetry
 Phys62.nb 63 5 Topological insulator with time-reversal symmetry It is impossible to have quantum Hall effect without breaking the time-reversal symmetry. xy xy. If we want xy to be invariant under, xy
Phys62.nb 63 5 Topological insulator with time-reversal symmetry It is impossible to have quantum Hall effect without breaking the time-reversal symmetry. xy xy. If we want xy to be invariant under, xy
Superstring in the plane-wave background with RR-flux as a conformal field theory
 0th December, 008 At Towards New Developments of QFT and Strings, RIKEN Superstring in the plane-wave background with RR-flux as a conformal field theory Naoto Yokoi Institute of Physics, University of
0th December, 008 At Towards New Developments of QFT and Strings, RIKEN Superstring in the plane-wave background with RR-flux as a conformal field theory Naoto Yokoi Institute of Physics, University of
Thanks to: NSF, EFRC (DOE)
 Mottness and Holography: A Discrete Marriage Thanks to: NSF, EFRC (DOE) Seungmin Hong M. Edalati R. G. Leigh emergent gravity spectral weight transfer 2-particle probe spectral weight transfer spectral
Mottness and Holography: A Discrete Marriage Thanks to: NSF, EFRC (DOE) Seungmin Hong M. Edalati R. G. Leigh emergent gravity spectral weight transfer 2-particle probe spectral weight transfer spectral
Math 265 (Butler) Practice Midterm III B (Solutions)
 Math 265 (Butler) Practice Midterm III B (Solutions). Set up (but do not evaluate) an integral for the surface area of the surface f(x, y) x 2 y y over the region x, y 4. We have that the surface are is
Math 265 (Butler) Practice Midterm III B (Solutions). Set up (but do not evaluate) an integral for the surface area of the surface f(x, y) x 2 y y over the region x, y 4. We have that the surface are is
Thanks to: NSF, EFRC (DOE)
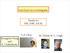 From Fermi Arcs to Holography Thanks to: NSF, EFRC (DOE) Seungmin Hong and S. Chakraborty T.-P. Choy M. Edalati R. G. Leigh Fermi Arcs P. Johnson, PRL 2011 Na-CCOC (Shen, Science 2006) La-Bi2201 (Meng,
From Fermi Arcs to Holography Thanks to: NSF, EFRC (DOE) Seungmin Hong and S. Chakraborty T.-P. Choy M. Edalati R. G. Leigh Fermi Arcs P. Johnson, PRL 2011 Na-CCOC (Shen, Science 2006) La-Bi2201 (Meng,
Nonlinear Control. Nonlinear Control Lecture # 2 Stability of Equilibrium Points
 Nonlinear Control Lecture # 2 Stability of Equilibrium Points Basic Concepts ẋ = f(x) f is locally Lipschitz over a domain D R n Suppose x D is an equilibrium point; that is, f( x) = 0 Characterize and
Nonlinear Control Lecture # 2 Stability of Equilibrium Points Basic Concepts ẋ = f(x) f is locally Lipschitz over a domain D R n Suppose x D is an equilibrium point; that is, f( x) = 0 Characterize and
